高中数学课件：简单的线性规划

合集下载

高二数学简单的线性规划2-PPT

4
的可行域内共有_______个整数点．
2．设z = x y，式中变量x，y满足
x y1

4x y 4 .
2 x 3 y 8 0

求z的最大值和最小值．
z max = 1，
z min = 3．
小结
练习：
3．教材P64练习1：
(1) 求z = 2x + y的最大值，使式
域内的点且平行于l的直线中，以经过
点A(5，2)的直线l2所对应的t最大，
大家有疑问的，可以询问和交流
可以互相讨论下，但要小声点
y
x 1
− 4 + 3 = 0
l2
6
5
l1
4
3
2
1
O
− 4 + 3 = 0
C
3 + 5 − 25 = 0
A
=1
B
1
2
3
4
5
6
7
x
以经过点B(1，1)的直线l1所对应的
2
1
O
C
3 + 5 − 25 = 0
A
=1
B
1
2
3
4
5
6
7
x
分析：不等式组表示的区域是图
中的ABC．
y
x 1
− 4 + 3 = 0
− 4 + 3 = 0
6
5
4
3
2
1
O
C
3 + 5 − 25 = 0
A
=1
B
1
2
3
4
5
6
7

高中数学新课标人教A版必修5课件线性规划

添加文档副标题
目录
01.
02.
03.
04.
05.
06.
线性规划是一种数学优化方法，用于求解线性目标函数在满足一组线性约束条件下的最优解。
线性规划的目标函数和约束条件都是线性的，即目标函数和约束条件中的变量和常数都是线性的。
线性规划的目标是找到一组决策变量，使得目标函数达到最大值或最小值，同时满足所有的约束条件。
线性规划在资源分配中的应用
资源分配问题的定义和分类
线性规划在资源分配问题中的求解方法
线性规划在资源分配问题中的实际应用案例
投资目标：最大化投资收益
投资约束：资金有限、风险控制等
投资策略：分散投资、风险对冲等
投资效果评估：投资回报率、风险调整后收益等
运输问题：在满足一定约束条件下，寻找最优的运输方案，以最小化运输成本或最大化运输收益
确定约束条件的类型，如等式约束、不等式约束等
确定约束条件的范围，如 x1+x2≤5等
确定约束条件的数量，如 x1+x2+x3=5等
目标函数是线性规划的核心，需要明确表示出要优化的目标
目标函数通常表示为最大化或最小化某个线性函数
目标函数中的变量需要与约束条件中的变量一致
目标函数中的系数需要是常数，不能含有变量
线性规划是研究线性约束条件下的优化问题的数学方法
线性规划的目标是找到一组决策变量，使得目标函数达到最大值或最小值
线性规划的几何意义在于，它可以将线性规划问题转化为几何问题，通过几何图形来直观地表示和解决问题
线性规划的几何意义可以帮助我们更好地理解和解决线性规划问题，提高解决问题的效率和准确性

高一数学§3.3.2简单的线性规划(1)

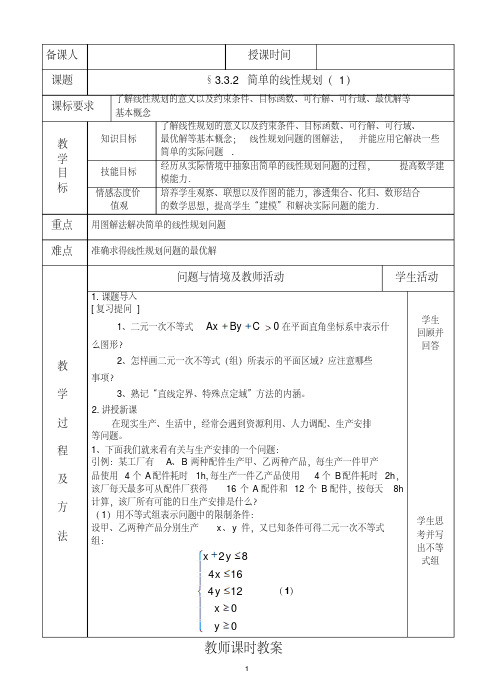
所以 zmax=2× 2-1=3.
（ 2）求 z=3x+5y 的最大值和最小值，使式中的 x、 y 满足约束条件
5x 3y 15, y x 1, x 5y 3.
教师课时教案
3
学生活动
学生完成学生板演
问题与情境及教师活动
解：不等式组所表示的平面区
域如图所示：
从图示可知，直线 3x+5y=t
在经过不等式组所表示的公共区
及
3
因此，问题可以转化为当直线
方 y
2z x 与不等式组（ 1）确
33
法定的平面区域有公共点时，在区域
内找一个点 P，使直线经过点 P 时
截距 z 最大。 3
（ 5）获得结果：
由上图可以看出，当实现
2z
y
x
3 3 金国直线 x=4 与直
z
14
线 x+2y-8=0 的交点 M（ 4， 2）时，截距 3 的值最大，最大值为 3 ，这
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解．
3、变换条件，加深理解
教探究：课本第 100 页的探究活动
（ 1）在上述问题中，如果生产一件甲产品获利
3 万元，每生产一件
学
乙产品获利 2 万元，有应当如何安排生产才能获得最大利润？
在换几组数据试试。
过（ 2）有上述过程，你能得出最优解与可行域之间的关系吗？
上.
3
2
x-y=0
1
11
O B(2, 2)
-2 -1
12
x
C(-1,-1) -1 A(2,-1)
x+y-1=0
2x+y=0

高中数学必修5 线性规划课件

A B A（3，4） B（4，8）
调整优值法
由z x y得y z x x z 可知，直线截距越小， z越小先令z 0, 作过原点的直线 y x 再对直线进行平移，可知，当直线经过点M时截距最小，z最小 18 x 2 x y 15 18 39 5 由 , 求得 , 故M（，） 5 5 x 3 y 27 y 39 5 又x、y只能取正整数，所以，找离点M最接近并且在区域里的正整数，得A（3， 9），B（4， 8）将A（3， 9）代入得z 3 9 12 将B（4， 8）代入得z 4 8 12 答：截第一种钢板 3张，第二种钢板 9张；或截第一种4张，第二种 8张，总张数最小，为 12张
y x 1 0 x 1 由 y x 1 0 求得 y 0 ，故
A（1，0）
故 z 的最大值为 zmax =2×1+0=2
[例] 设 x，y
x y 1 0 y 2x 1 0 满足约束条件 y x 1 0
线性规划问题的解决步骤数变形为y=kx+b的形式，
找截距与z的关系
3、令z=0, 先作出过原点的直线，定下直线形状
4、对直线进行平移，找出最优的点
5、联立边界直线方程，求出点坐标 6、将点坐标代入，求出最值
线性规划在实际中的应用
——生活中的最优化问题
每生产一件甲产品需要4个A配件，耗时1h；
例（课本87-88页）某工厂用A、B两种配件生产甲、乙两种产品，
每生产一件乙产品需要4个B配件,耗时2h；
该厂每天最多从配件厂获得16个A配件和12个B配件，而且每天工作时长为不能超过8小时；若每件甲产品获利2万元，每件乙产品获利3万元，问每天分别生产甲、乙产品多每天的获利达到最大？

高二数学简单的线性规划(第一课时)课件ppt--高中数学

由于A的任意性,故对于直线 x-y+1=0右下方任意点(x,y),都有x-y+1>0；
同理:对于直线上方的任意一点 (x,y),都有x-y+1<0.
点的集合{（x，y）|x-y+1>0}表示的是以直线L为边界的平面区域(不包括边界)
y
y=y0
A(x,y)
1 P(x0,y0)
-1
o
x
x-y+1=0
得出结论：
（1）二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域；
（2）在确定区域时，在直线的某一侧取一个特殊点(x0,y0) ，从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。一般在C≠0时，取原点作为特殊点；
y 二元一次不等式表示平面区域
o
x
横县职教中心覃春月
思考:
• 1、在平面直角坐标系中, 点的集合{（x，y）|xy+1=0}表示什么图形？
• 表示的是一条直线 • 即这条直线上的点都满足
条件: x-y+1=0 • 2、点的集合{（x，y）|x-
y+1>0}表示什么图形？
y x-y+1=0
ox观察源自1<0。猜想
（1）对直线L右下方的点（x，y）， x+y-1＞0 成立；
（2）对直线L左上方的点（x，y）， x+y-1＜0 成立.
证明
• 在直线x-y+1=0的下方任取一点 A（x，y），过点M作平行于x 轴的直线与直线x-y+1=0交于 P(x,y0)，有y=y0 ， x>x0,

人教版A版高中数学必修5：简单的线性规划问题_课件4

[解析] 设生产甲、乙两种产品分别为 x 件、y 件，总产值为 z 千元，则
4x＋3y≤120 2x＋y≤50 x≥0 y≥0
，z＝50x＋30y.
画出不等式组表示的平面区域即可行域如图．
易知直线 z＝50x＋30y 过点(15,20)时，取得最大值． zmax＝50×15＋30×20＝1 350. 答：生产甲、乙两种产品分别为 15 件、20 件，总收入最大是 1 350 千元．
为了在区域 OABC 内精确地找到这一点，我们平移直线 l0 到位置 l，使 l 通过平面区域 OABC，可见当 l 经过点 B 时，l 与 l0 的距离最大，∴d 最大．
解方程组x3＋x＋2y2＝y＝8010200 ，得点 B 的坐标(200,300)，代入式子①，得 tmax＝30×200＋40×300＝18 000. 答：用 200 工时生产甲种产品，用 300 工时生产乙种产品，能获得最大利润 18 000 元．
思路方法技巧
收益最大问题(利润、收入、产量等)
某工厂计划生产甲、乙两种产品，这两种产品都需要两种原料．生产甲产品 1 工时需要 A 种原料 3kg，B 种原料 1kg；生产乙产品 1 工时需要 A 种原料 2kg，B 种原料 2kg. 现有 A 种原料 1 200kg，B 种原料 800kg.如果生产甲产品每工时的平均利润是 30 元，生产乙产品每工时的平均利润是 40 元，问甲、乙两种产品各生产多少工时能使利润的总额最大？最大利润是多少？
[解析] 设调用甲型货车 x 辆，乙型货车 y 辆，则 0≤x≤4,0≤y≤8,20x＋10y≥100，即 2x＋y≥10，设运输费用为 t，则 t＝400x＋300y.
0≤x≤4 线性约束条件为0≤y≤8 ，

人教B版高中数学必修五课件3.5.2简单线性规划

由53xx＋＋25yy＝＝210500，，解得xy＝＝7111059900，
.
设点 A 的坐标为2700，970，点 B 的坐标为71090，11590，则不等式组(※)所表示的平面区域是四边形的边界及其内部 (如图中阴影部分)．
令 z＝0，得 7x＋10y＝0，即 y＝－170x.
解决简单线性规划的方法为图解法，就是用一组平行直线与某平面区域相交，研究直线在y轴上截距的最大值或最小值，从而求某些函数的最值．
2x＋y≤40 1.若变量 x，y 满足xx＋≥20y≤50
y≥0
，则 z＝3x＋2y 的最大
值是( ) A．90 C．70
B．80 D．40
【解析】由题意，满足二元一次不等式组的解的可行域如图所示．
高中数学课件
（金戈铁骑整理制作）
3.5.2 简单线性规划
1．在平面直角坐标系中，所有的点被直线x＋y－1＝0分成三类：即点在直线上，点在直线的区域，上点方在直线的区域．
2下．方二元一次不等式组表示的平面区域是其中的每个二元一
次不等式表示的平面区域的．公共部分
线性规划中的基本概念
名称
目标函数
由 z＝3x＋2y，得 y＝－32x＋2z.要求 z 的最大值，可求2z的最大值，即求斜率为－32的直线在可行域内在 y 轴上截距的最大值．
如上图，显然直线过 A 点时，在 y 轴上截距最大．联立2x＋x＋2yy＝＝4500 ，得xy＝＝1200 ， ∴A(10,20)，∴z＝3x＋2y 的最大值为 z＝3×10＋2×20 ＝70. 【答案】 C
x≥1
，所表示的平面区
域如图所示(阴影部分)
当直线 z＝2x＋y 经过可行域上的点 A 时，截距最大，即 z 最大，解方程组x3－x＋4y5＝y＝－235 ，得 A 的坐标为(5,2)．所以 zmax＝2×5＋2＝12. 当直线 z＝2x＋y 经过可行域上的点 B 时，截距最小，即 z 最小．解方程组xx－＝41y＝－3 ，得 B 的坐标为(1,1)．所以 zmin＝2x＋y＝2×1＋1＝3.

0051数学课件：简单的线性规划

坐标即为最优整解．
2.调整优解法：即先求非整数条件下的最优解，
调整Z的值使不定方程Ax+By=Z存在最大（小）的整点值，最后筛选出整点最优解．
巩固练习一
设每天应配制甲种饮料x杯，乙种饮料y杯，则
咖啡馆配制两种饮料．甲种饮料每杯含奶粉9g 、咖啡4g、糖 9 x 4 y 3600 4 x 5 y 2000 3g,乙种饮料每杯含奶粉4g 、咖啡5g、糖10g．已知每天原料的使用限额为奶粉3600g ，咖啡2000g 糖3000g,如果甲种饮 3x 10 y 3000 料每杯能获利0.7元，乙种饮料每杯能获利1.2元，每天在原料 x 0 的使用限额内饮料能全部售出，每天应配制两种饮料各多少目标函数为：z =0.7x +1.2y y 0 杯能获利最大？练习一.gsp 解：将已知数据列为下表：
直线x+y=12经过的整点是B(3,9)和C(4,8)，它们是最优解. 答（略）你能否猜测一下Z的最小值可能是多少?
3.最优解的几何意义是什么 (最优解可以转化为什么几何意义)?
结论2:
线性规划求最优整数解的一般方法:
1.平移找解法：即先打网格，描出可行域内的
整点，平移直线，最先经过或最后经过的整点
9 x + 4 y = 3600 _
得点C的坐标为（200，240）
小结
答:每天配制甲种饮料200杯,乙种饮料240杯可获取最大利润.
巩固练习二
某货运公司拟用集装箱托运甲.乙两种货物,一个大集装箱所装托 3 运货物的总体积不能超过24 m ,总重量不能超过1500kg,甲.乙两种货物每袋的体积.重量和可获得的利润,列表如下:
原料奶粉(g) 咖啡(g) 糖(g) 利润(元) 每配制1杯饮料消耗的原料甲种饮料 x 乙种饮料 y 9 4 3 0.7 4 5 10 1.2 原料限额 3600 2000 3000

高二数学简单的线性规划.ppt

四个步骤：
0 12 3 4 56
1.画 2.移
2x+3y=12 5x+4y=20
代数问题 3.求
4.答
(线性约束条件)
图解法
二.实际应用探索问题一
某工厂生产甲、乙两种产品.已知生产甲种产品1t需消耗A种矿石10t、B种矿石5t、煤4t；生产乙种产品1t需消耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、消耗B种
实际问题注意:
列表
寻找约束条件
设立变量
建立目标函数
转化
线性规划问题
1.约束条件要写全;
2.作图要准确,计算也要准确;
3.解题格式要规范.
探索问题二
某工厂现有两种大小不同规格的钢板可截成A、B、C三种规格，每张钢板可同时截得三种规格的小钢板的块数如下表所示：
规格类型钢板类型第一种来自板x张A规格总额达到yx最≥≥00大?
目标函数：z=600x+1000y.
分
原材
每吨产品消耗的原材料原材料限额
析
料甲产品(t) xt 乙产品(t) yt
问 A种矿石 10 1.本问4 题给定了哪些3原00材料(资源)?
题: B种矿石煤利润
5 2.该工4 厂生产哪些产2品00?
4 3.各种9 产品对原材料3(资60源)有怎样的要求? 600 4.该1工00厂0对原材料(资源)有何限定条件?
三.巩固练习
设每天应配制甲种饮料x杯，乙种饮料y杯，则咖啡9x馆配4 y制两36种00饮料．甲种饮料每杯含奶粉9g 、咖啡4g、糖 3的料g,使每34乙xx用杯种限能15饮0y额获y料为利2每30奶00杯0.070粉0含元3奶，60粉乙0g种4，g饮，咖料咖啡每啡20杯50g0能，g，获糖糖利1031g0.．20元0已g，,如知每果每天甲天在种原原饮料料解的杯：使能xy将用获00已限利知额最数内大据饮？列料为目能下标全函表部数：售为：出z ，=0.每7x天+1应.2y配(x制,y两 N种)饮料各多少

高中数学人教A版必修5第三章3.3.2简单的线性规划问题(二)课件

学段初中高中
硬件建设班级学生数配备教师数万元
45
2
26／班
40
3
54／班
教师年薪万元
2／人 2／人
分别用数学关系式和图形表示上述限制条件。若根据有关部门的规定，初中每人每年可收学费1600 元，高中每人每年可收学费2700元。那么开设初中班和高中班多少个？每年收费的学费总额最多？
解：设开设初中班x个，高中班y个。因办学规模以 20～30个班为宜，所以， 20≤x＋y≤30
2x+y=15 x+y=12 x+2y=18
x 27
x+3y=27
当直线经过点A时z=x+y=11.4, 但它不是最优整数解. 作直线x+y=12
B(3,9)和C(4,8)在直线上,且在可行域内, 整点是B(3,9)和C(4,8)，它们是最优解. 答（略）
{2x+y≥15, x+2y≥18, x+3y≥27, x≥0, x∈N* y≥0 y∈N*
目标函数t = x+y
y 15
B(3,9)
9
C(4,8)
A(18/5,39/5)
打网格线法
x+y =0
2 1 0 12 78
x
18
27
作出直线 x+y=0，
2x+y=15
x+2y=18 x+3y=27
当直线经过点A时t=x+y=11.4,但它不是最优整数解，
在可行域内打出网格线，将直线x+y=11.4继续向上平移，
7 x 7 y 5
14x 7 y 6
x
1 7
得M点的坐标为：

人教A版高中数学必修五课件3.3.2简单的线性规划问题2.pptx

5．已知线性目标函数 z＝3x＋2y，在线性约束条件
x＋y－3≥0 2x－y≤0 y≤a
下取得最大值时的最优解只有一个，则实数 a
的取值范围是________．
x＋y－3≥0
解析：作出线性约束条件2x－y≤0
y≤a
表示的平面
区域，
如图中阴影部分所示．
• 因为取得最大值时的最优解只有一个，所以目标函数对应的直线与平面区域的边界线不平行，根据图形及直线的斜率，可得实数a的取值范围是[2，＋∞)．
元．该企业在一个生产周期内消耗A原料不超过 13吨、B原料不超过18吨，那么该企业可获得最大利润是( )
• A．12万元
B．20万元
• C．25万元D．27万元
解析：设该企业在一个生产周期内各生产甲、乙产品
x、y 吨，获得利润 z 万元，根据题意，得
3x＋y≤13
2x＋3y≤18 x≥0
• (3)求：解方程组求最优解，进而求出目标函数的最大值和最小值．
• [注意] 画可行域时，要特别注意可行域各边的斜率与目标函数直线的斜率的大小关系，以便准确判断最优解．
• 2．最优解的确定
• 最优解的确定可有两种方法：
• (1)将目标函数的直线平行移动，最先通过或最后通过的顶点便是最优解．
交点 A(4,5)时，目标函数 z＝200x＋300y 取到最小值为 2 300
元，故所需租赁费最少为 2 300 元．
• 答案： 2300
• 2．某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨、B原料2吨；生产每吨乙产
品要用A原料1吨、B原料3吨．销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万
规格类型钢板类型

人教A版高中数学必修五课件《简单的线性规划》(21张)(共21张PPT)

高中数学课件
灿若寒星整理制作
简单的线性规划
教学目标
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念; 2.运用线性规划问题的图解法，解决一些简单的实际问题.
例1: 求z 2x y的最大值和最小值，
x - 4y -3 其中x, y满足下列条件 : 3x 5y 25
括周界)，目标函数z=x+ay取得最小值的最优解有无
数个，则a的一个可能值为( A )
(A)-3
(B)3 (C)-1 (D)1
5.在如图所示的坐标平面的可行域内(阴影部分且
包括周界)，目标函数z=x+ay取得最大值的最优解
有无数个，则a的一个可能值为( D )
(A)-3
(B)3 (C)-1 (D)1
5)求Z x2 y2的最值 x 1
y C(1, 22)
5
P
A(1,1)
0
x1
x 4 y 3
B(5,2)
x
3x 5 y 25
例2 ：若x, y满足下列条件: x - 4y -3 3x 5y 25
x 1
6)若 z=ax+y取得最大值的最优解
有无数个, 求实数a的值
y
22
C(1, )
5
x 4 y 3
A(1,1)
0
x1
B(5,2)
x
3x 5 y 25
例2 ：若x, y满足下列条件: x - 4y -3 3x 5y 25 x 1
7)若 z=ax+y取得最小值的最优解
有无数个, 求实数a的值
y C(1, 22)
1、画：画出线性约束条件所表示的可行域；

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

应该注意的几个问题：
1、若不等式中不含等号，则边界画成虚线，否则画成实线。 2、画图时应非常准确，否则将
得不到正确结果。
作业： P65 第1、3、7、8题
制作人：诸慧
xx2yy4100或
x2y1 0 x y40
y x －y + 4 = 0
4
－4
－1 o
1 2
Back
x x + 2y + 1 = 0
变题二：由直线 x + y + 2 = 0，x + 2y + 1 = 0 和
2x + y + 1 = 0 围成的三角形区域（包括边界）用
x y20
x
2
y
1
0
不等式可表示为 ___2_x___y___1__0__
x 0
变题三：求不等式组
y
0
表示的平
4x 3 y 12
面区域的面积及平面区域内的整点坐标。
3
x
4x + 3y －1 2 = 0
x y 1 ( x 0, y 0) x y 1 ( x 0, y 0) x y 1 ( x 0, y 0) x y 1 ( x 0, y 0)
y
∴ S=2
1
由图知：平面区域是边长为 2的正方形。
x－y+1=0
x－y－1=0
X 思考1：若直线与坐标轴垂
O
直的情况怎样分类？
问题2：一般地，如何画不等式 Ax + By + C > 0 表示的平面区域
y ？ Ax + By + C = 0
②
o①
x
二元一次不等式Ax+By+C>0 在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
由于对直线同一侧的所有点 (x,y)，把它代入Ax+By+C，所得实数的符号都相同，所以只需在此直线的某一侧取一个特殊点 (x0,y0) ，从Ax0+By0+C的正负可以判断出 Ax+By+C>0表示哪一侧的区域。
2x + y + 1 = 0 y
－2
x+y+2≥0 x + 2y + 1 ≤ 0 2x + y + 1 ≤ 0
Back
－1
1 2
o
1 2
－1
－2
x x + 2y + 1 = 0
x+y+2=0
y
4
o
Back
S 1 34 6 2
经检验：整点坐标为 ( 1 , 1 )、( 1 , 2 ) (2,1)
变题四：求不等式 | x | + | y | ≤1 所表示的平面区域的面积。
小结：
二元一次不等式Ax+By+C>0在平面直角坐标系中表示 _直__线__A_x_+_B_y_+_C__=_0_某_一__侧__所__ _有__点_组__成__的__平__面_区__域__。__
确定步骤： __直__线_定__界___、__特__殊__点_定__域___ 若C≠0，则 __直__线__定__界_、__原__点__定__域_.
－1 o
1
x
－1
x + y －1 = 0
Back
x+y+1=0
第一节二元一次不等式表示平面区域
问题1：在平面直坐标系中， x+y=0
表示的点的集合表示什么图形？
x+y>0 呢?
x+y＜0 呢? x-y+1>0 呢？
在平面直角坐标系中，所有的点都被直线 x + y = 0（如图所示）分成三类：
1、在直线上。 Y 2、在直线的左下方的平面区域内。
3、在直线的右上方的平面区域内。
一般在C≠0时，取原点作为特殊点。
应该注意的几个问题：
1、若不等式中不含等号，则边界画成虚线，否则画成实线。 2、画图时应非常准确，否则将
得不到正确结果。
例1：画出不等式 2x+y-6<0
表示的平面区域。
例2：画出不等式组 x y 5 0 x y 0 x 3
表示的平面区域
答案
变题一：画出不等式 ( x + 2y + 1 )( x －y + 4 ) ＜0 表示的平面区域。