特殊平行四边形中的五种折叠方式
特殊的平行四边形中的的图形变换模型之翻折(折叠)模型(解析版)

特殊的平行四边形中的的图形变换模型之翻折(折叠)模型几何变换中的翻折(折叠、对称)问题是历年中考的热点问题,试题立意新颖,变幻巧妙,主要考查学生的识图能力及灵活运用数学知识解决问题的能力。
翻折以矩形对称最常见,变化形式多样。
无论如何变化,解题工具无非全等、相似、勾股以及三角函数,从条件出发,找到每种对称下隐藏的结论,往往是解题关键。
本专题以各类几个图形(菱形、矩形、正方形等)为背景进行梳理及对应试题分析,方便掌握。
【知识储备】折叠问题的解决,大都是以轴对称图形的性质作为切入点,而数形变化,是解决这类问题的突破口。
有了“折”就有了”形”--轴对称图形、全等形;有了“折”就有了“数”--线段之间、角与角之间的数量关系。
"折” 就为“数”与“形”之间的转化搭起了桥梁。
特殊平行四边形中的折叠问题,还要考虑特殊平行四边形本身的性质,有时也需要用到计算工具:相似和勾股定理。
折叠的性质:重合部分是全等图形,对应边、对应角相等;对称点的连线被对称轴垂直平分。
【知识储备】1)矩形的翻折模型【模型解读】1(2023春·辽宁葫芦岛·八年级统考期末)如图,在矩形ABCD中,E是BC的中点,将△DEC沿DE翻折得到△DEC ,延长DC 交AB于点M,若AB=4,BC=6,则BM的长度为()A.94B.32C.12D.3【答案】A【分析】根据题意连接ME ,证明△BME ≌△C ME ,得出MC =BM =4-x ,在Rt △AMD 中运用勾股定理即可解答;【详解】连接ME ,∵AB =4,BC =6,ABCD 为矩形,∴AD =BC =6,DC =AB =4.∵E 是BC 的中点∴BE =CE =3∵△DEC 由△DEC 翻折得到,∴C ′E =CE =3,DC ′=DC =4,∠DC E =∠C =90°,∴∠MC E =180°-∠DC E =90°=∠B ,设AM =x ,则BM =4-x .在Rt △BEM 和Rt △C EM 中ME =ME BE =C ′E =3∴△BME ≌△C ME ∴MC =BM =4-x 在Rt △AMD 中AD 2+AM 2=MD 2即62+x 2=(4+4-x )2解得:x =74∴BM =4-x =94故选A【点睛】该题考查了矩形知识点和勾股定理的运用,掌握矩形性质和勾股定理是解答该题的关键2(2023春·陕西西安·八年级校考期末)如图,在矩形ABCD 中,AB =8,AD =4,E 是AB 上一个动点,F 是AD 上一点(点F 不与点D 重合).连接EF ,将△AEF 沿EF 翻折,使点A 的对应点A 落在边CD 上,连接EC ,若A E =CE ,则△A DF 的面积为()A.1B.1.5C.2D.2.5【答案】B【分析】由折叠可知AE =A E ,AF =A F ,设AE =A E =CE =x ,则BE =8-x ,在Rt △BCE 中,利用勾股定理可建立方程8-x 2+42=x 2,解得x =5,则AE =A E =CE =5,BE =3,再根据等腰三角形的性质得到A C =2CG =6,进而算出A D =2,设AF =A F =a ,则DF =4-a ,在Rt △A DF 中,利用勾股定理可建立方程4-a 2+22=a 2,解得a =52,则DF =32,再利用三角形面积公式计算即可求解.【详解】解:如图,过点E 作EG ⊥CD 于点G ,∵四边形ABCD 为矩形,AB =8,AD =4,∴AD =BC =4,AB =CD =8,∠B =∠D =90°,由折叠可知,AE =A E ,AF =A F ,∵A E =CE ,∴AE =A E =CE ,设AE =A E =CE =x ,则BE =AB -AE =8-x ,在Rt △BCE 中,BE 2+BC 2=CE 2,∴8-x 2+42=x 2,解得:x =5,∴AE =A E =CE =5,BE =3,∵∠B =∠BCG =∠CGE =90°,∴四边形BCGE 为矩形,∴CG =BE =3,∵A E =CE ,EG ⊥CD ,∴A C =2CG =6,∴A D =CD -A C =8-6=2,设AF =A F =a ,则DF =AD -AF =4-a ,在Rt △A DF 中,DF 2+A D 2=A F 2,∴4-a 2+22=a 2,解得:a =52,∴DF =32,∴S △A DF =12A D ⋅DF =12×2×32=1.5故选:B .【点睛】本题主要考查矩形的性质、折叠的性质、等腰三角形的性质、勾股定理,熟练掌握折叠的性质以及勾股定理是解题的关键.3(2023春·安徽安庆·九年级校联考阶段练习)如图,长方形ABCD 沿着对角线BD 翻折,点C 落在点C 处,BC 与AD 相交于点E ,若AB =3,AE =1,求BC 的长.【答案】10+1【分析】根据翻折的性质,证明△AEB ≅△C ED ,然后求出ED ,最后根据勾股定理即可求出结果.【详解】由翻折的性质可知,在△AEB 与△C ED 中,∠A =∠C∠AEB =∠C ED AB =C D∴△AEB ≅△C ED ∴AE =EC ,∵AB =3,∴BE =AB 2+AE 2=10,∵ED =BE ,∴AD =AE +ED =10+1,∵长方形ABCD ,AD =BC ,∴BC =10+1.【点睛】本题考查了全等三角形的判定及性质、勾股定理和矩形的性质,掌握全等三角形的判定及性质是解题的关键.4(2023春·湖北·八年级专题练习)如图,在长方形ABCD 中,AB =8,BC =6,P 为AD 上一点,将△ABP 沿BP 翻折至△EBP ,PE ,BE 与CD 分别相交于点O ,F ,且OE =OD .则AP 的长为()A.4.5B.4.6C.4.7D.4.8【答案】D【分析】由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,证明△ODP≌△OEF(ASA),得出OP=OF,PD=FE,设AP=EP=x,则DP=FE=6-x,DF=x,求出CF=8-x,BF=8-6-x=2+x,根据勾股定理得出方程,解方程即可.【详解】解:∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,根据题意得:△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=8,∵∠D=∠E,OD=OE,∠DOP=∠EOF,∴△ODP≌△OEF(ASA),∴OP=OF,PD=FE,∴DF= EP,设AP=EP=x,则DP=FE=6-x,DF=x,∴CF=8-x,BF=8-6-x=2+x,根据勾股定理得:BC2+CF2=BF2,即62+8-x2,解得:x=4.8,∴AP=4.8,故选:D2=x+2【点睛】本题考查了矩形的性质、折叠的性质、全等三角形的判定与性质以及勾股定理的运用,熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.5(2023春·陕西商洛·八年级统考期末)如图,在矩形ABCD中,AB=12,BC=24,将矩形折叠,使点C与点A重合,则AF的长为()A.20B.18C.16D.15【答案】D【分析】设BE=x,则CE=BC-BE=24-x,根据勾股定理列出关于x的方程122+x2=24-x2,据此即可求解.【详解】解:设BE=x,则CE=BC-BE=24-x,∵沿EF翻折后点C与点A重合,∴AE=CE=24-x,在Rt△ABE中,AB2+BE2=AE2,即122+x2=24-x2,解得x=9,∴AE=24-9=15,由翻折的性质得,∠AEF=∠CEF,∵矩形ABCD的对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AE=AF=15,故选:D.【点睛】本题主要考查了折叠的性质,勾股定理,矩形的性质,解题的关键是作出辅助线,熟练掌握折叠的性质和矩形的性质.6(2023春·江苏宿迁·八年级统考期末)如图,在矩形ABCD中,AB=6,BC=8.点O为矩形ABCD的对称中心,点E为边AB上的动点,连接EO并延长交CD于点F.将四边形AEFD沿着EF翻折,得到四边形A EFD ,边A E交边BC于点G,连接OG、OC,则△OGC的面积的最小值为()A.18-3B.92+37 C.12-372D.6+372【答案】D【分析】在EA上截取EM=EG,连接OM,证明△MOE≌△GOE,所以OM=OG,即可得OM最短时,OG也就最短,而当OM⊥AB时,OM最短,且OM=4=OG,再过点O作OH⊥BC,得OH=3,又因为OC=5,就可以根据勾股定理计算GH、HC的长,从而计算出最小面积.【详解】解:在EA上截取EM=EG,连接OM,由折叠得:∠MEO=∠GEO,又∵EO=EO,∴△MOE≌△GOE SAS,∴OM=OG,∴OM最短时,OG也就最短,而当OM⊥AB时,OM最短,此时,∵点O为矩形ABCD的对称中心,∴OM=12BC=4=OG,即OG的最小值是4,在△OGC中,∵点O为矩形ABCD的对称中心,∴OC长度是矩形对角线长度的一半,即是5,定值,∠BCO度数也不变,是定值,∴当OG=4最小值时,ΔOGC面积最小.过点O作OH⊥BC,∵点O为矩形ABCD的对称中心, ∴OH=12AB=3,∴Rt△OGH中,GH=OG2-OH2=42-32= 7,Rt△OHC中,HC=OC2-OH2=52-32=4,∴GC=GH+HC=7+4,∴△OGC面积的最小值是12×GC×OH=12×(7+4)×3=327+6.故选:D.【点睛】本题考查矩形的性质、全等三角形的判定与性质及垂线段最短等知识,解题关键是找到OG最小值.7(2023春·浙江金华·八年级统考期末)如图,在矩形ABCD中,AD=3,AB=5,点P,Q分别为AB,AD上的动点,将△PBC沿PC翻折得到△PEC,将△PAQ沿PQ翻折得到△PFQ在动点P,Q所有位置中,当F,E,P三点共线,CF=10时,AP=.【答案】3【分析】利用矩形和翻折的性质求出CE =CB =3,BP =EP ,AP =FP ,∠CEP =∠B =90°,在Rt △CEF 中利用勾股定理求出EF =1,设BP =x ,则EP =x ,AP =5-x ,FP =1+x ,根据AP =FP 可构建关于x 的方程,然求解即可解答.【详解】解:在矩形ABCD 中,AD =3,AB =5,∴BC =AD =3,∠B =90°,∵翻折,∴CE =CB =3,BP =EP ,AP =FP ,∠CEP =∠B =90°,∴∠CEF =90°,又CF =10,∴EF =CF 2-CE 2=1,设BP =x ,则EP =x ,AP =5-x ,FP =1+x ,∴1+x =5-x ,∴x =2,∴AP =3.故答案为:3.【点睛】本题考查矩形的性质,翻折的性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题.8(2023秋·山西·九年级专题练习)综合与实践:在综合与实践课上,老师让同学们以“矩形纸片的折叠”为主题开展数学活动.在矩形ABCD 中,E 为AB 边上一点,F 为AD 边上一点,连接CE 、CF ,分别将△BCE 和△CDF 沿CE 、CF 翻折,点D 、B 的对应点分别为点G 、H ,且C 、H 、G 三点共线.(1)如图1,若F 为AD 边的中点,AB =BC =6,点G 与点H 重合,则∠ECF =°,BE =;(2)如图2,若F 为AD 的中点,CG 平分∠ECF ,AB =2+1,BC =2,求∠ECF 的度数及BE 的长;(3)AB =5,AD =3,若F 为AD 的三等分点,请直接写出BE 的长.【答案】(1)45;2(2)∠ECF =45°;BE =22-2(3)2或97【分析】(1)根据正方形的性质和翻折的性质,可得出∠ECF =12∠BCD =12×90°=45°;设BE =x ,用x 表示出Rt △AEF 的三条边,然后根据勾股定理列出方程,即可得出BE 的长;(2)如图,由折叠性质和CG 平分∠ECF ,得出∠1=∠2=∠3=∠4,即可求出∠ECF 的度数;先证明△CBM 和△EHM 是等腰直角三角形,得出BM =BC =2,EM =2BE ,即可求出BE 的长;(3)根据F 为AD 的三等分点,分两种情况:当AF =2DF 时,过点E 作EP ∥GH ,交FG 的延长线于点P ,连接EF ,证明Rt △EFP ≌Rt △FEA ,得出AE =FP ,进而求出BE 的长;当DF =2AF 时,点E 作EP ∥GH ,交FG 的延长线于点P ,连接EF ,根据EF 2=AF 2+AE 2=EP 2+FP 2,计算即可求出BE 的长.【详解】(1)∵AB =BC ,四边形ABCD 是矩形,∴四边形ABCD 是正方形,∴AD =BC =6,∠BCD =90°,∵将△BCE 和△CDF 沿CE 、CF 翻折,点D 、B 的对应点分别为点G 、H ,∴∠BCE =∠GCE ,∠DCF =∠GCF ,∵∠BCD =90°,∴∠ECF =12∠BCD =12×90°=45°,∵F 为AD 的中点,∴DF =12AD =3,∵将△BCE 和△CDF 沿CE 、CF 翻折,点D 、B 的对应点分别为点G 、H ,∴BE =EG ,DF =FG =3,设BE =x ,则AE =6-x ,∴EF =3+x ,∵EF 2=AE 2+AF 2,∴3+x 2=6-x 2+32,∴x =2,∴BE =2.故答案为:45;2;(2)如图2,延长CG ,交AB 于点M ,∵CG 平分∠ECF ,∴∠2=∠4,由折叠的性质可知,∠1=∠2,∠3=∠4,∴∠1=∠2=∠3=∠4=14∠BCD =22.5°,∴∠ECF =45°,∵CD ∥AB ,∠EMH =∠DCM =45°,∴△CBM 和△EHM 均为等腰直角三角形,∴BM =BC =2,EM =2BE ,∴BM =BE +EM =2,即BE +2BE =2,解得BE =22-2.(3)分两种情况:①当AF =2DF 时,如图3,过点E 作EP ∥GH ,交FG 的延长线于点P ,连接EF ,则四边形GHEP 为矩形,GH =EP ,EH =GP ,由折叠的性质可知,CD =CG =5,BC =CH =3,∴HG =CG -CH =2,∵AF =2DF ,∴AF =2,DF =FG =1,∴AF =EP ,在Rt △EFP 和Rt △FEA 中,AF =EP EF =EF ,∴Rt △EFP ≌Rt △FEA (HL ),∴AE =FP ,设BE =EH =a ,FP =GP +FG =a +1,AE =FP =5-a ,∴a +1=5-a ,解得a =2,∴BE =2.②当DF =2AF 时,如图4,过点E 作EP ∥GH ,交FG 的延长线于点P ,连接EF ,则四边形GHEP 为矩形,GH =EP ,EH =GP ,由折叠的性质可知,CD =CG =5,BC =CH =3,∴EP =HG =CG -CH =2,∵DF =2AF ,∴AF =1,DF =FG =2,设BE =EH =a ,FP =GP +FG =a +2,AE =5-a ,∵EF 2=AF 2+AE 2=EP 2+FP 2,∴12+5-a 2=22+a +2 2,解得a =97,∴BE =97.综上可知,BE 的长为2或97.【点睛】本题主要综合考查了矩形的折叠问题,涉及到正方形的性质,矩形的判定和性质,轴对称的性质,全等三角形的判定和性质,勾股定理等知识,属于压轴题,难度较大,熟练掌握并灵活运用相关知识进行分类讨论是解题的关键.2)菱形的翻折模型【模型解读】9(2023·四川成都·模拟预测)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为.【答案】2.8【分析】作EH⊥BD于H,根据折叠的性质得到EG=EA,根据菱形的性质、等边三角形的判定定理得到△ABD为等边三角形,得到AB=BD,根据勾股定理列出方程,解方程即可.【详解】解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=12∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8-x,在Rt△EHB中,BH=12x,EH=32x,在Rt△EHG中,EG2=EH2+GH2,即(8-x)2=32x2+6-12x2,解得,x=2.8,即BE=2.8,故答案为:2.8.【点睛】本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.10(2023·安徽·统考一模)如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连结A'C,则A'C长度的最小值是( ).A.7B.7-1C.3D.2【答案】B【分析】根据题意,在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动,当A′C取最小值时,由两点之间线段最短知此时M、A′、C三点共线,得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.【详解】如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,过点M作MF⊥DC于点F,∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,∴2MD=AD=CD=2,∠FDM=60°,∴∠FMD=30°,∴FD=12MD=12,∴FM=DM×cos30°=32,∴MC=FM2+CF2=7,∴A′C=MC-MA′=7-1.故选B.11(2023·山东八年级统考期末)如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD 的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为()A.18B.17C.16D.15【答案】B【分析】连接BP ,BD ,证明ΔBCD 是等边三角形,证得∠ABP =∠CPB =90°,由折叠可得AM =MP ,由MP 2=BM 2+BP 2可求出MP 的长,进而得出答案.【详解】解:如图,连接BP ,BD ,∵四边形ABCD 为菱形,∠A =60°,∴AB =BC =CD ,∠A =60°=∠C ,∴ΔBCD 是等边三角形,∵P 是CD 中点,∴DP =CP =12CD ,BP ⊥CD ,∠PBC =30°,∴CP =12BC ,BP =3CP ,∵CD ⎳AB ,∴∠ABP =∠CPB =90°,由折叠可得AM =MP ,设AB =BC =CD =2a ,∴BP =3a ,∵MP 2=BM 2+BP 2,∴MP 2=3a 2+(2a -AM )2,即MP 2=3a 2+(2a -MP )2∴AM =MP =74a ,∴BM =AB -AM =AB -MP =14a ,∴BM AM=17.故答案为:B .【点睛】本题主要考查折叠的性质、菱形的性质、勾股定理及等边三角形的性质与判定,熟练掌握折叠的性质、菱形的性质、勾股定理及等边三角形的性质与判定是解题的关键.12(2023秋·广西九年级专题练习)如图,在菱形纸片ABCD 中,∠A =60°,P 为AB 中点.折叠该纸片使点C 落在点C 处且点P 在DC 上,折痕为DE ,则∠CED 的大小为()A.40°B.45°C.60°D.75°【答案】D 【分析】连接BD ,易得△DAB 为等边三角形,根据三线合一,易得∠DPA =90°,利用菱形的性质,易得:∠PDC =90°,∠C =60°,根据折叠的性质,易得∠CDE =12∠PDC =45°,再利用三角形的内角和求出∠CED 的度数即可.【详解】解:∵在菱形纸片ABCD 中,∠A =60°,∴∠C =∠A =60°,AD =AB ,AB ∥CD ,连接BD ,∴△DAB 为等边三角形,∵P 为AB 中点,∴DP ⊥AB ,∵AB ∥CD ,∴PD ⊥DC ,∴∠PDC =90°,∵折叠该纸片使点C 落在点C 处且点P 在DC 上,折痕为DE ,∴∠CDE =12∠PDC =45°,∴∠CED =180°-∠CDE -∠C =75°;故选D .【点睛】本题考查菱形的性质,等边三角形的判定和性质,折叠的性质,三角形的内角和个定理.熟练掌握并灵活运用相关知识点,是解题的关键.13(2023春·浙江·八年级专题练习)对角线长分别为6和8的菱形ABCD 如图所示,点O 为对角线的交点,过点O 折叠菱形,使B ,B 两点重合,MN 是折痕.若B M =1.5,则CN 的长为()A.3.5B.4.5C.5.5D.6.5【答案】A【分析】连接AC 、BD ,利用菱形的性质得OC =12AC =3,OB =OD =12BD =4,∠COD =90°,再利用勾股定理计算出CD =5,由ASA 证得△OBM ≌△ODN 得到DN =BM ,然后根据折叠的性质得BM =B M =1.5,则DN =1.5,即可得出结果.【详解】解:连接AC 、BD ,如图,∵点O 为菱形ABCD 的对角线的交点,∴OC =12AC =3,OB =OD =12BD =4,∠COD =90°,在Rt △COD 中,CD =OC 2+OD 2=32+42=5,∵AB ∥CD ,∴∠MBO =∠NDO ,在△OBM 和△ODN 中,∠MBO =∠NDOOB =OD ∠BOM =∠DON,∴△OBM ≌△ODN ASA ,∴DN =BM ,∵过点O 折叠菱形,使B ,B 两点重合,MN 是折痕,∴BM =B M =1.5,∴DN =1.5,∴CN =CD -DN =5-1.5=3.5,故选:A .【点睛】本题考查了菱形与折叠问题,熟练掌握菱形的性质,勾股定理,全等三角形的性质与判定和折叠的性质是解题的关键.14(2023·山东九年级课时练习)如图,在折叠千纸鹤时,其中某一步需要将如图所示的菱形纸片ABCD 分别沿AM ,AN 所在直线进行折叠,使得菱形的两边AB ,AD 重合于AO .若此时∠MON =80°,则∠AMO =.【答案】30°/30度【分析】根据菱形的性质得∠B =∠D ,∠B +∠BAD =180°,再由折叠的性质得∠B =∠AOM ,∠D =∠AON ,∠BAM =∠OAM =∠DAN =∠OAN =14∠BAD ,所以∠AOM =∠AON =12(360°-∠MON )=140°,所以∠B =∠AOM =140°,从而可求得∠BAD =40°,继而求得∠OAM =10°,再由三角形内角和定理求解即可.【详解】解:∵四边形ABCD 为菱形,∴∠B =∠D ,∠B +∠BAD =180°,由折叠的性质得:∠B =∠AOM ,∠D =∠AON ,∠BAM =∠OAM =∠DAN =∠OAN =14∠BAD ,∵∠MON =80°,∴∠AOM =∠AON =12(360°-80°)=140°,∴∠B =∠AOM =140°,∴∠BAD =40°,∴∠OAM =10°,∴∠AMO =180°-140°-10°=30°,故答案为:30°.【点睛】本题考查菱形的性质,折叠的性质,三角形内角和定理,熟练掌握菱形的性质、折叠的性质是解题的关键.3)正方形的翻折模型【模型解读】15(2023·湖南郴州·八年级校考期末)如图,正方形ABCD 的边长为4,E 是AD 边的中点,连接BE ,将△ABE 沿直线BE 翻折至△FBE ,延长EF 交CD 于点G ,则CG 的长度是()A.23B.34C.43D.32【答案】C【分析】连接BG ,根据折叠的性质和正方形的性质可得AB =BF =BC =4,AE =FE =12AD =2=DE ,∠A =∠BFE =90°=∠C ,即可证明Rt △BFG ≌Rt △BCG 得到FG =CG ,设CG =FG =x ,则DG=4-x ,EG =2+x ,在Rt △DEG 中,由勾股定理进行求解即可.【详解】解:如图所示,连接BG ,∵四边形ABCD 是正方形,∴AB =BC =DC =4,∠A =∠ABC =∠C =90°,由折叠的性质可得,AB=BF=BC=4,AE=FE=12AD=2=DE,∠A=∠BFE=90°=∠C,∵∠BFE+∠BFG=180°,∴∠C=∠BFG=90°,又∵BG=BG,∴Rt△BFG≌Rt△BCG(HL),∴FG=CG,设CG=FG=x,则DG=4-x,EG=2+x,在Rt△DEG中,由勾股定理得,EG2=DE2+DG2,∴(2+x)2=22+(4-x)2,解得x=43,即CG=43,故选C.【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,全等三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.16(2023·江苏·八年级假期作业)如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,则BF2=()A.42+4B.6+42C.12D.8+42【答案】D【分析】点F作FG⊥BC交于G点,设正方形的边长为x,则AC=2x,由折叠可知,DE=EF,AD= AF,∠D=∠EFA=90°,可得DE=2,EC=x-2,AC=2x,在Rt△EFC中,由勾股定理可得(x-2)2 =4+(2x-x)2,解得x,即为正方形的边长为22+2,再求出FC=2,由∠ACB=45°,可求FG=CG =2,BG=2+2,在Rt△BFG中,由勾股定理可得BF2=(2+2)2+2=8+42.【详解】解:过点F作FG⊥BC交于G点,由折叠可知,DE=EF,AD=AF,∠D=∠EFA=90°,设正方形的边长为x,∵EF=2,∴DE=2,EC=x-2,AC=2x,在Rt△EFC中,EC2=FE2+FC2,∴(x-2)2=4+(2x-x)2,解得x =22+2,∴FC =2x -x =2,∵∠ACB =45°,∴FG =CG =2,∴BG =2+2,在Rt △BFG 中,BF 2=BG 2+GF 2=(2+2)2+2=8+42,故选:D .【点睛】本题考查正方形性质,翻折的性质,熟练掌握翻折的性质,灵活应用勾股定理是解题的关键.17(2023·江苏·九年级专题练习)如图,ABCD 是一张边长为4cm 的正方形纸片,E ,F 分别为AB ,CD 的中点,沿过点D 的折痕将A 角翻折,使得点A 落在EF 上的点A ′处,则EG =cm .【答案】43-6【分析】由ABCD 是一张边长为4cm 的正方形纸片,E ,F 分别为AB ,CD 的中点,可得AE =DF =2cm ,EF =AD =4cm ,由翻折的性质可得AG =A ′G ,AD =A ′D ,在Rt △DFA ′与Rt △A ′EG 中,用勾股定理可求得答案.【详解】解:∵ABCD 是一张边长为4cm 的正方形纸片,E 、F 分别为AB ,CD 的中点,∴AE =DF =2cm ,EF =AD =4cm ,∵沿过点D 的折痕将A 角翻折,使得点A 落在EF 上的点A ′处,∴AG =A ′G ,AD =A ′D =4cm ,在Rt △DFA ′中,A ′F =A ′D 2-DF 2=42-22=23cm ,∴A ′E =4-23 cm ,在Rt △A ′EG 中,设EG =x ,则A ′G =AG =(2-x )cm ,∴A ′G 2=A ′E 2+EG 2,即2-x 2=x 2+4-23 2,解得x =43-6.故答案为:43-6.【点睛】本题考查了正方形的性质及图形的翻折问题;利用相关知识找出等量关系,两次利用勾股定理是正确解答本题的关键.18(2023·山西朔州·校联考模拟预测)如图,在正方形ABCD 中,AB =2,将其沿EF 翻折,使∠EFC =120°,顶点B 恰好落在线段AD 上的点G 处,点C 的对应点为点H .则线段AE 的长为.【答案】23【分析】设AE =x ,则BE =2-x ,由翻折性质,得EG =EB =2-x ,∠GEF =∠BEF =60°,所以∠AEG =60°,在Rt △AEG 中,利用三角函数可求出x ,从而得到线段AE 的长.【详解】解:设AE =x ,∵正方形ABCD 中,AB =2,∴BE =2-x ,AB ∥CD ,∵∠EFC =120°,∴∠BEF =60°,∵四边形EFHG 是四边形EFCB 折叠得到,∴∠GEF =∠BEF =60°,EG =BE =2-x ,∴∠AEG =180°-∠GEF -∠BEF =60°,在Rt△AGE中,cos∠AEG=AEEG,即cos60°=x2-x=12,解得x=23,经检验x=23是原方程的解,∴原方程的解为x=23,∴AE=23,故答案为:23.【点睛】本题考查翻折变换,正方形的性质,解直角三角形,熟练运用相关图形的性质是解题的关键.19(2023·广东九年级课时练习)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,则下列结论:①△ABG≌△AFG;②∠AGB+∠AED=135°③GF=3;④AG⎳CF;其中正确的有(填序号).【答案】①②③④【分析】根据折叠,得到AD=AF,∠D=∠AFE=90°,推出AB=AF,∠AFG=∠B=90°,可证明Rt△ABG≌Rt△AFG,即可判断①正确;根据∠DAE=∠EAF,∠BAG=∠FAG,进而可得∠GAE=45°,根据三角形内角和定理即可得∠AEF+∠ADF=135°,得到∠AGB+∠AED=135°,进而判断②正确;设BG=GF=x,则CG=6-x,EG=x+2,CE=4,在Rt△EGC中,根据勾股定理建立方程(x+2)2= (6-x)2+42,解方程可得GF=3,即可判断③正确;根据BG=FG=3,得到CG=BC-BG=6-3=3,得到CG=FG,推出∠GCF=∠GFC,根据∠AGB=∠AGF,得到∠BGF=2∠AGF=2∠GFC,得到∠AGF=∠GFC,推出AG∥CF,即可判断④正确【详解】∵四边形ABCD是正方形,∴∠D=∠ABC=∠DAB=∠BCD=90°,AB=BC=CD=AD=6,∵CD=3DE,∴DE=2,∴CE=4,∵将△ADE沿AE对折至△AFE,∴∠AFE=∠ADE=90°,AF=AD,EF=DE=2,∴∠AFG=∠ABG=90°,AF=AB,在Rt△ABG和Rt△AFG中,AB=AF AG=AG,∴Rt△ABG≌Rt△AFG(HL),∴①正确;∵将△ADE沿AE对折至△AFE,∴∠DAE=∠EAF,∵Rt△ABG≌Rt△AFG,∴∠BAG=∠FAG,∵∠DAE+∠EAF+∠BAG+∠FAG=∠DAB=90°,∴∠EAG=∠EAF+∠FAG=12∠DAB=45°,∴∠AEF+∠ADF=135°,∴∠AGB+∠AED=135°,∴②正确;设BG=GF=x,则CG=6-x,EG=x+2,∵CE=4,∴(x+2)2=(6-x)2+42,解得x=3,∴BG=GF=3,∴③正确;∵BG=FG=3,∴CG=BC-BG=6-3=3,∴CG=FG,∴∠GCF=∠GFC,∵∠AGB=∠AGF,∴∠BGF=2∠AGF=2∠GFC,∴∠AGF=∠GFC,∴AG∥CF∴④正确;故答案为:①②③④.【点睛】本题考查了正方形性质,折叠图形全等的性质,三角形全等的判断和性质,三角形内角和定理,勾股定理,熟练掌握以上知识是解题的关键.20(2023·江苏扬州·校考二模)如图,将正方形ABCD沿着BE、BF翻折,点A、C的对应点分别是点A 、C ,若∠A BC =14°,则∠EBF=.【答案】38°【分析】由正方形的性质及折叠的性质可得∠ABC=90°,∠ABE=∠A BE,∠CBF=∠C BF,利用角之间的和差关系可得2∠A BE+2∠C BF=90°+∠A BC =104°,进而求得∠A BE+∠C BF=52°,再利用∠EBF=∠A BE+∠C BF-∠A BC 即可求得结果.【详解】解:∵四边形ABCD是正方形,∴∠ABC=90°,由折叠可知,∠ABE=∠A BE,∠CBF=∠C BF,∵∠A BF=∠C BF-∠A BC ,∠ABE+∠A BE+∠A BF+∠CBF=90°,∴2∠A BE+2∠C BF-∠A BC =90°,即:2∠A BE+2∠C BF=90°+∠A BC =104°,∴∠A BE+∠C BF =52°,∴∠EBF=∠A BE+∠C BF-∠A BC =52°-14°=38°,故答案为:38°.【点睛】本题考查正方形与折叠的性质,利用正方形与折叠的性质得到∠A BE+∠C BF的度数是解决问题的关键.21(2023春·江苏宿迁·八年级统考期末)问题情境:如图1,在正方形ABCD中,AB=6,点F是边AD上一点(点F不与A,D重合),将△CDF沿直线CF翻折,点D落在点E处.(1)如图2,当点E落在对角线AC上时,求DF的长.(2)如图3,连接AC,BD,BD分别交CF,AC于点M,点O,连接OE并延长交AD于点G,当M为OD中点时,试判断OG与CF的位置关系,并说明理由.(3)如图4,在线段CE上取一点Q,且使CQ=2,连接AE,BQ,则在点F从点A运动到点D的过程中,AE+BQ的值是否存在最小值?如果存在,请求出其值;若果不存在,请说明理由.【答案】(1)62-6(2)CF∥OG,理由见解析.(3)213【分析】(1)可证得△FEA为等腰直角三角形,AF=2EF,结合DF=EF,可得AD=DF+AF=DF+ 2DF.(2)连接DE,交FM于点H,可知DH=EH,根据三角形的中位线定理,即可求得OG与CF的位置关系.(3)在线段CB上取一点P,使CP=CQ=2,连接AP,EP,可证得△CBQ≌△CPE,则AE +BQ=AE+EP,观察图形可知,当点A,E,P在同一条直线上时,AE+EP最小,最小值为AP.【详解】(1)根据折叠的性质可知DF=EF,∠D=∠FEC=90°,∴∠FEA=90°.∵∠FAE=45°,∴△FEA为等腰直角三角形.∴EF=EA.∴AF2=EF2+AE2=2EF2.∴AF=2EF.∴AF=2DF.∴AD=DF+AF=DF+2DF=6.∴DF=62-6.(2)CF∥OG,理由如下:如图所示,连接DE,交FM于点H.根据题意可知CF 为线段DE 的垂直平分线,∴DH =EH .∵M 为OD 中点,∴MH ∥OE ,即CF ∥OG .(3)如图所示,在线段CB 上取一点P ,使CP =CQ =2,连接AP ,EP .在△CBQ 和△CPE 中,CQ =CP∠QCB =∠PCE CB =CE∴△CBQ ≌△CPE .∴BQ =EP .∴AE +BQ =AE +EP .观察图形可知,当点A ,E ,P 在同一条直线上时,AE +EP 最小,最小值为AP .∴AP =AB 2+BP 2=62+42=213.【点睛】本题主要考查图形折叠的性质、全等三角形的判定及性质、勾股定理、等腰三角形的判定及性质、三角形的中位线定理,能根据题意作出辅助线是解题的关键.课后专项训练1(2023·湖北随州·八年级统考期末)如图,在菱形纸片ABCD 中,AB =4,∠A =60°,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,点F ,G 分别在边AB,AD 上,则EF 的长为()A.72 B.94 C.196 D.733【答案】A【分析】连接BE ,BD ,则△BCD 是等边三角形,则求出BE 的长度,由折叠的性质和勾股定理,即可求出EF 的长度.【详解】解:如图,连接BE ,BD ,∵AB =4=BC =CD ,∠A =60°=∠C ,∴△BCD 是等边三角形,∵E 是CD 中点∴DE =2=CE ,BE ⊥CD ,∠EBC =30°,∴BE =3CE =23,∵CD ∥AB ,∴∠ABE =∠CEB =90°,由折叠可得AF =EF ,∵EF 2=BE 2+BF 2,∴EF 2=12+(4-EF )2,∴EF =72.故选:A .【点睛】本题考查了折叠问题,菱形的性质,勾股定理,关键是添加恰当的辅助线构造直角三角形,利用勾股定理求线段长度.2(2023春·江西新余·八年级统考期末)如图,正方形ABCD 的边长为6,点E 是BC 上的一点,连接AE 并延长,交射线DC 于点F ,将△ABE 沿直线AE 翻折,点B 落在点N 处,AN 的延长线交DC 于点M ,当AB =2CF 时,则NM 的长为()A.12B.1C.32D.54【答案】A【分析】由折叠的性质可得AN =AB =6,∠BAE =∠NAE ,再由平行线的性质得到∠BAE =∠F ,则可证明∠NAE =∠F 得到AM =FM ,设CM =x ,则DM =6-x ,AM =FM =3+x ,在Rt △ADM 中,由勾股定理得3+x 2=62+6-x 2,解方程求出AM =132,则NM =AM -AN =12.【详解】解:∵△ABE 沿直线AE 翻折,点B 落在点N 处,∴AN =AB =6,∠BAE =∠NAE ,∵正方形ABCD 中,AB ∥CD ,∴∠BAE =∠F ,∴∠NAE =∠F ,∴AM =FM ,设CM =x ,∵AB =2CF =6,∴CF =3,∴DM =6-x ,AM =FM =3+x ,在Rt △ADM 中,由勾股定理得,AM 2=AD 2+DM 2,即3+x 2=62+6-x 2,解得x =72,∴AM =3+72=132,∴NM =AM -AN =132-6=12.故选:A .【点睛】本题主要考查了正方形的性质,勾股定理,等腰三角形的判定,证明AM =FM 是解题的关键.3(2023春·江苏宿迁·八年级校考阶段练习)如图,正方形ABCD 的边长为4,点E 在边CD 上,且CE =1,连结AE ,点F 在边AD 上,连结BF ,把△ABF 沿BF 翻折,点A 恰好落在AE 上的点G 处,下列结论:①AE =BF ;②AD =3DF ;③S △ABF =6;④GE =0.2,其中正确的是()A.①②③④B.①③④C.①②③D.①③【答案】B 【分析】根据翻折的性质证△ABF ≌△DAE (ASA ),得出AF =DE =3,BF =AE ,即可判断①正确;根据DF =AD -AF =4-3=1,即可判断②错误;由勾股定理得出BF =5,由S △ABF 求出即可求得③正确;根据S △ABF =12AB •AF =12BF •AH ,求出AH ,即可判断④正确,进而得出答案.【详解】解:∵四边形ABCD 为正方形,∴AB =AD =CD =4,∠BAD =∠D =90°,∵CE =1,∴DE =3,由折叠的性质可知,△ABF ≌△GBF ,BF 垂直平分AG ,∴BF ⊥AE ,AH =GH ,∴∠BAH +∠ABH =90°,∵∠FAH +∠BAH =90°,∴∠ABH =∠FAH ,在△ABF和△DAE中,∠BAF=∠D AB=AD∠ABF=∠DAE,∴△ABF≌△DAE(ASA),∴AF=DE=3,BF=AE,故①正确;∵DF=AD-AF=4-3=1,∴AD=4DF,故②错误;在Rt△ABF中,∵BF=AB2+AF2=42+32=5∴S△ABF=12AB•AF=12×4×3=6,故③正确;∵S△ABF=12AB•AF=12BF•AH,∴4×3=5AH,∴AH=125,∴AG=2AH=245,∵AE=BF=5,∴GE=AE-AG=5-245=0.2,故④正确;综上所述:正确的是①③④,故选:B.【点睛】本题考查了翻折变换,全等三角形的判定与性质,勾股定理,正方形的性质,解决本题的关键是掌握翻折的性质.4(2023春·山西长治·八年级统考期末)如图,在菱形ABCD中,∠B=60°,将边AB沿AF折叠得到AB ,AB交CD于点E,当E为CD中点时,∠EFC的大小为()A.28°B.75°C.40°D.30°【答案】D【分析】延长AE交BC的延长线于点H,过点A作AI⊥BH于点I,可证△ADE≌△HCE,故CH=AD= BC=AB,即BH=2AB,即可求解.【详解】解:延长AE交BC的延长线于点H,过点A作AI⊥BH于点I∵AD∥BC,∴∠D=∠ECH,∵E为CD中点,∴DE=CE,∵∠AED=∠HEC,∴△ADE≌△HCE,∵在菱形ABCD中,∴CH=AD=BC=AB,∴BH=2AB,∵AI⊥BH,∠B=60°,∴∠BAI=30°,BI=12AB,AI=AB2-BI2=32AB,∵HI=BH-BI=2AB-12AB=32AB,∴在Rt△AIH中:AH=AI2+HI2=3AB,∴AH=2AI,∠H=30°,∴∠BAH=90°=∠BAF+∠HAF,由折叠可知:∠BAF=∠HAF=45°,∴∠BFE=2∠AFB=2180°-∠B-∠BAF=150°,∴∠EFC=180°-∠BFE=30°,故选:D.【点睛】本题考查了菱形的性质、全等三角形的判定与性质、含30°角的直角三角形以及折叠的性质.掌握相关几何结论是解题关键.5(2023春·黑龙江哈尔滨·八年级统考期末)将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=23,折叠后,点C落在AD边上的C 处,并且点B落在EC 边上的B 处.则BC的长为()A.6B.43C.4D.33【答案】A【分析】由勾股定理得出232,求出BE=2,AE=4,根据翻折和对边平行可得△AEC2+BE2=2BE和△CC E为等边三角形,那么就得到EC=EC =AE=4,相加即可.【详解】解:连接CC ,在Rt△ABE中,∠BAE=30°,AB=23,AB2+BE2=AE2,∴AE=2BE,∠AEB =∠AEB=60°,∴232+BE2=2BE2,∴BE=2,∴AE=4,∵四边形ABCD是矩形,∴AD∥BC,∴∠C AE=∠AEB=60°,∴△AEC 为等边三角形,同理△CC E也为等边三角形,∴EC=EC =AE=4,∴BC=BE+EC=2+4=6,故选:A.【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理等边三角形的判定和性质,正确的作出辅助线是解题的关键.6(2023春·浙江杭州·八年级统考期末)如图,将菱形ABCD沿AE折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设∠ABE=α,∠BAE=β,∠C=γ,则关系正确的是()A.γ=α+2β-180°B.3β+γ=180°C.3α+2β=360°D.2α+γ=180°【答案】C【分析】可求∠AEB=180°-α-β,∠CED=2α+2β-180°,可求∠ADF=∠CED=2α+2β-180°,可证∠ADF=∠AFD,即可求解.【详解】解:∵∠ABE=α,∠BAE=β,∴∠AEB=180°-α-β,根据折叠可知,∠AEF=∠AEB=180°-α-β,∠AFE=∠ABE=α,AB=AF,∴∠CED=180°-2(180°-α-β)=2α+2β-180°,在菱形ABCD中,AD∥BC,AB=AD,∴∠ADF=∠CED=2α+2β-180°,AD=AF,∴∠ADF=∠AFD,∵∠AFD =180°-α,∴180°-α=2α+2β-180°,∴3α+2β=360°.故选:C .【点睛】本题主要考查了折叠的性质,菱形的性质,三角形的内角和定理,等腰三角形的性质,掌握相关的性质是解题的关键.7(2023·广东江门·统考二模)如图,在矩形片ABCD 中,边AB =4,AD =2,将矩形片ABCD 沿EF 折叠,使点A 与点C 重合,折叠后得到的图形是图中阴影部分.给出下列结论:①四边形AECF 是菱形;②BE 的长是1.5;③EF 的长为5;④图中阴影部分的面积为5.5,其中正确的结论有()A.1个B.2个C.3个D.4个【答案】D 【分析】根据矩形、折叠性质即可得出CF =CE =AE =AF ,则证明结论①正确;设DF =x ,故DF =BE =x ,在Rt △ADF 中,利用勾股定理即可求解结论②正确;过点F 作FH ⊥AB 于点H ,利用矩形判定与性质并结合勾股定理求得EF 的长,则可推出结论③正确;由DF =BE 可知阴影部分的面积为矩形ABCD 面积的一半与△CGF 面积的和,利用面积公式即可求得结果,证明结论④正确.【详解】解:∵四边形ABCD 是矩形,∴AB ∥CD ,∴∠AEF =∠CFE ,由折叠性质可知:AE =CE ,AF =CF ,∠AEF =∠CEF ,∴∠CFE =∠CEF ,∴CF =CE ,∴CF =CE =AE =AF ,∴四边形AECF 是菱形;故①正确;∵四边形AECF 是菱形,∴CF =AE ,∵四边形ABCD 是矩形,AB =4,AD =2,∴AB =CD =4,∠D =90°,∴AB -CF =CD -AE ,即DF =BE ,设DF =x ,则CF =AF =4-x ,在Rt △ADF 中,DF 2+AD 2=AF 2,即x 2+22=(4-x )2解得x =1.5,即BE 的长是1.5;故②正确;过点F 作FH ⊥AB 于点H ,∴四边形ADFH 是矩形,∴FH =AD =2,AH =DF =1.5,∵AE =AB -BE =2.5,∴HE =AE -AH =1,由勾股定理得EF =FH 2+HE 2=22+12=5;故③正确;∵DF =BE ,AD =GC =2,DF =GF =32,∴S 阴影部分=S 四边形BCFE +S △CGF ,=12S 矩形ABCD +S △CGF ,=12AB •AD +12CG •GF ,=12×4×2+12×2×32,=4+32=112;故④正确.故选:D .【点睛】本题考查了四边形的综合问题,熟练掌握菱形的判定与性质、矩形的判定与性质及折叠的性质等知识是解题的关键.。
平行四边形折叠问题解题技巧

平行四边形折叠问题解题技巧平行四边形折叠问题解题技巧什么是平行四边形折叠问题平行四边形折叠问题是一种数学问题,要求将一块平行四边形纸张折叠成特定的形状。
解决这个问题需要一些技巧和方法。
以下是一些常用的技巧,可以帮助你解题。
技巧一:注意对称性•在折叠平行四边形时,要注意纸张的对称性。
利用对称性可以简化问题,并找到更快的解决方案。
•如果可以发现平行四边形纸张具有对称性,可以根据对称性进行折叠,将问题简化为更小的子问题。
技巧二:利用角度相等•在平行四边形折叠问题中,角度是一个重要的概念。
角度相等的性质可以帮助我们确定折叠的方式。
•如果已知某个角度相等,可以通过将纸张折叠使得两个角度重合,从而找到解题的关键位置。
技巧三:利用边长比例•平行四边形的边长比例也是一个重要的信息。
通过观察边长比例,可以推导出纸张的折叠方式。
•如果已知两个边长的比例,可以利用这个比例关系进行折叠,从而找到解题的关键位置。
技巧四:分析折痕•折痕是平行四边形折叠问题中的关键点。
分析折痕的特点可以帮助我们确定折叠的方式。
•观察折痕的位置、形状和角度,可以推断出纸张的折叠方式,并找到最终的解答。
技巧五:尝试反向思考•在解决平行四边形折叠问题时,有时候可以尝试反向思考。
即从最终的形状出发,逆向推导出折叠的方式。
•这种方法可以帮助我们更直观地理解问题,从而找到更有效的解题方法。
技巧六:多练习、多实践•最后,最重要的是多练习、多实践。
通过反复练习和实践,可以加深对平行四边形折叠问题的理解,掌握更多的解题技巧。
•在实践中遇到问题不要气馁,可以寻求他人的帮助或参考相关资料,不断提升自己的解题能力。
以上是解决平行四边形折叠问题常用的技巧和方法。
通过灵活运用这些技巧,相信你能够轻松解决各种平行四边形折叠问题。
祝你成功!(以上仅为参考,具体文章内容可以根据实际需要进行修改和补充。
)。
平行四边形折叠问题

平行四边形折叠问题
平行四边形折叠问题是一个几何问题,它涉及到将一个平行四边形沿着其边界线进行折叠,使得一些特定的条件得到满足。
具体来说,给定一个平行四边形,我们可以将它的两个相对边折叠在一起,形成一个三角形或者一个平行四边形。
问题的目标通常是找到能够实现特定条件的折叠方式。
有一些常见的平行四边形折叠问题,例如:
1. 平行四边形的对角线折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得对角线之间的夹角保持不变。
2. 平行四边形的三角形折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得折叠后形成的是一个三角形。
3. 平行四边形的正方形折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得折叠后形成的是一个正方形。
对于这些问题,一般可以通过几何知识和数学推理来解决。
可以使用平行四边形的性质、角度关系、对称性等来推导出正确的折叠方式。
北师大版九年级数学上学期题型全攻略专题01 特殊平行四边形中的折叠问题全梳理(解析版)

专题01特殊平行四边形中的折叠问题全梳理目录【方法归纳】 (1)【考法一、三角形翻折问题】 (1)【考法二、四边形翻折问题】 (16)【课后练习】 (28)【方法归纳】1.折叠的基本性质:翻折前后对应的边与角相等;2.对于翻折都不确定的情况,注意分类讨论,避免漏掉解;3.方程思想:灵活设未知数,通过勾股定理建立方程,解出答案4.综合性:把折叠性质与四边形性质相结合,建立边角之间的关系。
【考法一、矩形翻折问题】例.如图,在矩形OABC 中8AB =,4BC =,点D 为对角线OB 中点,点E 在OC 所在的直线上运动,连结DE ,把ODE 沿DE 翻折,点O 的对应点为点F ,连结BF .(1)当点F 在OC 下方时(如图1),求证:DE BF ∥.(2)当点F 落在矩形的对称轴上时,求EF 的长.(3)是否存在点E ,使得以D ,E ,F ,B 为顶点的四边形是平行四边形?若存在,求OE 的长;若不存在,请说明理由.当四边形△中,在Rt ABO222=+=OB AB AO8BC OC⊥∴∥,且D为OBDM BC中位线,DM∴为OCBOE EF BD DO ∴==,,25OE OD ∴==;如图,当四边形DEBF 为平行四边形时,DF OD BE ∴=,25BE ∴=,在Rt BEC △中,EC =826OE ∴=-=;DF OD BD DF == ,25BE OD ∴==,在Rt BCE 中,2CE BE =-在矩形ABCD 中,8AB =,6AD =,现将纸片折叠,点D 的对应点记为点P ,折痕为EF (点E 、F 是折痕与矩形的边的交点),再将纸片还原.【初步思考】(1)若点P落在矩形ABCD的边AB上(如图①)当点P与点A重合时,DEF∠=_____︒,当点E与点A重合时,DEF∠=______︒;【深入探究】(2)若点P落在矩形ABCD的内部(如图②),且点E、F分别在AD、DC边上,AP的最小值是______;【拓展延伸】(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图③)在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请求出线段AE的长度;若不存在,请说明理由.【答案】(1)90;45(2)2(3)存在某一情况,使得线段AM与线段DE的长度相等,线段AE的长度为65或4211【分析】(1)当点P与点A重合时,画出图形可得结论;当点E与点A重合时,则EF平分DAB∠,即可得出答案;(2)当F与C重合,点P在对角线AC上时,AP有最小值,根据折叠的性质求8CD PC==,由勾股定理求10AC=,即可得出结果;(3)分两种情况根据全等三角形的判定和性质以及勾股定理解答即可.【详解】解:(1)四边形ABCD是矩形,90DAB D∴∠=∠=︒,当点P与点A重合时,EF是AD的中垂线,90DEF∴∠=︒,当点E与点A重合时,如图,则EF平分DAB∠,==,则AF=设DF PF x当A,P,F在一直线上时,当x最大为8时,AP最小值为四边形ABCD是矩形,A ADC B∴∠=∠=∠=90∠由折叠的性质得:EPM ,AM DE=∴=,AM EP四边形ABCD是矩形,∴∠=∠=∠=︒,DAM ADC B90∠=∠由折叠的性质得:EPC ADC ∴∠=∠=︒,GAM GPE90变式2.【问题情境】折纸操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘,下面是折纸过程.【动手操作】步骤1:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,展平纸片;步骤2:点M 为边AD 上任意一点(与点A ,D 不重合),ABM 沿BM 折叠得到A BM '△,折痕BM 交EF 于点N .【问题探究】(1)如图1,当点A 的对称点A '落在EF 上时,连接AN .求证:四边形ANA M '为菱形;(2)已知2BC AB =,继续对折矩形纸片ABCD ,使AB 与DC 重合,折痕GH 与EF 交于点O .将ABM 沿BM 折叠,连接MO ,若点A 的对称点A '恰好落在线段MO 上,此时2AM =.①尺规作图:请在图2中用直尺和圆规,作点A 的对称点A '(保留作图痕迹,不写作法);②求AB 的长度;【拓展迁移】如图3,在矩形纸片ABCD 的边AB 上取一点P ,折叠纸片,使P ,B 两点重合,展平纸片,得到折痕EF ;点B '为EF 上任意一点(与点E ,F 不重合),折叠纸片使B ,B '两点重合,得到折痕l 及点P 的对应点P ',折痕l 交EF 于点K ,展平纸片,连接BP ',KP '.(3)猜想P B K ∠'与BC P '∠的数量关系,并证明.【答案】(1)见解析;(2)①见解析;②6AB =;(3)3P BC BP K ''∠∠=,理由见解析【分析】(1)根据折叠可得出NA NA '=,MA MA '=,AMB A MB '∠=∠,,证明AD EF ∥,利用平行线的性质得出AMB MNA '∠=∠,则A MB MNA ''∠=∠,利用等角对等边得出MA NA ''=,即可得证;(2)①以M 为圆心,MA 为半径画弧交MO 于A '即可;②利用折叠的性质,矩形的判定与性质可得出2BH AB A B AG OG '====,证明()HL OA B OHB ' ≌,得出OA OH OG '==,在Rt MGO △中,根据勾股定理,可求出OG ,进而求出AB ;(3)连接PK ,BK ,延长BK 交P B ''于点M ,可证明EB B MBB ''≌ ,得出BE B M '=,90FEB BMB '∠=∠=︒,由折叠可得BK PK P K B K ''===,利用等边对等角和三线合一的性质可得出P BK BP K ''∠=∠,KBB KB B ''∠=∠,MB MP ''=,利用线段垂直平分线的性质BP BB ''=,利用三线合一性质可得出P BK KBB ''∠=∠,则P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)中BC EF ∥,可得出B BC KB B ''∠=∠,即可得证.【详解】(1)证明:连接AA ',∵ABM 沿BM 折叠,得到A BM '△,∴BM 垂直平分AA ',∴NA NA '=,MA MA '=,AMB A MB '∠=∠,由折叠可知:AEF BEF ∠=∠,∵180AEF BEF ∠+∠=︒,∴90BEF ∠=︒,∵四边形ABCD 为矩形,∴90DAB ∠=︒,∴90BEF DAB ∠=∠=︒,∴AD EF ∥,∴AMB MNA '∠=∠,∴A MB MNA ''∠=∠,∴MA NA ''=,∴MA NA NA MA ''===,∴四边形ANA M '为菱形;点A'即为所求,解:连接BO,由折叠可知:AB A B'=,MA 由(1)得90∠=∠=︒GHB HGA∵l为折痕,∴P B B PBB'''∠=∠,BP B P''=,l ∴KP KP'=,=,KB KB'∴KBB KB B''∠=∠,∵B B BB''=,∴BE B M '=,90FEB BMB '∠=∠=︒,由折叠可知:KP KB =,EP EB =,90FEB ∠=︒,∴KP KB '=,KP KB ''=∴P BK BP K ''∠=∠,MB MP ''=∴BP BB ''=,∴P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)可知BC EF ∥,∴B BC KB B ''∠=∠,∴3P BC BP K ''∠=∠.【点睛】本题考查了矩形与折叠,等腰三角形的判定与性质,全等三角形的判定与性质,线段垂直平分线的性质等知识,明确题意,灵活运用所学知识解决问题是解题的关键.变式3.如图1,在矩形ABCD 中,点E 是边AB 上的一点,连接DE .(1)若DE 平分ADC ∠,点G 是CD 上的一点,连接EC ,EG ,且EC EG =.过点C 作CQ EG⊥于Q ,CQ 延长线交ED 于H ,过点H 作HP CD ⊥于P ,如图.①填空:AED △的形状是______三角形;②求证:PHC BEC△△≌(2)将图1的矩形ABCD 画在纸上,若DE 平分ADC ∠,沿过点E 的直线折叠,点C 恰好落在AD 上的点C '处,点B 落在点B '处,得到折痕EF ,B C ''交AB 于点M ,如图.求证:MC ME '=.(3)如图,延长DE 交CB 的延长线于点K 使得AB BK =,此时恰好BE BC =,连接AC 交DK 于点J ,连接BJ .请证明:KJ AJ BJ >+.【答案】(1)①等腰直角;②见解析(2)见解析(3)见解析【分析】(1)①根据矩形的性质和角平分线的性质可得45AED ADE ∠=∠=︒,进而得出结果;②可证得BCE PCH ∠=∠,EC HC =,90HPC B ︒∠=∠=,进而得出结论;(2)连接C E ',可证得Rt Rt EC A C EB ''' ≌,可得C EA EC B '''∠=∠,根据等角对等边即可得出结论;(3)在线段EK 上取点I ,使得KI AJ =,连接BI ,可证KBE ABC ≌△△,得BKE BAC ∠=∠,在证KBI ABJ ≌△△,得KBI ABJ ∠=∠,90IBJ KBA ︒∠=∠=,得出IJ BJ >,进一步得出结论.【详解】(1)① 四边形ABCD 是矩形,∴90A ADC ∠=∠=︒,DE 平分ADC ∠,∴1452ADE ADC ∠=∠=︒,∴9045AED ADE ∠=︒-∠=︒,∴AED ADE ∠=∠,∴AE DE =,∴AED △等腰直角三角形,故答案为:等腰直角②证明:如图,过点E 作EW CD ⊥于W .EC EG = ,EGC ECG ∴∠=∠,CH EG ⊥ ,90HCP EGC ∴∠+∠=︒,90BCE ECG ∠︒∠+= ,BCE PCH ∴∠=∠,45EDW DEW ∠︒∠== ,45EHC EDW PCH PCH ∴∠=∠︒+∠=+∠,DEC DEW CEW ∠=∠+∠,EW BC ∥,BCE CEW PCH ∴∠=∠=∠,DEC EHC ∴∠=∠,EC HC ∴=,90HPC B ∠=∠=︒PHC BEC ∴△△≌.(2)证明:如图,连接C E ',由(1)知,AED △为等腰直角三角形,AD AE ∴=,四边形ABCD 是矩形,AD BC ∴=,90EAC B '∠=∠=︒,由折叠知,B C BC ''=,B B '∠=∠,AE B C ''∴=,EAC B ''∠=∠,又EC C E ''=,在Rt EC A '△和Rt C EB ''△中,EC C E ''=,AE B C ''=,∴Rt Rt EC A C EB ''' ≌,C EA EC B '''∴∠=∠,MC ME '∴=.(3)如图,在线段EK 上取点I ,使得KI AJ =,连接BI ,在AJB 与KIB △中,BK AB =,ABC ABK ∠=∠,BE BC =,KBE ABC ∴△△≌,BKE BAC ∴∠=∠.KI AJ = ,BK AB =,BKE BAC ∠=∠,KBI ABJ ∴△△≌,KBI ABJ ∴∠=∠,90IBJ IBA ABJ IBA KBI KBA ∴∠=∠+∠=∠+∠=∠=︒,IBJ ∴△为直角三角形,IJ BJ ∴>,KJ AJ BJ ∴>+.【点睛】本题是四边形综合题,考查了等腰直角三角形的判定和性质,矩形的性质,全等三角形的判定和性质,轴对称的性质,准确添加常用辅助线,构造特殊三角形和证明全等三角形是解本题的关键。
2024年平行四边形中的折叠问题课件

2024年平行四边形中的折叠问题课件.一、教学内容本节课我们将探讨教材第十二章“几何变换”中的折叠问题,特别是平行四边形的折叠。
详细内容包括:理解平行四边形的基本性质,掌握折叠过程中的对称性和不变量,运用这些性质解决折叠问题。
二、教学目标1. 理解平行四边形的性质,并能运用性质解决折叠问题。
2. 通过折叠活动,培养学生的空间想象能力和逻辑思维能力。
3. 提高学生运用数学知识解决实际问题的能力。
三、教学难点与重点教学难点:理解折叠过程中平行四边形的对称性和不变量。
教学重点:平行四边形性质的应用,折叠问题的解决方法。
四、教具与学具准备1. 教具:多媒体课件,平行四边形的模型。
2. 学具:剪刀,彩纸,尺子,圆规。
五、教学过程1. 实践情景引入:展示生活中的折叠实例,如纸飞机、纸盒等,让学生感受折叠在生活中的应用。
2. 知识讲解:(1)回顾平行四边形的性质。
(2)介绍折叠过程中平行四边形的对称性和不变量。
3. 例题讲解:(1)给出一个平行四边形折叠问题,引导学生分析问题,找出关键信息。
(2)示范解题过程,强调平行四边形性质的应用。
4. 随堂练习:让学生独立解决一个类似的折叠问题,巩固所学知识。
5. 小组讨论:学生分组讨论解决折叠问题的方法,分享解题心得。
六、板书设计1. 平行四边形的性质2. 折叠过程中的对称性和不变量3. 折叠问题的解题步骤七、作业设计答案:折叠后的形状为一个三角形。
2. 作业题目:已知平行四边形ABCD,对角线AC、BD相交于点O,沿对角线AC折叠,求折叠后的形状。
答案:折叠后的形状为一个三角形。
八、课后反思及拓展延伸1. 反思:本节课通过实践情景引入,让学生感受到了折叠的趣味性。
在讲解过程中,注重引导学生运用平行四边形的性质解决问题。
2. 拓展延伸:鼓励学生探究其他多边形的折叠问题,培养学生的探究意识和创新精神。
重点和难点解析1. 实践情景引入的选择与设计。
2. 知识讲解中对平行四边形性质的回顾与强调。
特殊平行四边形:折叠问题

折叠问题1.如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠EFB =65°,则∠AED ′为 度.2.如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ′处,折痕为EF ,若∠ABE =20°,那么∠EFC ′的度数为 度.3.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为 度.4.如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,︒>∠60BEG ,现沿直线EG 将纸片折叠,使点B 落在约片上的点H 处,连接AH ,则与BEG ∠相等的角有 个。
A.4B. 3C.2D.1EDBC′FCD ′A5.如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是6.如图,在梯形ABCD 中,AD ∥BC ,AD =2,AB =3,BC =6,沿AE•翻折梯形ABCD ,使点B 落在AD 的延长线上,记为B ′,连结B ′E 交CD 于F ,则DE:FC=A. 13B. 14C. 15D. 167.如图,在梯形ABCD 中,∠DCB =90°,AB ∥CD ,AB =25,BC =24. 将该梯形折叠,点A 恰好与点D 重合,BE 为折痕,那么AD 的长度为_______.8.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是 . 9.如图2是一张矩形纸片ABCD ,AD =10cm ,若将纸片沿DE 折叠,使DC 落在DA 上,点C 的对应点为点F ,若BE =6cm ,则CD 的长是A B CDMNA 'B ' F E DB A C①② 3 410.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长 是11.如图,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则A'G 的长是 。
初三数学多姿多彩的平行四边形折叠问题

多姿多彩的平行四边形折叠问题康海芯折叠问题是操作与运算相结合的问题,它可以产生许多美丽的图案。
通过这类问题还可以探究图形存在的某些内在的规律,并进行有关计算。
解决折叠问题的关键,是根据轴对称的性质,弄清折叠前后哪些量变化了、哪些量没有变,弄清折叠前后哪些条件可以利用。
本文将以中考题为例,谈谈平行四边形折叠问题的类型和解法,供同学们参考。
一、平行四边形的折叠例1 (2007年·长春)如图1,将平行四边形纸条ABCD沿EF折叠,点A、B分别落在A′B′处,线段FB′与AD交于点M。
(1)试判断△MEF的形状,并证明你的结论。
(2)如图2,将纸条的另一部分CFMD沿MN折叠,点C、D分别落在C′、D′处,且使MD′经过点F。
试判断四边形MNFE的形状,并证明你的结论。
(3)当∠BFE= 时,四边形MNFE是菱形。
解析:(1)△MEF为等腰三角形,利用“∠MFE=∠BFE=∠MEF”来证明即可。
(2)四边形MNFE是平行四边形,利用“一组对边平行且相等的四边形是平行四边形”或“两组对边分别平行的四边形是平行四边形”来证明就可以。
与(1)同理,可证△FMN 也为等腰三角形。
从而ME=MF=NF。
或利用两等腰三角形顶角相等则底角也相等来证明(因AD∥BC,∠EMF=MFN,故∠FMN=∠MFE)。
(3)若四边形MNFE是菱形,则∠EFM=∠NFM,又∠EFM=∠EFB,且∠EFM+∠NFM+∠EFB=180°,所以∠BFE=60°。
评注:解结论探究型题时,要善于根据图形和已知条件,先由观察直观得出一些结论。
二、矩形的折叠例2 (2006年·郴州)如图3,矩形纸片ABCD的边长分别为a、b(a<)b。
将纸片任意翻折(如图4),折痕为PQ(P在边BC上,Q在边CD上),使顶点C落在矩形ABCD内的点C′处,PC′的延长线交直线AD于M。
再将纸片的另一部分翻折,使A落在直线PM上的点A′处(如图5),折痕为MN。
第十八章微专题七特殊平行四边形中的折叠问题(教案)-2022-2023学年八年级下册数学(人教版)

4.折叠问题的实际应用:结合实际生活中常见的折叠问题,让学生学会运用所学知识解决实际问题。
5.折叠问题的拓展思考:引导学生思考折叠问题在其他几何图形中的应用,提高学生的创新能力和几何直观。
二、核心素养目标
-培养学生运用折叠方法解决问题的能力,使学生能够将理论知识与实际操作相结合。
举例:以矩形为例,重点讲解其对折后的图形仍为矩形,且对折线为矩形的对角线,对折前后矩形的面积相等但形状可能不同。
2.教学难点
-理解和掌握矩形、菱形、梯形折叠过程中几何量的变化规律,尤其是折叠后产生的新图形与原图形之间的关系。
最后,我认为在今后的教学中,还应加强对学生的鼓励和表扬,让他们在学习过程中感受到成功的喜悦,从而激发他们的学习兴趣和积极性。同时,我将不断学习,提升自身的教育教学水平,为学生们提供更优质的教学服务。
1.培养学生空间观念和几何直观,通过折叠问题的学习,让学生能够理解和把握图形的折叠特征,提高对几何图形变换的认识。
2.培养学生逻辑推理和问题解决能力,使学生能够运用折叠方法分析解决特殊平行四边形相关问题,形成严密的逻辑思维。
3.培养学生数学抽象和数学建模素养,让学生在折叠问题的探索过程中,学会提炼关键信息,构建数学模型,为解决实际问题奠定基础。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了特殊平行四边形折叠的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对折叠问题的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
北师大版数学九年级上册:第一章 特殊平行四边形——特殊平行四边形的折叠问题(含答案)
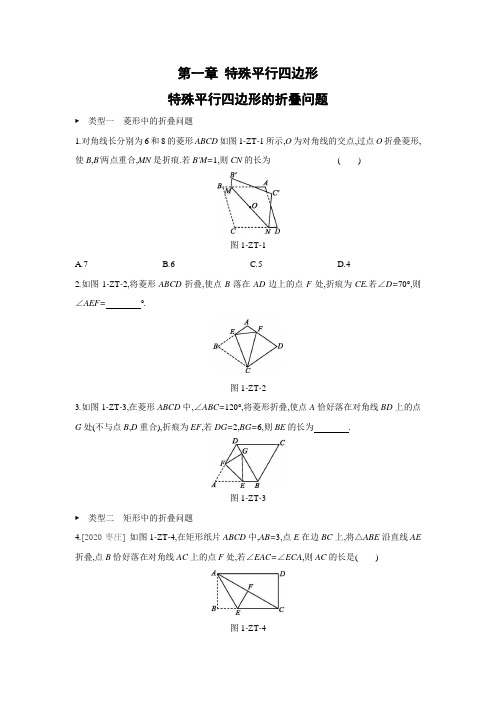
第一章特殊平行四边形特殊平行四边形的折叠问题▶类型一菱形中的折叠问题1.对角线长分别为6和8的菱形ABCD如图1-ZT-1所示,O为对角线的交点,过点O折叠菱形,使B,B'两点重合,MN是折痕.若B'M=1,则CN的长为()图1-ZT-1A.7B.6C.5D.42.如图1-ZT-2,将菱形ABCD折叠,使点B落在AD边上的点F处,折痕为CE.若∠D=70°,则∠AEF=°.图1-ZT-23.如图1-ZT-3,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与点B,D重合),折痕为EF,若DG=2,BG=6,则BE的长为.图1-ZT-3▶类型二矩形中的折叠问题4.[2020·枣庄]如图1-ZT-4,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE 折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是()图1-ZT-4A.3√3B.4C.5D.65.[2020·青岛]如图1-ZT-5,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为()图1-ZT-5A.√5B.32√5C.2√5D.4√56.[2020·衢州]如图1-ZT-6,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为()图1-ZT-6A.√2B.√2+12C.√5+12D.437.如图1-ZT-7,在矩形ABCD中,AB=6,BC=8,E为AD的中点,F为AB上一点,将△AEF沿EF 折叠后,点A恰好落到CF上的点G处,求折痕EF的长.图1-ZT-7▶类型三正方形中的折叠问题8.[2020·广东]如图1-ZT-8,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上的点B'处,则BE的长度为()图1-ZT-8A.1B.√2C.√3D.29.如图1-ZT-9,在平面直角坐标系中,正方形OABC的顶点A的坐标为(0,2),E是线段BC上一点,且∠AEB=67.5°,沿AE折叠正方形后点B落在点F处,那么点F的坐标为.图1-ZT-9参考答案1.D [解析] 连接AC ,BD ,如图.∵O 为菱形ABCD 对角线的交点,∴OC=12AC=3,OB=OD=12BD=4,∠COD=90°.在Rt △COD 中,CD=√32+42=5. ∵AB ∥CD ,∴∠MBO=∠NDO. 又∵∠BOM=∠DON ,OB=OD , ∴△OBM ≌△ODN ,∴DN=BM.∵过点O 折叠菱形ABCD ,使B ,B'两点重合,MN 是折痕, ∴BM=B'M=1,∴DN=1, ∴CN=CD-DN=5-1=4.故选D .2.30 [解析] ∵四边形ABCD 是菱形,∠D=70°, ∴∠B=70°,∠A=110°.∵将菱形ABCD 折叠,使点B 落在AD 边上的点F 处, ∴∠B=∠EFC=70°,CF=BC=CD , 则∠CFD=∠D=70°, ∴∠AFE=180°-70°-70°=40°,∴∠AEF=180°-∠A-∠AFE=30°.故答案为30. 3.2.8[解析] 如图,过点E 作EH ⊥BD 于点H.由折叠的性质可知EG=EA. 由题意得BD=DG+BG=8. ∵四边形ABCD 是菱形,∴AD=AB ,∠ABD=∠CBD=12∠ABC=60°,∴△ABD 为等边三角形,∠BEH=30°, ∴AB=BD=8.设BE=x ,则EG=AE=8-x.在Rt △EHB 中,BH=12x ,EH=√BE 2-BH 2=√32x.在Rt △EHG 中,EG 2=EH 2+GH 2, 即(8-x )2=(√32x )2+(6-12x )2,解得x=2.8,即BE=2.8. 故答案为2.8.4.D [解析] ∵将△ABE 沿直线AE 折叠,点B 恰好落在对角线AC 上的点F 处, ∴AF=AB ,∠AFE=∠B=90°,∴EF ⊥AC , ∵∠EAC=∠ECA ,∴AE=CE ,∴AF=CF , ∴AC=2AB=6. 故选D .5.C [解析] ∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠EFC=∠AEF . 由折叠得∠EFC=∠AFE ,∴∠AFE=∠AEF ,∴AE=AF=5. 由折叠得FC=AF ,OA=OC ,∴BC=3+5=8. 在Rt △ABF 中,AB=√AF 2-BF 2=√52-32=4. 在Rt △ABC 中,AC=√AB 2+BC 2=√42+82=4√5, ∴OA=OC=2√5.故选C .6.A [解析] 由折叠补全图形如图所示.∵四边形ABCD 是矩形,∴∠ADC=∠A=90°,AD=BC=1,CD=AB. 由第一次折叠得∠ADE=12∠ADC=45°, ∴∠AED=∠ADE=45°, ∴AE=AD=1.在Rt △ADE 中,根据勾股定理,得DE=√2AD=√2. 由第二次折叠知CD=DE=√2, ∴AB=√2. 故选A .7.解:∵四边形ABCD 是矩形,∴AB=CD=6,BC=AD=8,∠A=∠D=90°.如图,连接CE.∵E 为AD 的中点, ∴AE=DE=4.由折叠可得AE=GE ,∠EGF=∠A=90°, ∴DE=GE.又∵∠D=90°,∴∠EGC=∠D=90°. 又∵CE=CE.∴Rt △CDE ≌Rt △CGE (HL), ∴CD=CG=6.设AF=x ,则GF=x ,BF=6-x ,则CF=6+x. 在Rt △BCF 中,BF 2+BC 2=CF 2, 即(6-x )2+82=(6+x )2,解得x=83,∴AF=83.在Rt △AEF 中,EF=√AE 2+AF 2=√42+(83) 2=43√13. 8.D [解析] ∵四边形ABCD 是正方形, ∴AB ∥CD ,∠A=90°, ∴∠EFD=∠BEF=60°.∵将四边形EBCF 沿EF 折叠,点B 恰好落在AD 边上, ∴∠BEF=∠FEB'=60°,BE=B'E , ∴∠AEB'=180°-∠BEF-∠FEB'=60°, ∴∠AB'E=30°,∴B'E=2AE. 设BE=x ,则B'E=x ,AE=3-x ,∴2(3-x)=x,解得x=2.故选D.9.(-√2,2-√2)[解析] 如图,过点F作FD⊥CO于点D,FG⊥AO于点G.∵∠AEB=67.5°,沿AE折叠后点B落在点F处,∴∠BAE=∠EAF=22.5°,AF=AB=2,∴∠F AG=45°,∴FG=AG=√2,∴GO=2-√2,∴点F的坐标为(-√2,2-√2).故答案为(-√2,2-√2).。
最新人教版数学八年级下册第十八章《平行四边形-数学活:平行四边形中的翻折变换》优质教学课件

∴∠ABC=90°.
∴∠3=90°-60°=30°,
∴∠1=∠2=∠3=30°
在图中,你能找出所有30°的角吗?60°的角呢?还有其他度数的角吗?
G
还有120 ° 和150 °的角
利用折纸得到60°、30°、15°的角
【综合与实践】在线上教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动--折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.实践发现:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,把纸片展平,连接AN,如图①.
八年级 下册
第18章 平行四边形
——数学活动:平行四边形中的翻折变换
学习目标: 1.能折出60°,30°,15°的角,学会应用。 2.通过折叠活动,加深对轴对称、全等三角形、特 殊的三角形、四边形等知识的认识; 3.经历折叠、观察、推理、交流、反思等数学活动 过程,积累数学活动经验.学习重点: 折纸做60°,30°,15°的角,学会应用.
D
6.矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=10,CD=6,则BE=____。
特殊平行四边形中的五种折叠方式

特殊平行四边形中的五种折叠方式下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!特殊平行四边形中的五种折叠方式在数学中,特殊平行四边形指的是有特殊属性的四边形,例如菱形和正方形。
特殊平行四边形折叠问题

特殊平行四边形折叠问题嘿,伙计们!今天我们要聊一聊一个非常有趣的话题——特殊平行四边形折叠问题。
这个问题听起来好像很复杂,但其实它就像是我们生活中的一道谜题,只要我们用心去思考,就一定能找到答案。
让我们来简单了解一下什么是平行四边形。
平行四边形就是那种有两组对边分别平行的四边形。
你可能会觉得这个概念有点儿抽象,那我们就用一个简单的例子来说明。
比如说,我们可以把一张纸折成一个长方形,这就是一个特殊的平行四边形。
因为它的两组对边分别是平行的,而且这两组对边的长度相等。
那么,问题来了:如果我们把这张纸再次折叠,使得它的一边重合在一起,那么这个新的平行四边形是什么样子的呢?这个问题看似简单,但实际上却充满了挑战。
因为在这个过程中,我们需要保证折叠后的图形仍然满足平行四边形的条件,也就是说,它的两组对边仍然是平行的,而且这两组对边的长度相等。
为了解决这个问题,我们可以尝试从不同的角度去思考。
我们可以观察一下原始的长方形是如何折叠成新的平行四边形的。
是不是发现了一个规律:当我们把长方形的一个角折叠到另一个角时,它的两组对边仍然保持平行,而且这两组对边的长度也保持相等。
这就告诉我们,只要我们在折叠过程中保持这个规律,就能得到一个满足条件的平行四边形。
这个过程并不是一帆风顺的。
有时候,我们可能会遇到一些困难,比如说折叠后的图形不再满足平行四边形的条件。
这时候,我们就需要重新审视我们的折叠方法,看看是不是哪里出了问题。
也许我们需要调整一下折叠的角度,或者改变一下折叠的方式。
只要我们不放弃,总是能找到解决问题的方法。
在现实生活中,特殊平行四边形折叠问题也有很多实际应用。
比如说,在建筑工地上,工人们需要把钢筋网折叠成一个方便搬运和安装的形式。
这就需要他们根据钢筋网的结构特点,合理地设计折叠方案。
又比如说,在科学实验中,研究人员可能会需要制作一些特殊的平行四边形装置,以便于进行各种实验和观测。
这些装置的设计和制作过程,都需要运用到特殊平行四边形折叠问题的解决方法。
初二数学四边形的折叠问题技巧

初二数学:四边形的折叠问题技巧四边形是几何学中重要的图形之一,它具有丰富的性质和应用。
在数学学习中,我们常常会遇到与四边形相关的问题。
其中一个有趣且常见的问题就是四边形的折叠问题。
本文将介绍四边形折叠问题的基本概念和解题技巧,帮助初中生更好地理解和解决这类问题。
什么是四边形的折叠问题?四边形的折叠问题是指给定一个四边形,在保持边长不变的情况下,把它折叠成二维平面上的一个点或一条线段。
常见的四边形包括正方形、长方形、平行四边形和梯形等。
这类问题常常涉及如何折叠和旋转四边形,并要求计算折叠后的形状、面积、体积等数值。
基本概念在解决四边形的折叠问题之前,先了解一些基本概念是很有帮助的。
1.边长:四边形的每条边的长度,通常用a、b、c和d表示。
2.对角线:连接四边形的两个非相邻顶点的线段,通常用e和f表示。
3.高度:以顶点为基点,垂直于底边或顶边的线段的长度,通常用h表示。
4.面积:四边形所围成的区域的大小,通常用S表示。
折叠技巧解决四边形折叠问题的关键在于理解形状的变化和如何利用对称性质。
下面将介绍常见四边形的折叠技巧。
正方形折叠技巧正方形是最简单的四边形之一,它的所有边长相等,对角线相等且互相垂直。
当折叠一个正方形时,我们可以沿着对角线折叠,从而使正方形折叠成一个边长等于对角线长度的等边三角形。
长方形折叠技巧长方形是另一种常见的四边形,它拥有两组相等的边长,且相邻边互相垂直。
当折叠一个长方形时,我们可以沿着较短的一组边折叠,从而使长方形折叠成一个等腰直角三角形。
平行四边形折叠技巧平行四边形具有两对平行边,对角线互相交叉,但长度不相等。
当折叠一个平行四边形时,我们可以选择沿着任意一条对角线折叠。
如果选择沿着短对角线折叠,平行四边形会折叠成一个与原平行四边形等面积的直角梯形;如果选择沿着长对角线折叠,平行四边形会折叠成一个与原平行四边形相等的直角三角形。
梯形折叠技巧梯形的特点是两边平行,而另外两边不平行。
特殊平行四边形的折叠

※ 在知识上有哪些收获? ※ 学到了哪些好的思想方法? ※ 还存在什么疑问?
ChongQingShiQiJiangQuTongHuiZhongXue
我小结
1.一种变换
折叠 实质 轴对称
2.两种思想: 方程思想
数形结合的思想
谢谢大家,欢迎批评指正!
ChongQingShiQiJiangQuTongHuiZhongXue
我展示
如图,正方形ABCD中,AB=3,点E在边CD上, 且CD=3DE.将△ADE沿AE对折至△AFE,延 长EF交边BC于点G,连接AG,CF. 求证:点G是BC的中点。
ChongQingShiQiJiangQuTongHuiZhongXue
我探索
如图,矩形纸片ABCD中AB=6cm,AD=8cm,在
BC上找一点F,沿DF折叠矩形ABCD,使C点
落在对角线BD上的点E处,此时折痕DF的长是
多少?Aຫໍສະໝຸດ 8D6 6
4x
B
8-x
xC
ChongQingShiQiJiangQuTongHuiZhongXue
我探索
如图,在边长为10的正方形ABCD中,E是边 CD的中点,将△ADE沿AE对折△AFE,延长 EF交边BC于点G,连接AG. (1)求证:△ABG≌△AFG; (2)求BG的长.
义务教育教科书 数学 八年级 下册
专题
特殊平行四边形折叠问题
ChongQingShiQiJiangQuTongHuiZhongXue
我热身
已知在Rt△ABC中直角边长分别为6和8,当 AC边折到AB边上时,点C的对应点是点E, AD是折痕,求CD的长。
x
ChongQingShiQiJiangQuTongHuiZhongXue
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(四)特殊平行四边形中的五种折叠方式
►方式一把一个顶点折叠到一边上
1.如图4-ZT-1,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处.若AE=5,BF=3,则CD的长是() A.7 B.8 C.9 D.10
图4-ZT-1
2.如图4-ZT-2,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,△BEF沿EF折叠得到△GEF,且点G在边AD上.若EG⊥AC,AB=6 2,则FG的长为
________.
图4-ZT-2
3.如图4-ZT-3,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D 落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求CE
DE的值.
图4-ZT-3
►方式二把一个顶点折叠到对角线上
4.如图4-ZT-4所示,矩形纸片ABCD中,已知AD=8,折叠纸片使点B落在对角线AC上的点F处,折痕为AE,且EF=3,则AB的长为()
A.3 B.4 C.5 D.6
图4-ZT -4
5.如图4-ZT -5所示,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为CE ,且点D 落在对角线上的点D ′处.若AB =3,AD =4,则ED 的长为( )
A.32 B .3 C .1 D.43
图4-ZT -5 ► 方式三 把一个顶点折叠到另一个顶点上
6.把一张矩形纸片ABCD 按图4-ZT -6所示方式折叠,使顶点B 和点D 重合,折痕为EF ,若AB =3 cm ,BC =5 cm ,则重叠部分△DEF 的面积为______cm 2.
图4-ZT -6
7.如图4-ZT -7所示,将矩形ABCD 沿直线EF 折叠,使点C 与点A 重合,折痕交AD 于点E ,交BC 于点F ,连接CE .
(1)求证:四边形AFCE 为菱形;
(2)设AE =a ,ED =b ,DC =c ,请写出a ,b ,c 三者之间的数量关系,并说明理由.
图4-ZT -7
► 方式四 把一个顶点折叠到图形外或图形内 8.如图4-ZT -8,已知正方形ABCD 的对角线长为2 2,将正方形ABCD 沿直线EF 折叠,则图中阴影部分的周长为( )
A .8 2
B .4 2
C .8
D .6
图4-ZT -8
9.如图4-ZT -9,在矩形ABCD 中,AB =4,AD =6,E 是AB 边的中点,F 是线段BC 上的动点,将△EBF 沿EF 所在直线折叠得到△EB ′F ,连接B ′D ,则B ′D 的最小值是( )
A .2 10-2
B .6
C .2 13-2
D .4
图4-ZT-9
10.如图4-ZT-10,矩形ABCD中,点P,Q分别是边AD和BC的中点,沿过点C 的直线折叠矩形ABCD,使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ 于点G.若线段BC的长为3,则线段FG的长为________.
图4-ZT-10
11.如图4-ZT-11,在矩形ABCD中,E是AB边的中点,沿EC折叠矩形ABCD,使点B落在点P处,折痕为EC,连接AP并延长交CD于点F,连接BP.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
图4-ZT-11
►方式五多次折叠
12.2018·资阳如图4-ZT-12,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙、无重叠的四边形EFGH,EH=12 cm,EF=16 cm,则边AD的长是() A.12 cm B.16 cm
C.20 cm D.28 cm
图4-ZT-12
13.准备一张矩形纸片ABCD,按如图4-ZT-13所示操作:
将△ABE沿BE翻折,使点A落在对角线BD上的点M处,将△CDF沿DF翻折,使点C落在对角线BD上的点N处.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
图4-ZT-13
14.如图4-ZT-14①,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平;沿EF折叠,使顶点A落在折痕DE上的点G处;再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图②.
(1)求证:EG=CH;
(2)已知AF=2,求AD和AB的长.
图4-ZT-14
详解详析
1.[解析] C 由折叠的性质得EF =AE =5.由勾股定理得BE =4,∴AB =CD =9. 2.[答案] 3 6
[解析] ∵四边形ABCD 是菱形,∠BAD =120°,∴∠B =60°,∠BAC =60°. ∵EG ⊥AC ,∴∠AEG =30°.
由折叠可知,∠BEF =1
2
×(180°-∠AEG )=75°,
∴∠BFE =180°-(∠B +∠BEF )=45°.∴∠BFG =90°,即FG ⊥BC . ∴FG =BC 边上的高=3 6.
3.解:(1)证明:由折叠的性质得∠1=∠2,ED =EF ,GD =GF . ∵FG ∥CD ,∴∠1=∠3,则∠2=∠3,∴EF =GF ,
(方法一)(如图①)∴ED =EF =GD =GF ,∴四边形DEFG 为菱形. (方法二)(如图①)∴ED =GF .
又∵ED ∥GF ,∴四边形DEFG 为平行四边形. 又∵EF =GF ,∴▱DEFG 为菱形.
(方法三)连接DF 交AE 于点O (如图②),则EG ⊥DF ,DO =FO . ∵EF =GF ,EG ⊥DF ,∴OG =OE ,
∴四边形DEFG 为平行四边形,∴▱DEFG 为菱形.
(2)设DE =x ,则FE =DE =x ,CE =8-x . 在Rt △EFC 中,CF 2+CE 2=EF 2,
即42+(8-x )2=x 2,解得x =5,∴CE =8-x =3,∴CE DE =3
5.
4.[答案] D 5.[答案] A 6.[答案]
5110
[解析] 设ED =x cm ,则根据折叠和矩形的性质,得A ′E =AE =(5-x )cm ,A ′D =AB =3 cm.
根据勾股定理,得ED 2=A ′E 2+A ′D 2,
即x 2=(5-x )2+32,解得x =
175
, ∴S △DEF =12×175×3=51
10
(cm 2).
7.解:(1)证明:∵四边形ABCD 是矩形,
∴AD ∥BC ,∴∠AEF =∠CFE .
由折叠的性质,可得∠AFE =∠CFE ,AF =CF , ∴∠AEF =∠AFE ,。
