§4.7 周期信号的傅里叶变换
傅里叶变换及反变换
1 2{F [j(0) ]F [j(0) ] }
F ( j )
1
m 0 m
P( j)
( )
( )
0
0
0
R( j)
1 2
0
0
0
F ( j )
1
m 0 m
f (t)
r(t)
y1(t)
低通
滤波
y(t)
cos(0t) cos(0t)
R( j)
1 2
0 ( )
0
P( j)
0 ( )
§4.5 连续时间傅里叶变换的性质
复习
F(j)= f(t)ejtdt
f(t)21 F(j)ejtd
1 唯一性: 2 线性特性: 3 奇偶特性: 4 共轭特性: 5 对称特性: 6 时域展缩特性: 7 时移特性:
9 时域微分特性: 10 频域微分特性: 11 时域卷积定理: 12 频域卷积定理:
偶信号的频谱是偶函数,奇信 号的频谱是奇函数。
F(j) f(t)ejtdt令t
f()ejd f()关e于jtd F(j)
f(t) F (j) , 则 f* (t) F * ( j)
证F (: j)= f (t)ejtd可 t F 得 *(j)= f*(t)ejtdt
F *(j)= f *(t)ejtdt
0
1 4
20
0
0
Y1( j)
1
1
2
4
0
20
Y ( j) 1
2
0
4.7 傅里叶反 变换
要解决的问题:由F( jw)求 f(t)
f(t)21 F (j)ejtd
利用傅里叶变换的互易对称性 部分分式展开
模板傅里叶变换(周期和非周期信号).ppt

0
-0 -0 0
0
-0 -0 -0 0 0 0 0
双边频(谱a) 幅(度D频o谱uble Side Band)
-
π 4
-
π 4
-
π 2
(b) 相位频谱
单边频谱(Single Side Band)
三角函数 形式的频 谱图
cn 2
1
11
2
0
0 0 0
(a) 振幅频谱
优选文档
π n
4
0
0
0
0
-
π 4
-
π 2
n1
c0 a0
cn an2 bn2
优选文档
a0
1 T
T
2 -T
f (t) dt
2
an
2 T
T
2 T
2
f (t) cosn0t dt
bn
2 T
T
2 T
2
f (t)sin n0t dt
2
周期信号的傅里叶变换——傅里叶级数
1、 三角函数式傅里叶级数
若周期函数 f (t) 满足狄里赫利( Dirichlet)条件:
2. T不变,τ减小,则频谱的幅度也将减小,谱线密度 保持不变,但包络过零点的间隔将增大。
A
F0 T
优选文档
Back 31
优选文档
32
非周期信号的傅立里叶变换
两个重要公式:
f ( t ) F( ) : F( ) f ( t )e jtdt
F( ) f (t ):
F -1F( ) f ( t ) 1 F( )e jtd
2
2
dt
2
T1
2
傅里叶变换(周期和非周期信号)

常用信号的傅里叶变换

ω1 Sa (ω 1t ) 2 cos ω c t f 5 ( t ) = f ( t ) 2 cos ω c t = π
东南大学 信息科学与工程学院
若再有 6 (ω ) = (ω ωc )t1
f 6 (t ) = f 5 (t t1 )
则
若又有 7
=
2ω1
π
Sa [ω1 (t t1 )] cos[ ω c (t t1 )]
东南大学 信息科学与工程学院
8. 周期信号
An jnΩt 2π fT (t ) = ∑ e , Ω = T n=∞ 2
+∞
+∞ +∞
An FT ( jω) = ∑ 2πδ(ω nΩ) = π ∑ An δ(ω nΩ) 则 n=∞ 2 n=∞
东南大学 信息科学与工程学院
9. 周期性冲激序列
f (t ) = =
π 4ω = {δ(ω+ ωc ) + δ(ω ωc )}+ 2 2 2 j(ω ωc )
东南大学 信息科学与工程学院
东南大学 信息科学与工程学院
4. 尺度变换(比例)性质:
1 ω f ( at ) F( j ) |a | a , a ≠ 0
< Bτ = 常数 >
例:
f ( at t 0 ) ?
j
ω
a
t0
=
dF ( j ω ) j ω dF ( j ω ) j e = e dω dω
j (ω +
π
2
)
东南大学 信息科学与工程学院
8. 卷积定理 (1) 时域卷积定理: f1 (t ) * f 2 (t ) F1 ( jω) F2 ( jω)
第3章周期信号的傅里叶变换

,
对方程取傅里叶变换,得
jY ( j ) 2Y ( j ) F ( j )
由上式可得该系统的频率响应函数 Y ( j ) 1 H ( j ) F ( j ) j 2
1 f ( t ) e ( t ) F ( j ) j 1
t
1 Y ( j ) H ( j )F ( j ) ( j 2)( j 1) 1 1 j 1 j 2
3.3 §周期信号的傅里叶变换
一、 正、余弦函数的傅里叶变换
1 2 ( )
根据频移特性得
e e
j 0 t j 0 t
2 ( 0 ) 2 ( 0 )
所以,正、余弦函数的傅里叶变换为
1 j 0t cos( 0 t ) (e e j0t ) [ ( 0 ) ( 0 )] 2
T 2 T 2
1 jnt T (t )e dt T
T 2 T 2
(t )e
jnt
1 dt T
1 [ T ( t )] 2 ( n ) ( n ) ℱ n T n 令 ( ) ( n )
Y ( j ) H ( j ) F ( j )
称为系统的幅频特性(或幅频响应)
称为系统的相频特性(或相频响应)
( ) y ( ) f ( )
H ( j ) 是 的偶函数, ( )是 的奇函数。
幅频特性和相频特性的物理含义:
幅频特性代表系统对不同频率输入信号放大或衰减的 倍数. 相频特性代表系统对不同频率输入信号相移的大小.
e
cos 0 t
e
j 0 t
常用信号的傅里叶变换

常用信号的傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的数学工具。
对于任意一个周期信号,傅里叶变换可以将其表示成一系列正弦波的叠加形式,从而更好地理解和处理信号。
在实际应用中,有很多信号都需要进行傅里叶变换。
下面介绍一些常用信号的傅里叶变换。
1. 正弦信号正弦信号是一种最基本的周期信号,其函数形式为y=sin(wt),其中w为角频率。
通过傅里叶变换,可以将正弦信号表示为一组频率为w的正弦波的叠加形式,即:y(t) = A1*sin(wt) + A2*sin(2wt) + A3*sin(3wt) + …其中,An为振幅,表示第n个正弦波的幅度。
2. 方波信号方波信号是一种由周期为T的矩形波形组成的信号,其函数形式为:y(t) = sgn(sin(wt))其中,sgn表示符号函数,即当sin(wt)>0时,sgn(sin(wt))=1,否则sgn(sin(wt))=-1。
通过傅里叶变换,可以将方波信号表示为一组频率为w的正弦波的叠加形式,即:y(t) = (4/pi)*[sin(wt) + (1/3)*sin(3wt) + (1/5)*sin(5wt) + …]3. 带限信号带限信号是指信号的频率范围有限,通常是指截止频率为一定值的信号。
通过傅里叶变换,可以将带限信号表示为一组频率在一定范围内的正弦波的叠加形式,即:y(t) = (1/2*pi)*Int[-w0,w0]{F(w)*e^(jwt)dw}其中,F(w)为信号的频谱,w0为信号的截止频率,Int表示积分运算。
以上三种信号只是常用信号中的一部分,实际应用中还有很多其他类型的信号需要进行傅里叶变换。
傅里叶变换不仅可以分析信号的频域特性,还可以用于信号的滤波、压缩、编码等方面,具有广泛的应用价值。
傅里叶变换性质及常见函数傅里叶变换总结,表格打印版
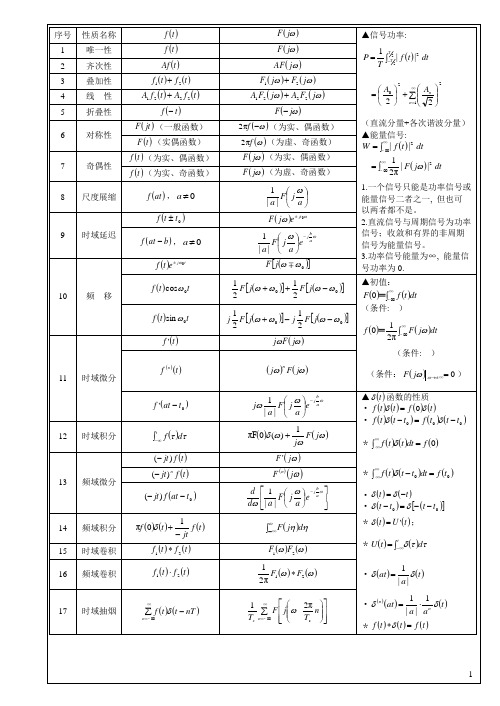
(为虚、奇函数)
7
奇偶性
(为实、偶函数)
(为实、偶函数)
(为实、奇函数)
(为虚、奇函数)
8
尺度展缩
,
9
时域延迟
,
10
频移
▲初值:
(条件:)
(条件:)
(条件: )
11
时域微分
▲ 函数的性质
·
·
*
*
·
·
* ;
*
·
·
*
*
·
12
时域积分
பைடு நூலகம்13
频域微分
14
频域积分
15
时域卷积
16
频域卷积
17
时域抽烟
序号
性质名称
▲信号功率:
(直流分量+各次谐波分量)
▲能量信号:
1.一个信号只能是功率信号或
能量信号二者之一,但也可
以两者都不是。
2.直流信号与周期信号为功率
信号;收敛和有界的非周期
信号为能量信号。
3.功率信号能量为∞,能量信
号功率为0.
1
唯一性
2
齐次性
3
叠加性
4
线性
5
折叠性
6
对称性
(一般函数)
(为实、偶函数)
18
频域抽样
常用时间信号傅里叶变换
常用非周期信号的傅里叶变换
周期信号的傅里叶变换
序号
↔
1
1
↔
2
↔
3
单位直流信号1
↔
4
5
6
一般周期信号
↔
其中
或,
或 ,
一般周期信号的傅立叶变换.

存在的
▪ 周期信号的频谱是离散的,其频谱密度, 即傅立叶变换是一系列冲击函数
§4.6周期信号的傅立叶变换
二、傅立叶级数FS与其单脉冲的傅立叶变换FT的
关系
f (t)
Fn
1 T1
F0 (
j )
f0 (t)
Fn
1 T1
F0 (
j)
n1
F0 ( j)
§4.6周期信号的傅立叶变换
§4.6周期信号的傅立叶变换
▪ 一般周期信号的傅立叶变换 ▪ 傅立叶级数FS与其单脉冲的傅立叶变
换FT的关系 ▪ 正余弦信号的傅立叶变换FT ▪ 周期单位冲激序列的FS和 FT ▪ 周期矩形脉冲的FS和FT ▪ 周期矩形脉冲与单矩形脉冲的关系
§4.6周期信号的傅立叶变换
一、一般周期信号的傅立叶变换
▪ 有限长余弦 f0(t) 看成矩形 G(t) 乘cos1t
▪ 有限长余弦求极限,得到无限长余弦
f0 (t) G(t) cos1t G(t)(e j1t e j1t ) / 2
F0 (
j )
1 [G(
2
1)
G(
1)]
2
Sa[(
1 )
2
]
2
Sa[(
1 )
2
]
§4.6周期信号的傅立叶变换
cos1t
1
(
n1 )
§4.6周期信号的傅立叶变换
小结——单脉冲和周期信号的傅立叶变换的 比较
▪ 单脉冲的频谱 F0( j) 是连续谱,它 的大小是有限值;
▪ 周期信号的谱 F( j) 是离散谱,含
谱密度概念,它的大小用冲激表
示;
常用信号的傅里叶变换

常用信号的傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学工具。
它是以法国数学家傅里叶的名字命名的,用于分析信号的频谱成分。
在信号处理和通信领域,傅里叶变换被广泛应用于信号的频谱分析、滤波、解调和压缩等方面。
1. 正弦信号的傅里叶变换正弦信号是最简单的周期信号之一,它可以表示为一个频率和幅度确定的正弦函数。
对于一个正弦信号,它的傅里叶变换是一个由两个峰值组成的频谱图。
其中一个峰值位于正弦信号的频率上,另一个峰值位于负频率上,其幅度与正弦信号的幅度相等。
2. 方波信号的傅里叶变换方波信号是一种以方波函数为基础的周期信号。
方波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个由多个峰值组成的频谱图。
频谱图上的峰值对应于方波信号中各个频率的成分。
3. 矩形脉冲信号的傅里叶变换矩形脉冲信号是一种在有限时间内突然变化的信号。
它在时域上表现为一个宽度有限的矩形脉冲,其傅里叶变换是一个以脉冲宽度为主要参数的频谱图。
频谱图上的峰值表示了矩形脉冲信号中各个频率的成分。
4. 高斯信号的傅里叶变换高斯信号是一种以高斯函数为基础的连续非周期信号。
高斯信号在时域上呈钟形分布,其傅里叶变换是一个以高斯函数为形状的频谱图。
频谱图上的峰值表示了高斯信号中各个频率的成分。
5. 三角波信号的傅里叶变换三角波信号是一种以三角函数为基础的周期信号。
三角波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个以基频为主要参数的频谱图。
频谱图上的峰值对应于三角波信号中各个频率的成分。
6. 音频信号的傅里叶变换音频信号是一种连续时间的信号,它可以通过傅里叶变换转换为频域信号进行分析。
音频信号的傅里叶变换可以得到音频信号的频谱图,从而可以对音频信号进行频谱分析、滤波和合成等操作。
7. 语音信号的傅里叶变换语音信号是一种声音信号,它可以通过傅里叶变换转换为频域信号进行分析。
语音信号的傅里叶变换可以得到语音信号的频谱图,从而可以对语音信号进行声音分析、语音识别和语音合成等操作。
第四章(1)周期信号的傅里叶级数和频谱

1 j n jnt f ( t ) An e e 2 n
1 j n j n 令复数量 2 An e Fn e Fn
,称其为复
Fn
傅里叶系数,简称傅里叶系数。其模为
,
相角为 n , 则得傅里叶级数的指数形式为 :
f (t )
n
F e
n
jnt
复傅里叶系数
n 2 , 4 , 6 , 8 ,...... n 1 , 3 , 5 , 7 ,.....
, 0 bn 4 n ,
4
1 1 1 f t [sin t sin3t sin5t .... sinnt ...] 3 5 n
2
0
T 2
2 an 0 T
n 0,1 , 2 , 3,.......
2 bn T 2 T
0
T 2 T 2
f ( t ) si nnt dt
2 T2 (1) si nnt dt T
0
T 2 0
si nnt dt
T 2
2 1 2 1 cosnt cosnt T T n T n 0
a0 an cos(nt ) bn sin(nt ) 2 n1 n 1 2 其中 an , bn 称为傅里叶系数, 。 T
那么,傅里叶系数如何求得呢?
T 2 T 2
a0 1 2 T
f ( t )dt
T 2 2 an T f ( t ) cos(nt )dt T 2 T b 2 2 f ( t ) sin( t )dt n n T T 2
A0 1 1 j n jnt j n jnt Ane e Ane e 2 2 n 1 2 n 1
第4章傅里叶变换ppt课件

23
例题4.6 求正弦波的频谱
解:
x(t)si n0tej0t
ej0t 2j
1 a1 2 j
a-1
- 1 2j
X(j)j(0)j(0)
可编辑课件PPT
24
ej0t ej0t
x(t)co0st 2
a1
1 2
a-1
1 2
X (j ) ( 0 ) ( 0 )
本例的结论在信号调制理论中有着广泛的应用
可编辑课件PPT
12
例题4.2 求 x(t)(t) 的频谱。
解
X(j)x(t)ejtdt (t)ejtdt
(t)ej0dt1
可编辑课件PPT
13
单位冲激信号的频谱是常数1,或者说,在所有 的频率点上,频谱的值都是恒定的。
这个例子的物理含义非常广泛,它意味着,尖脉 冲信号的频谱非常宽,会对处于不同接收频率的电子 设备产生干扰。
X(jk0)ejk0t
0
面X 积 (jk0)ej k0t 0 k 0
X(j)ejtd
X(jk0)ejk0t0
k
可编辑课件PPT
10
0 0
傅里叶反变换
x(t)21 X(j)ejtd
一种分解
可编辑课件PPT
11
傅里叶变换
频谱
傅里叶正变换
X(j) x(t)ejtdt
F
F1
x(t)X(j) X(j)x(t)
可编辑课件PPT
2
抽样函数或者称为采样函数:
Sa(x) sinx x
S(ax)S(a x) 偶函数
通过罗必塔法则,可以得到
Sa(0) 1
Sa()0
x 抽样函数右边的第一个过零点在
第四章(5)周期信号的傅里叶变换

�
fT ( t )e
dt
∞
fT ( t )] = ∑ Fne jn t ] = ∑ Fn [e jn t ] [ [
n = ∞
∞
n = ∞
= 2π
n = ∞
∑ Fnδ (ω n )
∞
[ f
Tபைடு நூலகம்
( t )] =
[ ∑ F e
n = ∞ ∞ n n = ∞ n
∞
jn t
]=
n = ∞
∑ F [e
n
∞
δ (t )
∞
∴ δ T ( t ) δ (ω )
1
δT(t )
-3 -2 - 0 2 3
ω 周期冲激序列的傅立叶变换
-3T -2T -T 0 T 2T3T t
图 4.6-3 周期冲激序列
可见: 的单位冲激序列, 可见:时域中周期为 T 的单位冲激序列,在频域中是 周期为 ,强度为
的冲激序列. 的冲激序列.其中 =
j
ωT 2
1 1 2 nT Fn = F0 ( jω) ω= n = Sa ( )e T 2 4 1 2 nπ jnπ = Sa ( )e 2 2 得到: 得到:
j
nT 2
1 2 nπ jnπ jnt f T ( t ) = ∑ Sa ( )e e 2 n = ∞ 2
+∞
本节小结
1,正弦,余弦函数的傅里叶变换 ,正弦, 2,周期信号的傅里叶变换 , 3,傅里叶系数与傅里叶变换的关系 ,
T 2 T 2
1 jn t δ T ( t )e dt = T
∞
∫
T 2 T 2
δ ( t )e
jn t
1 dt = T
常用信号的傅里叶变换

常用信号的傅里叶变换
傅里叶变换是一种将函数从时域(时间域)转换到频域(频率域)的数学技术。
在信号处理中,傅里叶变换可以用来分析各种信号的频率成分。
下面是一些常见信号的傅里叶变换:
1. 正弦信号:正弦信号是基本的周期信号,其傅里叶变换是两个峰值的Delta函数,分别位于正负频率轴上。
峰值的高度与正弦信号的振幅成正比。
2. 方波信号:方波信号的傅里叶变换是一系列的Delta函数,位于基频和其倍频的频率轴上。
每个Delta函数的幅值与方波的斜率成正比。
3. 三角波信号:三角波信号的傅里叶变换是一系列的Delta函数,位于基频和其奇倍频的频率轴上。
每个Delta函数的幅值与三角波的斜率成正比,而且随着频率的增加而逐渐减小。
4. 窗函数信号:窗函数信号可以用来限制一个信号的频率范围。
常见的窗函数信号有矩形窗、汉宁窗、汉明窗等。
它们的傅里叶变换都是一系列的Delta函数,位于基频和其倍频的频率轴上。
不同的窗函数有不同的幅值分布。
5. 常见滤波器的傅里叶变换:滤波器可以用来去除一个信号的某些频率成分。
常见的滤波器有低通滤波器、高通滤波器、带通滤波器、带阻滤波器等。
它们的傅里叶变换都有不同的频率响应曲线,用来描述信号在不同频率上的响应情况。
以上是一些常见信号的傅里叶变换,它们可以用来分析和处理各
种实际的信号。
在实际应用中,傅里叶变换经常和其它技术一起使用,如滤波、采样、量化等,以实现更复杂的信号处理任务。
典型周期信号的傅里叶级数

d
X(j)ejt
X(jk0)ej0t
x(t)21 X(j)ejtd1
0
2 T
k 0
0
于是,对非周期信号,有傅里叶变换对:
x(t)
1
2
X( j)ejtd 1
反
X( j)
x(t)e jtdt
2正
(e j t )
复 杂 信 号 = 系 数 ( ) 基 本 信 号 ( )
系 数 ( ) = 复 杂 信 号 ( 与 ) 基 本 信 号 ( )
F(j)ejtd
F( ) f(t)ejtdt
也是常用的形式
傅立叶变换的理解
周期信号的叶 指级 f数 T(t数 )型 Fn傅 ejn1t表 里明,
n
周期信号可限 以多 分个 解 n 频 1、 为 复率 无 振为 F幅 n的为 指
数分 ejn1t量 的离散和;
非周期信 傅号 里的 叶变 f(t)换 1
周期矩形脉冲信号的三角形式傅里叶级数为
f(t)E T 1 2 T E 1n 1Sa(n 2 1 )cosn1t
F n1 2(anjn b )1 2anE T 1 S(n a 21 )
f(t)的指数形式的傅里叶级数为
f(t)E S(an 1 )ejn 1t
T1 n
2
2、频谱 c0
E T1
规律收. 敛
例1:试将图示周期矩形脉冲信号 展开为(1)三角型和(2)指数型傅里 叶级数。
T
f (t)
A
T
22
t
解(: 1) f (t)是偶函数,故只含 数有 项常 和余弦项。
T
a0T 1
2 T
f(t)d t 2 T
2AdtA
周期信号的傅里叶变换

1 Xn T
n T1 2 T 1 1 2 jn 1 t X e n
x( t )e jn 1t dt
4
单周期信号的傅里叶变换
X d ( ) xd ( t )e j tdt Nhomakorabeadt
1 Xn T1
T1 2 T 1 2
x( t )e jn 1t dt
x(t)
xs(t) x( t ) T xs(t)
0
t
0
T
2T
3T
t
11
调制信号x(t)
抽样
xs(t)
数字信号 量化编码 载波信号
这是由于傅里叶变换反映的是频谱密度概念,周期 信号在各谐振点上,具有有限幅度,说明在这些谐振频 点上其频谐密度趋于无限大,所以变成冲激函数。 这也说明了傅里叶级数可看作傅里叶变换的一种特 例。 三、周期信号与单周期信号频谱间的关系 周期信号x(t)在时域上可以看作是它的单周期信号 xd(t)的周期延拓。已知周期信号的傅里叶级数为:
X ( )
n
0
T1
t
jn1t e
X
n
2 ( n 1 )
n 1 E 1 Sa ( n 1 ) 2 n
9
x0(t) E
E
X0() 2/
0
t E/T1 x(t) E Xn
2/
2.3.4 周期信号的傅里叶变换
前面在推导傅里叶变换时,是将非周期信号看成是 周期信号T 无穷大的周期信号的极限,从而导出了频谱 密度函数的概念。 本节将这概念推广去求周期信号的频谱密度函数 ,即 求周期信号的傅里叶变换,从而得出傅里叶级数是傅里叶 变换的特例的结论。 周期信号是不满足绝对可积条件的,同样它也仅仅在 频谱中引入冲激函数后,傅里叶变换才存在。 因为周期信号可以展成傅里叶级数,即展成一系列不 同频率的复指数分量或正弦、余弦分量的叠加。下面先 求复指数、正弦、余弦分量的傅里叶变换,在此基础上再 求任意周期信号的傅里叶变换。
