线性定常系统的综合
线性定常系统的综合

(5-17)
15
比较上述两种基本形式的反馈可以看出,输 出反馈中的 HC 与状态反馈中的 K 相当。但由于 m<n ,所以 H 可供选择的自由度远比 K 小,因而 输出反馈只能相当于一种部分状态反馈。只有当 C=I时,HC=K,才能等同于全状态反馈。
因此,在不增加补偿器的条件下,输出反馈 的效果显然不如状态反馈系统好。但输出反馈在 技术实现上的方便性则是其突出优点。
k A BK , B, C
可见,状态反馈阵 K 的引入,并不增加系统 的维数,但可通过 K 的选择自由地改变闭环系统 的特征值,从而使系统获得所要求的性能。
10
5.1.2 输出反馈
输出反馈是采用输出矢量 y 构成线性反馈律。 在经典控制理论中主要讨论这种反馈形式。
11
受控系统 0 A, B, C , D
可见引入状态反馈 K=[-1 0] 后,闭环系统保 持能控性不变,却破坏了系统的能观性 。
28
实际上这反映在传递函数上出现了零极点相 消现象。
因为
s 1 0 1 s W0 s csI A b 0 1 2 1 s 1 s 1
23
同理,第三块
A BK 2 B A2 B ABKB BKAB BKBKB
的列矢量可用[B AB A2B]的线性组合表示。 其余各分块类同。 因此 Qck可看作是由 Qc0经初等变换得到的, 而矩阵作初等变换并不改变矩阵的秩。所以Qck与 Qc0 的秩相同,定理得证。
u H Cx Du v HCx HDu v
(5-10)
整理得
u I HD1 HCx v
(5-11)
再把式(5-11)代入(5-7)求得
第5章_线性定常系统的综合

一、综合问题
给定系统状态空间描述:
Ax Bu, x y Cx
x(0) x0
t 0
(1)
A、B、C均为常阵且给定。 再给出所期望的性能指标:
1)对系统状态运动期望形式所规定的某些特征量。
2)对其运动过程所规定的某种期望形式或需取极小 (或极大)值的一个性能函数。 综合:寻找一个控制作用 u ,使得在其作用下,系统 运动的行为满足所给出的期望性能指标。
3. 状态反馈和输出反馈的基本结构形式均不太适用于工程实 际问题。状态反馈和输出反馈的通用结构形式较适用于工程 实际问题。带观测器的状态反馈系统,可解决系统状态不能 测量时的状态重构问题;带有补偿器的输出反馈系统,可解 决输出反馈基本结构形式不能任意配置极点的问题。 4. 状态反馈能保持原受控系统的能控性,但不一定能保持原 受控系统的能观测性。输出反馈能同时保持原受控系统的能 控性和能观测性。 5. 输出反馈是在物理上可构成的,状态反馈是在物理上不能 构成的。基此,输出反馈优于状态反馈。 6. 扩展状态反馈(即带状态观测器状态反馈系统)和扩展输出 反馈(即动态输出反馈系统)是等价的。
故(A BK)B的列向量可由 [B, AB]的列向量的线性 组合来表示。
结论1证明(续)
同理
2 (A BK) B (A BK)(A BK)B (A BK)(AB BKB)
A 2B ABKB BKAB BKBKB
2 故(A BK) B的列向量可由[B, AB, A 2B]的列向量的线性组 合表示。 n 1 以此类推(A BK) B的列向量可由[B, AB, A 2B A n 1B]的列向量
受控系统为: Ax Bu x y Cx 反馈控制规律 : u Hy v HCx v
线性定常系统的综合

2 它的列可由 B AB A B 的列的线性组合得到;
其余各分块类同。 所以有: rankMc rankMck
2. 状态反馈有可能改变系统的能观性。 例如单输入-单输出系统,状态反馈能改变系统的 极点分布,但不会影响系统的零点分布,这样就有可 能使传递函数出现零、极点相消现象。使系统不再是 既能控又能观的,前面已说明状态反馈不改变系统的 能控性,所以只能是影响系统的能观性了。
无零、极点相消现象,系统仍然是既能控又能观的。
5.2 极点配置
如何利用状态反馈与输出反馈来进行线性定常连续系统的极 点配置,即通过状态反馈阵K的选择,使得状态反馈闭环系统的 极点恰好处于预先选择的一组期望极点上。 问题一,闭环极点可任意配置的条件; 问题二,如何设计反馈增益阵使闭环极点配置在期望极点处。
能控性矩阵
0 1 M b Ak b 1 0
满秩,状态反馈系统能控; 不满秩,状态反馈系统不能观;
能观性矩阵: N
c 0 1 0 0 cA k
实际上,此时闭环系统的传递函数为:
s 1 0 1 s 1 0 s Gk ( s) 0 1 2 0 1 2 0 s 1 s 0 s 1 s
Qoh 的每一分块的行由 Qo 相应分块的行线性组 与1一样, Qoh 可以看作是 Qo 经初等变换的结果,而初等 合而成, 变换不改变矩阵的秩,因此能观性不变。
例 系统
0 1 0 x= x+ u 1 0 1 y 0 1 x
系统的传递函数为:
s 1 0 G ( s) c ( sI A) b = 0 1 1 1 s s 1 0 1 s 2 0 1 2 s 1 1 s 1 s 1
第五章线性定常系统的设计与综合-课件

(4)以便一个多输入—多输出系统实现“一个输入只控制一个输出”作 为
性能指标,相应的综合问题称为解耦控制问题。
优化型性能指标常取一个相对于状态 x 和控制 u 的二次型积分性能指标,
其形式为:
J(u()) (xTQxuTRu)dt 0
R正定对称;常阵
Q正定对称或半正 常定 阵对 (且 A,称 Q12)为能观测。
第五章 线性定常系统的设计与综合
二 输出反馈 输出反馈,就是将系统的输出量回馈到系统的 输入端,与参考输入一起,对受控对象进行控 制。在现代控制理论中,带输出反馈结构的控 制系统,根据反馈信号回馈点的位置不同,有 两种基本结构。 一种是反馈信号回馈至输入矩阵B的后端, 或者说,回馈点在状态微分处。图5-2为多输 入多输出系统输出反馈的这种结构型式。另一 种是反馈信号回馈至输入距阵B的前端,或者 说,回馈点在参考信号的入口处。图5-3为多 输入多输出系统输出反馈的这种结构型式。
(3)
其中:k 为 p×n常阵,状态反馈矩阵。
F为 p×q常阵,输出反馈矩阵。
v—参考输入向量。 2) 性能指标的类型
性能指标 非优化型性能指标:是一类不等式型的指标,即只要性能达
到或好于期望指标就算实现了综合目标。
优化型性能指标: 是一类极值型指标,综合的目的是要使
性能指标在所有可能值中取为极小(或
通过状态反馈构成闭环系统
x (ABK)xBu y(CDK)xDu
第五章 线性定常系统的设计与综合
一般D=0,可化简为
x (ABK)xBu yCx
闭环传递函数矩阵为
W k(s ) C (s IA B) 1 K B
状态反馈矩阵K的引入,并不增加系统的维 数,但可通过K的选择自由地改变闭环系统 的特征值,从而使系统获得所要求的性能。
现代控制工程理论与应用

C bn bn1 ... b1
其传递函数为
b1s n1 b2 s n2 ... bn1s bn W0 (s) n s a1 s n1 ... an1s an
设状态反馈矩阵为
K [k n, kn1,...,k1 ]
于是
0 1 0 0 A BK ... 0 0 (an k n ) (an 1 k n 1 ) ... ... ... ... ... 0 0 ... 0 1 (a2 k 2 ) (a1 k1 ) 0 0
D(t )
v(t )
Ax Bv x y Cx Dv
B(t )
x
A(t )
x(t )
C(t )
y(t )
D(t )
u(t )
v(t )
_
B(t )
x
A(t )
x(t )
C(t )
y(t )
H
线性反馈控制律为:
v u Hy u H (Cx Dv) u HCx HDv
(3)在选取所希望的极点位置时,需要研究它们 对系统品质的影响,以及它们与零点分布状况的 关系。此外,还要考虑工程实际情况。 (4)要考虑抗干扰及低灵敏度问题。应使系统具 有较强的抑制干扰能力,对系统参数变化不敏感。 4.2.2 单输入单输出状态反馈系统极点配置法
定理1
对单输入单输出系统
Ax Bv x y Cx
ai = ?, ai* = ?
小结: 对完全可控的单输入单输出系统,极点配置 不改变系统零点分布状态。 由于n阶系统含有n个可以调节的参数,因此 状态反馈对系统品质改进程度远比输出反馈好。
现代控制理论知识点复习

第一章 控制系统的状态空间表达式1. 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况; C 输出矩阵,表示输出与每个状态变量间的组成关系, D 直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
③由描述系统的输入输出动态方程式(微分方程)或传递函数,建立系统的状态空间表达式,即实现问题。
线性反馈控制系统的基本结构及其特点

求得ωb≈9.0;综合考虑响应速度和带宽要求,取ωn=10。于是,
闭环主导极点为s1,2=-7.07±j7.07,取非主导极点为s3=-10ωn=100。
第6章 线性定常系统的综合
(3)确定状态反馈矩阵K。状态反馈系统的特征多项式为
第6章 线性定常系统的综合
定理6.6-受控系统(A,B,C)通过状态反馈实现解耦控制的
环极点任意配置的充要条件是该受控系统状态完全可观。
证 根据对偶原理,如果受控系统Σ0(A,B,C)可观,则对偶系
统Σ0(AT,BT,CT)必然可控,因而可以任意配置(AT-CTHT)的特征
值。而(AT-CTHT)的特征值与(A-HC)的特征值是相同的,故当
且仅当Σ0(A,B,C)可观时,可以任意配置(A-HC)的特征值。
减小ζ,这就会使系统最大超调 Mp 增大。可见只靠调整增益
K 无法同时使ζ和ωn 都取最佳值。这从根轨迹来看,由于可调
参数只有 K,故系统特征根,即闭环极点只能在系统的根轨迹
这条线上,而无法在根轨迹以外的s 平面的其他点上实现。
第6章 线性定常系统的综合
方法二:状态反馈法。
第6章 线性定常系统的综合
图6-9 模拟结构图
第6章 线性定常系统的综合
第6章 线性定常系统的综合
第6章 线性定常系统的综合
图6-10 加入状态反馈后的模拟结构图
第6章 线性定常系统的综合
6.2.2 输出反馈极点配置
输出反馈有两种方式
(1)采用从输出到ሶ 反馈,如图6-3所示。
定理6.4 对受控系统采用从输出到ሶ 的线性反馈实现闭
图6-4 控制系统结构图
现代控制理论试题与答案

现代控制理论1.经典-现代控制区别:经典控制理论中,对一个线性定常系统,可用常微分方程或传递函数加以描述,可将某个单变量作为输出,直接和输入联系起来;现代控制理论用状态空间法分析系统,系统的动态特性用状态变量构成的一阶微分方程组描述,不再局限于输入量,输出量,误差量,为提高系统性能提供了有力的工具.可以应用于非线性,时变系统,多输入-多输出系统以及随机过程.2.实现-描述由描述系统输入-输出动态关系的运动方程式或传递函数,建立系统的状态空间表达式,这样问题叫实现问题.实现是非唯一的.3.对偶原理系统=∑1A1,B1,C1和=∑2A2,B2,C2是互为对偶的两个系统,则∑1的能控性等价于∑2的能观性, ∑1的能观性等价于∑2的能控性.或者说,若∑1是状态完全能控的完全能观的,则∑2是状态完全能观的完全能控的.对偶系统的传递函数矩阵互为转置4.对线性定常系统∑0=A,B,C,状态观测器存在的充要条件是的不能观子系统为渐近稳定第一章控制系统的状态空间表达式1.状态方程:由系统状态变量构成的一阶微分方程组2.输出方程:在指定系统输出的情况下,该输出与状态变量间的函数关系式3.状态空间表达式:状态方程和输出方程总合,构成对一个系统完整动态描述4.友矩阵:主对角线上方元素均为1:最后一行元素可取任意值;其余元素均为05.非奇异变换:x=Tz,z=T-1x;z=T-1ATz+T-1Bu,y=CTz+为任意非奇异阵变换矩阵,空间表达式非唯一6.同一系统,经非奇异变换后,特征值不变;特征多项式的系数为系统的不变量第二章控制系统状态空间表达式的解1.状态转移矩阵:eAt,记作Φt2.线性定常非齐次方程的解:xt=Φtx0+∫t0Φt-τBuτdτ第三章线性控制系统的能控能观性1.能控:使系统由某一初始状态xt0,转移到指定的任一终端状态xtf,称此状态是能控的.若系统的所有状态都是能控的,称系统是状态完全能控2.系统的能控性,取决于状态方程中系统矩阵A和控制矩阵b3.一般系统能控性充要条件:1在T-1B中对应于相同特征值的部分,它与每个约旦块最后一行相对应的一行元素没有全为0.2T-1B中对于互异特征值部分,它的各行元素没有全为0的4.在系统矩阵为约旦标准型的情况下,系统能观的充要条件是C中对应每个约旦块开头的一列的元素不全为05.约旦标准型对于状态转移矩阵的计算,可控可观性分析方便;状态反馈则化为能控标准型;状态观测器则化为能观标准型6.最小实现问题:根据给定传递函数阵求对应的状态空间表达式,其解无穷多,但其中维数最小的那个状态空间表达式是最常用的.第五章线性定常系统综合1.状态反馈:将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入相加形成控制律,作为受控系统的控制输入.K为rn维状态反馈系数阵或状态反馈增益阵2.输出反馈:采用输出矢量y构成线性反馈律H为输出反馈增益阵3.从输出到状态矢量导数x的反馈:A+GC4.线性反馈:不增加新状态变量,系统开环与闭环同维,反馈增益阵都是常矩阵动态补偿器:引入一个动态子系统来改善系统性能5.1状态反馈不改变受控系统的能控性2输出反馈不改变受控系统的能控性和能观性6.极点配置问题:通过选择反馈增益阵,将闭环系统的极点恰好配置在根平面上所期望的位置,以获得所希望的动态性能1采用状态反馈对系统任意配置极点的充要条件是∑0完全能控2对完全能控的单输入-单输出系统,通过带动态补偿器的输出反馈实现极点任意配置的充要条件1∑0完全能控2动态补偿器的阶数为n-13对系统用从输出到x线性反馈实现闭环极点任意配置充要条件是完全能观7.传递函数没有零极点对消现象,能控能观8.对完全能控的单输入-单输出系统,不能采用输出线性反馈来实现闭环系统极点的任意配置9.系统镇定:保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定1对系统采用状态反馈能镇定的充要条件是其不能控子系统渐近稳定2对系统通过输出反馈能镇定的充要条件是其结构分解中的能控且能观子系统是输出反馈能镇定的,其余子系统是渐近稳定的3对系统采用输出到x反馈实现镇定充要条件是其不能观子系统为渐近稳定10.解耦问题:寻求适当的控制规律,使输入输出相互关联的多变量系统的实现每个输出仅受相应的一个输入所控制,每个输入也仅能控制相应的一个输出 11.系统解耦方法:前馈补偿器解耦和状态反馈解耦 12.全维观测器:维数和受控系统维数相同的观测器现代控制理论试题1 ①已知系统u u uy y 222++=+ ,试求其状态空间最小实现;5分 ②设系统的状态方程及输出方程为11000101;0111x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =试判定系统的能控性;5分2 已知系统的状态空间表达式为00001⎛⎫⎡⎤=+ ⎪⎢⎥⎝⎭⎣⎦x x u t ;[]x y 01=; ⎥⎦⎤⎢⎣⎡=11)0(x 试求当0;≥=t t u 时,系统的输出)(t y ;10分 3给定系统的状态空间表达式为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100100110100013 ,211021y x -⎡⎤=⎢⎥⎣⎦ 试确定该系统能否状态反馈解耦,若能,则将其解耦10分 4 给定系统的状态空间表达式为设计一个具有特征值为 1 1 1---,,的全维状态观测器10分 5 ①已知非线性系统 ⎩⎨⎧--=+-=2112211sin 2x a x xx x x试求系统的平衡点,并确定出可以保证系统大范围渐近稳定的1a 的范围;5分② 判定系统11221223x x x x x x =-+⎧⎨=--⎩在原点的稳定性;5分6 已知系统 u x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=110011 试将其化为能控标准型;10分 7 已知子系统1∑ 111121011x x u -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,[]1110y x = 求出串联后系统现代控制理论试题1 ① 取拉氏变换知 )()2()()22(33s u s s s y s ++=+21121)1(21)(2213++-=+++=s s s s s g 3分其状态空间最小实现为u x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=101110 ; 21021+⎥⎦⎤⎢⎣⎡=x y 2分② 1n c u B ABA B -⎡⎤=⎣⎦012111101⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,秩为2,系统状态不完全能控; 2 解 02210(,)0.50.51⎛⎫Φ= ⎪-⎝⎭t t t t , 0()(,0)(0)(,)()tx t t x t B d τττ=Φ+Φ⎰ 1y = 3解 [][]100211101101c B ⎡⎤⎢⎥=-=-⎢⎥⎢⎥⎣⎦, [][]200021102101c B ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦所以120d d ==,121121E E E -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦; 1111213--⎡⎤=⎢⎥⎣⎦E 又因为E 非奇异,所以能用实现解耦控制; 2分12630011c A F c A ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦1分 求出u kx Lv =-+4 解 令122E E E E ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 代入系统得()123120()011100101sE sI A EC sE s E --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--=---⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭理想特征多项式为*332()(1)331f x s s s s =-=+++ 列方程,比较系数求得 001E ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 全维状态观测器为[]ˆˆx A EC x Bu Ey =-++ 12020ˆ01100,00111x u y --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦5 解 ①显然原点为一个平衡点,根据克拉索夫斯基方法,可知 因为 02<-;所以,当0)cos 21(42cos 21cos 212211111>--=----x a a x x时,该系统在原点大范围渐近稳定;解上述不等式知,491>a 时,不等式恒成立; 即491>a 时,系统在原点大范围渐近稳定; ② 解 2114523I A λλλλλ+--==+++,两个特征根均具有负实部,系统大范围一致渐近稳定;2分6 解 1210c u ⎡⎤=⎢⎥⎣⎦,1112201c u -⎡⎤=⎢⎥-⎣⎦ [][][]1111221122010101c p u -⎡⎤===-⎢⎥-⎣⎦[][]11112122221100p p A ⎡⎤==-=⎢⎥⎣⎦11221112211,11P P --⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦能控标准型为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=101010 7 解 组合系统状态空间表达式为[]1200101001,00010011010010x x u y x -⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=+=⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦5分组合系统传递函数为21()()()G s G s G s = 2分21331(1)(1)(1)(1)s s s s s s s ++=⨯=+-+-+ 3分。
线性定常系统的状态空间分析与综合2

从系统的机理出发
例 建立如右图所示机械系统的状
态空间表达式,并画出系统的状态图。
k F
根据牛顿第二定理有
m
或表示成
F ky f dy m d 2 y
dt
dt 2
d 2 y dy m dt2 f dt ky F
y f
机械位移系统
选择位移 y 和速度dy / dt为状态变量,令 x1 y, x2 dy / dt
同一个系统,状态变量的选取不是惟一的。 对于一般的物理系统,状态变量的个数应等于储能元 件的个数。
基本概念
用状态变量来表征系统时,还有如下基本概念:
状态向量 把描述系统的 n个状态变量 x1(t), x2 (t), , xn (t) 看作向
量x(t) 的分量,则x(t) 称为 n 维状态向量,记作
状态空间
x1(t)
x1
x(t
)
x2
(t
),
简记为
x
x2
xn
(t
)
xn
以状态变量 x1, x2, , xn为坐标轴所张成的n维空间,
称为状态空间。系统在任意时刻的状态,在状态空间中是一个
点,随时间推移,状态在变化,在状态空间中绘出一条轨迹,
称为状态轨线。
基本概念
状态方程 由系统的状态变量构成的一阶微分方程组,
则
x&1
x2
,
x&2
k m
x1
f m
x2
1 m
F,
y
x1
从系统的机理出发
用向量—矩阵表示的状态空间表达式为
x&1 x&2
0
k
m
1 f
线性系统的状态综合

的差异来判断原系统的稳定性。这种方法需要找到合适的参考系统。
03
频域分析法
对于线性时变系统,可以通过傅里叶变换等方法将其转换到频域进行分
析。通过观察系统频率响应的特性来判断系统的稳定性。这种方法适用
于具有周期性变化系数的线性时变系统。
05
线性系统的状态综合方法
状态反馈控制
状态反馈控制器的设计
控制器参数优化
线性系统的状态综合
目
CONTENCT
录
• 引言 • 线性系统的状态空间描述 • 线性系统的能控性和能观性 • 线性系统的稳定性分析 • 线性系统的状态综合方法 • 线性系统状态综合的应用实例
01
引言
线性系统的基本概念
线性系统定义
线性系统是指其输出与输入之间满足线性叠加原理 的系统,即输出的变化量与输入的变化量成正比。
优化设计
基于状态综合结果,对机械系统的 结构、参数和控制策略进行优化设 计,提高系统的动态性能和稳定性。
电力系统状态综合
1 2 3
稳态分析
通过测量电力系统的电压、电流和功率等参数, 分析系统的稳态特性,评估系统的供电质量和稳 定性。
暂态过程分析
利用状态综合技术对电力系统的暂态过程进行建 模和分析,研究系统在故障、切换和操作等情况 下的动态行为。
在实际应用中,通常希望一个系统既具有能控性又 具有能观性,这样可以更好地对系统进行状态综合 和控制设计。
04
线性系统的稳定性分析
稳定性的定义和分类
稳Hale Waihona Puke 性定义系统受到扰动后,能够恢复到原来的 平衡状态或者趋近于另一个新的平衡 状态的能力。
稳定性分类
根据系统受到扰动后的表现,可分为 渐近稳定、临界稳定(或中立稳定) 和不稳定三类。
现代控制理论第一章(吴忠强版)

吴忠强
目
录
第一章 控制系统的状态空间表达式 第二章 控制系统状态空间表达式的解 第三章 线性控制系统的能控性与能观性 第四章 控制系统的李亚普诺夫稳定性 第五章 线性定常系统的综合 第六章 最优控制系统设计 参考文献
内容简介
•
本书系统的介绍了现代控制理论的 基本内容,包括控制系统的状态空间描 述、运动分析与离散化、李亚普诺夫稳 定性分析、能控性与能观性、状态反馈 与状态观测器、最优控制系统设计。每 章配有一定的例题和习题.
b11 b 21 B bn1
b12 b 22 bn 2
b1 r b2 r b nr
y1 y2 y ym
——m维输出矢量;
—— n r 输入(或控制)矩阵;
c 11 c 12 c 21 c 22 C c m1 c m 2
1
式(1-3)就是图1-1系统的输出方程,它的矩阵表示为
y 1
T
0
x1 x2
或
y C x
T
y c x
T
(1-4)
式中
c
1
0
六、状态空间表达式
l 状态方程和输出方程总合起来,构成对一个系统完整的动态 描述,称为系统的状态空间表达式, 在经典控制理论中,用指定某个输出量的高阶微分方程来描 述系统的动态过程。如图1-1所示的系统,在以 uc 作输出时, 从式(1-1)消去中间变量i ,得到二阶微分方程为
回到式(1-5)或式(1-6)的二阶系统,若改选 u C 和 u c 作为 两个状态变量,即令 x 1 u C ,
x2 uc
第五章(线性定常系统的综合)
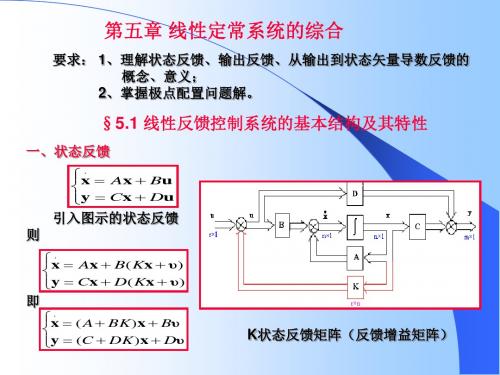
能控。 不能观。
0 rank( N ) rank 0
1 1 0
2、输出反馈不改变受控系统的能控性与能观性
§5.2 极点配置问题
给出系统的期望极点,确定增益矩阵。 一、采用状态反馈 1、定理 采用状态反馈对系统Σ0(A,b,C)任意配置极点的充要条件是: Σ0完全能控。 2、给定极点,求状态反馈增益K
13 可得 G 40 1 2 s
§5.3 系统的镇定、解耦和状态观测器
一、系统的镇定 系统镇定: Σ0(A,B,C)通过反馈使其极点均具有负实部,保证系 统为渐近稳定。 系统状态反馈能镇定: Σ0(A,B,C)通过状态反馈使其极点均具有 负实部,保证系统为渐近稳定。 系统输出反馈能镇定: Σ0(A,B,C)通过输出反馈使其极点均具有 负实部,保证系统为渐近稳定。 二、系统解耦 1、概念 使具有输入和输出个数相同的MIMO系统的每一输出只受一个输入 控制,称为系统的解耦。 2、实现方法 ①使用前馈补偿器 (见 P183 图5-9)
比较有
3 K 2 4 2 K1 6 K 4 0
得
K [ 4
4
1]
注意:当状态空间表达式不同时,结果亦不同。 二、采用输出反馈 定理1: 对于完全能控的SISO系统Σ0(A,b,C),不能采用输出线 性反馈来实现闭环系统极点的任意配置。 定理2:对于完全能控的SISO系统Σ0(A,b,C),通过带动态补偿 器的输出反馈实现闭环系统极点的任意配置的充要条件是: ① Σ0完全能观; ②动态补偿器的阶数为n-1。
. ~
~
其解为: x e ( AGC )t x(0) ①若 x(0) 0 ②若 x(0) 0
~
~
~
现代控制理论课后习题及答案
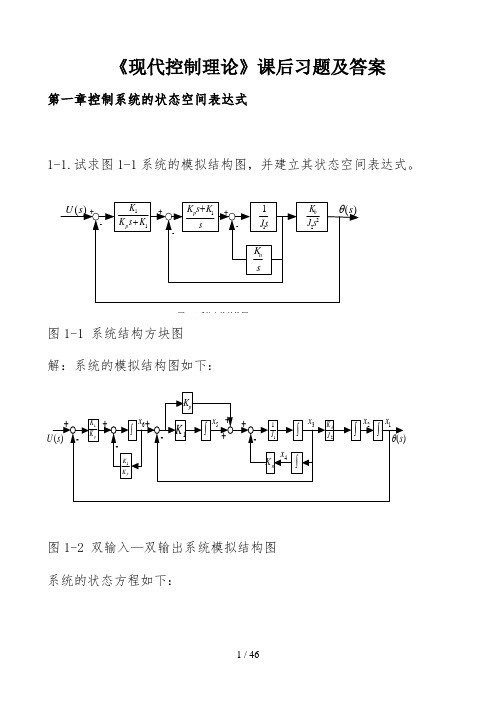
《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图图1-1 系统结构方块图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图图1-3 电路图解:由图,令32211,,x u x i x i c===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论

5.1.2 输出反馈
设线性定常系统为
Ax Bu x y Cx Du
其输入u ,状态变量 x,输出量y 的维数分别是r,n,m 状态反馈控制律 u Fv Hy
F输入变换阵
D
H输出反馈阵
+ +
v
+
F
u
B
+ +
∫
A
x
C
y
H
u Fv Hy Fv H (Cx Du )
0 0 0 s 3 18s 2 72s det(sI A) 1 s 6 0 1 s 12 0
a 0= 0,a1= 72,a2=18
5.2.1状态反馈极点配置
计算由期望闭环极点组决定的特征多项式
3 2 f ( s) ( s * ) ( s 2 )( s 1 j )( s 1 j ) s 4 s 6s 4 i * i 1 3
性能指标的类型
性能指标实质上是对所要综合的控制系统在运动过程行为 上的一种规定。
非优化型性能指标 (不等式型) 优化性型能指标 (极值型)
(1)镇定问题 (2)极点配置 (3)解耦控制 (4)跟踪问题
J (u()) ( x T Qx uT Ru)dt
0
5.1 反馈控制系统的基本结构
0 1 0 0 0 0 1 0 A bc K 0 0 0 0 1 (an 1 kn 1 ) (a0 k0 ) (a1 k1 )
sI ( Ac bc K ) s n ( an 1 kn 1 ) s n 1 ( a1 k1 ) s ( a0 k0 )
第13讲 反馈与极点配置

➢ 状态反馈闭环系统的系统结构可如图5-1所示
vu
+
B
x'
+
-
+
A
x
y
C
开环系统
K
图5-1 状态反馈系统的结构图
状态反馈的描述式(2/3)
u=-Kx+v 状态反馈闭环系统的状态空间模型可描述如下:
➢ 设开环系统状态空间模型和状态反馈律分别记为
x Ax Bu
y
Cx
u Kx v
其中K为rn维的实矩阵,称为状态反馈矩阵;v为r维的输入向 量,亦称为伺服输入。
❖ 该问题称为系统鲁棒性问题。
❖ 基于提高系统鲁棒性的控制综合方法也称为鲁 棒控制方法。
下面,本章将就这些系统综合的主要问题,如 ➢ 极点配置、 ➢ 镇定、 ➢ 解耦与 ➢ 观测器问题,
基于状态反馈理论作细致讨论。
概述(12/12)
5.1 状态反馈与输出反馈
状态反馈与输出反馈(1/3)
控制理论最基本的任务是,对给定的被控系统设计能满足所 期望的性能指标的闭环控制系统,即寻找反馈控制律。
➢ 状态反馈和输出反馈是控制系统设计中两种主要的反馈 策略,其意义分别为将观测到的状态和输出取作反馈量以 构成反馈律,实现对系统的闭环控制,以达到期望的对系 统的性能指标要求。
➢ 在经典控制理论中,一般只考虑由系统的输出变量来构成 反馈律,即输出反馈。
➢ 在现代控制理论的状态空间分析方法中,多考虑采用状态 变量来构成反馈律,即状态反馈。
rank[I-A+BK B]=n
来判定,而
r[I -A BK
B] r [I -A
I B] K
0IBiblioteka r[I-A
线性定常系统的综合
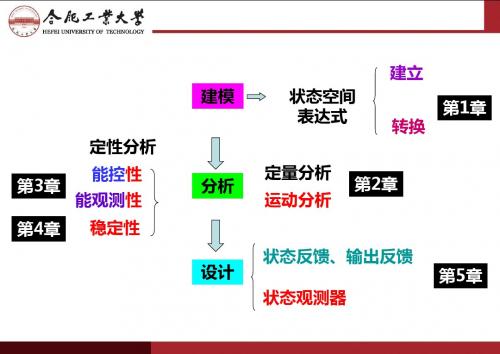
状态反馈
( A BK ) x Bv x y Cx (A BHC ) x Bv x y Cx
输出反馈
反馈信息上:状态反馈优于输出反馈 状态反馈是一种完全的系统信息反馈。 输出反馈是一种不完全的系统信息反馈。 由于反馈引自系统输出,所以输出反馈不影响系统的可观测性
1
0.5
0
-0.5
-1.5
-2
Im [s]平面 Re
Im
[s]平面 Re
2阶系统
2阶系统
3阶系统 1阶系统 1阶系统
3阶系统
期望的极点的选择
– 对于 n 阶系统,必须给出 n 个期望的极点 – 期望的极点必须是实数或成对出现的共轭复数 – 期望的极点必须体现对闭环系统的性能品质指标等的要求
极点配置:设法使闭环系统的极点位于s平面上的一组 合理的、具有期望性能指标的极点 经典控制理论
– 超前校正、滞后校正、PID校正,通过改变极点的位置来改 善性能指标,本质上均属于极点配置方法
现代控制理论
– 如何选择状态反馈阵K,使得闭环系统的极点位于期望极点 上
Ax Bu 线性定常系统(单输入单输出) x
4)输出矩阵由C变成(C-DK) ; 系统的瞬态性能主要由系数矩阵A决定。 通过适当的方法选择反馈阵K,就可以使系统达到希望的控制 目的。
D
v
u
B
x
A
K r n
x
C
ym1
一般D=0
Ax Bu x 原系统: y Cx
G( s) C( sI A) 1 B
推论:输出反馈不改变系统的能控性
现代控制理论试题(详细答案)-现控题目

现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是,能观测的状态变量个数是cvcvx 。
2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程(4分/个)解 1. 能控的状态变量个数是2,能观测的状态变量个数是1。
状态变量个数是2。
…..(4分)2.选取状态变量1x y =,2x y =,3x y =,可得 …..….…….(1分)12233131835x x x x x x x u y x ===--+= …..….…….(1分)写成010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦…..….…….(1分)[]100y x = …..….…….(1分)二、1给出线性定常系统(1)()(),()()x k Ax k Bu k y k Cx k +=+=能控的定义。
(3分)2已知系统[]210 020,011003x x y x ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦,判定该系统是否完全能观?(5分)解 1.答:若存在控制向量序列(),(1),,(1)u k u k u k N ++-,时系统从第k 步的状态()x k 开始,在第N 步达到零状态,即()0x N =,其中N 是大于0的有限数,那么就称此系统在第k 步上是能控的。
若对每一个k ,系统的所有状态都是能控的,就称系统是状态完全能控的,简称能控。
…..….…….(3分) 2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….(1分) [][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….(1分) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=940320110 2CA CA C U O ………………..……….(1分) rank 2O U n =<,所以该系统不完全能观……..….…….(2分)三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 线性定常系统的综合6-1 已知系统状态方程为:()100102301010100x x uy x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3.解: 由()100102301010100x x u y x •-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=可得:(1) 加入状态反馈阵()012K k k k =,闭环系统特征多项式为:32002012()det[()](2)(1)(2322)f I A bK k k k k k k λλλλλ=--=++++-+--+-(2) 根据给定的极点值,得期望特征多项式:*32()(1)(2)(3)6116f λλλλλλλ=+++=+++(3) 比较()f λ与*()f λ各对应项系数,可得:0124,0,8;k k k ===即:()408K =6-2 有系统:()2100111,0x x u y x•-⎛⎫⎛⎫=+ ⎪ ⎪-⎝⎭⎝⎭= (1) 画出模拟结构图。
(2) 若动态性能不能满足要求,可否任意配置极点? (3) 若指定极点为-3,-3,求状态反馈阵。
解(1) 模拟结构图如下:(2) 判断系统的能控性;0111c U ⎡⎤=⎢⎥-⎣⎦满秩,系统完全能控,可以任意配置极点。
(3)加入状态反馈阵01(,)K k k =,闭环系统特征多项式为:()2101()det[()](3)22f I A bK k k k λλλλ=--=+++++ 根据给定的极点值,得期望特征多项式:*2()(3)(3)69f λλλλλ=++=++比较()f λ与*()f λ各对应项系数,可解得:011,3k k ==即:[1,3]K =6-3 设系统的传递函数为:(1)(2)(1)(2)(3)s s s s s -++-+试问可否用状态反馈将其传递函数变成:1(2)(3)s s s -++若能,试求状态反馈阵,并画出系统结构图。
解:若希望采用状态反馈将(1)(2)(1)(2)(3)s s s s s -++-+变成1(2)(3)s s s -++,则根据状态反馈不改变系统传递函数的零点的原理,可知经过状态反馈之后的系统传递函数必为()()212(2)(3)s s s s -+++。
因此期望的特征多项式为232(2)(3)71612λλλλλ++=+++由于原系统的传递函数为232(1)(2)2(1)(2)(3)256s s s s s s s s s s -++-=+-++--,则状态反馈阵[]18215K =。
6-4 是判断下列系统通过状态反馈能否镇定。
210402105,00200517050A b -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪⎪ ⎪==- ⎪ ⎪- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭解:该系统为约旦标准型,很显然,其不能控不能所对应的特征值具有负实部,是渐进稳定的,因此可以通过状态反馈进行镇定。
6-5 设系统状态方程为:01000010100010001101x x u •⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭(1) 判断系统能否稳定。
系统能否镇定。
(2) 若能,试设计状态反馈使之稳定。
解:(1)()4100010det 000100110I A λλλλλλλ-⎡⎤⎢⎥⎢⎥-===⎢⎥-⎢⎥⎣⎦= 原系统处于临界稳定状态。
010110100101110110c U ⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥--⎣⎦,可知矩阵满秩,系统完全能控,所以可以通过状态反馈实现系统的镇定。
(2)自定义期望的系统极点,然后采用极点配置的方法进行即可。
6-6 设计一前馈补偿器,使系统:1112()11(1)s s W s s s s ⎛⎫ ⎪++⎪= ⎪ ⎪+⎝⎭解耦,且解耦后的极点为-1,-1,-2,-2.解:根据题意可知解耦后的系统传递函数矩阵为()()212101()102s W s s ⎛⎫⎪+ ⎪= ⎪⎪ ⎪+⎝⎭, 则前馈补偿器为()()()12211101121110(1)2d s s s W s s s s s -⎛⎫⎛⎫ ⎪ ⎪+++ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭+⎝⎭, 所以()()()()()()2232122122d s s s s W s s s s s s +⎛⎫- ⎪++⎪= ⎪+- ⎪ ⎪+++⎝⎭6-7 已知系统:100100230110101100011x x u y x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭(1) 判别系统能否用状态反馈实现解耦。
(2) 设计状态反馈使系统解耦,且极点为-1,-2,-3. 解:原系统的传递函数矩阵为:()()()()1101001010002301011101011011012s W s C sI A B s s s s s --+⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=-=+⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤⎢⎥+⎢⎥=⎢⎥⎢⎥++⎣⎦系统存在耦合。
下面判断系统能否通过状态反馈进行解耦:[][]0110101011001c A B ⎡⎤⎢⎥==≠⎢⎥⎢⎥-⎣⎦0,所以10d =;[][][][]02121001101000110010011023011010101c A B c A B ⎡⎤⎢⎥===⎢⎥⎢⎥-⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥=--=≠⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦00所以21d =。
因此1212100122d d c A D c A ⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦,1010010011221001E DB ⎡⎤⎡⎤⎡⎤⎢⎥===⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥-⎣⎦, 可知E 为非奇异阵,所以该系统不能通过状态反馈的办法实现解耦。
6-8 已知系统:()01000110x x u y x•⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭= 试设计一状态观测器,使观测器的极点为-r,-2r(r>0). 解 (1) 检验能观性因10,,01o c U cA ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭满秩系统能观可构造全维观测器.(2) 原系统的对偶系统为:[]001,,01100TT TA c b ⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦()201det ,0,0T I A a a λλ-===所以另观测器的期望多项式为()()22232r r r r λλλλ++=++则2012,3a r a r **==所以()22,3T KE r r ==下面求转换矩阵1100101100110T TT T TTP A cc A cc P -⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦所以原系统对应的()1222012,3321032TTE E P r r r r r E r -⎡⎤⎡⎤=⋅==⎢⎥⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦对应的全维观测器为:223103ˆˆ()2012rr x A Ec x bu Ey x u y rr -⎛⎫⎛⎫⎛⎫=-++=++ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭g6-9* 已知系统:()21001110x x uy x•-⎛⎫⎛⎫=+ ⎪ ⎪-⎝⎭⎝⎭= 设状态变量2x 不能测取,试设计全维和降维观测器,使观测器极点为-3,-3.解:[]201,,01110TT TA c b -⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦()201det 32,2,3T I A a a λλλ-=++==所以另观测器的期望多项式为()22369λλλ+=++则019,6a a **==所以()7,3T KE ==下面求转换矩阵1101131100111T TT T TTP A cc A cc P -⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥-⎣⎦所以原系统对应的()[]1017,3341134TTE E P E -⎡⎤=⋅==⎢⎥-⎣⎦⎡⎤=⎢⎥⎣⎦对应的全维观测器为:5103ˆˆ()4114x A Ec x bu Ey x u y -⎛⎫⎛⎫⎛⎫=-++=++ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭g6-11* 设受控对象传递函数为31s : (1)设计状态反馈,使闭环极点配置为13,2--± 解:期望的特征多项式为()3201211344322223,4,4j j a a a λλλλλλ***⎛⎫⎛⎫++-++=+++ ⎪⎪⎝⎭⎝⎭=== 原系统0120,0,0a a a ===所以[]344K=。
