最新切线长定理(共33张PPT)课件PPT
合集下载
《切线长定理》PPT课件

E O CD
P
OA⊥PA,OB ⊥PB,AB ⊥OP
B
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC (3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP (4)写出图中所有的等腰三角形 △ABP △AOB
(5)若PA=4、PD=2,求半径OA
外切圆的半径:交点到三
内切圆的半径:交点到三
角形任意一个定点的距离。 h 角形任意一边的垂直距离。15
分析题目已知:如
图, △ABC的内切圆
⊙O与BC 、CA、
AB 分别相交于点
A
D 、 E 、 F ,且
E
AB=9厘米,BC
FO
=14厘米,CA =13
厘米,求AF、BD、 B D CE的长。
h
C
16
A
几何语言: PA、PB分别切⊙O于A、B
PA = PB ∠OPA=∠OPB
反思:切线长定理为证明线段相等、角相 等提 供了新的方法
h
6
我们学过的切线,常有 六五个 性质:
1、切线和圆只有一个公共点; 2、切线和圆心的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。 6、从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
解:设Rt△ABC的内切圆与三边相切于D、E、F,
连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
A
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
F
设AD= x , BE= y ,CE= r
人教版九年级上册 24.2.4 切线长定理 课件
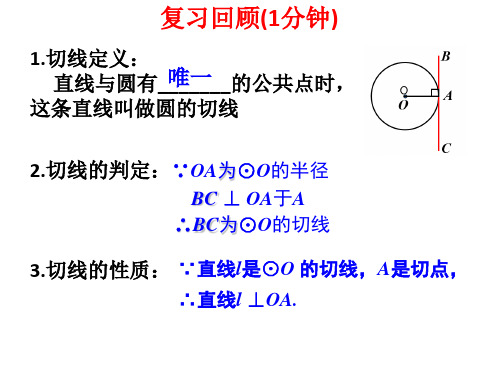
探究一:切线长定理 问题1:上节课我们学习了过圆上一点作已知圆的切线 (如左图所示),如果点P是圆外一点,又怎么作该圆的 切线呢?过圆外的一点作圆的切线,可以作几条?
A
P O
B
A
O.
P
B
1.切线长的定义: 经过圆外一点作圆的
切线,这点和切点之间的 线段的长叫做切线长.
A
O P
2.切线长与切线的区别在哪里?
名称
外心:三 角形外接 圆的圆心
确定方法
三角形三边
中垂线的交
点
B
图形
A
O
性质
1.OA=OB=OC 2.外心不一定 在三角形的内 部.
内心:三 角形内切 圆的圆心
三角形三条 角平分线的 交点
B
A
O C
1.到三边的距离相等; 2.OA、OB、OC分 别平分∠BAC、 ∠ABC、∠ACB 3.内心在三角形内
易错点
(1)切线是直线,不能度量.
(2)切线长是线段的长,可以度量.
A
2、已知PA、PB与⊙O相切
于点A、B,⊙O的半径为2 (1)若四边形OABP的周
2 30°
长为10,则PA= 3 。
2
(2)若∠APB=60°,则PA=
。B
3.如图,PA、PB、CD分别切⊙ O于A、B、E,CD交 PA,PB于C、D,已知PA=7cm,求△PCD的周长.
O 最大的圆与三角 形三边都相切
问题2:如何画出这个圆呢?
已知:△ABC. 求作:和△ABC的各边都相切的圆.
A
N
O
B
D
作法: 1.作∠B和∠C的平分线BM和 CN,交点为O. 2.过点O作OD⊥BC.垂足为D. M 3.以O为圆心,OD为半径作 圆O.
切线长定理(共33张PPT)

试用文字语言叙述你所发现的结论
切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等。
几何语言:
反思:切线长定理为证明线段相等、角相等提供新的方法
O
P
A
B
试一试
A
P
O
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
a+b-c
2
ab
a+b+c
· O
A
B
C
D
E
F
O
A
B
C
D
E
思考:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。 求证:AC∥OP
P
A
C
B
D
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有相等的线段
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等。
几何语言:
反思:切线长定理为证明线段相等、角相等提供新的方法
O
P
A
B
试一试
A
P
O
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
a+b-c
2
ab
a+b+c
· O
A
B
C
D
E
F
O
A
B
C
D
E
思考:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。 求证:AC∥OP
P
A
C
B
D
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有相等的线段
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
切线长定理PPT课件

求AF、BD、CE的长.
解: ∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
设AF=x(cm), BD=y(cm),CE=z(cm)
x+y=9
x=4
则有 y+z=14 解得 y=5
x+z=13
z=9
∴ AF=4(cm), BD=5(cm), CE=9(cm).
第十七页,共26页。
F
设AD= x , BE= y ,CE= r
D O·
则有
x+r=b y+r=a x+y=c
解得
r=
a+b-c
2
C
E
B
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= a+b-c或r=
2 第十八页,共26页。
ab
a+b+c
思考:如图,AB是⊙O的直径,
AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
AL
B
补充:圆的外切四边形的两组对边的和相等.
第十五页,共26页。
想一想
A
反思:在解决有关圆的
切线长问题时,往往需
。
要我们构建基本图形。 O
P
B
(1)分别连结圆心和切点 (2)连结两切点
(3)连结圆心和圆外一点
第十六页,共26页。
例题3
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
C E
C E
D
D
F
A
·O
B
A
O
B
第十九页,共26页。
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。
解: ∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
设AF=x(cm), BD=y(cm),CE=z(cm)
x+y=9
x=4
则有 y+z=14 解得 y=5
x+z=13
z=9
∴ AF=4(cm), BD=5(cm), CE=9(cm).
第十七页,共26页。
F
设AD= x , BE= y ,CE= r
D O·
则有
x+r=b y+r=a x+y=c
解得
r=
a+b-c
2
C
E
B
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= a+b-c或r=
2 第十八页,共26页。
ab
a+b+c
思考:如图,AB是⊙O的直径,
AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
AL
B
补充:圆的外切四边形的两组对边的和相等.
第十五页,共26页。
想一想
A
反思:在解决有关圆的
切线长问题时,往往需
。
要我们构建基本图形。 O
P
B
(1)分别连结圆心和切点 (2)连结两切点
(3)连结圆心和圆外一点
第十六页,共26页。
例题3
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
C E
C E
D
D
F
A
·O
B
A
O
B
第十九页,共26页。
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。
最新人教版初中九年级上册数学《切线长定理》精品课件

E O CD
P
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP
B
(2)写出图中与∠OAC相等的角和图中相等的线段;
∠OAC=∠OBC=∠APC=∠BPC,
OA=OB=OD=OE,PA=PB,AC=BC.
(3)写出图中所有的全等三角形; △AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
D
C
因此,AF=4,BD=5,CE=9.
随堂演练
基础巩固
1.如图,△ABC的内切圆⊙O与BC,CA,AB 分别相切于点D,E,F,且AB=11cm, BC=14cm,CA=13cm,则AF的长为( C )
A.3cm
B.4cm
C.5cm
D.9cm
2.如图,点O是△ABC的内心,若∠BAC=86°, 则∠BOC=(C ) A.172° B.130° C.133° D.100°
5.如图,一个油桶靠在墙 边,量得WY =1.65m, 并且XY⊥WY,这个油桶 底面半径是多少?
解:设圆心为O,连接OW,OX. ∵YW,YX均是⊙O的切线, ∴OW⊥WY,OX⊥XY, 又∵XY⊥WY, ∴∠OWY=∠OXY=∠WYX=90°, ∴四边形OWYX是矩形,又∵OW=OX. ∴四边形OWYX是正方形. ∴OW=WY=1.65m. 即这个油桶底面半径是1.65m.
P.
A
B
. O
(1)知道什么是圆的切线长,能叙述并证明切线长定理. (2)会作三角形的内切圆,知道三角形内心的含义和性质. (3)能用切线长定理和三角形内心的性质来解决简单的问题.
推进新课
知识点1 切线长定理
画一画:1.如何过⊙O外一点P画出⊙O的切线?
人教版数学九年级上册24.2.3切线长定理课件(共26张PPT)

三角形外心、内心的区别:
名称
外心
内心
图形
性质
三角形的外心到三角形三个 三角形的内心到三角形
顶点的距离相等
三条边的距离相等
位置 外心不一定在三角形内部 内心一定OC=90°+
1 2
∠A
例2 如图, △ABC的内切圆⊙O与BC,CA, AB
分别相交于点D , E , F ,且AB=9,BC =14,
CA =13,求AF,BD,CE的长.
解:设AF=x,则AE=x,
A
CD=CE=AC-AE=13-x,
E
BD=BF=AB-AF=9-x.
F
由BD+CD=BC,可得
(13-x)+(9-x)=14.解得,x=4. B
D
C
因此,AF=4,BD=5,CE=9.
随堂练习 1.如图,△ABC的内切圆⊙O与BC,CA,AB分 别相切于点D,E,F,且AB=11cm,BC=14cm, CA=13cm,则AF的长为( C ) A.3cm B.4cm C.5cm D.9cm
解:∵ 点O是△ABC的内心,
∴∠OBC= 1 ∠ABC= 1 ×50°=25°,
2
2
∴∠OCB= 1 ∠ACB = 1×75°=37.5° ,
2
2
∴∠BOC=180°-25°-37.5°=117.5° B
A O
C
【选自教材P100 练习 第2题】
5. △ABC的内切圆半径为r, △ABC的周长为l,求△ABC的
2.如图,点O是△ABC的内心,若∠BAC=86°, 则∠BOC=( C ) A.172° B.130° C.133° D.100°
3.如图,已知VP、VQ为⊙T的切线,P,Q为
34第三课时切线长定理用课件
22cm
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
《切线长定理》ppt

新课学习
复习:切线的判定定理:
经过半径的外端并且垂直于这 条半径的直线是圆的切线.
1.经过半径的外端; 2.与半径垂直.
OA是⊙O的半径 几何应用: OA⊥L于A
.O
L A
L是⊙O的切线.
复习:切线的性质定理:
圆的切线垂直于过切 点的半径
几何应用:
∵L是⊙O的切线 , ∴OA⊥L
.O
L A
证明切线时,添加辅助线的两种方法:
内切圆的概念
与三角形各边相切的圆叫做 三角形的内切圆,内切圆的 圆心是三角形三条角平分线 的交点,叫做三角形的内心。
图中,哪些线段相等?
B
A
D
F O
EC
外接圆
经过三角形的三个顶点 可以作一个圆,这个圆 叫做三角形的外接圆, B 外接圆的圆心是三角形 三条边的垂直平分线的 交点,叫做这个三角形 的外心。
(1)如果已知直线经过圆上一点,则连结这点和圆心, 得到辅助半径,再证所作半径与这直线垂直。
简称:与圆有交点时,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则 过圆心作直线的垂线段为辅助线,再证垂线段长等 于半径长。
简称:与圆没有交点时,作垂直,证半径。
想一想:过圆外一点可以引圆的几条切 线?
A C
注意:
三角形的内心和外心的区别: 内心是三角形三条角平分线的交点,
外心是三角形三条边的垂直平分线的交点。
练一练
1、与三角形各边相切的圆叫做三角形的 ________
2、经过三角形的三个顶点可以作一个圆,这个圆 叫做三角形的________
3、三角形_____的圆心,是三角形三条______ 的交点,叫做三角形的内心。
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
复习:切线的判定定理:
经过半径的外端并且垂直于这 条半径的直线是圆的切线.
1.经过半径的外端; 2.与半径垂直.
OA是⊙O的半径 几何应用: OA⊥L于A
.O
L A
L是⊙O的切线.
复习:切线的性质定理:
圆的切线垂直于过切 点的半径
几何应用:
∵L是⊙O的切线 , ∴OA⊥L
.O
L A
证明切线时,添加辅助线的两种方法:
内切圆的概念
与三角形各边相切的圆叫做 三角形的内切圆,内切圆的 圆心是三角形三条角平分线 的交点,叫做三角形的内心。
图中,哪些线段相等?
B
A
D
F O
EC
外接圆
经过三角形的三个顶点 可以作一个圆,这个圆 叫做三角形的外接圆, B 外接圆的圆心是三角形 三条边的垂直平分线的 交点,叫做这个三角形 的外心。
(1)如果已知直线经过圆上一点,则连结这点和圆心, 得到辅助半径,再证所作半径与这直线垂直。
简称:与圆有交点时,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则 过圆心作直线的垂线段为辅助线,再证垂线段长等 于半径长。
简称:与圆没有交点时,作垂直,证半径。
想一想:过圆外一点可以引圆的几条切 线?
A C
注意:
三角形的内心和外心的区别: 内心是三角形三条角平分线的交点,
外心是三角形三条边的垂直平分线的交点。
练一练
1、与三角形各边相切的圆叫做三角形的 ________
2、经过三角形的三个顶点可以作一个圆,这个圆 叫做三角形的________
3、三角形_____的圆心,是三角形三条______ 的交点,叫做三角形的内心。
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
初中九年级下册数学《切线长定理》PPT精品课件

切线长定理
2020/11/20
1
A
O
P
2020/11/20
B
过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这点 到圆的切线长。
2
A
O
P
B
• 切线是直线,不能度量;
• 切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
2020/11/20
3
A
1
O
M的两条切线,
内切圆圆心:三角形三个 内角平分线的交点。
内切圆的半径:交点到三 角形任意一边的垂直距离。
2020/11/20
9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2020/11/20
10
有什么关系? 又OA=OB,OP=OP, 地理课件:
历史课件:
∴Rt△AOP≌Rt△BOP(HL)
∴PA=PB,∠1=∠2
2020/11/20
4
A
O
P
B
• 切线长定理:
• 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
2020/11/20
5
切线长定理的拓展
A
D
O HC
P
B
(1)写出图中所有的垂直关系
(2)图中有哪些线段相等(除半径 外)、弧相等?
2020/11/20
6
2020/11/20
7
o.
o.
2020/11/20
8
三角形外接圆
C
2020/11/20
1
A
O
P
2020/11/20
B
过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这点 到圆的切线长。
2
A
O
P
B
• 切线是直线,不能度量;
• 切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
2020/11/20
3
A
1
O
M的两条切线,
内切圆圆心:三角形三个 内角平分线的交点。
内切圆的半径:交点到三 角形任意一边的垂直距离。
2020/11/20
9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2020/11/20
10
有什么关系? 又OA=OB,OP=OP, 地理课件:
历史课件:
∴Rt△AOP≌Rt△BOP(HL)
∴PA=PB,∠1=∠2
2020/11/20
4
A
O
P
B
• 切线长定理:
• 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
2020/11/20
5
切线长定理的拓展
A
D
O HC
P
B
(1)写出图中所有的垂直关系
(2)图中有哪些线段相等(除半径 外)、弧相等?
2020/11/20
6
2020/11/20
7
o.
o.
2020/11/20
8
三角形外接圆
C
人教版九年级数学上册《切线长定理》PPT

。
OM
P
OP垂直平分AB
A
证明:∵PA、PB是⊙O的切线,点A,B是切点.
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线.
∴OP垂直平分AB.
反思:在解决有关圆的
A
切线长问题时,往往需
要我们构建基本图形.
。
O
P
B (1)分别连结圆心和切点 (2)连结两切点
(3)连结圆心和圆外一点
F
· 连结OA、OB、OC、OD、OE、OF, O
则OD⊥AB,OE⊥BC,OF⊥ABC.
∴S△ABC=S△AOB+S△BOC +S△AOC
C E
= =
1 12
AB·OD+
l·r
1 2
BC·OE+
12AC·OF
2
设△ABC的三边为a、b、c,面积为S,
2S 则△ABC的内切圆的半径 r= a+b+c
切线长定理 从圆外一
B
点可以引圆的两条切线,它
们的切线长相等,这一点和
圆心的连线平分两条切线的
。
O
P
夹角.
A
几何语言: PA、PB分别切⊙O于A、B
PA=PB ∠OPA=∠OPB
反思:切线长定理为证明பைடு நூலகம்段相等、角相 等提供了新的方法.
B 若连结两切点A、B,交
OP于点M.你又能得出什
么新的结论?请给出证 明.
4.解决问题,加深理解
例 △ABC 的内切圆 ⊙O 与 BC,CA,AB 分别相 切于点 D,E,F,且 AB=9,BC=14,CA=13.
求 AF,BD,CE 的长.
A E
F
B
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内切圆的半径
r=
a+b-c
2
或r=
ab
a+b+c
思考:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
C E
C E
D
D
F
A
·O
B
A
O
B
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。
求证:AC∥OP CA
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
A
D
F O
B
EC
思考
三角形的内切圆的有关计算
如图,△ABC的内切圆的半径为r, △ABC的周长为l,
求△ABC的面积S.
A
解:设△ABC的内切圆与三边相切于D、E、F,
连结OA、OB、OC、OD、OE、OF, D
OD
P
B
课堂小结
切线长定理 从圆外一点引圆的两条切线,它 们的切线长相等,圆心和这一点的连线平分两
条切线的夹角。
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB OP垂直平分AB
切线长定理为证明线段相等,角 相等,弧相等,垂直关系提供了理论 依据。必须掌握并能灵活应用。
练习.如图,△ABC中,∠C =90º,它的
切线长定理
从圆外一点引
A
圆的两条切线,
它们的切线长
相等。
O
P
几何语言: B PA = PB
PA、PB分别切⊙O于A、B ∠OPA=∠OPB
反思:切线长定理为证明线段相等、角相 等提供新的方法
试一试
若连结两切点A、B,AB交OP于点M.你又能得 出什么新的结论?并给出证明. B
OP垂直平分AB
OM
PA=PB
A
E
O
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
Q
∴周长为24cm
P
B
F
变式:如图所示PA、PB分别切 圆O于A、B,并与圆O的切线分别相交于 C、D,已知PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
A
D
P
·O
E
C B
例题2
例2、如图,四边形ABCD的边AB、BC、CD、DA和 圆⊙O分别相切于点L、M、N、P,
∠OAC=∠OBC=∠APC=∠BPC
(3)写出图中所有相等的线段
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
例题1
已知:如图,PA、PB是⊙O的切线,切点分别是
A、B,Q为AB上一点,过Q点作⊙O的切线,交
PA、PB于E、F点,已知PA=12CM,求△PEF的
周长。
易证EQ=EA, FQ=FB,
连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
A
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
F
设AD= x , BE= y ,CE= r
D O·
则有
x+r=b y+r=a x+y=c
解得
r=
a+b-c
2
C
E
B
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
∴PA = PB ∠OPA=∠OPB ∴PC=PC
∴ △PCA ≌ △PCB ∴AC=BC
探究:PA、PB是⊙O的两条切
A
线,A、B为切点,直线OP交于
⊙O于点D、E,交AB于C。 E O C D
P
(1)写出图中所有的垂直关系
B
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中与∠OAC相等的角
P
B
(1)分别连结圆心和切点 (2)连结两切点
(3)连结圆心和圆外一点
例题3
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm, 求AF、BD、CE的长.
解: ∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
设AF=x(cm), BD=y(cm),CE=z(cm)
求证: AD+BC=AB+CD 证明:由切线长定理得
C N
∴AL=AP,LB=MB,NC=MCD,
DN=DP
M O
P
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
AL
B
补充:圆的外切四边形的两组对边的和相等.
想一想
A
反思:在解决有关圆的
切线长问题时,往往需
。
要我们构建基本图形。 O
过圆外一点可以引圆的几条切线?
A
O。
P
B
尺规作图:
过⊙O外一点作⊙O的切线
A
OO ·
P
B
比一比
在经过圆外一点的切线上,这一点和切点之间的线 段的长叫做这点到圆的切线长。
A
O
·
P
B
B
切线与切线长是一回事吗?它们有什么区别与联 系呢? 切线:不可以度量。切线长:可以度量。
A
1
O
2
P
B
思考:已知⊙O切线PA、PB,A、B 为切点,把圆沿着直线OP对折,你能 发现什么?
P
A 证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB ∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
若延长PO交⊙O于点C,连结CA、CB,你又 能得出什么新的结论?并给出证明.
B
CA=CB
。
P
C
O
A 证明:∵PA,PB是⊙O的切线,点A,B是切点
证一证
请证明你所发现的结论。 B
PA = PB
∠OPA=∠OPB
O
P
A 证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL)
试用文字语言 叙述你所发现 的结论
∴ PA = PB ∠OPA=∠OPB
切线长定理(共33张PPT)
切线的性质定理:
圆的切线垂直于过切 点的半径
几何应用:
∵L是⊙O的切线 , ∴OA⊥L
.O
L A
切线的判定定理:
经过半径的外端并且垂直于这 条半径的直线是圆的切线.
1.经过半径的外端; 2.与半径垂直.
OA是⊙O的半径 几何应用: OA⊥l于A
.O
L A
l是⊙O的切线.
x+y=9
x=4
则有 y+z=14 解得 y=5
x+z=13
z=9
∴ AF=4(cm), BD=5(cm), CE=9(cm).
变式
如图,Rt△ABC中,∠C=90°,BC=
a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:
Rt△ABC的内切圆的半径 r.
解:设Rt△ABC的内切圆与三边相切于D、E、F,
F
则OD⊥AB,OE⊥BC,OF⊥AC.
O·
∴S△ABC=S△AOB+S△BOC +S△AOC B
=
1 2
AB·OD+
1 2
BC·OE+
1 2
AC·OF
=
1 2
l·r
C E
设△ABC的三边为a、b、c,面积为S,
