高中数学必修1基本初等函数拔高训练

合集下载

人教版高中数学必修一习题基础综合拔高摘录汇集

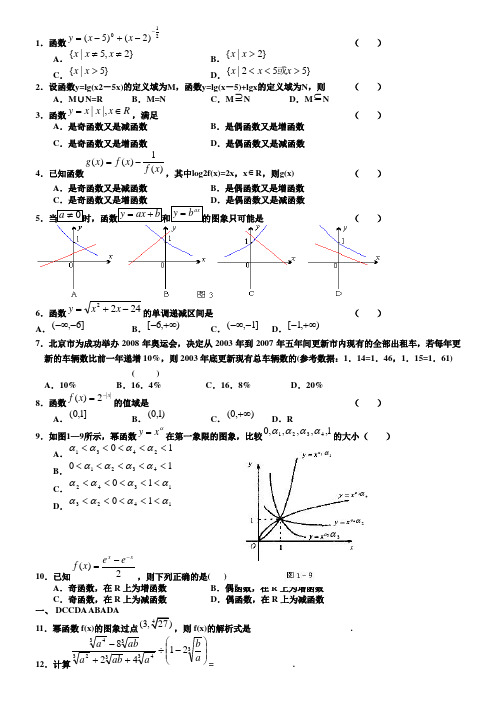
1．函数210)2()5(--+-=x x y （）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或 2．设函数y=lg(x2－5x)的定义域为M ，函数y=lg(x －5)+lgx 的定义域为N ，则（） A ．M ∪N=R B ．M=N C ．M ⊇N D ．M ⊆N 3．函数R x x x y ∈=|,|，满足（）A ．是奇函数又是减函数B ．是偶函数又是增函数C ．是奇函数又是增函数D ．是偶函数又是减函数4．已知函数)(1)()(x f x f x g -=，其中log2f(x)=2x ，x ∈R ，则g(x)（） A ．是奇函数又是减函数 B ．是偶函数又是增函数 C ．是奇函数又是增函数D ．是偶函数又是减函数5（）6．函数2422-+=x x y 的单调递减区间是（）A ．]6,(--∞B ．),6[+∞-C ．]1,(--∞D ．),1[+∞-7．北京市为成功举办2008年奥运会，决定从2003年到2007年五年间更新市内现有的全部出租车，若每年更新的车辆数比前一年递增10%，则2003年底更新现有总车辆数的(参考数据：1．14=1．46，1．15=1．61) ( )A ．10%B ．16．4%C ．16．8%D ．20%8．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R9．如图1—9所示，幂函数αx y =在第一象限的图象，比较1,,,,,04321αααα的大小（）A ．102431<<<<<ααααB ．104321<<<<<ααααC ．134210αααα<<<<<D ．142310αααα<<<<<10．已知2)(xx e e x f --=，则下列正确的是( )A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数一、 DCCDA ABADA11．幂函数f(x)的图象过点，则f(x)的解析式是.12．计算⎪⎪⎭⎫ ⎝⎛-÷++-33433233421428a b a ab a ab a = . 1α3α4α2α13．将函数xy 2=的图象向左平移一个单位，得到图象C1，再将C1向上平移一个单位得到图象C2，作出C2关于直线y=x 对称的图象C3，则C3的解析式为 . 11、)0()(34≥=x x x f 12、32a 13、1)1(log 2--=x y15．（12分）求函数23log (253)y x x =--的单调区间。

高一数学基本初等函数提高训练及答案

数学1（必修）第二章基本初等函数（1）一、选择题1 函数]1,0[)1(log )(在++=x a x f a x 上的最大值和最小值之和为a ，则a 的值为（） A41 B 21 C2 D 4 2 已知log (2)a y ax =-在[0,1]上是x 的减函数，则a 的取值范围是( ) A （0，1） B （1，2） C （0，2）D ∞[2，+） 3 对于10<<a ，给出下列四个不等式①)11(log )1(log a a a a +<+ ②)11(log )1(log a a a a +>+ ③a a a a 111++< ④a a a a 111++>其中成立的是（）A ①与③B ①与④C ②与③D ②与④4 设函数1()()lg 1f x f x x =+，则(10)f 的值为（）A 1B 1-C 10D 101 5 定义在R 上的任意函数()f x 都可以表示成一个奇函数()g x 与一个偶函数()h x 之和，如果()lg(101),x f x x R =+∈，那么( )A ()g x x =，()lg(10101)x x h x -=++B lg(101)()2x x g x ++=，x lg(101)()2x h x +-= C ()2x g x =，()lg(101)2x x h x =+- D ()2x g x =-， lg(101)()2x x h x ++= 6 若ln 2ln 3ln 5,,235a b c ===,则( ) A a b c << B c b a <<C c a b <<D b a c <<二、填空题1 若函数()12log 22++=x ax y 的定义域为R ，则a 的范围为__________2 若函数()12log 22++=x ax y 的值域为R ，则a 的范围为__________3 函数y =______；值域是______4 若函数()11x m f x a =+-是奇函数，则m 为__________5 求值：22log 3321272log 8-⨯+=__________ 三、解答题1 解方程：（1）40.2540.25log (3)log (3)log (1)log (21)x x x x -++=-++（2）2(lg )lg 1020x x x +=2 求函数11()()142x x y =-+在[]3,2x ∈-上的值域 3 已知()1log 3x f x =+，()2log 2x g x =,试比较()f x 与()g x 的大小 4 已知()()110212x f x x x ⎛⎫=+≠ ⎪-⎝⎭， ⑴判断()f x 的奇偶性； ⑵证明()0f x >（数学1必修）第二章基本初等函数（1）参考答案一、选择题1 B 当1a >时1log 21,log 21,,2a a a a a ++==-=与1a >矛盾；当01a <<时11log 2,log 21,2a a a a a ++==-=； 2 B 令[]2,0,0,1u ax a =->是的递减区间，∴1a >而0u >须恒成立，∴min 20u a =->，即2a <，∴12a <<；3 D 由10<<a 得111,11,a a a a<<+<+②和④都是对的； 4 A 11(10)()1,()(10)1,(10)(10)111010f f f f f f =+=-+=-++ 5 C ()()(),()()()()(),f x g x h x f x g x h x g x h x =+-=-+-=-+6 C a b c =====二、填空题1 (1,)+∞ 2210ax x ++>恒成立，则0440a a >⎧⎨∆=-<⎩，得1a > 2 []0,1 221ax x ++须取遍所有的正实数，当0a =时，21x +符合条件；当0a ≠时，则0440a a >⎧⎨∆=-≥⎩，得01a <≤，即01a ≤≤3 [)[)0,,0,1+∞ 111()0,()1,022x x x -≥≤≥；11()0,01()1,22x x >≤-<4 2 ()()11011x x m m f x f x a a --+=+++=--5 19 293(3)18lg1019-⨯-+=+=三、解答题1 解：（1）40.2540.25log (3)log (3)log (1)log (21)x x x x -++=-++ 33121x x x x -+=-+，得7x =或0x =，经检验0x =为所求（2）2(lg )lg lg lg lg 1020,(10)20x x x x x x x +=+= 10,x =1或10，经检验10,x =1或10为所求 2 解：21111()()1[()]()14222x x x x y =-+=-+ 而[]3,2x ∈-，则11()842x ≤≤ 当11()22x =时，min 34y =；当1()82x =时，max 57y = ∴值域为3[,57]43 解：3()()1log 32log 21log 4x x x f x g x -=+-=+，当31log 04x +>，即01x <<或43x >时，()()f x g x >；当31log 04x +=，即43x =时，()()f x g x =；当31log 04x +<，即413x <<时，()()f x g x < 4 解：（1）1121()()212221x x x x f x x +=+=⋅-- 2121()()221221x x x x x x f x f x --++-=-⋅=⋅=--，为偶函数（2）21()221x x x f x +=⋅-，当0x >，则210x ->，即()0f x >；当0x <，则210x -<，即()0f x >，∴()0f x >。

高中数学必修一拔高试题(试题复习)

目录第一讲集合概念及其基本运算第二讲函数的概念及解析式第三讲函数的定义域及值域第四讲函数的值域第五讲函数的单调性第六讲函数的奇偶性与周期性第七讲函数的最值第八讲指数运算及指数函数第九讲对数运算及对数函数第十讲幂函数及函数性质综合运用第一讲集合的概念及其基本运算知识点一元素与集合的关系1.已知A ＝{a ＋2，(a ＋1)2，a 2＋3a ＋3}，若1∈A ，则实数a 构成的集合B 的元素个数是( ) A ．0 B ．1 C ．2 D ．3知识点二集合与集合的关系1.已知集合A ＝{x|x 2－3x ＋2＝0，x∈R }，B ＝{x|0＜x<5，x∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( )A ．1B ．2C ．3D ．4【变式探究】 (1)数集X ＝{x|x ＝(2n ＋1)π，n∈Z }与Y ＝{y|y ＝(4k±1)π，k∈Z }之间的关系是( )A ．X ⊂YB ．Y ⊂XC ．X ＝YD ．X≠Y(2)设U ＝{1，2，3，4}，M ＝{x∈U|x 2－5x ＋p ＝0}，若∁U M ＝{2，3}，则实数p 的值是( ) A ．－4 B ．4 C ．－6 D ．6 知识点三集合的运算1.若全集U ＝{x∈R |x 2≤4}，则集合A ＝{x∈R ||x ＋1|≤1}的补集A C U 为( )A ．{x∈R |0<x<2}B ．{x∈R |0≤x<2}C．{x∈R |0<x≤2} D．{x∈R |0≤x≤2} 2.已知全集U ＝{0，1，2，3，4，5，6，7，8，9}，集合A ＝{0，1，3，5，8}，集合B ＝{2，4，5，6，8}，则(AC U )∩(B C U )＝( )A ．{5，8}B ．{7，9}C ．{0，1，3}D ．{2，4，6}【变式探究1】若全集U ＝{a ，b ，c ，d ，e ，f}，A ＝{b ，d}，B ＝{a ，c}，则集合{e ，f}＝( ) A ．A∪B B．A∩B C．(A C U )∩(B C U ) D ．(A C U )∪(B C U ) 典型例题：例1：满足M ⊆{a 1,a 2,a 3,a 4},且M∩{a 1 ,a 2, a 3}={a 1,a 2}的集合M 的个数是 ( )A.1B.2C.3D.4例2：设A={x|1<x<2}，B={x|x ＞a}，若A B ，则a 的取值范围是______变式练习：1.设集合M =｛x ｜－1≤x ＜2｝，N =｛x ｜x －k ≤0｝，若M ∩N ≠，则k 的取值范围是 2.已知全集}{R x x I∈=，集合}31{≥≤=x x x A 或，集合}1{+<<=k x k x B ，且=B AC I I )(，则实数k 的取值范围是3.若集合},012{2R x x ax x M ∈=++=只有一个元素，则实数的范围是4.集合A = {x | –1＜x ＜1}，B = {x | x ＜a }，（1）若A ∩B =∅，求a 的取值范围；（2）若A ∪B = {x | x ＜1}，求a 的取值范围.例3：设A = {x | x 2 – 8x + 15 = 0}，B = {x | ax – 1 = 0}，若B A ⊆，求实数a 组成的集合，并写出它的所有非空真子集.例4：定义集合A B 、的一种运算：121*{|A B x x x x x A ==+∈，， 2}x B ∈，若{123}A =，，，{12}B =，，则B A *中所有元素的和为．例5：设A 为实数集，满足a A ∈⇒11A a∈-,1A ∉, （1）若2A ∈,求A;（2）A 能否为单元素集？若能把它求出来，若不能，说明理由；（3）求证：若a A ∈,则11Aa -∈基础练习：1. 由实数x,－x,｜x ｜,332,x x -所组成的集合，最多含（）（A ）2个元素（B ）3个元素（C ）4个元素（D ）5个元素2. 下列结论中，不正确的是( )A.若a ∈N ，则-a ∉NB.若a ∈Z ，则a 2∈ZC.若a ∈Q ，则｜a ｜∈QD.若a ∈R ，则R a ∈33. 已知A ，B 均为集合U={1,3,5,7,9}子集，且A∩B={3},C U B∩A={9},则A=（）（A ）{1,3} (B){3,7,9} (C){3,5,9} (D){3,9}4. 设集合A={1, 3, a}, B={1, a 2-a+1}，若B ⊆A, 则A ∪B=__________5. 满足{}0,1,2{0,1,2,3,4,5}A ⊆的集合A 的个数是_____个。

高中数学必修一第二章基本初等函数 2-1 指数函数课时提升作业及解析

a>0 且 a≠1.
(1)求 a 的值.
(2)求函数 y=f (x≥0)的值域.
【解析】(1)函数图象经过点
,所以 a2-1= ,则 a= .
,其中
(2)由(1)知函数为 f(x)=
(x≥0),由 x≥0,得 x-1≥-1.于是 0<
≤
=2,所以函数的值域为(0,2].
(20 分钟 40 分) 一、选择题(每小题 5 分,共 10 分) 1.(2015·南昌高一检测)函数 f(x)=ax-b 的图象如图所示,其中 a,b 均为常数,则下列结论正确的是 ( )
【解题指南】从直线位置得出 b 与 1 的大小及 a 的正负,从而判断 y=bax 的增减性. 【解析】选 A.选项 A 中,由直线位置可知 a>0,0<b<1,所以 y=bax 为减函数,故 A 正确.选项 B 中 a>0,b>1,所以 y=bax 为增函数,故 B 项不正确.选项 C 中,a<0,b>1,
2.(2015·昆明高一检测)化简[
的结果为 ( )
A.5
B.
C.-
D.-5
【解析】选 B.[
=(
= == .
【补偿训练】计算[(- )2 的结果是 ( )
A.
B.-
C.
D.-
【解析】选 C.[(- )2 =(
=( )-1= = ,故选 C.
3.
+(-1)-1÷0.75-2+
=( )
A.
B.
C.-
D.-
所以
= =.
的值.
课时提升作业(2)
指数幂及运算
(15 分钟 30 分) 一、选择题(每小题 4 分,共 12 分)

(word完整版)高中数学必修1基本初等函数拔高训练

数学1（必修）第二章基本初等函数（1）
[提高训练C 组]
一、选择题
1. 函数上的最大值和最小值之和为 , 则的值为（）
2． A. B. C. D.
已知在上是的减函数, 则的取值范围是( )
. A....B... C.... D..
3．对于 , 给出下列四个不等式
①)11(log )1(log a a a a +<+ ②)11(log )1(log a a a a +>+ ③a a a a 111++< ④a a a a 1
11++> 其中成立的是（）
A. ①与③
B. ①与④
C. ②与③
D. ②与④
4．设函数 , 则的值为（）
A. B. C. D.
5. 定义在上的任意函数都可以表示成一个奇函数与一个偶函数之和, 如果 , 那么( )
A. ,
B. ,
C ． ,
D ． ,
6. 若 ,则( )
A. B. C. D.
二、填空题
1. 若函数的定义域为 , 则的范围为__________。

2．若函数的值域为 , 则的范围为__________。

3. 函数的定义域是______；值域是______.
4．若函数是奇函数, 则为__________。

5. 求值： __________。

三、解答题
1. 解方程: （1）
（2）2(lg )lg 10
20x x x +=
2. 求函数在上的值域。

3. 已知, ,试比较与的大小。

4. 已知,
⑴判断的奇偶性；⑵证明.。

高一数学必修一第二章基本初等函数练习题难题带答案

高一数学必修一基本初等函数一．选择题（共30小题）1．设a＝log43，b＝log54，c＝2﹣0.01，则a，b，c的大小关系为（）A．b＜a＜c B．a＜b＜c C．a＜c＜b D．b＜c＜a2．已知a＝3ln2π，b＝2ln3π，c＝3lnπ2，则下列选项正确的是（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a3．函数f（x）＝（|x|﹣7）e|x|则（）A．B．f（0.76）＜f（60.5）＜f（log0.76）C．D．4．已知P（x，y）为函数f（x）＝图象上一动点，则的最大值为（）A．B．C．2D．5．设a＝3，b＝3log3π，c＝πlogπ3，则a，b，c的大小关系为（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a6．若a＝0.220.33，b＝0.330.22，c＝log0.330.22，则（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a7．已知a，b，c∈R，满足＝＝﹣＜0，则a，b，c的大小关系为（）A．c＞a＞b B．a＞c＞b C．c＞b＞a D．b＞a＞c8．已知2a＝log2|a|，，c＝sin c+1，则实数a，b，c的大小关系是（）A．b＜a＜c B．a＜b＜c C．c＜b＜a D．a＜c＜b9．已知实数a，b，c分别满足2a＝﹣a，log0.5b＝b，log2c＝，那么（）A．a＜b＜c B．a＜c＜b C．b＜c＜a D．c＜b＜a10．已知a＝log1213，b＝（），c＝log1314，则a，b，c的大小关系为（）A．a＞b＞c B．c＞a＞b C．b＞c＞a D．a＞c＞b11．已知a＞b＞0，ab＝1，设，则log x2x，log y2y，log z2z的大小关系为（）A．log x2x＞log y2y＞log z2z B．log y2y＞log z2z＞log x2xC．log x2x＞log z2z＞log y2y D．log y2y＞log x2x＞log z2z12．已知，，c＝log23，则a，b，c的大小关系为（）A．b＞a＞c B．a＞c＞b C．a＞b＞c D．b＞c＞a13．下列命题为真命题的个数是（）①②③A．0B．1C．2D．314．设，实数c满足e﹣c＝lnc，（其中e为自然常数），则（）A．a＞b＞c B．b＞c＞a C．b＞a＞c D．c＞b＞a15．若实数x，y，z满足，则x，y，z的大小关系是（）A．x＜y＜z B．x＜z＜y C．z＜x＜y D．z＜y＜x16．已知x1＝ln，x2＝e，x3满足e＝lnx3，则下列各选项正确的是（）A．x1＜x3＜x2B．x1＜x2＜x3C．x2＜x1＜x3D．x3＜x1＜x217．已知t＞1，x＝log2t，y＝log3t，z＝log5t，则（）A．2x＜3y＜5z B．5z＜2x＜3y C．3y＜5z＜2x D．3y＜2x＜5z18．已知定义在R上的函数y＝f（x）对任意的x都满足f（x+2）＝f（x），当﹣1≤x＜1时，f（x）＝x3．若函数g（x）＝f（x）﹣log a|x|恰有6个不同零点，则a的取值范围是（）A．（，]∪（5，7] B．（，]∪（5，7]C．（，]∪（3，5] D．（，]∪（3，5]19．已知函数f（x）＝，g（x）＝x2﹣2x，设a为实数，若存在实数m，使f（m）﹣2g（a）＝0，则实数a的取值范围为（）A．[﹣1，+∞）B．（﹣∞，﹣1]∪[3，+∞）C．[﹣1，3] D．（﹣∞，3]20．已知函数y＝f（x）（x∈R）满足f（x+2）＝2f（x），且x∈[﹣1，1]时，f（x）＝﹣|x|+1，则当x∈[﹣10，10]时，y＝f（x）与g（x）＝log4|x|的图象的交点个数为（）A．13B．12C．11D．1021．设a＝log46，，，则（）A．a＞b＞c B．b＞c＞a C．a＞c＞b D．c＞b＞a22．已知实数a＞0，b＞0，a≠1，且满足lnb＝，则下列判断正确的是（）A．a＞b B．a＜b C．log a b＞1D．log a b＜123．设a＝π﹣e，b＝lnπ﹣1，c＝eπ﹣e e，则（）A．a＜b＜c B．b＜c＜a C．c＜b＜a D．b＜a＜c24．若函数f（x）＝在区间[2019，2020]上的最大值是M，最小值是m，则M﹣m（）A．与a无关，但与b有关B．与a无关，且与b无关C．与a有关，但与b无关D．与a有关，且与b有关25．正数a，b满足1+log2a＝2+log3b＝3+log6（a+b），则的值是（）A．B．C．D．26．已知实数a，b，c，d满足，则（a﹣c）2+（b﹣d）2的最小值为（）A．8B．4C．2D．27．函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A在直线mx+ny+2＝0上（其中m，n＞0），则的最小值等于（）A．10B．8C．6D．428．若m，n，p∈（0，1），且log3m＝log5n＝lgp，则（）A．B．C．D．29．已知a＝log2e，b＝ln3，c＝log，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．b＞c＞a30．若函数f（x）＝ln（ax2﹣2x+3）的值域为R，则实数a的取值范围是（）A．[0，]B．（，+∞）C．（﹣∞，]D．（0，]二．填空题（共6小题）31．已知函数f（x）在R上连续，对任意x∈R都有f（﹣3﹣x）＝f（1+x）；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；若f（2a﹣1）＜f（3a﹣2），则实数a的取值范围是．32．若存在正数x，y，使得（y﹣2ex）（lny﹣lnx）z+x＝0（其中e为自然对数的底数），则实数z的取值范围是33．已知函数f（x）＝log2（x+2）与g（x）＝（x﹣a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）＝g（x2），则实数a的取值范围是．34．已知函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，令h（x）＝f（1﹣|x|），则关于函数h（x）有以下命题：（1）h（x）的图象关于原点（0，0）对称；（2）h（x）的图象关于y轴对称；（3）h（x）的最小值为0；（4）h（x）在区间（﹣1，0）上单调递增．中正确的是．35．设a，b为非零实数，x∈R，若，则＝．36．函数f（x）＝log2x在区间[a，2a]（a＞0）上的最大值与最小值之差为．三．解答题（共4小题）37．已知函数f（x）＝的图象关于原点对称，其中a为常数．（1）求a的值；（2）当x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，求实数m的取值范围；（3）若关于x的方程f（x）＝（x+k）在[2，3]上有解，求k的取值范围．38．已知函数f（x）＝log a（2﹣x）﹣log a（2+x）（a＞0且a≠1），且1是函数y＝f（x）+x的零点．（1）求实数a的值；（2）求使f（x）＞0的实数x的取值范围．39．已知函数f（x）＝（a2﹣3a+3）a x是指数函数．（1）求f（x）的解析式；（2）判断函数F（x）＝f（x）﹣f（﹣x）的奇偶性，并证明；（3）解不等式log a（1﹣x）＞log a（x+2）．40．已知f（x）是定义在R上的偶函数，且x≤0时，f（x）＝（﹣x+1）（1）求f（3）+f（﹣1）；（2）求函数f（x）的解析式；（3）若f（a﹣1）＜﹣1，求实数a的取值范围．参考答案与试题解析一．选择题（共30小题）1．【解答】解：因为0＝log41＜a＝log43＜log44＝1，0＜b＝log54＜log55＝1，c＝2﹣0.01＞2≈0.92，log54＝≈0.86，＝＝log43×log45＜（）2＝（）2＜1，∴a，b，c的大小关系为a＜b＜c．故选：B．2．【解答】解：，，＝，∵6π＞0，∴a，b，c的大小比较可以转化为的大小比较．设f（x）＝，则f′（x）＝，当x＝e时，f′（x）＝0，当x＞e时，f′（x）＜0，当0＜x＜e时，f′（x）＞0∴f（x）在（e，+∞）上，f（x）单调递减，∵e＜3＜π＜4∴，∴b＞c＞a，故选：D．3．【解答】解，60.5＞1＞0.76＞0＞log0.76，函数f（x）为偶函数，则，当x＞0时，f（x）＝（x﹣7）e x，则f′（x）＝（x﹣6）e x，易知函数f（x）在（0，6）上单调递减，又，故，即﹣log0.76＜6，又，故，即﹣log0.76＞3，则0＜0.76＜1＜60.5＜﹣log0.76＜6，所以f（0.76）＞f（60.5）＞f（﹣log0.76）＝f（log0.76），故选：D．4．【解答】解：设Q（，1），原点O，则＝（，1），＝（x，y），∴即．∴当OP与f（x）在y轴右侧相切时取最大值，设直线y＝kx（k＞0）与函数f（x）相切于点P0（x0，y0），y′＝k，f′（x）＝2x，则，解得．即切点P0（，），∴，即的最大值为．故选：D．5．【解答】解：构造函数f（x）＝（x＞1），则f′（x）＝，当x∈（1，e2）时，f′（x）＞0，则f（x）在（1，e2）上为增函数，∴f（π）＞f（3），即＞，∴＞，即3log3π＞πlogπ3，则b＞c；设g（x）＝，则g′（x）＝，当x＞3时，g′（x）＞30ln3﹣1＞0，∴g（x）在（3，+∞）上为增函数，则g（π）＞g（3）＝0，即＞π，则3π＞π3．又πlogπ3＝＞．∴a＜c＜b．故选：B．6．【解答】解：由1＞a＝0.220.33＞0，1＞b＝0.330.22＞0，c＝log0.330.22＞log0.330.33＝1，所以c＞a，且c＞b；又ln0.220.33＝0.33ln0.22，ln0.330.22＝0.22ln0.33；不妨设0.33ln0.22＜0.22ln0.33，则有＜；构造函数f（x）＝，x＞0，所以f′（x）＝，令f′（x）＝0，解得x＝e；所以x∈（0，e）时，f′（x）＞0，f（x）是单调增函数；所以f（0.22）＜f（0.33），即＜，所以b＞a；综上知，c＞b＞a．故选：D．7．【解答】解：已知a，b，c∈R，令＝＝﹣＝﹣1，则：，所以c＞1．由于3b＞0，且，故lnb＜0，解得0＜b＜1，同理2a＞0，且，故lna＜0，解得0＜a＜1．由于0＜a＜1，0＜b＜1，＝＝﹣＜0，所以2a＜3b，故lnb＜lna，整理得b＜a，所以c＞1＞a＞b＞0．故选：A．8．【解答】解：作出函数y＝2x和y＝log2|x|的图象，由图1可知，交点A的横坐标a＜0；作出函数y＝和y＝的图象，由图2可知，交点B的横坐标0＜b＜1；作出函数y＝x和y＝sin x+1的图象，由图3可知，交点C的横坐标c＞1所以，a＜b＜c．故选：B．9．【解答】解：∵log0.5b＝﹣log2b＝b，∴log2b＝﹣b，在同一坐标系内画出函数y＝2x，y＝﹣x，y＝log2x，y＝的图象．可知a＜0＜b＜1＜c．故选：A．10．【解答】解：＝，∵＝＜1，∴log1314＜log1213，且log1314＞1，，∴a＞c＞b．故选：D．11．【解答】解：，＝，，∵a＞b＞0，ab＝1，∴a＞1＞b＞0，∴，log2（a+b）＜2，∴，∴，∴，又0＜，∴，∴log y2y＞log z2z＞log x2x．故选：B．12．【解答】解：根据指数运算与对数运算的性质，＞3，1＜＜2，1＜c＝log23＜2，设b＝，c＝log23，由于函数m＝log2t为增函数，由于的值接近于4，所以a＞b＞c．故选：C．13．【解答】解：构造函数f（x）＝，x∈（0，+∞），∴，令f'（x）＝0得：x＝e，∵当x∈（0，e）时，f'（x）＞0，f（x）单调递增；当x∈（e，+∞）时，f'（x）＜0，f（x）单调递减，∴f（e）＞f（3）＞f（π），即，故①正确，②错误，构造函数g（x）＝，x∈（0，+∞），∵，令g'（x）＝0得：x＝e，∵当x∈（0，e）时，g'（x）＜0，g（x）单调递减；当x∈（e，+∞）时，g'（x）＞0，g（x）单调递增，∴g（e）＜g（3），即0＜，∴ln3＜，∴，故③正确，∴真命题的个数是2个，故选：C．14．【解答】解：∵e﹣c＞0，∴lnc＞0，∴c＞1，∴，∴，∴1＜c＜2，又，∴b＞c＞a．故选：B．15．【解答】解：设＝p，∴p＞0，设y1＝log2x，y2＝log3y，y3＝2z，作出3个函数的图象，如图所示：由图可知：z＜x＜y，故选：C．16．【解答】解：依题意，因为y＝lnx为（0，+∞）上的增函数，所以x1＝ln＜ln1＝0；因为y＝e x为R上的增函数，且e x＞0，所以0＜x2＝e＜e0＝1；x3满足e＝lnx3，所以x3＞0，所以＞0，所以lnx3＞0＝ln1，又因为y＝lnx为（0，+∞）的增函数，所以x3＞1，综上：x1＜x2＜x3．故选：B．17．【解答】解：∵t＞1，∴lgt＞0．又0＜lg2＜lg3＜lg5，∴2x＝2＞0，3y＝3＞0，5z＝＞0，∴＝＞1，可得5z＞2x．＝＞1．可得2x＞3y．综上可得：3y＜2x＜5z．故选：D．18．【解答】解：首先将函数g（x）＝f（x）﹣log a|x|恰有6个零点，这个问题转化成f（x）＝log a|x|的交点来解决．数形结合：如图，f（x+2）＝f（x），知道周期为2，当﹣1＜x≤1时，f（x）＝x3图象可以画出来，同理左右平移各2个单位，得到在（﹣7，7）上面的图象，以下分两种情况：（1）当a＞1时，log a|x|如图所示，左侧有4个交点，右侧2个，此时应满足log a5≤1＜log a7，即log a5≤log a a＜log a7，所以5≤a＜7．（2）当0＜a＜1时，log a|x|与f（x）交点，左侧有2个交点，右侧4个，此时应满足log a5＞﹣1，log a7≤﹣1，即log a5＜﹣log a a≤log a7，所以5＜a﹣1≤7．故≤a＜综上所述，a的取值范围是：5≤a＜7或≤a＜，故选：A．19．【解答】解：∵g（x）＝x2﹣2x，设a为实数，∴2g（a）＝2a2﹣4a，a∈R，∵y＝2a2﹣4a，a∈R，∴当a＝1时，y最小值＝﹣2，∵函数f（x）＝，f（﹣7）＝6，f（e﹣2）＝﹣2，∴值域为[﹣2，6]∵存在实数m，使f（m）﹣2g（a）＝0，∴﹣2≤2a2﹣4a≤6，即﹣1≤a≤3，故选：C．20．【解答】解：由题意，函数f（x）满足：定义域为R，且f（x+2）＝2f（x），当x∈[﹣1，1]时，f（x）＝﹣|x|+1；在同一坐标系中画出满足条件的函数f（x）与函数y＝log4|x|的图象，如图：由图象知，两个函数的图象在区间[﹣10，10]内共有11个交点；故选：C．21．【解答】解：，，，∵0＜log34＜log35＜log36，∴，∴a＞b＞c．故选：A．22．【解答】解：∵lnb＝，∴lnb﹣lna＝，构造函数∴f（x）＝；∴＝＝；∴≥0；∴f（x）在（0，+∞）单调递增．且f（1）＝0；当x∈（0，1）时，f（x）＜0，当x∈（1．+∞）时f（x）＞0；∵a≠1∴当0＜a＜1时，f（a）＜0⇒0即lnb﹣lna＜0⇒b＜a，∴lnb＜lna＜0⇒⇒log a b＞1，当a＞1时，f（a）＞0⇒即lnb﹣lna＞0⇒b＞a，∴lnb＞lna＞0⇒⇒log a b＞1，故选：C．23．【解答】解：∵a＝π﹣e＞0，b＝lnπ﹣1＝lnπ﹣lne＞0，c＝eπ﹣e e＞0；设y＝lnx，则＝，表示了连接两点（π，lnπ），（e，lne）的割线的斜率，而y'＝，当x＞1时，曲线切线的斜率0＜k＜1；故0＜＝＜1，故b＜a；设y＝e x，则＝，表示了连接两点（π，eπ），（e，e e）的割线的斜率，而y'＝e x，当x＞1时，曲线切线的斜率k＞1；故＝＞1，故c＞a；故b＜a＜c；故选：D．24．【解答】解：，令，则y＝2019t2+bt+a的最大值是M，最小值是m，而a是影响图象的上下平移，此时最大和最小值同步变大或变小，故M﹣m与a无关，而b是影响图象的左右平移，故M﹣m与b有关，故选：A．25．【解答】解，依题意，设1+log2a＝2+log3b＝3+log6（a+b）＝k，则a＝2k﹣1，b＝3k﹣2，a+b＝6k﹣3，所以＝＝＝＝＝，故选：A．26．【解答】解：∵实数a，b，c，d满足，∴b＝lna，d＝c+1．考查函数y＝lnx，与y＝x+1．∴（a﹣c）2+（b﹣d）2就是曲线y＝lnx与直线y＝x+1之间的距离的平方值，对曲线y＝lnx求导：y′＝，与直线y＝x+1平行的切线斜率k＝1＝，解得：x＝1，将x＝1代入y＝lnx得：y＝0，即切点坐标为（1，0），∴切点（1，0）到直线y＝x+1的距离d＝＝，即d2＝2，则（a﹣c）2+（b﹣d）2的最小值为2．故选：C．27．【解答】解：令x+3＝1，求得x＝﹣2，可得函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A（﹣2，﹣1），若点A在直线mx+ny+2＝0上（其中m，n＞0），则﹣2m﹣n+2＝0，即2m+n＝2．由基本不等式可得2≥2，即mn≤，即≥2，当且仅当2m＝n＝1时，取等号．则＝＝≥4，故选：D．28．【解答】解：∵m，n，p∈（0，1），且log3m＝log5n＝lgp＝k，∴lgm，lgn，lgp＜0，m＝3k，n＝5k，p＝10k，∴＝＝，＝＝，＝＝，因为，＝53＝125，所以，同理＝5×5＝25，＝10，所以，所以＞0，又因为y＝x k（k＜0）在（0，+∞）上单调递减，∴即＜＜．故选：A．29．【解答】解：根据题意，c＝log＝ln2＜lne＝1，则c＜1，ln3＞ln2，∴c＜b，a＝log2e＞log22＝1，即a＞c，ln3﹣log2e＝ln3﹣＝，∵2＝lne2＞ln6＝ln2+ln3＞2，∴＜1，即ln2ln3＜1，则ln3﹣log2e＝ln3﹣＝＜0，即ln3＜log2e，即a＞b，综上a＞b＞c，故选：A．30．【解答】解：若函数f（x）＝ln（ax2﹣2x+3）的值域为R，即有t＝ax2﹣2x+3取得一切的正数，当a＝0时，t＝3﹣2x取得一切的正数，成立；当a＜0不成立；当a＞0，△≥0即4﹣12a≥0，解得0＜a≤，综上可得0≤a≤．故选：A．二．填空题（共6小题）31．【解答】解：由f（﹣3﹣x）＝f（1+x）可知函数f（x）关于直线x＝﹣1对称；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；可知函数f（x）在区间（﹣∞，﹣1）上单调递减，由对称性可知函数f（x）在区间（﹣1，+∞）上单调递增，不妨设f（x）＝（x+1）2，则由f（2a﹣1）＜f（3a﹣2）可得4a2＜（3a﹣1）2，整理得5a2﹣6a+1＞0，即（a﹣1）（5a﹣1）＞0，解得或a＞1，所以实数a的取值范围是．故答案为：．32．【解答】解：则（y﹣2ex）（lny﹣lnx）z+x＝0可化为：，令t＝，得（t﹣2e）lnt＝﹣．令f（t）＝（t﹣2e）lnt，（t＞0），则f′（t）＝g（t）＝lnt+1﹣，则g′（t）＝，故g（t）为（0，+∞）上的增函数，又因为f′（e）＝g（e）＝1+1﹣2＝0，故当t∈（0，e）时，f′（t）＜0，当t＞e时，f′（t）＞0，所以f（t）在（0，e）上单调递减，在（e，+∞）上单调递增，所以f（t）在（0，+∞）存在最小值f（e）＝﹣e，即f（t）的值域为（﹣e，+∞），∴﹣∈（﹣e，+∞），所以z∈（﹣∞，0）∪[，+∞），故填：（﹣∞，0）∪[，+∞），33．【解答】解：∵x1∈[2，6），∴f（2）≤f（x1）＜f（6），即2≤f（x1）＜3，∴f（x1）的值域为[2，3）．g（x）的图象开口向上，对称轴为x＝a，（1）若a≤0，则g（x）在[0，2]上是增函数，∴g（0）≤g（x2）≤g（2），即g（x2）的值域为[a2+1，a2﹣4a+5]，∴，解得﹣1≤a≤0．（2）若a≥2，则g（x）在[0，2]上是减函数，∴g（2）≤g（x2）≤g（1），即g（x2）的值域为[a2﹣4a+5，a2+1]，∴，解得2≤a≤3．（3）若0＜a≤1，则g min（x）＝g（a）＝1，g max（x）＝g（2）＝a2﹣4a+5，∴g（x）的值域为[1，a2﹣4a+5]，∴，解得0．（4）若1＜a＜2，则g min（x）＝g（a）＝1，g max（x）＝g（0）＝a2+1，∴g（x）的值域为[1，a2+1]，∴，解得a＜2．综上，a的取值范围是[﹣1，0]∪[2，3]∪（0，2﹣）∪（，2）＝[﹣1，2﹣]∪[，3]．故答案为[﹣1，2﹣]∪[，3]．34．【解答】解：由于函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，故函数f（x）与函数g（x）＝2x互为反函数．故函数f（x）＝log2x．∴h（x）＝f（1﹣|x|）＝log2（1﹣|x|），故函数h（x）是偶函数，图象关于y对称，故（2）正确而（1）不正确．函数h（x）的定义域为（﹣1，1），在（﹣1，0）上是增函数，在（0，1）上是减函数，故（4）正确．故当x＝0时，函数h（x）取得最大值为0，故（3）不正确．故答案为②④．35．【解答】解：由成立，得＝（sin2x+cos2x）2，化简得：，即，∴，又sin2x+cos2x＝1，得，．∴．则＝＝•（sin2x+cos2x）＝．故答案为：．36．【解答】解：∵f（x）＝log2x在区间[a，2a]上是增函数，∴f（x）max﹣f（x）min＝f（2a）﹣f（a）＝log22a﹣log2a＝1．故答案为：1．三．解答题（共4小题）37．【解答】解：（1）函数f（x）＝的图象关于原点对称，∴f（x）+f（﹣x）＝0，即+＝0，∴（）＝0，∴＝1恒成立，即1﹣a2x2＝1﹣x2，即（a2﹣1）x2＝0恒成立，所以a2﹣1＝0，解得a＝±1，又a＝1时，f（x）＝无意义，故a＝﹣1；（2）x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，即+（x﹣1）＜m，∴（x+1）＜m在（1，+∞）恒成立，由于y＝（x+1）是减函数，故当x＝1，函数取到最大值﹣1，∴m≥﹣1，即实数m的取值范围是m≥﹣1；（3）f（x）＝在[2，3]上是增函数，g（x）＝（x+k）在[2，3]上是减函数，∴只需要即可保证关于x的方程f（x）＝（x+k）在[2，3]上有解，下解此不等式组．代入函数解析式得，解得﹣1≤k≤1，即当﹣1≤k≤1时关于x的方程f（x）＝（x+k）在[2，3]上有解．38．【解答】解：（1）∵1是函数y＝f（x）+x的零点，∴f（1）＝﹣1，即log a（2﹣1）﹣log a（2+1）+1＝0，即log a3＝1，解得a＝3．（2）由（1）可知函数f（x）是递增函数，f（x）＞0得log3（2﹣x）＞log3（2+x），所以：有解得﹣2＜x＜0，所使f（x）＞0的实数x的取值集合为{x|﹣2＜x＜0}．39．【解答】解：（1）a2﹣3a+3＝1，可得a＝2或a＝1（舍去），∴f（x）＝2x；（2）F（x）＝2x﹣2﹣x，∴F（﹣x）＝﹣F（x），∴F（x）是奇函数；（3）不等式：log2（1﹣x）＞log2（x+2），即1﹣x＞x+2＞0，∴﹣2＜x＜﹣，解集为{x|﹣2＜x＜﹣}．40．【解答】解：（I）∵f（x）是定义在R上的偶函数，x≤0时，f（x）＝（﹣x+1），∴f（3）+f（﹣1）＝f（﹣3）+f（﹣1）＝4+2＝﹣2﹣1＝﹣3；（II）令x＞0，则﹣x＜0，f（﹣x）＝（x+1）＝f（x）∴x＞0时，f（x）＝（x+1），则f（x）＝．（Ⅲ）∵f（x）＝（﹣x+1）在（﹣∞，0]上为增函数，∴f（x）在（0，+∞）上为减函数∵f（a﹣1）＜﹣1＝f（1）∴|a﹣1|＞1，∴a＞2或a＜0。

2022版数学人教A版必修1基础训练：第二章+基本初等函数(Ⅰ)综合拔高练含解析

第二章基本初等函数(Ⅰ)2.1~2.3综合拔高练五年高考练考点1指数式与对数式的恒等变形1.(2020课标全国Ⅲ,4,5分,)logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的,其中K为最大确诊病例数.当单位:天)的logistic模型:I(t)=K1+e-0.23(t-53)I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)()A.60B.63C.66D.692.(2020新高考Ⅰ,6,5分,)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=e rt描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)()A.1.2天B.1.8天C.2.5天D.3.5天考点2指数函数、对数函数和幂函数的综合运用3.(2019课标全国Ⅰ,3,5分,)已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<cB.a<c<bC.c<a<bD.b<c<a)-0.8,c=log0.70.8,则a,b,c的大小关系为4.(2020天津,6,5分,)设a=30.7,b=(13()A.a<b<cB.b<a<cC.b<c<aD.c<a<b5.(2020课标全国Ⅰ,12,5分,)若2a+log2a=4b+2log4b,则()A.a >2bB.a <2bC.a >b 2D.a 0,且a ≠1)的图象可能是( )8.(2018课标全国Ⅲ,7,5分,)下列函数中,其图象与函数y =ln x 的图象关于直线x =1对称的是( ) A.y =ln (1-x ) B.y =ln (2-x ) C.y =ln (1+x )D.y =ln (2+x )9.(2020课标全国Ⅱ,11,5分,)若2x -2y <3-x -3-y ,则( )A.ln (y -x +1)>0B.ln (y -x +1)<0C.ln|x -y |>0D.ln|x -y |<010.(2020课标全国Ⅲ,12,5分,)已知55<84,134<85.设a =log 53,b =log 85,c =log 138,则( )A.a <b <cB.b <a <cC.b <c <aD.c <a <b考点3含参数的指数函数、对数函数问题的解法11.(2019课标全国Ⅱ,14,5分,)已知f(x)是奇函数,且当x<0时,f(x)=-e ax.若f(ln 2)=8,则a=.12.(2018课标全国Ⅰ,13,5分,)已知函数f(x)=log2(x2+a),若f(3)=1,则a=.强基计划13.(2018复旦大学自主招生试题,16,)设方程log3x3+log273x=-43的两个根为a和b,求a+b的值.三年模拟练1.(2020宁夏大学附属中学高二期中,)函数f(x)=ln x-√x+1的图象大致为()2.(2020山东潍坊高一上期中,)已知a=log32,b=314,c=ln23,则a,b,c的大小关系为()A.a>b>cB.b>a>cC.c>b>aD.c>a>b3.(2020安徽舒城中学高二开学考试,)设函数f (x )={31-x ,x ≤1,1-log 3x ,x >1,则满足f (x )≤3的x 的取值范围是 ( ) A.[0,+∞) B.[-1,3] C.[0,3]D.[1,+∞)4.(2019湖南长郡中学高一上第一次模块检测,)设x ∈R ,用[x ]表示不超过x 的最大整数,则y =[x ]称为高斯函数,例如:[-3.5]=-4,[2.1]=2.已知函数f (x )=e x 1+e x -12,则函数y =[f (x )]的值域是 ( )A.{0,1}B.{1}C.{-1,0,1}D.{-1,0}5.(2019山东师大附中高一上第一次学分认定考试,)设0<a <1,函数f (x )=log a (a 2x -2a x -2),使f (x )<0的x 的取值范围是 ( ) A.(-∞,0) B.(log a 3,+∞) C.(-∞,log a 3) D.(0,+∞)6.(2020四川成都外国语学校高一期中,)已知函数f (x )=|log 2x |(x ≤2),若a ≠b ,且f (a )=f (b ),则a +b 的取值范围是( ) A.(1,52]B.(2,52] C.(2,+∞)D.[1,2]7.()下列判断正确的是 (填序号).①若f (x )=x 2-2ax 在[1,+∞)上为增函数,则a =1; ②函数y =ln (x 2+1)的值域是R ; ③函数y =2|x |的最小值为1;④在同一平面直角坐标系中,函数y =2x与y =(12)x的图象关于y 轴对称.8.(2020江西九江高一期末,)已知函数f (x )=(12)x,函数g (x )=log 2x.(1)若g (mx 2+2x +m )的定义域为R ,求实数m 的取值范围;(2)当x ∈[-1,1]时,函数y =[f (x )]2-2af (x )+3的最小值为1,求实数a 的值.9.(2020山东菏泽一中高一月考,)2019年7月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N 随时间T (单位:年)的衰变规律满足N =N 0·2-T 5730(N 0表示碳14原有的质量),则经过5 730年后,碳14的质量变为原来的 ;经过测定,良渚古城遗址文物样本中碳14的质量是原来的37至12,据此推测良渚古城存在的时期距今约在5 730年到年之间.(参考数据:lg 2≈0.3,lg 7≈0.84,lg 3≈0.48)答案全解全析第二章基本初等函数(Ⅰ)2.1~2.3综合拔高练五年高考练1.C2.B3.B4.D5.B6.D7.D8.B9.A 10.A1.答案 C信息提取 ①I (t )=K 1+e -0.23(t -53); ②I (t *)=0.95K ,求t *.数学建模以新冠肺炎疫情为情境,构建logistic 模型,通过解方程I (t *)=K 1+e -0.23(t *-53)=0.95K 求值. 解析因为I (t )=K 1+e -0.23(t -53),所以I (t *)=K 1+e -0.23(t *-53)=0.95K ,整理得e 0.23(t *-53)=19, 所以0.23(t *-53)=ln 19≈3, 解得t *≈66.故选C . 2.答案 B信息提取 ①累计感染病例数I (t )与时间t (单位:天)满足:I (t )=e rt ;②指数增长率r 与R 0,T 近似满足R 0=1+rT ;③R 0=3.28,T =6;④累计感染病例数增加1倍所需的时间. 数学建模以基本再生数与新冠疫情感染的变化规律为情境,构建指数函数模型:I (t )=e rt ,根据R 0=3.28,T =6,R 0=1+rT 求出r ,将参数代入给定的函数模型,写出表达式I (t )=e rt =e 0.38t ,设累计感染病例数增加1倍需要的时间为t 1天,列出方程I (t 1)=2I (0)进行求解.解析因为R 0=3.28,T =6,R 0=1+rT ,所以r =3.28-16=0.38,所以I (t )=e rt =e 0.38t ,设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为t 1天,则I (t 1)=2I (0),即e 0.38t 1=2,所以0.38t 1=ln 2,所以t 1=ln20.38≈0.690.38≈1.8.故选B . 3.B ∵a =log 20.2<log 21=0,b =20.2>20=1,c =0.20.3∈(0,1),∴a <c 1,b =(13)-0.8=30.8>30.7=a ,c =log 0.70.8<log 0.70.7=1,所以c <1<a <b.故选D .5.B 2a +log 2a =22b +log 2b <22b +log 2(2b ), 令f (x )=2x +log 2x ,则f (a )<f (2b ), 又易知f (x )在(0,+∞)上单调递增, 所以a <2b ,故选B .6.D{|2x +1|>0,|2x -1|>0⇒x ∈x x ≠±12,x ∈R ,∴函数f (x )的定义域关于原点对称, 又∵f (-x )=ln|-2x +1|-ln|-2x -1|=ln|2x -1|-ln|2x +1|=-f (x ),∴f (x )是奇函数,排除A 、C ;当x ∈(-12,12)时,f (x )=ln (2x +1)-ln (1-2x ),易知y =ln (2x +1)在-12,12上单调递增,y =ln (1-2x )在-12,12上单调递减,∴函数f (x )在-12,12上单调递增,排除B .故选D . 7.D 对于函数y =log a (x +12),当y =0时,有x +12=1,得x =12,即y =log a (x +12)的图象恒过定点(12,0),排除选项A 、C ;函数y =1a x 与y =log a(x +12)在各自定义域上单调性相反,排除选项B ,故选D .8.B y =ln x 的图象过点(1,0),点(1,0)关于直线x =1的对称点还是(1,0),结合选项可知,只有y =ln (2-x )的图象过点(1,0).故选B . 9.A 因为2x -2y <3-x -3-y , 所以2x -3-x <2y -3-y . 设f (x )=2x -3-x ,易知y =2x 在R 上是增函数,y =3-x 在R 上是减函数, 所以f (x )在R 上为增函数. 由2x -3-x <2y -3-y 得x <y ,所以y -x +1>1,所以ln (y -x +1)>0,故选A .10.A 因为(845)5=84>55,所以845>5,所以45=log 8845>log 85=b ,即b <45.因为(1345)5=134<85,所以1345<8,所以45=log 131345<log 138=c ,即c >45.又2 187=37<55=3 125,所以lg 37<lg 55,所以7lg 3<5lg 5,所以lg3lg5<57,所以a =lg3lg5<57<45,而85<57,所以5lg 8<7lg 5,所以lg5lg8>57,所以b =lg5lg8>57,所以c >b >a. 11.答案 -3解析由x >0可得-x <0,由f (x )是奇函数可知f (-x )=-f (x ), ∴x >0时, f (x )=-f (-x )=-[-e a (-x )]=e -ax ,则f (ln 2)=e -a ln 2=8, ∴-a ln 2=ln 8=3ln 2,∴a =-3. 12.答案 -7解析由f (3)=log 2(9+a )=1,得9+a =2,即a =-7.13.解析利用对数的换底公式把方程log 3x 3+log 273x =-43化为11+log 3x+1+log 3x3=-43, 化简得(1+log 3x )2+4(1+log 3x )+3=0, 解得1+log 3x =-1或1+log 3x =-3, 即log 3x =-2或log 3x =-4,因此x =19或x =181,从而a +b =19+181=1081.三年模拟练1.A2.B3.A4.D5.C6.B1.A 当x ∈(0,e -1)时,ln x <-1,ln x +1<0,所以f (x )=ln x -√x +1<0,故排除B 、C ;由f (e )=ln e-√e +1=2-√e >0,可排除D .故选A .2.B 因为a =log 32∈(0,1),b =314>1,c =ln 23<0,所以a ,b ,c 的大小关系为b >a >c.故选B . 3.A 由函数f (x )={31-x ,x ≤1,1-log 3x ,x >1满足f (x )≤3,可得当x ≤1时,31-x ≤3,即1-x ≤1,解得x ≥0,此时0≤x ≤1;当x >1时,1-log 3x ≤3,即log 3x ≥-2=log 33-2,解得x ≥19,此时x >1. 综上,x 的取值范围是[0,+∞).故选A .4.D 由题知f (x )=e x1+e x -12=e x+1-1e x +1-12=12-1e x +1. ∵e x >0,∴e x +1>1,∴-12<12-1e x +1<12. 当-12<12-1e x +1<0时,[f (x )]=-1; 当0≤12-1e x +1<12时,[f (x )]=0. 因此y =[f (x )]的值域是{-1,0},故选D . 5.C 由f (x )<0,得log a (a 2x -2a x -2)<log a 1. ∵0<a <1,∴a 2x -2a x -2>1, 即(a x )2-2a x -3>0, 即(a x -3)(a x +1)>0,又a x +1>0,∴a x -3>0,∴a x >3=a log a 3,由0<a <1,得x <log a 3,故选C .6.B 作出函数f (x )=|log 2x |(x ≤2)的图象,如图.因为f (a )=f (b )且a ≠b ,所以不妨设a <b , 当f (x )=|log 2x |=1时,解得x =2或x =12, 所以12≤a <1<b ≤2, 由f (a )=f (b ),得|log 2a |=|log 2b |,去绝对值可得-log 2a =log 2b , 所以log 2a +log 2b =0, 所以log 2(ab )=0, 即ab =1,所以a +b =a +1a, 设g (a )=a +1a ,a ∈[12,1). 易知函数g (a )=a +1a 在12,1上单调递减,所以a +b ∈(2,52],故选B . 7.答案 ③④解析由f (x )=x 2-2ax 在[1,+∞)上为增函数,知a ≤1,①错误;由y =ln (x 2+1)≥ln 1=0,知其值域为[0,+∞),②错误;借助图象知③④正确. 8.解析 (1)g (mx 2+2x +m )=log 2(mx 2+2x +m ), ∵g (mx 2+2x +m )的定义域为R , ∴mx 2+2x +m >0恒成立, 当m =0时,不符合,当m ≠0时,需满足{m >0,4-4m 2<0,解得m >1, ∴实数m 的取值范围为(1,+∞). (2)令t =f (x )=(12)x,当x ∈[-1,1]时,t ∈[12,2], 则函数y =[f (x )]2-2af (x )+3化为y =t 2-2at +3=(t -a )2+3-a 2,t ∈[12,2]. ①当a >2时,可得当t =2时,y 取最小值,且y min =7-4a =1,解得a =32(舍去); ②当12≤a ≤2时, 可得当t =a 时,y 取最小值,且y min =3-a 2=1,解得a =-√2(舍)或a =√2; ③当a <12时, 可得当t =12时,y 取最小值,且y min =134-a =1,解得a =94(舍去). 综上,a =√2. 9.答案12;6 876信息提取 ①样本中碳14的质量N 随时间T (单位:年)的衰变规律满足N =N 0·2-T5730(N 0表示碳14原有的质量);②碳14的质量是原来的37至12.数学建模以良渚古城遗址考古测定的放射性物质衰变规律为情境,构建指数函数模型N =N 0·2-T5730,把T =5 730代入N =N 0·2-T5730,求出碳14的质量与原来的关系;令2-T5730>37,两边同时取以2为底的对数,结合给定的对数值求出T 的范围.解析 ∵N =N 0·2-T5730,∴当T =5 730时,N =N 0·2-1=12N 0, ∴经过5 730年后,碳14的质量变为原来的12. 由题意可知2-T5730>37, 两边同时取以2为底的对数, 得log 22-T5730>log 237, ∴-T 5730>lg 37lg2=lg3-lg7lg2≈-1.2,∴T <6 876,∴推测良渚古城存在的时期距今约在5 730年到6 876年之间.。

2021新教材人教版高中数学A版必修第一册模块练习题--3.1~3.2综合拔高练

3.1~3.2综合拔高练五年高考练考点1 函数的概念与表示 1.(2019江苏,4,5分,)函数y=√7+6x -x 2的定义域是 . 2.(2016浙江,12,6分,)设函数f(x)=x 3+3x 2+1.已知a ≠0,且f(x)-f(a)=(x-b)(x-a)2,x ∈R,则实数a= ,b= . 考点2 分段函数的应用 3.(2019课标全国Ⅱ,12,5分,)设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x ∈(0,1]时, f(x)=x(x-1).若对任意x ∈(-∞,m],都有f(x)≥-89,则m 的取值范围是( )A.(-∞,94]B.(-∞,73]C.(-∞,52] D.(-∞,83] 4.(2018天津,14,5分,)已知a ∈R,函数f(x)={x 2+2x +a -2,x ≤0,-x 2+2x -2a,x >0.若对任意x ∈[-3,+∞), f(x)≤|x|恒成立,则a 的取值范围是 .考点3 函数基本性质的综合运用 5.(2018课标全国Ⅱ,11,5分,)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( ) A.-50 B.0 C .2 D .50 6.(2019浙江,16,5分,)已知a ∈R,函数f(x)=ax 3-x.若存在t ∈R,使得|f(t+2)-f(t)|≤23,则实数a 的最大值是 .强基计划7.(2018中国科技大学自主招生试题,6改编,)已知定义在(0,+∞)上的函数f(x)是单射(即如果x,y ∈(0,+∞),且x ≠y,都有f(x)≠f(y)),对任意的x>0,有xf(x)>1, f(xf(x)-1)=2,则f(2)= .三年模拟练应用实践1.(2020黑龙江大庆实验中学高一上月考,)设f(x)={√x,0<x <1,2(x -1),x ≥1,若f(a)=f(a+1),则f (1a-1)=( ) A.8 B .6 C.4 D .22.(2020山东德州高一上期中,)已知函数f(x)是定义在R 上的单调函数,A(0,1),B(2,-1)是其图象上的两点,则不等式|f(x-1)|>1的解集为( )A.(-1,1)B.(-∞,-1)∪(1,+∞)C.(1,3)D.(-∞,1)∪(3,+∞)3.(2020黑龙江哈三中高一上第一次阶段性验收,)已知函数f(x)={(x +1)2,x ≤-1,2x +2,-1<x <1,1x,x ≥1,若f(a)>1,则实数a 的取值范围是( )A.(-∞,-2)∪(-12,+∞)B.(-12,12)C.(-∞,-2)∪(-12,1) D.(-2,12)∪(1,+∞)4.(多选)(2020山东菏泽高一上期末联考,)下列关于函数f(x)=√x 2-x 4|x -1|-1的性质描述正确的是( 易错 ) A. f(x)的定义域为[-1,0)∪(0,1] B. f(x)的值域为(-1,1) C. f(x)在定义域上是增函数 D. f(x)的图象关于原点对称 5.(多选)(2020山东日照高一上期中,)下列结论正确的有( )A.函数f(x)=(x-1)0+√x +1的定义域为(-1,1)∪(1,+∞)B.函数y=f(x)(x ∈[-1,1])的图象与y 轴有且只有一个交点C.“k>1”是“函数f(x)=(k-1)x+k(k ∈R)为增函数”的充要条件D.若奇函数y=f(x)在x=0处有定义,则f(0)=0 6.(多选)(2020山东淄博高一上期中,)我们把定义域为[0,+∞)且同时满足以下两个条件的函数f(x)称为“Ω函数”: (1)对任意的x ∈[0,+∞),总有f(x)≥0;(2)若x ≥0,y ≥0,则有f(x+y)≥f(x)+f(y)成立,下列判断正确的是( ) A.若f(x)为“Ω函数”,则f(0)=0B.若f(x)为“Ω函数”,则f(x)在[0,+∞)上为增函数C.函数g(x)={0,x ∈Q,1,x ∉Q 在[0,+∞)上是“Ω函数”D.函数g(x)=x 2+x 在[0,+∞)上是“Ω函数”7.(2020河北石家庄二中高一上月考,)已知函数f(x)={-x 24,0<x ≤4,4-2x,x >4,函数h(x)(x ≠0)为偶函数,且当x>0时,h(x)=f(x).若h(t)>h(2),则实数t 的取值范围为 . 8.(2020天津六校高一上期中联考,)已知函数f(x)=x 2-4x+10(x ∈[m,n])的值域为[3m,3n],则2m+n= . 9.(2020黑龙江哈师大附中高一上期中,)下列说法正确的是 .(填序号)(1)函数f(x)=-2x在(0,+∞)上单调递减; (2)函数y=2x(x ∈N)的图象是一条直线;(3)已知函数f(x)={x 2+1(x ≤0),-2x(x >0),若f(x)=10,则x 的值为-3或-5;(4)若函数y=x 2+(2a-1)x+1的减区间是(-∞,2],则a=-32;(5)若函数f(x)满足R 上的任意实数x 1,x 2(x 1≠x 2),(x 1-x 2)[f(x 1)-f(x 2)]<0恒成立,则f(x)在R 上单调递减. 10.(2020河北承德一中高一上月考,)已知函数f(√x +2)=3x+1x+2,函数g(x)=1-2x+√x +2.(1)求函数f(x)的解析式,并写出其定义域; (2)求函数g(x)的值域.11.(2020湖南衡阳一中高一上期中,)已知函数f(x)对任意的实数a,b 都有f(a+b)=f(a)+f(b),且当x>0时,有f(x)>0.(1)求证:f(x)在R上为增函数;(2)求证:f(x)是R上的奇函数;(3)若f(1)=1,解不等式f(x2)-f(x+2)>4.迁移创新12.(2020山东烟台高一上期中,)经过函数性质的学习,我们知道“函数y=f(x)的图象关于y轴成轴对称图形”的充要条件是“y=f(x)为偶函数”.(1)若f(x)为偶函数,且当x≤0时,f(x)=2x-1,求f(x)的解析式,并求不等式f(x)>f(2x-1)的解集;(2)某数学学习小组针对上述结论进行探究,得到一个真命题:“函数y=f(x)的图象关于直线x=a成轴对称图形”的充要条件是“y=f(x+a)为偶函数”.若函数g(x)的图象关于直线x=1对称,且当x≥1时,g(x)=x2-1.x①求g(x)的解析式;②求不等式g(x)>g(3x-1)的解集.答案全解全析五年高考练1.答案 [-1,7]解析由题意可得7+6x-x 2≥0,即x 2-6x-7≤0,解得-1≤x ≤7,故该函数的定义域是[-1,7]. 2.答案 -2;1 解析f(x)-f(a)=x 3-a 3+3(x 2-a 2)=(x-a)[x 2+ax+a 2+3(x+a)]=(x-a)[x 2+(a+3)·x+a 2+3a]=(x-a)(x-a)(x-b),则x 2+(a+3)x+a 2+3a=x 2-(a+b)x+ab,即{a +3=-(a +b),a 2+3a =ab,解得{a =-2,b =1. 3.B 由题可知,当x ∈(0,1]时, f(x)=x(x-1)=x 2-x,则当x=12时, f(x)min =-14,且当x=13时, f(x)=-29.当x ∈(1,2]时,x-1∈(0,1],则f(x)=2f(x-1).当x ∈(-1,0]时,x+1∈(0,1],则 f(x)=12f(x+1).∴若x ∈(1,2],则当x=32时, f(x)min =-12,且x=43时, f(x)=-49.同理,若x ∈(2,3],则当x=52时, f(x)min =-1,且x=73时, f(x)=-89.∴函数f(x)的大致图象如图所示.∵f(x)≥-89对任意x ∈(-∞,m]恒成立,∴当x ∈(-∞,m]时, f(x)min ≥-89,由图可知m ≤73.故选B.4.答案 [18,2]解析当x>0时, f(x)=-x 2+2x-2a,此时只需-x 2+2x-2a ≤x 恒成立, 即2a ≥-x 2+x 恒成立,因为x>0时,y=-x 2+x 的最大值为14,所以a ≥18;当-3≤x ≤0时, f(x)=x 2+2x+a-2, 此时只需x 2+2x+a-2≤-x 恒成立, 即a ≤-x 2-3x+2恒成立,因为-3≤x ≤0时,y=-x 2-3x+2的最小值为2, 所以a ≤2.故a 的取值范围为[18,2].5.C 因为f(x)是定义在(-∞,+∞)上的奇函数, 所以f(-x)=-f(x)①,且f(0)=0. 又因为f(1-x)=f(1+x), 所以f(-x)=f(2+x)②. 由①②可得f(x+2)=-f(x), 则有f(x+4)=f(x). 由f(1)=2,得f(-1)=-2,于是有f(2)=f(0)=0, f(3)=f(-1)=-2,f(4)=f(0)=0, f(5)=f(1)=2, f(6)=f(2)=0,……,所以f(1)+f(2)+f(3)+…+f(50)=12×[f(1)+f(2)+f(3)+f(4)]+f(49)+f(50)=12×0+f(1)+f(2)=2+0=2. 6.答案 43解析 |f(t+2)-f(t)|=|a(t+2)3-(t+2)-(at 3-t)|=|a(6t 2+12t+8)-2|.令m=6t 2+12t+8=6(t+1)2+2,则m ∈[2,+∞),设g(m)=f(t+2)-f(t)=am-2, |am-2|≤23,当a=0时,g(m)=-2,不符合题意;当a>0时,g(m)∈[2a-2,+∞),∵|g(m)|≤23有解,∴2a-2≤23,得0<a ≤43;当a<0时,g(m)∈(-∞,2a -2],∵|g(m)|≤23有解,∴2a-2≥-23,得a ≥23,与a<0矛盾.综上可知,0<a ≤43,即a 的最大值为43.7.答案 1解析由函数f(x)是单射,且f(xf(x)-1)=2,得xf(x)-1是常数,令xf(x)-1=t(x>0),则f(x)=t+1x ,且f(t)=2①,因此tf(t)-1=t,所以f(tf(t)-1)=2,由f(t)=2,得f(2t-1)=2②,由①②及函数f(x)是单射得t=2t-1,解得t=1,所以f(x)=2x (x>0),所以f(2)=1.三年模拟练应用实践1.C 由题意知,当a ∈(0,1)时,若f(a)=f(a+1),则√a =2a,解得a=14,则f (1a-1)=f(3)=2×(3-1)=4;当a ∈[1,+∞)时,若f(a)=f(a+1),则2(a-1)=2a,显然无解. 综上可得f (1a -1)=4,故选C.2.D 由题意可知f(0)=1,f(2)=-1, 又知f(x)是定义在R 上的单调函数, 所以f(x)在R 上单调递减.由|f(x-1)|>1得f(x-1)>1或f(x-1)<-1, 即f(x-1)>f(0)或f(x-1)<f(2), 所以x-1<0或x-1>2, 解得x<1或x>3,故选D.3.C 当a ≤-1时,由f(a)=(a+1)2>1,解得a>0或a<-2,故a<-2; 当-1<a<1时,由f(a)=2a+2>1,解得a>-12,故-12<a<1;当a ≥1时,由f(a)=1a>1,解得0<a<1,故无解.综上所述,a 的取值范围是(-∞,-2)∪(-12,1),故选C.4.ABD 由{x 2-x 4≥0,|x -1|-1≠0,得-1≤x ≤1且x ≠0,此时f(x)=√x 2-x 4-(x -1)-1=√x 2-x 4-x=|x|√1-x 2-x,因此A 正确;当0<x ≤1时, f(x)=-√1-x 2∈(-1,0],当-1≤x<0时, f(x)=√1-x 2∈[0,1),故f(x)的值域为(-1,1),B 正确;易知f(x)在定义域上不是增函数,选项C 错误;又f(-x)=|-x|√1-(-x)2-(-x)=|x|√1-x 2x=-f(x),则f(x)是奇函数,其图象关于原点对称,D 正确.故选ABD.易错警示研究函数的性质时,应先求定义域,再化简解析式.不求定义域就化简解析式可能会导致定义域发生变化,从而导致解题错误;化简解析式有一定的必要性,若不化简解析式,可能会反映不出函数的本质,从而导致问题不能解决.5.BCD 选项A 中,由{x -1≠0,x +1≥0,得x ≥-1且x ≠1,A 错误;选项B 中,由y=f(x)在x=0处有意义,因此f(x)的图象与y 轴有且只有一个公共点,B 正确;选项C 中,若k>1,则k-1>0,f(x)=(k-1)x+k 是增函数,反过来也成立,C 正确;选项D 中,由f(x)是奇函数知f(-x)=-f(x),又x=0处有定义,因此f(-0)=-f(0),即2f(0)=0,f(0)=0,D 正确,故选BCD.6.AD 对于选项A,由条件(1)知,f(x)≥0,则f(0)≥0,由条件(2)知, f(0+0)≥f(0)+f(0),即f(0)≤0,所以f(0)=0,A 正确; 对于选项B,当f(x)=0(x ∈[0,+∞))时,符合条件(1),(2), f(x)是“Ω函数”,但f(x)在[0,+∞)上不是增函数,B 错误; 对于选项C,取x=2-√2,y=2+√2,则g(2-√2)=1,g(2+√2)=1,g((2-√2)+(2+√2))=g(4)=0,不满足g(x+y)≥g(x)+g(y),所以g(x)不是“Ω函数”,C 错误;对于选项D,g(x)=x 2+x 在[0,+∞)上单调递增,所以g(x)≥g(0)=0,满足条件(1),又g(x+y)-g(x)-g(y)=[(x+y)2+(x+y)]-(x 2+x)-(y 2+y)=2xy,当x ≥0,y ≥0时,2xy ≥0,此时g(x+y)≥g(x)+g(y),满足条件(2),D 正确.故选AD.7.答案 (-2,0)∪(0,2)解析因为当x>0时,h(x)=f(x),所以当x>0时,h(x)={-x 24,0<x ≤4,4-2x,x >4,易知函数h(x)在(0,+∞)上单调递减,又函数h(x)(x ≠0)为偶函数,且h(t)>h(2),所以h(|t|)>h(2),所以0<|t|<2,所以{t ≠0,|t|<2,即{t ≠0,-2<t <2,解得-2<t<0或0<t<2.8.答案 9解析 ∵f(x)=x 2-4x+10=(x-2)2+6≥6,∴3m ≥6,∴m ≥2,又函数f(x)图象的对称轴为x=2,∴函数f(x)在[m,n]上单调递增. ∴f(m)=3m,f(n)=3n,即m 2-4m+10=3m,n 2-4n+10=3n,解得m=2或m=5,n=2或n=5,又m<n,∴m=2,n=5,∴2m+n=4+5=9,故答案为9.9.答案 (4)(5)解析函数f(x)=-2x 在(0,+∞)上单调递增,故(1)错误;函数y=2x(x ∈N)的图象是间断的点,故(2)错误;函数f(x)={x 2+1(x ≤0),-2x(x >0),若f(x)=10,则x 的值为-3,故(3)错误;若函数y=x 2+(2a-1)x+1的减区间是(-∞,2],则-2a -12=2,即a=-32,故(4)正确;若函数f(x)满足R 上的任意实数x 1,x 2(x 1≠x 2),(x 1-x 2)[f(x 1)-f(x 2)]<0恒成立,则当x 1>x 2时, f(x 1)<f(x 2),当x 1<x 2时,f(x 1)>f(x 2),所以f(x)在R 上单调递减,故(5)正确.故答案为(4)(5).10.解析 (1)令t=√x +2,t>2,则x=(t-2)2,∴f(t)=3(t-2)2+1(t -2)2+2, ∴f(x)=3(x-2)2+1(x -2)2+2,其定义域为(2,+∞). (2)令t=√x +2,t ≥0,则x=t 2-2,∴y=1-2(t 2-2)+t=-2t 2+t+5,t ≥0,当t=14时,y 取得最大值,最大值为418,所以原函数的值域为(-∞,418]. 11.解析 (1)证明:任取x 1,x 2∈R,且x 1<x 2,则f(x 2)-f(x 1)=f(x 2-x 1+x 1)-f(x 1), ∵对任意的实数a,b 都有f(a+b)=f(a)+f(b),∴f(x2-x1+x1)=f(x2-x1)+f(x1),∴f(x2)-f(x1)=f(x2-x1),∵当x>0时,f(x)>0,且x2-x1>0,∴f(x2-x1)>0,∴f(x2)>f(x1),即y=f(x)在R上为增函数.(2)证明:∵对任意的实数a,b都有f(a+b)=f(a)+f(b),∴令a=b=0,则f(0)=f(0)+f(0)=2f(0),∴f(0)=0,令a=x,b=-x,则f(x-x)=f(x)+f(-x)=f(0)=0,∴f(-x)=-f(x),即函数y=f(x)为R上的奇函数.(3)若f(1)=1,则f(2)=2f(1)=2,f(4)=2f(2)=4,∴不等式f(x2)-f(x+2)>4等价于f(x2)-f(x+2)>f(4),由(2)知f(x)为奇函数,∴-f(x+2)=f(-x-2),∴f(x2)-f(x+2)=f(x2)+f(-x-2),∴f(x2-x-2)>f(4),又由(1)知,f(x)在R上为增函数,∴x2-x-2>4,即x2-x-6>0,∴x>3或x<-2.∴原不等式的解集为(-∞,-2)∪(3,+∞).迁移创新12.解析(1)设x>0,则-x<0,则f(-x)=2·(-x)-1=-2x-1,又f(x)为偶函数,所以f(x)=f(-x)=-2x-1.所以f(x)={2x-1,x≤0, -2x-1,x>0.因为f(x)为偶函数,且f(x)在[0,+∞)上是减函数,所以f(x)>f(2x-1)等价于|x|<|2x-1|,即x2<(2x-1)2,解得x<13或x>1.所以不等式的解集是{x|x<13或x>1}.(2)①因为g(x)的图象关于直线x=1对称,所以y=g(x+1)为偶函数,所以g(1+x)=g(1-x),即g(x)=g(2-x)对任意x∈R恒成立.又当x<1时,2-x>1,所以g(x)=(2-x)2-12-x =x 2-4x+4+1x -2. 所以g(x)={x 2-1x,x ≥1,x 2-4x +4+1x -2,x <1.②任取x 1,x 2∈[1,+∞),且x 1<x 2,则g(x 1)-g(x 2)=x 12-1x 1-(x 22-1x 2)=(x 1-x 2)(x 1+x 2+1x 1x 2), 因为x 1<x 2,所以x 1-x 2<0,又x 1+x 2>0,1x 1x 2>0,所以(x 1-x 2)(x 1+x 2+1x 1x 2)<0,即g(x 1)<g(x 2).所以函数y=g(x)在[1,+∞)上是增函数,又因为函数g(x)的图象关于直线x=1对称, 所以g(x)>g(3x-1)等价于|x-1|>|3x-2|, 即(x-1)2>(3x-2)2,解得12<x<34. 所以不等式的解集为{x |12<x <34}.。

高中必修一基本初等函数精选考题归纳(小班提高版)(精华版)

高中数学必修一基本初等函数单元总复习一,指数函数及其性质指数函数二、对数与对数运算（1）对数的定义①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数． ②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么 ①加法：log log log ()a a a M N MN +=②减法：log log log a a aM M N N-=③数乘：log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b na a nM M b n R b=≠∈⑥换底公式：log log (0,1)log b a b NN b b a=>≠且三、对数函数及其性质四、幂函数（1）幂函数的定义一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（3）幂函数的性质图象分布：1,幂函数图象分布在第一、二、三象限，第四象限无图象．2,幂函数是偶函数时，图象分布在第一、二象限(图象关于y 轴对称)；3,是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限．4,过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)． 5,单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴．6,奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当qpα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则qp y x =是奇函数，若p 为奇数q 为偶数时，则q p y x =是偶函数，若p 为偶数q 为奇数时，则q py x =是非奇非偶函数．7,图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．五,经典考题讲解:1．下列函数与x y =有相同图象的一个函数是（）A ．2x y = B ．xx y 2=C ．)10(log ≠>=a a a y xa 且 D ．x a a y log =2．三个数60.70.70.76log 6，，的大小关系为（） A . 60.70.70.7log 66<+=a a b x y a 的图象过两点(1,0)-和(0,1)，则( )A ．2,2a b ==B ．2a b ==C ．2,1a b ==D ．a b =4．已知x x f 26log )(=，那么)8(f 等于（）A ．34 B ．8 C ．18 D ．215．下列函数中是奇函数的有几个（）①11x x a y a +=- ②2lg(1)33x y x -=+- ③x y x = ④1log 1a x y x +=-A ．1B ．2C ．3D ．46、12log <a (a>0且a ≠1),a 的取值范围为（）A 、2>a B 、2110<<<<a a 或 C 、210><<a a 或 D 、21<<a7．若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍，则a 的值为( ) A ．42 B ．22C ．41D ．218．函数]1,0[)1(log )(在++=x a x f a x 上的最大值和最小值之和为a ，则a 的值为（） A ．41 B ．21C ．2D ．49．若f x x (ln )=+34，则f x ()的表达式为（） A ．3ln x B ．3ln 4x + C ．3xe D ．34xe +10．函数)10()(≠>=a a a x f x 且对于任意的实数都有：A 、)()()(y f x f xy f =B 、)()()(y f x f xy f +=C 、)()()(y f x f y x f =+D 、)()()(y f x f y x f +=+11、已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （）A ．奇函数B ．偶函数C ．既奇又偶函数D ．非奇非偶函数 12、若,则的元素个数为( )12313．函数lg y x =( )A ．是偶函数，在区间(,0)-∞ 上单调递增B ．是偶函数，在区间(,0)-∞上单调递减C ．是奇函数，在区间(0,)+∞ 上单调递增D ．是奇函数，在区间(0,)+∞上单调递减14．已知函数=-=+-=)(.)(.11lg)(a f b a f xxx f 则若（） A ．b B ．b - C ．b 1 D ．1b-15．对于10<<a ，给出下列四个不等式①)11(log )1(log a a a a +<+ ②)11(log )1(log aa a a +>+ ③aaaa111++< ④aaaa 111++>其中成立的是（）A ．①与③B ．①与④C ．②与③D ．②与④16、比较下列各组数大小：（1）0.53.1 2.33.1 （2）0.323-⎛⎫⎪⎝⎭0.2423-⎛⎫⎪⎝⎭（3） 2.52.3- 0.10.2-17、已知下列不等式，试比较n m ,的大小：（1）nm22< （2）nm 2.02.0< （3）)10(<<<a a a n m18．计算：(log )log log 2222545415-++= 。

人教版高中数学必修一《基本初等函数》课后提升练习及答案

第二章基本初等函数(Ⅰ)2．1 指数函数2．1.1 根式与分数指数幂1．27的平方根与立方根分别是( ) A ．3 3，3 B ．±3 3，3 C ．3 3，±3 D ．±3 3，±3 2.44(2)-的运算结果是( )A ．2B ．－2C ．±2D ．不确定3．若a 2－2a ＋1＝a －1，则实数a 的取值范围是( ) A ．[1，＋∞) B ．(－∞，1) C ．(1，＋∞) D ．(－∞，1] 4．下列式子中，正确的是( ) A.416＝±2 B.364-＝－4 C.66(3)-＝－3D ．55(2)-＝25．下列根式与分数指数幂的互化中，正确的是( ) A ．－x ＝12()x -(x >0) B.26y ＝13y (y <0)C ．34x -＝341x ⎛⎫⎪⎝⎭(x >0)D ．13x -＝－3x (x ≠0)6．设a ，b ∈R ，下列各式总能成立的是( ) A ．(3a －3b )3＝a －b B.2244()a b +＝a 2＋b 2 C.44a －44b ＝a －b D.88()a b +＝a ＋b7．计算：()n n a b -＋()n n a b +(a 1，n ∈N *)．8．化简：6＋4 2＋6－4 2＝__________.9．化简：44(3.14π)-＋55()a b-＋66(π10)π10--＝()A．1 B．－1 C．3 D．－310．已知a，b是方程x2－6x＋4＝0的两根，且a＞b＞0，求a－ba＋b的值．2.1.2 指数幂的运算1．化简1327125-⎛⎫⎪⎝⎭的结果是( )A.35B.53 C ．3 D ．52．计算[(－2)2]12-的值为( )A. 2 B ．－ 2C.22 D ．－22 3．若(1－2x )12-有意义，则x 的取值范围是( )A ．x ∈RB ．x ∈R ，且x ≠12C ．x >12D ．x <124．设a ≥0，计算369a 2·639a 2的结果是( ) A ．a 8 B ．a 4 C ．a 2 D ．a5．211.533[(0.027)]-的值为( ) A.103 B ．3 C ．－13D ．66．计算：(－1.8)0＋(1.5)－2×23338⎛⎫⎪⎝⎭＋329＝________.73322114423()a b ab b a b a⋅8．化简：a b 3b a 3a 2b＝__________. 9．若x >0，则(2x 14＋332)(2x 14－332)－4x12-(x －x 12)＝__________.10．已知f (x )＝e x－e －x，g (x )＝e x＋e －x(e ＝2.718…)． (1)求[f (x )]2－[g (x )]2的值；(2)设f (x )f (y )＝4，g (x )g (y )＝8，求g (x ＋y )g (x －y )的值．2.1.3指数函数及其图象1．下列以x为自变量的函数中，是指数函数的是()A．y＝(－4)x B．y＝λx(λ>1)C．y＝－4x D．y＝a x＋2(a>0，且a≠1)2．y＝2x＋2－x的奇偶性为()A．奇函数B．偶函数C．既是偶函数又是奇函数D．既不是奇函数也不是偶函数3．函数f(x)＝1－2x的定义域是()A．(－∞，0] B．[0，＋∞)C．(－∞，0) D．(－∞，＋∞)4．已知0＜a＜1，b＜－1，则函数f(x)＝a x＋b的图象不经过()A．第一象限B．第二象限C．第三象限D．第四象限5．如图K2-1-1所示的韦恩图中，A，B是非空集合，定义集合A#B为阴影部分所表示的集合．若x，y∈R，A＝{x|y＝2x－x2}，B＝{y|y＝3x(x>0)}，则A#B为()图K2-1-1A．{x|0<x<2}B．{x|1<x≤2}C．{x|0≤x≤1或x≥2}D．{x|0≤x≤1或x>2}6．函数y＝a|x|(a>1)的图象是()A B C D7．求函数y＝16－4x的值域．8．已知f(x)是偶函数，且当x>0时，f(x)＝10x，则当x<0时，f(x)＝()A．10x B．10－xC．－10x D．－10－x9．对于函数f(x)定义域中任意的x1，x2(x1≠x2)，有如下结论：①f (x 1＋x 2)＝f (x 1)·f (x 2)； ②f (x 1·x 2)＝f (x 1)＋f (x 2)； ③f (x 1)－f (x 2)x 1－x 2<0；④f (x 1)－1x 1<0(x 1≠0)；⑤f (－x 1)＝1f (x 1).当f (x )＝⎝⎛⎭⎫12x时，上述结论中，正确结论的序号是____________．10．(1)当x ＞0时，函数f (x )＝(a 2－1)x的值总大于1，求实数a 的取值范围；(2)对于任意实数a ，函数y ＝a x －3＋3的图象恒过哪一点？2.1.4 指数函数的性质及其应用1.⎝⎛⎭⎫1323，34，⎝⎛⎭⎫13－2的大小关系是( ) A.⎝⎛⎭⎫1323<⎝⎛⎭⎫13－2<34 B.⎝⎛⎭⎫1323<34<⎝⎛⎭⎫－132 C.⎝⎛⎭⎫13－2<⎝⎛⎭⎫1323<34 D.⎝⎛⎭⎫13－2<34<⎝⎛⎭⎫13232．若⎝⎛⎭⎫122a ＋1<⎝⎛⎭⎫123－2a，则实数a 的取值范围为( )A ．(1，＋∞) B.⎝⎛⎭⎫12，＋∞ C ．(－∞，1) D.⎝⎛⎭⎫－∞，12 3．下列选项中，函数y ＝|2x－2|的图象是( )4．函数y ＝a x在[0,1]上的最大值与最小值之和为3，则函数y ＝3a x －1在[0,1]上的最大值为( )A ．6B ．1C ．3 D.325．(2014年四川泸州二模)已知在同一直角坐标系中，指数函数y ＝a x 和y ＝b x 的图象如图K2-1-2，则下列关系中正确的是( )图K2-1-2A ．a ＜b ＜1B ．b ＜a ＜1C ．a ＞b ＞1D ．b ＞a ＞16．下列函数中，既是偶函数，又在(0，＋∞)上单调递增的函数是( ) A ．y ＝x 3 B ．y ＝|x |＋1C ．y ＝－x 2＋1D ．y ＝2－|x |7．已知函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x (x ≥4)，f (x ＋1) (x ＜4)，求f (3)的值．8．设函数f (x )＝⎩⎪⎨⎪⎧2－x， x ∈(－∞，1)，x 2， x ∈[1，＋∞).若f (x )>4，则x 的取值范围是________________．9．函数f (x )＝2213x x-⎛⎫⎪⎝⎭的值域为__________．10．已知f (x )＝10x－10－x10x ＋10－x.(1)判断函数f (x )的奇偶性；(2)证明f (x )是定义域内的增函数； (3)求f (x )的值域．2.2 对数函数2．2.1 对数与对数运算1．下列各组指数式与对数式互化，不正确的是( ) A ．23＝8与log 28＝3B ．1327-＝13与log 2713＝－13C ．(－2)5＝－32与log －2(－32)＝5D ．100＝1与lg1＝02．已知函数f (x )＝log 2(x ＋1)，若f (a )＝1，则a ＝( ) A ．0 B ．1 C ．2 D ．33．以下四个命题：①若log x 3＝3，则x ＝9；②若log 4x ＝12，则x ＝2；③若3logx ＝0，则x ＝3；④若15log x ＝－3，则x ＝125.其中是真命题的个数是( )A ．1个B ．2个C ．3个D ．4个4．方程3log 2x ＝14的解是( )A ．x ＝19B ．x ＝33C ．x ＝ 3D ．x ＝95．若f (e x )＝x ，则f (e)＝( ) A ．1 B ．e e C ．2e D ．06．设集合P ＝{3，log 2a }，Q ＝{a ，b }，若P ∩Q ＝{0}，则P ∪Q ＝( ) A ．{3,0} B ．{3,0,1} C ．{3,0,2} D ．{3,0,1,2}7．求下列各式中x 的取值范围： (1)log (x －1)(x ＋2)； (2)log (x ＋3)(x ＋3)．8．设f (x )＝⎩⎪⎨⎪⎧lg x ，x >0，10x ，x ≤0，则f [f (－2)]＝__________.9．已知23a ＝49(a >0) ，则23log a ＝__________.10．(1)若f (log 2x )＝x ，求f ⎝⎛⎭⎫12的值；(2)若log 2[log 3(log 4x )]＝0，log 3[log 4(log 2y )]＝0，求x ＋y 的值．2.2.2 对数的性质及其应用1．计算log 23·log 32的结果为( ) A ．1 B ．－1 C ．2 D ．－22.(2013年陕西)设a ，b ，c 均为不等于1的正实数，则下列等式中恒成立的是( ) A ．log a b ·log c b ＝log c a B ．log a b ·log c a ＝log c b C ．log a bc ＝log a b ·log a c D ．log a (b ＋c )＝log a b ＋log a c3．(2014年四川泸州一模)2lg2－lg 125的值为( )A ．1B ．2C ．3D ．44．lg12.5－lg 58＋lg0.5＝( )A ．－1B ．1C ．2D ．－25．若log 513·log 36·log 6x ＝2，则x ＝( )A ．9 B.19C ．25 D.1256．设2a ＝5b ＝m ，且1a ＋1b＝2，则m ＝( )A.10 B ．10 C ．20 D ．1007．计算：lg2·lg 52＋lg0.2·lg40.8．已知lg2＝a ，lg3＝b ，用a ，b 表示log 1245＝______________. 9．已知log 83＝p ，log 35＝q ，以含p ，q 的式子表示lg2.10．已知lg a和lg b是关于x的方程x2－x＋m＝0的两个根，而关于x的方程x2－(lg a)x －(1＋lg a)＝0有两个相等的实根．求实数a，b和m的值．2.2.3 对数函数及其性质(1)1．若log 2a ＜0，⎝⎛⎭⎫12b＞1，则( ) A ．a ＞1，b ＞0 B ．a ＞1，b ＜0 C ．0＜a ＜1, b ＞0 D ．0＜a ＜1, b ＜02．(2014年广东揭阳一模)已知集合A ＝{x |y ＝lg(x ＋3)}，B ＝{x |x ≥2}，则下列结论正确的是( )A ．－3∈AB ．3∉BC ．A ∪B ＝BD ．A ∩B ＝B3．函数y ＝log 2x 与y ＝log 12x 的图象关于( )A ．x 轴对称B ．y 轴对称B ．原点对称 D ．直线y ＝x 对称4．函数y ＝1log 0.5(4x －3)的定义域为( )A.⎝⎛⎭⎫34，1B.⎝⎛⎭⎫34，＋∞ C ．(1，＋∞) D.⎝⎛⎭⎫34，1∪(1，＋∞)5．若函数f (x )＝log a (x ＋1)(a >0，a ≠1)的定义域和值域都是[0,1]，则a ＝( ) A.13 B. 2 C.22D ．2 6．已知a >0，且a ≠1，函数y ＝a x 与y ＝log a (－x )的图象只能是图中的( )7．若函数y ＝log a (x ＋b )(a >0，a ≠1)的图象过点(－1,0)和(0,1)，求a ，b 的值．8．已知A ＝{x |2≤x ≤π}，定义在A 上的函数y ＝log a x (a ＞0，且a ≠1)的最大值比最小值大1，则底数a 的值为( )A.2πB.π2C ．π－2 D.π2或2π9．设a ＝log 54，b ＝(log 53)2，c ＝log 45，则( ) A ．a <c 0)．(1)求函数f (x )的定义域；(2)若函数f (x )在区间[10，＋∞)上是增函数，求实数k 的取值范围．2.2.4 对数函数及其性质(2)1．已知函数y ＝a x 与y ＝log a x (a ＞0，且a ≠1)，下列说法不正确的是( ) A ．两者的图象都关于直线y ＝x 对称B ．前者的定义域、值域分别是后者的值域、定义域C ．两函数在各自的定义域内的增减性相同D ．y ＝a x 的图象经过平移可得到y ＝log a x 的图象2．若函数y ＝f (x )的反函数图象过点(1,5)，则函数y ＝f (x )的图象必过点( ) A ．(1,1) B ．(1,5) C ．(5,1) D ．(5,5)3．点(4,16)在函数y ＝log a x 的反函数的图象上，则a ＝( ) A ．2 B ．4 C ．8 D ．164．已知a ＝log 23.6，b ＝log 43.2，c ＝log 43.6，则( ) A ．a >b >c B ．a >c >b C ．b >a >c D ．c >a >b 5．若0<x <y <1，则( ) A ．3y <3x B ．log x 3<log y 3C ．log 4x <log 4y D.⎝⎛⎭⎫14x <⎝⎛⎭⎫14y6．设log a 23＜1，则实数a 的取值范围是( )A ．0＜a ＜23 B.23＜a ＜1C ．0＜a ＜23或a ＞1D ．a ＞237．在下面函数中，与函数f (x )＝lg 1＋x1－x有相同奇偶性的是( )A ．y ＝x 3＋1B ．y ＝e 0－1e 0＋1C ．y ＝|2x ＋1|＋|2x －1|D ．y ＝x ＋1x8．函数y ＝ln(4＋3x －x 2)的单调递增区间是___________．9．对于函数f (x )定义域中的任意x 1，x 2(x 1≠x 2)，有如下结论： ①f (x 1＋x 2)＝f (x 1)·f (x 2); ② f (x 1·x 2)＝f (x 1)＋f (x 2)； ③f (x 1)－f (x 2)x 1－x 2>0；④f ⎝⎛⎭⎫x 1＋x 22<f (x 1)＋f (x 2)2.当f (x )＝lg x 时，上述结论中，正确结论的序号是____________．10．设f (x )＝log 12⎝ ⎛⎭⎪⎫1－ax x －1为奇函数，a 为常数， (1)求a 的值；(2)证明f (x )在(1，＋∞)上单调递增；(3)若对于[3,4]上的每一个x 值，不等式f (x )＞⎝⎛⎭⎫12x＋m 恒成立，求实数m 的取值范围．2.2.5对数函数及其性质(3)1．设a＝log132，b＝log133，c＝⎝⎛⎭⎫120.3，则()A．a<b<c B．a<c<bC．b<c<a D．b<a<c2．将函数y＝3x－2的图象向左平移2个单位，再将所得图象关于直线y＝x对称后，所得图象的函数解析式为()A．y＝4＋log3x B．y＝log3(x－4)C．y＝log3x D．y＝2＋log3x3．方程log2x＝x2－2的实根有()A．3个B．2个C．1个D．0个4．设函数f(x)＝log a(x＋b)(a>0，a≠1)的图象过点(2,1)，其反函数的图象过点(2,8)，则a＋b＝()A．3 B．4C．5 D．65．如图K2-2-1，给出函数y＝a x，y＝log a x，y＝log(a＋1)x，y＝(a－1)x2的图象，则与函数y＝a x，y＝log a x，y＝log(a＋1)x，y＝(a－1)x2依次对应的图象是()图K2-2-1A．①②③④B．①③②④C．②③①④D．①④③②6．函数y＝e|ln x|－|x－1|的图象大致是()7．已知函数f(x)＝log a(2x＋b－1)(a>0，a≠1)的图象如图K2-2-2，则a，b满足的关系是()图K2-2-2A ．0<a －1<b <1B ．0<b <a －1<1C ．0<b －1<a <1D ．0<a －1<b －1<18．下列函数的图象中，经过平移或翻折后不能与函数y ＝log 2x 的图象重合的函数是( )A ．y ＝2xB ．y ＝log 12xC ．y ＝4x2 D ．y ＝log 21x＋19．若函数f (x )＝log a (x ＋x 2＋2a 2)是奇函数，求a 的值．10．已知函数f (x )＝log a (1－x )＋log a (x ＋3)(0<a <1)． (1)求函数f (x )的定义域； (2)求方程f (x )＝0的解；(3)若函数f (x )的最小值为－4，求a 的值．2.3 幂函数1．所有幂函数的图象都经过的定点的坐标是( ) A ．(0,0) B ．(0,1)C ．(1,1)D ．(－1，－1) 2．下列说法正确的是( ) A ．y ＝x 4是幂函数，也是偶函数 B ．y ＝－x 3是幂函数，也是减函数 C ．y ＝x 是增函数，也是偶函数 D ．y ＝x 0不是偶函数3．已知幂函数f (x )的图象经过点⎝⎛⎭⎫2，22，则f (4)的值为( )A ．16 B.116C.12D ．2 4．下列函数中，既是偶函数，又是在区间(0，＋∞)上单调递减的函数为( )A ．y ＝x －2B ．y ＝x －1C ．y ＝x 2D ．y ＝x 135．当x ∈(1，＋∞)时，下列函数的图象全在直线y ＝x 下方的偶函数是( ) A ．y ＝x 12B ．y ＝x －2C ．y ＝x 2D ．y ＝x －16．设a ＝0.712，b ＝0.812，c ＝log 30.7，则( ) A ．c <b <a B ．c <a <b C ．a <b <c D ．b <a <c 7．若幂函数y ＝(m 2－3m ＋3)x 22m m --的图象不经过坐标原点，求实数m 的取值范围．8．给出函数的一组解析式如下：①y ＝13x -；②y ＝23x -；③y ＝12x -；④y ＝23x ；⑤y ＝13x ；⑥y ＝12x ；⑦y ＝32x ；⑧y ＝x 3；⑨y ＝x －3；⑩y ＝32x -.回答下列问题： (1)图象关于y 轴对称的函数有__________； (2)图象关于原点对称的函数有__________． 9．请把相应的幂函数图象代号填入表格．①y＝23x；②y＝x－2；③y＝12x；④y＝x－1；⑤13431253x10．已知函数f(x)＝(m2－m－1)x－5m－3，当m为何值时，f(x)是：(1)幂函数；(2)幂函数，且是(0，＋∞)上的增函数；(3)正比例函数；(4)反比例函数；(5)二次函数．第二章基本初等函数(Ⅰ) 2．1 指数函数2．1.1 根式与分数指数幂 1．B 2.A 3.A4．B 解析：A2；C＝|－3|＝3；D 错，5＝－2.5．C 解析：A 错，－x ＝－x 12(x >0)；B(－y )13(y <0)；D 错，x 13-x ≠0)． 6．B7．解：当n 为奇数时，原式＝a －b ＋a ＋b ＝2a ；当n 为偶数时，原式＝b －a －a －b ＝－2a .8．4 解析：原式＝22＋2×2×2＋(2)2＋22－2×2×2＋(2)2 ＝(2＋2)2＋(2－2)2 ＝2＋2＋2－2＝4.9．B 解析：∵3.14<π<10，＝π－3.143.14－π＝－1＝10－ππ－10＝－1 1.故原式＝－1＋1－1＝－1.10．解：∵a ，b 是方程x 2－6x ＋4＝0的两根， ∴⎩⎪⎨⎪⎧a ＋b ＝6，ab ＝4. ∵a ＞b ＞0，∴⎝ ⎛⎭⎪⎫a －b a ＋b 2＝(a ＋b )2－4ab a ＋b ＋2ab ＝2010＝2. ∴a －b a ＋b ＝ 2.2．1.2 指数幂的运算 1．B2．C 解析：[(－2)2]12-＝(2)122⎛⎫⨯- ⎪⎝⎭＝(2)－1＝22. 3．D4．C 解析：原式＝2936a ⨯⎛⎫ ⎪⎝⎭·2936a ⨯⎛⎫ ⎪⎝⎭＝a 2.5．A 解析：原式＝⎝⎛⎭⎫3102313323⎛⎫⨯⨯-⨯ ⎪⎝⎭＝103. 6．29 解析：原式＝1＋⎝⎛⎭⎫232×⎝⎛⎭⎫32233⨯＋3223⨯ ＝1＋1＋27＝29.7．解：原式＝12323311233()()a b a b ab b a -⋅⋅＝113133a+-+·212233b+--＝8133a b .解析：原式＝⎝ ⎛⎭⎪⎫a b 3 b a 3 a 2b 12＝a 12·b 32-·⎝⎛⎭⎫b a 3 a 2b 14＝a 12·b 32-·b 14·a 34-⎝⎛⎭⎫a 2b 18＝a1324-·b3124-+·a 28b 18-＝a1144-+·b5148--＝a 0b118-＝9．－23 解析：(2x 14＋332)(2x 14－332)－4x12-(x －x 12)＝4x 12－33－4x 12＋4＝－23. 10．解：(1)[f (x )]2－[g (x )]2 ＝[f (x )＋g (x )]·[f (x )－g (x )]＝2·e x·(－2e －x ) ＝－4e 0＝－4.(2)f (x )f (y )＝(e x －e －x )(e y －e －y )＝e x ＋y ＋e －(x ＋y )－e x －y －e －(x －y ) ＝g (x ＋y )－g (x －y )＝4， ①同法可得g (x )g (y )＝g (x ＋y )＋g (x －y )＝8. ②由①②解方程组⎩⎪⎨⎪⎧g (x ＋y )－g (x －y )＝4，g (x ＋y )＋g (x －y )＝8.解得g (x ＋y )＝6，g (x －y )＝2， ∴g (x ＋y )g (x －y )＝62＝3.2．1.3 指数函数及其图象 1．B 2.B 3.A4．A 解析：g (x )＝a x 的图象经过一、二象限，f (x )＝a x ＋b 是将g (x )＝a x 的图象向下平移|b |(b ＜－1)个单位而得，因而图象不经过第一象限．5．D 解析：A ＝{x |y ＝2x －x 2}＝{x |2x －x 2≥0}＝{x |0≤x ≤2}，B ＝{y |y ＝3x (x >0)}＝{y |y >1}，则A ∪B ＝{x |x ≥0}，A ∩B ＝{x |1<x ≤2}，根据新运算，得A #B ＝∁A ∪B (A ∩B )＝{x |0≤x ≤1或x >2}．故选D.6．B 解析：函数关于y 轴对称．7．解：∵4x >0，∴0≤16－4x <16，∴0≤16－4x <4.8．B 解析：设x <0，则－x >0，f (－x )＝10－x ，∵f (x )为偶函数．∴f (x )＝f (－x )＝10－x .9．①③④⑤ 解析：因为f (x )＝⎝⎛⎭⎫12x ，f (x 1＋x 2)＝122x x +＝12x ·22x ＝f (x 1)·f (x 2)，所以①成立，②不成立；显然函数f (x )＝⎝⎛⎭⎫12x 单调递减，即f (x 1)－f (x 2)x 1－x 2<0，故③成立；当x 1<0时，f (x 1)>1，f (x 1)－1x 1<0，当x 1>0时，0<f (x 1)<1，f (x 1)－1x 1<0，故④成立；f (－x 1)＝⎝⎛⎭⎫121x -＝12x ＝1f (x 1)，故⑤成立． 10．解：(1)∵当x ＞0时，f (x )＝(a 2－1)x 的值总大于1， ∴a 2－1＞1.∴a 2＞2.∴a ＞2或a ＜－ 2.(2)∵函数y ＝a x －3的图象恒过定点(3,1)，∴函数y ＝a x －3＋3的图象恒过定点(3,4)．2．1.4 指数函数的性质及其应用 1．A 2.B3．B 解析：由y ＝|2x－2|＝⎩⎪⎨⎪⎧2x －2， (x ≥1)，－2x＋2， (x ≤1)，分两部分：一部分为y 1＝2x －2(x ≥1)，只须将y ＝2x 的图象沿y 轴的负半轴平移2个单位即可，另一部分为y 2＝－2x ＋2(x ≤1)，只须将y ＝2x 的图象对称于x 轴的图象y ＝－2x ，然后再沿y 轴的正半轴平移2个单位，即可得到y ＝－2x ＋2的图象．故选B.4．C 解析：由于函数y ＝a x 在[0,1]上是单调的，因此最大值与最小值都在端点处取到，故有a 0＋a 1＝3，解得a ＝2，因此函数y ＝3a x －1在[0,1]上是单调递增函数，最大值当x ＝1时取到，即为3.5．C 解析：很显然a ，b 均大于1；且y ＝b x 函数图象比y ＝a x 变化趋势小，故b ＜a ，综上所述，a ＞b ＞1.6．B7．解：f (3)＝f (3＋1)＝f (4)＝⎝⎛⎭⎫124＝116. 8．(－∞，－2)∪(2，＋∞)9．(0,3] 解析：设y ＝⎝⎛⎭⎫13u ，u ＝x 2－2x ，∵函数y ＝⎝⎛⎭⎫13u 是单调减函数，∴函数y ＝f (x )与u ＝x 2－2x 增减性相反．∵u 有最小值－1，无最大值，∴y 有最大值⎝⎛⎭⎫13－1＝3，无最小值．又由指数函数值域y >0知所求函数的值域为(0,3]．10．(1)解：∵f (x )的定义域是R ，且f (－x )＝10－x －10x10－x ＋10x＝－f (x )，∴f (x )是奇函数．(2)证法一：f (x )＝10x －10－x 10x ＋10－x ＝102x －1102x＋1＝1－2102x ＋1. 令x 2＞x 1，则f (x 2)－f (x 1)＝2221101x ⎛⎫- ⎪+⎝⎭－1221101x ⎛⎫- ⎪+⎝⎭＝212122222(1010)(101)(101)x x x x ⨯-++， ∵y ＝10x 为增函数，∴当x 2＞x 1时，2210x －1210x ＞0. 又∵1210x ＋1＞0,2210x ＋1＞0，故当x 2＞x 1时，f (x 2)－f (x 1)＞0，即f (x 2)＞f (x 1)． ∴f (x )是增函数．证法二：考虑复合函数的增减性．由f (x )＝10x －10－x 10x ＋10－x ＝1－2102x＋1. ∵y ＝10x 为增函数，∴y ＝102x ＋1为增函数，y ＝2102x ＋1为减函数，y ＝－2102x ＋1为增函数，y ＝1－2102x ＋1为增函数．∴f (x )＝10x －10－x10x ＋10－x在定义域内是增函数．(3)解：令y ＝f (x )．由y ＝102x －1102x ＋1，解得102x ＝1＋y1－y.∵102x ＞0，∴1＋y1－y＞0，解得－1＜y ＜1.即f (x )的值域为(－1,1)．2．2 对数函数2．2.1 对数与对数运算 1．C 2.B 3.B 4.A5．A 解析：令e x ＝t ，则x ＝ln t ，∴f (t )＝ln t .∴f (e)＝lne ＝1. 6．B 解析：log 2a ＝0，∴a ＝1.从而b ＝0，P ∪Q ＝{3,0,1}． 7．解：(1)由题意知⎩⎪⎨⎪⎧x ＋2>0，x －1>0，x －1≠1，解得x >1，且x ≠2.故x 的取值范围为(1,2)∪(2，＋∞)．(2)由题意知⎩⎪⎨⎪⎧x ＋3>0，x ＋3≠1，解得x >－3，且x ≠－2.故x 的取值范围为(－3，－2)∪(－2，＋∞)．8．－2 解析：∵x ＝－2<0，∴f (－2)＝10－2＝1100>0，∴f (10－2)＝lg10－2＝－2，即f [f (－2)]＝－2.9．3 解析：(a 23)32＝⎣⎡⎦⎤⎝⎛⎭⎫23232⇒a ＝⎝⎛⎭⎫233⇒log 23a ＝log 23⎝⎛⎭⎫233＝3. 10．解：(1)令log 2x ＝t ，则2t＝x .因为f (log 2x )＝x ，所以f (t )＝2t .所以f ⎝⎛⎭⎫12＝212＝ 2.(2)因为log 2[log 3(log 4x )]＝0，所以log 3(log 4x )＝1.所以log 4x ＝3，所以x ＝43＝64. 又因为log 3[log 4(log 2y )]＝0. 所以log 4(log 2y )＝1.所以log 2y ＝4.所以y ＝24＝16. 所以x ＋y ＝64＋16＝80.2．2.2 对数的性质及其应用 1．A 2.B 3.B4．B 解析：方法一：原式＝lg 10023－lg 1024＋lg 12＝lg100－lg23－lg10＋lg24＋lg1－lg2 ＝lg102－3lg2－1＋4lg2－lg2＝2－1＝1.方法二：原式＝lg 12.5×1258＝lg10＝1.5．D6．A 解析：∵1a ＋1b＝log m 2＋log m 5＝log m 10＝2，∴m 2＝10.又∵m >0，∴m ＝10.7．解：原式＝lg2·lg 1022＋lg 210·lg(22×10)＝lg2(1－2lg2)＋(lg2－1)(2lg2＋1)＝lg2－2(lg2)2＋2(lg2)2－2lg2＋lg2－1＝－1.8.2b ＋1－a 2a ＋b 解析：log 1245＝lg45lg12＝2lg3＋lg52lg2＋lg3＝2b ＋1－a2a ＋b.9．解：由log 83＝p ，得 lg3lg8＝p ，即lg3＝3lg2·p . ① 由log 35＝q ，得lg5lg3＝q ，即1－lg2＝lg3·q . ②①代入②中，得1－lg2＝3lg2·pq . ∴(3pq ＋1)lg2＝1.∵3pq ＋1≠0，∴lg2＝13pq ＋1.10．解：∵lg a 和lg b 是关于x 的方程x 2－x ＋m ＝0的两个根， ∴lg a ＋lg b ＝1， ① lg a ·lg b ＝m . ②∵关于x 的方程x 2－(lg a )x －(1＋lg a )＝0有两个相等的实根，∴Δ＝(lg a )2＋4(1＋lg a )＝0.∴lg a ＝－2，即a ＝1100.将lg a ＝－2代入①，得lg b ＝3.∴b ＝1000.再将lg a ＝－2，lg b ＝3代入②，得m ＝－6.综上所述，a ＝1100，b ＝1000，m ＝－6.2．2.3 对数函数及其性质(1)1．D 解析：由log 2a <0，得0<a <1.由⎝⎛⎭⎫12b>1，得b <0.故选D. 2．D3．A 解析：y ＝log 12x ＝－log 2x . 4．A 解析：由⎩⎪⎨⎪⎧log 0.5(4x －3)>0，4x －3>0，解得34<x <1.5．D6．B 解析：y ＝log a (－x )与y ＝log a x 关于y 轴对称． 7．a ＝2，b ＝2 8．D9．D 解析：∵log 45>1,0<log 54<1,0<log 53<1， ∴(log 53)2<log 54<log 45.∴b <a <c .故选D.10．解：(1)由kx －1x －1>0，得(kx －1)(x －1)>0.又∵k >0，∴⎝⎛⎭⎫x －1k (x －1)>0. 当k ＝1时，函数f (x )的定义域为{x |x ≠1}；由0<k <1时，函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x <1或x >1k ，当k >1时，函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x <1k 或x >1. (2)f (x )＝ln k (x －1)＋k －1x －1＝ln ⎝ ⎛⎭⎪⎫k ＋k －1x －1，∵函数f (x )在区间[10，＋∞)上是增函数，∴k －1<0，即k <1.又由10k －110－1>0，得k >110.综上所述，实数k 的取值范围为110<k <1.2．2.4 对数函数及其性质(2) 1．D 2.C 3.A4．B 解析：∵a ＝log 23.6>log 22＝1.又∵y ＝log 4x ，x ∈(0，＋∞)为单调递增函数， ∴log 43.2<log 43.6<log 44＝1，∴b <c <a . 5．C6．C 解析：由log a 23＜1＝log a a ，得(1)当0＜a ＜1时，由y ＝log a x 是减函数，得0＜a ＜23；(2)当a ＞1时，由y ＝log a x 是增函数，得a ＞23，∴a ＞1.综合(1)(2)，得0＜a ＜23或a ＞1.7．D 解析：f (x )的定义域为(－1,1)，且对定义域内任意x ，f (－x )＝lg 1－x 1＋x ＝lg ⎝ ⎛⎭⎪⎫1＋x 1－x －1＝－lg 1＋x 1－x＝－f (x )；又可以验证f ⎝⎛⎭⎫－12≠f ⎝⎛⎭⎫12，因此，f (x )是奇函数但不是偶函数．用同样的方法可有：y ＝x 3＋1既不是奇函数又不是偶函数；y ＝e 0－1e 0＋1＝0(x ∈R )既是奇函数又是偶函数；y ＝|2x ＋1|＋|2x －1|是偶函数而不是奇函数，只有y ＝12x －1＋12是奇函数但不是偶函数．故选D.8.⎝⎛⎦⎤－1，32 解析：令u (x )＝4＋3x －x 2，又∵4＋3x －x 2＞0⇒x 2－3x －4＜0，解得－1＜x ＜4.又u (x )＝－x 2＋3x ＋4＝－⎝⎛⎭⎫x －322＋254，对称轴为x ＝32，开口向下的抛物线；u (x )在⎝⎛⎦⎤－1， 32上是增函数，在⎝⎛⎭⎫32，4上是减函数，又y ＝ln u (x )是定义域上的增函数，根据复合函数的单调性，y ＝ln(4＋3x －x 2)在⎝⎛⎦⎤－1， 32上是增函数． 9．②③10．(1)解：∵f (x )是奇函数，∴f (－x )＝－f (x )．∴log 121＋ax －x －1＝－log 121－ax x －1⇔1＋ax －x －1＝x －11－ax ＞0⇒1－a 2x 2＝1－x 2⇒a ＝±1.检验a ＝1(舍)，∴a ＝－1.(2)证明：任取x 1＞x 2＞1，∴x 1－1＞x 2－1＞0.∴0＜2x 1－1＜2x 2－1⇒0＜1＋2x 1－1＜1＋2x 2－1⇒0＜x 1＋1x 1－1＜x 2＋1x 2－1⇒log 12x 1＋1x 1－1＞log 12x 2＋1x 2－1，即f (x 1)＞f (x 2)．∴f (x )在(1，＋∞)内单调递增．(3)解：f (x )－⎝⎛⎭⎫12x＞m 恒成立．令g (x )＝f (x )－⎝⎛⎭⎫12x.只需g (x )min ＞m ，用定义可以证g (x )在[3,4]上是增函数，∴g (x )min ＝g (3)＝－98.∴当m ＜－98时原式恒成立．2．2.5 对数函数及其性质(3)1．D 解析：c ＝⎝⎛⎭⎫120.3>0，a ＝log 132<0，b ＝log 123<0，并且log 132>log 133，所以c >a >b .2．C 解析：y ＝3x －2的图象向左平移2个单位得到y ＝3x的图象，其反函数为y ＝log 3x . 3．B 4.B 5.B 6.D 7.A 8．C 解析：将A 项函数沿着直线y ＝x 对折即可得到函数y ＝log 2x .将B 沿着x 轴对折，将D 向下平移1个单位再沿x 轴对折即可．9.22提示：利用奇函数的定义或f (0)＝0. 10．解：(1)要使函数有意义，则有⎩⎪⎨⎪⎧1－x >0，x ＋3>0，解得－3<x <1.所以函数f (x )的定义域为(－3,1)．(2)函数可化为f (x )＝log a (1－x )(x ＋3)＝log a (－x 2－2x ＋3)，由f (x )＝0，得－x 2－2x ＋3＝1，即x 2＋2x －2＝0，x ＝－1±3. ∵－1±3∈(－3,1)，∴方程f (x )＝0的解为－1±3.(3)函数可化为f (x )＝log a (－x 2－2x ＋3) ＝log a [－(x ＋1)2＋4]，∵－3<x <1，∴0<－(x ＋1)2＋4≤4.∵0<a <1，∴log a [－(x ＋1)2＋4]≥log a 4，即f (x )min ＝log a 4.由log a 4＝－4，得a －4＝4.∴a ＝4－14＝22.2．3 幂函数 1．C 2.A3．C 解析：设f (x )＝x α，则有2α＝22，解得α＝－12，即f (x )＝x 12-，所以f (4)＝412-＝12. 4．A 5.B 6.B7．解：⎩⎪⎨⎪⎧m 2－3m ＋3＝1，m 2－m －2≤0，解得m ＝1或m ＝2.8．(1)②④ (2)①⑤⑧⑨9．依次是E ，C ，A ，G ，B ，D ，H ，F10．解：(1)若f (x )是幂函数，故m 2－m －1＝1，即m 2－m －2＝0.解得m ＝2或m ＝－1.(2)若f (x )是幂函数且又是(0，＋∞)上的增函数，则⎩⎪⎨⎪⎧m 2－m －1＝1，－5m －3>0.所以m ＝－1. (3)若f (x )是正比例函数，则－5m －3＝1，解得m ＝－45.此时m 2－m －1≠0，故m ＝－45.(4)若f (x )是反比例函数，则－5m －3＝－1，则m ＝－25，此时m 2－m －1≠0，故m ＝－25.(5)若f (x )是二次函数，则－5m －3＝2，即m ＝－1，此时m 2－m －1≠0，故m ＝－1. 综上所述，当m ＝2或m ＝－1时，f (x )是幂函数；当m ＝－1时，f (x )既是幂函数，又是(0，＋∞)上的增函数；当m ＝－45时，f (x )是正比例函数；当m ＝－25时，f (x )是反比例函数；当m ＝－1时，f (x )是二次函数．。

人教B版数学高一版必修1教材习题点拨第三章基本初等函数(Ⅰ)

教材习题点拨思考与交流 1．略2．注意(n a )n 和na n (n ＞1且n ∈N ＋)的区别．①(n a )n 中：当n 为大于1的奇数时，na 对任意的a ∈R 都有意义，它表示a 在实数范围内有唯一的一个n 次方根，即(na )n ＝a ；当n 是大于1的偶数时，n a 只有当a ≥0时才有意义，a ＜0时无意义，na (a ≥0)表示a 在实数范围内的一个n 次方根，(na )n ＝a .②式子n a n 对任意a ∈R 都有意义，当n 为奇数时，n a n ＝a ；当n 为偶数时，na n ＝|a |＝⎩⎪⎨⎪⎧a (a ≥0)，－a (a <0). 3．幂的运算法则是①a m ·a n ＝a m ＋n ；②a m ÷a n ＝a m －n ；③(a m )n ＝a mn ；④(ab )m ＝a m ·b m . 4．对数恒等式：log =a bab .证明：设a N ＝b ，由对数的意义得log a b ＝N ，两边取以a 为底的指数得a log a b ＝a N ＝b ，所以log =a ba b .对数的运算法则．①log a (MN )＝log a M ＋log a N (a ＞0，a ≠1，M ＞0，N ＞0)．证明：设log a M ＝p ，log a N ＝q .由对数的定义可知：M ＝a p ，N ＝a q ， ∴MN ＝a p ·a q ＝a p ＋q ，∴log a (MN )＝log a a p ＋q ＝p ＋q ＝log a M ＋log a N . ②log a ⎝⎛⎭⎫M N ＝log a M －log a N (a ＞0，a ≠1，M ＞0，N ＞0)．证明：设log a M ＝p ，log a N ＝q . 由对数的定义得M ＝a p ，N ＝a q ， ∴M N ＝a p aq ＝a p －q . ∴log a M N ＝log a a p －q ＝p －q ＝log a M －log a N ，③log a M n ＝n log a M (a ＞0，a ≠1，M ＞0，n ∈R )．证明：设log a M ＝p ，由对数定义知M ＝a p ， ∴M n ＝(a p )n ＝a np ，∴log a M n ＝log a a np ＝np ＝n ·log a M .④log a nM ＝1nlog a M (a ＞0，a ≠1，M ＞0，n ∈R )．证明：设log a M ＝p ，由对数定义可得M ＝a p，∴11=()=p p nnnM a a ，∴log a nM ＝log p na a ＝p n ＝1nlog a M .5．常用对数是以10为底的对数，自然对数是以e ＝2.718 28…为底的对数，换底公式为log a b ＝log c blog c a(a ＞0，a ≠1，b ＞0，c ＞0，c ≠1)，作用略，合理即可．6．对数函数与指数函数性质对照表.7．略 8．略 9．略巩固与提高1．(1)4；(2)27；(3)(0,1)；(4)(1,0)； (5)(1,1)；(6)－2； (7)4313⎛⎫ ⎪⎝⎭；(8)0.778 1； (9){x |1＜x ≤2}；(10)2.2．解：(1)5×325×625＝221221362362555=5=55++⨯⨯(2)log 32×log 25×log 53＝lg2lg3×lg5lg2×lg3lg5＝1.(3)log 2⎝⎛⎭⎫log 232－log 234＋log 26＝log 2(log 2256)＝log 28＝3. 3．解：(1)121=8x y -有意义，需2x －1≠0，即x ≠12，即定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ∈R 且x ≠12. (2)y ＝1－⎝⎛⎭⎫12x有意义，需1－⎝⎛⎭⎫12x ≥0，所以定义域为[0，＋∞)．(3)函数y ＝log a (2－x )(a ＞0，且a ≠1)有意义，需2－x ＞0，所以定义域为(－∞，2)．(4)函数y ＝log a (1＋x )2(a ＞0，且a ≠1)有意义，需1＋x ≠0，所以定义域为{x |x ∈R ，且x ≠－1}． 4．5．解：函数f (x )＝log 2(－x )与g (x )＝x ＋1的图象如图所示．由图象可知f (x )＜g (x )的解为－1＜x ＜0.6．证明：函数f (x )的定义域为R . 又f (－x )＝a －x －a x 2＝－a x －a －x2＝－f (x )， ∴f (x )为奇函数．7．解：∵f (x )的定义域为[1,3]，又函数为f (lg x )，∴1≤lg x ≤3，即10≤x ≤1 000，则f (lg x )的定义域为[10,1 000]． 8．解：设这9年的平均增长率为x ，则800.05＝60.24(1＋x )9， (1＋x )9＝800.0560.24＝13.281 0，两边取常用对数，得9lg(1＋x )＝lg 13.281 0， ∴9lg(1＋x )≈1.123 2，则lg(1＋x )＝0.124 8， ∴1＋x ＝1.332 907，则x ＝0.332 907≈33.3%. ∴年平均增长率为33.3%. 9．解：当A 1＝100时，11lg lg 2521=10A R ＝25A 1＝250；当A 2＝156.25时，R 2＝25A 2＝312.5；当A 3＝169时，R 3＝25A 3＝325. ∴R 1＜R 2＜R 3.10．略 11．略自测与评估1．(1)B (2)B 解析：(1)∵(lg 8－1)2＝1－lg 8，故选B. (2)∵12=a b (a ＞0且a ≠1)， ∴log a b ＝12，即2log a b ＝1.故选B.2．证明：(1)f (a )·f (b )＝3a ·3b ＝3a ＋b ＝f (a ＋b )． (2)f (a )÷f (b )＝3a ÷3b ＝3a －b ＝f (a －b )． 3．解：函数f (x )的定义域为{x |x ∈R 且x ≠0}， f (－x )＝(a －x ＋1)(－x )a －x －1＝⎝⎛⎭⎫1a x ＋1(－x )1a x－1＝(1＋a x )(－x )1－a x ＝(a x ＋1)x a x －1＝f (x )，所以f (x )为偶函数．4．解：(1)∵2＞1，且2m ＜2n ，∴m ＜n . (2)∵0.2＜1且log 0.2m ＞log 0.2n ， ∴m ＜n .(3)∴a m ＜a n (0＜a ＜1)，∴m ＞n . (4)∵log a m ＞log a n (a ＞1)，∴m ＞n .5．解：由log 2[log 3(log 4x )]＝0得log 3(log 4x )＝1，即log 4x ＝3， ∴x ＝43＝64；由log 3[log 4(log 2y )]＝0得log 4(log 2y )＝1，即log 2y ＝4， ∴y ＝24＝16. ∴x ＋y ＝64＋16＝80.6．解：∵f (lg x )的定义域为[0.1,100]，即0.1≤x ≤100， ∴－1≤lg x ≤2，则f (x )的定义域为[－1,2]．由－1≤x2≤2，得－2≤x ≤4，∴f ⎝⎛⎭⎫x 2的定义域为[－2,4]．7．解：当x 0≤0时，2－x 0－1＞1，即022x >－－，∴－x 0＞1，从而x 0＜－1；当x 0＞0时，120>1x ，从而x 0＞1.综上知x 0＜－1或x 0＞1.图象如图所示．8．解：取得银行利息金额＝3×5 000× 2.7%＝405(元)，应纳税金额＝405×20%＝81(元)，实际取出金额＝5 000＋405－81＝5 324(元)．。

必修一基本初等函数练习题(含详细答案解析)

必修一基本初等函数练习题（含详细答案解析）一、选择题1．对数式log32－(2＋3)的值是()．A．－1 B．0 C．1 D．不存在1．A解析：log32－(2＋3)＝log32－(2－3)－1，故选A．2．当a＞1时，在同一坐标系中，函数y＝a－x与y＝log a x的图象是()．A B C D2．A解析：当a＞1时，y＝log a x单调递增，y＝a－x单调递减，故选A．3．如果0＜a＜1，那么下列不等式中正确的是()．A．(1－a)31＞(1－a)21B．log1－a(1＋a)＞0C．(1－a)3＞(1＋a)2D．(1－a)1+a＞13．A解析：取特殊值a＝21，可立否选项B，C，D，所以正确选项是A．4．函数y＝log a x，y＝log b x，y＝log c x，y＝log d x的图象如图所示，则a，b，c，d的大小顺序是()．A．1＜d＜c＜a＜bB．c＜d＜1＜a＜bC．c＜d＜1＜b＜aD．d＜c＜1＜a＜b4．B解析：画出直线y＝1与四个函数图象的交点，它们的横坐标的值，分别为a，b，c，d的值，由图形可得正确结果为B．(第4题)5．已知f (x 6)＝log 2 x ，那么f (8)等于( )． A ．34 B ．8 C ．18 D ．21 5．D6．如果函数f (x )＝x 2－(a －1)x ＋5在区间⎪⎭⎫⎝⎛121 ，上是减函数，那么实数a 的取值范围是( )．A ． a ≤2B ．a ＞3C ．2≤a ≤3D ．a ≥36．D7．函数f (x )＝2－x －1的定义域、值域是( )． A ．定义域是R ，值域是RB ．定义域是R ，值域为(0，＋∞)C ．定义域是R ，值域是(－1，＋∞)D ．定义域是(0，＋∞)，值域为R7．C＋∞)．8．已知－1＜a ＜0，则( )．A ．(0.2)a ＜a⎪⎭⎫⎝⎛21＜2aB ．2a ＜a⎪⎭⎫⎝⎛21＜(0.2)aC ．2a ＜(0.2)a ＜a⎪⎭⎫⎝⎛21D ．a⎪⎭⎫⎝⎛21＜(0.2)a ＜2a8．B9．已知函数f (x )＝⎩⎨⎧+-1 log 1≤413＞，，)(x x x a x a a是(－∞，＋∞)上的减函数，那么a 的取值范围是( )．A ．(0，1)B ．⎪⎭⎫ ⎝⎛310，C ．⎪⎭⎫⎢⎣⎡3171，D ．⎪⎭⎫⎢⎣⎡171，9．C解析：由f (x )在R 上是减函数，∴ f (x )在(1，＋∞)上单减，由对数函数单调性，即0上是减函数，为了满足单调区间的定义，f (x )在(－∞，1］上的最小值7a －1要大于等于f (x )在［1，＋∞)上的最大值0，才能保证f (x )在R 上是减函数．10．已知y ＝log a (2－ax )在［0，1］上是x 的减函数，则a 的取值范围是( )． A ．(0，1) B ．(1，2) C ．(0，2) D ．［2，＋∞)10．B解析：先求函数的定义域，由2－ax ＞0，有ax ＜2，因为a 是对数的底，故有a ＞0且若0＜a ＜1，当x 在［0，1］上增大时，2－ax 减小，从而log a (2－ax )增大，即函数 y ＝log a (2－ax )在［0，1］上是单调递增的，这与题意不符.若1＜a ＜2，当x 在［0，1］上增大时，2－ax 减小，从而log a (2－ax )减小，即函数 y ＝log a (2－ax )在［0，1］上是单调递减的．所以a 的取值范围应是(1，2)，故选择B ．二、填空题11．满足2－x ＞2x 的 x 的取值范围是．11．参考答案：(－∞，0)．解析：∵ －x ＞x ，∴ x ＜0．12．已知函数f (x )＝log 0.5(－x 2＋4x ＋5)，则f (3)与f (4)的大小关系为． 12．参考答案：f (3)＜f (4)．解析：∵ f (3)＝log 0.5 8，f (4)＝log 0.5 5，∴ f (3)＜f (4)． 13．64log 2log 273的值为_____．14．已知函数f (x )＝⎪⎩⎪⎨⎧，≤ ，，＞，020log 3x x x x 则⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛91f f 的值为_____．15．函数y ＝)－(34log 5.0x 的定义域为．16．已知函数f (x )＝a －121+x，若f (x )为奇函数，则a ＝________．解析：∵ f (x )为奇函数，三、解答题17．设函数f (x )＝x 2＋(lg a ＋2)x ＋lg b ，满足f (－1)＝－2，且任取x ∈R ，都有f (x )≥2x ，求实数a ，b 的值．17．参考答案：a ＝100，b ＝10．解析：由f (－1)＝－2，得1－lg a ＋lg b ＝0 ①，由f (x )≥2x ，得x 2＋x lg a ＋lg b ≥0 (x ∈R )．∴Δ＝(lg a )2－4lg b ≤0 ②．联立①②，得(1－lg b )2≤0，∴ lg b ＝1，即b ＝10，代入①，即得a ＝100．18．已知函数f (x )＝lg (ax 2＋2x ＋1) ．(1)若函数f (x )的定义域为R ，求实数a 的取值范围； (2)若函数f (x )的值域为R ，求实数a 的取值范围．18．参考答案：(1) a 的取值范围是(1，＋∞) ，(2) a 的取值范围是[0，1]．解析：(1)欲使函数f (x )的定义域为R ，只须ax 2＋2x ＋1＞0对x ∈R 恒成立，所以有⎩⎨⎧0 ＜440a －a ＞，解得a ＞1，即得a 的取值范围是(1，＋∞)； (2)欲使函数 f (x )的值域为R ，即要ax 2＋2x ＋1 能够取到(0，＋∞) 的所有值．②当a ≠0时，应有⎩⎨⎧0 ≥440a －a ＝＞Δ⇒ 0＜a ≤1．当x ∈(－∞，x 1)∪(x 2，＋∞)时满足要求(其中x 1，x 2是方程ax 2＋2x ＋1＝0的二根)．综上，a 的取值范围是[0，1]．19．求下列函数的定义域、值域、单调区间： (1)y ＝4x ＋2x +1＋1； (2)y ＝2＋3231x －x ⎪⎭⎫⎝⎛．19．参考答案：(1)定义域为R ．令t ＝2x (t ＞0)，y ＝t 2＋2t ＋1＝(t ＋1)2＞1， ∴ 值域为{y | y ＞1}．t ＝2x 的底数2＞1，故t ＝2x 在x ∈R 上单调递增；而 y ＝t 2＋2t ＋1在t ∈(0，＋∞)上单调递增，故函数y ＝4x ＋2x ＋1＋1在(－∞，＋∞)上单调递增．20．已知函数f(x)＝log a(x＋1)，g(x)＝log a(1－x)，其中a＞0，a≠1．(1)求函数f(x)－g(x)的定义域；(2)判断f(x)－g(x)的奇偶性，并说明理由；(3)求使f(x)－g(x)＞0成立的x的集合．20．参考答案：(1){x |－1＜x＜1}；(2)奇函数；(3)当0＜a＜1时，－1＜x＜0；当a＞1时，0＜x＜1．(2)设F(x)＝f(x)－g(x)，其定义域为(－1，1)，且F(－x)＝f(－x)－g(－x)＝log a(－x＋1)－log a(1＋x)＝－［log a(1＋x)－log a(1－x)］＝－F(x)，所以f(x)－g(x)是奇函数．(3)f(x)－g(x)＞0即log a(x＋1)－log a(1－x)＞0有log a(x＋1)＞log a(1－x)．。

高中数学必修1基本初等函数专项练习(附答案解析)

高中数学必修1基本初等函数专项练习一、单选题1.降雨量是气象部门观测的重要数据，日降雨量是指一天内降落在地面单位面积雨水层的深度(单位：毫米)｡我国古代就有关于降雨量测量方法的记载，古代数学名著《数书九章》中有“天池盆测雨”题：天池盆(圆台形状)盆口直径二尺八寸，盆底直径为一尺二寸，盆深一尺八寸｡若盆中积水深九寸，则平地降雨量是几寸(注：一尺等于十寸，一寸等于103厘米)?已知某隧道的积水程度与日降水量的关系如下表所示：如果某天该隧道的日降水量按照“天池盆测雨”题中数据计算，则该隧道的积水程度为（） A. 一级 B. 二级 C. 三级 D. 四级2.已知函数y=f （x ）的图象与函数y=log a x （a ＞0且a≠1）的图象关于直线y=x 对称，如果函数g （x ）=f （x ）[f （x ）﹣3a 2﹣1]（a ＞0，且a≠1）在区间[0，+∞）上是增函数，那么a 的取值范围是（）A. [0，23] B. [√33， 1） C. [1，√3] D. [32 ， +∞）3.已知幂函数 f(x)=x a 的图象经过函数 g(x)=a x−2−12 （ a >0 且 a ≠1 ）的图象所过的定点，则幂函数 f(x) 不具有的特性是（）A. 在定义域内有单调递减区间B. 图象过定点 (1,1)C. 是奇函数D. 其定义域是 R 4.“ a 3>b 3 ”是“ log 7a >log 7b ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 5.“ lna >lnb ”是“ 1a <1b ”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 6.设 a =(53)16，b=(35)−15，c=ln 23 ，则a ，b ，c 的大小关系是（）A. a ＞b ＞cB. b ＞a ＞cC. b ＞c ＞aD. a ＞c ＞b 7.已知函数 f(x)=(m 2−m −1)x m 2−4m+3是幂函数，且其图像与 y 轴没有交点，则实数 m = （）A. 或B.C. D.8.已知x ，y 为正实数，则（）A. 2lgx+lgy =2lgx +2lgyB. 2lg （x+y ）=2lgx •2lgyC. 2lgx•lgy =2lgx +2lgyD. 2lg （xy ）=2lgx •2lgy 9.下列选项正确的是（）A. log a （x+y ）=log a x+log a yB. log a x y = log a xlog ayC. （log a x ）2=2log a xD.log a x n=log a √x n10.幂函数f （x ）=（m 2﹣m ﹣1）x m 2+m −3 在x ∈（0，+∞）上是减函数，则m=（） A. ﹣1 B. 2 C. ﹣1或2 D. 1 11.以下不等式中错误的是（）A. log 50.7<log 58.1B. log 0.26>log 0.27C. log 0.15<log 1.23D. log a 4<log a 7(a >0 且 a ≠1)12.若幂函数f （x ）的图象过点（16，8），则f （x ）<f （x 2）的解集为（） A. （–∞，0）∪（1，+∞） B. （0，1） C. （–∞，0） D. （1，+∞） 13.下列各式中成立的是（）A. (mn)7=n 7m 17 B. √(−3)412=√−33 C. √x 3+y 34=(x +y)34 D. √√93=√33 14.若2a =5b =100，则下列关系中，一定成立的是（）A. 2a+2b=abB. a+b=abC. a+b=10D. ab=10 15.已知函数f （x ）=|2x ﹣a2|，其在区间[0，1]上单调递增，则a 的取值范围为（）A. [0，1]B. [﹣1，0]C. [﹣1，1]D. [﹣12 ， 12] 16.函数 f(x)=a 2x−3−5 （ a >0 且 a ≠1 ）的图象恒过点（） A. （32 ， -4） B. （32 ， -5） C. (0,1) D. (0,−5) 17.下列三个数：a=ln 32-32 ， b=lnπ﹣π，c=ln3﹣3，大小顺序正确的是（）A. a ＞c ＞bB. a ＞b ＞cC. b ＞c ＞aD. b ＞a ＞c18.对于任意实数x ，符号[x]表示x 的整数部分，即[x]是不超过x 的最大整数，例如[2]=2；[2.1]=2；[-2.2]=-3, 这个函数[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用。

人教B版高中数学必修一第三章《基本初等函数I》讲解与例题+综合测试(7份).docx

3.4函数的应用(II)QJy I (.Hl / H?S li IJHi E \ J I \ L \1.函数模型所谓数学模型是指对客观实际的特征或数量关系进行抽象概括，用形式化的数学语言表述一种数学结构.数学模型剔除了事物中一切与研究目标无木质联系的各种属性，在纯粹状态下研究数量关系和空间形式，函数就是重要的数学模型，用函数解决方程问题，使求解变得容易进行，这是数学模型间的相互转换在发挥作用.而用函数解决实际问题，则体现了数学模型是联系数学与现实世界的桥梁.本节涉及的函数模型有：⑴指数函数模型：y=G//+c(b>0, bHl, aHO),当b>\, d>0时，其增长特点是随着自变量的增大，函数值增大的速度越来越快，常形象地称为指数爆炸.(2)对数函数模型:y=mlog(l x+n(m^O f a>0, aHl),当aAl,加>0时，其增长的特点是随着自变量的增大，函数值增大的速度越来越慢.(3)帚函数模型：y=a-x n+b(a^O),其中最常见的是二次函数模型y=ax2+bx~\~c(a0), 当d>0时，其特点是随着自变量的增大，函数值先减小，后増大.在以上几种函数模型的选择与建立时，要注意函数图彖的直观运用，分析图象特点，分析变量x的范围，同时还要与实际问题结合，如取整等.【例1 — 1】据报道，全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度，设2012年的冬季冰雪覆盖面积为加，从2012年起，经过兀年后，北冰洋冬季冰雪覆盖面积)，与x的函数关系式是()A. ^=0.9550 -mB. >,=(l-O.O55O)-mC. y=0.9550_x-/?zD. y=(l-O.O55O_v)-/n解析：设每年的冰雪覆盖面积减少率为d.・・・50年内覆盖面积减少了5%,1・・・(1—a)5°=l—5%,解得0=1 — 0.9550.1 △・••从2012年起，经过x年后，冰雪覆盖面积尸加1一(1一0.95巧F二加095込答案：A【例1一2】某公司为应对金融危机的影响，拟投资100万元，有两种投资可供选择：一种是年利率1%,按单利计算，5年后收回本金和利息；另一种是年利率3%,按每年复利一次计算，5年后收回本金和利息.哪一种投资更有利？这种投资比另一种投资5年可多得利息多少元？(结果精确到0.01万元)分析：这是一个单利和复利所获得收益多少的比较问题.可先按单利和复利讣算5年后的本利和分别是多少，再通过比较作答.解：本金100万元，年利率1%,按单利计算，5年后的本利和是100X(l + l%X5) = 105(万元).本金100万元，年利率3%,按每年复利一次计算，5年后的本利和是100X(1 + 3%『a 115.93(万元).由此可见按年利率3%每年复利一次投资要比按年利率1%单利投资更有利，5年后多得利息约10.93万元.谈重点利息的计算利息分单利和复利两种.单利是只有木金牛息，利息不再牛息，而复利是把前一期的本利和作为本金再牛息，两种情况要注意区分.我国现行定期储蓄中的自动转存业务类似复利计•息的储蓄，如某人存入本金。

2022版数学人教A版必修1基础训练：第二章基本初等函数(Ⅰ)本章复习提升含解析

第二章基本初等函数(Ⅰ)本章复习提升易混易错练易错点1 利用指数、对数运算性质进行运算时忽视公式中的限定条件导致错误 1.()下列结论中正确的个数为( )①当a <0时,(a2)32=a3;②√a n n=|a |(n >0);③函数y =(x-2)12-(3x -7)0的定义域是(2,+∞);④若100a =5,10b =2,则2a +b =1. A.0 B.1 C.2 D.3 2.()计算:(1)5log 25(1-√3)2+3log 9(1+√3)2;(2)√(-8)33+√(√3-2)44-√(2-√3)33.易错点2 研究指数、对数函数时忽视对底数分0<a <1和a >1两种情况讨论导致错误 3.(2019湖北武昌实验中学高一上期中,)若log a 12<2,则a 的取值范围是( )A.(√22,+∞)B.(0,√22) C.(√22,1) D.(0,√22)∪(1,+∞)4.()若函数f (x )=a x +log a (x +1)在[0,1]上的最大值和最小值之和为a ,则a 的值为 . 5.()已知log a (2a +1)<log a (3a -1),其中a >0且a ≠1,求实数a 的取值范围.6.()已知函数f (x )=log a (8-ax )(a >0,且a ≠1).(1)若f (x )<2,求实数x 的取值范围;(2)若f (x )>1在区间[1,2]上恒成立,求实数a 的取值范围.易错点3 研究指数、对数函数时忽视定义域与值域导致错误 7.()已知f (x )是定义在R 上的奇函数,若f (x )在(0,+∞)上是增函数,且f (13)=0,则不等式f (lo g 18x )<0的解集为 ( ) A.(0,12)B.(12,+∞) C.(12,1)∪(2,+∞) D.(0,12)∪(2,+∞) 8.()若函数f (x )=log a (6-ax )在[0,2]上为减函数,则a 的取值范围是( )A.(0,1)B.(1,3)C.(1,+∞)D.[3,+∞) 9.()若函数f (x )=lo g 12(x 2-ax +3a )在区间(2,+∞)上是减函数,则a 的取值范围为( )A.(-∞,4]B.(-4,4]C.[-4,4)D.[-4,4]10.(2020山东枣庄高一上期末,)已知f (x )={3x -4,x >1,3x ,x ≤1,若a 0,且c≠1)是“减半函数”,则t的取值范围为()A.(0,1)B.(0,1]C.(-∞,18) D.(0,18)2.(2020江苏镇江高一期中,)已知函数y=f(x)是二次函数,且满足f(0)=3,f(1)=f(3)=0.(1)求y=f(x)的解析式;(2)求函数y=f(log2x),x∈[2,8]的最小值;(3)若x∈[1,t](t>1),试将y=f(x)的最小值表示成关于t的函数g(t).二、数形结合思想在解决函数问题中的应用3.()如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是()A.{x|-1<x≤0}B.{x|-1≤x≤1}C.{x|-1<x≤1}D.{x|-1<x≤2}4.()若实数a,b满足a+lg a=8,b+10b=8,则a+b=.5.()已知函数f (x )={|log 2x |,0<x ≤8,x 2-20x +99,x >8,若a ,b ,c ,d 互不相同,且a 1,若f (x )在(-∞,+∞)上单调递增,则实数a 的取值范围为 ( ) A.(1,2) B.(2,3) C.(2,3]D.(2,+∞)7.(2019浙江嘉兴一中高一上期中,)设函数f (x )=e |ln x |(e 为自然对数的底数),若x 1≠x 2且f (x 1)=f (x 2),则下列结论一定不成立的是 ( ) A.x 2 f (x 1)>1 B.x 2 f (x 1)<1C.x 2 f (x 1)=1D.x 2 f (x 1)<x 1 f (x 2)8.()设函数f (x )={21-x ,x ≤1,1-log 2x ,x >1,则满足f (x )≤2的x 的取值范围是 .四、转化与化归思想在解决函数问题中的应用 9.(2019吉林省实验中学高一上期中,)定义域为R 的函数f (x ),对任意实数x 均有f (-x )=-f (x ),f (2-x )=f (2+x )成立,若当2<x <4时,f (x )=2x -3+log 2(x -1),则f (-1)= .10.(2020山东菏泽高一上期末联考,)设函数f (x )=1ex +a e x (a 为常数),若对任意x ∈R ,f (x )≥3恒成立,则实数a 的取值范围是 . 11.()若3x =4y =36,则2x +1y= .五、特殊与一般思想在解决函数问题中的应用 12.()设f (x )为定义在R 上的奇函数.当x ≥0时, f (x )=2x +2x +b (b 为常数),则f (-1)= ( ) A.1 B.-1 C.-3 D.313. ()已知定义域为R 的函数f (x )=-2x +b2x+1+a是奇函数,求a ,b 的值.答案全解全析第二章基本初等函数(Ⅰ)本章复习提升易混易错练1.B 3.D 7.C 8.B9.D1.B ①中,当a <0时,(a 2)32=[(a 2)12]3=(-a )3=-a 3,∴①不正确;②中,若a =-2,n =3,则√(-2)33=-2≠|-2|,∴②不正确;③中,由{x -2≥0,3x -7≠0,得x ≥2且x ≠73,故其定义域为[2,73)∪(73,+∞),∴③不正确;④中,∵100a=5,即102a =5,10b =2,∴102a ×10b =102a +b =10,∴2a +b =1,∴④正确. 2.解析 (1)原式=25log 25(√3-1)+9log 9(1+√3)=√3-1+1+√3=2√3. (2)原式=-8+|√3-2|-(2-√3)=-8+2-√3-2+√3=-8.3.D 当a >1时,由log a 12<2,得log a 12<log a a 2,因此a 2>12,解得a >√22或a <-√22,又a >1,所以a >1;当0<a <1时,由log a 12<2,得log a 12<log a a 2,因此0<a 2<12,解得-√22<a <√22,且a ≠0,又0<a <1,所以0<a <√22.综上,a 的取值范围是0,√22∪(1,+∞).故选D . 易错警示由于对数函数的图象、单调性等受底数a 的影响,所以在底数未知的情况下应先讨论底数与1的大小关系,一般分0<a <1,a >1两种情况. 4.答案12解析当a >1时,y =a x 与y =log a (x +1)在[0,1]上都是增函数,因此f (x )=a x +log a (x +1)在[0,1]上是增函数,∴f (x )max =f (1)=a +log a 2,f (x )min =f (0)=a 0+log a 1=1,∴a +log a 2+1=a ,∴log a 2=-1=log a 1a ,解得a =12(舍去); 当0<a <1时,y =a x 与y =log a (x +1)在[0,1]上都是减函数,因此f (x )=a x +log a (x +1)在[0,1]上是减函数,∴f (x )max =f (0)=a 0+log a (0+1)=1, f (x )min =f (1)=a +log a 2,∴a +log a 2+1=a ,∴log a 2=-1=log a 1a ,解得a =12. 综上所述,a =12. 易错警示解决与对数函数有关的问题时需注意两点:(1)务必先研究函数的定义域;(2)注意对数自身(如真数、底数的取值)要满足的条件,特别是在研究复合函数的单调性时,除了按照“同增异减”的规律讨论之外,还要特别注意真数大于零. 5.解析当a >1时,原不等式等价于{2a +1<3a -1,2a +1>0,3a -1>0,所以a >2;当0<a <1时,原不等式等价于{2a +1>3a -1,3a -1>0,2a +1>0,所以13<a <1. 综上所述,a 的取值范围是13,1∪(2,+∞). 6.解析 (1)当a >1时,由f (x )<2,即log a (8-ax )<log a a 2,得0<8-ax <a 2,所以8a -a <x <8a; 当0<a <1时,由f (x )<2=log a a 2,得8-ax >a 2,所以x <8a-a. 因此当a >1时,x 的取值范围是{x|8a -a <x <8a}; 当0<a <1时,x 的取值范围是{x|x <8a-a}. (2)当a >1时,f (x )=log a (8-ax )在[1,2]上是减函数,由f (x )>1在区间[1,2]上恒成立,得f (x )min =log a (8-2a )>1,且在x ∈[1,2]上8-ax >0,即log a (8-2a )>log a a ,且8-2a >0,解得1<a <83. 当0<a <1时,f (x )=log a (8-ax )在[1,2]上是增函数,由f (x )>1在区间[1,2]上恒成立,得f (x )min =log a (8-a )>1,且在x ∈[1,2]上8-ax >0,即log a (8-a )>log a a ,且8-2a >0,所以a >4,且a <4,故a 不存在. 综上可知,实数a 的取值范围是1,83.7.C ∵f (x )是定义在R 上的奇函数,且在(0,+∞)上是增函数,f (13)=0,∴f (x )在(-∞,0)上也为增函数,f (-13)=0.画出f (x )的大致图象如图所示.结合图象,由f (lo g 18x )<0,可得0<lo g 18x <13或lo g 18x <-13,解得12<x <1或x >2,即不等式f (lo g 18x )<0的解集为(12,1)∪(2,+∞).8.B 设u =6-ax ,则函数f (x )由y =log a u ,u =6-ax 复合而成.因为a >0,所以u =6-ax 是减函数,那么函数y =log a u 就是增函数,所以a >1.因为[0,2]为定义域的子集,且u =6-ax 是减函数,所以当x =2时,u =6-ax 取得最小值,所以6-2a >0,解得a <3. 综上,得1<a <3,故选B . 9.D 设u =x 2-ax +3a ,则函数f (x )由y =lo g 12u ,u =x 2-ax +3a 复合而成.因为y =lo g 12u 是减函数,所以u =x 2-ax +3a 在(2,+∞)上单调递增, 从而a 2≤2,解得a ≤4. 又当x ∈(2,+∞)时,u =x 2-ax +3a >0, 所以当x =2时,u =4-2a +3a ≥0, 解得a ≥-4.所以-4≤a ≤4.故选D . 易错警示f (x )在(2,+∞)上为减函数,既要考虑单调性,又要考虑f (x )在(2,+∞)上有意义,解题时注意对数的真数大于0. 10.答案 (-∞,8]解析依题意,得a ≤1<b ,由f (a )=f (b ),得3a =3b -4,即3b =3a +4. 设S =a +3b =a +3a +4.∵函数S =a +3a +4在(-∞,1]上单调递增, ∴S ≤1+31+4=8,∴S 的取值范围是(-∞,8].思想方法练1.D 3.C 6.C 7.B 12.C1.D 显然f (x )是定义域上的单调递增函数,因此,若f (x )是“减半函数”,则{f (a )=a2,f (b )=b 2,即f (x )=x2有两个不等实根.故根据函数的性质构建关于a ,b 的方程组. log c (2c x+t )=x2,即2c x+t =c x2.令c x2=u ,则u >0,且2u 2-u +t =0.依题意知方程有两个不等正根,换元后构造关于u 的一元二次方程,根据方程根的情况,应用“三个二次”的关系求解. ∴{Δ=1-4×2×t >0,t 2>0,解得0<t <18,故选D . 2.解析 (1)设函数f (x )的解析式为f (x )=ax 2+bx +c (a ≠0),设出函数f (x )=ax 2+bx +c (a ≠0),根据题意,用待定系数法求出函数的解析式. 因为f (0)=c =3,所以f (x )=ax 2+bx +3, 又f (1)=f (3)=0,所以{a +b +3=0,9a +3b +3=0,解得{a =1,b =-4.所以f (x )=x 2-4x +3.(2)令t =log 2x ,∵x ∈[2,8],∴t ∈[1,3]. 则y =t 2-4t +3=(t -2)2-1,t ∈[1,3],用换元法,令t =log 2x ,构造二次函数求最值. 所以当t =2,即x =4时,y min =-1.所以函数y =f (log 2x ),x ∈[2,8]的最小值为-1. (3)f (x )=x 2-4x +3,x ∈[1,t ](t >1),定轴动区间问题,讨论区间端点t 与对称轴的相对位置. ①当1<t ≤2时,f (x )在[1,t ]上单调递减, 所以当x =t 时,f (x )有最小值t 2-4t +3;②当t >2时,f (x )在[1,2]上单调递减,在[2,t ]上单调递增, 所以当x =2时,f (x )有最小值-1,即此时g (t )=-1.综上,g (t )={t 2-4t +3,1<t ≤2,-1,t >2.3.C 作出函数y =log 2(x +1)的图象,如图所示.借助函数的图象求解不等式.在已有折线图中画出函数y =log 2(x +1)的图象,求出交点,以交点为分界点分析不等式的解集.结合图象得,BC 所在直线的解析式为y =-x +2,由{y =-x +2,y =log2(x +1),得{x =1,y =1, ∴不等式f (x )≥log 2(x +1)的解集为{x |-1<x ≤1}.4.答案 8解析依题意得lg a =8-a ,10b =8-b ,在同一平面直角坐标系内作出函数y =lg x ,y =10x ,y =8-x ,y =x 的图象,如图所示.由图可知,A ,B 的横坐标即为a ,b.由y =lg x 与y =10x 互为反函数知,交点A ,B 关于直线y =x 对称,故a +b =8.作出函数图象,把满足等式的a ,b 转化为函数图象交点的横坐标,结合互为反函数的图象的对称性分析坐标之间的关系. 5.答案 (96,99)解析画出函数y =f (x )和y =t 的图象,如图所示.设a ,b ,c ,d 分别为y =f (x )的图象与直线y =t 交点的横坐标.画出函数y =f (x )与y =t 的图象,问题转化为有四个交点时,横坐标乘积的范围,结合图象利用函数的性质解决该问题.由图可知,|log 2a |=-log 2a =log 2b ,即a ·b =1,c+d 2=10,且8<c <9,所以abcd =cd =c (20-c ).令g (c )=c (20-c ),8<c <9,因为函数g (c )的图象开口向下,对称轴方程为c =10,所以g (c )在(8,9)上单调递增,g (8)<g (c )<g (9),所以g (c )∈(96,99),即abcd 的取值范围是(96,99). 6.C 因为f (x )在(-∞,+∞)上单调递增,所以{a -2>0,a >1,a -2-1≤0,故2<a ≤3.所以a 的取值范围为(2,3].根据参数a 的不同,分析各段函数的单调性,根据整个函数的单调性,分析各段函数端点处函数值之间的关系. 7.B 由题知, f (x )=e |ln x |={x ,x ≥1,1x,0<x <1.按照自变量x 的不同取值范围把f (x )化为分段函数.由x ≥1时, f (x )=x 是增函数,0<x <1时,f (x )=1x 是减函数知,0<x 1<1≤x 2或0<x 2<1≤x 1. 分析分段函数的单调性,从而确定x 1,x 2分别在两个区间内. 当0<x 1<1≤x 2时, f (x 1)=1x 1, f (x 2)=x 2, ∴x 1x 2=1,∴x 2·f (x 1)=x 2x 1>1,x 1·f (x 2)=x 1·x 2=1,从而x 2 f (x 1)>x 1 f (x 2).此时A 成立. 当0<x 2<1≤x 1时, f (x 2)=1x 2, f (x 1)=x 1, ∴x 1x 2=1,∴x 2 f (x 1)=x 2·x 1=1,x 1·f (x 2)=x 1x 2>1, 从而x 2 f (x 1)<x 1 f (x 2).此时C 、D 成立. 因此无论何种情况,B 一定不成立,故选B . 8.答案 [0,+∞)解析当x ≤1时,令f (x )≤2,即21-x ≤2,解得x ≥0,所以0≤x ≤1; 当x >1时,令f (x )≤2,即1-log 2x ≤2,解得x ≥12,所以x >1. 综上,x 的取值范围是[0,+∞). 9.答案 -2解析由题意得,f (-1)=-f (1)=-f (2-1)=-f (2+1)=-f (3)=-[23-3+log 2(3-1)]=-(20+log 22)=-2.要想利用已知式求值,必须把自变量转化为区间(2,4)内的数. 10.答案94,+∞解析 f (x )≥3⇔1e x +a e x ≥3⇔a ≥3e x -1(e x )2.将含参的恒成立问题通过变形转化为有关参数的不等式问题.令t =1e x ,则t >0,则a ≥3t -t 2,①设g (t )=-t 2+3t =-t -322+94,t >0, 则当t =32时,g (t )max =94. 又不等式①恒成立,∴a ≥94, 把参数满足的不等式转化为函数最值问题.故a 的取值范围是94,+∞. 11.答案 1解析已知3x =4y =36,取以6为底的对数,将指数式化为对数式,得x log 63=y log 64=2, 应用指数与对数关系将指数式转化为对数式.∴2x =log 63,2y=log 64, 即1y =log 62,故2x +1y=log 63+log 62=1. 12.C 由f (x )是定义在R 上的奇函数知, f (0)=20+0+b =0,解得b =-1, 应用定义在R 上的奇函数的性质:f (0)=0,求b. ∴f (-1)=-f (1)=-(21+2-1)=-3,故选C .13.解析因为f (x )是定义在R 上的奇函数,所以f (0)=0,即-1+b2+a =0,解得b =1,所以f (x )=-2x +12x+1+a .由-f (x )=f (-x ),知--2x +12x+1+a =-2-x+12-x+1+a ,化简,得2x +1+a =2+a ·2x ,即(a -2)(2x -1)=0.由(a -2)(2x -1)=0对任意x ∈R 都成立,得a =2.故a =2,b =1.思维升华在处理函数奇偶性问题时,遇到定义域为R 的奇函数,应用性质f (0)=0,可以快速找到解决问题的突破口,使复杂的问题简单化.。