高中数学必修五模块综合测试-人教B版
人教B版人教B版高中数学必修五必修模块5测试样题B版答案及评分参考.docx
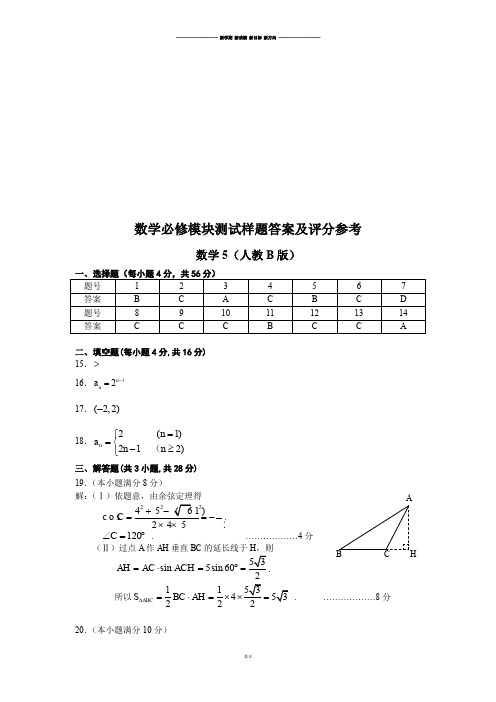
数学必修模块测试样题答案及评分参考数学5(人教B 版)一、选择题(每小题4分,共56分)题号 1 2 3 4 5 6 7 答案 B C A C B C D 题号 8 9 10 11 12 13 14 答案CCCBCCA二、填空题(每小题4分,共16分) 15.> 16.12n n a -= 17.(2,2)-18. 2(1)2 1 2)n n a n n =⎧=⎨-≥⎩(三、解答题(共3小题,共28分) 19.(本小题满分8分) 解:(Ⅰ)依题意,由余弦定理得22245(61)1c o s2452C +-==-⨯⨯. 120C ∠=︒ . ………………4分(Ⅱ)过点A 作AH 垂直BC 的延长线于H ,则53sin 5sin 602AH AC ACH =⋅=︒=. 所以1153453222ABCS BC AH ∆=⋅=⨯⨯= . ………………8分20.(本小题满分10分)B C AH解:设水池底面的长为x 米,则宽为48003x米,易知0x >,又设水池总造价为y 元. 根据题意,有48001600150120(2323)3y x x=⨯+⨯+⨯⨯ 1600240000720()x x=++16002400007202x x≥+⨯⋅ 297600=. 当1600,x x=即40x =时,等号成立. 所以,将水池的底面设计成边长为40米的正方形时,总造价最低,最低总造价为297600元..………………10分21.(本小题满分10分) 解:(Ⅰ)答案如图所示:………………3分 (Ⅱ)易知,后一个图形中的着色三角形个数是前一个的3倍,所以,着色三角形的个数的通项公式为:13n n b -=. ………………6分(Ⅲ)由题意知(1)2n n n a +=,11(1)23231n n n n n c n n --+⨯⨯=⋅+=, 所以 01113233n n S n -=⋅+⋅++⋅ ①12131323(1)33n n n S n n -=⋅+⋅++-⋅+⋅ ② ①-②得 0112(333)3n n n S n --=+++-⋅2n S -=13313nn n --⋅-. 即 (21)31()4n n n S n -+=∈N + . ………………10分。
高中数学人教B版必修五 模块综合测评2

模块综合测评(二)(时间分钟,满分分)一、选择题(本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的).数列,…的通项可能是()..+.--【解析】取=时,=,排除、,取=时,=,排除.【答案】.不等式-->的解集是().{≤-或≥}.{<-或>}.{<<}.{-≤≤}【解析】不等式化为-->,所以(-)(+)>,所以<-或>.【答案】.在正项等比数列{}中,和为方程-+=的两根,则··等于()...【解析】∵{}是等比数列且由题意得·==(>),∴··==.【答案】.下列不等式一定成立的是().> (>).+)≥(≠π,∈).+≥(∈)>(∈)【解析】.在△中,角,,的对边分别为,,,=,且=,则△的面积等于().【解析】∵=,∴由正弦定理得=,∴=.∵=,∴△的面积==××=,故选.【答案】.等比数列{}前项的积为,若是一个确定的常数,那么数列,,,中也是常数的项是() 【导学号:】...【解析】由等比数列的性质得===,而=,故为常数.【答案】.已知不等式--<的解集为,不等式+-<的解集为,不等式++<的解集是∩,那么+等于().-..-【解析】由题意:={-<<},={-<<},∩={-<<},由根与系数的关系可知:=-,=-,∴+=-.【答案】.古诗云:远望巍巍塔七层,红光点点倍加增.共灯三百八十一,请问尖头。
人教B版人教B版高中数学必修五必修5综合测试.docx

高中数学学习材料马鸣风萧萧*整理制作必修5综合测试(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在下列四个选项中,只有一项是符合题意的)1.已知集合M={x|x(x-1)3≥0},N={y|y=3x2+1,x∈R},则M∩N等于()A.{x|x>1}B.{x|x≥1}C.{x|x≥1或x<0}D.∅解析∵M=(-∞,0]∪(1,+∞),N=[1,+∞),∴M∩N=(1,+∞).答案 A2.已知数列{a n}中,a1=1,2na n+1=(n+1)a n,则数列{a n}的通项公式为()A.n2n B.n2n-1C.n2n -1D.n +12n解析 2a 2=2a 1,2×2a 3=3a 2,2×3a 4=4a 3,…, 2(n -1)a n =na n -1.上述式子相乘,2n -1a n =na 1, ∵a 1=1,∴a n =n2n -1.答案 B3.设x ∈R ,记不超过x 的最大整数为[x ],令{x }=x -[x ],则⎩⎨⎧⎭⎬⎫5+12,⎣⎢⎡⎦⎥⎤5+12,5+12( ) A .是等差数列但不是等比数列 B .是等比数列但不是等差数列 C .既是等差数列又是等比数列 D .既不是等差数列也不是等比数列解析 可分别求得⎣⎢⎡⎦⎥⎤5+12=1,⎩⎨⎧⎭⎬⎫5+12=5-12,则等比数列性质易得三者构成等比数列.答案 B4.在各项都为正数的等比数列{a n }中,首项a 1=3,前三项和为21,则a 3+a 4+a 5=( )A .33B .72C .84D .189解析 ∵a 1+a 2+a 3=21,a 1=3,∴q =2,或q =-3. ∵a n >0,∴q =2,a 3+a 4+a 5=(a 1+a 2+a 3)q 2=21×4=84. 答案 C5.已知a ,b 为非零实数,且a <b ,则下列命题成立的是( ) A .a 2<b 2 B .a 2b <ab 2C .2a-2b<0 D.1a >1b解析 ∵y =2x 在R 上单调递增,a <b ,∴2a <2b . ∴2a -2b <0. 答案 C6.二次方程x 2+(a 2+1)x +a -2=0,有一个根比1大,另一个根比-1小,则a 的取值范围是( )A .-3<a <1B .-2<a <0C .-1<a <0D .0<a <2解析 令f (x )=x 2+(a 2+1)x +a -2,由题意,可知f (1)<0,f (-1)<0,∴a ∈(-1,0).答案 C7.已知O 为直角坐标系原点,P ,Q 的坐标满足不等式组⎩⎪⎨⎪⎧4x +3y -25≤0,x -2y +2≤0,x -1≥0,则cos ∠POQ 的最小值为( )A.22 B.32 C.12D .0解析 画出可行域如图阴影部分,若P ,Q 在可行域内,则∠POQ ∈⎝ ⎛⎭⎪⎫0,π2,结合余弦函数单调性,可知当P ,Q 位于可行域的边界点时,cos ∠POQ 最小,由⎩⎪⎨⎪⎧x -1=0,4x +3y -25=0,得P (1,7);由⎩⎪⎨⎪⎧x -2y +2=0,4x +3y -25=0,得Q (4,3). 所以(cos ∠POQ )min =1×4+3×712+7242+32=22.答案 A8.对每一个正整数n ,抛物线y =(n 2+n )x 2-(2n +1)x +1与x 轴相交于A n ,B n 两点,|A n B n |表示该两点间的距离,则|A 1B 1| +|A 2B 2|+…+|A 2009B 2009|=( )A.20062007 B.20072008 C.20082009D.20092010解析 ∵|A n B n |=1n -1n +1,∴|A 1B 1|+|A 2B 2|+…+|A n B n |=11-12+12-13+…+1n -1n +1=n n +1,∴|A 1B 1|+|A 2B 2|+…+|A 2009B 2009|=20092010. 答案 D9.已知函数y =ax 2+bx +c (a ≠0)的图象经过点(-1,3)和(1,1)两点,若0<c <1,则a 的取值范围是( )A .(1,3)B .(1,2)C .[2,3)D .[1,3]解析 ∵⎩⎪⎨⎪⎧a -b +c =3,a +b +c =1,∴a +c =2,c =2-a .∵0<c <1,∴0<2-a <1,∴1<a <2.答案 B10.在△ABC 中,已知∠A <∠B (∠B ≠90°),那么下列结论一定成立的是( )A .cot A <cotB B .tan A <tan BC .cos A <cos BD .sin A <sin B解析 ∵∠A <∠B ,∴a <b , ∵a sin A =bsin B ,∴sin A <sin B . 答案 D11.如图,D ,C ,B 三点在地面同一直线上,DC =a ,从C ,D 两点测得A 点的仰角分别为β,α(α<β),则A 点离地面的高度AB =( )A.a sin αsin βsin (β-α)B.a sin αsin βcos (α-β)C.a sin αcos βsin (β-α)D.a cos αsin βcos (α-β)解析 在△ADC 中,∠DAC =β-α,∴a sin (β-α)=ACsin α,∴AC =a sin αsin (β-α),∴AB =AC ·sin β=a sin αsin βsin (β-α),故选A.答案 A12.已知a ,b ,a +b 成等差数列,a ,b ,ab 成等比数列,且0<log m (ab )<1,则m 的取值范围是( )A .(0,1)B .(1,+∞)C .(0,8)D .(8,+∞)解析 ∵a ,b ,a +b 成等差数列, ∴2b =2a +b ,b =2a . ∵a ,b ,ab 成等比数列, ∴a ≠0,b ≠0,b 2=a 2b ,∴b =a 2. ∴a 2=2a ,a =2,∴b =4,∴ab =8. ∵0<log m (ab )<1,∴m >8. 答案 D二、填空题(每题5分,共4个小题,共20分)13.函数y =3xx 2+x +1(x <0)的值域是________.解析 y =3x +1x +1,∵x <0,∴x +1x ≤-2.∴x +1x +1≤-1,∴y ∈[-3,0). 答案 y ∈[-3,0)14.已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -3≤0,x +3y -3≥0,y -1≤0,若目标函数z =ax +y (其中a >0)仅在点(3,0)处取得最大值,则a 的取值范围为________.解析 作出该不等式组表示的可行域,∵a >0,且仅在点(3,0)处取得最大值,∴a >12.答案 a >1215.已知△ABC 中,三个内角∠A ,∠B ,∠C 的对边分别是a ,b ,c ,若△ABC 的面积为S ,且2S =(a +b )2-c 2,则tan C 的值为________.解析 ∵2S =ab sin C =(a +b )2-c 2, c 2=a 2+b 2+2ab -ab sin C , ∴2ab -ab sin C =-2ab cos C . ∴sin C -2cos C =2.∴sin 2C +4cos 2C -4sin C cos C =4. ∴tan 2C +4-4tan C =4tan 2C +4. ∴3tan 2C +4tan C =0.∴tan C =0(舍),或tan C =-43. 答案 -4316.①数列{a n }的前n 项和为S n =n 2+2n (n ∈N *),则1a n +1+1a n +2+…+1a 2n≥15;②数列{a n }满足a 1=2,a n +1=2a n -1(n ∈N *),则a 11=1023; ③数列{a n }满足a n +1=1-14a n,b n =22a n -1(n ∈N *),则数列{b n }是从第二项开始的等比数列;④已知a 1+3a 2+5a 3+…+(2n -1)a n =2n +1(n ∈N *),则a n =2n -1. 以上命题正确的有________. 解析 ∵S n =n 2+2n ,∴a n =2n +1,1a n +1+1a n +2+…+1a 2n=12n +3+12n +5+…+14n +1≥n 4n +1=14+1n ≥15,当且仅当n =1时等号成立,故①正确;∵a n +1=2a n -1,∴a n +1-1=2(a n -1).∴a n +1-1a n -1=2.∴{a n -1}是等比数列,a n -1=2n -1.∴a n =2n -1+1, a 11=210+1=1025,故②错误;b n +1=22a n +1-1=22⎝ ⎛⎭⎪⎫1-14a n -1=22a n -1+2 =b n +2,∴{b n }是公差为2的等差数列,故③错误; ④中当n =1时,a 1=22=4,不满足a n =2n -1,∴④错误.答案 ①三、解答题(本题共6小题,共70分,其中17题10分,18、19、20、21、22题每题12分.解答应写出文字说明,证明过程或演算步骤)17.(10分)在△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,且a =3,b 2+c 2-2bc =3.(1)求∠A ;(2)设cos B =45,求边c 的大小. 解 (1)∵a 2=b 2+c 2-2bc cos A , ∴b 2+c 2-2bc cos A =3.∴2bc =2bc cos A ,∴cos A =22,∴∠A =π4.(2)∵cos B =45,∴sin B =35,∴sin C =sin(A +B )=sin A cos B +cos A sin B =22×45+22×35=7210.a sin A =c sin C ,∴c =a sin C sin A =3·721022=735. 18.(12分)在锐角△ABC 中,a ,b ,c 分别为∠A ,∠B ,∠C 所对的边,且3a =2c sin A .(1)确定∠C 的大小;(2)若c =7,△ABC 的面积为332,求a +b 的值. 解 (1)由3a =2c sin A 及正弦定理,得a c =2sin A 3=sin Asin C ,∵sin A ≠0,∴sin C =32.∴△ABC 是锐角三角形,∴∠C =π3. (2)解法1:∵c =7,∠C =π3.由面积公式得 12ab sin π3=332,即ab =6.① 由余弦定理,得a 2+b 2-2ab cos π3=7,即a 2+b 2-ab =7.②由②变形得(a +b )2=25,故a +b =5. 解法2:前同解法1,联立①、②得⎩⎪⎨⎪⎧ a 2+b 2-ab =7,ab =6,⇔⎩⎪⎨⎪⎧a 2+b 2=13,ab =6, 消去b 并整理,得a 4-13a 2+36=0,解得a 2=4,或a 2=9.所以⎩⎪⎨⎪⎧ a =2,b =3,或⎩⎪⎨⎪⎧a =3,b =2,故a +b =5.19.(12分)解关于x 的不等式ax +1x +a >1(其中|a |≠1).解 ax +1-x -a x +a>0⇔(x +a )[(a -1)x +1-a ]>0.当a -1>0时,原不等式变为(x +a )(x -1)>0,其解集为{x |x >1,或x <-a }.当-1<a <1时,原不等式变为(x +a )(x -1)<0,其解集为{x |-a <x <1}.当a <-1时,原不等式变为(x +a )(x -1)<0,其解集为{x |1<x <-a }.20.(12分)已知函数f (x )=2x-12|x |. (1)若f (x )=2,求x 的值;(2)若2t f (2t )+mf (t )≥0对于t ∈[1,2]恒成立,求实数m 的取值范围.解 (1)当x <0时,f (x )=0;当x ≥0时,f (x )=2x -12x .由条件可知,2x -12x =2,即22x -2·2x -1=0,解得2x =1±2.∵2x >0,∴x =log 2(1+2).(2)当t ∈[1,2]时,2t ⎝ ⎛⎭⎪⎫22t-122t +m ⎝ ⎛⎭⎪⎫2t -12t ≥0, 即m (22t -1)≥-(24t -1).∵22t -1>0,∴m ≥-(22t +1).∵t ∈[1,2],∴-(1+22t )∈[-17,-5].故m 的取值范围是[-5,+∞).21.(12分)已知数列{a n }中,已知a 1=1,a n +1=2n +2n a n (n =3ax 2).(1)证明:数列{a n n }是等比数列;(2)求数列{a n }的前n 项和S n .解 (1)∵a n +1=2n +2n a n =2(n +1)n a n ,∴a 2=2×21a 1,a 3=2×32a 2,a 4=2×43a 3,…,a n =2×n n -1a n -1. 上述式子相乘,a n =2n -1·na 1,∴a n =n ·2n -1.(2)S n =1×20+2×2+3×22+…+n ×2n -1, 2S n =1×21+2×22+…+(n -1)×2n -1+n ×2n , 两式相减,-S n =1+2+22+…+2n -1-n ×2n ,∴-S n =1-2n1-2-n ×2n . ∴S n =(n -1)·2n +1.22.(12分)已知{a n }是一个公差大于0的等差数列,且满足a 3a 6=55,a 2+a 7=16.(1)求数列{a n }的通项公式;(2)若数列{a n }和数列{b n }满足等式:a n =b 12+b 222+b 323+…+b n 2n (n 为正整数),求数列{b n }的前n 项和S n .解 (1)设等差数列{a n }的公差为d ,则依题设d >0, 由a 2+a 7=16,得2a 1+7d =16.①由a 3·a 6=55,得(a 1+2d )(a 1+5d )=55.② 由①得2a 1=16-7d ,将其代入②得(16-3d )(16+3d )=220,即256-9d 2=220.∴d 2=4,又d >0,∴d =2,代入①得a 1=1. ∴a n =1+(n -1)·2=2n -1.(2)令c n =b n 2n ,则有a n =c 1+c 2+…+c n ,a n +1=c 1+c 2+…+c n +1.两式相减,得a n +1-a n =c n +1.由(1)得a 1=1,a n +1-a n =2.∴c n +1=2,c n =2(n ≥2),即当n ≥2时,b n =2n +1.又当n =1时,b 1=2a 1=2,∴b n =⎩⎪⎨⎪⎧2 (n =1),2n +1 (n ≥2).于是S n =b 1+b 2+b 3…+b n =2+23+24+…+2n +1=2+22+23+24+…+2n +1-4=2(2n +1-1)2-1-4=2n +2-6,即S n =2n +2-6.。
人教B版人教B版高中数学必修五必修模块5测试样题B版答案及评分参考

数学必修模块测试样题答案及评分参考数学5(人教B版)二、填空题(每小题4分,共16分)15.>16.12nna-=17.(2,2)-18.2 (1)2 1 2)nnan n=⎧=⎨-≥⎩(三、解答题(共3小题,共28分)19.(本小题满分8分)解:(Ⅰ)依题意,由余弦定理得1cos2C==-.120C∠=︒.………………4分(Ⅱ)过点A作AH垂直BC的延长线于H,则sin5sin602AH AC ACH=⋅=︒=.A所以114222ABC S BC AH ∆=⋅=⨯⨯=.………………8分20.(本小题满分10分)解:设水池底面的长为x 米,则宽为48003x米,易知0x >,又设水池总造价为y 元. 根据题意,有48001600150120(2323)3y x x=⨯+⨯+⨯⨯ 1600240000720()x x=++240000720≥+⨯ 297600=.当1600,x x=即40x =时,等号成立. 所以,将水池的底面设计成边长为40米的正方形时,总造价最低,最低总造价为297600元..………………10分21.(本小题满分10分) 解:(Ⅰ)答案如图所示:………………3分 (Ⅱ)易知,后一个图形中的着色三角形个数是前一个的3倍,所以,着色三角形的个数的通项公式为:13n n b -=.………………6分(Ⅲ)由题意知(1)2n n n a +=,11(1)23231n n n n n c n n --+⨯⨯=⋅+=, 所以01113233n n S n -=⋅+⋅++⋅L ①12131323(1)33n n n S n n -=⋅+⋅++-⋅+⋅L ②①-②得0112(333)3n nn S n --=+++-⋅L2n S -=13313nn n --⋅-. 即(21)31()4n n n S n -+=∈N +.………………10分。
人教B版人教B版高中数学必修五本册综合检测.doc

高中数学学习材料马鸣风萧萧*整理制作本册综合检测(时间:120分钟满分:150分)一、选择题(本大题共12个小题,每个小题5分,共60分,每小题给出的四个备选答案中,有且仅有一个是符合题目要求的) 1.a∈R,且a2+a<0,那么-a,-a3,a2的大小关系是() A.a2>-a3>-a B.-a>a2>-a3C.-a3>a2>-a D.a2>-a>-a3[答案] B[解析]∵a2+a<0,∴-1<a<0.令a=-12,-a3=18,a2=14,排除A、C、D,故选B.2.已知全集U=R,集合A={x|x2-2x>0},则∁U A等于() A.{x|0≤x≤2} B.{x|0<x<2}C.{x|x<0或x>2} D.{x|x≤0或x≥2}[答案] A[解析]∵x2-2x>0,∴x>2或x<0,∴A={x|x>2或x<0},∴∁U A={x|0≤x≤2}.3.已知等差数列{a n}中,a2=4,a6=12,则公差d等于()A.12B.32 C .2 D .3[答案] C[解析] ∵a 2=4,a 6=12, ∴a 6-a 12=4d =8,∴d =2.4.在△ABC 中,由已知条件解三角形,其中有两解的是( ) A .b =20,A =45°,C =80° B .a =30,c =28,B =60° C .a =14,b =16,A =45° D .a =12,c =15,A =120° [答案] C[解析] A 中A =45°,C =80°,B =55°,△ABC 为锐角三角形,有唯一解;B 中,已知两边及其夹角,求第三边,有唯一解;C 中,已知两边及其一边对角,b >a ,∴B >45°,且由正弦定理知sin B =16sin45°14=427,∴C 有两种可能,或者为锐角或者为钝角,有两解;D 中,c >a ,A =120°,无解,故选C.5.设S n 是等差数列{a n }的前n 项和,若a 5a 3=59,则S 9S 5等于( )A .1B .-1C .2 D.12[答案] A[解析] ∵{a n }为等差数列,S n 为前n 项和,∴S 9=9(a 1+a 9)2=9×2a 52=9a 5,S 5=5(a 1+a 5)2=5×2a 32=5a 3,∴S 9S 5=9a 55a 3=95×59=1. 6.已知等比数列{a n }的各项均为正数,公比q ≠1,设P =a 3+a 92,Q =a 5·a 7,则P 与Q 的大小关系是( )A .P >QB .P <QC .P =QD .无法确定[答案] A[解析] 由等比知识得,Q =a 5·a 7=a 3·a 9 而P =a 3+a 92且a 3>0,a 9>0,a 3≠a 9∴a 3+a 92>a 3·a 9,即P >Q .7.若0<a 1<a 2,0<b 1<b 2,且a 1+a 2=b 1+b 2=1,则下列代数式中值最大的是( )A .a 1b 1+a 2b 2B .a 1a 2+b 1b 2C .a 1b 2+a 2b 1 D.12 [答案] A[解析] 解法一:令a 1=14,a 2=34,b 1=14,b 2=34,则a 1b 1+a 2b 2=1016=58, a 1a 2+b 1b 2=616=38, a 1b 2+a 2b 1=616=38,∴最大的数应是a 1b 1+a 2b 2. 解法二:作差法.∵a 1+a 2=1=b 1+b 2且0<a 1<a 2,0<b 1<b 2, ∴a 2=1-a 1>a 1,b 2=1-b 1>b 1, ∴0<a 1<12,0<b 1<12.又a 1b 1+a 2b 2=a 1b 1+(1-a 1)(1-b 1) =2a 1b 1+1-a 1-b 1,a 1a 2+b 1b 2=a 1(1-a 1)+b 1(1-b 1)=a 1+b 1-a 21-b 21,a 1b 2+a 2b 1=a 1(1-b 1)+b 1(1-a 1) =a 1+b 1-2a 1b 1.∴(a 1b 2+a 2b 1)-(a 1a 2+b 1b 2)=a 21+b 21-2a 1b 1=(a 1-b 1)2≥0, ∴a 1b 2+a 2b 1≥a 1a 2+b 1b 2.∵(a 1b 1+a 2b 2)-(a 1b 2+a 2b 1)=4a 1b 1+1-2a 1-2b 1 =1-2a 1+2b 1(2a 1-1)=(2a 1-1)(2b 1-1) =4(a 1-12)(b 1-12)>0,∴a 1b 1+a 2b 2>a 1b 2+a 2b 1.∵(a 1b 1+a 2b 2)-12=2a 1b 1+12-a 1-b 1=b 1(2a 1-1)-12(2a 1-1)=(2a 1-1)(b 1-12)=2(a 1-12)(b 1-12)>0,∴a 1b 1+a 2b 2>12.综上可知,最大的数应为a 1b 1+a 2b 2.8.已知△ABC 中,AB =3,AC =1且B =30°,则△ABC 的面积等于( )A.32B.34C.32或 3 D.34或32[答案] D[解析] c =AB =3,b =AC =1,B =30°. 由于c sin B =3×12=32,c sin B <b <c ,∴符合条件的三角形有两个 ∵b sin B =csin C ,即112=3sin C. ∴sin C =32.∴C =60°或120°,∵A =90°或30°,∴S △ABC =32或34.9.等比数列{a n }前n 项的积为T n ,若a 3a 6a 18是一个确定的常数,那么数列T 10,T 13,T 17,T 25中也是常数的项是( )A .T 10B .T 13C .T 17D .T 25[答案] C[解析] a 3·a 6·a 18=a 9q 6·a 9q 3·a 9·q 9=a 39是一个确定常数,∴a 9为确定的常数.T 17=a 1·a 2·…·a 17=(a 3)17,∴选C.10.函数y =log 2(x +1x -1+5)(x >1)的最小值为( )A .-3B .3C .4D .-4[答案] B[解析] x >1,x -1>0 y =log 2(x +1x -1+5)=log 2(x -1+1x -1+6) ≥log 2(2+6)=log 28=3.11.某粮店用一杆不准确的天平(两臂长不相等)称大米,某顾客要购买20kg 大米,售货员先将10kg 的砝码放入左盘,置大米于右盘使之平衡后给顾客,然后又将10kg 砝码放入右盘,置大米于右盘平衡后再给顾客,则( )A .粮店吃亏B .顾客吃亏C .都不吃亏D .不一定[答案] A[解析] 设天平支点为O ,左盘的臂长为a ,右盘的臂长为b ,两次称的粮食的质量分别为m 1,m 2.则有⎩⎪⎨⎪⎧10a =m 1bm 2a =10b,即⎩⎪⎨⎪⎧m 1=10a bm 2=10b a.∴m 1+m 2=10a b +10b a =10(a b +ba )>20(∵a ≠b ), 因此粮店吃亏,故选择A.12.一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品,甲每件4元,乙每件7元,甲商品每件卖出去后可赚1元,乙每件卖出去后可赚1.8元.若要使赚的钱最多,那么该商贩购买甲、乙两种商品的件数应分别为( )A .甲7件,乙3件B .甲9件,乙2件C .甲4件,乙5件D .甲2件,乙6件[答案] D[解析] 设该商贩购买甲、乙两种商品的件数为x 件和y 件,此时该商贩赚的钱为z 元,则由题意可得⎩⎪⎨⎪⎧4x +7y ≤50x ,y ∈N*,z =x +1.8y . 如图所示,经分析可知,要使z 最大,则只需通过点(2,6),∴当x =2,y =6时,z max =2+1.8×6=12.8.故选择D.二、填空题(本大题共4个小题,每个小题4分,共16分.将正确答案填在题中横线上)13.如图,在高出地面30m 的小山顶C 上建造一座电视塔,今在距离B 点60m 的地面上取一点A ,在此点测得CD 所张的角为45°,则电视塔的高度是____________.[答案] 150m[解析]设∠BAC=α,则tan α=BCAB=3060=12,tan A=tan(45°+α)=1+tan α1-tan α=1+121-12=3,∴BD=AB tan A=60×3=180.∴CD=BD-BC=150.14.一个正整数表如下(表中下一行中数的数的个数是上一行中的个数的2倍):第1行 1第2行2 3第3行4567…………则第9行中的第4个数是________.[答案]259[解析]由数表知表中各行数的个数构成一个以1为首项,公比为2的等比数列,前8行数的个数共有1-281-2=255个,故第9行中的第4个数是259.15.不等式(x2-4)(x-6)2≤0的解集是________.[答案]{x|-2≤x≤2或x=6}[解析]原不等式变形得(x+2)(x-2)(x-6)2≤0,∴-2≤x≤2或x=6.16.(2011·陕西文)如图,点(x,y)在四边形ABCD内部和边界上运动,那么2x-y的最小值为________.[答案] 1[解析]令b=2x-y,则y=2x-b,如图所示,作斜率为2的平行线y=2x-b,当经过点A时,直线在y轴上的截距最大,为-b,此时b=2x -y取得最小值,为b=2×1-1=1.三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)△ABC中,a、b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=30°,△ABC的面积为32,求b.[解析]∵a,b,c成等差数列,∴2b=a+c,平方得a2+c2=4b2-2ac,又S△ABC=32且∠B=30°.∴由S△ABC=12ac sin B=12ac sin30°=ac4=32,得ac=6,∴a2+c2=4b2-12.由余弦定理cos B =a 2+c 2-b 22ac =b 2-44=32,又b >0解得b =1+ 3.18.(本小题满分12分)(2011·宿州高二检测)已知函数f (x )=-3x 2+a (6-a )x +c .(1)当c =19时,解关于a 的不等式f (1)>0.(2)若关于x 的不等式f (x )>0的解集是(-1,3),求实数a ,c 的值. [解析] (1)由已知有:f (1)=3+a (6-a )+19>0., 即a 2-6a -16<0,解得:-2<a <8. 所以不等式的解集为:(-2,8).(2)由关于x 的不等式f (x )>0的解集是(-1,3)可知:-1,3是关于x 的方程3x 2-a (6-a )x -c =0的两个根,则有⎩⎪⎨⎪⎧Δ>0-1+3=a (6-a )3-1×3=-c 3,解得:a =3±3,c =9.19.(本小题满分12分)已知等比数列{a n }中,a 1=64,公比q ≠1,a 2,a 3,a 4又分别是某等差数列的第7项,第3项,第1项.(1)求a n ;(2)设b n =log 2a n ,求数列{|b n |}的前n 项和T n . [解析] (1)依题意有a 2-a 4=3(a 3-a 4), 即2a 1q 3-3a 1q 2+a 1q =0, ∴2q 2-3q +1=0.∵q ≠1,∴q =12,故a n =64×(12)n -1.(2)b n =log 2[64×(12)n -1]=7-n . ∴|b n |=⎩⎪⎨⎪⎧7-n (n ≤7)n -7 (n >7), 当n ≤7时,T n =n (13-n )2; 当n >7时,T n =T 7+(n -7)(n -6)2=21+(n -7)(n -6)2. 故T n =⎩⎨⎧n (13-n )2 (n ≤7)(n -7)(n -6)2+21 (n >7).20.(本小题满分12分)(2011·大纲全国卷文)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a sin A +c sin C -2a sin C =b sin B .(1)求B ;(2)若A =75°,b =2,求a ,c .[解析] (1)由正弦定理得a 2+c 2-2ac =b 2,由余弦定理得b 2=a 2+c 2-2ac cos B ,由cos B =22.又B 为三角形的内角,因此B =45°. (2)sin A =sin(30°+45°)=sin30°cos45°+cos30°sin45°=2+64. 故a =b sin A sin B =2+62=1+3, c =b sin C sin B =2×sin60°sin45°= 6.21.(本小题满分12分)已知等比数列{a n }的前n 项和为S n =a ·2n +b 且a 1=3.(1)求a 、b 的值及数列{a n }的通项公式;(2)设b n =n a n,求{b n }的前n 项和T n . [解析] (1)由已知,得⎩⎪⎨⎪⎧ 3=2a +b , ①3+a 2=4a +b , ②3+a 2+a 3=8a +b , ③解得a 2=2a ,a 3=4a ,∴公比q =a 3a 2=2. a 23=2a 3=2,∴a =3代入①得b =-3. ∴a n =3·2n -1.(2)b n =n a n=n 3·2n -1, T n =13(1+22+222+…+n 2n -1) ④ 12T n =13(12+222+…+n -12n -1+n 2n ) ⑤④-⑤得:12T n =13(1+12+122+…+12n -1-n 2n ) =13(1-12n 1-12-n 2n) =13(2-12n -1-n 2n )=23(1-12n -n 2n +1), ∴T n =43(1-12n -n 2n +1). 22.(本小题满分14分)围建一个面积为360m 2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m 的进出口,如图所示,已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为x (单位:米),修建此矩形场地围墙的总费用为y (单位:元).(1)将y 表示为x 的函数;(2)试确定x ,使修建此矩形场地围墙的总费用最小,并求最小总费用.[解析] (1)设矩形的另一边长为a m ,则y =45x +180(x -2)+180×2a =225x +360a -360.由已知xa =360,得a =360x ,∴y =225x +3602x -360(x >0).(2)∵x >0,∴225x +3602x ≥2225×3602=10800.∴y =225x +3602x -360≥10440.当且仅当225x =3602x 时,等号成立.即当x =24m 时,修建围墙的总费用最小,最小总费用是10440元.。
2022高中数学 综合模块测试15 新人教B版必修5

必修5综合模块测试15(人教B 版必修5)一、选择题:本大题共12小题,每小题5分,共60分 1、不等式01312>+-x x 的解集是( )A .}2131|{>-<x x x 或B .}2131|{<<-x xC .}21|{>x xD .}31|{->x x2、在数列1,2,2,3,3,3,4,4,4,4,……中,第25项为 ( ).A .25B .6C .7D .83、若A 、B 、C 是△ABC 的内角,coA ·coB>inA ·inB ,则此三角形一定是 ( )A .锐角三角形B .直角三角形C .钝角三角形D .不能确定 4.关于的不等式)1,(0-∞>+的解集为b ax ,则关于的不等式0)2)((>+-x a bx 的解集为( ) A .(-2,1) B .),1()2,(+∞-⋃--∞ C .(-2,-1) D .),1()2,(+∞⋃--∞ 5、若不等式)1,2(0)(2->--=的解集为c x ax x f ,则函数)(x f y -=的图象是( )6、数列{}n a 的前n 项和S n ,且212≥+-=n ,n a n 则时,下列不等式成立的是( ) A .n n na S na <<1 B .n n S na na <<1 C .n n na na S <<1 D .1na S na n n <<7、已知不等式1()()9ax y x y++≥对任意正实数,x y 恒成立,则正实数a 的最小值为 ( )(A)8 (B)6 (C )4 (D )28.关于x 的不等式x x x 352>--的解集是( )A }1x 5{-≤≥或x xB }1x 5{-<>或x xC }5x 1{<<-xD }5x 1{≤≤-x 9.在一幢10米高的楼顶测得对面一塔吊顶的仰角为060,塔基的俯角为045,那么这座塔吊的高是 A )331(10+B )31(10+C )26(5+D )26(2+10.已知+∈R b a ,且111=+ba ,则b a +的最小值为( ) B.8 C 4 D 111.已知△ABC 中,A 、B 、C 分别是三个内角,a 、b 、c 分别是角A 、B 、C 的对边。
2022高中数学 综合模块测试24 新人教B版必修5

必修5综合模块测试24(人教B 版必修5)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、在ABC ∆中,一定成立的等式是( )()sin sin A a A b B = ()cos cos B a A b B =()sin sin C a B b A = ()cos cos D a B b A =2、等比数列{}n a 的前n 项和2n n S a =+,则a =( )A 4-B 2-C 0D 1-3、ABC ∆中,2()()a c a c b bc +-=+,则A =( )(A )︒120 (B )︒60 (C )︒30 (D )︒1504、已知14和4的等差中项为1a,等比中项为b ,则 A a b = B a b < C a b > D 以上结论都不正确 5、等比数列{}n a 中,1010S =,2040S =,则30S =( )A70 B90 C 130 D 1606、数列{}n a 中,+∈≠N n a n ,0,12211,2,(1)n n a a a n a +===-且≥,则2008a =( ) A 12- B 1- C 1 D 2 7、台风中心从A 地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B 在A 的正东40千米处,B 城市处于危险区内的时间为( ) A 小时 B1小时 C 小时 D2小时8、等差数列{}n a 中,2517S =,那么71319a a a ++= A 5150 B 5125 C2 D 4925 9、在△ABC 中,∠A =60°, a =6, b =4, 满足条件的△ABCA 无解B 只有一解C 有两解D 不能确定10、一个正项等比数列{}n a 中,225)()(1088977=+++a a a a a a ,则=+97a a ( ) A20 B15 C10 D511、某人为了观看2022年奥运会,从2022年起,每年5月10日到银行存入a 元定期储蓄,若年利率为p 且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年5月10日将所有的存款及利息全部取回,则可取回的钱的总数(元)为( )(A )()[]118-+p p a (B )8)1(p a +(C )()()[]p p p a +-+117 (D )()()[]p p p a +-+118 12、一正整数表如下,表中下一行中的数的个数是上一行中数的个数的2倍,则第9行中按从左到右顺序的第4个数是A132 B255 C259 D260第Ⅱ卷(非选择题 共60分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.13、若A 是△ABC 的一个内角,且inAcoA=32,则△ABC 的形状是_______14、等差数列{}n a 的前n 项和为n S ,且53655,S S -=则4a =15、锐角三角形ABC 中,a 、b 、c 分别是三内角A 、B 、C 的对边 设B=2A ,则a b 的取值范围是_____________________16、若数列{n a }满足++∈+=N n x x n n ,lg 1lg 1且10010021=++x x x则101102103200lg()x x x x ++++的值为三、解答题:本大题共4小题,满分44分.解答应写出文字说明,证明过程或演算步骤.17、(本题满分10分)已知等差数列{n a },252, 5.a a ==(1)求{n a }的通项公式;(2令11n n n b a a +=*()n N ∈,求数列}{n b 的前n 项和S n18、(本题满分10分)ABC ∆中,三内角A 、B 、C 所对边分别为a 、b 、c 。
人教B版高中数学必修五模块检测(人教实验B版).docx

达捷致模鑫达捷
达捷致块鑫达捷
达捷致检鑫达捷
达捷致测鑫达捷
达捷致题鑫达捷
达捷致(鑫达捷
达捷致人鑫达捷
达捷致教鑫达捷
达捷致实鑫达捷
达捷致验B 鑫达捷
达捷致版鑫达捷
达捷致必鑫达捷
达捷致
修5)鑫达捷
达捷致一、鑫达捷
达捷致选
鑫达捷
达捷致择
鑫达捷
达捷致题
鑫达捷
达捷致(
鑫达捷
达捷致每
鑫达捷
达捷致小
鑫达捷
达捷致题
鑫达捷
达捷致5
鑫达捷
达捷致分,鑫达捷
达捷致共
鑫达捷
达捷致60
鑫达捷
达捷致分)鑫达捷
达捷致1
鑫达捷
达捷致.
鑫达捷
达捷致如
鑫达捷
达捷致图,鑫达捷
达捷致一
鑫达捷
达捷致货
鑫达捷
达捷致轮
鑫达捷
达捷致航
鑫达捷
达捷致行
鑫达捷
达捷致到
鑫达捷
达捷致M
鑫达捷
达捷致处,鑫达捷
达捷致测
鑫达捷
达捷致得
鑫达捷
达捷致灯
鑫达捷
达捷致塔
鑫达捷
达捷致S
鑫达捷
达捷致在
鑫达捷
达捷致货
鑫达捷
达捷致轮
鑫达捷
达捷致的
鑫达捷
达捷致北
鑫达捷。
人教B版高中数学必修五模块检测.doc

模块检测(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.不等式1x <12的解集是( )A .(-∞,2)B .(2,+∞)C .(0,2)D .(-∞,0)∪(2,+∞)解析 1x <12⇔1x -12<0⇔2-x 2x <0⇔x -22x >0⇔x <0或x >2.答案 D2.等比数列{a n }的前n 项和为S n ,且4a 1,2a 2,a 3成等差数列.若a 1=1,则S 4=( ) A .7 B .8 C .15D .16解析 ∵4a 1,2a 2,a 3成等差数列, ∴4a 2=4a 1+a 3.∵{a n }是等比数列,∴4a 1·q =4a 1+a 1q 2. ∵a 1=1,∴q 2-4q +4=0,∴q =2, ∴S 4=1×1-241-2=15.答案 C3.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c .若(a 2+c 2-b 2)·tan B =3ac ,则角B 的值为( )A.π6B.π3 C.π6或5π6D.π3或2π3解析 ∵a 2+c 2-b 22ac =cos B ,结合已知等式得cos B ·tan B =32,∴sin B =32,故选D. 答案 D4.等差数列中,3(a 3+a 5)+2(a 7+a 10+a 13)=24,则该数列前13项的和是( ) A .156 B .52 C .26D .13解析 ∵a 3+a 5=2a 4,a 7+a 10+a 13=3a 10,∴6(a 4+a 10)=24,a 4+a 10=4, ∴S 13=13a 1+a 132=13a 4+a 102=26,故选C.答案 C5.在△ABC 中,∠A =60°,b =1,其面积为3,则a +b +csin A +sin B +sin C等于( )A .3 3 B.2393 C.2633D.292解析 ∵S △ABC =12bc sin A ,∴3=12×1·c sin 60°∴c =4,a 2=b 2+c 2-2bc cos A =13, ∴a +b +c sin A +sin B +sin C =a sin A =2393.答案 B6.已知{a n }为等差数列,a 1+a 3+a 5=105,a 2+a 4+a 6=99.以S n 表示{a n }的前n 项和,则使得S n 达到最大值的n 是( )A .21B .20C .19D .18解析 ∵{a n }为等差数列, ∴a 1+a 3+a 5=105⇒a 3=35,a 2+a 4+a 6=99⇒a 4=33, d =a 4-a 3=33-35=-2,∴{a n }是递减数列,a n =a 3+(n -3)d =35+(n -3)×(-2)=-2n +41,由a n ≥0得-2n +41≥0,∴n ≤412,∴当n ≤20时,a n >0, ∴n =20时,S n 最大,故选B. 答案 B7.已知O 是坐标原点,点A (-1,1),若点M (x ,y )为平面区域⎩⎪⎨⎪⎧x +y ≥2x ≤1y ≤2上的一个动点,则OA →·OM →的取值范围是( )A .[-1,0]B .[0,1]C .[0,2]D .[-1,2]解析 可行域如图,M 点落在△FBC 内.设M (x ,y ),令z =OA →·OM →=-x +y ,易得z max =-0+2=2,z min =-1+1=0,即z ∈[0,2],故选C.答案 C8.数列{a n }中,a 2=2,a 6=0且数列{1a n +1}是等差数列,则a 4= ( )A.12B.13C.14D.16解析 设数列{1a n +1}的公差为d , 由4d =1a 6+1-1a 2+1得d =16, ∴1a 4+1=12+1+2×16,解得a 4=12,故选A. 答案 A9.不等式组⎩⎪⎨⎪⎧x -1>a 2,x -4<2a 有解,则实数a 的取值范围是( )A .(-1,3)B .(-∞,-1)∪(3,+∞)C .(-3,1)D .(-∞,-3)∪(1,+∞)解析 不等式组即⎩⎪⎨⎪⎧x >a 2+1,x <2a +4,若有解,则a 2+1<2a +4,解得-1<a <3.答案 A10.已知等比数列{a n }满足a n >0,n =1,2,…,且a 5·a 2n -5=22n(n ≥3),则当n ≥1时,log 2a 1+log 2a 3+…+log 2a 2n -1=( )A .(n -1)2B .n 2C .(n +1)2D .n (2n -1)解析 ∵a 5·a 2n -5=22n=a n 2,a n >0, ∴a n =2n,∴log 2a 1+log 2a 3+…+log 2a 2n -1 =log 2(a 1a 3…a 2n -1) =log 221+3+…+(2n -1)=log 22n 2=n 2.故选B. 答案 B11.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c .若a 2-b 2=3bc ,sin C =23sinB ,则∠A =( )A .30°B .60°C .120°D .150°解析 sin C =23sin B ⇒c =23b ,a 2-b 2=3bc ⇒a 2-b 2-c 2=3bc -c 2⇒b 2+c 2-a 2=c 2-3bc , ∴cos A =b 2+c 2-a 22bc =c 2-3bc 2bc =c 22bc -32=c 2b -32=232-32=32,∴在△ABC 中,∠A =30°. 答案 A12.已知正项等比数列{a n },a 1=2,又b n =log 2a n ,且{b n }的前n 项和为T n ,当且仅当n =7时T n 最大,则数列{a n }的公比q 的取值范围是( )A .217<q <216B .2-16<q <2-17C .q <2-16或q >2-17D .q >216或q <217解析 因为b n =log 2a n =log 2(a 1·qn -1)=1+(n -1)·log 2q ,所以b n +1-b n =log 2q ,所以{b n }是等差数列,又当且仅当n =7时T n 最大,所以⎩⎪⎨⎪⎧b 7>0,b 8<0⇒⎩⎪⎨⎪⎧1+6log 2q >0,1+7log 2q <0⇒-16<log 2q <-17⇒2-16<q <2-17,故选B.答案 B二、填空题(本大题共4小题,每小题5分,共20分)13.在等比数列{a n }中,若公比q =4,且前3项之和等于21,则该数列的通项公式a n=________.解析 由a 1+4a 1+16a 1=21,∴a 1=1,∴a n =4n -1.答案 4n -114.在△ABC 中,若b =1,c =3,∠C =2π3,则a =________.解析 ∵c 2=a 2+b 2-2ab cos C , ∴(3)2=a 2+12-2a ·1·cos 23π,∴a 2+a -2=0,∴(a +2)(a -1)=0, ∴a =1或a =-2(舍去). 答案 115.已知△ABC 的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC 的面积为__________.解析 设三边长依次为a ,a +4,a +8,则a >0,则有(a +8)2=a 2+(a +4)2-2a (a +4)cos120°=3a 2+12a +16,即有2a 2-4a -48=0,解得a =-4(舍去)或a =6.故有S △ABC =12×6×10×sin120°=15 3.答案 15 3 16.对任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围是________.解析 由x x 2+3x +1≤a 恒成立,所以a ≥(xx 2+3x +1)max而x x 2+3x +1=1x +1x+3≤12x ·1x+3=15 当且仅当x =1x 时等号成立,∴a ≥15.答案 [15,+∞)三、解答题(本大题共6小题,共70分) 17.(10分)不等式kx 2-2x +6k <0(k ≠0)(1)若不等式的解集是{x |x <-3或x >-2},求k 的值. (2)若不等式的解集为R ,求k 的取值范围. 解 (1)因为不等式的解集为{x |x <-3或x >-2}, 所以-3,-2是方程kx 2-2x +6k =0的两根,且k <0 ∴⎩⎪⎨⎪⎧-3-2=2k ,-3×-2=6,即k =-25.(2)若不等式的解集为R .则⎩⎪⎨⎪⎧k <0,Δ=4-4k ·6k <0,即⎩⎪⎨⎪⎧k <0,1-6k 2<0,解得:k <-66. 18.(12分)在△ABC 中,角A ,B ,C 成等差数列,并且sin A ·sin C =cos 2B ,三角形的面积S △ABC =43,求三边a ,b ,c .解 ∵角A ,B ,C 成等差数列,∴A +C =2B ,A +B +C =180°,∴B =60°, 所以sin A sin C =cos 260°= 14.①又S △ABC =43=12ac sin B ,得ac =16.② 由①②得:ac sin A sin C =(a sin A )2=64=(c sin C)2,所以a sin A =csin C=8.由b =a sin Bsin A=8sin B =8sin 60°=43, 根据cos B =a 2+c 2-b 22ac =12,∴a 2+c 2-b 2=ac ,(a +c )2-b 2=3ac , ∴(a +c )2=48+48=96, ∴a +c =4 6.③联立③与②得a =2(6+2),c =2(6-2),或a =2(6-2),c =2(6+2). 19.(12分)某村计划建造一个室内面积为72 m 2的矩形蔬菜温室.在温室内,沿左、右两则与后侧内墙各保留1 m 宽的通道,沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?解 设矩形温室的左侧边长为a m ,后侧边长为b m ,则ab =72,蔬菜的种植面积S =(a -4)(b -2)=ab -4b -2a +8=80-2(a +2b )≤80-42ab =32(m 2)当且仅当a =2b ,即a =12,b =6时,S max =32.所以矩形温室的边长6 m,12 m 时,蔬菜的种植面积最大,最大种植面积是32 m 2. 20.(12分)设数列{a n }的前n 项和为S n =2n 2,{b n }为等比数列,且a 1=b 1,b 2(a 2-a 1)=b 1.(1)求数列{a n }和{b n }的通项公式; (2)设c n =a nb n,求数列{c n }的前n 项和T n . 解 (1)当n ≥2时,a n =S n -S n -1=2n 2-2(n -1)2=4n -2,当n =1时,a 1=S 1=2满足上式, 故{a n }的通项公式为a n =4n -2.设{b n }的公比为q ,由已知条件b 2(a 2-a 1)=b 1知,b 1=2,b 2=12,所以q =14,∴b n =b 1qn -1=2×14n -1,即b n =24n -1.(2)∵c n =a n b n =4n -224n -1=(2n -1)4n -1,∴T n =c 1+c 2+…+c n =[1+3×41+5×42+…+(2n -1)4n -1].4T n =[1×4+3×42+5×42+…+(2n -3)4n -1+(2n -1)4n].两式相减得:3T n =-1-2(41+42+43+…+4n -1)+(2n -1)4n =13[(6n -5)4n+5].∴T n =19[(6n -5)4n+5].21.(12分)已知f (x )=ax 2+(b -8)x -a -ab ,当x ∈(-3,2)时,f (x )>0;x ∈(-∞,-3)∪(2,+∞)时,f (x )<0.(1)求y =f (x )的解析式;(2)c 为何值时,ax 2+bx +c ≤0的解集为R . 解 (1)由x ∈(-3,2)时,f (x )>0;x ∈(-∞,-3)∪(2,+∞)时,f (x )<0知:-3,2是方程ax 2+(b -8)x -a -ab =0的两根⎩⎪⎨⎪⎧-3+2=-b -8a ,-3×2=-a -ab a⇒⎩⎪⎨⎪⎧a =-3,b =5.∴f (x )=-3x 2-3x +18.(2)由a <0,知二次函数y =ax 2+bx +c 的图象开口向下.要使-3x 2+5x +c ≤0的解集为R ,只需Δ≤0,即25+12c ≤0⇔c ≤-2512.∴当c ≤-2512时,ax 2+bx +c ≤0的解集为R .22.(12分)设{a n }为等差数列,S n 为数列{a n }的前n 项和,已知S 7=21,S 15=-75,T n为数列{S n n}的前n 项和,求T n 的最大值.解 设等差数列{a n }公差为d ,则S n =na 1+12n (n -1)d .∵S 7=21,S 15=-75,∴⎩⎪⎨⎪⎧7a 1+21d =21,15a +105d =-75,即⎩⎪⎨⎪⎧a 1+3d =3,a 1+7d =-5,解得a 1=9,d =-2. ∴S n =na 1+n n -12d =9n -(n 2-n )=10n -n 2.则S nn=10-n . ∵S n +1n +1-S nn=-1, ∴数列{S n n}是以9为首项,公差为-1的等差数列. 则T n =n ·[9+10-n ]2=-12n 2+192n=-12(n -192)2+3618.∵n ∈N *,∴当n =9或n =10时,T n 有最大值45.。
人教B版高中数学必修五模块测试样题

高中数学学习资料金戈铁骑整理制作数学模块测试样题数学 5人教B 版考 : 90 分卷 分: 100 分一、 :本大 共14 小 ,每小 4 分,共56 分 .在每小 出的四个 中,只有一 是吻合要求的 .40km / h140km/ h的路 , 指示司机在前面路段行 ,使汽 的速度v 不超 ,.限速写成不等式就是A. v40B. v 40C. v 40D. v402 ABC 中,A, B, C 所 的 分a, b, c, 以下关系正确的选项是.在 △A. cosC a 2 b 2 c 2B. cosC a 2b 2c 2 C. cosCa 2b 2c 2a 2b 2c 22abD. cosCab3.不等式 ( x2)(x 1) 0 的解集A. x x 2或x 1B. x 2 x 1C. x x1或x 2D. x 1 x 24. 届 代奥运会召开 表以下:年份 1896 年1900 年1904 年⋯ 2008 年届数1 23⋯nn 的5. S n 是等差数列a n 的前 n 和,若是 S 10120 ,那么 a 1a 10 的 是6.不等式 x 2 y 1 0表示的平面地域在直x 2y 1 0 的A. 左上方B.左下方C.右上方D.右下方7.在 △ ABC 中,A, B, C 所 的 分a, b, c ,若 a 2 b 2 c 2 0, △ABC 是A. 锐角三角形B.直角三角形C.等腰三角形D. 钝角三角形8.以下列图, C 、D 、A 三点在同一水平线上,AB 是塔的中轴线,在 C 、D 两处测得塔顶部 B 处的仰角分别是和,若是 C 、D间的距离是 a ,测角仪高为b ,则塔高为a cos cosbB.a cos cos A.cos()cos()C 1D 1a sin sinasinsinCDbD.C.)sin( )sin(9.在△ ABC 中 ,A, B, C 所对的边分别为a,b,c ,若 a 8, B 60,C 75,则 b 等于A. 42B. 4 3C. 4 6 32D.10bd3a 、 、 c 、 ,以下命题:.对于任意实数① 若 a b , c 0 ,则 ac bc ;② 若 ab ,则 ac 2 bc 2; ③ 若 ac2bc2,则 ab ; ④ 若 a 1 1b ,则 ba中,真命题为A. ①B. ②C. ③D. ④x211.已知实数 x 、 y 满足拘束条件y2 ,则 z 2x 4 y 的最大值为xy612.已知等差数列a n 的公差为 2,若 a 1 ,a 3 , a 4 成等比数列 , 则 a 1 等于A. 4B. 6C.8D. 1013.若 a n 为递减数列 ,则 a n的通项公式可以为A. a n2n 3B. a nn 2 3n 1 C. a n1D. a n( 1)n2n a c ad bc ,若x 32 0 14.在 R 上定义运算dxx1 成立,则 x 的取值范围是b2A. ( 4,1)B. ( 1,4)C. (, 4) (1, )D. (, 1) (4, )二、填空题:本大题共 4 小题,每题 4 分,共 16 分 .把答案填在题中横线上 .15.比较大小: ( x 2)( x 3)x 2x 7(填入 “ ”,“ ”,“ =之”一) .BA 1A16.在各项均为正数的等比数列a n中,已知a11, a2a36, 则数列a n的通项公式为.17 .若函数f (x) log2(x2ax1)的定义域为 R ,则实数a的取值范围是.18.数列{ a n}的前 n 项和为S n n21( n N*),则它的通项公式是_______.三、解答题:本大题共 3 小题,共28 分 .解答应写出文字说明,证明过程或演算步骤. 19.(本小题满分8 分)在△ ABC 中 ,A, B, C 所对的边分别为a,b, c ,已知a4, b 5, c61 .(Ⅰ)求 C 的大小;(Ⅱ)求△ ABC 的面积 .20.(本小题满分10 分)某工厂修建一个长方体无盖蓄水池,其容积为4800 立方米 ,深度为 3 米 .若是池底每平方米的造价为 150 元 ,池壁每平方米的造价为 120 元 ,怎样设计水池能使总造价最低 ?最低造价是多少元 ?21.(本小题满分10 分)(Ⅰ)下面图形由单位正方形组成,请观察图 1 至图 4 的规律,并依此规律,在横线上方处画出合适的图形;图1图2图3图4(Ⅱ)以下列图中的三角形称为希尔宾斯基三角形,在以下列图四个三角形中,着色三角形的个数依次组成数列的前四项,依此着色方案连续对三角形着色,求着色三角形的个数的通项公式 b n;(Ⅲ)依照(Ⅰ)中规律,连续用单位正方形绘图,记每个图形中单位正方形的个数为a n (n 1,2,3, ) , 定 c n2a n b n,求数列 { c n } 的前 n 和 S n .n 1数学必修模块测试样题答案及评分参照数学 5(人教 B 版)一、 (每小4 分,共 56 分)号1 2 3 4 5 6 7答案 B C A C B C D号8 9 10 11 12 13 14答案 CCCBCCA二、 填空 ( 每小 4 分,共16分 )15.16. a n 2n 117. (2,2)18. a n2(n 1)2n 1 ( n2)三、解答 (共3小 ,共 28分)19.(本小 分8 分)解:(Ⅰ)依 意,由余弦定理得A4252( 612)1c o sC24 5.2C120.⋯⋯⋯⋯⋯⋯4 分(Ⅱ) 点 A 作 AH 垂直 BC 的延 于 H ,BCH5 3AHAC sin ACH 5sin 60.2所以 S ABC1BC AH1 5 3 .⋯⋯⋯⋯⋯⋯ 8 分2 42 5 3220.(本小 分 10 分)解: 水池底面的x 米,4800米,易知 x 0 ,又 水池 造价y 元.3x依照意,有y1504800120(23x216003)31600)x240000720(xx240000720 2x 1600x297600.当 x1600 ,即x40 ,等号成立.x所以,将水池的底面成40 米的正方形,造价最低,最低造价 297600元..⋯⋯⋯⋯⋯⋯10 分21.(本小分10 分)解:(Ⅰ)答案如所示:⋯⋯⋯⋯⋯⋯ 3 分(Ⅱ)易知,后一个形中的着色三角形个数是前一个的 3 倍,所以,着色三角形的个数的通公式:b n3n 1.⋯⋯⋯⋯⋯⋯ 6 分n(n1)2n(n1) 3n 1(Ⅲ)由意知a n, c n 2=n 3n 1,2n1所以S n121nn31①333S n 1 31 2 32(n 1) 3n 1n 3n②①-②得2S n(30313n 1 )n 3n2S n= 1 3n n 3n.13即 S n( 2n 1 )n 31(n N+ ).⋯⋯⋯⋯⋯⋯ 10 分4。
高中数学 综合模块测试36 新人教B版必修5

高中数学 综合模块测试36 新人教B 版必修5一、选择题1.如果33log log 4m n +=,那么n m +的最小值是( ) A .4B .34C .9D .182、数列{}n a 的通项为n a =12-n ,*N n ∈,其前n 项和为n S ,则使n S >48成立的n 的最小值为( )A .7B .8C .9D .103、若不等式897x +<和不等式022>-+bx ax 的解集相同,则a 、b 的值为( ) A .a =﹣8 b =﹣10 B .a =﹣4 b =﹣9 C .a =﹣1 b =9 D .a =﹣1b =2 4、△ABC 中,若2cosc a B =,则△ABC 的形状为( )A .直角三角形B .等腰三角形C .等边三角形D .锐角三角形5、在首项为21,公比为12的等比数列中,最接近1的项是( ) A .第三项 B .第四项 C .第五项 D .第六项 6、在等比数列{}n a 中,117a a ⋅=6,144a a +=5,则1020a a 等于( )A .32B .23C .23或32D .﹣32或﹣237、△ABC 中,已知()()a b c b c a bc +++-=,则A 的度数等于( )A .120 B .60 C .150 D .308、数列{}n a 中,1a =15,2331-=+n n a a (*N n ∈),则该数列中相邻两项的乘积是负数的是( ) A .2221a aB .2322a aC .2423a aD .2524a a9、某厂去年的产值记为1,计划在今后五年内每年的产值比上年增长10%,则从今年起到第五年,这个厂的总产值为( )A .41.1B .51.1 C .610(1.11)⨯- D . 511(1.11)⨯-10、已知钝角△ABC 的最长边为2,其余两边的长为a 、b ,则集合{}b y a x y x P ===,|),(所表示的平面图形面积等于( )A .2B .2-πC .4D .24-π 二、填空题11、在△ABC 中,已知BC=12,A=60°,B=45°,则AC= 12.函数2lg(12)y x x =+-的定义域是13.数列{}n a 的前n 项和*23()n n s a n N =-∈,则5a =14、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ,则y x z 32+=的最大值为15、《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。
高中数学 模块综合检测 新人教B版必修5

模块综合检测(时间120分钟 满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若f (x )=3x 2-x +1,g (x )=2x 2+x -1,则f (x )与g (x )的大小关系为( ) A .f (x )>g (x ) B .f (x )=g (x ) C .f (x )<g (x )D .随x 值变化而变化解析:选A 因为f (x )-g (x )=(3x 2-x +1)-(2x 2+x -1)=x 2-2x +2=(x -1)2+1>0,所以f (x )>g (x ).2.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =2,b =3,B =60°,那么角A 等于( )A .135°B .90°C .45°D .30°解析:选C 由正弦定理知a sin A =bsin B, ∴sin A =a sin Bb =2sin 60°3=22. 又a <b ,B =60°,∴A <60°,∴A =45°.3.若a 1=1,a n +1=a n3a n +1,则给出的数列{a n }的第4项是( )A.116B.117C.110D.125解析:选C a 2=a 13a 1+1=13+1=14,a 3=a 23a 2+1=1434+1=17,a 4=a 33a 3+1=1737+1=110. 4.若关于x 的不等式x 2-3ax +2>0的解集为(-∞,1)∪(m ,+∞),则a +m =( ) A .-1 B .1 C .2D .3解析:选D 由题意,知1,m 是方程x 2-3ax +2=0的两个根,则由根与系数的关系,得⎩⎪⎨⎪⎧1+m =3a ,1×m =2,解得⎩⎪⎨⎪⎧a =1,m =2,所以a +m =3,故选D.5.已知x >0,y >0,且x +y =8,则(1+x )(1+y )的最大值为( ) A .16 B .25 C .9D .36解析:选B (1+x )(1+y )≤⎣⎢⎡⎦⎥⎤+x ++y 22=⎣⎢⎡⎦⎥⎤2+x +y 22=⎝ ⎛⎭⎪⎫2+822=25,因此当且仅当1+x =1+y 即x =y =4时,(1+x )(1+y )取最大值25,故选B.6.已知数列{a n }为等差数列,且a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于( ) A .40 B .42 C .43D .45解析:选B 设等差数列{a n }的公差为d , 则2a 1+3d =13,∴d =3,故a 4+a 5+a 6=3a 1+12d =3×2+12×3=42.7.钝角三角形ABC 的面积是12,AB =1,BC =2,则AC =( )A .5 B. 5 C .2D .1 解析:选 B ∵S △ABC =12AB ·BC sin B =12×1×2sin B =12,∴sin B =22,∴B =45°或135°,若B =45°,则由余弦定理得AC =1,∴△ABC 为直角三角形,不符合题意,因此B =135°,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos B =1+2-2×1×2×⎝ ⎛⎭⎪⎫-22=5,∴AC =5,此时△ABC 为钝角三角形,符合题意.故选B.8.已知S n 为正项等比数列{a n }的前n 项和,S 3=3a 1+2a 2,且a 2-12,a 4,a 5成等差数列,则a 1=( )A .2 B.12 C.14D .4解析:选C 设数列{a n }的公比为q (q >0),则由S 3=3a 1+2a 2可得q 2-q -2=0,解得q =2或q =-1(舍去),又a 2-12,a 4,a 5成等差数列,所以2a 4=a 2-12+a 5,即a 2=12,所以a 1=14.9.在△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( ) A.32B.332C.3+62D.3+394解析:选B 由余弦定理得AB 2+4-2·AB ×2×cos 60°=7,解得AB =3或AB =-1(舍去),设BC 边上的高为x ,由三角形面积关系得12·BC ·x =12AB ·BC ·sin 60°,解得x =332,故选B.10.某汽车公司有两家装配厂,生产甲、乙两种不同型的汽车,若A 厂每小时可完成1辆甲型车和2辆乙型车;B 厂每小时可完成3辆甲型车和1辆乙型车.今欲制造40辆甲型车和40辆乙型车,若要使所费的总工作时数最少,那么这两家工厂工作的时间分别为( )A .16,8B .15,9C .17,7D .14,10解析:选A 设A 工厂工作x 小时,B 工厂工作y 小时,总工作时数为z ,则目标函数为z =x +y ,约束条件为⎩⎪⎨⎪⎧x +3y ≥40,2x +y ≥40,x ≥0,y ≥0作出可行域如图所示,由图知当直线l :y =-x +z过Q 点时,z 最小,解方程组⎩⎪⎨⎪⎧x +3y =40,2x +y =40,得Q (16,8),故A 厂工作16小时,B 厂工作8小时,可使所费的总工作时数最少.11.若log 4(3x +4b )=log 2ab ,则a +b 的最小值是( ) A .6+2 3 B .7+2 3 C .6+4 3D .7+4 3解析:选D 由log 4(3a +4b )=log 2ab ,得12log 2(3a +4b )=12log 2(ab ),所以3a +4b =ab ,即3b +4a=1.所以a +b =(a +b )⎝ ⎛⎭⎪⎫3b +4a=3a b +4ba +7≥43+7,当且仅当3ab =4b a,即a =23+4,b =3+23时取等号,故选D.12.已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +y ≤2,y ≥0.若z =ax +y 的最大值为4,则a =( )A .3B .2C .-2D .-3解析:选B 画出不等式组表示的平面区域如图阴影部分所示,若z =ax +y 的最大值为4,则最优解为x =1,y =1或x =2,y =0,经检验x =2,y =0符合题意,∴2a +0=4,此时a =2,故选B.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中的横线上)13.若实数x ,y 满足xy =1,则x 2+2y 2的最小值为________. 解析:因为实数x ,y 满足xy =1,所以x 2+2y 2≥2x 2·2y 2=2xy2=22,并且仅当x 2=2y 2且xy =1,即x 2=2y 2=2时等号成立,故x 2+2y 2的最小值为2 2.答案:2 214.已知△ABC 的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC 的面积为________.解析:由于三边长构成公差为4的等差数列, 故可设三边长分别为x -4,x ,x +4.由一个内角为120°,知其必是最长边x +4所对的角. 由余弦定理得,(x +4)2=x 2+(x -4)2-2x (x -4)·cos 120°, ∴2x 2-20x =0,∴x =0(舍去)或x =10, ∴S △ABC =12×(10-4)×10×sin 120°=15 3.答案:15 315.设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =________. 解析:∵a n +1=S n +1-S n ,a n +1=S n S n +1, ∴S n +1-S n =S n S n +1.∵S n ≠0,∴1S n -1S n +1=1,即1S n +1-1S n=-1.又1S 1=-1,∴⎩⎨⎧⎭⎬⎫1S n 是首项为-1,公差为-1的等差数列.∴1S n=-1+(n -1)×(-1)=-n ,∴S n =-1n.答案:-1n16.若a >0,b >0,a +b =2,则下列不等式①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④1a+1b≥2,对满足条件的a ,b 恒成立的是________.(填序号)解析:因为ab ≤⎝⎛⎭⎪⎫a +b 22=1,所以①正确;因为(a +b )2=a +b +2ab =2+2ab ≤2+a +b =4,故②不正确;a 2+b 2≥a +b22=2,所以③正确;1a +1b =a +b ab =2ab≥2,所以④正确.答案:①③④三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明、证明过程或演算步骤)17.(10分)等差数列{a n }的前n 项和记为S n ,已知a 10=30,a 20=50. (1)求通项a n ; (2)若S n =242,求n .解:(1)设{a n }的首项为a 1,公差为d ,则⎩⎪⎨⎪⎧a 1+9d =30,a 1+19d =50.解得⎩⎪⎨⎪⎧a 1=12,d =2.∴通项a n =a 1+(n -1)d =10+2n . (2)由S n =na 1+n n -2d =242,得12n +n n -2×2=242,解得n =11,或n =-22(舍去).故n =11.18.(12分)已知f (x )=2x 2+bx +c ,不等式f (x )<0的解集是(0,5). (1)求f (x )的解析式;(2)若对于任意的x ∈[-1,1],不等式f (x )+t ≤2恒成立,求t 的取值范围. 解:(1)因为f (x )=2x 2+bx +c ,不等式f (x )<0的解集是(0,5), 所以2x 2+bx +c <0的解集是(0,5), 所以0和5是方程2x 2+bx +c =0的两个根, 由根与系数的关系,知-b 2=5,c2=0,所以b =-10,c =0,所以f (x )=2x 2-10x .(2)对任意的x ∈[-1,1],f (x )+t ≤2恒成立等价于对任意的x ∈[-1,1],2x 2-10x +t -2≤0恒成立.设g (x )=2x 2-10x +t -2,则由二次函数的图象可知g (x )=2x 2-10x +t -2在区间[-1,1]上为减函数,所以g (x )max =g (-1)=10+t ,所以10+t ≤0,即t ≤-10,所以t 的取值范围为(-∞,-10].19.(12分)已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5=-5. (1)求{a n }的通项公式; (2)求数列⎩⎨⎧⎭⎬⎫1a 2n -1a 2n +1的前n 项和.解:(1)设{a n }的公差为d ,则S n =na 1+n n -2d .由已知可得⎩⎪⎨⎪⎧3a 1+3d =0,5a 1+10d =-5.解得a 1=1,d =-1.故{a n }的通项公式为a n =2-n . (2)由(1)知1a 2n -1a 2n +1=1-2n-2n=12⎝ ⎛⎭⎪⎫12n -3-12n -1,从而数列⎩⎨⎧⎭⎬⎫1a 2n -1a 2n +1的前n 项和为12( 1-1-11+11-13+…+12n -3-12n -1 )=n1-2n. 20.(12分)某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C 处进行该仪器的垂直弹射,观察点A ,B 两地相距100 m ,∠BAC =60°,在A 地听到弹射声音的时间比B 地晚217s .A 地测得该仪器在C 处时的俯角为15°,A 地测得最高点H 的仰角为30°,求该仪器的垂直弹射高度CH .(声音的传播速度为340 m/s)解:由题意,设AC =x m , 则BC =x -217×340=(x -40)m ,在△ABC 内,由余弦定理:BC 2=BA 2+CA 2-2·BA ·CA ·cos∠BAC , 即(x -40)2=1002+x 2-100x ,解得x =420.在△ACH 中,AC =420 m ,∠CAH =30°+15°=45°,∠CHA =90°-30°=60°, 由正弦定理:CH sin ∠CAH =ACsin ∠AHC ,可得CH =AC ·sin∠CAHsin ∠AHC=1406(m).即该仪器的垂直弹射高度CH 为140 6 m.21.(12分)在△ABC 中,BC =6,点D 在BC 边上,且(2AC -AB )cos A =BC cos C . (1)求角A 的大小;(2)若AD 为△ABC 的中线,且AC =23,求AD 的长;(3)若AD 为△ABC 的高,且AD =33,求证:△ABC 为等边三角形.解:(1)由(2AC -AB )cos A =BC cos C 及正弦定理,有(2sin B -sin C )cos A =sin A cos C , 得2sin B cos A =sin C cos A +sin A cos C =sin(A +C )=sin B ,所以cos A =12.因为0°<A <180°,所以A =60°. (2)由正弦定理BC sin A =ACsin B,得sin B =AC sin A BC =12. 因为A +B <180°,所以B =30°,所以C =90°. 因为D 是BC 的中点,所以DC =3, 由勾股定理,得AD =AC 2+DC 2=21.(3)证明:因为12AD ·BC =12AB ·AC sin A ,且AD =33,BC =6,sin A =32,所以AB ·AC=36.因为BC 2=AB 2+AC 2-2AB ·AC cos A , 所以AB 2+AC 2=72,所以AB =AC =6=BC , 所以△ABC 为等边三角形.22.(12分)已知数列{a n }的前n 项和S n 和通项a n 满足2S n +a n =1,数列{b n }中,b 1=1,b 2=12,2b n +1=1b n +1b n +2(n ∈N +).(1)求数列{a n },{b n }的通项公式;(2)数列{c n }满足c n =a n b n ,求证:c 1+c 2+c 3+…+c n <34.解:(1)由2S n +a n =1,得S n =12(1-a n ).当n ≥2时,a n =S n -S n -1=12(1-a n )-12(1-a n -1)=-12a n +12a n -1,即2a n =-a n +a n -1,∴a n a n -1=13(由题意可知a n -1≠0). ∴{a n }是公比为13的等比数列,而S 1=a 1=12(1-a 1),∴a 1=13,∴a n =13×⎝ ⎛⎭⎪⎫13n -1=⎝ ⎛⎭⎪⎫13n.由2b n +1=1b n +1b n +2,1b 1=1,1b 2=2,得d =1b 2-1b 1=1⎝ ⎛⎭⎪⎫d 为等差数列⎩⎨⎧⎭⎬⎫1b n 的公差,∴1b n =n ,∴b n =1n.(2)证明:c n =a n b n =n ⎝ ⎛⎭⎪⎫13n,设T n =c 1+c 2+…+c n ,则T n =1×⎝ ⎛⎭⎪⎫131+2×⎝ ⎛⎭⎪⎫132+3×⎝ ⎛⎭⎪⎫133+…+n ×⎝ ⎛⎭⎪⎫13n ,13T n =1×⎝ ⎛⎭⎪⎫132+2×⎝ ⎛⎭⎪⎫133+…+(n -1)×⎝ ⎛⎭⎪⎫13n +n ×⎝ ⎛⎭⎪⎫13n +1,由错位相减,得23T n =13+⎝ ⎛⎭⎪⎫132+…+⎝ ⎛⎭⎪⎫13n -n ×⎝ ⎛⎭⎪⎫13n +1=13⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13n 1-13-n ×⎝ ⎛⎭⎪⎫13n +1=12-12×⎝ ⎛⎭⎪⎫13n-n ×⎝ ⎛⎭⎪⎫13n +1,所以T n =34-34×⎝ ⎛⎭⎪⎫13n -12n ×⎝ ⎛⎭⎪⎫13n =34-2n +34×13n <34.。
高中数学 综合模块测试29 新人教B版必修5

高中数学 综合模块测试29 新人教B 版必修5一、选择题(每小题5分,10小题,共50分)1、在ABC ∆中,︒===452232B b a ,,,则A 为( )A .︒︒︒︒︒︒30.15030.60.12060D CB 或或2、在ABC ∆中,bc c b a++=222,则A 等于( )A ︒︒︒︒30.45.60.120.D C B3、在ABC ∆中,1660=︒=b A ,,面积3220=S ,则a 等于( ) A. 610.B. 75C . 49 D. 514、在下列通项公式中,一定不是数列2,4,8,…的通项公式的是( )A .nn a 2= B .22+-=n n a n C .n a n 2= D .632553223+-+-=n n n a n 5、等比数列{}n a 的首项1a =1,公比为q ,前n 项和是n S ,则数列⎭⎬⎫⎩⎨⎧n a 1的前n 项和是( )A .1-n S B .nn qS - C .nn qS -1 D .11--n n q S6、在等差数列{}n a 中,前四项之和为40,最后四项之和为80,所有项之和是210, 则项数n 为( )A .12B .14C .15D .167、等差数列{}n a 的前n 项和是n S ,若10173=+a a ,则=19S ( )A .55B .95C .100D .1908、已知方程04)2(2,02222=+-+=++x a x a x x 有且只有一个方程有两个不相等 的实数根,则实数a 的取值范围是( )A .21<a 或4>a B .210<≤a 或4>a C .210≤<a 或4≥a D .421≤<a9、已知y x y x 222log log )(log +=+,则y x +的取值范围是( )A .]1,0(B .),2[+∞C .]4,0(D .),4[+∞10、(文科)⎪⎪⎩⎪⎪⎨⎧≥≥-<-<+0011234x y y x y x 表示的平面区域内的整点的个数是( )A .8个B .5个C .4个D .2个10、(理科)在约束条件0024x y y x s y x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩下,当5s 3≤≤时,目标函数32z x y =+的最大值的变化范围是( )A.[6,15]B. [7,15]C. [6,8] D . [7,8]第二部分(非选择题)二、填空题(每小题5分,4小题,共20分)11、在△ABC 中,BC=2,AC=2,C=1500,则△ABC 的面积为12、当x 取值范围是 时,函数122-+=x x y 的值大于零 13、在等比数列}{n a 中,08,204321=+=+a a a a ,则=10S14、(文科)不等式组6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩表示的平面区域的面积是14、(理科)观察下列的图形中小正方形的个数,则第n 个图中有 个 小正方形.三、解答题(15小题10分,16小题12分,17、18小题13分,19、20小题16分) 15、已知{}n a 是等差数列,其中1425,16a a ==(1)数列{}n a 从哪一项开始小于0 (2)求13519a a a a ++++值。
高中数学 综合模块测试23 新人教B版必修5

高中数学 综合模块测试23 新人教B 版必修5一、选择题:(本大题共12小题,每小题5分,共60分,) 1.如图,这是一个正六边形的序列,则第n 个图形的边数为( ).A. 5n-1B. 6nC. 5n+1D.4n+22.在等比数列{}n a 中T n 表示前n 项的积,若T 5 =1,则( ) A .13=a B .11=a C .14=a D .15=a3.在△ABC 中,根据下列条件解三角形,则其中有两个解的是( ) A .b = 10,A = 45°,B = 70° B .a = 60,c = 48,B = 100° C .a = 7,b = 5,A = 80° D .a = 14,b = 16,A = 45°4.一个只有有限项的等差数列,它的前5项的和为34,最后5项的和为146,所有项的和为234,则它的第七项等于( )A. 22B. 21C. 19D. 185. 已知△ABC 的周长为9,且4:2:3sin :sin :sin =C B A ,则cosC 的值为 ( )A .41-B .41C .32-D .32 6.不等式(1)20x x -+≥的解集是( )A {|1}x x >B {|1}x x ≥C {|21}x x x ≥-≠且D {|21}x x x =-≥或7.某工厂第一年的产量为A ,第二年的增长率为a,第三年的增长率为b ,这两年的平均增长率为x,则( )A .2a b x +=B.2a b x +≤ C . 2a b x +> D. 2a bx +≥ 8.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12,则△ABC 为( )A.三边均不相等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形 9. 设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z=ax+by (a>0,b>0)的值是最大值为12,则23a b +的最小值为( ). A.625 B.38 C. 311 D. 410.若250ax x b -+>解集为{|32}x x -<<,则250bx x a -+>解集为 ( )A .11{|}32x x -<< B .{|32}x x -<< C . 11{|}32x x x <->或 D .{|32}x x x <->或 11已知点(3,A ,O 是坐标原点,点(,)P x y的坐标满足0200y x y -≤+≥⎨⎪≥⎪⎩,设z 为OA 在OP上的投影,则z=|OA |cos ,OA OP 〈〉的取值范围是( ).A.[,B.[3,3]-C.[,3]D.[3,-12.正奇数集合{1,3,5,…},现在由小到大按第n 组有(2n -1)个奇数进行分组: {1}, {3,5,7}, {9,11,13,15,17},… (第一组) (第二组) (第三组) 则2009位于第( )组中.A. 33B. 32 C . 31 D. 30二、填空题:(本题共小题,每小题5分,共20分.) 13. 等差数列{a n }中,10a <,n S 为前n 项和,且316S S =,则nS取最小值时,n 的值为____14.△ABC 的三个角A<B<C,且2B=A+C,最大边为最小边的2倍,则三内角之比为 .15.设220,0,12b a b a ≥≥+=,则的最大值为 16.若对任意实数]1,1[-∈x ,不等式230x mx m ++<恒成立,则实数m 的取值范围是 . 三、解答题:(共70分) 17.(本题10分)设ABC ∆的内角C B A ,,的对边分别为c b a ,,,且满足A b a sin =. (Ⅰ)求B 的大小;(Ⅱ)求C A cos cos +的取值范围.18. (本小题满分12分)如图所示,动物园要围成相同面积的长方形虎笼四间,一面可以利用原有的墙,其他各面用钢筋网围成。
高中数学 综合模块测试12 新人教B版必修5

高中数学 综合模块测试12 新人教B 版必修5一、选择题(每小题5分,共50分)1、某体育宫第一排有5个座位,第二排有7个座位,第三排有9个座位,依次类推,那么第十五排有( )个座位。
A .27B .33C .45D .51 2、下列结论正确的是( )A .若ac>bc ,则a>bB .若a 2>b 2,则a>bC .若a>b,c<0,则 a+c<b+cD .若a <b ,则a<b 3、等比数列{}n a 中,S 2=7,S 6=91,则S 4=( )A )28B )32C )35D )494、已知非负实数x ,y 满足2380x y +-≤且3270x y +-≤,则x y +的最大值是( )A .73 B .83C .2D . 3 5、已知数列{}n a 的前n 项和2(1)n S n n =+,则5a 的值为( )A .80B .40C .20D .10 6、设4321,,,a a a a 成等比数列,其公比为2,则432122a a a a ++的值为( )A .41 B .21 C .81D .17、不等式组13y x x y y <⎧⎪+≤⎨⎪≥-⎩表示的区域为D ,点P (0,-2),Q (0,0),则( )A. P ∉D ,且Q ∉DB. P ∉D ,且Q ∈DC. P ∈D ,且Q ∉DD. P ∈D ,且Q ∈D8、在△ABC 中,a= 3 +1, b= 3 -1, c=10 ,则△ABC 中最大角的度数为( )A. 600B.900C.1200D.15009、若实数a 、b 满足2a b +=,则33a b +的最小值是 ( )A .18B .6C .D .10、若2()1f x x ax =-+能取到负值,则a 的范围是 ( )A.2a ≠±B.-2<a <2C.a >2或a <-2D.1<a <3 二、填空题(5×4=20分)11、a 克糖水中含有b 克塘(a>b>0),若在糖水中加入x 克糖,则糖水变甜了。
高中数学 模块精选综合测试1 新人教B版必修5

模块精选综合测试(一)(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a <1,b >1,那么下列命题中正确的是( ) A.1a >1bB.b a>1 C.a 2<b 2D.ab <a +b【解析】 利用特值法,令a =-2,b =2. 则1a <1b ,A 错;b a<0,B 错;a 2=b 2,C 错.【答案】 D2.一个等差数列的第5项a 5=10,且a 1+a 2+a 3=3,则有( )【导学号:18082141】A.a 1=-2,d =3B.a 1=2,d =-3C.a 1=-3,d =2D.a 1=3,d =-2【解析】 ∵a 1+a 2+a 3=3且2a 2=a 1+a 3,∴a 2=1.又∵a 5=a 2+3d =1+3d =10,d =3.∴a 1=a 2-d =1-3=-2. 【答案】 A3.已知△ABC 的三个内角之比为∠A ∶∠B ∶∠C =3∶2∶1,那么对应的三边之比a ∶b ∶c 等于( )A.3∶2∶1B.3∶2∶1C.3∶2∶1D.2∶3∶1【解析】 ∵∠A ∶∠B ∶∠C =3∶2∶1,∠A +∠B +∠C =180°, ∴∠A =90°,∠B =60°,∠C =30°. ∴a ∶b ∶c =sin 90°∶sin 60°∶sin 30° =1∶32∶12=2∶3∶1. 【答案】 D4.在坐标平面上,不等式组⎩⎪⎨⎪⎧y ≥x -1,y ≤-3|x |+1所表示的平面区域的面积为( )A. 2B.32C.322D.2【解析】 由题意得,图中阴影部分面积即为所求.B ,C 两点横坐标分别为-1,12.∴S △ABC =12×2×⎪⎪⎪⎪⎪⎪12--=32. 【答案】 B5.已知△ABC 中,内角A ,B ,C 所对边长分别为a ,b ,c ,若∠A =π3,b =2a cos B ,c=1,则△ABC 的面积等于( )A.32B.34C.36D.38【解析】 由正弦定理得sin B =2sin A cos B ,故tan B =2sin A =2sin π3=3,又∠B ∈(0,π),所以∠B =π3.又∠A =∠B =π3,则△ABC 是正三角形,所以S △ABC =12bc sin A =12×1×1×32=34.【答案】 B6.等差数列的第二,三,六项顺次成等比数列,且该等差数列不是常数数列,则这个等比数列的公比为( )A.3B.4C.5D.6【解析】 设等差数列的首项为a 1,公差为d , 则a 2=a 1+d ,a 3=a 1+2d ,a 6=a 1+5d , 又∵a 2·a 6=a 23,∴(a 1+2d )2=(a 1+d )(a 1+5d ), ∴d =-2a 1,∴q =a 3a 2=3. 【答案】 A7.若不等式x 2+ax +1≥0对一切x ∈⎝ ⎛⎦⎥⎤0,12恒成立,则a 的最小值为( )【导学号:18082142】A.0B.-2C.-52D.-3【解析】 x 2+ax +1≥0在x ∈⎝ ⎛⎦⎥⎤0,12上恒成立⇔ax ≥-x 2-1⇔a ≥⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫x +1x max ,∵x+1x ≥52, ∴-⎝ ⎛⎭⎪⎫x +1x ≤-52,∴a ≥-52. 【答案】 C8.已知{a n }是等差数列,公差d 不为零,前n 项和是S n ,若a 3,a 4,a 8成等比数列,则( ) A.a 1d >0,dS 4>0 B.a 1d <0,dS 4<0 C.a 1d >0,dS 4<0D.a 1d <0,dS 4>0【解析】 ∵a 3,a 4,a 8成等比数列,∴a 24=a 3a 8,∴(a 1+3d )2=(a 1+2d )(a 1+7d ),展开整理,得-3a 1d =5d 2,即a 1d =-53d 2.∵d ≠0,∴a 1d <0.∵S n =na 1+n n -2d ,∴S 4=4a 1+6d ,dS 4=4a 1d +6d 2=-23d 2<0.【答案】 B9.已知数列{a n }满足a 1=1,a n +1=a n +2n,则a 10等于( ) A.1 024B.1 023C.2 048D.2 046【解析】 a 1=1,a 2-a 1=2,a 3-a 2=22,a 4-a 3=23,…,a 10-a 9=29, 上面各式相加,得a 10=1+2+22+…+29=1-2101-2=210-1=1 023,故选B.【答案】 B10.设x ,y ∈R ,a >1,b >1.若a x =b y=3,a +b =23,则1x +1y的最大值为( )A.2B.32C.1D.12【解析】 ∵23=a +b ≥2ab ,∴ab ≤3. 由a x=b y=3得x =log a 3,y =log b 3,∴1x +1y =1log a 3+1log b 3=log 3a +log 3b =log 3ab ≤log 33=1.故选C. 【答案】 C11.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若∠B =2∠A ,a =1,b =3,则c =( ) A.2 3 B.2 C. 2 D.1【解析】 由正弦定理得:a sin A =bsin B, ∵∠B =2∠A ,a =1,b =3, ∴1sin A =32sin A cos A. ∵A 为三角形的内角,∴sin A ≠0. ∴cos A =32. 又0<∠A <π,∴∠A =π6,∴∠B =2∠A =π3.∴∠C =π-∠A -∠B =π2,∴△ABC 为直角三角形.由勾股定理得c =12+32=2.【答案】 B12.一个等比数列前三项的积为2,最后三项的积为4,且所有项的积为64,则该数列有( )A.13项B.12项C.11项D.10项【解析】 设该数列的前三项分别为a 1,a 1q ,a 1q 2,后三项分别为a 1qn -3,a 1qn -2,a 1qn-1.所以前三项之积a 31q 3=2,后三项之积a 31q3n -6=4,两式相乘,得a 61q3(n -1)=8,即a 21qn -1=2.又a 1·a 1q ·a 1q 2·…·a 1q n -1=64,所以a n1·qn n -2=64,即(a 21qn -1)n=642,即2n=642,所以n =12.【答案】 B二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.在△ABC 中,BC =2,∠B =π3,当△ABC 的面积等于32时,sin C =________.【导学号:18082143】【解析】 由三角形的面积公式,得S =12AB ·BC sin π3=32,易求得AB =1,由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC ·cos π3,得AC =3,再由三角形的面积公式,得S =12AC ·BC sin C =32,即可得出sin C =12. 【答案】 1214.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤4,x -y ≤2,3x -y ≥0,则3x +y 的最大值是________.【解析】 画出可行域,如图阴影部分所示,设z =3x +y ,则y =-3x +z ,平移直线y =-3x 知当直线y =-3x +z 过点A 时,z 取得最大值.由⎩⎪⎨⎪⎧x +y =4,x -y =2,可得A (3,1).故z max =3×3+1=10.【答案】 1015.国家为了加强对烟酒生产的宏观管理,实行征收附加税政策.现知某种酒每瓶70元,不加附加税时,每年大约产销100万瓶,若政府征收附加税,每销售100元要征税k 元(叫做税率k %),则每年的产销量将减少10k 万瓶.要使每年在此项经营中所收取附加税金不少于112万元,则k 的取值范围为________.【解析】 设产销量为每年x 万瓶,则销售收入每年70x 万元,从中征收的税金为70x ·k %万元,其中x =100-10k .由题意,得70(100-10k )k %≥112,整理得k 2-10k +16≤0,解得2≤k ≤8.【答案】 [2,8]16.设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N +,则a 1=________,S 5=________.【解析】 ∵a n +1=2S n +1, ∴S n +1-S n =2S n +1, ∴S n +1=3S n +1, ∴S n +1+12=3⎝⎛⎭⎪⎫S n +12,∴数列⎩⎨⎧⎭⎬⎫S n +12是公比为3的等比数列,∴S 2+12S 1+12=3.又S 2=4,∴S 1=1,∴a 1=1, ∴S 5+12=⎝ ⎛⎭⎪⎫S 1+12×34=32×34=2432,∴S 5=121. 【答案】 1 121三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若m =(a 2+c 2-b 2,-3a ),n =(tan B ,c ),且m ⊥n ,求∠B 的值.【解】 由m ⊥n 得(a 2+c 2-b 2)·tan B -3a ·c =0,即(a 2+c 2-b 2)tan B =3ac ,得a 2+c 2-b 2=3ac tan B,所以cos B =a 2+c 2-b 22ac =32tan B,即tan B cos B =32,即sin B =32, 所以∠B =π3或∠B =2π3.18.(本小题满分12分)在等差数列{a n }中,S 9=-36,S 13=-104,在等比数列{b n }中,b 5=a 5,b 7=a 7, 求b 6.【解】 ∵S 9=-36=9a 5,∴a 5=-4, ∵S 13=-104=13a 7,∴a 7=-8. ∴b 26=b 5·b 7=a 5 ·a 7=32. ∴b 6=±4 2.19.(本小题满分12分)已知数列{log 2(a n -1)}为等差数列,且a 1=3,a 3=9. (1)求数列{a n }的通项公式; (2)求数列{a n }的前n 项和S n .【解】 (1)设等差数列{log 2(a n -1)}的公差为d .由a 1=3,a 3=9,得2(log 22+d )=log 22+log 28,解得d =1,∴log 2(a n -1)=1+(n -1)×1=n ,∴a n =2n+1.(2)∵a n =2n+1,∴S n =a 1+a 2+…+a n =(2+1)+(22+1)+…+(2n +1)=(2+22+ (2))+n =-2n1-2+n =2n +1+n -2.20.(本小题满分12分)解关于x 的不等式ax 2-2≥2x -ax (a ∈R ).【导学号:18082144】【解】 原不等式可化为ax 2+(a -2)x -2≥0⇒(ax -2)(x +1)≥0.(1)当a =0时,原不等式化为x +1≤0⇒x ≤-1;(2)当a >0时,原不等式化为⎝ ⎛⎭⎪⎫x -2a (x +1)≥0⇒x ≥2a或x ≤-1;(3)当a <0时,原不等式化为⎝⎛⎭⎪⎫x -2a (x +1)≤0.①当2a >-1,即a <-2时,原不等式等价于-1≤x ≤2a;②当2a =-1,即a =-2时,原不等式等价于x =-1; ③当2a<-1,即-2<a <0时,原不等式等价于2a≤x ≤-1.综上所述:当a <-2时,原不等式的解集为⎣⎢⎡⎦⎥⎤-1,2a ;当a =-2时,原不等式的解集为{-1}; 当-2<a <0时,原不等式的解集为⎣⎢⎡⎦⎥⎤2a ,-1;当a =0时,原不等式的解集为(-∞,-1];当a >0时,原不等式的解集为(-∞,-1]∪⎣⎢⎡⎭⎪⎫2a,+∞.21.(本小题满分12分)如图1,在扇形AOB 中,圆心角等于60°,半径为2,在弧AB 上有一动点P (不与点A ,B 重合),过点P 引平行于OB 的直线和OA 交于点C ,设∠AOP =θ,求△POC 的面积的最大值及此时θ的值.图1【解】 ∵CP ∥OB ,∴∠CPO =∠POB =60°-θ,∠OCP =120°. 在△POC 中,由正弦定理得:OPsin∠PCO =CPsin θ,即2sin 120°=CP sin θ,∴CP =43sin θ. 又∵OC-θ=2sin 120°,∴OC =43sin(60°-θ).∴△POC 的面积为S △POC =12CP ·OC sin 120°=12×43sin θ·43sin(60°-θ)×32 =43sin θsin(60°-θ)=43sin θ⎝ ⎛⎭⎪⎫32cos θ-12sin θ=23sin(2θ+30°)-33,θ∈(0°,60°).∴当θ=30°时,△POC 的面积取得最大值33. 22.(本小题满分12分)某厂用甲、乙两种原料生产A ,B 两种产品,制造1 t A,1 t B 产品需要的各种原料数、可得到利润以及工厂现有各种原料数如下表:(2)每吨B 产品的利润在什么范围变化时,原最优解不变?当超出这个范围时,最优解有何变化?【解】 (1)生产A ,B 两种产品分别为x t ,y t ,则利润z =5x +3y ,x ,y 满足⎩⎪⎨⎪⎧2x +y ≤14,x +3y ≤18,x ≥0,y ≥0,作出可行域如图: 当直线5x +3y =z 过点B ⎝ ⎛⎭⎪⎫245,225时,z 取最大值3715,即生产A 产品245 t ,B 产品225 t时,可得最大利润.(2)设每吨B 产品利润为m 万元,则目标函数是z =5x +my ,直线斜率k =-5m,又k AB =-2,k CB =-13,要使最优解仍为B 点,则-2≤-5m ≤-13,解得52≤m ≤15,则B 产品的利润在52万元/t 与15万元/t 之间时,原最优解仍为生产A 产品245 t ,B 产品225 t ,若B 产品的利润超过15万元/t ,则最优解为C (0,6),即只生产B 产品6 t ,若B 产品利润低于52万元/t ,则最优解为A (7,0),即只生产A 产品7 t.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修五模块综合测试 人教B 版(满分150分,测试时间120分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M={x|-4≤x≤7},N={x|x 2-x-12>0},则M∩N 为( )A.{x|-4≤x<-3或4<x≤7}B.{x|-4<x≤-3或4≤x<7}C.{x|x≤-3或x >4}D.{x|x <-3或x≥4} 解析:N={x|x <-3或x >4},借助数轴,进行集合的运算,如图.得M∩N={x|-4≤x<-3或4<x≤7}.故选A. 答案:A2.若A 是△ABC 的一个内角,且sinA+cosA=32,则△ABC 的形状是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定 解析:由sinA+cosA=32,得sinAcosA=185-<0. 又∵0<A <π,∴2π<A <π.故∠A 为钝角. 答案:C3.一群羊中,每只羊的重量数均为整千克数,其总重量为65千克,已知最轻的一只羊重7千克,除去一只10千克的羊外,其余各只羊的千克数恰能组成一等差数列,则这群羊共有( )A.6只B.5只C.8只D.7只解析:设这群羊共有n+1只,公差为d (d ∈N *). 由题意,得7n+d n n 2)1(-=55,整理,得14n+n (n-1)d=110. 分别把A 、B 、C 、D 代入验证,只有B 符合题意,此时n=5,d=2. 答案:A4.已知点P (x ,y )在经过A (3,0)、B (1,1)两点的直线上,那么2x +4y的最小值是( ) A.22 B.42 C.16 D.不存在 解析:可求AB 的直线方程为x+2y=3.∴2x +4y =2x +22y≥242222222322=+=•+y x y x . 答案:B5.若实数x 、y 满足不等式组⎪⎩⎪⎨⎧≥--≥-≥.022,0,0y x y x y 则w=11+-x y 的取值范围是( )A.[-1,31] B.[31,21-]C.[21-,+∞) D.[21-,1] 解析:作出不等式组表示的平面区域如下图所示.据题意,即求点M (x ,y )与点P (-1,1)连线斜率的取值范围.由图可知w min =211101-=---,w max <1,∴w∈[21-,1].答案:D6.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是P n =P 0(1+k )n(k >-1),其中P n 为预测期人口数,P 0为初期人口数,k 为预测期内年增长率,n 为预测期间隔年数.如果在某一时期有-1<k <0,那么在这期间人口数( ) A.呈上升趋势 B.呈下降趋势 C.摆动变化 D.不变解析:P n+1-P n =P 0(1+k )n+1-P 0(1+k )n =P 0(1+k )n (1+k-1)=P 0(1+k )n·k,∵-1<k <0,∴0<1+k <1.∴(1+k )n>0.又∵P 0>0,k <0,∴P 0(1+k )n·k<0. 即P n+1-P n <0,∴P n+1<P n . 答案:B7.设b >0,二次函数y=ax 2+bx+a 2-1的图象为下列之一,则a 的值为( )A.1B.-1C.251-- D.251+- 解析:由前两个图可知b=0,不合题意.根据后两个图过原点可知a 2-1=0,即a=-1或a=1.当a=1时,函数为y=x 2+bx ,其图象与x 轴交于(0,0)及(-b ,0)两点,不合题意;当a=-1时,函数为y=-x 2+bx ,其图象与x 轴交于(0,0)及(b ,0)两点,第三个图符合.故选B. 答案:B8.已知凸函数的性质定理:如果函数f (x )在区间D 上是凸函数,则对于区间内的任意x 1,x 2,…,x n ,有n 1[f (x 1)+f (x 2)+…+f(x n )]≤)(21nx x x f n Λ++.已知y=sinx 在区间(0,π)上是凸函数,那么在△ABC 中,sinA+sinB+sinC 的最大值为( ) A.2 B.233 C.23D.3解析:据题意得31(sinA+sinB+sinC )≤233sin 3sin ==++πC B A . ∴sinA+sinB+sinC≤233. 答案:B 9.已知yx 35+=2(x >0,y >0),则xy 的最小值是( ) A.12 B.14 C.15 D.18 解析:∵x>0,y >0,∴2=xyy x 15235≥+. ∴xy≥15,当且仅当yx 35=等号成立. 答案:C10.已知x 、y 满足条件⎪⎩⎪⎨⎧≤≥+≥+-.3,0,05x y x y x 则2x+4y 的最小值为( )A.6B.-6C.12D.-12 解析:作出平面区域如下图所示,令z=2x+4y ,欲求z 的最小值,即求y=421zx +-在y 轴上截距的最小值.可以看出当直线过点(3,-3)时,纵截距最小. ∴z min =2×3+4×(-3)=-6.故选B.答案:B11.设集合P={m|-1<m <0},Q={m∈R |mx 2+4mx-4<0,对任意实数x 恒成立},则下列关系中成立的是( ) A.PQ B.QP C.P=Q D.P∩Q=∅解析:由mx 2+4mx-4<0对x ∈R 恒成立⇒⎩⎨⎧<+=∆<⇒0161602m m m -1<m <0. 当m=0时,-4<0.∴Q={m|-1<m≤0}.∴P Q.答案:A12.在锐角三角形中,a 、b 、c 分别是内角A 、B 、C 的对边,设B=2A ,则ab的取值范围是( )A.(-2,2)B.(2,3)C.(2,2)D.(0,2)解析:C=π-3A.由0<B <2π,0<C <2π,得6.230,220ππππ⇒⎪⎪⎩⎪⎪⎨⎧<-<<<A A <A <4π. 由正弦定理得AAA B a b B b A a sin 2sin sin sin sin sin ==⇒===2cosA.而22<cosA <23, ∴2<ab<3.故选B. 答案:B二、填空题(把答案填在题中横线上.本大题共4小题,每小题4分,共16分)13.在等差数列{a n }中,当a r =a s (r≠s)时,{a n }必定是常数数列.然而在等比数列{a n }中,对正整数r 、s (r≠s),当a r =a s 时,非常数数列{a n }的一个例子是_____________.解析:因为在等差数列{a n }中,当a r =a s 时公差必为0,所以{a n }必定是常数数列,而在等比数列{a n }中,当a r =a s 时公比为±1,当公比为1时是常数数列,当公比为-1时,为摆动数列,所以要符合题意只要任写出一个摆动数列即可. 答案:a ,-a ,a ,-a ,…(a≠0)14.在等差数列{a n }中,已知a 1+a 3+a 5=18,a n-4+a n-2+a n =108,S n =420,则n=___________. 解析:∵(a 1+a 3+a 5)+(a n -4+a n-2+a n )=3(a 1+a n )=126,∴a 1+a n =42. 又S n =2422)(1⨯=+n a a n n =420,∴n=20. 答案:2015.已知函数y=f (x )是偶函数,当x >0时,f (x )=x+x4.当x∈[-3,-1]时,记f (x )的最大值为m ,最小值为n ,则m-n=______________.解析:∵y=f(x )是偶函数,∴即求f (x )在x ∈[1,3]上的最值. ∵x>0时,f (x )=x+x4≥4(x=2时,等号成立), ∴n=f(x )min =4.而m=f (x )max =f (1)=5,∴m -n=5-4=1. 答案:116.设x 、y∈R +,S=x+y ,P=xy ,以下四个命题中正确命题的序号是_________________.(把你认为正确的命题序号都填上)①若P 为定值m ,则S 有最大值m 2;②若S=P ,则P 有最大值4;③若S=P ,则S 有最小值4;④若S 2≥kP 总成立,则k 的取值范围为k≤4. 解析:P 为定值m 时,S 应有最小值m 2,故①不正确.S=P 时,x+y=xy ⇒xy≥xy xy ⇒2≥2⇒xy≥4⇒P min =4,∴②也不正确.由S=P ⇒x+y=xy≤4)(2y x +⇒x+y≥4⇒S min =4,∴③正确.S 2≥kP ⇒k≤P S 2,又xy xy xy xy xy y x P S 222222+≥++==4,∴(PS 2)min =4.∴k≤4. ∴④正确.答案:③④三、解答题(答案应写出文字说明、证明过程或演算步骤.本大题共6小题,共74分)17.(本题满分12分)在△ABC 中,已知角A 、B 、C 所对的三条边分别是a 、b 、c 且满足b 2=ac.(1)求证:0<B≤3π;(2)求函数y=B B B cos sin sin 12++的值域.(1)证明:∵b 2=ac ,∴cosB=21222222222=-≥-+=-+ac ac ac ac ac c a ac b c a . 又∵0<B <π,∴0<B≤3π. (2)解:y=B B B B B B B cos sin )cos (sin cos sin 2sin 12++=++=sinB+cosB=2sin (B+4π).∵0<B≤3π,∴12744πππ≤+<B .∴当B+44ππ=,即B=4π时,y max =2.当B+44ππ=时,y min =2×22=1.∴y∈(1,2).18.(本题满分12分)集合A={x|x 2-5x+4≤0},B={x|x 2-2ax+a+2≤0},若B ⊆A 且B≠∅,求a 的取值范围.解:由A={x|x 2-5x+4≤0}⇒A={x|1≤x≤4}.令f (x )=x 2-2ax+a+2. ∵B A 且B≠∅,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤<<-≤≥⇒⎪⎪⎩⎪⎪⎨⎧≥-≥-<<≥--⇒⎪⎪⎩⎪⎪⎨⎧≥≥<<≥∆.718,3,41,12.0718,03,41,02.0)4(,0)1(,41,02a a a a a a a a a a f f a 或⇒2≤a≤718.19.(本题满分12分)在△ABC 中,三内角A 、B 、C 成等差数列,角B 的对边b 为1,求证:1<a+c≤2.证法一:∵2B=A+C,又A+B+C=180°,∴B=60°,C=120°-A. 由正弦定理得︒==60sin 1sin sin C c A a , 再由合分比定理得a+c=332(sinA+sinC )=332[sinA+sin (120°-A )]=2sin (A+30°)≤2,再由两边之和大于第三边,∴1<a+c. ∴1<a+c≤2.证法二:先得B=60°(同上得).再利用余弦定理知cosB=ac b c a 2222-+,即acb c a 221222-+=,即(a+c )2-1=3ac≤2)2(3c a +. 解得a+c≤2.又∵a+c>1,∴1<a+c≤2.20.(本题满分12分)某商场预计全年分批购入每台价值为2 000元的电视机共3 600台.每批都购入x 台(x∈N *),且每批均需付运费400元.贮存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43 600元.现在全年只有24 000元资金用于支付这笔费用,请问能否恰当安排每批进货的数量使资金够用?写出你的结论,并说明理由.解:依题意,当每批购入x 台时,全年需用保管费S=2 000x·k.∴全年需用去运输和保管总费用为y=x 3600·400+2 000x·k. ∵x=400时,y=43 600,代入上式得k=201,∴y=x1440000+100x≥x x 10014400002•=24 000.当且仅当x1440000=100x ,即x=120台时,y 取最小值24 000元. ∴只要安排每批进货120台,便可使资金够用.21.(本题满分12分)已知等比数列{a n }满足a 1+a 6=11,且a 3a 4=932. (1)求数列{a n }的通项a n ;(2)如果至少存在一个自然数m ,恰使132-m a ,2m a ,a m+1+94这三个数依次成等差数列,问这样的等比数列{a n }是否存在?若存在,求出通项公式;若不存在,请说明理由.解:(1)由题意得⎪⎩⎪⎨⎧==⎪⎪⎩⎪⎪⎨⎧==⇒⎪⎩⎪⎨⎧=•=+.2,3121,332932,11113121511q a q a q a q a q a a 或∴a n =31)21(3321=-n ×26-n 或a n =31·2n-1. (2)对a n =31·2n-1,若存在题设要求的m ,则2(31·2m-1)2=32·31·2m-2+31·2m +94. ∴(2m)2-7·2m+8=0. ∴2m=8,m=3. 对a n =31·26-n ,若存在题设要求的m ,同理有(26-m )2-11·26-m-8=0. 而Δ=112+16×8不是完全平方数,故此时所需的m 不存在. 综上所述,满足条件的等比数列存在,且有a n =31·2n-1. 22.(本题满分14分)已知二次函数f (x )的二次项系数为a ,且不等式f (x )>-2x 的解集为(1,3).(1)若方程f (x )+6a=0有两个相等的根,求f (x )的解析式; (2)若f (x )的最大值为正数,求a 的取值范围.解:(1)设f (x )=ax 2+bx+c ,则不等式f (x )>-2x 为ax 2+(b+2)x+c >0. ∵不等式的解集为(1,3), ∴a<0,ab 2+-=4,ac=3, 即a <0,b=-4a-2,c=3a.∵方程ax 2+bx+6a+c=0有两个相等的根,∴Δ=b 2-4a (6a+c )=0.把b 、c 分别代入Δ中,得5a 2-4a-1=0.解得a=51-,a=1(舍). ∴b=56-,c=53-.∴f(x )的解析式为f (x )=5356512---x x . (2)由(1)知a <0,所以当x=ab2-时,函数f (x )取到最大值.由题设,得a (a b 2-)2+b·(ab2-)+c >0.代入b 、c 并整理,得a 2+4a+1>0. 解得a <-2-3或a >-2+3.又∵a<0,∴a 的取值范围为(-∞,-2-3)∪(-2+3,0).。
