第十二章《轴对称》单元测试题

合集下载

人教版八年级上第十二章轴对称测试题

第十二章轴对称单元测试题一、选择题(每小题5分，其25分)1．下列四个图案中，轴对称图形的个数是( )2．下列命题中，不正确的是( )(A)关于直线对称的两个三角形一定全等. (B)两个圆形纸片随意平放在水平桌面上构成轴对称图形.(C)若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线.(D)等腰三角形一边上的高、中线及这边对角平分线重台.3．下列四个图案中．具有一个共有性质则下面四个数字中，满足上述性质的一个是( ) (A)6 (B)7 (C)8 (D)94.等腰三角形的一个内角是50。

，则另外两个角的度数分别是( )(A) 65°，65°. (B) 50°,80°． (C) 65°，65°或50°，80°. (D) 50°,50°. 5.如果等腰三角形两边长是6cm 和3cm ,那么它的周长是( )(A) 9cm (B) 12cm (C) 1215cm cm 或 (D) 15cm .二、填空题(每小题5分，共20分)6．等腰三角形是对称图形，它至少有条对称轴.7．小明上午在理发店理发时，从镜子内看到背后墙上普通时钟的时针与分针的位置如图所示，此时时间是 .8．已知△ABC 是轴对称图形．且三条高的交点恰好是C 点，则△ABC 的形状是 .9．已知点A(一2，4)，B(2，4)，C(1．2)，D(1-2)，E(一3，1)，F(3，1)是平面坐标系内的6个点，选择其中三个点连成一个三角形，剩下三个点连成另一个三角形，若这两个三角形关于y 轴对称，就称为一组对称三角形，那么，坐标系中可找出组对称三角形． 10．如图，△ABC 中，AB=AC ．∠A=36°，AB 的中垂线DE 交AC 于D ，交AB 于E.下述结论(1)BD 平分∠ABC ；(2)AD=BD=BC ；(3)△BDC 的周长等于AB+BC ；(4)D 是AC 中点，其中正确的命题序号是 .三、画一画11.(6分)以“○○，△△，＿＿＿”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形.四、解答题12．(10分)在△ABC 中,∠C=90°，DE 垂直平分斜边AB ，分别交AB 、BC 于D 、E 。

第12章轴对称单元综合测评(含答案)

第12章轴对称单元综合测评一、选择题（每小题3分，共30分）题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获，我们设计的试卷主要就是从这点出发，所以从你下载这张试卷开始，就与知识接近了一步。

1．下列图形中一定是轴对称图形的是（）A．梯形B．直角三角形C．等腰三角形D．平行四边形2．已知△ABC在直角坐标系中的位置如图所示，如果△A'B'C'与△ABC关于y轴对称，那么点A的对应点A'的坐标为（）A．（－4，2）B．（－4，－2）C．（4，－2）D．（4，2）（第2题）（第3题）（第4题）3．如图，如果直线m是多边形ABCDE的对称轴，其中∠A＝130°，∠B＝110°．那么∠BCD 的度数等于（）A．40°B．50°C．60°D．70°4．如图，△ABC中，∠B＝90°，AB＝6，BC＝8，将△ABC沿DE折叠，使点C落在AB 边上的C′处，并且C′D//BC，则C′D的长是（）A．409B．509C．154D．2545．在平面直角坐标系中，已知A（2，－2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（）A．2个B．3个C．4个D．5个6．下列图形中对称轴条数最多的是（）A．正方形B．长方形C．等腰三角形D．等边三角形7．下列图案中，是轴对称的是（）A．（1）（2）B．（1）（3）（4） C．（1）（4）D．（2）（3）8．如图，有一矩形纸片ABCD，AB＝10，AD＝6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（）A．4 B．5 C．8 D．109．如图，在△ABC中，AB＝AC，D为AC边上一点，且BD＝BC＝AD．•则∠A等于（）A．30°B．36°C．45°D．72°10．如图，在等腰三角形ABC中，AB＝AC，∠A＝44°，CD⊥AB于D，则∠DCB等于（）A．44°B．68°C．46°D．22°二、填空题（每小题3分，共30分）11．正六边形的对称轴有_____________条．12．在△ABC中，AB ＝AC，AB的中垂线与AC所在直线相交所得的锐角是50°，则∠B 的度数为_____________．13．若等腰三角形的两边长分别为6和8，则该等腰三角形的周长为_____________．14．一条船5点从灯塔C南偏东42°的A处出发，以16海里/时的速度向正北航行，8点到达B处，此时灯塔C在船的北偏西84°方向，则船距离灯塔C_____________海里．（第14题）（第15题）15．如图，D、E为AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B＝500，则∠BDF＝_____________．16．如图，在△ABC中，AB＝AC，∠A＝50︒，BD为∠ABC的平分线，则∠BDC的度数为_____________．17．如图，由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是a，则六边形的周长是_____________．18．一个顶角为40︒的等腰三角形纸片，剪去顶角后，得到一个四边形，则∠1＋∠2＝_____________度．19．如图，在△ABC中，AB＝AC，∠BAD＝20°，且AE＝•AD，则∠CDE＝_____________．20．如图，沿大正三角形的对称轴对折，则互相重合的两个小三角形内的单项式的乘积为_____________．三、解答题（每小题8分，共40分）21．图中的大正三角形是由9个相同的小正三角形拼成的，将其部分涂黑，如图（1），（2）所示．观察图（1），图（2）中涂黑部分构成的图案．它们具有如下性质：①都是轴对称图形，②涂黑部分都是三个小正三角形．请你在图（3），图（4）内分别设计一个新图案，使图案具有上述两个特征．22．如图，已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分，求它的底边长．23．如图，△ABC是等边三角形，BD是AC边上的高，延长BC到E使CE＝CD．试判断DB与DE之间的大小关系，并说明理由．24．如图，△ABC中, D、E分别是AC、AB上的点, BD与CE交于点O．给出下列三个条件：①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD．（1）上述三个条件中，哪两个．．条件．．可判定△ABC是等腰三角形(用序号写出所有情形)；（2）选择第（1）小题中的一种情形, 证明△ABC是等腰三角形．25．如图，有一块三角形田地，AB ＝AC ＝10m ，作AB 的垂直平分线ED 交AC 于D ，交AB 于E ，量得△BDC 的周长为17m ，请你替测量人员计算BC 的长．参考答案一、1．C 2．D 3．C 4．A 5．C 6．A 7．B 8．C 9．B 10．D二、11．6 12．40︒或20︒ 13．20或22 14．48 15．80︒ 16．825 17．30a 18．220 19．10︒ 20．a ，22a b ，32a b 三、21．图略． 22．7cm 或11cm ．23．关系：DE ＝DB ．∵CD ＝CE ，∴∠E ＝∠EDC ，又∵∠ACB ＝60°，∴∠E ＝30°，又∵∠DBC ＝30°，∴∠E ＝∠DBC ，•∴DB ＝DE ． 24．（1）情形一：①和③；情形二：②和③．（2）选择情形一．证明：∵∠EOB ＝∠COD ，∠EBO ＝∠DCO ，BE ＝CD ．∴△BEO ≌△CDO ．∴BO ＝CO ．∴∠OBC ＝∠OCB ． ∴∠EBO ＋∠OBC ＝∠DCO ＋∠OCB ，即∠ABC ＝∠ACB ． ∴AB ＝AC ．∴△ABC 是等腰三角形．25．∵ED 是AB 的垂直平分线，∴DA ＝DB.又∵△BDC 的周长为17m ，AB ＝AC ＝10m ，∴BD+DC+BC ＝17，∴DA+DC+BC ＝17，即AC+BC ＝17． ∴10+BC ＝17，∴BC ＝7m ．可以编辑的试卷（可以删除）。

八年级数学第十二章轴对称整章水平测试(含答案)

八年级数学第十二章轴对称整章水平测试（含答案）
八年级数学24分)
1、下列说法正确的是（）
A轴对称涉及两个图形，轴对称图形涉及一个图形
B如果两条线段互相垂直平分，那幺这两条线段互为对称轴
C所有直角三角形都不是轴对称图形
D有两个内角相等的三角形不是轴对称图形
2、若等腰三角形的一边长为10，另一边长为7，则它的周长为
（）
A17B24C27D24或27
3、若一个三角形的三个外角的度数之比为5∶4∶5，则这个三角形
是（）
A等腰三角形，但不是等边三角形，也不是等腰直角三角形
B直角三角形，但不是等腰三角形
C等腰直角三角形
D等边三角形
4、等腰三角形底边长为5cm,一腰上的中线分其周长的两部分的差为
3cm，则腰长为（）
A2cmB8cmC2cm或8cmD以上答案都不对
5、下列说法正确的个数有（）
⑴等边三角形有三条对称轴⑵四边形有四条对称轴⑶等腰三角形的
一边长为4，另一边长为9，则它的周长为17或22⑷一个三角形中至少有
两个锐角
A1个B2个C3个D4个
请下载附件：
《八年级数学第十二章轴对称整章水平测试》
（本地下载）
点击下一页查看试题答案

第十二章轴对称单元测试题

D C B A 八年级数学第十二章轴对称测试题（时限：100分钟总分：100分）班级姓名座号总分一、选择题（本大题共12小题，每小题2分，共24分）1．下列图形中：①角，②正方形，③梯形，④圆，⑤菱形，⑥平行四边形，其中是轴对称图形的有（）A 、2个B 、3个C 、4个D 、5个2．长方形的对称轴有（）A 、2条B 、4条C 、6条D 、无数条3．把一张长方形的纸沿对角线折叠，则重合部分是（）A 、直角三角形B 、长方形C 、等边三角形D 、等腰三角形4．等腰三角形是轴对称图形，它的对称轴是（）A.过顶点的直线B.底边上的高C.底边的中线D.顶角平分线所在的直线.5．等腰三角形底边上的高等于腰的一半，则它的顶角度数为（）A 、60°B 、90°C 、100°D 、120°6．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；•③三个外角（每个顶点处各取一个外角）都相等的三角形；•④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A ．①②③B ．①②④C ．①③D ．①②③④7．下列图形中不是轴对称图形的是（）8．如图所示是一只停泊在平静水面的小船，它的“倒影”应是图中的（）9．等腰三角形的一个内角是50°，则另外两个角的度数分别为（）A.65°，65°B.50°，80°C.65°，65°或50°，80°D.50°，50°C D BA第1个第2个第3个第4个第5个第6个 21题⑴L10．已知点P （1，a ）与Q （b ，2）关于x 轴成轴对称，又有点Q （b ，2）与点M （m ，n ）关于y 轴成轴对称，则m －n 的值为（）A ．3 B.－3 C. 1 D. －111．将一等边三角形剪去一个角后，∠BDE ＋∠CEDA 、120°B 、240°C 、300°D 、1360°12．下图是按一定规律摆放的图案，按此规律，第2011个图案与第1~4个图案中相同的是（只填数字）二、填空题13．点A （－2，1）关于y 轴的对称点的坐标是，点A 关于x 的对称点的坐标是。

轴对称单元测试题及答案

轴对称单元测试题及答案一、选择题（每题2分，共20分）1. 下列图形中，哪一个是轴对称图形？A. 圆形B. 三角形C. 正方形D. 五边形2. 如果一个图形关于某条直线对称，那么这条直线被称为该图形的什么？A. 对称轴B. 中心线C. 垂直线D. 平行线3. 一个图形的轴对称图形与其本身是否完全重合？A. 是B. 否C. 有时是D. 不确定4. 轴对称图形的对称轴可以有多少条？A. 只有一条B. 至少一条C. 无数条D. 没有5. 下列哪个图形不是轴对称图形？A. 等边三角形B. 等腰梯形C. 矩形D. 正五边形二、填空题（每空1分，共10分）6. 轴对称图形的对称轴是________。

7. 如果一个图形关于点O对称，那么这个点O被称为该图形的________。

8. 一个轴对称图形的对称轴可以是一条________或多条________。

9. 轴对称图形的对称轴将图形分成两个完全________的部分。

10. 轴对称图形的对称轴是图形上所有点到________的距离相等的直线。

三、判断题（每题1分，共10分）11. 所有圆形都是轴对称图形。

（）12. 轴对称图形的对称轴可以是曲线。

（）13. 轴对称图形的对称轴一定经过图形的中心。

（）14. 一个图形的轴对称图形与原图形是完全相同的。

（）15. 轴对称图形的对称轴是唯一的。

（）四、简答题（每题5分，共10分）16. 请解释什么是轴对称图形，并给出一个例子。

17. 描述如何确定一个图形是否是轴对称图形。

五、应用题（每题5分，共10分）18. 给定一个矩形，如果将其沿一条对角线折叠，这条对角线是否是该矩形的对称轴？为什么？19. 如果一个图形关于某条直线对称，那么这条直线上的所有点是否也是对称的？请解释。

六、解答题（每题5分，共10分）20. 给定一个等边三角形ABC，如果点A关于对称轴l对称到点A'，求证点B和点C也关于对称轴l对称。

答案一、选择题1. A2. A3. A4. B5. D二、填空题6. 对称轴7. 对称中心8. 直线，直线9. 重合10. 对称轴三、判断题11. √12. ×13. ×14. √15. ×四、简答题16. 轴对称图形是指一个图形关于某条直线（对称轴）对称，这条直线将图形分成两个完全相同的部分。

第12章轴对称测试题

八级年数学上册班级：姓名：时间：编制：马尉平审阅：审批：第12章轴对称单元水平测试题一．选择题（每小题3分，共30分）成绩：1、下列轴对称图形中，对称轴最多的是（）（A）等腰直角三角形（B）线段（C）正方形（D）圆2、以下汽车标志中，不是轴对称图形的是（）（A）（B）（C）（D）3、如果一个等腰三角形的周长为15cm，一边长为3cm，那么腰长为（）A、3cmB、6cmC、5cmD、3cm或6cm4、已知点A（4，-6）关于x轴对称的点的坐标是：（）A．（4，6） B.（-4,6） C.(-4,-6) D.(6,-4)5、下列命题中，不正确的是（）（A）关于直线对称的两个三角形一定全等；（B）两个圆形纸片随意平放在水平桌面上构成轴对称图形；（C）若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线；（D）等腰三角形一边上的高、中线及这边对角平分线重合．6、等腰三角形两腰分别为3和7，那么它的周长为（）（A）10 （B）13 （C）17 （D）13或177、△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（）（A）300（B）360（C）450（D）7008、如图，在△ABC中，AB的中垂线交BC于点E，若BE=2则A、E两点的距离是（）.D.1 2A.4B.2C.39.在Rt△ABC中，如右图所示，∠C=90°，∠CAB=60°，AD平分∠CAB，点D到AB的距离DE=3.8 cm，则BC等于（）A.3.8 cmB.7.6 cmC.11.4 cmD.11.2 cm10. 如图已知: AB＝AC＝BD, 那么∠1与∠2之间的关系满足（）A.∠1＝2∠2B.2∠1＋∠2＝180°C.∠1＋3∠2＝180°D.3∠1－∠2＝180二、填空题：（第空3分，共30分）11、到线段两个端点距离相等的点的集合是________.12、在镜中看到的一串数字是“”，则这串数字是。

第12章轴对称综合复习测试题(一)及答案

第十二章《轴对称》综合复习测试题题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获，我们设计的试卷主要就是从这点出发，所以从你下载这张试卷开始，就与知识接近了一步。

一、选择题（每小题3分，共24分）1．下列图形，关于直线m对称的是（）2.下列图案都是轴对称图形，对称轴的条数最多的是（）3.下列叙述正确的语句是( )A.等腰三角形两腰上的高相等B.等腰三角形的高、中线、角平分线互相重合C.顶角相等的两个等腰三角形全等D.两腰相等的两个等腰三角形全等4．如图1，如果M点在∠ANB的角平分线上，AM⊥AN，BM⊥BN，那么和AM相等的线段一定是（）A．BM B．BN C．MN D．AN5．等腰三角形两条边长分别为12、15，则这个三角形的周长为（）A．27 B．39 C．42 D．39或426．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（）A．40°B．50°C．60°D．30°7.将一张正方形的纸片按下图方式三次折叠，沿MN裁剪，则可得( ).A A2.2等腰三角形的性质A A DDCDMNA B C DA B C Dm m m mA BM图1AB C DEBEA F DCA ．多个等腰直角三角形B ．一个等腰直角三角形和一个正方形C ．四个相同的正方形D ．两个相同的正方形8.如图2，在△ABC 中，AB ＝AC ，D 为BC 的中点，E 为AC 边上一点，且有AE=AD ，∠EDC=18°，则∠B 的度数是（）．A ．36°B ．46°C ．54°D ．72°图2 图3 二、填空题（每小题3分，共24分）1.如图3，若□ABCD 与□EBCF 关于BC 所在直线对称，∠ABE ＝90°，则∠F ＝ ° 2．如图4，OC 是∠AOB 的平分线，点P 在OC 上，PD ⊥OA 于D 点，PD=6，则P 到OB 的距离为__________cm.3．如图5，已知：在ABC ∆中，CD 是角平分线，BC DE //交AC 于E ，若cm DE 7=，cm AE 5=，则=AC _______cm .4．一辆汽车沿︒30角的山坡从山底开到山顶，共走了4000m ，那么此山的高度是_____m. 5．在等腰三角形ABC 中，若∠A=70°，则∠B= 。

轴对称单元测试题(含答案--高质量)

1第十二章轴对称提升训练一、选择题（每小题3%，共30分）1.下面四组图形中,右边与左边成轴对称的是（）A.B. C. D.2.下列图形中一定有4条对称轴的是（）A.长方形B.正方形C.等边三角形D.等腰直角三角形3.下列图形:①两个点;②线段;③角;④长方形;⑤两条相交直线;⑥三角形,其中一定是轴对称图形的有（）A.5个B.3个C.4个D.6个 4.如图1:射线BA,CA 相交于点A,连接BC,已知AB=AC,∠B=400, 则∠CAE 的度数为（）A.400B.600C.800D.10005.等腰三角形是轴对称图形,它的对称轴有（）A.1条B.2条C.3条D.1条或3条图1 6.如图2:在△ABC 中,DE 垂直平分AB,AE 平分∠BAC,若∠C=900,则∠B 的度数为（）A.30B.200C.400D.250图27.底和腰不等的等腰三角形中,它的角平分线、中线、高共有线段（） A.9条 B.6条 C.7条 D.3条8.如图3:在△ABC 中,AB=AC,∠A=36,BD,CE 分别平分∠ABC 和∠ACB,相交于点F,则图中等腰三角形共有（）A.7个B.8个C.6个D.9个图3 9.如图4:如果直线m 是多边形ABCDE 的对称轴,其中∠A=1300, ∠B=1000,则∠BCD 的度数为（） A.700B.800C.600D.90010.等腰三角形一腰上的高与另一腰的夹角为300,则顶角的度数为（）图4 A.600B.1200C.600或1500D.600或1200二、填空题（每小题3%，共15%）11.从镜子中看到背后墙上电子钟的示意数为 ,这时的实际时间为______. 12.在△ABC 中,AB=AC,AD ⊥BC 于D,由以上两个条件可得_________________.(写出一个结论即可)13.如图5:在△ABC 中, ∠A=900,BD 平分∠ABC,交AC于点D,已知AD=4.3㎝,则D 到BC 边的距离为__________. 图5 14.如果等腰三角形的三边长均为整数且周长为10,则它的三边长分别为______________.15.如图:有一张长方形纸片ABCD,AB=3,AD=1.8,将纸片折叠,使AD 边落在AB 边上,折痕为AE,再将△AED 以DE 为折痕向右折叠,AE 与BC 相交于点F,则CF 的长为__________.三、解答题（每小题5%，共30分）16.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.17.如图: △ABC 中,∠C=900.(1)请你以AC 所在的直线为对称轴,作出△ABC 的轴对称图形;(2)作出后所得的三角形与△ABC 是否组成一个等腰三角形?为什么?18.等腰△ABC 的腰AB=10㎝,AB 的垂直平分线交另一腰AC 于点D , △BCD 的周长为18㎝,求底边BC 的长.BCAE BC A ED ABCD E F A BCDEm ABCD A B CDA B C A D B C A D B C E AC F ED B219.如图:已知在△ABC 中,AB=AC,AE ∥BC,试说明AE 平分∠DAC.20.如图:一艘轮船在上午8时从A 处出发,以20海里/时的速度由南向北航行,在A 处测得小岛P 在北偏西24度,9点45分到达B 处,这时测得小岛P 在北偏西48度,求B 处到小岛P 的距离.21.如图:在△ABC 中,AB=AC,BF=DF,DC=DE,∠A=300,求∠EDF 的度数.四、解答题（22，23，24小题每小题6%，25题7%，共25%）22.如图:在△ABC 中,AB=AC,D 为BC 中点,DE ⊥AB 于E,DF ⊥AC 于F,则有DE=DF,你能说说其中的道理吗?23.如图: △ABC 中,若AD 平分∠BAC,CE ∥AD,CE 交BA 的延长线于E,问△ACE 是什么三角形?为什么?24.如图:在等边△ABC 中,BD 平分∠ABC,延长BC 到F,使CD=CF,连结DF. (1) 小刚说:BD=DF,他说得对吗?为什么?(2)小红说:把“BD 平分∠ABC”的条件改一改,也能得到同样的结论,你认为可以如何改呢?请说明你的理由.25.如图:在△ABC 中,AB=AC,P 为BC 边上任意一点,PF ⊥AB 于F,PE ⊥AC 于E,若AC 边上的高BD=a.(1)试说明PE ＋PF=a;(2)若点P 在BC 的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a 的关系式,不需要说明理由.A B CDE AB P A B CD E FA BD CE AB C D FA B C D F E A BCPFED。

轴对称测试题及答案

轴对称测试题及答案 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】DCBA新人教版八年级数学上册第十二章轴对称测试题及答案一、选择题（本大题共12小题，每小题2分，共24分）1.下列几何图形中，是轴对称图形且对称轴的条数大于1的有（）⑴ 长方形； ⑵正方形； ⑶圆； ⑷三角形； ⑸线段； ⑹射线； ⑺直线. A. 3个 B. 4个 C. 5个 D. 6个2.下列说法正确的是（）A.任何一个图形都有对称轴B.两个全等三角形一定关于某直线对称C.若△ABC 与△DEF 成轴对称，则△ABC ≌△DEFD.点A ，点B 在直线L 两旁，且AB 与直线L 交于点O ，若AO ＝BO ，则点A 与点B关于直线L 对称 3.如图所示是一只停泊在平静水面的小船，它的“倒影”应是图中的（）4.在平面直角坐标系中，有点A （2，－1），点A 关于y 轴的对称点是（） A.（－2，－1） B.（－2，1） C.（2，1） D.（1，－2）5.已知点A 的坐标为（1，4），则点A 关于x 轴对称的点的纵坐标为（） A. 1 B. －1 C. 4 D. －46.等腰三角形是轴对称图形，它的对称轴是（）A.过顶点的直线B.底边上的高C.底边的中线D.顶角平分线所在的直线. 7.已知点A （－2，1）与点B 关于直线x ＝1成轴对称，则点B 的坐标为（） A.（4，1） B.（4，－1） C.（－4，1） D.（－4，－1） 8.已知点P （1，a ）与Q （b ，2）关于x 轴成轴对称，又有点Q （b ，2）与点M （m ，n ）关于y 轴成轴对称，则m －n 的值为（）A. 3B.－3C. 1D. －19.等腰三角形的一个内角是50°，则另外两个角的度数分别为（）第14题°，65° °，80° °，65°或50°，80° °，50°10.等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角为（） A. 30° B. 150° C. 30°或150° °11.等腰三角形底边长为6cm ，一腰上的中线把它的周长分成两部分的差为2cm ，则腰长为（）A. 4cmB. 8cmC. 4cm 或8cmD. 以上都不对12.已知∠AOB ＝30°，点P 在∠AOB 的内部，点P 1和点P 关于OA 对称，点P 2和点P 关于OB 对称，则P 1、O 、P 2三点构成的三角形是（）A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形二、填空题：（本大题共8小题，每小题3分，共24分）13.等边三角形是轴对称图形，它有条对称轴. A 1B 1C 1与△ABC 关于y 轴对称，那么点A 的对应点A 1的是 .16.已知∠AOB ＝30°，点P 在OA 上，且OP ＝2，点P 关于直线OB 的对称点是Q ，则PQ ＝ .17.等腰三角形顶角为30°，腰长是4cm ，则三角形的面积为 .18.点P （1，2）关于直线y ＝1对称的点的坐标是；关于直线x ＝1对称的的坐标是 .19.三角形三内角度数之比为1∶2∶3，最大边长是8cm ，则最小边的长是 . 20.在△ABC 和△ADC 中，下列3个论断：①AB ＝AD ；②∠BAC ＝∠DAC ；③BC ＝DC.将两个论断作为条件，另一个论断作为结论构成一个命题，写出一个真命题：21题⑵BEDCBAPDCBAPE DCB A .三、解答题：（本大题共52分）21.（每小题5分，共10分）作图题：（不写作法，保留作图痕迹）⑴ 如图，已知线段AB 和直线L ，作出与线段AB 关于直线L 对称的图形.⑵ 已知∠AOB 和C 、D 两点，求作一点P ，使PC ＝PD ，且P 到∠AOB 两边的距离相等.22.（5B （－1，0），C （－4，3）.⑴求出△ABC 的面积.⑵ 在图形中作出△ABC 关于y 轴的对称图形△A 1B 1C 1. ⑶ 写出点A 1，B 1，C 1的坐标.23.（5分）如图所示，梯形ABCD 关y 轴对称，点A 的坐标为（－3，3），点B 的坐标为（－2，0）.⑴ 写出点C 和点D 的坐标； ⑵ 求出梯形ABCD 的面积.24.（5分）如图，△ABC 中，DE 是AC 的垂直平分线，AE ＝3cm ，△ABD 的周长为13cm.求△ABC 的周长.25.（6分）如图，D 是等边三角形ABC 内一点，DB ＝DA ，BP ＝AB ，∠DPB ＝∠DBC.求证：∠BPD ＝30°.26.（8分）如图，△ABC 为任意三角形，以边AB 、AC为边分别向外作等边三角形ABD 和等边三角形ACE ，连接CD 、BE 并且相交于点P.求证：⑴CD ＝BE. ⑵∠BPC ＝120°NMF E CB AED CB A27.（6分）下面有三个结论：⑴等腰三角形两底角的平分线的交点到底边两端的距离相等.⑵等腰三角形两腰上中线的交点到底边两端的距离相等.⑶等腰三角形两腰上的高的交点到底边两端的距离相等.请你任选一个结论进行证明.28.（7分）如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6，AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，求证：BM＝MN＝NC.参考答案和提示：一、选择题：；；；；；；；；；；；；二、填空题：13. 3；14.（－1，3）；15. 4点40分；16. 2；17. 4cm2；18.（1，0），（1，2）；19.4cm；20.等腰三角形的顶角平分线和底边上的中线重合.三、解答题：21.略；22.⑴＝×5×3＝（平方单位）；⑵略；⑶A1（1，5），B1（1，0）；C1（4，3）.23.⑴C（2，0），D（3，3）.⑵＝（4＋6）×3＝15（平方单位）.24.∵DE是线段AC的垂直平分线∴AD＝CD∵△ABD的周长为13cm∴AB＋BC＝13cm∵AE＝3cm∴AC＝2AE＝6cm. ∴△ABC的周长为：AB＋BC＋AC＝19cm.25.连接CD，并延度CD交AB于E，证CE垂直平分AB，可得∠DCB＝30°再证△BDC≌△BDP即可.26.略；27.略28.连接MA、NA，证明：MA＝NA＝MN.。

第12章轴对称单元水平测试题

第12章轴对称单元水平测试题一．选择题（每小题3分，共30分）1．下列说法中，正确的是（）A、有一边相等的两个等腰三角形全等B、有一边相等的两个等腰直角三角形全等C、有一边相等的两个直角三角形全等D、有一边相等的两个等边三角形全等2、如果一个等腰三角形的周长为15cm，一边长为3cm，那么腰长为（）A、3cmB、6cmC、5cmD、3cm或6cm3、若三角形中最大内角是60°，则这个三角形是（）A、不等边三角形B、等腰三角形C、等边三角形D、不能确定4、如果三角形中两条边的垂直平分线的交点在第三条边上，那么这个三角形是（）A、锐角三角形B、钝角三角形C、直角三角形D、等边三角形5、下列说法中，正确的是（）A、两个关于某直线对称的图形是全等图形B、两个图形全等，它们一定关于某直线对称C、两个全等三角形对应点连线的垂直平分线就是它们的对称轴D、两个三角形关于某直线对称，对称点一定在直线两旁6、若△ABC的三边满足a2+b2+c2=ab+bc+ca,则△ABC的形状是（）A、直角三角形B、等腰直角三角形C、锐角三角形D、等边三角形7、如图，AB=AC，D为BC中点，图中全等三角形（）A.1对B.2对C.3对D.4对8、已知△ABC中，∠A=∠B= 3∠C，则∠C的大小为（）9、若a、b、c为三角形的三条边长，则-(a+b+c)+｜a-b-c｜-｜b-c-a｜+｜c-b-a｜=（）(A)2(a-b-c)(B)2(b-a-c)(C)2(c-a-b)(D)2(a+b+c) 10、ABCD的边长AB=5cm，那么它的两条对角线AC、BD的长可能是（）A．4cm和6cm B．3cm和7cmC．4cm和8cm D．2cm和12cm二．填空题（每小题3分，共30分）11、△ABC的一边为5．另外两边的长是方程2x2-12x+m=0的两根，那么，m的取值范围是_____．12、一个三角形的周长为偶数，其中两条边的长分别是4和1997，则满足条件的三角形的个数是_____．13、等腰三角形底边长为7cm，它的周长不大于25cm，则它的腰长x的取值范围是______．14、如果三角形三个外角度数的比为3∶4∶5，那么三个内角的度数为______。

【八年级数学试题】初二数学上册第12章轴对称单元过关试题(带答案)

初二数学上册第12章轴对称单元过关试题（带答案）
一、选择题（每题2分，共4___，b=__-5__。

3点(-2，1)点关于x轴对称的点坐标为_(-2，-1 )__；关于轴对称的点坐标为_(2，1)_。

4等腰三角形中的一个角等于100°，则另外两个内角的度数分别为_40 °_40°_。

5已知△ABc中∠AcB=90°，cD⊥AB于点D，∠A=30°，Bc=2c，则AD=___3c_ _
6Rt△ABc中，cD是斜边AB上的高，∠B=30°，AD=2c，则AB 的长度是___8___c。

7已知等腰三角形中的一边长为5，另一边长为9，则它的周长为_19或23__。

8 如下图，点D在Ac上，点E在AB上，且AB=Ac，Bc=BD，AD=DE=BE，则∠A=__45°_
9如图，DE是△ABc中Ac边的垂直平分线，若Bc=8c，AB=10c，则△ABD的周长为___18__。

10如图，△ABc是等边三角形，cD是∠AcB的平分线，过点D 作Bc的平行线交Ac于点E，已知△ABc的边长为a，则Ec的边长是_ _05a__。

三、解答题（共60分）
1如图，Ac和BD相交于点，且AB//Dc，c=D，求证A =B。

证明∵c=D
∴∠D=∠c（等边对等角）
∵AB//Dc
∴∠B =∠D，∠A =∠c（两直线平行，内错角相等）
∴∠A =∠B
∴A=B。

人教版数学八年级上册第12章轴对称单元测试题(一)

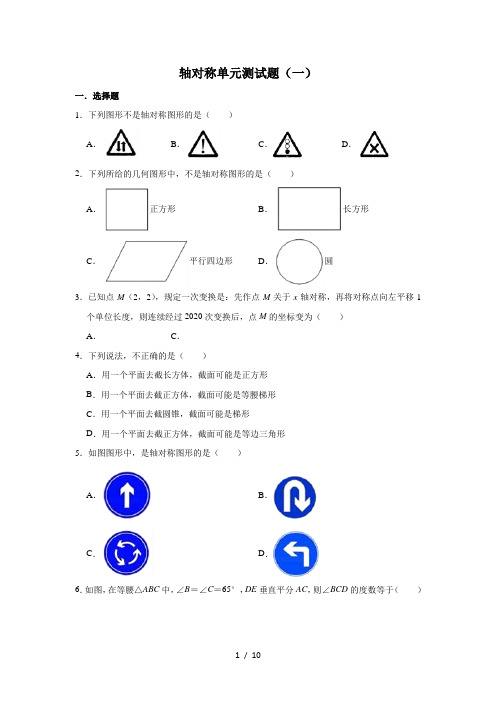
轴对称单元测试题（一）一．选择题1．下列图形不是轴对称图形的是（）A．B．C．D．2．下列所给的几何图形中，不是轴对称图形的是（）A．正方形B．长方形C．平行四边形D．圆3．已知点M（2，2），规定一次变换是：先作点M关于x轴对称，再将对称点向左平移1个单位长度，则连续经过2020次变换后，点M的坐标变为（）A．C．4．下列说法，不正确的是（）A．用一个平面去截长方体，截面可能是正方形B．用一个平面去截正方体，截面可能是等腰梯形C．用一个平面去截圆锥，截面可能是梯形D．用一个平面去截正方体，截面可能是等边三角形5．如图图形中，是轴对称图形的是（）A．B．C．D．6．如图，在等腰△ABC中，∠B＝∠C＝65°，DE垂直平分AC，则∠BCD的度数等于（）A．10°B．15°C．20°D．25°7．以方程组，的解作等腰三角形两边的长，则得到的三角形周长是（）A．6B．8C．10D．8或108．△ABC中，AB＝AC，∠BAC＝100°，两腰AB、AC的垂直平分线交于点P，则（）A．点P在△ABC外B．点P在△ABC底边上C．点P在△ABC内D．点P的位置与△ABC的边长有关9．如图，△ABC中，∠B＝60°，∠C＝50°，点D是BC上任一点，点E和点F分别是点D关于AB和AC的对称点，连接AE和AF，则∠EAF的度数是（）A．140°B．135°C．120°D．100°10．如图，在△ABC中，AB＝AC，点D在CA的延长线上，DE⊥BC于点E，∠BAC＝100°，则∠D＝（）A．40°B．50°C．60°D．80°二．填空题11．点P（﹣4，9）关于x轴对称点P′的坐标是．12．已知等腰三角形两边长分别为6cm、4cm，则它的周长为．13．如图，在△ABC中，AB＝AC＝10，DE垂直平分AB，交AB于点D，交AC于点E，△BEC的周长是17，则BC＝．14．如图在△ABC中MP，NQ分别垂直平分AB、AC，若BC的长度为9，则△APQ的周长是．15．如图，△ABC中，AB＝6cm，AC＝8cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为．三．解答题16．等腰三角形ABC中，一腰AC上的中线BD把三角形的周长分为12cm和15cm两部分，求此三角形的腰和底边的长．17．求证：到线段两端距离相等的点在线段的垂直平分线上．已知：；求证：．18．如图，在长方形网格中有一个△ABC．（1）画出△ABC关于y轴对称的△A1B1C1．（2）若网格中的最小正方形边长为1，求△A1B1C1的面积．19．如图，△ABC中，AB＝AC，D为AC的中点，DE⊥AB于E，DF⊥BC于F，且DE＝DF，求证：∠A＝∠B．参考答案与试题解析一．选择题1．【解答】解：A、不是轴对称图形，故本选项符合题意；B、是轴对称图形，故本选项不符合题意；C、是轴对称图形，故本选项不符合题意；D、是轴对称图形，故本选项不符合题意．故选：A．2．【解答】解：正方形、长方形、圆是轴对称图形，平行四边形不是轴对称图形，故选：C．3．【解答】解：由题可得，第2019次变换后的点M在x轴下方，∴点M的纵坐标为2，横坐标为2﹣2020×1＝﹣2018，∴点M的坐标变为（﹣2018，﹣2），故选：B．4．【解答】解：A．用一个平面去截长方体，截面可能是正方形，故该选项正确，不符合题意；B．用一个平面去截正方体，截面可能是等腰梯形，故该选项正确，不符合题意；C．用一个平面去截圆锥，截面不可能是梯形，故该选项错误，符合题意；D．用一个平面去截正方体，截面可能是等边三角形，故该选项正确，不符合题意；故选：C．5．【解答】解：A、是轴对称图形，故本选项符合题意；B、不是轴对称图形，故本选项不合题意；C、不是轴对称图形，故本选项不合题意；D、不是轴对称图形，故本选项不合题意．故选：A．6．【解答】解：∵∠ABC＝∠ACB＝65°．∴∠A＝50°，∵DE垂直平分AC，∴AD＝CD，∴∠A＝∠ACD＝50°，∴∠BCD＝∠ACB﹣∠ACD＝15°．故选：B．7．【解答】解：方程组，得，若4为腰，三边长为4，4，2，周长为4+4+2＝10；若2为腰，三边长为2，2，4，不能构成三角形．故选：C．8．【解答】解：如图所示，设垂直平分线MN、OQ相交于点P．∵AB＝AC，∴∠ABC＝∠C．∵∠BAC＝100°，∴∠ABC＝（180°﹣100°）÷2＝40°．∵AM＝AB，AO＝AC，∴AM＝AO．又AP＝AP，∴Rt△AMP≌Rt△AOP，∴∠P AM＝∠P AC＝50°．∵MN垂直平分AB，∴P A＝PB．∴∠PBA＝∠P AB＝50°＞∠ABC，∴点P在△ABC的外部．故选：A．9．【解答】解：如图，∵D点分别以AB、AC为对称轴，画出对称点E、F，∴∠EAB＝∠BAD，∠F AC＝∠CAD，∵∠B＝60°，∠C＝50°，∴∠BAC＝∠BAD+∠DAC＝180°﹣60°﹣50°＝70°，∴∠EAF＝2∠BAC＝140°，故选：A．10．【解答】解：∵AB＝AC，∠BAC＝100°，∴∠C＝∠B＝40°，∵DE⊥BC于点E，∴∠D＝90°﹣∠C＝50°，故选：B．二．填空题11．【解答】解：点P（﹣4，9）关于x轴对称点P′的坐标是：（﹣4，﹣9）．故答案为：（﹣4，﹣9）．12．【解答】解：当4为底时，其它两边都为6，4、6、6可以构成三角形，周长为16（cm）；当4为腰时，其它两边为4和6，4、4、6可以构成三角形，周长为14（cm）．综上所述，该等腰三角形的周长是14cm或16cm．故答案为：14cm或16cm．13．【解答】解：∵DE垂直平分AB，∴AE＝BE，∵△BEC的周长是17，∴BC+BE+CE＝17，∴BC+AE+CE＝17，∴AC+BC＝17，∵AC＝10，∴10+BC＝17，∴BC＝7，故答案为：7．14．【解答】解：∵在△ABC中，MP，NO分别垂直平分AB、AC，∴AP＝BP，AQ＝CQ，∵BC＝9，∴△APQ的周长是AP+PQ+AQ＝BP+PQ+CQ＝BC＝9，故答案为：9．15．【解答】解：∵BC的垂直平分线l与AC相交于点D，∴BD＝CD，∵AB＝6cm，AC＝8cm，∴△ABD的周长为AB+BD+AD＝AB+CD+AD＝AB+AC＝6+8＝14（cm），故答案为：14cm．三．解答题16．【解答】解：设腰长为xcm，①腰长与腰长的一半是12cm时，x+x＝12，解得x＝8，所以，底边＝15﹣8＝11，所以8cm、8cm、11cm能组成三角形；②腰长与腰长的一半是15cm时，x+x＝15，解得x＝10，所以，底边＝12﹣×10＝7，所以，三角形的三边为10cm、10cm、7cm，能组成三角形，综上所述，此三角形的腰和底边的长分别为8cm、11cm或10cm、7cm．17．【解答】已知：如图，QA＝QB，求证：点Q在线段AB的垂直平分线上．证明：当点Q在线段AB上时，∵QA＝QB∴点Q为线段AB的中点，∴点Q在线段AB的垂直平分线上；当点Q在线段AB外时，过点Q作QM⊥AB，垂足为点M，如图，则∠QMA＝∠QMB＝90°，在Rt△QMA和Rt△QMB中，，∴Rt△QMA≌Rt△QMB（HL），∴AM＝BM，∴点Q在线段AB的垂直平分线上．综上所述，即到线段两端距离相等的点在线段的垂直平分线上．18．【解答】解：（1）△A1B1C1即为所求；（2）△A1B1C1的面积为：3×5﹣×2×3﹣×2×3﹣×1×5＝15﹣3﹣3﹣2.5＝6.5．19．【解答】证明：∵DE⊥AB，DF⊥BC，垂足分别为点E，F，∴∠AED＝∠CFD＝90°，∵D为AC的中点，∴AD＝DC，在Rt△ADE和Rt△CDF中，∵，∴Rt△ADE≌Rt△CDF，∴∠A＝∠C，∵AB＝AC，∴∠C＝∠B。

八年级(初二)上册数学第十二章轴对称测试题(附答案)

第十二章轴对称一、填空题(每小题2分，共20分)1、等腰三角形是对称图形，它至少有条对称轴.2、等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为 _______________ .3、已知△ABC 是轴对称图形．且三条高的交点恰好是C 点，则△ABC 的形状是 ___________.4、直线y=kx+4与坐标轴围成的三角形是等腰三角形，则k=5、已知点P(一3，2)，点P 关于X 轴的对称点坐标为 ____6、Rt △ABC 中，∠ACB=90°，CD 是高，∠A=30°，BD=5cm ，则AB=7、观察上图中的图片，请说出图中小亮衣服上的数字是：8、如果等腰三角形一腰上的高与腰的夹角为30°，则该三角形的顶角的度数为 9、已知点A(一2，4)，B(2，4)，C(1，2)，D(-1，2)，E(一3，1)，F(3，1)是平面坐标系内的6个点，选择其中三个点连成一个三角形，剩下三个点连成另一个三角形，若这两个三角形关于y 轴对称，就称为一组对称三角形，那么，坐标系中可找出 ____________组对称三角形．10、小强拿了一张正方形的纸如图（1），沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是二、选择题(每小题3分，共18分)第6B ADC12、下列命题中，不正确的是( )(A)关于直线对称的两个三角形一定全等.(B)两个大小一样的圆形纸片随意平放在水平桌面上构成轴对称图形. (C)若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线. (D)等腰三角形一边上的高、中线及这边对角平分线重台.13、将长方形ABCD 沿折痕EF 折叠，使CD 落在GH 的位置，若∠BGH=55°，则∠HEF=（） (A)55° (B) 65°(C)72.5 (D)75° 12、等腰三角形的一个内角是50。

八年级数学上册第12章《轴对称图形》单元综合检测试题(含解析)(新版)新人教版

第12章《轴对称图形》一、选择题1.下列标志中，可以看作是轴对称图形的是（）2.正方形对称轴的条数是（）A.1B.1C.1D.13.点P (2，－5)关于x 轴对称的点的坐标为A.(－2， 5)B.(2，5)C.(－2，－5)D.(2，－5)4.如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段PA ＝5，则线段PB 的长度为（） A.6 B.5 C.4 D.35.将一张正方形纸片按如图1，图2所示的方向对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，再得到的图案是（）6.如图，在△ABC 中，点D 、E 分别是边AB 、AC 的中点，∠B ＝50°，∠A ＝26°，将△ABC 沿DE 折叠，点A 的对应点是点A ′，则∠AEA ′的度数是（） A.145° B.152°C.158°D.160°7.在等腰△ABC 中，AB ＝AC ，其周长为20cm ，则AB 边的取值范围是（）A.1cm ＜AB ＜4cmB.5cm ＜AB ＜10cmC.4cm ＜AB ＜8cmD.4cm ＜AB ＜10cm8.从一个等腰三角形纸片的底角顶点出发，能将其剪成两个等腰三角形纸片，则原等腰三角形纸片的底角等于（）DC B APD CBA ABCDA.72°B.5407⎛⎫ ⎪⎝⎭C.144°D.72°，或5407⎛⎫ ⎪⎝⎭9.如图，点P 是∠AOB 外的一点，点M ，N 分别是∠AOB 两边上的点，点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上.若PM ＝2.5cm ，PN＝3cm ，MN ＝4cm ，则线段QR 的长为（）cm A.4.5 B.5.5 C.6.5 D.710.如图所示，已知△ABC 和△ADE 均是等边三角形，点B 、C 、E 在同一条直线上，AE 与BD 交于点O ，AE 与CD 交于点G ，AG 与BD 交于点F ，连结OC 、FG ，则下列结论：①AE ＝BD ；②AG ＝BF ；③FG ∥BE ；④∠BOC ＝∠EOC ，其中正确的结论个数（）A.1个B.2个C.3个D.4个二、填空题11.如图，在Rt △ABC 中，∠ABC ＝90°，AC ＝10cm ，点D 为AC 的中点，则BD ＝＿＿＿cm.12.如图，∠A ＝30°，∠C ′＝60°，△ABC 与△A ′B ′C ′关于直线l 对称，则∠B ＝＿＿＿.13.已知OC 是∠AOB 的平分线，点P 在OC 上，PD ⊥OA ，PE ⊥OB ，垂足分别为点D 、E ，PD ＝10，则PE 的长度为＿＿＿.14.如图，在Rt △ABC 中，∠C ＝90°，D 为AB 的中点，DE ⊥AC 于点E ，∠A ＝30°，AB ＝8，则DE 的长度是＿＿＿. B ′A ′B C A C ′ l C B AD MR PO B A NQG FO D C B A E D C BA E15.如图，在等腰三角形纸片ABC 中，AB ＝AC ，∠A ＝50°，折叠该纸片，使点A 落在点B 处，折痕为DE ，则∠CBE ＝＿＿＿.16.如图，在△ABC 中，按以下步骤作图：①分别以点B 、C 为圆心，以大于12BC 的长为半径作弧，两弧相交于M 、N 两点；②作直线MN 交AB 于点D ，连接CD .若CD ＝AC ，∠B ＝25°，则∠ACB 的度数为＿＿＿.17.在一次夏令营活动中，小明同学从营地A 出发，要到A 地的北偏东60°方向的C 处，他先沿正东方向走了200m 到达B 地，再沿北偏东30°方向走，恰能到达目的地C （如图），那么，由此可知，B 、C 两地相距＿＿＿m.18.如图，在第1个△A 1BC 中，∠B ＝30°，A 1B ＝CB ；在边A 1B 上任取一点D ，延长CA 1到A 2，使A 1A 2＝A 1D ，得到第2个△A 1A 2D ；在边A 2D 上任取一点E ，延长A 1A 2到A 3，使A 2A 3＝A 2E ，得到第3个△A 2A 3E ，…按此做法继续下去，则第n 个三角形中以A n 为顶点的内角度数是＿＿＿.三、解答题 19.在平面直角坐标系中，已知点A (－3，1)，B (－1，0)，C (－2，－1)，请在图中画出△ABC ，并画出与△ABC 关于y 轴对称的图形.20.如图，△ABC 与△DEF 关于直线l 对称，请用无刻度的直尺，在下面两个图中分别作出直线l .21.如图，在等边△ABC 中，AB ＝2，点P 是AB 边上任意一点（点P 可以与点A 重合），过点P 作PE ⊥BC ，垂足为E ，过点E 作EF ⊥AC ，垂足为F ，过点F 作FQ ⊥AB ，垂足为Q ，求当BP 的长等于多少时，点P 与点Q 重合？F C E B D A F C E B A (D ) D CB AE C A A AA CB D E F …22.如图，在△ABC 中，点D 在AB 上，且CD ＝CB ，点E 为BD 的中点，点F 为AC 的中点，连结EF 交CD 于点M ，连接AM .（1）求证：EF ＝12AC . （2）若∠BAC ＝45°，求线段AM 、DM 、BC 之间的数量关系.23.如图，O 为△ABC 内部一点，OB ＝312，P 、R 为O 分别以直线AB 、直线BC 为对称轴的对称点.（1）请指出当∠ABC 在什么角度时，会使得PR 的长度等于7？并完整说明PR 的长度为何在此时会等于7的理由.（2）承（1）小题，请判断当∠ABC 不是你指出的角度时，PR 的长度是小于7还是会大于7？并完整说明你判断的理由.24.如图，在△ABC 中，点D ，E 分别在边AC ，AB 上，BD 与CE 交于点O ，给出下列三个条件：①∠EBO ＝∠DCO ；②BE ＝CD ；③OB ＝OC .（1）上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？（用序号写出所有成立的情形）（2）请选择（1）中的一种情形，写出证明过程.25.如图，在等边三角形ABC 中，点D ，E 分别在边BC ，AC 上，且DE ∥AB ，过点E 作EF⊥DE ，交BC 的延长线于点F .（1）求∠F 的度数.（2）若CD ＝2，求DF 的长.26.如图，已知△BAD 和△BCE 均为等腰直角三角形，∠BAD ＝∠BCE ＝90°，点M 为DE 的中点.过点E 与AD 平行的直线交射线AM 于点N .（1）当A ，B ，C 三点在同一直线上时（如图1），求证：M 为AN 的中点.AB CD E O E D C B A F P C B AE F Q P R B D CB A E F M（2）将如图1中△BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时（如图2），求证：△CAN 为等腰直角三角形.（3）将如图1中△BCE 绕点旋转到图3的位置时，（2）中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由.27.如图，△ABC 中，AB ＝AC ，∠A ＝36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC ）（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是＿＿＿度和＿＿＿度.（2）在图2中画2条线段，使图中有4个等腰三角形.（3）继续按以上操作发现：在△ABC 中画n 条线段，则图中有＿＿＿个等腰三角形，其中有＿＿＿个黄金等腰三角形.28.（1）操作发现：如图①，D 是等边△ABC 边BA 上一动点（点D 与点B 不重合），连结DC ，以DC 为边在BC 上方作等边△DCF ，连结AF .你能发现线段AF 与BD 之间的数量关系吗？并证明你发现的结论.（2）类比猜想：如图②，当动点D 运动至等边△ABC 边BA 的延长线上时，其它作法与（1）相同.猜想AF 与BD 在（1）中的结论是否仍然成立？（3）深入探究：Ⅰ.如图③，当动点D 在等边△ABC 边BA 上运动时（点D 与点B 不重合），连接DC ，以DC 为边在其上方、下方分别作等边△DCF 和等边△DCF ′，连接AF 、BF ′，探究AF 、BF ′与AB 有何等量关系？并证明你探究的结论.Ⅱ.如图④，当动点D 运动至等边△ABC 边BA 的延长线上运动时，其它作法与图③相同.Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论.F DC B A 图① FD C B A 图② F D C B A 图③ F ′ F AC F ′D 图④B DC B A E M N图1 D C B A E M N 图2 DC B A E M N 图3 图1 C B A E F 图2 C B A E 图3C B A参考答案：一、1.D.点拨：A 、不是轴对称图形，不符合题意；B 、不是轴对称图形，不符合题意；C 、不是轴对称图形，不符合题意；D 、是轴对称图形，符合题意.故应选D .2.D.3.B.点拨：把点P (2，－5)的纵坐标－5改成它的相反数5，即可得到点P 关于x 轴对称点的坐标.4.B.点拨：由根据线段垂直平分线性质可以直接判断线段PA 与线段PB 的长度相等.5.B.点拨：按照图中的顺序向右上翻折，向左上角翻折，剪去左上角，展开得到图形B .故应选B .6.B.点拨：∵D 、E 分别是边AB 、AC 的中点，∴DE ∥BC ，∴∠ADE ＝∠B ＝50°，∵∠A ＝26°，∴∠ADE ＝180°－50°－26°＝104°；再由折叠可知：∠AED ＝∠A ′ED ＝104°，∴∠AEA ′＝360°－104°－104°＝152°.7.B.点拨：∵在等腰△ABC 中，AB ＝AC ，其周长为20cm ，∴设AB ＝AC ＝x ，则BC ＝20－2x cm ，∴2x ＞20－2x ，且20－2x ＞0，解得5cm ＜x ＜10cm.故应选B .8.D.点拨：如图，等腰三角形ABC 中，因为AB ＝AC ，所以∠ABC ＝∠C ，设顶角为α、底角为β，则根据三角形三内角和为180°，得α+2β＝180.此时，由于过B 点画直线交AC 于D ，则△ADB 与△BDC 都是等腰三角形，若AD ＝DB ＝BC ，则β＝2α，α+2β＝180°，解得α＝36°，β＝72°；若AD ＝DB ，BC ＝DC ，则β＝3α，α+2β＝180°，解得α＝7180，β＝7540 .所以原等腰三角形纸片的底角等于72°，或5407⎛⎫ ⎪⎝⎭.故应选D .9.A.点拨：∵点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上，∴PM ＝MQ ，PN ＝NR .∵PM ＝2.5cm ，PN ＝3cm ，MN ＝4cm ，∴RN =3cm ，MQ ＝2.5cm ，NQ ＝MN －MQ ＝4－2.5＝1.5（cm ），则线段QR 的长为：RN +NQ ＝3+1.5＝4.5（cm ）.故应选A .10.D.点拨：因为BC ＝AC ，∠BCD ＝∠ACE ＝120°，CD ＝CE ，所以△BCD ≌△ACE ，从而得①AE ＝BD 是正确的；又因为△BCD ≌△ACE ，所以∠FBC ＝∠GAC ，根据BC ＝AC ，∠BCF ＝∠ACG ＝60°，得△BCF ≌△ACG ，所以②AG ＝BF 是正确的；由△BCF ≌△ACG ，得CF ＝CG ，而∠FCG ＝60°，所以∠CGF ＝∠CFG ＝∠FCG ＝60°，所以③FG ∥BE 是正确的；如图，过C 作CM ⊥BD 于M ，CN ⊥AE 于N ，易得△BCM ≌△CAN ，所以CM ＝CN ，所以④∠BOC ＝∠EOC 是正确的.故应选D .二、11.5. 12.90°.点拨：因为△ABC 与△A ′B ′C ′关于直线l 对称，∠C ′＝60°，所以∠C ′＝∠C ＝60°，在△ABC 中，因为∠A ＝30°，所以∠B ＝180°－30°－60°＝90°. G F O D C B AE M N D C B A13.10.点拨：由角平分线的性质及题中已知条件可得PD ＝PE ，又因为PD ＝10，所以PE ＝10.14.2.点拨：∵D 为AB 的中点，AB ＝8，∴AD ＝4，∵ DE ⊥AC 于点E ，∴∠DEA ＝90°，∵∠A ＝30°，∴DE ＝12AD ＝2； 15.15°.点拨：∵折叠该纸片，使点A 落在点B 处，折痕为DE ，∴EA ＝EB ，∴∠EBA ＝∠A .又∵AB ＝AC ，∠A ＝50°，∴∠B ＝65°，∠EBA ＝50°，∴∠CBE ＝15°.16.105°.点拨：由①的作图可知CD ＝BD ，∴∠DCB ＝∠B ＝25°，∴∠ADC ＝50°.又∵CD ＝AC ，∴∠A ＝∠ADC ＝50°，∴∠ACD ＝80°，∴∠ACB ＝80°+25°＝105°.17.200.点拨：由条件，得∠ABC ＝90°+30°＝120°，∠BAC ＝90°－60°＝30°，所以∠ACB ＝180°－∠ABC －∠BAC ＝180°－120°－30°＝30°，所以∠ACB ＝∠BAC ，所以BC ＝AB ＝200，即B 、C 两地相距200m. 18.(12)n －1·75°.点拨：∵A 1B ＝CB ，∠B ＝30°，∴∠C ＝∠BA 1C ＝12(180°－∠B )＝75°，又∵A 1A 2＝A 1D ，∴∠A 1A 2D ＝∠A 1DA 2＝12∠DA 1C ＝12×75°（三角形外角等于不相邻两内角之和）＝2112-×75°＝2112-⎛⎫ ⎪⎝⎭×75°；同样，∵A 2A 3＝A 2E ，∴∠A 2A 3E ＝∠A 2EA 3＝12∠DA 2A 1＝12×12×75°＝14×75°＝3112-×75°＝3112-⎛⎫ ⎪⎝⎭×75°；同理，∠A 3A 4F ＝∠A 3FA 4＝12∠EA 3A 2＝4112-⎛⎫ ⎪⎝⎭×75°；…第n 个三角形中以A n 为顶点的内角度数是112n -⎛⎫ ⎪⎝⎭×75°. 三、19.如图，△ABC 就是所求的三角形，A ，B ，C 三点关于y 轴的对称点分别为A ′(3，1)，B ′(1，0)，C ′(2，－1)，△A ′B ′C ′就是△ABC 关于y 轴对称的图形.20.如图1和2所示中的直线l 就是分别所求作的对称轴.21.设BP ＝x ，在Rt △PBE 中，∠BPE ＝30°，所以BE ＝12x ，则EC ＝2－12x ，在Rt △EFC 中，∠FEC ＝30°，所以FC ＝12EC ＝1－14x ，所以AF ＝2－FC ＝2－(1－14x )＝1+14x ，同理，AQ ＝12AF ＝12+18x ，当点P 与点Q 重合时，有BP +AQ ＝2，即x +(12+18x )＝2，解得图2 F C E B D A l 图1 F C E B A (D ) lx＝43，故当BP＝43时，点P与点Q重合.22.（1）证明：∵CD＝CB，E为BD的中点，∴CE⊥BD，∴∠AEC＝90°.又∵F为AC的中点，∴EF＝12AC.（2）∵∠BAC＝45°，∠AEC＝90°，∴∠ACE＝∠BAC＝45°，∴AE＝CE.又∵F为AC的中点，∴EF⊥AC，∴EF为AC的垂直平分线，∴AM＝CM，∴AM+DM＝CM+DM ＝CD.又∵CD＝CB，∴AM+DM＝BC.23.（1）∠ABC＝90°时，PR＝7.证明：连接PB、RB，∵P、R为O分别以直线AB、直线BC为对称轴的对称点，∴PB＝OB＝312，RB＝OB＝312，∵∠ABC＝90°，∴∠ABP+∠CBR＝∠ABO+∠CBO＝∠ABC＝90°，∴点P、B、R三点共线，∴PR＝2×312＝7.（2）PR的长度是小于7.理由：∠ABC≠90°，则点P、B、R三点不在同一直线上，∴PB+BR＞PR，∵PB+BR＝2OB＝2×312＝7，∴PR＜7.24.（1）①②、①③.（2）选①②证明如下：在△BOE和△COD中，∵∠EBO＝∠DCO，∠EOB＝∠DOC，BE＝CD，∴△BOE≌△COD（AAS），∴BO＝CO，∠OBC＝∠OCB，∴∠EOB+∠OBC ＝∠DOC+∠OCB，即∠ABC＝∠ACB，∴AB＝AC，即△ABC是等腰三角形.25.（1）∵三角形ABC为等边三角形，∴∠B＝60°，∵DE∥AB，∴∠EDC＝∠B＝60°，∵EF⊥DE，∴∠DEF＝90°，∴∠F＝90°－∠EDC＝30°.（2）∵∠ACB＝60°，∠EDC＝60°，∴△EDC是等边三角形，∴ED＝DC＝2，∵∠DEF＝90°，∠F＝30°，∴DF＝2DE＝4.26.（1）∵点M为DE的中点，∴DM＝ME．∵AD∥EN，∴∠ADM＝∠NEM，又∵∠DMA＝∠EMN，∴△DMA≌△EMN，∴AM＝MN，即M为AN的中点.（2）由（1）中△DMA≌△EMN可知DA＝EN，又∵DA＝AB，∴AB＝NE，∵∠ABC＝∠NEC＝135°，BC＝CE，∴△ABC≌△NEC，∴AC＝CN，∠ACB＝∠NCE，∵∠BCE＝∠BCN+∠NCE＝90°，∴∠BCN+∠ACB＝90°，∴∠CAN＝90°，∴△CAN为等腰直角三角形.（3）由（2）可知AB＝NE，BC＝CE.又∵∠ABC＝360°－45°－45°－∠DBE＝270°－∠DBE＝270°－(180°－∠BDE－∠BED)＝90°+∠BDE+∠BED＝90°+∠ADM－45°+∠BED＝45+∠MEN+∠BED＝∠CEN，∴△ABC≌△NEC，再同（2）可证△CAN 为等腰直角三角形，∴（2）中的结论是否仍然成立.27.（1）如图1所示.∵AB＝AC，∠A＝36°，∴当AE＝BE，则∠A＝∠ABE＝36°，则∠AEB＝108°，则∠EBC＝36°，∴这2个等腰三角形的顶角度数分别是108度和36度.（2）画法不惟一.如，如图2所示.四个等腰三角形分别是：△ABE，△BCE，△BEF，△CEF.（3）如图3所示.当1条直线可得到2个等腰三角形；当2条直线可得到4个等腰三角形；当3条直线可得到6个等腰三角形；…∴在△ABC中画n条线段，则图中有2n个等腰三角形，其中有n个黄金等腰三角形.28.（1）AF＝BD.证明：因为△ABC和△DCF均是等边三角形，所以∠ACB＝∠DCF，所以∠ACB－∠ACD＝∠DCF－∠ACD，即∠BCD＝∠ACF.在△BDC和△AFC中，BC＝AC，∠BCD＝∠ACF，DC＝FC，所以△BDC≌△AFC，所以AF＝BD.（2）仍然成立.证法同（1）.（3）Ⅰ：AF+BF′＝AB.证明：由（1）可证AF＝BD，同理可证△ADC≌△BF′C，所以BF′＝AD，所以AF+BF′＝AB.Ⅱ.在Ⅰ中的结论不成立，新结论是：AF－BF′＝AB.证明：同（1）可证△BDC≌△AFC，所以AF＝BD，同理可证△ADC≌△BF′C，所以BF′＝AD，因为BD－AD＝AB，所以AF－BF′＝AB.。

轴对称单元测试题

轴对称单元测试题一、选择题（每题 3 分，共 30 分）1、下列图形中，不是轴对称图形的是（）A 线段B 角C 平行四边形D 等腰三角形2、点 P（－2，1）关于 x 轴对称的点的坐标为（）A （－2，－1）B （2，1）C （2，－1）D （1，－2）3、等腰三角形的一个内角是 50°，则另外两个角的度数分别是（）A 65°，65°B 50°，80°C 65°，65°或 50°，80°D 无法确定4、下列说法正确的是（）A 对称轴是一条直线B 两个全等的三角形一定关于某条直线对称C 若△ABC 与△A'B'C'关于直线 l 对称，则△ABC 与△A'B'C'全等D 若线段 AB 和 A'B'关于直线 l 对称，则 AB ＝ A'B'5、如图，在△ABC 中，AB ＝ AC，∠A ＝ 36°，BD 平分∠ABC交 AC 于点 D，则图中的等腰三角形有（）A 1 个B 2 个C 3 个D 4 个6、如图，在△ABC 中，∠C ＝ 90°，DE 垂直平分 AB，若∠CAD ：∠DAB ＝ 2 ： 1，则∠B 的度数为（）A 20°B 225°C 25°D 30°7、已知等腰三角形的两边长分别为 3 和 6，则它的周长为（）A 9B 12C 15D 12 或 158、如图，在四边形 ABCD 中，AD∥BC，∠B ＝ 90°，AD ＝ 3，BC ＝ 5，AB ＝ 4，把线段 CD 以点 D 为中心逆时针旋转 90°到 DE 位置，连接 AE，则 AE 的长为（）A 4B 5C 6D 79、如图，在 Rt△ABC 中，∠C ＝ 90°，AB 的垂直平分线交 BC 于点 D，若∠CAD ：∠DAB ＝ 1 ： 2，则∠B 的度数为（）A 20°B 225°C 25°D 30°10、如图，在△ABC 中，AB ＝ AC，∠A ＝ 120°，BC ＝ 6cm，AB 的垂直平分线交 BC 于点 M，交 AB 于点 E，AC 的垂直平分线交BC 于点 N，交 AC 于点 F，则 MN 的长为（）A 2cmB 3cmC 4cmD 5cm二、填空题（每题 3 分，共 30 分）11、等边三角形有_____条对称轴。

八年级数学十二章轴对称单元测试题1

ABDC (A) (B) (C)(D)ABCDlO第十二章《轴对称》单元测试卷总分一、细心填一填：（4′×10＝40′）1．在日常生活中，事物所呈现的对称性能给人们以平衡与和谐的美感. 我们的汉语也有类似的情况，请写出轴对称图形的汉字有（请举出两个例子，笔画的粗细和书写的字体可忽略不计）. 2. 如右图,△ABC 中,AB=AC,AD ⊥BC,BD=5,则CD=______. 3. 等边三角形的内角都等于________. 4 等腰三角形的对称轴最多有___________条.5. 等腰三角形一个底角是30°,则它的顶角是__________.6.等腰三角形中，已知两边的长分别是9和4，则周长为_______.7.观察字母A 、E 、H 、O 、T 、W 、X 、Z ，______________. 8.小强从镜子中看到的电子表的读数是，则电子表的实际读数是________。

9.由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）.请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑，使它成为轴对称图形.10.如图,四边形ABCD 沿直线l 对折后互相重合,如果AD ∥BC ，有下列结论:①AB ∥CD ②AB=CD ③AB ⊥BC ④AO=OC ，其中正确的结论是___________.(把你认为正确的结论的序号都填上)二、精心选一选：（5′×10＝50′）11.下列平面图形中，不是轴对称图形的是（）学校班级姓名号码12.下列图形:①角②两相交直线③圆④正方形,其中轴对称图形有 ( )(A)4个 (B)3个 (C)2个 (D)1个13.圆、正方形、长方形、等腰梯形中有唯一条对称轴的是（） (A)圆 (B)正方形 (C)长方形 (D)等腰梯形14.点(3,-2)关于x 轴的对称点是 ( )(A )(-3,-2) (B )(3,2) (C )(-3,2) (D )(3,-2)15.下列长度的三线段,能组成等腰三角形的是（）(A) 1,1,2 (B) 2,2,5 (C) 3,3,5 (D) 3,4,516.如图，已知AC ∥BD ，OA=OC ，则下列结论不一定成立的是（）（A ）∠B=∠D （B ）∠A=∠B （C ）OA=OB （D ）AD=BC17.等腰三角形的一个角是80°,则它的底角是（）(A) 50° (B) 80° (C) 50°或80° (D) 20°或80°18.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )（A ）锐角三角形. （B ）直角三角形. （C ）钝角三角形. （D ）不能确定. 19.若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是（）（A ）75°或30° （B ）75° （C ）15° （D ）75°和15°20.已知∠AOB=30°,点P 在∠AOB 内部,P 1与P 关于OB 对称,P 2与P 关于OA 对称,则P 1,O,P 2三点构成的三角形是 ( )(A)直角三角形 (B)钝角三角形 (C)等腰三角形 (D)等边三角形三、用心解一解：（7′+7′+8′+8′+10′+10′+10′＝60′）21.把图中（实线部分）补成以虚线L 为对称轴的轴对称图形，你会得到一只美丽的蝴蝶图案.AB CD O22、如图，A 、B 是两个蓄水池，都在河流a 的同侧，为了方便灌溉作物，•要在河边建一个抽水站，将河水送到A 、B 两地，问该站建在河边什么地方，•可使所修的渠道最短，试在图中确定该点（保留作图痕迹）23、如图,在△ABC 中,AB=AD=DC, ∠B+∠C=120°,求∠BAD 的度数.24、如图，在△ABC 中，D 是BC 的中点，DE ⊥AB 于E ，DF ⊥AC 于点F ，且BE=CF.求证：AD ⊥BC ．E CBAFA B DC25、如图:△ABC 和△ADE 是等边三角形.证明：BD=CE.26、如图,AD ⊥BC,BD=DC,点C 在AE 的垂直平分线上,AB+BD 与DE 的长度有什么关系?并加以证明.27、如图，一艘轮船从点A 向正北方向航行，每小时航行15海里，小岛P 在轮船的北偏西15°，2小时后轮船航行到点B ，小岛P 此时在轮船的北偏西30°方向，在小岛P 的周围18海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由。

新人教版八年级数学《轴对称》单元测试题及答案

第十二章《轴对于称》尝试题之阳早格格创做座号：结果：一、采用题（每题2分，同20分）1.如图，下列图案是尔国几家银止的标记，其中是轴对于称图形的有（C）个个个个2.下列图形中对于称轴最多的是（A）A.圆B.正圆形C.等腰三角形D.少圆形3.下列图形中纷歧定为轴对于称图形的是（C）A.等腰三角形B.正五角星C.梯形D.少圆形4.下列图形：①角；②二相接曲角；③圆；④正圆形.其中轴对于称图形有（A）个个个个5.下列道法中，精确的是（A）A.闭于某曲线对于称的二个三角形是齐等三角形B.齐等三角形是闭于某曲线对于称的C.二个图形闭于某曲线对于称，则那二个图形一定分别位于那条曲线的二侧D.有一条公同边变得二个齐等三角形闭于公同边天圆的曲线对于称6.下列道法精确的是（D）A.等腰三角形的下、中线、角仄分线互相沉合B.顶角相等的二个等腰三角形齐等C.等腰三角形一边没有成一是另一边的二倍D.等腰三角形的二个底角相等7.已知等腰三角形的一个中角等于100°，则它的顶角是（C）°°°或者20° D.没有克没有及决定Array 8.△ABC中，AB=AC，中角∠CAD=100°，则∠B的度数（B）°°°°9.如图，正在已知△ABC中，AB=AC， BD=DC，则下列论断中过失的是（A）A.∠BAC=∠BB.∠1=∠⊥BC D.∠B=∠C10.到△ABC的三个顶面距离相等到的面是(D)A.三条中线的接面B.三条角仄分线的接面C.三条下线的接面 D 三条边的笔曲仄分线的接面二、挖空题（每题2分，同20分）1.△ABC 中，AB=AC ，∠A=∠C ，则∠B=___60°__2.如果面P （4，-5）战面Q(a ，b)闭于y 轴对于称，则a=___-4___，b=__-5__.3.面(-2，1)面闭于x 轴对于称的面坐标为_(-2，-1)__；闭于y 轴对于称的面坐标为_(2，1)_.4.等腰三角形中的一个角等于100°，则其余二个内角的度数分别为_40°_40°_.5.已知△ABC 中∠ACB=90°，CD ⊥AB 于面D ，∠A=30°，BC=2cm ，则AD=___3cm __6.Rt △ABC 中，CD 是斜边AB 上的下，∠B=30°，AD=2cm ，则AB 的少度是___8___cm.5，另一边少为9，则它的周少为_19或者23__.8.如下图，面D 正在AC 上，面E 正在AB 上，且AB=AC ，BC=BD ，AD=DE=BE ，则∠A=__45°_9.如图，DE 是△ABC 中AC 边的笔曲仄分线，若BC=8cm ，AB=10cm ，则△ABD 的周少为___18__.10.如图，△ABC 是等边三角形，CD 是∠ACB 的仄分线，过面D 做BC 的仄止线接AC 于面E ，已知△ABC 的边少为a ，则EC 的边少是____.三、解问题（同60分）1.如图，AC 战BD 相接于面O ，且AB//DC ，OC=OD ，供证：OA=OB.道明：∵OC=OD ∴∠D=∠C （等边对于等角） ∵AB//DC∴∠B =∠D ，∠A =∠C （二曲线仄止，内错角相等）∴∠A =∠B∴OA=OB2.如图，面D 、E 正在△ABC 的边BC 上，AD=AE ，AB=AC ，道明BD=EC.道明：过面A ，做AF ⊥BC.∵AD=AE ，AF ⊥BC∴DF=EF （三线合一）∵AB=AC ，AF ⊥BCA BB CF∴BF=CF（三线合一）∴BF- DF =CF- EF即BD=EC3.如图，面D、E正在△ABC的边BC上，AD=AE，BD=EC，道明AB=AC.道明：∵AD=AE∴∠ADC =∠AEB（等边对于等角）∴∠ADB =∠AEC（等角的补角相等）正在△ABD战△ACE中AD=AE∠ADB =∠AEBD=EC∴△ABD≌△ACE（SAS）∴AB=AC4.正在△ABC中，AB=AC，面D正在AC上，且BD=BC=AD.供△ABC各角的度数.参照课原50页例1四、做图题（生存做图痕迹）（1）做线段AB的中垂线EF（5分）（2）做∠AOB的角仄分线OC（5分）（3）要正在公路MN上建一个车站P，使得P背A，B二个场合的距离战最小，请正在图中绘出P的位子.（10分）。

轴对称单元测试(最新整理)

20、如图，在⊿ABC 中，∠ABC 和∠ACB 的平分线交于点 O，过 O 点作 EF∥BC，
交 AB 于 E，交 AC 于 F，BE=5cm，CF=3cm，求 EF 的长．
A
O
E
F
B
C
21、如图：AD 为△ABC 的高，∠B=2∠C，求证：CD=AB+BD．
A
B
C
D
22、如图已知:D、E 分别是△ABC 的边 BC、AB 上的点，BD=BE，AC=AD，∠B=60 °求证：AE=CD+DE。
6、如图 3，△ABC 与△A1B1C1 关于直线 MN 对称，P 为 MN 上任一点，下列结论中错误的是( )
A．△AA1P 是等腰三角形
B．MN 垂直平分 AA1，CC1
C．△ABC 与△A1B1C1 面积相等 D．直线 AB、A1B1 的交点不一定在 MN 上
7、如图 4，BC=BD，AD=AE，DE=CE，∠A=36°，则∠
A．含 30°角的直角三角形；
B．顶角是 30 的等腰三角形；
C．等边三角形
D．等腰直角三角形.
4．如图 1：等边三角形 ABC 中，BD＝CE，AD 与 BE 相交于点 P，则
∠APE 的度数是（）
A．45°
B．55°
C．60°
D．75°
A
A
M
A
A'
E P
B
C
D
图1
DF
E
B
图2
CBΒιβλιοθήκη PB'C C'
A
D
14、若 D 为△ABC 的边 BC 上一点，且 AD=BD，AB=AC=CD，