高等数学第3章参考答案

合集下载

高等数学第三章课后习题答案

第三章中值定理与导数的应用1. 验证拉格朗日中值定理对函数x x f ln )(=在区间[]e ,1上的正确性。

解：函数()ln f x x =在区间[1,]e 上连续，在区间(1,)e 内可导，故()f x 在[1,]e 上满足拉格朗日中值定理的条件。

又xx f 1)(='，解方程,111,1)1()()(-=--='e e f e f f ξξ即得),1(1e e ∈-=ξ。

因此，拉格朗日中值定理对函数()ln f x x =在区间[1,]e 上是正确的。

2．不求函数)4)(3)(2)(1()(----=x x x x x f 的导数，说明方程0)('=x f 有几个实根，并指出它们所在的区间。

解：函数上连续，分别在区间[3,4][2,3],2],,1[)(x f 上在区间(3,4)(2,3),2),,1(可导，且(1)(2)(3)(4)0f f f f ====。

由罗尔定理知，至少存在),2,1(1∈ξ),3,2(2∈ξ),4,3(3∈ξ使),3,2,1( 0)(=='i f i ξ即方程'()0f x =有至少三个实根。

又因方程'()0f x =为三次方程，故它至多有三个实根。

因此，方程'()0f x =有且只有三个实根，分别位于区间(1,2),(2,3),(3,4)内。

3．若方程 01110=+++--x a x a x a n n n 有一个正根,0x 证明:方程0)1(12110=++-+---n n n a x n a nxa 必有一个小于0x 的正根。

解：取函数()1011nn n f x a x a xa x --=+++。

0()[0,]f x x 在上连续，在0(0,)x 内可导，且0(0)()0,f f x ==由罗尔定理知至少存在一点()00,x ξ∈使'()0,f ξ=即方程12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根。

高等数学李伟版课后习题答案第三章

⾼等数学李伟版课后习题答案第三章习题3—1（A ）1．判断下列叙述是否正确，并说明理由：（1）函数的极值与最值是不同的，最值⼀定是极值，但极值未必是最值；（2）函数的图形在极值点处⼀定存在着⽔平的切线；（3）连续函数的零点定理与罗尔定理都可以⽤来判断函数是否存在零点，⼆者没有差别；（4）虽然拉格朗⽇中值公式是⼀个等式，但将()f ξ'进⾏放⼤或缩⼩就可以⽤拉格朗⽇中值公式证明不等式，不过这类不等式中⼀定要含（或隐含）有某函数的两个值的差．答：（1）不正确．最值可以在区间端点取得，但是由于在区间端点处不定义极值，因此最值不⼀定是极值；⽽极值未必是最值这是显然的．（2）不正确．例如32x y =在0=x 点处取极值，但是曲线在点)00(，却没有⽔平切线．（3）不正确．前者是判断)(x f 是否有零点的，后者是判断)(x f '是否有零点的．（4）正确．⼀类是明显含有)()(a f b f -的；另⼀类是暗含着)()(0x f x f -的． 2．验证函数2)1(e x y -=在区间]20[，上满⾜罗尔定理，并求出定理中的ξ．解：显然2)1(e x y -=在闭区间]20[，上连续，在开区间)20(，内可导，且e )2()0(==y y ，于是函数2)1(ex y -=在区间]20[，上满⾜罗尔定理的条件，2)1(e )1(2)(x x x y ---='，由0)(='ξy ，有0e )1(22)1(=---ξξ，得1=ξ，∈ξ)20(，，所以定理的结论也成⽴．3．验证函数1232-+=x x y 在区间]11[，-上满⾜拉格朗⽇中值定理，并求出公式中的ξ．解：显然1232-+=x x y 在闭区间]11[，-连续，在开区间)11(，-内可导，于是函数1232-+=x x y 在区间]11[，-上满⾜拉格朗⽇中值定理的条件，26)(+='x x y ，2)1(1)1()1(=----y y ，由)()1(1)1()1(ξy y y '=----，有226=+ξ，得0=ξ，∈ξ)11(，-，所以定理的结论也成⽴．4．对函数x x x f cos )(+=、x x g cos )(=在区间]20[π，上验证柯西中值定理的正确性，并求出定理中的ξ．解：显然函数x x x f cos )(+=、x x g cos )(=在闭区间]20[π，上连续，在开区间)20(π，内可导，且x x f sin 1)(-='，x x g sin )(-='，在区间)20(π，内0)(≠'x g ，于是函数x x x f cos )(+=、x x g cos )(=在区间]20[π，上满⾜柯西定理的条件，⼜21)0()2/()0()2/(πππ-=--g g f f ，由)()()0()2/()0()2/(ξξππg f g g f f ''=--，有ξξπsin sin 121--=-，即πξ2sin =，由于∈ξ)20(π，，得πξ2arcsin=，所以定理的结论也成⽴．5．在)(∞+-∞，内证明x x cot arc arctan +恒为常数，并验证2cot arc arctan π≡+x x ．证明：设x x x f cot arc arctan )(+=，显然)(x f 在)(∞+-∞，内可导，且-+='211)(x x f 0112≡+x，由拉格朗⽇定理的推论，得在)(∞+-∞，内x x cot arc arctan +恒为常数，设C x f ≡)(，⽤0=x 代⼊，得2π=C ，所以2cot arc arctan π≡+x x ．6．不求出函数2()(4)f x x x =-的导数，说明0)(='x f 有⼏个实根，并指出所在区间．解：显然2()(4)f x x x =-有三个零点20±==x x ，，⽤这三点作两个区间]20[]02[，、，-，在闭区间]02[，-上)(x f 连续，在开区间)02(，-内)(x f 可导，⼜0)0()2(==-f f 于是)(x f 在]02[，-满⾜罗尔定理，所以⾄少有∈1ξ)02(，-，使得0)(1='ξf ，同理⾄少有∈2ξ)20(，，使得0)(2='ξf ，所以0)(='x f ⾄少有两个实根．⼜因为)(x f 是三次多项式，有)(x f '时⼆次多项式，于是0)(='x f 是⼆次代数⽅程，由代数基本定理，得0)(='x f ⾄多有两个实根．综上，0)(='x f 恰有两个实根，且分别位于区间)02(，-与)20(，内．7．证明下列不等式：（1）对任何实数b a ，，证明cos cos a b a b -≤-；（2）当0>x 时，x x xx<+<+)1ln(1．证明：（1）当b a =时，cos cos a b a b -≤-显然成⽴．当b a <时，取函数x x f cos )(=，显然)(x f 在闭区间][b a ，上连续，在开间)(b a ，内可导，由拉格朗⽇定理，有∈ξ)(b a ，，使得))(()()(b a f b f a f -'=-ξ，即)(sin cos cos b a b a -?-=-ξ，所以)()(sin cos cos b a b a b a -≤-?-=-ξ．当b a >时，只要将上⾯的区间][b a ，换为][a b ，，不等式依然成⽴．所以，对任何实数b a ，，都有cos cos a b a b -≤-．（2）取函数)1ln()(t t f +=，当0>x 时，函数)1ln()(t t f +=在闭区间]0[x ，上连续，在开区间)0(x ，内可导，根据拉格朗⽇定理，有∈ξ)0(x ，，使得ξξ+='1)(xf ．因为x <<ξ0，则x xx x x =+<+<+0111ξ，所以x x x x <+<+)1ln(1． 8．若函数)(x f 在区间),(b a 具有⼆阶导数，且)()()(321x f x f x f ==，其中21x x a <<b x <<3，证明在区间)(3,1x x 内⾄少有⼀点ξ，使得0)(=''ξf ．证明：根据已知，函数)(x f 在区间][21x x ，及][32x x ，上满⾜罗尔定理，于是有∈1ξ)(21x x ，，∈2ξ)(32x x ，（其中21ξξ<），所得0)(1='ξf ，0)(2='ξf ．再根据已知及)()(21ξξf f '='，函数)(x f '在区间][21ξξ，上满⾜罗尔定理，所以有∈ξ)(21ξξ，?)(3,1x x ，所得0)(=''ξf ，即在区间)(3,1x x 内⾄少有⼀点ξ，使得0)(=''ξf ．习题3—1（B ）1．在2004年北京国际马拉松⽐赛中，我国运动员以2⼩时19分26秒的成绩夺得了⼥⼦组冠军．试⽤微分中值定理说明她在⽐赛中⾄少有两个时刻的速度恰好为18. 157km/h （马拉松⽐赛距离全长为42.195km ）．解：设该运动员在时刻t 时跑了)(t s s =（km ），此刻才速度为)()(t s t v v '==（km/h ），为解决问题的需要，假定)(t s 有连续导数．设起跑时0=t ，到达终点时0t t =，则3238888889.20≈t ，对函数)(t s 在区间]0[0t ，上⽤拉格朗⽇定理，有00t <<ξ，所得)()(0)0()(00ξξv s t s t s ='=--，⽽15706.183238888889.2195.420)0()(00≈=--t s t s km/h ，所以157.1815706.18)(>≈ξv ．对)(t v 在区间]0[ξ，及][0t ，ξ上分别使⽤连续函数的介值定理（注意，0)0(=v0)(0=t v ，则数值18. 157分别介于两个区间端点处函数值之间），于是有)0(1ξξ，∈，)0(2，ξξ∈，使得157.18)(1=ξv ，157.18)(2=ξv，这表明该运动员在⽐赛中⾄少有两个时刻的速度恰好为18. 157km/h ．2．若函数)(x f 在闭区间][b a ，上连续，在开区间），（b a 内可导，且0)(>'x f ，证明⽅程0)(=x f 在开区间），（b a 内⾄多有⼀个实根．证明：采⽤反证法，若⽅程0)(=x f 在开区间），（b a 有两个（或两个以上）不同的实根21x x <，即0)()(21==x f x f ，根据已知函数)(x f 在][21x x ，上满⾜罗尔定理，于是有∈ξ)()(21b a x x ，，?，使得0)(='ξf ，与在开区间），（b a 内0)(>'x f ⽭盾，所以⽅程0)(=x f 在开区间），（b a 内⾄多有⼀个实根．（注：本题结论也适⽤于⽆穷区间） 3．证明⽅程015=-+x x 只有⼀个正根．证明：设1)(4-+=x x x f （)(∞+-∞∈，x ），则014)(4>+='x x f ，根据上题结果，⽅程015=-+x x 在)(∞+-∞，内⾄多有⼀个实根．取闭区间]10[，，函数1)(4-+=x x x f 在]10[，上连续，且01)0(<-=f ，01)1(>=f ，由零点定理，有)10(，∈ξ，使得0)(=ξf ，从⽽⽅程015=-+x x 在)0(∞+，内⾄少有⼀个实根．综上，⽅程015=-+x x 只有⼀个正根，且位于区间)10(，内． 4．若在),(+∞-∞内恒有k x f =')(，证明b kx x f +=)(．证明：（⽅法1）设函数kx x f x F -=)()(，则0)()(≡-'='k x f x F ，根据拉格朗⽇定理的推论)(x F 恒为常数，设C kx x f x F ≡-=)()(，⽤0=x 代⼊，得)0(f C =，记b f =)0(，则b C kx x f x F ==-=)()(，所以b kx x f +=)(．（⽅法2）记b f =)0(，∈?x ),(+∞-∞，若0=x ，则满⾜b kx x f +=)(；若0≠x ，对函数)(t f 以x t t ==，0为端点的闭区间上⽤拉格朗⽇定理，则有ξ介于0与x 之间，使得)0)(()0()(-'=-x f f x f ξ，即kx b x f =-)(，所以b kx x f +=)(．5．若函数)(x f 在区间)0(∞+，可导，且满⾜0)()(2≡-'x f x f x ，1)1(=f ，证明x x f =)(.证明：设函数xx f x F )()(=（∈x )0(∞+，），则xx x f x f x x x x f x x f x F 2)()(22/)()()(-'=-'='，由0)()(2≡-'x f x f x ，得0)(≡'x F ，根据拉格朗⽇定理的推论)(x F 恒为常数，设C xx f x F ==)()(，⽤1=x 代⼊，且由1)1(=f ，得1=C ，所以1)()(==xx f x F ，即x x f =)(．6．证明下列不等式（1）当0>x 时，证明x x+>1e ；（2）对任何实数x ，证明x x arctan ≥．证明：（1）取函数t t f e )(=（]0[x t ，∈）显然函数)(t f 在区间]0[x ，上满⾜拉格朗⽇定理，则有∈ξ)0(x ，，使得)0)(()0()(-'=-x f f x f ξ，即x xξe 1e =-，所以 x x x+>+=1e 1e ξ．（2）当0=x 时，显然x x arctan ≥．当0≠x 时，取函数t t f arctan )(=，对)(t f 在以x t t ==，0为端点的闭区间上⽤拉格朗⽇定理，则有ξ介于0与x 之间，使得)0)(()0()(-'=-x f f x f ξ，即21arct an ξ+=xx ，所以x x x <+=21arctan ξ．综上，对任何实数x ，都有x x arctan ≥．7．若函数)(x f 在闭区间[1-，1]上连续，在开区间（1-，1）内可导，M f =)0(（其中0>M ），且M x f <')(．在闭区间[1-，1]上证明M x f 2)(<．证明：对∈?x [1-，1]，当0=x 时，M M f 2)0(<=，．不等式成⽴．当0≠x 时，根据已知，函数)(t f 在以x t t ==，0为端点的区间上满⾜拉格朗⽇定理，则有ξ介于0与x 之间，使得)0)(()0()(-'=-x f fx f ξ，即x f M x f )()(ξ'=-，所以，M x f x f +'=)()(ξ，从⽽M M f M x f M x f x f 2)()()()(<+'≤+'≤+'=ξξξ．综上，在闭区间[1-，1]上恒有M x f 2)(<．8．若函数)(x f 在闭区间]0[a ，上连续，在开区间)0(a ，内可导，且0)(=a f ，证明在开区间)0(a ，内⾄少存在⼀点ξ，使得0)()(='+ξξξf f ．证明：设函数)()(x xf x F =（∈x ]0[a ，），则0)(0)0(==a F F ，，再根据已知，函数)(x F 在区间],0[a 满⾜罗尔定理，则有∈ξ)0(a ，，使得0)(='ξf ．⽽)()()(ξξξξf f f '+='，于是0)()(='+ξξξf f ．所以，在开区间)0(a ，内⾄少存在⼀点ξ，使得0)()(='+ξξξf f ．习题3—2（A ）1．判断下列叙述是否正确？并说明理由（1）洛必达法则是利⽤函数的柯西中值定理得到的，因此不能利⽤洛必达法则直接求数列极限；（2）凡属“00”，“∞∞”型不定式，都可以⽤洛必达法则来求其的极限值；（3）型如””，“”，“”，“”，““0100∞∞-∞∞?∞型的不定式，要想⽤洛必达法则，需先通过变形．⽐如“0?∞”型要变型成为“00”，“∞∞”型，”，”，““00∞-∞””，““01∞∞型要先通过变型，转化为“0?∞”型的不定式，然后再化为基本类型.答：（1）正确．因为数列是离散型变量，对它是不能求导的，要想对数列的“不定式”极限使⽤洛必达法则，⾸先要根据“海涅定理”将数列极限转换为普通函数极限，然后再使⽤洛必达法则．（2）不正确．如0sin 1sinlim 20=→xx x x （00型）、1cos sin lim -=-+∞→x x x x x （∞∞型）、11lim 2=++∞→x x x （∞∞型）都不能⽤洛⽐达法则求得极限值．（3）正确．可参见本节3.其他类型的不定式极限的求法，但是“∞-∞”型通常是直接化为“00”，“∞∞”型． 2．⽤洛必达法则求下列极限：（1）x x x --→e 1ln lim e ；（2）11lim 1--→n m x x x （0≠mn ）；（3）x x x 5tan 3sin limπ→；（4）2e e cos 1lim 0-+--→x x x x；（5）1sec tan 2lim0-→x x x x ；（6）xxx 3tan tan lim 2/π→；（7）x x x 2cot lim 0→；（8）x x x cot arc lim +∞→；（9）)sin 11(lim 0x x x -→；（10）111lim()ln 1x x x →--；（11）xx x tan 0lim +→；（12）)1ln(1)(lim x x x ++∞→；（13）21)(cos lim x x x →；（14）nn n ln lim∞→；解：（1）e11/1lim e 1ln lime e -=-=--→→x x x x x ．（2）==----→→1111lim 11lim n m x nm x nx mx x x nm．（3）=-?-==→→22)1(535sec 53cos 3lim 5tan 3sin limx x x x x x ππ53-．（4）=+=-=-+--→-→-→x x x x x x x x x x x x e e cos lim e e sin lim 2e e cos 1lim00021．（5）===-=-→→→→xxx x x x x x x x x x x x tan 4lim tan sec 4lim 1sec 2lim 1sec tan 2lim002004． (6) =---=-=?=→→→→x xx x xx x x x x x x x x sin 3sin 3lim cos 3cos lim )cos 3cos 3sin sin (lim 3tan tan lim2/2/2/2/ππππ3．（7）===→→→x x x x x x x x 2sec 21lim 2tan lim 2cot lim 200021．（8）=+=-+-==+∞→+∞→+∞→+∞→22221lim /1)1/(1lim 1/cot arc lim cot arc lim xx x x x x x x x x x x 1．（9）=-=-=-=-=-→→→→→2sin lim 21cos lim sin lim sin sin lim )sin 11( lim 002000xx x x x x x x x x x x x x x x x 0．（10）xx x x x x x x x x x x x /)1(ln /11lim ln )1(ln 1lim )11ln 1(lim 111-+-=---=--→→→=+=-+-=→→2ln 1lim 1ln 1lim11x x x x x x x 21．（11）设xxy tan =，则x x y ln tan ln =，因为0lim /1/1lim /1ln lim ln lim ln tan lim ln lim 0200=-=-====++++++→→→→→→x xxx x x x x x y x x x x x x ，所以， ==+→0tan 0e lim xx x 1．（12）设)1ln(1)(x x y +=，则)1ln(ln 21)1ln(ln ln x xx x y +=+=，因为 21)11(lim 21)1/(1/1lim 21)1ln(ln lim 21ln lim =+=+=+= +∞→+∞→+∞→+∞→x x x x x y x x x x ，所以 ==++∞→21)1ln(1e )(lim x x x e ．（13）设21)(cos x x y =，则2cos ln ln x xy =，因为 21cos 2sin lim cos ln lim ln lim 0200-=-==→→→x x x x x y x x x ，所以==-→2 110e )(cos lim 2x x x e1．（14）根据海涅定理，====+∞→+∞→+∞→∞→xxx xx nn x x x n 2lim2/1/1limln limln lim0．3．验证极限xx xx x cos 2sin 2lim -+∞→存在，并说明不能⽤洛必达法则求得．解：=-+=-+=-+∞→∞→0102/)cos 2(1/)(sin 2lim cos 2sin 2limx x x x x x x x x x 2．因为极限xxx x x x x x sin 21cos 2lim )cos 2()sin 2(lim++='-'+∞→∞→不存在，因为此极限不能⽤洛必达法则求得．4．验证极限x x x x sin )/1sin(lim 20→存在，并说明不能⽤洛必达法则求得．解：=?=?=→→→011sin lim sin lim sin )/1sin(lim0020xx x x x x x x x x 0．因为极限xx x x x x x x x cos )/1sin()/1sin(2lim)(sin ])/1sin([lim 020-=''→→不存在，因为此极限不能⽤洛必达法则求得．习题3—2（B ）1．⽤洛必达法则求下列极限：（1）311lnarctan 2limx x xx x -+-→；（2）xx x x 30sin arcsin lim -→（3）)tan 11(lim 220xx x -→；（4）]e )11[(lim -+∞→xx x x ； (5) 260)sin (lim x x xx →；（6）n n nn b a )2(lim +∞→（00>>b a ，）．解：（1）原式30)1ln()1ln(arctan 2limx x x x x -++-=→=--=--+-+=→→)1(34lim 3111112lim 40220x x x x x x x 34-．（2）原式2220220301311lim 31/11lim arcsin lim xx x x x x x x x x x ---=--=-=→→→=-=--=→→22022032/lim 311lim xx x x x x 61-．（3）原式30022220tan lim tan lim tan tan lim xxx x x x x x x x x x x -?+=-=→→→ ==-=-=→→→22022030tan lim 3231sec lim 2tan lim 2x x xx x x x x x x 32．（4）令t x 1=，则原式21010)1ln()1()1(lim e )1(lim tt t t t t t t t tt ++-+=-+→→ =+-=-+-=++-=→→→t t t t t t t t t t t )1ln(lim 2e 21)1ln(1lim e )1ln()1(lim e 002 02 e -．（5）令6)sin (x x x y =，则2sin ln 6ln x x xy =，因为 30200sin cos lim 3)sin cos 2sin /6(lim ln lim xxx x x x x x x x x y x x x -=-?=→→→ 13sin lim 320-=-=→x x x x ，所以==-→160e )sin (lim x x xx e 1．（6）令=n x nn nb a )2(+，则]2ln )[ln(ln -+=n n n b a n x ，再令x t 1=，因为 tb a b a x x t t t xx x n n 2ln )ln(lim ]2ln )[ln(lim ln lim 011-+=-+=→+∞→∞→ ab b a ba b b a a t t t t t ln 2ln ln ln ln lim 0=+=++=→，所以==+∞→abnn nn b a ln e )2(lim ab ．2．当0→x 时，若)(e )(2c bx ax x f x ++-=是⽐2x ⾼阶的⽆穷⼩，求常数c b a 、、．解：根据已知，有0)(e lim220=++-→x c bx ax x x ，由分母极限为零，则有分⼦极限也为零，于是01)]([e lim 2x =-=++-→c c bx ax x ，得1=c ，此时02)2(e lim )(e lim 0220=+-=++-→→x b ax x c bx ax x x x x ，再由分⼦极限为零，同样得1=b ，进⽽022122e lim 2)12(e lim )(e lim 00220=-=-=+-=++-→→→a a x ax x c bx ax x x x x x x ，得21=a ，所以1121===c b a ，，时，当0→x 时，)(e )(2c bx ax x f x ++-=是⽐2x ⾼阶的⽆穷⼩．3.若函数)(x f 有⼆阶导数，且2)0(,1)0(,0)0(=''='=f f f ，求极限2)(limxxx f x -→．解：1)0(210)0()(lim 2121)(lim )(lim002=''=-'-'=-'=-→→→f x f x f x x f x x x f x x x ．（注：根据题⽬所给条件，不能保证)(x f ''连续，所以只能⽤⼀次洛⽐达法则，再⽤⼆阶导数的分析定义）习题3—3（A ）1．判断下列叙述是否正确？并说明理由：（1）只要函数在点0x 有n 阶导数，就⼀定能写出该函数的泰勒多项式．⼀个函数的泰勒多项式永远都不会与这个函数恒等，⼆者相差⼀个不恒为零的余项；（2）⼀个函数在某点附近展开带有拉格朗⽇余项的n 阶泰勒公式是它的n 次泰勒多项式加上与该函数的n 阶导数有关的所谓拉格朗⽇型的余项；（3）在应⽤泰勒公式时，⼀般⽤带拉格朗⽇型余项的泰勒公式⽐较⽅便．答：（1）前者正确，其根据是泰勒多项式的定义；后者不正确．当)(x f 本⾝是⼀个n 次多项式时，有0)(≡x R n ，这时函数的泰勒多项式恒等于这个函数．（2）不正确．拉格朗⽇型的余项与函数)(x f 的1+n 阶导数有关．（3）不正确．利⽤泰勒公式求极限时就要⽤带有⽪亚诺余项的泰勒公式，⼀般在对余项进⾏定量分析时使⽤带拉格朗⽇型余项的泰勒公式，在对余项进⾏定性分析时使⽤带⽪亚诺型余项的泰勒公式．2．写出函数x x f arctan )(=的带有佩亚诺型余项的三阶麦克劳林公式．解：因为211)(x x f +='，)1(2)(2x x x f +-=''，322)1(62)(x x x f ++-='''，于是 2)0(0)0(1)0(0)0(-='''=''='=f f f f ，，，，代⼊到)(!3)0(!2)0()0()0()(332x o x f x f x f f x f +'''+'+'+=中，得 )(3arctan 33x o x x x +-=． 3．按1-x 的乘幂形式改写多项式1)(234++++=x x x x x f ．解：因为1234)(23+++='x x x x f ，2612)(2++=''x x x f ，624)(+='''x x f ，24)()4(=x f ，更⾼阶导数都为零，于是，，，20)1(10)1(5)1(=''='=f f f 30)1(='''f ，24)0()4(=f ，将其带⼊到)()1(!4)1()1(!3)1()1(!2)1()1)(1()1()(44)4(32x R x f x f x f x f f x f +-+-'''+-'+-'+=中，得 432)1()1(5)1(10)1(105)(-+-+-+-+=x x x x x f（其中5)5(4)1(!5)()(-=x f x R ξ恒为零）． 4．将函数1)(+=x xx f 在1x =点展开为带有佩亚诺型余项的三阶泰勒公式．解：因为111)(+-=x x f ，则2)1(1)(+='x x f ，3)1(2)(+-=''x x f ，4)1(6)(+='''x x f ，于是83)1(41)0(41)1(21)1(='''-=''='=f f f f ，，，，将其带⼊到 ))1(()1(!3)1()1(!2)1()1)(1()1()(332-+-'''+-'+-'+=x o x f x f x f f x f 中，得))1((16)1(8)1(41211332-+-+---+=+x o x x x x x ． 5．写出函数xx x f e )(=的带有拉格朗⽇型余项的n 阶麦克劳林公式．解：因为)(e )()(k x x f x k +=（1321+=n n k ，，，，，）（参见习题2.5（B ）3），于是，k fk =)0()(（n k ，，，，210=），=+=++1)1()!1()()(n n n x n x f x R θ1)!1(e )1(++++n x x n x n θθ，将其带⼊到)(!)0(!2)0()0()0()()(2x R x n f x f x f f x f n nn +++'+'+= ，得 132)!1(e )1()!1(!2e +++++-++++=n x n xx n x n n x x x x x θθ )10(<<θ．6．将函数xx f 1)(=按(1)x +的乘幂展开为带有拉格朗⽇型余项的n 阶泰勒公式．解：因为1)(!)1()(+-=k k k xk x f，于是!)1()(k f k -=-（13210+=n n k ，，，，，，）， 1211211)1()1()1()1()!1()!1()1()1()!1()()(+++++++++-=+++-=++=n n n n n n n n n x x n n x n f x R ξξξ，将其代⼊到中)()1(!)1()1(!2)1()1)(1()1()()(2x R x n f x f x f f x f n n n ++-+++-'++-'+-= ，得2112)1()1()1()1()1(11++++-++--+-+--=n n n nx x x x x ξ（ξ介于1-与x 之间）．习题3—3（B ）1．为了修建跨越沙漠的⾼速公路，测量员测量海拔⾼度差时，必须考虑地球是⼀个球体⽽表⾯不是⽔平，从⽽对测量的结果加以修正．（1）如果R 表⽰地球的半径，L 是⾼速公路的长度．证明修正量为R RLR C -=sec ． (2)利⽤泰勒公式证明3422452R L R L C +≈．（3）当⾼速公路长100公⾥时，⽐较（1）和（2）中两个修正量（地球半径取6370公⾥）．证明：（1）由αR L =，有R L =α，⼜在直⾓三⾓形ODB 中，CR R+=αcos ，于是R C R L+==1s e cs e c α，由此得R RLR C -=sec ．（2）先将x x f sec )(=展开为4阶麦克劳林公式，为此求得x x x f tan sec )(='，x x x x f 32s e c t a n s e c )(+=''，x x x x x f tan sec 5tan sec )(33+='''，x x x x x x f5234)4(s e c 5t a n s e c 18tan sec )(++=，，，，，，5)0(0)0(1)0(0)0(1)0()4(=='''=''='=f f f f f 于是 )(245211sec 442x R x x x +++=；当1<2245211sec x x x ++≈，取R L x =，得442224521sec RL R L R L ++≈，于是≈-=R R L R C sec 3422452R L R L +．（3）按公式R RLR C -=sec计算，得修正量为785010135.0)1(≈C ，按公式3422452RL R L C +≈计算，得修正量为785009957.0)2(≈C ，它们相差⼤约为000000178.0)2()1(≈-C C ．2．写出函数212e)(x x f -=的带佩亚诺型余项的n 2阶麦克劳林公式．解：由)(!!3!21e 32nn tt o n t t t t ++++++= ，令22x t -=，得 )]2(!2)1(!62!42!221[e eee223624222122n n n nn x x x o n x x x x +?-++?-?+?-==--)(]!)!2()1(!!6!!4!!21[e 22642n n n x o n x x x x +-++-+-= ，按规律，由于nx2项的后⼀项为22+n x，所以余项也可以⽤)(12+n xo ．3．写出函数x x f 2sin )(=的带⽪亚诺型余项的m 2阶麦克劳林公式．解：x x 2cos 2121sin 2-=)2()!2()2()1(!6)2(!4)2(!2)2(1[2121222642m m mn x o m x x x x +-++-+--=)()!2(2)1(4523122121642m m m m x o x m x x x +-+-+-=-- ，同上⼀题，余项也可以⽤)(12+m x o ．（注意：像2、3题⽤变量代换写泰勒公式的⽅法只使⽤于带有佩亚诺型余项的泰勒公式，不适⽤带有拉格朗⽇型余项的泰勒公式，否则得到的余项不再是拉格朗⽇型余项） 4．应⽤三阶泰勒公式计算下列各数的近似值，并估计误差：（1）330；（2）18sin ．解：（1）取函数31)(x x f +=，展开为三阶麦克劳林公式，有31154323)1(3108159311)(x xx x x x x f θ+?-+-+=+=，3339/11332730+?=+=，现取9/1=x ，)59049572912711(3303+-+≈，误差为54431089.19310-?R ， 10725.3)000085.0001372.0037037.01(3)59049572912711(3303=+-+≈+-+≈；（2）⽤x sin 的麦克劳林公式，取1018π==x ，得53)10(!5)cos()10(!311018sin πθππx +-=，则3)10(!311018sin ππ-≈，误差为5531055.2)10(!51-?≈<≤πR3090.030899.000517.031416.018sin ≈=-≈．5．利⽤泰勒公式求下列极限：（1）642/012/e cos lim 2x x x x x +--→；（2）x x x x x x x sin )1(sin e lim 20+-→．解：（1）原式64636426 642012/)](!32821[)](!62421[lim xx x o x x x x o x x x x ++?-+--+-+-=→ 3607)(360/7lim 6660=+=→x x o x x ．（2）原式3233220)](6/)][(2/1[lim x x x x o x x x o x x x --+-+++=→ 31)(3/lim3330=+=→x x o x x ．6．设函数)(x f 在区间][b a ，上有⼆阶连续导数，证明：有)(b a ，∈ξ使得)(4)()2(2)()(2ξf a b b a f b f a f ''-=+-+．证明：将函数)(x f y =在20ba x +=点展开为⼀阶泰勒公式，有 20000)(!2)())(()()(x x f x x x f x f x f -''+-'+=η.（η介于x 与0x 之间）分别⽤b x a x ==、代⼊上式，得 201000)(!2)())(()()(x a f x a x f x f a f -''+-'+=η 4)(!2)(2)2()2(21b a f b a b a f b a f -''+-+'++=η（21b a a +<<η），202000)(!2)())(()()(x b f x b x f x f b f -''+-'+=η 4)(!2)(2)2()2(22a b f a b b a f b a f -''+-+'++=η（b b a <<+22η），上两式相加，得]2)()([4)()2(2)()(212ηηf f a b b a f b f a f ''+''-++=+，由)(x f ''连续，根据习题1-7（B ）4，得)(2)()(21ξηηf f f ''=''+''（)(b a ，∈ξ），于是，)(4)()2(2)()(2ξf a b b a f b f a f ''-++=+，所以，有)(b a ，∈ξ使得)(4)()2(2)()(2ξf a b b a f b f a f ''-=+-+． 7．若函数)(x f 有⼆阶导数，0)(>''x f ，且1)(lim=→xx f x ，⽤泰勒公式证明x x f ≥)(. 证明：由函数)(x f 可导，及1)(lim=→xx f x ，得1)0(0)0(='=f f ，，将)(x f 展开为⼀阶麦克劳林公式，有22)()(x f x x f ξ''+=（ξ介于0与x 之间），由0)(>''x f ，得x x f x x f ≥''+=22)()(ξ．8．设函数)(x f 在区间]20[，上⼆次可微，)2()0(f f =，且M x f ≤'')(，对任何]20[，∈x ，证明M x f ≤')(．证明：对任何∈x ]20[，，将函数)(t f y =在x t =点展开为⼀阶泰勒公式，有 2)(!2)())(()()(x t f x t x f x f t f -''+-'+=ξ.（ξ介于x 与t 之间）分别⽤20==t t 、代⼊上式，得 21!2)()()()0(x f x x f x f f ξ''+'-=，（x <<10ξ）（1） 22)2(!2)()2)(()()2(x f x x f x f f -''+-'+=ξ，（22<<ξx ）（2）（2）-（1），并由条件)2()0(f f =，有 ])()2)(([21)(202122x f x f x f ξξ''--''+'=，即])()2)(([41)(2122x f x f x f ξξ''--''-='，所以M x x M x x M x f =+-?≤+-≤'222])2[(4])2[(4)(．习题3—4（A ）1．下列叙述是否正确？并按照你的判断说明理由：（1）设函数()f x 在区间[,]a b 上连续，在(,)a b 内可导，那么()f x 在区间[,]a b 上单调增加（减少）的充分必要条件是对任意的(,)x a b ∈，0)(>'x f （0)(<'x f ）；（2）函数的极⼤值点与极⼩值点都可能不是唯⼀的，并且在其驻点与不可导点处均取得极值；（3）判定极值存在的第⼀充分条件是根据驻点两侧导数的符号来确定该驻点是否为极值点，第⼆充分条件是根据函数在其驻点处⼆阶导数的符号来判定该驻点是否为极值点；（4）在区间I 上连续的函数，其最⼤值点或最⼩值点⼀定是它的极值点.答：（1）不正确．如3x y =在]11[，-上单调增加，⽽032≥='x y ．（2）前者正确，后者不正确．驻点与不可导点是取得极值必要条件不是充分条件，如函数3x y =有驻点0=x ，⽽3x y =在0=x 点不取极值；⼜如函数3x y =有不可导点0=x ，⽽3x y =在0=x 点也不取极值．（3）前者不正确，后者正确．第⼀充分条件对连续函数的不可导点也适⽤．（4）不正确．函数的最⼤（⼩）值点可以是闭区间端点，这时的最值点就不是极值点． 2．证明函数x x x f arcsin )(-=在]11[，-上单调减少．解：在开区间)11(，-内，0111)(2≤--='xx f ，且等号只在0=x 点成⽴，所以)(x f 在开区间)11(，-内单调减少，⼜因为函数x x x f arcsin )(-=在区间]11[，-的左、右端点处分别右连续、左连续，所以x x x f arcsin )(-=在]11[，-上单调减少． 3．求下列函数的单调区间和极值：（1）323y x x =-；（2）xx y 12+=；（3）3232x x y +?=；（4）2exy x =；（5）x x y -+=)1ln(；（6）)1ln(2-=x y ．解：（1）定义域为)(∞+-∞，，)2(3632-=-='x x x x y ，由0='y ，得驻点0=x ，2=x ，函数没有不可导点．单增区间为：)2[]0(∞+-∞，、，，单减区间为：]20[，，极⼤值为：0)0(=y ，极⼩值为：4)2(-=y ．（2）定义域为)0()0(∞+-∞，，，221xx y -='，由0='y ，得驻点1±=x ，在定义域内函数没有不可导点．单增区间为：)1[]1(∞+--∞，、，，单减区间为：]10()01[，、，-，极⼤值为：2)1(-=-y ，极⼩值为：2)1(=y ．（3）定义域为)(∞+-∞，，2233)1(2xx y ?+='，由0='y ，得驻点1-=x ，不可导点0=x ．单增区间为：)1[∞+-，，单减区间为：]1(--∞，，⽆极⼤值，极⼩值为：1)1(-=-y ．（4）定义域为)0()0(∞+-∞，，，3)2(e xx y x -='，由0='y ，得驻点2=x ，在定义域内函数没有不可导点．单增区间为：、，)0(-∞)2[∞+，，单减区间为：]20(，，⽆极⼤值，极⼩值为：4/e )2(2=y ．（5）定义域为)1(∞+-，，xxy +-='1，由0='y ，得驻点0=x ，在定义域内函数没有不可导点．单增区间为：]01(，-，单减区间为：)0[∞+，，极⼤值为：0)0(=y ，⽆极⼩值．（6）定义域为)1()1(∞+--∞，，，122-='x xy ，在定义域内0≠'y ，且没有不可导点．单增区间为：)1(∞+，，单减区间为：)1(--∞，，既⽆极⼤值，也⽆极⼩值．4．求下列函数在指定区间的最⼤值M 和最⼩值m ：（1）163)(24+-=x x x f ，]20[，∈x ；（2）11)(+-=x x x f ，]40[，∈x ．解：（1）)1(121212)(23-=-='x x x x x f ，由0)(='x f ，得1=x （10-==x x ，都不在)20(，内），⽐较数值25)2(2)1(1)0(=-==f f f ，，，得163)(24+-=x x x f 在。

国防科大高等数学教材答案

国防科大高等数学教材答案为了方便学生对国防科大高等数学教材的学习，以下给出一些答案供参考。

这些答案将涵盖教材中的一些练习题和案例，帮助学生巩固和加深对相关数学概念和技巧的理解。

1. 第一章：函数与极限
1.1 作业题答案
1.2 难题解答
2. 第二章：导数与微分
2.1 作业题答案
2.2 难题解答
3. 第三章：不定积分
3.1 作业题答案
3.2 难题解答
4. 第四章：定积分及其应用
4.1 作业题答案
4.2 难题解答
5. 第五章：微分方程
5.1 作业题答案
5.2 难题解答
6. 第六章：多元函数微分学
6.1 作业题答案
6.2 难题解答
7. 第七章：多重积分
7.1 作业题答案
7.2 难题解答
8. 第八章：曲线积分与曲面积分 8.1 作业题答案
8.2 难题解答
9. 第九章：级数与幂级数
9.1 作业题答案
9.2 难题解答
10. 第十章：常微分方程
10.1 作业题答案
10.2 难题解答
请注意，这里提供的仅仅是一些答案供参考，在学习时应当注重理解思路和方法，而非仅仅背诵答案。

数学的学习过程需要通过自我思考和思维训练，才能真正掌握其中的知识和技巧。

希望以上答案能对学生们的学习有所帮助。

祝愿大家在国防科大高等数学课程中取得好成绩！。

北大版高等数学第三章积分的计算及应用答案习题

习题3.22222222222222222222111.ln ln ln ln 222111ln ln ln .222224111122.1212212ax ax ax ax ax ax ax ax ax ax ax ax x x xdx xdx x x d xx x x x x x dx x xdx x C x x e dx x de x e e dx x e xe dxa a a a ax x e xde x e e e dx a a a a a x e a ==-=-=-=-+==-=-=-=-+=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰求下列不定积分：2223223222122122.1113.sin 2cos 2cos 2cos 222211cos 2sin 2.244.arcsin arcsin arcsin arcsin 11arcsin 21ax ax ax ax ax x xde x e e e C a a a ax e x C aa a x xdx xd x x x xdxx x x C xdx x x xd x x x x x x x x =-++⎛⎫=-++ ⎪⎝⎭=-=-+=-++=-=--=+=-⎰⎰⎰⎰⎰⎰2arcsin 1.x x C - 2222222222225.arctan arctan arctan arctan 11(1)1arctan arctan ln(1).2121116.cos3cos3cos3cos32221313cos3sin 3cos3sin 322241x x x x x x x x xdxxdx x x xd x x x x d x x x x x x C x I e xdx xde e x e d xe x e xdx e x xde =-=-++=-=-+++===-=+=+=⎰⎰⎰⎰⎰⎰⎰⎰⎰()()22222223cos3sin 33cos324139cos3sin 3,2444131cos3sin 32cos33sin 3.132413sin 37.sin 3sin 33cos3sin 33cos3sin 33x x x x x x x x x x x x x x x e x e x e xdx e x e x I I x x e C x x e C xI dx xde e x e xdxee x xde e x e -------+-=+-⎛⎫=++=++ ⎪⎝⎭==-=-+=--=--⎰⎰⎰⎰⎰()cos33sin 3x x e xdx -+⎰()sin 33(cos33),1sin 33cos3(sin 33cos3).1010x x x x xe x e x I e I e x e x C x x C -----=--+=--+=-++ ()()22222222118.sin sin sin cos 1sin cos 1sin cos sin 1sin cos .11sin cos ,1(sin co ax axax ax ax ax ax ax ax ax ax ax ax axb I e bxdx bxde e bx e bxdx a a abe bx bxde a a be bx e bx b e bxdx a a be bx e bx bI a ab I e bx e bx b a a a e I a bx b a b ===-=-=-+=-+⎛⎫=- ⎪⎝⎭+=-+⎰⎰⎰⎰⎰s ).bx C +222222222222229.1919191921919191919,1911119ln(319)2231119ln(319).26I x dx x x x x x x dx x x I x I x x x Cx x x C =+=++=++⎛⎫=++- +⎝⎛⎫=+- +⎝=++++=+++⎰⎰2222222222210.cosh sinh sinh sinh sinh cosh .11.ln(1)ln(1)ln(1)ln(1)ln(1)1.112.(arccos )(arccos )21(arccos )2arcco x xdx xd x x x xdx x x x C x x dx x x x xd x x x x x x x x x C x x dx x x dxxx x ==-=-++=++-++=+-=++++=+-=-⎰⎰⎰⎰⎰⎰)222s 1(arccos )211x x x x x dx-=--+⎰⎰22(arccos )212.x x x x x C =---+()2222222222arccos 1113.arccos (1)21arccos 12(1)2(1)1arccos .2(1)2114.arctan arctan 2(1)1arctan .,,22122arctan ,11arc x xdx xdx x x x x x x C x xxdx x x x xxdx x x x u x u dx udu xxdx u uduu u C x u =--=+---=++--=+====+==-+++⎰⎰⎰⎰⎰12()2arctan (arctan )(1)arctan .xdx x x x x C x x x x C x x x C =-+=+=+⎰ 22222222arcsin 1arcsin 15.arcsin 1arcsin 0)1/1arcsin arcsin ln |1/1/11/1arcsin ln(11ln arcsin ln(11ln ||(0)(x x dx xd x x x x x x x x x x x x x x C x x x x x x Cx x x x C x x⎛⎫=-=-+ ⎪⎝⎭-=-+>-=--=---+-=-+--+=-+--+≠⎰⎰原函数为偶函数424322442423442442434).1(ln )12ln 16.(ln )(ln )444(ln )1(ln )1ln ln 4248(ln )1(ln )1ln ln .482488x x x xdx x x dx x dx xx x x x x xdx xdx x x x x x x x x dx x x C ==-=-=-=-+=-++⎰⎰⎰⎰⎰⎰223/225/225/2arctan 1arctan (1)1217.arctan (1)(1)2(1)23x xdx xd x xd x x x -+⎛⎫==-+ ⎪++⎝⎭⎰⎰⎰223/225/2arctan 1.tan ,(/2,/2).sec ,3(1)3(1)x dx x u u dx udu x x ππ=-+=∈-=++⎰ 3225/23322325/223/222323/223/22cos (1sin )sin (1)11sin sin ,3311arctan arctan 11(1)3(1)3311arctan 1.3(1)39(1)1dx udu u d u x u u C C x x x xdx x C x x x x x x C x x x ==-=+⎛⎫=-+=+++⎛⎫⎛⎫⎪=-++⎪++++⎭=-+++++⎰⎰⎰⎰ 222222222222222222222118.ln(1)ln(1)211ln(1)22111ln(1)221111ln(1)12221111ln(1)1ln(1)ln(1)222221ln(12x x x dx x x dx x x x x x x x x x x x x dx x x x x x x x x x x Cx x ++=++=++-+=++-+=++-+++⎛⎫+++=++-++++ ⎪ ⎪⎝⎭=++⎰⎰22211)1ln(1.44x x x x x C -++++。

高等数学课后习题答案第三章

习题三1(1)解：所给函数在定义域(,)−∞+∞内连续、可导，且2612186(1)(3)y x x x x ′=−−=+−可得函数的两个驻点：121,3x x =−=,在(,1),(1,3),(3,)−∞−−+∞内，y ′分别取+，–，+号，故知函数在(,1],[3,)−∞−+∞内单调增加，在[1,3]−内单调减少.(2)解:函数有一个间断点0x =在定义域外，在定义域内处处可导，且282y x ′=−，则函数有驻点2x =，在部分区间(0,2]内，0y ′<；在[2,)+∞内y ′>0，故知函数在[2,)+∞内单调增加，而在(0,2]内单调减少.(3)解:函数定义域为(,)−∞+∞，0y ′=>,故函数在(,)−∞+∞上单调增加.(4)解:函数定义域为(,)−∞+∞,22(1)(21)y x x ′=+−，则函数有驻点:11,2x x =−=,在1(,]2−∞内，0y ′<，函数单调减少；在1[,)2+∞内，0y ′>，函数单调增加.(5)解:函数定义域为[0,)+∞，11e e e ()n x n x x n y nx x x n x −−−−−′=−=−函数的驻点为0,x x n ==,在[0,]n 上0y ′>，函数单调增加；在[,]n +∞上0y ′<，函数单调减少.(6)解:函数定义域为(,)−∞+∞,πsin 2, [π,π], ,2πsin 2, [π,π], .2x x x n n n y x x x n n n ⎧+∈+∈⎪⎪=⎨⎪−∈−∈⎪⎩Z Z 1)当π[π,π]2x n n ∈+时，12cos 2y x ′=+，则1π0cos 2[π,π23y x x n n ′≥⇔≥−⇔∈+；πππ0cos 2[π,π]232y x x n n ′≤⇔≤−⇔∈++.2)当π[π,π]2x n n ∈−时，12cos 2y x ′=−，则1ππ0cos 2[π,π]226y x x n n ′≥⇔≤⇔∈−−1π0cos 2[π,π]26y x x n n ′≤⇔≥⇔∈−.综上所述，函数单调增加区间为πππ[,)223k k k z +∈，函数单调减少区间为ππππ[,)2322k k k z ++∈.(7)解:函数定义域为(,)−∞+∞.4453345(2)(21)4(2)(21)2(21)(1811)(2)y x x x x x x x ′=−++−+⋅=+−−函数驻点为123111,,2218x x x =−==,在1(,]2+∞−内，0y ′>,函数单调增加，在111[,]218−上，0y ′<,函数单调减少，在11[,2]18上，0y ′>,函数单调增加，在[2,)+∞内，0y ′>,函数单调增加.故函数的单调区间为:1(,]2−∞−，111[,218−，11[,)18+∞.2.(1)证明:令()sin tan 2,f x x x x =−−则22(1cos )(cos cos 1)()cos x x x f x x −++′=,当π02x <<时，()0,()f x f x ′>为严格单调增加的函数，故()(0)0f x f >=,即sin 2tan 2.x x x −>(2)证明:令2()=e sin 12xx f x x −+−−,则()=e cos xf x x x −′−+−,()=e sin 1e (sin 1)0x x f x x x −−′′−−=−+<,则()f x ′为严格单调减少的函数,故()(0)0f x f ′′<=,即()f x 为严格单调减少的函数,从而()(0)0f x f <=,即2e sin 1.2xx x −+<+3.证明:设()sin f x x x =−，则()cos 10,f x x =−≤()f x 为严格单调减少的函数，因此()f x 至多只有一个实根.而(0)0f =，即0x =为()f x 的一个实根，故()f x 只有一个实根0x =，也就是sin x x =只有一个实根.4.(1)解:22y x ′=−,令0y ′=，得驻点1x =.又因20y ′′=>，故1x =为极小值点，且极小值为(1)2y =.(2)解:266y x x ′=−,令0y ′=，得驻点120,1x x ==,126y x ′′=−,010,0x x y y ==′′′′<>,故极大值为(0)0y =，极小值为(1)1y =−.(3)解:2612186(3)(1)y x x x x ′=−−=−+,令0y ′=，得驻点121,3x x =−=.1212y x ′′=−,130,0x x y y =−=′′′′<>,故极大值为(1)17y −=，极小值为(3)47y =−.(4)解:1101y x ′=−=+，令0y ′=，得驻点0x =.201,0(1)x y y x =′′′′=>+,故(0)0y =为极大值.(5)解:32444(1)y x x x x ′=−+=−，令0y ′=，得驻点1231,0,1x x x =−==.210124, 0,0,x x y x y y =±=′′′′′′=−+<>故(1)1y ±=为极大值，(0)0y =为极小值.(6)解:1y ′=,令0y ′=，得驻点13,4x =且在定义域(,1]−∞内有一不可导点21x =，当34x >时，0y ′<;当34x <时，0y ′>,故134x =为极大值点，且极大值为35()44y =.因为函数定义域为1x ≤，故1x =不是极值点.(7)解:y ′=,令0y ′=，得驻点125x =.当125x >时，0y ′<；当125x <，0y ′>,故极大值为12()5y =.(8)解:2131x y x x +=+++,22(2)(1)x x y x x −+′=++,令0y ′=，得驻点122,0x x =−=.2223(22)(1)2(21)(2)(1)x x x x x x y x x −−+++++′′=++200,0x x y y =−=′′′′><,故极大值为(0)4y =，极小值为8(2)3y −=.(9)解:e (cos sin )x y x x ′=−,令0y ′=，得驻点ππ (0,1,2,)4k x k k =+=±±⋯.2e sin x y x ′′=−，ππ2π(21)π440,0x k x k y y =+=++′′′′<>，故2π2π 4k x k =+为极大值点，其对应的极大值为π2π42()k k y x +=;21π(21)π 4k x k +=++为极小值点，对应的极小值为π(21)π421()k k y x +++=.(10)解:11211ln (ln )xxxy x x x x x −′′==,令0y ′=，得驻点e x =.当e x >时，0y ′<，当e x <时，0y ′>,故极大值为1e(e)e y =.(11)解:2e e x xy −′=−,令0y ′=，得驻点ln 22x =−.ln 222e e ,0x x x y y −=−′′′′=+>,故极小值为ln 2()2y −=.(12)解:y ′=，无驻点.y 的定义域为(,)−∞+∞，且y 在x =1处不可导，当x >1时0y ′<，当x <1时，0y ′>，故有极大值为(1)2y =.(13)解:y ′=无驻点.y 在1x =−处不可导，但y ′恒小于0，故y 无极值.(14)解:21sec 0y x ′=+>,y 为严格单调增加函数，无极值点.5.证明：232y ax bx c ′=++，令0y ′=，得方程2320ax bx c ++=，由于22(2)4(3)4(3)0b a c b ac ∆=−=−<，那么0y ′=无实数根，不满足必要条件，从而y 无极值.6.解：f (x )为可导函数，故在π3x =处取得极值，必有π3π0()(cos cos3)3x f a x x =′==+，得a =2.又π3π0((2sin 3sin 3)3x f x x =′′=<=−−，所以π3x =是极大值点，极大值为π()3f =7.（1）解：y 的定义域为(,0)−∞，322(27)0x y x +′==，得唯一驻点x =－3且当(,3]x ∈−∞−时，0y ′<，y 单调递减；当[3,0)x ∈−时，0y ′>，y 单调递增,因此x =－3为y 的最小值点，最小值为f (－3)=27.又lim ()x f x →−∞=+∞，故f (x )无最大值.(2)解：10y ′==，在(5,1)−上得唯一驻点34x =，又53,(1)1,(5)544y y y ⎛⎞==−=−⎜⎟⎝⎠ ,故函数()f x 在[－5，1]上的最大值为545−.(3).解：函数在(－1，3)中仅有两个驻点x =0及x =2，而y (－1)=－5，y (0)=2，y (2)=－14，y (3)=11,故在[－1，3]上，函数的最大值是11，最小值为－14.8.解：20y ax b ′=+=得2b x a =−不可能属于以0和ba 为端点的闭区间上,而22(0)0,b b y y a a ⎛⎞==⎜⎟⎝⎠,故当a >0时，函数的最大值为22b b y a a ⎛⎞=⎜⎟⎝⎠，最小值为(0)0y =;当a <0时，函数的最大值为(0)0y =，最小值为22b b y a a ⎛⎞=⎜⎟⎝⎠.9.解：令y =,y ′===令0y ′=得x =1000.因为在(0，1000)上0y ′>，在(1000,)+∞上0y ′<,所以x =1000为函数y的极大值点，也是最大值点，max (1000)y y ==.故数列的最大项为1000a =.10.证明：11,01111(),01111,11x x x a f x x ax x a x a x x a ⎧+<⎪−−+⎪⎪=+≤≤⎨+−+⎪⎪+>⎪++−⎩当x <0时，()()2211()011f x x x a ′=+>−−+;当0<x <a 时，()()2211()11f x x x a ′=−++−+;此时令()0f x ′=，得驻点2a x =，且422a f a ⎛⎞=⎜⎟+⎝⎠，当x >a 时，()()2211()011f x x x a ′=−−<++−,又lim ()0x f x →∞=，且2(0)()1a f f a a +==+.而()f x 的最大值只可能在驻点，分界点，及无穷远点处取得故{}max 242(),,0121a af x a a a++==+++.11.解：设圆柱体的高为h ,，223πππ4V h r h h =⋅=−令0V ′=,得.h =即圆柱体的高为3r 时，其体积为最大.12.解：由题设知21π22x xy a⎛⎞+⋅=⎜⎟⎝⎠得21π18π8a x a y x x x −==−截面的周长212112π()2πππ,2424π2()1,4a a l x x y x x x x x x x x al x x=++⋅=+−+=++′=+−令()0l x ′=得唯一驻点x =，即为最小值点.即当x =.13.解：所需电线为()(03)()L x x L x =<<′=在0<x <3得唯一驻点x =1.2(km)，即变压器设在输电干线离A 处1.2km 时，所需电线最短.14.解：设小正方形边长为x 时方盒的容积最大.232222(2)44128V a x x x ax a xV x ax a =−⋅=−+′=−+令0V ′=得驻点2a x =(不合题意，舍去)，6a x =.即小正方形边长为6a时方盒容积最大.15.(1)解：42,20y x y ′′′=−=−<，故知曲线在(,)−∞+∞内的图形是凸的.(2)解：cosh ,sinh .y x y x ′′′==由sinh x 的图形知，当(0,)x ∈+∞时，0y ′′>，当(,0)x ∈−∞时，0y ′′<，故y =sinh x 的曲线图形在(,0]−∞内是凸的，在[0,)+∞内是凹的.(3)解：23121,0y y x x ′′′=−=>，故曲线图形在(0,)+∞是凹的.(4)解：2arctan 1x y x x ′=++，2220(1)y x ′′=>+故曲线图形在(,)−∞+∞内是凹的.16.(1)；解：23103y x x ′=−+610y x ′′=−，令0y ′′=可得53x =.当53x <时，0y ′′<，故曲线在5(,)3−∞内是凸弧；当53x >时，0y ′′>，故曲线在5[,)3+∞内是凹弧.因此520,327⎛⎞⎜⎟⎝⎠是曲线的唯一拐点.(2)解：(1)e , e (2)x xy x y x −−′′′=−=−令0y ′′=，得x =2当x >2时，0y ′′>，即曲线在[2,)+∞内是凹的；当x <2时，0y ′′<，即曲线在(,2]−∞内是凸的.因此(2，2e －2)为唯一的拐点.(3)；解：324(1)e , e 12(1)0x x y x y x ′′′=++=++>故函数的图形在(,)−∞+∞内是凹的，没有拐点.(4)解：222222(1), 1(1)x x y y x x −′′′==++令0y ′′=得x =－1或x =1.当－1<x <1时，0y ′′>，即曲线在[－1，1]内是凹的.当x >1或x <－1时，0y ′′<，即在(,1],[1,)−∞−+∞内曲线是凸的.因此拐点为(－1，ln2)，(1，ln2).(5)；解：arctan arctan 222112e ,e1(1)x xx y y x x −′′′==++ 令0y ′′=得12x =.当12x >时，0y ′′<，即曲线在1[,)2+∞内是凸的；当12x <时，0y ′′>，即曲线在1(,]2−∞内是凹的，故有唯一拐点1arctan 21(,e )2.(6)解：函数y 的定义域为(0，+∞)且在定义域内二阶可导.324(12ln 4),144ln .y x x y x x ′′′=−= 令0y ′′=，在(0，+∞)，得x =1.当x >1时，0y ′′>，即曲线在[1,)+∞内是凹的;当0<x <1时，0y ′′<，即曲线在(0，1]内是凸的，故有唯一拐点(1，－7).17.(1);证明：令()nf x x =12(),()(1)0n n f x nx f x n n x −−′′′==−> ，则曲线y =f (x )是凹的，因此,x y R +∀∈，()()22f x f y x y f ++⎛⎞<⎜⎟⎝⎠,即1()22nn n x y x y +⎛⎞<+⎜⎟⎝⎠.(2);证明：令f (x )=e x()e ,()e 0x x f x f x ′′′==> .则曲线y =f (x )是凹的，,,x y R x y∀∈≠ 则()()22f x f y x y f ++⎛⎞<⎜⎟⎝⎠即2e e e2x yx y ++<.(3)证明：令f (x )=x ln x (x >0)1()ln 1,()0(0)f x x f x x x′′′=+=>> 则曲线()y f x =是凹的，,x y R +∀∈，x ≠y ，有()()22f x f y x y f ++⎛⎞<⎜⎟⎝⎠即1ln (ln ln )222x y x y x x y y ++<+，即ln ln ()ln2x y x x y y x y ++>+.18.(1)解：22223d 33d 3(1),d 2d 4y t y t xt x t +−==令22d 0d yx =，得t =1或t =－1则x =1，y =4或x =1，y =－4当t >1或t <－1时，22d 0d yx >，曲线是凹的，当0<t <1或－1<t <0时，22d 0d yx <，曲线是凸的，故曲线有两个拐点(1，4)，(1，－4).(2)解：32d 22sin cos 2sin cos d 2(csc )y a xa θθθθθ⋅⋅==−⋅−222442222d 11(6sin cos 2sin )sin cos (3tan )d 2(csc )y x a a θθθθθθ=−+⋅=⋅−−令22d 0d y x =，得π3θ=或π3θ=−，不妨设a >0tan θ>>时，即ππ33θ−<<时，22d 0d y x >，当tan θ>或tan θ<π3θ<−或π3θ>时，22d 0d y x <,故当参数π3θ=或π3θ=−时，都是y的拐点，且拐点为3,2a ⎞⎟⎠及3,2a ⎛⎞⎜⎟⎝⎠.19.证明：22221(1)x x y x −++′=+，y ′′=令0y ′′=，得1,22x x x =−=+=−当(,1)x ∈−∞−时，0y ′′<；当(1,2x ∈−时0y ′′>；当(22x ∈−+时0y ′′<；当(2)x ∈++∞时0y ′′>,因此，曲线有三个拐点(－1，－1)，(2−+.因为111212−−+因此三个拐点在一条直线上.20.解：y′=3ax 2+2bx ,y″=6ax +2b 依题意有3620a b a b +=⎧⎨+=⎩解得39,22a b =−=.21.解：令f (x )=ax 3+bx 2+cx +d联立f (－2)=44，f ′(－2)=0，f (1)=－10，f ″(1)=0可解得a =1，b =－3，c =－24，d =16.22.解：224(3),12(1)y kx x y k x ′′′=−=− 令0y ′′=，解得x =±1，代入原曲线方程得y =4k ，只要k ≠0，可验证(1，4k )，(－1，4k )是曲线的拐点.18x k y =±′=±，那么拐点处的法线斜率等于18k ∓，法线方程为18y x k =∓.由于(1，4k )，(－1，4k )在此法线上，因此148k k =±,得22321, 321k k ==−(舍去)故8k ==±.23.答：因00()()0f x f x ′′′==，且0()0f x ′′′≠，则x =x 0不是极值点.又在0(,)U x δ�中，000()()()()()()f x f x x x f x x f ηη′′′′′′′′′′=+−=−，故()f x ′′在0x 左侧与0()f x ′′′异号，在0x 右侧与0()f x ′′′同号，故()f x 在x =x 0左、右两侧凹凸性不同，即00(,())x f x 是拐点.24.(1)；解：函数的定义域为(－∞，+∞),且为奇函数,2222222223121(1)(1)2(3)(1)x x x y x x x x y x +−−′==++−′′=+令0y ′=，可得1x =±，令0y ′′=，得x =0，,当x→∞时，y→0，故y=0是一条水平渐近线.函数有极大值1(1)2f=，极小值1(1)2f−=−，有3个拐点，分别为,⎛⎜⎝(0，0)，，作图如上所示.(2)解：函数定义域为(－∞，+∞)，且为奇函数,2222114(1)yxxyx′=−+′′=+令y′=0，可得x=±1，令y″=0，可得x=0.列表讨论如下：x0(0，1)1(1，∞)y′－0+y″0++y0极小又()2lim lim(1arctan)1x xf xxx x→∞→∞=−=且lim[()]lim(2arctan)πx xf x x x→+∞→+∞−=−=−故πy x=−是斜渐近线，由对称性知πy x=+亦是渐近线.函数有极小值π(1)12y=−，极大值π(1)12y−=−.(0，0)为拐点.作图如上所示.(3)；解：函数的定义域为,1x R x∈≠−.22232(1)(2)(1)(1)(1)2(1)x x x x xy xx xyx+−+′==≠−++′′=+令y′=得x=0，x=－2当(,2]x∈−∞−时，0,()y f x′>单调增加；当[2,1)x∈−−时，0,()y f x′<单调减少；当(1,0]x∈−时，0,()y f x′<单调减少；当[0,)x∈+∞时，0,()y f x′>单调增加,故函数有极大值f(－2)=－4，有极小值f(0)=0又211lim()lim1x xxf xx→−→−==∞+，故x=－1为无穷型间断点且为铅直渐近线.又因()lim1xf xx→∞=，且2lim(())lim11x xxf x x xx→∞→∞⎡⎤−==−−⎢⎥+⎣⎦，故曲线另有一斜渐近线y=x－1.综上所述，曲线图形为：(4)解：函数定义域为(－∞，+∞).22(1)(1)22(1)e e 2(241)x x y x y x x −−−−′=−−′′=⋅−+令0y ′=，得x =1.令0y ′′=，得1x =±.当(,1]x ∈−∞时，0,y ′>函数单调增加；当[1,)x ∈+∞时，0,y ′<函数单调减少；当(,1[1)x ∈−∞−++∞∪时，0y ′′>，曲线是凹的；当[1,122x ∈−+时，0y ′′<，曲线是凸的,故函数有极大值f (1)=1，两个拐点：1122(1,e ),(1,e )22A B −−−+，又lim ()0x f x →∞=，故曲线有水平渐近线y =0.图形如下：25.(1)解：2e ()0(1e )cxcx Ac g x −−′=>+，g (x )在(－∞，+∞)内单调增加，222244e e 2(1e )e e (1e )()(1e )(1e )cx cx cx cx cx cx cx cx Ac Ac Ac g x −−−−−−−−−+⋅+⋅−−′′==++当x >0时，()0,()g x g x ′′<在(0，+∞)内是凸的.当x <0时，()0,()g x g x ′′>在(－∞，0)内是凹的.当x =0时，()2A g x =.且lim ()0,lim ()x x g x g x A→−∞→+∞==.故曲线有两条渐近线y =0，y =A .且A 为该种动物数量(在特定环境中)最大值，即承载容量.如图：(2)解：()()1e 1e cx cxA Ag x g x A −−+=+=++.(3)证明：∵()1e 1e e c x T cx cT A Ay B B −+−−==++取e1cTB −=，得ln B T c =即曲线1e cx A y B −=+是对g (x )的图像沿水平方向作了ln B T c =个单位的平移.26.解：324d π,π,.3d r V r A r v t === 2d d d 4πd d d d d d 8πd d d V V rr v t r t A A r r v t r t=⋅=⋅=⋅=⋅27.解：d d de e .d d d a a r r a a t t ϕϕϕωωϕ=⋅=⋅⋅=28.解：22cos 2cos sin sin 2x a y a a ϕϕϕϕ⎧=⎨==⎩d d d 22cos (sin )2sin 2,d d d d d d 2cos 22cos .d d d x x a a t t y y a a t t ϕϕϕωωϕϕϕϕωωϕϕ=⋅=⋅⋅−⋅=−=⋅=⋅=29.解：方程22169400x y +=两边同时对t 求导，得d d 32180d d x yx y t t⋅+⋅=由d d d d x y tt −=.得161832,9y x y x == 代入椭圆方程得：29x =，163,.3x y =±=±即所求点为1616,3,3,33⎛⎞⎛⎞−−⎜⎟⎜⎟⎝⎠⎝⎠.30.解：当水深为h时，横截面为212s h ==体积为22212V sh h ′====d d 2d d V hh t t=⋅当h =0.5m 时，31d 3m min d Vt −=⋅.故有d 320.5d ht =⋅，得d d h t =(m 3·min －1).31.解：设t 小时后，人与船相距s公里，则d d s s t ===且120d 8.16d t st ==≈(km ·h－1)32.解：d d d 236.d d d y y xx x t x t=⋅=⋅=当x =2时，d 6212d yt =×=(cm ·s －1).33.证明：如图，设在t 时刻，人影的长度为y m.则53456y y t=+化简得d 7280,40,40d yy t y t t ===(m ·min －1).即人影的长度的增长率为常值.34.解：y =－(x －2)2+4，故抛物线顶点为(2，4)当x =2时，0,2y y ′′′==− ，故23/22.(1)y k y ′′==′+35.解：sinh ,cosh .y x y x ′′′== 当x =0时，0,1y y ′′′== ，故23/21.(1)y k y ′′==′+36.解：cos ,sin y x y x ′′′==−.当π2x =时，0,1y y ′′′==− ，故23/21.(1)y k y ′′==′+37.解：2tan ,sec y x y x ′′′== 故223/223/2sec cos (1)(1tan )y x k x y x ′′===′++1sec R x k ==.38.解：22d d 3sin cos d tan d d 3cos sin d y y a t t t t x x a t tt ===−−，22224d d d(tan )1sec 1(tan )d d d d 3cos sin 3sin cos d y t t t x x x ta t t a t t t −−=−=⋅==−，故423/2123sin cos [1(tan )]3sin 2a t t k t a t==+−且当t =t 0时，23sin 2k a t =.39.解：cos ,sin y x y x ′′′==− .23/223/2(1cos )1sin ,sin (1cos )x x R k x R x +===+ 显然R 最小就是k 最大，225/22cos (1sin )(1cos )x x k x +′=+令0k ′=，得π2x =为唯一驻点.在π0,2⎛⎞⎜⎟⎝⎠内，0k ′>，在π,π2⎛⎞⎜⎟⎝⎠内，0k ′<.所以π2x =为k 的极大值点，从而也是最大值点，此时最小曲率半径为23/2π2(1cos )1sin x x R x=+==.40.解：由ln 0y x y =⎧⎨=⎩解得交点为(1，0).1112111,11.x x x x y x y x ====′==′′=−=−故曲率中心212(1,0)(1)312x y y x y y y y αβ=⎧′′⎡⎤+==−⎪⎢′′⎣⎦⎪⎨′⎡⎤+⎪==−+⎢⎥⎪′′⎣⎦⎩曲率半径为R =.故曲率圆方程为：22(3)(2)8x y −++=.41.解：0010,5000x x y y ==′′′==，23/2(1)5000y R y ′+==′′飞行员在飞机俯冲时受到的向心力22702005605000mv F R ⋅===(牛顿)故座椅对飞行员的反力560709.81246F =+×=(牛顿).42.解：(1)边际成本为：()(300 1.1) 1.1.C q q ′′=+=(2)利润函数为2()()() 3.90.003300() 3.90.006L q R q C q q q L q q=−=−−′=−令()0L q ′=,得650q =即为获得最大利润时的产量.(3)盈亏平衡时：R (q )=C (q )即 3.9q －0.003q 2－300=0q 2－1300q +100000=0解得q =1218(舍去)，q =82.43.解：(1)利润函数为32322()70.010.6130.010.66()0.03 1.26L q q q q q q q qL q q q =−+−=−+−′=−+−令()0L q ′=，得231206000q q −+=即2402000q q −+=得20q =−(舍去)2034.q =+≈此时，32(34)0.01340.63463496.56L =−×+×−×=(元)(2)设价格提高x 元，此时利润函数为2()(7)(342)(34)220379.44L x x x C x x =+−−=−++令()0L x′=,得5x=(5)121.5696.56L=>故应该提高价格，且应提高5元.44.(1)解：y′=a即为边际函数.弹性为：1Ey axa xEx ax b ax b =⋅⋅=++,增长率为：yaax b γ=+.(2)解：边际函数为：y′=ab e bx弹性为：1eebxbxEyab x bx Ex a=⋅⋅=,增长率为：eebxy bxabbaγ==.(3)解：边际函数为：y′=ax a－1.弹性为：11aaEyax x a Ex x−=⋅⋅=,增长率为：1.ay aax ax x γ−==45.解：因弹性的经济意义为：当自变量x变动1%，则其函数值将变动% EyEx⎛⎞⎜⎟⎝⎠.故当价格分别提高10%，20%时，需求量将分别提高0.8×10%=8%，0.8×20%=16%.46.解：人均收入年增长率=国民收入的年增长率－人口增长率=7.1%－1.2%=5.9%.。

高等数学线性代数习题答案第三章

第三章习题3-11．设s =12gt ２，求2d d t s t=．解：22221214()(2)2lim lim 22t t t g g ds s t s dt t t t →→=-⨯-==-- 21lim (2)22t g t g →=+= 2．设f (x )=1x，求f '(x 0) (x 0≠0)．解：1211()()()f x x x x--'''===00201()(0)f x x x '=-≠ 3．试求过点（3，8）且与曲线2y x =相切的直线方程。

解：设切点为00(,)x y ，则切线的斜率为002x x y x ='=，切线方程为0002()y y x xx -=-。

由已知直线过点(3,8),得 00082(3)y x x -=- (1)又点00(,)x y 在曲线2y x =上，故200y x = (2)由(1),(2)式可解得002,4x y ==或004,16x y ==，故所求直线方程为44(2)y x -=-或168(4)y x -=-。

也即440x y --=或8160x y --=。

4．下列各题中均假定f ′(x 0)存在，按照导数定义观察下列极限，指出A 表示什么：(1) 0limx ∆→00()()f x x f x x-∆-∆=A ;(2) f (x 0)=0, 0limx x →0()f x x x-＝A ； (3) 0limh →00()()f x h f x h h+--=A ．解：(1)0000000()()[()]()limlim ()x x f x x f x f x x f x f x x x→-→--+--'=-=--0()A f x '∴=- (2)00000()()()limlim ()x x x x f x f x f x f x x x x x →→-'=-=---0()A f x '∴=-(3)000()()limh f x h f x h h→+--00000[()()][()()]lim h f x h f x f x h f x h→+----=000000()()[()]()lim lim h h f x h f x f x h f x h h→-→+-+--=+-000()()2()f x f x f x '''=+= 02()A f x '∴=5．求下列函数的导数： (1) y (2) y ；(3) y 322x ．解：(1)12y x x ==11221()2y x x -''∴=== (2)23y x -=225133322()33y x x x ----''∴==-=-=(3)2152362y xx xx -==15661()6y x x-''∴===6．讨论函数y x =0点处的连续性和可导性．解：30lim 0(0)x x f →==000()(0)0lim lim 0x x x f x f x x →→→-===∞-∴函数y =0x =点处连续但不可导。

文科高等数学第三版教材答案

文科高等数学第三版教材答案第一章：函数及其图像1. 函数的概念及性质函数是一种特殊的关系，它将一个集合中的每个元素都映射到另一个集合中的唯一元素。

函数有定义域和值域，可以用图像来表示。

2. 函数的表示方法函数可以用函数表、公式、图像等方式表示。

其中，函数表是一种列出定义域与值域对应关系的方式，而函数公式则是通过数学表达式来表示。

3. 常见的函数类型常见的函数类型包括线性函数、幂函数、指数函数、对数函数、三角函数等。

不同类型的函数有不同的性质和特点。

4. 函数的性质函数有奇偶性、单调性、周期性等性质。

奇偶性指的是函数的对称性，单调性指的是函数在定义域内的增减性，周期性指的是函数具有重复性。

5. 函数的限制函数的限制是指函数在某些条件下的取值范围。

常见的限制包括定义域的限制、值域的限制以及其他约束条件的限制。

第二章：导数与微分1. 导数的定义与性质导数是函数在某一点处的变化率，表示函数曲线在该点处的切线斜率。

导数具有线性性、乘法性、和法则、差法则等性质。

2. 导数的计算方法导数的计算方法包括求导法则、链式法则、参数法则等。

其中，求导法则包括常规函数的求导公式，链式法则适用于复合函数的求导，参数法则适用于含有参数的函数的求导。

3. 函数的凹凸性与拐点函数的凹凸性与拐点与其导数的变化有关。

例如，函数的二阶导数大于零时，函数凹，二阶导数小于零时，函数凸，二阶导数为零时，可能存在拐点。

4. 微分的概念与应用微分表示函数在某一点处的变化量，是导数的微小改变量。

微分在近似计算、极值问题等方面有广泛的应用。

第三章：不定积分与定积分1. 不定积分的基本概念不定积分是确定函数的原函数的过程，表示函数在一个区间内的积分。

不定积分可以通过求导的逆运算来求得。

2. 基本积分法和基本积分公式基本积分法包括基本积分公式、分部积分法、换元积分法等。

基本积分公式是一些常见函数的不定积分公式，可以直接应用于计算。

3. 定积分的基本概念与性质定积分是确定函数在一个区间内的面积的过程，可以看作是在坐标轴下所夹图形的面积。

高数同济第五版答案第3章

习题3-1 1.验证罗尔定理对函数y =ln sin x 在区间]65,6[p p 上的正确性.解因为y =ln ln sin sin x 在区间]65,6[p p 上连续, 在)65,6(p p 内可导, 且)65()6(pp y y =, 所以由罗尔定理知, 至少存在一点)65,6(pp x Î, 使得y ¢(x )=cot x =0.由y ¢(x )=cot x =0得)65,6(2pp p Î.因此确有)65,6(2pp p x Î=, 使y ¢(x )=cot x =0.2.验证拉格朗日中值定理对函数y =4x 3-5x 2+x -2在区间[0, 1]上的正确性.解因为y =4x 3-5x 2+x -2在区间[0, 1]上连续, 在(0, 1)内可导, 由拉格朗日中值定理知, 至少存在一点x Î(0, 1), 使001)0()1()(=--=¢yy y x .由y ¢(x )=12x2-10x +1=0得)1,0(12135Î±=x .因此确有)1,0(12135Î±=x , 使01)0()1()(--=¢y y y x .3.对函数f (x )=sin x 及F (x )=x +cos x 在区间]2,0[p 上验证柯西中值定理的正确性.解因为f (x )=sin x 及F (x )=x +cos x 在区间]2,0[p 上连续, 在)2,0(p 可导, 且F ¢(x )=1-sin x 在)2,0(p 内不为0, 所以由柯西中值定理知至少存在一点)2,0(px Î, 使得)()()0()2()0()2(x x p p F f F F f f ¢¢=--.令)0()2()0()2()()(F F f f x F x f --=¢¢p p , 即22sin 1cos -=-p x x .化简得14)2(8sin 2-+-=p x . 易证114)2(802<-+-<p , 所以14)2(8sin 2-+-=p x 在)2,0(p 内有解, 即确实存在)2,0(px Î, 使得)()()0()2()0()2(x x p p F f F F f f ¢¢=--.4. 试证明对函数y =px 2+qx +r 应用拉格朗日中值定理时所求得的点x 总是位于区间的正中间.证明证明证明因为函数y =px 2+qx +r 在闭区间[a , b ]上连续, 在开区间(a , b )内可导, 由拉格朗日中值定理, 至少存在一点x Î(a , b ), 使得y (b )-y (a )=y ¢(x )(b -a ), 即 (pb 2+qb +r )-(pa 2+qa +r )=(2p x +q )(b -a ). 化间上式得化间上式得p (b -a )(b +a )=2p x (b -a ),故2b a +=x .5. 不用求出函数f (x )=(x -1)(x -2)(x -3)(x -4)的导数，说明方程f ¢(x )=0有几个实根, 并指出它们所在的区间.解由于f (x )在[1, 2]上连续, 在(1, 2)内可导, 且f (1)=f (2)=0, 所以由罗尔定理可知, 存在x 1Î(1, 2), 使f ¢(x 1)=0. 同理存在x 2Î(2, 3), 使f ¢(x 2)=0; 存在x 3Î(3, 4), 使f ¢(x 3)=0. 显然x 1、x 2、x 3都是方程f ¢(x )=0的根. 注意到方程f ¢(x )=0是三次方程, 它至多能有三个实根, 现已发现它的三个实根, 故它们也就是方程f ¢(x )=0的全部根. 6. 证明恒等式: 2arccos arcsi n p=+x x (-1£x £1).证明证明设f (x )= arcsin x +arccos x . 因为因为 01111)(22º---=¢xxx f ,所以f (x )ºC , 其中C 是一常数. 因此2arccos arcsin )0()(p=+==x x f x f , 即2arccos arcsin p=+x x .7. 若方程a 0x n+a 1x n -1+ × × × + a n -1x =0有一个正根x 0, 证明方程证明方程 a 0nx n -1+a 1(n -1)x n -2 + × × × +a n -1 =0 必有一个小于x 0的正根.证明证明设F (x )=a 0x n +a 1x n -1+ × × × + a n -1x , 由于F (x )在[0, x 0]上连续, 在(0, x 0)内可导, 且F (0)=F (x 0)=0, 根据罗尔定理, 至少存在一点x Î(0, x 0), 使F ¢(x )=0, 即方程即方程 a 0nx n -1+a 1(n -1)xn -2 + × × × +a n -1 =0 必有一个小于x 0的正根.8. 若函数f (x )在(a , b )内具有二阶导数, 且f (x 1)=f (x 2)=f (x 3), 其中a <x 1<x 2<x 3<b , 证明: 在(x 1, x 3)内至少有一点x , 使得f ¢¢(x )=0. 证明证明由于f (x )在[x 1, x 2]上连续, 在(x 1, x 2)内可导, 且f (x 1)=f (x 2), 根据罗尔定理, 至少存在一点x 1Î(x 1, x 2), 使f ¢(x 1)=0. 同理存在一点x 2Î(x 2, x 3), 使f ¢(x 2)=0. 又由于f ¢(x )在[x 1, x 2]上连续, 在(x 1, x 2)内可导, 且f ¢(x 1)=f ¢(x 2)=0, 根据罗尔定理, 至少存在一点x Î(x 1, x 2)Ì(x 1, x 3), 使f ¢¢(x )=0. 9. 设a >b >0, n >1, 证明:nb n -1(a -b )<a n-b n<na n -1(a -b ) .证明证明设f (x )=x n, 则f (x )在[b , a ]上连续, 在(b , a )内可导, 由拉格朗日中值定理, 存在x Î(b , a ), , 使 f (a )-f (b )=f ¢(x )(a -b ), 即a n -b n =n x n -1(a -b ).因为因为 nb n -1(a -b )<n x n -1(a -b )< na n -1(a -b ),所以所以 nb n -1(a -b )<a n -b n < na n -1(a -b ) . 10. 设a >b >0, 证明:bb a b a a b a -<<-ln . 证明证明设f (x )=ln x , 则f (x )在区间[b , a ]上连续, 在区间(b , a )内可导, 由拉格朗日中值定理, 存在x Î(b , a ), , 使f (a )-f (b )=f ¢(x )(a -b ), 即)(1ln ln b a b a -=-x.因为b <x <a , 所以所以)(1ln ln )(1b a b b a b a a -<-<-, 即bb a b a a b a -<<-ln . 11. 证明下列不等式:(1)|arctan a -arctan b |£|a -b |; (2)当x >1时, e x>e ×x . 证明证明 (1)设f (x )=arctan x , 则f (x )在[a , b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在x Î(a , b ), 使f (b )-f (a )=f ¢(x )(b -a ), 即)(11arctan arctan 2ab a b -+=-x,所以||||11|arctan arctan |2a b a b a b -£-+=-x, 即|arctan a -arctan b |£|a -b |. (2)设f (x )=e x, 则f (x )在区间[1, x ]上连续, 在区间(1, x )内可导, 由拉格朗日中值定理, 存在x Î(1, x ), 使 f (x )-f (1)=f ¢(x )(x -1), 即 e x -e =e x(x -1). 因为x >1, 所以所以e x -e =e x (x -1)>e (x -1), 即e x >e ×x .12. 证明方程x 5+x -1=0只有一个正根.证明证明设f (x )=x 5+x -1, 则f (x )是[0, +¥)内的连续函数.因为f (0)=-1, f (1)=1, f (0)f (1)<0, 所以函数在(0, 1)内至少有一个零点, 即x 5+x -1=0至少有一个正根.假如方程至少有两个正根, 则由罗尔定理, f ¢(x )存在零点, 但f ¢(x )=5x 4+1¹0, 矛盾. 这说明方程只能有一个正根.13. 设f (x )、g (x )在[a ,b ]上连续, 在(a , b )内可导, 证明在(a , b )内有一点x , 使 )()()()()()()()()(xx g a g f a f a b b g a g b f a f ¢¢-=.解设)()()()()(x g a g x f a f x =j , 则j (x )在[a ,b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在x Î(a ,b ), 使 j (b )-j (a )=j ¢(x )(b -a ),即 úûùêëé¢¢+¢¢-=-)()()()()(])([)(])([)()()()()()()()()(x x x x g a g f a f g a g f a f a b a g a g a f a f b g a g b f a f . 因此因此 )()()()()()()()()(xx g a g f a f a b b g a g b f a f ¢¢-=.14. 证明: 若函数.f (x )在(-¥, +¥)内满足关系式f ¢(x )=f (x ), 且f (0)=1则f (x )=e x. 证明证明令x ex f x )()(=j , 则在(-¥, +¥)内有内有0)()()()()(2222º-=-¢=¢xxx x eex f e x f ee xf e x f x j , 所以在(-¥, +¥)内j (x )为常数.因此j (x )=j (0)=1, 从而f (x )=e x. 15. 设函数y =f (x )在x =0的某邻域内具有n 阶导数, 且f (0)=f ¢(0)= × × × =f (n -1)(0)=0, 试用柯西中值定理证明: !)()()(n x fx x f n n q =(0<q <1).证明证明根据柯西中值定理 111)(0)0()()(-¢=--=n nn f x f x f xx f x x (x 1介于0与x 之间),2221111111)1()(0)0()()(-----¢¢=×-¢-¢=¢n n n n n n f n n f f n f x x x x x x (x 2介于0与x 1之间),3332222222)2)(1()(0)1()1()0()()1()(------¢¢¢=×---¢¢-¢¢=-¢¢n n n n n n n f n n n n f f n n f x x x x x x (x 3介于0与x 2之间), 依次下去可得依次下去可得 !)(02)1(2 )1()0()(2)1()()(1)1(1)1(11)1(n fn n n n ffn n fn n n n n n n n n x x xx x=××××--××××--=××××--------(x n 介于0与x n -1之间), 所以!)()()(n fxx f n n n x =由于x n 可以表示为x n =qx (0<q <1), 所以!)()()(n x fx x f n n q = (0<q <1).习题3-2 1. 用洛必达法则求下列极限:解 (1)111lim 111lim )1ln(lim 0=+=+=+®®®xxxx x x x . (2)2cos limsin lim=+=--®-®xeex ee xxx xxx .(3)a x a x a x ax a x cos 1cos lim sin sin lim ==--®®.(4)535sec 53cos 3lim 5tan 3sin lim2-==®®xx x xx x pp . (5)812csclim 41)2()2(2cot lim )2(sin ln lim 22222-=---=-×-=-®®®xx x x x x x x pppp p .(6)nm n m n m ax nnm m ax anm namx nxmx axa x -----®®===--1111lim lim .(7)177sec22sec lim 277tan 2tan lim 2722sec2tan 177sec 7tan 1lim 2tan ln 7tan ln lim220220=××==××××=++®®++®®+®+®x x xx x xx x xxx x x x .(8))sin (cos 23)3sin (3cos 2lim 31cos 3cos lim 3133sec sec lim 3tan tan lim 22222222x x x x x x x x x x x x x x -×-==×=®®®®pp p p3sin 3sin 3limcos 3cos lim22=---=-=®®xx xx x x pp.(9)122lim212lim1lim11)1(111limcot arc )11ln(lim 2222==+=++=+-×+=++¥®+¥®+¥®+¥®+¥®x x x x x xx xx x x xxxx.(10)xxxx x xx x x x x 220222cos 1lim cos1)1ln(cos lim cos sec )1ln(lim -=-+=-+®®®®(注: cos x ×ln(1+x 2)~x 2) 1sin lim )sin (cos 22lim 0==--=®®xx x x xx x .(11)2122sec1lim2tan lim 2cot lim2=×==®®®®x xx x x x xx .(12)+¥====+¥®+¥®®®1lim lim 1limlim 2101222ttttxx xx ete xee x (注: 当x ®0时, +¥®=21xt).(13)2121lim 11lim 1112lim 12121-=-=--=÷øöçèæ---®®®x x x x x x x x .(14)因为)1ln(lim )1(lim x a x x x x e xa +¥®¥®=+,而aa ax ax xxa xa xxa xa x x x x x x ==+=--×+=+=+¥®¥®¥®¥®¥®1limlim1)(11lim1)1ln(lim)1(ln(lim 22,所以所以ax a x x xx ee xa==++¥®¥®)1l n (lim )1(lim ..(15)因为xx x xxe xln sin 0sin 0lim lim +®+®=, ,而0cos sinlim cot csc 1lim csc ln lim ln sin lim 2=-=×-==+®+®+®+®xx xxx x x xx x x x x x ,所以所以1lim lim 0ln sin 0sin 0===+®+®ee x xx x xx .(16)因为xx xx exln tan tan 0)1(lim -+®=, ,而sinlim csc1lim cot ln lim ln tan lim 22000=-=-==+®+®+®+®xxxx x x x x x x x x ,所以所以1lim )1(lim 0ln tan 0tan 0===-+®+®e exx x x xx .2. 验证极限xxx x sin lim +¥®存在, 但不能用洛必达法则得出.解1)s i n 1(lim sin lim =+=+¥®¥®xx xxx xx , 极限xxx x si n lim +¥®是存在的.但)cos 1(lim 1cos 1lim )()sin (lim x xx x x xxx +=+=¢¢+¥®¥®¥®不存在, 不能用洛必达法则. 3. 验证极限xx x x sin 1sin lim2®存在, 但不能用洛必达法则得出. 解011sinsin limsin 1sinlim2=×=×=®®xx xx x x x x x , 极限xxx x sin 1sinlim2®是存在的.但xxxx x xx x x cos 1cos1sin2lim )(sin )1sin(lim 02-=¢¢®®®不存在, 不能用洛必达法则.4. 讨论函数ïïîïïíì£>+=-0 0 ])1([)(2111x e x ex x f x x在点x =0处的连续性. 解21)0(-=ef , )0(lim )(lim 212100f e ex f x x ===---®-®, ,因为因为]1)1ln(1[101100lim ])1([lim )(lim -+-®-®+®=+=x xx x xxx x e ex x f , ,而21)1(21lim 2111lim )1ln(lim ]1)1ln(1[1lim 00200-=+-=-+=-+=-++®+®+®+®x x x xx x x x x x x x x ,所以所以)0(lim ])1([lim )(lim 21]1)1ln(1[101100f e e ex x f x xx x xxx x ===+=--+-®-®+®.因此f (x )在点x =0处连续.习题3-3 1. 按(x -4)的幂展开多项式x 4-5x 3+x 2-3x +4. 解因为f (4)=-56, f ¢(4)=(4x 3-15x 2+2x -3)|x =4=21,f ¢¢(4)=(12x 2-30x +2)|x =4=74, f ¢¢¢(4)=(24x -30)|x =4=66,f (4)(4)=24,所以按(x -4)的幂展开的多项式为的幂展开的多项式为435234+-+-x x x x 4)4(32)4(!4)4()4(!3)4()4(!2)4()4)(4()4(-+-¢¢¢+-¢¢+-¢+=x fx f x f x f f=-56+21(x -4)+37(x -4)2+11(x -4)3+(x -4)4. 2. 应用麦克劳林公式, 按x 幂展开函数f (x )=(x 2-3x +1)3. 解因为因为 f ¢(x )=3(x 2-3x +1)2(2x -3),f ¢¢(x )=6(x 2-3x +1)(2x -3)2+6(x 2-3x +1)2=30(x 2-3x +1)(x 2-3x +2),f ¢¢¢(x )=30(2x -3)(x 2-3x +2)+30(x 2-3x +1)(2x -3)=30(2x -3)(2x 2-6x +3), f (4)(x )=60(2x 2-6x +3)+30(2x -3)(4x -6)=360(x 2-3x +2),f (5)(x )=360(2x -3), f (6)(x )=720;f (0)=1, f ¢(0)=-9, f ¢¢(0)=60, f ¢¢¢(0)=-270, f (4)(0)=720, f (5)(0)=-1080, f (6)(0)=720, 所以所以6)6(5)5(4)4(32!6)0(!5)0(!4)0(!3)0(!2)0()0()0()(xfx fx fx f x f x f f x f +++¢¢¢+¢¢+¢+==1-9x +30x 3-45x 3+30x 4-9x 5+x 6.3. 求函数x x f =)(按(x -4)的幂展开的带有拉格朗日型余项的3阶泰勒公式. 解因为24)4(==f 4121)4(421==¢=-x xf , 32141)4(423-=-=¢¢=-x xf ,328383)4(425×==¢¢¢=-x xf , 27)4(1615)(--=xx f,所以所以 4)4(32)4(!4)()4(!3)4()4(!2)4()4)(4()4(-+-¢¢¢+-¢¢+-¢+=x fx f x f x f f x x4732)4()]4(4[1615!41)4(5121)4(641)4(412--+×--+---+=x x x x x q(0<q <1).4. 求函数f (x )=ln x 按(x -2)的幂展开的带有佩亚诺型余项的n 阶泰勒公式. 解因为因为f ¢(x )=x -1, f ¢¢(x )=(-1)x -2, f ¢¢¢(x )=(-1)(-2)x -3, × × × , nn nnxn x n x f )!1()1()1( )2)(1()(1)(--=+-×××--=--;kk kk f 2)!1()1()2(1)(--=-(k =1, 2, × × ×, n +1) 所以所以])2[()2(!)2( )2(!3)2()2(!2)2()2)(2()2(ln )(32nn n x o x n fx f x f x f f x -+-+×××+-¢¢¢+-¢¢+-¢+=])2[()2(2)1( )2(231)2(221)2(212ln 13322nnnn x o x n x x x -+-×-+×××--×+-×--+=-.5. 求函数xxf 1)(=按(x +1)的幂展开的带有拉格朗日型余项的n 阶泰勒公式.解因为因为f (x )=x -1, f ¢(x )=(-1)x -2, f ¢¢(x )=(-1)(-2)x -3, × × × ,1)1()(!)1()()2)(1()(++--=-×××--=n nn n xn x n x f;!)1(!)1()1(1)(k k fk kk -=--=-+(k =1, 2, × × ×, n ),所以所以 )1(!3)1()1(!2)1()1)(1()1(132×××++-¢¢¢++-¢¢++-¢+-=x f x f x f f x1)1()()1()!1()()1(!)1(++++++-+n n nn x n fx n fx12132)1()]1(1[)1(])1()1()1()1(1[++++++--+++×××+++++++-=n n n n x x x x x x q (0<q <1). 6. 求函数f (x )=tan x 的带有拉格朗日型余项的3阶麦克劳林公式. 解因为因为f ¢(x )=sec 2x , f ¢¢(x )=2sec x ×sec x ×tan x =2sec 2x ×tan x , f ¢¢¢(x )=4sec x ×sec x ×tan 2x +2sec 4x =4sec 2x ×tan 2x +2sec 4x , f (4)(x )=8sec 2x ×tan 3x +8sec 4x ×tan x +8sec 4x ×tan x xx x 52cos)2(sinsin 8+=;f (0)=0, f ¢(0)=1, f ¢¢(0)=0, f ¢¢¢(0)=2, 所以所以 4523)(c o s 3]2)()[s i n s i n (31t a n x x x x x x x q q q +++=(0<q <1).7. 求函数f (x )=xe x的带有佩亚诺型余项的n 阶麦克劳林公式. 解因为因为 f ¢(x )=e x +x e x , f ¢¢(x )=e x +e x +x e x =2e x +x e x, f ¢¢¢(x )=2e x +e x +x e x =3e x +x e x , × × ×,f (n )(x )=ne x +xe x ; f (k )(0)=k (k =1, 2, × × ×, n ),所以所以 )(!)0( !3)0(!2)0()0()0()(32nn n xx o x n fx f x f x f f xe ++××××+¢¢¢+¢¢+¢+=)()!1(1!2132n n x o x n x x x +-×××+++=.8. 验证当210££x 时, 按公式62132xx x e x +++»计算e x的近似值时, 所产生的误差小于0.01, 并求e 的近似值, 使误差小于0.01.解因为公式62132xxx e x+++»右端为e x的三阶麦克劳林公式, 其余项为其余项为43!4)(xex R x=,所以当210££x 时，按公式62132xxx e x+++»计算e x的误差01.00045.0)21(!43|!4||)(|42143<»£=x ex R x.645.1)21(61)21(212113221»×+×++»=e e . 9. 应用三阶泰勒公式求下列各数的近似值, 并估计误差: (1)330;(2)sin 18°. 解 (1)设3)(x x f =, 则f (x )在x 0=27点展开成三阶泰勒公式为点展开成三阶泰勒公式为2353233)27)(2792(!21)27(273127)(-×-×+-×+==--x x x x f4311338)27)(8180(!41)27)(272710(!31--×+-××+--x x x(x 介于27与x 之间).于是于是 33823532333)272710(!313)2792(!21327312730×××+××-×+××+»---10724.3)3531311(31063»+-+»,其误差为其误差为5114311431131088.13!4803278180!41|3)8180(!41||)30(|---´=×=×××<×-×=x R .(2) 已知已知 43!4s i n!31s i n x x x x x +-=(x 介于0与x 之间),所以所以 sin 18°3090.0)10(!311010sin 3»-»=p p p ,其误差为44431003.2)10(!46sin|)10(!4sin ||)10(|-´=<=p pp x pR .10. 利用泰勒公式求下列极限: (1))23(lim 434323x x xx x --++¥®;(2))]1ln([cos lim 222x x x ex xx -+--®;(3)222sin )(cos 1211lim 2xe x xx xx -+-+®.解 (1)ttt xx xx x x x t x x 43434343232131lim 12131lim )23(lim --+=--+=--++®+¥®+¥®.因为)(1313to t t ++=+,)(211214t o t t +-=-, 所以所以23])(23[lim )](211[)](1[lim )23(lim 00434323=+=+--++=--++®+®+¥®t t o tt o t t o t x x x x t t x .(2)])1ln(1[)](41!21211[)](!41!211[lim )]1ln([cos lim 13442442222x x xx x x x o x x x o x x x x x ex -++×+--++-=-+-®-®010)1l n (1)(121lim 1134=+=-++-=-®ex xx o x xx .(3)244244244222220))](!211())(!41!211[()](!43!211[211lim sin )(cos 1211lim 2xx o x x x o x x x o x x x xe x xx x xx +++-++-+-+-+=-+-+®®12123!43)(241123)(!43lim )(241123)(!43lim 2424404264440-=-=+--+=×+--+=®®xx o x x x o x o x x x x o x x x .习题3-4 1. 判定函数f (x )=arctan x -x 单调性. 解因为011111)(22£+-=-+=¢xxx f , 且仅当x =0时等号成立, 所以f (x )在(-¥, +¥)内单调减少.2. 判定函数f (x )=x +cos x (0£x £2p )的单调性. 解因为f ¢(x )=1-sin x ³0, 所以f (x )=x +cos x 在[0, 2p ]上单调增加.3. 确定下列函数的单调区间: (1) y =2x 3-6x 2-18x -7; (2)x x y 82+=(x >0); (3)xx x y 6941023+-=;(4))1ln(2x x y ++=; (5) y =(x -1)(x +1)3; (6))0.())(2(32>--=a x a a x y ; (7) y =x n e -x(n >0, x ³0);(8)y =x +|sin 2x |. 解 (1) y ¢=6x 2-12x -18=6(x -3)(x +1)=0, 令y ¢=0得驻点x 1=-1, x 2=3. 列表得列表得可见函数在(-¥, -1]和[3, +¥)内单调增加, 在[-1, 3]内单调减少. (2) 0)2)(2(28222=+-=-=¢xx x xy ,令y ¢=0得驻点x 1=2, x 2=-2(舍去).因为当x >2时, y >0; 当0<x <2时, y ¢<0, 所以函数在(0, 2]内单调减少, 在[2, +¥)内单调x (-¥, -1) -1 (-1, 3) 3 (3, +¥) y ¢ + 0 - 0 +y ↗ ↘ ↗增加. (3)223)694()1)(12(60x x x x x y +----=¢, 令y ¢=0得驻点211=x ,x 2=1, 不可导点为x =0. 列表得列表得x (-¥, 0) 0 (0, 21) 21 (21, 1) 1 (1, +¥) y ¢- 不存在不存在-0 + 0 - y↘↘０↗↘可见函数在(-¥, 0), ]21,0(, [1, +¥)内单调减少, 在]1,21[上单调增加. (4)因为011)1221(11222>+=++++=¢xxx xx y , 所以函数在(-¥, +¥)内单调增加.(5) y ¢=(x +1)3+3(x -1)(x +1)22)1)(21(4+-=x x . 因为当21<x 时, y ¢<0; 当21>x 时, y ¢>0, 所以函数在]21 ,(-¥内单调减少, 在) ,21[¥+内单调增加. (6)32)()2(3)32(x a a x a x y ----=¢, 驻点为321a x =, 不可导点为22a x =, x 3=a .列表得列表得x )2,(a -¥2a)32 ,2(a a32a ),32(a aa (a , +¥) y ¢ + 不存在不存在 + 0 - 不存在不存在 +y↗↗↘↗可见函数在)2 ,(a -¥, ]32 ,2(aa , (a , +¥)内单调增加, 在) ,32[a a 内单调减少.(7)y ¢=e -x x n -1(n -x ), 驻点为x =n . 因为当0<x <n 时,y ¢>0; 当x >n 时, y ¢<0, 所以函数在[0, n ]上单调增加, 在[n , +¥)内单调减少.(8)ïïîïïíì+<<+-+££+=p p p p p p p k x k x x k x k x x y 2 2sin 2 2sin (k =0, ±1, ±2, × × ×),ïïîïïíì+<<+-+££+=¢pp p p p p p k x k x k x k x y 2 2cos 212 2cos 21(k =0, ±1, ±2, × × ×).y ¢是以p 为周期的函数, 在[0, p ]内令y ¢=0, 得驻点21p =x , 652p =x , 不可导点为23p =x .列表得列表得x )3,0(p3p)2,3(p p2p)65 ,2(p p65p ) ,65(p py ¢ + 0 - 不存在不存在 + 0 - y↗↘ ↗↘根据函数在[0, p ]上的单调性及y ¢在(-¥, +¥)的周期性可知函数在]32,2[ppp+k k 上单调增加,在]22 ,32[pp p p++k k 上单调减少(k =0, ±1, ±2, × × ×). 4. 证明下列不等式: (1)当x >0时, xx +>+1211;(2)当x >0时, 221)1ln(1x x x x +>+++; (3)当20p<<x 时, sin x +tan x >2x ; (4)当20p<<x 时, 331tan x x x +>;(5)当x >4时, 2x>x 2; 证明证明 (1)设xx x f +-+=1211)(, 则f (x )在[0, +¥)内是连续的. 因为因为x x f +-=¢12121)(01211>+-+=x x ,所以f (x )在(0, +¥)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01211>+-+x x ,也就是也就是 x x +>+1211.(2)设221)1ln(1)(x x x x x f +-+++=, 则f (x )在[0, +¥)内是连续的. 因为因为0)1l n (1)11(11)1l n ()(22222>++=+-++×++×+++=¢x x xx xx xx x x x x f , 所以f (x )在(0, +¥)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即01)1l n (122>+-+++x x xx , 也就是也就是 221)1l n (1x x xx +>+++. (3)设f (x )=sin x +tan x -2x , 则f (x )在)2 ,0[p内连续,f ¢(x )=cos x +sec 2x -2xx x x 22cos ]cos )1)[(cos 1(cos ---=.因为在)2,0(p 内cos x -1<0, cos 2x -1<0,-cos x <0, 所以f ¢(x )>0, 从而f (x )在)2,0(p 内单调增加, 因此当20p<<x 时,f (x )>f (0)=0, 即 sin x +tan x -2x >0, 也就是也就是 sin x +tan x >2x . (4)设331tan )(x x x x f --=, 则f (x )在)2 ,0[p内连续,))(t a n (t a nt a n 1s e c )(2222x x x x x x x x x f +-=-=--=¢. 因为当20p<<x 时, tan x >x , tan x +x >0, 所以f ¢(x )在)2,0(p 内单调增加, 因此当20p<<x 时,f (x )>f (0)=0, 即 031t a n 3>--x x x ,也就是也就是 231tan x x x +>.(5)设f (x )=x ln2-2ln x , 则f (x )在[4, +¥)内连续, 因为因为 0422ln 224ln 22ln )(=->-=-=¢e x x x f ,所以当x >4时, f ¢(x )>0, 即f (x )内单调增加.因此当x >4时, f (x )>f (4)=0, 即x ln2-2ln x >0, 也就是也就是2x>x 2. 5. 讨论方程ln x =ax (其中a >0)有几个实根？有几个实根？解设f (x )=ln x -ax . 则f (x )在(0, +¥)内连续, xax a xx f -=-=¢11)(, 驻点为ax 1=.因为当a x 10<<时, f ¢(x )>0, 所以f (x )在)1,0(a内单调增加; 当ax 1>时, f ¢(x )<0, 所以f (x )在) ,1(¥+a内单调减少. 又因为当x ®0及x ®+¥时, f (x )®-¥, 所以如果011ln )1(>-=aa f ,即ea 1<, 则方程有且仅有两个实根; 如果011ln )1(<-=aa f , 即ea 1>, 则方程没有实根. 如果11ln )1(=-=aa f , 即ea1=, 则方程仅有一个实根.6. 单调函数的导函数是否必为单调函数？研究下面这个例子: f (x )=x +sin x .解单调函数的导函数不一定为单调函数.例如f (x )=x +sin x 在(-¥,+¥)内是单调增加的, 但其导数不是单调函数. 事实上, f ¢(x )=1+cos x ³0, 这就明f (x )在(-¥, +¥)内是单调增加的. f ¢¢(x )=-sin x 在(-¥, +¥)内不保持确定的符号, 故f ¢(x )在(-¥, +¥)内不是单调的.7. 判定下列曲线的凹凸性: (1) y =4x -x 2; (2) y =sh x ;(3)xy 11+= (x >0);(4) y =x arctan x x ; 解 (1)y ¢=4-2x ,y ¢¢=-2, 因为y ¢¢<0, 所以曲线在(-¥, +¥)内是凸的.(2)y ¢=ch x , y ¢¢=sh x . 令y ¢¢=0, 得x =0. 因为当x <0时, y ¢¢=sh x <0; 当x >0时, y ¢¢=sh x >0, 所以曲线在(-¥, 0]内是凸的, 在[0, +¥)内是凹的. (3)21xy -=¢, 32xy =¢¢.因为当x >0时, y ¢¢>0, 所以曲线在(0, +¥)内是凹的. (4)21arctan xx x y ++=¢,22)1(2x y +=¢¢.因为在(-¥, +¥)内, y ¢¢>0, 所以曲线y =x arctg x 在(-¥, +¥)内是凹的.8. 求下列函数图形的拐点及凹或凸的区间: (1).y =x 3-5x 2+3x +5 ;(2) y =xe -x ; (3) y =(x +1)4+e x ;(4) y =ln(x 2+1); (5) y =e arctan x ;(6) y =x 4(12ln x -7), 解 (1)y ¢=3x 2-10x +3,y ¢¢=6x -10. 令y ¢¢=0, 得35=x .因为当35<x 时, y ¢¢<0; 当35>x 时, y ¢¢>0, 所以曲线在]35 ,(-¥内是是凸的, 在),35[¥+内是凹的, 拐点为)2720,35(.(2)y ¢=e -x-xe -x, y ¢¢=-e -x-e -x+x e -x=e -x(x -2). 令y ¢¢=0, 得x =2. 因为当x <2时, y ¢¢<0; 当x >2时, y ¢¢>0, 所以曲线在(-¥, 2]内是凸的, 在[2, +¥)内是凹的,拐点为(2, 2e -2). (3)y ¢=4(x +1)3+e x , y ¢¢=12(x +1)2+e x . 因为在(-¥, +¥)内, y ¢¢>0, 所以曲线y =(x +1)4+e x的在(-¥, +¥)内是凹的, 无拐点. (4)122+=¢x xy , 22222)1()1)(1(2)1(22)1(2++--=+×-+=¢¢x x x x xx x y . 令y ¢¢=0, 得x 1=-1,x 2=1. 列表得列表得可见曲线在(-¥, -1]和[1, +¥)内是凸的, 在[-1, 1]内是凹的, 拐点为(-1, ln2)和(1, ln2). (5)2arctan 11xe y x+×=¢,)21(12arctan x xey x-+=¢¢. 令y ¢¢=0得, 21=x .因为当21<x 时, y ¢¢>0; 当21>x 时, y ¢¢<0, 所以曲线y =earctg x在]21,(-¥内是凹的, 在) ,21[¥+内是凸的, 拐点是),21(21arctan e .(6) y ¢=4x 3(12ln x -7)+12x 3, y ¢¢=144x 2×ln x . 令y ¢¢=0, 得x =1. 因为当0<x <1时, y ¢¢<0; 当x >1时, y ¢¢>0, 所以曲线在(0, 1]内是凸的, 在[1, +¥)内是凹的, 拐点为(1, -7).9. 利用函数图形的凹凸性, 证明下列不等式:(1) nnny x y x )2()(21+>+ (x >0,y >0, x ¹y , n >1); x (-¥, -1) -1 (-1, 1) 1 (1, +¥) y ¢¢-0 +0 -y Ç ln2 拐点拐点È ln2 拐点拐点Ç(2))(22y x ee e y x yx ¹>++;(3)2ln)(ln ln y x y x y y x x ++>+ (x >0,y >0, x ¹y ). 证明证明 (1)设f (t )=t n, 则f ¢(t )=nt n -1, f ¢¢(t )=n (n -1)t n -2. 因为当t >0时, f ¢¢(t )>0, 所以曲线f (t )=tn 在区间(0, +¥)内是凹的. 由定义, 对任意的x >0, y >0, x ¹y 有 )2()]()([21y x f y f x f +>+,即 nnn y x y x )2()(21+>+.(2)设f (t )=e t, 则f ¢(t )=e t, f ¢¢(t )=e t. 因为f ¢¢(t )>0, 所以曲线f (t )=e t在(-¥, +¥)内是凹的.由定义, 对任意的x , y Î(-¥, +¥),x ¹y 有 )2()]()([21yx f y f x f +>+, 即)(22y x ee e y x yx¹>++.(3)设f (t )=t ln t , 则 f ¢(t )=ln t +1, t t f 1)(=¢¢. 因为当t >0时, f ¢¢(t )>0, 所以函数f (t )=t ln t 的图形在(0, +¥)内是凹的. 由定义, 对任意的x >0,y >0, x ¹y 有 )2()]()([21y x f y f x f +>+, 即 2ln )(ln ln y x y x y y x x ++>+.10. 试证明曲线112+-=x x y 有三个拐点位于同一直线上.证明证明 222)1(12+++-=¢x x x y , 323223)1()]32()][32()[1(2)1(2662++---+=++--=¢¢x x x x x x x x y .令y ¢¢=0, 得x 1=-1, 322-=x , 323+=x . 例表得例表得x (-¥. -1) -1 )32 ,1(-- 32-)32 ,32(+- 32+),32(¥++y ¢-0 +0 - 0 +。

同济大学版高等数学课后习题答案第3章

习题3-11. 验证罗尔定理对函数y =ln sin x 在区间]65 ,6[ππ上的正确性.解因为y =ln sin x 在区间]65 ,6[ππ上连续, 在)65 ,6(ππ内可导, 且)65()6(ππy y =,所以由罗尔定理知, 至少存在一点)65 ,6(ππξ∈, 使得y '(ξ)=cot ξ=0.由y '(x )=cot x =0得)65 ,6(2πππ∈.因此确有)65 ,6(2πππξ∈=, 使y '(ξ)=cot ξ=0.2. 验证拉格朗日中值定理对函数y =4x 3-5x 2+x -2在区间[0, 1]上的正确性. 解因为y =4x 3-5x 2+x -2在区间[0, 1]上连续, 在(0, 1)内可导, 由拉格朗日中值定理知, 至少存在一点ξ∈(0, 1), 使001)0()1()(=--='y y y ξ. 由y '(x )=12x 2-10x +1=0得)1 ,0(12135∈±=x .因此确有)1 ,0(12135∈±=ξ, 使01)0()1()(--='y y y ξ.3. 对函数f (x )=sin x 及F (x )=x +cos x 在区间]2 ,0[π上验证柯西中值定理的正确性.解因为f (x )=sin x 及F (x )=x +cos x 在区间]2 ,0[π上连续, 在)2 ,0(π可导, 且F '(x )=1-sin x 在)2 ,0(π内不为0, 所以由柯西中值定理知至少存在一点)2 ,0(πξ∈, 使得)()()0()2()0()2(ξξππF f F F f f ''=--. 令)0()2()0()2()()(F F f f x F x f --=''ππ, 即22sin 1cos -=-πx x . 化简得14)2(8si n 2-+-=πx . 易证114)2(802<-+-<π, 所以14)2(8si n 2-+-=πx 在)2 ,0(π内有解, 即确实存在)2 ,0(πξ∈, 使得 )()()0()2()0()2(ξξππF f F F f f ''=--. 4. 试证明对函数y =px 2+qx +r 应用拉格朗日中值定理时所求得的点ξ总是位于区间的正中间.证明因为函数y =px 2+qx +r 在闭区间[a , b ]上连续, 在开区间(a , b )内可导, 由拉格朗日中值定理, 至少存在一点ξ∈(a , b ), 使得y (b )-y (a )=y '(ξ)(b -a ), 即 (pb 2+qb +r )-(pa 2+qa +r )=(2p ξ+q )(b -a ). 化间上式得p (b -a )(b +a )=2p ξ (b -a ), 故2b a +=ξ.5. 不用求出函数f (x )=(x -1)(x -2)(x -3)(x -4)的导数，说明方程f '(x )=0有几个实根, 并指出它们所在的区间.解由于f (x )在[1, 2]上连续, 在(1, 2)内可导, 且f (1)=f (2)=0, 所以由罗尔定理可知, 存在ξ1∈(1, 2), 使f '(ξ1)=0. 同理存在ξ2∈(2, 3), 使f '(ξ2)=0; 存在ξ3∈(3, 4), 使f '(ξ3)=0. 显然ξ1、ξ2、ξ 3都是方程f '(x )=0的根. 注意到方程f '(x )=0是三次方程, 它至多能有三个实根, 现已发现它的三个实根, 故它们也就是方程f '(x )=0的全部根.6. 证明恒等式: 2arccos arcsin π=+x x (-1≤x ≤1).证明设f (x )= arcsin x +arccos x . 因为 01111)(22≡---='x x x f , 所以f (x )≡C , 其中C 是一常数.因此2arccos arcsin )0()(π=+==x x f x f , 即2arccos arcsin π=+x x .7. 若方程a 0x n +a 1x n -1+ ⋅ ⋅ ⋅ + a n -1x =0有一个正根x 0, 证明方程 a 0nx n -1+a 1(n -1)x n -2 + ⋅ ⋅ ⋅ +a n -1 =0必有一个小于x 0的正根.证明设F (x )=a 0x n +a 1x n -1+ ⋅ ⋅ ⋅ + a n -1x , 由于F (x )在[0, x 0]上连续, 在(0, x 0)内可导, 且F (0)=F (x 0)=0, 根据罗尔定理, 至少存在一点ξ∈(0, x 0), 使F '(ξ)=0, 即方程 a 0nx n -1+a 1(n -1)x n -2 + ⋅ ⋅ ⋅ +a n -1 =0 必有一个小于x 0的正根.8. 若函数f (x )在(a , b )内具有二阶导数, 且f (x 1)=f (x 2)=f (x 3), 其中a <x 1<x 2<x 3<b , 证明:在(x 1, x 3)内至少有一点ξ, 使得f ''(ξ)=0.证明由于f (x )在[x 1, x 2]上连续, 在(x 1, x 2)内可导, 且f (x 1)=f (x 2), 根据罗尔定理, 至少存在一点ξ1∈(x 1, x 2), 使f '(ξ1)=0. 同理存在一点ξ2∈(x 2, x 3), 使f '(ξ2)=0. 又由于f '(x )在[ξ1, ξ2]上连续, 在(ξ1, ξ2)内可导, 且f '(ξ1)=f '(ξ2)=0, 根据罗尔定理, 至少存在一点ξ ∈(ξ1, ξ2)⊂(x 1, x 3), 使f ''(ξ )=0. 9. 设a >b >0, n >1, 证明: nb n -1(a -b )<a n -b n <na n -1(a -b ) .证明设f (x )=x n , 则f (x )在[b , a ]上连续, 在(b , a )内可导, 由拉格朗日中值定理, 存在ξ∈(b , a ), 使f (a )-f (b )=f '(ξ)(a -b ), 即a n -b n =n ξ n -1(a -b ). 因为 nb n -1(a -b )<n ξ n -1(a -b )< na n -1(a -b ), 所以 nb n -1(a -b )<a n -b n < na n -1(a -b ) . 10. 设a >b >0, 证明: bb a b a a b a -<<-ln .证明设f (x )=ln x , 则f (x )在区间[b , a ]上连续, 在区间(b , a )内可导, 由拉格朗日中值定理, 存在ξ∈(b , a ), 使f (a )-f (b )=f '(ξ)(a -b ), 即)(1ln ln b a b a -=-ξ.因为b <ξ<a , 所以)(1ln ln )(1b a b b a b a a -<-<-, 即b b a b a a b a -<<-ln .11. 证明下列不等式: (1)|arctan a -arctan b |≤|a -b |; (2)当x >1时, e x >e ⋅x .证明 (1)设f (x )=arctan x , 则f (x )在[a , b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在ξ∈(a , b ), 使f (b )-f (a )=f '(ξ)(b -a ), 即)(11arctan arctan 2a b a b -+=-ξ,所以||||11|arctan arctan |2a b a b a b -≤-+=-ξ, 即|arctan a -arctan b |≤|a -b |.(2)设f (x )=e x , 则f (x )在区间[1, x ]上连续, 在区间(1, x )内可导, 由拉格朗日中值定理, 存在ξ∈(1, x ), 使f (x )-f (1)=f '(ξ)(x -1), 即 e x -e =e ξ (x -1). 因为ξ >1, 所以e x -e =e ξ (x -1)>e (x -1), 即e x >e ⋅x . 12. 证明方程x 5+x -1=0只有一个正根.证明设f (x )=x 5+x -1, 则f (x )是[0, +∞)内的连续函数.因为f (0)=-1, f (1)=1, f (0)f (1)<0, 所以函数在(0, 1)内至少有一个零点, 即x 5+x -1=0至少有一个正根.假如方程至少有两个正根, 则由罗尔定理, f '(x )存在零点, 但f '(x )=5x 4+1≠0, 矛盾. 这说明方程只能有一个正根.13. 设f (x )、g (x )在[a , b ]上连续, 在(a , b )内可导, 证明在(a , b )内有一点ξ, 使)()()()()()()()()(ξξg a g f a f a b b g a g b f a f ''-=.解设)()()()()(x g a g x f a f x =ϕ, 则ϕ(x )在[a , b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在ξ∈(a , b ), 使 ϕ(b )-ϕ(a )=ϕ'(ξ)(b -a ), 即⎥⎦⎤⎢⎣⎡''+''-=-)()()()()(])([)(])([)()()()()()()()()(ξξξξg a g f a f g a g f a f a b a g a g a f a f b g a g b f a f . 因此)()()()()()()()()(ξξg a g f a f a b b g a g b f a f ''-=.14. 证明: 若函数.f (x )在(-∞, +∞)内满足关系式f '(x )=f (x ), 且f (0)=1则f (x )=e x .证明令x ex f x )()(=ϕ, 则在(-∞, +∞)内有 0)()()()()(2222≡-=-'='xx x x ee xf e x f e e x f e x f x ϕ, 所以在(-∞, +∞)内ϕ(x )为常数.因此ϕ(x )=ϕ(0)=1, 从而f (x )=e x .15. 设函数y =f (x )在x =0的某邻域内具有n 阶导数, 且f (0)=f '(0)= ⋅ ⋅ ⋅ =f(n -1)(0)=0, 试用柯西中值定理证明:!)()()(n x f xx f n n θ= (0<θ<1).证明根据柯西中值定理111)(0)0()()(-'=--=n n n f x f x f x x f ξξ(ξ1介于0与x 之间),2221111111)1()(0)0()()(-----''=⋅-'-'='n n n n n n f n n f f n f ξξξξξξ(ξ2介于0与ξ1之间), 3332222222)2)(1()(0)1()1()0()()1()(------'''=⋅---''-''=-''n n n n n n n f n n n n f f n n f ξξξξξξ(ξ3介于0与ξ2之间),依次下去可得!)(02 )1(2 )1()0()(2 )1()()(1)1(1)1(11)1(n f n n n n f f n n f n n n n n n n n n ξξξξξ=⋅⋅⋅⋅--⋅⋅⋅⋅--=⋅⋅⋅⋅--------(ξn 介于0与ξn -1之间),所以!)()()(n f xx f n n n ξ=.由于ξn 可以表示为ξn =θ x (0<θ<1), 所以!)()()(n x f xx f n n θ= (0<θ<1).习题3-21. 用洛必达法则求下列极限:(1)xx x )1ln(lim 0+→;(2)xe e xx x sin lim 0-→-;(3)ax a x a x --→sin sin lim ;(4)xx x 5tan 3sin lim π→;(5)22)2(sin ln lim x x x -→ππ;(6)n n m m a x ax ax --→lim ;(7)xx x 2tan ln 7tan ln lim 0+→;(8)xx x 3tan tan lim 2π→;(9)x arc x x cot )11ln(lim++∞→; (10)xx x x cos sec )1ln(lim 20-+→;(11)x x x 2cot lim 0→;(12)2120lim x x ex →;(13))1112(lim 21---→x x x ;(14)x x x a )1(lim +∞→;(15)x x x sin 0lim +→;(16)x x xtan 0)1(lim +→. 解 (1)111lim 111lim )1ln(lim000=+=+=+→→→x x xx x x x . (2)2cos lim sin lim00=+=--→-→xe e x e e x x x x x x .(3)a x ax a x a x a x cos 1cos lim sin sin lim ==--→→.(4)535sec 53cos3lim 5tan 3sin lim 2-==→→x x x x x x ππ. (5)812csc lim 41)2()2(2cot lim )2(sin ln lim 22222-=---=-⋅-=-→→→x x x x x x x x πππππ. (6)n m n m n m a x n n m m a x a n m namx nx mx a x a x -----→→===--1111lim lim .(7)22sec 2tan 177sec 7tan 1lim 2tan ln 7tan ln lim 2200⋅⋅⋅⋅=+→+→x xx x x x x x177s e c 22s e c l i m 277t a n 2t a n l i m 272200=⋅⋅==+→+→x x x x x x . (8)x x x x x x x x x 2222222cos 3cos lim 3133sec sec lim 3tan tan lim πππ→→→=⋅= )s i n (c o s 23)3s i n (3c o s 2lim 312x x x x x -⋅-=→πxx x c o s 3c o s l i m2π→-= 3s i n3s i n 3l i m2=---=→x x x π. (9)22221lim 11)1(111lim cot arc )11ln(lim xx x xx x x x x x x ++=+--⋅+=++∞→+∞→+∞→122lim 212lim ==+=+∞→+∞→x x x x .(10)x x xx x x x x x x x 22022020cos 1lim cos 1)1ln(cos lim cos sec )1ln(lim -=-+=-+→→→1s i n lim )sin (cos 22lim00==--=→→x x x x x x x . (注: cos x ⋅ln(1+x 2)~x 2) (11)2122sec 1lim 2tan lim2cot lim 2000=⋅==→→→x x x x x x x x .(12)+∞====+∞→+∞→→→1lim lim 1limlim 21012022tt t t x x x x e t e x e ex (注: 当x →0时, +∞→=21xt . (13)2121lim 11lim 1112lim 12121-=-=--=⎪⎭⎫ ⎝⎛---→→→x x x x x x x x . (14)因为)1ln(lim )1(lim x ax x x x exa +∞→∞→=+, 而 221)(11lim 1)1ln(lim )1(ln(lim xx a x ax x a x a x x x x --⋅+=+=+∞→∞→∞→a a a x ax x x ==+=∞→∞→1lim lim ,所以 a x ax x x x e e xa ==++∞→∞→)1l n (l i m )1(l i m. .(15)因为x x x x x e x ln sin 0sin 0lim lim +→+→=,而 x x x x x x x x x x c o tc s c 1lim csc ln lim ln sin lim 000⋅-==+→+→+→c o s s i n l i m 20=-=+→xx x x ,所以 1lim lim 0ln sin 0sin 0===+→+→e e x x x x x x .(16)因为x x x x e xln tan tan 0)1(lim -+→=, 而 xx x x x x x x x 2000c s c 1limcot ln lim ln tan lim -==+→+→+→ 0s i n l i m 20=-=+→xx x ,所以 1l i m )1(l i m 0ln tan 0tan 0===-+→+→e e x x x x x x .2. 验证极限x x x x sin lim +∞→存在, 但不能用洛必达法则得出.解 1)s i n 1(l i m s i n l i m =+=+∞→∞→x x x x x x x , 极限x x x x sin lim +∞→是存在的. 但)cos 1(lim 1cos 1lim )()sin (limx x x x x x x x +=+=''+∞→∞→∞→不存在, 不能用洛必达法则. 3. 验证极限xx x x sin 1sin lim20→存在, 但不能用洛必达法则得出. 解 0011sin sin lim sin 1sin lim020=⋅=⋅=→→xx x x x x x x x , 极限x x x x sin 1sin lim 20→是存在的. 但xx x x x x x x x cos 1cos 1sin 2lim )(sin )1sin (lim020-=''→→不存在, 不能用洛必达法则. 4. 讨论函数⎪⎪⎩⎪⎪⎨⎧≤>+=-0 0])1([)(2111x e x ex x f x x 在点x =0处的连续性. 解 21)0(-=e f ,)0(lim)(lim 21210f e e x f x x ===---→-→,因为]1)1l n (1[101100lim])1([lim )(lim -+-→-→+→=+=x x x x x x x x e ex x f ,而 200)1l n (l i m]1)1l n (1[1l i m x xx x x x x x -+=-++→+→ 21)1(21lim 2111lim 00-=+-=-+=+→+→x x x x x ,所以]1)1l n (1[101100lim])1([lim )(lim -+-→-→+→=+=x x x x x x x x e ex x f)0(21f e ==-.因此f (x )在点x =0处连续. 习题3-31. 按(x -4)的幂展开多项式x 4-5x 3+x 2-3x +4. 解设f (x )=x 4-5x 3+x 2-3x +4. 因为 f (4)=-56,f '(4)=(4x 3-15x 2+2x -3)|x =4=21, f ''(4)=(12x 2-30x +2)|x =4=74, f '''(4)=(24x -30)|x =4=66, f (4)(4)=24, 所以4)4(32)4(!4)4()4(!3)4()4(!2)4()4)(4()4()(-+-'''+-''+-'+=x f x f x f x f f x f =-56+21(x -4)+37(x -4)2+11(x -4)3+(x -4)4.2. 应用麦克劳林公式, 按x 幂展开函数f (x )=(x 2-3x +1)3. 解因为f '(x )=3(x 2-3x +1)2(2x -3),f ''(x )=6(x 2-3x +1)(2x -3)2+6(x 2-3x +1)2=30(x 2-3x +1)(x 2-3x +2), f '''(x )=30(2x -3)(x 2-3x +2)+30(x 2-3x +1)(2x -3)=30(2x -3)(2x 2-6x +3), f (4)(x )=60(2x 2-6x +3)+30(2x -3)(4x -6)=360(x 2-3x +2), f (5)(x )=360(2x -3), f (6)(x )=720;f (0)=1, f '(0)=-9, f ''(0)=60, f '''(0)=-270, f (4)(0)=720, f (5)(0)=-1080, f (6)(0)=720, 所以6)6(5)5(4)4(32!6)0(!5)0(!4)0(!3)0(!2)0()0()0()(x f x f x f x f x f x f f x f +++'''+''+'+= =1-9x +30x 3-45x 3+30x 4-9x 5+x 6.3. 求函数x x f =)(按(x -4)的幂展开的带有拉格朗日型余项的3阶泰勒公式. 解因为24)4(==f , 4121)4(421=='=-x x f , 32141)4(423-=-=''=-x x f ,328383)4(425⋅=='''=-x x f , 27)4(1615)(--=x x f , 所以 4)4(32)4(!4)()4(!3)4()4(!2)4()4)(4()4(-+-'''+-''+-'+=x f x f x f x f f x ξ 4732)4()]4(4[1615!41)4(5121)4(641)4(412--+⋅--+---+=x x x x x θ(0<θ<1). 4. 求函数f (x )=ln x 按(x -2)的幂展开的带有佩亚诺型余项的n 阶泰勒公式. 解因为f '(x )=x -1, f ''(x )=(-1)x -2, f '''(x )=(-1)(-2)x -3 , ⋅ ⋅ ⋅ ,nn nn x n x n x f )!1()1()1( )2)(1()(1)(--=+-⋅⋅⋅--=--;kk k k f 2)!1()1()2(1)(--=-(k =1, 2, ⋅ ⋅ ⋅, n +1),所以])2[()2(!)2( )2(!3)2()2(!2)2()2)(2()2(ln )(32n n n x o x n f x f x f x f f x -+-+⋅⋅⋅+-'''+-''+-'+= ])2[()2(2)1( )2(231)2(221)2(212ln 13322n n n n x o x n x x x -+-⋅-+⋅⋅⋅--⋅+-⋅--+=-. 5. 求函数x x f 1)(=按(x +1)的幂展开的带有拉格朗日型余项的n 阶泰勒公式.解因为f (x )=x -1, f '(x )=(-1)x -2, f ''(x )=(-1)(-2)x -3 , ⋅ ⋅ ⋅ , 1)1()(!)1()( )2)(1()(++--=-⋅⋅⋅--=n n n n xn xn x f;!)1(!)1()1(1)(k k fk k k -=--=-+(k =1, 2, ⋅ ⋅ ⋅, n ),所以 )1(!3)1()1(!2)1()1)(1()1(132⋅⋅⋅++-'''++-''++-'+-=x f x f x f f x 1)1()()1()!1()()1(!)1(++++++-+n n nn x n f x n f ξ 12132)1()]1(1[)1(])1( )1()1()1(1[++++++--+++⋅⋅⋅+++++++-=n n n nx x x x x x θ (0<θ<1).6. 求函数f (x )=tan x 的带有拉格朗日型余项的3阶麦克劳林公式. 解因为 f '(x )=sec 2x ,f ''(x )=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x ,f '''(x )=4sec x ⋅sec x ⋅tan 2x +2sec 4x =4sec 2x ⋅tan 2x +2sec 4x ,f (4)(x )=8sec 2x ⋅tan 3x +8sec 4x ⋅tan x +8sec 4x ⋅tan x xx x 52cos )2(sin sin 8+=;f (0)=0, f '(0)=1, f ''(0)=0, f '''(0)=2,所以 4523)(c o s 3]2)()[s i n s i n (31t a n x x x x x x x θθθ+++=(0<θ<1). 7. 求函数f (x )=xe x 的带有佩亚诺型余项的n 阶麦克劳林公式. 解因为 f '(x )=e x +xe x ,f ''(x )=e x +e x +xe x =2e x +xe x , f '''(x )=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅, f (n )(x )=ne x +xe x ;f (k )(0)=k (k =1, 2, ⋅ ⋅ ⋅, n ),所以 )(!)0( !3)0(!2)0()0()0()(32n n n xx o x n f x f x f x f f xe ++⋅⋅⋅⋅+'''+''+'+= )()!1(1 !2132n n x o x n x x x +-⋅⋅⋅+++=.8. 验证当210≤≤x 时, 按公式62132x x x e x +++≈计算e x 的近似值时, 所产生的误差小于0.01, 并求e 的近似值, 使误差小于0.01.解因为公式62132xx x e x+++≈右端为e x 的三阶麦克劳林公式, 其余项为43!4)(x e x R ξ=,所以当210≤≤x 时，按公式62132x x x e x+++≈计算e x 的误差01.00045.0)21(!43|!4||)(|42143<≈≤=x e x R ξ.645.1)21(61)21(212113221≈⋅+⋅++≈=e e .9. 应用三阶泰勒公式求下列各数的近似值, 并估计误差: (1)330; (2)sin18︒.解 (1)设3)(x x f =, 则f (x )在x 0=27点展开成三阶泰勒公式为2353233)27)(2792(!21)27(273127)(-⋅-⋅+-⋅+==--x x x x f4311338)27)(8180(!41)27)(272710(!31--⋅+-⋅⋅+--x x ξ(ξ介于27与x 之间).于是33823532333)272710(!313)2792(!21327312730⋅⋅⋅+⋅⋅-⋅+⋅⋅+≈---10724.3)3531311(31063≈+-+≈, 其误差为5114311431131088.13!4803278180!41|3)8180(!41||)30(|---⨯=⋅=⋅⋅⋅<⋅-⋅=ξR .(2) 已知43!4s i n !31s i nx x x x ξ+-=(ξ介于0与x 之间), 所以 sin 18︒3090.0)10(!311010sin 3≈-≈=πππ,其误差为44431003.2)10(!46sin |)10(!4sin ||)10(|-⨯=<=πππξπR . 10. 利用泰勒公式求下列极限: (1))23(lim 434323x x x x x --++∞→;(2))]1ln([cos lim222x x x e x x x -+--→;(3)2220sin )(cos 1211lim 2x e x x x x x -+-+→. 解 (1)tt t xx x x x x x t x x 430434343232131lim 12131lim)23(lim --+=--+=--++→+∞→+∞→.因为)(1313t o t t ++=+,)(211214t o t t +-=-, 所以23])(23[lim )](211[)](1[lim)23(lim 00434323=+=+--++=--++→+→+∞→t t o t t o t t o t x x x x t t x . (2)])1ln(1[)](41!21211[)](!41!211[lim)]1ln([cos lim1344244202202x x xx x xx o x x x o x x x x x e x -++⋅+--++-=-+-→-→ 010)1l n (1)(121lim 11340=+=-++-=-→ex x x o x xx .(3)2442442442202220))](!211())(!41!211[()](!43!211[211lim sin )(cos 1211lim 2xx o x x x o x x x o x x x x e x x x x x x +++-++-+-+-+=-+-+→→ 12123!43)(241123)(!43lim )(241123)(!43lim 2424404264440-=-=+--+=⋅+--+=→→x x o x x x o x o x x x x o x x x . 习题3-41. 判定函数f (x )=arctan x -x 单调性.解因为011111)(22≤+-=-+='xx x f , 且仅当x =0时等号成立, 所以f (x )在(-∞,+∞)内单调减少.2. 判定函数f (x )=x +cos x (0≤x ≤2π)的单调性.解因为f '(x )=1-sin x ≥0, 所以f (x )=x +cos x 在[0, 2π]上单调增加. 3. 确定下列函数的单调区间: (1) y =2x 3-6x 2-18x -7; (2)xx y 82+=(x >0);(3)x x x y 6941023+-=;(4))1ln(2x x y ++=; (5) y =(x -1)(x +1)3;(6))0())(2(32>--=a x a a x y ; (7) y =x n e -x (n >0, x ≥0); (8)y =x +|sin 2x |.解 (1) y '=6x 2-12x -18=6(x -3)(x +1)=0, 令y '=0得驻点x 1=-1, x 2=3. 列表得x (-∞, -1) -1 (-1, 3) 3 (3, +∞) y ' + 0 - 0 + y↗↘↗可见函数在(-∞, -1]和[3, +∞)内单调增加, 在[-1, 3]内单调减少.(2) 0)2)(2(28222=+-=-='x x x x y ,令y '=0得驻点x 1=2, x 2=-2(舍去).因为当x >2时, y >0; 当0<x <2时, y '<0, 所以函数在(0, 2]内单调减少, 在[2, +∞)内单调增加. (3)223)694()1)(12(60x x x x x y +----=', 令y '=0得驻点211=x , x 2=1, 不可导点为x =0. 列表得x (-∞, 0) 0 (0, 21) 21 (21, 1) 1 (1, +∞)y ' - 不存在 - 0 + 0 - y↘↘↗↘可见函数在(-∞, 0), ]21 ,0(, [1, +∞)内单调减少, 在]1 ,21[上单调增加.(4)因为011)1221(11222>+=++++='x x x x x y , 所以函数在(-∞, +∞)内单调增加.(5) y '=(x +1)3+3(x -1)(x +1)22)1)(21(4+-=x x . 因为当21<x 时, y '<0; 当21>x 时,y '>0, 所以函数在]21 ,(-∞内单调减少, 在) ,21[∞+内单调增加.(6)32)()2(3)32(x a a x a x y ----=', 驻点为321a x =, 不可导点为22a x =, x 3=a .列表得x )2 ,(a -∞2a )32 ,2(a a 32a ) ,32(a aa (a , +∞) y ' + 不存在 + 0 - 不存在 + y↗↗↘↗可见函数在)2 ,(a -∞, ]32 ,2(a a , (a , +∞)内单调增加, 在) ,32[a a 内单调减少.(7)y '=e -x x n -1(n -x ), 驻点为x =n . 因为当0<x <n 时, y '>0; 当x >n 时, y '<0, 所以函数在[0, n ]上单调增加, 在[n , +∞)内单调减少.(8)⎪⎩⎪⎨⎧+<<+-+≤≤+=πππππππk x k x x k x k x x y 2 2sin 2 2sin (k =0, ±1, ±2, ⋅ ⋅ ⋅),⎪⎩⎪⎨⎧+<<+-+≤≤+='πππππππk x k x k x k x y 2 2cos 212 2cos 21(k =0, ±1, ±2, ⋅ ⋅ ⋅).y '是以π为周期的函数, 在[0, π]内令y '=0, 得驻点21π=x , 652π=x , 不可导点为23π=x .列表得x )3 ,0(π3π )2,3(ππ 2π)65 ,2(ππ 65π ) ,65(ππ y ' + 0 - 不存在+ 0 - y↗↘↗↘根据函数在[0, π]上的单调性及y '在(-∞, +∞)的周期性可知函数在]32 ,2[πππ+k k 上单调增加, 在]22 ,32[ππππ++k k 上单调减少(k =0, ±1, ±2, ⋅ ⋅ ⋅).4. 证明下列不等式: (1)当x >0时, x x +>+1211;(2)当x >0时, 221)1ln(1x x x x +>+++; (3)当20π<<x 时, sin x +tan x >2x ;(4)当20π<<x 时, 331tan x x x +>;(5)当x >4时, 2x >x 2;证明 (1)设x x x f +-+=1211)(, 则f (x )在[0, +∞)内是连续的. 因为x x f +-='12121)(01211>+-+=xx , 所以f (x )在(0, +∞)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01211>+-+x x , 也就是 x x +>+1211.(2)设221)1ln(1)(x x x x x f +-+++=, 则f (x )在[0, +∞)内是连续的. 因为0)1l n (1)11(11)1l n ()(22222>++=+-++⋅++⋅+++='x x x x x x x x x x xx f ,所以f (x )在(0, +∞)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01)1l n (122>+-+++x x x x , 也就是 221)1l n (1x x x x +>+++.(3)设f (x )=sin x +tan x -2x , 则f (x )在)2,0[π内连续,f '(x )=cos x +sec 2x -2xx x x 22cos ]cos )1)[(cos 1(cos ---=.因为在)2,0(π内cos x -1<0, cos 2x -1<0, -cos x <0, 所以f '(x )>0, 从而f (x )在)2 ,0(π内单调增加, 因此当20π<<x 时, f (x )>f (0)=0, 即 sin x +tan x -2x >0, 也就是 sin x +tan x >2x .(4)设331tan )(x x x x f --=, 则f (x )在)2 ,0[π内连续,))(t a n (t a n t a n 1s e c )(2222x x x x x x x x x f +-=-=--='.因为当20π<<x 时, tan x >x , tan x +x >0, 所以f '(x )在)2 ,0(π内单调增加, 因此当20π<<x 时, f (x )>f (0)=0, 即031t a n 3>--x x x ,也就是 231t a n x x x +>.(5)设f (x )=x ln2-2ln x , 则f (x )在[4, +∞)内连续, 因为 0422ln 224ln 22ln )(=->-=-='e x x x f ,所以当x >4时, f '(x )>0, 即f (x )内单调增加.因此当x >4时, f (x )>f (4)=0, 即x ln2-2ln x >0, 也就是2x >x 2. 5. 讨论方程ln x =ax (其中a >0)有几个实根？解设f (x )=ln x -ax . 则f (x )在(0, +∞)内连续, x ax a x x f -=-='11)(, 驻点为ax 1=.因为当a x 10<<时, f '(x )>0, 所以f (x )在)1 ,0(a 内单调增加; 当ax 1>时, f '(x )<0,所以f (x )在) ,1(∞+a内单调减少. 又因为当x →0及x →+∞时, f (x )→-∞, 所以如果011ln )1(>-=a a f , 即e a 1<, 则方程有且仅有两个实根; 如果011ln )1(<-=aa f , 即e a 1>, 则方程没有实根. 如果011ln )1(=-=a a f , 即e a 1=, 则方程仅有一个实根. 6. 单调函数的导函数是否必为单调函数？研究下面这个例子: f (x )=x +sin x .解单调函数的导函数不一定为单调函数.例如f (x )=x +sin x 在(-∞,+∞)内是单调增加的, 但其导数不是单调函数. 事实上,f '(x )=1+cos x ≥0,这就明f (x )在(-∞, +∞)内是单调增加的. f ''(x )=-sin x 在(-∞, +∞)内不保持确定的符号, 故f '(x )在(-∞, +∞)内不是单调的.7. 判定下列曲线的凹凸性: (1) y =4x -x 2 ; (2) y =sh x ; (3)xy 11+=(x >0);(4) y =x arctan x ; 解 (1)y '=4-2x , y ''=-2,因为y ''<0, 所以曲线在(-∞, +∞)内是凸的. (2)y '=ch x , y ''=sh x . 令y ''=0, 得x =0.因为当x <0时, y ''=sh x <0; 当x >0时, y ''=sh x >0, 所以曲线在(-∞, 0]内是凸的, 在[0, +∞)内是凹的.(3)21xy -=', 32x y =''.因为当x >0时, y ''>0, 所以曲线在(0, +∞)内是凹的.(4)21arctan xx x y ++=',22)1(2x y +=''. 因为在(-∞, +∞)内, y ''>0, 所以曲线y =x arctg x 在(-∞, +∞)内是凹的.8. 求下列函数图形的拐点及凹或凸的区间: (1).y =x 3-5x 2+3x +5 ; (2) y =xe -x ; (3) y =(x +1)4+e x ; (4) y =ln(x 2+1); (5) y =e arctan x ; (6) y =x 4(12ln x -7),解 (1)y '=3x 2-10x +3, y ''=6x -10. 令y ''=0, 得35=x .因为当35<x 时, y ''<0; 当35>x 时, y ''>0, 所以曲线在]35 ,(-∞内是凸的, 在) ,35[∞+内是凹的, 拐点为)2720 ,35(. (2)y '=e -x -xe -x , y ''=-e -x -e -x +xe -x =e -x (x -2). 令y ''=0, 得x =2.因为当x <2时, y ''<0; 当x >2时, y ''>0, 所以曲线在(-∞, 2]内是凸的, 在[2, +∞)内是凹的, 拐点为(2, 2e -2).(3)y '=4(x +1)3+e x , y ''=12(x +1)2+e x .因为在(-∞, +∞)内, y ''>0, 所以曲线y =(x +1)4+e x 的在(-∞, +∞)内是凹的, 无拐点.(4)122+='x x y , 22222)1()1)(1(2)1(22)1(2++--=+⋅-+=''x x x x x x x y . 令y ''=0, 得x 1=-1, x 2=1. 列表得可见曲线在(-∞, -1]和[1, +∞)内是凸的, 在[-1, 1]内是凹的, 拐点为(-1, ln2)和(1, ln2).(5)2arctan 11x e y x+⋅=',)21(12arctan x x e y x -+=''. 令y ''=0得, 21=x . 因为当21<x 时, y ''>0; 当21>x 时, y ''<0, 所以曲线y =e arctg x 在]21 ,(-∞内是凹的,在) ,21[∞+内是凸的, 拐点是) ,21(21arctane. (6) y '=4x 3(12ln x -7)+12x 3, y ''=144x 2⋅ln x . 令y ''=0, 得x =1.因为当0<x <1时, y ''<0; 当x >1时, y ''>0, 所以曲线在(0, 1]内是凸的, 在[1, +∞)内是凹的, 拐点为(1, -7).9. 利用函数图形的凹凸性, 证明下列不等式:(1) nn n y x y x )2()(21+>+(x >0, y >0, x ≠y , n >1); (2))(22y x e e e yx y x ≠>++;(3)2ln)(ln ln yx y x y y x x ++>+ (x >0, y >0, x ≠y ). 证明 (1)设f (t )=t n , 则f '(t )=nt n -1, f ''(t )=n (n -1)t n -2. 因为当t >0时, f ''(t )>0, 所以曲线f (t )=t n 在区间(0, +∞)内是凹的. 由定义, 对任意的x >0, y >0, x ≠y 有)2()]()([21yx f y f x f +>+, x (-∞, -1) -1 (-1, 1) 1 (1, +∞) y '' - 0 + 0 - y⋂ln2 拐点⋃ln2 拐点⋂即 nn n y x y x )2()(21+>+. (2)设f (t )=e t , 则f '(t )=e t , f ''(t )=e t . 因为f ''(t )>0, 所以曲线f (t )=e t 在(-∞, +∞)内是凹的. 由定义, 对任意的x , y ∈(-∞, +∞), x ≠y 有)2()]()([21yx f y f x f +>+, 即)(22y x e e e yx y x ≠>++.(3)设f (t )=t ln t , 则 f '(t )=ln t +1, tt f 1)(=''.因为当t >0时, f ''(t )>0, 所以函数f (t )=t ln t 的图形在(0, +∞)内是凹的. 由定义, 对任意的x >0, y >0, x ≠y 有)2()]()([21yx f y f x f +>+, 即 2ln )(ln ln yx y x y y x x ++>+.10. 试证明曲线112+-=x x y 有三个拐点位于同一直线上.证明 222)1(12+++-='x x x y , 323223)1()]32()][32()[1(2)1(2662++---+=++--=''x x x x x x x x y . 令y ''=0, 得x 1=-1, 322-=x , 323+=x . 例表得 x (-∞. -1) -1 )32 ,1(-- 32- )32 ,32(+-32+ ) ,32(∞++y ' - 0 + 0- 0+ y⋂-1⋃)32(431--⋂)32(431++ ⋃可见拐点为(-1, -1), ))32(431 ,32(---, ))32(431 ,32(+++. 因为41)1(32)1()32(431=-------, 41)1(32)1()32(431=--+--++,所以这三个拐点在一条直线上.11. 问a 、b 为何值时, 点(1, 3)为曲线y =ax 3+bx 2的拐点？解 y '=3ax 2+2bx , y ''=6ax +2b . 要使(1, 3)成为曲线y =ax 3+bx 2的拐点, 必须y (1)=3且y ''(1)=0, 即a +b =3且6a +2b =0, 解此方程组得23-=a , 29=b .12. 试决定曲线y =ax 3+bx 2+cx +d 中的a 、b 、c 、d , 使得x =-2处曲线有水平切线, (1, -10)为拐点, 且点(-2, 44)在曲线上. 解 y '=3ax 2+2bx +c , y ''=6ax +2b . 依条件有⎪⎩⎪⎨⎧=''=-'-==-0)1(0)2(10)1(44)2(y y y y , 即⎪⎩⎪⎨⎧=+=+--=+++=+-+-02604121044248b a c b a d c b a d c b a .解之得a =1, b =-3, c =-24, d =16.13. 试决定y =k (x 2-3)2中k 的值, 使曲线的拐点处的法线通过原点. 解y '=4kx 3-12kx , y ''=12k (x -1)(x +1). 令y ''=0, 得x 1=-1, x 2=1.因为在x 1=-1的两侧y ''是异号的, 又当x =-1时y =4k , 所以点(-1, 4k )是拐点. 因为y '(-1)=8k , 所以过拐点(-1, 4k )的法线方程为)1(814+-=-x k k y . 要使法线过原点, 则(0, 0)应满足法线方程, 即kk 814-=-, 82±=k .同理, 因为在x 1=1的两侧y ''是异号的, 又当x =1时y =4k , 所以点(1, 4k )也是拐点.因为y '(1)=-8k , 所以过拐点(-1, 4k )的法线方程为)1(814-=-x k k y . 要使法线过原点, 则(0, 0)应满足法线方程, 即kk 814-=-, 82±=k .因此当82±=k 时, 该曲线的拐点处的法线通过原点.14. 设y =f (x )在x =x 0的某邻域内具有三阶连续导数, 如果f ''(x 0)=0, 而f '''(x 0)≠0, 试问 (x 0, f (x 0))是否为拐点？为什么？解不妨设f '''(x 0)>0. 由f '''(x )的连续性, 存在x 0的某一邻域(x 0-δ, x 0+δ), 在此邻域内有f '''(x )>0. 由拉格朗日中值定理, 有f ''(x )-f ''(x 0)=f '''(ξ)(x -x 0) (ξ介于x 0与x 之间), 即 f ''(x )=f '''(ξ)(x -x 0).因为当x 0-δ<x <x 0时, f ''(x )<0; 当x 0<x <x 0+δ 时, f ''(x )>0, 所以(x 0, f (x 0))是拐点.习题3-51. 求函数的极值: (1) y =2x 3-6x 2-18x +7; (2) y =x -ln(1+x ) ; (3) y =-x 4+2x 2 ; (4)x x y -+=1; (5)25431xx y ++=;(6)144322++++=x x x x y ;(7) y =e x cos x ;(8)xx y 1=;(9)31)1(23+-=x y ;(10) y =x +tan x .解 (1)函数的定义为(-∞, +∞), y '=6x 2-12x -18=6(x 2-2x -3)=6(x -3)(x +1), 驻点为x 1=-1, x 2=3. 列表x (-∞, -1) -1 (-1, 3) 3 (3, +∞) y ' + 0 - 0 + y↗17极大值↘-47极小值↗可见函数在x =-1处取得极大值17, 在x =3处取得极小值-47. (2)函数的定义为(-1, +∞), xxx y +=+-='1111, 驻点为x =0. 因为当-1<x <0时, y '<0; 当x >0时, y '>0, 所以函数在x =0处取得极小值, 极小值为y (0)=0. (3)函数的定义为(-∞, +∞),y '=-4x 3+4x =-4x (x 2-1), y ''=-12x 2+4, 令y '=0, 得x 1=0, x 2=-1, x 3=1.因为y ''(0)=4>0, y ''(-1)=-8<0, y ''(1)=-8<0, 所以y (0)=0是函数的极小值, y (-1)=1和y (1)=1是函数的极大值.(4)函数的定义域为(-∞, 1], )112(1243121121211+---=---=--='x x x xx xy ,令y '=0, 得驻点43=x .因为当43<x 时, y '>0; 当143<<x 时, y '<0, 所以45)1(=y 为函数的极大值.(5)函数的定义为(-∞, +∞), 32)54()512(5x x y +--=', 驻点为512=x . 因为当512<x 时, y '>0; 当512>x 时, y '<0, 所以函数在512=x 处取得极大值, 极大值为10205)512(=y . (6)函数的定义为(-∞, +∞), 22)1()2(+++-='x x x x y , 驻点为x 1=0, x 2=-2.列表x (-∞, -2) -2(-2, 0) 0 (0, +∞) y ' - 0+ 0 - y↘38极小值 ↗4极大值↘可见函数在x =-2处取得极小值38, 在x =0处取得极大值4.(7)函数的定义域为(-∞, +∞). y '=e x (cos x -sin x ), y ''=-e x sin x .令y '=0, 得驻点ππk x 24+=, ππ)1(24++=k x , (k =0, ±1, ±2, ⋅ ⋅ ⋅).因为0)24(<+''ππk y , 所以22)24(24⋅=++ππππk e k y 是函数的极大值.因为y ''0])1(24[>++ππk , 所以22])1(24[)1(24⋅-=++++ππππk e k y 是函数的极小值. (8)函数xx y 1=的定义域为(0, +∞),)ln 1(121x x x y x-⋅='.令y '=0, 得驻点x =e .因为当x <e 时, y '>0; 当x >e 时, y '<0, 所以ee e y 1)(=为函数f (x )的极大值.(9)函数的定义域为(-∞, +∞), 3/2)1(132+-='x y , 因为y '<0, 所以函数在(-∞, +∞)是单调减少的, 无极值.(10)函数y =x +tg x 的定义域为ππk x +≠2(k =0, ±1, ±2, ⋅ ⋅ ⋅). 因为y '=1+sec 2x >0, 所以函数f (x )无极值.2. 试证明: 如果函数y =ax 3+bx 2+cx +d 满足条件b 2 -3ac <0, 那么这函数没有极值 . 证明y '=3a x 2+2b x +c . 由b 2 -3ac <0, 知a ≠0. 于是配方得到 y '=3a x 2+2b x +c ab ac a b x a a c x a b x a 33)3(3)332(32222-++=++=,因3ac -b 2>0, 所以当a >0时, y '>0; 当a <0时, y '<0. 因此y =ax 3+bx 2+cx +d 是单调函数, 没有极值.3. 试问a 为何值时, 函数x x a x f 3sin 31sin )(+=在3π=x 处取得极值？它是极大值还是极小值？并求此极值.解 f '(x )=a cos x +cos 3x , f ''(x )=-a sin x -3 sin x . 要使函数f (x )在3π=x 处取得极值, 必有0)3(='πf , 即0121=-⋅a , a =2 . 当a =2时, 0232)3(<⋅-=''πf . 因此, 当a =2时, 函数f (x )在3π=x 处取得极值, 而且取得极大值, 极大值为3)23(=f . 4. 求下列函数的最大值、最小值:(1) y =2x 3-3x 2 , -1≤x ≤4; (2) y =x 4-8x 2+2, -1≤x ≤3 ; (3)x x y -+=1, -5≤x ≤1.解 (1)y '=6x 2-6x =6x (x -1), 令y '=0, 得x 1=0, x 2=1. 计算函数值得y (-1)=-5, y (0)=0, y (1)=-1, y (4)=80,经比较得出函数的最小值为y (-1)=-5, 最大值为y (4)=80.(2)y '=4x 3-16x =4x (x 2-4), 令y '=0, 得x 1=0, x 2=-2(舍去), x 3=2. 计算函数值得 y (-1)=-5, y (0)=2, y (2)=-14, y (3)=11,经比较得出函数的最小值为y (2)=-14, 最大值为y (3)=11.(3)xy --='1211, 令y '=0, 得43=x . 计算函数值得65)5(+-=-y , 45)43(=y , y (1)=1,经比较得出函数的最小值为65)5(+-=-y , 最大值为45)43(=y .5. 问函数y =2x 3-6x 2-18x -7(1≤x ≤4)在何处取得最大值？并求出它的最大值. 解 y '=6x 2-12x -18=6(x -3)(x +1), 函数f (x )在1≤x ≤4内的驻点为x =3. 比较函数值:f (1)=-29, f (3)=-61, f (4)=-47,函数f (x )在x =1处取得最大值, 最大值为f (1)=-29. 6. 问函数xx y 542-=(x <0)在何处取得最小值？解 2542x x y +=', 在(-∞, 0)的驻点为x =-3. 因为 31082x y -='', 0271082)3(>+=-''y , 所以函数在x =-3处取得极小值. 又因为驻点只有一个, 所以这个极小值也就是最小值, 即函数在x =-3处取得最小值, 最小值为27)3(=-y .7. 问函数12+=x x y (x ≥0)在何处取得最大值？解 222)1(1+-='x x y . 函数在(0, +∞)内的驻点为x =1.因为当0<x <1时, y '>0; 当x >1时y '<0, 所以函数在x =1处取得极大值. 又因为函数在 (0, +∞)内只有一个驻点, 所以此极大值也是函数的最大值, 即函数在x =1处取得最大值, 最大值为f (1)=21. 8. 某车间靠墙壁要盖一间长方形小屋, 现有存砖只够砌20cm 长的墙壁, 问应围成怎样的长方形才能使这间小屋的面积最大？解设宽为x 长为y , 则2x +y =20, y =20-2x , 于是面积为 S = xy =x (20-2x )=20x -2x 2. S '=20-4x =4(10-x ), S ''=-4.。

高等数学：高数第三章自测题答案

第三章单元自测题答案一、填空题：1．满足，2=ξ； 2．满足,3415=ξ； 3． 3； 4． 1-=a ，4-=b ．二、选择题:1. B ；2.A ；3.C ；4.A ；5.B .三、计算下列各题: 1.解 ∞→x lim 1lim 1lim 11lim )1(0011==-=-=-→→∞→u u u u x x x e ue xe e x . 2.解 2000)1ln(lim )1ln()1ln(lim )1)1ln(1(lim xx x x x x x x x x x x +-=++-=-+→→→21)1(2lim 2111lim 00=+=+-=→→x x x x x x x . 3.解设21)(cos x x y =，取对数有2cos ln ln xx y = 因为212tan lim cos ln lim 020-=-=→→x x x x x x ，所以21cos ln 01022lim )(cos lim -→→==e e x x xx x x . 四、应用题:1.解函数的定义域为),(+∞-∞，因为 x x x e x x e x xe y ----=-=')24(2422,令0='y ，解得2,021==x x .当,0,0<'<y x 当,0,20>'<<y x 当,0,2<'>y x因此,]2,0[为单调增加区间，]0,(-∞)和),2[+∞为单调减少区间.2.解函数的定义域为),(+∞-∞，因为2222)1(22,12x x y x x y +-=''+=', 令0=''y ，解得1,121=-=x x .当,0,1<''-<y x 时当11<<-x 时,0>''y ,当0,1<''>y x 时，故曲线的凹区间为]1,1[-，凸区间为]1,(--∞和),1[+∞.拐点为)2ln ,1(-，)2ln ,1(.3.解 )5,0(2,2,01232∈=±==-='x x x y 解得, 70)5(,5)0(,11)2(==-=f f f ,故,70max =f 11min -=f .4.解 ,26,232b ax y bx ax y +=''+='由已知得0)2(=''y ，即6,0212b a b a -==+. 又)5,2(为曲线23bx ax y +=上的点,因此有815,42653=+⋅-=b b b .于是16581561-=⋅-=a . 5.解由已知得x y 2=，且72=xyh ，于是有236xh =，长方体带盖箱子的表面积)362362(2)(2)(222x x x x x yh xh xy x S S ⋅+⋅+=++== )0(,21642>+=x x x 因为22168)(x x x S -='，令0)(='x S ，解得唯一驻点3=x ，由问题实际意义知，当长3=x m 时，箱子的用料最省，此时宽m y 6=，高m h 4=.五、证明题:1.证明令x x f ln )(=，显然)(x f 在],[b a 上满足拉格朗日中值定理条件，于是有 ))(()()(a b f a f b f -'=-ξ,)(b a <<ξ,即 ξa b a b a b -==-ln ln ln ，)(b a <<ξ，因为b a <<<ξ0，所以aa b a b b a b -<-<-ξ，因此aa b a b b a b -<<-ln . 2.证明令221)1ln()(x x x x f +-+=，则)(x f 在],0[x 上连续，且xx x x x f +=+-+='1111)(2，当0>x 时，0)(>'x f ，所以)(x f 在),0[+∞上单调增加，又0)0(=f ，从而，当0>x 时有)0()(f x f >，即当0>x 时，221)1ln(x x x ->+. 3.证明令1)(5-+=x x x f ，则)(x f 在区间]2,0[上连续,且0122)2(,01)0(5>-+=<-=f f ，由零点定理知方程015=-+x x 在区间)2,0(内有一正根.又在),(+∞-∞内，,015)(4>+='x x f 故)(x f 在),(+∞-∞上单调增加, 因此正根唯一，即方程015=-+x x 只有一个正根.。

北大版高等数学第三章积分的计算及应用答案习题3.5

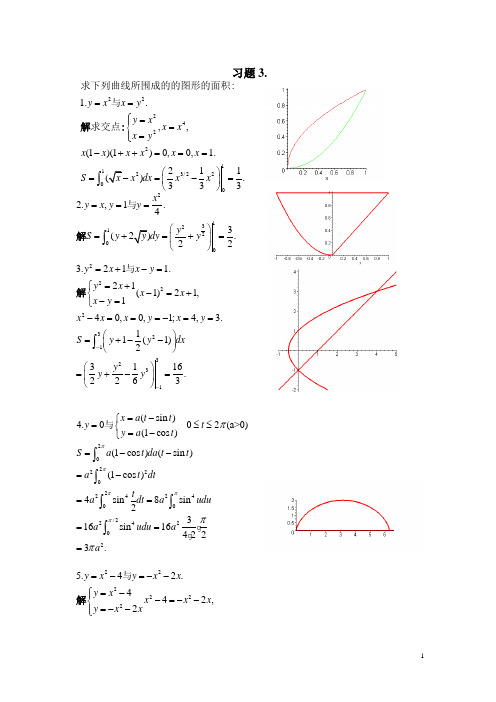
习题3.2132122.,1.43(.22xy x y yyS y d y y===⎛⎫=+=+=⎪⎝⎭⎰与解222232132313.21 1.21(1)21,140,0,1;4, 3.11(1)23116.2263y x x yy xx xx yx x x y x yS y y d xyy y--=+-=⎧=+-=+⎨-=⎩-===-==⎛⎫=+--⎪⎝⎭⎛⎫=+-=⎪⎝⎭⎰与解2222225.42.442,2y x y x xy xx x xy x x=-=--⎧=-⎪-=--⎨=--⎪⎩与解2224221123/22: 1..,,(1)(1)0,0, 1.211).333 y x x yy xx xx yx x x x x xS x d x x x==⎧=⎪=⎨=⎪⎩-++===⎛⎫==-=⎪⎝⎭⎰求下列曲线所围成的的图形的面积与求交点解:22222242400/22422(sin)4.0 02(a>0)(1co s)(1co s)(sin)(1co s)4sin8sin2316sin164223.x a t ty ty a tS a t d a t ta t d tta d t a ud ua ud u aaππππππππ=-⎧=≤≤⎨=-⎩=--=-=====⎰⎰⎰⎰⎰与212122212213222240,(22)(2)0,2, 1.(24)(224)249.3x x x x x x S x x x d xx x d xx x x ---+-=-+==-==---+=--+⎛⎫=--+= ⎪⎝⎭⎰⎰222222424222222122212220216.8().28181424320,4320,(8)(4)08()4,4,2,212122424arcsin23x y y x x y x x y xx x x uu u u u u u x x x S x d x x d x Sπ-+==⎧+=⎪+=⎨=⎪⎩+-==+-=+-==-===-=⎛⎫=⎪⎝⎭⎛⎫= ⎪⎝⎭⎛==+⎝⎰⎰与分上下两部分舍解244826.33πππ⎛⎫=-+=- ⎪⎝⎭22221211222213227.4 2.442220,(2)(1)0,2, 1.(42)6()96.322yx y x y x x x y x x x x x x x S x x dx x x dxx x ---=-=+⎧=--=+⎨=+⎩+-=+-==-==---=-+⎛⎫=-+= ⎪⎝⎭⎰⎰与解22/422/42008.co s 2(0).1co s 22sin 2|.2r a a a d a a ππϕϕϕϕ=>==⎰其求双纽线所围图形的面积1解S =422/32/32/333/2226200/2372/23723:9.(0).co s ,02.sin 22sin 3co s sin 6sin co s 6sin (1sin )6428326175391a x y a a x a t t y a t V y d x a ta t td ta t td t at t d ta πππππππππ+=>⎧=⎪≤≤⎨=⎪⎩====-⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭⎰⎰⎰⎰求下列曲线围成的平面图形绕轴旋转所成旋转体的体积解3.05a πln 3ln 3220ln 32010.1,ln 3,.(1)(21)12ln 3.2xxxxx xy e x y e V e d x ee d xe e x ππππ=-===-=-+⎛⎫=-+= ⎪⎝⎭⎰⎰231/32/31/32/322/37/32/37/3:11.,0(0,0).,()33.77b b a y x x y b a b x ayV ay d y a y abπππ===>>====⎰求下列平面曲线围成的平面图形绕轴旋转所成旋转体的体积及解13.()[,](0)()2().2(),2().b ab ay f x a b a y f x x a x b y V xf x d x d x d V xf x d x V xf x d x πππ=>======⎰⎰设在区间上连续且不取负值，试用微元法推导：由曲线，直线，及轴围成的平面图形绕轴旋转所成立体的体积为厚度的圆筒的体积解21111111211112.0,.8ln 8ln 8ln |ln 1812881.eeee ee x x y e yy V d yyyd y y y y d y yd ye y e e ππππππ-----====⎡⎤=-⎢⎥⎣⎦⎡⎤=-+⎢⎥⎣⎦⎡⎤=-+⎢⎥⎣⎦⎡⎤⎡⎤=--=-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰解2211222211122214.,1,22222222()2.xx xx x xy e x x x y V xe d x xd e x e e d x e e ee e e e e ππππππ===⎡⎤==⎢⎥⎣⎦⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤=---=⎣⎦⎰⎰⎰求曲线及轴所围成的平面图形绕轴旋转所成的立体的体积.解22223233215.:.3().1()|31(())33aa a ha ha h h V h a y f x a h x a V a x d x a h x h a h a a h h a πππππ--⎛⎫=-⎪⎝⎭==-≤≤⎡⎤=-=-⎢⎥⎣⎦⎡⎤⎛⎫=---=- ⎪⎢⎥⎣⎦⎝⎭⎰证明半径为高为的球缺的体积为证3230320/22017.sin .3sin co s ,33sin 3136sin 6.222r a r a s a a d a d a a πππθθθθθθπθθπ='======⎰⎰⎰ 求曲线的全长解3322/22/218.cos ,sin .3cos (sin ),3sin cos 143sin cos 12sin |6.2x a t y a t x a t t y at t s a t tdx a t a ππ==''=-====⎰ 求向星形线的弧长解322313433211116.13.621.221114.2623x y x x xx y xs x x xd x x x =+=='=-=⎡⎤+==-=⎢⎥⎣⎦⎰⎰求曲线在到之间的弧长解12220.2co s 2(0)d x ra a L L θ=>=⎰试证双纽线的全长可表为2022202/4522222221.1(02)4.2214144co s sec sectan sec tan (2)sectan sec tan (2)(2),1nn n n n n n n n xy x x x y x S xd x d x xI xd x xd xx x n x xd xx x n I n I I n ππππ-----=+≤≤'=⎛⎫=+ ⎪⎝⎭=====--=--+-=-⎰⎰⎰⎰⎰⎰求抛物线绕旋转所得的旋转体的侧面积.解 222sectan .11n n n x x I n ---+-00019.(1co s ).(sin )24co s 8sin8.22r a r a s a a d x a a πππθθθθθ=+'=-====⎰⎰求心脏线的全长解22/40/40/40/40/40/4024sin 2,2sin 2/,4)rr a r a r s d xππππππθθθθθθ''=-=-========⎰⎰⎰⎰⎰⎰证10⎰335313131311sec tan sec tan sec tan 444422133sec tan sec tan ln(tan sec ).488I x x I x x x x I x x x x x x C ⎛⎫=+=++ ⎪⎝⎭=++++3/41334(sec tan sec tan ln(tan sec ))|4883ln(12S x x x x x x πππ=+++=+2222/20/201022.(0),.co s ,02,sin ,co s .sin 224co s 444a x yb a abxa tt x a ty b t y b t S b td t b t b uua bππππππππ+=<≤=⎧''≤≤=-=⎨=⎩===-====⎰⎰⎰ 求1分别绕长短轴旋转而成的椭球面的面积解12/20/201222arcsin 2arcsin 2.22s 4sin 444ln 2()b u aa b S a td ta t a uuba b ππεεεπεπππππ-⎤⎥⎣⎦⎛⎫= ⎪⎝⎭=====-⎰⎰⎰ 122(22ln(1).u ba ab ππεε⎤+⎥⎥⎦⎡⎤=++⎢⎥⎣⎦22223.(,0)x y a a h y a h a y +=-≤≤<<计算圆弧绕轴旋转所得球冠的面积.101020025.10m ()(70.2)(70.2)70.180(k g ).26..co s 0.,0sin sin 2[co s ]|.2(0,).27.,x x m x d x x x a x a tt y a t a ta d taay t aaππρπππππ=+⎡⎤=+=+=⎣⎦=⎧=≤≤⎨=⎩==-=⎰⎰0有一细棒长已知距左端点x 处的线密度是k g /m 求这细棒的质量.求半径为的均匀半圆周的重心坐标由对称性,x 重心坐标有一均匀细杆解解/54/522../5./.l l l M l M M M l J x d x x d xllρ==+⎰⎰长为质量为计算细杆绕距离一端处的转动惯量解/54/533213.3375l l M x M x M l ll=+=[]2arcsin 22arcsin22arcsin2co s arcsin .sin 222co s sin 212.a haa h aa ha x a t a h t y a ta S t a td ta t a h a a h a πππππππππ---=⎧-≤≤⎨=⎩===-⎡⎤=-=⎢⎥⎣⎦⎰⎰解a h -a ()23/23/2123/21125/21224.(1co s ).2(1co s )sin 2(1co s )sin 21co s co s 2(1)2)32.5r a S a a d a d a x d x a x a πππθθπθθθπθθθπθθπππ--=+'=+=+=-+=+=+=⎰求心脏线绕极轴旋转所成的旋转体的侧面积000解r =-a s i n.222422222223228.,,,.2.2.221.4229.,,,,33,,13aa a M MMM xd x d m xd x aaa M xd x M x J xM a aaM a h aMMa M y x d m x d x x d x h a h h h a h d ρπππρρπππ=====⎛⎫===== ⎪⎝⎭⎰设有一均匀圆盘半径为质量为求它对于通过其圆心且与盘垂直的轴之转动惯量有一均匀的圆锥形陀螺质量为底半径为高为试求此陀螺关于其对称轴的转动惯量.解=解2245225425555201132213133.2251030.,2k g /m.29.8.29.89.8259.8().hha a M J d m x x d x h h a M a M x J x d x M a hhd W xd x W xd x x J ⎛⎫== ⎪⎝⎭=======⎰⎰楼顶上有一绳索沿墙壁下垂该绳索的密度为若绳索下垂部分长为5m ,求将下垂部分全部拉到楼顶所需做的功.解2231.()[,],,(),,,(),(),().32.48m ,64m ,164,06424,,9b a y f x a b y f x x a x b x y d S f x d x d F p d S g xf x d x F g xf x d x y a x a a x ρρρ=========-=-=⎰ 设在上连续非负将由及轴围成的曲边梯形垂直放置于水中使轴与水平面相齐求水对此曲边梯形的压力.一水闸门的边界线为一抛物线,沿水平面的宽度为最低处在水面下求水对闸门的的压力.解解642828356,64,08,64,0.6(64)(2)126452428.8.35F g y u y u y u y u F g u u u d y u ug g ρρρρ=±===-=====-⎡⎤=-=⎢⎥⎣⎦⎰⎰ 时时6424。

高等数学课后题答案(西工大版)第3章

2 1− x ex + sin x
=
1 2
.
(2)
lim
ln(1 + x2 )
⎜⎛ 0 ⎟⎞
⎝0⎠
====
lim
2x 1+ x2
x→0 sec x − cos x
x→0 tan x sec x + sin x
=
lim
x→0
sin
x
⋅
1
2 +x
2
x(sec2 x
+
1)
2
= lim 1 + x 2 = 1
⎝π
⎠
⎝π
⎠
ln⎜⎛ 2 arctan x ⎟⎞
lim ln y = lim x ln⎜⎛ 2 arctan x ⎟⎞ = lim
x →+∞
x→+∞ ⎝ π
⎠ x→+∞
⎝π x −1
⎠
1 21
⎜⎛ 0 ⎟⎞
=⎝=0=⎠ = lim x →+∞
2 arctan x π 1 + x2 π
− x−2
=
−
lim
令
f
(x)
=
ex x
,
g(x)
=
1 x
,易验证
f
(x)
和
g(x)
在 [x1,
x2 ] 上满足柯西中值定理的条件,于
是存在 ξ ∈ (x1, x2 ) ,使得
f (x2 ) − f (x1 ) = f '(ξ ) , g(x2 ) − g(x1 ) g'(ξ )
e x2 − e x1
xex− ex
x2 x1 = x2

高等数学教材第三版答案

高等数学教材第三版答案为了方便广大高等数学学习者更好地学习，我特意整理了高等数学教材第三版的答案，希望能对大家的学习有所帮助。

下面是对教材中各章节习题的答案解析。

第一章微分学1.1 函数与极限1.2 导数与微分1.3 微分中值定理与导数的应用第二章积分学2.1 定积分2.2 反常积分2.3 定积分的应用第三章无穷级数3.1 数项级数3.2 幂级数3.3 函数项级数第四章高次方程及其解法4.1 代数方程与代数方程的根4.2 高次代数方程的整数根与有理根4.3高次代数方程的正根与实根4.4高次代数方程的复根第五章傅立叶级数5.1 傅立叶级数的定义与性质5.2 奇延拓与偶延拓5.3 傅立叶级数的收敛性第六章偏微分方程6.1 偏导数与偏微分方程6.2 一阶线性偏微分方程6.3 高阶线性偏微分方程第七章多元函数微分学7.1 多元函数的极限与连续7.2 一阶偏导数与全微分7.3 高阶偏导数与多元函数微分学应用第八章向量代数与空间解析几何8.1 向量代数8.2 空间解析几何8.3 平面与直线的夹角与距离第九章多元函数积分学9.1 二重积分9.2 三重积分9.3 三重积分的应用第十章曲线积分与曲面积分10.1 第一类曲线积分10.2 第二类曲线积分10.3 曲面积分第十一章广义重积分与格林公式11.1 广义重积分11.2 格林公式及其应用11.3 闭曲线上格林公式的应用第十二章级数的一致收敛性12.1 函数项级数的一致收敛性12.2 幂级数的一致收敛性12.3 一致收敛性的应用第十三章线性代数初步13.1 行列式13.2 向量空间与线性方程组13.3 特征值与特征向量第十四章线性代数进阶14.1 线性空间与线性映射14.2 矩阵与线性映射14.3 特征多项式与相似矩阵注意：以上只是教材中各章节的题目答案简要解析，建议在学习过程中，除了参考答案之外，还需要仔细研读教材中的知识点，并通过大量的练习来巩固和加深理解。

高等数学第四版教材答案

高等数学第四版教材答案第一章导数与微分1.1 函数与极限在这一章中，我们将学习函数的性质以及如何计算函数的极限。

了解函数的极限是理解微积分的基础。

1.2 导数的定义与性质导数是描述函数变化率的概念。

我们将研究导数的定义、性质以及常见函数的导数。

1.3 高阶导数与隐函数求导高阶导数是导数的导数。

我们将学习如何计算高阶导数，并介绍隐函数求导的方法。

1.4 微分微分是导数的应用之一，它可以帮助我们更好地理解函数的变化。

我们将研究微分的概念和性质，并解决一些应用问题。

第二章微分学的应用2.1 极值与最值极值是函数取得的最大值或最小值。

我们将研究如何找到函数的极值，并解决一些极值应用问题。

2.2 中值定理中值定理是微分学中重要的定理之一，它描述了函数在某个区间内的平均变化率与瞬时变化率相等的关系。

我们将学习中值定理的几种形式以及其应用。

2.3 函数的单调性与曲线的凹凸性函数的单调性描述了函数的增减趋势，曲线的凹凸性则描述了函数曲线的弯曲程度。

我们将学习如何确定函数的单调区间和凹凸区间，并解决相关的应用问题。

第三章定积分3.1 定积分的概念与性质定积分是微积分中的一个重要概念，它描述了曲线下面积的大小。

我们将学习定积分的定义、性质以及计算方法。

3.2 定积分的几何应用定积分的几何应用包括计算曲线下面积、计算旋转体的体积等。

我们将解决一些相关的几何应用问题。

3.3 定积分的物理应用定积分在物理学中也有广泛的应用，如计算质点的质量、计算功、计算质心等。

我们将学习如何应用定积分解决物理问题。

第四章微分方程4.1 微分方程的基本概念微分方程是描述函数与其导数之间关系的方程。

我们将学习微分方程的基本概念，并分析一些简单的微分方程。

4.2 一阶线性微分方程一阶线性微分方程是一类特殊的微分方程，其解可以通过积分得到。

我们将学习一阶线性微分方程的解法以及应用。

4.3 高阶线性微分方程高阶线性微分方程是多个导数的函数关系。

我们将学习高阶线性微分方程的解法，并解决一些实际问题。

高等数学教材参考答案大一

高等数学教材参考答案大一第一章：数列与极限1. 数列的概念和性质数列是按照一定规则排列的一串数，可以用公式表达表示。

数列有很多重要的性质，如有界性、单调性等。

2. 数列的极限数列的极限是指当数列的项随着自变量趋于无穷大时，数列的值逐渐趋近于某个常数。

可以用极限的定义来求解数列的极限。

3. 数列极限的运算法则数列的极限具有一些运算法则，如极限的加法、乘法、倒数等。

应用这些法则可以简化数列极限的求解过程。

4. 无穷大与无穷小无穷大是指数列在无限接近无穷大时的情况，无穷小是指数列在无限接近零时的情况。

无穷大与无穷小具有一些重要的性质和关系。

第二章：连续性与导数1. 函数的连续性函数的连续性是指函数在某一点上是否存在极限，以及该极限与函数在该点上的取值是否一致。

可以通过极限的定义和连续函数的性质来判断函数的连续性。

2. 函数的导数函数的导数是指函数在某一点上的变化率，可以用导数的定义和求导公式来求解函数的导数。

导数有一些重要的性质，如导数的和、差、积、商等。

3. 函数的微分函数的微分是指函数在某一点上的变化量，可以用微分的定义和微分公式来求解函数的微分。

微分和导数有一定的关系，可以根据微分和导数的定义来推导微分与导数的关系。

4. 高阶导数与凹凸性高阶导数是指函数的导数的导数，可以用高阶导数的定义和求导公式来求解函数的高阶导数。

高阶导数与函数的凹凸性有一定的关系，可以通过高阶导数来判断函数的凹凸性。

第三章：定积分与不定积分1. 定积分的概念定积分是指函数在一个区间上的加权平均值，可以用定积分的定义和性质来求解定积分。

定积分有一些重要的性质，如定积分的线性性、可加性等。

2. 定积分的计算定积分的计算可以通过换元法、分部积分法等方法来进行。

通过掌握积分公式和积分表可以简化定积分的计算过程。

3. 不定积分的概念不定积分是指函数的原函数，可以用不定积分的定义和性质来求解不定积分。

不定积分有一些重要的性质，如不定积分的线性性、和定积分的关系等。

武忠祥《2016高等数学辅导讲义》第三章解答

25.【解】应填
. 4
原式 lim
1 1 1 ( 1 )2 1 ( 2 )2 1 ( n 1)2 1 x 2 dx 0 n n n n n 4
26.【解】应填
2 2 1 2 x 2 2 .原式 1 cos x d x sin d x . 0 0 2
7.【解】应选(B).
c 3 x ,故 c 90 3
3 n 2 1 n 1 1 ， n n 1
an
3 2n
n n 1 0
(1 x ) d(1 x n )
e t 偶函数，则 e t dt 奇函数.
0
原式 2

π 2 0
π
cos 2 x sin 2 xdx 2 2 (1 sin 2 x ) sin 2 xdx
0
π . 8
21.【解】
原式
π π π π 2 4 cos x cos x d x | cos x | sin xdx 0 0 2 2 2
1 1 x x e sin nx d x cos nx 0 0 e d n 1
1
27.【解】应填 0.
1 1 1 1 1 1 x e x cos nx e x cos nx d x 1 e cos n 0 e cos nx d x 0 n n n 0
1 n 2
1 (1 x ) n
n 3 n 1 n 2 0
3 n 2 3 n 1 2 故 lim nan lim 1 1 ( 1 e ) 1. n n n 1

重大高等数学上教材答案

重大高等数学上教材答案在高等数学教学中，教材答案是学生们学习和掌握数学知识的一种重要辅助工具。

通过查阅教材答案，学生可以及时了解自己的学习进展，并对自己的错题进行复习和纠正。

本文将为大家提供重大高等数学上教材的答案。

第一章：函数及其图像1.1 函数的概念题目1：判断下列是否为函数解答：a) 是函数，因为一个自变量x只对应一个唯一的函数值y。

b) 不是函数，因为一个自变量x对应两个函数值y1和y2。

...第二章：极限与连续2.1 极限的定义题目1：计算极限解答：a) 当x趋于0时，sinx/x的极限是1。

b) 当x趋于正无穷时，e^x/x的极限是正无穷。

...2.2 连续的概念题目2：判断函数在指定点是否连续解答：a) 函数在x=2处连续。

b) 函数在x=0处不连续，因为左极限不等于右极限。

...第三章：导数与微分3.1 导数的概念题目1：求函数的导数解答：a) f(x)的导数为f'(x)=2x。

b) g(x)的导数为g'(x)=3cosx。

...3.2 导数的运算法则题目2：利用导数的运算法则，求函数的导数解答：a) h(x)=3x^2，则h'(x)=6x。

b) f(x)=sinx+2x^3，则f'(x)=cosx+6x^2。

...第四章：定积分4.1 定积分的概念题目1：计算定积分解答：a) ∫[0,1] (2x+1)dx = 2∫[0,1] xdx + ∫[0,1] dx = 2(1/2) + 1 = 2。

b) ∫[-π,π] sinx dx = 0。

...4.2 定积分的计算方法题目2：利用定积分的计算方法，计算定积分解答：a) ∫[0,1] x^2 dx = 1/3。

b) ∫[1,2] (x^3+2x-1) dx = (1/4)x^4 + x^2 - x ∣[1,2] = (1/4)2^4 + 2^2 - 2 - ((1/4)1^4 + 1^2 - 1) = 5.5。

高等数学第3版答案

高等数学第3版答案【篇一：中国人民大学出版社(第四版)高等数学一第3章课后习题详解】t>习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值?。

（1）f(x)?2x2?x?3,[?1,1.5]；（2）f(x)?x?x,[0,3]。

知识点：罗尔中值定理。

2解：（1）∵f(x)?2x?x?3在[?1, 1.5]上连续，在(?1,1.5)内可导，且f(?1)?f(1.5)?0，∴（2）∵∴1?(?1,1.5)即为所求。

4f(x)?x?x在[0,3]上连续，在(0,3)内可导，且f(0)?f(3)?0， f(x)?x?x 在[0,3]上满足罗尔定理的条件。

令y?4x3?5x2?x?2在区间[0,1]上的正确性。

f(1)?f(0)1?032知识点：拉格朗日中值定理。

可验证定理的正确性。

1]连续，在(0,1)内可导，∴y?4x?5x?x?2在解：∵y?f(x)?4x?5x?x?2在[0,1]上满足拉格朗日中值定理的条件。

又区间[0,f?(?)?32f(1)??2,f(0)??2，f?(x)?12x2?10x?1，∴要使f(1)?f(0)5?0，只要：??(0,1)，1?012∴???1?012★3.已知函数。

解：要使的?。

f(2)?f(1)32?1★★4.试证明对函数总是位于区间的正中间。

证明：不妨设所讨论的区间为[a,b]，则函数y?px2?qx?r在[a,b]上连续，在(a,b)内可导，从而有f(b)?f(a)(pb2?qb?r)?(pa2?qa?r)b?ab?ab?a，结论成立。

2★5.函数f(x)?x3与g(x)?x2?1在区间[1,2]上是否满足柯西定理的所有条件？如满足，请求出满知识点：柯西中值定理。

思路：根据柯西中值定理的条件和结论，求解方程便为所求。

解：∵f(x)?x3及g(x)?x2?1在[1,2]上连续，在(1,2)内可导，且在(1,2)内的每一点处有g?(x)?2x?0，所以满足柯西中值定理的条件。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章第1节 1 B 。

2 A 。

3 C 。

4 B 。

5 C 。

6、证：设)1,0(1arctan1arcsin )(22∈-+-=x xx x x f 。

由于0)(='x f 。

所以C x f ≡)(，)1,0(∈x 。

为了确定C ，取21=x 得26331arctan23arcsin)21(πππ=+=+==f C 。

故)1,0(,21arctan1arcsin22∈=-+-x xx x π。

7、证：设nx x f =)(，则)(x f 在],[a b 上连续，在),(a b 内可导。

于是由拉格朗日定理知存在),(a b ∈ξ使得))((')()(b a f b f a f -=-ξ，即)(1b a n b a n nn-=--ξ，其中a b <<ξ。

因此有)()(11b a nab a b a nbn n n n -<-<---。

8、证：若b a =，显然有||0|arctan arctan |b a b a -==-。

若b a ≠，不妨设b a <。

设x x f arctan )(=，则)(x f 在],[b a 上连续，在),(b a 内可导。

由拉格朗日定理知存在),(b a ∈ξ，使得))(()()(b a f b f a f -'=-ξ，即)(11arctan arctan 2b a b a -+=-ξ，其中b a <<ξ。

因此b a b a b a -≤-+=-211arctan arctan ξ。

9、证：设)()(x xf x g =，则)(x g 在],[b a 上连续，在),(b a 内可导，且)(')()('x xf x f x g +=。

由拉格朗日中值定理知存在),(b a ∈ξ使得)()()(ξg a b a g b g '=--，即)()()()(ξξξf f ab a af b bf '+=--。

10、证：设x x f x F sin )()(=，则)(x F 在],[π0连续，在),(π0内可导，且0)()0(==πF F 。

由罗尔定理知存在),0(πξ∈使得0)('=ξF 。

而x x f x x f x F cos )(sin )(')('+=，故有0cos )(sin )('=+ξξξξf f 。

11、证：任取),(,00b a x x x ∈∆+，则由题设知x M xx f x x f ∆≤∆-∆+≤)()(000。

因此由夹挤定理知0)()(lim000=∆-∆+→∆xx f x x f x ，即0)(0='x f 由0x 的任意性知)('x f 在),(b a 内恒为零，因此)(x f 为常值函数。

12、证：设nx x g =)(，则)(x g 在0=x 的某邻域内具有n 阶导数，且0)0()0(')0()1(====-n gg g 。

对函数)(),(x g x f 在以0和x 为端点的区间上应用柯西中值定理可得 222221111111)1()()('')('')0(')(')0()()()(')()0()()0()()()()(---''==-'-'='='=--==n n nn n f g f g g f f n f g f g x g f x f x g x f xx f ξξξξξξξξξξ!)()()()0()()0()()()()()()()1(1)1()1(1)1(1)1(1)1(n fgf ggf f gf n n n n n n n n n n n n n n n n ξξξξξξξ==--===---------- ，其中1ξ在0和x 之间，2ξ在0和1ξ之间，……，n ξ在0和1-n ξ之间。

因此n ξ在0和x 之间，记x n θξ=)10(<<θ。

故有!)()()(n x fxx f n nθ=。

第2节 1B 。

2．0。

3 . 81-。

4 .1。

5 . 1。

6 . π2-e7 .xx x exx x xxx x xx ln )1ln()1(lim ln )1ln()1lim2ln sin 02sin 0+-=+-++→→（=1ln ln lim 2=⋅+→xx x x x x 。

8． ())0(1lim 21110f e e x xxx ≠=⎥⎥⎦⎤⎢⎢⎣⎡+-+→，故函数在0=x 处不连续。

9．1)0(210)0()(lim 2121)(lim )(lim 0020=''=-'-'=-'=-→→→f x f x f x x f x x x f x x x 。

10. 5,4=-=B A第3节：1．解：)())((!1))((''21))((')()(00)(200000x R x x x fn x x x f x x x f x f x f n nn +-++-+-+=)()1()1()1()1(12x R x x x n nn+--++-+--= 。

其中1211)1()1()1()1()!1()()(+++++--=-+=n n n n n n x x n fx R ξξ。

2)()0(!1)0(''21)0(')0()()(2x R x fn x f x f f x f n n n +++++= ()32()2!1!nn xxx x R x n =+++++- 。

其中11)1()!1()1()!1()()(++++++=+=n n n n xn e n x n fx R ξξξ。

3．当0→x 时，44~sinx x 。

又)(!4!21cos 442x o xxx ++-=，)()2(!2121422222x o xxex+-+-=-，所以121)](8121[)](241211[limsincos lim4442442422-=++--++-=-→-→xx o x xx o x x xe x x xx 。

4 .作变换令xt 1=，则有，原式21)](2[lim)1ln(lim2222=+--=+-=→→tt o tt t tt t t t 。

或用罗比达法则：原式21)1(21lim 2111lim)1ln(lim0020=+=+-=+-=→→→t t t t t t t t t 。

5 .31)(31lim tan )1(sin lim3332=+=+-→→xx o x xx x x x e x xx 。

6 .作变换xt 1=，则有，原式31)](611[)](611[lim)1()1(lim6/16/10=+--++=--+=→→t t o t t o t tt t t t 。

7．证明：首先注意到)(x f 在],[b a 上连续。

由题设知)(x f 在),(b a 内可导，且0)()(==b f a f ，这样由罗尔定理知至少存在一点),(1b a ∈ξ使得0)('1=ξf 。

又由题设知)('x f 在],[1b ξ上连续，在),(1b ξ内可导，且0)(')('1==b f f ξ，由罗尔定理知存在),(12b ξξ∈使得0)(''2=ξf 。

依此类推可知，存在b n <-1ξ使得0)(1)1(=--n n fξ。

由于)()1(x fn -在],[1b n -ξ上连续，在),(1b n -ξ内可导及0)()()1(1)1(==---b ffn n n ξ，所以据罗尔定理知存在),(1b n -∈ξξ使得0)()(=ξn f 。

8．证：设],[,ln )(b a x x x F ∈=。

显然)(x F 在],[b a 上连续，在),(b a 内可导，且01)(≠='xx F 。

这样对函数)(),(x F x f 在],[b a 上应用柯西中值定理知，至少存在一点),(b a ∈ξ使得)(')(')()()()(ξξF f b F a F b f a f =--⇒()()'()ln ln 1/f b f a f b aξξ-=-。

即ab f a f b f ln)(')()(ξξ=-。

第4节 1D 2D 3A 4 A 5 当x <-1时，y '>0,函数单调增加；当-1<x <3时，y '<0,函数单调减小；当x >3时，y '>0,函数单调增加；6．当x <-1时，y '<0,函数单调减小；当-1<x <1，y '>0,函数单调增加；当x >1时，y '<0,函数单调减小；7．证：设221)1ln(1)(x x x x x f +-+++=，则f(x)在[0,+∞)上连续，在(0,+∞)内可导，且f(0)=0,0)1ln()(2>++='x x x f ，所以f(x)在[0，+∞)上单调递增，当x>0时，f(x)>f(0)=0，即221)1ln(1x x x x +>+++8．证明：设361sin )(x x x x f +-=，则f(x)在[0,+∞)上有连续导数，且f(0)=0,2211cos )(x x x f +-=',且0)0(='f ，x x x f +-=''sin )(，且0)0(=''f ，01cos )(≥+-='''x x f ，所以)(x f ''在[0,+∞)单调递增，当x>0时，0)(>''x f ,从而0)0()(='>'f x f ，所以f(x)在[0,+∞)单调递增，f(x)>f(0)，即361sin x x x ->9．证明：设f(t)=e t ，则f '(t)=e t ，f "(t)=e t >0，函数图像是凹的，所以有⎪⎭⎫⎝⎛+>+22)()(y x f y f x f ，即22yx y x ee e +>+10．解：设f(x)=lnx-ax ，f(x)在(0,+∞)内连续，且可导。

0x1)x (f ,a x1)x (f 2<-=''-='。

令f '(x)=0，得a1x =。

1a ln 1a 1ln a 1f --=-=⎪⎭⎫⎝⎛是最大值。