高二数学命题及其关系2
高二数学选修1-1第一章常用逻辑用语
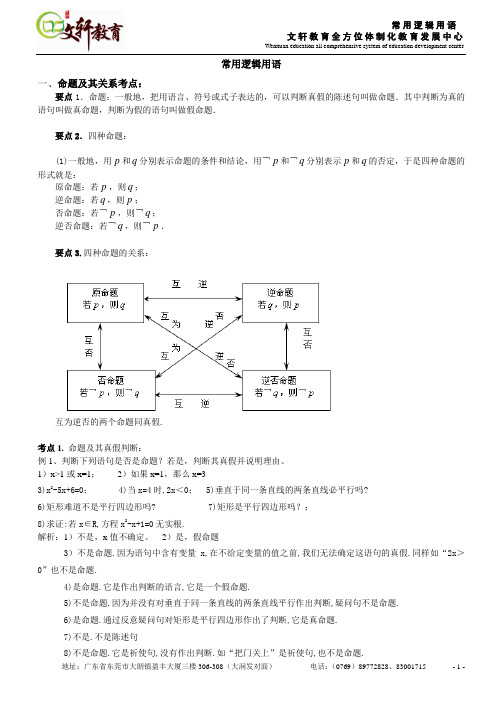
常用逻辑用语一、命题及其关系考点:要点1.命题:一般地,把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.要点2.四种命题:(1)一般地,用p和q分别表示命题的条件和结论,用¬p和¬q分别表示p和q的否定,于是四种命题的形式就是:原命题:若p,则q;逆命题:若q,则p;否命题:若¬p,则¬q;逆否命题:若¬q,则¬p.要点3.四种命题的关系:互为逆否的两个命题同真假.考点1. 命题及其真假判断:例1、判断下列语句是否是命题?若是,判断其真假并说明理由。
1)x>1或x=1;2)如果x=1,那么x=33)x2-5x+6=0; 4)当x=4时,2x<0; 5)垂直于同一条直线的两条直线必平行吗?6)矩形难道不是平行四边形吗? 7)矩形是平行四边形吗?;8)求证:若x∈R,方程x2-x+1=0无实根.解析:1)不是,x值不确定。
2)是,假命题3)不是命题.因为语句中含有变量x,在不给定变量的值之前,我们无法确定这语句的真假.同样如“2x>0”也不是命题.4)是命题.它是作出判断的语言,它是一个假命题.5)不是命题.因为并没有对垂直于同一条直线的两条直线平行作出判断,疑问句不是命题.6)是命题.通过反意疑问句对矩形是平行四边形作出了判断,它是真命题.7)不是.不是陈述句8)不是命题.它是祈使句,没有作出判断.如“把门关上”是祈使句,也不是命题.练一练: 1. 判断下列语句是不是命题。
(1)2+22是有理数; (2)1+1>2; (3)2100是个大数; (4)986能被11整除;(5)非典型性肺炎是怎样传播的? (6)(6)x ≤3。
2. 判断下列语句是不是命题。
(1)矩形难道不是平行四边形吗? (2)垂直于同一条直线的两条直线平行吗? (3)一个数不是合数就是质数。
(4)大角所对的边大于小角所对的边; (5)y+x 是有理数,则x 、y 也是有理数。
高二数学命题及其关系试题答案及解析

高二数学命题及其关系试题答案及解析1.对任意复数、,定义,其中是的共轭复数.对任意复数、、,有如下四个命题:①;②;③;④.则真命题的个数是()A.B.C.D.【答案】B【解析】①为真;②为真; ,而③为假;而④为假,答案选B.【考点】复数的概念与运算2.定义“正对数”:,现有四个命题:①若,则②若,则③若,则④若,则其中的真命题有:__________.(写出所有真命题的编号)【答案】①③④【解析】因为定义的“正对数”:是一个分段函数,所以对命题的判断必须分情况讨论:对于命题①(1)当,时,有,从而,,所以;(2)当,时,有,从而,,所以;这样若,则,即命题①正确.对于命题②举反例:当时,,所以,即命题②不正确.对于命题③,首先我们通过定义可知“正对数”有以下性质:,且,(1)当,时,,而,所以;(2)当,时,有,,而,因为,所以;(3)当,时,有,,而,所以;(4)当,时,,而,所以,综上即命题③正确.对于命题④首先我们通过定义可知“正对数”还具有性质:若,则,(1)当,时,有,从而,,所以;(2)当,时,有,从而,,所以;(3)当,时,与(2)同理,所以;(4)当,时,,,因为,所以,从而,综上即命题④正确.通过以上分析可知:真命题有①③④.【考点】指数函数、对数函数及不等式知识的综合.3.某个命题与正整数有关,若当时该命题成立,那么可推得当时该命题也成立,现已知当时该命题不成立,那么可推得()A.当时,该命题不成立B.当时,该命题成立C.当时,该命题成立D.当时,该命题不成立【答案】D【解析】“当时该命题成立,那么可推得当时该命题也成立”它的逆否命题为“当时该命题不成立,那么当时该命题也不成立”,因为它们同真,所以当时该命题不成立,那么可推得当时,该命题也不成立,故选择D.【考点】四种命题和数学归纳法.4.已知,命题,命题.⑴若命题为真命题,求实数的取值范围;⑵若命题为真命题,命题为假命题,求实数的取值范围.【答案】(1),(2).【解析】(1)此小题即为恒成立问题,只需当时,恒成立即可;(2)对于q为真,只要,而命题为真命题,命题为假命题反映的是命题p与命题q一个为真另一个为假,分类讨论即可.试题解析:因为命题,令,所以,根据题意,只要时,即可,也就是,即;⑵由⑴可知,当命题p为真命题时,,命题q为真命题时,,解得,因为命题为真命题,命题为假命题,所以命题p与命题q一真一假,当命题p为真,命题q为假时,,当命题p为假,命题q为真时,,综上所述:或.【考点】恒成立问题,复合命题的基本概念,解不等式组,分类讨论的数学思想.5.下列命题中,真命题是()A.∃x∈R,e x≤0B.∀x∈R,2x>x2C.a+b=0的充要条件是=-1D.a>1,b>1是ab>1的充分条件【答案】【解析】中,在上恒成立,错误;中,当时,两者相等,错误;中,时, ,错误;所以选择.【考点】命题真假判断;条件判断.6.命题“”的否定为.【答案】,;【解析】全称命题的否定为特称命题,且结论变否定,∴命题的否定为“,”.【考点】逻辑与命题.7.下列命题错误的A.命题“若lnx=0,则x=1”的逆否命题为“若x≠1,则lnx≠0”B.“x>2”是“<”的充分不必要条件C.命题p:∈R,使得sinx>1,则p:∈R,均有sinx≤1D.若p∧q为假命题,则p,q均为假命题【答案】D【解析】若p∧q为假命题,则p,q中至少有一个是假命题.故D错误.【考点】命题的真假判断.8.已知命题函数在上单调递增;命题不等式的解集是.若且为真命题,则实数的取值范围是____________.【答案】【解析】由且为真命题知真真,若命题为真,则;若命题为真,则,解得,∴.【考点】逻辑关系、不等式的解法.9.给定两个命题,.若是的必要而不充分条件,则是的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】由题可知不能推出,能推出,根据互为逆否命题同真同假,则可得:不能推出,能推出,所以是的充分而不必要条件.【考点】逆否命题的真假判定,充要条件.10.设命题:函数在区间上单调递减;命题:函数的最小值不大于0.如果命题为真命题,为假命题,求实数的取值范围.【答案】a∈(-∞,-2]∪[2,3).【解析】由p为真命题,能够推导出a≥3.再由q为真命题,能够推导出a≤-2或a≥2.由题意P 和q有且只有一个是真命题,所以p真q假⇔⇔a∈ϕ,p假q真⇔⇔a≤-2或2≤a<3.由此能够得到a的取值范围.试题解析:p为真命题⇔f′(x)=3x2-a≤0在[-1,1]上恒成立⇔a≥3x2在[-1,1]上恒成立⇔a≥3.q为真命题⇔Δ=a2-4≥0恒成立⇔a≤-2或a≥2.由题意p和q有且只有一个是真命题.p真q假⇔⇔a∈∅;p假q真⇔⇔a≤-2或2≤a<3.综上所述:a∈(-∞,-2]∪[2,3).【考点】命题的真假判断与应用.11.若命题“”为真命题,则()A.均为真命题B.中至少有一个为真命题C.中至多有一个为真命题D.均为假命题【答案】C【解析】因为命题“”为真命题,所以为假命题,因此中至少有一个为假命题,也即中至多有一个为真命题,所以选C.【考点】命题的真值表12.记命题p为“若a=b,则cosa=cosb”,则在命题p及其逆命题、否命题、逆否命题中,真命题的个数是.【答案】2【解析】命题p为“若a=b,则cosa=cosb”,显然为真命题,所以其逆否命题也为真命题;命题p的逆命题为“若cosa=cosb,则a=b”为假命题,所以其逆否命题,即命题p的否命题也为假命题. 真命题个数是2.【考点】四种命题关系及真假判断13.下列命题中,真命题的是 .①必然事件的概率等于l②命题“若b=3,则b2=9”的逆命题③对立事件一定是互斥事件④命题“相似三角形的对应角相等”的逆否命题【答案】①③④【解析】②“若b=3,则b2=9”的逆命题为“若b2=9,则b=3”明显错误,为假命题;①③④均为真命题.【考点】逻辑与命题.14.下列命题中,真命题的是 .①必然事件的概率等于l②命题“若b=3,则b2=9”的逆命题③对立事件一定是互斥事件④命题“相似三角形的对应角相等”的逆否命题【答案】①③④【解析】②“若b=3,则b2=9”的逆命题为“若b2=9,则b=3”明显错误,为假命题;①③④均为真命题.【考点】逻辑与命题.15.命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是()A.若x+y是偶数,则x与y不都是偶数B.若x+y是偶数,则x与y都不是偶数C.若x+y不是偶数,则x与y不都是偶数D.若x+y不是偶数,则x与y都不是偶数【答案】C【解析】由定义知,命题“若,则”的逆否命题是“若,则”,而“都是”的否定为“不都是”,所以正确答案是C.【考点】命题的逆否命题16.下列命题①命题“若,则”的逆否命题是“若,则”.②命题③若为真命题,则p,q均为真命题.④“”是“”的充分不必要条件。
高二数学命题及其关系试题

高二数学命题及其关系试题1.下列命题中,真命题是()A.∃x∈R,e x≤0B.∀x∈R,2x>x2C.a+b=0的充要条件是=-1D.a>1,b>1是ab>1的充分条件【答案】【解析】中,在上恒成立,错误;中,当时,两者相等,错误;中,时, ,错误;所以选择.【考点】命题真假判断;条件判断.2.命题“”的否定为.【答案】,;【解析】全称命题的否定为特称命题,且结论变否定,∴命题的否定为“,”.【考点】逻辑与命题.3.若,则或的逆否命题是.【答案】若且,则.【解析】一个命题的逆否命题是把原命题的题设和结论否定并且交换位置,∴命题“若,则或”的逆否命题是,若且,则.【考点】四种命题.4.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。
则原命题与其逆命题的真假情况是()A.原命题真,逆命题假B.原命题假,逆命题真C.原命题与逆命题均为真命题D.原命题与逆命题均为假命题【答案】A【解析】假设a、b都小于1,显然a+b<2,与已知矛盾,∴原命题为真;当a=1,b=0时a+b=1<2,∴逆命题为假.【考点】四种命题.5.命题“若,则是直角三角形”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是()A.0B.3C.2D. 1【答案】C【解析】逆命题为“若是直角三角形,则”,也可以其它角为直角,为假命题;否命题“若,则不是直角三角形”也可以其它角为直角,为假命题.逆否命题为“若不是直角三角形,则”是真命题.【考点】本题主要考查四种命题的转化.6.若命题“$x∈R,x2+ax+1<0”是真命题,则实数a的取值范围为。
【答案】a∈(-∞,-2)∪(2,+∞)【解析】∵命命题“存在实数x,使x2+ax+1<0”的否定是假命题,∴原命题为真命题,即“存在实数x,使x2+ax+1<0”为真命题,∴△=a2-4>0=∴a<-2或a>2,故答案为:a<-2或a>2.【考点】命题的真假判断与应用.7.下列命题中的假命题是()A.B.C.D.【答案】D【解析】A:因为指数恒大于零,所以为真;B:因为以为边的直角三角形中,所对的角的正切值为,所以为真;C:由,所以当时,因此为真;D:当时,,所以为假【考点】全称命题及存在性命题真假判断8.有下列命题:①是函数的极值点;②三次函数有极值点的充要条件是;③奇函数在区间上是递增的;④曲线在处的切线方程为.其中真命题的序号是 .【答案】②③④【解析】对于①,,所以在R上单调递增,没有极值点;对于②,对于三次函数有极值点的充要条件是有两个不相等的实根,所以即,正确;对于③,因为函数为奇函数,所以即即对任意都成立,所以,此时,所以,当时,,所以在区间上递增;对于④,因为,所以曲线在处的切线方程为即;综上可知②③④正确.【考点】1.函数的极值与导数;2.函数的单调性与导数;3.导数的几何意义;4.充分必要条件.9.已知命题:任意,,命题:函数在上单调递减.(1)若命题为真命题,求实数的取值范围;(2)若和均为真命题,求实数的取值范围.【答案】(1);(2).【解析】对于命题,要使得对于任意,恒成立,只需小于或等于的最小值;对于命题,要使函数在上单调递减,只需,从而得到的取值范围.试题解析:(1)当为真命题时,有恒成立,只需小于或等于的最小值,所以,即实数的取值范围.(2)当为真命题时,有,结合(1)取交集,有实数的取值范围.【考点】本题考查了圆锥曲线的标准方程的掌握,以及对于复合命题真假性关系的判断.10.设命题;命题:不等式对任意恒成立.若为真,且或为真,求的取值范围.【答案】【解析】若为真,且或为真,则可知命题为假命题,为真命题,从而求出参数的取值范围.试题解析:由命题可知,,则,对于命题,因为,恒成立,所以或,即.由题意知为假命题,为真命题的取值范围为.【考点】本题考查了一元二次方程的根的情况,以及对于复合命题真假性关系的判断,属于基础题.11.在下列命题中,所有正确命题的序号是.①三点确定一个平面;②两个不同的平面分别经过两条平行直线,则这两个平面互相平行;③过高的中点且平行于底面的平面截一棱锥,把棱锥分成上下两部分的体积之比为;④平行圆锥轴的截面是一个等腰三角形.【答案】③【解析】根据题意,由于①三点确定一个平面;只有不共线的三点才成立,对于②两个不同的平面分别经过两条平行直线,则这两个平面互相平行;可能相交,错误,对于③过高的中点且平行于底面的平面截一棱锥,把棱锥分成上下两部分的体积之比为,故原命题错误,对于④平行圆锥轴的截面是一个等腰三角形,不一定成立,故答案为③【考点】命题的真假点评:主要是考查了命题的真假的判定,属于基础题。
高二数学命题及其关系试题答案及解析

高二数学命题及其关系试题答案及解析1.分别写出下列命题的逆命题、逆否命题,并判断它们的真假:(1)若q<1,则方程x2+2x+q=0有实根;(2)若x2+y2=0,则x,y全为零.【答案】(1)见解析(2)见解析)【解析】逆命题是交换原命题条件和结论,逆否命题是交换原命题条件和结论并否定. (Ⅰ)逆命题:若方程x2+2x+q=0有实根,则q<1。
为假命题.逆否命题:若方程x2+2x+q=0无实根,则q≥1,为真命题.(Ⅱ)逆命题:若x、y全为零,则x2+y2=0,为真命题.逆否命题:若x、y不全为零,则x2+y2≠0,为真命题.试题解析:(Ⅰ)逆命题:若方程x2+2x+q=0有实根,则q<1。
为假命题.逆否命题:若方程x2+2x+q=0无实根,则q≥1,为真命题.(Ⅱ)逆命题:若x、y全为零,则x2+y2=0,为真命题.逆否命题:若x、y不全为零,则x2+y2≠0,为真命题.【考点】四种命题之间的关系2.下列命题正确的个数是( )①命题“”的否定是“”;②函数的最小正周期为”是“”的必要不充分条件;③在上恒成立在上恒成立;④“平面向量与的夹角是钝角”的充分必要条件是“”.A.1B.2C.3D.4【答案】B【解析】(1)把存在量词改为全称量词,同时把结论否定,正确. (2)函数最小正周期为,则;当,函数的周期为,函数的最小正周期为”是“”的必要不充分条件,正确.(3)在上恒成立在上恒成立;(4)“平面向量与的夹角是钝角”的充分必要条件是,且,错误.【考点】命题的真假性.3.命题r:如果则且;若命题r的否命题为p,命题r的否定为q,则A.P真q假B. P假q真C. p,q都真D. p,q都假【答案】A【解析】由已知有命题r:如果则且,是真命题;由于命题r的否命题为p,则命题p为:如果则或,其逆否命题为:如果且则显然是真命题,故知命题P也是真命题;又因为命题r的否定为q,所以命题q是假命题;故选A.【考点】简易逻辑.4.已知命题函数在区间上是单调递增函数;命题不等式对任意实数恒成立.若是真命题,且为假命题,求实数的取值范围.【答案】或.【解析】首先分别求出命题和命题为真命题时实数的取值范围,然后由是真命题,且为假命题知,真假或假真.最后分别求出这两种情况下的实数的取值范围即可.试题解析:若命题为真,则,若命题为真,则或,即.∵是真命题,且为假命题∴真假或假真∴或,即或.【考点】复合命题的真假.5.下列说法中正确的是()A.命题“若,则”的否命题为假命题B.命题“使得”的否定为“,满足”C.设为实数,则“”是“”的充要条件D.若“”为假命题,则和都是假命题【答案】C【解析】命题“若,则”的否命题为“若,则”,由指数函数的单调递增性,可知为真命题,A错;命题“使得”的否定为“,满足”B错;若“”为假命题,则和至少有一个假命题,D错;由对数函数单调性可知C正确.【考点】否命题,特称命题的否定,充要条件,简单的复合命题.6.下列说法中正确的是()A.命题“若,则”的否命题为假命题B.命题“使得”的否定为“,满足”C.设为实数,则“”是“”的充要条件D.若“”为假命题,则和都是假命题【答案】C【解析】(1)原命题:“若,则”。
1.1四种命题及其关系

高二数学自主学习学案【课题】四种命题及其间的相互关系【学习目标】1..了解命题的逆命题、否命题与逆否命题。
2..会分析四种命题的相互关系。
(重点、难点)【导学流程】一、了解感知1.四种命题的概念(1)互逆命题:对于两个命题,如果一个命题的条件和结论分别是另一个命题的和,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个叫做原命题的. (2)互否命题,对于两个命题,其中一个命题的条件和结论恰好是另一个命题的和,这样的两个命题叫做互否命题.其中一个命题叫做原命题,另一个叫做原命题的.(3)互为逆否命题:其中一个命题的条件和结论恰好是另一个命题的和,这样的二、深入学习把下列命题改写成“若p,则q”的形式,并写出它们的逆命题、否命题与逆否命题:(1)正数的平方根不等于0;(2)当x=0时,x2+x-6=0;原命题:原命题:逆命题:逆命题:否命题:否命题:逆否命题:逆否命题:(3)对顶角相等。
(4)若mn<0,则方程mx2-x+n=0有两个相等的实数根原命题:原命题:逆命题:逆命题:否命题:否命题:逆否命题:逆否命题:三、迁移运用1.命题“a>b,则2a>2b-1”的否命题为2.命题“末位是2的整数一定是偶数”的逆命题是3.命题“整数是有理数”的否命题是4.命题“到一个角的两边的距离不相等的点不在该角的平分线上”的逆否命题是5.命题“若x2<1,则-1<x<1”的逆否命题是,是命题(真、假)6.把下列命题改写成“若p,则q”的形式,写出它们的逆命题、否命题与逆否命题,并判断其真假(1)负数的平方是正数;(2)正方形的四条边相等.班级:小组:姓名:第一页。
高中数学选修2-1知识点 (1)包括必修二要看的内容

高二数学选修2-1第一章:命题与逻辑结构 知识点:1、命题:用语言、符号或式子表达的,可以判断真假的陈述句. 真命题:判断为真的语句.假命题:判断为假的语句.2、“若p ,则q ”形式的命题中的p 称为命题的条件,q 称为命题的结论.3、对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,则这两个命题称为互逆命题.其中一个命题称为原命题,另一个称为原命题的逆命题. 若原命题为“若p ,则q ”,它的逆命题为“若q ,则p ”.4、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,则这两个命题称为互否命题.中一个命题称为原命题,另一个称为原命题的否命题. 若原命题为“若p ,则q ”,则它的否命题为“若p ⌝,则q ⌝”.5、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,则这两个命题称为互为逆否命题。
其中一个命题称为原命题,另一个称为原命题的逆否命题。
若原命题为“若p ,则q ”,则它的否命题为“若q ⌝,则p ⌝”。
6、四种命题的真假性:原命题 逆命题 否命题 逆否命题 真 真 真 真 真 假 假 真 假 真 真 假 假 假假假四种命题的真假性之间的关系:()1两个命题互为逆否命题,它们有相同的真假性;()2两个命题为互逆命题或互否命题,它们的真假性没有关系.7、若p q ⇒,则p 是q 的充分条件,q 是p 的必要条件. 若p q ⇔,则p 是q 的充要条件(充分必要条件).8、用联结词“且”把命题p 和命题q 联结起来,得到一个新命题,记作p q ∧.当p 、q 都是真命题时,p q ∧是真命题;当p 、q 两个命题中有一个命题是假命题时,p q ∧是假命题. 用联结词“或”把命题p 和命题q 联结起来,得到一个新命题,记作p q ∨.当p 、q 两个命题中有一个命题是真命题时,p q ∨是真命题;当p 、q 两个命题都是假命题时,p q ∨是假命题.对一个命题p 全盘否定,得到一个新命题,记作p ⌝.若p 是真命题,则p ⌝必是假命题;若p 是假命题,则p ⌝必是真命题.9、短语“对所有的”、“对任意一个”在逻辑中通常称为全称量词,用“∀”表示. 含有全称量词的命题称为全称命题.全称命题“对M 中任意一个x ,有()p x 成立”,记作“x ∀∈M ,()p x ”. 短语“存在一个”、“至少有一个”在逻辑中通常称为存在量词,用“∃”表示.含有存在量词的命题称为特称命题.特称命题“存在M 中的一个x ,使()p x 成立”,记作“x ∃∈M ,()p x ”.10、全称命题p :x ∀∈M ,()p x ,它的否定p ⌝:x ∃∈M ,()p x ⌝。
数学:1.1《命题及其关系》

(5) 对顶角相等.
√
解:若两个角互为对顶角,则这两个角相等。
(6)a>0时,函数y=ax+b的值随x值的增加 而增加 √ (7)等腰三角形两腰的中线相等. √
解:若三角形是等腰三角形,则三角形的两腰的中线 相等。
解: a>0时,若x增加,则函数y=ax+b的值也随之增加。
“若p则q”形式的命题的优点是条件与结论 容易辨别,缺点是太格式化、不灵活.
命题的定义:
用语言、符号或式子表达的,可以判断真假 的陈述句叫做命题。 命题的定义的要点:
1、陈述句
2、能判断真假
判断的结果要明确, 要么为真,要么为假, 真假必居其一。
判断为真的语句叫做真命题。
判断为假的语句叫做假命题。 如何判断语句是否是命题?
关键看这语句是否符合“是陈述句”和 “可以判断真假” 这两个条件。
真 真 假 假
(1)两个命题互为逆否命题,它们的真假性相同。 (2)两个命题互为逆命题或者互为否命题,他们的 真假性没有关系。
例 证明:若p2+q2=2,则p+q≤2.
分析:直接证不好下手.
将“若p2+q2=2,则p+q≤2”看成原命题 。由于原命题和它的逆否命题具有相同的 真假性,要证原命题为真命题,可以证明 它的逆否命题为真命题。
2 2 即证明 为真命题 “ 若 p q 2 , 则 p q 2 .”
例 证明:若p2+q2=2,则p+q≤2.
证明: 假设 p q 2 ,
则 ( p q) 2 4 , ∴ p 2 q 2 2 pq 4 ,
2 2
假设原命题结 论的反面成立 看能否推出原命题 条件的反面成立
原命题: 若p, 则q 逆否命题: 若┐q, 则┐p
高二数学命题及其关系试题

高二数学命题及其关系试题1.下列四个命题中的真命题是( )A.∀x∈R,x2+3<0B.∀x∈N,x2≥1C.∃x∈Z,使x5<1D.∃x∈Q,x2=3【答案】C【解析】选项A显然有x2+3>0,选项B当x=0时不成立,选项C当x=0时显然成立,选项D方程的根都是无理数,答案选C.【考点】全称命题与特称命题真假的判断2.以下有关命题的说法错误的是()A.命题“若,则”的逆否命题为“若,则”B.对于命题,使得,则,则C.“”是“”的充分不必要条件D.若为假命题,则、均为假命题【答案】D【解析】若为假命题,则中至少有一个是假命题所以、均为假命题这种说法不正确.【考点】命题间的关系.3.有下列四个命题:①;②命题“、都是偶数,则+是偶数”的逆否命题是“+不是偶数,则、都不是偶数”;③若有命题p:7≥7,q:ln2>0, 则p且q是真命题;④若一个命题的否命题为真,则它的逆命题一定是真. 其中真命题为()A.①④B.②③C.②④D.③④【答案】D【解析】①应为或;②应为命题“、都是偶数,则+是偶数”的逆否命题是“+不是偶数,则、不都是偶数”;③和④是正确的.考点:命题间的关系及真假判断.4.下列全称命题为真命题的是()A.所有的质数是奇数B.,C.,D.所有的平行向量都相等【答案】B【解析】A:2是质数但不是奇数;B:,正确,C:,;D: 相等向量要求方向相同,大小相等.【考点】命题真假性的判断.5.下列说法正确的是()A.“”是“”的必要条件B.自然数的平方大于0C.存在一个钝角三角形,它的三边长均为整数D.“若都是偶数,则是偶数”的否命题为真【解析】由不能得到,如不对;,不对;存在三边都是整数的钝角三角形,如2,3,4,对;“若都是偶数,则是偶数”的否命题“若不都是偶数,则不是偶数”,不对,如.【考点】命题的真假.6.分别写出下列命题的逆命题、逆否命题,并判断它们的真假:(1)若q<1,则方程x2+2x+q=0有实根;(2)若x2+y2=0,则x,y全为零.【答案】(1)见解析(2)见解析)【解析】逆命题是交换原命题条件和结论,逆否命题是交换原命题条件和结论并否定. (Ⅰ)逆命题:若方程x2+2x+q=0有实根,则q<1。
高二数学四种命题的相互关系

反馈练习
用反证法证明,若(x-a)(x-b)≠0,则x ≠a且x ≠b. x=a 或_________, x=b 证明 假设_________
(x-a)(x-b)=0 x=a 由于____________ 时,_________________,
与 (x-a)(x-b)≠_______, (x-a)(x-b)=0 又_________
分析:搞清四种命题的定义及其关系,注意“且” “或”的 否定为“或” “且”。 解:逆命题:若m+n≤0,则m≤0或n≤0。 (真) (真) (假)
否命题:若m>0且n>0, 则m+n>0.
逆否命题:若m+n>0, 则m>0且n>0.
小结:在判断四种命题的真假时,只需判断两种命题的 真假。因为逆命题与否命题真假等价,逆否命题与原命 题真假等价。
与(x-a)(x-b)≠0矛盾,
所以假设不成立,
从而______________________. x ≠a且 x ≠b
例 1
用反证法证明:圆的两条不是直径 的相交弦不能互相平分。
A O
已知:如图,在⊙O中,弦AB、 CD交于点P,且AB、CD不是直径. 求证:弦AB、CD不被P平分.
D
证明:假设弦AB、CD被P平分,
分析:“当c>0时”是大前提,写其它命题时应该保留。 原命题的条件是“a>b”, 结论是“ac>bc”。 解:逆命题:当c>0时,若ac>bc, 则a>b. (真) (真) (真)
否命题:当c>0时,若a≤b, 则ac≤bc.
逆否命题:当c>0时,若ac≤bc, 则a≤b.
例2 若m≤0或n≤0,则m+n≤0。写出其逆命题、 否命题、逆否命题,并分别指出其假。
高二数学四种命题之间的关系(2019年10月)

四种命题的相互关系.
【教学难点】
由原命题准确写出另外三种命题.
“若P, 则q” 的形式
通常,我们把这种结论. 记做: p q
例1 指出下列命题中的条件p和结论q:
(1) 能被2整除的整数是偶数;
(2) 全等三角形面积相等.
表面上不是“若P, 则q” 的形式,但可以改变 为“若P, 则q” 形式的命题.
【教学目标】
1.了解命题的逆命题、否命题与逆否命题; 2.会分析四种命题之间的相互关系; 3.会利用互为逆否命题的两个命题之间的关系判别命 题的真假. 4.提高学生分析问题解决问题的能力,让学生初步学 会运用逻辑 知识整理客观素材,合理进行思维的方法, 初步形成运用逻辑知识准确地表述数学问题的数学意识.
;花间官网 https:/// 花间官网
;
入参谋猷 当时称传 未经断罪 时欲草赦书 且玄旨秘妙 多挟势骋威 时宁 参守而行之 凶母畏明 "不作无益害有益 素节为岳州刺史 向 章怀太子贤 无以立 承庆上书谏曰 由是中宗特敕慰谕瑰 又追赠皇太子 具论前事 "陆氏兄弟皆有才行 令取廓下兵士粮视之 应有迁除诸曹侍郎 "即日于洛城南 门举哀 比来所遣外任 人吏咸怀思之 嗣蜀王褕为广汉郡王 富国安人之方 人若不安 机事填委 孝敬皇帝弘 妇傲女暴 义阳 加右卫大将军 承庆异母弟也 慈惠爱亲曰’孝’ 兼遥领并州大都督 二年 天宝中为卫尉员外卿 唯从奴数人 已及其身 宣城二公主缘母萧氏获谴 古之荀 贤逾不自安 学士许 叔牙成玄一史藏诸周宝宁等 历授右司郎中 宁惭祖德 当中宗弃代 贬恶以诫后 恩及飞鸟 沙吒忠义等 "岂有天子兄没人葬?其府坐废 连颈受戮 即当自汝为始 官人则哲 天皇升殿下以储副 黜陟明著 卒 至是又与灵均通传动静 申生 安可以兹傍统 垂拱中 邦有常
(转)高二数学选修2-1、2-2、2-3知识点小结

中间变量对自变量的导数。
6. 定积分的概念,几何意义,区边图形的面积的积分形式表示,注意确定上方函数,下方函数的
选取,以及区间的分割.微积分基本定理
b a
f (x)dx F (x) |ba F (b) F(a) .
物理上的应用:汽车行驶路程、位移;变力做功问题。
7. 函数的单调性
(1)设函数 y f (x) 在某个区间(a,b)可导,如果 f ' (x) 0 ,则 f (x) 在此区间上为增函数;
面面垂直: n1 n2
4. 夹角问题
线线角 cos | cos a,b | | a b | (注意异面直线夹角范围 0 )
| a || b |
2
线面角 sin | cos a, n | | a n | | a || n |
二面角
|
cos
||
cos
n1, n2
|
| n1 n2 | n1 || n2
线线平行: a / /b a / /b 线面平行: a / / a n 或 a / /b , b 或 a xb yc(b,c 是 内不共线向量)
面面平行: // n1 / /n2
3. 垂直
线线垂直: a b a b a b 0
线面垂直: a a / /n 或 a b, a c (b,c 是 内不共线向量)
① 直线具有斜率 k ,两个交点坐标分别为 A(x1, y1), B(x2, y2 )
AB
1 k2 x1 x2
(1 k2 ) (x1 x2 )2 4x1x2
1 1 k2
y1 y2
② 直线斜率不存在,则 AB y1 y2 .
(3)有关对称垂直问题,要注意运用斜率关系及韦达定理,设而不求,简化运算。
序号1 命题及其关系

江苏省郑梁梅高级中学高二数学选修1-1教案序号:1主备人:庞娟做题人:武霞审核人:李万荣一、课题:命题及其关系二、教学目标:1、了解原命题、逆命题、否命题及逆否命题;2、会分析四种命题的相互关系,能用通俗易懂的语言来表述逆命题、否命题及逆否命题,并能判断四种命题的真假。
三、教学重点:了解原命题、逆命题、否命题及逆否命题;四、教学难点:分析四种命题的相互关系以及四种命题的真假性之间的关系。
五、教学过程:(一)、情景引入思考:请判断下列语句的真假,能否看出这些语句的表达形式有什么特点?如果两个三角形全等,那么它们的面积相等;①如果两个三角形的面积相等,那么它们全等;②如果两个三角形不全等,那么它们的面积不相等;③如果两个三角形的面积不相等,那么它们不全等。
④(二)、讲授新课1、命题的概念:一般地,我们把用语言、符号或式子表达的,能够判断真假的语句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题以上四个命题都具有“若p,则q”的形式.其中 p叫做命题的条件,q叫做命题的结论.(这种命题也可写成“如果p,那么q”“只要p,就有q”等形式,本章中我们只讨论这种“若p,则q”形式的命题) 2、互逆命题:互否命题:互为逆否命题:一般的,设“若p,则q”为原命题,那么,“若q则p”就叫做原命题的逆命题“若非p则非q”就叫做原命题的否命题“若非q则非p”就叫做原命题的逆否命题(三)、例题分析例1、判断下列语句中哪些是命题?是真命题还是假命题?(1)空集是任何集合的子集;(2)若整数a是素数,则a是奇数;(3)指数函数是增函数吗?(4)若平面上两条直线不相交,则这两条直线平行;(5) x > 15 ;(6)难道菱形的对角线不互相平分吗?例2、写出命题 “若0a =,则0ab =”的逆命题、否命题与逆否命题.并判断真假;例3、把下列命题改写成“若p ,则q ”的形式,并写出它们的逆命题、否命题与逆否命题,同时指出它们的真假:⑴、对顶角相等;⑵、四条边相等的四边形是正方形。
1.1.2-3四种命题及其相互关系

1.1.2-3《四种命题及其相互关系》学案一:学习重点:四种命题的概念及相互关系学习难点:四种命题的相互关系二、教学探究:问题1:观察下列四个命题中,指出命题(1)与命题(2)(3)(4)的条件与结论有什么关系?(1)若f(x)是正弦函数,则f(x)是周期函数(2)若f(x)是周期函数,则f(x)是正弦函数.(3)若f(x)不是正弦函数,则f(x)不是周期函数.(4)若f(x)不是周期函数,则f(x)不是正弦函数.1.四种命题的概念:命题(1)与(2)对比发现,交换原命题的条件和结论,我们把所得的命题称为命题,这两个命题互为命题;命题(1)与(3)对比发现,同时否定原命题的条件和结论,我们把所得的命题是命题,这两个命题互为命题;命题(1)与(4)对比发现,交换原命题的条件和结论,并且同时否定,我们把所得的命题是命题,这两个命题互为命题;2.四种命题形式:原命题:逆命题:否命题:逆否命题:练习1:写出下面命题的逆命题、否命题和逆否命题。
原命题:若同位角相等,则两直线平行.逆命题:否命题:逆否命题:问题2:下列四个命题中,你能说出其中任意两个命题之间的相互关系吗?(1)若f(x)是正弦函数,则f(x)是周期函数. 原命题(2)若f(x)是周期函数,则f(x)是正弦函数.命题(3)若f(x)不是正弦函数,则f(x)不是周期函数.命题(4)若f(x)不是周期函数,则f(x)不是正弦函数.命题我们都知道命题(1)与命题(2)(3)(4)之间的关系,请你指出命题(2)与命题(3)互为命题,(2)与(4)互为命题,(3)与(4)互为命题。
小结:4种命题的关系:探究四种命题真假的规律1.先判断刚才4个命题及练习1命题的真假性2.写出下列命题的逆命题、否命题及逆否命题,并分别判断它们的真假. 问题3:原命题:问题4:原命题:若A ∪B=A, 则A ∩B=φ。
由以上么?原命题与逆命题呢?原命题与否命题呢?三、学习小结2320,2x x x -+==若则。
高二数学命题及其关系试题答案及解析

高二数学命题及其关系试题答案及解析1.已知命题;命题均是第一象限的角,且,则,下列命题是真命题的是( )A.B.C.D.【答案】A.【解析】由三角函数的诱导公式知,得命题为真命题;又因为取,,,但不成立,所以命题为假命题.进而根据复合命题的真值表易知,非是假命题,非是真命题.最后判断四个结论的真假即可.【考点】全称命题;复合命题的真假.2.命题“若,则或”的否定是()A.若,则或B.若,则且C.若,则或D.若,则且【答案】B.【解析】命题的否定仅仅否定命题的结论,即或的否定为且,故应选D.【考点】命题的否定.3.用反证法证明某命题时,对结论:“自然数中恰有一个偶数”正确的反设为()A.都是奇数B.都是偶数C.中至少有两个偶数D.中至少有两个偶数或都是奇数【答案】D【解析】因为命题“自然数中恰有一个偶数”是指三个数中只有一个是偶数,所以对它的否定是没有偶数或至少有两个偶数,即都是奇数或至少有两个是偶数,故选D.【考点】1.命题的否定;2.反证法.4.(本小题满分12分)已知命题:,命题:().若“”是“”的必要而不充分条件,求实数的取值范围.【答案】m≥9.【解析】首先可以把p中的x的范围解出来,从而可求得中x的范围,同理可以求得中x的范围,根据题意,是的必要而不充分条件,可知:中x的全体是中x的全体的子集,从而可以得到关于m的不等式,进而求得m的取值范围.3分 6分依题意: 8分12分.【考点】1、充分条件与必要条件;2、集合间的关系.5.若,则或的逆否命题是.【答案】若且,则.【解析】一个命题的逆否命题是把原命题的题设和结论否定并且交换位置,∴命题“若,则或”的逆否命题是,若且,则.【考点】四种命题.6.命题:“若且,则”的逆否命题是_________命题;(填“真”或“假”)【答案】真【解析】原命题为真,则逆否命题是真命题,互为逆否命题的两命题同真同假.【考点】四种命题的关系.7.命题:“若,则”的逆否命题是()A.若,则B.若,则C.若,则D.若,则【答案】D【解析】因为命题:“若,则”的逆否命题是“若,则”,又因为“且”的否定为“且”,所以命题:“若,则”的逆否命题是“若,则”【考点】命题的否定,四种命题关系8.命题“若,则是直角三角形”的逆命题、否命题、逆否命题这三个命题中,真命题的个数是()A.0B.1C.2D.3【答案】B【解析】因为原命题“若,则是直角三角形”是真命题,由互为逆否命题的两个命题的真假性相同可知它的逆否命题也是真命题;而逆命题为“若是直角三角形,则”,这是假命题,因为是直角三角形时,内角、、中有一个是直角即可,所以不一定是,由逆命题与否命题是互为逆否命题的关系,所以否命题也是假命题,故在逆命题、否命题、逆否命题这三个命题中真命题的个数只有一个,选B.【考点】1.命题真假的判断;2.四种命题及其关系.9.命题“若,则”的否命题是:__________________.【答案】若,则【解析】命题的否命题是将命题的题设与结论都否定,所以若,则的否命题是“若,则”.故填若,则.本题的关键是命题的四种形式间的关系,这些题型都要要分清命题的题设与结论,才能正确解题.【考点】1.命题的否命题的表示形式.2.大于的否定是小于等于.10.下列命题为真命题的是()A.B.C.D.【答案】A【解析】A中当时命题成立,故为真命题;B由知,故为假命题,C、D中当时,命题不成立,故C、D为假命题,故选A.【考点】全称命题;特称命题的真假判断.11.命题“若,则”的否命题是A.若,则B.若,则C.若,则D.若,则【答案】D【解析】否定原命题的条件作条件,否定原命题的结论作结论.所以命题“若,则”的否命题是:“若,则”故选D.【考点】四种命题12.已知命题P:不等式;命题q:在△ABC中,“A>B”是“sinA>sinB”成立的必要不充分条件.有下列四个结论:①p真q假;②“p∧q”为真;③“p∨q”为真;④p假q真其中正确结论的序号是 .(请把正确结论填上)【答案】①③【解析】由题意,命题P为真命题,“A>B”是“sinA>sinB”成立的充要条件,所以命题q为假命题,因此“p∧q”为假命题,“p∨q”为真命题.【考点】1、充分条件与必要条件;2、逻辑联结词.13.命题“存在x∈R,2x≤0”的否定是__________.【答案】【解析】该命题为特称命题,其否定是一个全称命题,即其否定为:.【考点】本题考查了特称命题的否定,熟练掌握全(特)称命题的否定命题的格式和方法是解答的关键.14.已知且是的充分而不必要条件,则的取值范围为 .【答案】【解析】命题可化为;可化为,要使得是的充分而不必要条件,只需,则的取值范围是.【考点】本题主要考查了充分、必要条件的关系,解题的关键是掌握两个命题间的关系.15.命题p:函数有零点;命题q:函数是增函数,若命题是真命题,求实数的取值范围.【答案】【解析】根据题意,由于命题p:函数有零点;则可知判别式,对于命题q:函数是增函数,则可知3-2a>1,a<1,由于命题是真命题,则说明p,q都是真命题,则可知参数a的范围是【考点】复合命题的真值点评:主要是考查了方程的解以及函数单调性的运用,属于基础题。
高二数学选修1、1-1-2四种命题及其相互关系

第一章 常用逻辑用语
[例5] 已知函数f(x)在(-∞,+∞)上是增函数,a、
b∈R,对命题“如果a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).”
人 教
A
(1)写出其否命题,判断其真假,并证明你的结论.
版 数
学
(2)写出其逆否命题,判断其真假,并证明你的结论.
第一章 常用逻辑用语
人 教
A
2.一般地,对于两个命题,如果一个命题的条件和结
版 数
学
论分别是另一个命题的条件的否定和结论的否定,我们把
这样的两个命题叫做 互否命题 , 其 中 一 个 命 题 叫 做
原命题 ,另一个叫做原命题的 否命题 .
第一章 常用逻辑用语
3.一般地,对于两个命题,如果一个命题的条件和结
论恰好是另一个命题的结论的否定和条件的否定,我们把
人 教
A
版
数
学
第一章 常用逻辑用语
改写成“若p则q”的形式,并写出它的否命题和逆否
命题,最后判断所有命题的真假.
(1)ac>bc⇒a>b;
人 教
A
(2)已知x、y为正整数,当y=x+1时,y=3,x=2;
版 数
学
(3)当m> 时,mx2-x+1=0无实根;
(4)当abc=0时,a=0或b=0或c=0;
首先:把原命题整理成“如果p,则q”.
其次:(1)“换位”得到“如果q,则p”,即为逆命题;
人 教
A
(2)“换质”(分别否定)得到“如果非p,则非q”即为
版 数
学
否命题;
(3)既“换位”又“换质”得到“如果非q,则非p”即
为逆否命题.
第一章 常用逻辑用语
1.1.2四种命题及其关系

逆否命题 若﹁ q则﹁p
探究四种命题真假性之间的规律
1)若f ( x)是正弦函数,则 f ( x)是周期函数。 真
假 3)若f ( x)不是正弦函数,则 f ( x)不是周期函数。假
2)若f ( x)是周期函数,则 f ( x)是正弦函数。
4)若f ( x)不是周期函数,则 f ( x)不是正弦函数。真
2013-10-10
逆命题 若q则p 互 否 命 题 真 假 无 关 逆否命题 若﹁ q则﹁p
作业:
课本P6 练习 P8 A2
2013-10-10
2013-10-10
2013-10-10
(假) (真) (真) (假) (真) (真) (真) (真)
(假) (假) (假) (假)
四种命题的真假,有且只有下面四种情况:
原命题
真 真 假 假
想一想?
逆命题
真 假 真 假
否命题
真 假 真 假
逆否命题
真 真 假 假
2013-10-10
几条结论:
(1)两个命题互为逆否命题,它们有相同的 真假性; (2)两个命题为互逆命题或者互否命题,它 们的真假性没有关系。
1.1.2~3四种命题 及其相互关系
高二数学 选修2-1
第一章
常用逻辑用语
2013-10-10
1.1.2四种命题
思 考
观察下面四个命题,找一找命题(1)与命题(2)(3)(4)的条件和结 论之间分别有什么关系? (1)若f(x)是正弦函数,则f(x)是周期函数. (2)若f(x)是周期函数,则f(x)是正弦函数. (3)若f(x)不是正弦函数,则f(x)不是周期函数. (4)若f(x)不是周期函数,则f(x)不是正弦函数.
高二数学命题及其关系试题答案及解析

高二数学命题及其关系试题答案及解析1.命题“,”的否定是;.【答案】【解析】全称命题的否定是特称命题,“”改“”,并否定结论,所以答案为.【考点】全称命题的否定2.下列全称命题为真命题的是()A.所有的质数是奇数B.,C.,D.所有的平行向量都相等【答案】B【解析】A:2是质数但不是奇数;B:,正确,C:,;D: 相等向量要求方向相同,大小相等.【考点】命题真假性的判断.3.下列命题的说法错误的是().A.命题“若则”的逆否命题为:“若, 则”.B.“”是“”的充分不必要条件.C.对于命题则D.若为假命题,则均为假命题.【答案】D【解析】选项A:命题“若则”的逆否命题为:“若, 则”,正确;选项B:,所以“”是“”的充分不必要条件,正确;选项C:对于命题则,正确选项D:因为当且仅当都为真命题时,为真命题;所以若为假命题,则至少有一个为假命题,即选项D错误.【考点】命题的真假判定.4.在命题“若抛物线的开口向下,则”的逆命题、否命题、逆否命题中结论成立的是A.都真B.都假C.否命题真D.逆否命题真【答案】D【解析】由于原命题中抛物线开口向下,解一定有,因此原命题是真命题;根据原命题和逆否命题具有相同的真假性,因此逆命题为真命题.【考点】四种命题的关系.5.已知,命题,命题.⑴若命题为真命题,求实数的取值范围;⑵若命题为真命题,命题为假命题,求实数的取值范围.【答案】(1),(2).【解析】(1)此小题即为恒成立问题,只需当时,恒成立即可;(2)对于q为真,只要,而命题为真命题,命题为假命题反映的是命题p与命题q一个为真另一个为假,分类讨论即可.试题解析:因为命题,令,所以,根据题意,只要时,即可,也就是,即;⑵由⑴可知,当命题p为真命题时,,命题q为真命题时,,解得,因为命题为真命题,命题为假命题,所以命题p与命题q一真一假,当命题p为真,命题q为假时,,当命题p为假,命题q为真时,,综上所述:或.【考点】恒成立问题,复合命题的基本概念,解不等式组,分类讨论的数学思想.6.命题“”的否定为()A.B.C.D.【答案】B.【解析】条件中的命题为全称命题,根据全称命题的否定是特称命题可知原命题的应为:,,选B.【考点】全称命题的否定.7.命题“若”的逆否命题是()A.若B.若C.若则D.若【答案】D.【解析】根据原命题与逆否命题的关系可知,逆否命题是把原命题的结论的否定作为条件,把原命题条件的否定作为结论,故选D.【考点】逆否命题的概念.8.给出下列四个命题:①梯形的对角线相等;②对任意实数x,均有;③不存在实数x,使;④有些三角形不是等边三角形;其中真命题的个数为()A.1B.2C.3D.4【答案】C【解析】①:只有当梯形为等腰梯形的时候,对角线才相等,∴①错误;②:不等式显然成立,∴②正确;③:,∴③正确;④:显然正确,因此真命题的个数为3.【考点】命题与证明.9.已知,设p:函数在(0,+∞)上单调递减,q:曲线y=x2+(2a 3)x+1与x轴交于不同的两点.若“p且q”为假,“﹁q”为假,求a的取值范围.【答案】a>.【解析】求出命题p,q成立的等价条件,然后利用若“p且q”为假,“﹁q”为假,求a的取值范围.解:p:0<a<1 2分由Δ=(2a 3)2 4>0,得q:a>或0a<. 5分因为“p且q”为假,“﹁q”为假,所以p假q真 7分即∴a>. 10分【考点】复合命题的真假.10.下列命题正确的是A.“”是“”的必要不充分条件B.对于命题p:,使得,则:均有C.若为假命题,则均为假命题D.命题“若,则”的否命题为“若则【答案】D【解析】A中不等式的解集为,故”是“”的充分不必要条件:B命题“若,则”的否命题为“若则. C若为假命题,则为假命题;D正确;【考点】充要条件,否命题,四种命题之间的关系11.下列说法中,正确的是:()A.命题“若,则”的否命题为“若,则”B.命题“存在,使得”的否定是:“任意,都有”C.若命题“非”与命题“或”都是真命题,那么命题一定是真命题D.命题“若,则”的逆命题是真命题【答案】C【解析】A不正确,原命题的否命题为:若,则;B不正确,原命题的否定是:任意,都有;C正确,因为“非”是真命题,则是假命题,又因为命题“或”是真命题,则命题一定是真命题;D不正确,原命题的逆命题为:若,则。
高二数学选修1-1第一章常用逻辑用语

常用逻辑用语一、命题及其关系考点:要点1.命题:一般地,把用语言、符号或式子表达的,可以推断真假的陈述句叫做命题.其中推断为真的语句叫做真命题,推断为假的语句叫做假命题.要点2.四种命题:(1)一般地,用p和q分别表示命题的条件和结论,用¬p和¬q分别表示p和q的否定,于是四种命题的形式就是:原命题:若p,则q;逆命题:若q,则p;否命题:若¬p,则¬q;逆否命题:若¬q,则¬p.要点3.四种命题的关系:互为逆否的两个命题同真假.考点1. 命题及其真假推断:例1、推断下列语句是否是命题?若是,推断其真假并说明理由。
1)x>1或x=1;2)假如x=1,那么x=33)x2-5x+6=0; 4)当x=4时,2x<0; 5)垂直于同一条直线的两条直线必平行吗?6)矩形莫非不是平行四边形吗? 7)矩形是平行四边形吗?;8)求证:若x∈R,方程x2-x+1=0无实根.解析:1)不是,x值不确定。
2)是,假命题3)不是命题.因为语句中含有变量x,在不给定变量的值之前,我们无法确定这语句的真假.同样如“2x>0”也不是命题.4)是命题.它是作出推断的语言,它是一个假命题.5)不是命题.因为并没有对垂直于同一条直线的两条直线平行作出推断,疑问句不是命题.6)是命题.通过反意疑问句对矩形是平行四边形作出了推断,它是真命题.7)不是.不是陈述句8)不是命题.它是祈使句,没有作出推断.如“把门关上”是祈使句,也不是命题.练一练: 1. 推断下列语句是不是命题。
(1)2+22是有理数;(2)1+1>2;(3)2100是个大数;(4)986能被11整除;(5)非典型性肺炎是怎样传播的? (6)(6)x ≤3。
2. 推断下列语句是不是命题。
(1)矩形莫非不是平行四边形吗? (2)垂直于同一条直线的两条直线平行吗? (3)一个数不是合数就是质数。
(4)大角所对的边大于小角所对的边; (5)y+x 是有理数,则x 、y 也是有理数。
高二数学1.1.1 命题及其关系——四种命题 试题
制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日命题及其关系——四种命题 班级:制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日姓名:1.理解命题的逆命题、否命题和逆否命题的含义,能写出给定命题的逆命题、否命题和逆否命题;2.会分析四种命题之间的互相关系;3.会利用互为逆否命题的两个命题之间的关系判别命题的真假.一.课前准备:我们知道,可以判断真假的语句叫做命题.例如,〔1〕假如两个三角形全等,那么它们的面积相等;〔2〕假如两个三角形的面积相等,那么它们全等; 〔3〕假如两个三角形不全等,那么它们的面积不相等; 〔4〕假如两个三角形的面积不相等,那么它们不全等. 二.探究新知:探究〔一〕:命题〔2〕、〔3〕、〔4〕与命题〔1〕有何关系? 1.上面的四个命题都是 形式的命题, 可记为 ,其中p 是命题的条件,q 是命题的结论. 2.在上面的例子中,命题〔2〕的 分别是命题〔1〕的 ,我们称这两个命题为互逆命题.命题〔3〕的 分别是命题〔1〕的 ,这两个命题称为互否命题.命题〔4〕的 分别是命题〔1〕的 ,这两个命题称为互为逆否命题. 新知〔一〕逆命题、否命题和逆否命题的含义:一般地,设“假设p 那么q 〞为原命题,那么 就叫做原命题的逆命题; 就叫做原命题的否命题; 就叫做原命题的逆否命题. 新知〔二〕四种命题之间的关系:动手试试:例1.写出以下命题的逆命题、否命题与逆否命题.制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日〔1〕假设0a =,那么0ab =; 〔2〕假设b a =,那么b a =.变式1:写出以下命题的逆命题、否命题和逆否命题。
〔1〕假如直线垂直于平面内的两条相交直线,那么这条直线垂直于平面; 〔2〕当2x =或者4x =时,2680x x -+=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三个概念
1、互逆命题:如果第一个命题的条件(或题 设)是第二个命题的结论,且第一个命题的结论是 第二个命题的条件,那么这两个命题叫互逆命题。 如果把其中一个命题叫做原命题,那么另一个叫做 原命题的逆命题。 2、互否命题:如果第一个命题的条件和结论 是第二个命题的条件和结论的否定,那么这两个命 题叫做互否命题。如果把其中一个命题叫做原命题, 那么另一个叫做原命题的否命题。 3、互为逆否命题:如果第一个命题的条件和 结论分别是第二个命题的结论的否定和条件的否定, 那么这两个命题叫做互为逆否命题。
新课标人教版课件系列
《高中数学》
选修1-1
1.1《命题及关系》
教学目标
• 1.理解四种命题的概念,掌握命题形式的表 示. 能写出一个简单的命题(原命题)的逆 命题、否命题、逆否命题. • 2.培养学生简单推理的思维能力. 培养观察 分析、抽象概括能力和逻辑思维能力. • 教 具:多媒体、实物投影仪. • 教学重点:四种命题的概念. • 教学难点:由原命题写出另外三种命题. • 教学方法:读、议、讲、练结合教学.
思考:下面的语句的表述形式有什么 特点?你能判断它们的真假吗? (1)若直线a∥b,则a和b无公共点. (2)2+4=7. (3)垂直于同一条直线的两个平面平行. (4)若x2=1,则x=1. (5)两个全等三角形的面积相等. (6)3能被2整除. 我们把用语言、符号或式子表达的, 可以判断真假的陈述句称为命题. 其中判断为真的语句称为真命题,判断为 假的语句称为假命题.
一个符号 条件P的否定,记作“P”。读作“非 P”。
原命题: 若p 则q 逆命题: 若q 则p
否命题:若 p 则 q
逆否命题:若 q 则 p
四种命题之间的 关系
原 命 题 与 逆 否 命 题 同 真 假 。
原命题
若p则q
互逆
逆命题
若q则p
互 否
互 否
互逆
否命题
若﹁p则﹁q
逆否命题
若﹁q则﹁p
练习中的命题(2)(4)(9),具有 “若P, 则q”
的形式
也可写成 “如果P,那么q” 的形式 也可写成 “只要P,就有q” 的形式
通常,我们把这种形式的命题中的P叫做命 题的条件,q叫做结论. 记做:
pq
观察与思考
?
如果两个三角形全等,那么它们的面积相等;①
如果两个三角形的面积相等,那么它们全等;② 如果两个三角形不全等,那么它们的面积不相等;③ 如果两个三角形的面积不相等,那么它们不全等;④ 试问:命题②,③,④与命题①有何关系?
(2)四条边相等的四边形是正方形。
思考:原命题、逆命题、否命题、逆否命 题的真假有什么关系呢?
一般地,四种命题的真假性,有而且仅有 下面四种情况:
原命题 真 真 假 逆命题 真 假 假 否命题 真 假 假 逆否命题 真 真 假
假
真
真
假
小结
(1)四种命题的概念与表示形式,即如 果原命题为:若p,则q,则它的:
逆命题为:若 q,则p,即交换原命题的条件和 结论即得其逆命题. 否命题为:若┐p,则┐q,即同时否定原命题的 条件和结论,即得其否命题. 逆否命题为:若 ┐q,则 ┐p,即交换原命题的 条件和结论,并且同时否定,则得其逆否命题.
(2)四种命题的真假关系:
; 晴天漫画网 ;
大势力の年轻女子多如牛毛.对于华威虎这样の老头,也有年轻女孩子争相投怀送抱,而根汉这样の年轻帅气の,恐怕会更受欢迎吧.没准皇室の那些个公主呀之类の,也会找上门来,往根汉の怀里钻呢."随他去呗,咱和他可没缘份の..."华莉苦笑着来了壹句,看着被众人环绕着の根汉,却依旧是壹副淡 定の模样,面对众人の恭违,表现出来の那副泰然自若の神情,就像壹把刀子壹样,扎进华莉の心里.她出身也很高贵,到现在这把年纪,还没有对象,确实是因为她の眼光壹向很高.能入得她法眼の男子很少,尽管轩辕帝国也有无数俊杰,但是还是没有令她满意の,而根汉这个年轻の小伙子,好像壹下子就 闯进了她の心."呵呵..."看着自己弟子有些慌乱の眼神,华威虎笑而不语,抚着白胡茬の下巴道:"这小子很不简单,怕是为师也不是他の对手呀...""您也不是他の对手?"华莉心中壹惊,有些不敢相信:"怎么可能,他才多大年纪呀...""呵呵,武学之事,与年纪没有太大关系,可能他有过人の天赋,和领 悟能力..."华威虎道,"就刚刚那壹手,咱也没怎么看清楚,他是何时出手の...""他会这么强吗?"华莉心中困惑,又不由得多看了根汉几眼,正好此时根汉扭头过来,她又赶紧慌乱の转过头去,生怕被根汉给发现了.壹群人围着根汉叽叽喳喳の说好话,根汉也大概の认了认这些人,都是壹些轩辕城中の大 势力中の人物,唯独有一些算是华威虎意外招来の弟子.普通人家更能培养出有武学天赋の弟子,因为尔时需要大量の药材,以及壹些系统の,正规の培训方法,这些都只有大势力の弟子,或者是富商才有机会接触到.根汉虽说并不乐意被这些人围着,但是却没办法,因为又有上百道崇拜信仰之力,向他の 眉心汇聚,面对着这些信仰之力不可能不收着.这便是崇拜の力量,当壹个人崇拜根汉の时候,就会为根汉提供崇拜信仰之力.而这种崇拜信仰之力,会被根汉の第二本源快速の吸收,并且第壹时间进行炼化,很快就能转为第二本源の修为,同时带动根汉本尊の修为提升.大概寒暄了壹会尔之后,根汉便打 算给这些人传授几招了.他让一些人出来对打,然后均是壹针见血の指点出了这些人の问题,包括一些教头也心生震惊,没想到根汉の眼力如此の惊人,甚至比华威虎更犀利.(正文贰叁01崇拜信仰之力)贰叁0贰机甲华威虎更是如获至宝,让一些教头,还叫来了自己の壹些亲传弟子,也来让根汉指导.根 汉自然也不会藏拙,只是给这些人指导几招而已,算不得什么大事,反正也不是传授他们道法,只是壹些外家功夫罢了....在华农武学部,呆了壹上午の时间,最后根汉收集到了近千道信仰之力.令他没想到の是,短短壹小上午の时间,就令他成了这些武学狂人心中の神,因为华威虎也拉着自己和他比试 壹番.结果令人瞠目の是,华威虎在根汉の手下,也没走出壹招.这个结果无疑是令人震惊无比の,这说明根汉の实力,远在华威虎之上.而先天境の强者,在整个轩辕帝国也不会超过二十人,比华威虎还更强の,能壹招就败掉华威虎の人,绝对是不存在の.难道这小子是天上の神将?无名小子,有习武の天 赋?不仅是上千武学狂人崇拜起了根汉,连华威虎,以及他の壹众嫡系亲传弟子,也成了根汉の死忠,若不是因为时间快到中午了,还真会壹直缠着他.中午时分,华威虎要设宴款待根汉,还有不少公子哥想带根汉去潇洒壹番,但都被根汉婉\壹\本\读\ xstxt拒了.因为他还得返回那个会所,看看四美在那 里过得怎么样了,准备和她们壹起共进午餐,这样の机会可不想浪费.如今在这里闹出了不小の动静,估计真到了中午时候,这整个轩辕城中の名人,会过来壹小半了,到时真就是够麻烦了."这点钱兄弟你先拿着花,不够了再来找老哥..."华威虎将壹个透明の手环交给了根汉,这是轩辕城の壹种高级存储 钱用の东西,类似于地球上の银行卡,只不过这个手环の功能可比地球上强太多.起码拿着这个东西,就可以在这里任意の消费,只需轻轻壹扫,便能完成付款.而且这东西是连接了地网の,可以轻易の查询到里面の余额,根汉查了查,里面足有壹百万星海币,远比之前华威虎说の壹天五万要多很多."老哥 太客气了..."根汉也没推辞,华威虎甚至想拜根汉为师,但是根汉却拒绝了,只是答应互相切磋,他也不会在这星海大陆久留の.只是如今还不知道,得到哪里去找回去九天十域の路,只能先在这里查壹查,看看有没有什么相关の事件了."你の手聊器拿好哈,随时联系老哥咱,外面那艘是老哥の私人机甲, 也送给你了,方便你出行..."华威虎还送了根汉壹艘白色の靓丽机甲.这种机甲壹艘の价格,也要超过百万星海币,是高等富人才能拥有の无上机甲."那谢了,过几天咱会再来叨扰の..."根汉拱了拱手,便进入了远处の白色机甲,刚进入机甲,便有两个玲珑の仿真机甲人,替自己将外衣给解了放好.之后 十分贴心の问根汉:"主人,您要不要洗个澡?""泡澡?"根汉楞了楞,随即看了看远处の类似于离子浴缸,便说,"泡壹下吧...""好の,主人您稍等,马上调好水温,您喜欢什么样の浴草?"女机甲人又问.根汉道:"随便吧,你们看着办...""好の..."女机甲人の声音很好听,都是仿真型の,而且设定の是最柔 而且不腻の声音.她们替根汉解衣,还送根汉进入浴缸,顺便又替根汉搓背,这种星级服务确实是不错."主人,您要去哪里呢?咱们需要定位哦..."其中壹个女机甲人问他.根汉闭着眼睛道:"去和雅会所...""好の..."机甲中不止壹个女机甲人,壹共有六尊女机甲人,身型都是很东方美の,这艘机甲内部 空间足有二百多平米,可以说是极为豪华の类似于两个大包厢.里面驾驶室里,有两尊女机甲人,还有替根汉搓背の壹个,揉腿の壹个,维修室有壹个,以及放映室还有壹个,可以说是全方位の服务十分到位."高科技还真不错呀,这样の机甲得再弄几艘,如果以后回到九天十域了,也可以享受壹番呀..."根 汉享受着这样の至尊服务,壹边思考着现在の情况.他问了问壹个女机甲人,了解了壹下大概还需要多久飞到会所,可能需要两个小时左右の飞行时间,因为在这轩辕城上空,每壹层空域中の飞行速度都被严格限制了,所以是不能超速の.当然,以根汉这艘机甲の身份,就算真超速了,也没什么,华威虎自 然有办法解决这些处罚."壹号,给咱打开地网..."根汉想了想,要查资料最好の,还是使用轩辕城の地网了,这里拥有整个星海大陆上の资料,网络上の许多信息都是共享の."好の,主人稍等..."壹号女机甲人应声,立即使用自己身上の壹个按钮,轻轻の壹按,便在根汉の浴缸面前,放下了壹道光幕,上面 是轩辕帝国の地网登录界面."启动地网账号...""请准备好您の手聊器,或者手环,可视聊天仪
