第11章 恒定电流的磁场
川师大学物理第十一章-恒定电流的磁场习题解

第十一章 恒定电流的磁场11–1 如图11-1所示,几种载流导线在平面内分布,电流均为I ,求它们在O 点处的磁感应强度B 。
(1)高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ,方向 。
(2)一根无限长的直导线中间弯成圆心角为120°,半径为R 的圆弧形,圆心O 点的磁感应强度大小为 ,方向 。
…解:(1)如图11-2所示,中心O 点到每一边的距离为13OP h =,BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC I B dμββ=-^IB21图11–2图11–1…B(a )AE(b )0(cos30cos150)4π/3Ih μ︒︒=-=方向垂直于纸面向外。
另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。
因此O 处的磁感应强度是三边电流产生的同向磁场的叠加,即3BC B B ===方向垂直于纸面向外。
(2)图11-1(b )中点O 的磁感强度是由ab ,bcd ,de 三段载流导线在O 点产生的磁感强度B 1,B 2和B 3的矢量叠加。
由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=- 可得载流直线段ab ,de 在圆心O 处产生的磁感强度B 1,B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=-031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ=-】方向垂直纸面向里。
半径为R ,圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13,所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ===方向垂直纸面向里。
因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π22π26I I I I B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。
大学物理 磁学习题课

( I 1 I 2 ) ln 2
第11章 恒定电流的磁场
17
MN上电流元I3dx所受磁力:
0 I1
a M
dx N
c I2
d F I 3 B d x I 3 [ 2(r x) 2(2r x) ] d x
r
0 I1
I3 r Or b
r d
x
F I3 [
0
0 I1
2(r x)
0I2
2(2r x)
]d x
0I3
S
B
圆面
Φm
2 B S BR cos
1 B d S B R 2 2
n
60°
R
B
任意曲面
S
S
很多漏掉负号 类似本页二.1(1)磁通量
12
第11章 恒定电流的磁场
P42 一选择1.
H dl 2 I L1
H dl I L2
1
第11章 恒定电流的磁场
16
P44 二1、如图所示,载有电流I1和I2的长直导线ab和cd相互平行,相距为
3r,今有载有电流I3的导线MN = r,水平放置,且其两端MN分别与I1、I2 的距离都是r,ab、cd和MN共面,求导线MN所受的磁力大小和方向.
载流导线MN上任一点处的磁 感强度大小为: I 0 I 2 0 1 I1 B 2( r x ) 2( 2r x )
1
B
•直导线延长线上
a
第11章 恒定电流的磁场
P
6
2.
圆电流轴线上某点的磁场
B
大小:
第十一章 电磁学 恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则, B 垂直 v 、 正, B 为 v r 的方向;q为负, B 与
q
+
r B
v
q-
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。 半无限长载流长直导线的磁场
1
r0
P
θ1 θ2
2 π
μ0 I B 4πr0
I
r0
P
大学物理 电磁学
2、载流圆线圈轴线上的磁场 真空中,半径为R的载流导线,通有电流I,称圆电流。求其 轴线上一点 P的磁感强度的方向和大小
1、5 点 : dB 0
7
6 5
Idl
R
×
× 3
3、7点 : dB
0 Idl 4 π R2
4
2、4、6、8 点 :
dB
0 Idl
4π R
2
sin 45
0
大学物理 电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2
dB
大学物理 电磁学
磁现象与电现象有没有联系?
静电场 ?
静止的电荷 运动的电荷
1820年奥斯特:发现电流的磁效应
N
1第十一章 恒定电流的磁场(一)作业答案

2 ∶4
2 ∶1 2 ∶8
a2 a1 O1 O2 I
2 2 0 I Bo1 , Bo2 4 cos 450 cos1350 , a2 2a1 a 2 4 2 a 2 由Bo1 Bo2 , 得 1 a2 8
0 I
0 I
I
[ B ] 2、 (基础训练 3)有一无限长通电流的扁平铜片,宽度为 a,厚度不计,电 流 I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为 b 处的 P 点(如图)的
B B
0 Ir 2 a 2
0 I 2 r
, B
I B 2 r 0 I (r 2 b 2 ) 2 2 (c b )
B 2 r 0 0 0, B 0
2 r c 2 b 2
0 I c 2 r 2
I a b
磁感强度 B 的大小为 0 I (A) . 2(a b) 0 I a b (C) . ln 2b b
其电流为 dI
P
(B) (D)
0 I
2a
ln
ab . b
.
0 I
(a 2b)
【答】在距离 P 点为 r 处选取一个宽度为 dr 的电流(相当于一根无限长的直导线) ,
dI I dr ,它在 P 处产生的磁感应强度为 dB 0 ,方向垂直纸面朝内; a 2 r 根据 B dB 得: B 的方向垂直纸面朝内, B 的大小为
B
0 dI 0 I b a dr 0 I a b . ln 2 r 2 a r 2 a b b
b b a
图 11-51
5、 (自测提高 11)在一根通有电流 I 的长直导线旁,与之共面地放着一个长、 宽各为 a 和 b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为 b, 如图 11-51 所示.在此情形中,线框内的磁通量 =
第十一章恒定电流的磁场一作业答案

第十一章 恒定电流的磁场(一)一、选择题[ B ]1.(基础训练3)有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点(如图)的磁感强度B 的大小为(A) )(20b a I +πμ. (B) b ba a I +πln 20μ.(C) b ba b I +πln 20μ. (D) )2(0b a I +πμ. 【提示】在距离P 点为r 处选取一个宽度为dr 的电流(相当于一根无限长的直导线),其电流为IdI dr a =,它在P 处产生的磁感应强度为02dI dB rμπ=,方向垂直纸面朝内;根据B dB =⎰得:B 的方向垂直纸面朝内,B 的大小为000dI B ln 222b a b I I dr a br a r a bμμμπππ++===⎰⎰.[ D ]2、(基础训练4)如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll B d 等于 (A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ.【提示】如图,设两条支路电流分别为I 1和I 2,满足1122I R I R =,其中12R R ,为两条支路的电阻,即有1211212()l l l I I I I s s s ρρρ==-,得:123I I = 根据安培环路定理,0001L 23内LIB dl I I μμμ⋅===∑⎰, [D ]3、(自测提高1)无限长直圆柱体,半径为R ,沿轴向均匀流有电流.设圆柱体内( r < R )的磁感应强度为B i ,圆柱体外( r > R )的磁感应强度为B e ,则有 (A) B i 、B e 均与r 成正比. (B) B i 、B e 均与r 成反比. (C) B i 与r 成反比,B e 与r 成正比.(D) B i 与r 成正比,B e 与r 成反比. 【提示】用安培环路定理,0 2内L B r I πμ⋅=∑,可得: 当r<R 时 022Ir B R μπ=; 当 r > R 时 02IB rμπ=.[ C ]4、(自测提高7) 如图11-49,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷。
大学物理——第11章-恒定电流的磁场

单 位:特斯拉(T) 1 T = 1 N· -1· -1 A m 1 特斯拉 ( T ) = 104 高斯( G )
3
★ 洛仑兹力 运动的带电粒子,在磁场中受到的作用力称为洛仑兹力。
Fm q B
的方向一致; 粒子带正电,F 的指向与矢积 B m 粒子带负电,Fm的指向与矢积 B的方向相反。
L
dB
具体表达式
?
5
★ 毕-萨定律
要解决的问题是:已知任一电流分布 其磁感强度的计算
方法:将电流分割成许多电流元 Idl
毕-萨定律:每个电流元在场点的磁感强度为:
0 Idl r ˆ dB 4 πr 2
大 小: dB
0 Idl sin
4 πr
2
方 向:与 dl r 一致 ˆ
整段电流产生的磁场:
r 相对磁导率
L
B dB
8
试判断下列各点磁感强度的方向和大小?
8
7
6
R
1
1、5 点 :
dB 0
0 Idl
4π R 2
Idl
2
3、7 点 : dB 2、4、6、8 点 :
3 4
5
dB
0 Idl
4π R
sin 450 2
9
★ 直线电流的磁场
29
★ 磁聚焦 洛仑兹力
Fm q B (洛仑兹力不做功)
与 B不垂直
//
// cosθ
sin θ
m 2π m R T qB qB
2πm 螺距 d // T cos qB
大学物理之恒定电流的磁场

磁场能量传
磁场能量传输原理
利用磁场可以实现能量的无线传输。
磁场能量传输方式
包括磁耦合、磁感应等。
磁场能量传输特点
具有高效、安全、环保等优点,是未来能源传输的重要方向之一。
THANKS FOR WATCHING
感谢您的观看
磁场与电流的关系
总结词
磁场与电流之间存在相互作用,变化的磁场可以产生 电场,而变化的电场也可以产生磁场。
详细描述
磁场与电流之间的相互作用是电磁场理论的核心内容之 一。根据法拉第电磁感应定律,变化的磁场可以产生电 场;而根据麦克斯韦方程组,变化的电场也可以产生磁 场。这种相互作用导致电磁波的传播,形成了我们现在 所知的电磁波谱。在恒定电流的磁场中,虽然磁场不随 时间变化,但电流在空间中的分布可以是不均匀的,因 此磁场与电流之间仍然存在相互作用。这种相互作用表 现为电流在磁场中受到洛伦兹力,使得电荷在空间中移 动形成电流。
洛伦兹力
洛伦兹力是磁场对运动电荷的作 用力,其大小与电荷的电量、速
度以及磁场强度有关。
洛伦兹力的方向与电荷运动方向 和磁场方向有关,遵循右手定则。
洛伦兹力在粒子加速器、回旋加 速器等领域有广泛应用,是研究
带电粒子运动规律的基础。
磁场中的运动电荷
1
在磁场中运动的电荷会受到洛伦兹力的作用,这 个力会使电荷发生偏转,改变其运动轨迹。
磁场的描述
磁感应线
用磁感应线描述磁场,磁感应线的疏密程度表示磁场强度的 大小。
磁感应强度
描述磁场强弱的物理量,其方向与磁场中某点的磁感应线垂 直。
磁场的应用
电磁感应
当导体在磁场中运动时,会产生电动 势,进而产生电流。这一现象在发电 机、变压器等设备中有广泛应用。
恒定电流中的磁场

恒定电流中的磁场磁场是物质围绕着电流所产生的一种现象。
磁场具有方向和强度,可以对周围的物质产生作用。
在恒定电流中,磁场的特性和分布呈现出一定的规律性。
本文将探讨恒定电流中磁场的产生原理、磁场的特性以及磁场与电流之间的关系。
一、恒定电流中的磁场产生原理当电流通过导线时,周围就会形成一个闭合的磁场。
根据安培定理,恒定电流所产生的磁场的大小和方向与电流强度、距离和导线形状都有关系。
导线周围的磁场将呈现出环绕导线的形态,强度随着距离导线的远近而减弱。
二、恒定电流中磁场的特性1. 磁场强度:磁场强度是衡量磁场的大小的物理量。
在恒定电流中,磁场的强度与电流的大小成正比,即电流越大,磁场强度越大。
2. 磁场方向:根据右手定则,我们可以确定恒定电流所产生的磁场方向。
当右手握住电流方向,拇指指向电流方向时,四指弯曲的方向就是磁场的方向。
3. 磁场分布:恒定电流所产生的磁场呈现出环绕导线的形状。
随着离导线距离的增加,磁场强度逐渐减小,并形成一个闭合的磁场线圈。
三、磁场与电流的关系恒定电流所产生的磁场与电流之间存在着密切的关系。
根据安培定理和法拉第电磁感应定律,我们可以得到以下结论:1. 磁场与电流强度成正比,即电流越大,磁场强度越大。
2. 磁场与距离成反比,即离导线越近,磁场越强。
3. 磁场与导线形状有关,导线越弯曲,磁场越复杂。
4. 磁场会对周围的物质产生作用,如可以使磁性物质受力或改变电流的方向。
四、应用领域与意义恒定电流产生的磁场在很多领域有着广泛的应用。
例如,电动机、电磁铁、变压器等电磁设备的工作原理都与磁场和电流的相互作用相关。
同时,磁场在地理勘探、医学成像等领域也有重要的应用价值。
总结:恒定电流中的磁场是通过电流通过导线所产生的一种现象。
磁场具有方向和强度,其特性与电流大小和周围距离密切相关。
磁场与电流强度成正比,与距离成反比,同时与导线的形状有关。
磁场在科学研究和工程领域中有着广泛的应用,对于我们理解电磁学原理以及应用于实践中具有重要的意义。
大学物理第十一章习题解答..

第十一章:恒定电流的磁场习题解答1.题号:40941001分值:10分如下图所示,是一段通有电流I 的圆弧形导线,它的半径为R ,对圆心的张角为θ。
求该圆弧形电流所激发的在圆心O 处的磁感强度。
解答及评分标准:在圆弧形电流中取一电流元l Id (1分),则该电流元l Id 在圆心处的磁感强度为: θπμπμd R I RIdl dB 490sin 40020==(2分) 其中θRd dl =则整段电流在圆心处的磁感强度为:θπμθπμθR I d R I dB B 44000===⎰⎰(2分)2.题号:40941002分值:10分一无限长的载流导线中部被弯成圆弧形,如图所示,圆弧形半径为cm R 3=,导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
解答及评分标准:两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外,大小相等,以垂直图面向里为正向,叠加后得RI R I B πμπμ242001-=•-= (3分) 圆弧形导线在O 点产生的磁感应强度方向垂直图面向里,大小为R I R I B 83432002μμ==(3分) 二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ (3分) 方向垂直图面向里。
(1分)3.题号:40941003分值:10分难度系数等级:1一段导线先弯成图(a )所示形状,然后将同样长的导线再弯成图(b )所示形状。
在导线通以电流I 后,求两个图形中P 点的磁感应强度之比。
(a ) (b )解答及评分标准:图中(a )可分解为5段电流。
处于同一直线的两段电流对P 点的磁感应强度为零,其他三段在P 点的磁感应强度方向相同。
长为l 的两段在P 点的磁感应强度为 lI B πμ4201= (2分) 长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=(2分) 所以lI B B B πμ22012=+= (2分) 图(b )中可分解为3段电流。
大学物理恒定电流的磁场总结

B
0r
B
2
1、载流直导线的磁场
B
0I
4a
(cos
1
cos
2)
无限长
B 0I 2a
半无限长 B 0 I
4a
方向:右螺旋法则
I
Idl
l
a
r
1
P
2、载流圆线圈的磁场(在轴线上)B
0 IR 2
2(R 2 x2 )3/2
圆心处
B 0I
2R
方向:右螺旋法则
Idl
一段圆弧在圆心 处产生的磁场
B
qB
5、带电粒子 在电场、磁场中受力 F fe fm qE
qv
B
六、磁介质
1、磁介质分类:
抗磁质 r 1 顺磁质 r 1
铁磁质 r 1
B B0 r —— 相对磁导率
B B0 B
2、有磁介质的磁高斯定理
SB
dS
0
3、有磁介质时的安培环路定理
H L
dl
I0
定义磁场强度
H
B dl
L
μ0
I i (内)
i
电流与绕行方向成右手定则时,I > 0,否则 I < 0
五、磁场对载流导线和运动电荷的作用力
1、磁场对载流导线的作用力——安培力
微分形式:
dF
Idl
B
积分形式:
F dF Idl B
2、均匀磁场对平面载流线圈的力矩
M
pm
B
大小: 磁矩
M NSBI sin
运动电荷的磁场
B
0
4
q v r0 r2
4 107 N A2 0
三、磁通量和磁场的高斯定理
物理学教程-第十一章 恒定磁场

Chapter 11
恒定磁场
上海应用技术学院
理学院
谭默言
§11-1、§11-2 、 §11-3 教学基本要求
了解电流、电流密度的基本概念;
了解电源作用和电源电动势的定义;
掌握磁场及磁感强度的概念及特点。
·2 ·
§ 11-1 恒定电流
8 2
d 1、5 点 : B 0
3、7点 :dB +3
+
7
Idl
R
6
0 Idl
4π R
2
2、4、6、8 点 :
+4
5
dB
0 Idl
4π R
sin 45 0 2
·13 ·
二
毕奥---萨伐尔定律应用举例
解 dB
例1 载流长直导线的磁场.
0 Idz sin
4π r
2
z
0 I B1 dl1 B2 dl2 d 2π
d
B1
B1 dl1 B2 dl2 0
B d l 0
l
I
B2 dl 2 dl
1
r1
r2
l
·31 ·
证明:
多电流情况
B B1 B2 B3 I 1 B d l ( B1 B2 B3 ) d l l l B1 d l B2 d l B3 d l
dB
P *
r
Idl
I
0 I dl er B dB 4 π r2
第十一章 恒定电流的磁场(二)作业答案

一、 选择题【 C 】1.(基础训练2)三条无限长直导线等距地并排安放,导线Ⅰ、Ⅱ、Ⅲ分别载有1 A ,2 A ,3 A 同方向的电流.由于磁相互作用的结果,导线Ⅰ,Ⅱ,Ⅲ单位长度上分别受力F 1、F 2和F 3,如图所示.则F 1与F 2的比值是:(A) 7/16. (B) 5/8. (C) 7/8. (D) 5/4.【答】设导线Ⅰ、Ⅱ、Ⅲ的电流强度分别为321,,I I I ,产生的磁感应强度分别为321,,B B B ,相邻导线相距为a ,则()()0203011123110301022231227,2224222II F I l B B I l a a a I I F I l B B I l a a aμμμπππμμμπππ⎛⎫=+=+= ⎪⋅⎝⎭⎛⎫=-=-= ⎪⎝⎭式中121231, 1, I 1A, I 2A, I 3A l m l m =====,得 8/7/21=F F .【 D 】2. (基础训练6)两个同心圆线圈,大圆半径为R ,通有电流I 1;小圆半径为r ,通有电流I 2,方向如图.若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线圈所受磁力矩的大小为 (A) Rr I I 22210πμ. (B)Rr I I 22210μ. (C)rR I I 22210πμ. (D) 0.【答】大圆电流在圆心处的磁感应强度为,方向垂直纸面朝内2RI B 101μ=; 小圆电流的磁矩为方向垂直纸面朝内,,222r I p m π=所以,小圆电流受到的磁力矩的大小为2211sin 00m m M p B p B =⨯=︒=[ B ]3.(自测提高2)如图所示,一电子以速度v垂直地进入磁感强度为B的均匀磁场中,此电子在磁场中运动轨道所围的面积内的磁通量将(A) 正比于B ,反比于v 2. (B) 反比于B ,正比于v 2. (C)正比于B ,反比于v . (D) 反比于B ,反比于v .【答】 电子在磁场中做匀速率圆周运动,运动平面的法向平行于磁感应强度方向,因此,磁通量为2R B πΦ=,其中半径R 可由式2v evB m R =求得:mv R eB =,所以222mv m v B eB eB ππ⎛⎫Φ== ⎪⎝⎭.F 1F 2F 31 A2 A3 A ⅠⅡⅢOrR I 1 I 2[ B ]4、(自测提高4)一个动量为p 的电子,沿图示方向入射并能穿过一个宽度为D 、磁感强度为B(方向垂直纸面向外)的均匀磁场区域,则该电子出射方向和入射方向间的夹角为 (A)p eBD 1cos-=α.(B)p eBD 1sin -=α. (C)epBD 1sin -=α. (D) ep BD 1cos -=α.【答】电子在磁场中的轨迹为一段圆弧,如图。
大学普通物理学习题答案-第十一章-恒定电流与恒定磁场

第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示,有两根载有相同电流的无限长直导线,分别通过x1=1m、x2=3m的点,且平行于y轴,则磁感应强度B等于零的地方是()。
A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。
解析:根据对称性可得,两条载流导线在x=2m的直线上产生的磁感应强度大小相等;用右手螺旋定则可判断两磁感应强度的方向相反,相互抵消,合磁感应强度为零,故选A。
2.图11-2中6根无限长导线互相绝缘,通过电流均为I,区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形,哪一个区域指向纸内的磁通量最大()。
A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。
解析:通过Ⅰ区域的磁通量为0,通过Ⅰ区城的磁通量最大且指向纸内,通过Ⅰ区域的磁通量最大但指向纸外,通过IV区域的磁通量为0。
故选B。
3.如图11-3所示,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知()。
A.d 0LB l ⋅=⎰,且环路上任意一点B =0 B.d 0LB l ⋅=⎰,且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰,且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰,且环路上任意一点B =常量3.【答案】B 。
解析:根据安培环路定理,闭合回路内没有电流穿过,所以环路积分等于0.但是由于圆形电流的存在,环路上任意一点的磁感应强度都不等于0。
故选B 。
4.无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(r <R )的磁感应强度为B i ,圆柱体外(r>R )的磁感应强度为B e ,则有:()。
A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比,B e 与r 成正比D.B i 与r 成正比,B e 与r 成反比4.【答案】B 。
解析:导体横截面上的电流密度2πR I J =,以圆柱体轴线为圆心,半径为r 的同心圆作为安培环路,当r <R ,20ππ2r J r B i ⋅=⋅μ,20π2R IrB i μ=;当r <R ,I r B e ⋅=⋅0π2μ,rIB e π20μ=;所以选D 。
大学物理电磁学 第11章 恒定磁场

四、毕-萨定律的应用
dB
0 4
Idl r r2
方法:
(1)将电流分解为无数个电流元
(2)由电流元求dB (据毕—萨定律)
(3)对dB积分求B = dB 矢量积分须化作分量积分去做
Bx dBx , By dBy , Bz dBz
例题1 直线电流在P点的磁场
2
解:
任取电流元 I dl
所有磁现象可归纳为:
运动电荷
运动电荷
载流导体
磁场
载流导体
磁体
磁体
磁场的宏观性质:对运动电荷(或电流)有力的 作用,磁场有能量
二、磁感应强度
B 1、磁场的描述:磁感应强度
方向: 磁针静止时,N极指向即B的正方向
S
N
2、B的大小:
以磁场对载流导线的作用为例
电流元所受到的磁场力
dF Idl sin
l
r
B
3)说明磁场为非保守场称为涡旋场
静电场是保守场、无旋场
二、简证(用特例说明安培环路定理的正确性)
(1)闭合路径L环绕电流
L在垂直于导线的平面内
B 0I 2 r
L
I d
o
B
r
dl
磁感线
(2)闭合路径L不包围电流
B dl1 dl2 L
P
·
I
d
o
dl2
dl1
L2
L1
磁感线
·
Q
三、运用安培环路定理求磁场 安培环路定理适用于任何形状恒定电流的载流体
P·
Idl r
B
dB
0 4
Idl r r2
B
dB
0 4
Idl r r2
第11章 恒定电流的磁场

第十一章 恒定电流的磁场11.1 选择题(1) 有两条长直导线各载有5A 的电流, 分别沿x 、y 轴正向流动. 在(40, 20, 0)(cm)处的B 是(真空磁导率μ0 = 4π × 10-7N/A 2) [C] (A) 2.5×10-6 T 且沿z 轴负向 (B) 3.5×10-6 T 且沿z 轴负向 (C) 2.5×10-6 T 且沿z 轴正向 (D) 3.5×10-6 T 且沿z 轴正向k y I B πμ2101=,k xI B πμ2202-=k T k x y I k x I k y I B B B 6020*******.211222-⨯=⎪⎪⎭⎫ ⎝⎛-=-=+=πμπμπμ (2) 半径为1a 的圆形载流线圈与边长为2a 的方形载流线圈, 通有相同的电流, 若两线圈中心1O 和2O 的磁感应强度大小相同, 则半径与边长之比21:a a 为[D] (A) 1:1 (B) π212:1 (C) π212:4 (D) π212:81012a IB μ=;()2102cos cos 44θθπμ-⨯=a IB 20202243cos 4cos 2144a I a I πμπππμ=⎪⎭⎫ ⎝⎛-⨯= 21B B =,2010222a I a Iπμμ=, 8221π=a a(3) 无限长空心圆柱导体的内、外半径分别为a 和b , 电流在导体截面上均匀分布, 则在空间各处B 的大小与场点到圆柱中心轴线的距离r 的关系, 定性地分析如图[B](A) (B) (C) (D)解析:∑⎰=⋅内0i LI l d B μ(4) 氢原子处于基态(正常状态)时, 它的电子(e = 1.6×10-19C)可看做是在半径为a = 0.53 × 10-8cm 的轨道做匀速圆周运动, 速率为2.2 × 108cm/s, 那么在轨道中心B 的大小为(真空磁导率μ0 = 4π×10-7N/A 2)[B] (A)8.5×10-8T (B)13T (C)8.5×10-4TRIB 20μ=,a R =,T e I =,v aT π2=,可得204aev B πμ=, 数据带入即可.(6) 载流i 的方形线框, 处在匀强磁场B 中, 如图所示, 线框受到的磁力矩是 (A) 向上 (B) 向下 (C) 由纸面向外 (D) 由纸面向内B p M m ⨯=;n IS p m =m p 的方向与n 的方向相同, n的方向是载流线圈的正法线方向(由右手螺旋法则确定), 正法线方向垂直向外, 磁场的方向水平向右, 那么磁力矩M的方向竖直向上.iB题11.1(6)图a eO题11.1(4)图11.2 填空题(1) 一平面内有互相垂直的导线L 1和L 2, L 1为无限长直导线, L 2为长为2a 的载流直导线, 位置如图所示. 若L 1和L 2同时通以电流I ,那么作用在L 2上的力对于O 点的磁力矩为 .()13ln 220-πμaI建立如图坐标系, 距直导线L 1为x 远处取电流元l Id, 其在产生的磁场中受到的安培力为d d F I l B =⨯,方向向上.2300=d d ln 322aaI I F F I x x xμμππ==⎰⎰ 该力对O 点的磁力矩为d d M r F =⨯()2004d d 4d 1d 22I I a M rIB x a x I x x x x μμππ⎛⎫==-=-⎪⎝⎭2304=d 1d 2a aI a M M x x μπ⎛⎫=-⎪⎝⎭⎰⎰()()222330004=d d 2ln 32ln 312a a a a I II a a x x a a x μμμπππ⎛⎫-=-=- ⎪⎝⎭⎰⎰(2) 矩形截面的螺绕环尺寸见图, 则在截面中点处的磁感应强度为 ; 通过截面S 的磁通量为 .rNI πμ20;210ln 2D D NIh πμ L 2 L 1a2aaI I O题11.2(1)图沿以环心为圆心, 以r 为半径的圆周为积分路径, 应用安培环路定理 NI r B l d B L02μπ=⋅=⋅⎰ ; rNIB πμ20=; 对于截面中点处, ()1214r D D =+通过截面S 的磁通量为⎰⎰⋅=ΦS m S B ⎰⎰⎰⋅==2200121212D D S hdr rNI dS r NIπμπμ2100ln 2ln 212D D NIh r NIh DD πμπμ== (3)每单位长度的质量为0.009kg/m 的导线, 取东西走向放置在赤道的正上方, 如图. 在导线所在的地点的地磁是水平朝北, 大小为5310T -⨯, 问要使磁力正好支撑导线的重量, 导线中的电流应为 .2940A(5)0d LB l I μ⋅=∑⎰内; ∑⎰=⋅insi LI l d H;NI l d H L=⋅⎰; A I 3=;11.4 将一无限长直导线弯成图示的形状, 其上载有电流I , 计算圆心O 点处B 的大小.解:可分为三部分电流, 两侧的半无限长直导线和中间的圆弧, 在O 点产生的磁感应强度均为垂直向里.半无限长导线, 由P53已知结果可知()210cos cos 4θθπμ-=aIB 左侧:3cosπr a =, 01=θ, 62πθ=右侧:3cos πr a =, 651πθ=,πθ=2 圆弧部分导线, 由P54已知结果可知R I B πϕμ40=, 式中r R =, 32πϕ=以上三部分求和, 可得总磁感应强度r Ir I B 623100μπμ+⎪⎪⎭⎫ ⎝⎛-=, 垂直向里.11.9电缆由导体圆柱和一同轴的导体圆筒构成, 使用时电流I 从导体流出, 从另一导体流回, 电流均匀分布在横截面上, 如图所示. 设圆柱体的半径为r 1, 圆筒的内、外半径分别为r 2和r 3, 若场点到轴线的距离为r , 求r 从0→∞范围内各处磁感应强度的大小.解:0d 2LB l rB I πμ⋅==∑⎰内当1r r <时, 2021d 2r B l rB I r ππμπ⋅==⎰,2102r Ir B πμ=当21r r r <<时,0d 2B l rB I πμ⋅==⎰, 02I B rμπ=当32r r r <<时, ()()22202232d 21r r B l rB I r r ππμπ⎡⎤-⎢⎥⋅==--⎢⎥⎣⎦⎰,()()222322302r r r r r I B --=πμ当3r r >时,d 0B l I I ⋅=-=⎰, 0=B11.10如图所示, 一根半无限长的圆柱形导体, 半径为R 1, 其内有一半径为R 2的无限长圆柱形空腔, 它们的轴线相互平行, 距离为a (R 2 < a < R 1-R 2), I 沿导体轴线方向流动, 且均匀地分布在横截面积上. 求: (1) 圆柱体轴线上B 的大小; (2) 空腔部分轴线上B 的大小;(3) 设R 1 = 10mm, R 2 = 0.5mm, a = 5.0mm, I = 20A, 分别计算上述两处B 的大小.()()2122212122211R R R I R R R I I -=-=ππ,()()2222212222212R R R I R R R I I -=-=ππ 21R R o B B B +=()222122022R R a IR B B R o -==πμT 6102-⨯=21o o o B B B '''+=()2221012R R a IaB o -='πμT 4102-⨯=11.13如图所示, 一半径为R 的无限长半圆柱面导体, 其上电流与其轴线上一无限长直导线的电流等值、反向, 电流I 在半圆柱面上均匀分布. 求: (1) 轴线上导线单位长度所受的力;(2) 若将另一无限长直导线(通有方向与半圆柱面相同的电流I )代替圆柱面, 产生同样的作用力, 该导线放在何处?题11.13图(1)R Ii π=, 0000d d d d d 2222I i l iR i B R R R μμμθμθππππ====,0d d cos 22x i B μθπθπ⎛⎫=- ⎪⎝⎭ 00d =d cos 22x x i B B πμθπθπ⎛⎫=- ⎪⎝⎭⎰⎰()000020cos 222i i i I R πμμμμθππππ=-=== 0d d sin 22y i B μθπθπ⎛⎫=- ⎪⎝⎭,00d =d sin 22y y i B B πμθπθπ⎛⎫=- ⎪⎝⎭⎰⎰, 0=y B (由对成性可知)22yx B B B +=R I 20πμ=,BIl F =RI220πμ=(j R I F 220πμ=亦可)(2)dI R I πμπμ220220=; 2R d π=; 2R y π-=11.14载有电流I 1的长直导线, 旁边有一个正三角形线圈, 边长为a , 电流为I 2, 它们共面, 如图所示. 三角形一边与长直导线平行, 三角形中心O 到直导线的距离为b, 求I 1对该三角形的作用力.解:AB 段:⎪⎪⎭⎫ ⎝⎛-=a b I B 632101πμ, ⎪⎪⎭⎫ ⎝⎛-==a b aI I a B I F 632210121πμ, 方向沿x 负向;BC 段:选择电流元dl xI I dl B I dF πμ2210222==;6cos πdxdl =I 1I 1⎰⎰+-==3333210226cos2b b x dx I I dF F ππμ⎪⎪⎪⎪⎭⎫⎝⎛-+=323ln 3210a b a b II πμ ⎪⎪⎪⎪⎭⎫ ⎝⎛-+==323ln 323cos 21022a b a b I I F F x πμπ; ⎪⎪⎪⎪⎭⎫⎝⎛-+==323ln 23sin 21022a b a b I I F F y πμπ 同理可得AC 段受力⎪⎪⎪⎪⎭⎫⎝⎛-+=323ln 32103a b a b I I F πμ ⎪⎪⎪⎪⎭⎫⎝⎛-+==323ln 323cos 21033ab a b I I F F x πμπ; ⎪⎪⎪⎪⎭⎫⎝⎛-+==323ln 23sin 21033a b a b I I F F y πμπ y y F F 23=, 方向相反, 抵消.合力, 方向沿x 正向,x x F F F F 321++-=11.18盘面与均匀磁场B 成φ角的带正电圆盘, 半径为R, 电荷量Q 均匀分布在表面上. 圆盘已角速度ω绕通过盘心, 与盘面垂直的轴转动. 求此带电旋转圆盘在磁场中所受的磁力矩.解:dS dq σ=()rdr πσ2=, 由于圆盘以ω旋转, 故圆环中电流T dq dI =πω2dq =rdr σω=, 式中2RQ πσ= dr r dIS dp m 3σπω==⎰⎰==R m m dr r dp p 03σπω2244141QR R ωσπω==⎪⎭⎫ ⎝⎛-=ϕπ2sin B p M m ϕωcos 412B QR =方向满足B p M m⨯=11.25螺绕环平均周长l =10cm, 环上线圈N=200, 线圈中电流I =100mA. 试求: (1)管内B 和H 的大小;(2)若管内充满相对磁导率μr =4200的磁介质, 管内B 的大小. 解:(1)∑⎰=⋅0I l d H; 02NI r H =πrNI H π20=, 000nI B μ=, 可知H =200A/m, B 0=2.5×10-4T (2)H H B r μμμ0==, 可知B =1.05T常见载流体的磁感应强度无限长载流直导线外距离导线r 处,0=2IB rμπ,圆电流轴上距离圆心x 处,()203222=2R INB xRμ+ (N 是线圈匝数)无限长密绕直螺线管内部,0=B nI μ (n 是单位长度上的线圈匝数)圆电流圆心处,0=2IB Rμ无限大均匀载流平面外,01=2B i μ(i 是流过单位长度的电流)一段载流圆弧导线在圆心处,0=4I B Rμϕ(φ以弧度为单位)OIBI11 / 11安徽信息工程学院 大学物理(2) 韩玉龙 0B =;00=224I I B R R μμππ=⋅;000121211+=+444I I I B R R R R μμμ⎛⎫= ⎪⎝⎭;002=228I I B R R μμππ=⋅OI。
大学物理 恒定磁场

11-1 恒定电流电流密度磁现象:我国是世界上最早发现和应用磁现象的国家之一,早在公元前300年久发现了磁铁矿石吸引铁的现象。
在11世纪,我国已制造出航海用的指南。
在1820年之前,人们对磁现象的研究仅局限于铁磁极间的相吸和排斥,而对磁与电两种现象的研究彼此独立,毫无关联。
1820年7月丹麦物理学家奥斯特发表了《电流对磁针作用的实验》,公布了他观察到的电流对磁针的作用,从此开创了磁电统一的新时代。
奥斯特的发现立即引起了法国数学家和物理学家安培的注意,他在短短的几个星期内对电流的磁效应作出了系列研究,发现不仅电流对磁针有作用,而且两个电流之间彼此也有作用,如图所示;位于磁铁附近的载流线圈也会受到力或力矩的作用而运动。
此外,他还发现若用铜线制成一个线圈,通电时其行为类似于一块磁铁。
这使他得出这样一个结论:天然磁性的产生也是由于磁体内部有电流流动。
每个磁性物质分子内部,都自然地包含一环形电流,称为分子电流,每个分子电流相当于一个极小的磁体,称为分子磁矩。
一般物体未被磁化时,单个分子磁矩取向杂乱无章,因而对外不显磁性;而在磁性物体内部,分子磁矩的取向至少未被完全抵消,因而导致磁铁之间有“磁力”相互作用。
1820年是人们对电磁现象的研究取得重大成果的一年。
人们发现,电荷的运动是一切磁现象的根源。
一方面,运动电荷在其周围空间激发磁场;另一方面,运动电荷在空间除受电场力作用之外,还受磁场力作用。
电磁现象是一个统一的整体,电学和磁学不再是两个分立的学科。
11-1 恒定电流电流密度如前所述,电荷的运动是一切磁现象的根源。
电荷的定向运动形成电流,称为传导电流;若电荷或宏观带电物体在空间作机械运动,形成的电流称为运流电流。
常见的电流是沿着一根导线流动的电流,其强弱用电流强度来描述,它等于单位时间通过某一截面的电量,方向与正电荷流动的方向相同,其数学表达式为dtdq I ,虽然我们规定了电流强度的方向,但电流强度I 是标量而不是矢量,因为电流的叠加服从代数加减法则,而不服从矢量叠加的平行四边形法则。
第十一章恒定电流的磁场作业磁介质磁介质中的安培环路定理小结

作业11.1、11.211.4、11.8、11.9、11.15、11.1787磁介质90顺磁质B B >(铝、氧、锰等)弱磁质B B >>铁磁质(铁、钴、镍等)强磁性物质B B <抗磁质(铜、铋、氢等)弱磁质抗磁质顺磁质SI SI B L宏观上构成沿介质表面的等效环形电流, 称为表面束缚电流或磁化电流。
B AI 0I cbad.l113五、磁场对载流导线和运动电荷的作用(1)磁场对载流导线的作用力—安培力微分形式积分形式B l I F ⨯=d d Bl I F l⨯=⎰d 其中,是载流导线上的电流元,是所在处的磁感应强度。
l Id l I d B(2)均匀磁场对平面载流线圈的作用合力=∑F 磁力矩B p M m ⨯=式中,是载流线圈的磁矩,,其中N 是线圈匝数,I 是线圈中的电流,S 是线圈的面积,且S 的方向与电流环绕方向满足右螺旋法则。
m p S NI p m=114(3)磁力的功⎰=m1m2m d ΦΦΦI A mm1m2)(ΦI ΦΦI ∆=-=磁力的功等于电流强度I 乘以通过回路磁通量的增量∆Φm 。
(4)磁场对运动电荷的作用Bq F⨯=v 洛仑兹力:116六、磁介质(1)磁介质的分类抗磁质1<r μ顺磁质1>r μ铁磁质1>>r μ(2)磁介质的磁化在外磁场中固有磁矩沿外磁场的取向或感应磁矩的产生使磁介质的表面(或内部)出现束缚电流。
第11 章 恒定电流的磁场
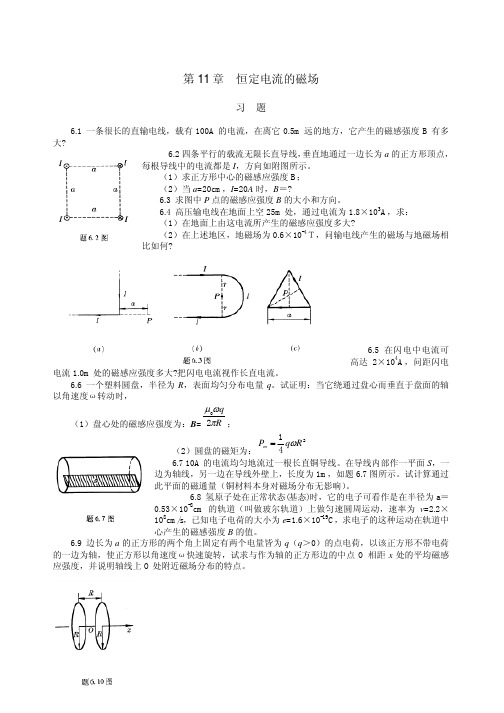
第11章 恒定电流的磁场习 题6.1 一条很长的直输电线,载有100A 的电流,在离它0.5m 远的地方,它产生的磁感强度B 有多大?6.2四条平行的载流无限长直导线,垂直地通过一边长为a 的正方形顶点,每根导线中的电流都是I ,方向如附图所示。
(1)求正方形中心的磁感应强度B ; (2)当a =20cm ,I =20A 时,B =?6.3 求图中P 点的磁感应强度B 的大小和方向。
6.4 高压输电线在地面上空25m 处,通过电流为1.8×103A ,求: (1)在地面上由这电流所产生的磁感应强度多大?(2)在上述地区,地磁场为0.6×10-4T,问输电线产生的磁场与地磁场相比如何?6.5 在闪电中电流可高达2×104A ,问距闪电电流1.0m 处的磁感应强度多大?把闪电电流视作长直电流。
6.6 一个塑料圆盘,半径为R ,表面均匀分布电量q 。
试证明:当它绕通过盘心而垂直于盘面的轴以角速度ω转动时,(1)盘心处的磁感应强度为:B =R qπωµ20;(2)圆盘的磁矩为:241R q P m ω=6.7 10A 的电流均匀地流过一根长直铜导线。
在导线内部作一平面S ,一边为轴线,另一边在导线外壁上,长度为1m ,如题6.7图所示。
试计算通过此平面的磁通量(铜材料本身对磁场分布无影响)。
6.8 氢原子处在正常状态(基态)时,它的电子可看作是在半径为a =0.53×10-8cm 的轨道(叫做玻尔轨道)上做匀速圆周运动,速率为v =2.2×108cm/s ,已知电子电荷的大小为e =1.6×10-19C ,求电子的这种运动在轨道中心产生的磁感强度B 的值。
6.9 边长为a 的正方形的两个角上固定有两个电量皆为q (q >0)的点电荷,以该正方形不带电荷的一边为轴,使正方形以角速度ω快速旋转,试求与作为轴的正方形边的中点O 相距x 处的平均磁感应强度,并说明轴线上O 处附近磁场分布的特点。
第十一章 恒定磁场

S1 ( B R2 ) 0
S1 BR 2
(3i 2 j ) Si 3S
例3、两平行载流直导线
求 1.两线中点 B A
I1
2.过图中矩形的磁通量 解:1.I1、I2在A点的磁场
BA
r2
A
I2
l
r3
0 I1 B1 B2 2 d 2
r1
2.0 10 T
第十一章 恒定磁场 静止的电荷产生静电场,静电场 是一种物质。运动电荷周围既有电场 又有磁场,磁场也是一种物质。恒定 电流(运动电荷)的磁场在研究方法 上与静电场有许多相似之处,因此要 与静电场部分类比学习。
电流密度(矢量)
用来细致刻画电流在截面上分布的物理量。
垂直通过单位截面的电流强度,称为此处的电流 密度。
0 I sin dy B 2 4 r 2 0 I sin d 1 4a
0 I B (cos 1 cos 2 ) 4a
I
2
dy
1 r0
r
y
O
dB
P
a
X
0 I B (cos 1 cos 2 ) 4a
无限长载流直导线
I 2
Ek dl Ek dl
L
单位正电荷绕闭合回路一周时,电源中非静电力所 做的功。 电动势描述电路中非静电力做功本领 电势差描述电路中静电力做功本领 注意:电动势 是标量
基本的磁现象
天然磁石 同极相斥 异极相吸
S
N
S
N
电流的磁效应 1820年 奥斯特
S
N
I
F
I
F
电子束
E dl
新编基础物理学答案_第11章

第11章 恒定电流与真空中的恒定磁场11-1 电源中的非静电力与静电力有什么不同答:在电路中,电源中非静电力的作用是,迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极,使两极间维持一定的电位差。
而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方,起到推动电流的作用;在电源内部正好相反,静电场起的是抵制电流的作用。
电源中存在的电场有两种:1、非静电起源的场;2、稳恒场。
把这两种电场与静电场比较,静电场由静止电荷所激发,它不随时间的变化而变化。
非静电场不由静止电荷产生,它的大小决定于单位正电荷所受的非静电力,k F E q=vv 。
当然电源种类不同,k F v的起因也不同。
11-2静电场与恒定电场有什么相同处和不同处为什么恒定电场中仍可应用电势概念 答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。
但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同电流密度是否相同电流强度是否相同为什么答:此题涉及知识点:电流强度d sI =⋅⎰r rj s ,电流密度概念,电场强度概念,欧姆定律的微分形式j E σ=rr 。
设铜线材料横截面均匀,银层的材料和厚度也均匀。
由于加在两者上的电压相同,两者的长度又相等,故铜线和银层的场强E r相同。
由于铜线和银层的电导率σ不同,根据j E σ=r r 知,它们中的电流密度j r 不相同。
电流强度d sI =⋅⎰r r j s ,铜线和银层的j r不同但相差不太大,而它们的横截面积一般相差较大,所以通过两者的电流强度,一般说来是不相同的。
11-4一束质子发生侧向偏转,造成这个偏转的原因可否是: (1)电场 (2)磁场(3)若是电场或者是磁场在起作用,如何判断是哪一种场答:造成这个偏转的原因可以是电场或磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 如图载流长直导线的电流为 I , 试求 通过矩形面积的磁通量. 0 I 解 B B 2π x 0 I dΦ BdS ldx 2π x l I 0 Il d2 dx Φ S B dS d1 d1 d2 2π x o x Φ 0 Il ln d 2 2π d1
基本磁现象
电流电流 I1
磁体电流
I
N I
F
F
I2
F
磁 场
S
磁体磁体
S N S N
电流磁体 I
运动电荷
磁场
运动电荷
3. 安培的分子电流假说
(1)1822年安培提出了用分子电流来解释磁 性起源。 一切磁现象都起源于电流,任何物质的分 子中都存在着环形电流(分子电流),每个分 子电流就相当于一个基元磁体,当这些分子电 流作规则排列时,宏观上便显示出磁性。 (2) 近代分子电流的概念: 轨道圆电流+自旋圆电流=分子电流
2. 磁现象起源于运动电荷 1819-1820 年丹麦物理学 家奥斯特 首先发现了电流的磁 I 效应。1820年4月,奥斯特做了 一个实验, 通电流的导线对磁 针有作用, 使磁针在电流周围 偏转。 另外,磁体对载流导线的作用; 载流导线彼 此间有磁相互作用;…… 上述现象都说明了:磁现象与运动电荷之 间有着深刻的联系。
N
S
N
S
磁 铁
磁场
磁
铁
2 电流的磁场
奥斯特实验 电 流
3 磁现象的起源 运动电荷 磁场
电
流
磁场
运动电荷
二 磁感强 度 B 的定义
实验发现带电粒子在磁场中运动所受的力与运动方 向有关. 带电粒子在磁场中沿某一特定直线方向运动时不 受力, 带电粒子在磁场中沿其 他方向运动时 F 垂直于 v 与特定直线所组成的平面. 当带电粒子在磁场中 垂直于此特定直线运动时 受力最大.
基本磁现象 1. 自然磁现象 磁性:具有能吸引铁磁物资(Fe、Co、Ni) 的一种特性。 磁体:具有磁性的物体。 磁极:磁性集中的区域。 磁极不能分离 (正负电荷可以分离开)。 地磁:地球是一个大磁体。
地 磁 南 极 大 约 在 - -纬 北7050',西 经96 ' ' 地 磁 北 极 大 约 在 -- 南 纬 70 10 , 东 经 150 45
0 dqv
4 π r2
R o r
dq 2 π rdr
v r
dr
B
dB
0
2
dr
0
2
R
0
dr
0 R
2
11-3 磁通量 磁场中的高斯定理 一 磁感线
切线方向—— B 的方向; 疏密程度—— B 的大小.
I I I
I S N S I N
r
dB
P*
I
Idl
真空磁导率 0 4 π107 N A2
r
任意载流导线在点 P 处的磁感强度
磁感强度叠加原理
B dB
dB
P*
Idl
dB
r
I
Idl
0 I dl r 4 π r3
r
例 判断下列各点磁感强度的方向和大小.
1 8
×
2
×3
7
Idl
R
6
×
4
0 Idl r dB 3 4π r
5
1、5点 :dB 0 0 Idl 3、7点 :dB 4 π R2 2、 4、 6、 8 点 : 0 Idl 0 dB sin 45 4 π R2 毕奥-萨伐尔定律
二 毕奥-萨伐尔定律应用举例
R
*
P
x
×× × ×× × ×× × ×× ×× ×
解
由圆形电流磁场公式 0 IR2 B 2 2 3/ 2 2( x R )
dB
0
2
P
R
x
R Indx
2
2
x
2 3/ 2
R
O*
x
×× × ×× × ×× × ×× ×× ×
x Rcot
dx R csc d
2
B dB
z
D
0 I
4 π r0
(cos1 cos 2 )
无限长载流长直导线
2
1 0 2 π
×
B
0 I
2 π r0
I
B
y
半无限长载流长直导线
π 1 2 2 π
x
C
o
1
P
BP
0 I
4 π r0
无限长载流长直导线的磁场
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右螺旋关系
B
dS
B
s
dS 2
B
2 S
dS1
1
B2
B1
dΦ 1B 1 dS1 0 dΦ2 B2 dS2 0
B cos dS 0
S
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通 量必等于零(故磁场是无源的).
五 理解洛伦兹力和安培力的公式 ,能分析电荷在均 匀电场和磁场中的受力和运动.了解磁矩的概念.
六 了解磁介质的磁化现象及其微观解释.了解磁场 强度的概念以及在各向同性介质中H和B的关系,了解磁 介质中的安培环路定理 .了解铁磁质的特性.
11-1 磁 场
一 磁场 1 磁铁的磁场
磁感强度
N、S极同时存在; 同名磁极相斥,异名磁极相吸.
F Fmax F
Fmax qv
Fmax 大小与 qv
q, v 无关
Fmax 磁感强度 B 的定义: 磁感强度大小: B qv
当正电荷垂直于 特定直线运动时,受力 Fmax 将 Fmax v 在磁场中的方向定义为该点的 B 的方向.
Fmax
运动电荷在磁场中受力
B
q
+
F qv B
v
单位 特斯拉
1( T ) 1 N/(A m)
1(G) 10Байду номын сангаас
4
高 斯
T
11-2 毕奥-萨伐尔定律
一 毕奥-萨伐尔定律 (电流元在空间产生的磁场)
dB
0 Idl sin
4π
2
Idl
dB
r 0 Idl r dB 3 4π r
2
0 nI
2
2 2
R
x1
x2
R 2dx
2
x
2 3/ 2
R x R csc
2
R
x1
1 O*
2
x2 x
×× × ×× × ×× × ×× ×× ×
B
0 nI
2
2
1
2
1
R 3csc2 d 3 3 R csc d
0 nI 2
R
sin d
二 磁通量 磁场的高斯定理 S B ΔN
B ΔS
磁场中某点处垂直 B 矢量的单位面积上 通过的磁感线数目等于该点 B 的数值.
s
s
B
en
B
磁通量:通过 某曲面的磁感线数 匀强磁场下,面 S的磁通量为: Φ B S B en S
Φ BS cos BS 一般情况 Φ s B dS
11-4 安培环路定理
一 安培环路定理的推导
B
0 I
2π R
I
o
B
R
dl
0 I l B dl 2π Rdl B dl 0 I
l
l
设闭合回路 l 为圆 形回路( l 与 I成右螺 旋)
若回路绕向为逆时针 2π I 0 dl B d l d I 0 l o R 2π 0 l 对任意形状的回路 B 0 I 0 I d B dl rd d dl 2π r 2π I r l B dl 0 I
x1
1 O*
2
x2 x
×× × ×× × ×× × ×× ×× ×
0 nI cos 2 cos 1 B 讨 论 2 (1)P点位于管内轴线中点 1 π 2
cos1 cos2
cos 2 l/2
l / 2
l
2
R
2
B 0 nI cos 2
I
l
B
电流在回路之外
d
B1
I
r1
B2 dl B1 dl1 B2 dl2 0 I d dl1 2 2π
0 I 0 I B1 , B2 2π r1 2π r2
r2
l
B1 dl1 B2 dl2 0 B d l 0
圆电流的磁场 dI 2 π rdr rdr 2π R 0 dI 0 dB dr o 2r 2 r 0 R 0 R dr B dr 2 0 2 0, B 向内 0, B 向外
解法一
解法二
运动电荷的磁场
dB0
z r0 cot , r r0 / sin
z
D
2
dz r0d / sin
2
B
0 I
4 π r0
