新人教版九年级下册初三数学29.2三视图优秀PPT课件

合集下载

(人教版)数学九年级下29.2.1三视图课件(共23张PPT)(优质课件)

23
尝试画出下列实物的三视图：
课件在线
24
画出下面一些基本几何体的三视图：
圆柱正三棱柱球
（1）（2）（3）
课件在线
11
你会画圆柱的三视图吗？试一试吧！
演示
课件在线
12
圆柱的三视图：
高平齐
主视图
长对正
俯视图
课件在线
左视图
宽相等
13
正三棱柱的三视图：
高平齐
长对正
可见轮廓线用实线绘制，不可见的轮廓线用虚线绘制
课件在线
宽相等
14
在水平面内得到的由上向下观察物体的视图，叫做俯视图；
在侧面内得到由左向右观察物体的视图，叫做左视图。
课件在线
7
1.三视图
从左面看
主视图
从上面看
正面
主视图
左视图
俯视图
从正面看
将三个投影面展开在一个平面内，得到这个物体的一张三
视图.
课件在线
8
2.三视图的位置规定：
主视图是俯视图
俯视图
左视图在主视图在右边
课件在线
9
3.三视图的对应规律
主视图和俯视图 ----长对正
高平齐
主视图
左视图高
主视图和左视图长对正 ----高平齐
俯视图和左视图
长
宽
宽俯视图
宽相等
----宽相等
注意：一定要将边缘、棱、顶点都体现出来，
看得见线画成实线，看不见部分的轮
课廓件在线线画成虚线。
10
例1：
球的三视图：
主视图
左视图
俯视图
课件在线
15
再总结

《三视图》PPT优秀教学课件1

在正面内得到的由前向后观察物体的视图，叫做
；
(1)画一个几何体的三视图前要观察几何体，在观察时一定要使视线与观察面垂直；
支架可以看作是由两个大小不相等的长方体构成的组合体.
画视图的外轮廓线时一定要将边缘、棱、顶点都体现出来.
17．用小立方块搭一个几何体，使它的主视图和俯视图如图所示，俯视图中的小正方形中的数字和字母表示该位置小立方块的个数，试回答下列问题：
)
解：(1)→B，(2)→C，(3)→A
16．(练习变式)如图，请你根据三视图画出该物体的立体图并说明
该物体的具体名称．
17．用小立方块搭一个几何体，使它的主视图和俯视图如图所示，俯视图中的小正方形中的数字和字母表示该位置小立方块的个数，试回答下列问题：
A．长方体 B．四棱锥 C．三棱锥 D．圆锥
解：(1)x＝3，z＝1 (2)y＝1或2；
画三视图时，看得见部分的轮廓线画成实线，因被其他部分遮挡而看不见部分的轮廓线画成虚线.
5．(襄阳中考)一个几何体的三视图如图所示，则这个几何体是（
）
主视图与俯视图最左侧在一条竖直线上，最右侧在一条竖直线上；
解：(1)x＝3，z＝1 (2)y＝1或2；
2．如图是某几何体的俯视图，该几何体可能是(
A
B
C
D
看不到，用虚线
2.画出如图所示的几何体的三视图．
4．(2019·贺州)如图是某几何体的三视图，则该几何体是 ( )
(1)确定主视图的位置，画出主视图；
画组合体的三视图时，可采用图形分解法，即先将组合体分解成若干个简单的几何体，再分别画出这些简单几何体的三视图，最后按照原组合体将各视图组合在一起.
14．如图由一些完全相同的小正方体搭成的几何体的俯视图和左视图，组成这个几何体的小正方体的个数是____________.

新人教版九年级数学下册29.2.三视图 (42张PPT)

主视图
主视图
左视图高
正面
长宽俯视图
宽
画法示例1：画法要点（二）
主视图左视图
高平齐
高
长宽俯视图
宽
正方形
正方形
长对正
宽相等
三视图画法示例2 线面分析
前、后两棱面是正平面，正面投影反映实形，水平投影和侧面投影积聚成直线段. 其余四个侧棱面是铅垂面，它们的水平投影都积聚成直线，并与正六边形的边线重合，在正面投影和侧面投影面上的投影为类似形（矩形）.
根据三视图描述形状
例1 .(教材98页例5)根据三视图说出立体图形的名称．
分析：由三视图想象立体图形时，要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面，然后再综合起来考虑整体图形．
解. ⑴.从三个方向看立体图形，图象都是矩形，可以想象出：整体是长方体，如图所示． ⑵.从正面、侧面看立体图形，图象都是等腰三角形；从上面看，图象是圆；可以想象出：整体是圆锥，如图所示
师生互动：画圆锥体的三视图（教材96页）
基本几何体的三视图：
⑴.正方体的三视图都是正方形;
⑵.圆柱的三视图中有两个是长方形，另一个是圆; ⑶.圆锥的三视图中有两个是三角形，另一个是圆和一个点; ⑷.四棱锥的三视图中有两个是三角形，另一个是矩形和它的对角线; ⑸.球体的三视图都是圆形.
……
例2.(教材97页例2）画出下列所示支架（一种小零件）的三视图，其中支架的两个台阶的高度和宽度相等.
型加深.
绘制六棱柱的三视图
我们一起再来重新画一下！
主视图左视图
俯视图
例1.(教材96页例1）画出下列图中基本几何体的三视图.
分析：画几何体的三视图时，要注意从三个方面观察它们，注意“长对正，宽平齐，高相等.”注意看得见的轮廓线用实线，看不见的轮廓线用虚线.

人教版九年级数学下册29.2 三视图(课件)(共32张PPT)

务于生活，为了我们的美好生活，为了祖国的繁荣富强，让我们一起珍惜时间，共同努力吧！
在侧面内得到由左向右观察物体的视图，叫做左视图。
三视图的位置
从上面看
主视图
正面
主视图
左视图
从左面看
俯视图
从正面看
将三个投影面展开在一个平面内，得到这个物体的一张三视图.
三视图的对应规律
主视图和俯视图 ----长对正
高平齐
主视图
左视图高
主视图和左视图长对正 ----高平齐
长
宽
宽
俯视图和左视图
在本次阅兵式中展出了不少先进的武器:
看一看
看一看
聪明的同学,你发现了吗?以上几幅图是从哪几个角度来展示的.
学习目标
※知识目标：知道三视图的概念。 ※能力目标：会画简单几何体的三视图,及归纳总结知识的能力. ※情感目标：培养学生合作交流的意识，热爱祖国的情感。
自学指导
自学课本94页—97页，完成以下内容： 1、知道什么是视图，什么是三视图。 2、掌握三视图的位置关系。 3、知道三视图的对应规律。自学5分钟，看看哪个同学自学效果好。
猜猜他们是什么关系？
看问题不能只看单方面
三个互相垂直的平面作为投影面
从上面看
从三个角度观察长方体的投影（视图）
从左面看
从正面看
知识要点
一个物体在三个投影面内进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图；
在水平面内得到的由上向下观察物体的视图，叫做俯视图；
高平齐
长对正
可见轮廓线用实线绘制，不可见的轮廓线用虚线绘制
宽相等
球的三视图：

人教版九年级数学下册课件：29.2三视图 (共31张PPT)

圆锥体是由圆锥侧面和底面所围成的立体图形。圆锥面是一条母线绕与它相交的旋转轴旋转而成的。
母线
旋转轴
3、圆柱体的投影
旋转轴
D
A
B
C
水平投影为一圆，反映顶、底圆的图形，
圆柱面上所有竖线都积聚在该圆周上。
母线
例、画下例几何体的三视图
例、画下例几何体的三视图
延
伸
拓
展
我思我进步
回味无穷
三视图
用小立方块搭出符合下列三视图的几何体：
主视图
左视图
俯视图
下列是一个物体的三视图，请描述出它的形状
主视图
左视图
俯视图
主视图
左视图
俯视图
探究根据三视图想它的立体图形，它是由几块小正方体组成的？
谢谢同学们的合作！
再见
温故知新我们生活在一个丰富多彩的图形世界中，同
一个图形，从各个方向看，形状可能不尽相同，这就是视图问题，在七年级（上）的学习中，我们已经学习了立方体及其简单组合体的三种视图，你还记得是哪三种视图吗？
你能画出下图的主视图、左视图和俯视图吗？
主
左
视
视
图
图
俯视图
三视图的形成1
物体向投影面投影所得到的图形称为视图。
从左向右正投影，在投影面得到的投影，称为左视图（从左向右看）；
从上向下正投影，在投影面得到的投影，称为俯视图（从上向下看）。
宽高
长主视图
长
长俯视图
高
高
左视图
宽
长对正,
宽
高平齐,
宽相等.
议一议
⒈下图中物体的形状分别可以看成什么样的几何体？

29.2 三视图人教版九年级下册课件(共23张)

巩固知识
1.一个直六棱柱和长方体如图所示放置.你能说出下面 (a),(b),(c)三个视图分别是从哪个方向看到的吗?
( 第1题 )
(a)
(b)
2.用4个小立方块搭成的几何体如图.请画出它的三视图.
(c)
( 第2题 )
更上一层楼
3.一个圆柱如图,从正面看到的是什么图形?从上面看到的是什么图形?从左面看到的是什么图形?
主视图
左视图
高平齐
主视方向图3-18
长对正
宽相等
俯视图图3-19
1.说出圆锥、球、正方体的三视图各是什么图形.
圆锥, 球的三视图.
主
视
主视图左视图
图
俯视图
左视图
俯视图
立方体的三视图都是正方形。
主视图左视图俯视图
如图，圆柱的主视图和左视图都是长方形，俯视图是圆。
主视图左视图
俯视图和左视图共同反映了物体前后方向的尺寸, 通常称之为“宽相等”; “长对正,高平齐,宽相等”是画三视图必须遵循的法则.
在画三视图时,一般先画主视图,再把左视图画在主视图的右边,把俯视图画在主视图的下面.
一个长方体的立体图如图3-18所示,请画它的三视图.
重画一次解: 所求三视图如图3-19.
猜猜他们是什么关系？
看必为
事须了从能
物多完方整
不能
面确观切察的
只物表体达
看
。物体
单
的形
方面
状和大
小
பைடு நூலகம்
，
你认识吗？
你认识吗？
你认识吗？
观察物体从哪些方面去考虑呢？

人教版九年级数学下册29.2三视图课件25张ppt

横看成岭侧成峰 ,
苏轼
题西林壁
由立体图到视图
当我们从某一个方向观察一个物体时，所看到的图形叫做物体的一个视图。
由立体图到视图
数学中我们一般只从正面、上面、左面这三个不同方向看同一几何体，这就是今天学习的三视图。
定义：
主视图：从正面看到的图形；俯视图：从上面看到的图形；左视图：从左面看到的图形；主视图、俯视图,左视图合称三视图.
三视图
请欣赏漫画并回答：为什么会出现争执？
漫画 “6”与“9”
不同角度
猜猜他们是什么关系？
看事物不能只看单方面
要学会从多个角度看待问题
多角度思考
只缘身在此山中 .
不识庐山真面目 ,
远近高低各不同 .
例1.桌上放着一个长方体、一个棱锥和一个圆柱，请说出下面的三幅图分别面看
（请说明理由）
（1）主视图
（2）左视图
（3）俯视图
例2：由5个相同的正方体搭成的几何体如
图所示，
从上面看
从左面看
从正面看
搭一搭、画一画：搭得快、画得好
由5个相同的正方体搭成几何体 • 每个小组搭出一个图形（体现小组的特色） • 小组同学画出它的三视图（不妨设正方体的边长为1厘米） • 小组合作交流、小组展示
数学冲刺：我最棒
例3.三视图相同，立体图形是否唯一确定？
主视图
左视图
俯视图
本节课里我的收获是……
学到了什么？
从正面看
实物图
平面图
从左面看
立体图

人教版九年级数学下册第二十九章《29-2 三视图》优课件(共57张PPT)

不识庐山真面目，只缘身在此山中。
——苏轼
, . , .
只不远缘识近身庐高在山低此真各山面不中目同
横看成题岭苏西侧轼林成壁峰
下列是一个物体的三视图，请描述出它的形状
主视图左视图
俯视图
用小立方块搭出符合下列三视图的几何体：
主视图
左视图
俯视图
下列是一个物体的三视图，请描述出它的形状
三视图的对应规律
主视图和俯视图 ----长对齐主视图和左视图 ----高对齐
俯视图和左视图 ----宽对齐
圆锥体
下面所给的三视图表示什么几何体? 圆锥
画下例几何体的三视图
延
伸
拓
展
画下例几何体的三视图
主视图左视图
三视图
主视图
左视图
宽
宽
老师提示: 俯视图
俯视图
在画图时,看的见部分的轮廓通常画成实线,看不见部分
错误的三视图 —长未对正
错误的三视图
—高不平齐
错误的三视图 —宽不相等
P123 2
正视图
球的三视图
侧视图
俯视图
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
正视图
侧视图
俯视图
注意：不可见的轮廓线，用虚线画出。
那怎样画一个空间几何体的三视图呢?请同学们看底下图的三视图.
三视图
你能指出这些图形分别从哪个角度观察得到的吗?
俯
左
正面
将三个投影面展开在一个平面内，得到这一物体的一张三视图
三视图是主视图、俯视图、左视图的统称。它是从三个方向分别表示物体形状的一种常用视图。

人教版九年级数学下册《三视图》PPT课件

正面
例 3 画出下面简单组合体的三视图．
解：其三视图如下：
主视图Biblioteka 左视图俯视图练一练找出对应的的三视图. 主视图 ( A ) 左视图 ( A ) 俯视图 ( B )
A
B
C
1. 下图的几何体中，主视图、左视图、俯视图均相同
的是
( D)
A
B
C
D
2. 一个几何体的三视图形状都相同，大小均等，那么
这个几何体不可以是
( D)
A. 球
B. 正六面体 C. 正方体 D. 圆柱
3．如图摆放的几何体的俯视图是
( B)
A
B
C
D
4．将矩形硬纸板绕它的一条边旋转 180° 所形成的
几何体的主视图和俯视图不可能是
(C)
A．矩形、矩形
B．半圆、矩形
C．圆、矩形
D．矩形、半圆
5．下图中①表示的是组合在一起的模块，那么这个
模块的俯视图是
第二十九章投影与视图
29.2 三视图
第1课时三视图
情境引入 “横看成岭侧成峰，远近高低各不同．不识庐山真面目，只缘身在此山中．”你能说明是什么原因吗？
观察与思考
三视图的概念及关系
下图为某飞机的设计图，你能指出这些设计图是
从哪几个方向来描绘物体的吗？
当我们从某一方向观察一个物体时，所看到的图形叫做物体的一个视图．视图也可以看作物体在某一个方向的光线下的正投影，对于同一物体，如果从不同方向观察，所得到的视图可能不同．本章中我们只讨论三视图.
1. 三个投影面我们用三个互相
垂直的平面（例如：墙角处的三面墙面）作为投影面，其中正对着我们的叫正面，正面下方的叫水平面，右边的叫做侧面.

202X人教版九年级数学下册29.2 三视图(1)课件(20张ppt)

在水平面内得到的由上向下观察物体的视图，叫做俯视图
在侧面内得到由左向右观察物体的视图，叫做左视图．
主视图
投影面
左视图
正面
俯视图
侧面水平面
合作探究达成目标
三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高，左视图与俯视图表示同一物体的宽，因此三个视图的大小是互相联系的，画三视图时，三个视图要放在正确的位置
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
• 10、人的志向通常和他们的能力成正比例。2021/3/122021/3/122021/3/123/12/2021 10:22:50 AM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/122021/3/122021/3/12Mar-2112-Mar-21 • 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/122021/3/122021/3/12Friday, March 12, 2021 • 13、志不立，天下无可成之事。2021/3/122021/3/122021/3/122021/3/123/12/2021
合作探究达成目标

29.2 三视图人教版九年级下册课件(共38张)

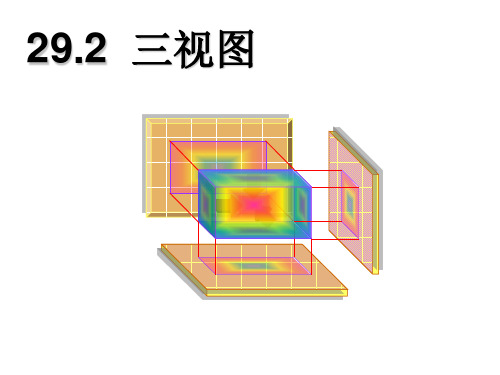
正视图
左视图
俯视图
我相信你一定能画出这个复杂几何体的三视图！
随堂练习
• 1找出图中每一物品所对应的主视图。
（A）
（B）
（C）
（D）
主视图（ B ）左视图（ B ）俯视图（ C ）
A
B
C
考考你
主视图（ A ）左视图（ A ）俯视图（ B ）
A
B
C
试一试：
• 1、如下图几何体，请画出这个物体的三种视图。
29.2 三视图
看一看
看一看
你能说出这三个视图分别是从哪个方向观察这本
书得到的吗？
当我们从某一个角度观察一个物体时, 所看到的图象叫做物体的一个视图
为了全面反映物体形状，在生活中我们应从不同角度，多个视图去反映物体的形状。
我们用三个互相垂直的平面作为投影面
其中：正对着我们的叫正面，正面下方的叫水平面，左边的叫做侧面。
正面
主视图
左视图
俯视图
如将物右三体图个的将：投一三影张个面三投展视影开图面在.展一开个在平从一正面面个看内平，面得内到，一得张到三这视个图。
2、三视图的位置规定：
主视图
左视图
主视图要在左上边
它的下方应是俯视图
俯视图
左视图坐落在右边
3.三视图的对应规律
主视图和俯视图 ----长对正
主视图和左视图 ----高平齐
主主视主主视图视视图图图
左左左左视视视视图图图图
俯俯俯俯视视视视图图图图
第二课时
下面所给的三视图表示什么几何体? 圆锥
例根据三视图说出立体图形的名称
例5 根据物体的三视图，描述物体的形状.

人教版九年级数学下册第二十九章《29-2三视图》优质课课件(共21张PPT)

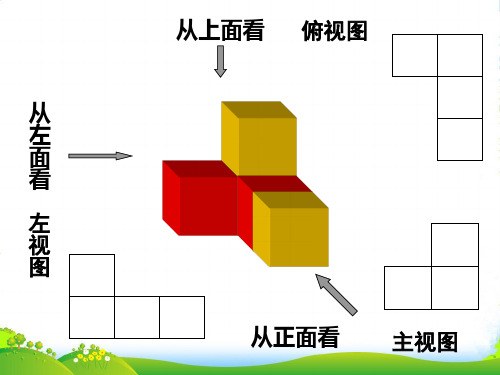
三视图
左面视图图俯形视图
面看
么
•11、即使是普通孩子，只要教育得法，也会成为不平凡的人。 •12、首先是教师品格的陶冶，行为的教育，然后才是专门知识和技能的训练。 •13、儿童是中心，教育的措施便围绕他们而组织起来。 •14、孩子在快乐的时候，他学习任何东西都比较容易。 •15、生活即教育，社会即学校，教学做合一。 •16、当在学校所学的一切全都忘记之后，还剩下来的才是教育。2021年10月19日星期二2021/10/192021/10/192021/10/19 •17、播种行为，可以收获习惯；播种习惯，可以收获性格；播种性格，可以收获命运。2021年10月2021/10/192021/10/192021/10/1910/19/2021 •18、我们发现了儿童有创造力，认识了儿童有创造力，就须进一步把儿童的创造力解放出来2021/10/192021/10/19October 19, 2021 •19、人自身有一种力量，用许多方式按照本人意愿控制和影响这种力量，一旦他这样做，就会影响到对他的教育和对他发生作用的环境。 2021/10/192021/10/192021/10/192021/10/19
中的数字表示在该位置小正方
1
体的个数。
你能摆出这个几何体吗？
试画出这个几何体的正视图与侧视图。
主视图：
侧视图：
21 2
21
不用摆出这个几何体，你能画出这个几何体的主视图与左视图吗？
12
思考方法
先根据俯视图确定主视图有列，
正视图：
再根据数字确定每列的方块有个，
主视图有 3 列，第一列的方块有 1 个，第二列的方块有 2 个，第三列的方块有 1 个，左视图有 2 列，第一列的方块有 2 个，

初中数学人教版九年级下册《29.2 三视图》 (共19张PPT)

左视图
B. 8
C. 12
俯视图
D. 24
10
2. 如图是一个几何体的三视图．根据图示，可计算
出该几何体的侧面积为
104π ．
主
左
视
视
13
图
图
俯
8
视
2020/6/7
图8
11
3. 如图是某几何体的三视图及相关数据(单位：cm)，则该几何体的侧面积为 2π cm2.
主视图
2020/6/7
左视图
俯视图
3
解析：根据三视图得到圆锥的底面圆的直径为88，即底面圆的半径r为4，圆锥的高为3，所以圆锥的母线长 l 32 42 ，5
所以这个圆锥的侧面积是π×4×5=20π．
2020/6/7
9
课堂检测
1. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为 ( B )
A. 6
2020/6/7
15
解：长方体，其体积为 10×12×15=1800(cm3).
2020/6/7
主视图
12
15 12 10
左视图俯视图
7
课堂练习
2. 如图是一个几何体的三视图，根据图中提供的数据(单
位：cm)，可求得这个几何体的体积为 3 cm3
.
3
1
1
主视图左视图俯视图
2020/6/7
8
已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积为 20π ．
钢板的面积 (图中尺寸单位：mm). 分析：
1. 应先由三视图想象出
密封罐的立体形状；
2020/6/7
2. 画出物体的展开图 . 3

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

• 画物体的三视图时,要符合如下原则:
• 位置：主视图左视图
•
俯视图
• 大小：长对正,高平齐,宽相等.
课堂检测
1. 画出下列立体图形的三视图.
（底面是矩形，四条棱相等）
2. 指出左面三个平面图形是右面这个物体的三视图中的哪个视图.
（主视图) （俯视图) （左视图)
如图所示长方体的长、宽、高分别为 5cm、4cm、3cm，画出这个长方体的三视图.
4cm
5cm
3cm
讨论：①这个长方体的三视图分别是什么形状的？
②主视图、左视图和俯视图中的长方形的长、宽、高分别为多少厘米？ ③主视图和左视图中有没有相同的线段？主
视图和俯视图呢？左视图和俯视图呢？
主视图
c ba
a(长)
高
长对正
平齐
a(长)
b（宽）
左
c（高）
视图
b（宽）
宽相等
主左俯视视视图图图反反反映映映了了了物物物体体体的的的高高长度度度和和和长宽宽度度度
c（高）
b（宽）
a(长)
还学过的正方体、圆柱、圆锥、四棱锥．
你能画出正方体的三视图吗？
高平齐
主视图
左视图
高平齐:主视图和左视图都反映了物体上下方向的Leabharlann 寸.左视图俯视图
主俯长 3cm 对正
5cm 主左高平齐 4cm 3cm
主视图
左视图
5cm 俯
左宽 4cm
相等
俯视图
位置关系：主视图为主，左视图在主视图正右方，俯视图在主视图正下方.必须相互对齐，不能错位.
三视图能反映物体真实的形状和长、宽、高.
三视图之间的投影规律
主
视图
c（高）
俯视图
三视图是主视图、俯视图、左视图的统称.它是从三个方向分别表示物体形状的一种常用视图.
一个物体在三个投影面内同时进行正投影，
在正面得到的由前向后观察物体的视图，叫主视图（从前面看）；
在水平面内得到的由上向下观察物体的视图，叫俯视图（从上面看）；
在侧面内得到由左向右观察物体的视图，叫左视图（从左面看）.
第二十九章投影与视图
29.2 三视图（1）
猜猜他们是什么关系？
看事物不能只看单方面
• 当我们从某一角度观察一个物体时，所看到的图象叫做物体的一个视图．视图也可以看作物体在某一个角度的光线下的投影，对于同一物体，如果从不同角度观察，所得到的视图可能不同．
俯视图
你会画圆柱的三视图吗？试一试吧！
主视图
左视图
宽相等
俯视图
宽相等:俯视图和左视图都反映了物体前后方向的尺寸.
高平齐
长对正
主视图 .
俯视图
左视图
宽相等
画出如图所示四棱锥的三视图.
正视图
左视图
俯视图
小结反馈
三视图
• 三视图
• 主视图——从正面看到的图
• 左视图——从左面看到的图
• 俯视图——从上面看到的图
对长方体的六个面进行正投影，并思考选择用怎样的视图能够表达长方体的形状和尺寸?
4cm
5cm 3cm
由立体图形到视图
我们用三个互相垂直的平面（例如：墙角处的三面墙壁）作为投影面，其中正对着我们的叫正面，正面下方的叫水平面，右边的叫做侧面.
正面
将三个投影面展开在一个平面内，得到这一物体的一张三视图.