3的倍数的特征3
3的倍数特征
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
25
26
27
28
29
30
31
32
33
34
35
36
37
28
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
3的倍数特征:各个数位上的数字之()是3的倍数,这个数一定是3的倍数。
二、深入学习。
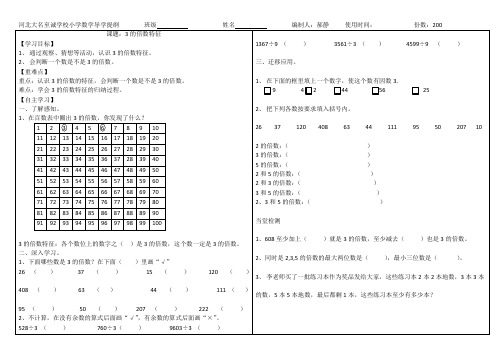
1、下面哪些数是3的倍数?在下面()里画“√”
26()37()15()120()
408()63()44()111()
河北大名至诚学校小学数学导学提纲班级姓名编制人:郝静使用时间:份数:200
课题:3的倍数特征
3的倍数的特征

3的倍数的特征教学内容分析3的倍数的特征是在因数和倍数的基础上进行教学的,是求最大公因数、最小公倍数的重要基础,也是学习约分和通分的必要前提。
因此,使学生熟练地掌握2、5、3的倍数的特征,具有十分重要的意义。
教材是先教学2、5的倍数的特征,再教学3的倍数的特征。
因为2、5的倍数的特征仅仅体现在个位上的数,比较明显,容易理解。
而3的倍数的特征,不能只从个位上的数来判定,必须把其各位上的数相加,看所得的和是否是3的倍数来判断,学生理解起来有一定的困难,因此,把它放在2、5的倍数的特征后面教学。
教学对象分析苏霍姆林斯基说:“在小学面临的许多任务中,首要的任务是教会儿童学习”。
这里的学习指学习方法,3的倍数的特征,有规律可循,容易上成机械刻板,枯燥无味的课,学生能死套规律判断,但学生的能力没能培养,智力得不到开发。
本课的设计旨在扬弃“满堂灌”的教学,取而代之以启发与发现相结合的教学方法,点拨学生大胆猜想,动手实践,去发现规律,使全体学生积极参与,积极思考,激发学生学习的积极性。
教学目标:1、经历在100以内的自然数表中找3的倍数的活动,在活动的基础上感悟3的倍数的特征,并尝试用自己的语言总结特征。
2、在探索活动中,感受数学的奥妙;在运用规律中,体验数学的价值。
教学重、难点:是3的倍数的数的特征。
教学流程图教学过程:一、提出课题,寻找3的特征。
师:同学们,我们已经知道了2、5的倍数的特征,那么3的倍数会有什么特征呢?谁能猜测一下?生1:个位上是3、6、9的数是3的倍数。
生2:不对,个位上是3、6、9的数不定是3的倍数,如l 3、l 6、19都不是3的倍数。
生3:另外,像60、12、24、27、18等数个位上不是3、6、9,但这些数都是3的倍数。
师:看来只观察个位不能确定是不是3的倍数,那么3的倍数到底有什么特征呢?今天我们共同来研究。
(揭示课题)师:先请在下表中找出3的倍数,并做上记号。
(教师出示百以内数表,学生人手一张。
3的倍数的特征

暂停一下
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54Biblioteka 576063
66
69
72
75
78
81
84
87
90
93
96
99
个位和十位上的数字相加之和都等于9。
9
18 1+8=9
27 2+7=9
36 3+6=9
45 4+5=9
54
5+4=9
63
6+3=9
72 81
7+2=9 8+1=9
个位和十位上的 数字相加之和: 9+2=11, 11 ÷3=3……2
如果是三位数或更多数位的数,我们的发现还成立吗?
暂停一下
3的倍数的特征:
一个数各个数位上的数字之和是3 的倍数,这个数就是3的倍数。
北师大版 五年级上册 第三单元 倍数与因数
学习目标:
√ 经历探索3的倍数的特征的过程,理解3 的倍数的特征。
√ 能判断一个数是否是3的倍数。 √ 发展分析、比较、猜测、验证的能力。
2的倍数的特征:个位上是2、4、6、8、0的数都是 2的倍数。
5的倍数的特征:个位上是0或5的数都是5的倍数。
个位上是3、6、9的数是3的 倍数。
个位上是3、6、9的数不一定 是3的倍数,如:23、26、29
都不是3的倍数。
请在百数表中圈出3的倍数,你发现了什么?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
第二单元《3的倍数的特征》教案

5.3的倍数在日常生活中的应用。
二、核心素养目标
《3的倍数的特征》教学旨在培养学生的以下核心素养:
1.数学抽象:通过探究和归纳,使学生理解数的倍数概念,提高数学抽象思维能力。
2.逻辑推理:培养学生运用逻辑推理方法,分析并证明3的倍数的特征,增强推理能力。
3.数学建模:让学生运用所学知识解决实际问题,建立数学模型,提高数学建模素养。
-重点三:分析数列中3的倍数的规律,如每隔两个数出现一个3的倍数等。
-重点四:结合实际情境,让学生学会将数学知识应用于生活,如购物时如何判断总价是否为3的倍数。
2.教学难点
(1)理解并掌握如何运用各位数字之和判断一个数是否为3的倍数。
(2)在数列中找出并应用3的倍数的规律。
(3)将抽象的数学概念应用于解决具体问题。
五、教学反思
在今天的课堂中,我们探讨了《3的倍数的特征》,整体教学过程让我有了以下几点思考。
首先,我发现同学们对3的倍数的概念掌握得还不错,但在运用各位数字之和判断一个数是否为3的倍数时,部分同学还是感到有些困难。这一点让我意识到,在今后的教学中,需要加强对这一知识点的讲解和练习,让学生更好地理解并运用这一方法。
其次,在实践活动环节,同学们分组讨论和实验操作的过程中,我注意到他们对3的倍数在实际生活中的应用有了更深刻的认识。但同时,我也发现有些小组在讨论时,观点较为片面,未能全面考虑到3的倍数在各种情境下的应用。针对这一问题,我计划在接下来的课堂中,引入更多丰富多样的实例,激发学生的思考,帮助他们更好地将数学知识应用于实际生活。
3.重点难点解析:在讲授过程中,我会特别强调3的倍数的定义和判断方法这两个重点。对于难点部分,如理解各位数字之和与3的倍数的关系,我会通过举例和图示来帮助大家理解。
小学五年级数学《3的倍数的特征》认知教案

小学五年级数学《3的倍数的特征》认知教案一、教学目标1.理解3的倍数的概念,能够正确地说出3的倍数是指能够被3整除的数。
2.理解3的倍数的特征,能够正确地说出3的倍数的末尾数字一定是0、3、6、9。
3.能够运用所学知识解决实际问题。
二、教学重点1.理解3的倍数的概念。
2.掌握3的倍数的特征。
三、教学难点1.通过实际问题理解3的倍数的特征。
2.运用所学知识解决实际问题。
四、教学过程1.导入新知识(1)引导学生对3的倍数的概念进行探讨。
(2)通过举例的方式让学生体会3的倍数与非3的倍数的区别。
2.概念解析(1)给学生呈现一些3的倍数,让他们观察和比较这些数的特点,引导他们慢慢得到3的倍数的特征:末尾数字一定是0、3、6、9。
(2)让学生知道“三的倍数”是指能够被3整除的数,并培养学生用“n÷3=整数”来判断一个数是不是3的倍数的能力。
3.结论总结通过练习,让学生巩固所学知识,掌握3的倍数的特征,在运用所学知识解决实际问题时更加得心应手,提高数学思维和解决问题的能力。
五、示例练习1.以下哪些数是3的倍数?A.63B. 98C. 105D. 1572. 找出下列数中所有是3的倍数的数:24,17,81,12,76,93,353. 小明家剩下26元钱,想买8个1元橘子,需花费多少元?若小明是用10元的纸币付款,须找零多少元?六、扩展与延伸1.小数的除法和3的倍数有什么关系?2.对于4位数abcd(a,b,c,d为数字),若它是3的倍数,则它的数码和(即a+b+c+d)一定是几?七、教学反思通过本节课的教学,学生们对3的倍数的概念、特征有了一定的认识和理解,能够解决一些简单的实际问题,但需要注意的是,在实际生活中,需要运用数学知识解决一些更加复杂的问题,因此教师需要多注重拓展与延伸,让学生更好地运用所学知识解决不同的问题。
是3的倍数的特征

是3的倍数的特征
3的倍数的特征有以下几个方面:
1.整除性质:3的倍数具有整除3的性质,即一个数能够被3整除,那么它就是3的倍数。
例如,6除以3的结果是2,说明6是3的倍数。
2.数位和:一个数的各个位数之和如果能够被3整除,那么这个数也是3的倍数。
例如,123的各个位数之和是6,因为6能被3整除,所以123是3的倍数。
3.末尾为0:为0、3、6、9的数字都能被3整除,因此如果一个数的末尾是0、3、6、9中的一个,那么它就是3的倍数。
4.各位数字之和为3的倍数:如果一个数的各位数字之和能够被3整除,那么这个数也是3的倍数。
例如,624的各位数字之和是12,因为12能被3整除,所以624是3的倍数。
5.间隔为3的倍数:如果一个数的个位数和十位数的差能被3整除,那么这个数也是3的倍数。
例如,27的个位数为7,十位数为2,它们的差为5,5不能被3整除,所以27不是3的倍数;而30的个位数为0,十位数为3,它们的差为3,3能被3整除,所以30是3的倍数。
即个位数与十位数之差能被3整除。
6.整数规律:3的倍数的个位数如果是0、3、6、9,那么这个数还是3的倍数。
如果一个数的个位数是0、3、6、9,那么它一定能被3整除,并且这个规律也可以递归应用于数的每一位。
例如,231的个位数为1,因此它不是3的倍数;而234的个位数为4,因此可以通过判断234除以10后的结果是否是3的倍数来判断234是否是3的倍数。
这些都是3的倍数的特征,根据这些特征可以判断一个数是否是3的倍数。
同时,这些特征也可以用于解决一些与3的倍数有关的问题,例如编写算法求解3的倍数的个数或者求给定范围内3的倍数之和等。
3的倍数的特征范文

3的倍数的特征范文
3的倍数是指能被3整除的数,以下是3的倍数的一些特征:
1.个位数为0、3、6、9:一个数能被3整除的条件是,这个数的每
位数字之和能被3整除。
个位数为0、3、6、9的数的每位数字之和一定
能被3整除。
例如,12、21、33、600等都是3的倍数。
2.末尾两位为00:如果一个数的末尾两位都是0,那么这个数一定能
被3整除。
例如,300、900、1200等都是3的倍数。
3.数字之和能被3整除:一个数的每位数字之和能被3整除的话,那
么这个数一定能被3整除。
例如,342的数字之和为3+4+2=9,能被3整除,所以342是3的倍数。
4.前N项和为3的倍数:如果一个数的前N项和是3的倍数,那么这
个数一定是3的倍数。
例如,1+2+3=6是3的倍数,所以6是3的倍数。
5.数字反序后也是3的倍数:如果一个数的每位数字反序之后得到的
数也是3的倍数,那么这个数一定是3的倍数。
例如,24的反序数为42,42也是3的倍数,所以24是3的倍数。
6.如果一个数的末尾两位与该数除以100的余数相等,那么它是3的
倍数。
例如,156的末尾两位是56,156除以100的余数也是56,所以
156是3的倍数。
7.一个数的十位数减去个位数的差是3的倍数:一个数的十位数减去
个位数的差是3的倍数时,那么这个数就是3的倍数。
例如,93的十位
数减去个位数的差是9-3=6,6是3的倍数,所以93是3的倍数。
通过以上特征,我们可以很容易地判断一个数是否是3的倍数。
3的倍数特征以及原因分析

3的倍数特征以及原因
分析
本页仅作为文档封面,使用时可以删除
This document is for reference only-rar21year.March
3的倍数特征以及原因分析
我研究了一下3的倍数特征以及它的原因分析,首先,我画了一张百数图,然后把一百以内的3的倍数标了出来,它们分别是:3、6、9、12、15、18、21。
90、99。
然后慢慢地观察这些数,我就发现,如果用这些数上的每一位的数字加起来,就是3的倍数,他们分别是:3、6、9、3、6、9。
就这样一直循环下去,所以我得出了一个结论:“只要是3的倍数,无论多少位,所有位上的数字相加起来的和就一定是3的倍数。
如果加起来不是3的倍数,那这个数本身就不是3的倍数。
”后来我又研究,为什么3的倍数特征是这样的呢,我就拿三位数来举例。
一个三位数,假设它是ABC,那就是由100A+10B+C组成的,如果它能被3整除,又有99A+9B肯定能被3整除,所以它们的差A+B+C也就肯定是3的倍数,A+B+C就是所有位上的数字相加起来的和。
这个结论:“只要是3的倍数,无论多少位,所有位上的数字相加起来的和就一定是3的倍数。
如果加起来不是3的倍数,那这个数本身就不是3的倍数。
”通过试验后,它是成立的。
3的倍数的特征

探索新知
在计数器上分别表示出几个3的倍数,看看各用了多少个珠。
探索新知
一个数各数位上数的和是3的倍数,这 个数一定是3的倍数。
探索新知 判断下列数是不是3的倍数。
42 134 78 268
4+2=6 6是3的倍数。
所以42是3的倍数。
7+8=15 15是3的倍数。 所以78是3的倍数。
1+3+4=8 8不是3的倍数。 所以134不是3的倍数。
分析:设这三个连续的自然数是n-1,n ,n+1,则3个连续自然数的和是3n。是 3的倍数。同样方法可知3个连续奇数或 偶数的和也是3的倍数。
课堂小结
3的倍数的特征 一个数,每个数位上的数字的和是3的倍数, 这个数就是3的倍数。
Hale Waihona Puke 学习目标● 1、经历探索3的倍数的特征的过程,知道3 的倍数的特征,能正确判断一个数是不是3的 倍数。重点、难点 ● 2.在探索3的倍数的特征的过程中,进一步 培养观察、比较、分析、归纳,以及数学表达 的能力,感受数学思维的严谨性及数学结论的 确定性,激发学生学习兴趣。
情景导入
小游戏:你说我猜 你说出一个整数,老师马上 说出它是不是3的倍数
2 4 5 8 47 96
易错提醒
下面用数字卡片摆出的数中,哪些是3的倍数 ?在每个数后面增加一张卡片,使这三个数成为3 的倍数。
2 4 5 8 47 96
错误解答:
583、58 3、58 3、476、479、476是3的倍数。
错解分析:3的倍数的特征是一个数,每个数位上的数字的
和是3的倍数,这个数就是3的倍数。末尾是3的 倍数的数不一定是3的倍数。
探索新知
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
3的倍数的特征

3的倍数的特征当我们将一个整数除以3时,得到的余数只可能是0、1或2、如果余数是0,那么这个整数就是3的倍数;如果余数是1或2,那么这个整数就不是3的倍数。
以下是3的倍数的一些特征:1.数字和为3的倍数:一个整数的每位数字相加得到的和如果是3的倍数,那么这个整数也是3的倍数。
例如,108的每位数字相加得到的和是9,是3的倍数,所以108也是3的倍数。
2.末尾数字为0、3、6或9:如果一个整数的个位数字是0、3、6或9,那么它一定是3的倍数。
例如,90、27和42都是3的倍数。
3. 同余模运算:如果两个整数对3的余数相等,那么它们的差也是3的倍数。
例如,对于任意整数a和b,如果a ≡ b (mod 3),那么a -b是3的倍数。
4.逆向思考:如果我们能够证明一个数不是3的倍数,那么它一定不是3的倍数。
例如,对于一个整数,如果它的个位数字之和不是3的倍数,那么这个整数肯定不是3的倍数。
5.数字位数之和不断相加:如果一个整数的所有位数之和不是3的倍数,那么这个整数也不是3的倍数。
我们可以将这个整数的所有位数相加,如果和大于9,再将和的各位数字相加,直到和小于10为止。
如果得到的最终和是3的倍数,那么这个整数也是3的倍数。
6.除法法则:当一个整数除以9的余数是0时,它一定是3的倍数。
因为3和9都是3的倍数,所以3的倍数也一定是9的倍数。
总结起来,判断一个数是否是3的倍数,可以使用以下方法:1.将整数的每位数字相加,如果和是3的倍数,那么这个整数也是3的倍数。
2.判断整数的个位数字是否是0、3、6或9,如果是,那么这个整数是3的倍数。
3.判断整数对3的余数是否相等,如果相等,那么这两个整数的差也是3的倍数。
4.判断整数的个位数字之和是否是3的倍数,如果不是,那么这个整数不是3的倍数。
5.判断整数的位数之和是否是3的倍数,直到和小于10为止。
如果最终和是3的倍数,那么这个整数也是3的倍数。
6.判断整数除以9的余数是否是0,如果是,那么这个整数是3的倍数。
3的倍数特征

84
判断下列数是否是3的倍数。
78
判断下列数是否是3的倍数。
269
判断下列数是否是3的倍数。
256
判断下列数是否是3的倍数。
1001
判断下列数是否是3的倍数。
2050
判断下列数是否是3的倍数。
482
判断下列数是否是3的倍数。
356
判断下列数是否是3的倍数。
444
判断下列数是否是3的倍数。
111
判断下列数是否是3的倍数。461判断下列数是否是3的倍数。
7777
在□里填上一个合适的数字,使这个 数是3的倍数,各有几种填法?
16□2 617□
56□3 5□41
判断下面这个数是否是3的倍数:
396336933631
声音太小,没底气?
1
3 石榴下 颜 上 色 4TEN 5 6 7 9
谈谈你有什么收获?
小故事:
阿凡提去书店买书,定价12.36元,买一 本,又帮同学捎两本,老板按了按计算机对他 说共需要37.58元,自己人,那8分不要了,拿 37.5元就可以了!阿凡提一听就反问到:“老 板不要骗小孩子哟!”老板笑着说:“哪能呢? 如果骗你了,这三本书就白送给你!” 阿凡提听了非常高兴!拿起书就走了,老 板气的说不出话来。
强尼知道,这个年轻人故意为难他,他亲 切的问其中的一个孩子:“小朋友,你几岁 了?”年轻人不等孩子回答,马上接过话来: “你猜不出来了吧?他是我儿子,今年3岁了” 话音刚落,强尼就用手铐把他铐了起来。
你看懂了吗?
作业布置:
课本:试一试 练一练第1、2题
拓展题:要使4□3 □既是2的倍数,又是3 的倍数,同时还不能是5的倍数, □有几种 填法(供学习有余力者)
《3的倍数的特征》(教案)

《3的倍数的特征》(教案)《3的倍数的特征》(教案)一、教学目标1.能够理解什么是3的倍数,举一些例子。
2.能够掌握3的倍数的特征,能够运用情景理解。
3.能够解决一些简单的3的倍数的问题。
二、教学准备1.课件、黑板、粉笔、3的倍数的卡片。
2.绘本《三只小熊找蜂蜜》三、教学过程1.导入环节(1)引入话题: “同学们,你们知道什么是3的倍数吗?”(2)播放图片:上课之前,我准备了一些图片,让学生看看,里面都有几个物品,问学生物品的数量是几的倍数,并让学生手举出答案卡。
2.理论知识部分(1)讲解什么是3的倍数。
(2)讲解3的倍数的特征,即末尾数为0的数、2位数且个位数和十位数之和为3的数、满足4的倍数并且个位数是2的数等等,让学生自己探讨一下还有哪些特征。
(3)通过课件展示一些使用3的倍数的例子,例如日历、时钟等。
3.练习环节(1)使用卡片游戏:“老师已经准备了很多数字卡片,让我们来玩一个游戏。
大家抽取一张卡片,然后根据这个数字卡片,做出一个201的数,看看这个数是否可以整除3,如果可以整除3,就说明他是3的倍数。
”(2)带领学生做一些3的倍数的练习,如小学数学下册P27 题目。
4.拓展环节(1)阅读绘本《三只小熊找蜂蜜》。
在故事中,小熊们分别采摘到了5瓶、6瓶和7瓶的蜂蜜,但是要平分给3只小熊,他们该怎么做呢?通过这个故事,学生可以将理论知识和现实生活中的问题联系起来。
(2)结合学生们现实生活中接触到的事物,教师可以提出一些问题,如根据3的倍数的特征,学生发现我们身边还有哪些是3的倍数,这样可以激发学生的思考和发散思维能力。
三、教学反思通过这节课,学生们了解到了什么是3的倍数,以及3的倍数具有哪些特征,并能运用所学知识解决简单的问题。
通过卡片游戏、练习以及与现实生活结合的拓展环节来实现对学生的检测和巩固,同时也激发了学生们的思维能力和发散思维能力。
在教学过程中,教师应该注重实际操作和生动形象的展示。
3的倍数的特征是什么

3的倍数的特征是什么1.定义:一个数如果能被3整除,那么它就是3的倍数。
也就是说,存在一个整数k,使得3k等于这个数。
例如,6是3的倍数,因为2乘以3等于62.数字和位数的特性:一个数是否是3的倍数可以通过它的位数之和来判断。
如果一个数的各个位上的数字之和能够被3整除,那么这个数也能被3整除。
例如,123的各个位上的数字之和是1+2+3=6,6能够被3整除,所以123是3的倍数。
3.除法规则:一个数是否是3的倍数可以通过它的除数规则来判断。
如果一个数的各个位上的数字之和能够被3整除,那么这个数也能被3整除。
例如,123的各个位上的数字之和是1+2+3=6,6能够被3整除,所以123是3的倍数。
4.末位规则:一个数是否是3的倍数还可以通过它的末位数字来判断。
如果一个数的末位数字是0、3、6、9中的任意一个,那么这个数就是3的倍数。
因为3乘以任意一个末位数字得到的结果都能被3整除。
例如,72的末位数字是2,所以72不是3的倍数;而75的末位数字是5,所以75是3的倍数。
5.间隔法则:一个数是否是3的倍数还可以通过其间隔规则来判断。
如果一个数的各个数字之间的间隔(差值)综合能被3整除,那么这个数也能被3整除。
例如,540的各个数字之间的间隔是(5-4)+(4-0)=1+4=5,5不能被3整除,所以540不是3的倍数;而537的各个数字之间的间隔是(5-3)+(3-7)=2+4=6,6能够被3整除,所以537是3的倍数。
6.九法规则:一个数是否是3的倍数还可以通过九法规则来判断。
将一个数的各个位上的数字相加,如果得到的结果大于9,那么再将这个结果的各个位上的数字相加,继续这个过程,直到得到的结果小于或等于9、如果得到的结果等于3、6或9,那么这个数就是3的倍数。
例如,927的各个位上的数字之和为9+2+7=18,18大于9,再将18的各个位上的数字相加得到1+8=9,所以927是3的倍数。
综上所述,以上是3的倍数的特征。
3 的倍数的特征
第三单元长方体和正方体体积
课题:1认识常用的体积单位
年级
年级
备课教师
杨信华
使用教师
教学目标
知识与技能目标:使学生理解体积的意义.
方法与过程目标:认识常用的体积单位:立方米、立方分米、立方厘米,培养初步的空间观念。。
情感态度与价值观目标:使学生知道计量一个物体的体积有多大,要看它包含多少个体积单位。
新课
一、探究发现,总结概念:
1、师:学生独立思考,然后全班交流。
2、师:这样的四个小正方形能拼出几个不同的长方形?
学生各自独立思考,想像后举手回答。
3、师:同学们再想一下,如果有12个这样的小正方形,你能拼出几个不同的长方形?
师:我看到许多同学不用画就已经知道了。(指名说一说)
4、师:同学们,如果给出的正方形的个数越多,那拼出的不同的长方形的个数——,你觉得会怎么样?
课题:3的倍数的特征
年级
年级
备课教师
使用教师
教学目标
知识与技能目标:经历在100以内的自然数表中找3的倍数的活动,在活动的基础上感悟3的倍数的特征,并尝试用自己的语言总结特征。
方法与过程目标:在探索活动中,感受数学的奥妙.
情感态度与价值观目标:在运用规律中,体验数学的价值。
教学重点
尝试用自己的语言总结特征。
师:这表从哪来呢?
(教师出示百以内数表)这上面是1到100这100个数,它不是质数表,你们能不能想办法找出100以内的质数,制成质数表?谁来说说自己的想法?(让学生充分发表自己的想法。)
2、让学生动手制作质数表。
3、集体交流方法。
小结
这节课你在激烈的讨论中有什么收获?
作业
练习四第1、2题。
3的倍数特征

√ )
看谁能用最快的方法判断出 5169这个四位数是否是3的倍 数。
因为5+1+6+9=21 所以5169是3的倍数。
• 1 ﹑ 一个数同时是3﹑ 5的倍数,这个 数有 什么 特征? • 2 ﹑ 一个数同时是2 ﹑3﹑5的倍数,这 个数有什么特征?
这个数的个位上是0或5,并且 各数位上数的和是3的倍数。 这个数的个位上是0,并且 各数位上数的和是3的倍数。
36 46
7 17 27
37 47
8 18 28
38 48
9 19 29
39 49
10 20 30
40 50
51
61 71 81 91
52
62 72 82 92
53
63 73 83 93
54
64 74 84 86 96
57
67 77 87 97
58
68 78 88 98
51
61 71 81 91
52
62 72 82 92
53
63 73 83 93
54
64 74 84 94
55
65 75 85 95
56
66 76 86 96
57
67 77 87 97
58
68 78 88 98
59
69 79 89 99
60
70 80 90 100
3的倍数的特征:
一个数各位上的数的和 是3的倍数,这个数就 一定是3的倍数。
32 42
3 13 23
33 43
4 14 24
34 44
5 15 25
35 45
6 16 26
36 46
7 17 27
3的倍数特征

3的倍数的特征
总结延伸:
1. 通过这节课,你学到了什么?有什么感受? 2. 阅读第34页“你知道吗”,认识“完全数(完美数)。”
下课,再见!
3的倍数的特征
练一练:你能很快说出哪几题的得数有余数吗?
48÷3 57÷3 342÷3 567÷3 802÷3
3的倍数的特征
练一练:在每个 里填一个数字,使组成的数是3的倍数。
7
12
20
35
3的倍数的特征
练一练:
从0、5、6、7中选出3个数字,组成是3的倍数的三位数。一共可以 组成多少个?
3的倍数的特征
3的倍数的特征
利用计数器,任选一个3的倍数,并把它拨出来。
在计数器上拨出的3的倍数,所用的珠的个数都是3的倍数。
3的倍数的特征
练一练:
在29、45、51、67、86、96中,哪些是3倍数?
45
51ห้องสมุดไป่ตู้
96
3的倍数的特征
回顾反思:
1. 在学习3的倍数的特征时,我们经历了哪些探究过程? 2. 根据刚才的操作,你能说说3的倍数有怎样的特征吗?
3的倍数的特征
3的倍数的特征
3的倍数的特征
我们今天要研究3的倍数特征,你能猜一猜3的倍数有哪些特征吗?
你们打算如何验证猜想?
3的倍数的特征
请大家在百数表中把3的倍数都圈出来。
观察这些3的倍数,想一想你刚才的猜想真确吗?
3的倍数的特征
利用计数器,任选一个3的倍数,并把它拨出来。
仔细观察这几个3的倍数所用的珠的个数,你能发现什么吗?
