第六章 均匀平面波的反射与透射
第6章 均匀平面波的反射与透射

Er
kr
Hr
Et
θt kt
Ht
也称P波或P分量 (E的方向平行 入射面);因其 磁场H只有y分 量,又常称为T M波(叙述方便, 文献中常出现, 不严格)。
z
垂直极化波 指入射波电场垂直于入射面。
Ei Hi
介质1 介质2
ki
θi θ r
Er
kr
(驻波波节)
波节 波腹
E
z
磁场强度的振幅
2 H1 (t Eim cos( β1 z
最大值2Eim/1,其位置
1
最小值0,其位置
nλ1 β1 z nπ z , n 0,1, 2 , ... 2 (波腹)
π λ1 β1 z (2n 1 z (2n 1 , n 0,1, 2 , ... 2 4
若为理想介质,1=0, 1c= 1为实数。
2
界面上反射波的平均功率密度:
* 1 Sav,r Re Er H r z 0 2 * 1 E rm ˆ Re ex Erm e y ˆ η , 2 1c
2 2 Γ Eim 1 ˆ Re ez * 2 η1c
ˆ e x 100e
j ( βz π 2
ˆ e x 200 sin βz je-j π 2
z<0区域的磁场:
H H i (z H r (z 1 100 j ( βzπ 2 j ( βz π 2 ˆ ˆ e y 100e ey e η0 η0 ˆ ey 200 cos βz e -j π 2 η0
第6章 均匀平面电磁波的反射与透射

Γ =
S −1 S +1
6、平均能流密度 媒质1 媒质1 媒质2 媒质2
S1av
E 2 im 1 = Re[ E1合 × H *1合 ] = ez (1 − Γ 2 ) 2 2η1
E 2 im 2 1 = Re[ E t × H *t ] = e z τ 2 2η 2
S 2 av
可以证明, 可以证明, S1av = S 2 av
η1c
Eime−γ1z − ey
1
η1c
Erme+γ1z
2区透射波
E2 = Et = ex Etme−γ 2 z H2 = Ht = ez × 1
η2c
Et = ey
1
η2c
Etme−γ 2 z
z=0处 由于没有感应面电流, 在z=0处,由于没有感应面电流,故分界面两侧其电场和磁场的切向分量连续
Eim + Erm = Etm
反射波 en1
−
Ei = Eime
Et = Etme
x
+ − jk1en1 r
反射波电场
Er = Erme
−
− jk1en1 r
+ − jk2en2 r
H1r 1r
Et
折射波 e 透射波
+ n2
反射波 en1
x
n 媒质1 媒质1
E1r θ 1r r E1ii θi 1
入射波 en1
+
θt
Ht
z 媒质2 媒质2 n 媒质1 媒质1
η1c
Erme+γ1z
η1
Eim[(1+Γ)e− jβ1z − 2Γ cos β1z]
表达式中第一项包含行波因子 1)表达式中第一项包含行波因子 e − jkz ,表示振幅为 (1 + Γ) Eim +z方向传播的行波。 方向传播的行波 沿+z方向传播的行波。
第六章-3 均匀平面波的反射和透射
1
(1)
2
(2)
3
(n-2) (n-1) n
(3) (n-3) (n-2) (n-1)
1
2
(1) (2)
3
(n-2)
(n-1)ef
(3) (n-3) (n-2)
1
(1)
1 H 2 ez E2
2
6.67 ey cos(3 109 t 20 z ) 60 e y 0.036 cos(3 109 t 20 z ) A/m
电子科技大学编写 高等教育出版社出版
电磁场与电磁波
第6章 均匀平面波的反射与透射
14
例 6.1.4 已知媒质1的εr1=4、μr1=1、σ1=0 ; 媒质2 的εr2=10、
2ef
1
ห้องสมุดไป่ตู้
2
(1) (2)
3
(n-2)ef
(3) (n-3)
电子科技大学编写
高等教育出版社出版
电磁场与电磁波
第6章 均匀平面波的反射与透射
9
2、四分之一波长匹配层 设两种理想介质的波阻抗分别为η1 与η2 ,为了消除分界面 的反射,可在两种理想介质中间插入厚度为四分之一波长(该 波长是指平面波在夹层中的波长)的理想介质夹层,如图所示。 首先求出第一个分界面上的等效波
4
1、 多层介质中的场量关系与等效波阻抗
媒质①和②中存在两种平面波,其一是向正 z 方向传播的波,
另一是向负 z 方向传播的波,在媒质③中仅存在向正 z 方向传播
的波 。因此,各个媒质中的电场强度可以分别表示为
电磁场与电磁波均匀平面波的反射与透射

ey
1
2c
Etme 2z
其中
2 j
2 2c j
2 2 1
j
2 2
2c
2 2c
2 2
1
j
2 2
1 2
• 电磁场与电磁波 •
第六章 均匀平面波的反射与透射
三、反射系数和透射系数
根据边界条件,电场强度的切向分量在任何边界上均是连 续的,同时考虑到所讨论的有限电导率边界上不可能存在表面 电流,因而磁场强度的切向分量也是连续的。于是在z=0的边 界上满足下列关系:
6.1.2 对理想导体平面的垂直入射
如下图所示,媒质1为理想介质(1=0),媒质2为理想导体 (2=),则媒质2的本征阻抗为
• 电磁场与电磁波 •
2c
2 2c
第六章 均匀平面波的反射与透射
1
2 2
1
j 2 2
2
0
0 1
表明电磁能量全部被边界反射,无任何能 量进入媒质2中,这种情况称为全反射。
Er
(z)
ex
(
Eim
e
1z
Erme1z
)
H1(z)
Hi
(z)
Hr
(z)
ey
1
1c
( Eim e 1z
Erme1z )
• 电磁场与电磁波 •
第六章 均匀平面波的反射与透射
二、媒质2中平面波的电场和磁场
E2
(z)
Et
(z)
ex
Etme
2z
H2(z)
Ht (z)
ez
1
2c
Et (z)
余弦函数变化,即
E1(z) 2Eim sin 1z
电磁场与电磁波-第六章-均匀平面波的反射和透射
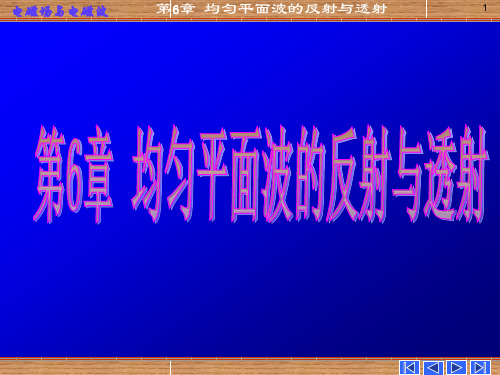
磁场的波节点恰好是电场的
波腹点;而磁场的波腹点恰好
是电场的波节点。
E1、H1在空间上错开λ/ 4。 E1、H1在时间上有π/ 2 的相移 坡印廷矢量的平均值为零,不发生能量传输过程,仅在两 个波节间进行电场能量和磁场能的交换。
电磁场与电磁波
第6章 均匀平面波的反射与透射
12
例6.1.1 一均匀平面波沿+z方向传播,其电场强度矢量为
1c
e 1 z
ey
Erm
1c
e1z
电磁场与电磁波
第6章 均匀平面波的反射与透射
6
媒质2中的透射波:
Et (z)
ex
Et
me
2
z
,
Ht (z)
ey
Etm
2c
e 2z
2 jk2c j
2 2c j
2 2 (1
j 2 )1 2 2
2c
2 2c
2 2
(1
j 2 2
)1 2
Er (z)
ex100e
j
z
e
j
1 2
ey 200e j z
反射波的磁场为
Hr
(z)
1
0
(ez
Er
)
1
0
(ex
200e
jz
ey100e
jz
e
j 2
)
电磁场与电磁波ห้องสมุดไป่ตู้
第6章 均匀平面波的反射与透射
14
在区域 z < 0 的合成波电场和磁场分别为
j1
E1 Ei Er ex j200e 2 sin z ey j400sin z
H1
Hi
均匀平面波的反射和透射课件

波的传播速度与介质有关,与频率和波长无关。
平面波的传播特性
平面波的定义
波面是一系列平行的平面的波。
平面波的传播特性
波在传播过程中,波面保持为平面,且波速与波长成正比。
02
均匀平面波的反射
反射定律
01
反射定律总结了波在界面上的反射行为,指出 入射波、反射波和折射波之间的关系。
02
入射波、反射波和折射波的振幅、相位和传播 方向满足一定的关系。
均匀平面波的反射和透射课件
$number {01}
目录
• 引言 • 均匀平面波的反射 • 均匀平面波的透射 • 均匀平面波的反射和透射实例 • 均匀平面波的反射和透射的应用 • 结论与展望
01 引言
波的基本概念
1 2
3
波动
物体振动产生波,波在空间中传播形成波场。
波形
波的形状和大小随时间变化,波形包括正弦波、方波等。
电磁波在通信中的应用
01
02
03
无线通信
利用电磁波传输信息,实 现无线通信,如手机、无 线网络等。
有线通信
利用电缆传输信息,实现 有线通信,如电话、互联 网等。
卫星通信
利用卫星反射和透射电磁 波,实现远距离通信,如 卫星电话、卫星电视等。
06
结论与展望
总结均匀平面波的反射和透射的规律
要点一
总结词
反射波的相位也会发生变化,这 取决于入射角、界面性质和传播 方向。
在某些情况下,反射波的振幅可 能会超过入射波的振幅,这被称 为反射增强。
在其他情况下,反射波的振幅可 能会小于入射波的振幅,这被称 为反射减弱。
03
均匀平面波的透射
透射定律
谢处方《电磁场与电磁波》(第4版)课后习题-第6章 均匀平面波的反射与透射【圣才出品】

第6章 均匀平面波的反射与透射(一)思考题6.1 试述反射系数和透射系数的定义,它们之间存在什么关系?答:(1)反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数;透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。
(2)反射系数Γ和透射系数τ之间的关系为:6.2 什么是驻波?它与行波有何区别?答:频率和振幅均相同,振动方向一致,传播方向相反的两列波叠加后形成的波叫驻波。
行波在介质中传播时,其波等相面随时间前移,而驻波的波形不向前推进。
6.3 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,反射系数大于0?在什么情况下,反射系数小于0?答:均匀平面波垂直入射到两种理想媒质分界时,当时,反射系数Γ>0;当时,反射系数Γ<0。
6.4 均匀平面波向理想导体表面垂直入射时,理想导体外面的合成波具有什么特点?答:均匀平面波向理想导体表面入射时,理想导体外面的合成波具有特点如下:合成波电场和磁场的驻波在时间上有的相移,在空间上也错开了且在导体边界上,电场为零。
驻波的坡印廷矢量的平均值为零,不发生电磁能量的传输过程,仅在两个波节之间进行电场能量和磁场能量的交换。
6.5 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,分界面上的合成波电场为最大值?在什么情况下,分界面上的合成波电场为最小值?答:当均匀平面波垂直入射到两种理想媒质分界面时,的位置时,分界面上的合成波电场为最大值。
的位置时,分界面上的合成波电场为最小值。
6.6 一个右旋圆极化波垂直入射到两种媒质分界面上,其反射波是什么极化波?答:右旋圆极化。
6.7 试述驻波比的定义,它与反射系数之间有什么关系?答:驻波比的定义是合成波的电场强度的最大值与最小值之比,即6.8 什么是波阻抗?在什么情况下波阻抗等于媒质的本征阻抗?答:在空间任意点,均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗,在均匀无耗各向同性的无界媒质中,均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。
第六章均匀平面波的反射与透射

t 4 t 0
t 2
y t 2
x
t 4 2
t 0
y
t 3
t
4
x
4
3 4
t 7 4
t 3 2
t 4 t 0
t 2
1. 对于确定的时间 t ,总场在空间成正余弦分布,在 kx nπ 处,电场恒定为零,而磁场
jk1x
ez
Emi
1
1 e jk1x
2
j cos k1x
E2 Et ey Emi e jk2x
H2
=
Ht
ez
Emi
1
e jk2x
S
E1 max
1
E1 min 1
总场是行驻波
S 1 S 1
1
电子工业出版社
第六章 均匀平面波的反射与透射
电磁波的传播与分布问题除了与基本方程 有关外,还与边界条件密切相关
6.1 均匀平面波对分界面的垂直入射
6.1.1 均匀平面波对理想导体分界面的垂直入射
y
Ei ey Emi e jkx
Ei
ki
Hi
Hi
ez
Emi
e jkx
x
O
假设电场方向不变,而磁场方向反向
幅度为最大值;在 kx nπ π 处,磁场恒定为零,而电场幅度为最大值,电场和磁场的 2
零点以及最大值点相差 。 4
2.对于固定的空间位置,电场和磁场随时间是震荡变化的,但相位相差 π 。 2
3.总场的平均坡印廷矢量为
Sav
1 2
第六章-平面电磁波的反射和透射

z=0分界面处的反射系数
0
E1r 0 E1i 0
Z2 (0) 1 Z2 (0) 1
上式中的Z2(0)表示区域2中z=0处的等效波阻抗:
Z2 (0)
2
3 2
j2 j3
tan k2d tan k2d
区域2和区域3中的入射波电场振幅为
E2i 0
1
1 0 e j2k2d
E e jk2d 1i 0
E3i 0
H1i
H1r
ey
1
1
(E1i0e jk1z
E1r0e jk1z )
区域2(0≤z≤d)中的合成电磁波:
E2
E2i
E2r
ex [E2i0e jk2 ( zd )
E e ] jk2 ( zd ) 2r0
H2
H2i
H2r
ey [E2i0e jk2 ( zd )
E e ] jk2 ( zd ) 2r0
区域3(z≥d)中的合成电磁波:
E1m 2 1 Eim 2 1
E2m 22 Eim 2 1
6.1.27 6.1.28
反射系数和透射系数的关系为
1
区域Ⅰ(z<0)中任意点的合成电场强度和磁场强度可表示为
E1 Ei Er ex Eim (e j1z e j1z ) ex Eime j1z (1 e j21z ) ex Eim[(1 )e j1z (e j1z e j1z )]
驻波系数:S Emax 1 Emin 1
因为Γ=-1~1,所以ρ=1~∞。 当|Γ|=0、ρ=1时,为行波状态,
区域Ⅰ中无反射波,因此全部入射波功率都透入区域Ⅱ。
E2 Et exTEi0e jk2z
H2
Ht
第6章 均匀平面波的反射和透射

1
2
由于界面上是驻波电场的最小点,故 1
而反射系数 2 1 2 1
式中 1 0 , 2
2 2
r r
0
2
2
1 3
0
又因为2区的波长 2
0 0 r r 6
r r 36
r 1 r 9
z
求得
H JS
x
ey
ex
2
Eim
1
2 Eim c
0
cos
os
i cos(k1z
e jk1x sin i
i
cos
i
)e
jk1
x
sin
i
电磁场理论
第6章 均匀平面波的反射与透射
66
能流密度的平均值
Sav
1 2
Re(E
H*)
1 2
Re[Ey
z)
电磁场理论
第6章 均匀平面波的反射与透射
57
例 6.3.1 一圆极化波以入射角θi=π/ 3 从媒质1(参数为μ= μ0、ε=4ε0 )斜入射至空气。试求临界角,并指出此时反射波
是什么极化?
解:临界角为
c arcsin
2 1
arcsin
0 4 0
波的电场和磁场;(5)导体表面上的感应电流密度和电荷密度。
解:(1)由题意可知, kix kiz 2π ,所以
ki exkix ezkiz (ex ez ) 2π, k ki 2π
第6章 均匀平面波的反射与透射-4

实数
2 1
0
同相位
2 1
0
半波损失
25
媒质1中平面波的电场和磁场
合成波
均匀平面波的反射与透射
j 1 z E1 ( z ) ex Eim (1 )e j 2 sin 1 z
E1 ( z ) ex Eim (1 ) cos(1 z t ) 2 sin 1 z sin t
1
2
//
( 2 / 1 ) cos i 2 / 1 sin i ( 2 / 1 ) cos i 2 / 1 sin 2 i
全反射
1
2 arcsin c 使透射角 t 的入射角称为临界角 2 2 1
11
均匀平面波的反射与透射
2. 全透射
//
// 0
2
( 2 / 1 ) cos i 2 / 1 sin i ( 2 / 1 ) cos i 2 / 1 sin 2 i
0
( 2 / 1 ) cos i 2 / 1 sin 2 i 0
jk 2 x sin t
i
E Etm e e k z jk x sin Etm e e
t 1 1
jk 2 z cos t
1 cos t 1 sin 2 i 2
5
均匀平面波的反射与透射
表面波(隐矢波、倏失波)
6
均匀平面波的反射与透射
表面波(隐矢波、倏失波)
( 2 / 1 ) (1 sin i ) 2 / 1 sin i
2 2 2
2 b i arcsin 1 2
第6章 均匀平面波的反射与透射

v v v v Etm − jk2 z − jk2 z k 2 = ω µ 2ε 2 Et = ex Etm e ⇒ H t = e y e
η2
媒质1中总的电场、磁场为: 媒质 中总的电场、磁场为: 中总的电场
v v v v − jk1 z jk1 z E合 = Ei + Er = ex ( Eim e + Erm e ) v v v v 1 − jk1 z jk1 z H 合 = H i + H r = e y ( Eim e − Erm e )
已知入射波电场强度矢量为
r 1 r r − jk1 z Ei = ( e x − je y ) E 0 e 2 ( k1 = ω µ 0 ε 0 )
解:(1)因为入射波电场强度矢量为
r 1 r r Ei = (ex − jey ) E0 e − jk1z , k1 = ω µ0ε 0 2
反射系数和透射系数为
Erm η 2 − η1 = 定义: 定义:反射系数 Γ = Eim η1 + η 2 Etm 2η2 透射系数 τ = = Eim η1 + η2 则 v v jk1 z Er = ex ΓEim e v v − jk2 z Et = exτ Eim e
媒质1中合成波为: 媒质 中合成波为: 中合成波为
π λ
λ
ωt = 0
ωt =
π
4
ωt =
π
2
ωt =
3π ωt = π 5π ωt = 4 4
Ex
ωt =
3π 7π ωt = 2π ωt = 2 4
Hy
−
3λ 2
−λ
−
λ
2
0
z
− 5λ 4
平面波的全反射和全透射现象

思考:
—圆极化波以布儒斯特角斜入射时,反射波是什么极化波?
折射波是什么极化波? 圆极化波可以分解为:
'垂直极化波 、平行极化波
不可能发生全折射现象 能发生全折射现象
结论: 反射波中只有垂直方向的线极化波; 折射波为椭圆极化波。
小结:平面波的全反射和全折射现象 1全反射:当电磁波入射到两种介质分界面上,在介质2中 没
6.13平面波的全反射和全折射现象
1、 全反射现象 2、 全折射现象
1 ,全反射现象
全反射:当电磁波入射到两种介质分界面上,
在介质2中没有折射波的现象。
全反射现象包括两种情况:
(1) 理想导体的全反射 (2) 理想介质的全反射
(2)理想介质的全反射
sin q
时
由折射定律可知: sin q V *2卩2
当勻日1 > £恥时,必然有et > q。
如果入射角增大到某个角度时,恰好使q二90o则:
sin90o "迎=arcsin sin。 V 时2
*2外 3 = & q = arcsin 冬 时
丫 賢i
临界角
讨论:
当耳> Oc时,有sin^t > 1 , 此时
0,不是实数角,而是复数角。
则:cos 0t = 土 j 冬 sin2 0 -1
2 cos 4B = 2 cos 4
若 卩\=M =卩o
COS 4 =
4 = arcsin
布儒斯特角或偏振角
(2)对垂直极化波的情况
亿"〃g 0 % cosQ—0 cos Q = 0
丄 % COSQ +% COSQ ‘2 1/1 t
均匀平面电磁波的反射与透射要点
E
z 媒质2 2 媒质1
n
E 入射波 en
r i
H
媒质2 2
z
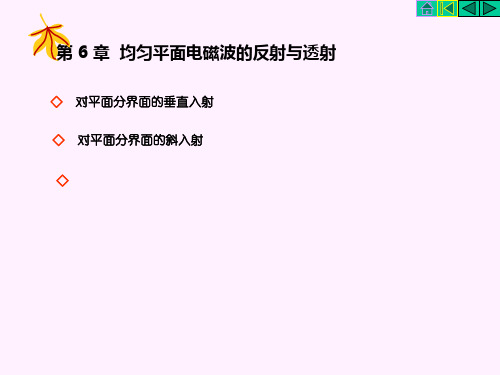
平行极化波
垂直极化波
对理想导体平面斜入射
(1) 平行极化波的斜入射
入射线方向单位矢量 en ex sin i ez cosi
反射线方向单位矢量 en ex sin r ez cosr
均匀平面波垂直入设到理
想导体平面上
入射波
Ei ex Eime j z
Hi 1
e z Ei e y
1
Eim e j z
E e x Eim e j z e j z e x 2jEim sin z
电磁波不能穿入理想导体,到达 分界面时将被反射回来。
t 0
2E e y Re im cos z e jt 2E e y im cos z cos t
t
3 t 5 t t t 4 2 4 4 Ex
t
3 7 t 2 t 2 4
式中 v p
◇ 沿电磁波传播方向(x方向)不存在磁场分量,这种波称为横磁波,简称TM波。
Ex 总是零。故 ◇ 当 sin kz cosi 0 或 kz cos i z cosi n n 0,1, 2,... 时, z 在 插入一导体板,将不会改变此导体板与原理想导体分界面之 2cosi 间的场分布。这就是平行板波导的原理。
4、驻波系数
(描述波的起伏程度)
E合 S E合
max min
1 1
S 1 S 1
5、平均能流密度 1 E 2 im ˆz S1av Re[E1合 H *1合 ] e (1 2 ) 媒质1 2 21 媒质2
均匀平面波的反射和透射---对分界面的斜入射

θr θi
θt
O
z
y
11:24
反射波
x
透射波
θr θi O
θt
z
入射波
y
11:24
基本问题:
分别求解入射波和透射波空间的电磁场 v v v v uv v uv v uv v uv − j k uv − j k r r ⋅ i 入射波空间: E1 (r ) = E i (r ) + E r (r ) = E im e + E rm e r ⋅ 透射波空间:
⋅
z =0
k1 sin θi = k1 sin θ r = k2 sin θ t
11:24
Snell定理
反射波与透射波的方向(反射定律和折射定律)
斯耐尔反射定律: 由 k1 sin θi = k1 sin θ r ,得 分界面 2 1 ki z n θt kt x
θ r = θi ——反射角θr等于入射角θi
11:24
平行极化入射时的反射系数与折射系数(续)
反射系数
透射系数
ε1 = ε 0 , ε 2 = 2.25ε 0,
布儒斯特角θb :使平行极化波的反射系数等于0 的角。
11:24
菲涅尔公式的另外一种表达式
在理想电介质中:
Γ⊥ =
cos θi − ε 2 ε1 − sin θi cos θi + ε 2 ε1 − sin θi
v v uv v uv v uv − j k ⋅r E 2 (r ) = E t (r ) = E tm e t
问题核心: uv v 已知 E im , k i uv uv v v 求解 E rm , E tm ; k r , k t 利用关系:边界条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S2av
i 2 E 1 * Re E2 H 2 ex m 2 2 22
E1 H1
y
H1
x
71 31 51 31 1 1 1 4 4 2 4 2 4
x
3 21 71 31 51 1 1 1 1 2 4 4 4 2 4
6.1.3均匀平面波对导电媒质分界面的垂直入射
2 1 2 1
22 2 1
所不同的是:
1)导电媒质的特征阻抗为复数,因此电场和磁场不同相;
2)反射系数和透射系数此时均为复数,反射波、透射波和入
射波存在相位差 3) 相位差的大小由介质特性决定,不再是0°或180°。
kr
Er Hr
O
1
e jk1x
e jk1x
E ey E e
r r m
jk1x
H r ez
H ez
t
r Em
Ei
E
H
t
t
x
k
t
1
H
i
k
i
E ey E e
t
t jk2 x m
2
t Em
e jk2 x
1 1 1
1 , 1
2 , 2
2
2 2
k1 11
2 . 当 2 1 时 , 反 射 系 数 0 , 反 射 电 场 与 入 射 电 场 反 相 位 。 在
i 2k1x 2nπ π (n 0,1, 2,3...) 处,电场达到最大值 Em 1 ;在 2k1x 2nπ 处,电场达到
i i 最小值 Em 在介质交界面上, 左边的总电场和右边的透射场都等于最小值 Em 1 。 1 。
(3)由电场透射系数可以得到海水中透射波 的电磁场为
反射系数:
2 1 0.889 0.8 2 1 1.111
22 0.222 0.2 2 1 1.111
E2 E t ex Eme jk2 z , H 2 = H t e y
(4)趋肤深度
t
2
t
4
t 0
t
x
2
3 4
t
x
4
3 4
t
7 4
t
3 2
t
4
t
t 0
2
y
t
2
t
4
t 0
2
x
y
t
3 4
t
3 4
4
x
7 t 4
3 t 2
t
22 t i 2 1 i Em E Em Em 2 1 2 1 2 1 22 2 1 1 2 1
r m
当介质交界面位于 x
d
i jk1 ( x d ) E i e y Em e r i jk1 ( x d ) E e y Em e t i jk1 ( x d ) E e y Em e
Er H
r
kr
H ez
r
r Em
e jkx
r jkx E r ey Em e
y
E ey E e
tot
i jkx m
ey E e
r m jkx
r jkx m
ki
Ei
Hi
x 0 电场需要满足切向电场为0
x
O
E Hr
r
E
kr
tot
ey E e
r m
i jkx m
4
t
t 0
2
1. 对于确定的时间 t ,总场在空间成正余弦分布,在 kx nπ 处,电场恒定为零,而磁场 幅度为最大值;在 kx nπ 零点以及最大值点相差
π 处,磁场恒定为零,而电场幅度为最大值,电场和磁场的 2
。 4
2.对于固定的空间位置,电场和磁场随时间是震荡变化的,但相位相差 3.总场的平均坡印廷矢量为
E e
x 0
0
E E
i m
交界面上,入射电 场与反射电场方向 相反或相位差180°
其他点上如何???
总场是纯驻波
E
tot
ey E
i m
e
jkx
e
jkx
e 2 jE
y
i m
sin kx H
tot
ez
i Em
e
jkx
e
jkx
e
i 2Em z
1
jk2 ( x d )
(1 1 )
1 jk d (e 2e jk d ) 2
2 2
E2 e y 1 Em e H 2 ez 1
2e
23 2 2 2 3 3 2 3 2
2
t
Em
jk2 ( x d ) jk2 ( x d ) e e 2
H
i 3
i k3
1
e jk1x
1 表征介质1中所有左
O
d
行的电磁波与入射电 x 磁波的比值
E1 e y Em e
H1 ez Em
jk1 x
1e
jk1 x
1 1 1 (e jk2d 2e jk2d )
1
1
e
jk1 x
1e
jk1 x
jk2 ( x d )
例题 6-2 常用 X 波段雷达若工作于 10GHz 频率,沿 e z 方向垂直入射到 z 0 的海水
( r 81, r 1, 4) 表面,试求
(1)电场反射系数和电场透射系数 (2)海水上方空间的电磁场分布 (3)海平面下方电磁场分布 (4)海水的趋肤深度
解: (1)海水上方空气的特征阻抗为1 0 377 , 海水的特征阻抗
E1 e x Em e jk0 z e jk0 z ,
0 0 2 j / 81 0 j 4 / 2 1010
0.1110e
1 j arc tg(0.088889) 2
H1 e y
Em
0
e
jk0 z
e jk0 z
i E jk1 x jk1x jk1x H1 = H i H r e z e jk1x e jk1x = e z m 1 e e e 1 1 i Em
ez
t
i Em
jk1 x 1 e 2 j cos k1 x 1
cos kx
i i E tot x, t Re E tot e jt = Re e y 2 jEm sin kxe jt e y 2 Em sin kx sin t
i i 2 E 2 E H tot x, t Re H tot e jt Re ez m cos kxe jt ez m cos kx cos t y y
k2 2 2
电磁波必须满足切向电场连续和切向磁场连续两个边界条件
Ei E r
x 0 i r e y Em Em x 0
Et
x 0
x 0
t e y Em
Hi Hr
x 0
i r ez Em Em /1
Ht
x 0
t ez Em / 2
E2 E ey E e
H 2 = H t ez
i Em
i jk2 x m
1
e jk2 x
总场是行驻波
S1av
S
E1 max E1 min
1 1
E1
S 1 S 1
y
i 2 E 1 Re E1 H1* ex m 1 2 2 21
E3 E = ey1 2 Eme
i 2 Em 1 1 i Sav Re E H Re ex 2 jEm sin kx ez cos kx 0 2 2
π 。 2
6.1.2均匀平面波对理想介质分界面的垂直入射
y
i jk1x H i ez Ei ey Em e
i Em
电子工业出版社
第六章 均匀平面波的反射与透射
电磁波的传播与分布问题除了与基本方程 有关外,还与边界条件密切相关
6.1.1 均匀平面波对理想导体分界面的垂直入射
y
i jkx E i ey Em e
6.1 均匀平面波对分界面的垂直入射
ki
Ei
H
i
H i ez
i Em
e jkx
x
O
假设电场方向不变,而磁场方向反向
3.磁场最大值和最小值出现的位置正好与电场错开
。 4
例 题 6-1 全 球定 位 系统 (GPS) 已经 在军 用和 民 用电 子系 统中 大量 使 用, 设工 作于 1.575GHz 的 GPS 右旋圆极化平面波从自由空间垂直照射到 r 2.25 的聚乙烯介 试求 (1)反射波电磁场复数表达式 (2)透射波电磁场复数表达式 (3)判断反射电磁波极化
y
E1i ey Eme jk1x
1 , 1 x
E1r
2 , 2
r E2
3 , 3
H ez
