平面波反射与透射
地球物理勘探 1-4地震波的反射、透射和折射

r
r
▪ 式中正负号的确定方法为:r 的x分量沿x轴增大为正,反之为负;
▪
r 的z分量沿z轴增大为正,反之为负.
▪ 根据P波和s波的质点振动特性,可得5个位移矢量各自在x,z方向得 位移分量u和w为(见书图1-12 和(1.4-5)式)
▪ 将位移分量代入位移边界条件:(见书(1.4-6)式)
▪ 及应力边界条件: (见书(1.4-7)式)
Q
V2 T
e
T f
:入射角(入射线和界面法线的夹角)
:反射角(反射线和界面法线的夹角) 1
:透射角(透射线和界面法线的夹角)
2
4.1 平面波的反射和透射
▪ 从图中可看出: AS BQ V1 T,
▪
ABQ ASQ 90
▪
共边 AQ
▪ 可证明:
• 另一类是一定的密度比和速度比条件下,反射系数 与入射角的关系。(见书P24)
21
22
4.4 地震面波
一、面波的分类
在三维空间中,凡是能量向整个空间中传播的波,都称为 体波。例如在弹性分界面上形成的反射、折射、透射波,它 们随着时间的增加,在整个弹性空间的介质内传播。
能量只分配在弹性界面附近的波称为面波( 在Z方向振 幅呈指数衰减)。常见的面波有三类:
12
4.2 在弹性分界面上波的转换,
能量分配,法向入射和倾斜入射
4.2.5 倾斜入射、折射波的形成
1、 非法向入射的情况(称为倾斜入射)。
设 有
Vp,i1,入Vp射,i 角和透射角分别为 和 ,根 据斯 奈尔定律,
sin VP,i sin
VP,i1
总能找到一个入射角 i,pp使
均匀平面波的反射和透射matlab -回复

均匀平面波的反射和透射matlab -回复均匀平面波的反射和透射(matlab)引言:均匀平面波的反射和透射是电磁波传播中的基本现象之一。
通过研究波在边界上的反射和透射行为,我们可以更好地理解电磁波的传播规律和性质。
在本文中,我们将使用MATLAB编程来模拟均匀平面波的反射和透射现象,并详细介绍每一步的操作。
第一步:定义均匀平面波首先,我们需要定义一个均匀平面波的初始状态。
假设我们有一个平面波在z轴上传播,其电场分量Ez(x, y, t)可以由下述公式表示:Ez(x, y, t) = E0 * exp(j*(kx*x + ky*y - ωt))其中,E0表示电场强度的振幅,kx和ky分别表示波矢在x和y方向上的分量,ω表示角频率,t表示时间。
我们可以在MATLAB中定义这个函数,并设定合适的参数。
例如:MATLABE0 = 1; 设置电场强度的振幅kx = 2*pi; 设置波矢在x方向上的分量ky = 3*pi; 设置波矢在y方向上的分量omega = 10; 设置角频率t = 0; 设置初始时间定义均匀平面波函数Ez = (x, y) E0 * exp(1j * (kx*x + ky*y - omega*t));第二步:绘制均匀平面波的图像在前面的步骤中,我们定义了一个函数Ez(x, y),用来描述均匀平面波在空间中的电场分布情况。
为了更直观地理解该函数的特性,我们可以使用MATLAB绘制二维图像。
MATLAB[X, Y] = meshgrid(-10:0.1:10); 定义绘制图像所需的坐标点Z = angle(Ez(X, Y)); 计算相位,并将其作为图像的颜色映射绘制二维图像figure;imagesc(X(1,:), Y(:,1), Z);xlabel('x');ylabel('y');colorbar;运行以上代码后,我们将得到一个二维图像,其中不同位置的颜色表示该位置上电场分量的相位。
垂直入射平面波在分界面上的反射和折射2学时ppt课件

过分界面进入空气中的能量只有入射声能的千分之一。
例题2:
2、平面波垂直入射时的反射和透射
具体计算“绝对软”和“绝对硬” 边界条件下声场 性质及边界上声压和振速的特点。
声波由水入射到空气中
“绝对软”边
声波由空气入射到水中
Du
u~t x,t u~ix,t
x
边
界
振速折射系数
振速折射系数:谐和平面波入射到分界面上,在分界 面处复透射振速与复入射振速的比值。
(2)反射系数和折射系数 2、平面波垂直入射时的反射和透射 则有:
R p~ p ~ p r i x x ,,ttx 0p p r ia a 2 2 c c 2 2 1 1 c c 1 1 Z Z 2 2 Z Z 1 1 声压反射系数
那么
u ia
u ra
u ta
u ia
p ia
1c1
入射波振速振幅
反射波振速振幅
透射波振速振幅
u ra
p ra
1c1
u ta
p ta
2c2
(2)反射系数和折射系数 2、平面波垂直入射时的反射和透射 所以,有
p 1 ~ p i ~ p r p ie a j t k 1 x p r e j a t k 1 x
处的声压是入射波的两倍;反射波质点振速和入射 波质点振速幅度大小相等、符号相反,在分界面上 合成质点振速为零;
(2)反射系数和折射系数 2、平面波垂直入射时的反射和透射 讨论:(4) “绝对硬”边界
③发生了全反射,在介质Ⅰ中入射波与反射波叠加
形成了驻波,分界面处恰是振速波节和声压波腹;
3.5.2 平面波垂直入射时的反射与透射
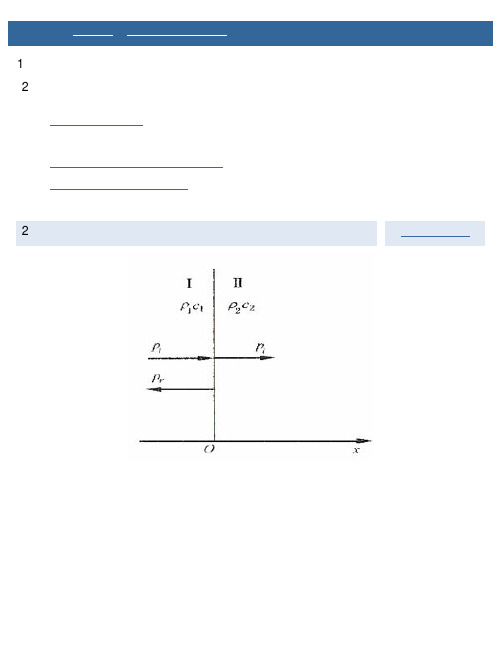
设媒质 I 和媒质 II 的特性阻抗分别为 和? ,它们分界面的坐标为 ( 见图 3-5-2 ) ,如果一列声压为 的平面声波从媒质 I 垂直入射到分界在媒质中求解一维声波方程 ( 3-1-7 ) 式可得声压入的形式,为( 3-5-5 )由§ 4.5 的讨论可知,上式第一项代表沿 x 方向前进的波,也就是原来已知的入射波 p i ,所以这里的常数 A 就是入射波的幅值 p ia ;第二项代表向负 x 方向行进的波,它实际代表了入射波遇到分界面以后在媒质 I 中产生的反射波,记为 p r 、即有 ,因此 ( 3-5-5 ) 式可改写为( 3-5-6 )即媒质 I 中的声场为入射波与反射波之和。
媒质 II 中的声场 p 2 的一般解形式上仍为 ( 3-5-5 ) 式,但由于媒质 II 无限延伸,不会出现向负 x 方向传播的波,所以这里只需保留 ( 3-5-5 ) 式中的第一项,它实际上代表了透入媒质 II 的透射波,记为 p i ,即得( 3-5-7 )运用 (4 — 3 — 11) 式可求得媒质 I 、媒质 II 中的质点振速 v 1 及 v 2 分别为( 3-5-8 )式中现在通过声学边界条件来确定反射、透射的大小。
据声学边界条件知,在 x = 0 的分界面处应有声压连续及法向质点速度连续( 3-5-9 )联合 ( 3-5-8 ) 式及 ( 3-5-9 ) 式即可求得在分界面上反射波声压与入射波声压之比 r p ,反射波质点速度与入射波质点速度之比 r v ,透射波声压与入射波声压之比 t p 以及透射波质点速度与人射波质点速度之比 t p 分别为( 3-5-10 )式中由此可见,声波在分界面上反射与透射的大小仅决定于媒质的特性阻抗,这再次说明媒质的特性阻抗对声传播有着重要的影响。
现分几种情况讨论:1 )由 ( 3-5-10 ) 式得这表明声波没有反射,即全部透射,也就是说即使存在着两种不同媒质的分界面,但只要两种媒质的特性阻抗相等,那么对声的传播讲来,分界面就好像不存在一样。
谢处方《电磁场与电磁波》(第4版)章节习题-第6章 均匀平面波的反射与透射【圣才出品】

第6章 均匀平面波的反射与透射一、判断题电磁波垂直入射至两种媒质分界面时,反射系数与透射系数之间的关系为ρτ1+=。
( )ρτ【答案】√二、填空题电磁波从理想介质1垂直向理想介质2入射,介质1和2的本征阻抗分别为30Ω和70Ω,则分界面处的反射系数Γ和透射系数τ分别是_______,_______。
【答案】0.4;1.4三、简答题1.简述平面电磁波在媒质分界面处的反射现象和折射现象满足的斯耐尔(Snell )定律;并具体说明什么条件下发生全反射现象,什么是临界角,给出临界角的计算公式。
答:(1)斯耐尔(Snell )定律:①反射线和折射线都在入射面内;②反射角等于入射角,即;r i θθ=③折射角的正弦值与入射角的正弦值之比等于入射波所在的媒质的折射率与折射波所在媒质的折射率之比,即,式中sin sin ii n n ττθθ=n =(2)全反射现象:①理想导体全反射。
在电磁波入射到理想导体表面时,由理想导体表面切向电场为零的条件,反射系数为±1,称为理想导体全反射现象;②理想介质全反射。
当电磁波由光密介质入射到光疏介质时,由于,根据斯耐12n n >尔定律有。
当入射角增加到某一个角度时,折射角就可能等于。
因此,i τθθ>i θπ2c θ<τθπ2在时,就没有向介质2内传播的电磁波存在,即发生全反射现象。
c θθ>能使的入射角称为临界角,有:π2τθ=c θ21sin c n n θ==2.什么是电磁波在媒质分界面的全反射现象和全折射现象?什么是临界角和布儒斯特角?一个任意极化波由空气斜入射到一介质界面,以什么角度入射才能使反射波为线极化波?说明原因。
答:(1)当电磁波由光密介质入射到光疏介质时,由于,根据斯耐尔定律有12n n >。
当入射角增加到某一个角度时,折射角就可能等于。
因此,在i τθθ>i θπ2C θ<τθπ2时,就没有向介质2内传播的电磁波存在,即发生全反射现象。
电磁波在不同分界面的反射与透射的简单分析

目录摘要 (1)关键词 (1)Abstract (1)Key words (1)引言(或绪论) (1)1 理论基础 (2)1.1 均匀平面波 (2)1.2对导电媒质分界面的垂直入射 (2)1.3全反射与全透射 (3)2 均匀平面波对理想介质分界面的斜入射 (4)2.1垂直极化波 (4)2.2平行极化波 (6)3 均匀平面波对理想导体分界面的斜入射 (4)3.1垂直极化波 (9)3.2平行极化波 (9)参考文献 (10)电磁波在不同分界面的反射与透射的简单分析摘要:由于不同媒质其媒质参数不同, 电磁波入射到媒质分界面时会产生反射和透射现象。
通过对电磁波在分界面上反射和透射的理论分析, 讨论反射波、透射波振幅、方向随入射角的变化。
关键词:边界条件; 反射系数; 平行极化;全反射Reflection and transmission characteristics of electromagnetic waves on interface of different mediumsStudent majoring in elecnomic information engineering JingXinpingTutor Jinhua OuyangAbstract:Due to the different parameters with different mediums, electromagneticwaves incidencing on the interface between mediums will produce the phenomenon ofreflection and transmission. This paper discusses amplitude, direction characteristics of reflected wave and transmission wave versus the angle of incidence throughanalyzing the formula.Key words: boundary condition; reflection coefficient;parallel polarization; allreflection引言随着电磁波技术在通讯、勘探等诸多领域的不断发展, 电磁波在介质中的传播问题也越来越重要[ 1] 。
电磁场与电磁波-第六章-均匀平面波的反射和透射
(
z)
z 0
Er (z) (ex jey )Eme
jz
0
所以反射波是沿-z方向传播的左旋圆极化波
电磁场与电磁波
第6章 均匀平面波的反射与透射
16
(2)在z<0区域的总电场强度
E1(z,
Re
Re
t()ex RejeyE)ie(zj)zE(r(ezx)
(ex
je
y
)
j2 sin
1= 2= 0
则
1 j1 j 11
2 j2 j 22
1c 1
1 1
, 2c
2
2 2
2 1 , 22
2 1
2 1
讨论
x
介质1:
1, 1
Ei
ki
Hi
kr
Er Hr
介质2:
2, 2
Et
kt
Ht
y
z
z=0
当η2>η1时,Γ> 0,反射波电场与入射波电场同相
当η2<η1时,Γ< 0,反射波电场与入射波电场反相
ex
Eim
(e
j1z
e
) j1z
H1(z) Hi (z) Hr (z) ey
媒质2中的透射波:
E2
(z)
Et
(z)
ex
Eime
j2 z
Eim
1
(e j1z
e j1z )
H2(z)
Ht
(z)
ey
Eim 2
e
j2 z
电磁场与电磁波
第6章 均匀平面波的反射与透射
20
合成波的特点
E1(z) ex Eim (e j1z e ) j1z ex Eim (1 )e j1z (e j1z e j1z ) ex Eim (1 )e j1z j2 sin 1z
谢处方《电磁场与电磁波》(第4版)课后习题-第6章 均匀平面波的反射与透射【圣才出品】

第6章 均匀平面波的反射与透射(一)思考题6.1 试述反射系数和透射系数的定义,它们之间存在什么关系?答:(1)反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数;透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。
(2)反射系数Γ和透射系数τ之间的关系为:6.2 什么是驻波?它与行波有何区别?答:频率和振幅均相同,振动方向一致,传播方向相反的两列波叠加后形成的波叫驻波。
行波在介质中传播时,其波等相面随时间前移,而驻波的波形不向前推进。
6.3 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,反射系数大于0?在什么情况下,反射系数小于0?答:均匀平面波垂直入射到两种理想媒质分界时,当时,反射系数Γ>0;当时,反射系数Γ<0。
6.4 均匀平面波向理想导体表面垂直入射时,理想导体外面的合成波具有什么特点?答:均匀平面波向理想导体表面入射时,理想导体外面的合成波具有特点如下:合成波电场和磁场的驻波在时间上有的相移,在空间上也错开了且在导体边界上,电场为零。
驻波的坡印廷矢量的平均值为零,不发生电磁能量的传输过程,仅在两个波节之间进行电场能量和磁场能量的交换。
6.5 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,分界面上的合成波电场为最大值?在什么情况下,分界面上的合成波电场为最小值?答:当均匀平面波垂直入射到两种理想媒质分界面时,的位置时,分界面上的合成波电场为最大值。
的位置时,分界面上的合成波电场为最小值。
6.6 一个右旋圆极化波垂直入射到两种媒质分界面上,其反射波是什么极化波?答:右旋圆极化。
6.7 试述驻波比的定义,它与反射系数之间有什么关系?答:驻波比的定义是合成波的电场强度的最大值与最小值之比,即6.8 什么是波阻抗?在什么情况下波阻抗等于媒质的本征阻抗?答:在空间任意点,均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗,在均匀无耗各向同性的无界媒质中,均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。
第六章均匀平面波的反射与透射

t 4 t 0
t 2
y t 2
x
t 4 2
t 0
y
t 3
t
4
x
4
3 4
t 7 4
t 3 2
t 4 t 0
t 2
1. 对于确定的时间 t ,总场在空间成正余弦分布,在 kx nπ 处,电场恒定为零,而磁场
jk1x
ez
Emi
1
1 e jk1x
2
j cos k1x
E2 Et ey Emi e jk2x
H2
=
Ht
ez
Emi
1
e jk2x
S
E1 max
1
E1 min 1
总场是行驻波
S 1 S 1
1
电子工业出版社
第六章 均匀平面波的反射与透射
电磁波的传播与分布问题除了与基本方程 有关外,还与边界条件密切相关
6.1 均匀平面波对分界面的垂直入射
6.1.1 均匀平面波对理想导体分界面的垂直入射
y
Ei ey Emi e jkx
Ei
ki
Hi
Hi
ez
Emi
e jkx
x
O
假设电场方向不变,而磁场方向反向
幅度为最大值;在 kx nπ π 处,磁场恒定为零,而电场幅度为最大值,电场和磁场的 2
零点以及最大值点相差 。 4
2.对于固定的空间位置,电场和磁场随时间是震荡变化的,但相位相差 π 。 2
3.总场的平均坡印廷矢量为
Sav
1 2
平面波的全反射和全透射现象

6.13 平面波的全反射和全折射现象
1、全反射现象 2、全折射现象
1、全反射现象
全反射:当电磁波入射到两种介质分界面上,
在介质2中没有折射波的现象。 全反射现象包括两种情况:
x ,
Er
(1)理想导体的全反射
(2)理想介质的全反射
z
Ei
(2)理想介质的全反射
由折射定律可知:
sin t sin i
折射定律: sint 1 sini 2
cost 1 cosi 2
i t
但由于 1 2 ,因此 i t 。
结论:垂直极化波斜入射时,不可能发生全折射现象。
思考:
一圆极化波以布儒斯特角斜入射时,反射波是什么极化波?
折射波是什么极化波? 圆极化波可以分解为:
垂直极化波 平行极化波
不可能发生全折射现象 能发生全折射现象
结论: 反射波中只有垂直方向的线极化波; 折射波为椭圆极化波。
小结:平面波的全反射和全折射现象
1、全反射:当电磁波入射到两种介质分界面上,在介质2中 没有折射波的现象。
理想导体的全反射
理想介质的全反射,条件 i c
2、全折射:当入射波以布儒斯特角入射时,入射波在分界面 处全部折射进第二种媒质中,不发生反射的现象。
1 2
sin B
sin2 B
2 1 2
折射定律
1 cosB 2 cost
若 1 2 0
cost
2 1
cosB
B arcsin
2 1 2
或:
B arctan
2 1
布儒斯特角或偏振角
(2)对垂直极化波的情况
地震波的反射投射和折射

§地震波的反射、透射和折射序:在§中讨论了无限均匀完全弹性介质中波的传播情况。
当地震波遇到岩层界面时,波的动力学特点会发生变化。
地震勘探利用界面上的反射、透射和折射波。
一、平面波的反射及透射同光线在非均匀介质中传播一样,地震波在遇到弹性分界面时,也要发生反射和透射。
首先讨论平面波的反射与透射。
(一)斯奈尔(snell)定律1.费马原理(最小时间原理)波从一点传播到另一点,以所需时间最小来取传播路径。
如图,波从P1点传到P2点。
速度均匀时,走路径①,直线,t最小,s也最小。
速度变化时,走路径②,曲线,t最小,s不最小。
注意:时间最小,不一定路程最小(取决于速度)。
P 1 P2路径①路径②例1:人要去火车站(见图)。
方法①从A步行到B,路程短,用时却多。
方法②从A步行到C,再坐车到B,路程长,用时却少。
步行速度V 1 V 2>>V 1 汽车速度V 2 例2:尽快地将信从A 送到B① 傻瓜路径 ② 经验路径③ 最小时间路径,满足透射定律:21sin sin V V βα=②A2.反射定律、透射定律、斯奈尔定律波遇到两种介质的分界面,就发生反射和透射(注:地震透射、物理折射)。
(1) 反射定律:反射波位于法平面内,反射角=入射角。
注:法平面——入射线与界面法线构成的平面,也叫入射平面或射线平面。
O S地面 入射角=反射角与下式等价:111sin sin V V αα= (1) (2) 透射定律透射线位于法平面内,入射角与透射角满足下列关系:221sin sin V V αα= (2) (3) 斯奈尔定律综合(1)和(2)式,有P V V V ===22111sin sin sin ααα 这就是斯奈尔定律,P 叫射线参数....。
推广到水平层状介质有:P V V V nn ====αααsin ......sin sin 2211 () 注:斯奈尔定律满足费马原理,上例2中把信由A 送到B 路径③是最小时间路径,它满足透射定律(用高等数学求极值可证明)。
电磁波第六章均匀平面波的反射与透射

(3) 媒质1为空气,媒质2为良导体:将产生趋肤效应
良导体→ 2c (1 j)
f (1 j) 1
j (1 j) f
,2c , , ;
反射大、透射小 :电磁波很难进入良导体内部
(4) 两理想介质的分界面,即1= 2= 0,则得到实数值的
2 1 , 22
2 1
2 1
1c 1c
Em1
Em 2
Em1
22c 2c 1c
Em1
反射系数 透射系数
Em1 2c 1c Em1 2c 1c
Em 2 Em1
22c 2c 1c
7
电磁场与电磁波 第六章__均匀平面波的反射与透射
反射系数Γ:反射波电场的振幅与入射波电场振幅之比
透射系数τ:透射波电场的振幅与入射波电场振幅之比 ~ 的关系:1
入射面 Ei
Ei //
Er // 反射波
入射波 Ei^
ki i
Er
r
kr Er^
x
分界面
Et //
t
y
Et
Et^ z
透射波 kt
均匀平面波对理想介质分界面的斜入射
θ : 入射角, θ′ : 反射角, θ′′: 折射角
i , r , t
入射面:入射波矢量与分 界面法线所在的平面 26
H最大,E 最小
E
E
E1
E2
E1 E2
5 1 4
1
3 1 4
1 2
1 4
o
Γ > 0 时合成波电场振幅
z
5 1 4
1
3 1 4
1 2
1 4
o
z
Γ <0 时合成波电场振幅
声学基础4.10平面声波的反射 折射与透射

⑤Z1 (Z1>> Z2).R=-1,D=0
称完全软边界.反射波声压与入射波声压大小相等, 相位相反,在界面上的合成声压为零;在界面处,入 射波与反射波的振速大小相等,相位相同,界面上的 合成振速为入射波的两倍.
折射波声压为零—无折射波产生;在界面处,介质2 中的质点有相当于入射波振速两倍的速度,但由于 介质2 “完全柔软”,故介质2中没有波动传播.也为全 反射.从水向空气入射就近于这种情况.
0.5 0.4
00
IRI 560
2a 1800
00
反射系数,相角随入射角的变化曲线
4.10.4平面声波通过介质层时的反射和折射 讨论垂直入射的情况 利用前面的结果可知, 各介 质中的声压和振速分别为: 介质I中
(e)
介质Ⅱ中 (f)
介质Ⅲ中 (g)
介质层的输入阻抗、反射和折射系数 在x = 0处的声学边界条件为
由上式可见,反射系数与折射系数只与两交界面介 质的波阻抗及入射角有关.
为了以下讨论方便,令
密度比
介质2对1的折射率
由 得
R,D可写为:
讨论:
①全透射
当声波入射角 i 满足
得到:
这时没有反射波,声波全部进入介质 2.所以 0 称
为全透射角.
并不是对任意的两种介质(m 和 n)都可以出现全 透射现象.出现全透射的条件:
○ 注意事项: – 存在反射波的的平面声场中,输入阻抗一般不等 于介质的特性阻抗,也不是实数,这是有界平面波 声场区别于无限介质平面行波场很重要的特征. 不仅平面波如此,对其他声场也是这样.
R表达式及透射系数的计算 将(m)代入(i)中
或者 由(ha)式左边消去B1求得
代入下图,可以把前面公
3.5.3 平面波斜入射时的反射与透射

轴有一个夹角 ,因为波的行进方( 3-2-5 )图 3-5-3这时同一波阵而上不同位置的点 ( x , y , z ) 因为有相同的 x 坐标,因此声压的振幅和相位均相同,即这些位置上的声压都以 ( 3-2-5 ) 式描述。
仔细分析一下,发现 ( 3-2-5 ) 式中的 x 值实际上代表的是位置矢量 r 在波阵面法线方向 ( 这里恰巧为 x 轴 ) 上的投影。
如图 3-5-3(a) 。
如果设想一列沿空间任意方向行进的平面波,也会发现,那时波阵面上的不同位置也因为位置矢量在波阵而法线方向上的投影相等而具有相同的声压,见图图 3-5-3(b) 。
所以我们可以把 ( 3-2-5 ) 式中的 x 一般化地理解为声场某点的位置矢量 r 在波阵面法线上的投影,它等于波阵面法线的单位矢量 与位置矢量 r = x i + y j + z k 的标量积,即这里的 为波阵面法线与 三个坐标轴间的夹角, 为该法线的方向余弦。
只是在现在的法线方向与 x 轴重合的情况有 , 。
这样 ( 3-2-5 ) 式就可一般化地写成如果令 k n = k ,它代表波阵面法线方向上长度为 k 的矢量,称为波矢量 ( 简称波矢 ) ,则上式成为( 3-5-13 )这就是我们由 (4 — 5 — 5) 式推广得到的沿空间任意方向行进的平面波的表示式,其中 k 为波矢, r 为位置矢量。
因为所以 (4 — l0 — 14) 式也可写成( 3-5-14 )今后只要己知平面波传播方向的方向余弦 ,就可以用 (4 — l0 — 15) 式表示空间一点 (x , y , z) 的声压。
由声压 p ,应用 (4 - 3 - 11) 式即可求得空间任意一点 (x , y , z) 的质点速度沿三个坐标的分量( 3-5-15 )现在再回到斜入射问题。
当有一列行进方向仍在 xy 在平面内、但与 x 轴夹角为 的平面声波入射于分界面上时,根据刚才的讨论,对该入射平面波有,所以按 ( 3-5-14 ) 式及 ( 3-5-15 ) 式,声压 p 及质点速度沿 x 方向的分量分别为( 3-5-16 )式中 。
平面波的全反射和全透射现象

思考:
—圆极化波以布儒斯特角斜入射时,反射波是什么极化波?
折射波是什么极化波? 圆极化波可以分解为:
'垂直极化波 、平行极化波
不可能发生全折射现象 能发生全折射现象
结论: 反射波中只有垂直方向的线极化波; 折射波为椭圆极化波。
小结:平面波的全反射和全折射现象 1全反射:当电磁波入射到两种介质分界面上,在介质2中 没
6.13平面波的全反射和全折射现象
1、 全反射现象 2、 全折射现象
1 ,全反射现象
全反射:当电磁波入射到两种介质分界面上,
在介质2中没有折射波的现象。
全反射现象包括两种情况:
(1) 理想导体的全反射 (2) 理想介质的全反射
(2)理想介质的全反射
sin q
时
由折射定律可知: sin q V *2卩2
当勻日1 > £恥时,必然有et > q。
如果入射角增大到某个角度时,恰好使q二90o则:
sin90o "迎=arcsin sin。 V 时2
*2外 3 = & q = arcsin 冬 时
丫 賢i
临界角
讨论:
当耳> Oc时,有sin^t > 1 , 此时
0,不是实数角,而是复数角。
则:cos 0t = 土 j 冬 sin2 0 -1
2 cos 4B = 2 cos 4
若 卩\=M =卩o
COS 4 =
4 = arcsin
布儒斯特角或偏振角
(2)对垂直极化波的情况
亿"〃g 0 % cosQ—0 cos Q = 0
丄 % COSQ +% COSQ ‘2 1/1 t
P波入射反射、透射系数推导14页

P波入射Zoeppritz方程的推导根据弹性力学的假设,介质是均匀各向同性的无限大介质,平面波是一种最简单的波动形式,其以波面为平面的形式在介质中传播,即平面波在垂直于波传播的任一平面上,各点的振动是同相的,实际上并不存在激发平面波的震源,所以它是一个数学抽象了的波动过程。
点震源激发的球面波向四面八方传播,当其距震源足够远时,在这个地方研究一个局部的等相位面,可以将其看成一个平面波。
在理论上,任何类型的波都可以用平面波的合成形式来表示,所以平面波是波动现象中最基本的形式,也是理论研究和实际应用的基础。
在地震勘探中,讨论在两种不同的介质分界面上的波的传播现象是十分重要的。
一般分为两种情况进行讨论,第一种,我们所研究的地球介质按其物性变化是分层的,具有层装结构。
因此,讨论两种弹性性质不同的介质分界面上波的传播情况。
第二种,地球表面是一个特殊的分界面,它将无限介质划分为两个半空间。
地面以上的空气介质,其密度与地面以下的岩石或海平面以下的海水层及岩石层的密度相比可以忽略。
因此,地球表面可以看成是一个弹性半空间表面,称为自由面,其上的应力作用为零。
根据本文所讨论的地质模型所涉及到的地质灾害,我们只讨论波在第一种介质分界面情况下波的传播,即平面波在弹性分界面上的反射与透射。
1.1波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所示:关于位函数我们首先看:沿任意方向传播的平面波。
设N r是一个任意取定的单位方向矢量。
N li mj nk =++r r r r(1)下面来看沿N r方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f fx y z V t∂∂∂∂++=∂∂∂∂(2)这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
cos1
Vp
y sin 1
)
改写为 U1 A1 sin(t f1x g1 y)
f1
cos1
Vp
;
g1
sin Vp
1
设入射波为拉伸波,即质点的运动方向与波的前进方 向相反,于是可以知道在入射波中质点的位移分量为:
u1 U1 cos1, v1 U1 sin 1
假设与自由界面作用后,只有纵波反射,且反射纵波 的位移函数为:
假定yoz面的左边为真空,由于没有传播振动的介质,故不会 产生透射问题,全部入射波都在界面上被反射。
P1入射纵波
P1S1反射横波 P11反射纵波
设一平面纵波与x轴夹角为α1的方向入射到自由界面; 设入射纵波中质点的位移函数(即波动方程的解)为:
2U t 2
Vp2
2U r 2
U1
A1
sin (t
在此波动中,质点的位移函数与z无关,且位移在z方向的分量 w=0
因为在自由界面上既有入射波带来的位移,又有反射 波带来的位移。所以在假定只有反射纵波的时候,有
u u1 u2; v v1 v2
U1 A1 sin(t f1x g1 y) U2 A2 sin(t f2 x g2 y 1) u1 U1 cos1, v1 U1 sin 1 u2 U2 cos2 , v2 U2 sin 2
u u1 u2 u3; v v1 v2 v3 U1 A1 sin(t f1x g1y) u1 U1 cos1, v1 U1 sin1
U2 A2 sin(t f2x g2 y 1) u2 U2 cos2, v2 U2 sin2
U3 A3 sin(t f3x g3 y 2 ) u3 U3 sin 2 , v3 U3 cos 2
U2 A2 sin(t f2 x g2 y 1)
f2
cos2
Vp
; g2Βιβλιοθήκη sin2Vpf2前面的负号原因:反射波相对于x轴而言,是正向传播。
δ1为常数,表示由反射所引起的相位改变。
仍假设反射波为拉伸波,在此波动中质点的位移分量为:
u2 U2 cos2 , v2 U2 sin 2
问题:确定反射波的各参数
• 如果平面波的传播方向与z轴垂直(即在xoy面或平行于 xoy的平面内),弹性动力学问题中的场变量都依赖于x和 y两维,此时弹性动力学问题为二维问题,这 时讨论分层 介质波传播问题就是讨论这样二维弹性动力学问题。
§7-1平面波在自由界面上的反射
一、平面纵波在自由界面上的反射 设半无限弹性介质的自由表面为yoz面,z轴与图面垂直。
方法:由边界条件可以确定
边界条件:在自由界面上位移不受任何限制,即应力等于零;
即在x=0的平面上,对于y与t的任意值有
x xy xz 0
由广义胡克定理和几何方程可以得到:
[ x ]x0
t
2
u x x0
0
[ xy ]x0
u
y
v
x
x0
0
[ xz ]x0
u z
w x x0
0自然满足
形变传播时,两部分的传播速度不同。在震源附近,两部分还未分开, 所以波经过处的形变是复杂的。在较远的地方,波阵面就分成两个。胀缩波 传播较快,波阵面上的质点位移和传播方向一致,所以叫做纵波,一般用字 母P(Primary)表示。较慢的叫畸变波,质点位移和传播方向垂直,所以叫做 横波,一般用字母S(shear)表示。在均匀的介质中,波阵面在震源附近是曲 面,但在相当距离后就趋近于平面。为简单起见,现只讨论平面波。
代入边界条件可以得到:
A1
(
2 cos2 1) cos(t
Vp
[
A1
sin
21
cos(t
g1y) g1y)
A2( 2 cos2 2) A2 sin 22 cos(t
cos(t g2 y 1 g2 y 1)] 0
)
0
对于y的任意值,为了使第一式得到满足,必须有
(1)g1 g2 (即1 1); (2)1 0, A1 A2或1 , A1 A2
上面两式是等价的,说明经过自由界面的反射,位移的位相 改变了π,但是将其代入第二式却不能使第二式得到满足。 于是我们可以知道仅有一反射的纵波,是不能同时满足边界 上无正应力和无剪应力的边界条件的。
现在我们证明还有一反射的横波,入射纵波、反射纵波、反 射横波代入可以同时满足边界上的边界条件。
设反射横波的传播方向与x轴的夹角为β2,相应于此波质点 的位移函数为:
第七章 平面波的反射与透射
在无限弹性介质中有无旋波(纵波)和等容波(横波)这两种弹性波 的传播。
但是实际介质内部,一般都会存在分界面。如地表表面、岩层的分界 面。
通常把实际地层称为层状介质。本章研究弹性波在传播的过程中遇到 分界面的情况。
纵波和横波 地震波到达之处,介质就产生形变。由力学定律知道,任何 小的形变都可以分解为两部分:一部分表示胀缩,即变体积而不变形状;另 一部分表示畸变,即变形状而不变体积。
三点说明
• 因为地球介质在短暂力(如爆炸)的作用下,在离开震源 稍远的大部分地区 可看成弹性体,并且地球半径比地震 波波长大得多,所以可将地球看作半无限大弹性介质,同 时,可近似将地震波视为平面波。
• 任何复杂的波都可看成一系列不同振幅,不同频率及波长 谐波的叠加,因此仅讨论一个平面谐波入射到自由界面的 情形即可。
地震P波(纵波)和S波(横波)运行时弹性岩石运动的形态
纵波:间隔形成压缩带(密集带)和膨胀带(稀疏带),传播 方向与振动方向一致,波速―― Vp
横波:传播方向与振动方向相垂直,波速――Vs 水平面内分量:称SV波 垂直面内分量:称SH波
§7-1平面波在自由界面上的反射
自由界面:指地表应力为零的界面,半无限 弹性体的界面就是自由界面。由于地球表 面大气压相对于地球内部压力来说是十分 小的,在讨论中可把大气压忽略不计,于 是地球表面可以看作自由界面。
U3 A3 sin(t f3x g3 y 2 )
f3
cos Vs
2
;
g3
sin Vs
2
考虑到横波中质点的位移与传播方向垂直,且假定z方向无 运动,因此振动必然发生在oxy平面内,这样,在次波动中质 点的位移分量为:
u3 U3 sin 2 , v3 U3 cos 2
入射纵波、反射纵波、反射横波同时存在,在自由界面上 质点的位移分量为:
