平板边界层实验报告
平板划线法实验报告

平板划线法实验报告导语:平板划线法实验是一种重要的实验方法,是描述地面上的凹凸侧界的常用方法。
该实验用以测量海岸线、山脉、河流谷等地质特征,在地质技术活动中发挥着重要作用。
本文主要介绍了平板划线法实验的原理、器材介绍、实验方法以及数据记录等内容,旨在为读者提供一份平板划线法实验报告,以帮助读者更好地理解和掌握该实验方法。
一、实验原理平板划线法实验是一种基于直线剖面的地面调查方法,主要是把一个宏观大尺度的地形调查结果用多条水平的直线剖面去描述。
它根据地形变化的规律来把一个宏观区域分割成若干划线,从而形成的一组具有特征的划线框架,又称作“划线网”,主要用于描述地面上的凹凸侧界,如海岸线、山脉、河流谷等。
二、器材介绍平板划线法实验所用的器材包括:水准仪、探点架、测距尺、画线画板等。
其中水准仪是主要的设备,是用来水平、高程测量的仪器;探点架是用来测量凹凸深度的,它的底座有微量水平调整;测距尺是用来测量划线之间的距离;画线画板是用来将测量出的结果记录在图纸上的。
三、实验方法1. 测量基准点:首先,用水准仪测量一个基准点,确定地面的水平坐标系;2. 测量基准线:然后,从基准点开始,沿着目标凹凸边界测量出一条水平线,即为基准线;3. 描绘凹凸边界:接着,纵向依次划出几条垂直于基准线的直线,距离基准线有一定距离;4. 测量线距:最后,用测距尺测量出平板网格的线距,并用画板画出来。
四、数据记录测量完后的数据应该记录妥当,其包括基准点和基准线以及平板网格等信息。
包括:1. 基准点:基准点的水平坐标、高程;2. 基准线:基准线的起点及终点水平坐标、高程;3. 网格:每条网格线的起点及终点水平坐标;4. 线距:每行网格之间的线距。
五、总结平板划线法实验是一种常见的实验方法,它可以有效地描述地面的凹凸侧界。
本文简单介绍了该实验的原理、器材介绍、实验方法以及数据记录等内容,以帮助读者更好地理解和掌握该实验方法。
平板边界层速度剖面的测定讲义2

2009年04月20~22日平板附面层速度剖面与厚度的测定一、实验目的:1.熟悉附面层速度分布和厚度的测量方法。
2.具体测定平板附面层层流与湍流附面层的速度分布及其厚度。
3.把实验结果与理论计算结果进行比较,分析其差异产生的原因。
二、实验原理:粘性匀质不可压缩流体,测量边界层内的速度,仍利用风速管(皮托管)测风速的原理,即测出某点的总压P0和静压P后再换算成该点的速度,因为边界层很薄,其厚度往往只有几mm到十几mm,因而只能用极细的探针去探测边界层内的压力。
由于在边界层内部满足∂(P)/∂(Y)=0,即静压P沿着平板的法线方向不变,因此,可以用壁面上的静压P来表示边界层内法线上所有不同高度的静压。
于是,本实验将一根微总压管装在一标架上,使微总压管以很小的间距上下移动,测出不同高度处的总压P0(y)后,即可算出法线上离壁面y处的速度。
实验时,把总压管由壁面逐步往上移动,则测出的总压越来越大。
当移动到某一高度以后,再继续往上移动几个间距,这时所测到的总压已不再随高度的变化而变化。
记录下数据,经软件分析后可得速度边界层厚度和速度剖面,并与理论曲线对照。
理论分析中总是假定从平板(或物体)的前缘(或驻点)就开始形成层流或湍流边界层。
实际上绕流体的运动常常是组合边界层问题,即在物体的前部分首先形成层流边界层,在它的后部分形成湍流边界层,在它们之间还有一个过渡段。
过渡段从层流的失稳点(层流不稳定点)开始直到流动成为完全湍流之点(湍流过渡点)结束。
性质介于两者之间。
为了读出压力的微小变化,本实验采用压力传感器,采用总压和静压之差,将其采集的压力信号转换成电信号,再通过放大器进行信号放大后,输入A/D转换器,由计算机直接计算出速度值。
由于速度剖面是以无量纲形式画成的,因此,不需要计算一点的速度,只要计算出速度的相对值就可以了。
计算各高度上的u y/v和y/δ的值,以y/δ为纵坐标,u y/v为横坐标作图(其中v是边界层δ处所对应的边界层外缘处的速度,相当于来流速度),从流速分布图上判断各测点处是层流还是湍流边界层。
平板边界层实验指导1213

平板边界层实验指导一.实验目的1)测量平板边界层流速剖面,加深对边界层概念的认识;了解层流和湍流边界层的差异。
2)掌握热线风速仪和皮托管测速技术。
二.实验原理U 大Re 数绕平板流动,在平板边界附近有一个薄层,流速从平板处的零值,经过该层迅速增大到接近来流速度U ,此薄层被称为边界层。
通常定义0.99u =处到平板的距离为边界层厚度。
在平板的前段,边界层内流动呈层流状态,即层流边界层。
建立直角坐标系如图1,原点在平板前端,x 轴沿来流方向,轴垂直平板。
定义局地雷诺数y Re x Uxν=,ν为流体的运动学粘性系数。
从平板前端向后,在某个x 位置以后,Re x 足够大,边界层内流动变得不稳定;继续向后,当Re x 超过临界值Re xc 后,边界层内流动发展为湍流。
Re xc 被称为转捩雷诺数,其大小受多种因素影响,包括来流湍流度、平板粗糙度和其他扰动等。
对光滑平板边界层的观测研究表明,在低湍流度风洞中(湍流度低于1%),Re xc 可达;对于较大的来流湍流度,Re 610xc 也可以低至几千甚至几百。
在层流边界层中,粘性力与惯性力同量级。
除平板前端外(Re 100x <),层流边界层流速剖面满足Blasius 解,即()u Uf η′=,f满足200,0,1f ff f f f ηη′′′′′+=⎧⎪′===⎨⎪′=∞=⎩--------------------(1)其中η=该速度剖面如图2所示。
相应地,层流边界层厚度c δ≈从固壁向外,湍流边界层可分为粘性底层、过渡区和湍流核心区。
在粘性底层内,分子粘性应力远大于湍应力,流速呈线性分布。
在湍流核心区,情况正好相反,分子粘性可略,流速呈对数分布。
设u u u +∗=,yu y ν∗+=,其中u为脉动平均流速,u ∗=为摩擦风速,wτ为壁面上的切应力,ρ为流体密度。
在粘性底层u y +=+,-------(2-1) 在湍流核心区1ln u y κ++=C +,-------(2-2)常数和由实验确定。
微尺度射流、平板边界层及叶栅流动实验研究

南京航空航天大学硕士学位论文微尺度射流、平板边界层及叶栅流动实验研究姓名:***申请学位级别:硕士专业:航空宇航推进理论与工程指导教师:梁德旺;黄国平20060101南京航空航天大学硕士学位论文摘要本文以某型微型涡轮喷气发动机研制为背景,以认识微尺度下粘性流体流动状态及其机理和微涡轮叶栅通道内部流动特性为目的,设计并搭建了除本实验外还可供其他流体力学实验使用的微型风洞,并在该微型风洞基础上进行了微尺度射流实验、微尺度壁面边界层实验和微尺度涡轮叶栅实验。
微射流实验在出口宽度固定为20mm情况下,选取了3种不同出口高度:2mm,3mm和5mm,并通过改变速度使出口高度雷诺数在约20000到约55000之间改变,实验得到了流动图谱和微射流数学模型。
实验发现微射流中内外层流体微团之间的动量交换较常规大尺度下减弱,掺混变得相对缓慢,射流特征半厚度相对减小,从而初始段扩张角和基本段极角都有所减小。
该实验还同时研究了下游较远处射流流动情形,发现其掺混强度在微尺度二维平面射流和常规三维射流之间。
微尺度平板边界层实验选取从总长度为15mm的微平板前缘8mm到14mm之间的7个站位,4种马赫数,13个不同雷诺数(从35000到150000)的实验状态,发现了该尺度下边界层流动的一些新的特点,如形状因子比常规大尺寸下充分发展湍流状态的形状因子更小等。
微尺度叶栅实验使用弦长5.64mm的VKI-1叶型,选取了4种安装角度,3种叶尖间隙,4种出口主流马赫数状态的实验,得到了叶栅出口的总损失分布云图,发现微尺度叶栅栅后高损失区域与栅距的比例较常规大尺度下明显增大;同时对叶栅出口流动损失进行了分析,发现为了提高涡轮的效率,需要尽可能减小叶尖间隙并选择合适的安装角度(针对本实验中叶栅,最佳安装角为45~50度)。
关键词微流动微射流平板边界层流动涡轮叶栅Experimental Research on Micro Jet Flow , Flat Plate Boundary Layer Flow & Turbine Cascades FlowAbstractThis dissertation has on the research and design of a Micro Turbine Engine as background and it is for the purpose of comprehending viscous flow behaviors in micro scaled conditions and that in the mini-turbine cascades. A mini wind tunnel is designed and set up which also can be used in other micro flow experiments. On the basis of this mini wind tunnel, three mini flow experiments, including micro jet experiment, micro boundary layer experiment and mini-turbine cascades experiment, have been carried out.The micro jet experiment is under conditions of 3 different heights, 2mm, 3mm and 5mm of 2D (2 dimensional) rectangle jet outlet and the width of each is same, 20mm. 5 Reynolds numbers vary from 20,000 to 55,000.The experiment characters tell that compared with that of the normal scaled jet flow, the dilution power of this micro jet becomes weaker. Furthermore, the flow in the far down stream are also researched. The diluting power of the flow within this area is between that of 2D micro jets and normal scale 3D jets.The micro boundary layer experiment is carried out from 8mm to 14mm of a 15mm-long micro plane. Re numbers vary from 35,000 to 150,000 and 4 different Mach numbers are selected. Some new characters are discovered, such as velocity curve factor is smaller than that of well developed normal scale turbulence Boundary Layer.VKI-1 cascade with 5.64mm chord is adopted in mini-turbine cascades experiment. 4 assembly angles, 3 different blade tip clearances and 4 Mach number statuses are chosed as status variables. From 12 total pressure distribution maps, a conclusion is formed that ratio of high-loss area to full width of cascades period is large that that of normal scaled cascedes. Based on effiociency analysis,it has been found that narrower blade tip clearance and right assembly angle lead to utmost efficience. (e.g. 45~50 degree for this micro VKI-1 cascades)Keywords: Micro Flow, Micro Fluid, Micro jet(s), Flat Plate Boundary Layer Flow, Turbinary Cascades.承诺书本人郑重声明:所呈交的学位论文,是本人在导师的指导下,独立进行研究工作所取得的成果。
平板边界层实验报告

平板边界层实验报告引言平板边界层实验是一种常见的流体力学实验方法,用于研究在流体与固体界面发生的各种现象和特性。
通过实验可以获取边界层厚度、速度剖面、摩擦系数等参数,对于理解流体边界层的特性具有重要意义。
本实验报告将详细介绍平板边界层实验的原理、实验装置、实验过程和实验结果,并对实验结果进行分析和讨论。
实验原理在实验中,我们使用平板边界层实验装置对流体的边界层进行研究。
其原理基于以下几点:1.边界层理论:边界层是指流体流动过程中处于流体与固体物体之间的一层流动区域,其特点是速度梯度较大、流动剪切应力较高。
边界层的特性对于流体的运动、传热和传质等过程具有重要影响。
2.平板边界层:平板边界层是指位于平板表面附近的边界层,它是边界层研究中最常见的情况之一。
通过对平板边界层的研究,可以深入理解边界层的结构、特性及其对流体流动的影响。
3.流动速度剖面:边界层中流体的速度随距离平板表面的距离而变化,一般呈现一定的速度剖面形态。
通过测量流体速度剖面,可以确定边界层的厚度和速度分布特性。
实验装置实验装置由以下几个主要部分组成:1.平板:平板用于产生平板边界层。
通常采用光滑的表面,材质多为金属或塑料。
2.流体:实验中常使用空气或水作为流体介质。
流体通过输送装置注入到实验装置中。
3.流量计:流量计用于精确测量流体的流量,以保证实验条件的准确性。
4.速度测量装置:速度测量装置用于测量流体在平板边界层中的速度。
常见的测量方法包括热线法、激光多普勒测速法等。
5.数据记录系统:数据记录系统用于记录实验过程中获得的各项数据,包括流体流量、速度剖面等。
实验步骤本实验的具体步骤如下:1.准备工作:清洁实验装置,确保平板表面光滑且无杂质。
2.实验装置搭建:按照实验要求搭建实验装置,包括安装平板、连接流体输送装置和速度测量装置。
3.流体注入:启动流体输送装置,将流体注入实验装置中,并调节流量控制阀以控制流体的流量。
4.测速:使用速度测量装置对流体在平板边界层中的速度进行测量。
清华水力学实验18平边

γ 2g(
s
⋅l
⋅
N
+ψ
)
γa
式中:空气重度 γ a ;酒精重度 γ s ;微压计斜管中液柱长度 l ;毕托管修正系数ϕ ;微压
计修正系数ψ ; N = n ;微压计常数因子 n .
0.81
实验设备
实验在空气动力学多功能实验装置上进行。该多功能实验台相当于一个小型风洞,它包
平边-1
括风机、稳压箱、收缩段与试验段等。风机提供风源,风量由调节阀调节,气流经风道送入 稳压箱,稳压箱下接收缩段,在收缩段进口装设阻尼网以均化气流,出口接各种试验段。实 验后的气流从实验台面上的孔口吸入风机,以供循环使用。
进行平板边界层实验时,在实验段中心轴线位置安装一长为 L=300mm 的铝制平板,其一 面光滑一面粗糙。平板能沿轴线上下移动,以便选择不同的量测断面。
在实验段出口装一小型毕托管,连接一个千分卡尺,用以调节和记录毕托管的横向位置, 将毕托管刚接触到平板时的位置作为量测的起始点,此时指示灯发亮。
毕托管与微压计相连,以测定各点流速。
2. 为什么在量测断面处的层内外压强,都可按均布的大气压来考虑。
注意事项
1. 千分卡尺应缓慢旋转以防碰伤毕托管。 2. 实验过程中实验台两侧阀门不能动,实验台面泄流口不能有物体阻挡气流。 3. 若多功能实验台为两台共用一个通风机,实验时应尽量避免互相干扰。
平边-4
5. 接通电源,取走实验台面上的活动板,开启调节阀到最大位置,当流动稳定后,记录第 二测点的微压计读数 l 值。
6. 反时针旋转千份卡尺使毕托管远离实验板以改变测点位置,它每转一圈其 y 值增加 0.5mm每转一小格则增加 0.01mm. 测点在紧靠平板处布置要密,间距约 0.02mm至 0.03mm,随 y 增加间隔可逐渐增加为 0.05mm,0.3mm甚至为 1mm,测点总数约 25 左右。 每次量测需有一定稳定时间,并记下相应千分卡尺读数 y′′ 和微压计读数 l . 测点坐标为 y = ( y′′ − y′) + b . 当微压计读数 l 不再继续变化时,表明测点已达主流区。在主流区中需任
平板边界层测试实验
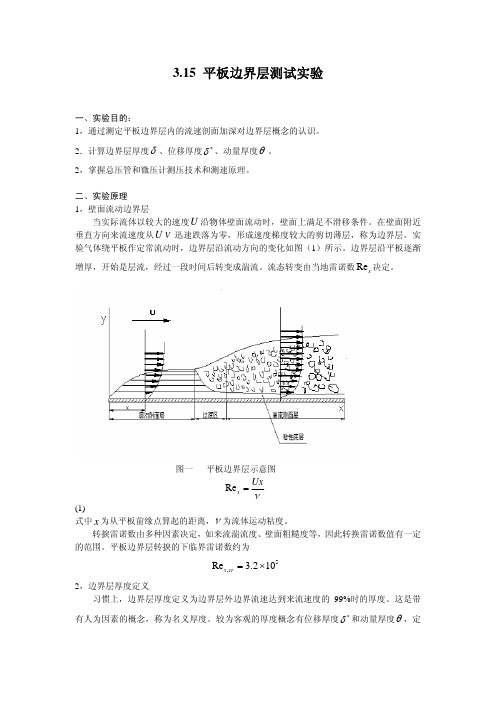
增厚,开始是层流,经过一段时间后转变成湍流。流态转变由当地雷诺数 Rex 决定。
图一 平板边界层示意图
Rex
=
Ux ν
(1)
式中 x 为从平板前缘点算起的距离,ν 为流体运动粘度。
转捩雷诺数由多种因素决定,如来流湍流度、壁面粗糙度等,因此转换雷诺数值有一定
的范围。平板边界层转捩的下临界雷诺数约为
Rex,cr = 3.2 ×105
2,边界层厚度定义 习惯上,边界层厚度定义为边界层外边界流速达到来流速度的 99%时的厚度。这是带
有人为因素的概念,称为名义厚度。较为客观的厚度概念有位移厚度 δ ∗ 和动量厚度θ ,定
义如下 , (2) (3)
∫ δ ∗ = δ (1 − u )dy
3.15 平板边界层测试实验
一、实验目的: 1,通过测定平板边界层内的流速剖面加深对边界层概念的认识。
2.计算边界层厚度 δ 、位移厚度 δ ∗ 、动量厚度θ 。
2,掌握总压管和微压计测压技术和测速原理。
二、实验原理 1,壁面流动边界层
当实际流体以较大的速度U 沿物体壁面流动时,壁面上满足不滑移条件。在ห้องสมุดไป่ตู้面附近 垂直方向来流速度从U V 迅速跌落为零,形成速度梯度较大的剪切薄层,称为边界层。实
0
U
∫ θ = δ u (1 − u )dy 0U U
式中 u( y) 为边界层内速度分布函数。
如 果 测 得 了 边 界 层 的 速 度 分 布 曲 线 u( y) , 就 可 以 分 别 画 出 (1 − u ) �����������������������������������������������������������
流体力学平板边界层内的流速分布实验报告电子版

平板边界层内的流速分布实验实验日期 2011-5-21 小组成员:李超,郭静文(93班)等 报告人 周楠 能动95 09031125实验目的1) 测量离平板前缘任意截面边界层内的速度分布; 2) 根据速度分布确定边界层厚度; 3) 了解风洞结构及测量仪器。
仪器设备吸入式风洞、大气压强计、温度计、微压计、U 型测压管、平板模型、总压探针及三维坐标架。
其中仪器的重要参数包括:(1)吸入式低速风洞P max =P a , 工作截面尺寸300mm ×300mm;(2)风洞的气体流速u max <25m/s, M<0.3,所以风洞内气体流动可以看成二维不可压缩流动即ρ=ρa(3)平板尺寸325mm ×200mm (4)总压探针头部直径:d=0.9mm实验原理1 流体在大雷诺数下绕物体流动时,由于流体粘性的作用,与物体表面接触的流体速度为零,然后沿法向很快增至主流速度,这层贴近物体表面,沿着法向有很大速度梯度的流动薄层,称为边界层;2 在边界层内,速度梯度很大,不能忽略流体的粘性,因此流动作实际流动u x 和p o 都在变化且u x <v ∞,p o <p a ;而在边界层外,流体粘性对流动的影响很小,可作理想流体分析,即总压p o =p a ,来流速度v ∞不变;3 对于平板而言,各点静压相同;4 对平板模型解N-S 方程可得总压与静压之关系22x o j u p p ρ=+5 任意点速度为x u =其中Δh 为总压与静压的压差水柱高度,本次实验中采用电测法测量静压和总压的压差Δp ,所以x u =6 边界层的厚度由下列条件确定,在该点边界层的流速与主流速相差1%时规定为边界层的边界,该点距平板的距离为边界层的厚度δ。
7 空气的密度ρ可以根据理想气体状态方程以及测量得到的实验室温度和大气压可得,pM RT ρ=。
实验步骤1 调整U型测压管和微压计,使管内两液面保持水平。
平板边界层实验报告

X 层= 340mm
Re层
v1x层
83096.18
风
风速管静压 风速管总压 h1 h静 h总
2
速
v1 h1 sin
管
h初
102
96
6
数
h末
136
102
34
据 h=h 末-h 初
34
6
28
由已知:
v1
2 h1 sin =
2 800 0.028 sin10 =8.01m/s 0.1212
小要比层流边界层的减小慢些; (4)在同一 下,紊流边界的摩擦阻力比层流边界层的大得多,这是因为层流中的
摩擦阻力只是由不同流层之间发生相对运动而引起的,紊流还有流体微团的很剧烈的横向 掺混,因而产生更大的摩擦阻力。
3. 用边界层厚度的经验公式求出δ层和δ紊 ,再与实验求得的δ层和δ紊作比较,分析产
生误差的原因。
2.实验曲线:
(自备坐标纸画出 vi f ( yi ) 曲线)
v1
1.
计算出各
yi 点处的
vi v1
,并求出δ层,δ紊。
2. 在坐标纸上画出 vi v1
f ( yi ) ,用曲线板连成光滑曲线,并比较层流边界层和紊流边
界层速度分布的差别。
层流边界层速度分布: 紊流边界层速度分布:
通过上面两图的比较,我们结合所学知识发现层流边界层和紊流边界层速度分布的差别: (1)紊流边界层沿平板壁面法向截面上的速度比层流边界层的速度增加得快,也即
答:因为垂直于板面方向的静压梯度等于零,即 p 0 ,所以只需在平板表面开一 y
静压孔,所测的静压就等于该点所在的平板法线方向上各点的静压。
总压排管
平板边界层实验报告

平板边界层实验报告一、实验目的本次实验旨在通过测量平板边界层的速度分布、压力分布和阻力系数等参数,了解平板边界层的特性及其对流体运动的影响。
二、实验原理平板边界层是指流体在与固体表面接触时,由于黏性作用而形成的一层极薄的流动区域。
在平板上方,流体速度逐渐增大,而在靠近平板表面处,由于黏性作用,流体速度减小并趋于零。
因此,在平板表面附近会形成一个速度梯度很大的区域,即平板边界层。
本次实验采用热线法测量平板边界层速度分布,并利用静压法测量压力分布。
根据这些数据可以计算出阻力系数等参数。
三、实验装置本次实验所使用的装置如下:1. 平板:宽300mm,长600mm,厚10mm。
2. 电源:直流电源。
3. 流量计:利用热线法测量气流速度。
4. 压力传感器:利用静压法测量气流压力。
5. 数据采集系统:将测得的数据传输到计算机上进行处理。
四、实验步骤1. 将平板放置在风洞中央,并调整风洞风速为指定值。
2. 开始测量速度分布。
将热线传感器插入平板上,并通过电源对其加热,使其温度高于周围空气。
当气流通过热线时,由于黏性作用,会导致热线周围的空气速度发生变化。
通过测量热线电阻的变化,可以计算出气流速度。
3. 测量压力分布。
将静压传感器插入平板上,并记录不同位置处的静压值。
4. 根据测得的数据计算出阻力系数等参数。
五、实验结果及分析1. 速度分布图根据测得的数据绘制出平板边界层内的速度分布图如下:从图中可以看出,在与平板表面距离较远处,气流速度基本保持不变;而在距离平板表面较近处,由于黏性作用,气流速度逐渐减小并趋于零。
因此,在平板表面附近会形成一个速度梯度很大的区域,即平板边界层。
2. 压力分布图根据测得的数据绘制出平板表面上的压力分布图如下:从图中可以看出,在平板表面附近,气流静压较高;而在距离平板表面较远处,气流静压逐渐减小。
这是由于在平板表面附近,由于黏性作用,气流速度减小,因此气流静压会增大。
3. 阻力系数计算根据测得的数据可以计算出阻力系数等参数。
平板边界层实验

平板边界层实验(一)(一)实验目的1.测定平板边界层内的流速分布,从而确定流速分布指数规律、边界层名义厚度δ、位移厚度1δ、动量厚度2δ、能量厚度3δ。
2.掌握毕托管和测压计的测速原理和量测技能。
(二)DQS 系列空气动力学多功能实验装置:该装置相当于小型风洞,为组装式结构。
由主机和多种易更换实验段组成,流量可以控制。
风机提供气流,在压出段设有流量调节阀门,气流通过风道进稳压箱流速减慢进入阻尼网,阻尼网由二层细密钢丝网构成,可将流体较大尺度的旋涡破碎,使气流均匀地进入收缩段,经过收缩段可将收缩段进口的速度不均匀度缩小n 2倍,n 为收缩比,本收缩段的收缩比较大。
收缩曲线应用波兰人维托辛斯基曲线。
收缩段出口接各种实验段,实验排放的气流由实验台面的孔口进吸音箱回到风机入口,如图1所示。
多管测压计,设有可改变角度的测压排管及调平设置,当测某点压强时取与大气连通的测压管与该点测压管的读数差,即为测点的压强水头,如图2所示。
1.稳压箱1.测压管2.收缩段 2.角度盘3.风道 3.支架4.调节阀门4.联通管5.通风机 5.输液管6.吸音箱 6.酒精库7.阻尼网 7.通气管图 1 图 2 (三)实验段简图稳压箱内的气流经过阻尼网及收缩段均匀进入实验段,在实验段轴心位置安装一块一面光滑一面粗糙的平板,平板可沿轴线滑动,在实验段的出口装有精致的鸭咀形毕托管,其头部厚度仅有0.3㎜,并配有千分卡尺,灯光显示设置和多管测压计,见图1-1。
(三)实验原理及计算式1.平板紊流边界层的流速分布实际流体因存在粘性,紧贴壁面的流体将粘附于固体表面,其相对速度为零,沿壁面法向随着与壁面距离的增加,流体的速度逐渐增大,当距离为δ时,其速度达到未受扰动的主流流速∞u ,这个厚度为δ的薄层称为边界层,通常规定从壁面到∞=u u x 99.0处的距离作为边界层的厚度。
边界层的厚度沿平板长度方向是顺流渐增的,在平板迎流的前段是层流边界层,如果平板足够长,则边界层可以过渡到紊流,判别过渡位置的特征值是雷诺数x Re ,如图1-2所示。
实验四 空气纵掠平板时流动边界层和热边界层的测量

实验四空气纵掠平板时流动边界层和热边界层的测量一、试验目的1、了解流体流过热固体表面时形成流动边界层和热边界层的特性。
2、了解流体的流速和固体表面温度对流动边界层和热边界层的影响。
二、实验原理当实际流体流过固体表面时,在接触表面的地方因为粘性作用的缘故,其速度为零,离开表面处,速度逐渐增加,至一定厚度以后,其速度不再增加,即与主流速度相等,这种在固体表面附近流体速度发生剧烈变化的簿层称之为流动边界层(又称速度边界层)。
其厚度记为δ。
根据流体的雷诺准数不同,形成的边界层可分为层流边界层和紊流边界层,边界层的厚度定义为流体速度等于99 %主流速度处至固体表面速度为零处的厚度。
在对流换热条件下,主流与壁面之间存在着温度差。
实验观察同样发现,在壁面附近的一个簿层内,流体温度在壁面的法线方向上发生剧烈的变化,而在此簿层之外,流体的温度梯度几乎等于零。
流动边界层的概念可以推广到对流换热中去,固体表面附近流体温度发生剧烈变化的这一簿层称为温度边界层或热边界层,其厚度记为δt。
对于纵掠平板的对流换热,一般也以过余温度为来流过余温度的99 %处定义为δt的外边界,而且除液态金属及高粘性的流体外,热边界层的厚度δt在数量级上是个与运动边界层厚度δ相当的小量。
在测量平板局部换热系数后,仍保持平板相同的热状态不变,可以利用边界层速度分布、温度分布测量机构,即用全压探头测量边界层内全压的变化,以及用测温探头测量边界层内温度的变化。
最后测出流动边界层厚度δ和温度边界层厚度δt。
三、实验设备测量流动边界层厚度δ和温度边界层厚度δt的装置见图4—1。
测温探头3与4和测压探头5一同固定在位移机构6上,由于边界层的厚度很小,用千分表来精确测量二探头的位移。
位移机构上固定探头处有一微调件,可以调节探头的伸出距离,使二探头处于对平板壁面有同样的相对位置。
探头接触平板壁的初始位置由一电回路上的指示灯来确定。
边界层速度分布、温度分布测量机构是装压在试验风道出口处,所测边界层截面位置紧靠空气流射流出口,因此全压管所反映的即为气流的动压。
平板边界层实验
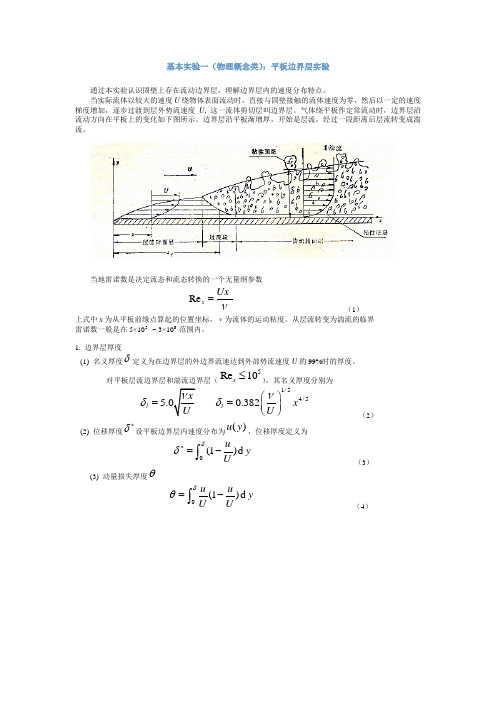
基本实验一(物理概念类):平板边界层实验
通过本实验认识固壁上存在流动边界层,理解边界层内的速度分布特点。
当实际流体以较大的速度U 绕物体表面流动时,直接与固壁接触的流体速度为零,然后以一定的速度梯度增加,逐步过渡到层外势流速度U , 这一流体剪切层叫边界层。
气体绕平板作定常流动时,边界层沿流动方向在平板上的变化如下图所示。
边界层沿平板渐增厚,开始是层流,经过一段距离后层流转变成湍流。
当地雷诺数是决定流态和流态转换的一个无量纲参数 Re x Ux ν
= (1)
上式中x 为从平板前缘点算起的位置坐标,ν为流体的运动粘度。
从层流转变为湍流的临界
雷诺数一般是在5×105 ~ 3×106 范围内。
1. 边界层厚度
(1) 名义厚度δ定义为在边界层的外边界流速达到外部势流速度U 的99%时的厚度。
对平板层流边界层和湍流边界层(5Re 10x ≤),其名义厚度分别为 1/54/55.0
0.382l t x x U
U ννδδ⎛⎫== ⎪⎝⎭ (2) (2) 位移厚度δ*设平板边界层内速度分布为()u y ,位移厚度定义为
0(1)d u y U δδ*=-⎰ (3)
(3) 动量损失厚度θ
0(1)d u u y U U δθ=-⎰ (4)。
平板边界层内的流速分布实验

平板边界层内的流速分布实验(一).实验目的测定平板上离前缘某一定点处边界层内的流速分布及其厚度。
(二)仪器设备吸入式风洞~大气压强计~温度计~微压计~U形测压管~平板模型~总压探针及三维坐标架。
(三)实验原理1.边界层外为理想流体(总压P0=P a和速度V无穷不变)。
2.边界层内为实际流体(P0和u x都在变化,Po<Pa,u x<V无穷)3.对平板而言:⊿P/⊿x=0,⊿P/⊿y=0,各点静压相同)4.任一点的总压,静压,速度之间的关系为:P o=P j+u x^2*ρ/25.任一点的速度:ux=(2*g*⊿h(ρ水-ρ)/ρ)^0.56.边界层厚度δ的定义:在外边界上的速度ux与来流速度V无穷相差1%的点,该点据平板壁面的垂直距离为边界层厚度)(四)数据处理(1)当x=150mm时,Re=2.031*10^5,可以认为是层流,当X=250mm时,Re=3.38*10^5,为紊流(2)在图一和图二中,X=150mm,实际曲线与紊流理论曲线更接近,因此为紊流在图二和图三中,X=250mm,实际曲线与紊流理论曲线更接近,因此为紊流(3)计算得X=150mm时,层流边界层为14.35mm,紊流边界层为2.125mm根据实验数据分析得实际边界层厚度约5.15mm,接近紊流X=250mm时,层流边界层厚度为18.527mm,紊流边界层为3.92mm,实验得实际边界层厚度约6.80mm,接近紊流。
(4)数据记录及分析如下5 56 182 93 99 35 91159 8 8.4526.3221.3120.9998 21.4271.00420.6110.96620.8570.9771 0 99.4525.621.3411.0008 21.4271.00421.2450.99621.1930.993图一X为150毫米时的速度分布曲线图二X为250mm时的速度分布曲线图三X为250mm时的速度分布曲线图四X为250mm时的速度分布曲线。
平板边界层速度分布测量

平板边界层速度分布测量实验指导书实验目的:通过零迎角平板流动的流速测量,获取流速沿物面法向分布。
学习总压管测速。
实验装置和仪器:(1)风洞:回流开口小型风洞,试验段见右图,矩形有机玻璃管道中夹放一金属板,来流沿管道被该板分开,从出口流出。
出口截面的静压为大气压。
(2)偏平总压探针头:偏平总压探针头顶可在出口截面内水平移动,移动量由微分尺控制。
(3)酒精斜管压力计:斜角θ=30º,系数K=1.0,一头通大气,另一头接总压探头。
实验原理:测量原理,就是伯努利定理:不计重力,气流的动压和静压之和为总压。
设总压为P 0,则 )(])()([21)(220y P y v y u y P ++=ρ (1) y 为探头中心距平板的距离,u 、v 分别为平行于平板的流速和平板法向的流速, p 为当地静压,ρ为气流的密度。
因为 a P y P ≡)( , u v <<由(1)可得ρ])([2)(0a P y P y u -= (2)实验步骤:图 风洞试验段示意图(1)实验室大气参数读取和记录;(2)探头零位确定;(3)压力计底座水平调解,测压管液面零刻度调节;(4)风洞开车;(5)调节好探头距平板的距离y ,从压力计读取并记录相应的压力值Po-Pa实验要求:测压时,每移动探头至新位置,应等待几秒钟,在压力平衡后再读取数据。
测量中,观察随探头离开平板距离的增大,压力的变化趋势。
实验报告要求:(1)实验参数:大气压P a (毫米汞柱) ,大气温度t (︒C ) ,大气密度 )(15.273)(464.0C t mmHg P o a +⨯=ρ (公斤/米3) 。
测量为之举平板前缘的距离X ;(2)测压原始数据,及由(2)是换算成流速,给出曲线y y u -)(;(3)找出不随距离y 而变的速度值,记为U 1,并找出满足u(y)= U 1的最小的y值作为δ,给出曲线δ//)(1y U y u -。
边界层实习报告

实习报告一、实习背景与目的近年来,随着我国经济的快速发展,对能源的需求日益增加,风电行业得到了迅猛发展。
为了更好地了解风电行业的发展现状和技术特点,提高自己的实践能力,我选择了风电场边界层实习。
本次实习的主要目的是:1. 了解风电场的边界层现象及其对风电场运行的影响;2. 学习风电场的设计、施工、运行和管理等方面的知识;3. 提高自己的实际操作能力和团队合作能力。
二、实习内容与过程1. 实习前的准备在实习前,我通过查阅资料和请教老师,对风电场的基本概念、边界层现象以及风电场的运行管理等方面的知识进行了系统的学习,为实习打下了坚实的基础。
2. 实习过程实习期间,我参与了风电场的日常运行维护工作,重点关注了风电场的边界层现象。
在实际操作中,我深刻体会到了边界层现象对风电场运行的影响,如湍流、剪切层等。
此外,我还学习了风电场的设计、施工、运行和管理等方面的知识,对风电场的整体运行有了更深入的了解。
3. 实习成果通过实习,我总结了风电场边界层现象对风电场运行的影响,并提出了相应的优化措施。
同时,我还撰写了实习报告,对实习期间的学习和收获进行了梳理和总结。
三、实习收获与反思1. 实习收获通过本次实习,我收获颇丰,主要体现在以下几个方面:(1)理论知识与实践相结合:通过实习,我将所学的风电场相关知识应用到实际操作中,加深了对理论知识的理解,提高了自己的实践能力。
(2)团队协作:在实习过程中,我与同事们共同承担工作任务,学会了沟通协调,提高了团队合作能力。
(3)问题解决能力:在面对风电场运行中的问题时,我学会了分析问题、提出解决方案,并加以实施,锻炼了解决实际问题的能力。
2. 实习反思在实习过程中,我也发现了自己在理论知识掌握、实际操作能力、团队协作等方面存在的不足。
在今后的工作中,我将努力学习,不断提高自己的综合素质,为我国风电行业的发展贡献自己的力量。
四、总结本次风电场边界层实习让我对风电场的运行管理和边界层现象有了更深入的了解,提高了自己的实践能力和团队合作能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学实验
平板边界层实验报告
班级
姓名
实验日期
指导教师
北京航空航天大学流体力学研究所
流体力学实验
平板边界层实验报告
一、实验目的
测定平板边界层内的流速分布,并比较层流边界层及紊流边界层的速度分布的差别。
二、实验设备
本实验使用的是一个二维开路闭口低速风洞,在该风洞实验段中装有两块平板,以分别测量层流及紊流边界层的速度分布。
为测量速度分布,在平板板面上安装有总压排管及静压管。
这些测压管分别用橡皮管连接到多管压力计上,通过测量多管压力计液柱高度推算出速度来,具体原理见后。
为测出实验段风速,在实验段侧壁上装有风速管,风速管的总压孔及静压孔也分别用橡皮管连接于多管压力计上,装备情况见图1。
图1
三、实验原理
当气流流过平板时由于粘性作用使紧贴平板表面处的流速为零,离开板面速度就逐渐增大,最后达到相当于无粘时的气流速度。
对平板来说,就等于来流速度了。
由于空气粘性很小,只要来流速度不是很小时,流速变化大的区域只局限在靠近板面很薄的一层气流
内,这一薄层气流通常叫作边界层。
人为地规定,自板面起,沿着它的法线方向,至达到99%无粘时的速度处的距离,称为边界层厚度δ。
不可压流场中,每一点处的总压P 0,等于该点处的静压和动压
1
2
2ρv 之和。
p p v 021
2=+
ρ 则 v p p =
-20()
ρ
(1)
因此只需测出边界层内各点处的静压p ,总压p 0,就可计算出各点的速度来。
但考虑到垂直平板方向的静压梯度等于零(即∂∂p y /=0),我们只需在平板表面开一静压孔,所测的静压就等于该点所在的平板法线方向上各点的静压。
要测边界层内的速度分布就只要测出沿平板法线上各点的总压即可。
p i 0──为各测点的总压。
p i ──为各测点的静压。
v i ──为各测点的速度。
γ ──为多管压力计所使用的液体重度(公斤/米3)。
∆h i ──为各测点总压管与静压管的液柱高度差。
ρ ──为空气的密度,实验时可依据当时室温及大气压强由表查出。
φ ──为多管压力计的倾斜角。
根据(1)式,边界层内各测点处的速度为 v h i i =
2
ρ
γφ∆sin (2)
通常边界层内的速度分布用无量纲的形式表示为
v v f y i i
1=()δ
y i 为各测点至板面的高度,δ 为边界层厚度,v 1为边界层外边界上的速度,对平板
来说即为来流速度。
v 1可通过风速管的静压管和总压管在多管压力计上的液柱高度差∆h 1,由下式算出: v h 112
=ρ
γφ∆sin (3) 由(2)式和(3)式,可得
v v h h i
i
1
1
=∆∆ (4)
测量总压用的排管是由一组很细的空心钢管组成。
为了能同时测量较多的点,又避免各总压管之间过分接近,产生相互间的干扰,所以将总压排管倾斜安装在平板上,并用橡皮管连到多管压力计上。
总压排管倾斜后,各测点就不在平板同一法线上。
考虑到二维流动的特点,这仍可视为同一法线上所测的结果。
总压排管各测量点的y i 值用高度尺量出。
根据(4)式,求出各y i 点的v v i 1值后,用线性插值求出v v i
1
=0.99处所对应的y 值,即
为边界层厚度δ。
最后画出v v f y
i i
=
()δ
的曲线,如图2所示。
四、实验步骤
1. 记录两个总压排管离开平板前缘的距离x 层和x 紊。
测量出各总压管离板面的高度y i 。
2. 检查各总压排管及静压孔、风速管和多管压力计的连接是否合适。
橡皮管是否有闭塞
或漏气现象。
3. 记录多管压力计的倾斜角φ。
4. 测量多管压力计的液柱重度γ,记下当日大气压及室温,由表和曲线查出空气密度ρ
及运动粘性系数ν。
5. 调整多管压力计液柱的高度,记下初读数h 初。
6. 开风洞调到所需风速。
测层流边界层时风速要比较小;测紊流边界层时风速要比较大。
7. 当多管压力计稳定后,记下末读数h 末。
8. 关闭风洞,整理实验场地。
将记录交给老师检查。
9. 整理实验数据,写好实验报告。
五.实验数据记录及处理
1. 实验数据记录
多管压力计倾斜角 φ =10
大气压强 P =756.81mmHg 室 温 t =22.5C
空气密度 ρ=0.1212千克·秒2
/米
4
运动粘性系数 υ =51.51810-⨯米2
/秒
多管压力计液体重度 γ=800千克 /米3
2.层流边界层实验数据记录及计算结果:
X 层=340mm 1Re 83096.18v x υ==层层
由已知:
v h 112
=
ργφ∆sin 8.01m/s
==υ层层x v 1Re 5
3.710.340
1.51810
-⨯⨯=83096.18
使用以上的数据,用Matlab采用多项式拟合的方式,得到在如图区间范围内的曲线方程为:
令y=0.99得:
实数解:6.272980216
虚数解:5.059587957 + 0.9745630270 i,
-0.3325213419 + 2.056467537 i,
-0.3325213419 - 2.056467537 i,
5.059587957 - 0.9745630270 i
结合如图曲线观察,取解X=6.272980216
3.紊流边界层实验数据记录及计算结果表: X 紊=1105mm 1Re 853863.64v x
==紊
紊
sin10
=
=
υ
紊
紊x v 1Re 5
11.73 1.105
1.51810
-⨯⨯=853863.64
使用以上的数据,用Matlab采用多项是拟合的方式,得到在如图区间范围内的曲线方程为:
令y=0.99得:
实数解:13.30967841, 16.53270960, 19.95144869
虚数解:3.148596321 + 3.331806442 i, 3.148596321 - 3.331806442 i
结合如图曲线观察,取解X=19.95144869
2.实验曲线:
(自备坐标纸画出v
v
f
y
i i
1
=()
δ曲线)
1.计算出各y i点处的v
v
i
1
,并求出δ层,δ紊。
2.在坐标纸上画出v
v
f
y
i i
1
=()
δ,用曲线板连成光滑曲线,并比较层流边界层和紊流边
界层速度分布的差别。
层流边界层速度分布:
紊流边界层速度分布:
通过上面两图的比较,我们结合所学知识发现层流边界层和紊流边界层速度分布的差别:
(1)紊流边界层沿平板壁面法向截面上的速度比层流边界层的速度增加得快,也即是说紊流边界层的速度分布曲线比层流边界层的速度分布曲线要饱满得多,这与圆管的情况相似;
(2)沿平板壁面紊流边界层的厚度比层流边界的厚度增加得快,因为紊流的δ与X 45成比例,而层流的δ则与X
12成比例,在紊流边界层内流体微团发生横向运动,容易促使厚度
迅速增长;
(3)在其他条件相同的条件下,沿平板壁面上紊流边界层的切向应力沿着壁面的减小要比层流边界层的减小慢些;
(4)在同一Re L 下,紊流边界的摩擦阻力比层流边界层的大得多,这是因为层流中的摩擦阻力只是由不同流层之间发生相对运动而引起的,紊流还有流体微团的很剧烈的横向掺混,因而产生更大的摩擦阻力。
3. 用边界层厚度的经验公式求出δ层和δ紊 ,再与实验求得的δ层和δ紊作比较,分析产
生误差的原因。
由层流边界层厚度经验公式δ=
5 5.89737mm δ==层 由紊流边界层厚度经验公
式δ=
,0.38327.560mm δ==紊 边界层厚度实验值δ层=6.27mm ,δ紊=19.95mm
显然,层流实验的测量值偏大,紊流实验的测量值偏小。
4. 回答问题:
(1) 如何提高实验的精确度?本实验在测量中采取了哪些措施?
答:本实验中,通过多管压力计的排列倾斜一定角度来消除多管压力计之间的影响。
(2) 如何判断边界层是层流边界层还是紊流边界层?
答:层流边界层的压强比紊流边界层低,因此层流边界层多管测压计的液面高度比
紊流边界层高,由此可以判断。
(3) 为什么测量v 的分布时只测物面静压而不需测沿法线上各点的静压? 答:因为垂直于板面方向的静压梯度等于零,即0p y
∂=∂,所以只需在平板表面开一静压孔,所测的静压就等于该点所在的平板法线方向上各点的静压。
