高一数学综合测试试卷
高一数学必修一综合测试题(含答案)

高一数学必修一综合测试题(含答案)一、选择题(每题5分,共50分)1、已知集合M={0,1,2},N={xx=2a,a∈M},则集合MN=A、{ }B、{0,1}C、{1,2}D、{0,2}答案:B解析:将M中的元素代入N中得到:N={2,4,8},与M 的交集为{0,1},故MN={0,1}。
2、若f(lgx)=x,则f(3)=()A、lg3B、3C、10D、310答案:C解析:将x=3代入f(lgx)=x中得到f(lg3)=3,又因为lg3=0.477,所以f(0.477)=3,即f(3)=10^0.477=3.03.3、函数f(x)=x−1x−2的定义域为()A、[1,2)∪(2,+∞)B、(1,+∞)C、[1,2)D、[1,+∞)答案:A解析:由于分母不能为0,所以x-2≠0,即x≠2.又因为对于x<1,分母小于分子,所以x-1<0,即x<1.所以定义域为[1,2)∪(2,+∞)。
4、设a=log13,b=23,则().A、a<b<cB、c<b<aC、c<a<bD、b<a<c答案:A解析:a=log13=log33-log32=1/2-log32,b=23=8,c=2^3=8,所以a<b=c。
5、若102x=25,则10−x等于()A、−15B、51C、150D、0.2答案:B解析:由102x=25可得x=log10(25)/log10(102)=1.3979,所以10^-x=1/10^1.3979=0.1995≈0.2.6、要使g(x)=3x+1+t的图象不经过第二象限,则t的取值范围为A.t≤−1B.t<−1C.t≤−3D.t≥−3答案:B解析:当x=0时,y=1+t,要使图像不经过第二象限,则1+t>0,即t>-1.又因为g(x)的斜率为正数,所以对于任意的x,g(x)的值都大于1+t,所以t< -1.7、函数y=2x,x≥1x,x<1的图像为()答案:见下图。
新人教版高一数学必修一综合测试含答案解析

高一数学必修一综合测试一、单项选择 (每题5分 共12小题 60分) 1.函数210)2()5(--+-=x x y( )A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或2.设函数y =lg(x 2-5x )的定义域为M ,函数y =lg(x -5)+lg x 的定义域为N ,则( )A .M ∪N=RB .M=NC .M ⊇ND .M ⊆N3.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是( )4.函数2422-+=x x y 的单调递减区间是( )A .]6,(--∞B .),6[+∞-C .]1,(--∞D .),1[+∞-5. 函数y =的定义域为( ) A 、(],2-∞ B 、(],1-∞ C 、11,,222⎛⎫⎛⎤-∞ ⎪ ⎥⎝⎭⎝⎦ D 、11,,222⎛⎫⎛⎫-∞ ⎪ ⎪⎝⎭⎝⎭6. 已知(1)f x +的定义域为[2,3]-,则(21)f x -定义域是 ( )A.5[0,]2B.[1,4]-C.[5,5]-D.[3,7]-7.函数()f x 定义域为R +,对任意,x y R +∈都有()()()f xy f x f y =+ 又(8)3f =,则f =A.12B.1C.12-8.若偶函数)(x f 在(]1,-∞-上是增函数,则下列关系式中成立的是( )A .)2()1()23(f f f <-<- B .)2()23()1(f f f <-<-C .)23()1()2(-<-<f f fD .)1()23()2(-<-<f f f9.下列四个命题:(1)函数f x ()在0x >时是增函数,0x <也是增函数,所以)(x f 是增函数;(2)若函数2()2f x ax bx =++与x 轴没有交点,则280b a -<且0a >;(3) 223y x x =--的递增区间为[)1,+∞;(4) 1y x =+和y =表示相等函数。
2023-2024学年高一上数学必修一综合测试卷(附答案解析)

解析:当 c=0 时,A 不成立;当 a=-1,b=-2 时,B 不成立;
由不等式的性质知 C 不成立;若 a> b,则一定能推出 a>b,故 D 成
立.
3.命题“∃x∈R,x3-x2+1>0”的否定是( A )
A.∀x∈R,x3-x2+1≤0 B.∀x∈R,x3-x2+1>0
C.∃x∈R,x3-x2+1≤0 D.不存在 x∈R,x3-x2+1≤0
的取值范围是( A )
A.[2,6)
B.(2,6)
C.(-∞,2]∪(6,+∞)
D.(-∞,2)∪(6,+∞)
解析:①当 a=2 时,1>0 成立,故 a=2 符合条件;②当 a≠2 时,
a-2>0,
必须满足 Δ=a-22-4a-2<0,
解得 2<a<6.由①②可知,a∈
[2,6).故选 A.
二、多项选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小
2
4
sinx
在
1π,3π 22
上单调递减,故
y=
π,3π 2sin2x 在 4 4 上单调递减,故
题给出的四个选项中,有多个选项符合题目要求.全部选对的得 5 分,
部分选对的得 3 分,有选错的得 0 分)
9.下列函数是偶函数的是( CD )
A.f(x)=tanx B.f(x)=sinx C.f(x)=cosx D.f(x)=lg|x|
解析:根据题意,依次分析选项:对于 A,f(x)=tanx,是正切函
解析:存在量词命题“∃x∈M,p(x)”的否定为全称量词命题“∀
x∈M,綈 p(x)”,故选 A.
4. 22cos375°+ 22sin375°的值为( A )
高一数学必修测试题及答案
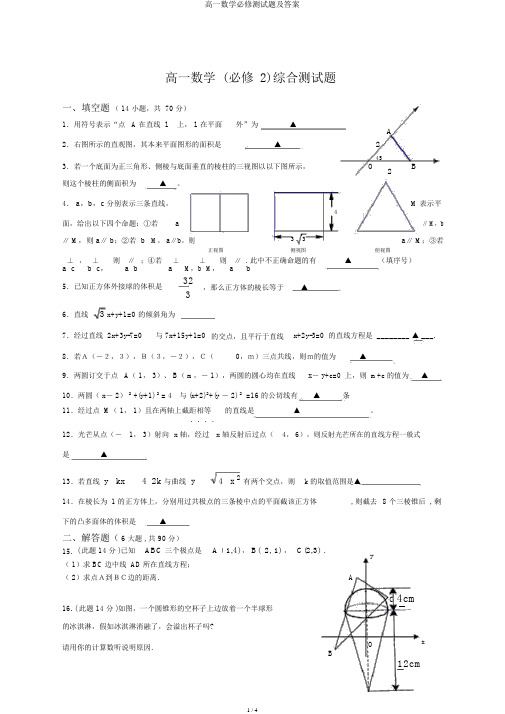
高一数学 (必修 2)综合测试题一、填空题( 14 小题,共 70 分)1.用符号表示“点 A 在直线l上, l在平面外”为▲A 2.右图所示的直观图,其本来平面图形的面积是▲23.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图以以下图所示,O 45B2则这个棱柱的侧面积为▲。
4.a,b,c分别表示三条直线,4M表示平面,给出以下四个命题:①若a∥ M,b ∥ M,则 a∥ b;②若 b M, a∥b,则33a∥ M;③若正视图侧视图俯视图⊥,⊥则∥;④若⊥⊥M,则a∥ . 此中不正确命题的有▲(填序号)a cb c, a b a M,b b5.已知正方体外接球的体积是32,那么正方体的棱长等于▲36.直线 3 x+y+1=0的倾斜角为7.经过直线 2x+3y-7=0与 7x+15y+1=0的交点,且平行于直线x+2y-3=0 的直线方程是 ________ ▲ ___. 8.若A(-2,3),B(3,-2),C(0,m)三点共线,则m的值为▲9.两圆订交于点 A( 1, 3)、 B( m,- 1),两圆的圆心均在直线x- y+c=0上,则 m+c的值为▲10.两圆( x― 2)2 +(y+1) 2 = 4与 (x+2)2+(y ― 2) 2 =16 的公切线有▲条11.经过点 M( 1, 1)且在两轴上截距相等的直线是▲。
....12.光芒从点(―1, 3)射向x 轴,经过x 轴反射后过点(4, 6),则反射光芒所在的直线方程一般式是▲13.若直线y kx 4 2k 与曲线y4x 2有两个交点,则k 的取值范围是▲14.在棱长为 1 的正方体上,分别用过共极点的三条棱中点的平面截该正方体, 则截去8 个三棱锥后 , 剩下的凸多面体的体积是▲二、解答题( 6 大题 , 共 90 分)15.( 此题 14 分 )已知ABC 三个极点是 A (1,4), B( 2, 1) ,C(2,3).y( 1)求 BC边中线 AD所在直线方程;( 2)求点A到BC边的距离.AC 4cm16.( 此题 14 分 )如图,一个圆锥形的空杯子上边放着一个半球形的冰淇淋,假如冰淇淋消融了,会溢出杯子吗?请用你的计算数听说明原因.O xB12cm17. (本 15 分 )如, ABCD是正方形, O是正方形的中心,PO 底面 ABCD, E 是 PC的中点.P求:( 1)PA∥平面 BDE;(2)平面 PAC 平面 BDE.18. (本15 分 )已知直 l 点P(1,1),并与直 l 1:x E- y+3=0 和l2:2x+y - 6=0 分交于点A、B,若段 AB 被点 P 平分,求:(Ⅰ)直l 的方程;D C (Ⅱ)以 O心且被l 截得的弦8 5的的方程.O5A B19.( 本16 分) 已知数a足 0<a<2,直l1:ax- 2y- 2a+4=0 和l2:2x+a2y- 2a2- 4=0 与两坐成一个四形。
高中数学新教材必修第一册综合测试数学试题(含参考答案)

新教材必修第一册综合测试数学试题(含答案)高一数学本试卷共4页,22小题,全卷满分150分,考试时间120分钟。一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.(1)集合2{|20}A x x x =--,{|10}B x x =-<,则()A B ⋂=A.{|1}x xB.{|11}x x -<C.{|1}x x <-D.{|21}x x -<(2)函数为()f x =的定义域( ) A.1,2⎛⎫-+∞ ⎪⎝⎭ B.1,2⎡⎫-+∞⎪⎢⎣⎭C.()1,00,2⎛⎫-⋃+∞ ⎪⎝⎭ D.()1,00,2⎡⎫-⋃+∞⎪⎢⎣⎭(3)“0lgx <”是“2x <”的 ( ) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(4)已已知知512x log =,1012y ⎛⎫= ⎪⎝⎭,132z =,则( )A.x y z <<B.x z y <<C.y x z <<D.z x y <<(5)下列函数中,既是偶函数又在区间()0,+∞上单调递增的函数是( ) A. 1||y lnx = B.||2x y =C.y cosx =D.3y x =(6)已知定义在R 上的函数()f x 的图象是连续不断的且有如下对应值表:那么函数()()2g x f x x =-一定存在零点的区间是( ) A.((),1-∞B.()1,2C.()2,3D.()3,4(7)将函数23y sin x π⎛⎫=-⎪⎝⎭的图象向右平移6π个的单位长度,再将所得到的函数图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),则所得到的图象的函数解析式为( ) A. 23y sin x π⎛⎫=-⎪⎝⎭ B.243y sin x π⎛⎫=-⎪⎝⎭C.2y sin x π⎛⎫=- ⎪⎝⎭D.42y sin x π⎛⎫=-⎪⎝⎭ (8)中国的5G 技术领先世界,5G 技术的数学原理之一便是著名的香农公式: 21S C Wlog N ⎛⎫=+⎪⎝⎭它表示:在受噪声干扰的信道中,最大信息传递速度C 取决于信道带宽W 、信道内信号的平均功率S 、信道内部的高斯噪声功率N 的大小。其中SN叫做信噪比,当信噪比较大时,公式中真数中的1可以忽略不计。按照香农公式,若不改变带宽W,而将信噪比SN从1000提升至8000,则C 大约增加了(20.3010lg ≈,30.4771lg ≈)( ) A.10%B.30%C.60%D.90%二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得3分,有选错的得0分.请把正确选项在答题卡中的相应位置涂黑. (9)在下列四组函数中,()f x 与()g x 表示同一函数的是( )A.()1f x x =-,()2g x =B.()|3|,|f x x g =-(),g x =C.()f x x =,()10xg x lg =D.()f x =()g x =(10)幂函数223a a y x --=是奇函数,且在()0,+∞是减函数,则整数a 的值是( )A.0B.1C.2D.3(11)下列结论正确的是( )A.当1x 时,2B.当54x <时, 14245x x -+-的最小值是5C.当0x ≠时, 1x x+的最小值是2D.设0x >,0y >,且2x y +=,则14x y+的最小值是92(12)已知函数()()f x Asin x ωϕ=+,0,0,||2A πωϕ⎛⎫>><⎪⎝⎭部分图象如图所示,下列说法不正确是( )A.()f x 的图象关于直线23x π=对称B.()f x 的图象关于点5,012π⎛⎫-⎪⎝⎭对称 C.将函数22y x cos x =-的图象向左平移2π个单位得到函数()f x 的图象 D.若方程()f x m =在,02π⎡⎤-⎢⎥⎣⎦上有两个不相等的实数根,则m的取值范围是(2,- 三、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡的相应位置上. (13)18427242cos cos cos sin ︒︒︒︒⋅-⋅=____. (14)已知3cos sin cos sin αααα+=-,则4tan πα⎛⎫+= ⎪⎝⎭____.(15)已知函数32,1()log (1),1x x f x x x ⎧≤=⎨->⎩,且()01f x =,则0x =____.(16)已知关于x 的不等式20ax bx c -+的解集为{|12}x x ,则20cx bx a ++的解集为____.四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.解答应写出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效. (17)(本小题满分10分) 已知02πα<<,且513sin α=.(I)求tan α的值;(II)求2sin 22sin()sin 2cos ()sin 22απααπαα--++的值.已知函数()11xf x lnx-=+. (I)判断并证明函数()f x 的奇偶性; (Ⅱ)若()()2f m f m --=,求实数m 的值.(19)(本小题满分12分)已知函数()()2f x Asin x ϕ=+(A,ϕ是常数,0A >,0,x R ϕπ<<∈)在8x π=时取得最大值3.(1)求()f x 的最小正周期; (Ⅱ)求()f x 的解析式; (Ⅲ)若18f πα⎛⎫+=- ⎪⎝⎭,求sin α.(20)(本小题满分12分)某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系**20025,1002530,t t t N P t t t N⎧+<<∈=⎨-+≤≤∈⎩,该商品在30天内日销售量Q(件)与时间t(天)之间满足一次函数关系,具体数据如下表:(I)根据表中提供的数据,求出日销售量关于时间t 的函数表达式; (Ⅱ)求该商品在这30天中的第几天的日销售金额最大,最大值是多少?设函数()2f x cos x a =++ (I)写出函数()f x 的最小正周期及单调递减区间; (Ⅱ)当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()f x 的最大值与最小值的和32,求不等式()1f x >的解集.(22)(本小题满分12分)已知函数()313xxa f x +=+是R 上的奇函数(I)求a;(Ⅱ)用定义法讨论()f x 在R 上的单调性; (III)若21121042xx f k k f -⎛⎫⎛⎫-⋅++> ⎪ ⎪⎝⎭⎝⎭在x ∈R 上恒成立,求k 的取值范围.新教材必修第一册综合测试数学试题答案高一数学一、单项选择题:本大题共8小题,每小题5分,共40分.(1)B (2)D (3)A (4)A (5)B (6)B(7)A(8)B二、多项选择题:本大题共4小题,每小题5分,共20分.(9)BC (10)AC (11)AD (12)ABC三、填空题:本大题共4小题,每小题5分,共20分.(13)21(14)3(15)0或4(16)1{|1,}2x x x ≤-≥-或四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.(17)解:(Ⅰ)因为135sin =α,20πα<<,所以12cos 13α===,……………………………………4分故125cos sin tan ==ααα.……………………………………5分(Ⅱ)222sin 22sin()sin 2sin cos 2sin 2sin 2sin cos 2cos ()sin 22απαααααπααααα---=+++…………………7分cos sin 1tan sin cos 1tan αααααα--==++…………………9分51712517112-==+.…………………10分(18)(Ⅰ)解:()1ln 1xf x x-=+是奇函数.证明:要10,1xx->+等价于()()110,x x +->即11,x -<<故()1ln1xf x x-=+的定义域为()1,1,-关于原点对称又因为()()1111ln ln ln .111x x x f x f x x x x -+--⎛⎫-===-=- ⎪-++⎝⎭所以()1ln1xf x x-=+是奇函数.…………6分(Ⅱ)由(1)知,()f x 是奇函数,则()()0f m f m +-=,联立()()()()02f m f m f m f m +-=--=⎧⎪⎨⎪⎩得()=1f m ,即1ln 1,1m m -=+解得1.1em e-=+…………12分(19)(Ⅰ))(x f 的最小正周期ππ==22T ………………2分(列式1分,计算1分)(Ⅱ)依题意3=A ………………………………………4分3)82sin(3=+⨯ϕπ…………………………………5分因为4544πϕππ<+<且1)4sin(=+ϕπ…………………6分所以24πϕπ=+,4πϕ=…………………………………7分)42sin(3)(π+=x x f ……………………………………8分(Ⅲ)由18(-=+παf 得122sin(3-=+πα…………………9分即312cos -=α……………………………………………10分所以31sin 212-=-α……………………………………11分36sin ±=α………………………………………………12分.(20)(Ⅰ)设日销售量Q 关于时间t 的函数表达式为Q kt b =+,依题意得:3551030k b k b =+⎧⎨=+⎩,解之得:140k b =-⎧⎨=⎩,所以日销售量Q 关于时间t 的函数表达式为40Q t =-+((0,30]t ∈,t N *∈,).(Ⅱ)设商品的日销售金额为y (元),依题意:y PQ =,所以(20)(40)025,,(100)(40)2530,.t t t t N y t t t t N **⎧+-+<<∈=⎨-+-+≤≤∈⎩,即:2220800025,,14040002530,.t t t t N y t t t t N **⎧-++<<∈=⎨-+≤≤∈⎩.当(0,25)t ∈,t N *∈时,2(10)900y t =--+,当10t =时,max 900y =;当[25,30]t ∈,t N *∈时,2(70)900y t =--,当25t =时,max 1125y =;所以该商品在这30天中的第25天的日销售金额最大,为1125元.(21)解:(Ⅰ)31cos 2()sin 222xf x x a +=++……1分1sin(262x a π=+++,……3分T π∴=,……4分令3222262k x k πππππ+≤+≤+,Z k ∈,∴263k x k ππππ+≤≤+,Z k ∈,∴函数)(x f 的递减区间为:2[,],63k k k Z ππππ++∈.……6分(Ⅱ)由[,63x ππ∈-得:52666x πππ-≤+≤,max min 3(),()2f x a f x a ∴=+=,……8分33022a a a ∴++=⇒=,……9分∴1()1sin(2)62f x x π>⇒+>,52226663k x k k x k ππππππππ∴+<+<+⇒<<+,Z k ∈,……11分又⎦⎤⎢⎣⎡-∈3,6ππx ,∴不等式1)(>x f 的解集为{|0}3x x π<<.……12分(22)(Ⅰ) 函数()313xxa f x +=+是R 上的奇函数()()331313x xx x a a f x f x --++∴-==-=-++即3133113x xx xa a +--=++即()()3131xxa +=-+解得1a =-;(Ⅱ)由(1)知()3131-=+x xf x ()()12121231313131x x x x f x f x ---=-++()()()()()()122112313131313131x x x x x x -+--+=++()()()12122333131x x x x -=++设12x x <,则12033x x <<故12330x x -<,1310x +>,2310x +>故()()120f x f x -<即()()12f x f x <()f x ∴是R 上的增函数.(Ⅲ)()f x 是R 上的奇函数,()f x 是R 上的增函数21121042x x f k k f -⎛⎫⎛⎫∴-⋅++> ⎪ ⎪⎝⎭⎝⎭在x ∈R 上恒成立等价于2111122244x x xf f k k f k k -⎛⎫⎛⎫⎛⎫+>--⋅=⋅-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴等价于2112142x x k k -⋅-<+在x ∈R 上恒成立即()2212420xx k k +⋅+⋅->在x ∈R 上恒成立“*”令20x t =>则“*”式等价于()22140k t t k ++->对0t >时恒成立“**”①当210k +=,即12k =-时“**”为1402t +>对0t >时恒成立②当210k +≠,即12k ≠时,“**”对0t >时恒成立须()210164210k k k +>⎧⎨∆=++<⎩或2102021k k k +>⎧⎪⎪-≤⎨+⎪-≥⎪⎩解得102k -<≤综上,k 的取值范围是1,02⎡⎤-⎢⎥⎣⎦.。
高一数学必修1综合测试卷

高中数学必修1测试题第I 卷(选择题)满分150分 考试时间:120分钟一、选择题(一共12道小题,每小题5分,共60分,每道小题只有一个正确答案,请把你认为对的选项填在相应的位置) 1.设集合{}3,2ln A x =,{},B x y =,若{}0AB =,则2x y +的值是( )A. 1B. 2C. 0D.1e2.设1232,2().((2))log (1)2x e x f x f f x x -⎧<⎪=⎨-≥⎪⎩,则的值为,( ) A .0 B .1 C .2 D .33.若01x y <<<,则( ) A .33y x <B .log 3log 3x y <C .44log log x y < D4.函数y =)A .[1,2]B .[1,2)C .1(,1]2D .1[,1]25.已知函数⎩⎨⎧>≤=+.0,log ,0,3)(21x x x x f x 若()30>x f ,则0x 的取值范围是( )A .80>xB .00<x 或80>xC .800<<xD .00<x 或800<<x . 6. 已知集合{}R x x x M ∈>-=,02|,则M ∪N 等于( ). A .{x|x≥1} B .{x|1≤x<2} C .{x|x >2} D .{x|x >2或x <0} 7)A. C.1) D.(1,2) 8.记函数13x y -=+的反函数为()y g x =,则(10)g =( ) A.2.B.2-.C.3.D.1-. 9.下列四组中的f(x),g(x),表示同一个函数的是( )A .f(x)=1,g(x)=x 0B .f(x)=x -1,g(x)1C .f(x)=x 2,g(x)=4D .f(x)=x 3,g(x)10.函数243,[0,3]y x x x =-+∈的值域为 ( )A.[0,3]B.[-1,0]C.[-1,3]D.[0,2]11.下列函数中,满足“对任意的时,都有”的是( ) A. C .D 12.已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数,那么a 的取值范围是( )A.(0,1) B .1(0,)3C .11[,)73D .1[,1)7第II 卷(非选择题)二、填空题(一共4道小题,每小题5分,共20分)13. 计算:不等式1)12(log 3≤-x 的解集为 . 14.的值是____________. 15.已知幂函数()a f x x =的图象过点 16.设函数()f x 是定义在R 上的偶函数,当0x ≥时,()21xf x =+.若()3f a =,则实数a 的值为 .三、解答题(一共7道小题,共70分,解答题应写出必要的文字说明、演算过程与步骤) 17.(一共10分,每小题5分)求下列各式的值. (1)355log +-145log ;(2)3948(log 2log 2)(log 3log 3)+⋅+;()f x ()1212,0,,x x x x ∈+∞<当()()12f x f x <()244f x x x =-+()2xf x =2lg 50lg 4lg -+18. (本题满分12分)已知函数()lg(3)lg(3)f x x x =++-. (1)求函数()f x 的定义域;(2)判断函数()f x 的奇偶性,并说明理由.19. (本小题满分12分)已知函数)10()0()0(1)(≠>⎩⎨⎧<≥+=a a x x x a x f x 且;(1)若2)1(=f ,求a 的值,并作出)(x f 的图象; (2)当R x ∈时,恒有)0()(f x f ≤求a 的取值范围。
高一数学必修一必修二综合测试卷(有答案)

高一数学试题四(考试时间:120分钟 试卷满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 下列说法正确的是( )A . 经过三点确定一个平面B . 经过一条直线和一个点确定一个平面C . 四边形确定一个平面D . 两两相交且不共点的三条直线确定一个平面2. 下列哪个函数的定义域与函数()15xf x ⎛⎫= ⎪⎝⎭的值域相同( )A . 2y x x =+B . ln 2y x x =-C . 1y x =D . 1y x x=+3. 已知集合12|log 1A x x ⎧⎫=>-⎨⎬⎩⎭,{}|22xB x =>,则A B =( )A . 1,22⎛⎫ ⎪⎝⎭B . 1,2⎛⎫+∞⎪⎝⎭C . ()0,+∞D . ()0,24. 已知圆锥的侧面展开图是一个半圆,则其母线与底面半径之比为( ) A . 1B .2C .3D . 25. 已知函数()2f x x x a =++在区间()0,1上有零点,则实数a 的取值范围是( ) A . 1,4⎛⎤-∞ ⎥⎝⎦B . 1,4⎛⎫-∞ ⎪⎝⎭C . ()2,0-D . []2,0-6. 函数()()10,1x f x a a a -=>≠的图象恒过点A ,则下列函数中图象不经过点A 的是( )A . 1y x =-B . 2y x =-C . 21xy =-D . ()2log 2y x =7. 正四面体ABCD 中,E ,F 分别为棱AD ,BC 的中点,则异面直线EF 与CD 所成的角为( ) A .6π B .4π C . 3π D . 2π8. 已知函数()212log 3y x ax a =-+在[)2,+∞上为减函数,则实数a 的取值范围是( )A . 4a ≤B . 4a ≥C . 4a <-或4a ≥D . 44a -<≤9. 某几何体的三视图如图所示,该几何体表面上的点P 与点Q 在正视图与侧视图上的对应点分别为A ,B ,则在该几何体表面上,从点P 到点Q 的路径中,最短路径的长度为( ) A .5B .6 C . 22D .1010. 已知函数()ln 1f x x =-,()223g x x x =-++,用{}min ,m n 表示m ,n 中最小值,设()()(){}min ,h x f x g x =,则函数()h x 的零点个数为( )A . 1B . 2C . 3D . 411. 已知()g x 为偶函数,()h x 为奇函数,且满足()()2x g x h x -=.若存在[]1,1x ∈-,使得不等式()()0m g x h x ⋅+≤有解,则实数m 的最大值为( )A .315-B . 35-C . 1D . -1 12. 无论x ,y ,z 同为三条不同的直线还是同为三个不同的平面,给出下列说法:①若//x y ,//x z ,则//y z ;②若x y ⊥,x z ⊥,则y z ⊥;③若x y ⊥,//y z ,则x z ⊥;④若x 与y 无公共点,y 与z 无公共点,则x 与z 无公共点; ⑤若x ,y ,z 两两相交,则交点可以有一个,三个或无数个.其中说法正确的序号为( ) A . ①③B . ①③⑤C . ①③④⑤D . ①④⑤二、填空题(本大题共4小题,每小题5分,共20分) 13. 设函数()()xxf x e aea R -=+∈,若()f x 为奇函数,则a =______.14. 一个正四棱锥的侧棱长与底面边长相等,体积为423,则它的侧面积为______. 15. 已知函数()f x 为定义在[]2,3a -上的偶函数,在[]0,3上单调递减,并且()22522a f m m f m ⎛⎫-- ⎪⎝⎭>-+-,则m 的取值范围是______.16. 正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为______.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17. 如图所示,在正方体1111ABCD A B C D -中,E 、F 分别是AB 和1AA 的中点.求证:CE ,1D F ,DA 交于一点.18. 已知函数()21x ax b f x x +=++是定义域为R 的奇函数. (1)求实数a 和b 的值,判断并证明函数()f x 在()1,+∞上的单调性;(2)已知0k <,且不等式()()22310f t t f k -++-<对任意的t R ∈恒成立,求实数k 的取值范围.19. 食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入P 、种黄瓜的年收入Q 与投入a (单位:万元)满足8042P a =+,11204Q a =+.设甲大棚的投入为x (单位:万元),每年两个大棚的总收益为()f x (单位:万元). (1)求()50f 的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益()f x 最大?20. 已知幂函数()()3*p N x x f p -=∈的图象关于y 轴对称,且在()0,+∞上为增函数. (1)求不等式()()22132pp x x +<-的解集;(2)设()()()log 0,1a f x ax g x a a =->≠⎡⎤⎣⎦,是否存在实数a ,使()g x 在区间[]2,3上的最大值为2,若存在,求出a 的值,若不存在,请说明理由.21. 已知函数()11439x xm f x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭.(1)当2m =-时,求函数()f x 在(),0-∞上的值域;(2)若对任意[)0,x ∈+∞,总有()6f x ≤成立,求实数m 的取值范围.22. 在菱形ABCD 中,2AB =且60ABC ∠=︒,点M ,N 分别是棱CD ,AD 的中点,将四边形ANMC 沿着AC 转动,使得EF 与MN 重合,形成如图所示多面体,分别取BF ,DE 的中点P ,Q .(1)求证://PQ 平面ABCD ;(2)若平面AFEC ⊥平面ABCD ,求多面体ABCDFE 的体积.参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1-5:DBCDC6-10:ABDCC11-12:AB1.【解析】A 选项考查公理2,即三点必须不在同一条直线上,才能确定一个平面;B 选项如果点在直线上,则该直线和这个点不能确定一个平面;C 选项中的四边形有可能是空间四边形,故选D .2.【解析】函数()15xf x ⎛⎫= ⎪⎝⎭的值域为()0,+∞,函数2y x x =+的定义域为R ,函数ln 2y x x =-的定义域为()0,+∞;函数1y x x=+的定义域为()(),00,-∞+∞,函数1y x=的定义域为()(),00,-∞+∞,故选B .3.【解析】由{}12|log 1|02A x x x x ⎧⎫=>-=<<⎨⎬⎩⎭,{}1|22|2xx x x B =⎧⎫>=>⎨⎬⎩⎭,则()0,A B =+∞,故选C .4.【解析】由已知可得2r l ππ=,所以2l r =,故2lr=.故选D . 5.【解析】函数()2f x x x a =++的图象的对称轴为12x =-,故函数在区间()0,1上单调递增,再根据函数()f x 在()0,1上有零点,可得()()00120f a f a =<⎧⎪⎨=+>⎪⎩,解20a -<<,故选C .6.【解析】函数()()10,1x f y ax a a -=>≠=的图象恒过点A ,即10x -=,可得1x =,那么1y =.∴恒过点()1,1A .把1x =,1y =带入各选项,只有A 没有经过A 点.故选A . 7.【解析】略8.【解析】()23g x x ax a =-+,则()230x a a g x x =-+>在[)2,+∞恒成立,且()23g x x ax a =-+在[)2,+∞上为增函数,所以22a≤且()240g a =+>,所以44a -<≤.故选D .9.【解析】由题,几何体如图所示(1)前面和右面组成一面此时222222PQ =+=.(2)前面和上面在一个平面此时223110PQ =+=,2210<,故选C . 10.【解析】作出函数()f x 和()g x 的图象如图,两个图象的下面部分图象,由()2230g x x x =-++=,得1x =-,或3x =,由()ln 10f x x =-=,得x e =或1x e=,∵()0g e >,∴当0x >时,函数()h x 的零点个数为3个,故选C .11.【解析】由()()2xg x h x -=,及()g x 为偶函数,()h x 为奇函数,得()222x xg x -+=,()222x x h x --=.由()()0m g x h x ⋅+≤得224121224141x x x x x x x m ----≤==-+++,∵2141x y =-+为增函数,∴max 231415x ⎛⎫+= ⎪+⎝⎭,故选A . 12.【解析】由平行于同一直线的两直线平行,平行于同一平面的两平面平行,可得①正确;由垂直于同一直线的两直线平行、相交或异面;垂直于同一平面的两平面相交或平行,可得②错误;由垂直于两平行直线中的一条,也垂直于另一条;垂直于两平行平面中的一个,也垂直于另一个,可得③正确;若一条直线与另两条直线无公共点,可得另两条直线可以相交;若一个平面与另两个平面无公共点,可得另两个平面无公共点;可得④错误.若三条直线两两相交,则交点可以有一个或三个,若三个平面两两相交,则交点有无数个.故选B . 二、填空题(本大题共4小题,每小题5分,共20分)13. -1 14. 43 15. 1122m -≤< 16. 4π13.【解析】若函数()x x f x e ae -=+为奇函数,则()()f x f x -=-,即()x x x x ae ae e e --+=-+,即()()10x x e a e -++=对任意的x 恒成立,则10a +=,得1a =-. 14.【解析】设正四棱锥的侧棱长与底面边长相等为2a ,则24ABCD S a =,2222422h PB BO a a a =-=-=,则31442233V a =⨯=,则1a =,则 22142242BC PF a a a S ⎛⎫=⨯⨯⨯=⨯⨯- ⎪⎝⎭侧24343a ==.15.【解析】由题设可得230a -+=,即5a =,故()()22122f m f m m -->-+-可化()()22122f m f m m +>-+,又2113m ≤+≤,21223m m ≤-+≤,故2211222m m m m +<-+⇒<,且12m ≥-.故应填答案1122m -≤<.16.【解析】将四面体ABCD 放置于正方体中,如图所示可得正方体的外接球就是四面体ABCD 的外接球,∵正四面体ABCD 的棱长为4,∴正方体的棱长为22, 可得外接球半径R 满足()22322R =⨯,解得6R =.E 为棱BC 的中点,过E 作其外接球的截面,当截面到球心O 的距离最大时,截面圆的面积达最小值,此时球心O 到截面的距离等于正方体棱长的一半,可得截面圆的半径为222r R =-=,得到截面圆的面积最小值为24S r ππ==.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【解析】证明:如图所示,连接1CD 、EF 、1A B ,因为E 、F 分别是AB 和1AA 的中点, 所以1//EF A B 且112EF A B =.即:1//EF CD ,且112EF CD =, 所以四边形1CD FE 是梯形,所以CE 与1D F 必相交,设交点为P ,则P CE ∈,且1P D F ∈,又CE ⊂平面ABCD , 且1D F ⊂平面11A ADD ,所以P ∈平面ABCD ,且P ∈平面11A ADD , 又平面ABCD平面11A ADD AD =,所以P AD ∈,所以CE 、1D F 、DA 三线交于一点.18.【解析】(1)因为()()f x f x -=-,所以2211x a x ax bx x bx -+--=-+++, ∴0a b ==,()21xf x x =+, 任取()12,1,x x ∈+∞,且12x x <,()()1212221211x xf x f x x x -=-++()()()()21122212111x x x x x x --=++, ∵210x x ->,1210x x ->,()()2212110x x ++>,∴()f x 在()1,+∞单调递减.(2)()()2231f t t f k -+<--,()()2231f t t f k -+<-, ∵2232t t -+≥,11k ->,∴2231t t k -+>-, 即()211k t >---, ∵t R ∈≤,∴()1,0k ∈-. 19.【解析】(1)由题可知:甲大棚投入50万元,则乙大棚投入150万元, 所以()1804250150120277.5450f =+⨯+⨯+=. (2)依题意得202018020020x x x ≥⎧⇒≤≤⎨-≥⎩.故()()142250201804x x f x x =-++≤≤. 令25,65t x ⎡⎤=∈⎣⎦,则()()2211422508228244f x t t t =-++=--+,当82t =,即128x =时,()max 282f x =,所以投入甲大棚128万元,乙大棚72万元时,总收益最大, 且最大收益为282万元. 20.【解析】(1)由已知得30p ->且*p N ∈,所以1p =或2p =, 当2p =时,()3p f x x -=为奇函数,不合题意, 当1p =时,()2f x x =.所以不等式()()22132pp x x +<-变为()()1122132x x +<-, 则0132x x ≤+<-,解得213x -≤<. 所以不等式()()22132p p x x +<-的解集为21,3⎡⎫-⎪⎢⎣⎭.(2)()()2log a a g x x x =-,令()2h x x ax =-,由()0h x >得()(),0,x a ∈-∞+∞,因为()g x 在[]2,3上有定义,所以02a <<且1a ≠, 所以()2h x x ax =-在[]2,3上为增函数,当12a <<时,()()()max 3log 932a g x g a ==-=, 即2390a a +-=,∴3352a -±=,又12a <<, ∴3352a -+=. 当01a <<时,()()()max 2log 422a g x g a ==-=,即2240a a +-=,∴15a =-±,此时解不成立.综上:3352a -+=. 21.【解析】(1)当2m =-时,设13xt ⎛⎫= ⎪⎝⎭,∵(),0x ∈-∞,∴()1,t ∈+∞,∴()()222413t t t y g t -+=-=+=,对称轴1t =,图像开口向上,∴()g t 在()1,t ∈+∞为增函数, ∴()3g t >,∴()f x 的值域为()3,+∞.(2)由题意知,()6f x ≤在[)0,+∞上恒成立,即11239xxm ⎛⎫⎛⎫⋅≤- ⎪ ⎪⎝⎭⎝⎭,∴1233xx m ≤⋅-在[)0,x ∈+∞恒成立,则只需当[)0,x ∈+∞时,min 1233x x m ⎛⎫≤⋅- ⎪⎝⎭,设3xt =,()12h t t t=-,由[)0,x ∈+∞得1t ≥,设121t t ≤<,则()()()()12121212210t t t t h t h t t t -+-=<,所以()h t 在[)1,+∞上递增,()h t 在[)1,+∞上的最小值为()11h =,所以实数m 的取值范围为(],1-∞. 22.【解析】(1)取BE 中点R ,连接PR ,QR ,BD ,由P ,Q 分别是BF ,DE 的中点, ∴//PR EF ,//QR BD ,又∵//EF AC ,∴//PR 平面ABCD ,//QR 平面ABCD ,又∵PR QR R =,∴平面//PQR 平面ABCD ,又∵PQ ⊂平面PQR , ∴//PQ 平面ABCD .(2)连接AC ,设AC ,BD 交于点O , ∴BD AC ⊥,又∵平面AFEC ⊥平面ABCD , 平面AFEC平面ABCD AC =,∴BD ⊥平面AFEC .∴多面体ABCDFE 可以分解为四棱锥B ACEF -和四棱锥D ACEF -, 菱形ABCD 中,2AB =且60ABC ∠=︒知:2AC =,23BD =,12ACEF ==, 设梯形EFAC 的面积为()133244EFAC BD EF AC S =+⋅=, 1332ABCDFE EFAC V S BD =⋅⋅=.。
2024届山东省青岛市高一上数学期末综合测试试题含解析

注意事项: 1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。 2.答题时请按要求用笔。 3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。 4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。 5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
BD1 3 3 【点睛】考查了异面直线所成角的计算方法,关键得出直线 AD1 与 EF 所成角即为∠AD1B ,难度中等 12、 2 【解析】根据直线一般式,两直线平行则有 A1B2 A2B1 0 ,代入即可求解. 【详解】由题意,直线 x y 2 0 与直线 ax 2y 0 平行,
则有1 (2) 1 a 0 a 2 故答案为: 2
3
,
则反射光线所在直线方程 y 3 3 1 x 4 4 1
即: 4x 5y 1 0
故选 A 10、D 【解析】把方程的根转化为二次函数的零点问题,恰有一个零点属于(0,1),分为三种情况,即可得解.
【详解】方程 x2 (m 2)x 2m 1 0 对应的二次函数设为: f x x2 (m 2)x 2m 1
(m 2)2 42m 1 0 ,解得 m 6 2 7 ,
当 m 6 2 7 时,方程 x2 (m 2)x 2m 1 0 的根为 2 7 ,不合题意;
若 m 6 2 7 ,方程 x2 (m 2)x 2m 1 0 的根为 7 2 ,符合题意
综上:实数
m
的取值范围为
不一定有对任意 x R , f x 0 ,所以 A 错误,
对于 B,当函数 y f x 的图像关于原点成中心对称,可知 f (x) f (x) ,函数 f (x) 为奇函数,所以 B 错误,
高一数学考试题

高一期末综合测试卷一、单项选择题:本题10小题,每小题4分,共52分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合}2,2{},03|{2-=≥-∈=B x x R x A ,则=⋂B A C R )(( )A.∅B.}2{-C.}2{D.}22{,-2.已知函数)1(-x f 的定义域为]3,(-∞,则函数)22(xx f -定义域为( ) A.]2,1[ B.)2,1[ C.),2[]1,(+∞⋃-∞ D. ),2(]1,(+∞⋃-∞3.不等式022>-x x 的解集为( )A. ),2(+∞B.)2,(-∞C.)2,0(D.),2()0,(+∞⋃-∞4.设4.0log5.0log 454.04.0===c b a ,,,则c b a ,,的大小关系是( )A.c b a <<B.a c b <<C.b a c <<D.a b c <<5.设}20|{},20|{≤≤=≤≤=y y N x x M ,给出下列四个图形,其中能表示从集合M 到集合N 的函数关系的有( )① ② ③ ④A. 0个B. 1个C. 2个D. 3个6.下列选项中叙述正确的是( )A.三角形的内角是第一象限角或第二象限角B.锐角一定是第一象限的角C.小于90°的角一定是锐角D.终边相同的角一定相等7.若点P )2018cos ,2018(sin ︒︒,则P 在( )A.第一象限B.第二象限C.第三象限D.第四象限8.下列结论错误的是( )A.命题“若4=x ,则0432=--x x ”为真命题.B.“4=x ”是“0432=--x x ”的充分不必要条件C.已知命题p “若0>m ,则方程02=-+m x x 有实数根”,则命题p 的否定为真命题D.命题“若022=+n m ,则0=m 且0=n ”的为真命题9.已知函数x x x f )21(|lg |)(-=有两个零点21,x x ,则有( )A.021<x xB.121=x xC.121>x xD.1021<<x xA.在],0[π上是增函数,在]2,[ππ上是减函数C.在]2,[ππ上是增函数,在],0[π上是减函数二、多项选择题(本大题共3小题,每小题4分,共12分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,选对但不全的得2分,有选错的得0分)11.设R b a ∈,,若0||>-b a ,则下列不等式中正确的是( )A.0>-a bB.033<+b aC.0>+a bD.022>-b a交点,则k 的取值不可能是( )A.1B.2C. 3D.-1三、填空题:本题共4小题,每小题4分,共16分.16.当0>a 且1≠a 时,函数1)1(log )(+-=x x f a 的图像恒过点A ,若点A 在直线n mx y +=上,三、解答题:本题共6分,共82分.解答应写出文字说明、证明过程或演算步骤.18.(本小题满分12分)用二分法求函数632)(23--+=x x x x f 的一个正零点(精确到0.1).19.(本题满分14分)设全集U=R ,集合}0124|{2≥-+=x x x A ,}.|{},3|1||{a x x C x x B <=<-= (1)求B A ⋂;(2)若C B A C U ⊆⋂])[(,求实数a 的取值范围.20.(本小题满分14分)求证:)(x f 在),(+∞a 上是减函数.21.(本小题满分14分)某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为10000辆,本年度为适应市场需求,计划适度增加投入成本,提高产品的档次.若每辆车投入成本增加的比例为)10(<<x x ,则出厂价相应的提高比例为x 75.0,同时预计年销售量增加的比例为.6.0x(1)写出本年度预计的年利润y 与投入成本增加的比例x 的关系式;(2)投入成本增加的比例多大时,本年度预计的年利润最大?最大值是多少?22.(本小题满分14分)已知.)(sin )cot()23tan()2cos()sin()(2αππαπααπαπ----+---=a f (1)化简);(αf(2)若21)(=αf ,求ααααcos sin cos sin -+的值.23.(本小题满分14分)某医药研究所最近研制了一种新药,对防治SARS有显著疗效.在实验中,据微机监测,如果成人按规定量单次服用,服药后每毫升血液中含药量y(微克)与时间t(小时)之间近似拟合如图所示的曲线:(1)写出图中表示的含药量y与时间t的函数关系式);y(tf(2)根据临床测定,如果成人每毫升血液中的含药量不少于4微克,则该药物能抑制其病原生长,但每次服药后一小时内再次服药,则用药量过大,会对身体产生副作用.假若SARS病人按规定剂量服药,第一次服药时间是早晨7:00,晚上10:00左右就寝后不再服药,问患者一天中应怎样安排服药的时间和次数,治疗效果最佳?答案:1.C2.D3.D4.D5.B6.B7.C8.C9.D10.A11.CD12.ACD13.AC17.}2≥xxx,且{≠-1|18.列表如下:正零点的近似值为1.719.(1)}42|{<≤=⋂x x B A ;(2)2≥a .0)()(0,010,21212112<-⇒><-⇒<<>>x g x g x x x x a a x x综上,)(x f 在),(+∞a 上是减函数.21.(1))6.01(10000)]1()75.01(2.1[x x x y +⨯+-+==.10),103(2002<<++-x x x(2)考虑到晚上10:00左右就寝后不再服药,故一天中安排四次服药为宜,服药时间分别为早晨7:00,上午11:00,下午16:00和晚上20:30.。
华大新2025届高一数学第一学期期末综合测试试题含解析

f
(x)
tan
2
x
3
1
的对称中心是
k 2
6
,1
,
k Z
,
其中正确命题的序号是________.
16.已知定义在区间[a 2023, 2024]上的奇函数 f (x) 满足: f (2 x) f (x) ,且当 x [1, 0] 时,
f (x) a log2 (b x) ,则 f (2021) f (2022) ____________.
【解析】可直接根据题意转化为方程 x x 1 2x 2t 有两个根,然后利用分类讨论思想去掉绝对值再利用判别式即
可求得各个 t 的值
【详解】由题意得方程 x x 1 2x 2t 有两个不等实根,
当方程有两个非负根时,
令 x 0 时,则方程为 x x 1 2x 2t ,整理得 x2 3x 2t 0
4sin
0
(1)求
tan
4
的值;
(2)求
sin
2
2
的值.
20.如图,已知在正四棱锥 P ABCD 中, M 为侧棱 PD 的中点,
(1)证明: PB / /平面ACM ;
连接 AC、BD 相交于点 O
(2)证明: 平面ACM 平面PBD ;
(3)设 AB 2 ,若质点从点 A 沿平面 PAD 与平面 PCD 的表 棱锥 P ABCD 的体积
AO ∴ AOA 60 .
故选:C
【点睛】本题考查了二面角的平面角的作法,重点考查了运算能力,属基础题. 7、B 【解析】由三角函数的定义即可得到结果.
【详解】∵ 480 角的终边上一点 (4, a) , ∴ tan 480 tan1200 3 a ,
高一数学必修一综合测试题(含标准答案)

高一数学必修一综合测试题(含标准答案) 高一数学期中考试试卷满分:120分考试时间:90分钟一、选择题(每题5分,共50分)1、已知集合M={0,1,2},N={x=2a,a∈M},则集合MN=()A、{ }B、{0,1}C、{1,2}D、{0,2}2、若f(lgx)=x,则f(3)=()A、lg3B、3C、D、3103、函数f(x)=(x-1)/(x-2)的定义域为()A、[1,2)∪(2,+∞)B、(1,+∞)C、[1,2)D、[1,+∞)4.设a=log3,b=1/2,c=2/3,则()A a<b<cB c<b<aC c<a<bD b<a<c5、若(1+x)/(1-x)=5,则x^2+1/x^2=()A、1B、5C、6D、256、已知函数f(x+1)=x^2-x+3,那么f(x-1)/f(x+5)的表达式是()A、(x-2)/(x+6)B、(x^2-x-3)/(x^2-11x+30)C、(x+6)/(x-2)D、x(x-2)/(x^2-5x+9)7、函数y=-|x-2|的图像为()见图片8、函数y=f(x)在R上为增函数,且f(2m)>f(-m+9),则实数m的取值范围是().A.(-∞,-3) B.(0,+∞) C.(3,+∞) D.(-∞,-3)∪(3,+∞)9、若loga(a+1)<loga(2a),则a的取值范围是()A、0110.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且当x∈[-1,0]时f(x)=2,则f(log28)等于()A.3 B.-2 C.2 D.8二、填空题(每题4分,共20分)11.当a>0且a≠1时,函数f(x)=a^x-2x-3必过定点(2,1/a)。
12.函数y=-|x-3|x的递减区间为(-∞,3)。
13、在f(x)=x+2(a-1)x+2在(-∞,4]上单调递减,则a的取值的集合为(0,2)。
吉林省公主岭市第三中学2025届高一数学第一学期期末综合测试试题含解析

所以,命题“ x0 R ,使得 x03 ax02 bx0 c 0 ”的否定是 xR , x3 ax2 bx c 0 .
故选:B
2、D
【解析】令 x= 1 ,y=1,则有 f( 1 )=f( 1 )+f(1),
2
2
2
故 f(1)=0;
令 x= 1 ,y=2,则有 f(1)=f( 1 )+f(2),
7.
sin
11 6
cos
3
(
)
A.1
B.0
C.-1
D. 3
2
8.下列关于函数 f (x) 的图象中,可以直观判断方程 f (x) 2 0 在 (-,0) 上有解的是
A.
B.
C.
D.
9.设角 的终边经过点 P(3,4) ,那么 cos( 2 ) 2
7 A.
25
B. 7 25
24
C.
25
∴ x 2 0,x 2,
a 2,1 ,
a 22 12 5 ,
故选:A 【点睛】本题主要考查平面向量垂直的坐标表示,考查平面向量的模,属于基础题 6、A
【解析】因为两条直线平行,所以: 2m 1 6 m 3 1 7
解得 m=1 故选 A. 点睛:本题主要考查直线的方程,两条直线平行与斜率的关系,属于简单题.对直线位置关系的考查是热点命题方向之一,
分别观察直线 y=2 与函数 f(x)的图象在(-∞,0)上交点的情况,
选项 A,B,C 无交点,D 有交点, 故选 D 点睛:这个题目考查了方程有解的问题,把函数的零点转化为方程的解,再把方程的解转化为函数图象的交点,特别 是利用分离参数法转化为动直线与函数图象交点问题,要求图像的画法要准确 9、D
高一数学综合测试含答案

:L高一数学综合测试题(一)一、选择题1.给出以下四个命题: ①若a b >,则11a b<;②若22ac bc >,则a b >; ③若||a b >,则a b >;④若a b >,则22a b >A.②④B. ②③C. ①②D.①③2.如图所示的直观图的原平面图形是( )A.任意三角形B.直角梯形C.任意四边形D.平行四边形3.三视图如图所示的几何体是( )A. 三棱锥B. 四棱锥C. 四棱台D.三棱台4.已知ABC中,4,30a b A ===︒,则B 等于( )A. 30°B.30°或150°C.60°D.60°或120°5.已知0,0a b ≥≥,且2a b +=,则( )A.12ab ≤ B.12ab ≥C.222a b +≥D.223a b +≤6.等差数列{}n a 的前n 项和为n S ,若242,10S S ==,则6S 等于( )A.12B.18C.24D.427、已知点(),P x y 在不等式组2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩表示的平面区域内运动,则z x y =-的取值范围是( )A. []2,1--B.[]2,1-C.[]1,2-D.[]1,28.在ABC 中,260,B b ac =︒=,则这个三角形是( )A.不等边三角形B.等边三角形C.等腰三角形D.直角三角形9.两直线()12:0,:10l ax by l a x y b +=-++=,若直线12l l 、同时平行于直线:230l x y ++=,则,a b 的值为( )A. 3,32a b ==- B.2,33a b ==- C.3,32a b == D.2,33a b ==10、已知S ,A ,B ,C 是球O 表面上的点,SA ⊥平面,,1,2A B C A B B C S A A B B C ⊥==O 的表面积等于( )A. 4πB.3πC. 2πD.π11、直三棱柱111ABC A B C -中,若90BAC ∠=︒,1AB AC AA ==,则异面直线1BA 与1AC 所成的角等于( ) A. 30°B.45°C. 60°D.90°12.,四个顶点在同一球面上,则此球的体积为( )A.2π B. π二、填空题13.20y -++=绕点()1,2-旋转30°,所得到的直线方程是 。
湖北省武汉第二中学2024届高一数学第二学期期末综合测试试题含解析

湖北省武汉第二中学2024届高一数学第二学期期末综合测试试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.无论m 取何实数,直线:120l mx y m +-+=恒过一定点,则该定点坐标为( )A .()-21,B .()2,1--C .()2,1D .()2,1-2.在∆ABC 中,222sin sin sin sin sin A B C B C +-≤.则的取值范围是( )A .(0,6π] B .[6π,π) C .(0,3π] D .[3π,π) 3.中国古代数学名著《算法统宗》中有这样一个问题:“三百七十里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行数里,请公仔细算相还”.其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问从第几天开始,走的路程少于30里( ) A .3B .4C .5D .64.已知角终边上一点,则的值为( ) A .B .C .D .5.若函数()()12,1,1,1,x x f x f x x -⎧≤⎪=⎨->⎪⎩则20192f ⎛⎫= ⎪⎝⎭( ) A .12B .22 C .2D .22-6.三棱锥P ABC -中,底面ABC ∆是边长为2的正三角形,PA ⊥底面ABC ,且2PA =,则此三棱锥外接球的半径为( )A .B .C .2D .7.我国古代数学名著《九章算术》第六章“均输”中有这样一个问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”(注:“均输”即按比例分配,此处是指五人所得成等差数列;“钱”是古代的一种计量单位),则分得最少的一个得到( ) A .13钱 B .23钱 C .56钱 D .1钱8.曲线221169x y +=与曲线22(0)169x y k k +=>的()A .长轴长相等B .短轴长相等C .焦距相等D .离心率相等9.ABC ∆的斜二测直观图如图所示,则原ABC ∆的面积为( )A .22B .1C .2D .210.如图,矩形ABCD 中,AB =2,AD =1,P 是对角线AC 上一点,25AP AC =,过点P 的直线分别交DA 的延长线,AB ,DC 于点M ,E ,N .若,DM mDA DN nDC == (m >0,n >0),则2m +3n 的最小值是( )A .65 B .125 C .245D .485二、填空题:本大题共6小题,每小题5分,共30分。
高一数学必修综合测试题套附答案

高一数学必修综合测试题套附答案高一数学综合检测题(1)一、选择题:(每小题5分,共60分,请将所选答案填在括号内)1.已知集合M⊂{4,7,8},且M中至多有一个偶数,则这样的集合共有()。
A) 3个 (B) 4个 (C) 5个 (D) 6个2.已知S={x|x=2n,n∈Z},T={x|x=4k±1,k∈Z},则()。
A) S⊂T (B) T⊂S (C) S≠T (D) S=T3.已知集合P={y|y=−x^2+2,x∈R},Q={y|y=−x+2,x∈R},那么P∩Q等于()。
A) (,2),(1,1) (B) {(,2),(1,1)} (C) {1,2} (D){y|y≤2}4.不等式ax^2+ax−4<0的解集为R,则a的取值范围是()。
A) −16≤a−16 (C) −1605.已知f(x)=x−5(x≥6)f(x+4)(x<6)则f(3)的值为()。
A) 2 (B) 5 (C) 4 (D) 36.函数y=x^2−4x+3,x∈[0,3]的值域为()。
A) [0,3] (B) [−1,0] (C) [−1,3] (D) [0,2]7.函数y=(2k+1)x+b在(-∞,+∞)上是减函数,则()。
A) k>−1/2 (B) k−1 (D) k<−18.若函数f(x)=x^2+2(a−1)x+2在区间(−∞,4]内递减,那么实数a的取值范围为()。
A) a≤−3 (B) a≥−3 (C) a≤5 (D) a≥39.函数y=(2a^2−3a+2)ax是指数函数,则a的取值范围是()。
A) a>0,a≠1 (B) a=1 (C) a=1/2 (D) a=1或a=1/210.已知函数f(x)=4+ax−1的图象恒过定点p,则点p的坐标是()。
A) (1,5) (B) (1,4) (C) (0,4) (D) (4,4)11.函数y=log(3x−2)的定义域是()。
高一数学测试试题及答案

高一数学测试试题及答案一、选择题(每题4分,共40分)1. 下列函数中,为奇函数的是()A. y = x^2B. y = x^3C. y = |x|D. y = sin(x)2. 已知集合A={1, 2, 3},B={2, 3, 4},则A∩B等于()A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3, 4}3. 函数f(x) = x^2 - 4x + 4的对称轴是()A. x = -2B. x = 2C. x = 0D. x = 44. 计算(2x - 1)^5的展开式中,x^3的系数是()A. 10B. -10C. 20D. -205. 已知等差数列{a_n}的首项a_1=3,公差d=2,则a_5等于()B. 11C. 9D. 76. 函数y = 2x + 3的图象与x轴的交点坐标是()A. (-3/2, 0)B. (3/2, 0)C. (-1.5, 0)D. (1.5, 0)7. 已知函数f(x) = 2x^2 - 3x + 1,求f(-1)的值()A. 6B. 4C. 2D. 08. 圆x^2 + y^2 = 4的圆心坐标是()A. (0, 0)B. (2, 2)C. (-2, -2)D. (1, 1)9. 已知向量a = (3, 1),向量b = (-1, 2),则向量a与向量b的点积为()A. -1B. 1C. 5D. -510. 计算sin(π/6)的值是()B. √3/2C. 1/√2D. √2/2二、填空题(每题4分,共20分)1. 函数y = x^2 - 6x + 9的最小值是______。
2. 已知等比数列{a_n}的首项a_1=2,公比q=3,则a_4等于______。
3. 函数f(x) = 3x - 5的反函数是______。
4. 已知向量a = (2, -3),向量b = (4, -6),则向量a与向量b平行,向量a与向量b的夹角是______。
5. 计算cos(π/3)的值是______。
高一数学期末综合能力测试

期末综合能力测试班级 姓名 学号 得分一、选择题1、全集R ,若M={x|x ≥1},N={x|0≤x<5}则C U MUC U N 是( )A {x|x ≥0}B {x| x ≥5或x <1 C{x|x ≤1或x >5} D{x|x <0或x ≥5 2若(x ,y )在映射f 的作用下,象为[(x+y ),(x-y )],那么(-1,5)在映射f 下的原象是( )A (4,6)B (2,-3)C (6,4)D (-3,2)3、下列函数中既不是奇函数也不是偶函数的是( )A y=a x +a-xBy=log a x x -+11 Cy=2212-+-x x D y=(1-x )x x -+11 4、f (x )=2x ,g (x )=3x ,h (x )=(21)x ,当x ∈(-)0,∞时,它们的函数值的大小关系是( ) A h (x )<g (x )<f (x ) B g (x )<f (x )<h (x )Cg (x )<h (x )<f (x ) Df (x )<g (x )<h (x )5、定义在R 上的偶函数f (x )在(0,∞)上为增函数,且f (31)=0,则满足f (log 81x )>0的x 的取值范围是( )A (0,21 ) B ( 21 ,1)∪(2,∞) C (2,∞) D (0,21 )∪(2,∞)6、若指数函数y=f (x )的反函数图象经过点(2,-1),则此指数函数是( )A y=(21)xB y=2xC y=3x Dy=(31)x 7、若数列a 1,a 2,a 3,……a n ,是公差不为零的等差数列,则下列四个数列: ① lga 1,lga 2,lga 3,……lga n ……②21a ,22a ,……2n a ……③a 1a 2,a 2a 3,……a n a n+1…… ④a 1+a 2,a 2+a 3,……a n +a n+1…… 其中是等比数列的为( )A ①B ②C ③D ④8、若实数a 、b 、c 成等比数列,那么函数y=ax 2+bx+c 的图象与x 轴的交点的个数为( )A 0B 1C 2D 不确定9、在数列{a n }中,a 1=-60,a n+1=a n +3,那么S 30 =|a 1|+|a 2|+……+|a 30|等于( )A –445B 765C 1080D 310510、“lg (x-1)、lgx 、lg (x+1)成等差数列”是“x-1、x 、x+1成等比数列”的( )A 充分但非必要条件B 必要但非充分条件C 充要条件D 既不充分又非必要条件11、某商品降价10%,欲恢复原价,则应提价的百分率是( ) A 10% B 10101% C 11% D 1191 12、已知函数f (x )=log a |x+1|在(-1,0)上有f (x )>0,那么下列命题正确的是( )A f (x )在(-∞,0)上为增函数B f (x )在(-∞,0)上为减函数C f (x )在(-∞,-1)上为增函数D f (x )在(-∞,-1)上为减函数13、数列{a n }中,a 1,a 2=1+2,a 3=1+2+22,a 4=1+2+22+23,……a n =1+2+22+23+…………+2n-1 那么前99项的和是( )A 299-101 B299-99 C 2100-101 D 2100-9914、甲工厂八年来某产品总产量y 与时间t (年)的函数关系如右图,下列说法:(1)前三年中产量增长的速度越来越快;(2)前三年中产量增长的速度越来越快;(3)第三年后,这种产品停止生产;第三年后,年产量保持不变,其中说法正确的是( )A (2)(3) B (2)(4) C (1)(3) D (1)(4)二、填空题15、f (x )的定义域为(-1,1],那么f (x 2-1)的定义域是 16、-1+3-5+……+(-1)n (2n-1)=17、给出下列四个命题:(1) 在同一坐标系中函数y=f (x )的图象与函数y=-f (x )的图象关于x 轴对称(2)在同一坐标系中函数y=f (x )的图象与函数y=f (|x|)的图象关于y 轴对称(3)对于任意实数x ,函数y=f (x )恒满足f (-x )=-f (x ),则函数y=-f (x )的图象关于坐标原点对称(4)函数y=a -x与函数y=log a (-x )(a >0,a ≠1)的图象关于直线y=x 对称 其中正确命题的序号是三、解答题18、 已知x ∈R ,集合A={-3,x2,x+1},B={x-3,2x-1,x2+1},如果A B={-3},求A B19、已知数列{a n }为递减的等差数列,且a 2+a 8=56 ,a 4a 6=775,试求数列前n 项的最大值和取最大值时的n 值20若奇函数f (x )在定义域(-1,1)上是减函数(1) 求满足0)1()1(2<-+-a f a f 的a 的取值集合M(2) 对于(1)中的a ,求函数])1(1[log )(2x x a ax f --=的定义域21、数列{a n}为正项等比数列,它的前n项和为80,其中数值最大的项为54,前2n项和为6560。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学综合测试试卷【模拟试题】一. 选择题:本大题共10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请把所选答案的标号字母填在题后的括号内。
1. 设θθ|{=A 为锐角},θθ|{=B 为小于︒90的角},θθ|{=C 为第一象限的角},则下面正确的是( )A. A=B=CB. C A ≠⊂C. B C A =⋂D. C B A =⋂ 2. )619cos(π-的值等于( ) A.21 B.21- C. 23 D. 23-3. 若命题0:=x p ,命题0:=a x q ,则命题q 是命题p 的( ) A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4. 角α终边在直线x y 2=上,则下面结论中正确的是( ) A. 552sin =αB. 55cos -=α C. 2tan =αD. 2tan ±=α5. 函数)225sin(x y -=π是( ) A. 最小正周期为π的偶函数B. 最小正周期为π的奇函数C. 最小正周期为π2的偶函数D. 最小正周期为π的非奇非偶函数6. 设=a (23,αsin ),)31,(cos α=b ,且b a //,则锐角α为( ) A. 30° B. 60° C. 45° D. 75°7. 已知两点P 1(1-,6-),P 2(3,0),点P (37-,y )分有向线段21P P 所成的比为λ,则λ,y 的值为( )A. 8,41-B. 8,41-C. 8,41--D. 81,4 8. 已知1||=a ,2||=b ,且(b a -)和a 垂直,则a 与b 的夹角是( )A. 90°B. 60°C. 45°D. 30° 9. 要得到函数)32sin(π-=x y 的图象,只要将x y 2sin =的图象( )A. 向右平移6π个单位 B. 向左平移6π个单位 C. 向右平移3π个单位D. 向左平移3π个单位10.(I )(只重点校做)当函数x x y sin 3cos 2-=取得最大值时,x tan 的值是( ) A.23 B. 23- C. 13 D. 4 (II )(只非重点校做) 函数x x y cos sin +=,]2,0[π∈x 的最大值是( )A. 1B. 22C. 2D. 2二. 填空题:本大题共5个小题,每小题3分,共15分。
请把答案直接填在题中横线上。
11. 函数1sin 2-=x y 的定义域为 。
12. ABC ∆中,AB=3,AC=2,︒=∠60BAC ,则BC 边的长为 。
13. 已知)1,2(--=a ,)3,4(-=b ,则a 与b 的夹角的余弦值是 。
14. 已知a x a x 7)(23=-+且)3,1(=a ,则=||x 。
15.(I )(只重点校做)把函数5422+-=x x y 按向量a 平移,得22x y =的图象,且b a ⊥,)1,1(-=c ,4=⋅c b ,则=b 。
(II )(只非重点校做)把函数322++=x x y 的图象c ,按)1,3(-=a 平移到c ',则c '的函数解析式是 。
三. 解答题:本大题共6个小题,共55分,解答应写出文字说明,演算步骤或证明过程。
16.(本小题满分10分) 已知53sin =α,),2(ππα∈ 求)4sin(πα-,)3cos(πα+及α2tan 的值。
17.(本小题满分8分) 已知2||=a ,3||=b ,a 与b 的夹角为︒45,求使向量b a λ+与b a +λ的夹角为锐角时λ的取值范围。
18.(本小题满分8分) (I )(只重点校做) 已知βα<<02π<,且αcos 、βcos 是方程02150sin )50sin 2(22=-︒+︒-x x 的两根,求)2tan(αβ-的值。
(II )(只非重点校做) 已知20πβα<<<,且αtan 、βtan 是方程0652=+-x x 的两根,求)2tan(αβ-的值。
19.(本小题满分9分)已知函数x x x x y 22cos cos sin 32sin -+=,R x ∈,(1)求函数y 的最大值,并求y 取得最大值时,自变量x 的集合; (2)求函数y 的单调递减区间。
20.(本小题10分)设两个非零向量1e 和2e 不共线(1)如果21e e AB +=,2182e e BC +=,)(321e e CD -=,求证A 、B 、D 三点共线; (2)试确定实数k ,使21e e k +和21e k e +共线;(3)(只重点校做,非重点校不做)若2||1=e ,3||2=e ,1e 与2e 的夹角为︒60,试确定实数k ,使21e e k +与21e k e +垂直。
21.(本小题10分)已知向量)23sin,23(cos x x a =,)2sin ,2(cos x x b -=,且]2,0[π∈x ,(1)求b a ⋅及||b a +;(2)(只非重点校做,重点校不做)求函数||2)(b a b a x f +-⋅=的最小值; (3)(只重点校做,非重点校不做)若||2)(b a b a x f +-⋅=λ的最小值是23-,求实数λ的值。
【试题答案】一. 选择题:(每小题3分,共30分)1. B2. D3. B4. C5. A6. C7. C8. C9. A 10.(I )B (II )C二. 填空题:(每小题3分,共15分) 11. },65262|{Z k k x k x ∈+≤≤+ππππ 12.7 13. 55-14. 10 15.(I )(3,1-) (II )171122+-=x x y三. 解答题:(共55分,以下各题为累计得分,其他解法请相应给分) 16. 解: ∵ 53sin =α ),2(ππα∈ ∴ 54)53(1sin 1cos 22-=--=--=αα(2分)435453cos sin tan -=-==ααα(4分)∴ 210722)54(22534sincos 4cossin )4sin(=⨯--⨯=-=-παπαπα(6分)10334235321)54(3sinsin 3coscos )3cos(+-=⨯-⨯-=-=+παπαπα(8分) 724)43(1)43(2tan 1tan 22tan 22-=---⨯=--=ααα(10分) 17. 解:由已知得0)()(>+⋅+b a b a λλ(2分) 即0)(222>⋅+++⋅b a b a b a λλ(3分) 又 ∵ 3cos ||||==⋅αb a b a (5分) ∴ 031132>++λλ(6分))(b a b a +=+λμλ ⎩⎨⎧==μλμλ1 ∴ 1±=λ 解得68511--<λ或68511+->λ且1≠λ 18. 解:(I )∵ βα<<02π<∴ 0cos cos >>βα由韦达定理得⎪⎩⎪⎨⎧-︒=⋅︒=+)2(2150sin cos cos )1(50sin 2cos cos 2βαβα(2分) ∴ ︒=-+=-50cos 2cos cos 4)cos (cos cos cos 2βαβαβα(3)(4分)由(1)、(3)可得︒=︒+︒=︒+︒=5cos )4550sin(250cos 250sin 2cos α(5分)︒=︒=︒-︒=︒-︒=85cos 5sin )4550sin(250cos 250sin 2cos β(6分)∵ 20πα<<,20πβ<< ∴︒=5α,︒=85β(7分)∴ 3275tan )2tan(+=︒=-αβ(8分) (II )∵ 20πβα<<< ∴ βαtan tan <由韦达定理得⎩⎨⎧=⋅=+6tan tan 5tan tan βαβα(2分)解得⎩⎨⎧==3tan 2tan βα(4分) ∴ 342122tan 1tan 22tan 22-=-⨯=-=ααα(6分) ∴ 913)34(31)34(32tan tan 12tan tan )2tan(-=-⨯+--=⋅+-=-αβαβαβ(8分) 19. 解:)62sin(2)212cos 232(sin 22cos 2sin 3π-=-=-=x x xx x y (3分) (I )y 的最大值为2,当)62sin(π-x 1= 即2262πππ+=-k x 时即ππ31+=k x ∴ y 取最大值时自变量x 的集合为},3|{Z k k x x ∈+=ππ(6分)(II )由题意知πππππ2326222+≤-≤+k x k ,Z k ∈,解得+≤≤+πππk x k 31π65,即函数y 的单调递减区间是]65,3[ππππ++k k Z k ∈(9分)20. 解:(I )∵ AB e e e e e e CD BC BD 5)(5)(382212121=+=-++=+= ∴ BD 与AB 共线 ∴ A 、B 、D 三点共线;重点校3分,非重点校5分 (II )由题意可知存在非零实数λ使)(2121e k e e e k +=+λ 即2121e k e e e k λλ+=+∴ ⎩⎨⎧==1λλk k 解得1±=k (重点校6分,非重点校10分)(III )由题意知0)()(2121=+⋅+e k e e e k即0)1(2221221=+⋅++e k e e k e k又 ∵ 4||2121==e e ,2222||e e =9=,3213260cos ||||2121=⨯⨯=︒=⋅e e e e 即09)1(342=+++k k k 化简得031332=++k k 即613313±-=k (重点校10分) 21. 解:(I )x xx x x b a 2cos 2sin 23sin 2cos 23cos=-=⋅(1分) 22222)(||b b a a b a b a +⋅+=+=+(2分)又 ∵ 123sin 23cos||2222=+==x x a a (3分) 12sin 2cos ||2222=+==xx b b (4分)x b a 2cos =⋅∴ x x x b a 22cos 4)2cos 1(22cos 22||=+=+=+(5分) 又 ∵ ]2,0[π∈x∴ x b a cos 2||=+(6分)(II )x x b a b a x f cos 42cos ||2)(-=+-⋅= 3)1(cos 21cos 4cos 222--=--=x x x ∵ ]2,0[π∈x ∴ ]1,0[cos ∈x∴ 当1cos =x 时,)(x f 有最小值3-(非重点校10分)(III )1cos 4cos 2cos 42cos )(2--=-=x x x x x f λλ 2221)(cos 2λλ---=x (重点校7分) 设t x =cos ,则]1,0[∈t2221)(2)()(λλϕ---==t t x f ]1,0[∈t(1)当0<λ时,)0(ϕ最小,1)0(-=ϕ与最小值为23-矛盾; (2)当10≤≤λ时,)(λϕ最小,此时有2321)(2-=--=λλϕ 21=λ(3)当1>λ时,)1(ϕ最小,此时有2341)1(-=-=λϕ,85=λ与1>λ矛盾综上可知21=λ(重点校10分)。
