周源(最小表示法)
NOI国家集训队论文分类(至2008)(摘抄自C博客)

摘抄自C博客组合数学计数与统计2001 - 符文杰:《Pólya原理及其应用》2003 - 许智磊:《浅谈补集转化思想在统计问题中的应用》2007 - 周冬:《生成树的计数及其应用》2008 - 陈瑜希《Pólya计数法的应用》数位问题2009 - 高逸涵《数位计数问题解法研究》2009 - 刘聪《浅谈数位类统计问题》动态统计2004 - 薛矛:《解决动态统计问题的两把利刃》2007 - 余江伟:《如何解决动态统计问题》博弈2002 - 张一飞:《由感性认识到理性认识——透析一类搏弈游戏的解答过程》2007 - 王晓珂:《解析一类组合游戏》2009 - 曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》2009 - 方展鹏《浅谈如何解决不平等博弈问题》2009 - 贾志豪《组合游戏略述——浅谈SG游戏的若干拓展及变形》母函数2009 - 毛杰明《母函数的性质及应用》拟阵2007 - 刘雨辰:《对拟阵的初步研究》线性规划2007 - 李宇骞:《浅谈信息学竞赛中的线性规划——简洁高效的单纯形法实现与应用》置换群2005 - 潘震皓:《置换群快速幂运算研究与探讨》问答交互2003 - 高正宇:《答案只有一个——浅谈问答式交互问题》猜数问题2003 - 张宁:《猜数问题的研究:<聪明的学生>一题的推广》2006 - 龙凡:《一类猜数问题的研究》数据结构数据结构2005 - 何林:《数据关系的简化》2006 - 朱晨光:《基本数据结构在信息学竞赛中的应用》2007 - 何森:《浅谈数据的合理组织》2008 - 曹钦翔《数据结构的提炼与压缩》结构联合2001 - 高寒蕊:《从圆桌问题谈数据结构的综合运用》2005 - 黄刚:《数据结构的联合》块状链表2005 - 蒋炎岩:《数据结构的联合——块状链表》2008 - 苏煜《对块状链表的一点研究》动态树2006 - 陈首元:《维护森林连通性——动态树》2007 - 袁昕颢:《动态树及其应用》左偏树2005 - 黄源河:《左偏树的特点及其应用》跳表2005 - 魏冉:《让算法的效率“跳起来”!——浅谈“跳跃表”的相关操作及其应用》2009 - 李骥扬《线段跳表——跳表的一个拓展》SBT2007 - 陈启峰:《Size Balance Tree》线段树2004 - 林涛:《线段树的应用》单调队列2006 - 汤泽:《浅析队列在一类单调性问题中的应用》哈希表2005 - 李羽修:《Hash函数的设计优化》2007 - 杨弋:《Hash在信息学竞赛中的一类应用》Splay2004 - 杨思雨:《伸展树的基本操作与应用》图论图论2005 - 任恺:《图论的基本思想及方法》模型建立2004 - 黄源河:《浅谈图论模型的建立与应用》2004 - 肖天:《“分层图思想”及其在信息学竞赛中的应用》网络流2001 - 江鹏:《从一道题目的解法试谈网络流的构造与算法》2002 - 金恺:《浅谈网络流算法的应用》2007 - 胡伯涛:《最小割模型在信息学竞赛中的应用》2007 - 王欣上:《浅谈基于分层思想的网络流算法》2008 - 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》最短路2006 - 余远铭:《最短路算法及其应用》2008 - 吕子鉷《浅谈最短径路问题中的分层思想》2009 - 姜碧野《SPFA算法的优化及应用》欧拉路2007 - 仇荣琦:《欧拉回路性质与应用探究》差分约束系统2006 - 冯威:《数与图的完美结合——浅析差分约束系统》平面图2003 - 刘才良:《平面图在信息学中的应用》2007 - 古楠:《平面嵌入》2-SAT2003 - 伍昱:《由对称性解2-SAT问题》最小生成树2004 - 吴景岳:《最小生成树算法及其应用》2004 - 汪汀:《最小生成树问题的拓展》二分图2005 - 王俊:《浅析二分图匹配在信息学竞赛中的应用》Voronoi图2006 - 王栋:《浅析平面Voronoi图的构造及应用》偶图2002 - 孙方成:《偶图的算法及应用》树树2002 - 周文超:《树结构在程序设计中的运用》2005 - 栗师:《树的乐园——一些与树有关的题目》路径问题2009 - 漆子超《分治算法在树的路径问题中的应用》最近公共祖先2007 - 郭华阳:《RMQ与LCA问题》划分问题2004 - 贝小辉:《浅析树的划分问题》数论欧几里得算法2009 - 金斌《欧几里得算法的应用》同余方程2003 - 姜尚仆:《模线性方程的应用——用数论方法解决整数问题》搜索搜索2001 - 骆骥:《由“汽车问题”浅谈深度搜索的一个方面——搜索对象与策略的重要性》2002 - 王知昆:《搜索顺序的选择》2005 - 汪汀:《参数搜索的应用》启发式2009 - 周而进《浅谈估价函数在信息学竞赛中的应用》优化2003 - 金恺:《探寻深度优先搜索中的优化技巧——从正方形剖分问题谈起》2003 - 刘一鸣:《一类搜索的优化思想——数据有序化》2006 - 黄晓愉:《深度优先搜索问题的优化技巧》背包问题2009 - 徐持衡《浅谈几类背包题》匹配2004 - 楼天城:《匹配算法在搜索问题中的巧用》概率概率2009 - 梅诗珂《信息学竞赛中概率问题求解初探》数学期望2009 - 汤可因《浅析竞赛中一类数学期望问题的解决方法》字符串字符串2003 - 周源:《浅析“最小表示法”思想在字符串循环同构问题中的应用》多串匹配2004 - 朱泽园:《多串匹配算法及其启示》2006 - 王赟:《Trie图的构建、活用与改进》2009 - 董华星《浅析字母树在信息学竞赛中的应用》后缀数组2004 - 许智磊:《后缀数组》2009 - 罗穗骞《后缀数组——处理字符串的有力工具》字符串匹配2003 - 饶向荣:《病毒的DNA———剖析一道字符匹配问题解析过程》2003 - 林希德:《求最大重复子串》动态规划动态规划2001 - 俞玮:《基本动态规划问题的扩展》2006 - 黄劲松:《贪婪的动态规划》2009 - 徐源盛《对一类动态规划问题的研究》状态压缩2008 - 陈丹琦《基于连通性状态压缩的动态规划问题》状态设计2008 - 刘弈《浅谈信息学中状态的合理设计与应用》树形DP2007 - 陈瑜希:《多角度思考创造性思维——运用树型动态规划解题的思路和方法探析》优化2001 - 毛子青:《动态规划算法的优化技巧》2003 - 项荣璟:《充分利用问题性质——例析动态规划的“个性化”优化》2004 - 朱晨光:《优化,再优化!——从《鹰蛋》一题浅析对动态规划算法的优化》2007 - 杨哲:《凸完全单调性的加强与应用》计算几何立体几何2003 - 陆可昱:《长方体体积并》2008 - 高亦陶《从立体几何问题看降低编程复杂度》计算几何思想2004 - 金恺:《极限法——解决几何最优化问题的捷径》2008 - 程芃祺《计算几何中的二分思想》2008 - 顾研《浅谈随机化思想在几何问题中的应用》圆2007 - 高逸涵:《与圆有关的离散化》半平面交2002 - 李澎煦:《半平面交的算法及其应用》2006 - 朱泽园:《半平面交的新算法及其实用价值》矩阵矩阵2008 - 俞华程《矩阵乘法在信息学中的应用》高斯消元2002 - 何江舟:《用高斯消元法解线性方程组》数学方法数学思想2002 - 何林:《猜想及其应用》2003 - 邵烜程:《数学思想助你一臂之力》数学归纳法2009 - 张昆玮《数学归纳法与解题之道》多项式2002 - 张家琳:《多项式乘法》数形结合2004 - 周源:《浅谈数形结合思想在信息学竞赛中的应用》黄金分割2005 - 杨思雨:《美,无处不在——浅谈“黄金分割”和信息学的联系》其他算法遗传算法2002 - 张宁:《遗传算法的特点及其应用》2005 - 钱自强:《关于遗传算法应用的分析与研究》信息论2003 - 侯启明:《信息论在信息学竞赛中的简单应用》染色与构造2002 - 杨旻旻:《构造法——解题的最短路径》2003 - 方奇:《染色法和构造法在棋盘上的应用》一类问题区间2008 - 周小博《浅谈信息学竞赛中的区间问题》序2005 - 龙凡:《序的应用》系2006 - 汪晔:《信息学中的参考系与坐标系》物理问题2008 - 方戈《浅析信息学竞赛中一类与物理有关的问题》编码与译码2008 - 周梦宇《码之道—浅谈信息学竞赛中的编码与译码问题》对策问题2002 - 骆骥:《浅析解“对策问题”的两种思路》优化算法优化2002 - 孙林春:《让我们做得更好——从解法谈程序优化》2004 - 胡伟栋:《减少冗余与算法优化》2005 - 杨弋:《从<小H的小屋>的解法谈算法的优化》2006 - 贾由:《由图论算法浅析算法优化》程序优化2006 - 周以苏:《论反汇编在时间常数优化中的应用》2009 - 骆可强《论程序底层优化的一些方法与技巧》语言C++2004 - 韩文弢:《论C++语言在信息学竞赛中的应用》策略策略2004 - 李锐喆:《细节——不可忽视的要素》2005 - 朱泽园:《回到起点——一种突破性思维》2006 - 陈启峰:《“约制、放宽”方法在解题中的应用》2006 - 李天翼:《从特殊情况考虑》2007 - 陈雪:《问题中的变与不变》2008 - 肖汉骏《例谈信息学竞赛分析中的“深”与“广”》倍增2005 - 朱晨光:《浅析倍增思想在信息学竞赛中的应用》二分2002 - 李睿:《二分法与统计问题》2002 - 许智磊:《二分,再二分!——从Mobiles(IOI2001)一题看多重二分》2005 - 杨俊:《二分策略在信息学竞赛中的应用》调整2006 - 唐文斌:《“调整”思想在信息学中的应用》随机化2007 - 刘家骅:《浅谈随机化在信息学竞赛中的应用》非完美算法2005 - 胡伟栋:《浅析非完美算法在信息学竞赛中的应用》2008 - 任一恒《非完美算法初探》提交答案题2003 - 雷环中:《结果提交类问题》守恒思想2004 - 何林:《信息学中守恒法的应用》极限法2003 - 王知昆:《浅谈用极大化思想解决最大子矩形问题》贪心2008 - 高逸涵《部分贪心思想在信息学竞赛中的应用》压缩法2005 - 周源:《压去冗余缩得精华——浅谈信息学竞赛中的“压缩法”》逆向思维2005 - 唐文斌:《正难则反——浅谈逆向思维在解题中的应用》穷举2004 - 鬲融:《浅谈特殊穷举思想的应用》目标转换2002 - 戴德承:《退一步海阔天空——“目标转化思想”的若干应用》2004 - 栗师:《转化目标在解题中的应用》类比2006 - 周戈林:《浅谈类比思想》分割与合并2006 - 俞鑫:《棋盘中的棋盘——浅谈棋盘的分割思想》2007 - 杨沐:《浅析信息学中的“分”与“合”》平衡思想2008 - 郑暾《平衡规划——浅析一类平衡思想的应用》。
2024版圆周率ppt课件

2024/1/26
24
06
圆周率趣味知识
2024/1/26
25
记忆技巧分享
01
02
03
谐音记忆法
利用数字的谐音进行记忆, 如“山巅一寺一壶酒 (3.14159)”。
2024/1/26
故事记忆法
将圆周率的数字串编成一 个有趣的故事,通过联想 进行记忆。
歌曲记忆法
将圆周率的数字串谱成歌 曲,通过旋律和歌词进行 记忆。
28
THANK YOU
感谢观看
2024/1/26
29
2024/1/26
16
04
圆周率在数学中地位
2024/1/26
17
数学基础作用
圆周率是数学中的一 个重要常数,它代表 了圆的周长与直径之 比。
圆周率的精确值对于 数学理论的推导和证 明具有重要意义。
2024/1/26
圆周率在数学中扮演 着基础角色,涉及到 圆的面积、体积、弧 长等计算。
18
在几何、代数等领域应用
2024/1/26
多边形逼近法
通过构造与圆外切或内接的多边形,利用多边形周长与直径的 比值来逼近圆周率。随着多边形边数的增加,这个比值会越来 越接近π。
蒙特卡罗方法
这是一种基于概率的算法。通过随机生成大量点,并计算落在 圆内点的比例来估算圆的面积,进而求得圆周率的近似值。
10
分析法
2024/1/26
无穷级数法
利用一些与π有关的无穷级数公式, 通过逐项相加来得到π的近似值。 如莱布尼茨级数、欧拉公式等。
连分数法
将π表示为连分数的形式,通过截 断连分数并计算其近似值来得到π 的近似值。这种方法可以得到较高 精度的近似值。
元素周期律

△
金属性:Na > Mg 镁与盐酸反应比铝与盐酸反应更剧烈。
Mg + 2HCl = MgCl2 + H2↑
镁
铝
2Al + 6HCl = 2AlCl3 + 3H2↑
金属性:Mg > Al
Al2O3既能与盐酸反应,也能与NaOH反应,属两性氧化物。
Al2O3 + 6HCl = 2AlCl3 + 3H2O
同一主族元素 金属性和非金属变化
• 预测:从上到下,失电子能力逐渐增强,得 电子能力逐渐减弱。∴元素金属性逐渐增强, 非金属性逐渐减弱。 • 以碱金属和卤族元素为例: 碱金属:从上到下,金属性逐渐增强 卤素:从上到下,非金属性逐渐减弱, 金属性逐渐增强。
思考:
Li
元素的性质呈现出周期性的变化,那 么这种周而复始是不是又回到了原来的起点了呢? 每一主族的元素性质相似,是不是完全相同?
NaOH溶液→
Al2O3 + 2NaOH = H2O + 2NaAlO2
←Al(OH)3
偏铝酸钠
AlCl3溶液 → 稀硫酸→
AlCl3 + 3NaOH = Al(OH)3↓+ 3NaCl 2Al(OH)3 + 3H2SO4 = Al2(SO4)3+6H2O
←Al2(SO4)3 溶液Al(OH)3→ NaOH源自液→和钠与水的反应作对比。
Conclusion 结论
1. 锂、钠、钾都能与水反应 2. 反应越来越剧烈。
Preduction演示
1.铷与铯能与水反应吗? 2.反应剧烈程度如何?
碱金属单质与水反应
Li
Na
K
Rb
Cs
Conclusion 结论
循环字符串的最小表示(自学)

循环字符串的最小表示drizzlecrj整理循环同构问题:给出两个串:s1 = “babba”和s2 = “bbaba”,其中两者均看成环状的,即首尾是相接的,问:从s1的哪里断开可以得到和s2一样的串或者两者用不会相同?本题就是从s1的第2个字符’a’后面断开,可以得到与s2一样的串。
这个问题就是同构问题。
下面一步一步分析:1.朴素算法(O(nm)):即尝试s1的n个断开点,与s2进行比较,如果相同则找到同构位置,否则找不到。
该算法仅适用于n, m规模较小情况,对于n, m 都在10000规模的长度,明显速度太慢。
2.转换为模式匹配:对于此类问题,已经有一个很好的转换思路了,即:首先构造新的模型:S=s1+s1为主串,s2为模式串。
如果s1和s2是循环同构的,那么s2就一定可以在S中找到匹配。
否则找不到匹配则两则不能同构。
而在S中寻找s2的匹配是有很多O(N+M)级的算法了,KMP算法就是这样一个优秀的算法,所以本问题转换为模式匹配后应用KMP算法,可以在O(n+m)的时间内获得问题的解。
3.下面再来看看“最小表示法”在此类问题中的应用(算法思路来源于国家队的一位队员--周源),它也可以在O(n+n)时间内求解,更大的优势还有无需KMP算法的Next数组,仅需要两个指针即可。
一.从小问题谈起:问题:有两列数a1,a2…an和b1,b2…bn ,不记顺序,判断它们是否相同。
eg:{an} = {2, 3, 5, 7};{bn} = {2, 7, 5 3}。
一眼可见两者是相同的,但是对于计算机来说,如果采用枚举算法,那么比较次数将是:n*(n-1)*(n-2)….*2*1 = n! 量级。
阶乘增长之快,时间上是无法忍受的。
抓住问题的本质:如果两列数相同,那么它们排序之后从头到尾肯定一样!则问题在O(nlogn)时间解决。
可见这个问题的本质就在于排序(非降序)之后的序列是原序列的“最小表示”,如果两个序列的“最小表示”相同则两者就相同,否则就不相同。
周期表
19 20 21 22 23 37 38 39 40 41 55 56 87 88
57 71
89103
24 42 74
25 43
27 28 29 30 31 32 33 34 35 36 45 46 47 48 49 50 51 52 53 54 77 78 79 80 81 82 83 84 85 86
3 、 A 、 B 、 C 、 D4 种短周期元素的原子序数依次 增大。 A、D同族,B、 C同周期。 A、B组成的化 合物甲为气态,其中A、B原子数之比为4:1。由 A、 C组成的两种化合物乙和丙都为液态,乙中A、 C原子数之比为1:1,丙中为2:1。由 D、 C组成 的两种化合物丁和戊都为固态,丁中D、C原子数 之比为1:1,戊中为2:1。 写出分子式:甲 CH4 乙 H2O2 丙 H2O , 丁 Na2O2 戊 Na2O ; 写出B元素的氧化物跟丁发生反应的化学方程式:
元素周期表中的规律及技巧 1、核外电子层数=周期数 2、主族元素的最外层电子数=主族序数=最高正化合价 3、质子数=原子序数=原子核外电子数 4、主族元素的最高正价=主族序数; 负价的绝对值=8—主族序数 5、族序数等于周期数的元素 ;族序数等于周期数2倍的元 素 ;族序数等于周期数3倍的元素 . 6、周期数是族序数2倍的元素 ,3倍的元素 . 7、最高正价与最低负价代数和为零的短周期元素 . 8、最高正价是最低负价绝对值3倍的短周期元素 . 9、除H外,原子半径最小的元素 . 10、短周期中其离子半径最大的元素 . 11、最高化合价不等于族序数的元素 .
原子半径周期性递变图
元素化合价周期性递变图
+7 +6 +5 +4 +3 +2 +1 -1 -2 -3 -4
1.1 元素周期表

▪3 5
▪3 6
▪5
▪3 7
▪3 8
▪3 9
▪4 0
▪4 1
▪4 2
▪4 3
▪4 4
▪4 5
▪4 6
▪4 7
▪4 8
▪4 9
▪5 0
▪5 1
▪5 2
▪5 3
▪5 4
▪6
▪5 5
▪5 6
▪5 771
▪7 2
▪7 3
▪7 4
▪7 5
▪7 6
▪7 7
▪7 8
▪7 9
▪8 0
▪8 1
▪8 2
▪8 3
▪8 4
同钠与氧气的反应比较。
[实验现象] 金属钾被加热后熔成金属小球,并且剧烈燃 烧,发出紫色火焰。
比钠剧烈
(2)钾与H20的反应 在小烧杯中放入一些水,然后
取绿豆大的钾,吸干表面的煤油, 投入到小烧杯中,观察现象。 [实验现象]金属钾浮在水面上,剧烈反应,听到微
弱的爆鸣声,并且出现紫色的火光。
2K+2H2O=2KOH+H2
2M + 2H2O === 2MOH + H2↑
碱金属的化学性质
与O2反应
Li
Na
反应不如钠 点燃剧烈
剧烈,生成 燃烧,生
Li2O
成Na2O2
K
Rb Cs
燃烧更加剧 遇空气立即遇空气立即
烈生成比过 燃烧,生成燃烧,生成
氧化物复杂 更复杂的氧更复杂的氧
的氧化物 化物
化物
剧烈,生 更剧烈,生 轻微的爆炸,遇水立即燃遇水立即燃
元素名称 核电 荷数
原子结构 最外层 电子层 示意图 电子数 数
碱 锂 Li
国家集训队论文分类

2007 - 胡伯涛:《最小割模型在信息学竞赛中的应用》
2007 - 王欣上:《浅谈基于分层思想的网络流算法》
2008 - 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》
最短路
2006 - 余远铭:《最短路算法及其应用》
2008 - 吕子鉷《浅谈最短径路问题中的分层思想》
2009 - 刘聪《浅谈数位类统计问题》
动态统计
2004 - 薛矛:《解决动态统计问题的两把利刃》
2007 - 余江伟:《如何解决动态统计问题》
博弈
2002 - 张一飞:《由感性认识到理性认识——透析一类搏弈游戏的解答过程》
2007 - 王晓珂:《解析一类组合游戏》
2009 - 曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》
国家集训队论文分类
组合数学
计数与统计
2001 - 符文杰:《Pólya原理及其应用》
2003 - 许智磊:《浅谈补集转化思想在统计问题中的应用》
2007 - 周冬:《生成树的计数及其应用》
2008 - 陈瑜希《Pólya计数法的应用》
数位问题
2009 - 高逸涵《数位计数问题解法研究》
置换群
2005 - 潘震皓: - 高正宇:《答案只有一个——浅谈问答式交互问题》
猜数问题
2003 - 张宁:《猜数问题的研究:<聪明的学生>一题的推广》
2006 - 龙凡:《一类猜数问题的研究》
数据结构
数据结构
2005 - 何林:《数据关系的简化》
最小生成树
2004 - 吴景岳:《最小生成树算法及其应用》
高考化学-元素周期律 总结

知识结构图:一·周期表结构二·“位,构,性”的相互推导元素周期律三·原子结构四·碱金属五·卤素一.周期表结构1. 元素周期表注意:①元素周期表的上界②金属与非金属的边界线2.3.每个周期元素的总数和每个周期过渡元素的总数二.“位、构、性”的相互推导 失电子能力↓⇒金属性↑1.结构与性质 原子半径↑⇒F↓得电子能力↓⇒非金属性↓(1)原子核对最外层电子的引力核电核数↓ ⇒F↓半径↓ 半径↑ (主)同周期 F↓ 同主族 F↓ 质子数↑ 质子数↓(次) 多⇒得电子(2)最外层电子数 少⇒失电子ⅡA ⅢA 二三 X X+1 四五 X X+11 六七 X X+25221r q q G F =4 ⇒共用电子对(3)化合价与结构的关系:最高正价数=最外层电子数最低负价数=8-最外层电子2.位置与结构(1) 周期数=电子数主族序数=3.位置与性质(1)递变规律化合价 +1 +7递变规律 -4 -1原子半径↓,金属性↓,非金属性↑相似性 化合价相同递变性 原子半径↑金属性 ↑非金属性↓Ⅳ:- 4,+2,+4Ⅴ:-3,+3,+5(特殊的氮:-3~+5)Ⅵ:-2,+4,+6Ⅶ:-1,+1,+3,+5,+7成正比:失电子能力,还原性,单质与水,与酸,水化物的碱性(2成反比:阳离子的氧化性成正比:得电子能力,氧化性,单质与氢气,氢化物的稳定性,(3 最高价氧化物对应的水化物的酸性成反比:阴离子的还原性(4)无氧酸的酸性:①同周期:与非金属性成正比,HCl >H 2S②同主族:与非金属性成反比,HF <HCl <HBr <HI三.原子结构 原子:Z 个原子核1.原子构成(X A Z ) 电子:Z 个2.两个等量关系3.核素4.同位素5.核素的相对原子质量≈核素的质量数Ar (X A Z )=)(C X A Z 12121m )m( 6.元素的相对原子质量中子:A-Z 个例:Ar (O )=Ar (O 16)·a %+Ar (O 17)·b %+Ar (O 18)·c %7.核外电子排布规律(1)22n (个)(2)最外层≤8(He≤2)次外层≤18倒数第三层≤32(3)能量最低8.半径的比较规律同周期:从左到右,r↓ (1)原子半径同主族:从上到下,r↓都不同:左下与右上,r 左下>r 右上 ;左上与右下,无法比较电子数相同 同主族:从上到下,r↓ 同周期:阴离子>阳离子,且都从左到右减小(3)同一元素的不同离子:电子数↑⇒r↑四.碱金属①物理性质:银白色,柔软,密度小,熔、沸点低,导热导电性很好 ②化合价:+1③活泼金属,易失去电子④单质还原性很强 ⑤MOH 都是强碱⑥单质易与O 2、卤素单质,硫反应⑦单质易与H 2O 、酸反应⑧单质不能从盐溶液中置换出金属①从上到下单质的溶沸点减小②单质的密度增大2.递变性 ③原子半径↑④离子半径↑⑤金属性↑①Cs 略带金色光泽3.特殊性 ②ρ(Na )>ρ(K ) Li 2O③与O 2反应 M+O 2 Na 2O 2KO 2 (钾以后的更复杂)五.卤素质子数↑⇒r 电荷数↑⇒r ↓ (2)离子半径 1.相似性①物理性质:单质熔、沸点都比较低 ②化合价:-1,+2,+3,+5,+7 ③活泼非金属,易得电子 ④单质氧化性很强 ⑤H 2+X 2→HX ⑥X 2+H 2O→HX +HXO(F 2除外) ⑦X 2+NaOH→NaX+NaXO+H 2O(F 2除外) ⑧X 2+M→MX n⑨卤代反应⑩加成反应①从上到下单质的熔、沸点,密度增大②单质的状态:气→液→固③单质的颜色变深2.递变性 ④非金属性减弱⑤原子、离子半径增大,⑥HX 的酸性增强⑦X 2+H 2O→HX+HXO 的反应强度减弱①氟的化合价只有-1,没有正价②氟没有含氧酸③2F 2+2H 2O=4HF+O 2 ④F 2+NaOH= NaF+OF 2↑+H 2O⑤F 2不能置换其他卤化物水溶液中的卤素,直接和水反应 ⑥I 2和Fe 反应生成Fe 2+ I 2+Fe→FeI 2 (Fe+X 2→FeX 3)3.特殊性 1.相似性。
2元素周期律与元素周期表
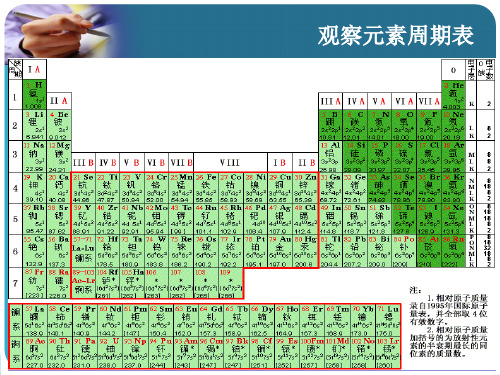
He 氦 2 2 1 2 -- 4.003 0
接上表
Li 锂 3 2,1 2 1 0.152 6.941 +1 Be 铍 4 2,2 2 2 0.089 9.012 +2 B 硼 5 2,3 2 3 0.082 10.81 +3 C 碳 6 2,4 2 4 0.077 12.01 +4,-4 N 氮 7 2,5 2 5 0.075 14.01 +5,-3 O 氧 8 2,6 2 6 0.074 16.00 -2 F 氟 9 2,7 2 7 0.071 19.00 -1 Ne 氖 10 2,8 2 8 -- 20.18 0
接上表
Na 钠 11 2,8,1 3 1 0.168 22.99 +1 Mg 镁 12 2,8,2 3 2 0.160 24.31 +2 Al 铝 13 2,8,3 3 3 0.143 26.98 +3 Si 硅 14 2,8,4 3 4 0.117 28.09 +4,-4 P 磷 15 2,8,5 3 5 0.110 30.97 +5,-3 S 硫 16 2,8,6 3 6 0.102 32.06 +6,-2 Cl 氯 17 2,8,7 3 7 0.099 35.45 +7,-1 Ar 氩 18 2,8,8 3 8 -- 39.95 0
❖同一竖行(同主族):层多径大。从上到下,原子半 径依次增大
❖同种元素:价高径小。化合价越高,半径越小。
❖同结构: 序高径小。 电子层相同的离子。离子序数 越大,半径越小。
(3)原子序数——元素最高正价最低负价坐标图
+7 +6 +5 +4 +3 +2 +1
-1 -2 -3 -4
【高中化学】元素周期律PPT课件52(3份)2

1
2 3 4 5 6 7 最强
金 属 性 逐 渐 增 强
非 金 属 性 逐 渐 增 At 强
金属性逐渐增强
思考与交流
你能理解“位(位置)——构(结构)—— 性(性质)”三者之间的关系吗?
原子结构 电子层数 金属性、非金属 最外层电子数 性强弱 原子结构决定元素在周期表中的位 周期数= 电子层数 (主族)最外层电子数 置和性质。元素在周期表中的位置, 主族序数=最外层电子数 = 最高正价数 反映了元素的原子结构和元素的性 非金属最高正价+|最低负价|= 8 原子序数= 核电荷数 表中位置
本节内容结束
1、不要做刺猬,能不与人结仇就不与人结仇,谁也不跟谁一辈子,有些事情没必要记在心上。 2、相遇总是猝不及防,而离别多是蓄谋已久,总有一些人会慢慢淡出你的生活,你要学会接受而不是怀念。 3、其实每个人都很清楚自己想要什么,但并不是谁都有勇气表达出来。渐渐才知道,心口如一,是一种何等的强大! 4、有些路看起来很近,可是走下去却很远的,缺少耐心的人永远走不到头。人生,一半是现实,一半是梦想。 5、你心里最崇拜谁,不必变成那个人,而是用那个人的精神和方法,去变成你自己。 6、过去的事情就让它过去,一定要放下。学会狠心,学会独立,学会微笑,学会丢弃不值得的感情。 7、成功不是让周围的人都羡慕你,称赞你,而是让周围的人都需要你,离不开你。 8、生活本来很不易,不必事事渴求别人的理解和认同,静静的过自己的生活。心若不动,风又奈何。你若不伤,岁月无恙。 9、命运要你成长的时候,总会安排一些让你不顺心的人或事刺激你。 10、你迷茫的原因往往只有一个,那就是在本该拼命去努力的年纪,想得太多,做得太少。 11、有一些人的出现,就是来给我们开眼的。所以,你一定要禁得起假话,受得住敷衍,忍得住欺骗,忘得了承诺,放得下一切。 12、不要像个落难者,告诉别人你的不幸。逢人只说三分话,不可全抛一片心。 13、人生的路,靠的是自己一步步去走,真正能保护你的,是你自己的选择。而真正能伤害你的,也是一样,自己的选择。 14、不要那么敏感,也不要那么心软,太敏感和太心软的人,肯定过得不快乐,别人随便的一句话,你都要胡思乱想一整天。 15、不要轻易去依赖一个人,它会成为你的习惯,当分别来临,你失去的不是某个人,而是你精神的支柱;无论何时何地,都要学会独立行走 ,它会让你走得更坦然些。 16、在不违背原则的情况下,对别人要宽容,能帮就帮,千万不要把人逼绝了,给人留条后路,懂得从内心欣赏别人,虽然这很多时候很难 。 17、做不了决定的时候,让时间帮你决定。如果还是无法决定,做了再说。宁愿犯错,不留遗憾! 18、不要太高估自己在集体中的力量,因为当你选择离开时,就会发现即使没有你,太阳照常升起。 19、时间不仅让你看透别人,也让你认清自己。很多时候,就是在跌跌拌拌中,我们学会了生活。 20、与其等着别人来爱你,不如自己努力爱自己,对自己好点,因为一辈子不长,对身边的人好点,因为下辈子不一定能够遇见。
PIVAS的职业风险和防护

PIVAS的职业风险和防护摘要】通过认识PIVAS中存在的种种职业风险危害,并积极采取相应的安全防护措施,更加完善静脉配置中心的优化管理。
【关键词】 PIVAS 职业风险防护措施【中图分类号】R471 【文献标识码】B 【文章编号】2095-1752(2013)30-0266-02随着静脉配置中心在临床上的开展,配置中心的工作人员所面临的职业危害引起了广泛的注意,工作人员在PIVAS中长期受到噪音、锐器伤、辐射、化学消毒剂,工作强度等危害,因此我们需要采取安全有效的防护措施,降低可能导致职业病的各种危害,防患于未然。
1 分析PIVAS中存在的职业风险因素1.1物理因素(1)噪音:为确保静脉配置中心空气洁净达到万级标准及局部环境达到百级标准,抽排风设备及中央空调需要24小时运行,因此空调风机及加药时震荡器等噪声时刻存在。
电脑、打印机、冰箱等设备发出的噪音,长期会引起耳聋,听力下降,机体植物神经紊乱,甚至会引起内分泌功能紊乱等疾病[1]。
(2)锐器损伤:为PIVAS中最常见的损伤,如被安瓿玻璃划伤、扎伤、配药时针头扎伤,清洁物品时皮肤损伤,还有药物微粉不慎溅入眼中等。
(3)辐射:紫外线是PIVAS用于环境消毒的主要方法,它对人体的伤害主要表现在暴露的皮肤和眼睛上,引起皮肤老化,甚至皮肤癌,白内障,眼睛灼伤。
紫外灯发出的臭氧,长期接触会增加呼吸和心血管疾病的死亡率。
长期接触电磁辐射的人群也可能受累积效应影响,易产生身体系统各方面的损伤。
1.2化学因素(1)药物:医务人员每天反复接触各种药物,通过皮肤接触、呼吸道吸入,其过敏反应率明显高于普通人员。
因在PIVAS集中配置大量细胞毒药物和抗生素,长期暴露在这些药物之下,有可能损害器官、致流产、致畸!(2)化学消毒剂:消毒剂具有一定的挥发性、刺激性、和腐蚀性。
PIVAS医务人员需要每天使用含氯消毒剂和75%乙醇等进行消毒,挥发性的消毒剂能直接被鼻、口、眼等暴露的粘膜吸收,易引起皮肤过敏、头痛、鼻炎、呼吸道等刺激症状。
元素周期律(第二课时)

(2)比较原子半径大小的规律:
①电子层数不同时,电子层数越多,原子半径越大。
②电子层相同时,核电荷数越大,原子半径越小。
元素周期表中的同 周期主族元素从左到 右,原子半径的变化 趋势如何?应如何理 解这种趋势?周期表 中的同主族元素从上 到下,原子半径的变 化趋势如何?应如何 理解这种趋势?
原子半径的周期性变化
P
S
Cl
光照或点 燃反应 高氯酸 HClO4 最强酸
磷蒸气与 加热反 氢气反应 应 磷酸 H3PO4 中强酸 硫酸 H2SO4 强酸
非金属性:Si < P < S < Cl 综上所述: Na
Mg
Al
Si
P
S
Cl
金属性逐渐减弱,非金属性逐渐增强
元素的金属性与非金属性
规律: ①、同周期元素的金属性,随荷电荷数的增加 而减小,如:Na>Mg>Al;非金属性,随荷电荷 数的增加而增大,如:Si<P<S<Cl。 ②、同主族元素的金属性,随荷电荷数的增加 而增大,如:Li<Na<K<Rb<Cs;非金属性,随荷 电荷数的增加而减小,如:F>Cl>Br>I。 ③、金属活动性顺序表: K>Ca>Mg>Al>Zn>Fe>Sn>Pb>(H)>Cu>Hg>Ag >Pt>Au
(3)电负性的应用
一般认为: 电负性 1.8的元素为非金属元素,电负 性数值越大,元素的非金属性越强。 大于 电负性 1.8的元素为金属元素。电负性 数值越小,元素的金属性越强。
①判断元素金属性和非金属性的强弱。
小于
电负性等于1.8的元素为半金属或准金属元素
元素周期表

核素
1. 原子的构成、原子核的构成是怎样的?
原子
{ 核外电子
原子核 {
质子 中子
如果忽略电子的质量,将原子核内所有 的质子和中子的相对质量取近似整数值加起 来,所得的数值,我们称之为质量数。
质量数=质子数+中子数 质量数 —— A
核电荷数 —— Z (核内质子数)
X
——元素符号
同种元素的原子的质子数 如:11H、21H、相等,但中子数不一定相等。 3 H就各为一 我们把具有一定数目的质子 1 种核素,他们 和一定数目的中子的一种原子叫 都是氢的同位 做核素。 素。 同一元素的不同核素互称 同位素。
1.按原子序数递增的顺序从左到右排列 2.将电子层数相同元素排成一个横行(7) 3.把最外电子数相同的元素排成一个纵行(18)
(二)、构造
2 短 周 第二周期: 8 期 第三周期:
第一周:
8 注意:周期序数由电子层层数决定
18 长 第四周期: 周 第五周期: 18 期 第六周期: 32
不完全周期
第七周期: 26
镧57La – 镥71Lu 共15 种元素称镧系元素 锕89Ac – 铹103Lr 共15 种元素称锕系元素
• 把最外层电子数相同的元素按电子层数递增的顺序从上到下排 成纵行——族。
族的分类
主族
副族 长周期 元素 7
零族
Ⅷ族
包含元素 长、短周期 元素 表示 个数 7
稀有气体 8、9、10 元素 纵行 0 1 Ⅷ 1
许多元素都有同位素,如氧、碳、铀等,同位 素在日常生活、工农业生产和科学研究中有着重要的用 途……Leabharlann ⅠA,ⅡA等 ⅠB,ⅡB等
思考:为什么我们将稀有气体元素称为零族元素? ——它们很稳定,它们的化合价通常情况下为0。 结构:(七主、七副、零八族); 最外层电子数决定。 主族序 数由
第一节 元素周期表

元素周期表
上学科网,下精品资料!
问题
随着原子序数的递增,原子半径有什么变化? 随着原子序数的递增,原子半径有什么变化?
答⑴ 原子半径出现周期性变化 不够具体!是从大到小,还是从小到大? 不够具体!是从大到小,还是从小到大? 答⑵ 原子半径由大逐渐变小 岂不是氢原子的半径最大, 号元素的原子 岂不是氢原子的半径最大,112号元素的原子 半径最小吗,可见结论是错误的。 半径最小吗,可见结论是错误的。 错在没有“电子层数相同”这个前提 前提和 错在没有“电子层数相同”这个前提和“稀有 气 体元素原子除外”这个特例。 体元素原子除外”这个特例。 特例
三个短周期,七个主族和零族的元素符 三个短周期,七个主族和零族的元素符 号和名称。 号和名称。 零族元素(稀有气体) 零族元素(稀有气体)的原子序数
练习
号元素: 第6号元素: 号元素
推算原子序数为6,13,34,53,88,82的 的 推算原子序数为
元素在周期表中的位置。 元素在周期表中的位置。
6-2=4 第二周期第Ⅳ 第二周期第ⅣA 族。 第三周期第Ⅲ 第三周期第ⅢA 族。 第四周期第Ⅵ 第四周期第ⅥA 族。 第五周期第Ⅶ 第五周期第ⅦA 族。 第七周期第Ⅱ 第七周期第ⅡA 族。 第六周期第Ⅳ 第六周期第ⅣA 族。
副族: 副族: B , ⅡB , ⅢB , ⅣB ,ⅤB , ⅥB , ⅦB Ⅰ Ⅴ 族
纵向) (纵向) 共七个副族
第VIII 族:三个纵行,位于Ⅶ B 与ⅠB中间 三个纵行,位于Ⅶ 中间 零族: 零族: 稀有气体元素
主族序数 = 最外层电子数
请您回答
氦元素原子最外层有两个电子, 氦元素原子最外层有两个电子,为什么 不把它排在ⅡA族 不把它排在ⅡA族? ⅡA K层填充两个电子已达饱和,性质与ⅡA 层填充两个电子已达饱和,性质与ⅡA 族的元素完全不同。 族的元素完全不同。 卤族元素和氧族元素分别是周期表的哪 一族? 一族? ⅦA、 ⅦA、ⅥA
人教版版高中化学必修二元素周期表
8 . 日 地 距离 适中, 使得表 面温度 适宜, 有液态 水存在 ;体积 和质量 适中, 产生适 当的引 力,形 成稳定 的大气 层,具 有适合 生物呼 吸的空 气;地 球运动 周期适 中,有 利于适 宜温度 的形成 。
9 . 联 系 文章 的主题 或作者 的情感 态度揣 摩词语 的含义 ,一般 分析具 有深层 含义或 特定意 义的词 语,点 明中心 或主旨 的词语 等依据 此法。
一、元素周期表的历史
1.第一张元素周期表 (1)时间: 1869年 (2)绘制者: 俄国化学家——门捷列夫 (3)排序依据:将元素按照相对原子质量由小到大依次排列 (4)结构特点:将化学性质相似的元素放在一个纵行 (5)意义: 揭示了化学元素的内在联系——里程碑 2.现行元素周期表
(1)排序依据:按照原子序数 (2)原子序数:原子的核电荷数 (3)结构特点:
10
—— 8 种
18
—— 18 种 36
—— 18 种 54
—— 32 种 86 —— 26 种 118
主族 共 7 个主族,包括短周期和长周期元素
族
副族 共 7 个副族,只包括在长周期中
(16个族) 第VIII族 包括第8、9、10 纵行
(18个纵行) 0 族
稀有气体元素
周 第七
Ⅷ
期主
表 族七
里 。副
数和
周零
期族
1,
2 3 4 5
最 后 莫 忘
6
7
横行叫周期,共有七周期; 三四分长短,第七不完全。 纵行称作族,共有十六族; 二、三分主副,先主后副族; VIII族最特殊,三行是一族; 二次分主副,副后是主族。 一、八依次现,一、零再一遍。 锕、镧各十五,均属IIIB族。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
IOI2003冬令营演示文稿 安徽 周源
构造新的算法
首先构造新的模型: S=s1+s1为主串,s2为模式串。 如果s1和s2是循环同构的, 那么s2就一定可以在S中找到匹配!
IOI2003冬令营演示文稿 安徽 周源
匹配算法:理论的下界
在S中寻找s2的匹配是有很多O(N)级的算法的。 本题最优算法的时空复杂度均为O(N)级。 这已经是理论的下界了。
s2=‘c d a b’
IOI2003冬令营演示文稿 安徽 周源
明确几个记号和概念
⑹.设有两个映射f1,f2:A→A, 定义f1和f2的连接f1•f2(x)=f1(f2(x))。
IOI2003冬令营演示文稿 安徽 周源
问题的数学语言表达形式
给定两个长度相等的字符串,|s1|=|s2|, 判断它们是否是循环同构的。
所以s1(x-1)不可能是s1的最小表示! 因此M(s1)>i+k, 指针i滑到u[i+k+1]处仍可以保证小于等于M(s1)!
u:
1
…
i
…
x
…
i+k i+k+1
…
|s1|…
s1(x-1)的前几个字符 一定是s1的其他循环表示的前几个字符 w: 1 … j … j+(x-i)
大于
… j+k j+k+1 … |s2|…
设s1=‘babba’,s2=‘bbaba’。
i i 因为u[i+k]>w[j+k] 所以移动指针i
比较失败时k=0
u=‘b a b b a b a b b a’ w=‘b b a b a b b a b a’
j 不相等
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
设s1=‘babba’,s2=‘bbaba’。
“最小表示法”就是可以应用于此类题目的一种思 想: 确立一种T中事物 将s和t化成规定大小关系
的大小关系 根据F中的变化规则 中的最小者m1和m2 m1≠m2 如果 m1=m2 可以证明, s和t不是本质相同
t
本质相同
m2
本质相同
m1
本质相同
s
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
其中F满足两个条件: ⑴.任意t∈T,一定能在F中一系列映射的连接 的作用下,仍被映射至t。即任意一个事物t∈T, 它和自己是F本质相同的。 即“本质相同”这个概念具有自反性。 ⑵. 任意s,t∈T,若在F的一系列映射作用下, s和t是F本质相同的。那么一定有另一系列属于 F的映射作用下,t和s是F本质相同的。 即“本质相同”这个概念具有对称性。
s串: 1 2… i … j … |s|
S(1)串: 2…
i
…
j
…
|s|
1
IOI2003冬令营演示文稿 安徽 周源
明确几个记号和概念
⑸.如果字符串s1可以经过有限次循环得到 s2,则称s1和s2是循环同构的。例如:
s1=‘a b c d’
一次循环
‘b c d a’
一次循环
s1和 s2 是循 环同 构的 !
小结:引例
这道题虽然简单,却给了我们一个重要的启示: 当某两个对象有多种表达形式,且需要判 断它们在某种变化规则下是否能够达到一 个相同的形式时,可以将它们都按一定规 则变化成其所有表达形式中的最小者,然 后只需要比较两个“最小者”是否相等即 可!
IOI2003冬令营演示文稿 安徽 周源
定义:“最小表示法”
s=‘b b b a a b’
如M(‘bbbaab’)=4
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
现在换一种思路:
设u=s1+s1,w=s2+s2并设指针i,j指向u,w第一个字符
s1: 1
… |s1|
u: w:
1 1
… …
|s1| |s1|+1 … 2*|s1| |s2| |s2|+1 … 2*|s2|
IOI2003冬令营演示文稿 安徽 周源
枚举算法
易知,s1的不同的循环串最多只有|s1|个, 即s1,s1(1),s1(2),…s1(|s1|-1), 所以只需要把他们一一枚举, 然后分别与s2比较即可。
IOI2003冬令营演示文稿 安徽 周源
枚举算法 Time Limit Exceeded!
优点:思维简单,易于实现。 时间复杂度是O(N2)级(N=|s1|=|s2|)。 如果N大一些,几十万,几百万……
IOI2003冬令营演示文稿 安徽 周源
小结:枚举和匹配算法
很容易得到的枚举算法显然不能满足大数据的要求, 于是我们从算法的执行过程入手, 探查到了枚举算法的实质:模式匹配。 最后,通过巧妙的构造、转换模型, 直接套用模式匹配算法,得到了O(N)级的算法。
IOI2003冬令营演示文稿 安徽 周源
IOI2003冬令营演示文稿 安徽 周源
浅析“最小表示法”思想 在字符串循环同构问题中的应用
安徽省芜湖市第一中学 周 源
IOI2003冬令营演示文稿 安徽 周源
前言
“最小表示法”比起动态规划、贪心等思想, 最小表示法”比起动态规划、贪心等思想, 最小表示法 在当今竞赛中似乎并不是很常见。但是 在当今竞赛中似乎并不是很常见。 在解决判断“同构” 在解决判断 “同构 ”一类问题中却起着 重要的作用。 重要的作用。 本文即将讨论字符串中的同构问题, 本文即将讨论字符串中的同构问题 , 如何 巧妙地运用最小表示法来解题呢, 巧妙地运用最小表示法来解题呢 ,让我 们继续一起思考吧。 们继续一起思考吧。
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
同理,当u[i+k]<w[j+k]的时候,可以将指针j滑到w[j+k+1]处! 也就是说,两指针向后滑动比较失败以后,
指向较大字符的指针向后滑动k+1个位置。
下面让我们将这种方法应用于一个实例。
IOI2003冬令营演示文稿 安徽 周源
[分析]
由于题目要求“不记顺序”,因此每一列数的不 同形式高达n!种之多! 如果要一一枚举,显然是不科学的。
如果两列数是相同的,那么将它们排 序之后得到的数列一定也是相同的。 {an}:4 2 6 3 {bn}:6 2 3 4
排序后
{an}:2 3 4 6 {bn}:2 3 4 6
相同
IOI2003冬令营演示文稿 安徽 周源
⑴.|s|=length(s),即s的长度。 ⑵.s[i]为s的第i个字符。 ⑶.s[i→j]=copy(s,i,j-i+1)。 这里1≤ i≤ j≤ |s|。
s[i→j]
s串:
1
…
i
…
j
…
|s|
IOI2003冬令营演示文稿 安徽 周源
明确几个记号和概念
⑷.定义s的一次循环s(1)=s[2→|s|]+s[1]; s的k次循环(k>1)s(k)为s(k-1)的一次循环; s的0次循环s(0)=s。
IOI2003冬令营演示文稿 安徽 周源
问题引入
有两条环状的项链,每条项链上各有N个多种 颜色的珍珠,相同颜色的珍珠,被视为相同。 问题:判断两条项链是否相同。 简单分析:由于项链是环状的,因此循环以 后的项链被视为相同的,如图的两条项链就 是一样的。
IOI2003冬令营演示文稿 安徽 周源
明确几个记号和概念
IOI2003冬令营演示文稿 安徽 周源
求一个字符串的最小表示
直到j=n。 在上述步骤中,始终保持了i<j,这样就不 会出现i=j而直接停止的情况。实际上, 对于长度为n的字符串的n种同构,上述 方法是都判断了的,只是,对于不满足 的就直接跳过了。这类似于用较人体法 国优解去推更优解,直到推出最优解。 那么,什么情况下,
s2: 1
… |s2|IBiblioteka I2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
现在换一种思路:
如果s1和s2是循环同构的,那么当i,j分别指向M(s1),M(s2)时, 一定可以得到u[i→i+|s1|-1]=w[j→j+|s2|-1],迅速输出正确解。 |s1|
i u: w: 1 1 … M(s1) … … … 2*|s1|
u: 1 … i … x … i+k i+k+1 大于 j+k j+k+1 … … |s1|…
“最小表示法”在本题的应用
相等
w: 1 … j … j+(x-i) … …
|s2|…
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用 很容易就得到u[x→i+k]>w[j+(x-i)→j+k]。
i i 因为u[i+k]>w[j+k] 所以移动指针i
比较失败时k=2
u=‘b a b b a b a b b a’ w=‘b b a b a b b a b a’
j 不相等
IOI2003冬令营演示文稿 安徽 周源
“最小表示法”在本题的应用
设s1=‘babba’,s2=‘bbaba’。
i
u=‘b a b b a b a b b a’ w=‘b b a b a b b a b a’
IOI2003冬令营演示文稿 安徽 周源
因为u[x]在u[i]后(x-i)个位置, 对应的可以找到在w[j]后(x-i)个位置的w[j+(x-i)], 同样对应的有u[x+1]和w[j+(x+1-i)],u[x+2]和w[j+(x+2)-i], 直到u[i+k-1]和w[j+k-1]。 它们都是相等的, 即有u[x→i+k-1]=w[j+(x-i)→j+k-1]。
