上海市各区县历年中考数学模拟压轴题汇总及答案
2019-2020年上海各区数学中考一模压轴题分类汇编-18题含详解
专题2020年分类汇编-18题专题一图形的翻折【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在等腰梯形ABCD中,AD∥BC,sin C=45,AB=9,AD=6,点E、F分别在边AB、BC上,联结EF,将△BEF沿着EF所在直线翻折,使BF的对应线段B′F经过顶点A,B′F交对角线BD于点P,当B′F⊥AB时,AP的长为.2.(2019秋•青浦区期末)已知,在矩形纸片ABCD中,AB=5cm,点E、F分别是边AB、CD的中点,折叠矩形纸片ABCD,折痕BM交AD边于点M,在折叠的过程中,如果点A 恰好落在线段EF上,那么边AD的长至少是cm.3.(2019秋•闵行区期末)如图,在等腰△ABC中,AB=AC=4,BC=6,点D在底边BC 上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为.4.(2019秋•杨浦区期末)在Rt△ABC中,∠A=90°,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B 所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=.5.(2019秋•崇明区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,D是AC的中点,点E在边AB上,将△ADE沿DE翻折,使得点A落在点A′处,当A′E⊥AB时,则A′A=.6.(2019秋•静安区期末)如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为.专题二图形的旋转【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG 的正切值是.2.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为.3.(2019秋•长宁、金山区期末)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B 的对应点是点B′,则BB′的长等于.4.(2019秋•松江区期末)如图,矩形ABCD中,AD=1,AB=k,将矩形ABCD绕着点B 顺时针旋转90°得到矩形A′BC′D′,联结AD′,分别交边CD,A′B于E、F,如果AE D′F,那么k=.5.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为.6.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是.7.(2019秋•普陀区期末)如图,在RtΔABC中,∠C=90°,AC=5,sinB=513,点P为边BC上一点,PC=3,将△ABC绕点P旋转得到△A'B'C'(点A,B、C分别与点A'、B'、C'对应).使B'C'∥AB,边A'C'与边AB交于点G,那么A'G 的长等于.专题三其他题型【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是.2.(2019秋•宝山区期末)如图,点A在直线34y x上,如果把抛物线y=x²沿OA方向平移5个单位,那么平移后的抛物线的表达式为__.专题2020年分类汇编-18题专题一图形的翻折【历年真题】1.(2019秋•虹口区期末)如图,在等腰梯形ABCD中,AD∥BC,sin C=45,AB=9,AD=6,点E、F分别在边AB、BC上,联结EF,将△BEF沿着EF所在直线翻折,使BF的对应线段B′F经过顶点A,B′F交对角线BD于点P,当B′F⊥AB时,AP的长为24 7.【考点】相似三角形的判定与性质;解直角三角形;等腰梯形的性质;翻折变换(折叠问题).【专题】图形的相似;解直角三角形及其应用;应用意识.【分析】解直角三角形求出BF,AF,再利用相似三角形的性质求解即可.【解答】解:如图,∵FB′⊥AB,∴∠BAF=90°,∵四边形ABCD是等腰梯形,∴∠ABC=∠C,∴sin∠ABC=sin∠C=AFBF=45,设AF=4k,BF=5k,则AB=9=3k,∴k=3,∴AF=12,BF=15,∵AD∥BF,∴△APD∽△FPB,∴PA AD62=== PF BF155,∴PA=27AF=247,故答案为24 7.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.2.(2019秋•青浦区期末)已知,在矩形纸片ABCD 中,AB =5cm ,点E 、F 分别是边AB 、CD 的中点,折叠矩形纸片ABCD ,折痕BM 交AD 边于点M ,在折叠的过程中,如果点A恰好落在线段EF 上,那么边AD .【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;推理能力.【分析】根据已知条件得到AE =DF =BE =CF ,求得四边形AEFD 是矩形,得到EF =AD ,∠AEN =∠BEN =90°,根据折叠的性质得到BN =AB ,根据直角三角形的性质得到∠BNE =30°,于是得到EN =32BN 到结论.【解答】解:如图,∵在矩形纸片ABCD 中,点E 、F 分别是边AB 、CD 的中点,∴AE =DF =BE =CF ,∴四边形AEFD 是矩形,∴EF =AD ,∠AEN =∠BEN =90°,∵折叠矩形纸片ABCD ,折痕BM 交AD 边于点M ,∴BN =AB ,∵BE =12AB ,∴BE =12BN ,∴∠BNE =30°,∵AB =5cm ,∴EN =32BN∴EF ≥EN 时,点A 恰好落在线段EF 上,即AD∴边AD 的长至少是【点评】本题考查了翻折变换(折叠问题),矩形的性质,直角三角形的性质,正确的识别图形是解题的关键.3.(2019秋•闵行区期末)如图,在等腰△ABC 中,AB =AC =4,BC =6,点D 在底边BC上,且∠DAC =∠ACD ,将△ACD 沿着AD 所在直线翻折,使得点C 落到点E 处,联结BE ,那么BE 的长为1.【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.【专题】平移、旋转与对称;推理能力.【分析】只要证明△ABD∽△MBE,得AB BDBM BE=,只要求出BM、BD即可解决问题.【解答】解:∵AB=AC,∴∠ABC=∠C,∵∠DAC=∠ACD,∴∠DAC=∠ABC,∵∠C=∠C,∴△CAD∽△CBA,∴CA CDCB AC=,∴464CD=,∴CD=83,BD=BC﹣CD=103,∵∠DAM=∠DAC=∠DBA,∠ADM=∠ADB,∴△ADM∽△BDA,∴AD DMBD DA=,即8310833DM=,∴DM=3215,MB=BD﹣DM=65,∵∠ABM=∠C=∠MED,∴A、B、E、D四点共圆,∴∠ADB=∠BEM,∠EBM=∠EAD=∠ABD,∴△ABD∽△MBE,(不用四点共圆,可以先证明△BMA∽△EMD,推出△BME∽AMD,推出∠ADB=∠BEM也可以!)∴AB BD BM BE=,∴BE=BD BMAB=1.故答案为:1.【点评】本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是充分利用相似三角形的性质解决问题,本题需要三次相似解决问题,题目比较难.4.(2019秋•杨浦区期末)在Rt△ABC中,∠A=90°,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=4或【考点】翻折变换(折叠问题);勾股定理;三角形中位线定理.【专题】平移、旋转与对称;推理能力.【分析】当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,根据对称的性质和平行线可得:A1C=A1E=4,根据直角三角形斜边中线的性质得:BC=2A1B=8,最后利用勾股定理可得AB的长;②当∠A1FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.【解答】解:当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,∵△A1BC与△ABC关于BC所在直线对称,∴A1C=AC=4,∠ACB=∠A1CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A1EF,∴AC∥A1E,∴∠ACB=∠A1EC,∴∠A1CB=∠A1EC,∴A1C=A1E=4,Rt△A1CB中,∵E是斜边BC的中点,∴BC=2A1E=8,由勾股定理得:AB2=BC2﹣AC2,∴AB=;②当∠A1FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A1BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA1=45°,∴△ABC是等腰直角三角形,∴AB=AC=4;综上所述,AB的长为或4;故答案为:4;【点评】本题考查了翻折变换(折叠问题),三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质,并利用分类讨论的思想解决问题.5.(2019秋•崇明区期末)如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,D 是AC的中点,点E 在边AB 上,将△ADE 沿DE 翻折,使得点A 落在点A ′处,当A ′E ⊥AB 时,则A ′A =2825或425.【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;解直角三角形及其应用.【分析】分两种情形分别求解,作DF ⊥AB 于F ,连接AA ′.想办法求出AE ,利用等腰直角三角形的性质求出AA ′即可.【解答】解:如图,作DF ⊥AB 于F ,连接AA ′.在Rt △ACB 中,BC 22AB AC -=6,∵∠DAF =∠BAC ,∠AFD =∠C =90°,∴△AFD ∽△ACB ,∴DF AD AF BC AB AC ==,∴46108DF AF ==,∴DF =125,AF =165,∵A′E⊥AB,∴∠AEA′=90°,由翻折不变性可知:∠AED=45°,∴EF=DF=125,∴AE=A′E=125+165=285,∴AA′=2825,如图,作DF⊥AB于F,当EA′⊥AB时,同法可得AE=165﹣125=45,AA AE=425.故答案为2825或425.【点评】本题考查翻折变换,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.6.(2019秋•静安区期末)如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为1 7.【考点】翻折变换(折叠问题);解直角三角形;等边三角形的判定与性质;菱形的性质.【专题】矩形菱形正方形;解直角三角形及其应用.【分析】如图,连接BD.设BC=2a.在Rt△BEF中,求出EF,BF即可解决问题.【解答】解:如图,连接BD.设BC=2a.∵四边形ABC都是菱形,∴AB=BC=CD=AD=2a,∠A=∠C=60°,∴△BDC是等边三角形,∵DE=EC=a,∴BE⊥CD,∴BE=a,∵AB∥CD,BE⊥CD,∴BE⊥AB,∴∠EBF=90°,设AF=EF=x,在Rt△EFB中,则有x2=(2a﹣x)2+a)2,∴x=74a,∴AF=EF=74a,BF=AB﹣AF=4a,∴cos∠EFB=14774aBFaEF==,故答案为1 7.【点评】本题考查菱形的性质,解翻折变换,直角三角形等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.专题二图形的旋转【历年真题】1.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG的正切值是1.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;应用意识.【分析】连接BD,BF,EG.利用四点共圆证明∠BEG=∠BFD=45°即可.【解答】解:连接BD,BF,EG.由题意:BD=BF,∠DBF=90°,∵DG=GF,∴BG⊥DF,∴∠BGF=∠BEF=90°,∴B,G,E,F四点共圆,∠BEG=∠BFD=45°,∴∠BEG的正切值是1.故答案为1.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,四点共圆,锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,属于中考常考题型.2.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为【考点】三角形综合题.【专题】图形的全等;等腰三角形与直角三角形;矩形菱形正方形;图形的相似;推理能力.【分析】分两种情况:①点A在E'D'的延长线上时;②点A在线段D'E'的延长线上时;然后分类讨论,求出线段BD的长各是多少即可.【解答】解:如图1,当点A在E'D'的延长线上时,∵∠C=90°,AC=2,BC=4,∴AB==2,∵点D、E分别是边BC、AB的中点,∴DE∥AC,DE=12AC=1,BD=12BC=2,∴∠EDB=∠ACB=90°,∵将△BDE绕着点B旋转,∴∠BD'E'=∠BDE=90°,D'E'=DE=1,BD=BD'=2,∵在Rt△ABC和Rt△BAD'中,D'B=AC=2,AB=BA,∴Rt△ABC≌Rt△BAD'(HL),∴AD'=BC,且AC=D'B,∴四边形ACBD'是平行四边形,且∠ACB=90°,∴四边形ACBD'是矩形,∴CD'=AB=如图2,当点A在线段D'E'的延长线上时,∵∠AD 'B =90°,∴AD '==4,∴AE '=AD '﹣D 'E '=3,∵将△BDE 绕着点B 旋转,∴∠ABC =∠E 'BD ',∵'12BE AB ==BD BC ,∴△ABE '∽△CBD ',∴''AE AB CD BC=,∴'3254CD =,∴CD '故答案为:.【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质,勾股定理等知识,解题的关键是理解题意,正确寻找相似三角形解决问题,属于中考常考题型.3.(2019秋•长宁、金山区期末)如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =4点P 在边BC 上,联结AP ,将△ABP 绕着点A 旋转,使得点P 与边AC 的中点M 重合,点B的对应点是点B ′,则BB ′的长等于5.【考点】旋转的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,延长AB '交BC 于E ,过点B '作B 'D ⊥AB 于点D ,由勾股定理可求AC 的长,由旋转的性质可求AP=AM ,∠PAB =∠CAE ,AB =AB '=2,通过证明△ABP ∽△CBA ,可得∠PAB =∠C ,可得CE =AE ,由勾股定理可求CE ,BE 的长,由相似三角形的性质可求B 'D ,BD 的长,即可求解.【解答】解:如图,延长AB '交BC 于E ,过点B '作B 'D ⊥AB 于点D ,∵∠ABC =90°,AB =2,BC =4,∴AC ==∵点M 是AC 中点,∴AM ∵将△ABP 绕着点A 旋转,使得点P 与边AC 的中点M 重合,∴AP =AM ,∠PAB =∠CAE ,AB =AB '=2,∵AP 2=AB 2+PB 2,∴PB =1,∵BA PB =2=BC AB,且∠ABP =∠ABC =90°,∴△ABP ∽△CBA ,∴∠PAB =∠C ,∴∠C =∠CAE ,∴CE =AE ,∵AE 2=AB 2+BE 2,∴CE 2=4+(4﹣CE )2,∴CE =AE =52,∴BE =32,∵B 'D ∥BC ,∴△AB 'D ∽△AEB ,∴''AB AD B D AE AB BE ==,∴'253222AD B D ==,∴AD =85,B 'D =65,∴BD =25,∴BB '=2105,故答案为:5.【点评】本题考查了旋转的性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理等知识,求出CE 的长是本题的关键.4.(2019秋•松江区期末)如图,矩形ABCD 中,AD =1,AB =k ,将矩形ABCD 绕着点B顺时针旋转90°得到矩形A ′BC ′D ′,联结AD ′,分别交边CD ,A ′B 于E 、F ,如果AED ′F ,那么k【考点】旋转的性质;相似三角形的判定与性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】由矩形的性质和旋转的性质可求AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,通过证明△ADE ∽△FA 'D ',可得''''AD DE AE A F A D D F==,可求DE ,A 'F 的长,通过证明△A 'D 'F ∽△CEF ,由相似三角形的性质可求解.【解答】解:∵将矩形ABCD 绕着点B 顺时针旋转90°得到矩形A ′BC ′D ′,∴AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,∴A 'D '∥BA ∥CD∴∠A 'D 'F =∠FEC =∠DEA ,且∠D =∠A '=90°,∴△ADE ∽△FA 'D ',∴''''AD DE AE A F A D D F==,且AED ′F ,∴DEA 'D ',A 'FAD =22,∵∠A '=∠DCF =90°,∠A 'FD '=∠EFC ,∴△A 'D 'F ∽△CEF ,∴'''EC FC A D A F =,∴''212222k k A D ---=∴k+1,+1.【点评】本题考查了旋转的性质,矩形的性质,相似三角形的判定和性质,利用相似三角形的性质求DE ,A 'F 的长是本题的关键.5.(2019秋•嘉定区期末)在△ABC 中,∠ACB =90°,AB =10,cos A =35(如图),把△ABC 绕着点C 按照顺时针的方向旋转,将A 、B 的对应点分别记为点A '、B '.如果A 'B '恰好经过点A ,那么点A 与点A '的距离为365.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】如图,过点C 作CE ⊥A 'B ',由锐角三角函数可求AC =6,由旋转的性质可得AC =A 'C =6,∠A '=∠BAC ,即可求A 'E 的长,由等腰三角形的性质可求AA '的长.【解答】解:如图,过点C 作CE ⊥A 'B ',∵在△ABC 中,∠ACB =90°,AB =10,cos ∠BAC =35,∴AC =6,∵把△ABC 绕着点C 按照顺时针的方向旋转,∴AC =A 'C =6,∠A '=∠BAC ,∵cos ∠A '=cos ∠BAC ==35,∴A 'E =185,∵AC =A 'C ,CE ⊥A 'B ',∴AA '=2A 'E =365,故答案我:365.【点评】本题考查了旋转的性质,等腰三角形的性质,锐角三角函数的应用,求出A 'E 的长是本题的关键.6.(2019秋•徐汇区期末)如图,在矩形ABCD 中,AB =3,AD =4,将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',点A 的对应点A '在对角线AC 上,点C 、D 分别与点C '、D '对应,A ′D '与边BC 交于点E ,那么BE 的长是258.【考点】旋转的性质;相似三角形的性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,由勾股定理可求AC =5,由面积法可求BF =125,由勾股定理可求AF =95,由旋转的性质可得AB =BA ',∠BAD =∠BA 'D '=90°,可求CA '=75,由等腰三角形的性质可求HC 的长,通过证明△EHC ∽△ABC ,可得EC BC HC AC ,可求EC 的长,即可求解.【解答】解:如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,∵AB =3,AD =4,∠ABC =90°,∴AC ===5,∵S △ABC =12AB ×BC =12AC ×BF ,∴3×4=5BF ,∴BF =125∴AF 22144925AB BF -=-95,∵将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',∴AB =BA ',∠BAD =∠BA 'D '=90°,且BF ⊥AC ,∴∠BAC =∠BA 'A ,AF =A 'F =95,∠BA 'A +∠EA 'C =90°,∴A 'C =AC ﹣AA '=75,∵∠BA 'A +∠EA 'C =90°,∠BAA '+∠ACB =90°,∴∠ACB =∠EA 'C ,∴A 'E =EC ,且EH ⊥AC ,∴A 'H =HC =12A 'C =710,∵∠ACB =∠ECH ,∠ABC =∠EHC =90°,∴△EHC ∽△ABC ,∴BC HC AC EC =∴74105EC =∴EC =78,∴BE =BC ﹣EC =4﹣78=258,故答案为:258.【点评】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定和性质,求出HC 的长是本题的关键.7.(2019秋•普陀区期末)如图,在RtΔABC 中,∠C=90°,AC=5,sinB=513,点P 为边BC 上一点,PC=3,将△ABC 绕点P 旋转得到△A'B'C'(点A ,B 、C 分别与点A'、B'、C'对应).使B'C'∥AB ,边A'C'与边AB 交于点G ,那么A'G 的长等于2013.【考点】旋转的性质;解直角三角形;平行线的判定,图形的旋转【专题】矩形菱形正方形;平移,旋转与对称;解直角一角形及其应用;应用意识。
上海市历年中考数学试题、模拟题汇编及答案

上海中考试题、模拟题汇编及答案20PP 年上海市初中毕业统一学业考试数学卷 20PP 年上海市初中毕业统一学业考试 20PP 年上海市初中毕业生统一学业考试20PP 年上海市初中毕业生统一学业考试数学试题及答案评分要点20PP 年上海市中考数学试题及答案上海市黄浦区20PP 年九年级数学学业 考试模拟考试 上海市青浦区20PP 学年度九年级数学学业 模拟考试 20PP 上海金山中考 数学模拟试卷--数学 20PP 上海浦东新中考数学预测卷--数学20PP 年上海市初中毕业统一学业考试数学卷(满分150分,考试时间100分钟)、选择题(本大题共 6题,每题4分,满分24分)1. 下列实数中,是无理数的为(C )A. 3.14B. 1C. . 3【解析】无理数即为无限不循环小数,则选 C 。
k2. 在平面直角坐标系中,反比例函数 P = - ( k v 0 )图像的两支分别在(XA.第一、三象限B.第二、四象限C.第一、二象限【解析】设K=-1,则P=2时,P= _丄,点在第四象限;当 P=-2时,P=丄,在第二象限,所以图像过2 2第二、四象限,即使选 B 3.已知一元二次方程 P 2+ P —1 = 0 ,下列判断正确的是( B )A .该方程有两个相等的实数根 B.该方程有两个不相等的实数根 C.该方程无实数根D.该方程根的情况不确定【解析】根据二次方程的根的判别式: A=b 2—4ac=(1 j —4心江(―1 )=5>0,所以方程有两个不相等的实数根,所以选 B4. 某市五月份连续五天的日最高气温分别为 23、20、20、21、26 (单位:°C),这组数据的中位数和众数分别是(D ) A. 22 C, 26°CB. 22 C, 20°CC. 21 C, 26°CD. 21 C, 20°C【解析】中位数定义:将所有数学按从小到大顺序排列后,当数字个数为奇数时即中间那个数为中位 数,当数字的个数为偶数时即中间那两个数的平均数为中位数。
2023上海各区中考一模数学压轴题

中考模拟数学试卷一、单项选择题(共12分)1.如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()A.4对 B.3对C.2对D.1对2.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3 D.x1=0,x2=33.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3D.x1=0,x2=34.如图,以A、B、C为顶点的三角形与以D、E、F为顶点的三角形相似,则这两个三角形的相似比为()A.2:1 B.3:1 C.4:3 D.3:25.如图,一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了()A.4圈B.3圈C.5圈D.3.5圈二、填空题(共24分)1.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30∘方向,同时测得岛礁P正东方向上的避风港M在北偏东60∘方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达()。
(结果保留根号)|与(tanB−√3)2互为相反数,则∠C的度数2.已知△ABC,若有|sinA−12是。
三、解答题3.如图,在四边形A BCD中,A D∥BC,A B⊥BC,点E在A B上,∠DEC=90°。
求证:△ADE∽△BEC。
1.如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积。
2.如图,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C,在x轴的正半轴上(C在B的右侧),BC=2,AB=2根号3,△ADC与△ABC关于AC所在的直线对称。
上海初三数学各区一模压轴题汇总套全

上海初三数学各区一模压轴题汇总套全TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-2016~2017学年度上海市各区初三一模数学压轴题汇总(18+24+25)共15套整理 廖老师宝山区一模压轴题18(宝山)如图,D 为直角ABC 的斜边AB 上一点,DE AB 交AC 于E ,如果AED 沿着DE 翻折,A 恰好与B 重合,联结CD 交BE 于F ,如果8AC ,1tan 2A ,那么:___________.CF DF24(宝山)如图,二次函数232(0)2y ax x a 的图像与x 轴交于A B 、两点,与y 轴交于点,C 已知点(4,0)A .(1)求抛物线与直线AC 的函数解析式;(2)若点(,)D m n 是抛物线在第二象限的部分上的一动点,四边形OCDA 的面积为S ,求S 关于m 的函数关系;(3)若点E 为抛物线上任意一点,点F 为x 轴上任意一点,当以A C E F 、、、为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E 的坐标.25(宝山)如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P Q 、同时从点B 出发,点P 以1/cm s 的速度沿着折线BE ED DC 运动到点C 时停止,点Q 以2/cm s 的速度沿着BC 运动到点C 时停止。
设P Q 、同时出发t 秒时,BPQ 的面积为2ycm ,已知y 与t 的函数关系图像如图(2)(其中曲线OG 为抛物线的一部分,其余各部分均为线段).(1)试根据图(2)求05t 时,BPQ 的面积y 关于t 的函数解析式;(2)求出线段BC BE ED 、、的长度;(3)当t 为多少秒时,以B P Q 、、为顶点的三角形和ABE 相似;(4)如图(3)过点E 作EF BC 于F ,BEF 绕点B 按顺时针方向旋转一定角度,如果BEF 中E F 、的对应点H I 、恰好和射线BE CD 、的交点G 在一条直线,求此时C I 、两点之间的距离.崇明县一模压轴题18(崇明)如图,已知 ABC ∆中,45ABC ∠=,AH BC ⊥于点H ,点D 在AH 上,且DH CH =,联结BD ,将BHD 绕点H 旋转,得到EHF ∆(点B 、D 分别与点E 、F 对应),联结AE ,当点F 落在AC 上时,(F 不与C 重合)如果4BC =,tan 3C =,那么AE 的长为 ;24(崇明)在平面直角坐标系中,抛物线235y x bx c =-++与y 轴交于点(0,3)A ,与x轴的正半轴交于点(5,0)B ,点D 在线段OB 上,且1OD = ,联结AD 、将线段AD 绕着点D 顺时针旋转90︒,得到线段DE ,过点E 作直线l x ⊥轴,垂足为H ,交抛物线于点F .(1)求这条抛物线的解析式;(2)联结DF ,求cot EDF ∠的值;(3)点G 在直线l 上,且45EDG ︒∠=,求点G 的坐标.25(崇明)在ABC ∆中,90ACB ︒∠=,3cot 2A =,AC =,以BC 为斜边向右侧作等腰直角EBC ∆,P 是BE 延长线上一点,联结PC ,以PC 为直角边向下方作等腰直角PCD ∆,CD 交线段BE 于点F ,联结BD .(1)求证:PC CE CD BC =; (2)若PE x =,BDP ∆的面积为y ,求y 关于x 的函数解析式,并写出定义域;(3)当BDF ∆为等腰三角形时,求PE 的长.奉贤区一模压轴题18(奉贤)如图3,在矩形ABCD 中,AB =6,AD =3,点P 是边AD 上的一点,联结BP ,将△ABP 沿着BP 所在直线翻折得到△EBP ,点A 落在点E 处,边BE 与边CD 相交于点G ,如果CG=2DG ,那么DP 的长是__ ____.24(奉贤)如图,在平面直角坐标系中xOy 中,抛物线2y x bx c =-++与x 轴相交于点A (-1,0)和点B ,与y 轴相交于点C (0,3),抛物线的顶点为点D ,联结AC 、BC 、DB 、DC .(1)求这条抛物线的表达式及顶点D 的坐标;(2)求证:△ACO ∽△DBC ;(3)如果点E 在x 轴上,且在点B 的右侧,∠BCE=∠ACO ,求点E 的坐标。
2020-2021年上海各区数学中考一模压轴题分类汇编-24题含详解
专题2021年上海各区分类汇编-24题专题一二次函数与角度问题【知识梳理】【历年真题】1.(2020秋•闵行区期末)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.2.(2020秋•长宁区期末)已知在平面直角坐标系xOy中,抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),与y轴交于点C.(1)求抛物线的表达式;(2)点D是抛物线上的点,且位于线段BC上方,联结CD.①如果点D的横坐标为2.求cot∠DCB的值;②如果∠DCB=2∠CBO,求点D的坐标.3.(2020秋•青浦区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.(1)求该抛物线的表达式及点C的坐标;(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.4.(2020秋•虹口区期末)如图,在平面直角坐标系xOy中,已知点A(﹣1,0)、B(3,0)、C(0,3),抛物线y=ax2+bx+c经过A、B两点.(1)当该抛物线经过点C时,求该抛物线的表达式;(2)在(1)题的条件下,点P为该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;(3)如果抛物线y=ax2+bx+c的顶点D位于△BOC内,求a的取值范围.5.(2020秋•松江区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),与y轴交于点C.(1)求这个抛物线的表达式;(2)如果点P是抛物线位于第二象限上一点,PC交x轴于点D,23 PDDC .①求P点坐标;②点Q在x轴上,如果∠QCA=∠PCB,求点Q的坐标.6.(2020秋•奉贤区期末)如图,在平面直角坐标系xOy中,抛物线y=﹣12x2+bx+c与x轴正半轴交于点A(4,0),与y轴交于点B(0,2),点C在该抛物线上且在第一象限.(1)求该抛物线的表达式;(2)将该抛物线向下平移m个单位,使得点C落在线段AB上的点D处,当AD=3BD时,求m的值;(3)连接BC,当∠CBA=2∠BAO时,求点C的坐标.专题二二次函数与相似三角形【知识梳理】【历年真题】1.(2020秋•崇明区期末)如图,已知对称轴为直线x=﹣1的抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(1,0).(1)求点B的坐标及抛物线的表达式;(2)记抛物线的顶点为P,对称轴与线段BC的交点为Q,将线段PQ绕点Q,按顺时针方向旋转120°,请判断旋转后点P的对应点P′是否还在抛物线上,并说明理由;(3)在x轴上是否存在点M,使△MOC与△BCP相似?若不存在,请说明理由;若存在,请直接写出点M的坐标【不必书写求解过程】.2.(2020秋•黄浦区期末)如图,平面直角坐标系内直线y=x+4与x轴、y轴分别交于点A、B,点C是线段OB的中点.(1)求直线AC的表达式;(2)若抛物线y=ax2+bx+c经过点C,且其顶点位于线段OA上(不含端点O、A).①用含b的代数式表示a,并写出1b c的取值范围;②设该抛物线与直线y=x+4在第一象限内的交点为点D,试问:△DBC与△DAC能否相似?如果能,请求此时抛物线的表达式;如果不能,请说明理由.3.(2020秋•浦东新区期末)二次函数y=ax2+bx+c(a≠0)的图象经过点A(2,4)、B(5,0)和O(0,0).(1)求二次函数的解析式;(2)联结AO,过点B作BC⊥AO于点C,与该二次函数图象的对称轴交于点P,联结AP,求∠BAP的余切值;(3)在(2)的条件下,点M在经过点A且与x轴垂直的直线上,当△AMO与△ABP相似时,求点M的坐标.4.(2020秋•普陀区期末)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+1与y轴交于点A,顶点B的坐标为(2,﹣1).(1)直接写出点A的坐标,并求抛物线的表达式;(2)设点C在x轴上,且∠CAB=90°,直线AC与抛物线的另一个交点为点D.①求点C、D的坐标;②将抛物线y=ax2+bx+1沿着射线BD的方向平移;平移后的抛物线顶点仍在线段BD上;点A的对应点为点P.设线段AB与x轴的交点为点Q,如果△ADP与△CBQ相似,求点P的坐标.专题三二次函数与其他【知识梳理】【历年真题】1.(2020秋•嘉定区期末)在平面直角坐标系xOy中,已知点A(﹣1,2),点B(1,6),点C(1,4),如果抛物线y=ax2+bx+3(a≠0)恰好经过这三个点之中的两个点.(1)试推断抛物线y=ax2+bx+3经过点A、B、C之中的哪两个点?简述理由;(2)求常数a与b的值;(3)将抛物线y=ax2+bx+3先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移t(t >0)个单位长度,如果所得到的新抛物线经过点C(1,4),设这个新抛物线的顶点是D,试探究△ABD的形状.2.(2020秋•金山区期末)在平面直角坐标系xOy中,直线y=﹣34x+2与直线y=12x﹣3相交于点A,抛物线y=ax2+bx﹣1(a≠0)经过点A.(1)求点A的坐标;(2)若抛物线y=ax2+bx﹣1向上平移两个单位后,经过点(1,﹣2),求抛物线y=ax2+bx﹣1的表达式;(3)若抛物线y=a'x2+b'x+c(a'<0)与y=ax2+bx﹣1关于x轴对称,且这两条抛物线的顶点分别是点P'与点P,当S△OPP′=3时,求抛物线y=ax2+bx﹣1的表达式.3.(2020秋•徐汇区期末)已知二次函数y=ax2﹣2ax+a+4(a<0)的大致图象如图所示,这个函数图象的顶点为点D.(1)求该函数图象的开口方向、对称轴及点D的坐标;(2)设该函数图象与y轴正半轴交于点C,与x轴正半轴交于点B,图象的对称轴与x轴交于点A,如果DC⊥BC,1tan 3DBC ∠=,求该二次函数的解析式;(3)在(2)的条件下,设点M 在第一象限该函数的图象上,且点M 的横坐标为t (t >1),如果△ACM 的面积是258,求点M 的坐标.4.(2020秋•静安区期末)如图,在平面直角坐标系xOy 中,直线y =﹣x +m (m >0)与x 轴、y 轴分别交于点A ,B ,抛物线y =ax 2+bx +4(a ≠0)经过点A ,且与y 轴相交于点C ,∠OCA =∠OAB .(1)求直线AB 的表达式;(2)如果点D 在线段AB 的延长线上,且AD =AC ,求经过点D 的抛物线y =ax 2+bx +4的表达式;(3)如果抛物线y =ax 2+bx +4的对称轴与线段AB 、AC 分别相交于点E ,F ,且EF =1,求此抛物线的顶点坐标.5.(2020秋•杨浦区期末)已知在平面直角坐标系xOy 中,抛物线y =﹣(x ﹣m )2+4与y轴交于点B ,与x 轴交于点C 、D (点C 在点D 左侧),顶点A 在第一象限,异于顶点A 的点P (1,n )在该抛物线上.(1)如果点P 与点C 重合,求线段AP 的长;(2)如果抛物线经过原点,点Q是抛物线上一点,tan∠OPQ=3,求点Q的坐标;(3)如果直线PB与x轴的负半轴相交,求m的取值范围.专题四二次函数与平行四边形【知识梳理】【历年真题】1.(2020秋•宝山区期末)已知抛物线y=ax2+bx(a≠0)经过A(4,0),B(﹣1,3)两点,抛物线的对称轴与x轴交于点C,点D与点B关于抛物线的对称轴对称,联结BC、BD.(1)求该抛物线的表达式以及对称轴;(2)点E在线段BC上,当∠CED=∠OBD时,求点E的坐标;(3)点M在对称轴上,点N在抛物线上,当以点O、A、M、N为顶点的四边形是平行四边形时,求这个平行四边形的面积.专题2021年上海各区分类汇编-24题专题一二次函数与角度问题【历年真题】1.(2020秋•闵行区期末)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.【考点】二次函数综合题.【专题】二次函数图象及其性质;图形的相似;推理能力;应用意识.【分析】(1)先求出点M坐标,M'的坐标,代入解析式可求解;(2)先求出点C坐标,C'的坐标,利用回归点的定义可求解;(3)通过证明△CEF∽△CDE,可得CF CECE CD,可求CF=10,即可求解.【解答】解:(1)抛物线y=﹣x2+2x+4是回归抛物线,理由如下:∵点M在抛物线y=﹣x2+2x+4上,∴y=﹣4+4+4=4,∴点M(2,4),∴点M关于坐标原点O的对称点M'(﹣2,﹣4),当x=﹣2时,y=﹣4﹣4+4=﹣4,∴点M'在抛物线上,∴抛物线y=﹣x2+2x+4是回归抛物线;(2)∵点C为回归抛物线y=﹣x2﹣2x+c的顶点,∴点C(﹣1,c+1),∴点C关于原点O的对称点C'(1,﹣c﹣1),∵点C是这条抛物线的回归点,∴﹣c﹣1=﹣1﹣2+c,∴c=1,∴抛物线解析式为:y=﹣x2﹣2x+1;(3)∵抛物线y=﹣x2﹣2x+1,∴对称点为x=﹣1,∴点D(﹣1,0),点C(﹣1,2),∴直线CO解析式为y=﹣2x,联立方程组2212y x xy x⎧=--+⎨=-⎩,∴1212xy=⎧⎨=-⎩,2212xy=-⎧⎨=⎩,点E(1,﹣2),在△CEF和△CDE中,∠CFE=∠CED,∠FCE=∠ECD,∴△CEF∽△CDE,∴CF CECE CD=,∴CE2=CD•CF,∴(﹣1﹣1)2+(2+2)2=2CF,∴CF=10,∴F(﹣1,﹣8).【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,理解新定义并运用是解题的关键.2.(2020秋•长宁区期末)已知在平面直角坐标系xOy中,抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),与y轴交于点C.(1)求抛物线的表达式;(2)点D是抛物线上的点,且位于线段BC上方,联结CD.①如果点D的横坐标为2.求cot∠DCB的值;②如果∠DCB=2∠CBO,求点D的坐标.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)将点A,B坐标代入抛物线解析式中,解方程组,即可得出结论;(2)①先求出点D坐标,进而求出BC,CD,DB,判断出△BDC是直角三角形,即可得出结论;②构造出等腰三角形,利用对称性求出点F的坐标,进而求出直线CF的解析式,进而联立抛物线解析式,解方程组,即可得出结论.【解答】解:(1)∵抛物线y=ax2+bx+2经过点A(﹣3,﹣6)、B(6,0),∴932636620a ba b-+=-⎧⎨++=⎩,∴1353ab⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的表达式为y=﹣13x2+53x+2;(2)①如图1,由(1)知,抛物线的解析式为y=﹣13x2+53x+2,当x=0时,y=2,∴C(0,2),当x=2时,y=﹣13×4+53×2+2=4,∴D(2,4),∵B(6,0),∴CD2=(2﹣0)2+(4﹣2)2=8,BC2=(6﹣0)2+(0﹣2)2=40,DB2=(6﹣2)2+(0﹣4)2=32,∴CD2+BC2=DB2,∴△BCD是直角三角形,∠BDC=90°,在Rt△BDC中,CD=,BD=,∴cot∠DCB=12 CDBD==;②如图2,过点C作CE∥x轴,则∠BCE=∠CBO,∵∠DCB=2∠CBO,∴∠DCE=∠BCE,过点B作BE⊥CE,并延长交CD的延长线于F,∵C(0,2),B(6,0),∴F(6,4),设直线CF的解析式为y=kx+2,∴6k+2=4,∴k=1 3,∴直线CF的解析式为y=13x+2①,∵抛物线的解析式为y=﹣13x2+53x+2②,联立①②,解得2xy=⎧⎨=⎩或4103xy=⎧⎪⎨=⎪⎩,∴D(4,10 3).【点评】此题是二次函数综合题,主要考查了待定系数法,勾股定理的逆定理,等腰三角形的性质,构造出等腰三角形是解本题的关键.3.(2020秋•青浦区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.(1)求该抛物线的表达式及点C的坐标;(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.【考点】二次函数综合题.【专题】二次函数的应用;图形的相似;解直角三角形及其应用;应用意识.【分析】(1)利用待定系数法可求解析式;(2)过D作DE⊥AC交CA延长线于E,通过证明∴△EAD∽△OAC,由相似三角形的性质可求ED=2,EC=,即可求解;(3)由角的数量关系可求∠ACP =∠BAP ,由锐角三角函数可求解.【解答】解:(1)将点A (﹣4,0)和点B (2,0)代入抛物线y =ax 2+bx ﹣4,可得164404240a ab --=⎧⎨+-=⎩,解得:12a =,1b =∴抛物线的解析式为2142y x x =+-,当x =0时,y =﹣4,∴C (0,﹣4);(2)如图1,过D 作DE ⊥AC 交CA 延长线于E ,∵C (0,﹣4),点A (﹣4,0),∴OA =OC =4,∴AC =,∵∠EAD =∠OAC ,∠DEA =∠COA ,∴△EAD ∽△OAC ,∴DE EA DA CO OA CA ===,∴44DE EA ==∴DE =EA =,∴EC =,∴DE 1tan ACD==EC 3∠;(3)如图2,过点P 作PF ⊥x 轴于F ,设21(,4)2P t t t +-,∵∠OCD =∠CAP ,∴∠OCA +∠ACD =∠CAB +∠BAP ,∴45°+∠ACD=45°+∠BAP,∴∠ACD=∠BAP,∴1 tan BAP=tan ACD=3∠∠,∴tan∠BAP=21t+t-4PF12==AF t+43,∴83t 或t=﹣4(舍去),∴820 (,) 39 P.【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,锐角三角函数等知识,灵活运用这些性质解决问题是本题的关键.4.(2020秋•虹口区期末)如图,在平面直角坐标系xOy中,已知点A(﹣1,0)、B(3,0)、C(0,3),抛物线y=ax2+bx+c经过A、B两点.(1)当该抛物线经过点C时,求该抛物线的表达式;(2)在(1)题的条件下,点P为该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;(3)如果抛物线y=ax2+bx+c的顶点D位于△BOC内,求a的取值范围.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)设抛物线的解析式为y=a(x﹣3)(x+1),将点C的坐标代入求得a的值,可得抛物线的解析式;(2)先根据点B和C的坐标证明△OCB是等腰直角三角形,得∠OBC=∠OCB=45°,根据等式的性质得:∠OAC =∠PBO,利用三角函数列式可得OE的长,利用待定系数法求PB的解析式,联立抛物线和直线PB的解析式组成方程组可得点P的坐标即可;(3)先确定抛物线的对称轴,计算边界点D的坐标和对应a的值,根据图形可知:符合条件的a一定是负数,从而得解.【解答】解:(1)设抛物线的解析式为y=a(x﹣3)(x+1).将点C的坐标(0,3)代入得:﹣3a=3,解得:a=﹣1,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图1,设PB交y轴于点E,∵C(0,3),B(3,0),∴OB=OC=3,∵∠COB=90°,∴∠OCB=∠OBC=45°,又∵∠ACB=∠PCB,∴∠ACB﹣∠OCB=∠PBC﹣∠OBC,即∠OCA=∠PBO,∴tan∠OCA=tan∠PBO,即OA OE OC OB=,∴133OE=,∴OE=1,∵点P在第三象限,∴E(0,﹣1),设PB的解析式为:y=kx+b(k≠0),把E(0,﹣1)和B(3,0)代入得:130bk b=-⎧⎨+=⎩,解得:131kb⎧=⎪⎨⎪=-⎩,∴PB的解析式为:y=13x﹣1,则223113y x xb x⎧=-++⎪⎨=-⎪⎩,解得:113xy=⎧⎨=⎩或2243139xy⎧=-⎪⎪⎨⎪=-⎪⎩,∴P(﹣43,﹣139);(3)∵抛物线y=ax2+bx+c经过A、B两点,∴对称轴是:直线x=312-=1,∵B(3,0)、C(0,3),同理得BC的解析式为:y=﹣x+3,当x=1时,y=2,当顶点D(1,2)时,设抛物线的解析式为y=a(x﹣3)(x+1),把顶点D(1,2)代入得:a=﹣1 2,∴抛物线y=ax2+bx+c的顶点D位于△BOC内,a的取值范围是﹣12<a<0.【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,三角函数,对称的性质,二次函数的性质等知识,熟知利用方程组的解确定两函数的交点坐标是本题的关键.5.(2020秋•松江区期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),与y轴交于点C.(1)求这个抛物线的表达式;(2)如果点P是抛物线位于第二象限上一点,PC交x轴于点D,23 PDDC=.①求P点坐标;②点Q在x轴上,如果∠QCA=∠PCB,求点Q的坐标.【考点】二次函数综合题.【专题】二次函数的应用;图形的全等;图形的相似;应用意识.【分析】(1)由待定系数法可求解析式;(2)①过点P作PE⊥x轴于E,由平行线分线段成比例可求PE的长,代入解析式可求解;②分两种情况讨论,利用全等三角形的性质和相似三角形的性质可求解.【解答】解:(1)∵抛物线y=ax2+bx﹣2经过点A(2,0)和B(﹣1,﹣1),∴120422a ba b-=--⎧⎨=+-⎩,解得:2313ab⎧=⎪⎪⎨⎪=-⎪⎩,∴抛物线解析式为:y=23x2﹣13x﹣2;(2)①如图1,过点P作PE⊥x轴于E,∵抛物线y=ax2+bx﹣2与y轴交于点C,∴点C(0,﹣2),∴OC=2,∵PE∥OC,∴23PE PDOC DC===EDDO,∴PE=43,∴43=23x2﹣13x﹣2,∴x=﹣2或x=52(不合题意舍去),∴点P(﹣2,4 3);②如图2,过点B作BH⊥CO于H,由①可知DO==,∵B(﹣1,﹣1),点C(0,﹣2),A(2,0)∴OA=OC=2,BH=CH=1,∴∠BCH=45°=∠OCA,∴∠BCA=90°,当点Q在线段AO上时,∵∠QCA=∠PCB,∴∠DCO=∠QCO,又∵CO=CO,∠DOC=∠QOC=90°,∴△DOC≌△QOC(ASA),∴DO=QO=6 5,∴点Q坐标为(65,0),当点Q'在射线OA上时,∵∠Q'CA=∠PCB,∴∠DCQ'=90°,∴∠CDO +∠DQ 'C =90°,∠DCO +∠CDO =90°,∴∠DQ 'C =∠DCO ,又∵∠DOC =∠Q 'OC =90°,∴△DOC ∽△COQ ',∴'DO CO OC Q O=,∴4=65×Q 'O ,∴Q 'O =103,∴点Q '(103,0),综上所述:点Q 坐标为(65,0)或(103,0).【点评】本题二次函数综合题,考查了待定系数法求解析式,二次函数的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,灵活运用这些知识解决问题是解题的关键.6.(2020秋•奉贤区期末)如图,在平面直角坐标系xOy 中,抛物线y =﹣12x 2+bx +c 与x 轴正半轴交于点A (4,0),与y 轴交于点B (0,2),点C 在该抛物线上且在第一象限.(1)求该抛物线的表达式;(2)将该抛物线向下平移m 个单位,使得点C 落在线段AB 上的点D 处,当AD =3BD 时,求m 的值;(3)连接BC ,当∠CBA =2∠BAO 时,求点C的坐标.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)利用待定系数法求抛物线的解析式即可;(2)如图1,过点D 作DG ⊥x 轴于G ,利用平行证明△ADG ∽△ABO ,列比例式可以计算OG 和DG 的长,从而得D (1,32),最后由平移的性质可得m 的值;(3)如图2,作辅助线,构建等腰△ABF ,确定点F 的坐标,计算BF 的解析式,联立抛物线和BF 的解析式,方程组的一个解就是点C 的坐标.【解答】解:(1)把点A (4,0)和点B (0,2)代入抛物线y =﹣12x 2+bx +c 中得:1-16+4b+c=02c=2⎧⨯⎪⎨⎪⎩,解得:3b=-2c=2⎧⎪⎨⎪⎩,∴抛物线的解析式为:y=﹣12x2+32x+2;(2)如图1,过点D作DG⊥x轴于G,∴DG∥OB,∴△ADG∽△ABO,∴AD DG AG AB OB OA==,∵AD=3BD,∴AG=3OG,∵A(4,0),B(0,2),∴OA=4,OB=2,∴OG=1,DG=3 2,∵D(1,3 2),由平移得:点C的横坐标为1,当x=1时,y=﹣12×1+32×1+2=3,∴m=3﹣32=32;(3)∵∠CBA=2∠BAO,点C在该抛物线上且在第一象限,∴点C在AB的上方,如图2,过A作AF⊥x轴于A,交BC的延长线于点F,过B作BE⊥AF于点E,∴BE∥OA,∴∠BAO=∠ABE,∵∠CBA=2∠BAO=∠ABE+∠EBF,∴∠FBE=∠ABE,∵∠BEF=∠AEB=90°,∴∠F=∠BAF,∴AB=BF,∴AE=EF=OB=2,∴F(4,4),设BF的解析式为:y=kx+n,则402k nn+=⎧⎨=⎩,解得:122kn⎧=⎪⎨⎪=⎩,∴BF的解析式为:y=12x+2,∴212213222y xy x x⎧=+⎪⎪⎨⎪=++⎪⎩,解得2xy=⎧⎨=⎩或23xy=⎧⎨=⎩,∴C(2,3).【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰三角形的性质和相似三角形的判定与性质;会利用待定系数法求抛物线和一次函数的解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用数形结合的思想解决数学问题.专题二二次函数与相似三角形【历年真题】1.(2020秋•崇明区期末)如图,已知对称轴为直线x=﹣1的抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(1,0).(1)求点B的坐标及抛物线的表达式;(2)记抛物线的顶点为P,对称轴与线段BC的交点为Q,将线段PQ绕点Q,按顺时针方向旋转120°,请判断旋转后点P的对应点P′是否还在抛物线上,并说明理由;(3)在x轴上是否存在点M,使△MOC与△BCP相似?若不存在,请说明理由;若存在,请直接写出点M的坐标【不必书写求解过程】.【考点】二次函数综合题.【专题】代数几何综合题;推理能力.【分析】(1)构建方程组求解即可.(2)如图1中,过点P′作P′H⊥PQ于H.求出点P′的坐标,即可判断.(3)首先证明∠PCB=90°,由PC:BC=1:3,推出OM:OC=1:3或OC:OM=1:3,推出OM=1或9,由此即可解决问题.【解答】解:(1)由题意,3012a bba++=⎧⎪⎨-=-⎪⎩,解得12ab=-⎧⎨=-⎩,∴抛物线的解析式y=﹣x2﹣2x+3,令y=0,则﹣x2﹣2x+3=0,解得x=1或﹣3,∴B(﹣3,0).(2)点P′在抛物线上,理由:如图1中,过点P′作P′H⊥PQ于H.∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点P(﹣1,4),∵B(﹣3,0),C(0,3),∴直线BC的解析式为y=x+3,∵PQ∥y轴,∴Q(﹣1,2),∴PQ=2,在Rt△P′QH中,∠P′HQ=90°,∠P′QH=180°﹣120°=60°,P′Q=PQ=2,∴PH=P′Q•sin60PH=P′Q•cos60°=1,∴P1,1),当x﹣1时,y1)2﹣2﹣1)+3=1,∴点P′在抛物线上.(3)存在.如图2中,连接PB,PC.∵B(﹣3,0),P(﹣1,4),C(0,3),∴BC=,PC,PB=∴PB2=PC2+CB2,∴∠PCB=90°,PC:BC=:=1:3,当MO:OC=1:3或OC:MO=1:3时,△COM与△BCP相似,∴OM=1或9,∴满足条件的点M的坐标为(1,0)或(﹣1,0)或(9,0)或(﹣9,0).【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会利用参数构建方程组解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.2.(2020秋•黄浦区期末)如图,平面直角坐标系内直线y=x+4与x轴、y轴分别交于点A、B,点C是线段OB的中点.(1)求直线AC的表达式;(2)若抛物线y=ax2+bx+c经过点C,且其顶点位于线段OA上(不含端点O、A).①用含b的代数式表示a,并写出1b c的取值范围;②设该抛物线与直线y=x+4在第一象限内的交点为点D,试问:△DBC与△DAC能否相似?如果能,请求此时抛物线的表达式;如果不能,请说明理由.【考点】二次函数综合题.【专题】代数几何综合题;推理能力.【分析】(1)求出A,C两点坐标,利用待定系数法解决问题即可.(2)①根据顶点的纵坐标为0,对称轴在线段OA上,构建方程与不等式即可解决问题.②能相似.利用相似三角形的性质构建方程,求出点D的坐标,再利用待定系数法解决问题即可.【解答】解:(1)∵直线y=x+4与x轴、y轴分别交于点A、B,∴A(﹣4,0),B(0,4),∴OA=OB=4,∵BC=OC=2,∴C(0,2),设直线AC的解析式为y=mx+n,则有240n m n =⎧⎨-+=⎩,解得122m n ⎧=-⎪⎨⎪=⎩,∴直线AC 的解析式为y =12x +2.(2)①由题意,2240402c b ac b a ⎧⎪=⎪-=⎨⎪⎪-<-<⎩,∴a =18b 2,1>1b>0.②能相似.如图,在Rt △AOC 中,∠AOC =90°,OA =4,OC =2,∴AC=2,∵△△DBC 与△DAC 相似,∠CDB =∠ADC ,∴当∠BCD =∠DAC 时,△DCB ∽△DAC ,∴55DC CB DA AC ===,∵点D 在直线y =x +4上,∴可以假设D (t ,t +4),5=,解得t =1或﹣32(舍弃),经检验,t =1是方程的根,∴D (1,5),∵抛物线y =ax 2+bx +2经过D (1,5),∴a +b +2=5,∴a +b =3,∵a =18b 2,∴3﹣b =18b 2,∴b 2+8b ﹣24=0,∴b =﹣4﹣,∴a =7﹣∴抛物线的解析式为y =(7﹣x 2+(﹣x +2.【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程或不等式解决问题,属于中考压轴题.3.(2020秋•浦东新区期末)二次函数y=ax2+bx+c(a≠0)的图象经过点A(2,4)、B(5,0)和O(0,0).(1)求二次函数的解析式;(2)联结AO,过点B作BC⊥AO于点C,与该二次函数图象的对称轴交于点P,联结AP,求∠BAP的余切值;(3)在(2)的条件下,点M在经过点A且与x轴垂直的直线上,当△AMO与△ABP相似时,求点M的坐标.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)利用待定系数法,即可得出结论;(2)先判断出OB=AB,进而判断出△OBP≌△ABP,得出∠BOP=∠BAP,再求出直线BC的解析式,求出点P 的坐标,构造直角三角形,即可得出结论;(3)先判断出∠OAE=∠OBC,进而得出OM=AM或OA=OM,即可得出结论.【解答】解:(1)二次函数y=ax2+bx+c(a≠0)的图象经过点B(5,0)和O(0,0),∴设二次函数的解析式为y=ax(x﹣5),将点A(2,4)代入y=ax(x﹣5)中,得4=a×2(2﹣5),∴a=﹣2 3,∴二次函数的解析式为y=﹣23x(x﹣5)=﹣23x2+103x;(2)如图1,连接OP,∵A(2,4)、B(5,0)和O(0,0),∴OB=5,AB5,∴OB=AB,∵BC⊥OA,∴BC是OA的垂直平分线,∴AP=OP,∵BP=BP∴△OBP≌△ABP(SSS),∴∠BOP=∠BAP,∵AC=OC,A(2,4),∴点C(1,2),∴直线BC的解析式为y=﹣12x+52,由(1)知,二次函数的解析式为y=﹣23x2+103x,∴对称轴为直线x=52,∴P(52,54),∴OD=52,PD=54,∴cot∠BAP=cot∠BOP=ODPD=2;(3)∵BC⊥OA,AE⊥OB,∴∠ACB=∠AEB=90°,∵∠AMC=∠BME,∴∠OAE=∠OBC,∵点P在抛物线的对称轴上,∴OP=PB,∴△BOP是等腰三角形,∵△AMO与△ABP相似,∴△AMO与△OBP相似,∴OM=AM或OA=OM,设M(2,m),当OM=AM时,OM=AM=4﹣m,在Rt△OEM中,EM=m,根据勾股定理得,OM2﹣EM2=OE2,∴(4﹣m)2﹣m2=4,∴m=3 2,当OA=OM时,AE=M'E,∴M'(2,﹣4)即满足条件的点M的坐标为(2,32)或(2,﹣4).4.(2020秋•普陀区期末)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+1与y轴交于点A,顶点B的坐标为(2,﹣1).(1)直接写出点A的坐标,并求抛物线的表达式;(2)设点C在x轴上,且∠CAB=90°,直线AC与抛物线的另一个交点为点D.①求点C、D的坐标;②将抛物线y=ax2+bx+1沿着射线BD的方向平移;平移后的抛物线顶点仍在线段BD上;点A的对应点为点P.设线段AB与x轴的交点为点Q,如果△ADP与△CBQ相似,求点P的坐标.【考点】二次函数综合题.【专题】压轴题;应用意识.【分析】(1)先令x=0可得y=1,得点A的坐标,根据抛物线的顶点B(2,﹣1),利用待定系数法可得抛物线的表达式;(2)①根据点A和B的坐标得∠BAO=45°,所以∠CAO=45°,可知△ACO是等腰直角三角形,可得C的坐标,从而得AC的解析式,联立方程组可得直线AC与抛物线的交点D的坐标;②先证明∠PAD=∠ADB=∠BCQ,设P(m,2m+1),根据平移后B的对称点B'在线段BD上可知0≤m≤4,如果△ADP与△CBQ相似,存在两种情况:AP ADCQ BC=或AP ADBC CQ=,列方程可得结论.【解答】解:(1)当x =0时,y =1,∴A (0,1),设抛物线的解析式为:y =a (x ﹣2)2﹣1,把A (0,1)代入得:1=a (0﹣2)2﹣1,∴a=,∴抛物线的表达式为:y =(x ﹣2)2﹣1;(2)①如图1,∵A (0,1),B (2,﹣1),∴∠BAO =45°,∵∠CAB =90°,∴∠CAO =45°,∴OC =OA =1,∴C (﹣1,0),设AC 的解析式为:y =kx +m ,则01k m m -+=⎧⎨=⎩,解得:11k m =⎧⎨=⎩,∴AC 的解析式为:y =x +1,则211(2)12y x y x =+⎧⎪⎨=--⎪⎩,解得:1101x y =⎧⎨=⎩或2267x y =⎧⎨=⎩,∴D (6,7);②∵A (0,1),B (2,﹣1),同理得直线AB 的解析式为:y =﹣x +1,∴Q (1,0),∴CQ =2,BC=∵D (6,7),A (0,1),∴AD=AB=如图2,同理得:直线BD 的解析式为:y =2x ﹣5,由平移得:AP ∥BD ,则直线AP 的解析式为:y =2x +1,∴∠PAD =∠ADB ,∵tan ∠BCQ =13AB AD==tan ∠ADB ,∴∠PAD =∠BCQ ,设抛物线平移后的顶点为B ',P (m ,2m +1),则AP 5m ,B '(m +2,2m ﹣1),∵抛物线y =ax 2+bx +1沿着射线BD 的方向平移;平移后的抛物线顶点仍在线段BD 上,∴0≤m ≤4,如果△ADP 与△CBQ 相似,有以下两种情况:i )当AP AD CQ BC =时,即562210m =,解得:m =2.4,∴P (2.4,5.8);ii )当AP AD BC CQ =562210m=,解得:m =6(不符合题意,舍去),综上,P (2.4,5.8).【点评】本题是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数和一次函数的解析式,两点的距离公式,相似三角形的性质和判定,平移的性质等知识,解题时,注意数形结合,使抽象的问题变得具体化,降低了解题的难度.专题三二次函数与其他【历年真题】1.(2020秋•嘉定区期末)在平面直角坐标系xOy 中,已知点A (﹣1,2),点B (1,6),点C (1,4),如果抛物线y =ax 2+bx +3(a ≠0)恰好经过这三个点之中的两个点.(1)试推断抛物线y =ax 2+bx +3经过点A 、B 、C 之中的哪两个点?简述理由;(2)求常数a与b的值;(3)将抛物线y=ax2+bx+3先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移t(t >0)个单位长度,如果所得到的新抛物线经过点C(1,4),设这个新抛物线的顶点是D,试探究△ABD的形状.【考点】二次函数综合题.【专题】综合题;推理能力.【分析】(1)先求出抛物线必经过点E(0,3),再判断出BC∥y轴,再判断出点A、E、C在同一条直线上,即可得出结论;(2)将点A,B坐标代入抛物线解析式中,即可得而出结论;(3)先用t表示出新抛物线的解析式,再将点C坐标代入,即可得出新抛物线的解析式,最后求出AB,AD,BD 即可得出结论.【解答】解:(1)抛物线与y轴的交点记作点E,针对于抛物线y=ax2+bx+3,当x=0时,y=3,∴抛物线与y轴的交点E的坐标为(0,3),∵点B(1,6),点C(1,4),∴BC∥y轴,∴抛物线y=ax2+bx+3经过点B、C两点中其中的一点,而点A(﹣1,2),E(0,3),C(1,4),∴点A,E,C从左到右,横坐标依次增加1,纵坐标也依次增加1,∴点A,E,C再同一条直线上,∴点C不在物线y=ax2+bx+3上,即抛物线y=ax2+bx+3经过点A、B、C之中的A、B两个点;(2)将点A(﹣1,2)、B(1,6)代入抛物线y=ax2+bx+3中,得3236 a ba b-+=⎧⎨++=⎩,∴12ab=⎧⎨=⎩,即a,b的值分别为1,2;(3)由(2)知,a=1,b=2,∴抛物线的解析式为y=x2+2x+3=(x+1)2+2,由平移得,平移后新抛物线的解析式为y=(x+1﹣t)2+2﹣2,即新抛物线的解析式为y=(x+1﹣t)2,∵抛物线经过点C(1,4),∴4=(1+1﹣t)2,∴t=0(舍)或t=4,∴新抛物线的解析式为y=(x﹣3)2,∴顶点D(3,0),∵点A(﹣1,2)、B(1,6),∴AB=AD=BD=∴AB=AD,AB2+AD2=20+20=40=BD2,∴△ABD是等腰直角三角形.【点评】此题是二次函数综合题,主要考查了待定系数法,平移的规律,两点间的距离公式,等腰直角三角形的判定,判断出抛物线必经过点E是解本题的关键.2.(2020秋•金山区期末)在平面直角坐标系xOy中,直线y=﹣34x+2与直线y=12x﹣3相交于点A,抛物线y=ax2+bx﹣1(a≠0)经过点A.(1)求点A的坐标;(2)若抛物线y=ax2+bx﹣1向上平移两个单位后,经过点(1,﹣2),求抛物线y=ax2+bx﹣1的表达式;(3)若抛物线y=a'x2+b'x+c(a'<0)与y=ax2+bx﹣1关于x轴对称,且这两条抛物线的顶点分别是点P'与点P,当S△OPP′=3时,求抛物线y=ax2+bx﹣1的表达式.【考点】二次函数综合题.【专题】代数几何综合题;二次函数图象及其性质;平移、旋转与对称;运算能力;推理能力.【分析】(1)联立两直线解析式,解二元一次方程组即可得出答案;(2)由抛物线经过点A可得出b=﹣4a,由平移的性质可得出答案;(3)求出顶点P的坐标为(2,﹣4a﹣1),由轴对称的性质可得出P'的坐标,求出PP'的长,根据三角形的面积公式可得出方程,解方程可得出答案.【解答】解:(1)∵直线y=﹣34x+2与直线y=12x﹣3相交于点A,∴324132y xy x⎧=-+⎪⎪⎨⎪=-⎪⎩,解得:41xy=⎧⎨=-⎩;∴点A的坐标为(4,﹣1).(2)∵抛物线y=ax2+bx﹣1(a≠0)经过点A(4,﹣1),∴16a+4b﹣1=﹣1,即b=﹣4a,∴y=ax2﹣4ax﹣1,∴平移后的抛物线的表达式是y =ax 2﹣4ax +1,∴﹣2=a ﹣4a +1,解得:a =1,∴抛物线y =ax 2+bx ﹣1的表达式是:y =x 2﹣4x ﹣1.(3)如图,∵y =ax 2﹣4ax ﹣1=a (x ﹣2)2﹣4a ﹣1,∴P (2,﹣4a ﹣1),∵抛物线y =a 'x 2+b 'x +c (a '<0)与y =ax 2﹣4ax ﹣1关于x 轴对称,∴P '(2,4a +1),∵a '<0,∴a >0,∴P 'P =8a +2,又∵OD =2,S △OPP '=12×OD ×PP ',∴12(82)32a ⨯⨯+=,解得:a =18,∴抛物线y =ax 2+bx ﹣1的表达式是y =21182x x -x ﹣1.【点评】本题是二次函数综合题,考查了求两直线的交点坐标,二次函数的性质,待定系数法,平移的性质,轴对称的性质,三角形的面积公式,利用参数列出方程是本题的关键.3.(2020秋•徐汇区期末)已知二次函数y =ax 2﹣2ax +a +4(a <0)的大致图象如图所示,这个函数图象的顶点为点D .(1)求该函数图象的开口方向、对称轴及点D 的坐标;(2)设该函数图象与y 轴正半轴交于点C ,与x 轴正半轴交于点B ,图象的对称轴与x 轴交于点A ,如果DC ⊥BC ,1tan 3DBC ∠=,求该二次函数的解析式;(3)在(2)的条件下,设点M 在第一象限该函数的图象上,且点M 的横坐标为t (t >1),如果△ACM 的面积是258,求点M 的坐标.。
2019-2020年上海各区数学中考一模压轴题分类汇编-25题含详解

专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD中,AD AB=5,tan A=2,点E在射线AD上,过点E作EF⊥AD,垂足为点E,交射线AB于点F,交射线CB于点G,联结CE、CF,设AE=m.(1)当点E在边AD上时,①求△CEF的面积;(用含m的代数式表示)②当S△DCE=4S△BFG时,求AE:ED的值;(2)当点E在边AD的延长线上时,如果△AEF与△CFG相似,求m的值.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.专题二动点函数背景下的面积问题【知识梳理】【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE 的长.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.专题三动点函数背景下的等腰三角形【知识梳理】【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.2.(2019秋•青浦区期末)如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.(1)求证:EQ∥DC;(2)当BP>BQ时,如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.4.(2019秋•崇明区期末)如图,在△ABC中,AB=AC=10,BC=16,点D为BC边上的一个动点(点D不与点B、点C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F.(1)求证:AB•CE=BD•CD;(2)当DF平分∠ADC时,求AE的长;(3)当△AEF是等腰三角形时,求BD的长.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.专题四动点函数背景下的线段问题【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;=y,求y关于x的函数关系式(不需要写函数的定义域);(2)当点D在BC的延长线上时,设AG=x,S△DAF(3)如果AG=8,求DE的长.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.专题四动点函数背景下四边形【知识梳理】【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.3.(2019秋•徐汇区期末)如图,在△ABC中,AB=AC=5,BC=6,点D是边AB上的动点(点D不与点AB重合),点G在边AB的延长线上,∠CDE=∠A,∠GBE=∠ABC,DE与边BC交于点F.(1)求cos A的值;(2)当∠A=2∠ACD时,求AD的长;(3)点D在边AB上运动的过程中,AD:BE的值是否会发生变化?如果不变化,请求AD:BE的值;如果变化,请说明理由.4.(2019秋•普陀区期末)如图,在梯形ABCD中,AD//BC,∠C=90°,AD=2,BC=5,DC=3,点E在边BC上,tan∠AEC=3,点M是射线DC上一个动点(不与点D、C重合),联结BM交射线AE于点N,设DM=x,AN=y.(1)求BE的长;(2)当动点M在线段DC上时,试求y与x之间的函数解析式,并写出函数的定义域;(3)当动点M运动时,直线BM与直线AE的夹角等于45°,请直接写出这时线段DM的长.专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD 中,AD AB =5,tan A =2,点E 在射线AD 上,过点E 作EF ⊥AD ,垂足为点E ,交射线AB 于点F ,交射线CB 于点G ,联结CE 、CF ,设AE =m .(1)当点E 在边AD 上时,①求△CEF 的面积;(用含m 的代数式表示)②当S △DCE =4S △BFG 时,求AE :ED 的值;(2)当点E 在边AD 的延长线上时,如果△AEF 与△CFG 相似,求m 的值.【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)①先根据三角函数表示出EF ,再用勾股定理表示出AF ,再判断出△AEF ∽△BGF ,得出比例式表示出CG ,即可得出结论;②先表示出FG ,再用S △DCE =4S △BFG 建立方程求出m ,即可得出结论;(2)分两种情况:①当△AEF ∽△CGF 时,得出∠AFE =∠CFG ,进而得出BG =12BC =52,FG =BG tan ∠CBFBF =52,进而得出AF =AB +BF =5+52=152,最后判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论;②当△AEF ∽△CGF 时,先判断出∠AFC =90°,进而得出CF =2BF ,再根据勾股定理得,求出BF =1,得出AF =AB +BF =6,同理:BG =,再判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论.【解答】解:(1)①∵EF ⊥AD ,∴∠AEF =90°,在Rt △AEF 中,tan A =2,AE =m ,∴EF =AE tan A =2m ,根据勾股定理得,AF ,∵AB =5,∴BF =5,∵四边形ABCD 是平行四边形,∴BC =AD AD ∥BC ,∴∠G =∠AEF =90°,∴△AEF ∽△BGF ,∴AE AFBG BF =,∴m BG =,∴BG m ,∴CG =BC +BG =m =m ,∴S △CEF =12EF •CG =12•2m •(m )=m ﹣m 2;②由①知,△AEF ∽△BGF ,∴BF FG AF EF =,∴FG =BFAF •EF •2m =2m ),∴EG =EF +FG =2m +2﹣m )=∴S △CDE =12DE •EG =12(m )•5,S △BFG =12BG •FG =12m )•2m ﹣m )2,S △DCE =4S △BFG 时,∴5=4m )2,∴m m =354,∴DE =AD ﹣AE ﹣4=4,∴AE :ED =354:54=3,即:AE :ED 的值为3;(2)∵四边形ABCD 是平行四边形,∴BC =AD ,AD ∥BC ,∵EF ⊥AD ,∴EF ⊥BC ,∴∠AEF =∠CGF =90°,∵△AEF 与△CFG 相似,∴①当△AEF ∽△CGF 时,如图1,∴∠AFE =∠CFG ,∵EF ⊥BC ,∴BG =12BC =52,∵AD ∥BC ,∴∠CBF =∠A ,∵tan A =2,∴tan ∠CBF =2,在Rt △BGF 中,FG =BG tan ∠CBF根据勾股定理得,BF 52,∴AF =AB +BF =5+52=152,∵BC∥AD,∴△BGF∽△AEF,∴BG BFAE AF=,∴,∴m =35 2;②当△AEF∽△CGF时,如图2,∴∠EAF=∠GFC,∵∠EAF+∠AFE=90°,∴∠GFC+∠AFE=90°,∴∠AFC=90°,∵AD∥BC,∴∠CBF=∠A,∴tan∠CBF=tan A=2,在Rt△BFC中,CF=BF•∠CBF=2BF,根据勾股定理得,BF2+CF2=BC2,∴BF2+4BF2)2,∴BF=1,∴AF=AB+BF=6,在Rt△BGF中,同理:BG =5 5,∵AD∥BC,∴△BGF∽△AEF,∴AE AFBG BF=6155=,∴m =655.即:如果△AEF与△CFG相似,m 的值为35 2或.【点评】此题是相似形综合题,主要考查了平行四边形的性质,锐角三角函数,三角形的面积公式,相似三角形的判定和性质,用方程的思想解决问题是解本题的关键.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ ,直线PQ 与直线BC 交于点E ,如果△QCE 与△BCP 相似,求线段BP 的长.【考点】相似形综合题.【专题】几何综合题;应用意识.【分析】(1)如图1中,作PH ⊥BC 于H .解直角三角形求出BH ,PH ,在Rt △PCH 中,理由勾股定理即可解决问题.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .证明△POQ ∽△BOC ,推出∠OPQ =∠OBC =30°=∠PCQ ,推出PQ =CQ =y ,推出PC ,在Rt △PHB 中,BH =12x ,PH =2x ,根据PC 2=PH 2+CH 2,可得结论.(3)分两种情形:①如图2中,若直线QP 交直线BC 于B 点左侧于E .②如图3中,若直线QP 交直线BC 于C 点右侧于E .分别求解即可.【解答】解:(1)如图1中,作PH ⊥BC 于H .∵四边形ABCD 是菱形,∴AB =BC =4,AD ∥BC ,∴∠A +∠ABC =180°,∵∠A =120°,∴∠PBH =60°,∵PB =3,∠PHB =90°,∴BH =PB •cos60°=32,PH =PB •sin60°=332,∴CH =BC ﹣BH =4﹣32=52,∴PC =.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .∵四边形ABCD 是菱形,∴∠ABD =∠CBD =30°,∵∠PCQ =30°,∴∠PBO =∠QCO ,∵∠POB=∠QOC,∴△POB∽△QOC,∴PO BOQO CO=,∴PO QOBO CO=,∵∠POQ=∠BOC,∴△POQ∽△BOC,∴∠OPQ=∠OBC=30°=∠PCQ,∴PQ=CQ=y,∴PC y,在Rt△PHB中,BH=12x,PH=32x,∵PC2=PH2+CH2,∴3y2=(2x)2+(4﹣12x)2,∴y=3(0≤x<8).(3)①如图2中,若直线QP交直线BC于B点左侧于E.此时∠CQE=120°,∵∠PBC=60°,∴△PBC中,不存在角与∠CQE相等,此时△QCE与△BCP不可能相似.②如图3中,若直线QP交直线BC于C点右侧于E.则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,∵∠PCB>∠E,∴只可能∠BCP=∠QCE=75°,作CF⊥AB于F,则BF=2,CF=PCF=45°,∴PF=CF=,此时PB=2+2,③如图4中,当点P在AB的延长线上时,∵△QCE 与△BCP 相似,∴∠CQE =∠CBP =120°,∴∠QCE =∠PCB =15°,作CF ⊥AB 于F .∵∠FCB =30°,∴∠FCP =45°,∴BF =12BC =2,CF =PF =23∴PB =3﹣2.综上所述,满足条件的PB 的值为3或232.【点评】本题考查相似形综合题,考查了菱形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.专题二动点函数背景下的面积问题【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE的长.【考点】三角形综合题.【专题】等腰三角形与直角三角形;应用意识.【分析】(1)过点E 作EG ⊥BC ,垂足为点G .AE =x ,则EC =2﹣x .根据BG =EG 构建方程求出x 即可解决问题.(2)①证明△AEF ∽△BEC ,可得22BCE AEF S BE S AE∆∆=,由此构建关系式即可解决问题.②分两种情形:当∠CAD <120°时,当120°<∠CAD <180°时,分别求解即可解决问题.【解答】解:(1)∵△ABC 是等边三角形,∴AB =BC =AC =2,∠BAC =∠ABC =∠ACB =60°.∵AD =AC ,∴AD =AB ,∴∠ABD =∠ADB ,∵∠ABD +∠ADB +∠BAC +∠CAD =180°,∠CAD =90°,∠ABD =15°,∴∠EBC =45°.过点E 作EG ⊥BC ,垂足为点G.设AE =x ,则EC =2﹣x .在Rt △CGE 中,∠ACB =60°,∴3sin ACB=)2EG EC x =- ∠,1cos ACB=12CG EC x =- ∠,∴BG =2﹣CG =1+12x ,在Rt △BGE 中,∠EBC =45°,∴131)22x x +=-,解得4x =-.所以线段AE的长是4-.(2)①设∠ABD =α,则∠BDA =α,∠DAC =∠BAD ﹣∠BAC =120°﹣2α.∵AD =AC ,AH ⊥CD ,∴1CAF=DAC=60-2α ∠∠,又∵∠AEF =60°+α,∴∠AFE =60°,∴∠AFE =∠ACB ,又∵∠AEF =∠BEC ,∴△AEF ∽△BEC ,∴22BCE AEF S BE S AE∆∆=,由(1)得在Rt △CGE 中,BG =1+12x,EG )2x =-,∴BE 2=BG 2+EG 2=x 2﹣2x +4,∴2224x x y x-+=(0<x <2).②当∠CAD <120°时,y =7,则有7=2224x x x-+,整理得3x 2+x ﹣2=0,解得x =23或﹣1(舍弃),2AE=3.当120°<∠CAD <180°时,同法可得22+24x x y x +=当y=7时,7=22+24x xx,整理得3x2﹣x﹣2=0,解得x=﹣23(舍弃)或1,∴AE=1.【点评】本题属于三角形综合题,考查了等边三角形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.【考点】相似形综合题.【专题】分类讨论;图形的相似;推理能力.【分析】(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=5,推出CO=CG=5,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF 时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.【解答】解:(1)如图1,延长FC交OM于点G,∵∠BCG+∠CGB=90°,∠MON+∠CGB=90°,∴∠BCG=∠MON,则tan∠BCG=tan∠MON=2,∴BG=2BC=4,CG=,在Rt△AOE中,设OE=a,由tan∠MON=2,可得OA a,则OG+6,OF=OG=a+,∴EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=∵CD平分∠FCO,∴∠FCD=∠DCO,∵CD∥OM,∴∠FCD=∠CGO,∠DCO=∠COG,∴∠CGO=∠COG,∴CO=CG=在Rt△COB中,由BC2+BO2=OC2,得22++2)2=(2,解得a1=﹣655(舍去),a2=255,∴OF=a+5=5,cos∠COF=45 OFOC=,∴sin∠COF=3 5;(3)当D在∠MON内部时,①如图3﹣1,△FDA∽△FDC时,此时CD=AD=2,∴m=2;②当△FDA∽△CDF时,如图3﹣2,延长CD交ON于点Q,过F作FP⊥CQ于P,则∠FDC=∠FDA=135°,∴∠FDP=45°,∵PC=FP•tan∠PFC=FP•tan∠MON=2FP=2DP=CD+DP,∴FP=PD=CD=m,∴FD m,∵△FDA∽△CDF,∴FD CD DA FD=,∴FD==,∴m=1;当D在∠MON外部时,∠ADF>90°,∠DFC>90°,∴∠ADF =∠DFC ,∴∠DFI =∠FDI ,ID =IF ,①如图3﹣3,△FDA ∽△DFC 时,此时△FDA ≌△DFC ,∴CF =AD =2,∵∠DAF =∠FCD =∠FHD ,∴A 、O 重合,延长BC 交ON 于R ,∴FR =2CF =4,CR =BR =,∴m =CD =AB =12BR =;②如图3﹣4,△FDA ∽△CFD 时,设CF =(t >0),延长BC 交ON 于R ,过F 作FS ⊥CD 于S ,∵△DFC ≌△FDH ,∴DH =FC ,∴ID =IF =12CF ,∴IS =t ,FS =2t ,CS =4t ,DS )t ,DH =FC =,∵△FDA ∽△CFD ,∴AD DF DF FC=,∴DF 2=AD •FC =2DH =t ,∵DF 2=DS 2+FS 2,∴=4t 2+)2t 2,解得t 1=512-,t 2=0(舍去),∴DH =t =52=AD ,矛盾,综上所述:m =1或m =2,或m =【点评】本题考查了解直角三角形,等腰三角形的性质,相似三角形的判定与性质等,解题关键是注意分类讨论思想的运用.专题三动点函数背景下的等腰三角形【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.【考点】几何变换综合题.【专题】几何综合题;应用意识.【分析】(1)证明∠ACD=∠EDB=∠B,推出tan∠ACD=tan∠B,可得AD ACAC AB=,由此构建方程即可解决问题.(2)如图1中,作EH⊥BD于H.证明△ACD∽△HDE,推出AC ADDH EH=,由此构建关系式即可解决问题.(3)分两种情形:①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N.利用角平分线的性质定理求出BD即可.②如图3﹣2中,当CB′交BA的延长线于K时,同法可得BD.【解答】解:(1)∵ED=EB,∴∠EDB=∠B,∵CD⊥DE,∴∠CDE=∠A=90°,∵∠ACD+∠ADC=90°,∠ADC+∠EDH=90°,∴∠ACD=∠EDB=∠B,∴tan∠ACD=tan∠B,∴AD ACAC AB=,∴334AD=,∴94AD=.(2)如图1中,作EH⊥BD于H.在Rt△ACB中,∵∠A=90°,AC=3,AB=4,∴BC=5,∵BE=y,∴EH=35y,BH=45y,DH=AB﹣AD﹣BH=4﹣x﹣45y,∵∠A=∠DHE=90°,∠ACD=∠EDH,∴△ACD∽△HDE,∴AC AD=DH EH,∴3x=434-x-55y y,∴220594x xyx-=+(0<x<4).(3)①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N∵AC =AB ′=3,AE ⊥CB ′,∴CE ='EB ='12CB =52,∴AE 22225113()22AC CE -=-,由△ACE ∽△KCA ,可得AK =3115,CK =185,∴BK =AB ﹣AK =4﹣3115,∵∠DCK =∠DCB ,DM ⊥CM ,DN ⊥CB ,∴DM =DN ,∴181185215252CDK CDB CK DM S DK CK S DB CB BC DN ∆∆===== ,∴BD =2543BK =10043151143,∴AD =AB ﹣BD =4﹣(10043151143)=7242151143.②如图3﹣2中,当CB ′交BA 的延长线于K 时,同法可得BD =2543BK =10043151143,∴AD =AB ﹣BD =7242﹣151143.【点评】本题属于几何变换综合题,考查了解直角三角形,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.2.(2019秋•青浦区期末)如图,在梯形ABCD 中,AD ∥BC ,BC =BD =10,CD =4,AD=6.点P 是线段BD 上的动点,点E 、Q 分别是线段DA 、BD 上的点,且DE =DQ =BP ,联结EP 、EQ .(1)求证:EQ ∥DC ;(2)当BP >BQ 时,如果△EPQ 是以EQ 为腰的等腰三角形,求线段BP 的长;(3)当BP =m (0<m <5)时,求∠PEQ 的正切值.(用含m 的式子表示)【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)先利用两边对应成比例,夹角相等,判断出△DEQ ∽△BCD ,得出∠DQE =∠BDC ,即可得出结论;(2)先用△DEQ ∽△BCD ,得出比例式表示出EQ ,再分两种情况,建立方程求解,即可得出结论;(3)先判得出△PHQ ∽△BGD ,得出PH PQ HQ BG BD GD ==,进而表示出HQ =1025m -,PH =26(102)5m -,即可得出结论.【解答】解:(1)∵AD ∥BC ,∴∠EDQ =∠DBC ,∵DE =DQ ,BD =BC ,∴1DE DQ =,BD BC =1,∴DE BD DQ BC=,∴△DEQ ∽△BCD ,∴∠DQE =∠BDC ,∴EQ ∥CD ;(2)设BP =x ,则DQ =x ,QP =2x ﹣10,∵△DEQ∽△BCD,∴EQ QDDC BC=,∴410EQ x=,∴EQ=25x,∵△EPQ是以EQ为腰的等腰三角形,∴Ⅰ、当EQ=EP时,∴∠EQP=∠EPQ,∵DE=DQ,∴∠EQP=∠QED,∴∠EPQ=∠QED,∴△EQP∽△DEQ,∴,∴EQ2=DE•QP,∴(25x)2=(2x﹣10)•x,解得,x=0(舍)或x=12523<6,即:BP=12523,Ⅱ、当QE=QP时,25x=2x﹣10,解得,x=254>6,此种情况不存在,即:BP=125 23;(3)如图,过点P作PH⊥EQ,交EQ的延长线于点H,过点B作BG⊥DC,垂足为点G,∵BD=BC,BG⊥DC,∴DG=2,BG=,∵BP=DQ=m,∴PQ=10﹣2m,∵EQ∥DC,∴∠PQH=∠BDG,∵∠PHQ=∠BGD=90°,∴△PHQ∽△BGD,∴PH PQ HQBG BD GD==102102m HQ-==,∴HQ=1025m-,PH=2)5m-,∴EH=102255m m-+=2,∴tan∠PEQ=PHEH=2)5m-12⨯=﹣5m.【点评】此题是相似形综合题,主要考查了相似三角形的判定和性质,平行线的性质,锐角三角函数,用方程的思想解决问题是解本题的关键.3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.【考点】相似形综合题.【专题】图形的相似;推理能力.【分析】(1)由点G是Rt△ABC的重心,证明CF⊥AB,即∠AFC=90°,利用外角的性质即可证明结论;(2)过点B作BH⊥CD于点H,先证△CAD≌△BCH,得出BH=CD=2,CH=AD=x,DH=2﹣x,再证△ADE ∽△BHE,利用合比性质即可求出结论;(3)分两种情况讨论,当GC=GD时,如图2﹣1,取AC的中点M,联结MD,可证AD=CH=12CD=1;当CG=CD时,如图2﹣2,可由重心分别求出CF,AC,CD的长,可由勾股定理求出AD的长.【解答】(1)证明:∵点G是Rt△ABC的重心,∴CF是Rt△ABC的中线,又∵在Rt△ABC中,AC=BC,∠ACB=90°,∴CF⊥AB,即∠AFC=90°,∵∠DEF=∠ADE+∠DAE=∠EFC+∠ECF,且∠ADE=∠EFC=90°,∴∠DAB=∠DCF;(2)解:如图1,过点B作BH⊥CD于点H,则∠CBH+∠BCH=90°,又∵∠BCH+∠ACD=90°,∴∠ACD=∠CBH,又∵∠ADC=∠CHB=90°,AC=CB,∴△CAD≌△BCH,∴BH=CD=2,CH=AD=x,DH=2﹣x,∵∠ADC=∠CHB=∠BHD=90°,∴AD∥BH,∴△ADE∽△BHE,∴AD DEBH EH=,∴2x DEEH=,∴22x DE EH DHEH EH++==,∴4-2xEH=x+2,∴2424(02)22x xy CE CH HE x xx x-+==+=+=<≤++;(3)解:当GC=GD时,如图2﹣1,取AC的中点M,联结MD,那么MD=MC,联结MG,MG⊥CD,且直线MG经过点B,那么BH与MG共线,又CH =AD ,那么AD =CH =12CD =1;当CG =CD 时,如图2﹣2,即CG =2,点G 为△ABC 的重心,∴332CF CG ==,∴AB =2CF =6,∴22AC AB ==,∴AD ==;综上所述,AD =1【点评】本题考查了函数,相似三角形的判定与性质,重心的性质等,解题关键是熟练掌握重心的性质.4.(2019秋•崇明区期末)如图,在△ABC 中,AB =AC =10,BC =16,点D 为BC 边上的一个动点(点D 不与点B 、点C 重合).以D 为顶点作∠ADE =∠B ,射线DE 交AC 边于点E ,过点A 作AF ⊥AD 交射线DE 于点F .(1)求证:AB •CE =BD •CD ;(2)当DF 平分∠ADC 时,求AE 的长;(3)当△AEF 是等腰三角形时,求BD 的长.【考点】相似形综合题.【专题】几何综合题;图形的相似;推理能力.【分析】(1)根据等腰三角形的性质得到∠B =∠C ,根据三角形的外角性质得到∠BAD =∠CDE ,得到△BAD ∽△CDE ,根据相似三角形的性质证明结论;(2)证明DF ∥AB ,根据平行线的性质得到AE BD AC BC =,证明△BDA ∽△BAC ,根据相似三角形的性质列式计算,得到答案;(3)分点F 在DE 的延长线上、点F 在线段DE 上两种情况,根据等腰三角形的性质计算即可.【解答】(1)证明:∵AB =AC ,∴∠B =∠C ,∠ADC =∠BAD +∠B ,∠ADE =∠B ,∴∠BAD =∠CDE ,又∠B =∠C ,∴△BAD ∽△CDE ,∴AB BD CD CE=,即AB •CE =BD •CD ;(2)解:∵DF 平分∠ADC ,∴∠ADE =∠CDE ,∵∠CDE =∠BAD ,∴∠ADE =∠BAD ,∴DF ∥AB ,∴AE BD AC BC=,∵∠BAD =∠ADE =∠B ,∴∠BAD =∠C ,又∠B =∠B ,∴△BDA ∽△BAC ,∴BD BA BA BC =,即101016BD =解得,254BD =,∴2541016AE =,解得,AE =12532;(3)解:作AH ⊥BC 于H ,∵AB =AC ,AH ⊥BC ,∴BH =HC =12BC =8,由勾股定理得,AH 22221086AB BH -=-=,∴tan B =AH BH =34,∴tan ∠ADF =AF AD =34,设AF =3x ,则AD =4x ,由勾股定理得,DF 22AD AF +=5x ,∵△BAD ∽△CDE ,∴AD AB DE CD =,当点F在DE的延长线上,FA=FE时,DE=5x﹣3x=2x,∴1042xCD x=,解得,CD=5,∴BD=BC﹣CD=11,当EA=EF时,DE=EF=2.5x,∴1042.5xCD x=,解得,CD=254,∴BD=BC﹣CD=39 4;当AE=AF=3x时,DE=75x,∴10475xCD x=,解得,CD=72,∴BD=BC﹣CD=252;当点F在线段DE上时,∠AFE为钝角,∴只有FA=FE=3x,则DE=8x,∴1048x CD x=,解得,CD=20>16,不合题意,∴△AEF是等腰三角形时,BD的长为11或394或252.【点评】本题考查的是相似三角形的判定和性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.【考点】几何变换综合题.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】(1)通过证明△ODE ∽△OCA ,可得2()DEO OAC S OD S OC∆∆=,即可求解;(2)通过证明△OEM ∽△BAC ,可得∠EOM =∠ABC =36°,分两种情况讨论可求解;(3)分四种情况讨论,由等腰三角形的性质可求解.【解答】解:(1)∵OC 是△ABC 中AB 边的中线,△ABC 的面积为26,∴S △OAC =13,∵DE ∥AC ,∴△ODE ∽△OCA ,∠OEM =∠OAC ,∴2()DEO OAC S OD S OC∆∆=,且OD =k ⋅OC ,∴S △ODE =13k 2,(2)∵△ODE ∽△OCA ,∴OE OD DE k OA OC AC ===,∵OC 是△ABC 中AB 边的中线,点M 是DE 的中点,∴AB =2AO ,EM =12DE ,∴2OE k EM AB AC==,且∠OEM =∠OAC ,∴△OEM ∽△BAC ,∴∠EOM =∠ABC =36°,如图2,当0<α<144°时,∵∠AON =∠B +∠ONB ,∴∠AOE +∠EOM =∠B +∠ONB ∴y =α如图3,当144°<α<180°时,∵∠BON =∠EOM ﹣∠BOE =36°﹣(180°﹣α)∴∠NOB =α﹣144°,∵∠BNO =∠ABC ﹣∠NOB =36°﹣(α﹣144°)=180°﹣α;(3)当0<α<144°时,若OB=ON,则∠ABC=∠BNO=36°=α,若OB=BN,则∠ONB=180362-=72°=α,若ON=BN,则∠ABC=∠BON=36°,∴∠ONB=180°﹣2×36°=108°=α,当144°<α<180°时,若OB=BN,则∠N=∠NOB=18°=180°﹣α,∴α=162°.【点评】本题是几何变换综合题,考查了相似三角形的判定和性质,旋转的性质,等腰三角形的性质等知识,证明△OEM∽△BAC是本题的关键.专题四动点函数背景下的线段问题【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);(3)如果AG=8,求DE的长.【考点】三角形综合题.【专题】几何综合题;等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识.【分析】(1)求出AC=3,可得∠DAC=∠FBC,则tan∠FBC=tan∠DAC=23 DCAC=;(2)由条件可得∠AGF=∠CBF,可得AF CFAG BC=,可用x表示CF和AF的长,求出CD,则S△DAF=12AF CD,可用x表示结果;(3)分两种情况,①当点D 在BC 的延长线上时,②当点D 在BC 的边上时,可求出AE 长AD 的长,则DE =AD ﹣AE 可求出.【解答】解:(1)∵∠ACB =90°,BC =4,sin ∠ABC =35,∴设AC =3x ,AB =5x ,∴(3x )2+16=(5x )2,∴x =1,即AC =3,∵BE ⊥AD ,∴∠AEF =90°,∵∠AFE =∠CFB ,∴∠DAC =∠FBC ,∴tan ∠FBC =tan ∠DAC =23DC AC =;(2)∵AG ∥BD ,∴∠AGF =∠CBF ,∴tan ∠AGF =tan ∠CBF ,∴AF CF AG BC =,AG AF BC CF =,∴34x CF CF-=,∴124CF x =+.∴12334AF CF x =-=-+=34x x+.∵∠EAF =∠CBF ,∴CD CF AC BC =,∴94CD x =+,∴S △DAF =12AF CD =2193272442(4)x x x x x ⨯⨯=+++;(3)①当点D 在BC 的延长线上时,如图1,∵AG =8,BC =4,AG ∥BD ,∴21AG AF BC CF ==,∴AF =2CF ,∵AC =3,∴AF =2,CF =1,∴CF 1tan AGE=tan CBF==BC 4∠∠,∴AE 1=GE 4,设AE =x ,GE =4x ,∴x 2+16x 2=82,解得x =,即AE .同理tan ∠DAC =tan ∠CBF ,∴DC 1=AC 4,∴DC =34,∴AD∴DE AD AE=-=②当点D在BC的边上时,如图2,∵AG∥BD,AG=8,BC=4,∴8241AG AFBC CF===.∴AF=6,∵∠EAF=∠CBF=∠ABC,∴cos∠EAF=cos∠ABC,∴654AE=,∴245AE=,同理AC BCAD AB=,∴345AD=,∴154AD=.∴DE=AE﹣AD=241521 5420-=.综合以上可得DE的长为191768或2120.【点评】本题是三角形综合题,考查了勾股定理,平行线的性质,三角形的面积,锐角三角函数等知识,熟练掌握锐角三角函数的定义是解题的关键.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.【考点】相似三角形的判定与性质;等腰三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)根据相似三角形的判定定理进行判定即可;(2)由相似三角形的性质即可得出答案;(3)由等腰直角三角形的性质、相似三角形的判定与性质即可得出答案.【解答】解:(1)与△ACD 相似的三角形有:△ABE 、△ADE ,理由如下:∵AB 2=BE •DC ,∴BE AB AB DC=,∵AB =AC ,∴∠B =∠C ,BE AC AB DC =,∴△ABE ∽△DCA .∵△ABE ∽△DCA ,∴∠AED =∠DAC .∵∠AED =∠C +∠EAC ,∠DAC =∠DAE +∠EAC ,∴∠DAE =∠C .∴△ADE ∽△CDA ;(2)∵△ADE ∽△CDA ,又∵DF 平分∠ADC ,∴DG DE AD DF AD CD==,设CE =a ,则DE =3CE =3a ,CD =4a ,∴34a AD AD a=,解得:AD =23a ,∴23342DG AD a DF CD a ===;(3)∵∠BAC =90°,AB =AC ,∴∠B =∠C =45°,∴∠DAE =∠C =45°∵DG ⊥AE ,∴∠DAG =∠ADF =45°,∴AG =DG =22AD =22×236a ,∴EG 2222(3)(6)3DE DG a a -=-a ,∴AE =AG +EG =(63)a ,∵∠AED =∠DAC ,∴△ADE ∽△DFA ,∴AD AE DF AD=,∴22AD AE ==a ,∴24DG DF +==.【点评】本题考查了相似三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识;熟记相似三角形的判定定理是解题的关键.专题四动点函数背景下四边形【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt △ABC 中,∠C =90°,AC =8,BC =6,点P 、Q 分别在边AC 、射线CB 上,且AP =CQ ,过点P 作PM ⊥AB ,垂足为点M ,联结PQ ,以PM 、PQ 为邻边作平行四边形PQNM ,设AP =x ,平行四边形PQNM 的面积为y .(1)当平行四边形PQNM 为矩形时,求∠PQM 的正切值;(2)当点N 在△ABC 内,求y 关于x 的函数解析式,并写出它的定义域;(3)当过点P 且平行于BC 的直线经过平行四边形PQNM 一边的中点时,直接写出x 的值.【考点】四边形综合题.【专题】几何综合题;应用意识.【分析】(1)当四边形PQMN 是矩形时,PQ ∥AB .根据tan ∠PQM =PM PQ求解即可.(2)如图1中,延长QN 交AB 于K .求出MK ,PM ,根据y =PM •MK 求解即可.(3)分两种情形:①如图3﹣1中,当平分MN 时,D 为MN 的中点,作NE ∥BC 交PQ 于E ,作NH ⊥CB 交CB 的延长线于H ,EG ⊥BC 于G .根据EG =12PC 构建方程求解.②如图3﹣2中,当平分NQ 时,D 是NQ 的中点,作DH ⊥CB 交CB 的延长线于H .根据PC =GH 构建方程求解即可.【解答】解:(1)在Rt △ACB 中,∵∠C =90°,AC =8,BC =6,∴AB ==10,当四边形PQMN是矩形时,PQ∥AB.∴tan∠PQM=PMPQ=3955253PACQ=.(2)如图1中,延长QN交AB于K.由题意BQ=6﹣x,QN=PM=35x,AM=45x,KQ=45BQ=2445x-,BK=35BQ=1835x-,∴MK=AB﹣AM﹣BK=325x-,∵QN<QK,∴35x<2445x-,∴x<247,∴y=PM•MK=296325x x-(0<x<247).(3)①如图3﹣1中,当平分MN时,D为MN的中点,作NE∥BC交PQ于E,作NH⊥CB交CB的延长线于H,EG⊥BC于G.∵PD∥BC,EN∥BC,∴PD∥NE,∵PE∥DN,∴四边形PDNE是平行四边形,∴PE=DN,∵DN=DM,PQ=MN,∴PE=EQ,∵EG∥PC,∴CG=GQ,∴EG=12PC,∵四边形EGHN是矩形,∴NH=EG=35NQ=35PM=925x,PC=8﹣x,∴925x=12•(8﹣x),解得x=20043.②如图3﹣2中,当平分NQ时,D是NQ的中点,作DH⊥CB交CB的延长线于H.∵DH=PC,∴8﹣x=12•925x,解得x=40059,综上所述,满足条件x的值为20043或40059.【点评】本题属于四边形综合题,考查了平行四边形的性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.【考点】相似三角形的判定与性质;解直角三角形;等腰三角形的性质.【专题】图形的相似;应用意识.【分析】(1)根据两角对应相等的两个三角形相似证明即可.(2)证明△PAB∽△PCA,利用相似三角形的性质解决问题即可.(3)分三种情形:AB=AC,AB=BC,AC=BC分别求解即可解决问题.【解答】证明:(1)∵∠ABP +∠BAP +∠APB =180°,∠APB +∠BAC =180°,∴∠ABP +∠BAP +∠APB =∠APB +∠BAC ,即∠ABP +∠BAP +∠APB =∠APB +∠BAP +∠CAP ,∴∠ABP =∠CAP ,又∵∠APB =∠APC ,∴△PAB ∽△PCA .(2)如图1中,∵∠APB +∠BAC =180°,∠APB =120°,∴∠BAC =60°,在△ABC 中,∵∠ABC =90°,∠BAC =60°,∴,又∵△PAB ∽△PCA ,∴12PB PA AB PA PC AC ===,∴14PB PB PA PC PA PC == ,即4PC PB =.(3)∵∠BAC =45°,∠APB +∠BAC =180°,∠APB =∠APC ,∴∠APB =∠APC =135°.∴∠BPC =360°﹣∠APB ﹣∠APC =360°﹣135°﹣135°=90°,∵△PCA ∽△PAB ,∴PA PC AC PB PA AB==,∴163.①如图2中,当△ABC 是等腰三角形,且AB =AC 时,2tan PBC=()=1PC AC PB AB =∠.②如图3中,当△ABC 是等腰三角形,且AB =BC 时,∠ACB =∠BAC =45°,∠ABC =90°,易得2AC AB ,∴2tan PBC=()=2PC AC PB AB=∠.③如图10﹣4,当△ABC 是等腰三角形,且AC =BC 时,∠ABC =∠BAC =45°,∠ACB =90°,易得2=2AC AB ,∴21tan PBC=()=2PC AC PB AB =∠.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.3.(2019秋•徐汇区期末)如图,在△ABC 中,AB =AC =5,BC =6,点D 是边AB 上的动点(点D 不与点AB 重合),点G 在边AB 的延长线上,∠CDE =∠A ,∠GBE =∠ABC ,DE 与边BC 交于点F .(1)求cos A 的值;(2)当∠A =2∠ACD 时,求AD 的长;(3)点D 在边AB 上运动的过程中,AD :BE 的值是否会发生变化?如果不变化,请求AD :BE 的值;如果变化,请说明理由.【考点】三角形综合题.。
马井堂上海市各区县历年中考数学模拟压轴题汇总

上海市各区县历年中考数学二模试卷压轴题汇总1. 已知,如图,△ABC 是等边三角形,过AC 边上的点D 作 DG //BC ,交AB 于点G ,在GD 的延长线上取点E ,使DE=DC ,连接AE 、BD .(1)求证:△AGE ≌△DAB ;(2)过点E 作EF //DB ,交BC 于点F ,连AF ,求∠AEF 的度数.D A C GE F2、 如图,菱形OABC 放在平面直角坐标系内,点A 在x 轴的正半轴上,点B 在第一象限,其坐标为(8,4).抛物线2bx c y ax ++=过点O 、A 、C .(1)求抛物线的解析式?(2)将菱形向左平移,设抛物线与线段AB 的交点为D,连接CD .① 当点C 又在抛物线上时求点D的坐标?② 当△BCD 是直角三角形时,3、如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC= 4.(1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴;(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的距离相等.如果存在,求出P点坐标;如果不存在,请说明理由.4、 如图,AD//BC ,点E 、F 在BC 上,∠1=∠2,AF ⊥DE ,垂足为点O. (1)求证:四边形AEFD 是菱形;(2)若BE=EF=FC ,求∠BAD+∠ADC 的度数;(3)若BE=EF=FC ,设AB = m ,CD = n ,求四边形ABCD 的面积.21OFEDCBA5、如图,在平面直角坐标系中,抛物线6422++-=x x y 与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于C 点,顶点为D.过点C 、D 的直线与x 轴交于E 点,以OE 为直径画⊙O 1,交直线CD 于P 、E 两点. (1)求E 点的坐标;(2)联结PO 1、PA.求证:BCD ∆~A PO 1∆;(3) ①以点O 2 (0,m)为圆心画⊙O 2,使得⊙O 2与⊙O 1相切,当⊙O 2经过点C 时,求实数m 的值;②在①的情形下,试在坐标轴上找一点O 3,以O 3为圆心画⊙O 3,使得⊙O 3与⊙O 1、⊙O 2同时相切.直接写出满足条件的点O 3的坐标(不需写出计算过程).6.如图,EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别交于点E、F.(1)求证:四边形BFDE是菱形;(2)若E为线段AD的中点,求证:AB⊥BD.EA DOB F C7. 在平面直角坐标系中,抛物线2y x bx c =++经过点(0,2)和点(3,5).(1)求该抛物线的表达式并写出顶点坐标;(2)点P 为抛物线上一动点,如果直径为4的⊙P 与y 轴相切,求点P 的坐标.bx c ++8. 如图,在Rt △ABC 中,∠BAC = 90°,AB =3,AC =4,AD 是BC 边上的高,点E 、F 分别是AB 边和AC 边上的动点,且∠EDF = 90°.(1)求DE ︰DF 的值;(2)联结EF ,设点B 与点E 间的距离为x ,△DEF 的面积为y ,求y 关于x 的函数解析式,并写出x 的取值范围; (3)设直线DF 与直线AB 相交于点G ,△EFG 能否成为等腰三角形?若能,请直接写出线段BE 的长;若不能,请说明理由.CE FA备用图1BCD 备用图2BCA A9. 如图,已知抛物线c bx x y ++-=2与x 轴负半轴交于点A ,与y 轴正半轴交于点B ,且OB OA =.(1) 求c b +的值;(2) 若点C 在抛物线上,且四边形OABC 是平行四边形,试求抛物线的解析式; (3) 在(2)的条件下,作∠OBC 的角平分线,10.如图1,已知⊙O的半径长为1,PQ是⊙O的直径,点M是PQ延长线上一点,以点M为圆心作圆,与⊙O交于A、B两点,联结PA并延长,交⊙M于另外一点C.(1) 若AB恰好是⊙O的直径,设OM=x,AC=y,试在图2中画出符合要求的大致图形,并求y关于x的函数解析式;(2) 联结OA、MA、MC,若OA⊥MA,且△OMA与△PMC相似,求OM的长度和⊙M的半径长;(3) 是否存在⊙M,使得AB、AC恰好是一个正五边形的两条边?若存在,试求OM的长度和⊙M的半径长;若不存在,试说明理由.图2上海市各区县历年中考数学二模试卷压轴题答案1.(1)∵△ABC 是等边三角形,DG //BC ,∴△AGD 是等边三角形.AG =GD =AD ,∠AGD =60°.∵DE =DC ,∴GE =GD +DE =AD +DC =AC =AB .∵∠AGD =∠BAD ,AG =AD ,∴△AGE ≌△DAB . …………………………(5分) (2)由(1)知AE =BD ,∠ABD =∠AEG …………………………………………(6分) ∵EF ∥DB ,DG ∥BC ,∴四边形BFED 是平行四边形 ………………………… (7分) ∴∠DBC =∠DEF ,∴∠AEF=∠AEG +∠DEF =∠ABD +∠DBC=∠ABC =60°(8分)2、(本题12分)(1)A (0,3),C(3,0) ∵3m=3 ∴m=1∴抛物线的解析式为322++-=x x y ………2分(2)∵m=1 ∴322++-=x x y ∴AO=3 点32,(2++-x x x D ),连结OD当y=0时,即0322=++-x x ,解得x 1=-1 x 2=3 ∴OC=3∴S= S △AOD + S △DOC =292923)32(32132122++-=++-⨯⨯+⨯x x x x x ∴S 与x 的函数关系式S=2929232++-x x (0<x <3) …………………………4分当232=-=a b x 符合(0<x <3) S 最大值=863)23(4)29(29)23(44422=-⨯-⨯-⨯=-a b ac ……6分(3)…………………………………………7分假设存在点P ,使AC 把△PCD 分成面积之比为2:1的两部分,分两种情况讨论: (ⅰ)当△CDE 与△CEP 的面积之比为2:1时,DE=2EP ∴DP=3EP即)3(3322+-=++-x x x 整理得:0652=+-x x解得;21=x 32=x (不合题意,舍去), 此时点P 的坐标是(2,0)… 9分 (ⅱ)当△CEP 与△CDE 的面积之比为2:1时, EP DE 21=, ∴EP DP 23= 即)3(23322+-=++-x x x 整理得:03722=+-x x BED PO xy3453OA OC AOC Rt ECP EP PC x==∴∴∠=︒∴==-为等腰54321OFEDCB A 解得:213=x 34=x (不合题意,舍去),此时点P 的坐标是(21,0) …………………………………………11分综上所述,使直线AC 把△PCD 分成面积之比为2:1两部分的点P 存在,点P 的坐标是(2,0)或(21,0)……………………… 12分3、(12分)解:(1) ( 6分)∵C(2,4), BC=4 且 BC//OA ∴ B(6,4) 1分设抛物线为c bx ax y ++=2()0≠a将O(0,0),C(2,4),B(6,4)代入得⎪⎩⎪⎨⎧=+=++=)3(4636)2(424)1(0b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=03831c b a 3分∴x x y 38312+-= 1分∴顶点)316,4( 对称轴:直线4=x 2分(2) (6分)据题意,设),(a a P 或),(a a P -()0≠a 1分将),(a a P 代入抛物线得a a a =+-38312 解得0,521==a a (舍) 2分将),(a a P -代入抛物线得a a a -=+-38312 解得0,1121==a a (舍) 2分∴符合条件的点)5,5(p 和)11,11(-p 1分4、(12分)(1)( 4分)证明:(方法一)∵AF ⊥DE∴∠1+∠3=90° 即:∠3=90°-∠1∴∠2+∠4=90° 即:∠4=90°-∠2又∵∠1=∠2 ∴∠3=∠4 ∴AE = EF∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5∴AE = AD ∴EF = AD 2分 ∵AD//EF ∴四边形AEFD 是平行四边形 1分 又∵AE = AD∴四边形AEFD 是菱形 1分(方法二)∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5∵AF ⊥DE ∴∠AOE=∠AOD =90°在△AEO 和△ADO 中⎪⎩⎪⎨⎧=∠=∠∠=∠AO AO AOD AOE 51 ∴△AEO ≅△ADO ∴EO=OD在△AEO 和△FEO 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FOE AOE EO EO 21∴△AEO ≅△FEO ∴AO=FO 2分 ∴AF 与ED 互相平分 1分 ∴四边形AEFD 是平行四边形 又∵AF ⊥DE ∴四边形AEFD 是菱形 1分 (2)( 5分)∵菱形AEFD ∴AD=EF ∵BE=EF ∴AD=BE又∵AD//BC ∴四边形ABED 是平行四边形 1分 ∴AB//DE ∴∠BAF=∠EOF同理可知 四边形AFCD 是平行四边形 ∴AF//DC ∴∠EDC=∠EOF又∵AF ⊥ED ∴∠EOF=∠AOD=90° ∴∠BAF=∠EDC=∠EOF=90° 2分 ∴∠5 +∠6=90° 1分∴∠BAD+∠ADC=∠BAF+∠6 +∠5+∠EDC =270° 1分(3)( 3分)由(2)知∠BAF =90°平行四边形AFCD ∴AF=CD=n又∵AB=m mn 21AF AB 21S ABF =⋅=∆ 1分 由(2)知 平行四边形ABED ∴DE=AB=m 由(1)知OD=m DE 21= mn 21OD AF S AFCD =⋅=四边形 1分 mn S AFCD ABCD =+=∆四边形四边形S S ABF 1分5、(14分)解:(1) ( 3分)()81264222+--=++-=x x x y ∴)8,1(),6,0(D C 1分设直线CD:()0≠+=k b kx y 将C 、D 代入得⎩⎨⎧+==686k b 解得⎩⎨⎧==62b k∴CD 直线解析式:62+=x y 1分 )0,3(-E 1分 (2) ( 4分)令y=0 得06422=++-x x 解得3,121=-=x x ∴)0,3()0,1(B A - 1分又∵)0,0(O 、)0,3(-E ∴以OE 为直径的圆心)0,(231-O 、半径231=r .设)62,(+t t P 由231=PO 得232223)62()(=+++t t 解得3,25121-=-=t t (舍) ∴),(56512-P 2分∴585=PA 211=AO54321OFEDCB A6又 5=DC 53=CB 172=DB∴5211===PADBPO CB AO DC 1分 ∴BC D ∆~A PO 1∆ (3) ( 7分)① )0,(231-O 231=r),0(2m O 据题意,显然点2O 在点C 下方 m C O r -==622当⊙O 2与⊙O 1外切时 2121r r O O +=代入得()()m m -+=+6232223 解得 2,51821==m m (舍)2分 当⊙O 2与⊙O 1内切时 2121r r O O -=代入得()()m m --=+6232223 解得 518,221==m m (舍) 2分 ∴2,51821==m m ② ⎪⎭⎫ ⎝⎛518,03O ⎪⎭⎫ ⎝⎛-710,03O ⎪⎭⎫ ⎝⎛0,233O ⎪⎭⎫ ⎝⎛-0,14453O ⎪⎭⎫ ⎝⎛1514,03O ()2,03O ⎪⎭⎫⎝⎛0,2213O 3分6、.证明:(1)∵四边形ABCD 是平行四边形∴ED ∥BF ,得∠EDB =∠FBD ……………………………………………………(2分)∵EF 垂直平分BD∴BO=DO ,∠DOE =∠BOF =90°∴△DOE ≌△BOF ……………………………………………………………………(2分) ∴ EO=FO∴四边形BFDE 是平行四边形 ……………………………………………………(1分) 又∵EF ⊥BD∴四边形BFDE 是菱形 ……………………………………………………………(1分) (2)∵四边形BFDE 是菱形∴ED=BF ∵AE=ED∴AE=BF ………………………………………………………………………………(2分) 又∵AE ∥BF∴四边形ABFE 是平行四边形………………………………………………………(1分) ∴AB ∥EF ……………………………………………………………………………(1分) ∴∠ABD =∠DOE ……………………………………………………………………(1分) ∵∠DOE =90° ∴∠ABD =90°即AB ⊥BD ……………………………………………………………………………(1分)7.解:(1)把(0,2)、(3,5)分别代入2y x bx c =++得 2593cb c =⎧⎨=++⎩解得22b c =-⎧⎨=⎩……………………………………………(3分) ∴抛物线的解析式为222y x x =-+ ………………………………………………(1分) ∴抛物线的顶点为(1,1)………………………………………………………………(2分) (2)设点P 到y 轴的距离为d ,⊙P 的半径为r∵⊙P 与y 轴相切 ∴1422d r ==⨯= ∴点P 的横坐标为2±…………………………………………………………………(2分)当2x =时, 2y = ∴点P 的坐标为(2,2) …………………………………(2分)当2x =-时,10y = ∴点P 的坐标为(2,10)- ………………………………(2分)∴点P 的坐标为(2,2)或(2,10)-.8.解:(1)∵∠BAC = 90° ∴∠B +∠C =90°,∵AD 是BC 边上的高 ∴∠DAC +∠C =90°∴∠B =∠DAC ………………………………………………………………………(1分) 又∵∠EDF = 90°∴∠BDE +∠EDA =∠ADF +∠EDA = 90° ∴∠BDE =∠ADF∴△BED ∽△AFD ……………………………………………………………………(1分)∴DE BDDF AD =…………………………………………………………………………(1分) ∵3cot 4BD AB B AD AC === ∴DE ︰DF =34…………………………………………………………………………(1分)(2)由△BED ∽△AFD 得34BE BD AF AD ==∴4433AF BE x == …………………………………………………………………(1分)∵BE x = ∴3AE x =-∵∠BAC = 90°∴2222425(3)()6939EF x x x x =-+=-+………………………………………(1分) ∵DE ︰D F =3︰4,∠EDF =90°∴ED =35EF ,FD =45EF …………………………………………………………………(1分) ∴216225y ED FD EF =⋅=∴22365432525y x x =-+ (03)x ≤≤ ………………………………………………(2分) (3)能. BE 的长为543255或.……………………………………………………………(5分)(说明:BE 的长一个正确得3分,全对得5分)9、解:(1)由题意得:点B 的坐标为),0(c ,其中0>c ,c OB = (1分) ∵OB OA =,点A 在x 轴的负半轴上,∴点A 的坐标为)0,(c - (1分)∵点A 在抛物线c bx x y ++-=2上,∴c bc c +--=20 (1分)∴ 1=+c b (因为0>c ) (1分)(2)∵四边形OABC 是平行四边形∴c AO BC ==,又BC ∥x 轴,点B 的坐标为),0(c∴点C 的坐标为),(c c (1分) 又点C 在抛物线上,∴c bc c c ++-=2∴0=-c b 或0=c (舍去) (1分) 又 由(1)知:1=+c b ∴21=b ,21=c . 抛物线的解析式为21212++-=x x y . (2分) (3)过点P 作⊥PM y 轴,⊥PN BC ,垂足分别为M 、N ∵ BP 平分CBO ∠ ∴ PN PM = (1分) 设点P 的坐标为)2121(2++-x x x , ∴x x x =++--)2121(212 (1分) 解得:23=x 或0=x (舍去) (1分) 所以,点P 的坐标为)21,23(- (1分)10、(1)图画正确 (1分)过点M 作AC MN ⊥,垂足为N∴y NC AN 21== 由题意得:AB PM ⊥, 又AB 是圆O 的直径∴1==OP OA ∴︒=∠45APO , 2=PA∴y PN 212+=(1分) 在Rt △PNM 中,PMPNNPM =∠cos 又x PM +=1,︒=∠45NPM∴ 22121245cos =++=︒x y∴ y 关于x 的函数解析式为22-=x y (1>x ) (2分)(2)设圆M 的半径为r因为 OA ⊥MA ,∴∠OAM=90°,12+=r OM又△OMA 与△PMC 相似,所以△PMC 是直角三角形。
2020-2021年上海各区数学中考一模压轴题分类汇编-18题含详解
专题2021年分类汇编-18题专题一图形的翻折【知识梳理】【历年真题】1.(2020秋•崇明区期末)在△ABC中,AB=,∠B=45°,∠C=60°.点D为线段AB的中点,点E在边AC上,连接DE,沿直线DE将△ADE折叠得到△A′DE.连接AA′,当A′E⊥AC时,则线段AA′的长为.2.(2020秋•长宁区期末17)如图,矩形ABCD沿对角线BD翻折后,点C落在点E处.联结CE交边AD于点F.如果DF=1,BC=4,那么AE的长等于.3.(2020秋•虹口区期末)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D是BC的中点,点E在边AB上,将△BDE沿直线DE翻折,使得点B落在同一平面内的点B'处,线段B'D交边AB于点F,联结AB'.当△AB'F是直角三角形时,BE的长为.5.(2020秋•松江区期末)如图,已知矩形纸片ABCD,点E在边AB上,且BE=1,将△CBE沿直线CE翻折,使点B落在对角线AC上的点F处,联结DF,如果点D、F、E在同一直线上,则线段AE的长为.6.(2020秋•普陀区期末)如图,在▱ABCD中,点E在边BC上,将△ABE沿着直线AE翻折得到△AFE,点B的对应点F恰好落在线段DE上,线段AF的延长线交边CD于点G,如果BE:EC=3:2,那么AF:FG的值等于.专题二图形的旋转【知识梳理】【历年真题】1.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=55(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为.2.(2020秋•闵行区期末)如图,在Rt△ABC中,∠ACB=90°,AB=3,tan B=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=.3.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为.4.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为.5.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP =.6.(2020秋•奉贤区期末)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD 是△ABC 的角平分线,将Rt △ABC 绕点A 旋转,如果点C 落在射线CD 上,点B 落在点E 处,联结DE ,那么∠AED 的正切值为.专题三定义新图形【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC3AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.2.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=.3.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为.4.(2020秋•徐汇区期末)如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=45,ED=5,如果△ECD的面积是6,那么BC的长是.5.(2020秋•金山区期末)已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=12,CE=GE,那么BD的长等于.6.(2020秋•黄浦区期末)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为.专题2021年分类汇编-18题专题一图形的翻折【历年真题】1.(2020秋•崇明区期末)在△ABC中,AB=,∠B=45°,∠C=60°.点D为线段AB的中点,点E在边AC上,连接DE,沿直线DE将△ADE折叠得到△A′DE.连接AA′,当A′E⊥AC时,则线段AA′的长为2.【考点】翻折变换(折叠问题).【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;运算能力;推理能力.【分析】画出相应的图形,结合图形通过作高构造直角三角形,求出AM=BM=4,进而求出AC,再利用相似三角形的性质和判定求出AE,根据对称在Rt△AEF中求出AF即可.【解答】解:如图,过点A作AM⊥BC,垂足为M,在Rt△ABM中,∠B=45°,AB=,∴AM=BM=AB•sin∠B=4,在Rt△ACM中,AM=4,∠C=60°,∴AC=AM4=sin C sin60∠,又∵A′E⊥AC,∴∠A′EC=90°,由折叠得∠AED=∠A′ED=12(180°﹣90°)=45°,AA′⊥DE,∵∠AED=45°=∠B,∠DAE=∠CAB,∴△DAE∽△CAB,∴AE AD=AB DC,∵点D为线段AB的中点,∴AD=BD=12AB=,833AE=,在Rt△AEF中,AF=EF=AE•sin∠AED=×2,∴AA′=2AF=,故答案为:.【点评】本题考查轴对称的性质,相似三角形的判定和性质,解直角三角形,掌握轴对称、相似三角形的性质以及解直角三角形是解决问题的关键.2.(2020秋•长宁区期末17)如图,矩形ABCD 沿对角线BD 翻折后,点C 落在点E 处.联结CE 交边AD 于点F .如果DF =1,BC =4,那么AE 的长等于655.【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形菱形正方形;推理能力.【分析】首先根据题意得到EG =CG ,CE ⊥BD ,证明△CDF ∽△BCD 和△CDG ∽△BDC ,可计算CD 和CG 的长,再证明△EFD ∽△AED ,可得AE 的长.【解答】解:由折叠得:CE ⊥BD ,CG =EG ,∴∠DGF =90°,∴∠DFG +∠FDG =90°,∵四边形ABCD 是矩形,∴∠ADC =∠BCD =90°,∴∠ADG +∠CDG =90°,∴∠CDG =∠DFG ,∵∠CDF =∠BCD =90°,∴△CDF ∽△BCD ,∴CD DF =BC CD,∵AB =4,DF =1,∴CD 1=4CD,∴CD =2,由勾股定理得:CF =221+2=5,BD 222+45,同理得:△CDG∽△BDC,∴CD CG=BD BCCG4,∴CG =455,∴CE=2CG =85 5,∴EF=CE﹣CF =855=355,∵DF1=ED2,ED21==AD42,且∠EDF=∠AED,∴△EFD∽△AED,∴EF DF=AE DE ,即15=AE2,∴AE【点评】本题主要考查了几何变换中的翻折变换、相似三角形的性质和判定、矩形的性质、勾股定理;熟练掌握翻折变换和矩形的性质,利用相似三角形列比例式是本题的关键.3.(2020秋•虹口区期末)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D是BC的中点,点E在边AB上,将△BDE沿直线DE翻折,使得点B落在同一平面内的点B'处,线段B'D交边AB于点F,联结AB'.当△AB'F是直角三角形时,BE的长为2或40 17.【考点】翻折变换(折叠问题);相似三角形的判定与性质;勾股定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】分两种情况画出图形,①方法一:如图1,当∠AFB′=90°时,由相似三角形的性质及直角三角形的性质可求出答案;方法二:过点E作EH⊥BC于点H,设EH=3a,BE=5a,则BH=4a,由BF的长列出方程,解方程求出a即可;②方法一如图2,当∠AB′F=90°时,由相似三角形的性质及直角三角形的性质可求出答案.方法二:过点E作EG⊥BD于点G,设EG=3a,BG=4a,BE=5a,得出9442a a+=,求出a的值则可得出答案.【解答】解:①方法一:如图1,当∠AFB′=90°时.在Rt △ABC 中,∵AC =6,BC =8,∴AB 22226810AC BC +=+=,∵D 是BC 的中点,∴BD =CD =12BC =4,∵∠AFB '=∠BFD =90°,∠ACB =90°,∴∠DFB =∠ACB ,又∵∠DBF =∠ABC ,∴△BDF ∽△BAC ,∴BF BD BC AB =,即4810BF =,解得:BF =165,设BE =B 'E =x ,则EF =165﹣x ,∵∠B =∠FB 'E ,∴sin ∠B =sin ∠FB 'E ,∴'AC EF AB B E =,∴166510x x-=,解得x =2.∴BE =2.方法二:过点E 作EH ⊥BC 于点H ,设EH =3a ,BE =5a ,则BH =4a ,∵将△BDE 沿直线DE 翻折,∴EF =3a ,∴BF =8a =BD •cos ∠B =4×45,∴a =25,∴BE =5a =2;②如图2中,当∠AB ′F =90°时,连接AD ,作EH ⊥AB ′交AB ′的延长线于H.∵AD =AD ,CD =DB ′,∴Rt △ADC ≌Rt △ADB ′(HL ),∴AC =AB ′=6,∵将△BDE 沿直线DE 翻折,∴∠B =∠DB 'E ,∵AB '⊥DB ',EH ⊥AH ,∴DB '∥EH ,∴∠DB 'E =∠B 'EH ,∴∠B =∠B 'EH ,∴sin ∠B =sin ∠B 'EH ,设BE =x ,则B 'H =35x ,EH =45x ,在Rt △AEH 中,AH 2+EH 2=AE 2,∴22234(6)()(10)55x x x ++=-,解得x =4017,∴BE =4017.则BE 的长为2或4017.方法二:过点E 作EG ⊥BD 于点G ,设EG =3a ,BG =4a ,BE =5a ,∴DG =EG ×32=92a ,∵DG +GB =DB ,∴9442a a +=,∴a =817,∴BE =4017.故答案为:2或4017.【点评】本题考查了翻折变换、勾股定理、解直角三角形、相似三角形的判定与性质、全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想解决问题.5.(2020秋•松江区期末)如图,已知矩形纸片ABCD ,点E 在边AB 上,且BE =1,将△CBE 沿直线CE 翻折,使点B 落在对角线AC 上的点F 处,联结DF ,如果点D 、F 、E 在同一直线上,则线段AE 的长为152+.【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;运算能力;推理能力.【分析】根据矩形的性质得到AD =BC ,∠ADC =∠B =∠DAE =90°,根据折叠的性质得到CF =BC ,∠CFE =∠B =90°,EF =BE =1,DC =DE ,证明△AEF ∽△DEA ,根据相似三角形的性质即可得到结论.【解答】解:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠ADC =∠B =∠DAE =90°,∵把△BCE 沿直线CE 对折,使点B 落在对角线AC 上的点F 处,∴CF =BC ,∠CFE =∠B =90°,EF =BE =1,∠CEB =∠CEF ,∵矩形ABCD 中,DC ∥AB ,∴∠DCE =∠CEB ,∴∠CEF =∠DCE ,∴DC =DE ,设AE=x,则AB=CD=DE=x+1,∵∠AFE=∠CFD=90°,∴∠AFE=∠DAE=90°,∵∠AEF=∠DEA,∴△AEF∽△DEA,∴AF DEEF AE=,∴11x xx+=,解得x=152+或x=152(舍去),∴AE=12.故答案为:15 2.【点评】本题考查了翻折变换(折叠问题),平行线的性质,相似三角形的判定和性质,矩形的性质,正确的识别图形是解题的关键.6.(2020秋•普陀区期末)如图,在▱ABCD中,点E在边BC上,将△ABE沿着直线AE翻折得到△AFE,点B的对应点F恰好落在线段DE上,线段AF的延长线交边CD于点G,如果BE:EC=3:2,那么AF:FG的值等于214.【考点】相似三角形的判定与性质;平行四边形的性质;翻折变换(折叠问题).【专题】多边形与平行四边形;平移、旋转与对称;图形的相似;推理能力.【分析】延长BC,AG交于点H,设BE=3x,EC=2x,由平行四边形的性质可得AD=BC=5x,AD∥BC,由折叠的性质可得∠AEB=∠AEF,BE=EF=3x,通过证明△ADF∽△HEF,△ADG∽△HCG,可求AF=425y,FG=AG﹣AF=85y,即可求解.【解答】解:如图,延长BC,AG交于点H,∵BE:EC=3:2,∴设BE=3x,EC=2x,∵四边形ABCD是平行四边形,∴AD=BC=5x,AD∥BC,∴∠DAE=∠AEB,∵将△ABE沿着直线AE翻折得到△AFE,∴∠AEB=∠AEF,BE=EF=3x,∴∠DAE=∠AED,∴AD=DE=5x,∴DF=2x,∵AD∥BC,∴△ADF∽△HEF,∴AD DF AFEH EF FH==,∴523x AFEH FH==,∴EH=152x,AF=23FH,∴CH=EH﹣EC =x,∵AD∥BC,∴△ADG∽△HCG,∴AD AGCH GH=,∴51011112x AGGHx==,∴设AG=10y,GH=11y,∴AH=21y,∴AF=215y×2=425y,∴FG=AG﹣AF=85y,∴AF:FG=21:4=21 4,故答案为21 4.【点评】本题考查了相似三角形的判定和性质,折叠的性质,平行四边形的性质,灵活运用这些性质进行推理是解题的关键.专题二图形的旋转【历年真题】1.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=5(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为【考点】旋转的性质;解直角三角形.【专题】分类讨论;平移、旋转与对称;几何直观.【分析】根据△AA′C为直角三角形,分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形;②当点B'在线段AC的延长线上时,△AA′C为直角三角形,依据线段的和差关系进行计算即可得到点A与点B'的距离.【解答】解:分两种情况:①当点B '在线段AC 上时,△AA ′C 为直角三角形,∵∠ACB =90°,AB =10,sin A =5,∴BC =AB ×55=10×55=∴B 'C =AC =,∴AB '=AC ﹣B 'C =②当点B '在线段AC 的延长线上时,△AA ′C 为直角三角形,同理可得,B 'C =AC =,∴AB '=AC +B 'C =综上所述,点A 与点B '的距离为故答案为:【点评】本题考查了旋转的性质,勾股定理,锐角三角函数的应用,运用分类思想是本题的关键.2.(2020秋•闵行区期末)如图,在Rt △ABC 中,∠ACB =90°,AB =3,tan B =.将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,点C 落在点E 处,射线DE 与边AB 相交于点F ,那么BF =3【考点】旋转的性质;解直角三角形.【专题】平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.【分析】过点F 作FG ⊥AC 于点G ,由旋转的性质得出∠B =∠D ,得出tan ∠B =tan ∠D =12FG GD =,由平行线的性质得出∠B =∠AFG ,设AG =x ,则FG =2x ,则2132x x =+,求出AG =1,则可得出答案.【解答】解:如图,过点F 作FG ⊥AC 于点G ,∵将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,∴∠B =∠D ,∴tan ∠B =tan ∠D =12FG GD =,∵∠ACB =∠FGA =90°,∴BC ∥FG ,∴∠B =∠AFG ,∴tan ∠B =tan ∠AFG =12AG FG =,设AG =x ,则FG =2x ,∴2132x x =+,解得x =1,∴AG =1,FG =2,∴AF 225FG AG +=∴BF =AB ﹣AF =35.故答案为:35【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.3.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】过C 作CE ⊥AB 于E ,根据勾股定理和正切的定义得到AC =,BC =,根据三角形面积得到CE =6,再根据旋转的性质和相似三角形的判定与性质即可求解.【解答】解:过C 作CE ⊥AB 于E ,∵tan B =23,∴23AC BC =,设AC =2x ,则BC =3x ,在Rt △ABC 中,AB =13,解得x =AC =,BC =,S △ABC =12AC •BC =12AB •CE ,即12××312×13×CE ,解得CE =6,∵tan B =CE EB =23,∴EB =9,∵将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',∴∠B =∠B ′,AC =AC ′,∵CE ⊥AB ,∴AE ′=AE =AB ﹣BE =13﹣9=4,∴A ′B =AB ﹣A ′E =9﹣4=5,∵∠A ′DB =∠CDB ′,∴△A ′DB ∽△B ′DC ,∴'CD A D =''CB A B ='CB A B ..【点评】本题考查了勾股定理,解直角三角形,旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.4.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为622.【考点】旋转的性质;平行线的性质.【专题】平移、旋转与对称;推理能力.【分析】由旋转的性质和等腰三角形的性质可求∠B 1AB =30°,由直角三角形的性质可求DB 1=2DE ,DB =3﹣DE ,即可求解.【解答】解:如图,过点D 作DE ⊥AB 1于E,∵∠B =45°,∠C =60°,∴∠CAB =75°,∵BB 1∥AC ,∴∠CAB =∠ABB 1=75°,∵将△ABC 绕点A 旋转,∴AB =AB 1,∠AB 1C 1=∠ABC =45°,∴∠AB 1B =∠ABB 1=75°,∴∠B 1AB =30°,又∵DE ⊥AB 1,∠AB 1C 1=45°,∴AD =2DE ,AE=DE ,DE =B 1E ,∴AB 1DE +DE =AB ,DB 1DE ,∴DB =AB ﹣ADDE ﹣DE ,∴1BD B D622=,故答案为:2.【点评】本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质,灵活运用这些性质进行推理是本题的关键.5.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP﹣1.【考点】旋转的性质;解直角三角形;等腰直角三角形;三角形中位线定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;推理能力.【分析】分两种情形:①当点D 在线段PC 上时,延长AD 交BC 的延长线于H .证明AD =DC 即可解决问题.②当点P 在线段CD 上时,同法可证:DA =DC 解决问题.【解答】解:如图1,当点D 在线段PC 上时,延长AD 交BC 的延长线于H.∵CE =EA ,CF =FB ,∴EF ∥AB ,∴∠EFC =∠ABC =45°,∵∠PAO =45°,∴∠PAO =∠OFH ,∵∠POA =∠FOH ,∴∠H =∠APO ,∵∠APC =90°,EA =EC ,∴PE =EA =EC ,∴∠EPA =∠EAP =∠BAH ,∴∠H =∠BAH ,∴BH =BA ,∵∠ADP =∠BDC =45°,∴∠ADB =90°,∴BD ⊥AH ,∴∠DBA =∠DBC =22.5°,∵∠ADB =∠ACB =90°,∴A ,D ,C ,B 四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,AP=PD=2a,∴PC=a+2a,∴tan∠CAP=22122a aCPAP+==;如图2中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD =2 2 a,∴PC=a ﹣22 a,∴tan∠CAP=22122a aCPAP+==,∵点P在线段EF上,∴情形1,不满足条件,情形2满足条件,﹣1.【点评】本题考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.6.(2020秋•奉贤区期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是△ABC的角平分线,将Rt△ABC绕点A旋转,如果点C落在射线CD上,点B落在点E处,联结DE,那么∠AED的正切值为3 7.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】设点C落在射线CD上的点C'处,由勾股定理可求AB=5,由旋转的性质可得∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',由平行线分线段成比例可求AD的长,即可求解.【解答】解:如图,设点C落在射线CD上的点C'处,∵∠ACB=90°,AC=3,BC=4,∴AB=5,∵CD是△ABC的角平分线,∴∠ACD=∠DCB=45°,∵将Rt△ABC绕点A旋转,∴∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',∴∠CAC'=90°=∠EAB,∴AC'∥BC,∴'34AD ACDB BC==,∴AD=157,∴tan∠AED=37 ADAE=,故答案为:3 7.【点评】本题考查了旋转的性质,勾股定理,锐角三角函数,平行线的性质等知识,灵活运用这些性质解决问题是本题的关键.专题三定义新图形【历年真题】1.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于414.【考点】相似图形;三角形中位线定理.【专题】图形的相似;推理能力.【分析】利用相似三角形的性质求出BC长,再利用等腰三角形的性质和勾股定理计算出EF的长即可.【解答】解:如图所示:∵AB=AC,AD=CD,△ABC∽△DAC,∴AC2=BC•AD,∵AC AD=32,∴CB=2,∵△ABC∽△DAC,∴∠ACB=∠CAD,∴CB∥AD,∵AB=AC,F为BC中点,∴AF⊥CB,BF=CF=1,∴∠AFC=90°,∵CB∥AD,∴∠FAE=∠AFC=90°,∵AC Rt△AFC中AF==,∵AD=32,E为AD中点,∴AE=34,∴EF414 =.故答案为:41 4.【点评】此题主要考查了相似三角形的性质,以及等腰三角形的性质和勾股定理,关键是掌握相似三角形对应边成比例、对应角相等.2.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=或.【考点】相似图形.【专题】图形的相似;推理能力.【分析】如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.利用相似三角形的性质,构建方程求解即可.【解答】解:如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.过点A作AE⊥BC于E,过点D作DF⊥BC于F,则四边形AEFD是矩形,∴AD=EF,∵AB=CD=2,AD∥BC,∴四边形ABCD是等腰梯形,∴∠ABE=∠DCF=60°,BE=AB•cos60°=1,CF=CD•cos60°=1,∴EF=BC﹣BE﹣CF=6,∴AD=EF=6,DQ=6﹣x,∵△BAQ∽△QDC,∴AB AQ=QD CD,∴x(6﹣x)=4,解得x=3±5,∴AQ=3±5故答案为:5或3-5【点评】本题考查相似三角形的判定和性质,等腰梯形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.3.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为2.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】先求出BD =8,CD =4,再求出MH =4,DH =2,设BE =x ,得出CE =12﹣x ,CF =3+x ,EH =10﹣x ,再判断出△EHM ∽△ECF ,得出比例式,建立方程求解,即可得出结论.【解答】解:如图,∵点D 是BC 上一点,BC =12,∴BD :CD =2:1,∴BD =8,CD =4,过点M 作MH ∥AC 交CD 于H ,∴△DHM ∽△DCA ,∴MH DH =AC DM CD AD=,∴点M 是AD 的中点,∴AD =2DM ,∵AC =8,∴MH DH 1=842=,∴MH =4,DH =2,过点M 作MG ∥AB 交BD 于G ,同理得,BG =DG =4,∵AB =10,BC =12,AC =8,∴△ABC 的周长为10+12+8=30,∵过AD 中点M 的直线将△ABC 分成周长相等的两部分,∴CE +CF =15,设BE =x ,则CE =12﹣x ,∴CF =15﹣(12﹣x )=3+x ,EH =CE ﹣CH =CE ﹣(CD ﹣DH )=12﹣x ﹣2=10﹣x ,∵MH ∥AC ,∴△EHM ∽△ECF ,∴MH EH =CF CE ,∴410-=3+12x x x-,∴x =2或x =9,当x =9时,CF =12>AC ,点F 不在边AC 上,此种情况不符合题意,即BE =x =2,故答案为:2.【点评】此题主要考查了相似三角形的判定和性质,构造出相似三角形是解本题的关键.4.(2020秋•徐汇区期末)如图,在△ABC 中,∠ABC =120°,AB =12,点D 在边AC 上,点E 在边BC 上,sin ∠ADE =45,ED =5,如果△ECD 的面积是6,那么BC 的长是﹣6.【考点】解直角三角形;三角形的面积.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .解直角三角形求出BH ,CH 即可解决问题.【解答】解:如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .∵∠ABC =120°,∴∠ABH =180°﹣∠ABC =60°,∵AB =12,∠H =90°,∴BH =AB •cos60°=6,AH =AB •sin60°=,∵EF ⊥DF ,DE =5,∴sin ∠ADE =EF DE =45,∴EF =4,∴DF 3==,∵S △CDE =6,∴12•CD •EF =6,∴CD =3,∴CF =CD +DF =6,∵tan C =EF AH CF CH =,∴4636CH=,∴CH =,∴BC =CH ﹣BH =6.故答案为:﹣6.【点评】本题考查解直角三角形,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.5.(2020秋•金山区期末)已知在Rt △ABC 中,∠C =90°,BC =1,AC =2,以点C 为直角顶点的Rt △DCE 的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若tan ∠CED=12,CE =GE ,那么BD 的长等于2+【考点】解直角三角形;勾股定理.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点A 作AH ⊥CE 于H .想办法证明AK =AC ,推出HK =CH ,推出AK =AD =2,即可解决问题.【解答】解:如图,过点A 作AH ⊥CE 于H .∵tan ∠CED =12=tan ∠BAC ,∴∠E =∠BAC ,∵CE =EG ,∴∠CGE =∠ECG ,∵∠BAC+∠GAK=180°,∴∠E+∠GAK=180°,∴∠AGE+∠AKE=180°,∵∠AKE+∠AKC=180°,∴∠AKC=∠CGE,∴∠AKC=∠ACK,∴AC=AK=2,∵AH⊥CK,∴KH=CH,∵∠AHE=∠DCK=90°,∴AH∥CD,∴KA=AD,∴DK=2AK=4,AD=AK=2,∵∠ACB=90°,BC=1,AC=2,∴AB=∴BD=AB+AD=,故答案为:【点评】本题考查解直角三角形,勾股定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.6.(2020秋·黄浦区期末)已知一个矩形的两邻边长之比为1:2.5.一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为2:1或1:2或1:1.【考点】相似多边形的性质;矩形的性质,四手拉手模型【专题】图形的相似;推理能力.【分析】如图,设AB=a,AD=2.5a,AE=x,则DE=2.5a-x,利用相似多边形的性质,构建方程求解,另外两个矩形全等也符合题意.【解答】解:如图,设AB=a,AD=2.5a,,AE=x,则DE=2.5a-x.∵矩形ABFE∽矩形EDCF∴AE EF=EF DE∴=2.5x aa a x-整理得,x2-2.5xa+a2=0,解得x=2a或0.5a,∴矩形ABFE与矩形EDCF相似,相似比为2:1或1:2.当E,F分别是AD,BC的中点时,两个矩形全等,也符合题意,相似比为:1:1故答案为:2:1或1:2或1:1.【点评】本题考查相似多边形的性质,解题的关键是学会利用参数构建方程求解,属干电考常考题型。
2019-2020年上海市中考数学各地区模拟试题分类:圆压轴题专项(含解析)
2019-2020年上海市中考数学各地区模拟试题分类:圆压轴题专项1.(2020•长宁区二模)已知AB是⊙O的一条弦,点C在⊙O上,联结CO并延长,交弦AB于点D,且CD=CB.(1)如图1,如果BO平分∠ABC,求证:=;(2)如图2,如果AO⊥OB,求AD:DB的值;(3)延长线段AO交弦BC于点E,如果△EOB是等腰三角形,且⊙O的半径长等于2,求弦BC的长.2.(2020•浦东新区二模)已知:如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=16,点O为斜边AB的中点,以O为圆心,5为半径的圆与BC相交于E、F两点,联结OE、OC.(1)求EF的长;(2)求∠COE的正弦值.3.(2020•崇明区二模)如图已知⊙O经过A、B两点,AB=6,C是的中点,联结OC 交弦AB与点D,CD=1.(1)求圆⊙O的半径;(2)过点B、点O分别作点AO、AB的平行线,交于点G,E是⊙O上一点,联结EG 交⊙O于点F,当EF=AB,求sin∠OGE的值.4.(2020•宝山区二模)已知:如图,⊙O与⊙P相切于点A,如果过点A的直线BC交⊙O 于点B,交⊙P于点C,OD⊥AB于点D,PE⊥AC于点E.求:(1)求的值;(2)如果⊙O和⊙P的半径比为3:5,求的值.5.(2020•闵行区一模)在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D 在劣弧AB上,联结CO并延长交线段AB于点F,联结OA、OB.当OA=,且tan∠OAB =.(1)求弦CD的长;(2)如果△AOF是直角三角形,求线段EF的长;(3)如果S△CEF =4S△BOF,求线段AF的长.6.(2020•宝山区一模)如图,直线l:y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x 的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.求:(1)点B1的坐标和∠A1OB1的度数;(2)弦A4B3的弦心距的长度.7.(2020•闵行区一模)如图,梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=4,tan B=3.以AB为直径作⊙O,交边DC于E、F两点.(1)求证:DE=CF;(2)求:直径AB的长.8.(2020•都江堰市模拟)如图,已知Rt△ABC中,∠ACB=90°,AC=,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.(1)求半径OB的长;(2)如果点P是弧AB的中点,联结PC,求∠PCB的正切值;(3)如果BA平分∠PBC,延长BP、CA交于点D,求线段DP的长.9.(2020•亳州模拟)如图,⊙O1和⊙O2相交于A、B两点,O1O2与AB交于点C,O2A 的延长线交⊙O1于点D,点E为AD的中点,AE=AC,联结OE.(1)求证:O1E=O1C;(2)如果O1O2=10,O1E=6,求⊙O2的半径长.10.(2019•杨浦区三模)△ABC中,∠ACB=90°,tan B=,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.(1)如图1,当点E、G分别在边BC、AC上,且CE=CG时,请判断圆A与圆O的位置关系,并证明你的结论;(2)当圆O与圆A存在公共弦MN时(如图2),设OB=x,MN=y,求y关于x的函数解析式,并写出定义域;(3)设圆A与边AB的交点为F,联结OE、EF,当△OEF为以OE为腰的等腰三角形时,求圆O的半径长.11.(2019•青浦区二模)已知:在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点,以CD为直径的⊙Q分别交BC、BA于点F、E,点E位于点D下方,连接EF交CD于点G.(1)如图1,如果BC=2,求DE的长;(2)如图2,设BC=x,=y,求y关于x的函数关系式及其定义域;(3)如图3,连接CE,如果CG=CE,求BC的长.12.(2019•浦东新区二模)已知AB是圆O的一条弦,P是圆O上一点,过点O作MN⊥AP,垂足为点M,并交射线AB于点N,圆O的半径为5,AB=8.(1)当P是优弧的中点时(如图),求弦AP的长;(2)当点N与点B重合时,试判断:以圆O为圆心,为半径的圆与直线AP的位置关系,并说明理由;(3)当∠BNO=∠BON,且圆N与圆O相切时,求圆N半径的长.13.(2019•静安区二模)已知:如图8,梯形ABCD中,AD∥BC,AD=2,AB=BC=CD =6.动点P在射线BA上,以BP为半径的⊙P交边BC于点E(点E与点C不重合),联结PE、PC.设BP=x,PC=y.(1)求证:PE∥DC;(2)求y关于x的函数解析式,并写出定义域;(3)联结PD,当∠PDC=∠B时,以D为圆心半径为R的⊙D与⊙P相交,求R的取值范围.14.(2019•普陀区二模)如图1,在Rt△ABC中,∠ACB=90°,AB=5,cos∠BAC=,点O是边AC上一个动点(不与A、C重合),以点O为圆心,AO为半径作⊙O,⊙O 与射线AB交于点D,以点C为圆心,CD为半径作⊙C,设OA=x.(1)如图2,当点D与点B重合时,求x的值;(2)当点D在线段AB上,如果⊙C与AB的另一个交点E在线段AD上时,设AE=y,试求y与x之间的函数解析式,并写出x的取值范围;(3)在点O的运动过程中,如果⊙C与线段AB只有一个公共点,请直接写出x的取值范围.15.(2019•嘉定区二模)在圆O中,AB是圆O的直径,AB=10,点C是圆O上一点(与点A、B不重合),点M是弦BC的中点.(1)如图1,如果AM交OC于点E,求OE:CE的值;(2)如图2,如果AM⊥OC于点E,求sin∠ABC的值;(3)如图3,如果AB:BC=5:4,点D为弦BC上一动点,过点D作DF⊥OC,交半径OC于点H,与射线BO交于圆内点F.探究一:如果设BD=x,FO=y,求y关于x 的函数解析式及其定义域;探究二:如果以点O为圆心,OF为半径的圆经过点D,直接写出此时BD的长度;请你完成上述两个探究.16.(2019•虹口区二模)如图,AD∥BC,∠ABC=90°,AD=3,AB=4,点P为射线BC 上一动点,以P为圆心,BP长为半径作⊙P,交射线BC于点Q,联结BD、AQ相交于点G,⊙P与线段BD、AQ分别相交于点E、F.(1)如果BE=FQ,求⊙P的半径;(2)设BP=x,FQ=y,求y关于x的函数关系式,并写出x的取值范围;(3)联结PE、PF,如果四边形EGFP是梯形,求BE的长.17.(2019•长宁区二模)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P在边AC上(点P与点A不重合),以点P为圆心,PA为半径作⊙P交边AB于另一点D,ED⊥DP,交边BC于点E.(1)求证:BE=DE;(2)若BE=x,AD=y,求y关于x的函数关系式并写出定义域;(3)延长ED交CA的延长线于点F,联结BP,若△BDP与△DAF相似,求线段AD的长.18.(2019•宝山区二模)如图已知:AB是圆O的直径,AB=10,点C为圆O上异于点A、B的一点,点M为弦BC的中点.(1)如果AM交OC于点E,求OE:CE的值;(2)如果AM⊥OC于点E,求∠ABC的正弦值;(3)如果AB:BC=5:4,D为BC上一动点,过D作DF⊥OC,交OC于点H,与射线BO交于圆内点F,请完成下列探究.探究一:设BD=x,FO=y,求y关于x的函数解析式及其定义域.探究二:如果点D在以O为圆心,OF为半径的圆上,写出此时BD的长度.19.(2019•徐汇区二模)如图,△ABC中,AC=BC=10,cos C=,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.(1)当⊙P与边BC相切时,求⊙P的半径.(2)连接BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围.(3)在(2)的条件下,当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时,求相交所得的公共弦的长20.(2019•金山区二模)如图,在Rt△ABC中,∠C=90°,AC=16cm,AB=20cm,动点D由点C向点A以每秒1cm速度在边AC上运动,动点E由点C向点B以每秒cm速度在边BC上运动,若点D,点E从点C同时出发,运动t秒(t>0),联结DE.(1)求证:△DCE∽△BCA.(2)设经过点D、C、E三点的圆为⊙P.①当⊙P与边AB相切时,求t的值.②在点D、点E运动过程中,若⊙P与边AB交于点F、G(点F在点G左侧),联结CP并延长CP交边AB于点M,当△PFM与△CDE相似时,求t的值.参考答案一.解答1.(1)证明:如图1中,∵BO平分∠ABC,∴∠ABO=∠CBO,∵OB=OA=OC,∴∠A=∠ABO,∠C=∠OBC,∴∠A=∠C,∵OB=OB,∴△OBA≌△OBC(AAS),∴AB=BC,∴=.(2)解:如图2中,作DM⊥OB于M,DN⊥OA于N,设OM=a.∵OA⊥OB,∴∠MON=∠DMO=∠DNO=90°,∴四边形DMON是矩形,∴DN=OM=a,∵OA=OB,∠AOB=90°,∴∠A=∠ABO=45°,∵OC=OB,CD=CB,∴∠C=∠OBC,∠CDB=∠CBD,∵∠C+∠CDB+∠CBD=180°,∴3∠C+90°=180°,∴∠C=30°,∴∠CDB=∠CBD=75°,∵∠DMB=90°,∴∠MDB=∠DBM=45°,∴DM=BM,∠ODM=30°,∴DM=OM=a,DN=DM=a,AD=DN=a,∴==.(3)解:如图3﹣1中,当BO=BE时,∵CD=CB,∴∠CDB=∠CBD,∴∠A+∠AOD=∠OBA+∠OBC,∵∠A=∠ABO,∴∠AOD=∠OBC=∠C,∵AOD=∠COE,∴∠C=∠COE=∠CBO,∵∠C=∠C,∴△OCE∽△BCO,∴=,∴=,∴EC2+2EC﹣4=0,解得EC=﹣1+或﹣1﹣(舍弃),∴BC=+1.如图3﹣2中,当EO=EB时,同法可证△OEB是等腰直角三角形,∴EO=EB=EC=OB=,∴BC=2,∵∠OEB=∠C+∠COE>∠OBE,∴OE≠OB,综上所述,BC的值为+1或2.2.解:(1)作OM⊥EF于M,如图,则EM=FM,∵∠ACB=90°,∴OM⊥BC,∴OM=AC=×8=4,在Rt△OEM中,EM==3,∴EF=2EM=6;(2)CM=BC=8,∴CE=8﹣3=5,∴CE=OE,∴∠OEC=∠OCE,在Rt△OCM中,OC==4,∴sin∠OCM===,∴∠COE的正弦值为.3.解:(1)∵AB=6,C是的中点,CD=1,∴OC⊥AB且OC平分AB,∴AD=3,∠ODA=90°,设OA=r,则OD=r﹣1,∴r2=32+(r﹣1)2,解得,r=5,即圆⊙O的半径为5;(2)作OH⊥EF于点H,∵AB=EF,OD=r﹣1=4,∴OH=OD=4,∠OHG=90°,∵OA∥BG,OG∥AB,∴四边形OABG是平行四边形,∴OG=AB,∵AB=6,∴OG=6,∴sin∠OGH===,即sin∠OGE=.4.解:(1)∵OD⊥AB,PE⊥AC,OD过O,PE过P,∴AD=AB,AE=AC,∴;(2)连接OP,OP必过切点A,连接OB、CP,∵OB=OA,PA=PC,∴∠OBA=∠OAB=∠PAC=∠PCA,即∠OBA=∠PCA,∠BAO=∠PAC,∴△OOA∽△CPA,∴=,∵⊙O和⊙P的半径比为3:5,即=,∴=.5.解:(1)如图,过点O作OH⊥AB于点H,∵tan∠OAB==,∴设OH=a,AH=2a,∵AO2=OH2+AH2=5,∴a=1,∴OH=1,AH=2,∵OH⊥AB,∴AB=2AH=4,∵弧AC=弧BD∴=,∴AB=CD=4;(2)∵OA=OB,∴∠OAF=∠OBA,∴∠OAF=∠ECF,①当∠AFO=90°时,∵OA=,tan∠OBA=,∴OC=OA=,OF=1,AB=4,∴EF=CF•tan∠ECF=CF•tan∠OBA=;②当∠AOF=90°时,∵OA=OB,∴∠OAF=∠OBA,∴tan∠OAF=tan∠OBA=,∵OA=,∴OF=OA•tan∠OAF=,∴AF=,∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,∴△OFA∽△EFC,∴==,∴EF=OF=,即:EF=或;(3)如图,连接OE ,∵∠ECB =∠EBC ,∴CE =EB ,∵OE =OE ,OB =OC ,∴△OEC ≌△OEB ,∴S △OEC =S △OEB ,∵S △CEF =4S △BOF ,∴S △CEO +S △EOF =4(S △BOE ﹣S △EOF ), ∴=, ∴=,∴FO =CO =,∴OH ==1,∴HF ==,∴AF =AH +HF =2+.6.解:(1)∵直线的解析式y =x ,∴tan ∠A 1OB 1==, ∴∠A 1OB 1=60°,OA 1=1,∴A 1B 1=,OA 2=OB 1=2, ∴B 1(1,).(2)连接A 4B 3,作OH ⊥A 4B 3于H .由题意OA1=1,OA2=2,OA3=4,OA4=8,∵OA4=OB3,OH⊥A4B3,∴∠A4OH=∠A4OB3=30°,∴OH=OA4•cos30°=8×=4.7.(1)证明:过点O作OH⊥DC,垂足为H.∵AD∥BC,∠ADC=90°,OH⊥DC,∴∠BCN=∠OHC=∠ADC=90°.∴AD∥OH∥BC.又∵OA=OB.∴DH=HC.∵OH⊥DC,OH过圆心,∴EH=HF,∴DH﹣EH=HC﹣HF.即:DE=CF.(2)解:过点A作AG⊥BC,垂足为点G,∠AGB=90°,∵∠AGB=∠BCN=90°,∴AG∥DC.∵AD∥BC,∴AD=CG.∵AD=2,BC=4,∴BG=BC﹣CG=2.在Rt△AGB中,∵tan B=3,∴AG=BG•tan B=2×3=6.在Rt△AGB中,AB2=AG2+BG2∴AB=.8.解:(1)∵Rt△ABC中,∠ACB=90°,AC=,BC=16,∴AB==12,如图1,过O作OH⊥AB于H,则BH=AB=6,∵∠BHO=∠ACB=90°,∠B=∠B,∴△BHO∽△BCA,∴,∴=,∴OB=9;(2)如图2,连接OP交AB于H,过P作PE⊥BC于E,∵点P是弧AB的中点,∴OP⊥AB,AH=BH=AB=6,在Rt△BHO中,OH===3,在△POE与△BOH中,,∴△POE≌△BOH(AAS),∴PE=HB=6,OE=OH=3,∴CE=BC﹣OB+OE=10,∴∠PCB的正切值==;(3)如图3,过A作AE⊥BD于E,连接CP,∵BA平分∠PBC,AC⊥BC,∴AE=AC=4,∵∠AED=∠ACB=90°,∠D=∠D,∴△ADE∽△BDC,∴=,设DE=x,∴=,∴AD=,在Rt△ACB与Rt△AEB中,,∴Rt△ACB≌Rt△AEB(HL),∴BE=BC=16,∵CD2+BC2=BD2,∴(4+)2+162=(16+x)2,解得:x=,∴AD=,BD=16+=,∴CD=,∴OB=9,过O作OF⊥PB交PB于F,则△OBF∽△DBC,∴,∴=,∴BF=7,∴PB=2BF=14,∴PD=BD﹣BP=.9.(1)证明:连接O1A,∵点E为AD的中点,∴O1E⊥AD,∵⊙O1和⊙O2相交于A、B两点,O1O2与AB交于点C,∴O1C⊥AB,在Rt△O1EA和Rt△O1CA中,,∴Rt△O1EA≌Rt△O1CA(HL)∴O1E=O1C;(2)解:设⊙O2的半径长为r,∵O1E=O1C=6,∴O2C=10﹣6=4,在Rt△O1EO2中,O2E==8,则AC=AE=8﹣r,在Rt△ACO2中,O2A2=AC2+O2C2,即r2=(8﹣r)2+42,解得,r=5,即⊙O2的半径长为5.10.解:(1)圆A与圆O外切,理由如下:∵∠ACB=90°,tan B=,AB=5,∴AC=3,BC=4,作OP⊥BE于P,如图1所示:则PB=PE,OP∥AC,∴=,设PB=PE=x,则CG=CE=4﹣2x,∴OB==x,AG=AC﹣CG=2x﹣1,∵AG=OB,∴2x﹣1=x,解得:x=,∴OB═,∴OA=AB﹣OB=5﹣==2OB,∴圆A与圆O外切;(2)连接OM,如图2所示:∵圆O与圆A存在公共弦MN,∴OA与MN垂直平分,∴∠ODM=90°,DM=MN=y,AD=OD=(5﹣x),由勾股定理得:DM2=OM2﹣OD2,即(y)2=x2﹣()2,整理得:y2=3x2+10x﹣25,∴y=(<x<5);(3)分三种情况:①当圆O与圆A外切,OE=OF时,圆O与圆A外切,圆O的半径长OB=;②当OE=FE时,圆O与圆A相交,如图3所示:作EH⊥OF于H,则OF=OH=﹣OB,∵∠B=∠B,∠EHB=90°=∠C,∴△BEH∽△BAC,∴=,∴EH==,在Rt△OEH中,由勾股定理得:()2+(﹣OB)2=OE2=OB2,解得:OB=;③当O与A重合时,OE=OF,F与B重合,OE=AB=5;综上所述,当△OEF为以OE为腰的等腰三角形时,圆O的半径长为或或5.11.解:(1)如图1中,连接CE.在Rt△ACB中,∵∠ACB=90°,AC=1,BC=2,∴AB==,∵CD是⊙Q的直径,∴∠CED=90°,∴CE⊥AB,∵BD=AD,∴CD=AB=,∵•AB•CE=•BC•AC,∴CE=,在Rt△CDE中,DE===.(2)如图2中,连接CE,设AC交⊙Q于K,连接FK,DF,DK.∵∠FCK=90°,∴FK是⊙Q的直径,∴直线FK经过点Q,∵CD是⊙Q的直径,∴∠CFD=∠CKD=90°,∴DF⊥BC,DK⊥AC,∵DC=DB=DA,∴BF=CF,CK=AK,∴FK∥AB,∴=,∵BC=x,AC=1,∴AB=,∴DC=DB=DA=,∵△ACE∽△ABC,∴可得AE=,∴DE=AD﹣AE=﹣,∴=,∴=,∴y=(x>1).(3)如图3中,连接FK.∵CE=CG,∴∠CEG=∠CGE,∵∠FKC=∠CEG,∵FK∥AB,∴∠FKC=∠A,∵DC=DA,∴∠A=∠DCA,∴∠A=∠DCA=∠CEG=∠CGE,∴∠CDA=∠ECG,∴EC=DE,由(2)可知:=﹣,整理得:x2﹣2x﹣1=0,∴x=1+或1﹣(舍弃),∴BC=1+.12.解:(1)连接PO并延长交弦AB于点H,如图1所示:∵P是优弧的中点,PH经过圆心O,∴PH⊥AB,AH=BH,在△AOH中,∠AHO=90°,AH=AB=4,AO=5,∴OH===3,在△APH中,∠AHP=90°,PH=OP+OH=5+3=8,∴AP===4;(2)当点N与点B重合时,以点O为圆心,为半径的圆与直线AP相交;理由如下:作OG⊥AB于G,如图2所示:∵∠OBG=∠ABM,∠OGB=∠AMB,∴△OBG∽△ABM,∴=,即=,解得:BM=,∴OM=﹣5=,∵<,∴当点N与点B重合时,以点O为圆心,为半径的圆与直线AP相交;(3)①当点N在线段AB延长线上时,当圆N与圆O相外切时,作OD⊥AB于D,如图3所示:∵OA=OB=5,∴AD=DB=AB=4,∴OD===3,∵∠BNO=∠BON,∴BN=OB=5,∴DN=DB+BN=9,在Rt△ODN中,由勾股定理得:ON===3,∵圆N与圆O相切,∴圆N半径=ON﹣5=3﹣5;当圆N与圆O相内切时,圆N半径=ON+5=3+5;②当点N在线段AB上时,此时点P在弦AB的下方,点N在圆O内部,如图4所示:作OE⊥AB于E,则AE=BE=4,OE==3,∵∠BNO=∠BON,∴BN=OB=5,∴EN=BN=BE=1,在Rt△OEN中,由勾股定理得:ON===,∴圆N半径为5﹣或5+;综上所述,当∠BNO=∠BON,且圆N与圆O相切时,圆N半径的长为3﹣5或3+5或5﹣或5+.13.(1)∵证明:梯形ABCD,AB=CD,∴∠B=∠DCB,∵PB=PE,∴∠B=∠PEB,∴∠DCB=∠PEB,∴PE∥CD;(2)解:分别过P、A、D作BC的垂线,垂足分别为点H、F、G.∵梯形ABCD中,AD∥BC,AF⊥BC,DG⊥BC,PH⊥BC,∴四边形ADGF是矩形,PH∥AF,∵AD=2,BC=DC=6,∴BF=FG=GC=2,在Rt△ABF中,AF===4,∵PH∥AF,∴==,即==,∴PH=x,BH=x,∴CH=6﹣x,在Rt△PHC中,PC=,∴y=,即y=(0<x<9);(3)解:作EM∥PD交DC于M.∵PE∥DC,∴四边形PDME是平行四边形.∴PE=DM=x,即MC=6﹣x,∴PD=ME,∠PDC=∠EMC,又∵∠PDC=∠B,∠B=∠DCB,∴∠DCB=∠EMC=∠PBE=∠PEB.∴△PBE∽△ECM,∴=,即=,解得:x=,即BE=,∴PD=EC=6﹣=,当两圆外切时,PD=r P+R,即R=0(舍去);当两圆内切时,PD=r P﹣R,即R1=0(舍去),R2=;即两圆相交时,0<R<.14.解:(1)如图1中,在Rt△ABC中,∵∠ACB=90°,AB=5,cos∠BAC=,∴AC=4,BC===3,∵OA=OB=x,∴OC=4﹣x,在Rt△BOC中,∵OB2=BC2+OC2,∴x2=32+(4﹣x)2,∴x=(2)如图2中,作CH⊥AB于H,OG⊥AB于G,EK⊥AC于K,连接CE.∵•AB•CH=•BC•AC,∴CH=,AH=,∵OD=OA=x,OG⊥AD,∴AG=DG=OA•cos A=x,∴AD=x,DH=x﹣,∴CD2=()2+(x﹣)2,∵AK=AE•cos A=y,EK=y,∴CE2=(4﹣y)2+(y)2,∵CD=CE,∴()2+(x﹣)2=(4﹣y)2+(y)2,∴x2﹣x=y2﹣y,∴(y﹣)2=(x﹣2)2,∵y<,x>2,∴﹣y=x﹣,∴y=﹣x+(2<x≤).(3)①如图3﹣1中,当⊙C经过点B时,易知:BH=DH=,∴BD=,∴AD=5﹣=,∴x=,∴x=,观察图象可知:当0<x<时,⊙C与线段AB只有一个公共点.②如图3﹣2中,当⊙C与AB相切时,CD⊥AB,易知OA=2,此时x=2,③如图3﹣3中,当<x<4时,⊙C与线段AB只有一个公共点.综上所述,当0<x<或x=2或<x<4时,⊙C与线段AB只有一个公共点.15.解:(1)过点O作ON∥BC交AM于点N,如图1∴,,∵∴∵点M是弦BC的中点∴BM=MC∴,∴OE:CE=1:2;(2)联结OM,如图2∵点M是弦BC的中点,OM经过圆心O ∴OM⊥BC,∠OMC=90°,∵AM⊥OC,∴∠MEO=90°∴∠OMC=∠MEO=90°,又∵∠MOC=∠EOM∴△MOC∽△EOM;∴,∵OE:CE=1:2∴,∵OB=OC∴∠ABC=∠OCM在直角△MOC中,∴;(3)探究一:如图3,过点D作DL⊥DF交BO于点L,取BC中点M,连接OM∵DF⊥OC,∴DL∥OC,∴∠LDB=∠C=∠B∴BL=DL,∵AB=10,AB:BC=5:4,∴BC=8,OC=5,∵BM=CM=4,∴cos∠OCM=∵DL∥OC,∴设BD=x,则CD=8﹣x,∴BL=DL=x,CH=(8﹣x),OH=OC﹣CH=5﹣(8﹣x),∵OH∥DL,∴,∴=;∴y关于x的函数解析式是定义域是,探究二:∵以O为圆心,OF为半径的圆经过D,∴OF=OD,∵DF⊥OC,∴OC垂直平分DF,FO=OL,∴y=5﹣x,∴,解得:x=,∴BD=.16.解:(1)∵BE=FQ,∴∠BPE=∠FPQ,∵PE=PB,∴∠EBP=(180°﹣∠EPB),同理∠FQP=(180°﹣∠FPQ),∴∠EBP=∠FQP,∵AD∥BC,∴∠ADB=∠EBP,∴∠FQP=∠ADB,∴tan∠FQP=tan∠ADB=,设⊙P的半径为r,则tan∠FQP==,∴=,解得:r=,∴⊙P的半径为;(2)过点P作PM⊥FQ,垂足为点M,如图1所示:在Rt△ABQ中,cos∠AQB====,在Rt△PQM中,QM=PQ cos∠AQB=,∵PM⊥FQ,PF=PQ,∴FQ=2QM=,∴,当圆与D点相交时,x最大,作DH⊥BC于H,如图2所示:则PD=PB=x,DH=AB=4,BH=AD=3,则PH=BP﹣BH=x﹣3,在Rt△PDH中,由勾股定理得:42+(x﹣3)2=x2,解得:x=,∴x的取值范围为:;(3)设BP=x,分两种情况:①EP∥AQ时,∴∠BEP=∠BGQ,∵PB=PE,∴∠PBE=∠BEP,∴∠BGQ=∠PBE,∴QG=QB=2x,同理:AG=AD=3,在Rt△ABQ中,由勾股定理得:42+(2x)2=(3+2x)2,解得:x=,∴QG=QB=2x=,∵EP∥AQ,PB=PQ,∴BE=EG,∵AD∥BC,∴=,即=,解得:BG=,∴BE=BG=;②PF∥BD时,同①得:BG=BQ=2x,DG=AD=3,在Rt△ABD中,由勾股定理得:42+32=(3+2x)2,解得:x=1或x=﹣4(舍去),∴BQ=2,∴BP=1,作PN⊥BG于N,则BE=2BN,如图3所示:∵AD∥BC,∴∠PBN=∠ADB,∴cos∠PBN=cos∠ADB=,即=,∴BN=,∴BE=2BN=;综上所述,或.17.(1)证明:∵ED⊥DP,∴∠EDP=90°.∴∠BDE+∠PDA=90°.又∵∠ACB=90°,∴∠B+∠PAD=90°.∵PD=PA,∴∠PDA=∠PAD.∴∠BDE=∠B.∴BE=DE.(2)∵AD=y,BD=BA﹣AD=5﹣y.过点E作EH⊥BD垂足为点H,由(1)知BE=DE,∴.在Rt△EHB中,∠EHB=90°,∴.在Rt△ABC中,∠ACB=90°,AC=3,BC=4.∴AB=5.∴.∴,∴.(3)设PD=a,则,在等腰△PDA中,,易得在Rt△PDF中,∠PDF=90°,.∴,.若△BDP∽△DAF又∠BDP=∠DAF①当∠DBP=∠ADF时,即,解得a=3,此时.②当∠DBP=∠F时,即,解得,此时.综上所述,若△BDP与△DAF相似,线段AD的长为或.18.解:(1)如图1,过点O作ON∥BC交AM于点N,∵点O是AB的中点,∴点N是AM的中点,∴ON=BM,∵点M为弦BC的中点,∴BM=CM,∴ON=CM,∵ON∥BC,∴=;(2)如图1,连接OM,∵点M为弦BC的中点,∴OM⊥BC,∵AM⊥OC于点E,∴∴∠OME+∠CME=∠CME+∠C=90°,∴∠OME=∠MCE,∴△OME∽△MCE,∴ME2=OE•CE,设OE=x,则CE=2x,ME=x,在Rt△MCE中,CM==x,∴sin∠ECM===∴sin∠ABC=;(3)探究一:如图2,过点D作DL⊥DF交BO于点L,∵DF⊥OC,∴DL∥OC,∴∠LDB=∠C=∠B,∴BL=DL,∵AB=10,AB:BC=5:4,设BD=x,则CD=8﹣x,BL=DL=x,CH=,OH=OC﹣CH=5﹣(8﹣x),∵OH∥DL,∴=,∴,∴y=(其中);探究二:∵以O为圆心,OF为半径的圆经过D,∴OF=OD,∵DF⊥OC,∴OC垂直平分DF,FO=OL,∴y=5﹣x,∴,解得:x=,∴BD=.19.解:(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cos C=,则sin C=,sin C===,解得:R=;(2)在△ABC中,AC=BC=10,cos C=,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH=BC sin C=8,同理可得:CH=6,HA=4,AB=4,则:tan∠CAB=2BP==,DA=x,则BD=4﹣x,如下图所示,PA=PD,∴∠PAD=∠CAB=∠CBA=β,PD∥BE,tanβ=2,则cosβ=,sinβ=,EB=BD cosβ=(4﹣x)×=4﹣x,∴PD∥BE,∴,即:=,整理得:y=(0<x<10);(3)以EP为直径作圆Q如下图所示,点D在圆P上,EP是圆Q的直径,则点D也在圆Q上,故GD为相交所得的公共弦,设∠DCP=∠PDC=∠α,GD是公共弦,则GD⊥PE,则∠PED=∠BDE,∵∠EDP=90°,∴∠PDE+∠EPD=90°=∠EPD+∠GDP,故∠PED=∠EDP=∠α,由(2)知tan∠BAC=tanβ=2,故tan,则cosα=,则AD=AG=x,在Rt△EPD中,ED=2PD=2x,在Rt△BED中,ED=2x,则EB=ED=x,则EC=CB﹣BE=10﹣x,在Rt△CGE中,CG=AC﹣AG=10﹣2x,cos∠C===,解得:x=;GD=2PD cosα=2x cosα=2××=.20.(1)证明:由题意得:CD=t,CE=t,由勾股定理得,BC==12,=,==,∴=,又∠C=∠C,∴△DCE∽△BCA;(2)①连结CP并延长CP交AB于点H,∵∠ACB=90°,∴DE是⊙P的直径,即P为DE中点,∴CP=DP=PE=DE,∴∠PCE=∠PEC,∵△DCE∽△BCA,∴∠CDE=∠B,∵∠CDE+∠CED=90°,∴∠B+∠HCB=90°,即CH⊥AB,∵⊙P与边AB相切,∴点H为切点,CH为⊙P的直径,∵sin A==,∴=,解得,CH=,∴DE=,sin A=sin∠CED==,即=,解得,CD=,∴t=;②由题意得,0<t≤12,即0<t≤9,∵CD=t,CE=t,∴DE==t,由①得,CM=,CP=DE=t,CM⊥AB,∴PM=﹣t,PF=CP=t,∠PMF=90°,当△FMP∽△DCE时,=,即=,解得,t=;当△PMF∽△DCE时,=,即=,解得,t=;∴综上所述:当△PFM与△CDE相似时.t=或t=.。
2020-2021年上海各区数学中考一模压轴题分类汇编-25题含详解
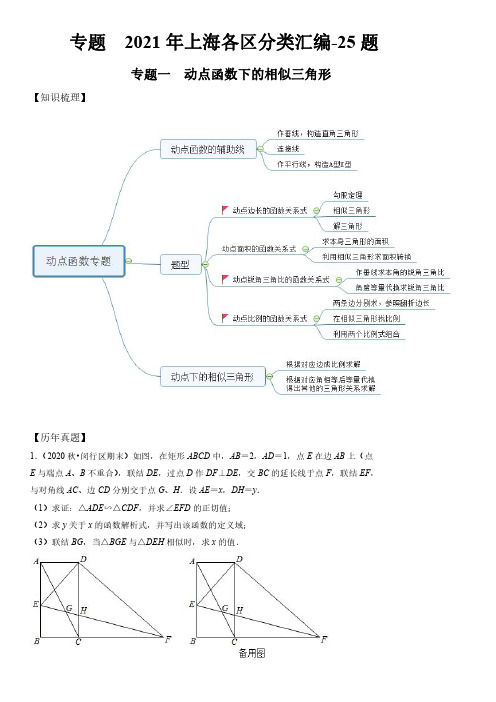
可得: y 2x2 2 (0<x<2); 2x 1
(3)BE=2﹣x,DH=y,DE= 1 x2 ,EH= 1 ( y x)2 ,
∴ EG AE ,∴EG= AE EH ,
GH CH
AE CH
∵∠BEG=∠DHE,
若△BEG 与△DHE 相似,则有两种情况,
【知识梳理】
专题二 动点函数背景下的面积问题
【历年真题】
1.(2020 秋•静安区期末)已知∠MAN 是锐角,点 B、C 在边 AM 上,点 D 在边 AN 上,∠
EBD=∠MAN,且 CE∥BD,sin∠MAN= 3 ,AB=5,AC=9. 5
(1)如图 1,当 CE 与边 AN 相交于点 F 时,求证:DF•CE=BC•BE; (2)当点 E 在边 AN 上时,求 AD 的长; (3)当点 E 在∠MAN 外部时,设 AD=x,△BCE 的面积为 y,求 y 与 x 之间的函数解析式,并写出定义域.
⊙O 的半径为 5,tan∠OAC= 3 . 4
(1)求弦 AC 的长. (2)当点 E 在线段 OA 上时,若△DOE 与△AEC 相似,求∠DCA 的正切值. (3)当 OE=1 时,求点 A 与点 D 之间的距离(直接写出答案).
3.(2020 秋•黄浦区期末)如图,四边形 ABCD 中,AB=AD=4,CB=CD=3,∠ABC=
4.(2020 秋•奉贤区期末)已知⊙O 的直径 AB=4,点 P 为弧 AB 上一点,联结 PA、PO, 点 C 为劣弧 AP 上一点(点 C 不与点 A、P 重合),联结 BC 交 PA、PO 于点 D、E.
(1)如图,当 cos∠CBO= 7 时,求 BC 的长; 8
2018-2019学年上海中考数学各区一模压轴题汇编

目录Ⅰ第18题(填空小压轴) (2)【2019届一模徐汇】 (2)【2019届一模浦东】 (2)【2019届一模杨浦】 (3)【2019届一模普陀】 (3)【2019届一模奉贤】 (3)【2019届一模松江】 (3)【2019届一模嘉定】 (4)【2019届一模青浦】 (4)【2019届一模青浦】 (4)【2019届一模静安】 (5)【2019届一模宝山】 (5)【2019届一模长宁】 (5)【2019届一模金山】 (6)【2019届一模闵行】 (6)【2019届一模虹口】 (6)Ⅱ第23题(几何证明题) (7)【2019届一模徐汇】 (7)【2019届一模浦东】 (7)【2019届一模杨浦】 (7)【2019届一模普陀】 (8)【2019届一模奉贤】 (8)【2019届一模松江】 (9)【2019届一模嘉定】 (9)【2019届一模青浦】 (10)【2019届一模静安】 (10)【2019届一模宝山】 (11)【2019届一模长宁】 (11)【2019届一模金山】 (12)【2019届一模闵行】 (12)【2019届一模虹口】 (13)Ⅲ第24题(二次函数综合) (13)【2019届一模徐汇】 (13)【2019届一模浦东】 (14)【2019届一模普陀】 (16)【2019届一模奉贤】 (16)【2019届一模松江】 (17)【2019届一模嘉定】 (18)【2019届一模青浦】 (19)【2019届一模静安】 (20)【2019届一模宝山】 (21)【2019届一模长宁】 (22)【2019届一模金山】 (23)【2019届一模闵行】 (24)【2019届一模虹口】 (25)Ⅳ第25题(压轴题) (25)【2019届一模徐汇】 (25)【2019届一模浦东】 (26)【2019届一模杨浦】 (27)【2019届一模普陀】 (28)【2019届一模奉贤】 (29)【2019届一模松江】 (30)【2019届一模嘉定】 (31)【2019届一模青浦】 (32)【2019届一模静安】 (33)【2019届一模宝山】 (33)【2019届一模长宁】 (34)【2019届一模金山】 (35)【2019届一模闵行】 (36)【2019届一模虹口】 (37)Ⅰ第18题(填空小压轴)【2019届一模徐汇】18.在梯形ABCD中,AB∥DC,∠B=90°,BC=6,CD=2,3tan4A=.点E为BC上一点,过点E作EF∥AD交边AB于点F.将△BEF沿直线EF翻折得到△GEF,当EG过点D时,BE的长为▲ .【2019届一模浦东】18. 将矩形纸片ABCD沿直线AP折叠,使点D落在原矩形ABCD的边BC上的点E处,如果∠AED的余弦值为35,那么ABBC=__________.(第18题图)【2019届一模杨浦】18.Rt △ABC 中,∠C =90°,AC =3,BC =2,将此三角形绕点A 旋转,当点B 落在直线BC 上的点D 处时,点C 落在点E 处,此时点E 到直线BC 的距离为 ▲ .【2019届一模普陀】18.如图5,△ABC 中,8AB AC ==,3cos 4B =,点D 在边BC 上,将△ABD 沿直线AD 翻折得到△AED ,点B 的对应点为点E ,AE 与边BC 相交于点F ,如果2BD =,那么EF = ▲ .【2019届一模奉贤】18.如图5,在△ABC 中,AB =AC =5,3sin =5C ,将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应,AD 与边BC 交于点F .如果AE //BC ,那么BF 的长是 ▲ .【2019届一模松江】18.如图,在直角坐标平面xoy 中,点A 坐标为(3,2),∠AOB =90°,∠OAB =30°,ABACB(第18题图)图 5ABCD图5ABC与x 轴交于点C ,那么AC :BC 的值为______.【2019届一模嘉定】18.在△ABC 中,°=∠90ACB ,点D 、E 分别在边BC 、AC 上,AE AC 3=,°=∠45CDE (如图3),△DCE沿直线DE 翻折,翻折后的点C 落在△ABC 内部的点F ,直线AF 与边BC 相交于点G ,如果AE BG =,那么=B tan ▲ .【2019届一模青浦】17.如图,在Rt △ABC 中,∠ACB=90°,AC=1,tan ∠CAB=2,将△ABC 绕点A 旋转后,点B 落在AC 的延长线上的点D ,点C 落在点E ,DE 与直线BC 相交于点F ,那么CF= ▲ .【2019届一模青浦】18.对于封闭的平面图形,如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上,那么这样的点S 称为“亮点”. 如图,对于封闭图形ABCDE ,S 1是“亮点”,S 2不是“亮点”,如果AB ∥DE ,AE ∥DC , AB=2,AE=1,∠B=∠C= 60°,那么该图形中所有“亮点” 组成的图形的面积为 ▲ .【2019届一模静安】18.如图6,将矩形ABCD 沿对角线BD 所在直线翻折后,点A 与点E 重合,且ED 交BC 于点F ,联结AE .如果2tan 3DFC ∠=,那么BDAE的值是 ▲ .【2019届一模宝山】18.如图4,Rt △ABC 中,∠ACB =90°,AC =4,BC =5,点P 为AC 上一点,将△BCP 沿直线BP 翻折,点C 落在C ’处,连接AC ’,若AC ’∥BC ,则CP 的长为 ▲ .【2019届一模长宁】18.如图,点P 在平行四边形ABCD 的边BC 上,将ABP ∆沿直线AP 翻折,点B 恰好落在边AD 的垂直平分线上,如果5=AB ,8=AD ,34tan =B ,那么BP 的长为 ▲ . AC(图4)B(第18题图)图6F BA CDEA【2019届一模金山】18.如图,在ABC Rt ∆中,o90=∠C ,8=AC ,6=BC .在边AB 上取一点O ,使BC BO =,以点O 为旋转中心,把ABC ∆逆时针旋转o90,得到C B A ′′′∆(点A 、B 、C 的对应点分别是点A ′、B ′、C ′),那么ABC ∆与C B A ′′′∆的重叠部分的面积是 ▲ .【2019届一模闵行】18.如图,在Rt △ABC 中,∠ACB = 90°,BC = 3,AC = 4,点D 为边AB 上一点.将△BCD 沿直线CD 翻折,点B 落在点E 处,联结AE .如果AE // CD ,那么BE = ▲ .【2019届一模虹口】18.如图,正方形ABCD 的边长为4,点O 为对角线AC 、BD 的交点,点E 为边AB 的中点,△BED 绕着点B 旋转至△BD 1E 1,如果点D 、E 、D 1在同一直线上,那么EE 1的长为 ▲ .ABC第18题OABC (第18题图)A DE OⅡ第23题(几何证明题)【2019届一模徐汇】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,已知菱形ABCD,点E是AB的中点,AF BC⊥于点F,联结EF、ED、DF,DE交AF于点G,且2AE EG ED=⋅.(1) 求证:DE EF⊥;(2) 求证:22BC DF BF=⋅.【2019届一模浦东】23.(本题满分12分,其中每小题各6分)已知:如图8,在平行四边形ABCD中,M是边BC的中点,E是边BA延长线上的一点,联结EM,分别交线段AD于点F、AC于点G.(1)求证:GF EF GM EM=;(2)当22BC BA BE=⋅时,求证:∠EMB=∠ACD.【2019届一模杨浦】23.(本题满分12分,每小题各6分)B(第23题图)(图8)D B已知:如图,在△ABC 中,点D 在边AB 上,点E 在线段CD 上,且∠ACD =∠B =∠BAE. (1)求证:AD DEBC AC=; (2)当点E 为CD 中点时,求证:22AE ABCE AD=.【2019届一模普陀】23.(本题满分12分)已知:如图9,△ADE 的顶点E 在△ABC 的边BC 上,DE 与AB 相交于点F ,AE AF AB =⋅2,DAF EAC ∠=∠.(1)求证:△ADE ∽△ACB ;(2)求证:DF CE DE CB=.【2019届一模奉贤】23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图9,在△ABC 中,点D 在边AC 上,BD 的垂直平分线交CA 的延长线于点E , (第23题图)ECF图9ABDE交BD 于点F ,联结BE ,EC EA ED •=2. (1)求证:∠EBA =∠C ;(2)如果BD =CD ,求证:AC AD AB •=2.【2019届一模松江】23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:如图,在梯形ABCD 中,AD ∥BC ,AB=DC ,E 是对角线AC 上一点,且AC ·CE=AD ·BC . (1)求证:∠DCA=∠EBC ;(2)延长BE 交AD 于F ,求证:AB 2=AF ·AD .【2019届一模嘉定】23.(本题满分12分,每小题6分)如图6,已知点D 在△ABC 的外部,AD //BC ,点E 在边AB 上,AE BC AD AB ⋅=⋅. (1)求证:AED BAC ∠=∠;(2)在边AC 取一点F ,如果D AFE ∠=∠,ABCDEF图9(第23题图)EDCBAF(第23题图)EDCBAD A求证:ACAFBC AD =.【2019届一模青浦】23.(本题满分12分,第(1)小题7分,第(2)小题5分)已知:如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,点F 在DE 的延长线上,AD=AF ,AE CE DE EF ⋅=⋅.(1)求证:△ADE ∽△ACD ;(2)如果AE BD EF AF ⋅=⋅,求证:AB=AC .【2019届一模静安】23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)已知:如图9,在ABC ∆中,点D 、E 分别在边BC 和AB 上,且AD AC =,EB ED =,分别延长ED 、AC 交于点F .(1)求证:ABD ∆∽FDC ∆;(2)求证:2AE BE EF =⋅.ABCDEF(第23题图) 图9AC BDEF【2019届一模宝山】23.(本题满分12分)地铁10号线某站点出口横截面平面图如图8所示,电梯AB 的两端分别距顶部9.9米和2.4米,在距电梯起点A 端6米的P 处,用1.5米的测角仪测得电梯终端B 处的仰角为14°,求电梯AB 的坡度与长度. 参考数据:,,.【2019届一模长宁】23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,点D 、E 分别在ABC ∆的边AC 、AB 上,延长DE 、CB 交 于点F ,且AC AD AB AE ⋅=⋅. (1)求证:C FEB ∠=∠;(2)联结AF ,若FD CD AB FB =,求证:FB AC AB EF ⋅=⋅.24.014sin ≈°25.014tan ≈°97.014cos ≈°Q 9.9米 B出口顶部1.5米(图8) AP 6米 2.4米°14 第23题图CEDABF【2019届一模金山】23.如图,M 是平行四边形ABCD 的对角线上的一点,射线AM 与BC 交于点F ,与DC 的延长线交于点H .(1)求证:MH MF AM ⋅=2.(2)若DM BD BC ⋅=2,求证:ADC AMB ∠=∠.【2019届一模闵行】23.(本题共2小题,每小题6分,满分12分)如图,在△ABC 中,点D 为边BC 上一点,且AD = AB ,AE ⊥BC ,垂足为点E .过点D 作DF // AB ,交边AC 于点F ,联结EF ,212EF BD EC =⋅. (1)求证:△EDF ∽△EFC ; (2)如果14EDF ADC S S =V V ,求证:AB = BD .ABCD HF M第23题ABCDE F(第23题图)【2019届一模虹口】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在△ABC 中,AB=AC ,D 是边BC 的中点,DE ⊥AC ,垂足为点E . (1)求证:DE CD AD CE ⋅=⋅;(2)设F 为DE 的中点,联结AF 、BE ,求证:=AF BC AD BE ⋅⋅.Ⅲ第24题(二次函数综合)【2019届一模徐汇】24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,在平面直角坐标系xoy 中,顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ,AO =OB =2,120AOB ∠=o .(1)求该抛物线的表达式; (2)联结AM ,求AOM S V ;(3)将抛物线C 1向上平移得到抛物线C 2,抛物线C 2与x 轴分别交于点E 、F (点E 在点F 的左侧),如果△MBF 与△AOM 相似,求所有符合条件的抛物线C 2的表达式.(第24题图)第23题图E【2019届一模浦东】24. (本题满分12分,其中每小题各4分)已知:如图9,在平面直角坐标系xOy 中,直线12y x b =−+与x 轴相交于点A ,与y 轴相交于点B . 抛物线244y ax ax =−+经过点A 和点B ,并与x 轴相交于另一点C ,对称轴与x 轴相交于点D .(1)求抛物线的表达式; (2)求证: △BOD ∽△AOB ;(3)如果点P 在线段AB 上,且∠BCP =∠DBO , 求点P 的坐标.【2019届一模杨浦】24.(本题满分12分,每小题各4分)在平面直角坐标系xOy 中,抛物线2(0)y ax bx c a =++?与y 轴交于点C (0,2), 它的顶点为D (1,m ),且1tan 3COD ?. (1)求m 的值及抛物线的表达式;(2)将此抛物线向上平移后与x 轴正半轴交于点A ,与y 轴交于点B ,且OA =OB .若点A 是由原抛物线上的点E 平移所得,求点E 的坐标;(3)在(2)的条件下,点P 是抛物线对称轴上的一点(位于x 轴上方),且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3-1 -2 -3 (第24题图)【2019届一模普陀】24.(本题满分12分)如图10,在平面直角坐标系中,抛物线23y ax bx =+−(0)a ≠与x 轴交于点A ()1,0−和点B ,且3OB OA =,与y 轴交于点C ,此抛物线顶点为点D .(1)求抛物线的表达式及点D 的坐标;(2)如果点E 是y 轴上的一点(点E 与点C 不重合),当BE DE ⊥时,求点E 的坐标; (3)如果点F 是抛物线上的一点,且135FBD ∠=o ,求点F 的坐标.【2019届一模奉贤】24.(本题满分12分,每小题满分6分)如图10,在平面直角坐标系中,直线AB 与抛物线2y ax bx =+交于点A (6,0)和点B (1,-5). (1)求这条抛物线的表达式和直线AB 的表达式; xOy xOy 图10(2)如果点C 在直线AB 上,且∠BOC 的正切值是32, 求点C 的坐标.【2019届一模松江】24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图,抛物线c bx x y ++−=221经过点A (﹣2,0),点B (0,4). (1)求这条抛物线的表达式;(2)P 是抛物线对称轴上的点,联结AB 、PB ,如果∠PBO=∠BAO ,求点P 的坐标;(3)将抛物线沿y 轴向下平移m 个单位,所得新抛物线与y 轴交于点D ,过点D 作DE ∥x 轴交新抛物线于点E ,射线EO 交新抛物线于点F ,如果EO =2OF ,求m 的值.【2019届一模嘉定】24.(本题满分12分,每小题4分)在平面直角坐标系xOy (如图7)中,抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ,与y 轴的交点为C .(1)试求这个抛物线的表达式;(2)如果这个抛物线的顶点为M ,求△AMC(3)如果这个抛物线的对称轴与直线BC 交于点D (第24题图)y xOBA在线段AB 上,且°=∠45DOE ,求点E 的坐标.【2019届一模青浦】24.(本题满分12分, 其中第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,将抛物线2y x =−平移后经过点A (-1,0)、B (4,0),且平移后的抛物线与y 轴交于点C (如图).(1)求平移后的抛物线的表达式;(2)如果点D 在线段CB 上,且CD CAD 的正弦值;(3)点E 在y 轴上且位于点C 的上方,点P 在直线BC 上,点Q 在平移后的抛物线上,如果四边形ECPQ 是菱形,求点Q 的坐标.【2019届一模静安】24.(本题满分12分,其中第(1)小题4分,第(2)小题3分,第(3)小题5分)在平面直角坐标系xOy 中(如图10),已知抛物线2(0)y ax bx c a ++≠的图像经过点(40)B ,、(53)D ,,设它与x 轴的另一个交点为A (点A 在点B 的左侧),且ABD ∆的面积是3. (1)求该抛物线的表达式; (2)求ADB ∠的正切值;(3)若抛物线与y 轴交于点C ,直线CD 交x 轴于点E ,点P 在射线AD 上,当APE ∆与ABD ∆相似时,求点P 的坐标.(第24题图)(备用图)BD ﹒﹒【2019届一模宝山】24.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图9,已知:二次函数的图像交x 轴正半轴于点A ,顶点为P ,一次函数的图像交x 轴于点B ,交y 轴于点C , ∠OCA 的正切值为. (1)求二次函数的解析式与顶点P 坐标;(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若,求m 的值.2y x bx =+132y x =−23A CO (图9)【2019届一模长宁】24.(本题满分12分,每小题4分)如图,在直角坐标平面内,抛物线经过原点O 、点)3,1(B ,又与x 轴正半轴相交于点A ,°=∠45BAO ,点P 是线段AB 上的一点,过点P 作OB PM //,与抛物线交于点M ,且点M 在第一象限内. (1)求抛物线的表达式;(2)若AOB BMP ∠=∠,求点P 的坐标;(3)过点M 作x MC ⊥轴,分别交直线AB 、x 轴于点N 、C ,若ANC ∆的面积等于PMN ∆的面积的2倍,求NCMN 的值. 第24题图xO A By备用图xO A By【2019届一模金山】24.已知抛物线c bx x y ++=2经过点()6,0A ,点()3,1B ,直线1l :()0≠=k kx y ,直线2l :2−−=x y ,直线1l 经过抛物线c bx x y ++=2的顶点P ,且1l 与2l 相交于点C ,直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移,使抛物线的顶点在直线2l 上(此时抛物线的顶点记为M ),再把抛物线左右平移,使抛物线的顶点在直线1l 上(此时抛物线的顶点记为N ). (1)求抛物线c bx x y ++=2的解析式.(2)判断以点N 为圆心,半径长为4的圆与直线2l 的位置关系,并说明理由.(3)设点F 、H 在直线1l 上(点H 在点F 的下方),当MHF ∆与OAB ∆相似时,求点F 、H 的坐标(直接写出结果). 第24题【2019届一模闵行】24.(本题共3小题,每小题4分,满分12分)已知:在平面直角坐标系xOy中,抛物线2y a x b x=+经过点A(5,0)、B(-3,4),抛物线的对称轴与x 轴相交于点D.(1)求抛物线的表达式;(2)联结OB、BD.求∠BDO的余切值;(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.xO(第24题图)【2019届一模虹口】24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy 中,抛物线2y x bx c =−++与x 轴相交于原点O 和点B (4,0),点A (3,m )在抛物线上.(1)求抛物线的表达式,并写出它的对称轴; (2)求tan ∠OAB 的值;(3)点D 在抛物线的对称轴上,如果∠BAD =45°,求点D 的坐标.Ⅳ第25题(压轴题)【2019届一模徐汇】25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长;(2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域;(3)当△DFC 是等腰三角形时,求AD 的长.OAy xB【2019届一模浦东】25. (本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C重合,小三角尺的顶点D、E分别在大三角尺的直角边AC、BC上,此时小三角尺的斜边DE恰好经过大三角尺的重心G. 已知∠A=∠CDE=30°,AB=12.(1)求小三角尺的直角边CD的长;(2)将小三角尺绕点C逆时针旋转,当点D第一次落在大三角尺的边AB上时(如图10-2),求点B、E之间的距离;(3)在小三角尺绕点C旋转的过程中,当直线DE经过点A时,求∠BAE的正弦值.(第25题图1)(第25题图)CE【2019届一模杨浦】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD 中,AD //BC ,AB ⊥BC ,AD =3,AB =6,DF ⊥DC 分别交射线AB 、射线CB 于点E 、F . (1)当点E 为边AB 的中点时(如图1),求BC 的长;(2)当点E 在边AB 上时(如图2),联结CE ,试问:∠DCE 的大小是否确定?若确定,请求出∠DCE 的正切值;若不确定,则设AE =x ,∠DCE 的正切值为y ,请求出y 关于x 的函数解析式,并写出定义域; (3)当△AEF 的面积为3时,求△DCE 的面积.A BC D EF (图1) (第25题图) A B C D E F (图2)【2019届一模普陀】25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=°,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=°,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.A BCP OABCPO图11①图11②【2019届一模奉贤】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.图11ABC D F E G 备用图ABC D【2019届一模松江】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD =,且CE =2,ED =3,求线段PD 的长. (备用图2)ABCD(备用图1)ABCD(第25题图)ABPCD E【2019届一模嘉定】25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.A 备用图BDCA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C【2019届一模青浦】25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长. NHGFEDC AB (第25题图)图11ABCPQM【2019届一模静安】25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC ∆中,6AB =,9AC=,tan ABC ∠.过点B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.【2019届一模宝山】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.【2019届一模长宁】25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且°=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域; AP 备用图A BCD A(图10)(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.【2019届一模金山】25.已知多边形ABCDEF 是⊙O 的内接正六边形,联结AC 、FD ,点H 是射线AF 上的一个动点,联结CH ,直线CH 交射线DF 于点G ,作CH MH ⊥交CD 的延长线于点M ,设⊙O 的半径为()0>r r . (1)求证:四边形ACDF 是矩形.(2)当CH 经过点E 时,⊙M 与⊙O 外切,求⊙M 的半径(用r 的代数式表示).(3)设()o900<<=∠ααHCD ,求点C 、M 、H 、F 构成的四边形的面积(用r 及含α的三角比的式子表示). 第25题图图2 BFEC NDA MB FCE N A DM图1备用图BC NAMA B FOHEO【2019届一模闵行】25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,5cos13ABC∠=.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,AG yDG=.(1)求AB的长;(2)当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;(3)如果23ABEFABCDSS=四边形四边形,求线段CE的长.A DFGA D【2019届一模虹口】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F . (1)如果cos ∠DBC =23,求EF 的长;(2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEFS y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长. 第25题备用图第25题图EABCFDG。
上海市中考数学压轴题专项训练(含答案)

上海市20XX 年中考数学压轴题专项训练1.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)如图,已知抛物线2y x bx c =++经过()01A -,、()43B -,两点. (1)求抛物线的解析式; (2 求tan ABO ∠的值;(3)过点B 作BC ⊥x 轴,垂足为点C ,点M 是抛物线上一点,直线MN 平行于y 轴交直线AB 于点N ,如果M 、N 、B 、C 为顶点的四边形是平行四边形,求点N 的坐标.1.解:(1)将A (0,-1)、B (4,-3)分别代入2y x bx c =++得1,1643c b c =-⎧⎨++=-⎩, ………………………………………………………………(1分)解,得9,12b c =-=-…………………………………………………………………(1分) 所以抛物线的解析式为2912y x x =--……………………………………………(1分)(2)过点B 作BC ⊥x 轴,垂足为C ,过点A 作AH ⊥OB ,垂足为点H ………(1分)在Rt AOH ∆中,OA =1,4sin sin ,5AOH OBC ∠=∠=……………………………(1分) ∴4sin 5AH OA AOH =∠=,∴322,55OH BH OB OH ==-=, ………………(1分)在Rt ABH ∆中,4222tan 5511AH ABO BH ∠==÷=………………………………(1分) (3)直线AB 的解析式为112y x =--, ……………………………………………(1分)设点M 的坐标为29(,1)2m m m --,点N 坐标为1(,1)2m m --那么MN =2291(1)(1)422m m m m m -----=-; …………………………(1分)∵M 、N 、B 、C 为顶点的四边形是平行四边形,∴MN =BC =3解方程24m m -=3得2m = ……………………………………………(1分) 解方程243m m -+=得1m =或3m =; ………………………………………(1分)所以符合题意的点N 有4个35(22),(22),(1,),(3,)22---- ……………………………………………………………………………………(1分)2.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)在Rt △ABC 中,∠ACB = 90°,经过点B 的直线l (l 不与直线AB 重合)与直线BC 的夹角等于∠ABC ,分别过点C 、点A 作直线l 的垂线,垂足分别为点D 、点E .(1)如图1,当点E 与点B 重合时,若AE =4,判断以C 点为圆心CD 长为半径的圆C 与直线AB 的位置关系并说明理由;(2)如图2,当点E 在DB 延长线上时,求证:AE =2CD ;(3)记直线CE 与直线AB 相交于点F ,若56CF EF =,CD = 4,求BD 的长.2.解:(1)过点C 作CF ⊥AB ,垂足为点F. ……………………………………………(1分) ∵∠AED =90°,∠ABC =∠CBD ,∴∠ABC =∠CBD =45°,∵∠ACB =90°,∠ABC =45°,AE =4,∴CF =2,BC =1分) 又∵∠CBD =∠ABC =45°,CD ⊥l ,∴CD =2, …………………………………………(1分) ∴CD =CF =2,∴圆C 与直线AB 相切.……………………………………………………(1分) (2)证明:延长AC 交直线l 于点G . ………………………………………………(1分) ∵∠ACB = 90°,∠ABC =∠GBC ,∴∠BAC =∠BGC .∴AB = GB .…………………………………………………………………………………(1分) ∴AC = GC .…………………………………………………………………………………(1分) ∵AE ⊥l ,CD ⊥l ,∴AE ∥CD .A CDB (E )l(第25题图1)(第25题图2)ACD ElB∴12CD GC AE GA ==. …………………………………………………………………………(1分) ∴AE = 2CD . ………………………………………………………………………………(1分) (3)(I )如图1,当点E 在DB 延长线上时:过点C 作CG ∥l 交AB 于点H ,交AE 于点G ,则∠CBD =∠HCB . ∵∠ABC =∠CBD ,∴∠ABC =∠HCB .∴CH = BH .………(1分) ∵∠ACB = 90°,∴∠ABC +∠BAC =∠HCB +∠HCA = 90°. ∴∠BAC =∠HCA .∴CH = AH = BH .∵CG ∥l ,∴56CH CF BE EF ==. 设CH = 5x ,则BE = 6x ,AB = 10x .在Rt △ABE 中,8AE x ==.由(2)知AE = 2CD = 8,∴88x =,得1x =. ∴CH = 5,BE = 6,AB = 10.∵CG ∥l ,∴12HG AH BE AB ==,∴HG =3.……………………(1分) ∴CG = CH + HG = 8.易证四边形CDEG 是矩形,∴DE = CG = 8.∴2BD DE BE =-=.…………………………………………(1分) (II )如图2,当点E 在DB 上时:同理可得CH = 5,BE = 6,HG = 3.…………………………(1分) ∴2DE CG CH HG ==-=.∴BD =DE + BE = 8.…………………………………………………………………………(1分) 综上所述,BD 的长为2或8.3.已知点A (2,﹣2)和点B (﹣4,n )在抛物线y=ax 2(a ≠0)上. (1)求a 的值及点B 的坐标;(2)点P 在y 轴上,且△ABP 是以AB 为直角边的三角形,求点P 的坐标;(3)将抛物线y=ax 2(a ≠0)向右并向下平移,记平移后点A 的对应点为A ′,点B 的对应点为B ′,若四边形ABB ′A ′为正方形,求此时抛物线的表达式.(第25题图1)A CD ElGBHF B(第25题图2)A CD lGE HF【考点】二次函数图象上点的坐标特征;坐标与图形变化-平移.【分析】(1)把点A(2,﹣2)代入y=ax2,得到a,再把点B代入抛物线解析式即可解决问题.(2)求出直线AB解析式,再分别求出过点A垂直于AB的直线的解析式,过点B垂直于直线AB的解析式即可解决问题.(3)先求出点A′坐标,确定是如何平移的,再确定抛物线顶点的坐标即可解决问题.【解答】解:(1)把点A(2,﹣2)代入y=ax2,得到a=﹣,∴抛物线为y=﹣x2,∴x=﹣4时,y=﹣8,∴点B坐标(﹣4,﹣8),∴a=﹣,点B坐标(﹣4,﹣8).(2)设直线AB为y=kx+b,则有,解得,∴直线AB为y=x﹣4,∴过点B垂直AB的直线为y=﹣x﹣12,与y轴交于点P(0,﹣12),过点A垂直AB的直线为y=﹣x,与y轴交于点P′(0,0),∴点P在y轴上,且△ABP是以AB为直角边的三角形时.点P坐标为(0,0),或(0,﹣12).(3)如图四边形ABB′A′是正方形,过点A作y轴的垂线,过点B、点A′作x轴的垂线得到点E、F.∵直线AB解析式为y=﹣x﹣12,∴△ABF,△AA′E都是等腰直角三角形,∵AB=AA′==6,∴AE=A′E=6,∴点A′坐标为(8,﹣8),∴点A到点A′是向右平移6个单位,向下平移6个单位得到,∴抛物线y=﹣x2的顶点(0,0),向右平移6个单位,向下平移6个单位得到(6,﹣6),∴此时抛物线为y=﹣(x﹣6)2﹣6.4.已知,AB=5,tan∠ABM=,点C、D、E为动点,其中点C、D在射线BM上(点C在点D的左侧),点E和点D分别在射线BA的两侧,且AC=AD,AB=AE,∠CAD=∠BAE.(1)当点C与点B重合时(如图1),联结ED,求ED的长;(2)当EA∥BM时(如图2),求四边形AEBD的面积;(3)联结CE,当△ACE是等腰三角形时,求点B、C间的距离.【考点】三角形综合题.【分析】(1)如图1中,延长BA交DE于F,作AH⊥BD于H,先证明BF⊥DE,EF=DF,再利用△ABH∽△DBF,得=,求出DF即可解决问题.=BD•AH,计算即可.(2)先证明四边形ADBE是平行四边形,根据S平行四边形ADBE(3)由题意AC≠AE,EC≠AC,只有EA=EC,利用四点共圆先证明四边形ADBE是平行四边形,求出DH、CH即可解决问题.【解答】解:(1)如图1中,延长BA交DE于F,作AH⊥BD于H.在RT△ABH中,∵∠AHB=90°,∴sin∠ABH==,∴AH=3,BH==4,∵AB=AD,AH⊥BD,∴BH=DH=4,在△ABE 和△ABD中,,∴△ABD≌△ABE,∴BE=BD,∠ABE=∠ABD,∴BF⊥DE,EF=DF,∵∠ABH=∠DBF,∠AHB=∠BFD,∴△ABH∽△DBF,∴=,∴DF=,∴DE=2DF=.(2)如图2中,作AH⊥BD于H.∵AC=AD,AB=AE,∠CAD=∠BAE,∴∠AEB=∠ABE=∠ACD=∠ADC,∵AE∥BD,∴∠AEB+∠EBD=180°,∴∠EBD+∠ADC=180°,∴EB∥AD,∵AE∥BD,∴四边形ADBE是平行四边形,∴BD=AE=AB=5,AH=3,=BD•AH=15.∴S平行四边形ADBE(3)由题意AC≠AE,EC≠AC,只有EA=EC.如图3中,∵∠ACD=∠AEB(已证),∴A、C、B、E四点共圆,∵AE=EC=AB,∴=,∴=,∴∠AEC=∠ABC,∴AE∥BD,由(2)可知四边形ADBE是平行四边形,∴AE=BD=AB=5,∵AH=3,BH=4,∴DH=BD﹣BH=1,∵AC=AD,AH⊥CD,∴CH=HD=1,∴BC=BD﹣CD=3.5.如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.(1)求这个二次函数的解析式;(2)联结AC,求∠BAC的正切值;(3)点P为直线AB上一点,若△ACP为直角三角形,求点P的坐标.【分析】(1)先把A点坐标代入y=x+m求出m得到直线AB的解析式为y=x+1,这可求出直线与y轴的交点B的坐标,然后把A点和B点坐标代入y=x2+bx+c中得到关于b、c的方程组,再解方程组求出b、c即可得到抛物线解析式;(2)如图,先抛物线解析式配成顶点式得到C(1,0),再利用两点间的距离公式计算出BC2=2,AB2=18,AC2=20,然后利用勾股定理的逆定理可证明△ABC为直角三角形,∠ACB=90°,于是利用正切的定义计算tan∠BAC的值;(3)分类讨论:当∠APC=90°时,有(2)得点P在B点处,此时P点坐标为(0,1);当∠ACP=90°时,利用(2)中结论得tan∠PAC==,则PC=AC,设P(t,t+1),然后利用两点间的距离公式得到方程t2+(t+1﹣1)2=20,再解方程求出t即可得到时P点坐标.【解答】解:(1)把A(3,4)代入y=x+m得3+m=4,解得m=1∴直线AB的解析式为y=x+1,∵当x=0时,y=x+1=1,∴B(0,1),把B(0,1),A(3,4)代入y=x2+bx+c得,解得,∴抛物线解析式为y=x2﹣2x+1;(2)如图,∵y=x2﹣2x+1=(x﹣1)2,∴C(1,0),∴BC2=12+12=2,AB2=32+(4﹣1)2=18,AC2=(3﹣1)2+42=20,而2+18=20,∴BC2+AB2=AC2,∴△ABC为直角三角形,∠ACB=90°,∴tan∠BAC===;(3)当∠APC=90°时,点P在B点处,此时P点坐标为(0,1);当∠ACP=90°时,∵tan∠PAC==,∴PC=AC,设P(t,t+1),∴t2+(t+1﹣1)2=20,解得t1=﹣,t2=(舍去),此时P点坐标为(﹣,﹣ +1),综上所述,满足条件的P点坐标为(0,1)或(﹣,﹣ +1).【点评】本题考查了二次函数的综合题:熟练掌握二次函数的性质和一次函数图象上点的坐标特征;能运用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式;能利用勾股定理的逆定理证明直角三角形.6.如图,▱ABCD中,AB=8,AD=10,sinA=,E、F分别是边AB、BC上动点(点E不与A、B重合),且∠EDF=∠DAB,DF延长线交射线AB于G.(1)若DE⊥AB时,求DE的长度;(2)设AE=x,BG=y,求y关于x的函数解析式,并写出函数的定义域;(3)当△BGF为等腰三角形时,求AE的长度.【分析】(1)DE⊥AB时,根据sinA=即可解决问题.(2)如图2中,作DM⊥AB于M,根据DG2=DM2+MG2=AGEG,列出等式即可解决问题.(3)分三种情形①BF=BG,②FB=FG,③GB=GF,根据BF∥AD,得出比例式,列方程即可解决.【解答】解:(1)如图1中,∵DE⊥AB,∴sinA==,∵AD=10,∴DE=8.(2)如图2中,作DM⊥AB于M,由(1)可知DM=8,AM=6,MG=AB﹣AM=8﹣6=2,∴DG2=DM2+MG2,∵∠DGE=∠DGA,∠GDE=∠A,∴△DGE∽△AGD,∴=,∴DG2=AGEG,∴DM2+MG2=AGEG,∴82+(2+y)2=(8+y)(8+y﹣x),∴y=(0<x<8)(3)①当BF=FG时,∵BF∥AD,∴=,∴AD=AG=10,∴y=2,即=2,解得x=2,∴AE=2.②当FB=FG时,∵BF∥AD,∴=,∴AD=DG=10,∵DM⊥AG,∴AM=MB=6,∴AG=12,∴y=4,即=4,解得x=.③当GB=GF时,∵BF∥AD,∠GBF=∠BFG,∴∠A=∠GBF,∠ADG=∠BFG,∴∠A=∠ADG,∵∠A=∠EDG,∴∠EDG=∠ADG,∴此时点E与点A重合,不合题意.综上所述AE=2或时,△BFG是等腰三角形.【点评】本题考查四边形综合题、锐角三角函数、相似三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,学会用方程的思想解决问题,属于中考常考题型.。
上海初三数学一模压轴题汇总各区题

崇明23.(本题满分12分,每小题各6分)如图,点E 是正方形ABCD 的边BC 延长线上一点,联结DE ,过顶点B 作BF DE ⊥,垂足为F ,BF 交边DC 于点G .(1)求证:GD AB DF BG ⋅=⋅; (2)联结CF ,求证:45CFB ∠=︒.崇明24.(本题满分12分,每小题各4分)如图,抛物线243y x bx c =-++过点(3,0)A ,(0,2)B .(,0)M m 为线段OA 上一个动点(点P 、N ((((第23题图) ABDE C GF(第24题图)(备用图)A崇明25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分) 如图,已知ABC △中,90ACB ∠=︒,8AC =,4cos 5A =,D 是AB 边的中点,E 是AC 边上一点,联结DE ,过点D 作DF DE ⊥交BC 边于点F ,联结EF . (1)如图1,当DE AC ⊥时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,DFE ∠的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出DFE ∠的正切值;(3)如图3,联结CD 交EF 于点Q ,当CQF △是等腰三角形时,请直接写出....BF 的长.金山23. (本题满分12分,每小题6分)如图,已知在Rt △ABC 中,∠ACB=90°,AC >BC ,CD 是Rt △ABC 的高,E 是AC的中点,ED 的延长线与CB 的延长线相交于点F .(1)求证:DF 是BF 和CF 的比例中项;(2)在AB 上取一点G ,如果AE :AC=AG :AD ,求证:EG :CF=ED :DF .金山24. (本题满分12分,每小题4分)平面直角坐标系xOy 中(如图),已知抛物线23yax bx 与y 轴相交于点C ,与x 轴正半轴相交于点A ,OA OC ,与x 轴的另一个交点为B ,对称轴是直线1x ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(第25题图1)A BCDFEBD FECA(第25题图2) B DFECA(第25题图3)(2)抛物线的对称轴与x 轴相交于点M ,求∠PMC 的正切值; (3)点Q 在y 轴上,且△BCQ 与△CMP 相似,求点Q 的坐标.金山25. (本题满分14分,第(1)小题3分,第(2)小题5分,第(3)小题6分)如图,已知在△ABC 中,45,cos 5ABACB,P 是边AB 一点,以P 为圆心,PB 为半径的P 与边BC 的另一个交点为D ,联结PD 、AD . (1)求△ABC 的面积;(2)设PB =x ,△APD 的面积为y ,求y 关于x 的函数关系式,并写出定义域;(3)如果△APD 是直角三角形,求PB 的长.青浦23.(本题满分12分,第(1)小题4分,第(2)小题8分)如图8,已知点D 、E 分别在△ABC 的边AC 、BC 上,线段BD 与AE 交于点F ,且CD CA CE CB ⋅=⋅.(1)求证:∠CAE =∠CBD ;(2)若BEABEC AC=,求证:AB AD AF AE ⋅=⋅.青浦24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图9,在平面直角坐标系xOy 中,抛物线()20y ax bx c a =++>与x 轴相交于点AB CDE FA(-1,0)和点B,与y轴交于点C,对称轴为直线1x .(1)求点C的坐标(用含a的代数式表示);(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F 与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.青浦25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)如图10,在边长为2的正方形ABCD 中,点P 是边AD 上的动点(点P 不与点A 、点D 重合),点Q 是边CD 上一点,联结PB 、PQ ,且∠PBC =∠BPQ .(1)当QD =QC 时,求∠ABP 的正切值;(2)设AP =x ,CQ =y ,求y 关于x 的函数解析式;(3)联结BQ ,在△PBQ 中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.黄浦23、(本题满分12分)如图,BD 是ABC △的角平分线,点E 位于边BC 上,已知BD 是BA 与BE 的比例中项. (1)求证:12CDE ABC ∠=∠(2)求证:AD CD AB CE ⋅=⋅ 黄浦24、(本题满分12分)在平面直角坐标系xOy 中,对称轴为直线1x =的抛物线28y ax bx =++过点QPD CBAA B CDED CBA()2,0-.(1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y 方向平移若干个单位,所得抛物线的顶点为D ,与y 轴的交点为B ,与x 轴负半轴交于点A ,过点B 作x 轴的平行线交所得抛物线于点C ,若AC BD ∥,试求平移后所得抛物线的表达式.黄浦25、(本题满分14分)如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积; (2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域. 松江23.(本题满分12分,每小题6分)已知四边形ABCD 中,∠BAD =∠BDC =90°,2BD AD BC =⋅. (1)求证:AD ∥BC ;(2)过点A 作AE ∥CD 交BC 于点E .请完善图形并求证:2CD BE BC =⋅. 松江24.(本题满分12分,每小题4分)如图,在平面直角坐标系xOy中,抛物线2=++的对称轴为直线x=1,抛物线y x bx c与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.(1)求点A的坐标和抛物线的表达式;(2)当AE:EP=1:2时,求点E的坐标;(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.松江25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.闵行23.(本题共2小题,每小题6分,满分12分)如图,已知在△ABC中,∠BAC =2∠B,AD平分∠BAC,DF//BE,点E在线段BA的延长线上,联结DE,交AC于点G,且A∠E =∠C.(1)求证:2=⋅;AD AF AB(2)求证:AD BE DE AB⋅=⋅.闵行24.(本题共3题,每小题4分,满分12分)抛物线23(0)=++≠经过点A(1-,0),y ax bx a且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.闵行25.(共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边上中线,点E在边AC上,点F在边BC上,且∠EDA=∠FDB,联结EF、DC交于点G.(1)当∠EDF =90°时,求AE 的长;(2)CE = x ,CF = y ,求y 关于x 的函数关系式,并指出x 的取值范围;(3)如果△CFG 是等腰三角形,求CF 与CE 的比值.浦东23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)如图,已知,在锐角△ABC 中,CE ⊥AB 于点E ,点D 在边AC 上,联结BD 交CE 于点F ,且DF FB FC EF ⋅=⋅.(1)求证:BD ⊥AC ;(2)联结AF ,求证:AF BE BC EF ⋅=⋅. 浦东24.(本题满分12分,每小题4分)已知抛物线y =ax 2+bx +5与x 轴交于点A (1,0)和点B (5,0),顶点为M .点C 在x 轴的负半轴上,且AC =AB ,点D 的坐标为(0,3),直线l 经过点C 、D .(1)求抛物线的表达式;(2)点P 是直线l 在第三象限上的点,联结AP ,且线段CP 是线段CA 、CB 的比例中项,求tan ∠CPA 的值;(3)在(2)的条件下,联结AM 、BM ,在直线PM 上是否存在点E ,使得∠AEM =∠AMB .AB CABEFGA若存在,求出点E的坐标;若不存在,请说明理由.浦东25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D 为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED 交射线AC于点G.(1)求证:△EFG∽△AEG;(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;(3)联结DF,当△EFD是等腰三角形时,请直接..写出FG的长度.D、E上,F,且EF⋅(1AC⋅;(2)当AB =12,AC =9,AE =8时,求BD 的长与△△ADE ECFS S 的值. 虹口24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy 中,抛物线与x 轴相交于点A (-2,0)、B (4,0),与y 轴交于点C (0,-4),BC 与抛物线的对称轴相交于点D .(1)求该抛物线的表达式,并直接写出点D 的坐标;(2)过点A 作AE ⊥AC 交抛物线于点E ,求点E 的坐标;(3)在(2)的条件下,点F 在射线AE 上,若△ADF ∽△ABC ,求点F 的坐标. 虹口25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知AB =5,AD =4,AD ∥BM ,3cos 5B =(如图),点C 、E 分别为射线BM 上的动点(点C 、E 都不与点B 重合),联结AC 、AE ,使得∠DAE =∠BAC ,射线EA 交射线CD 于点F .设BC =x ,AF y AC=. (1)如图1,当x =4时,求AF 的长;(2)当点E 在点C 的右侧时,求y 关于x 的函数关系式,并写出函数的定义域;(3)联结BD 交AE 于点P ,若△ADP 是等腰三角形,直接写出x 的值.普陀23. (本题满分12分)已知:如图9,四边形ABCD 的对角线AC 和BD 相交于点E ,2,AD DC DC DE DB ==⋅.求证:(1)BCE ADE ∽;(2)··AB BC BD BE =. 普陀24.(本题满分12分,每小题满分各4分) 如图10,在平面直角坐标系中,已知抛物线22y ax ax c +=+(其中a c 、为常数,且0a <)与x 轴交于点A ,它的坐标是()3, 0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4.(1)求该抛物线的表达式;(2)求CAB ∠的正切值;(3)如果点P 是抛物线上的一点,且ABP CAO ∠=∠,试直接写出点P 的坐标. 普陀25.(本题满分14分,第(1)小题满分3分,第(1)小题满分5分,第(1)小题满分6分)如图11,BAC ∠的余切值为2,AB =D 是线段AB 上的一动点(点D 不与点A B 、重合),以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上,且点F 在点E 的右侧.联结BG ,并延长BG ,交射线EC 于点P .(1)点D 在运动时,下列的线段和角中,______是始终保持不变的量(填序号);图9B D①AF ; ②FP ; ③BP ; ④BDG ∠; ⑤GAC ∠; ⑥BPA ∠;(2)设正方形的边长为x ,线段AP 的长为y ,求y 与x 之间的函数关系式,并写出定义域;(3)如果PFG 与AFG 相似,但面积不相等,求此时正方形的边长.嘉定23.(本题满分12分,每小题6分)如图6,已知梯形ABCD 中,AD ∥BC ,CD AB =,点E 在对角线AC 上,且满足BAC ADE ∠=∠.(1)求证:BC DE AE CD ⋅=⋅;(2)以点A 为圆心,AB 长为半径画弧交边BC 于点F ,联结AF .求证:CA CE AF ⋅=2.嘉定24.(本题满分12分,每小题4分)已知在平面直角坐标系xOy (如图7)中,已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B . (1)求该抛物线的表达式;(2)设该抛物线的对称轴与x 轴的交点为C ,第四象限内的点D 在该抛物线的对称轴上,如果以点A 、C 、D 所组成的三角形与△AOB 相似,求点D 的坐标;(3)设点E 在该抛物线的对称轴上,它的纵坐标是1,联结AE 、BE ,求ABE ∠sin .嘉定25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在正方形ABCD 中,8=AB ,点P 在边CD 上,43tan =∠PBC ,点Q 是在射线BP 上的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直.(1)如图8,当点R 与点D 重合时,求PQ 的长;(2)如图9,试探索:MQ RM 的比值是否随点Q 的运动而发生变化若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图10,若点Q 在线段BP 上,设x PQ =,y RM =,求y 关于x 的函数关系式,并写出它的定义域.12ABCD ,BD AD 上一点,作45EBC ∠=,联结CE ,交DB 于点F . (1)求证:ABE ∽DBC ;B C 图8A B C 图9B C图10(2)如果56BC BD =,求BCE BDA S S 的值.静安24. (本题满分12分,第1小题4分,第2小题8分)在平面直角坐标系xOy 中(如图),已知抛物线253y ax bx =+-经过点(1,0)A -、(5,0)B .(1)求此抛物线顶点C 的坐标;(2)联结AC 交y 轴于点D ,联结BD 、BC ,过点C 作CH BD ⊥,垂足为点H ,抛物线对称轴交x 轴于点G ,联结HG ,求HG 的长.静安25. (本题满分14分,第1小题4分,第2小题6分,第3小题4分) 已知:如图,四边形ABCD 中,090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠.(1)求证:四边形ABCD 是菱形;(2)如果点E 在对角线AC 上,联结BE 并延长,交边DC 于点G ,交线段AD 的延长线于点F (点F 可与点D 重合),AFB ACB ∠=∠,设AB 长度是a (a 实常数,且0a >),,AC x AF y ==,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题的条件下,当CGE 是等腰三角形时,求AC 的长.(计算结果用含a 的代数式表示)长宁23.(本题满分12分,第(1)小题6分,第(2)小题6分)F EA B C如图,在∆ABC 中,点D 在边BC 上,联结AD ,∠ADB=∠CDE ,DE 交边AC 于点E ,DE 交BA 延长线于点F ,且DF DE AD ⋅=2.(1)求证:BFD ∆∽CAD ∆;(2)求证:AD AB DE BF ⋅=⋅.长宁24.(本题满分12分,每小题4分) 在直角坐标平面内,直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ,且与x 轴的另一个交点为点B . 点D 在该抛物线上,且位于直线AC 的上方.(1)求上述抛物线的表达式;(2)联结BC 、BD ,且BD 交AC 于点E ,如果∆ABE 的面积与∆ABC 的面积之比为4:5,求∠DBA 的余切值;(3)过点D 作DF ⊥AC ,垂足为点F ,联结CD . 若∆CFD 与∆AOC 相似,求点D 的坐标.长宁25.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分)已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D 重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E .设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求∆ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域;(3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.徐汇23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)如图在△ABC 中,AB =AC ,点D 、E 、F 分别在边BC 、AB 、AC 上,且∠ADE =∠B , ∠ADF =∠C ,线段EF 交线段AD 于点G .(1)求证:AE =AF ;(2)若DF CF DE AE =,求证:四边形EBDF 是平行四边形. 徐汇24.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分) 如图,在平面直角坐标系xOy 中,直线y =kx (k ≠0)沿着y 轴向上平移3个单位长DC BA D CB A F E P DC B A第25题图度后,与x轴交于点B(3,0),与y轴交于点C,抛物线2=++过点B、C且与y x bx cx轴的另一个交点为A.(1)求直线BC及该抛物线的表达式;(2)设该抛物线的顶点为D,求△DBC的面积;(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.徐汇25.(本题满分14分,第(1)小题3分,第(2)小题7分,第(3)小题4分)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.杨浦23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:梯形ABCD中,AD//BC,AD=AB,对角线AC、BD交于点E,点F在边BC上,Array且∠BEF=∠BAC.(1)求证:△AED∽△CFE;B CF(2)当EF//DC时,求证:AE=DE.杨浦24.(本题满分12分,第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy中,抛物线2221=-+--+交 y轴于点为A,顶点为D,对称y x mx m m轴与x轴交于点H.(1)求顶点D的坐标(用含m的代数式表示);(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线22=-+的位置,求平移的方向y x x和距离;(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.杨浦25.(本题满分14分,第(1)、(2)小题各6分,第(3)小题2分)已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB 上.(1)如图1,当EP⊥BC时,求CN的长;(2)如图2,当EP⊥AC时,求AM的长;(3)请写出线段CP的长的取值范围,及当CP的长最大时MN的长.奉贤23.(本题满分 12 分,每小题满分各 6 分)已知:如图 8,四边形90ABCD DCB ∠=︒,,对角线 BD ⊥AD ,点 E 是边 AB 的中点,CE 与 BD 相交于点 F ,2·BD AB BC =.(1) 求证:BD 平分∠ABC ;(2) 求证:··BE CF BC EF =.奉贤24. (本题满分 12 分,每小题满分各 4 分)如图9,在平面直角坐标系xOy 中,抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ,与y 轴相交于点(0,3)C -,经过点A 的射线AM 与y 轴相交于点E ,与抛物线的另一个交点为点F ,且13AE EF =. (1)求这条抛物线的表达式,并写出它的对称轴;(2)求FAB ∠的余切值;(3)点D 是点C 关于抛物线对称轴的对称点,点 P 是 y 轴上一点,且AFP DAB ∠=∠,求点 P 的坐标.奉贤25.(本题满分 14 分,第(1)小题满分 3 分,第(1)小题满分 5 分,第(1)小题满分 6 分)已知:如图10,在梯形ABCD 中,//,90,2AB CD D AD CD ∠===,点E 在边AD 上(不与点A 、D 重合),45,CEB EB ∠=与对角线AC 相交于点F ,设DE x =.(1)用含x 的代数式表示线段CF 的长;(2)如果把CAE 的周长记作CAE C ,BAF 的周长记作BAF C ,设CAE BAF Cy C =,求y 关于x 的函数关系式,并写出它的定义域; (3)当ABE ∠的正切值是35时,求AB 的长. 宝山23、(满分12分,每小题各6分)如图,ABC 中,AB AC =,过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ,联结BF ,交AC 于点G .(1)求证:AE EG AC CG=; (2)若AH 平分BAC ∠,交BF 于H ,求证:BH 是HG 和HF 的比例中项.宝山24、(满分12分,每小题各4分)设,a b 是任意两个不等实数,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],a b ,对于一个函数,如果它的自变量x 与函数值y 满足:当m x n ≤≤时,有m y n ≤≤,我们就此称此函数是闭区间[],m n 上的“闭函数”。
上海市历年中考数学试题、模拟题汇编及答案

上海中考试题、模拟题汇编及答案20PP 年上海市初中毕业统一学业考试数学卷 20PP 年上海市初中毕业统一学业考试 20PP 年上海市初中毕业生统一学业考试20PP 年上海市初中毕业生统一学业考试数学试题及答案评分要点20PP 年上海市中考数学试题及答案上海市黄浦区20PP 年九年级数学学业 考试模拟考试 上海市青浦区20PP 学年度九年级数学学业 模拟考试 20PP 上海金山中考 数学模拟试卷--数学 20PP 上海浦东新中考数学预测卷--数学20PP 年上海市初中毕业统一学业考试数学卷(满分150分,考试时间100分钟)、选择题(本大题共 6题,每题4分,满分24分)1. 下列实数中,是无理数的为(C )A. 3.14B. 1C. . 3【解析】无理数即为无限不循环小数,则选 C 。
k2. 在平面直角坐标系中,反比例函数 P = - ( k v 0 )图像的两支分别在(XA.第一、三象限B.第二、四象限C.第一、二象限【解析】设K=-1,则P=2时,P= _丄,点在第四象限;当 P=-2时,P=丄,在第二象限,所以图像过2 2第二、四象限,即使选 B 3.已知一元二次方程 P 2+ P —1 = 0 ,下列判断正确的是( B )A .该方程有两个相等的实数根 B.该方程有两个不相等的实数根 C.该方程无实数根D.该方程根的情况不确定【解析】根据二次方程的根的判别式: A=b 2—4ac=(1 j —4心江(―1 )=5>0,所以方程有两个不相等的实数根,所以选 B4. 某市五月份连续五天的日最高气温分别为 23、20、20、21、26 (单位:°C),这组数据的中位数和众数分别是(D ) A. 22 C, 26°CB. 22 C, 20°CC. 21 C, 26°CD. 21 C, 20°C【解析】中位数定义:将所有数学按从小到大顺序排列后,当数字个数为奇数时即中间那个数为中位 数,当数字的个数为偶数时即中间那两个数的平均数为中位数。
2020-2021年上海各区数学中考一模压轴题分类汇编-23题含详解
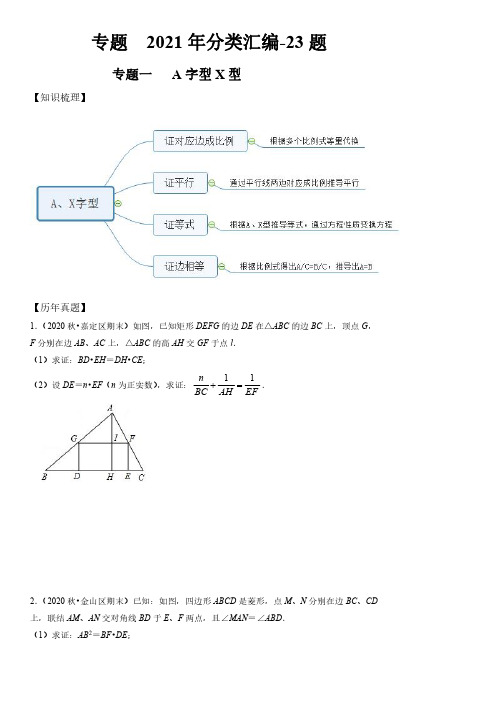
专题2021年分类汇编-23题专题一A字型X型【知识梳理】【历年真题】1.(2020秋•嘉定区期末)如图,已知矩形DEFG的边DE在△ABC的边BC上,顶点G,F分别在边AB、AC上,△ABC的高AH交GF于点l.(1)求证:BD•EH=DH•CE;(2)设DE=n•EF(n为正实数),求证:11nBC AH EF+=.2.(2020秋•金山区期末)已知:如图,四边形ABCD是菱形,点M、N分别在边BC、CD 上,联结AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.(1)求证:AB2=BF•DE;(2)若BE DNDE DC=,求证:EF∥MN.3.(2020秋•黄浦区期末)某班级的“数学学习小组心得分享课”上,小智跟同学们分享了关于梯形的两个正确的研究结论:①如图1,在梯形ABCD中,AD∥BC,过对角线交点的直线与两底分别交于点M、N,则AM CNDM BN=;②如图2,在梯形ABCD中,AD∥BC,过两腰延长线交点P的直线与两底分别交于点K、L,则AK BLDK CL=.接着小明也跟同学们分享了关于梯形的一个推断:过梯形对角线交点且平行于底边的直线被梯形两腰所截,截得的线段被梯形对角线的交点平分.(1)经讨论,大家都认为小明所给出的推断是正确的.请你结合图示(见答题卷)写出已知、求证,并给出你的证明;(2)小组还出了一个作图题考同学们:只用直尺将图3中两条平行的线段AB、CD同时平分.请保留作图过程痕迹,并说明你作图方法的正确性(可以直接运用小智和小明得到的正确结论).(注意:请务必在试卷的图示中完成作图草稿,在答题卷上直接用2B铅笔或水笔完成作图,不要涂改.)专题二相似三角形之等量代换【知识梳理】【历年真题】1.(2020秋•闵行区期末)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA 的延长线于点D,交EA的延长线于点F,且AF•CD=BC•AD.(1)求证:AE⊥BC;(2)如果BE=CE,求证:BC2=2BD•AC.2.(2020秋•徐汇区期末)如图,在△ACB中,点D、E分别在边BC、AC上,AD=AB,BE=CE,AD与BE交于点F,且AF•DF=BF•EF.求证:(1)∠ADC=∠BEC;(2)AF•CD=EF•AC.3.(2020秋•青浦区期末)已知:如图,在四边形ABCD中,AB=AD,AC、BD相交于点E,AE⋅CE=DE⋅BE(1)求证:△ABE∽△ACB;(2)如果DA2=DE•DB,求证:AB•EC=BC•AE.4.(2020秋•虹口区期末)如图,在△ABC中,点D、G在边AC上,点E在边BC上,DB =DC,EG∥AB,AE、BD交于点F,BF=AG.(1)求证:△BFE∼△CGE;(2)当∠AEG=∠C时,求证:AB2=AG•AC.5.(2020秋•奉贤区期末)如图,在四边形ABCD中,∠B=∠DCB,联结AC,点E在边BC上,且∠CDE=∠CAD,DE与AC交于点F,CE•CB=AB•CD.(1)求证:AD∥BC;(2)当AD=DE时,求证:AF2=CF•CA.6.(2020秋•杨浦区期末)已知:如图,在梯形ABCD中,AD∥BC,对角线BD、AC相交于点E,过点A作AF∥DC,交对角线BD于点F.(1)求证:DF DE=BD BE;(2)如果∠ADB=∠ACD,求证:线段CD是线段DF、BE的比例中项.专题三相似三角形之面积比【知识梳理】【历年真题】1.(2020秋•崇明区期末)已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED =∠ABC,联结BE、CD相交于点F.(1)求证:∠ABE=∠ACD;(2)如果ED=EC,求证:22DF EF BD BE.2.(2020秋•长宁区期末)已知:如图,在Rt△ABC中,∠ACB=90°,CH⊥AB,垂足为点H.点D在边BC上,联结AD,交CH于点E,且CE=CD.(1)求证:△ACE∽△ABD;(2)求证:△ACD的面积是△ACE的面积与△ABD的面积的比例中项.3.(2020秋•静安区期末)已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE ∥BC,AD2=AE•AC.求证:(1)△BCD∽△CDE;(2)22CD AD BC AB.专题四相似三角形综合题【知识梳理】【历年真题】1.(2020秋•浦东新区期末)Rt△ABC中,∠ACB=90°,点D、E分别为边AB、BC上的点,且CD=CA,DE⊥AB.(1)求证:CA2=CE•CB;(2)联结AE,取AE的中点M,联结CM并延长与AB交于点H,求证:CH⊥AB.2.(2020秋•普陀区期末)已知:如图,AD∥BC,∠ABD=∠C,AE⊥BD,DF⊥BC,点E、F分别为垂足.(1)求证:AE BD DF BC;(2)联结EF,如果∠ADB=∠BDF,求证:DF•DC=EF•BC.3.(2020秋•松江区期末)如图,已知在▱ABCD中,E是边AD上一点,联结BE、CE,延长BA、CE相交于点F,CE2=DE•BC.(1)求证:∠EBC=∠DCE;(2)求证:BE•EF=BF•AE.专题2021年分类汇编-23题专题一A 字型X 型【历年真题】1.(2020秋•嘉定区期末)如图,已知矩形DEFG 的边DE 在△ABC 的边BC 上,顶点G ,F 分别在边AB 、AC 上,△ABC 的高AH 交GF 于点l .(1)求证:BD •EH =DH •CE ;(2)设DE =n •EF (n 为正实数),求证:11n BC AH EF+=.【考点】相似三角形的判定与性质;矩形的性质.【专题】证明题;图形的相似;推理能力.【分析】(1)根据已知条件证明△BDG ∽△ABH ,△FEC ∽△ACH ,对应边成比例整理即可得结;(2)根据已知条件证明△AGF ∽△ABC ,对应边成比例即可证明结论.【解答】(1)证明:∵四边形DEFG 是矩形,∴GD ⊥BC ,FE ⊥BC ,DG =EF ,∵AH ⊥BC ,∴GD ∥AH ∥FE ,∴BD BG =DH GA CE FC =HE FA∵GF ∥BC ∴BG FC =GA FA ∴BD CE =DH EH∴BD •EH =DH •CE ;(2)证明:∵DF ∥BC ,∴△AGF ∽△ABC ,∴GF AF =BC AC ,∵FC EF =AC AH ,∴GF EF 1BC AH AF FC AC AC+=+=,∵GF =DE =n •EF ,∴1n EF EF BC AH += ,∴11n BC AH EF+=.【点评】本题考查了相似三角形的判定与性质、矩形的性质,解决本题的关键是掌握相似三角形的判定与性质.2.(2020秋•金山区期末)已知:如图,四边形ABCD 是菱形,点M 、N 分别在边BC 、CD上,联结AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.(1)求证:AB2=BF•DE;(2)若BE DNDE DC=,求证:EF∥MN.【考点】相似三角形的判定与性质;菱形的性质.【专题】线段、角、相交线与平行线;矩形菱形正方形;图形的相似;推理能力.【分析】(1)由菱形的性质得AB=AD,则∠ABD=∠ADB,易证∠AED=∠BAF,则△AED∽△FAB,得AD DE BF AB=,即AD•AB=BF•DE,即可得出结论;(2)由菱形的性质得AD=BC,AD∥BC,则△BME∽△DAE,得BE BMDE AD=,进而证出BM DNBC DC=,则MN∥BD即可.【解答】证明:(1)∵四边形ABCD是菱形,∴AB=AD,∴∠ABD=∠ADB,∵∠AED=∠ABD+∠BAE,∠BAF=∠MAN+∠BAE,∠MAN=∠ABD,∴∠AED=∠BAF,∴△AED∽△FAB,∴AD DEBF AB=,即AD•AB=BF•DE,∴AB2=BF•DE;(2)∵四边形ABCD是菱形,∴AD=BC,AD∥BC,∴△BME∽△DAE,∴BE BM DE AD=,∵BE DNDE DC=,∴BM DNAD DC=,∴BM DNBC DC=,∴MN∥BD,∴EF∥MN.【点评】本题考查了相似三角形的判定与性质、菱形的性质、平行线的判定与性质等知识;熟练掌握菱形的性质,证明三角形相似是解题的关键.3.(2020秋•黄浦区期末)某班级的“数学学习小组心得分享课”上,小智跟同学们分享了关于梯形的两个正确的研究结论:③如图1,在梯形ABCD中,AD∥BC,过对角线交点的直线与两底分别交于点M、N,则AM CNDM BN=;④如图2,在梯形ABCD中,AD∥BC,过两腰延长线交点P的直线与两底分别交于点K、L,则AK BLDK CL=.接着小明也跟同学们分享了关于梯形的一个推断:过梯形对角线交点且平行于底边的直线被梯形两腰所截,截得的线段被梯形对角线的交点平分.(1)经讨论,大家都认为小明所给出的推断是正确的.请你结合图示(见答题卷)写出已知、求证,并给出你的证明;(2)小组还出了一个作图题考同学们:只用直尺将图3中两条平行的线段AB、CD同时平分.请保留作图过程痕迹,并说明你作图方法的正确性(可以直接运用小智和小明得到的正确结论).(注意:请务必在试卷的图示中完成作图草稿,在答题卷上直接用2B铅笔或水笔完成作图,不要涂改.)【考点】相似三角形的判定与性质;梯形.【专题】图形的相似;几何直观;推理能力.【分析】(1)写出已知,求证,证明即可.(2)连接CA,DB,延长CA交DB延长线于点F,连接AD,BC交于点F,作直线EF交AB于点M,交CD于点N,点M,N即为所求作.【解答】解:(1)已知:如图,四边形ABCD是梯形,AD∥BC,AC与BD交于点O,EF经过点O,且EF∥BC,求证:OE=OF.证明:∵EF∥BC,∴△AEO∽△ABC,△DOF∽△DBC,∴OE AO=BC AC,OF DO=BC DB,∵AD∥BC,∴AO DO=AC DB,∴EO OF=BC BC,∴EO=OF.(2)如图3中,点M,N即为所求作.【点评】本题考查相似三角形的判定和性质,梯形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.专题二相似三角形之等量代换【历年真题】1.(2020秋•闵行区期末)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA 的延长线于点D,交EA的延长线于点F,且AF•CD=BC•AD.(1)求证:AE⊥BC;(2)如果BE=CE,求证:BC2=2BD•AC.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)通过证明△ADF∽△CDB,可得∠F=∠B,由余角的性质可求解;(2)通过证明△ABE∽△CBD,可得AB BEBC BD=,可得结论.【解答】证明:(1)∵AF•CD=BC•AD,∴AF BCAD CD=,设AF BCAD CD==k,∴AF=kAD,BC=kCD,∴DF=AD,BD CD,∴DF AD BD CD=,又∵∠ADF=∠BDC,∴△ADF∽△CDB,∴∠F=∠B,∵∠B+∠BCD=90°,∴∠F+∠BCD=90°,∴AE⊥BC;方法2:∵AF•CD=BC•AD,∴AF BC AD CD=,又∵∠ADF=∠BDC=90°,∴△FAD∽△BCD,∴∠B=∠F,∵∠B+∠BCD=90°,∴∠F+∠BCD=90°,∴AE⊥BC;(2)∵BE=CE,AE⊥BC,∴AB=AC,∵∠ABE=∠DBC,∠BDC=∠AEB=90°,∴△ABE∽△CBD,∴AB BE BC BD=,∴BC•12BC=AB•BD,∴BC2=2BD•AC.【点评】本题考查了相似三角形的判定和性质,掌握相似三角形的判定定理是本题的关键.2.(2020秋•徐汇区期末)如图,在△ACB中,点D、E分别在边BC、AC上,AD=AB,BE=CE,AD与BE交于点F,且AF•DF=BF•EF.求证:(1)∠ADC=∠BEC;(2)AF•CD=EF•AC.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)利用AF•DF=BF•EF和∠AFE=∠BFD可判断△AFE∽△BFD,所以∠AEF=∠BDF,然后根据等角的补角相等得到结论;(2)由△AFE∽△BFD得到∠EAF=∠FBD,∠AEF=∠BDF,再证明∠EAF=∠C,∠ABC=∠AEF,于是可证明△AEF∽△CBA,利用相似比得到AF EFAC AB=,然后证明AD=AB=CD,从而得到结论.【解答】证明:(1)∵AF•DF=BF•EF,∴AF EF BF DF=,而∠AFE=∠BFD,∴△AFE∽△BFD,∴∠AEF=∠BDF,∵∠AEF+∠BEC=180°,∠BDF+∠ADC=180°,∴∠ADC=∠BEC;(2)∵△AFE∽△BFD,∴∠EAF=∠FBD,∠AEF=∠BDF,∵EB=EC,AB=AD,∴∠EBC=∠C,∠ADB=∠ABD,∴∠EAF=∠C,∠ABC=∠AEF,∴△AEF∽△CBA,∴AF EFAC AB,∴EF•AC=AB•AF∵∠DAC=∠C,∴AD=CD,∴AB=AD=CD,∴EF•AC=CD•AF,即AF•CD=EF•AC.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;可利用相似三角形的性质得到对应角相等,通过相似比进行几何计算.3.(2020秋•青浦区期末)已知:如图,在四边形ABCD中,AB=AD,AC、BD相交于点E,AE⋅CE=DE⋅BE(1)求证:△ABE∽△ACB;(2)如果DA2=DE•DB,求证:AB•EC=BC•AE.【考点】相似三角形的判定与性质.【专题】证明题;图形的相似;推理能力.【分析】(1)根据AE⋅CE=DE⋅BE,∠AED=∠BEC,可得△ADE∽△BCE,得∠DAE=∠CBE,∠ADE=∠BCE,根据AB=AD,进而可以证明结论;(2)根据DA2=DE•DB,∠ADB=∠ADE,可得△ADB∽△ADE,对应边成比例,结合(1)△ADE∽△CBE对应边成比例,进而可得结论.【解答】证明:(1)∵AE⋅CE=DE⋅BE,∠AED=∠BEC,∴△ADE∽△BCE,∴∠DAE=∠CBE,∠ADE=∠BCE,∵AB=AD,∴∠ADB=∠ABE,∴∠ABE=∠ACB,∵∠BAE=∠CAB,∴△ABE∽△ACB;(2)∵DA2=DE•DB,∠ADB=∠ADE,∴△ADB∽△EDA,∴AB AD AE DE=,∵△ABE∽△ACB,∴AD DE BC EC=,∴AD BCDE EC=,∴AB BCAE EC=,∴AB•EC=BC•AE.【点评】本题考查了相似三角形的判定与性质,解决本题的关键是掌握相似三角形的判定与性质.4.(2020秋•虹口区期末)如图,在△ABC中,点D、G在边AC上,点E在边BC上,DB=DC,EG∥AB,AE、BD交于点F,BF=AG.(1)求证:△BFE∼△CGE;(2)当∠AEG=∠C时,求证:AB2=AG•AC.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)由平行线分线段成比例可得CE CGBE AG=,进而可得CE CGBE BF=,由等腰三角形的性质可得∠DBC=∠DCB,由相似三角形的判定可得结论;(2)通过证明△ABE∽△CBA,可得AB BEAC AB=,可得结论.【解答】证明:(1)∵DB=DC,∴∠DBC=∠DCB,∵EG∥AB,∴CE CG BE AG=,∵BF=AG,∴CE CG BE BF=,∴△BFE∼△CGE;(2)∵△BFE∼△CGE,∴∠BEF=∠GEC,∠BFE=∠EGC,∵∠AEG=∠C,∠GEB=∠AEG+∠AEB=∠C+∠EGC,∴∠AEB=∠EGC,∴∠BEF=∠GEC=∠BFE=∠EGC,∴BE=BF,EC=GC,∴BE=AG,∵GE∥AB,∴∠AEG=∠BAE,∴∠BAE=∠C,又∵∠ABE=∠ABC,∴△ABE∽△CBA,∴AB BE AC AB=,∴AB 2=AC •BE =AC •AG .【点评】本题考查了相似三角形的判定和性质,等腰三角形的性质,证明△ABE ∽△CBA 是本题的关键.5.(2020秋•奉贤区期末)如图,在四边形ABCD 中,∠B =∠DCB ,联结AC ,点E 在边BC 上,且∠CDE =∠CAD ,DE 与AC 交于点F ,CE •CB =AB •CD .(1)求证:AD ∥BC ;(2)当AD =DE 时,求证:AF 2=CF •CA.【考点】相似三角形的判定与性质.【专题】图形的全等;图形的相似;推理能力.【分析】(1)通过证明△ABC ∽△ECD ,可得∠CDE =∠ACB =∠CAD ,可得结论;(2)由“ASA ”可证△ADF ≌△DEC ,可得AF =CD ,通过证明△ADC ∽△DFC ,可得CD CF AC CD=,可得结论.【解答】证明:(1)∵CE •CB =AB •CD ,∴AB BC EC DC=,又∵∠B =∠DCB ,∴△ABC ∽△ECD ,∴∠CDE =∠ACB ,∵∠CDE =∠CAD ,∴∠DAC =∠ACB ,∴AD ∥BC ;(2)∵AD ∥BC ,∴∠ADF =∠DEC ,在△ADF 和△DEC 中,DAC=CDE AD=DE ADF=DEC ⎧⎪⎨⎪⎩∠∠∠∠,∴△ADF ≌△DEC (ASA ),∴AF =CD ,∵∠CDE =∠DAC ,∠DCA =∠DCF ,∴△ADC ∽△DFC ,∴CD CF AC CD=,∴CD 2=CF •CA ,∴AF 2=CF •CA .【点评】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行线的性质,证明AF =CD 是本题的关键.6.(2020秋•杨浦区期末)已知:如图,在梯形ABCD中,AD∥BC,对角线BD、AC相交于点E,过点A作AF∥DC,交对角线BD于点F.(1)求证:DF DE=BD BE;(2)如果∠ADB=∠ACD,求证:线段CD是线段DF、BE的比例中项.【考点】相似三角形的判定与性质;梯形.【专题】图形的相似;推理能力.【分析】(1)根据平行线的性质和等量代换证明∠DAF=∠BCD,则可证明△DAF∽△BCD,利用相似比得到AD DF=BC BD,再证明△ADE∽△CBE,则AD DE=BC BE,然后利用等量代换得到结论;(2)证明△DCE∽△DBC,则根据相似比得DC2=DE•DB,再利用(1)中的结论得到DF DE=BD BE,利用等量代换得到DC2=DF•BE,从而得到结论.【解答】证明:(1)∵AD∥BC,∴∠CBD=∠ADF,∠ADC+∠BCD=180°,∵AF∥CD,∴∠ADC+∠DAF=180°,∴∠DAF=∠BCD,∴△DAF∽△BCD,∴AD DF=BC BD,∵AD∥BC,∴△ADE∽△CBE,∴AD DE=BC BE,∴DF DE=BD BE;(2)∵∠ADB=∠ACD,∠ADB=∠CBD,∴∠ECD=∠CBD,而∠CDE=∠BDC,∴△DCE∽△DBC,∴DC DE=BD DC,∴DC2=DE•DB,∵DF DE=BD BE,∴DE•DB=DF•BE,∴DC2=DF•BE,即线段CD是线段DF、BE的比例中项.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;可利用相似三角形的性质得到对应角相等,通过相似比进行几何计算.也考查了梯形的性质.专题三相似三角形之面积比【历年真题】1.(2020秋•崇明区期末)已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED =∠ABC,联结BE、CD相交于点F.(1)求证:∠ABE=∠ACD;(2)如果ED=EC,求证:22DF EF BD BE=.【考点】相似三角形的判定与性质.【专题】证明题;图形的相似;推理能力.【分析】(1)根据已知条件证明△ADE∽△ACB,可得AE ABAD AC=,根据∠A=∠A,证明△ADC∽△AEB,即可得结论;(2)根据已知条件证明△EDF∽△EBD,可得DF EF DEBD DE BE==,进而可得结论.【解答】(1)证明:∵∠AED=∠ABC,∠A=∠A,∴△ADE∽△ACB,∴AE AB AD AC=,∵∠A=∠A,∴△ADC∽△AEB,∴∠ABE=∠ACD;(2)证明:∵ED=EC,∴∠EDC=∠ECD,∴∠EDC=∠EBD,∵∠DEF=∠DEB,∴△EDF∽△EBD,∴DF EF DEBD DE BE==,2()DF EF DEBD DE BE= ,∴22DF EF BD BE=.【点评】本题考查了相似三角形的判定和性质,熟练运用相似三角形的判定和性质是解题的关键.2.(2020秋•长宁区期末)已知:如图,在Rt △ABC 中,∠ACB =90°,CH ⊥AB ,垂足为点H .点D 在边BC 上,联结AD ,交CH 于点E ,且CE =CD .(1)求证:△ACE ∽△ABD ;(2)求证:△ACD 的面积是△ACE 的面积与△ABD的面积的比例中项.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)根据同角的余角相等得到∠ACH =∠CBH ,根据等腰三角形的性质得到∠CED =∠CDE ,进而得到∠AEC =∠ADB ,根据相似三角形的判定定理证明结论;(2)过点B 作BG ∥AC 交AD 的延长线于点G ,根据相似三角形的性质得到AD BD AE CD=,根据相似三角形的面积公式计算,证明结论.【解答】证明:(1)∵AC ⊥BC ,CH ⊥AB ,∴∠ACB =∠AHC =90°,∴∠ACH =∠CBH ,∵CE =CD ,∴∠CED =∠CDE ,∴∠AEC =∠ADB ,∴△ACE ∽△ABD ;(2)过点B 作BG ∥AC 交AD 的延长线于点G ,∴∠CAD =∠G ,∵△ACE ∽△ABD ,∴AD BD AE CD =,∠CAD =∠BAD ,∴∠BAD =∠G ,∴AB =BG ,∵BG ∥AC ,∴△ADC ∽△GDB ,∴BG BD AC CD =,∴AD BD AE CD=,∴ACD ABD ACE ACDS S S S ∆∆∆∆=,∴△ACD 的面积是△ACE 的面积与△ABD 的面积的比例中项.【点评】本题考查的是相似三角形的判定和性质、掌握相似三角形的判定定理和性质定理是解题的关键.3.(2020秋•静安区期末)已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD2=AE•AC.求证:(1)△BCD∽△CDE;(2)22CD AD BC AB=.【考点】相似三角形的判定与性质;平行线分线段成比例.【专题】图形的相似;推理能力.【分析】(1)由题意可证△ADE∽△ACD,可得∠ADE=∠ACD,由平行线的性质可得∠EDC=∠DCB,∠B=∠ADE=∠ACD,可得结论;(2)由相似三角形的性质可得CD DEBC CD=,可得22CD CD DE DEBC BC CD BC=⋅=,由平行线分线段成比例可得结论.【解答】证明:(1)∵AD2=AE•AC,∴AD AC AE AD=,又∵∠A=∠A,∴△ADE∽△ACD,∴∠ADE=∠ACD,∵DE∥BC,∴∠EDC=∠DCB,∠B=∠ADE,∴∠B=∠ACD,∴△BCD∽△CDE;(2)∵△BCD∽△CDE,∴CD DE BC CD=,∴22CD CD DE DE BC BC CD BC=⋅=,∵DE∥BC,∴DE ADBC AB=,∴22CD ADBC AB=.【点评】本题考查了相似三角形的判定和性质,掌握相似三角形的判定定理是本题的关键.专题四相似三角形综合题【历年真题】1.(2020秋•浦东新区期末)Rt△ABC中,∠ACB=90°,点D、E分别为边AB、BC上的点,且CD=CA,DE⊥AB.(1)求证:CA2=CE•CB;(2)联结AE,取AE的中点M,联结CM并延长与AB交于点H,求证:CH⊥AB.【考点】相似三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)通过证明△DCE∽△BCD,可得DC CEBC CD=,可得结论;(2)由直角三角形的性质可得AM=ME=CM,进而可得∠MCE=∠MEC,通过证明点A,点C,点E,点D四点共圆,可得∠AEC=∠ADC,由余角的性质可得结论.【解答】证明:(1)∵DE⊥AB,∴∠EDB=∠ACB=90°,∴∠A+∠B=90°=∠B+∠DEB,∴∠A=∠DEB,∵CA=CD,∴∠A=∠CDA,∴∠CDA=∠DEB,∴∠CDB=∠CED,又∵∠DCE=∠DCB,∴△DCE∽△BCD,∴DC CE BC CD=,∴CD2=CE•CB,∴CA2=CE•CB;(2)如图,∵∠ACE是直角三角形,点M是AE中点,∴AM=ME=CM,∴∠MCE=∠MEC,∵∠ACB=∠ADE=90°,∴点A,点C,点E,点D四点共圆,∴∠AEC=∠ADC,∴∠AEC=∠MCE=∠ADC=∠CAD,又∵∠MCE+∠ACH=90°,∴∠CAD+∠ACH=90°,∴CH⊥AB.【点评】本题考查了相似三角形的判定和性质,等腰三角形的性质,掌握相似三角形的判定定理是本题的关键.2.(2020秋•普陀区期末)已知:如图,AD ∥BC ,∠ABD =∠C ,AE ⊥BD ,DF ⊥BC ,点E 、F 分别为垂足.(1)求证:AE BD DF BC=;(2)联结EF ,如果∠ADB =∠BDF ,求证:DF •DC =EF •BC .【考点】相似三角形的判定与性质;等腰三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)证明△ABD ∽△DCB ,由相似三角形的性质得出AB BD DC BC =,证明△ABD ∽△DCB ,由相似三角形的性质得出AE BD DF BC=,则可得出结论;(2)证明△ADB ∽△EDF ,由相似三角形的性质得出∠ABD =∠EFD ,证明△EDF ∽△DBC ,得出DF EF BC DC =,则可得出结论.【解答】(1)证明:∵AE ⊥BD ,DF ⊥BC ,∴∠AEB =∠DFC =90°,∵∠ABD =∠C ,∴△ABE ∽△DCF ,∴AE AB DF DC=,∵AD ∥BC ,∴∠ADB =∠DBC ,∴△ABD ∽△DCB ,∴AB BD DC BC =,∴AE BD DF BC =;(2)证明:∵∠ADB =∠DBF ,∠ADB =∠BDF ,∠BFD =90°,∴∠DBF =∠BDF ,∴∠DBF =ADE =45°,∴△AED 和△BFD 都是等腰直角三角形,∴AD BD DE DF==又∵∠ADE =∠BDF ,∴△ADB ∽△EDF ,∴∠ABD =∠EFD ,∵∠ABD =∠C ,∴∠EFD =∠C ,∵∠EDF =∠DBC ,∴△EDF ∽△DBC ,∴DF EF BC DC=,∴DF •DC =EF •BC .【点评】本题考查了平行线的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.3.(2020秋•松江区期末)如图,已知在▱ABCD中,E是边AD上一点,联结BE、CE,延长BA、CE相交于点F,CE2=DE•BC.(1)求证:∠EBC=∠DCE;(2)求证:BE•EF=BF•AE.【考点】相似三角形的判定与性质;平行四边形的性质.【专题】多边形与平行四边形;平移、旋转与对称;推理能力.【分析】(1)通过证明△DEC∽△ECB,可得结论;(2)通过证明△ABE∽△EBF,可得△ABE∽△EBF,可得结论.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DEC=∠BCE,∵CE2=DE•BC,∴DE CE=CE BC,∴△DEC∽△ECB,∴∠EBC=∠DCE;(2)∵AD∥BC,AB∥CD,∴∠AEB=∠EBC,∠F=∠ECD,∴∠AEB=∠F,又∵∠ABE=∠EBF,∴△ABE∽△EBF,∴BE EF=BF AE,∴BE•EF=BE•AE.【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,熟练运用相似三角形的判定定理是本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(本小题满分10分)已知,如图,△ABC 是等边三角形,过AC 边上的点D 作 DG //BC ,交AB 于点G ,在GD 的延长线上取点E ,使DE=DC ,连接AE 、BD . (1)求证:△AGE ≌△DAB ;(2)过点E 作EF //DB ,交BC 于点F ,连AF ,求∠AEF 的度数.2、(本小题满分12分)如图,菱形OABC 放在平面直角坐标系内,点A 在x 轴的正半轴B 在第一象限,其坐标为(8,4).抛物线2bx c y ax ++=过点O 、A (1)求抛物线的解析式?(2)将菱形向左平移,设抛物线与线段AB 的交点为D,连接CD .①当点C 又在抛物线上时求点D的坐标?② 当△BCD 是直角三角形时,求菱形的平移的距离?3、(本题12分)如图,在平面直角坐标系中,等腰梯形OABC ,BC= 4.(1)求过O 、C 、B 三点的抛物线解析式,并写出顶点坐标和对称轴;(2)经过O 、C 、B 三点的抛物线上是否存在P 点(与原点O 不重合)求出P 点坐标;如果不存在,请说明理由.4、 (本题12分)如图,AD//BC ,点E 、F 在BC 上,∠1=∠2,AF ⊥DE ,垂足为点O. (1)求证:四边形AEFD 是菱形;(2)若BE=EF=FC ,求∠BAD+∠ADC 的度数;(3)若BE=EF=FC ,设AB = m ,CD = n ,求四边形ABCD 的面积. 5、 (本题14分)如图,在平面直角坐标系中,抛物线6422++-=x x y 与 x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于C 点,顶点为D.过点 C 、D 的直线与x 轴交于E 点,以OE 为直径画⊙O 1,交直线CD 于P 、E 两点.(1)求E 点的坐标;(2)联结PO 1、PA.求证:BCD ∆~A PO 1∆;(3) ①以点O 2 (0,m)为圆心画⊙O 2,使得⊙O 2与⊙O 1相切,当⊙O 2经过点C 时,求实数m 的值;②在①的情形下,试在坐标轴上找一点O 3,以O 3为圆心画⊙O 3,使得⊙O 3与⊙O 1、⊙O 2同时相切.直接写出满足条件的点O 3的坐标(不需写出计算过程). 6.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,EF 是平行四边形ABCD 的对角线BD 的垂直平分线,EF 与边AD 、BC 分别交于点E 、F . (1)求证:四边形BFDE 是菱形;(2)若E 为线段AD 的中点,求证:AB ⊥BD .7.(本题满分12分,第(1)小题6分,第(2)小题6在平面直角坐标系中,抛物线2y x bx c =++经过点((1)求该抛物线的表达式并写出顶点坐标;(2)点P 为抛物线上一动点,如果直径为4的 ⊙P 与y 轴相切,求点P 的坐标.8.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,在Rt △ABC 中,∠BAC = 90°,AB =3,AC =4,AD 是BC 边上的高,点E 、F 分别是AB 边和AC 边上的动点,且∠EDF = 90°.(1)求DE ︰DF 的值;(2)联结EF ,设点B 与点E 间的距离为x ,△DEF 的面积为y ,求y 关于x 的函数解析式,并写出x 的取值范围;(3)设直线DF 与直线AB 相交于点G ,△EFG 能否成为等腰三角形?若能,请直接写出线段BE 的长;若不能,请说明理由.9.(本题满分12分,每小题各4如图10,已知抛物线y -=OB OA =.(1)求c b +的值; (2) 若点C (3) 在(2)的条件下,作∠OBC 与抛物线交于点P ,求点P 的坐标10.(本题满分14分,第(1)如图11,已知⊙O 的半径长为⊙O 交于A 、B 两点,联结PA (1) 若AB 恰好是⊙O 的直径,设OM=x ,AC=y ,试在图12中画出符合要求的大致图形,并求y 关于x 的函数解析式;(2) 联结OA 、MA 、MC ,若OA ⊥MA ,且△OMA 与△PMC 相似,求OM 的长度和⊙M 的半径长;(3) 是否存在⊙M ,使得AB 、AC 恰好是一个正五边形的两条边?若存在,试求OM 的长度和⊙M 的半径长;若不存在,试说明理由. BC .DC =AGE ≌△DAB . …………………………(5分) AEG …………………………………………(6分) 是平行四边形 ………………………… (7分) +∠DEF =∠ABD +∠DBC=∠ABC =60°(8分) (1)A (0,3),C(3,0) ∵3m=3 ∴m=1∴抛物线的解析式为322++-=x x y ………2分(2)∵m=1 ∴322++-=x x y ∴AO=3BED PO xy第25题图 B C D EFA图12点32,(2++-x xx D ),连结OD当y=0时,即0322=++-x x ,解得x 1=-1 x 2=3 ∴OC=3∴S= S △AOD + S △DOC =292923)32(32132122++-=++-⨯⨯+⨯x x x x x ∴S 与x 的函数关系式S=2929232++-x x (0<x <3) …………………………4分当232=-=a b x 符合(0<x <3) S 最大值=863)23(4)29(29)23(44422=-⨯-⨯-⨯=-a b ac ……6分(3)…………………………………………7分假设存在点P ,使AC 把△PCD 分成面积之比为2:1的两部分,分两种情况讨论:(ⅰ)当△CDE 与△CEP 的面积之比为2:1时,DE=2EP ∴DP=3EP即)3(3322+-=++-x x x 整理得:0652=+-x x解得;21=x 32=x (不合题意,舍去), 此时点P 的坐标是(2,0)… 9分 (ⅱ)当△CEP 与△CDE 的面积之比为2:1时, EP DE 21=, ∴EP DP 23= 即)3(23322+-=++-x x x整理得:03722=+-x x 解得:213=x 34=x (不合题意,舍去),此时点P 的坐标是(21,0)…………………………………………11分综上所述,使直线AC 把△PCD 分成面积之比为2:1两部分的点P 存在,点P 的坐标是(2,0)或(21,0)……………………… 12分3、(12分)解:(1) ( 6分)∵C(2,4), BC=4 且 BC//OA ∴ B(6,4) 1分设抛物线为c bx ax y ++=2()0≠a将O(0,0),C(2,4),B(6,4)代入得⎪⎩⎪⎨⎧=+=++=)3(4636)2(424)1(0b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=03831c b a 3分∴x x y 38312+-= 1分∴顶点)316,4( 对称轴:直线4=x 2分(2) (6分)据题意,设),(a a P 或),(a a P -()0≠a 1分3453OA OC AOC RtECP EP PC x==∴∴∠=︒∴==-为等腰54321OFE DCBA将),(a a P 代入抛物线得a a a =+-38312 解得0,521==a a (舍) 2分将),(a a P -代入抛物线得a a a -=+-38312 解得0,1121==a a (舍) 2分∴符合条件的点)5,5(p 和)11,11(-p 1分4、(12分)(1)( 4分)证明:(方法一)∵AF ⊥DE∴∠1+∠3=90° 即:∠3=90°-∠1∴∠2+∠4=90° 即:∠4=90°-∠2 又∵∠1=∠2 ∴∠3=∠4 ∴AE = EF∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5 ∴AE = AD ∴EF = AD 2分 ∵AD//EF∴四边形AEFD 是平行四边形 1分 又∵AE = AD∴四边形AEFD 是菱形 1分(方法二)∵AD//BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5∵AF ⊥DE ∴∠AOE=∠AOD =90°在△AEO 和△ADO 中⎪⎩⎪⎨⎧=∠=∠∠=∠AO AO AOD AOE 51 ∴△AEO ≅△ADO ∴EO=OD在△AEO 和△FEO 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FOE AOE EO EO 21∴△AEO ≅△FEO ∴AO=FO 2分 ∴AF 与ED 互相平分 1分 ∴四边形AEFD 是平行四边形 又∵AF ⊥DE∴四边形AEFD 是菱形 1分(2)( 5分)∵菱形AEFD ∴AD=EF ∵BE=EF ∴AD=BE又∵AD//BC ∴四边形ABED 是平行四边形 1分 ∴AB//DE ∴∠BAF=∠EOF同理可知 四边形AFCD 是平行四边形 ∴AF//DC ∴∠EDC=∠EOF 又∵AF ⊥ED ∴∠EOF=∠AOD=90° ∴∠BAF=∠EDC=∠EOF=90° 2分 ∴∠5 +∠6=90° 1分∴∠BAD+∠ADC=∠BAF+∠6 +∠5+∠EDC =270° 1分(3)( 3分)由(2)知∠BAF =90°平行四边形AFCD ∴AF=CD=n又∵AB=mmn 21AF AB 21S ABF =⋅=∆ 1分 由(2)知 平行四边形ABED ∴DE=AB=m54321OFE DCBA6由(1)知OD=m DE 21= mn 21OD AF S AFCD =⋅=四边形 1分 mn S AFCD ABCD =+=∆四边形四边形S S ABF 1分5、(14分)解:(1) ( 3分)()81264222+--=++-=x x x y ∴)8,1(),6,0(D C 1分设直线CD:()0≠+=k b kx y 将C 、D 代入得⎩⎨⎧+==686k b 解得⎩⎨⎧==62b k∴CD 直线解析式:62+=x y 1分 )0,3(-E 1分 (2) ( 4分)令y=0 得06422=++-x x 解得3,121=-=x x ∴)0,3()0,1(B A - 1分又∵)0,0(O 、)0,3(-E ∴以OE 为直径的圆心)0,(231-O 、半径231=r .设)62,(+t t P 由231=PO 得232223)62()(=+++t t 解得3,25121-=-=t t (舍) ∴),(56512-P 2分∴585=PA 211=AO又 5=DC 53=CB 172=DB∴5211===PADBPO CB AO DC 1分 ∴BCD ∆~A PO 1∆ (3) ( 7分)① )0,(231-O 231=r),0(2m O 据题意,显然点2O 在点C 下方 m C O r -==622当⊙O 2与⊙O 1外切时 2121r r O O +=代入得()()m m -+=+6232223 解得 2,51821==m m (舍)2分 当⊙O 2与⊙O 1内切时2121r r O O -=代入得()()m m --=+6232223 解得 518,221==m m (舍) 2分 ∴2,51821==m m② ⎪⎭⎫ ⎝⎛518,03O ⎪⎭⎫ ⎝⎛-710,03O ⎪⎭⎫ ⎝⎛0,233O ⎪⎭⎫ ⎝⎛-0,14453O ⎪⎭⎫⎝⎛1514,03O ()2,03O ⎪⎭⎫ ⎝⎛0,2213O 3分6、.证明:(1)∵四边形ABCD 是平行四边形∴ED ∥BF ,得∠EDB =∠FBD ……………………………………………………(2分) ∵EF 垂直平分BD∴BO=DO ,∠DOE =∠BOF =90°∴△DOE ≌△BOF ……………………………………………………………………(2分) ∴ EO=FO∴四边形BFDE 是平行四边形 ……………………………………………………(1分) 又∵EF ⊥BD∴四边形BFDE 是菱形 ……………………………………………………………(1分) (2)∵四边形BFDE 是菱形∴ED=BF ∵AE=ED∴AE=BF ………………………………………………………………………………(2分) 又∵AE ∥BF∴四边形ABFE 是平行四边形………………………………………………………(1分) ∴AB ∥EF ……………………………………………………………………………(1分) ∴∠ABD =∠DOE ……………………………………………………………………(1分) ∵∠DOE =90° ∴∠ABD =90°即AB ⊥BD ……………………………………………………………………………(1分) 7.解:(1)把(0,2)、(3,5)分别代入2y x bx c =++得2593cb c =⎧⎨=++⎩解得 22b c =-⎧⎨=⎩……………………………………………(3分) ∴抛物线的解析式为222y x x =-+ ………………………………………………(1分) ∴抛物线的顶点为(1,1)………………………………………………………………(2分) (2)设点P 到y 轴的距离为d ,⊙P 的半径为r∵⊙P 与y 轴相切 ∴1422dr ==⨯= ∴点P 的横坐标为2±…………………………………………………………………(2分)当2x =时, 2y = ∴点P 的坐标为(2,2) …………………………………(2分)当2x =-时,10y = ∴点P 的坐标为(2,10)- ………………………………(2分) ∴点P 的坐标为(2,2)或(2,10)-.8.解:(1)∵∠BAC = 90° ∴∠B +∠C =90°,∵AD 是BC 边上的高 ∴∠DAC +∠C =90°∴∠B =∠DAC ………………………………………………………………………(1分)又∵∠EDF = 90°∴∠BDE +∠EDA =∠ADF +∠EDA = 90° ∴∠BDE =∠ADF∴△BED ∽△AFD ……………………………………………………………………(1分)∴DE BDDF AD =…………………………………………………………………………(1分) ∵3cot 4BD AB B AD AC === ∴DE ︰DF =34…………………………………………………………………………(1分)(2)由△BED ∽△AFD 得34BE BD AF AD ==∴4433AF BE x == …………………………………………………………………(1分)∵BE x = ∴3AE x =-∵∠BAC = 90° ∴2222425(3)()6939EFx x x x =-+=-+………………………………………(1分)∵DE ︰D F =3︰4,∠EDF =90°∴ED =35EF ,FD =45EF …………………………………………………………………(1分) ∴216225y ED FD EF =⋅=∴22365432525y x x =-+ (03)x ≤≤ ………………………………………………(2分)(3)能. BE 的长为543255或.……………………………………………………………(5分) (说明:BE 的长一个正确得3分,全对得5分)9、解:(1)由题意得:点B 的坐标为),0(c ,其中0>c ,c OB = (1分)∵OB OA =,点A 在x 轴的负半轴上,∴点A 的坐标为)0,(c - (1分)∵点A 在抛物线c bx x y ++-=2上,∴c bc c +--=20 (1分) ∴ 1=+c b (因为0>c) (1分)(2)∵四边形OABC 是平行四边形∴c AO BC ==,又BC ∥x 轴,点B 的坐标为),0(c∴点C 的坐标为),(c c (1分) 又点C 在抛物线上, ∴c bc c c ++-=2∴0=-c b 或0=c (舍去) (1分)又 由(1)知:1=+c b ∴21=b,21=c . 抛物线的解析式为21212++-=x x y . (2分) (3)过点P 作⊥PM y 轴,⊥PN BC ,垂足分别为M 、N∵BP 平分CBO ∠ ∴ PN PM = (1分)设点P 的坐标为)2121(2++-x x x , ∴x x x =++--)2121(212 (1分) 解得:23=x 或0=x (舍去) (1分) 所以,点P 的坐标为)21,23(- (1分) 10、(1)图画正确 (1分)过点M 作AC MN⊥,垂足为N ∴y NC AN 21==由题意得:AB PM ⊥, 又AB 是圆O 的直径∴1==OP OA ∴︒=∠45APO , 2=PA∴y PN212+= (1分) 在Rt △PNM 中,PMPNNPM =∠cos 又x PM+=1,︒=∠45NPM∴ 22121245cos =++=︒x y∴ y 关于x 的函数解析式为22-=x y (1>x ) (2分)(2)设圆M 的半径为r因为 OA ⊥MA ,∴∠OAM=90°,12+=r OM又△OMA 与△PMC 相似,所以△PMC 是直角三角形。
