2013新人教版七年级上第一章有理数复习课课件ppt
合集下载
第1章 有理数 人教版七年级数学上册单元复习课件(共38张PPT)

知识点四:有理数的混合运算 有理数的运算有加法、减法、乘法、除法和乘方.进行混合 运算时,运算顺序是: (1)先乘方,再乘除,最后加减; (2)同级运算,按从左到右的顺序进行; (3)如有括号,先做括号内的运算,按小括号、中括号、大 括号依次进行.
13.【例1】下面的说法正确的是( D ) A.有理数的绝对值一定比0大 B.有理数的相反数一定比0小 C.若两个数的绝对值相等,则这两个数相等 D.互为相反数的两个数的绝对值相等
20.【例8】(创新题)观察下列所给的式子,解答下列问题: 1+3=22; 1+3+5=32; 1+3+5+7=42; 1+3+5+7+9=52;…. (1)1+3+5+7+…+29= 225 ; (2)1+3+5+…+(2n-1)= n2 ;(n为正整数) (3)21+23+25+…+57+59= 800 .
16.【例4】(创新题)若x为有理数,式子2 023-|x+2|存在最
大值,则这个最大值是( B )
A.2 022
B.2 023
C.2 024
D.2 025
小结:直接利用绝对值的性质得出|x+2|的最小值为0.
小结:明确有理数混合运算的计算方法,并合理运用运算律.
18.【例6】(全国视野)(2022泸州改编)若(a-2)2+|b+3|=0, 求ab的值. 解:由题意得a-2=0,b+3=0, 可得a=2,b=-3, 所以ab=2×(-3)=-6.
(3)相反数:只有符号不同的两个数叫做互为相反数,0的相 反数是0. 互为相反数的两个数到原点的距离相等.
(4)绝对值:一个数在数轴上对应的点到原点的距离叫做这 个数的绝对值. 一个正数的绝对值是它本身;一个负数的绝对值是它的相反 数;0的绝对值是0. (5)倒数:乘积是1的两个数互为倒数.
人教版七年级数学上册第一章有理数复习课件(37张PPT)

第一章 有理数
类型四
非负数性质的应用
a2≥0 , | a| ≥0 , 即一个数的平方或一个数的绝对值都不会
是负数,这一点在解题中用处很大,特别是若几个非负数的 和是 0,则这几个数都为 0.
若|a+1|+(b-2)2=0,试求(a+b)9+a6.
[解析] 若要求(a+b)9+a6 的值,需求 a,b 的值,但题中只有 一个等式,似乎无从下手,但从题目的特点来考虑,|a+1|与 (b-2) 为非负数,和又为 0,故问题得解.
> > < ; a+b____0; a-b____0; b+c____0
b > < > b-c____0; ab____0; ____0. c
第一章 有理数
[解析] 互为相反数的两个数表示的点关于原点对称,比较两 个数的绝对值的大小可直接观察其与原点距离的大小,有理 数运算结果的符号可根据法则来确定.在数轴上表示数-a,
第一章 有理数
1 1 3 2 1 1 3 7 2 7 (2) - - -2 + 2 + - - 3 =- + 2 + 2 - - 3 = 3 4 8 3 2 3 4 8 3 2 1 3 7 2 3 1 1 1 -2+24-8+23-33=18-13=24. 1 1 1 3 1 1 2 1 2 (3) ÷-2 + 11 +2 -13 ×24 - × - 3= 4 2 4 3 4 (- 0.2 ) 16 5 45 7 55 1 1 45 7 55 + + - ×24- =- + ×24+ ×24- ×24+ 4 3 4 40 4 3 4 1 3 -5
[点析] (1)利用数轴把问题中“数”和数轴上的“点”结合起 来,就是数形结合,这样可以直观地解决问题.(2)本题所用
人教版数学七年级上册(新) 单元复习课件:第一章《有理数》(共15张PPT)

2 7 5
㈠正数与负数 1、正数与负数的概念: ①正数:大于0的数。 ②负数:小于0的数。带“-”号的数并不都是负数 ③0既不是正数,也不是负数。 2、正数与负数的意义:在实际中表示意义相反的量。
知识要点
(1)相反意义的量包含两个要素:一是它们的意义要相反;二 是它们都具有数量。如前进8m与前进5m,上升与下降不是相反 意义的量;因为前者意义相同,后者缺少数量。 (2)与一个量成相反意义的量不止一个,如与上升2m成相反意 义的量就很多,如:下降1m,下降0.2m,…… (3)在同一问题中,用正、负数表示具有相反意义的量。对于 两个具有相反意义的量,把哪一种意义规定为正,带有任意性, 不过习惯上把向东、上升、盈利、运进、增加、收入等规定为正, 把它们的相反量规定为负的。
负数的绝对值是它的相反数; 0的绝对值是0. ③互为相反数的两个数的绝对值相等。 即︱a︱=︱-a︱且︱a-b︱=︱b-a︱ ④利用绝对值比较大小:两个负数,绝对值大的反而小。其步骤 如下:第一步分别求出两个负数的绝对值,第二步比较这两个绝 对值的大小,第三步根据性质比较。
6、倒数: 1 ①乘积是1的两个数叫作互为倒数。a的倒数是 a (a≠0),0没 有倒数。 ②如果a与b互为倒数,那么ab=1. 例:求下列各数的倒数:2,-2.5,-5 7、实数比大小: ①利用数轴:数轴上两个点表示的数,右边的总比左边的大; 正数大于0,负数小于0,正数大于负数。 ②利用绝对值比较负数大小:两个负数大小,绝对值大的反而小.
-4 2 -2 -4 -3 –2 –1 0 1 2
4 3 4
5、绝对值: ①数轴上看,一个数的绝对值就是表示这个数的点与原点的距离 叫做a的绝对值。 a的绝对值就是数a所表示点到原点的距离。表示成︱a︱。 (︱a︱≥0,一个数的绝对值是非负数) a a
人教版七年级数学上册 第一章 有理数复习课件(共51张PPT)

01
复习课
有理数
1. 正__整_数__、__零_、__负__整_数统称整数,试举例说明。
2. 正_分__数__、_负__分__数___统称分数,试举例说明。
3. __整__数__、_分__数____统称有理数。
有理数的分类表
整数 有 理 数 分数
正整数 0
自然数
(非负整数)
负整数
正分数 负分数
有理数的分类
②下列说法正确的是( )A A.–1/4的相反数是0.25
B.4的相反数是-0.25
C.0.25的倒数是-0.25,
D.0.25的相反数的倒数是-0.25
③用-a表示的数一定是( D) A.负数 B.正数 C.正数或负数 D.都不对
④一个数的相反数是最小的正整数,那么这个数 是( A)
A .–1 B. 1 C .±1 D. 0
A.“向东5米”与“向西10米”不是相反意义的 量; B.如果汽球上升25米记作+25米,那么-15米
的意义就是下降-15米; C.如果气温下降6℃记作-6℃,那么+8℃的意
义就是零上8℃; D.若将高1米设为标准0,高1.20米记作+0.20
米,那么-0.05米所表示的高是0.95米.
6.正数、负数在实际生活中的应用
8.05×106
解:⑴ 0.07010 ,精确到 十万分位(或精确到0.00001),
有四个有效数字: 7,0,1,0
⑵ 103.2万 ,精确到 千位
有四个有效数字 1,0,3, 2 (3) 2.4千,精确到 百位, 有二个有效数字2,4
(4) 8.05×106 ,精确到 万位,
有三个有效数字 8,0,5
小测验
1. 22 2 22
复习课
有理数
1. 正__整_数__、__零_、__负__整_数统称整数,试举例说明。
2. 正_分__数__、_负__分__数___统称分数,试举例说明。
3. __整__数__、_分__数____统称有理数。
有理数的分类表
整数 有 理 数 分数
正整数 0
自然数
(非负整数)
负整数
正分数 负分数
有理数的分类
②下列说法正确的是( )A A.–1/4的相反数是0.25
B.4的相反数是-0.25
C.0.25的倒数是-0.25,
D.0.25的相反数的倒数是-0.25
③用-a表示的数一定是( D) A.负数 B.正数 C.正数或负数 D.都不对
④一个数的相反数是最小的正整数,那么这个数 是( A)
A .–1 B. 1 C .±1 D. 0
A.“向东5米”与“向西10米”不是相反意义的 量; B.如果汽球上升25米记作+25米,那么-15米
的意义就是下降-15米; C.如果气温下降6℃记作-6℃,那么+8℃的意
义就是零上8℃; D.若将高1米设为标准0,高1.20米记作+0.20
米,那么-0.05米所表示的高是0.95米.
6.正数、负数在实际生活中的应用
8.05×106
解:⑴ 0.07010 ,精确到 十万分位(或精确到0.00001),
有四个有效数字: 7,0,1,0
⑵ 103.2万 ,精确到 千位
有四个有效数字 1,0,3, 2 (3) 2.4千,精确到 百位, 有二个有效数字2,4
(4) 8.05×106 ,精确到 万位,
有三个有效数字 8,0,5
小测验
1. 22 2 22
人教版七年级数学上册第一章《有理数》复习PPT课件

2/ 3 化简(1)-|-2/3|=___ ;
1/
由绝对值求数
3. 若|a|=3,则a=____ -1 ±3 ;|a+1|=0,则a=____ 若|a+1|=3,则a=____ 2,-4
1 4、已知a>0,ab<0,化简|a-b+4|-|b-a-3|=_____ 。
5、若
a a
> ,若 =1,则a____0
×
×
考点二:有理数的分类
一、按整数、分数分类:
整数
正整数 0 负整数 正分数 负分数
二、按正数、负数分类:
正有理数
正整数
正分数
有 理 数
有 理 数
0 负有理数
分数
负整数 负分数
1、0和正数 叫非负数 2、0和负数 叫非正数
3、0和负整数 叫非正整数
4、0和正整数叫非负整数 也叫自然数
分数 。 5、有限小数和无限循环小数属于_____
下列各式中用了哪条运算律?如何用字母表示? 1、(-4) × 8=8 ×(-4) ab=ba 乘法交换律: 2、[(-8)+5]+(-4)=(-8)+[5+(-4)] 加法结合律:( a+b)+c=a+(b+c) 2 1 2 1 3、 (6) [ ( )] (6) (6) ( ) 3 2 3 2 分配律: a(b+c)=ab+bc 4、[29×(-5/6)] ×(-12)=29×[(-5/6) ×(-12)] 乘法结合律:(ab)c=a(bc) 5、(-8)+(-9)=(-9)+(-8) 加法交换律: a+b=b+a
乘法三结合 1、积为整数结合 解 题 技 能
七年级上数学第一章复习-课件
,正这方样向的直线叫做
数轴
返回
数轴三要素: 原点、单位长度、正方向
绝对值的几何意义
一般地,数轴上表示数a的点与 原点的距离叫做数a的绝对值 .记作|a|
返回
绝对值的代数意义:
(1) 当a是正数时, |a|= a (2) 当a是负数时, |a|=- a
(3) 当a=0时, |a|=0
定义:只有符号不同的两个数 叫互为相反数, 0的相反数是0; 数a的相反数是-a
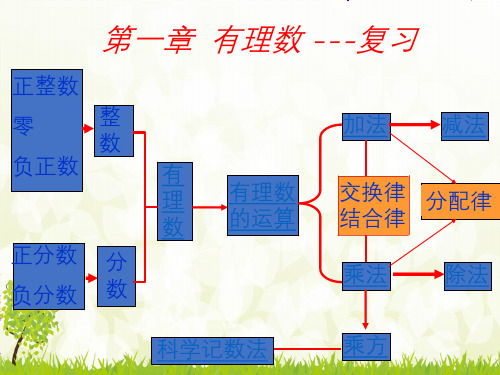
第一章 有理数 ---复习
正整数
零
整
数
负正数
有
理
数
正分数 分
负分数 数
有理数 的运算
加法 减法
交换律 分配律 结合律
乘法
除法
科学记数法
乘方
数轴
有
理
绝对值
数
相反数
有理数的比较大小
返回
数轴
-2
-1
0
1
2
画一条水平直线,在直线上取一点表
示0(这个点叫原点),选取某一长度作
为 单位长度,规定直线上向右的方向为
返回
友情提 示
•有理数的混合运算顺序
• 先乘方,再乘除,最后加减; • 同级运算,从左到右进行; • 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进
行.
返回
把一个大于10的数表示 成a×10n 的形式(其中a是整数
数位只有一位的数,且1 ≤ a
<10 ,n是正整数),使用的
是科学记数法。
;
返回
这种求几个相同因数的积的运算,叫做
乘方,乘方的结果叫做幂.在 an中,a叫作底
数,n叫做指数, 读作a的n次方, 看作是a
人教版七年级数学上册第一章有理数复习(1)ppr优秀课件

第1章有理数 复习(1)
复习目标 (一)知识目标:
理解四个重要概念: 有理数、数轴、相反数、绝对值。 (二 )能力目标:
初步领会有理数大小的比较方法. (三)重点和难点
重点是四个重要概念的理解. 难点是绝对值的应用。
本章的知识点回顾
①有理数:
有理数
整数和分数
统称为有理数
正整数
整数
零
负整数
分数
正分数 负分数
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。 • 二、补笔记 • 上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一
甲
0
乙
4.若 1a1a,则a一定
2
2
A.负数 B.正数 C.非正数 D.非负数
5 .|x|=1,则x与-3的差为( )
A. 4
B. -2
C. 4或2
D. 2
a=2,等式不 成立,a=-2或0, 等式成立
C.
∵|x|=1,∴ x=±1 1-(-3)=4. -1-(-3) =-1+3=2
∴选C.
负数 分数
二选择题: 9、下列说法不具有相反意义的量的是( )
(A)向东2.5千米和向西2千米 (B)上升3米和下降1.5米 (C)零上6 ℃ 和零下5 ℃ (D)收入5000元和亏损5000元
10、在-4,-9,-
,自-我01评.1中定,最大的数是( )
100
(A) -4 (B) -9 (C) -
复习目标 (一)知识目标:
理解四个重要概念: 有理数、数轴、相反数、绝对值。 (二 )能力目标:
初步领会有理数大小的比较方法. (三)重点和难点
重点是四个重要概念的理解. 难点是绝对值的应用。
本章的知识点回顾
①有理数:
有理数
整数和分数
统称为有理数
正整数
整数
零
负整数
分数
正分数 负分数
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。 • 二、补笔记 • 上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一
甲
0
乙
4.若 1a1a,则a一定
2
2
A.负数 B.正数 C.非正数 D.非负数
5 .|x|=1,则x与-3的差为( )
A. 4
B. -2
C. 4或2
D. 2
a=2,等式不 成立,a=-2或0, 等式成立
C.
∵|x|=1,∴ x=±1 1-(-3)=4. -1-(-3) =-1+3=2
∴选C.
负数 分数
二选择题: 9、下列说法不具有相反意义的量的是( )
(A)向东2.5千米和向西2千米 (B)上升3米和下降1.5米 (C)零上6 ℃ 和零下5 ℃ (D)收入5000元和亏损5000元
10、在-4,-9,-
,自-我01评.1中定,最大的数是( )
100
(A) -4 (B) -9 (C) -
最新七年级数学上:第1章有理数复习课件人教新课标版ppt课件

( 3 )、 0.531(2.75)71
4
2
解: -(-12)-(-25)-18+(-10) 8 ( 1 ) 5 ( 0 . 2 5 )
4
= 12+25-18-10 = 37-28
8 1 5 0 .2 5 4
=9
0 .5 3 1 ( 2 .7 5 ) 7 1
4
2
0 .5 3 1 2 .7 5 7 1
1. _规__定_了__原_点_、__正_方__向_和__单_位_长__度_的__直_线__叫数轴。 2. 练习1、在数轴上画出表示下列各数的点,并按从大
到小的顺序排列,用“>”号连接起来。 4, -|-2|, -4.5, 1, 0。
3. ①比-3大的负整数是__-_2_,_-_1_; ②已知m是整数且 -4<m<3,则m为____-3_,_-_2_,_-_1,__0,__1_,。2 ③有理数中, 最大的负整数是__,最-1 小的正整数是__。最1 大的非正
数是__。0 ④与原点的距离为三个单位的点有__个,2
他们分别表示的有理数是__ 和-3__。+3
选择题:
在数轴上,原点及原点左边所表示的数是( D ) A整数 B负数 C非负数 D非正数
下列语句中正确的是( D ) A数轴上的点只能表示整数 B数轴上的点 只能表示分数 C数轴上的点只能表示有理 数 D所有有理数都可以用数轴上的点表示 出来
A C
–01.2/45的的相倒反数数是是-00.2.255,,B
4的相反数是-0.25,
D 0.25的相反数的倒数是-0.25
③用-a表示的数一定是(D) A .负数 B. 正数 C .正数或负数 D.都不对
④一个数的相反数是最小的正整数,那么这个数 是(A)
人教版七年级上册第一章有理数 复习课件(15张PPT)

互为相反数的两个数相加得0.一个数同0 相加,仍得这个数。
(2)运算律:加法交换律:a+b=b+a;加法 结合律:(a+b)+c=a+(b+c)
2、有理数的减法: 减法法则:减去一个数,等于加上这个 数的相反数。a-b=a+ (-b) 引入相反数后,加减混合运算可以统一 为加法运算。
四、有理数的乘除法 1、有理数的乘法: (1)乘法法则:两数相乘,同号得正, 异号得负,并把绝对值相乘。任何数同 0相乘,都得0. 倒数:乘积是1的两个数互为倒数。 多个有理数相乘,可以把它们按顺序依 次相乘。
6、绝对值:一般地,数轴上表示数a的点与
原点的距离叫做数a的绝对值,记作 a
a(a≥0)
a=
-a(a<0)
两个负数,绝 对值大的反而 小
三、有理数的加减法 1、有理数的加法:
(1)加法法则: 同号两数相加,取相同的符号,并把绝
对值相加; 绝对值不相等的异号两数相加,取绝对
值较大的加数的符号,并用较大的绝对值减 去较小的绝对值。
整数
零
或
正整数 零 负数
负整数 负数
负分数
正分数 分数 负分数
3、“0”表示的意义
(1)0既不是正数也不是负数 (2)0是整数 (3)0不是表示没有,有时表示一种趋于 正负的状态 (4)0是最小) 0等相反数是0 (7) 0的绝对值是0 (8) 0没有倒数 (9) 0乘以任何数都为0 (10) 0除以任何不为0的数都为0.
人教版初中数学讲义
空白演示
在第此一输 入章您 的有封理面数副 标 题
一、正数和负数
1、正数、负数: 大于零的数叫做正数, 小于零的数叫做负数。
(2)运算律:加法交换律:a+b=b+a;加法 结合律:(a+b)+c=a+(b+c)
2、有理数的减法: 减法法则:减去一个数,等于加上这个 数的相反数。a-b=a+ (-b) 引入相反数后,加减混合运算可以统一 为加法运算。
四、有理数的乘除法 1、有理数的乘法: (1)乘法法则:两数相乘,同号得正, 异号得负,并把绝对值相乘。任何数同 0相乘,都得0. 倒数:乘积是1的两个数互为倒数。 多个有理数相乘,可以把它们按顺序依 次相乘。
6、绝对值:一般地,数轴上表示数a的点与
原点的距离叫做数a的绝对值,记作 a
a(a≥0)
a=
-a(a<0)
两个负数,绝 对值大的反而 小
三、有理数的加减法 1、有理数的加法:
(1)加法法则: 同号两数相加,取相同的符号,并把绝
对值相加; 绝对值不相等的异号两数相加,取绝对
值较大的加数的符号,并用较大的绝对值减 去较小的绝对值。
整数
零
或
正整数 零 负数
负整数 负数
负分数
正分数 分数 负分数
3、“0”表示的意义
(1)0既不是正数也不是负数 (2)0是整数 (3)0不是表示没有,有时表示一种趋于 正负的状态 (4)0是最小) 0等相反数是0 (7) 0的绝对值是0 (8) 0没有倒数 (9) 0乘以任何数都为0 (10) 0除以任何不为0的数都为0.
人教版初中数学讲义
空白演示
在第此一输 入章您 的有封理面数副 标 题
一、正数和负数
1、正数、负数: 大于零的数叫做正数, 小于零的数叫做负数。
第一章有理数复习课-人教版七年级数学上册课件(共19张PPT) (1)

、正方向 、单位长度 的直线,
2021/6/27
学习赢得智慧人生
3
数学是思维的体操
(三)、相反数的概念 像2和-2、-5和5、2.5和-2.5这样,只有 符号不同的两个 数叫做互为相反数; 0的相反数是 0 。
一般地:若a为任一有理数,则a的相反数为-a
相反数的相关性质:
体现了怎样
1、相反数的几何意义:
位.
2021/6/27
学习赢得智慧人生
14
数学是思维的体操
综合训练
1.一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记 录如下(单位:米): +5,-3,+10,-8,-6,+12,-10; (1)守门员是否 回到了原来的位置? (2)守门员离开球门的位置最远是多少? (3)守门员一共走 了多少路程?
(3)有理数乘法法则
(4)有理数除法法则
(5)有理数的乘方:求几个 相同因数的积的运算,叫做有理
数的乘方。
即:an=aa…aaa(有n个a)
有理数运算律:
交换律
结合律
分配律
有理数混合运算顺序:
(1)先乘方,再乘除,最后算加减
(2)同级运算,从左到右进行
(3)如果有括号,先做括号内的运算,按 小括号,中括号,大括号依次进行。
学习赢得智慧人生
2
数学是思维的体操
知识链接
一、有理数及相关概念
(一)有理数的分类
1.正_整__数_、__0_、_负__整_数__统称整数,试举例说明。 2.__正_分__数_和__负_分__数__统称分数,试举例说明。 3.____整__数_和__分_数__统称有理数。
(二)数轴 规定了 原点、 叫数轴
人教版七年级上册第一章 有理数复习课件(13张PPT)

辨别精确度是根据精确度按要求取近似数的逆用,辨别时,易出现不知依 据哪个数位的数来辨别,或不会数数位,特别是用科学记数法表示的数,不能 根据具1体情形来处理数据,从而导致辨别出错。若要判断精确到的数位,则要 找准精- 3确后的数,再将该数还原以确定数位。
四、数学思想
数形结合思想就是将代数问题与几何图形结合起来进行分析研究,它可以把 抽象的数转化为直观的图形,从而使复杂的问题简单化,这是数学中常用的方法 之一。本章引入数轴就是实现数形结合的雏形,把数在数轴上用点表示出来,会 给解决问题带来方便。 例:有理数a>0,b<0,|a|<|b|,试判断a,b,-a,-b之间的大小关系。
决简单的问题。
一、
本 章 学 习 目
标
情感与态度
体验数学活动充满着探 索性和创造性;感受证 明过程的严谨性以及结 论的确定性。使学生感 知数学知识具有普遍的 联系性 。
二、知识内容结构
知识内容层次分明:主要采取渗透说理的方式, 引导学生自主探索,激发学生进行思考,促进合 作交流。
锁定目标∙全局把握
化简绝对值必须先判断该数的正负性,再根据绝对值的性质写出结果,特别 是当绝对值符号内是字母时,如果没有说明其符号,就得分类讨论;此外还易忽 略一对相反数的绝对值是相等的,而出现已知绝对值求解时漏解。 例:若|a|=|-4|,则a= _______. 错解:a=-4
三、易错点分析
例1:如果|a+2|+(b-1)2=0,那么(a+b)2019的值是( ) 例2:如果|a+6|与(b-2)2互为相反数,那么b-a的值是( ) 例3:如果2|a-3|+(2b-1)2=0,那么-2a-b的值是( )
13.|x-3|=3-x,则x的取值范围是_________.
四、数学思想
数形结合思想就是将代数问题与几何图形结合起来进行分析研究,它可以把 抽象的数转化为直观的图形,从而使复杂的问题简单化,这是数学中常用的方法 之一。本章引入数轴就是实现数形结合的雏形,把数在数轴上用点表示出来,会 给解决问题带来方便。 例:有理数a>0,b<0,|a|<|b|,试判断a,b,-a,-b之间的大小关系。
决简单的问题。
一、
本 章 学 习 目
标
情感与态度
体验数学活动充满着探 索性和创造性;感受证 明过程的严谨性以及结 论的确定性。使学生感 知数学知识具有普遍的 联系性 。
二、知识内容结构
知识内容层次分明:主要采取渗透说理的方式, 引导学生自主探索,激发学生进行思考,促进合 作交流。
锁定目标∙全局把握
化简绝对值必须先判断该数的正负性,再根据绝对值的性质写出结果,特别 是当绝对值符号内是字母时,如果没有说明其符号,就得分类讨论;此外还易忽 略一对相反数的绝对值是相等的,而出现已知绝对值求解时漏解。 例:若|a|=|-4|,则a= _______. 错解:a=-4
三、易错点分析
例1:如果|a+2|+(b-1)2=0,那么(a+b)2019的值是( ) 例2:如果|a+6|与(b-2)2互为相反数,那么b-a的值是( ) 例3:如果2|a-3|+(2b-1)2=0,那么-2a-b的值是( )
13.|x-3|=3-x,则x的取值范围是_________.
数学:第一章有理数总复习课件ppt新人教版七年级上

[基础练习] 1☆如图所示的图形为四位同学画的数轴,其中正确的是
()
2☆在数轴上画出表示下列各数的点,并按从大到小的顺 序排列,用“>”号连接起来。
4, -|-2|, -4.5, 1, 0。
3★ ①比-3大的负整数是__-_2_,__-_; ②已知m是整数且 -4<m<3,则m为____-_3,__1-2_,__-1_,_0_,__1,。2 ③有理数中, 最大的负整数是__,最-1小的正整数是__。最1 大的非正
__________。 • 3☆绝对值等于其相反数的数一定是( )
A.负数 B.正数 • C.负数或零 D.正数或零 • 4★ ,x 则7x=______; , 则 x=x___7____;
精品文档
5★如果,则的取值范围是( )
的点与原点的距离。
3
4
2
-3 –2 –1 0 1 2 3 4
1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= a ; 2) 若a<0,则︱a︱= -a ;
若a =0,则︱a︱= 0 ;
3) 对任何有理数精品a文档,总有︱a︱≥0.
• [基础练习] • 1☆—2的绝对值表示它离开原点的距离是
个单位,记作 . • 2☆ |-8|= ; -|-5|= ; 绝对值等于4的数是
() • A.负数; B.正数; C精.品负文档数或零; D.非负数
5、用-a表示的数一定是( )D A .负数 B. 正数 C .正数或负数 D.正数或负数或0 6、一个数的相反数是最小的正整数,那么这个数是( ) A .–1 B. 1AC .±1 D. 0 7、①互为相反的两个数在数轴上位于原点两旁( ) ②③在只一要个符数号前不面同添,上这“两-个”号数,就它是就相成反了数一(个)负数(× )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(×)
3:有理数的分类
正整数 整数 负整数 0 正分数 分数 负分数 负数 0
正数
3:有理数的分类 1, -0.1, -789, 25, π, 0, -20, -3.14, 200%, 6/7
正整数集{ 1, 25, 200%, …} 负整数集{ -789,-20 …} 正分数集{ 6/7 …} 负分数集{ -0.1, -3.14 …} 正有理数集{ 1, 25,200%,6/7 …} 负有理数集{ -0.1,-789, -20,-3.14 …} 自然数集{ …} 1, 25, 0, 200% 有理数集 {1, -0.1, -789, 25, 0, -20, -3.14, 200%, 6/7…}
3) 对任何有理数a,︱a︱一定是非负数.
6:绝对值 判断: (1)|5|=|-5| (2)|-0.3|=|0.3| (3)|3|>0 (4)|-1.4|>0 (5)有理数的绝对值一定是正数 (6)若a=b,则|a|=|b| (7)若|a|=|b|,则a=b (8)若|a|=-a,则a必为负数
(√ ) (√ ) (√ ) (√ ) ( ×) (√ ) ( ×) ( ×)
2
2007
的值.
2、已知:(a b) | b 4 | 0, 求a b 的值
2 2
3、若(a - 1) 与 | b - 2 | 互为相反数,求a b
2
3
3
4:数 轴
1、在数轴上,原点及原点左边所表示的数( D)
A整数 B负数 C非负数 D非正数 2、下列语句中正确的是( D) A数轴上的点只能表示整数 B数轴上的点只能表示分数 C数轴上的点只能表示有理数 D所有有理数都可以用数轴上的点表示出来 3、若两个有理数在数轴上的对应点分别在原点的两侧, 则这两个数相除所得的商( B ) A.一定是正数 B.一定是负数 C.等于零 D、正、负数不确定
非负整数集{ 1, 25, 0, 200%,
„}
3:有理数的分类
判断:
(1)整数一定是自然数(×)
(2)自然数一定是整数(√ )
填空:
最小的自然数是 最小的正整数是
0 ,
最大的负整数是 -1 ,
1 ,
最大的非正数是 0 .
4:数 轴
规定了原点、正方向和单位长度的直线 叫数轴.
-3 –2 –1
负数
D.以上都不对
3.上升9记作+9,那么上升6又下降8后记作
-2
.
2:正负数的概念 判断题: ①不带“-”号的数都是正数 (×) ②带“+”号的数都是正数 ( ×) ③如果a是正数,那么-a一定是负数(√ ) ④不存在既不是正数,也不是负数的数(×) ⑤一个有理数不是正数就是负数 (×)
⑥0℃表示没有温度
B )
3、下列各式中,是互为倒数的是( C ) A、a-b和b-a C、1÷m和m÷1 B、(-1)×(-1)和-(1÷1) 2 D、2÷6和 6
6:绝对值
数a的绝对值就是数轴上表示数a的点与原点的距离。 1)数a的绝对值记作︱a︱; 2)
若a>0,则︱a︱= a ; 若a<0,则︱a︱= -a ; 若a =0,则︱a︱= 0 ;
综合练习2: 已知有理数a、b、c在数轴上的位置如图, 化简|a|-|a+b|+|c-a|+|b+c|
b
a0
c
综合练习3:
绝对值等于本身的数 相反数等于本身的数 正数和零
0
1,-1
倒数等于本身的数
平方等于本身的数
0,1
0,1,-1
立方等于本身的数
……
课后作业:
1、已知a、b互为相反数,c、d互为倒数,m是绝 对值最小的数,求 (a m b) (m cd )
第一章:有理数复习课
1:正负数的意义
具有相反意义的量
1.下列语句中,含有相反意义的两个量是( C ) A.盈利1千元和收入2千元 B.上升8米和后退8米
C.存入1千元和取出2千元
D.超过2厘米和上涨2厘米
2.如果零上6℃记作+3,则这个问题中,0表示的是( A )
A.零上3 。c
B.零下3 。C
C. 0
0
1
2
3
4
< 0
<
正数
4:数 轴
1.两个有理数表示较大的数的点离原点的距离较近( ) ×
2 2.与原点的距离为三个单位的点有__个,他们分别表
示的有理数是__和__。 +3 -3
2 3.与+3表示的点距离2000个单位的点有__个,他们
-1997 2003 分别表示的有理数是__ __ 和__ __ 。 5 4.+3表示的点与-2表示的点距离是__个单位。
5:相反数
只有符号不同的两个数,叫做互为相反数.
(1)数a的相反数是-a. (2)0的相反数是0. (3)若a、b互为相反数,则a+b=0.
5:相反数
1.一个数的相反数是最小的正整数,这个数是( A ) A .–1 B. 1 C .±1 D. 0 2.互为相反数的两个数在数轴上位于原点两旁(×) 3.位于原点两旁的数是互为相反数(×)
4. 只要符号不同,这两个数就是相反数(×)
5.表示相反意义的量的两个数互为相反数(×) 6.若-a=-8,则-a的相反数是 8
-(-4)的相反数是
-4
5:相反数
1、若a+b=0,则a÷b的值为 ( D
A、-意义
a 1 的值( b
2、a、b互为相反数且都不为0,则 a b 1 A、-1 B、0 C、1 D、2
6:绝对值
1)绝对值等于它本身的数是正数(
×
)
2)绝对值等于它的相反数的数是负数( × ) 3)正数的绝对值大于负数的绝对值( 4) 绝对值较大的数较大(×) 5)任何数的绝对值都不是负数( ) √ 6)若
×)
a a
=1,则a____0,若 >
a a
=-1,则a____0. <
综合练习1: (1)若(x-1)2+|y+4|=0,则3x+5y=____ (2)若|a-3|+ |3a-4b|=0,则-2a+8b=____ (3)|3-|+|4- |=____ (4)已知|x|=3,|y|=2,且x<y,则x+y=____
