概率论期中试卷大字
概率论与数理统计期中试题(一)

概率论与数理统计期中试题(一)《概率论与数理统计》期中试题(一)姓名班级学号成绩一、填空题(每小题4分,共12分)1.设事件仅发生一个的概率为0.3,且,则至少有一个不发生的概率为__________.2.设随机变量服从泊松分布,且,则______.3.设随机变量在区间上服从均匀分布,则随机变量在区间内的概率密度为_________.二、单项选择题(每小题4分,共16分)1.设为三个事件,且相互独立,则以下结论中不正确的是(A)若,则与也独立. (B)若,则与也独立.(C)若,则与也独立.(D)若,则与也独立. ()2.设随机变量的分布函数为,则的值为(A). (B). (C). (D). ()3.设随机变量和不相关,则下列结论中正确的是(A)与独立. (B).(C). (D).4.设离散型随机变量和的联合概率分布为若独立,则的值为(A). (A). (C)(D). ()三、(12分)已知一批产品中90%是合格品,检查时,一个合格品被误认为是次品的概率为0.05,一个次品被误认为是合格品的概率为0.02,求(1)一个产品经检查后被认为是合格品的概率;(2)一个经检查后被认为是合格品的产品确是合格品的概率.四、(12分)从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是2/5. 设为途中遇到红灯的次数,求的分布列、分布函数、数学期望和方差.五、(12分)设二维随机变量在区域上服从均匀分布. 求关于的边缘概率密度;六、(12分)向一目标射击,目标中心为坐标原点,已知命中点的横坐标和纵坐标相互独立,且均服从分布. 求(1)命中环形区域的概率;(2)命中点到目标中心距离的数学期望.七、(12分)设, 求的概率密度.Y X0200.10.2010.30.050.120.1500.1八、(12分)已知离散型随机向量的概率分布为求.。
最新概率论与数理统计期中考试试题1

概率论与数理统计期中考试试题1一.选择题(每题4分,共20分)1.设,,A B C 为三个随机事件,,,A B C 中至少有一个发生,正确的表示是( ) A. ABC B. ABC C. AB C D. A B C2.一个袋子中有5个红球,3个白球,2个黑球,现任取三个球恰为一红,一白,一黑的概率为 ( ) A.12 B. 14 C. 13 D. 153.设,A B 为随机事件,()0.5,()0.6,(|)0.8P A P B P B A ===,则()P AB =( )A .0.7 B. 0.8 C. 0.6 D. 0.44. 一电话总机每分钟收到呼唤的次数服从参数为2的泊松分布,则某一分钟恰有4次呼唤的概率为( )A.423e - B. 223e - C. 212e - D. 312e - 5.若连续性随机变量2(,)X N μσ,则X Z μσ-= ( )A .2(,)ZN μσ B. 2(0,)Z N σ C. (0,1)ZN D. (1,0)Z N二. 填空题(每题4分,共20分)6. 已知1()2P A =,且,A B 互不相容,则()P AB =7. 老张今年年初买了一份为期一年的保险,保险公司赔付情况如下:若投保人在投保后一年内因意外死亡,则公司赔付30万元;若投保人因其他原因死亡,则公司赔付10万元;若投保人在投保期末生存,则公司无需付给任何费用。
若投保人在一年内因意外死亡的概率为0.0002,因其他原因死亡的概率为0.0050,则保险公司赔付金额为0元的概率为 8. 设连续性随机变量X 具有分布函数0,1()ln ,11,x F x x x e x e <⎧⎪=≤<⎨⎪≥⎩则概率密度函数()f x = 9. 设连续型随机变量2(3,2)XN ,则{}2<5P X ≤=(注: (1)=0.8413,(0.5)=0.6915φφ)10. 设离散型随机变量X 的分布律为10120.20.30.10.4X-⎛⎫ ⎪⎝⎭,则2(1)Y X =-的分布律为三.解答题(每题8分,共48分)11. 将9名新生随机地平均分配到两个班级中去,这9名新生中有3名是优秀生。
《概率论与数理统计》期中考试试题汇总,DOC

《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( )A .A 1A 2B .21A AC .21A AD .21A A2345C 68.将3个球放入5个盒子中,则3个盒子中各有一球的概率为=________.9.从a 个白球和b 个黑球中不放回的任取k 次球,第k 次取的黑球的概率是=.10.设随机变量X ~U (0,5),且21Y X =-,则Y 的概率密度2f Y (y )=________.11.设二维随机变量(X ,Y )的概率密度f (x ,y )=⎩⎨⎧≤≤≤≤,y x ,其他,0,10,101则P {X +Y ≤1}=________. 12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59⎛⎫ ⎪⎝⎭,则相关系数,X Y ρ=________. 13.二维随机变量(X ,Y )(1,3,16,25,0.5)N -,则X ;Z X Y =-+.(-1,31),(2,0),且取这些值的概率依次为61,a ,121,125. 求(1)a =?并写出(X ,Y )的分布律;(2)(X ,Y )关于X ,Y 的边缘分布律;问X ,Y 是否独立;(3){0}P X Y +<;(4)1X Y =的条件分布律;(5)相关系数,X Y ρ18.(8分)设测量距离时产生的随机误差X ~N (0,102)(单位:m),现作三次独立测量,记Y 为三次测量中误差绝对值大于19.6的次数,已知Φ(1.96)=0.975.(1)求每次测量中误差绝对值大于19.6的概率p ;(2)问Y 服从何种分布,并写出其分布律;求E (Y ).1取出的3件中恰有一件次品的概率为( )A .601B .457C .51D .157 2.下列选项不正确的是()A .互为对立的事件一定互斥B .互为独立的事件不一定互斥C .互为独立的随机变量一定是不相关的D .不相关的随机变量一定是独立的3.某种电子元件的使用寿命X (单位:小时)的概率密度为42100,100;()0,100,x p x x x ⎧≥⎪=⎨⎪<⎩任取一只电子元件,则它的使用寿命在150小时以内的概率为( )A .41B .31C .21D .32 4.若随机变量,X Y 不相关,则下列等式中不成立的是.A5A 6A 79.设随机变量X ~E (1),且21Y X =-,则Y 的概率密度f Y (y )=________.10.设随机变量X ~B (4,32),则{}1P X <=___________. 11.已知随机变量X 的分布函数为0,6;6(),66121,6,x x F x x x ≤-⎧⎪+⎪=-<<⎨⎪≥⎪⎩,则X 的概率密度p (x )=______________.12.设二维随机变量(,)X Y 的协方差矩阵是90.60.625⎛⎫⎪⎝⎭,则相关系数,X Y ρ=________. 13.二维随机变量(X ,Y )(2,3,9,16,0.4)N -,则X;Z X Y =-+. 14.随机变量X 的概率密度函数为,0()0,0x X e x f x x -⎧>=⎨≤⎩,Y 的概率密度函数为1,12()3Y y f y ⎧-<<⎪=⎨,,X Y 相互独立,且Z X Y =+的概率密度函数为()z f z = 试求:(1)常数α,β;(2)(X ,Y )关于X ,Y 的边缘分布律;问X ,Y 是6否独立;(3)X 的分布函数F(x);(4){1}P X Y +<;(5)1X Y =的条件分布律;(6)相关系数,X Y ρ18.(8分)设顾客在某银行窗口等待服务的时间X (单位:分钟)具有概率密度()3103x e x p x -⎧>⎪=⎨,;某顾客在窗口等待服务,若超过9分钟,他就离视机,厂方获得利润50万元,但如果因销售不出而积压在仓库里,则每一万台需支付库存费10万元,问29寸彩色电视机的年产量应定为多少台,才能使厂方的平均收益最大?《概率论与数理统计》期中试卷试题(五)一、选择题(共5题,每题2分,共计12分)1.下列选项正确的是()A.互为对立事件一定是互不相容的B.互为独立的事件一定是互不相容的C.互为独立的随机变量一定是不相关的 D.不相关的随机变量不二、填空题:(每小题2分,共18分)7.同时扔4枚均匀硬币,则至多有一枚硬币正面向上的概率为________.8.将3个球放入6个盒子中,则3个盒子中各有一球的概率为=________.89.从a 个白球和b 个黑球中不放回的任取3次球,第3次取的黑球的概率是=.10.公共汽车站每隔5分钟有一辆汽车到站,乘客到站的时刻是任意的,则一个乘客候车时间不超过3分钟的概率为 (1,2,9,16,0)N -;2Z X =-. 率密度函数51,050,0x e x x ->≤的概率密,(,)X Y 相互独立,且X Y +的概率密度函数为(z f 在某区域有一架飞机,雷达以99%的概率探测到并报警。
概率论期中考试试卷及答案

概率论期中考试试卷及答案1、将4个不同的球随机地放在5个不同的盒子里,求下列事件的概率: (1) 4个球全在一个盒子里; (2) 恰有一个盒子有2个球、 解:把4个球随机放入5个盒子中共有45=625种等可能结果、 (1)A={4个球全在一个盒子里}共有5种等可能结果,故P(A)=5/625=1/125 (2) 5个盒子中选一个放两个球,再选两个各放一球有302415=C C 种方法4个球中取2个放在一个盒子里,其她2个各放在一个盒子里有12种方法因此,B={恰有一个盒子有2个球}共有12×30=360种等可能结果、 故12572625360)(==B P2、某货运码头仅能容纳一只船卸货,而,甲乙两船在码头卸货时间分别为1小时与2小时,设甲、乙在24小时内随时可能到达,求它们中间任何一船都不需要等待码头空出的概率。
解:设x,y 分别为两船到达码头的时刻。
由于两船随时可以到达,故x,y 分别等可能地在[0,60]上取值,如右图 方形区域,记为Ω。
设A 为“两船不碰面”,则表现为阴影部分。
222024,024024,024,2111()24576,()2322506.522()()0.8793()x y x y x y y x m m A m A P A m Ω≤<≤<≤<≤<->->Ω===⨯+⨯===Ω={(x,y)},A={(x,y)或},有所以,3、设商场出售的某种商品由三个厂家供货,其供应量之比就是3:1:1,且第一、二、三厂家的正品率依次为98%、98%、96%,若在该商场随机购买一件商品,求:(1) 该件商品就是次品的概率。
(2) 该件次品就是由第一厂家生产的概率。
解:厦门大学概统课程期中试卷____学院___系___年级___专业考试时间 2013、11、81231122331,(1)()()(|)()(|)()(|)=60%*(1-98%)+20%*(1-98%)+20%*(1-96%) =0.024(2) (|)A B B B P A P B P A B P B P A B P B P A B P B A =++=设为该产品为次品,,分别为三个厂家产品,则由全概率公式可知由贝叶斯公式可知111()()(|)60%*(1-98%)()()0.024 =0.5P AB P B P A B P A P A ==4、甲乙丙三台机床独立工作,在同一时间内她们不需要工人照顾的概率分别为0、7,08,0、9,求在这段时间内,最多只有一台机床需人照顾的概率。
《概率论与数理统计》期中考试试题汇总

系数 X ,Y
18.(8 分) 设测量距离时产生的随机误差 X~N(0,102)(单位:m),现作三次独 立测量,记 Y 为三次测量中误差绝对值大于 19.6 的次数,已知Φ(1.96)=0.975.
(1)求每次测量中误差绝对值大于 19.6 的概率 p; (2)问 Y 服从何种分布,并写出其分布律;求 E(Y).
fY
( y)
1
2
, 1
y
1 , (X ,Y )
相互独立,且
Z
X
Y
的概率密度函数为
fz (z)
0, others
15. 设 随 机 变 量 X , E(X ) 3, D(X ) 1 , 则 应 用 切 比 雪 夫 不 等 式 估 计 得 3
P{| X 3|1}
三、计算题(本题共 5 小题,共 70 分)
2
D. 2
3
4.若随机变量 X ,Y 不相关,则下列等式中不成立的是
.
A. D(X Y ) DX DY
B. Cov(X ,Y ) 0
C. E(XY ) EX EY
D. D(XY ) DX DY
5.设随机变量 X 与 Y 相互独立,X 服从参数 1 为的泊松分布,Y~B(6,1 ),则 D(X-Y)=( )
pY ( y) , X 与 Y 是否独立;(4) 概率 P{Y X} , (5)求 Z X Y 的概率密度; (6)相关系数 X ,Y
20.(10 分)假定暑假市场上对冰淇淋的需求量是随机变量 X 盒,它服从区间[200, 400]上的均匀分布,设每售出一盒冰淇淋可为小店挣得 1 元,但假如销售不出而 屯积于冰箱,则每盒赔 3 元。问小店应组织多少货源,才能使平均收益最大?
《概率论与数理统计》期中考试试题汇总,DOC

《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i=1,2,B 表示事件“仅第一次射击命中目标”,则B=()A .A 1A 2B .21A AC .21A AD .21A A 2.某人每次射击命中目标的概率为p(0<p<1),他向目标连续射击,则第一次未中第二次命中的概率为()A .p 2B .(1-p)2C .1-2p D .p(1-p)3.已知P(A)=0.4,P(B)=0.5,且A B ,则P(A|B)=()A .0 B .0.4 C .0.8 D .14.一批产品中有5%不合格品,而合格品中一等品占60%,从这批产品中任取一件,则该件产品是一等品的概率为()A .0.2B .0.30C .0.38D .0.57 5.下列选项正确的是()A .互为对立事件一定是互不相容的B .互为独立的事件一定是互不相容的C .互为独立的随机变量一定是不相关的D .不相关的随机变量不一定是独立的6.设随机变量X 与Y 相互独立,X 服从参数2为的指数分布,Y ~B(6,21),则D(X-Y)=( ) A .1B .74C .54D .12二、填空题(本题共9小题,每小题2分,共18分)7.同时扔3枚均匀硬币,则至多有一枚硬币正面向上的概率为________.8.将3个球放入5个盒子中,则3个盒子中各有一球的概率为= ________. 9.从a 个白球和b 个黑球中不放回的任取k 次球,第k 次取的黑球的概率是= .10.设随机变量X ~U (0,5),且21Y X ,则Y 的概率密度f Y (y)=________.11.设二维随机变量(X ,Y)的概率密度 f (x,y)=,y x ,其他,0,10,101则P{X+Y ≤1}=________.12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59,则相关系数,X Y = ________.13. 二维随机变量(X ,Y)(1,3,16,25,0.5)N ,则X ;Z X Y .。
概率统计中期考试试题及答案

概率统计中期考试试题及答案 一选择题1 设A ,B ,C 为三个独立事件,则下列等式中不成立的是( ) (A ) )()()(B P A P B A P = (B ) )()()(B P A P B A P = (C ) )()()(C P A P AC P = (B ) )()()()(C P B P A P ABC P =解 A ,B ,C 为三个独立事件 ,则A 与B 相互独立 )()()(B P A P B A P = 所以 (B )不成立2 如果事件A 与B 相互对立,则下面结论错误的是( ) (A ) A+B 是必然事件 (B )B A +是必然事件 (C ) B A 是不可能事件 (D )A 与B 一定不互斥解 如图 :事件A 与B 相互对立,则 A B ==,Φ=B A所以(D )是错误的 3 给出下列命:(1) 互斥事件一定对立 (2) 对立事件一定互斥 (3) 互斥事件不一定对立(4) 事件A 与B 的和事件的概率一定大于事件A 的概率 (5) 事件A 与B 互斥,则P(A)=1-P(B) 其中命题正确的个数为( )(A) 0 (B) 1 (C) 2 (D) 3 解 (1) 错误 (2) 正确 (3) 正确(4) 如果 A B ⊆,则 )()(A P B A P =+ 所以错误(5) 事件A 与B 互斥,则)()()(B P A P B A P +=+ 但)(B A P +不一定等于1 所以错误4 一个员工一周需要值班二天,其中恰有一天是星期六的概率为( ) ( A) 1/7 (B) 2/7 (C) 1/49 (D) 2/49 解 A={ 恰有一天是星期六} 726)(27==C A P 5 有三个相识的人某天各自乘火车外出,假设火车有10节车厢,那么至少有二人在车厢内相遇的概率( )(A) 29/200 (B) 7/25 (C) 29/144 (D) 7/18 解 A={至少有二人在车厢内相遇} 则2571089101)(1)(3=⨯⨯-=-=A P A P二 填空题1 袋中3红球,2白球,每次取1个,取后放回,再放入相同颜色的球1个,则连续三次取得红球的概率 解 i A 第i 次取红球(i=1,2,3)则 )|()|()()(213121321A A A P A A P A P A A A P =756453⨯⨯=72= 2 有两箱同类的零件,第一箱有50只,其中有10件一等品,第二箱有30只,其中有18件一等品,今从两箱中任取一箱,然后从该箱中取零件两次,每次取一只,不放回,则第一次取到一等品的概率是解 A------取到第一只箱子 B------第一次取到红球)|()()|()()(A B P A P A B P A P B P +=4.0301821501021=⨯+⨯=3某射手命中率为0.9,他射击10次恰好中9次的概率为 解 X------10次射击命中的次数,则 )9.0,10(~B X1.09.0}9{9910C X P ===0.387424设8支枪中已有5支经试射校正,有3支未校正,一射手用校正过的枪命中率为0.8,用未校正过的枪命中率为0.3,今从8支枪中选一支进行射击,结果中靶,则所用枪是校正过的概率为解 A------取到校正过的枪 B-----射击命中目标 )|()()|()()(A B P A P A B P A P B P += 3.0838.085⨯+⨯=)()|()()()()|(B P A B P A P B P AB P B A P ==3.0838.0858.085⨯+⨯⨯==0.8163275 设随机变量X 的分布律为 kb k X P )32(}{== (k=1,2,3,…) 则常数b=解 132132)32(1=-=∑∞=b b k k5.0=⇒b6 事件A ,B ,C 三事件相互独立,A 发生的概率为1/2,A ,B ,C 同时发生的概率为1/24,A ,B ,C 都不发生的概率为1/4,则A ,B ,C 只有一个发生的概率为 解 事件A ,B ,C 三事件相互独立21)(=A P 241)()()()(==C P B P A P ABC P 41))(1))((1))((1()()()()(=---==C P B P A P C P B P A P C B A P 则 31)(=B P 41)(=C P )()()()(P P P P ++=++)()()()()()()()()(C P B P A P C P B P A P C P B P A P ++=413221433121433221⨯⨯+⨯⨯+⨯⨯=2411=7设某项实验成功率是失败率的2倍,用X 表示一次实验成功的次数,则P{X=0}= 解 A={成功} 则 32)(=A P 31)0(==X P 8 已知a A P =)( b B P =)( c B A P =+)( 则 =)(B A P 解 )()()])[()(B P B A P B B A P B A P -+=-+==c-b9 从1到100共100个整数中任取一个数,在已知这个数是3的倍数的条件下,这个数能被5整除的概率为解 A={这个数是3的倍数} B={这个数能被5整除}则 112100331006)()()|(===A P AB P A B P三 设连续型随机变量的分布函数为 ⎪⎩⎪⎨⎧≥<≤<=111000)(2x x Axx x F 求(1)A=? (2)P{0.3<X<0.7} (3) X 的概率密度解 (1)因为为F(x)连续函数,特别地,在X=1处连续, 有A=1(2) 4.03.07.0)3.0()7.0(}7.03.0{22=-=-=<<F F X P(3) ⎪⎩⎪⎨⎧≥<≤<='=1010200)()(x x x x x F x f四 测量到某目标的距离时发生的随机误差X 具有概率密度3200)20(22401)(--=x ex f π求在一次测量中误差的绝对值不超过30米的概率 解 224020213200)20(24012401)(⎪⎭⎫ ⎝⎛----==x x eex f ππ)40,20(~2N X)25.1()25.0()402030()402030(}3030{}30|{|-Φ-Φ=--Φ--Φ=≤≤-=≤X P X P 4931.018944.05981.0)]25.1(1[)25.0(=-+=Φ--Φ=五 设随机变量X 服从均匀分布U (0,1),试求Xe Y = 概率密度函数与分布函数解 )1,0(~U X ⎪⎩⎪⎨⎧≥<≤<=1010100)(x x x x f Xx e y =单调上升,其反函数为: y x ln = 导数为: yx y 1='(1) Xe Y = 概率密度函数为:|)(|))(()(y h y h f y f X Y '∙=⎪⎪⎩⎪⎪⎨⎧≥<≤<=1ln 01ln 010ln 0y y y y ⎪⎪⎩⎪⎪⎨⎧≥<≤<=e y e y y y 0111(2) 分布函数为 dy y f y F Y Y ⎰=)()(⎪⎩⎪⎨⎧≥<≤+<=e y c e y c y y c 3211ln 1根据)(y F Y 的连续性,及,0)(=-∞Y F 1)(=+∞Y F 有 1,0,0321===c c c所以 =)(y F Y ⎪⎩⎪⎨⎧≥<≤<=e y e y y y 11ln 10。
概率论与数理统计试题期中考试-答案

概率论与数理统计课程期中考试考试时间:90分钟姓名:班级:学号:一、单项选择题(本大题共有5个小题,每小题4分,共20分)1,设..~(100,0.1)R V X B,1..~()2R V Yπ,且X和Y相互独立,令72+-=YXZ,则D(Z)=(D )。
A:7 B:8 C:10 D:11 2,若P(A)=1/2,P(B|A)=1/3,则P(AB)=( B )A:1/2 B: 1/3 C: 5/6 D:1/63,设X的概率密度函数为30()xke xf x-⎧>=⎨⎩其它,则=k( C )A:1/3 B:1/9 C: 3 D: 94, 如果X,Y为两个随机变量,满足COV(X,Y)=0,下列命题中正确的是( A )。
A:X,Y不相关B:X,Y相互独立C:D(XY) =D(X)+D(Y) D:D(X-Y) =D(X)-D(Y)5,在8片药中有4片是安慰剂,从中任取3片,则取到2片是安慰剂的概率为( B )A:1/4 B :3/7 C:1/2 D:6/7二、填空题(本大题共有6个小题,每空2分,共20分)4 A,B为两个随机事件,若P(A)=0.4,P(B)=0.6,P(B A)=0.2.则P(AB)= 0.4 ,P(AB)= 0.25 甲乙两人独立射击,击中目标的概率分别为0.8,0.7,现在两人同时射击同一目标,则目标被击中的概率为 0.946.若某产品平均数量为73,均方差为7,利用切比雪夫不等式估计数量在52~94之间的概率为 8/97.在8件产品中有2件次品。
从中随机抽取2次,每次抽取一件,做不放回抽取。
则两次都是正品的概率为 15/28 抽取的产品分别有一正品和一件次品的概率为 3/7 ,第二次取出的产品为次品的概率为 1/48若X~N(2,1),Y~U[1,4],X,Y互相独立,则E(X+2Y-XY+2)= 4 ,D(X-2Y+3)=49 设D(X)=D(Y)=2,0.3XY ρ=,则D(X-Y)= 2.8三、解答题(本大题共有3个小题,共32分)10(7分)病树主人外出,委托邻居浇水。
概率论期中测试答案

概率论与数理统计期中测试答案一、 单项选择题1.当事件A 、B 同时发生时,事件C 必发生,则( B )(A) ()()()1-+≤B P A P C P (B) ()()()1-+≥B P A P C P (C) ()()AB P C P = (D) ()()B A P C P ⋃=2.设随机变量X 的概率密度是()x f ,则下列函数中一定可以作为概率密度的是( )(A) ()x f 2 (B) ()x f 2 (C) ()x f - (D) ()x f 3.设1{0,0}5P X Y ≥≥=,2{0}{0}5P X P Y ≥=≥=,则{max{,}0}P X Y ≥=( )(A)15 (B) 25 (C) 35 (D) 454.设,X Y 相互独立,X 服从()0,2上的均匀分布,Y 的概率密度函数为,0()0,0y Y e y f y y -⎧≥=⎨<⎩,则{}1P X Y +≥=( )(A) 11e -- (B) 21e -- (C) 212e -- (D) 110.5e -- 二 填空题1 设随机变量X 服从参数为λ的指数分布, 则=>}{DX X P 1/e .2 设和ξη是两个相互独立且均服从正态分布N (0,21)的随机变量,则=-|)(|ηξE3 设随机变量X 和Y 的数学期望分别为-2和2,方差分别为1和4,而相关系数为-0.5,则根据切比雪夫不等式有≤≥+}6|{|Y X P 1/12.4 设平面区域D 由曲线所围成及直线2,1,01e x x y xy ====,二维随机变量(X ,Y )在区域D 上服从均匀分布,则(X ,Y )关于X 的边缘概率密度在x =2处的值为1/4。
三 计算题1、自动包装机把白色和淡黄色的乒乓球混装入盒子,每盒装12只,已知每盒内装有的白球的个数是等可能的。
为检查某一盒子内装有白球的数量,从盒中任取一球发现是白球,求此盒中装的全是白球的概率。
概率统计期中考答案版

《_》 期中考试 (一、四)班级 ______ ___ 姓名 _______学号 _ ___一、选择题(共6题,每题3分,共计18分) 1. 事件C 发生导致事件A 发生, 则 B 。
A. A 是C 的子事件 B. C 是A 的子事件 C. A C = D .()()P C P A >2. 设事件B A ,两个事件,111(),(),()2310P A P B P AB ===,则()P A B = B 。
A .1115 B .415 C .56 D .16(逆事件概率,加法公式,()1()1[()()()]P A B P A B P A P B P AB =-=-+-U )3. 设X ~2(,)N μσ,那么当σ增大时,{2}P X μσ-< C 。
A .增大B .减少C .不变D .增减不定 (随机变量的标准正态化,2(2)1=Φ-)4. 已知B A ,是两个事件,X ,Y 是两个随机变量,下列选项正确的是(C )A . 如果B A ,互不相容,则A 与B 是对立事件B . 如果B A ,互不相容,且()()0,0>>B P A P ,则B A ,互相独立C . Y X 与互相独立,则Y X 与不相关D . Y X 与相关,则相关系数1ρ=5.已知2,1,(,)1,DX DY Cov X Y === 则(2)D X Y -= ( C ) (A) 3; (B) 11; (C) 5; (D) 7 (考查公式(2)4()()2cov(2,)D X Y D X D Y X Y -=+-)6.若X,Y 为两个随机变量,则下列等式中成立的是( A ) A.EY EX Y X E +=+)( B.DY DX Y X D +=+)( C.DXY DX DY =⋅ D.EXY EX EY =⋅二、填空题(共6题,每题3分,共计18分)1. 设三次独立试验中,事件A 出现的概率相等,如果已知A 至少出现一次的概率等于2719,则事件A 在一次试验中出现的概率为13. (考查贝努里概型)2.设顾客在某银行窗口等待服务的时间X (单位:分钟)具有概率密度 某顾客在窗口等待服务,若超过9分钟,他就离开. (1)该顾客未等到服务而离开窗口的概率P {X >9}= 3e -(2)若该顾客一个月内要去银行5次,以Y 表示他未等到服务而离开窗口的次数,即事件{X >9}在5次中发生的次数,P {Y =0}= 35(1)e -- 3.设随机变量X ~)2,1(2N ,(1){ 2.2}P X <= 0.7257 (2){ 1.6 5.8}P X -≤<= 0.895 (3){ 3.5}P X ≤= 0.8822((0.6)0.7257Φ=(2.4)0.9918,Φ=(1.3)0.9032Φ=(1.25)0.8944,Φ=(2.25)0.9878Φ=)4.,,,X Y Z W 是独立的随机变量,X 服从二项分布1(4,)2B ,Y 为参数为2的指数分布,Z 为参数为3的泊松分布,W 是服从[2,4]-上的均匀分布, ()D Y Z -= 13/4 ,(2)E Z W += 7 ,[(1)]E XY X Z +-= -2 。
《概率论与数理统计》期中考试试习题汇总

欢迎阅读《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( )A .A 1A 2B .21A AC .21A AD .21A A2.某人每次射击命中目标的概率为p (0<p <1),他向目标连续射击,则第一次未中第二次命中的概率为( ) A .p 223.已知A .0 4率为(A .0.25A C 6.A .1- 7.8.将39.从a 10.11.12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59⎛⎫⎪⎝⎭,则相关系数,X Y ρ= ________.13. 二维随机变量(X ,Y )(1,3,16,25,0.5)N -,则X;Z X Y=-+ .14. 随机变量X 的概率密度函数为51,0()50,0x X e x f x x -⎧>⎪=⎨⎪≤⎩,Y 的概率密度函数为1,11()20,Y y f y others ⎧-<<⎪=⎨⎪⎩,(,)X Y相互独立,且Z X Y =+的概率密度函数为()z f z =15. 设随机变量X , 1()3,()3E X D X ==,则应用切比雪夫不等式估计得{|3|1}P X -≥≤三、计算题(本题共5小题,共70分)16.(8分)某物品成箱出售,每箱20件,假设各箱含0,1和2件次品的概率分别是0.7,0.2和0.1,顾客在购买时,售货员随机取出一箱,顾客开箱任取4件检查,若无次品,顾客则买下该箱物品,否则退货.试求:(1) 顾客买下该箱物品的概率;(2) 现顾客买下该箱物品,问该箱物品确实17.(20求(1)a (3){P X Y +18.(8为三次(1)(2)19.(24求: (1) ;(4) 概率{P Y 20.(101.一批产品共10件,其中有2件次品,从这批产品中任取3件,则取出的3件中恰有一件次品的概率为( ) A .601 B .457 C .51 D .157 2.下列选项不正确的是( ) A .互为对立的事件一定互斥B .互为独立的事件不一定互斥C .互为独立的随机变量一定是不相关的D .不相关的随机变量一定是独立的3.某种电子元件的使用寿命X (单位:小时)的概率密度为2100,100;()0,100,x p x x x ⎧≥⎪=⎨⎪<⎩ 任取一只电子元件,则它的使用寿命在150小时以内的概率为( ) A .41 B .31 C .21 D .324.若随机变量,X Y 不相关,则下列等式中不成立的是 . A .DY DX Y X D +=+)( B. 0),(=Y X Cov C. (E 5.A .1-6.则常数x A .7.8. 将29. 10. 11. 已密度p (x 12.13. 二维随机变量(X ,Y )(2,3,9,16,0.4)N -,则X;Z X Y=-+ .14. 随机变量X 的概率密度函数为,0()0,0x X e x f x x -⎧>=⎨≤⎩,Y 的概率密度函数为1,12()30,Y y f y others⎧-<<⎪=⎨⎪⎩,,X Y 相互独立,且Z X Y =+的概率密度函数为()z f z =15. 设随机变量X,1()1,()3E X D X==,则应用切比雪夫不等式估计得{13}P X-<<≥三、计算题(本大题共5小题,共70分)16.(8分)据市场调查显示,月人均收入低于1万元,1至3万元,以及高于3万元的家庭在今后五年内有购置家用高级小轿车意向的概率分别为 0.1,0.2 和 0.7.假定今后五年内家庭月人均收入X 服从正态分布N (2, 0.82 ).试求:(1) 求今后五年内家庭有购置高级小轿车意向的概率;(2) 若已知某家庭在今后五年内有购置高级小轿车意向,求该家庭月人均收入在1至3万元的概率.17(1),Y)关问X,Y)相关18{X>9}(1)X Y的条件概率密度函数;(5)相关系数,X Yρ20.(10分)设市场上每年对某厂生产的29寸彩色电视机的需求量是随机变量X(单位:万台),它均匀分布于[10,20].每出售一万台电视机,厂方获得利润50万元,但如果因销售不出而积压在仓库里,则每一万台需支付库存费10万元,问29寸彩色电视机的年产量应定为多少台,才能使厂方的平均收益最大?《概率论与数理统计》期中试卷试题(五)一、选择题(共5题,每题2分,共计12分)1.下列选项正确的是()A .互为对立事件一定是互不相容的B .互为独立的事件一定是互不相容的C .互为独立的随机变量一定是不相关的D .不相关的随机变量不一定是独立的2. 设事件B A ,两个事件,111(),(),()2310P A P B P AB ===,则()P A B = 。
概率论期中测试试卷

1.据多年来的气象记录知甲、乙两城市在一年内的雨天分布是均等的,且雨天的比例甲市占20%,乙市占18%,两市同时下雨占12%.求
(1) 某一天两市中至少有一市下雨的概率;
(2) 乙市下雨的条件下, 甲市也下雨的概率;
(3) 甲市下雨的条件下, 乙市也下雨的概率.
2. 设随机变量X 的概率密度为: +∞<<∞-=-x Ae
x f x ,)(||
求: (1)系数A ; (2)(01)P X <<.
3. 某厂甲、乙、丙三个车间生产同一种产品, 其产量分别占全厂总产量的40%, 38%, 22%, 经检验知各车间的次品率分别为0.04, 0.03, 0.05. 现从该种产品中任意取一件进行检查,求这件产品是次品的概率.
4. 设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧>>=+-.,
0;0,0,),()(其他y x Ae y x f y x 试求:(1)常数A ; (2) 概率)(Y X P ≤
5. 设随机变量X 的概率密度 ⎩⎨⎧≤≤=其他,
010,2)(x x x f
求X Y -=1的概率密度.。
最新概率论期中考试试卷及答案

精品文档1.将4个不同的球随机地放在5个不同的盒子里,求下列事件的概率: (1) 4个球全在一个盒子里; (2) 恰有一个盒子有2个球.解:把4个球随机放入5个盒子中共有45=625种等可能结果. (1)A={4个球全在一个盒子里}共有5种等可能结果,故P(A)=5/625=1/125 (2) 5个盒子中选一个放两个球,再选两个各放一球有302415=C C 种方法4个球中取2个放在一个盒子里,其他2个各放在一个盒子里有12种方法因此,B={恰有一个盒子有2个球}共有12×30=360种等可能结果. 故12572625360)(==B P2.某货运码头仅能容纳一只船卸货,而,甲乙两船在码头卸货时间分别为1小时和2小时,设甲、乙在24小时内随时可能到达,求它们中间任何一船都不需要等待码头空出的概率。
解:设x,y 分别为两船到达码头的时刻。
由于两船随时可以到达,故x,y 分别等可能地在[0,60]上取值,如右图 方形区域,记为Ω。
设A 为“两船不碰面”,则表现为阴影部分。
222024,024024,024,2111()24576,()2322506.522()()0.8793()x y x y x y y x m m A m A P A m Ω≤<≤<≤<≤<->->Ω===⨯+⨯===Ω={(x,y)},A={(x,y)或},有所以,3.设商场出售的某种商品由三个厂家供货,其供应量之比是3:1:1,且第一、二、三厂家的正品率依次为98%、98%、96%,若在该商场随机购买一件商品,求:(1) 该件商品是次品的概率。
(2) 该件次品是由第一厂家生产的概率。
厦门大学概统课程期中试卷____学院___系___年级___专业考试时间 2013.11.8解:1231122331,(1)()()(|)()(|)()(|)=60%*(1-98%)+20%*(1-98%)+20%*(1-96%) =0.024(2) (|)A B B B P A P B P A B P B P A B P B P A B P B A =++=设为该产品为次品,,分别为三个厂家产品,则由全概率公式可知由贝叶斯公式可知111()()(|)60%*(1-98%)()()0.024=0.5P AB P B P A B P A P A ==4.甲乙丙三台机床独立工作,在同一时间内他们不需要工人照顾的概率分别为0.7,08,0.9,求在这段时间内,最多只有一台机床需人照顾的概率。
概率统计期中试题及答案

一、填空题1、设A,B 为两个随机事件, P(A)=0.5, P(A ∪B)=0.7,若A 与B 互斥,则P (B)= 0.2 。
2、从5双不同的鞋子中任取4只,则这4只鞋子中至少有两只鞋子配成一双的概率为 13/21 。
3、三个人进行射击,令A i 表示“第i 人击中目标”,则至少有两人击中目标为12132A A A A A A ++。
4、四人独立的破译密码,他们能译出的概率分别为1/5 , 1/4 ,1/3 ,1/6 , 则密码能被译出的概率 2/3 。
5、在相同条件下相互独立地进行 5 次射击,每次射击时击中目标的概率为 0.6 ,求击中目标的次数 X 的分布及最有可能击中次数为 B(5,0.6) ;3 。
6、设(X , Y )的联合概率分布列为则Z=max(X,Y)的分布列为7、某人连续向一目标射击,每次命中目标的概率为3/4,他连续射击直到命中为止,则射击次数为3的概率是 3/64 。
8、已知 (X , Y )的联合概率密度⎩⎨⎧>≤≤=-其它0,10,4),(2y x xe y x f y ,则E X = 2/3 。
9、若随机变量X ~N (-2,4),Y ~N (3,9),且X 与Y 相互独立。
设Z =2X -Y +5,则Z ~ N (-2,25) 。
X 和Y 的分布分别为:则(2)P X Y +==1/6 。
二、市场上出售的某种商品由三个厂家同时供货,其供应量第一厂家为第二厂家的两倍,第二、第三厂家相等,且第一、第二、第三厂家的次品率依次为2%,2%,4%。
在市场上随机购买一件商品,问(1)该件商品为正品的概率是多少?(2)若该件商品为次品,则它是第一厂家生产的概率为多少?解:设任购一件商品,它恰好来自第i 家厂生产的事件记为Ai ,i=1、2、3;设该商品恰好是次品事件记为B 。
(1))|()()|()()|()()(332211A B P A P A B P A P A B P A P B P ++= 025.040104.04102.04102.042==⨯+⨯+⨯=()1()0.975P B P B =-=(2)1111()()(|)(|)()()P A B P A P B A P A B P B P B ==2/40.020.40.025⨯==三、已知离散型随机变量X 分布函数为:()⎪⎩⎪⎨⎧≥<≤<≤<=41428.0214.010x x x x x F 。
《概率论与数理统计》期中试卷

杉达 各 专业 2007 级 专科《概率论与数理统计》期中试卷A 评析一、单项选择题(在每小题的四个备选答案中选出一个正确答案,每小题3分,共21分。
)1.设事件A 与B 相互独立,且P(A)>0, P(B)>0,则下列等式成立的是 ( )A 、AB=∅B 、P(AB ¯)=P(A)P(B ¯)C 、P(B)=1-P(A)D 、P(B |A¯)=0 【讲评】考点:事件的相互独立的性质。
如果事件A 与事件B 满足P(AB)=P(A)P(B),则称事件A 与事件B 相互独立。
本题: 因为A 与B 独立⇔事件A 与事件B  ̄独立⇔ P(AB¯)=P(A)P(B ¯) 选B 。
2.设甲、乙两人向同一目标射击,事件A, B 分别表示甲、乙击中目标,则AB¯¯表示 ( )A 、两人都没有击中目标B 、两人都击中了目标C 、至少有一人击中目标.D 、至少有一人没有击中目标.【讲评】考点:事件的运算的算律与实际意义。
对偶律:AB¯¯=A ¯∪B ¯ 本题: 因为AB ¯¯=A ¯∪B ¯,所以其实际意义为至少有一人没有击中目标. 选D 。
3.一批产品共10件,其中有3件次品,从这批产品中任取3件,则取出的3件中恰有一件次品的概率为 ( )A 、1/60B 、21/40C 、1/5D 、7/15【讲评】考点:P(A)=A 包含样本总个数样本点总数=N(A)N(S), 本题: N(S)= C 103=10×9×8/3! = 120 . N(A)= C 31×C 72= 63,P(A)=N(A)/N(S)=63/120 = 21/40 .选B 。
4.下列各函数中可作为随机变量分布函数的是 ( )A 、F 1(x)=⎩⎨⎧2x 0≤x ≤1 0 其他B 、F 2(x)=⎩⎨⎧0 x<0x 0≤x<11 x ≥1C 、F 3(x)=⎩⎨⎧-1 x<-1x -1≤x<11 x ≥1D 、F 4(x)=⎩⎨⎧0 x<02x 0≤x<12 x ≥1【讲评】考点:分布函数的性质。
概率统计期中考试试题

概率统计期中考试试题一、填空题一、填空题1设C B A ,,是三个随机事件,则A 、B 、C 中至多有2个事件发生可表示为个事件发生可表示为 . 2.掷一颗骰子,A 表示表示 “ 出现偶数点出现偶数点 ”,B 表示“ 点数小于4 ”, 则B A -表示表示 . 3.设C B A ,,是三个随机事件,()()()14P A P B P C ===,()16P AC =,()0P AB =、()0P BC =,则C B A ,,至少发生一个的概率为至少发生一个的概率为 . 4.设B A ,为两个随机事件,()0.6P A =,()0.2P A B -=,则()P AB = . 5.一批零件的次品率为0.2, 连取三次, 每次一件(有放回), 则三次中恰有两次取到次品的概率为则三次中恰有两次取到次品的概率为 . 6. 若随机变量X 在(1,6)上服从均匀分布,则方程210a aX ++=,有实根的概率,有实根的概率 。
7.设随机变量X 服从参数为(2,p )的二项分布,随机变量Y 服从参数为(3,p )的二项分布,若9/5}1{=³X P 则}1{³Y P 。
8.已知某厂的产品中2%有缺陷,求100件产品中3件有缺陷的概率件有缺陷的概率 。
9.在抛两枚均匀硬币中出现两个正面、一正一反、和两个反面的概率分别为0.25,0.5,0.25,若把两枚均匀硬币连抛6次,两个正面出现1次,一正一反出现3次,两个反面出现2次的概率是次的概率是 。
10.设(,)X Y 的概率密度为(),0,0(,)0,x y ce x y f x y others -+ì>>ï=íïî,则常数c 是 。
二、单项选择题二、单项选择题1.对掷一枚硬币的试验, “出现正面”称为(称为( )。
(A ) 随机事件随机事件 (B ) 必然事件必然事件 (C ) 不可能事件不可能事件 (D ) 样本空间样本空间2.设A 和B 是任意两个概率不为零的互斥事件,则下列结论中肯定正确的是(是任意两个概率不为零的互斥事件,则下列结论中肯定正确的是( )。
数学081082概率论期中试卷

1绍兴文理学院 2009 学年 1 学期数学 专业 08 级《概率论》期中试卷(答题卷)(考试形式: 闭卷 )(共10分)设考试时共有N 张不同的考签,现有n 个学生参加考试(N n ≥),每人随机地从中抽取一张,,求在考试结束之后至少有一张考签没有被抽到的概率. (共10分)设.)(,)(,)(r B A P q B P p A P === 试求:)(),(B A P B A P(共10 分)某城有N 辆汽车,车牌号从1到N,有一个人将他遇到的该城市的n 辆汽车的车牌号码(可)一一抄下,假设每一次这个人遇到这N 辆汽车中的任何一辆的机会是相同的,)1(N k k ≤≤的概率.四、(共15分)设一只盒子中装有a 个红球和b 个黑球,每次随机地取出一个球,记,2,1==i i R i 次取出的是红球,第 试分别对有放回和不放回抽样讨论事件21R R 与的独立性五、(共15分)设随机变量X 的分布函数为⎩⎨⎧<≥+-=-000)1(1)(x x e x x F x试求概率密度函数并求)10(≤≤X P2六、(共15分)一工厂生产的某种设备的寿命X (以年计)服从指数分布,且已知这种设备的平均寿命为4年。
工厂规定,出售的设备若在一年之内损坏可予以调换。
若工厂出售一台设备赢利100元,调换一台设备需花费300元。
试求厂方出售一台设备净赢利的数学期望。
七、(共10分)设),(~2σμN X ,令X e Y =,试求Y 的k 阶矩k EY八、(共15分)设随机变量X 服从)2,2(ππ-上的均匀分布,令X Y tan =,试求:(1)Y 的密度函数. (2) EY 是否存在?。
概率论期中试卷
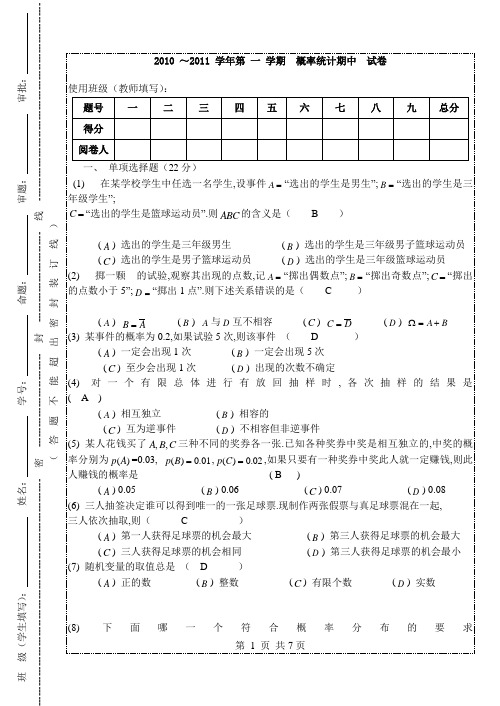
第 1 页 共7页班 级(学生填写): 姓名: 学号: 命题: 审题: 审批: ------------------------------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 -----------------------------------------------------------(答题不能超出密封装订线)2010 ~2011 学年第 一 学期 概率统计期中 试卷使用班级(教师填写):一、单项选择题(分) (1) 在某学校学生中任选一名学生,设事件A =“选出的学生是男生”;B =“选出的学生是三年级学生”;C =“选出的学生是篮球运动员”.则ABC 的含义是( B )(A ) 选出的学生是三年级男生 (B ) 选出的学生是三年级男子篮球运动员 (C ) 选出的学生是男子篮球运动员 (D ) 选出的学生是三年级篮球运动员 (2) 掷一颗 的试验,观察其出现的点数,记A =“掷出偶数点”;B =“掷出奇数点”;C =“掷出的点数小于5”;D =“掷出1点”.则下述关系错误的是( C )(A ) B A = (B ) A 与D 互不相容 (C ) C D = (D ) A B Ω=+(3) 某事件的概率为0.2,如果试验5次,则该事件 ( D )(A ) 一定会出现1次 (B ) 一定会出现5次(C ) 至少会出现1次 (D ) 出现的次数不确定(4) 对一个有限总体进行有放回抽样时,各次抽样的结果是 ( A )(A ) 相互独立 (B ) 相容的 (C ) 互为逆事件 (D ) 不相容但非逆事件(5) 某人花钱买了,,A B C 三种不同的奖券各一张.已知各种奖券中奖是相互独立的,中奖的概率分别为()p A =0.03, ()0.01p B =,()0.02p C =,如果只要有一种奖券中奖此人就一定赚钱,则此人赚钱的概率是 ( B )(A ) 0.05 (B ) 0.06 (C ) 0.07 (D ) 0.08 (6) 三人抽签决定谁可以得到唯一的一张足球票.现制作两张假票与真足球票混在一起,三人依次抽取,则( C )(A ) 第一人获得足球票的机会最大 (B ) 第三人获得足球票的机会最大(C ) 三人获得足球票的机会相同 (D ) 第三人获得足球票的机会最小 (7) 随机变量的取值总是 ( D )(A ) 正的数 (B ) 整数 (C ) 有限个数 (D ) 实数 (8)下面哪一个符合概率分布的要求第 2 页 (共8 页) 2 ( A )(A ) }{(1,2,3)6xp X x x === (B ) }{(1,2,3)4xp X x x === (C ) }{(1,1,3)3x p X x x ===- (D ) }{2(1,1,3)8x p X x x ===-(9) 两人独立破译密码,他们能单独译出的概率分别为11,54则此密码被译出的概率为( C )11()54A + (B )1154⨯ 1111()5454c +-⨯ (10) 设连续型随机变量X 的分布函数是()F x ,密度函数是()f x ,则}{p X x == ( C )(A )()F x (B )()f x (C ) 0 (D ) 以上都不对(11)设 E(X)=μ,Var(X)=2s ,则对任意常数 C , 必有( D )222222222(1) [()]()(2) [()][()](3) [()][()](4) [()][()]μμμ-=--=--<--≥-E X C E X C E X C E X E X C E X E X C E X二 填空题(每小题3分,共18分)1、设 随 机 变 量X 的 分 布 函 数 为()00sin 0212x F x A xx x ππ⎧⎪<⎪⎪=≤<⎨⎪⎪≥⎪⎩则 A = 1 。
(完整版)概率期中(理工)
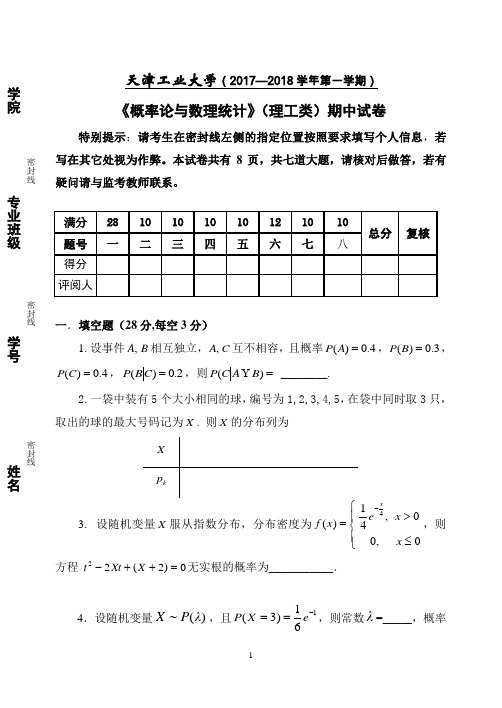
天津工业大学(2017—2018学年第一学期)《概率论与数理统计》(理工类)期中试卷特别提示:请考生在密封线左侧的指定位置按照要求填写个人信息,若写在其它处视为作弊。
本试卷共有8页,共七道大题,请核对后做答,若有疑问请与监考教师联系。
一.填空题(28分,每空3分)1.设事件B A ,相互独立,C A ,互不相容,且概率4.0)(=A P ,3.0)(=B P ,4.0)(=C P ,2.0)(=C B P ,则=)(B A C P Y ________.2.一袋中装有5个大小相同的球,编号为1,2,3,4,5,在袋中同时取3只,取出的球的最大号码记为X . 则X 的分布列为3. 设随机变量X 服从指数分布,分布密度为⎪⎩⎪⎨⎧≤>=-0,0,41)(4x x e x f x,则方程0)2(22=++-X Xt t 无实根的概率为___________.4.设随机变量)(~λP X ,且1613)(-==e X P ,则常数λ=_____,概率 -----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名=≥)1(X P ___________.5.设随机变量),(Y X 的联合分布列为则=Y时的条件分布列为6.设随机变量)2,1(~N X ,)4,3(~N Y ,且Y X ,相互独立,则~432+-Y X7.=))((Y X E E二.(10分)某市发生了一起出租车肇事逃逸案且已排除其他城市出租车作案可能,唯一目击者陈述是绿色车;该市出租车只有蓝绿两种颜色,各占95% 和5%;经警方测试,目击者对蓝绿两色的辨认准确概率均为95%.记事件A 为“该市一辆出租车是绿色”,B 为“该目击者判定一辆出租车是绿色”. (1)写出概率)(A P ,)(A P ;(2)写出条件概率)(A B P ,)(A B P ;(3)求目击者将该市任意一辆出租车判定为绿色的概率;(4)试分析警方可否根据目击者陈述只排查绿色出租车.-----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名----------------------装订线----------------------------------------装订线----------------------------------------装订线---------------------------------------------三.(10分)设某型号器件的寿命X 的概率密度为⎪⎩⎪⎨⎧≤>=0100,0 1000 ,1000)(2x x x x f现有5只此型号器件,它们损坏与否相互独立,试求这5只中没有寿命大于1500小时的概率.四.(10分)设随机变量X 的概率密度函数为⎩⎨⎧<<+=else x b ax x f X ,010 ,)(且已知85)21(=>X P . (1)求常数b a ,的值;(2)求Xe Y =的概率密度函数)(yf Y .-----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名----------------------装订线----------------------------------------装订线----------------------------------------装订线---------------------------------------------五.(10分)设随机变量Y ,X 相互独立,下表给出了联合分布列和边缘分布列中的部分数值.(1)请将其余数值填入表中括号里; (2)Y X Z +=1的分布列为(3))(2Y ,X max Z =的分布列为六、(12分)设二维随机变量),(Y X 的联合分布密度为⎪⎩⎪⎨⎧-≤≤=else xy y x f ,0 10,43),(2当(1) 求)(2X Y P >(2) 求边缘分布密度)(x f X ;(3) 求条件密度)(x y f X Y ;-----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名----------------------装订线----------------------------------------装订线----------------------------------------装订线---------------------------------------------七、(10分)设某商店经销某种商品,每月的销售量是随机变量且相互独立,都服从[0,1]上的均匀分布,即分布密度均为⎩⎨⎧≤≤=它其当 ,0 10,1)(x x f求两个月的总销售量Z 的概率分布密度)(z f Z .八、(10分)一个部件包括20个部分,每部分的长度是一个随机变量,它们是相互独立的,且服从同一分布,其期望为5.1mm ,均方差为05.0mm .规定该部件的总长度为)1.030(±mm 时产品合格,计算产品合格的概率.。
概率统计期中考试试卷

概率论与数理统计期中考试试卷一、填空题(每题3分,共15分)1.3人独立的破译一份密码,他们能单独译出的概率分别为41,31,51,则此密码被破译出的概率为 ___________. 2.已知X 的密度函数为⎩⎨⎧<<=其它,010,2)(x x x f ,用Y 表示对X 的3次独立重复观察中事件⎭⎬⎫⎩⎨⎧≤21X 出现的次数,则._________}2{==Y P3. 从五个数1,2,3,4,5中任选3个数,用X 表示这3个数中最大的一个,则________}4{=≥X P .4. 设)4,1(~N X ,,8413.0)1(0=Φ,9986.0)3(0=Φ则._________}31{=≤≤X P5. 已知X 的密度函数为+∞<<-∞=-x Ae x f x ,)(,则._________=A二.计算题(共85分)1.(15分)一种玻璃杯成箱出售,每箱10只,每箱不含次品的概率为0.8,每箱含有1只次品或2只次品的概率都为0.1,一顾客为了决定是否购买该产品,随机的查看箱中的3只,若无次品则买下,否则退回,试求: (1)随机选取一箱玻璃杯,顾客买下该箱玻璃杯的概率。
(2)假设顾客已经买下一箱玻璃杯,问箱中没有次品的概率。
2.(10分)已知1.0)(,6.0)(,4.0)(===B A P B P A P ,求)(),(),(A B P B A P B A P +3.(10分)已知⎩⎨⎧<<++=其它,010,)(~2x c bx ax x f X ,15.0,5.0==DX EX ,求c b a ,,4.(15分)已知]2,2[~-U X ,122+=X Y ,求Y 的密度函数)(y f Y5.(15分)已知离散型随机变量Y X ,相互独立,其联合分布及边缘分布如下表所示:(1)请将表格填写完整 (2)计算DY EY DX EX ,,,6.(20分)设二维随机向量),(Y X 概率密度为⎩⎨⎧<<<<=其它,0x y 0,1x 0,xy )y x,(f A ,(1)求常数A (2)求边缘密度)(),(y f x f Y X (3)判断Y X ,是否相互独立,并说明理由(4)求)1(≤+Y X P。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期中试卷
一. 填空(22分)
1.设C B A ,,为三个随机事件,用C B A ,,表示下列事件:
C B A ,,中至少有一事件发生__________, 其对立事件为______________.
2. 己知()5.0=A P ,()6.0=B P , ()8.0|=A B P ,则()B A P = .
3.设随机变量ξ服从[1,3]上的均匀分布,则)1(ξE = .
4. 设二维随机变量()Y X ,的联合密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他,010,10,),(y x kxy y x f ,则=k .
5. 设()(),
6.0,3.0=+=B A P A P 那么(1)若A 和B 互不相容,则()=B P ,
(2)若A 和B 相互独立,则()=B P ,(3)若B A ⊂,则()=B P .
6.若⎪⎭⎫ ⎝⎛51,10~B ξ,则()2
ξE =_________. 7.设随机变量()2
,2~σN X ,且()3.042=<<X P ,
则()=<0X P .
8.设4=DX ,9=DY ,()5.0,=Y X R ,则()=-Y X D 2 .
二、选择题: (21分)
1.某人射击时,中靶的概率为3/4,如果射击直到中靶为止,则射击次数为3的概率为( ).
3)43(. A 41)43(.2⨯ B 43)41(.2⨯ C 3
)41(. D
2. 若存在常数()0,≠a b a ,使得b a +=ξη,则()ηξ,R 为( ). ()1,..1.1.<-ηξR D a a
C B A
3. 设()0,,~2>σσμξN ,则随着σ的增大,概率()σμξ<-P ( ).
单调增大 A . 单调减小 B . 保持不变 C . 非单调变化 D .
4.设ηξ,是两个随机变量,则有( )正确.
()的相关矩和是ηξηξ,.R A ()的相关矩
和是**ηξηξ,.R B ()的绝对值可以大于一ηξ,.R C ()1,.=+=ηξξηηξR a b D 的充要条件存在线性关系和
5.设随机变量ξ的分布律为() ,,,2,1,n k b k P k ===λξ,则下列选项中正确的是( ). 1110.--=<<λλb A 且 110.-=<<λλb B 且
110.1-=<<-λλb C 且 1110.-+=<<λλb D 且
6.如果X 与Y 不相关,则( ).
()()()Y D X D Y X D A +=+. ()()()Y D X D Y X D B -=-.
()()()Y D X D XY D C =. 相互独立
与Y X D . 7. 设 ,,,,21n X X X 为独立同分布的随机变量序列,且()2,~σμN X
i , ,,,2,1n i =,则下列选项中错误的是( ) A) ⎪⎪⎭⎫ ⎝⎛∑=n n N X n n i i
21,~1σμ B) ⎪⎪⎭
⎫ ⎝⎛∑=n N X n n i i
21,~1σμ C) ()21,~σμn n N X
n i i ∑= D) 11lim 1=⎪⎪⎭⎫ ⎝⎛<-∑=∞→εμn i i n X n P
三、 (10分)库中有同样规格的产品10箱,其中5箱是甲厂,3箱是乙厂,2箱是丙厂生产的,甲、乙、丙厂产品的次品率分别为1/10,1/15,1/20, 现随机抽取一箱并从中任取一件产品。
求取出的产品是合格品的概率.
四、(16分) 设随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤<=111
000)(2x x Ax x x F
(1)求常数A ; (2)求X 落在⎪⎭
⎫ ⎝⎛-21,1内的概率; (3)求X 的密度函数. (4)求13+=X Y 的概率密度
五、(8分)某射手有三发子弹,每次射击命中目标的概率为0.8,如果命中了
就停止射击,如果不命中就一直射到子弹用尽.求子弹剩余数的分布律和分布函数.
六、(8分) 某地抽样调查结果表明,考生的外语成绩(百分制)近似服从
正态分布()2
12,72~N X ,试求考生成绩在60分至84分之间的概率.
七、(15分)设二维随机变量(X ,Y )的分布率为
求:(1)求a (2) ()()()Y X X D X E ,cov ,, (3)()Y X R ,; (4)()Y X D -
(5)()Y X Z ,max =的分布律;
8.设随机变量X 与Y 独立,其概率密度分别为
()⎩⎨⎧≤≤=其它 x x f X ,010,1, ()⎩⎨⎧≤>=-0,00,y y e y f y Y 求随机变量Y X Z +=的概率密度.。
