函数演示
《指数函数》指数函数与对数函数PPT演示课件

和友谊,从那些无所不能的狱友们弄到一把铁捶和一张明星的海报。一年又一年的监狱生活,带走了
对他来说,简直就是希望和救星,他找到监狱长,救他,说这是他可以翻案的机会,只要找到那名犯人,再加上他的学生做证,他就
讨论:
1
1
(1)如果 a<0,如 y=(-4)x,这时对于 x=4,x=2等,在实数范围内函数值
不存在;
(2)如果 a=0,
当 > 0 时, 恒等于 0,
当 ≤ 0 时, 无意义;
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
指数函数与对数函数
4.2 指数函数
-1-
首页
课标阐释
思维脉络
1.理解指数函数的概念和意义,
能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并
能解决与指数函数有关的定义
域、值域、定点问题.
3.逐步体会指数函数在实际问
题中的应用.
课前篇
自主预习
整部片子比较压抑,可能因为是讲述在监狱里发生的事情吧,但看完后心情却久久不能平静,那样的荡气回肠,那样的震憾人心!一
一
二
个年轻有为的银行家安迪,因为与妻子发生口角气跑了妻子,而当天妻子与她的情人双双被枪杀在床上,他成为最有杀人动机的嫌疑
犯,加上口吐莲花的律师,就这样,一个年轻有为的银行家被送了肖申克监狱。在监狱里发生了许多的事情,先是被老犯人们打赌,
第一晚谁会扛不住最先哭泣,最有权威的老犯人阿瑞看他白白净净,瘦瘦弱弱的样子,押了他两盒烟的赌注,第一次就让阿瑞输了赌
人教版二次函数与一元二次方程PPT演示课件

一元二次方程与二次函数 川流不息的人群热闹地挤在小小的骑廊下,或单独一人,或三三两两。有的低头私语,有的莞尔窃笑,没有大声的喧哗和吵闹,似乎谁都不愿破坏平和的气氛。放眼长长的一条街道,逛街的人都好象在做服装秀,尤其是那些披红戴绿穿着入时的少男少女,是中山路上最亮丽的风景。 有什么关系?
川流不息的人群热闹地挤在小小的骑 廊下, 或单独 一人, 或三三 两两。 有的低 头私语 ,有的 莞尔窃 笑,没 有大声 的喧哗 和吵闹 ,似乎 谁都不 愿破坏 平和的 气氛。 放眼长 长的一 条街道 ,逛街 的人都 好象在 做服装 秀,尤 其是那 些披红 戴绿穿 着入时 的少男 少女, 是中山 路上最 亮丽的 风景。
飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
川流不息的人群热闹地挤在小小的骑 廊下, 或单独 一人, 或三三 两两。 有的低 头私语 ,有的 莞尔窃 笑,没 有大声 的喧哗 和吵闹 ,似乎 谁都不 愿破坏 平和的 气氛。 放眼长 长的一 条街道 ,逛街 的人都 好象在 做服装 秀,尤 其是那 些披红 戴绿穿 着入时 的少男 少女, 是中山 路上最 亮丽的 风景。
考虑下列问题: (1)球的飞行高度能否达到 15 m? 若能,需要多少时间?
川流不息的人群热闹地挤在小小的骑 廊下, 或单独 一人, 或三三 两两。 有的低 头私语 ,有的 莞尔窃 笑,没 有大声 的喧哗 和吵闹 ,似乎 谁都不 愿破坏 平和的 气氛。 放眼长 长的一 条街道 ,逛街 的人都 好象在 做服装 秀,尤 其是那 些披红 戴绿穿 着入时 的少男 少女, 是中山 路上最 亮丽的 风景。
19.1.2函数的图像PPT演示课件

间?
x/min
12
应用
例2 下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x 表示时间,y 表
示小明离家的距离,小明家、食堂、图书馆在同一直线
上.
y/km
0.8 0.6
O
8
25 28
根据图象回答下列问题:
(2)小明在食堂吃早餐用了多少时间?
58
68
x/min
13
应用
例2 下图反映的过程是小明从家去食堂吃早餐,
19.1.2函数的图象(1)
1.一辆汽车的油箱中现有汽油50升,如果不再加 油,那么油箱中的油量y(升)随行驶里程x(公 里)的增加而减少,平均耗油量为0.1升/公里。
(1)写出表示y与x的函数关系的式子。 (2)指出自变量x的取值范围 (3)汽车行驶200公里时,油箱中还有多少油?
2
2.求下列函数中自变量的取值范围
上.
y/km
0.8 0.6
O
8
25 28
58
68
根据图象回答下列问题:
(5)图书馆离小明家多远?小明从图书馆回家的平均
速度是多少?
x/min
16
练习1:
300
y(米)
(1)小强让爷爷先上多少米?
60米
(2)山顶高多少米?谁先爬上山顶?
山顶离山脚的距离有300米,小强先爬上山顶.
240
180
爷爷
120
按照横坐标从小到大的顺序把描出的点用 平滑曲线依次连接起来
11
应用
例2. 下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x 表示时间,y 表
示小明离家的距离,小明家、食堂、图书馆在同一直线
幂函数 举例

4.1.2 数 幂函数举例
指数
对数
对数
1 . a n = a×a×a×…×a ( n 个 a 连乘 )
a 0 =1( a ≠ 0),
a
–n
=
1 an
(a ≠ 0, n N+),
a
1
n=
√na (a>0),
a
mn =
√na
m(a>0,m,n
N+,且
m n
为既约分数).
四个过桥人
有一处地势险恶的峡谷,涧底奔腾着湍急的水流,而所谓的桥则 是几根横亘在悬崖峭壁间光秃秃的铁索。一行四人来到桥头,一个盲 人、一个聋子,以及两个耳聪目明的正常人。四个人一个接一个抓住 铁索,凌空行进。
总 这个函数在 (0, ) 内是减函数.
结
函数的图像不经过坐标原点,
但是经过点(1,1).
二、幂函数应用
例 画出下列函数的图象:
(1)y = x;
(2)y = x
1 2
;
(3)y = x 2 ; 列表
(4)y = x -1 .
1 2
二、幂函数应用
例2 画出下列函数的图象:
(1)y = x;
(2)y = x
二、幂函数应用
例1 写出下列函数的定义域:
(1)y = x 3 ;
1
(2)y = x 2 ;
(3)y = x -2 ;
(4)y
=
x-
3 2
.
1 解:(3)函数 y = x-2,即 y = x2 ,
定义域为(-∞,0)∪(0,+∞);
二、幂函数应用
例1 写出下列函数的定义域:
(1)y = x 3 ;
y = x2,y = x3,y = x 及 y = x-1. 这些函数表达式的共同特征是什么? 你还能举出类似的函数吗?
反比例函数的图象PPT演示文稿

正比例函数
y=kx ( k≠0 )
直线 位置 一三 象限
k y =x ( k是常数,k≠0 )
反比例函数
双曲线 一三 象限
K>0
增减 y随x的增大而 y随x的增大而减小 性 增大 二四 二四 位置 象限 象限 增减 y随x的增大 而减小 性
K<0
y随x的增大 而增大
练习
5 二,四 象限,在每 1.函数 y = x 的图像在第_____ 增大 . y 个象限内,y 随 x 的增大而_____ 1 1 2. 双曲线 y = 3x 经过点(-3,___ 9 ) x m-2 3.函数 y = x 的图像在二、四象限,则m的 取值范围是 ____ m < 2. 1 减小 4.对于函数 y = 2x ,当 x<0时,y 随x的_____ 三 而增大,这部分图像在第 ________ 象限.
列表注意问题: ①列表时自变量取值要均匀和对称 ②x≠0 ③选整数较好计算和描点.
议一议:
比较反比例函数 和y= ①位置; ②变化趋势; ③与坐标轴的关系 有什么相同点和不同点?
6 y= x 6 x
y
的图象的
6 y=x
0 x
y
x
0
6 y= x
填表 分析 正比 例函 数和 反比 例函 数的 区别
函数 解析 式
y
y
(A)
0
x
(B)
0
x
y y 3.设x为一切实数,在下列 函数中,当x减小时,y的 (C) 0 0 x (D) x 值总是增大的函数是( C ) (A) y = -5x -1 ( B)y= x 2 (C)y=-2x+2; (D)y=4x.
课堂小结
函数几何画板课件 (5)

304(1) 奇函数
[适用章节]
数学(上册)第3.1.4节函数的奇偶性.
[使用目的]
教师通过使用课件直观演示奇函数定义的内涵,加深对奇函数定义的理解,是数形结合的具体体现.
[操作说明]
1 . 按钮“动画”,可以用来观察)
(x
f的值的关系;用鼠标拖动x可
f-和)
(x
更从容地观察显示)
f的值的关系.
(x
(x
f-和)
2 . 按钮“旋转180度”可以显示图象以坐标原点为中心旋转180度,与原图象重合.显示奇函数的图象以坐标原点为中心对称.
3 .双击函数解析式,可以自行改变函数解析式,教师可以自己再设计一两个奇函数和学生一起研究.。
if函数套用公式

if函数套用公式
在电子表格软件中,IF函数通常用于在满足特定条件时返回一个值,否则返回另一个值。
可以通过嵌套使用IF函数来实现更复杂的条件逻辑。
下面是一个简单的示例,演示如何嵌套使用IF函数:
假设有两个单元格A1和B1,你想根据A1的值执行不同的操作:
```excel
=IF(A1 > 0, "A1大于零", "A1不大于零")
```
上述公式的意思是,如果A1大于零,则返回字符串"A1大于零",否则返回字符串"A1不大于零"。
如果要添加更多条件,可以使用嵌套的IF函数。
例如:
```excel
=IF(A1 > 0, "A1大于零", IF(A1 = 0, "A1等于零", "A1小于零"))
```
这个公式首先检查A1是否大于零,如果是,则返回"A1大于零";如果不是,则进一步检查A1是否等于零,如果是,则返回"A1等于零",否则返回"A1小于零"。
你可以根据实际需求继续嵌套IF函数,但请注意,过度的嵌套可能会使公式难以理解和维护。
在这种情况下,考虑使用其他函数(如VLOOKUP、INDEX、MATCH等)或者将逻辑拆分成多个单独的公式,以提高可读性。
一次函数的图像和性质PPT演示课件

1.下列函数中,是正比例函数的是
A.y=-8x
B.y=-x8
C.y=5x2+6
D.y=-0.5x-1
2.一次函数 y=x-2 的图象不经过 ( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
( A)
•32
3.已知正比例函数 y=kx(k≠0)的图象经过点(1,-2),则正比例
函数的解析式为
考点聚焦
考点1 一次函数与正比例函数的概念
•1
考点2 一次函数的图象和性质 (2)正比例函数与一次函数的性质
第一、三 象限
第二、四 象限
•2
第一、二、 三象限
第一、三、 四象限
第一、二、 四象限
第二、三、 四象限
•3
考点3 两条直线的位置关系
k1≠k2 k1=k2,b1≠b2
•4
考点4 两直线的交点坐标及一次函数的图象与坐标 轴围成的三角形的面积
•21
变式题
5.已知直线 y=kx+b 经过点(k,3)和(1,k),则 k
的值为( B )
A. 3
B.± 3
C. 2
D.± 2
•22
变式题
▪ 6、在平面直角坐标系中,点O为原点,直线y
=kx+b交x轴于点A(-2,0),交y轴于点
B.若△AOB的面积为8,则k的值为( D ) ▪ A.1 B.2 C.-2或4 D.4或-4
图10-2 •26
变式题
▪ 1(1)根据图象信息可求得关于x的不等式 ▪ kx+b>0的解集为____________ ▪ (2)根据图象信息可求得关于x的不等式 ▪ kx+b≥0的解集为____________ ▪ (3)根据图象信息可求得关于x的不等式 ▪ kx+b≤0的解集为____________
函数的奇偶性PPT演示文稿

二、运用: 关注一半 ①对称性研究图象 ②函数值 ③单调性(奇不变偶变)
|x| 画出y=(1/2)
、y=-x/(1+|x|)的图 象,并研究其值域、单调区间。
重要思想:数形结合
例4:若奇函数f(x)在[-3,-2] 上是减函数,且最大值为6,则f(x) 在[2,3]上 A.是减函数且最大值-6 B.是减函数且最小值-6 C.是增函数且最大值-6 D.是增函数且最小值-6 变:已知函数f(x)是偶函数,y=f(x-2) 在[0,2]上是单调减函数,比较
2、对于定义域是R的任意奇函数f(x) 都有( ) A.f(x)―f(―x)>0(x∈R B.f(x)―f(―x)≤0(x∈R) C.f(x)•f(―x)≤0(x∈R) D.f(x)•f(―x)>0(x∈R)
3、函数y=f(x)与y=g(x)有相同的定 义域R,且定义域中任何x都有 f(x)+f(-x)=0,g(x)•g(-x)=1, 若g(x)=1的解是x=0, 则函数F(x)=2f(x)/[g(x)-1]+f(x)是 A.奇函数 B.偶函数 C.既奇又偶 D.非奇非偶
2
分段函数
2
x x (4) f ( x) x (a 0, a 1) a 1 2
(5) y log a ( x x 1)( a 0, a 1)
2
一奇偶性的判断: 若定义在[3-a,5]
上的函数 f(x) 是奇函数, 法1、定义法: 则a=?
①定义域是否正负对称
偶函数:f(-x)=f(x)→f(x)=f(-x)=f(|x|) ②尽量化简 等价式:f(x) -f(-x)=0(适用于对数形式) f(x)/f(-x)= 1(适用于指数形式) ③研究 f(x)与f(-x)=-f(x) f(-x)的关系式 奇函数: , 等价式: ___________________________
二次函数的图像和性质演示文稿(共81张PPT)

a的绝对值越大,开口越小
关于y轴对称
(0,k)
顶点是最低点
在对称轴左侧递减
在对称轴右侧递增
顶点是最高点
在对称轴左侧递增
在对称轴右侧递减
探究
画出二次函数
y 1(x1)2 2
y 12(x、1)2
的图像,并考虑它们的开口方向、对称轴和顶
点.
解:列表
x … -3 -2 -1 0 1 2 3 …
y1(x1)2 … -2
x … –1.5 –1 –0.5 0 0.5 1 1.5 … y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 … y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
问题1:当自变量x取同 一数值时,这两个函数 的函数值之间有什么关
系?反映在图象上,相应
的两个点之间的位置又
口方向、对称轴和顶点坐标,并填写下表.
y=ax2
向上 y轴 (0,0)
向下
y轴 (0,0)
4、二次函数y=2x2+1的图象与二次函数y= 2x2的图象开口方向、对称轴和顶点坐标是否
相同?它们有什么关系?我们应该采取什么 方法来研究这个问题?
画出函数y=2x2和函数y= 2x2+1的图象,并
加以比较
y2x2 1
y 2x2
x … –1 –0.6 –0.3 0 0.3 0.6 1 …
y=3x2 … 3 1.08 0.27 0 0.27 1.08 3 …
y=3x2–1 … 2 0.08 –0.73 – 1 –0.73 0.08 2 …
(2)二次函数 y=3x²-1 的图象
与二次函数
y=3x²的图象有
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
Excel高级函数使用IFOR和COUNTIFS函数进行复杂条件判断和计数

Excel高级函数使用IFOR和COUNTIFS函数进行复杂条件判断和计数Excel是一款功能强大的电子表格软件,广泛应用于各行各业的数据处理和分析工作中。
在实际使用中,经常会遇到需要根据多个条件进行判断和计数的情况。
IFOR函数和COUNTIFS函数作为Excel的高级函数,可以有效地帮助我们处理这些复杂的条件判断和计数任务。
本文将详细介绍IFOR函数和COUNTIFS函数的使用方法,并通过实例分析展示它们的应用。
一、IFOR函数的使用方法IFOR函数是Excel的逻辑函数之一,用于根据指定的条件进行判断,返回相应的结果。
其基本语法如下:=IFOR(条件,值1,条件1,值2,条件2...[默认值])其中,条件是要进行判断的条件表达式,值1、值2等是对应条件满足时需要返回的结果,[默认值]是可选的默认返回值。
IFOR函数支持多个条件的判断,当满足第一个条件时返回对应的值,如果不满足,则继续判断下一个条件,直到找到满足的条件为止。
如果所有条件都不满足,就返回默认值或者空值。
下面通过一个实例演示IFOR函数的使用方法。
假设我们有一个学生成绩表格,其中包含学生的姓名、科目和成绩。
现在需要根据学生的科目和成绩进行评级,并将评级结果填写到表格中。
首先,在评级列中输入IFOR函数,设置第一个条件为科目为"数学",对应的评级为"优秀"。
条件2为科目为"英语",对应的评级为"良好"。
条件3为科目为"物理",对应的评级为"及格"。
最后,设置[默认值]为"未评级"。
接下来,将IFOR函数拖拽填充到其他单元格中,即可自动根据不同的科目生成对应的评级结果。
二、COUNTIFS函数的使用方法COUNTIFS函数是Excel的统计函数之一,用于根据多个条件进行统计计数。
其基本语法如下:=COUNTIFS(范围1,条件1,范围2,条件2...)其中,范围1、范围2等是要计数的范围,条件1、条件2等是对应范围的计数条件。
如何在Excel中使用MAXIF函数进行条件最大值查找

如何在Excel中使用MAXIF函数进行条件最大值查找Excel是一款功能强大的电子表格软件,在数据处理和分析方面有着广泛的应用。
其中,MAXIF函数是Excel中的一个非常实用的函数,能够帮助用户在满足指定条件的数据中找到最大值。
本文将介绍如何在Excel中使用MAXIF函数进行条件最大值查找。
一、MAXIF函数的基本语法在使用MAXIF函数之前,我们需要先了解其基本语法。
MAXIF函数的基本语法如下:=MAXIFS(最大数的范围,条件范围1,条件1,[条件范围2,条件2]...)其中,参数的含义如下:- 最大数的范围:指定要进行最大值查找的数据范围;- 条件范围1:指定第一个条件的数据范围;- 条件1:指定第一个条件;- 条件范围2:(可选)指定第二个条件的数据范围;- 条件2:(可选)指定第二个条件;- ...MAXIF函数的返回值为满足所有条件的数据范围中的最大值。
下面我们通过一个具体的案例来演示如何使用MAXIF函数。
二、案例演示假设我们现在有一份销售数据表格,其中包含了产品名称、销售额和销售月份三列数据。
我们想要找到某个产品在某个月份中的最高销售额。
下面是这份表格的示例数据:产品名称销售额(万元)销售月份产品A 10 1月产品B 20 1月产品C 15 1月产品A 25 2月产品B 18 2月产品C 22 2月现在,我们要找到产品A在1月份中的最高销售额。
我们可以按照以下步骤进行操作:1. 创建一个新的单元格,用于输入MAXIF函数。
2. 输入MAXIF函数的开头部分:“=MAXIF(”。
3. 选择“销售额(万元)”列作为最大数的范围,进行最大值查找。
此时,我们可以使用鼠标拖动的方式选中整列数据,或手动输入数据范围,例如“A2:A7”。
4. 输入逗号(,),继续输入条件范围1:“销售月份”列。
5. 输入逗号(,),再输入条件1:“1月”。
6. 输入右括号()并按下回车键,即可得到产品A在1月份中的最高销售额。
excel计算余数的函数

excel计算余数的函数在E某cel中,我们可以使用函数来计算余数。
E某cel提供了几个函数可以帮助我们进行这样的计算,包括MOD函数、IF函数、以及一些数学运算函数。
下面将为您详细介绍和演示这些函数的用法。
1.MOD函数:MOD函数是E某cel中用于计算余数的函数。
其语法如下:=MOD(数值,除数)其中,数值是要进行计算余数的数值,除数是用来除以数值的数值。
示例:假设我们要计算16除以5的余数,我们可以使用MOD函数进行计算:=MOD(16,5)计算结果为1,表示16除以5的余数为1。
除了使用具体的数值,我们也可以使用单元格引用来计算余数。
例如,将16和5分别放在单元格A1和B1中,我们可以使用以下公式进行计算:=MOD(A1,B1)计算结果仍然为1。
2.IF函数:如果我们想在进行求余数的时候添加一些条件,我们可以使用IF函数来实现。
IF函数的语法如下:=IF(条件,值为真时的结果,值为假时的结果)其中,条件是一个逻辑表达式,如果为真则返回值为真时的结果,如果为假则返回值为假时的结果。
示例:假设我们要计算100除以3的余数,但是如果100小于10,则返回0。
我们可以使用IF函数进行如下计算:=IF(100<10,0,MOD(100,3))在这个例子中,100小于10,因此IF函数会返回0。
3.数学运算函数:除了MOD函数和IF函数,我们还可以使用E某cel中的一些数学运算函数来计算余数。
这些函数包括除法运算、取整函数以及求余函数等。
例如,我们可以使用INT函数来计算余数。
INT函数用于获取一个数的整数部分,其语法如下:=数值-INT(数值)我们可以使用该函数来计算余数,如下所示:=100-INT(100/3)某3这个公式将100除以3,然后将商与3相乘,再用100减去这个结果,得到余数。
这只是几个可以在E某cel中计算余数的函数的例子,E某cel还提供了其他更多的函数可以用于这样的计算。
excel ifs的使用

excel ifs的使用Excel是一个功能强大的电子表格软件,它提供了多种函数和工具,能够帮助用户进行数据分析、计算和处理。
其中,IFS函数是Excel 中一种常用的逻辑函数,用于根据多个条件进行判断和返回结果。
本文将介绍IFS函数的使用方法,并通过实例演示其在实际工作中的应用。
一、IFS函数的基本概念和语法IFS函数是Excel 2016及以上版本新增的函数,它的作用是根据多个条件进行判断,并返回满足条件的结果。
IFS函数的语法如下:IFS(条件1, 结果1, 条件2, 结果2, …, [条件n, 结果n])其中,条件1、条件2等表示要判断的条件,结果1、结果2等表示满足条件时要返回的结果。
IFS函数会按照条件的顺序进行判断,一旦某个条件满足,就返回对应的结果,并停止继续判断其他条件。
二、实例演示为了更好地理解和掌握IFS函数的使用,下面将通过几个实例来演示其具体应用。
1. 判断学生成绩等级假设有一份学生成绩单,其中A1单元格为学生成绩,要求根据不同的分数段判断学生的等级。
根据通常的标准,90分以上为优秀,80-89分为良好,70-79分为中等,60-69分为及格,60分以下为不及格。
可以使用IFS函数来实现判断,公式如下:=IFS(A1>=90, "优秀", A1>=80, "良好", A1>=70, "中等", A1>=60, "及格", A1<60, "不及格")这样,根据学生成绩的不同,即可自动返回对应的等级。
2. 判断奖金发放额度假设某公司根据员工的绩效评级来确定发放的奖金额度,绩效评级分为A、B、C、D四个等级,对应的奖金额度分别为5000元、3000元、1000元和0元。
可以使用IFS函数来实现判断,公式如下:=IFS(A1="A", 5000, A1="B", 3000, A1="C", 1000, A1="D", 0)这样,根据员工的绩效评级,即可自动返回对应的奖金额度。
Excel工作表中最常用的10个函数,中文解读,动图演示,易学易用
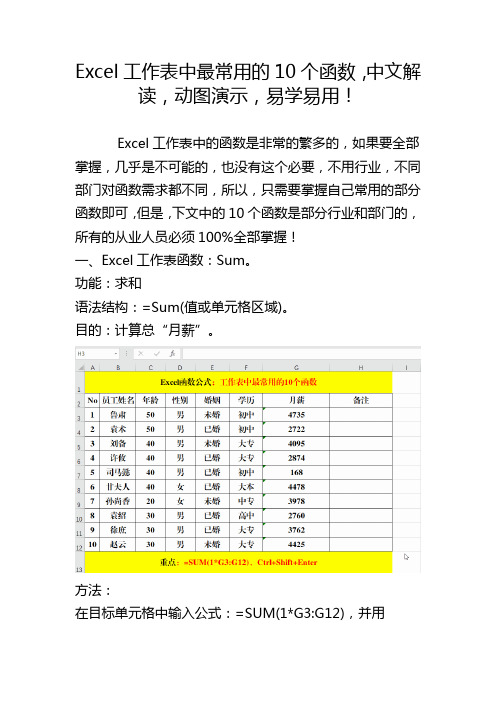
Excel工作表中最常用的10个函数,中文解读,动图演示,易学易用!Excel工作表中的函数是非常的繁多的,如果要全部掌握,几乎是不可能的,也没有这个必要,不用行业,不同部门对函数需求都不同,所以,只需要掌握自己常用的部分函数即可,但是,下文中的10个函数是部分行业和部门的,所有的从业人员必须100%全部掌握!一、Excel工作表函数:Sum。
功能:求和语法结构:=Sum(值或单元格区域)。
目的:计算总“月薪”。
方法:在目标单元格中输入公式:=SUM(1*G3:G12),并用Ctrl+Shift+Enter填充即可。
解读:因为“月薪”为文本型数值,所以直接用Sum函数求和时,得到的结果为0,此时我们需要将每个值转换为数值,所以给每个值乘以1,然后用Sum函数求和即可。
二、Excel工作表函数:If功能:判断是否满足某个条件,如果满足则返回一个值,如果不满足则返回另一个值。
语法结构:=IF(判断条件,条件为真时的返回值,条件为假时的返回值)。
目的:“月薪”>4000,返回“高”,>3000,返回“中”,否则返回“底”。
方法:在目标单元格中输入公式:=IF(G3>4000,"高",IF(G3>3000,"中","低"))。
解读:If函数除了常规的判断之外,还可以嵌套使用,公式的含义为:如果当前单元格的值>4000,则直接返回“高”,终止判断,否则继续执行当前单元格的值是否>3000,如果大于,返回“中”,否则返回“低”。
三、Excel工作表函数:Lookup功能:从单行或单列或数组中查找一个值。
Lookup具有两种形式:向量形式和数组形式。
(一)向量形式功能:从单行或单列中查找查找指定的值,返回第二个单行或单列中相同位置的值。
语法结构:=Lookup(查找值,查找值所在的范围,[返回值所在的范围])。
当“查找值所在的范围”和“返回值所在的范围”相同时,可以省略“返回值所在的范围”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.函数的概念 (1)在一个变化过程中,我们称数值__________的 量为变量,有些数值是 的,称它们为常量. (2)一般地,在一个变化过程中,如果有两个变量x 1.函数的概念 与y,并且对于 x在其取值范围内的每一个确定的 (1)在一个变化过程中,我们称数值 __________的量为变量,有些数值是 值,y都有 的,称它们为常量. 的值与其对应,那么就说,x (2)一般地,在一个变化过程中,如果有两 是 ,y是 x的函数. 个变量x与y,并且对于x在其取值范围内的 每一个确定的值,y都有 的值与其对 (3)用来表示函数关系的数学式子,叫做函数解析 应,那么就说,x是 ,y是x的函数. (3)用来表示函数关系的数学式子,叫做函 式或函数关系式.
例题讲解
(详见《金钥匙P36》)重点是: • 1、知识点1中的例1 • 2、知识点3中的跟踪训练3 • 3、知识点4中的跟踪训练
课 堂 通过本节课的复习,你 感 对 函数 有哪些新的认识? 悟
有哪些收获与体会?学科网
温馨提示: 画图象时要注意自变量取值范围,当图象有端点 时,要注意端点是否有等号,有等号时画实心 点,无等号时画空心圆圈.
自变量取值范围的确定方法 求函数自变量的取值范围时,首先要考虑自变量的取值必须使解析 式有意义. 1.自变量以整式形式出现,它的取值范围是全体实数. 2.自变量以分式形式出现,它的取值范围是使分母不为零的实 数. 3.当自变量以偶次方根形式出现,它的取值范围是使被开方数为 非负数;以奇次方根出现时,它的取值范围为全体实数. 4.当自变量出现在零次幂或负整数幂的底数中,它的取值范围是 使________________. 5.在一个函数关系式中,同时有几种代数式,函数自变量的取值 范围应是各种代数式中自变量取值范围的公共部分.
数解析式或函数关系式.
2.函数的表示法及自变量的取值范围 (1)函数有三种表示方法: , , ,这三 种方法有时可以互相转化. (2)当函数解析式表示实际问题或几何问题时,其自变 量的取值范围必须符合 意义或 意义. 3.函数的图象 对于一个函数,把自变量x和函数y的 每对对应值分别作为点的 与 在平面内描出相 应的点,组成这些点的图形叫这个函数的图象. (1)画函数图象,一般按下列步骤进行:列表、描点、 连线.学科网 (2)图象上任一点的坐标是解析式方程的一个解;反之 以解析式方程的任意一个解为坐标的点一定在函数图 象上.
