xxxx年中考数学压轴题52
中考数学压轴题50题精选及答案(全)(1)

3yMDCPAOQB x中考数学压轴题 50 题精选【001】如图,已知抛物线 y = a (x -1)2+ 3 (a≠0)经过点 A (-2,0) ,抛物线的顶点为 D ,过O 作射线OM ∥ AD .过顶点 D 平行于 x 轴的直线交射线OM 于点C , B 在 x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点 P 从点O 出发,以每秒 1 个长度单位的速度沿射线OM 运动,设点 P 运动的时间为t (s ) .问当t 为何值时,四边形 DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC = OB ,动点 P 和动点Q 分别从点O 和点 B 同时出发,分别以每秒 1 个长度单位和 2 个长度单位的速度沿OC 和 BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t (s ) ,连接 PQ ,当t 为何值时,四边形 BCPQ 的面积最小?并求出最小值及此时PQ 的长.BEQDPC【002】如图 16,在 R t△ABC 中,∠C =90°,AC = 3,AB = 5.点 P 从点 C 出发沿 C A 以每秒 1 个单位长的速度向点 A 匀速运动,到达点 A 后立刻以原来的速度沿 A C 返回;点 Q 从点 A 出发沿 A B 以每秒 1 个单位长的速度向点 B 匀速运动.伴随着 P 、Q 的运动,D E 保持垂直平分 P Q ,且交 P Q 于点D ,交折线 Q B -B C -C P 于点E .点 P 、Q 同时出发,当点 Q 到达点 B 时停止运动,点 P 也随之停止.设点 P 、Q 运动的时间是 t 秒(t >0).(1)当 t = 2 时,AP =,点 Q 到 A C 的距离是;(2)在点 P 从 C 向 A 运动的过程中,求△APQ 的面积 S 与t 的函数关系式;(不必写出 t 的取值范围)(3)在点 E 从 B 向 C 运动的过程中,四边形 Q B E D 能否成为直角梯形?若能,求 t 的值.若不能,请说明理由;(4)当 D E 经过点 C 时,请直.接.写出 t 的值. A图 16【003】如图,在平面直角坐标系中,已知矩形A B C D的三个顶点B(4,0)、C(8,0)、D(8,8). 抛物线y=a x2+b x过A、C两点.(1)直接写出点 A 的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒 1 个单位长度,运动时间为t秒.过点P作P E⊥A B交A C于点E,① 过点E作E F⊥A D于点F,交抛物线于点G.当t为何值时,线段E G最长?②连接E Q.在点P、Q运动的过程中,判断有几个时刻使得△C E Q是等腰三角形?请直接写出相应的t值。
(完整)中考数学压轴题精选含答案

一、解答题1.如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),与y轴交于点A (0,a),且a、p满足+(p﹣1)2=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP 的面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ是以BC为底边的等腰直角三角形,直角顶点为Q,若存在,请求出点Q坐标;若不存在,请说明理由.2.已知:如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,以OA,OC为边作矩形ABCO,矩形ABCO的面积是36.(1)求直线AC的解析式.(2)点P为线段AB上一点,点Q为第一象限内一点,连接PO,PQ,∠OPQ=90°,且OP=PQ,设AP的长为t,点Q的横坐标为d,求d与t的函数关系式.(不要求写出自变量t的取值范围)(3)在(2)的条件下,过点Q作QE∥PO交AB的延长线于点E,作∠POC的平分线OF交PE于点F,交PQ于点K,若KQ=2EF,求点Q的坐标.3.如图1,ΔABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点.(1)求证:∠BDE=∠ACD;(2)若DE=2DF,过点E作EG//AC交AB于点G,求证:AB=2AG;(3)将“点D在BA的延长线上,点E在BC上”改为“点D在AB上,点E在CB的延长线上”,“点F是DE与AC的交点”改为“点F是ED的延长线与AC的交点”,其它条件不变,如图2.①求证:AB·BE=AD·BC;②若DE=4DF,请直接写出SΔABC:SΔDEC的值.4.在平面直角坐标系xOy中,⊙O的半径为1.对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O的以点A为中心的“关联线段”是;(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A 为中心的“关联线段”,求t的值;(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.5.综合与探究如图,在平面直角坐标系中,点()0,10A ,点B 是x 轴的正半轴上的一个动点,连接AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90°,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(),0t(1)当6t =时,点M 的坐标是 ;(2)用含t 的代数式表示点C 的坐标;(3)是否存在点B ,使四边形AOBD 为矩形?若存在,请求出点B 的坐标;若不存在,请说明理由;(4)在点B 的运动过程中,平面内是否存在一点N ,使得以A 、B 、N 、D 为顶点的四边形是菱形?若存在,请直接写出点N 的纵坐标(不必要写横坐标);若不存在,请说明理由.6.抛物线1C :211211y x t x t ---≠=()()()与x 轴交于A 、B 两点(点A 在点B 的左侧)(1)若2t -=,求线段AB 的长;(2)猜想:随着t 的变化,A 、B 两点是否会有一定点?若会,请求出该定点的坐标;若不会,请说明理由;(3)求线段AB 的长(用t 表示)(4)若1t >,将抛物线1C 经过适当平移后,得到抛物线2C :221y x t t --=()+,A 、B 的对应点分别为D m (、n ),2E m (+、n ); ①求抛物线2C 的解析式;②将抛物线2C 位于直线DE 下方的部分沿直线DE 向上翻折,连同G 在DE 上方的部分组成一个新图形,记为图形G ,若直线132y x b b -=+(<)与圆形G 有且只有两个公共点,求b 的取值范围.7.如图1,直线l 1:y =kx 与直线l 2:y =﹣12x +b 相交于点A (4,3),直线l 2:y =﹣12x +b 与x 轴交于点B ,点E 为线段AB 上一动点,过点E 作EF ∥y 轴交直线l 1于点F ,连接BF .(1)求k、b的值;(2)如图2,若点F坐标为(8,6),∠OFE的角平分线交x轴于点M.①求线段OM的长;②点N在直线l1的上方,当△OFN和△OFM全等时,直接写出点N的坐标.8.如图,△ABC为等腰三角形,AB=AC,将CA绕点C顺时针旋转至CD,连接AD,E为直线CD上一点,连接AE;(1)如图1,若∠BAC=60°,∠ACD=90°,E为CD中点,23AB=,求△BCE的面积;(2)如图2,若∠ACD=90°,点E在线段CD上且∠DAE+∠ABC=90°,AE的延长线与BC的延长线交于点F,连接DF,求证:2=;BC DF(3)如图3,AB=1,∠BAC=90°,∠ACD=105°,若BE恰好平分∠AEC,点P为线段AE上的动点,点E′与点E关于直线DP对称,AE′与CD交于点Q,连接CE′,当'+-''的值最小时,直接写出CQ的值.2CE AE CE9.如图1,已知数轴上的点A、B对应的数分别是﹣5和1.(1)若P到点A、B的距离相等,求点P对应的数;(2)动点P从点A出发,以2个单位/秒的速度向右运动,设运动时间为t秒,问:是否存在某个时刻t,恰好使得P到点A的距离是点P到点B的距离的2倍?若存在,请求出t 的值;若不存在,请说明理由;(3)如图2在数轴上的点M和点N处各竖立一个挡板(点M在原点左侧,点N在原点右侧且OM>ON),数轴上甲、乙两个弹珠同时从原点出发,甲弹珠以2个单位/秒的速度沿数轴向右运动,乙弹珠以5个单位/秒的速度沿数轴向左运动.当弹珠遇到挡板后立即以原速度向反方向运动,若甲、乙两个弹珠相遇的位置恰好到点M和点N的距离相等,试探究点M对应的数m与点N对应的数n是否满足某种数量关系,请写出它们的关系式,并说明理由.10.在平面直角坐标系xOy中,已知点A(1,0)和点B(5,0).对于线段AB和直线AB外的一点C,给出如下定义:点C到线段AB两个端点的连线所构成的夹角∠ACB叫做线段AB关于点C的可视角,其中点C叫做线段AB的可视点.(1)在点D(-2,2)、E(1,4)、F(3,-2)中,使得线段AB的可视角为45°的可视点是;(2)⊙P为经过A,B两点的圆,点M是⊙P上线段AB的一个可视点.① 当AB为⊙P的直径时,线段AB的可视角∠AMB为度;② 当⊙P的半径为4时,线段AB的可视角∠AMB为度;(3)已知点N为y轴上的一个动点,当线段AB的可视角∠ANB最大时,求点N的坐标.11.图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在ABC中,AB AC∠=,MN分别为AB、BC边上一=,BACα点,连接MN,且MN AC∥,将ABC绕点B在平面内旋转.(1)观察猜想 ABC 绕点B 旋转到如图2所示的位置,若60α=︒,则AM CN 的值为______. (2)类比探究 若90α=︒,将ABC 绕点B 旋转到如图3所示的位置,求AM CN 的值. (3)拓展应用若90α=︒,M 为AB 的中点,4AB =,当AM BN ⊥时,请直接写出CN 的值.12.如图1,抛物线y 14=-x 2+bx +c 经过点C (6,0),顶点为B ,对称轴x =2与x 轴相交于点A ,D 为线段BC 的中点.(1)求抛物线的解析式;(2)P 为线段BC 上任意一点,M 为x 轴上一动点,连接MP ,以点M 为中心,将△MPC 逆时针旋转90°,记点P 的对应点为E ,点C 的对应点为F .当直线EF 与抛物线y 14=-x 2+bx +c 只有一个交点时,求点M 的坐标.(3)△MPC 在(2)的旋转变换下,若PC 2=2).①求证:EA =ED .②当点E 在(1)所求的抛物线上时,求线段CM 的长.13.如图1,在平面直角坐标系中,已知△ABC 中,∠ABC =90°,B (4,0),C (8,0),tan∠ACB =2,抛物线y =ax 2+bx 经过A ,C 两点.(1)求点A的坐标及抛物线的解析式;(2)如图2,过点A作AD⊥AB交BC的垂线于点D,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG取得最大值?最大值是多少?②连接EQ,在点P,Q运动过程中,t为何值时,使得△CEQ与△ABC相似?14.在平面直角坐标系中,抛物线:与x轴交于点A,B(点B 在点A的右侧).抛物线顶点为C点,△ABC为等腰直角三角形.(1)求此抛物线解析式.(2)若直线与抛物线有两个交点,且这两个交点与抛物线的顶点所围成的三角形面积等于6,求k的值.(3)若点,且点E,D关于点C对称,过点D作直线2l交抛物线于点M,N,过点E作直线轴,过点N作于点F,求证:点M,C,F三点共线.15.如图1:抛物线y=ax2+bx﹣4交x轴于点A、B,连接AC、BC,tan∠ABC=1,tan∠BAC=4.(1)抛物线的解析式为;(2)点P在第三象限的抛物线上,连接PC、PA,若点P横坐标为t,△PAC的面积为S,求S与t的函数关系式;(3)如图2,在(2)的条件下,当S=6时,点G为第四象限抛物线上一点,连接PG,CH ⊥PG 于点H ,连接OH ,若tan∠OHG 34=,求GH 的长. 16.已知抛物线24y ax bx =++(a ≠0)与x 轴交于点A (3-,0)、B (2,0),与y 轴交于点C ,直线y mx n =+经过两点A 、C .(1)求a ,b 的值;(2)如图1,点Р在已知抛物线上,且位于第二象限,当四边形PABC 的面积最大时,求点P 的坐标.(3)如图2,将已知抛物线向左平移12个单位,再向下平移2个单位.记平移后的抛物线为'y ,若抛物线'y 与原抛物线的对称轴交于点Q .点E 是新抛物线'y 的对称轴上一动点,在(2)的条件下,当△PQE 是等腰三角形时,请直接写出点E 的坐标.17.如图,已知四边形ABCD 内接于⊙O ,直径DF 交BC 于点G .(1)如图1,求证:∠BAD -∠BCF =90°;(2)如图2,连接AC ,当∠BAC =∠CFD +∠ACD 时,求证:CA =CB ;(3)如图3,在(2)的条件下,AC 交DF 于点H ,∠BAC =∠DGB ,45CG BG =,AC =9,求△CDH 的面积.18.同学们学过正方形与等腰三角形发现它们都是轴对称图形,它们之间有很多相似,在正边形ABCD 中,E 是对角线AC 上一点(不与点A 、C 重合),以AD 、AE 为邻边作平行四边形AEGD ,GE 交CD 于点M ,连接CG .(1)如图1,当12AE AC <时,过点E 作EF BE ⊥交CD 于点F ,连接GF 并延长交AC 于点H .求证:EB EF =;(2)在ABC 中,AB AC =,90BAC ∠=︒.过点A 作直线AP ,点C 关于直线AP 的对称点为点D ,连接BD ,CD 直线BD 交直线AP 于点E .如图2,①依题意补全图形;②请用等式表示线段EB ,ED ,BC 之间的数量关系,并予以证明.19.已知抛物线y 14=-kx 212-(k ﹣2)x +2与y 轴交于点A ,与x 轴交于B 、C (点B 在点C 的左边).(1)直接写出点B 的坐标;(2)当k =1时(如图),求:①在直线AC 上方的抛物线上一点M ,求点M 到直线AC 的最大距离及此时点M 的坐标;②将线段OA 绕x 轴上的动点P (m ,0)顺时针旋转90°得到线段O ′A ′,若线段O ′A ′与抛物线只有一个公共点,请结合函数图象,求m 的取值范围.20.如图,在平面直角坐标系中,抛物线的对称轴是直线1x =,且与x 轴交于A ,B 两点,与y 轴交于点()0,3C -,OB OC =.(1)求抛物线的解析式.(2)在抛物线上是否存在点Q,使得BCQ△是以BC为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.(3)设抛物线上的一点P的横坐标为m,且在直线BC的下方,求使BCP的面积为最大整数时点P的坐标.【参考答案】**科目模拟测试一、解答题1.(1)y=3x-3;(2)(-2,3);(3)Q的坐标为(-72,0)或(0,74)或(0,132)【解析】【分析】(1)根据算术平方根的非负性及偶次方的非负性得到a+3=0,p-1=0,求出a,p,得到点P,A的坐标,设直线AP的解析式为y=kx+b,利用待定系数法求出函数解析式;(2)过M作MD交x轴于D,连接AD,由MD,△MAP的面积等于6,顶点△DAP的面积等于6,求出DP,得到点D坐标,求出直线DM的解析式,即可求出M的坐标;(3)设B(t,3t-3),分三种情况,①当点Q在轴负半轴时,过B作BE⊥x轴于E,证明△BEQ≌△QNC(AAS),得到O Q=QE-OE=ON+QN,即4-t=2+3-3t,求出t值即可;②当Q在y轴正半轴上时,过C作CF⊥y轴于F,过B作BG⊥y轴于G,证明△CQF≌△QBG(AAS),得到O Q=OG-QG=OF-QF,即3t-3-2=4-t,求出t即可;③当Q在y轴正半轴上时,过点C作CF⊥y轴于F,过B作BT⊥y轴于T,同②可证△CFQ≌△QTB(AAS),得到OQ=OT+QT=OF+QF,即3t-3+2=4+t,求出t值即可.(1)解:∵+(p﹣1)2=0.∴a+3=0,p-1=0,解得a=-3,p=1,∴P(1,0),A(0,-3),设直线AP的解析式为y=kx+b,∴,解得,∴直线AP的解析式为y=3x-3;(2)解:过M作MD交x轴于D,连接AD,∵MD,△MAP的面积等于6,∴△DAP的面积等于6,∴,即,∴DP=4,∴D(-3,0)设直线DM的解析式为y=3x+c,则,∴c=9,∴直线DM的解析式为y=3x+9,令x=-2,得y=3,∴M(-2,3);(3)解:存在设B(t,3t-3),①当点Q在x轴负半轴时,过B作BE⊥x轴于E,如图,∴OE=t,BE=3-3t,∵△BCQ是以BC为底边的等腰直角三角形,∴BQ=CQ,∠BQC=90°,∴∠BQE=90°-∠NQC=∠QCN,又∵∠BEQ=∠QN C,∴△BEQ≌△QNC(AAS),∴QN=BE=3-3t,QE=CN=4,∴OQ=QE-OE=ON+QN,即4-t=2+3-3t,∴t=12,∴OQ=72,∴Q(-72,0);②当Q在y轴正半轴上时,过C作CF⊥y轴于F,过B作BG⊥y轴于G,如图,∴BG=t,OG=3t-3,∵△BCQ是以BC为底边的等腰直角三角形,∴BQ=CQ,∠BCQ=90°,∴∠CQF=90°-∠BQG=∠GBQ,又∵∠CFQ=∠BGQ=90°,∴△CQF≌△QBG(AAS),∴CF=QG=2,QF=BG=t,∴O Q=OG-QG=OF-QF,即3t-3-2=4-t,∴t=94,∴OQ=4-t=74,∴Q(0,74);③当Q在y轴正半轴上时,过点C作CF⊥y轴于F,过B作BT⊥y轴于T,如图,∴BT=t,OT=3t-3,同②可证△CFQ≌△QTB(AAS),∴CF=BT=t,QF=CF=2,∴O Q=OT+QT=OF+QF,即3t-3+2=4+t,∴t=52,∴OQ=4+t=132,∴Q(0,132);综上,Q的坐标为(-72,0)或(0,74)或(0,132).【点睛】此题是一次函数与图形的综合题,考查了待定系数法求函数解析式,全等三角形的判定即性质,等腰直角三角形的性质,算术平方根的非负性及偶次方的非负性,熟记全等三角形的判定即性质是解题的关键.2.(1)直线AC的解析式为y=﹣x+6;(2)d=4-t;(3)Q(212,1).【解析】【分析】(1)先由解析式求出得A、C点的坐标,得OA=OC,得四边形ABCO为正方形,再根据正方形的面积求得边长,便可得b的值;(2)过点Q作QG⊥AB交AB延长沿于点G,证明Rt△AOP≌Rt△GPQ(AAS),得到AP=GQ,进而求得结论便可;(3)过点P作PH⊥OF于点H,延长PH交EQ的延长线于点R,EQ的延长线与x轴交于点N,过Q作QM⊥x轴于点M.证明Rt△AOP≌Rt△GPQ(CCS),得PK=QR,∠R=∠OKP,再证明∠R=∠FPR,得EP=ER,再证FE=NR,设FE=NR=k,NQ=m,在Rt△PQE中,由勾股定理列出方程,得到k与m的关系,解Rt△PQE得tan∠PEQ,进而把这个函数值运用到△OAP中,求得t的值,再运用(2)中结论得Q的纵坐标d的值,再运用到△QNM中求得NM,NQ的值,进而求得ON,便可得Q的横坐标的值.【详解】解:(1)∵直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,A b C b,∴(,0),(0,)∴OA=OC=b,∴矩形ABCO为正方形,∵矩形ABCO的面积是36.∴b=6,即直线AC的解析式为y=﹣x+6;(2)如图,过点Q作QG⊥AB交AB延长沿于点G,∵∠OPQ=90°,∴∠APO+∠GPQ=90°,∵∠APO+∠AOP=90°,∴∠AOP=∠GPQ,∵在矩形ABCO,∠OAP=90°,QG⊥AB,∴∠QGP=∠OAP=90°,∵PQ=OP,∴Rt△AOP≌Rt△GPQ(AAS),∴AP=GQ,∵AP=t,∴GQ=t,∴d=4-t;(2)过点P 作PH ⊥OF 于点H ,延长PH 交EQ 的延长线于点R ,EQ 的延长线与y 轴交于点N ,过Q 作QM ⊥y 轴于点M .则AP =t ,QM =d ,且d =6-t .∵OF 平分∠POC ,∴∠POF =∠COF =∠PFO ,∴PF =PO ,∵PH ⊥OF ,∠OPQ =90°,∴∠OPH =∠FPH ,∠KPH =∠POH ,在△OPK 和△PQR 中,90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩====, ∴△OPK ≌△PQR (ASA ),∴PK =QR ,∠R =∠OKP ,∵∠OKP +∠POK =∠POK +∠OPH =90°,∴∠OKP =∠OPH ,∴∠R =∠OPH ,∵PO =PF ,PH ⊥OF ,∴∠OPH =∠FPH ,∴∠R =∠FPR ,∴EP =ER ,∵PE ∥ON ,OP ∥EN ,∴四边形OPEN 是平行四边形,∴EN =PO =PF ,∴PE -PF =ER -EN ,∴FE =NR ,设FE=NR=k,则KQ=2FE=2k,又设NQ=m,∴PK=QR=m+k,∴PQ=m+3k,∴PO=EN=PF=m+3k,∴QE=EN-QR=m+3k-m=3k,PE=PF+FE=4k+m,在Rt△PQE中,∵PE2=PQ2+QE2,∴(4k+m)2=(3k+m)2+(3k)2,∴k1=0(舍去),k2=m,∴PQ=4m,QE=3m,∴tan∠PEN=43 PQQE=,∵OP∥EN,∴∠OPA=∠PEN,∴tan∠APO=43,∵AO=6,∴AP=4.5,∴t=4.5,∴QM=d=6-t=1.5,∵PE∥OC,∴∠QNM=∠PEN,∴tan∠QNM=tan∠PEN=43,∴NM=9 tan8QMQNM=∠,∴m=NQ158 =,∴PE=ON=4k+m=5m=758,∴OM=ON+NM=212,∴Q(212,1).【点睛】本题是一次函数与四边形的综合题,主要考查了一次函数的图象与性质,全等三角形的性质与判定,正方形的性质,旋转的性质,解直角三角形的应用,等腰三角形的性质与判定,平行四边形的性质与判定,是一道综合性极强的题目,解决这类问题常用到数形结合、方程和转化等数学思想方法.构造全等三角形是解题的关键,也是问题的突破口.3.(1)见解析;(2)见解析;(3)①见解析;②16:15.【解析】【分析】(1)运用等腰三角形的性质及三角形的外角性质就可解决问题.(2)如图1,证明△DCA ≌△EDG (AAS ),得AD =EG ,根据等腰三角形的判定得:DG =AB ,由平行线分线段成比例定理得:2DE DG DF AD ==,由此可得结论; (3)①如图2,作辅助线,构建三角形全等,证明△DCA ≌△EDG (AAS ),得DA =EG ,再证明△ACB ∽△GEB ,列比例式可得结论;②如图3,作辅助线,构建△ABC 和△DCE 的高线,先得14AF AD EG DG ==,设AF =a ,则EG =AD =4a ,DG =16a ,根据AH ∥PD ,得123164PD BD a AH AB a ===,设PD =3h ,AH =4h ,根据EG ∥AC ,同理得41164BG BE a AB BC a ===,设BE =y ,BC =4y ,利用三角形面积公式代入可得结论.【详解】(1)证明:∵AC =AB ,∴∠ACB =∠B ,∵DC =DE ,∴∠DCE =∠DEC ,∴∠ACD +∠ACB =∠B +∠BDE ,∴∠BDE =∠ACD ;(2)证明:如图1,∵EG ∥AC ,∴∠DAC =∠DGE ,∠BEG =∠ACB ,由(1)知:∠DCA =∠BDE ,∵DC =DE ,∴△DCA ≌△EDG (AAS ),∴AD =EG ,∵∠B =∠ACB =∠BEG ,∴EG =BG =AD ,∵DE =2DF ,AF ∥EG , ∴2DE DG DF AD==, ∴DG =2AD =2AG ,∴AB =DG =2AG ;(3)解:①如图2,过点E 作EG ∥AC ,交AB 的延长线于点G ,则有∠A =∠G ,∵AB =AC ,CD =DE ,∴∠ACB =∠ABC ,∠DCE =∠DEC ,∴∠ACD +∠DCE =∠EDG +∠DEC ,∴∠ACD =∠EDG ,在△DCA 和△EDG 中,∵ACD EDG A G CD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△DCA ≌△EDG (AAS ).∴DA =EG ,∵AC ∥EG ,∴△ACB ∽△GEB ,∴AC BC EG BE=, ∵EG =AD ,AC =AB ,∴AB •BE =AD •BC ;②如图3,过A 作AH ⊥BC 于H ,过D 作DP ⊥BC 于P ,则AH ∥PD ,∴AF AD DF EG DG DE==,∵DE=4DF,∴14 AF ADEG DG==,设AF=a,则EG=AD=4a,DG=16a,∵∠ACB=∠ABC,∴∠GBE=∠BEG,∴BG=EG=4a,∴BD=12a,∵AH∥PD,∴123164 PD BD aAH AB a===,设PD=3h,AH=4h,∵EG∥AC,∴41164 BG BE aAB BC a===,设BE=y,BC=4y,∴S△ABC=12BC•AH=4?42y h=162yh=8yh,S△DCE=12CE•PD=5?32y h=152yh,∴S△ABC:S△DEC=8yh:152yh=16:15.【点睛】本题是三角形的综合题,考查了相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质和判定等知识,第三问有难度,利用参数表示各线段的长是本题的关键,综合性较强.4.(1)B2C2;(23)OA最小值为1,相应的BC=OA最大值为2,相应的BC=【解析】【分析】(1)结合题意,根据旋转和圆的性质分析,即可得到答案;(2)根据题意,分B C''在x轴上方和x轴上方两种情况;根据等边三角形、勾股定理、全等三角形的性质,得AD OD==(3)结合题意,得当AC'为⊙O的直径时,OA取最小值;当A、B'、O三点共线时,OA 取最大值;根据勾股定理、等腰三角形的性质计算,即可得到答案.【详解】(1)线段B 1C 1绕点A 旋转得到的11B C '',均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”;线段B 2C 2绕点A 旋转得到的22B C '',如下图:∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”;线段B 3C 3绕点A 旋转得到的33B C '',均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”;故答案为:B 2C 2;(2)∵△ABC 是边长为1的等边三角形,点A (0,t ),⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况:当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:∵1OB OC ''== ∴1122B D B C '''==∴2232OD OB B D ''=-= ∵△ABC 是边长为1的等边三角形,即△AB C ''是边长为1的等边三角形,∴AC D OC D ''∠=∠,AD B C ''⊥∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =;当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:同理,3AO AD OD =+=∴()0,3A -;∴t 3=-;∴3t =或3-;(3)当AC '为⊙O 的直径时,OA 取最小值,如下图:∴OA 最小值为1,90AB C ''∠=︒∴223BC B C AC AB ''''==-=当A 、B '、O 三点共线时,OA 取最大值,2OA AC '== ,如下图:作AE OC '⊥交OC '于点E ,作C F AO '⊥交AO 于点F ,如下图∵2OA AC '== ∴1122OE OC '== ∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '== ∴2214OF OC C F ''=-= ∴34B F OB OF ''=-= ∴26BC B C C F B F ''''==+=∴OA 最小值为1,相应的3BC =;OA 最大值为2,相应的62BC =. 【点睛】 本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识;解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质,从而完成求解.5.(1)(3,5)M ,(2)1(5,)2C t t +;(3)(20,0)B ;(4)154或10. 【解析】【分析】(1)利用中点坐标公式计算即可.(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .证明()MEB BFC AAS ∆≅∆,利用全等三角形的性质即可解决问题.(3)如图2中,存在.由题意当CF OA =时,可证四边形AOBD 是矩形,构建方程即可解决问题.(4)分三种情形:①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为6.③因为BD AB ≠,所以不存在以AD 为对角线的菱形.【详解】解:(1)如图1中,(0,10)A ,(6,0)B ,AM BM =,(3,5)M ∴,(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .//ME OA ,AM BM =,12OE EB t ∴==,152ME OA ==, 90MEB CFB CBM ∠=∠=∠=︒,90MBE CBF ∴∠+∠=︒,90MBE BME ∠+∠=︒,BME CBF ∴∠=∠,BM BC =,()MEB BFC AAS ∴∆≅∆,5BF ME ∴==,12CF BE t ==, 5OF OB BF t ∴=+=+,1(5,)2C t t ∴+. (3)存在.如图2中,作ME OB ⊥于E ,CF x ⊥轴于F .理由:由题意当=10CF OA =时,//OA CF ,∴四边形AOFC 是平行四边形,90AOF ∠=︒,∴四边形AOFC 是矩形,90DAO AOB DBO ∴∠=∠=∠=︒,∴四边形AOBD 是矩形,又∵由(2)得12CF BE t ==,即:1102t =,解得:20t =.(20,0)B ∴. (4)①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.AD BD =,BAD ABD ∴∠=∠,//BD y 轴,OAB ABD ∴∠=∠,OAB BAD ∴∠=∠.tan tan OAB BAD ∴∠=∠, ∴12OB BC OA BA ==,即1102t =, 5t ∴=,5OB ∴=,设AN NB m ==,在Rt OBN △中,则有2225(10)m m =+-,解得254m =, 25151044ON OA AN ∴=-=-=, ∴点N 的纵坐标为154. ②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为10.③BD AB ≠,∴不存在以AD 为对角线的菱形.综上所述,满足条件的点N 的纵坐标为154或10. 【点睛】本题属于四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,翻折变换,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.6.(1)6;(2)会,(1,0);(3)22t -;(4)①y 2=(x -2)2+1;②52<b <3. 【解析】【分析】(1)根据题意令y 1=0,解得x ,即AB 点的横坐标,进而即可求得AB 的长;(2)由题意可知当x =1时,y 1=0,进而可以得出该定点的坐标;(3)由(1)可知AB 点的横坐标,进而即可用t 表示线段AB 的长;(4)①由题意可知t >1时,点A 、B 的坐标分别为:(1,0),(2t -1,0),进而依据AB =DE ,即可求解;②根据题意将点D 、E 的坐标代入抛物线表达式得:m =1,故点D 、E 的坐标为:(1,2)、(3,2),当直线过点D 时,2=-12×1+b ,解得:b =52,同理直线过点E 时,b =72,而b <3,即可求解. 【详解】解:(1)令y 1=0,解得:x =1或2t -1,当t =-2,则x =1或-5,所以线段AB =1-(2t -1)=2-2t =6; (2)会有一定点,理由如下:当x =1时,y 1=0,所以会有一定点(1,0);(3)由(1)可知当y 1=0,解得:x =1或2t -1,所以线段AB 的长为:1(21)22t t --=-;(4)①t >1时,点A 、B 的坐标分别为:(1,0),(2t -1,0),因为平移距离相等可得AB =DE ,即2t -1-1=m +2-m =2,解得:t =2,所以点B (3,1),把t =2,代入221y x t t --=()+, 可得抛物线C 2的解析式为:y 2=(x -2)2+1;②将点D 、E 的坐标代入抛物线表达式得:n =(m -2)2+1=(m +2-2)2+1,解得:m =1,故点D 、E 的坐标为:(1,2)、(3,2);图象G 如下图所示,当直线过点D 时,2=-12×1+b ,解得:b =52, 同理直线过点E 时,b =72,而b <3, 所以b 的取值范围为:52<b <3. 【点睛】 本题考查的是二次函数综合运用,涉及到一次函数、图形过定点等,其中(3),要注意分类讨论避免遗漏.7.(1)34k =,5b =;(2)①OM =5;②()3,6N 或724,55N ⎛⎫ ⎪⎝⎭【解析】【分析】(1)分别将将(4,3)A 代入y kx =和12y x b =-+中,求解即可; (2)①设直线AB 与y 轴交与点C ,与FM 交于点D ,证明△AFD ≌△EFD ,得到AD =ED ,利用中点坐标公式求得点D 坐标,用待定系数法求得直线FD 的函数表达式,令0y =,即可求得点M 的坐标,从而求得OM ;②点N 在直线l 1的上方,当△OFN 和△OFM 全等时,满足题意的点N 有两个,分别画出相关的图形,分类讨论求解即可.【详解】解:(1)∵直线l 1:y kx =和直线l 2:12y x b =-+相交于点A ∴将(4,3)A 代入y kx =中,得:43k =解得:34k = ∴将(4,3)A 代入12y x b =-+中,得:1432b -⨯+= 解得:5b =∴3,54k b == (2)① 设直线AB 与y 轴交与点C ,与FM 交于点D ,如下图:∵34k =,5b = ∴直线l 1的函数表达式为34y x =,直线l 2的函数表达式为152y x =-+ ∵(4,3)A∴22345OA +设直线AB 与y 轴交与点C ,与FM 交于点D则()0,5C∴5OC =∴5OA OC ==∴∠OCA =∠OAC∵//FE y 轴∴∠OCA =∠FEA又∵∠OAC =∠FAE∴∠FAE =∠FEA∴FA =FE又∵FM 是∠OFE 的角平分线∴∠AFM =∠EFM又∵FD =FD∴△AFD ≌△EFD∴AD =ED∴点D 为AE 的中点∵//FE y 轴∴点F 和点E 的横坐标相同将8x =代入152y x =-+中,得1y = ∴()8,1E∵(4,3)A ,()8,1E∴()6,2D设线段FM 所在的直线函数表达式为()0y ax b a =+≠将()()8,6,6,2F D 代入y ax b =+中,得:8662k b k b +=⎧⎨+=⎩解得:210k b =⎧⎨=-⎩∴线段FM 所在的直线函数表达式为210y x =-令0y =,得2100x -=解得:5x =∴()5,0M∴OM =5② 当,OFN FOM 全等时,有两种情况,情况一,如下图所示:∵OFN FOM ≅△△∴∠OFN =∠FOM ,FN =OM ,ON =FM∴//FN OM∵OM =5∴FN =5,8F x =∴853N x =-=,6N F y y ==∴()3,6N情况二,当△OMF 和△ONF 关于直线l 1对称时,如下图所示:∵OFN FOM ≅△△∴ON =OM =5,∠NOF =∠MOF∵OP =OP∴△NOP ≌△MOP∴PN =PM∵()8,6F ∴226810OF + 又∵1122OMF F S OM y OF PM =⋅=⋅ ∴F OM y OF PM ⋅=⋅ ∴56==310PM ⨯ ∴MN =2PM =6,OP 2222534OM PM -- ∵1122OMN N S MN OP OM y =⋅=⋅△ ∴642455N y ⨯== ∴2222247555N N x ON y ⎛⎫=-=- ⎪⎝⎭∴724,55N ⎛⎫ ⎪⎝⎭ 综上所述,满足题意点有两个,分别是:()3,6N 或724,55N ⎛⎫ ⎪⎝⎭ 【点睛】本题考查用待定系数法求一次函数表达式,三角形全等的性质和证明,两条直角交点的求法以及三角形的等面积法等知识点,牢记相关内容并能灵活应用数形结合思想解题是本题的关键.8.(1)32;(2)见解析;(3)222- 【解析】【分析】(1)过点,,A E D 分别作BC 的垂线,垂足分别为,,H I G ,连接BE ,证明Rt AHC Rt CGD △≌△,根据含30度角的直角三角形的性质求得CE ,进而求得EI ,根据三角形的面积公式求解即可;(2)过点,A D 分别作BC 的垂线,交BC 及BC 的延长线于点,H G ,证明Rt AHC Rt CGD △≌△,进而可得HAF △是等腰直角三角形,DGF 是等腰直角三角形,即可证明2222DF DG HC BC ===,即2BC DF =; (3)延长,EA EC ,过点B 分别作,BN EN BM CM ⊥⊥,垂足分别为,N N ,解直角三角形Rt ABN △可得45ABN ∠=︒,进而可得30AEC NEM ∠=∠=︒,进求得DE 的长度,由点P 为线段AE 上的动点,点E ′与点E 关于直线DP 对称,AE ′与CD 交于点Q ,连接CE ′,构造相似三角形,在线段DC 上截取322DF =-,连接E F ',则CDE E DF ''△∽△,求得目标等量关系()21E F CE ''=-,根据()221CE AE CE CE AE E F AE AF '''''+-=-+=+≥''则当,,A E F '三点共线时,取得最小值,此时Q 点与F 点重合,根据CQ CF CD FD ==-即可求得答案.【详解】(1)如图,过点,,A E D 分别作BC 的垂线,垂足分别为,,H I G ,连接BE ,AB =AC ,将CA 绕点C 顺时针旋转至CD ,AC CD ∴=∠BAC =60°,ABC ∴是等边三角形,AC CD ∴=,60BAC ∠=︒AH BC ⊥ 1302CAH CAB ∴∠=∠=︒ ,AH HC DG GC ⊥⊥,∠ACD =90°,90AHC CGD ∴∠=∠=︒90ACH DCG ACH HAC ∴∠+∠=∠+∠=︒DCG HAC ∴∠=∠Rt AHC Rt CGD ∴△≌△HC GD ∴=,30CAH DCG ∠=∠=︒ E 为CD 中点,23AB =, 11322CE CD AB ∴=== 在Rt CEI △中,30ECI ∠=︒1322EI CE ∴== 1133232222BCE S BC EI ∴=⋅⋅=⨯⨯=△ (2)如图,过点,A D 分别作BC 的垂线,交BC 及BC 的延长线于点,H G ,,AH HC DG GC ⊥⊥,∠ACD =90°,90AHC CGD ∴∠=∠=︒90ACH DCG ACH HAC ∴∠+∠=∠+∠=︒DCG HAC ∴∠=∠Rt AHC Rt CGD ∴△≌△AH CG ∴=,DG HC =AC CD =, AH BC ⊥∴BAH HAC ∠=∠,90ABC BAH ∠+∠=︒∠DAE +∠ABC =90°,DAE HAC DCG ∴∠=∠=∠AC CD =,∠ACD =90°,45DAC ∴∠=︒DAE EAC CAH EAC ∴∠+∠=∠+∠45HAF =∠=︒即45HAF ∠=︒HAF ∴△是等腰直角三角形AH HF ∴=CG HF ∴=CG CF HF CF ∴-=-即HC FG =又DG HC =FG DG ∴= ∴DGF 是等腰直角三角形 2222DF DG HC BC ∴=== 即2BC DF =(3)如图,延长,EA EC ,过点B 分别作,BN EN BM CM ⊥⊥,垂足分别为,N N ,BE 恰好平分∠AEC ,BM BN ∴=∠BAC =90°,∠ACD =105°,AB =AC ,AB =1,在Rt ABC 中,2BC 45ABC ACB ∴∠=∠=︒150BCE ACB ACE ∴∠=∠+∠=︒30BCM ∴∠=︒60CBM ∴∠=︒22BM ∴= 2BN BM ∴==在Rt ABN △中21,AB BN ==2cos BN ABN AB ∴∠==45ABN ∴∠=︒90NBC ∴∠=︒9060150NBM NBC CBM ∴∠=∠+∠=︒+︒=︒在四边形ENBM 中,90,150M N NBM ∠=∠=︒∠=︒30AEC NEM ∴∠=∠=︒ 1152BEC AEC ∴∠==︒ 又30BCM BEC CBE ∠=∠+∠=︒15CBE CEB ∴∠=∠=︒CB CE ∴=2= 1CD CA AB ===21DE CE CD ∴=-=-如图,点P 为线段AE 上的动点,点E ′与点E 关于直线DP 对称,AE ′与CD 交于点Q ,连接CE ′, ∴21DE DE '==-211DE CD '-= 若211DF E D -=',则322DF =- 在线段DC 上截取322DF =-,连接E F ',则DF ED E D CD'=',又E DF CDE ''∠=∠ CDE E DF ''∴△∽△ 21CE CD E F E D '∴==''-()21E F CE ''= ∴()221CE AE CE CE AE E F AE AF '''''+-=+=+≥'' 则当,,A E F '三点共线时,取得最小值,此时Q 点与F 点重合,此时1(322)22CQ CF CD FD ==-=--=【点睛】本题考查了三角形全等的性质与判定,相似三角形的性质与判定,角平分线的性质,解直角三角形,第三问是阿氏圆模型,找到点F 的位置是解题的关键.9.(1)点P 对应的数为-2;(2)当t =2或6时,恰好使得P 到点A 的距离是点P 到点B 的距离的2倍;(3)m +13n =0.【解析】【分析】(1)设点P 对应的数为x ,表示出BP 与PA ,根据BP =PA 求出x 的值,即可确定出点P 对应的数;(2)表示出点P 对应的数,进而表示出PA 与PB ,根据PA =2PB 求出t 的值即可;(3)因为OM >ON ,只有甲乙均反弹之后在中点相遇一种情况,设点M 对应的数为m ,点N 对应的数为n ,时间为t ,则M 、N 的中点对应的数为2m n +,根据甲、乙两个弹珠相遇的位置恰好到点M 和点N 的距离相等列出关系式即可.【详解】解:(1)点A 、B 对应的数分别是﹣5和1,设点P 对应的数为x ,则BP =1-x ,PA =x +5,∵BP =PA ,∴1-x =x +5,解得:x =-2,∴点P 对应的数为-2;(2)P 对应的数为-5+2t ,∴PA =2t ,PB =|-5+2t -1|=|2t -6|,∵PA =2PB ,∴2t =2|2t -6|,当t =2t -6时,t =6;当t +2t -6=0时,t =2;答:当t =2或6时,恰好使得P 到点A 的距离是点P 到点B 的距离的2倍;(3)设点M 对应的数为m ,点N 对应的数为n ,时间为t ,则M 、N 的中点对应的数为2m n +, ∴MN =n -m ,OM =-m ,ON =n ,∴()()252502t t n m m n t m m ⎧+=-⎪+⎨⎛⎫=-+- ⎪⎪⎝⎭⎩,即()()351073352t n m n m t ⎧=-⎪⎨-=⎪⎩, 化简得m +13n =0.【点睛】本题考查了二元一次方程的应用,数轴,两点间的距离,运用分类讨论思想、方程思想及数形结合思想是解题的关键.10.(1)点E(2)① 90;② 30或150(3)N(00,【解析】【分析】(1)AE、BE、AB满足勾股定理,且AE=AB,可知ABE△为等腰直角三角形,则∠AEB=45°,故E点可使线段AB的可视角为45°.(2)①由半径所对的圆周角为90°即可得出∠AMB为90°.②连接AP、BP,即可得出ABP△为等边三角形,由圆周角定理即可求得∠AMB为30°或150°.(3)以AB为弦作圆M且过点N,由圆周角定理可得出当圆心角AMB最大时,圆周角ANB最大,由直线与圆的位置关系得出当y轴与圆M相切时圆心角AMB最大,进而可求得N点坐标.(1)连接AE,BE∵AE=4,AB=4,AE⊥AB∴ABE△为等腰直角三角形∴∠AEB=45°.故使得线段AB的可视角为45°的可视点是点E.(2)①有题意可知,此时AB为⊙P直径由半径所对的圆周角为90°可知∠AMB为90°②当⊙P的半径为4时,AB为⊙P一条弦,连接AP,BP∵BP=AP=4,AB=4∴ABP△为等边三角形∴∠APB=60°当点M在圆心一侧由圆周角定理知∠AMB=当点M不在圆心一侧由内切四边形性质可知∠AMB=180°-30°=150°。
中考数学压轴题60例(选择题)

中考数学压轴题60例(选择题)一、选择题(共60小题)1.(2015•遵义)将正方形ABCD 绕点A 按逆时针方向旋转30°,得正方形AB 1C 1D 1,B 1C 1交CD于点E ,AB=,则四边形AB 1ED 的内切圆半径为( ). C . D.2.(2015•遵义)如图,四边形ABCD 中,∠C=50°,∠B=∠D=90°,E 、F 分别是BC 、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为( )3.(2015•自贡)如图,在矩形ABCD 中,AB=4,AD=6,E 是AB 边的中点,F 是线段BC 上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是()22﹣4.(2015•株洲)有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是()的一个根,那么5.(2015•镇江)如图,坐标原点O为矩形ABCD 的对称中心,顶点A的坐标为(1,t),AB∥x 轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,=k.已知关于x,y的二元一次方程(m ,n 是实数)无解,在以m ,n 为坐标(记为(m ,n )的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k •t 的值等于( )A .B .1 C . D .6.(2015•枣庄)如图是二次函数y=ax 2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y 1),(1,y 2)是抛物线上的两点,则y 1=y 2.上述说法正确的是( )A . ①②④B . ③④C . ①③④D .①②7.(2015•岳阳)如图,在△ABC 中,AB=CB ,以AB 为直径的⊙O 交AC 于点D .过点C 作CF∥AB,在CF 上取一点E ,使DE=CD ,连接AE .对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE 为⊙O的切线,一定正确的结论全部包含其中的选项是()A.①②B.①②③C.①④D.①②④8.(2015•营口)如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是()A.25°B.30°C.35°D.40°9.(2015•盐城)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG,动点P 从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( ). . C . D .10.(2015•烟台)如图,Rt△ABC 中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG 的一边CD 在直线AB 上,且点D 与点A 重合,现将正方形DEFG 沿A ﹣B 的方向以每秒1个单位的速度匀速运动,当点D 与点B 重合时停止,则在这个运动过程中,正方形DEFG 与△ABC 的重合部分的面积S 与运动时间t 之间的函数关系图象大致是( ). .C .D .11.(2015•雅安)如图所示,MN 是⊙O 的直径,作AB⊥MN,垂足为点D ,连接AM ,AN ,点C 为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是()12.(2015•宿迁)在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P在反比例函数y=的图象上,若△PAB为直角三角形,13.(2015•孝感)如图,二次函数y=ax2+bx+c (a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②>0;③ac﹣b+1=0;④OA•OB=﹣.其中正确结论的个数是()14.(2015•西宁)如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y 和x ,则y 与x 的函数图象大致是( ). B .C . .15.(2015•武汉)如图,△ABC,△EFG 均是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FC 相交于点M .当△EFG 绕点D 旋转时,线段BM 长的最小值是( )A.2﹣B.+1 C.D.﹣116.(2015•无锡)如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB 上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB 分别交于点E、F,则线段B′F的长为()A.B.C.D.17.(2015•潍坊)已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c >0.其中正确结论的个数是()A1 B2 C3 D418.(2015•天水)如图,AB 为半圆所在⊙O 的直径,弦CD 为定长且小于⊙O 的半径(C 点与A 点不重合),CF⊥CD 交AB 于点F ,DE⊥CD 交AB 于点E ,G 为半圆弧上的中点.当点C 在上运动时,设的长为x ,CF+DE=y .则下列图象中,能表示y 与x 的函数关系的图象大致是( ). . C . D .19.(2015•泰州)如图,△ABC 中,AB=AC ,D 是BC 的中点,AC 的垂直平分线分别交AC 、AD 、AB 于点E 、O 、F ,则图中全等三角形的对数是( )20.(2015•遂宁)二次函数y=ax 2+bx+c (a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c <0,其中正确的个数是()A.2 B.3 C.4 D.521.(2015•绥化)如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A.1个B.2个C.3个D.4个22.(2015•十堰)如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为()A2B3C D23.(2015•日照)如图是抛物线y 1=ax 2+bx+c (a≠0)图象的一部分,抛物线的顶点坐标A (1,3),与x 轴的一个交点B (4,0),直线y 2=mx+n (m≠0)与抛物线交于A ,B 两点,下列结论: ①2a+b=0;②abc>0;③方程ax 2+bx+c=3有两个相等的实数根;④抛物线与x 轴的另一个交点是(﹣1,0);⑤当1<x <4时,有y 2<y 1, 其中正确的是( )24.(2015•泉州)在同一平面直角坐标系中,函数y=ax 2+bx 与y=bx+a 的图象可能是( ) . .C .D .25.(2015•庆阳)在如图所示的平面直角坐标系中,△OA 1B 1是边长为2的等边三角形,作△B 2A 2B 1与△OA 1B 1关于点B 1成中心对称,再作△B 2A 3B 3与△B 2A 2B 1关于点B 2成中心对称,如此作下去,则△B 2n A 2n+1B 2n+1(n 是正整数)的顶点A 2n+1的坐标是( )A . (4n ﹣1,)B . (2n ﹣1,)C . (4n+1,)D . (2n+1,) 26.(2015•钦州)如图,AD 是△ABC 的角平分线,则AB :AC 等于( )A . BD :CDB . AD :CDC . BC :AD D . BC :AC 27.(2015•齐齐哈尔)如图,在钝角△ABC 中,分别以AB 和AC 为斜边向△ABC 的外侧作等腰直角三角形ABE 和等腰直角三角形ACF ,EM 平分∠AEB 交AB 于点M ,取BC 中点D ,AC 中点N ,连接DN 、DE 、DF .下列结论:①EM=DN;②S △CDN =S 四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )28.(2015•盘锦)如图,边长为1的正方形ABCD ,点M 从点A 出发以每秒1个单位长度的速度向点B 运动,点N 从点A 出发以每秒3个单位长度的速度沿A→D→C→B 的路径向点B 运动,当一个点到达点B 时,另一个点也随之停止运动,设△AMN 的面积为s ,运动时间为t 秒,则能大致反映s 与t 的函数关系的图象是( )..C ..29.(2015•宁德)如图,在平面直角坐标系中,点A 1,A 2,A 3…都在x 轴上,点B 1,B 2,B 3…都在直线y=x 上,△OA 1B 1,△B 1A 1A 2,△B 2B 1A 2,△B 2A 2A 3,△B 3B 2A 3…都是等腰直角三角形,且OA 1=1,则点B 2015的坐标是( )A.(22014,22014)B.(22015,22015)C.(22014,22015)D.(22015,22014)30.(2015•内江)如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y 轴.若双曲线y=与正方形ABCD有公共点,则k 的取值范围为()A.1<k<9 B.2≤k≤34C.1≤k≤16D.4≤k<1631.(2015•南通)如图,AB为⊙O的直径,C 为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为()A2.5 B2.8 C3 D3.232.(2015•南宁)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为()33.(2015•南充)关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y 的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m﹣1)2+(n﹣1)2≥2;③﹣1≤2m ﹣2n≤1,其中正确结论的个数是()34.(2015•南昌)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()35.(2015•牡丹江)如图,在△ABC 中,AB=BC ,∠ABC=90°,BM 是AC 边中线,点D ,E 分别在边AC 和BC 上,DB=DE ,EF⊥AC 于点F ,以下结论: (1)∠DBM=∠CDE; (2)S △BDE <S 四边形BMFE ; (3)CD •EN=BN •BD ; (4)AC=2DF .其中正确结论的个数是( )36.(2015•梅州)对于二次函数y=﹣x 2+2x .有下列四个结论:①它的对称轴是直线x=1;②设y 1=﹣x 12+2x 1,y 2=﹣x 22+2x 2,则当x 2>x 1时,有y 2>y 1;③它的图象与x 轴的两个交点是(0,0)和(2,0);④当0<x <2时,y >0.其中正确的结论的个数为( )37.(2015•辽阳)如图,点A 是双曲线y=﹣在第二象限分支上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为底作等腰△ABC,且∠ACB=120°,点C 在第一象限,随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线y=上运动,则k 的值为( )38.(2015•凉山州)二次函数y=ax 2+bx+c (a≠0)的图象如图所示,下列说法: ①2a+b=0②当﹣1≤x≤3时,y <0 ③若(x 1,y 1)、(x 2,y 2)在函数图象上,当x 1<x 2时,y 1<y 2 ④9a+3b+c=0其中正确的是( )39.(2015•连云港)如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是()40.(2015•莱芜)如图,在矩形ABCD 中,AB=2a ,AD=a ,矩形边上一动点P 沿A→B→C→D 的路径移动.设点P 经过的路径长为x ,PD 2=y ,则下列能大致反映y 与x 的函数关系的图象是( )..C .D .41.(2015•酒泉)如图,矩形ABCD 中,AB=3,BC=5,点P 是BC 边上的一个动点(点P 与点B 、C 都不重合),现将△PCD 沿直线PD 折叠,使点C 落到点F 处;过点P 作∠BPF 的角平分线交AB 于点E .设BP=x ,BE=y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )..C .D .42.(2015•荆州)如图,正方形ABCD 的边长为3cm ,动点P 从B 点出发以3cm/s 的速度沿着边BC ﹣CD ﹣DA 运动,到达A 点停止运动;另一动点Q 同时从B 点出发,以1cm/s 的速度沿着边BA 向A 点运动,到达A 点停止运动.设P 点运动时间为x (s ),△BPQ 的面积为y (cm 2),则y 关于x 的函数图象是( )....43.(2015•荆门)如图,点A ,B ,C 在一条直线上,△ABD,△BCE 均为等边三角形,连接AE 和CD ,AE 分别交CD ,BD 于点M ,P ,CD 交BE 于点Q ,连接PQ ,BM ,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ 为等边三角形;④MB 平分∠AMC, 其中结论正确的有()44.(2015•济南)如图,抛物线y=﹣2x 2+8x ﹣6与x 轴交于点A 、B ,把抛物线在x 轴及其上方的部分记作C 1,将C 1向右平移得C 2,C 2与x 轴交于点B ,D .若直线y=x+m 与C 1、C 2共有3个不同的交点,则m 的取值范围是( ). ﹣ ﹣45.(2015•黄石)如图是自行车骑行训练场地的一部分,半圆O 的直径AB=100,在半圆弧上有一运动员C 从B 点沿半圆周匀速运动到M (最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A 点停止.设运动时间为t ,点B 到直线OC 的距离为d ,则下列图象能大致刻画d 与t 之间的关系是( )..C .D .46.(2015•黑龙江)如图,正方形ABCD 中,点E 是AD 边中点,BD 、CE 交于点H ,BE 、AH 交于点G ,则下列结论:①AG⊥BE;②BG=4GE;③S △BHE =S △CHD ;④∠AHB=∠EHD.其中正确的个数是( )47.(2015•菏泽)如图,在平面直角坐标系xOy 中,直线y=x 经过点A ,作AB⊥x 轴于点B ,将△ABO 绕点B 逆时针旋转60°得到△CBD.若点B 的坐标为(2,0),则点C 的坐标为( ),),)(﹣,(﹣,48.(2015•河南)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O 1、O 2、O 3,…组成一条平滑的曲线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是()A.(2014,0)B.(2015,﹣1)C.(2015,1)D.(2016,0)49.(2015•河池)我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P 个数是()A.6 B.8 C.10 D.1250.(2015•河北)如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是()51.(2015•河北)如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则()52.(2015•桂林)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是()53.(2015•广元)如图,矩形ABCD 中,AB=3,BC=4,点P 从A 点出发,按A→B→C 的方向在AB 和BC 上移动.记PA=x ,点D 到直线PA 的距离为y ,则y 关于x 的函数大致图象是( ). . C . D .54.(2015•抚顺)如图,将矩形ABCD 绕点A 旋转至矩形AB′C′D′位置,此时AC 的中点恰好与D 点重合,AB′交CD 于点E .若AB=3,则△AEC 的面积为( )2 55.(2015•鄂州)在平面直角坐标系中,正方形A 1B 1C 1D 1、D 1E 1E 2B 2、A 2B 2C 2D 2、D 2E 3E 4B 3、A 3B 3C 3D 3…按如图所示的方式放置,其中点B 1在y 轴上,点C 1、E 1、E 2、C 2、E 3、E 4、C 3…在x 轴上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O=60°,B 1C 1∥B 2C 2∥B 3C 3…则正方形A 2015B 2015C 2015D 2015的边长是( )(()()()56.(2015•滨州)如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转,若∠BOA 的两边分别与函数y=﹣、y=的图象交于B 、A 两点,则∠OAB 的大小的变化趋势为( )57.(2015•本溪)如图,在△ABC 中,∠C=90°,点P 是斜边AB 的中点,点M 从点C 向点A 匀速运动,点N 从点B 向点C 匀速运动,已知两点同时出发,同时到达终点,连接PM 、PN 、MN ,在整个运动过程中,△PMN 的面积S 与运动时间t 的函数关系图象大致是( )..C .D .58.(2015•巴彦淖尔)如图1,E 为矩形ABCD 边AD 上的一点,点P 从点B 沿折线BE ﹣ED ﹣DC 运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是2cm/s .若P 、Q 同时开始运动,设运动时间为t (s ),△BPQ 的面积为y (cm 2),已知y 与t 的函数关系图象如图2,则下列结论错误的是( )sin∠EBC=59.(2015•眉山)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()C60.(2015•徐州)若函数y=kx﹣b的图象如图所示,则关于x的不等式k(x﹣3)﹣b>0的解集为()2015年全国中考数学压轴题60例(选择题卷)参考答案与试题解析一、选择题(共60小题) 1.(2015•遵义)将正方形ABCD 绕点A 按逆时针方向旋转30°,得正方形AB 1C 1D 1,B 1C 1交CD 于点E ,AB=,则四边形AB 1ED 的内切圆半径为( ).C . D.AB=,解答:解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,】则∠OAF=30°,∠AB1O=45°,故B1F=OF=OA,设B1F=x,则AF=﹣x,故(﹣x)2+x2=(2x)2,解得x=或x=(舍去),∴四边形AB1ED的内切圆半径为:.故选:B.点评:本题考查了旋转的性质三角形的内切圆,正方形的性质,要熟练掌握正方形的性质及直角三角形的性质,是解答此题的关键.2.(2015•遵义)如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.50°B.60°C.70°D.80°3.(2015•自贡)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是()22﹣∴DE=,∴DB′=24.(2015•株洲)有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是()的一个根,那么﹣4ac≥0,符号相同,>得c+所以是方程5.(2015•镇江)如图,坐标原点O 为矩形ABCD 的对称中心,顶点A 的坐标为(1,t ),AB∥x轴,矩形A′B′C′D′与矩形ABCD 是位似图形,点O 为位似中心,点A′,B′分别是点A ,B 的对应点,=k .已知关于x ,y 的二元一次方程(m ,n 是实数)无解,在以m ,n 为坐标(记为(m ,n )的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k •t 的值等于( ) D的二元一次方程的图象只经过点的图象经过点的图象经过点图形,=k的二元一次方程(m≠3)n=由的图象经过点的图象经过点6.(2015•枣庄)如图是二次函数y=ax 2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y 1),(1,y 2)是抛物线上的两点,则y 1=y 2.上述说法正确的是( ),∴﹣的对称点的坐标7.(2015•岳阳)如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是()与∴与点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了等腰三角形的性质、平行线的性质和相似三角形的判定.8.(2015•营口)如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是()A.25°B.30°C.35°D.40°考点:轴对称-最短路线问题.菁优网版权所有专题:压轴题.得出∠AOB=∠COD,证出△OCDOB=∠COD,9.(2015•盐城)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P从点A 出发,沿A→D→E→F→G→B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( ). . C . D .10.(2015•烟台)如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG 的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是()..C.D.0≤t≤2时;2∴AC=AB×cos30°=8×=4=4∴CH=AC×AH=0≤t≤2S==t2S=﹣=242S=2)tan30°2]tan60°=[]t+2+6]×[﹣t﹣+2t+4﹣230﹣2S=11.(2015•雅安)如图所示,MN 是⊙O 的直径,作AB⊥MN,垂足为点D ,连接AM ,AN ,点C 为上一点,且=,连接CM ,交AB 于点E ,交AN 于点F ,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF .其中正确结论的个数是( )是直径得出②正确,==∴AD=BD,=∵=∴==,∴AE=MF12.(2015•宿迁)在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P在反比例函数y=的图象上,若△PAB为直角三角形,则满足条件的点P的个数为(),(()。
(完整)中考数学压轴题精选含答案

一、解答题1.如图,ABC 为O 的内接三角形,AB 为O 的直径,过点A 作O 的切线交BC 的延长线干点D .(1)求证:ABC ∽;(2)若E 为AD 上一点,使得,连接OE ,求证:OE 平分;(3)若点F 为直径AB 下方半圆的中点,连接CF 交AB 于点G ,且,2AB =,求CG的长.2.如图,在Rt △AOD 中,∠AOD =90°,以点O 为圆心、OA 为半径作⊙O .延长AD 、OD ,分别交⊙O 于点C 、E ,点B 是OD 延长线上一点,且有BC =BD .(1)求证:BC 是⊙O 的切线;(2)若∠OAD =30°,CD =3,求弧CE 长. (3)若OD =3,DE =1,求BE .3.如图①,直线:24l y x =-+分别交x 轴和y 轴于点A 和点B ,将AOB 绕点O 逆时针旋转90︒得到COD △.抛物线2:4h y ax bx =++经过A 、B 、D 三点.(1)求抛物线h的表达式;(2)若与y轴平行的直线m以1秒钟一个单位长的速度从y轴向左平移,交线段CD于点M、交抛物线h于点N,求线段MN的最大值;(3)如图②,点E为抛物线h的顶点,点P是抛物线h在第二象限的上一动点(不与点D、B重合),连接PE,以PE为边作图示一侧的正方形PEFG.随着点P的运动,正方形的大小、位置也随之改变,当顶点G恰好落在y轴的负半轴时,试求出此时点P的坐标.4.已知有理数a,b,c在数轴上对应的点分别为A,B,C,其中b是最小的正整数,a,c满足()2a c++-=.250a______,b=______,c=______;(1)填空:=(2)点A,B,C分别以每秒4个单位长度,1个单位长度,1个单位长度的速度在数轴上同时向右运动,设运动时间为t秒.①当AC长为6时,求t的值;②当点A在点C左侧时(不考虑点A与B,C重合的情况),是否存在一个常数m使得+⋅的值在某段运动过程中不随t的改变而改变?若存在,求出m的值;若不存2AC m AB在,请说明理由.5.如图,抛物线2=-++与x轴相交于A B、两点,与y轴交于点C,顶点为D,抛y x2x3物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求线段DE的长.(2)联结OE,若点G在抛物线的对称轴上,且BEG与COE相似,请直接写出点G的坐标.(3)设点P为x轴上的一点,且tan4,时,求点P的坐∠+∠=∠=DAO DPOαα标.6.已知抛物线经过()30A -,,()1,0B ,52,2C ⎛⎫⎪⎝⎭三点,其对称轴交x 轴于点H ,一次函数()0y kx b k =+≠的图象经过点C ,与抛物线交于另一点D (点D 在点C 的左边),与抛物线的对称轴交于点E . (1)求抛物线的解析式;(2)在抛物线上是否存在点F ,使得点A 、B 、E 、F 构成的四边形是平行四边形,如果存在,求出点F 的坐标,若不存在请说明理由(3)设∠CEH=α,∠EAH =β,当αβ>时,直接写出k 的取值范围7.已知二次函数y =﹣x 2+2x +m +1. (1)当m =2时. ①求函数顶点坐标;②当n ≤x ≤n +1时,该函数的最大值为3,求n 的值.(2)当x ≤2时,函数图象上有且只有2个点到x 轴的距离为2,求m 的取值范围. (3)已知点P 为二次函数上一点,点P 的横坐标为﹣3m +2,点M 的坐标为(2m ,m ),以PM 为对角线构造矩形PQMN ,矩形的各边与坐标轴垂直,当抛物线在矩形PQMN 内部的函数部分y 随着x 的增大而增大时,直接写出m 的取值范围.8.如图,在△ABC 中,∠ACB =90°,AC =3,BC =4.点P 从点A 出发,在线段AB 上以每秒1个单位长度的速度向终点B 运动,连接CP .设点P 运动的时间为t 秒. (1)填空:AB = ;(2)当t 为何值时,CP 平分∠ACB ; (3)当t 为何值时,△BCP 为等腰三角形.9.在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △面积最大时,求出点P 的坐标; (3)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A C M Q 、、、为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,说明理由.10.在平面直角坐标系xOy 中,已知抛物线y =x 2﹣2x ﹣3与x 轴交于A 、B 两点,与y 轴交于C 点,D 为抛物线顶点.(1)连接AD ,交y 轴于点E ,P 是抛物线上的一个动点.①如图一,点P 是第一象限的抛物线上的一点,连接PD 交x 轴于F ,连接,若,求点P 的坐标.②如图二,点P 在第四象限的抛物线上,连接AP 、BE 交于点G ,若,则w 有最大值还是最小值?w 的最值是多少?(2)如图三,点P 是第四象限抛物线上的一点,过A 、B 、P 三点作圆N ,过点P 作PM x ⊥轴,垂足为I ,交圆N 于点M ,点P 在运动过程中,线段是否变化?若有变化,求出MI 的取值范围;若不变,求出其定值.(3)点Q 是抛物线对称轴上一动点,连接OQ 、AQ ,设AOQ 外接圆圆心为H ,当的值最大时,请直接写出点H 的坐标.11.已知,E 为正方形ABCD 中CD 边上一点,连接BE ,过点C 作CF ⊥BE 交AD 于F ,垂足为G .(1)如图1,求证:CE =DF ;(2)如图2,连接AG 、BF ,交于点H ,求证:∠ABF =∠AGF ; (3)如图3,在(2)的条件下,若AG =AB =11,求线段GH 的长.12.如图1,在平面直角坐标系中,直线4y x =+与x 轴、y 轴分别交于A 、B 两点,抛物线2y x bx c =-++经过A 、B 两点,并且与x 轴交于另一点C (点C 在点A 的右侧),点P 是抛物线上一动点.(1)求抛物线的解析式;(2)若点P 是第二象限内抛物线上的一个动点,过点P 作PD ∥y 轴交AB 于点D ,点E 为线段DB 上一点,且DE =,过点E 作EF ∥PD 交抛物线于点F ,当点P 运动到什么位置时,四边形PDEF 的面积最大?并求出此时点P 的坐标;(3)如图2,点F 为AO 的中点,连接BF ,点G 为y 轴负半轴上一点,且GO =2,沿x 轴向右平移直线AG ,记平移过程的直线为,直线交x 轴于点M ,交直线AB 于点N .是否存在点M ,使得△FMN 为等腰三角形,若存在,直接写出....平移后点M 的坐标;若不存在,请说明理由.13.如图,在正方形OABC 中,AB =4,点E 是线段OA (不含端点)边上一动点,作△ABE 的外接圆交AC 于点D .抛物线y =ax 2﹣x +c 过点O ,E .(1)求证:∠BDE =90°;(2)如图1,若抛物线恰好经过点B ,求此时点D 的坐标; (3)如图2,AC 与BE 交于点F .①请问点E 在运动的过程中,CF ⋅AD 是定值吗?如果是,请求出这个值,如果不是,请说明理由; ②若,求点E 坐标及a 的值.14.(1)[感知]如图1,在正△ABC 的外角∠CAH 内引射线AM ,作点C 关于AM 的对称点E (点E 在∠CAH 内),连接BE ,BE 、CE 分别交AM 于点F 、G .求∠FEG 的度数.(2)[探究]把(1)中的“正△ABC ”改为“正方形ABDC ,其余条件不变,如图2,类比探究,可得: ①∠FEG = °;②猜想线段BF 、AF 、FG 之间的数量关系,并说明理由.(3)[拓展]如图3,点A 在射线BH 上,AB =AC ,∠BAC =α(0°<α<180°),在∠CAH 内引射线AM ,作点C 关于AM 的对称点E (点E 在∠CAH 内),连接BE ,BE 、CE 分别交AM 于点F .G .则线段BF 、AF 、GF 之间的数量关系为 .15.定义:在平面直角坐标系中,对于任意两点()11,A x y ,()22,B x y ,如果点(),M x y 满足122x x x -=,122y y y -=,那么称点M 是点A 、B 的“双减点”. 例如:()4,5A -,()6,1B -、当点(),T x y 满足4652x --==-,()5132y --==,则称点()5,3M -是点A 、B 的“双减点”.(1)写出点()1,3A -,()1,4B -的“双减点”C 的坐标;(2)点()6,4E -,点4,43F m m --⎛⎫⎪⎝⎭,点(),M x y 是点E 、F 的“双减点”.求y 与x 之间的函数关系式;(3)在(2)的条件下,y 与x 之间的函数图象与y 轴、x 轴分别交于点A 、C 两点,B 点坐标为3,0,若点E 在平面直角坐标系内,在直线AC 上是否存在点F ,使以A 、B 、E 、F 为顶点的四边形为菱形?若存在,请求出F 点的坐标;若不存在,请说明理由. 16.如图,在平面直角坐标系中,已知AOB CDA △△≌,且1OA =,()0,2B ,抛物线24y ax ax a =+-经过点C .(1)求抛物线的解析式.(2)在抛物线(对称轴的右侧)上是否存在一点P ,使△ABP 是以AB 为直角边的等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(3)若x 轴上有一点E 的横坐标为2a ,过点E 作y 轴的平行线交抛物线于点F ,抛物线对称轴与x 轴交于点G ,Q 为抛物线(对称轴的左侧)上一动点,是否存在点Q 使GF 为EFQ ∠的平分线?若存在,求出点Q 的坐标;若不存在,请说明理由.17.已知抛物线y =﹣x 2+bx +c 与x 轴交于点A (m ﹣2,0)和B (2m +1,0)(点A 在点B 的左侧),与y 轴相交于点C ,顶点为P ,对称轴为l :x =1.(1)求抛物线解析式;(2)直线y =kx +2(k ≠0)与抛物线相交于两点M (x 1,y 1),N (x 2,y 2)(x 1<x 2),当|x 1﹣x 2|最小时,求抛物线与直线的交点M 和N 的坐标;(3)首尾顺次连接点O 、B 、P 、C 构成多边形的周长为L ,若线段OB 在x 轴上移动,求L 最小值时点O 、B 移动后的坐标及L 的最小值.18.已知AB 、CD 为O 的两条弦,//AB CD .(1)如图1,求证弧AC =弧BD ;(2)如图2,连接AC 、BC 、OA 、BD ,弦BC 与半径OA 相交于点G ,延长AO 交CD 于点E ,连接BE ,使BE BD =,若OA BC ⊥,求证:四边形ABEC 为菱形;(3)在(2)的条件下,CH 与O 相切于点C ,连接CO 并延长交BE 于点F ,延长BE 交CH 于点H ,11OF =,24sin 25BDC ∠=,求CH 长. 19.如图,圆心M (3,0),半径为5的⊙M 交x 轴于A 、B 两点,交y 轴于C 点,抛物线2y ax bx c =++经过A 、B 、C 三点.(1)求抛物线的解析式.(2)求圆M 上一动点P 到该抛物线的顶点Q 的距离的最小值?并求出此时P 点的坐标. (3)若OC 的中点为F ,请问抛物线上是否存在一点G ,使得∠FBG =45°,若存在,求出点G 的坐标,若不存在,请说明理由.20.如图1,在平面直角坐标系中,已知抛物线y =ax 2+bx -4(a ≠0)经过点A (-2,0)和点B (4,0).(1)求这条抛物线所对应的函数表达式;(2)点P为抛物线上第一象限内一点,若S△ABC=2S△PBC,求点P的坐标;(3)如图2,点D是第二象限内抛物线上一点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.【参考答案】**科目模拟测试一、解答题1.(1)见解析(2)见解析(3)【解析】【分析】(1)由圆周角定理和切线的性质可知,又因为,即可证明;(2)连接OE交圆于点H,连接OC,由,利用等腰三角形的性质和判定可证,从而得出OE是AC的垂直平分线,从而解决问题;(3)过点G作于K,由点F在半圆的中点,得,得,,得,可求出,从而解决问题.(1)解:证明:为O的直径,,过点A作O的切线交BC的延长线于点D,,,又,;(2)证明:如图,连接OE交圆于点H,连接OC,,,,,,,OC是O的半径,,垂直平分AC,∴,平分;(3)如图,在中,,2AB=,,过点G作于K,,,点F为直径AB下方半圆的中点,,,,,在Rt ABC∆中,,,由勾股定理得,,,,,,,在中,,.【点睛】本题是圆的综合题,主要考查了圆的切线的性质,圆周角定理,相似三角形的判定与性质,勾股定理,三角函数等知识,根据得出线段之间的数量关系是解题的关键.2.(1)见详解;(2)12π;(3)16【解析】【分析】(1)连接CO,先证∠BCD=∠ADO,由∠A+∠ADO=90°,可得∠OCA+∠BCD=90°,进而即可得到结论;(2)先证BCD△是等边三角形,∠BOC=30°,求出OC=3,利用弧长公式即可求解;(3)过点O作ON⊥AD,过点B作BM⊥CD,利用勾股定理和面积法求出ON=125,AN=165,结合垂径定理和等腰三角形的性质得DM=710,最后利用锐角三家函数即可求解.【详解】解:(1)连接CO,∵BC=BD,∴∠BDC=∠BCD,∵∠BDC=∠ADO,∴∠BCD=∠ADO,∵OA=OC,∴∠A=∠OCA,∵∠AOD=90°,∴∠A+∠ADO=90°,∴∠OCA+∠BCD=90°,即OC⊥BC,∴BC是⊙O的切线;(2)∵∠OAD=30°,∴∠OCA=∠OAD=30°,∠AOC=180°-30°-30°=120°,∠ADO=∠BDC=90°-30°=60°,∴∠BOC=120°-90°=30°,又∵BC=BD,∴BCD△是等边三角形,∴CB=CD=3,∵OC⊥BC,∴OC=3×3=3,∴30311802CEππ⨯==;(3)过点O作ON⊥AD,过点B作BM⊥CD,∵OD=3,DE=1,∴AO=EO=3+1=4,∴AD22345+=,∴ON=125 OD OAAD⨯=,∴AN221216455⎛⎫-=⎪⎝⎭,∴AC=2AN=325,∴CD=325-5=75,∵BD=BC,∴DM=75÷2=710,∵∠BDM=∠ADO,∴cos∠BDM=cos∠ADO,即:35 DM ODBD AB==,∴BD =53DM =710×53=76,∴BE =76-1=16. 【点睛】本题主要考查圆和三角形的综合,掌握勾股定理,切线的判定定理,垂径定理,锐角三角函数的定义是解题的关键.3.(1)2142y x x =--+;(2)258;(3)P 点的坐标为552222⎛-- ⎝ 【解析】 【分析】(1)先由直线l 的解析式得出A 、B 的坐标,再根据旋转的性质得出D 点坐标,然后用待定系数法求出抛物线解析式;(2)设出N 点横坐标,纵坐标用横坐示表示,同时表示出M 点坐标,而MN 的长度为N 点与M 点的纵坐标之差,得出MN 的长度是N 点横坐标的二次函数,利用配方法求出最值;(3)作PH y ⊥轴于H ,交抛物线对称轴于K ,可得到PKE GHP △≌△,从而得到PK GH =,EK PH =,利用配方法可得到顶点91,2E ⎛⎫- ⎪⎝⎭,然后设21,42P m m m ⎛⎫--+ ⎪⎝⎭,则有21122EK m m =++,PH m =-,可得到关于m 的方程,解出即可.【详解】解:(1)直线:24l y x =-+交x 轴于点A 、交y 轴于点B , (2,0)A ∴,(0,4)B ,将AOB 绕点O 逆时针旋转90︒得到COD △, (4,0)D ∴-,(0,2)C ,设过点A ,B ,D 的抛物线h 的解析式为:(4)(2)y a x x =+-,将B 点坐标代入可得:4(04)(02)a =+-,解得12a =-∴抛物线h 的解析式为2142y x x =--+;(2)由(4,0)D -,(0,2)C , 则直线CD 的解析式为122y x =+, 设N 点坐标为21,42n n n ⎛⎫--+ ⎪⎝⎭,则M 点坐标为1,22n n ⎛⎫+ ⎪⎝⎭,222111313254222222228MN n n n n n n ⎛⎫⎛⎫∴=--+-+=--+=-++ ⎪ ⎪⎝⎭⎝⎭,∴当32n =-时,MN 最大,最大值为258; (3)若G 点在y 轴上,如图,作PH y ⊥轴于H ,交抛物线对称轴于K ,正方形,PEFG90,EPK GPH GPH PGH,EPKPGH同理:,PEK GPH在PKE △和GHP △中,EPKPGHPE GP PEK GPH,PKE GHP ∴△≌△, PK GH ∴=,EK PH =对2142y x x =--+,配方得219(1)22y x =-++,则顶点91,2E ⎛⎫- ⎪⎝⎭,设21,42P m m m ⎛⎫--+ ⎪⎝⎭,则有22911142222EK m m m m =++-=++,PH m =-, 21122m m m ∴-=++,解得23m =-P ∴点的坐标为5523,323,322⎛-- ⎝. 【点睛】本题是二次函数综合题,主要考查了一次函数图象上坐标点的特征,待定系数法求二次函数解析式,利用纵坐标之差表示竖直方向线段的长度,利用配方法求二次函数最值,正方形的性质、全等三角形的判定与性质、解一元二次方程等众多知识点,综合性强,难度较大.对于(3)问,根据正方形的性质巧妙构造出全等三角形,从而得出线段相等而列出方程是解答的关键和要点.4.(1)2,1,5-;(2)①13或133;②存在,m 的值为2-或2.【解析】 【分析】(1)根据正整数的定义、绝对值的非负性、偶次方的非负性分别可求出,,b a c 的值; (2)①先求出运动t 秒后,点,A C 所表示的数,再分点A 在点C 左侧和点A 在点C 右侧两种情况,然后根据数轴的定义建立方程,解方程即可得;②先求出运动t 秒后,点,,A B C 所表示的数,从而可得AC 的长,再分点A 在点B 左侧和点A 在点B 右侧两种情况,分别求出AB 的值,代入化简,然后根据整式的无关型问题求解即可得. 【详解】解:(1)b 是最小的正整数,1b ∴=,()2250a c ++-=, 20,50a c ∴+=-=,解得2,5a c =-=, 故答案为:2,1,5-;(2)①由题意,运动t 后,点A 所表示的数是42t -,点C 所表示的数是5t +, 当点A 在点C 左侧时,5(42)6AC t t =+--=,解得13t =, 当点A 在点C 右侧时,42(5)6AC t t =--+=,解得133t =, 综上,t 的值为13或133;②由题意,运动t 后,点A 所表示的数是42t -,点B 所表示的数是1t +,点C 所表示的数是5t +,当421t t -=+时,13t =, 当425t t -=+时,73t =, 因为点A 在点C 左侧, 所以5(42)73AC t t t =+--=-,当点A 在点B 左侧,即01t <<时,1(42)33AB t t t =+--=-, 则22(73)(33)314(36)AC m AB t m t m m t +⋅=-+-=+-+, 由360m +=得:2m =-,即在01t <<运动时间内,当2m =-时,2AC m AB +⋅的值不随t 的改变而改变; 当点A 在点B 右侧,即713t <<时,42(1)33AB t t t =--+=-,则22(73)(33)143(36)AC m AB t m t m m t +⋅=-+-=-+-, 由360m -=得:2m =, 即在713t <<运动时间内,当2m =时,2AC m AB +⋅的值不随t 的改变而改变; 综上,存在一个常数m 使得2AC m AB +⋅的值在某段运动过程中不随t 的改变而改变,m 的值为2-或2. 【点睛】本题考查了数轴、一元一次方程的应用、绝对值和偶次方的非负性、整式等知识点,较难的是题(2)②,正确分两种情况讨论是解题关键.5.(1)2;(2)(1,4)-或21,3⎛⎫⎪⎝⎭;(3)(19,0)或(17,0)-【解析】 【分析】(1)根据抛物线的解析式可求得与坐标轴的坐标及顶点坐标,从而易得OB =OC ,由EF ⊥OB 即可求得EF 的长,从而求得DE 的长;(2)设点G 的坐标为(1,x ),分两种情况考虑:△COE ∽△EGB 和△COE ∽△EBG ,根据相似三角形的性质即可求得x 的值,从而可求得点G 的坐标;(3)分两种情况考虑:点P 在点A 的右侧和点P 在点A 的左侧;当点P 在点A 的右侧时,由D (1,4),则tan 4DOF ∠=,得出∠α =∠DOF ,然后根据三角形外角的性质可求得∠DPO =∠ADO ,进而可得△ADP ∽△AOD ,由相似三角形的性质可求得OP 的长,从而求得P 点的坐标;当点P 在点A 的左侧时, 作点P 关于抛物线对称轴的对称点P ',则点P '也满足题意. 【详解】(1)当2y x x =-++23=0时,解方程得:1213x x =-=, ∴抛物线2y x x =-++23与x 轴的交点坐标分别为A (-1,0)、B (3,0) ∴OB =3∵在2y x x =-++23中,当x =0时,3y = ∴抛物线与y 轴的交点C 的坐标为(0,3) ∴OC =3∵2223(1)4y x x x =-++=--+ ∴抛物线的顶点坐标为D (1,4) ∴DF =4,OF =1 ∵OB =OC =3,OC ⊥OB ∴∠OCB =∠OBC =45° ∵EF ⊥OB∴∠FEB =∠OBC =45° ∴EF =BF =OB -OF =3-1=2∴DE =DF -EF =4-2=2 (2)设点G 的坐标为(1,x )在Rt △OBC 及Rt △FBE 中,由勾股定理得:BC =BE ===∴CE BE BE =-==①若△COE ∽△EGB 则有OC EGCE BE=,∠GEB =∠OCE =45° 即OC ∙BE =CE ∙EG ∴点G 只能在点E 下方∵由(1)可得点E 的坐标为(1,2) ∴EG =2-x∴3)x ⨯=- 解得:x =-4即点G 的坐标为(1,-4) ②若△COE ∽△EBG 则有OC BECE EG=,∠BEG =∠OCE =45° 即OC ∙EG =CE ∙BE ∴点G 只能在点E 下方 ∴EG =2-x∴3(2)x ⨯-=解得:23x =即点G 的坐标为21,3⎛⎫⎪⎝⎭综上所述,满足条件的点G 的坐标为(1,4)-或21,3⎛⎫⎪⎝⎭(3)①如图,当点P 在点A 的左侧时,连接DP 、DA 、DO ∵tan 4DFDOF OF∠==,tan 4α= ∴∠DOF =∠α=∠DAO +∠DPO ,∠DOF =∠PDO +∠DPO ∴∠DAO =∠PDO ∴△OAD ∽△ODP ∴OA ODOD OP=,即2OD OA OP = ∵22211617OD OF DF =+=+= ∵OA =1 ∴OP =17∴点P 的坐标为(-17,0)②当点P 在点A 的右侧时,作点P (-17,0)关于抛物线的对称轴的对称点P ',则DP O DPO '∠=∠∴DAO DP O α'∠+∠=∠此时点P '满足题意,且其坐标为(19,0)综上所述,满足条件的点P 的坐标为(19,0)或(17,0)- 【点睛】本题考查了求二次函数与x 轴的交点、顶点坐标,相似三角形的判定与性质,勾股定理等知识,求得三角形相似是关键.注意分类讨论.6.(1)y =12x 2+x −32;(2)(3,6)或(-5,6)或(−1,-2);(3)−12<k <56且k ≠0或56<k <43【解析】 【分析】(1)把A (−3,0),B (1,0),52,2C ⎛⎫ ⎪⎝⎭代入y =ax 2+bx +c ,解方程组即可;(2)把C 点坐标代入直线CD ,得2k +b =52,分两种情况:①若AB 为平行四边形的边时,②若AB 为平行四边形的对角线时,得关于k 、b 的方程组,解方程组即可求解; (3)分两种情况:①当E 点在x 轴上方时,②E 点在x 轴下方时,根据当α=β时,列方程,可求出k 的值,进而求出k 的取值范围. 【详解】解:(1)设抛物线的解析式为y =ax 2+bx +c , ∵抛物线经过A (−3,0),B (1,0),C (2,52)三点, ∴93005422a b c a b c a b c ⎧⎪-+=⎪++=⎨⎪⎪++=⎩,∴12132a b c ⎧⎪⎪⎨⎪⎪-⎩===, ∴抛物线的解析式为y =12x 2+x −32; (2)如图1所示,将C 点坐标代入直线CD ,得2k +b =52, 当x =−1时,y =−k +b ,即E (−1,−k +b ).①若AB 为平行四边形的边时,则F (-1+4,−k +b )或F (-1-4,−k +b ),即:F (3,−k +b )或F (-5,−k +b ), 把F (3,−k +b )代入y =12x 2+x −32,得−k +b =6, 把F (-5,−k +b ),代入y =12x 2+x −32,得−k +b =6, 又∵2k +b =52, ∴k =76-,b =296∴F (3,6)或(-5,6);②若AB 为平行四边形的对角线时,则F 和E 关于x 轴对称, ∴F (−1,k -b ), ∴k -b =-2, 又∵2k +b =52, ∴k =16,b =136,∴F (−1,-2),综上所述:F 的坐标为(3,6)或(-5,6)或(−1,-2); (3)如图2所示,①当E点在x轴上方时,如图2所示,当α=β时,∵∠EHA=90°,∴∠AEC=90°,∴∠AEH=∠EGH,∵∠AHF=∠FHG=90°,∴AHF FHG∽,∴AE AH EG EH=,∵A (−3,0),E(−1,−k+b),G(bk-,0),∴()()2222221k bk bbk bk+-+=-+⎛⎫-++-+⎪⎝⎭,∴k2−bk−2=0,联立方程220522k bkk b⎧--=⎪⎨+=⎪⎩,解得k=−12(k=43舍去),随着E点向下移动,∠CEH的度数越来越大,∠EAH的度数越来越小,当E点和H点重合时(如图3所示),α和β均等于0,此时联立方程522k bk b⎧+⎪⎨⎪-+⎩==,解得5656kb⎧=⎪⎪⎨⎪=⎪⎩,因此当−12<k <56且k ≠0时,α>β;②E 点在x 轴下方时,如图4所示,当α=β时, ∵∠EHA =90°, ∴∠AEC =90°, 根据①可得此时k =43(k =−12舍去),随着E 点向下移动,∠CEH 的度数越来越小,∠EAH 的度数越来越大,因此当56<k <43时,α>β.综上所述可得,当α>β时,k 取值范围为−12<k <56且k ≠0或56<k <43.【点睛】本题考查的是一次函数、二次函数和相似三角形的判定和性质的综合应用,掌握待定系数法求函数解析式和数形结合思想方法是解题的关键.7.(1)①()1,4;②2n =或1n =-;(2)1m 或0m =或43m -<≤-;(3)12m ≤ 【解析】 【分析】(1)①根据顶点坐标的计算公式计算即可;②分两种情况讨论,根据二次函数的图象性质计算即可;(2)分三种情况讨论,再根据当x ≤2时,函数图象上有且只有2个点到x 轴的距离为2,列不等式组即可;(3)根据点P 和点M 横坐标的位置及二次函数的图象性质列不等式组即可; 【详解】(1)当m =2时,函数解析式为2y x 2x 3=-++, ①2122b xa ,24124444ac b y a ---===-,∴顶点坐标是()1,4;②∵2y x 2x 3=-++,10a =-<, ∴开口方向向下,对称轴为:1,x =当1n >时,则x n =时,2233y n n =-++=,此时函数值最大,220,n n ∴-=解得:2n =(0n =舍去), 当11n +<,即0n <时, ∴1x n =+时,3y =最大, ∴()()212133n n -++++=, 解得:1n =-(1n =舍去) 综上:2n =或1n =-; (2)221,y x x m =-+++()()2241148,m m ∴=-⨯-⨯+=+ 当480m +>即2m >-时, 如图,当2x =时,1,y m =+根据当x ≤2时,函数图象上有且只有2个点到x 轴的距离为2可知,12,m +> 1,m ∴>m ∴的范围是 1.m >当1x =时,22,y m =+= 此时符合题意, 则0,m =当当480m +<即2m <-时,如图,根据当x ≤2时,函数图象上有且只有2个点到x 轴的距离为2可知,同理可得:2212m m +>-⎧⎨+≤-⎩解得:43,m -<≤-所以m 的范围是:4 3.m -<≤- 综上:1m 或0m =或4 3.m -<≤- (3)2221(1)2y x x m x m =-+++=--++∴抛物线的顶点坐标为(1,2m +),对称轴为直线1x = ∵点P 的横坐标为﹣3m +2,∴点P 的坐标为(﹣3m +2,2971m m -++)∵以PM 为对角线构造矩形PQMN ,矩形的各边与坐标轴垂直,抛物线在矩形PQMN 内部的函数部分y 随着x 的增大而增大, ∴矩形中抛物线为对称轴左侧的部分,即1x ≤ 又点M 的坐标为(2m ,m ),∴2971121m m m m ⎧-++≥+⎨≤⎩ ∴102m ≤< ∵点P 在二次函数的图象上, 当点M 点在点P 的左侧时 ∴232m m <-+ ∴25m <∴232m m <-+∴25 m<∴25 m<当点M点在点P的右侧时∴232m m-+>∴25 m>∴21 52m≤<故当抛物线在矩形PQMN内部的函数部分y随着x的增大而增大时,12 m≤【点睛】本题主要考查了二次函数综合应用,二次函数的图象与性质,不等式组的解法,清晰的分类讨论是解题的关键.8.(1)5;(2)157t=;(3)1t=或52t=【解析】【分析】(1)直接运用勾股定理求解即可;(2)当CP平分∠ACB时,作PM⊥BC于M点,PN⊥AC于N点,作CQ⊥AB于Q点,利用等面积法分别表示△APC和△BPC,进而得出AP ACBP BC=,从而建立分式方程求解并检验即可;(3)根据等腰三角形的性质进行分类讨论,结合勾股定理求解即可.【详解】解:(1)由勾股定理:2222AB AC BC345++=,故答案为:4;(2)当CP平分∠ACB时,如图所示,作PM⊥BC于M点,PN⊥AC于N点,作CQ⊥AB于Q点,则由角平分线的性质得:PM=PN,∵1122APCS AP CQ AC PN==,1122BPCS BP CQ BC PM==,∴11221122APCBPCAP CQ AC PNSS BP CQ BC PM==,即:AP AC BP BC=,由题意,AP t=,则5BP AB AP t=-=-,∴3 54tt=-,解得:157t=,经检验,157t=是上述分式方程的解,∴当157t=时,CP平分∠ACB;(3)①若BC=BP,如图所示,此时,BP=BC=4,AP=AB-BP=1,∴t=1;②若CP=BP,如图所示,此时,作CT⊥AB于T点,∵1122ABCS AC BC AB CT==,∴125 CT=,在Rt△CBT中,2216 5BT BC CT-,∵AP t=,∴5BP t=-,5CP t=-,∴()169555PT BT BP t t =-=--=-, 在Rt △CPT 中,222CP CT PT =+, 即:()222129555t t ⎛⎫⎛⎫-=+- ⎪ ⎪⎝⎭⎝⎭, 解得:52t =;③若CP =CB ,由于P 在线段AB 上运动,则CP =CB 的情况不成立,故舍去; 综上,当1t =或52t =时,满足△BCP 为等腰三角形. 【点睛】本题考查了勾股定理和等腰三角形的性质,解决本题的关键是正确理解题意,熟练掌握勾股定理,能够根据等腰三角形的性质进行分类讨论解决.9.(1)224233y x x =--+;(2)35(,)22P -(3)存在,12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【解析】 【分析】(1)根据待定系数法求抛物线解析式;(2)设224(,)33P t t --根据(1)的结论求得C 的坐标,进而求得AC 的解析式,过P 作PD ⊥x 轴交AC 于点D ,进而求得PD 的长,根据12APC C A S PD x x =⋅⋅-△求得APCS的表达式,进而根据二次函数的性质求得取得最大值时,t 的值,进而求得P 点的坐标; (3)分情况讨论,①//CM AQ ,②//AC MQ ,根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标. 【详解】(1)二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+(2)抛物线224233y x x =--+与y 轴交于点C ,令0x =,则2y =(0,2)C ∴设直线AC 的解析式为y kx b =+,由(3,0)A -,(0,2)C ,则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩∴直线AC 的解析式为223y x =+, 如图,过P 作PD ⊥x 轴交AC 于点D ,设224(,)33P t t --,则2(,2)3D t t +,2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APCC A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时,APCS取得最大值,此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P -(3)存在,理由如下抛物线解析式为224233y x x =--+()228133x =-++∴抛物线的对称轴为直线1x =①如图,当//CM AQ 时,Q 点在x 轴上,//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称,(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时,如图,设M 的纵坐标为n ,四边形ACQM 是平行四边形,点A ,Q 在x 轴上,则,AQ MC 的交点也在x 轴上, 202n +∴=解得2n =- 设(,2)M m -, 2242233x x ∴-=--+解得1x =-(12)M ∴--A 点到C 点是横坐标加3,纵坐标加2∴M 点到Q 点也是横坐标加3,纵坐标加2即(13,0)Q -±34(2(2Q Q ∴综上所述,存在点Q ,使得以A C M Q 、、、为顶点的四边形是平行四边形,Q 点的坐标为12(1,0),(5,0)Q Q --,34(2(2Q Q .【点睛】本题考查了二次函数综合,待定系数法,二次函数最值,二次函数的图象与性质,平行四边形的性质,综合运用以上知识是解题的关键.10.(1)①,②w 有最小值,w 的最值是(2)不变,(3)或【解析】 【分析】(1)①根据题意先求得各点的坐标,求得AD 的解析式,进而求得点E 的坐标,通过计算可得,进而可得,由可得出,依题意,设,解方程求解即可;②根据已知条件设,求得直线AP 的解析式,直线BE 的解析式,联立即可求得点G 的坐标,根据,令,根据二次函数的性质求得的最大值,即可求得的最小值;(2)根据题意过点N 作,依题意,点N 为ABP △的外心,N 为AB 垂直平分线上的点则点N 在抛物线的对称轴1x =上,设,,()1,0A -,()3,0B ,根据建立方程,解得,进而求得,即可求得;(3)作的外心H ,作轴,则,进而可得H 在AO 的垂直平分线上运动,根据题意当最大转为求当取得最小值时,最大,进而根据点到直线的距离,垂线段最短,即可求得,求得,勾股定理求得,即可求得点H 的坐标,根据对称性求得另一个坐标. (1)抛物线y =x 2﹣2x ﹣3与x 轴交于A 、B 两点,与y 轴交于C 点,D 为抛物线顶点. 令0x =,解得3y =-,则()0,3C - 令0y =,则,解得121,3x x =-=则,则①设直线AD 的解析式为y kx b =+ 则 解得令0x =,则,,依题意,设解得(舍)②点P 在第四象限的抛物线上,AP 、BE 交于点G ,如图,设,()1,0A -设直线AP 的解析式为则解得∴设直线AP 的解析式为设直线BE 的解析式为11y k x b =+∴直线BE 的解析式为联立解得∴=令存在最大值,则存在最小值当时,存在最大值,最大值为则的最小值为∴ w 有最小值,w 的最值是(2) 不变,,理由如下,如图,过点N 作,依题意,点N 为ABP △的外心N 为AB 垂直平分线上的点,即点N 在抛物线的对称轴1x =上, PM x ⊥,,轴,∴设,,()1,0A -,()3,0B ,N 为ABP △的外心,,则即解得即(3) 如图,作的外心H ,作轴,则H在AO的垂直平分线上运动依题意,当最大时,即最大时,是的外心,,即当最大,最大则当取得最小值时,最大,即当HQ⊥直线x=1时,取得最小值时,此时∴在中,.根据对称性,则存在.综上所述,或.【点睛】本题考查了三角形的外心,垂径定理,抛物线与三角形面积计算,二次函数的性质求最值问题,抛物线与圆综合,运用转化思想是解题的关键.11.(1)证明见解析,(2)证明见解析,(3)6 【解析】 【分析】(1)证明△BCE ≌△CDF 即可;(2)取BF 中点O ,连接OA 、OG ,证明A 、B 、G 、F 四点共圆即可;(3)作AK ⊥BG 于K ,HN ⊥AB 于N ,GM ⊥AB 于M ,根据等腰三角形的性质得出12BK AK ,进而得出∠BAG 的正切值,求出AH 长即可. 【详解】(1)证明∵四边形ABCD 是正方形, ∴CB =CD ,∠BCD =90°, ∵CF ⊥BE , ∴∠BGC =90°,∴∠CBE +∠GCB =90°,∠GCB +∠DCF =90°, ∴∠CBE =∠DCF , ∴△CBE ≌△DCF (AAS ), ∴CE =DF ;(2)取BF 中点O ,连接OA 、OG , ∵∠BAF =90°, ∴OA =OF =OB , 同理,OG =OF =OB ,∴A 、B 、G 、F 四点在以O 为圆心,OA 为半径的圆上,如图所示, ∴∠ABF =∠AGF ;(3)作AK ⊥BG 于K ,HN ⊥AB 于N ,GM ⊥AB 于M , ∵四边形ABCD 是正方形, ∴AB =CB ,∠ABC =90°, ∵AK ⊥BG , ∴∠AKB =90°,∴∠BAK +∠ABK =90°,∠ABK +∠CBG =90°, ∴∠BAK =∠CBG , ∴△BAK ≌△CBG (AAS ), ∴AK =BG ; ∵AG =AB =11, ∴1122BK BG AK ==, ∴1tan tan 2BAK CBG ∠=∠=, ∴BC =2EC ,由(1)得,DC =2DF , ∴1tan 2ABF ∠=, ∴12NH BN = ∵MG ∥CB , ∴∠MGB =∠CBG , ∴MG =2MB ,AM =11-MB , 222(11)(2)11MB MB -+=,解得,1225MB =,20MB =(舍去), 335AM =,445MG =, ∴4tan 3MAG ∠=,∴43NH AN =, ∵12NH BN =, ∴32114BN AN NH NH +=+=, 解得,4NH =,则3AN =,225AH AN NH =+=,GH =11-5=6.【点睛】本题考查了全等三角形的判定与性质,等腰三角形的性质,解直角三角形,圆周角定理等知识,解题关键是恰当的作辅助线,熟练运用相关性质进行推理证明.12.(1)(2)点P 的坐标为(−3,4) (3)存在,点M 的坐标为:,,【解析】 【分析】(1)由直线方程可求得A 、B 两点的坐标,代入抛物线解析式可求得b 、c 的值,可求得抛物线解析式,再令y =0可求得C 点坐标;(2)过E 作EH ⊥PD 于H ,可求得EH ,设出P 点坐标,则可表示出D 、E 、F 的坐标,从而可表示出PD 和EF ,利用梯形面积公式可表示出四边形PDEF 的面积,根据二次函数的最值,可求得P 点坐标;(3)可求得直线AG 和A ′G ′的方程,从而可表示出M 、N 点的坐标,从而可表示出MN 、FM 、FN 的长,分MN =FM 、MN =FN 和FM =FN 三种情况分别求解即可.(1)∵直线4y x =+与x 轴、y 轴分别交于A 、B 两点,∴A (−4,0),B (0,4). ∵抛物线2y x bx c =-++经过A 、B 两点,∴.解得.∴抛物线的解析式为.(2)如图,过点E作EH⊥PD于点H,则EH∥OA.∵OA=OB=4,∴∠OAB=45°.∴∠HDE=45°,且DE=.∴HE=HD=2.设点P的坐标为(a,--3a+4),则点D为(a,a+4),点E为(a+2,a+6),点F为(a+2,--7a-6).∴|PD|=-−3a+4-(a+4)=--4a,|EF|=--7a-6-(a+6)=--8a-12.∴S四边形PDEF=HE×(PD+EF)= ×2(--4a--8a-12)=-2-12a-12=-2(a+3)2+6.∴当a=-3时,S四边形PDEF有最大值6.此时点P的坐标为(−3,4).(3)满足条件的点M的坐标为:,,.理由如下:∵OG=2,∴点G的坐标为(0,-2),且A(-4,0).=+,把A、G坐标代入可得,解得.设直线AG的方程为y kx n。
中考数学压轴题(完整版)

中考数学压轴题(完整版)临近中考,学生要有一定的自主性,光跟着老师跑没用。
因为每位学生对知识点的掌握程度不同,复习进度也不同。
查字典数学网初中频道为大家提供了中考数学压轴题,希望能够切实的帮助到大家。
A级基础题1.要使分式1x-1有意义,那么x的取值范围应满足()A.x=1B.x0C.x1D.x=02.(2019年贵州黔西南州)分式x2-1x+1的值为零,那么x的值为()A.-1B.0C.1D.13.(2019年山东滨州)化简a3a,正确结果为()A.aB.a2C.a-1D.a-24.约分:56x3yz448x5y2z=________;x2-9x2-2x-3=________.5.a-ba+b=15,那么ab=__________.6.当x=______时,分式x2-2x-3x-3的值为零.7.(2019年广东汕头模拟)化简:1x-4+1x+42x2-16.8.(2019年浙江衢州)先化简x2x-1+11-x,再选取一个你喜欢的数代入求值.9.先化简,再求值:m2-4m+4m2-1m-2m-1+2m-1,其中m=2.B级中等题10.(2019年山东泰安)化简:2mm+2-mm-2mm2-4=________.11.(2019年河北)假设x+y=1,且x0,那么x+2xy+y2xx+yx的值为____ ____.12.(2019年贵州遵义)实数a满足a2+2a-15=0,求1a+1-a+2a2-1a+1a+2a 2-2a+1的值.C级拔尖题13.(2019年四川内江)三个数x,y,z满足xyx+y=-2,yzz+y=34,zxz+ x=-34,那么xyzxy+yz+zx的值为________.14.先化简再求值:ab+ab2-1+b-1b2-2b+1,其中b-2+36a2+b2-12ab=0.分式1.C2.D3.B4.7z36x2y x+3x+15.326.-17.解:原式=x+4+x-4x+4x-4x+4x-42=x+4+x-42=x.8.解:原式=x2-1x-1=x+1,当x=2时,原式=3(除x=1外的任何实数都可以).9.解:原式=m-22m+1m-1m-1m-2+2m-1=m-2m+1+2m-1=m-2m-1+2m+1 m+1m-1=m2-m+4m+1m-1,当m=2时,原式=4-2+43=2.10.m-6 11.112.解:原式=1a+1-a+2a+1a-1a-12a+1a+2=1a+1-a-1a+12=2a+12,∵a2+2a-15=0,(a+1)2=16.原式=216=18.13.-4 解析:由xyx+y=-2,得x+yxy=-12,裂项得1y+1x=-12.同理1z+1y=43,1x+1z=-43.所以1y+1x+1z+1y+1x+1z=-12+43-43=-12,1z+1y+1x=-14.于是xy+yz+zxxyz=1z+1y+1x=-14,所以xyzxy+yz+zx=-4.家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练工作,孩子一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。
初三数学压轴题含答案

1.如图,直线3y x =-+与x 轴,y 轴分别相交于点B ,点C ,经过B C ,两点的抛物线2y ax bx c =++与x 轴的另一交点为A ,顶点为P ,且对称轴是直线2x =.(1)求A 点的坐标;(2)求该抛物线的函数表达式;(3)连结AC .请问在x 轴上是否存在点Q ,使得以点P B Q ,,为顶点的三角形与ABC △相似,若存在,请求出点Q 的坐标;若不存在,请说明理由.[解]直线3y x =-+与x 轴相交于点B ,∴当0y =时,3x =,∴点B 的坐标为(30),. 又抛物线过x 轴上的AB ,两点, 且对称轴为2x =,根据抛物线的对称性,∴点A 的坐标为(10),. (2)3y x =-+过点C ,易知(03)C ,,3c ∴=.又抛物线2y ax bx c =++过点(10)(30)A B ,,,,309330a b a b +==⎧∴⎨++=⎩,. 解得14a b =⎧⎨=-⎩,.243y x x ∴=-+. (3)连结PB ,由2243(2)1y x x x =-+=--,得(21)P -,,设抛物线的对称轴交x 轴于点M ,在Rt PBM △中,1PM MB ==,452PBM PB ∴==,∠.由点(30)(03)B C ,,,易得3OB OC ==,在等腰直角三角形OBC 中,45ABC =∠,由勾股定理,得32BC =. 假设在x 轴上存在点Q ,使得以点P B Q ,,为顶点的三角形与ABC △相似. ①当BQ PBBC AB=,45PBQ ABC ==∠∠时,PBQ ABC △∽△. 即2232BQ =,3BQ ∴=,又3BO =,∴点Q 与点O 重合,1Q ∴的坐标是(00),. ②当QB PB AB BC=,45QBP ABC ==∠∠时,QBP ABC △∽△. AB CPO y2x =AB C PO xy2x =即2232QB =,23QB ∴=.273333OB OQ OB QB =∴=-=-=,, 2Q ∴的坐标是703⎛⎫⎪⎝⎭,.180********PBx BAC PBx BAC =-=<∴≠,,∠∠∠∠. ∴点Q 不可能在B 点右侧的x 轴上综上所述,在x 轴上存在两点127(00)03Q Q ⎛⎫ ⎪⎝⎭,,,,能使得以点P B Q ,,为顶点的三角形与ABC △相似。
数学数学中考数学压轴题试题及解析

一、中考数学压轴题1.如图,等腰△ABC,AB=CB,边AC落在x轴上,点B落在y轴上,将△ABC沿y轴翻折,得到△ADC(1)直接写出四边形ABCD的形状:______;(2)在x轴上取一点E,使OE=OB,连结BE,作AF⊥BC交BE于点F.①直接写出AF与AD的关系:____(如果后面的问题需要,可以直接使用,不需要再证明);②取BF的中点G,连接OG,判断OG与AD的数量关系,并说明理由;(3)若四边形ABCD的周长为8,直接写出GE2+GF2=____.2.如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为.(2)如图3,当∠EPF=90°,F P平分∠EFC时,求证:EP平分∠AEF;(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.①若∠EPF=60°,则∠EQF=.②猜想∠EPF与∠EQF的数量关系,并说明理由;3.如图1,正方形CEFG 绕正方形ABCD 的顶点C 旋转,连接AF ,点M 是AF 中点. (1)当点G 在BC 上时,如图2,连接BM 、MG ,求证:BM =MG ;(2)在旋转过程中,当点B 、G 、F 三点在同一直线上,若AB =5,CE =3,则MF = ;(3)在旋转过程中,当点G 在对角线AC 上时,连接DG 、MG ,请你画出图形,探究DG 、MG 的数量关系,并说明理由.4.已知.在Rt △OAB 中,∠OAB=90°,∠BOA=30°,OA=23,若以O 为坐标原点,OA 所在直线为x 轴,建立如图所示的平面直角坐标系,点B 在第一象限内,将Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处.(1)求经过点O ,C ,A 三点的抛物线的解析式.(2)若点M 是抛物线上一点,且位于线段OC 的上方,连接MO 、MC ,问:点M 位于何处时三角形MOC 的面积最大?并求出三角形MOC 的最大面积.(3)抛物线上是否存在一点P ,使∠OAP=∠BOC ?若存在,请求出此时点P 的坐标;若不存在,请说明理由.5.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度1y (米/分钟)与时间x (分钟)前2分钟满足二次函数21y ax ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.(1)求第一颗弹珠的速度1y (米/分钟)与时间x (分钟)之间的函数关系式;(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度2y (米/分钟)与弹出第一颗弹珠后的时间x (分钟)之间的函数关系式;(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.6.已知:如图,二次函数213222y x x =-++的图象交x 轴于A 点和B 点(A 点在B 点左则),交y 轴于E 点,作直线,EB D 是直线EB 上方抛物线上的一个动点.过D 点作 直线l 平行于直线.EB M 是直线 EB 上的任意点,N 是直线l 上的任意点,连接,MO NO ,始终保持MON ∠为90︒,以MO 和ON 边,作矩形MONC .(1)在D 点移动过程中,求出当DEB ∆的面积最大时点D 的坐标;在DEB ∆的面积最大 时,求矩形MONC 的面积的最小值.(2)在DEB ∆的面积最大时,线段ON 交直线EB 于点G ,当点,,,D N G B 四个点组成平行 四边形时,求此时线段ON 与抛物线的交点坐标.7.如图,已知正方形ABCD 中,4,BC AC BD =、相交于点O ,过点A 作射线AM AC ⊥,点E 是射线AM 上一动点,连接OE 交AB 于点F ,以OE 为一边,作正方形OEGH ,且点A 在正方形OEGH 的内部,连接DH .(1)求证:EDO EAO ∆≅∆;(2)设BF x =,正方形OEGH 的边长为y ,求y 关于x 的函数关系式,并写出定义域;(3)连接AG ,当AEG ∆是等腰三角形时,求BF 的长.8.如图,在菱形ABCD 中,AB a ,60ABC ∠=︒,过点A 作AE BC ⊥,垂足为E ,AF CD ⊥,垂足为F .(1)连接EF ,用等式表示线段EF 与EC 的数量关系,并说明理由;(2)连接BF ,过点A 作AK BF ⊥,垂足为K ,求BK 的长(用含a 的代数式表示); (3)延长线段CB 到G ,延长线段DC 到H ,且BG CH =,连接AG ,GH ,AH . ①判断AGH 的形状,并说明理由; ②若12,(33)2ADH a S ==+,求sin GAB ∠的值.9.如图,直线y =12x ﹣2与x 轴交于点B ,与y 轴交于点A ,抛物线y =ax 2﹣32x+c 经过A ,B 两点,与x 轴的另一交点为C .(1)求抛物线的解析式;(2)M 为抛物线上一点,直线AM 与x 轴交于点N ,当32MN AN =时,求点M 的坐标; (3)P 为抛物线上的动点,连接AP ,当∠PAB 与△AOB 的一个内角相等时,直接写出点P 的坐标.10.定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在ABC ∆与AED ∆中,,BA BC EA ED == ,且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”,设它们的顶角为α,连接,EB DC ,则称DC EB 会为“关联比". 下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”,且90α︒=时, ①在图1中,若点E 落在AB 上,则“关联比”DC EB=②在图2中,探究ABE ∆与ACD ∆的关系,并求出“关联比”DC EB的值.[类比探究]()2如图3,①当ABC ∆与AED ∆为“关联等腰三角形”,且120a ︒=时,“关联比”DC EB = ②猜想:当ABC ∆与AED ∆为“关联等腰三角形”,且n α=︒时,“关联比”DC EB= (直接写出结果,用含n 的式子表示)[迁移运用] ()3如图4, ABC ∆与AED ∆为“关联等腰三角形”.若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点,且1PA =,点E 为PB 上一动点,求点E 自点B 运动至点P 时,点D 所经过的路径长.11.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(13),(13)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.12.如图1,平面直角坐标系xoy 中,A (-4,3),反比例函数(0)k y k x=<的图象分别交矩形ABOC 的两边AC ,BC 于E ,F (E ,F 不与A 重合),沿着EF 将矩形ABOC 折叠使A ,D 重合.(1)①如图2,当点D 恰好在矩形ABOC 的对角线BC 上时,求CE 的长;②若折叠后点D 落在矩形ABOC 内(不包括边界),求线段CE 长度的取值范围. (2)若折叠后,△ABD 是等腰三角形,请直接写出此时点D 的坐标.13.在平行四边形ABCD 中,60B ∠=︒,点E ,F 分别在边AB ,AD 上,且60ECF ∠=︒.(1)如图1,若AB BC =,求证:AE AF BC +=;(2)如图2,若4AB BC ==,且点E 为AB 的中点,连接BF 交CE 于点M ,求FM ;(3)如图3,若AB kBC =,探究线段BE 、DF 、BC 三之间的数量关系,说明理由.14.在平面直角坐标系xOy 中,点A 为x 轴上的动点,点B 为x 轴上方的动点,连接OA ,OB ,AB .(1)如图1,当点B 在y 轴上,且满足OAB ∠的角平分线与OBA ∠的角平分线交于点P ,请直接写出P ∠的度数;(2)如图2,当点B 在y 轴上,OAB ∠的角平分线与OBA ∠的角平分线交于点P ,点C在BP 的延长线上,且满足45AOC ∠=︒,求OAB OCB∠∠;(3)如图3,当点B 在第一象限内,点P 是AOB ∆内一点,点M ,N 分别是线段OA ,OB 上一点,满足:1902APB AOB ∠=︒+∠,PM PN =,180ONP OMP ∠+∠=︒.以下结论:①OM ON =;②AP 平分OAB ∠;③BP 平分OBA ∠;④AM BN AB +=.正确的是:________.(请填写正确结论序号,并选择一个正确的结论证明,简写证明过程).15.如图,在矩形ABCD 中,6AB cm =,8AD cm =,连接BD ,将ABD △绕B 点作顺时针方向旋转得到A B D '''△(B ′与B 重合),且点D '刚好落在BC 的延长上,A D ''与CD 相交于点E .(1)求矩形ABCD 与A B D '''△重叠部分(如图1中阴影部分A B CE '')的面积; (2)将A B D '''△以每秒2cm 的速度沿直线BC 向右平移,如图2,当B ′移动到C 点时停止移动.设矩形ABCD 与A B D '''△重叠部分的面积为y ,移动的时间为x ,请你直接写出y 关于x 的函数关系式,并指出自变量x 的取值范围;(3)在(2)的平移过程中,是否存在这样的时间x ,使得AA B ''△成为等腰三角形?若存在,请你直接写出对应的x 的值,若不存在,请你说明理由.16.如图,在平面直角坐标系中,点O 为坐标原点,直线y =-x + m 交 y 轴的正半轴于点A ,交x 轴的正半轴于点B ,过点A 的直线AF 交x 轴的负半轴于点F ,∠AFO=45°. (1)求∠FAB 的度数;(2)点 P 是线段OB 上一点,过点P 作 PQ ⊥OB 交直线 FA 于点Q ,连接 BQ ,取 BQ 的中点C ,连接AP 、AC 、CP ,过点C 作 CR ⊥AP 于点R ,设 BQ 的长为d ,CR 的长为h ,求d 与 h 的函数关系式(不要求写出自变量h 的取值范围);(3)在(2)的条件下,过点 C 作 CE ⊥OB 于点E ,CE 交 AB 于点D ,连接 AE ,∠AEC=2∠DAP ,EP=2,作线段 CD 关于直线AB 的对称线段DS ,求直线PS 与直线 AF 的交点K 的坐标.17.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式.18.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 19.如图1,D 是等边△ABC 外一点,且AD =AC ,连接BD ,∠CAD 的角平分交BD 于E . (1)求证:∠ABD =∠D ;(2)求∠AEB 的度数;(3)△ABC 的中线AF 交BD 于G (如图2),若BG =DE ,求AF DE的值.20.问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰ABC 中,AB AC =,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点,D E ,若5,6AB BC ==,求线段BP 的取值范围,并求AD CE +的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB '、CC '、DD '.若你是此次项目设计的负责人,要使三条运输轨道的距离之和()BB CC DD '''++最小,你能不能按照要求进行规划,请通过计算说明.21.(操作发现)如图1,ABC ∆为等腰直角三角形,90ACB ∠=︒,先将三角板的90︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于45︒),旋转后三角板的一直角边与AB 交于点D .在三角板另一直角边上取一点F ,使CF CD =,线段AB 上取点E ,使45DCE ∠=︒,连接AF ,EF .(1)请求出EAF ∠的度数?(2)DE 与EF 相等吗?请说明理由;(类比探究)如图2,ABC ∆为等边三角形,先将三角板中的60︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于30).旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ,使CF CD =,线段AB 上取点E ,使30DCE ∠=︒,连接AF ,EF .(3)直接写出EAF ∠=_________度;(4)若1AE =,2BD =,求线段DE 的长度.22.如图,平行四边形ABCD 中,AB ⊥AC ,AB =2,AC =4.对角线AC 、BD 相交于点O ,将直线AC 绕点O 顺时针旋转α°(0°<α<180°),分别交直线BC 、AD 于点E 、F .(1)当α=_____°时,四边形ABEF 是平行四边形;(2)在旋转的过程中,从A 、B 、C 、D 、E 、F 中任意4个点为顶点构造四边形, ①当α=_______°时,构造的四边形是菱形;②若构造的四边形是矩形,求该矩形的两边长.23.在综合与实践课上老师将直尺摆放在三角板上,使直尺与三角板的边分别交于点P 、M 、N 、Q ,(1)如图①所示.当∠CNG =42°,求∠HMC 的度数.(写出证明过程)(2)将直尺向下平移至图 2 位置,使直尺的边缘通过点 C ,交 AB 于点 P ,直尺另一侧与三角形交于 N 、Q 两点。
(完整)中考数学压轴题精选含答案

一、解答题1.平面直角坐标系中,点在y轴正半轴,点在x轴正半轴,以线段AB为边在第一象限内作等边ABC,点C关于y轴的对称点为点D,连接AD,BD,且BD交y 轴于点E.(1)补全图形,并填空;①若点,则点D的坐标是__________;②若,则________.(2)若,求证:AD垂直平分BC;(3)若时,探究的数量关系,并证明.2.如图,在平面直角坐标系中,已知一次函数y=kx+b(k>0,b>0)的图象与x轴交于A,与y轴交于C.双曲线y=ax(x>0)的图象交一次函数的图像于第一象限内的点B,BD⊥x轴于D.E是AB中点,直线DE交y轴于F,连接AF.(1)若k=1,点B(2,6)时.①求一次函数和反比例函数的解析式;②求AFD的面积.(2)当k=2,a=12时,求AFD的面积.(3)求证:当k,b,a为任意常数时,AFD的面积恒等于1 2 a3.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.(1)如图1,当∠MBN 绕B 点旋转到AE =CF 时,求证:AE +CF =EF .(2)如图2,当∠MBN 绕B 点旋转到AE ≠CF 时,上述结论是否成立?若成立,请给予证明;若不成立,线段AE ,CF ,EF 又有怎样的数量关系?请写出你的猜想,并证明. (3)当∠MBN 绕B 点继续旋转到图3位置时,AE =10,CF =2.求EF 的长度.4.抛物线212y x mx n =-++与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,已知(1,0)A -,(0,2)C .(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点P ,使PCD 是以CD 为腰的等腰三角形?如果存在,求出P 点的坐标;如果不存在,请说明理由;(3)点E 是线段BC 上的一个动点,过点E 作x 轴的垂线与抛物线相交于点F ,当四边形CDBF 的面积最大时,求点E 的坐标.5.如果抛物线1C 的顶点在抛物线2C 上,同时,抛物线2C 的顶点在抛物线1C 上,那么我们称抛物线1C 与2C 关联.(1)已知抛物线①221y x x =+-,判断下列抛物线②221y x x =-++;③221y x x =++与已知抛物线①是否关联,并说明理由.(2)抛物线211:(1)28C y x =+-,动点P 的坐标为(,2)t ,将抛物线绕点(,2)P t 旋转180︒得到抛物线2C ,若抛物线1C 与2C 关联,求抛物线2C 的解析式.(3)点A 为抛物线211:(1)28C y x =+-的顶点,点B 为与抛物线1C 关联的抛物线顶点,是否存在以AB 为斜边的等腰直角ABC ,使其直角顶点C 在y 轴上,若存在,求出C 点的坐标;若不存在,请说明理由.6.已知二次函数2y x bx c =+-图象通过两点(1,),(2,10)P a Q a . (1)如果a ,b ,c 是整数,且8c b a <<,求a ,b ,c 值.(2)设二次函数2y x bx c =+-图象和x 轴交点为A 、B ,和y 轴交点为C .如果有关x 方程20x bx c +-=两个根都是整数,求ABC 面积.7.如图1,直线AB 与x 轴,y 轴分别交于A ,B 两点,点C 在x 轴负半轴上,这三个点的坐标分别为A (4,0),B (0,4),C (−1,0) . (1)请求出直线AB 的解析式;(2)连接BC,若点E是线段AC上的一个动点(不与A,C重合),过点E作EF//BC交AB于点F,当△BEF的面积是52时,求点E的坐标;(3)如图2,将点B向右平移1个单位长度得到点D,在x轴上存在动点P,若∠DCO+∠DPO=∠α,当tan∠α=4时,请直接写出点P的坐标.8.如图①,在平面直角坐标系中,点A、B的坐标分别为A(4,0)、B(0,3),连结AB.抛物线经过点B,且对称轴是直线.(1)求抛物线的函数关系式.(2)将图①中的△ABO沿x轴向左平移得到△DCE(如图②),当四边形ABCD是菱形时,说明点C和点D都在该抛物线上.(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),过点M作MN∥y轴交直线CD于点N.设点M的横坐标为m,线段MN的长为l.求l与m之间的函数关系式.(4)在(3)的条件下,直接写出m为何值时,以M、N、C、E为顶点的四边形是平行四边形.9.如图1,ABC内接于O,弦AE交BC于点D,连接BO,且ABO DAC∠∠.(1)求证:AE BC⊥;(2)如图2,点F在弧AC上,连接CF、BF,BF交AE于点M,若ACF OBC∠=∠,求证:MD ED=;(3)如图3,在(2)的条件下,3AM=时,求弦CF∠=∠,若10BFC EACBM=,3的长.10.如图,在△ABC中,AB=6,AC=BC=5,CD⊥AB于点D,点P从点A出发,以每秒5个单位长度的速度沿折线AC—CB向终点B运动,当点P不与A,B,C重合时,过点P作PQ⊥AB交AB于点Q,过点P作PM⊥PQ,使得PM=2PQ,点M、点D在PQ的同侧,连结MQ,设点P的运动时间为t(s)(1)线段CD=.(2)当点P在线段BC上时,PC=.(用含t的代数式表示)(3)当点M落在△BCD的内部时,求t的取值范围;(4)连结CM,当△CPM为锐角三角形时,直接写出t的取值范围.11.在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,过点A作AE⊥BC于点E.(1)如图1,求证:AE=CE;(2)如图2,点F是线段CE.上一点,CF=BE,FG⊥BC交BD于点G,连接AG,求证:AG=BE+FG;(3)如图3,在(2)的条件下,若EF=10,FG=7,求AG的长.12.在ABC中,AB AC=,D是边AC上一点,F是边AB上一点,连接BD、CF交于点E,连接AE,且.(1)如图1,若90BAC∠=︒,,,求点B到AE的距离;(2)如图2,若E为BD中点,连接FD,FD平分,G为CF上一点,且,求证:;(3)如图3,若,12△沿着AB翻折得,点H为的BC=,将ABD中点,连接HA、HC,当周长最小时,请直接写出的值.13.如图1,抛物线y=ax2+bx+3过点A(﹣1,0),点B(3,0),与y轴交于点C.M是抛物线任意一点,过点M作直线l⊥x轴,交x轴于点E,设M的横坐标为m(0<m<3).(1)求抛物线的解析式及tan∠OBC的值;(2)当m=1时,P是直线l上的点且在第一象限内,若△ACP是直角三角形时,求点P的坐标;(3)如图2,连接BC,连接AM交y轴于点N,交BC于点D,连接BM,设△BDM的面积为S1,△CDN的面积为S2,求S1﹣S2的最大值.14.如图,抛物线y=ax2+bx+2与直线AB相交于A(﹣1,0),B(3,2),与x轴交于另一点C.(1)求抛物线的解析式;(2)在y上是否存在一点E,使四边形ABCE为矩形,若存在,请求出点E的坐标;若不存在,请说明理由;DB的最小值.(3)以C为圆心,1为半径作⊙C,D为⊙O上一动点,求DA+5515.如图,已知抛物线y=ax2+bx+5(a≠0)与x轴交于点A(﹣5,0),点B(1,0)(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点,连接BD.直线y=经过点A,且与y轴交于点E.(1)求抛物线的解析式;(2)点N是抛物线上的一点,当△BDN是以DN为腰的等腰三角形时,求点N的坐标;(3)点F为线段AE上的一点,点G为线段OA上的一点,连接FG,并延长FG与线段BD 交于点H(点H在第一象限),当∠EFG=3∠BAE且HG=2FG时,求出点F的坐标.16.如图1,点A,点B的坐标分别(a,0),(0,b),且b=+4,将线段BA绕点B逆时针旋转90°得到线段BC.(1)直接写出a = ,b = ,点C 的坐标为 ;(2)如图2,作CD ⊥x 轴于点D ,点M 是BD 的中点,点N 在△OBD 内部,ON ⊥DN ,求证:2MN +ON =DN .(3)如图3,点P 是第二象限内的一个动点,若∠OPB =90°,求线段CP 的最大值. 17.如图,在长方形ABCD 中,10AB =,9BC =,点E 在AB 上,点G 在AD 上,AEFG 为正方形.点M ,N 分别为BC ,CD 上的动点,MO BC ⊥,NO CD ⊥,且点O 始终在正方形AEFG 的内部,MO 交EF 于点P ,NO 交FG 于点Q .(1)设CM AE a ==,①用含a 的代数式表示四边形EBMP 的周长;②若四边形OPFQ ,GQND 的周长之和恰好为四边形EBMP 周长的两倍,求a 的值. (2)设3CM x =,2CN x =,AE n CN =,是否存在正整数x ,n ,使得EBMP GQND S S =四边形四边形若存在,求出x ,n 的值;若不存在,请说明理由.18.如图,抛物线24y ax bx =++的对称轴是直线x =3,与x 轴交于()2,0A -,B 两点,与y 轴交于点C .(1)求抛物线的函数表达式;(2)若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,若3MN =,求点M 的坐标;(3)设点D ,E 是直线3x =上两动点,且1DE =,点D 在点E 上方,求四边形ACDE 周长的最小值.19.已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B (1,0)两点,与y 轴交于点()03C -,.(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图象上位于第三象限内的点,若点D 的横坐标为m ,ACD △的面积为S ,求S 与m 之间的函数关系式,并写出ACD △的面积取得最大值时点D 的坐标; (3)M 是二次函数图象对称轴上的点,在二次函数图象上是否存在点N .使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).20.如图1,已知二次函数y =ax 232+x +c 的图象与y 轴交于点C (0,4),与x 轴交于点A 、点B ,点B 坐标为(8,0).(1)请直接写出二次函数的解析式;(2)在直线BC 上方的抛物线上是否存在点P ,使△PBC 的面积为16?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的结论下,过点P作PF⊥x轴于点F,交直线BC于点E,连接AE,点N是抛物线对称轴上的动点,在抛物线上是否存在点M,使得以M、N、A、E为顶点的四边形是平行四边形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.【参考答案】**科目模拟测试一、解答题1.(1)①D(-2,3) ②∠BEO=60°;(2)答案见解析;(3)DE= AE+2EO,证明见解析.【解析】【分析】(1)①根据关于y轴的对称的性质可得答案,关于y轴的对称的两点,横坐标互为相反数,纵坐标不变;②根据C、D两点关于y轴的对称,可知y轴是线段CD的垂直平分线,得AD=AC、∠CAF=∠DAF,然后由等边△ABC得AC=AB,最后得AD=AB,∠ADB=∠ABD,即可得答案;(2)由|a−3|+b2−6b+9=0,得a=b,得∠BAO=45°,然后根据平角得∠CAF的度数、∠CAG的度数,即可得答案;(3)先证∠EBO=30°,得BE=2EO,然后作HE=AE,证△ADE≌△ABH,得DE=BH,最后证BH= AE+2EO,即可得答案.(1)解:补全图形如下图①∵C、D两点关于y轴的对称的两点,∴横坐标互为相反数,纵坐标不变,∵C(2,3),∴D(-2,3);②∵C、D两点关于y轴的对称,∠CAD=140°,=70°∴∠CAF=∠DAF=140°×12∵△ABC是等边三角形,∴∠CAB=60°,AC=AB,∴∠BAE=180°-70°-60°=50°,∵C、D两点关于y轴的对称,∴AD=AC,∴AD=AB,∴∠ADB=∠ABD=[180°-(360°-140°-60°)] ×1=10°2∴∠BEO=∠BAE+∠ABD=50°+10°=60°;(2)如下图:延长DA交BC于点G,∵|a−3|+b2−6b+9=0,∴|a−3|+(b−3)2=0,∴a=b=3,∴AO=BO,∴∠BAO=45°,∴∠CAF=180°-45°-60°=75°,∴∠CAG=180°-75°-75°=30°,∴∠BAG=60°-30°=30°,∴∠CAG=∠BAG,∴AD垂直平分BC;(3)如下图:作HE=AE,连接AH,∵C、D两点关于y轴的对称,∴∠CAF=∠DAF,∴∠CAE=∠DAE,∵∠CAE=60°+∠BAO,∴∠DAE=60°+∠BAO,∴∠DAB=60°+2∠BAO,=60°-∠BAO,∴∠DBA=[ 180°-(60°+2∠BAO)] ×12∴∠BEO=∠BAO+∠DBA=∠BAO+60°-∠BAO=60°,∴∠EBO=30°,∵∠AOB=90°,∴BE=2EO,∵HE=AE,∠BEA=∠AEH=60°,∴△AEH是等边三角形,∴AH=AE,∠HAE=60°,∴∠DAH=∠BAO,∵∠DAE=∠DAH+60°,∠BAH=∠BAO+60°,∴∠DAE=∠BAH,在△ADE和△ABH中,,∴△ADE≌△ABH,∴DE =BH , ∵HE =AE ,BE =2EO , ∴BH =BE +HE = AE +2EO , ∴DE = AE +2EO . 【点睛】本题考查了关于y 轴的对称的性质、等边三角形的性质、三角形的内角与外角的性质,垂直平分线的判定、在直角三角形中,30°的所对的边是斜边的一半、全等三角形的判定和性质,做题的关键是作辅助线,构造△ADE ≌△ABH .2.(1)①y =x +4,12y x=; ②6;(2)6;(3)见解析 【解析】 【分析】(1)①把点B (2,6)分别代入y =x +b 和y =kx (x >0),根据待定系数法即可求得; ②求出D ,E 的坐标,求出直线DE 的解析式,得到F 点坐标,故可求出△ADF 的面积; (2)联立两函数求出B 点坐标,再得到E 点坐标,求出直线DE 的解析式,从而得到F 点坐标,根据三角形的面积公式即可求出AFD 的面积 (3)与(2)同理即可求解. 【详解】解:(1)①∵一次函数y =x +b 的图象与反比例函数y =ax(x >0)的图象交于B ,B (2,6), ∴6=2+b ,6=2a , ∴b =4,a =12,∴一次函数解析式为y =x +4,反比例函数解析式为12y x=; ②令一次函数y =x +4=0 解得x =-4 ∴A (-4,0)∵E 是AB 中点,B (2,6) ∴E (-1,3) ∵BD ⊥x 轴于D ∴D (2,0)设直线DE 的解析式为y =mx +n ,代入E (-1,3)、D (2,0)得302m nm n =-+⎧⎨=+⎩解得12m n =-⎧⎨=⎩∴直线DE 的解析式为y =-x +2,令x =0,得y =2 ∴F (0,2) ∴OF =2 ∴AFD 的面积为1162622AD OF ⨯=⨯⨯=; (2)∵一次函数y =2x +b ,反比例函数12y x= 联立得2x +b =12x∴2x 2+bx -12=0解得xx舍去)∴B由A (12b -,0)得到E∵D0)设直线DE 的解析式为y =mx +n ,代入ED)得0m n m n ⎧=⎪=+⎪⎩解得2m n =-⎧⎪⎨=⎪⎩∴直线DE 的解析式为y =-2x令x =0,y∴F (0∴OF∵A (12b -,0),D0) ∴AD =12b∴AFD的面积为11622AD OF ⨯==;(3)∵一次函数y =kx +b ,反比例函数ay x= 联立得kx 2+bx -a =0解得xx舍去)∴B由A (bk -,0)得到E∵D0)设直线DE 的解析式为y =mx +n ,代入ED)得0m n m n ⎧=+⎪=+⎪⎩解得m kn =-⎧⎪⎨=⎪⎩∴直线DE 的解析式为y =-kx令x =0,y∴F (0∴OF∵A (bk -,0),D0)∴AD =b k∴AFD的面积为11212282ak AD OF a k ⨯===.【点睛】本题是反比例函数与一次函数的交点问题,解题的关键是熟知待定系数法求函数的解析式,三角形的面积及一元二次方程的解法.3.(1)见解析;(2)成立,理由见解析;(3)EF =8. 【解析】 【分析】(1)根据SAS 证明Rt △ABE ≌Rt △CBF ,求得BF =BE ,易求得△BEF 是等边三角形,可得BF =2CF ,即可解题;(2)将Rt △ABE 顺时针旋转120°,可得FG =CG +CF =AE +CF ,易证∠GBF =∠EBF =60°,即可求证△GBF ≌△EBF ,可得FG =EF ,即可解题;(3)将Rt △ABE 顺时针旋转120°,可得FG =CG -CF =AE -CF ,易证∠GBF =∠EBF =60°,即可求证△GBF ≌△EBF ,可得FG =EF ,即可解题. 【详解】证明:(1)∵Rt △ABE 和Rt △CBF 中,AB =BC ,CF =AE ,∠C =∠A =90°, ∴Rt △ABE ≌Rt △CBF (SAS ), ∴∠CBF =∠ABE ,BF =BE , ∵∠ABC =120°,∠MBN =60°,∴∠CBF =∠ABE =30°,△BEF 是等边三角形, ∴BF =2CF ,BE =2AE ,BF =EF , ∴EF =BF =2CF =AE +CF ; (2)成立,理由如下:如图2,将Rt △ABE 顺时针旋转120°,∵AB =BC ,∠ABC =120°,∴A 点与C 点重合,AE =CG ,BG =BE , ∵∠BCG =∠BCF =90°, ∴点G 、C 、F 共线, ∴FG =CG +CF =AE +CF ,∵∠ABC =120°,∠MBN =60°,∠ABE =∠CBG , ∴∠GBF =60°, 在△GBF 和△EBF 中, 60BG BE GBF EBF BF BF =⎧⎪∠=∠=︒⎨⎪=⎩,∴△GBF ≌△EBF (SAS ), ∴FG =EF , ∴EF =AE +CF ;(3)如图3,将Rt △ABE 顺时针旋转120°,∵AB =BC ,∠ABC =120°,∴A 点与C 点重合,AE =CG ,BG =BE , ∵∠BCG =∠BCD =90°, ∴点G 、C 、D 共线, ∴FG =CG +CF =AE +CF , ∵∠ABC =∠ABE +∠CBE =120°, ∴∠CBG +∠CBE =∠GBE =120°, ∵∠MBN =60°, ∴∠GBF =60°, 在△BFG 和△BFE 中, 60BG BE GBF EBF BF BF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△BFG ≌△BFE ,(SAS ) ∴GF =EF ,∴EF =AE -CF =10-2=8. 【点睛】本题考查了全等三角形的判定和性质,30°角所对直角边是斜边一半的性质,旋转的性质等知识点,本题中求证△BFG ≌△BFE 是解题的关键.4.(1)213222y x x =-++;(2)存在,13(,4)2P ,235(,)22P ,335(,)22P -;(3)点()2,1E【解析】 【分析】(1)把()1,0A -,()0,2C 代入抛物线的解析式,利用待定系数法求解即可;(2)先求解抛物线的对称轴3,2x = 再求解CD 的长,由CDP 是以CD 为腰的等腰三角形,可得123CP DP DP CD ===.再作CH ⊥对称轴于点H ,从而可得答案; (3)先求解()4,0B .再求解直线BC 的解析式为122y x =-+.过点C 作CM EF ⊥于M ,设1,22E a a ⎛⎫-+ ⎪⎝⎭,213,222F a a a ⎛⎫-++ ⎪⎝⎭,根据BCDCEFBEFCDBF S SSS=++四边形111222BD OC EF CM EF BN =⋅+⋅+⋅列函数关系式,从而可得答案. 【详解】解:(1)∵抛物线212y x mx n =-++经过()1,0A -,()0,2C ,∴10,22,m n n ⎧--+=⎪⎨⎪=⎩解得3,22.m n ⎧=⎪⎨⎪=⎩ ∴抛物线的解析式为213222y x x =-++.(2)∵22131325222228y x x x ⎛⎫=-++=--+⎪⎝⎭, ∴抛物线的对称轴是直线32x =. ∴32OD =. ∵()0,2C ,∴2OC =.在Rt OCD △中,由勾股定理,得2235222CD ⎛⎫=+ ⎪⎝⎭. ∵CDP 是以CD 为腰的等腰三角形, ∴123CP DP DP CD ===. 作CH ⊥对称轴于点H , ∴12HP HD ==.∴14DP =.∴13(,4)2P ,235(,)22P ,335(,)22P -. (3)当0y =时,由2132022x x -++=,解得11x =-,24x =,∴()4,0B .设直线BC 的解析式为y kx b =+,得2,40,b k b =⎧⎨+=⎩解得1,22.k b ⎧=-⎪⎨⎪=⎩∴直线BC 的解析式为122y x =-+. 过点C 作CM EF ⊥于M ,设1,22E a a ⎛⎫-+ ⎪⎝⎭,213,222F a a a ⎛⎫-++ ⎪⎝⎭,∴2213112222222EF a a a a a ⎛⎫=-++--+=-+ ⎪⎝⎭.∵BCDCEFBEFCDBF S SSS=++四边形111222BD OC EF CM EF BN =⋅+⋅+⋅ 2215111122(4)2222222a a a a a a ⎛⎫⎛⎫=⨯⨯+-++--+ ⎪ ⎪⎝⎭⎝⎭225134(2)22a a a =-++=--+. ∴根据题意04a ≤≤,∴当2a =时,CDBF S 四边形的最大值为132,此时点()2,1E . 【点睛】本题考查的是利用待定系数法求解抛物线的解析式,二次函数与等腰三角形,图形面积的最值问题,灵活运用二次函数的图象与性质解决问题是解题的关键.5.(1)①、②关联,理由见解析;(2)21(7)68y x =--+或21(9)68y x =-++;(3)存在,(0,1)或(0,3+420,3-42 【解析】 【分析】(1)首先求得抛物线①的顶点坐标,然后检验是否此点在抛物线②与③上,再求得抛物线②的顶点坐标,检验是否在抛物线①上即可求得答案;(2)首先求得抛物线C 1的顶点坐标,则可得:点P 在直线y =2上,则可作辅助线:作M 关于P 的对称点N ,分别过点M 、N 作直线y =2的垂线,垂足为E ,F ,则可求得:点N 的坐标,利用顶点式即可求得结果;(3)分别从当A ,B ,C 逆时针分布时与当A ,B ,C 顺时针分布时分析,根据全等三角形的知识,即可求得点C 的坐标,注意别漏解. 【详解】解:(1)∵①抛物线y =x 2+2x -1=(x +1)2-2的顶点坐标为M (-1,-2), ∴②当x =-1时,y =-x 2+2x +1=-1-2+1=-2, ∴点M 在抛物线②上;∵③当x =-1时,y =x 2+2x +1=1-2+1=0, ∴点M 不在抛物线③上; ∴抛物线①与抛物线②有关联;∵抛物线②y =-x 2+2x +1=-(x -1)2+2,其顶点坐标为(1,2), 经验算:(1,2)在抛物线①上, ∴抛物线①、②是关联的;(2)抛物线C 1:211:(1)28C y x =+-的顶点M 的坐标为(-1,-2),∵动点P 的坐标为(t ,2), ∴点P 在直线y =2上,作M 关于P 的对称点N ,分别过点M 、N 作直线y =2的垂线,垂足为E ,F ,则ME =NF =4,∴点N 的纵坐标为6,当y =6时,21(1)268x +-=,解得:x 1=7,x 2=-9,①设抛物C 2的解析式为:y =a (x -7)2+6, ∵点M (-1,-2)在抛物线C 2上, ∴-2=a (-1-7)2+6,∴a =18-,∴抛物线C 2的解析式为:21(7)68y x =--+,②设抛物C 2的解析式为:y =a (x +9)2+6, ∵点M (-1,-2)在抛物线C 2上, ∴-2=a (-1+9)2+6,∴a =18-,∴抛物线C 2的解析式为:21(9)68y x =-++;(3)点C 在y 轴上的一动点,以AC 为腰作等腰直角△ABC ,令C 的坐标为(0,c ),则点B 的坐标分两类:①当A ,B ,C 逆时针分布时,如图中B 点,过点A ,B 作y 轴的垂线,垂足分别为H ,F , 在等腰直角△ABC 中,AC =BC ,∠ACB =90°,即∠ACH +∠BCH =90°, ∵∠ACH +∠CAH =90°,∴∠CAH =∠BCH ,又∠AHC =∠BFC =90°, 则△BCF ≌△CAH (AAS ),∴CF =AH =1,BF =CH =c +2,点B 的坐标为(c +2,c -1),当点B 在抛物线C 1:y =221(1)8x +-上时,c -1=18(c +2+1)2-2,解得:c =1.②当A ,B ,C 顺时针分布时,如图中B ′点,过点B ′作y 轴的垂线,垂足为D , 同理可得:点B ′的坐标为(-c -2,c +1),当点B ′在抛物线C 1:y =18(x +1)2-2上时,c +1=18(-c -2+1)2-2,解得:c =3+42c =3-42综上所述,存在三个符合条件的等腰直角三角形,其中C 点的坐标分别为:C 1(0,1),C 2(0,3+42C 3(0,3-42【点睛】此题考查了待定系数法求二次函数的解析式以及二次函数的顶点坐标的求解方法,全等三角形的性质等知识.此题综合性很强,难度较大,注意数形结合思想与分类讨论思想的应用.6.(1)a=2,b=15,c=14;(2)1【解析】【分析】(1)代入两点坐标,求得b、c(用a表示),再由已知c<b<8a,联立不等式组求得a、b、c的值;(2)设出程x2+bx-c=0的两个根,根据根与系数的关系与因式分解求得两根,得出函数解析式,进一步求得图象与x、y轴的交点A、B、C三点解答问题.【详解】解:点P(1,a)、Q(2,10a)在二次函数y=x2+bx-c的图象上,故1+b-c=a,4+2b-c=10a,解得b=9a-3,c=8a-2;(1)由c<b<8a知8293 938a aa a-<-⎧⎨-<⎩,解得1<a<3,又a为整数,所以a=2,b=9a-3=15,c=8a-2=14;(2)设m,n是方程的两个整数根,且m≤n.由根与系数的关系可得m+n=-b=3-9a,mn=-c=2-8a,消去a,得9mn-8(m+n)=-6,两边同时乘以9,得81mn-72(m+n)=-54,分解因式,得(9m-8)(9n-8)=10.∴9819810mn-=⎧⎨-=⎩或9810981mn-=-⎧⎨-=-⎩或985982mn-=-⎧⎨-=-⎩或982985mn-=⎧⎨-=⎩,解得:12mn=⎧⎨=⎩或2979mn⎧=-⎪⎪⎨⎪=⎪⎩或1323mn⎧=⎪⎪⎨⎪=⎪⎩或109139mn⎧=⎪⎪⎨⎪=⎪⎩;又∵m,n是整数,所以后面三组解舍去,故m=1,n=2.因此,b=-(m+n)=-3,c=-mn=-2,二次函数的解析式为y=x2-3x+2.令y=0,则x=1或x=2,令x=0,则y=2,∴点A、B的坐标为(1,0)和(2,0),点C的坐标为(0,2),∴△ABC的面积为12×(2−1)×2=1.【点睛】此题主要考查二次函数图象上点的坐标特点、根与系数的关系、不等式组、以及三角形的面积计算公式.7.(1)4y x =-+;(2)点E 坐标为3,02⎛⎫⎪⎝⎭;(3)点P 的坐标为(19,0)或(-17,0).【解析】 【分析】(1)利用待定系数法即可求解;(2)同理利用待定系数法求得直线BC 的解析式为y =4x +4,再求得直线EF 的解析式,联立求得点F 的坐标,利用BEF OAB OBE AEF S S S S ∆∆∆∆=--列式求解即可; (3)计算得到tan 4DGDOG OG∠==,推出∠α=∠DOG ,∠DPO =∠CDO ,设点P 的坐标为(p ,0),分p <0和p >0两种情况讨论,利用相似三角形的判定和性质求解即可. 【详解】解:(1)∵直线AB 经过点A (4,0),B (0,4), ∴设直线AB 的解析式为y =kx +4, 把A (4,0)代入得:4k +4=0, 解得:k =-1,∴直线AB 的解析式为y =-x +4; (2)设点E (m ,0),同理求得直线BC 的解析式为y =4x +4, ∵EF //BC ,∴设直线EF 的解析式为:4y x n =+,将点E 坐标代入上式并解得:04m n =+, ∴4n m =-,∴直线EF 的解析式为:44y x m =-, ∴444x x m -+=-, 解得:()415x m =+, 把x 的值代入4y x =-+,得1645my -=.∴点F 坐标为4416455m m +-⎛⎫⎪⎝⎭,, ()1111645444422252BEF OAB OBE AEF m S S S S m m -=--=⨯⨯-⨯--⨯=△△△△,解得:32m =, ∴点E 坐标为302⎛⎫⎪⎝⎭,; (3)将点B (0,4)向右平移1个单位长度得到点D ,则D (1,4), 过点D 作DG ⊥x 轴于点G ,则∠OGD =90°,OG =1,GD =4,CG =2, ∴tan 4DGDOG OG∠==,OD =22224117DG OG +=+=, 在Rt △CDG 中,CD =22222425CG DG +=+=, ∵tan ∠α=4, ∴∠α=∠DOG ,∵∠DCO +∠DPO =∠α,∠DCO +∠CDO =∠DOG , ∴∠DPO =∠CDO , ∵点P 在x 轴上∴设点P 的坐标为(p ,0),当p <0时,PO =-p ,∵∠POD =∠DOC ,∠DPO =∠CDO , ∴△POD ~△DOC , ∴PO DODO CO=, ∴PO =2171DO CO ==17,此时,点P 的坐标为(-17,0);当p>0时,PO=p,PC=p+1,∵∠PCD=∠DCO,∠DPC=∠ODC,∴△PCD~△DCO,∴PC DC DC CO=,∴PC=(22201DCCO==,∴p=PC-1=19,此时,点P的坐标为(19,0);综上,点P的坐标为(19,0)或(-17,0).【点睛】本题是一次函数综合题,主要考查了待定系数法,角平分线的性质,相似三角形的性质和判定,三角形函数等,分类讨论是解第(3)问的关键.8.(1) y=;(2)见解析;(3)l=或l=;(4)m=或或−3时,以点M、N、C、E为顶点的四边形是平行四边形.【解析】【分析】(1)把点B的坐标代入抛物线解析式、联合对称轴x=列出关于系数b、c的方程组,通过解方程组来求它们的值;(2)由平移的性质易求点C、D的坐标,将它们的坐标分别代入抛物线解析式进行验证即可;(3)根据点C、D的坐标易求直线CD的解析式为y=.根据已知条件知点M、N 的横坐标都是m,则l的值就是点M、N的纵坐标之差.(4)由平行四边形的对边相等的性质推知MN=CE=3,利用所求的l与m间的函数式可以求得相应的m的值.【详解】解:(1)由已知,得,解得,∴二次函数的解析式为y=;(2)在Rt△ABO中,∵OA=4,OB=3,∴AB=5.又∵四边形ABCD是菱形,∴BC=AD=AB=5.∵△ABO沿x轴向左平移得到△DCE,∴CE=OB=3.∴C(−5,3)、D(−1,0).当x=−5时,y==3,当x=−1时,y==0,∴C、D在该抛物线上;(3)设直线CD的解析式为y=kx+b,则,解得,∴y=,∵MN//y轴,∴M、N的横坐标均为m,当M在直线CD的上方时,有l=MN=()−()=;当M在直线CD的下方时,有l=MN=()− ()=.∴l与m之间的函数解析式为l=或l=.(4)由于MN//CE,要使以点M、N、C、E为顶点的四边形是平行四边形,只需MN=CE=3,当=3时,解得;当=3时,解得.即当m=或或−3时,以点M、N、C、E为顶点的四边形是平行四边形.【点睛】本题综合考查了待定系数法求一次函数、二次函数解析式,平行四边形的性质.在求有关动点问题时要注意分析题意分情况讨论结果.9.(1)见解析;(2)见解析;(3)53.【解析】【分析】(1)作⊙O的直径AF,连接BF,证明∠ACD+∠CAE=90°即可;(2)连接BE,利用角的转换证明∠BMD=∠BEM,从而可得BM=BE,进而根据等腰三角形三线合一即可得出结论;(3)如图3,证明BEM AEB得2=即可求出DE长,进而由勾股定理求出BE EM AEBD,再由相交线弦定理求出CD,即可得出CE长,EC FC=.=可得EC FC【详解】解:(1)如图1,作⊙O的直径AF,连接BF,∴∠AFB+∠OAB=90°,∵OA=OB,∴∠ABO=∠OAB,又∵∠DAC=∠ABO,∴∠DAC=∠ABO=∠OAB.∵AB AB=∵∠AFB=∠ACD,∵AF是直径∴∠AFB+∠OAB=90°,∴∠ACD+∠CAE=90°,∴∠ADC=90°,即AE⊥BC;(2)连接BE,∵AF AF=∴∠ACF=∠ABF,又∵∠ACF=∠OBC,∴∠ABF=∠OBC,∴∠ABO+∠OBF=∠FBC+∠OBF,∴∠ABO=∠FBC,∵∠DAC=∠ABO,∴∠DAC=∠MBC,∵∠BMD+∠MBC=∠ACD+∠DAC=90°,∴∠BMD=∠ACD,∵AB AB=∴∠BEM=∠ACD,∴∠BMD=∠BEM,∴BM=BE,∵AE⊥BC,∴MD=ED;(3)如图2,连接EC,∵BC BC=∴BFC BAC∠=∠,∵3BFC EAC∠=∠,∴3BAC EAC∠=∠,∴2BAE BAC EAC EAC∠=∠-∠=∠,∵EBC FBC DAC∠=∠=∠,∴=2MBE EBC FBC EAC∠=∠+∠∠,∴MBE BAE∠=∠,又∵E E∠=∠,∴BEM AEB,∴BE AE EM BE=,∵10BM BE=3AM= 1010=1010=∴=2EM,由(2)可知MD =ED ,BM =BE ,∴1DM DE ==,314AD AM DM =+=+=在Rt BDM 中,BD =,在Rt BDA 中,AB =, ∵=BE BE , ∴BAD DCE ∠=∠, 又∵BDA CDE ∠=∠, ∴BDA EDC ,∴=EC DE AB BD,即1=53EC ∴5=3EC ,∵CAE FBC ∠=∠, ∴EC FC =,∴5=3EC FC =【点睛】本题是圆的综合题,主要考查了圆周角定理,涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点,解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系,从而利用相似或勾股定理解题.10.(1)4;(2);(3)或;(4)或.【解析】 【分析】(1)首先根据等腰三角形三线合一的性质得到,然后根据勾股定理即可求出线段CD 的长度;(2)根据点P 运动的速度求出点P 运动的路程,然后减去AC 的长度即可求出PC 的长度;(3)分两种情况,当点P 在线段AC 上时和点P 在线段BC 上时,分别利用相似三角形的性质计算出点M 在线段CD 上时和点M 在线段BC 上时的时间,即可求出t 的取值范围; (4)分两种情况,当点P 在线段AC 上时和点P 在线段BC 上时,分别得出点M 在线段CD 上时和点M 在线段BC 上时是直角三角形,然后利用相似三角形的性质求出t 的值,即可得出△CPM 为锐角三角形时t 的取值范围. 【详解】解:(1)∵在△ABC 中,AC =BC =5 ∴ABC ∆是等腰三角形 ∵CD ⊥AB 于点D∴(三线合一)∴在中,由勾股定理得,故答案为:4;(2)∵点P从点A出发,以每秒5个单位长度的速度沿折线AC—CB向终点B运动∴点P运动的路程为5t∴当点P在线段BC上时,故答案为:;(3)当点P在线段AC上时,由题意得,,AC=5,如图所示,当点M在线段CD上时,∵PQ⊥AB,CD⊥AB,∴∴∴∴,即,解得:,,∴,∵PM=2PQ,∴,∵CD⊥AB,PQ⊥AB,PM⊥PQ,∴四边形PQDM是矩形,∴,∴,解得:,如图所示,当点M在线段BC上时,同理可得,,,,,,∵PQ⊥AB,PM⊥PQ,∴∴∴∴,即,解得:,∴当时,点M落在△BCD的内部;如图所示,当点P在线段BC上时,当点M在线段CD上时,设,则,同理可得,四边形MDQP是矩形,,∴,,∴,即,解得:,∴,∴,∴,当点P运动到B点时,,∴当时,点M落在△BCD的内部,综上所述,当点M落在△BCD的内部时,t的取值范围是或;(4)当点M在线段CD上时,,即是直角三角形,由(3)可得,此时,当时,如图所示,∵,,,则,,∵,,又∵,∴∴,即,解得:,∴当时,是锐角三角形;当点M在线段BC上时,当时,即是直角三角形,如图所示,设,则,,,,同理可得,,∴,即,解得:,∴,∴,∵当点M在CD上时,此时,即是直角三角形,由(3)可得,此时,∴当时,是锐角三角形,∴综上所述,当△CPM为锐角三角形时,t的取值范围是或.【点睛】此题考查了相似三角形的性质和判定,等腰三角形的性质,勾股定理,三角形动点问题等知识,解题的关键是根据题意画出相应的图形,分情况讨论利用相似三角形的性质求解.11.(1)见详解;(2)见详解;(3)29 2【解析】【分析】(1)过点D作DM⊥AE于点M,证明ABE△≌DAM△,即可得到结论;(2)延长GF到点M,使FM=BE,则BE+FG=MG,先证明ABE△≌BMF,再证明ABG≌MBG△,进而即可得到结论;(3)过点G作GN⊥AE,设BE=x,则AG=BE+FG=x+7,AN= 3+x,结合勾股定理,列出方程,进而即可求解.【详解】解:(1)过点D作DM⊥AE于点M,∵∠DME=∠MEC=∠C=90°,∴四边形CDME是矩形,∴DM=CE,又∵∠BAD=∠AMD=90°,∴∠1+∠EAD=∠2+∠EAD=90°,∴∠1=∠2,在ABE△和DAM△中,∵1290AMD AEB AB AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴ABE △≌DAM △, ∴AE=DM , ∴AE =CE ;(2)延长GF 到点M ,使FM =BE ,则BE +FG =MG ,∵BE =CF , ∴BF =CE =AE , 在ABE △和BMF 中,∵90AE BF AEB BFM BE MF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴ABE △≌BMF , ∴∠BAE =∠MBF ,AB =BM , ∵∠BAE +∠ABE =90°, ∴∠MBF +∠ABE =90°, ∴∠ABM =90°, ∵∠BAD =90°,AB =AD , ∴∠A BD=45°, ∴∠DBM =45°, ∴∠ABD =∠DBM , ∴ABG ≌MBG △, ∴AG=MG=BE +FG ;(3)过点G 作GN ⊥AE ,设BE =x ,则AG =BE +FG =x +7,∵∠GNE =∠NEF=EFG =90°, ∴四边形EFGN 是矩形, ∴NG =EF =10,EN=FG =7, 又∵AE =BF =10+x , ∴AN =AE -EN =10+x -7=3+x ,在直角ANG 中,()()2223107x x ++=+,解得:x =152, ∴AG =x +7=152+7=292.【点睛】本题主要考查矩形的性质,全等三角形的判定和性质,勾股定理,等腰自交三角形的性质,添加辅助线构造全等三角形,掌握“截长补短法”是解题的关键.12.3(2)证明见解析 (3)【解析】 【分析】(1)如图所示,过点B作BG⊥AE交AE延长线于G,先证明∠ACF=∠GAB,即可证明△ABG≌△CAE得到BG=AE,由勾股定理得,再由,得到,则点B到AE的距离为(2)如图所示,延长AE到H使得,AE=HE,连接DH,CH,先证明△AEB≌△HED得到AB=HD=AC,∠ABE=∠HDE,则∠HCD=∠HDC,AB∥DH,从而推出∠BAC=∠HDC=∠HCD,再证明CE是AH的垂直平分线,得到AC=HC,则∠ACE=∠HCE,即∠HCA=2∠ACE,然后推出∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD,GD=GC,即可证明△AFD≌△GFD(AAS),得到AF=GF,则CF=GF+CG=AF+DG;(3)如图所示,连接,延长交BC于F,作直线BE⊥BC,由翻折的性质可知,,,,然后证明,得到,则点D在线段BC的垂直平分线上,即AF⊥BC,求出,由H 是的中点,得到直线A关于点H的对称点A'在直线BE上,则要使△AHC的周长最小,则要最小,即最小,即当A'、C、H、三点共线时有最小值,如图所示,连接交于,交AF于P,连接BP,先证明,得到,由平行线之间的间距相等,得到,然后求出,再证明,求出,由此求解即可.(1)解:如图所示,过点B作BG⊥AE交AE延长线于G,∵AE⊥CF,AG⊥BG,∴∠BAC=∠AGB=∠AEF=∠AEC=90°,∠AFC+∠ACF=90°,∴∠FAE+∠AFE=90°,∴∠ACF=∠GAB,又∵AB=CA,∴△ABG≌△CAE(AAS),∴BG=AE,在直角△AFC中,由勾股定理得,∵,∴,∴点B到AE(2)解:如图所示,延长AE到H使得,AE=HE,连接DH,CH,∵FD平分∠AFC,∴∠AFD=∠CFD,∵E是BD的中点,∴BE=DE,又∵AE=HE,∠AEB=∠HED,∴△AEB≌△HED(SAS),∴AB=HD=AC,∠ABE=∠HDE,∴∠HCD=∠HDC,∴∠BAC=∠HDC=∠HCD,∴∠ACE=∠HCE,即∠HCA=2∠ACE,∵∠GDC=∠GCD,∠FGD=∠GDC+∠GCD,∴∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD,GD=GC,又∵FD=FD,∠AFD=∠GFD,∴△AFD≌△GFD(AAS),∴AF=GF,∴CF=GF+CG=AF+DG;(3)解:如图所示,连接,延长交BC于F,作直线BE⊥BC,由翻折的性质可知,,,,∴,又∵AB=AC,,∴,∴,∴点D在线段BC的垂直平分线上,即AF⊥BC,∴,∵H是的中点,∴直线A关于点H的对称点A'在直线BE上,∴,∴要使△AHC的周长最小,则要最小,即最小,∴当A'、C、H、三点共线时有最小值,如图所示,连接交于,交AF于P,连接BP,∵BE⊥BC,AF⊥BC,∴,∴,,又∵,∴,∴,∵,BC⊥BE,∴,∵平行线之间的间距相等,∴∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∴AB=2AF,∴,∴,∴,∵P在线段BC的垂直平分线上,∴PB=PC,∴∠PBC=∠PCB,∵,∴,∴,∴,∴,∴,∴,∴【点睛】本题主要考查了全等三角形的性质与判定,线段垂直平分线的性质,等腰三角形的性质与判定,含30度角的直角三角形的性质,勾股定理,平行线的性质与判定等等,熟练掌握相关知识是解题的关键.13.(1)y=﹣x2+2x+3,1(2)(1,1)或(1,2)或(1,83)(3)【解析】【分析】(1)用待定系数法即可求解;(2)①当为直角时,证明,则,即,即可求解;②当为直角时,同理可解;③当为直角时,同理可解;(3);,即可求解.(1)解:设抛物线的表达式为,则,则,解得1a=-,故抛物线的表达式为2y x2x3=-++,则;(2)解:当1m=时,则直线l为抛物线的对称轴,如图1,连接AC,设点(1,)P m,①当为直角时,则,,,,过点C作于点N,,,,,即,∴,解得1m=或2,故点P的坐标为(1,1)或(1,2);②当为直角时,同理可得:点P'的坐标为8 (1,)3;③当为直角时,。
数学中考压轴题大全(含答案、详细解析版)

( 2) A( 3,0) B (5,4)
C (0,4) ………… 5 分
C
1
A 01
B x
把点 A 坐标代入 y ax2 5ax 4 中,解得 a
1
……… 6 分
6
y
1 x2
5 x
4 …………………………………………
7分
66
y
M
( 3)存在符合条件的点 P 共有 3 个.以下分三类情形探索.
A
1
N
令 x=20,y=60 ,得 k=60
①
令 x=100,y=100 ,得 a× 802+ k=100
②
由①②解得
1 a
160 , k 60
∴y
1
2
x 20 60 。……… 14 分
160
2 、(常州)已知 A( 1, m) 与 B(2, m 3 3) 是反比例函数
y
k
图象上的两个点.
x
( 1)求 k 的值;
( 3)过原点 O 的另一条直线 l 交双曲线 y k ( k 0) 于 P, Q 两 x
一象限),若由点 A, B, P, Q 为顶点组成的四边形面积为 24 ,求点
y A
解: (1) ∵点 A横坐标为 4 , ∴当 x = 4 时, y = 2 .
O B
点( P 点在第 P 的坐标. x
∴ 点 A的坐标为( 4 , 2 ) .
∴ S = S 梯形 PEFA △POA = 6 .
∴ 1 (2
8 ) (m 4)
6,
2m
解得 m = 8 , m = - 2 ( 舍去 ) .
∴ P(8, 1) .
∴ 点 P的坐标是 P( 2,4)或 P( 8, 1).
(完整)中考数学压轴题精选附答案

一、解答题1.如图,已知正方形ABCD ,将AD 绕点A 逆时针方向旋转到AP 的位置,分别过点作,垂足分别为点E 、F .(1)求证:;(2)联结,如果,求的正切值; (3)联结,如果,求n 的值.2.在ABC 中,AB BC =,45B ∠=︒,AD 为BC 边上的高. (1)如图1,若1AD =,求线段CD 的长度;(2)如图2,点E ,点F 在AB 边上,且满足AE BF =,连接CE ,CF 分别交线段AD 于点M ,点N ,若点M 为线段CE 的中点,求证:2AN CD AB +=;(3)在(2)问条件下,若2AC =,点K 为AC 边上一动点,点Р为ACF 内一点且满足ACP CAD ∠=∠,当PK PA +取最小值时,请直接写出CPK S △的值.3.如图,点D 、E 分别在等边△ABC 的边AB 、BC 上,且BD =CE ,CD ,AE 交于点F . (1)求∠AFD 的度数;(2)如图2,若D ,E ,M ,N 分别是△ABC 各边上的三等分点,BM ,CD 交于Q .若△ABC 的面积为S ,则四边形ANQF 的面积为______;(只写出答案即可,不要求写解题过程)(3)如图3,延长CD 到点P ,使∠BPD =30°,设AF =a ,CF =b ,请用含a ,b 的式子表示PC 的长,并说明理由.4.如图1,在平面直角坐标系xOy中,矩形OABC的顶点A、C的坐标分别为(0,6)、(5,0),点P为线段OA上的一个动点,将矩形OABC在直线PC上方的部分沿直线PC翻折,点B落在点D处,点A落在点E处,直线CD交y轴于点F.(1)如图2,当点P与点A重合时,求点F的坐标;(2)点P从A向O运动的过程中,点D、P、C、B能否构成菱形,若能,求出符合条件的点D的坐标,若不能,请说明理由;(3)点P从A向O运动的过程中,当△DPC的重心刚好落在y轴上时,求出此时点P的坐标.5.问题提出(1)如图①,在△ABC中,BC=2,将△ABC绕点B顺时针旋转60°得到△A′B′C′,则CC′=;问题探究(2)如图②,在△ABC中,AB=BC=3,∠ABC=30°,点P为△ABC内一点,连接PA、PB、PC,求PA+PB+PC的最小值,并说明理由;问题解决(3)如图③,在四边形ABCD中,AD∥BC,AB=6,AD=4,∠ABC=∠BCD=60°.在四边形ABCD内部有一点,满足∠APD=120°,连接BP、CP,点Q为△BPC内的任意一点,是否存在一点P和一点Q,使得PQ+BQ+CQ有最小值?若存在,请求出这个最小值;若不存在,请说明理由.6.折叠变换是特殊的轴对称变换,我们生活中常对矩形纸片进行折叠,这其中蕴含着丰富的数学知识和思想.(1)如图1,矩形ABCD中,AB=6,BC=4,点E是DC的中点,将矩形ABCD沿BE折叠,点C落在点F的位置.①求证:DF∥BE;②求DF的长度.(2)如图2,在直角坐标系中,把矩形OABC沿对角线AC所在的直线折叠,点B落在点D处,AD与y轴交于点E,OA=2,OC=23,点G是直线AC上的一个动点,在坐标平面内存在点H,使得以点E,A,G,H为顶点的四边形是菱形,请直接写出点H坐标.7.“数学建模”是中学数学的核心素养,平时学习过程中能归纳一些几何模型,解决几何问题就能起到事半功倍的作用.(1)如图1,正方形ABCD中,45=;∠=︒,且DE BFEAF=,求证:EG AG(2)如图2,正方形ABCD中,45∠=︒,延长EF交AB的延长线于点G,(1)中的EAF结论还成立吗?请说明理由;⊥,垂足为点Q,交AF于点N,连结DN,求(3)如图3在(2)的条件下,作GQ AE证:45∠=︒.NDC8.如图,在平面直角坐标系中,点B的坐标是(0,2),动点A从原点O出发,沿着x 轴正方向移动,△ABP是以AB为斜边的等腰直角三角形(点A、B、P顺时针方向排列),当点A与原点O重合时,得到等腰直角△OBC(此时点P与点C重合).(1)BC=;当OA=2时,点P的坐标是;(2)设动点A的坐标为(t,0)(t≥0).①点A在移动过程中,△ABP的顶点P在射线OC上吗?请说明理由;②用含t的代数式表示点P的坐标为:(,);(3)分别过点P、A做x轴、y轴的平行线,两条平行线交于点Q,是否存在这样的Q,使得△AQB是等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.9.抛物线y=ax2+b经过点A(4,0),B(0,﹣4),直线EC过点E(4,﹣1),C (0,﹣3),点P是抛物线上点A、B间的动点(不含端点A、B),过P作PD⊥x轴于点D,连接PC、PE.(1)求抛物线与直线CE的解析式;(2)求证:PC+PD为定值;(3)若△PEC的面积为1,求满足条件的点P的坐标.10.如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=8,CD=2m(m>2),P为CD中点,以P为圆心,CP为半径作半圆P,交线段AC于点E,交线段AD于点F.(1)当E为CA中点时,①求证:E是弧CF的中点.②求此时m的值.(2)连结PF,若PF平行△ABC的某一边时求出满足条件的m值.(3)连结PE,将PE绕着点E顺时针旋转90°得到EP',连结AP',当AP'⊥AC时,求此时CE的长.11.已知抛物线214y x bx c =-++与直线AC 相交于A 、C 两点,且()2,0A -、()4,3C .(1)填空:b =______,c =______;(2)长度为5的线段DE 在线段AC 上移动,点G 与点F 在上述抛物线上,且线段DG 与EF 始终平行于y 轴.①连接FG ,求四边形DEFG 的面积的最大值,并求出对应点D 的坐标;②CH AB ⊥,垂足为点H ,线段DE 在移动的过程中,是否存在点D ,使△DEG 与△ACH 相似?若存在,请求出此时点D 的坐标;若不存在,试说明理由. 12.如图,抛物线交x 轴于A ,B 两点,交y 轴于点C ,直线经过点B ,C .(1)求抛物线的解析式;(2)抛物线的对称轴l 与直线BC 相交于点P ,连接AC ,AP ,判定△APC 的形状,并说明理由;(3)在直线BC 上是否存在点M ,使AM 与直线BC 的夹角等于∠ACB 的2倍?若存在,请求出点M 的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,矩形OABC ,点A 在y 轴上,点C 在x 轴上,其中B(﹣2,3),已知抛物线y=﹣34x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE,DE,若S△BDE=4S△ABE,求E点坐标;(3)如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q,连接AP,AQ,PQ,若△APQ为直角三角形,请直接写出P点坐标.14.如图,已知二次函数的解析式为y=﹣12x2+bx+c,A(-1,0),C(4,0),P为二次函数上的动点.(1)求二次函数的解析式.(2)若P在第一象限上,求S△BCP的最大值.(3)在x轴上是否存在点Q,使得BQ=BP且BP⊥BQ若存在,请直接写出所有点Q的坐标,若不存在,请说明理由.15.(1)[感知]如图1,在正△ABC的外角∠CAH内引射线AM,作点C关于AM的对称点E(点E在∠CAH内),连接BE,BE、CE分别交AM于点F、G.求∠FEG的度数.(2)[探究]把(1)中的“正△ABC”改为“正方形ABDC,其余条件不变,如图2,类比探究,可得:①∠FEG=°;②猜想线段BF、AF、FG之间的数量关系,并说明理由.(3)[拓展]如图3,点A在射线BH上,AB=AC,∠BAC=α(0°<α<180°),在∠CAH 内引射线AM,作点C关于AM的对称点E(点E在∠CAH内),连接BE,BE、CE分别交AM于点F.G.则线段BF、AF、GF之间的数量关系为.16.在平面直角坐标系中,抛物线:与x轴交于点A,B(点B 在点A的右侧).抛物线顶点为C点,△ABC为等腰直角三角形.(1)求此抛物线解析式.(2)若直线与抛物线有两个交点,且这两个交点与抛物线的顶点所围成的三角形面积等于6,求k的值.(3)若点,且点E,D关于点C对称,过点D作直线2l交抛物线于点M,N,过点E作直线轴,过点N作于点F,求证:点M,C,F三点共线.17.在平面直角坐标系中,抛物线交x轴于A、B两点(点A在点B的左),交y轴于点C(1)当3a =时,①如图1,求△ABC 的面积; ②如图2,若抛物线上有一点P ,且,求点P 的坐标(2)过点B 且与抛物线仅有一个交点的直线y kx b =+交y 轴于点D ,求的值.18.已知:在⊙O 中,弦AC ⊥BD 于点E ,连接OC 、BC 、CD .(1)如图1,求证:∠B +∠OCD =90°.(2)如图2,连接OE 、OD ,若EO 平分∠AED ,求证:2=CD OC .(3)如图3,在(2)的条件下,延长OE 交⊙O 于点F ,连接FC 、FD ,点K 为OD 上一点,KC 交FD 于点H ,FD 交OC 于点G ,若CK =5,552DG =,∠ODF =2∠KCD 时,求FC 的长. 19.问题提出:如图①所示,在矩形AOCB 和矩形ODEF 中,CO FOk AO DO==,点A ,O ,D 不在同一直线上,连接,AD CF .HO 是AOD △的中线,那么,HO CF 之间存在怎样的关系?HO CF的数量关(1)问题探究:先将问题特殊化,如图②所示,当1k=且90AOD∠=︒时,,系是________,位置关系是________.(2)问题拓展:再探究一般情形如图③所示,当1k=,90∠≠︒时,证明(1)中的结论AOD仍然成立.HO CF之间存在怎样的关系(数量关系用k表示)?(3)问题解决:回归图①所示,探究,20.如图,△ABC为等腰三角形,AB=AC,将CA绕点C顺时针旋转至CD,连接AD,E 为直线CD上一点,连接AE;(1)如图1,若∠BAC=60°,∠ACD=90°,E为CD中点,23AB=,求△BCE的面积;(2)如图2,若∠ACD=90°,点E在线段CD上且∠DAE+∠ABC=90°,AE的延长线与BC的延长线交于点F,连接DF,求证:2=;BC DF(3)如图3,AB=1,∠BAC=90°,∠ACD=105°,若BE恰好平分∠AEC,点P为线段AE上的动点,点E′与点E关于直线DP对称,AE′与CD交于点Q,连接CE′,当'+-''的值最小时,直接写出CQ的值.2CE AE CE【参考答案】**科目模拟测试一、解答题1.(1)证明见解析;(2)2;3(3)30【解析】【分析】(1)作CG⊥CE,交FD延长线于G点,可根据题意得出四边形FECG为矩形,再结合矩形和正方形的性质推出△BCE≌△DCG,从而得到CE=CG,即四边形FECG为正方形,即可证得结论;(2)在(1)的基础之上,连接CF,首先通过旋转的性质和三角形的内角定理推出△CEF 和△DFP均为等腰直角三角形,进而利用相似三角形的判定与性质推出PF和EF之间的关系,从而表示出BE的长度,即可求出∠BCE的正切值,再根据余角的关系证明∠ABP=∠BCE,即可得出结论;(3)根据正方形的性质以及前面两个问题的求解过程推断出A、C、D、F四点共圆,即可得到在变化过程中,∠AFC始终为90°,从而在Rt△ACF中运用特殊角的三角函数值求解角度即可得出结论.(1):如图所示,作CG⊥CE,交FD延长线于G点,∵CE⊥BP,DF⊥BP,CG⊥CE,∴∠EFG=∠FEC=∠ECG=∠BEC=90°,∴四边形FECG为矩形,∠G=90°,∵四边形ABCD为正方形,∴∠BCD=90°,BC=DC,∵∠BCD=∠BCE+∠ECD,∠ECG=∠ECD+∠DCG,∴∠BCE+∠ECD=∠ECD+∠DCG,即:∠BCE=∠DCG,在△BCE和△DCG中,∴△BCE≌△DCG(AAS),∴CE=CG,∴四边形FECG为正方形,∴CE=EF;(2)解:如图所示,连接CF,由(1)知,CE=EF,CE⊥EF,则△CEF为等腰直角三角形,由旋转的性质得:∠PAD=n°,AP=AD,∴∠PAB=90°+n°,∠APD=12(180°-∠PAD)=90°-12n°,∵AP=AB,∴∠APB=12(180°-∠PAB)=45°-12n°,∴∠FPD=∠APD-∠APB=45°,∵DF⊥AB,∴∠DFP=90°,∴△DFP也为等腰直角三角形,PF=DF,∴△DFP∽△CEF,∵,∴,设PF= DF=x,则FE=CE=3x,由(1)知四边形CEFG为正方形,∴FG=FE=3x,∴DG=FG-DF=2x,∵△BCE≌△DCG,∴BE=DG=2x,∴在Rt△BEC中,,∵∠ABP+∠EBC=90°,∠EBC+∠BCE=90°,∴∠ABP=∠BCE,∴;(3)解:∵,∴如图所示,连接AF和对角线AC,由(2)可知,∠EFC=45°,∠EFD=90°,∴∠CFD=45°,∵AC为正方形ABCD的对角线,∴∠CAD=45°,AC2,∴∠CAD=∠CFD,∴点A、C、D、F四点共圆,∴∠AFC=∠ADC=90°,∵AF=22AB,∴AF=12AC,则在Rt△AFC中,,∵∠ACF为锐角,∴∠ACF=30°,∠FAC=90°-30°=60°,∵∠CAD=45°,∴∠FAD=60°-45°=15°,∵AP=AD,AF=AF,PF=DF,∴△AFP≌△AFD,∴∠FAD=∠FAP=15°,∴∠PAD=30°,∴n=30.【点睛】本题考查正方形的判定与性质,相似三角形的判定与性质,以及旋转的性质和解直角三角形等,掌握图形的基本性质和判定方法,具有较强的综合分析能力是解题关键.2.(121;(2)证明见解析;(321- 【解析】【分析】(1)证明,AD BD = 再利用勾股定理求解,,AB BC 从而可得答案;(2)如图,过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥ 证明,EHM CDM ≌ 可得22,AE EH CD == 同理:22,BF FQ BQ == 而,AE BF = 再证明,FQC DCA ≌ 可得,FCQ CAD ∠=∠ 再证明,AF AN = 从而可得结论;(3)如图,记CP 与AB 的交点为,L 由(2)得:45,ACF BAD ∠=∠=︒ 证明,22.5,CF CA CAD =∠=︒ 可得CP 平分,ACF ∠ 则,A F 关于直线CP 对称,,PF PA = 过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+= 所以PA PK +最短,设,PK n = 则1,21,PF PA n AK ==-= 再利用勾股定理求解,n 即可得到答案.【详解】解:(1)45B ∠=︒,AD 为BC 边上的高,90,45,ADB B BAD ∴∠=︒∠=∠=︒221,112,AD BD AB ∴==+=AB BC =,2,2 1.BC CD BC BD ∴=-=(2)如图,过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥则90,EHM CDM ∠=∠=︒ M 为CE 的中点,,HME DMC ∠=∠,EM CM ∴=,EHM CDM ∴≌,EH CD ∴=45,90,BAD AHE EHM ∠=︒∠=∠=︒22,AE EH CD ∴==同理:22,BF FQ BQ == 而,AE BF =,FQ BQ CD EH ∴===,BD CQ AD ∴==90,ADC CQF ∠=∠=︒,FQC DCA ∴≌,FCQ CAD ∴∠=∠,AB BC =,BAC BCA ∴∠=∠,BAD ACF ∴∠=∠ 而,B BAD ∠=∠,,B FCQ AFN ANF ACF CAD ∠+∠=∠∠=∠+∠,AFN ANF ∴∠=∠,AF AN ∴=2.AN CD AF AE AF BF AB ∴=+=+=(3)如图,记CP 与AB 的交点为,L 由(2)得:45,ACF BAD ∠=∠=︒,45,BA BC B =∠=︒67.5,BAC BCA ∴∠=∠=︒67.5,CFA BAC ∴∠=︒=∠,22.5,CF CA CAD ∴=∠=︒22.5,ACP CAD ∠=∠=︒CP ∴平分,ACF ∠,,CP AF AL FL ∴⊥=则,A F 关于直线CP 对称,,PF PA =过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+=所以PA PK +最短,2,AC ∴= 则2,CF = 而45,ACF ∠=︒1,CK FK ∴==设,PK n = 则1,21,PF PA n AK ==-=())222121,n n ∴-=+ 解得:21,n = )121121.22CPK S ∴=⨯⨯= 【点睛】本题考查的是全等三角形的判定与性质,等腰直角三角形的判定与性质,等腰三角形的判定与性质,勾股定理的应用,本题综合性较强,是压轴题,知识的系统化是解题的关键.3.(1)60°;(2)13S ;(3)a +2b ,理由见解析 【解析】【分析】(1)由等边三角形的性质AB =AC =BC ,∠ABC =∠ACE =∠BAC =60°,且BD =CE ,可证△BDC ≌△CEA ,由三角形的外角性质可求∠AFD 的度数;(2)由等边三角形的性质可得BD =CE =AM =DN ,且AB =AC =BC ,∠ABC =∠ACE =∠BAC =60°,可证△ABM ≌△CAE ≌△BCD 和△BDQ ≌△CEF ,由全等三角形的性质和三等分点性质,可求四边形ANQF 的面积;(3)在AC 上截取AM =CE ,由题意可证△BHC ≌△CFA ,可得BH =CF =b ,AF =CH =a ,∠PHB =60°,即可求PC 的长.【详解】解:(1)∵△ABC 是等边三角形∴AB =AC =BC ,∠ABC =∠ACE =∠BAC =60°,且BD =CE ,∴△BDC≌△CEA(SAS),∴∠CAE=∠BCD,∵∠AFD=∠CAE+∠ACF=∠BCD+∠ACD=∠ACB,∴∠AFD=60°;(2)∵D,E,M,N分别是△ABC各边上的三等分点,∴BD=CE=AM=DN,且AB=AC=BC,∠ABC=∠ACE=∠BAC=60°,∴△ABM≌△CAE≌△BCD(SAS),∴∠CAE=∠ABM=∠BCD,∠AMB=∠AEC=∠BDC,且BD=CE,∴△BDQ≌△CEF(ASA),∴S△BDQ=S△CEF,∵BD=DN,∴S△BDQ=S△DNQ=S△CEF,∵D,E是AB,BC上三等分点,∴S△BDC=S△CEA=13S△ABC=13S,∵四边形ANQF的面积=S△ABC-S△AEC-S△DNQ-S四边形DFEB=S-13S-13S=13S;(3)PC=a+2b.理由如下:如图,在AC上截取AM=CE,即AM=CE=BD,∵AM=CE=BD,∠ABC=∠BAC=∠ACB=60°,AB=AC=CB.∴△CBD≌△ACE≌△BAM(SAS),∴∠CAE=∠BCD=∠ABM,且∠ABC=∠ACE,∴∠MBC=∠ACD,且BC=AC,∠EAC=∠BCD,∴△BHC≌△CFA(ASA),∴BH=CF=b,AF=CH=a,∵∠PHB=∠MBH+∠HCB=∠ABM+∠MBC=∠ABC,∴∠PHB=60°,且∠BPD=30°,∴∠PBH=90°,且∠BPH=30°,∴PH=2BH=2b,∴PC=PH+HC=a+2b.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等边三角形的性质,三角形的外角的性质,添加恰当的辅助线构造全等三角形是本题的关键.4.(1)F(0,3112);(2)能,D(0,-31);(3)P的坐标为(0,5)或(0,1).【解析】【分析】(1)由矩形的性质和折叠的性质,求出AF=CF,设OF=x,然后利用勾股定理求出x,即可得到答案;(2)当四边形DPBC为菱形时,PB∥DC,PD∥BC,利用菱形的性质和勾股定理求出31AP ,然后求出OD的长度,即可得到答案;(3)当重心在y轴上时,F一定是DC的中点,过D作DH⊥x轴于H,利用勾股定理求出DH=4,然后得到点D的坐标,即可求出点P的坐标.【详解】解:(1)如图:在矩形OABC中,OA∥BC,∴∠1=∠2,又∵∠2=∠3,∴∠1=∠3,∴AF=FC,设OF=x,∴AF=FC=6-x,∴(6-x)2=x2+52,解得:x=31 12,∴F(0,31 12)(2)能,当四边形DPBC为菱形时,PB∥DC,PD∥BC,∴点D在y轴上,且PB=BC=6,在Rt△APB中,AP2+AB2=PB2,∴AP2=62-(5)2,∴AP=31,∵AO=PD=6,∴OD=31,∴D(0,-31);(3)当重心在y轴上时,F一定是DC的中点,过D作DH⊥x轴于H,∴OH=OC5∴CH=5∴DH2246(25)∴D5454)当D54)时,F(0,2),∴AP=1(6-4)=12∴OP=5,∴P(0,5)当D(-5,-4)时,F(0,-2),AP=12(6+4)=5,∴OP=1,∴P(0,1)综上,P的坐标为(0,5)或(0,1).【点睛】本题考查了矩形的性质,折叠的性质,勾股定理,坐标与图形等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线进行解题.5.(1)2;(2)32;(3)存在,223 3【解析】【分析】(1)如图①,根据等边三角形的判定和性质解决问题即可.(2)如图②,将△ABP绕点B逆时针旋转60°得到△BFE,连接PF,EC.易证PA+PB+PC=PC+PF+EF,因为PC+PF+EF≥EC,推出当P,F在直线EC上时,PA+PB+PC的值最小,求出EC的长即可解决问题.(3)如图③−1中,将△PBQ绕点B逆时针旋转60°得到△EBG,则PQ=EG,△BQG是等边三角形,易知PQ+BQ+CQ=EG+GQ+QC≥EC,推出EC的值最小时,QP+QB+QC的值最小,如图③−2中,延长BA交CD的延长线于J,作△ADJ的外接圆⊙O,将线段BO,BP绕点B逆时针旋转60°得到线段BO′,BE,连接EO′,OB,OP.易证△BEO′≌△BPO(SAS),推出EO′=OP=433,推出点E的运动轨迹是以O′为圆心,433为半径的圆,推出当点E在线段CO′上时,EC的值最小,最小值=CO′−EO′.【详解】(1)如图①,由旋转的性质可知:△BCC′是等边三角形,∴CC′=BC=2,故答案为2.(2)如图②,将△ABP 绕点B 逆时针旋转60°得到△BFE ,连接PF ,EC .由旋转的性质可知:△PBF 是等边三角形,∴PB =PF ,∵PA =EF ,∴PA +PB +PC =PC +PF +EF ,∵PC +PF +EF ≥EC ,∴当P ,F 在直线EC 上时,PA +PB +PC 的值最小,根据旋转以及翻折的性质可得BC =BE =BA =3,∵,30EBF ABP ABP PBC ∠=∠∠+∠=︒,∴90FBP EBF PBC ∠+∠+=︒,∵EB ⊥BC ,∴EC =2BC =32,∴PA +PB +PC 的最小值为32.(3)如图③﹣1中,将△PBQ 绕点B 逆时针旋转60°得到△EBG ,则PQ =EG ,△BQG 是等边三角形,∴BQ =QG ,PQ =EG ,∴PQ +BQ +CQ =EG +GQ +QC ≥EC ,∴EC 的值最小时,QP +QB +QC 的值最小,如图③﹣2中,延长BA 交CD 的延长线于J ,作△ADJ 的外接圆⊙O ,将线段BO ,BP 绕点B 逆时针旋转60°得到线段BO ′,BE ,连接EO ′,OB ,OP .∵,,BO BO BE BP O BE OBP ==∠=∠'',∴△BEO ′≌△BPO (SAS ),∴EO ′=OP ,∵∠APD +∠AJD =180°,∴A ,P ,D ,J 四点共圆,∴OP 43 ∴EO 43, ∴点E 的运动轨迹是以O 43为半径的圆, ∴当点E 在线段CO ′上时,EC 的值最小,最小值=CO ′﹣EO ′,连接OO ′,延长OO ′到R ,使得O ′R =OO ′,连接BR ,则∠OBR =90°,作RH ⊥CB 交CB 的延长线于H ,O ′T ⊥CH 于T ,OM ⊥BC 于M .在Rt △OBM 中,BM =5,OM 113 ∴OB 22OM BM +113 ∴BR 3=14,由△BHR ∽△OMB , ∴RH BM =BR OB, ∴RH =3∵HR ∥O ′T ∥OM ,OO ′=RO ′,∴TM =TH ,∴O ′T =2RH OM +133 ∴BT 22O B O T -''3,∴CO ,∴CO ′﹣EO∴QP +QB +QC 【点睛】 本题属于四边形综合题,考查了旋转变换,全等三角形的判定和性质,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.6.(1)①见解析;②185;(2)在坐标平面内存在点2,03H ⎛⎫ ⎪⎝⎭或4,H ⎛ ⎝⎭或2H ⎫⎪⎝⎭或2H ⎛⎫+ ⎪⎝⎭使得以点E ,A ,G ,H 为顶点的四边形是菱形. 【解析】【分析】(1)①由折叠的性质可知EF =EC ,∠BEF =∠BEC ,E 是CD 的中点,得到DE =EC =EF ,则∠EDF =∠EFD ,即可证明∠EDF =∠BEC ,得到DF ∥BE ;②过点E 作EG ⊥DF 于G ,先证明△EGD ∽△BCE ,得到DE DG BE CE=,利用勾股定理求出5BE ,由此求解即可;(2)先证明△CDE ≌△AEO 得到AE =CE ,设OE x =,则AE CE OC OE x ==-=,由222AE OE OA =+,得到()2222x x =+,可求得E ⎛ ⎝⎭,AE =求出直线AC的解析式为y =+,设(,G a +,(),H m n ,然后分当AE 是菱形的对角线时,则AG =EG ,当AG 是菱形的对角线时,AE =EG ,当AH 为菱形对角线时,AE =AG ,三种情况进行讨论求解即可.【详解】解:(1)①由折叠的性质可知EF =EC ,∠BEF =∠BEC ,∵E 是CD 的中点,∴DE =EC =EF ,∴∠EDF =∠EFD ,∵∠FEC =∠EDF +∠EFD =∠BEF +∠BEC ,∴∠EDF =∠BEC ,∴DF ∥BE ;②如图所示,过点E 作EG ⊥DF 于G ,∴FD=2DG,∵四边形ABCD是矩形,∴CD=AB=6,∠C=90°,∵∠EGD=∠BCE,∠EDG=∠BEC,∴△EGD∽△BCE,∴DE DG BE CE=,∵E为CD中点,∴132DE CE CD===,∴225 BE BC CE=+=,∴353DG =,∴95 DG=,∴185 DF=;(2)∵2OA=,3OC=∴A(2,0),C(0,23∵四边形OABC是矩形,∴BC=OA,∠ABC=90°,由折叠的性质可知CD=CB=OA,∠CDE=∠AOE=90°,又∵∠CED=∠AEO,∴△CDE≌△AOE(AAS),∴AE=CE,设OE x=,则3AE CE OC OE x==-=,∵222AE OE OA=+,∴()222232x x=+,解得23 x=∴23E⎛⎝⎭,43AE=设直线AC的解析式为y kx b=+,∴20k b b +=⎧⎪⎨=⎪⎩,∴k b ⎧=⎪⎨=⎪⎩, ∴直线AC的解析式为y =+设(,G a +,(),H m n ,∴AGEG =当AE 是菱形的对角线时,则AG =EG ,∴()(222a -++=22a ⎛++ ⎝⎭,解得43a =, 由AE 与HG的中点坐标相同得:0222032a m ++⎧=⎪⎪⎨⎪=⎪⎩ 解得230m n ⎧=⎪⎨⎪=⎩; ∴2,03H ⎛⎫ ⎪⎝⎭当AG 是菱形的对角线时,AE =EG ,22163a ⎛++= ⎝⎭, 解得2a =或0a =(舍去),由AG 与EH的中点坐标相同得2202232m n ++⎧=⎪⎪= 解得4m n =⎧⎪⎨=⎪⎩∴4,H ⎛ ⎝⎭; 当AH 为菱形对角线时,AE =AG ,∴()()221623233a a -+-+=, 解得2323a =±, 由AH 与EG 的中点坐标相同得2022233230322m a a n ++⎧=⎪⎪⎨-++⎪+=⎪⎩, 解得2332323m n ⎧=⎪⎪⎨⎪=-⎪⎩或2332323m n ⎧=-⎪⎪⎨⎪=+⎪⎩; ∴2323,233H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫-+ ⎪⎝⎭; ∴综上所述,在坐标平面内存在点2,03H ⎛⎫ ⎪⎝⎭或234,3H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫-+ ⎪⎝⎭使得以点E ,A ,G ,H 为顶点的四边形是菱形.【点睛】本题主要考查了坐标与图形,一次函数与几何综合,全等三角形的性质与判定,等腰三角形的性质与判定,平行线的判定,矩形的性质,菱形的性质等等,解题的关键在于能够熟练掌握相关知识进行求解.7.(1)见解析;(2)结论依然成立,理由见解析;(3)见解析【解析】【分析】(1)根据半角旋转模型,把△ABF 逆时针旋转90°,则AB 与AD 重合,设F 对应的点为M ,即可证明AME AFE ≅,得到AEM AEF ∠=∠,再结合AEM EAG ∠=∠,可得AEM AEF ∠=∠,可得EG AG =;(2)结论依然成立,证明方法与(1)一样;(3)又等腰三角形三线合一的性质可得GQ 垂直平分EA ,可得△ANE 是等腰直角三角形,可得A 、D 、E 、N 四点共圆,根据圆周角45NDC EAN ∠=∠=︒【详解】(1)把△ABF 逆时针旋转90°,则AB 与AD 重合,设F 对应的点为M ,∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB ∥CD∴AEM EAG ∠=∠∴AEG EAG ∠=∠∴EG AG =(2)结论依然成立,EG AG =把△ABF 逆时针旋转90°,则AB 与AD 重合,设F 对应的点为M ,∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB ∥CD∴AEM EAG ∠=∠∴AEG EAG ∠=∠∴EG AG =(3)连接EN由(2)得EG AG =∵GQ AE ⊥∴GQ 垂直平分AE∴EN =AN∵45EAF ∠=︒∴90ANE ADE ∠=︒=∠∴A 、D 、E 、N 四点在以AE 为直径的同一个圆上,∴45NDC EAN ∠=∠=︒.【点睛】本题考查半角旋转模型,熟练根据模型做出辅助线是解题的关键.第(3)问根据四点共圆证明是本题的难点.8.(12 ;(2,2);(2)① 在,理由见解析; ②22t +,22t +;(3)存在,(2,2)(6,4)【解析】【分析】(1)作PM ⊥y 轴于M ,PN ⊥OA 于N ,根据全等三角形的判定及性质可得:PMB PNA ≌,PM PN =,BM AN =,再依据正方形的判定及性质即可得出结果;(2)①利用角平分线的判定定理证明OP 平分AOB ∠即可;②由(1)可知:22OM OB OA t =+=+,即可得出点P 的坐标;(3)过点A 作平行于y 轴的直线交过点M 作平行于x 轴的直线于点Q ,连接QB ,由(1)(2)结论可知:2,2t Q t +⎛⎫ ⎪⎝⎭,可得22t QA +=,根据点坐标及勾股定理确定QB 、AB 长度,然后分三种情况讨论三角形为等腰三角形,得出一元二次方程求解即可得.【详解】 解:(1)作PM ⊥y 轴于M ,PN ⊥OA 于N .∵OBC 是等腰直角三角形,2OB =,∴222BC OC OB +=,∴2BC =∵90PMB PNA PNO MON ∠=∠=∠=∠=︒,∴90MPN BPA ∠=∠=︒,四边形PMON 是矩形,∴MPB NPA ∠=∠,∵PBA △是等腰直角三角形,∴PB PA =,在PMB △与PNA 中,PMB PNA MPB NPA PB PA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴PMB PNA ≌,∴PM PN =,BM AN =,∴24OB OA OM BM ON AN OM +=-++==,∴2OM ON ==,∴四边形PMON 是正方形,∴()2,2P ,2,(2,2);(2)①由(1)可知:四边形PMON 是正方形,PM PN =,如图所示,∵PM OB ⊥,PN OA ⊥,∴OP 平分AOB ∠,∵45BOC ∠=︒,∴OC 平分AOB ∠,∴点P 在射线OC 上;②由(1)可知:22OM OB OA t =+=+, ∴22t OM ON +==, ∴22,22t t P ++⎛⎫ ⎪⎝⎭, 故答案为22,22t t ++; (3)如图,过点A 作平行于y 轴的直线交过点M 作平行于x 轴的直线于点Q ,连接QB ,由(1)可知:四边形PMON 是正方形,PM PN =,点()0,2B ,(),0A t ,由(2)可知:22,22t t P ++⎛⎫ ⎪⎝⎭, ∴点2,2t Q t +⎛⎫ ⎪⎝⎭, ∴22t QA +=, 根据勾股定理可得:222252124t QB t t t +⎛⎫=+-=-+ ⎪⎝⎭ 22224AB t t ++①当QA QB =时,即22t += 化简可得:220t t -=,解得:2t =或0=t (题中已给,舍去), ∴222t +=, 故点()2,2Q ;②当QA AB =时,即22t +, 化简可得:234120t t -+=, ()2443120∆=--⨯⨯<,方程无解,故这种情况不存在;③当QB AB =时,= 化简可得:24120t t --=,解得:6t =或2t =-(舍去), ∴242t +=, 故点()6,4Q ;综上可得:点()6,4Q 或()2,2Q .【点睛】题目主要考查等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质角平分线的性质、勾股定理等知识点,理解题意,作出相应辅助线,综合运用这些知识点是解题关键.9.(1)2144y x =-,132y x =-;(2)见解析;(3)1(12)P +,2(13)P 【解析】【分析】(1)将A (4,0),B (0,﹣4)的坐标代入y =ax 2+b ,利用待定系数法得抛物线解析式,再将点E (4,﹣1),C (0,﹣3)的坐标代入y =mx +n 可得问题的答案;(2)设点21,44P t t ⎛⎫- ⎪⎝⎭ ,0<t <4,如图,过点P 作PF ⊥y 轴于点F ,从而得PF 、PD 、PC 、FC 的长度,从而得到答案;(3)设DP 与EC 的交点为G ,设21,44P x x ⎛⎫- ⎪⎝⎭,①当点G 在点P 上方时,根据三角形面积公式可得答案;②当点G 在点P 下方时,根据三角形面积公式可得答案. 【详解】解:(1)将A (4,0),B (0,﹣4)的坐标代入y =ax 2+b ,得1604a b b +=⎧⎨=-⎩,解得,144a b ⎧=⎪⎨⎪=-⎩ ,∴抛物线的解析式为2144y x =-, 设直线CE 为y =mx +n ,将点E (4,﹣1),C (0,﹣3)的坐标代入y =mx +n 得,413m n n +=-⎧⎨=-⎩, 解得,123m n ⎧=⎪⎨⎪=-⎩ ,∴直线CE 的解析式是132y x =-;(2)证明:设点21,44P t t ⎛⎫- ⎪⎝⎭,0<t <4,如图,过点P 作PF ⊥y 轴于点F ,则PF =t ,221143144FC t t =-+=- ,2144PD t =- ,222222111111444PC t t t t ⎛⎫⎛⎫=+-=+=+ ⎪ ⎪⎝⎭⎝⎭ ,所以221114544PC PD t t ⎛⎫⎛⎫+=++-= ⎪ ⎪⎝⎭⎝⎭ 为定值;(3)解:方法一:设DP 与EC 的交点为G ,设21,44P x x ⎛⎫- ⎪⎝⎭,①如图,当点G 在点P 上方时,()2211115434122422PEC S x x x ⎡⎤⎛⎫⎛⎫=⨯⨯---=--+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦△ ,∵S △PEC =1 , ∴()2151122x --+=, 解得:113x =+ ,213x =- (负根舍去), ∴()213134342y =+-=- ,即1313,32P ⎛⎫=+- ⎪ ⎪⎝⎭, ②如图,当点G 在点P 下方时,()2211115443124222PEC S x x x ⎡⎤⎛⎫⎛⎫=⨯⨯---=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦△,∵S △PEC =1, ∴()2151122x --= , 解得:317x =,417x =(负根舍去),∴()217174242y =⨯+-=-,即2717,22P ⎛⎫+- ⎪ ⎪⎝⎭, 综上所述,满足条件的点有1313,32P ⎛⎫=+- ⎪ ⎪⎝⎭,2717,22P ⎛⎫+- ⎪ ⎪⎝⎭. 方法二:如图,分别过点P ,E 作PF ⊥CE ,EH ⊥y 轴,垂足为F ,H ,PD 交CE 于点G ,在Rt △EHC 中,EH =4,HC =2, ∴2225CE EH HC +=, ∵S △PEC =1, ∴12CE PF =1, 即5PF =, ∵PF ⊥CE ,PG ⊥EH , ∴△PFG ∽△CHE , ∴PG ECPF EH= , 255= , 解得12PG =, ∴过点P 与直线CE 平行,且与直线CE 5的直线有两条:1522y x =- 或1722y x =- ,依题意得:21441522y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得:1x =(负根舍去),∴1x =+2y =- ,∴112P ⎛⎫ ⎪ ⎪⎝⎭, 21441722y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得:1x =∴1x =+3y = ,∴2(13)P +,综上所述,满足条件的点有1(12)P +,2(13)P +-. 【点睛】此题考查的是二次函数综合题目,掌握待定系数法求解析式、由坐标得线段长度、相似三角形的判定与性质是解决此题关键.10.(1)①见解析;②5m =;(2)m的值为6;(3)CE =【解析】 【分析】(1)①连接DE ,证明ADC ∆是等腰三角形,根据“三线合一”的性质可得ADE CDE ∠=∠,证得EC EF =,从而可得结论;②根据勾股定理得到AC =,由E 为AC 中点得EC =DEC CBA ,由相似三角形的性质列出比例式,求出m 的值即可;(2)分PF //AC 和PF //BC 两种情况求解即可; (3)设CE =x ,作PG ⊥AC ,则2xGE =,AE x = 证明PGE EAP '≅得AP GE '=,再证明AP E BAC ',列比例式求出x 的值即可.【详解】解:(1)如图,连接DE∵CD是圆P的直径,∴∠DEC=90°,即DE⊥AC∵E为CA中点∴AE=CE∴AD=CD∴ADE CDE∠=∠∴EC EF=∴E是CF的中点;②在Rt△ABC中,∠B=90°,AB=4,BC=8,∴22224845AC AB BC=+=+=∵E是AC的中点∴114525 22EC AC==⨯=∵AB//CD,90B∠=︒∴90B DCB∠+∠=︒∴90DCB∠=︒,即90DCE BCA∠+∠=︒∵90CDE DCE∠+∠=︒∴CDE BCA∠=∠又90B DEC∠=∠=︒∴DEC CBA∆∆∽∴CE DCAB AC=,即252=445m解得,5m=;(2)分两种情况:①当PF//AC时,如图,则有PDF CDA∆∆∴PF PDAC CD =,即245PF m m=∴25=PF ∴25m =②当PF //BC 时,如图,过点A 作AH ⊥DC ,垂足为H ,则四边形AHCB 是矩形, ∴AH //BC ,HC =AB =4,AH =BC =8 ∴PF //AH ∵90DCB ∠=︒ ∴90FPD ∠=︒ ∴45PDF PFD ∠=∠=︒ ∴45HAD HDA ∠=∠=︒ ∴DH =AH ,即248m -= 解得,6m =综上,m 的值为25或6;(3)过点P 作PG AC ⊥于点G ,如图,∵PE =PC∴1,2GE CE EPG CPG =∠=∠∵90PEP '∠=︒ ∴90P EA PEG '∠+∠=︒ 又90PEG GPE ∠+∠=︒ ∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒,PE P E '= ∴P AE EPG '∆≅∆ ∴AP GE '=设CE x =,则,2x AE x GE AP '===∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒ ∴GPC BCA ∠=∠ ∴EPG BCP ∠=∠ ∴P EA BCA '∠=∠ 又90P AE B '∠=∠=︒ ∴AP EBAC '∆∆∴AP ABAE BC'=48x=∴x =CE =【点睛】本题主要考查了全等三角形的判定与性质,圆的基本概念,相似三角形的判定与性质,正确作出辅助线以及进行分类讨论是解答本题的关键.11.(1)1,3;(2)①4;D (0,1);②存在这样的D 使△DEG 与△ACH相似,坐标为1⎛ ⎝ 【解析】 【分析】(1)将A (-2,0),C (4,3)代入抛物线方程214y x bx c =-++得b 与c 的值即可;(2)①过D 作EF 垂线交FE 延长线于P ,过C 作CH LAB 于H ,从而求出EP =1,DP =2,再求出直线AC 的函数关系式,D (x ,12x +1),则E (x +2,12x +2),G (x ,2134x x -++),F (x +2,()()212234x x -++++),最后列出关于四边形DEFG 的面积的关系式,再求其最大值;②分∠DGE =∠CAH 及∠GDE =∠CAH 两种情况进行讨论,设1,12D m m ⎛+⎫ ⎪⎝⎭,则21,34G m m m ⎛⎫-++ ⎪⎝⎭,根据三角函数值求出GD 的长,令其等于用坐标表示的GD 长,解方程求出满足要求的解即可,进而可得坐标. (1)将A (-2, 0),C (4, 3)代入抛物线方程214y x bx c =-++得:()221443412204b c b c ⎧-⨯++=⎪⎪⎨⎪-⨯--+=⎪⎩, 解得:13b c =⎧⎨=⎩,故答案为 1,3; (2)①解:如图,过D 作EF 垂线交FE 延长线于P ,过C 作CH ⊥AB 于H则DP AB ∥,∠EDP = ∠CAH ,且CH =3,AH =4+2=6, 故tan ∠EDP =tan ∠CAH =CH :AH =12,又DE 5 ∴EP =1,DP =2设直线AC 方程y =kx +a ,将A ,C 坐标代入得:2043k a k a -+=⎧⎨+=⎩,解得112a k =⎧⎪⎨=⎪⎩,设D (x ,12x +1),则E (x +2,12x +2),G (x ,2134x x -++),F (x +2,()()212234x x -++++), ∴1S S S ()2DEFG DPFG DEP DP GD FP EP =-=+- 22111131(2)(2)324242x x x x x x ⎛⎫⎛⎫=-++-+-++++-+ ⎪ ⎪⎝⎭⎝⎭ 2142x =-+ 故当x =0时,四边形面积最大为4,此时D (0,1); ②解:由题意知,DG CH ∥ ∴GDE ACH ∠=∠ ∵6AH =,3CH = ∴2235AC AH CH +∴sinCH CAH AC ∠==1tan 2CH CAH AH ∠== 由题意知△DEG 与△ACH 相似分两种情况求解: 情况一:90DGE ∠=︒时,DEG CAH ∽ ∴1tan tan 2DG DEG CAH GE ∠==∠= ∴2GE DG =∵DE 解得1DG =设1,12D m m ⎛+⎫ ⎪⎝⎭,则21,34G m m m ⎛⎫-++ ⎪⎝⎭∴21131142m m m -++--=整理得2240m m --=∴m =解得11m =21m =当1m =(1112y =⨯+=∴1D ⎛ ⎝⎭; 情况二:90DEG ∠=︒时,DGE CAH ∽ ∴sin sinDE DGE CAH DG ∠==∠=∴5DG =∴21131542m m m -++--=整理得22120m m -+= ∵()224120=--⨯< ∴方程无解,此时不存在;综上所述,存在这样的D 使△DEG 与△ACH 相似,坐标为1⎛ ⎝⎭. 【点睛】本题考查了二次函数综合,二次函数与几何图形面积问题及二次函数与相似相结合问题,勾股定理,三角函数值等知识.解题的关键在于熟练掌握二次函数的性质及几何图形有关性质.12.(1)(2)ACP △为直角三角形,理由见解析 (3)存在,点M 的坐标为或【解析】 【分析】(1)根据一次函数的解析式可求得()5,0B ,,再把这两点的坐标分别代入二次函数解析式,即可求得; (2) 抛物线的对称轴为直线3x =,可分别求得点A 、C 、P 的坐标,分别求得、、,根据勾股定理的逆定理即可证得;(3)分点M 在PA 左边和右边两种情况分别计算,根据两点间距离公式及等腰三角形判定与性质即可分别求得. (1) 解:由,得点B 的坐标为,点C 的坐标为.把()5,0B ,代入抛物线,得,解得1a =-,,∴抛物线的解析式为;(2)解:ACP △为直角三角形. 理由如下: 抛物线的对称轴为直线3x =, 当3x =时,, ∴点P 的坐标为,当0y =时,,得1x =或5,∴点A 的坐标为.∵, ∴. 同理,,,∴, ∴ACP △为直角三角形;(3)解:存在点M ,使AM 与直线BC 的夹角等于ACB ∠的2倍. 分两种情况:①点M 在PA 左边时,如图, ∵,,∴,∴,M在直线上,∵点1M的坐标为.设点1根据题意,得,,∴,解得,M的坐标为.∴点1②点M在PA右边时,如图,此时,∴,∵,∴点P是的中点∵,,∴.综上所述,点M的坐标为或.【点睛】本题考查了利用待定系数法求二次函数的解析式,两点间距离公式,勾股定理的逆定理,解决(3)的关键是分两种情况分别计算13.(1)(2)E(23,53)(3)(﹣2,1)或(﹣2,3)或(﹣2,9)【解析】【分析】(1)由矩形的性质及已知,易得点A的坐标,把A、B两点的坐标代入解析式中可得关于b、c的方程组,解方程组即可;(2)设E(m,﹣34m2﹣32m+3),由题意易得BD、AB的长,则可把△BDE、△ABE的面积表示出来,由S△BDE=4S△ABE得关于m的方程,解方程即可;(3)用待定系数法可求得直线DE的解析式;分三种情况:当P、B重合时,易得△APQ 是等腰直角三角形,从而问题解决;当点P在线段DB的延长线,且AP⊥AQ时,过点Q 作QM⊥AB交BA的延长线于点M,易证△PAB∽△AQM,设P(﹣2,t),由相似三角形的性质可得关于t的方程,解方程即可求得t;当PQ⊥AQ时,易得AP∥DE,则可求得直线AP的解析式,易得点P的坐标.(1)∵B(﹣2,3),矩形OABC,∴A(0,3),∵抛物线y=﹣34x2+bx+c经过点A和点B,∴,∴,∴y=﹣34x2﹣32x+3;(2)∵D(﹣2,﹣1),∴BD=4,设E(m,﹣34m2﹣32m+3),∴S△BDE=12×4×(m+2)=2(m+2),∵AB=2,∴,∵S△BDE=4S△ABE,∴2(m+2)=4(),。
(完整)中考数学压轴题精选及答案

一、解答题1.在△ABC中,AB = BC,∠ABC=90°.(1)如图1,已知DE⊥BC,垂足为D,若∠DBE=60°,AC=22,BD=3,求线段AE的长;(2)如图2,若点D在△ABC内部,点F是CD的中点,且∠BAD=∠CBF,求证:∠DBF=45°;(3)如图3,点A与点'A关于直线BC对称,点D是△'A AC内部一动点,∠ADC=90°.若AC=4,则线段'A D的长是否有最小值,如果有,请直接写出这个最小值;如果没有,请说明理由.2.如图,在△ABC中,AB=AC,⊙是△ABC的外接圆,连接BO并延长交边AC于点D.(1)如图1,求证:∠BAC=2∠ABD;(2)如图2,过点B作BH⊥AC于点H,延长BH交⊙O于点G,连接OC,CG,OC交BG于点F,求证:BF=2HG;(3)如图3,在(2)的条件下,若AD=2,CD=3,求线段BF的长.3.在等腰Rt ABC中,AB AC∠=︒.=,90BAC(1)如图1,D,E是等腰Rt ABC斜边BC上两动点,且45DAE∠=︒,在等腰Rt ABC 外侧作CAF BAE≅△△,连接DF.问:①DCF∠=__________度.②AED与AFD是否全等?请说明理由;③当3BE=,7CE=时,求DE的长;(2)如图2,点D是等腰Rt ABC斜边BC所在射线CB上的一动点,连接AD,以点A为直角顶点作等腰Rt ADE△(点E在点D的顺时针方向上),当4BD=,12BC=时,直接可出DE的长.4.直线y=﹣x+6与x轴、y轴分别交于点A,点B.点P为线段AB上一动点(与点A,B不重合).过点P作PM⊥OA于点M,以OB,OM为邻边作矩形BOMN.点Q在直线BN上,且PQ⊥OP.(1)如图1,①判断△APM的形状,并说明理由;②求证:△PNQ≌△OMP;③若∠PQN=22.5°,直接写出点P的坐标.(2)作射线OQ交直线AB于点K,∠OPQ的角平分线交边OB于点G.若BGOG=35,①当∠PKQ为钝角时,直接写出线段PK的长;②当∠PKQ为锐角时,直接写出BK2+AP2的值.5.在矩形ABCD中,3OA=,6AB=.分别以OA,OC边所在的直线为x轴,y轴建立如图所示的平面直角坐标系.(1)如图1,将OAC 沿对角线AC 翻折,交AB 于点P ,求点P 的坐标; (2)如图2,已知H 是AB 上一点,且32HBC S =△,OG CH ⊥于点P ,求四边形OAHP 的面积;(3)如图3,点()0,5D ,点E 是OB 上一点,且2OE BE =,M 是直线DE 上的一个动点,在x 轴上方的平面内是否存在另一个点N ,使以O 、D 、M 、N 为顶点的四边形是菱形?若存在,直接写出点N 的坐标;若不存在,请说明理由.6.如图,AB 是ABC 的外接圆O 的直径,点D 在半圆上,DC 与AB 交于点E ,过点C 作CF ⊥DC 交DB 的延长线于点F ,交圆O 于点G .(1)求证:ABC ∽DCF ;(2)当∠1=∠2,DF =105,AE :EC =1:2时,求圆O 的半径.(3)在(2)的条件下,连接DG 交BC 于点M ,则OMB DGF S S =:△△ (直接写出答案).7.如图,在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A (4,0)、B (0,4)、C .其对称轴l 交x 轴于点D ,交直线AB 于点F ,交抛物线于点E .(1)求抛物线的解析式;(2)点P为直线l上的动点,求△PBC周长的最小值;(3)点N为直线AB上的一点(点N不与点F重合),在抛物线上是否存在一点M,使以点E、F、N、M为顶点的四边形为平行四边形?若存在,直接写出点M的坐标,若不存在,说明理由.8.如图,在平面直角坐标系xOy中,抛物线与x轴交于两点与y轴交于点C,点M是抛物线的顶点,抛物线的对称轴l与BC交于点D,与x轴交于点E.(1)求抛物线的对称轴及B点的坐标(2)如果,求抛物线的表达式;(3)在(2)的条件下,已知点F是该抛物线对称轴上一点,且在线段BC的下方,,求点F的坐标9.如图,四边形ABCD中,AD∥BC,AB=10,CD=45,动点P从点A沿着A-B-C 运动,同时点Q从点D沿着D-A运动,它们同时到达终点,设点P运动的路程为x,AQ的长度为y,且2163y x=-+.(1)求AD,BC的长和四边形ABCD的面积.(2)连接PQ,设△APQ的面积为S,在P,Q的运动过程中,S是否存在最大值,若存在,求出S的最大值;若不存在,请说明理由.(3)当PQ与四边形ABCD其中一边垂直时,求所有满足要求的x的值.10.如图,在平面直角坐标系中,矩形OABC,点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣34x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE,DE,若S△BDE=4S△ABE,求E点坐标;(3)如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q,连接AP,AQ,PQ,若△APQ为直角三角形,请直接写出P点坐标.11.在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.(1)当点P在线段ED上时(如图1),求证:BE=PD 3;(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PF的长.12.已知抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C (0,﹣3),顶点D 坐标为(1,﹣4).(1)求抛物线的解析式;(2)如图1,抛物线在第四象限的图象上有一点M ,求四边形ABMC 面积的最大值及此时点M 的坐标;(3)如图2,直线CD 交x 轴于点E ,若点P 是线段EC 上的一个动点,是否存在以点P 、E 、O 为顶点的三角形与ABC ∆相似.若存在,请直接写出点P 的坐标;若不存在,请说明理由.13.如图,已知抛物线23y ax bx =++经过点1,0A 和点()3,0B ,与y 轴交于点C .(1)求抛物线的表达式;(2)若P 是直线BC 下方的抛物线上一个动点,(不点B ,C 重合),过点P 作y 轴的平行线交直线BC 于点D , ①求线段PD 长度的最大值.②若PBD △为直角三角形,求出P 点坐标(3)点E 为y 轴上一动点,连接AE ,BE ,形成AEB ∠,当AEB ∠的度数最大时,求点E 的坐标.14.已知等边△ABC 边长为6,D 为边AB 上一点,E 为直线AC 上一点,连接DE ,将DE 绕点D 顺时针旋转90°得到线段DF .(1)如图1,若∠AED =90°,过点F 作FG ⊥AC 于点G ,求AFFG的值; (2)若AD =x ,AF 的最小值为y , ①若x =4,求y 的值; ②直接写出y 与x 的关系式.15.如图①,Rt ABC 和Rt BDE 重叠放置在一起,∠ABC =∠DBE =90°,且AB =2BC ,BD =2BE .(1)观察猜想:图①中线段AD 与CE 的数量关系是 ,位置关系是 ;(2)探究证明:把BDE 绕点B 顺时针旋转到图②的位置,连接AD ,CE ,判断线段AD 与CE 的数量关系和位置关系如何,并说明理由;(3)拓展延伸:若BC 5BE =1,当旋转角α=∠ACB 时,请直接写出线段AD 的长度. 16.如图,抛物线与x 轴交于A 、B 两点( 点A 在点B 的左侧),点B 坐标()3,0,抛物线与y 轴交于点()0,3C -,点D 为抛物线顶点,对称轴1x =与x 轴交于点E ,连接BC 、EC .(1)求抛物线的解析式;(2)点P 是BC 下方异于点D 的抛物线上一动点,若PBCEBCS S=,求此时点P 的坐标;(3)点Q 是抛物线上一动点,点M 是平面上一点,若以点B 、C 、Q 、M 为顶点的四边形为矩形,直接写出满足条件的点Q 的横坐标.17.如图(1),ABC 中,90ABC ∠=︒,AB BC =,点D 是AC 的中点,点E 在CD 上(点E 不与点D 和点C 重合),AG BE ⊥于点G ,交BD 于点F ,连接DG .(1)求证:ADF BDE △≌△;(2)设GF a =,GE b =,GD c =,证明:2a b c +=;(3)如图(2),延长AG 交BC 于点M ,若点M 是BC 中点,点N 是AB 的中点,请证明点N 、F 、C 三点共线.18.已知,如图1,Rt△ABC 中,AB =AC ,∠BAC =90°,D 为△ABC 外一点,且∠ADC =90°,E 为BC 中点,AF ∥BC ,连接EF 交AD 于点G ,且EF ⊥ED 交AC 于点H ,AF =1.(1)若13AHCH,求EF的长;(2)在(1)的条件下,求CD的值;(3)如图2,连接BD,BG,若BD=AC,求证:BG⊥AD.19.如图1,抛物线y=ax2﹣2ax+3与x轴交于A、B两点,且B(3,0),与y轴交于点C,一次函数y=kx+b的图象l与抛物线在第一象限交于点P.(1)直接写出抛物线的解析式;(2)若∠PCB=∠ACO,求P点的坐标;(3)如图2,若b=1,直线l与抛物线的另一个交点为D,过点D作DE∥y轴交直线PC于E,请说明点E一定在某条确定的直线上运动,求出这条直线的解析式.20.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)若点M在直线BH上运动,点N在x轴上运动,是否存在以点C、M、N为顶点的三角形为等腰直角三角形?若存在,求出其值;若不存在,请说明理由.【参考答案】**科目模拟测试一、解答题 1.(1)27 (2)见解析 (3)252- 【解析】 【分析】(1)如图1中,过点E 作EQ AB ⊥,交AB 延长线于点Q ,则四边形BQED 是矩形,解直角三角形求出AQ ,QE 即可解决问题.(2)如图2中,在BF 上取一点M ,使得BM AD =,并且延长MF 至点H ,使MF FH =,连接CM ,DH .利用全等三角形的性质证明H FMC DBH ∠=∠=∠,再证明290DBH ∠=︒即可解决问题.(3)如图3中,取AC 的中点F ,连接A F ',DF ,过点F 作FT AB ⊥于T .解直角三角形求出DF ,FA ',判断出当A ',D ,F 共线时,DA '的值最小于是得到结论. (1)解:如图1中,过点E 作EQ AB ⊥,交AB 延长线于点Q ,则四边形BQED 是矩形,3BD QE ∴==在Rt BQE ∆中,30QBE ∠=︒,223BE BD ∴==,33BQ QE ==,在Rt ABC ∆中,22AB BC ===,5AQ ∴=,在中,;(2)如图2中,在BF 上取一点M ,使得BM AD =,并且延长MF 至点H ,使MF FH =,连接CM ,DH .在和中,,,,,是CD 的中点,,在和中,,,,, ,H FMC DBH ∠=∠=∠,又是的外角,,,,;(3)如图3中,取AC 的中点F ,连接A F ',DF ,过点F 作FT AB ⊥于T .,90ABC∠=︒,4AC=,,,,FT AB⊥,,,,,,,AF CF=,,,,∴当A',D,F共线时,DA'的值最小,此时,故线段的长最小值是52.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形或全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.2.(1)证明见解析;(2)证明见解析,(3)157 BF=【解析】【分析】(1)连接OA并延长AO交BC于E,证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论,(2)利用直角三角形两锐角互余、圆周角定理进行导角,得出MCG△和△FCG是等腰三角形,得出BM=MC=FG=CG,MH=HG,进而由BF=BM+MH-FH=FG-FH+HG,得出结论;(3)过O点作OP⊥AC,由垂径定理得出12 PD=,再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==,由勾股定理进而可求BH,再利用相似三角形对应边成比例求出HG,即可得BF长.【详解】解:(1)连接OA并延长AO交BC于E,∵AB=AC,∴AB AC=,∵AE过圆心O,∴AE BC⊥,BE EC=,∴∠BAC=2∠BAE,∵OA=OB,∴∠ABD=∠BAE,∴∠BAC=2∠ABD;(2)如解图(2),连接OA并延长AO交BC于E,AE交BF于M,连接MC,设2BACα∠=,则ABD BAE EACα∠=∠=∠=∵AE=EC,AE⊥BC,∴BM=MC,∴∠MBC=∠MCB,∵BG⊥AC,AE⊥BC,∴∠EAC+∠ACE=90°,∠HBC+∠ACE=90°,∴EAC HBC MCBα∠=∠=∠=,∴2CMG MBC MCBα∠=∠+∠=,∵BC BC=,∴2G BAC α∠=∠=,∴∠G =∠CMG ,∴CG =CM =BM ,∵AC ⊥BG ,∴MH =HG ,∵OA =OC ,∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-,∵180FCG CFG G ∠=︒-∠-∠,即180(90)290FCG ααα∠=︒-︒--=︒-,∴FCG CFG ∠=∠,∴FG =CG ,∴BM =MC =FG =CG ,又∵MH =HG ,∴BF =BM +MH -FH =FG -FH +HG ,∴BF =2HG .(3)过O 点作OP ⊥AC ,如解图(3)∵AO 是∠BAC 的角平分线,∴点O 到AB 、AC 的距离相等, ∴ABO ADO SAB BO S AD OD==, ∵AD =2,CD =3,∴AB =AC =5, ∴5=2BO OD ,即:2=7OD BD , ∵OP ⊥AC ,∴52AP PC ==,12PD =, ∵BH AC ⊥, ∴OP //BH ,∴27DP OP OD DH BH BD ===, ∴7724DH DP ==,∴154AH AD DH =+=,5-4HC DC DH ==,∵在Rt ABH 中,BH == ∵BAH G ∠=∠,AHB GHC ∠=∠,∴AHB GHC △△, ∴AH BH HG CH = 即:AH HC BH HG =,51544=⨯,∴HG =, 由(2)得BF =2HG ,∴BF = 【点睛】本题是圆的综合题,主要考查了圆周角定理,涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点,解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系,从而利用相似或勾股定理解题.3.(1)①90︒;②全等,证明见解析;③29=7DE ;(2)DE 的值为 【解析】【分析】(1)①先由等腰直角三角形的性质得∠B =∠ACB =45°,再由全等三角形的性质得∠ACF =∠B =45°,即可得出答案; ②先证出∠DAE =∠DAF ,再由DA =DA ,AE =AF ,即可得出结论; ③设DE =x ,则CD =7-x .在Rt △DCF 中,由勾股定理得DF 2=CD 2+CF 2,则x 2=(7-x )2+32,解方程即可;(2)分两种情形:①当点D 在线段BC 上时,连接BE ,由△EAD ≌△ADC ,推出∠ABE =∠C =45°,BE =CD =8,推出∠EBD =90°,由勾股定理即可得出答案; ②当点D 在CB 的延长线上时,同法可得DE 的长.【详解】解:(1)①∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°,∵△CAF ≌△BAE ,∴∠ACF =∠B =45°,∴∠DCF =∠ACB +∠ACF =45°+45°=90°,故答案为:90;②△AED ≌△AFD ,理由如下:∵△CAF≌△BAE,∴AF=AE,∠CAF=∠BAE,∵∠BAC=90°,∴∠CAE+∠BAE=∠CAE+∠CAF=∠BAC=90°,∵∠DAE=45°,∴∠DAF=90°-45°=45°,∴∠DAE=∠DAF,又∵DA=DA,AE=AF,∴△AED≌△AFD(SAS);③∵△CAF≌△BAE,∴CF=BE=3,设DE=x,则CD=7-x,由①得:∠DCF=90°,由②得:△AED≌△AFD,∴DE=DF=x,在Rt△DCF中,由勾股定理得:DF2=CD2+CF2,即x2=(7-x)2+32,∴297x,∴29=7 DE;(2)①当点D在线段BC上时,连接BE,如图2所示:∵△ADE是等腰直角三角形,∠EAD=90°,∴AE=AD,∠BAC=∠EAD,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=45°,BE=CD=BC-BD=12-4=8,∴∠EBD=90°,∴22228445DE BE BD+=+②当点D在CB的延长线上时,连接BE,如图3所示:同①得:△EAB≌△DAC(SAS),∠EBD=90°,∴BE=CD=BC+BD=12+4=16,∴2222164417DE BE BD=++=综上所述,DE的值为45417【点睛】本题是三角形综合题目,考查了等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的判定、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题.4.(1)①等腰直角三角形,理由见解析,②证明见解析,③(63232)-,,(2)52,②225 2【解析】【分析】(1)①求出直线y=﹣x+6与x轴、y轴交点坐标,得出∠BAO=45°即可证明;②由①得出BN=PN=OM,再根据PQ⊥OP得出∠PQB=∠OPM,即可证明△PNQ≌△OMP;③∠PQN=22.5°,可得BQ=PB,设点P坐标为(a,-a+6),列出关于a的方程求解即可;(2)①证△OPG∽△OBP,求出OP长,得出P点坐标,再证△OPB∽△KPO,求出PK 的长即可;②类似①得出P点坐标,求出PK的长即可.【详解】解:(1)①△APM是等腰直角三角形,理由如下:y=﹣x+6与x轴、y轴分别交于点A,点B.当x=0时,y=6,当y=0时,x=6,则点A(6,0)点B(0,6);∴OA =OB ,∴∠BAO =45°,∵PM ⊥OA ,∴∠BAO =∠MPA =45°,∴PM =PA ,∴△APM 是等腰直角三角形;②由①同理可得BN =PN ,∵BN =OM ,∴PN =OM ,∵PQ ⊥OP ,∴∠QPN +∠OPM =90°,∵∠POM +∠OPM =90°,∴∠POM =∠QPN ,∵∠PMO =∠PNQ =90°,∴△PNQ ≌△OMP ;③设点P 坐标为(a ,-a +6),∵∠PQN =22.5°,∠PBN =45°,∴∠PQN =∠BPQ =22.5°,∴BQ =PB ,∵△PNQ ≌△OMP ;∴QN =PM=-a +6,6a a +=-+,解得,6a =-则点P 坐标为(6-;(2)∵BG OG =35,OB =6, ∴94BG =,154OG =, ①∵∠OPQ 的角平分线交边OB 于点G ,∴∠OPG =∠OBA =45°,∵∠PGO =45°+∠BPG ,∠BPO =45°+∠BPG ,∴∠PGO =∠BPO ,∴△OPG ∽△OBP ,∴OP OG OB OP =,即1546OP OP=,解得OP = 设点P 坐标为(a ,-a +6),222(6)a a +-+=,解得,132a =,292a =; 当∠PKQ 为钝角时,92a =,P 坐标为93()22,, 则32AP =,92BP =, ∵∠POK =∠OBA =45°,∠BPO =∠BPO ,∴△OPB ∽△KPO , ∴OP PB KP OP =,即3109222310KP =,解得52KP =;②当∠PKQ 为锐角时,32a =,P 坐标为39()22,, 则92AP =32BP = 由①得,310OP =OP PB KP OP =即3103222310KP ,152KP = 1523262BK == BK 2+AP 2=22922252+=2()).【点睛】本题考查了一次函数与图形,全等三角形的判定与性质,相似三角形的判定与性质,解题关键是熟练运用相关定理进行推理证明.5.(1)153,4P ⎛⎫ ⎪⎝⎭;(2)11110;(3)存在,(125,5N -,()24,8N ,355,2N ⎛⎫- ⎪⎝⎭. 【解析】【分析】(1)根据翻折的性质得出△BCP ≌△O 'AP ,再利用勾股定理得出结论;(2)先求出直线CH 和OG 的解析式,联立解得H 的坐标,再根据OCP OAHP OAHC S S S =-四边形梯形得出结果;(3)分三种情况讨论:①当OD =DM =MN =NO =5时,②当OD =DN =MN =MO =5时,③当OM =MD =DN =NO =5时.【详解】(1)∵四边形OABC 是矩形,∴OA =BC =3,OC =AB =6,由翻折得3OA OA ,∠O '=∠AOC =90°,在△BCP 与△O 'AP 中,∠B =90°,∠BPC =∠O 'PA ,BC =O 'A =2,∴△BCP ≌△O 'AP ,∴BP =O 'P ,设BP =O 'P =x ,则AP =AB -BP =6-x ,在Rt △AP O '中,222O P O A AP ''+=,则2223(6)x x +=-,解得94x =, ∴AP =6-x =6-94=154,则15(3,)4P ; (2)1133222HBCSBC BH BH BH =⋅=⨯⨯=,则3322BH =, ∴BH =1,AH =AB -BH =6-1=5, ∴H (3,5), ∵(0,6),(3,5)C H ,∴设直线CH 为:y mx n =+,过点(0,6),(3,5)C H ,∴6053n m n =+⎧⎨=+⎩,解得:136m n ⎧=-⎪⎨⎪=⎩, ∴直线CH 为:163y x =-+,∵OG ⊥CH ,且13CH K =-,∴3OG K =,∴直线OG 为:3y x =,联立3163y xy x =⎧⎪⎨=-+⎪⎩,解得95x =, 当95x =时,275y = ,∴927(,)55H ,∵33()22OAHC S AH OC OA =+⋅÷=梯形,OCPOAHP OAHC S S S =-四边形梯形,∴33271112510OAHP S =-=四边形;(3)设DM 与AB 交于F ,与x 轴交于H , ∵OD ∥AB ,∴△ODE ∽△BFE , ∴OE ODBE BF =, ∴2=ODBF, ∵D (0,5), ∴OD =5, ∴BF=522OD =, ∴AF =AB -BF =6-52=72, ∴F (3,72); 设直线DF :y kx b =+,过点D (0,5),F (3,72), ∴50732b k b =+⎧⎪⎨=+⎪⎩,解得512b k =⎧⎪⎨=-⎪⎩,∴直线DF :152y x =-+,当OD =DM =MN =NO =5时,如图,作MP ⊥y 轴交于点P ,则MP ∥x 轴, ∴△MPD ∽△FOD , ∴MP PD MDOF OD FD==, 直线DF :152y x =-+,当y =0时,x =10,∴H (10,0),则DH =10,FD =222251055OD DF +=+=,则10555MP PD ==, ∴MP =25,PD =5, ∴(25,55)M -+,∴25N M x x ==-,555N M y y MN =-=+-=5, ∴(25,5)N -;②当OD =DN =MN =MO =5时,如图,延长MN 交x 轴于点P ,则MP ⊥x 轴, ∵M 在152y x =-+上,∴设M (a ,15)2a -+,在Rt △DPM 中,222OP PM OM +=,∴2221(5)52a a +-+=,解得124,0a a ==(舍去),∴M (4,3),∴MP =3+MN =3+5=8, ∴N (4,8);③当OM =MD =DN =NO =5时,如图,连接NM ,交OD 于点P ,则MN 垂直平分OD , ∴52M N y y OP ===,则15522M x -+=, ∴5M x =, ∴5N M x x -=,∴5(5,)2N -;综上所述:N 点的坐标为(25,5)-,(4,8),5(5,)2-.【点睛】本题考查了全等三角形的判定与性质,勾股定理,相似三角形的判定与性质及一次函数的性质,解题的关键是灵活运用这些性质.6.(1)证明见解析;(2)254;(3)544【解析】【分析】(1)证明90ACB DCF,结合,A CDF从而可得答案;(2)连接OD,先证明△AEC∽△DCF,可得DC=10,DE=CE=5,AE=52,设⊙O的半径为r,则OE=52r,OD=r,根据勾股定理列方程可解答;(3)如图,连接BG,根据圆周角定理可得DG是⊙O的直径,根据勾股定理计算CG的长,得FG的长,知FG=DG,根据等腰三角形三线合一的性质得BD=BF,证明△OBM∽△GCM,得OD:OM:MG=11:5:6,根据同高三角形面积的关系可得结论.【详解】(1)证明:∵AB是△ABC的外接圆⊙O的直径,,CF DC∴90,ACB DCF,A CDF∴ABC∽DCF;(2)解:如图,连接OD,∵12,∠=∠∴AD AC=,∴AB⊥CD,∴∠AEC=90°,∵DC⊥CF,∴∠DCF=90°,∴∠AEC=∠DCF,∵∠A=∠ADB,∴△AEC∽△DCF,∴AE CE DC CF,∵AE:EC=1:2,∴DC:CF=1:2,∵DF=52222105,DC DC∴DC=10,(负根舍去)20,CF∵OA⊥CD,∴DE=CE=5,AE=52,设⊙O的半径为r,则OE=52r,OD=r,在Rt△ODE中,由勾股定理得:OD2=DE2+OE2,∴222552r r,解得:254r=,答:圆O的半径为254;(3)解:如图,连接BG,∵∠DCG=90°,∴DG是⊙O的直径,∴∠DBG=90°,由(2)知:CD=10,DG=252,由勾股定理得:222225151022 CG DG CD,∴FG=CF﹣CG=15252022DG,∵90,DCG∴90,DBG∠=︒ BG⊥DF,∴BD=BF,∴S△DBG=S△BGF,∵S △DGF=12FG•CD=12512510222,∴S△DGB=1254,∵∠DEB=∠DCG=90°,∴OB CG∥,∴△OBM ∽△GCM , ∴25541562OM OB MG CG, ∴OD :OM :MG =11:5:6, ∴S △OMB =512562522488, ∴S △OMB :S △DGF =62588:1255244. 故答案为:544. 【点睛】本题考查垂径定理,圆周角定理,相似三角形的性质和判定,三角形面积,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形和等腰三角形解决问题,属于中考常考题型.7.(1)234y x x =-++ (2)(3)存在,(52,)或(,-)或(,-)【解析】 【分析】(1)把点A (4,0)、B (0,4)代入抛物线y =-x 2+bx +c 中,求得b 和c 即可; (2)作点B 关于直线l 的对称轴B ′,连接B ′C 交l 于一点P ,点P 即为使△PBC 周长最小的点,由对称可知,PB ′=PB ,即△PBC 周长的最小值为:BC +CB ′;(3)设M (m ,-m 2+3m +4),①当EF 为边时,则EF ∥MN ,则N (m ,-m +4),所以NM =EF =,即|-m 2+3m +4-(-m +4)|=,求出m 的值,代入即可;②当EF 为对角线时,EF 的中点为(32,),由中点坐标公式可求得点N 的坐标,再由点N 是直线AB上一点,可知-3+m +4=m 2-3m +,解得m 的值即可.(1)解:把点A (4,0)、B (0,4)代入抛物线y =-x 2+bx +c 中, 得,,解得,∴抛物线的解析式为:y =-x 2+3x +4; (2)解:由抛物线解析式可知,对称轴直线l :x =32,∵点A(4,0),∴点C(-1,0),如图,作点B关于直线l的对称轴B′,连接B′C交l于一点P,点P即为使△PBC周长最小的点,此时B′(3,4),设直线B′C的解析式为y=kx+b1,∴,解得:,∴直线B′C的解析式为:y=x+1,把x=32代入得:y=32+1=52,∴P(32,52),∵B(0,4),C(-1,0),B′(3,4),∴BC=,CB′=2∴△PBC周长的最小值为:;(3)解:存在,以点E、F、N、M为顶点的四边形为平行四边形的点M的坐标为(52,)或(,-)或(,-).理由如下:由抛物线解析式可知,E(32,),∵A(4,0)、B(0,4),∴直线AB的解析式为:y=-x+4,∴F(32,52).∴EF=.设M(m,-m2+3m+4),①当EF为边时,则EF∥MN,∴N(m,-m+4),∴NM=EF=,即|-m2+3m+4-(-m+4)|=,解得m=32(舍)或52或或,∴M(52,)或(,-)或(,-).②当EF为对角线时,EF的中点为(32,),∴点N的坐标为(3-m,m2-3m+),∴-3+m+4=m2-3m+,解得m=32(舍),m=52,∴M(52,).综上,满足以点E、F、N、M为顶点的四边形为平行四边形的点M的坐标为(52,)或(,-)或(,-).【点睛】本题主要考查了待定系数法求函数解析式,平行四边形存在性问题,解题过程中注意需要分类讨论.8.(1)对称轴是,B(4,0)(2)y=(3)F(32,-5)【解析】【分析】(1)根据二次函数抛物线的性质,可求出对称轴,即可得B点的坐标;(2)二次函数的y轴平行于对称轴,根据平行线分线段成比例用含a的代数式表示DE的长,MD=158,可表示M的纵坐标,然后把M的横坐标代入y=ax2−3ax−4a,可得到关于a的方程,求出a的值,即可得答案;(3)先证△AOC∽△COB,得∠BCO=∠CAO,再求出∠CAO=∠CFB,得△AGC∽△FGB,根据相似三角形对于高的比等于相似比,可得答案.(1)解:∵二次函数y=ax2−3ax−4a,∴对称轴是 ,∵A (−1,0), ∵1+1.5=2.5, ∴1.5+2.5=4, ∴B (4,0); (2)∵二次函数y =ax 2−3ax −4a ,C 在y 轴上,∴C 的横坐标是0,纵坐标是−4a , ∵y 轴平行于对称轴, ∴ , ∴, ∵ , ∵MD =158, ∵M 的纵坐标是+158∵M 的横坐标是对称轴x , ∴ ,∴+158=,解这个方程组得:12a =- ,∴y =ax 2−3ax −4a =12- x 2-3×(12-)x -4×(12-)=;(3)假设F 点在如图所示的位置上,连接AC 、CF 、BF ,CF 与AB 相交于点G ,由(2)可知:AO=1,CO=2,BO=4,∴,∴,∵∠AOC=∠COB=90°,∴△AOC∽△COB,∴∠BCO=∠CAO,∵∠CFB=∠BCO,∴∠CAO=∠CFB,∵∠AGC=∠FGB,∴△AGC∽△FGB,∴,设EF=x,∵BF2=BE2+EF2=,AC2=22+12=5,CO2=22=4,∴=,解这个方程组得:x1=5,x2=-5,∵点F在线段BC的下方,∴x1=5(舍去),∴F(32,-5).【点睛】本题考查了二次函数的性质、平行线分线段成比例、一元一次方程的解法、一元二次方程方程的解法、相似三角形的判定与性质,做题的关键是相似三角形的判定与性质的灵活运用.9.(1)120;(2)存在,最大值为1123;(3)24043x=或487x=或12x=【解析】【分析】(1)当x=0时,当y=0时,分别求解得出对应线段的长度,过点B作BM⊥AD,过点D 作DN⊥BC,求出高,即可求解;(2)分情况讨论(点P在线段AB上、当P在BC上时),得出△APQ的面积的函数表达式,根据函数性质求解即可;(3)分三种情况讨论,利用三角形相似的性质求解即可.【详解】解(1):由题意:∵P,Q两点同时到达终点,所以,当x=0时,y=16,即AD=16;当y=0时,x=24,所以BC=14过点B作BM⊥AD,过点D作DN⊥BC,如下图:又∵AD∥BC,可知四边形BMDN为矩形设AM=m,∴MD=16-m,即BN=16-m,∴CN=m-2,根据BM=DN,可得:102-m2=2(45)-(m-2)2,解得m=6.即BM=8,4CN=∴四边形ABCD的面积为:(16+14)×8÷2=120(2)当点P在线段AB上时,010x<≤,作PE AD⊥,如下图,则//PE BM,∴APE ABM△∽△∴AP PE AEAB BM AM==,即45PE x=,35AE x=21124432(16)2235155 APQS AQ PE x x x x=⨯=-+⨯=-+△对称轴为12x=,0a<又∵010x<≤∴10x=时,APQS最大,为1123当P在BC上时,1024x≤≤,186423APQS AQ BM x=⨯=-+△k<,APQS随x的增大而减小,综上所述,APQS的最大值为1123(3)当PQ AB⊥时,如下图:∴APQ AMB△∽△∴AP AQAM AB=,即2163610xx-+=,解得487x=当PQ BC⊥时,可得BP MQ=,即2101663x x-=-+-解得12x=当PQ CD⊥时,如下图:∵//AD BC,∴C QDH∠=∠又∵90H CND PEQ∠=∠=∠=︒,PQE DQH∠=∠∴PEQ DHQ CND△∽△∽△∴PE CN EQ DN=由(1)(2)得45PE x=,35AE x=,4CN=,8DN=∴231635 EQ x x =-+-∴4452381635xx x=-+-,解得24043x=综上所得24043x=或487x=或12x=【点睛】本题考查了一次函数图象和性质,二次函数最值问题,三角形面积,勾股定理,相似三角形的判定和性质等,是一道关于四边形的综合题,解题关键是熟练掌握并运用二次函数性质、相似三角形的判定和性质等相关知识,并应用数形结合思想、方程思想和分类讨论思想解决问题.10.(1)(2)E(23,53)(3)(﹣2,1)或(﹣2,3)或(﹣2,9)【解析】【分析】(1)由矩形的性质及已知,易得点A的坐标,把A、B两点的坐标代入解析式中可得关于b、c的方程组,解方程组即可;(2)设E(m,﹣34m2﹣32m+3),由题意易得BD、AB的长,则可把△BDE、△ABE的面积表示出来,由S△BDE=4S△ABE得关于m的方程,解方程即可;(3)用待定系数法可求得直线DE的解析式;分三种情况:当P、B重合时,易得△APQ 是等腰直角三角形,从而问题解决;当点P在线段DB的延长线,且AP⊥AQ时,过点Q 作QM⊥AB交BA的延长线于点M,易证△PAB∽△AQM,设P(﹣2,t),由相似三角形的性质可得关于t的方程,解方程即可求得t;当PQ⊥AQ时,易得AP∥DE,则可求得直线AP的解析式,易得点P的坐标.(1)∵B(﹣2,3),矩形OABC,∴A(0,3),∵抛物线y=﹣34x2+bx+c经过点A和点B,∴,∴,∴y=﹣34x2﹣32x+3;(2)∵D(﹣2,﹣1),∴BD=4,设E(m,﹣34m2﹣32m+3),∴S△BDE=12×4×(m+2)=2(m+2),∵AB=2,∴,∵S△BDE=4S△ABE,∴2(m+2)=4(),解得m=﹣2或m=23,∵E点在y轴由侧,∴m=23,∴E;(3)∵E,D(﹣2,﹣1),设直线DE的解析式为y=kx+b,∴,∴,∴y=x+1,∴直线与y轴的交点为(0,1),如图1,当P点与B点重合,Q点为(0,1),此时△APQ为等腰直角三角形,∴P(﹣2,3);如图2,过点Q作QM⊥AB交BA的延长线于点M,∵∠PAQ=90°,∠PBA=90°,∠QME=90°,∴∠PAB=∠AQM,∴△PAB∽△AQM,∴=,设P(﹣2,t),∵直线DE的解析式为y=x+1,PQ⊥DE,∴∠PDQ=45°,∴Q(,),∴PB=t﹣3,AB=2,AM=,QM=﹣3=,∴,∴t =9, ∴P (﹣2,9);如图3,当PQ ⊥AP 时,∵∠PAQ +∠AQP =90°,∠AQP +∠AQE =90°,∴∠APQ =∠AQE ,∴AP //DE ,∴直线AP 的解析式为y =x +3,∴P (﹣2,1);综上所述:P 点的坐标为(﹣2,1)或(﹣2,3)或(﹣2,9).【点睛】本题是二次函数的综合,考查了待定系数法求函数解析式,相似三角形的判定与性质,直角三角形的性质,解一元二次方程,三角形面积等知识,涉及分类讨论思想、方程思想.11.(1)见解析;(2)23y x =-;(3421【解析】【分析】(1)过点E 作EM ⊥QP 垂足为M ;在Rt △EQP 中,易得∠EBD =∠EDB =30°;进而可得PE 3,且BE =DE .故可证得BE =PD 3. (2)点P 从点E 出发沿射线ED 运动,所以分当点P 在线段ED 上时与当点P 在线段ED 的延长线上时两种情况讨论,根据所作的辅助线,可得y 与x 的关系;(3)连接PC 交BD 于点N ,可得∠QPC =90°,进而可得△PNG ∽△QPC ,可得PG PNQC PQ,解可得PG的长,再证明△PNG∽△PFC,利用相似三角形的性质即可求解.【详解】(1)证明:∵∠A=90°,∠ABE=30°,∴∠AEB=60°.∵EB=ED,∴∠EBD=∠EDB=30°.∵PQ∥BD,∴∠EQP=∠EBD.∠EPQ=∠EDB.∴∠EPQ=∠EQP=30°,∴EQ=EP.过点E作EM⊥QP垂足为M.则PQ=2PM.∵∠EPM=30°,∴PM=3PE,PE=3PQ.∵BE=DE=PD+PE,∴BE=PD+3PQ.(2)解:由题意知AE=12BE,∴DE=BE=2AE.∵AD=BC=6,∴2AE=DE=BE=4.当点P在线段ED上时(如图1),过点Q作QH⊥AD于点H,则QH=12PQ=12x.由(1)得PD=BE 3,即PD3.∴y=12PD•QH=−32+x.当点P在线段ED的延长线上时(如图2),过点Q作QH′⊥DA交DA延长线于点H′,∴QH′=12x.过点E作EM′⊥PQ于点M′,同理可得EP=EQ=3PQ,∴BE=3PQ-PD,∴PD=3x-4,∴y=12PD•QH′=3x2−x.(3)解:连接PC交BD于点N(如图3).∵点P是线段ED中点,∴EP=PD=2,PQ3∵DC=AB=AE•tan3∴PC22PD DC+.∴cos∠DPC=12 PDPC=.∴∠DPC=60°.∴∠QPC=180°-∠EPQ-∠DPC=90°.∵PQ∥BD,∴∠PND=∠QPC=90°.∴PN=12PD=1.QC22PQ PC+7.∵∠PGN=90°-∠FPC,∠PCF=90°-∠FPC,∴∠PGN=∠PCF.∵∠PNG=∠QPC=90°,∴△PNG ∽△QPC , ∴PG PN QC PQ=, ∴PG∵∠PNG =∠PFC =90°,∠NPG =∠FPC ,∴△PNG ∽△PFC , ∴PF PC PN PG =,即1PF =, ∴PF【点睛】本题考查相似三角形的判定和性质,解直角三角形,注意某个图形无法解答时,常常放到其他图形中,利用图形间的角、边关系求解.12.(1)抛物线表达式为:2(1)4y x =--;(2)点M 坐标3(2,15)4时,四边形ABMC 面积的最大值758; (3)当点P 坐标为(1,2)--或3(4-,9)4-时,点P 、E 、O 为顶点的三角形与ABC ∆相似【解析】【分析】(1)利用二次函数的顶点式求解;(2)将四边形ABMC 进行分割,分成ABC ∆,∆CMN ,BMN ∆的和,ABC ∆的面积是定值,求出直线BC 的表达式,当点M 在移动时,表示出线段MN 的长度,从而计算出∆CMN ,BMN ∆面积和的最大值,进而求解;(3)利用三角形相似的判定条件,两边对应成比例且夹角相等进行求解,通过求直线CD 的表达式,得到E 点的坐标,从而求出OEC OBC ∠=∠,分情况讨论两边成比例的情况,进而求出点EP 的长度,再借助解直角三角形进行求解.(1)解:设抛物线的表达式为2(1)4y a x =--,∴将点(0,3)C -代入得:43a -=-,解得1a =,∴抛物线表达式为:()214y x =--;(2)解:连接BC ,作MN y ∥轴交BC 于点N ,作BE MN ⊥,CF MN ⊥,如图所示:由(1)知,抛物线表达式为22(1)423y x x x =--=--, 令0y =,可解得11x =-,23x =, ∴点A 坐标(1,0)-,点B 坐标(3,0),设直线BC 的表达式为y kx b =+,将点B (3,0),(0,3)C -代入得:303k b b +=⎧⎨=-⎩, ∴直线BC 表达式为3y x =-, 设M 点2(,23)m m m --,则点(,3)N m m -,222393(23)3()24N M MN y y m m m m m m =-=----=-+=--+, ΔΔABC BCM ABMC S S S ∴=+四边形ΔΔΔABC CMN BMN S S S =++111222AB OC MN CF MN BE =⨯⨯+⨯⨯+⨯⨯ 1143()22MN CF BE =⨯⨯+⨯⨯+ 1632MN =+⨯⨯ 23375()228m =--+, 当32m =时,即点M 坐标3(2,15)4时,四边形ABMC 面积的最大值758; (3) 解:如图所示,作PQ 垂直x 轴,设直线:CD y px q =+,将点C ,D 分别代入得,4{3p q q +=-=-,解得1{3p q =-=-, ∴直线:3CD y x =--,当0y =时,解得3x =-,∴点E 坐标为(3,0)-,3OE OC OB ===,45OEC OBC ∴∠=∠=︒,在Rt OBC ∆中,223332BC +=①当ΔΔBAC EPO ∽时,AB EP BC EO=332EP =,解得22EP = 在Rt ΔEPQ 中,45OEC ∠=︒,sin 45PQ EP∴︒=,解得2PQ =, 2EQ PQ ∴==,此时点P 坐标(1,2)--; ②当ΔΔBAC EOP ∽时,BA EO BC EP =332EP =,解得92EP = 在Rt ΔEPQ 中,45OEC ∠=︒,sin 45PQ EP ∴︒=,解得94PQ =, 94EQ PQ ∴==,此时点P 坐标3(4-,9)4-; 综上所述,当点P 坐标为()1,2--或39,44⎛⎫-- ⎪⎝⎭时,点P 、E 、O 为顶点的三角形与ABC ∆相似.【点睛】本题是二次函数的综合应用题,主要考查了待定系数法求函数解析式,直角坐标系内多边形面积的求法,三角形相似的判定.第2问的解题关键是能够将四边形面积进行分割计算,并且能够表示出线段MN 的长度,从而建立函数关系进行求解,第3问的解题关键是利用三角形相似求出线段EP 的长度,再借助解直角三角形进行求解.13.(1)y =x 2-4x +3(2)①94;②(1,0);(3)0(或0(, 【解析】【分析】(1)用待定系数法求解析式即可;(2)①根据抛物线解析式设出P 点坐标,用待定系数法求出直线BC 的解析式,确定D 点的坐标,根据二次函数的性质得出PD 的最大值即可;②分情况讨论求出P 点的坐标即可;(3)作△ABE 的外接圆,根据圆心在抛物线的对称轴上,且当半径最小时∠AEB 有最大值,即外接圆与y 轴相切时,求出此时的E 点坐标即可.(1)解:(1)∵抛物线y =ax 2+bx +3经过点A (1,0)和点B (3,0), ∴30,9330a b a b ++=⎧⎨++=⎩解得14a b =⎧⎨=-⎩∴抛物线的解析式为:y =x 2-4x +3;(2)①设P (m ,m 2-4m +3),由抛物线解析式知,C (0,3),设直线BC 的解析式为y =sx +t , 将点B 、C 坐标代入得30,3s t t +=⎧⎨=⎩解得13s t =-⎧⎨=⎩∴直线BC 的解析式为y =-x +3,∴D (m ,-m +3),∴PD =(-m +3)-(m 2-4m +3)=-m 2+3m =239(),24m =-+ ∴当32m =时,PD 有最大值为9;4(3) ②若△PBD 为直角三角形,则存在以下两种情况:(Ⅰ)如下图,当P 点与A 点重合时△PBD 为直角三角形,即P(1,0),(Ⅱ)如下图,当∠DBP=90°时,∵OB=OC=3,∴∠DBO=45°,∴此时△BPD为等腰直角三角形,由(Ⅰ)知PD=-m2+3m,且BD=BP,∴-m2+3m=2(3-m),且|-m2-4m+3|=-m+3此时无解,∴P点坐标为(1,0);(3)如下图,作△ABE的外接圆M,则圆心M在AB的垂直平分线上,即抛物线的对称轴上,AB长度不变,要使∠AEB最大则当⊙M半径最小时,即⊙M与y轴相切时,设E(0,e),则M(2,e),且AM=EM=2,||e ∴∴E 点的坐标为0(或0(, 【点睛】本题主要考查二次函数的综合知识,熟练掌握二次函数的性质及分类讨论思想是解题的关键.14.(2)①2;②(()11062y x x =< 【解析】【分析】(1)设AD =2a ,解直角三角形ADE ,表示AE 和DE ,可得四边形DEGF 是正方形,解直角三角形AGF ,表示出AF ,即可得出结果;(2)①作DG ⊥AB ,截取DG =AD ,作直线GF 交AC 于M ,交直线AB 于H ,可以证明ADE GDF ≌,从而得出60DGF A ∠=∠=︒,得出点F 的运动轨迹,然后解直角三角形DGH ,再解直角三角形AHM ,即可得出结果;②由①得,点F 的运动轨迹,然后解直角三角形DGH ,再解直角三角形AHM ,进而得出y 与x 的函数关系式.(1)设AD =2a , ABC 是等边三角形,60CAB ∴∠=︒,90AED ∠=︒,sin 2sin 60DE AD ABC a ∴=⋅∠=⨯︒=,12AE AD a ==, FG AC ⊥,90FGE ∴∠=︒,90DEG EDF ∠=∠=︒,∴四边形DEGF 是矩形,DE DF =,∴矩形DEFG 是正方形,∴GE FG DE ===,AG AE EG a ∴=+=,在Rt△AFG 中,由勾股定理得,AF=。
中考数学压轴题含答案

中考数学压轴题含答案一、选择题1、下列图形中,既是轴对称图形,又是中心对称图形的是()A.菱形B.平行四边形C.矩形(答案:C)2、如果一个三角形的三条边的平方相等,那么这个三角形一定是()A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形(答案:A)3、下列说法正确的是()A.所有的质数都是奇数B.所有的偶数都是合数C.一个数的因数一定比它的倍数小D.自然数一定是正数(答案:A)二、填空题1、若a-b=2,a+b=7,则a²-b²=(答案:14)2、我们学过的数有整数和分数,整数的运算律在分数运算中(答案:同样适用)。
3、一个长方形的周长是20cm,长和宽的比是3:2,则长方形的面积是(答案:60平方厘米)。
三、解答题1、一个圆柱体底面半径为r,高为h,它的体积是多少?(答案:πr²h)2、有一块三角形的土地,底边长为120米,高为90米,这块土地的面积是多少?(答案:5400平方米)3、对于一个给定的整数n,如果它是3的倍数,那么我们就称它为“三的倍数”,否则我们就称它为“非三的倍数”。
现在有一个整数n,它是“三的倍数”,我们可以得出哪些结论?(答案:n+1、n+2、n+3、...、2n都是“三的倍数”,因为它们都可以被3整除。
)中考数学压轴题100题及答案在中考数学考试中,压轴题往往是最具挑战性和最能检验考生数学能力的题目。
为了帮助同学们更好地理解和掌握中考数学的压轴题,本文将分享100道经典的中考数学压轴题及其答案。
一、选择题1、在一个等边三角形中,边长为6,下列哪个选项的面积最接近这个等边三角形的面积?A. 20B. 25C. 30D. 35答案:B解析:等边三角形的面积可以通过计算得出,边长为6的等边三角形的面积为:436293约为28.2,因此选项B最接近。
2、如果一个多边形的内角和是外角和的2倍,那么这个多边形的边数是多少?A. 4B. 6C. 8D. 10答案:C解析:根据多边形的内角和公式和外角和为360度,可列出方程求解。
中考数学压轴题60例共164页文档

中考数学压轴题60例(解答题)一、解答题(共60小题)1.(2019•遵义)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).(1)求抛物线的解析式;(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.2.(2019•株洲)已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.(1)当点P运动到使Q、C两点重合时(如图1),求AP的长;(2)点P在运动过程中,有几个位置(几种情况)使△CQD的面积为?(直接写出答案)(3)当△CQD的面积为,且Q位于以CD为直径的上半圆,CQ>QD时(如图2),求AP的长.3.(2019•长沙)在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.(1)求函数y=x+2的图象上所有“中国结”的坐标;(2)若函数y=(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?4.(2019•岳阳)已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系:.(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA 与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.5.(2019•玉林)已知:一次函数y=﹣2x+10的图象与反比例函数y=(k>0)的图象相交于A,B两点(A在B的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若=,求△ABC的面积.6.(2019•烟台)【问题提出】如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF试证明:AB=DB+AF【类比探究】(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.7.(2019•湘西州)如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.(1)求抛物线的解析式;(2)问:当t为何值时,△APQ为直角三角形;(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标;(4)设抛物线顶点为M,连接BP,BM,MQ,问:是否存在t的值,使以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.8.(2019•湘潭)如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.(1)求二次函数的解析式;(2)如图1,当△BPQ为直角三角形时,求t的值;(3)如图2,当t<2时,延长QP交y轴于点M,在抛物线上是否存在一点N,使得PQ 的中点恰为MN的中点?若存在,求出点N的坐标与t的值;若不存在,请说明理由.9.(2019•咸宁)如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x 轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.10.(2019•通辽)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形(1)求该抛物线的解析式;(2)求点P的坐标;(3)求证:CE=EF;(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2=(+1)2].11.(2019•天津)已知二次函数y=x2+bx+c(b,c为常数).(Ⅰ)当b=2,c=﹣3时,求二次函数的最小值;(Ⅱ)当c=5时,若在函数值y=l的怙况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.12.(2019•泰州)已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.13.(2019•沈阳)如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A 在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA 或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.(1)求点A和点C的坐标;(2)当0<t<30时,求m关于t的函数关系式;(3)当m=35时,请直接写出t的值;(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.14.(2019•日照)如图,抛物线y=x2+mx+n与直线y=﹣x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).(Ⅰ)求抛物线的解析式和tan∠BAC的值;(Ⅱ)在(Ⅰ)条件下:(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE 以每秒一个单位速度运动到E点,再沿线段EA以每秒个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?15.(2019•泉州)(1)如图1是某个多面体的表面展开图.①请你写出这个多面体的名称,并指出图中哪三个字母表示多面体的同一点;②如果沿BC、GH将展开图剪成三块,恰好拼成一个矩形,那么△BMC应满足什么条件?(不必说理)(2)如果将一个三棱柱的表面展开图剪成四块,恰好拼成一个三角形,如图2,那么该三棱柱的侧面积与表面积的比值是多少?为什么?(注:以上剪拼中所有接缝均忽略不计)16.(2019•潜江)已知抛物线经过A(﹣3,0),B(1,0),C(2,)三点,其对称轴交x轴于点H,一次函数y=kx+b(k≠0)的图象经过点C,与抛物线交于另一点D(点D在点C的左边),与抛物线的对称轴交于点E.(1)求抛物线的解析式;(2)如图1,当S△EOC=S△EAB时,求一次函数的解析式;(3)如图2,设∠CEH=α,∠EAH=β,当α>β时,直接写出k的取值范围.17.(2019•齐齐哈尔)如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO 的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求线段AB的长;(2)求直线CE的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.18.(2019•莆田)在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.特殊发现:如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).问题探究:把图1中的△AEF绕着点A顺时针旋转.(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)19.(2019•宁夏)如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.(1)计算A1C1的长;(2)当α=30°时,证明:B1C1∥AB;(3)若a=,当α=45°时,计算两个三角板重叠部分图形的面积;(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.(参考数据:sin15°=,cos15°=,tan15°=2﹣,sin75°=,cos75°=,tan75°=2+)20.(2019•南通)如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC 上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.(1)求证:PQ∥AB;(2)若点D在∠BAC的平分线上,求CP的长;(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.21.(2019•南宁)在平面直角坐标系中,已知A、B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限,(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积.(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,A、B两点的横坐标的乘积是否为常数?如果是,请给予证明;如果不是,请说明理由.(3)在(2)的条件下,若直线y=﹣2x﹣2分别交直线AB,y轴于点P、C,直线AB交y 轴于点D,且∠BPC=∠OCP,求点P的坐标.22.(2019•绵阳)已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.23.(2019•梅州)如图,过原点的直线y=k1x和y=k2x与反比例函数y=的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.(1)四边形ABCD一定是四边形;(直接填写结果)(2)四边形ABCD可能是矩形吗?若可能,试求此时k1,k2之间的关系式;若不能,说明理由;(3)设P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=图象上的任意两点,a=,b=,试判断a,b的大小关系,并说明理由.24.(2019•娄底)如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)当AB=3,BP=2PC,求QM的长;(3)当BP=m,PC=n时,求AM的长.25.(2019•辽阳)如图1,平面直角坐标系中,直线y=﹣x+3与抛物线y=ax2+x+c相交于A,B两点,其中点A在x轴上,点B在y轴上.(1)求抛物线的解析式;(2)在抛物线上存在一点M,使△MAB是以AB为直角边的直角三角形,求点M的坐标;(3)如图2,点E为线段AB上一点,BE=2,以BE为腰作等腰Rt△BDE,使它与△AOB 在直线AB的同侧,∠BED=90°,△BDE沿着BA方向以每秒一个单位的速度运动,当点B 与A重合时停止运动,设运动时间为t秒,△BDE与△AOB重叠部分的面积为S,直接写出S关于t的函数关系式,并写出自变量t的取值范围.26.(2019•锦州)如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.(1)求该抛物线的解析式;(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x 轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.27.(2019•锦州)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.28.(2019•济南)如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.29.(2019•济南)如图1,点A(8,1)、B(n,8)都在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.(1)求m的值和直线AB的函数关系式;(2)动点P从O点出发,以每秒2个单位长度的速度沿折线OD﹣DB向B点运动,同时动点Q从O点出发,以每秒1个单位长度的速度沿折线OC向C点运动,当动点P运动到D时,点Q也停止运动,设运动的时间为t秒.①设△OPQ的面积为S,写出S与t的函数关系式;②如图2,当的P在线段OD上运动时,如果作△OPQ关于直线PQ的对称图形△O′PQ,是否存在某时刻t,使得点O′恰好落在反比例函数的图象上?若存在,求O′的坐标和t的值;若不存在,请说明理由.30.(2019•黄石)已知双曲线y=(x>0),直线l1:y﹣=k(x﹣)(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+.(1)若k=﹣1,求△OAB的面积S;(2)若AB=,求k的值;(3)设N(0,2),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(x1,y1),B (x2,y2)则A,B两点间的距离为AB=)31.(2019•黄冈)我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.(1)求W关于x的函数关系式,并写出自变量x的取值范围;(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,最多可节约3400元,求a的值.32.(2019•呼伦贝尔)直线y=x﹣6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.(1)画出当t=2时,四边形ABEF沿直线EF折叠后的四边形CDEF(不写画法);(2)在点E运动过程中,CD交x轴于点G,交y轴于点H,试探究t为何值时,△CGF的面积为;(3)设四边形CDEF落在第一象限内的图形面积为S,求S关于t的函数解析式,并求出S 的最大值.33.(2019•黑龙江)如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB 绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2﹣6x+8=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求△OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.34.(2019•河南)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.35.(2019•贵阳)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C 落在AD边上的点M处,折痕为PE,此时PD=3.(1)求MP的值;(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)36.(2019•贵港)已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:①线段PB=,PC=;②猜想:PA2,PB2,PQ2三者之间的数量关系为;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)37.(2019•广西)在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.(1)求证:△CMN∽△BAM;(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y 的最大值;(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.38.(2019•甘南州)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,﹣4),B(x1,0),C(x2,0)三点,且|x2﹣x1|=5.(1)求b,c的值;(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.39.(2019•丹东)在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP 时,猜想此时PE与PF的数量关系,并给出证明;当BD=m•BP时,请直接写出PE与PF 的数量关系.40.(2019•大连)如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2,点P,Q同时从点D出发,以相同的速度分别沿射线DC、射线DA运动,过点Q作AC的垂线段QR,使QR=PQ,连接PR,当点Q到达点A时,点P,Q同时停止运动.设PQ=x,△PQR与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤,<x≤m时,函数的解析式不同).(1)填空:n的值为;(2)求S关于x的函数关系式,并写出x的取值范围.41.(2019•成都)已知AC,EC分别是四边形ABCD和EFDG的对角线,点E在△ABC内,∠CAE+∠CBE=90°.(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.(i)求证:△CAE∽△CBF;(ii)若BE=1,AE=2,求CE的长;(2)如图②,当四边形ABCD和EFCG均为矩形,且==k时,若BE=1,AE=2,CE=3,求k的值;(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)42.(2019•常州)如图,反比例函数y=的图象与一次函数y=x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.43.(2019•北京)在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D 不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.(1)若点P在线段CD上,如图1.①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)44.(2019•包头)已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.(1)求该抛物线的解析式及点D的坐标;(2)连接AC,CD,BD,BC,设△AOC,△BOC,△BCD的面积分别为S1,S2和S3,用等式表示S1,S2,S3之间的数量关系,并说明理由;(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时刻直线MN 的解析式;若不存在,请说明理由.45.(2019•重庆)如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标.46.(2019•重庆)如图1,在平面直角坐标系中,抛物线y=﹣x2+x+3交x轴于A,B两点(点A在点B的左侧),交y轴于点W,顶点为C,抛物线的对称轴与x轴的交点为D.(1)求直线BC的解析式;(2)点E(m,0),F(m+2,0)为x轴上两点,其中2<m<4,EE′,FF′分别垂直于x轴,交抛物线于点E′,F′,交BC于点M,N,当ME′+NF′的值最大时,在y轴上找一点R,使|RF′﹣RE′|的值最大,请求出R点的坐标及|RF′﹣RE′|的最大值;(3)如图2,已知x轴上一点P(,0),现以P为顶点,2为边长在x轴上方作等边三角形QPG,使GP⊥x轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P 到达点A时停止,记平移后的△QPG为△Q′P′G′.设△Q′P′G′与△ADC的重叠部分面积为s.当Q′到x轴的距离与点Q′到直线AW的距离相等时,求s的值.47.(2019•漳州)如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.(1)填空:点C的坐标为(,),点D的坐标为(,);(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?48.(2019•营口)如图1,一条抛物线与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C,且当x=﹣1和x=3时,y的值相等,直线y=x﹣与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.(1)求这条抛物线的表达式.(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为t秒.①若使△BPQ为直角三角形,请求出所有符合条件的t值;②求t为何值时,四边形ACQP的面积有最小值,最小值是多少?(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥x轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿x轴向左平移m个单位长度(0<m<2),将平移后的三角形与△ODM重叠部分的面积记为S,求S与m的函数关系式.49.(2019•威海)已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣).(1)求抛物线l2的函数表达式;(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.50.(2019•泉州)阅读理解抛物线y=x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.问题解决如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.(1)写出点C的坐标,并说明∠ECF=90°;(2)在△PEF中,M为EF中点,P为动点.①求证:PE2+PF2=2(PM2+EM2);②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.51.(2019•青岛)已知,如图①,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD 沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:(1)当t为何值时,PQ∥MN?(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.52.(2019•龙岩)如图,已知点D在双曲线y=(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.(1)写出点D的坐标并求出抛物线的解析式;(2)证明∠ACO=∠OBC;。
初中数学的中考数学必做的36道压轴题

中考必做的36道压轴题及变式训练第一题夯实双基“步步高”,强化条件是“路标”例1(北京,23,7分)在平面直角坐标系x O y 中,抛物线222--=mx mx y (0≠m )与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)设直线l 与直线AB 关于该抛物线的对称轴对称,求直线l 的解析式;(3)若该抛物线在12-<<-x 这一段位于直线l 的上方,并且在32<<x 这一段位于直线AB 的下方,求该抛物线的解析式.解:(1)当x =0时,y =-2.∴A (0,-2).抛物线对称轴为x =212mm--=,∴B (1,0).(2)易得A 点关于对称轴的对称点为A (2,-2)则直线l 经过A 、B .没直线的解析式为y =kx +b 则22,0.k b k b +=-⎧⎨+=⎩解得2,2.k b =-⎧⎨=⎩∴直线的解析式为y =-2x +2.(3)∵抛物线对称轴为x =1抛物体在2<x <3这一段与在-1<x <0这一段关于对称轴对称,结合图象可以观察到抛物线在-2<x <1这一段位于直线l 的上方,在-1<x <0这一段位于直线l 的下方.∴抛物线与直线l 的交点横坐标为-1;当x =-1时,y =-2x (-1)+2=4则抛物线过点(-1,4)当x =-1时,m +2m -2=4,m =2∴抛物线解析为y =2x 2-4x -2.连接(江苏南京,26,9分)已知二次函数y =a (x -m )2-a (x -m )(a 、m 为常数,且a ≠0).(1)求证:不论a 与m 为何值,该函数的图象与x 轴总有两个公共点;(2)设该函数的图象的顶点为C .与x 轴交于A 、B 两点,与y 轴交于点D .①当△ABC 的面积等于1时,求a 的值;②当△ABC 的面积与△ABD 的面积相等时,求m 的值.【答案】(1)证明:y =a (x -m )2-a (x -m )=ax 2-(2am +a )x +am 2+am .因为当a ≠0时,[-(2am +a )]2-4a (am 2+am )=a 2>0.所以,方程ax 2-(2am +a )x +am 2+am =0有两个不相等的实数根.所以,不论a 与m 为何值,该函数的图象与x 轴总有两个公共点.………3分(2)解:①y =a (x -m )2-a (x -m )=a (x -212+m )2-4a,所以,点C 的坐标为(212+m ,-4a).当y =0时,a (x -m )2-a (x -m )=0.解得x 1=m ,x 2=m +1.所以AB =1.当△ABC 的面积等于1时,21×1×4a -=1.所以21×1×(-4a )=1,或21×1×4a=1.所以a =-8,或a =8.②当x =0时,y =am 2+am .所以点D 的坐标为(0,am 2+am ).当△ABC 的面积与△ABD 的面积相等时,21×1×4a -=21×1×amam +221×1×(-4a )=21×1×(am 2+am ),或21×1×4a =21×1×(am 2+am ).所以m =-21,或m =221--,或m =221+-.………9分变式:(北京,23,7分)已知二次函数23(1)2(2)2y t x t x =++++在0x =和2x =时的函数值相等。
中考数学 中考数学压轴题测试试题及答案
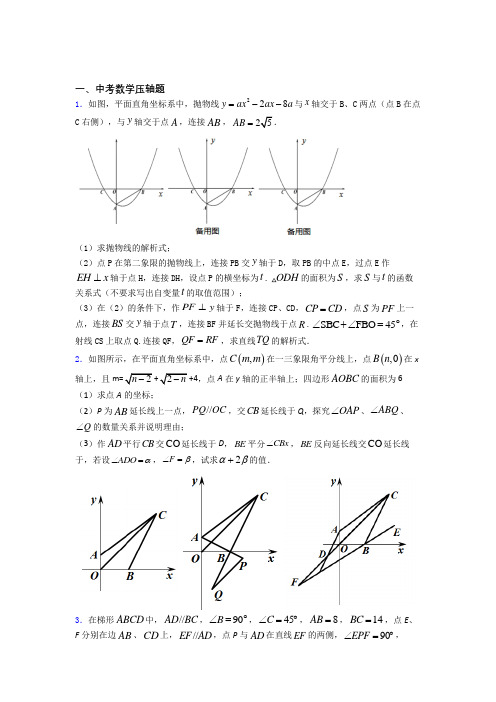
一、中考数学压轴题1.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式.2.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且m=2n -+2n -+4,点A 在y 轴的正半轴上;四边形AOBC 的面积为6 (1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.3.在梯形ABCD 中,//AD BC ,90B ∠=︒,45C ∠=︒,8AB =,14BC =,点E 、F 分别在边AB 、CD 上,//EF AD ,点P 与AD 在直线EF 的两侧,90EPF ∠=︒,PE PF =,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE x =,MN y =.(1)求边AD 的长;(2)如图,当点P 在梯形ABCD 内部时,求关于x 的函数解析式,并写出定义域; (3)如果MN 的长为2,求梯形AEFD 的面积.4.如图,90EOF ∠=︒,矩形ABCD 的边BA 、BC 分别在OF 、OE 上,4AB =,3BC =,矩形ABCD 沿射线OD 方向,以每秒1个单位长度的速度运动.同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动,当点P 到达点C 时,矩形ABCD 也停止运动,设点P 的运动时间为()t s ,PDO △的面积为S . (1)分别写出点B 到OF 、OE 的距离(用含t 的代数式表示);(2)当点P 不与矩形ABCD 的顶点重合时,求S 与t 之间的函数关系式;(3)设点P 到BD 的距离为h ,当15h OD =时,求t 的值; (4)若在点P 出发的同时,点Q 从点B 以每秒43个单位长度的速度向终点A 运动,当点Q 停止运动时,点P 与矩形ABCD 也停止运动,设点A 关于PQ 的对称点为E ,当PQE 的一边与CDB △的一边平行时,直接写出线段OD 的长.5.如图,在ABC ∆中,14AB =,45B ∠=︒,4tan 3A =,点D 为AB 中点.动点P 从点D 出发,沿DA 方向以每秒1个单位长度的速度向终点A 运动,点P 关于点D 对称点为点Q ,以PQ 为边向上作正方形PQMN .设点P 的运动时间为t 秒.(1)当t =_______秒时,点N 落在AC 边上.(2)设正方形PQMN 与ABC ∆重叠部分面积为S ,当点N 在ABC ∆内部时,求S 关于t 的函数关系式.(3)当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时,直接写出t 的值.6.如图,在平面直角坐标系xoy 中,直线122y x =-+与x 轴交于点B ,与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点.(1)求抛物线的解析式;(2)点M 为抛物线对称轴上一动点,当BM CM -的值最小时,请你求出点M 的坐标;(3)抛物线上是否存在点N ,过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似?若存在,请直接写出点N 的坐标;若不存在,请说明理由.7.小明研究了这样一道几何题:如图1,在ABC 中,把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB ',把AC 绕点A 逆时针旋转β得到AC ',连接B C ''.当180a β+=︒时,请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么?以下是他的研究过程:特例验证:(1)①如图2,当ABC 为等边三角形时,猜想AD 与BC 的数量关系为AD =_______BC ;②如图3,当90BAC ∠=︒,8BC =时,则AD 长为________. 猜想论证:(2)在图1中,当ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.拓展应用:(3)如图4,在四边形ABCD ,90C ∠=︒,120A B ∠+∠=︒,123BC =,6CD =,63DA =,在四边形内部是否存在点P ,使PDC △与PAB △之间满足小明探究的问题中的边角关系?若存在,请画出点P 的位置(保留作图痕迹,不需要说明)并直接写出PDC △的边DC 上的中线PQ 的长度;若不存在,说明理由.8.在平面直角坐标系中,点O 为坐标原点,抛物线(2)()y a x x m =++与x 轴交于点A C 、(点A 在点C 的左侧),与y 轴正半轴交于点B ,24OC OB ==.(1)如图1,求a m 、的值;(2)如图2,抛物线的顶点坐标是M ,点D 是第一象限抛物线上的一点,连接AD 交抛物线的对称轴于点N ,设点D 的横坐标是t ,线段MN 的长为d ,求d 与t 的函数关系式;(3)如图3,在(2)的条件下,当154d =时,过点D 作DE x 轴交抛物线于点E ,点P 是x 轴下方抛物线上的一个动点,连接PE 交x 轴于点F ,直线211y x b =+经过点D 交EF 于点G ,连接CG ,过点E 作EH CG 交DG 于点H ,若3CFG EGH S S =△△,求点P 的坐标.9.(1)如图1,A 是⊙O 上一动点,P 是⊙O 外一点,在图中作出PA 最小时的点A . (2)如图2,Rt △ABC 中,∠C =90°,AC =8,BC =6,以点C 为圆心的⊙C 的半径是3.6,Q 是⊙C 上一动点,在线段AB 上确定点P 的位置,使PQ 的长最小,并求出其最小值. (3)如图3,矩形ABCD 中,AB =6,BC =9,以D 为圆心,3为半径作⊙D ,E 为⊙D 上一动点,连接AE ,以AE 为直角边作Rt △AEF ,∠EAF =90°,tan ∠AEF =13,试探究四边形ADCF 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.10.如图,正方形ABCD 的边长为8,M 是AB 的中点,P 是BC 边上的动点,连结PM ,以点P 为圆心,PM 长为半径作⊙P .(1)当BP = 时,△MBP ~△DCP ;(2)当⊙P 与正方形ABCD 的边相切时,求BP 的长;(3)设⊙P 的半径为x ,请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围.11.如图,在平面直角坐标系中,Rt ABC △的斜边在AB 在x 轴上,点C 在y 轴上90ACB ∠=︒,OC 、OB 的长分别是一元二次方程2680x x -+=的两个根,且OC OB <.(1)求点A 的坐标;(2)D 是线段AB 上的一个动点(点D 不与点A ,B 重合),过点D 的直线l 与y 轴平行,直线l 交边AC 或边BC 于点P ,设点D 的横坐标为t ,线段DP 的长为d ,求d 关于t 的函数解析式;(3)在(2)的条件下,当12d =时,请你直接写出点P 的坐标.12.已知:如图①,在等腰直角ABC ∆中,斜边2AC =.(1)请你在图①的AC 边上求作一点P ,使得90APB ∠=︒;(2)如图②,在(1)问的条件下,将AC 边沿BC 方向平移,使得点A 、P 、C 对应点分别为E 、Q 、D ,连接AQ ,BQ .若平移的距离为1,求AQB ∠的大小及此时四边形ABDE 的面积;(3)将AC 边沿BC 方向平移m 个单位至ED ,是否存在这样的m ,使得在直线DE 上有一点M ,满足30AMB ∠=︒,且此时四边形ABDE 的面积最大?若存在,求出四边形ABDE 面积的最大值及平移距离m 的值;若不存在,请说明理由.13.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 14.如图①,在△ABC 中,∠ACB =90°,∠B =30°,AC =1,D 为AB 的中点,EF 为△ACD 的中位线,四边形EFGH 为△ACD 的内接矩形(矩形的四个顶点均在△ACD 的边上). (1)计算矩形EFGH 的面积;(2)将矩形EFGH 沿AB 向右平移,F 落在BC 上时停止移动.在平移过程中,当矩形与△CBD 重叠部分的面积为3时,求矩形平移的距离; (3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形1111E F G H ,将矩形1111E F G H 绕1G 点按顺时针方向旋转,当1H 落在CD 上时停止转动,旋转后的矩形记为矩形2212E F G H ,设旋转角为α,求cos α的值.15.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH 、AH 、BD 的数量关系.请说明理由.16.已知抛物线2y ax bx c =++过点(6,0)A -,(2,0)B ,(0,3)C -.(1)求此抛物线的解析式;(2)若点H 是该抛物线第三象限的任意一点,求四边形OCHA 的最大面积;(3)若点Q 在y 轴上,点G 为该抛物线的顶点,且45GQA ∠=︒,求点Q 的坐标.17.定义:将函数l 的图象绕点P (m ,0)旋转180°,得到新的函数l '的图象,我们称函数l '是函数关于点P 的相关函数.例如:当m =1时,函数y =(x +1)2+5关于点P (1,0)的相关函数为y =﹣(x ﹣3)2﹣5.(1)当m =0时①一次函数y =x ﹣1关于点P 的相关函数为 ; ②点(12,﹣98)在二次函数y =﹣ax 2﹣ax +1(a ≠0)关于点P 的相关函数的图象上,求a 的值.(2)函数y =(x ﹣1)2+2关于点P 的相关函数y =﹣(x +3)2﹣2,则m = ; (3)当m ﹣1≤x ≤m +2时,函数y =x 2﹣mx ﹣12m 2关于点P (m ,0)的相关函数的最大值为6,求m 的值.18.已知四边形ABCD 为矩形,对角线AC 、BD 相交于点O ,AD =AO .点E 、F 为矩形边上的两个动点,且∠EOF =60°.(1)如图1,当点E 、F 分别位于AB 、AD 边上时,若∠OEB =75°,求证:DF =AE ; (2)如图2,当点E 、F 同时位于AB 边上时,若∠OFB =75°,试说明AF 与BE 的数量关系;(3)如图3,当点E 、F 同时在AB 边上运动时,将△OEF 沿OE 所在直线翻折至△OEP ,取线段CB 的中点Q .连接PQ ,若AD =2a (a >0),则当PQ 最短时,求PF 之长.19.如图,在矩形ABCD中,点E为BC的中点,连接AE,过点D作DF AE⊥于点F,过点C作CN DF⊥于点N,延长CN交AD于点M.(1)求证:AM MD=(2)连接CF,并延长CF交AB于G①若2AB=,求CF的长度;②探究当ABAD为何值时,点G恰好为AB的中点.20.已知菱形ABCD中,∠ABC=60°,AB=4,点M在BC边上,过点M作PM∥AB交对角线BD于点P,连接PC.(1)如图1,当BM=1时,求PC的长;(2)如图2,设AM与BD交于点E,当∠PCM=45°时,求证:BEDE=33+;(3)如图3,取PC的中点Q,连接MQ,AQ.①请探究AQ和MQ之间的数量关系,并写出探究过程;②△AMQ的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.21.在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A 顺时针旋转90°,得到线段AE,连接DE.(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.(3)如图3,点F为线段DE中点,AB=2a,求出动点D从B运动到C,点F经过的路径长度.22.在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=()A.180° B.270° C.360° D.540°(1)请写出这道题的正确选项;(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.23.发现来源于探究.小亮进行数学探究活动,作边长为a的正方形ABCD和边长为b的正方形AEFG(a>b),开始时,点E在AB上,如图1.将正方形AEFG绕点A逆时针方向旋转.(1)如图2,小亮将正方形AEFG绕点A逆时针方向旋转,连接BE、DG,当点G恰好落在线段BE上时,小亮发现DG⊥BE,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG 的长.(2)如图3,小亮旋转正方形AEFG ,点E 在DA 的延长线上,连接BF 、DF .当FG 平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示).24.已知,抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ,B ,且B 点的坐标为()2,0.(1)求该抛物线的解析式.(2)如图1,若点P 是线段AB 上的一动点,过点P 作//PE AC ,交BC 于E ,连接CP ,求PCE ∆面积的最大值.(3)如图2,若直线y x m =+与线段AC 交于点M ,与线段BC 交于点N ,是否存在M ,N ,使得OMN ∆为直角三角形,若存在,请求出m 的值;若不存在,请说明理由.25.如图,在平面直角坐标系中,矩形ABCD 的顶点,A D 在坐标轴上,两点的坐标分别是点()0,,A m 点(),0,D m 且m 满足:322m m -+62=边AB 与x 轴交于点,E 点F 是边AD 上一动点,连接FB ,分别与x 轴,y 轴交于点,P 点,H 且FD BE =.(1)求m 的值;(2)若45,APF ∠=︒求证:AHF HFA ∠=∠;(3)若点F 的纵坐标为,n 则线段HF 的长为 .(用含n 的代数式表示)【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.H解析:(1)211242y x x =--;(2)213S 242t t =---;(3)7433y x =-+ 【解析】【分析】(1)先把B 、C 两点坐标求解出来,再根据待定系数法即可把函数解析式求解出来;(2) 过点P 作PK x ⊥轴于点K ,PF y ⊥轴于点F ,把OH 、OD 的长度用t 表示出来,再根据ODH ∆的面积为S ,即可表示出S 与t 的函数关系式;(3)先证明PKC COD ∆≅∆,再过点R 作RN x ⊥轴,设211m,242R m m ⎛⎫-- ⎪⎝⎭,连接RC 、RO ,作CL RO ⊥于L ,求出Q 点的坐标,再利用待定系数法即可把直线TQ 的解析式求解出来;【详解】(1)∵228y ax ax a =--与x 轴交于B 、C 两点∴令0y =,即2280ax ax a --=解得14x =,22x =-由题意得,∴B(4,0),C(2,0)-在Rt OAB 中,4OB =,25AB =.∴22OA 2AB OB =-=∴()0,2A -∴82a -=-∴14a = ∴抛物线的解析式为211242y x x =-- (2)过点P 作PK x ⊥轴于点K ,PF y ⊥轴于点F∴PKO PFO 90∠=∠=︒,FOK 90∠=︒∴四边形FPKO 为矩形∴FO PK =∵E 为PB 的中点∴PE BE =∵EH BK ⊥∴PKB EHB 90∠=∠=︒∴PK //EH ∴BH BM HK PM= ∴BH HK = ∵211,242P t t t ⎛⎫-- ⎪⎝⎭ ∴211PK OF 242t t ==--,OK PF t ==- ∴BK 4t =- ∴1t BH BK 222==- ∴t t OH 42222⎛⎫=--=+ ⎪⎝⎭ ∵OD PK tan DBO OB BK ∠==, 即21441422t t OD t--=- ∴OD t 2=-- ∴211t 13S OD OH (t 2)2222242t t ⎛⎫=⋅=--+=--- ⎪⎝⎭, (3)∵OK t =-,OC 2=,∴CK OD t 2==--,∵CP CD =,PKC COD 90∠=∠=︒,∴PKC COD ∆≅∆,∴PK OC 2==,∴2OF = ∴OF 1tan FBO OB 2∠== 过点R 作RN x ⊥轴,如图设211m,242R m m ⎛⎫-- ⎪⎝⎭∴RN 1tan FBO BN 2∠==, ∴211214242m m m --=- 解得4m =-或4m =(舍去),∴R(4,4)- ∴CN 1tan CRN RN 2∠== ∴CRN FBO ∠=∠连接RC 、RO ,作CL RO ⊥于L ,如上图∵RN ON =∴45NRO RON NRC CRO ∠=∠=∠+∠=︒,∴LC LO =,RO 42=, ∴CL OL 2==, ∴CL 1tan CRO RL 3∠=, ∵SBC FBO 45∠+∠=︒, ∴OT 1tan TBO OB 3∠==, ∴4OT 3=,2TF 3=, ∴4T 0,3⎛⎫ ⎪⎝⎭∵//PF OB ,∴2FT 13tan FST FS 3FS ∠=== ∴2FS =,∴FS CO OF 2===,∴QC BC ⊥∵QF FB =,QSF BOF 90∠=∠=︒,∴QFS BFO ∆≅∆∴QS OB 4==∴(2,6)Q -设直线TQ 的解析式为y kx b =+ ∴2643k b b -+=⎧⎪⎨=⎪⎩ 解得7343k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线TQ 的解析式为7433y x =-+. 【点睛】本题主要考查了二次函数的综合应用,涉及到用待定系数法求解函数解析式、一次函数、全等三角形、图形的面积计算、矩形的性质、解直角三角形等相关知识,灵活运用所学知识是解题的关键. 2.A解析:(1)A (0,1)(2)结论:∠ABQ +∠OAB ﹣∠Q =135°.(3)α+2β=45°.【解析】【分析】(1)利用二次根式的性质求出m 、n 的值,求出B 、C 两点坐标,由S 四边形AOBC =S △OBC +S △AOC ,推出12×2×4+12×OA ×4=6,求出OA 即可; (2)如图2中,结论:∠ABQ +∠OAB ﹣∠Q =135°.根据三角形内角和定理,三角形的外角的性质即可解决问题;(3)由AD ∥BC ,推出∠ADC =∠DCB =α,由BE 平分∠CBx ,推出∠CBE =∠EBx ,由∠CBE =∠F +∠OCB =α+β,推出∠OBF =∠EBx =α+β,由OC 平分∠AOB ,可得∠COB =45°=∠F +∠OBF =α+(α+β),由此即可解决问题;【详解】解:(1)由题意2020n n -≥⎧⎨-≥⎩,,得,解得n =2,∴m=4,B(2,0),C(4,4).如图:∵S四边形AOBC=S△OBC+S△AOC,∴12×2×4+12×OA×4=6,∴OA=1,∴A(0,1).(2)结论:∠ABQ+∠OAB﹣∠Q=135°.如图:理由如下:∵OC∥PQ,∴∠Q=∠OCB,∵∠ABQ=∠1+∠OCB=∠1+∠Q,∠1=180°﹣∠OAB﹣∠AOC=180°﹣∠OAB﹣45°=135°﹣∠OAB,∴∠ABQ=∠Q+135°﹣∠OAB,∴∠ABQ+∠OAB﹣∠Q=135°.(3)如图:∵AD∥BC,∴∠ADC=∠DCB=α,∵BE平分∠CBx,∴∠CBE=∠EBx,∵∠CBE=∠F+∠OCB=α+β,∴∠OBF=∠EBx=α+β,∵C(4,4),∴OC平分∠AOB,∴∠COB=45°=∠F+∠OBF=α+(α+β),∴α+2β=45°.【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题,属于压轴题.3.D解析:(1)6;(2)y=-3x+10(1≤x<103);(2)1769或32【解析】【分析】(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.【详解】(1)如下图,过点D作BC的垂线,交BC于点H∵∠C=45°,DH ⊥BC∴△DHC 是等腰直角三角形∵四边形ABCD 是梯形,∠B=90°∴四边形ABHD 是矩形,∴DH=AB=8∴HC=8∴BH=BC -HC=6∴AD=6(2)如下图,过点P 作EF 的垂线,交EF 于点Q ,反向延长交BC 于点R ,DH 与EF 交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理,PR=12y ∵AB=8,∴EB=8-x∵EB=QR∴8-x=()11622x y ++ 化简得:y=-3x+10 ∵y >0,∴x <103 当点N 与点B 重合时,x 可取得最小值则BC=NM+MC=NM+EF=-3x+10+614x +=,解得x=1∴1≤x <103(3)情况一:点P 在梯形ABCD 内,即(2)中的图形 ∵MN=2,即y=2,代入(2)中的关系式可得:x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二:点P 在梯形ABCD 外,图形如下:与(2)相同,可得y=3x -10则当y=2时,x=4,即AE=4∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质,难点在于第(2)问中确定x 的取值范围,需要一定的空间想象能力. 4.B解析:(1)35t ,45t ;(2)当0<t <3时,224655S t t =--+;当3<t <7时,23391052S t t =+-;(3)75;(4)132,7713,477 【解析】【分析】(1)过点B 作x 轴垂线,利用相似三角形可求得; (2)分2种情况,一种是点P 在AD 上,另一种是点P 在CD 上,然后利用三角形面积公式可求得;(3)直接令15h OD =即可求出; (4)存在3种情况,第一种是:QP ∥BD ,第二种是EP ∥CD 或EQ ∥CB ,第三种是QE ∥BD ,分别按照几何性质分析求解.【详解】(1)如下图,过点B 作x 轴垂线,垂足为点M根据平移的特点,可得∠BOM=∠DBA∵∠BMO=∠DAB=90°,∴△BMO ∽△DAB∵AB=4,AD=BC=3∴BD=5∵BM OM BO DA BA BD==,OB=t ∴BM=35t ,OM=45t (2)情况一:当0<t <3时,图形如下,过点P 作OD 的垂线,交OD 于点N∵∠NDP=∠BDA ,∠PND=∠BAD ,∴△PND ∽△BAD∵AP=t ,∴PD=3-t∵PN BA PD BD =,∴PN=()435t - 图中,OD=5+t ∴()()243124562555OBD t S t t t -=+=--+ 情况二:当3<t <7时,图形如下,过点P 作OD 的垂线,交OD 于点N图中,PD=t -3,OD=5+t同理,△PND ∽△BCD ,可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- (3)情况一:当0<t <3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得:t=75情况二:当3<t <7时则h=PN=()335t - ∵15h OD =∴()33555t t -+= 解得:t=7(舍)(4)情况一:QP ∥BD ,图形如下由题意可得:BQ=43t ,AP=t ,则QA=4-43t ,DP=3-t ∵BD ∥QP∴QA PA QB PD= 代入得:4()2243t t =-解得:t=32∴OD=5+t=132 情况二:如下图,EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点∴EP=PA ,EQ=QA ,QP=QP∴△APQ ≌△EPQ∵EP ∥CD ,CD ⊥AD∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形,AQ=PA∴4-43t t = 解得:t=127∴OD=5+t=477 情况三:如下图,QE ∥BD ,延长QE 交DA 于点N∵△APQ ≌△EPQ ,∴∠QEP=∠QAP=90°∴△ENP 是等腰直角三角形∵QN ∥BD ,∴∠NQA=∠DBA ,∠A=∠A∴△QNA ∽△BDA∵BQ=43t ,AP=t ,QA=4-43t ,DP=3-t ∴QN QA AN BD BA AD== ∴QN=5-43t ,NA=3-t ∴EN=QN -QE=QN -QA=1-3t ,NP=NA -AP=3-2t ,EP=PA=t ∴在Rt △ENP 中,()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得:t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题,解题关键是利用相似将图形中各边用t 表示出来.5.A解析:(1)145;(2)2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩;(3)t 的值为477或727.【解析】【分析】(1)如下图,根据4tan 3A =,可得出PN 与AP 的关系,从而求出t 的值; (2)如下图,存在2种情况,一种是点M 在△ABC 内,另一种是点M 在△ABC 外部,分别根据正方形和三角形求面积的公式可求解;(3)如下图,存在2种情况,一种是PM 所在的直线将△ABC 的面积平分,另一种是QN 所在的直线将△ABC 的面积平分.【详解】(1)如图1,点N 在AC 上图1由题意可知:PD=DQ=t ,AP=7-t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =,即2473t t =- 解得:t=145 (2)①如图2,图2四边形PQMN 是正方形,90BQM ∴∠=︒,45B ∠=︒,BQ MQ ∴=,即72t t -=解得73t =, 故当0t <≤73时,22(2)4S t t ==; ②如图3,图390BQF ∠=︒,45B ∠=︒,7BQ FQ t ∴==-,45BFQ MFE ∠=∠=︒,则37MF MQ QF t =-=-,90M ∠=︒,37ME MF t ∴==-, 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭; 综上,2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩. (3)如下图,过点C 作AB 的垂线,交AB 于点G图4∵4tan 3A = ∴设CG=4x ,则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14,解得:x=2∴1148562ABC S== ∴1282ABCS = 情况一:PM 所在的直线平分△ABC 的面积,如下图,PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形,∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB-PA=14-(7-t)=7+t∴7+t=47t=477-情况二:如下图,QN所在线段平分△ABC的面积,QF交AC于点F,过点F作AB的垂线,交AB于点H图6同理,28AFQS=∵四边形PQMN是正方形,∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y,则AH=3y,HQ=FH=4y,∴AQ=7y∴174282AFQS y y==,解得:2∵AQ=AB-QB=14-(7-t)=7+t ∴2解得:7∴综上得:t 的值为7或7.【点睛】本题考查动点问题,解题关键是根据动点的变化情况,适当划分为几种不同的形式分别分析求解.6.B解析:(1)213222y x x =-++;(2)3(,0)2;(3)存在;(0,2)N 或(3,2)N 或(2,3)--N 或(5,18)--N【解析】【分析】(1)由直线122y x =-+可得B 、C 两点的坐标,根据二次函数的对称轴求得A 点坐标,可设抛物线的解析式为(1)(4)y a x x =+-,将C 点坐标代入可求得a ,即可得抛物线的解析式;(2)根据绝对值的性质得出BM CM -的值最小时,点M 为BC 的垂直平分线与直线32x =的交点,求得BC 垂直平分线的解析式,联立直线32x =即可求得点M ; (3)分四种情况进行讨论,设出N 的坐标,根据相似三角形的对应边成比例的性质,求得N 的横坐标与纵坐标的关系,然后联立抛物线解析式即可求解.【详解】 解:∵直线122y x =-+与x 轴交于点B ,与y 轴交于点C , ∴当y =0时,即1022x =-+,解得:x =4,则点B 的坐标为(4,0), 当x =0时,10222=-⨯+=y ,则点C 的坐标为(0,2),由二次函数的对称性可知:点A 与点B 关于直线32x =对称, ∴点A 的坐标为(1,0)-,∵抛物线与x 轴的交点为点(1,0),(4,0)A B -,∴可设抛物线的解析式为(1)(4)y a x x =+-,又∵抛物线过点(0,2)C ,∴2(01)(04)a =+-,解得:12a =-, ∴2113(1)(4)2222y x x x x =-+-=-++∴抛物线的解析式为213222y x x =-++; (2)如图1,连结CM 、BM ,作线段BC 的垂直平分线l 分别交BC 、直线32x =于点'、N M ,则N 为BC 中点;由绝对值的性质可得:0≥-BM CM ,∴当BM CM -的值最小时,即0=-BM CM ,则此时CM BM =, ∴点M 为l 与直线32x =的交点,此时M 与'M 重合, 设l 的解析式为:y kx b =+,∵直线BC 的解析式为:122y x =-+,BC l ⊥ ∴112-⋅=-k ,解得:2k =,则l 的解析式可化为:2y x b =+, 由(4,0),(0,2)B C 得点N 的坐标为(2,1),将(2,1)N 代入2y x b =+得: 14b =+,解得:3b =-,∴23y x =-,将32x =代入23y x =-,得323=02=⨯-y ,即3'(,0)2M , ∴当BM CM -的值最小时,点M 的坐标为3(,0)2,(3)抛物线上存在点N ,使得以点、、B N H 为顶点的三角形与ABC 相似; ∵(1,0),(4,0),(0,2)-A B C∴1,4==OA OB ,2OC =,5AB =, ∴2222125=+=+=AC OA OC 22224225BC OB OC =+=+=, ∵22252025+=+==AC BC AB ,∴ABC 为直角三角形,90ACB ∠=︒,∵NH x ⊥轴,∴90∠=︒NHB ,则90∠=∠=︒NHB ACB ,如图2所示,分四种情况,点N 的坐标分别为1234、、、N N N N ,设点N 的坐标为(,)m n ,①当点1N 在x 轴的上方,要使11N BH ABC ,则11∠=∠N BH ABC ,则此时点1N 与点C 重合,则此时点1H 与点O 重合,则11≅N BH ABC ,满足题意,∴此时点1N 的坐标为(0,2);②当点2N 在x 轴的上方,要使22BN H ABC ,则2222==N H BC BH AC , ∴24=-n m,即28n m =-+,代入抛物线的解析式得: 21328222mm m ,化简得:27120m m , 解得:13m =,24m =(不符合题意,故舍去),将3m =代入抛物线解析式得:2n =,∴此时点2N 的坐标为(3,2);③当点3N 在x 轴的下方,要使33N BH ABC ,则3332==BH BC N H AC , ∴42-=-m n ,即42-=m n ,代入抛物线的解析式得:24132222m m m ,化简得:2280m m --=,解得:12m =-,24m =(不符合题意,故舍去),将2m =-代入抛物线解析式得:3n =-,∴此时点3N 的坐标为(2,3)--;④当点4N 在x 轴的下方,要使44BN H ABC ,则4442==N H BC BH AC , ∴24-=-n m,即28=-n m ,代入抛物线的解析式得: 21328222m m m ,化简得:2200m m , 解得:15m =-,24m =(不符合题意,故舍去),将5m =-代入抛物线解析式得:18n =-,∴此时点4N 的坐标为(5,18)--;综上所述,抛物线存在点N 的坐标为(0,2)或(3,2)或(2,3)--或(5,18)--使得以点、、B N H 为顶点的三角形与ABC 相似.【点睛】本题主要考查了一次函数与二次函数的性质、相似三角形的性质,运用数形结合与分类讨论的方法是解题的关键.7.(1)①12;②4,(2)12AD BC =;理由见解析,(3)存在; 【解析】 【分析】 (1)①首先证明ADB '∆是含有30的直角三角形,可得1122AD AB BC '==,即可解决问题;②首先证明BAC B AC ''∆∆≌,根据直角三角形斜边中线定理即可解决问题. (2)AD 与BC 的数量关系为12AD BC =,如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',先证四边形AC MB ''是平行四边形,再证明BAC AB M '∆∆≌,即可解决问题.(3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,做直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,先证明PA PD =,PB PC =,再证明+180APD BPC ∠∠=︒,即可得出结论,再在Rt PDQ ∆中,根据勾股定理,即可求出PQ 的长.【详解】(1)①如图2,∵ABC ∆是等边三角形,把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ',∴===AB AC BC AB AC ''=,又∵AD 是AB C ''△边B C ''上的中线,∴=DB DC '',∴AD B C ''⊥,即90ADB '∠=︒,∵60BAC ∠=︒,180BAC B AC ''∠+∠=︒,∴120B AC ''∠=︒,∴=30B C ''∠∠=︒,∴在ADB '∆中,90ADB '∠=︒,30B '∠=︒, ∴1122AD AB BC '==. 故答案为:12. ②如图3,∵90BAC ∠=︒,+=180BAC B AC ''∠∠︒,∴==90BAC B AC ''∠∠︒,即ABC ∆和AB C ''∆为直角三角形,∵把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ', ∴=AB AB ',=AC AC ',∴在ABC ∆和AB C ''∆中,===AB AB BAC B AC AC AC '''∠'⎧⎪∠⎨⎪⎩∴BAC B AC ''∆∆≌,∴=BC B C '',∵AD 是AB C ''△边B C ''上的中线,AB C ''∆为直角三角形,∴1122AD B B C C ''==, 又∵8BC =, ∴11=8=422AD BC =⨯. 故答案为:4. (2)12AD BC =, 如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',图5∵=B D DC '',AD DM =,∴四边形AC MB ''是平行四边形,∴AC B M AC ''==,∵+=180BAC B AC ''∠∠︒,+=180B AC AB M '''∠∠︒,∴=BAC AB M '∠∠,∵=AB AB ',∴在BAC ∆和AB M '∆中,==AC B M BAC AB M AB AB ''=⎧'⎪∠∠⎨⎪⎩∴BAC AB M '∆∆≌,∴BC AM =, ∴12AD BC =. (3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,作直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,图6∵+=120A B ∠∠︒,∴=180=60M A B ∠︒-∠-∠︒, ∵=90C ∠︒,∴=180=30MDC M MCD ∠︒-∠-∠︒,在Rt DCM ∆中,∵=6CD ,=90DCM ∠︒,=30MDC ∠︒, ∴=23CM =43DM =60M ∠︒, 在Rt BEM ∆中,∵=90BEM ∠︒,143BM BC CM =+==30MDC ∠︒,∴1732EM BM ==, ∴33DE EM DM =-=,∵=63AD =AE DE ,∵BE AD ⊥,∴PA PD =,PB PC =,在Rt CDF ∆中,∵=6CD ,CF∴tan CDF ∠=∴60CDF CPF =︒=∠∠,∴FCP CFD ∆∆≌,∴CD PF =,∵//CD PF ,∴四边形CDPF 是矩形,∴=90CDP ∠︒,∴=60ADP ADC CDP ∠∠-∠=︒,∴ADP ∆是等边三角形,∴=PA PD AD =∵=60BPF CPF ∠∠=︒,∴120BPC ∠=︒,∴+180APD BPC ∠∠=︒,∴PDC ∆与PAB ∆之间满足小明探究的问题中的边角关系,在Rt PDQ ∆中,∵=90PDQ ∠︒,PD PA AD ===132DQ CD ==,∴PQ ==【点睛】本题考查了三角形的综合问题.掌握全等三角形的性质以及判定定理、直角三角形斜边中线定理、解直角三角形、勾股定理、中线的性质是解题的关键.在处理三角形的边旋转问题时,旋转前后边长不变,根据已知角度变化,求得线段之间关系.在证明某点是否存在问题时,先假设这点存在,能求出相关线段或坐标,即证实存在性. 8.B解析:(1)14a =,4m =-;(2)3344d t =-;(3)220,39P ⎛⎫- ⎪⎝⎭. 【解析】【分析】(1)根据24OC OB ==得出B,C 的坐标,令(2)()0y a x x m =++=即可求出m 的值,将B 的坐标代入抛物线的解析式中即可求出a 的值;(2)过点D 作DI AC ⊥于点I ,设MN 与x 轴的交点为J ,先利用抛物线的解析式求出M 的坐标,然后利用平行线分线段成比例有AF NF AE DE =,代入相应的值计算即可得出答案; (3)先根据154d =求出此时D,E 的坐标,然后将点D 的坐标代入211y x b =+中求出直线的解析式,设G 点的坐标为232(,)1111m m +,利用待定系数法求出直线GE 的解析式,进而求出F 的坐标及CFG S ,然后利用待定系数法求出GC,EH 的解析式,进而求出H 点的坐标,然后表示出EGH S,然后利用3CFG EGH S S =△△求出m的值,进而求出直线GE 的解析式,通过直线GE 的解析式与抛物线解析式联立即可求出P 点的坐标. 【详解】(1)24OC OB ==(0,2),(4,0)B C ∴- .令(2)()0y a x x m =++=,解得2,x x m =-=-,4m ∴-= ,4m ∴=- ,∴抛物线的解析式为(2)(4)y a x x =+- ,将点(0,2)B -代入得,82a -=-,解得14a = ; (2)如图,过点D 作DI AC ⊥于点I ,设MN 与x 轴的交点为J ,∵1,44a m ==- , 2119(2)(4)(1)444y x x x ∴=+-=--, 9(1,)4M ∴- . ∵点D 的横坐标是t ,∴211(,2)42D t t t --, 211242DI t t ∴=--. MN x ⊥轴,DI x ⊥轴,//NM DI ∴ ,AJ NJAI DI∴=.NM d=,291(2)4112242dt t t---∴=+--,解得3344d t=-;(3)如图,当154d=时,3315444d t=-=,解得6t=,此时D的坐标为(6,4).//DE x轴,∴点E的纵坐标也是4,令1(2)(4)44y x x=+-=,解得4x=-或6x=,∴(4,4)E-.∵直线211y x b=+经过点D,∴26411b⨯+=,解得3211b=,∴2321111y x=+.设点G的坐标为232(,)1111m m+,设直线EG的解析式为y kx b=+,将232(4,4),(,)1111E G m m -+代入解析式中得 442321111k b mk b m -+=⎧⎪⎨+=+⎪⎩ 解得2121144521281144m k m m b m -⎧=⎪⎪+⎨+⎪=⎪+⎩∴直线EG 解析式为2125212811441144m m y x m m -+=+++ , 令0y = ,即21252128011441144m m x m m -++=++,解得26646m x m+=- , 2664(,0)6m F m+∴- , ∴26643040466m m CF m m ++=-=--, 113040232(3040)(16)()226111111(6)CFG G m m m S CF y m m m +++∴=⋅=⨯⨯+=-- . 设直线GC 的解析式为y ax c =+ , 将232(4,0),(,)1111C G m m +代入解析式中得 402321111a c ma c m +=⎧⎪⎨+=+⎪⎩ 解得232114481281144m a m m c m +⎧=⎪⎪-⎨+⎪=-⎪-⎩∴直线GC 解析式为232812811441144m m y x m m ++=--- . ∵EH CG , ∴设直线EH 解析式为2321144m y x n m +=+-, 将点(4,4)E -代入得232(4)41144m n m +⨯-+=-, 解得52481144m n m -=- , ∴直线EH 解析式为232524811441144m m y x m m +-=+--. 将直线GD 的解析式与直线EH 的解析式联立,23211232524811441144y x x m m y x m m ⎧=+⎪⎪⎨+-⎪=+⎪--⎩解得422811m x m y +⎧=-⎪⎪⎨-⎪=⎪⎩∴428(,)211m m H +--, 11341520()10()221111EGH EDG EDH H G m m S S S ED y y ++∴=-=⋅-=⨯⨯-=- . ∵3CFG EGH S S =△△,∴(3040)(16)11(6)m m m ++-15203()11m +=⨯-, 解得154m =-或43m =-. 当154m =-时,GE 的解析式为4433y x =--, 将直线GE 的解析式与抛物线的解析式联立, 2443311242y x y x x ⎧=--⎪⎪⎨⎪=--⎪⎩解得23209x y ⎧=⎪⎪⎨⎪=-⎪⎩或44x y =-⎧⎨=⎩(点E 的坐标,舍去), ∴220(,)39P -; 当43m =-时,GE 的解析式为122y x =-+, 将直线GE 的解析式与抛物线的解析式联立212211242y x y x x ⎧=-+⎪⎪⎨⎪=--⎪⎩解得40x y =⎧⎨=⎩(点C 的坐标,舍去) 或44x y =-⎧⎨=⎩(点E 的坐标,舍去), ∴综上所述,点P的坐标为220(,)39P- . 【点睛】本题主要考查二次函数,一次函数与几何综合,难度较大,尤其是计算量太大,容易出错,掌握待定系数法,平行线分线段成比例,合理的设出点的坐标并准确的计算是解题的关键. 9.A解析:(1)作图见解析;(2)PQ 长最短是1.2;(3)四边形ADCF 面积最大值是812+,最小值是812- 【解析】【分析】(1)连接线段OP 交⊙C 于A ,点A 即为所求;(2)过C 作CP ⊥AB 于Q ,P ,交⊙C 于Q ,这时PQ 最短,根据勾股定理以及三角形的面积公式即可求出其最小值;(3)△ACF的面积有最大和最小值,取AB的中点G,连接FG,DE,证明△FAG~△EAD,进而证明点F在以G为圆心1为半径的圆上运动,过G作GH⊥AC于H,交⊙G于F1,GH 反向延长线交⊙G于F2,①当F在F1时,△ACF面积最小,分别求出△ACD的面积和△ACF 的面积的最小值即可得出四边形ADCF的面积的最小值;②当F在F2时,四边形ADCF的面积有最大值,在⊙G上任取异于点F2的点P,作PM⊥AC于M,作GN⊥PM于N,利用矩形的判定与性质以及三角形的面积公式即可得出得出四边形ADCF的面积的最大值.【详解】解:(1)连接线段OP交⊙C于A,点A即为所求,如图1所示;(2)过C作CP⊥AB于Q,P,交⊙C于Q,这时PQ最短.理由:分别在线段AB,⊙C上任取点P',点Q',连接P',Q',CQ',如图2,由于CP⊥AB,根据垂线段最短,CP≤CQ'+P'Q',∴CO+PQ≤CQ'+P'Q',又∵CQ=CQ',∴PQ<P'Q',即PQ最短.在Rt△ABC中22228610AB AC BC=+=+=,1122ABCS AC BC AB CP∆=•=•,∴684.810AC BCCPAB•⨯===,∴PQ=CP﹣CQ=6.8﹣3.6=1.2,∴22226 4.8 3.6BP BC CP-=-=.当P在点B左侧3.6米处时,PQ长最短是1.2.(3)△ACF的面积有最大和最小值.如图3,取AB的中点G,连接FG,DE.∵∠EAF=90°,1 tan3AEF∠=,∴13 AF AE=。
中考数学压轴题(有答案)

- --中考初中数学压轴题精选(有答案)一.解答题(共30小题)1.(2014•)如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A 在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.(1)求B、C两点的坐标;(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q 为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.2.(2014•)如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=4cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)(1)如图①,连接OA、AC,则∠OAC的度数为_________°;(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值围(解答时可以利用备用图画出相关示意图).3.(2014•)如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.(1)若直线AB与有两个交点F、G.①求∠CFE的度数;②用含b的代数式表示FG2,并直接写出b的取值围;(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.4.(2014•)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.5.(2014•)在平面直角坐标系xOy中,点M(,),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM 的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是上的动点.(1)写出∠AMB的度数;(2)点Q在射线OP上,且OP•OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E.①当动点P与点B重合时,求点E的坐标;②连接QD,设点Q的纵坐标为t,△QOD的面积为S.求S与t的函数关系式及S的取值围.6.(2014•)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)(1)【理解与应用】如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为_________.(2)【类比与推理】如图3,矩形ABCD的对角线AC,BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA 交BD于点F,求PE+PF的值;(3)【拓展与延伸】如图4,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.7.(2014•)已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.8.(2014•)已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.(1)如图①,在矩形ABCD中,AB=3,BC=4,如果BC边上存在点P,使△APD为等腰三角形,那么请画出满足条件的一个等腰三角形△APD,并求出此时BP的长;(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长;问题解决(3)有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM 的长,若不存在,请说明理由.10.(2014•)如图,在⊙O的接△ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,=,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值围)11.(2014•)木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:方案一:直接锯一个半径最大的圆;方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.(1)写出方案一中圆的半径;(2)通过计算说明方案二和方案三中,哪个圆的半径较大?(3)在方案四中,设CE=x(0<x<1),圆的半径为y.①求y关于x的函数解析式;②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.(1)试说明四边形EFCG是矩形;(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;②求点G移动路线的长.13.(2014•东昌府区三模)已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O 是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sinC=时,求⊙O的半径.14.(2014•模拟)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB•r1+AC•r2=AB•h,∴r1+r2=h(1)理解与应用如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形任一点”,即:已知边长为2的等边△ABC任意一点P到各边的距离分别为r1,r2,r3,试证明:.(2)类比与推理边长为2的正方形任意一点到各边的距离的和等于_________;(3)拓展与延伸若边长为2的正n边形A1A2…An部任意一点P到各边的距离为r1,r2,…r n,请问r1+r2+…r n是否为定值(用含n 的式子表示),如果是,请合理猜测出这个定值.15.(2014•名校一模)如图△ABC中∠A=90°,以AB为直径的⊙O交BC于D,E为AC边中点,求证:DE是⊙O 的切线.16.(2014•灌南县模拟)如图,AB是⊙O的直径,AC是弦,∠ACD=∠AOC,AD⊥CD于点D.(1)求证:CD是⊙O的切线;(2)若AB=10,AD=2,求AC的长.17.(2014•普陀区二模)如图,在等腰△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),过D作射线DE交AB边于E,使∠BDE=∠A,以D为圆心、DC的长为半径作⊙D.(1)设BD=x,AE=y,求y关于x的函数关系式,并写出定义域.(2)当⊙D与AB边相切时,求BD的长.(3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD的长为多少时,⊙D与⊙E相切?18.(2014•模拟)如图,矩形ABCD的边AB=4,BC=3.一简易量角器放置在矩形ABCD,其零度线即半圆O的直径与边AB重合,点A处是0刻度,点B处是180刻度.P点是量角器的半圆弧上一动点,过P点的切线与边BC、CD(或其延长线)分别交于点E、F.设点P的刻度数为n,∠P AB=α.(1)当n=136时,α=_________,求出α与n的关系式;(2)在P点的运动过程中,线段EB与EP有怎样的数量关系,请予证明;(3)在P点的运动过程中,F点在直线CD上的位置随着α的变化而变化,当F点在线段CD上时、在CD的延长线上时、在DC的延长线上时,对应的α值分别是多少?(参考数据:tan56.3°≈1.5)(4)连接BP,在P点的运动过程中,是否存在△ABP与△CEF相似的情况?若存在,求出此时n的值以及相应的EF的长;若不存在,请说明理由.19.(2014•一模)如图,正方形ABCD的边长是8cm,以正方形的中心O为圆心,EF为直径的半圆切AB于M、切BC于N,已知C为BG的中点,AG交CD于H.P,Q同时从A出发,P以1cm/s的速度沿折线ADCG运动,Q以cm/s的速速沿线段AG方向运动,P,Q中有一点到达终点时,整个运动停止.P,Q运动的时间记为t.(1)当t=4时,求证:△PEF≌△MEF;(2)当0≤t≤8时,试判断PQ与CD的位置关系;(3)当t>8时,是否存在t使得=?若存在请求出所有t的值,若不存在,请说明理由.20.(2013•)如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.(1)求证:AC平分∠BAD;(2)若CD=1,AC=,求⊙O的半径长.21.(2013•襄阳)如图,△ABC接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;(2)若AC=6,BC=8,求线段PD的长.22.(2013•)如图,⊙O的直径AB=10,C、D是圆上的两点,且.设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.(1)求证:DF⊥AF.(2)求OG的长.23.(2013•德阳)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.(1)求证:PC=PG;(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为时,求弦ED的长.24.(2013•贺州)已知:⊙O的直径为3,线段AC=4,直线AC和PM分别与⊙O相切于点A,M.(1)求证:点P是线段AC的中点;(2)求sin∠PMC的值.25.(2013•)已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN 于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.26.(2013•)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE 交⊙O于点F,连接AF,AF的延长线交DE于点P.(1)求证:DE是⊙O的切线;(2)求tan∠ABE的值;(3)若OA=2,求线段AP的长.27.(2013•)如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.28.(2013•)如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求证:EF是⊙0的切线.(2)如果⊙0的半径为5,sin∠ADE=,求BF的长.29.(2013•)如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切于点B,连接BA并延长交⊙A于点D,交ON于点E.(1)求证:ON是⊙A的切线;(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)30.(2013•)如图,AB是⊙O的直径,∠B=∠CAD.(1)求证:AC是⊙O的切线;(2)若点E是的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.参考答案与试题解析一.解答题(共30小题)1.(2014•)如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A 在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.(1)求B、C两点的坐标;(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.考点:圆的综合题.专题:压轴题.分析:(1)连接P A,运用垂径定理及勾股定理即可求出圆的半径,从而可以求出B、C两点的坐标.(2)由于圆P是中心对称图形,显然射线AP与圆P的交点就是所需画的点M,连接MB、MC即可;易证四边形ACMB是矩形;过点M作MH⊥BC,垂足为H,易证△MHP≌△AOP,从而求出MH、OH的长,进而得到点M的坐标.(3)易证点E、M、B、G在以点Q为圆心,QB为半径的圆上,从而得到∠MQG=2∠MBG.易得∠OCA=60°,从而得到∠MBG=60°,进而得到∠MQG=120°,所以∠MQG是定值.解答:解:(1)连接PA,如图1所示.∵PO⊥AD,∴AO=DO.∵AD=2,∴OA=.∵点P坐标为(﹣1,0),∴OP=1.∴PA==2.∴BP=CP=2.∴B(﹣3,0),C(1,0).(2)连接AP,延长AP交⊙P于点M,连接MB、MC.如图2所示,线段MB、MC即为所求作.四边形ACMB是矩形.理由如下:∵△MCB由△ABC绕点P旋转180°所得,∴四边形ACMB是平行四边形.∵BC是⊙P的直径,∴∠CAB=90°.∴平行四边形ACMB是矩形.过点M作MH⊥BC,垂足为H,如图2所示.在△MHP和△AOP中,∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,∴△MHP≌△AOP.∴MH=OA=,PH=PO=1.∴OH=2.∴点M的坐标为(﹣2,).(3)在旋转过程中∠MQG的大小不变.∵四边形ACMB是矩形,∴∠BMC=90°.∵EG⊥BO,∴∠BGE=90°.∴∠BMC=∠BGE=90°.∵点Q是BE的中点,∴QM=QE=QB=QG.∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.∴∠MQG=2∠MBG.∵∠COA=90°,OC=1,OA=,∴tan∠OCA==.∴∠OCA=60°.∴∠MBC=∠BCA=60°.∴∠MQG=120°.∴在旋转过程中∠MQG的大小不变,始终等于120°.点评:本题考查了垂径定理、勾股定理、全等三角形的判定与性质、矩形的判定与性质、圆周角定理、特殊角的三角函数、图形的旋转等知识,综合性比较强.证明点E、M、B、G在以点Q为圆心,QB为半径的圆上是解决第三小题的关键.2.(2014•)如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=4cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)(1)如图①,连接OA、AC,则∠OAC的度数为105°;(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值围(解答时可以利用备用图画出相关示意图).考点:圆的综合题.专题:几何综合题;压轴题.分析:(1)利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°,∠DAC=60°,进而得出答案;(2)首先得出,∠C1A1D1=60°,再利用A1E=AA1﹣OO1﹣2=t﹣2,求出t的值,进而得出OO1=3t得出答案即可;(3)①当直线AC与⊙O第一次相切时,设移动时间为t1,②当直线AC与⊙O第二次相切时,设移动时间为t2,分别求出即可.解答:解:(1)∵l1⊥l2,⊙O与l1,l2都相切,∴∠OAD=45°,∵AB=4cm,AD=4cm,∴CD=4cm,∴tan∠DAC===,∴∠DAC=60°,∴∠OAC的度数为:∠OAD+∠DAC=105°,故答案为:105;(2)如图位置二,当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,连接O1E,可得O1E=2,O1E⊥l1,在Rt△A1D1C1中,∵A1D1=4,C1D1=4,∴tan∠C1A1D1=,∴∠C1A1D1=60°,在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,∴A1E==,∵A1E=AA1﹣OO1﹣2=t﹣2,∴t﹣2=,∴t=+2,∴OO1=3t=2+6;(3)①当直线AC与⊙O第一次相切时,设移动时间为t1,如图,此时⊙O移动到⊙O2的位置,矩形ABCD移动到A2B2C2D2的位置,设⊙O2与直线l1,A2C2分别相切于点F,G,连接O2F,O2G,O2A2,∴O2F⊥l1,O2G⊥A2C2,由(2)得,∠C2A2D2=60°,∴∠GA2F=120°,∴∠O2A2F=60°,在Rt△A2O2F中,O2F=2,∴A2F=,∵OO2=3t1,AF=AA2+A2F=4t1+,∴4t1+﹣3t1=2,∴t1=2﹣,②当直线AC与⊙O第二次相切时,设移动时间为t2,记第一次相切时为位置一,点O1,A1,C1共线时位置二,第二次相切时为位置三,由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等,∴+2﹣(2﹣)=t2﹣(+2),解得:t2=2+2,综上所述,当d<2时,t的取值围是:2﹣<t<2+2.点评:此题主要考查了切线的性质以及锐角三角函数关系等知识,利用分类讨论以及数形结合t的值是解题关键.3.(2014•)如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.(1)若直线AB与有两个交点F、G.①求∠CFE的度数;②用含b的代数式表示FG2,并直接写出b的取值围;(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.考点:圆的综合题.专题:几何综合题;压轴题.分析:(1)连接CD,EA,利用同一条弦所对的圆周角相等求行∠CFE=45°,(2)作OM⊥AB点M,连接OF,利用两条直线垂直相交求出交点M的坐标,利用勾股定理求出FM2,再求出FG2,再根据式子写出b的围,(3)当b=5时,直线与圆相切,存在点P,使∠CPE=45°,再利用△APO∽△AOB和△AMP∽△AOB相似得出点P的坐标,再求出OP所在的直线解析式.解答:解:(1)①如图,∵∠COE=90°∴∠CFE=∠COE=45°,(圆周角定理)②方法一:如图,作OM⊥AB点M,连接OF,∵OM⊥AB,直线的函数式为:y=﹣x+b,∴OM所在的直线函数式为:y=x,∴交点M(b,b)∴OM2=(b)2+(b)2,∵OF=4,∴FM2=OF2﹣OM2=42﹣(b)2﹣(b)2,∵FM=FG,∴FG2=4FM2=4×[42﹣(b)2﹣(b)2]=64﹣b2=64×(1﹣b2),∵直线AB与有两个交点F、G.∴4≤b<5,∴FG2=64×(1﹣b2)(4≤b<5)方法二:①如图,作OM⊥AB点M,连接OF,∵直线的函数式为:y=﹣x+b,∴B的坐标为(0,b),A的坐标为(b,0),∴AB==b,∴sin∠BAO===,∴sin∠MAO===,∴OM=b,∴在RT△OMF中,FM==∵FG=2FM,∴FG2=4FM2=4(42﹣b2)=64﹣﹣b2=64×(1﹣b2),∵直线AB与有两个交点F、G.∴4≤b<5,∴FG2=64×(1﹣b2)(4≤b<5)(2)如图,当b=5时,直线与圆相切,∵在直角坐标系中,∠COE=90°,∴∠CPE=∠ODC=45°,∴存在点P,使∠CPE=45°,连接OP,∵P是切点,∴OP⊥AB,∴△APO∽△AOB,∴=,∵OP=r=4,OB=5,AO=,∴=即AP=,∵AB===,作PM⊥AO交AO于点M,设P的坐标为(x,y),∵△AMP∽△AOB,∴=∴=,∴y=,∴x=OM===∴点P的坐标为(,).点评:本题主要考查了圆与一次函数的知识,解题的关键是作出辅助线,利用三角形相似求出点P的坐标.4.(2014•)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.考点:圆的综合题.专题:压轴题.分析:(1)当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,直接利用勾股定理求出AC进而得出答案;(2)首先得出四边形APCE是菱形,进而得出CM的长,进而利用锐角三角函数关系得出CP以及EF的长;(3)∠GAE≠∠BGC,只能∠AGE=∠AEG,利用AD∥BC,得出△GAE∽△GBC,进而求出即可.解答:解:(1)如图1,设⊙O的半径为r,当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,∴BH=AB•cosB=4,∴AH=3,CH=4,∴AC==5,∴此时CP=r=5;(2)如图2,若AP∥CE,APCE为平行四边形,∵CE=CP,∴四边形APCE是菱形,连接AC、EP,则AC⊥EP,∴AM=CM=,由(1)知,AB=AC,则∠ACB=∠B,∴CP=CE==,∴EF=2=;(3)如图3:过点C作CN⊥AD于点N,设AQ⊥BC,∵=cosB,AB=5,∴BQ=4,AN=QC=BC﹣BQ=4.∵cosB=,∴∠B<45°,∵∠BCG<90°,∴∠BGC>45°,∴∠BGC>∠B=∠GAE,即∠BGC≠∠GAE,又∠AEG=∠BCG≥∠ACB=∠B=∠GAE,∴当∠AEG=∠GAE时,A、E、G重合,则△AGE不存在.即∠AEG≠∠GAE∴只能∠AGE=∠AEG,∵AD∥BC,∴△GAE∽△GBC,∴=,即=,解得:AE=3,EN=AN﹣AE=1,∴CE===.点评:此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,利用分类讨论得出△AGE是等腰三角形时只能∠AGE=∠AEG进而求出是解题关键.5.(2014•)在平面直角坐标系xOy中,点M(,),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM 的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是上的动点.(1)写出∠AMB的度数;(2)点Q在射线OP上,且OP•OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E.①当动点P与点B重合时,求点E的坐标;②连接QD,设点Q的纵坐标为t,△QOD的面积为S.求S与t的函数关系式及S的取值围.考点:圆的综合题.专题:几何综合题;压轴题.分析:(1)首先过点M作MH⊥OD于点H,由点M(,),可得∠MOH=45°,OH=MH=,继而求得∠AOM=45°,又由OM=AM,可得△AOM是等腰直角三角形,继而可求得∠AMB的度数;(2)①由OH=MH=,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,又由动点P与点B重合时,OP•OQ=20,可求得OQ的长,继而求得答案;②由OD=2,Q的纵坐标为t,即可得S=,然后分别从当动点P与B点重合时,过点Q作QF⊥x轴,垂足为F点,与当动点P与A点重合时,Q点在y轴上,去分析求解即可求得答案.解答:解:(1)过点M作MH⊥OD于点H,∵点M(,),∴OH=MH=,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°,∵OM=AM,∴∠OAM=∠AOM=45°,∴∠AMO=90°,∴∠AMB=90°;(2)①∵OH=MH=,MH⊥OD,∴OM==2,OD=2OH=2,∴OB=4,∵动点P与点B重合时,OP•OQ=20,∴OQ=5,∵∠OQE=90°,∠POE=45°,∴OE=5,∴E点坐标为(5,0)②∵OD=2,Q的纵坐标为t,∴S=.如图2,当动点P与B点重合时,过点Q作QF⊥x轴,垂足为F点,∵OP=4,OP•OQ=20,∴OQ=5,∵∠OFC=90°,∠QOD=45°,∴t=QF=,此时S=;如图3,当动点P与A点重合时,Q点在y轴上,∴OP=2,∵OP•OQ=20,∴t=OQ=5,此时S=;∴S的取值围为5≤S≤10.点评:此题考查了垂径定理、等腰直角三角形的性质以及勾股定理等知识.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想、分类讨论思想与方程思想的应用.6.(2014•)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)(1)【理解与应用】如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为.(2)【类比与推理】如图3,矩形ABCD的对角线AC,BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA 交BD于点F,求PE+PF的值;(3)【拓展与延伸】如图4,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.考点:圆的综合题;等边三角形的判定与性质;矩形的性质;正方形的性质;弦切角定理;相似三角形的判定与性质.专题:压轴题;探究型.分析:(1)易证:OA=OB,∠AOB=90°,直接运用阅读材料中的结论即可解决问题.(2)易证:OA=OB=OC=0D=,然后由条件PE∥OB,PF∥AO可证△AEP∽△AOB,△BFP∽△BOA,从而可得==1,进而求出EP+FP=.(3)易证:AD=BC=4.仿照(2)中的解法即可求出PE+PF=4,因而PE+PF是定值.解答:解:(1)如图2,∵四边形ABCD是正方形,∴OA=OB=OC=OD,∠ABC=∠AOB=90°.∵AB=BC=2,∴AC=2.∴OA=.∵OA=OB,∠AOB=90°,PE⊥OA,PF⊥OB,∴PE+PF=OA=.(2)如图3,∵四边形ABCD是矩形,∴OA=OB=OC=OD,∠DAB=90°.∵AB=4,AD=3,∴BD=5.∴OA=OB=OC=OD=.∵PE∥OB,PF∥AO,∴△AEP∽△AOB,△BFP∽△BOA.∴,.∴==1.∴+=1.∴EP+FP=.∴PE+PF的值为.(3)当∠ADG=∠BCH=30°时,PE+PF是定值.理由:连接OA、OB、OC、OD,如图4∵DG与⊙O相切,∴∠GDA=∠ABD.∵∠ADG=30°,∴∠ABD=30°.∴∠AOD=2∠ABD=60°.∵OA=OD,∴△AOD是等边三角形.∴AD=OA=4.同理可得:BC=4.∵PE∥BC,PF∥AD,∴△AEP∽△ACB,△BFP∽△BDA.∴,.∴==1.∴=1.∴PE+PF=4.∴当∠ADG=∠BCH=30°时,PE+PF=4.点评:本题考查了正方形的性质、矩形的性质、弦切角定理、相似三角形的判定与性质、等边三角形的判定与性质等知识,考查了类比联想的能力,由一定的综合性.要求PE+PF的值,想到将相似所得的比式相加是解决本题的关键.7.(2014•)已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC 相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.考点:圆的综合题;待定系数法求一次函数解析式;垂线段最短;勾股定理;切线长定理;相似三角形的判定与性质.专题:综合题;压轴题;存在型;分类讨论.分析:(1)只需先求出AC中点P的坐标,然后用待定系数法即可求出直线DP的解析式.(2)由于△DOM与△ABC相似,对应关系不确定,可分两种情况进行讨论,利用三角形相似求出OM的长,即可求出点M的坐标.(3)易证S△PED=S△PFD.从而有S四边形DEPF=2S△PED=DE.由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣.根据“点到直线之间,垂线段最短”可得:当DP⊥AC时,DP最短,此时DE也最短,对应的四边形DEPF的面积最小.借助于三角形相似,即可求出DP⊥AC时DP的值,就可求出四边形DEPF面积的最小值.解答:解:(1)过点P作PH∥OA,交OC于点H,如图1所示.∵PH∥OA,∴△CHP∽△COA.∴==.∵点P是AC中点,∴CP=CA.∴HP=OA,CH=CO.∵A(3,0)、C(0,4),∴OA=3,OC=4.∴HP=,CH=2.∴OH=2.∵PH∥OA,∠COA=90°,∴∠CHP=∠COA=90°.∴点P的坐标为(,2).设直线DP的解析式为y=kx+b,∵D(0,﹣5),P(,2)在直线DP上,∴∴∴直线DP的解析式为y=x﹣5.(2)①若△DOM∽△ABC,图2(1)所示,∵△DOM∽△ABC,∴=.∵点B坐标为(3,4),点D的坐标为(0.﹣5),∴BC=3,AB=4,OD=5.∴=.∴OM=.∵点M在x轴的正半轴上,∴点M的坐标为(,0)②若△DOM∽△CBA,如图2(2)所示,∵△DOM∽△CBA,∵BC=3,AB=4,OD=5,∴=.∴OM=.∵点M在x轴的正半轴上,∴点M的坐标为(,0).综上所述:若△DOM与△CBA相似,则点M的坐标为(,0)或(,0).(3)∵OA=3,OC=4,∠AOC=90°,∴AC=5.∴PE=PF=AC=.∵DE、DF都与⊙P相切,∴DE=DF,∠DEP=∠DFP=90°.∴S△PED=S△PFD.∴S=2S△PED四边形DEPF=2×PE•DE=PE•DE=DE.∵∠DEP=90°,∴DE2=DP2﹣PE2.=DP2﹣.根据“点到直线之间,垂线段最短”可得:当DP⊥AC时,DP最短,此时DE取到最小值,四边形DEPF的面积最小.∵DP⊥AC,∴∠DPC=90°.∴∠AOC=∠DPC.∵∠OCA=∠PCD,∠AOC=∠DPC,∴△AOC∽△DPC.∴=.∵AO=3,AC=5,DC=4﹣(﹣5)=9,∴=.∴DP=.∴DE2=DP2﹣=.∴DE=,∴S=DE四边形DEPF=.∴四边形DEPF面积的最小值为.点评:本题考查了相似三角形的判定与性质、用待定系数法求直线的解析式、切线长定理、勾股定理、垂线段最短等知识,考查了分类讨论的思想.将求DE的最小值转化为求DP的最小值是解决第3小题的关键.另外,要注意“△DOM与△ABC相似”与“△DOM∽△ABC“之间的区别.8.(2014•)已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.考点:圆的综合题.专题:压轴题.分析:(1)连接PM,PN,运用△PMF≌△PNE证明;(2)分两种情况:①当t>1时,点E在y轴的负半轴上;②当0<t≤1时,点E在y轴的正半轴或原点上,再根据(1)求解,(3)分两种情况,当1<t<2时,当t>2时,三角形相似时还各有两种情况,根据比例式求出时间t.解答:证明:(1)如图,连接PM,PN,∵⊙P与x轴,y轴分别相切于点M和点N,∴PM⊥MF,PN⊥ON且PM=PN,∴∠PMF=∠PNE=90°且∠NPM=90°,∵PE⊥PF,∠NPE=∠MPF=90°﹣∠MPE,在△PMF和△PNE中,,∴△PMF≌△PNE(ASA),∴PE=PF;(2)解:分两种情况:①当t>1时,点E在y轴的负半轴上,如图1,由(1)得△PMF≌△PNE,∴NE=MF=t,PM=PN=1,∴b=OF=OM+MF=1+t,a=NE﹣ON=t﹣1,∴b﹣a=1+t﹣(t﹣1)=2,∴b=2+a,②0<t≤1时,如图2,点E在y轴的正半轴或原点上,同理可证△PMF≌△PNE,∴b=OF=OM+MF=1+t,a=OE=ON﹣NE=1﹣t,∴b+a=1+t+1﹣t=2,∴b=2﹣a.综上所述,当t>1时,b=2+a;当0<t≤1时,b=2﹣a;。
中考数学压轴题60例选择题

中考数学压轴题60例(选择题)一、选择题(共60小题)1.(2015•)将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD 于点E,AB=,则四边形AB1ED的切圆半径为()A.B.C.D.2.(2015•)如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.50°B.60°C.70°D.80°3.(2015•)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是()A. 2﹣2 B.6 C.2﹣2 D.44.(2015•株洲)有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是()A.如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根B.如果方程M的两根符号相同,那么方程N的两根符号也相同C.如果5是方程M的一个根,那么是方程N的一个根D.如果方程M和方程N有一个相同的根,那么这个根必是x=15.(2015•)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x 轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,=k.已知关于x,y的二元一次方程(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于()A.B.1 C.D.6.(2015•枣庄)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说确的是()A.①②④B.③④C.①③④D.①②7.(2015•)如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是()A.①②B.①②③C.①④D.①②④8.(2015•)如图,点P是∠AOB任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是()A.25°B.30°C.35°D.40°9.(2015•)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是()A.B.C.D.10.(2015•)如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG 的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC 的重合部分的面积S与运动时间t之间的函数关系图象大致是()A.B.C.D.11.(2015•)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C 为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是()A. 2 B.3 C.4 D.5 12.(2015•宿迁)在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P 在反比例函数y=的图象上,若△PAB为直角三角形,则满足条件的点P的个数为()A. 2个B.4个C.5个D.6个13.(2015•)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②>0;③ac﹣b+1=0;④OA•OB=﹣.其中正确结论的个数是()A. 4 B.3 C.2 D.114.(2015•)如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是()A.B.C.D.15.(2015•)如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A. 2﹣B.+1 C.D.﹣1 16.(2015•)如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A 落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为()A.B.C.D.17.(2015•潍坊)已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是()A. 1 B.2 C.3 D.4 18.(2015•)如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A 点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.19.(2015•)如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是()A. 1对B.2对C.3对D.4对20.(2015•)二次函数y=ax2+bx+c(a ≠0)的图象如图所示,下列结论:①2a+b>0;②abc <0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是()A. 2 B.3 C.4 D.5 21.(2015•)如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A. 1个B.2个C.3个D.4个22.(2015•)如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为()A . 2B .3C.D.23.(2015•日照)如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A (1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是()A.①②③B.①③④C.①③⑤D.②④⑤24.(2015•)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是()A.B.C.D.25.(2015•庆阳)在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2n A2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是()A.(4n﹣1,)B.(2n﹣1,)C.(4n+1,)D.(2n+1,)26.(2015•)如图,AD是△ABC的角平分线,则AB:AC等于()A. BD:CD B.AD:CD C.BC:AD D.BC:AC 27.(2015•)如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是()A. 1个B.2个C.3个D.4个28.(2015•)如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是()A.B.C.D.29.(2015•)如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是()A.(22014,22014)B.(22015,22015)C.(22014,22015)D.(22015,22014)30.(2015•江)如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD有公共点,则k的取值围为()A. 1<k<9 B.2≤k≤34C.1≤k≤16D.4≤k<16 31.(2015•)如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为()A. 2.5 B.2.8 C.3 D.3.2 32.(2015•)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为()A. 4 B.5 C.6 D.7 33.(2015•)关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m﹣1)2+(n﹣1)2≥2;③﹣1≤2m﹣2n≤1,其中正确结论的个数是()A. 0个B.1个C.2个D.3个34.(2015•)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧35.(2015•)如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:(1)∠DBM=∠CDE;(2)S△BDE<S四边形BMFE;(3)CD•EN=BN•BD;(4)AC=2DF.其中正确结论的个数是()A. 1 B.2 C.3 D.4 36.(2015•)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为()A. 1 B.2 C.3 D.4 37.(2015•)如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为()A. 1 B.2 C.3 D.4 38.(2015•凉山州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当﹣1≤x≤3时,y<0③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2④9a+3b+c=0其中正确的是()A.①②④B.①④C.①②③D.③④39.(2015•)如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是()A.第24天的销售量为200件B.第10天销售一件产品的利润是15元C.第12天与第30天这两天的日销售利润相等D.第30天的日销售利润是750元40.(2015•莱芜)如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D 的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是()A.B.C.D.41.(2015•)如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PCD沿直线PD折叠,使点C落到点F处;过点P作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.42.(2015•荆州)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是()A.B.C.D.43.(2015•)如图,点A,B,C在一条直线上,△ABD,△BCE 均为等边三角形,连接AE和CD ,AE分别交CD,BD 于点M,P ,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有()A. 1个B.2个C.3个D.4个44.(2015•)如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值围是()A.﹣2<m<B.﹣3<m<﹣C.﹣3<m<﹣2 D.﹣3<m<﹣45.(2015•)如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是()A.B.C.D.46.(2015•)如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的个数是()A. 1 B.2 C.3 D.4 47.(2015•)如图,在平面直角坐标系xOy中,直线y=x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为()A.(﹣1,)B.(﹣2,)C.(﹣,1)D.(﹣,2)48.(2015•)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是()A.(2014,0)B.(2015,﹣1)C.(2015,1)D.(2016,0)49.(2015•)我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是()A. 6 B.8 C.10 D.1250.(2015•)如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是()A.②③B.②⑤C.①③④D.④⑤51.(2015•)如图是甲、乙两不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则()A.甲、乙都可以B.甲、乙都不可以C.甲不可以、乙可以D.甲可以、乙不可以52.(2015•)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A 时,点F运动的路径长是()A. 8 B.10 C.3πD.5π53.(2015•)如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是()A.B.C.D.54.(2015•)如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为()A. 3 B.1.5 C.2D.55.(2015•)在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是()A.()2014B.()2015C.()2015D.()201456.(2015•滨州)如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA 的两边分别与函数y=﹣、y=的图象交于B、A两点,则∠OAB的大小的变化趋势为()A.逐渐变小B.逐渐变大C.时大时小D.保持不变57.(2015•)如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A 匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是()A.B.C.D.58.(2015•巴彦淖尔)如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE﹣ED ﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是2cm/s.若P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系图象如图2,则下列结论错误的是()A. AE=12cmB.sin∠EBC=C.当0<t≤8时,y=t2D.当t=9s时,△PBQ是等腰三角形59.(2015•眉山)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.460.(2015•)若函数y=kx﹣b的图象如图所示,则关于x的不等式k(x﹣3)﹣b>0的解集为()A. x<2 B.x>2 C.x<5 D.x>52015年全国中考数学压轴题60例(选择题卷)参考答案与试题解析一、选择题(共60小题)1.(2015•)将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD 于点E,AB=,则四边形AB1ED的切圆半径为()A.B.C.D.考点:三角形的切圆与心;正方形的性质;旋转的性质.专题:压轴题.分析:作∠DAF与∠AB1G的角平分线交于点O,则O即为该圆的圆心,过O作OF⊥AB1,AB=,再根据直角三角形的性质便可求出OF的长,即该四边形切圆的圆心.解答:解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,】则∠OAF=30°,∠AB1O=45°,故B1F=OF=OA,设B1F=x,则AF=﹣x,故(﹣x)2+x2=(2x)2,解得x=或x=(舍去),∴四边形AB1ED的切圆半径为:.故选:B.点评:本题考查了旋转的性质三角形的切圆,正方形的性质,要熟练掌握正方形的性质及直角三角形的性质,是解答此题的关键.2.(2015•)如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.50°B.60°C.70°D.80°考点:轴对称-最短路线问题.专题:压轴题.分析:据要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=50°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.解答:解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,∵∠C=50°,∴∠DAB=130°,∴∠HAA′=50°,∴∠AA′E+∠A″=∠HAA′=50°,∵∠EA′A=∠EAA′,∠FAD=∠A″,∴∠EAA′+∠A″AF=50°,∴∠EAF=130°﹣50°=80°,故选:D.点评:本题考查的是轴对称﹣最短路线问题,涉及到平面最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出E,F的位置是解题关键.3.(2015•)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是()A. 2﹣2 B.6 C.2﹣2 D.4考点:翻折变换(折叠问题).专题:压轴题.分析:当∠BFE=∠DEF,点B′在DE上时,此时B′D的值最小,根据勾股定理求出DE,根据折叠的性质可知B′E=BE=2,DE﹣B′E即为所求.解答:解:如图,当∠BFE=∠DEF,点B′在DE上时,此时B′D的值最小,根据折叠的性质,△EBF≌△EB′F,∴EB′⊥FD,∴EB′=EB,∵E是AB边的中点,AB=4,∴AE=EB′=2,∵AB=6,∴DE==2,∴DB′=2﹣2.故选:A.点评:本题主要考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,确定点B′在何位置时,B′D的值最小,是解决问题的关键.4.(2015•株洲)有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是()A.如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根B.如果方程M的两根符号相同,那么方程N的两根符号也相同C.如果5是方程M的一个根,那么是方程N的一个根D.如果方程M和方程N有一个相同的根,那么这个根必是x=1考点:根的判别式;一元二次方程的解;根与系数的关系.专题:压轴题.分析:利用根的判别式判断A;利用根与系数的关系判断B;利用一元二次方程的解的定义判断C与D.解答:解:A、如果方程M有两个相等的实数根,那么△=b2﹣4ac=0,所以方程N也有两个相等的实数根,结论正确,不符合题意;B、如果方程M的两根符号相同,那么方程N的两根符号也相同,那么△=b2﹣4ac≥0,>0,所以a与c符号相同,>0,所以方程N的两根符号也相同,结论正确,不符合题意;C、如果5是方程M的一个根,那么25a+5b+c=0,两边同时除以25,得c+b+a=0,所以是方程N的一个根,结论正确,不符合题意;D、如果方程M和方程N有一个相同的根,那么ax2+bx+c=cx2+bx+a,(a﹣c)x2=a﹣c,由a≠c,得x2=1,x=±1,结论错误,符合题意;故选:D.点评:本题考查了一元二次方程根的情况与判别式△的关系:△>0⇔方程有两个不相等的实数根;△=0⇔方程有两个相等的实数根;△<0⇔方程没有实数根.也考查了根与系数的关系,一元二次方程的解的定义.5.(2015•)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x 轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,=k.已知关于x,y的二元一次方程(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于()A.B.1 C.D.考点:位似变换;二元一次方程组的解;坐标与图形性质.专题:压轴题.分析:首先求出点A′的坐标为(k,kt),再根据关于x,y的二元一次方程(m,n是实数)无解,可得mn=3,且n≠1;然后根据以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,可得反比例函数n=的图象只经过点A′或C′;最后分两种情况讨论:(1)若反比例函数n=的图象经过点A′时;(2)若反比例函数n=的图象经过点C′时;求出k•t的值等于多少即可.解答:解:∵矩形A′B′C′D′与矩形ABCD是位似图形,=k,顶点A的坐标为(1,t),∴点A′的坐标为(k,kt),∵关于x,y的二元一次方程(m,n是实数)无解,∴mn=3,且n≠1,即n=(m≠3),∵以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,∴反比例函数n=的图象只经过点A′或C′,由,可得mnx﹣3x+4=3n+1,(1)若反比例函数n=的图象经过点A′,∵mn=3,3x﹣3x+4=3kt+1,解得kt=1.(2)若反比例函数n=的图象经过点C′,∵mn=3,3x﹣3x+4=﹣3kt+1,解得kt=﹣1,∵k>0,t>0,∴kt=﹣1不符合题意,∴kt=1.故选:B.点评:(1)此题主要考查了位似变换问题,要熟练掌握,解答此题的关键是要明确:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.(2)此题还考查了二元一次方程组的求解方法,以及坐标与图形的性质,要熟练掌握.6.(2015•枣庄)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说确的是()A.①②④B.③④C.①③④D.①②考点:二次函数图象与系数的关系.专题:压轴题.分析:①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号;②根据对称轴求出b=﹣a;③把x=2代入函数关系式,结合图象判断函数值与0的大小关系;④求出点(0,y1)关于直线x=的对称点的坐标,根据对称轴即可判断y1和y2的大小.解答:解:①∵二次函数的图象开口向下,∴a<0,∵二次函数的图象交y轴的正半轴于一点,∴c>0,∵对称轴是直线x=,∴﹣,∴b=﹣a>0,∴abc<0.故①正确;②∵由①中知b=﹣a,∴a+b=0,故②正确;③把x=2代入y=ax2+bx+c得:y=4a+2b+c,∵抛物线经过点(2,0),∴当x=2时,y=0,即4a+2b+c=0.故③错误;④∵(0,y1)关于直线x=的对称点的坐标是(1,y1),∴y1=y2.故④正确;综上所述,正确的结论是①②④.故选:A点评:本题考查了二次函数的图象和系数的关系的应用,注意:当a>0时,二次函数的图象开口向上,当a<0时,二次函数的图象开口向下.7.(2015•)如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是()A.①②B.①②③C.①④D.①②④考点:切线的判定;相似三角形的判定与性质.专题:压轴题.分析:根据圆周角定理得∠ADB=90°,则BD⊥AC,于是根据等腰三角形的性质可判断AD=DC,则可对①进行判断;利用等腰三角形的性质和平行线的性质可证明∠1=∠2=∠3=∠4,则根据相似三角形的判定方法得到△CBA∽△CDE,于是可对②进行判断;由于不能确定∠1等于45°,则不能确定与相等,则可对③进行判断;利用DA=DC=DE可判断∠AEC=90°,即CE⊥AE,根据平行线的性质得到AB⊥AE,然后根据切线的判定定理得AE为⊙O的切线,于是可对④进行判断.解答:解:∵AB为直径,∴∠ADB=90°,∴BD⊥AC,而AB=CB,∴AD=DC,所以①正确;∵AB=CB,∴∠1=∠2,而CD=ED,∴∠3=∠4,∵CF∥AB,∴∠1=∠3,∴∠1=∠2=∠3=∠4,∴△CBA∽△CDE,所以②正确;∵△ABC不能确定为直角三角形,∴∠1不能确定等于45°,∴与不能确定相等,所以③错误;∵DA=DC=DE,∴点E在以AC为直径的圆上,∴∠AEC=90°,∴CE⊥AE,而CF∥AB,∴AB⊥AE,∴AE为⊙O的切线,所以④正确.故选:D.点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了等腰三角形的性质、平行线的性质和相似三角形的判定.8.(2015•)如图,点P是∠AOB任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是()A.25°B.30°C.35°D.40°考点:轴对称-最短路线问题.专题:压轴题.分析:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=CM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB=∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.解答:解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:∵点P关于OA的对称点为D,关于OB的对称点为C,∴PM=DM,OP=OD,∠DOA=∠POA;∵点P关于OB的对称点为C,∴PN=,OP=OC,∠COB=∠POB,∴OC=OP=OD,∠AOB=∠COD,∵△PMN周长的最小值是5cm,∴PM+PN+MN=5,∴DM++MN=5,即CD=5=OP,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°;故选:B.点评:本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.9.(2015•)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是()A.B.C.D.考点:动点问题的函数图象.专题:压轴题.分析:根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.解答:解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;故选:B.点评:本题考查的是动点问题的函数图象,正确分析点P 在不同的线段上△ABP的面积S与时间t的关系是解题的关键.10.(2015•)如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG 的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC 的重合部分的面积S与运动时间t之间的函数关系图象大致是()A.B.C.D.考点:动点问题的函数图象.专题:压轴题.分析:首先根据Rt△ABC中∠C=90°,∠BAC=30°,AB=8,分别求出AC、BC,以及AB边上的高各是多少;然后根据图示,分三种情况:(1)当0≤t≤2时;(2)当2时;(3)当6<t≤8时;分别求出正方形DEFG与△ABC的重合部分的面积S的表达式,进而判断出正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是哪个即可.解答:解:如图1,CH是AB边上的高,与AB相交于点H,∵∠C=90°,∠BAC=30°,AB=8,∴AC=AB×cos30°=8×=4,BC=AB×sin30°=8×=4,∴CH=AC×,AH=,(1)当0≤t≤2时,S==t2;(2)当2时,S=﹣=t2[t2﹣4t+12]=2t﹣2(3)当6<t≤8时,S=[(t﹣2)•tan30°]×[6﹣(t﹣2)]×[(8﹣t)•tan60°]×(t﹣6)=[]×[﹣t+2+6]×[﹣t]×(t﹣6)=﹣t2+2t+4﹣t2﹣30=﹣t2﹣26综上,可得S=∴正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是A图象.故选:A.点评:(1)此题主要考查了动点问题的函数图象,解答此类问题的关键是通过看图获取信息,并能解决生活中的实际问题,用图象解决问题时,要理清图象的含义即学会识图.(2)此题还考查了直角三角形的性质和应用,以及三角形、梯形的面积的求法,要熟练掌握.11.(2015•)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C 为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是()A. 2 B.3 C.4 D.5考点:圆周角定理;垂径定理.专题:压轴题.分析:根据AB⊥MN,垂径定理得出①③正确,利用MN是直径得出②正确,==,得出④正确,结合②④得出⑤正确即可.解答:解:∵MN是⊙O的直径,AB⊥MN,∴AD=BD,=,∠MAN=90°(①②③正确)∵=,∴==,∴∠ACM+∠ANM=∠MOB(④正确)∵∠MAE=∠AME,∴AE=ME,∠EAF=∠AFM,∴AE=EF,∴AE=MF(⑤正确).正确的结论共5个.故选:D.点评:此题考查圆周角定理,垂径定理,以及直角三角形斜边上的中线等于斜边的一半等知识.12.(2015•宿迁)在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P 在反比例函数y=的图象上,若△PAB为直角三角形,则满足条件的点P的个数为()A. 2个B.4个C.5个D.6个考点:反比例函数图象上点的坐标特征;圆周角定理.专题:压轴题.分析:分类讨论:①当∠PAB=90°时,则P点的横坐标为﹣3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,),根据两点间的距离公式和勾股定理可得(x+3)2+()2+(x﹣3)2+()2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.解答:解:①当∠PAB=90°时,P点的横坐标为﹣3,把x=﹣3代入y=得y=﹣,所以此时P点有1个;②当∠APB=90°,设P(x,),PA2=(x+3)2+()2,PB2=(x﹣3)2+()2,AB2=(3+3)2=36,因为PA2+PB2=AB2,所以(x+3)2+()2+(x﹣3)2+()2=36,整理得x4﹣9x2+4=0,所以x2=,或x2=,所以此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,把x=3代入y=得y=,所以此时P点有1个;综上所述,满足条件的P点有6个.故选:D.点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.13.(2015•)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:。
往年中考数学试卷压轴题

今年中考数学试卷的压轴题是一道几何综合题,题目如下:已知等腰三角形ABC中,AB=AC,BC=10,点D是边BC的中点,点E是边AB上的一点,且∠BAC=30°,∠BEC=90°。
求点E的轨迹方程。
二、解题思路1. 分析题意,明确求解目标为点E的轨迹方程。
2. 利用等腰三角形的性质,推导出∠ABC=∠ACB=75°。
3. 利用勾股定理,求出BD和CD的长度。
4. 分析∠BEC=90°,得出点E在以BC为直径的圆上。
5. 利用点E在圆上的性质,列出轨迹方程。
三、详细解答1. 已知AB=AC,∠BAC=30°,可得∠ABC=∠ACB=75°。
2. 在等腰三角形ABC中,点D是边BC的中点,所以BD=CD=BC/2=5。
3. 根据勾股定理,可得AB=√(BD²+AD²),其中AD=AB/2=√(BD²+(AB/2)²)=√(5²+(5√3)²)=5√3。
4. 由∠BEC=90°,可得点E在以BC为直径的圆上。
5. 设点E的坐标为(x, y),则点E到点B和点C的距离相等,即√[(x-5)²+y²]=√[(x+5)²+y²]。
6. 对上述方程进行化简,得到(x-5)²+y²=(x+5)²+y²,即x²-10x+25=x²+10x+25。
7. 化简得到-10x=10x,即x=0。
8. 将x=0代入原方程,得到y²=25,即y=±5。
9. 因此,点E的轨迹方程为x=0,y=±5。
四、总结本题是一道典型的几何综合题,考查了等腰三角形的性质、勾股定理、圆的性质以及轨迹方程的求解。
解题过程中,需要注意以下几点:1. 利用等腰三角形的性质,推导出角度关系。
2. 运用勾股定理,求解边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xxxxxx
8
6
4
2
15
10
5
A B D
2
5
10
15
C
4
6
8
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0), B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
8
6
4
2
15
10
5
A B D
2
5
10
15
C
4
6
8
(1)∵二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0), B(2,0),C(0,-2),a+b+c=0①,4a+2b+c=0,c=-2③, ①②③联立方程组,解得:a=-1,b=3,c=-2. y = x2 + 3∙x 2。
2
D F E
5ห้องสมุดไป่ตู้
10
15
C
4
6
②当点E2的坐标为(m,
8
2-m 2
)时,点F1的坐标
为(m-1, 2-m
2-m 2
2
),∵点F1在抛物线的图象上, 7
=-(m-1) +3(m-1)-2,m3= ,m2=2(舍去), 2 2 5 3 3 3 F1( ,- ),SABEF1• = . 2 4 4 4
xxxxxxxxxxx
xxxxxx
DE
OA
6
4
2
15
10
5
OA B
2
D F E
5
10
15
C
4
6
8
(3)在(2)成立的条件下,抛物线上是否存在一点F, 使得四边形ABEF为平行四边形?若存在,请求出m的值 及四边形ABEF的面积;若不存在,请说明理由.
6
4
2
15
10
5
OA B
2
D F E
5
10
15
C
4
6
8
(3)假设抛物线上存在一点F,使得四边形为平行四边形, 则EF=AB=1,点F的横坐标为m-1,
8
6
4
2
15
10
5
OA B
2
D
5
10
15
C
4
E
6
8
m-2 1 ①当 = 时,即 = ,DE=2m-4, DE OC DE 2 ∵点在第四象限,.E1(m,4-2m)
BD
OA
6
4
2
15
10
5
OA B
2
D E
5
10
15
C
4
6
8
DE 1 m-2 ②当 = 时,即 = ,DE= , DB OC m-2 2 2 2-m ∵点在第四象限,.E1(m, ) 2
8
6
4
2
15
10
5
OA B
2
D
5
10
15
C
4
E
6
8
(2)在直线x=m(m>2)上有一点E(点E在第四象限), 使得以E、D、B为顶点的三角形与以A、O、C为顶点的 三角形相似,求点E坐标(用含m的代数式表示);
8
6
4
2
15
10
5
OA B
2
D
5
10
15
C
4
E
6
8
(2)∵ BDE AOC, BD OA DE AO = ,或 = DE OC BD OC
6
4
2
15
10
5
OA B
2
5 D
10
15
C
4
6
F E
8
①当点E1的坐标为(m,4-2m)时,点F1的坐标
为(m-1,4-2m),∵点F1在抛物线的图象上, 4-2m=-(m-1)2+3(m-1)-2,m1=5,m2=2(舍去), F1(4,-6),SABEF1•6=6.
6
4
2
15
10
5
OA B
