第三章线性规划的解法习题解答090426y
线性规划问题求解例题和知识点总结

线性规划问题求解例题和知识点总结线性规划是运筹学中研究较早、发展较快、应用广泛且方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。
在实际生活中,很多问题都可以归结为线性规划问题,例如资源分配、生产计划、运输调度等。
下面我们将通过一些具体的例题来深入理解线性规划问题,并对相关知识点进行总结。
一、线性规划问题的基本概念线性规划问题是在一组线性约束条件下,求一个线性目标函数的最大值或最小值的问题。
其数学模型一般可以表示为:目标函数:$Z = c_1x_1 + c_2x_2 +\cdots + c_nx_n$约束条件:$\begin{cases}a_{11}x_1 + a_{12}x_2 +\cdots +a_{1n}x_n \leq b_1 \\ a_{21}x_1 + a_{22}x_2 +\cdots +a_{2n}x_n \leq b_2 \\\cdots \\ a_{m1}x_1 + a_{m2}x_2 +\cdots + a_{mn}x_n \leq b_m \\ x_1, x_2, \cdots, x_n \geq0\end{cases}$其中,$x_1, x_2, \cdots, x_n$是决策变量,$c_1, c_2, \cdots, c_n$是目标函数的系数,$a_{ij}$是约束条件的系数,$b_1, b_2, \cdots, b_m$是约束条件的右端项。
二、线性规划问题的求解方法1、图解法对于只有两个决策变量的线性规划问题,可以使用图解法来求解。
其步骤如下:(1)画出约束条件所对应的可行域。
(2)画出目标函数的等值线。
(3)根据目标函数的优化方向,平移等值线,找出最优解所在的顶点。
例如,求解线性规划问题:目标函数:$Z = 2x + 3y$约束条件:$\begin{cases}x + 2y \leq 8 \\ 2x + y \leq 10\\ x \geq 0, y \geq 0\end{cases}$首先,画出约束条件所对应的可行域:对于$x + 2y \leq 8$,当$x = 0$时,$y = 4$;当$y = 0$时,$x =8$,连接这两点得到直线$x +2y =8$,并取直线下方的区域。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析

《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析第一篇:《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析《管理运筹学》第四版课后习题解析第3章线性规划问题的计算机求解1.解:⑴甲、乙两种柜的日产量是分别是4和8,这时最大利润是2720⑵每多生产一件乙柜,可以使总利润提高13.333元⑶常数项的上下限是指常数项在指定的范围内变化时,与其对应的约束条件的对偶价格不变。
比如油漆时间变为100,因为100在40和160之间,所以其对偶价格不变仍为13.333 ⑷不变,因为还在120和480之间。
2.解:⑴不是,因为上面得到的最优解不为整数解,而本题需要的是整数解⑵最优解为(4,8).解:⑴农用车有12辆剩余⑵大于300 ⑶每增加一辆大卡车,总运费降低192元4.解:计算机得出的解不为整数解,平移取点得整数最优解为(10,8)5.解:圆桌和衣柜的生产件数分别是350和100件,这时最大利润是3100元相差值为0代表,不需要对相应的目标系数进行改进就可以生产该产品。
最优解不变,因为C1允许增加量20-6=14;C2允许减少量为10-3=7,所有允许增加百分比和允许减少百分比之和(7.5-6)/14+(10-9)/7〈100%,所以最优解不变。
6.解:(1)x1=150,x2=70;目标函数最优值103 000。
(2)1、3车间的加工工时数已使用完;2、4车间的加工工时数没用完;没用完的加工工时数为2车间330小时,4车间15小时。
(3)50,0,200,0。
含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
(4)3车间,因为增加的利润最大。
(5)在400到正无穷的范围内变化,最优产品的组合不变。
(6)不变,因为在[0,500]的范围内。
(7)所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件1的右边值在[200,440]变化,对偶价格仍为50(同理解释其他约束条件)。
线性规划题及答案

线性规划题型及解法一、已知线性约束条件,探求线性目标关系最值问题例1、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ,则y x z 32+=的最大值为 。
二、已知线性约束条件,探求非线性目标关系最值问题例2、已知1,10,220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则22x y +的最小值是 . “()()2221++-y x ”值域?三、约束条件设计参数形式,考查目标函数最值范围问题。
例3、在约束条件024x y y x s y x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩下,当35s ≤≤时,目标函数32z x y =+的最大值的变化范围是()A.[6,15]B. [7,15]C. [6,8]D. [7,8]四、已知平面区域,逆向考查约束条件。
例4、已知双曲线224x y -=的两条渐近线与直线3x =围成一个三角形区域,表示该区域的不等式组是()(A)0003x y x y x -≥⎧⎪+≥⎨⎪≤≤⎩ (B)0003x y x y x -≥⎧⎪+≤⎨⎪≤≤⎩(C) 0003x y x y x -≤⎧⎪+≤⎨⎪≤≤⎩ (D) 0003x y x y x -≤⎧⎪+≥⎨⎪≤≤⎩五、已知最优解成立条件,探求目标函数参数范围问题。
例5已知变量x ,y 满足约束条件1422x y x y ≤+≤⎧⎨-≤-≤⎩ 若目标函数z ax y =+(其中0a >)仅在点(3,1)处取得最大值,则a 的取值范围为 。
六、设计线性规划,探求平面区域的面积问题例6在平面直角坐标系中,不等式组20200x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域的面积是()(A)(B)4 (C) (D)2七、研究线性规划中的整点最优解问题例7、某公司招收男职员x 名,女职员y 名,x 和y 须满足约束条件⎪⎩⎪⎨⎧≤≥+-≥-.112,932,22115x y x y x 则1010z x y =+的最大值是(A)80(B) 85 (C) 90 (D)95 八、比值问题 当目标函数形如bx ay z --=时,可把z 看作是动点()y x P ,与定点()a b Q ,连线的斜率,这样目标函数的最值就转化为PQ 连线斜率的最值。
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决在给定约束条件下求解线性目标函数的最优解的问题。
本文将介绍一个线性规划题及其答案,以帮助您更好地理解和应用线性规划。
题目描述:某工厂生产两种产品A和B。
每单位产品A需要3个工时和2个材料单位,每单位产品B需要4个工时和1个材料单位。
工厂每天有总共24个工时和10个材料单位可用。
产品A的利润为100元/单位,产品B的利润为80元/单位。
问工厂每天应该生产多少单位的产品A和产品B,以最大化利润?解答步骤:1. 确定决策变量:设工厂每天生产的产品A的单位数为x,产品B的单位数为y。
2. 建立目标函数:目标是最大化利润,因此目标函数为:Z = 100x + 80y。
3. 建立约束条件:根据题目描述,工厂每天可用的工时为24个,每单位产品A需要3个工时,每单位产品B需要4个工时,因此工时的约束条件为:3x + 4y ≤ 24。
工厂每天可用的材料单位为10个,每单位产品A需要2个材料单位,每单位产品B需要1个材料单位,因此材料单位的约束条件为:2x + y ≤ 10。
另外,生产的产品数量不能为负数,即:x ≥ 0,y ≥ 0。
4. 构建线性规划模型:综合考虑目标函数和约束条件,可以得到线性规划模型如下:Maximize Z = 100x + 80ySubject to:3x + 4y ≤ 242x + y ≤ 10x ≥ 0y ≥ 05. 解答最优解:通过线性规划求解器或图形法等方法,可以求解出最优解。
假设最优解为x*和y*,则工厂每天应该生产x*单位的产品A和y*单位的产品B,以最大化利润。
答案解析:通过线性规划求解器求解上述线性规划模型,得到最优解为x* = 4,y* = 4。
即工厂每天应该生产4个单位的产品A和4个单位的产品B,以最大化利润。
利润最大化时的最优解下,工厂每天使用的工时为3x* + 4y* = 3*4 + 4*4 = 24个,使用的材料单位为2x* + y* = 2*4 + 4 = 12个。
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
在实际应用中,线性规划常常用于资源分配、生产计划、运输问题等领域。
本文将为您提供一道线性规划题目及其详细解答,帮助您更好地理解和掌握线性规划的基本原理和求解方法。
题目描述:某食品加工厂生产两种产品:A和B。
每单位产品A需要3小时的加工时间和2小时的包装时间,每单位产品B需要2小时的加工时间和4小时的包装时间。
加工厂每天有8小时的加工时间和10小时的包装时间可用。
已知产品A的利润为300元/单位,产品B的利润为400元/单位。
现在需要确定每种产品的生产数量,以最大化总利润。
解答步骤:1. 建立数学模型:设产品A的生产数量为x,产品B的生产数量为y。
目标函数:最大化总利润,即最大化Z = 300x + 400y。
约束条件:加工时间和包装时间的限制。
加工时间约束:3x + 2y ≤ 8。
包装时间约束:2x + 4y ≤ 10。
非负约束:x ≥ 0,y ≥ 0。
2. 图形解法:将约束条件转化为直线的形式,并绘制在坐标系中。
然后确定可行域,即满足约束条件的可行解区域。
加工时间约束对应的直线为:3x + 2y = 8。
包装时间约束对应的直线为:2x + 4y = 10。
将两条直线绘制在坐标系中,并找出它们的交点,即可行域的顶点。
3. 确定最优解:在可行域的顶点中,计算目标函数的值,找出使目标函数取得最大值的顶点。
计算Z = 300x + 400y 在可行域的顶点 (x, y) 处的值,并比较得出最大值。
4. 计算最优解:根据计算结果,确定最优解对应的生产数量。
解答过程:1. 建立数学模型:设产品A的生产数量为x,产品B的生产数量为y。
目标函数:Z = 300x + 400y。
约束条件:3x + 2y ≤ 8,2x + 4y ≤ 10,x ≥ 0,y ≥ 0。
2. 图形解法:将约束条件转化为直线的形式:加工时间约束:3x + 2y = 8,即 y = (8 - 3x) / 2。
《管理运筹学》第四版课后习题答案
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
当 c1 不变时 ,c2 在 负无穷 到 6.4 的范 围内变 化,最优 解不 变。 (5)约 束条件 1 的右 边值 在 780 000,1500 000 变化,对偶价格仍 为 0.057(其他同理) 。 (6)不能,因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ,理由
4.25 3.6
11.解: 设圆 桌和衣柜的生 产件数分 别为 x、y,所获 利润为 z,则 z=6x+10y.
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域.平移 6x+ 10y=0 ,如图
y0
2x y 800
x 350
得
即 C(350,100) .当直线 6x+ 10y=0 即 3x+ 5y=0 平移
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
线性规划题及答案

线性规划题及答案引言概述:线性规划是一种数学优化方法,用于在一组线性约束条件下寻找使目标函数取得最大(最小)值的变量值。
在实际生活和工作中,线性规划常常被用于资源分配、生产计划、运输问题等方面。
本文将介绍一些常见的线性规划题目,并给出相应的答案。
一、资源分配问题1.1 问题描述:某公司有两个生产部门A和B,每天生产产品X和Y。
部门A每天生产产品X需要消耗3个单位的资源,生产产品Y需要消耗2个单位的资源;部门B每天生产产品X需要消耗2个单位的资源,生产产品Y需要消耗4个单位的资源。
公司每天有20个单位的资源可供分配,如何分配资源才能使得产出最大化?1.2 解答:设部门A每天生产产品X的数量为x,生产产品Y的数量为y;部门B每天生产产品X的数量为u,生产产品Y的数量为v。
根据题目描述,可以建立如下线性规划模型:Maximize Z = 3x + 2y + 2u + 4vSubject to:3x + 2y + 2u + 4v <= 20x, y, u, v >= 0通过线性规划求解器可以得到最优解。
二、生产计划问题2.1 问题描述:某工厂有两个生产车间,每天生产产品P和Q。
车间1每天生产产品P需要花费5个单位的时间,生产产品Q需要花费3个单位的时间;车间2每天生产产品P需要花费4个单位的时间,生产产品Q需要花费6个单位的时间。
工厂每天有40个单位的时间可供分配,如何安排生产计划才能使得产量最大化?2.2 解答:设车间1每天生产产品P的数量为x,生产产品Q的数量为y;车间2每天生产产品P的数量为u,生产产品Q的数量为v。
根据题目描述,可以建立如下线性规划模型:Maximize Z = 5x + 3y + 4u + 6vSubject to:5x + 3y + 4u + 6v <= 40x, y, u, v >= 0通过线性规划求解器可以得到最优解。
三、运输问题3.1 问题描述:某公司有两个仓库和三个销售点,每个仓库有一定数量的产品可供销售点购买。
线性规划题及答案

线性规划题及答案一、问题描述某公司生产两种产品A和B,每个产品的生产需要消耗不同的资源,并且每个产品的销售利润也不同。
公司希望通过线性规划来确定生产计划,以最大化利润。
已知产品A每个单位的生产需要消耗2个资源1和3个资源2,每个单位的销售利润为10元;产品B每个单位的生产需要消耗4个资源1和1个资源2,每个单位的销售利润为15元。
公司目前有10个资源1和12个资源2可供使用。
二、数学建模1. 假设生产产品A的数量为x,生产产品B的数量为y。
2. 根据资源的消耗情况,可以得到以下约束条件:2x + 4y ≤ 10 (资源1的消耗)3x + y ≤ 12 (资源2的消耗)x ≥ 0, y ≥ 0 (生产数量为非负数)3. 目标是最大化利润,即最大化销售收入减去生产成本:最大化 Z = 10x + 15y三、线性规划求解1. 将目标函数和约束条件转化为标准形式:目标函数:最大化 Z = 10x + 15y约束条件:2x + 4y ≤ 103x + y ≤ 12x ≥ 0, y ≥ 02. 通过图形法求解线性规划问题:a. 绘制约束条件的图形:画出2x + 4y = 10和3x + y = 12的直线,并标出可行域。
b. 确定可行域内的顶点:可行域的顶点为(0, 0),(0, 2.5),(4, 0),(2, 3)。
c. 计算目标函数在每个顶点处的值:分别计算Z = 10x + 15y在(0, 0),(0, 2.5),(4, 0),(2, 3)四个顶点处的值。
Z(0, 0) = 0Z(0, 2.5) = 37.5Z(4, 0) = 40Z(2, 3) = 80d. 比较所有顶点处的目标函数值,确定最优解:最优解为Z = 80,即在生产2个单位的产品A和3个单位的产品B时,可以获得最大利润80元。
四、结论根据线性规划的结果,公司在资源充足的情况下,应该生产2个单位的产品A和3个单位的产品B,以最大化利润。
此时,公司可以获得80元的最大利润。
线性规划题及答案

线性规划题及答案一、问题描述某公司生产两种产品A和B,每一个产品都需要通过两个工序进行加工。
每一个工序的加工时间和利润都不相同。
现在需要确定每一个产品在两个工序上的加工时间和产量,以最大化总利润。
请根据以下要求进行线性规划求解。
二、问题分析1. 产品A在工序1上的加工时间为x1小时,产品A在工序2上的加工时间为x2小时。
2. 产品B在工序1上的加工时间为y1小时,产品B在工序2上的加工时间为y2小时。
3. 产品A在工序1上的产量为a1个,产品A在工序2上的产量为a2个。
4. 产品B在工序1上的产量为b1个,产品B在工序2上的产量为b2个。
5. 产品A在工序1上的利润为p1元/个,产品A在工序2上的利润为p2元/个。
6. 产品B在工序1上的利润为q1元/个,产品B在工序2上的利润为q2元/个。
三、目标函数和约束条件1. 目标函数:最大化总利润Z = p1 * a1 + p2 * a2 + q1 * b1 + q2 * b2。
2. 约束条件:a) 工序1的总加工时间:x1 + y1 ≤ 100小时。
b) 工序2的总加工时间:x2 + y2 ≤ 80小时。
c) 产品A的总产量:a1 + a2 ≤ 200个。
d) 产品B的总产量:b1 + b2 ≤ 150个。
e) 非负约束:x1, x2, y1, y2, a1, a2, b1, b2 ≥ 0。
四、线性规划模型最大化总利润Z = p1 * a1 + p2 * a2 + q1 * b1 + q2 * b2,满足约束条件:x1 + y1 ≤ 100,x2 + y2 ≤ 80,a1 + a2 ≤ 200,b1 + b2 ≤ 150,x1, x2, y1, y2, a1, a2, b1, b2 ≥ 0。
五、求解过程1. 根据线性规划模型,我们可以使用线性规划求解方法求解该问题。
2. 根据目标函数和约束条件,可以建立线性规划模型,并使用线性规划求解器进行求解。
3. 求解得到最优解,即每一个产品在两个工序上的加工时间和产量,以及最大化的总利润。
第三章线性规划问题的解法

(1)用图解法求解; (2)将模型化为标准型; (3)计算基可行解,并标出在图中位置。
min z = − x + 2 x
1
2
max z ′ = x1 − 2 x2 ≤ = 2 − x1 + x2 +x3 ≤ +x4= 6 x1 + 2 x2 x , x ,x x ≥ 0 1 2 3, 4
1. 图解法的步骤 (1)做约束的图形
x
2
先做非负约束的图形; 再做资源约束的图形。
以例1为例,其约束为
9 x + 4 x ≤ 360 4 x + 5 x ≤ 200 s.t 3 x + 10 x ≤ 300 x , x ≥ 0
1 2 1 2 1 2 1 2
0
x
1
问题:不等式的几何意义是什么?怎样做图?
这就得到初始基可行解x16121243换入变量换出变量12934换人变量换出变量主元素以4为主元素进行旋转运算或迭代运算即初等行变换使p是得到新表检查该表的所有检验数这时有x应为换入变量
第一节、线性规划模型的图解法
图解法是用画图的方式求解线性规划的一种 方法。它虽然只能用于解二维(两个变量) 的问题,但其主要作用并不在于求解,而是 在于能够直观地说明线性规划解的一些重要 性质。
−1 −1 2 2 2
T 2
上二组概念间的联系: 系数阵A中可找出若干个基B 每个基B都对应于一个基本解 非负的基本解就是基可行解 几种解之间的关系:
基可行解 非可行解 可行解 基本解
问题:基本可行解是可行域中的哪些点?
练习:对于下面的线性规划
min z = − x + 2 x
管理运筹学课后练习答案
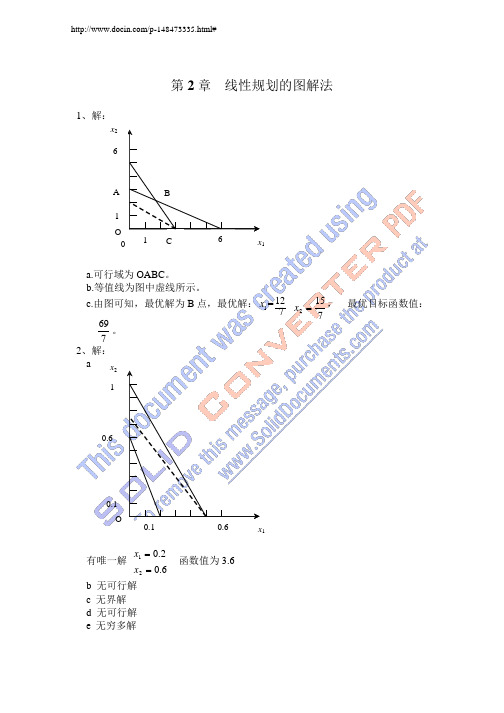
/p-148473335.html#第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12 c.由图可知,最优解为 B 点,最优解: x 1 = 7 69 。
7 2、解:15 x 2 = 7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f = 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 39 x 1 + 2x 2 + s 1 = 30 3x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ε 0= 4 x 1 6x 3 0s 1 0s 23x 1 x 2 s 1 = 6 x 1 + 2x 2 + s 2 = 10 7 x 1 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ε 0max f= x ' + 2x ' 2 x '' 0s 0s''' 3x 1 + 5x 25x 2+ s 1 = 70 2 x ' 5x ' + 5x '' = 50122 ' ' '' 3x 1 + 2 x 2 2x 2s 2 = 30' ' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ε 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 95x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ε 0s 1 = 2, s 2 = 05 、解:标准形式: min f= 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 s 1 = 20 3x 1 + 3x 2 s 2 = 18 4 x 1 + 9x 2 s 3 = 36x 1 , x 2 , s 1 , s 2 , s 3 ε 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 δc 1 δ 3c 2 δ c 2 δ 6d x 1 = 6x 2 = 4e x 1 [4,8]x 2 = 16 2x 1f 变化。
运筹学课后习题答案
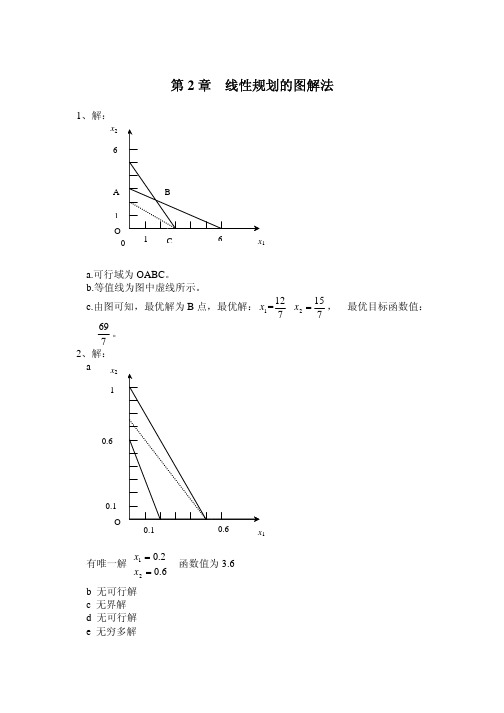
s1 = 2, s2 = 0
5 、解: 标准形式: min f = 11x1 + 8x2 + 0s1 + 0s2 + 0s3
10x1 + 2x2 − s1 = 20 3x1 + 3x2 − s2 = 18 4x1 + 9x2 − s3 = 36 x1, x2 , s1, s2 , s3 ≥ 0
s1 = 0, s2 = 0, s3 = 13 6 、解:
3 车间每增加 1 工时,总利润增加 200 元 2、4 车间每增加 1 工时,总利润不增加。 d 3 车间,因为增加的利润最大 e 在 400 到正无穷的范围内变化,最优产品的组合不变
f 不变 因为在 [0,500]的范围内
g 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条
件 1 的右边值在 [200,440]变化,对偶价格仍为 50(同理解释其他约束条件)
2、解:从上午 11 时到下午 10 时分成 11 个班次,设 xi 表示第 i 班次安排的临时 工的人数,则可列出下面的数学模型: min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11) s.t. x1+1 ≥ 9 x1+x2+1 ≥ 9 x1+x2+x3+2 ≥ 9 x1+x2+x3+x4+2 ≥ 3
x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0, x10=0,x11=0 最优值为 320。
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
管理运筹学(第3版)章后习题解析(上)课后习题答案
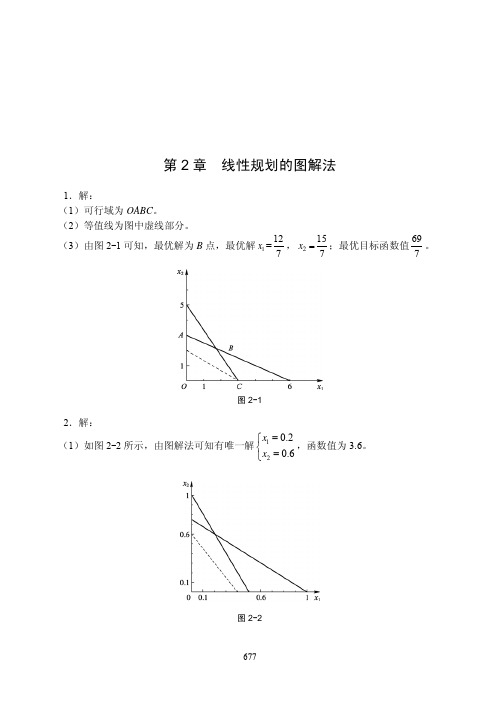
《管理运筹学》(第3版)章后习题解析第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++ 12112212121236210764,,,0x x s x x s x x x x s s −−=++=−=≥(3)标准形式12212min 2200f x x x s s ′′′′=−+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s ′′′−+−+=′′′′−+=′′′′+−−=′′′′≥4.解: 标准形式1212max 10500z x x s s =+++ 1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量(0,0) 最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++ 121122123121231022033184936,,,,0x x s x x s x x s x x s s s +−=+−=+−=≥剩余变量(0, 0, 13) 最优解为 x 1=1,x 2=5。
线性规划题及答案

线性规划题型及解法一、已知线性约束条件,探求线性目标关系最值问题例1、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ,则y x z 32+=的最大值为 。
二、已知线性约束条件,探求非线性目标关系最值问题例2、已知1,10,220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则22x y +的最小值是 . “()()2221++-y x ”值域?三、约束条件设计参数形式,考查目标函数最值范围问题。
例3、在约束条件0024x y y x sy x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩下,当35s ≤≤时,目标函数32z x y =+的最大值的变化范围是()A.[6,15]B. [7,15]C. [6,8]D. [7,8]四、已知平面区域,逆向考查约束条件。
例4、已知双曲线224x y -=的两条渐近线与直线3x =围成一个三角形区域,表示该区域的不等式组是()(A)0003x y x y x -≥⎧⎪+≥⎨⎪≤≤⎩ (B)0003x y x y x -≥⎧⎪+≤⎨⎪≤≤⎩ (C) 0003x y x y x -≤⎧⎪+≤⎨⎪≤≤⎩ (D) 0003x y x y x -≤⎧⎪+≥⎨⎪≤≤⎩五、已知最优解成立条件,探求目标函数参数范围问题。
例5已知变量x ,y 满足约束条件1422x y x y ≤+≤⎧⎨-≤-≤⎩若目标函数z ax y =+(其中0a >)仅在点(3,1)处取得最大值,则a 的取值范围为 。
六、设计线性规划,探求平面区域的面积问题例6在平面直角坐标系中,不等式组20200x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域的面积是()(A)(C) (D)2七、研究线性规划中的整点最优解问题例7、某公司招收男职员x 名,女职员y 名,x 和y 须满足约束条件⎪⎩⎪⎨⎧≤≥+-≥-.112,932,22115x y x y x 则1010z x y =+的最大值是(A)80 (B) 85 (C) 90 (D)95八、比值问题 当目标函数形如bx a y z --=时,可把z 看作是动点()y x P ,与定点()a b Q ,连线的斜率,这样目标函数的最值就转化为PQ 连线斜率的最值。
《管理运筹学》第四版课后习题解析(上)
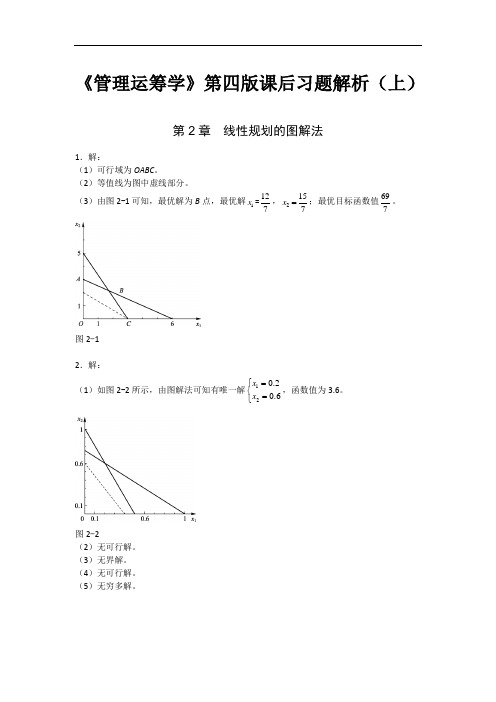
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解1x=127,2157x=;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6xx=⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
精选文档(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解: 标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量(0,0) 最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13) 最优解为 x 1=1,x 2=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章线性规划的解法§3.1重点、难点提要一、线性规划问题的图解法及几何意义1.图解法。
线性规划问题采用在平面上作图的方法求解,这种方法称为图解法。
图解法具有简单、直观、容易理解的特点,而且从几何的角度说明了线性规划方法的思路,所以,图解法还有助于了解一般线性规划问题的实质和求解的原理。
(1)图解法适用于求解只有两个或三个变量的线性规划问题,求解的具体步骤为:1)在平面上建立直角坐标系;2)图示约束条件,找出可行域。
具体做法是画出所有约束方程(约束条件取等式)对应的直线,用原点判定直线的哪一边符合约束条件,从而找出所有约束条件都同时满足的公共平面区域,即得可行域。
求出约束直线之间,以及约束直线与坐标轴的所有交点,即可行域的所有顶点;3)图示目标函数直线。
给定目标函数Z一个特定的值k,画出相应的目标函数等值线;4)将目标函数直线沿其法线方向向可行域边界平移,直至与可行域边界第一次相切为止,这个切点就是最优点。
具体地,当k值发生变化时,等值线将平行移动。
对于目标函数最大化问题,找出目标函数值增加的方向(即坐标系纵轴值增大的方向),等值线平行上移到可行域(阴影部分)的临界点,最终交点就是取得目标函数最大值的最优解;对于目标函数最小化问题,找出目标函数值减少的方向(即坐标系纵轴值减少的方向),等值线平行下移到可行域(阴影部分)的临界点,最终交点就是取得目标函数最小值的最优解。
(2)线性规划问题的几种可能结果:1)有唯一最优解;2)有无穷多个最优解;3)无最优解(无解或只有无界解)。
2.重要结论。
(1)线性规划的可行域为一个凸集,每一个可行解对应该凸集中的一个点;(2)每一个基可行解对应可行域的一个顶点。
若可行解集非空,则必有顶点存在,从而,有可行解必有基可行解。
(3)一个基可行解对应约束方程组系数矩阵中一组线性无关的列向量,对于n 个变量m 个约束方程的线性规划问题,基可行解的个数不会超过!!()!m n n m n m C =-。
(4)如果最优解存在,则最优解或最优解之一(具有无穷多个解的情形),一定可在可行域的凸集的某个顶点上找到。
二、线性规划模型的标准形式与标准化线性规划模型的形式有多种多样,这给求解线性规划问题带来不便。
虽然图解法对线性规划模型的形式没有限制,但它对变量个数有约束。
为寻求统一规范的求解方法,我们定义线性规划模型的标准形式,将线性规划模型的所有形式都转化为标准形式进行研究。
1.线性规划模型的标准形式11211122112122222122,,,max ..n nn n n n m m mn n m n a x a x a x b a x a x a x b a x a x a x b x x x z c x c x c x s t +++=⎧⎪+++=⎪⎪⎨⎪+++=⎪≥⎪⎩=+++1111123-1 其中,0,1,2,,i b i m ≥= 标准形式(3-1)具有几种等价的表示形式。
(1)一般形式 1,2,,1,2,,max ..n j jj nij j i j jc x a x b i m x j n z s t ==⎧==⎪⎨⎪≥=⎩=∑∑110(2)矩阵形式 max .z cXAX b s t X ==⎧⎨≥⎩0(3)向量形式max ..nj j j cXx b X z s t =⎧=⎪⎨⎪≥⎩=∑P 10 其中n n m m mn a a a a a a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦A 111212122212, 11,,)(,n c c c c =,12m b b b b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,2n x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=X 1 12,1,2,,j j j mj a a j n a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦P 线性规划模型标准形式中的一般形式、矩阵形式和向量形式等三种表达形式是等价的,在应用中可根据需要灵活使用。
2.线性规划模型的标准形式的特点线性规划模型的标准形式具有四个特点:(1)目标函数是最大化类型:max cX z =(2)约束条件均由等式组成:AX b =(3)决策变量均为非负:X ≥0(4)资源常数项非负:≥b 03.线性规划模型的标准化 根据线性规划模型标准形式的特点,我们可以将其它形式的线性规划模型转化为标准形式,这种转化过程称为线性规划模型的标准化。
(1)目标函数的转化。
若原问题的目标函数是最小化,即min n j j j c x z ==∑1则可将原目标函数乘以-1,等价转化为最大化问题max min()nj j j c x z z ='=-=-∑1转化后的问题与原问题有相同的最优解。
(2)约束条件的转化。
约束条件的转化是将不等式约束转化为等式约束。
如果约束条件为n ijj i j a x b =≤∑1则引入松弛变量0n i x +≥,将其转化为等价的等式约束条件n ijj n i i j a x x b +=+=∑1如果约束条件为n ijj i j a x b =≥∑1则引入剩余变量0n i x +≥,将其转化为等价的等式约束条件n ijj n i i j a x x b +=-=∑1总之,若原问题的约束条件中,约束为“≤”型,则左边+松驰变量转化为等式约束;若约束为“≥”型,则左边-剩余变量转化为等式约束。
(3)变量约束的转化。
如果原问题中某变量非正,即0j x ≤,则令0j j x x '=-≥;如果原问题中某变量j x 是自由变量(即无非负限制),则可令,0,0j j j j j x x x x x ''''''=-≥≥将变换后的变量代入原问题,得到的转化后的问题与原问题具有相同的最优解。
(4)资源常量的转化。
如果某个资源常量0i b ≤,则先将0i b ≤所在的约束式两边乘以-1使得0i i b b '=-≥后,再将不等约束化为等式约束。
三、单纯形法原理与基本思路丹捷格(G .B .Dantzig )在1947年提出的求解线性规划问题的单纯形法,使线性规划在理论上渐趋成熟,在实际应用中日益广泛和深入。
单纯形法的原理:如果线性规划问题的可行域D 非空,则可从D 的某一顶点X 0出发,判断它是否最优;如果不是,则沿着边界找其邻近的另一个顶点,新顶点应该比原顶点更优,再次判优;如果不是,再次沿着边界找其邻近的顶点,再判优。
通过逐次迭代,直至找出最优解或判定问题无解。
单纯形法的原理表明,单纯形法是一种迭代算法。
根据单纯形法的原理,可得出单纯形法求解的基本思路:(1)求线性规划问题(LP )的初始基可行解X 0,并将线性规划问题的相关数据简单明了、恰当地表示出来(制成单纯形表);(2)判别X 0是否为最优解。
为此,需要给出一个基可行解是否为最优的判别准则;(3)如果X 0不是最优解,则应另求基可行解X 1,且使得 C T X 1< C T X 0(至少C T X 1≤ C T X 0)。
同时,由X 0相应的单纯形表给出X 1相应的单纯形表。
这里,需要给出X 1迭代X 0的换基迭代(进基、出基)原则(4)若X 1仍非最优解,则视X 1为X 0重复步骤(3),直至线性规划问题求得最优解,或判定目标函数在D 内无下界。
四、用单纯形法求解线性规划模型的具体步骤1.第1步,找出初始基,建立初始单纯形表。
如果在标准型线性规划模型中,约束条件系数矩阵中至少含有一个单位子矩阵B ,不妨设B =(12,,,m P P P )(单位子矩阵B 称为基,其对应的变量B X 称为基变量,对应的价值(费用)系数记为B C ,其余变量N X 为非基变量),且目标函数中不含基变量,则可简便地确定初始基可行解。
在线性规划模型中,令非基变量0j x =,求出基变量i x 的值,即得初始基可行解。
注意,在实际问题中,直接确定初始基B 是比较困难的。
2.第2步,判断最优,检验各非基变量j x 的检验数1j B j j C B P c σ-=-。
(1)若所有的0j σ≥,则基B 为最优基,相应的基可行解即为基最优解,停止计算;(2)若某个负检验数0j σ<,它所对应的列向量的全部分量112(,,,)0T s s s ms B P a a a -=≤,则该线性规划问题的目标函数值无上界,即线性规划问题具有无界解,停止计算;(3)若某个负检验数0j σ<所对应的列向量有正分量,则基B 不是最优基。
转第3步。
3.第3步,换基迭代。
(1)确定换入变量s x ,单纯形表从左至右选择检验数为负的进基。
(2)确定换出变量r x ,单纯形表中按最小比值原则从上至下选择变量出基。
根据确定θ的规则,对k P 列计算θ=min {i ik b a ︱ik a >0}=l lkb a ,确定l x 为出基变量,该规则称为最小比值原则。
再返回第2步。
四、改进单纯形法求解线性规划模型的具体步骤1.设线性规划的标准形式为max .0Z s t ==⎧⎨≥⎩CXAX b X 其中,()()()0ij m n n a r m n b ⨯===<≥12A P ,P ,P A ,,。
在标准形式中,设矩阵B 为基,则有B B N N SB N S B N S max X X X X X X ..X ,X ,X 0zC C B N I b s t =++⋅++=⎧⎨≥⎩0其中,B N S X X X ,,分别为基变量、非基变量和松弛变量;B N C C 与分别为基变量和非基变量的价值系数;N I 与分别为非基变量系数矩阵和单位阵。
在目标函数中消除基变量,则有111111max ()..0B B N N B SB N S B N S zC B b C B N C X C B X X B NX B X B b s t X X X ------=---⎧++=⎪⎨≥⎪⎩,,于是,可建立对应于基B 的矩阵形式的单纯形表T (B ):表3-1 矩阵形式的单纯形表T (B )表中的1B C B -称为单纯形乘子,它是一个m 维的行向量。
对于基B ,可给出线性规划模型的简洁形式的单纯形表T (B ):表3-2 矩阵简洁形式的单纯形表T (B )2.检验数的本质对于标准形式的线性规划模型 max .0Z CXAX b s t X ==⎧⎨≥⎩ 它的变量之间有着确定的数量关系,即由约束方程组AX b =所确定的关系,目标函数中的各个变量间当然也有相同的数量关系。
如果把约束方程组确定的变量间的数量关系反映到目标函数中,则目标函数的表达式就等价地变为另一种形式。
比如,对于选定的可行基B ,把约束方程组AX b =变形,把每一个基变量都用非基变量和常数表达出来,再把这些表达式代入目标函数,则目标函数的新的表达式中将不再含有基变量(或者说在目标函数的新的表达式中.基变量的系数全是0),这时目标函数新的表达式中各个变量的系数就是此变量的检验数。
