2020年春人教版九年级数学下册学案27.2.1 第4课时 两角分别相等的两个三角形相似
【人教版】九年级数学下册:27.2.1第4课时两角分别相等的两个三角形相似教案

相像三角形的判断第 4 课时两角分别相等的两个三角形相像1.理解“两角分别相等的两个三角形相像”的含义,能分清条件和结论,并能用文字、图形和符号语言表示; (要点 )2.会运用“两角分别相等的两个三角形相像”判断两个三角形相像,并解决简单的问题. (难点 )一、情境导入与伙伴合作,一人画△ ABC,另一人画△ A′ B′ C′,使得∠ A 和∠ A ′都等于给定的∠α,∠ B 和∠ B′都等于给定的∠β,比较你们画的两个三角形,∠ C 与∠ C′相等吗?对应边的比AB AC BC,,相等吗?这样的两个三角形相像吗?和同学们沟通.二、合作研究研究点:两角分别相等的两个三角形相像【种类一】利用判断定理证明两个三角形相像如图,在等边△ ABC 中, D 为 BC 边上一点, E 为 AB 边上一点,且∠ ADE = 60° .(1)求证:△ ABD ∽△ DCE ;(2)若 BD = 3,CE=2,求△ ABC 的边长.分析: (1)由题有∠ B=∠ C= 60°,利用三角形外角的知识得出∠BAD=∠ CDE,即可证明△ ABD ∽△ DCE ; (2) 依据△ ABD ∽△ DCE ,列出比率式,即可求出△ ABC的边长.(1)证明:在△ ABD 中,∠ ADC=∠ B+∠ BAD ,又∠ ADC=∠ ADE+∠ EDC,而∠ B=∠ADE = 60°,∴∠ BAD =∠ CDE.在△ ABD 和△ DCE 中,∠ BAD =∠ CDE ,∠B=∠ C=60°,∴△ ABD ∽△ DCE ;AB = BD,∴x=3,∴ x=(2)解:设 AB=x,则 DC= x- 3,由△ ABD ∽△ DCE ,∴DC DE x-329.即等边△ ABC 的边长为 9.方法总结:本题主假如利用“两角分别相等的两个三角形相像” ,解答本题的要点是利用三角形的外角的知识得出角相等.变式训练:见《学练优》本课时练习“讲堂达标训练”第5题【种类二】增添条件证明三角形相像如图,在△ ABC 中, D 为 AB 边上的一点,要使△ABC∽△ AED 建立,还需要添加一个条件为____________.分析:∵∠ ABC=∠ AED,∠A=∠A,∴△ABC∽△AED ,故增添条件∠ ABC=∠ AED 即可AD AE求得△ABC∽△AED.同理可得∠ADE =∠C或∠AED=∠B或AC=AB能够得出AD AE△ ABC ∽△ AED .故答案为∠ ADE=∠ C 或∠ AED=∠ B 或AC=AB.方法总结:娴熟掌握相像三角形的各样判断方法是解题要点.变式训练:见《学练优》本课时练习“讲堂达标训练”第3题【种类三】相像三角形与圆的综合应用如图, AB 为⊙ O 的直径, C 为⊙ O 上一点, CD⊥AB 于点 D ,交 AE 于点 G,弦CE 交 AB 于点 F,求证: AC 2= AG·AE.分析:延伸 CG,交⊙O 于点 M ,连结 AM,依据圆周角定理,可证明∠ ACG=∠ E,根据相像三角形的判断定理,可证明△ CAG∽△ EAC,依据相像三角形对应边成比率,可得出结论.︵︵证明:延伸 CG,交⊙ O 于点 M,连结 AM,∵ AB⊥CM ,∴ AC=AM,∴∠ ACG=∠ E,又∵∠ CAG=∠ EAC,∴△ CAG∽△ EAC,∴ACAE=AGAC,∴ AC2= AG·AE.方法总结:相像三角形与圆的知识综合时,常常要用到圆的一些性质找寻角的等量关系证明三角形相像.变式训练:见《学练优》本课时练习“课后稳固提高”第 3 题【种类四】相像三角形与四边形知识的综合如图,在 ?ABCD 中,过点 B 作 BE ⊥CD,垂足为 E,连结 AE, F 为 AE 上一点,且∠BFE=∠ C.若 AB =8, BE= 6, AD =7,求 BF 的长.分析:可经过证明∠ BAF =∠ AED,∠AFB =∠ D,证得△ ABF ∽△ EAD ,可得出对于AB,AE ,AD ,BF 的比率关系.已知AD , AB 的长,只要求出AE 的长即可.可在直角三角形ABE 顶用勾股定理求出AE 的长,从而求出BF 的长.解:在平行四边形ABCD 中,∵ AB∥CD,∴∠ BAF =∠ AED.∵∠ AFB +∠ BFE = 180°,∠D +∠ C=180°,∠ BFE =∠ C,∴∠ AFB=∠ D,∴△ ABF ∽△ EAD .∵ BE⊥ CD,AB∥ CD ,∴ BE⊥ AB,∴∠ ABE= 90°,∴ AE=AB2+ BE2=82+ 62= 10.∵△ ABF ∽△ EAD,∴BF=ADAB,∴BF=8,∴ BF= 5.6.AE710方法总结:相像三角形与四边形知识综合时,常常要用到平行四边形的一些性质找寻角的等量关系证明三角形相像.变式训练:见《学练优》本课时练习“课后稳固提高”第7 题【种类五】相像三角形与二次函数的综合如图,在△ ABC 中,∠ C= 90°, BC= 5m, AB= 10m.M 点在线段CA 上,从C 向 A 运动,速度为1m/s;同时 N 点在线段AB 上,从 A 向 B 运动,速度为2m/s.运动时间为ts.(1)当 t 为什么值时,△AMN 的面积为 6m2?(2)当 t 为什么值时,△AMN 的面积最大?并求出这个最大值.分析: (1) 作 NH ⊥ AC 于 H ,证得△ ANH∽△ ABC,从而获得比率式,而后用t 表示出NH ,依据△AMN 的面积为6m2,获得对于t 的方程求得t 值即可; (2)依据三角形的面积计算获得相关t 的二次函数求最值即可.解: (1)在 Rt△ABC 中,∵ AB2=BC2+AC2,∴ AC= 5 3m.如图,作NH⊥ AC 于 H,∴∠NHA =∠ C=90°,∵∠ A 是公共角,∴△ NHA ∽△ BCA,∴AN=NH,即2t=NH,∴ NH ABBC10 51= t ,∴ S△AMN=2t(5 3-t)= 6,解得 t1=3, t2= 43(舍去 ),故当 t 为3秒时,△ AMN 的面积为 6m2.13- t)=-12- 5 3t+75)+7515 3 2+75,∴当 t=53(2)S△AMN= t(52(t4=-(t-2)2时,S 最2222 752大值=2 m .方法总结:解题的要点是依据证得的相像三角形获得比率式,从而解决问题.三、板书设计1.三角形相像的判断定理:两角分别相等的两个三角形相像;2.应用判断定理解决简单的问题.在研究式教课中教师是学生学习的组织者、指引者、合作者、共同研究者,教课过程中鼓舞学生勇敢研究,指引学生关注过程,实时一定学生的表现,鼓舞创新.备课时应多考虑学生学法的打破,教课时只在要点处点拨,在不足时增补.与学生同等地沟通,创建民主、和睦的学习气氛 .。
部审人教版九年级数学下册学案27.2.1第4课时两角分别相等的两个三角形相似

2 页 共 4 页
小结:三角形相似的判定方法4: 的两个三角形相似. 几何语言: 证明: 三、巩固提升 如图,Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上一点,AE=5,ED⊥AB,垂足为D.求AD的长. 解: 由三角形相似的条件可知,如果两个直角三角形满足_______或△ABC和△A/B/C/相似吗? 自己画图证明。 自己动脑完成看谁最先做出来
4 页 共 4 页
六.2.1 相似三角形的判定 第4课时 两角分别相等的两个三角形相似 学习目标: 1.掌握“两角对应相等,两个三角形相似”的判定方法. 2.能够运用三角形相似的条件解决简单的问题. 学习重点:三角形相似的判定方法4——“两角对应相等,两个三角形相似”. 学习难点:三角形相似的判定方法4的运用. 教具:三角板 学法指导:自主完成一、认真阅读教材小组合作交流完成二、三、四、五 学习过程 备注 一、复习导学: 1、我们已学习过哪些判定三角形相似的方法? 2、如图,△ABC中,点D在AB上,如果AC2=AD?AB,那么△ACD与△ABC相似吗?说说你的理由. 二、探究新知: 问题1:观察两副三角板其中同样度数的两个三角尺相似吗?说说理由。 问题2:作△ABC和△A/B/C/ 使得∠A=∠ A/ ,∠B=∠B/,这时它们的第三个角满足∠C=∠C/ 吗?分别度量这两个三角形的边长,计算△ABC和△A/B/C/的对应边的比是否相等? 自主完成 把你的结果与邻座的同学比较,你们的结论一样吗?
3 页 共 4 页
_____,那么这两个直角三角形相似. 四、思考探究: 对于两个直角三角形,我们还可以用“HL”判定它们全等。那么,满足斜边的比等于一组直角边的比的两个直角三角形相似吗? 已知:如图,Rt△ABC与Rt△A/B/C/中,∠C=∠C/ =90°, AB:A/B/=AC:A/ C/ .求证: Rt△ABC∽Rt△A/B/C/ 结论:_________________________________________________ 五、能力提升: 1、已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长. 2、已知:如图,△ABC 的高AD、BE交于点F.求证:AFEFBFFD=. 小组交流展示讲解
人教版数学九年级下册27.2.1 第4课时 两角分别相等的两个三角形相似

6.如图,AB=AC,∠A=36°,BD 是∠ABC 的平 分线,求证:△ABC∽△BDC. 证明:∵AB=AC,∠A=36°, ∴∠ABC=∠C=72°. ∵BD 是∠ABC 的平分线, ∴∠ABD=∠DBC=36°, ∴∠A=∠CBD, 又∵∠C=∠C,∴△ABC∽△BDC.
5.如图,在△ABC 中,∠C=90°,DM⊥AB 于点 M , DN⊥BC 于 点 N , 交 AB 于 点 E. 求 证 : △DME∽△BCA. 证明:∵∠C=90°,DM⊥AB 于点 M,DN⊥BC 于 点 N, ∴∠C=∠ENB=∠DME=90°, ∴AC∥DN,∴∠DEM=∠A.
在△DME 与△BCA 中, DEM A, DME C, ∴△DME∽△BCA.
1.已知一个三角形的两个内角分别是 40°,60°,另
一个三角形的两个内角分别是 40°,80°,则这两个
三角形( C )
A.一定不相似 B.不一定相似
C.一定相似
D.不能确定
2.如图,在△ABC 与△ADE 中,∠C=∠AED=90°, 点 E 在 AB 上,那么添加下列一个条件后,仍无法 判定△ABC∽△DAE 的是( A ) A.∠B=∠D B. AC AB
DE AD C.AD∥BC D.∠BAC=∠D
3.如图,∠C=∠E=90°,AC=3,AB=4,AE=2
8
当 AD=____3____时,Rt△ABC∽Rt△ADE.
4.如图,点 D 是△ABC 中 AC 边上的一点. (1)若∠1=_∠__C_B__A_,则△CBD∽△CAB; (2)若∠2=_∠__A____,则△CBD∽△CAB.
而 AC=3,DB=156,
∴AD
AD
16 5
=9,
人教版九年级数学下册27.2.1 第4课时 两角分别相等的两个三角形相似

2
D
B
2 C
练一练 在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=∠C′=90°,
依据下列各组条件判定这两个三角形是否相似. (1) ∠A=35°,∠B′=55°: 相似 ;
(2) AC=3,BC=4,A′C′=6,B′C′=8: 相似 ;
(3) AB=10,AC=8,A′B′=25,B′C′=15: 相似 .
AB 2 AC 2 B C
k 2 AB2 k 2 AC2 B C
kBC k. BC
A' A
∴ _BB_CC_ _AAB_B _ A_ACC_ .
∴ Rt △ABC ∽ Rt △A′B′C′. C
B C'
B'
归纳: 由此得到另一个判定直角三角形相似的方法:
B
C
B'
C'
2. 如图,⊙O 的弦 AB,CD 相交于点 P,若 PA=3, PB = 8,PC = 4,则 PD = 6 .
C A
P B
O
D
二 判定两个直角三角形相似
例2 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,
AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足
B
A A'
C B' C'
练一练
如图,△ABC中,DE∥BC,EF∥AB,求证:
△ADE∽△EFC.
A
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C, ∠A=∠FEC.
D
E
∴ △ADE∽△EFC.
B
F
C
典例精析
例1 如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°, ∠E=80 °,∠F=60 ° .求证:△ABC ∽△DEF.
人教版九年级数学下册全册配套教案设计第4课时两角分别相等的两个三角形相似

27.2.1 相似三角形的判定第4课时 两角分别相等的两个三角形相似1.理解“两角分别相等的两个三角形相似”的含义,能分清条件和结论,并能用文字、图形和符号语言表示;(重点)2.会运用“两角分别相等的两个三角形相似”判定两个三角形相似,并解决简单的问题.(难点)一、情境导入与同伴合作,一人画△ABC ,另一人画△A ′B ′C ′,使得∠A 和∠A ′都等于给定的∠α,∠B 和∠B ′都等于给定的∠β,比较你们画的两个三角形,∠C 与∠C ′相等吗?对应边的比AB A ′B ′,AC A ′C ′,BC B ′C ′相等吗?这样的两个三角形相似吗?和同学们交流. 二、合作探究探究点:两角分别相等的两个三角形相似【类型一】 利用判定定理证明两个三角形相似如图,在等边△ABC 中,D 为BC 边上一点,E 为AB 边上一点,且∠ADE =60°.(1)求证:△ABD ∽△DCE ;(2)若BD =3,CE =2,求△ABC 的边长.解析:(1)由题有∠B =∠C =60°,利用三角形外角的知识得出∠BAD =∠CDE ,即可证明△ABD ∽△DCE ;(2)根据△ABD ∽△DCE ,列出比例式,即可求出△ABC 的边长.(1)证明:在△ABD 中,∠ADC =∠B +∠BAD ,又∠ADC =∠ADE +∠EDC ,而∠B =∠ADE =60°,∴∠BAD =∠CDE .在△ABD 和△DCE 中,∠BAD =∠CDE ,∠B =∠C =60°,∴△ABD ∽△DCE ;(2)解:设AB =x ,则DC =x -3,由△ABD ∽△DCE ,∴AB DC =BD DE ,∴x x -3=32,∴x =9.即等边△ABC 的边长为9.方法总结:本题主要是利用“两角分别相等的两个三角形相似”,解答此题的关键是利用三角形的外角的知识得出角相等.变式训练:见《学练优》本课时练习“课堂达标训练” 第5题【类型二】 添加条件证明三角形相似如图,在△ABC 中,D 为AB 边上的一点,要使△ABC ∽△AED 成立,还需要添加一个条件为____________.解析:∵∠ABC =∠AED ,∠A =∠A ,∴△ABC ∽△AED ,故添加条件∠ABC =∠AED 即可求得△ABC ∽△AED .同理可得∠ADE =∠C 或∠AED =∠B 或AD AC =AE AB可以得出△ABC ∽△AED .故答案为∠ADE =∠C 或∠AED =∠B 或AD AC =AE AB. 方法总结:熟练掌握相似三角形的各种判定方法是解题关键.变式训练:见《学练优》本课时练习“课堂达标训练” 第3题【类型三】 相似三角形与圆的综合应用如图,AB 为⊙O 的直径,C 为⊙O 上一点,CD ⊥AB 于点D ,交AE 于点G ,弦CE 交AB 于点F ,求证:AC 2=AG ·AE .解析:延长CG ,交⊙O 于点M ,连接AM ,根据圆周角定理,可证明∠ACG =∠E ,根据相似三角形的判定定理,可证明△CAG ∽△EAC ,根据相似三角形对应边成比例,可得出结论.证明:延长CG ,交⊙O 于点M ,连接AM ,∵AB ⊥CM ,∴AC ︵=AM ︵,∴∠ACG =∠E ,又∵∠CAG =∠EAC ,∴△CAG ∽△EAC ,∴AC AE =AG AC,∴AC 2=AG ·AE . 方法总结:相似三角形与圆的知识综合时,往往要用到圆的一些性质寻找角的等量关系证明三角形相似.变式训练:见《学练优》本课时练习“课后巩固提升”第3题【类型四】 相似三角形与四边形知识的综合如图,在▱ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连接AE ,F 为AE 上一点,且∠BFE =∠C .若AB =8,BE =6,AD =7,求BF 的长.解析:可通过证明∠BAF =∠AED ,∠AFB =∠D ,证得△ABF ∽△EAD ,可得出关于AB ,AE ,AD ,BF 的比例关系.已知AD ,AB 的长,只需求出AE 的长即可.可在直角三角形ABE 中用勾股定理求出AE 的长,进而求出BF 的长.解:在平行四边形ABCD 中,∵AB ∥CD ,∴∠BAF =∠AED .∵∠AFB +∠BFE =180°,∠D +∠C =180°,∠BFE =∠C ,∴∠AFB =∠D ,∴△ABF ∽△EAD .∵BE ⊥CD ,AB ∥CD ,∴BE ⊥AB ,∴∠ABE =90°,∴AE =AB 2+BE 2=82+62=10.∵△ABF ∽△EAD ,∴BF AD=AB AE ,∴BF 7=810,∴BF =5.6. 方法总结:相似三角形与四边形知识综合时,往往要用到平行四边形的一些性质寻找角的等量关系证明三角形相似.变式训练:见《学练优》本课时练习“课后巩固提升”第7题【类型五】 相似三角形与二次函数的综合如图,在△ABC 中,∠C =90°,BC =5m ,AB =10m.M 点在线段CA 上,从C向A 运动,速度为1m/s ;同时N 点在线段AB 上,从A 向B 运动,速度为2m/s.运动时间为t s.(1)当t 为何值时,△AMN 的面积为6m 2?(2)当t 为何值时,△AMN 的面积最大?并求出这个最大值.解析:(1)作NH ⊥AC 于H ,证得△ANH ∽△ABC ,从而得到比例式,然后用t 表示出NH ,根据△AMN 的面积为6m 2,得到关于t 的方程求得t 值即可;(2)根据三角形的面积计算得到有关t 的二次函数求最值即可.解:(1)在Rt △ABC 中,∵AB 2=BC 2+AC 2,∴AC =53m.如图,作NH ⊥AC 于H ,∴∠NHA =∠C =90°,∵∠A 是公共角,∴△NHA ∽△BCA ,∴AN AB =NH BC ,即2t 10=NH 5,∴NH=t ,∴S △AMN = 12t (53-t )=6,解得t 1=3,t 2=43(舍去),故当t 为3秒时,△AMN 的面积为6m 2.(2)S △AMN =12t (53-t )=-12(t 2-53t +754)+752=-12(t -532)2+752,∴当t =532时,S 最大值=752m 2. 方法总结:解题的关键是根据证得的相似三角形得到比例式,从而解决问题.三、板书设计1.三角形相似的判定定理:两角分别相等的两个三角形相似;2.应用判定定理解决简单的问题.在探究式教学中教师是学生学习的组织者、引导者、合作者、共同研究者,教学过程中鼓励学生大胆探索,引导学生关注过程,及时肯定学生的表现,鼓励创新.备课时应多考虑学生学法的突破,教学时只在关键处点拨,在不足时补充.与学生平等地交流,创设民主、和谐的学习氛围.。
2020年春人教版九年级数学下册 27.2.1 第4课时 两角分别相等的两个三角形相似.bak
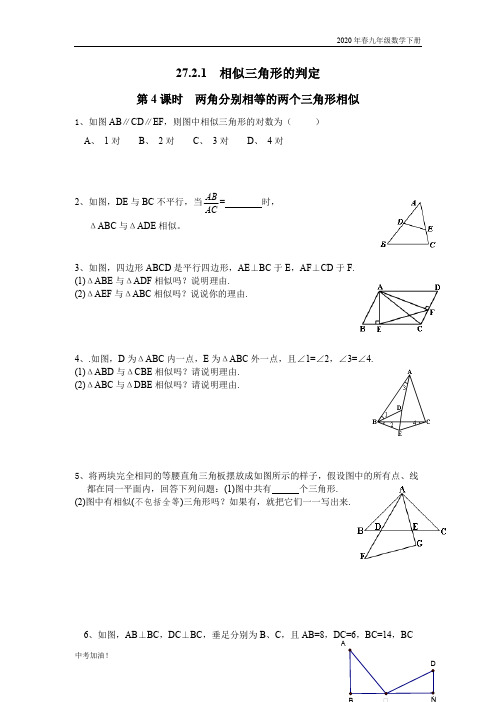
27.2.1 相似三角形的判定第4课时两角分别相等的两个三角形相似1、如图AB∥CD∥EF,则图中相似三角形的对数为()A、1对B、2对C、3对D、4对AB2、如图,DE与BC不平行,当= 时,ΔABC与ΔADE相似。
3、如图,四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F.(1)ΔABE与ΔADF相似吗?说明理由.(2)ΔAEF与ΔABC相似吗?说说你的理由.4、.如图,D为ΔABC内一点,E为ΔABC外一点,且∠1=∠2,∠3=∠4.(1)ΔABD与ΔCBE相似吗?请说明理由.(2)ΔABC与ΔDBE相似吗?请说明理由.5、将两块完全相同的等腰直角三角板摆放成如图所示的样子,假设图中的所有点、线都在同一平面内,回答下列问题:(1)图中共有个三角形.(2)图中有相似(不包括全等)三角形吗?如果有,就把它们一一写出来.6、如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BCA上是否存在点P 使△ABP 与△DCP 相似?若有,有几个?并求出此时BP 的长,若没有,请说明理由。
7、已知:如图,CE 是Rt ΔABC 的斜边AB 上的高,BG ⊥AP.求证:CE 2=ED ·EP.8、.如图,在直角梯形ABCD 中,AB//CD ,,在7,3,2,===⊥AD AB CD AB DA AD 上能否找到一点P ,使三角形PAB 和三角形PCD 相似?若能,共有几个符合条件的点P ?并求相应PD 的长。
若不能,说明理由。
D CPA B9、如图:AB 是等腰直角三角形ABC 的斜边,点M 在边AC 上,点N 在边BC 上,沿直线MN 将△MCN 翻折,使点C 落在AB 上,设其落点为P ,①当P 是边AB 中点时,求证:;CN CM PB PA =②当P 不是边AB 中点时,是否仍成立?请证明你的结论;CN CM PB PA =C M N A P B。
【人教版】九年级数学下册:27.2.1第4课时两角分别相等的两个三角形相似学案

相像三角形的判断第 4 课时两角分别相等的两个三角形相像学习目标:1.掌握“两角对应相等,两个三角形相像”的判断方法.2.能够运用三角形相像的条件解决简单的问题.学习要点 :三角形相像的判断方法4——“两角对应相等,两个三角形相像”.学习难点 :三角形相像的判断方法4的运用.教具 :三角板学法指导:自主达成一、仔细阅读教材小组合作沟通达成二、三、四、五学习过程备注一、复习导学 :1、我们已学习过哪些判断三角形相像的方法?2、如图,△ABC 中,点 D 在 AB 上,假如自主达成AC 2=AD?AB ,那么△ACD 与△ABC 相像吗?谈谈你的原因.二、研究新知:问题 1:察看两副三角板此中相同度数的两个三角尺相像吗?谈谈原因。
把你的结果问题 2:作△ABC 和△A / //使得∠ A=∠ A/∠∠B/,这时它们与邻座的同B C, B=的第三个角知足∠ C=∠ C/吗?分别胸怀这两个三角形的边长,计学比较,你算△ABC 和△A /B/C/的对应边的比能否相等?们的结论一样吗?△ABC和///△ABC相小结:三角形相像的判断方法4:自己绘图证的两个三角形相像.明。
几何语言:证明:三、稳固提高如图, Rt △ABC 中,∠ C=90°, AB=10 , AC=8.E 是AC 上一点,AE=5, ED⊥ AB ,垂足为 D.求AD 的长 .解:自己动脑完成看谁最初做出来由三角形相像的条件可知,假如两个直角三角形知足_______或_____,那么这两个直角三角形相像.四、思虑研究:关于两个直角三角形,我们还能够用“HL”判断它们全等。
那么,知足斜边的比等于一组直角边的比的两个直角三角形相像吗?已知 :如图, Rt△ ABC 与 Rt △A/B/C/中,∠ C=∠C/ =90°,AB :A / B/ =AC: A / C/ .求证 : Rt△ABC ∽Rt△A/B/C/结论: _________________________________________________五、能力提高:1、已知:如图,矩形 ABCD 中,E 为 BC 上一点, DF⊥ AE 于 F,若 AB=4 ,AD=5 ,AE=6,求 DF 的长.小组沟通展示解说2、已知:如图,△ABC 的高 AD 、BE交于点 F.求证:AF=EF.BF FD六、小结。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27.2.1 相似三角形的判定
第4课时 两角分别相等的两个三角形相似
学习目标:
1.掌握“两角对应相等,两个三角形相似”的判定方法.2.能够运用三角形相似的条件解决简单的问题.
学习重点:三角形相似的判定方法4——“两角对应相等,两个三角形相似”.学习难点:三角形相似的判定方法4的运用.教具:三角板
学法指导:自主完成一、认真阅读教材小组合作交流完成二、三、四、五
学习过程
备注
一、复习导学:
1、我们已学习过哪些判定三角形相似的方法?
2、如图,△ABC 中,点D 在AB 上,如果AC 2=AD•AB ,那么△ACD 与△ABC 相似吗?说说你的理由.
二、探究新知:
问题1:观察两副三角板其中同样度数的两个三角尺相似吗?说说理由。
问题2:作△ABC 和△A /B /C / 使得∠A=∠ A / ,∠B=∠B /,这时它们的第三个角满足∠C=∠C / 吗?分别度量这两个三角形的边长,计算△ABC 和△A /B /C /的对应边的比是否相等?
自主完成
把你的结果
与邻座的同学比较,你们的结论一样吗?△ABC 和
小结:三角形相似的判定方法4:的两个三角形相似.几何语言:
证明:
三、巩固提升
如图,Rt △ABC 中,∠C=90°,AB=10,AC=8.E 是AC 上一点,AE=5,ED ⊥AB ,垂足为D.求AD 的长.
解:
由三角形相似的条件可知,如果两个直角三角形满足_______或_____,那么这两个直角三角形相似.
△A /B /C /相似吗?
自己画图证明。
自己动脑完成看谁最先做出来
四、思考探究:
对于两个直角三角形,我们还可以用“HL”
判定它们全等。
那么,满足斜边的比等于一组直角边的比的两个直角三角形相似吗?
已知:如图,Rt △ABC 与Rt △A /B /C /中,∠C=∠C / =90°,AB :A /B /=AC :A / C / .求证: Rt △ABC ∽Rt △A /B /C /
结论:_________________________________________________
五、能力提升:
1、已知:如图,矩形ABCD 中,E 为BC 上一点,DF ⊥AE 于F ,若AB=4,AD=5,AE=6,求DF 的长.
2、已知:如图,△ABC
的高AD 、BE 交于点F .求证:
.AF EF
BF FD
小组交流展示讲解
六、小结。
