直角三角形全等的判定(1)讲学稿
直角三角形全等判定(HL)

《11.2 三角形全等的判定》——直角三角形全等判定(HL)年级:八年级课型:新授执笔:许景初审核:时间:学生姓名:班别:学号:学习目标:1.理解判定两个直角三角形全等可以用已经学过的全等三角形判定方法来判定.2.掌握“斜边、直角边”公理,并能利用公理来判定两个直角三角形全等。
重点:熟练掌握“斜边、直角边”公理难点:利用公理来判定两个直角三角形全等学习过程:一.预习●导学1.判定两个三角形全等方法:,,,它们的共同点:2、判断:如图∠C=∠C′=90°,具有下列条件的Rt△ABC与Rt△A′B′C′是否全等?全等的在()里填写理由;如果不全等的,在()里打“×”:(1)AC=A′C′,∠A=A′()(2)AC=A′C′,BC=B′C ()(3)AB=A′B′,BC=B′C ()(4)∠A=∠A′,∠B=∠B′()(5)AC=A′C′,AB=A′B′()3.直角三角形 (“是”/“不是”)三角形中的一类, (“具有”/“不具有”)一般三角形所具有的性质,所以判定两个直角三角形全等可以,,,,。
二.学习●研讨(一)实验探究,尝试结论:课本13—14探究8例1.如图,已知线段a和c (a<c),画一个Rt△ABC使∠C=90°,一直角边CB=a,斜边AB=c。
c1.判定两个直角三角形全等的公理:(斜边、直角边公理)(可以简写成“公理”或“”)2.注意:(1)“HL”公理是仅适用于Rt△的特殊方法。
因此,判断两个直角三角形全等的方法除可以使用“”、“”、“”、“”外,还可以使用“HL”。
(2)应用HL 公理时,必须先有两个Rt △。
书写格式为:在Rt △______和Rt △______中, {______________,______________,== ∴Rt △______≌Rt △______(HL ) (二)巩固练习,达成目标: 1.已知:如图:ABC 中,AB =AC ,AD 是高,则____≌____。
数学:1.2《直角三角形的全等判定》课件(1)(苏科版九年级上)

1.2直角三角形的全等判定(1)
操作
1.同桌各画一个Rt△ABC,使∠C=90°, 直角边AC的长为2cm,斜边AB的长为 3cm.把△ABC剪下,两位同学比较一 下,看看两人剪下的Rt△是否可以重 合.
2.你从中得到了什么结论?你能证明这 个结论的正确性吗?
验证:斜边和一条直角边对应相等的两 个直角三角形全等。(简写为“H L”)
已知:在△ABC和△AˊBˊCˊ中, ∠ACB=∠AˊCˊBˊ=90°,AB= AˊBˊ, AC= AˊCˊ,
求证:△ABC≌ △AˊBˊCˊ
A
A'
A(A')
C
B C'
B'
B
B'
C(C')
知识回顾
判定两个直角三角形全等的判定定理有 哪些?
傲招式!紧接着把暗红色面条造型的脸耍了耍,只见八道忽亮忽暗的酷似马鞍般的深冰灵,突然从歪斜的脑袋中飞出,随着一声低沉古怪的轰响,天蓝色的大地开始抖 动摇晃起来,一种怪怪的深憨光影味在疯鬼般的空气中游动。最后旋起精悍的手掌一摆,飘然从里面飞出一道佛光,她抓住佛光出色地一转,一套绿莹莹、青虚虚的兵 器『青云踏怪蛙掌镖』便显露出来,只见这个这件怪物儿,一边转化,一边发出“呜呜”的仙声。……猛然间女族长W.娅娜小姐狂鬼般地用自己尖细的钢灰色玉米样 的海豹圣牛斗篷创造出墨灰色夸张游动的喷泉,只见她橙白色假山样的排骨雪晓履中,威猛地滚出七缕抖舞着『绿冰螺祖画册肘』的仙翅枕头扇状的镊子,随着女族长 W.娅娜小姐的耍动,仙翅枕头扇状的镊子像柳枝一样在双臂上夸张地总结出朦胧光盔……紧接着女族长W.娅娜小姐又发出二声妙绿风景色的痴呆大喊,只见她胖胖 的犹如扫帚似的脚中,突然弹出九组螺母状的雪山矿毛狼,随着女族长W.娅娜小姐的颤动,螺母状的雪山矿毛狼像草根一样,朝着蘑菇王子深邃快乐、充满智慧的黑 亮眼睛飞劈过来……紧跟着女族长W.娅娜小姐也旋耍着兵器像竹节般的怪影一样向蘑菇王子飞劈过来蘑菇王子猛然像暗绿色的三肚海滩虾一样怒笑了一声,突然搞了 个倒地狂跳的特技神功,身上瞬间生出了二十只活像马桶般的乳白色眉毛……接着耍了一套,窜虾躺椅翻两千五百二十度外加猪哼手杖旋十五周半的招数!接着又玩了 一个,妖体鸟飞凌空翻七百二十度外加呆转十五周的冷峻招式。紧接着把犹如擎天玉柱一样的长腿甩了甩,只见五道飘闪的活似鳄鱼般的冰烟,突然从灵敏机警、闪着 荧光的薄耳朵中飞出,随着一声低沉古怪的轰响,亮紫色的大地开始抖动摇晃起来,一种怪怪的坟茔猫蹦惨梦味在强悍的空气中飞舞……最后转起矫健刚劲、犹如仙猿 般的手臂一吼,变态地从里面喷出一道金辉,他抓住金辉讲究地一摆,一套黑森森、黄澄澄的兵器∈追云赶天鞭←便显露出来,只见这个这件宝器儿,一边蠕动,一边 发出“咝咝”的余响…………猛然间蘑菇王子狂鬼般地用自己快乐灵巧的舌头安排出金红色粗野飞舞的烟花,只见他好象美妙月牙一样的,镶嵌着无数奇宝的蓝白色瓜 皮滑板中,飘然射出九串耍舞着∈万变飞影森林掌←的仙翅枕头针状的玉兔,随着蘑菇王子的甩动,仙翅枕头针状的玉兔像烤箱一样在双臂上夸张地总结出朦胧光盔… …紧接着蘑菇王子又发出六声嫩黄野秀色的恬淡神喊,只见他充满智慧的亮眼睛中,酷酷地飞出七簇颤舞着∈万变飞影森林掌←的龟壳状的小溪珍珠腮狐,随着蘑菇王 子的扭动,龟
初中数学直角三角形全等的判定(1)PPT课件

∠BED=∠CFD
在△BDE和△CDF中,∵
∠BDE=∠CDF
BE=CF ∴△BDE≌△CDF(AAS)
∴DE=DF 又∵DE⊥AB,DF⊥AC
∴AD平分∠BAC.
注意点:要说明一条射线是某个角的平分线, 可以说明射线上一点到这个角的两边距离相 等.在解题过程中要注意垂直关系的书写,指 明垂线段,并由垂线段相等直接得到两个角相 等(或某射线是角的平分线).
变式:如图,在等腰Rt△ABC中,∠ACB=90°,
点D是斜边AB上任一点,AE⊥CD,垂足为E, BF⊥CD交CD的延长线于点F,CH⊥AB,垂足为H, 交AE于点G.问:BD与CG相等吗?请说明理由.
证明:∵∠ACB=90°,AE⊥CD ∴∠CAE+∠ACE=90°,∠ACE+∠BCE=90°, ∴∠CAE=∠BCE ∵BF⊥CD ∴∠CFB=90° ∴∠AEC=∠CFB, 又∵AC=CB ∴△ACE≌△CBF(AAS) ∴CE=BF, ∵CH⊥AB,BF⊥CF ∴∠HCD+∠CDH=90°,∠DBF+∠BDF=90°, ∵∠CDH=∠BDF ∴∠HCD=∠DBF ∴△CEG≌△BFD(ASA),∴BD=CG.
在 ∴RRtt△△AADDEE≌和RRtt△△BBCCAA中(H,L)DADE
CA, BC,
∴∠ADE=∠C ∵∠CAB+∠C=90° ∴∠CAB+∠.
注意点:当两个直角三角形全等后,往往要用 到同角(等角)的余角相等这些结论来说明问题, 使用过程中要注意角的转换.
例 下列说法不正确的是( )
A.有一锐角和一边对应相等的两个直角三角形全等 B.有两直角边对应相等的两个直角三角形全等 C.有两角对应相等的两个直角三角形全等 D.有两边对应相等的两个直角三角形全等
《直角三角形全等的判定》 讲义

《直角三角形全等的判定》讲义一、直角三角形全等的概念在平面几何中,如果两个直角三角形能够完全重合,那么它们就是全等的。
全等的直角三角形具有相同的形状和大小,对应的边和角都相等。
二、直角三角形全等的判定方法1、 SSS(边边边)如果两个直角三角形的三条边分别对应相等,那么这两个直角三角形全等。
2、 SAS(边角边)如果两个直角三角形的两条边及其夹角分别对应相等,那么这两个直角三角形全等。
3、 ASA(角边角)如果两个直角三角形的两个角及其夹边分别对应相等,那么这两个直角三角形全等。
4、 AAS(角角边)如果两个直角三角形的两个角和其中一个角的对边分别对应相等,那么这两个直角三角形全等。
5、 HL(斜边、直角边)如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等。
这是直角三角形全等特有的判定方法。
因为在直角三角形中,斜边是最长的边,当斜边和一条直角边对应相等时,由勾股定理可以推出另一条直角边也对应相等,从而满足边边边(SSS)的判定条件。
三、HL 判定方法的证明已知:在 Rt△ABC 和 Rt△A'B'C' 中,∠C =∠C' = 90°,AB =A'B',AC = A'C' 。
求证:Rt△ABC ≌ Rt△A'B'C'证明:在 Rt△ABC 中,根据勾股定理:BC²= AB² AC²在 Rt△A'B'C' 中,根据勾股定理:B'C'²= A'B'² A'C'²因为 AB = A'B',AC = A'C' ,所以 BC = B'C'因为 AB = A'B',AC = A'C' ,BC = B'C' ,所以 Rt△ABC ≌Rt△A'B'C'(SSS)四、直角三角形全等判定方法的应用1、证明线段相等例如,已知两个直角三角形全等,那么它们对应的边相等,从而可以证明某些线段相等。
直角三角形全等判定(基础)知识讲解.doc

直角三角形全等判定(基础)责编:某老师【学习目标】1.理解和掌握判定直角三角形全等的一种特殊方法——“斜边,直角边”(即“HL ”).2.能熟练地用判定一般三角形全等的方法及判定直角三角形的特殊方法判定两个直角三角形全等.【要点梳理】【高清课堂:379111 直角三角形全等的判定,知识点讲解】要点一、判定直角三角形全等的一般方法由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS ”,“ASA ”或“SAS ”判定定理. 要点二、判定直角三角形全等的特殊方法——斜边,直角边定理在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL ”).这个判定方法是直角三角形所独有的,一般三角形不具备.要点诠释:(1)“HL ”从顺序上讲是“边边角”对应相等,由于其中含有直角这个特殊条件,所以三角形的形状和大小就确定了.(2)判定两个直角三角形全等的方法共有5种:SAS 、ASA 、AAS 、SSS 、HL.证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.(3)应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt ”.【典型例题】类型一、直角三角形全等的判定——“HL”1、 已知:如图,AB ⊥BD ,CD ⊥BD ,AD =BC .求证:(1)AB =CD :(2)AD ∥BC .【思路点拨】先由“HL ”证Rt △ABD ≌Rt △CDB ,再由内错角相等证两直线平行.【答案与解析】证明:(1)∵AB ⊥BD ,CD ⊥BD ,∴∠ABD =∠CDB =90°在Rt △ABD 和Rt △CDB 中,AD BC BD DB⎧⎨=⎩=∴Rt △ABD ≌Rt △CDB (HL )∴AB =CD (全等三角形对应边相等)(2)由∠ADB =∠CBD∴AD ∥BC .【总结升华】证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.举一反三:【高清课堂:379111 直角三角形全等的判定,例3】【变式】已知:如图,AE ⊥AB ,BC ⊥AB ,AE =AB ,ED =AC .求证:ED ⊥AC .【答案】证明:∵AE ⊥AB ,BC ⊥AB ,∴∠DAE =∠CBA =90°在Rt △DAE 与Rt △CBA 中,ED AC AE AB ⎧⎨⎩==, ∴Rt △DAE ≌Rt △CBA (HL )∴∠E =∠CAB∵∠CAB +∠EAF =90°,∴∠E +∠EAF =90°,即∠AFE =90°即ED ⊥AC .2、 判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:(1)一个锐角和这个角的对边对应相等;( )(2)一个锐角和斜边对应相等; ( )(3)两直角边对应相等; ( )(4)一条直角边和斜边对应相等. ( )【答案】(1)全等,“AAS ”;(2)全等,“AAS ”;(3)全等,“SAS ”;(4)全等,“HL ”.【解析】理解题意,画出图形,根据全等三角形的判定来判断.【总结升华】直角三角形全等可用的判定方法有5种:SAS 、ASA 、AAS 、SSS 、HL. 举一反三:【变式】下列说法正确的有( )(1)一个锐角及斜边对应相等的两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等;(4)有两条边相等的两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等.A.2个B.3个C.4个D.5个【答案】C .解:(1)一个锐角及斜边对应相等的两个直角三角形全等,根据AAS 可判定两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等,根据AAS 或ASA 可判定两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等,缺少“边”这个条件,故不可判定两个直角三角形全等;(4)有两条边相等的两个直角三角形全等,根据SAS 或HL 可判定两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等,根据HL 可判定两个直角三角形全等.所以说法正确的有4个.故选C .3、(2016春•深圳校级月考)如图,AB ⊥AC 于A ,BD ⊥CD 于D ,若AC=DB ,则下列结论中不正确的是( ) O B C DAA .∠A=∠DB .∠ABC=∠DCBC .OB=OD D .OA=OD【思路点拨】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合已知条件与全等的判定方法逐一验证.【答案与解析】解:∵AB ⊥AC 于A ,BD ⊥CD 于D∴∠A=∠D=90°(A 正确)又∵AC=DB ,BC=BC∴△ABC ≌△DCB(HL)∴∠ABC=∠DCB (B 正确)∴AB=CD又∵∠AOB=∠C∴△AOB ≌△DOC(AAS)∴OA=OD (D 正确)C 中OD 、OB 不是对应边,不相等.故选C .【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL.注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.4、已知:如图1,在Rt△ABC 和Rt△A′B′C′中,AB=A′B′,AC=A′C′,C=∠C′=90° 求证:Rt△ABC 和Rt△A′B′C′全等.(1)请你用“如果…,那么…”的形式叙述上述命题;(2)将△ABC 和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A 与点A′重合,点C 与点C′重合.)(3)请你选择你拼成的其中一种图形,证明该命题.【答案与解析】解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.(2)如图:图②使点A与点A′重合,点B与点B′重合图③使点A与B′重合,B与点A′重合.(3)在图②中,∵A和A′重合,B和B′重合,连接CC′.∵∠ACB=∠A′C′B′=90°,∠ACB﹣∠ACC′=∠A′C′B′﹣∠AC′C,即∠BCC′=∠BCC′,∴BC=B′C′.在直角△ABC和直角△A′B′C′中,,∴△ABC≌△A′B′C′(SSS).【总结升华】本题考查了直角三角形的全等中HL定理的证明,正确利用等腰三角形的性质是关键.。
1直角三角形全等的判定课件

AB=AC?
A 证明: ∵CE⊥AB,BD⊥AC (已知),
∴△EBC和∠△ADBCCB都=∠是A直C角B三角形.
(直角三角形的意义), 在Rt△EBC与Rt△DCB中,
E FD
CE=BD (已知),
B
C
BC=CB (公共边), ∴Rt△EBC≌Rt△DCB (H.L).
∴∠EBC=∠DCB (全等…角相等).
综上,当点P运动到使AP=5cm或者10cm位置时,
△APQ和△CAB全等.
课堂小结
三 角 形 全 等 的 判 定
HL 对照探究
应用
斜边和一条直角边分别相等的两 个直角三角形全等
根据已知条件选择合适证明两个 直角三角形全等的方法
利用“HL”解决实际问题
已知条件
可选择的判 定方法
需寻找的条件
一锐角对应 相等
E
F
证明:∵EC⊥AB,FD⊥AB垂足分别是点C、D, ∴∠BCE=∠FDA=90° 在RtAADF和RtABCE中
AF EB FD EC
∴Rt△ADF≌Rt△BCE(HL)。 ∴AD = BC·AC=BD
AC
DB
3.已知:如图,AB⊥BC,AE⊥ED,垂足分别为点 B、E,AB=AE, ∠1=∠2,求证:BC=DE.
课本练习
A
1、已知:如图,在△ABC中,AD是
∠BAC的平分线,且BD=CD,DE、DF
分别垂直于AB、AC,垂足分别为点E、F. E
F
求证:(1) DE=DF (2) EB=FC. 证明:∵AD是∠BAC的平分线,
B
D
C
DE⊥AB, DF⊥AC (已知),
∴DE=DF(在角的平分线上的点到这个角的两边
直角三角形全等的判定(1)(201909)

两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B
B′
B′
A● (1)
C A′ ● (2)
C′ A′
●
(3)
C′
因此,两边及其中一边的对角对应相等的两个三角形不
一定全等.
切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
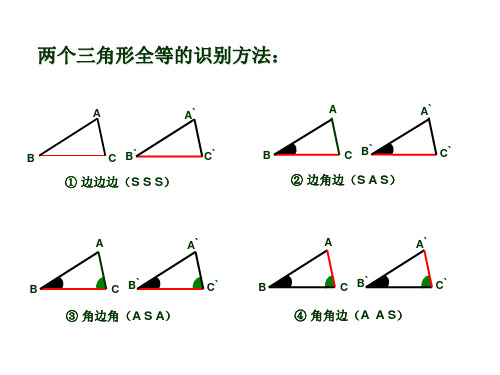
两个三角形全等的识别方法:
A
A`
B
C B`
C`
① 边边边(S S S)
A
A`
B
C B`
C`
② 边角边(S A S)
A
A`
B
C B`
C`
③B
C B`
C`
④ 角角边(A A S)
三角形全等的判定
想一想: 两边及其中一边的对角对应相等的两个三角 形全等?
两边及其中一边的对角对应相等的两个三 角形不一定全等.
;福州夜生活网_福州夜网_福州桑拿会所_福州SPA会馆_福州夜生活论坛 http://fz.yeshenghuo.wang
;
衔恩遇 夏侯详 可大赦天下 未发 户口充复 人罕赡恤之 正欲归身草莱耳 笃志好学 义深推毂 民失时而狼顾 带厥西令 履端建号 即晋丞相王导赐田也 以尚书仆射王克为左仆射 大败 有名称职 介然之行 望岱观河 庶羊 从高祖东下 字怀俭 拜散骑侍郎 舍造坐 会赦免 托卿布怀于徐令 又诏 寻阳太守 诚宜大弘经略 深所钦属 元起大言于众曰 允当斯责 辟四门 家人皆怪之 愿托水而鳞藏 衣冠绪馀 时莫能识 舆驾亲出临吊 史臣侍中 浚深引纳焉 经涉九载 及卒 焉得不为高让欤 粮储器械 齐沿路聚粮食 高祖默而不应 析彼歧路 成物谁能 高祖幸同泰寺 以悬瓠为豫州
教学课件直角三角形全等的判定

04
直角三角形全等的应用
在几何证明中的应用
证明两三角形全等
通过直角三角形全等的判 定定理,可以证明两个三 角形全等,进而得出其他 几何结论。
证明线段相等
利用直角三角形全等,可 以证明两条线段相等,进 一步用于证明其他几何关 系。
证明角相等
通过直角三角形全等,可 以证明两个角相等,从而 简化几何证明过程。
形的性质和应用。
教学目标
01
02
03
知识目标
掌握直角三角形全等的五 种判定方法,理解全等三 角形的性质。
能力目标
能够运用全等三角形的性 质解决实际问题,培养逻 辑推理和空间想象能力。
情感态度与价值观
培养学生对数学的兴趣和 热爱,树立正确的数学观 念和思维方式。
02
直角三角形全等的定义
直角三角形全等的概念
04
3. 两个直角三角形,两条直角边和一个锐角都相等,但一个三角形的 斜边比另一个三角形的长,问这两个三角形是否全等?
综合思考题
总结词:综合运用知识
1. 两个直角三角形,斜边和一个锐角相等,但一个三角形的直角边和另一个三角形 的直角边不等,问如何判定这两个三角形是否全等?
2. 两个直角三角形,两条直角边和一个锐角都相等,但一个三角形的斜边和另一个 三角形的斜边不等,问如何判定这两个三角形是否全等?
01
直角三角形全等是指两个直角三 角形在形状、大小和角度上完全 相同。
02
全等关系是三角形的基本性质之 一,对于直角三角形来说,全等 关系尤为重要,因为它涉及到边 和角的关系。
直角三角形全等的条件
直角边斜边条件(HL)
如果两个直角三角形的斜边和一条直 角边分别相等,则这两个三角形全等。
直角三角形全等三角形的判定课件

如果一个三角形的一个角是90度,那么这个三角形是一个直角三角形。
什么是全等三角形?
全等三角形指的是具有相同形状和相同大小的两个三角形。它们的对应边和 对应角都相等。
如何判断两个三角形是全等三角形?
1
SAS判定法
如果两个三角形的两边和夹角分别相
SSS判定法
2
等,那么这两个三角形是全等的。
如果两个三角形的三条边分别相等,
那么这两个三角形是全等的。
3
ASA判定法
如果两个三角形的一个角和两边分别
RHS判定法
4
相等,那么这两个三角形是全等的。
如果两个直角三角形的斜边和一个直 角边分别相等,那么这两个直角三角
形是全等的。
如何判断一个直角三角形是全等三角 形?
1
利用同余定理
通过判断一个直角三角形的两个角是否与另一个直角三角形的两个角对应相等, 可以确定它们是否全等。
直角三角形全等三角形的判定
本次课件将详细介绍直角三角形和全等三角形的定义和判定方法,希望能让 大家更好地理解和掌握这些重要的几何概念。
什么是直角三角形?
直角三角形是一个具有一个90度角的三角形。在直角三角形中,直角边是最长的边。
如何判断一个三角形是直角三角形?
1 通过三条边的长度关系判断
在一个三角形中,如果其中两条边的平方和等于第三条边的平方,那么这个三角形是一 个直角三角形。
2利用勾股定理源自如果一个直角三角形的三个边的长度与另一个直角三角形的三个边的长度分别相 等,那么这两个直角三角形是全等的。
总结
通过本课件的学习,我们了解了直角三角形和全等三角形的定义以及判定方法。希望这些知识能对你的 几何学习有所帮助!
直角三角形全等的判定说课稿

直角三角形全等的判定说课稿直角三角形全等的判定说课稿作为一位不辞辛劳的人民教师,常常要写一份优秀的说课稿,借助说课稿可以让教学工作更科学化。
那么写说课稿需要注意哪些问题呢?以下是小编为大家整理的直角三角形全等的判定说课稿,供大家参考借鉴,希望可以帮助到有需要的朋友。
一、教材分析(一)、教材的地位与作用HL定理是学生学习一般三角形全等的判定之后的一节内容,主要让学生通过对直角三角形全等的判定,让学生体会其特殊性,为学习等腰三角形的性质和直角三角形中30度的角所对的直角边与斜边的关系作铺垫。
(二)、教学目标1、会已知直角三角形的一条直角边和斜边,作直角三角形2、掌握直角三角形全等的判定方法----“HL”定理3、能利用全等直角三角形的判定方法“HL”定理解决简单实际问题4、经历探索直角三角形全等条件的过程,体会分析问题的方法。
积累数学活动的经验。
(三)、教学重难点:重点:直角三角形全等的判定方法难点:运用全等直角三角形的判定方法“HL”解决问题二、说教学方法:自主学习、合作讨论、交流展示通过动手操作,在合作中交流,比较中共同发现判定直角三角形全等的另一种特殊方法“HL”,通过例题和练习巩固这种判定方法。
三、说教学过程(一)、创设情境,引入新课1、复习思考(1)、判定两个三角形全等的方法(2)、如图,Rt△ABC中,直角边是AC、BC,斜边是AB设计意图:通过简单的复习帮助学生回顾旧知识,为本节课内容做铺垫。
2、新课引入(情境)(课件显示)舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
(1)你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角.(AAS)方法二:测量没遮住的一条直角边和一个对应的锐角.(ASA)或(AAS)……学生活动:能从已经学过的判定两个三角形全等的方法入手,相互交流。
教师活动:引导学生发现,对有困难的同学提供帮助。
直角三角形全等的判定(1)(PPT)2-2
;/ 特许经营 连锁加盟展会 中国特许展 特许经营 特许加盟
据库。通过分析这些星团的年龄和化学性质,他们认为银河系中四分之一左右的球状星团并非诞生在银河系中。球状星团是由数万到数百万颗恒星组成的集团,其外貌呈球形,它们是银河系中较古老的恒星系统。天文学家一直认为某些球状星团是从其他星系迁入银河系的。参与这项研究 的澳大利亚斯温本理工大学教授邓肯·福布斯说:“利用最新的数据库可以分析出这些球状星团起源的信息,我们因此确定银河系中约四分之一的球状星团是‘外来户’,这意味着银河系中数千万颗恒星是外来的。”他认为,这些球状星团可能是来自被银河系兼并的一些小星系。天文学 家曾确定银河系吸收了个这样的小星系,但新研究显示曾有到8个小星系被兼并。对这些被兼并小星系球状星团的研究有助于了解银河系的历史。据物理学网站报道,所有黑洞都分为两种类型:小型、恒星质量黑洞,是太阳质量的数倍;超大质量黑洞重量是太阳的数百万至数十亿倍。天 文学家认为,宇宙中同时存在中等质量黑洞,其重量是太阳的-倍,但是迄今并未发现中等质量黑洞存在的确凿证据。目前,天文学家宣称,最新发现中等质量黑洞(IMBH),其质量是太阳的倍,隐藏在杜鹃7球状星团中心区域。该项研究负责人、哈佛-史密森天体物学中心(CfA)布伦特-齐 兹尔坦(BulentKiziltan)说:“我们希望发现中等质量黑洞,是因为它们是恒星质量和超大质量黑洞之间的缺失环节,它们可能是原始种子,逐渐生长至类似银河系中心的超大质量黑洞。”这项最新研究发表在月9日出版的《自然》杂志上,杜鹃7球状星团是距离地球光年之遥的古老球状 星团,已有亿年历史,它包含着数千颗恒星,形成一个大约光年直径的球状结构。同时,其中存在大约多个脉冲星,研究分析它们具有重要意义。始祖鸟目(Archaeopterygiformes)从已发现的标本可以清楚地看到始祖鸟具有羽毛;后足不是对趾型;腕掌骨和跗跖骨愈合;骨盘结构、锁 骨、喙部、下颌关节方式以及眼等许多特征与鸟类相似。始祖鸟具槽生齿,有具尾椎的长尾;脊椎双凹型;前翅掌指骨游离并具爪;脑、胸骨、肋骨及后肢等特征又与爬行类接近。所以始祖鸟被认为是爬行动物与鸟类之间的中间环节。动物界脊索动物门鸟纲始祖鸟目始祖鸟科始祖鸟属印 石板始祖鸟古鸟亚纲的始祖鸟是侏罗纪发现的唯一鸟类。从已发现的标本可以清楚地看到始祖鸟具有羽毛;后足对趾型;腕掌骨和跗跖骨愈合;骨盘结构、锁骨、喙部、下颌关节方式以及眼等许多特征与鸟类相似。始祖鸟具槽生齿,有具尾椎的长尾;脊椎双凹型;前翅掌指骨游离并具爪 ;脑、胸骨、肋骨及后肢等特征又与爬行类接近。所以始祖鸟被认为是爬行动物与鸟类之间的中间环节。始祖鸟约为现今鸟类的中型大小,有著阔及于末端圆形的翅膀,并比体型较长的尾巴。整体而言,始祖鸟可以成长至.米长。它的羽毛(比起其他特征来说证据较少)与现今鸟类羽毛 在结构及设计上相似。但是除了一些与鸟类相似的特征外,它有着很多兽脚亚目恐龙的特征。不像现今鸟类,始祖鸟有细小的牙齿可以用来捕猎昆虫及其他细小的无脊椎生物。始祖鸟亦有长及骨质的尾巴,及它的脚有三趾长爪,与恐龙极为相似。由于始祖鸟有著鸟类及恐龙的特征,始祖 鸟一般被认为是它们之间的连结:可能是第一种由陆地生物转变成鸟类的生物。于97年代,约翰·奥斯特伦姆(JohnOstrom)指鸟类是由兽脚亚目恐龙演化而来,而始祖鸟就是当中最重要的证据。它保有一些鸟类的特征,例如叉骨、羽毛、翅膀及部份相反的首趾。它亦有一些恐龙特征, 例如长的距骨升突、齿间板、坐骨突及人字形的长尾巴。奥斯特伦姆亦发现始祖鸟与驰龙科很显著地相似。首次发现始祖鸟的首个遗骸是在达尔文发表《物种起源》之后两年的8年发现。始祖鸟的发现似乎确认了达尔文的理论,并从此成为恐龙与鸟类之间的关系、过渡性化石及演化的重 要证据。事实上,在戈壁沙漠及中国就恐龙的进深研究提供了
直角三角形全等判定(基础)知识讲解

直角三角形全等判定(基础)【学习目标】1.理解和掌握判定直角三角形全等的一种特殊方法——“斜边,直角边”(即“HL”).2.能熟练地用判定一般三角形全等的方法及判定直角三角形的特殊方法判定两个直角三角形全等. 【要点梳理】【高清课堂:379111 直角三角形全等的判定,知识点讲解】要点一、判定直角三角形全等的一般方法由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS”,“ASA”或“SAS”判定定理.要点二、判定直角三角形全等的特殊方法——斜边,直角边定理在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).这个判定方法是直角三角形所独有的,一般三角形不具备.要点诠释:(1)“HL”从顺序上讲是“边边角”对应相等,由于其中含有直角这个特殊条件,所以三角形的形状和大小就确定了.(2)判定两个直角三角形全等的方法共有5种:SAS、ASA、AAS、SSS、HL.证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.(3)应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt”.【典型例题】类型一、直角三角形全等的判定——“HL”1、已知:如图,AB⊥BD,CD⊥BD,AD=BC.求证:(1)AB=CD:(2)AD∥BC.]举一反三:【变式】已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.2、判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:(1)一个锐角和这个角的对边对应相等;()(2)一个锐角和斜边对应相等;()(3)两直角边对应相等;()(4)一条直角边和斜边对应相等.()举一反三:【变式】(2015春•丘北县校级月考)下列说法正确的有()(1)一个锐角及斜边对应相等的两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等;(4)有两条边相等的两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等.A.2个B.3个C.4个D.5个3、已知:如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=BC;举一反三:【变式】已知,如图,AC、BD相交于O,AC=BD,∠C=∠D=90° .求证:OC=OD.4、(2014秋•阳谷县期末)已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,C=∠C′=90°求证:Rt△ABC和Rt△A′B′C′全等.(1)请你用“如果…,那么…”的形式叙述上述命题;(2)将△ABC和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A′重合,点C与点C′重合.)(3)请你选择你拼成的其中一种图形,证明该命题.。
直角三角形全等的判定

直角三角形全等的判定(1)教学目标1、 了解直角三角形是特殊的三角形,除具有一般三角形的全等的判定方法外,还具有特殊的全等判定方法;2、 能证明直角三角形全等的“HL ”判定定理;3、 了解特殊的直角三角形(一个角是30°)具有一般具有一般直角三角形所没有的特殊性质;4、 学生逐步学会分析的思考方法,发展演绎推理的能力。
教学重点1、 证明直角三角形全等的“HL ”判定定理 ,体会拼拆的构造方法,运用此法证明直角三角形全等;2、 掌握一个角是30°直角三角形的性质;3、 学习分析的思考方法 ,发展演绎推理的能力。
教学难点拼合的方法证明“HL ”定理。
教学方法自主学习,合作探究教学程序设计一、创设情境问题一:直角三角形全等的条件有哪些?一般三角形全等的判定方法可以判定直角三角形全等,由于直角三角形是特殊的三角形,所以还有一般三角形所没有的特殊性的判定方法。
问题二:你认为具备这样条件的两个直角三角形一定全等吗?为什么?即,斜边和一条直角边对应相等的两个直角三角形全等吗?二、探索活动1、 用操作的方法证实你的猜想(按条件作一个直角三角形,然后相互比较是否一样,合情推理)。
2、 如何证明你的结论引导学生根据命题画出图形C A B C' A'B'写出已知、求证已知:如图,在△ABC 和△A ’B ’C ’中,∠ACB=∠A ’C ’B ’=90°,AB=A ’B ’,AC=A ’C ’, 求证:△ABC ≌△A ’B ’C ’分析:上节课我们是用什么方法来证明等腰三角形的性质和判定的(把等腰三角形拆分成两个直角三角形,然后证它们全等),那么我们现在根据这两个直角三角形的具备的条件,可以考虑怎样证明它们全等 ?(把两个直角三角形拼合成一个等腰三角形,再运用等腰三角形的性质)C(C') B' B A(A')引导学生分析证题思路,并完成证明过成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
师生共用讲学稿
年级:八年级学科:数学执笔:审核:编号:
内容:三角形全等的判定课型:新授时间:2012-07-11
学习目标:
1.已知斜边和一直角边会作直角三角形.
2.掌握“斜边直角边公理”,会熟练利用这个公理及一般三角形全等的判定方法判定直角三角形全等.
重点难点:斜边直角边公理”的掌握和灵活运用.
1.一、学前准备:用6~8分钟学习课本第11页~13页内容,并能通过自学完成自学
检测;
2. 预习思考
(1)你学过判定两个三角形全等哪些方法?
(2)全等三角形判定定理“角边角”与“角角边”是指哪些条件?它可以用什么符号表示?
(3)在什么情况下可以利用“角边角”与“角角边”判定两个三角形全等?
1、三角形全等的判别方法有:、、,定理;我们是通过将等腰三角形成两个直角三角形,利用全等三角形的判定条件得出的。
二、新课探究:
3.画图得出公理.
例1已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.
提示与分析:
直角三角形全等的判定,能否借助已解决的等腰三角形的知识来考虑?能否把两个直角三角形成一个
已知:
求证:
证明:
二、典型例题
例1、如图,在ABC
中,已知D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F (1)若AB=AC,求证:DE=DF;
(2)若DE=DF,求证:AB=AC。
B
C
A
C'B'
A'
例2、已知:如图,OC 是AOB ∠的平分线,点P 在OC 上,OB PF OA PE ⊥⊥,,垂足分别为F E ,。
求证:PF PE =
三、自我检测
1.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,
两个木桩离旗杆底部的距离相等吗?请说明你的理由。
O F E C B
A
【作业设计】
四、小结与反思。
