广东中考数学专题训练(二)：几何综合题(圆题)

合集下载

中考数学总复习《圆综合解答题》专题训练-附答案

中考数学总复习《圆综合解答题》专题训练-附答案学校：___________班级：___________姓名：___________考号：___________ 1．如图△ABC内接于⊙O AB、CD是⊙O的直径E是DA长线上一点且∠CED=∠CAB．(1)求证：CE是⊙O的切线；求线段CE的长．(2)若DE=3√5tanB=122．如图在△ABC中AB=AC以AB为直径作⊙O交BC于点D．过点D作DE⊥AC 垂足为E延长CA交⊙O于点F．(1)求证：DE是⊙O的切线；⊙O的半径为5 求线段CF的长．(2)若tanB=123．如图△ABC内接于⊙O直径DE⊙AB于点F交BC于点M DE的延长线与AC的延长线交于点N连接AM．（1）求证：AM＝BM；（2）若AM⊙BM DE＝8 ⊙N＝15° 求BC的长．4．如图△ABC内接于⊙O AB是⊙O的直径D是⊙O上的一点CO平分∠BCD CE⊥AD垂足为E AB与CD相交于点F．(1)求证：CE是⊙O的切线；时求CE的长．(2)当⊙O的半径为5sinB=355．如图1 锐角△ABC内接于⊙O⊙BAC=60°若⊙O的半径为2√3．(1)求BC的长度；(2)如图2 过点A作AH⊙BC于点H若AB+AC=12 求AH的长度．6．如图AB是⊙O的直径M是OA的中点弦CD⊥AB于点M过点D作DE⊥CA交CA的延长线于点E．(1)连接AD则∠AOD=_______；(2)求证：DE 与⊙O 相切；(3)点F 在BC ⏜上 ∠CDF =45° DF 交AB 于点N ．若DE =6 求FN 的长．7．如图 AB 是⊙O 的直径点C 为⊙O 上一点 OF ⊥BC 垂足为F 交⊙O 于点E AE 与BC 交于点H 点D 为OE 的延长线上一点且∠ODB =∠AEC ．(1)求证：BD 是⊙O 的切线(2)求证：CE 2=EH ⋅EA(3)若⊙O 的半径为52 sinA =35 求BH 和DF 的长． 8．如图在⊙ABC 中 ⊙C=90° 点O 在AC 上以OA 为半径的⊙O 交AB 于点D BD 的垂直平分线交BC 于点E 交BD 于点F 连接DE ．（1）求证：直线DE 是⊙O 的切线（2）若AB=5 BC=4 OA=1 求线段DE 的长．9．如图 AB 是⊙O 的直径弦CD 与AB 交于点E 过点B 的切线BP 与CD 的延长线交于点P 连接OC CB ．(1)求证：AE ·EB =CE ·ED(2)若⊙O 的半径为 3 OE =2BE CE DE =95 求tan∠OBC 的值及DP 的长．10．如图菱形ABCD中AB=4以AB为直径作⊙O交AC于点E过点E作EF⊥AD于点F．(1)求证：EF是⊙O的切线(2)连接OF若∠BAD=60°求OF的长．(3)在（2）的条件下若点G是⊙O上的一个动点则线段CG的取值范围是什么？11．如图点C在以AB为直径的半圆O上（点C不与A B两点重合）点D是弧AC的中点DE⊥AB于点E连接AC交DE于点F连接OF过点D作半圆O的切线DP 交BA的延长线于点P．(1)求证：AC∥DP(2)求证：AC=2DE的值．(3)连接CE CP若AE⊙EO=1⊙2求CECP12．如图1 AB为⊙O直径CB与⊙O相切于点B D为⊙O上一点连接AD OC若AD//OC．（1）求证：CD为⊙O的切线（2）如图2 过点A作AE⊥AB交CD延长线于点E连接BD交OC于点F若AB=3AE=12求BF的长．13．已知：如图在⊙O中∠PAD=∠AEP AF=CF AB是⊙O的直径CD⊥AB于点G．(1)求证：AP是⊙O的切线．(2)若AG=4tan∠DAG=2求△ADE的面积．(3)在（2）的条件下求DQ的长．14．如图已知AB是⊙O的直径点E是⊙O上异于A B的点点F是弧EB的中点连接AE AF BF过点F作FC⊙AE交AE的延长线于点C交AB的延长线于点D⊙ADC的平分线DG交AF于点G交FB于点H．(1)求证：CD是⊙O的切线(2)求sin⊙FHG的值(3)若GH＝4√2HB＝2 求⊙O的直径．15．如图⊙O的两条弦AB、CD互相垂直垂足为E且AB=CD．(1)求证：AC=BD．(2)若OF⊥CD于F OG⊥AB于G问四边形OFEG是何特殊四边形？并说明理由．(3)若CE=1，DE=3求⊙O的半径．16．【问题提出】如图1 △ABC为⊙O内接三角形已知BC=a圆的半径为R 探究a R sin∠A之间的关系．【解决问题】如图2 若∠A为锐角连接BO并延长交⊙O于点D连接DC则∠A=∠D在△DBC中BD为⊙O的直径BC=a所以BD=2R,∠BCD=90°．所以在Rt△DBC中建立a R sin∠D的关系为________________．所以在⊙O内接三角形△ABC中a R sin∠A之间的关系为________________．类比锐角求法当∠A为直角和钝角时都有此结论．【结论应用】已知三角形△ABC中∠B=60°,AC=4则△ABC外接圆的面积为________．17．已知AB为⊙O的直径PA PC是⊙O的的切线切点分别为A C过点C作CD//AB交⊙O于D．（1）如图当P D O共线时若半径为r求证CD=r（2）如图当P D O不共线时若DE=2CE=8求tan∠POA．18．如图1 已知矩形ABCD中AB=2√3AD=3 点E为射线BC上一点连接DE以DE为直径作⊙O（1）如图2 当BE=1时求证：AB是⊙O的切线（2）如图3 当点E为BC的中点时连接AE交⊙O于点F连接CF求证：CF=CD （3）当点E在射线BC上运动时整个运动过程中CF长度是否存在最小值？若存在请直接写出CF长度的最小值若不存在请说明理由．19．已知四边形ABCD为⊙O的内接四边形直径AC与对角线BD相交于点E作CH⊥BD于H CH与过A点的直线相交于点F∠FAD=∠ABD.（1）求证：AF为⊙O的切线（2）若BD平分∠ABC求证：DA=DC（3）在（2）的条件下N为AF的中点连接EN若∠AED+∠AEN=135°⊙O 的半径为2√2求EN的长.20．如图1 直线l1⊥l2于点M以l1上的点O为圆心画圆交l1于点A B交l2于点C D OM＝4 CD＝6 点E为弧AD上的动点CE交AB于点F AG⊙CE 于点G连接DG AC AD．（1）求⊙O的半径长（2）若⊙CAD＝40° 求劣弧弧AD的长（3）如图2 连接DE是否存在常数k使CE−DE=k·EG成立？若存在请求出k的值若不存在请说明理由（4）若DG⊙AB则DG的长为（5）当点G在AD的右侧时请直接写出⊙ADG面积的最大值．参考答案1．（1）证明：⊙AB是⊙O的直径⊙∠ACB=90°⊙∠CAB+∠B=90°⊙∠CED=∠CAB∠B=∠D⊙∠CED+∠D=90°⊙∠DCE=∠ACB=90°⊙CD⊥CE⊙CD是⊙O的直径即OC是⊙O半径⊙CE是⊙O的切线（2）由（1）知CD⊥CE在Rt△ABC和Rt△DEC中⊙∠B=∠D tanB=12⊙tan∠B=tan∠D=CECD =12⊙CD=2CE在Rt△CDE中CD2+CE2=DE2DE=3√5⊙(2CE)2+CE2=(3√5)2解得CE=3（负值舍去）即线段CE的长为3．2．解：（1）⊙OB=OD⊙∠ABC=∠ODB⊙AB=AC⊙∠ABC=∠ACB⊙∠ODB=∠ACB⊙OD∥AC⊙DE⊥AC OD是半径⊙DE⊥OD⊙DE是⊙O的切线．（2）连接BF AD⊙⊙O的半径为5 AB为直径⊙AB=10∠ADB=90°∠BFC=90°⊙tanB=1设AD=x则BD=2x2在Rt△ABD中由勾股定理得：AD2+BD2=AB2即x2+(2x)2=102解得：x=2√5或x=−2√5（舍去）⊙BD=2x=4√5⊙AB=AC∠ADB=90°⊙BD=CD⊙BC=2BD=8√5由（1）知OD∥AC⊙∠ODB=∠C⊙OB=OD⊙∠B=∠ODB=∠C⊙tanC=tanB=1即CF=2BF2在Rt△BCF中BF2+CF2=BC2即BF2+(2BF)2=(8√5)2解得BF=8或BF=−8（舍去）⊙CF=2BF=16．3．（1）证明：⊙直径DE⊙AB于点F⊙AF＝BF⊙AM＝BM（2）连接AO BO如图由（1）可得AM＝BM⊙AM⊙BM⊙⊙MAF＝⊙MBF＝45°⊙⊙CMN＝⊙BMF＝45°⊙AO＝BO DE⊙AB∠AOB⊙⊙AOF＝⊙BOF＝12⊙⊙N＝15°⊙⊙ACM＝⊙CMN+⊙N＝60° 即⊙ACB＝60°∠AOB．⊙⊙ACB＝12⊙⊙AOF＝⊙ACB＝60°．⊙DE＝8⊙AO＝4．得AF＝2√3在Rt⊙AOF中由sin∠AOF=AFAO在Rt⊙AMF中AM＝√2AF＝2√6．得BM= AM＝2√6得CM＝2√2在Rt⊙ACM中由tan∠ACM=AMCM⊙BC＝CM+BM＝2√2+2√6．4．（1）证明：⊙弧AC=弧AC⊙∠ADC=∠B．⊙OB=OC⊙∠B=∠OCB．⊙CO平分∠BCD⊙∠OCB=∠OCD⊙∠ADC=∠OCD．⊙CE⊥AD⊙∠ADC+∠ECD=90°⊙∠OCD+∠ECD=90°即CE⊥OC．⊙OC为⊙O的半径⊙CE是⊙O的切线．（2）连接OD得OD=OC⊙∠ODC=∠OCD．⊙∠OCD=∠OCB=∠B⊙∠ODC=∠B⊙CO=CO⊙△OCD≌△OCB⊙CD=CB．⊙AB是⊙O的直径⊙∠ACB=90°⊙AC=AB⋅sinB=10×35=6⊙CB=√AB2−AC2=√102−62=8⊙CD=8⊙CE=CD⋅sin∠ADC=CD⋅sinB=8×35=245．5．解：（1）连接OB OC过点O作OD⊙BC于点D⊙BD =CD =12BC⊙⊙A =60°⊙⊙BOC =2⊙A =120°⊙OB =OC⊙⊙OBC =⊙OCB =180°−∠BOC2=30°⊙OB =2√3⊙BD =OB •cos30°=2√3×√32=3⊙BC =2BD =6．（2）设点G 为此三角形ABC 内切圆的圆心（角平分线的交点）过G 分别向ABAC BC 作垂线GM GN GQ⊙GM =GN =GQ CQ =CN BQ =BM AM =AN⊙AM +AN =AB +AC -BC =6⊙AM =AN =3．在Rt △AGM 中⊙⊙GAM =30°⊙GM =√3⊙S △ABC =12BC •AH =S △ABG +S △BCG +S △ACG=12AB •GM +12BC •GQ +12AC •GN=12GM（AB+AC+CB）=9√3∵BC=6, S△ABC=12BC•AH⊙AH=3√3．6．（1）解：如图1 连接OD AD⊙AB是⊙O的直径CD⊥AB⊙AB垂直平分CD⊙M是OA的中点⊙OM=12OA=12OD⊙cos∠DOM=OMOD =12⊙∠DOM=60°即∠AOD=60°故答案为：60°（2）解：⊙CD⊥AB AB是⊙O的直径⊙CM=MD⊙M是OA的中点⊙AM=MO又⊙∠AMC=∠DMO⊙△AMC≌△OMD⊙∠ACM=∠ODM⊙CA∥OD⊙DE⊥CA⊙∠E=90°⊙∠ODE=180°−∠E=90°⊙DE⊥OD⊙DE与⊙O相切（3）如图2 连接CF CN⊙OA⊥CD于M⊙M是CD中点⊙NC=ND⊙∠CDF=45°⊙∠NCD=∠NDC=45°⊙∠CND=90°⊙∠CNF=90°由（1）可知∠AOD=60°∠AOD=30°⊙∠ACD=12在Rt△CDE中∠E=90°∠ECD=30°DE=6=12⊙CD=DEsin30°在Rt△CND中∠CND=90°∠CDN=45°CD=12⊙CN=CD•sin45°=6√2⊙∠AOD=60°，OA=OD⊙△OAD是等边三角形⊙∠OAD=60°∠CAD=2∠OAD=120°⊙∠CFD=180°−∠CAD=60°在Rt△CNF中∠CNF=90°∠CFN=60°CN=6√2 =2√6．⊙FN=CNtan60°7．（1）证明：如图1所示⊙∠ODB=∠AEC∠AEC=∠ABC⊙∠ODB=∠ABC⊙OF⊥BC⊙∠BFD=90°⊙∠ODB+∠DBF=90°⊙∠ABC+∠DBF=90°即∠OBD=90°⊙BD⊥OB⊙AB是⊙O的直径⊙BD是⊙O的切线（2）证明：连接AC如图2所示⊙OF⊥BC⊙弧BE=弧CE⊙∠CAE=∠ECB⊙∠CEA=∠HEC⊙△AEC ∽△CEH⊙CE EH =EACE⊙CE 2=EH ⋅EA（3）解：连接BE 如图3所示⊙AB 是⊙O 的直径⊙∠AEB =90°⊙⊙O 的半径为52 sin∠BAE =35 ⊙AB =5 BE =AB ⋅sin∠BAE =5×35=3 ⊙EA =√AB 2−BE 2=4⊙弧BE =弧CE⊙BE =CE =3⊙CE 2=EH ⋅EA⊙EH =94⊙在Rt △BEH 中 BH =√BE 2+EH 2=√32+(94)2=154 ⊙∠A =∠C⊙sinC =sinA⊙OF ⊥BC 垂足为F⊙在Rt △CFE 中 FE =CE ⋅sinC =3×35=95 ⊙CF =√CE 2−EF 2=√32−(95)2=125 ⊙BF =CF =125⊙OF =√BO 2−BF 2=√(52)2−(125)2=710 ⊙∠ODB =∠ABC⊙tan∠ODB =tan∠ABC⊙BFDF =OFBF⊙BF 2=OF ⋅DF⊙(125)2=710DF ⊙DF =28835．8．解：（1）连接OD 如图⊙EF 垂直平分BD⊙ED=EB⊙⊙EDB=⊙B⊙OA=OD⊙⊙A=⊙ODA⊙⊙A+⊙B=90°⊙⊙ODA+⊙EDB=90°⊙⊙ODE=90°⊙OD⊙DE⊙直线DE 是⊙O 的切线（2）作OH⊙AD 于H 如图则AH=DH 在Rt △OAB 中 sinA=BC AB =45在Rt △OAH 中 sinA=OH OA =45⊙OH=45⊙AH=√12−(45)2=35⊙AD=2AH=65 ⊙BD=5﹣65=195⊙BF=12BD=1910在Rt⊙ABC 中 cosB=45 在Rt⊙BEF 中 cosB=BF BE =45⊙BE=54×1910=198 ⊙线段DE 的长为198．9．(（1）证明：连接AD∵∠A =∠BCD ∠AED =∠CEB ∴ΔAED ∽ΔCEB∴ AECE =EDEB∴AE ·EB =CE ·ED（2）解：∵⊙O 的半径为 3 ∴OA =OB =OC =3∵OE =2BE∴OE =2 BE =1 AE =5 ∵ CEDE =95 ∴设CE =9x DE =5x∵AE ·EB =CE ·ED∴5×1=9x ·5x解得：x 1=13 x 2=−13（不合题意舍去） ∴CE =9x =3 DE =5x =53 过点C 作CF ⊥AB 于F∵OC =CE =3∴OF =EF =12OE =1∴BF =2在RtΔOCF中∵∠CFO=90°∴CF2+OF2=OC2∴CF=2√2在RtΔCFB中∵∠CFB=90°∴tan∠OBC=CFBF =2√22=√2∵CF⊥AB于F∴∠CFB=90°∵BP是⊙O的切线AB是⊙O的直径∴∠EBP=90°∴∠CFB=∠EBP在ΔCFE和ΔPBE中{∠CFB=∠PBE EF=BE ∠FEC=∠BEP∴ΔCFE≅ΔPBE(ASA)∴EP=CE=3∴DP=EP−ED=3−53=43．10．:解：（1）证明：如图连接OE．⊙四边形ABCD是菱形∴∠CAD=∠CAB∵OA=OE∴∠CAB=∠OEA∴∠CAD=∠OEA∴OE∥AD∵EF⊥AD∴OE⊥EF又⊙OE是⊙O的半径⊙EF是⊙O的切线．（2）解：如图连接BE．⊙AB是⊙O的直径∴∠AEB=90°∵∠BAD=60°∴∠CAD=∠CAB=30°在Rt△ABE中AE=AB·cos30°=2√3在Rt△AEF中EF=AE·sin30°=√3AB=2在Rt△OEF中OE=12⊙OF=√OE2+EF2=√4+3=√7．（3）解：如图过点C作CM垂直AB交AB延长线于点M由（2）知∠BAD=60°∴∠ACB=∠CAB=30°，∠CBM=60°∴AB=BC=4，BM=2，CM=2√3∴AM=6，OM=6−2=4．⊙OC=√OM2+CM2=√42+(2√3)2=2√7⊙CG近=2√7−2CE远=2√7+2⊙线段CG的取值范围是：2√7−2≤CG≤2√7+211．（1）证明：连接OD∵D为弧AC的中点∴OD⊥AC又∵DP为⊙O的切线∴OD⊥DP∴AC∥DP（2）证明：∵DE⊥AB∴∠DEO=90°由（1）可知OD⊥AC设垂足为点M∴∠OMA=90°∴∠DEO=∠OMA AC=2AM又∵∠DOE=∠AOM OD=OA∴△ODE≌△OAM(AAS)∴DE=AM∴AC=2AM=2DE（3）解：连接OD OC CE CP∵∠ODP=∠OED=90°∠DOE=∠DOP ∴△DOE∽△POD∴ODOP =OEOD∴OD2=OE⋅OP ∵OC=OD∴OC2=OE⋅OP∴OCOE =OPOC又∵∠COE=∠POC ∴△COE∽△POC∴CECP =OEOC∵AE:EO=1:2∴OEOA =23∴OEOC =23∴CECP =23．12．解：（1）连接OD⊙CB与⊙O相切于点B⊙OB⊥BC⊙AD//OC⊙∠A=∠COB,∠ADO=∠DOC⊙OA=OD⊙∠A=∠ADO=∠COB=∠DOC⊙△DOC≌△BOC(SAS)⊙∠ODC=∠OBC=90°⊙OD⊥DC又OD为⊙O半径⊙CD为⊙O的切线（2）解：设CB=x⊙AE⊥EB⊙AE为⊙O的切线⊙CD CB为⊙O的切线⊙ED=AE=4,CD=CB=x,∠DOC=∠BCO⊙BD⊥OC过点E作EM⊥BC于M则EM=12,CM=x−4⊙(4+x)2=122+(x−4)2解得x=9⊙CB=9⊙OC=√62+92=3√13⊙AB是直径且AD⊙OC⊙⊙OFB=⊙ADB=⊙OBC=90°又⊙⊙COB=⊙BOF⊙⊙OBF⊙⊙OCB⊙OB BF =OCBC⊙BF=OB⋅BCOC =6×93√13=1813√1313．（1）证明：如图所示连接AC ⊙AB是⊙O的直径CD⊥AB⊙弧AD=弧AC⊙∠AEP=∠ADC⊙∠PAD=∠AEP⊙∠PAD=∠ADC⊙AP∥CD⊙AP⊥AB⊙AB是⊙O的直径⊙AP是⊙O的切线（2）解：如图所示连接BD⊙AF=CF⊙∠FAC=∠FCA⊙弧CE=弧AD⊙弧AD=弧AC⊙弧AD=弧AC=弧CE⊙∠ADG=∠QDG⊙AB⊥CD⊙∠AGD=∠QGD=90°又⊙OG=OG⊙△AGD≌△OGD(ASA)⊙QG=AG=4∠DQG=∠DAG=2在Rt△ADG中tan∠DAG=DGAG⊙DG=2AG=8⊙QD=√DG2+QG2=4√5连接OD过点E作EH⊥AB于H设圆O的半径为r则OG=r−4在Rt△ODG中由勾股定理得OD2=OG2+DG2⊙r2=(r−4)2+82解得r=10⊙AB=20⊙BQ=12⊙∠AEQ=∠DBQ，∠EAQ=∠BDQ⊙△AQE∽△DQB⊙QE BQ =AQDQ即QE12=84√5⊙QE=12√55⊙∠EQH=∠DQG=∠DAG⊙在Rt△EQH中tan∠EQH=EHQH=2⊙EH=2QH⊙EH2+QH2=QE2⊙4QH2+QH2=1445⊙QH=125⊙EH=245⊙S△ADE=S△ADQ+S△AEQ=12AQ⋅DG+12AQ⋅EH=12×8×8+12×8×245=70.4．（3）解：由（2）得DQ=4√5．14．（1）证明：连接OF．⊙OA＝OF⊙⊙OAF＝⊙OF A⊙EF̂=FB̂,⊙⊙CAF＝⊙F AB⊙⊙CAF＝⊙AFO⊙OF∥AC⊙AC⊙CD⊙OF⊙CD⊙OF是半径⊙CD是⊙O的切线．（2）⊙AB是直径⊙⊙AFB＝90°⊙OF⊙CD⊙⊙OFD＝⊙AFB＝90°⊙⊙AFO＝⊙DFB⊙⊙OAF＝⊙OF A⊙⊙DFB＝⊙OAF⊙GD平分⊙ADF⊙⊙ADG＝⊙FDG⊙⊙FGH＝⊙OAF+⊙ADG⊙FHG＝⊙DFB+⊙FDG⊙⊙FGH＝⊙FHG＝45°⊙sin⊙FHG=sin45°=√22（3）解：过点H作HM⊙DF于点M HN⊙AD于点N．⊙HD平分⊙ADF⊙HM＝HNS△DHF⊙S△DHB= FH⊙HB=DF ⊙DB⊙⊙FGH是等腰直角三角形GH＝4√2⊙FH＝FG＝4⊙DF DB =42=2设DB＝k DF＝2k⊙⊙FDB＝⊙ADF⊙DFB＝⊙DAF ⊙⊙DFB⊙⊙DAF⊙DF2＝DB•DA⊙AD＝4k⊙GD平分⊙ADF⊙FG AG =DFAD=12⊙AG＝8⊙⊙AFB＝90° AF＝12 FB＝6∴AB=√AF2+BF2=√122+622=6√5⊙⊙O的直径为6√515．（1）证明：⊙AB=CD⊙弧AB=弧CD⊙弧AB−弧BC=弧CD−弧BC即弧AC=弧BD⊙AC=BD（2）解：四边形OFEG是正方形.理由如下：⊙AB⊥CD OF⊥CD OG⊥AB⊙∠AED=∠OGE=∠OFE=90°⊙四边形OFEG是矩形．如图连接OA OD．⊙OF⊥CD OG⊥AB⊙CF=DF AG=BG．⊙CD=AB⊙AG=DF．⊙OG=√OA2−AG2OF=√OD2−DF2OA=OD⊙OG=OF⊙四边形OFEG是正方形（3）解：⊙CE=1 DE=3⊙CD=4⊙CF=DF=2⊙EF=CF-CE=2-1=1．⊙四边形OFEG是正方形⊙OF=EF=1．在Rt△OED中OD=√OF2+DF2=√5⊙⊙O的半径为√5．16．:解：【解决问题】如图连接BO并延长交⊙O于点D连接DC则∠A=∠D 在△DBC中⊙BD为⊙O的直径BC=a⊙BD=2R,∠BCD=90°⊙sinD=BCBD =a2R⊙sinA=a2R故答案为：sinD=a2R sinA=a2R【结论应用】解：设△ABC外接圆的半径为R ⊙∠B=60°,AC=4⊙sinB=AC2R⊙√3 2=42R解得：R=43√3⊙△ABC外接圆的面积为π×(43√3)2=163π．故答案为：163π17．（1）证明：连接OC⊙PA PC是⊙O的切线切点分别为A C ⊙PA=PC∠PAO=∠PCO=90°在RtΔPAO和RtΔPCO中{PA=PCPO=PO⊙RtΔPAO≌RtΔPCO(HL)⊙∠POA=∠POC⊙CD//AB⊙∠CDO=∠DOA⊙∠CDO=∠COD⊙CD=OC=r（2）解：设OP交CD于E连接OC过O作OH⊥CD于点H由（1）可知RtΔPAO≌RtΔPCO⊙∠POA=∠POC⊙CD//AB⊙∠CEO=∠EOA⊙∠CEO=∠COE⊙CE=CO=8⊙CD=CE+ED=10⊙OH⊥CD⊙CH=DH=5⊙EH=DH−DE=3在RtΔCHO中⊙OH=√OC2−CH2=√82−52=√39在RtΔOHE中⊙tan∠POA=tan∠HEO=OHEH =√393⊙tan∠POA=√393．18．解：（1）如图过点O作OM⊥AB且OM的反向延长线交CD于点N．由题意可知四边形BCNM为矩形⊙MN=AD=3⊙O为圆心即O为DE中点⊙N为DC中点即线段ON为△DEC中位线又⊙CE=BC−BE=3−1=2⊙ON=12CE=1⊙OM=MN -ON=3-1=2．在Rt △DEC 中 DE =√CD 2+CE 2=√(2√3)2+22=4． ⊙OD=DE=OM=2．即AB 为⊙O 的切线．（2）设⊙O 与AD 交于点G 连接CG EG DF FG ⊙DE 为直径⊙∠EGD =∠EFD =90°．⊙∠GEC =90°⊙CG 为直径．⊙∠CFG =∠CDG =90°⊙E 为BC 中点⊙G 为AD 中点在Rt △AFD 中 FG 为中线⊙AG=DG=FG在Rt △CFG 和Rt △CDG 中 {FG =DG CG =CG⊙△CFG ≅△CDG(HL)．⊙CF=CD ．（3）如图取AD 中点H 连接CH FH FD ．由（2）可知FH =12AD =32 在Rt △CDH 中 CH =√CD 2+HD 2=√(2√3)2+(32)2=√572 ⊙CF ≥CH −FH =√572−32． ⊙当F 点在CH 上时CF 长有最小值最小值为√572−32．19．解：（1）⊙AC 为⊙O 的直径⊙⊙ADC =90°⊙⊙DAC +⊙DCA =90°．⊙弧AD =弧AD⊙⊙ABD =⊙DCA ．⊙⊙F AD =⊙ABD⊙⊙F AD =⊙DCA⊙⊙F AD +⊙DAC =90°⊙CA ⊙AF⊙AF 为⊙O 的切线．（2）连接OD ．⊙弧AD =弧AD⊙⊙ABD=1⊙AOD．2⊙弧DC=弧DC⊙DOC．⊙⊙DBC=12⊙BD平分⊙ABC⊙⊙ABD=⊙DBC⊙⊙DOA=⊙DOC⊙DA=DC．（3）连接OD交CF于M作EP⊙AD于P．⊙AC为⊙O的直径⊙⊙ADC=90°．⊙DA=DC⊙DO⊙AC⊙⊙F AC=⊙DOC=90° AD=DC=√(2√2)2+(2√2)2=4 ⊙⊙DAC=⊙DCA=45° AF⊙OM．⊙AO=OCAF．⊙OM=12⊙⊙ODE+⊙DEO=90° ⊙OCM+⊙DEO=90°⊙⊙ODE=⊙OCM．⊙⊙DOE=⊙COM OD=OC⊙⊙ODE⊙⊙OCM⊙OE=OM．设OM=m⊙OE =m AE =2√2−m AP =PE =2−√22m⊙DP =2+√22m ． ⊙⊙AED +⊙AEN =135° ⊙AED +⊙ADE =135°⊙⊙AEN =⊙ADE ．⊙⊙EAN =⊙DPE⊙⊙EAN ⊙⊙DPE⊙AE DP =AN PE ⊙2√2−m 2+√22m =m2−√22m⊙m =2√23⊙AN =2√23 AE =4√23由勾股定理得：NE =2√103．20．解：（1）连接OD⊙AB 是⊙O 的直径 l 1⊥l 2 CD ＝6⊙CM =DM =12CD =3在Rt △DOM 中 OM ＝4⊙OD=√OM2+CM2=5即⊙O的半径长为5（2）⊙AB是⊙O的直径l1⊥l2⊙弧BC=弧BD⊙∠BAD=∠BAC=12∠CAD=20°⊙∠BOD=2∠BAD=40°⊙∠AOD=180°−∠BOD=140°⊙劣弧弧AD的长为140×π×5180=35π9（3）存在常数k=2理由如下：如图在CG上截取CH=DE连接AH AE⊙AB垂直平分CD⊙AC=AD又⊙⊙ACH=⊙ADE⊙⊙ACH⊙⊙ADE（SAS）⊙AH=AE⊙ AG⊙HE⊙HG=EG⊙CE-DE=2EG⊙k=2（4）⊙DG⊙AB⊙⊙CFM⊙⊙CGD⊙FM DG =CFCG=CMCD=12⊙CF=FG DG=2FM⊙⊙CMF=⊙AGF⊙CFM=⊙AFG ⊙⊙CFM⊙⊙AFG⊙CF AF =FMFG⊙FM×AF=CF×FG=CF2设FM=x则AF=9-x⊙x(9−x)=32+x2解得：x=32或3⊙DG=3或6（5）如图取AC的中点P当PG⊙AD时⊙ADG的面积最大在Rt△AMC中⊙CMA=90° CM=3 AM=OA+OM=5+4=9⊙AD=AC=√CM2+AM2=√32+92=3√10在Rt△AGC中⊙CGA=90° 点P为AC的中点⊙PG=12AC=3√102过点C作CN⊙AD于点N在Rt⊙CDN和Rt⊙ADM中⊙⊙CND=⊙AMD=90° ⊙CDN=⊙ADM ⊙Rt⊙CDN~Rt⊙ADM⊙CN AM =CDAD⊙CN=AM⋅CDAD =9×63√10=9√105设PG交AD于点K ⊙PK⊙AD CN⊙AD ⊙PK⊙CN⊙⊙APK⊙⊙CAN⊙PK CN =APAC=12⊙PK=12CN=9√1010⊙GK=PG−PK=3√102−9√1010=3√105⊙⊙ADG面积的最大值为12AD⋅GK=12×3√10×3√105=9．。

2023年九年级中考数学高频考点专题训练圆的综合题(含解析)

2023年中考数学高频考点专题训练--圆的综合题1．已知：△ABC内接于△O，直径AM平分△BAC．（1）如图1，求证AB＝AC；（2）如图2，弦FG分别交AB、AC于点D、E，AE＝BD，当△ADE+△DEC＝90°时，连接CD，直径AM分别交DE、CD、BC于N、H、R，若CD△AB，求证：△NDC＝△ACB；（3）在（2）的条件下，若DE长为√2，求△ACH的面积．2．在平面直角坐标系xOy中，对于点P，Q和图形G，给出如下定义：若图形G上存在一点C，使△PQC＝90°，则称点Q为点P关于图形G的一个“直角联络点”，称Rt△PCQ为其对应的“联络三角形”．如图为点P关于图形G的一个“直角联络点”及其对应的“联络三角形”的示例．（1）已知点A（4，0），B（4，4）①在点Q1（2，2），Q2（4，﹣1）中，点O关于点A的“直角联络点”是；②点E的坐标为（2，m），若点E是点O关于线段AB的“直角联络点”，直接写出m的取值范围；（2）△T的圆心为（t，0），半径为√10，直线y＝﹣x+2与x，y轴分别交于H，K两点，若在△T上存在一点P，使得点P关于△T的一个“直角联络点”在线段HK 上，且其对应的“联络三角形”是底边长为2的等腰三角形，直接写出t的取值范围．3．对于平面直角坐标系xOy中的点P和△C，给出如下定义：若△C上存在一个点M，使得PM = MC，则称点P为△C的“等径点”．已知点D (12，13)，E(0，2√3)，F (−2，0)．（1）当△O的半径为1时，①在点D，E，F中，△O的“等径点”是；②作直线EF，若直线EF上的点T（m，n）是△O的“等径点”，求m的取值范围．（2）过点E作EG△EF交x轴于点G，若△EFG上的所有点都是某个圆的“等径点”，求这个圆的半径r的取值范围．4．问题背景：如图①，在四边形ADBC中，△ACB=△ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE 是等腰直角三角形，所以CE= √2CD，从而得出结论：AC+BC= √2CD．简单应用：（1）在图①中，若AC= √2，BC=2 √2，则CD=．（2）如图③，AB是△O的直径，点C、D在△上，AD̂= BD̂，若AB=13，BC=12，求CD的长．拓展规律：（3）如图④，△ACB=△ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD 的长（用含m，n的代数式表示）（4）如图⑤，△ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= 1 3AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是．5．如图，等边三角形ABC中，AB= 2√3，AH△BC于点H，过点B作BD△AB交线段AH的延长线于点D，连结CD. 点E为线段AD上一点(不与点A，D重合)，过点E作EF△AB交BC于点F，以EF为直径作△O. 设AE的长为x.（1）求线段CD的长度.（2）当点E在线段AH上时，用含x的代数式表示EF的长度.（3）当△O与四边形ABDC的一边所在直线相切时，求所有满足条件的x的值. 6．如图1，⊙O是ΔABC的外接圆，AB是直径，D是⊙O外一点且满足∠DCA=∠B，连接AD.（1）求证：CD是⊙O的切线；（2）若AD⊥CD，AB=8，AD=6，求AC的长；（3）如图2，当∠DAB=45°时，AD与⊙O交于E点，试写出AC、EC、BC 之间的数量关系并证明.7．问题探究（1）如图1，在△ABC中，BC=8，D为BC上一点，AD=6，则△ABC面积的最大值是。

广东省2024年九年级中考数学一轮复习：圆模拟练习(含解析)

2024年广东省九年级数学一轮复习：圆模拟练习一、单选题1．（2023·广东广州·中考真题）如图，的内切圆与，，分别相切于点D，E，F，若的半径为r，，则的值和的大小分别为（）A．2r，B．0，C．2r，D．0，2．（2023·广东·中考真题）如图，是的直径，，则（）A．B．C．D．3．（2023·广东清远·二模）如图，在边长为4正方形中，点E在以B为圆心的弧上，射线交于F，连接，若，则（）．A．2B．C．D．4．（2023·广东河·一模）如图，为⊙O的直径，是⊙O的弦，点是上的一点，且．若，，则的长为（）A．B．C．D．5．（2023·广东湛江·一模）如图，、是的直径，弦，弧为，则的度数为（）A．B．C．D．6．（2023·广东佛山·一模）如图，点A、B、C在上，，则（）A．18°B．36°C．72°D．144°7．（2023·广东深圳·模拟预测）下列说法中正确的一项是（）A．经过三点有且只有一个圆B．在圆中，长度相等的弦所对的圆心角相等C．有一组对边平行，一组对角相等的四边形是平行四边形D．有两条边相等的直角三角形全等8．（2023·广东清远·模拟预测）如图，是半的直径，点在半上，．是上的一个动点，连接，过点作于，连接．在点移动的过程中，的最小值为（）A．B．C．D．29．（2023·广东云浮·一模）如图，切于C，点D从C出发，以每秒的速度沿方向运动，运动1秒时，运动2秒时长是（）A．B．C．D．10．（2023·广东深圳·二模）如图，在中，，，，D是上一动点，于E，交于点F，则的最大值是（）A．B．C．D．11．（2023·广东阳江·二模）如果一个正多边形的中心角是，那么这个正多边形的边数是（）A．4B．6C．8D．1012．（2023·广东广州·二模）如图，正六边形内接于，点是上的一点，则的度数为（）A．B．C．D．13．（2023·广东深圳·模拟预测）如图，在中，，以点B为圆心，长为半径画弧，交边于点D，则的长为（）A．B．C．D．14．（2023·广东珠海·一模）如图，切于两点，若，的半径为，则阴影部分的面积为（）A．B．C．D．二、填空题15．（2023·广东深圳·中考真题）如图，在中，为直径，C为圆上一点，的角平分线与交于点D，若，则°．16．（2023·广东东莞·一模）如图，四边形为的内接四边形，，则的度数为．17．（2023·广东广州·一模）如图，是的弦，交于点P，过点B的直线交的延长线于点C，若，，，则的长为．18．（2023·广东梅州·一模）如图，是上的三个点，，则度数是．19．（2023·广东东莞·一模）如图，在平面直角坐标系中，已知，以点C为圆心的圆与y轴相切，点A、B在x轴上，且．点P为上的动点，，则长度的最小值为．20．（2023·广东广州·一模）如图，在中，为直径，点M为延长线上的一点，与相切于点C，圆周上有另一点D与点C分居直径两侧，且使得，连接．现有下列结论：①与相切；②四边形是菱形；③；④．其中正确的结论是（填序号）．21．（2023·广东揭阳·一模）一个正多边形的中心角为36°，则这个正多边形的内角和为度．22．（2023·广东东莞·三模）如图，和是两个完全重合的直角三角板，，斜边长为三角板绕直角顶点顺时针旋转，当点落在边上时，则点所转过的路径长为．23．（2023·广东潮州·一模）如图，正方形的边长为2，分别以为圆心，以正方形的边长为半径的圆相交于点，那么图中阴影部分的面积为．三、解答题24．（2023·广东广州·中考真题）如图，在平面直角坐标系v中，点，，所在圆的圆心为O．将向右平移5个单位，得到（点A平移后的对应点为C）．(1)点D的坐标是___________，所在圆的圆心坐标是___________；(2)在图中画出，并连接，；(3)求由，，，首尾依次相接所围成的封闭图形的周长．（结果保留）25．（2023·广东·中考真题）综合探究如图1，在矩形中，对角线相交于点，点关于的对称点为，连接交于点，连接．(1)求证：；(2)以点为圆心，为半径作圆．①如图2，与相切，求证：；②如图3，与相切，，求的面积．26．（2023·广东东莞·一模）如图，在中，，延长到点D，以为直径作，交的延长线于点E，延长到点F，使．(1)求证：是的切线；(2)若的半径为5，，，求的长．27．（2023·广东汕头·一模）如图，内接于．是直径，过点作直线，且是的切线．(1)求证：．(2)设是弧的中点，连接交于点，过点作于点，交于点．①求证：．②若，，试求的长．28．（2023·广东肇庆·二模）如图，在中，，平分交于点，为上一点，经过点，的分别交，于点，连接交于点．(1)求证：是的切线；(2)若，半径为4，在圆O上取点P，使，求点P到直线的距离．29．（2023·广东茂名·一模）张师傅要将一张残缺的圆形轮片恢复原貌（如图），已知轮片的一条弦的垂直平分线交弧于点，交弦于点，测得，．(1)请你帮张师傅找出此残片所在圆的圆心（尺规作图，不写作法，保留作图痕迹）；(2)求（1）中所作圆的半径．30．（2023·广东河·三模）【发现问题】爱好数学的小明在做作业时碰到这样的一道题目：如图，点为坐标原点，的半径为，点．动点在上，连接，作等边（，，为顺时针顺序），求的最大值；【解决问题】小明经过多次的尝试与探索，终于得到解题思路：在图中，连接，以为边在的左侧作等边，连接．（）请你找出图中与相等的线段，并说明理由；（）线段的最大值为．【灵活运用】（）如图，在平面直角坐标系中，点的坐标为，点的坐标为，点为线段外一动点，且，，，求线段长的最大值及此时点的坐标．【迁移拓展】（）如图③，，点是以为直径的半圆上不同于的一个动点，以为边作等边，请直接写出的最值．参考答案：1．D【分析】如图，连接．利用切线长定理，圆周角定理，切线的性质解决问题即可．【详解】解：如图，连接．∵的内切圆与，，分别相切于点D，E，F，∴，∴，，∴，∴．故选：D．【点睛】本题考查三角形的内切圆与内心，圆周角定理，切线的性质等知识，解题的关键是掌握切线的性质，属于中考常考题型．2．B【分析】根据圆周角定理可进行求解．【详解】解：∵是的直径，∴，∵，∴，∵，∴；故选B．【点睛】本题主要考查圆周角的相关性质，熟练掌握直径所对圆周角为直角是解题的关键．3．B【分析】如图，连接，过点B作于点H，根据圆的性质和等腰三角形的性质可定，再结合正方形的性质可得；再证可得，即；然后再根据勾股定理列方程即可解答．【详解】解：如图，连接，过点B作于点H，∵点E在以B为圆心的弧上，∴，∵，∴，∵四边形是正方形，∴，∴，∵，∴，∴，∴，在中，，∴，∴或（舍去）．故选：B．【点睛】本题主要考查了圆的基本性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识点，灵活运用相关知识成为解答本题的关键．4．B【分析】连接，交于，根据垂径定理推论，再由垂径定理，再由勾股定理计算，的长，从而求得的长，此题考查了圆周角定理，垂径定理和勾股定理的性质，正确作出辅助线是解题的关键．【详解】解：连接，交于，∵，∴点是的中点，∴，，∴，∵，∴，∴，∴，∵为的直径，∴，∴，故选：．5．C【分析】连接，利用等边对等角，弦，圆心角，弧的关系，平行线的性质计算即可.【详解】连接，解：∵弧为，∴，∵，∴，∵，∴，故选：C．【点睛】本题考查了等边对等角，弦，圆心角，弧的关系，平行线的性质，熟练掌握平行线的性质，圆的性质是解题的关键.6．C【分析】本题考查圆周角定理，根据对边对等角，三角形的内角和定理，求出的度数，根据同弧所对的圆周角等于圆心角的一半，即可得出结果．【详解】解：∵点A、B、C在上，∴，∴，∴，∴；故选C．7．C【分析】根据确定圆的条件对A进行判断；根据弦与圆心角关系对B进行判断；根据平行四边形的判定方法对C进行判断；根据全等三角形的判定对D进行判断．【详解】解：A、经过不在同一直线上的三点有且只有一个圆，故此选项错误；B、在同圆或等圆中，长度相等的弦所对的圆心角相等，故此选项错误；C、有一组对边平行，一组对角相等的四边形是平行四边形，故此选项正确；D、有两条边相等的直角三角形不一定全等，故此选项错误．故选：C．【点睛】此题主要考查了确定圆的条件、弦与圆心角的关系、平行四边形的判定及全等三角形的判定方法等知识，正确有关图形的判定与性质是解题关键．8．D【分析】以为直径画圆，圆心为，连接、，在点移动的过程中，点在以为直径的圆上运动，当、、共线时，的值最小，最小值为，利用勾股定理求出即可解决问题．【详解】解：如图，以为直径画圆，圆心为，连接、，，∵，∴，∴在点移动的过程中，点在以为直径的圆上运动，∵是直径，∴，在中，∵，∴，在中，，∵，∴当、、共线时，的值最小，最小值为，故选：D．【点睛】本题主要考查了勾股定理、点与圆的位置关系等知识，解题的关键是确定点的运动轨迹是在以为直径的圆上运动，属于中考填空题中的压轴题．9．C【分析】本题考查切线的性质、勾股定理，掌握切线性质是关键．先证得，再利用勾股定理求解即可．【详解】解：∵切于C，∴，∵点D从C出发，以每秒的速度沿方向运动，∴运动1秒时，又∵运动1秒时，∴在中，由勾股定理得：，∵运动2秒时长为，∴此时．故选：C．10．B【分析】取的中点O，连接，，延长交于T．证明，推出点E在以O为圆心，为半径的圆上运动，推出当与相切时，的值最大，根据切线的性质、平行线的性质及含30度角的直角三角形的性质即可得出答案．【详解】解：如图，取的中点O，连接，，延长交于T．∵，，，∴，∴，，∵，∴，∴E在上，∵，∴，∴点E在以O为圆心，为半径的圆上运动，∵，∴当与相切时，的值最大，∵直线，直线都是的切线，∴，∴，∵，，∴，∵，，∴，∴，∵，，∴，∵，∴，∴，∴，∴，∴的最大值为．故选：B．【点睛】本题考查直角三角形角的性质、直线与圆的位置关系、线段的垂直平分线的性质等知识，解题的关键是发现点E在以O为圆心，为半径的圆上运动，并推出与相切时，的值最大．11．C【分析】根据正多边形的边数周角中心角，计算即可得解．【详解】解：这个多边形的边数是，故选：C．【点睛】本题考查的是正多边形的中心角的有关计算；熟记正多边形的中心角与边数的关系是解题的关键．12．B【分析】利用圆内接正多边形中心角及同弧所多对的圆周角是圆心角一半定理即可．【详解】如图，连接，，∵六边形是圆内接正六边形，∴，∴，故选：．【点睛】本题考查圆内接正多边形和圆周角定理，解此题的关键是熟练掌握圆内接正多边形中心角计算和圆周角定理角度计算．13．B【分析】根据直角三角形的性质得到，根据已知条件得到是等边三角形，由等边三角形的性质即可得到结论．【详解】解：连接，，，，，，以点为圆心，长为半径画弧，交边于点，是等边三角形，，，故选：B．【点睛】本题考查了含角的直角三角形的性质，等边三角形的判定和性质及弧长公式，熟练掌握直角三角形的性质是解题的关键．14．B【分析】如图所示，连接，可证，，，根据含角的直角三角形的性质可计算出的值，由此可算出四边形的面积，再根据四边形的性质，算出的角度，可算出扇形的面积，由此即可求解．【详解】解：如图所示，连接，∵切于，，∴，，∴是的角平分线，则，∵，是公共边，∴，∴，在中，，∴，∴，∴，在四边形中，，∴，∴，∴，故选：．【点睛】本题主要考查扇形，不规则图像面积的计算方法，掌握圆的基础知识，扇形的面积计算方法，不规则图形面积的计算方法是解题的关键．15．35【分析】由题意易得，，则有，然后问题可求解．【详解】解：∵是的直径，∴，∵，，∴，∴，∵平分，∴；故答案为35．【点睛】本题主要考查圆周角的性质，熟练掌握直径所对圆周角为直角是解题的关键．16．/70度【分析】本题考查圆内接四边形的性质，掌握圆内接四边形对角互补是解题关键．直接利用圆内接四边形对角互补与邻补角的性质推导可得出答案．【详解】解：∵四边形为的内接四边形，，即，，故答案为：．17．4【分析】由垂直定义得，根据等腰三角形的性质由得，根据对顶角相等得，所以，而，所以，设，则，在中，根据勾股定理得到，然后解方程即可．【详解】解：连接，如图所示：∵，∴，∴，∵，∴，而，∴，∵，∴，∴，∴为直角三角形，设，则，在中，，，∵，∴，解得：，即的长为4．故答案为：4．【点睛】本题考查了圆的基本知识，等腰三角形的性质以及勾股定理，垂线定义理解，正确应用勾股定理求出的长是解题关键．18．【分析】由圆周角定理即可得到答案．【详解】解：，，故答案为：．【点睛】本题主要考查了圆周角定理，熟练掌握圆周角定理：同弧所对的圆周角等于圆心角的一半，是解题的关键．19．4【分析】本题考查了切线的性质，坐标和图形的性质，圆周角定理，找到的最小值是解题的关键．连接，交上一点P，以O为圆心，以为半径作，交x轴于A、B，此时的长度最小，根据勾股定理和题意求得，则的最小长度为4．【详解】解：连接，交⊙C上一点P，以O为圆心，以为半径作，交x轴于A、B，此时的长度最小，∵，∴，∵以点C为圆心的圆与y轴相切．∴的半径为3，∴，∴，∵是直径，∴，∴长度的最小值为4，故答案为：4．20．①②③④【分析】本题考查了全等三角形的判定及性质、切线的判定及性质、菱形的判定及性质、含角的直角三角形的特征，利用得，可得，再根据切线的判定及性质可判断①，利用三角形的判定及性质得，再根据菱形的判定即可判断②，利用含角的直角三角形的特征可判断③，利用菱形的性质可判断④，熟练掌握相关的判定及性质是解题的关键．【详解】解：连接，，，，，，，与相切于点C，，，是的直径，与相切；故①正确；，，，，，，，∴四边形是菱形，故②正确；，，，，，，，，故③正确；∵四边形是菱形，，，故④正确；故答案为：①②③④．21．1440【分析】依据正多边形的中心角和为求得边数，再依据多边形内角和公式代入求解即可．【详解】解：因为正多边形的中心角为36°，且中心角和为，所以这个多边形边数：，则这个多边形的内角和为：．故答案为：．【点睛】本题考查了正多边形内角和公式、中心角性质，通过中心角求得边数是解题的关键．22．【分析】本题主要考查了旋转的性质，求弧长，等边三角形的性质与判定，含30度角的直角三角形的性质，根据三角形内角和和含度的直角三角形三边的关系得到，，再根据旋转的性质得，于是可判断为等边三角形，所以，然后根据弧长公式计算弧的长度即可．【详解】解：，，，，，三角板绕直角顶点顺时针旋转，点落在边上，∴，∴为等边三角形，∴弧的长度，即点所转过的路径长．故答案为：．23．【分析】本题考查了等边三角形的判定与性质、扇形面积、弓形面积的计算，连接，过点作，易得为等边三角形，从而利用割补法求得阴影部分的面积即可，准确识图，添加适当的辅助线构造规则图形是解此题的关键．【详解】解：如图，连接，过点作，由题意可得，为等边三角形，，，，，，∴弓形的面积为，∴空白部分的面积为，∴阴影部分的面积为，故答案为：．24．(1)，(2)见解析(3)【分析】（1）根据平移的性质，即可解答；（2）以点为圆心，2为半径画弧，即可得出；（3）根据弧长公式求出，根据平移的性质得出，根据勾股定理求出，最后相加即可．【详解】（1）解：∵，所在圆的圆心为，∴，所在圆的圆心坐标是，故答案为：，；（2）解：如图所示：即为所求；（3）解：连接，∵，，∴的半径为2，∴，∵将向右平移5个单位，得到，∴，∴，∴由，，，首尾依次相接所围成的封闭图形的周长．【点睛】本题主要考查了平移的性质，求弧长，勾股定理，解题的关键是掌握平移前后对应点连线相等，弧长公式，以及勾股定理的内容．25．(1)见解析(2)①见解析；②【分析】（1）由点关于的对称点为可知点E是的中点，，从而得到是的中位线，继而得到，从而证明；（2）①过点O作于点F，延长交于点G，先证明得到，由与相切，得到，继而得到，从而证明是的角平分线，即，，求得，利用直角三角形两锐角互余得到，从而得到，即，最后利用含度角的直角三角形的性质得出；②先证明四边形是正方形，得到，再利用是的中位线得到，从而得到，，再利用平行线的性质得到，从而证明是等腰直角三角形，，设，求得，在中，即，解得，从而得到的面积为．【详解】（1）∵点关于的对称点为，∴点E是的中点，，又∵四边形是矩形，∴O是的中点，∴是的中位线，∴∴，∴（2）①过点O作于点F，延长交于点G，则，∵四边形是矩形，∴，，∴，．∵，，，∴，∴．∵与相切，为半径，，∴，∴又∵即，，∴是的角平分线，即，设，则，又∵∴∴又∵，即是直角三角形，∴，即解得：，∴，即，在中，，，∴，∴；②过点O作于点H，∵与相切，∴，∵∴四边形是矩形，又∵，∴四边形是正方形，∴，又∵是的中位线，∴∴∴又∵，∴又∵，∴又∵，∴是等腰直角三角形，，设，则∴在中，，即∴∴的面积为：【点睛】本题考查矩形的性质，圆的切线的性质，含度角的直角三角形的性质，等腰直角三角形的性质与判定，中位线的性质定理，角平分线的判定定理等知识，掌握相关知识并正确作出辅助线是解题的关键．26．(1)见详解(2)【分析】（1）连接，根据，，可得，，再根据，，可得，即有半径，问题得证；（2）连接，过O点作于点，利用垂径定理可得，，即，再证明，即有，设，即，在和中，有，，即，解方程即可求解．【详解】（1）证明：连接，如图，∵，，∴，，∵，∴，∵，，，∴，∴半径，∴是的切线；（2）解：连接，过O点作于点，如图，∵，，，的半径为5，∴，，即：，∵，，，∴，∴，设，即，∵，，∴在中，有；在中，有∴，解得：，∴．【点睛】本题考查了切线的判定与性质，等边对等角，全等三角形的判定与性质以及勾股定理等知识，掌握切线的判定与性质是解答本题的关键．27．(1)见解析(2)①见解析；②1【分析】（1）由直径所对的圆周角等于得出，由切线的性质定理得出，即可得出结论；（2）①由等弧所对的圆周角相等得出，由直角所对的圆周角为90°得出，由垂直的定义得出，等量代换得出，即可得出结论；②连接、，作，交的延长线于点，由角平分线的性质得出，由全等三角形的判定得出和，得出，，代入计算即可求出的值．【详解】（1）证明：是直径，，；是的切线；∴，，∴；（2）解：①是弧的中点，，是直径，，∵，，，，．②连接、，作，交的延长线于点．，，，，在与中，，，，是弧的中点，，在与中，，．．，即，．【点睛】本题考查了圆周角定理，切线的性质，全等三角形的性质和判定，角平分线的性质，熟练掌握各性质定理是解答此题的关键．28．(1)见解析(2)或【分析】（1）连接，可得，从而可证，即可求证；（2）①过点作交的延长线于点，并连接、，，过作交于，可求，从而可求，，进而可求，即可求解；②连接，，，过点作交于点，连接，同理可求，，可证，可得与重合，可求，即可求解．【详解】（1）解：如图，连接，，，是的平分线，，，，，点在上，是的切线；（2）解：①如图，过点作交的延长线于点，并连接、，，过作交于，，，，，，是的平分线，，，，，，，在中，，，，在中，，，，，，，点到直线的距离是；②如图，连接，，，过点作交于点，连接，同理可求，，，，，与重合，，在中，，，，，，点到直线的距离是；综上所述：或．【点睛】本题考查了切线的判定，勾股定理，等腰三角形的性质，直角三角形的特征，根据题意作出辅助线，掌握相关的性质是解题的关键．29．(1)见解析(2)【分析】（1）由垂径定理知，垂直于弦的直径是弦的中垂线，故作，的中垂线交于点，则点是弧所在圆的圆心；（2）在中，由勾股定理得出方程，解方程可求得半径的长．【详解】（1）解：作弦的垂直平分线与弦的垂直平分线交于点，以为圆心长为半径作圆就是此残片所在的圆，如图1所示．（2）连接，如图2所示：设，∵，，∴，则根据勾股定理列方程：，解得：．答：圆的半径为．【点睛】本题考查了作图，垂径定理，中垂线的性质，勾股定理；熟练掌握垂径定理，由勾股定理得出方程是解决问题（2）的关键．30．（）结论：，理由见解析；（）；（），；（）的最大值为，的最小值为．【分析】()结论：．只要证明即可；()利用三角形的三边关系即可解决问题；()连接，将绕着点顺时针旋转得到，连接，得到是等腰直角三角形，根据全等三角形的性质得到，，根据当在线段的延长线时，线段取得最大值，即可得到最大值为；过作轴于，根据等腰直角三角形的性质，即可得到结论；()如图中，以为边作等边三角形，由，推出，推出欲求的最大值，只要求出的最大值即可，由定值，，推出点在以为直径的上运动，由图象可知，当点在上方，时，的值最大．【详解】解：（）如图中，结论：，理由：∵、都是等边三角形，∴，，，∴，∴，∴；（）在中，，∴当共线，∴的最大值为，∴的最大值为．故答案为：；（）如图，连接，∵将绕着点顺时针旋转得到，连接，则是等腰直角三角形，∴，，∵的坐标为，点的坐标为，∴，，∴，∴线段长的最大值线段长的最大值，∴当在线段的延长线时，线段取得最大值（如图中），最大值，∵，∴最大值为；如图，过作轴于，∵是等腰直角三角形，∴，∴，∴；（）如图中，以为边作等边三角形，∵，∴，∵，，∴，∴，∴欲求的最大值，只要求出的最大值即可，∵定值，，∴点在以为直径的半圆上运动，由图象可知，当点在上方，时，的值最大，最大值，∴AC的最大值为；当点在线段的右侧时，以为边作等边，∵，∴，且，，∴，∴，∴欲求的最小值，只要求出的最小值即可，∵定值，，∴点在以为直径的上运动，由图象可知，当点在的上方，时，的值最小，的最小值，∴的最小值为；综上所述，的最大值为，AC的最小值为．【点睛】本题考查了圆的有关知识、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质，正确的作出辅助线构造全等三角形是解题的关键．。

广东省2019中考数学第二部分题型研究题型五圆的综合题

题型五圆的综合题针对演练1. 如图、AB 是⊙O 的弦、AB ＝4、过圆心O 的直线垂直AB 于点D 、交⊙O 于点C 和点E 、连接AC 、BC 、OB 、cos ∠ACB ＝13、延长OE 到点F 、使EF ＝2OE .(1)求证：∠BOE ＝∠ACB ; (2)求⊙O 的半径；(3)求证：BF 是⊙O 的切线．第1题图2. 如图、AB 为⊙O 的直径、点C 为圆外一点、连接AC 、 BC 、分别与⊙O 相交于点D 、点E 、且AD DE 、过点D 作DF ⊥BC 于点F 、连接BD 、DE 、AE .(1)求证：DF 是⊙O 的切线；(2)试判断△DEC 的形状、并说明理由；(3)若⊙O 的半径为5、AC ＝12、求sin ∠EAB 的值．第2题图3. (2016长沙9分)如图、四边形ABCD内接于⊙O、对角线AC为⊙O的直径、过点C 作AC的垂线交AD的延长线于点E、点F为CE的中点、连接DB、DC、DF.(1)求∠CDE的度数；(2)求证：DF是⊙O的切线；(3)若AC＝25DE、求tan∠ABD的值．第3题图4. (2016德州10分)如图、⊙O是△ABC的外接圆、AE平分∠BAC交⊙O于点E、交BC 于点D、过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系、并说明理由；(2)若∠ABC的平分线BF交AD于点F、求证：BE＝EF;(3)在(2)的条件下、若DE＝4、DF＝3、求AF的长．第4题图5. (2015永州)如图、已知△ABC内接于⊙O、且AB＝AC、直径AD交BC于点E、F是OE 上的一点、使CF∥BD.(1)求证：BE＝CE；(2)试判断四边形BFCD的形状、并说明理由；(3)若BC＝8、AD＝10、求CD的长．第5题图6. (2015省卷24、9分)⊙O是△ABC的外接圆、AB是直径、过BC的中点P作⊙O的直径PG交弦BC于点D、连接AG、CP、PB.(1)如图①、若D是线段OP的中点、求∠BAC的度数；(2)如图②、在DG上取一点K、使DK＝DP、连接CK、求证：四边形AGKC是平行四边形；(3)如图③、取CP的中点E、连接ED并延长ED交AB于点H、连接PH、求证：PH⊥AB.第6题图7. (2017原创)如图、AB 切⊙O 于点B 、AD 交⊙O 于点C 和点D 、点E 为DC 的中点、连接OE 交CD 于点F 、连接BE 交CD 于点G .(1)求证：AB ＝AG ；(2)若DG ＝DE 、求证：GB 2＝GC ·GA ；(3)在(2)的条件下、若tan D ＝34、EG ＝10、求⊙O 的半径．第7题图8. (2015达州)在△ABC 的外接圆⊙O 中、△ABC 的外角平分线CD 交⊙O 于点D 、F 为AD上一点、且AF BC 、连接DF 、并延长DF 交BA 的延长线于点E .(1)判断DB 与DA 的数量关系、并说明理由； (2)求证：△BCD ≌△AFD ；(3)若∠ACM ＝120°、⊙O 的半径为5、DC ＝6、求DE 的长．第8题图9. 如图、AB 为⊙O 的直径、P 是BA 延长线上一点、PC 切⊙O 于点C 、CG 是⊙O 的弦、CG ⊥AB 、垂足为点D .(1)求证：△ACD ∽△ABC ； (2)求证：∠PCA ＝∠ABC ；(3)过点A 作AE ∥PC 交⊙O 于点E 、交CG 于点F 、连接BE 、若sin P ＝35、CF ＝5、求BE的长．第9题图10. (2016大庆9分)如图、在Rt △ABC 中、∠C ＝90°、以BC 为直径的⊙O 交斜边AB 于点M 、若H 是AC 的中点、连接MH.(1)求证：MH 为⊙O 的切线；(2)若MH ＝32、tan ∠ABC ＝34、求⊙O 的半径；(3)在(2)的条件下分别过点A 、B 作⊙O 的切线、两切线交于点D 、AD 与⊙O 相切于N点、过N 点作NQ ⊥BC 、垂足为E 、且交⊙O 于Q 点、求线段NQ 的长度．第10题图11. 如图、△ABC 为⊙O 的内接三角形、P 为BC 延长线上一点、∠PAC ＝∠B 、AD 为⊙O 的直径、过C 作CG ⊥AD 交AD 于E 、交AB 于F 、交⊙O 于G.(1)判断直线PA 与⊙O 的位置关系、并说明理由；(2)求证：AG 2＝AF ·AB ；(3)若⊙O 的直径为10、AC ＝25、AB ＝45、求△AFG 的面积．第11题图12. (2016鄂州10分)如图、在Rt △ABC 中、∠ACB ＝90°、AO 是△ABC 的角平分线、以O 为圆心、OC 为半径作⊙O .(1)求证：AB 是⊙O 的切线；(2)已知AO 交⊙O 于点E 、延长AO 交⊙O 于点D 、tan D ＝12、求AEAC 的值；(3)在(2)的条件下、设⊙O 的半径为3、求AB 的长．第12题图【答案】1．(1)证明：如解图、连接OA 、第1题解图∵CE ⊥AB 、 ∴AD ＝BD ＝2、AE BE 、∴∠ACE ＝∠BCE 、∠AOE ＝∠BOE 、又∵∠AOB ＝2∠ACB 、 ∴∠BOE ＝∠ACB ； (2)解：∵cos ∠ACB ＝13、∴cos ∠BOD ＝13、在Rt △BOD 中、设OD ＝x 、则OB ＝3x 、∵OD 2＋BD 2＝OB 2、 ∴x 2＋22＝(3x )2、解得x ＝22、 ∴OB ＝3x ＝322、即⊙O 的半径为322；(3)证明：∵FE ＝2OE 、 ∴OF ＝3OE ＝922、∴OB OF ＝13、 ∵OD OB ＝13、 ∴OB OF ＝OD OB、∵∠BOF ＝∠DOB 、 ∴△OBF ∽△ODB 、∴∠OBF ＝∠ODB ＝90°、即OB ⊥BF 、 ∵OB 是⊙O 的半径、 ∴BF 是⊙O 的切线．2．(1)证明：如解图、连接DO 、交AE 于点G 、则DO ＝BO 、第2题解图∴∠ABD ＝∠ODB 、 ∵AD DE =、∴∠ABD ＝∠EBD 、 ∴∠ODB ＝∠EBD 、 ∴DO ∥BC 、∴∠ODF ＝∠CFD 、 ∵DF ⊥BC 、∴∠CFD ＝90°、∴∠ODF ＝90°、即OD ⊥DF 、又∵OD 为⊙O 的半径、 ∴DF 是⊙O 的切线；(2)解：△DEC 是等腰三角形、理由如下： ∵AB 是⊙O 的直径、 ∴∠ADB ＝∠CDB ＝90°、又∵BD ＝BD 、∠ABD ＝∠EBD 、 ∴△ABD ≌△CBD (ASA)、 ∴AD ＝CD . ∵AD DE =、∴AD ＝DE 、 ∴CD ＝DE 、∴△DEC 是等腰三角形； (3)解：由(2)可知AD ＝12AC ＝6、∵AD DE =、∴OD ⊥AE 、∠ABD ＝∠DAE 、 ∴sin ∠DAE ＝DG AD. 在Rt △ADB 中、sin ∠ABD ＝AD AB ＝610、 ∴DG 6＝610、 ∴DG ＝3.6、∴OG ＝OD －DG ＝1.4、∴在Rt △AGO 中、sin ∠EAB ＝OG OA ＝1.45＝725. 3．(1)解：∵AC 为⊙O 的直径、∴∠ADC ＝90°、∴∠CDE ＝90°；………………………………………………(2分)第3题解图(2)证明：如解图、连接OD 、∵∠CDE ＝90°、F 为CE 中点、∴DF ＝12CE ＝CF 、 ∴∠FDC ＝∠FCD .又∵OD ＝OC 、∴∠ODC ＝∠OCD 、∴∠ODC ＋∠FDC ＝∠OCD ＋∠FCD 、∴∠ODF ＝∠OCF 、∵EC ⊥AC 、∴∠OCF ＝90°、∴∠ODF ＝90°、即OD ⊥DF 、又∵OD 为⊙O 的半径、∴DF 为⊙O 的切线；…………………………………………(5分)(3)解：在△ACD 与△ECA 中、∵∠ADC ＝∠ACE ＝90°、∠EAC ＝∠CAD 、∴△ACD ∽△AEC 、∴AC AE ＝AD AC∴AC 2＝AD ·AE 、又∵AC ＝25DE 、∴20DE 2＝(AE －DE )·AE∴AE ＝5DE 、∴AD ＝4DE 、∵在Rt △ACD 中、AC 2＝AD 2＋CD 2、∴CD ＝2DE 、又∵在⊙O 中、∠ABD ＝∠ACD 、∴tan ∠ABD ＝tan ∠ACD ＝AD CD＝2. …………………………(9分)4．(1)解：直线l 与⊙O 相切．理由如下：如解图、连接OE 、OB 、OC .第4题解图∵AE 平分∠BAC 、∴∠BAE ＝∠CAE 、∴BE CE =、∴∠BOE ＝∠COE 、又∵OB ＝OC 、∴OE ⊥BC 、∵l ∥BC 、∴OE ⊥l 、又∵OE 为⊙O 的半径、∴直线l 与⊙O 相切；…………………………………………(3分)(2)证明：∵BF 平分∠ABC 、∴∠ABF ＝∠CBF 、又∵∠CBE ＝∠CAE ＝∠BAE 、∴∠CBE ＋∠CBF ＝∠BAE ＋∠ABF .又∵∠EBF ＝∠CBE ＋∠CBF 、∠EFB ＝∠BAE ＋∠ABF 、∴∠EBF ＝∠EFB 、∴BE ＝EF ；……………………………………………………(6分)(3)解：∵BE ＝EF 、DE ＝4、DF ＝3、∴BE ＝EF ＝DE ＋DF ＝7、∵BE CE =、∴∠DBE ＝∠BAE 、∵∠DEB ＝∠BEA 、∴△BED ∽△AEB 、∴DE BE ＝BE AE 、即47＝7AE、解得AE ＝494、…………………………………………………(9分) ∴AF ＝AE －EF ＝494－7＝214.………………………………(10分) 5．(1)证明：∵AD 是⊙O 的直径、∴∠ABD ＝∠ACD ＝90°、在Rt △ABD 和Rt △ACD 中、⎩⎪⎨⎪⎧AB ＝AC AD ＝AD 、 ∴Rt △ABD ≌Rt △ACD (HL)、∴∠BAD ＝∠CAD 、∵AB ＝AC 、∴AD 垂直平分BC 、∴BE ＝CE ；(2)解：四边形BFCD 是菱形．理由如下：∵AD 是⊙O 的直径、AB ＝AC 、∴AD ⊥BC 、BE ＝CE 、∵CF ∥BD 、∴∠FCE ＝∠DBE 、在△BED 和△CEF 中、⎩⎪⎨⎪⎧∠DBE ＝∠FCE BE ＝CE∠BED ＝∠CEF ＝90°、 ∴△BED ≌△CEF (ASA)、∴BD ＝CF 、∴四边形BFCD 是平行四边形、∵∠BAD ＝∠CAD 、∴BD ＝CD 、∴四边形BFCD 是菱形；(3)解：∵AD 是⊙O 的直径、AD ⊥BC 、BE ＝CE 、∴∠ECD ＝∠CAE 、∵∠AEC ＝∠DEC ＝90°、∴Rt △CDE ∽Rt △ACE 、∴DE CE ＝CE AE、∴CE 2＝DE ·AE 、设DE ＝x 、则AE ＝AD －DE ＝10－x 、∵BC ＝8、∴CE ＝12BC ＝4、 ∴42＝x (10－x )、解得x ＝2或x ＝8(舍去)、在Rt △CED 中、 CD ＝CE 2＋DE 2＝42＋22＝2 5.6．(1)解：∵点P 为BC 的中点、PG 为⊙O 的直径、∴BP ＝PC 、PG ⊥BC 、CD ＝BD 、∴∠ODB ＝90°、∵D 为OP 的中点、∴OD ＝12OP ＝12OB 、 ∴∠OBD ＝30°、∵AB 为⊙O 的直径、∴∠ACB ＝90°、∴∠BAC ＝60°；………………………………………………(3分)(2)证明：由(1)知、CD ＝BD 、在△PDB 和△KDC 中、⎩⎪⎨⎪⎧BD ＝CD ∠BDP ＝∠CDK DP ＝DK、∴△PDB ≌△KDC (SAS)、∴BP ＝CK 、∠BPO ＝∠CKD 、∵∠AOG ＝∠BOP 、∴AG ＝BP 、∴AG ＝CK 、∵OP ＝OB 、∴∠OBP ＝∠BPO 、又∵∠G ＝∠OBP 、∴∠G ＝∠BPO ＝∠CKD 、∴AG ∥CK 、∴四边形AGKC 是平行四边形；……………………………(6分)(3)证明：∵CE ＝PE 、CD ＝BD 、∴DE ∥PB 、即DH ∥PB 、∵∠G ＝∠BPO 、∴PB ∥AG 、∴DH ∥AG 、∴∠OAG ＝∠OHD 、∠G ＝∠ODH .∵OA ＝OG 、∴∠OAG ＝∠G 、∴∠ODH ＝∠OHD 、∴OD ＝OH 、在△OBD 和△OPH 中、⎩⎪⎨⎪⎧OD ＝OH ∠DOB ＝∠HOP OB ＝OP、∴△OBD ≌△OPH (SAS)、∴∠OHP ＝∠ODB ＝90°、∴PH ⊥AB . ……………………………………………………(9分)7．(1)证明：如解图、连接OB 、第7题解图∵AB 为⊙O 的切线、∴OB ⊥AB 、∴∠ABG ＋∠OBG ＝90°、∵点E 为DC 的中点、∴OE ⊥CD 、∴∠OEG ＋∠FGE ＝90°、又∵OB ＝OE 、∴∠OBG ＝∠OEG 、∴∠ABG ＝∠FGE 、∵∠BGA ＝∠FGE 、∴∠ABG ＝∠BGA 、∴AB ＝AG ；(2)证明：如解图、连接BC 、∵DG ＝DE 、∴∠DGE ＝∠DEG 、由(1)得∠ABG ＝∠BGA 、又∵∠BGA ＝∠DGE 、∴∠A ＝∠GDE 、∵∠GBC ＝∠GDE 、∴∠GBC ＝∠A 、∵∠BGC ＝∠AGB 、∴△GBC ∽△GAB 、∴GB GA ＝GC GB、∴GB 2＝GC ·GA ；(3)解：如解图、连接OD 、 ∵在Rt △DEF 中、tan ∠EDF ＝EF DF ＝34、 ∴设EF ＝3x 、则DF ＝4x 、由勾股定理得DE ＝5x 、∵DG ＝DE 、∴DG ＝5x 、∴GF ＝DG －DF ＝x .在Rt △EFG 中、由勾股定理得GF 2＋EF 2＝EG 2、即x 2＋(3x )2＝(10)2、解得x ＝1、设⊙O 半径为r 、在Rt △ODF 中、OD ＝r 、OF ＝r －3、DF ＝4、由勾股定理得OF 2＋FD 2＝OD 2、即(r －3)2＋42＝r 2、解得r ＝256、 ∴⊙O 的半径为256. 8．(1)解：DB ＝DA .理由如下：∵CD 平分∠ACM 、∴∠MCD ＝∠ACD 、∵∠ACD 和∠ABD 都是AD 所对的圆周角、∴∠ACD ＝∠ABD 、∴∠MCD ＝∠ABD 、又∵∠MCD ＝∠BAD 、∴∠BAD ＝∠ABD 、∴DB ＝DA ；(2)证明：如解图、连接AF 、第8题解图∵AD ＝BD 、∴AD BD =、 ∵AF BC =、 ∴DF CD =、∴AF ＝BC 、DF ＝DC 、在△BCD 和△AFD 中、⎩⎪⎨⎪⎧BD ＝AD BC ＝AF DC ＝DF、∴△BCD ≌△AFD (SSS)；(3)解：∵∠ACM ＝120°、∴∠MCD ＝∠ACD ＝60°、∴∠ABD ＝∠BAD ＝∠BDA ＝60°、∴△ABD 是等边三角形、如解图、连接DO 并延长与AB 交于点G 、则∠ADO ＝30°、过点O 作OH ⊥AD 于点H 、则AD ＝2DH ＝2OD ·cos30°＝53、∵∠ADF ＋∠DAF ＝∠AFE ＝∠ACD ＝60°、∠ADE ＋∠E ＝∠BAD ＝60°、 ∴∠DAF ＝∠E 、∵∠ADF ＝∠EDA 、∴△ADF ∽△EDA 、∴DA DE ＝DF DA、 ∴DE ＝DA 2DF、 ∵DF ＝DC ＝6、DA ＝53、∴DE ＝252. 9．(1)证明：∵AB 是⊙O 直径、∴∠ACB ＝90°、∵CG ⊥AB 、∴∠ADC ＝∠ACB ＝90°、∵∠CAD ＝∠BAC 、∴△ACD ∽△ABC ；(2)证明：如解图、连接OC .第9题解图∵PC 切⊙O 于点C 、∴OC ⊥PC 、∴∠PCO ＝90°、∴∠PCA ＋∠OCA ＝90°、∵∠ACB ＝90°、∴∠ABC ＋∠OAC ＝90°、∵OC ＝OA 、∴∠OCA ＝∠OAC 、∴∠PCA ＝∠ABC ；(3)解：∵AE ∥PC 、∴∠PCA ＝∠CAF 、∵AB ⊥CG 、∴AC AG 、∴∠ABC ＝∠ACF 、∵∠PCA ＝∠ABC 、∴∠CAF ＝∠ABC 、∴∠ACF ＝∠CAF 、∴FA ＝FC 、∵CF ＝5、∴AF ＝5、∵AE ∥PC 、∴∠FAD ＝∠P 、∵sin P ＝35、 ∴sin ∠FAD ＝35、 ∴FD ＝3、AD ＝4、CD ＝8、在Rt △COD 中、设CO ＝r 、则有r 2＝(r －4)2＋82、∴r ＝10、∴AB ＝2r ＝20、∵AB 是⊙O 的直径、∴∠AEB ＝90°、∴sin ∠EAB ＝35、 ∴BE AB ＝35、205∴BE ＝12.10．(1)证明：如解图①、连接OM 、CM 、第10题解图①∵BC 为⊙O 的直径、∴∠AMC ＝∠BMC ＝90°、∵H 是AC 的中点、∴HC ＝HM ＝12AC 、 ∴∠HMC ＝∠HCM 、∵OM ＝OC 、∴∠OMC ＝∠OCM 、∴∠OMH ＝∠OCH 、∵∠ACB ＝90°＝∠OCH 、∴∠OMH ＝90°、即OM ⊥MH 、又∵OM 为⊙O 的半径、∴MH 为⊙O 的切线；…………………………………………(3分)(2)解：∵MH ＝32、 ∴AC ＝2MH ＝3、在Rt △ABC 中、tan ∠ABC ＝AC BC ＝34、 ∴BC ＝4、故⊙O 的半径为2；……………………………………………(5分)(3)解：如解图②、过点D 作DP ⊥AC 于点P 、连接ON 、第10题解图②则DP ＝BC ＝4、BD ＝PC 、设DB ＝DN ＝x 、则AP ＝3－x 、∵AN ＝AC ＝3、∴AD ＝x ＋3.在Rt △ADP 中、由勾股定理得、(x ＋3)2－(3－x )2＝42、3∴DN ＝BD ＝43、AD ＝133、 ∵QN ⊥BC 、AC ⊥BC 、BD ⊥BC 、∴AC ∥NQ ∥DB 、∴DN AD ＝BE BC 、即43133＝BE 4、 ∴BE ＝1613、 ∴OE ＝OB －BE ＝1013、 ∴EN ＝ON 2－OE 2＝2413、 ∴NQ ＝2EN ＝4813.……………………………………………(9分) 11．(1)解：直线PA 与⊙O 相切．理由如下：∵AD 为⊙O 的直径、 CG ⊥AD 、∴AD 垂直且平分CG 、∴AC ＝AG 、∴∠ACG ＝∠AGC 、∵∠AGC ＝∠B 、∠PAC ＝∠B 、∴∠PAC ＝∠ACG 、∴PA ∥CG 、∵CG ⊥AD 、∴PA ⊥AD 、又∵AD 为⊙O 的直径∴直线PA 是⊙O 的切线；【一题多解】如解图①、连接DC 、第11题解图①则∠B ＝∠ADC 、∵AD 是⊙O 的直径、∴∠ACD ＝90°、∴∠ADC ＋∠DAC ＝90°.又∵∠PAC ＝∠B 、∴∠ADC ＝∠PAC 、∴∠PAC ＋∠DAC ＝90°、即DA ⊥PA 、∴PA 是⊙O 的切线．(2)证明：由垂径定理得AC AG =、 ∴∠ACG ＝∠B 、∵∠CAB ＝∠FAC 、∴△ABC ∽△ACF 、∴AC AF ＝AB AC、∴AC 2＝AF ·AB 、又∵AC ＝AG 、∴AG 2＝AF ·AB ；【一题多解】此题还可以通过连接BG 、证明△GAB ∽△FAG 、从而证得AG 2＝AF ·AB .(3)解：由(2)得AG 2＝AF ·AB 、∵AG ＝AC ＝25、AB ＝45、∴(25)2＝45AF 、∴AF ＝5、如解图②、连接BD 、则∠ABD ＝90°、第11题解图②由勾股定理得BD ＝AD 2－AB 2＝102－（45）2＝25、∵∠AEF ＝∠ABD ＝90°、∠EAF ＝∠BAD 、∴△AEF ∽△ABD 、 ∴AE AB ＝AF AD ＝EF BD、 ∴AE45＝510＝EF 25、 ∴AE ＝2、EF ＝1、在Rt △ACE 中、由勾股定理、得CE 2＝AC 2－AE 2、∴CE ＝（25）2－22＝4、∵CE ＝EG 、∴EG ＝4、∴FG ＝EG －EF ＝ 4－1＝3、 ∴1132322AFG S FG AE ==⨯⨯=△. 12．(1)证明：如解图、过点O 作OF ⊥AB 于点F 、第12题解图∵AO 平分∠CAB 、OC ⊥AC 、垂足为点F 、∴OF ＝OC 、即OF 为⊙O 的半径、∴AB 是⊙O 的切线；…………………………………………(3分)(2)解：如解图、过点D 作DP ⊥AC 交AC 延长线于点P 、 ∵∠ACB ＝90°、DP ⊥AC 、∴CO ∥DP 、∵OC ＝OD 、∴∠OCD ＝∠ODC ＝∠CDP 、∵tan ∠CDO ＝12、 ∴tan ∠OCD ＝12. 连接DQ 、设DQ ＝a 、则CD ＝2a 、CQ ＝5a 、∴CO ＝OD ＝OE ＝5a 2、在Rt △CPD 中、设CP ＝b 、则DP ＝2b 、CD ＝5b 、∴b ＝255a 、则PC ＝255a 、PD ＝455a 、 ∵CO ∥DP 、∴△ACO ∽△APD 、∴OC PD ＝AC AP ＝AO AD 、即5a 2455a ＝AC 255a ＋AC ＝AO 5a 2＋AO 、解得AC ＝253a 、AO ＝556a 、 ∴AE ＝AO －OE ＝556a －5a 2＝53a 、 ∴AE AC ＝53a 253a ＝12；……………………………………………(7分) (3)解：由(2)知AE AC ＝12、设AE ＝c 、则AC ＝2c 、在Rt △ACO 中、(2c )2＋32＝(c ＋3)2、解得c ＝2、∴AF ＝AC ＝2c ＝4、在△BFO 和△BCA 中、⎩⎪⎨⎪⎧∠B ＝∠B ∠BFO ＝∠BCA 、∴△BFO ∽△BCA 、 ∴BF BC ＝FO CA ＝BO AB、设BF ＝x 、BO ＝y 、 ∴x3＋y ＝34＝y 4＋x 、解得：x ＝727、y ＝757、 ∴AB ＝AF ＋BF ＝4＋727＝1007. ……………………………(10分)。

中考数学复习专题：几何综合题（含答案解析）

中考数学复习专题：⼏何综合题（含答案解析）⼏何综合题1.已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD 的延长线于点H ．（1）如图1，若60BAC ∠=?①直接写出B ∠和ACB ∠的度数；②若AB =2，求AC 和AH 的长；（2）如图2，⽤等式表⽰线段AH 与AB +AC 之间的数量关系，并证明．答案：（1）①75B ∠=?，45ACB ∠=?；②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=?，AD=2可得DE =1，AE 3=. Rt △CDE 中，由45ACD ∠=?，DE=1，可得EC =1. ∴AC 31=.Rt △ACH 中，由30DAC ∠=?，可得AH 33+=；（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH .易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =，∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==.2.正⽅形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图1，当045α?<②⽤等式表⽰NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α?<CDBA图1备⽤图C DBAM答案：（1）①补全的图形如图7所⽰．（2）当45°<α<90°时，=1802NCE BAM ∠?-∠．证明：如图8，连接CM ，设射线AM 与CD 的交点为H ．∵四边形ABCD 为正⽅形，∴∠BAD=∠ADC=∠BCD=90°，直线BD为正⽅形ABCD的对称轴，点A与点C关于直线BD对称．∵射线AM与线段BD交于点M，∴∠BAM=∠BCM=α．-．∴∠1=∠2=90α∵CE⊥AM，∴∠CEH=90°，∠3+∠5=90°．⼜∵∠1+∠4=90°，∠4=∠5，∴∠1=∠3．-．∴∠3=∠2=90α∵点N与点M关于直线CE对称，-∠．∴∠NCE=∠MCE=∠2+∠3=1802BAM（313. 如图，已知60AOB ∠=?，点P 为射线OA 上的⼀个动点，过点P 作PE OB ⊥，交OB 于点E ，点D 在AOB ∠内，且满⾜DPA OPE ∠=∠，6DP PE +=. （1）当DP PE =时，求DE 的长；（2）在点P 的运动过程中，请判断是否存在⼀个定点M ，证明你的判断.答案：（1）作PF ⊥DE 交DE 于F . ∵PE ⊥BO ，60AOB ∠=o，∴30OPE ∠=o.∴30DPA OPE ∠=∠=o.∴120EPD ∠=o∴cos30DF PD =??=∴2DE DF ==（2）当M 点在射线OA 上且满⾜OM =DMME的值不变，始终为1.理由如下：当点P 与点M 不重合时，延长EP 到K 使得PK PD =.∵,DPA OPE OPE KPA ∠=∠∠=∠,∴KPA DPA ∠=∠. ∴KPMDPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △. ∴MKMD =.作ML ⊥OE 于L ,MN ⊥EK 于N . ∵3,60MO MOL =∠=o，∴sin 603ML MO =?=o.∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ，∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MKME =.∴ME MKMD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成⽴.4. 如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上⼀动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中⼼，顺时针旋转120°，分别交射线AD 于点F ，G. （1）依题意补全图形；（2）若∠ACE=α，求∠AFC 的⼤⼩（⽤含α的式⼦表⽰）；（3）⽤等式表⽰线段AE 、AF 与CG 之间的数量关系，并证明．答案：（1）补全的图形如图所⽰.（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°，∴∠DAC=∠BAC= 30°. ∴∠AGC=30°. ∴∠AFC =α+30°.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. ∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ，∴△ACE ≌△GCF. ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠?= ∴AG =3CG .即AF+AE =3CG .5.如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N . （1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，⽤等式表⽰线段AM ，CN 之间的数量关系，并证明．答案：（1）如图；ABCE（2）45°；（3）结论：AM CN．证明：作AG⊥EC的延长线于点G．∵点B与点D关于CE对称，∴CE是BD的垂直平分线．∴CB=CD．∴∠1=∠2=α．∵CA=CB，∴CA=CD．∴∠3=∠CAD．∵∠4=90°，∴∠3=12（180°-∠ACD）=12（180°-90°-α-α）=45°-α．∵∠4=90°，CE是BD的垂直平分线，∴∠1+∠7=90°，∠1+∠6=90°．∴∠6=∠7．∵AG⊥EC，∴∠G=90°=∠8．∴在△BCN和△CAG中，∠8=∠G，∠7=∠6，BC=CA，∴△BCN≌△CAG．∴CN=AG．∵Rt△AMG中，∠G=90°，∠5=45°，∴AM AG．∴AM CN．6.在正⽅形ABCD中，M是BC边上⼀点，点P在射线AM上，将线段AP绕点A顺时针旋转90°得到线段AQ，连接BP，DQ．（1）依题意补全图1；答案：（1）补全图形略（2）①证明：连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ，∴AQ AP =，90QAP ∠=°．∵四边形ABCD 是正⽅形，∴AD AB =，90DAB ∠=°．∴12∠=∠．∴△ADQ ≌△ABP ．∴DQ BP =，3Q ∠=∠．∵在Rt QAP ?中，90Q QPA ∠+∠=°，∴390BPD QPA ∠=∠+∠=°．∵在Rt BPD ?中，222DP BP BD +=，⼜∵DQ BP =，222BD AB =，∴2222DP DQ AB +=．②BP AB =．7.如图，在等腰直⾓△ABC 中，∠CAB=90°，F 是AB 边上⼀点，作射线CF ，过点B 作BG ⊥C F 于点G ，连接AG ．（1）求证：∠ABG =∠ACF ；（2）⽤等式表⽰线段C G ，AG ，BG 之间∵∠CAB=90°. ∵ BG ⊥CF 于点G ，∴∠BGF =∠CAB =90°. ∵∠GFB =∠CFA . ∴∠ABG =∠ACF .（2）CG =2AG +BG .证明：在CG 上截取CH =BG ，连接AH ，∵△ABC 是等腰直⾓三⾓形，∴∠CAB =90°，AB =AC . ∵∠ABG =∠ACH . ∴△ABG ≌△ACH . ∴ AG =AH ,∠GAB =∠HAC . ∴∠GAH =90°. ∴ 222AG AH GH +=. ∴ GH =2AG . ∴ CG =CH +GH =2AG +BG .8.如图，在正⽅形ABCD 中，E 是BC 边上⼀点，连接AE ，延长CB ⾄点F ，使BF=BE ，过点F 作FH ⊥AE 于点H ，射线FH 分别交AB 、CD 于点M 、N ，交对⾓线AC 于点P ，连接AF ．（1）依题意补全图形；（2）求证：∠FAC =∠APF ；（3）判断线段FM 与PN 的数量关系，并加以证明．答案：（1）补全图如图所⽰．（2）证明∵正⽅形ABCD ，∴∠BAC =∠BCA =45°，∠ABC =90°，∴∠PAH =45°-∠BAE ．∵FH ⊥AE ．EDCBAM H PDAC∴∠APF=45°+∠BAE．∵BF=BE，∴AF=AE，∠BAF=∠BAE．∴∠FAC=45°+∠BAF．∴∠FAC=∠APF．（3）判断：FM=PN．证明：过B作BQ∥MN交CD于点Q，∴MN=BQ，BQ⊥AE．∵正⽅形ABCD，∴AB=BC，∠ABC=∠BCD=90°．∴∠BAE=∠CBQ．∴△ABE≌△BCQ．∴AE=BQ．∴AE=MN．∵∠FAC=∠APF，∴FP=MN．∴FM=PN．9.如图所⽰，点P位于等边ABC△的内部，且∠ACP=∠CBP．(1) ∠BPC的度数为________°；(2) 延长BP⾄点D，使得PD=PC，连接AD，CD．①依题意，补全图形；②证明：AD+CD=BD；(3)在(2)的条件下，若BD的长为2，求四边形ABCD的⾯积．M HPD AC解：(1)120°. ----------------------------2分(2)①∵如图1所⽰.②在等边ABC △中，60ACB ∠=?，∴60.ACP BCP ∠+∠=? ∵=ACP CBP ∠∠，∴60.CBP BCP ∠+∠=?∴()180120.BPC CBP BCP ∠=?-∠+∠=?∴18060.CPD BPC ∠=?-∠=? ∵=PD PC ，∴CDP △为等边三⾓形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=?，∴.ACD BCP ∠=∠在ACD △和BCP △中，AC BC ACD BCP CD CP =??∠=∠??=?，，，∴()SAS ACD BCP △≌△. ∴.AD BP =∴.AD CD BP PD BD +=+=-----------------------------------------4分（3）如图2，作BM AD ⊥于点M ，BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=?，∴=60.ADB CDB ∠∠=?∴=60.ADB CDB ∠∠=?D∴=BM BN BD == ⼜由（2）得，=2AD CD BD +=，ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =22==-----------------------------------7分10.如图1，在等边三⾓形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A的对应点E 落在射线BC 上，连接BQ ，设∠DAQ =α（0°＜α＜60°且α≠30°）. （1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE （⽤含α的式⼦表⽰）；②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE ，AC ，CQ 之间的数量关系.解：（1）①3-． ………………………………………………………………………… 1分② 0≤QL．……………………………………………………………… 2分（2）设直线+33y x =与x 轴，y 轴的交点分别为点A ，点B，可得A ，(0,3)B ．∴OA =3OB =，30OAB ∠=?．由0≤Q①如图13，当⊙D 与x 轴相切时，相应的圆⼼1D 满⾜题意，其横坐标取到最⼤值．作11D E x ⊥轴于点1E ，可得11D E ∥OB ，111D E AE BO AO=．∵⊙D 的半径为1，∴ 111D E =．∴1AE =11OE OA AE =-=．∴1D x =②如图14，当⊙D与直线y =相切时，相应的圆⼼2D 满⾜题意，其横坐标取到最⼩值．作22D E x ⊥轴于点2E ，则22D E ⊥OA ．设直线y =与直线+3y =的交点为F ．可得60AOF ∠=?，OF ⊥AB ．则9cos 2AF OA OAF =?∠==．图13∵⊙D 的半径为1，∴ 21D F =．∴2272AD AF D F =-=．=?∠72==，22OE OA AE =-=．∴2D x =．由①②可得，D x≤D x≤． ………………………………………… 5分（3）画图见图15．．……………………………… 7分11.如图，在等边ABC △中， ,D E 分别是边,AC BC 上的点，且CD CE = ,30DBC ∠对称，连接,AF FE ，FE 交BD 于G .（1）连接,DE DF ，则,DE DF 之间的数量关系是；（2）若DBC α∠=，求FEC ∠的⼤⼩; （⽤α的式⼦表⽰）（3）⽤等式表⽰线段,BG GF 和FA 之间的数量关系，并证明.GFEDCBA图15（1）DE DF =；（2）解：连接DE ，DF ，∵△ABC 是等边三⾓形，∴60C ∠=?. ∵DBC α∠=，∴120BDC α∠=?-.∴120BDF BDC α∠=∠=?-，DF DC =. ∴1202FDC α∠=?+. 由（1）知DE DF =.∴F ，E ，C 在以D 为圆⼼，DC 为半径的圆上.∴1602FEC FDC ∠=∠=?+α.（3）BG GF FA =+.理由如下：连接BF ，延长AF ，BD 交于点H ，∵△ABC 是等边三⾓形，∴60ABC BAC ∠=∠=?，AB BC CA ==. ∵点C 与点F 关于BD 对称，∴BF BC =，FBD CBD ∠=∠.GFEDCBA∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=，则602ABF α∠=?-. ∴60BAF α∠=?+. ∴FAD α∠=.∴FAD DBC ∠=∠.由（2）知60FEC α∠=?+. ∴60BGE FEC DBC ∠=∠-∠=?. ∴120FGB ∠=?，60FGD ∠=?.四边形AFGB 中，360120AFE FAB ABG FGB ∠=?-∠-∠-∠=?. ∴60HFG ∠=?.∴△FGH 是等边三⾓形. ∴FH FG =，60H ∠=?. ∵CD CE =，∴DA EB =.在△AHD 与△BGE 中，,,.AHD BGE HAD GBE AD BE ∠=∠??∠=∠??=?∴△△AHD BGE ?. ∴BG AH =.∵AH HF FA GF FA =+=+，∴BG GF FA =+．HGFEDCBA12.如图，在△ABC中，AB=AC，∠BAC=90°，M是BC的中点，延长AM到点D，AE= AD，∠EAD=90°，CE交AB于点F，CD=DF.（1）∠CAD= 度；（2）求∠CDF的度数；（3）⽤等式表⽰线段CD和CE之间的数量关系，并证明.解：（1）45 ……………………………………………………………1分（2）解：如图，连接DB.∵90，°，M是BC的中点，AB AC BAC=∠=∴∠BAD=∠CAD=45°.∴△BAD≌△CAD. ………………………………2分∴∠DBA=∠DCA，BD = CD.∵CD=DF,∴B D=DF. ………………………………………3分∴∠DBA=∠DFB=∠DCA.∵∠DFB+∠DFA =180°,∴∠DCA+∠DFA =180°.∴∠BAC+∠CDF =180°.∴∠CDF =90°. ………………………………………4分21CD. ……………………………………5分（3）CE=)证明：∵90∠=°，EAD∴∠EAF =∠DAF =45°. ∵AD =AE ，∴△EAF ≌△DAF . …………………………………6分∴DF =EF .由②可知，CF. …………………………7分∴CE=)1C D .13.如图，正⽅形ABCD 中，点E 是BC 边上的⼀个动点，连接AE ，将线段AE 绕点A 逆时针旋转90°，得到AF ，连接EF ，交对⾓线BD 于点G ，连接AG ．（1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．解：（1）图形补全后如图…………………1分（2）结论：AG ⊥EF ． …………………2分证明：连接FD ，过F 点FM ∥BC ，交BD 的延长线于点M ．∵四边形ABCD 是正⽅形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC =90°，∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ，A BC ED∴AE=AF ，∠FAE =90°．∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分∴∠FDA =∠EBA =90°，FD=BE ．∵∠ADC =90°，∴∠FDA +∠ADC =180°。

中考数学圆综合题专题训练

中考数学圆综合题专题训练（第11天）1.如图，以△ABC 的BC 边为直径作⊙O ，分别交AC 、AB 于E 、F 两点，过A 作⊙O 的切线，切点为D ，且点E 、F 为劣弧CD ︵的三等分点．（1）求证：AD ∥BC ；（2）求∠DAC 的大小．2．（成都某校自主招生）如图，在直角坐标系中，点B （－1－3，0），C （1＋3，0），△ABC 的内切圆的圆心是I （－1，1），求△ABC 的面积．3．（四川德阳）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O 的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB 的延长线于G．（1）求证：FC＝FB；（2）求证：CG是⊙O的切线；（3）若FB＝FE＝2，求⊙O的半径．4．（四川广安）如图，在△ABC中，∠ABC＝∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB＝2∠BCP．（1）求证：直线CP是⊙O的切线．（2）若BC＝25，sin∠BCP＝55，求点B到AC的距离．（3）在第（2）的条件下，求△ACP的周长．CP5．（四川泸州）如图，△ABC 内接于⊙O ，AB 是⊙O 的直径，C 是AD ︵的中点，弦CE ⊥AB 于点H ，连接AD ，分别交CE 、BC 于点P 、Q ，连接BD ．（1）求证：P 是线段AQ 的中点；（2）若⊙O 的半径为5，AQ ＝152，求弦CE 的长．B中考数学圆综合题专题训练（第12天）6．（四川宜宾）如图，⊙O1、⊙O2相交于P、Q两点，其中⊙O1的半径r1＝2，⊙O2的半径r2＝2．过点Q作CD⊥PQ，分别交⊙O1和⊙O2于点C、D，连接CP、DP，过点Q任作一直线AB交⊙O1和⊙O2于点A、B，连接AP、BP、AC、DB，且AC与DB的延长线交于点E．（1）求证：P APB＝2；（2）若PQ＝2，试求∠E度数．7．（四川资阳）如图，在△ABC 中，AB ＝AC ，∠A ＝30°，以AB 为直径的⊙O 交BC 于点D ，交AC 于点E ，连接DE ，过点B 作BP ∥DE ，交⊙O 于点P ，连接EP 、CP 、OP ．（1）求证：BD ＝DC ；（2）求∠BOP 的度数；（3）求证：CP 是⊙O 的切线．AC BD OE P8．（四川某校自主招生）如图，等腰Rt△ABC的直角边AB、AC分别与⊙O相切于点E、D，AD＝3，DC＝5，直线FG与AC、BC分别交于点F、G，且∠CFG＝60°．（1）求阴影部分的面积；FG与⊙O的位置关系，并说明理由．9．如图，在平面直角坐标系中，半径分别为m、n（0＜m＜n）的两圆⊙O1和⊙O2相交于P，Q两点，且点P（4，1），两圆同时与两坐标轴相切，⊙O1与x轴、y轴分别切于点M、N，⊙O2与x轴、y轴分别切于点R、H．（1）求两圆的圆心O1、O2所在直线的解析式；（2）求两圆的圆心O1、O2之间的距离d；（3）令四边形PO1QO2的面积为S1，四边形RMO1O2的面积为S2．试探究：是否存在一条经过P、Q两点、开口向下，且在x轴上截得的线段长为|S1－S2|2d的抛物线？若存在，请求出此抛物线的解析式；若不存在，请说明理由．中考数学圆综合题专题训练（第13天）10．（湖南怀化）如图，已知AB 是⊙O 的弦，OB ＝4，∠OBC ＝30°，点C 是弦AB 上任意一点（不与点A 、B 重合），连接CO 并延长CO 交⊙O 于点D ，连接AD 、DB ．（1）当∠ADC ＝18°时，求∠DOB 的度数；（2）若AC ＝23，求证△ACD ∽△OCB ．ACBDO11．（湖南湘潭）如图，在⊙O 上位于直径AB 的异侧有定点C 和动点P ，AC ＝12AB ，点P在半圆弧AB 上运动（不与A 、B 两点重合），过点C 作直线PB 的垂线CD 交PB 于D 点．（1）如图1，求证：△PCD ∽△ABC ；（2）当点P 运动到什么位置时，△PCD ≌△ABC ？请在图2中画出△PCD 并说明理由；（3）如图3，当点P 运动到CP ⊥AB 时，求∠BCD 的度数．B 图2D图1B图312．（湖南张家界）如图，⊙O 的直径AB ＝4，C 为圆周上一点，AC ＝2，过点C 作⊙O 的切线DC ，点P 为优弧CBA ︵上一动点（不与A 、C 重合）．（1）求∠APC 与∠ACD 的度数；（2）当点P 移动到CB ︵的中点时，证明：四边形ACPO 是菱形；（3）P 点移动到什么位置时，由点A 、P 、C 三点构成的三角形与△ABC 全等，请说明理由．B13．（湖北鄂州）如图，梯形ABCD是等腰梯形，且AD∥BC，O是腰CD的中点，以CD长为直径作圆，交BC于E，过E作EH⊥AB于H．（1）求证：OE∥AB；（2）若EH＝12CD，求证：AB是⊙O的切线；（3）若BE＝4BH，求BHCE的值．中考数学圆综合题专题训练（第14天）14．（湖北恩施）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE＝CB．（1）求证：BC是⊙O的切线；（2）连接AF，BF，求∠ABF的度数；（3）如果CD＝15，BE＝10，sin A＝513，求⊙O的半径．C15．（湖北十堰）如图1，⊙O 是△ABC 的外接圆，AB 是直径，OD ∥AC ，且∠CBD ＝∠BAC ，OD 交⊙O 于点E ．（1）求证：BD 是⊙O 的切线．（2）若点E 为线段OD 的中点，证明：以O 、A 、C 、E 为顶点的四边形是菱形；（3）作CF ⊥AB 于点F ，连接AD 交CF 于点G （如图2）．求FGFC的值．ACB ODE图1A CB ODE图2F G16．（湖北襄阳）如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E，F，过点B作PO 的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．（1）求证：直线PA为⊙O的切线；（2）试探究线段EF，OD，OP之间的等量关系，并加以证明；（3）若BC＝6，tan∠F＝12，求cos∠ACB的值和线段PE的长．AC BO D EPF17．（湖北某校自主招生）已知扇形AOB 的半径为6，圆心角为90°，E 是半径OA 上一点，F 是AB ︵上一点．将扇形AOB 沿EF 对折，使得折叠后的图形恰好与半径OB 相切于点G ．（1）若OE ＝4，求折痕EF 的长；（2）若G 是OB 中点，求OE 和折痕EF 的长；（3）点E 可移动的最大距离是多少？B中考数学圆综合题专题训练（第15天）18．（湖北某校自主招生）如图，在平面直角坐标系中，点A的坐标为（2，0），以点A为圆心，2为半径的⊙A与x轴交于O、B两点，OC为弦，∠AOC＝60°，P是x轴上的一动点，直线CP交⊙A于点Q，连接OQ、AQ．Array（1）当△OCQ是等腰三角形时，求点P的坐标；（2）当△APQ是等腰三角形时，求∠OCQ的度数．19．（湖北模拟）如图，在△ABC中，AB＝AC，且⊙O内切于△ABC，D、E、F是切点，CF 交⊙O于G，EG延长线交BC于M，AG交⊙O于K．（1）求证：△MCG∽△MEC；（2）若EM⊥BC，求cos∠FAK的值．20．（湖北模拟）已知矩形ABCD中，半径为r的两个等圆⊙O1、⊙O2外切，且⊙O1与边AB、BC相切，⊙O2与边BC相切．点E是边CD上一点，将△ADE沿AE翻折得△AD′E，AD′恰好与⊙O2相切于点D′．若AD＝3，折痕AE的长为10．（1）求r的值；（2）求证：矩形ABCD为正方形．D E。

中考数学综合专题训练【几何综合题】(几何)精品解析

中考数学综合专题训练【几何综合题】（几何）精品解析在中考中.几何综合题主要考察了利用图形变换（平移、旋转、轴对称）证明线段、角的数量关系及动态几何问题。

学生通常需要在熟悉基本几何图形及其辅助线添加的基础上.将几何综合题目分解为基本问题.转化为基本图形或者可与基本图形、方法类比.从而使问题得到解决。

在解决几何综合题时.重点在思路.在老师讲解及学生解题时.对于较复杂的图形.根据题目叙述重复绘图过程可以帮助学生分解出基本条件和图形.将新题目与已有经验建立联系从而找到思路.之后绘制思路流程图往往能够帮助学生把握题目的脉络；在做完题之后.注重解题反思.总结题目中的基本图形及辅助线添加方法.将题目归类整理；对于典型的题目.可以解析题目条件.通过拓展题目条件或改变条件.给出题目的变式.从而对于题目及相应方法有更深入的理解。

同时.在授课过程中.将同一类型的几何综合题成组出现.分析讲解.对学生积累对图形的“感觉”有一定帮助。

一.考试说明要求图形与证明中要求：会用归纳和类比进行简单的推理。

图形的认识中要求：会运用几何图形的相关知识和方法（两点之间的距离.等腰三角形、等边三角形、直角三角形的知识.全等三角形的知识和方法.平行四边形的知识.矩形、菱形和正方形的知识.直角三角形的性质.圆的性质）解决有关问题；能运用三角函数解决与直角三角形相关的简单实际问题；能综合运用几何知识解决与圆周角有关的问题；能解决与切线有关的问题。

图形与变换中要求：能运用轴对称、平移、旋转的知识解决简单问题。

二.基本图形及辅助线解决几何综合题.是需要厚积而薄发.所谓的“几何感觉”.是建立在足够的知识积累的基础上的.熟悉基本图形及常用的辅助线.在遇到特定条件时能够及时联想到对应的模型.找到“新”问题与“旧”模型间的关联.明确努力方向.才能进一步综合应用数学知识来解决问题。

在中档几何题目教学中注重对基本图形及辅助线的积累是非常必要的。

举例：1、与相似及圆有关的基本图形2、正方形中的基本图形3、基本辅助线（1）角平分线——过角平分线上的点向角的两边作垂线（角平分线的性质）、翻折；（2）与中点相关——倍长中线（八字全等）.中位线.直角三角形斜边中线；（3）共端点的等线段——旋转基本图形（60°.90°）.构造圆；垂直平分线.角平分线——翻折；转移线段——平移基本图形（线段）线段间有特殊关系时.翻折；（4）特殊图形的辅助线及其迁移．．．．——梯形的辅助线（什么时候需要这样添加？）等作双高——上底、下底、高、腰（等腰梯形）三推一；面积；锐角三角函数平移腰——上下底之差；两底角有特殊关系（延长两腰）；梯形——三角形平移对角线——上下底之和；对角线有特殊位置、数量关系。

2021年九年级中考复习数学考点提分专练——几何专题：《圆的提高题》(二)

九年级中考复习数学考点提分专练——几何专题《圆的提高题》（二）1．如图，⊙O是直角三角形ABC的外接圆，直径AC＝4，过C点作⊙O的切线，与AB延长线交于点D，M为CD的中点，连接BM，OM，且BC与OM相交于点N．（1）求证：BM与⊙O相切；（2）当∠A＝60°时，求弦AB和弧AB所夹图形的面积；（3）在（2）的条件下，在⊙O的圆上取点F，使∠ABF＝15°，求点F到直线AB的距离．2．如图，已知四边形ABCD内接于⊙O，AC⊥BD于E，＝．（1）求证：∠BDC＝2∠ADB；（2）若直径BM交AC于点N，AD﹣BN＝2，BC＝8，求⊙O的半径．3．如图，在平面直角坐标系xOy中，过⊙T外一点P引它的两条切线，切点分别为M，N，若60°≤∠MPN＜180°，则称P为⊙T的环绕点．（1）当⊙O半径为1时，①在P1（1，0），P2（1，1），P3（0，2）中，⊙O的环绕点是；②直线y＝x+b与x轴交于点A，与y轴交于点B，若线段AB上存在⊙O的环绕点，求b的取值范围；（2）⊙T的半径为1，圆心为（0，t），以为圆心，为半径的所有圆构成图形H，若在图形H上存在⊙T的环绕点，直接写出t的取值范围．4．如图，△ABC内接于⊙O，AB是⊙O的直径，C是中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD．（1）求证：P是线段AQ的中点；（2）若⊙O的半径为5，D是的中点，求弦CE的长．5．如图，MB，MD是⊙O的两条弦，点A，C分别在弧MB，弧MD上，且AB＝CD，点M是弧AC的中点．（1）求证：MB＝MD；（2）过O作OE⊥MB于E，OE＝1，⊙O的半径是2，求MD的长．6．如图，△ABC内接于⊙O，AB是⊙O的直径，AC＝6，CB＝8，CE平分∠ACB交⊙O于E，交AB于点D，过点E作MN∥AB分别交CA、CB延长线于M，N．（1）补全图形，并证明MN是⊙O的切线．（2）分别求MN、CD的长．7．如图，AB为⊙O的直径，AC，BE为⊙O上位于AB异侧的两条弦，连接BC，CE，延长AB到点D，使得∠BCD＝∠A．（1）求证：CD是⊙O的切线；（2）当AC＝CE时，①求证：BC2＝BEBD；②若BD＝3BE，AC＝2，求⊙O的半径r．8．如图，⊙O与△ABC的AB边相切于点B，与AC、BC边分别交于点D、E，DE∥OA，BE是⊙O的直径．（1）求证：AC是⊙O的切线；（2）若∠C＝30°，AB＝3，求DE的长．9．如图，四边形ABCD内接于⊙O，对角线BD是⊙O的直径，AC平分∠BAD，过点C作CG∥BD交AD的延长线于点G．（1）求证：CG是⊙O的切线；（2）若AB＝3，AD＝5，求AC的长．10．在平面直角坐标系xOy中，对于△ABC，点P在BC边的垂直平分线上，若以点P为圆心，PB为半径的⨀P与△ABC三条边的公共点个数之和不小于3，则称点P为△ABC关于边BC的“Math点”．如图所示，点P即为△ABC关于边BC的“Math点”．已知点P （0，4），Q（a，0）．（1）如图1，a＝4，在点A（1，0）、B（2，2）、C（，）、D（5，5）中，△POQ关于边PQ的“Math点”为．（2）如图2，，①已知D（0，8），点E为△POQ关于边PQ的“Math点”，请直接写出线段DE的长度的取值范围；②将△POQ绕原点O旋转一周，直线交x轴、y轴于点M、N，若线段MN上存在△POQ关于边PQ的“Math点”，求b的取值范围．参考答案1．解：∵∠A＝600，OA＝OB，∴△ABO为等边三角形，∴∠AOB＝60，∵AC＝4，∴OA＝2，∴S阴影＝S扇形AOB﹣S△AOB＝﹣×22＝﹣；（3）①如图1：∠ABF＝15°时，∠AOF＝30°，过点O作OH⊥AB，过F作FP⊥OH，FG⊥BA，由（2）知∠AOB＝60°，∴∠AOH＝30°，∴∠FOP＝60°．Rt△FPO中，∠FOP＝60°，OF＝2，∴OP＝1．Rt△AOH中，AO＝2，∠AOH＝30°，∴OH＝，∴FG＝HP＝﹣1．②如图2：∠ABF＝15°时，∠AOF＝30°，等边△ABO中，OF平分∠AOB，∴OF⊥AB．Rt△AOH中，AO＝2，∠AOH＝30°，∴OH＝，∴FH＝2﹣．综上所述，点F到直线AB的距离是﹣1或2﹣．2．（1）证明：如图1，作直径DG，交AC于F，交BC于P，交⊙O于G，连接CG，∵＝．∴DG⊥BC，BD＝CD，∴∠CBD＝∠BCD，∵AC⊥BD，∴∠DEF＝90°，∵∠CPF＝90°，∴∠DEF＝∠CPF，∵∠DFE＝∠CFP，∴∠EDF＝∠ACB＝∠ADB＝∠CDG，∴∠BDC＝2∠ADB；（2）解：如图2，作直径DG，交AC于F，交BC于P，交⊙O于G，连接CG，BG，由（1）知：∠ADB＝∠BDG＝∠CDG，∴＝，∴∠CBG＝∠BCA，∴BG∥AC，∴∠ONF＝∠OBG，∠OFN＝∠OGB，∵OB＝OG，∴∠OBG＝∠OGB，∴∠ONF＝∠OFN，∴OF＝ON，∵AC⊥BD，∠ADB＝∠FDB，∴∠DAE＝∠AFD，∴AB＝DF，同理得：CF＝CG，∴AD﹣BN，＝DF﹣BN＝OD+OF﹣（OB﹣ON）＝OF+ON＝2，∴OF＝ON＝1，∵CF＝CG，CP⊥FG，∴FP＝PG，设FP＝a，则OB＝OG＝2a+1，FP＝a+1，∵DG⊥BC，且BC＝8，∴BP＝BC＝4，Rt△OBP中，OB2＝OP2+BP2，∴（2a+1）2＝（a+1）2+42，3a2+2a﹣16＝0，（a﹣2）（3a+8）＝0，∴a1＝2，a2＝﹣（舍），∴⊙O的半径OG＝2a+1＝5．3．解：（1）①如图，PM，PN是⊙T的两条切线，M，N为切点，连接TM，TN．当∠MPN＝60°时，∵PT平分∠MPN，∵∠TPM＝∠TPN＝30°，∵TM⊥PM，TN⊥PN，∴∠PMT＝∠PNT＝90°，∴TP＝2TM，以T为圆心，TP为半径作⊙T，观察图象可知：当60°≤∠MPN＜180°时，⊙T的环绕点在图中的圆环内部（包括大圆上的点不包括小圆上的点）．如图1中，以O为圆心2为半径作⊙O，观察图象可知，P2，P3是⊙O的环绕点，故答案为：P2，P3．②如图2中，设小圆交y轴的正半轴与于E．当直线y＝x+b经过点E时，b＝1．当直线y＝x+b与大圆相切于K（在第二象限）时，连接OK，由题意B（0，b），A（﹣b，0），∴OB＝b，OA＝b，AB＝＝b，∵OK＝2，ABOK＝OAOB，∴b×2＝bb，解得b＝2，观察图象可知，当1＜b≤2时，线段AB上存在⊙O的环绕点，根据对称性可知：当﹣2≤b＜﹣1时，线段AB上存在⊙O的环绕点，综上所述，满足条件的b的取值范围为1＜b≤2或﹣2≤b＜﹣1．（2）如图3中，不妨设E（m，m），则点E在直线y＝x时，∵m＞0，∴点E在射线OE上运动，作EM⊥x轴，∵E（m，m），∴OM＝m，EM＝，∴以E（m，m）（m＞0）为圆心，m为半径的⊙E与x轴相切，作⊙E的切线ON，观察图象可知，以E（m，m）（m＞0）为圆心，m为半径的所有圆构成图形H，图形H即为∠MON的内部，包括射线OM，ON上．当⊙T的圆心在y轴的正半轴上时，假设以T为圆心，2为半径的圆与射线ON相切于D，连接TD．∵tan∠EOM＝＝，∴∠EOM＝30°，∵ON，OM是⊙E的切线，∴∠EON＝∠EOM＝30°，∴∠TOD＝30°，∴OT＝2DT＝4，∴T（0，4），当⊙T的圆心在y轴的负半轴上时，且经过点O（0，0）时，T（0，﹣2），观察图象可知，当﹣2＜t≤4时，在图形H上存在⊙T的环绕点．4．（1）证明：∵CE⊥AB，AB是直径，∴，又∵∴，∴∠CAD＝∠ACE，∴AP＝CP，∵AB是⊙O的直径，∴∠ACB＝90˚，∴∠ACE+∠BCP＝90°，∠CAD+∠CQA＝90°，∴∠BCP＝∠CQA，∴CP＝PQ，∴AP＝PQ，即P是线段AQ的中点；（2）解：∵，AB是直径，∴∠ACB＝90˚，∠ABC＝30˚，又∵AB＝5×2＝10，∴AC＝5，BC＝5，∴CH＝BC＝，又∵CE⊥AB，∴CH＝EH，∴CE＝2CH＝2×＝5．5．证明：（1）∵AB＝CD，∴＝，又∵点M是弧AC的中点，∴＝，∴+＝+，即：＝，∴MB＝MD；（2）过O作OE⊥MB于E，则ME＝BE，连接OM，在Rt△MOE中，OE＝1，⊙O的半径OM＝2，∴ME＝＝＝，∴MD＝MB＝2ME＝2．6．证明：（1）补全图形如图所示，连接OE，∵AB是⊙O的直径，∴∠ACB＝90°，又∵CE平分∠ACB，∴∠ACE＝∠BCE＝∠ACB＝45°，∴∠AOE＝2∠ACE＝90°，∴OE⊥AB，又∵MN∥AB，∴OE⊥MN，∴MN是⊙O的切线；（2）过点C作CQ⊥MN，垂足为Q，交AB于点P，则CQ⊥AB，在Rt△ABC中，∵AC＝6，BC＝8，∴AB＝＝＝10∴OE＝PQ＝OA＝OB＝5，由三角形的面积公式得，ACBC＝ABCP，∴6×8＝10CP，∴CP＝4.8，∴CQ＝4.8+5＝9.8，∵AB∥MN，∴△CAB∽△CMN，∴＝，即＝，∴MN＝，连接BE，则BE＝AE，在Rt△ABE中，AE＝BE＝×AB＝5，∵EN是⊙O的切线，∴∠BEN＝∠BCE＝∠ACE，∵ACBE是⊙O的内接四边形，∴∠EBN＝∠CAB，∴△AEC∽△BNE，∴＝，即＝，∴BN＝，∵∠ACE＝∠ECN，∠CAE＝∠CEN，∴△CAE∽△CEN，∴＝，即＝，解得，CE＝7，又∵∠ACD＝∠ECB，∠CAD＝∠CEB，∴△ACD∽△ECB，∴＝，即＝，解得，CD＝，∴MN＝，CD＝．7．①∵∠BAE＝∠BCE，∴∠CAE＝∠CAB+∠BAE＝∠CAB+∠BCE，∵∠BCD＝∠CAB，∴∠CAE＝∠BCD+∠BCE＝∠DCE，∵AC＝CE，∴∠CAE＝∠AEC，∴∠AEC＝∠DCE，∴CD∥AE，∴∠BAE＝∠D，∵∠BAE＝∠BCE，∴∠BCE＝∠D，∵∠CAB和∠CEB是所对的圆周角，∴∠CEB＝∠CAB，∵∠BCD＝∠CAB，∴∠CEB＝∠BCD，∵∠BAE＝∠D，∴△BCE∽△BDC，∴，∴BC2＝BEBD；②如图2，连接OC，AE，设BE＝x（x＞0），∵BD＝3BE，∴BD＝3x，由①知，BC2＝BEB，∴BC＝x，由①知，△BCE∽△BDC，∴，∵CE＝AC＝2，∴，∴CD＝2，在Rt△OCD中，OD＝OB+BD＝r+3x，根据勾股定理得，OC2+CD2＝OD2，∴r2+（2）2＝（r+3x）2，∴3x2+2rx﹣4＝0（Ⅰ），在Rt△ABC中，根据勾股定理得，AC2+BC2＝AB2，∴22+（x）2＝（2r）2，∴3x2﹣4r2+4＝0（Ⅱ），（Ⅰ）+（Ⅱ）得，6x2+2rx﹣4r2＝0，∴3x2+rx﹣2r2＝0，∴（3x﹣2r）（x+r）＝0，∵r＞0，x＞0，∴x+r＞0，∴3x﹣2r＝0，∴x＝r，将x＝r代入（Ⅱ）得，3×（r）2﹣4r2+4＝0，∴r＝（舍去负值），即⊙O的半径r为．8．证明：（1）连接OD，∵AB与⊙O相切于点B，∴∠ABO＝90°，∵DE∥OA，∴∠OED＝∠BOA，∠EDO＝∠AOD，又∵OD＝OE＝OB，∴∠OED＝∠ODE，在△ABO和△ADO中，∵OB＝OD，∠BOA＝∠DOA，AO＝AO，∴△ABO≌△ADO（SAS），∴∠ADO＝∠ABO＝90°，即OD⊥AC，∴AC是⊙O的切线；（2）∵∠C＝30°，∠ODC＝90°，∴∠DOE＝90°﹣30°＝60°，又∵OD＝OE，∴△ODE是正三角形，∴OD＝OE＝DE＝OB，在Rt△ABO中，∠AOB＝60°，AB＝3，∴OB＝＝＝，∴DE＝．9．证明：（1）如图，连接OC，∵BD是⊙O的直径，∴∠BAD＝90°，∴∠BAC＝∠DAC＝∠BAD＝45°，∴∠BOC＝2∠DAC＝90°，∴OC⊥BD，又∵CG∥BD，∴OC⊥CG，∴CG是⊙O的切线；（2）∵BD是⊙O的直径，∴∠BAD＝∠BCD＝90°，又∵AC平分∠BAD，∴∠BAC＝∠DAC，∴BC＝CD，在Rt△ABD中，BD＝＝＝，在Rt△BCD中，BC＝CD＝BD＝×＝，∵CG是⊙O的切线；∴∠DCG＝∠DAC＝∠BAC，∠ACG＝∠ABC，又∵∠CDG＝∠ABC，∴△ABC∽△CDG，∴＝，即＝，∴DG＝，由∠ACG＝∠ABC，∠BAC＝∠DAC可得△ABC∽△ACG，∴＝，即＝，解得，AC＝4．10．解：（1）根据“Math点”的定义，观察图象可知，△POQ关于边PQ的“Math点”为B、C．故答案为：B，C．（2）如图2中，∵P（0，4），Q（4，0），∴OP＝4，OQ＝4，∴tan∠PQO＝，∴∠PQO＝30°，①当点E与PQ的中点K重合时，点E是△POQ关于边PQ的“Math点”，此时E（2，2），∵D（0，8），∴DE＝＝4，当⊙E′与x轴相切于点Q时，E′（4，8），∴DE′＝4，观察图象可知，当点E在线段KE′上时，点E为△POQ关于边PQ的“Math点”，∵E′Q⊥OQ，∴∠E′QO＝90°，∴∠E′QK＝60°，∴∠E′KQ＝90°，∴∠EE′Q＝30°，∵DE′∥OQ，∴∠DE′K＝60°，∵DE′＝DK，∴△DE′K是等边三角形，∵点D到E′K的距离的最小值为4sin60°＝6，∴．②如图3中，分别以O为圆心，2和4为半径画圆，当线段MN与图中圆环有交点时，线段MN上存在△POQ关于边PQ的“Math点”，当直线MN与小圆相切时，b＝±4，当直线MN与大圆相切时，b＝±8，观察图象可知，满足条件的b的值为：或．。

中考数学《圆的综合》专题训练(含有答案)

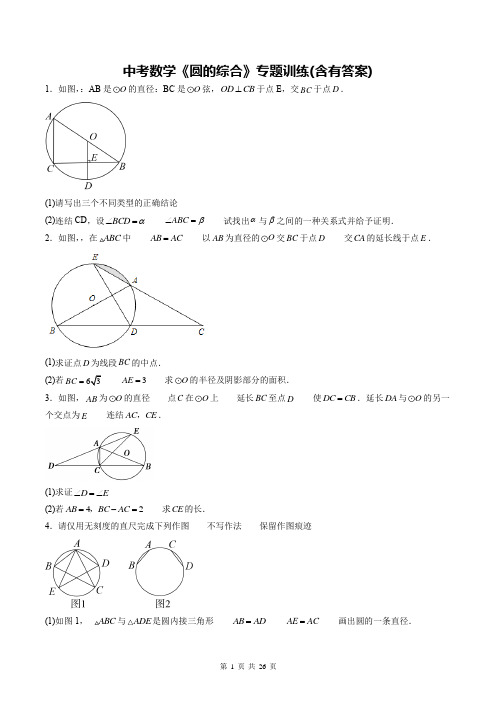
中考数学《圆的综合》专题训练(含有答案)1．如图，：AB 是O 的直径：BC 是O 弦，OD CB ⊥于点E ，交BC 于点D ．(1)请写出三个不同类型的正确结论(2)连结CD ，设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明．2．如图，，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E ．(1)求证点D 为线段BC 的中点．(2)若63BC = 3AE = 求O 的半径及阴影部分的面积．3．如图，AB 为O 的直径点C 在O 上延长BC 至点D 使DC CB =．延长DA 与O 的另一个交点为E 连结AC CE ，．(1)求证D E ∠=∠(2)若42AB BC AC =-=，求CE 的长．4．请仅用无刻度的直尺完成下列作图不写作法保留作图痕迹(1)如图1， ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径．(2)如图2 ， AB CD 是圆的两条弦 AB CD =且不相互平行画出圆的一条直径． 5．如图，AB 是O 的直径点D 在AB 的延长线上点C 在O 上 ,30CA CD CDA =∠=︒．(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离．6．如图，点C 在以AB 为直径的O 上过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC ．(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长．7．如图，已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点连接EF ．(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长．8．如图， AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E ．(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长．9．如图， AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F ．(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长． 10．如图，所示 AB 是O 的直径点D 在AB 上点C 在O 上 AD AC =CD 的延长线交O 于点E ．(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积．11．如图， ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠．(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长． 12．如图，四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB ．(1)求ABD ∠的度数 (2)求BAD ∠的度数．13．如图，四边形ABCD 是O 的内接四边形且对角线BD 为O 的直径过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠．(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长．14．如图，在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置．(1)若正方形的边长是8 4BP =．求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长．15．如图， AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点若CDB BFD ∠=∠．(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长． 16．如图，O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E ．(1)如图，① 若70C ∠=︒ 求E ∠的大小 (2)如图，① 若AE AB = 求E ∠的大小．17．已知如图，直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E ．(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径．18．已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =．(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值．参考答案与解析1．(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】（1）AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理．（2）连接,CD DB 根据四边形ACDB 为圆内接四边形可以得到290αβ+=︒．【解析】（1）解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等．（2）如图，连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒．【点评】本题考查了圆的一些基本性质且有一定的开放性垂径定理圆内接四边形的性质掌握圆的相关知识． 2．(1)见解析 (2)半径为3 39π324S =阴【分析】（1）连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点（2）根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】（1）连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点．（2）①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-（舍去） 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质相似三角形的判定和性质不规则图形面积的计算熟练掌握相关知识点是解题的关键． 3．(1)见解析 (2)CE 的长为17【分析】（1）由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠（2）设BC x = 则2AC x =- 在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长由（1）知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】（1）证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠（2）解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由（1）得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理三角形全等的判定与性质等腰三角形的性质勾股定理解直角三角形熟练掌握圆周角定理三角形全等的判定与性质等腰三角形的性质是解题的关键． 4．(1)见解析 (2)见解析【分析】（1）设BC DE 交于点G 连接AG 交圆于点F 即可作答（2）连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答．【解析】（1）如图，设BC DE 交于点G 连接AG 并延长交圆于点F线段AF 即为所求证明如图， BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径（2）如图，连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求．证明方法同（1）．【点评】本题主要考查了垂径定理圆周角定理以及全等三角形的判定与性质等知识掌握圆周角定理以及垂径定理是解答本题的关键． 5．(1)见解析 (2)9【分析】（1）已知点C 在O 上先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系．（2）要求点A 到CD 所在直线的距离先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE ．【解析】（1）①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒．连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线即直线CD 与O 相切．（2）过点A 作AE CD ⊥ 垂足为E ．在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==．【点评】此题考查的知识点是切线的判定与性质解题的关键是运用直角三角形的性质及30°角所对直角边的性质．6．(1)见解析 (2)252AB =．【分析】（1）连接OC 由DE 为O 的切线得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径可知90ACB ∠=︒ 最后根据等角的余角相等可得结论（2）在Rt CAD △中利用锐角三角函数定义求出CD 的长根据勾股定理求出AD 的长由（1）易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长．【解析】（1）解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠（2）在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由（1）可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质以及解直角三角形熟练掌握切线的判定与性质是解本题的关键． 7．(1)证明见解析 (2)125AB =【分析】（1）连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线（2）根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可．【解析】（1）证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线（2）解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由（1）知 EFD △为直角三角形且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明圆的基本性质以及勾股定理解三角形等掌握切线的证明方法熟练运用圆中的基本性质是解题关键．8．(1)见解析(2)半径为2 123AE =【分析】（1）根据点C 为弧BD 的中点得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解（2）连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式进而即可求解．【解析】（1）证明连接OC 如图，点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线．（2）解连接BC 如图，AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2．设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定相似三角形的性质与判定掌握切线的判定以及相似三角形的性质与判定是解题的关键．9．(1)见解析(2)3【分析】（1）连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质证明ADC AOF ∠∠=．（2）利用平行线分线段成比例定理计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解．【解析】（1）如图，连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=．（2）如图，连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=．【点评】本题考查了切线的性质等腰三角形的三线合一性质平行线分线段成比例定理相似三角形的性质与判定熟练掌握切线的性质相似三角形的性质与判定是解题的关键．10．(1)证明过程见解析 (2)142π-【分析】（1）AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证（2）如图，所示（见解析）连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解．【解析】（1）证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线．（2）解如图，所示连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-．【点评】本题主要考查圆的基础知识掌握圆的切线的证明方法扇形面积的计算方法是解题的关键．11．(1)见解析(2)3【分析】（1）连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可（2）根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例即可求解．【解析】（1）证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线（2）①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=．【点评】本题主要考查了切线的判定和性质圆周角定理相似三角形的判定和性质以及解直角三角形解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质．12．(1)30︒(2)100︒【分析】（1）根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解（2）根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质即可求解．【解析】（1）解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ （2）解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒．【点评】本题主要考查了圆内接四边形的性质圆周角定理等知识熟练掌握圆内接四边形的性质圆周角定理是解题的关键．13．(1)见解析(2)AD 的长是25【分析】（1）连接OA 根据已知条件证明OA AE ⊥即可解决问题（2）作OF CD ⊥ 则四边形OAEF 是矩形且132DF CD ==由此可求得DE 的长在Rt OFD △中勾股定理求出OF 即AE 的长在Rt AED △中利用勾股定理求DA ．【解析】（1）证明如图，连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒．①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线（2）解过点O 作OF CD ⊥于F ．①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===，．①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质垂径定理圆周角定理勾股定理解决本题的关键是掌握切线的判定与性质．14．(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形根据公式计算即可．(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可．【解析】（1）如图， ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==， ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影．（2）连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =．【点评】本题考查了正方形的性质旋转的性质阴影面积的计算扇形面积公式勾股定理熟练掌握旋转的性质阴影面积的计算扇形面积公式勾股定理是解题的关键．15．(1)证明见解析(2)10DF =【分析】（1）因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论（2）利用勾股定理先求解AC 再利用垂径定理得出AE 的长可得OE 的长证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长．【解析】（1）①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线（2）①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =．经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质垂径定理圆周角定理切线的判定以及平行线的判定掌握相似三角形的判定与性质垂径定理圆周角定理以及平行线的判定是解题的关键．16．(1)50︒(2)30︒【分析】（1）连接OA 先由切线的性质得OAE ∠的度数求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案（2）连接OA 根据等腰三角形的性质及切线的性质列方程求解即可．【解析】（1）连接OA ．如图，①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒．（2）连接OA 如图，①设E x ∠=．AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=． AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒．【点评】本题主要考查了切线的性质等腰三角形的性质圆周角的性质三角形内角和的性质用方程思想解决几何问题关键是熟悉掌握这些性质．17．(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长再由ACD ADE ∽ 根据相似三角形的性质列出比例式代入数据即可求得圆的半径．【解析】（1）证明如图，连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线（2）解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图，连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm ．【点评】本题考查圆了切线的判定；等边对等角平行线的判定与性质圆周角定理勾股定理相似三角形的判定和性质等知识在圆中学会正确添加辅助线是解决问题的关键．18．(1)见解析 (2)49【分析】（1）欲证~CBA FDC ，只要证明两个角对应相等就可以．可以转化为证明DE BC =就可以（2）由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案．【解析】（1）证明①四边形ABCD 内接于O①CBA CDF ∠=∠．①DE BC =①BCA DCE ∠=∠．①~CBA FDC（2）解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===．【点评】本题考查的是圆的综合题；涉及弧、弦的关系；等腰三角形的性质；相似三角形的判定与性质；锐角三角函数；掌握相似三角形的判定和性质是解答此题的关键．。

广东省2013年中考数学专题训练(二)及答案

第9题第8题2013年广东省数学中考专题训练二一、选择题(本大题8小题，每小题4分，共32分)1、已知点P (3，－2)与点Q 关于x 轴对称，则Q 点的坐标为( )A ．(－3，2)B ．(－3，－2)C ．(3，2)D ．(3，－2) 2、4的平方根是( ) A ．±2B ．2C ．±2D ．23、2009年3月5日，温家宝总理在《政府工作报告》中，讲述了六大民生新亮点，其中之一就是全部免除了西部地区和部分中部地区农村义务教育阶段约52000000名学生的学杂费。

这个数据保留两个有效数字用科学记数法表示为( ) A ．52×107B ．5.2×107C ．5.2×108D ．52×1084、下图是由几个相同的小正方体搭成的一个几何体，它的俯视图是( )5、如图，已知a ∥b ，∠1=40︒，则∠2=( ). A ．140︒B ．120︒C ．40︒D ．50︒6、已知一个多边形的内角和等于900，则这个多边形的边数是( ) A ．6B ．7C ．8D ．97、不等式组152320xx -⎧>3⎪⎨⎪-<⎩的解集的情况为( ) A ．x <－1 B ．x <32 C ．－1<x <32D ．无解8、如图，图中正方形ABCD 的边长为4，则图中阴影部分的面积为( ) A ．16－4π B ．32－8π C ．8π－16 D ．无法确定二、填空题(本大题5小题，每题4分，共20分)9、如图，AB 是⊙O 的直径，点C 在⊙O 上，OD ∥BC ，若OD =1，则BC 的长为． 10、若代数式3-x 有意义，则实数x 的取值范围为． 11、写出一个图象位于第二、四象限的反比例函数的表达式是___________．12、关于x 的一元二次方程x 2－2x +m =0有两个实数根，则m 的取值范围是．(第5题)bac2113、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第n 个图形需_____根火柴棒．(第一个图形)(第二个图形)(第三个图形)三、解答题14、计算： ︒--π+----458143321022sin ).()()(16、解方程：11262213x x=---17、先化简，后求值：121111122+--÷+--+-x x x x x ，其中x =－320、如图，在平行四边形ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ，BD 与AE 、AF 分别相交于G 、H ．(1)求证：△ABE ∽△ADF ；(2)若AG =AH ，求证：四边形ABCD 是菱形．22、如图，已知⊙O 的直径AB 垂直于弦CD 于点E ，过C 点作CG ∥AD 交AB 的延长线于点G ，连接CO 并延长交AD 于点F ，且CF ⊥AD ． (1)试问：CG 是⊙O 的切线吗？说明理由；ADBGEHF(第20题)AF(2)求证：E为OB的中点；(3)若AB=8，求CD的长．参考答案一、选择题(本大题8小题，每小题4分，共32分)二、填空题(本大题共5小题，每小题4分，共20分) 9． 2 10．x ≥3 11．y =－x1(答案不唯一) 12．m ≤1 13．6(n +1) 三、解答题(本大题共5小题，每小题7分，共35分)14．解：原式=4－3+1－22×22=4－3+1－2 =016．解：原方程可化为：1122(31)231x x =+-- 1=314x -+ 313x -=-23x =-经检验23x =-是原方程的解 17．解：原式=112111122-+-⨯-++-x x x x x =11111112--⨯-++-x )x ()x )(x (x=x x ++-1111 =212x -当x =3-时原式=1223122-=-=--)(20．解：(1)∵AE ⊥BC ，AF ⊥CD ，∴∠AEB =∠AFD =90°．∵四边形ABCD 是平行四边形，∴∠ABE =∠ADF ． ∴△ABE ∽△ADF(2) ∵△ABE ∽△ADF ，∴∠BAG =∠DAH ． ∵AG =AH ，∴∠AGH =∠AHG ， ∴∠AGB =∠AHD ． ∴△ABG ≌△ADH ．∴AD AB =． ∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形．22．(1)解：是⊙O 的切线理由：CG AD ∥180FCG CFD ∴∠+∠=CF AD ⊥90CFD ∴∠= 90FCG ∴∠= 即OC ⊥CG ．∴CG 是⊙O 的切线．ADBGEHF(第20题)(2)证明：连接BD ，AB 为⊙O 的直径90ADB ∴∠=又90AFO ∠=ADB AFO ∴∠=∠CF BD ∴∥ BDE OCE ∴△∽△BE DEOE CE∴=AE CD ⊥ 且AE 过圆心O CE DE ∴=BE OE ∴=∴点E 为OB 的中点．(3)解：8AB = 142OC AB ∴== 又BE OE = 2OE ∴= AB CD ⊥ ∴CE =32242222=-=-OE OC2CD CE ∴==。

2020年九年级数学中考几何图形综合题专题训练(含答案)

2020年九年级数学中考几何图形综合题专题训练1、如图，在▱ABCD 中，点E 在边BC 上，点F 在边AD 的延长线上，且DF=BE ，BE 与CD 交于点G（1）求证：BD ∥EF ；（2）若=，BE=4，求EC 的长．2、如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，∠BAC ＝60°，AD 平分∠BAC 交BC 于点D ，过点D 作DE ∥AC 交AB 于点E .点M 是线段AD 上的动点，连接BM 并延长分别交DE ，AC 于点F ，G .(1)求CD 的长；(2)若点M 是线段AD 的中点，求EF DF的值；(3)请问当DM 的长满足什么条件时，在线段DE 上恰好只有一点P ，使得∠CPG ＝60°？3、如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．（1）求证：△AC D∽△BFD；（2）当tan∠ABD=1，AC=3时，求BF的长．4、如图，▱ABCD的对角线AC、BD交于点O，EF过点O且与BC、AD分别交于点E、F．试猜想线段AE、CF的关系，并说明理由．5、如图，平行四边形ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF（1）根据题意，补全原形；（2）求证：BE=DF．6、如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G.(1)猜想并证明线段FG与CG的数量关系；(2)若将图①中的正方形改成矩形，其他条件不变，如图②，那么线段FG与CG之间的数量关系是否改变？请证明你的结论；(3)若将图①中的正方形改成平行四边形，其他条件不变，如图③，那么线段FG与CG 之间的数量关系是否会改变？请证明你的结论．7、如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．8、如图，□A BCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。

2021年中考数学一轮复习专题突破训练：几何压轴—圆的综合(二)

2021年九年级数学中考一轮复习专题突破训练：几何压轴—圆的综合（二）1．如图，点C在以AB为直径的⊙O上．AE与过点C的切线垂直，垂足为D，AD交⊙O于点E，过B作BF∥AE交⊙O于点F，连接CF．（1）求证：∠B＝2∠F；（2）已知AE＝8，DE＝2，求CF的长．2．如图，在等腰△ABC中，AB＝AC，以AC为直径的⊙O与BC相交于点D，过点D作DE⊥AB 交CA的延长线于点E，垂足为点F．（1）判断DE与⊙O的位置关系，并说明理由．（2）若⊙O的半径R＝3，cos∠E＝，求EF的长．3．已知，⊙O中，＝，D是⊙O上的点，OC⊥BD．（1）如图①，求证＝；（2）如图②，连接AB，BC，CD，DA，若∠A＝70°，求∠BCD，∠ADB的大小．4．已知⊙O是△ABC的外接圆，CE为⊙O的直径，交AB于点F，连接AO并延长交BC于点D，AD⊥BC．（1）如图1，求证：∠BFC＝3∠BAD；（2）如图2，连接AE、BE，过点A作AG⊥CE，垂足为G．求证：CE＝BE+2EG；（3）如图3，在（2）的条件下，连接DG交AB于点H，若GH＝2，AG＝4，求△CDG 的面积．5．已知：如图，⊙O内两条弦AB、CD，且AB⊥CD于E，OA为⊙O半径，连接AC、BD．（1）求证：∠OAC＝∠BCD；（2）作EN⊥BD于N，延长NE交AC于点H．求证：AH＝CH；（3）在（2）的条件下，作∠EHF＝60°交AB于点F，点P在FE上，连接PC交HN于点L，当EL＝HF＝，CL＝8，BE＝2PF时，求⊙O的半径．6．如图，AB是半圆O的直径，半径OC⊥AB，OB＝2，D是OB的中点，点E是弧BC上的动点，连接AE，DE．（1）当点E是弧BC的中点时，求△ADE的面积；（2）若tan∠AED＝，求AE的长；（3）点F是半径OC上一动点，设点E到直线OC的距离为m，当△DEF是等腰直角三角形时，求m的值．7．如图，在矩形ABCD中，点O在对角线BD上，以OB的长为半径的圆O与AB，BD分别交于点E，F，连接DE，且∠ADE＝∠BDC．（1）判断直线DE与⊙O的位置关系，并证明你的结论；（2）若BC＝6，CD＝8，AE＝4.5，求⊙O的半径．8．如图，在△ABC 中，∠ACB ＝90°，CA ＝CB ，点O 在△ABC 的内部，⊙O 经过B ，C 两点，交AB 于点D ，连接CO 并延长交AB 于点G ，以GD ，GC 为邻边作平行四边形GDEC ．（1）判断DE 与⊙O 的位置关系，并说明理由；（2）若DE ＝17，CE ＝13，求⊙O 的半径．9．在△ABC 中，以AB 边上的中线CD 为直径作圆，如果与边AB 有交点E （不与点D 重合），那么称为△ABC 的C ﹣中线弧．例如，如图中是△ABC 的C ﹣中线弧．在平面直角坐标系xOy 中，已知△ABC 存在C ﹣中线弧，其中点A 与坐标原点O 重合，点B 的坐标为（2t ，0）（t ＞0）．（1）当t ＝2时，①在点C 1（﹣3，2），C 2（0，2），C 3（2，4），C 4（4，2）中，满足条件的点C 是；②若在直线y ＝kx （k ＞0）上存在点P 是△ABC 的C ﹣中线弧所在圆的圆心，其中CD ＝4，求k 的取值范围；（2）若△ABC的C﹣中线弧所在圆的圆心为定点P（2，2），直接写出t的取值范围．10．如图，点A，点C在以BD为直径的⊙O上过点A作AE∥BC交CD的延长线于点E，且∠DAE＝∠ABD．（1）求证：AE是⊙O的切线．（2）若⊙O的半径为5．CD＝6，求AD的长．参考答案1．（1）证明：连接OC，∵CD是⊙O的切线，∴OC⊥CD，∵AD⊥CD，∴OC∥AD，∴∠BOC＝∠DAB，由圆周角定理得，∠BOC＝2∠F，∴∠DAB＝2∠F，∵AD∥BF，∴∠B＝∠DAB，∴∠B＝2∠F；（2）解：连接AF、AC，延长CO交⊙O于H，过O作OG⊥AE于G，∵OC∥AD，AE∥BF，∴OC∥BF，∴∠BFC＝∠HCF，∵∠B＝2∠F，∴∠B＝2∠HCF，∵∠ACF＝∠B，∴∠ACF＝2∠HCF，∴∠ACH＝∠HCF，∴＝，∴CH垂直平分AF，∴CF＝AC，∵OG⊥AE，∴AG＝EG＝4，∴GD＝GE+ED＝4+2＝6，∵∠OGD＝∠D＝∠OCD＝90°，∴四边形OCDG是矩形，∴OC＝GD＝6，OG＝CD，∵OA＝OC＝6，AG＝4，∴OG＝＝＝2，∴DC＝2，在Rt△ADC中，AC＝＝＝2∴CF＝AC＝2．2．解：（1）DE与⊙O相切，理由：连接OD，∵OD＝OC，∴∠ODC＝∠OCD，∵AB＝AC，∴∠B═∠C，∴∠B＝∠ODC，∴AB∥OD，∵DE⊥AB，∴OD⊥DE，∴DE是⊙O的切线；（2）∵DE⊥AB，cos∠E＝，∴＝，∴＝，∵AB∥OD，∴△AEF∽△OED，∴＝，∵OA＝OD＝R＝3，∴＝，∴EA＝2，∵＝，∴EF＝×2＝．3．（1）证明：∵OC⊥BD，OC过O，∴＝，∵＝，∴＝；（2）解：∵四边形ABD是圆内接四边形，∴∠A+∠BCD＝180°，∵∠A＝70°，∴∠BCD＝110°，∵＝，∴∠CBD＝∠CDB＝（180°﹣∠BCD）＝35°，∵＝，∴∠ADB＝∠CDB＝35°．4．（1）证明：如图1，∵AD⊥BC，AD是过圆心的线段，∴BD＝CD．∴AB＝AC．∴∠BAD＝∠CAO．∵OA＝OC，∴∠OAC＝∠OCA．∵∠BFC＝∠FAC+∠ACF，∴∠BFC＝3∠BAD；（2）如图2，在CE上截取CP＝BE，连接AP．∵＝．∴∠EBA＝∠FCA．∵AB＝AC，∴△EBA≌△PCA（SAS）．∴AE＝AP．∵AG⊥EC，∴EG＝PG．∴CE＝BE+2EG．（3）∵∠AGO＝∠CDO，AO＝CO，∠AOG＝∠COD，∴△AGO≌△CDO（AAS）．∴OG＝OD，AG＝CD．∴∠OGD＝∠ODG＝∠OAC＝∠OCA．∴AC∥DG．∴四边形AGMC是平行四边形．∵BD＝CD，∴DH＝AC．如图3，过点C作CN⊥DG，CM⊥GC交GD延长线于点M，∴四边形AGMC是平行四边形，∴CM＝AG＝CD＝4．设AC＝m，则DH＝m．∴DN＝MN＝m﹣1．∴sin∠CGM＝sin∠MCN．∴＝，即＝．∴m1＝20，m2＝﹣16．过点D作DQ⊥CG于Q．∵GC＝8，DG＝12，∴DQ＝．＝CG•DQ＝×8×＝48．∴S△CDG∴△CDG的面积是48．5．证明：（1）如图1，连接CO，∵OA＝OC，∴∠OAC＝∠OCA，∵∠OAC+∠OCA+∠AOC＝180°，∴2∠OAC+∠AOC＝180°，∵∠AOC＝2∠ABC，∴∠OAC+∠ABC＝90°，∵AB⊥CD，∴∠ABC+∠BCD＝90°，∴∠OAC＝∠BCD；（2）∵EN⊥BD，AB⊥CD，∴∠DEN+∠CDN＝90°，∠AEH+∠DEN＝90°，∴∠AEH＝∠CDN，又∵∠CDB＝∠CAB，∴∠CAB＝∠AEH，∴AH＝HE，∵∠CAB+∠ACE＝∠AEH+∠CEH＝90°，∴CH＝HE，∴AH＝CH；（3）如图3，延长HF至Q，使HQ＝HE，连接EQ，在AF上取点T，使QT＝QF，过点L作LR⊥CD于R，∵AH＝CH＝HE＝HQ，∠FHE＝60°，∴△HEQ是等边三角形，∴HQ＝HE＝QE，∠HQE＝∠HEQ＝∠QHE＝60°，∵EL＝HF＝，∴FQ＝HL，设∠AHQ＝2α，则∠CHE＝180°﹣2α﹣60°＝120°﹣2α，∴∠AEH＝∠HAE＝60﹣α，∴∠AEQ＝60°﹣∠AEH＝α，∴∠AFQ＝60°+α，∵TQ＝FQ，∴∠ETQ＝∠AFQ＝60°+α，∴∠TQE＝180°﹣α﹣（60°+α）＝120°﹣α；∴∠TQE＝∠CHL，又∵QE＝CH，QF＝HL，∴△ETQ≌△CLH（SAS），∴CL＝ET＝8，∠HCL＝∠TEQ＝α，∵HC＝HE，∠CHE＝120°﹣2α，∴∠HCE＝∠HEC＝30°+α，∵LR⊥CD，∴LR＝CL＝4，CR＝LR＝4，∴RE＝＝＝2，∴CE＝6，∵∠PCE＝30°，CE⊥AB，∴EC＝PE，CP＝2PE，∴PE＝6，CP＝12，∴PL＝CP﹣CL＝4，∵CH＝HE，HG⊥CE，∴CG＝GE＝3，∵HG∥LR，∴，∴＝，∴HE＝3＝AH＝HC，∵∠CPE＝∠EHF＝60°，∠PEL＝∠HEF，∴△PEL∽△HEF，∴，∴，∴EF＝7，∴PF＝1，∵BE＝2PF，∴BE＝2，∴BC＝＝＝4∵AH＝CH，∴OH⊥AC，∴tan∠CAO＝tan∠BCE＝，∴＝，∴AO＝．6．解：（1）如图，作EH⊥AB，连接OE，∵OB＝2，D是OB的中点，∴OD＝DB＝1，设DH＝a，则OH＝1+a，∵点E是弧BC中点，∴∠COE＝∠EOH＝45°，∴EH＝OH＝1+a，∵OE2＝EH2+OH2，∴4＝2（1+a）2，解得a＝﹣1∴EH＝OH＝，＝×3×＝；∴S△ADE（2）如图2，连接BE，过点D作DN⊥AE，∵tan∠AED＝＝，∴设DN＝3a，NE＝2a，∵AB是直径，∴∠AEB＝90°＝∠AND，∴BE∥DN，∴，∴∴AN＝6a，∵AN2+DN2＝AD2，∴36a2+9a2＝9，∴a＝，∴AE＝AN+NE＝6a+2a＝；（3）①当点D为等腰直角三角形直角顶点时，如图设DH＝a，∵∠DOF＝∠EDF＝∠EDH＝90°，∴∠FDO+∠OFD＝90°，∠FDO+∠EDH＝90°，∴∠OFD＝∠EDH，且DF＝DE，∠DOF＝∠EHD＝90°，∴△ODF≌△EDH（AAS）∴OD＝EH＝1，在Rt△ABE中，EH2＝AH•BH（1）2＝（3+a）•（1﹣a）解得a＝﹣1+，（负值舍去）∴m＝；当点E为等腰直角三角形直角顶点时，如图同理可证：△EFG≌△EDH，设DH＝a，则GE＝a，EH＝CG＝1+a，在Rt△ABE中，EH2＝AH•BH（1+a）2＝（3+a）•（1﹣a）解得a＝﹣1+，（负值舍去）∴m＝；当点F为等腰直角三角形直角顶点时，如图同理可证：△EFM≌△ODF，设OF＝a，则ME＝a，MF＝OD＝1，∴EH＝a+1，在Rt△ABE中，EH2＝AH•BH（a+1）2＝（2+a）•（2﹣a）解得a＝（负值舍去）∴m＝．7．解：（1）直线DE与⊙O相切，证明：连接OE，∵四边形ABCD是矩形，∴AB∥CD，∴∠EBD＝∠BDC，∵OB＝OE，∴∠EBD＝∠BEO，∵∠ADE＝∠BDC，∴∠BEO＝∠EBD＝∠BDC＝∠ADE，∵四边形ABCD是矩形，∴∠ADC＝90°，∴∠EOD+∠EDO＝∠EBD+∠BEO+∠EDO＝∠BDC+∠ADE+∠EDO＝∠ADC＝90°，∴∠OED＝180°﹣（∠EOD+∠EDO）＝180°﹣90°＝90°，即OE⊥ED，∵OE为半径，∴直线DE与⊙O相切；（2）解：∵四边形ABCD是矩形，∴∠A＝∠C＝90°，在Rt△DCB中，∠C＝90°，∴BD＝，∵四边形ABCD是矩形，∴AD＝BC＝6，在Rt△ADE中，∠A＝90°，∴ED＝，设⊙O的半径为R，在Rt△DOE中，DO2＝DE2+OE2，，解得：R＝，即⊙O的半径是．（2）第二种方法：解：∵四边形ABCD是矩形，∴∠A＝∠C＝90°，在Rt△DCB中，∠C＝90°，∴BD＝，∵AB＝CD＝8，AE＝4.5，∴BE＝8﹣4.5＝3.5，作OG⊥BE于G，则BG＝EG＝BE＝，∵OG∥AD，∴，即，∴OB＝，即⊙O的半径是．8．（1）DE是⊙O的切线；证明：连接OD，∵∠ACB＝90°，CA＝CB，∴∠ABC＝45°，∴∠COD＝2∠ABC＝90°，又∵四边形GDEC是平行四边形，∴DE∥CG，∴∠EDO+∠COD＝180°，∴∠EDO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：设⊙O的半径为r，∵四边形GDEC 为平行四边形，∴DG ＝CE ＝13，CG ＝DE ＝17，∵∠DOG ＝90°∴OD 2+OG 2＝DG 2，即r 2+（17﹣r ）2＝132，解得r 1＝5，r 2＝12，当r ＝5时，OG ＝12，点G 在⊙O 外，∴r ＝5不成立，舍去，∴r ＝12．9．解：（1）当t ＝2时，点B 的坐标为（4，0），∵点D 是AB 的中点，∴D （2，0），①如图1，过点C 作CE ⊥AB 于E ，则∠CED ＝90°，∴CE ⊥AB ，即点C 和点E 的横坐标相同，∵点E 是以CD 为直径与边AB 的交点，∴0≤AE ≤4，∵点E 与点D 重合，∴AE ≠2，∴点E 的横坐标大于等于0小于等于4，且不等于2，即点E 的横坐标大于等于0小于等于4，且不等于2，∵点C 1（﹣3，2），C 2（0，2），C 3（2，4），C 4（4，2）， ∴只有点C 2，C 4的横坐标满足条件，故答案为C 2，C 4；②∵△ABC 的中线CD ＝4，∴点C在以点D为圆心4为半径的弧上，由①知，点C的横坐标大于等于0小于等于4，且不等于2，∴点C在如图2所示的上（点H（2，4）除外），∵点P是以CD为半径的圆的圆心，∴点P在如图2所示的上（点G（2，2）除外），在Rt△ODC中，AD＝2，DC＝4，根据勾股定理得，OC＝2，∴C（0，2），同理：C'（4，2），∵点P是DC的中点，∴P（1，），同理：点P'（3，），当直线y＝kx过点P（1，）时，得，当直线y＝kx过点P'（3，）时，得，当直线y＝kx过点G（2，2）时，得k＝1，结合图形，可得k的取值范围是且k≠1；（2）同（1）①知，点E的横坐标大于等于0小于等于2t，且不等于t，∵点D是AB的中点，且B（2t，0），∴D（t，0），当点E在线段AD上时，AE＝t﹣2（t﹣2）＝﹣t+4≥0，∴t≤4，当点E在线段BE上时，AE＝2（2﹣t）+t≤2t，∴t≥，∴且t≠2．10．解：（1）证明：如图，连接OA，∴OA＝OB，∴∠ABD＝∠OAB，∵∠DAE＝∠ABD，∴∠OAB＝∠DAE，∵OA＝OD，∴∠OAD＝∠ODA，∵BD为⊙O的直径，∴∠BAD＝90°，∴∠OAB+∠OAD＝90°，∴∠DAE+∠OAD＝90°，∴∠OAE＝90°，∴OA⊥AE，∴AE是⊙O的切线；（2）作OF⊥BC于点F，∵OA⊥AE，AE∥BC，∴点A、O、F在同一条直线上，∵BD是直径，∴∠BCD＝90°，∴∠AED＝90°，∴四边形AECF是矩形，∴AF＝EC，AE＝FC，∵⊙O的半径为5，即BD＝10，∵CD＝6，∴BC＝＝8，∴BF＝FC＝4，OF＝CD＝3，∴CE＝AF＝AO+OF＝5+3＝8，∴DE＝CE﹣CD＝8﹣6＝2，∵AE＝FC＝4，∴AD＝＝2．。

决战2021年九年级中考复习数学考点满分专练——几何专题：《圆的综合》(二)

决战2021年九年级中考复习数学考点满分专练——几何专题：《圆的综合》（二）1．如图，在△ABC的边BC上取一点O，以O为圆心，OC为半径画⊙O，⊙O与边AB相切于点D，AC＝AD，连接OA交⊙O于点E，连接CE，并延长交线段AB于点F．（1）求证：AC是⊙O的切线；（2）若AB＝10，tan B＝，求⊙O的半径；（3）若F是AB的中点，试探究BD+CE与AF的数量关系并说明理由．2．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．3．如图，在△ABC中，AB＝AC．以AB为直径的⊙O与BC交于点E，与AC交于点D点，点F在边AC的延长线上，且∠CBF＝∠BAC．（1）试说明FB是⊙O的切线；（2）过点C作CG⊥AF，垂足为C．若CF＝4，BG＝3，求⊙O的半径；（3）连接DE，设△CDE的面积为S1，△ABC的面积为S2，若＝，AB＝10，求BC 的长．4．已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r．（1）如图1，点C在点A，B之间的优弧上，∠MPN＝80°，求∠ACB的度数；（2）如图2，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，∠APB的度数应为多少？请说明理由；（3）若PC交⊙O于点D，求第（2）问中对应的阴影部分的周长（用含r的式子表示）．5．如图1，AB是⊙O的直径，直线AM与⊙O相切于点A，直线BN与⊙O相切于点B，点C（异于点A）在AM上，点D在⊙O上，且CD＝CA，延长CD与BN相交于点E，连接AD并延长交BN于点F．（1）求证：CE是⊙O的切线；（2）求证：BE＝EF；（3）如图2，连接EO并延长与⊙O分别相交于点G、H，连接BH．若AB＝6，AC＝4，求tan∠BHE．6．已知：四边形ABCD内接于⊙O，连接AC、BD，∠BAD+2∠ACB＝180°．（1）如图1，求证：点A为弧BD的中点；（2）如图2，点E为弦BD上一点，延长BA至点F，使得AF＝AB，连接FE交AD于点P，过点P作PH⊥AF于点H，AF＝2AH+AP，求证：AH：AB＝PE：BE；（3）在（2）的条件下，如图3，连接AE，并延长AE交⊙O于点M，连接CM，并延长CM交AD的延长线于点N，连接FD，∠MND＝∠MED，DF＝12﹒sin∠ACB，MN＝，求AH的长．7．如图1，在△ABC中，∠ACB＝90°，∠ABC的角平分线交AC上点E，过点E作BE的垂线交AB于点F，△BEF的外接圆⊙O与CB交于点D．（1）求证：AC是⊙O的切线；（2）若BC＝9，EH＝3，求⊙O的半径长；（3）如图2，在（2）的条件下，过C作CP⊥AB于P，求CP的长．8．在图1至图3中，⊙O的直径BC＝30，AC切⊙O于点C，AC＝40，连接AB交⊙O于点D，连接CD，P是线段CD上一点，连接PB．（1）如图1，当点P，O的距离最小时，求PD的长；（2）如图2，若射线AP过圆心O，交⊙O于点E，F，求tan F的值；（3）如图3，作DH⊥PB于点H，连接CH，直接写出CH的最小值．9．如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于D，且BD＝8cm．点M从点A出发，沿AC方向匀速运动，速度为2cm/s；同时直线PQ由点B出发沿BA方向匀速运动，速度为1cm/s，运动过程中始终保持PQ∥AC，直线PQ交AB于P，交BC于Q，连接PM，设运动时间为t（s），0＜t≤5．（1）CM＝，PQ＝，BQ＝；（用含t的式子表示）（2）当四边形PQCM是平行四边形时，求t的值；（3）当点M在线段PC的垂直平分线上时，求t的值；（4）是否存在时刻t，使以PM为直径的圆与△ABC的边相切？若存在，直接写出t的值；若不存在，请说明理由．10．如图，A，B，C，D四点都在OO上，弧AC＝弧BC，连接AB，CD、AD，∠ADC＝45°．（1）如图1，AB是⊙O的直径；（2）如图2，过点B作BE⊥CD于点E，点F在弧AC上，连接BF交CD于点G，∠FGC＝2∠BAD，求证：BA平分∠FBE；（3）如图3，在（2）的条件下，MN与⊙O相切于点M，交EB的延长线于点N，连接AM，若2∠MAD+∠FBA＝135°，MN＝AB，EN＝26，求线段CD的长．参考答案1．解：（1）如图，连接OD，∵⊙O与边AB相切于点D，∴OD⊥AB，即∠ADO＝90°，∵AO＝AO，AC＝AD，OC＝OD，∴△ACO≌△ADO（SSS），∴∠ADO＝∠ACO＝90°，又∵OC是半径，∴AC是⊙O的切线；（2）∵tan B＝＝，∴设AC＝4x，BC＝3x，∵AC2+BC2＝AB2，∴16x2+9x2＝100，∴x＝2，∴BC＝6，∵AC＝AD＝8，AB＝10，∴BD＝2，∵OB2＝OD2+BD2，∴（6﹣OC）2＝OC2+4，∴OC＝，故⊙O的半径为；（3）AF＝CE+BD，理由如下：连接OD，DE，由（1）可知：△ACO≌△ADO，∴∠ACO＝∠ADO＝90°，∠AOC＝∠AOD，又∵CO＝DO，OE＝OE，∴△COE≌△DOE（SAS），∴∠OCE＝∠ODE，∵OC＝OE＝OD，∴∠OCE＝∠OEC＝∠OED＝∠ODE，∴∠DEF＝180°﹣∠OEC﹣∠OED＝180°﹣2∠OCE，∵点F是AB中点，∠ACB＝90°，∴CF＝BF＝AF，∴∠FCB＝∠FBC，∴∠DFE＝180°﹣∠BCF﹣∠CBF＝180°﹣2∠OCE，∴∠DEF＝∠DFE，∴DE＝DF＝CE，∴AF＝BF＝DF+BD＝CE+BD．12．解：（1）∵BE平分∠ABC，CE平分∠ACD，∴∠E＝∠ECD﹣∠EBD＝（∠ACD﹣∠ABC）＝α，（2）如图1，延长BC到点T，∵四边形FBCD内接于⊙O，∴∠FDC+∠FBC＝180°，又∵∠FDE+∠FDC＝180°，∴∠FDE＝∠FBC，∵DF平分∠ADE，∴∠ADF＝∠FDE，∵∠ADF＝∠ABF，∴∠ABF＝∠FBC，∴BE是∠ABC的平分线，∵＝，∴∠ACD＝∠BFD，∵∠BFD+∠BCD＝180°，∠DCT+∠BCD＝180°，∴∠DCT＝∠BFD，∴∠ACD＝∠DCT，∴CE是△ABC的外角平分线，∴∠BEC是△ABC中∠BAC的遥望角．（3）①如图2，连接CF，∵∠BEC是△ABC中∠BAC的遥望角，∴∠BAC＝2∠BEC，∵∠BFC＝∠BAC，∴∠BFC＝2∠BEC，∵∠BFC＝∠BEC+∠FCE，∴∠BEC＝∠FCE，∵∠FCE＝∠F AD，∴∠BEC＝∠F AD，又∵∠FDE＝∠FDA，FD＝FD，∴△FDE≌△FDA（AAS），∴DE＝DA，∴∠AED＝∠DAE，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠AED+∠DAE＝90°，∴∠AED＝∠DAE＝45°，②如图3，过点A作AG⊥BE于点G，过点F作FM⊥CE于点M，∵AC是⊙O的直径，∴∠ABC＝90°，∵BE平分∠ABC，∴∠F AC＝∠EBC＝∠ABC＝45°，∵∠AED＝45°，∴∠AED＝∠F AC，∵∠FED＝∠F AD，∴∠AED﹣∠FED＝∠F AC﹣∠F AD，∴∠AEG＝∠CAD，∵∠EGA＝∠ADC＝90°，∴△EGA∽△ADC，∴，∵在Rt△ABG中，AB＝8，∠ABG＝45°，∴AG＝，在Rt△ADE中，AE＝AD，∴，∴，在Rt△ADC中，AD2+DC2＝AC2，∴设AD＝4x，AC＝5x，则有（4x）2+52＝（5x）2，∴x＝，∴ED＝AD＝，∴CE＝CD+DE＝，∵∠BEC＝∠FCE，∴FC＝FE，∵FM⊥CE，∴EM＝CE＝，∴DM＝DE﹣EM＝，∵∠FDM＝45°，∴FM＝DM＝，∴S△DEF＝DE•FM＝．13．解：如图，（1）证明：连接AE，∵AB是直径，∴∠AEB＝90°，又∵AB＝AC，∴∠BAE＝BAC，∴∠CBF＝∠BAE，∵∠BAE+∠ABE＝90°，∴∠CBF+∠ABE＝90°，即AB⊥BF∵AB是直径，∴FB与⊙O相切．所以FB是⊙O的切线；（2）∵AB＝AC，∴∠ABC＝∠ACB，∵AB⊥BF，CG⊥AC，∴∠ABC+∠GBC＝∠ACB+∠BCG，∴∠GBC＝∠BCG，∴BG＝CG＝3．∵CG＝3，CF＝4，∴FG＝5，∴FB＝8，∵tan∠F＝＝，∴AB＝6，∴⊙O的半径为3．答：⊙O的半径为3．（3）连接BD，∵AB是直径，∴∠ADB＝90°，∵AB＝AC，AE⊥BC，∴E为BC中点，∴S△CDE＝S△DEB，∵＝，设S1＝a，S2＝5a，∴S△BCD＝2a，S△ABD＝3a，∴＝，∴＝，∵AB＝AC＝10，∴AD＝6，CD＝4，∵在Rt△ABD中，BD＝＝8，∴在Rt△BCD中，BC＝＝4．答：BC的长为4．14．解：（1）如图1，连接OA，OB，∵P A，PB为⊙O的切线，∴∠P AO＝∠PBO＝90°，∵∠APB+∠P AO+∠PBO+∠AOB＝360°，∴∠APB+∠AOB＝180°，∵∠APB＝80°，∴∠AOB＝100°，∴∠ACB＝50°；（2）如图2，当∠APB＝60°时，四边形APBC是菱形，连接OA，OB，由（1）可知，∠AOB+∠APB＝180°，∵∠APB＝60°，∴∠AOB＝120°，∴∠ACB＝60°＝∠APB，∵点C运动到PC距离最大，∴PC经过圆心，∵P A，PB为⊙O的切线，∴P A＝PB，∠APC＝∠BPC＝30°，又∵PC＝PC，∴△APC≌△BPC（SAS），∴∠ACP＝∠BCP＝30°，AC＝BC，∴∠APC＝∠ACP＝30°，∴AP＝AC，∴AP＝AC＝PB＝BC，∴四边形APBC是菱形；（3）∵⊙O的半径为r，∴OA＝r，OP＝2r，∴AP＝r，PD＝r，∵∠AOP＝90°﹣∠APO＝60°，∴的长度＝＝，∴阴影部分的周长＝P A+PD+＝r+r+r＝（+1+）r．15．解：（1）如图1中，连接OD，∵CD＝CA，∴∠CAD＝∠CDA，∵OA＝OD∴∠OAD＝∠ODA，∵直线AM与⊙O相切于点A，∴∠CAO＝∠CAD+∠OAD＝90°，∴∠ODC＝∠CDA+∠ODA＝90°，∴CE是⊙O的切线．（2）如图1中，连接BD，∵OD＝OB，∴∠ODB＝∠OBD，∵CE是⊙O的切线，BF是⊙O的切线，∴∠OBD＝∠ODE＝90°，∴∠EDB＝∠EBD，∴ED＝EB，∵AM⊥AB，BN⊥AB，∴AM∥BN，∴∠CAD＝∠BFD，∵∠CAD＝∠CDA＝∠EDF，∴∠BFD＝∠EDF，∴EF＝ED，∴BE＝EF．（3）如图2中，过E点作EL⊥AM于L，则四边形ABEL是矩形，设BE＝x，则CL＝4﹣x，CE＝4+x，∴（4+x）2＝（4﹣x）2+62，解得：x＝，∴，∵∠BOE＝2∠BHE，∴，解得：tan∠BHE＝或﹣3（﹣3不合题意舍去），∴tan∠BHE＝．补充方法：如图2中，作HJ⊥EB交EB的延长线于J．∵tan∠BOE＝＝，∴可以假设BE＝3k，OB＝4k，则OE＝5k，∵OB∥HJ，∴＝＝，∴＝＝，∴HJ＝k，EJ＝k，∴BJ＝EJ﹣BE＝k﹣3k＝k∴tan∠BHJ＝＝，∵∠BHE＝∠HBA＝∠BHJ，∴tan∠BHE＝．16．（1）证明：连接OA、OB、OD，∵∠BAD+2∠ACB＝180°，∠BAD+∠BCD＝180°，∴2∠ACB＝∠BCD，即∠ACB＝∠ACD，∵∠AOD＝2∠ACD，∠AOB＝2ACB，∴∠AOD＝∠AOB，∴，即点A为弧AB的中点；（2）在HF上截取点Q，使HQ＝AH，连接PQ、AE，∵PH⊥AF，∴PH是AQ的垂直平分线，∴P A＝PQ，∴∠P AQ＝∠PQA，AH＝HQ，∴QF＝AF﹣AQ＝AF﹣2AH，又∵PQ＝AP＝AF﹣2AH，∴PQ＝QF，∴∠F＝∠FPQ＝PQA＝P AQ，∵，∴∠ABD＝∠ADB＝P AQ，∴∠F＝∠ABD，∴EB＝EF，∵AB＝AF，∵FH⊥BF，∴∠EAF＝∠PHF＝90°，∴EA∥PH，∴＝，又∵AF＝AB，EF＝BE，∴＝；（3）连接MD、MB，∵，，∴∠AMB＝∠AMD，∠MBD＝∠MAD，∴∠MED＝∠AMB+∠MBD，∠MDN＝∠AMD+∠MAD，∴∠MED＝∠MDN，∵∠MED＝∠MND，∴∠MDN＝∠MND，∴MD＝MN＝，∵，∴AB＝AD，∵AB＝AF，∴AD＝AF，∴∠ADF＝∠AFD，由（1）知∠ABD＝∠BDA，∴∠BDF＝∠ADF+∠ADB＝（∠ADF+∠AFD+∠ABD+∠BDA）＝×180°＝90°，∴DF＝12•sin∠ACB＝12•sin∠ABD＝12×，∴BF＝12，∴AF＝AB＝6，由（2）知∠MAB＝∠MAF＝90°，∴∠MDB＝90°，∴∠MDB+∠BDF＝180°，∴M、D、F共线，∵，∴∠ABD＝∠AMD，∴sin∠ABD＝sin∠AMD，∴＝，即＝，∴DF1＝，DF2＝﹣10（舍去），∴BD＝＝，∵∠BMD+∠BAD＝180°，∠P AH+∠BAD＝180°，∴∠BMD＝∠P AH，∴tan∠BMD＝＝＝＝tan∠P AH，tan∠PFH＝tan∠EBA＝＝，设PH＝24k，则AH＝7k，FH＝32k，∴32k+7k＝6，∴k＝，∴AH＝7k＝．17．（1）证明：连接OE．如图1所示：∵BE⊥EF，∴∠BEF＝90°，∴BF是圆O的直径，∴OB＝OE，∴∠OBE＝∠OEB，∵BE平分∠ABC，∴∠CBE＝∠OBE，∴∠OEB＝∠CBE，∴OE∥BC，∴∠AEO＝∠C＝90°，∴AC⊥OE，∴AC是⊙O的切线；（2）解：∵∠ACB＝90°，∴EC⊥BC，∵BE平分∠ABC，EH⊥AB，∴EH＝EC，∠BHE＝90°，在Rt△BHE和Rt△BCE中，，∴Rt△BHE≌Rt△BCE（HL），∴BH＝BC＝9，∵BE⊥EF，∴∠BEF＝90°＝∠BHE，BF是圆O的直径，∴BE＝＝＝3，∵∠EBH＝∠FBE，∴△BEH∽△BFE，∴＝，即＝，解得：BF＝10，∴⊙O的半径长＝BF＝5；（3）解：连接OE，如图2所示：由（2）得：OE＝OF＝5，EC＝EH＝3，∵EH⊥AB，∴OH＝＝＝4，在Rt△OHE中，cos∠EOA＝＝，在Rt△EOA中，cos∠EOA＝＝，∴OA＝OE＝，∴AE＝＝＝，∴AC＝AE+EC＝+3＝，，∵AB＝OB+OA＝5+＝，∠ACB＝90°，∴△ABC的面积＝AB×CP＝BC×AC，∴CP＝＝＝．18．解：（1）如图1，连接OP，∵AC切⊙O于点C，∴AC⊥BC．∵BC＝30，AC＝40，∴AB＝50．由S△ABC＝AB•CD＝AC•BC，即，解得CD＝24，当OP⊥CD时，点P，O的距离最小，此时．（2）如图2，连接CE，∵EF为⊙O的直径，∴∠ECF＝90°．由（1）知，∠ACB＝90°，由AO2＝AC2+OC2，得（AE+15）2＝402+152，解得．∵∠ACB＝∠ECF＝90°，∴∠ACE＝∠BCF＝∠AFC．又∠CAE＝∠F AC，∴△ACE∽△AFC，∴．∴．（3）CH的最小值为．解：如图3，以BD为直径作⊙G，则G为BD的中点，DG＝9，∵DH⊥PB，∴点H总在⊙G上，GH＝9，∴当点C，H，G在一条直线上时，CH最小，此时，，，即CH的最小值为．19．解：（1）∵AB＝AC＝10cm，BD⊥AC，BD＝8cm．∴由勾股定理可得：AD＝6cm，∴DC＝4cm，∴在Rt△BDC中，BC＝＝4cm，由题意得：CM＝AC﹣AM＝（10﹣2t）cm，BP＝tcm；∵PQ∥AC，∴△BPQ∽△BAC，∴＝＝，∴＝＝，∴PQ＝tcm，BQ＝cm；故答案为：（10﹣2t）cm，tcm，cm；（2）当四边形PQCM是平行四边形时，PQ∥AC且PQ＝CM，∴t＝10﹣2t，解得s．∴四边形PQCM是平行四边形时，s；（3）当点M在线段PC的垂线平分线上时，MP＝MC，过点M作ME⊥AB于点E，如图所示：在Rt△ABD中，∵AB＝10cm，BD＝8cm，∴cm，∴，在Rt△AEM中，∵AM＝2t，，∴，∴，∴，解得：t1＝0（舍去），s，∴当点M在线段PC的垂直平分线上时，s；（4）存在t＝或或或，使以PM为直径的圆与△ABC的边相切．①与AC相切，即PM⊥AC，＝cos A，∴＝，∴t＝；②与AB相切，即MP⊥AB，＝cos A，∴＝，∴；③与BC相切，即PM中点O到BC距离为，如图，设切点为K，连接EK，则EK⊥BC，作PG⊥BC于G，AS⊥BC于S，MH⊥BC于H，PN⊥AC，则EK∥PG∥AS∥MH，∵BC＝4cm，AB＝AC，AS⊥BC，∴BS＝2cm，∴AS＝＝4cm，∴PG：BP＝AS：AB＝4：10＝2：5，∴PG＝cm；同理：MH：CM＝AS：AC＝4：10＝2：5，∴MH＝（10﹣2t）cm．∵E为PM的中点，∴K为GH的中点，∴EK是梯形PGHM的中位线，∴EK＝＝（10﹣t）cm，∵PM＝2EK，∴PM＝（10﹣t）cm．∵＝cos A＝，AP＝（10﹣t）cm，∴AN＝（10﹣t）＝（6﹣t），∴MN＝|AN﹣AM|＝|6﹣t﹣2t|＝|6﹣t|cm；∵BD⊥AC，PN⊥AC，∴PN∥BD，∴△APN∽△ABD，∴＝，∵BD＝8cm，AP＝（10﹣t）cm，AB＝10cm，∴PN＝×8＝（8﹣t）cm，∴在Rt△PMN中，由勾股定理得：+＝，整理得：33t2﹣140t+100＝0，解得：或．综上，存在t＝或或或，使以PM为直径的圆与△ABC的边相切．20．解（1）如图1，连接BD．∵＝，∴∠BDC＝∠ADC＝45°，∴∠ADB＝90°，∴AB是圆O的直径．（2）如图2，连接OG、OD、BD．则OA＝OD＝OB，∴∠OAD＝∠ODA，∠OBD＝∠ODB，∴∠DOB＝∠OAD+∠ODA＝2∠BAD，∵∠FGC＝2∠BAD，∴∠DOB＝∠FGC＝∠BGD，∴B、G、O、D四点共圆，∴∠ODE＝∠OBG，∵BE⊥CD，∠BDC＝45°，∴∠EBD＝45°＝∠EDB，∴∠OBE＝∠ODE＝∠OBG，∴BA平分∠FBE．（3）如图3，连接AC、BC、CO、DO、EO、BD．∵AC＝BC，∴AC＝BC，∵AB为直径，∴∠ACB＝90°，∠CAB＝∠CBA＝45°，CO⊥AB，延长CO交圆O于点K，则∠DOK＝∠OCD+∠ODC＝2∠ODC＝2∠OBE＝2∠FBA，连接DM、OM，则∠MOD＝2∠MAD，∵2∠MAD+∠FBA＝135°，∴∠MOD+∠FBA＝135°，∴2∠MOD+2∠FBA＝270°，∴2∠MOD+∠DOK＝270°，∵∠AOM+∠DOM+∠KOK＝270°，∴∠AOM＝∠DOM，∴AM＝DM，连接MO并延长交AD于H，则∠MHA＝∠MHD＝90°，AH＝DH，设MH与BC交于点R，连接AR，则AR＝DR，∵∠ADC＝45°，∴∠ARD＝∠ARC＝90°，△ADR是等腰直角三角形，∴∠BRH＝∠ARH＝45°∵∠ACR+∠BCE＝∠BCE+∠CBE＝90°，∴∠ACR＝∠CBE，∴△ACR≌△CBE（AAS），∴CR＝BE＝ED，作EQ⊥MN于Q，则∠EQN＝∠EQM＝90°，连接OE，则OE垂直平分BD，∴OE∥AD∥MN，∴四边形OEQM是矩形，∴OM＝EQ，OE＝MQ，延长DB交MN于点P，∵∠PBN＝∠EBD＝45°，∴∠BNP＝45°，∴△EQN是等腰直角三角形，∴EQ＝QN＝EN＝13，∴OA＝OB＝OC＝OD＝OM═13，AB＝2OA＝26，∴BC＝OC＝26，∵MN＝AB＝20，∴OE＝MQ＝MN﹣QN＝20﹣13＝7，∵∠ORE＝45°，∠EOR＝90°，∴△OER是等腰直角三角形，∴RE＝OE＝14，设BE＝CR＝x，则CE＝14+x，在Rt△CBE中：BC2＝CE2+BE2，∴262＝（x+14）2+x2，解得x＝10，∴CD＝CR+RE+DE＝10+14+10＝34．。

中考数学几何圆专题训练

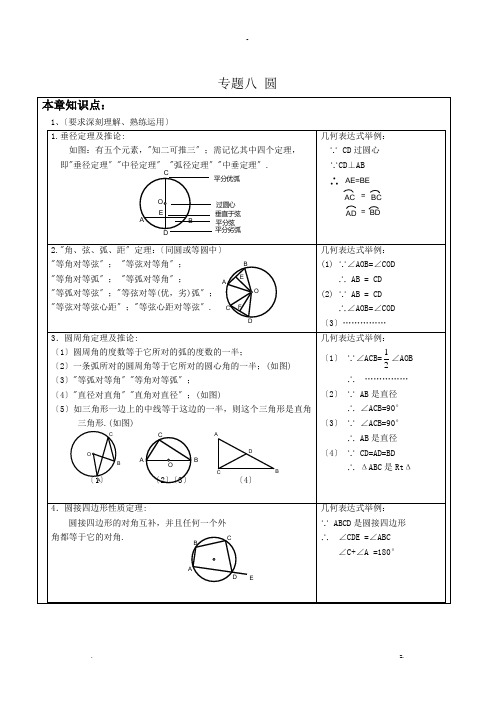
专题八圆图2ED CB AoABC第5ABC 第6OD E2.圆柱与圆锥的侧面展开图：〔1〕圆柱的侧面积：S 圆柱侧 =2πrh ； (r:底面半径；h:圆柱高)〔2〕圆锥的侧面积：S 圆锥侧 =LR 21=πrR. 〔L=2πr ，R 是圆锥母线长；r 是底面半径〕四常识：1．圆是轴对称和中心对称图形.2．圆心角的度数等于它所对弧的度数. 3．三角形的外心 ⇔ 两边中垂线的交点 ⇔ 三角形的外接圆的圆心；三角形的心 ⇔ 两角平分线的交点 ⇔ 三角形的切圆的圆心.4．直线与圆的位置关系：〔其中d 表示圆心到直线的距离；其中r 表示圆的半径〕直线与圆相交 ⇔ d ＜r ；直线与圆相切 ⇔ d=r ；直线与圆相离 ⇔ d ＞r.5．圆与圆的位置关系：〔其中d 表示圆心到圆心的距离，其中R 、r 表示两个圆的半径且R ≥r 〕两圆外离 ⇔ d ＞R+r ；两圆外切 ⇔ d=R+r ；两圆相交 ⇔ R-r ＜d ＜R+r ；两圆切 ⇔ d=R-r ；两圆含 ⇔ d ＜R-r.6．证直线与圆相切，常利用："交点连半径证垂直〞和"不知交点作垂直证半径〞的方法加辅助线.圆中考专题练习一：选择题。

1. 〔2010红河自治州〕如图2，BD 是⊙O 的直径，⊙O 的弦AC ⊥BD 于点E ，假设∠AOD=60°，则∠DBC 的度数为〔〕A.30°B.40°C.50°D.60°2、〔11〕．如上图，AB 是⊙O 的弦，半径OA ＝2，∠AOB ＝120°，则弦AB 的长是〔〕．〔A 〕22 〔B 〕32 〔C 〕5〔D 〕533、〔2011省〕9.如图，点A 、B 、P 在⊙O 上，点P 为动点，要是△ABP 为等腰三角形，则所有符合条件的点P 有〔〕A 1个B 2个C 3个D 4个 4、〔2011〕，〕如下图，在圆O 有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC 的长为〔〕A ．19B ．16C ．18D ．205、〔11·〕如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝3，BC ＝5，假设把Rt △ABC 绕直线AC 旋转一周，则所得圆锥的侧面积等于〔〕A ．6πB ．9πC ．12πD ．15π 6、〔2010·〕．如图，⊙O 的直径AB ⊥弦CD 于点E ．以下结论中一定．．正确的选项是〔〕第9题图 A BCA ．AE ＝OEB ．CE ＝DEC ．OE ＝12CE D ．∠AOC ＝60°7、〔〕圆O 1、圆O 2的半径不相等，圆O 1的半径长为3，假设圆O 2上的点A 满足AO 1 = 3，则圆O 1与圆O 2的位置关系是〔〕 A.相交或相切 B.相切或相离 C.相交或含 D.相切或含8. 〔莱芜〕圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为〔〕A ．2.5B ．5C ．10D ．159、〔10·〕．如图，等腰梯形ABCD 接于半圆D ，且AB = 1，BC = 2，则OA =〔〕．A ．231+ B ．2 C ．323+ D ．251+ 10、〔2010〕如图，在△ABC 中，AB = AC ，AB = 8，BC = 12，分别以 AB 、AC 为直径作半圆，则图中阴影局部的面积是〔〕A ．64127π-B ．1632π-C ．16247π-D ．16127π-11、〔10年〕9. 现有一个圆心角为90，半径为cm 8的扇形纸片，用它恰好围成一个圆锥的侧面〔接缝忽略不计〕.该圆锥底面圆的半径为A ． cm 4B ．cm 3C ．cm 2D ．cm 1二：填空 1、〔11)如图6，直线AB 是⊙O 的切线，A 为切点，OB 交⊙O 于点C ，点D 在⊙O 上，且∠OBA=40°，则∠ADC=______．2、〔10年〕如图，△ABC 接于⊙O ，AC 是⊙O 的直径，∠ACB ＝500，点D 是BAC 上一点，则∠D ＝______3、(2011市)如图，正方形ABCD 边长为4，以BC 为直径的半圆O 交对角线BD 于E ．则直线CD 与⊙O 的位置关系是，阴影局部面积为(结果保存π)．4、〔10株洲市〕15．两圆的圆心距5d =，它们的半径分别是一元二次方程2540x x -+=的两个根，这两圆的位置关系是.5、〔10〕如图，在ABC ∆中，AB 为O 的直径，60,70B C ∠=∠=，则BOD ∠的度数是_______度．6、(2011中考题18)．如图，A 、B 两点的坐标分别为()230，、(0，2)，P 是△AOB 外接圆上的一点，且∠AOP=45°，则点P 的坐标为． 7、〔2010年〕．假设一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是___________．C B AODABDOE〔第15题〕三：解答题 1、〔10〕如图，△ABC 接于⊙O ，AB ＝6,AC ＝4,D 是AB 边上一点，P 是优弧BAC 的中点，连结PA 、PB 、PC 、PD.(1)当BD 的长度为多少时，△PAD 是以AD 为底边的等腰三角形？并证明；〔2〕假设cos ∠PCB=55，求PA 的长. 2、〔10市〕．如图，△ABC 中，AB=BC ，以AB 为直径的⊙O 交AC 于点D ，过D 作DE ⊥BC ，垂足为E ，连结OE ，CD=3，∠ACB=30°.〔1〕求证：DE 是⊙O 的切线；〔2〕分别求AB ，OE 的长；3、〔2010市〕如图，AB 是⊙O 的直径，弦DE 垂直平分半径OA ，C 为垂足，弦DF 与半径OB 相交于点P ，连结EF 、EO ，假设DE ＝23，∠DPA ＝45°．〔1〕求⊙O 的半径；〔2〕求图中阴影局部的面积．4、〔2011〕25．〔此题总分值10分〕如图，⊙O 是△ABC 的外接圆，FH 是⊙O 的切线，切点为F ，FH ∥BC ，连结AF 交BC 于E ，∠ABC 的平分线BD 交AF 于D ，连结BF ．〔1〕证明：AF 平分∠BAC ；〔2〕证明：BF ＝FD ；〔3〕假设EF ＝4，DE ＝3，求AD 的长．5、〔10年〕26.〔此题总分值10分〕如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 的延长线交于点P ，AC=PC ，∠COB=2∠PCB.〔1〕求证：PC 是⊙O 的切线；〔2〕求证：BC=21AB ；〔3〕点M 是弧AB 的中点，CM 交AB 于点N ，假设AB=4，求MN ·MC 的值. 6、〔11〕如图，△ABC 接于⊙O ，且∠B = 60︒．过点C 作圆的切线l 与直径AD 的延长线交于点E ，AF ⊥l ，垂足为F ，CG ⊥AD ，垂足为G ．〔1〕求证：△ACF ≌△ACG ；〔2〕假设AF = 43，求图中阴影局部的面积．7、(11、27)．(此题总分值9分)如图，在等腰梯形ABCD 中，AD ∥BC ．O 是CD 边的中点，以O 为圆心，OC 长为半径作圆，交BC 边于点E ．过E 作EH ⊥AB ，垂足为H ．⊙O 与AB 边相切，切点为F (1)求证：OE ∥AB ；(2)求证：EH=12AB ；(3)假设14BH BE =，求BHCE的值．近年中考题A BCDEO BD FAO G ECl20．〔本小题总分值10分〕如图10，在O ⊙中，60ACB BDC ∠=∠=°，23cm AC =．〔1〕求BAC ∠的度数；〔2〕求O ⊙的周长．23、〔2008〕〔12分〕如图9，射线AM 交一圆于点B 、C ，射线AN 交该圆于点D 、E ，且BC DE = 〔1〕求证：AC=AE〔2〕利用尺规作图，分别作线段CE 的垂直平分线与∠MCE 的平分线，两线交于点F 〔保存作图痕迹，不写作法〕求证：EF 平分∠CEN 24．〔2010，24，14分〕如图，⊙O 的半径为1，点P 是⊙O 上一点，弦AB 垂直平分线段OP ，点D 是APB 上任一点〔与端点A 、B 不重合〕，DE ⊥AB 于点E ，以点D 为圆心、DE 长为半径作⊙D ，分别过点A 、B作⊙D 的切线，两条切线相交于点C ．〔1〕求弦AB 的长；〔2〕判断∠ACB 是否为定值，假设是，求出∠ACB 的大小；否则，请说明理由；〔3〕记△ABC 的面积为S ，假设2SDE ＝3△ABC 的周长.25. 〔2011市，25，14分〕如图7，⊙O 中AB 是直径，C 是⊙O 上一点，∠ABC =45°，等腰直角三角形DCE 中 ∠DCE 是直角，点D 在线段AC 上．〔1〕证明：B 、C 、E 三点共线；〔2〕假设M 是线段BE 的中点，N 是线段AD 的中点，证明：MN=2OM ；〔3〕将△DCE 绕点C 逆时针旋转α〔0°＜α＜90°〕后，记为△D 1CE 1〔图8〕，假设M 1是线段BE 1的中点，N 1是线段AD 1的中点，M 1N 1=2OM 1是否成立？假设是，请证明；假设不是，说明理由．CP DOBAEAOCB图10 图9局部答案：一：选择题1、A2、B3、D4、 D5、D6、B7、A8、C9、A 10、D 11、C二：填空1、25 2、40 3、相切、-6π 4、外切 5、100 6、)13,13(++ 7、 3 三：解答题： 1、解：〔1〕当BD ＝AC ＝4时，△PAD 是以AD 为底边的等腰三角形∵P 是优弧BAC 的中点 ∴弧PB ＝弧PC ∴PB ＝PC ∵BD ＝AC ＝4 ∠PBD=∠PCA ∴△PBD ≌△PCA ∴PA=PD 即△PAD 是以AD 为底边的等腰三角形〔2〕由〔1〕可知，当BD ＝4时，PD ＝PA ，AD ＝AB-BD ＝6-4＝2过点P 作PE ⊥AD 于E ，则AE ＝21AD=1 ∵∠PCB=∠PAD ∴cos ∠PAD=cos ∠PCB=55=PA AE ∴PA=5 2、〔1〕∵AB 是直径，∴∠ADB=90°∴OD ⊥DE ，∴DE 是⊙O 的切线. 〔2〕在 30,3,=∠=∆ACB CD CBD Rt 中，5、解：〔1〕∵OA=OC,∴∠A=∠ACO ∵∠COB=2∠A ,∠COB=2∠PCB ∴∠A=∠ACO=∠PCB ∵AB 是⊙O 的直径 ∴∠ACO+∠OCB=90°∴∠PCB+∠OCB=90°,即OC ⊥CP∵OC 是⊙O 的半径 ∴PC 是⊙O 的切线〔2〕∵PC=AC ∴∠A=∠P ∴∠A=∠ACO=∠PCB=∠P ∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB∴∠CBO=∠COB ∴BC=OC ∴BC=21AB(3)连接MA,MB ∵点M 是弧AB 的中点 ∴弧AM=弧BM ∴∠ACM=∠BCM∵∠ACM=∠ABM ∴∠BCM=∠ABM ∵∠BMC=∠BMN ∴△MBN ∽△MCB∴BM MNMC BM =∴BM 2=MC ·MN ∵AB 是⊙O 的直径，弧AM=弧BM ∴∠AMB=90°,AM=BM ∵AB=4 ∴BM=22∴MC ·MN=BM 2=86：〔1〕如图，连结CD ，OC ，则∠ADC =∠B = 60︒．∵AC ⊥CD ，CG ⊥AD ，∴∠ACG =∠ADC = 60︒．由于 ∠ODC = 60︒，OC = OD ，∴△OCD 为正三角形，得 ∠DCO = 60︒．由OC ⊥l ，得 ∠ECD = 30︒，∴∠A B CD 1E 1M 1ON 1图8A BCDEMN O图7ECG = 30︒ + 30︒ = 60︒．进而 ∠ACF = 180︒－2×60︒ = 60︒，∴△ACF ≌△ACG ．〔2〕在Rt △ACF 中，∠ACF = 60︒，AF = 43，得 CF = 4．在Rt △OCG 中，∠COG = 60︒，CG = CF = 4，得 OC =38．在Rt △CEO 中，OE =316．于是 S 阴影 = S △CEO －S 扇形COD =36060212OC CG OE ⋅-⋅π=9)33(32π-．25、【答案】〔1〕∵AB 为⊙O 直径∴∠ACB=90°∵△DCE 为等腰直角三角形 ∴∠ACE=90°∴∠BCE=90°+90°=180°∴B 、C 、E 三点共线．〔2〕连接BD ，AE ，ON ．∵∠ACB=90°，∠ABC =45°∴AB=AC ∵DC=DE∠ACB=∠ACE=90°∴△BCD ≌△ACE ∴AE=BD ，∠DBE=∠EAC ∴∠DBE+∠BEA=90° ∴BD ⊥AE ∵O ，N 为中点∴ON ∥BD ，ON=12BD同理OM ∥AE ，OM=12AE ∴OM ⊥ON ，OM=ON ∴MN=2OM〔3〕成立证明：同〔2〕旋转后∠BCD 1=∠BCE 1=90°－∠ACD 1所以仍有△BCD 1≌△ACE 1，所以△ACE 1是由△BCD 1绕点C 顺时针旋转90°而得到的，故BD 1⊥AE 1 其余证明过程与〔2〕完全一样．。

2021年广东省中考数学最新圆的综合练习

广东中考圆的综合
1.如图，在△ABC的边BC上取一点O，以O为圆心，OC为半径画⊙O，⊙O与边AB相切
于点D，AC＝AD，连接OA交⊙O于点E，连接CE，并延长交线段AB于点F．
（1）求证：AC是⊙O的切线；
（2）若AB＝10，tan B=4
3，求⊙O的半径．
2.如图，AD是O的直径，PA与O相切于点A，连接OP，过点A作AB OP
⊥，垂足为C，交O于点B，连接PB并延长交AD的延长线于点E，连接BD．
（1）求证：PB是O的切线；
（2）若6
BD=，8
AB=，求sin E
∠．
3.如图，已知AB 是⊙O 的直径，AC ，BC 是⊙O 的弦，OE ∥AC 交BC 于E ，过点B 作⊙O 的切线交OE 的延长线于点D ，连接DC 并延长交BA 的延长线于点F ．
（1）求证：DC 是⊙O 的切线；
（2）若∠ABC ＝30°，AB ＝8，求线段CF 的长．
4.如图，已知AB 是O 的直径，CB AB ⊥，CD 切圆O 于点D ，连AC ，BD ，AC 与BD 交于点M ．
（1）求证：//AD OC ；
（2）若3CD =，2AD =，求CM MA
的值．。

1.2021年广东中考数学压轴题几何综合问题(PDF版)(1)

第二课时圆的综合问题1. 如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C，使DC=BD，连接AC，过点D 作DE⊥AC，垂足为E．（1）求证：DE 为⊙O 的切线；（2）若⊙O 的半径为5，∠BAC=60°，求DE 的长．（1）证明：如图，连接OD．∵OA=OB，CD=BD，∴OD∥AC．∴∠0DE=∠CED．又∵DE⊥AC，∴∠CED=90°．∴∠ODE=90°，即OD⊥DE．∴DE 是⊙O 的切线．（2）解：∵OD∥AC，∠BAC=60°，∴∠BOD=∠BAC=60°，∠C=∠0DB．又∵OB=OD，∴△BOD 是等边三角形．∴∠C=∠ODB=60°，CD=BD=5．∵DE⊥AC，∴DE=CD•sin∠C=5×sin60°=．2.如图，AB 是⊙O 的直径，延长弦BD 到点C，使DC=BD，连接AC，过点D 作DE⊥AC，垂足为E．（1）判断直线DE 与⊙O 的位置关系，并证明你的结论；（2）若⊙O 的半径为6，∠BAC=60°，延长ED 交AB 延长线于点F，求阴影部分的面积．【解】（1）直线DE 与⊙O 的位置关系是相切，﹣证明：连接 OD ， ∵AO=BO ，BD=DC ， ∴OD ∥AC ， ∵DE ⊥AC ， ∴DE ⊥OD ， ∵OD 为半径，直线 DE 是⊙O 的切线，即直线 DE 与⊙O 的位置关系是相切；（2）解：∵OD ∥AC ，∠BAC=60°，∴∠DOB=∠A=60°， ∵DE 是⊙O 切线， ∴∠ODF=90°， ∴∠F=30°， ∴FO=2OD=12，由勾股定理得，∴阴影部分的面积 S=S △ODF ﹣S 扇形DOB = ×6×6=18﹣6π．3.如图所示，在 Rt △OBC 中，∠OBC=90°，以 O 为圆心，OB 为半径的⊙O 交 BO 的延长线于 A ， BD ⊥OC 于 D ，交⊙O 于 E ，连接 CE 并延长交直线 AB 于 P ．（1）求证：CE 是⊙O 的切线．（2）若，⊙O 的半径为 5，求 PE 的长？（1）证明：连接 EO ， ∴△EOB 为等腰三角形， ∵BD ⊥OC 于 D ， ∴∠DOB=∠DOE ， ∴△CEO ≌△CBO ， ∵∠OBC=90°， ∴OE ⊥PC ， ∴CE 是⊙O 的切线．（2）解：∵OE ⊥PC ，∠OBC=90°，∴∠EOP=∠BCP，∴△PEO∽△PBC，∵OE=5，BC=EC=，∴，设PE=3x，PB=4x，∴（3x+）2﹣（4x）2=（）2，解方程得：x（40﹣7x）=0，x1=0（舍去），∴PE= ．4.如图所示，CD 为⊙O 的直径，AD、AB、BC 分别与⊙O 相切于点D、E、C（AD＜BC）．连接DE 并延长与直线BC 相交于点P，连接OB．（1）求证：BC=BP；（2）若DE•OB=40，求AD•BC 的值；（3）在（2）条件下，若S△ADE ：S△PBE=16：25，求四边形ABCD 的面积．解：（1）证明：连接OE，如下图①，∵BC、AB 分别与⊙O 相切于点C、E，∴∠OCB=∠OEB=90°，在RT△OCB 与RT△OEB 中，RT△OCB∽RT△OEB（HL）∴∠COB=∠EOB∵同弧所对的圆周角是其所对的圆心角的一半，∴∠COB=∠COE=∠CDP，∴DP∥OB，又点O 是CD 的中点，∴OB 是△CDP 的中位线，∴BC=BP（2）连接OA、OE、CE，如下图②所示∵CD 是⊙O 的直径，∴∠DEC=90°，又BC 与⊙O 相切于点C，∴∠DEC=∠OCB=90°，又∠4=∠6∴△DEC∽△OCB，∴∴DE•OB=OC•DC=40∴DC=2OC OC2=20，OC=2 ，∵又∠1=∠2，∠3=∠4，∴∠1+∠4=90°，又∠1+∠5=90°，∴∠4=∠5∴△ADO∽△OCB∴∴AD•BC=OC•OD=OC2=20即：AD•BC=20（3）∵AD、BC 分别与⊙O 相切于点D、C，如图②所示，∴CD⊥AD，CD⊥PC，∴AD∥PB∴△ADE∽△BPE∴==，∴，即BC=BP又∵AD•BC=20∴BC2=25即：BC=5∴S 四边形（AD+BC）•2OC=OC（AD+BP）=2 BC=2 ×5=18即：四边形ABCD 的面积为5.如图，已知AB 是⊙O 直径，BC 是⊙O 的弦，弦ED⊥AB 于点F，交BC 于点G，过点C 作⊙O 的切线与ED 的延长线交于点P．（1）求证：PC=PG；（2）点C 在劣弧AD 上运动时，其他条件不变，若点G 是BC 的中点，试探究CG、BF、BO 三者之间的数量关系，并写出证明过程；（3）在满足（2）的条件下，已知⊙O 的半径为5，若点O 到BC 的距离为时，求弦ED 的长．【解】（1）证明：连结OC，如图，∵PC 为⊙O 的切线，∴OC⊥PC，∴∠OCG+∠PCG=90°，∵ED⊥AB，∴∠B+∠BGF=90°，∵OB=OC，∴∠B=∠OCG，∴∠PCG=∠BGF，而∠BGF=∠PGC，∴∠PGC=∠PCG，∴PC=PG；（2）解：CG、BF、BO 三者之间的数量关系为CG2=BO•BF．理由如下：连结OG，如图，∵点G 是BC 的中点，∴OG⊥BC，BG=CG，∴∠OGB=90°，∵∠OBG=∠GBF，∴Rt△BOG∽Rt△BGF，∴BG：BF=BO：BG，∴BG2=BO•BF，∴CG2=BO•BF；（3）解：连结OE，如图，由（2）得OG⊥BC，∴OG=，在Rt△OBG 中，OB=5，∴BG==2，由（2）得BG2=BO•BF，∴BF==4，∴OF=1，在Rt△OEF 中=2，∵AB⊥ED，∴EF=DF，∴DE=2EF=4．6.如图所示，AB 是⊙O 的直径，AE 是弦，C 是劣弧AE 的中点，过C 作CD⊥AB 于点D，CD 交AE 于点F，过C 作CG∥AE 交BA 的延长线于点G．（1）求证：CG 是⊙O 的切线．（2）求证：AF=CF．（3）若∠EAB=30°，CF=2，求GA 的长．【解】（1）证明：连结OC，如图，∵C 是劣弧AE 的中点，∴OC⊥AE，∵CG∥AE，∴CG⊥OC，∴CG 是⊙O 的切线；（2）证明：连结AC、BC，∵AB 是⊙O 的直径，∴∠ACB=90°，∴∠2+∠BCD=90°，而CD⊥AB，∴∠B+∠BCD=90°，∴∠B=∠2，∵C 是劣弧AE 的中点，∴=，∴∠1=∠B，∴∠1=∠2，∴AF=CF；（3）解：在Rt△ADF 中，∠DAF=30°，FA=FC=2，∴DF=AF=1，∴AD=DF=，∵AF∥CG，∴DA：AG=DF：CF，：AG=1：2，∴AG=2．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

广东中考数学专题训练（二）：几何综合题（圆题）
一、命题特点与方法分析
以考纲规定，“几何综合题”为数学解答题（三）中出现的题型．一般出现在该题组的第2题（即试卷第24题），近四年来都是以圆为主体图形，考察几何证明．
近四年考点概况：
也相对复杂．难度也较高（尤其是14、15年），考查学生综合多方面知识进行几何证明的能力．
本题除了常规的证明以外，主要的命题特点有以下两种：
1．改编自常考图形，有可能成为作辅助线的依据．如16年的构图中包含弦切角定理的常用图，17年第（2）问则显然是“切线+垂直+半径相等”得出角平分线的考察，依此就不难判断出辅助线的构造，应该对常考图形有一定的识别能力．
2．利用数量关系求出特殊角．如15年第（1）问，17年第（3）问，这常常是容易被遗忘的点，在做这类题目的时候，首先要通过设问推敲，其次在观察题干中是否有给出角度的条件，如果没有，一般就是通过数量关系求出特殊角．
二、例题训练
1．如图，⊙O 为∆ABC 外接圆，BC 为⊙O 直径，BC =4．点D 在⊙O 上，连接OA
、CD 和BD ，AC 与BD 交于点E
，并作
AF ⊥
BC 交
BD
于点G ，点G 为BE 中点，连
接
OG ．（1）求证：OA ∥CD ；
（2）若∠DBC =2∠DBA ，求BD 的长；
（3）求证：FG =
2
DE ．
2．如图，⊙O为 ABC外接圆，AB为⊙O直径，AB=4．⊙O切线CD交BA延长线于点D，∠ACB平分线交⊙O于点E，并以DC 为边向下作∠DCF=∠CAB交⊙O于点F，连接AF．
（1）求证：∠DCF=∠D+∠B；
（2）若AF=3
2
，AD=
5
2
，求线段AC的长；
（3）若CE
，求证：AB⊥CF．
3．如图，⊙O为 ABC外接圆，BC为⊙O直径．作AD=AC，
连接AD、CD和BD，AB与CD交于点E，过点B作⊙O 切线，并作点E作EF⊥DC交切线于点G．
（1）求证：∠DAC=∠G+90°；
（2）求证：CF=GF；
（3）若EF
BD
=
2
3
，求证：AE=DE．
4．如图，⊙O 为 ABC 外接圆，AB 为⊙O 直径．连
接CO ，并作AD ∥CO 交⊙O 于点D ，过点D 作
⊙O 切线DE 交CO 延长线于点E ，连接BE ，作
AF ⊥CO 交BC 于点G ，交BE 于点H ，连接OG ．
（1）若CF =2，OF =3，求AC 的长；
（2）求证：BE 是⊙O 的切线；
（3）若2AF AH DE =23
，求证：OG ⊥AB ．
三、例题解析
答案：
1．（1）难度中等，关键是推出∠DBA =∠ACB ；
（2）难度中等，关键是推出∠DBC =45°；
（3）难度大，OA 与BD 交于点H ，关键是利用OG 为∆BEC 中位线推出GH =2
DE ，再利用全等三角形推出FG =GH ．
【考点：圆的性质（垂径定理）、三角函数、三角形中位线、全等三角形】
2．（1）难度中等，关键是推出∠DCA =∠B ；
（2）难度中等，关键是推出∠F =∠B ，从而得出∆AFC ∽∆ACD ；
（3）难度大，关键是通过作下角平分线的常规辅助线得到全等三角形，通过转化边长和
∠ACE =45°的条件推出AC +BC AB =4解出AC =2，BC 出30°．
【考点：圆的性质、三角函数、相似三角形、全等三角形、角平分线的性质】
3．（1）难度低，关键是推出∠G =∠DCB ；
（2）难度中等，关键是推出BF =EF ，再推出三角形全等；
（3）难度较大，利用平行截割推出2BF =FC ，再利用第（2）问结论转换边长推出∠G =30°，
进而推出∠ADC =∠BAD =30°．
【考点：圆的性质（切线）、三角函数、全等三角形、平行截割、等腰三角形】
4．（1）难度中等，关键是推出∆AFC ∽∆ACB ；
（2）难度中等，关键是利用AD ∥CO 得到∆DOE ≌∆BOE ；
（3）难度大，关键是推出∆AFO ∽∆ABH ，进而推出AF •AH =2OB 2，=BE ，
推出∠AOC =60°，利用∆ACG ≌∆AOG 得出OG ⊥AB ．
【考点：圆的性质（切线）、相似三角形、全等三角形、三角函数】
解析：主要的命题特点与例题对应：
1．改编自常考图形．
【题1（1），题2（1），题4（2）】
2．利用数量关系求出特殊角．
【题1（2），题2（3），题3（3），题4（3）】。