2015春人教版数学七下53《平行线的性质》习题精选

合集下载

人教版七年级数学下册第五章平行线的性质作业复习试题(含答案) (39)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)已知：如图所示，∠1＝∠2，∠3＝∠B，AC∠DE，且B，C，D在一条直线上．求证：AE∠BD．【答案】见解析【解析】试题分析：根据AC∥DE得出∥2＝∥4，结合∥1＝∥2得出∥1＝∥4，从而说明AB∥CE，即∥B+∥BCE＝180°，根据∥B＝∥3得到∥3+∥BCE＝180°，从而说明平行.试题解析：∥ AC∥DE，∥∥2＝∥4∥∥1＝∥2，∥∥1＝∥4.∥AB∥CE∥∥B+∥BCE＝180°∥∥B＝∥3，∥∥3+∥BCE＝180°∥AE∥BD.考点：平行线的性质与判定82．已知：如图，∠ADE＝∠B，∠DEC＝115°．求∠C的度数．【答案】∥C=65°．【解析】【分析】【详解】解：∵∵ADE＝∵B∵DE∵BC∵∵DEC+∵C=180°∵∵C=180°-∵DEC =180°-115°=65°83．如图,已知CD⊥AB，GF⊥AB,∠B=∠ADE，试说明∠1=∠2．【答案】说明见解析.【解析】试题分析：利用平行线的判定及性质，通过证明∥1=∥BCD=∥2达到目的．试题解析：∥∥B=∥ADE（已知），∥DE∥BC（同位角相等，两直线平行）∥∥1=∥DCB．（两直线平行，内错角相等）∥CD∥AB，GF∥AB，∥CD∥FG（平面内，垂直于同一条直线的两条直线平行），∥∥2=∥DCB．（两直线平行，同位角相等）∥∥1=∥2．（等量代换）考点：1.平行线的判定与性质；2.垂线．84．如图AB∥CD．∠1=∠2，∠3=∠4，试说明AD∥BE．解：∵AB∥CD（已知）∴∠4=∠（）∵∠3=∠4（已知）∴∠3=∠（）∵∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF（即∠=∠（）∴∠3=∠∴AD∥BE（）【答案】BAF；两直线平行，同位角相等；BAF；等量代换；等式的性质；角的和差；CAD；内错角相等，两直线平行．【解析】【详解】解：∵AB∥CD（已知），∴∠4=∠BAE（两直线平行，同位角相等）；∵∠3=∠4（已知），∴∠3=∠BAE（等量代换）；∵∠1=∠2（已知），∴∠1+∠CAF=∠2+∠CAF（等式的性质），即∠BAE=∠DAC，∴∠3=∠DAC（等量代换），∴AD∥BE（内错角相等，两直线平行）．85．已知：如图，CD∠AB于D，DE∠BC，EF∠AB于F，求证：∠FED=∠BCD．【答案】见解析【解析】试题分析：由垂直于同一条直线的两直线平行得到CD与EF平行，利用两直线平行得到一对内错角相等，再由DE与BC平行，利用两直线平行得到另一对内错角相等，等量代换即可得证．证明：∥CD∥AB，EF∥AB，∥CD∥EF，∥∥FED=∥EDC，∥DE∥BC，∥∥EDC=∥BCD，∥∥FED=∥BCD．考点：平行线的判定与性质．86．（1）如图甲，AB∥CD，试问∥2与∥1+∥3的关系是什么，为什么；（2）如图乙，AB∥CD，试问∥2+∥4与∥1+∥3+∥5一样大吗，为什么；（3）如图丙，AB∥CD，试问∥2+∥4+∥6与∥1+∥3+∥5+∥7哪个大；为什么；你能将它们推广到一般情况吗．请写出你的结论．【答案】（1）∵2=∵1+∵3；理由见解析；（2）一样大；理由见解析；（3）∵2+∵4+∵6=∵1+∵3+∵5+∵7；理由见解析；开口朝左的所有角度之和与开口朝右的所有角度之和相等．【解析】【分析】（1）首先过点E作EF∵AB，由AB∵CD，可得AB∵CD∵EF，根据平行线的性质，易得∵2=∵BEF+∵CEF=∵1+∵3；（2）首先分别过点E，G，M，作EF∵AB，GH∵AB，MN∵AB，由AB∵CD，可得AB∵CD∵EF∵GH∵MN，由平行线的性质，可得∵2+∵4=∵1+∵3+∵5．（3）首先分别过点E，G，M，K，P，作EF∵AB，GH∵AB，MN∵AB，KL∵AB，PQ∵AB，由AB∵CD，可得AB∵CD∵EF∵GH∵MN∵KL∵PQ，然后利用平行线的性质，即可证得∵2+∵4+∵6=∵1+∵3+∵5+∵7．【详解】解：（1）∵2=∵1+∵3．过点E作EF∵AB，∵AB∵CD，∵AB∵CD∵EF，∵∵BEF=∵1，∵CEF=∵3，∵∵2=∵BEF+∵CEF=∵1+∵3；（2）∵2+∵4=∵1+∵3+∵5．分别过点E，G，M，作EF∵AB，GH∵AB，MN∵AB，∵AB∵CD，∵AB∵CD∵EF∵GH∵MN，∵∵1=∵BEF，∵FEG=∵EGH，∵HGM=∵GMN，∵CMN=∵5，∵∵2+∵4=∵BEF+∵FEG+∵GMN+∵CMN=∵1+∵EGH+∵MGH+∵5=∵1+∵3+∵5；（3）∵2+∵4+∵6=∵1+∵3+∵5+∵7．分别过点E，G，M，K，P，作EF∵AB，GH∵AB，MN∵AB，KL∵AB，PQ∵AB，∵AB∵CD，∵AB∵CD∵EF∵GH∵MN∵KL∵PQ，∵∵1=∵BEF，∵FEG=∵EGH，∵HGM=∵GMN，∵KMN=∵LKM，∵LKP=∵KPQ，∵QPC=∵7，∵∵2+∵4+∵6=∵1+∵3+∵5+∵7．归纳：开口朝左的所有角度之和与开口朝右的所有角度之和相等．【点睛】本题考查平行线的性质．87．如图，EF∠AD，∠1=∠2，∠BAC=80°．将求∠AGD的过程填写完整．解：因为EF∠AD，所以∠2= （）．又因为∠1=∠2，所以∠1=∠3（）．所以AB∠（）．所以∠BAC+ =180°（）．因为∠BAC=80°，所以∠AGD= ．【答案】见解析.【解析】【分析】【详解】∵EF∵AD，∵∵2=∵3（两直线平行，同位角相等）；又∵∵1=∵2，∵∵1=∵3（等量代换），∵AB∵DG（内错角相等，两直线平行），∵∵BAC+∵AGD=180°（两直线平行，同旁内角互补），∵∵BAC=80°，∵∵AGD=100°．88．如图，已知直线a∠b,∠3=131°，求∠1、∠2的度数（填理由或数学式）解：∠∠3=131°（）又∠∠3=∠1 （）∠∠1=（）（）∠ a∠b（）∠∠1＋∠2=180°（）∠∠2=（）（）【答案】已知，对顶角相等，131°，等量代换，已知，两直线平行，同旁内角互补，等式的性质．【解析】【分析】先根据对顶角相等求出∵1，再根据两直线平行，同旁内角互补列式计算即可得【详解】解：∵∵3=131°（已知）又∵∵3=∵1 （对顶角相等）∵∵1=131°（等量代换）∵a∵b （已知）∵∵1+∵2=180°（两直线平行，同旁内角互补）∵∵2=49°（等式的性质）．89．已知：AB∠CD，∠B +∠D＝180 ，判断直线BC与ED的位置关系并请说明理由.【答案】BC∥DE，证明过程见解析．【解析】试题分析：根据平行线的性质可以得到∥B=∥C，根据等式的性质可得∥C+∥D=180°从而说明BC∥ED.试题解析：∥AB∥CD ∥∥B=∥C ∥∥B+∥D=180°∥∥C+∥D=180°∥BC∥ED.考点：平行线的性质与判断.90．如图所示，已知AB∥CD，分别探索下列四个图形中∥P与∥A，∥C 的关系，请你从所得的四个关系中任选一个加以说明．【答案】答案见解析【解析】【分析】本题考查的是平行线的性质以及平行线的判定定理．（1）（2）都需要用到辅助线利用两直线平行，内错角相等的定理加以证明；（3）（4）是利用两直线平行，同位角相等的定理和三角形外角的性质加以证明．【详解】解：如图：（1）∵A+∵C+∵P=360；（2）∵A+∵C=∵P；（3）∵A+∵P=∵C；（4）∵C+∵P=∵A．说明理由（以第三个为例）：已知AB∵CD，根据两直线平行，同位角相等及三角形的一个外角等于两不相邻内角之和，可得∵C=∵A+∵P．【点睛】本题考查平行线的性质；三角形的外角性质．。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (59)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图BC∥DE，∥B=∥D，AB 和CD 平行吗？填空并写出理由．解：AB∥CD，理由如下：∥BC∥DE（）∥∥D=∥（）∥∥D=∥B（）∥∥B=（）（）∥AB∥CD（）【答案】已知，两直线平行内错角相等，已知，∠C，等量代换，内错角相等，两直线平行．【解析】【分析】根据平行线的判定和性质一一判断即可；【详解】解：AB∠CD，理由如下：∠BC∠DE（已知）∠∠D=∠C（两直线平行内错角相等）∠∠D=∠B（已知）∠∠B=（∠C）（等量代换）∠AB∠CD（内错角相等两直线平行）．故答案为：已知，两直线平行内错角相等，已知，∠C，等量代换，内错角相等，两直线平行．【点睛】本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．82．如图，直线AB∥CD，直线EF 与AB 相交于点P，与CD 相交于点Q，且PM∥EF，若∥1=68°，求∥2 的度数．【答案】∠2=22°．【解析】【分析】根据平行线的性质求得∠1=∠QPA=50°，由于∠2+∠QPA=90°，即可求得∠2的度数．【详解】解：∠AB∠CD，∠1=68°，∠∠1=∠QPA=68°．∠PM∠EF，∠∠2+∠QPA=90°．∠∠2+68°=90°，∠∠2=22°．【点睛】本题考查了平行线的性质，熟练掌握平行线的性质是本题的关键．83．（原题）已知直线AB∥CD，点P为平行线AB，CD之间的一点．如图1，若∥ABP=50°，∥CDP=60°，BE平分∥ABP，DE平分∥CDP，求∥BED的度数．（探究）如图2，当点P在直线AB的上方时，若∥ABP=α，∥CDP=β，∥ABP 和∥CDP的平分线交于点E1，∥ABE1与∥CDE1的角平分线交于点E2，∥ABE2与∥CDE2的角平分线交于点E3，…以此类推，求∥E n的度数．（变式）如图3，∥ABP的角平分线的反向延长线和∥CDP的补角的角平分线交于点E，试猜想∥P与∥E的数量关系，并说明理由．（β﹣α）；【变式】∠DEB=90°【答案】【原题】55°；【探究】∠E n的度数为12n﹣1∠P．理由见解析.2【解析】【分析】过E 作EF ∠AB ，依据平行线的性质，即可得到∠BED=∠BEF+∠DEF=∠ABE+∠CDE ，依据角平分线即可得出∠BED 的度数；【探究】依据平行线的性质以及三角形外角性质，求得∠E 1=12（β﹣α），∠E 2=14（β﹣α），∠E 3=18（β﹣α），以此类推∠E n 的度数为12n （β﹣α）；【变式】过E 作EG ∠AB ，进而得出∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE ，再根据平行线的性质以及三角形外角性质，即可得到∠DEB=90°﹣12（∠CDP ﹣∠ABP ）=90°﹣12（∠AHP ﹣∠ABP ）=90°﹣12∠P ．【详解】如图1，过E 作EF ∠AB ，而AB ∠CD ，∠AB ∠CD ∠EF ，∠∠ABE=∠FEB ，∠CDE=∠FED ，∠∠BED=∠BEF+∠DEF=∠ABE+∠CDE ，又∵∠ABP=50°，∠CDP=60°，BE 平分∠ABP ，DE 平分∠CDP ，∠∠ABE=12∠ABP=25°，∠CDE=12∠CDP=30°， ∠∠BED=25°+30°=55°，故答案为55°；【探究】如图2，∠∠ABP 和∠CDP 的平分线交于点E 1，∠∠ABE 1=12∠ABP=12α，∠CDE 1=12∠CDP=12， ∠AB ∠CD ，∠∠CDF=∠AFE1=12β，∠∠E1=∠AFE1﹣∠ABE1=12β﹣12α=12（β﹣α），∠∠ABE1与∠CDE1的角平分线交于点E2，∠∠ABE2=12∠ABE1=14α，∠CDE2=12∠CDE1=14β，∠AB∠CD，∠∠CDG=∠AGE2=14β，∠∠E2=∠AGE2﹣∠ABE2=14（β﹣α），同理可得，∠E3=18（β﹣α），以此类推，∠E n的度数为12n（β﹣α）．【变式】∠DEB=90°﹣12∠P．理由如下：如图3，过E作EG∠AB，而AB∠CD，∠AB∠CD∠EG，∠∠MBE=∠BEG，∠FDE=∠GED，∠∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE，又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，∠∠FDE=12∠PDF=12（180°﹣∠CDP），∠ABQ=12∠ABP，∠∠DEB=12∠ABP+12（180°﹣∠CDP）=90°﹣12（∠CDP﹣∠ABP），∠AB∠CD，∠∠CDP=∠AHP，∠∠DEB=90°﹣12（∠CDP﹣∠ABP）=90°﹣12（∠AHP﹣∠ABP）=90°﹣12∠P．【点睛】本题考查了平行线性质以及三角形外角性质的应用，解题的关键是正确作出辅助线，构造出平行线求解．84．如图，已知∥A=∥F，∥C=∥D，请问BD与CE平行吗？并说明理由．【答案】平行．理由见解析.【解析】【分析】由∠A=∠F可判定AC∠DF，可得到∠ABD=∠D=∠C，可判定BD∠CE．【详解】平行．理由如下：∠∠A=∠F，∠AC∠DF，∠∠ABD=∠D，且∠C=∠D∠∠ABD=∠C，∠BD∠CE．【点睛】本题主要考查平行线的判定和性质，掌握平行线的判定和性质是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行，同旁内角互补．85．已知直线AB∥CD，直线EF与AB，CD分别相交于点E，F．（1）如图1，若∥1=60°，求∥2，∥3的度数．（2）若点P是平面内的一个动点，连结PE，PF，探索∥EPF，∥PEB，∥PFD 三个角之间的关系．①当点P在图（2）的位置时，可得∥EPF=∥PEB+∥PFD请阅读下面的解答过程并填空（理由或数学式）解：如图2，过点P作MN∥AB则∥EPM=∥PEB（）∥AB∥CD（已知）MN∥AB（作图）∥MN∥CD（）∥∥MPF=∥PFD（）∥_____=∥PEB+∥PFD（等式的性质）即：∥EPF=∥PEB+∥PFD②拓展应用，当点P在图3的位置时，此时∥EPF=80°，∥PEB=156°，则∥PFD=_____度．③当点P在图4的位置时，请直接写出∥EPF，∥PEB，∥PFD三个角之间关系_____．【答案】（1）∠2=60°，∠3=60°；（2）①两直线平行，内错角相等；如果两条直线都和第三条直线平行，那么这两条直线也互相平行；两直线平行，内错角相等；∠EPM+∠FPM；②124；③∠EPF+∠PFD=∠PEB．【解析】【分析】（1）根据对顶角相等求∠2，根据两直线平行，同位角相等求∠3；（2）①过点P作MN∠AB，根据平行线的性质得∠EPM=∠PEB，且有MN∠CD，所以∠MPF=∠PFD，然后利用等式性质易得∠EPF=∠PEB+∠PFD．②同①；③利用平行线的性质和三角形的外角性质得到三个角之间的关系．【详解】（1）∠∠2=∠1，∠1=60°∠∠2=60°，∠AB∠CD∠∠3=∠1=60°；（2）①如图2，过点P作MN∠AB，则∠EPM=∠PEB（两直线平行，内错角相等）∠AB∠CD（已知），MN∠AB，∠MN∠CD（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）∠∠MPF=∠PFD（两直线平行，内错角相等）∠∠EPM+∠MPF=∠PEB+∠PFD（等式的性质）即∠EPF=∠PEB+∠PFD；故答案为两直线平行，内错角相等；如果两条直线都和第三条直线平行，那么这两条直线也互相平行；两直线平行，内错角相等；∠EPM+∠MPF；②过点P作PM∠AB，如图3所示：则∠PEB+∠EPM=180°，∠MPF+∠PFD=180°，∠∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°，即∠EPF+∠PEB+∠PFD=360°，∠∠PFD=360°﹣80°﹣156°=124°；故答案为124；③∠EPF+∠PFD=∠PEB．故答案为∠EPF+∠PFD=∠PEB．【点睛】本题考查了平行线的判定与性质、三角形的外角性质；熟练掌握平行线的判定与性质，正确作出辅助线是解决问题的关键．86．如图，直线AB∥CD，EF⊥CD，F为垂足，∠GEF=30°，求∠1的度数．【答案】120°【解析】【分析】由EF⊥CD，∠GEF=30°，根据直角三角形中两个锐角互余，即可求得∠EGF 的度数，根据邻补角的定义得到∠CGE的度数，又由两直线平行，同位角相等，即可求得∠1的度数．【详解】∵EF⊥CD于点F，∴∠EFG=90°，∴∠EGF=90°﹣∠GEF=90°﹣30°=60°，∵∠CGE+∠EGF=180°，∴∠CGE=180°﹣60°=120°，∵AB∥CD，∴∠1=∠CGE=120°（两直线平行，同位角相等）．【点睛】此题考查了平行线的性质与直角三角形的性质．此题比较简单，注意掌握两直线平行，同位角相等定理的应用．87．如图，CD∥AB于点D，GF∥AB于点F，∥B＝∥ADE.请你判断∠1与∠2的关系，并证明你的结论．【答案】∠1＝∠2，证明详见解析.【解析】【分析】由CD∠AB，GF∠AB，根据平行线的判定方法得CD∠GF，再根据平行线的性质得∠2=∠BCD；由∠B=∠ADE，根据同位角相等，两直线平行得DE∠BC，则利用平行线的性质得∠1=∠BCD，然后利用等量代换即可得到∠1=∠2．【详解】解：∠1＝∠2.证明：∵∠B＝∠ADE，∠DE∠BC，∠∠1＝∠DCB.又∵CD∠AB，GF∠AB，∠CD∠FG，∠∠2＝∠DCB，∠∠1＝∠2【点睛】本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．88．如图，AB∥DE，∥1＝∥2，试判断AE与DC的位置关系，并说明理由．【答案】AE∠DC，理由详见解析.【解析】【分析】判断两直线的位置关系，通过角与角的数量关系，从而证明直线平行【详解】解：AE∠DC.理由：∵AB∠DE，∠∠1＝∠AED，又∵∠1＝∠2，∠∠2＝∠AED，∠AE∠DC【点睛】解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．89．如图，AB∥CD，∥ABE＝∥DCF.求证：∠E＝∥F.【答案】详见解析.【解析】【分析】根据两直线平行内错角相等可得，∠ABC=∠BCD，结合已知又可知∠EBC=∠FCB，所以BE∠CF（内错角相等，两直线平行）从而证两角相等．【详解】证明：∵AB∠CD，∠∠ABC＝∠BCD.又∵∠ABE＝∠DCF，∠∠ABC－∠ABE＝∠BCD－∠DCF，即∠EBC＝∠FCB，∠BE∠CF，∠∠E＝∠F【点睛】本题考查了平行线的性质和判定，以及角的和差关系，灵活运用相关知识是解题关键．90．如图，在△ABC中，AD⊥BC，垂足为D，点E在AB上，EF⊥BC，垂足为F．(1)AD与EF平行吗？为什么？(2)如果∠1＝∠2，且∠3＝115°，求∠BAC的度数．【答案】（1）AD与EF平行；（2）115°．【解析】【分析】（1）根据在同一平面内，垂直于同一条直线的两直线平行可判断AD∥EF；（2）根据平行线的性质由AD∥EF得∠2=∠BAD，而∠1=∠2，所以∠1=∠BAD，则可根据平行线的判定方法得到AB∥DG，然后利用平行线的性质得∠BAC=∠3=115°．【详解】解：（1）AD与EF平行．理由如下：∠AD∠BC，EF∠BC，∠AD∠EF；（2）∠AD∠EF，∠∠2=∠BAD，而∠1=∠2，∠∠1=∠BAD，∠AB∠DG，∠∠BAC=∠3=115°．【点睛】本题考查了平行线的判定与性质：内错角相等，两直线平行；两直线平行，同位角相等；在同一平面内，垂直于同一条直线的两直线平行．。

人教版七年级数学下册第五章平行线的性质习试（含答案）（53）

⼈教版七年级数学下册第五章平⾏线的性质习试（含答案）（53）⼈教版七年级数学下册第五章平⾏线的性质复习试题（含答案)如图，a∥b，点A在直线a上，点B，C在直线b上，AC⊥b，如果AB=5cm，BC=3cm，那么平⾏线a，b之间的距离为（）A．5cm B．4cm C．3cm D．不能确定【答案】B【解析】【分析】从⼀条平⾏线上的任意⼀点到另⼀条直线作垂线，垂线段的长度叫两条平⾏线之间的距离，并由勾股定理可得出答案．【详解】解：∵AC⊥b，∴△ABC是直⾓三⾓形，∵AB=5cm，BC=3cm，∴（cm），∴平⾏线a、b之间的距离是：AC=4cm．故选：B．【点睛】本题考查了平⾏线之间的距离，以及勾股定理，关键是掌握平⾏线之间距离的定义，以及勾股定理的运⽤．22．如图，⼀副直⾓三⾓板按如图所⽰放置，若AB∥DF，则∠BCF的度数为（）A．30°B．45°C．60°D．90°【答案】C【解析】【分析】利⽤平⾏线的性质解决问题即可．【详解】解：∵AB∥DF，∠B=60°，∴∠BCF=∠B=60°，故选：C．【点睛】此题考查平⾏线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．23．如图，在甲、⼄两地之间要修⼀条笔直的公路，在甲地测得公路的⾛向是北偏东48．．°，甲、⼄两地同时开⼯，要使公路准确接通，⼄地所修公路的⾛．．．向应是（）A．南偏西48°B．北偏东42°C．北偏东48°D．南偏西42°【答案】A【解析】【分析】根据⽅位⾓的概念，结合图形，利⽤平⾏线的性质解答即可．【详解】解：如图所⽰，∵同是正北⽅向，AB CD，∴//∠=∠=?，∴1248∴⼄地所修公路的⾛向应是南偏西48°．故选：A．【点睛】本题考查的知识点是平⾏线的性质以及⽅位⾓的概念，熟知⽅位⾓的定义是解此题的关键．24．如图，a∥b，∠α与∠β是⼀对同旁内⾓，若∠α＝50°，则∠β的度数为（）A．130°B．50°C．50°或130°D．⽆法确定【答案】A【解析】【分析】根据两直线平⾏，同旁内⾓互补，即可求出．【详解】解：∵a∥b，∴∠α+∠β=180°，∵∠α＝50°∴∠β=180°-50°=130°，故答案为：A．【点睛】本题考查了平⾏线的性质，解题的关键是熟知两直线平⾏，同旁内⾓互补．25．如图，将⼀副三⾓板和⼀张对边平⾏的纸条按下列⽅式摆放，两个三⾓板的⼀直⾓边重合，含45°⾓的直⾓三⾓板的斜边与纸条⼀边重合，含30°⾓的三⾓板的⼀个顶点在纸条的另⼀边上，则∠1的度数是（）A．10°B．15°C．20°D．25°【解析】【分析】先根据平⾏线的性质得出∠BCD的度数，进⽽可得出结论．【详解】解：如下图所⽰：∠AB∠CD，∠∠BCD＝∠ABC＝45°，∠∠1＝∠BCD﹣∠BCE＝45°﹣30°＝15°．故选：B．【点睛】本题考查的是平⾏线的性质，熟知平⾏线的性质与三⾓板的特点是解答此题的关键．m n，将⼀直⾓三⾓尺的直⾓顶点放在直线m上，已知26．如图，直线//∠=?，则2135∠的度数为（）A．135°B．145°C．120°D．125°【答案】D【分析】根据两直线平⾏，内错⾓相等求出∠4，根据余⾓的性质求出∠3，再根据补⾓的性质求解即可．【详解】如图：∵//m n ，∠1=35°，∴∠4=∠1=35°（两直线平⾏，内错⾓相等），∴∠3=90°-∠4=90°-35°=55°，∴∠2=180°-∠3=180°-55°=125°．故选：D ．【点睛】本题主要考查了两直线平⾏，内错⾓相等的性质以及余⾓、补⾓的性质，熟练掌握性质定理是解题的关键．27．如图，已知//AB DE ，则B C D ∠∠∠、、之间的数量关系是（）A ．180BCD ?∠+∠+∠= B ．180B C D ?∠-∠+∠=C ．180D B C ?∠-∠+∠=D ．180D B C ?∠-∠-∠=【答案】B【解析】【分析】过C 点作CF ∥AB ，即可判断CF ∥DE ，根据“两直线平⾏，内错⾓相等，同旁内⾓互补”求解即可．【详解】过C 点作CF ∥AB ，∵AB ∥DE∴CF ∥DE∴∠B=∠BCF ，∠DCF+∠D=180°∴∠B-∠BCD+∠D=180°故选：B【点睛】本题考查的是平⾏线的性质，掌握平⾏线的性质定理是关键．⼆、填空题28．为了增强学⽣体质，某学校将“抖空⽵”引阳光体育⼀⼩时活动，图1是⼀位同学抖空⽵时的⼀个瞬间，⼩明把它抽象成图2的数学问题：已知//,80,110AB CD EAB ECD ∠=?∠=?，则E ∠的度数是_____．【答案】30°【解析】【分析】过E 点作EF ∥AB ，由两直线平⾏，同旁内⾓互补即可求解.【详解】解：过E 点作EF ∥AB ，如下图所⽰：∵EF ∥AB ，∴∠EAB+∠AEF=180°，⼜∠EAB=80°∴∠AEF=100°∵EF ∥AB ，AB ∥CD∴EF ∥CD∴∠CEF+∠ECD=180°，⼜∠ECD=110°∴∠CEF=70°∴∠AEC=∠AEF-∠CEF=100°-70°=30°.故答案为：30°.【点睛】本题考查平⾏线的构造及平⾏线的性质，关键是能想到过E点作EF∥AB，再利⽤两直线平⾏同旁内⾓互补即可解决.29．⼭上的⼀段观光索道如图所⽰，索道⽀撑架均为相平⾏（AM∥CN），且每两个⽀撑架之间的索道均是直的，若∠MAB＝60°，∠NCB＝40°，则∠ABC ＝_____°．【答案】100°【解析】【分析】利⽤平⾏线的性质得到∠ABE＝∠MAB＝60°，∠CBE＝∠NCB＝40°，然后计算∠ABE+∠CBE即可．【详解】解：如图，延长DB ⾄点E，∵AM∥BD，∴∠ABE＝∠MAB＝60°，∵CN∥BD，∴∠CBE＝∠NCB＝40°，∴∠ABC ＝∠ABE+∠CBE ＝60°+40°＝100°．故答案为100．【点睛】本题考查了平⾏线性质：两直线平⾏，同位⾓相等；两直线平⾏，同旁内⾓互补；两直线平⾏，内错⾓相等．30．如图，∠AEM ＝∠DFN ＝a ，∠EMN ＝∠MNF ＝b ，∠PEM ＝12∠AEM ，∠MNP ＝12∠FNP ，∠BEP ，∠NFD 的⾓平分线交于点I ，若∠I ＝∠P ，则a 和b 的数量关系为_____（⽤含a 的式⼦表⽰b ）．【答案】81209a b =-?．【解析】【分析】分别过点P 、I 作ME ∥PH ，AB ∥GI ，设∠AME=2x ，∠PNF=2y ，知∠PEM=x ，∠MNP=y ，由PH ∥ME 知∠EPH=x ，由EM ∥FN 知PH ∥FN ，据此得∠HPN=2y ，∠EPN=x+2y ，同理知3902 EIF x x ∠?-+＝，根据∠EPN=∠EIF 可得答案．【详解】分别过点P 、I 作ME ∥PH ，AB ∥GI ，设∠AME ＝2x ，∠PNF ＝2y ，则∠PEM ＝x ，∠MNP ＝y ，∴∠DFN ＝2x ，∵PH ∥ME ，∴∠EPH ＝x ，∵EM ∥FN ，∴PH ∥FN ，∴∠HPN ＝2y ，∠EPN ＝x +2y ，同理，3902EIF x x ∠?-+＝，∵∠EPN ＝∠EIF ，∴3902x x ?-+＝x +2y ，∴339042b ?-a ＝，∴91358b a =?-，∴81209b -?a ＝，故答案为：81209b -?a ＝．【点睛】本题主要考查平⾏线的判定与性质，解题的关键是熟练掌握平⾏线的判定与性质．。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (100)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)直线l1∥l2，一块含45°角的直角三角板如图放置．若∠1＝75°，则∠2＝_____度．【答案】30【解析】【分析】给图中各角标上序号，由直线l1∥l2可得出∠4＝∠1＝75°，由三角形外角的性质及等腰直角三角形的性质可求出∠3的度数，再利用对顶角相等即可求出∠2的度数．【详解】解：给图中各角标上序号，如图所示．∵直线l1∥l2，∴∠4＝∠1＝75°．∵∠4＝∠3+45°，∴∠3＝∠4﹣45°＝30°，∴∠2＝∠3＝30°．故答案为30．【点睛】本题考查了等腰直角三角形、平行线的性质以及三角形外角的性质，利用三角形外角的性质，求出∠3的度数是解题的关键．92．如图，已知AB ∥CD ，OE 平分∠AOD ，OF ⊥OE ，∠CDO ＝50°，则∠DOF ＝_____度．【答案】25【解析】【分析】要求∠DOF 的度数，结合已知条件，只需求得∠DOE 的度数．显然根据平行线的性质以及角平分线的定义就可求解．【详解】解：∵AB ∥CD ，OE 平分∠AOD ，∠CDO ＝50°，∴∠AOD ＝180°﹣∠CDO ＝180°﹣50°＝130°，111306522AOE DOE AOD ∠=∠=∠=⨯︒=︒． ∵OF ⊥OE ，∴∠EOF ＝90°．∴∠DOF ＝∠EOF ﹣∠DOE ＝90°﹣65°＝25°．【点睛】本题考查了平行线的性质及角平分线的性质，是中学阶段的常规题．93．如图，//a b ，将三角尺的直角顶点落在直线a 上，若160∠=︒, 250∠=︒，则3∠=________．【答案】70°【解析】【分析】结合三角形内角和定理得到∠4=70°，然后由对顶角相等和“两直线平行，同位角相等”求得∠3的度数．【详解】如图，∵∠1=60°，∠2=50°，∴∠4=180°-∠1-∠2=70°．∴∠5=∠4=70°∵a ∥b ，∴∠3=∠5=70°，故答案是：70°．【点睛】考查了平行线的性质，解题的关键是利用三角形内角和定理求得∠4的度数．94．如图，直线a∥b，∠1＝55°，则∠2＝_____．【答案】125°．【解析】【分析】先根据平行线的性质求出∠3的度数，再由两角互补的性质求出∠2的度数即可．【详解】∵直线a∥b，∠1＝55°，∴∠3＝∠1＝55°，∵∠2+∠3＝180°，∴∠3＝180°﹣∠2＝180°﹣55°＝125°．故答案为：125°．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．熟练的掌握平行线的性质是关键.95．如图，易拉罐的上下底面互相平行，吸管放在罐内时，∠1=110°，则∠2=_____【答案】70°【解析】【分析】先根据对顶角相等求出∠1的对顶角，再根据两直线平行，同旁内角互补求解即可．【详解】解：如图∵∠1=110°，∴∠3=∠1=110°，∵易拉罐的上下底面互相平行，∴∠2=180°-∠3=180°-110°=70°．故答案为70．【点睛】本题主要考查了平行线的性质，准确识图并熟记性质是解题的关键．96．如图，直线a∥b，∠1=120°，则∠2的度数为________．【答案】60°【解析】【分析】如图，根据平角的定义求出∠3的度数，根据平行线的性质得出∠2=∠3，代入求出即可．【详解】如图，∵∠1+∠3=180°，∴∠3=180°-∠1=60°，∵a//b，∴∠2=∠3=60°，故答案为：60°【点睛】本题考查了平行线的性质的应用，两直线平行，同位角相等；两直线平行，同位角相等；两直线平行，同旁内角互补；熟练掌握平行线的性质是解题关键.97．如图，一束平行太阳光照射到每个内角都相等的五边形上，若∠1＝47°，则∠2＝_____．【答案】25°【解析】【分析】先根据正五边形的性质求出∠3的度数，再由平行线的性质即可得出结论．【详解】解：∵图中是正五边形．∴∠3＝108°．∵太阳光线互相平行，∠1＝47°，∴∠2＝180°﹣∠1﹣∠3＝180°﹣47°﹣108°＝25°．故答案为：25°．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补，解题的关键是：根据正五边形的性质求出∠3的度数．98．如图，∠1+∠2=180°，∠3=∠B，求证：EF∥BC，请你补充完成下面的推导过程．证明：∵∠1+∠2=180°（已知）∠2=∠4（）∴∠+∠4=180°（等量代换）∴DF∥AB（）∴∠B=∠FDH（）∵∠3=∠B（）∴∠3=∠（）∴EF∥BC（）【答案】详见解析【解析】【分析】先依据同旁内角互补,两直线平行,即可得到EF∥BC.再根据平行线的性质即可得出∠B=∠FDH,进而得到3=∠FDH,即可依据内错角相等,两直线平行,判定EF∥BC【详解】证明：∵∠1+∠2=180°（已知）∠2=∠4（对顶角相等）∴∠ 1 +∠4=180°（等量代换）∴DF∥AB（同旁内角互补，两直线平行）∴∠B=∠FDH（两直线平行，同位角相等）∵∠3=∠B（已知）∴∠3=∠FDH （等量代换）∴EF∥BC（内错角相等，两直线平行）【点睛】本题考查了平行线的性质和判定,补角定义的应用,能运用平行线的性质和判定进行推理是解此题的关键99．如图，已知∠ACB＝90°，直线MN∥AB，若∠1＝33°，则∠2＝_____°．【答案】57【解析】【分析】直接利用已知得出∠ACN的度数，再利用平行线的性质得出答案．【详解】解：∵∠ACB＝90°，∠1＝33°，∴∠ACN＝57°，∵直线MN∥AB，∴∠2＝∠ACN＝57°．故答案为：57°．【点睛】此题主要考查了平行线的性质，正确得出∠ACN的度数是解题关键．100．如图，AB∥EG∥CD，EF平分∠BED，若∠D＝69°，∠GEF＝21°，则∠B＝_____°．【答案】27【解析】【分析】根据平行线的性质求出∠GED＝∠D，∠B＝∠BEG，根据角平分线的定义求出∠BEF＝∠DEF，即可求出答案．【详解】解：∵AB∥EG∥CD，∠D＝69°，∴∠GED＝∠D＝69°，∵∠GEF＝21°，∴∠DEF＝∠GED﹣∠GEF＝48°，∵EF平分∠BED，∴∠BEF＝∠DEF＝48°，∴∠BEG＝∠BEF﹣∠GEF＝48°﹣21°＝27°，∵AB∥EG，∴∠B＝∠BEG＝27°，故答案为：27．【点睛】本题考查了角平分线的定义和平行线的性质，能根据平行线的性质求出∠GED＝∠D和∠B＝∠BEG是解此题的关键．。

人教版七年级数学下册第五章平行线的性质习试(含答案) (51)

人教版七年级数学下册第五章平行线的性质复习试题（含答案)一、单选题1．如图，在横线本上面画了两条平行线AB∥CD，则下列等式一定成立的是（）A．∠3＝2∠1 B．∠3＝∠2+90° C．∠2+∠1＝90° D．∠3+∠1＝180°【答案】D【解析】【分析】利用AB∥CD得到∠1＝∠4，利用横线都平行得到∠2＝∠4，∠3＝∠5，则∠1＝∠2，从而得到∠1+∠3＝180°，∠2+∠3＝180°，即可解决问题．【详解】解：如图，∵AB∥CD，∴∠1＝∠4，∵横线都平行，∴∠2＝∠4，∠3＝∠5，∴∠1＝∠2，∵∠4+∠5＝180°，∴∠1+∠3＝180°，∠2+∠3＝180°．故选：D．【点睛】本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．2．下列命题正确的是（）A．相等的角是对顶角B．两条直线被第三条直线所截，同位角相等C．同旁内角互补D．在同一平面内，垂直于同一条直线的两条直线平行【答案】D【解析】【分析】根据对顶角、平行线的性质和判定判断即可．【详解】解：A、相等的角不一定是对顶角，不符合题意；B、两条平行线被第三条直线所截，同位角相等，选项未没有平行的条件，故错误，不符合题意；C、两直线平行，同旁内角互补，选项未没有平行的条件，故错误，不符合题意；D、在同一平面内，垂直于同一条直线的两条直线平行，正确，符合题意；故选：D．【点睛】本题考查了命题的真假判断．判断命题的真假关键是要熟悉课本中的性质定理．3．如图，直线a∥b，∠1=40º，则∠2=（）A．40ºB．60ºC．100ºD．140º【答案】D【解析】【分析】如解题所示，根据平角的定义即可求出∠3，然后根据两直线平行，同位角相等即可求出结论．【详解】解：如图所示∵∠1=40°∴∠3=180°－∠1=140°∵a∥b∴∠2=∠3=140°故选D．【点睛】此题考查的是平行线的性质，掌握两直线平行，同位角相等是解决此题的关键．4．下列图形中，∠1与∠2不是互补关系的是（）A．B．C．D．【答案】C【解析】【分析】根据互补的两个角的和为180︒判定即可．【详解】解：A．∠1与∠2是互补关系，故本选项不合题意；B．由平行线的性质可知∠1与∠2是互补关系，故本选项不合题意；C．由对顶角的定义可知∠1与∠2是对顶角，不一定具有互补关系，故本选项符合题意；D．∠1+∠2=180°，即∠1与∠2是互补关系，故本选项不合题意．故选：C．【点睛】本题主要考查了补角的定义、邻补角、对顶角、平行线的性质，熟记补角的定义是解答本题的关键．m n，将含有45︒角的三角板ABC的直角顶点C放在直线n 5．如图，直线//∠+∠等于（）上，则12A．30B．40︒C．45︒D．60︒【答案】C【解析】【分析】首先过点A作l∥m，由直线l∥m，可得n∥l∥m，由两直线平行，内错角相等，即可求得答案：∠1+∠2=∠3+∠4的度数．【详解】解：如图，过点A 作l ∥m ，则∠1=∠3．又∵m ∥n ，∴l ∥n ，∴∠4=∠2，∴∠1+∠2=∠3+∠4=45°．故选：C ．【点睛】本题考查了平行线的性质．此题难度不大，注意辅助线的作法，注意掌握“两直线平行，内错角相等”性质定理的应用．6．如图，已知AB CD ∥，150∠=，245∠=，则CAD ∠等于（）A ．75°B ．80°C ．90°D ．85°【答案】D【解析】【分析】先根据平行线的性质得出245BAD ∠=∠=︒，然后利用平角的定义得出∠=︒-∠+∠，即可求解．CAD BAD180(1)【详解】//AB CD，∴∠=∠=︒．245BAD∠+∠+∠=︒，BAD CAD1180CAD BAD∴∠=︒-∠+∠=︒-︒+︒=︒．180(1)180(5045)85故选：D．【点睛】本题主要考查平行线的性质及平角的定义，掌握平行线的性质是解题的关键．7．一副三角板如图放置，点D在CB的延长线上，EF∥CD，∠C=∠EDF=90°，∠A=45°，∠EFD=30°，则∠DFB=( )A．15°B．20°C．25°D．30°【答案】A【解析】【分析】直接利用三角板的特点，结合平行线的性质得出∠BFE=45°，进而得出答案．【详解】由题意可得：∠EFD=30°，∠ABC=45°，∵EF∥CD，∴∠BFE=∠ABC=45°，∴∠DFB=45°-30°=15°．故选：A．【点睛】此题主要考查了平行线的性质，根据平行线的性质得出∠BFE的度数是解题关键．8．如图，已知直线AB与CD平行，直线EF与AB，CD分别交于点E，F，若∠1=125°，则∠2=( )A．65°B．55°C．50°D．45°【答案】B【解析】【分析】利用平行线的性质解决问题即可．【详解】∵∠1=125°，∴∠AEC=180°-125°=55°，∵AB∥CD，∴∠2=∠AEC=55°，故选：B．【点睛】本题考查平行线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．9．如图，下列命题：①若∠1＝∠2，则∠D＝∠4；②若∠C＝∠D，则∠4＝∠C；③若∠A＝∠F，则∠1＝∠2；④若∠1＝∠2，∠C＝∠D，则∠A＝∠F；⑤若∠C＝∠D，∠A＝∠F，则∠1＝∠2．其中正确的个数有（）个．A．1 B．2 C．3 D．4【答案】C【解析】【分析】根据平行线的性质和判定进行判断即可．【详解】解：①若∠1＝∠2，可得∠3＝∠2，可得DB∥EC，则∠D＝∠4，正确；②若∠C＝∠D，得不出∠4＝∠C，错误；③若∠A＝∠F，得不出∠1＝∠2，错误；④若∠1＝∠2，∠C＝∠D，则∠A＝∠F，正确；⑤若∠C＝∠D，∠A＝∠F，则∠1＝∠2，正确．故选：C．【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．10．如图，若AB ∥DE ，∠B ＝130°，∠D ＝35°，则∠C 的度数为（）A ．80°B ．85°C ．90°D ．95°【答案】B【解析】【分析】过C 作//CM AB ，进而可证出////AB CM DE ，根据平行线的性质可得1180B ∠+∠=︒，230D ∠=∠=︒，进而可得BCD ∠的度数．【详解】解：过C 作CM ∥AB ，∵AB ∥DE ，∴AB ∥CM ∥DE ，∴∠1+∠B ＝180°，∠2＝∠D ＝35°，∵∠B ＝130°，∴∠1＝50°，∴∠BCD ＝∠1+∠2＝85°，故选：B ．【点睛】本题主要考查了平行线的性质，关键是掌握两直线平行内错角相等，同旁内角互补．。

人教版初中数学七年级下《5.3平行线的性质》同步练习题(含答案)

人教版初中数学七年级下《5.3平行线的性质》同步练习题《平行线的性质》同步练习1课堂作业1．下列图形表示平面内直线AB∥CD的是()A．B．C．D．2．下列说法正确的是()A．同一平面内没有公共点的两条线段平行B．两条不相交的直线是平行线C．同一平面内没有公共点的两条线平行D．同一平面内没有公共点的两条射线平行3．经过直线外一点画直线，下列说法错误的是()A．可以画无数条直线与这条直线相交B．可以画无数条直线与这条直线平行C．能且只能画一条直线与这条直线平行D．能且只能画一条直线与这条直线垂直4．如图，写出图中所有的平行线：________．5．根据下列要求画图：(1)如图①，过点A画MN∥BC；(2)如图②，过点P画PE∥OB，交OA于点E；(3)如图③，过点C画CE∥DA，交AB于点E，交DB于点H；过点C画CF∥DB，交AB的延长线于点F．课后作业6．在同一平面内，一条直线与另外两条平行直线的位置关系是()A．一定与两条平行直线相交B．与两条平行直线中的一条平行，而与另一条相交C．一定与两条平行直线平行D．与两条平行直线都平行或都相交7．下列说法：①一条直线的平行线只有一条；②过一点与已知直线平行的直线只有一条；③因为a∥b，c∥d，所以a∥d；④经过直线外一点，有且只有一条直线与这条直线平行．其中，正确的有() A．1个B．2个C．3个D．4个8．a、b、c是平面上的任意三条直线，它们的交点可以有()A．1个或2个或3个B．0个或1个或2个或3个C．1个或2个D．以上都不正确9．已知直线a、b都过点M，且直线a∥l，b∥l，那么直线a、b是同一条直线，根据是________．10．将一张长方形的硬纸片ABCD对折后打开，折痕为EF，把长方形ABEF平摊在桌面上．另一面CDFE无论怎样改变位置，总有CD∥AB，理由是________．11．如图，P为直线AB外一点，读下列语句画图形：(1)过点P画PC⊥AB，垂足为C；(2)过点P画PD∥AB；(3)观察图形，猜想PC与PD的位置关系(不要求说明理由)．12．如图，直线AB、CD是一条河的两岸，并且AB∥CD，E为直线AB、CD外一点，现想过点E画岸CD的平行线，只需过点E画岸AB的平行线即可．画图，并说明理由．13．如图，AD∥BC，AE＝BE．(1)过点E画EF∥BC，交DC于点F．(2)AD与EF平行吗？为什么？(3)通过测量，试判断等式DF＝CF与1()2EF AD BC=+是否成立．答案[课堂作业]1．B2．C3．B4．AB∥CD，EF∥BH5．略[课后作业]6．D7．A8．B9．经过直线外一点，有且只有一条直线与已知直线平行10．如果两条直线都与第三条直线平行，那么这两条直线也互相平行11．(1)如图所示(2)如图所示(3)PC⊥PD12．图略理由：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．13．(1)略(2)略(3)两个等式都成立《平行线的性质》同步练习21．平面内两条________的直线叫平行线，如果直线a与直线b平行可记为______，读作_________．2．经过直线外一点，__________与这条直线平行．3．如果两条直线和第三条直线______，那么这两条直线平行；若a∥b，b•∥c，•则_______．4．在同一平面内，•不互相重合的两条直线位置关系有_____•种，•它们是____，______．5．在同一平面内L1与L2没有公共点，则L1______L2．6．在同一平面内L1和L2有一个公共点，则L1与L2______．7．在同一平面内，不重合的两条直线的位置关系有_______种，分别是________．8．（经典题）设a，b，c为平面内三条不同直线：（1）若a∥b，c⊥a，则b与c的位置关系是______；（2）若a∥b，b∥c，则a与c的位置关系是______．9．（合作探究题）在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为0个，因为a∥b∥c，如图（1）所示．乙：同一平面内三条直线交点个数只有1个，因为a，b，c交于同一点O，如图（2）所示．以上说法谁对谁错？为什么？10．请举出一例生活中平行线的例子，如笔直铁路上铁轨是互相平行的直线．举例：__________________参考答案1．不相交，a∥b，a平行于b2．有且只有一条直线3．都平行，a∥c4．2，相交，平行5．∥6．相交7．2，相交，平行8．（1）b⊥C（2）a∥c（点拨：画图来判定）9．甲，乙说法都不对，各自少了三种情况．a∥b，c与a，b相交如图（1），a，b，•c两两相交如图（2），所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况．解题规律：三条直线在同一平面的位置关系有四种情况，有1个交点，2个交点，•3个交点和0个交点．10．窗户的柱子《平行线的性质》同步练习31．公路两旁的两根电线杆位置关系是________．2．练习本中的横线格中的横线段是_______，如图所示．3．如图所示，AB∥CD，EF与AB，CD相交，EF与AB交于点_____，•EF•与CD•交于______．4．下列说法不正确的是（）A．过马路的斑马线是平行线B．100米跑道的跑道线是平行线C．若a∥b，b∥d，则a⊥dD．过直线外一点有且只有一条直线与已知直线平行5．下列说法正确的是（）A．同一平面内不相交的两线段必平行B．同一平面内不相交的两射线必平行C．同一平面内不相交的一条线段与一条直线必平行D．同一平面内不相交的两条直线必平行6．如图所示，在这些四边形AB不平行于CD的是（）7．（原创题）如图所示，在∠AOB内有一点P．（1）过P画L1∥OA；（2）过P画L2∥OB；（3）用量角器量一量L1与L2相交的角与∠O的大小有怎样关系？8．如图所示，在5×5的网格中，AC是网格中最长的线段，请画出两条线段与AC平行并且过网格的格点．9．（教材变式题）“垂直于同一条直线的两直线平行”，•运用这一性质可以说明铺设铁轨互相平行的道理．如图所示，已知∠2是直角，再度量出∠1或∠3就会知道铁轨平行不平行？方案一：若量得∠3=90°，结合∠2情况，说明理由．方案二：若量得∠1=90°，结合∠2情况，说明理由．10．（原创题）如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：（1）请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；（2）EF与A′B′有何位置关系？CC′与DH有何位置关系？参考答案1．平行关系2．互相平行的线段3．M，N4．C（点拨：用平行线定义来判定）5．D（点拨：A，B，C都有可能相交）．6．D（点拨：A是平行四边形，B是梯形，C是正方形．）7．（1），（2）如图所示，（3）L1与L2夹角有两个，∠1，∠2，∠1=∠O，∠2+∠O=•180°，所以L1和L2夹角与∠O相等或互补．思路点拨：注意∠2与∠O是互补关系，易漏掉．8．如图所示：EF∥AC，PQ∥AC，MN∥AC，且它们都过格点．解题技巧：过网格格点，EF，PQ，MN与竖直线AB都成45°角，AC与AB成45°，由同位角相等得两直线平行．9．方案一：如果量∠3=90°，而∠2=90°∴两铁轨都与枕木垂直，那么两铁轨就平行．方案二：如果量得∠1=90°，而∠2=90°，∴两铁轨都与枕木垂直，那么两铁轨就平行．思路点拨：运用已知定理及垂直的定义来说明．10．（1）正面：AB∥EF，AE∥MF等等；上面：A′B′∥AB，C′D′∥CD等等；右侧：•DD′∥HR，DH∥D′R（2）EF∥A′B′，CC′⊥DH思路点：（1）在同一平面的两线段平行，假设延长看有无交点；（2）•不在同一平面的线段位置关系判断，可通过两个平面的交线来判定．。

人教版七年级数学下册第五章平行线的性质复习试题（含答案）（53）

线的性质和判定进行推理和证明，题目比较典型．
三、填空题 77 ．将一副三角板按如图放置，小明得到下列结论： ①如果 ∠2 ＝30 °，则有 AC ∥DE ；②∠ BAE+ ∠ CAD ＝180 ° ；③如果 BC ∥ AD ，则有 ∠2 ＝30 ° ； ④ 如果 ∠ CAD ＝ 150 ° ，则 ∠4 ＝ ∠C；那么其中正确的结论有 ________
【答案】见解析【解析】【分析】首先易证 AD ∥ BC ，得到 ADC C 180 ，然后根据 ∠5 ∠C 证明 AF∥CD ，最后由 2 AGD ， 1 2 即可证明 AB∥DE . 【详解】 ∵ 3 4， ∴ AD ∥ BC ， ∴ ADC C 180 ，又∵ ∠5 ∠C ， ∴ ADC 5 180 ， ∴ AF∥CD ， ∴ 2 AGD ，
又∵∠ C=45 °，∠1+ ∠2=90 °， ∴∠ 3=45 °， ∴∠ 2=90 °－45 °=45 °，故 ③错误； ∵∠ D=30 °，∠CAD=150 °， ∴∠ CAD+ ∠ D=180 °， ∴AC//DE ， ∴∠ 4= ∠ C，故 ④正确．故答案为： ①②④ 【点睛】此题考查平行线的判定定理和性质，角的关系，解题关键在于利用判定定理进行判断 78 ．如图，把一块含有 45 °角的直角三角板的两个顶点放在直尺的对边上．如果 ∠1=15 °，那么 ∠2 的度数是 _______
【点睛直线平行，内错角相等． 79 ．有一条直的宽纸带折叠成如图所示，则 ∠1 的度数为 _____度．
【答案】 75 【解析】【分析】根据平行线的性质得出 ∠EDC= ∠EFA=30 °，∠1+ ∠BDC=180 °，根据折叠求出 ∠EDB=75 °，代入求出即可．【详解】 ∵AB∥CD ，

2015春人教版数学七下53《平行线的性质》习题及答案

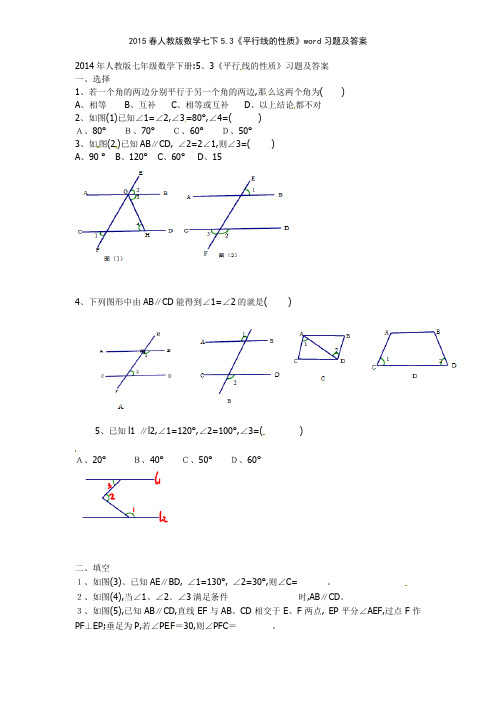
2014年人教版七年级数学下册:5、3《平行线的性质》习题及答案一、选择1、若一个角的两边分别平行于另一个角的两边,那么这两个角为( )A、相等B、互补C、相等或互补D、以上结论都不对2、如图(1)已知∠1=∠2,∠3=80°,∠4=()Ａ、80°Ｂ、70°Ｃ、60°Ｄ、50°3、如图(2)已知AB∥CD, ∠2=2∠1,则∠3=( )A、90 °B、120°C、60°D、154、下列图形中由AB∥CD能得到∠1=∠2的就是( )5、已知l1 ∥l2,∠1=120°,∠2=100°,∠3=()Ａ、20°Ｂ、40°Ｃ、50°Ｄ、60°二、填空１、如图(3)、已知AE∥BD, ∠1=130°, ∠2=30°,则∠C= 。

２、如图(4),当∠1、∠2、∠3满足条件时,AB∥CD。

３、如图(5),已知AB∥CD,直线EF与AB、CD相交于E、F两点, EP平分∠AEF,过点F作PF⊥EP;垂足为P,若∠PE F＝30,则∠PFC＝。

４、如图(6),直线AB⊥l1,l1∥l2,∠1＝75°,则∠2＝。

5、如图(7),已知AB∥CD,则∠1、∠2、∠3之间的关系就是。

三、解答题。

１、如图,AB∥CD,直线FG平分∠AOE ,∠1＝40°,则∠2就是多少度？２、已知∠AGE=∠DHF,∠1＝∠2,则图中的平行线有几对？分别就是？为什么？３、如图,AB∥CD∥GF,∠1:∠Ｄ:∠Ｂ＝2:3:4,求∠1的度数？参考答案:一、１、C２、A３、C４、B５、B二、１、30２、∠1＝∠2+∠3３、60°４、165°５、∠2-∠3+∠1＝180° 三、略。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (93)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，直线a∥b，直线c分别与a，b相交，∠1＝55°，则∠2的度数为（）A．55°B．105°C．125°D．135°【答案】C【解析】【分析】先根据对顶角相等求出∠3的度数，再由平行线的性质求出∠2的度数即可．【详解】如图：∵∠1与∠3是对顶角，∠1＝55°，∴∠3＝55°．∵a∥b，∴∠2＝180°﹣∠3＝180°﹣55°＝125°．故选C．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．22．将一块三角板如图放置，∠ACB＝90°，∠ABC＝60°，点B，C分别在PQ，MN上，若PQ∥MN，∠ACM＝42°，则∠ABP的度数为( )A．45°B．42°C．21°D．12°【答案】D【解析】【分析】直接利用平行线的性质得出∠ACM＝∠QPC＝42°，进而得出∠ABP的度数．【详解】解：∵PQ∥MN，∴∠ACM＝∠QPC＝42°，∵∠PCQ＝90°，∴∠PQC＝48°，∴∠ABP＝60°﹣48°＝12°．故选D．【点睛】本题考查平行线的性质，正确应用平行线的性质是解题关键．23．如图，直线l1∥l2，且分别与直线l交于C、D两点，把一块含30o角的三角尺按如图所示的位置摆放，若∠1=53o，则∠2的度数是( )A ．93oB ．97oC ．103oD ．107o【答案】B【解析】【分析】依据l 1∥l 2，即可得到∠1=∠3=53°，再根据∠4=30°，即可得出∠2=180°-∠3-∠4=97°．【详解】解：如图，∵l 1∥l 2，∴∠1=∠3=53°，又∵∠4=30°，∴∠2=180°-∠3-∠4=180°-53°-30°=97°，故选B ．【点睛】此题主要考查了平行线的性质，三角板的特征，角度的计算，熟练掌握是解题的关键.24．如图，已知AE 平分BAC ∠，BE AE ⊥于E ，ED AC ，34BAE ∠=，那么BED ∠=（）A．134B．124C．114D．104【答案】B【解析】【分析】已知AE平分∠BAC，ED∥AC，根据两直线平行同旁内角互补，可求得∠DEA的度数，然后易求∠BED度数．【详解】解：∵AE平分∠BAC∴∠BAE＝∠CAE＝34°∵ED∥AC∴∠DEA＝180°−34°＝146°∵∠AED＋∠AEB＋∠BED＝360°∴∠BED＝360°−146°−90°＝124°．故选：B．【点睛】本题考查平行线的性质和角平分线的性质．熟知两直线平行，同旁内角互补是解题关键．25．如图，直线l1∥l2，将一直角三角尺按如图所示放置，使得直角顶点在直线l1上，两直角边分别与直线l1、l2相交形成锐角∠1、∠2且∠1＝25°，则∠2的度数为（）A．25°B．75°C．65°D．55°【答案】C【解析】【分析】依据∠1＝25°，∠BAC＝90°，即可得到∠3＝65°，再根据平行线的性质，即可得到∠2＝∠3＝65°．【详解】如图，∵∠1＝25°，∠BAC＝90°，∴∠3＝180°-90°-25°=65°，∵l1∥l2，∴∠2＝∠3＝65°，故选C．【点睛】本题考查的是平行线的性质，运用两直线平行，同位角相等是解答此题的关键．26．一副三角板如图放置，若AB∥DE，则∠1的度数为（）A ．105°B ．120°C ．135°D ．150°【答案】A【解析】【分析】利用平行线的性质以及三角形的内角和定理即可解决问题．【详解】解：如图，延长EF 交AB 于点H.AB DE ，BHE E 45?∠∠∴＝＝，1180B EHB 1803045105＝﹣﹣＝﹣﹣＝，∠∠∠∴︒︒︒︒︒故选A.【点睛】本题考查平行线的性质，三角形的内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．27．如图,E 为BC 上一点,AB ∥DE,∠1=∠2,则AE 与DC 的位置关系是( )A．相交B．平行C．垂直D．不能确定【答案】B【解析】【分析】根据AB∥DE可得∠1=∠AED,再由∠1=∠2可得∠AED=∠2,根据平行线的判定可得AE∥DC.【详解】AB∥DC;∵AB∥DE,∴∠1=∠AED∵∠1=∠2∴∠AED=∠2∴AE∥DC故选B【点睛】此题考查平行线的判定与性质，难度不大28．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠2＝42°，则∠1＝( )A．48°B．42°C．40°D．45°【答案】A【解析】【分析】由互余得出可求得∠3的度数，然后由两直线平行，同位角相等求得∠1的度数．【详解】如图，∵∠2＝42°，∴∠3＝90°﹣∠2＝48°，∴∠1＝48°．故选：A．【点睛】考查了平行线的性质．两直线平行，同位角相等的应用是解此题的关键．29．将一把直尺与一块含30°和60°角的三角板ABC按如图所示的位置放置，直尺的一边恰好经过点A，如果∠CDE＝50°，那么∠BAF的度数为（）A．15°B．20°C．30°D．40°【答案】B【解析】【分析】先根据∠CDE＝50°，得出∠CED＝40°，再根据DE∥AF，即可得到∠CAF＝40°，最后根据∠BAC＝60°，即可得出∠BAF的大小．【详解】解：由图可得，∠CDE＝50°，∠C＝90°，∴∠CED＝40°，又∵DE∥AF，∴∠CAF＝40°，∵∠BAC＝60°，∴∠BAF＝60°﹣40°＝20°，故选：B．【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用，解题时注意：两直线平行，同位角相等．30．如图，直线l1，l2，l3交于一点，直线l4∥l1，若∠1＝124°，2＝84°，则∠3的度数为（）A．30°B．40°C．45°D．60°【答案】B【解析】【分析】如图，首先运用平行线的性质求出∠AOB的大小，然后根据平角的定义求出∠3即可解决问题．【详解】解：如图，∵直线l4∥l1，∴∠1+∠AOB＝180°，而∠1＝124°，∴∠AOB＝56°，∴∠3＝180°﹣∠2﹣∠AOB＝180°﹣84°﹣56°＝40°，故选：B．【点睛】该题主要考查了平行线的性质及其应用，平角的定义，应牢固掌握平行线的性质，这是灵活运用、解题的基础和关键．。

人教版七年级数学下册5.3《平行线的性质》课时练习(简单答案)

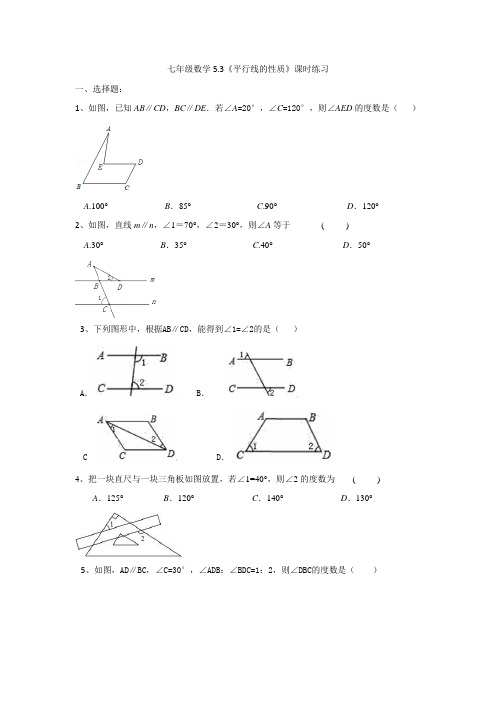
七年级数学5.3《平行线的性质》课时练习一、选择题：1、如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED的度数是（）A.100°B．85°C.90°D．120°2、如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于( )A.30°B．35°C.40°D．50°3、下列图形中，根据A B∥CD，能得到∠1=∠2 的是（）A．B．C D．4、把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为( )A．125°B．120°C．140°D．130°5、如图，AD∥B C，∠C=30°，∠AD B：∠BDC=1：2，则∠DBC 的度数是（）A．30° B．36° C．45° D．50°6、如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=80°，则∠BFD的度数是（）A．20°B．30°C．40°D．45°7、将一副直角三角板ABC和DEF如图放置(其中∠A=60︒，∠F=45︒)，使点E落在AC边上，且ED∥BC，则∠CEF的度数为（）A.15°B．35°C.20°D．22.5°8、如图，把一块三角板的直角顶点放在一直尺的一边上，若∠1=50°，则∠2 的度数为（）A．55° B．50° C．45° D．40°二、填空题：9、如图，AB∥CD，AD平分∠BAC，若∠BAD=70°，那么∠ACD的度数为。

DCBA10、如图，AB∥CD，点E在CB的延长线上，若∠ABE=60º，则∠ECD的度数为。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (80)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，直线a∥b，c与直线a、b分别相交于A、B两点，若∠1=50度，则∠2=____度．【答案】50【解析】【分析】根据平行线的性质可得∠1=∠3=50°，再由对顶角相等即可求得∠2 =50°．【详解】解：∵直线a∠b，∠1=50°，∠∠1=∠3=50°．∠∠2与∠3是对顶角，∠∠2=∠3=50°．故答案为50．【点睛】本题考查了平行线的性质，熟知平行线的性质是解题的关键.92．若∠α的两边与∠β的两边互相平行，当∠α=40°时，∠β=_____．【答案】40°或140°．【解析】【分析】两角可能相等，也可能互补.【详解】解：如图所示，可能有两种情况，二角可以是同位角关系时，则∠α=∠β=40°；当二角可以是同旁内角关系时，则∠α+∠β=180°，∠β=180°-∠α=180°-40°=140°.故∠β=40°或140°.【点睛】本题很容易忽略两角互补这种情况.93．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：______．【答案】∠2+∠3﹣∠1=180°．【解析】【分析】由OP∠QR∠ST可得∠3=∠QRS，∠2+∠QRP=180°.解：由QR∠ST可得∠3=∠QRS=∠QRP+∠1，由OP∠QR可得∠2+∠QRP=180°，则：∠3=∠QRP+∠1=180°-∠2+∠1，整理得，∠2+∠3﹣∠1=180°.【点睛】本题考查了平行线的性质.∠+∠+∠+∠+∠=__________．94．如图，两直线AB、CD平行，则12345【答案】720【解析】【分析】根据题意，通过添加平行线，利用内错角和同旁内角，把这五个角转化成4个180的角．【详解】分别过F点，G点，H点作2L，3L，4L平行于AB利用内错角和同旁内角，把这五个角转化一下，可得，有4个180的角，∴⨯=．1804720故答案为720．本题考查了平行线的性质：两直线平行，同旁内角互补，添加辅助线是解题关键．95．如图，∵DE∥BC（已知），∴∠1=____（____），∠2=_______（_____）又∵∠1=∠2（已知），∴∠B=∠C（____），∵∠3=∠B（已知），∴∠3=∠C （_________），∴DF∥AC（______）【答案】∠B 两直线平行，同位角相等∠C 两直线平行，同位角相等等量代换等量代换同位角相等，两直线平行【解析】【分析】根据两直线平行，同位角相等可得∠1=∠B，∠2=∠C，由∠3=∠C可根据同位角相等，两直线平行得到DF∥AC．【详解】∵DE∥BC（已知），∴∠1=∠B，（两直线平行，同位角相等）．∠2=∠C（两直线平行，同位角相等）．又∵∠1=∠2（已知），∴∠B=∠C．（等量代换）∵∠3=∠B（已知），∴∠3=∠C，（等量代换）∴DF∥AC （同位角相等，两直线平行）．故答案为：(1). ∠B (2). 两直线平行，同位角相等(3). ∠C (4). 两直线平行，同位角相等(5). 等量代换(6). 等量代换(7). 同位角相等，两直线平行【点睛】本题主要考查了平行线的判定与性质，灵活掌握平行线的判定是解题关键．96．如图，点D、E分别在AB、BC上，DE∥AC，AF∥BC，∠1＝70°，则∠2＝_____°．【答案】70【解析】【分析】根据两直线平行，同位角相等可得∠C=∠1，再根据两直线平行，内错角相等可得∠2=∠C．【详解】∵DE∥AC，∴∠C＝∠1＝70°，∵AF∥BC，∴∠2＝∠C＝70°．故答案为：70．【点睛】本题考查了平行线的性质，熟记性质并准确识图是解题的关键．97．如图，直线a，b分别与直线c，d相交，且∠1+∠3=135°，∠2﹣∠3=45°，若∠3=α，则∠4的度数为_____．【答案】180°﹣α【解析】【分析】如图，由∠1+∠3=135°，∠2﹣∠3=45°，可得∠1+∠2=180°，根据∠1+∠5=180°，可得∠2=∠5，由此可得a∥b，从而得∠3=∠6=α，根据邻补角的定义即可求得∠4=180°﹣α．【详解】解：如图，∵∠1+∠3=135°，∠2﹣∠3=45°，∴∠1+∠3+∠2﹣∠3=135°+45°=180°，∴∠1+∠2=180°，∵∠1+∠5=180°，∴∠2=∠5，∴a∥b，∴∠3=∠6=α，∴∠4=180°﹣α，故答案为180°﹣α．【点睛】本题考查了平行线的判定与性质、邻补角的定义，熟练掌握平行线的判定与性质定理是解题的关键．98．如图，AB∥CD，AE∥AC，∥ACE=65°，则∥BAE的度数为_____．【答案】25°【解析】【分析】【详解】∠AB∠CD，∠∠BAC=180°﹣∠ACE=115°，∠AE∠AC，∠∠CAE=90°，∠∠BAE=∠BAC﹣∠CAE=25°，故答案为25°．【点睛】本题主要考查平行线的性质：两直线平行，同旁内角互补.99．如图：若12∠=︒，则2∠=__________．l l，145【答案】135︒【解析】【分析】根据平行线的性质，得∠1的同位角是45°，再根据邻补角的定义，得：∠2=180°-45°=135°．【详解】∠=︒，∵1l∥2l, 145∴∠1的同位角是45︒，=︒-︒=︒.∴∠218045135故答案为：135︒【点睛】考查平行线的性质，掌握两直线平行，同位角相等是解题的关键.100．如图，把一张对边互相平行的纸条，折成如图所示，EF是折痕，若∥EFB=32°，则∥AEG的度数是__．【答案】116°【解析】【分析】先求出∠GEF，∠AEG=180°–2∠GEF.【详解】因为∠EFB=32°，又∵AE∥BF,折叠问题∴∠C´EF=∠GEF=∠EFB=32°，所以∠AEG=180°–2∠GEF=116°. 【点睛】知道折叠后哪些角相等是解题的关键.。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (51)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)一、单选题1．一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行∠=º,则2∠的大小是关系没有发生变化,若175A．75ºB．115ºC．65ºD．105º【答案】D【解析】【详解】∵AD∥BC，∠1=75°，∴∠3=∠1=75°，∵AB∥CD，∴∠2=180°-∠3=180°-75°=105°．故选D．2．如图，已知∠1=110°，∠2=70°，∠4=115°，则∠3的度数为（）A．65ºB．70ºC．97ºD．115º【答案】D【解析】【分析】因为∠2=∠5=70°，∠1=110°，所以a∥b，则∠4=∠3，故∠3度数可求．【详解】∵∵2=∵5=70°，∵1=110°，∵∵1+∵5=180°，∵a∵b（同旁内角互补两直线平行），∵∵4=∵3，∵∵4=115°，∵∵3=115°．故选D．【点睛】本题考查平行线的判定与性质，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．3．如图，已知AB∥CD∥EF，∥ABC=50°，∥CEF=150°，则∥BCE的值为（）．A．50°B．30°C．20°D．60°【答案】C【解析】【分析】【详解】解：∵AB∥CD∥EF，∴∠ABC=∠BCD=50°，∠CEF+∠ECD=180°；∴∠ECD=180°-∠CEF=30°，∴∠BCE=∠BCD-∠ECD=20°．故选：C．4．如图，小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上，已知∠1=55°，则∠2的度数为( )A．35°B．45°C．55°D．125°【答案】A【解析】【详解】试题分析：根据平行线的性质可得∠1=∠3，再根据平角定义可计算出∠3+∠2=90°，然后可算出∠2的度数．解：∵a∥b，∴∠1=∠3=55°，∵∠3+∠2+90°=180°，∴∠2+∠3=90°，∴∠2=90°﹣55°=35°，故选A．5．如图，装修工人向墙上钉木条，若∠2=110°，要使木条b与a平行，则∠1的度数等于（）A．55°B．70°C．90°D．110°【答案】B【解析】已知a∥b，∥∥3=∥2=110°，又∥3+∥1=180°，∥∥1=180°-∥3=180°-110°=70°故选B6．如图，给出下列条件：∥∥3=∥4;∥∥1=∥2；∥EF∥CD,且∥D=∥4；∥∥3+∥5=180°．其中，能推出AD∥BC的条件为（）A．∥∥∥B．∥∥∥C．∥∥∥D．∥∥∥【答案】C【解析】【分析】【详解】∵∵∵3=∵4，∵AD∵BC，正确；∵∵∵1=∵2，∵AB∵DC，（内错角相等，两直线平行），错误；∵∵EF∵CD，∵∵D=∵3，∵∵D=∵4，∵∵3=∵4，由同位角相等，两直线平行可得AD∵BC正确；∵∵∵3+∵5=180°，∵4+∵5=180°∵∵3=∵4，由同位角相等，两直线平行可得AD∵BC正确；故能推出AB∵DC的条件为∵∵∵．故选C．7．如图：已知AB∠CD，∠B=120度，∠D=150度，则∠O等于（）.A．50度B．60度C．80度D．90度【答案】D【解析】【分析】【详解】作OE∵AB，则OE∵CD，∵∵B+∵1=180°，∵D+∵2=180°；∵∵B+∵BOD+∵D=360°．又∵∵B=120°，∵D=150°，∵∵BOD=360°-∵B-∵D=90°．故选D．8．如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（）A．180°B．360°C．540°D．720°【答案】C【解析】【分析】【详解】解：作EM∥AB，FN∥AB，∵AB∥CD，∴AB∥EM∥FN∥CD．∴∠A+∠AEM=180°，∠MEF+∠EFN=180°，∠NFC+∠C=180°，∴∠A+∠AEF+∠EFC+∠C=540°．故选：C．9．如图，若a∠b，∠1=115°，则∠2=（）A．55°B．60°C．65°D．75°【答案】C【解析】试题分析：由a∥b，∥1=115°，根据两直线平行，同旁内角互补，即可求得∥2的度数．解：∥a∥b，∥∥1+∥2=180°，∥∥1=115°，∥∥2=65°．故选C．10．AB//CD,,则的度数是（）A．80°B．100°C．70°D．以上都不对【答案】B【解析】【分析】根据平行线的性质和邻补角的定义即可求解.【详解】解：∵AB∥CD，∵∠3=∠1=80°，∵∠2+∠3=180°，∴∠2=180°－∠3=100°.故选B.【点睛】本题考查了平行线的性质和邻补角的定义，属于基本题型，熟练掌握平行线的性质是解题的关键.。

人教版七年级数学下学期《5.3 平行线的性质》同步练习

5.3 平行线的性质一．选择题1．下列语句是命题的是（）A．画直线AB B．直线a∥bC．如果a∥b，b∥c，则a∥c D．点M与点N都在直线AB上2．下列命题中，真命题的个数是（）①过一点有且只有一条直线与已知直线平行；②过一点有且只有一条直线与已知直线垂直；③图形平移的方向一定是水平的；④内错角相等；⑤相等的角是对顶角；⑥垂线段最短A．3B．2C．1D．03．下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的．其中真命题的个数是（）A．2个B．3个C．4个D．5个4．下列选项中a，b的取值，可以说明“若a＞b，则|a|＞|b|”是假命题的反例为（）A．a＝﹣5 b＝﹣6B．a＝6 b＝5C．a＝﹣6 b＝5D．a＝6 b＝﹣5 5．下列命题中，逆命题为真命题的是（）A．对顶角相等B．邻补角互补C．两直线平行，同位角相等D．互余的两个角都小于90°6．如图是婴儿车的平面示意图，其中AB∥CD，∠1＝120°，∠3＝40°，那么∠2的度数为（）A．80°B．90°C．100°D．102°7．如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°8．能说明“锐角α，锐角β的和是锐角”是假命题的例证图是（）A．B．C．D．9．如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）A．30°B．40°C．50°D．60°10．若直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a，b间的距离是（）cm．A．2B．8C．2或8D．4二．填空题11．若a2＝b2，那么a＝b；请举出一个反例，说明该命题是假命题；12．把命题“两直线平行，同位角相等”改写成“如果…那么…”的形式是：．13．“同角的余角相等”，这个命题改写成如果…那么…形式应该为．三．解答题14．已知：如图，AD∥BE，∠1＝∠2，求证：∠A＝∠E．15．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．参考答案一．选择题1．解：C是用数学式子表达的可以判断真假的陈述句，是命题；A、B、D均不是可以判断真假的陈述句，没有题设和结论之分，都不是命题．故选：C．2．解：过直线外一点有且只有一条直线与已知直线平行，①是假命题；在同一平面内，过一点有且只有一条直线与已知直线垂直，②是假命题；图形平移的方向不一定是水平的，③是假命题；两直线平行，内错角相等，④是假命题；相等的角不一定是对顶角，⑤是假命题；垂线段最短，⑥是真命题，故选：C．3．解：①如果两个数的绝对值相等，那么这两个数的平方相等，是真命题；②两直线平行，内错角相等，原命题是假命题；③在同一平面内，垂直于同一条直线的两条直线互相平行，是真命题；④两个无理数的和不一定是无理数，原命题是假命题；⑤坐标平面内的点与有序数对是一一对应的，是真命题；故选：B．4．解：当a＝﹣5，b＝﹣6时，a＞b，但|a|＜|b|，∴“若a＞b，则|a|＞|b|”是假命题，故选：A．5．解：A、对顶角相等的逆命题是相等的角是对顶角，逆命题是假命题；B、邻补角互补的逆命题是互补的角是邻补角，逆命题是假命题；C、两直线平行，同位角相等逆命题是同位角相等，两直线平行，逆命题是真命题；D、互余的两个角都小于90°的逆命题是都小于90°的角互余，逆命题是假命题；故选：C．6．解：∵AB∥CD，∴∠A＝∠3＝40°，∵∠1＝120°，∴∠2＝∠1﹣∠A＝80°，故选：A．7．解：如图，∵a∥b，∴∠3＝∠2＝62°，∵∠3+∠1＝180°，∴∠1＝180°﹣62°＝118°．故选：C．8．解：例如C选项图中：三角形三个内角都是锐角，则∠α+∠β＞90°．故选：C．9．解：如图，∵∠BEF是△AEF的外角，∠1＝20°，∠F＝30°，∴∠BEF＝∠1+∠F＝50°，∵AB∥CD，∴∠2＝∠BEF＝50°，故选：C．10．解：分为两种情况：如图1，直线a，b间的距离是5cm﹣3cm＝2cm，如图2，直线a，b间的距离是5cm+3cm＝8cm，故选：C．二．填空题11．解：若a2＝b2，那么a＝b，是假命题．例如：22＝（﹣2）2＝4但是2≠﹣2．所以答案可以是：若22＝（﹣2）2＝4，但是2≠﹣2．12．解：“两直线平行，同位角相等”的条件是：“两直线平行”，结论为：“同位角相等”，∴写成“如果…，那么…”的形式为：“如果两直线平行，那么同位角相等”，故答案为：如果两直线平行，那么同位角相等．13．解：根据命题的特点，可以改写为：“如果两个角是同一个角的余角，那么这两个角相等”，故答案为：如果两个角是同一个角的余角，那么这两个角相等．三．解答题14．证明：∵AD∥BE，∴∠A＝∠3，∵∠1＝∠2，∴DE∥AC，∴∠E＝∠3，∴∠A＝∠EBC＝∠E．15．证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (75)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，已知∠1＝∠2＝90°，∠3＝30°，∠4＝60°，试确定图中有几对平行线，并说明你的理由．【答案】有两对平行线，分别是AB∥CD，EF∥HG，理由见解析.【解析】【分析】根据平行线定理即可解答.【详解】有两对平行线，分别是AB∥CD，EF∥HG.理由如下：因为∠1＝∠2＝90°，所以AB∥CD.因为∠3＝30°，所以∠5＝90°－30°＝60°.又因为∠4＝60°，所以∠4＝∠5，所以EF∥HG.【点睛】本题考查了平行线定理，正确识别同位角，内错角，同旁内角是解答本题的关键.42．（1）如图a示，AB∥CD，且点E在射线AB与CD之间，请说明∠AEC=∠A+∠C的理由．（2）现在如图b示，仍有AB∥CD，但点E在AB与CD的上方，①请尝试探索∠1，∠2，∠E三者的数量关系；②请说明理由．【答案】（1）证明见解析；（2）∠1+∠2-∠E=180°．【解析】【分析】（1）过点E作EF∥AB，由两直线平行，内错角相等，得到∠A=∠1，由平行的传递性得到EF // CD，再由平行线的性质得到∠2=∠C，由角的和差即可得到结论；（2）过点E作EF∥AB，类似可得到结论．【详解】解：（1）过点E作EF∥AB，∴∠A=∠1（两直线平行，内错角相等）．∵AB // CD（已知），∴EF // CD（平行的传递性），∴∠2=∠C（两直线平行，内错角相等）．∵∠AEC=∠1+∠2（图上可知），∴∠AEC=∠A+∠C（等量代换）；（2）∠1+∠2-∠E=180°．理由如下：过点E作EF∥AB，∴∠4+∠1=180°（两直线平行，同旁内角互补）．∵AB // CD（已知），∴EF // CD（平行的传递性），∴∠FEC=∠2（两直线平行，内错角相等），即∠3+∠4=∠2，∴∠4=∠2-∠3（等式性质），∴∠2-∠3+∠1=180°（等量代换），即∠1+∠2-∠AEC=180°．【点睛】本题考查了平行线的性质，作辅助线并熟记性质是解题的关键．43．已知：AD∠BC，垂足为D，EG∠BC，垂足为点G, EG交AB于点F，且AD平分∠BAC，试说明∠E＝∠AFE的理由.【答案】证明见解析【解析】试题分析：利用垂直于同一条直线的两条直线互相平行、平行线的判定和性质进行证明．试题解析：解：∵ AD ⊥BC ， EG ⊥BC （已知）∥∥ADC =∥EGD =90°（垂直的意义）∥EG // AD （同位角相等，两直线平行）∥∥E =∥CAD （两直线平行，同位角相等）∥AFE =∥BAD （两直线平行，内错角相等）∥ AD 平分∠BAC （已知）∥∥BAD =∥CAD （角平分线的意义）∥∥E =∥AFE （等量代换）44．如图，点B ，E 分别在直线AC 和DF 上，若AGB EHF ∠=∠，C D ∠=∠，可以证明A F ∠=∠.请完成下面证明过程中的各项“填空”.证明：∠AGB EHF ∠=∠（理由：______.）AGB ∠=______（对顶角相等）∠EHF DGF ∠=∠，∠DB EC （理由：______）∠∠______DBA =∠（两直线平行，同位角相等）又∵C D ∠=∠，∠DBA D ∠=∠，∠DF ______（内错角相等，两直线平行）∠A F ∠=∠（理由：______）【答案】见解析.【解析】【分析】根据对顶角相等推知同位角∠EHF＝∠DGF，从而证得两直线DB∥EC；然后由平行线的性质及已知得到内错角∠DBA＝∠D，即可根据平行线的判定定理推知两直线DF∥AC；最后由平行线的性质（两直线平行，内错角相等）证得∠A ＝∠F．【详解】解：∵∠AGB＝∠EHF（理由：已知），∠AGB＝∠DGF（对顶角相等），∴∠EHF＝∠DGF，∴DB∥EC（理由：同位角相等，两直线平行），∴∠C＝∠DBA （两直线平行，同位角相等），又∵∠C＝∠D（已知），∴∠DBA＝∠D（等量代换），∴DF∥AC（内错角相等，两直线平行），∴∠A＝∠F（理由：两直线平行，内错角相等）.故答案为：已知；∠DGF；同位角相等，两直线平行；C；AC；两直线平行，内错角相等．【点睛】本题考查了平行线的判定与性质．解答此题的关键是注意平行线的性质和判定定理的综合运用．45．如图，AB∠CD（1）若∠A=30°，∠C=60°，则∠AEC= ；（2）请猜想∠A、∠AEC、∠C之间有何数量关系？并说明理由．【答案】（1）90°；（2）∥AEC=∥A+∥C，理由见解析.【解析】【分析】（1）过点E作EF∥AB，根据平行线的性质可得∠AEC=∠A+∠C，根据已知角即可得出∠AEC的度数；（2）证明同（1）.【详解】（1）过点E作EF∥AB，∴∠A=∠AEF∵AB∥CD∴EF∥CD∵∠C=∠CEF∵∠AEC=∠AEF+∠CEF∴∠AEC=∠A+∠C.∵∠A=30°，∠C=60°∴∠AEC=90°；（2）∠AEC=∠A+∠C.证明同（1）.【点睛】本题考查了平行线的性质，解题的关键是熟练的掌握平行线的性质.46．如图，四边形ABCD中，，BE、CF分别是∠B、∠D的平分线.且∠A＝∠C ＝90°，试猜想BE与DF有何位置关系?请说明理由．【答案】BE∥DF，证明见解析【解析】【分析】根据四边形的内角和定理和∠A=∥C=90°，得∠ABC+∥ADC=180°；根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等，从而证明两条直线平行.【详解】解:∵四边形内角和等于360°，∠A＝∠C＝90°∥∥ABC+∥ADC＝180°∵BE、CF分别是∠B、∠D的平分线∥∥1+∥2＝90°∥在Rt∥DCF中，∥3+∥2＝90°∥∥1＝∥3∥BE∥DF【点睛】本题主要考查了平行线的判定与性质，注意平行线的性质和判定定理的综合运用.47．如图1，AB∥CD，点P为定点，E、F分别是AB、CD上的动点．(1)求证：∠P＝∠BEP＋∠PFD；(2)若点M为CD上一点，如图2，∠FMN＝∠BEP，且MN交PF于N.试说明∠EPF与∠PNM的数量关系，并证明你的结论；(3)移动E、F使得∠EPF＝90°，如图3，作∠PEG＝∠BEP，求∠AEG 与∠PFD度数的比值．【答案】（1）详见解析；（2）∠EPF＝∠PNM.（3）2∶1.【解析】【分析】（1）如图1，过点P作PG∥AB，根据平行线的性质进行证明；（2）利用（1）中的结果和三角形外角的性质可以推知∠EPF=∠PNM；（3）利用（1）中的结论得到∠1+∠2=90°，结合已知条件∠PEG=∠BEP，即∠1=∠3得到∠4=180°-2∠1，易求∠AEG与∠PFD度数的数量关系．【详解】解：(1)证明：如答图(1)，过点P作PG∥AB，则∠1＝∠BEP.又∵AB∥CD，∴PG∥CD，∴∠2＝∠PFD，∴∠EPF＝∠1＋∠2＝∠BEP＋∠PFD，即∠EPF＝∠BEP＋∠PF D.(2)∠EPF＝∠PNM.证明如下：由(1)知，∠EPF＝∠BEP＋∠PFD.如答图(2)，∵∠FMN＝∠BEP，∴∠EPF＝∠FMN＋∠PFD.又∵∠PNM＝∠FMN＋∠PFD，∴∠EPF＝∠PNM.(3)如答图(3)，∵由(1)知∠1＋∠2＝90°.∴∠2＝90°－∠1.又∵∠1＝∠3，∴∠4＝180°－2∠1＝2∠2，∴∠4∶∠2＝2∶1.即∠AEG与∠PFD度数的比值为2∶1.【点睛】本题考查了平行线的性质，三角形外角性质以及平角定义的运用，熟练掌握平行线的性质是解本题的关键．48．完成下面的证明过程如图，已知∠1+∠2=180°，∠B=∠DEF，求证：DE∠BC．证明：∠∠1+∠2=180°（已知），而∠2=∠3（），∠∠1+∠3=180°∠______∠______（）∠∠B=______（）∠∠B=∠DEF（已知）∠∠DEF=______（等量代换）∠DE∠BC（）【答案】对顶角相等EF AB 同旁内角互补，两直线平行∥CFE 两直线平行，同位角相等∥CFE 两直线平行【解析】【分析】先由对顶角相等可得：∠2=∠3，然后由∠1+∠2=180°，根据等量代换可得：∠1+∠3=180°，然后根据同旁内角互补两直线平行可得：EF∥AB，然后根据两直线平行同位角相等可得：∠B=∠CFE，然后由∠B=∠DEF，根据等量代换可得：∠CFE=∠DEF，然后根据内错角相等两直线平行即可得到：DE∥BC．【详解】证明：∵∠1+∠2=180°（已知），而∠2=∠3（对顶角相等），∴∠1+∠3=180°∴EF∥AB（同旁内角互补，两直线平行）∴∠B=∠CFE（两直线平行，同位角相等）∵∠B=∠DEF（已知）∴∠DEF=∠CFE（等量代换）∴DE∥BC（内错角相等，两直线平行）．【点睛】考查平行线的判定与性质，掌握平行线的判定定理与性质定理是解题的关键.49．如图，己知∠A=∠1，∠C=∠F，请问BC与EF平行吗？请说明理由．【答案】BC∥EF．理由见解析.【解析】【分析】因为∠A=∠1，根据同位角相等，两直线平行，得到AC∥DF，根据平行线的性质得到∠C＝∠CGF，等量代换得到∠CGF＝∠F，根据内错角相等，两直线平行即可判定BC∥EF.【详解】解：BC∥EF．理由：∵∠A=∠1，∴AC∥DF（同位角相等，两直线平行），∴∠C＝∠CGF（两直线平行，内错角相等）.∵∠C=∠F，∴∠CGF＝∠F，∴BC∥EF（内错角相等，两直线平行）．【点睛】考查平行线的判定与性质，掌握平行线的判定定理与性质定理是解题的关键.50．如图，∠AEF＝80°，且∠A＝x°，∠C＝y°，∠F＝z°|y－80－m|＋|z－40|＝0（m为常数，且0＜m＜100）(1) 求∠A、∠C的度数（用含m的代数式表示）(2) 求证：AB∠CD(3) 若∠A＝40°，∠BAM＝20°，∠EFM＝10°，直线AM与直线FM交于点M，直接写出∠AMF的度数【答案】(1) ∥A＝m＋20°，∥C＝m＋80°；(2)见解析；(3)50°、70°、30°、10°.【解析】【分析】（1）根据二次根式和绝对值的非负数性质解答即可；（2）过点F作FG∥AB，过点E作EH∥AB，可知EH//FG，根据平行线性质可证明∠BAE＝∠AEH＝m ＋20°，∠EFG＝∠FEH，进而证明∠EFG＝∠AEF－∠AEH＝80°－(m＋20°)＝60°－m，由∠CFG＋∠FCD＝y＋z＋80°－x＝80°＋m＋40°＋80°－m－20°＝180°，通过判定定理即可证明结论；（3）当∠A＝40°时，∠C＝100°，分情况讨论AM和FM的位置，计算即可；【详解】(1) |y－80－m|＋|z－40|＝0（m为常数，且0＜m＜100），∴x-m-20=0，y-80-m=0，z-40=0，∴∠A＝x°=m＋20°，∠C＝y°=m＋80°，z=40°，(2) 过点F作FG∥AB，过点E作EH∥AB，∴EH∥FG，∴∠BAE＝∠AEH＝m＋20°，∠EFG＝∠FEH，∴∠EFG＝∠AEF－∠AEH＝80°－(m＋20°)＝60°－m，∵∠CFG＋∠FCD＝y＋z＋80°－x＝80°＋m＋40°＋80°－m－20°＝180°，∴AB∥CD，(3) 当∠A＝40°时，∠C＝100°，如图，分为四种情况:延长FE交AM于N，∵∠BAE=40°，∠BAM=20°，∴∠MAE=20°，∵∠AEF=80°，∴∠ANE=80°-20°=60°，∴∠AMF=60°-10°=50°，∵∠AGF=∠MFE+∠AEF=10°+80°=90°，∴∠AMF=90°-∠MAE=70°，∵∠BAM=20°，∠BAE=40，°∴∠EAM=60°，∵∠AHF=∠MFE+∠AEF=90°，∴∠AMF=90°-∠EAM=30°，延长AE交FM于O，∵∠AEF=∠EFO+∠AOF=80°，∴∠AOF=80°-10°=70°，∴∠AMF=∠AOF-∠MAF=70°-60°=10°，综上所述：∥AMF的度数分别为：50°；70°；30°；10°.【点睛】本题考查平行线的性质和判定及三角形外角性质，同旁内角互补，两条直线平行；两条直线平行，内错角相等；三角形一个外角等于和它不相邻的两个内角的和；熟练掌握相关知识是解题关键.。

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (75)

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，直线//a b ，BD 为ABC ∠的平分线，158∠︒＝，则2∠的度数为（）A ．22°B ．32°C ．58°D ．61°【答案】D【解析】【分析】根据邻补角的定义得出∠ABC ，根据角平分线的定义得出∠ABD 的度数，再由平行线的性质即可得出结论．【详解】∵∠1=58°，∴∠ABC =122°．∵BD 为∠ABC 的平分线，∴∠ABD =61°．又∵a ∥b ，∴∠2=∠ABD =61°．【点睛】本题考查了对平行线的性质．掌握平行线的性质是解答本题的关键．（1）平行线性质：两直线平行，同位角相等、内错角相等、同旁内角互补；（2）角的相关性质：①互为邻补角的两角之和为180°，②互余的两角之和为90°，③对顶角相等，④一个角的平分线将这个角分成两个相等的角；（3）三角形的相关性质：①三角形的内角和等于180°，②三角形的一个外角等于与它不相邻的两个内角的和；（4）平行线性质求角度的思维方式：先观察所求角与已知角的位置关系，再选择合理的角进行等量代换，因此需要熟练掌握平行线的性质及平角、直角、三角形内角和、三角形内外角关系等知识的运用．42．已知直线12l l//，将一块含30角的直角三角板ABC按如图所示方式放置，∠=︒，则2∠等于（）若185A．35︒B．45︒C．55︒D．65︒【答案】D【解析】【分析】利用对顶角相等及三角形内角和定理，可求出∠4的度数，由直线l1∥l2，利用“两直线平行，内错角相等”可求出∠2的度数．【详解】∵∠A+∠3+∠4=180°，∠A=30°，∠3=∠1=85°，∴∠4=65°．∵直线l1∥l2，∴∠2=∠4=65°．故选：D ．【点睛】本题考查了平行线的性质以及三角形内角和定理，牢记“两直线平行，内错角相等”是解题的关键．43．如图，直线//a b ，185∠=︒，235∠=︒，则3∠的度数为（）A ．35︒B ．40︒C ．45︒D ．50︒【答案】D【解析】【分析】根据平行线的性质可得内错角相等，再根据邻补角和三角形内角和的性质可求出3∠的对顶角，即可求出结果．【详解】如图所示，∵//a b ，185∠=︒，∵4=85∠︒，∵4∠的邻补角=180-85=95︒︒︒，又∵235∠=︒，∵3∠的对顶角=180-95-35=50︒︒︒︒，∵3=50∠︒．故答案选D ．【点睛】本题主要考查了平行线的性质应用，与三角形内角和定理结合，准确利用对顶角的性质是关键．44．如图，将一块含的三角板叠放在直尺上．若，则A ．B ．C ．D ．【答案】D【解析】试题分析：如图，将一块含的三角板叠放在直尺上．若，直尺的对边是相互平行的，在根据对顶角的性质，所以在直尺的下方的三角形中一个角等于40∘，40∘+30∘=70∘（三角形的一个外角等于不相邻的两个内角之和）考点：平行线和对顶角及三角形外角定理点评：本题考查平行线和对顶角及三角形外角定理，熟悉平行线的性质，对顶角定理，和三角形的外角定理内容是解本题关键45．如图，直线AB CD 、相交于点E ， //DF AB ，若110AEC ∠=，则D ∠等于（）A ．70B ．80C ．90D ．100【答案】A【解析】【分析】由题意先根据补角的定义求出∠BEC 的度数，再由平行线的性质即可得出结论．【详解】解：∵∠AEC=110°，∴∠BEC=180°-110°=70°．∵DF ∥AB ，∴∠D=∠BCE=70°．故选：A ．【点睛】本题考查的是平行线的性质，注意掌握两直线平行，同位角相等这一平行线的性质．46．如图，12l l//，等边△ABC的顶点A、B分别在直线l1、l2，则∠1＋∠2＝（）A．30°B．40°C．50°D．60°【答案】D【解析】【分析】根据等边三角形的性质三个角都相等，再根据平行线的性质，两直线平行同旁内角互补，计算求解即可.【详解】解：∵12l l//,∴∠1+∠ABC+∠2+∠BAC=180°，∵△ABC是等边三角形，∴∠ABC=∠BAC=∠C=60°，∴∠1+∠2=180°-60°-60°=60°.故选D.【点睛】本题考查了等边三角形的性质和平行线的性质，解决本题的关键是熟练掌握两者的性质，能够判断出同旁内角互补.47．如图，有一块含有30角的直角三角板的两个顶点放在直尺的对边上．如∠=︒，那么1∠的度数是（）果246A．14︒B．15︒C．16︒D．17︒【答案】A【解析】【分析】如解图所示，依据∠ABC=60°，∠2=46°，即可得到∠EBC=14°，再根据BE∥CD，即可得出∠1=∠EBC=14°．【详解】解：如图，∵∠ABC=60°，∠2=46°，∴∠EBC=14°，∵BE∥CD，∴∠1=∠EBC=14°，故选A．【点睛】此题考查了平行线的性质，掌握两直线平行，内错角相等是解决此题的关键．48．将直尺和直角三角板按如图方式摆放（△ACB为直角），已知△1=30°，则△2的大小是( )A．30°B．45°C．60°D．65°【答案】C【解析】试题分析：先根据两角互余的性质求出∠3的度数，再由平行线的性质即可得出结论．∠∠1+∠3=90°，∠1=30°，∠∠3=60°．∠直尺的两边互相平行，∠∠2=∠3=60°．考点：平行线的性质49．如图，直线a∥b，若∠1=45°，∠2=55°，则∠3等于（）A．80°B．90°C．955°D．100°【答案】B【解析】试题分析：根据三角形外角的性质可得：∠4=∠1+∠2=45°+55°=100°，根据两直线平行同位角相等可得：∠3=∠4=100°50．如图，直线a，b被直线c所截，且a b，若∠1=70°，则∠2的度数是（）A．130°B．110°C．80°D．70°【答案】B【解析】【分析】由a∥b，根据两直线平行，同位角相等，即可求得∠3的度数，又由邻补角的定义即可求得∠2的度数．【详解】解：∵a∥b，∴∠3=∠1=70°，∵∠2+∠3=180°，∴∠2=110°，故选：B．【点睛】此题考查了平行线的性质与邻补角的定义，熟练掌握平行线的性质与邻补角的定义是解决本题的关键．。

人教版数学七年级下册-5.3平行线的性质作业

5.3平行线的性质1．如图所示，如果AD//BC，则：①∠1 =∠2；②∠3 =∠4；③∠1+∠3 =∠2+∠4；上述结论中一定正确的是( )A．只有①B．只有②C．①和②D．①、②、③答案：A说明：因为∠1与∠2是AD、BC被BD所截而成的内错角，所以由AD//BC可知∠1 =∠2成立；而AB与CD不一定平行，所以②、③难以确定是否正确；答案为A．2．如图，下列说法中正确的是( )A．因为∠2 =∠4，所以AD//BCB．因为∠BAD+∠D = 180º，所以AD//BCC．因为∠1 =∠3，所以AD//BCD．因为∠BAD+∠B = 180º，所以AB//CD答案：C说明：选项A，因为∠2与∠4是AB、CD被AC所截而成的内错角，所以由∠2 =∠4可知AB//CD，但无法得出AD//BC，A错；选项B，因为∠BAD与∠D是AB、CD被AD所截而成的同旁内角，所以由∠BAD+∠D = 180º可得AB//CD，但无法得到AD//BC，B错；选项C，因为∠1与∠3是AD、BC被AC所截而成的内错角，所以由∠1 =∠3可知AD//BC，选项C正确；选项D，因为∠BAD与∠B是AD、BC被AB所截而成的同旁内角，所以由∠BAD+∠B = 180º可知AD//BC，但无法得到AB//CD，D错；答案为C．3．图中，∠1和∠2是同位角的是( )答案：D说明：由同位角的概念可知，一条直线与两条直线相交，同位角位置相同且有一边在同一直线上，这样可以判断选项A、B、C中的∠1与∠2都不是同位角，只有选项D中的∠1与∠2是同位角，答案为D．4．如图，AB//CD则∠α等于( )A．50º B．80º C．85º D．95º答案：C说明：如图，过点E作EF//AB，因为AB//CD，所以EF//CD；因此，有∠ABE+∠BEF = 180º，∠FEC =∠ECD，则∠BEF = 60º，∠FEC = 25º，所以∠α=∠BEF+∠FEC = 85º，答案为C．5．如图，已知AB//CD，∠1 =∠2，∠E = nº，则∠F = ( )A．nº B．2nºC．90º−nº D．40º答案：A说明：因为AB//CD，知∠ABC =∠DCB，再由∠1 =∠2，得∠EBC =∠FCB，由此得到EB//FC，所以∠F =∠E = nº，答案为A．解答题：1．如图所示，已知：AE平分∠BAC，CE平分∠ACD，且AB∥CD．求证：∠1+∠2=90°．证明：因为AB∥CD，所以∠BAC+∠ACD=180°，又因为AE平分∠BAC，CE平分∠ACD，所以∠1 =∠BAC，∠2 =∠ACD，故∠1+∠2 =(∠BAC+∠ACD) =×180º = 90º．即∠1+∠2=90°．2．已知如图，AB//CD，∠ABE = 3∠DCE，∠DCE = 28º，求∠E的度数．解析：如图所示，∵∠1 = 3∠2，∠2 = 28º，∴∠1 = 3×28º = 84º∵AB//CD(已知)，∴∠3 =∠1 = 84º(两直线平行，同位角相等)又∵∠BFC =∠3(对顶角相等)∴∠BFC = 84º(等量代换)过F作FP//CE交BC于P∴∠4 =∠2 = 28º(两直线平行，内错角相等)∴∠5 =∠BFC−∠4 = 84º−28º = 56º∵FP//CE(辅助线作法)∴∠E =∠5 = 56º(两直线平行，同位角相等)。

人教版七年级下册第五章相交线与平行线 5.3 平行线的性质同步练习(含答案)

平行线的性质同步练习一、选择题1、如图，已知a∥b，∠1=75°，则∠2的度数是（）A．35° B．75°C．105° D．125°2、已知三条不同的直线a，b，c在同一平面内，下列四个命题：①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．其中是真命题的是（）A．①②③B．①② C．①②④ D．①③3、如图，直线AB、CD被直线EF所截，∠1=50°，下列说法错误的是（）A．如果∠5=50°，那么AB∥CD B．如果∠4=130°，那么AB∥CDC．如果∠3=130°，那么AB∥CD D．如果∠2=50°，那么AB∥CD4、某人在练车场上练习驾驶汽车，两次拐弯后的行驶方向与原来的方向相反，则两次拐弯的角度可能是（）A.第一次向左拐，第二次向右拐B. 第一次向左拐，第二次向右拐C.第一次向左拐，第二次向右拐D. 第一次向左拐，第二次向左拐5、如图，直线a∥b，直线c与直线a，b分别相交于点A，B，AM⊥b，垂足为点M．如果∠1=58°，那么∠2=（）A．32°B．58° C．42° D．122°6、．如图，AB∥CD，有图中α，β，γ三角之间的关系是（）A．α+β+γ=180° B．α﹣β+γ=180° C．α+β﹣γ=180° D．α+β+γ=360°7、如图，AB∥CD，DB⊥BC，∠2=50°，则∠1的度数是（）A．40°B．50° C．60° D．140°8、如图，把三角板的直角顶点放在直尺的一边上，若∠1=30°，则∠2的度数为（）A．60° B．50° C．40° D．30°9、如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）A．65°B．115°C．125°D．130°10、如图，直线AB∥CD，∠A=70°，∠C=40°，则∠E等于（）A．30°B．40° C．60° D．70°11、如图，直线a∥b，射线DC与直线a相交于点C，过点D作DE⊥b于点E，已知∠1=25°，则∠2的度数为( )A.115°B.125°C.155°D.165°12、．如图，将矩形纸片ABCD沿EF折叠（E、F分别是AD、BC上的点），使点B与四边形CDEF内一点B′重合，若∠B′FC=50°，则∠AEF等于（）A．110° B．115° C．120° D．130°二、填空题13、如图，已知则= ．14、已知AB∥CD，BE平分∠ABC，∠CDE＝150°，则∠C＝= ．15、如图，在△ABC中，已知∠B和∠C的平分线相交于点P，过点P作DE//BC交AB于D，交AC于E，若BD+CE=9，则DE的长为=16、AD为ΔABC的角平分线，DE∥AB交AC于E，若∠BAC=100°，则∠ADE= = 。

2015春人教版数学七下53《平行线的性质》习题精选

人教版七年级数学下册第五章平行线的性质作业复习试题(含答案) (39)

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (59)

人教版七年级数学下册第五章平行线的性质习试（含答案）（53）

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (100)

人教版七年级数学下册第五章平行线的性质习试(含答案) (51)

人教版初中数学七年级下《5.3平行线的性质》同步练习题(含答案)

人教版七年级数学下册第五章平行线的性质复习试题（含答案）（53）

2015春人教版数学七下53《平行线的性质》习题及答案

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (93)

人教版七年级数学下册5.3《平行线的性质》课时练习(简单答案)

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (80)

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (51)

人教版七年级数学下学期《5.3 平行线的性质》 同步练习

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (75)

人教版七年级数学下册第五章平行线的性质作业练习题(含答案) (75)

人教版数学七年级下册-5.3平行线的性质 作业

人教版七年级下册 第五章 相交线与平行线 5.3 平行线的性质 同步练习(含答案)

人教版七年级数学下学期《5.3 平行线的性质》同步练习

人教版数学七年级下册-5.3平行线的性质作业

人教版七年级下册第五章相交线与平行线 5.3 平行线的性质同步练习(含答案)