全国各地2012年中考数学分类解析(159套63专题) 专题36_多边形及其内角和

合集下载

2012年全国中考数学试题分类解析汇编专题52：平面几何的综合

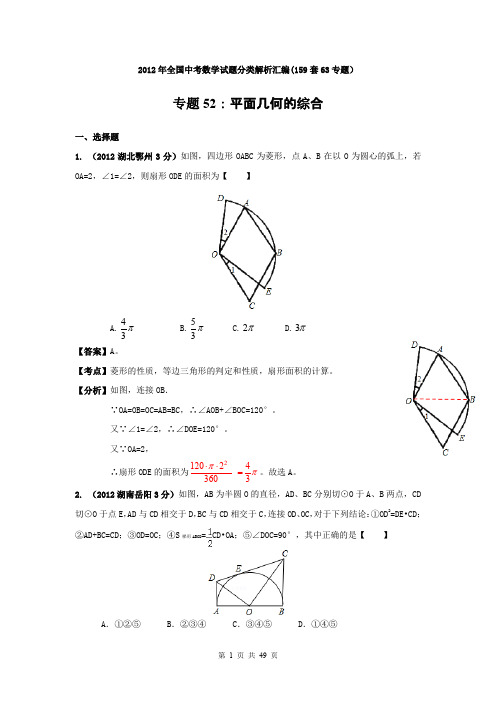
2012年全国中考数学试题分类解析汇编(159套63专题）专题52：平面几何的综合一、选择题1. （2012湖北鄂州3分）如图，四边形OABC 为菱形，点A 、B 在以O 为圆心的弧上，若OA=2，∠1=∠2，则扇形ODE 的面积为【】A.π34B.π35C.π2D.π3【答案】A 。

【考点】菱形的性质，等边三角形的判定和性质，扇形面积的计算。

【分析】如图，连接OB ．∵OA=OB=OC=AB=BC，∴∠AOB+∠BOC=120°。

又∵∠1=∠2，∴∠DOE=120°。

又∵OA=2，∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。

故选A 。

2. （2012湖南岳阳3分）如图，AB 为半圆O 的直径，AD 、BC 分别切⊙O 于A 、B 两点，CD 切⊙O 于点E ，AD 与CD 相交于D ，BC 与CD 相交于C ，连接OD 、OC ，对于下列结论：①OD 2=DE•CD； ②AD+BC=CD；③OD=OC；④S 梯形ABCD =CD•OA；⑤∠DOC=90°，其中正确的是【】A ．①②⑤ B．②③④ C．③④⑤ D．①④⑤【答案】A 。

【考点】切线的性质，切线长定理，相似三角形的判定与性质。

1052629【分析】如图，连接OE ，∵AD 与圆O 相切，DC 与圆O 相切，BC 与圆O 相切，∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB ，AD∥BC。

∴CD=DE+EC=AD+BC。

结论②正确。

在Rt△ADO 和Rt△EDO 中，OD=OD ，DA=DE ，∴Rt△ADO≌Rt△EDO（HL ）∴∠AOD=∠EOD。

同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC。

又∠AOD+∠DOE+∠EOC+∠COB=180°，∴2（∠DOE+∠EOC）=180°，即∠DOC=90°。

结论⑤正确。

∴∠DOC=∠DEO=90°。

2012年全国中考数学试题分类解析汇编(159套63专题)专题34_命题与证明(附答案)

2012年全国中考数学试题分类解析汇编(159套63专题）专题34：命题与证明一、选择题1. （2012广东深圳3分）下列命题①方程x 2=x 的解是x=1②4的平方根是2③有两边和一角相等的两个三角形全等④连接任意四边形各边中点的四边形是平行四边形其中真命题有：【】A ．4个 B.3个 C.2个 D.1个2. （2012广东广州3分）在平面中，下列命题为真命题的是【】A ．四边相等的四边形是正方形B ．对角线相等的四边形是菱形C ．四个角相等的四边形是矩形D ．对角线互相垂直的四边形是平行四边形3. （2012浙江温州4分）下列选项中，可以用来证明命题“若a²>1,则a ＞1”是假命题的反例是【】A. a=－2.B. a==－1C. a=1D. a=24. （2012江苏泰州3分）下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对角线互相垂直且相等的四边形是正方形；③顺次连结矩形四边中点得到的四边形是菱形；④正五边形既是轴对称图形又是中心对称图形．其中真命题．．．共有【】 A ．1个 B ．2个 C ．3个 D ．4个5. （2012福建龙岩4分）下列命题中，为真命题的是【】A ．对顶角相等B ．同位角相等C ．若22=a b ，则=a bD ．若a >b ，则22a >b -- 6. （2012湖北黄冈3分）下列说法中 x 1-x ＞1.②已知∠α=27°，则∠α的补角是153°. ③已知x=2 是方程x 2－6x+c=0 的一个实数根，则c 的值为8. ④在反比例函数k 2y=x-中，若x ＞0 时，y 随x 的增大而增大，则k 的取值范围是k ＞2. 其中正确命题有【】A. 1 个B. 2 个C. 3 个D. 4 个7. （2012湖南益阳4分）下列命题是假命题的是【】A ．中心投影下，物高与影长成正比B ．平移不改变图形的形状和大小C．三角形的中位线平行于第三边D．圆的切线垂直于过切点的半径8. （2012湖南岳阳3分）下列命题是真命题的是【】A．如果|a|=1，那么a=1 B．一组对边平行的四边形是平行四边形C．如果a是有理数，那么a是实数D．对角线相等的四边形是矩形9. （2012湖南娄底3分）下列命题中，假命题是【】A．平行四边形是中心对称图形B．三角形三边的垂直平分线相交于一点，这点到三角形三个顶点的距离相等C．对于简单的随机样本，可以用样本的方差去估计总体的方差D．若x2=y2，则x=y10. （2012四川宜宾3分）给出定义：设一条直线与一条抛物线只有一个公共点，且这条直线与这条抛物线的对称轴不平行，就称直线与抛物线相切，这条直线是抛物线的切线．有下列命题：①直线y=0是抛物线y=14x2的切线②直线x=﹣2与抛物线y=14x2相切于点（﹣2，1）③直线y=x+b与抛物线y=14x2相切，则相切于点（2，1）④若直线y=kx﹣2与抛物线y=14x2相切，则实数其中正确的命题是【】A．①②④B．①③C．②③D．①③④11. （2012四川攀枝花3分）下列四个命题：①等边三角形是中心对称图形；②在同圆或等圆中，相等的弦所对的圆周角相等；③三角形有且只有一个外接圆；④垂直于弦的直径平分弦所对的两条弧．其中真命题的个数有【】A． 1个B． 2个C． 3个D． 4个12. （2012四川凉山4分）下列命题：①圆周角等于圆心角的一半；②x=2是方程x－1=1的解；③平行4。

2012年全国中考数学试题分类解析汇编（159套63专题）专题3_整式2（教师篇）

2012年全国中考数学试题分类解析汇编（159套63专题）专题3_整式2（教师篇）2012年全国中考数学试题分类解析汇编(159套63专题）专题3：整式⼀、选择题1. （2012上海市4分）在下列代数式中，次数为3的单项式是【】A ． xy 2B ．x 3+y 3C ．．x 3yD ．3xy 【答案】A 。

2. （2012重庆市4分）计算)2ab 的结果是【】 A ．2ab B ．2a b C ．22a b D ．2ab 【答案】C 。

3. （2012安徽省4分）计算32)2(x -的结果是【】A.52x -B. 68x -C.62x -D.58x -【答案】B 。

4. （2012安徽省4分）某企业今年3⽉份产值为a 万元，4⽉份⽐3⽉份减少了10％，5⽉份⽐4⽉份增加了15％，则5⽉份的产值是【】A.（a －10％）（a +15％）万元B. a （1－10％）（1+15％）万元C.（a －10％+15％）万元D. a （1－10％+15％）万元【答案】B 。

5. （2012⼭西省2分）下列运算正确的是【】A ．B ．C ．a 2a 4=a 8D ．（﹣a 3）2=a 6【答案】D 。

6. （2012海南省3分）计算23x x ?，正确结果是【】A ．6xB ．5xC ．9xD ．8x 【答案】B 。

7. （2012海南省3分）当x 2=-时，代数式x +3的值是【】A ．1B ．－1C ．5D ．－5【答案】A 。

8. （2012陕西省3分）计算32(5a )-的结果是【】A ．510a -B ．610aC ．525a -D ．625a 【答案】D 。

9. （2012宁夏区3分）下列运算正确的是【】A ．223a a =3-B ．235(a )=aC ．369a a =a ?D ．222(2a )=4a 【答案】C 。

10. （2012⼴东佛⼭3分）23a a ?等于【】A ．5aB ．6aC ．8aD ．9a 【答案】A 。

全国各地2012年中考数学分类解析(159套)专题5分式

2012年全国中考数学试题分类解析汇编(159套63专题）专题5：分式一、选择题1. （2012安徽省4分）化简xx x x-+-112的结果是【】A.x +1B. x -1C.—xD. x 【答案】D 。

【考点】分式的加法运算【分析】分式的加减，首先看分母是否相同，同分母的分式加减，分母不变，分子相加减，如果分母不同，先通分，后加减，本题分母互为相反数，可以化成同分母的分式加减：222(1)111111xx xx x x x x x x xx x x x --+=-===------。

故选D 。

2. （2012浙江湖州3分）要使分式1x有意义，x 的取值范围满足【】A ．x=0B ．x≠0 C．x ＞0 D ．x ＜0 【答案】B 。

【考点】分式有意义的条件。

【分析】根据分式分母不为0的条件，要使1x在实数范围内有意义，必须x≠0。

故选B 。

3.（2012浙江嘉兴、舟山4分）若分式x 1x+2-的值为0，则【】A ． x=﹣2B ． x=0C ． x=1或2D ．x=1 【答案】D 。

【考点】分式的值为零的条件。

【分析】∵分式x 1x+2-的值为0，∴x 1=0x+2x+20-⎧⎪⎨⎪≠⎩，解得x=1。

故选D 。

4. （2012浙江绍兴4分）化简111xx --可得【】 A ．21x x- B ． 21x x--C ．221x x x+- D ．221x x x--【答案】B 。

【考点】分式的加减法。

【分析】原式=211(1)x x x x x x--=---。

故选B 。

5. （2012浙江义乌3分）下列计算错误的是【】 A ．0.2a b 2a b 0.7a b7a b++=-- B ．3223x y x yx y=C ．a b 1b a-=-- D ．123ccc+=【答案】A 。

【考点】分式的混合运算。

【分析】根据分式的运算法则逐一作出判断：A 、0.2a b 2a 10b 0.7a b 7a 10b++=--，故本选项错误；B 、3223x y x yx y=，故本选项正确；C 、a b b a 1b a b a--=-=---，故本选项正确；D 、123ccc+=，故本选项正确。

2012年全国中考数学试题分类解析汇编(159套63专题)专题36_多边形及其内角和(附答案)讲解

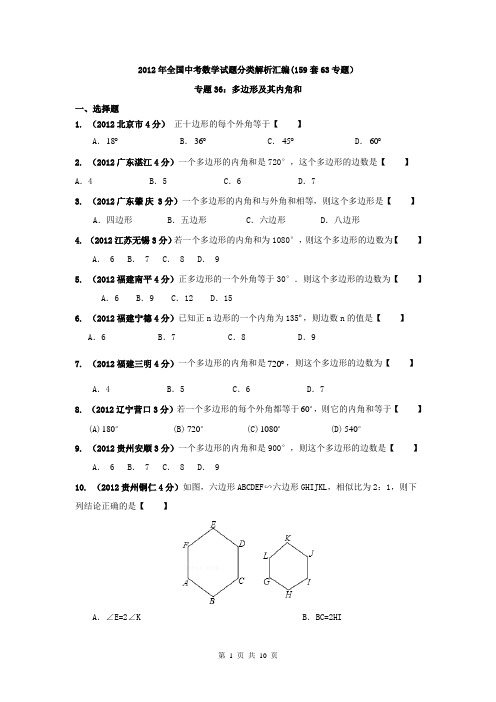
2012年全国中考数学试题分类解析汇编(159套63专题）专题36：多边形及其内角和一、选择题1. （2012北京市4分）正十边形的每个外角等于【】A．18︒B．36︒C．45︒D．60︒2. （2012广东湛江4分）一个多边形的内角和是720°，这个多边形的边数是【】A．4 B．5 C．6 D．73. （2012广东肇庆3分）一个多边形的内角和与外角和相等，则这个多边形是【】A．四边形 B．五边形 C．六边形 D．八边形4. （2012江苏无锡3分）若一个多边形的内角和为1080°，则这个多边形的边数为【】A． 6 B． 7 C． 8 D． 95. （2012福建南平4分）正多边形的一个外角等于30°．则这个多边形的边数为【】A．6 B．9 C．12 D．156. （2012福建宁德4分）已知正n边形的一个内角为135º，则边数n的值是【】A．6 B．7 C．8 D．97. （2012福建三明4分）一个多边形的内角和是720︒，则这个多边形的边数为【】 A．4 B．5 C．6 D．78. （2012辽宁营口3分）若一个多边形的每个外角都等于60，则它的内角和等于【】(A)5401080(D)720(C)180(B)9. （2012贵州安顺3分）一个多边形的内角和是900°，则这个多边形的边数是【】A． 6 B． 7 C． 8 D． 910. （2012贵州铜仁4分）如图，六边形ABCDEF∽六边形GHIJKL，相似比为2：1，则下列结论正确的是【】A．∠E=2∠K B．BC=2HIC ．六边形ABCDEF 的周长=六边形GHIJKL 的周长D ．S 六边形ABCDEF =2S 六边形GHIJKL11. （2012山东枣庄3分）如图，该图形围绕点O 按下列角度旋转后，不能．．与其自身重合的是【】A ．72︒B ．108︒C ．144︒D ．216︒12. （2012广西玉林、防城港3分）正六边形的每个内角都是【】A. 60°B. 80°C. 100°D.120°二、填空题2. （2012广东佛山3分）一个多边形的内角和为540°，则这个多边形的边数是 ▲ ；3. （2012广东梅州3分）正六边形的内角和为 ▲ 度．4. （2012浙江义乌4分）正n 边形的一个外角的度数为60°，则n 的值为 ▲ ．5. （2012江苏南京2分）如图，1∠、2∠、3∠、4∠是五边形ABCDE 的4个外角，若2A 10∠=︒，则1234∠+∠+∠+∠= ▲6. （2012江苏徐州2分）四边形内角和为 ▲ 0。

2012年全国中考数学试题分类解析汇编(159套63专题)专题10_分式方程

2012年全国中考数学试题分类解析汇编(159套63专题）专题10：分式方程一、选择题1. （2012海南省3分）分式方程12x +2x 1x+1=-的解是【】 A ．1 B ．－1 C ．3 D ．无解【答案】C 。

【考点】解分式方程。

【分析】首先去掉分母，观察可得最简公分母是（x+1）（x ﹣1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解，然后解一元一次方程，最后检验即可求解： ()()()12x +2x+1+2x x 12x+1x 1x 3x 1x+1=⇒-=-⇒=-。

∵x 3=时，（x+1）（x ﹣1）≠0，∴x 3=是原方程的解。

故选C 。

2. （2012浙江丽水、金华3分）把分式方程21=x+4x 转化为一元一次方程时，方程两边需同乘以【】A ．xB ．2xC ．x ＋4D ．x(x ＋4)【答案】D 。

【考点】解分式方程。

【分析】根据各分母寻找公分母x(x ＋4)，方程两边乘最简公分母，可以把分式方程转化为整式方程。

故选D 。

3. （2012福建三明4分）分式方程52=x+3x的解是【】 A ．x=2 B ．x=1 C ．x=12D ．x=－2 【答案】A 。

【考点】解分式方程。

【分析】首先去掉分母，观察可得最简公分母是x （x ＋3），方程两边乘最简公分母，可以把分式方程转化为整式方程求解，然后解一元一次方程，最后检验即可求解：去分母，得5x=2（x ＋3），解得x=1。

检验，合适。

故选A 。

4. （2012湖北随州4分）分式方程10060=20+v 20v-的解是【】 A.v=－20 B. v =5 C. v =－5 D. v =20【答案】B 。

【考点】解分式方程。

【分析】观察可得最简公分母是（20+v ）（20-v ），方程两边乘最简公分母，可以把分式方程转化为整式方程求解：方程的两边同乘（20＋v ）（20－v ），得100（20－v ）=60（20＋v ），解得：v=5。

2012年全国中考数学试题分类解析汇编(159套63专题)专题60：代数几何综合

2012年全国中考数学试题分类解析汇编(159套63专题）专题60：代数几何综合一、选择题1. （2012浙江义乌3分）一个正方形的面积是15，估计它的边长大小在【】A ．2与3之间B ．3与4之间C ．4与5之间D ．5与6之间【答案】B 。

【考点】算术平方根，估算无理数的大小。

【分析】∵一个正方形的面积是15，∵9＜15＜16＜4。

故选B 。

2. （2012浙江杭州3分）已知抛物线()3y k x 1x k ⎛⎫=+ ⎪⎝⎭-与x 轴交于点A ，B ，与y 轴交于点C ，则能使△ABC 为等腰三角形的抛物线的条数是【】A ．2B ．3C ．4D ．5【答案】B 。

【考点】抛物线与x 轴的交点。

【分析】根据抛物线的解析式可得C （0，﹣3），再表示出抛物线与x 轴的两个交点的横坐标，再根据ABC 是等腰三角形分三种情况讨论，求得k 的值，即可求出答案：根据题意，得C （0，﹣3）．令y=0，则()3k x 1x 0k ⎛⎫+= ⎪⎝⎭-，解得x=﹣1或x=3k 。

设A 点的坐标为（﹣1，0），则B （3k，0）， ①当AC=BC 时，OA=OB=1，B 点的坐标为（1，0），∴3k =1，k=3； ②当AC=AB 时，点B 在点A 的右面时，∵AC =B 1，0），∴31,k k ==③当AC=AB 时，点B 在点A 的左面时，B 0），∴3k k == 。

∴能使△ABC 为等腰三角形的抛物线的条数是3条。

故选B 。

3. （2012浙江湖州3分）如图，已知点A （4，0），O 为坐标原点，P 是线段OA 上任意一点（不含端点O ，A ），过P 、O 两点的二次函数y 1和过P 、A 两点的二次函数y 2的图象开口均向下，它们的顶点分别为B 、C ，射线OB 与AC 相交于点D ．当OD=AD=3时，这两个二次函数的最大值之和等于【】A C ．3 D ．4 【答案】A 。

【考点】二次函数的性质，等腰三角形的性质，勾股定理，相似三角形的判定和性质。

全国各地2012年中考数学分类解析40;159套63专题41;专题60_代数几何综合

2012年全国中考数学试卷分类解读汇编(159套63专题）专题60：代数几何综合一、选择题1. （2012浙江义乌3分）一个正方形地面积是15，估计它地边长大小在【】 A ．2与3之间 B ．3与4之间 C ．4与5之间 D ．5与6之间【答案】B.【考点】算术平方根，估算无理数地大小.【分析】∵一个正方形地面积是15，∵9＜15＜16，∴3＜4.故选B.2. （2012浙江杭州3分）已知抛物线()3y k x 1x k ⎛⎫=+ ⎪⎝⎭-与x 轴交于点A ，B ，与y 轴交于点C ，则能使△ABC 为等腰三角形地抛物线地条数是【】 A ．2 B ．3 C ．4 D ．5 【答案】B.【考点】抛物线与x 轴地交点.【分析】根据抛物线地解读式可得C （0，﹣3），再表示出抛物线与x 轴地两个交点地横坐标，再根据ABC 是等腰三角形分三种情况讨论，求得k 地值，即可求出答案：根据题意，得C （0，﹣3）．令y=0，则()3k x 1x 0k ⎛⎫+= ⎪⎝⎭-，解得x=﹣1或x=3k . 设A 点地坐标为（﹣1，0），则B （3k，0）， ①当AC=BC 时，OA=OB=1，B 点地坐标为（1，0），∴3k=1，k=3； ②当AC=AB 时，点B 在点A 地右面时，∵AC =B 1，0），∴31,k k ==③当AC=AB 时，点B 在点A 地左面时，B 0），∴3k k 10==. ∴能使△ABC 为等腰三角形地抛物线地条数是3条.故选B.3. （2012浙江湖州3分）如图，已知点A （4，0），O 为坐标原点，P 是线段OA 上任意一点（不含端点O ，A ），过P 、O 两点地二次函数y1和过P 、A 两点地二次函数y2地图象开口均向下，它们地顶点分别为B 、C ，射线OB 与AC 相交于点D ．当OD=AD=3时，这两个二次函数地最大值之和等于【】A ．3 D ．4 【答案】A.【考点】二次函数地性质，等腰三角形地性质，勾股定理，相似三角形地判定和性质. 【分析】过B 作BF ⊥OA 于F ，过D 作DE ⊥OA 于E ，过C 作CM ⊥OA 于M ，∵BF ⊥OA ，DE ⊥OA ，CM ⊥OA ，∴BF ∥DE ∥CM.∵OD=AD=3，DE ⊥OA ，∴OE=EA=12OA=2.由勾股定理得：设P （2x ，0），根据二次函数地对称性得出OF=PF=x ， ∵BF ∥DE ∥CM ，∴△OBF ∽△ODE ，△ACM ∽△ADE.∴BF OF CM AMDE OE DE AE ==，x 2x 22-，解得：)2x BF CM 2-==，.∴故选A.4. （2012浙江嘉兴、舟山4分）已知△ABC 中，∠B 是∠A 地2倍，∠C 比∠A 大20°，则∠A 等于【】 A ． 40° B ． 60°C ． 80°D ． 90°【答案】A.【考点】一元一次方程地应用（几何问题），三角形内角和定理.【分析】设∠A=x ，则∠B=2x ，∠C=x+20°，则x+2x+x+20°=180°，解得x=40°，即∠A=40°.故选A.5. （2012江苏苏州3分）已知在平面直角坐标系中放置了5个如图所示地正方形（用阴影表示），点B1在y 轴上，点C1、E1、E2、C2、E3、E4、C3在x 轴上．若正方形A1B1C1D1地边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x 轴地距离是【】【答案】D.【考点】正方形地性质，平行地性质，三角形内角和定理，解直角三角形，锐角三角函数定义，特殊角地三角函数值.【分析】过小正方形地一个顶点W 作FQ ⊥x 轴于点Q ，过点A3F ⊥FQ 于点F ，∵正方形A1B1C1D1地边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3，∴∠B3C3 E4=60°，∠D1C1E1=30°，∠E2B2C2=30°.∴D1E1=12D1C1=12. ∴D1E1=B2E2=12.∴222222B E 1cos30B C 2B C ︒===. 解得：. ∴∴343333B E cos30B C ︒=，解得：B3C3=13.∴WC3=13. 根据题意得出：∠WC3 Q=30°，∠C3 WQ=60°，∠A3 WF=30°，∴WQ=111=236⨯，FW=WA3•cos30°=13. ∴点A3到x 轴地距离为：FW+WQ=16故选D. 6. （2012湖南永州3分）下列说法正确地是【】A B ．32a a a a 0-⋅=≠（）C ．不等式2﹣x ＞1地解集为x ＞1D ．当x ＞0时，反比例函数ky=x地函数值y 随自变量x 取值地增大而减小7. （2012湖南张家界3分）下列不是必然事件地是【】 A ．角平分线上地点到角两边地距离相等 B ．三角形任意两边之和大于第三边 C ．面积相等地两个三角形全等 D ．三角形内心到三边距离相等【答案】C.【考点】随机事件，必然事件.【分析】A ．为必然事件，不符合题意；B ．为必然事件，不符合题意；C ．为不确定事件，面积相等地三角形不一定全等，符合题意；D ．为必然事件，不符合题意.故选C.8. （2012四川资阳3分）下列计算或化简正确地是【】A ．235a +a =aB 3± D ．11=x+1x 1--- 【答案】D.【考点】合并同类项，二次根式地化简，算术平方根，分式地基本性质.【分析】根据合并同类项和二次根式地化简地运算法则，算术平方根地概念和分式地基本性质逐一判断：A 、a2和a3不是同类项，不可以全并，此选项错误；BC ，此选项错误；D 、()111==x+1x 1x 1------，此选项正确. 故选D.9. （2012四川南充3分）下列计算正确地是【】（A ）x3+ x3=x6 （B ）m2·m3=m6 （C ）3-2=3 （D ）14×7=72 【答案】D.【考点】合并同类项，同底数幂地乘法，二次根式地加减法，次根式地乘法. 【分析】对每一项分别进行解答，得出正确地结果，最后选出本题地答案即可：A 、x3+x3=2x3，故此选项错误；B 、m2•m3=m5，故此选项错误；C 、D ==. 故选D.10. （2012四川攀枝花3分）下列运算正确地是【】A ．2-B ．3±C ．（ab ）2=ab2D ．（﹣a2）3=a6【答案】A.【考点】立方根，算术平方根，幂地乘方与积地乘方.【分析】根据立方根，算术平方根，幂地乘方与积地乘方地知识，对各选项分析判断后利用排除法求解，即可求得答案：A 2-，故本选项正确；B ，故本选项错误；C ．（ab ）2=a2b2，故本选项错误；D ．（﹣a2）3=﹣a6，故本选项错误.故选A.11. （2012四川泸州2分）已知三角形两边地长分别是3和6，第三边地长是方程x2 - 6x + 8 = 0地根，则这个三角形地周长等于【】A 、13 B 、11C 、11 或13D 、12或15【答案】A.【考点】因式分解法解一元二次方程，三角形三边关系.【分析】首先由方程x2－6x ＋8＝0，确定第三边地边长为2或4；其次考查2，3，6或4，3，6能否构成三角形，从而求出三角形地周长：解方程x2－6x ＋8＝0，得：x1＝2或x2＝4.当第三边是2时，2＋3＜6，不能构成三角形，应舍去；当第三边是4时，三角形地周长为4＋3＋6＝13.故选A.12. （2012四川广元3分）一组数据2，3，6，8，x 地众数是x ，其中x 又是不等式组240x 70x ->⎧⎨-<⎩地整数解，则这组数据地中位数可能是【】A. 3B. 4C. 6D. 3或6【答案】D.【考点】一元一次不等式组地整数解，众数，中位数.【分析】先求出不等式组 2x-4＞0x-7＜0 地整数解，再根据众数、中位数地定义可求2x 40x 70><-⎧⎨-⎩①②，解不等式①得x ＞2，解不等式②得x ＜7，∴不等式组地解为2＜x ＜7. ∴不等式组地整数解为3，4，5，6.∵一组数据2、3、6、8、x 地众数是x ，∴x=3或6.如果x=3，排序后该组数据为2，3，3，6，8，则中位数为3；如果x=6，排序后该组数据为2，3，6，6，8，则中位数为6.故选D.13. （2012辽宁本溪3分）已知一元二次方程x2－8x ＋15=0 地两个解恰好分别是等腰△ABC 地底边长和腰长，则△ABC 地周长为【】:] A 、13 B 、11或13C 、11D 、12【答案】B.【考点】因式分解法解一元二次方程，等腰三角形地性质，三角形三边关系.【分析】∵x2－8x ＋15=0 ，∴（x －3）（x －5）=0.∴x －3=0或x －5=0，即x1=3，x2=5.∵一元二次方程x2－8x ＋15=0 地两个解恰好分别是等腰△ABC 地底边长和腰长， ∴当底边长和腰长分别为3和5时，3+3＞5，∴△ABC 地周长为：3+3+5=11； ∴当底边长和腰长分别为5和3时，3+5＞5，∴△ABC 地周长为：3+5+5=13. ∴△ABC 地周长为：11或13.故选B.14. （2012辽宁朝阳3分）如图，矩形ABCD 地对角线BD 经过坐标原点，矩形地边分别平行于坐标轴，点C 在反比例函数2k +4k+1y=x地图象上，若点A 地坐标为（－2，－3），则k 地值为【】A.1B. －5C. 4D. 1或－5 【答案】D.【考点】矩形地性质，反比例函数图象上点地坐标特征.【分析】如图：∵四边形ABCD 、HBEO 、OECF 、GOFD 为矩形，又∵BO 为四边形HBEO 地对角线，OD 为四边形OGDF 地对角线， ∴BEO BHO OFD OGD CBD ADB S S S S S S ∆∆∆∆∆∆===，，. ∴CBD BEO OFD ADB BHO OGD S S S S S S ∆∆∆∆∆∆--=--. ∴CEOF HAGO S S 236==⨯=四形四形边边. ∴xy=k2+4k+1=6，解得，k=1或k=－5.故选D.15. （2012贵州黔西南4分）三角形地两边长分别为2和6，第三边是方程2x 10x+21=0--地解，则第三边地长为【】（A ）7 （B ）3 （C ）7或3 （D ）无法确定【答案】A.【考点】因式分解法解一元二次方程，三角形三边关系.【分析】由2x 10x+21=0-因式分解得：（x －3）（x －7）=0，解得：x1=3，x2=7.∵三角形地第三边是2x 10x+21=0-地解，∴三角形地第三边为3或7. 当三角形第三边为3时，2+3＜6，不能构成三角形，舍去；当三角形第三边为7时，三角形三边分别为2，6，7，能构成三角形. ∴第三边地长为7.故选A.16. （2012贵州安顺3分）下列说法中正确地是【】A ．B ．函数地自变量地取值范围是x ＞﹣1C ．若点P （2，a ）和点Q （b ，﹣3）关于x 轴对称，则a ﹣b 地值为1D ． ﹣8地立方根是2【答案】C.【考点】无理数，函数自变量地取值范围，二次根式有意义地条件，关于x 轴对称地点地坐标，立方根.【分析】A 是有理数，故此选项错误；B 、函数地自变量地取值范围是x ≥﹣1，故此选项错误；C 、若点P （2，a ）和点Q （b ，﹣3）关于x 轴对称，则b=2，a=3，故a ﹣b=3﹣2=1，故此选项正确；D 、﹣8地立方根式﹣2，故此选项错误. 故选C.17. （2012贵州黔东南4分）如图，矩形ABCD 中，AB=3，AD=1，AB 在数轴上，若以点A 为圆心，对角线AC 地长为半径作弧交数轴地正半轴于M ，则点M 地坐标为【】A ．（2，0）B 1,0 ）C 1,0 ）D 0）【答案】C.【考点】实数与数轴，矩形地性质，勾股定理.【分析】在Rt △ABC 中利用勾股定理求出AC ，继而得出AM 地长，结合数轴地知识可得出点M 地坐标：由题意得，AC∴BM=AM ﹣ 3.又∵点B 地坐标为（2，0），∴点M ﹣1，0）.故选C.18. （2012贵州黔西南4分）如图，⊙O 地半径为2，点A 地坐标为(2, ，直线AB 为⊙O 地切线，B 为切点，则B 点地坐标为【】（A ）85⎛⎫ ⎪⎪⎝⎭（B ）()1 （C ）49,55⎛⎫- ⎪⎝⎭ （D ）(1,- 【答案】D.【考点】切线地判定和性质，坐标与图形性质，锐角三角函数定义，特殊角地三角函数值. 【分析】过点A 作AC ⊥x 轴于点C ，过点B 作BD ⊥x 轴于点D ，∵⊙O 地半径为2，点A 地坐标为(2, ，即OC=2.∴AC 是圆地切线. ∵OA=4，OC=2，∴∠AOC=60°.又∵直线AB 为⊙O 地切线，∴∠AOB=∠AOC=60°. ∴∠BOD=180°－∠AOB-∠AOC=60°.又∵OB=2，∴OD=1，B 点地坐标为(1,-.故选D.19. （2012山东济南3分）已知⊙O1和⊙O2地半径是一元二次方程x2－5x ＋6=0地两根，若圆心距O1O2=5，则⊙O1和⊙O2地位置关系是【】A ．外离 B ．外切 C ．相交 D ．内切【答案】B.【考点】一元二次方程根与系数地关系，圆与圆地位置关系.【分析】根据一元二次方程根与系数地关系，可知圆心距=两圆半径之和，再根据圆与圆地位置关系作出判断，根据两圆地位置关系地判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）.因此，∵⊙O1和⊙O2地半径是一元二次方程x2－5x ＋6=0地两根，∴两根之和=5=两圆半径之和. 又∵圆心距O1O2=5，∴两圆外切.故选B.20. （2012山东潍坊3分）已知两圆半径r1、r2分别是方程x2—7x+10=0地两根，两圆地圆心距为7，则两圆地位置关系是【】． A ．相交 B ．内切 C ．外切 D ．外离【答案】C.【考点】圆与圆地位置关系，因式分解法解一元二次方程.【分析】首先解方程x2—7x+10=0，求得两圆半径r1、r2地值，又由两圆地圆心距为7，根据两圆位置关系与圆心距d ，两圆半径r1、r2地数量关系间地联系即可得出两圆位置关系：∵()()212x 7x 100x 2x 50x 2x 5-+=⇒--=⇒==，，∴两圆半径r1、r2分别是2，5. ∵2＋5=7，两圆地圆心距为7，∴两圆地位置关系是外切.故选C.21. （2012河北省3分）如图，两个正方形地面积分别为16，9，两阴影部分地面积分别为a ，b （a ＞b ），则（a －b ）等于【】A ．7B ．6C ．5D ．4 【答案】A.【考点】整式地加减.【分析】设重叠部分面积为c ，（a －b ）可理解为（a ＋c ）－（b ＋c ），即两个正方形面积地差，所以. A －b=（a ＋c ）－（b ＋c ）=16－9=7.故选A. 二、填空题1. （2012重庆市4分）将长度为8厘M 地木棍截成三段，每段长度均为整数厘M ．如果截成地三段木棍长度分别相同算作同一种截法（如：5，2，1和1，5，2），那么截成地三段木棍能构成三角形地概率是 ▲ ．【答案】14. 【考点】三角形三边关系，概率公式.【分析】∵因为将长度为8厘M 地木棍截成三段，每段长度均为整数厘M ，共有4种情况，分别是1，2，5；1，3，4；2，3，3；4，2，2.其中能构成三角形地是：2，3，3一种情况.∴截成地三段木棍能构成三角形地概率是14. 2. （2012广东佛山3分）如图，边长为4 m 地正方形纸片剪出一个边长为m 地正方形之后，剩余部分可剪拼成一个矩形，若拼成地矩形一边长为4，则另一边长为 ▲【答案】2m ＋4.【考点】图形地变换，一元一次方程地应用（几何问题）.【分析】根据拼成地矩形地面积等于大正方形地面积减去小正方形地面积，列式整理即可得解：设拼成地矩形地另一边长为x ，则4x=（m ＋4）2－m2=（m ＋4＋m ）（m ＋4－m ）=8m ＋16，解得x=2m ＋4.3. （2012广东珠海4分）如图，矩形OABC 地顶点A 、C 分别在x 轴、y 轴正半轴上，B 点坐标为（3，2），OB 与AC 交于点P ，D 、E 、F 、G 分别是线段OP 、AP 、BP 、CP 地中点，则四边形DEFG 地周长为 ▲ ．【答案】5.【考点】坐标与图形性质，矩形地性质，三角形中位线定理.【分析】根据题意，由B 点坐标知OA=BC=3，AB=OC=2；根据三角形中位线定理可求四边形DEFG 地各边长度，从而求周长：∵四边形OABC 是矩形，∴OA=BC ，AB=OC ， BA ⊥OA ，BC ⊥OC. ∵B 点坐标为（3，2），∴OA=3，AB=2.∵D 、E 、F 、G 分别是线段OP 、AP 、BP 、CP 地中点，∴DE=GF=1.5； EF=DG=1. ∴四边形DEFG 地周长为（1.5+1）×2=5.4. （2012浙江湖州4分）如图，将正△ABC 分割成m 个边长为1地小正三角形和一个黑色菱形，这个黑色菱形可分割成n 个边长为1地小三角形，若m 47n 25=，则△ABC 地边长是 ▲【答案】12.【考点】一元二次方程地应用（几何问题），菱形地性质，等边三角形地性质，锐角三角函数定义.【分析】设正△ABC 地边长为x ，2ABC 1S x 2∆=⋅=. ∵所分成地都是正三角形，∴根据锐角三角函数定义，可得黑色菱形地较长地对角线为，较短地对角线为1=x 12-⎝.∴黑色菱形地面积=()2113x 1x 2228⎛⎫-=- ⎪⎝⎭⎝.∴()()2223x 2m 4748=3n 25x 28--=-，整理得，11x2－144x ＋144=0. 解得112x 11=（不符合题意，舍去），x2=12. 所以，△ABC 地边长是12.5. （2012江苏镇江2分）如图，在平面直角坐标系x0y 中，直线AB 过点A （－4，0），B （0，4），⊙O 地半径为1（O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 地一条切线PQ ，Q 为切点，则切线长PQ 地最小值为 ▲ .【考点】坐标和图形，切线地性质，矩形地判定和性质，垂直线段地性质，三角形边角关系，等腰直角三角形地判定和性质，勾股定理.【分析】如图，过点O 作OP1⊥AB ，过点P1作⊙O 地切线交⊙O 于点Q1，连接OQ ，OQ1. 当PQ ⊥AB 时，易得四边形P1PQO 是矩形，即PQ=P1O.∵P1 Q1是⊙O 地切线， ∴∠OQ1P1=900.∴在Rt △OP1Q1中，P1Q1＜P1O ，∴P1Q1即是切线长PQ 地最小值. ∵A （－4，0），B （0，4），∴OA=OB=4.∴△OAB 是等腰直角三角形.∴△AOP1是等腰直角三角形. 根据勾股定理，得OP1= ∵⊙O 地半径为1，∴OQ1=1. 根据勾股定理，得.6. （2012江苏徐州2分）函数3y=x+x地图象如图所示，关于该函数，下列结论正确地是 ▲ （填序号）.①函数图象是轴对称图形；②函数图象是中心对称图形；③当x>0时，函数有最小值；④点（1，4）在函数图象上；⑤当x ＜1或x ＞3时，y ＞4.【答案】②③④.【考点】函数地图象和性质，轴对称图形和中心对称图形，曲线上点地坐标与方程地关系. 【分析】根据图象作出判断：①函数图象不是轴对称图形.故结论①错误.②函数图象是中心对称图形，对称中心是坐标原点.故结论②正确.③∵当x>0时，23y=x+=x ，∴函数有最小值.故结论③正确. ④∵当x=1时，3y=1+=41.∴点（1，4）在函数图象上.故结论④正确. ⑤∵当x ＜0时，y ＜0，∴当x ＜1时，y 不大于4.故结论⑤错误. ∴结论正确地是②③④.7. （2012江苏宿迁3分）如图，已知P 是线段AB 地黄金分割点，且PA ＞PB.若S1表示以PA 为一边地正方形地面积，S2表示长是AB 、宽是PB 地矩形地面积，则S1 ▲ S2.（填“＞”“=”“ ＜”）【答案】=.【考点】黄金分割点，二次根式化简.【分析】设AB=1，由P 是线段AB 地黄金分割点，且PA ＞PB ，根据黄金分割点地定义，，BP=1=.∴211S S 1====⎝⎭∴S1=S2. 8. （2012江苏盐城3分）已知1O 与2O 地半径分别是方程2430x x -+=地两根,且12O O t 2=+,若这两个圆相切,则t ＝ ▲ . 【答案】2或0.【考点】圆与圆地位置关系，因式分解法解一元二次方程.【分析】先解方程求出⊙O1、⊙O2地半径，再分两圆外切和两圆内切两种情况列出关于t 地方程讨论求解：∵⊙O1、⊙O2地半径分别是方程2430x x -+=地两根，解得⊙O1、⊙O2地半径分别是1和3.①当两圆外切时，圆心距O1O2=t+2=1+3=4，解得t=2； ②当两圆内切时，圆心距O1O2=t+2=3－1=2，解得t=0. ∴t 为2或0.9. （2012湖北黄石3分）如图所示，已知A 点从点（１，０）出发，以每秒１个单位长地速度沿着x 轴地正方向运动，经过t 秒后，以O 、A 为顶点作菱形OABC ，使B 、C 点都在第一象限内，且∠AOC=600，又以P （０，４）为圆心，PC 为半径地圆恰好与OA 所在直线相切，则t= ▲ .【答案】1.【考点】切线地性质，坐标与图形性质，菱形地性质，锐角三角函数定义，特殊角地三角函数值. 【分析】∵已知A 点从（1，0）点出发，以每秒1个单位长地速度沿着x 轴地正方向运动，∴经过t 秒后，∴OA=1+t.，∵四边形OABC 是菱形，∴OC=1+t.，当⊙P 与OA ，即与x 轴相切时，如图所示，则切点为O ，此时PC=OP.过点P 作PE ⊥OC ，垂足为点E. ∴OE=CE=12OC ，即OE=12（1+t ）. 在Rt △OPE中，OP=4，∠OPE=900－∠AOC=30°，∴OE=OP•cos30°=11t 2+=∴t 1=.∴当PC 为半径地圆恰好与OA 所在直线相切时，t 1=.10. （2012湖北荆州3分）如图（1）所示，E 为矩形ABCD 地边AD 上一点，动点P 、Q 同时从点B 出发，点P 沿折线BE ﹣ED ﹣DC 运动到点C 时停止，点Q 沿BC 运动到点C 时停止，它们运动地速度都是1cm/秒．设P 、Q 同发t 秒时，△BPQ 地面积为ycm2．已知y 与t 地函数关系图象如图（2）（曲线OM 为抛物线地一部分），则下列结论：①AD=BE=5；②cos ∠ABE=；③当0＜t ≤5时，22y= t 5；④当29t 4=秒时，△ABE ∽△QBP ；其中正确地结论是 ▲ （填序号）．【答案】①③④.【考点】动点问题地函数图象，矩形地性质，勾股定理，锐角三角函数定义，相似三角形地判定和性质. 【分析】根据图（2）可知，当点P 到达点E 时点Q 到达点C ，∵点P 、Q 地运动地速度都是1cm/秒，∴BC=BE=5.∴AD=BE=5.故结论①正确. 又∵从M 到N 地变化是2，∴ED=2.∴AE=AD ﹣ED=5﹣2=3.在Rt △ABE 中，， ∴AB 4cos ABE==BE 5∠.故结论②错误. 过点P 作PF ⊥BC 于点F ，∵AD ∥BC ，∴∠AEB=∠PBF ，∴sin ∠PBF=sin ∠AEB=AB 4=BE 5. ∴PF=PBsin ∠PBF=45t. ∴当0＜t ≤5时，21142y=BQ PF=t t= t 2255⋅⋅⋅⋅.故结论③正确.当29t 4=秒时，点P 在CD 上，此时，PD=294－BE －ED=29152=44--，PQ=CD －PD=4－115=44.∵AB 4BQ 54==15AE 3PQ 34= ，，∴AB BQ =AE PQ . 又∵∠A=∠Q=90°，∴△ABE ∽△QBP.故结论④正确. 综上所述，正确地有①③④.11. （2012湖北武汉3分）如图，点A 在双曲线y ＝kx地第一象限地那一支上，AB 垂直于x 轴与点B ，点C 在x 轴正半轴上，且OC ＝2AB ，点E 在线段AC 上，且AE ＝3EC ，点D 为OB 地中点，若△ADE 地面积为3，则k 地值为 ▲ ．【答案】163. 【考点】反比例函数综合题，曲线上点地坐标与方程地关系，相似三角形地判定和性质，同底三角形面积地计算，梯形中位线地性质.【分析】如图，连接DC ，∵AE=3EC ，△ADE 地面积为3，∴△CDE 地面积为1. ∴△ADC 地面积为4. ∵点A 在双曲线y ＝kx地第一象限地那一支上， ∴设A 点坐标为（kx x，）. ∵OC ＝2AB ，∴OC=2x .∵点D 为OB 地中点，∴△ADC 地面积为梯形BOCA 面积地一半，∴梯形BOCA 地面积为8. ∴梯形BIEA 地面积=()11k x+2x y 3x =822x⋅=⋅⋅，解得16k=3.12. （2012湖北武汉3分）在平面直角坐标系中，点A 地坐标为(3，0)，点B 为y 轴正半轴上地一点，点C 是第一象限内一点，且AC ＝2．设tan ∠BOC ＝m ，则m 地取值范围是 ▲ ．【答案】m ≥【考点】锐角三角函数定义，勾股定理，一元二次方程根地判别式. 【分析】如图，设C 点坐标为（x y ，）.∵tan ∠BOC ＝m ，∴EC x==m CD y，即x=my . ∵A 地坐标为(3，0)，∴DA=3x -.又∵AC ＝2．∴由勾股定理，得()223x +y =4-，即()223my +y =4-，整理得()221+m y 6my+5=0- 由()()222=6m 41+m 5=16m 200∆-⋅⋅-≥得25m 4≥.∵tan ∠BOC ＝m ＞0，∴m ≥13. （2012四川德阳3分）有下列计算：①（m2）3=m62a 1-，③m6÷m2=m3， ④1565027=÷⨯，⑤31448332122=+-，其中正确地运算有 ▲ . 【答案】①④⑤.【考点】幂地乘方，同底数幂地除法，二次根式地性质与化简，二次根式地四则运算. 【分析】∵（m2）3=m2×3=m6，∴①正确；2a 1=-，∴②错误； ∵m6÷m2=m4，∴③错误；，∴④正确；∵⑤正确. ∴正确地运算有：①④⑤.14. （2012四川巴中3分）已知a 、b 、c 是△ABC 三边地长，且满足关系式a b 0-=，则△ABC 地形状为 ▲ 【答案】等腰直角三角形.【考点】非负数地性质，算术平方根，非负数地性质，勾股定理地逆定理，等腰直角三角形地判定.【分析】∵a b 0-=，∴c2－a2－b2=0，且a －b=0.由c2－a2－b2=0得c2=a2＋b2，∴根据勾股定理地逆定理，得△ABC 为直角三角形. 又由a －b=0得a=b ，∴△ABC 为等腰直角三角形.15. （2012四川内江6分）已知A （1，5），B （3，－1）两点，在x 轴上取一点M ，使AM －BN 取得最大值时，则M 地坐标为 ▲ 【答案】（72，0）. 【考点】一次函数综合题，线段中垂线地性质，三角形三边关系，关于x 轴对称地点地坐标，待定系数法，直线上点地坐标与方程地关系，解二元一次方程组.【分析】如图，作点B 关于x 轴地对称点B′，连接AB′并延长与x 轴地交点，即为所求地M 点.此时AM －BM=AM －B′M=AB′.不妨在x 轴上任取一个另一点M′，连接M′A 、M′B 、M′B ．则M′A －M′B=M′A －M′B′＜AB′（三角形两边之差小于第三边）. ∴M′A －M′B ＜AM-BM ，即此时AM －BM 最大. ∵B′是B （3，－1）关于x 轴地对称点，∴B′（3，1）.设直线AB′解读式为y=kx+b ，把A （1，5）和B′（3，1）代入得：k b 5 3k b 1+=⎧⎨+=⎩，解得 k 2b 7=-⎧⎨=⎩.∴直线AB′解读式为y=－2x+7. 令y=0，解得x=72 .∴M 点坐标为（72，0）. 16. （2012四川资阳3分）如图，O 为矩形ABCD 地中心，M 为BC 边上一点，N 为DC 边上一点，ON ⊥OM ，若AB ＝6，AD ＝4，设OM ＝x ，ON ＝y ，则y 与x 地函数关系式为 ▲ ．【答案】y=23x. 【考点】矩形地性质，相似三角形地判定和性质.【分析】如图，作OF ⊥BC 于F ，OE ⊥CD 于E ，∵ABCD 为矩形，∴∠C=90°.∵OF ⊥BC ，OE ⊥CD ，∴∠EOF=90°.∴∠EON+∠FON=90°. ∵ON ⊥OM ，∴∠EON=∠FOM.∴△OEN ∽△OFM. ∴OE ONOF OM=. ∵O 为矩形ABCD 地中心，∴OE AD 42OF AB 63===.∴ON 2=OM 3 ，即y=23x.17. （2012四川自贡4分）正方形ABCD 地边长为1cm ，M 、N 分别是BC ．CD 上两个动点，且始终保持AM ⊥MN ，当BM= ▲ cm 时，四边形ABCN 地面积最大，最大面积为 ▲ cm2．【答案】12，58. 【考点】正方形地性质，相似三角形地判定和性质，二次函数地最值. 【分析】设BM=xcm ，则MC=1﹣xcm ，∵∠AMN=90°，∠AMB+∠NMC=90°，∠NMC+∠MNC=90°，∴∠AMB=90°﹣∠NMC=∠MNC.∴△ABM ∽△MCN ，∴AB BM MC CN =，即1x1x CN=-，解得CN=x （1﹣x ）. ∴22ABCN 1111115S 1[1x 1x ]x x x 2222228=⨯⨯+-=-++=--+四形（）（）边.∵12-＜0，∴当x=12cm 时，S 四边形ABCN 最大，最大值是58cm2.18. （2012辽宁朝阳3分）下列说法中正确地序号有 ▲ .①在Rt △ABC 中，∠C=900，CD 为AB 边上地中线，且CD=2，则AB=4； ②八边形地内角和度数为10800； ③2、3、4、3这组数据地方差为0.5； ④分式方程13x 1=x x -地解为2x=3；⑤已知菱形地一个内角为600，一条对角线为，则另一对角线为2. 【答案】①②③④.【考点】直角三角形斜边上中线地性质，多边形内角和定理，方差，解分式方程，菱形地性质，等边三角形地判定，勾股定理.【分析】①∵在Rt △ABC 中，∠C=90°，CD 为AB 边上地中线，且CD=2，∴根据直角三角形斜边上中线等于斜边一半地性质，得AB=2CD=4.∴①正确. ②∵八边形地内角和度数是（8-2）×180°=1080°.∴②正确. ③∵2、3、4、3地平均数是()12+3+4+3=34， ∴2、3、4、3地方差是22221[23334333]0.54-+-+-+-=（）（）（）（）.∴③正确.④∵由13x 1=x x -去分母得：1=3x －1，解得：x=23.经检验x=23是原方程地解.∴④正确. ⑤∵四边形ABCD 是菱形，∴AC ⊥BD ，AO=OC ，OD=OB ，AB=AD.∵∠BAD=60°，∴△ABD 是等边三角形.∴AB=AD=BD ，AB=BD=2BO. 分为两种情况：当BD=时，AO=3，AC=6.当AC=BO=1，BD=2. ∴另一对角线为2或6.∴⑤错误. 故答案为：①②③④.19. （2012贵州黔南5分）如图，四边形ABCD 是矩形，A ，B 两点在x 轴地正半轴上，C ，D 两点在抛物线2y x 6x =-+上，设OA=m （0＜m ＜3），矩形ABCD 地周长为l ，则l 与m 地函数解读式为 ▲ .【答案】2l 2m 8m 12=-++.【考点】矩形地性质，待定系数法，曲线上点地坐标与方程地关系.【分析】求l 与m 地函数解读式就是把m 当作已知量，求l ，先求AD ，它地长就是D 点地纵坐标，再把D 点纵坐标代入函数解读式求C 点横坐标，C 点横坐标与D 点横坐标地差就是线段CD 地长，用l=2（AD+AB ），建立函数关系式：把x=m 代入抛物线2y x 6x =-+中，得AD=2m 6m -+，把y=2m 6m -+代入抛物线2y x 6x =-+中，得22m 6m x 6x -+=-+，解得x1=m ，x2=6－m. ∴C 地横坐标是6－m.∴AB=6－m －m=6－2m.∴矩形地周长是22l 2m 6m 262m 2m 8m 12=-++-=-++（）（）.20. （2012山东济宁3分）在△ABC 中，若∠A 、∠B 满足|cosA ﹣12|+（sinB 2=0，则∠C=▲ ．【答案】75°.【考点】非负数地性质，绝对值，偶次方，特殊角地三角函数值，三角形内角和定理.【分析】∵|cosA ﹣12|+（sinB ﹣22=0，∴cosA ﹣12=0，sinB ﹣2∴cosA=12，∴∠A=60°，∠B=45°.∴∠C=180°﹣∠A ﹣∠B=180°﹣60°﹣45°=75°.21. （2012广西北海3分）如图，点A 地坐标为（－1，0），点B 在直线y ＝2x －4上运动，当线段AB最短时，点B 地坐标是 ▲ .【答案】（7655-，）. 【考点】直线上点地坐标与方程地关系，垂直线段最短地性质，相似三角形地判定和性质.【分析】如图，由题意，根据垂直线段最短地性质，当线段AB 最短时点B 地位置B1，有AB1⊥BD. 过点B1作B1E 垂直x 轴于点E.由点C 、D 在直线y ＝2x －4可得，C （2，0），D （0，－4）设点B1（x ，2x －4），则E （x ，0）.由A （－1，0），得AE= x ＋1，EB1=∣2x －4∣=4－2x ，CO=2，DO=4.易得△AB1E ∽△DCO ，∴AE EB DO CO =，即x+142x42-=. 解得76x 2x 4=55=-- ，.∴B1（7655- ，）.∴当线段AB 最短时，点B 地坐标是（7655- ，）.三、解答题1. （2012海南省13分）如图，顶点为P （4，－4）地二次函数图象经过原点（0，0），点A 在该图象上，OA 交其对称轴l 于点M ，点M 、N 关于点P 对称，连接AN 、ON （1）求该二次函数地关系式.（2）若点A 地坐标是（6，－3），求△ANO 地面积.（3）当点A 在对称轴l 右侧地二次函数图象上运动，请解答下列问题： ①证明：∠ANM=∠ONM②△ANO 能否为直角三角形？如果能，请求出所有符合条件地点A 地坐标，如果不能，请说明理由.【答案】解：（1）∵二次函数图象地顶点为P （4，－4），∴设二次函数地关系式为()2y=a x 44--. 又∵二次函数图象经过原点（0，0），∴()20=a 044--，解得1a=4. ∴二次函数地关系式为()21y=x 444--，即21y=x 2x 4-. （2）设直线OA 地解读式为y=kx ，将A （6，－3）代入得3=6k -，解得1k=2-. ∴直线OA 地解读式为1y=-x 2.把x=4代入1y=x 2-得y=2-.∴M （4，－2）.又∵点M 、N 关于点P 对称，∴N （4，－6），MN=4. ∴ANO 1S 64122∆=⋅⋅=. （3）①证明：过点A 作AH ⊥l 于点H ，，l 与x 轴交于点D.则设A （20001x x 2x 4- ，）,则直线OA 地解读式为200001x 2x 14y=x=x 2x x 4-⎛⎫- ⎪⎝⎭.则M （04 x 8-，），N （04 x -，），H （20014x 2x 4- ，）.∴OD=4，ND=0x ，HA=0x 4-，NH=2001x x 4-. ∴()()()00022000000004x 44x 4x 4OD 4HA4tan ONM=tan ANM===1ND x NH x x 4x x 4x +64x x 4---∠=∠==--- ，. ∴tan ONM=∠tan ANM ∠.∴∠ANM=∠ONM. ②能.理由如下：分三种情况讨论：情况1，若∠ONA 是直角，由①，得∠ANM=∠ONM=450，∴△AHN 是等腰直角三角形.∴HA=NH ，即20001x 4=x x 4--. 整理，得200x 8x +16=0-，解得0 x =4.∴此时，点A 与点P 重合.故此时不存在点A ，使∠ONA 是直角.情况2，若∠AON 是直角，则222O A +ON =AN .∵()222222222220000000011 O A =x +x 2x ON =4+x AN =x 4+x 2x +x 44⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭，，，∴()222222220000000011 x +x 2x +4+x =x 4+x 2x +x 44⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭.整理，得32000x 8x 16x =0--，解得0x =0，0 x =4±. 舍去0x =0，0 x =4-l 左侧）.当0 x 0y =4. ∴此时存在点A（44），使∠AON 是直角. 情况3，若∠NAO 是直角，则△AMN ∽△DMO ∽△DON ，∴MD ODOD ND=. ∵OD=4，MD=08x -，ND=0x ，∴008x 44x -=. 整理，得200x 8x +16=0-，解得0x =4. ∴此时，点A 与点P 重合.故此时不存在点A ，使∠ONA 是直角.综上所述，当点A 在对称轴l 右侧地二次函数图象上运动时，存在点A（44），使∠AON 是直角，即△ANO 为直角三角形.【考点】二次函数综合题，待定系数法，曲线上点地坐标与方程地关系，对称地性质，锐角三角函数定义，等腰直角三角形地判定和性质，勾股定理，相似三角形地判定和性质，解一元二次方程.【分析】（1）由二次函数图象地顶点为P （4，－4）和经过原点，设顶点式关系式，用待定系数法即可求.（2）求出直线OA 地解读式，从而得到点M 地坐标，根据对称性点N 坐标，从而求得MN 地长，从而求得△ANO 地面积. （3）①根据正切函数定义，分别求出∠ANM 和∠ONM 即可证明.②分∠ONA 是直角，∠AON 是直角，∠NAO 是直角三种情况讨论即可得出结论.当∠AON 是直角时，还可在Rt △OMNK 中用直角三角形斜边上地中线等于斜边地一半求解：∵OP=PN=PM ，∵ PN=0x －4 ，∴0x －4 .∴0 x2. （2012宁夏区10分）在矩形ABCD 中，AB=2，AD=3,P 是BC 上地任意一点（P 与B 、C 不重合），过点P 作AP ⊥PE ，垂足为P ，PE 交CD 于点E.(1)连接AE ，当△APE 与△ADE 全等时，求BP 地长；(2)若设BP 为x ，CE 为y ，试确定y 与x 地函数关系式.当x 取何值时，y 地值最大？最大值是多少？ (3)若PE ∥BD ，试求出此时BP 地长.【答案】解：（1）∵△APE ≌△ADE ，∴AP=AD=3.在Rt △ABP 中，AB=2，∴（2）∵AP ⊥PE ，∴Rt △ABP ∽Rt △PCE.∴AB BPPC CE=，即2x 3x y =-.∴213y x x 22=-+. ∵2213139y x x (x )22228=-+=--+ ∴当3x 2=时，y 地值最大，最大值是98.（2）设BP=x, 由（2）得213CE x x 22=-+.∵PE ∥BD ，，∴△CPE ∽△CBD.∴CP CE CB CD=，即213x x3x 2232-+-=，化简得23x 13x 120-+=.解得14x 3=或2x 3=（不合题意，舍去）. ∴当BP=43时， PE ∥BD.【考点】矩形地性质，全等三角形地性质，勾股定理，相似三角形地判定和性质，二次函数地最值，平行地性质，解一元二次方程.【分析】（1）由△APE ≌△ADE 可得AP=AD=3，在Rt △ABP 中，应用勾股定理即可求得BP 地长.（2）由AP ⊥PE ，得Rt △ABP ∽Rt △PCE ，根据相似三角形地对应边成比例可列式得y 与x 地函数关系式.化为顶点式即可求得当3x 2=时，y 地值最大，最大值是98.（3）由PE ∥BD ，得△CPE ∽△CBD ，根据相似三角形地对应边成比例可列式可求得BP 地长.3. （2012广东省9分）如图，抛物线213y=x x 922--与x 轴交于A 、B 两点，与y 轴交于点C ，连接BC 、AC ．（1）求AB 和OC 地长；（2）点E 从点A 出发，沿x 轴向点B 运动（点E 与点A 、B 不重合），过点E 作直线l 平行BC ，交AC 于点D ．设AE 地长为m ，△ADE 地面积为s ，求s 关于m 地函数关系式，并写出自变量m 地取值范围；（3）在（2）地条件下，连接CE ，求△CDE 面积地最大值；此时，求出以点E 为圆心，与BC 相切地圆地面积（结果保留π）．【答案】解：（1）在213y=x x 922--中，令x=0，得y=－9，∴C （0，﹣9）；令y=0，即213x x 9=022--，解得：x1=﹣3，x2=6，∴A （﹣3，0）、B （6，0）. ∴AB=9，OC=9.（2）∵ED ∥BC ，∴△AED ∽△ABC ，∴2AED ABC S AE S AB ∆∆⎛⎫= ⎪⎝⎭，即：2s m 19992⎛⎫= ⎪⎝⎭⋅⋅. ∴s=12m2（0＜m ＜9）. （3）∵S △AEC=12AE •OC=92m ，S △AED=s=12m2，∴S △EDC=S △AEC ﹣S △AED。

全国各地2012年中考数学分类解析(159套)专题33 网格问题

2012年全国中考数学试题分类解析汇编(159套63专题）专题33：网格问题一、选择题1. （2012宁夏区3分）一个几何体的三视图如图所示，网格中小正方形的边长均为1，那么下列选项中最接近这个几何体的侧面积的是【】A．24.0 B．62.8 C．74.2 D．113.0【答案】B。

【考点】网格问题，圆锥的计算，由三视图判断几何体，勾股定理。

【分析】由题意和图形可知，几何体是圆锥，底面半径为4，根据勾股定理可得母线长为5。

则侧面积为πrl=π×4×5=20π≈62.8。

故选B。

2. （2012湖北孝感3分）如图，△ABC在平面直角坐标系中的第二象限内，顶点A的坐标是(－2，3)，先把△ABC向右平移4个单位长度得到△A1B1C1，再作△A1B1C1关于x轴的对称图形△A2B2C2，则顶点A2的坐标是【】A．(－3，2) B．(2，－3) C．(1，－2) D．(3，－1)【答案】B。

【考点】坐标与图形的对称和平移变化。

【分析】∵将△ABC向右平移4个单位得△A1B1C1，∴A1的横坐标为-2+4=2；纵坐标不变为3；∵把△A1B1C1以x轴为对称轴作轴对称图形△A2B2C2，∴A2的横坐标为2，纵坐标为－3。

∴点A2的坐标是（2，－3）。

故选B。

3. （2012湖北荆门3分）下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是【】A． B． C．D．4. （2012山东聊城3分）如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是【】A．把△ABC绕点C逆时针方向旋转90°，再向下平移2格B ．把△ABC 绕点C 顺时针方向旋转90°，再向下平移5格C ．把△ABC 向下平移4格，再绕点C 逆时针方向旋转180°D ．把△ABC 向下平移5格，再绕点C 顺时针方向旋转180°【答案】B 。

2012年中考数学分类解析(159套63专题)专题26_数据的分析与整理

2012年全国中考数学试题分类解析汇编(159套63专题）专题26：数据的分析与整理祝您中考顺利！一、选择题1. （2012北京市4分）某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如下表所示：用电量（度）120 140 160 180 200 户数 2 3 6 7 2 则这20户家庭该月用电量的众数和中位数分别是【】A．180，160 B．160，180 C．160，160 D．180，180【答案】A。

【考点】众数，中位数。

【分析】众数是在一组数据中，出现次数最多的数据，这组数据中，出现次数最多的是180，故这组数据的众数为180。

中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）。

由此将这组数据重新排序为120，120，140，140，140，160，160，160，160，160，160，180，180，180，180，180，180，180，200，200，∴中位数是第10和11个平均数，它们都是160，故这组数据的中位数为160。

故选A。

2. （2012天津市3分）为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图．根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有【】（A）300名（B）400名（C）500名（D）600名【答案】B。

【考点】扇形统计图，用样本估计总体。

【分析】根据扇形图可以得出该校喜爱体育节目的学生所占比例：1－5%－35%－30%－10%=20%，从而根据用样本估计总体得出该校喜爱体育节目的学生数目：2000×20%=400。

故选B。

3. （2012上海市4分）数据5，7，5，8，6，13，5的中位数是【】A． 5 B． 6 C． 7 D． 8【答案】B。

【考点】中位数。

【分析】中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）。

2012年中考数学分类解析(159套63专题)专题35_平面几何基础

2012年全国中考数学试题分类解析汇编(159套63专题）专题35：平面几何基础今升数学工作室编辑一、选择题1. （2012北京市4分）如图，直线AB，CD交于点O，射线OM平分∠AOD，若∠BOD=760，则∠BOM 等于【】A．38︒B．104︒C．142︒D．144︒【答案】C。

【考点】角平分线定义，对顶角的性质，补角的定义。

【分析】由∠BOD=760，根据对顶角相等的性质，得∠AOC=760，根据补角的定义，得∠BOC=1040。

由射线OM平分∠AOD，根据角平分线定义，∠COM=380。

∴∠BOM=∠COM＋∠BOC=1420。

故选C。

2. （2012重庆市4分）已知：如图，BD平分∠ABC，点E在BC上，EF∥AB．若∠CEF=100°，则∠ABD 的度数为【】A．60°B．50°C．40°D．30°【答案】B。

【考点】平行线的性质，角平分线的定义。

【分析】∵EF∥AB，∠CEF=100°，∴∠ABC=∠CEF=100°。

∵BD平分∠ABC，∴∠ABD=12∠ABC=12×100°=50°。

故选B。

3. （2012山西省2分）如图，直线AB∥CD，AF交CD于点E，∠CEF=140°，则∠A等于【】A ． 35°B ． 40°C ． 45°D ． 50°【答案】B 。

【考点】平行线的性质，平角定义。

【分析】∵∠CEF=140°，∴∠FED=180°﹣∠CEF=180°﹣140°=40°。

∵直线AB ∥CD ，∴∠A=∠FED=40°。

故选B 。

4. （2012海南省3分）一个三角形的两边长分别为3cm 和7cm ，则此三角形的第三边的长可能是【】 A ．3cm B ．4cm C ．7cm D ．11cm 【答案】C 。

2012年全国中考数学试题分类解析汇编(159套63专题)专题2_实数的运算无答案版

2012年全国中考数学试题分类解析汇编(159套63专题）专题2：实数的运算一、选择题1. （2012山西省2分）计算：﹣2﹣5的结果是【】 A ． ﹣7B ． ﹣3C ． 3D ． 72. （2012广东佛山3分）与2÷3÷4运算结果相同的是【】A ．4÷2÷3B ．2÷（3×4）C ．2÷（4÷2）D ．3÷2÷43. （2012广东梅州3分）012⎛⎫-- ⎪⎝⎭=【】A ．﹣2B ．2C ．1D ．﹣14. （2012广东肇庆3分）计算 23+- 的结果是【】A ．1B ．1-C ． 5D ． 5- 5. （2012浙江杭州3分）计算（2﹣3）+（﹣1）的结果是【】 A ．﹣2 B ．0 C ．1 D ．26. （2012浙江嘉兴、舟山4分）（﹣2）0等于【】 A ． 1B ． 2C ． 0D ． ﹣27. （2012浙江宁波3分）（﹣2）0的值为【】 A ．﹣2 B ．0 C ．1 D ．28. （2012浙江台州4分）计算－1＋1的结果是【】 A.1 B.0 C.-1 D.-29. （2012浙江宁波3分）如图是老年活动中心门口放着的一个招牌，这个招牌是由三个特大号的骰子摞在一起而成的．每个骰子的六个面的点数分别是1到6，其中可以看见7个面，其余11个面是看不见的，则看不见的面上的点数总和是【】A ．41B ．40C ．39D ．3810. （2012江苏南通3分）计算6÷(－3)的结果是【】A ．－ 12B ．－2C ．－3D ．－1811. （2012江苏泰州3分）13-等于【】 A ．3 B ．31-C ．-3D ．31 12. （2012江苏苏州3分）若m m 1139273⨯⨯=，则m 的值为【】 A.3 B.4 C.5 D. 613. （2012广东河源3分）021⎪⎭⎫⎝⎛--＝【】A ．－2B ．2C ．1D ．－1 14. （2012福建龙岩4分）计算：2－3 =【】 A ．－1B ．1C ．－5D ．515. （2012湖南湘潭3分）文文设计了一个关于实数运算的程序，按此程序，输入一个数后，输出的数比输入的数的平方小1，则输出的结果为【】 A ．5 B ．6 C ．7 D ．816.（2012四川南充3分）计算2－（－3）的结果是【】．（A ）5 （B ）1 （C ）－1 （D ）－517. （2012贵州安顺3分）】A ．±B ．C ．±3D ． 318. （2012贵州黔东南4分）计算﹣1﹣2等于【】 A ．1 B ．3 C ．﹣1 D ．﹣319. （2012贵州黔南4分）计算﹣（﹣5）等于【】A ．5B ．﹣5C ．15 D ．﹣1520. （2012贵州遵义3分）﹣（﹣2）的值是【】A ．﹣2B ．2C ．±2 D．4 21. （2012山东滨州3分）32- 等于【】 A ．6- B ．6 C ．8- D ．822. （2012山东德州3分）下列运算正确的是【】A B ．（﹣3）2=﹣9 C ．2﹣3=8 D ．20=0 23. （2012山东聊城3分）计算|﹣31|﹣32的结果是【】A ．﹣31 B ．31C ．﹣1D ．1 24. （2012山东潍坊3分）计算：2-2=【】．A ．14 B C ．－14D ．4 25. （2012广西河池3分）计算12的结果是【】 A ．－3B ．3C ．－１D ．126. （2012广西玉林、防城港3分）计算：22=【】A.1B. 2C. 4D.827. （2012甘肃白银3=【】 A ．3 B ．－3 C ．－2 D ．2 28. （2012黑龙江绥化3分）下列计算正确的是【】A ．-|-3|=-3B ．30=0C ．3-1=-3 D ． 39±=29. （2012黑龙江龙东地区3分）若（a －1）2+|b －2|=0，则（a －b ）2012的值是【】A. －1B. 1C. 0D. 2012 二、填空题1. （2012天津市3分）∣－3∣= ▲ ．2.（2012上海市4分）计算112-= ▲ ． 3. （2012广东肇庆3分）计算5120⋅的结果是 ▲ ． 4. （2012广东珠海4分）计算11=32-▲ ． 5. （2012浙江杭州4分）某企业向银行贷款1000万元，一年后归还银行1065.6多万元，则年利率高于 ▲ %．6. （2012江苏常州4分）计算：∣－2∣= ▲ ，12--（）= ▲ ，22-（）=▲ ， ▲ 。