面积与微积分

合集下载

微积分求面积公式原理

微积分求面积公式原理微积分是数学中的一门重要学科，它研究的是变化和积分的关系。

在微积分中，面积是一个非常重要的概念，而求面积的公式则是微积分的核心内容之一。

本文将从微积分的角度，探讨面积公式的原理和推导过程。

在微积分中，我们常常需要求解曲线所围成的面积。

对于一个简单的凸曲线来说，我们可以通过直观的方法来求解。

比如，我们可以将曲线分割成若干个小矩形，然后将这些小矩形的面积相加，就可以得到整个曲线所围成的面积。

当我们将这些小矩形的宽度无限缩小，将其个数无限增大时，我们就可以得到曲线的精确面积。

然而，对于一些复杂的曲线来说，使用直观的方法求解面积是非常困难的甚至不可能的。

这时，我们就需要借助微积分的工具来求解面积。

微积分中的面积公式就是为了解决这个问题而产生的。

面积公式的推导过程可以通过积分来实现。

我们可以将曲线所围成的面积分成若干个小的区间，然后将每个小区间的面积相加，最后再将这些小区间的面积无限加和，就可以得到整个曲线所围成的面积。

具体来说，对于一个函数y=f(x)在区间[a,b]上的曲线，我们可以将其分成若干个小区间，每个小区间的长度为Δx。

然后我们可以在每个小区间上选择一个点(xi,yi)，然后计算这个小区间上的矩形面积。

这个矩形的宽度为Δx，高度为f(xi)。

接下来，我们将所有小区间的面积相加，即Σf(xi)Δx。

当我们将Δx 无限缩小，将小区间的个数无限增大时，Σf(xi)Δx就会无限接近于曲线所围成的面积。

用数学的语言来表达，即∫[a,b]f(x)dx = lim(Δx→0) Σf(xi)Δx这个式子就是面积公式的数学表达形式。

其中，∫[a,b]f(x)dx表示函数f(x)在区间[a,b]上的面积，lim(Δx→0)表示当Δx无限趋近于0时的极限值，Σf(xi)Δx表示所有小区间上的矩形面积之和。

通过面积公式，我们可以求解各种复杂曲线所围成的面积。

无论是抛物线、正弦曲线还是其他任何曲线，只要我们能够找到其对应的函数表达式，就可以使用面积公式来求解。

微积分圆面积的推导过程

微积分圆面积的推导过程
微积分中推导圆的面积是一个经典的问题，我们可以通过多种方法来推导圆的面积，其中最常见的方法是使用定积分。

下面我将从多个角度来解释这个问题。

首先，我们知道圆的面积公式是πr^2，其中r是圆的半径。

要推导这个公式，我们可以从圆的定义出发，假设我们要计算半径为r的圆的面积。

我们可以将圆分成许多细小的扇形，然后将这些扇形拼接成一个近似于圆的形状。

接着，我们可以计算每个扇形的面积，然后将这些面积相加，最后取极限得到圆的面积。

另一种方法是利用积分的概念。

我们可以将圆分成许多细小的扇形，每个扇形的面积可以近似为一个矩形的面积，然后我们可以对所有这些矩形的面积进行累加，最后取极限得到圆的面积。

具体来说，我们可以将圆分成许多扇形，每个扇形的面积可以表示为r 乘以扇形的弧长，然后对所有的扇形面积进行积分，即可得到圆的面积公式πr^2。

另外，我们还可以利用极坐标系来推导圆的面积公式。

在极坐标系中，圆的方程可以表示为r=cos(theta)，其中r是到原点的距
离，theta是与x轴的夹角。

我们可以利用极坐标系下的面积元素公式来推导圆的面积，然后对整个圆的面积元素进行积分，最终也可以得到圆的面积公式πr^2。

总之，推导圆的面积是微积分中的经典问题，可以通过分割成扇形、利用积分的概念以及极坐标系等多种方法来完成。

以上是我对微积分圆面积推导过程的多角度解释，希望能够帮助到你。

圆面积微积分推导

圆面积微积分推导
摘要：
一、圆面积公式回顾
1.圆面积公式
2.圆面积公式的推导
二、微积分基本概念
1.导数
2.积分
三、圆面积微积分推导
1.圆的面积与半径的关系
2.圆面积的导数
3.圆面积的积分
4.应用微积分推导圆面积公式
四、结论
1.圆面积公式推导完成
2.微积分在圆面积问题中的应用
正文：
一、圆面积公式回顾
圆是平面内到定点的距离等于定长的所有点的集合，其面积公式为：S = πr，其中r为圆的半径。

二、微积分基本概念
1.导数：导数是描述一条曲线（函数）在某一点处斜率的概念，用f"(x)表示。

2.积分：积分是导数的逆运算，表示求曲线下的面积，用∫表示。

三、圆面积微积分推导
1.圆的面积与半径的关系：圆的面积公式可以改写为S = 2πr * r。

2.圆面积的导数：对圆面积公式求导，得到dS/dr = 4πr。

3.圆面积的积分：对圆面积的导数进行积分，得到S = 2πr/3 + C。

4.应用微积分推导圆面积公式：将圆面积的积分结果与原公式S = πr进行对比，可得C = 0，从而得到圆面积公式S = πr。

四、结论
1.通过微积分的推导方法，我们成功地证明了圆面积公式S = πr的正确性。

微积分等于面积

微积分等于面积微积分是数学中的一门重要学科，它是研究极限、导数、积分等概念和方法的学科。

微积分的应用非常广泛，涉及到物理、化学、经济学、生物学等多个领域。

在微积分中，有一个非常重要的定理，那就是微积分等于面积。

微积分的基础是极限，极限是指当自变量趋近于某个值时，函数的取值趋近于某个值。

在微积分中，我们常常用极限来定义导数和积分。

导数是函数在某一点的变化率，而积分则是函数在某一区间内的面积。

在微积分中，我们可以通过求导来求函数的极值和拐点，从而确定函数的性质。

而通过积分，我们可以求出函数在某一区间内的面积，这个面积可以表示函数所代表的物理量，比如速度、加速度、质量等等。

微积分等于面积的定理是指，如果我们对一个函数进行积分，得到的结果就是该函数所代表的曲线下的面积。

这个定理在微积分中非常重要，因为它可以帮助我们求出很多物理量，比如速度、加速度、质量等等。

在微积分中，我们常常用定积分来求函数在某一区间内的面积。

定积分的计算方法非常简单，只需要将函数在该区间内的面积分成无数个小矩形，然后将这些小矩形的面积加起来，就可以得到函数在该区间内的面积。

除了定积分之外，微积分中还有一种重要的积分方法，那就是不定积分。

不定积分是指求出一个函数的原函数，也就是说，如果一个函数的导数是f(x)，那么它的原函数就是F(x)。

不定积分在微积分中非常重要，因为它可以帮助我们求出函数在任意一点的值。

总之，微积分是数学中的一门重要学科，它涉及到很多重要的概念和方法，比如极限、导数、积分等等。

微积分等于面积的定理是微积分中非常重要的一个定理，它可以帮助我们求出很多物理量，比如速度、加速度、质量等等。

在学习微积分的过程中，我们需要认真理解这个定理，并且掌握好定积分和不定积分的计算方法。

经济学微积分定积分的应用求面积体积

(3) 生产多少单位产品才能获得最大利润；
(4) 最大利润是多少?
解：(1)
C( x) C(0)
x
C(t)dt 200
x
(16 0.002t)dt
0
0
16x 0.001x2 200
(2) L( x) R( x) C( x) px C( x) (20 0.001x)x (16x 0.001x2 200) 0.002x2 4x 200
S
2

y

4

2
dy
18.
选x为积分变量
2
8
S 0 2x ( 2x ) dx 2 ( 2x ( x 4))dx 18.
例：求由曲线 y 1 与y x, x 2 所围面积。
x
解：画草图，
y y 1
x
2
1
S

1
(x

)dx x
c
d
b
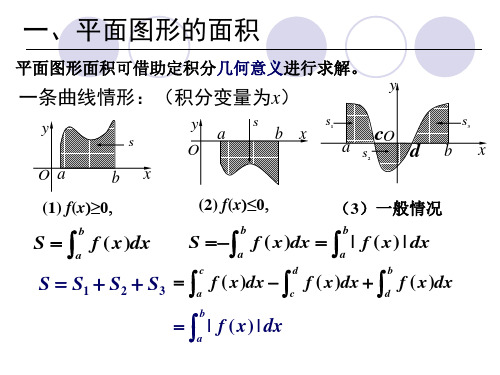
S S1 S2 S3
f ( x)dx
a
c
f ( x)dx
d
f ( x)dx
b
a | f ( x) | dx
由y f ( x), x a, x b及x轴所围图形的面积为
b
S a | f ( x) | dx
一条曲线（积分变量为y）
y
d
x (y)
y
d
y
d
x (y) e
c
c
c
O
x
O
x
O
x
(1) ( y) 0 (2) ( y) 0

面积微分和面积

面积微分和面积微积分在数学中的应用微积分，是一门关于极限、函数、导数和积分的数学学科。

在微积分中，面积微分是非常重要的一个概念，它是用来计算曲线下方的面积或者曲线围成的面积的。

本文将从基本概念、应用场景以及具体例子来解析面积微分与面积的关系。

一、基本概念——面积积分面积积分是在平面上对某个区域进行积分的一种方式，它的本质是在某个区域上把无限多个微小的面积相加，最终得到整个区域的总面积。

通常情况下，我们用∫∫D f(x, y) dxdy 来表示面积积分，其中 D 为被积区域，f(x, y) 为被积函数，dxdy 表示对 x 和 y 的积分。

以曲线 y = x²为例，我们可以通过面积积分来计算其围成的面积。

首先，我们需要找到积分的上下限，此时我们可以通过求解 y = x²和 y = 0 的交点得到。

根据积分的定义，我们需要在考虑的区域上找到无限个微小的面积，那么每个微小面积的大小就是ΔS =f(x, y)ΔxΔy，将此式中的Δ 替换成微分符号，最终的面积积分公式为：∫∫D f(x, y) dxdy = ∫₀¹ ∫₀x² 1 dydx如果我们要计算曲线 y = sin(x) 与 x 轴之间围成的面积，那么我们可以通过以下计算得出：∫π₀ ∫sin(x)₀ 1 dydx = ∫π₀ [y]sin(x)₀ᵖ dx = 2二、应用场景——面积微分与曲线下方面积面积微分可以被广泛应用于计算曲线围成的面积或者曲线下方的面积，例如在物理、工程学领域中。

比如说，在机械学中，为了求解活塞从轨迹曲线上移动的距离，我们需要计算曲线围成的面积。

在结构力学中，曲线下方的面积可以被用来计算物体的质心或者重心。

下面，举一个例子来说明如何通过面积微分来计算曲线下方的面积。

考虑曲线 y = x³，我们希望计算这个曲线在 x ∈ [0, 1] 的区间内围成的面积。

我们可以按照以下步骤进行计算：1. 找到积分的上下限——在此例中，我们需要计算 x ∈ [0, 1] 的区间内所围成的面积，因此积分的上下限应该为∫₁⁰2. 通过面积微分计算面积——我们可以用∫₁⁰x³dx 来计算这个曲线在 x ∈ [0, 1] 区间内所围成的面积3. 完成积分——将 x³带入 x 的积分公式中，得出：∫₁⁰ x³dx = [¼x⁴]₁⁰ = ¼因此，曲线 y = x³在 x ∈ [0, 1] 区间内围成的面积为 ¼。

如何运用微积分理论解决面积体积问题

如何运用微积分理论解决面积体积问题微积分是数学的一个重要分支，它以函数为对象研究极限、导数和积分等概念。

微积分的应用非常广泛，其中包括解决面积和体积问题。

本文将介绍如何运用微积分理论解决面积和体积问题，以帮助读者更好地理解和应用微积分知识。

一、面积问题的微积分解法在解决面积问题时，可以运用微积分中的定积分概念。

定积分表示曲线与坐标轴之间的面积，我们可以通过定积分求解不同形状的面积。

1. 矩形的面积我们首先考虑最简单的情况，矩形的面积。

假设一个矩形的长为a，宽为b，我们可以将其面积表示为：S = a * b。

2. 直角三角形的面积对于直角三角形，我们只需要知道两条直角边的长度，就可以计算出其面积。

假设直角三角形的直角边长分别为a和b，则面积可以表示为：S = 0.5 * a * b。

3. 弧线图形的面积当我们需要计算弧线图形的面积时，可以使用定积分来求解。

首先，我们需要找到弧线对应的函数表达式，并确定积分的上下限。

然后，利用定积分的计算方法，求解出曲线与x轴之间的面积。

二、体积问题的微积分解法在解决体积问题时，可以运用微积分中的定积分和旋转体的概念。

定积分可以帮助我们计算不同形状的体积。

1. 平面图形的旋转体体积对于平面图形的旋转体，我们可以通过定积分来计算其体积。

首先，我们需要找到平面图形对应的函数表达式，并确定积分的上下限。

然后，利用定积分的计算方法，求解出旋转体的体积。

2. 空间图形的体积对于空间图形，我们可以通过分解为多个平面图形，然后利用定积分来计算体积。

首先，我们需要确定空间图形的切面，然后对每个切面进行面积计算，最后通过定积分将各个切面的面积相加，得到整个空间图形的体积。

三、小结通过微积分理论，我们可以解决各种面积和体积问题。

对于面积问题，我们可以利用定积分来计算不同形状的面积，包括矩形、直角三角形和弧线图形等。

对于体积问题，我们可以利用定积分和旋转体的概念来计算平面图形的旋转体和空间图形的体积。

微积分中的定积分与面积

微积分中的定积分与面积微积分是数学中的一门重要学科，其研究对象主要是函数的性质和变化规律。

微积分中的定积分与面积是两个息息相关的概念，下面将对它们进行详细的介绍。

首先，我们来了解一下什么是定积分。

在微积分中，定积分是一个数的极限。

通过分割区间，将其分为无限多个小区间，并将区间内每个小区间的面积相加，就可以得到最终的定积分。

对于函数y=f(x)，在区间[a,b]上的定积分可以表示为∫[a,b]f(x)dx。

这个表示中的∫符号代表求和的意思，[a,b]表示积分的区间，f(x)表示被积函数。

dx是一个微小的自变量，代表区间的长度。

然后，我们来看一下定积分的几何意义。

定积分可以用来计算曲线与x轴之间的面积。

具体来说，如果f(x)表示的是曲线在某一点的纵坐标，那么区间[a,b]上的定积分就表示这段曲线与x轴之间的面积。

这里需要注意的是，在计算定积分时，需要将区间[a,b]分成无限多个小区间，并在每个小区间内选取一个代表性点，计算该点处函数值与小区间长度的乘积，再将它们相加。

而且，为了准确计算，小区间的长度必须无限接近于0。

当被积函数f(x)是正值函数时，定积分代表了曲线与x轴之间的面积。

当被积函数f(x)是负值函数时，定积分的值就是曲线与x轴之间的面积的负值。

当被积函数f(x)有正有负时，定积分的值等于曲线上方的面积减去曲线下方的面积。

定积分还有一个重要的性质，即可加性。

这意味着，如果将一个区间分成两段，那么整个区间上的定积分等于这两段定积分的和。

这个性质在实际计算中非常有用，可以将复杂的区间分割成多个简单的小区间，然后计算每个小区间的面积，最后再将它们相加。

除了计算曲线与x轴之间的面积，定积分还可以用来计算曲线的弧长、质量、力和功等问题。

例如，曲线的弧长可以通过定积分公式S=∫√(1+(dy/dx)^2)dx进行计算，其中dy/dx表示曲线的斜率。

另外，对于定积分应用中的一些特殊情况，有一些常用的公式和技巧可以简化计算。

微积分中的定积分与面积计算

微积分中的定积分与面积计算微积分是数学中的一个重要分支，包含了微分与积分两个方面。

在微积分中，定积分是一个非常重要的概念，它与面积计算密切相关。

本文将介绍定积分的概念、性质，以及如何利用定积分来计算曲线下的面积。

一、定积分的概念与性质定积分是微积分中的一个基本概念，它可以用来计算曲线与坐标轴之间的面积。

在数学中，定积分可以看作是一个函数在某个区间上的加权平均值。

具体来说，对于一个函数f(x)，我们可以将其分割成无穷多个小区间，每个小区间的长度为Δx。

然后，我们计算每个小区间上的函数值f(x)乘以Δx的乘积，并将所有乘积相加。

当Δx趋近于0时，这个和就收敛于一个确定的值，即定积分。

定积分的符号表示为∫f(x)dx，其中f(x)为被积函数，dx表示积分变量。

定积分的计算可以通过积分的定义和一系列的积分性质来完成。

其中，积分的定义是通过极限的概念来定义的，即∫f(x)dx = lim(Δx→0) Σf(x)Δx定积分具有一些重要的性质，包括线性性质、区间可加性、保号性等。

线性性质指的是定积分具有加法和数乘的性质，即∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx。

区间可加性指的是对于一个函数在不同区间上的定积分，可以将其分割成多个小区间的定积分的和。

保号性指的是如果一个函数在一个区间上恒大于等于0，则其定积分也大于等于0。

二、利用定积分计算曲线下的面积定积分与面积计算密切相关，可以用来计算曲线与坐标轴之间的面积。

具体来说，对于一个函数f(x)，我们可以通过定积分来计算其在某个区间[a, b]上的面积。

计算方法如下：1. 首先，我们需要确定被积函数f(x)以及积分的区间[a, b]。

2. 将区间[a, b]分成无穷多个小区间，每个小区间的长度为Δx。

3. 在每个小区间上选择一个代表点xi，计算对应的函数值f(xi)。

4. 计算每个小区间上的函数值f(xi)乘以Δx的乘积，并将所有乘积相加。

微积分中的曲线积分与面积计算方法

微积分中的曲线积分与面积计算方法微积分是数学中的一个重要分支，它包括微分和积分两大部分。

在微积分中，曲线积分和面积计算是其中两个重要的概念和计算方法。

本文将介绍曲线积分和面积计算的概念、性质以及具体的计算方法。

一、曲线积分曲线积分是微积分的一个重要概念，它描述了沿曲线的积分。

在数学中，曲线通常表示为参数方程或者向量函数。

曲线积分可以分为第一类曲线积分和第二类曲线积分两种形式。

1.第一类曲线积分第一类曲线积分也称为标量值曲线积分，它是将曲线上的每一点乘以一个标量函数后再对其进行累加。

数学上，第一类曲线积分的计算公式为：∫f(x,y)ds = ∫f(x(t),y(t))√(dx/dt)²+(dy/dt)²dt其中, f(x,y)是一个标量函数， (x(t),y(t))是曲线的参数方程，ds是曲线上的线元长度。

2.第二类曲线积分第二类曲线积分也称为矢量值曲线积分，它是将曲线上的每一点乘以一个向量函数后再对其进行累加。

数学上，第二类曲线积分的计算公式为：∫F·dr = ∫(Pdx+Qdy)其中，F=(P,Q)是一个矢量函数，dr=(dx,dy)是曲线上的切向量。

二、面积计算方法面积计算是微积分中另一个重要的应用领域。

对于一条曲线所围成的封闭区域，我们可以使用曲线积分来计算其面积。

在进行面积计算时，可以采用累加法或者使用格林公式。

1.累加法累加法是面积计算中常用的一种直观方法。

我们可以将封闭区域分成若干个小的图形，然后计算每个小图形的面积，最后将所有小图形的面积累加得到所求的面积。

2.格林公式格林公式是基于曲线积分的面积计算方法。

对于封闭曲线C，其包围的区域记为D，我们有如下公式：∫Pdx+Qdy = ∬D((∂Q/∂x) - (∂P/∂y))dA其中，D为封闭区域的面积，(∂Q/∂x)和(∂P/∂y)分别是矢量函数F=(P,Q)的偏导数。

总结：微积分中的曲线积分和面积计算是重要的概念和计算方法。

微积分中的积分与曲线面积计算

微积分中的积分与曲线面积计算微积分是数学中的一个重要分支，它涉及到函数的导数和积分。

而在微积分中，积分与曲线面积计算有着密切的关系。

本文将介绍微积分中的积分与曲线面积计算的相关概念和方法。

1. 积分的概念积分是微积分中的一个基本概念，它是对函数的一种运算。

在微积分中，积分可以看作是函数的反导数。

给定一个函数f(x)，它的积分可以表示为∫f(x)dx，其中dx表示对x的微小变化。

积分可以理解为函数曲线下的面积。

2. 定积分与不定积分在微积分中，积分分为定积分和不定积分两种形式。

定积分是对函数在一定区间上的积分，可以表示为∫a~bf(x)dx，其中a和b分别是积分的上限和下限。

定积分表示了函数在给定区间上的累积效果，可以用来计算曲线下的面积。

而不定积分则是对函数的一种反运算，表示函数的原函数。

3. 曲线面积的计算在微积分中，积分可以用来计算曲线下的面积。

对于一个函数f(x)，如果我们要计算它在[a, b]区间上的曲线下的面积，可以使用定积分来表示，即∫a~bf(x)dx。

这个积分的结果就是曲线下的面积。

4. 划分区间与近似计算在实际计算中，如果要计算复杂函数的曲线下的面积，通常会将区间划分成多个小区间，并在每个小区间上进行近似计算。

这种方法被称为数值积分或数值逼近。

常用的数值积分方法有梯形法则、辛普森法则等。

通过将区间划分成多个小区间，并在每个小区间上进行近似计算，可以得到曲线下的面积的近似值。

5. 曲线面积的应用曲线面积的计算在实际中有着广泛的应用。

例如，在物理学中，曲线下的面积可以表示物体的位移、速度和加速度等。

在经济学中，曲线下的面积可以表示某个时间段内的经济收益或成本。

在工程学中，曲线下的面积可以表示材料的体积或能量的消耗等。

因此，曲线面积的计算在各个领域都有着重要的应用价值。

综上所述，微积分中的积分与曲线面积计算有着密切的关系。

积分可以看作是函数的反导数，而曲线面积可以通过积分来计算。

通过划分区间和近似计算，我们可以得到曲线下的面积的近似值。

微积分中的积分与面积计算方法研究

微积分中的积分与面积计算方法研究微积分中的积分与面积计算方法是微积分学中的重要部分，它们在求解曲线下面积、曲线长度、体积、定积分等问题中起着至关重要的作用。

本文将从基本概念入手，详细介绍微积分中的积分与面积计算方法，并对几种常用的方法进行研究。

首先，我们来了解微积分中的积分概念。

在微积分中，积分是对函数的整体变化进行量化的数学工具。

通过积分运算，我们可以求取函数的面积、曲线长度、体积等。

基本概念包括不定积分和定积分。

不定积分表示函数的原函数，定积分表示函数在给定区间上的面积。

接下来，我们研究微积分中的面积计算方法。

一种常用的方法是求解曲线的下面积。

通过将曲线分割成若干个小矩形，在每个小矩形上计算面积，并将这些小矩形的面积加和，就可以得到曲线下的面积。

这种方法被称为黎曼和。

还有一种方法是使用梯形法则，将曲线分割成若干个小梯形，计算每个小梯形的面积，并将它们加和，即可得到曲线下的面积。

此外，还有较为复杂的辛普森法则和高斯-勒让德求积公式等方法，它们在特定情况下能够提供更精确的结果。

除了面积计算方法，微积分中的积分还可用于求解曲线的长度。

曲线的长度可以通过对曲线进行分割，计算每段曲线的长度，并将它们加和得到。

这种方法被称为弧长公式。

当曲线较为复杂时，可以使用数值方法进行求解，如欧拉法或龙格-库塔法等。

这些数值方法通过近似计算来获得曲线的长度。

在微积分中，积分还可以用于求解体积问题。

在求解立体体积时，可以通过构造适当的平行截面，将体积分割成无穷多个小体积，对每个小体积进行计算，并将它们加和起来，即可得到整个体积。

这种方法被称为截面法。

此外，还有其他方法如鉴别体积法和泛函法等，它们可以提供更加灵活和高效的体积计算方式。

最后，我们对几种常用的积分计算方法进行研究。

首先是不定积分，它是求取函数的原函数的过程。

常用的方法有换元法、分部积分法和三角代换法等。

这些方法通过对积分的转化与简化，使得求解更为方便。

另外，定积分是求取函数在给定区间上的面积的过程。

微积分的应用的面积体积与平均值

微积分的应用的面积体积与平均值微积分的应用：面积、体积与平均值微积分是数学中的一门重要学科，旨在研究函数的变化率与积分。

它不仅具有纯粹的数学理论意义，也广泛应用于其他学科，如物理学、工程学和经济学等。

其中，微积分在计算面积、体积以及求解平均值等问题上发挥了重要作用。

本文将探讨微积分在这些方面的应用。

一、面积的计算微积分可以帮助我们计算各种几何形状的面积。

其中，最基本的是计算矩形、三角形和圆形等常见几何形状的面积。

1. 矩形的面积计算矩形的面积等于其宽度乘以长度。

假设一个矩形的宽度为w，长度为l，则其面积S可以表示为S = w * l。

在利用微积分计算矩形的面积时，可以将其看作是宽度为w的矩形函数f(x)与长度为l的区间[a, b]之间的积分，即S = ∫[a,b]f(x) dx。

2. 三角形的面积计算三角形的面积等于其底边长度乘以高的一半。

假设一个三角形的底边长度为b，高为h，则其面积S可以表示为S = (1/2) * b * h。

同样，在利用微积分计算三角形的面积时，可以将其看作是底边长度为b的三角形函数f(x)与高为h的区间[a, b]之间的积分，即S = (1/2) *∫[a,b]f(x) dx。

3. 圆形的面积计算圆形的面积等于π乘以半径的平方。

假设一个圆形的半径为r，则其面积S可以表示为S = π * r^2。

通过微积分计算圆形的面积时，可以将其看作是半径为r的圆形函数f(x)在区间[a, b]上的积分，即S = π *∫[a,b]f(x) dx。

二、体积的计算微积分不仅可以计算几何形状的面积，还能够帮助我们计算各种几何体的体积。

下面以球体和圆柱体为例介绍微积分在体积计算中的应用。

1. 球体的体积计算球体的体积等于(4/3)乘以π乘以半径的立方。

假设一个球体的半径为r，则其体积V可以表示为V = (4/3) * π * r^3。

在微积分中，可以将球体看作半径为r的球体函数f(x)在区间[a, b]上的积分，即V = (4/3) * π * ∫[a,b]f(x) dx。

微积分计算面积举例

微积分计算面积举例
嘿，朋友们！今天咱就来讲讲微积分计算面积这事儿！你们知道吗，这可真是个超有意思的东西呢！
比如说，咱想象一下，有一块形状奇奇怪怪的地（就像那坑坑洼洼的月球表面一样），咱得知道它有多大面积。

这时候微积分不就派上用场啦！就好比你要给这块地围个篱笆，你得知道要准备多长的篱笆才行吧。

再看看日常生活中的蛋糕，一个圆形蛋糕，咱怎么精确算出上面那层奶油的面积呀？微积分呀！它就像一把神奇的钥匙，能打开面积计算的大门。

你想想，如果连个蛋糕奶油面积都算不清楚，那吃起来都没那么香了吧！哈哈！
还记得有一次，我和几个同学一起研究一个不规则图形的面积（那图形简直比毕加索的画还抽象）。

我们就像侦探一样，一点点用微积分去剖析它。

这个说这样算，那个说那样算，争论得可激烈了。

最后算出答案的时候，那种兴奋感，真的无法形容！就好像解开了一个超级大难题，那成就感爆棚啊！
还有一次，在课堂上老师给我们讲了个例子，说可以用微积分算一个奇怪瓶子的横截面积呢。

哇塞，当时我就在想，这也太神奇了吧，连个瓶子都能搞定！这岂是一般人能想到的呀。

所以啊，朋友们，微积分计算面积真的是超级重要又有趣的呢！它能让我们面对那些奇奇怪怪的形状不再迷茫，而是充满信心地去探索它们的面积。

真的，它就像我们探索面积世界的秘密武器一样，不用可就太可惜啦！赶紧去试试吧！。

微积分求sin面积

微积分求sin面积微积分是数学中的一个分支，主要研究函数的变化、变化率以及面积、体积等几何问题。

在微积分中，我们经常会遇到求解曲线下面积的问题，其中包括求解sin函数的面积。

要求sin函数的面积，通常是指求解sin函数在某个区间上的曲线与x轴之间的面积。

对于这个问题，我们可以通过微积分的方法来求解。

我们需要确定sin函数的区间。

由于sin函数的周期为2π，我们可以将区间限定在一个周期内，比如[0, 2π]。

然后，我们可以将这个区间分成若干个小区间，对每个小区间进行计算。

接下来，我们需要确定每个小区间的宽度。

我们可以将整个区间等分成n个小区间，每个小区间的宽度为Δx，即Δx = (2π-0)/n。

然后，我们可以在每个小区间上取一个点，将这个点的纵坐标代入sin函数得到一个面积的近似值。

为了求解整个区间的面积，我们可以将每个小区间的近似值相加。

即A ≈ Δx * (sin(x1) + sin(x2) + ... + sin(xn))，其中x1，x2， (x)为每个小区间上选择的点。

随着n越来越大，我们可以得到更加精确的面积近似值。

当n趋向于无穷大时，我们可以得到sin函数在整个区间上的准确面积。

除了上述方法外，我们还可以使用定积分的方法来求解sin函数的面积。

定积分是微积分中的一个重要概念，表示函数在某个区间上的面积。

对于sin函数在区间[0, 2π]上的面积，我们可以使用定积分的形式进行求解。

即A = ∫[0, 2π] sin(x)dx。

通过求解这个定积分，我们可以得到sin函数在整个区间上的准确面积。

在实际应用中，我们可以将sin函数的面积问题推广到任意区间上。

通过微积分的方法，我们可以求解任意函数在任意区间上的面积。

总结起来，求解sin函数的面积是微积分中的一个重要问题。

我们可以通过近似值的方法或者定积分的方法来求解。

无论是哪种方法，微积分都为我们提供了一种强大的工具，帮助我们解决各种几何问题。

三角形面积微积分

三角形面积微积分三角形是数学中十分重要的几何图形，的出现可以追溯到古希腊和罗马时期。

早期的几何学中，三角形被认为是最基本的几何图形，被认为具有特殊的性质，例如它的面积可以用三边的长度来确定。

种性质被称为“三角形面积公式”。

三角形的面积是许多数学问题的基础，此研究三角形面积的方法源源不断。

古希腊和罗马时期，三角形面积的计算可以通过根据三角形三边长度和内角求出其面积来实现。

种方法被称为“测地学”，在17世纪中叶得到了大量发展，以更精确地计算三角形面积。

然而，面临测地学无法解决的问题时，要运用其他方法来计算三角形面积。

三角形面积的微积分法是这类方法的代表，可以通过对三角形的底边和高进行微积分求解。

管微积分法并不容易，但它可以用来解决测地学方法所不能解决的问题，在三角形的研究中发挥着重要的作用。

三角形面积的微积分法可以用一个简单的实证示例来解释。

三角形的三条边长分别为a， b， c，三角形做如下坐标变换：x = a - bty = c - btz = bt由于三角形面积的定义是高乘以底的一半，此根据上式可以得出三角形面积的微积分：S = 1/2 * (x y)dt其中t是坐标变换中的参数，t从0到1时，三角形的面积S 就可以由上式计算出来。

从宏观上看，三角形面积的微积分是通过分析三角形的边长和内角的凸多边形面积的极限来实现的。

三角形面积的微积分可以用许多种方法来解决，例如可以使用Green公式或极端值技术，但不管采用哪种方法，需要计算三角形的变形面积。

虽然微积分是一种复杂的方法，但它却是三角形面积计算的关键技术。

今，积分法已经被用于许多数学问题的解决，例如最小矩形面积的计算、形的积分计算等等。

表明三角形面积的微积分确实是一种重要的技术，许多数学方面都有着广泛的应用。

由此可见，三角形面积的微积分是一种十分重要的数学方法，可以用来解决测地学方法难以解决的问题，帮助我们更好地研究三角形的特性及其衍生出的其他几何图形。

球面积微积分推导

球面积微积分推导球面积微积分是一门研究球体表面积的数学学科。

它通过对球体表面进行分割和求和，来推导球面积的公式。

这门学科的研究对象是球体的曲面积分，通过对球面上的微小曲面元的面积进行求和，来得到整个球面的面积。

在球面积微积分中，我们首先需要将球面分割成许多微小的曲面元。

这些微小的曲面元可以近似看作是平面，因此可以使用平面上的积分来计算其面积。

然后，我们将这些微小曲面元的面积进行累加，得到整个球面的面积。

为了更好地描述这个过程，让我们假设球体的半径为R。

我们可以将球面分割成许多纬线和经线相交形成的小矩形区域。

每个小矩形区域都可以看作是一个微小的曲面元。

我们可以选取一个纬线和一个经线作为边界，将球面分割成一个小矩形区域。

这个小矩形的宽度可以表示为Δφ，即纬线的间隔。

而长度可以表示为Δθ，即经线的间隔。

接下来，我们可以计算这个小矩形的面积。

由于这个小矩形可以近似看作是平面，其面积可以用平面上的面积公式计算。

假设这个小矩形的边长分别为Δφ和Δθ，那么它的面积可以表示为ΔS=Δφ·Δθ。

然后，我们将这个小矩形的面积进行累加。

我们可以让纬线的间隔Δφ趋近于0，使得纬线的数量无限增加。

同时，我们也可以让经线的间隔Δθ趋近于0，使得经线的数量无限增加。

这样，通过将这些小矩形的面积ΔS进行累加，就可以得到整个球面的面积S。

通过对ΔS进行求和的过程，我们可以得到球面积的公式：S=∫∫R^2 sinφ dφ dθ其中，R是球体的半径，φ是纬度角，θ是经度角。

球面积微积分是一门重要的数学学科，它在物理学、工程学等领域中有着广泛的应用。

通过研究球面积微积分，我们可以更好地理解球体的性质，并应用于实际问题的求解中。

球面积微积分是一门研究球体表面积的数学学科，通过对球面进行分割和求和，推导出球面积的公式。

它的研究对象是球体的曲面积分，通过对球面上的微小曲面元的面积进行求和，得到整个球面的面积。

这门学科的研究对于深入理解球体的形态和性质，以及解决与球体相关的实际问题具有重要意义。