清华大学理论力学lecture09A
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
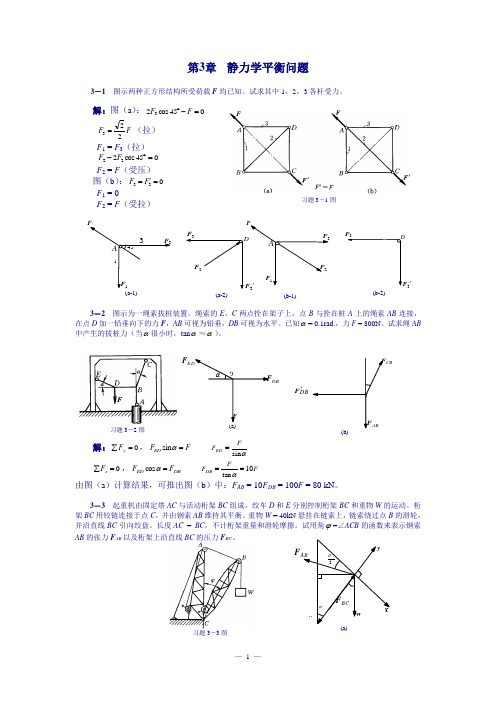
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
【最新试题库含答案】清华理论力学课后答案4

清华理论力学课后答案4篇一:理论力学课后习题答案第4章运动分析基础第4章运动分析基础4-1 小环A套在光滑的钢丝圈上运动,钢丝圈半径为R(如图所示)。
已知小环的初速度为v0,并且在运动过程中小环的速度和加速度成定角θ,且 0 <θ<?,试确定小环2A的运动规律。
22解:asin??a?v,a?v nRsin?R2vdvt1a?dv?acos??v,?dt t2??v00vdtRtan?Rtan?v?ds?v0Rtan?dtRtan??v0tstv0Rtan?ds??0?0Rtan??v0tdtAs?Rtan?lnRtan?Rtan??v0t习题4-1图2??x?3sint?x?4t?2t1.?, 2.?2y?2cos2t?y?3t?1.5t??4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的解:1.由已知得 3x = 4y ? v?5?5t?y?3?3t? ?a??5 ??y??3????4x????4?4t?x(1)为匀减速直线运动,轨迹如图(a),其v、a图像从略。
2.由已知,得arcsinx3?12arccosy242(b)习题4-2图化简得轨迹方程:y?2?x9(2)轨迹如图(b),其v、a图像从略。
4-3 点作圆周运动,孤坐标的原点在O点,顺钟向为孤坐标的正方向,运动方程为s?12?Rt2,式中s以厘米计,t以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y坐标值最大的位置时,求点的加速度在x和y轴上的投影。
解:v?s???Rt,at?v???R,an?v??2Rt2y坐标值最大的位置时:?s? ax?at??R,ay???R22R12?Rt2??22R,?t?1习题4-3图4-4 滑块A,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
试求滑块的速度随距离x 的变化规律。
解:设t = 0时AB长度为l0,则t时刻有:r (?t?arcta?arctan)r?l?x2?r2l0x2?r2对时间求导:?r??r2x22xx?r?rx ???xx2?r2???xxx?r224-5 凸轮顶板机构中,偏心凸轮的半径为R,偏心距OC = e,绕轴O以等角速转动,从而带动顶板A作平移。
理论力学第9章A

• 运动的特点
– 刚体的运动不仅仅是定轴转动和平面运动
• 实验手段的特点
– 不仅有物理实验还有计算机仿真实验
• 研究方法的特点
– 多学科交叉(数学、物理、力学、计算机)
2013-3-5 9
理论力学
• 问题(现象)的提出
学习上应注意的问题
– 问题是怎样产生的;原有的方法为什么不能(不易) 解决该问题;解决该问题有哪些“新”途径。
δx ≠ 0, F − 4ma = 0
23
理论力学
αB
x
A
§9-1 动力学普遍方程
例:图示系统在铅垂平面内运动,各物体的质量均为m,圆盘的半径为 R,绳索与圆盘间无相对滑动。求滑块的加速度和圆盘C 的角加速度。
应用动力学普遍方程
aA
B
αC θ
M IB
∑ (F + F
i =1 i
n
Ii
) ⋅ δri = 0
2013-3-5 22
理论力学
§9-1 动力学普遍方程
例:图示系统在铅垂平面内运动,各物体的质量均为m,均质圆盘的半径 为R,圆盘在地面上纯滚动,若板上作用有一个主动力F。求板的加速度。
α
M IC
FI
FI a
α
M IC
FI
F
∑ (F + F
i =1 i
n
应用动力学普遍方程
Ii
) ⋅ δri = 0
0
x0
1 + y '2 2 gy
dx
曲线方程为:
2013-3-5
x = c(θ − sin θ )
y = c(1 − cos θ )
15
理论力学
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
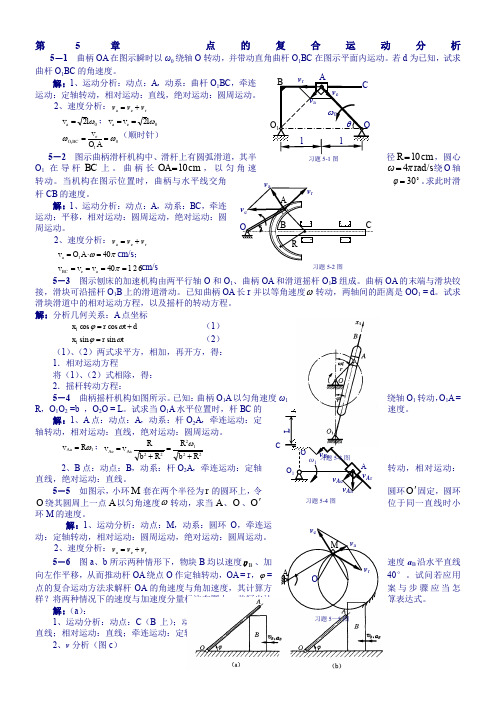
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
清华大学版理论力学课后习题答案大全 第10章动能定理及其应用习题解

A(a)O(a)第10章 动能定理及其应用10-1 计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A 、B 两点的速度方向如图示,B 点的速度为v B ,θ = 45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v (图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.222222163)2(2121)2(212121B B B C C C mv r v mr v m J mv T =⋅+=+=ω 2.222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2 图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]c o s 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
清华大学本校用理论力学课件8-1第二类拉格朗日方程

第二类拉格朗日方程
2019年2月21日
广义坐标中的达伦伯-拉格朗日原理
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
理想完整约束系统:广义坐标为q1, q2, …, qN
质点i矢径: ri ri ( q1 , q2 ,
, qN , t )
n i 1
n
ri ri qk qk k 1
Qk Q 0
* k
T d Q dt qk
* k
T q k
V 如主动力都是有势力: Qk qk
d T dt qk T V q qk k
d T dt qk
T q Qk , k 1,2, k
O
y x R
R
m
L ( J mR 2 sin 2 )
d L ( J mR2 sin2 ) 2mR2 sin cos dt
例4
解
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
d L L Q dt
第 二 类 拉 格 朗 日 方 程 及 其 应 用
应用拉格朗日方程的解题步骤为 判断系统是否为完整约束,主动力是否 有势,以决定能否应用拉格朗日方程以 及应用何种形式的拉格朗日方程。 确定系统的自由度数,选择合适的广义 坐标。
按所选的广义坐标,写出系统动能、势 能或广义力。
把动能、广义力或拉格朗日函数代入拉格 朗日方程。
n n d 1 1 2 2 mi ri mi ri dt qk i 1 2 qk i 1 2
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解

F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
理论力学课件 第九章动量定理,质点和质点系动量定理

5、解方程。
ω
O2
e
O1 θ
例9-3 如图所示,电动机外壳固
定在水平基础上,定子、转子的
质量分别为m1、m2。设定子质心 位 于 转 轴中 心 O1 , 由 于 制 造 误 差,转子质心O2 到O1的距离为
e,已知转子以匀角速度ω 转
动。求: 基础对电机总的水平和
铅垂反力
偏心转子
解:1、研究对象
如何建立受力和运动的关系?
建立运动特征量的变化与 力系作用量的关系
第9章 动量定理
第9章 动量定理
现代跳高为什么采用背越式?
9.1 质点和质点系动量定理
一、基本概念
1 质心
∑ rvC =
m i rvi m
∑ xC =
mi xi m
∑ yC =
mi yi m
∑ zC =
mi zi m
9.1 质点和质点系动量定理
x
m1g
Fx
M O Fy
Fx = −m2ω2e cosωt Fy = −m2ω 2e sin ωt + (m1 + m2 )g
由主动力直接引起的静约束力
Fx静 = 0
Fy静 = (m1 + m2 )g
由质点系运动引起的动约束力
vy
ω
O2
e
O1 θ m2 g
x
m1g
Fx
M O Fy
Fx动 = −m2ω 2e cosωt
9.1 质点和质点系动量定理
思考题:两个相同的均质杆 AB 和 AD 用铰链连接,每个杆的质量为m ,长
为L,在屏幕面内运动。已知铰链A的速度为u,两个杆的角速度为ω(转向
如图),求该瞬时系统的动量。
