第四章简支梁设计计算
钢结构简支梁设计计算书

计算依据:
1、《钢结构设计标准》GB50017-2017
一、基本参数
简支梁长L(m)
10
简支梁间距/受荷面宽B(m)
2.5
恒载标准值Gk(kN/m2)
3
活载标准值Qk(kN/m2)
2
恒载分项系数γG
1.2
活载分项系数γQ
1.4
挠度控制
1/250
材质
Q235
X轴塑性发展系数γx
1.05
满足要求!
2、连接板验算
两块拼接板的净截面积:A=2h×l-2×k×h×r =2×10×200-2×4×10×21.5=2280mm2
剪应力:τ= Vmax/A=84.73×103/2280=37.162N/mm2≤[τ]=125N/mm2
满足要求!
二、梁截面计算
截面类型
工字钢
截面型号
45a号工字钢
截面面积A(cm2)
102
截面惯性矩Ix(cm4)
32240
截面抵抗矩Wx(cm3)
1430
自重标准值gk(kN/m)
0.788
抗弯强度设计值[f](N/mm2)
205
抗剪强度设计值τ(N/mm2)
120
弹性模量E(N/mm2力极限状态:
q=γG(Gk×B+gk)+γQ×Qk×B=1.2×(3×2.5+0.788)+1.4×2×2.5=16.946kN/m
正常使用极限状态:
q'= Gk×B+gk+Qk×B=3×2.5+0.788+2×2.5=13.288kN/m
1、抗弯验算
Mmax=qL2/8=16.946×102/8=211.825 kN·m
4.1主梁内力计算与荷载横向分布计算

此桥在跨度内设有横隔梁,具有强大的横向连结刚性,且承重
结构的长宽比为
l 19.50 2.4>2 B 51.60
各根主梁的横截面均相等,梁数n=5,梁间距为1.60m
5
ai2
a12
a
2 2
a32
a42
a52
(21.60)2+1.602+0+(-1.60)2+(-21.60)2=25.60m2
恒载集度
g 9.76 1.00 3.67 2 16.43kN / m
பைடு நூலகம் 恒载跨中弯矩
M gl2 16.43 19.52 780 .94kN m
8
8
二、活载内力计算
汽车荷载
——车道荷载
汽车荷载等级 公路-I级 公路-II级
均布荷载标准值 qk
集中荷载标准值 Pk
10.5kN/m
计算跨径≤5m Pk =180kN 计算跨径≥50m Pk =360kN
荷载横向分布计算方法
【刚性横梁法】(偏心压力法)——把横隔梁视作刚性极大的梁; 【杠杆原理法】忽略主梁之间横向结构的联系; 【铰接板(梁)法】相邻板(梁)之间视为铰接,只传递剪力; 【刚接梁法】相邻主梁之间视为刚性连接,即传递剪力和弯矩; 【比拟正交异性板法】——将主梁和横隔梁的刚度换算成纵横两向
0.14
]
25
9.76 kN
/
m
(2)横隔梁
g2
[(1
0.08 0.14) (1.6 0.18) (0.15 0.16)] 25 40
2
2
2
/ 5 /19.5
1.00kN / m
(3)桥面铺装
g3
0.02
7
23
《混凝土结构设计原理》第四章_课堂笔记

《混凝土结构设计原理》第四章受弯构件正截面承载力计算课堂笔记◆知识点掌握:受弯构件是土木工程中用得最普遍的构件。
与构件计算轴线垂直的截面称为正截面,受弯构件正截面承载力计算就是满足要求:M≤Mu。
这里M为受弯构件正截面的设计弯矩,Mu为受弯构件正截面受弯承载力,是由正截面上的材料所产生的抗力,其计算及应用是本章的中心问题。
◆主要内容受弯构件的一般构造要求受弯构件正截面承载力的试验研究受弯构件正截面承载力的计算理论单筋矩形戴面受弯承载力计算双筋矩形截面受弯承载力计算T形截面受弯承载力计算◆学习要求1.深入理解适筋梁的三个受力阶段,配筋率对梁正截面破坏形态的影响及正截面抗弯承载力的截面应力计算图形。
2.熟练掌握单筋矩形、双筋矩形和T形截面受弯构件正截面设计和复核的握法,包括适用条件的验算。
重点难点◆本章的重点:1.适筋梁的受力阶段,配筋率对正截面破坏形态的影响及正截面抗弯承载力的截面应力计算图形。
2.单筋矩形、双筋矩形和T形截面受弯构件正截面抗弯承载力的计算。
本章的难点:重点1也是本章的难点。
一、受弯构件的一般构造(一)受弯构件常见截面形式结构中常用的梁、板是典型的受弯构件:受弯构件的常见截面形式的有矩形、T形、工字形、箱形、预制板常见的有空心板、槽型板等;为施工方便和结构整体性,也可采用预制和现浇结合,形成叠合梁和叠合板。
(二)受弯构件的截面尺寸为统一模板尺寸,方便施工,宜按下述采用:截面宽度b=120, 150 , 180、200、220、250、300以上级差为50mm。
截面高度h=250, 300,…、750、800mm,每次级差为50mm,800mm以上级差为100mm。
板的厚度与使用要求有关,板厚以10mm为模数。
但板的厚度不应过小。
(三)受弯构件材料选择与一般构造1.受弯构件的混凝土等级提高砼等级对增大正截面承载力的作用不显著。
受弯构件常用的混凝土等级是C20~C40。
2.受弯构件的混凝土保护层厚度纵向受力钢筋的外表面到截面边缘的最小垂直距离,称为混凝土保护层厚度,用c表示。
简支梁计算例题

简支梁计算例题设计任务:设计一个简支梁,已知梁的跨度L=6米,梁的截面尺寸为b×h=200×400毫米,承受均布荷载设计值q=70kN/m(包括自重),混凝土强度等级为C25,纵向受拉钢筋采用HRB400级钢筋,箍筋采用HPB300级钢筋。
1. 计算梁所受总弯矩M:M = qL²/ 8 = 70 ×6²/ 8 = 255 kN·m2. 计算梁的截面面积A:A = b ×h = 200 ×400 = 80000 mm²3. 计算梁的截面模量W:W = α×A ×fcm = 1.1 ×80000 ×30 = 2640000 N·mm4. 计算梁的抗弯承载力Mu:Mu = fcmw = 30 ×2640000 = 79200000 N·mm > M = 25500000 N·mm5. 计算梁的纵筋数量:由M/mho²+fyAs/s ≤fcd得出As ≥M/(mho²+ fy/s),其中fy为HRB400级钢筋的抗拉强度设计值,取值为360N/mm²。
通过计算得出As≥8176mm²,选用2Φ28的钢筋,As=12568mm²。
6. 计算箍筋数量:根据构造要求,选用Φ8@200的箍筋,每米长度内布置箍筋数量为n=1×100/200+1=2个。
7. 验算裂缝宽度:根据规范要求,裂缝宽度不应超过Wmax=0.3mm。
根据M/γfW≤Wmax,其中γf为受拉或受压区纵向普通钢筋的配筋率,取值为As/(bho),通过计算得出W≤Wmax。
8. 绘制施工图,标明梁的跨度、截面尺寸、纵向钢筋和箍筋的位置和规格。
结论:根据以上计算和验算,该简支梁的设计满足要求,可以用于实际工程中。
(完整版)梁的内力计算
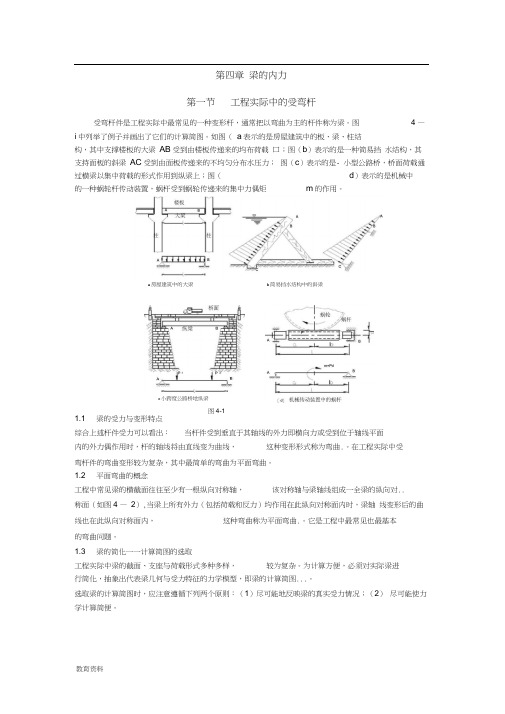
第四章梁的内力第一节工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图 4 —i中列举了例子并画出了它们的计算简图。
如图(a表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB受到由楼板传递来的均布荷载口;图(b)表示的是一种简易挡水结构,其支持面板的斜梁AC受到由面板传递来的不均匀分布水压力;图(c)表示的是- 小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d)表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m的作用。
1.1 梁的受力与变形特点综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲.。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对..称面(如图4 —2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲.。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化一一计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图...。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
a房屋建筑中的大梁c小跨度公路桥地纵梁图4-1b简易挡水结构中的斜梁图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1) 梁本身简化一一以轴线代替梁,梁的长度称为跨度; (2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等; (3) 支座简化——主要简化为以下三种典型支座:(a ) 活动铰支座(或辊轴支座),其构造图及支座简图如图4— 3 (a )所示。
混凝土第四章答案

第四章4.1一钢筋混凝土简支梁,计算跨度为6m ,截面尺寸b ×h =200mm×500mm ,混凝土强度等级C30,纵向受拉钢筋采用3C 20的HRB400级钢筋,环境类别为一类,试求该梁所能负担的均布荷载设计值(包括梁自重在内)?解:(1)确定基本参数查附表知C30级混凝土:2c 14.3N/mm f =,2t 1.43N/mm f =;HRB400级钢筋:2y 360N/mm f =;1 1.0α=,b 0.518ξ=;一类环境:25mm c =,s 22520235mm a c d =+=+=,0s 50035465mm h h a =-=-=;t min y 1.43max 0.2%.45max 0.2%.450.002360f f ρ⎧⎫⎪⎪⎧⎫==⨯=⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭,0,0 3C 20,2s 941mm A =。
(2)判断是否超筋y sb 01c 360941118.4mm<0.518465240.8mm 114.3200f A x h f b ξα⨯====⨯=⨯⨯ 不是超筋梁(3)判断是否少筋s min 9410.0094200500A bh ρρ===>⨯ 不是少筋梁(4)该梁能承担的弯矩设计值u y s 0118.4360941465137.5kN m 22x M f A h ⎛⎫⎛⎫=-=⨯⨯-=⋅ ⎪ ⎪⎝⎭⎝⎭ 故该梁能负担的均布荷载设计值:22088137.530.6kN/m 6M q l ⨯===4.3钢筋混凝土雨棚板,承受均布荷载,计算跨度1m ,垂直于计算跨度方向板的总宽度为6m ,取单位板宽b =1m 的板带计算,板厚100mm ,混凝土强度等级C30,HRB335级钢筋,环境类别为二类b ,单位宽度板带控制截面弯矩设计值 3.6kN m/m M =⋅。
要求计算雨棚板的受力钢筋截面面积,选用钢筋直径及间距,并绘出雨棚板的受力钢筋和分布钢筋平面布置图。
简支梁计算例题

简支梁计算例题(原创实用版)目录1.引言:简支梁的概述2.简支梁的计算方法3.计算例题4.总结正文【引言】简支梁是一种常见的梁式结构,主要用于承受横向载荷。
在工程设计中,简支梁的计算是必不可少的环节。
本文将介绍简支梁的计算方法,并通过例题进行具体讲解。
【简支梁的计算方法】简支梁的计算主要包括以下几个步骤:1.确定梁的材料和截面形状2.计算截面的惯性矩和截面模量3.计算梁的弯曲应力和弯矩4.根据梁的稳定性条件,确定梁的允许载荷【计算例题】假设有一根简支梁,材料为普通钢筋混凝土,截面为矩形,长为 4 米,宽为 0.2 米。
现需要计算该梁在承受最大弯矩时,允许的载荷。
首先,计算截面的惯性矩和截面模量。
矩形截面的惯性矩 I=(b*h^3)/12=(0.2*4^3)/12=0.0267m^4,截面模量 W=I/(b*h)=0.0267/(0.2*4)=0.0334m^2。
其次,计算梁的弯曲应力和弯矩。
假设最大弯矩为 M,根据弯矩公式M=F*L/4,其中 F 为梁的允许载荷,L 为梁的长度。
代入已知数值,得到M=F*4/4=F。
由于简支梁在弯曲时,弯曲应力σ=M/W,所以σ=F/W。
最后,根据简支梁的稳定性条件,确定梁的允许载荷。
假设梁的允许弯矩为 M",根据简支梁的稳定性条件 M"=2*W*σ",其中σ"为梁的允许弯曲应力。
代入已知数值,得到 M"=2*0.0334*0.6=0.04m^2。
因此,该梁在承受最大弯矩时,允许的载荷为 F=M"=0.04m^2。
【总结】通过以上例题,我们可以看出简支梁的计算过程主要包括确定梁的材料和截面形状、计算截面的惯性矩和截面模量、计算梁的弯曲应力和弯矩以及根据梁的稳定性条件确定梁的允许载荷。
第6讲 简支梁计算-第四部分 主梁内力 横隔梁计算 挠度验算

2016-03
第七节 横隔梁计算
一、横隔梁的内力影响线
由力的平衡条件可写出横隔梁任意截面r的内力计算公式
1.荷载P=1位于截面r的左侧时
左
M r R1 b1 R2 b2 1 e Ribi e
左
Qr R1 R2 1 Ri 1
2.荷载P=1位于截面r的右侧时:
左
M r R1 b1 R2 b2 Ribi
桥梁工程
2016-03
1)荷载横向分布系数
荷载横向分布系数计算结果
梁号 荷载分类
车辆荷载 0.504
0.4375
①
人群荷载 0.620
1.4220
桥梁工程
2016-03
2)主梁跨中截面弯矩 计算主梁弯矩时,对跨中的荷载横向分布系数与跨 内其他各点上采用相同的值 。
桥梁工程
2016-03
按式(2-6-5)进行计算,其中由 = 3.7Hz得:u=0.1767ln − 0.0157 = 0.215, = 1,双车道不折减( 是按两行汽车荷载 计算的) = 1178.5 , = 7.875 ⁄ 。
桥梁工程
2016-03
3)①号梁支点截面剪力计算
变化区段附加三角形重心处的影响线 2
= 1.0 × (19.5 − × 4.875 )⁄19.5 = 0.83 3
桥梁工程
2016-03
汽车荷载的支点剪力为:
, = (1 + ) [ (
++
1
_
)+ ( − ) ]
2
1
= 1.215 × 1 × [0.4375 × 1.2 × 178.5 × 1.0 + 0.504 × 7.875 × 2
第四章-简支梁设计计算(1)

第四章 简支梁(板)桥设计计算第一节 简支梁(板)桥主梁内力计算对于简支梁桥的一片主梁,知道了永久作用和通过荷载横向分布系数求得的可变作用,就可按工程力学的方法计算主梁截面的内力(弯矩M 和剪力Q ),有了截面内力,就可按结构设计原理进行该主梁的设计和验算。
对于跨径在10m 以内的一般小跨径混凝土简支梁(板)桥,通常只需计算跨中截面的最大弯矩和支点截面及跨中截面的剪力,跨中与支点之间各截面的剪力可以近似地按直线规律变化,弯矩可假设按二次抛物线规律变化,以简支梁的一个支点为坐标原点,其弯矩变化规律即为:)(42maxx l x lM M x -=(4-1) 式中:x M —主梁距离支点x 处的截面弯矩值;m ax M —主梁跨中最大设计弯矩值;l —主梁的计算跨径。
对于较大跨径的简支梁,一般还应计算跨径四分之一截面处的弯矩和剪力。
如果主梁沿桥轴方向截面有变化,例如梁肋宽度或梁高有变化,则还应计算截面变化处的主梁内力。
一 永久作用效应计算钢筋混凝土或预应力混凝土公路桥梁的永久作用,往往占全部设计荷载很大的比重(通常占60~90%),桥梁的跨径愈大,永久作用所占的比重也愈大。
因此,设计人员要准确地计算出作用于桥梁上的永久作用。
如果在设计之初通过一些近似途径(经验曲线、相近的标准设计或已建桥梁的资料等)估算桥梁的永久作用,则应按试算后确定的结构尺寸重新计算桥梁的永久作用。
在计算永久作用效应时,为简化起见,习惯上往往将沿桥跨分点作用的横隔梁重力、沿桥横向不等分布的铺装层重力以及作用于两侧人行道和栏杆等重力均匀分摊给各主梁承受。
因此,对于等截面梁桥的主梁,其永久作用可简单地按均布荷载进行计算。
如果需要精确计算,可根据桥梁施工情况,将人行道、栏杆、灯柱和管道等重力像可变作用计算那样,按荷载横向分布的规律进行分配。
对于组合式梁桥,应按实际施工组合的情况,分阶段计算其永久作用效应。
对于预应力混凝土简支梁桥,在施加预应力阶段,往往要利用梁体自重,或称先期永久作用,来抵消强大钢丝束张拉力在梁体上翼缘产生的拉应力。
第四章 简支梁(板)桥设计计算

对于人群均布荷载情况,在荷载横向分布系数变 化区段内所产生的三角形荷载对内力的影响,可 用下式计算:
a ΔQ A = (m0 − mc ) ⋅ qr ⋅ y 2
计算弯矩,Pk = 0.75 × [180 +
360 − 180 (19.5 − 5)] = 178.5 kN 50 − 5
qk = 7.875 kN / m
§4.2
荷载横向分布计算
4.2.1 荷载横向分布计算原理 荷载横向分布计算所针对的荷载主要是活 载,因此又叫做活载横向分布计算。 梁桥作用荷载P时,结构的刚性使P在x、y方 向内同时传布,所有主梁都以不同程度参与工作。 可类似单梁计算内力影响线的方法,截面的内力 值用内力影响面双值函数表示,即
485
2
160
160
160 横剖面
160
16
14 130
15 485 485 1996 485
纵剖面
解:(1) 永久作用集度 主梁:
0.08 + 0.14 g1 = [0.18 × 1.30 + ( )(1.60 − 0.18)] × 25.0 = 9.76 kN / m 2
横隔梁:边主梁横隔板:
附加剪力由式(4-5)计算:
a ′ ΔQ0 q = (1 + μ ) ⋅ ξ ⋅ (m0 − mc ) ⋅ qk ⋅ y 2 = 1.296 × 1 × (0.438 − 0.538) × 7.875 × 0.916 = −2.29 kN
由式(4-4),公路-II级作用下,边主梁支点 的最大剪力为:
485
250号混凝土垫层(6~12cm)
中主梁横隔板:
g = 2 × 0.063 = 1.26 kN / m
《简支梁设计计算》课件

梁的受力分布和大小。公式包括力
的平衡、力矩平衡和造成内力的外
载荷三大类。
3
剪切应力的计算
4
剪切应力是梁在横向内力作用下产
生的。它可以通过剪力公式进行计
算,需要考虑截面形状和材料特性
5
等因素。
简支梁的力学模型
简支梁的力学模型是由两个支座和 一个负载组成的简单模型。在受到 外力作用时,梁会发生弯曲和剪切 等应力。
简支梁设计计算的目的是为了保证结构的 安全可靠并满足使用要求。它需要考虑梁 的受力分析、截面形状及材料选择、尺寸 设计等因素。
梁的基本结构形式
梁的截面形式
梁的截面形式包括矩形、圆 形、T形、H形、工字形等多 种形式。在实际设计中,需 要根据实际情况和实用性选 择合适的截面形式。
材料选择与性能要求
梁的几何形状
梁的材料一般为钢、混凝土 或木材等。在选择材料时需 要考虑承载能力、使用寿命、 环保性等因素,并确保满足 相关国家标准和要求。
梁的几何形状包括直线型、 弧形、斜线型等多种形式。 在确定几何形状时需要考虑 实际情况、美观性和使用寿 命等因素。
简支梁的受力分析
1
静力平衡方程
2
通过应用静力平是梁在纵向内力作用下产 生的。它可以通过简单的公式进行 计算,需要考虑弹性模量、惯性矩 和受力位置等因素。
段内合力的计算
在一定跨度范围内,梁的内力分布 是复杂的。可以通过截面法和位移 法等方法计算出各段的受力状态。
简支梁的设计原则与方法
首先设计截面形 状和尺寸
在进行简支梁设计计算时, 需要首先确定梁的截面形 状和尺寸。这些参数应满 足结构安全、使用要求和 美观性等要求。
简支梁设计计算实例
1
简支梁(板)桥设计计算

各板截面相同, 1 2
得 p1i pi1
上式表明:单位荷载作用在1号梁上时任一板 梁所分配的荷载,等于单位荷载作用于任意板 梁上时1号板梁所分配到的荷载,即1号板梁荷 载横向影响线的竖标,以 1i 表示 。
24
第四章 简支梁(板)桥设计计算
1号板梁横向影响线的竖标为:
(x)
gi
sin
x
l
gi(x)=gisinπx (左侧的铰接力未示出)
11
第四章 简支梁(板)桥设计计算 §4.1 荷载横向分布计算
4.1.2 铰接板(梁)法
预制板用现浇混凝土铰缝连结成整体,铰缝 以传递剪力为主,抗弯刚度很弱,结构受力 状态,接近于数根并列而相互间横向铰接的 狭长板(梁)。
12
第四章 简支梁(板)桥设计计算
31g1 32 g2 33g3 34 g4 3 p 0
41g1 42 g2 43g3 44 g4 4 p 0
式中, ik 铰缝k内作用单位正弦铰接力,在铰缝i处引
起 的竖向相对位移
ip 外荷载p在铰缝i处引起的竖向位移
20
第四章 简支梁(板)桥设计计算
11
1
g1
21
g 2
1
g3
0
-1- g2 21 g3 1 g4 0
1 g3 21 g4 0
22
第四章 简支梁(板)桥设计计算
2 铰接板的荷载横向影响线和横向分布系数
荷载作用在1号板梁上,各块板梁的挠度和所分配
的荷载图式如图所示 弹性板梁,荷载挠度呈正比
p1
pi1 1i1 p1i 2 1i
22
33
44
2 w
b
混凝土桥课件 第四章 RCB预应力混凝土简支梁

梁端适当扩大; 桥规规定不小于14cm或上下翼缘板梗胁间腹板高的 1/20(有预箍)、1/15(无预箍) 4 下翼缘形状与尺寸:主要取决于力筋布置。
重心尽量靠下 管道净距满足规定 注意张拉端锚具 5 主梁荷载与内力计算:基本同钢筋混凝土梁。
2 力筋类型 高强钢丝、钢铰线、粗钢筋。 常用强度不低于850MPa IV级以上的精轧螺纹钢 近年来也多用高强、低松弛钢铰线。
3 力筋线形和力筋“绝缘”的目的和做法
*直线形和折线形 *折线形合理高但工艺复杂。 *多用直线形,端部、分批把硬质塑料管套在钢铰线
上绝缘,防止端部上翼缘混凝土开裂。
4 先张法梁抗剪
普通钢筋 (T20MnSi A3)
箍筋:跨中-1/8 2肢
φ10 @ 200mm
1/8- 1/16支座 加密 φ10 @ 100mm
1/16-梁端 4肢 φ10 @ 80mm
下翼缘处: 最下排预应力筋处 10根φ8纵 向非预应力筋,增强正截面抗裂性
为增强下翼缘的纵向抗裂性 设间距 100mm φ8封闭箍筋
2 30m跨T梁 梁长2996cm、梁高175cm 梁中心距 160cm(较大跨度180 cm) 上翼缘宽 158cm, 跨中腹板 16cm 下面有马蹄宽36cm 端部腹板 36cm
3 30m跨工形组合截面 5cm预制板做现浇桥面底模, 主梁力筋7φ5钢铰线 XM或QM锚具 预制部分(主梁、横隔板、桥面板)C50 现浇部分C30
第4章 预应力钢筋混凝土简支梁
第一节 后张法预应力混凝土简支梁标准设计及构造 第二节 先张法预应力混凝土简支梁标准设计简介 第三节 其他形式预应力混凝土简支梁简介 第四节 后张法预应力混凝土简支梁设计与计算 第五节 预应力混凝土简支梁的制造及架设
简支梁计算例题

简支梁计算例题摘要:1.引言:简支梁的概述2.计算方法:简支梁的内力计算3.例题:简支梁计算的具体步骤4.总结:简支梁计算的重要性正文:一、引言:简支梁的概述简支梁是指在两端支承,中间自由悬挂的梁。
它是工程中常见的一种结构形式,广泛应用于房屋建筑、桥梁、输电线路等领域。
简支梁的计算主要包括内力计算和挠度计算。
本文主要介绍简支梁的内力计算方法,并通过一个例题来说明具体的计算步骤。
二、计算方法:简支梁的内力计算简支梁的内力计算主要包括弯矩和剪力。
在计算时,一般采用静力平衡法或力矩平衡法。
其中,静力平衡法适用于简支梁在均布荷载作用下的内力计算;力矩平衡法则适用于简支梁在集中荷载作用下的内力计算。
三、例题:简支梁计算的具体步骤假设有一简支梁,梁的长度为L,截面尺寸为b×h,材料为钢筋混凝土,弹性模量为Ec,截面惯性矩为I。
在梁的中心施加一个均布荷载q,求梁在荷载作用下的弯矩和剪力。
1.根据均布荷载求梁的弯矩:首先,根据均布荷载的定义,求得荷载对梁端弯矩的影响。
设梁的一端受到的弯矩为M,则有:M = ql/82.根据弯矩求梁的剪力:根据静力平衡原理,梁在弯矩作用下,梁的剪力V 可表示为:V = M/Ec * h3.计算梁的挠度:根据力矩平衡原理,梁在荷载作用下的挠度f 可表示为:f = V * L / (Ec * I)四、总结:简支梁计算的重要性简支梁计算在工程中有着重要的意义。
通过计算,可以了解梁在荷载作用下的内力分布情况,从而为梁的材料选择、截面尺寸设计以及梁的强度分析提供依据。
混凝土简支梁的设计计算

H—— 板的H厚度。
《公路桥规》规定:
计算弯矩时:
0
≯l0
计算剪力时:
0
l0—— 板的净跨径。 t—— 板的厚度。
b—— 梁肋宽度。
2l /3
(b) 对几个靠近的相同荷载
如按上式计算所得的各有效分布宽度发生重叠时,应按相邻靠近的荷载一起计算其共有的有 效分布宽度。
a a 1 d l/3 a 2 2 H d l/3
(2)车辆荷载在板上的分布面积
沿行车方向 a12+2H 沿横向 b12+2H
图 6.3.2
H ——为铺装层厚度
当车辆荷载作用于桥面板上时作用于板面上的局部分布荷载为:
p P轮 a 1b1
P轮 ——轮重,汽车轴重P的1/2为。
图 6.3.2 车轮荷载在板面上的分布
3.板的有效工作宽度 (1)板的有效工作宽度的含义 (2)单向板的荷载有效工作宽度 (3)悬臂板的荷载有效工作宽度
③若实际上,行车道板和主梁梁肋的连接情况,既不是固接,也不是铰接,而应是考虑为弹 性固接。图5-44(c)
简便的算法: 对于弯矩,先计算出一个跨度相同的简支板的跨中弯矩M0,然后再根据实验及理论分析的
数据加以修正。
图5-44 主梁扭转对行车道板的影响
2)弯矩的计算 ①当<1/4时,(即主梁抗扭刚度较大) ②当≥1/4时,(即主梁抗扭刚度较小)
图 6.3.3 行车道板的 受力和变形状态
对板来讲:以宽度为a的板来承受车轮荷载产生的总弯矩,既可满足弯矩最大值的要求,计算 也方便。
对荷载而言:荷载只在a范围内有效,且均匀分布。一旦确定了a的值就可以确定作用在1范围 内的荷载集度p了。
通过对不同支承条件、不同荷载性质以及不同荷载位置情况下,随承压面大小变化的板有效 工作宽度与跨径的比值的分析,可知两边固结的板的有效工作宽度要比简支的板小3040%左右, 全跨满布的条形荷载的有效分布宽度也比局部分布荷载的小些。另外,荷载愈靠近支承边时, 其有效工作宽度也愈小。
简支梁计算公式总汇

简支梁计算公式总汇简支梁是一种常见的结构形式,在工程设计中经常使用。
它的计算公式是基于梁的力学性能来进行推导和计算的,下面将介绍简支梁计算公式的总汇。
1.简支梁的跨度和支点反力计算公式简支梁的跨度是指两个支点之间的距离,可以根据悬臂臂长和梁的长度来计算。
支点反力是指支点处的外力作用力,可以通过力的平衡方程来计算。
2.简支梁的弯矩计算公式简支梁的弯矩是指在梁上各点产生的弯曲力矩,可以通过力的平衡和弯矩平衡方程来计算。
弯矩与梁的截面惯性矩有关,可以通过梁的几何形状和材料特性来计算。
3.简支梁的剪力计算公式简支梁的剪力是指在梁上各点产生的剪切力,可以通过力的平衡和剪力平衡方程来计算。
剪力与梁的截面面积有关,可以通过梁的几何形状和材料特性来计算。
4.简支梁的挠度和挠度计算公式简支梁的挠度是指在梁上任意一点由于受力而产生的弯曲变形,可以通过力的平衡和挠度平衡方程来计算。
挠度与梁的弹性模量、截面惯性矩和梁的长度有关,可以通过梁的几何形状、材料特性和受力情况来计算。
5.简支梁的自振频率和频率计算公式简支梁的自振频率是指梁在受到外力或激励时的振动频率,可以通过梁的质量、刚度和长度来计算。
自振频率与梁的自重、材料特性和梁的长度有关,可以通过梁的几何形状、材料特性和支撑方式等来计算。
总结起来,简支梁的计算公式包括跨度和支点反力计算公式、弯矩计算公式、剪力计算公式、挠度计算公式和频率计算公式等。
通过这些公式,可以对简支梁的受力和变形进行准确的计算和分析,为工程设计提供参考依据。
但需要注意的是,在实际应用中还应考虑一些实际条件和约束,如荷载类型、荷载大小、梁的几何形状和材料特性等。
简支梁的周期计算

简支梁的周期计算简支梁是一种较为常见的结构形式,其两个端点可以完全自由地旋转,不受约束。
这种结构梁比较简单,可以用一维振动理论来描述和计算。
简支梁的自由振动方程可以表示为:m* d²u/dt² + k* u = 0其中,m是梁的质量,k是梁的刚度,u是梁的挠度,t是时间。
这是一个二阶线性常微分方程,可以通过解特征方程来得到解析解。
由于此处要求大于1200字,我将分几个方面来详细讲解简支梁的周期计算。
1.导出简支梁的振动方程2.计算简支梁的自然频率3.计算简支梁的周期首先,我们可以从简支梁的振动方程出发,推导得到简支梁的自然频率。
自然频率是梁在自由振动时的频率,是梁固有的特性。
可以用公式表示为:ω=√(k/m)其中,ω是自然频率,k是梁的刚度,m是梁的质量。
接下来,我们可以用自然频率来计算简支梁的周期。
周期是一个完整振动周期所需的时间,可以用公式表示为:T=2π/ω其中,T是周期,ω是自然频率。
对于简支梁,刚度k和质量m可以通过结构的几何形状和材料性质来确定。
例如,对于均匀截面的简支梁,可以用梁的截面面积A、杨氏模量E和长度L来计算刚度k和质量m。
刚度k可以通过以下公式计算:k=3EI/L³其中,E是杨氏模量,I是梁截面的惯性矩,L是梁的长度。
质量m可以通过以下公式计算:m=ρAL其中,ρ是梁的密度,A是梁的截面面积,L是梁的长度。
通过上述方法,我们可以计算出简支梁的自然频率ω和周期T。
需要注意的是,上述计算方法适用于假设简支梁是线性弹性结构的情况。
对于非线性情况,计算方法会有所不同。
此外,简支梁的几何形状和材料特性也会对周期的计算结果产生影响。
在实际工程中,为了保证结构的安全性和可靠性,设计时通常会将简支梁的自然频率控制在一定范围内。
频率过高或过低都可能导致结构出现问题,例如共振或不够刚性。
综上所述,简支梁的周期计算是工程设计中的重要问题。
通过推导梁的振动方程,计算自然频率和周期,可以帮助工程师合理地确定梁的材料和几何形状参数,确保结构的安全性和可靠性。
简支梁的剪力计算公式

简支梁的剪力计算公式简支梁是一种常见的结构形式,在建筑、机械等领域广泛应用。
在设计这种结构时,需要计算其面对荷载时的剪力,即作用于梁的横向拉力。
本文将介绍简支梁的剪力计算公式,并解释其基本原理。
一、剪力的定义和计算方法剪力是指作用于物体横向的拉力,常用符号为V。
对于简支梁而言,其剪力大小为距离荷载作用点的梁端距离x处的荷载分量,即V=Qx。
其中,Q表示单位长度的荷载大小,x表示距离荷载作用点的梁端距离。
在实际计算中,为了方便起见,可以将梁截面按纵向划分为若干小段,然后通过受力平衡,计算出每一小段的剪力大小,最终将所有小段的剪力加和得到梁整体的剪力大小。
二、剪力计算公式对于简支梁而言,其剪力的计算公式为:V=Qx其中,Q表示单位长度的荷载大小,x表示距离荷载作用点的梁端距离。
具体说来,可以将梁截面按纵向划分为若干小段,然后对每一个小段进行受力平衡,得到该小段的剪力大小。
这里以一段长度为dx的小段为例,其剪力大小可以通过以下公式计算:dV=Qdx其中,Q表示单位长度的荷载大小,dx表示小段长度。
最后将所有小段的剪力加和,即可得到整体的剪力大小。
三、剪力计算的基本原理简支梁在受荷载作用时,会在横向方向上产生拉力,即剪力。
这种拉力不仅取决于荷载的大小和分布,还与梁的固定方式、材料等因素有关。
因此,在进行剪力计算时,需要考虑这些因素对剪力大小的影响。
具体说来,剪力计算的基本原理是受力平衡。
在进行受力平衡时,需要将梁截面按纵向划分为若干小段,然后对每一小段分别进行受力分析。
根据受力平衡原理,梁的每一小段所受的剪力大小应该等于两侧的力的合力,即:V1+V2=Qdx其中,V1和V2分别表示小段左右两侧的剪力大小。
通过这个公式,可以计算出每一小段的剪力大小,并得到整体的剪力大小。
四、总结简支梁的剪力计算是建筑、机械等领域中的一项基本任务。
在实际应用中,可以将梁截面按纵向划分为若干小段,然后通过对每一小段进行受力分析,计算出其剪力大小。
简支梁长度问题回答

简支梁长度简支梁长度简支梁是一种常见的结构形式,它由两个支座支撑,中间悬挂着梁体。
在工程设计中,确定简支梁的长度是非常重要的一步,因为它直接影响着梁体的承载能力和使用寿命。
下面将从简支梁长度的定义、计算方法和影响因素三个方面进行探讨。
一、简支梁长度的定义简支梁长度指的是梁体两个支座之间的距离,通常用L表示。
在实际工程中,简支梁长度的确定需要考虑多种因素,如梁体的材料、截面形状、荷载情况等。
二、简支梁长度的计算方法简支梁长度的计算方法有多种,下面介绍两种常用的方法。
1. 基于荷载的计算方法在实际工程中,简支梁的长度通常是根据荷载来确定的。
具体计算方法如下:L = (5/384) * (wL^4 / EI)其中,w为梁体的均布荷载,L为梁体的长度,E为梁体的弹性模量,I为梁体的截面惯性矩。
2. 基于挠度的计算方法挠度是指梁体在受到荷载作用后产生的弯曲变形。
在实际工程中,可以通过挠度来确定简支梁的长度。
具体计算方法如下:L = (K * EI / w) ^ (1/3)其中,K为挠度系数,E为梁体的弹性模量,I为梁体的截面惯性矩,w为梁体的均布荷载。
三、简支梁长度的影响因素简支梁长度的确定需要考虑多种因素,下面列举几个比较重要的因素。
1. 梁体的材料不同材料的简支梁长度是不同的。
例如,钢材的简支梁长度比混凝土的简支梁长度要小。
2. 梁体的截面形状不同截面形状的简支梁长度也是不同的。
例如,矩形截面的简支梁长度比圆形截面的简支梁长度要小。
3. 荷载情况荷载大小和分布情况对简支梁长度的确定也有很大的影响。
荷载越大、分布越不均匀,简支梁的长度就越小。
总之,简支梁长度的确定是一个复杂的过程,需要考虑多种因素。
在实际工程中,需要根据具体情况选择合适的计算方法和参数,以确保简支梁的安全可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 简支梁(板)桥设计计算第一节 简支梁(板)桥主梁内力计算对于简支梁桥的一片主梁,知道了永久作用和通过荷载横向分布系数求得的可变作用,就可按工程力学的方法计算主梁截面的内力(弯矩M 和剪力Q ),有了截面内力,就可按结构设计原理进行该主梁的设计和验算。
对于跨径在10m 以内的一般小跨径混凝土简支梁(板)桥,通常只需计算跨中截面的最大弯矩和支点截面及跨中截面的剪力,跨中与支点之间各截面的剪力可以近似地按直线规律变化,弯矩可假设按二次抛物线规律变化,以简支梁的一个支点为坐标原点,其弯矩变化规律即为:)(42maxx l x lM M x -=(4-1) 式中:x M —主梁距离支点x 处的截面弯矩值;m ax M —主梁跨中最大设计弯矩值;l —主梁的计算跨径。
对于较大跨径的简支梁,一般还应计算跨径四分之一截面处的弯矩和剪力。
如果主梁沿桥轴方向截面有变化,例如梁肋宽度或梁高有变化,则还应计算截面变化处的主梁内力。
一 永久作用效应计算钢筋混凝土或预应力混凝土公路桥梁的永久作用,往往占全部设计荷载很大的比重(通常占60~90%),桥梁的跨径愈大,永久作用所占的比重也愈大。
因此,设计人员要准确地计算出作用于桥梁上的永久作用。
如果在设计之初通过一些近似途径(经验曲线、相近的标准设计或已建桥梁的资料等)估算桥梁的永久作用,则应按试算后确定的结构尺寸重新计算桥梁的永久作用。
在计算永久作用效应时,为简化起见,习惯上往往将沿桥跨分点作用的横隔梁重力、沿桥横向不等分布的铺装层重力以及作用于两侧人行道和栏杆等重力均匀分摊给各主梁承受。
因此,对于等截面梁桥的主梁,其永久作用可简单地按均布荷载进行计算。
如果需要精确计算,可根据桥梁施工情况,将人行道、栏杆、灯柱和管道等重力像可变作用计算那样,按荷载横向分布的规律进行分配。
对于组合式梁桥,应按实际施工组合的情况,分阶段计算其永久作用效应。
对于预应力混凝土简支梁桥,在施加预应力阶段,往往要利用梁体自重,或称先期永久作用,来抵消强大钢丝束张拉力在梁体上翼缘产生的拉应力。
在此情况下,也要将永久作用分成两个阶段(即先期永久作用和后期永久作用)来进行计算。
在特殊情况下,永久作用可能还要分成更多的阶段来计算。
得到永久作用集度值g 之后,就可按材料力学公式计算出梁内各截面的弯矩M 和剪力Q 。
当永久作用分阶段计算时,应按各阶段的永久作用集度值g i 来计算主梁内力,以便进行内力或应力组合。
下面通过一个计算实例来说明永久作用效应的计算方法。
例4-1:计算图4-1 所示标准跨径为20m 、由5片主梁组成的装配式钢筋混凝土简支梁桥主梁的永久作用效应,已知每侧的栏杆及人行道构件的永久作用为m kN /5。
160纵剖面横剖面160160160图4-1 装配式钢筋混凝土简支梁桥一般构造图(单位:cm )解:(1) 永久作用集度 主梁:m kN g /76.90.25)]18.060.1)(214.008.0(30.118.0[=⨯-++⨯= 横隔梁:边主梁:mkN g /63.050.19/}0.255216.015.0)218.060.1()]214.008.0(00.1{[2=⨯⨯+⨯-⨯+-= 中主梁:m kN g /26.1061.0212=⨯=桥面铺装层:mkN g /67.35/]0.2400.7)12.006.0(210.2300.702.0[3=⨯⨯++⨯⨯= 栏杆和人行道:m kN g /00.25/20.54=⨯= 作用于边主梁的全部永久作用集度为:∑=+++==m kN g g i /06.1600.267.363.076.9作用于中主梁的全部永久作用集度为:m kN g /69.1600.267.326.176.9=+++='(2)永久作用效应边主梁弯矩和剪力的力学计算模型如图4-2(a) 和( b) 所示,则:)(222x l gx x gx x gl M x -=⋅-⋅=)2(22x l ggx gl Q x -=-=各计算截面的剪力和弯矩值列于表4-1。
(a)g=2x(b)图4-2 永久作用效应力学计算模型二 可变作用效应计算公路桥梁的可变作用包括汽车荷载、人群荷载等几部分,求得可变作用的荷载横向分布系数(本章后叙)后,就可以具体确定作用在一根主梁上的可变作用,然后用工程力学方法计算主梁的可变作用效应。
截面可变作用效应计算的一般计算公式为:)()1(21Ω+⋅⋅+=k k k q m y P m S ξμ汽 (4-2) Ω=人人q m S 2 (4-3)式中:S —所求截面的弯矩或剪力;)1(μ+—汽车荷载的冲击系数,按《公桥通规》规定取值;ξ—多车道桥涵的汽车荷载横向折减系数,按《公桥通规》规定取用;1m —沿桥跨纵向与车道集中荷载k P 位置对应的荷载横向分布系数;2m —沿桥跨纵向与车道均布荷载k q 所布置的影响线面积中心位置对应的荷载横向分布系数,一般可取跨中荷载横向分布系数c m ;kP —车道集中荷载标准值;kq —车道均布荷载标准值;r q —纵向每延米人群荷载标准值;k y —沿桥跨纵向与k P 位置对应的内力影响线最大坐标值;Ω—弯矩、剪力影响线面积。
利用式(4-2)和式(4-3)计算支点截面处的剪力或靠近支点截面的剪力时,尚须计入由于荷载横向分布系数在梁端区段内发生变化所产生的影响,以支点截面为例,其计算公式为:A A A Q Q Q ∆+='(4-4)式中:'A Q —由式(4-2)或式(4-3)按不变的c m 计算的内力值,即由均布荷载k c q m 计算的内力值;A Q ∆—计及靠近支点处荷载横向分布系数变化而引起的内力增(或减)值。
A Q ∆的计算(见图4-3):对于车道均布荷载情况,在荷载横向分布系数变化区段内所产生的三角形荷载对内力的影响,可用式(4-5)计算:y q m m aQ k c A ⋅⋅-⋅⋅+=∆)(2)1(0ξμ (4-5)对于人群均布荷载情况,在荷载横向分布系数变化区段内所产生的三角形荷载对内力的影响,可用式(4-6)计算:y q m m aQ r c A ⋅⋅-=∆)(20 (4-6) 式中:a —荷载横向分布系数m 过渡段长度;q r —侧人行道顺桥向每延米的人群荷载标准值;y —m 变化区段附加三角形荷载重心位置对应的内力影响线坐标值;其余符号意义同前。
图4-3 支点剪力力学计算模型下面通过一个计算实例来说明可变作用效应的计算方法。
例4-2:以例4-1所示的标准跨径为20m 的5梁式装配式钢筋混凝土简支梁桥为实例,计算边主梁在公路-II 级和人群荷载2/0.3m kN q r =作用下的跨中截面最大弯矩、最大剪力以及支点截面的最大剪力。
荷载横向分布系数可按表4-2中的备注栏参阅有关例题。
解:(1)荷载横向分布系数汇总(2)计算跨中截面车辆荷载引起的最大弯矩 按式(4-2)计算,其中简支梁桥基频计算公式为ccm EI l f 22π=,对于单根主梁: 混凝土弹性模量E 取210/103m N ⨯,主梁跨中截面的截面惯性矩4066146.0m I c =,主梁跨中处的单位长度质量m kg m c /10995.03⨯=,831.510995.0066146.01035.19214.3231022=⨯⨯⨯⨯⨯==c c m EI l f π(Hz ), 根据表1-17,冲击系数296.00157.0ln 1767.0=-=f μ,296.1)1(=+μ,双车道不折减,1=ξ, 计算弯矩时,kN P k 5.178)]55.19(550180360180[75.0=---+⨯=,m kN q k /875.7=,按跨中弯矩影响线,计算得出弯矩影响线面积为: 22253.475.198181m l =⨯==Ω, 沿桥跨纵向与k P 位置对应的内力影响线最大坐标值875.44==ly k , 故得:mkN q m y P m M k c k k q l⋅=⨯⨯+⨯⨯⨯⨯=Ω⋅⋅+⋅⋅+=72.867)53.47875.7538.0875.45.178538.0(1296.1)()1(12ξμ,(3)计算跨中截面人群荷载引起的最大弯矩 m kN q m M r cr r l⋅=⨯⨯⨯=Ω⋅⋅=15.7353.47)75.00.3(684.02,(4)计算跨中截面车辆荷载引起的最大剪力鉴于跨中剪力影响线的较大坐标位于跨中部分(见图4-4),可采用全跨统一的荷载横向分布系数c m 进行计算。
计算剪力时,kN P k 2.2145.1782.1=⨯= 影响线的面积m 438.25.05.192121=⨯⨯⨯=Ω 故得:影响线公路-II 级图4-5 支点剪力力学计算模型对应于支点剪力影响线的最不利车道荷载布置如图4-5a 所示,荷载的横向分布系数图如图4-5b 所示。
m 变化区段内附加三角形荷载重心处的剪力影响线坐标为:916.05.19/)9.4315.19(1=⨯-⨯=y ,影响线面积为m 75.915.1921=⨯=Ω。
因此,按式(4-2) 计算,则得:kNq m y P m Q k c k k q 13.175)75.9875.7538.00.12.214438.0(1296.1)()1(10=⨯⨯+⨯⨯⨯⨯=Ω+⋅⋅+='ξμ附加剪力由式(4-5)计算:kNy q m m aQ k c q 29.2916.0875.7)538.0438.0(1296.1)(2)1(00-=⨯⨯-⨯⨯=⋅⋅-⋅⋅+='∆ξμ 由式(4-4),公路-II 级作用下,边主梁支点的最大剪力为:kN Q Q Q q q q 84.17229.213.1750'00=-=∆+=(7)计算支点截面人群荷载引起的最大剪力由式(4-3)和式(4-6)可得人群荷载引起的支点剪力为:916.0)75.00.3()684.0422.1(9.42175.9)75.00.3(684.0)(200⨯⨯⨯-⨯⨯+⨯⨯⨯=⋅-+Ω⋅⋅=y q m m aq m Q r c r c rkN 73.18=三 主梁内力组合和包络图为了按各种极限状态来设计钢筋混凝土或预应力混凝土梁(板)桥,需要确定主梁沿桥跨方向关键截面的作用效应组合设计值(或称为计算内力值),可将各类荷载引起的最不利作用效应分别乘以相应的荷载分项系数,按《公桥通规》规定的作用效应组合而得到计算内力值。
例4-3:已知例4-1所示的标准跨径为20m 的5梁式装配式钢筋混凝土简支梁桥中1号边主梁的内力值最大,利用例4-1和例4-2的计算结果确定控制设计的计算内力值。
解:(1)内力计算结果汇总(2)作用效应组合 结构重要性系数10=γ 1)作用效应基本组合时:跨中弯矩:)4.18.04.12.1(0r cq cg c M M M M ⨯⨯++=γm kN ⋅=⨯⨯+⨯+⨯⨯=78.2212)15.734.18.072.8674.14.7632.1(0.1梁端剪力:)4.18.04.12.1(00000r q g Q Q Q Q ⨯⨯++=γkN 82.450)73.184.18.084.1724.16.1562.1(0.1=⨯⨯+⨯+⨯⨯=2)作用短期效应组合时,车辆荷载不计冲击力: 跨中弯矩:r cq cg c M M M M 0.17.0++=m kN ⋅=⨯+⨯+=23.130515.730.154.6697.04.763梁端剪力:r cq cg c Q Q Q Q 0.17.0++=kN 68.26873.180.136.1337.06.156=⨯+⨯+=3)作用长期效应组合时,车辆荷载不计冲击力: 跨中弯矩:r cq cg c M M M M 4.04.0++=m kN ⋅=⨯+⨯+=48.106015.734.054.6694.04.763梁端剪力:r cq cg c Q Q Q Q 4.04.0++=kN 44.21773.184.036.1334.06.156=⨯+⨯+=如果在梁轴线上的各个截面处,将所采用控制设计的各效应组合设计值按适当的比例尺绘成纵坐标,连接这些坐标点而绘成的曲线,称为效应组合设计值(或称为内力组合设计值)的包络图,如图4-6所示。
