matlab四杆机构源程序
基于MATLAB的给定连杆预定位置的四杆机构设计

o x y, 以 M 为原 点 , 在连杆 上建 立 动坐标 系 Mx ' y , M
一 N 为 轴 的正 向。点 B、 C在 动 坐 标 系 的坐 标 为 ( z , Y s " ) 、( , Y c " ) , 在 固定坐标系的坐标为 ( , . y ) ,( c 、 , y c ) , 可 以得 到 :
hi gh e f f i ci e n c y .
Ke y wo r d s:f our b a r me c h a ni s m, M A TI A B, t h e pr e de t e r mi n e d po s i t i on
境 I : : _ 窑 曼 . 主 和 _ , 2 - n I  ̄ _ 性 数 学 模 型 的 建 立 它提 供 了一个 人机 交互 的系统环 境 , 并 以矩 阵 … … …一 ~ 一
便 地进 行T 程 数值 分析 、 优化 分析 、 数据 处 理和 自动 控制 , 也可 以 实现计 算 可视化 、 图形绘 制 图像处 理 和 仿 真 等功 能 , 在T 业 和研 究 领 域 具 有 极 大 的使 用 价 值, 逐 渐成 为 优化 领域 的 主要T 具之 一 。MATI AB 可 以快速 解决 传统 办 法 很 难 解 决 的 问 题 , 在 实 际 应
l y t i c a l me t h o d .Th i s p a p e r i s b a s e d o n t h e M ATI AB l a n g u a g e ,t h e d e s i g n o f f o u r b a r me c h a n i s m i s l i n k e d t o t h e p r e d e t e r — mi n e d p o s i t i o n g i v e n b y c o mp u l e r .Th e r e s u l t s s h o w t h a t t h i s me t h o d i s s i mp l e ,a n d t h e r e s u l t i s r e a s o n a b l e ,a c c u r a t e ,a n d
matlab4节点杆单元计算

篇下载MATLAB4节点杆单元计算在工程结构分析领域中,节点杆单元是一种常用的有限元分析方法。
它通过将结构划分成多个小单元,然后对每个小单元进行力学分析,最终得出整个结构的受力情况。
MATLAB作为一种强大的工程计算工具,被广泛应用于结构分析中。
本文将介绍如何利用MATLAB进行4节点杆单元计算,并提供相应的代码实例。
1. 理论背景在进行4节点杆单元计算之前,首先需要了解节点杆单元的基本理论。
节点杆单元是将结构划分为多个杆件,并在每个节点处考虑位移和受力。
通过分析每个杆件的受力平衡和位移关系,可以得出整个结构的受力和变形情况。
4节点杆单元是其中的一种常用的单元类型,它由4个节点和2个杆件组成,可以用来模拟各种不同形状和受力情况的结构。
2. MATLAB实现在MATLAB中,可以利用有限元分析工具箱进行4节点杆单元计算。
首先需要定义结构的几何形状和材料性质,并将其转化为有限元模型。
然后可以利用有限元分析工具箱提供的函数进行网格划分和边界条件设置。
接下来可以利用求解器进行结构的力学分析,并得出节点的位移和受力情况。
最后可以利用MATLAB的绘图工具对结果进行可视化展示。
3. 代码实例下面是一个简单的MATLAB代码实例,演示了如何利用有限元分析工具箱进行4节点杆单元计算:```matlab定义结构的几何形状和材料性质L = 1; 结构的长度A = 1; 结构的横截面积E = 1; 结构的弹性模量定义节点坐标node = [0, 0; 0, L; L, L; L, 0];定义单元节点关系element = [1, 2; 2, 3; 3, 4; 4, 1];网格划分和边界条件设置model = createpde();geometryFromEdges(model,(p)struct('p',p','e',[]),(p)ones(size(p,2 ),1));generateMesh(model);结构的力学分析structuralProperties(model,'YoungsModulus',E,'PoissonsRatio',0); structuralBC(model,'Edge',1,'Constraint','fixed');节点的位移和受力情况result = solve(model);可视化展示pdeplot(model,'XYData',result.displacement,'Deformation','on'); ```4. 结论通过以上代码实例,可以看到利用MATLAB进行4节点杆单元计算是非常简单和高效的。
四节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释

四节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释1.引言1.1 概述悬臂梁是一种常见的结构形式,在工程领域中被广泛应用。
四节点四边形单元是有限元分析中常用的元素类型,能够准确地模拟悬臂梁的受力情况。
Matlab是一种强大的数学工具,可以用来编程实现有限元分析。
本文旨在介绍如何利用Matlab进行四节点四边形单元悬臂梁的有限元编程,并对其进行分析和展望。
通过本文的研究,我们希望能够为工程实践提供一定的参考和指导,同时也为进一步的研究提供基础。
1.2 文章结构本文主要分为三个部分:引言、正文和结论。
引言部分将介绍文章的背景和目的,明确文章研究的问题和意义。
正文部分包括理论基础、Matlab有限元编程介绍和四节点四边形单元悬臂梁建模三个小节。
其中,理论基础将介绍与悬臂梁有关的理论知识,Matlab有限元编程介绍将详细介绍如何使用Matlab进行有限元分析,最后,四节点四边形单元悬臂梁建模将展示具体的悬臂梁建模过程。
结论部分将对实验结果进行分析与总结,探讨本研究的意义和潜在研究方向。
1.3 目的本文旨在利用Matlab编程实现四节点四边形单元悬臂梁的有限元分析,通过建立合适的数学模型,探索悬臂梁在受力状态下的力学特性。
具体目的包括:1. 建立悬臂梁的有限元数学模型,包括节点、单元和材料参数的设置;2. 实现悬臂梁在不同受力情况下的应力、应变、位移等力学性能的计算;3. 分析悬臂梁受力情况下的应力分布情况,探讨悬臂梁的破坏模式和极限承载能力;4. 验证Matlab编程方法的有效性和准确性,为工程实际中悬臂梁等复杂结构的有限元分析提供参考和借鉴。
通过本文的研究,旨在为工程实践提供可靠的数值计算工具和理论分析方法,为解决工程结构强度和稳定性问题提供一定的指导和参考价值。
2.正文2.1 理论基础在介绍四节点四边形单元悬臂梁的Matlab有限元编程之前,我们首先需要了解一些基本的理论知识。
悬臂梁是一种常见的结构形式,在工程领域中广泛应用于桥梁、建筑物等领域。
基于MATLAB的平面四连杆机构运动仿真

12端 点 B运 动分析 .
在 复 数 坐标 系 中 ,端 点 B的位 置 可 表 示 为 B ri,则 =2 ̄ e2
6
』Brn02 I =c2 I 2si O R 2s e o mB=r
速度分别为 :
( 5 ) 一
。
4
2
分 别 对 上 式 求 一 次 、二 次 导 数 ,得 到 B点 的 速 度 、加
[ ] 孙 桓 , 陈作 模 . 械 原 理 [ ] . 京 : 高 等 教 育 出版 社 1 机 M 北
2 0 . 0 6
( 转第 8 下 4页 )
1 00
5 0
>
一
5 0
。
10 0
图 4 交 替 反相 层 叠 下 相 电 压 波形 及 对 应 频谱
1 0. 0 0
lve i v re sa d DTC o rd v p lc t n .I E a so e l n etr n mo r e a p i ai s EE Tr n n i o
[ ] 刘风 君 ,多 电平 逆 变技 术及 其 应 用 [ ] , 京 :机 械 工 业 出 4 M 北
1 00 0 .
8 . 0O
.
5 0 0.
≮ 0
一
S O 0.
一
1 0. 0 0 0
^ 1 j f
1 0 2 0 0. 0. 3 0 400 0. . 500 6 0 . 0。
越
0 20 . 40 . 60 . 80 . 1 0 0.
t / ms
0
~
.
ll1 斟 s2 v t c西 m o2 B j
l 『 Is 一s i I 一 c ].∞ o h1 I l +s c o j
第三章 四连杆之MATLAB程式
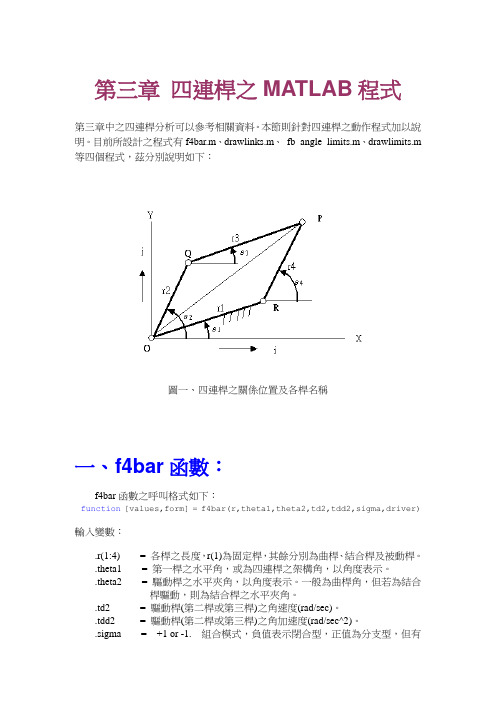
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式,茲分別說明如下:圖一、四連桿之關係位置及各桿名稱一、f4bar函數:f4bar函數之呼叫格式如下:function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數:.r(1:4) = 各桿之長度,r(1)為固定桿,其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角,或為四連桿之架構角,以角度表示。
.theta2 = 驅動桿之水平夾角,以角度表示。
一般為曲桿角,但若為結合桿驅動,則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式,負值表示閉合型,正值為分支型,但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數:.form = 組合狀態,0 :表示無法組合;1:可以正確組合.values = 輸出矩陣,其大小為 4 X 7,各行之資料分配如下:其中第一行之連桿位置向量,屬於單桿的位置向量。
第二行為各桿之水平夾角,第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量,第五行為向量,第六行為絕對量,第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中,以abs()這一個函數指令即可求得,而以函數angle()則可求得其夾角,雖然第二行與第七行之輸出亦有相對應之夾角。
例一:為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中,有框線者表示其為輸入值。
基于MATLAB软件的铰链四杆机构运动分析仿真软件开发

文章编号: 1009-3818(2002)02-0047-03基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发覃虹桥1 魏承辉2 罗佑新2(1华中科技大学材料学院 湖北武汉430074)(2常德师范学院机械工程系 湖南常德415003)摘 要: 建立了铰链四杆机构运动分析的数学模型,以MATLAB 程序设计语言为平台,将参数化设计与交互式相结合,设计了铰链四杆机构仿真软件,该软件具有方便用户的良好界面,并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到仿真结果,再将运行结果与设计要求相比较,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词: 铰链四杆机构;按钮;界面;仿真中图分类号: TH 311.52;TH 113.2+2 文献标识码: A铰链四杆机构的运动学分析是机构学中典型的机构运动分析之一,如果设计铰链四杆机构时能及时图示其运动轨迹和速度分析,从而将图示结果与设计要求相比较,可以及时修改设计中的偏差.目前,MALTAB 已经不再是/矩阵实验室0,而成为国际上最流行的科学与工程计算的软件工具,以及一种具有广泛应用前景的全新的计算机高级编程语言,它在国内外高校和科研部门正扮演着越来越重要的角色,功能也越来越大,不断适应新的要求提出新的解决办法.可以预见,在科学运算与科学绘图领域,MATLAB 语言将长期保持其独一无二的地位.然而,国内至今尚未见到采用MATLAB 开发的有关机构学的软件,笔者以MATLAB 的科学运算与绘图的强大功能开发了铰链机构运动仿真软件.1 铰链四杆机构运动轨迹仿真软件1.1 程序功能与数学模型1)程序功能 本程序可以进行铰链四杆机构的运动分析及位置求解.用户在铰链四杆机构运动分收稿日期:2002-12-10基金项目:湖南省教育厅科研资助项目(00C289)第一作者:覃虹桥(1959-)男高级工程师研究方向:机械设计制造析仿真软件里输入各种参数,即可自动演示不同的铰链四杆机构(曲柄摇杆机构、双曲柄机构、双摇杆机构)的运动.2)数学模型 已知AB=a ,BC =b ,C D =c ,AD=d .AB 为主动杆,以匀角速度逆时针旋转,AD 为机架,见图1.图1 铰链四杆机构运动简图Fig.1 plame four-linkage motion diagram分析:求B C 的运动轨迹,可找B 、C 两点坐标与转动角度51的关系,然后求51+d 51及B 、C 两点的坐标,即可求出运动轨迹.由图1有矢量方程:AB +BC =AD +DC ,则其分量方程为:a c os 51+b cos 52=d +c cos 53(1)a sin 51+b sin 52=c sin 53(2)将式(1)、(2)联立消去52并整理得:a 2+c 2+d 2-b 22ac +d c os 53a -d cos 51c -cos (51-53)=0(3)再改写为:sin 51sin 53+(cos 51-da)cos 53+a 2+c 2+d 2-b 22ac -d c os 51c=0(4)令r 1=sin 51,r 2=cos 51-d a ,r 2222第14卷第2期常德师范学院学报(自然科学版)Vol.14No.22002年6月Journal of Changde Teachers University(Natural Science Edition)Jun.2002则(4)化为:r 1sin 53+r 2cos 53=r 3(5)由三角恒等式求得:53=2arctg r 1?r 21+r 22-r 23r 2+r 3(6)式(6)两个解对应于机构的两种不同装配形式./+0对应于图1的实线,而/-0对应于图1的虚线.B 点坐标:B x =A x +a cos 51,B y =A y +a sin 51C 点坐示:C x =D x +c cos 53,C y =D y +a sin 53从运动杆的转角53,对时间求导可得DC 的角速度,由式(1)、(2)解出52按速度合成可求得BC 的转动角速度[2].1.2 程序框图以曲柄摇杆机构的运动仿真程度为例,程序框图如下:图2 程序框图Fig.2 Programming frame diagram1.3 程序代码采用MATLAB 开发图形界面,程序如下:%fourlinkages.mh_main=figure(.Units .,.normalized .,.Position .,[.3,.3,.5,.5],,.MenuBar .,.none .,.Name .,.四杆机构仿真.,.Number Title .,,.off .,.Resize .,.off .);h_axis=axes(.Units .,.normalized .,.Position .,[.12,.15,.6,.6],,.Tag .,.axPlot .,.Visible .,.on .,.XLim .,[-50,80<,.YLim .,-60,80]);h_text1=uicontrol (.Style .,.Text .,.Tag .,.myText1.,.Units .,,.normalized .,.Position .,[0.78,0.55,.05,.38],.String .,,.输入已知参数.,,.HorizontalAlignment .,.right .);h_te xt2=uicontrol(.Style .,.Text .,.Tag .,.myText2.,.Units .,,.nor malized .,.Position .,[0.15,0.90,.35,0.05],.String .,,.正在仿真,,OK !.,,.HorizontalAlignment .,.right .);a =20;b =50;c =40;d =50;fai =60;four_linkages0(a,b ,c,fai );%初始化图形h_edit1=uicontrol(.Style .,.Edit .,.Tag .,.myEdit1.,.Units .,,.normalized .,.Position .,[0.86,.85,.10,.1],.String .,.20.,,.HorizontalAlignment .,.right .);h_edit2=uicontrol(.Style .,.Edit .,.Tag .,.myEdit2.,.Units .,,.normalized .,.Position .,[0.86,.75,.10,.1],.String .,.50.,,.HorizontalAlignment .,.right .);h_edit3=uicontrol(.Style .,.Edit .,.Tag .,.myEdit3.,.Units .,,.normalized .,.Position .,[0.86,.65,.10,.1],.String .,.40.,,.HorizontalAlignment .,.right .);h_edit4=uicontrol(.Style .,.Edit .,.Tag .,.myEdit4.,.Units .,,.normalized .,.Position .,[0.86,.55,.10,.1],.String .,.60.,,.HorizontalAlignment .,.right .);h_list=uic ontrol(.Style .,.ListBox .,.Tag .,.myList .,.Units .,,.normalized .,.Position .,[0.78,.35,.20,.15],.String .,.正置|反置.,,.HorizontalAlignment .,.right .,.Value .,1);k=1;h_button1=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.25,.2,.1],.String .,,.运动轨迹仿真.,.CallBack .,,.hd1=findobj(gcf,..Tag ..,..myEdit1..);.,,.a =eval(get(hd1,..String ..));.,,.hd2=findobj(gcf,..Tag ..,..myEdit2..);.,,.b =eval(get(hd2,..String ..));.,,.hd3=findobj(gcf,..Tag ..,..myEdit3..);.,,.c =eval(get(hd3,..String ..));.,,.hd4=findobj(gcf,..Tag ..,..myEdit4..);.,,.d =eval(get(hd4,..String ..));.,,48常德师范学院学报(自然科学版)2002年.kk =get(findobj(gcf,..Ta g ..,..myList ..),..Value ..);.,,.four_linkages(a,b,c,d,kk ).]);%调用回调函数轨迹仿真.h_button2=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.15,.2,.1],.String .,,.角速度分析.,.CallBack .,.four_linkages1(a,b,c,d ,kk ).);h_button3=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.05,.2,.1],,.String .,.退出.,.CallBack .,.four_linkages2.);%调用回调函数退出系统在主程序中有3个回调函数和一个初始化函数,回调函数分别用轨迹仿真、运动分析和退出系统.回调函数程序按前述数学模型编程(程序略);初始化函数用程序运行时初始化界面的图形.运行程序产生以下界面(图3).图3 程序运行界面Fi g.3 Programming Interface在界面中输入已知参数,则可生成相应的图形.当输入a =20,b =50,c =40,d =60,装配形式选取正置时,如果选运动轨迹仿真,则得仿真轨迹(图4);如果装配形式选反置,进行轨迹仿真(图5).(注:图4 运动轨迹仿真(装配形式正置)Fi g.4 Moti on track simulation(positiveset)图5 运动轨迹仿真(装配形式为反置)Fig.5 Motion track simulation (in reverse positive set)在图4、5中为节省篇幅,这两个图形只选了对应图3的图形部分,界面的其它部分未剪取.).而当选取装配形式进行轨迹仿真后,可再选角速度分析,得到连杆与摇杆的角速度图形(略).2 结论1)自动演示不同的四杆机构的运动,模拟仿真运动轨迹与从动件的速度分析,有助于分析机构的速度、加速程度和机构的工作性能;2)采用MATLAB 语言开发机构仿真运动分析软件,开发界面容易,运行程序时无需编辑、连接,给使用者以极大的方便.只要输入数据,即可得到结果.将运行结果与设计要求相比较,从而引导设计者修改设计.参 考 文 献1 薛定宇.科学运算程序MATLAB5.3程序设计与应用[M ].北京:清华大学出版社,2000.2 孟宪源.现代机构手册(上)[M].北京:机械工业出版社,1994.3 王沫然.Si mulink4建模及动态仿真[M].北京:电子工业出版社,2002.THE DEVELOPMENT OF EMULATIONAL SOFTWARE FOR ANALYSIS OF MOTION IN PLANE GEMEL FOUR -LINKAGEBASED ON MATLAB SOFTWAREQING Hong -qiao 1 WEI CH eng -hui 2LU O You -xin 2(1T he material institute,Cen tral China University of Science and T echnology,Wuhan Hubei,430074)(2Department of Mechanical Engineering,Changde Teachers University,Changde Hunan 415003)Abstract A mathematical model of motion analysis was estab -lished in plane four-linkage,and emulational software was deve-loped .The software adop ted Matlab5.3.1as a desi gn language.It combined parametric design with interactive design and had good in -terface for user.Thus,i t was fas ter and more convenient to analyse linkage.The emulational result was obtained as soon as input param -eters was imported and the devisers can make decision-making of modification by the comparing emulational result with design de -mand.It provides an applied software and method for linkage.Key words Gemel Four -Linkage;button;interface;emula -tion(责任编校:谭长贵)49第2期覃虹桥 魏承辉 罗佑新 基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发。
运用MATLAB解决四杆机构问题

MATLAB 解题1.设有如图所示四杆机构,其中→R 4为机架(常矢),→R1为主动杆,→R3为从动杆,→R 2为连杆。
设在某一工作位置时各杆的角速度和角加速度分别取如下值:ω1=20 rad/s, ε1= 0;ω2=8.5 rad/s, ε2=-10 rad /s 2;ω3=13 rad/s, ε3=-160rad /s 2.试根据上述要求确定该机构尺寸比。
根据图(2),回路闭合方程可写为:→R 1 +→R 2 +→R 3=-→R 4 回路闭合方程对时间求导一次,利用(6)式,可得: 图2 ω1→R 1 +ω2→R 2 +ω3→R 3 = 0回路闭合方程对时间求导两次,利用(7)式,可得c 1→R 1 + c 2 →R 2 + c 3→R 3 = 0其中 c 1=ε1+j ω12 , c 2=ε2+j ω22, c 3=ε3+j ω32解关于→R 1 ,→R 2 和→R 3的线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→→→001111321321321R R R c c c ωωω→R 4 (13) 可得 →R 1=DDx →R 4, →R 2=DDy →R 4 , →R 3=DDz →R 4注意到上述解中含有相同的分母D,它是一个复数,不妨记为D =k<j α|,被它除的效果是把各杆的长度都缩小k 倍,同时方向都顺时针旋转α角,相当于机构不动,坐标轴逆时针旋转α角。
设计机构时,重要的是机构的形状与尺寸比例。
基于这种考虑,可设→R 4 / D =1,则有→R 1=D x =32320111c c ωω-=1230-j497.3 ; →R 2= D y =311030111c c ωω-=-3200-j1820 ; →R 3= D z =001112121c c ωω-=200+j1955 . 于是:→R 4 = -(→R 1 +→R 2+→R 3) = 1770+j362.3在坐标系上作出上述各杆矢量图,根据各杆矢量图作出机构的闭合矢量图,再根据实际需要选定某一杆长度,其它各杆长度按图比例相似放大。
matlab(四连杆优化设计)

机械优化设计在matlab中的应用东南大学机械工程学院**优化设计目的:在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。
最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方案的科学。
由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管理等,并取得了显著的经济效益和社会效益。
优化设计步骤:1. 机械优化设计的全过程一般可以分为如下几个步骤:1)建立优化设计的数学模型;2)选择适当的优化方法;3)编写计算机程序;4)准备必要的初始数据并伤及计算;5)对计算机求得的结果进行必要的分析。
其中建立优化设计数学模型是首要的和关键的一步,它是取得正确结果的前提。
优化方法的选取取决于数学模型的特点,例如优化问题规模的大小,目标函数和约束函数的性态以及计算精度等。
在比较各种可供选用的优化方法时,需要考虑的一个重要因素是计算机执行这些程序所花费的时间和费用,也即计算效率。
2. 建立数学模型的基本原则与步骤①设计变量的确定;设计变量是指在优化设计的过程中,不断进行修改,调整,一直处于变化的参数称为设计变量。
设计变量的全体实际上是一组变量,可用一个列向量表示:x= [彫Sa X4 ..................... 。
②目标函数的建立;选择目标函数是整个优化设计过程中最重要的决策之一。
当对某以设计性能有特定的要求,而这个要求有很难满足时,则针对这一性能进行优化会得到满意的效果。
目标函数是设计变量的函数,是一项设计所追求的指标的数学反映,因此它能够用来评价设计的优劣。
目标函数的一般表达式为:f(x)= f(X臣」甌巧捡.■…,要根据实际的设计要求来设计目标函数。
③约束条件的确定。
一个可行性设计必须满足某些设计限制条件,这些限制条件称为约束条件,简称约束。
由若干个约束条件构成目标函数的可行域,而可行域内的所有设计点都是满足设计要求的,一般情况下,其设计可行域可表示为(.r}S O tt =A (⑴三O L.2.. /J < FT在可行域中,任意设计点满足全部约束条件,称为可行解,但不是最优解,而优化设计就是要求出目标函数在可行域的最优解。
matlab四连杆机构代码实现

matlab四连杆机构代码实现
下面是一个使用MATLAB实现四连杆机构的简单示例代码:
```matlab
% 定义连杆参数
a = [2 3 2 3]; % 连杆长度
theta = [pi/4 pi/3 pi/2 pi/6]; % 连杆转角
% 计算连杆末端坐标
x = zeros(1,5);
y = zeros(1,5);
for i = 2:5
x(i) = x(i-1) + a(i-1) * cos(theta(i-1));
y(i) = y(i-1) + a(i-1) * sin(theta(i-1));
end
% 绘制机构图像
figure;
hold on;
axis equal;
for i = 1:4
line([x(i) x(i+1)], [y(i) y(i+1)], 'LineWidth', 2);
plot(x(i+1), y(i+1), 'ro', 'MarkerSize', 8);
end
```
在这个例子中,我们使用数组`a`存储了四个连杆的长度,使用数组`theta`存储了四个连杆的转角。
通过循环计算每个连杆末端的坐标,并使用MATLAB的`line`函数和`plot`函数绘制连杆和末端坐标点。
你可以根据实际情况修改连杆长度和转角,然后运行代码来生成相应的机构图像。
希望对你有帮助!。
用matlab分析四杆机构

首先创建函数 FoutBarPosition ,函数 fsolve 通过他确定 。
function t=fourbarposition(th,th2,L2,L3,L4,L1) t=[L2*cos(th2)+L3*cos(th(1))-L4*cos(th(2))- L1; …L2*sin(th2)+L3*sin(th(1))-L4*sin(th(2))];主程序如下:% 曲柄输入角度从 0 至 360 度,步长为 pi/6 th34=zeros(length(th2),2); %建立一个 N 行2列的零矩阵,第一列存放options=optimset('display','off'); %0 _3 ,第二列存放 0 _3figure(1)'k--A',x,y,'ko',xx,yy,'ks') title (' 连杆 3 的几个位置点 ') xlabel(' 水平方向 ') ylabel(' 垂直方向 ') axis equal %XY 坐标均衡 % 重新细分曲柄输入角度 0 _2,步长为 5 度th34=zeros(length(th2),2); options=optimset('display','off'); for m=1:length(th2)disp ' * * * 平面四杆机构的运动分析L1=304.8;L2=101.6;L3=254.0;L4=177.8;% 给定已知量,各杆长 L1,L2,L3,L4th2=[0:1/6:2]*pi;for m=1:length(th2) %建立for 循环,求解 0 _3 0 _4th34(m,:)=fsolve('fourbarposition',[1 1],…%调用fsove 函数求解关于 0 _3 0 _4options,th2(m),L2,L3,L4,L1); % 的非线性超越方程,结果保存在 th34 中end y=L2*sin(th2)+L3*sin(th34(:,1)'); % 连杆 3 的 D 端点 Y 坐标值 x=L2*cos(th2)+L3*cos(th34(:,1)'); % 连杆 3 的 D 端点 X 坐标值xx=[L2*cos(th2)]; % 连杆 3 的 C 端点 X 坐标值 yy=[L2*sin(th2)];% 连杆 3 的 C 端点 Y 坐标值plot([x;xx],[y;yy],'k',[0 L1],[0 0],%绘制连杆3的几个位置点th2=[0:2/72:2]*pi;th34(m,:)=fsolve('fourbarposition',[1 1], options,th2(m),L2,L3,L4,L1); endfigure(2) plot(th2*180/pi,th34(:,1)*180/pi,th2*180/pi,th34(:,2)*180/pi)% 绘制摇杆 4 的角位移关于曲柄 2 的角位移图axis([0 360 0 170]) % 确定 XY 边界值 grid % 图形加网格xlabel(' 主动件转角 \theta_2( 度 )') ylabel(' 从动件角位移 (度 )') title(' 角位移线图 ') text(120,120,' 摇杆 4 角位移 ') text(150,40,' 连杆 3 角位移 ') w2=250; % 设定曲柄角速度 for i=1:length(th2)A=[- L3*sin(th34(i,1)) L4*sin(th34(i,2)); L3*cos(th34(i,1)) -L4*cos(th34(i,2))]; B=[w2*L2*sin(th2(i)); -w2*L2*cos(th2(i))]; w=inv(A)*B; w3(i)=w(1); w4(i)=w(2); end figure(3)plot(th2*180/pi,w3,th2*180/pi,w4);% 绘制角速度线图axis([0 360 -175 200]) text(50,160,' 摇杆 4 角速度 (\omega_4)') text(220,130,' 连杆 3 角速度 (\omega_3)')plot(th2*180/pi,th34(:,1),th2*180/pi,th34(:,2)) 图%绘制连杆 3的角位移关于曲柄 2 的角位移grid xlabel(' 主动件转角 \theta_2( 度 )') ylabelC 从动件角速度(rad'cdot s^-l})') title (' 角速度线图 ') for i=1:length(th2)C=[-L3*sin(th34(i,1)) L4*sin(th34(i,2)); L3*cos(th34(i,1)) -L4*cos(th34(i,2))];D=[w2A2*L2*cos(th2(i))+w3(i)A2*L3*cos(th34(i,1))-w4(i)A2*L4*cos(th34(i,2));... w2A2*L2*si n( th2(i))+w3(i)^2*L3*s in (th34(i,1))-w4(i)A2*L4*si n( th34(i,2))]; a=inv(C)*D; a3(i)=a(1); a4(i)=a(2); endfigure(4) plot(th2*180/pi,a3,th2*180/pi,a4);axis([0 360 -70000 65000]) text(50,50000,' 摇杆 4 角加速度 (\alpha_4)') text(220,12000,' 连杆 3 角加速度 (\alpha_3)') grid曲柄转角 连杆转角 -摇杆转角 -连杆角速度 -摇杆角速度 -连杆加速度 -摇杆加速度 1.0e+004 *0 0.00440.0097 -0.0125-0.0125-0.54784.8458%绘制角加速度线图 xlabel (' 从动件角加速度 ')ylabel (' 从动件角加速度 (rad\cdot s^{-2})') title (' 角加速度线图 ')disp ' 曲柄转角连杆转角 -摇杆转角 -连杆角速度 -摇杆角速度 -连杆加速度 -摇杆加速度 ' ydcs=[th2'*180/pi,th34(:,1)*180/pi,th34(:,2)*180/pi,w3',w4',a3',a4']; disp(ydcs) >>* * * 平面四杆机构的运动分析0.0005 0.0042 0.0094 -0.0126 -0.0107 0.2300 5.5630 0.0010 0.0039 0.0092 -0.0124 -0.0086 0.8946 6.0520 0.0015 0.0037 0.0091 -0.0119 -0.0065 1.4143 6.2982 0.0020 0.0034 0.0090 -0.0114 -0.0043 1.7801 6.3174 0.0025 0.0032 0.0089 -0.0107 -0.0021 2.0027 6.1467 0.0030 0.0030 0.0089 -0.0100 0.0000 2.1046 5.8339 0.0035 0.0028 0.0089 -0.0093 0.0020 2.1134 5.4272 0.0040 0.0026 0.0090 -0.0085 0.0038 2.0566 4.9687 0.0045 0.0025 0.0091 -0.0078 0.0054 1.9578 4.4918 0.0050 0.0023 0.0092 -0.0072 0.0069 1.8356 4.0198 0.0055 0.0022 0.0093 -0.0065 0.0082 1.7040 3.5680 0.0060 0.0021 0.0095 -0.0060 0.0094 1.5725 3.1450 0.0065 0.0019 0.0097 -0.0055 0.0104 1.4474 2.7545 0.0070 0.0018 0.0099 -0.0050 0.0113 1.3328 2.3968 0.0075 0.0017 0.0102 -0.0045 0.0121 1.2307 2.0702 0.0080 0.0017 0.0104 -0.0041 0.0128 1.1425 1.7716 0.0085 0.0016 0.0107 -0.0037 0.0134 1.0687 1.4971 0.0090 0.0015 0.0110 -0.0034 0.0138 1.0095 1.2426 0.0095 0.0014 0.0112 -0.0030 0.0142 0.9653 1.0035 0.0100 0.0014 0.0115 -0.0027 0.0145 0.9364 0.7752 0.0105 0.0013 0.0118 -0.0024 0.0148 0.9232 0.5530 0.0110 0.0013 0.0121 -0.0020 0.0149 0.9269 0.3319 0.0115 0.0013 0.0124 -0.0017 0.0150 0.9485 0.1069 0.0120 0.0012 0.0127 -0.0014 0.0150 0.9899 -0.1276 0.0125 0.0012 0.0130 -0.0010 0.0149 1.0530 -0.3773 0.0130 0.0012 0.0133 -0.0006 0.0147 1.1404 -0.6481 0.0135 0.0012 0.0136 -0.0002 0.0145 1.2544 -0.9455 0.0140 0.0012 0.0139 0.0002 0.0141 1.3967 -1.2743 0.0145 0.0012 0.0142 0.0008 0.0136 1.5677 -1.63680.0150 0.0012 0.0144 0.0013 0.0129 1.7648 -2.0314 0.0155 0.0012 0.0147 0.0020 0.0121 1.9807 -2.4495 0.0160 0.0013 0.0149 0.0027 0.0112 2.2018 -2.8735 0.0165 0.0013 0.0151 0.0035 0.0101 2.4071 -3.2754 0.0170 0.0014 0.0153 0.0044 0.0089 2.5697 -3.6186 0.0175 0.0015 0.0155 0.0053 0.0076 2.6616 -3.8650 0.0180 0.0016 0.0156 0.0063 0.0063 2.6609 -3.9849 0.0185 0.0018 0.0157 0.0072 0.0049 2.5591 -3.9674 0.0190 0.0019 0.0158 0.0080 0.0035 2.3638 -3.8244 0.0195 0.0021 0.0159 0.0088 0.0022 2.0959 -3.5866 0.0200 0.0023 0.0159 0.0095 0.0010 1.7823 -3.2931 0.0205 0.0025 0.0159 0.0100 -0.0001 1.4487 -2.9815 0.0210 0.0027 0.0159 0.0105 -0.0011 1.1152 -2.6809 0.0215 0.0029 0.0159 0.0108 -0.0020 0.7942 -2.4103 0.0220 0.0031 0.0158 0.0111 -0.0028 0.4916 -2.1794 0.0225 0.0033 0.0158 0.0112 -0.0035 0.2086 -1.9913 0.0230 0.0036 0.0157 0.0112 -0.0042 -0.0565 -1.8450 0.0235 0.0038 0.0156 0.0111 -0.0048 -0.3071 -1.7375 0.0240 0.0040 0.0155 0.0110 -0.0054 -0.5475 -1.6650 0.0245 0.0042 0.0154 0.0108 -0.0060 -0.7817 -1.6233 0.0250 0.0044 0.0153 0.0104 -0.0065 -1.0139 -1.6089 0.0255 0.0046 0.0151 0.0100 -0.0071 -1.2479 -1.6181 0.0260 0.0048 0.0150 0.0096 -0.0077 -1.4868 -1.6480 0.0265 0.0050 0.0148 0.0090 -0.0082 -1.7336 -1.6955 0.0270 0.0052 0.0146 0.0084 -0.0088 -1.9905 -1.7574 0.0275 0.0054 0.0145 0.0076 -0.0095 -2.2588 -1.8304 0.0280 0.0055 0.0143 0.0068 -0.0101 -2.5391 -1.9100 0.0285 0.0056 0.0141 0.0058 -0.0108 -2.8305 -1.9910 0.0290 0.0057 0.0138 0.0048 -0.0115 -3.1300 -2.06600.0295 0.0058 0.0136 0.0037-0.0122 -3.4326 -2.1255 0.0300 0.0059 0.0133 0.0024 -0.0130 -3.7297 -2.1572 0.0305 0.0059 0.0131 0.0011 -0.0137 -4.0091 -2.1451 0.0310 0.0059 0.0128 -0.0004 -0.0145 -4.2538 -2.0696 0.0315 0.0059 0.0125 -0.0019 -0.0152 -4.4419 -1.9079 0.0320 0.0058 0.0122 -0.0035 -0.0158 -4.5473 -1.6352 0.0325 0.0058 0.0119 -0.0051 -0.0163 -4.5411 -1.2273 0.0330 0.0056 0.0115 -0.0066 -0.0166 -4.3954 -0.6661 0.0335 0.0055 0.0112 -0.0081 -0.0167 -4.0889 0.0551 0.0340 0.0053 0.0109 -0.0095 -0.0166 -3.6129 0.9243 0.0345 0.0051 0.0105 -0.0106 -0.0161 -2.9781 1.9058 0.0350 0.0049 0.0102 -0.0115 -0.0152 -2.2178 2.9395 0.0355 0.0047 0.0099 -0.0122 -0.0140 -1.3857 3.9473 0.03600.00440.0097-0.0125-0.0125-0.54784.8458图形输出图2连杆3的几个位置点-liOO•50 0 50 WQ 150200 苫 030a水平方向连秆了的几牛位,e 点从动件鶴速屋. 0)- hg § S O g §— 2g 8从动件fte移〔度)M Ilf■、III--疋■=r fcTi - ■-rl-Tr-r u TT ■ r r ■ T h T\ [搖杆個加速度圍V :・MlL50 100 ISO 200 250 m 350乩动斧S 加逋度图5角加速度线图11 I II…….丄J江谨杆埔加逮政幻Jj\IMl。
第三章 四连杆之MATLAB程式讲解
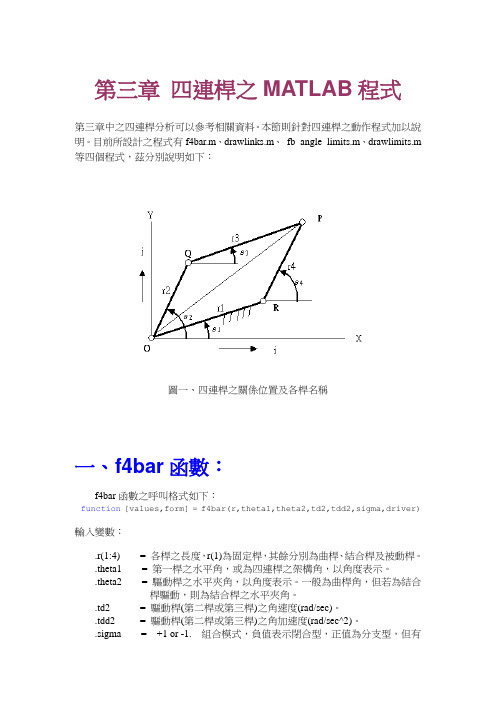
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式,茲分別說明如下:圖一、四連桿之關係位置及各桿名稱一、f4bar函數:f4bar函數之呼叫格式如下:function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數:.r(1:4) = 各桿之長度,r(1)為固定桿,其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角,或為四連桿之架構角,以角度表示。
.theta2 = 驅動桿之水平夾角,以角度表示。
一般為曲桿角,但若為結合桿驅動,則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式,負值表示閉合型,正值為分支型,但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數:.form = 組合狀態,0 :表示無法組合;1:可以正確組合.values = 輸出矩陣,其大小為 4 X 7,各行之資料分配如下:其中第一行之連桿位置向量,屬於單桿的位置向量。
第二行為各桿之水平夾角,第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量,第五行為向量,第六行為絕對量,第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中,以abs()這一個函數指令即可求得,而以函數angle()則可求得其夾角,雖然第二行與第七行之輸出亦有相對應之夾角。
例一:為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中,有框線者表示其為輸入值。
基于matlab的4连杆机构设计

基于matlab的4连杆机构设计第一篇:基于matlab的4连杆机构设计目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理................................................................................................1 1.3 机构的数学模型的建立.......................................................................................1 1.3.1建立机构的闭环矢量位置方程...................................................1 1.3.2求解方法.....................................................................2 2 基于MATLAB程序设计..........................................................................................4 2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出.............................................................................................7 3 基于MATLAB图形界面设计....................................................................................11 3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献………………………………………………………………………………………………18平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
Matlab在四杆机构运动分析中的应用

Matlab在四杆机构运动分析中的应用MATLAB软件由美国MathWorks公司于1982年推出,经过十几年的发展和竞争,现已成为国际公认的最优秀的科技应用软件之一。
MATLAB提供了强大的矩阵处理和绘图功能。
它主要包括两部分内容:核心函数和工具箱。
Matlab编程代码接近数学推导公式,简洁直观,与科技人员的思维方式和书写习惯相适应,操作简易,人机交互性能好,且可以方便迅速地用三维图形、图像、声音、动画等表达计算结果,拓展思路。
编制相应的M函数文件。
Pos.m用于求解位置、角度和角加速度。
th1为初始角度,w1为杆1角速度,其余为杆长。
将课本P35(i)、(ii)、(iii)式用MATLAB语言表述,即可编制为四杆机构求解函数文件pos.m。
function f=pos(th1,w1,l1,l2,l3,l4)syms x21 x31 x22 x32x1=th1*pi/180;x11=cos(x1);x12=sin(x1);eq1=l1*x11+l2*x21-l3*x31-l4;eq2=l1*x12+l2*x22-l3*x32;eq3=x21^2+x22^2-1;eq4=x31^2+x32^2-1;s=solve(eq1,eq2,eq3,eq4,x21,x22,x31,x32);s1=double(s.x21); s2=double(s.x22);s3=double(s.x31); s4=double(s.x32);x2=(acos(s1(1,1)))/pi*180;x3=(acos(s3(1,1)))/pi*180;A=[l2*s2(1,1),-l3*s4(1,1);l2*s1(1,1),-l3*s3(1,1)];B=[-l1*x12;-l1*x11];w=A\(w1*B);w2=w(1,1);w3=w(2,1);C=[-l2*w(1,1)*s1(1,1),l3*w(2,1)*s3(1,1);l2*w(1,1)*s2(1,1),-l3*w(2,1)*s4(1,1)];D=[w(1,1);w(2,1)];E=[-l1*w1*x11;l1*w1*x12];F=[l2*s2(1,1),-l3*s4(1,1);l2*s1(1,1),-l3*s3(1,1)];t=F\(C*D+w1*E);a2=t(1,1);a3=t(2,1);l1=cat(1,th1,w1,0);l2=cat(1,x2,w2,a2);l3=cat(1,x3,w3,a3);f=(cat(2,l1,l2,l3))';subplot(2,2,1);plot(th1,w2,'r-');hold on;title('连杆2角速度分析');subplot(2,2,2);plot(th1,a2,'b-');hold on;title('连杆2角加速度分析');subplot(2,2,3);plot(th1,w3,'r-');hold on;title('连杆3角速度分析');subplot(2,2,4);plot(th1,a3,'b-');hold on;title('连杆3角加速度分析');return在MA TLAB命令窗口输入命令:>> th1=60;w1=pi/3;l1=20;l2=30;l3=40;l4=45;>> function f=pos(th1,w1,l1,l2,l3,l4)60°,ω=pi/3时的值即可得到theta=采用实时动画的方法编写draw.m文件:function dw = draw(l1,l2,l3,l4,x1,x2,x3)figure(2);th1=x1*pi/180;th2=x2*pi/180;th3=x3*pi/180;x=0:0.001:l4;plot(x,0,'r-');axis([-25,70,-25,60]);hold onfor i=0:0.1:l1;s=i*cos(th1); c=i*sin(th1);plot(s,c,'b-');hold on;end;for x=0:0.1:l3;s2=x*cos(th3)+l4;c2=x*sin(th3);plot(s2,c2);hold on;endfor x=0:0.1:l2;s3=l1*cos(th1)+x*cos(th2); c3=l1*sin(th1)+x*sin(th2);plot(s3,c3);hold on;endreturn代入pos.m中所得的结果,输入命令:>>draw(l1,l2,l3,l4,y(1,1),y(2,1),y(3,1))即可得到当前位置下的四杆图形。
基于Matlab的四杆机构优化设计简介

·制造业信息化·Vol.22.,200922009机电产品开发与创新Development &Innovation of M achinery &E lectrical P roducts3,No.1Jan .,2010第23卷第1期2010年1月收稿日期:2009-11-06作者简介:李建霞,女,河南信阳人,教授。
主要从事计算机辅助设计教学与研究工作。
已发表核心期刊论文20余篇;王良才,男,山东济南人,副教授。
主要从事机械设计教学与研究工作。
已发表核心期刊论文10余篇。
0引言Matlab 语言是一种非常强大的工程计算语言,提供了非常丰富的Matlab 优化工具箱。
其优化工具箱有许多常用的优化算法,广泛应用于线性规划、二次规划、非线性优化、最小二乘法问题、非线性方程求解、多目标决策等问题,其函数表达简洁,优化算法选择灵活,参数设置自由,相比于其它很多成熟的优化程序具有明显的优越性。
机械优化设计是在现代机械设计理论发展基础上产生的一种新的设计方法,在机械零部件设计中取得了广泛的应用。
机械优化设计是在进行某种机械产品设计时,根据规定的约束条件,优选设计参数,使某项或几项设计指标获得最优值。
在进行优化设计时,首先要建立工程设计问题的数学模型,然后按照数学模型的特点选择优化方法及其计算程序,求得最优设计方案。
1四杆机构优化设计的数学模型四杆机构是机械传动的重要组成部分。
设计四杆机构通常使用作图法与实验法,这两种方法简单易行,但误差较大,运用解析法,能获得所要求的精度,然而用人工进行,整个设计过程是一项繁琐、冗长的工作,甚至可能无法实现。
采用Matlab 优化工具箱对四杆机构进行优化设计,不仅参数输入简单,而且编程工作量小,可更快捷准确地达到设计要求。
四杆机构种类很多,这里只以曲柄摇杆机构为例说明四杆机构优化设计方法。
Matlab 优化工具箱是一套功能强大的工程计算软件,集数值计算、符号运算、可视化建模、仿真和图形处理等多种功能于一体,被广泛应用于机械设计、自动控制和数理统计等工程领域。
基于MATLAB的四杆变幅机构结构参数分析(1)

作者简介:黄鹤辉(1947-),男,广西宜州市人,广西工学院副教授。
收稿日期:2002-12-17基于M A TLAB 的四杆变幅机构结构参数分析黄鹤辉,陈 晨(广西工学院机械工程系,广西柳州 545006)摘要:本文介绍利用M A TLAB [1]数值计算和数据可视化功能对门座式起重机四杆变幅机构结构参数进行分析,各参数变化时对运动规律的影响。
关键词:门座式起重机;四杆变幅机构;结构分析中图分类号:TB 11 文献标识码:A :1004-2148(2003)01-0029-04引言 四杆变幅机构是门座式起重机应用最广泛的一种装置。
它的设计要求是:在变幅过程中由物品引起的臂架力矩要尽量地小,变幅轨迹的最大铅垂落差要尽量地小,速度要均匀,机构重量要轻等。
由于四杆变幅机构结构参数较多,用一般的解析法或图解法很难分析其运动规律。
本文介绍利用M A TLAB 强大的数值计算功能和数据可视化功能,当初步选定某一结构方案后,计算臂架一定转角范围内象鼻梁端点(起吊点)的轨迹坐标和臂架力矩值并绘制曲线,并在其它参数确定的情况下将某一参数在一定范围内取不同值绘制轨迹曲线和力矩曲线,分析各参数对轨迹、力矩曲线的影响规律,为合理确定各参数提供直观、可靠的依据。
在此基础上,也可借助M A TLAB 优化工具箱的函数进行优化计算[2],最后再次将优化结果绘制曲线验证。
由于M A TALB 语言书写简洁,且无须设计者进行复杂的优化计算基础编程工作,易于在实际设计工作中推广应用。
1 四杆变幅机构运动分析[3] 四杆变幅机构结构简图如图1所示。
图中S m ax ,S m in —机构最大、最小的变幅值: h —起升高度;(x ,y )—象鼻梁E 点坐标;(x 0,y 0)—拉杆固定支点B 0的坐标;l 0—A 0B 0间的长度;l 0—臂架A 0D 的长度;l 2—象鼻梁后臂DB 的长度;l 3—拉杆B 0B 的长度;l 4—象鼻梁前臂D E 的长度;图1 四杆变幅机构Η—象鼻梁前后臂之间的夹角;Α—臂架的摆角;Β—拉杆的摆角;Υ—象鼻梁前臂与x 轴的夹角。
matlab四连杆 带代码

用Matlab对四连杆运动模拟引言四连杆机构因其结构灵活、能够传递动力并有效地实现预定动作,在很多领域得到了广泛应用。
进行连杆机构运动分析,传统方法主要是图解法或分析法,无论设计精度还是设计效率都相对低下,无法满足现代机械高速高精度的要求。
随着计算机技术的飞速发展,特别是以MATLAB为代表的数值计算软件的出现,为进行机构分析提供了有力的工具。
1、四连杆介绍1.1、四连杆介绍与分类所有运动副均为转动副的四杆机构称为铰链四杆机构,它是平面四杆机构的基本形式,其他四杆机构都可以看成是在它的基础上演化而来的。
选定其中一个构件作为机架之后,直接与机架链接的构件称为连架杆,不直接与机架连接的构件称为连杆,能够做整周回转的构件被称作曲柄,只能在某一角度范围内往复摆动的构件称为摇杆。
如果以转动副连接的两个构件可以做整周相对转动,则称之为整转副,反之称之为摆转副。
铰链四杆机构中,按照连架杆是否可以做整圆周转动,可以将其分为三种基本形式,即曲柄摇杆机构,双曲柄机构和双摇杆机构。
曲柄摇杆机构,两连架杆中一个为曲柄一个为摇杆的铰链四杆机构。
双曲柄机构,具有两个曲柄的铰链四杆机构称为双曲柄机构。
其特点是当主动曲柄连续等速转动时,从动曲柄一般做不等速转动。
在双曲柄机构中,如果两对边构件长度相等且平行,则成为平行四边形机构。
这种机构的传动特点是主动曲柄和从动曲柄均以相同的角速度转动,而连杆做平动。
双摇杆机构。
双摇杆机构是两连架杆均为摇杆的铰链四杆机构。
1.2、格拉霍夫定理杆长之和条件:平面四杆机构的最短杆和最长杆的长度之和小于或者等于其余两杆长度之和。
在铰链四杆机构中,如果某个转动副能够成为整转副,则它所连接的两个构件中,必有一个为最短杆,并且四个构件的长度关系满足杆长之和条件。
在有整装副存在的铰链四杆机构中,最短杆两端的转动副均为整转副。
此时,如果取最短杆为机架,则得到双曲柄机构;若取最短杆的任何一个相连构件为机架,则得到曲柄摇杆机构;如果取最短杆对面构件为机架,则得到双摇杆机构。
MATLAB程序:已知三个位置设计平面四杆机构求解程序(位移矩阵法)

%MATLAB程序:已知三个位置设计平面四杆机构求解程序(位移矩阵法)clear;clc;%凡是变量名前带v的为数值变量,不带的是符号变量vxp1=0; vyp1=0; vsita1=0*pi/180;vxp2=-2; vyp2=6; vsita2=40*pi/180;vxp3=-10; vyp3=8; vsita3=90*pi/180; %精确位置P1,P2,P3及各角度vsita12=vsita2-vsita1;vsita13=vsita3-vsita1;vxa=-10; vya=-2;vxd=-5; vyd=-2; %选定A,D点%所有数值均在此确定,更改此处即可解出不同数值的四杆机构位移矩阵方程syms xp1 yp1 xp2 yp2 xp3 yp3 sita12 sita13;syms xa ya xb1 yb1 xb2 yb2 xb3 yb3;f1='(xb2-xa)^2+(yb2-ya)^2=(xb1-xa)^2+(yb1-ya)^2';f2='(xb3-xa)^2+(yb3-ya)^2=(xb1-xa)^2+(yb1-ya)^2'; %前两个机构方程f3='xb2=cos(sita12)*xb1-sin(sita12)*yb1+xp2-xp1*cos(sita12)+yp1*sin(sita12)';f4='yb2=sin(sita12)*xb1+cos(sita12)*yb1+yp2-xp1*sin(sita12)-yp1*cos(sita12)'; %由第一个位移矩阵方程得出f5='xb3=cos(sita13)*xb1-sin(sita13)*yb1+xp3-xp1*cos(sita13)+yp1*sin(sita13)';f6='yb3=sin(sita13)*xb1+cos(sita13)*yb1+yp3-xp1*sin(sita13)-yp1*cos(sita13)'; %由第二个位移矩阵方程得出f1=subs(f1,{xa,ya},{vxa,vya});f2=subs(f2,{xa,ya},{vxa,vya});f3=subs(f3,{xp1,xp2,yp1,sita12},{vxp1,vxp2,vyp1,vsita12});f4=subs(f4,{xp1,yp1,yp2,sita12},{vxp1,vyp1,vyp2,vsita12});f5=subs(f5,{xp1,xp3,yp1,sita13},{vxp1,vxp3,vyp1,vsita13});f6=subs(f6,{xp1,yp1,yp3,sita13},{vxp1,vyp1,vyp3,vsita13}); %代入具体数值[xb1,xb2,xb3,yb1,yb2,yb3]=solve(f1,f2,f3,f4,f5,f6); %解方程vxb1=vpa(xb1);vyb1=vpa(yb1);vxb2=vpa(xb2);vyb2=vpa(yb2);vxb3=vpa(xb3);vyb3=vpa(yb3);(vxb1-vxa)^2+(vyb1-vya)^2;(vxb2-vxa)^2+(vyb2-vya)^2;(vxb3-vxa)^2+(vyb3-vya)^2; %去掉这三行分号可验证B点三个位置是否距离A点相等syms xd yd xc1 yc1 xc2 yc2 xc3 yc3;f7='(xc2-xd)^2+(yc2-yd)^2=(xc1-xd)^2+(yc1-yd)^2';f8='(xc3-xd)^2+(yc3-yd)^2=(xc1-xd)^2+(yc1-yd)^2'; %前两个机构方程f9='xc2=cos(sita12)*xc1-sin(sita12)*yc1+xp2-xp1*cos(sita12)+yp1*sin(sita12)';f10='yc2=sin(sita12)*xc1+cos(sita12)*yc1+yp2-xp1*sin(sita12)-yp1*cos(sita12)'; %由第一个位移矩阵方程得出f11='xc3=cos(sita13)*xc1-sin(sita13)*yc1+xp3-xp1*cos(sita13)+yp1*sin(sita13)';f12='yc3=sin(sita13)*xc1+cos(sita13)*yc1+yp3-xp1*sin(sita13)-yp1*cos(sita13)'; %由第二个位移矩阵方程得出f7=subs(f7,{xd,yd},{vxd,vyd});f8=subs(f8,{xd,yd},{vxd,vyd});f9=subs(f9,{xp1,xp2,yp1,sita12},{vxp1,vxp2,vyp1,vsita12});f10=subs(f10,{xp1,yp1,yp2,sita12},{vxp1,vyp1,vyp2,vsita12});f11=subs(f11,{xp1,xp3,yp1,sita13},{vxp1,vxp3,vyp1,vsita13});f12=subs(f12,{xp1,yp1,yp3,sita13},{vxp1,vyp1,vyp3,vsita13}); %代入具体数值[xc1,xc2,xc3,yc1,yc2,yc3]=solve(f7,f8,f9,f10,f11,f12); %解方程vxc1=vpa(xc1);vyc1=vpa(yc1);vxc2=vpa(xc2);vyc2=vpa(yc2);vxc3=vpa(xc3);vyc3=vpa(yc3);(vxc1-vxd)^2+(vyc1-vyd)^2;(vxc2-vxd)^2+(vyc2-vyd)^2;(vxc3-vxd)^2+(vyc3-vyd)^2; %去掉这三行分号可验证C点三个位置是否距离D点相等%最终答案xb1,yb1,xc1,yc1Lab=sqrt((vxb1-vxa)^2+(vyb1-vya)^2)Lbc=sqrt((vxb1-vxc1)^2+(vyb1-vyc1)^2)Lcd=sqrt((vxc1-vxd)^2+(vyc1-vyd)^2)Lad=sqrt((vxa-vxd)^2+(vya-vyd)^2) %得到四杆长'曲柄存在条件:'%得出四杆长后计算得到'可靠到位条件:'[vxc1-vxb1,vyc1-vyb1]*[vxc1-vxd,vyc1-vyd]'[vxc2-vxb2,vyc2-vyb2]*[vxc2-vxd,vyc2-vyd]'[vxc3-vxb3,vyc3-vyb3]*[vxc3-vxd,vyc3-vyd]''顺序到位条件:'%未完成输出结果:xb1 =(-7-4*sin(2/9*pi)+4*cos(2/9*pi))/(4*cos(2/9*pi)+4*sin(2/9*pi)-5)yb1 =-1xc1 =-6*(27+24*sin(2/9*pi)-64*cos(2/9*pi))/(-31*cos(2/9*pi)-5+39*sin(2/9*pi))yc1 =-2*(72*cos(2/9*pi)-175+192*sin(2/9*pi))/(-31*cos(2/9*pi)-5+39*sin(2/9*pi))Lab =1.0288436025165976748172169832223Lbc =2.9872531417317691216303250912289Lcd =6.9831476545729886023199865357226Lad =5ans =曲柄存在条件:ans =可靠到位条件:ans =14.605219997928496422368168445525ans =19.799913716084881287517588922012ans =20.814756669957613005391246805307ans =顺序到位条件:。
matlab

Matlab课程设计班级:机械081姓名:黄太林学号:20081110661.如图一所示四杆机构简图,由图可得:图1四杆机构L 2cos 2θ+ L 3cos 3θ- L 4cos 4θ -L 1cos 1θ=0 (1)L 2sin 2θ+ L 3sin 3θ- L 4sin 4θ -L 1sin 1θ=0 (2)令1θ=0,上式简化为:L 2cos 2θ+ L 3cos 3θ- L 4cos 4θ -L 1=0 (3) L 2sin 2θ+ L 3sin 3θ- L 4sin 4θ -L 1=0 (4) 杆2的端部线速度V 2=L 2w 2,连杆4的端部线速度)θ-θsin()θ-θsin(V = V 343224,V 4的速度方向为垂直于杆4并且同W 4一致。
且得3、4杆的角速度以及角加速度)-sin()-sin(=w 43324223θθθθL w L (5))θ-θsin()θ-θsin(=w 34432224L w L (6)3α=)θ-θsin(-)θ-θcos()θ-θcos()θ-θsin(α-43324434233242222422L w L w L w L L ++ (7) 4α=)θ-θsin(-)θ-θcos()θ-θcos()θ-θsin(α43424443233232222322L w L w L w L L ++ (8)2.由上述可知,当给定杆长和杆2的角速度w 2(匀速即02=α)时,杆4的的角速度和角加速度都是关于2θ的方程。
由方程(3)、(4)通过fsolve 函数可以得出3θ、4θ,代码如下(fun.m): function F=fun(X)global l1 l2 l3 l4 theta1 theta2 theta3=X(1); theta4=X(2);F(1)=l2*cos(theta2)+l3*cos(theta3)-l4*cos(theta4)-l1*cos(theta1); F(2)=l2*sin(theta2)+l3*sin(theta3)-l4*sin(theta4)-l1*sin(theta1); (注:theta1即1θ,theta2即2θ,theta3即3θ,theta4即4θ) 然后调用a=fsolve(@fun,[1,1]),则theta3=a(1),theta4=a(4),则可以确定此时各个杆件的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.角位移M函数:
function y=jweiyi(x)
% Input parameters
% x(1)=theta-1
% x(2)=theta-2 guess value
% x(3)=theta-3 guess value
% x(4)=r1
% x(5)=r2
% x(6)=r3
% x(7)=r4
% Output parameters
% y(1)=theta-2
% y(2)=theta-3
theta2=x(2);
theta3=x(3);
%
epsilon=1.0E-6;
%
f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);
x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];
%
while norm(f)>epsilon
J=[-x(5)*sin(theta2) x(6)*sin(theta3);x(5)*cos(theta2) -x(6)*cos(theta3)];
dth=inv(J)*(-1.0*f);
theta2=theta2+dth(1);
theta3=theta3+dth(2);
f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);
x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];
norm(f);
end;
y(1)=theta2;
y(2)=theta3;
2. r1旋转360°时,θ2,θ3的M文件程序:
r(1)=50;
r(2)=150;
r(3)=300;
r(4)=400;
dr=pi/180;
th(1)=0;
th(2)=58.4119*dr;
th(3)=154.7912*dr;
y=jweiyi([th(1),th(2),th(3),r(1),r(2),r(3),r(4)])
dth=1*dr;
for i=1:360
y=jweiyi([th(1),th(2),th(3),r(1),r(2),r(3),r(4)]);
th23(i,:)=[th(1)/dr,th(2)/dr,th(3)/dr];
th(1)=th(1)+dth;
th(2)=y(1);
th(3)=y(2);
end
figure(1)
plot(th23(:,1),th23(:,2),th23(:,1),th23(:,3),th23(:,1),th23(:,1)) axis([0,360,0,360])
grid on
title('角位移线图')
xlabel('曲柄转角th(1)')
ylabel('从动件转角th(2),th(3)')
text(300,50,'角th(2)')
text(300,150,'角th(3)')
text(200,200,'角th(1)')
3.角速度的M函数:
function y=rrrvel(x)
% Input parameters
%
% x(1)=theta-1
% x(2)=theta-2
% x(3)=theta-3
% x(4)=dtheta-1
% x(5)=r1
% x(6)=r2
% x(7)=r3
%
% Output parameters
%
% y(1)=dtheta-2
% y(2)=dtheta-3
%
A=[-x(6)*sin(x(2)) x(7)*sin(x(3));
x(6)*cos(x(2)) -x(7)*cos(x(3))];
B=[x(5)*sin(x(1));-x(5)*cos(x(1))]*x(4);
y=inv(A)*B;
4. r1旋转360°时ω2,ω3的M文件程序:
th(1)=0;
dr=pi/180;
dth(1)=36;
dth(2)=58.4119*dr;
dth(3)=154.7912*dr;
dth1=1*dr;
r(1)=50;
r(2)=150;
r(3)=300;
r(4)=400;
for j=1:360
x=rrrvel([th(1),dth(2),dth(3),dth(1),r(1),r(2),r(3)]);
y=jweiyi([th(1),dth(2),dth(3),r(1),r(2),r(3),r(4)]);
dth(2)=y(1);
dth(3)=y(2);
th(1)=th(1)+dth1;
dth23(j,:)=[th(1)/dr,x(1)/dr,x(2)/dr];
end
figure(2)
plot(dth23(:,1),dth23(:,2),dth23(:,1),dth23(:,3))
axis([0,360,-800,2000])
grid on
title('角速度线图')
xlabel('曲柄旋转角度')
ylabel('从动件角速度dth(2),dth(3)(rad/s)')
text(250,200,'连杆2角速度')
text(50,100,'摇杆3角速度')
5. r1旋转360°时,α2,α3程序M文件:
r(1)=50;
r(2)=150;
r(3)=300;
r(4)=400;
th(1)=0;
dr=pi/180;
dth(2)=58.4119*dr;
dth(3)=154.7912*dr;
dth(1)=36;
dth2=1*dr;
for k=1:360
x=rrrvel([th(1),dth(2),dth(3),dth(1),r(1),r(2),r(3)]);
y=jweiyi([th(1),dth(2),dth(3),r(1),r(2),r(3),r(4)]);
dth(2)=y(1);
dth(3)=y(2);
w1=x(1);
w2=x(2);
C=[-r(2)*sin(dth(2)),r(3)*sin(dth(3));r(2)*cos(dth(2)),-r(3)*cos(dth(3))];
D=-[-w1*r(2)*cos(dth(2)),w2*r(3)*cos(dth(3));-w2*r(2)*sin(dth(2)),w2*r(3)*sin(dth(3))]*[w1;w 2]+10*[10*r(1)*cos(th(1));10*r(1)*sin(th(1))];
a=inv(C)*D;
a2(k)=a(1);
a3(k)=a(2);
jiao(k)=th(1);
th(1)=th(1)+dth2;
end
figure(3)
plot(jiao/dr,a2,jiao/dr,a3)
axis([0,360,-5000,5000])
grid on
title('角加速度线图')
xlabel('曲柄旋转转角')
ylabel('从动件角加速度(rad/s^2)')
text(200,40,'连杆2的角加速度')
text(150,-40,'摇杆3的角加速度')。
