浙教版数学九年级下册《三角形的内切圆》习题
春九年级数学下册2.3三角形的内切圆同步练习新版浙教版0418141【含解析】

) )
第 1 页,共 4 页
14. 如图,AB 是 ⊙O 的直径,点 D 在 AB 的延长线上,DC 切 ⊙O 于 C ,若 ∠A = 25◦ ,则 ∠D 等于( ). ◦ A. 20 B. 30◦ C. 40◦ D. 50◦
15. 已知 △ABC 中,∠ABC = 50◦ ,∠ACB = 75◦ ,点 O 是 △ABC 的内心,则 ∠BOC 的大小为( A. 120◦ B. 117.5◦ C. 87.5◦ D. 55◦ 二、填空题 16. 圆的切线的性质定理是 17. 判断:三角形一定有内切圆 . .
26. 如图所示, AB 是 ⊙O 的弦, AC 是 ⊙O 的切线, A 为切点, BC 经过圆心. 若 ∠B = 25◦ , . 则 ∠C =
27. 如图所示,AD,AE ,CB 都是 ⊙ O 的切线,切点分别为 D,E ,F ,AD = 4 cm,则 cm. △ABC 的周长是
)
6. 已知 ⊙O 的半径为 4 cm,如果圆心 O 到直线 l 的距离为 3.5 cm,那么直线 l 与 ⊙O 的位置关系是( A. 相交 B. 相切 C. 相离 D. 不确定 7. 如果一个圆的半径是 8cm ,圆心到一条直线的距离也是 8cm ,那么这条直线和这个圆的位置关系是( A. 相离 B. 相交 C. 相切 D. 不能确定 8. 如图,BC 是 ⊙O 的直径,AD 是 ⊙O 的切线,切点为 D,AD 与 CB 的延长线交于点 1 A,∠C = 30◦ ,给出下面四个结论:x AD = DC ;y AB = BD;z AB = BC ;{ 2 BD = CD,其中正确的个数为( ) A. 4 个 B. 3 个 C. 2 个 D. 1 个 9. 如图所示,点 O 是 △ABC 的内心,过点 O 作 EF AB ,与 AC ,BC 分别交于点 E ,F , 则( ) A. EF > AE + BF B. EF < AE + BF C. EF = AE + BF D. EF ⩽ AE + BF 10. 如图所示,已知 O 是以数轴的原点 O 为圆心,半径为 1 的圆,∠AOB = 45◦ ,点 P 在数轴上 运动,若过点 P 且与 OA 平行的直线与 O 有公共点,设 OP = x,则 x 的取值范围是( ) √ √ √ √ B. − 2 ⩽ x ⩽ 2 C. −1 ⩽ x ⩽ 1 D. x > 2 A. 0 < x ⩽ 2 √ 11. 我们将直角坐标系中圆心坐标和半径均为整数的圆称为“整圆” , 如图, 直线 l: y = kx + 4 3 与 x 轴、y 轴分别交于 A,B 两点,∠OAB = 30◦ ,点 P 在 x 轴上,⊙P 与 l 相切,当 P 在线段 OA 上运动时,使得 ⊙P 成为整圆的点 P 个数是( ) A. 6 B. 8 C. 10 D. 12 12. 如图,AB 为 O 直径,BC 是 O 切线,∠CAB = 50◦ ,点 P 是边 BC 上(点 P 不与 点 B 、点 C 重合)的一个动点.某学习小组根据对点 P 的不同位置的探究,给出下 列结论,其中一定错误的是( ) A. ∠ABC = 90◦ B. ∠AP B = 40◦ C. P A = P C D. P A = 2P B ˜ 13. 如图所示,Rt△ABC 的内切圆 ⊙O 与两直角边 AB 、BC 分别相切于点 D 、E ,过劣弧 DE (不包括端点 D 、E )上任一点 P 作 ⊙O 的切线 M N 与 AB 、BC 分别交于点 M 、N ,若 ⊙O 的半径为 r,则 Rt△M BN 的周长为( ) 3 5 A. r B. r C. 2r D. r 2 2
切线长定理-三角形的内切圆(巩固篇)-2022-2023学年九年级数学下册基础知识专项讲练(浙教版)

专题2.9 切线长定理 三角形的内切圆(巩固篇)(专项练习)一、单选题1.直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( ) A .12B .14C .16D .182.如图,C 与AOB ∠的两边分别相切,其中OA 边与⊙C 相切于点P .若90AOB ∠=︒,4OP =,则OC 的长为( )A .8B .2C .42D .23.如图,在ABC ∆中,52AB AC BC +=,AD BC ⊥于D ,⊙O 为ABC ∆的内切圆,设⊙O 的半径为R ,AD 的长为h ,则Rh的值为( )A .12B .27C .13D .344.如图,O 是正方形ABCD 的对角线BD 上一点,⊙O 与边AB ,BC 都相切,点E ,F 分别在AD ,DC 上,现将⊙DEF 沿着EF 对折,折痕EF 与⊙O 相切,此时点D 恰好落在圆心O 处.若DE =2,则正方形ABCD 的边长是( )A .3B .4C .22D .225.如图,点E 是ABC 的内心,AE 的延长线和ABC 的外接圆相交于点D ,与BC 相交于点G ,则下列结论:⊙BAD CAD ∠=∠;⊙若60BAC ∠=︒,则120∠=︒BEC ;⊙若点G 为BC 的中点,则90BGD ∠=︒;⊙BD DE =.其中一定正确的个数是( )A .1B .2C .3D .46.如图,已知△ABC 内接于⊙O ,∠ABC =45°,∠C =65°,点D 是BC 的中点,则∠OAD 的大小为( )A .5°B .10°C .15°D .20°7.如图,点A ,B ,C ,D 都在半径为2的O 上,若直径,30AD BC D ⊥∠=︒,则弦BC 的长为( )A .4B .22C 3D .38.如图,已知AT 切O 于点T ,点B 在O 上,且60BOT ∠=︒,连结AB 并延长交O 于点C ,O 的半径为2,设AT m =,⊙当m 23BOC ∆是等腰直角三角形; ⊙若2m =,则62AC ⊙当23m =AB 与O 相切.以上列选项正确的有( ) A .⊙B .⊙C .⊙⊙D .⊙⊙9.如图,经过A 、C 两点的⊙O 与△ABC 的边BC 相切,与边AB 交于点D ,若⊙ADC =105°,BC =CD =3,则AD 的值为( )A .2B .2C 52D 7210.如图,在⊙O 中,点C 在优弧AB 上,将弧BC 沿BC 折叠后刚好经过AB 的中点D .若⊙O 5AB =4,则BC 的长是( )A .3B .2C .2D .3二、填空题11.如图,P A ,PB 是O 的切线,A ,B 为切点.若60APB ∠=︒,则AOP ∠的大小为______.12.如图,⊙O 是△ABC 的内切圆,与AB ,BC ,CA 的切点分别为D ,E ,F ,若⊙BDE +⊙CFE =110°,则⊙A 的度数是________︒.13.如图,矩形ABCO 的顶点A ,C 分别在x 轴、y 轴上,点B 的坐标为()4,3,⊙M 是AOC △的内切圆,点N ,点P 分别是⊙M ,x 轴上的动点,则BP PN +的最小值是______.14.如图,圆O 是四边形ABCD 的内切圆,若⊙BOC =118°,则⊙AOD =__.15.如图,在平面直角坐标系中,点()0,6A ,点()8,0B ,I 是OAB 的内心,则(1)AB=______;(2)点I关于x轴对称的点的坐标是______.16.如图,点I是⊙ABC的内心,连接AI并延长交⊙ABC的外接圆于点D,若⊙ACB=70°,则⊙DBI=_____°.17.如图,已知O的半径为m,点C为直径AB延长线上一点,BC m=.过点C任作一直线l,若l上总存在点P,使过P所作的O的两切线互相垂直,则ACP∠的最大值等于__.18.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则AMN周长的最小值为________.三、解答题19.已知ABC 的三边长分别为,,BC a AC b AB c ===,⊙为ABC 的内心,且⊙在ABC的边 BC AC AB 、、上的射影分别为D E F 、、. (1)若5,4,3a b c ===,求ABC 内切圆半径r ; (2)求证:2b c aAE AF +-==.20.已知关于x 的方程x 2﹣(k +1)x +14k 2+1=0的两根是一个直角三角形两直角边的长.(1)k 取何值时,方程有两个实数根;(2)若直角三角形的内切圆半径为12,求k 值.21.如图,四边形ABCD 内接于O ,AB 是O 的直径,过点D 作O 的切线交BC 的延长线于点E ,交BA 的延长线于点F ,且DE BE ⊥,过点A 作O 的切线交EF 于点G ,连接AC .(1) 求证:AD 平分GAC ∠;(2) 若AD =5,AB =9,求线段DE 的长.22.如图,在Rt △ABC 中,⊙ABC =90°,以AB 的中点O 为圆心,AB 为直径的圆交AC 于D ,E 是BC 的中点,DE 交BA 的延长线于F .(1) 求证:FD 是圆O 的切线; (2) 若BC =4,FB =8,求AB 的长.23.在O 中,弦CD 与直径AB 相交于点P ,16ABC ∠=︒. (1)如图⊙,若52BAD =︒∠,求APC ∠和CDB ∠的大小;(2)如图⊙,若CD AB ⊥,过点D 作O 的切线,与AB 的延长线相交于点E ,求E ∠的大小.24.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的“好角”.(1)如图1,⊙E 是ABC 中⊙A 的“好角”,若A α∠=,则E ∠=______;(用含α的代数式表示)(2)如图2,四边形ABCD 内接于O ,点D 是优弧ACB 的中点,直径BF ⊥弦AC ,BF 、CD 的延长线于点G ,延长BC 到点E .求证:⊙BGC 是ABC 中⊙BAC 的“好角”.(3)如图3,ABC 内接于O ,⊙BGC 是ABC 中⊙A 的“好角”,BG 过圆心O 交O 于点F ,O 的直径为8,45A ∠=︒,求FG .参考答案1.B 【分析】⊙I 切AB 于E ,切BC 于F ,切AC 于D ,连接IE ,IF ,ID ,得出正方形CDIF 推出CD=CF =1,根据切线长定理得出AD=AE ,BE=BF ,CF=CD ,求出AD+BF=AE+BE=AB =6,即可求出答案.解:如图,⊙I 切AB 于E ,切BC 于F ,切AC 于D ,连接IE ,IF ,ID ,则⊙CDI =⊙C =⊙CFI =90°,ID=IF =1,⊙四边形CDIF是正方形,⊙CD=CF=1,由切线长定理得:AD=AE,BE=BF,CF=CD,⊙直角三角形的外接圆半径为3,内切圆半径为1,⊙AB=6=AE+BE=BF+AD,即⊙ABC的周长是AC+BC+AB=AD+CD+CF+BF+AB=6+1+1+6=14,故选:B.【点拨】本题考查了直角三角形的外接圆与内切圆,正方形的性质和判定,切线的性质,切线长定理等知识点的综合运用.2.C【分析】如图所示,连接CP,由切线的性质和切线长定理得到⊙CPO=90°,⊙COP=45°,由此推出CP=OP=4,再根据勾股定理求解即可.解:如图所示,连接CP,⊙OA,OB都是圆C的切线,⊙AOB=90°,P为切点,⊙⊙CPO=90°,⊙COP=45°,⊙⊙PCO=⊙COP=45°,⊙CP=OP=4,⊙2242=+=,OC CP OP故选C.【点拨】本题主要考查了切线的性质,切线长定理,等腰直角三角形的性质与判定,勾股定理,熟知切线长定理是解题的关键.3.B【分析】O 分别与ABC ∆的三边切于P ,Q ,T ,连接OA OB OC OP OQ OT ,,,,,,利用ABC OAB OAC OBC S S S S ∆∆∆∆=++求出7142R h =,进一步得出结论. 解:如图,令O 分别与ABC ∆的三边切于P ,Q ,T ,连接OA OB OC OP OQ OT ,,,,,⊙,,OP AB OQ AC OT BC ⊥⊥⊥⊙ABC OAB OAC OBC S S S S ∆∆∆∆=++=111222AB OP AC OQ BC OT ⋅+⋅⋅+⋅⋅ =111222AB R AC R BC R ⋅+⋅⋅+⋅⋅ 1()2R AB AC BC =++ 又⊙52AB AC BC +=⊙17()2524ABC S R BC BC R BC ∆=+=⋅ 又⊙,AD BC AD h ⊥=⊙1122ABC S BC AD h BC ∆=⋅⋅=⋅⋅ ⊙7142R BC h BC ⋅=⋅⋅ ⊙7142R h = ⊙122774Rh == 故选:B .【点拨】此题主要考查了三角形的内切圆与内心,解答的关键是,充分利用已知条件将问题转化为求几个三角形面积的和.4.C【分析】延长FO 交AB 于点G ,根据折叠对称可以知道OF ⊙CD ,所以OG ⊙AB ,即点G 是切点,OD 交EF 于点H ,点H 是切点.结合图形可知OG =OH =HD =EH ,等于⊙O 的半径,先求出半径,然后求出正方形的边长.解:如图:延长FO 交AB 于点G ,则点G 是切点,OD 交EF 于点H ,则点H 是切点,⊙ABCD 是正方形,点O 在对角线BD 上,⊙DF =DE ,OF ⊙DC ,⊙GF ⊙DC ,⊙OG ⊙AB ,⊙OG =OH =HD =HE =AE ,且都等于圆的半径.在等腰直角三角形DEH 中,DE =2,⊙EH =DH 2AE .⊙AD =AE +DE 2+2.故选C .【点拨】本题考查的是切线的性质,利用切线的性质,结合正方形的特点求出正方形的边长.5.D【分析】根据点E 是ABC 的内心,可得BAD CAD ∠=∠,故⊙正确;连接BE ,CE ,可得⊙ABC +⊙ACB =2(⊙CBE +⊙BCE ),从而得到⊙CBE +⊙BCE =60°,进而得到⊙BEC =120°,故⊙正确; BAD CAD ∠=∠,得出BD CD =,再由点G 为BC 的中点,则90BGD ∠=︒成立,故⊙正确;根据点E 是ABC 的内心和三角形的外角的性质,可得()12BED BAC ABC ∠=∠+∠,再由圆周角定理可得()12DBE BAC ABC ∠=∠+∠,从而得到⊙DBE =⊙BED ,故⊙正确;即可求解.解:⊙点E 是ABC 的内心,⊙BAD CAD ∠=∠,故⊙正确;如图,连接BE ,CE ,⊙点E 是ABC 的内心,⊙⊙ABC =2⊙CBE ,⊙ACB =2⊙BCE ,⊙⊙ABC +⊙ACB =2(⊙CBE +⊙BCE ),⊙⊙BAC =60°,⊙⊙ABC +⊙ACB =120°,⊙⊙CBE +⊙BCE =60°,⊙⊙BEC =120°,故⊙正确;⊙点E 是ABC 的内心,⊙BAD CAD ∠=∠,⊙BD CD =,⊙点G 为BC 的中点,⊙线段AD 经过圆心O ,⊙90BGD ∠=︒成立,故⊙正确;⊙点E 是ABC 的内心,⊙11,22BAD CAD BAC ABE CBE ABC ∠=∠=∠∠=∠=∠, ⊙⊙BED =⊙BAD +⊙ABE ,⊙()12BED BAC ABC ∠=∠+∠, ⊙⊙CBD =⊙CAD ,⊙⊙DBE =⊙CBE +⊙CBD =⊙CBE +⊙CAD ,⊙()12DBE BAC ABC ∠=∠+∠, ⊙⊙DBE =⊙BED ,⊙BD DE =,故⊙正确;⊙正确的有4个.故选:D【点拨】本题主要考查了三角形的内心问题,圆周角定理,三角形的内角和等知识,熟练掌握三角形的内心问题,圆周角定理,三角形的内角和等知识是解题的关键.6.B【分析】连接OB ,根据圆周角定理求出⊙AOB ,得到⊙OAB 的度数,根据三角形内角和定理求出⊙BAC ,根据圆周角定理求出⊙BAD ,结合图形计算,得到答案.解:连接OB ,由圆周角定理得,⊙AOB=2⊙C=130°,⊙OA=OB ,⊙⊙OAB=12×(180°-130°)=25°,⊙⊙ABC=45°,⊙C=65°,⊙⊙BAC=180°-45°-65°=70°,⊙点D 是BC 的中点,⊙⊙BAD=⊙CAD=35°,⊙⊙OAD=⊙BAD -⊙OAB=10°,故选:B .【点拨】本题考查的是三角形的外接圆与外心,掌握圆周角定理、三角形内角和定理是解题的关键.7.D【分析】AD BC ⊥交BC 于点E ,连接OC ,由题意得==30DCO D ∠∠︒,根据三角形内角和定理得120COD ∠=︒,即60COE ∠=︒,可得30OCE ∠=︒,根据直角三角形的性质得112EO OC ==,在Rt CEO 中,根据勾股定理得3CE 解:如图所示,令AD BC ⊥交BC 于点E ,连接OC ,⊙=2OC OD =,=30D ∠︒,⊙==30DCO D ∠∠︒,⊙180=1803030=120COD DCO D ∠=︒-∠-∠︒-︒-︒︒,即180=180120=60COE COD ∠=︒-∠︒-︒︒,⊙180=180609030OCE COE OEC ∠=︒-∠-∠︒-︒-︒=︒,⊙112EO OC ==, 在Rt CEO 中,根据勾股定理得,2222213CE CO OE -=-=⊙直径AD BC ⊥,⊙BE CE =,即223BC CE ==故选:D .【点拨】本题考查了直角三角形的性质,勾股定理,垂径定理,解题的关键是掌握这些知识点.8.C【分析】根据题目所给条件,结合圆的性质,证明90∠=︒ABO 即可判断⊙⊙,根据等腰直角三角形的性质并结合圆的性质,应用勾股定理即可判断⊙解:如图,连接TB 、OA ,TB 、OA 相较于点G当23AT m ==2333tan 2AT AOT OT ∠===⊙30AOT ∠=︒⊙OA 垂直平分TB⊙30AOT AOB OAT OAB ∠=∠=︒∠=∠,又⊙AT 与O 相切⊙90ATO ∠=︒⊙60BOT ∠=︒⊙30ATB ∠=︒⊙60OAT OAB ∠=∠=︒⊙90AOB OAB ∠+∠=︒⊙90∠=︒ABO⊙AB 与O 相切则⊙错误;⊙正确;当2AT m ==时,OT AT =⊙AB 与O 相切45AOT OAT ∠=∠=︒∴60BOT ∠=︒∵604515AOB BOT AOT ∠=∠-∠=︒-︒=︒∴30ATB AT BT ∠=︒=∵,()1180752BAT ATB ∠=︒-∠=︒∴ 754530OAB BAT TAO ∠=∠-∠=︒-︒=︒∴153045OBC AOB OAB ∠=∠+∠=︒+︒=︒∴22222222BC OC OB =+=+∴作OE BC ⊥,则122OE CE BE BC ====22222222OA AT OT ++=∵()22222226AE OA OE --∴62AC AE CE =+=∴故⊙正确;故选:C【点拨】本题主要考查圆的性质,等边三角形的性质,以及勾股定理,掌握以上知识,并正确做出辅助线是解题的关键.9.A【分析】连接OC 、OD ,作OE AB ⊥于点E .易求出75CBD CDB ∠=∠=︒,30BCD ∠=︒.再由切线的性质,即可求出60OCD ∠=︒,即三角形OCD 为等边三角形.得出结论60ODC ∠=︒,3OC OD CD ===.从而即可求出45ADO ∠=︒,即三角形OED 为等腰直角三角形,由此即可求出DE 的长,最后根据垂径定理即可求出AD 的长.解:如图,连接OC 、OD ,作OE AB ⊥于点E .⊙BC CD =,⊙CBD CDB ∠=∠,⊙105ADC ∠=︒,⊙75CBD CDB ∠=∠=︒,⊙18027530BCD ∠=︒-⨯︒=︒.由题意可知OC BC ⊥,即90OCB ∠=︒,⊙903060OCD OCB BCD ∠=∠-∠=︒-︒=︒,⊙OD =OC ,⊙三角形OCD 为等边三角形.⊙60ODC ∠=︒,3OC OD CD ===.⊙1056045ADO ADC ODC ∠=∠-∠=︒-︒=︒,⊙三角形OED 为等腰直角三角形, ⊙22323DE === ⊙322232AD DE ===故选:A .【点拨】本题考查切线的性质,等腰三角形的性质,三角形外角的性质,等腰直角三角形与等边三角形的判定和性质以及垂径定理,综合性强.正确的连接辅助线是解答本题的关键.10.B【分析】连接OD 、AC 、DC 、OB 、OC ,作CE ⊙AB 于E ,OF ⊙CE 于F ,利用垂径定理得到OD ⊙AB ,则AD =BD =2,于是根据勾股定理可计算出OD =1,再利用折叠的性质可判断AC 和CD 所在的圆为等圆,则根据圆周角定理得到AC CD =,所以AC =DC ,利用等腰三角形的性质得AE =DE =1,接着证明四边形ODEF 为正方形得到OF =EF =1,然后计算出CF 后得到CE =BE =3,于是可得到BC 的长.解:如图,连接OD 、AC 、DC 、OB 、OC ,作CE ⊙AB 于E ,OF ⊙CE 于F ,⊙D 为AB 的中点,⊙OD ⊙AB ,⊙AD =BD =12AB =2,在Rt △OBD 中,OD 22541OB BD --=,⊙将BC 沿BC 折叠,⊙AC 和CD 所在的圆为等圆,⊙AC CD =,⊙AC =DC ,⊙AE =DE =1,⊙⊙ODE =⊙OFE =⊙DEF =90°,⊙四边形ODEF 是矩形,⊙DE =OD =1,⊙四边形ODEF 是正方形,⊙OF =EF =1,在Rt △OCF 中,CF 22512OC OF ,⊙CE =CF +EF =2+1=3,而BE =BD +DE =2+1=3,⊙BC 223332+=故选:B .【点拨】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理,垂径定理,勾股定理及正方形的判定和性质等.11.60°##60度【分析】先由切线的性质及切线长定理求出90,30PAO APO ∠=︒∠=︒,再根据直角三角形两锐角互余求解即可. 解: P A ,PB 是O 的切线,A ,B 为切点190,2PAO APO PAB ∴∠=︒∠=∠ 90APO AOP ∴∠+∠=︒60APB ∠=︒30APO ∴∠=︒60AOP ∴∠=︒故答案为:60°.【点拨】本题考查了切线的性质及切线长定理、直角三角形两锐角互余,熟练掌握知识点是解题的关键.12.40【分析】根据切线长定理,等腰三角形的性质以及三角形内角和定理推出⊙BDE +⊙BED +⊙B =180°,⊙CFE +⊙CEF +⊙C =180°,得到2(⊙BDE +⊙CFE )+⊙B +⊙C =360°,据此求解即可.解:⊙⊙O 是△ABC 的内切圆,与AB ,BC ,CA 的切点分别为D ,E ,F ,⊙BD =BE ,CE =CF ,⊙⊙BDE =⊙BED ,⊙CFE =⊙CEF ,⊙⊙BDE +⊙BED +⊙B =180°,⊙CFE +⊙CEF +⊙C =180°,即2⊙BDE +⊙B =180°,2⊙CFE +⊙C =180°,⊙2(⊙BDE +⊙CFE )+⊙B +⊙C =360°,⊙⊙BDE +⊙CFE =110°,⊙2×110°+⊙B +⊙C =360°,⊙⊙B +⊙C =140°,⊙⊙A =180°-(⊙B +⊙C )= 40°.故答案为:40.【点拨】本题考查了切线长定理,等腰三角形的判定和性质,三角形内角和定理,熟记各图形的性质并准确识图是解题的关键.13.4【分析】作点B 关于x 轴的对称点B ′,连接MB ′,交⊙M 于点N ,交x 轴于点P ,此时BP +PN 取得最小值,然后结合勾股定理及三角形的面积公式分析计算.解:作点B关于x轴的对称点B′,连接MB′,交⊙M于点N,交x轴于点P,过点M作MQ⊙x轴,交x轴于点E,过点B′作B′Q⊙MQ,⊙点B与点B′关于x轴对称,⊙PB+PN=PB′+PN,当N、P、B’在同一直线上且经过点M时取最小值.在Rt△ABC中,AC22OA OC,由⊙M是△AOC的内切圆,设⊙M的半径为r,⊙S△AOC=12(3r+4r+5r)=12×3×4,解得r=1,⊙ME=MN=1,⊙QB′=4-1=3,QM=3+1=4,⊙MB′=5,⊙PB′+PN=5-1=4,即PB+PN最小值为4,故答案为:4.【点拨】本题考查轴对称—最短路线问题,三角形内切圆,理解“两点之间,线段最短”,掌握轴对称的性质,通过添加辅助线构建直角三角形是解题关键.14.62°【分析】先根据切线长定理得到⊙1=12⊙ABC,⊙2=12⊙BCD,⊙3=12⊙ADC,⊙4=12⊙BAD,再利用三角形内角和计算出⊙1+⊙2=62°,则⊙ABC +⊙BCD =124°,然后利用四边形内角和得出⊙BAD +⊙ADC =236°,再求⊙3+⊙4=118°即可.解:⊙圆O 是四边形ABCD 的内切圆,⊙OA 平分ABC ,OC 平分⊙BCD ,OD 平分⊙ADC ,OA 平分⊙BAD ,⊙⊙1=12⊙ABC ,⊙2=12⊙BCD ,⊙3=12⊙ADC ,⊙4=12⊙BAD ,⊙⊙1+⊙2=180°﹣⊙BOC =180°﹣118°=62°,⊙⊙ABC +⊙BCD =2(⊙1+⊙2)=2×62°=124°,⊙⊙BAD +⊙ADC =360°﹣(⊙ABC +⊙BCD )=360°﹣124°=236°,⊙⊙3+⊙4=12(⊙BAD +⊙ADC )=12×236°=118°, ⊙⊙AOD =180°﹣(⊙3+⊙4)=180°﹣118°=62°.故答案为:62°.【点拨】本题考查了四边形的内切圆.切线的性质和切线长定理,三角形内角和,掌握四边形的内切圆性质.切线的性质和切线长定理,三角形内角和是解题关键.15. 10 (2,-2)【分析】(1)利用勾股定理解答即可;(2)根据I 是OAB 的内心,利用OM =ON ,BM =BE ,AE =AN ,得出AE +BE =6-x +8-x =10,求解即可.解:(1)⊙点()0,6A ,点()8,0B ,⊙OA =6,OB =8,在Rt △OAB 中,AB 22226810OA OB ++;(2)连接OI ,BI ,AI ,过I 作IM ⊙OB ,IN ⊙OA ,IE ⊙AB ,⊙I 是OAB 的内心,⊙OM=ON,BM=BE,AE=AN,设OM=ON=x,则BM=BE=8-x,AN=AE=6-x,⊙AE+BE=6-x+8-x=10,解得:x=OM=ON=2,⊙I的坐标为(2,2),⊙点I关于x轴对称的点的坐标是(2,-2).【点拨】本题考查了勾股定理及三角形的内心,解题的关键是灵活运用性质解决实际问题.16.55【分析】由三角形的内心的性质可得⊙BAD=⊙CAD,⊙ABI=⊙CBI,由外角的性质和圆周角的性质可得⊙BID=⊙DBI,由三角形内角和定理可求解.解:⊙点I是⊙ABC的内心,⊙⊙BAD=⊙CAD,⊙ABI=⊙CBI,⊙⊙CAD=⊙CBD,⊙⊙BAD=⊙CBD,⊙⊙BID=⊙BAD+⊙ABI,⊙IBD=⊙CBI+⊙CBD,⊙⊙BID=⊙DBI,⊙⊙ACB=70°,⊙⊙ADB=70°,⊙⊙BID=⊙DBI=180702︒︒-=55°故答案为:55.【点拨】本题考查了三角形的内切圆与圆心,圆周角的定理,等腰三角形的性质等知识,证明⊙BID=⊙DBI是本题的关键.17.45︒【分析】根据切线的性质和已知条件先证得四边形PMON是正方形,从而求得2=,以OOP m为圆心,2m长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时⊙ACP 有最大值,作出图形,根据切线的性质得出OP⊙PC,根据勾股定理求得PC的长,从而证得⊙OPC是等腰直角三角形,即可证得⊙ACP的最大值为45°.解:PM、PN是过P所作的O的两切线且互相垂直,∴∠=︒,MON90∴四边形PMON是正方形,根据勾股定理求得2OP m=,∴点在以O2m长为半径作大圆O上,P以O为圆心,2m长为半径作大圆O,然后过C点作大O的切线,切点即为∠有最大值,如图所示,P点,此时ACPPC是大圆O的切线,∴⊥,OP PC2=,2OC m=,OP m222PC OC OP m∴-,∴=,OP PC∴,∠=︒45ACP∴∠的最大值等于45︒,ACP故答案为45︒.【点拨】本题考查了切线的性质,正方形的判定和性质,勾股定理的应用,解题的关键是求得P点的位置.18.4【分析】由正方形的性质,知点C 是点A 关于BD 的对称点,过点C 作CA ′⊙BD ,且使CA ′=1,连接AA ′交BD 于点N ,取NM =1,连接AM 、CM ,则点M 、N 为所求点,进而求解.解:⊙O 的面积为2π222BD =,则=AC ,由正方形的性质,知点C 是点A 关于BD 的对称点,过点C 作CA ′⊙BD ,且使CA ′=1,连接AA ′交BD 于点N ,取NM =1,连接AM 、CM ,则点M 、N 为所求点,理由:⊙A ′C ⊙MN ,且A ′C =MN ,则四边形MCA ′N 为平行四边形,则A ′N =CM =AM ,故⊙AMN 的周长=AM +AN +MN =AA ′+1为最小,则A ′A 22(22)1=+=3,则⊙AMN 的周长的最小值为3+1=4,故答案为:4.【点拨】本题考查了圆的性质、点的对称性、平行四边形的性质等,确定点M 、N 的位置是本题解题的关键.19.(1)1;(2)见分析【分析】(1)先得到⊙ABC 为直角三角形,再根据面积相等求出⊙ABC 内切圆的半径;(2)利用切线的判定与性质以及切线长定理得出AF=AE ,BF=BD ,CD=EC ,进而求出即可.解:(1)⊙5,4,3a b c ===,⊙⊙ABC 是直角三角形, 设⊙ABC 内切圆的半径为r ,由⊙ABC 的面积可得:()12AB BC AC r ⨯++=12AC AB ⨯⨯, 即()13452r ⨯++=1342⨯⨯, 解得:r=1,⊙⊙ABC 的内切圆半径为1;(2)⊙I 为⊙ABC 的内心,且I 在⊙ABC 的边BC ,AC ,AB 上的射影分别为D ,E ,F ,⊙D 、E 、F 分别是⊙I 的三边切点,⊙AF=AE ,BF=BD ,CD=EC ,设AE=AF=x ,则EC=b -x ,BF=c -x ,故BC=a=b -x+c -x ,整理得出:x=2b c a +-, 即AE=AF=2b c a +-. 【点拨】此题主要考查了三角形的内切圆与内心,利用切线长定理得出是解题关键.20.(1)k ≥32;(2)22+ 【分析】(1)根据一元二次方程根的判别式,方程有两个正实数根,则判别式⊙0,且两根的和与积都是正数,得出关于k 的不等式组,求出k 的取值范围.(2)根据切线性质得出直角三角形的内切圆半径与直角三角形三边的关系:2a b c r +-=,再结合勾股定理和根与系数的关系可求k 的值. 解:(1)设方程的两根为1x ,2x ,则⊙221(1)4(1)234k k k =+-+=-,方程有两个实数根,∴⊙0,即230k -,∴综上可知32k , ∴当32k ,方程有两个实数根; (2)如图,设直角三角形两直角边为BC =a ,AC =b ,斜边为AB =c ,其内切圆半径r ,⊙AB 、AC 、BC 是圆的切线,⊙90OEC OFC ∠=∠=︒,又⊙OE OF r ==,90C ∠=︒,⊙四边形OECF 是正方形,⊙==CE CF r ,又⊙AG AF =,BG BE =,⊙AC BC AB CE CF +=++,即2b a c r +=+,⊙12r =, ⊙1c a b =+-,即:又⊙222=c a b +,⊙222(-1)a b a b ++=,化简得:22()10ab a b -++=,又121a b x x k +=+=+,2121(1)4ab x x k ==+,⊙212(1)2(1)104k k +-++=,解得22=k 3222k =(舍去), k ∴的值为22【点拨】本题考查了三角形的内切圆与内心,根的判别式,根与系数的关系,解决本题的关键是首先利用判别式是非负数确定k 的取值范围,然后利用一元二次方程根与系数的关系和勾股定理以及内切圆的半径公式,把问题转化为解方程求得k 的值.21.(1)见分析1014【分析】(1)根据切线长定理得到GA =GD ,则⊙GAD =⊙GDA ,根据圆周角定理推出AC ⊙DE ,则⊙CAD =⊙GDA ,进而得到⊙GAD =⊙CAD ,据此即可得解;(2)连接OD,交AC于点H,根据切线的性质、平行线的性质推出OH是△ABC的中位线,AH=CH=12AC,则OH=12BC,设OH=x,则DH=92−x,BC=2x,解直角三角形得到AH1014(1)证明:⊙GA、GD是⊙O的切线,⊙GA=GD,⊙⊙GAD=⊙GDA,⊙AB是⊙O的直径,⊙⊙ACB=90°,⊙AC⊙BE,⊙DE⊙BE,⊙AC⊙DE,⊙⊙CAD=⊙GDA,⊙⊙GAD=⊙CAD,⊙AD平分⊙GAC;(2)解:连接OD,交AC于点H,⊙DE是⊙O的切线,⊙OD⊙DE,⊙⊙ODE=90°,由(1)知,AC⊙DE,⊙OD⊙AC,⊙AH=CH=12AC,⊙AHD=⊙CHD=90°,⊙OA=OB,⊙OH是△ABC的中位线,⊙OH =12BC , ⊙AB =9,⊙OD =92, 设OH =x ,则DH =92−x ,BC =2x , ⊙2222814AC AB BC x --==,⊙222814AH x -()=,⊙22814AH x -=, ⊙222AH AD DH -=,AD =5,⊙222819542x x ⎛⎫ -⎝--⎪⎭=, ⊙x =3118, ⊙AH 28110144x -= ⊙⊙HCE =180°−⊙ACB =90°=⊙ODE =⊙CHD ,⊙四边形CHDE 是矩形,⊙DE =CH =AH 1014 【点拨】此题考查了切线长定理、切线的判定与性质,熟记切线的判定定理与性质定理并作出合理的辅助线是解题的关键.22.(1)见分析171【分析】(1)连接OD ,BD ,根据直径所对的圆周角是直角,可得90ADB ∠=︒根据直角三角形斜边上的中线可得BE ED =,进而根据,OBD ODB EBD EDB ∠=∠∠=∠,等量代换可得90ODE ∠=︒,即可证明FD 是圆O 的切线;(2)利用勾股定理求得EF 的长,进而根据切线长定理求得ED ,即可求得FD ,在Rt ODF 中,勾股定理建立方程求得半径,进而求得AB 的长.解:(1)连接OD ,BD ,AB 是O 的直径,∴90ADB ∠=︒.OB OD =. OBD ODB ∴∠=∠. E 是BC 的中点,BE ED ∴=.EBD EDB ∴∠=∠.90ABC ∠=︒,90OBD EBD ∴∠+∠=︒. 90ODB EDB ∴∠+∠=. 即90ODE ∠=︒.OD 是半径,FD ∴是圆O 的切线;(2)如图,连接OD ,90,ABC E ∠=︒为BC 的中点,BC =4,FB =8, 2BE ∴=,BC 是O 的切线, ,EF BC 是O 的切线, 2ED EB ∴==.在Rt FBE △中,2,8BE FB ==,2282217EF ∴+=2172FD EF ED ∴=-=,设O 的半径为r ,则OA OD r ==,在Rt OFD 中,8,,172OF BF OB r OD r DF =-=-==,222OF OD DF ∴=+,即()()22282172r r -=+,解得171r -= 171AB ∴=.【点拨】本题考查了切线的性质与判定,勾股定理解直角三角形,切线长定理,掌握切线的性质与判定是解题的关键.23.(1)68APC ∠=︒;74CDB ∠=︒(2)58°【分析】(1)由同弧所对圆周角相等求得C ∠,进而求得APC ∠;连接AC ,求得BAC ∠,进而由同弧所对的圆周角相等求得CDB ∠.(2)连接OD ,求得PCB ∠,进而求得其所对圆心角BOD ∠,再由三角心外角和内角的关系求得E ∠.(1)解:⊙=BD BD⊙52C BAD ∠=∠=︒⊙68APC C ABC ∠=∠+∠=︒如图,连接AC ,⊙AB 为O 直径⊙90ACB ∠=︒⊙18074BAC ACB ABC ∠=︒-∠-∠=︒⊙=BC BC⊙74CDB BAC ∠=∠=︒(2)解:如图,连接OD⊙CD AB ⊥⊙90CPB ∠=︒⊙9074PCB PBC ∠=︒-∠=︒⊙在O 中,2BOD BCD ∠=∠⊙148BOD ∠=︒⊙DE 是O 的切线⊙OD DE ⊥即90ODE ∠=︒⊙90=58E BOD ∠=∠-︒︒.【点拨】本题考查圆与三角形的综合问题,熟练掌握三角形和圆的相关性质定理是解题的关键.24.(1)12α(2)见分析(3)FG =2 【分析】(1)根据角平分线的性质以及三角形外角定理,可知⊙A =⊙ACD -⊙ABC ,⊙E =⊙ECD -⊙EBC =12ACD ∠-12ABC ∠,由此可知⊙E =12A ∠=12α; (2)根据圆内接四边形的性质可知⊙DCB +⊙BAD =180°,可知⊙BAD =⊙DCE ,根据圆周角的定理可知⊙ACD =⊙DCE ,进而证得⊙ABF =⊙CBF ,根据“好角”的定义即可得出结论;(3)连接CF,根据“好角”的定义可知⊙G=12⊙A,即⊙G=12⊙BFC,由外角定理可知⊙G=⊙GCF,可知FG=CF,利用三角函数求得CF即可求得结果.(1)解:由题意得,⊙ABE=⊙CBE=12ABC∠,⊙ACE=⊙ECD=12ACD∠,⊙⊙ACD=⊙A+⊙ABC,⊙ECD=⊙E+⊙EBC,⊙⊙A=⊙ACD-⊙ABC,⊙E=⊙ECD-⊙EBC=12ACD∠-12ABC∠,⊙⊙E=12A∠=12α;(2)如图,⊙四边形ABCD内接于⊙O,⊙⊙DCB+⊙BAD=180°,又⊙⊙DCB+⊙DCE=180°,⊙⊙BAD=⊙DCE,⊙点D是优弧ACB的中点,⊙AD BD=,⊙⊙ACD=⊙BAD,⊙⊙ACD=⊙DCE,⊙CG是⊙ABC的外角平分线,⊙直径BF⊙弦AC⊙⊙AF CF=,⊙⊙ABF=⊙CBF,⊙BG是⊙ABC的平分线,⊙⊙BGC是⊙ABC中⊙BAC的“好角”;(3)如图3,连接CF⊙⊙⊙A=45°,⊙⊙BFC=45°.⊙BG过圆心O⊙⊙⊙BCF=90°.⊙⊙BGC是⊙ABC中⊙A的“好角”,⊙⊙G=12⊙A⊙⊙ ⊙A=⊙BFC;⊙⊙G=12⊙BFC⊙⊙⊙G=⊙GCF ⊙⊙FG=CF⊙⊙cos⊙BFC=CF BF,⊙CF=cos45°×BF2=2,⊙FG=2【点拨】本题考查的是圆的有关知识、全等三角形的判定和性质、等腰直角三角形的性质,掌握圆周角定理、三角形外角性质、全等三角形的判定定理和性质定理是解题的关键.。
浙教版数学九年级数学下册 2.2切线长2.3三角形的内切圆同步测试试题

切线长定理一、选择题(只有一个选项是正确的,请把它选出来)1. 点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,若PA=12,则PB的长为()(A)6. (B)8. (C)12. (D)14.2. (原创)如图1,点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,PO与AB交于点C,则图中直角三角形的个数为()(A)4个. (B)5个. (C)6个. (D)8个.图 13. 如图2,点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,E点是劣弧AB上一点,过E点的切线CD,交PA,PB分别于点D,C,若圆的半径为3,PO=5,则三角形PCD的周长为()(A)6. (B)8. (C)10. (D)12.图 24. (原创)如图3,点A是⊙O外一点,AB,AC是圆的切线,切点分别为B,C,若∠BOC=120°,则三角形ABC的形状是()(A)等腰三角形. (B)等边三角形. (C)等腰直角三角形. (D)直角三角形.图 3二、填空题(答案要简洁)5. (原创) 如图4,点A是⊙O外一点,AB,AC是圆的切线,切点分别为B,C,若AB⊥AC,则四边形ABOC的形状是 .图 46. (原创)如图5,点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,C是优弧AB上一点,且∠ACB=84°.则∠P的度数是 .图 57. (原创)如图6,点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,C是PA的中点,CD切圆O于点D,则AD,PD,PB三者之间的关系是 .图 68. (原创) 如图7,已知点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,B是OC 的中点,∠POB=70°,则∠APC的度数为 .图 7三、解答题9. (原创)如图8,已知半⊙O与等腰三角形ABC的边AB,AC分别相切,切点分为D,E,半圆的直径FG在边BC上.求证:DF=EG.图 810. (原创) 如图9,已知点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,连接AB,PO 二线交于点E,以AB为一边作矩形ABCD,连接OB,若OB=3,PO=5,求矩形ABCD的面积.图 9三角形的内切圆一、选择题(只有一个选项是正确的,请把它选出来)1.三角形的内心是()(A)三角形三条中线的交点.(B)三角形三条垂直平分线的交点.(C)三角形三条高线的交点.(D)三角形三条角平分线的交点.2. 如图1,⊙G是三角形ABC的内切圆,切点分别是D,E,F,则三角形EDF的形状是()(A)直角三角形. (B)锐角三角形. (C)等边三角形. (D)无法确定.3. 如图2,⊙O是三角形ABC的内切圆,切点分别是D,E,F,∠C=78°,则∠EDF的度数是()(A)51°. (B)62°. (C)78°. (D)84°.4. (原创) 如图3,圆与直角三角形ABC的三边都相切,切点分别是D,E,F,已知斜边AB=10,直角边BC=6,则CD,AE,BF 的长分别是 ( ) (A )2、6、4. (B )2、4、6. (C )2、4、5. (D )2、5、4.二、填空题(答案要简洁)5. (原创) Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,r 为半径作圆与三角形的三边都相切,则点A 到圆心的距离为_______.6.三角形ABC 的内心与外心重合,则三角形ABC 的形状是 .7. 如图4,Rt△ABC 的内切圆⊙O 与两直角边AB ,BC 分别相切与点D 、E ,过劣弧DE (不包括端点D ,E )上任一点P 作⊙O 的切线MN 与AB ,BC 分别交于点M ,N ,若⊙O 的半径为r ,则Rt△MBN 的周长为 .8. (原创) 如图4,CD 是Rt△ABC 斜边AB 上高,⊙E 是三角形ABC 的内切圆,半径为R ,⊙F 是三角形ACD 的内切圆,半径为1R ,⊙G 是三角形BCD 的内切圆,半径为2R ,设三角形ABC 的三边长分别为a,b,c ,则12R R R= .(用a,b,c 表示)三、解答题9. 原创如图5,,CD是Rt△ABC斜边AB上高,⊙1O是三角形ACD的内切圆,半径为1R,⊙2O是三角形BCD的内切圆,半径为2R,设三角形ABC的三边长分别为a,b,c.(1)用a,b,c分别表示1R,2R;(2)计算12RR的值.10.原创如图6,Rt△ABC中,⊙O是三角形ABC的内切圆,半径为1R;如图7,⊙1O,⊙2o是两个等圆,两圆外切,且⊙1O与AB,BC都相切,⊙2o与AC,BC都相切,半径为2R;如图8,⊙1O,⊙2o,⊙3O是等圆,自左到右依次外切,且⊙1O与AB,BC都相切,⊙3O与AC,BC都相切,半径为3R,设三角形ABC的三边长分别为a,b,c.(1)求1R,2R,3R;(2)有n个等圆⊙1O,⊙2o,⊙3O…⊙nO,自左到右依次外切,且⊙1O与AB,BC都相切,⊙nO与AC,BC都相切,半径为2R,仔细观察(1)中的规律,直接写出nR.探究题:如图9,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0与直角三角形的三边相切,圆的半径r.则r=2()abcc a b c++.(2)如图10,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0、⊙I是两个等圆,且⊙0与直角三角形的两边相切,⊙I与直角三角形的两边相切,⊙0与⊙I相外切,圆的半径r.则r=22()abcc a b c ab+++.(3)如图11,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0、⊙I是n个等圆中的两个,且⊙0与直角三角形的两边相切,⊙I与直角三角形的两边相切,n个等圆两两相切,圆的半径r,则r= .切线长定理一、选择题 1.(C )提示:根据切线长定理PB=12. 2. (C )提示:根据切线的性质,知道三角形PAO,PBO 是直角三角形,根据切线长定理,等腰三角形三线合一,知道三角形PAC,PBC,OAC,OBC 都是直角三角形. 3.(B )提示: 三角形PCD 的周长为PA+PB=2PA ,根据勾股定理,PA=4. 4.. (B ) 提示:利用切线性质,四边形内角,确定∠A=60°. 二、填空题 5. 正方形提示:切线性质,得到两个直角,矩形+邻边相等. 6. 12°提示:利用圆心角与圆周角关系定理,得∠AOB=168°,利用四边形内角和定理可求. 7. 222AD PD PB +=提示:根据切线长定理,得PA=PB,AC=CD=CP ,所以三角形APD 是直角三角形. 8. 60°提示:切线长定理,等腰三角形三线合一,确定∠APO=∠OPB=∠BPC=20°.三、解答题 9.证明:连接OA ,因为AD,AE 是圆的切线,所以OA 平分∠BAC ,AD=AE , 所以AB-AD=AC-AE ,所以BD=CE. 因为OA 平分∠BAC,AB=AC ,所以OB=OC,所以OB-OF=OC-OG ,所以BF=CG ,因为∠B=∠C ,所以△DBF ≌△EGC , 所以DF=EG.10.解:因为PB 是圆的切线,所以三角形POB 是直角三角形,所以PB=4, 所以BD=8.因为PA,PB 是圆的切线,所以PE ⊥AB ,所以PB g OB=PO g BE , 所以BE=125,所以AB=245, 所以2222248()5BD AB -=-325, 所以矩形的面积AB g AD=245×325=76825.三角形的内切圆一、选择题 1.(D )提示:根据三角形内心的定义判断. 2. (B )提示:连接EG,FG ,则∠EGF <180°,所以12∠EGF <90°,所以∠EDF 是锐角,同理可证其余两个角也是锐角.3. (A )提示:先求∠EOF=102°,后求解即可. 4.(A )提示:先求AC=8,再求CF=2,AE=6,BF=4.二、填空题提示:r=1,AC 上点A 到切点的距离为2,根据勾股定理求解. 6. 等边三角形提示:等边三角形的三线合一判定. 7.2r提示:三角形的周长为2BD ,BD 就是r. 8.a bc+ 提示:设CD=h ,AD=x ,BD=y ,则R=2a b c +-,1R =2h x b +-,2R =2h y a+- 所以1R +2R =2h x b +-+2h y a +-=2()2h x y a b ++-+=2()2h c a b +-+,因为h=ab c ,所以1R +2R =222()()22ab ab c a b cc a b c c +-++-+= =2222()()()22ab a b a b ca b a b c c c++-++-+==()()22a b a b c a b a b c a b R c c c++-++-+==•g ,所以12R R R +=a b c+.三、解答题 9.解:(1)因为三角形ABC 的面积是定值,所以CD=abc.易证△ADC ∽△ACB , 所以AD=2b c,因为⊙1O 是三角形ACD 的内切圆,半径为1R ,所以AD-1R +CD-1R =AC所以1R =2AD CD AC +-=2()22b abbb a bc c c c+-+-=; 同理可证, 2R =()2a a b c c+-;(2)因为1R =()2b a b c c +-,2R =()2a a b c c+-,所以12R R =b a .10. 解:(1)如图6 连接OA,OC,OB,因为⊙O 是三角形ABC 的内切圆,半径为1R ,三角形ABC 的三边长分别为a,b,c ,所以三角形AOC 的面积=12×AC ×1R ,三角形BOC 的面积=12×BC ×1R ,三角形AOB 的面积=12×AB ×1R ,三角形ABC 的面积=12×a ×b , 所以12×AC ×1R +12×BC ×1R +12×AB ×1R =12×a ×b , 所以1R =ab a c b ++;如图7 连接1O A, 1O C, 1O B, 等圆的半径为2R 三角形ABC 的三边长分别为a,b,c , 所以三角形A 1O C 的面积=12×AC ×22R ,三角形B 1O C 的面积=12×BC ×2R ,三角形A 1O B 的面积=12×AB ×2R ,三角形ABC 的面积=12×a ×b , 所以12×AC ×22R +12×BC ×2R +12×AB ×2R =12×a ×b , 所以2R =2ab a c b ++;同理可证,3R =3ab a c b++; (2)n R =ab a c nb ++.探究题:解:(1)连接OA,OC ,OB ,则三角形AOC 的面积=12×AC ×r ,三角形BOC 的面积=12×BC ×r , 三角形AOB 的面积=12×AB ×r ,三角形ABC 的面积=12×a ×b , 因为三角形AOC 的面积+三角形BOC 的面积+三角形AOB 的面积=三角形ABC 的面积, 所以12×AC ×r+12×BC ×r+12×AB ×r=12×a ×b , 所以12(a+b+c )r=12×a ×b,所以r=ab a b c ++,所以r=2()abc c a b c++. (2)连接OA,OC,IC,IB,OI,OE,IF,作高CD,交OI 于点G ,则三角形AOC 的面积=12×AC ×r ,三角形BIC 的面积=12×BC ×r ,三角形AOF 的面积=12×AF ×r ,三角形BIF 的面积=12×BF ×r ,三角形OIF 的面积=12×OI ×IF ,三角形OCI 的面积=12×OI ×CG ,三角形ABC 的面积=12×a ×b ,因为三角形AOC 的面积+三角形BIC 的面积+三角形AOF 的面积+三角形BIF 的面积+三角形OIF 的面积+三角形OCI 的面积=三角形ABC 的面积, 所以12×AC ×r+12×BC ×r+12×AF ×r+12×BF ×r+12×OI ×IF+12×OI ×CG=12×a ×b , 所以12(a+b+c )r+12×OI ×CD=12×a ×b,且CD=ab c ,整理得:r=22()abc c a b c ab +++.(3)规律隐藏在ab 分母中ab 的系数中,且系数与等圆的个数n 的关系是:系数=2(n-1),于是结论为r=221()()abc c a b c n ab +++-.。
浙教版九年级下数学《2.3三角形的内切圆》同步练习含答案

2.3 三角形的内切圆同步练习一、单选题1、下列说法:①平分弦的直径垂直于弦;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的内心到三条边的距离相等。
其中不正确的有()个。
A、1B、2C、3D、42、如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A、一处B、两处C、三处D、四处3、在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为()A、1.5,2.5B、2,5C、1,2.5D、2,2.54、如图, O为Rt△ABC内切圆, ∠C=90°, AO延长线交BC于D点,若AC=4, CD=1,则⊙O半径为()A、B、C、D、5、图中圆与圆之间不同的位置关系有()A、2种B、3种C、4种D、5种6、已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是()A、0<d<1B、d>5C、0<d<1或d>5D、0≤d<1或d>57、在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是 ( )A、B、1C、2D、8、如图4,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有()A、内切、相交B、外离、相交C、外切、外离D、外离、内切9、若⊙O1,⊙O2的半径分别是r1=5,r2=3,圆心距d=8,则这两个圆的位置关系是()A、内切B、相交C、外切D、外离10、⊙O1和⊙O2的半径分别为3cm和5cm,若O1O2=8cm,则⊙O1和⊙O2的位置关系是A、外切B、相交C、内切D、内含11、两圆的半径分别为R和r,圆心距d=3,且R、r是方程的两个根,则这两个圆的位置关系是()A、内切B、外切C、相交D、内含12、在△ABC中,O为内心,∠A=80°,则∠BOC=()A、140°B、135°C、130°D、125°13、如图,△ABC中,下面说法正确的个数是()个.①若O是△ABC的外心,∠A=50°,则∠BOC=100°;②若O是△ABC的内心,∠A=50°,则∠BOC=115°;③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;④△ABC的面积是12,周长是16,则其内切圆的半径是1.A、1B、2C、3D、4二、填空题14、若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为________ ,内切圆半径为________ .15、在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,⊙O是Rt△ABC的内切圆,则⊙O的面积是________(用含π的式子表示).16、如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是________17、如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O 切AB,BC,AC于点D,E,F,则AF的长为________.18、如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC 交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90º+∠A;②以E为圆心、BE为半径的圆与以F为圆心、CF 为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF=mn;④EF是△ABC的中位线.其中正确的结论是________.三、解答题19、如图,△ABC的周长为24,面积为24,求它的内切圆的半径.20、如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.(1)求⊙O的半径的长及线段AD的长;(2)设PH=x,PC=y,求y关于x的函数关系式.21、△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?22、在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.(1)求证:内切圆的半径r=1;(2)求tan∠OAG的值.23、如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.(1)求证:BD=DI;(2)若OI⊥AD,求的值.24、已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.(1)求证:EB=EN=EC;(2)求证:NE2=AE•DE.25、如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I 是△ABD的内心.求证:(1)OI是△IBD的外接圆的切线;(2)AB+AD=2BD.答案部分一、单选题1、【答案】D2、【答案】D3、【答案】C4、【答案】A5、【答案】A6、【答案】D7、【答案】B8、【答案】B 9、【答案】C10、【答案】A11、【答案】A12、【答案】C13、【答案】C二、填空题14、【答案】5;215、【答案】4πcm216、【答案】217、【答案】4.518、【答案】①②三、解答题19、【答案】解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,设它的内切圆的半径为r,则OD=OE=OF=r,∵S△ABC=S△AOB+S△OBC+S△OAC,∴•r•AB+•r•BC+•r•AC=24,∴r(AB+BC+AC)=24,∴r•24=24,∴r=2.即它的内切圆的半径为2.20、【答案】解:(1)连接AO、DO.设⊙O的半径为r.在Rt△ABC中,由勾股定理得AC==4,则⊙O的半径r=(AC+BC﹣AB)=(4+3﹣5)=1;∵CE、CF是⊙O的切线,∠ACB=90°,∴∠CFO=∠FCE=∠CEO=90°,CF=CE,∴四边形CEOF是正方形,∴CF=OF=1;又∵AD、AF是⊙O的切线,∴AF=AD;∴AF=AC﹣CF=AC﹣OF=4﹣1=3,即AD=3;(2)点P在线段AC上时.在Rt△ABC中,AB=5,AC=4,BC=3,∵∠C=90°,PH⊥AB,∴∠C=∠PHA=90°,∵∠A=∠A,∴△AHP∽△ACB,∴,即∴y=﹣x+4,即y与x的函数关系式是y=﹣x+4.21、【答案】解:∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,∴AF=AE,BF=BD,CD=CE.设AF=AE=x,则BF=BD=11﹣x,EC=DC=15﹣x.根据题意得11﹣x+15﹣x=16.解得;x=5cm.∴AF=5cm.BD=11﹣x=11﹣5=6cm,EC=15﹣x=10cm.∴AF=5cm,BD=6cm,EC=10cm.22、【答案】(1)证明:如图连结OE,OF,OG.∵⊙O是△ABC的内切圆,∠C=90°,∴四边形CEOF是正方形,∴CE=CF=r.又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5,∴(3﹣r)+(4﹣r)=5.解得r=1;(2)解:连结OA,在R t△AOG中,∵r=1,AG=3﹣r=2,tan∠OAG=.23、【答案】(1)证明:∵点I是△ABC的内心∴∠BAD=∠CAD,∠ABI=∠CBI∵∠CBD=∠CAD∴∠BAD=∠CBD∴∠BID=∠ABI+∠BAD,∠BAD=∠CAD=∠CBD,∵∠IBD=∠CBI+∠CBD,∴∠BID=∠IBD∴ID=BD;(2)解:连接OA、OD、BD和BI,∵OA=O D,OI⊥AD∴AI=ID,∵I为△ABC内心,∴∠BAD=∠BCD,∴弧BD=弧CD,∵弧CD=弧CD,∴∠BCD=∠BAD,∴∠DBI=∠BCD+∠CBI=∠CAD+∠CBI,=(∠BAC+∠ACB),∵∠DIB=∠DAB+∠ABI=(∠BAC+∠ABC),∴∠DIB=∠DBI,∴BD=ID=AI,,故OD⊥BC,记垂足为E,则有BE=BC,作IG⊥AB于G,又∠DBE=∠IAG,而BD=AI,∴Rt△BDE≌Rt△AIG,于是,AG=BE=BC,但AG=(AB+AC﹣BC),故AB+AC=2BC,∴=2.24、【答案】证明:(1)连接BN,∵点N为△A BC的内心,∴∠1=∠2,∠3=∠4.∴∠BCE=∠1,∴EB=EC.∵∠5与∠2都是弧EC所对的圆周角,∴∠5=∠2=∠1.∴∠4+∠5=∠3+∠1.∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,∴∠NBE=∠BNE.∴EB=EN.∴EB=EN=EC.(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,∴△BED∽△AEB.∴.即BE2=AE•DE.∵E B=EN,∴NE2=AE•DE.25、【答案】解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA∴∠CID=∠C DI,∴CI=CD.同理,CI=CB.故点C是△IBD的外心.连接OA,OC,∵I是AC的中点,且OA=OC,∴OI⊥AC,即OI⊥CI.∴OI是△IBD外接圆的切线.(2)由(1)可得:∵AC的中点I是△ABD的内心,∴∠BAC=∠CAD∴∠BDC=∠DAC=∠BAC,又∵∠ACD=∠DCF,∴△ADC∽△DFC,∴,∵AC=2CI∴AC=2CD∴AD=2DF同理可得:AB=2BF∴AB+AD=2BF+2DF=2BD.。
初中数学浙教版九年级下册2.3 三角形的内切圆 强化提升训练A卷

初中数学浙教版九年级下册2.3 三角形的内切圆强化提升训练A卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分) (2017八上·安陆期中) 如图,点O在△ABC内,且到三边的距离相等,若∠A=60 ,则∠BOC的大小为()A .B .C .D . 602. (2分)(2019·深圳模拟) 下列说法正确的是()A . 顺次连接矩形各边中点得到的四边形是矩形B . 三角形的三条角平分线交于一点,并且这一点到三个顶点的距离相等C . 既是矩形又是菱形的四边形不一定是正方形D . 直角三角形斜边上的中线等于斜边的一半3. (2分) (2018九上·商河期中) 如图,矩形ABCD中,,,且BE与DF之间的距离为3,则AE的长是)A .B .C .D .4. (2分) (2018九上·磴口期中) 中,,将绕点A逆时针旋转后,能与重合,如果,那么的长等于A . 3B .C .D . 不能确定5. (2分)(2019·桥东模拟) 如图,点E点为△ABC的内心,且EF⊥BC于点F,若∠BAC=38°,∠B=56°,则∠AEF的度数为()A . 163B . 164C . 165D . 1666. (2分) (2018八上·江岸期中) 如图,点是的角平分线上一点,于点,点是线段上一点.已知,,点为上一点.若满足,则的长度为()A . 3B . 4C . 5D . 3或57. (2分) (2019九上·沙坪坝期末) 如图,在△ABC中,AC=BC=4,∠ACB=90°,若点D是AB的中点,分别以点A,B为圆心, AB长为半径画弧,交AC于点E,交BC于点F,则图中阴影部分的面积是()A .B .C .D .8. (2分)如图,在△ABC中,∠A=70°.⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为()A . 160°B . 135°C . 125°D . 110°二、填空题 (共4题;共4分)9. (1分) (2018八上·武汉月考) 如图,已知P(3,3),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=________.10. (1分) (2019八下·瑞安期中) 如图,H是△ABC内一点,BH⊥CH,AH=6,CH =3,BH=4,D、E、F、G分别是AB、AC、CH、BH的中点,则四边形DEFG的周长是________.11. (1分) (2019九上·台州期末) 如图,在△ABC 中,∠A=70°,⊙O 截△ABC 的三边所得弦长相等,则∠BOC 的度数为________.12. (1分) (2017九上·建湖期末) 如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为________.三、综合题 (共4题;共51分)13. (10分)(2019·孝感) 如图,点是的内心,的延长线与的外接圆交于点,与交于点,延长、相交于点,的平分线交于点 .(1)求证:;(2)求证:;(3)若,,求的长.14. (11分) (2018九上·硚口月考) 如图,点E是△ABC的内心,AE的延长线和△ABC 的外接圆相交于点D,连接BE(1)若∠CBD=35°,求∠BAC及∠BEC的度数(2)求证:DE=DB15. (15分)如图1,已知∠ABC=90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.(1)求证:BE=BF;(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.16. (15分)我们引入如下概念,定义;到三角形的两条边的距离相等的点,叫做此三角形的准内心,举例:如图1,PE⊥BC,若PE=PD则P为△ABC的准内心(1)填空;根据准内心的概念,图1中的点P在∠BAC的________上.(2)应用;如图2,△ABC中,AC=BC=13,AB=10,准内心P在AB上,求P到AC 边的距离PD的长.(3)探究;已知△ABC为直角三角形,AC=BC=6,∠C=90°,准内心P在△ABC的边上,试探究PC的长.参考答案一、单选题 (共8题;共16分)1、答案:略2、答案:略3、答案:略4、答案:略5、答案:略6、答案:略7、答案:略8、答案:略二、填空题 (共4题;共4分)9、答案:略10、答案:略11、答案:略12、答案:略三、综合题 (共4题;共51分)13、答案:略14、答案:略15、答案:略16、答案:略。
2020浙教版九年级数学下 三角形的内切圆测试题
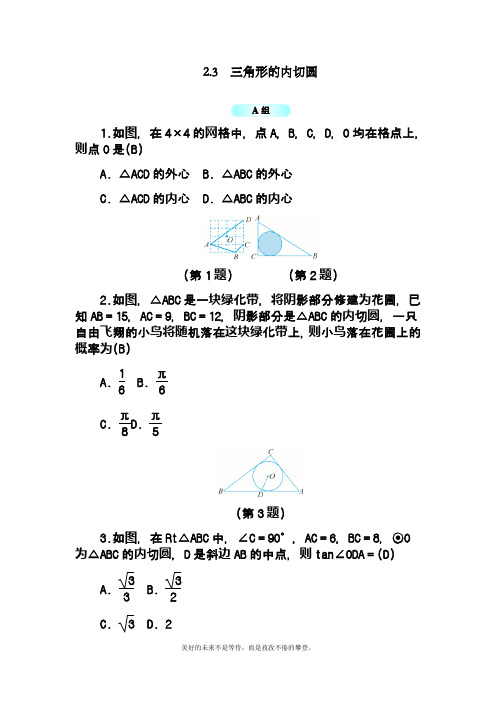
8.如图,△ABC中,∠A=m°.
(1)如图(1),当O是△ABC的内心时,求∠BOC的度数;
(2)如图(2),当O是△ABC的外心时,求∠BOC的度数;
(3)如图(3),当O是高线BD与CE的交点时,求∠BOC的度数.
9.如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是()
求证:DE=DB。
课堂小结:
(1)画已知三角形的内切圆
(2)三角形内切圆、三角形的内心、圆的外切三角形.
(3)利用作三角形的内角平分线,任意两条角平分线的交点就是内切圆的Hale Waihona Puke 心,交点到任意一边的距离是圆的半径.
(4)区别“内”与“外”,“接”与“切”;还应注意“连结内心和三角形顶点”这一辅助线的添加和应用.
(3)将条件中的“正三角形”改为“正方形”“正六边形”,你能得出怎样的结论?
(4)已知正n边形的边长为2a,请写出它的内切圆与外接圆组成的圆环面积.
12.如图,已知△ABC的内切圆⊙O分别和边BC,AC,AB切于D,E,F,如果AF=2,BD=7,CE=4.
(1)求△ABC的三边长;
(2)如果P为 上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.
(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
二、例题
例1、如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠FDE=70°,求∠A的度数。
例2、⊙I内切于△ABC,切点分别为D、E、F,试说明
2019-2020学年度最新浙教版九年级数学下册《三角形的内切圆》单元考点练习及答案解析一

2.3《三角形的内切圆》同步提升练习一、选择题1.下列命题正确的是()A.三角形的内心到三角形三个顶点的距离相等B.三角形的内心不一定在三角形的内部C.等边三角形的内心,外心重合D.一个圆一定有唯一一个外切三角形图2 图32.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,•则∠DOE=()A.70° B.110° C.120° D.130°3.如图3,△ABC中,∠A=45°,I是内心,则∠BIC=() A.112.5° B.112° C. 125° D.55°4.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为()A、1.5,2.5B、2,5C、1,2.5D、2,2.55.已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是()A、0<d<1B、d>5C、0<d<1或d>5D、0≤d<1或d>56.如图, O为Rt△ABC内切圆, ∠C=90°, AO延长线交BC于D 点,若AC=4, CD=1,则⊙O半径为()A、B、C、D、二、填空题7.若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为________ ,内切圆半径为________ .8.在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,⊙O是Rt△ABC 的内切圆,则⊙O的面积是 ________(用含π的式子表示).9.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是________10.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC 的内切圆⊙O切AB,BC,AC于点D,E,F,则AF的长为________.11.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90º+∠A;②以E为圆心、BE为半径的圆与以F 为圆心、CF为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF =mn;④EF是△ABC的中位线.其中正确的结论是________.三、解答题12.如图,△ABC,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.(1)求证:BF=CE;(2)若∠C=30°,CE=23,求AC的长.13.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是DEF上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.14.如图,已知正三角形ABC的边长为2a.(1)求它的内切圆与外接圆组成的圆环的面积;(2)根据计算结果,要求圆环的面积,•只需测量哪一条弦的大小就可算出圆环的面积;(3)将条件中的“正三角形”改为“正方形”“正六边形”,你能得出怎样的结论?(4)已知正n边形的边长为2a,请写出它的内切圆与外接圆组成的圆环面积.15.如图,已知△ABC的内切圆⊙O分别和边BC,AC,AB切于D,E,F,•如果AF=2,BD=7,CE=4.(1)求△ABC的三边长;(2)如果P为DF上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.参考答案1.B 2.B 3.A 4.C 5.C 6. A7.∠DMF 的大小一定,∠DMF=65°8.(1)90°+12m ° (2)2m ° (3)180°-m °9.AC=410.AC11.(1)πa 2 (2)弦AB 或BC 或(3)圆环的面积均为π·(2边长)2 (4)πa 2 12.(1)AB=9,BC=11,AC=6 (2)1413.(•1)2 (2)r=1222(3)n SSr a b c d a a a =++++++14.5(提示:连ID ,IE ,IF ,IB ,证四边形CEID 为正方形,求出ID=CE=2,证BF=BE=4,OF=1,再在Rt △IFO 中求IO )15.(1)AB+CD=AD+BC ,证明略 (2)4m。
浙教版九年级数学下册培优练习附答案:2.3三角形的内切圆

一、选择题(共15小题)1.已知 ㈠的半径是,,点"到同一平面内直线■'的距离为:-,则直线 与“的位置关系是A.相交B.相切C.相离D.无法判断"-■ ■,贝卩--■- 的大小是C.亍D. I"5. 已知的半径为 ,如果圆心厂到直线■的距离为」,那么直线■' 与•的位置关系是 A.相交B.相切C.相离D.不确定6. 在平面直角坐标系 一中,以点一-为圆心,-为半径的圆A.与'•轴相交,与■轴相切B.与“轴相离,与■轴相交C.与-轴相切,与轴相交D.与,轴相切,与1轴相离2.3三角形的内切圆2.的半径是“,点"到直线的距离为-,则直线;;与 的位置关系为A.相离B.相切C.相交D.内含3.如图,—和行是■的切线,点;和丹是切点,「是一的直径,已知A. ■-- C. ■4.已知 的半径是、直线,是 的切线,则点仃到直线:的距离是A. 一B.「7. 如图,宀是■-的直径,.:,是的切线,切点为打,与*」的延长线交于点!,: =「「,给出下面四个结论:①8.如图,丿'为■的直径“延长线上的一点,二与■相切,切点为<, 点门是 上一点,连接已知.:=.「=「.下列结论:(1) 与:相切;(2 )四边形―是菱形;(3); ( 4):「.其中正确的个数为A. |个B. '个C.:个D.'个9. 若等腰直角三角形的外接圆半径的长为-,则其内切圆半径的长为 A. x -B. - ■ 2 2C. - - .D. 」10. 如图,「是 的弦,「是'的切线,:为切点,-经过圆心,若*,贝S -的大小等于A. B. C. - D.11. 在平面直角坐标系 中,点二’的坐标为:..如果以原点为圆心, 半径为」的'上存B 」个C.:个D. L 个2,其中正确的个数为在点丫,使得八门,那么的取值范围是B -1<C. 0 I" W 112.如图,’ .:■中,—一「一•• -,一 - - , - :■圆心所作的半圆分别与:•,宀相切于点",厂,C.14.如图,等边皿匚的周长为■,半径是|的 心从与、相切于点打的 位置出发,在:甘外部按顺时针方向沿三角形滚动,又回到与::相切于点门的位置,贝S 心自转了,以斜边…’上的一点仃为 则为13.如图,亠:是•的直径,.::、八是•的弦, g ,那么二丁等于a ::、汀是 的切线,切点B. ■■■C.-C.-周A.C. ■-、填空题(共6小题)16.如图,•二是 的直径,点匚在—的延长线上,—•切•于点。
春九年级数学下册2.3三角形的内切圆同步练习新版浙教版0315115【含解析】

三、解答题 15. 任何三角形都有一个内切圆,任何四边形是否一定有一个内切圆? 请举例说明. 16. 如图,在 △ABC 中,AB = AC ,以 AB 为直径的 ⊙O 交 BC 于点 D,过点 D 作 DE ⊥ AC 于点 E .求证:DE 是 ⊙O 的切线.
17. 已知:如图,直线 P A 交 ⊙O 于 A,E 两点,P A 的垂线 DC ,DC 切 ⊙O 于点 C ,过 A 点 作 ⊙O 的直径 AB .若 DC = 4,DA = 2,求 ⊙O 的直径.
2.3 三角形的内切圆 一、选择题 1. 如图所示,∠AOB = 30◦ ,P 为边 OA 上一点,且 OP = 5 cm,若以 P 为圆心,r 为半径的 圆与 OB 相切,则半径 r 为 ) √( √ 5 3 5 5 3 A. 5 cm B. cm C. cm D. cm 2 2 3 2. 如图所示,AB 是 O 的弦,BC 与 O 相切于点 B ,连接 OA,OB ,若 ∠ABC = 70◦ ,则 ∠A 等于( ) A. 15◦ B. 20◦ C. 30◦ D. 70◦
第 3 页,共 3 页
2.3 三角形的内切圆—答案
一、选择题 1 2 3 4 5 6 7 C B B B C B A 1. 如图所示,过点 P 作 P D ⊥ OB 于点 D. 8 B
第 2 页,共 3 页
19. 如图,在 △ABC 中,在 AB 上取一点 E ,以 BE 为直径的 ⊙O 恰与 AC 相切于点 D,若 AE = 2 cm,AD = 4 cm. (1) 求 ⊙O 的直径 BE 的长; (2) 求 CD 的长.
20. 如图所示, P 是 ⊙O 外一点, P A, P B 分别和 ⊙O 切于 A, B 两点, P A = P B = 4 cm, ˜ 上任意一点,过点 C 作 ⊙O 的切线,分别交 P A,P B 于点 ∠P = 40◦ ,C 是 AB D,E ,求: (1) △P DE 的周长; (2) ∠DOE 的度数.
(浙教版)九年级数学下册 同步备课系列专题2.3 三角形的内切圆(作业)

第2章直线与圆的位置关系2.3 三角形的内切圆一、单选题1.如图,已知正方形ABCD的边长是8,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是()A.4B.4C.4D.4【答案】B【分析】作DC关于AB的对称点D′C′,以BC中的O为圆心作半圆O,连D′O分别交AB及半圆O于P、G.将PD+PG转化为D′G找到最小值.【详解】取点D关于直线AB的对称点D′.以BC中点O为圆心,OB为半径画半圆.连接OD′交AB于点P,交半圆O于点G,连BG.连CG并延长交AB于点E.由以上作图可知,BG⊥EC于G.PD+PG=PD′+PG=D′G由两点之间线段最短可知,此时PD+PG最小.∵D′C′=8,OC′=12∴D′O=∴D′G=4∴PD+PG的最小值为4故选B.【点睛】本题考查与圆有关的线段和的最小值问题,通常思想是将线段之和转化为固定两点之间的线段和最短. 2.如图,在O 中,AB 是直径,点D 是O 上一点,点C 是弧AD 的中点,CE AB ⊥于点E ,过点D 的切线交EC 的延长线于点G ,连接AD ,分别交CE ,CB 于点PQ .连接AC ,关于下列结论:①BAD ∠= ABC ∠;②GP GD =;③点P 是ACQ ∆的外心,其中正确结论是( )A .①②B .①③C .②③D .①②③【答案】C【分析】 由于AC 与BD 不一定相等,根据圆周角定理可知①错误;连接OD ,利用切线的性质,可得出∠GPD =∠GDP ,利用等角对等边可得出GP =GD ,可知②正确;先由垂径定理得到A 为CF 的中点,再由C 为AD 的中点,得到CD AF =,根据等弧所对的圆周角相等可得出∠CAP =∠ACP ,利用等角对等边可得出AP =CP ,又AB 为直径得到∠ACQ 为直角,由等角的余角相等可得出∠PCQ =∠PQC ,得出CP =PQ ,即P 为直角三角形ACQ 斜边上的中点,即为直角三角形ACQ 的外心,可知③正确;【详解】∵在⊙O 中,AB 是直径,点D 是⊙O 上一点,点C 是弧AD 的中点,∴AC =CD ≠BD ,∴∠BAD ≠∠ABC ,故①错误;连接OD ,则OD ⊥GD ,∠OAD =∠ODA ,∵∠ODA +∠GDP =90︒,∠EPA +∠EAP =∠EAP +∠GPD =90︒,∴∠GPD =∠GDP ;∴GP =GD ,故②正确;∵弦CF ⊥AB 于点E ,∴A 为CF 的中点,即AF AC =,又∵C 为AD 的中点,∴AC CD =,∴CD AF =,∴∠CAP =∠ACP ,∴AP =CP .∵AB 为圆O 的直径,∴∠ACQ =90︒,∴∠PCQ =∠PQC ,∴PC =PQ ,∴AP =PQ ,即P 为Rt △ACQ 斜边AQ 的中点,∴P 为Rt △ACQ 的外心,故③正确;故选C .【点睛】此题是圆的综合题,其中涉及到切线的性质,圆周角定理,垂径定理,圆心角、弧、弦的关系定理,相似三角形的判定与性质,以及三角形的外接圆与圆心,平行线的判定,熟练掌握性质及定理是解决本题的关键.3.如图,把ABC ∆剪成三部分,边AB ,BC ,AC 放在同一直线l 上,点O 都落在直线MN 上,直线//MN l .在ABC ∆中,若130BOC ∠=︒,则BAC ∠的度数为( )A .70︒B .75︒C .80︒D .85︒【答案】C【分析】 首先利用平行线间的距离处处相等,得到点O 是△ABC 的内心,点O 为三个内角平分线的交点,从而容易得到∠BOC=90°+12∠BAC ,通过计算即可得到答案. 【详解】解:如图,过点O 分别作OD ⊥AC 于D ,OE ⊥AB 于E ,OF ⊥BC 于F ,∵直线MN ∥l ,∴OD=OE=OF ,∴点O 是△ABC 的内心,点O 为三个内角平分线的交点,∴∠BOC=180-12(180-∠BAC )=90°+12∠BAC=130°, ∴∠BAC=80°.故选C.【点睛】本题考查了平行线的性质及三角形内心的性质及判定,利用平行线间的距离处处相等判定点O 是△ABC 的内心是解题的关键.4.一个等腰直角三角形的内切圆与外接圆的半径之比为( )A B .2 C 1 D 1【分析】设等腰直角三角形的直角边是1.根据直角三角形的内切圆半径是两条直角边的和与斜边的差的一半,得其内切圆半径是22-;其外接圆半径是斜边的一半,得其外接圆半径是2.所以它们21. 【详解】解:设等腰直角三角形的直角边是1;∵内切圆半径是22-,外接圆半径是2,1. 故选:D .【点睛】本题考查三角形的内切圆与外接圆的知识,解题的关键是熟记直角三角形外接圆的半径和内切圆的半径公式:直角三角形的内切圆半径等于两条直角边的和与斜边的差的一半;直角三角形外接圆的半径是斜边的一半.5.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?“其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”则该圆的直径为( )A .6步B .5步C .4步D .3步【分析】根据勾股定理求出直角三角形的斜边,可确定出内切圆半径,即可求得直径.【详解】=17,则该直角三角形能容纳的圆形(内切圆)半径r=815172+-=3(步),即直径为6步, 故选:A .【点睛】本题考查三角形的内切圆与内心,掌握Rt △ABC 中,三边长为a ,b ,c (斜边),其内切圆半径r=2a b c +-是解题的关键.6.下列关于三角形的内心说法正确的是( )A .内心是三角形三条角平分线的交点B .内心是三角形三边中垂线的交点C .内心到三角形三个顶点的距离相等D .钝角三角形的内心在三角形外【答案】A【分析】根据三角形内心定义即可得到答案.【详解】∵内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心,∴A 正确,B 、C 、D 均错误,故选:A.【点睛】此题考查三角形的内心,熟记定义是解题的关键.7.如图,点E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点D ,连接BD ,BE ,CE ,若∠CBD=32°,则∠BEC 的度数为( )A .128°B .126°C .122°D .120°【答案】C【分析】 根据圆周角定理推论可求∠CAD=32°,再根据三角形内心的定义可求∠BAC ,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB ,再根据三角形内角和定理可求∠BEC 的度数.【详解】在⊙O 中,∵∠CBD=32°,∵∠CAD=32°,∵点E 是△ABC 的内心,∴∠BAC=64°,∴∠EBC+∠ECB=(180°-64°)÷2=58°,∴∠BEC=180°-58°=122°.故选:C .【点睛】考查了三角形的内切圆与内心,圆周角定理推论,三角形内角和定理,关键是得到∠EBC+∠ECB 的度数. 8.如图,O 的直径AB 与弦CD 的延长线交于点E ,若DE OB =,84AOC ∠=,则E ∠=( )A .28B .42C .21D .20【答案】A【分析】 根据示意图结合已知条件可得出,2E DOE OCD ODC E ∠=∠∠=∠=∠,因此,1804COD E ∠=︒-∠,即可得出180(18044)8E E =︒-∠-︒-∠,计算即可得出答案.【详解】解:∵DE OB =∴DE OD =∴,2E DOE OCD ODC E ∠=∠∠=∠=∠∴1804COD E ∠=︒-∠∴180(18044)8E E =︒-∠-︒-∠∴28E ∠=︒故选:A .【点睛】本题考查的知识点是圆的综合题目,根据示意图得出,2E DOE OCD ODC E ∠=∠∠=∠=∠是解此题的关键.二、填空题9.阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:已知:ABC.求作:ABC 的内切圆.小明的作法如下:如图2,()1作ABC ∠,ACB ∠的平分线BE 和CF ,两线相交于点O ;()2过点O 作OD BC ⊥,垂足为点D ;()3点O 为圆心,OD 长为半径作O.所以,O 即为所求作的圆.请回答:该尺规作图的依据是______.【答案】到角两边距离相等的点在角平分线上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线.【分析】根据三角形的内切圆,三角形的内心的定义,角平分线的性质即可解答.【详解】解:该尺规作图的依据是到角两边距离相等的点在角平分线上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线;故答案为到角两边距离相等的点在角平分线上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线.【点睛】此题主要考查了复杂作图,三角形的内切圆与内心,关键是掌握角平分线的性质.10.边长分别为3、4、5的三角形的内切圆半径与外接圆半径之比为________.【答案】1:2.5【解析】设三角形为△ABC,∵32+42=52,∴△ABC为直角三角形,∴外接圆的直径为5,∴外接圆的半径为2.5,设内切圆的半径为r,∵S△ABC=12,AB+BC+CA,•r,即12×3×4=12×,3+4+5,r,解得r=1,∴该三角形内切圆半径与外接圆半径之比为1,2.5,故答案是,1,2.5,11.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为cm.【答案】r=103【解析】试题分析:如图,设,ABC的内切圆半径为r,由勾股定理得AD=12,再由切线长定理得AE=8,根据勾股定理求得r 即可.试题解析:如图,,AB=AC=13cm ,BC=10cm ,,BD=5cm ,,AD=12cm ,根据切线长定理,AE=AB -BE=AB -BD=13-5=8,设,ABC 的内切圆半径为r ,,AO=12-r ,,(12-r )2-r 2=64,解得r=103.考点:1.三角形的内切圆与内心;2.等腰三角形的性质.12.如图,已知点O 是ABC ∆的内心,若120BOC ∠=,则A ∠=__________.【答案】60【分析】先利用120BOC ∠=,可求出∠OBC +∠OCB ,再利用三角形的内心即为三个内角角平分线的交点,可求出∠ABC +∠ACB ,然后就可求出∠A.【详解】∵120BOC ∠=∴∠OBC +∠OCB=180°-∠BOC=60°又∵点O 是ABC ∆的内心∴BO、CO 分别平分∠ABC 和∠ACB∴∠ABC +∠ACB=2(∠OBC +∠OCB )=120°∴∠A=180°-(∠ABC +∠ACB )=60°故答案为:60【点睛】此题考查的是三角形内心的定义和三角形内角和定理.13.如图,在O 中,弦4AB =,点C 在AB 上移动,连结OC ,过点C 作CD OC ⊥交O 于点D ,则CD 的最大值为__________.【答案】2【分析】连接OD ,根据勾股定理求出CD ,利用垂线段最短得到当OC ⊥AB 时,OC 最小,根据垂径定理计算即可;【详解】如图,连接OD ,∵CD ⊥OC ,∴∠DCO=90︒,∴CD当OC 的值最小时,CD 的值最大,OC ⊥AB 时,OC 最小,此时D 、B 两点重合,∴CD=CB=12AB=2,即CD 的最大值为2; 故答案为:2.【点睛】本题主要考查了勾股定理,垂径定理,掌握勾股定理,垂径定理是解题的关键.14.在ABC ∆中,70A ∠=︒,若O 为ABC ∆的外心,则BOC ∠=______度;若O 为ABC ∆的内心,则BOC ∠=______度.【答案】140 125【分析】若O 为ABC ∆的外心,根据圆周角定理,即可求解;若O 为ABC ∆的内心,根据内心是角平分线的交点,再结合三角形的内角和定理即可求解.【详解】解:如图一,点O 是三角形的外心.根据圆周角定理,得∠BOC=2∠A=140°;如图二,点O 是三角形的内心.∴BO 、CO 平分∠ABC 、∠ACB ,∴∠BOC=180°-(∠OBC+∠OCB )=180°-12(∠ABC+∠ACB ) =180°-12(180°-∠A ) =90°+12∠A=125°.故答案为140,125.【点睛】本题考查三角形外心和内心的定义,熟练掌握圆周角定理,熟记内心为三角形三个内角平分线的交点是解题的关键.三、解答题15.如图,点D 是ABC 外接圆的圆心,点O 是ABC 内切圆的圆心,已知110A ∠=︒,求BOC ∠和BDC ∠的度数.【答案】145BOC ∠=︒,140BDC ∠=︒【分析】如图,在D 上取点H ,连接,,BH CH 由圆的内接四边形的性质求解H ∠, 再利用圆周角定理求解,BDC ∠ O 为ABC 的内心,可得,OB OC 分别平分,,ABC ACB ∠∠结合三角形的内角和定理可得()()1118022OBC OCB ABC ACB A ∠+∠=∠+∠=︒-∠,再利用内角和定理可得BOC ∠的大小. 【详解】解:如图,在D 上取点H ,连接,,BH CH四边形ABHC 为D 的内接四边形,110A ∠=︒,18011070H ∴∠=︒-︒=︒,2140,BDC H ∴∠=∠=︒O 为ABC 的内心,,OB OC ∴分别平分,,ABC ACB ∠∠11,,22OBC ABC OCB ACB ∴∠=∠∠=∠ ()()1118022OBC OCB ABC ACB A ∴∠+∠=∠+∠=︒-∠ ()1180110352=⨯︒-︒=︒, ()180********.BOC OBC OCB ∴∠=︒-∠+∠=︒-︒=︒【点睛】本题考查的是圆的内接四边形的性质,圆周角定理的应用,三角形内心的含义,三角形的内角和定理,掌握以上知识是解题的关键.16.如图所示,AB 为☉O 的直径,CD 是☉O 的弦,AB ,CD 的延长线交于点E ,已知AB=2DE ,∠AEC=20°.求∠AOC 的度数.【答案】∠AOC=60°.【分析】连接OD ,如图,由AB,2DE,AB,2OD 得到OD,DE ,根据等腰三角形的性质得∠DOE,∠E,20°,再利用三角形外角性质得到∠CDO,40°,加上∠C,∠ODC,40°,然后再利用三角形外角性质即可计算出∠AOC,【详解】解:连接OD.∵AB=2DE ,AB=2OD ,∴OD=DE ,∴∠DOE=∠E=20°,∴∠CDO=∠DOE+∠E=40°,∵OC=OD ,∴∠C=∠ODC=40°,∴∠AOC=∠C+∠E=60°.【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.17.如图,AB 是O 的直径,点D 是O 上一点,DC AB ⊥于点C .(1)如图①,连接,OD BD ,若点C 是AO 的中点,求ODB ∠的大小;(2)如图②,过点D 作O 的切线,交AB 的延长线于点E ,DF OE 交O 于点F ,且DF OE =.若O 的半径为2,求CE 的长.【答案】(1)30°;(2【分析】(1)连接AD ,根据已知条件可得出AD=OD=OA ,因此,AOD 是等边三角形,得出DAO 60∠=︒,继而得出30ODB OBD ∠=∠=︒;(2)连接, OF OD ,可得四边形OFDE 为平行四边形,有2OF OD DE ===,DE 为圆的切线,90ODE ∠=︒,因此,ODE 为等腰直角三角形,可求出OE 的值,进一步求出CE 的长.【详解】解:(I )如图,连接AD ,∵点C 是AO 的中点,∴AC OC =,∵DC AB ⊥,∴AD OD =,∵OA OD =,∴OA OD AD ==,∴AOD △为等边三角形,∴60AOD ∠=︒,∴30OBD ∠=︒,∵OB OD =,∴30ODB OBD ∠=∠=︒.(2)如图,连接, OF OD ,∵DE 为O 的切线,∴90ODE ∠=︒,∵,DF OE DF OE =,∴四边形OFDE 为平行四边形,∴2OF OD DE ===,∴ODE 为等腰直角三角形,∴OE =∵DC AB ⊥,∴12CE OE == 【点睛】本题是一道关于圆的综合题目,涉及到的知识点有圆的切线的性质,等边三角形的性质,平行四边形的判定及性质,勾股定理等,属于容易题,失分原因:(1)不能根据AC OC =判断出AOD △是等边三角形;(2)不能正确的作出辅助线证明四边形OFDE 是平行四边形;未能掌握等腰直角三角形的性质. 18.如图:在三角形ABC 中,AB=5,AC=7,BC=8,求其内切圆的半径.【分析】作AD BC ⊥,根据勾股定理求解ABC S,再结合内切圆的性质,利用等面积转换的方法求解即可. 【详解】如图,作AD BC ⊥,设BD x =,则8CD x =-,由勾股定理可知:2222AB BD AC CD -=-,则()2225498x x -=--,解得52x =,则2AD =,故11822ABC S BC AD ==⨯=△ 由三角形的内切圆性质,可得:()12ABC S r AB BC AC =++△2578ABC S r AB BC AC ∴===++++△.【点睛】本题考查了勾股定理计算以及三角形的内切圆性质,能够灵活利用三角形的面积转换是解决问题的关键. 19.在同一平面直角坐标系中有6个点:A (1,1),B (−3,−1),C (−3,1),D (−2,−2),E (−2,−3),F (0,−4).(1)画出△ABC 的外接圆P ,则点D 与P 的位置关系___;(2)△ABC 的外接圆的半径=___,△ABC 的内切圆的半径=___.(3)若将直线EF 沿y 轴向上平移,当它经过点D 时,设此时的直线为1l ,则直线1l 与⊙P 的位置关系____【答案】(1)见解析,在圆上;(2)△ABC ABC 的内切圆的半径:3(3)直线与圆相交【分析】(1)分别找出AC 与BC 的垂直平分线,交于点P ,即为圆心,求出AP 的长即为圆的半径,画出圆P ,如图所示,求出D 到圆心P 的距离,与半径比较即可做出判断;(2)求出三角形ABC 的外接圆半径,内切圆半径即可;(3)根据图形及直线与圆的位置关系即可判断.【详解】(1)画出△ABC 的外接圆P ,如图所示,∵DP r ===,∴点D 与P 的位置关系是点在圆上;故答案为:在圆上;(2)△ABC 的外接圆的半径AP ABC 的内切圆的半径为242+-3=3(3)画图之后由网格图得,直线与圆相交故答案为:相交. 【点睛】此题属于圆的综合题,涉及的知识有:待定系数法求一次函数解析式,两点间的距离公式,点与圆的位置关系,以及直线与圆的位置关系,熟练掌握公式及性质是解本题的关键.20.如图,在ABC 中,8AB =,6AC =,O 是其内部一点,AO 平分BAC ∠,连接OC ,在AB 上取一点D ,使6AD =,连接OD .(1)求证:ADO △△ACO △;(2)若130AOD ∠=︒,连接CD ,求OCD ∠的度数;(3)若O 是ABC 的内心,过O 作OM BC ⊥于M ,求CM 的取值范围.【答案】(1)详见解析;(2)40︒;(3)06CM <<.【分析】(1)由SAS 证明三角形全等;(2)根据全等三角形对应边相等、对应角相等的性质,解得100DOC ∠=︒,再由等腰三角形等边对等角的性质解题即可;(3)过O 作ON AC ⊥于N ,OQ AB ⊥于Q ,由于三角形内心是三角形三个内角平分线的交点,可知OCN OCM ∠=∠,再由ASA 证明OCN ,OCM ,最后有全等三角形对应边相等的性质,解得CN CM =,同理解得BM BQ =,AN AQ =,根据三角形三边关系解出答案即可.【详解】解:(1)证明:,6AD AC ==,DAO CAO ∠=∠,AO AO =,,ADO △,ACO △.(2),ADO △,ACO △,,OD OC =,130AOD AOC ∠=∠=︒,,100DOC ∠=︒,,OD OC =,,40OCD ODC ∠=∠=︒.(3)过O 作ON AC ⊥于N ,OQ AB ⊥于Q ,,O 是ABC 的内心,,OCN OCM ∠=∠,,OC OC =,90ONC OMC ∠=∠=︒,,OCN ,OCM ,,CN CM =.同理可得BM BQ =,AN AQ =,,AN CN CM BM BQ AQ AB BC AC +++++=++,,22CM AB AB AC BC +=++,,22BC CM =+,,214BC <<,,22214CM <+<,,06CM <<【点睛】本题考查全等三角形的判定与性质、三角形内心的性质、等腰三角形的性质、三角形三边关系等知识,是重要考点,难度较易,掌握相关知识是解题关键.。
2019-2020学年度最新浙教版九年级数学下册《三角形的内切圆》单元考点练习及答案解析
2.3 三角形的内切圆1.如图,在4×4的网格中,点A ,B ,C ,D ,O 均在格点上,则点O 是(B)A. △ACD 的外心B. △ABC 的外心C. △ACD 的内心D. △ABC 的内心(第1题) (第2题)2.如图,△ABC 是一块绿化带,将阴影部分修建为花圃,已知AB =15,AC =9,BC =12,阴影部分是△ABC 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为(B)A. 16B. π6C. π8D. π5(第3题)3.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,⊙O 为△ABC 的内切圆,D 是斜边AB 的中点,则tan ∠ODA =(D) A. 33 B. 32 C. 3 D. 24.如图,⊙O 是△ABC 的内切圆,若∠ABC =70°,∠ACB =40°,则∠BOC = 125° .(第4题) (第5题)5.如图,△ABC 的内心在x 轴上,点B 的坐标是(2,0),点C 的坐标是(0,-2),点A 的坐标是(-3,b),若反比例函数y =k x(x<0)的图象经过点A ,则k =-15 . 6.如图,在矩形ABCD 中,AB =4,BC =3,连结AC ,⊙P 和⊙Q 分别是△ABC 和△ADC 的内切圆,求PQ 的长.(第6题)【解】 ∵四边形ABCD 为矩形,∴△ACD ≌△CAB ,∴⊙P 和⊙Q 的半径相等.在Rt △ABC 中,∵AB =4,BC =3,∴AC =AB 2+BC 2=5,∴⊙P 的半径r =3+4-52=1. 如解图,连结PQ ,过点Q 作QE ∥DA ,交⊙Q 于点E ,连结PE.(第6题解)∵BC =3,⊙Q 与⊙P 的半径都为1,∴易得PE ∥AB.∴∠QEP =90°.在Rt △QEP 中,∵QE =BC -2r =3-2=1,EP =AB -2r =4-2=2,∴PQ =QE 2+EP 2=12+22= 5.7.如图,在△ABC 中,AC =AB =10,BC =12,⊙O 内切于△ABC ,切点分别为D ,E ,F.(第7题)(1)求△ADE 的周长.(2)求内切圆的面积.【解】 (1)连结AF ,BO ,CO.∵AC =AB =10,BC =12,⊙O 内切于△ABC ,切点分别为D ,E ,F ,∴AF 过圆心O 且AF ⊥BC ,AD =AE ,∴BD =BF =CF =CE =6,∴AD =AE =4.∵AB =AC ,∴AD AB =AE AC. 又∵∠DAE =∠BAC ,∴△ADE ∽△ABC.∴DE BC =AD AB =410=25.∴DE =25×12=245.∴△ADE的周长为4+4+245=645.(2)连结OD.由(1),得AF=AB2-BF2=102-62=8.设FO=r,则AO=8-r.∵OD2+AD2=AO2,∴r2+42=(8-r)2,∴r=3,∴内切圆的面积为π×32=9π.8.如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在边AD,BC上,连结OG,DG,若OG⊥DG.且⊙O的半径长为1,则下列结论中,不成立的是(A)(第8题)A. CD+DF=4B. CD-DF=23-3C. BC+AB=23+4D. BC-AB=2(第8题解)【解】如解图,设⊙O与BC的切点为M,连结MO并延长,交AD于点N.由折叠,知OG =DG.∵OG ⊥DG ,∴∠MGO +∠CGD =90°.又∵∠MOG +∠MGO =90°,∴∠MOG =∠CGD.在△OMG 和△GCD 中,∵⎩⎪⎨⎪⎧∠OMG =∠GCD =90°,∠MOG =∠CGD ,OG =GD ,∴△OMG ≌△GCD(AAS).∴GC =OM =1.∴CD =MG =BC -BM -GC =BC -2.∵AB =CD ,∴BC -AB =2.设AB =a ,BC =b ,AC =c.由⊙O 是Rt △ABC 的内切圆可得r =12(a +b -c), ∴c =a +b -2.在Rt △ABC 中,由勾股定理,得a 2+b 2=(a +b -2)2, 整理,得2ab -4a -4b +4=0.又∵BC -AB =2,即b =2+a ,代入,得2a(2+a)-4a -4(2+a)+4=0,解得a 1=1+3,a 2=1-3(不合题意,舍去).∴b =3+ 3.∴BC +AB =23+4.设DF =x.在Rt △ONF 中,∵FN =3+3-1-x =2+3-x ,OF =x ,ON =1+3-1=3,∴(2+3-x)2+(3)2=x 2,解得x =4- 3.∴CD -DF =3+1-(4-3)=23-3,CD +DF =3+1+(4-3)=5.综上所述,只有选项A 不成立.(第9题)9.如图,在平面直角坐标系中,有一正方形AOBC.反比例函数y =k x的图象经过正方形AOBC 对角线的交点,半径为4-22的圆内切于△ABC ,求k 的值.【解】 如解图,过正方形对角线的交点D 作DN ⊥BO 于点N.设圆心为Q ,切点为H ,E ,连结HQ ,QE.设点D(x ,y).∵反比例函数y =k x的图象经过正方形AOBC 的对角线的交点D ,(第9题解)∴DO=CD,NO=DN.易得HQ=QE,HC=CE,QH⊥AC,QE⊥BC,∠ACB=90°,∴四边形HQEC是正方形.∵半径为4-22的圆内切于△ABC,∴DQ=HQ=4-2 2.∵HQ2+HC2=QC2,∴QC2=2HQ2=2×(4-22)2=(42-4)2,∴QC=42-4,∴CD=42-4+4-22=22,∴DO=2 2.∵NO2+DN2=DO2=(22)2=8,∴2NO2=8,∴NO2=4,∴DN·NO=4,即xy=k=4.(第10题)10.如图,⊙O是以∠ACB为直角的△ABC的内切圆,切点分别是D,E,F.(1)填空:当AC=BC(答案不唯一)时,EF∥AB(填上符合题目要求的一个条件即可).(2)当EF∥AB时,设⊙O的半径r=1,DE,AC的延长线交于点G,求GF的长.【解】(1)由题意,易得CE=CF,∴∠CFE=∠CEF.∵AC=BC,∴∠A=∠B,∴∠A =12(180°-∠C)=∠CFE ,∴EF ∥AB. ∴当AC =BC 时,EF ∥AB.(2)连结OE ,OF.易得四边形OECF 为正方形,∴CE =CF =r =1,∴EF = 2.∵EF ∥AB ,CE =CF ,∴AC =BC.∵∠ACB =90°,∴AB =2AC.∴r =1=AC +BC -AB 2=(2-2)AC 2,解得AC =2+ 2.∴BC =2+2,AB =2 2+2.∴AD =AF =2+1.∵EF ∥AB ,∴△GEF ∽△GDA.∴GF GA =EF DA ,即GF 2+1+GF =2 2+1, 解得GF =2+2.(第11题)11.如图,在△ABC 中,AC =BC ,I 为△ABC 的内心,O 为BC上一点,过B ,I 两点的⊙O 交BC 于点D ,tan ∠CBI =13,AB =6. (1)求线段BD 的长.(2)求线段BC 的长.【解】 (1)如解图,连结CI 并延长交AB 于点E ,连结ID. ∵I 是△ABC 的内心,(第11题解)∴BI 平分∠ABC ,CI 平分∠ACB.又∵AC =BC ,∴CE 垂直平分AB ,∴BE =12AB =3. ∵∠ABI =∠CBI ,tan ∠CBI =13,∴IE BE =DI BI =13. ∴IE =1,∴BI =BE 2+EI 2=10.∴DI =103.∴BD =BI 2+DI 2=103. (2)∵BI ,CI 分别平分∠ABC ,∠ACB ,∴∠BIC =90°+12∠A =90°+12∠ABC =90°+∠IBC , ∴∠IBC =∠BIC -90°.∵∠DIC =∠BIC -90°,∴∠IBC =∠DIC.又∵∠BCI =∠ICD ,∴△BIC ∽△IDC.∴BI ID =BC IC. ∵CI =CE -IE =BC 2-9-1,∴BC=3(BC2-9-1),解得BC=154(负值舍去).12.如图①~④,在直角边长分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,在图⑩中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,求S1+S2+S3+…+S10的值.(第12题)【解】在图①中,∵三角形的两直角边长分别为3和4,∴斜边长为5,∴内切圆半径r=3+4-52=1,∴内切圆面积S=πr2=π.(第12题解) 在图②中标出字母如解图所示.∵S△ABC=12×3×4=12×5×CD,∴CD=12 5.由勾股定理,得AD =32-⎝ ⎛⎭⎪⎪⎫1252=95, ∴BD =5-95=165. 同①可得⊙O 的半径=95+125-32=35,⊙E 的半径=125+165-42=45, ∴S ⊙O +S ⊙E =π×⎝ ⎛⎭⎪⎪⎫352+π×⎝ ⎛⎭⎪⎪⎫452=π. ……由上述规律可知,在图⑩中,S 1+S 2+S 3+…+S 10=π.13.如图,D 是△ABC 的内心,E 是△ABD 的内心,F 是△BDE的内心,若∠BFE 的度数为整数,则∠BFE 至少是多少度?(第13题)【解】 ∵D 是△ABC 的内心,∴AD ,BD 分别是∠BAC 和∠ABC 的平分线,∴∠BAD =12∠BAC ,∠ABD =12∠ABC. ∵∠ABC +∠BAC +∠ACB =180°,∴∠ABC +∠BAC =180°-∠ACB ,∴∠BAD +∠ABD =12∠ABC +12∠BAC =90°-12∠ACB. ∵∠BAD +∠ABD +∠ADB =180°,∴∠ADB =180°-(∠BAD +∠ABD)=90°+12∠ACB. ∵E 是△ABD 的内心,∴DE 是∠ADB 的平分线,∴∠BDE =12∠ADB =45°+14∠ACB.同理可得∠BFE =90°+12∠BDE.∴∠BFE =90°+12⎝ ⎛⎭⎪⎪⎫45°+14∠ACB=90°+22°+4°+∠ACB 8=112°+4°+∠ACB 8.要使∠BFE 最小,且度数为整数,则∠ACB =4°, 此时∠BFE 为113°.故∠BFE 至少为113°.。
初中数学浙教版九年级下册第二章2.3三角形的内切圆练习题-普通用卷

初中数学浙教版九年级下册第二章2.3三角形的内切圆练习题一、选择题1.如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为()A. 110°B. 125°C. 130°D. 140°2.下列说法正确的是()A. 顺次连接矩形各边中点得到的四边形是矩形B. 三角形的三条角平分线交于一点,并且这一点到三个顶点的距离相等C. 既是矩形又是菱形的四边形不一定是正方形D. 直角三角形斜边上的中线等于斜边的一半3.如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为()A. 100°B. 160°C. 80°D. 130°4.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是()A. 9cmB. 12cmC. 15cmD. 18cm5.三角形的内心是()A. 三条边的中垂线的交点B. 三条中线的交点C. 三个内角平分线的交点D. 三条高的交点6.当一个三角形的内心与外心重合时,这个三角形一定是()A. 直角三角形B. 等腰直角三角形C. 钝角三角形D. 等边三角形7.在△ABC中,AO,BO分别平分∠BAC,∠ABC,则点O是△ABC的()A. 外心B. 内心C. 中线交点D. 高线交点8.下列说法:①三角形的内心到三边的距离相等;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;④过平面内三点一定可以做圆;其中正确的有()个.A. 0个B. 1个C. 2个D. 3个9.如图,⊙O是△ABC的内切圆,则点O是△ABC的()A. 三条边的垂直平分线的交点B. 三条角平分线的交点C. 三条中线的交点D. 三条高的交点10.如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( )A. 2B. 3C. √3D. 2√3二、填空题11.如图,⊙I是△ABC的内切圆,D、E、F为三个切点.若∠DEF=52°,则∠A的度数为____________________12.13.14.如图,已知⊙O是△ABC的内切圆,切点分别为D,E,F,若AE=1,CD=2,BF=3,且△ABC的面积为6,则内切圆的半径r为.15.直角三角形的两条直角边长为6,8,则其外接圆半径是_______,内切圆半径是_______16.如图所示的网格由边长为1个单位长度的小正方形组成,点A、B、C在直角坐标系中的坐标分别为(3,6),(−3,3),(7,−2),则△ABC内心的坐标为________.17.18.19.如图,△ABC的内切圆与三边分别切于点D,E,F,若∠C=90°,AD=3,BD=5,则△ABC的面积为_____.20.三、解答题21.如图,已知点I是△ABC的内心,AI交BC于D,交外接圆O于E,求证:22.(1)IE=EC;(2)IE2=ED⋅EA.23.已知:如图,⊙O是Rt▵ABC的内切圆,∠C=90∘.24.25.(1)若AC=8cm,BC=6cm,求⊙O的半径r;26.(2)若AC=b,BC=a,AB=c,求⊙O的半径r.27.28.29.30.31.32.33.34.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.求证:DE=DB.35.36.37.38.如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是弧APB上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.(1)求弦AB的长;(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;=4√3,求△ABC的周长.(3)记△ABC的面积为S,若SDE答案和解析1.【答案】B【解析】【分析】本题考查了三角形内切圆的相关知识,掌握圆周角定理、三角形的内心的定义是解题的关键.基本解题思路:由O为△ABC的外心,根据外心的性质可得到∠A=12∠BOC,进而根据三角形内角和定理,得到∠ABC+∠ACB的值;根据三角形的内心的定义得到∠IBC=12∠ABC,∠ICB=12∠ACB,再根据三角形内角和定理,得到∠BIC=180°−∠IBC−∠ICB,综合这两步即可求出∠BIC的值.【解答】解:根据圆周角定理得到∠A=12∠BOC=70∘,根据三角形的内心的性质得到BI平分∠ABC,CI平分∠ACB,∴∠IBC+∠ICB=12(∠ABC+∠ACB)=12×(180∘−70∘)=55∘,∴∠BIC=180∘−55∘=125∘.故答案选B.2.【答案】D【解析】解:A、顺次连接矩形各边中点得到的四边形是菱形,故本选项错误;B、三角形的三条角平分线交于一点,并且这一点到三边的距离相等,故本选项错误;C、既是矩形又是菱形的四边形一定是正方形,故本选项错误;D、直角三角形斜边上的中线等于斜边的一半,故本选项正确.故选:D.根据三角形的中位线定理可得顺次连接矩形各边中点得到的四边形是菱形;三角形的三条角平分线的交点是三角形的内心,这一点到三边的距离相等;矩形的对角线平分且相等,菱形的对角线平分且垂直,则对角线平分、相等且垂直的四边形为正方形;直角三角形的性质是斜边上的中线等于斜边的一半.本题考查了三角形的内切圆和内心、直角三角形的性质、三角形的中位线定理、矩形、正方形的性质,此题综合性较强,难度适中.3.【答案】D【解析】解:∵∠A=80°,∴∠ABC+∠ACB=180°−∠A=100°,∵点O是△ABC的内心,(∠ABC+∠ACB)=50°,∴∠OBC+∠OCB=12∴∠BOC=180°−50°=130°.故选:D.根据∠A=80°,求出∠ABC+∠ACB,再根据点O是△ABC的内心,求出∠OBC+∠OCB,根据三角形内角和定理求出∠BOC的度数即可.本题考查了三角形的内切圆与内心,三角形内角和定理,圆周角定理的应用,主要考查学生运用定理进行推理和计算的能力.4.【答案】B【解析】【分析】此题主要考查了三角形的内切圆、切线长定理;由切线长定理得出AM+AN+MN= AD+AE是解题关键.利用切线长定理得出DM=MF,FN=EN,AD=AE,进而得出答案.【解答】解:如图所示:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=6cm,∴设E、F分别是⊙O的切点,故D M=MF,FN=EN,AD=AE,∴△AMN的周长=AM+AN+MN=AD+AE=6+6=12(cm).故选B.5.【答案】C【解析】【分析】本题主要考查了三角形内心的概念,解题的关键是要熟记内心的定义.利用三角形的三条角平分线的交点叫做三角形的内心直接求解即可.【解答】解:三角形的内心为三条角平分线的交点.故选C.6.【答案】D【解析】解:根据等边三角形的性质可知,一个三角形的外心与内心恰好重合,这个三角形是等边三角形.故选:D.根据内心和外心的概念,三角形的内心是三个内角平分线的交点,外心是三边的垂直平分线的交点;再根据等边三角形中三线合一性质,所以一个三角形的外心与内心恰好重合,这个三角形是等边三角形.本题考查三角形的内切圆与内心、三角形外接圆与外心、等边三角形、等腰直角三角形,解决本题的关键是掌握以上知识,属于基础题.7.【答案】B【解析】【试题解析】【分析】本题考查了三角形的内切圆与内心,解决本题的关键是区分三角形的内切圆与外接圆的定义.根据三角形的内心是三角形三个内角角平分线的交点即可得结论.【解答】解:∵AO,BO分别平分∠BAC,∠ABC,∴点O是△ABC的内心.故选B.8.【答案】B【解析】解:①正确,三角形的内心到三边的距离相等;②错误,在同圆或等圆中,相等的圆心角所对的弧相等;③错误,如果平分的弦是直径,那么平分弦的直径不垂直于弦;④错误,不在同一条直线上的三点确定一个圆;故选:B.根据三角形的内切圆与内心、角平分线的性质、垂径定理等知识逐一进行判断即可.本题考查了三角形的内切圆与内心、角平分线的性质、垂径定理,解决本题的关键是掌握以上知识.9.【答案】B【解析】【分析】本题考查了三角形的内切圆与内心;熟练掌握三角形的内切圆的圆心性质是关键.根据三角形的内切圆得出点O到三边的距离相等,即可得出结论.【解答】解:∵⊙O是△ABC的内切圆,则点O到三边的距离相等,∴点O是△ABC的三条角平分线的交点;故选B.10.【答案】D【解析】【分析】本题主要考查等边三角形的性质、三角形内切圆的性质,关键在于作辅助线构建直角三角形.要求三角形的边长,已知内切圆半径,可过内心向正三角形的一边作垂线,连接顶点与内切圆心,构造直角三角形求解.【解答】解:如图,过O点作OD⊥AB于点D,则OD=1,∵△ABC是正三角形,∴∠BAC=60°,AB=2AD,∵O是△ABC的内心,∴∠OAD=30°,Rt△OAD中,∠OAD=30°,OD=1,∴AD=OD=√3,tan30∘∴AB=2AD=2√3.故选D.11.【答案】76°【解析】【分析】本题考查了三角形的内切圆和内心,常作的辅助线是连接圆心和切点.连接DI,FI,根据圆周角定理求得∠DIF,再根据四边形的内角和定理和切线的性质求得∠A的度数.【解答】解:连接DI,FI,∵∠DEF=52°,∴∠DIF=104°,∵⊙I是△ABC的内切圆,D,E,F为三个切点,∴∠IDA=∠IFA=90°,∴∠A=360°−90°−90°−104°=76°.故答案为76°.12.【答案】1【解析】×三【分析】此题主要考查了切线长定理以及三角形的内切圆,明确三角形的面积=12角形的周长×三角形内切圆半径是解题关键.根据切线长定理得出AF=AE,EC=CD,×三角形的周长×三角形DB=BF,进而得出△ABC的周长,最后根据三角形的面积=12内切圆半径求解即可.【解答】解:∵⊙O是△ABC的内切圆,切点分别为D,E,F,∴OF⊥AB,OE⊥AC,OD⊥BC,AF=AE=1,EC=CD=2,DB=BF=3,∴△ABC的周长为2×(1+2+3)=12.连接OA,OB,OC,则△ABC的面积等于△AOC,△AOB,△COB的面积之和,则AB⋅r2+AC⋅r2+BC⋅r2=6,∴r2(AB+AC+BC)=6,∴12×12×r=6,解得r=1.∴△ABC的内切圆的半径r为1.13.【答案】5;2【解析】【试题解析】解:如图,∵AC=8,BC=6,∴AB=10,∴外接圆半径为5,设内切圆的半径为r,∴CE=CF=r,∴AD=AF=8−r,BD=BE=6−r,∴6−r+8−r=10,解得r=2.故答案为:5;2.根据直角三角形外接圆的圆心是斜边的中点,由勾股定理求得斜边,设内切圆的半径为r,由切线长定理得6−r+8−r=10,求解即可.本题考查了三角形的内切圆和内心,以及外心,注:直角三角形的外心是斜边的中点.14.【答案】(2,3)【解析】解:如图,点I即为△ABC的内心.所以△ABC内心I的坐标为(2,3).故答案为:(2,3).根据点A、B、C在直角坐标系中的坐标分别为(3,6),(−3,3),(7,−2),建立直角坐标系,根据等腰三角形三线合一,利用网格确定△ABC内心的坐标即可.本题考查了三角形的内切圆与内心、坐标与图形性质,解决本题的关键是掌握三角形的内心定义.15.【答案】15【解析】【分析】此题主要考查了切线长定理以及勾股定理,三角形的面积有关知识,直接利用切线长定理得出AD=AF=3,BD=BE=5,FC=EC,再结合勾股定理得出FC的长,进而得出答案.【解答】解:∵Rt△ABC的内切圆⊙I分别与斜边AB、直角边BC、CA切于点D、E、F,AD=3,BD=5,∴AD=AF=3,BD=BE=5,FC=EC,设FC=EC=x,则(3+x)2+(5+x)2=82,整理得,x2+8x−5=0,解得:x1=−4+√31,x2=−4−√31(不合题意舍去),则AC=−1+√31,BC=1+√31,×(−1+√31)(1+√31)=15,故Rt△ABC的面积为12故答案为15.16.【答案】证明:(1)连接IC,∵点I是△ABC的内心,∴∠ACI=∠BCI,∠BAE=∠CAE.又∵∠BAE=∠BCE,∴∠CAE=∠BCE.∴∠CAE+∠ACI=∠ICB+∠BCE.∴∠EIC=∠ICE.∴IE=EC;(2)由(1)可知:∠CAE=∠BCE.又∵∠AEC=∠DEC,∴△DCE∽△CAE,∴CEAE =DECE,∴CE2=DE⋅EA,∵IE=EC,∴IE2=DE⋅EA.【解析】本题主要考查的是圆周角定理及其推论、三角形的内心和相似三角形的判定及性质.(1)连接IC,根据三角形的内心得出∠ACI=∠BCI,∠BAE=∠CAE,根据同弧圆周角相等,得出∠BAE=∠BCE,推出∠CAE=∠BCE,即可解答;(2)根据(1)得出△DCE∽△CAE,再根据相似三角形的性质即可解答.17.【答案】解:(1)如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,根据勾股定理AB=√AC2+BC2=10cm,四边形OFCD中,OD=OF,∠ODC=∠OFC=∠C=90°,则四边形OFCD是正方形;由切线长定理,得:AD=AE,CD=CF,BE=BF,(AC+BC−AB),则CD=CF=12(8+6−10)=2.即:r=12(2)当AC=b,BC=a,AB=c,(AC+BC−AB),由(1)可得:CD=CF=12(a+b−c).即:r=12(a+b−c).则⊙O的半径r为:12【解析】此题主要考查直角三角形内切圆的性质及半径的求法.利用切线长定理得出四边形OFCD是正方形是解题关键.(1)首先设AC、AB、BC与⊙O的切点分别为D、E、F;易证得四边形OFCD是正方形;(AC+BC−AB),由此代入可求出r的长;那么根据切线长定理可得:CD=CF=12(2)由(1)代入可求出r的长.18.【答案】证明:连接BE∵E 是△ABC 的内心∴∠BAD =∠CAD∠ABE =∠CBE又∵∠CBD =∠CAD∴∠BED =∠BAD +∠ABE =∠CAD +∠CBE∠DBE =∠CBD +∠CBE =∠CAD +∠CBE∴∠BED =∠DBE∴△BDE 是等腰三角形∴DE =DB【解析】连接BE ,由三角形的内心得出∠BAD =∠CAD ,∠ABE =∠CBE ,再由三角形的外角性质和圆周角定理得出∠DEB =∠DBE ,即可得出结论.本题考查了三角形的外心与内心、等腰三角形的判定等知识;本题综合性强,根据圆周角定理得出角的数量关系是解题的关键.19.【答案】 解:(1)连接OA ,取OP 与AB 的交点为F ,则有OA =1.∵弦AB 垂直平分线段OP ,∴OF =12OP =12,AF =BF ,在Rt △OAF 中,∵AF =√OA 2−OF 2=√12−(12)2=√32, ∴AB =2AF =√3.(2)∠ACB 是定值.理由:连接AD 、BD ,由(1),OF =12,AF =√32, 又AO =1,∴∠OAF =30°,∴∠AOP =60°,∴∠AOB =120°,∵点D 为△ABC 的内心,∴∠CAB =2∠DAE ,∠CBA =2∠DBA ,∵∠DAE +∠DBA =12∠AOD +12∠DOB =12∠AOB =60°,∴∠CAB +∠CBA =120°,∴∠ACB =60°.(3)记△ABC 的周长为l ,取AC ,BC 与⊙D 的切点分别为G ,H ,连接OD .连接DG ,DC ,DH ,则有DG =DH =DE ,DG ⊥AC ,DH ⊥BC ,∴S =S △ABD +S △ACD +S △BCD=12AB ⋅DE +12BC ⋅DH +12AC ⋅DG =12(AB +BC +AC)⋅DE =12l ⋅DE , ∵S DE 2=4√3,∴12l⋅DE DE 2=4√3,∴l =8√3DE ,∵CG ,CH 是⊙D 的切线,∴∠GCD =12∠ACB =30°,∴在Rt △CGD 中,CD =2DG ,CG =√3DG =√3DE ,∴CH =CG =√3DE ,又由切线长定理可知AG =AE ,BH =BE ,∴l =AB +BC +AC =2√3+2√3DE =8√3DE ,解得DE =13,∴△ABC 的周长为8√33.【解析】本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起,需要考生从前往后按顺序解题,前面问题为后面问题的解决提供思路,是一道难度较大的综合题.(1)连接OA,OP与AB的交点为F,则△OAF为直角三角形,且OA=1,OF=12,借助勾股定理可求得AF的长;(2)要判断∠ACB是否为定值,只需判定∠CAB+∠ABC的值是否是定值,由于⊙D是△ABC的内切圆,所以AD和BD分别为∠CAB和∠ABC的角平分线,因此只要∠DAE+∠DBA是定值,那么CAB+∠ABC就是定值,而∠DAE+∠DBA等于弧AB所对的圆周角,这个值等于∠AOB值的一半;(3)由题可知S=S△ABD+S△ACD+S△BCD=12DE(AB+AC+BC),又因为SDE2=4√3,所以AB+AC+BC=8√3DE,由于DH=DG=DE,所以在Rt△CDH中,CH=√3DH=√3DE,同理可得CG=√3DE,又由于AG=AE,BE=BH,所以AB+AC+BC=CG+ CH+AG+AB+BH=2√3DE+2√3,可得8√3DE=2√3DE+2√3,解得:DE=13,代入AB+AC+BC=8√3DE,即可求得周长为8√33.。
浙教版九年级数学下册作业本:2.3 三角形的内切圆

2.3 三角形的内切圆1.三角形内切圆定义:与三角形三边相切的圆叫做三角形的内切圆.2.三角形的内心是__________________________交点.3.如图,⊙I 内切于△ABC ,切点分别为D ,E ,F .(1)∠BIC =90°+12∠BAC ;∠DEF =90°-12∠BAC ; (2)△ABC 三边长分别为a ,b ,c ,⊙I 的半径为r ,则有S △ABC =12r (a +b +c ); (3)若∠ACB =90°,AC =b ,BC =a ,AB =c ,则内切圆半径r =CE =a +b -c 2.A 组 基础训练1.下列命题正确的是( )A .三角形的内心到三角形三个顶点的距离相等B .三角形的内心不一定在三角形的内部C .等边三角形的内心,外心重合D .一个圆一定有唯一一个外切三角形第2题图2.如图所示,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,则∠DOE等于()A.70°B.110°C.120°D.130°第3题图3.如图,⊙I是△ABC的内切圆,D,E,F为三个切点,若∠DEF=52°,则∠A的度数为()A.76°B.68°C.52°D.38°4.Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为() A.1.5,2.5B.2,5 C.1,2.5D.2,2.55.如图,∠A=70°,若O为△ABC的外心,则∠BOC=________,若O为△ABC 的内心,则∠BOC=________.第5题图第6题图6.如图,△ABC的三边分别切⊙O于点D,E,F.若AB=7,BC=8,AC=9,则BE =_______,CF=_______.7.⊙O是边长为2的等边△ABC的内切圆,则⊙O的半径为________.8.已知△ABC的面积为4cm2,周长为10cm,则△ABC的内切圆半径为________cm.第9题图9.如图,在Rt△ABC中,∠C=90°,△ABC的内切圆⊙O切AB于点D,切BC 于点E,切AC于点F,AD=4,BD=6,求Rt△ABC的面积.10.如图,在△ABC中,AB=AC,内切圆⊙O与边BC,AC,AB分别切于D,E,F.(1)求证:BF=CE;(2)若∠C=30°,CE=23,求AC的长.第10题图B组自主提高第11题图11.(遵义中考)将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=3,则四边形AB1ED的内切圆半径为()A.3+12 B.3-32C.3+13 D.3-33第12题图12.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,DC =1,则⊙O 的半径等于________.13.如图,点I 是△ABC 的内心,AI 的延长线交边BC 于点D ,交△ABC 的外接圆于点E.(1)求证:IE =BE ;(2)若IE =4,AE =8,求DE 的长.第13题图C 组 综合运用14.如图,在锐角△ABC 中,BC =5,sin ∠BAC =45,点I 为三角形ABC 的内心,AB =BC ,求AI 的长.第14题图参考答案【课堂笔记】2.三角形的三条角平分线的【课时训练】1-4.CBAC 5.140° 125° 6.3 5 7.33 8.45 9.连结OE ,OF ,OD ,设△ABC 的内切圆⊙O 的半径为r.∵△ABC 的内切圆⊙O 切AB 于点D ,切BC 于点E ,切AC 于点F ,∴∠OFC =∠OEC =∠C =90°,AF =AD =4,BD =BE =6,∴四边形OECF 是矩形.∵OE =OF ,∴四边形OECF 是正方形.在Rt △ABC 中,AB 2=BC 2+AC 2,∴102=(6+r)2+(4+r)2,解得r =2或r =-12(舍去),∴BC =8,AC =6,∴Rt △ABC 的面积为12×6×8=24.第10题图10.(1)证明:∵AE ,AF 是⊙O 的切线,∴AE =AF ,又∵AC =AB ,∴AC -AE =AB -AF ,∴CE =BF ,即BF =CE ; (2)连结AO 、OD ,∵O 是△ABC 的内心,∴OA 平分∠BAC ,∵⊙O 是△ABC 的内切圆,D 是切点,∴OD ⊥BC ;又∵AC =AB ,∴A 、O 、D 三点共线,即AD ⊥BC ,∵CD 、CE 是⊙O 的切线,∴CD =CE =23,∴在Rt △ACD 中,由∠C =30°,CD =23,得AC =CD cos 30°=2332=4. 11.B 12.45 13.(1)连结IB.∵点I 是△ABC 的内心,∴∠BAD =∠CAD ,∠ABI =∠IBD.第13题图又∵∠BIE =∠BAD +∠ABI ,∴∠BIE =∠CAD +∠IBD =∠DBE +∠IBD =∠IBE ,∴BE =IE; (2)在△BED 和△AEB 中,∵∠EBD =∠CAD =∠EAB ,∠BED =∠AEB ,∴△BED ∽△AEB ,∴BE AE =DE BE .∵IE =4,∴BE =4.∵AE =8,∴DE =BE 2AE=2.第14题图14.连结CI ,BI ,且延长BI 交AC 于点F ,过点I 作IG ⊥BC 于点G ,IE ⊥AB 于点E.∵AB =BC =5,点I 为△ABC 的内心,∴BF ⊥AC ,AF =CF.在Rt △ABF 中,∵sin ∠BAC =45=BF AB,∴BF =4.∴AF =BA 2-BF 2=3,∴AC =6.∵点I 是△ABC 的内心,IE ⊥AB ,IF ⊥AC ,IG ⊥BC ,∴IE =IF =IG.∴S △ABC =12(AB +AC +BC)·IF =12AC ·BF ,∴IF =AC ·BF AB +AC +BC =6×45+5+6=32,∴AI =AF 2+IF 2=32 5.。
浙教版九年级数学下册练习题:2.3 三角形的内切圆

2.3 三角形的内切圆A组1.如图,⊙O是△ABC的内切圆,则O是△ABC的(B)A. 三条边的垂直平分线的交点B. 三条角平分线的交点C. 三条中线的交点D. 三条高的交点,(第1题)),(第2题))2.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为(B)A. 16 B.π6 C.π8 D.π5(第3题)3.如图,在平面直角坐标系xOy中,点A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为(A)A. (-2,3)B. (-3,2)C. (3,-2)D. (2,-3)4.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC的内切圆,D是斜边AB的中点,则tan∠ODA=(D),(第4题))A.33 B.32 C.3 D. 25.已知△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,∠A=75°,∠B=45°,则∠EOF=__120°__.6.如图,⊙O为△ABC的内切圆,切点分别为D,E,F,∠C=90°,BC=3,AC=4.(1)求△ABC的面积.(2)求⊙O的半径.(3)求AF的长.,(第6题)),(第6题解)) 【解】(1)∵∠C=90°,BC=3,AC=4,∴S△ABC=12×3×4=6.(2)由勾股定理,得AB=AC2+BC2=5,∴r=AC+BC-AB2=3+4-52=1,即⊙O的半径为1.(3)如解图,连结OE,OD.易知四边形OECD为正方形,∴CD=OE=1,∴AF=AD=4-1=3.7.如图,I为△ABC的内心,AB=4,AC=3,BC=2.将∠ACB平移使其顶点与点I重合,角的两边与AB边相交于点E,F,求图中阴影部分的周长.,(第7题)),(第7题解)) 【解】连结IA.∵I是△ABC的内心,∴∠CAI=∠BAI.由平移的性质,得IE∥AC,∴∠CAI=∠EIA,∴∠BAI=∠EIA,∴AE=IE.同理,IF=BF,∴C△IEF=IE+EF+IF=AE+EF+FB=AB=4.B组(第8题)8.如图,△ABC的内心在x轴上,点B的坐标是(2,0),点C的坐标是(0,-2),点A的坐标是(-3,b),若反比例函数y=kx(x<0)的图象经过点A,则k=-15.【解】过点A作AD⊥x轴于点D.∵△ABC的内心在x轴上,∴∠ABO=∠OBC.在Rt△OBC中,∵tan∠OBC=OCOB=22=1,∴∠OBC=45°,∴∠ABO=45°.∵点B(2,0),C(0,-2),A(-3,b),∴AD=b,BD=2-(-3)=5.在Rt△ABD中,∵tan∠ABD=ADBD=b5=1,∴b=5,即点A(-3,5).∵反比例函数y=kx(x<0)的图象经过点A,∴k=-15.(第9题)9.如图,E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连结BD,BE,CE.若∠CBD=32°,则∠BEC的度数为__122°__.【解】∵∠CBD=32°,∴∠CAD=32°.∵E是△ABC的内心,∴∠BAC=2∠CAD=64°,∴∠EBC+∠ECB=(180°-64°)÷2=58°,∴∠BEC=180°-58°=122°.10.如图,⊙O是△ABC的外接圆,BC为⊙O的直径,E为△ABC的内心,连结AE并延长交⊙O于点D,连结BD并延长至点F,使得BD=DF,连结CF,BE.(1)求证:DB=DE.(2)求证:直线CF为⊙O的切线.,(第10题)),(第10题解))【解】 (1)∵E 是△ABC 的内心, ∴∠BAE =∠CAE ,∠EBA =∠EBC.∵∠BED =∠BAE +∠EBA ,∠DBE =∠EBC +∠DBC ,∠DBC =∠CAE , ∴∠DBE =∠BED ,∴DB =DE. (2)如解图,连结CD.∵AD 平分∠BAC ,∴∠DAB =∠DAC , ∴BD ︵=CD ︵.∴BD =CD.∵BD=DF,∴CD=DB=DF,∴∠BCF=90°,∴BC⊥CF,∴CF是⊙O的切线.(第11题)11.如图,⊙O是以∠ACB为直角的△ABC的内切圆,切点分别是D,E,F.(1)填空:当AC=BC(答案不唯一)时,EF∥AB(填上符合题目要求的一个条件即可).(2)当EF∥AB时,设⊙O的半径r为1,DE,AC的延长线相交于点G,求GF的长.【解】(1)由题意,易得CE=CF,∴∠CFE=∠CEF.∵AC=BC,∴∠A=∠B,∴∠A=12(180°-∠C)=∠CFE,∴EF∥AB,∴当AC=BC时,EF∥AB. (2)连结OE,OF.易得四边形OECF为正方形,∴CE=CF=r=1,∴EF= 2.∵EF∥AB,CE=CF,∴AC=BC.∵∠ACB=90°,∴AB=2AC.∴r=1=AC+BC-AB2=(2-2)AC2,解得AC=2+2,∴BC=2+2,AB=2 2+2,∴AD=AF=2+1.∵EF∥AB,∴△GEF∽△GDA,∴GFGA=EFDA,即GF2+1+GF=22+1,解得GF=2+2.12.如图,在△ABC中,AC=BC,I为△ABC的内心,O为BC边上的一点,过B,I两点的⊙O交BC于点D,tan∠CBI=13,AB=6.(1)求BD的长.(2)求BC的长.,(第12题)),(第12题解)) 【解】(1)如解图,连结CI并延长,交AB于点E,连结DI.∵I是△ABC的内心,∴BI平分∠ABC,CI平分∠ACB.又∵AC=BC,∴CE垂直平分AB,∴BE=12AB=3.∵∠ABI=∠CBI,tan∠CBI=1 3,∴EIBE=DIBI=13,∴IE=1,∴BI=BE2+EI2=10,∴DI=103,∴BD=BI2+DI2=103.(2)∵BI平分∠ABC,∴∠EBI=∠IBC,∴∠IBC=∠BIC-∠BEI=∠BIC-90°.∵∠DIC=∠BIC-90°,∴∠IBC=∠DIC.又∵∠BCI=∠ICD,∴△BIC∽△IDC,∴BIID=BCIC=3.∵CI=CE-EI=BC2-9-1,∴BC=3(BC2-9-1),解得BC=154(负值舍去).数学乐园13.如图①~④,在直角边长分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,在图⑩中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,求S1+S2+S3+…+S10的值.导学号:56250045,(第13题))【解】 在图①中,∵三角形的两直角边长分别为3和4,∴斜边长为5,∴内切圆半径r =3+4-52=1,∴内切圆面积S =πr 2=π.(第13题解)在图②中标出字母如解图所示.∵S △ABC =12×3×4=12×5×CD ,∴CD =125. 由勾股定理,得AD =32-⎝⎛⎭⎫1252=95, ∴BD =5-95=165. 同①可得⊙O 的半径=95+125-32=35,⊙E 的半径=125+165-42=45, ∴S ⊙O +S ⊙E =π×⎝⎛⎭⎫352+π×⎝⎛⎭⎫452=π. ……由上述规律可知,在图⑩中,S 1+S 2+S 3+…+S 10=π.。
浙教版数学九年级下册《三角形的内切圆》习题

《三角形的内切圆》习题1.如图1,⊙O内切于△ABC,切点为D,E,F.已知∠B=50°,∠C=60°,•连结OE,O F,DE,DF,那么∠EDF等于( )A.40°B.55°C.65°D.70°图1图2图32.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,•则∠DOE=( )A.70°B.110°C.120°D.130°3.如图3,△ABC中,∠A=45°,I是内心,则∠BIC=( )A.112.5°B.112°C.125°D.55°4.下列命题正确的是( )A.三角形的内心到三角形三个顶点的距离相等B.三角形的内心不一定在三角形的内部C.等边三角形的内心,外心重合D.一个圆一定有唯一一个外切三角形5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( ) A.1.5,2.5B.2,5C.1,2.5D.2,2.56.如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.(1)求证:BF=CE;(2)若∠C=30°,CE=23,求AC的长.7.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是DEF上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.8.如图,△ABC 中,∠A =m °.(1)如图(1),当O 是△ABC 的内心时,求∠BOC 的度数;(2)如图(2),当O 是△ABC 的外心时,求∠BOC 的度数;(3)如图(3),当O 是高线BD 与CE 的交点时,求∠BOC 的度数.9.如图,在半径为R 的圆内作一个内接正方形,•然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n 个内切圆,它的半径是( )A .(22)n RB .(12)n RC .(12)n -1RD .(22)n -1R10.如图,⊙O 为△ABC 的内切圆,∠C =90°,AO 的延长线交BC 于点D ,AC =4,•DC =1,则⊙O 的半径等于( )A .45B .54C .34D .5611.如图,已知正三角形ABC 的边长为2a .(1)求它的内切圆与外接圆组成的圆环的面积;(2)根据计算结果,要求圆环的面积,•只需测量哪一条弦的大小就可算出圆环的面积;(3)将条件中的“正三角形”改为“正方形”“正六边形”,你能得出怎样的结论?(4)已知正n 边形的边长为2a ,请写出它的内切圆与外接圆组成的圆环面积.初中数学试卷。
浙教版九年级数学下册2.3三角形的内切圆同步练习

浙教版九年级数学下册2.3三角形的内切圆同步练习学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列说法中,不正确的是( )A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列命题:①任意三角形一定有一个外接圆,并且只有一个外接圆; ②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形, 并且只有一个外切三角形,其中真命题共有( )A.1个B.2个C.3个D.4个3.已知如图所示,等边△ABC的边长为,下列以A为圆心的各圆中,半径是3cm的圆是( )A.B.C. D.4.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )A.70°B.90°C.60°D.45°5.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为()A.12(a+b+c)r B.2(a+b+c)C.13(a+b+c)r D.(a+b+c)r6.如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是()A.1 B.54C.127D.947.正三角形内切圆半径r与外接圆半径R之间的关系为()A.4R=5r B.3R=4r C.2R=3r D.R=2r8.若正方形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r∶R∶a=…()A.B.2C.D2:4 9.如图1,⊙O内切于△ABC,切点为D,E,F,已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于()A.40°B.55°C.65°D.70°10.若O是△ABC的内心,且∠BOC=100°,则∠A=()A.20°B.30°C.50°D.60°二、填空题11.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.12.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.13.如图,在半径为r的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆,那么这个内切圆的半径是________.14.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,DC=1,则⊙O的半径等于________.15.等腰直角△ABC中, ∠C=90度,斜边AB=6,则此三角形的内心与外心之间的距离是_________.16.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为_____.17.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,DC=1,则⊙O的半径等于________.18.将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB AB1ED的内切圆半径为_________三、解答题19.如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E.求证:ID=BD.20.如图,园林部门准备在公园的三条小道围成的地域内建造一个圆形喷水池,要求它的面积尽量大,请设计水池的半径与圆心.21.如图, △ABC中, AB=10, BC=8, AC=7, ⊙O为△ABC的内切圆, 切点分别是D, E, F. 求AD的长.22.如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.(1)求证:IE=BE;(2)若IE=4,AE=8,求DE的长.23.如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半求:(1)求BF+CE的值;(2)求△ABC的周长.24.已知:如图,P A、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.①若∠COP=∠DOP,求证:AC=BD;②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.25.如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D,E,F.(1)求证:BE=CE;(2)若∠A=90°,AB=AC=2,求⊙O的半径.参考答案1.C【解析】【分析】根据三角形的内心的性质得出A、B、D正确;根据切线的判定定理得出C不正确;即可得出结果.【详解】由三角形的内心是三角形三条内角平分线的交点,故可知A正确;由三角形内心的概念,可知锐角三角形、直角三角形、钝角三角形的内心都在三角形内部,故可知B正确;经过半径外端并且垂直于这条半径的直线是圆的切线,故可知C不正确;由三角形的内心是三角形三条内角平分线的交点,可知三角形的内心到三角形的三边的距离相等,故可知D正确.故选:C.【点睛】本题考查了三角形的内心与性质、切线的判定定理;熟练掌握三角形的内心性质与切线的判定定理是解决问题的关键.2.B【分析】根据外心与内心的概念,分别分析即可判断对错.三角形的外接圆是三条垂直平分线的交点,有且只有一个交点,所以任意三角形一定有一个外接圆,并且只有一个外接圆;反过来说圆的内接三角形可以无数多个;三角形的内切圆的圆心是三个内角平分线的交点,有且只有一个交点,所以任意一个三角形一定有一个内切圆,并且只有一个内切圆;反过来说圆的外切三角形可以有无数多个.【详解】三角形的外接圆是三条垂直平分线的交点,有且只有一个交点,所以任意三角形一定有一个外接圆,并且只有一个外接圆,①是对的;反过来说圆的内接三角形可以无数多个,所以②是错的;三角形的内切圆的圆心是三个内角平分线的交点,有且只有一个交点,所以任意一个三角形一定有一个内切圆,并且只有一个内切圆,③是对的;反过来说圆的外切三角形可以有无数多个,④是错误的.所以正确的命题有2个.故选B.【点睛】考查三角形外心与内心的概念,属于概念题.3.C【分析】过点O作AB的垂线OC,根据等边三角形的性质求出OC的长,然后与圆的半径比较确定选项.【详解】如图,过点O作OC⊥AB于C,则在Rt△AOC中,A=60°,∴×sin60°=3.所以OC=3cm,与圆的半径相等.故选C.【点睛】本题考查的是点与圆的位置关系,根据等边三角形的性质,求出等边三角形的高,把等边三角形的高与圆的半径比较,只有点C在圆上,线段AB上的其它点在圆外.4.B【解析】【分析】由于AD、DC、CB都是⊙O的切线,根据切线长定理知:∠ADO=∠CDO,∠DCO=∠BCO;而AD∥BC,则2∠ODC和2∠OCD互补,由此可求得∠DOC的度数.【详解】∵DA、CD、CB都与⊙O相切,∴∠ADO=∠ODC,∠OCD=∠OCB;∵AD∥BC,∴∠ADC+∠BCD=180°;∴∠ODC+∠OCD=90°,即∠DOC=90°;故选B.【点睛】此题主要考查的是切线长定理及平行线的性质,准确的确定角的关系是解题关键.5.A【解析】【分析】首先根据题意画出图,观察发现三角形ABC的内切圆半径,恰好是三角形ABC内三个三角形的高,因而可以通过面积S△ABC=S△AOB+S△BOC+S△AOC来计算.【详解】如图,可得S△ABC=S△AOB+S△BOC+S△AOC=12ABr+12BCr+12ACr=12(AB+BC+AC)r =12(a+b+c)r ,故选:A.【点睛】本题考查三角形的内切圆与内心.解决本题的关键是将求△ABC转化为求S△AOB、S△BOC、S△AOC.6.C【分析】设AC与⊙O相切于点D,连接OD,AO.在直角三角形ABC中,根据勾股定理,得BC=6,再证明BC=PC,所以可求∠BPC=45°.设⊙O的半径是r,根据三角形ABP的面积的两种表示方法,得2r+10r=12,解方程即可求解.【详解】解:设AC与⊙O相切于点D,连接OD,AO,⊙O的半径是r,∵∠C=90°,AC=8,AB=10,∴BC=6,∵PC=8-2=6,∴BC=PC;∴∠BPC=45°,∴S△APB=S△APO+S△AOB=S△ABC-S△BCP,1 2×2r+12×10r=12×6×8-12×6×62r+10r=12,解得r=1.故选A.【点睛】本题考查切线的性质,勾股定理.熟练运用勾股定理,根据已知条件发现特殊直角三角形,运用三角形面积的不同表示方法列方程求解.7.D【分析】正三角形的内心和外心重合,根据等腰三角形的三线合一,则正三角形的外接圆半径和内切圆的半径可以放在30°的直角三角形中,根据30°所对的直角边是斜边的一半,得R=2r.【详解】正三角形内切圆半径r与外接圆半径R之间的关系为R=2r.故选D.【点睛】熟记正三角形的外接圆半径是内切圆半径的2倍.8.B【解析】【分析】经过圆心O 作正方形一边AB 的垂线OC ,垂足是C .连接OA ,则在直角△OAC 中,∠O=45°.OC 是边心距r ,OA 即半径R .根据三角函数即可求解. 【详解】作出正方形的边心距,连接正方形的一个顶点和中心可得到一直角三角形.在中心的直角三角形的角为3604245︒÷÷=︒,∴内切圆的半径为 2a ,外接圆的半径为2,∴r R a =::.故选B .【点睛】本题考查的知识点是正多边形和圆,解题关键是构造直角三角形,把半径和边心距用边长表示出来.9.B【分析】由三角形内角和定理求出∠A=70°,然后根据切线的性质求得∠OEA=∠OFA=90°,再利用四边形内角和求得∠EOF=360°-∠A-∠OEA-∠OFA=110°,最后利用圆周角定理求解.【详解】解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,∴∠A=70°,∵⊙O 内切于△ABC ,切点分别为D 、E 、F ,∴∠OEA=∠OFA=90°,∴∠EOF=360°-∠A-∠OEA-∠OFA=110°,∴∠EDF=12∠EOF=55°. 故选B .【点睛】本题考查三角形的内切圆与内心;三角形内角和定理;多边形内角与外角;圆周角定理,熟练掌握相关定理综合应用是本题的解题关键.10.A【解析】【分析】根据三角形的内角和定理求出∠OCB+∠0BC=80°,根据三角形的内心求出∠ABC+∠ACB 的度数,根据三角形的内角和定理即可求出答案.【详解】∵∠BOC=100°,∴∠OCB+∠0BC=180°﹣∠BOC=80°,∵O是△ABC的内心,∴∠ABC+∠ACB=2(∠OBC+∠OCB)=160°,∴∠A=180°﹣(∠ABC+∠ACB)=20°.故选:A.【点睛】本题主要考查对三角形的内角和定理,角平分线的性质,三角形的内心等知识点的理解和掌握,能求出∠ABC+∠ACB的度数是解此题的关键.11.76°【分析】已知∠DEF=52o,根据同弧圆心角和圆周角的关系得到圆心角的大小,从而结合四边形内角和求出答案.【详解】解:已知∠DEF=52o∴∠DIF=104o(同弧所对的圆心角是圆周角的2倍)∠ADI=∠AFI=90o(切线的性质)∴∠A=76o.(四边形内角和定理)故答案为76︒.【点睛】此题重点考察学生对切线性质的理解,掌握同弧所对的圆心角是圆周角的2倍是解题的关键. 12.52【解析】【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.【详解】根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,∴AB+BC+CD+AD=52故填:52【点睛】此题主要考查了圆外切四边形的性质,对边和相等.13.2r【解析】【分析】△ABC为大⊙O的内接正三角形,小⊙O为△ABC的内切圆,与BC切于D,且OB=r,根据等边三角形的性质得到∠ABC=60°,根据内圆的性质以及内心的性质得到∠OBD=1 2∠ABC=30°,OD⊥BC,然后根据含30度的直角三角形三边的关系即可得到OD=12OB=12r.【详解】如图,△ABC为大⊙O的内接正三角形,小⊙O为△ABC的内切圆,与BC切于D,且OB=r,∵△ABC为正三角形,∴∠ABC=60°,∵小⊙O为△ABC的内切圆,与BC切于D,∴∠OBD=12∠ABC=30°,OD⊥BC,在Rt△OBD中,∠ODB=90°,∠OBD=30°,OB=r,∴OD=12OB=12r.故答案为:12r.【点睛】本题考查了三角形的内切圆与内心:与三角形三边都相切的圆叫三角形的内切圆,内切圆的圆心叫三角形的内心,三角形内心到三角形三边的距离相等.也考查了正三角形的性质以及含30度的直角三角形三边的关系.14.4 5【解析】【分析】设圆O与AC的切点为M,圆的半径为r,先证得△AOM∽△ADC,再根据相似三角形的对应边成比例即可求得结果.【详解】设圆O与AC的切点为M,圆的半径为r,如图,连接OM,∵∠C=90°∴CM=r,∵△AOM∽△ADC,∴OM:CD=AM:AC,即r:1=(4-r):4,解得r=45,故答案为:4 5 .【点睛】本题考查了三角形的内切圆和内心,解答本题的关键是作出辅助线OM,证得△AOM∽△ADC。
切线长定理-三角形的内切圆(基础篇)-2022-2023学年九年级数学下册基础知识专项讲练(浙教版)

专题2.8 切线长定理三角形的内切圆(基础篇)(专项练习)一、单选题1.用尺规作图作三角形的内切圆,用到了哪个基本作图()A.作一条线段等于已知线段B.作一个角等于已知角C.作一个角的平分线D.作一条线段的垂直平分线2.一个等腰直角三角形的内切圆与外接圆的半径之比为()A2B2C21D213.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为()A.4B.3C.2D.14.如图,PA、PB是O的切线,AC是O的直径,62P∠=,则BOC∠的度数为()A.60B.62C.31D.705.如图,从⊙O外一点P引圆的两条切线P A,PB,切点分别是A,B,若⊙APB=60°,P A=5,则弦AB的长是()A.52B532C.5D.36.如图,P A和PB是⊙O的两条切线,A,B为切点,点D在AB上,点E,F分别在线段P A和PB上,且AD=BF,BD=AE.若⊙P=α,则⊙EDF的度数为()A .90°﹣αB .32αC .2αD .90°﹣12α7.如图,已知PA 、PB 是O 的两条切线,A 、B 为切点,连接OP 交AB 于C ,交O 于D ,连接OA 、OB ,则图中等腰三角形、直角三角形的个数分别为( )A .1,2B .2,2C .2,6D .1,68.若Rt ABC 的外接圆半径为R ,内切圆半径为r ,则其内切圆的面积与Rt ABC 的面积比为( )A .22rr Rπ+ B .2rR rπ+ C .42rR rπ+ D .4rR rπ+9.已知⊙ABC 中,⊙ACB =90°,CD 、CE 分别是⊙ABC 中线和高线,则( )A .D 点是⊙ABC 的内心B .D 点是⊙ABC 的外心 C .E 点是⊙ABC 的内心D .E 点是⊙ABC 的外心10.如图,点E 是⊙ABC 的内心,AE 的延长线和⊙ABC 的外接圆相交于点D ,连接BD ,CE ,若⊙CBD =32°,则⊙BEC 的大小为( )A .64°B .120°C .122°D .128°二、填空题11.如图,已知点O 是ABC ∆的内心,若120BOC ∠=,则A ∠=__________.12.如图,Rt ⊙ABC 中,⊙C =90°,若AC =4,BC =3,则⊙ABC 的内切圆半径r =_____.13.如图,P 是⊙O 外一点,P A 、PB 分别和⊙O 切于A 、B ,C 是弧AB 上任意一点,过C 作⊙O 的切线分别交P A 、PB 于D 、E ,若△PDE 的周长为20cm ,则P A 长为__________.14.如图,AB 是⊙O 的直径,弦BC=2cm ,⊙ABC=60°.若动点P 以2cm/s 的速度从B 点出发沿着B→A 的方向运动,点Q 以1cm/s 的速度从A 点出发沿着A→C 的方向运动,当点P 到达点A 时,点Q 也随之停止运动.设运动时间为t (s ),当⊙APQ 是直角三角形时,t 的值为_________.15.如图所示,AB 、AC 为⊙O 的切线,B 和C 是切点,延长OB 到D ,使BD =OB ,连接AD .∠DAC =78°,那么∠AOD 等于_____度.16.如图,AB AC 、是O 的切线,B C 、为切点,连接BC .若50A ∠=︒,则ABC ∠=__________.17.在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8、BD =6,则菱形ABCD 的内切圆半径为 ________.18.如图,四边形ABCD 为O 的内接四边形,I 是BCD △的内心,点O 与点I 关于直线BD 对称,则A ∠的度数是__________.三、解答题19.如图,ABC 中,50,75ABC ACB ∠=︒∠=︒,点O 是ABC 的内心.求BOC ∠的度数.20.如图,Rt ABC 中,90ABC ∠=︒,O 为BC 上一点,以O 为圆心,OB 长为半径的圆恰好与AC 相切于点D ,交BC 于点E ,连接DO ,并延长交于O 点F .(1)求证:BAO F ∠=∠;(2)若3AD =,2CD =,求O 的半径及EF 的长.21.如图,线段AB 经过O 的圆心O ,交圆O 于点A ,C ,1BC =,AD 为O 的弦,连接BD ,30BAD ABD ∠=∠=︒,连接DO 并延长交O 于点E ,连接BE 交O 于点M .(1)求证:直线BD 是O 的切线; (2)求线段BM 的长.22.如图,点E 是ABC 的内心,AE 的延长线和ABC 的外接圆O 相交于点D ,过D 作直线DG ∥B C .(1)若80ACB ∠=︒,则ADB =∠______;AEB ∠= ______. (2)求证:DE CD =;(3)求证:DG 是O 的切线C .23.如图,在ABC 中,AB AC =,以AB 为直径的O 交BC 于点P ,交CA 的延长线于点D ,连接BD .(1)求作O的切线PQ,PQ交AC于点Q;(要求:尺规作图,不写作法,保留作图迹).(2)在(1)的条件下,求证:QC DQ24.如图,四边形ABCD是⊙O的内接四边形,AB = 6,BC = 8,⊙ABC = 90°,弧AD = 弧DC.(1)求边CD的长;(2)已知⊙ABE与⊙ABD关于直线AB对称.⊙尺规作图:作⊙ABE;(保留作图痕迹,不写作法)⊙连接DE,求线段DE的长.参考答案1.C【分析】根据三角形内心的定义解答.解:三角形的内切圆的圆心叫三角形的内心,是三角形三个角平分线的交点,⊙用尺规作图作三角形的内切圆,用到了作角的平分线的作法,故选:C.【点拨】此题考查了三角形内心的定义,正确理解定义是解题的关键.2.D【分析】设等腰直角三角形的直角边是12条直角边的和与斜边的差的一半,22-其外接圆半径是斜边的一半,22222-21.解:设等腰直角三角形的直角边是12;⊙22-外接圆半径是22,⊙2222-21.故选:D.【点拨】本题考查三角形的内切圆与外接圆的知识,解题的关键是熟记直角三角形外接圆的半径和内切圆的半径公式:直角三角形的内切圆半径等于两条直角边的和与斜边的差的一半;直角三角形外接圆的半径是斜边的一半.3.D【分析】设内切圆的半径为r,根据公式:12rC S三角形三角形,列出方程即可求出该三角形内切圆的半径.解:设内切圆的半径为r11262r解得:r=1故选D.【点拨】此题考查的是根据三角形的周长和面积,求内切圆的半径,掌握公式:1 2rC S三角形三角形是解决此题的关键.4.B【分析】(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出⊙PAB=59°,求出⊙BAC⊙BOC即可.解:PA,PB是⊙O的切线,∴AP=BP,⊙P=62°,∴⊙PAB=o o180-622=59°,AC是⊙O的直径,∴⊙PAC=90°,∴⊙BAC=90°-59°=31°,∴∠BOC=2⊙BAC=62°,故选B.【点拨】本题考查了等腰三角形的性质,切线长定理,切线的性质,圆周角定理等知识点的应用,题型较好,综合性比较强,通过做此题培养了学生分析问题和解决问题的能力.5.C【分析】先利用切线长定理得到P A=PB,再利用⊙APB=60°可判断⊙APB为等边三角形,然后根据等边三角形的性质求解.解:⊙P A,PB为⊙O的切线,⊙P A=PB,⊙⊙APB=60°,⊙⊙APB为等边三角形,⊙AB=P A=5.故选:C.【点拨】本题考查了切线长定理以及等边三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.6.D 【分析】根据切线性质,证得DAE △⊙FBD ,通过等量代换得出EDF DAE ∠=∠,再根据等腰三角形的性质,由⊙P =α,求得DAE ∠即可.解: ⊙P A 和PB 是⊙O 的两条切线,A ,B 为切点,⊙P A =PB ,⊙PAB PBA ∠=∠,即DAE DBF ∠=∠ 在DAE △与FBD 中, ⊙AD BF DAE DBF AE BD =⎧⎪∠=∠⎨⎪=⎩⊙DAE △⊙FBD (SAS ), ⊙DEA FDB ∠=∠, 在DAE △中,180DAE AED EDA ∠+∠+∠=︒,⊙DEA FDB ∠=∠,⊙180DAE FDB EDA ∠+∠+∠=︒, ⊙180EDF FDB EDA ∠+∠+∠=︒, ⊙EDF DAE ∠=∠, ⊙⊙P =α,P A =PB , ⊙PAB PBA ∠=∠⊙在PAB △中,1902BAP α∠=︒-,即1902DAE α∠=︒-,⊙EDF DAE ∠=∠, ⊙1902EDF α∠=︒-故选:D .【点拨】本题考查了切线的性质,全等三角形的性质以及等腰三角形的性质,通过全等证明,等量代换求得EDF DAE ∠=∠是解题关键.7.C 【分析】根据切线长定理及半径相等得,⊙APB 为等腰三角形,⊙AOB 为等腰三角形,共两个;根据切线长定理和等腰三角形三线合一的性质,直角三角形有:⊙AOC ,⊙AOP ,⊙APC ,⊙OBC ,⊙OBP ,⊙CBP ,共6个.解:因为OA 、OB 为圆O 的半径,所以OA =OB ,所以⊙AOB 为等腰三角形,根据切线长定理,PA =PB ,故⊙APB 为等腰三角形,共两个,根据切线长定理,PA =PB ,⊙APC =⊙BPC ,PC =PC ,所以⊙PAC⊙⊙PBC ,故AB⊙PE ,根据切线的性质定理⊙OAP =⊙OBP =90°,所以直角三角形有:⊙AOC ,⊙AOP ,⊙APC ,⊙OBC ,⊙OBP ,⊙CBP ,共6个.故选C .【点拨】此题综合考查了切线的性质和切线长定理及等腰三角形的判定,有利于培养同学们良好的思维品质.8.B【分析】画好符合题意的图形,由切线长定理可得:,,,CE CF r AE AG m BF BG n ======结合勾股定理可得:22,mn Rr r =+再求解直角三角形的面积()()21==22ACB S m r n r Rr r +++,从而可得直角三角形的内切圆的面积与直角三角形的面积之比.解:如图,由题意得:902ACB AB R ∠=︒=,,111O E O F O G r ===,由切线长定理可得:,,,CE CF r AE AG BF BG ====设,,AE AG m BF BG n ====()()()222m r n r m n ∴+++=+,2,m n R += ()2mn m n r r ∴=++,22,mn Rr r ∴=+而()()()211=+22ACB S m r n r mn mr nr r ++=++ ()221=222Rr r Rr r +++ 2=2Rr r +122.22O ABC Sr r S Rr r R r ππ∴==++故选B .【点拨】本题考查的是三角形的内切圆与三角形的外接圆,切线长定理,勾股定理的应用,掌握以上知识是解题的关键.9.B【分析】根据直角三角形斜边上的中线等于斜边的一半,可得D 是⊙ABC 的外心,据此即可求解.解:在△ABC 中,⊙ACB =90°,⊙CD 是△ABC 中线,⊙D 点是△ABC 的外心.故选:B .【点拨】本题考查了三角形的外心,直角三角形斜边上的中线等于斜边的一半,掌握以上知识是解题的关键.10.C【分析】根据圆周角定理可求⊙CAD=32°,再根据三角形内心的定义可求⊙BAC ,再根据三角形内角和定理和三角形内心的定义可求⊙EBC+⊙ECB ,再根据三角形内角和定理可求⊙BEC 的度数.解:在⊙O 中,⊙⊙CBD=32°,⊙⊙CAD=32°,⊙点E 是⊙ABC 的内心,⊙⊙BAC=64°,⊙⊙EBC+⊙ECB=(180°-64°)÷2=58°,⊙⊙BEC=180°-58°=122°.故选:C.【点拨】本题考查了三角形的内心,圆周角定理,三角形内角和定理,关键是得到⊙EBC+⊙ECB的度数.11.60【分析】先利用120BOC∠=,可求出⊙OBC+⊙OCB,再利用三角形的内心即为三个内角角平分线的交点,可求出⊙ABC+⊙ACB,然后就可求出⊙A.解:⊙120BOC∠=⊙⊙OBC+⊙OCB=180°-⊙BOC=60°∆的内心又⊙点O是ABC⊙BO、CO分别平分⊙ABC和⊙ACB⊙⊙ABC+⊙ACB=2(⊙OBC+⊙OCB)=120°⊙⊙A=180°-(⊙ABC+⊙ACB)=60°故答案为60【点拨】此题考查的是三角形内心的定义和三角形内角和定理.12.1解:如图,设⊙ABC的内切圆与各边相切于D,E,F,连接OD,OE,OF,则OE⊙BC,OF⊙AB,OD⊙AC,设半径为r,CD=r,⊙⊙C=90°,AC=4,BC=3,⊙AB=5,⊙BE=BF=3﹣r,AF=AD=4﹣r,⊙4﹣r+3﹣r=5,⊙r=1,⊙⊙ABC的内切圆的半径为1,故答案为1.13.10cm【分析】根据切线长定理,可将△PDE的周长转化为两条切线长的和,已知了△PDE的周长,即可求出切线的长.解:根据切线长定理得:AD=CD,CE=BE,P A=PB,则△PDE的周长=PD PE DE PD PE DC EC PA PB++=+++=+=2P A=20,∴P A=10.故答案为:10.cm【点拨】本题考查的是切线长定理,三角形的周长的计算,掌握切线长定理是解题的关键14.或3-解:因为AB是⊙O的直径,所以⊙ACB=90°,又因为BC=2,⊙ABC=60°;所以AB=2BC=4cm;因为运动时间为t(s),所以AQ=t,BP=2t,所以AP=4-2t,⊙当⊙AQP=90°时,因为⊙A=30°,AP=4-2t,所以PQ=2-t,AQ=3PQ,所以t=3(2-t),所以t=3-;⊙当⊙APQ=90°时,PQ=12AQ,AP=3PQ,所以4-2t=32t,解得t=,综上所述,当t的值为或3-时,⊙APQ是直角三角形.【点拨】1.圆的性质;2.直角三角形的判定与性质.15.64【分析】由已知条件推导出⊙CAO=⊙OAB=⊙BAD,⊙ABD=90°,由此根据⊙DAC=78°,能求出⊙AOD的大小.解:⊙AB、AC为⊙O的切线,B和C是切点,BD=OB,AB∴垂直平分OD,⊙CAO=⊙OABAO AD∴=∴⊙OAB=⊙BAD,⊙⊙CAO=⊙OAB=⊙BAD,⊙ABD=90°,⊙⊙DAC=78°,⊙⊙BAO=13⊙DAC=26°,⊙∠AOD=90°-26°=64°.故答案为:64.【点拨】本题考查角的大小的求法,解题时要认真审题,注意切线性质的灵活运用是解题的关键.16.65°【分析】根据切线长定理即可得出AB=AC,然后根据等边对等角和三角形的内角和定理即可求出结论.解:⊙AB AC、是O的切线,⊙AB=AC⊙⊙ABC=⊙ACB=12(180°-⊙A)=65°故答案为:65°.【点拨】此题考查的是切线长定理和等腰三角形的性质,掌握切线长定理和等边对等角是解决此题的关键.17.125##2.4【分析】根据菱形的性质,可得AC⊙BD,11,22AO AC DO BD==,再由勾股定理可得5AD=,然后设菱形ABCD的内切圆半径为r,根据三角形的面积,即可求解.解:在菱形ABCD中,AC⊙BD,11,22AO AC DO BD==,⊙AC=8、BD=6,⊙AO=4,DO=3,⊙225 AD AO DO+,设菱形ABCD 的内切圆半径为r ,⊙12AOD SAD r =⨯ , ⊙12AODS AO DO =⨯, ⊙1153422r ⨯=⨯⨯ ,解得:125r = , 即菱形ABCD 的内切圆半径为125. 故答案为:125【点拨】本题主要考查了菱形的性质,内切圆,熟练掌握菱形的性质是解题的关键. 18.72︒【分析】连接OB 、OD 、BI 、DI ,利用轴对称的性质证得四边形OBID 是菱形,得到⊙BOD =⊙BID ,⊙OBD =⊙BDO =⊙IBD =⊙IDB ,根据圆周角定理得到⊙BOD =2⊙A ,由圆内接四边形性质得到180A C ∠+∠=︒,求出⊙BID =180°-12A ∠,由此得到2⊙A =180°-12A ∠,求出⊙A =72︒. 解:连接OB 、OD 、BI 、DI ,⊙点O 与点I 关于直线BD 对称,⊙OB =BI ,OD =DI ,⊙OB =OD ,⊙OB =BI =OD =DI ,⊙四边形OBID 是菱形,⊙⊙BOD =⊙BID ,⊙OBD =⊙BDO =⊙IBD =⊙IDB ,⊙⊙BOD =2⊙A ,⊙BID =180°-(⊙IBD +⊙IDB ),⊙⊙IBD +⊙IDB =()11802C ︒-∠,180A C ∠+∠=︒, ⊙ ⊙IBD +⊙IDB =12A ∠,⊙⊙BID =180°-12A ∠, ⊙2⊙A =180°-12A ∠, 解得⊙A =72︒,故答案为:72︒.【点拨】此题考查了圆内接四边形对角互补的性质,三角形内心定义,菱形的判定及性质,三角形内角和定理,轴对称的性质,熟记各知识点是解题的关键.19.117.5°【分析】由点O 是ABC ∆的内心,50ABC ∠=︒,75ACB ∠=︒,根据三角形的内心是三角形三条角平分线的交点,即可求得OBC ∠与OCB ∠的度数,又由三角形内角和定理,即可求得BOC ∠的度数.解:点O 是ABC 的内心,50ABC ∠=︒,75ACB ∠=︒,11502522OBC ABC ∴∠=∠=⨯︒=︒,117537.522OCB ACB ∠=∠=⨯︒=︒, 1801802537.5117.5BOC OBC OCB ∴∠=︒-∠-∠=︒-︒-︒=︒.【点拨】此题考查了三角形内心的性质.此题难度不大,解题的关键是掌握三角形的内心是三角形三条角平分线的交点.20.(1)见分析(2)O 的半径为1.5,65EF =【分析】(1)连接DE ,根据切线长定理可得⊙BAO =⊙DAO ,⊙PDC =90°,从而得到⊙BAO =12⊙BAD ,从而得到⊙BAO =12()1902C COD ︒-∠=∠=⊙F ,即可求证; (2)根据切线长定理可得AB =AD =3,再由勾股定理可得BC =4,设O 的半径为x ,则OD =x ,OC =4-x ,在Rt COD 中,由勾股定理可得O 的半径为1.5,由(1)可得1tan tan 2F BAO =∠=,在Rt DEF △中,由勾股定理,即可求解. (1)证明:如图,连接DE ,⊙90ABC ∠=︒,⊙AB 与O 相切,⊙AD 与O 相切,⊙⊙BAO =⊙DAO ,⊙PDC =90°,⊙⊙BAO =12⊙BAD ,⊙⊙BAD =90°-⊙C ,⊙C =90°-⊙COD , ⊙⊙BAO =12()1902C COD ︒-∠=∠=⊙F ; (2)解:⊙AB 与O 相切,AD 与O 相切,⊙AB =AD =3,⊙CD =2,⊙AC =5,⊙BC =4,设O 的半径为x ,则OD =x ,OC =4-x ,在Rt COD 中,由勾股定理得:222OD CD OC +=,⊙()222x 24x +=-,解得:x =1.5,⊙O 的半径为1.5,即OB =1.5,⊙DF 为直径,DF =3,⊙⊙DEF =90°,⊙BAO F ∠=∠,⊙ 1.51tan tan 32OB F BAO AB =∠===, ⊙EF =2DE ,在Rt DEF △中,由勾股定理得:222DF DE EF =+,⊙222132EF EF ⎛⎫=+ ⎪⎝⎭,解得:65EF =65EF =(舍去).【点拨】本题主要考查了切线长定理,圆周角定理,勾股定理,熟练掌握切线长定理,圆周角定理是解题的关键.21.(1)见分析37 【分析】(1)根据圆周角定理可得260BOD BAD ∠=∠=︒,从而得到90ODB ∠=︒ ,即可求证; (2)连接DM ,Rt ⊙BOD 中,根据直角三角形的性质可得 BO =2OD ,从而得到1OD OC ==,3BD =DE O 为的直径,可得2DE =,90DME ∠=︒,从而得到7BE =,再由1122BDE S BD DE BE DM =⋅=⋅△,可得221DM =解.(1)证明:⊙⊙BOD =2⊙BAD ,⊙260BOD BAD ∠=∠=︒,又⊙30ABD ∠=︒,⊙90ODB ∠=︒ ,即OD BD ⊥,又⊙OD 为O 的半径,⊙直线BD 是O 的切线;(2)解:如图,连接DM ,Rt ⊙BOD 中,30DBO ∠=︒,⊙2BO OD OC BC ==+,又1BC =,OD OC =,⊙1OD OC ==,⊙3BD =⊙DE O 为的直径,⊙2DE =,90DME ∠=︒,在Rt ⊙BDE 中,227BE DE BD +⊙1122BDE S BD DE BE DM =⋅=⋅△, ⊙221BD DE DM BE ⋅= 在Rt ⊙BDM 中,2237BM BD DM =- 【点拨】本题主要考查了切线的判定,圆周角定理,直角三角形的性质,勾股定理等知识,熟练掌握切线的判定,圆周角定理,直角三角形的性质,勾股定理是解题的关键.22.(1)80°,130°;(2)见分析过程;(3)见分析过程.【分析】(1)由圆周角定理可得∠ACB =∠ADB =70°,由三角形的内心的性质可得∠AEB =125°;(2)由三角形的内心的性质可得AE 平分∠BAC ,BE 平分∠ABC ,可得∠BAE =∠CAE ,∠ABE =∠CBE ,由外角的性质可得∠BED =∠DBE ,可证DE =CD ;(3)由垂径定理可得OD ⊥BC ,由平行线的性质可得OD ⊥DG ,可得结论.(1)解:如图,连接BD ,OD ,∵AB AB =,∴∠ACB =∠ADB =80°,∴∠ABC +∠BAC =100°,∵点E 是△ABC 的内心,∴AE 平分∠BAC ,BE 平分∠ABC ,∴∠BAE =∠CAE ,∠ABE =∠CBE ,∴∠BAE +∠ABE =50°,∴∠AEB =130°,故答案为:80°,130°;(2)证明:∵∠BAE =∠CAE ,∴BD =CD ,∴BD =CD ,∵∠BAE =∠CAE =∠CBD ,∠ABE =∠CBE ,∴∠BED =∠BAE +∠ABE =∠CBD +∠CBE =∠DBE ,∴BD =DE ,∴DE =CD ;(3)证明:∵BD =CD ,∴OD ⊥BC ,∵DG ∥BC ,∴OD ⊥DG ,又∵OD 是半径,∴DG 是⊙O 的切线.【点拨】本题考查了三角形的内心,圆的有关性质,切线的判定和性质,灵活运用这些性质解决问题是解题的关键.23.(1)见详解;(2)见详解.【分析】(1)作射线OP ,以点P 为圆心,任意长为半径画弧交射线于M ,N ,以点M ,N 为圆心,大于12MN 为半径画弧,两弧交于点E ,作直线PE ,交AC 于点Q ,则直线PQ 即为所求;(2)如图,连接AP ,则BP =PC ,根据中位线的性质证得OP AC ∥,由切线的性质,平行线的性质证PQ AC ⊥,根据直径所对的圆周角是直角,得90D ∠=︒,证得PQ BD ∥问题得证.(1)解:如图所示,直线PQ 即为所求;(2)证明:如图,连接AP ,AB AC =,BP PC ∴=,OA OB =,OP AC ∴∥,OP 是O 的切线,OP PQ ∴⊥,PQ AC ∴⊥,AB 是O 的直径,90D ∴∠=︒ ,BD AC ⊥,BD DC ∴∥,1CQ PC DQ BP∴==, DQ CQ ∴=.【点拨】本题考查了圆的综合题、圆的半径相等、切线的判定和性质、直径所对的圆周角是直角、三角形中位线的判定和性质、平行线的判定和性质、等腰三角形的性质等知识,作辅助线是解决本题的关键.24.(1)52图见分析⊙14【分析】(1)先求出直径AC,再得到⊙ADC是等腰直角三角形,利用勾股定理即可求解;(2)⊙以B点为圆心,BD为半径,和以A点为圆心,AD为半径画弧,交点为E点,再顺次连接即可;⊙过A点作AH⊙BD,先求出BD的长,再证明⊙BDE是等腰直角三角形,故可求出DE 的长.解:(1)⊙AB = 6,BC = 8,⊙ABC = 90°,⊙AC22+=,AC是⊙O的直径6810⊙⊙ADC=90°⊙弧AD = 弧DC⊙AD=CD⊙⊙ADC是等腰直角三角形⊙AD2+CD2=AC2解得CD=52(2)⊙如图,⊙ABE为所求;⊙过A点作AH⊙BD,⊙弧AD = 弧DC⊙ABC=45°⊙⊙ABD=⊙CBD=12⊙⊙ABH是等腰直角三角形⊙AB2=BH2+AH2,AH=BH⊙AH=BH2⊙AD=CD2⊙在Rt⊙ADH中,DH2242-=AD AH⊙BD=BH+DH=2⊙⊙ABE与⊙ABD关于直线AB对称⊙⊙EBD=2⊙ABD=90°,BE=BD=2⊙⊙BDE是等腰直角三角形⊙DE2214+.BE BD【点拨】此题主要考查圆内的线段长度求解、尺规作图,解题的关键是熟知圆周角的性质、等腰直角三角形的判定与性质及对称性的应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《三角形的内切圆》习题
1.如图1,⊙O内切于△ABC,切点为D,E,F.已知∠B=50°,∠C=60°,•连结OE,O F,DE,DF,那么∠EDF等于( )
A.40°B.55°C.65°D.70°
图1图2图3
2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,•则∠DOE=( )
A.70°B.110°C.120°D.130°
3.如图3,△ABC中,∠A=45°,I是内心,则∠BIC=( )
A.112.5°B.112°C.125°D.55°
4.下列命题正确的是( )
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心,外心重合
D.一个圆一定有唯一一个外切三角形
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( ) A.1.5,2.5B.2,5C.1,2.5D.2,2.5
6.如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=23,求AC的长.
7.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是DEF上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.
1。
