随机过程-第二章答案
(解答)《随机过程》第二章习题

第二章 Markov 过程 习题解答1、 设}1,{≥n n ξ为相互独立同分布的随机变量序列,其分布为:01}0{,0}1{>-===>==p q P p P n n ξξ定义随机序列}2,{≥n X n 和}2,{≥n Y n 如下:⎪⎪⎩⎪⎪⎨⎧=========----;1,1,3;0,1,2;1,0,1;0,0,01111n nn n n n n nn X ξξξξξξξξ ⎩⎨⎧===-;,1;0,0,01其它n n n Y ξξ试问随机序列}2,{≥n X n 和}2,{≥n Y n 是否为马氏链?如果是的话,请写出其一步转移概率矩阵并研究各个状态的性质。
不是的话,请说明理由。
解:(1)显然,随机序列}2,{≥n X n 的状态空间为}3,2,1,0{=S 。
任意取S i i i j i n ∈-132,,,,, ,由于当i X n =给定时,即1,-n n ξξ的值给定时,就可以确定1+n X 的概率特性,即我们有:}{},,,,{12233111i X j X P i X i X i X i X j X P n n n n n n ========+--+因此}2,{≥n X n 是齐次马氏链,其一步转移概率矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=p qp q p q p qP 0000000 由于01,0>-=>p q p ,画出状态转移图,可知各个状态都相通,且都是非周期的,因此此链是不可约的遍历链。
(也可以利用02>P 判定此链是不可约的遍历链)(2)显然,}2,{≥n Y n 的状态空间为}1,0{=S ,由于:}1,1{}1,1,0{}1,10{23234234=========Y Y P Y Y Y P Y Y Y P}0,1{}0,1,0{}0,10{23234234=========Y Y P Y Y Y P Y Y Y P由}2,{≥n Y n 的定义,可知}1,1,1{}1,1,0{}0,1,1{}0,1,0{}1,0,1{}1,1{12312312312312323===⋃===⋃===⋃⋃===⋃======ξξξξξξξξξξξξξξξY Y}1,1,0,0{}0,1,0,0{}1,1,0{12341234234====⋃========ξξξξξξξξY Y Y}0,0,1{}0,1{12323======ξξξY Y , ∅====}0,1,0{234Y Y Y利用}1,{≥n n ξ是相互独立同分布的随机变量序列及其分布,我们有:322233}1,1{q q p pq Y Y P ++=== 223234}1,1,0{q p pq Y Y Y P +==== 223}0,1{pq Y Y P ===0}0,1,0{234====Y Y Y P即有:22222343}1,10{q p pq qp pq Y Y Y P +++==== 0}0,10{234====Y Y Y P由于01,0>-=>p q p ,因此有}0,10{}1,10{234234===≠===Y Y Y P Y Y Y P根据马氏链的定义可知}2,{≥n Y n 不是马氏链。
随机过程第二章作业及参考答案

第二章 平稳过程2. 设随机过程()sin X t Ut =,其中U 是在[]02π,上均匀分布的随机变量。
试证 (1)若t T ∈,而{}12T = ,,,则(){}12X t t = ,,,是平稳过程; (2)若t T ∈,而[)0T =+∞,,则(){}0X t t ≥,不是平稳过程。
证明:由题意,U 的分布密度为:()10220u f u ππ⎧<<⎪=⎨⎪⎩,,其它数学期望()()[]sin X m t E X t E Ut ==⎡⎤⎣⎦()()2220001111sin sin cos cos 212222ut du ut d ut ut t t t t ππππππππ=⋅==-=--⎰⎰.相关函数()()()()()sin sin X X R R t t E X t X t E Ut U t ττττ=+=+=⋅+⎡⎤⎡⎤⎣⎦⎣⎦,()()()2200111sin sin cos 2cos 222ut u t du ut u u du ππτττππ⎛⎫=⋅+⋅=⋅-+--⎡⎤ ⎪⎣⎦⎝⎭⎰⎰ ()()2220001111cos 2cos sin 2sin 442u t u du u t u t πππττττππττ⎡⎤=-+-=-+-⎡⎤⎢⎥⎣⎦+⎢⎥⎣⎦⎰()()11sin 22sin 2424t t πτπτπτπτ=-+++.(1)若t T ∈,而{}12T = ,,时,()0X m t =,()X R τ只与τ有关,二者均与t 无关,因此,(){}12X t t = ,,,是平稳过程。
(2)若t T ∈,而[)0T =+∞,时,()X m t 可能取到不是常数的值,所取到的值与t 有关,()X R τ取到的值也与t 有关,因此,(){}0X t t ≥,不是平稳过程。
3. 设随机过程()()0cos X t A t ωΦ=+,t -∞<<+∞其中0ω是常数,A 和Φ是独立随机变量。
《随机过程答案》第二章习题答案

第二章Markov 过程习题完整答案,请搜淘宝1、 设}1,{≥n n ξ为相互独立同分布的随机变量序列,其分布为:01}0{,0}1{>-===>==p q P p P n n ξξ定义随机序列}2,{≥n X n 和}2,{≥n Y n 如下:⎪⎪⎩⎪⎪⎨⎧=========----;1,1,3;0,1,2;1,0,1;0,0,01111n nn n n n n nn X ξξξξξξξξ ⎩⎨⎧===-;,1;0,0,01其它n n n Y ξξ试问随机序列}2,{≥n X n 和}2,{≥n Y n 是否为马氏链?如果是的话,请写出其一步转移概率矩阵并研究各个状态的性质。
不是的话,请说明理由。
2、 天气预拨模型如下:今日是否下雨依赖于前三天是否有雨(即一连三天有雨;前两天有雨,第三天是晴天;…),试将此问题归纳为马尔可夫链,并确定其状态空间。
如果过去一连三天有雨,今天有雨的概率是0.8;过去三天连续为晴天,而今天有雨的概率为0.2;在其它天气情况时,今日的天气和昨日相同的概率为0.6。
试求此马氏链的转移概率矩阵。
3、 设}0;{≥n X n 是一齐次马氏链,状态空间为}2,1,0{=S ,它的初始状态的概率分布为:4/1}0{0==X P ,2/1}1{0==X P ,4/1}2{0==X P ,它的一步转移转移概率矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=4341031313104341P (1) 计算概率:}1,1,0{210===X X X P ; (2) 计算)3(12)2(01,p p 。
4、 独立地连续抛掷一颗质地均匀的骰子,以n ξ表示前n 次抛掷出的最大点数,试证明}1;{≥n n ξ是一马氏链,并求其n 步转移概率矩阵。
5、 设有一个三个状态}2,1,0{=S 的齐次马氏链,它的一步转移概率矩阵为:⎪⎪⎪⎭⎫ ⎝⎛=33221100p q q p q p P 试求:(1) )3(01)2(01)1(01)3(00)2(00)1(00,,,,,f f f f f f ; (2) 确定状态分类,哪些属于常返的,哪些属于非常返的。
随机过程第一、二章测验题答案(2010)

随机过程测试题一答案每题10分1. 在一汽车工厂中,一辆汽车有两道工序是由机器人完成的。
其一是紧固三只螺栓,其二是焊接两处焊点。
以X 表示由机器人紧固的螺栓不良的数目,以Y 表示由机器人焊接的焊点不良的数目。
据积累资料知),(Y X 具有分布律: Y X 0 1 2 3 0 0.840 0.030 0.020 0.010 1 0.060 0.010 0.008 0.002 20.0100.0050.0040.001(1)求EX ;(2)求]|[j Y X E =,2,1,0=j ;(3)验证 ∑====2}{]|[j j Y P j Y X E EX .解: (1) X 的分布律为 X 0 1 2 3 P0.9100.0450.0320.013148.0=EX .(2) Y 的分布律为 Y 0 1 2 P0.9000.0800.0200=Y 时,X 的条件分布律为X|0=Y 0 123P0.840/0.90.030/0.90.020/0.90.010/0.991]0|[==Y X E ;1=Y 时,X 的条件分布律为X|1=Y 0 123P0.060/0.080.010/0.080.008/0.080.002/0.084.0]1|[==Y X E ;2=Y 时,X 的条件分布律为X|2=Y0 1 2 3P 0.010/0.02 0.005/0.02 0.004/0.02 0.001/0.028.0]2|[==Y X E .(3) EX j Y P j Y X E j ==⨯+⨯+⨯===∑=148.002.08.008.04.09.091}{]|[2.2.设二维随机变量),(Y X 的概率密度为⎩⎨⎧<<=-.,00,),(其他,y x e y x f y(1)求EX;(2)对任意0>y ,求]|[y Y X E =;(3)验证⎰+∞==0)(]|[dy y f y Y X E EX Y .解: (1)当0>x 时, X 的概率密度为x xy xX e dy e dy y x f x f -+∞-+∞===⎰⎰),()(.1)(0===⎰⎰+∞-+∞dx xe dx x xf EX x X .(2) 对任意0>y , Y 的概率密度为y yy yY ye dx e dx y x f y f --===⎰⎰0),()(.⎪⎩⎪⎨⎧<<==.,0,0,1)(),()|(|其他y x y y f y x f y x f Y Y X21)|(]|[0|ydx y xdx y x f x y Y X E yY X ====⎰⎰+∞ (3)EX dy ye y dy y f y Y X E y Y ==Γ=⋅==⎰⎰+∞-+∞1)3(212)(]|[03.写出六种常见分布(退化、二项、泊松、均匀、指数、正态)的特征函数.分布 记号 概率密度或分布律)x (f特征函数)t (ψ退化 {c} 1}{==c X Pict e0-1 b(1,p) .1,0,}{1===-x q p x X P x x q pe it +二项b(n,p) 独立同分布于b(1,p)的n 个r.v.的和..,,1,0,}{1n x q p C x X P x x x n ===-n it q pe )(+泊松 )(P λ.,2,1,0,!}{ ===-x e x x X P xλλ)1(-it e eλ均匀U(a,b))(1)(),(x I ab x f b a -=t a b i e e iatibt )(--标准正态 N(0,1)2221)(x e x f -=π22t e-正态),(N 2σμ222)(21)(σμσπ--=x e x f2)(2t t i eσμ-指数 )(E λ)()(),0(x I e x f x +∞-=λλit-λλ4.关于独立随机变量序列}{n X ,下列哪些命题是正确的. (1)若 ,2,1,||=+∞<k X E k ,则∏∏===nk k nk k EX X E 11;(2) 若 ,2,1,2=+∞<k EX k ,则∑∑===nk k n k n VarX X Var 11)(;(3) 设)(t f k 为k X 的特征函数,)(t f n S 为∑==nk k n X S 1的特征函数,则∏==nk k S t f t f n 1)()(.(4) 设)(t k φ为k X 的矩母函数,)(t n S φ为∑==nk k n X S 1的矩母函数,则∑==nk k S t t n1)()(φφ.解:(4)错,应为 ∏==nk k S t t 1)()(φφ.5.设ηξ,是相互独立,且都为均值0,方差1的随机变量,令t t X ηξ+=)(,求随机过程}0),({≥t t X 的均值函数和相关函数. 解:;0)()()]([)(=+==ηξμtE E t X E t X;1)()()()]([)(222t D t D t D t X D t x +=+=+==ηξηξσ.1)()()()()()]()([),(22ts E E s t tsE E s X t X E s t R x +=+++==ηξηξ6.X (t )=Y cos(t )+Z sin(t ), t >0,Y , Z 相互独立,且 EY =EZ =0,DY =DZ =σ2. 讨论随机过程{X (t ), t >0}的平稳性.解: 0sin cos )]([)(=+==tEZ tEY t X E t X μ;)]()([),(s X t X E s t R X =).cos(sin sin cos cos )()cos sin sin (cos sin sin cos cos 22222s t EZ s t EY s t YZ E s t s t EZ s t EY s t -=⋅+⋅=++⋅+⋅=σ因)(t X μ为常数,),(s t R X 仅与s t -=τ有关,故)}({t X 是宽平稳过程.7.在电报信号)(t X 的传输过程中,信号由不同的电流符号A A -,给出,而电流的发送又有一个任意的持续时间,电流符号的转换是随机的. 设)(t X 在],0(t 时间内的变号次数)(t N 是参数为λ的泊松过程,且可以表示为)()1)(0()(t N X t X -=,又设)0(X 与}0),({≥t t N 独立,且5.0})0({})0({=-===A X P A X P ,求}0),({≥t t X 的均值函数.解:=)]([t X E 0.8.考虑电子管中的电子发射问题,设单位时间内到达阳极的电子数目N 服从参数为λ的泊松分布. 每个电子携带的能量构成一个随机变量序列 ,,21X X 已知}{k X 与N 独立,}{k X 之间互不相关并且具有相同的均值和方差2,σμ==k k DX EX . 单位时间内阳极接收到的能量为∑==Nk kXS 1. 求S 的均值.解:∑∑+∞=====1}{]|[n Nk kn N P n N XE ES∑∑+∞====01}{][n nk k n N P X E ∑+∞===01}{n n N P nEX∑+∞===01}{n n N nP EX λμ=⋅=1EX EN .9.随机过程}0),({≥t t W 称为参数为2σ的维纳过程, 如果 (1) 0)0(=W ;(2),0t s <≤∀))(,0(~)()(2s t N s W t W --σ;(3) ,0v u t s <<<≤∀ 增量)()(s W t W -与)()(u W v W -相互独立.(1)求}0),({≥t t W 的均值函数)]([t W E 和相关函数)]()([s W t W E . (2)}0),({≥t t W 是否为宽平稳过程?证明:(1),0≥∀t ),0(~)(2t N t W σ, 故0)]([)(==t W E t W μ;又,0t s <≤∀))(,0(~)()(2s t N s W t W --σ, 且增量)()(s W t W -与)(s W 相互独立,故)]()([)]())()([()]()([),(s W s W E s W s W t W E s W t W E s t R W +-==s s W D s W E s W t W E 2)]([)]([)]()([σ=+-=从而),min(),(2s t s t R W σ=.(2)由于),(s t R W 与出发时刻),min(s t 有关,因而}0),({≥t t W 不是宽平稳过程.10. 下面四个随机过程中哪些不是宽平稳过程(A) 随机相位正弦波过程:}0),cos()({≥Φ+=t t t X λ,其中),(~ππ-ΦU ,λ是常数. (B) 白噪声序列: },1,0,{ =n X n 是一列两两互不相关(即m n X EX m n ≠=,0)的随机变量序列,且满足2,0σ==n n DX EX . (C) 移动平均序列:},2,1,0,{11 ±±==∑=-+n a X ki in i n ε,其中},2,1,0,{ ±±=n n ε为白噪声序列,k a a a ,,,21 为任意实数.(D) 强度为λ的泊松过程}0),({≥t t N ,其中)(t N 表示到时刻t 为止事件A 发生的次数. 解: D .。
南京大学随机过程练习题附中文解释及答案

8、(3.8)An unbiased die is successively rolled. Let X and Y denote, respectively, the number of rolls necessary to obtain a six and a five. Find (a) E[X], (b) E[X|Y=1] 相继地掷一颗不均匀的骰子。令 X 和 Y 分别记得到一个 6 和一个 5 所必须的抛 掷次数。求(a)E[X],(b)E[X|Y=1]。 重要:E[E[X|Y]]=E[X]
3、(4.32) Each of two switches is either on or off during a day. On day n, each switch will independently be on with probability [1+#of on switches during day n-1]/4. For instance, if both switches are on during day n-1, then each will independently be on during day n with probability3/4. What fraction of days are both switches on? What fractions are both off? 在一天中两个开关或者开或者关。在第 n 天,每个开关独立地处于开的概率是[1+ 第 n-1 天是开的开关数]/4。例如,如果在第 n-1 天两个开关都是开的,那么在第 n 天,每个开关独立地处于开的概率是 3/4。问两个开关都是开的天数的比例是 多少?两个开关都是关的天数的比例是多少?
随机过程答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设ln (),()(k Z F X E Z k =并求是常数)。
(仅供参考)随机信号分析与处理简明教程--第二章习题答案
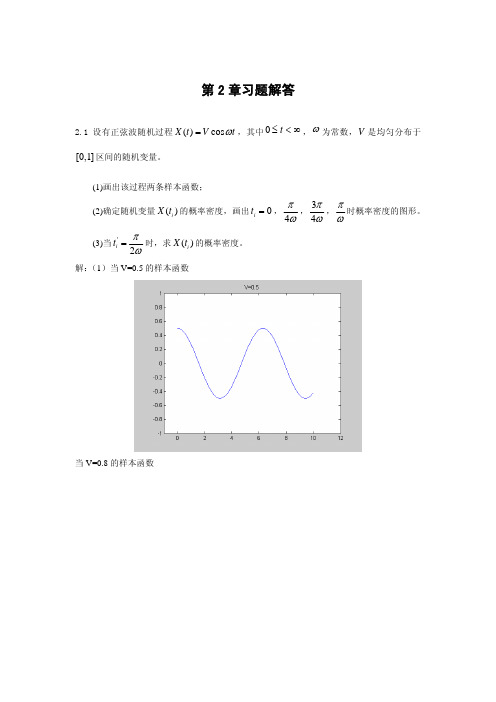
2.1 设有正弦波随机过程 X (t) = V cosωt ,其中 0 ≤ t < ∞ , ω 为常数,V 是均匀分布于 [0,1] 区间的随机变量。
(1)画出该过程两条样本函数;
(2)确定随机变量
X (ti ) 的概率密度,画出 ti
=
0,
π 4ω
,
3π 4ω
,π ω
时概率密度的图形。
δ
(y
−
A)
2.4 设随机过程 X (t) = b + Nt ,已知 b 为常量,N 为正态随机变量,其均值为 m,方差为σ 2 。
试求随机过程 X(t)的一维概率密度及其均值和方差。
解:易知 X(t)也是正态随机变量,只需要知道 X(t)的均值和方差就可以知道其概率密度。
均值: mX = E[ X (t)] = E[b + Nt] = b + tE[N ] = b + mt
⎪⎩0, 其他
⎪⎩0, 其他
求随机过程 X(t)的一维概率密度。
解:首先设Y (t) = a cos(ωt + Θ) ,其中 a 和ω 是常数, Θ 同上。
(由例 2.1.1 知道)Y(t)的一维概率密度为
⎧ fY ( y) = ⎪⎨π
1 ,
a2 − y2
⎪⎩0,
比较 X(t)和 Y(t),可以看出
fX ( x,t) = ∫ ∫ π
1 a2 − x2
fA (a) fΩ (ω ) dadΩ =
∫ ∫ A0 350
da
1
2a 1 da =
x π 250 a2 − x2 A02 100
⎧2 ⎪⎨π A02 ⎪⎩0,
A02 − x2 ,
随机过程-第二章答案

随机过程 2-1.[(1)][2cos(2)][2cos()]()2cos()(0)2cos()21E E E P P ξπθθπθθθθ=+===⨯+=⨯=222(0,1)[(0)(1)][2cos()2cos(2)]4[cos ]4(()cos (0)cos )22R E E E P P ξξξθθππθθθθθ==⋅+==⨯=⨯+=⨯=2-2.102010201020[()][cos sin ][cos ][sin ][]cos []sin 0E Z t E X t X t E X t E X t E X t E X t ωωωωωω=-=-=-=2222210201202222102012021202[()][cos sin sin 2][]cos []sin []sin 2[][]sin 2E Z t E X t X t X X t E X t E X t E X X t E X E X tωωωωωωσωσ=+-=+-=-=(2)()Z t 是两个独立的高斯随机变量的正交组合,所以()Z t 是一个高斯过程,通过上一问可得,()Z t 均值为0,方差为2σ,因此22_2()zf Z σ=(3)由于均值为零,因此1212122210102201021201222010*********(,)(,)[()()][cos cos sin sin cos ()]cos cos sin sin 0cos ()B t t R t t E Z t Z t E X t t X t t X X t t t t t t t t ωωωωωσωωσωωσω===+-+=+-=-2-4(1)12120102(,)[()()cos()cos()]R t t E m t m t t t ωθωθ=++;0[()][()cos()]E Z t E m t t ωθ=+由于θ与()m t 相互统计独立,而且()m t 是宽平稳随机过程,所以()m t 的均值为常数,因此上两式可以化为1212010212012012212012012012012(,)[()()][cos()cos()]1()[cos ()cos(()2)]211()[cos ()cos(()2)]221()cos ()2m m m R t t E m t m t E t t R t t E t t t t R t t t t t t d R t t t t πωθωθωωθωωθθπω=++=-⋅-+++=-⋅-+++⋅=-⋅-⎰自相关只与时间间隔有关;0[()][cos()]0m E Z t E t μωθ=+=,常数。
《概率论与随机过程》第2章习题答案
a2 2
cos(0
)
2.12
若随机过程并
t
的导数存在,求证:
t
d t
dt
dR t,t
dt
t
d t
dt
E
X
(t
)
lim
t 0
X (t
t) t
X (t)
证:
lim
t 0
3
f (x,6) 1 (x 2) (x 5) (x 7)
3
F(x,6) 1 U(x 2) U(x 5) U(x 7)
3
fX
(
x1,
x2
,
2,
6)
1 3
(
x1
3)
( x2
5)
( x1
4)
( x2
7)
(
x1
6)
F
x;1 以及二维分布
F
x1
,
x2
;
1 2
,1
解: f x, 1 0.5 x 0.5 x 1
2
Fx
x,
1 2
0.5 pcos
2
x
0.5 p2 *
1 2
x
0.5 px
0
3
3
E[X(6)]= 1 (2 5 7) 14
南京大学随机过程练习题附中文解释及答案

南京⼤学随机过程练习题附中⽂解释及答案(以第九版为准)第⼆章Random Variables 随机变量1、(2.16)An airline knows that 5percent of the people making reservations on a certain flight will not show up.Consequently,their policy is to sell 52tickets for a flight that can hold only 50passengers.What is the probability that there will be a seat available for every passenger who shows up?航空公司知道预订航班的⼈有5%最终不来搭乘航班。
因此,他们的政策是对于⼀个能容纳50个旅客的航班售52张票。
问每个出现的旅客都有位置的概率是多少?答:05.0*95.0*52-95.0-15152)()(2、(2.25略变动)Suppose that two teams are playing a series of games,each of which is independently won by team A with probability p and by team B with probability 1-p.The winner of the series is the first team to win i games.If i =4,find the probability that a total of 7games are played.Find the p that maximizes/minimizes this probability.假定两个队玩⼀系列游戏,A 队独⽴地赢的概率是p ,B 队独⽴地赢的概率是1-p 。
随机过程习题解答第1,2章

习题11. 令X(t)为二阶矩存在的随机过程,试证它是宽平稳的当且仅当EX(s)与E[X(s)X(s+t)]都不依赖s.证明:充分性:若X(t)为宽平稳的,则由定义知EX(t)=μ, EX(s)X(s+t)=r(t) 均与s 无关必要性:若EX(s)与EX(s)X(s+t)都与s 无关,说明EX(t)=常数, EX(s)X(s+t)为t 的函数2. 记1U ,...,n U 为在(0,1)中均匀分布的独立随机变量,对0 < t , x < 1定义I( t , x)=⎩⎨⎧>≤,,,,t x t x 01并记X(t)=),(11∑=nk k U t I n ,10≤≤t ,这是1U ,...,n U 的经验分布函数。
试求过程X (t )的均值和协方差函数。
解: EI ()k U t ,= P ()t U k ≤= t , D()),(k U t I = EI ()k U t ,-()2),(kU t EI= t -2t = t(1-t)j k ≠, cov ()),(),(j k U s I U t I ,=EI(t,k U )I(s,j U )-EI(t, k U )EI(s, j U ) = st -st=0k = j , cov ()),(),(j k U s I U t I ,= EI(t,k U )I(s,j U )-st = min(t,s)-stEX(t)=),(11∑=n k k U t EI n =∑=nk tn 11= tcov ())(),(s X t X =()()),(),,(cov 1),(),,(cov 1212j kjk nk k k U s I Ut I n U s I U t I n ∑∑≠=+=[]∑=nk st t s n12),min(1-=()st t s n-),min(13.令1Z ,2Z 为独立的正态分布随机变量,均值为0,方差为2σ,λ为实数,定义过程()t Sin Z t Cos Z t X λλ21+=.试求()t X 的均值函数和协方差函数,它是宽平稳的吗?Solution: ()221,0~,σN Z Z . 02221==EZ EZ .()()221σ==Z D Z D ,()0,21=Z Z Cov ,()0=t EX ,()()()()()[]s Sin Z s Cos Z t Sin Z t Cos Z E s X t X Cov λλλλ2121,+⋅+=[]t C o s S i n Z Z s t S i n C o s Z Z s t S i n S i n Z t C o s C o s Z E λλλλλλλλ12212221+++=()02++=s t S i n S i n s t C o s C o s λλλλσ =()[]λσs t Cos -2(){}t X 为宽平稳过程.4.Poisson 过程()0,≥t t X 满足(i )()00=X ;(ii)对s t >,()()s X t X -服从均值为()s t -λ的Poisson 分布;(iii )过程是有独立增量的.试求其均值函数和协方差函数.它是宽平稳的吗?Solution ()()()()t X t X E t EX λ=-=0,()()t t X D λ= ()()()()()s t s X t EX s X t X Cov λλ⋅-=,()()()()()ts s EX s X s X t X E 22λ-+-= ()()()()ts s EX s X D 220λ-++=()ts s s 22λλλ-+=()t s s λλλ-+=1 显然()t X 不是宽平稳的.5. ()t X 为第4题中的Poisson 过程,记()()()t X t X t y -+=1,试求过程()t y 的均值函数和协方差函数,并研究其平稳性. Solution ()λλ=⋅=1t Ey , ()()λ=t y DCov(y(t),y(s))=Ey(t)y(s)-Ey(t)y(s)=E(x(t+1)-x(t))(x(s+1)-x(s))-λ2(1)若s+1<t, 即s≤t-1,则Cov(y(t),y(s))=0-λ2=-λ2(2)若t<s+1≤t+1, 即t>s>t-1, 则Cov(y(t),y(s))=E[x(t+1)-x(s+1)+x(s+1)-x(t)][x(s+1)-x(t)+x(t)-x(s)] -λ2=E(x(t+1)-x(s+1))(x(s+1)-x(t))+E(x(t+1)-x(s+1))(x(t)-x(s))+E(x(s+1)-x(t))+E(x(s+1)-x(t))(x(t)-x(s))- λ2=λ(s+1-t)= λ-λ(t-s)- λ2(3) 若t<s<t+1Cov(y(t),y(s))= E [x(t+1)-x(s)+x(s)-x(t)] [x(s+1)-x(t+1)+x(t+1)-x(s)]- λ2 =(x(t+1)-x(s))(x(s+1)-x(t+1))+E(x(t+1)-x(s))(x(t+1)-x(s))+E(x(s)-x(t))(x(s+1)-x(t+1))+E(x(s)-x(t))(x(t+1)-x(s))- λ2=0+λ(t+1-s)+0-λ2=λ+λ(t-s)- λ2(4) 若s>t+1 Cov(y(t),y(s))=0-λ2=-λ2由此知,故方差只与t-s有关,与t,s无关故此过程为宽平稳的。
(仅供参考)随机信号分析与处理简明教程--第二章习题答案

⎧ 0,
(2)
FX
⎜⎛ ⎝
x1
,
x2
;
1 2
,1⎟⎞ ⎠
=
⎪⎩⎪⎨ 121,,
x1 < 0,−∞ < x2 < ∞; 0 ≤ x1 < 1, x2 ≥ −1;
x1 ≥ 1,
x1 ≥ 0, x2 < −1 x1 ≥ 1,−1 ≤ x2 < 2
x2 ≥ 2
2.3 设某信号源,每 T 秒产生一个幅度为 A 的方波脉冲,其脉冲宽度 X 为均匀分布于[0,T ]
当 ti
=
0 时,
fX
( x, t )
=
⎧1 ⎨⎩ 0
0< x <1 else
当 ti
=
π 4ω
时,
fX (x,t)
=
⎧⎪ ⎨ ⎪⎩
2 0
0<x< π 4ω
时,
fX (x,t)
=
⎧⎪ ⎨ ⎪⎩
2 0
− 2 2<x<0 else
当 ti
=
π ω
时,
fX
( x, t )
=
⎧1 ⎨⎩ 0
当kl时有rtsx2????????????eakutkt0utkt01uskt0uskt01ea2eut?k?t?ut?k?t?1us?k?t?us?k?t?1k0000eut?k?t0?ut?k?t0?1us?k?t0?us?k?t0?1kt00faa?2??0a0是在02中均匀分布的随机变量且与a统计独立为常量
D[ X (t)] = D[ Acosωt + B sin ωt] = D[ A]cos2 ωt + D[B]sin2 ωt = σ 2
随机过程_汪荣鑫_答案2,3,4

1.指出下面所给的习题中,哪些是平稳过程,哪些不是平稳过程? (1)设随机过程 X (t ) e
Xt
,t>0,其中 X 具有在区间 (0, T ) 中的均匀分布
解:∵ 该随机过程的数学期望为
mx (t ) EX (t ) e xt
0
T
1 1 1 Tt dx e xt T [e 1] const 0 T Tt Tt
E[cos( 0 t ) cos( 0 t 0 )]
1 E[cos 0 cos(2 0 t 0 2)] 2
1 1 E (cos 0 ) E cos(2 0 t 0 2) 2 2 1 1 2 1 1 cos 0 cos(2 0 t 0 2 )d cos 0 2 2 0 2 2
2
2 0
1 [1 cos 2t ] 2t
不是常数
3
3.设随机过程
X (t ) A cos( 0 t ), t
其中 0 是常数,A 与Φ 是独立随机变量。Φ 服从在区间(0,2π )中的均匀分布。A 服从 瑞利分布,其密度为
x x2 2 2 f ( x ) 2 e 0
EA
2
x2
0
x
2
x
2
e
x2 2
2
dx
0
x de
2
x2 2 2
x e
2
2
2
0
0
e
x2 2
2
d ( x ) 2
最新西安交通大学汪荣鑫随机过程第二版课后答案

西安交通大学汪荣鑫随机过程第二版课后答案------------------------------------------作者xxxx------------------------------------------日期xxxx随机过程习题解答第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ 0()k jtkk p q e∞==∑ =0()1jtkjt k pp qe qe ∞==-∑ 又20()kk k k q qE X kpq p kq pp p∞∞======∑∑ 222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 100()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰22201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
随机过程课后习题解答 毛用才 胡奇英
= 1 n e jtk
n k 1
P{xk
k}
1 n
( k 0, 2,n )
6、证函数 f (t) 1 为一特征函数,并求它所对应的随机变量的分布。
1 t2
nn
解 (1)
f (ti tk )i k
i1 k 1
5
= n i1
n
i k
k 1 1 (ti tk )2
t2
t3, t2
t3 ,t3 )
exp{
1 2
[(t1
t2
t3 )2
(t2
t3) t32 ]
2}
(2) fS1,S2,S3 (t1, t2 , t3 ) E{exp[ j(t1s1 t2s2 t3s3 )]}
= E{exp[ j((t1 t2 t3 )x1 (t2 t3 )x2 t3x3 ]}
2 1
X
2 2
X
2 1
X
2 3
X
2 2
X
2 3
]
3
4
E[
X
2 1
]
6
又
f
(t)
exp{
1 2
tBt '}
4 f
t12t22
n e i1 k 1 l1
n n
nn
1 e e =
jlti i
jltk k
n i1 l 1
k 1 l 1
nn
f (ti tk )i k 0
i1 k 1
非负定
(2)
f
(t)
e jt (1 e jnt ) n(1 e jt )
= e jt (1 e jt )(1 e jt e2 jt e(n1)tj )
随机过程第二章复习题及其解答基本概念

第二章1、随机过程若按状态空间与参数集分类可分为离散参数链,连续参数链,随机序列,随机过程四类.2、若{X(t), teT}是零均值的二阶矩过程,若对任意的tKtWtKs 则X(t)为正交增量过程的充分条件是E[X⑷-x fi][x(t4)-x(t3)J = 03、设随机过程X(t)=Y+Zt, t>0,其中Y, Z是相互独立的N (0,1) 随机变量,求{ X(t), t>0}的一维和二维概率密度族.解:由于X与Z是相互独立的正态随机变量,故其线性组合仍为正态随机变量,要计算{X(t), t〉0}的一、二维随机概率密度,只要计算数字特征叫(/)、D x (?)和Px (s, t)即可.iDx(t)=E (Y+Zt)=EY+tEZ=0, Dx (t)=D(Y+Zt)二DY+t'DZ 二1+F,B x(s, t)=EX(s)X(t)- m x(s) m3£(t)=E(Y+Zs) (Y+Zt)=l+st,t) _ 1 十st(PxG丿’瓦⑤叵貢血十旳(屮2),故随机过程{X(t), t>0}的一、二维概率密度分别为I Y2ft(x)=7^?W xp{-绪d'X* 2兀如旳二片讦 -eXP(令 [ 昙—2p j(】+:;;;+t2)+悬]},s,t>0,其中p = Px(s,t)4、设{X(t), tMO}是实正交增量过程,X(0)=0, V是标准正态随机变量,若对任意的tMO, X(t)与V相互独立,令Y(t)=X(t)+V,求随机过程(Y(t), tMO}的协方差函数.解:依题意知EX(t)=O, EV=O, DV=1,所以EY (t) =E [X (t)+V] =EX (t) +EV=O,12)=E(X(ti)+V) (X(t2)+V)=E [X (tD X (t2)) ]+EV2= O \(min (t b t2)) +1.5、试证明维纳过程是正态过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机过程 2-1.
[(1)][2cos(2)][2cos()]()2cos()(0)2cos()2
1
E E E P P ξπθθπ
θθθθ=+===⨯+=⨯=
2
22
(0,1)[(0)(1)][2cos()2cos(2)]4[cos ]4(()cos (0)cos )2
2
R E E E P P ξξξθθππθθθθθ==⋅+==⨯=⨯+=⨯=
2-2.
102010201020[()][cos sin ][cos ][sin ][]cos []sin 0
E Z t E X t X t E X t E X t E X t E X t ωωωωωω=-=-=-=
2
2
2
2
2
10201202
2
2
2
102012021202
[()][cos sin sin 2][]cos []sin []sin 2[][]sin 2E Z t E X t X t X X t E X t E X t E X X t E X E X t
ωωωωωωσωσ
=+-=+-=-=
(2)()Z t 是两个独立的高斯随机变量的正交组合,所以()Z t 是一个高斯过程,通过上一问可得,()Z t 均值为0,方差为2σ,因此
22
_2()z
f Z σ
=
(3)由于均值为零,因此
1212122
2
1010220102120122
2
010*********(,)(,)[()()]
[cos cos sin sin cos ()]cos cos sin sin 0cos ()
B t t R t t E Z t Z t E X t t X t t X X t t t t t t t t ωωωωωσωωσωωσω===+-+=+-=-
2-4
(1)12120102(,)[()()cos()cos()]R t t E m t m t t t ωθωθ=++;
0[()][()cos()]E Z t E m t t ωθ=+
由于θ与()m t 相互统计独立,而且()m t 是宽平稳随机过程,所以()m t 的均值为常数,因此上两式可以化为
12120102120120122120120
120
12012(,)[()()][cos()cos()]1()[cos ()cos(()2)]
211()[cos ()cos(()2)]
221()cos ()
2
m m m R t t E m t m t E t t R t t E t t t t R t t t t t t d R t t t t π
ωθωθωωθωω
θθπ
ω=++=-⋅-+++=-⋅-+++⋅
=-⋅
-⎰
自相关只与时间间隔有关;
0[()][cos()]0m E Z t E t μωθ=+=,常数。
所以()Z t 是宽平稳随机过程。
(2)峰值是
1/2
(3)
2
2
00
()()1[(
)()]
42
2
j z z a a P R e
d S S ωτ
ωττ
ωωωω+∞
--∞
=⋅+-=+⎰
功率1(0)2
S R ==
2-5.
2
2
2
()()j n n a
P R e
d a ωτ
ωττω
+∞
--∞
=
⋅=
+⎰
;
(0)2
a S R ==
2-7.
滤波器输出噪声的功率谱为:
2
0()()(),,02
n i c c n P H P B B ωωωωπωωπ==
+<<-其余为
则自相关函数
01()()2cos ()
j n n c a R P e
d n B S B ωτ
τωω
π
ωτπτ+∞
-∞
=
=⋅⎰
因为输入噪声是高斯白噪声,所以输出噪声也是高斯分布
[()][()](0)0o i E t E t H ξξ=⋅=
22
2
0[()][()][()][()]o o o o D t E t E t E t n B
ξξξξ=-==
所以输出的噪声一维概率密度为
2
02()n B
f ξ
ξ-
=
2-8. 1()1
H j RC ωω=
+
2
00
2
()()()1
()12
n P H P n RC ωωωω==
⋅+
对上式求傅立叶反变换得到自相关函数
0()4RC
n n R e
RC
τ
τ-
=
2-13.
输入噪声是高斯白噪声,经过滤波器之后是一个窄带高斯过程 求得输出均值和方差分别为
[()][()](0)0o i E t E t H ξξ=⋅=;
22
2
0[()][()][()][()]4o o o o D t E t E t E t n R C
ξξξξ=-==
所以输出噪声的一维概率密度函数为
2
2
00
2421()n n RC
RC
f ξ
ξ
ξ-
-
⋅
=
=。
