2017-2018学年江苏省宿迁市高一下学期3月月考数学试题5
苏科版江苏省宿迁市初二数学上学期第三次月考试卷

苏科版江苏省宿迁市初二数学上学期第三次月考试卷一、选择题1.在▱ABCD 中,已知∠A ﹣∠B=20°,则∠C=( ) A .80°B .90°C .100°D .110°2.如图,直线(0)y x b b =+>分别交x 轴、y 轴于点A 、B ,直线(0)y kx k =<与直线(0)y x b b =+>交于点C ,点C 在第二象限,过A 、B 两点分别作AD OC ⊥于D ,BE OC ⊥于E ,且8BE BO +=,4=AD ,则ED 的长为( )A .2B .32C .52D .13.下列成语描述的事件为随机事件的是( ) A .守株待兔B .水中捞月C .瓮中捉鳖D .水涨船高4.对函数31y x =-,下列说法正确的是( ) A .它的图象过点(3,1)- B .y 值随着x 值增大而减小 C .它的图象经过第二象限D .它的图象与y 轴交于负半轴5.下列各数中,是无理数的是( ) A .38B .39C .4-D .2276.下列图形中的五边形ABCDE 都是正五边形,则这些图形中的轴对称图形有( )A .1个B .2个C .3个D .4个7.下列运算正确的是( )A .236a a a ⋅=B .235()a a -=-C .109(0)a a a a ÷=≠D .4222()()bc bc b c -÷-=-8.下列图形是轴对称图形的是( )A .B .C .D .9.如图,给出下列四组条件:①AB =DE ,BC =EF ,AC =DF ;②AB =DE ,∠B =∠E ,BC =EF ;③∠B =∠E ,BC =EF ,∠C =∠F ;④AB =DE ,AC =DF ,∠B =∠E .其中能使△ABC ≌△DEF 的条件有( )A .1组B .2组C .3组D .4组10.如图(1),在四边形ABCD 中,AB CD ∥,90ABC ∠=︒,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为x ,ABP ∆的面积为y ,如果y 关于x 的函数图象如图(2)所示,则BCD ∆的面积是( )A .6B .5C .4D .311.已知△ABC 的三边长分别为3,4,5,△DEF 的三边长分别为3,3x ﹣2,2x +1,若这两个三角形全等,则x 的值为( ) A .2B .2或C .或D .2或或12.下列各式中,属于分式的是( )A .x ﹣1B .2mC .3b D .34(x+y ) 13.如图:若△ABE ≌△ACD ,且AB =6,AE =2,则EC 的长为( )A .2B .3C .4D .614.下列二次根式中属于最简二次根式的是( ) A 32B 24x y C y xD 24+x y15.设2的整数部分用a 表示,小数部分用b 表示,4﹣2的整数部分用c 表示,小数部分用d 表示,则b dac+值为( ) A .12 B .14C .212- D .2+12二、填空题16.在一个不透明的袋子中装有2个黄球和3个红球,每个除颜色外完全相同,将球摇匀从中任取一球:①恰好取出白球;②恰好取出红球;③恰好取出黄球,根据你的判断,将这些事件按发生的可能性从小到大顺序排列___________(只需填写序号).17.在平面直角坐标系xOy 中,我们把横、纵坐标都是整数的点叫做整点,已知点A (0,4),点B 是x 轴正半轴上的整点,记△AOB 内部(不包括边界)的整点个数为m ,当m =3时,则点B 的横坐标是_____.18.一次函数y =kx +b 的图像如图所示,则关于x 的不等式kx -m +b >0的解集是____.19.如图,数轴上点A 表示的数为a ,化简:a 244a a +-+=_____.20.若直线y x m =+与直线24y x =-+的交点在y 轴上,则m =_______. 21.若某个正数的两个平方根分别是21a +与25a -,则a =_______.22.如图,在平面直角坐标系中,已知点A(1,0)、B(0,2),如果将线段AB 绕点B 顺时针旋转90°至CB ,那么点C 的坐标是 .23.已知点M (1,a )和点N (2,b )是一次函数y =-2x +1图象上的两点,则a 与b 的大小关系是_________.24.已知函数y=x+m-2019 (m 是常数)是正比例函数,则m= ____________25.如图,在△ABC 中,∠C =90°,∠B =22.5°,DE 垂直平分AB 交BC 于点E ,EC =1,则三角形ACE 的面积为__.三、解答题26.如图,已知函数12y x =+的图像与y 轴交于点A ,一次函数2y kx b =+的图像经过点(0,4)B ,与x 轴交于点C ,与12y x =+的图像交于点D ,且点D 的坐标为2,3n ⎛⎫ ⎪⎝⎭.(1)求k 和b 的值;(2)若12y y >,则x 的取值范围是__________. (3)求四边形AOCD 的面积.27.如图,在ABC ∆中,AD BC ⊥,15AB =,12AD =,13AC =.求BC 的长.28.某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由. 29.计算或求值(1)计算:(2a+3b)(2a﹣b);(2)计算:(2x+y﹣1)2;(3)当a=2,b=﹣8,c=5时,求代数式242b b aca-+-的值;(4)先化简,再求值:(m+252m--)243mm-⨯-,其中m=12-.30.如图,已知直线l1:y1=x+b经过点A(﹣5,0),交y轴于点B,直线l2:y2=﹣2x﹣4与直线l1:y1=x+b交于点C,交y轴于点D.(1)求b的值;(2)求△BCD的面积;(3)当0≤y2<y1时,则x的取值范围是.(直接写出结果)31.计算:(1)2a b aa b b a ++--;(2)221(1)11xx x-÷+-.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】由四边形ABCD是平行四边形,可得∠A+∠B=180°,又由∠A-∠B=20°,即可求得∠A 的度数,继而求得答案.【详解】解:∵四边形ABCD是平行四边形,∴∠A+∠B=180°, ∵∠A-∠B=20°, ∴∠A=100°, ∴∠C=∠A=100°. 故选:C . 【点睛】此题考查了平行四边形的性质.注意平行四边形的对角相等,邻角互补.2.D解析:D 【解析】 【分析】图中直线y=x+b 与x 轴负半轴,y 轴正半轴分别交于A ,B 两点,可以根据两点的坐标得出OA=OB ,由此可证明△AOD ≌△OBE ,证出OC=AD ,BE=OD ,在Rt △OBE 中,运用勾股定理可求出BE 的长,再根据线段的差可求出DE 的长. 【详解】直线y=x+b(b >0)与x 轴的交点坐标A 为(-b ,0)与y 轴的交点坐标B 为(0,-b ), 所以,OA=OB , 又∵AD ⊥OC ,BE ⊥OC , ∴∠ADO=∠BEO=90°,∵∠DOA+∠DAO=90°,∠DOA+∠DOB=90°, ∴∠DAO=∠DOB , 在△DAO 和△BOE 中,DAO BOE ADO BEO OA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DAO ≌EOB , ∴OD=BE.AD=OE , ∵AD=4, ∴OE=4, ∵BE+BO=8, ∴B0=8-BE ,在Rt △OBE 中,222BO BE OE =+, ∴222(8)BE BE OE -=+ 解得,BE=3, ∴OD=3, ∴ED=OE-OD=4-3=1. 【点睛】此题主要考查了一次函数的应用以及全等三角形的判定与性质,根据全等三角形的性质求出OD=BE 是解题的关键.3.A解析:A 【解析】 【分析】根据事件发生的可能性大小判断相应事件的类型即可. 【详解】解:A.守株待兔是随机事件,故A 符合题意; B.水中捞月是不可能事件,故B 不符合题意; C.瓮中捉鳖是必然事件,故C 不符合题意; D.水涨船高是必然事件,故D 不符合题意; 故选:A . 【点睛】本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.4.D解析:D 【解析】 【分析】根据一次函数的性质,对每一项进行判断筛选即可. 【详解】A 将x=3代入31y x =-得:3×3-1=8,A 选项错;B .一次函数k >0,y 值随着x 值增大而增大,B 选项错;C .一次函数k >0,y 值随着x 值增大而增大,当x=0时,y=-1,故此函数的图像经过一、三、四象限,C 选项错;D .当x=0时,y=-1,一次函数的图象与y 轴交于负半轴,D 项正确. 故选D. 【点睛】本题考查了一次函数的性质,解决本题的关键是正确理解题意,熟练掌握一次函数的性质.5.B解析:B 【解析】 【分析】根据无理数的定义结合算术平方根和立方根逐一判断即可得. 【详解】2=,为有理数,故该选项错误;D. 42-=-,为有理数,故该选项错误;D. 227,为有理数,故该选项错误.故选B.【点睛】本题考查无理数的定义,立方根,算术平方根.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.6.D解析:D【解析】分析:直接利用轴对称图形的性质画出对称轴得出答案.详解:如图所示:直线l即为各图形的对称轴.,故选:D.点睛:此题主要考查了轴对称图形,正确把握轴对称图形的定义是解题关键.7.C解析:C【解析】【分析】根据同底数幂的乘法、除法、积的乘方和幂的乘方进行计算即可.【详解】A. a2⋅a3=a5,故A错误;B. (−a2)3=−a6,故B错误;C. a10÷a9=a(a≠0),故C正确;D. (−bc)4÷(−bc)2=b2c2,故D错误;故答案选C.【点睛】本题考查了同底数幂的相关知识点,解题的关键是熟练的掌握同底数幂的乘法与除法的运算.8.B解析:B【解析】【分析】根据轴对称图形的概念,一个图形沿一条直线对折后,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形. 据此进行选择即可.【详解】根据轴对称图形定义,图形A、C、D中不是轴对称图形,而B是轴对称图形.故选B【点睛】本题主要考查了轴对称图形的辨识,解答本题的关键是熟练掌握轴对称图形的概念.9.C解析:C【解析】【分析】根据全等三角形的判定方法:SSS、SAS、ASA及AAS,即可判定.【详解】①满足SSS,能判定三角形全等;②满足SAS,能判定三角形全等;③满足ASA,能判定三角形全等;④的条件是两边及其一边的对角分别对应相等,不能判定三角形全等.∴能使ABC DEF△≌△全等的条件有3组.故选:C.【点睛】本题考查全等三角形的判定,解题关键是熟练掌握各种判定方法并注意“两边及其一边的对角分别对应相等”不能判定三角形全等.10.D解析:D【解析】【分析】根据图1可知,可分P在BC上运动和P在CD上运动分别讨论,由此可得BC和CD的值,进而利用三角形面积公式可得BCD∆的面积.【详解】解:动点P从直角梯形ABCD的直角顶点B出发,沿BC,CD的顺序运动,当P在BC段运动,△ABP面积y随x的增大而增大;当P在CD段运动,因为△ABP的底边不变,高不变,所以面积y不变化.由图2可知,当0<x<2时,y随x的增大而增大;当2<x<5时,y的值不随x变化而变化.综上所述,BC=2,CD=5-2=3,故1123322BCDS CD BC∆.故选:D.【点睛】本题考查动点问题的函数图象,动点的图象问题是中考的常考题型,做此类题需要弄清横纵坐标的代表量,并观察确定图象分为几段,弄清每一段自变量与因变量的变化情况及变化的趋势,主要是正负增减及变化的快慢等. 匀速变化呈现直线段的形式,平行于x轴的直线代表未发生变化.11.A解析:A【解析】【分析】首先根据全等三角形的性质:全等三角形的对应边相等可得:3x-2与4是对应边,或3x-2与5是对应边,计算发现,3x-2=5时,2x-1≠4,故3x-2与5不是对应边.【详解】解:∵△ABC三边长分别为3,4,5,△DEF三边长分别为3,3x-2,2x-1,这两个三角形全等,①3x-2=4,解得:x=2,当x=2时,2x+1=5,两个三角形全等.②当3x-2=5,解得:x=,把x=代入2x+1≠4,∴3x-2与5不是对应边,两个三角形不全等.故选A.【点睛】此题主要考查了全等三角形的性质,分类讨论正确得出对应边是解题关键.12.B解析:B【解析】【分析】利用分式的定义判断即可.分式的分母中必须含有字母,分子分母均为整式.【详解】解:2m是分式,故选:B.【点睛】此题考查了分式的定义,熟练掌握分式的定义是解本题的关键.13.C解析:C【解析】【分析】根据全等三角形的对应边相等解答即可.【详解】解:∵△ABE≌△ACF,∴AC=AB=6,∴EC=AC﹣AE=6-2=4,故选:C.【点睛】本题考查的知识点是全等三角形的性质,熟记性质内容是解此题的关键.14.D解析:D【解析】【分析】最简二次根式即被开方数不含分母且不含能开得尽方的因数或因式,由此判断即可.【详解】解:AB2CD故选:D.【点睛】本题考查了最简二次根式,熟练掌握最简二次根式的概念是解题的关键.15.A解析:A【解析】【分析】和4的值,确定其整数部分,再用原数减去其整数部分可得小数部分,将求得的值代入求解即可.【详解】解:∵1<2<4,∴1<2.∴a=1,b﹣1,∵2<4<3∴c=2,d=4﹣2=2.∴b+d=1,ac=2.∴b dac=12.故选:A.【点睛】本题考查了实数的估算,灵活的利用估算确定无理数的整数部分与小数部分是解题的关键.二、填空题16.①③②【解析】【分析】根据可能性大小的求法,求出各个事件发生的可能性的大小,再按照大小顺序从小到大排列起来即可.【详解】解:根据题意,袋子中共5个球, 2个黄球和3个红球,故将球摇匀,从中解析:①③②【解析】【分析】根据可能性大小的求法,求出各个事件发生的可能性的大小,再按照大小顺序从小到大排列起来即可.【详解】解:根据题意,袋子中共5个球, 2个黄球和3个红球,故将球摇匀,从中任取1球,则①恰好取出白球的可能性为0,②恰好取出红球的可能性为35,③恰好取出黄球的可能性为25,故这些事件按发生的可能性从小到大的顺序排列是①③②.故答案为:①③②.【点睛】本题主要考查了可能性大小计算,即概率的计算方法,用到的知识点为:可能性等于所求情况数与总情况数之比,难度适中.17.3或4【解析】【分析】作出图形,然后根据图形判断出横坐标的可能值即可;【详解】解:如图当点B为(3,0),(4,0)记ΔAOB内部(不包括边界)的整点为(1,1),(1,2),(2,1解析:3或4【解析】【分析】作出图形,然后根据图形判断出横坐标的可能值即可;【详解】解:如图当点B 为(3,0),(4,0)记内部(不包括边界)的整点为(1,1),(1,2),(2,1)共三个点,故当时,则点的横坐标可能是3,4. 故填3,4.【点睛】 此题考查了点的坐标,关键是根据题意画出图形,找出点B 的横坐标与△AOB 内部(不包括边界)的整点m 之间的关系,考查数形结合的数学思想方法.18.【解析】【分析】先根据一次函数y=kx+b 的图象经过点(,m )可知,由图像可知,当时,,即可得出结论.【详解】解:有图像可知,一次函数y=kx+b 经过点(,m ),则当时,,由图像可知,解析:3x <-【解析】【分析】先根据一次函数y=kx+b 的图象经过点(3-,m )可知,由图像可知,当x 3<-时,kx b m +>,即可得出结论.【详解】解:有图像可知,一次函数y=kx+b 经过点(3-,m ),则当x 3=-时,kx b m +=,由图像可知,当x 3<-时,kx b m +>,∴0kx m b -+>的解集是:3x <-;故答案为:3x <-.【点睛】本题考查的是一次函数与一元一次不等式,能利用数形结合求出不等式的取值范围是解答此题的关键.19.【解析】【分析】直接利用二次根式的性质以及结合数轴得出a 的取值范围进而化简即可.【详解】由数轴可得:0<a <2,则a+=a+=a+(2﹣a )=2.故答案为2.【点睛】本题主要考查了解析:【解析】【分析】直接利用二次根式的性质以及结合数轴得出a 的取值范围进而化简即可.【详解】由数轴可得:0<a <2,则(2﹣a )=2. 故答案为2.【点睛】本题主要考查了二次根式的性质与化简,正确得出a 的取值范围是解题的关键. 20.4【解析】【分析】先求出直线与y 轴的交点坐标为(0,4),然后根据两直线相交的问题,把(0,4)代入即可求出m 的值.【详解】解:当x=0时,=4,则直线与y 轴的交点坐标为(0,4),把(解析:4【解析】【分析】先求出直线24y x =-+与y 轴的交点坐标为(0,4),然后根据两直线相交的问题,把(0,4)代入y x m =+即可求出m 的值.【详解】解:当x=0时,24y x =-+=4,则直线24y x =-+与y 轴的交点坐标为(0,4), 把(0,4)代入y x m =+得m=4,故答案为:4.本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.21.1【解析】【分析】根据一个正数的两个平方根互为相反数可得2a+1+2a-5=0,解方程求出a值即可.【详解】∵某个正数的两个平方根分别是2a+1与2a-5,∴2a+1+2a-5=0,解解析:1【解析】【分析】根据一个正数的两个平方根互为相反数可得2a+1+2a-5=0,解方程求出a值即可.【详解】∵某个正数的两个平方根分别是2a+1与2a-5,∴2a+1+2a-5=0,解得:a=1故答案为:1【点睛】本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.22..【解析】【分析】【详解】如图,过点C作CD⊥y轴于点D,∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,∴∠CBD=∠BAO,在△ABO与△BCD中,∠CBD=∠BAO,,.解析:(21)【解析】【分析】如图,过点C作CD⊥y轴于点D,∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,∴∠CBD=∠BAO,在△ABO与△BCD中,∠CBD=∠BAO,∠BDC=∠AOB, BC=AB,∴△ABO≌△BCD(AAS),∴CD=OB,BD=AO,∵点A(1,0),B(0,2),∴CD=2,BD=1,∴OD=OB-BD=1,又∵点C在第二象限,∴点C的坐标是(-2,1).23.a>b【解析】【分析】【详解】解:∵一次函数y=﹣2x+1中k=﹣2,∴该函数中y随着x的增大而减小,∵1<2,∴a>b.故答案为a>b.【点睛】本题考查一次函数图象上点的坐标特征解析:a>b【解析】【分析】【详解】解:∵一次函数y=﹣2x+1中k=﹣2,∴该函数中y随着x的增大而减小,∵1<2,∴a>b.故答案为a>b.【点睛】本题考查一次函数图象上点的坐标特征.【解析】【分析】根据正比例函数的定义,m-2019=0,从而求解.【详解】解:根据题意得:m-2019=0,解得:m=2019,故答案为2019.【点睛】本题主要考查了正比解析:2019【解析】【分析】根据正比例函数的定义,m-2019=0,从而求解.【详解】解:根据题意得:m-2019=0,解得:m=2019,故答案为2019.【点睛】本题主要考查了正比例函数的定义,形如y=kx(k是常数,k≠0)的函数,其中k叫做比例系数.正比例函数一定是一次函数,但一次函数不一定是正比例函数.25..【解析】【分析】由线段垂直平分线的性质可知EA=EB,由等边对等角的性质及外角的性质可得∠AEC=45°,易知△ACE为等腰直角三角形,可得CA长,利用三角形面积公式求解即可.【详解】解解析:12.【解析】【分析】由线段垂直平分线的性质可知EA=EB,由等边对等角的性质及外角的性质可得∠AEC=45°,易知△ACE为等腰直角三角形,可得CA长,利用三角形面积公式求解即可.【详解】解:∵DE垂直平分AB交BC于点E,∴∠EAB =∠B =22.5°,∴∠AEC =∠EAB +∠B =45°,∵∠C =90°,∴△ACE 为等腰直角三角形,∴CA =CE =1,∴三角形ACE 的面积=12×1×1=12. 故答案为:12. 【点睛】本题主要考查了线段垂直平分线的性质及等腰三角形的性质,线段垂直平分线上的点到线段两端的距离相等,等腰三角形的两底角相等,灵活利用这两个性质是解题的关键. 三、解答题26.(1)k 和b 的值分别为2-和4;(2)23x >;(3)103. 【解析】【分析】(1)根据点D 在函数y =x +2的图象上,即可求出n 的值;再利用待定系数法求出k ,b 的值;(2)根据图象,直接判断即可;(3)用三角形OBC 的面积减去三角形ABD 的面积即可.【详解】(1)函数12y x =+的图像过点D ,且点D 的坐标为2(,)3n ,则有28233n =+=. 所以点D 的坐标为28(,)33. 所以有4,28.33b k b =⎧⎪⎨+=⎪⎩ 解得2,4.k b =-⎧⎨=⎩所以k 和b 的值分别为2-和4. (2)由图象可知,函数y =kx +b 大于函数y =x +2时,图象在直线x =23的左侧, ∴x <23, 故答案为:x <23.(3)已知函数12y x =+的图像与y 轴交于点A ,则点A 坐标为(0,2).所以422AB OB OA =-=-=.函数2y kx b =+的图像与x 轴交于点C ,令20y =,则240x -+=.2x =.所以点C 坐标为(2,0).∴2OC =.则四边形AOCD 的面积等于112104222233BOC BAD S S ∆∆-=⨯⨯-=⨯⨯. 【点睛】本题主要考查一次函数的交点,解决此题时,明确二元一次方程组与一次函数的关系是解决此类问题的关键.第(3)小题中,求不规则图形的面积时,可以利用整体减去部分的方法进行计算.27.BC=14.【解析】【分析】根据垂直的性质和勾股定理,先求出线段BD 的长度,再求出线段CD 的长度,最后求和即可.【详解】 解:AD BC ⊥,90ADB ADC ∴∠=∠=︒ ∴在Rt ABD ∆中,9BD ===∴在Rt ACD ∆中,5CD ∴==9514BC BD CD =+=+=∴【点睛】本题考查了垂直的性质,勾股定理,解决本题的关键是正确理解垂直的性质,熟练掌握勾股定理中三边之间的关系.28.(1)1个甲种乒乓球的售价是5元,乙种售价是7元;(2)当购买甲种乒乓球150只,乙种乒乓球50只时最省钱.【解析】【分析】(1)设1个甲种乒乓球的售价是x 元,1个乙种乒乓球的售价是y 元,根据题意列出二元一次方程组,解方程组即可;(2)设购买甲种乒乓球a 只,则购买乙种乒乓球()200a -只,费用为w 元,根据题意列出费用关于a 的一次函数,根据一次函数的性质解答即可.【详解】(1)设1个甲种乒乓球的售价是x 元,1个乙种乒乓球的售价是y 元,35502331x y x y +=⎧⎨+=⎩,解得,57x y =⎧⎨=⎩, 答:1个甲种乒乓球的售价是5元,乙种售价是7元;(2)设购买甲种乒乓球a 只,则购买乙种乒乓球()200a -只,费用为w 元,()5720021400w a a a =+-=-+,∵()3200a a -,∴150a ≤,∴当150a =时,w 取得最小值,此时1100w =,20050a -=,答:当购买甲种乒乓球150只,乙种乒乓球50只时最省钱.【点睛】本题考查的是列二元一次方程组、一元一次不等式解实际问题/一次函数的性质等知识,解题的关键是学会利用一次函数的性质解决最值问题.29.(1)4a 2+4ab ﹣3b 2;(2)4x 2+4xy+y 2﹣4x ﹣2y ﹣1;(3)42+4)﹣2m ﹣6,-5【解析】【分析】(1)利用多项式乘多项式展开,然后合并即可;(2)利用完全平方公式计算;(3)先计算出24b ac -,然后计算代数式的值;(4)先把括号内通分,再把分子分母因式分解后约分得到原式26m =--,然后把m 的值代入计算即可.【详解】解:(1)原式224263a ab ab b =-+-22443a ab b =+-; (2)原式2(2)2(2)1x y x y =+-+-2244421x xy y x y =++---;(3)224(8)42524b ac -=--⨯⨯=,= (4)原式(2)(2)52(2)[]23m m m m m +---=--- (3)(3)2(2)23m m m m m +--=--- 2(3)m =-+26m =--,当12m =-时,原式12()652=-⨯--=-.本题考查了多项式乘法和、分式的化简求值以及代数式求值.掌握整式乘法和分式运算法则熟练运算是解题关键.30.(1)b =5;(2)272;(3)﹣3<x ≤﹣2 【解析】【分析】(1)把点A 的坐标代入直线l 1:y 1=x +b ,列出方程并解答;(2)利用两直线相交求得点C 的坐标,由直线l 2、l 1求得点B 、D 的坐标,根据三角形的面积公式解答;(3)结合图形直接得到答案.【详解】(1)把A (﹣5,0)代入y 1=x +b ,得﹣5+b =0解得b =5;(2)由(1)知,直线l 1:y 1=x +5,且B (0,5). 根题意知,524y x y x =+⎧⎨=--⎩. 解得32x y =-⎧⎨=⎩,即C (﹣3,2). 又由y 2=﹣2x ﹣4知,D (0,﹣4).所以 BD =9.所以S △BCD =12BD •|x C |=1932⨯⨯=272; (3)由(2)知,C (﹣3,2).当y =0时,﹣2x ﹣4=0,此时x =﹣2. 所以由图象知,当0≤y 2<y 1时,则x 的取值范围是﹣3<x ≤﹣2.故答案是:﹣3<x ≤﹣2.【点睛】此题主要考查一次函数性质的综合应用,熟练掌握,即可解题.31.(1)1-;(2)1x x-. 【解析】(1)根据异分母分式的加减法法则计算即可;(2)先把括号里的通分,再根据分式的除法法则计算即可.【详解】解:(1)原式=2a b a a b a b +--- =2a b a a b +-- =b a a b-- a b a b-=-- =1-; (2)原式=211(1)(1)1x x x x x +-+-⋅+ =1x x-. 【点睛】本题考查了分式的混合运算,在运算过程中,分子、分母能进行因式分解的先因式分解,熟练掌握分式的加减乘除运算是解题的关键.。
江苏省宿迁市宿迁中学2024届高三下学期一模考试化学试题含解析

江苏省宿迁市宿迁中学2024届高三下学期一模考试化学试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题只有一个选项符合题意)1、已知X、Y、Z、W、M均为短周期元素。
25℃时,其最高价氧化物对应的水化物(浓度均为0.01mol/L)溶液的pH和原子半径的关系如图所示。
下列说法不正确的是()A.X、M简单离子半径大小顺序:X>MB.Z的最高价氧化物水化物的化学式为H2ZO4C.X、Y、Z、W、M五种元素中只有一种是金属元素D.X的最简单氢化物与Z的氢化物反应后生成的化合物中既含离子键又含共价键2、以铁作阳极,利用电解原理可使废水中的污染物凝聚而分离,其工作原理如图所示。
下列说法错误的是()A.电极b为阴极B.a极的电极反应式:Fe-2e-=Fe2+C.处理废水时,溶液中可能发生反应:4Fe2++O2+8OH-+2H2O=4Fe(OH)3D.电路中每转移3 mol电子,生成1 mol Fe(OH)3胶粒3、下列离子方程式书写正确的是()A.向NaHSO4溶液中滴加过量的Ba(OH)2溶液:2H++SO42-+Ba2++2OH-=BaSO4↓+2H2OB.向Na2SiO3溶液中滴加稀盐酸:Na2SiO3+2H+=H2SiO3↓+2Na+C.向偏铝酸钠溶液中加入量过量HCl:AlO2-+4H+=Al3++2H2OD.过量的铁与稀硝酸Fe +4H++2NO3-=Fe3++2NO↑+2H2O4、铊(Tl)是某超导材料的组成元素之一,与铝同族,位于周期表第六周期。
Tl3+与银在酸性溶液中发生反应:Tl3++2Ag→Tl++2Ag+,下列推断正确的是()A.Tl+的最外层有1个电子B.Tl能形成+3价和+1价的化合物C.Tl3+氧化性比铝离子弱D.Tl+的还原性比Ag强5、《本草纲目》中的“石碱”条目下写道:“采蒿蓼之属……晒干烧灰,以原水淋汁……久则凝淀如石……浣衣发面,甚获利也。
2017-2018学年高一物理上学期第一次月考试题 (IV)

2017-2018学年高一物理上学期第一次月考试题 (IV)一、选择题(本大题共10小题,其中第1-6为单选,7-10为多选,共50分)1.下列说法正确的是()A.在苹果园摘苹果,找成熟的大的苹果,可将苹果视为质点B.导弹将目标锁定敌舰的要害,如弹药舱,可将敌舰视为质点C.计算飞机在两地间的往返时间,可将飞机视为质点D.设计月球车在月球表面抓月球土壤的动作,可将月球车视为质点2.以下说法正确的是()A.某时刻物体的速度为零,其一定处于静止状态B.物体速度变化量为负值时,它的加速度可能为正值C.物体速度变化很快,其加速度一定很大D.物体加速度的大小不断变小,则速度大小也不断变小3.一辆汽车以速度v匀速行驶了全程的一半,以行驶了另一半,则全程的平均速度为()A. B. C. D.4.甲、乙两物体从同一点出发且在同一条直线上运动,它们的位移-时间(x-t)图象如图所示,由图象可以得出在0-4s内()A.甲、乙两物体始终同向运动B.4s时甲、乙两物体间的距离最大C.甲的平均速度等于乙的平均速度D.甲、乙两物体间的最大距离为6m5.以10m/s的速度沿平直公路行驶的汽车,遇障碍物刹车后获得大小为a=4m/s2的加速度,刹车后第3s内,汽车走过的路程为()A.12.5mB.2mC.10mD.0.5m6.一物体以2m/s的初速度做匀加速直线运动,4s内位移为16m,则()A.物体的加速度为2m/s2B.4s内的平均速度为6m/sC.4s末的瞬时速度为6m/sD.第2s内的位移为6m7.xx年3月29日,中国女子冰壶队首次夺得世界冠军,如图所示,一冰壶以速度v垂直进入三个矩形区域做匀减速运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是()A.v1:v2:v3=::1B.v1:v2:v3=6:3:2C.t1:t2:t3=1::D.t1:t2:t3=(-):(-1):18.一质点在连续的6s内作匀加速直线运动,在第一个2s内位移为12m,最后一个2s内位移为36m,则下面说法正确的是()A.质点的加速度大小是6m/s2B.质点的加速度大小是3m/s2C.第1s末的速度大小是6m/sD.第1s末的速度大小是8m/s9.质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),则该质点()A.第1s内的位移是5mB.第2s末的速度是9m/sC.任意相邻的2s内位移差都是8mD.任意1s内的速度增量都是1m/s10.甲、乙两质点从同一位置出发,沿同一直线路面运动,它们的v-t图象如图所示.对这两质点在0~3s内运动的描述,下列说法正确的是()A.t=2s时,甲、乙两质点相遇B.在甲、乙两质点相遇前,t=1s时,甲、乙两质点相距最远C.甲质点的加速度比乙质点的加速度小D.t=3s时,乙质点在甲质点的前面二、实验题(共16分)11.如图所示,是某同学在做“研究匀加速直线运动”的实验中得到的纸带,在纸带上选取了A、B、C、D、E等5个计数点,每相邻两个计数点之间还有4个点没画出来,其相邻点间距离如图所示.(1)打点计时器从打下A点到打下C点的时间内,小车的平均速度是 ______ m/s(小数点后保留两位有效数字),这条纸带的 ______ (左或右)端与小车相连.(2)两计数点间的时间间隔着用T表示,则小车运动的加速度的计算式a= ______ (逐差法,用s和T表示).其大小为 ______ m/s2(小数点后保留两位有效数字).三、计算题(本大题共3小题,共34分)12.(10分)一辆汽车从O点由静止开始做匀加速直线运动,已知在2S内经过相距24m的A和B两点,汽车经过A点时的速度为10m/s,如图所示,求:(1)汽车的加速度.(2)A点与出发点O间的距离.13.(12分)从斜面上某一位置每隔0.1s释放一个相同的小球,在连续释放几个小球之后,对斜面上运动的小球拍下照片如图所示,测得AB=20cm,CD=30cm,试求:(1)小球沿斜面下滑的加速度多大?(2)拍摄时C球的速度多大?14.(12分)公路边随处可见“保持车距,注意刹车”警示语,这是因为在日常行车中,如果前后两车车距太小,容易发生追尾事故.下面我们来研究一下相关问题:A、B两车在同一直线上同方向做匀速直线运动,B车在前A车在后,速度分别为v B=15m/s,v A=20m/s.A车做匀减速直线运动时能获得的最大加速度是a m=0.5m/s2,为避免A,B相撞,请问A车至少应在离B车多远时开始以最大加速度减速,才能保证两车安全?高一物理第一次月考答案1.C2.C3.B4.C5.D6.C7.AD8.BC9.BC 10.BCD11.0.40;左;;0.8012.解:(1)汽车从A到B,根据位移公式有代入数据:解得:(2)汽车从O点到A点,根据速度位移公式有代入数据:答:(1)汽车的加速度为.(2)A点与出发点O间的距离为25m13.解:小球释放后做匀加速直线运动,且每相邻的两个小球的时间间隔相等,均为0.1 s,可以认为A、B、C、D是一个小球在不同时刻的位置.(1)BC-AB=CD-BC,BC-20=30-BC,解得BC=25cm相邻相等时间位移差为△x=5cm由推论△x=a T2可知,小球加速度为a==m/s2=5 m/s2.(2)由题意知B点对应AC段的中间时刻,可知B点的速度等于AC段上的平均速度,即v C=═m/s=2.75 m/s.答:(1)小球沿斜面下滑的加速度为(2)拍摄时C球的速度为2.75m/s14.解:设经过时间t,两车速度相等,有:v A-a m t=v B即:20-0.5t=15解得t=10s设两车最小间距为△x,有:△x=v A t-a m t2-v B t=(20×10-×0.5×102)-15×10=25m即A车至少应在离B车25m时开始以最大加速度减速.答:A车至少应在离B车25m时开始以最大加速度减速,才能保证两车安全.。
高一数学第一次月考试题与答案

2017-2018学年度高一数学9月月考试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________分卷I一、选择题(共12小题,每小题5.0分,共60分)1.已知集合M ={x ∈N +|2x ≥x 2},N ={-1,0,1,2},则(∁R M )∩N 等于( ) A . ∅ B . {-1} C . {1,2} D . {-1,0}2.已知集合P ={4,5,6},Q ={1,2,3},定义P ⊕Q ={x |x =p -q ,p ∈P ,q ∈Q },则集合P ⊕Q 的所有真子集的个数为( )A . 32B . 31C . 30D . 以上都不对3.定义A -B ={x |x ∈A ,且x ∉B },若A ={1,2,4,6,8,10},B ={1,4,8},则A -B 等于( ) A . {4,8} B . {1,2,6,10} C . {1} D . {2,6,10}4.下列各组函数中,表示同一个函数的是( ) A .y =x -1和y =B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2 D .f (x )=和g (x )=5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图像是( )A .B .C .D .6.下列三个函数:①y =3-x ;②y =;③y =x 2+2x -10.其中值域为R 的函数有( ) A .0个 B .1个 C .2个 D .3个 7.一次函数g (x )满足g [g (x )]=9x +8,则g (x )是( ) A .g (x )=9x +8 B .g (x )=3x +8C .g (x )=-3x -4D .g (x )=3x +2或g (x )=-3x -4 8.下列函数中,在[1,+∞)上为增函数的是( ) A .y =(x -2)2 B .y =|x -1| C .y =D .y =-(x +1)2 9.若非空数集A ={x |2a + ≤x ≤3a -5},B ={x |3≤x ≤ },则能使A ⊆B 成立的所有a 的集合是( ) A . {a | ≤a ≤9} B . {a |6≤a ≤9} C . {a |a ≤9} D . ∅10.若函数f (x )= ,, , ,φ(x )=, , , ,则当x <0时,f (φ(x ))为( ) A . -x B . -x 2C .XD .x 2 11.若函数f (x )=的最小值为f (0),则实数m 的取值范围是( )A . [-1,2]B . [-1,0]C . [1,2]D . [0,2]12.已知函数f (x )=4x 2-kx -8在区间(5,20)上既没有最大值也没有最小值,则实数k 的取值范围是( )A. [160,+∞) B. (-∞,40]C. (-∞,4 ]∪[ 6 ,+∞) D. (-∞, ]∪[8 ,+∞)分卷II二、填空题(共4小题,每小题5.0分,共20分)13.已知M={2,a,b},N={2a,2,b2},且M=N,则有序实数对(a,b)的值为________.14.已知函数y=f(x2-1)的定义域为{x|-2<x<3},则函数y=f(3x-1)的定义域为____________.15.设函数f(x)=, ,, ,若f(f(a))=2,则a=_________.16.已知函数y=f(x)的定义域为{1,2,3},值域为{1,2,3}的子集,且满足f[f(x)]=f(x),则这样的函数有________个.三、解答题(共6小题,,共70分)17.(10分)用单调性的定义证明函数f(x)=2x2+4x在[-1,+∞)上是增函数.18(12分).根据下列函数解析式求f(x).(1)已知f(x+1)=2x2+5x+2;(2)已知f=x3+3-1;(3)已知af(x)+f(-x)=bx,其中a≠± 19(12分).已知集合A={x| ≤x<7},B={x|3<x<10},C={x|x<a}.(1)求A∪B,(∁R A)∩B;(2)若A∩C≠∅,求a的取值范围.20(12分).经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-|t-10|.(1)试写出该种商品的日销售额y与时间t( ≤t≤ )的函数表达式;(2)求该种商品的日销售额y的最大值与最小值.21(12分).已知函数f(x)=(x-a)2-(a2+1)在区间[0,2]上的最大值为g(a),最小值为h(a)(a∈R).(1)求g(a)和h(a);(2)作出g (a )和h (a )的图像,并分别指出g (a )的最小值和h (a )的最大值各为多少?22(12分).已知函数f (x )的定义域是(0,+∞),当x >1时,f (x )>0,且f (x ·y )=f (x )+f (y ). (1)求f (1)的值;(2)证明:f (x )在定义域上是增函数;(3)如果f (3)=-1,求满足不等式f (x )-f (x - )≥ 的x 的取值范围.2017-2018学年度高一数学9月月考试卷答案解析1.【答案】D【解析】因为M ={1,2},所以(∁R M )∩N ={-1,0},故正确答案为D. 2.【答案】B【解析】由所定义的运算可知P ⊕Q ={1,2,3,4,5}, ∴P ⊕Q 的所有真子集的个数为25-1=31.故选B. 3.【答案】D【解析】A -B 是由所有属于A 但不属于B 的元素组成,所以A -B ={2,6,10}.故选D. 4.【答案】D【解析】A 中的函数定义域不同;B 中y =x 0的x 不能取0;C 中两函数的对应关系不同,故选D. 5.【答案】C【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图像一定是下降的,由此排除A ;再由小明骑车上学,开始时匀速行驶,可得出图像开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图像与x轴平行,由此排除D,后为了赶时间加快速度行驶,此一段时间段内函数图像下降的比较快,由此可确定C正确,B不正确.故选C.6.【答案】B【解析】7.【答案】D【解析】∵g(x)为一次函数,∴设g(x)=kx+b,∴g[g(x)]=k(kx+b)+b=k2x+kx+b,又∵g[g(x)]=9x+8,∴9,8,解得3,或3,4,∴g(x)=3x+2或g(x)=-3x-4.故选D.8.【答案】B【解析】y=(x-2)2在[2,+∞)上为增函数,在(-∞,2]为减函数;y=|x-1|= , ,,在[1,+∞)上为增函数,故选B.9.【答案】B 10.【答案】B【解析】x<0时,φ(x)=-x2<0,∴f(φ(x))=-x2.11.【答案】D【解析】当x≤ 时,f(x)=(x-m)2,f(x)min=f(0)=m2,所以对称轴x=m≥ .当x>0时,f(x)=x++m≥ +m=2+m,当且仅当x=,即x=1时取等号,所以f(x)min=2+m.因为f(x)的最小值为m2,所以m2≤ +m,所以 ≤m≤ .12.【答案】C【解析】由于二次函数f(x)=4x2-kx-8在区间(5,20)上既没有最大值也没有最小值,因此函数f(x)=4x2-kx-8在区间(5,20)上是单调函数.二次函数f(x)=4x2-kx-8图像的对称轴方程为x=8,因此8≤5或8≥ ,所以k≤4 或k≥ 6 .13.【答案】(0,1)或(4,)【解析】∵M={2,a,b},N={2a,2,b2},且M=N,∴或即或或4当a=0,b=0时,集合M={2,0,0}不成立,∴有序实数对(a,b)的值为(0,1)或(4,),故答案为(0,1)或(4,).14.【答案】{x| ≤x<3}【解析】∵函数y=f(x2-1)的定义域为{x|-2<x<3},∴-2<x<3.令g(x)=x2-1,则- ≤g(x)<8,故- ≤3x-1<8,即 ≤x<3,∴函数y=f(3x-1)的定义域为{x| ≤x<3}.15.【答案】【解析】若a≤ ,则f(a)=a2+2a+2=(a+1)2+1>0,所以-(a2+2a+2)2=2,无解;若a>0,则f(a)=-a2<0,所以(-a2)2+2(-a2)+2=2,解得a=.故a=.16.【答案】10【解析】∵f[f(x)]=f(x),∴f(x)=x,①若f:{ , ,3}→{ , ,3},可以有f(1)=1,f(2)=2,f(3)=3,此时只有1个函数;②若f:{ , ,3}→{ },此时满足f(1)=1;同理有f:{ , ,3}→{ };f:{ , ,3}→{3},共有3类不同的映射,因此有3个函数;③首先任选两个元素作为值域,则有3种情况.例如选出1,2,且对应关系f:{ , ,3}→{ , },此时满足f(1)=1,f(2)=2.则3可以对应1或2,又有2种情况,所以共有3× =6个函数.综上所述,一共有1+3+6=10个函数.17.【答案】设x1,x2是区间[-1,+∞)上的任意两个实数,且x1<x2,则f(x1)-f(x2)=(2+4x1)-(2+4x2)=2(-)+4(x1-x2)=2(x1-x2)(x1+x2+2).∵- ≤x1<x2,∴x1-x2<0,x1+x2+2>0,∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在[-1,+∞)上是增函数.18.【答案】(1)方法一(换元法)设x+1=t,则x=t-1,∴f(t)=2(t-1)2+5(t-1)+2=2t2+t-1,∴f(x)=2x2+x-1.方法二(整体代入法)∵f(x+1)=2x2+5x+2=2(x+1)2+(x+1)-1,∴f(x)=2x2+x-1.(2)(整体代入法)∵f=x3+3-1=3-3x2·-3x·-1=3-3-1,∴f(x)=x3-3x-1(x≥ 或x≤-2).(3)在原式中以-x替换x,得af(-x)+f(x)=-bx,于是得+ - = ,- + =-消去f(-x),得f(x)=.故f(x)的解析式为f(x)=x(a≠± ).19.【答案】(1)因为A={x| ≤x<7},B={x|3<x<10},所以A∪B={x| ≤x<10}.因为A={x| ≤x<7},所以∁R A={x|x<2或x≥7},则(∁R A)∩B={x|7≤x<10}.(2)因为A={x| ≤x<7},C={x|x<a},且A∩C≠∅,所以a>2.20.【答案】(1)y=g(t)·f(t)=(80-2t)·( -|t-10|)=(40-t)(40-|t-10|)=3 4 , ,4 5 ,(2)当 ≤t<10时,y的取值范围是[1 200,1 225],在t=5时,y取得最大值1 225;当 ≤t≤ 时,y的取值范围是[600,1 200],在t=20时,y取得最小值600.综上,第5天,日销售额y取得最大值1 225元;第20天,日销售额y取得最小值600元.21.【答案】( )∵f(x)=(x-a)2-(a2+1),又x∈[ , ],∴当a≤ 时,g(a)=f(2)=3-4a,h(a)=f(0)=-1;当0<a≤ 时,g(a)=f(2)=3-4a,h(a)=f(a)=-(a2+1);当1<a<2时,g(a)=f(0)=-1,h(a)=f(a)=-(a2+1);当a≥ 时,g(a)=f(0)=-1,h(a)=f(2)=3-4a.综上可知g(a)=3 4h(a)=3 4(2)g(a)和h(a)的图像分别为:由图像可知,函数y=g(a)的最小值为-1,函数y=h(a)的最大值为-1.【解析】22.【答案】(1)解令x=y=1,得f(1)=2f(1),故f(1)=0.(2)证明令y=,得f(1)=f(x)+f()=0,故f()=-f(x).任取x1,x2∈( ,+∞),且x1<x2,则f(x2)-f(x1)=f(x2)+f()=f().由于>1,故f()>0,从而f(x2)>f(x1).∴f(x)在(0,+∞)上是增函数.(3)解由于f(3)=-1,而f(3)=-f(3),故f(3)=1.在f(x·y)=f(x)+f(y)中,令x=y=3,得f(9)=f(3)+f(3)=2.故所给不等式可化为f(x)-f(x- )≥f(9),∴f(x)≥f[9(x-2)],∴x≤94.又∴ <x≤94,∴x的取值范围是94.【解析】。
高一数学第一次月考

县直高中2017-2018学年第一次月考高一数学试题一、选择题(本大题共12小题,每小题5分,共60分)1.集合{1,2,3}的真子集共有 ( )A 、5个B 、6个C 、7个D 、8个2. 以下四个图形中可以作为函数()y f x =的图象的是 ( )A .B .C .D .3.已知集合{}01|2=-=x x A ,则下列式子表示正确的有 ( ) ①A ∈1 ②{}A ∈-1 ③A ⊆φ ④{}A ⊆-1,1 A.1个 B.2个 C.3个 D.4个 4.图中的阴影表示的集合中是 ( )A .)(BC A u ⋂ B.)(A C B u ⋂ C .)(B A C u ⋂D .)(B A C u ⋃5.已知{}{}N M x y y N x y x M ⋂-==-==,1|,1|22等于 ( ) A.N B.M C.R D.φ6. 下列各组函数中为相等函数的是 ( )ABUA .1)(,)1()(2-=-=x x g x x fB .1)(,1)(-=-=t t g x x gC .11)(,1)(2-⋅+=-=x x x g x x f D .21()1,()1x f x x g x x -=+=-7. 函数2)21()(0++-=x x x f 的定义域是 ( ) A .)21,2(- B .[)+∞-,2C .),21()21,2[+∞⋃- D .),21(+∞8.若集合{}{}260,10A x x x B x mx =+-==+=,且A B ⊆,则m 的取值所构成的集合为 ( ) A.{-31,21} B.{31,21-} C.{31,21--} D.{31,21,0-}9.若函数1)12(2+-+=x a x y 在区间(-∞,2)上是减函数,则实数a 的取值范围是 ( )A. ⎪⎭⎫⎢⎣⎡+∞-,23B. ⎥⎦⎤ ⎝⎛-∞-23,C. ⎪⎭⎫⎢⎣⎡+∞,23D. ⎥⎦⎤ ⎝⎛∞-23,10. 定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++,()1 2.f =则=)3(f ( )A.12B.3C.6D.16 11.给出函数)(),(x g x f 如下表,则f (g (x ))的值域为 ( )A.{4,2}B.{1,3}C. {1,2,3,4}D. 以上情况都有可能12.设}4,3,2,1{=I , A 与B 是I 的子集, 若A ∩B =}3,1{,则称(A ,B )为一个“理想配集”.那么符合此条件的“理想配集”的个数是 (规定(A ,B )与(B ,A )是两个不同的“理想配集”) ( ) A. 4 B. 8 C. 9 D. 16二、填空题(本大题共4小题,每小题5分,共20分) 13.设全集{}4,3,2,1,0=U ,集合{} 3,2,1=A ,{}4,3,2=B ,则()=⋂B C A U ____.14.已知x x x f 2)12(2-=+,则=)3(f _____.15.若函数)(x f 的定义域为[-1,2],则函数)23(x f -的定义域是 .16.已知集合⎭⎬⎫⎩⎨⎧=1,,a ba A ,集合{}0,,2b a a B +=,且B A ⊆同时A B ⊆,则=+b a 2________.三、解答题(本大题共6题,共70分) 17.(本题满分10分)设全集{}{}31|,24|,≤<-=<≤-==x x B x x A R U ,求: (1)B A B A ⋃⋂,;(2))(,)(B C A B A C U U ⋂⋃.18.(本题满分12分)设集合{}{}01)1(2|,04|222=-+++==+=a x a x x B x x x A ,若A B A =⋃,求实数a 的取值集合.19.(本题满分12分)分别求下列函数的解析式: (1)已知()f x 是二次函数,且满足x x f x f f 2)()1(,1)0(=-+=,求()f x ; (2)已知23)1(2+-=-x x x f ,求()f x ;20.(本题满分12分) 求下列函数的值域. (1)[)5,1,642∈+-=x x x y . (2)112+-=x x y21.(本题满分12分)设函数xx f 32)(-=,(1)判断函数)(x f 在(0,+∞)上的单调性并用定义加以证明; (2)求函数)(x f 在区间[2,5]上的最大值与最小值.22.(本题满分12分)已知函数(1) 求)2(),3(f f -的值,并在给定的直角坐标系中画出函数)(x f 的图像;(2) 若21)(=a f ,求实数a 的取值集合;(3) 若m m f >)(,求实数m 的取值范围.⎪⎩⎪⎨⎧≥<<--≤+=)2()21()1(22)(2x x x x x x x f。
江苏省宿迁市2023-2024学年高二下学期6月期末考试数学试题(解析版)

高二年级调研测试数学本试卷共4页,19小题,满分150分,考试用时120分钟.注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.将条形码横贴在答题卡上“条形码粘贴处”.2.回答选择题时,选出每小题答案后,用2B 铅笔在答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上.如需改动,先划掉原来的答案,然后再写上新答案.不准使用铅笔和涂改液.不按以上要求作答无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 计算012456C C C ++=( )A. 20B. 21C. 35D. 36【答案】B 【解析】【分析】利用组合数计算公式计算可得结果.【详解】由组合数计算公式可得01245665C C C 152112×++=++=×. 故选:B2. 已知样本数据121x +,221x +,…,21n x +的平均数为5,则131x +,231x +,…,31n x +的平均数为( ) A. 6 B. 7C. 15D. 16【答案】B 【解析】【分析】根据平均数的性质即可得12,,,n x x x …的平均数为2,则可得到新的一组数据的平均数. 【详解】由题意,样本数据121x +,221x +,…,21n x +的平均数为5,设12,,,n x x x …的平均数为x , 即215+=x ,解得2x =,根据平均数性质知131x +,231x +,…,31n x +的平均数为317x +=. 故选:B3. 下表是大合唱比赛24个班级的得分情况,则80百分位数是( ) 得分 7 8 9 10 11 13 14 频数 4246242A. 13.5B. 10.5C. 12D. 13【答案】D 【解析】【分析】根据百分位数的定义求解即可.【详解】因为00248019.2×=,24个班级的得分按照从小到大排序, 可得80百分位数是第20个数为13. 故选:D4. 已知a ,b 为两条不同直线,α,β,γ为三个不同平面,则下列说法正确的是( ) A. 若a b ∥,b α⊂,则//a α B. 若//a α,b α⊂,则//a b C. //αγ,//βγ,则//αβ D. 若αγ⊥,βγ⊥,则//αβ【答案】C 【解析】【分析】由线线、线面、面面的位置关系即可求得本题. 【详解】若//a b ,b α⊂,则//a α或a α⊂,则A 错; 若//a α,b α⊂,则//a b 或a 与b 异面,则B 错;//αγ,//βγ,由平行的传递性可知,//αβ,则C 对;若αγ⊥,βγ⊥,则//αβ或相交.,D 错, 故选:C.5. 已知,,A B C 三点不共线,O 为平面ABC 外一点,下列条件中能确定,,,M A B C 四点共面的是( )的.A. OM OA OB OC =++B. 3OM OA OB BC =−−C. 1123OM OA OB OC =++D. 32OM OA OB BC =−−【答案】D 【解析】【分析】根据空间向量基本定理对选项逐个进行验证即可得出结论.【详解】由空间向量基本定理可知,若,,,M A B C 四点共面,则需满足存在实数,,x y z 使得OM xOA yOB zOC =++,且1x y z ++=, 显然选项A ,C 不成立;对于选项B ,由3OM OA OB BC =−−可得()33OM OA OB OC OB OA OC =−−−=− ,不合题意,即B 错误;对于D ,化简32OM OA OB BC =−−可得()323OM OA OB OC OB OA OB OC =−−−=−− ,满足()()3111+−+−=,可得D 正确; 故选:D6. 已知随机事件A ,B ,3()10P A =,1()2P B =,1(|)3P B A =,则(|)P A B =( ) A.15B.16 C.320D.110【答案】A 【解析】【分析】根据题意,由乘法公式代入计算可得()P AB ,再由条件概率公式,代入计算,即可得到结果. 【详解】因为3()10P A =,1()2P B =,1(|)3P B A =, 则()()131(|)31010P B A P A P AB ×=×==, 则()()1110(|)152P AB P A BP B ===. 故选:A7. 已知9290129(21)x a a x a x a x +=+++⋅⋅⋅+,则682424682222a a a a +++的值为( )A. 255B. 256C. 511D. 512【答案】A 【解析】【分析】利用二项式定理写出展开式的通项,令0x =求出0=1a ,分别令12x =、12x =−,再两式相加可得8202825622a a a +++=,再减去0a 即可. 【详解】令0x =,得0=1a , 令12x =,得93891202389251222222a a a a a a ++++++== , 令12x =−,得38912023********a a a a a a −+−++−= , 两式相加得82028251222a a a+++=, 得8202825622a a a +++= , 则682424682552222a a a a +++=. 故选:A.8. 某工厂有甲、乙、丙3个车间生产同一种产品,其中甲车间的产量占总产量的20%,乙车间占35%,丙车间占45%.已知这3个车间的次品率依次为5%,4%,2%,若从该厂生产的这种产品中取出1件为次 ) A.331000B.1033C.1433D.311【答案】C 【解析】【分析】根据题意,由全概率公式可得抽取到次品的概率,再由条件概率公式代入计算,即可求解. 【详解】记事件A 表示甲车间生产的产品, 记事件B 表示乙车间生产的产品, 记事件C 表示丙车间生产的产品, 记事件D 表示抽取到次品,则()()()0.2,0.35,0.45P A P B P C ===, ()()()0.05,0.04,0.02P D A P D B P D C ===,取到次品的概率为()()()()()()()P D P A P D A P B P D B P C P D C =++0.20.050.350.040.450.020.033=×+×+×=,若取到的是次品,此次品由乙车间生产的概率为:()()()()()()0.350.040.014140.0330.03333P B P D B P BD P B D P D P D ×=====.故选:C二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 下列选项中叙述正确有( )A. 在施肥量不过量的情况下,施肥量与粮食产量之间具有正相关关系B. 在公式1xy=中,变量y 与x 之间不具有相关关系C. 相关系数10.6r =时变量间的相关程度弱于20.8r =−时变量间的相关程度D. 某小区所有家庭年收入x (万元)与年支出y (万元)具有相关关系,其线性回归方程为ˆˆ0.8ybx =+.若20x =,16y =,则ˆ0.76b =. 【答案】ACD 【解析】【分析】AB 的正误,根据相关系数的性质可判断C 的正误,根据回归方程的性质可判断D 的正误.【详解】对于A ,在施肥量不过量的情况下,施肥量越大,粮食产量越高, 故两者之间具有正相关关系,故A 正确.对于B ,变量y 与x 之间函数关系,不是相关关系,故B 错误. 对于C ,因为210.80.6r r =>=,故相关系数10.6r =时变量间的相关程度弱于20.8r =−时变量间的相关程度,故C 正确.对于D ,因为回归直线过(),x y ,故ˆ16200.8b=×+,故ˆ0.76b =,故D 正确. 故选:ACD.10. 已知点(2,3,3)A −−,(2,5,1)B ,(1,4,0)C ,平面α经过线段AB 的中点D ,且与直线AB 垂直,下列选项中叙述正确的有( ) A. 线段AB 的长为36的是B. 点(1,2,1)P −在平面α内C. 线段AB 的中点D 的坐标为(0,4,1)−D. 直线CD 与平面α【答案】BCD 【解析】【分析】由空间两点间的距离公式即可得到线段AB 的长,判断A ;由AB ⊥平面α,垂足为点D ,PD AB ⊥,即可判断B ;由中点坐标公式可得点D 的坐标,判断C ;设直线CD 与平面α所成的角为β,sin cos ,AB CD AB CD AB CDβ⋅==,通过坐标运算可得,判断D.【详解】因为点(2,3,3)A −−,(2,5,1)B , 所以6AB =,故A 错误;设D 点的坐标为(),,x y z ,因为D 为线段AB 的中点,所以2235310,4,1222x y z −++−+======−, 则D 的坐标为(0,4,1)−,故C 正确;因为点(1,2,1)P −,则()1,2,0PD =− ,又()4,2,4AB =,则()()1,2,04,2,40PD AB ⋅=−⋅=,所以PD AB ⊥,即PD AB ⊥, 又AB ⊥平面α,垂足为点D ,即D ∈平面α,所以PD ⊂平面α,故B 正确;由(1,4,0)C ,(0,4,1)D −,得()1,0,1CD =−−,设直线CD 与平面α所成的角为β,则sin cos ,ABβ= ,故D 正确.故选:BCD.11. 甲袋中有2个红球、3个黄球,乙袋中有3个红球、2个黄球,同时从甲、乙两袋中取出2个球交换,分别记交换后甲、乙两个袋子中红球个数的数学期望为()E X 、()E Y ,方差为()D X 、()D Y ,则下列结论正确的是( )A. ()()5E X E Y +=B. ()()E X E Y <C. ()()D X D Y <D. ()()D X D Y =【答案】ABD 【解析】【分析】依题意可知不管如何交换红球个数始终只有5个,易知5X Y +=,利用期望值和方差性质可得A ,D 正确,C 错误;易知随机变量X 的所有可能取值为0,1,2,3,4,写出对应的概率并得出分布列,可得() 2.4E X =,()()5 2.6E Y E X =−=,可得B 正确.【详解】根据题意,记甲、乙两个袋子中红球个数分别为,X Y , 不管如何交换红球个数始终只有5个,易知5X Y +=,对于A ,由期望值性质可得()()()55E X E Y E Y =−=−,即()()5E X E Y +=,所以A 正确; 对于B ,易知随机变量X 的所有可能取值为0,1,2,3,4; 当从甲袋中取出2个红球,乙袋中取出2个黄球后交换,可得()()22222255C C 105C C 100P X P Y ====×=, 当从甲袋中取出1个红球,1个黄球,乙袋中取出2个黄球后交换,或者从甲袋中2个红球,乙袋中取出1个红球,1个黄球后交换,可得()()1111223232222555C C C C C 12314C C C 10025P X P Y ====+×==;当从甲袋中取出1个红球,1个黄球,乙袋中取出1个红球,1个黄球;或者从甲袋中取出2个红球,乙袋中取出取出2个红球;或者从甲袋中取出2个黄球,乙袋中取出取出2个黄球后交换,可得()()1111222223233322222222555555C C C C C C C C 422123C C C C C C 10050P X P Y ====×+×+×==; 当从甲袋中取出2个黄球,乙袋中取出1个红球,1个黄球;或者从甲袋中取出1个红球,1个黄球,乙袋中取出取出2个红球后交换,可得()()21111232323322225555C C C C C C 36932C C C C 10025P X P Y ====×+×==;当从甲袋中取出2个黄球,乙袋中取出2个红球后交换,可得()()22332255C C 941C C 100P X P Y ====×=,随机变量X 的分布列为所以期望值()132******** 2.4100255025100E X =×+×+×+×+×=, 可得()()5 2.6E Y E X =−=,即()()E X E Y <,可得B 正确; 对于C ,D ,由方差性质可得()()()()()251D Y D X D X D X =−=−=,即可得()()D X D Y =,所以C 错误,D 正确. 故选:ABD【点睛】关键点点睛:根据题意可得随机变量满足5X Y +=,利用期望值和方差性质可判断出AD 选项,再求出随机变量X 的分布列可得结论.三、填空题:本题共3小题,每小题5分,共15分.12. 已知随机变量X 服从正态分布()295,N σ,若(80)0.3P X <=,则(95110)P X ≤<=______. 【答案】0.2##15【解析】【分析】根据正态分布的对称性结合已知条件求解即可. 【详解】因为随机变量X 服从正态分布()295,N σ,(80)0.3P X <=, 所以(95110)(8095)0.5(80)0.2P X P X P X ≤<=<<=−<=, 故答案为:0.213. 如图,用四种不同颜色给图中的,,,,A B C D E 五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法共有______种.【答案】72 【解析】【分析】由图形可知点E 比较特殊,所以按照分类分步计数原理从点E 开始涂色计算可得结果.【详解】根据题意按照,,,,A B C D E 的顺序分5步进行涂色,第一步,点E 的涂色有14C 种,第二步,点A 的颜色与E 不同,其涂色有13C 种, 第三步,点B 的颜色与,A E 都不同,其涂色有12C 种,第四步,对点C 涂色,当,A C 同色时,点C 有1种选择;当,A C 不同色时,点C 有1种选择; 第五步,对点D 涂色,当,A C 同色时,点D 有2种选择;当,A C 不同色时,点D 有1种选择;根据分类分步计数原理可得,不同的涂色方法共有()111432C C C 121172×+×=种. 故答案为:7214. 如图,已知三棱锥−P ABC 的底面是边长为2的等边三角形,60APB ∠=°,D 为AB 中点,PA CD ⊥,则三棱锥−P ABC 的外接球表面积为______.【答案】20π3##20π3【解析】【分析】设PAB 外接圆的圆心为E ,三棱锥−P ABC 的外接球的球心为O ,连接OE , ABC 的外接圆的圆心为G ,连接OG ,OB ,可证四边形OGDE 为矩形,利用解直角三角形可求外接球半径,故可求其表面积.【详解】因为ABC 为等边三角形,D 为AB 中点,故CD AB ⊥, 而PA CD ⊥,PA AB A = ,,PA AB ⊂平面PAB ,所以CD ⊥平面PAB . 设PAB 外接圆的圆心为E ,三棱锥−P ABC 的外接球的球心为O ,连接,OE BE , 设ABC 的外接圆的圆心为G ,连接OG ,OB , 则OE ⊥平面PAB ,OG CD ⊥故//OE CD ,故,,,O G D E 共面,而DE ⊂平面PAB , 故CD DE ⊥,故四边形OGDE 为矩形.又12sinABBEAPB=×∠13OE DG CD===,故外接球半径为OB=,故外接球的表面积为1520π4π93×=,故答案为:20π3四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步聚.15.在()*23,Nnx n n≥∈的展开式中,第2,3,4项的二项式系数依次成等差数列.(1)证明展开式中不存在常数项;(2)求展开式中所有的有理项.【答案】(1)证明见解析;(2)7128x,4672x,280x,214x.【解析】【分析】(1)根据题意可求得7n=,利用二项展开式的通项可得展开式中不存在常数项;(2)由二项展开式的通项令x的指数为整数即可解得合适的k值,求出所有的有理项.【小问1详解】易知第2,3,4项的二项式系数依次为123C,C,Cn n n,可得132C+C2Cn n n=,即()()()121262n n n n nn−−−+=×,整理得()()270n n−−=,解得7n=或2n=(舍);所以二项式为72x,假设第1k+项为常数项,其中Nk∈,即可得()1777277C 22C kk k kkk k x x −−−−=为常数项,所以1702k k −−=, 解得14N 3k =∉,不合题意; 即假设不成立,所以展开式中不存在常数项; 【小问2详解】由(1)可知,二项展开式的通项()1777277C22C kk k kk k k x x−−−−=可得, 其中的有理项需满足17Z 2k k −−∈,即37Z 2k −∈,且7k ≤;当30,77Z 2k k =−=∈,此时有理项为707772C 128x x =; 当32,74Z 2k k =−=∈,此时有理项为524472C 672x x =; 当34,71Z 2k k =−=∈,此时有理项为3472C 280x x =; 当36,72Z 2k k =−=−∈,此时有理项为16272142C x x−=; 综上可知,展开式中所有的有理项为7128x ,4672x ,280x ,214x . 16. 某校天文社团将2名男生和4名女生分成两组,每组3人,分配到A ,B 两个班级招募新社员. (1)求到A 班招募新社员的3名学生中有2名女生的概率;(2)设到A ,B 两班招募新社员的男生人数分别为a ,b ,记X a b =−,求X 的分布列和方差. 【答案】(1)35(2)85【解析】【分析】(1)由古典概型的概率求解122436C C 3C 5P ==; (2)由题意,X 的可能取值为2,0,2−,算出对应概率()2P X =−,()0P X =,()2P X =,即可列出X 的分布列,再求出()E X ,进而由公式求出方差.【小问1详解】到A 班招募新社员的3名学生中有2名女生的概率为122436C C 3C 5P ==. 【小问2详解】由题意,X 的可能取值为2,0,2−,则()032436C C 12C 5P X =−==,()122436C C 30C 5P X ===,()212436C C 12C 5P X ===, 所以X 的分布列为则()1312020555E X =−×+×+×=, 所以()()()()22213182000205555D X =−−×+−×+−×=. 17. 如图,正三棱柱111ABC A B C 中,D 为AB 的中点.(1)求证:1BC ∥平面1ACD ; (2)当1AA AB的值为多少时,1AB ⊥平面1ACD ?请给出证明. 【答案】(1)证明见答案. (2 【解析】【分析】(1)连接1AC ,交1AC 于点O ,连接DO ,能证出1//BC DO ,则能证出1BC ∥平面1ACD.(2)先把1AB ⊥平面1ACD 当做条件,得出11AB A D ⊥,得出1AA AB的值,过程要正面分析. 【小问1详解】连接1AC ,交1AC 于点O ,连接DO , 因为O 是1AC 的中点,D 为AB 的中点, 所以DO 是1ABC 的中位线,即1//BC DO ,1BC ⊄平面1ACD ,DO ⊂平面1ACD , 所以1BC ∥平面1ACD . 【小问2详解】1AA AB =时,1AB ⊥平面1ACD ,证明如下:因为1AA AB =,11tan A AB ∴∠,111tan AA DA B AD ∠= 1111A AB DA B ∴∠=∠,1112DA B AA D π∠+∠= ,1112A AB AA D π∴∠+∠=,即11AB A D ⊥.因为三棱柱111ABC A B C 为正三棱柱,ABC ∴ 为正三角形,且1AA ⊥平面ABC ,1,CD AB CD AA ∴⊥⊥,1AB AA A ∩=,AB ⊂平面11ABB A ,1AA ⊂平面11ABB A ,CD 平面11ABB A ,因为1AB ⊂平面11ABB A ,所以1AB CD ⊥,1A D CD D = ,1,A D CD ⊂平面1ACD , 1AB ∴⊥平面1ACD .1AA AB∴18. 会员足够多的某知名户外健身俱乐部,为研究不高于40岁和高于40岁两类会员对服务质量的满意度.现随机抽取100名会员进行服务满意度调查,结果如下:年龄段满意度合计满意不满意 不高于40岁 50 20 70 高于40岁 25 5 30 合计7525100(1)问:能否认为,会员不高于40岁和高于40岁年龄结构对服务满意度有关;(2)用随机抽取的100名会员中的满意度频率代表俱乐部所有会员的满意度概率.从所有会员中随机抽取3人,记抽取的3人中,对服务满意的人数为X ,求X 的分布列和数学期望.参考公式:22()()()()()n ad bc a b c d a c b d χ−=++++(其中n a b c d =+++).参考数据:()20P x χ≥ 0.150.10 0.05 0.025 0.010 0.005 0.0010x2.072 2.7063.841 5.024 6.635 7.879 10.828【答案】(1)不能认为会员不高于40岁和高于40岁年龄结构对服务满意度有关. (2)分布列见解析;94. 【解析】【分析】(1)首先根据列联表中的数据结合公式计算2χ值,然后对照表格得到结论;(2)由表格可知,对服务满意的人的概率为34,且33,4X B∼,根据二项分布公式即可求解. 【小问1详解】 由列联表可知:2217100(5052520)100.587255 2.072730630χ××−×<××==≈, 所以不能认为会员不高于40岁和高于40岁年龄结构对服务满意度有关. 【小问2详解】由表格可知,对服务满意人的概率为34,且33,4X B∼, 则0,1,2,3X =,可得:()303110C 464P X ===,()2133191C 4464P X === , ()22331272C 4464P X ===,()3333273C 464P X === , 故X 的分布列如图:可得()39344EX =×=. 19. 如图,在三棱台ABC DEF −中,2AB BC AC ===,1AD DF FC ===,N 为DF 的中点,二面角D AC B −−的大小为θ.(1)求证:AC BN ⊥; (2)若π2θ=,求三棱台ABC DEF −的体积; (3)若A 到平面BCFE cos θ的值. 【答案】(1)证明见解析; (2)78(3)3cos 5θ=−的【解析】【分析】(1)利用三棱柱性质,根据线面垂直的判定定理可得AC ⊥平面BMN ,可证明结论; (2)由二面角定义并利用棱台的体积公式代入计算可得结果;(3)建立空间坐标系,求出平面BCFE 的法向量,利用点到平面距离的向量求法即可得出cos θ的值. 【小问1详解】取AC 的中点为M ,连接,NM BM ;如下图所示:易知平面//ABC 平面DEF ,且平面ABC ∩平面DACF AC =,平面DEF ∩平面DACF DF =; 所以//AC DF ,又因为1AD FC ==, 可得四边形DACF 为等腰梯形,且,M N 分别为,AC DF 的中点,所以MN AC ⊥, 因为2AB BC AC ===,所以BM AC ⊥, 易知BM MN M = ,且,BM MN ⊂平面BMN , 所以AC ⊥平面BMN ,又BN ⊂平面BMN ,所以AC BN ⊥; 【小问2详解】由二面角定义可得,二面角D AC B −−的平面角即为BMN ∠, 当π2θ=时,即π2BMN ∠=,因此可得MN ⊥平面ABC ,可知MN 即为三棱台的高,由1,2ADDF FC AC ====可得MN =;易知三棱台的上、下底面面积分别为DEFABC S S =因此三棱台ABC DEF −的体积为1738V =【小问3详解】由(1)知,BM AC ⊥,MN AC ⊥,二面角D AC B −−的平面角即为()0,πBMN θ∠=∈; 以M 为坐标原点,分别以,MA MB 所在直线为,x y 轴,过点M 作垂直于平面ABC 的垂线为z 轴建立如图所示的空间直角坐标系:可得()()()()1,0,0,1,0,0,,,0,0,0A C B N M θθ −,易知11,0,022NF MC==−,可得12F θθ − ;则()1,cos 2CBCF θθ =设平面BCFE 的一个法向量为(),,n x y z =,所以01cos sin 02n CB x n CF x y z θθ ⋅==⋅=++=, 令1y =,则1cos sin x z θθ−=,可得1cos sin n θθ−=; 显然()2,0,0AC =− ,由A 到平面BCFE,可得AC n n ⋅==,可得21cos 4sin θθ− =;整理得25cos 2cos 30θθ−−=,解得3cos 5θ=−或cos 1θ=; 又()0,πθ∈,可得3cos 5θ=−.【点睛】方法点睛:求解点到平面距离常用方法:(1)等体积法:通过转换顶点,利用体积相等可得点到面的距离;(2)向量法:求出平面的法向量,并利用点到平面距离的向量求法公式计算可得结果;。
2017-2018学年度第一学期高一第一次月考成绩统计表
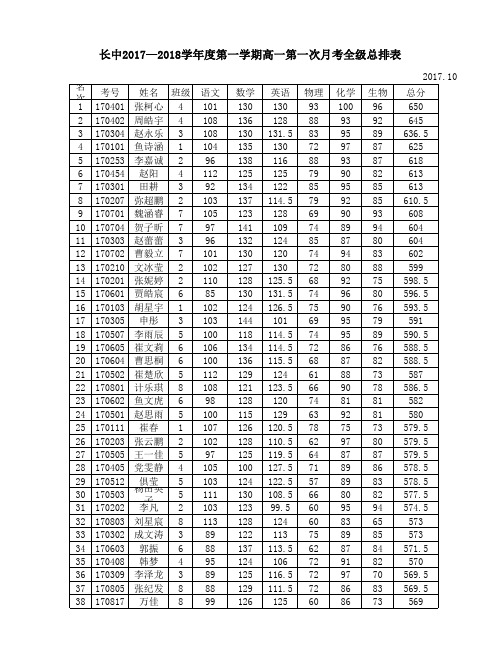
长中2017—018学年度第一学期高一第一次月考全级总排表
2017.10 名次 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 考号 170614 170104 170822 170712 170107 170834 170114 170115 170311 170708 171055 170318 170417 170815 170333 170519 170624 170217 170215 170308 170729 170514 170516 170617 170809 170811 170225 170711 170411 170610 170223 170406 170234 170108 170618 170211 170508 170616 姓名 班级 司梦晨 6 惠嘉康 1 胡叶叶 8 周逸飞 7 鱼朝阳 1 弥田 8 高金枝 1 尚甜甜 1 陈宝玲 3 李阳 7 杨广 10 杨扬 3 宇文雅 4 郭钾 8 黎佳昊 3 于莹莹 5 全宝婷 6 张晨 2 洪亦璇 2 李昭伟 3 解欣 7 陈雪彤 5 景凡 5 李一杰 6 党佳杰 8 尚国梁 8 罗睿青 2 剡心怡 7 梁娜 4 高星 6 曹亚鹏 2 曹锐洋 4 申岩 2 司帅 1 王帅 6 李煜 2 贾文丽 5 尚丁 6 语文 98 96 89 82 102 103 93 97 90 88 100 88 95 94 87 98 101 95 108 93 102 101 99 94 89 87 91 84 84 107 83 100 92 94 92 90 102 91 数学 117 126 117 119 101 126 112 109 107 120 118 101 103 119 113 115 124 92 97 108 120 116 111 113 138 118 114 123 118 125 123 98 111 102 133 113 112 110 英语 114 100 123.5 89.5 109 105.5 101.5 123 113 98.5 76 113 114.5 81.5 86.5 104 114.5 105.5 106.5 101.5 108 113 78 90.5 87 111.5 99 105 72 79.5 84.5 108.5 73 95.5 109.5 67.5 117 76 物理 57 60 67 67 70 48 66 50 58 65 64 61 63 62 80 59 42 69 47 45 56 42 62 55 44 57 65 56 74 50 62 69 80 68 56 70 52 67 化学 73 85 83 90 73 76 86 82 92 87 82 82 87 86 81 72 72 84 84 89 62 70 86 89 88 80 76 76 95 86 78 76 84 86 80 90 55 95 生物 77 68 54 86 78 74 74 71 71 72 89 83 64 84 79 78 72 79 79 85 72 78 84 78 73 65 72 73 73 68 84 62 73 67 42 82 74 73 总分 536 535 533.5 533.5 533 532.5 532.5 532 531 530.5 529 528 526.5 526.5 526.5 526 525.5 524.5 521.5 521.5 520 520 520 519.5 519 518.5 517 517 516 515.5 514.5 513.5 513 512.5 512.5 512.5 512 512
专题05 全称量词与存在量词(测)(解析版)

20.【必修第一册逆袭之路】判断下列命题的真假:
(1) ;(2) .
【答案】(1)假命题;(2)真命题.
【解析】(1) ;当 时, ,故 是假命题.
(2) .
取 ,计算得到: ,故 是真命题.
21.判断下列命题的真假:
(1) ;
(2) .
【答案】(1)真命题;(2)真命题.
【答案】(1)真命题;(2)真命题;(3)真命题;(4)假命题.
【解析】(1)实数包括有理数与无理数,其中无理数包括无限不循环小数如 等.故为真命题.
(2)等腰三角形有两条长度相等的边,但并不是每个三角形都有两条长度相等的边,故为真命题.
(3)四边长度相等的四边形为菱形,此时若相邻边互相垂直则为正方形,故为真命题.
【解析】(1) ;
,当 ,即 或 时 ,真命题;
(2) .
根据完全平方公式得到 ,故
真命题.
22.已知命题 ,若p为假命题,求实数m的取值范围.
【答案】
【解析】由题意得 ,∵p为假命题,∴ 为真命题.
当 时,对 不恒成立,不符合题意;当 时,得
∴ ∴ ,∴实数m的取值范围为 .
10.【必修第一册过关斩将】已知命题 , 为真命题,则实数m的取值范围是()
A. B. C. D.
【答案】A
【解析】由 , 为真命题,故 的取值不超过 ,即 .故选:A.
11.【海南省三亚市华侨学校2019-2020学年高一上学期期中】下列命题中是全称量词命题并且是真命题的是()
A. B.所有菱形的 条边都相等
A. B.
C. D.
【答案】C
【解析】
,故选C
5.【四川省南充高级中学2019-2020学年高二下学期期中】已知命题 为 , ,则命题 的否定为()
江苏省徐州高级中学2023届高三下学期3月月考数学试题

江苏省徐州高级中学2023届高三下学期3月月考数学试题学校:___________姓名:___________班级:___________考号:___________.2017-2021年,普通本专科招生人数逐年增加.普通本专科招生人数在2017-2018年增长最多.2017-2021年,普通高中招生人数在普通本专科、中等职业教育及普通高中招生总人数中所占比例逐年下降.2017-2021年,中等职业教育平均招生人数大约为608万10.一般地,如果一个凸n面体共有m个面是直角三角形,那么我们称这个凸n面体的直度为mn,则以下结论正确的是().三棱锥的直度的最大值为1.直度为34的三棱锥只有一种.四棱锥的直度的最大值为1(2)若()0EF DB l l =>uuu r uuu r ,求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.20.随着5G 网络信号的不断完善,5G 手机已经成为手机销售市场的明星.某地区手机专卖商场对已售出的1000部5G 手机的价格数据进行分析得到如图所示的频率分布直方图:(1)某夫妻两人到该商场准备购买价位在4500元以下的手机各一部,商场工作人员应顾客的要求按照分层抽样的方式提供了14部手机让其从中购买,假定选择每部手机是等可能的,求这两人至少选择一部价位在3500~4500元的手机的概率;(2)该商场在春节期间推出为期三天的“中奖打折”活动,活动规则如下:在一个不透明的容器中装有一白一黄两个除颜色外完全相同的乒乓球,顾客每次限抽一球,抽完后放回容器中摇晃均匀后再抽取下一次.若抽中白球得2分,抽中黄球得1分,得分为9分或10分时停止抽取,其中得9分为中奖,享受标价打n 折(*N n Î)优惠,得10分则未中奖按标价购买.设得i 分的概率为i P (1i =,2,…,10),其中01P =.(i )证明{}1ii P P--(10i <,且*N i Î)是等比数列;(ii )假定厂家在出售手机时的标价为进价的2倍,则厂家至少打几折才不致亏损?21.如图,在平面直角坐标系xOy 中,已知点()1,0F ,直线l :=1x -,P 为平面上的动点,过点P 作直线l 的垂线,垂足为点Q ,分别以PQ ,PF 为直径作圆1C 和圆2C ,且圆1C 和圆2C 交于P ,R 两点,且PQR PFR Ð=Ð.。
江苏省宿迁市泗阳县实验高级中学2023-2024学年高一下学期3月月考物理试题(解析版)

【答案】D
【解析】
【详解】A.小孩沿滑梯匀速下滑时,其动能不变,重力势能减小,故机械能不守恒,其实是有摩擦存在,将机械能转化成了内能,故A错误;
B.货物匀速下降,其动能不变,重力势能减小,它的机械能也不守恒,故B错误;
C.火箭加速上升,动能增大,重力势能也增大,故机械能增大,机械能不守恒,其实是外力对火箭做了功,故机械能会增大,故C错误;
15.如图所示,粗糙轻杆水平固定在竖直轻质转轴上 A点。质量为m的小球和轻弹簧套在轻杆上,小球与轻杆间的动摩擦因数为μ= ,弹簧原长为0.6L,左端固定在A点,右端与小球相连。长为L的细线一端系住小球,另一端系在转轴上的B点,AB间距离为0.6L。装置静止时将小球向左缓慢推到距A点0.4L处时松手,小球恰能保持静止。接着使装置由静止缓慢加速转动。已知小球与杆间最大静摩擦力等于滑动摩擦力,重力加速度为g,不计转轴所受摩擦。
(1)实验前,老师提供两种计时器:电磁打点计时器、电火花打点计时器。为减小“验证机械能守恒定律”的实验误差,实验时应用选择______打点计时器,其所需的电源为________。
(2)某同学正确的选择打点计时器后,用一质量为 的重物拉着纸带进行实验,选出点迹清晰的纸带,自起始点O测量出纸带上连续的四个点A、B、C、D到O点的距离,如图所示。已知打点计时器的打点频率为50Hz,当地重力加速度为 。则在打点计时器打O点到B点的这段时间内,重物动能的增加量为_________J、重力势能的减少量为_________J。(结果均保留二位有效数字)
A.在 内,合外力做 功为
B.在 内,合外力做的功为
C.在 内,摩擦力做的功为
D.在 内,摩擦力做的功为
【答案】A
【解析】
江苏省宿迁市2024届高三下学期调研测试数学试题

【详解】由题意得 A = {0,1, 2,3, 4} , B = {x x 被 3 除余数为 2 的整数} ,
\ A I B = {2} ,
故选:C. 2.D
【分析】根据复数的除法运算求得 z ,再求 z 在复平面内对应的点.
【详解】
z
=
5 3 + 4i
=
3 - 4i 5
,则对应点为
æ çè
3 5
,
所以原不等式的解集是 (-1,3) .
故选:A
解法二:特值当 x = 0 时, f (0) < f (3) ,排除 B,D,当 x = 1 时, f (1) < f (5) ,排除 C,
答案第21 页,共22 页
对 A:当 x Î(-1,3) 时, x2 < 2x + 3 ,因为函数 f (x) 是 R 上的增函数,所以
8.人工智能领域让贝叶斯公式:
P(
A
B)
=
P
(
B A) P
P(B)
(
A)
站在了世界中心位置,AI
换
脸是一项深度伪造技术,某视频网站利用该技术掺入了一些“AI”视频,“AI”视频占
有率为 0.001.某团队决定用 AI 对抗 AI,研究了深度鉴伪技术来甄别视频的真假.该
鉴伪技术的准确率是 0.98,即在该视频是伪造的情况下,它有 98% 的可能鉴定为
A.变量 X 的方差为 1,均值为 0
B. P ( X £ x) = 1- 2 f ( x)
C.函数 f ( x) 在 (0, +¥ ) 上是单调增函数 D. f (-x) = 1- f ( x)
10.在平面直角坐标系 xOy 中,已知抛物线 C : y2 = 4x,A, B 为抛物线 C 上两点下列说 法正确的是( )
江苏省宿迁市泗阳县实验高级中学2023-2024学年高一下学期5月月考物理试题

江苏省宿迁市泗阳县实验高级中学2023-2024学年高一下学期5月月考物理试题一、单选题1.关于电流强度,下列说法中正确的是A .导体中的电流强度越大,表示通过其横截面的电荷量越多B .在相同时间内,通过导体横截面的电荷量越多,导体中电流强度就越小C .通电时间越短,电流强度越大D .单位时间内通过导体横截面的电荷量越多,导体中电流强度越大 2.关于电动势,下列说法正确的是( )A .电源电动势越大说明电源把其他形式的能转化为电能的本领越大B .用电压表直接测量电源两极间电压得到的数值,实际上总略大于电源电动势的准确值C .电源电动势总等于内、外电路上的电压之和,所以它的数值与外电路的组成有关D .电源电动势等于电源正、负极之间的电势差3.一段长为L ,电阻为R 的均匀电阻丝,把它拉成3L 长的均匀细丝后,然后再切成等长的三段,则其中每一段电阻丝的阻值为( ) A .3RB .RC .3R D .9R 4.如图所示,一幢居民楼里住着生活水平各不相同的24户居民,所以整幢居民楼里有各种不同的电器,例如电炉、电视机、微波炉、电脑等等.停电时,用多用电表测得A 、B 间的电阻为R ;供电后,各家电器同时使用,测得A 、B 间电压为U ,进线电流为I ,则计算该幢居民楼用电的总功率可以用的公式是( )A .2P I R =B .2U P R=C .P IU =D .以上公式都可以5.如图所示,用甲、乙两种电路测R X的阻值,甲电路中伏特表和安培表的示数分别为3.0V和3.0mA,乙电路中伏特表和安培表示数分别为2.9V和4.0mA,则待测电阻RX的值应A.比1000Ω略大一些B.比1000Ω略小一些C.比725Ω略大一些D.比725Ω略小一些6.在如图所示电路中,电源电动势为E,内阻为r,R1、R2为定值电阻,电流表、电压表均为理想电表,现使R3阻值增大,则()A.V表读数变大B.A表读数变大C.R1两端的电压升高D.流过R2的电流减小7.一电流表的满偏电流I g=30 mA,内电阻R g=95 Ω,要把它改装成一个量程为0.6 A的电流表,应在电流表上()A.串联一个5.00 Ω的电阻B.并联一个5.00 Ω的电阻C.串联一个4.75 Ω的电阻D.并联一个4.75 Ω的电阻8.如图所示,一直流电动机与阻值R=9Ω的电阻串联在电源上,电源的电动势E=30V,内阻r=1Ω,闭合开关,用理想电压表测出电动机两端电压U=10V,已知电动机线圈的电阻R M=1Ω,则下列说法中正确的是()A.通过电动机的电流为10AB.电动机的输入功率为2WC .电源的输出功率为4WD .电动机的输出功率为16W9.如图为某控制电路的一部分,已知AA ′的输入电压为24 V ,如果电阻6k ΩR =,16k ΩR =,23k ΩR =,则BB ′不可能输出的电压是( )A .12 VB .8 VC .6 VD .3 V10.如图所示电路,闭合开关S ,两个灯泡都不亮,电流表指针几乎不动,而电压表指针有明显偏转,该电路的故障可能是( )A .电流表坏了或未接好B .从点a 经过灯1L 到点b 的电路中有断路C .灯2L 的灯丝断了或灯座未接通D .电流表和灯1L 、2L 都坏了11.如图所示,曲线C 1、C 2分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线。
江苏省宿迁市泗洪中学高一数学理月考试卷含解析

江苏省宿迁市泗洪中学高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 的三边分别为,且满足,,则此三角形是( ).等腰三角形.直角三角形.等腰直角三角形.等边三角形参考答案:D2. 已知,,则的值等于()A.B.C.D.参考答案:A略3. 函数的图象大致是( )A.B.C.D.参考答案:A【考点】余弦函数的图象.【专题】数形结合.【分析】由函数的解析式可以看出,函数的零点呈周期性出现,且法自变量趋向于正无穷大时,函数值在x轴上下震荡,幅度越来越小,而当自变量趋向于负无穷大时,函数值在x轴上下震荡,幅度越来越大,由此特征对四个选项进行判断,即可得出正确选项.【解答】解:∵函数∴函数的零点呈周期性出现,且法自变量趋向于正无穷大时,函数值在x轴上下震荡,幅度越来越小,而当自变量趋向于负无穷大时,函数值在x轴上下震荡,幅度越来越大,A选项符合题意;B选项振幅变化规律与函数的性质相悖,不正确;C选项是一个偶函数的图象,而已知的函数不是一个偶函数故不正确;D选项最高点离开原点的距离的变化趋势不符合题意,故不对.综上,A选项符合题意故选A【点评】本题考查余弦函数的图象,解题的关键是根据余弦函数的周期性得出其零点周期性出现,再就是根据分母随着自变量的变化推测出函数图象震荡幅度的变化,由这些规律对照四个选项选出正确答案.4. 设全集U={1,2,3,4,5,6,7},A={1,3,6},B={2,3,5,7},则A∩(?U B)等于()A.{3,4} B.{1,6} C.{2,5,7} D.{1,3,4,6}参考答案:B【考点】交、并、补集的混合运算.【分析】根据补集与交集的定义进行计算即可.【解答】解:全集U={1,2,3,4,5,6,7},B={2,3,5,7},∴?U B={1,4,6},又A={1,3,6},∴A∩(?U B)={1,6}.故选:B.5. 下列函数中最小值为2的是()A、 B、 C、 D、参考答案:D6. 已知x0是函数f(x)=2x+的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则()A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0 C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0参考答案:B【考点】函数零点的判定定理.【专题】函数的性质及应用.【分析】因为x0是函数f(x)=2x+的一个零点可得到f(x0)=0,再由函数f(x)的单调性可得到答案.【解答】解:∵x0是函数f(x)=2x+的一个零点∴f(x0)=0∵f(x)=2x+是单调递增函数,且x1∈(1,x0),x2∈(x0,+∞),∴f(x1)<f(x0)=0<f(x2)故选B.【点评】本题考查了函数零点的概念和函数单调性的问题,属中档题.7. 中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是()A. 2018年1月至4月的仓储指数比2017年同期波动性更大B. 2017年、2018年的最大仓储指数都出现在4月份C. 2018年全年仓储指数平均值明显低于2017年D. 2018年各月仓储指数的中位数与2017年各月仓储指数中位数差异明显参考答案:D 【分析】根据折线图逐一验证各选项.【详解】通过图象可看出,2018年1月至4月的仓储指数比2017年同期波动性更大, 这两年的最大仓储指数都出现在4月份, 2018年全年仓储指数平均值明显低于2017年,所以选项A,B,C的结论都正确;2018年各仓储指数的中位数与2017年各仓储指数中位数基本在52%,∴选项D的结论错误.故选:D.【点睛】本题考查折线图,考查基本分析判断能力,属基础题.8. (5分)函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)=,若关于x的方程2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是()A.(﹣,﹣)B.(﹣,﹣)C.(﹣,﹣)∪(﹣,﹣)D.(﹣,﹣)参考答案:B考点:根的存在性及根的个数判断;函数奇偶性的性质.专题:计算题;作图题;数形结合;函数的性质及应用.分析:作函数f(x)的图象,从而可化条件为方程x2+ax+b=0有两个根,且x1=,0<x2<;从而求a的取值范围.解答:由题意,作函数f(x)的图象如下,由图象可得,0≤f(x)≤f(2)=;∵关于x的方程2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,∴方程x2+ax+b=0有两个根,不妨设为x1,x2;且x1=,0<x2<;又∵﹣a=x1+x2,∴a∈(﹣,﹣);故选:B.点评:本题考查了函数的图象的作法与数形结合的思想应用,同时考查了二次方程的根与系数的关系应用,属于中档题.9. 在中,,则为()A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判定参考答案:C略10. (5分)已知向量=(3,﹣4),=(6,﹣3),=(2m,m+1).若,则实数m的值为()A.B.﹣3 C.D.﹣参考答案:B考点:平行向量与共线向量;平面向量的坐标运算.专题:平面向量及应用.分析:先求得得==(3,1),再由,则这两个向量的坐标对应成比例,解方程求得实数m的值,可得结论.解答:由题意可得==(3,1),若,则这两个向量的坐标对应成比例,即,解得m=﹣3,故选:B.点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,属于基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 定义在区间[0,5π]上的函数y=2sinx的图象与y=cosx的图象的交点个数为.参考答案:5【考点】正弦函数的图象;余弦函数的图象.【分析】画出函数y=2sinx与y=cosx在一个周期[0,2π]上的图象,即可得出结论.【解答】解:画出函数y=2sinx与y=cosx在一个周期[0,2π]上的图象如图实数:由图可知,在一个周期内,两函数图象在[0,π]上有1个交点,在(π,2π]上有1个交点, 所以函数y=2sinx 与y=cosx 在区间[0,5π]上图象共有5个交点. 故答案为:5.12. 定义在区间上的函数的图像与的图像的交点为P ,过点P 作PP 1垂直轴于点P 1,直线PP 1与的图像交于点P 2,则线段P 1P 2的长为________。
宿迁市2013-2014学年高二上学期第三次月考数学试题

.
2
)的图象如图所
示,为了得到 y sin x 的图象,只需把 y f ( x) 的图象 上所有点向右平移 个单位长度. 14.如图所示,在平面四边形 ABCD 中,若 AC=3,BD=2, → → → → 则(AB+DC)· (AC+BD)=_ _______.
二、解答题: (本大题共 6 道题,计 90 分.15~16 每小题 14 分,1,7~18 每小题 15 分,19~20 每小题 16 分,共计 90 分,解答应写出必要的文字说明、证明过程或演算步骤) → → 15.设两个非零向量 a 与 b 不共线. → → → → → → → → → (1)若AB= a + b ,BC=2 a +8 b ,CD=3( a - b ).求证:A,B,D 三点共线;
tsinθ =(-2ksinθ +16)sinθ =-2k(sinθ - )2+ . k k
4 ∵k>4,∴1> >0,
4
32
k
4 32 ∴当 sinθ = 时,tsinθ 取最大值为 .
k
k
32 由 =4,得 k=8,
k
6
π → 此时 θ = ,OC=(4,8). 6 → → ∴OA·OC=(8,0)·(4,8)=32.
7
9. (, 4) (4,1)
11. [
3
4 , 4
]
12. 1
6
14. 5
二、解答题: (本大题共 6 道题,计 90 分.15~16 每小题 14 分,1,7~18 每小题 15 分,19~20 每小题 16 分,共计 90 分,解答应写出必要的文字说明、证明过程或演算步骤) → → → 15.解析: (1)证明:∵AB=a+b,BC=2a+8b,CD=3(a-b), → → → ∴BD=BC+CD=2a+8b+3(a-b) → =2a+8b+3a-3b=5(a+b)=5AB. → → ∴AB,BD共线,
江苏省宿迁市泗洪中学2021年高一数学理月考试卷含解析

江苏省宿迁市泗洪中学2021年高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知集合,则()。
A. B. C. D.参考答案:D2. 已知向量,向量,且,那么x= ()A. 10B. 5C.D.参考答案:C【分析】利用向量平行的坐标表示求解即可。
【详解】因为向量,向量,且,所以,解得故选D.【点睛】本题考查向量平行的坐标表示,属于简单题。
3. 已知数列中,且,则此数列的通项公式为(▲)A. B. C. D.或参考答案:A略4. 已知组数据,,…,的平均数为2,方差为5,则数据2+1,2+1,…,2+1的平均数与方差分别为( )A. =4,=10B. =5,=11C. =5,=20D. =5,=21参考答案:C【分析】根据题意,利用数据的平均数和方差的性质分析可得答案.【详解】根据题意,数据,,,的平均数为2,方差为5,则数据,,,的平均数,其方差;故选:C.【点睛】本题考查数据的平均数、方差的计算,关键是掌握数据的平均数、方差的计算公式,属于基础题.5. 直线l过点(-1,2)且与直线垂直,则l的方程是()A. B.C.D.参考答案:A6. 已知集合,或,则().A.B.或C.D.或参考答案:C∵集合,集合或,∴集合.故选.7. 已知偶函数满足且时,,则方程的实数解共有()A .1个 B.4个 C .3个 D .2个参考答案:C略8. 若在实数范围内有意义,则x的取值范围是()A. x<3 B.x≤3 C.x>3 D.x≥3参考答案:D9. 已知全集U={0,1,2,3,4,5},集合M={0,3,5},N={1,4,5},则集合M∪(?U N)=()A.{5} B.{0,3} C.{0,2,3,5} D.{0,1,3,4,5}参考答案:C【考点】交、并、补集的混合运算.【专题】计算题.【分析】由全集U以及N,求出N的补集,找出M与N补集的并集即可.【解答】解:∵全集U={0,1,2,3,4,5},集合M={0,3,5},N={l,4,5},∴?U N={0,2,3},则M∪(?U N)={0,2,3,5}.故选C【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.10. (5分)已知sin(π+α)=,α为第三象限角,则tanα=()A.B.﹣C.D.﹣参考答案:A 考点:同角三角函数基本关系的运用.专题:三角函数的求值.分析:已知等式利用诱导公式化简求出sinα的值,根据α为第三象限角,利用同角三角函数间基本关系求出cosα的值,即可确定出tanα的值.解答:∵sin(π+α)=﹣sinα=,即sinα=﹣,α为第三象限角,∴cosα=﹣=﹣,则tanα==,故选:A.点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数满足:对于实数a的某些值,可以找到相应正数b,使得f(x)的定义域与值域相同,那么符合条件的实数a 的个数是.参考答案:2【考点】函数的值域;函数的定义域及其求法.【分析】由于函数解析式中,被开方式是一个类一元二次式,故我们可分a=0,a>0和a<0,三种情况,分别分析是否存在正实数b,使函数f(x)的定义域和值域相同,进而综合讨论结果,即可得到答案.【解答】解:(1)若a=0,则对于每个正数b,f(x)=的定义域和值域都是[0,+∞)故a=0满足条件.(2)若a>0,则对于正数b,的定义域为D=(﹣∞,﹣]∪[0,+∞),但f(x)的值域A?[0,+∞),故D≠A,即a>0不合条件;(3)若a <0,则对正数b ,定义域D=[0,﹣],(f (x ))max =,f (x )的值域为[0,],则﹣=?.综上所述:a 的值为0或﹣4. 故答案为2.【点评】本题考查的知识点是函数的定义域及其求法,函数的值域,二次函数的图象和性质,其中熟练掌握一次函数和二次函数的图象和性质是解答本题的关键,解答中易忽略a=0时,也满足条件,而错解为a=﹣4. 12. 在等腰直角三角形中,是斜边的中点,如果的长为,则的值为 ▲ .参考答案:4 略13. 设函数,则=参考答案:8 14. 计算:3﹣27﹣lg0.01+lne 3= .参考答案:【考点】对数的运算性质;有理数指数幂的化简求值. 【分析】利用对数和分数指数幂的运算法则求解.【解答】解: =4﹣9+2+3=0.故答案为:0.15. 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图所示.(Ⅰ)直方图中的值为___________; (Ⅱ)在这些用户中,用电量落在区间内的户数为_____________.参考答案:0.0044,70.16. 在平行四边形ABCD 中,AD=1,AB=2,∠BAD=60°,E 是CD 的中点,则·= .参考答案:﹣【考点】平面向量数量积的运算.【分析】由条件利用两个向量的数量积的定义求得=1,再根据=()?(﹣),运算求得结果.【解答】解:由题意可得=2×1×cos60°=1, ∴=()?(+)=()?(﹣)=﹣++=﹣×4+×1+1=﹣, 故答案为﹣.【点评】本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,属于中档题.17. 已知M={(x,y)|x2+y2=1,0<y ≤1},N={(x,y)|y=x+b,b ∈R},并且M ∩N ≠ ,那么b 的取值范围是 . 参考答案:略三、解答题:本大题共5小题,共72分。
2017-2018 学年.七中.高一下.第一次月考化学试卷及答案

2.能作为 Cl、Br、I 元素非金属性递变规律的判断依据的是( )
①Cl2、Br2、I2 的熔点
②Cl2、Br2、I2 的氧化性
③HCl、HBr、HI 的热稳定性
④HCl、HBr、HI 的酸性
A.①②③
B.②③
C.②③④
D.①②③④
器 3.下列各组物质中化学键的类型完全相同的是( )
A.NaCl MgCl2 Na2O
2017-2018 学年.七中.高一下.第一次月考.试卷及答案
一、选择题(共 16 小题,每小题 4 分,共 64 分)
1.中国科Lv
的名称为鉝。关于
293 116
Lv
的叙述错误的是
()
A.原子序数 116
B.中子数 177
C.核外电子数 116
D.质 子 数 177
B.H2O
辑 C.Na2S NaOH H2SO4
D.NH4Cl
MgO CO2 NaNO3 NH3
4.下列分子的电子式书写正确的是( )
编 A.氨气
C.氮气
B.四氯化碳 D.二氧化碳
捷PDF 5.下列反应过程中的能量变化与如图一致的是( )
迅A. 2Al + Fe2O3 高温 2Fe + Al2O3 C. C + H2O 高温 CO + H2
B. CaCO3 高温 CaO + CO2 ↑ D. C + CO2 ∆ 2CO
6.关于碱金属元素的说法中正确的是( ) A.ⅠA 族元素都是碱金属元素 B.碱金属单质可将铜从其盐溶液中置换出来 C.金属钾具有强还原性,K+具有强氧化性 D.Cs 常温下与水反应会发生爆炸
7.反应 3A(g) + B(g)=2C(g) + 2D(g) ,在不同条件下,用不同物质表示其反应速率,分别为 ①v(A) = 0.6mol ⋅ L−1 ⋅ min−1 ②v(B) = 0.45mol ⋅ L−1 ⋅ min−1 ③v(C) = 0.02mol ⋅ L−1 ⋅ min−1 ④v(D) = 0.45mol ⋅ L−1 ⋅ min−1
江苏省宿迁市沭阳县随园中学高三化学月考试题含解析

江苏省宿迁市沭阳县随园中学高三化学月考试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 同温同压下,在两个体积相同密闭容器中分别充入甲、乙两种气体,若甲的密度大于乙的密度,则下列说法正确的是( )A.甲的分子数比乙的分子数多 B.甲的物质的量比乙的物质的量少C.甲的气体摩尔体积比乙的气体摩尔体积小 D.甲的相对分子质量比乙的相对分子质量大参考答案:D略2. 化学与人类生活、社会可持续发展密切相关,下列措施有利于节能减排、保护环境的是()①研发易降解的生物农药;②加快化石燃料的开采与使用;③应用高效洁净的能源转换技术;④田间焚烧秸秆;⑤推广使用节能环保材料。
A.①③⑤B.②③⑤C.①②④D.②④⑤参考答案:A略3. 用某种仪器量一液体体积时,若平视时读数为n mL,仰视时读数为x mL,俯视时读数为y mL,若x>n>y,则所使用的仪器可能是A.量筒B.滴定管C.容量瓶D.分液漏斗参考答案:略4. 某元素的一个原子形成的离子可表示为abX n-,下列说法正确的是A.a bX n-含有的中子数为a+b B.a bX n-含有的电子数为a-n C.X原子的质量数为a+b+n D.X原子的质量约为b/6.02×1023参考答案:D5. 分子式为C8H10的芳香烃,苯环上的一溴取代物只有一种,该芳香烃的名称是()A.乙苯 B.邻二甲苯 C.间二甲苯 D.对二甲苯参考答案:D略6. 下列离子方程式书写正确的是()A.向50 mL 1 mol·L-1明矾溶液中滴入数滴0.1 mol·L-1Ba(OH)2溶液Al3++2SO42-+2Ba2++3OH- === Al(OH)3↓+2BaSO4↓B.向KI与稀硫酸的混合溶液中通入氧气:4H++O2+6I-=== 3I2+2H2OC.a mol FeBr2溶液中通入a mol Cl2:2Fe2++2Br-+2Cl2 = Br2+2Fe3++4C1-D.在澄清石灰水中加入适量碳酸氢镁溶液:Ca2++ OH-+ HCO3-==CaCO3↓+H2O参考答案:C7. 下列反应的离子方程式书写正确的是A. 铜溶于0.5mo/L 的硝酸: Cu+4H++2NO3- =Cu2++2NO2 ↑+2H2OB. Na2S2O3溶液中加入稀硫酸: 2S2O32-+ 4H+ =SO42-+ 3S ↓+ 2H2OC. 向Ba(OH)2溶液中加入少量的NH4HSO4溶液: Ba2++OH-+H++SO42-=BaSO4↓+H2OD. Ca(HCO3)2溶液与少量NaOH 溶液反应: HCO3-+Ca2+ +OH-=CaCO3↓+H2O参考答案:D铜溶于0.5mo/L的硝酸生成NO,离子方程式是3Cu+8H++2NO3- =3Cu2++2NO↑+4H2O,故A错误;Na2S2O3溶液中加入稀硫酸,+2价S发生歧化反应2生成S单质、SO2气体,反应离子方程式是S2O32-+ 2H+═SO2↑+S↓+H2O,故B错误;向Ba(OH)2溶液中加入少量的NH4HSO4溶液,反应离子方程式是Ba2++2OH-+H++SO42-+NH4+=BaSO4↓+H2O+,故C错误;Ca(HCO3)2溶液与少量NaOH 溶液反应生成碳酸钙、碳酸氢钠、水,反应离子方程式是: HCO3-+Ca2++OH-=CaCO3↓+H2O,故D正确。
江苏省宿迁市沭阳县沭阳如东实验学校2023-2024学年八年级下学期3月月考数学试题
江苏省宿迁市沭阳县沭阳如东实验学校2023-2024学年八年级下学期3月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列以数学家名字命名的图形中,既是轴对称图形又是中心对称图形的是( ) A .笛卡尔心形线 B .赵爽弦图C .莱洛三角形D .科克曲线2.以下调查中,适宜普查的是( )A .调查全班每位同学所穿鞋子的尺码B .调查某批次洗衣机的使用寿命C .调查公民保护环境的意识D .调查黄海湿地中现有鱼的种类 3.下列事件中,属于必然事件的是( )A .购买一张彩票,中奖B .三角形的两边之和大于第三边C .经过有交通信号灯的路口,遇到红灯D .对角线相等的四边形是矩形4.袋子里有8个红球,m 个白球,3个黑球,每个球除颜色外都相同,从中任意摸出一个球,若摸到红球的可能性最大,则m 的值不可能是( )A .1B .3C .5D .105.如图,ABC 与A B C '''关于点O 成中心对称,则下列结论不一定成立的是( )A .点A 与点A '是对称点B .BO B O '=C .ACB C A B '''∠=∠D .A ABC B C '''≌△△6.用反证法证明,“在ABC 中,A ∠、B ∠对边是a 、b .若A B ∠<∠,则a b <.”第一步应假设( )A .a b >B .a b =C .a b ≥D .a b ≤7.若顺次连接四边形ABCD 各边的中点所得四边形是菱形.则四边形ABCD 一定是 ( ) A .菱形B .对角线互相垂直的四边形C .矩形D .对角线相等的四边形8.如图,在四边形ABCD 中,,E F 分别是,AD BC 的中点.若6AB =,8,30,120CD ABD BDC =∠=︒∠=︒,则EF 的长是( )A .125B .3C .4D .5二、填空题9.学校为了了解500名初三学生的体重情况,从中抽取100名学生进行测量,样本容量是 .10.若要制作统计图来反映某品牌奶粉中蛋白质、钙、维生素糖和其他物质含量的百分比,最适当的统计图是 统计图.(填“折线”、“条形”或“扇形”)11.已知样本的数据个数为30,且被分成4组,第一组至第四组的数据个数之比为2∶4∶3∶1,则第三组的数据频率为 .12.在如图所示(A ,B ,C 三个区域)的图形中随机地撒一把豆子,豆子落在_________区域的可能性最大(填A 或B 或C ).13.如图,在ABC 中,,100AB AC BAC =∠=︒,在同一平面内,将ABC 绕点A 顺时针旋转到11AB C △的位置,连接1BB ,若11BB AC ∥,则1CAC ∠的度数是 .14.已知菱形ABCD 的两条对角线AC 、BD 的长分别是8cm 和6cm .则菱形的面积为 2cm .15.如图,ABC 中,,E F 分别是,AB AC 的中点,点D 在EF 上,延长AD 交BC 于,,6N BD AN AB ⊥=,8BC =,则DF = .16.如图,正方形ABCD 的边长为4,点,E F 分别在边,AD CD 上,若45EBF ∠=︒,则EDF 的周长等于 .17.如图,正方形ABCD 的边长为1,E 为与点D 不重合的动点,以DE 一边作正方形DEFG ,设1DE m =,点F G 、与点C 的距离分别为23,m m ,则123m m m ++的最小值为 .18.如图,点P 为ABCD Y 内一点(点P 不在BD 上),过点P 作,EF AD HG AB ∥∥,与各边分别相交于点E F G H 、、、.设四边形AEPH 的面积为2,四边形PGCF 的面积为8,则PBD △的面积为 .三、解答题19.如图,平面直角坐标系中,ABC 三个顶点的坐标分别为()()()3,5,5,3,2,2A B C −−−,将ABC 按照某种方式平移得到111A B C △,其中点A 的对应点1A 的坐标为()3,3.(1)请在图中画出;(2)已知111A B C △与222A B C △关于原点O 成中心对称,请在图中画出222A B C △,此时222A B C △与ABC 关于某点成中心对称,这一点的坐标为_______;20.如图,ABC 为等边三角形,P 是等边三角形ABC 内一点.ABP 经过逆时针旋转后到达ACQ 的位置.(1)图中BP 的对应边是_______,ABP ∠的对应角是∠_______;(2)APQ △是_______三角形;(3)若3,5,4PA PB PC ===,则APC ∠=_______度.21.环保部门为了解城区某一天18:00时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A、B、C、D、E五组,结果如下(每组含起点值,不含终点值):请解答下列问题:(1)请补全频数分布直方图;(2)在扇形统计图中C组对应的扇形圆心角的度数是______°;(3)若城区共有400个噪声测量点,请估计该城区这一天18:00时噪声声级低于70dB的测量点的个数.22.在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:a______;b=______;(1)按表格数据格式,表中的=(2)请估计:当次数s很大时,摸到白球的频率将会接近______(精确到0.1);(3)请推算:摸到红球的概率是_______(精确到0.1);(4)试估算:这一个不透明的口袋中红球有______只.AC BD相交于点O,点,E F在对角线BD上,且23.如图,平行四边形ABCD的对角线,AE EC CF FA.BE EF FD==,连接,,,(1)求证:四边形AECF 是平行四边形.(2)若ABE 的面积等于4,求CFO △的面积.24.如图,将矩形纸片ABCD 沿对角线BD 折叠,点C 落在点E 处,BE 交AD 于点F ,连接AE .(1)求证:BF=DF.(2)若BC=8,DC=6,求BF 的长.25.如图,ABCD Y 的面积为12,6,AC BD AC ==与BD 交于点O ,分别过点,C D 作,BD AC 的平行线相交于点F ,(1)求证:四边形OCFD 是菱形;(2)若点G 是CD 的中点,点P 是四边形OCFD 边上的动点,则PG 的最小值是_______. 26.如图,在△ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,AH 是边BC 上的高.(1)求证:四边形ADEF 是平行四边形;(2)求证:∠DHF=∠DEF .27.如图,在Rt △ABC 中,∠C =30°,AB =5,点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D 、E 运动的时间是t 秒(t >0).过点D 作DF ⊥BC 于点F ,连接DE 、EF .(1)求证:AE =DF .(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.(3)当t 为何值时,△DEF 为直角三角形?请说明理由.28.定义:对于一个四边形,我们把依次连结它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”.【概念理解】:下列四边形中一定是“中方四边形”的是_______.A .平行四边形;B .矩形;C .菱形;D .正方形.【问题解决】:如图2,以锐角ABC 的两边,AB AC 为边长,分别向外侧作正方形ABDE 和正方形ACFG ,连结,,BE EG GC .求证:四边形BCGE 是“中方四边形”:【拓展应用】:如图3,已知四边形ABCD 是“中方四边形”,,M N 分别是,AB CD 的中点.(1)试探索BD 与MN 的数量关系,并说明理由;(2)若AB CD +的最小值是4,则BD 的长度为_______.(不需要解答过程)。
江苏省宿迁市支口中学高三物理月考试题含解析

江苏省宿迁市支口中学高三物理月考试题含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. “蹦极”是一项刺激的极限运动,一个重为F0的运动员将一端固定的长弹性绳绑在踝关节处,从高处跳下,测得弹性绳的弹力F的大小随时间t的变化图像如图所示。
若将蹦极过程视为在竖直方向上的运动,且空气阻力不计,下列说法正确的是()A.t1~t2时间内运动员处于超重状态B.t3时刻运动员的速度最大C.t1~t3时间内运动员受到的弹力冲量和重力冲量大小相等D.t1~t5时间内运动员的机械能先减小后增大参考答案:D2. (单选)被拉直的绳子一端固定在天花板上,另一端系着小球。
小球从A点静止释放,运动到B点的过程中,不计空气阻力。
则()A.小球受到的拉力先变小后变大B.小球的切向加速度一直变大C.小球的机械能守恒D.小球的动能先变大后变小参考答案:C3. 三个完全相同物块1、2、3放在水平桌面上,它们与桌面间的动摩擦数都相同。
现用大小相同的外力F沿图示方向分别作用在1和2上,用F的外力沿水平方向作用在3上,使三者做加速运动。
令a1、a2、a3分别代表物块1、2、3的加速度,则()A. a1=a2=a3B. a1=a2,a2>a3C. a1>a2,a2< a3D. a1>a2,a2> a3参考答案:答案:C4. (单选)彩虹是悬浮于空气中的大量小水珠对阳光的色散造成的,如图所示为太阳光照射到空气中的一个小水珠发生反射和色散的光路示意图,其中a、b为两束频率不同的单色光。
对于这两束光,以下说法中正确的是()A.色光a如果是黄光,色光b可能是紫光B.如果太阳光在小水珠中的照射方向合适,可能会有一种或几种颜色的光发生全反射C.在同一装置用两种色光做双缝干涉实验,看到的a光的干涉条纹间距比b光的干涉条纹间距小D.同一介质中a光的波长小于b光的波长参考答案:A5. 经国际小行星命名委员会命名的“神舟星”和“杨利伟星”的轨道均处在火星和木星轨道之注:AU离)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一下学期3月月考数学试题
一、填空题(本大题共14小题,每小题5分,共70分。
) 1.
sin 22co s 38co s 22sin 38o
+=
2. ︒
︒+︒︒55cos 10cos 35cos 80cos
=
3.已知tan α、tan β是方程7x2-8x+1=0的两根,则tan 2
β
α+=
4.已知12
s in ,,132πααπ⎛⎫
=∈ ⎪⎝⎭
,则sin 2α=
5. 设4
o
x π
≤≤
=
6. 在△ABC 中,已知3=a ,4=b ,3
2sin
=
B ,则A
sin =
7.在△ABC 中,已知2
=
b
,1=c ,B=0
45,则=
a
8. 已知数列{a n }的首项,a 1=1,且a n =2a n -1+1(n ≥2),则a 5= 9.在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=450,则a 2+a 8= 10. 已知数列{a n }中a 3=2,a 7=1,又数列{1
1+n a }为等差数列,则a 11=
11. 数列1,
4
1,41,41,41,31,31,31,21,21,…的前100项的和为
12. 已知数列{a n }的前n 项和S n =n 2+2n +5,则a 6+a 7+a 8= ____.
13.在等差数列{a n }和{b n }中,a 1=25,b 1=75,a 100+b 100=100,则数列{a n +b n }的前100项的和为 14.若数列{a n }满足a 1=21
,a n =1-
1
1-n a ,n ≥2,n ∈N*,则a 2003=
二、解答题:本大题共6小题,共90分。
(解答应写出文字说明、证明过程或演算步骤)
15.(本题14分)在等差数列{}n a 中,已知10
5=a ,31
12
=a ,求20,n a a
16.(本题14分)已知锐角α,β满足cos α=5
3 cos(α+β)=13
5-
求cos β
17.(本题14分)已知cos (2α-β)=-14
11,sin (α-2β)=
7
3
4,且
4
π
<α<
2
π
,0<β<
4
π
,
求cos(α+β)的值。
18、(本题16分)在四边形ABCD 中∠ADB=∠BCD=75︒,∠ACB=∠BDC=45︒
,
DC=3
,
求: (1) AB 的长
(2) 四边形ABCD 的面积
19.(本题共16分)△ABC 中已知∠A=30°cosB=2sin B -C
sin 3
①求证:△ABC 是等腰三角形
②设D 是△ABC 外接圆直径BE 与AC 的交点,且AB=2 求:CD
AB 的值
20.(本题共16分)数列{a n }是首项为23,公差为整数的等差数列,且第六项为正,第七项为负. (1)求数列的公差.
(2)求前n 项和S n 的最大值. (3)当S n >0时,求n 的最大值.
高一数学试卷答案
一填空题(每小题5分,共70分)
1.
2
2.
2
3. 12
或-2 4. 120169
-
5. 2co s x
6. 2
1
7.
2
2
6+ 8. 31
9. 180 10. 2
1
11. 913
14
12. 45
13. 10000 14. -1
二、解答题(本大题共6小题,共90分。
解答时应写出必要的文字说明、演算步骤或证明过程)
15(14分) 解:【解法一】: ∵10
5=a ,31
12
=a ,则
⎩⎨
⎧=+=+31
1110411d a d a ⇒
⎩⎨
⎧=-=3
2
1d a …………………………………………………5分
∴5
3)1(1-=-+=n d n a a n
…………………………………………………10分
55
19120=+=d a a (14)
分
【解法二】:
1257311073
a a d d d =+⇒=+⇒=
2012
855a a
d =+=
5
3)12(12-=-+=n d n a a n
解:∵cos α=
5
3 ∴
sin α=
5
4……………………………………………………………2分
又∵cos(α+β)=13
5-<0
∴α+β为钝角 ∴sin(α+β)=13
12……………………………………………………………………………
…8分 ∴cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α
=65
335413
125313
5=⋅+⋅-
………14分
17.(14分) 解:∵
4
0,2
4π
βπ
απ
<
<<
<, ∴
4
π
<2α-β<π,-
4
π
<α-2β<
2
π
,
由cos(2α-β)=-14
11得,sin (2α-β)=143
5; (4)
分
由sin (α-2β)=7
3
4得,cos(α-2β)=
7
1 …………………………………………
8分
∴cos(α+β)=cos [(2α-β)-(α-2β)]
=cos(2α-β)cos(α-2β)+sin (2α-β)sin (α-2β) =-
14
11×
7
1+
14
3
5×
73
4=2
1
………………………………………………………………14分
【解】(1)因为∠BCD=75︒,∠ACB=45︒,所以∠ACD=30︒ , 又因为∠BDC=45︒,所以∠DAC=180︒-(75︒+ 45︒+ 30︒)=30︒, 所以, AD=DC=
3
…………………………………………………………2分
在∆BCD 中,∠CBD=180︒-(75︒+ 45︒)=60︒, 所以
︒
75
sin BD =
︒
60
sin DC ,
BD =
︒
︒
60
sin 75sin 3=
2
2
6+……………………………………………………6分
在∆ABD 中,AB 2=AD 2+ BD 2-2⨯AD ⨯BD ⨯cos75︒= 5, 所以, AB=5
…………………………………………………………10分
(2)S ABD ∆=
2
1⨯
AD ⨯BD ⨯sin75︒
=
4
3
2
3+
同理, S BCD ∆=
43
3+
所以四边形ABCD 的面积S=4
3
3
6+……………………………………16分
19.( 16分) 【解】 ①150
=+C B
°
)
150s i n (3s i n 2s i n 3s i n 2c o s B B C B B --=-=∴
)
s i n 2
3c o s 2
1(
3s i n 2B B B +
-=
t a n 23B ∴=
75
=∴
B …………………………………………………4分
从而
75
=C
∴
△ABC 是顶角为A 的等腰三角形。
(8)
分
②在△ABC 中由正弦定理
2
s i n 30
s i n 75
B C =
2
6-
=
∴BC
在△BCD 中由正弦定理
45
sin 2
660
sin -=
CD
3
3-
=∴CD
1
32-=
-=∴CD AD 3
33
313=
-
-=
∴
DC
AD ………………………………16分
20(16分)
【解】 (1)由已知a 6=a 1+5d =23+5d >0,a 7=a 1+6d =23+6d <0, 解得:-
5
23<d <-
6
23,又d ∈Z,
∴d =-4……………………………………………………………………4分 (2)∵d <0,∴{a n }是递减数列, 又a 6>0,a 7<0
∴当n =6时,S n 取得最大值,S 6=6×23+2
56⨯ (-4)=78 (10)
分 (3)S n =23n +2
)
1(-n n (-4)>0,整理得:n (50-4n )>0
∴0<n <
2
25
,又n ∈N*,
所求n 的最大值为12………………………………………………………………16分。
