积分变换第二章拉氏变换
第2章—拉普拉斯变换的数学方法
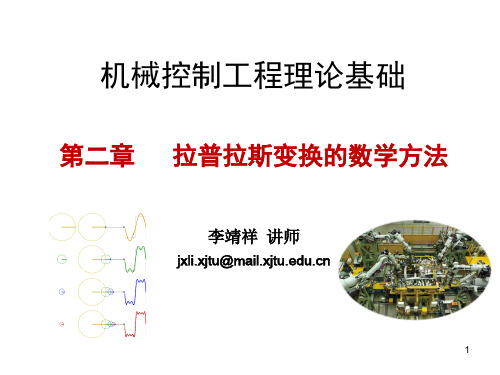
f t f t se st dt
27
若f(t)的二阶、三阶、……,各阶导函数存在,则:
L f n t s n F s s n 1 f 0 s n 2 f 0 f n 1 0
2.1 复数和复变函数
2. 复数的表示方法 (1) 点表示法
复平面
10
2. 复数的表示方法
(2) 向量表示法 模
s r 2 2
辐角 arctan
(3) 三角函数表示法和指数表示法
r cos
三角函数表示法
r sin
cos j sin
0
14
L[ f (t )] F ( s) f (t )e st dt
0
s为复数,s = σ + jω,称f(t)为原函数,F(s)为象函数。 拉氏变换F(s)存在条件:
(1) 在任一有限区间上, f(t)分段连续, (2)被积函数 f(t)e-st 绝对值收敛, 只有有限个间断点 即f(t)e-σt绝对可积
23
3. 周期函数的拉氏变换
设函数f(t)是以T为周期的周期函数,即f(t+nT)=f(t) ,n为整数。 则f(t)的拉氏变换为: L f t f t e st dt
0
f t e dt
T st 0
2T
T
f t e dt
st
L f at f e
0
s a
1 1 1 s a d f e d F a a 0 a a
s
26
6. 微分定理
若时间函数f(t)的拉氏变换为F(s),且其一阶导函数f’(t)存在,则
二章2拉氏变换ppt课件

五、拉氏变换求解线性微分方程
➢将微分方程通过拉氏变换变为 s 的代数方程; ➢解代数方程,得到有关变量的拉氏变换表达式; ➢应用拉氏反变换,得到微分方程的时域解。
A1 A2 A3 S S2 S3
A1
S S
1
2S
3
S
S 0
1 6
A2
S S
1
2S
3 S
2
S 2
1 2
A3
S S
1
2S
3 S
3
S 3
1 3
1
Y(S) 6
1 2
1 3
S S2 S3
yt 1 1 e2t 1 e3t
62 3
1 e2t 1 e3t
2
3
1
S 0.5
0.57 0.866
S S 0.52 0.8662 S 0.52 0.8662
f t 1 e0.5t cos 0.866 t 0.57e0.5t sin 0.866 t
3、A(S)=0有重极点
设A(S)=0有r个重极点,将F(S)展开成下列形式:
FS
S
A01
P0 r
1 !
例3:求
F
S
S
S 3
22 S
1
的反变换
将F(S)展开成下列形式:
FS
S
A01
22
A02
S 2
A3
S 1
A01
S
S 3
22 S
1 S
22
S 2
1
A02
d
ds
S
S 3
22 S
1 S
22
S
2
2
拉氏变换的数学方法解答

拉氏变换的数学方法解答拉氏变换是一种重要的数学工具,用于求解微分方程和积分方程。
它通过将时间域的函数转换为频率域的函数,从而简化了微分方程和积分方程的求解过程。
在本文中,我们将介绍拉氏变换的定义、性质以及如何使用拉氏变换来求解常见的微分方程。
首先,我们来介绍拉氏变换的定义。
拉氏变换是一种积分变换,它将一个在时间域上定义的函数f(t)转换为一个在复平面上定义的函数F(s)。
具体地,拉氏变换定义为:F(s) = L(f(t)) = ∫[0,∞] e^(-st) f(t) dt其中,s 是复变量,e^(-st) 是指数函数。
拉氏变换的结果 F(s) 是一个复函数,它描述了函数 f(t) 在频率域上的性质。
下面我们来介绍拉氏变换的一些基本性质。
首先,拉氏变换是线性的,即对于任意的函数f(t)和g(t),以及任意的常数a和b,有:L(af(t) + bg(t)) = aF(s) + bG(s)其中,F(s)和G(s)分别是f(t)和g(t)的拉氏变换。
其次,拉氏变换有一个重要的性质,即微分等式在变换后变为乘法等式。
具体地,对于一个函数f(t)和它的导数f'(t),有:L(f'(t))=sF(s)-f(0)其中,f(0)是函数f(t)在t=0时的值。
另外,拉氏变换还有一个重要的性质,即积分等式在变换后变为除法等式。
具体地,对于函数f(t)的积分F(t)和它的拉氏变换F(s),有:L(F(t))=1/sF(s)通过上述性质,我们可以将微分方程和积分方程通过拉氏变换转化为更简单的代数方程,从而求解微分方程和积分方程。
接下来,我们来介绍如何使用拉氏变换来解决常见的微分方程。
对于一个线性常系数微分方程:a_n*y^(n)(t)+a_(n-1)y^(n-1)(t)+...+a_1*y'(t)+a_0*y(t)=b(t)其中,y(t)是未知函数,a_i和b(t)是已知函数或常数。
我们可以将该微分方程转化为一个代数方程,通过拉氏变换求解。
第二章拉氏变换的数学方法

一、拉氏变换的定义: 拉氏变换的定义: 设f(t)是定义在(0,∞)区间上的时间函 ( )是定义在( , ) --st 为复数( ),用 乘以f( ) 数,又s为复数(s= σ +jw),用e 乘以 (t)后, 为复数 ), 再将它对t从 ∞ 进行积分,如果这个积分收 进行积分, 再将它对 从0 则这个积分便确定了一个以s为参量的复变函 敛,则这个积分便确定了一个以 为参量的复变函 数F(s); ( ); F(s)=L f(t) = ∞ f(t)e --stdt () () ()
L [d f(t)/ dt ] = s2 F(s) –s f(0)– f `(0) L [d f(t)/ dt] = s F(s) – f(0)
2
2
3、积分定理: 、积分定理: n n (--1) n L[ …. f(t) dt ]=(1/s ) F(s) + (1/s ) f (0) + n …..(1/s) f (--n) (0) (--n) (--1) (--2) f (0) , f (0) , ……, f (0)为 f(t) 的各重积分在 为 t= 0时的值,若初值为 0 则, 时的值, 时的值 L[ f (t) dt ]=(1/s) F(s) L[ f (t) dt 2 ]=(1/s2 ) F(s) L[ …. f (t) dtn ]=(1/sn ) F(s)
0
F(s)------象函数 象函数 f(t)-------原函数 原函数
二、几种典型函数的拉氏变换
加于控制系统中的外作用( 加于控制系统中的外作用(指给定值和 干扰)一般事先是不完全知道的, 干扰)一般事先是不完全知道的,而且常常随 时间任意变化。为了便于对系统进行理论分析, 时间任意变化。为了便于对系统进行理论分析, 工程实践中允许采用以下几种简单的时间函数 作为系统的典型输入, 单位阶跃函数、 作为系统的典型输入,即:单位阶跃函数、单 位斜坡函数、等加速函数、指数函数、正弦函 位斜坡函数、等加速函数、指数函数、 数以及单位脉冲函数等。 数以及单位脉冲函数等。
积分变换 拉氏变换

dx(t ) st lim e dt limsX ( s ) x(0) s s dt 0 0 lim sX ( s) lim x(0)
s s
lim x(t ) lim sX ( s)
t 0 s
lim x ( t ) lim sX ( s ) 6)终值定理 t s 0
6 (0) 5sY ( s) y (0) 6Y ( s) s Y ( s) sy (0) y s 2s 2 12s 6 1 5 4 Y ( s) s( s 2)(s 3) 5e 2t 4e 3t
st e Lx(t ) x(t )e st dt x(t )d s 0 0 st e st e x(t ) dx(t ) s 0 0 s
x(0) 1 dx(t ) st e dt s s 0 dt x ( 0) 1 d L x(t ) s s dt d L x(t ) sX ( s ) x(0) dt
(t ) 8 y (t ) 32y(t ) 4 (t ) y 例:解方程 解:将方程两边取拉氏变换,得
(0) y(0) 0 y
8s 32 Y ( s ) 4 4 4 Y (s) 2 s 8s 32 s 4 2 4 2 4 Lsin(4t ) 2 s 42 y (t ) e 4t sin(4t )
0
t 0
1
t 0
0 0
F (t ) (t )e jwt dt e jwt
0
1
x(t ) (t )dt lim
电路分析中拉氏变换如何理解与计算

电路分析中拉氏变换如何理解与计算拉氏变换是一种在电路分析中常用的数学工具,用于将微分方程转换为代数方程,从而简化电路分析的过程。
它基于拉氏变换的定义和拉氏变换的性质进行计算。
下面将详细介绍拉氏变换的概念、计算方法以及其在电路分析中的应用。
一、拉氏变换的概念与定义1.拉氏变换的定义拉氏变换是一种线性、时不变的积分变换,它将一个函数f(t)转换为复数域的函数F(s)。
拉氏变换定义如下:F(s) = L{f(t)} = ∫[e^(-st) * f(t)] dt其中,f(t)是定义在t≥0时间域上的函数,F(s)是定义在复平面上的函数,s=σ+jω是一个复数,σ和ω分别表示实部和虚部。
2.拉氏变换的性质拉氏变换具有一些重要的性质,这些性质是进行拉氏变换计算的基础。
以下是几个常用的性质:线性性质:对于常数a和b,以及函数f(t)和g(t),有L{a*f(t)+b*g(t)}=a*F(s)+b*G(s)。
时延性质:对于函数f(t)和其时延h(t)=f(t-τ),有L{h(t)}=e^(-sτ)*F(s)。
因果性质:对于定义在t≥0时间域上的函数f(t),如果f(t)=0当t<0,那么F(s)只在Re(s)>σ0的区域存在,其中σ0是f(t)中所有极点的实部的最大值。
二、拉氏变换的计算方法在实际计算中,为了将一个函数f(t)进行拉氏变换,通常需要先将其分解为更简单的函数的组合。
常用的计算方法有积分法、查表法和拉氏变换的性质。
1.积分法积分法是根据拉氏变换的定义进行计算,将函数 f(t) 乘以 e^(-st) 后积分。
这种方法适用于简单的函数,如指数函数、幂函数等。
2.查表法拉氏变换的常见函数对应关系可以通过查找拉氏变换表来获得。
在查表法中,将函数f(t)的拉氏变换直接从表格中找到。
这种方法适用于常见函数的变换计算,如单位阶跃函数、脉冲函数等。
3.拉氏变换的性质根据拉氏变换的性质,可以将一个复杂的函数分解成多个简单的函数,然后利用已知的变换对这些简单函数进行变换。
02第二章拉氏变换的数学方法

02第二章拉氏变换的数学方法拉氏变换是一种重要的数学工具,广泛应用于信号与系统、控制理论、电路分析、通信工程等领域。
本文将介绍拉氏变换的数学方法,包括拉氏变换的定义、性质和常见的拉氏变换对列表。
一、拉氏变换的定义拉氏变换是一种将时间域函数转换为频率域函数的数学工具。
对于一个连续时间函数f(t),其拉氏变换F(s)定义为:F(s) = L{f(t)} = ∫[0,∞] f(t)e^(-st)dt其中s是复变量,通常为一个复平面上的点。
拉氏变换可以将一个函数从时间域表示转换为频率域表示,提供了一种更便于分析和处理的数学工具。
二、拉氏变换的性质拉氏变换具有一些重要的性质,如线性性质、平移性质、尺度性质等。
下面简要介绍几个常用的性质:1.线性性质:如果f(t)和g(t)的拉氏变换分别为F(s)和G(s),那么对于任意常数a和b,有a*f(t)+b*g(t)的拉氏变换为a*F(s)+b*G(s)。
2. 平移性质:如果f(t)的拉氏变换为F(s),那么e^(-at)f(t)的拉氏变换为F(s+a)。
3. 尺度性质:如果f(t)的拉氏变换为F(s),那么f(at)的拉氏变换为(1/a)F(s/a)。
这些性质使得我们能够利用拉氏变换进行函数的变换和计算,简化了分析过程。
三、常见的拉氏变换对列表拉氏变换对列表是一些常见的函数及其在拉氏变换下的变换对。
常见的拉氏变换对列表如下:1.常数函数:L{1}=1/s2.单位阶跃函数:L{u(t)}=1/s3.单位冲激函数:L{δ(t)}=14. 指数函数:L{e^(at)} = 1/(s-a),其中a为实数5. 正弦函数:L{sin(ωt)} = ω/(s^2 + ω^2)6. 余弦函数:L{cos(ωt)} = s/(s^2 + ω^2)7. 方波函数:L{rect(t/T)} = (T/s) * sin(Ts/2)8. 指数衰减函数:L{e^(-at)u(t)} = 1/(s+a),其中a为正数这些变换对可以通过拉氏变换的定义进行推导得到,可以用于解决各种信号与系统的分析和计算问题。
第二章附录-拉氏变换

例3 : y(3) 3y 3y y 1, y(0) y(0) y(0) 0 求微分方程.
F (s)
1 s(s 1)3
b3 (s 1)3
b2 (s 1)2
b1 s 1
c4 s
b3
[
s(s
1 1)3
(s
1)3 ]s1
1
b2
d
ds
[
s(s
1 1)3
(s
1)3
]
s1
[d ds
(
1 s
一.拉氏变换
1.定义:设函数f(t)当t≥0时有定义,而且积
分
F (s) f (t)est dt
0
存在,则称F(s)是f(t)的拉普拉斯变换。
简称拉氏变换。记为 F (s) L[ f (t)]
f(t)称为 F(s)的拉氏逆变换。记为:
f (t) L1[F (s)]
2.常用函数的拉氏变换
单位阶跃函数1(t) f(t)
ci是常数
M (s) ci [ D(s) (s pi )]s pi
例1: F(s)
1
(s 1)(s 2)(s 3)
c1 c2 c3 s 1 s 2 s 3
c1
[ (s
1)(s
1 2)(s
3)
(s
1)]s 1
1 6
1
1
c2
[ (s
1)(s
2)(s
3)
(s
2)]s2
15
c3
[ (s
证:
a L[ f ( t )] f ( t )est dt
a 0a
令t / a ,则原式 f ( )esa ad aF(as)
0
(8)卷积定理
积分变换_(Laplace)课件与习题

§1 Laplace变换的概念
设指数衰减函数
(t
)
0, e
t
,
t0
( 0).
t0
考虑 f t t ,,有 f t u t =f t t 0.
若存在 0,使 lim et f t =0,则 + et f t dt .
t
-
那麽 f t u t et的傅氏积分总是存在的。
F [ f (t)u(t)et ] f (t)u(t)ete jtdt
L[ f (t)] F s f (t)estdt 0
f (t)称为F (s)的Laplace逆变换,记为f (t) L1[F (s)]. F (s)称为象函数,f (t)称为象原函数.
8
例1
求单位阶跃函数
u(t)
0 1
t 0 的拉氏变换. t 0
根据拉氏变换的定义, 有
L[u(t)] estd t 0
;
smL
t m
1 s
m!
L
t m
1 s m1
m!
(Re(s) 0).
26
练习: 求 f (t) cost 的Laplace变换.
解 因为
参见上节例3, 与这里方法不同
f (0) 1, f (0) 0, f (t) 2cost,
根据 微分性质 和线性性质
[2 cost] s2 [cost] sf (0) f (0),
对正整数n, 有
L[f
2
(n)
[(ct )o]sstn]F(
s2
s)
[scnos1
t] s,
f (0)
f (n1)(0).
所以
特[c别os地,t] 当sf2
积分变换_(Laplace)课件与习题

当函数f (t)在t<0时没有定义或者不需 要知道时, 可以认为当t<0时, f (t)0. 这时, Fourier变换的表达式为
[ f (t )] f (t )eitdt. 0
但是仍然需要f (t)在[0, )上绝对可积的条件,
这个要求限制了它的应用.
对定义在 [0,) 上的函数 f (t), 如果考虑
L[sin kt] sin kt estd t 0 1 (e jkt e jkt ) estd t 2j 0
j e(sjk)td t e(sjk)td t
20
0
j
2
s
1 jk
s
1 jk
s2
k
k2
,(Re(s)>0)
k L[sin kt] s2 k 2
5
§1 Laplace变换的概念
设指数衰减函数
(t
)
0, e
t
,
t0
( 0).
t0
考虑 f t t ,,有 f t u t =f t t 0.
若存在 0,使 lim et f t =0,则 + et f t dt .
t
-
那麽 f t u t et的傅氏积分总是存在的。
F [ f (t)u(t)et ] f (t)u(t)ete jtdt
0
0
这个积分在Re(s)>k时收敛, 而且有
e(sk )td t 1 e (sk )t 1
0
sk
0 sk
所以 L[ekt ] 1 (Re(s) k). sk
其实k为复数时上式也成立, 只是收敛区间为
Re(s)>Re(k)
10
练习: 求单位斜坡函数
拉氏变换的数学方法解答

L[cost]
s2
s
2
§2.4 典型时间函数的拉氏变换
§2.5 拉氏变换性质
例1:例L1:1Le12tec2tos3例cto1st: 33tLt3(1t)(e1st2)t s 1sc2oss1s322ts9ts32
ss6491(st64)
s
0
1
2s2 12s 6
K2
s(s
2)(s
(s 3)
2)
s
2
5
2s2 12s 6
K3
s(s
2)(s
(s 3)
3)
s
3
4
所以 可得
Y(s) 1 5 4 s s2 s3
y(t ) L1[Y (s)] 1 5e2t 4e3t
2. F(s)有重极点的情况
§2.6 拉氏反变换的数学方法
2. F(s)有重极点的情况
§2.6 拉氏反变换的数学方法
2. F(s)有重极点的情况
二、用MATLAB函数求解原函数
§2.7 用拉氏变换解微分方程
用拉氏变换解常微分方程,首先是通过拉氏变换将常微分 方程化为象函数的代数方程,然后求解象函数,最后利用 拉氏反变换求得微分方程的解。 其步骤如下:
§2.7 用拉氏变换解微分方程
§2.7 用拉氏变换解微分方程
§2.7 用拉氏变换解微分方程
§2.7 用拉氏变换解微分方程
§2.7 用拉氏变换解微分方程
§2.7 用拉氏变换解微分方程
作业:P36 2.1 (1)、(4) 2.2 (3)、(4) 2.3 2.6 (4) 2.8 (1)
拉氏变换_精品文档

拉氏变换什么是拉氏变换拉氏变换(Laplace Transform)是一种将函数从时间域转换到复频域的数学工具。
它在工程学科和物理学中有广泛的应用,特别是在控制系统分析和信号处理领域。
拉氏变换通过积分运算将一个函数从时间域(t-domain)变换到频域(s-domain),其中s是一个复变量。
拉氏变换的定义给定一个函数f(t),其拉氏变换F(s)定义为:F(s) = L{f(t)} = ∫[0, ∞] e^(-st) f(t) dt这里,s是复变量,e是自然对数的底数,t表示时间。
拉氏变换的性质拉氏变换具有许多有用的性质,以下是一些常见的性质:1.线性性质:L{af(t) + bg(t)} = aF(s) + bG(s),其中a和b是常数。
2.移位性质:L{f(t - a)} = e^(-as)F(s),其中a是常数。
3.初值定理:lim_[s→∞] sF(s) = f(0),其中f(0)是函数f(t)在t=0时的初值。
4.终值定理:lim_[s→0] sF(s) = lim_[t→∞] f(t),即函数f(t)在t→∞时的极限等于F(s)在s=0时的极限。
这些性质使得拉氏变换成为了解决微分方程问题以及计算复杂电路的有效工具。
拉氏变换的应用1. 信号处理在信号处理领域,拉氏变换用于分析和处理连续时间信号。
通过将信号从时间域转换到频域,可以更好地理解信号的频谱特性,并进行滤波、降噪、调制等处理。
2. 控制系统在控制系统分析中,拉氏变换被广泛用于研究和设计控制系统的性能和稳定性。
通过将控制系统表示为拉氏域的传输函数,可以方便地进行频率响应、稳定性分析和控制器设计。
3. 电路分析在电路分析中,拉氏变换用于求解电路的幅频特性、相频特性和传输函数。
通过将电路中的电压和电流转换到拉氏域,可以更方便地进行复杂电路的分析和计算。
4. 信号传输拉氏变换在信号传输中的应用非常广泛。
信号的拉氏变换可以帮助我们理解信号在传输过程中的衰减、失真和干扰等问题,从而优化信号传输的方案。
拉普拉斯积分变换

1
一、拉氏变换
1. 拉氏变换的概念
定义 设函数 f (t)当 t 0 时有定义,而且积分
f (t)est dt
(s是一个复参量)
0
在s的某一域内收敛,则由此积分所确定的函数
F (s) f (t)est dt 0
称为函数 f (t) 的拉普拉斯变换式(简称拉氏变换式)
34
此公式是一个复变函数的积分,通常计算起来 比较困难,但当F(s)满足一定条件时,可以用 留数学方法来计算这个反演积分,特别当F(s) 为有理函数时更为简单。
35
定理
若 s1, s2 , sn 是函数 F(s) 的所有奇点(适当选
取 使这些奇点全在 Re(s) 的范围内), 且当 s 时,F(s) 0 ,则有
根据定义,利用积分性质就可推出这个性质。 此性质表明:函数线性组合的拉氏变换等于各 函数拉氏变换的线性组合。
13
b. 微分性质 L f (t) sF (s) f (0)
证 由定义并利用分部积分法得
L f (t) f (t)estdt 0
f (t)est
0
s
0
f (t)estdt
s L f (t) f (0)
L (t)
(t) est dt
0
(t) est dt 0
(t) est dt est
t0 1
10
例7 求函数 f (t) e t (t) e tu(t)( 0)
的拉氏变换。
解 L f (t) f (t) estdt 0 e t (t) e tu(t) estdt 0
(Re(s) c)
这个性质表明:一个函数求导后取拉氏变换 等于这个函数的拉氏变换乘以参变数s,再减 去函数的初值。
拉氏变换定义,性质

拉氏变换的未来发展
理论完善
随着数学和工程领域的发展,拉普拉斯变换的理论体系将不断完 善,为解决更复杂的问题提供更有效的工具。
应用拓展
随着科技的不断进步,拉普拉斯变换的应用领域将不断拓展,例如 在人工智能、机器学习等领域的应用。
数值计算
随着计算机技术的发展,拉普拉斯变换的数值计算方法将更加精确 和高效,为实际应用提供更好的支持。
拉氏变换的定义
定义
拉普拉斯变换是一种将时域函数(通常是无限或有限时间内 的信号或系统响应)转换为复频域函数的方法。通过将时域 函数乘以相应的权函数,然后对结果进行积分,可以得到该 时域函数的拉普拉斯变换。
符号表示
通常使用符号 (L) 表示拉普拉斯变换,例如,如果 (f(t)) 是时 域函数,那么 (F(s)) 就是 (f(t)) 的拉普拉斯变换,其中 (s) 是 复频域变量。
时移性质
时移性质
若 $f(t)$ 是输入信号,$F(s)$ 是它的 拉氏变换,则 $f(t-a)$ 的拉氏变换为 $e^{-sa}F(s)$,其中 $a$ 是时移量。
应用
在系统分析中,时移性质可用于分析 系统的稳定性和动态响应。
频移性质
Hale Waihona Puke 频移性质若 $f(t)$ 是输入信号,$F(s)$ 是它的 拉氏变换,则 $f(at)$ 的拉氏变换为 $frac{1}{|a|}F(frac{s}{a})$,其中 $a$ 是频移量。
拉氏变换定义、性质
目录
• 引言 • 拉氏变换的性质 • 拉氏变换的应用 • 结论
01 引言
拉氏变换的背景和重要性
背景
拉普拉斯变换是18世纪末由法国科学家拉普拉斯提出的一种数学工具,主要用 于解决初值问题,即求解微分方程时,需要给出初始条件的问题。
积分变换第二章拉氏变换

则:
∞ f (t ) L = ∫s F ( s )d s . t
∞ ∞ ∞ f (t ) 一般地 , 有L n = ∫ d s ∫ d s⋯ ∫ F ( s )d s s s s t n次
17
例9 求函数
sht f (t ) = t
d L [ f ( t )] = −L [ tf ( t )] Re( s ) > c ds
推论
d n n L [ f ( t )] = ( −1) L[t f ( t )] Re( s ) > c n ds
n
10
f ( t ) = t 2 cos kt (k为实数 的拉氏变换 为实数) 例4 求 为实数 的拉氏变换.
2
2.拉氏变换的存在定理 若函数 (t)满足 拉氏变换的存在定理 若函数f 满足 满足: (1) 在t ≥ 0的任一有限区间上分段连续 的任一有限区间上分段连续; 的任一有限区间上分段连续 (2) 当t→+∞时, f (t)的增长速度不超过某一指数函数 即存 →+∞时 的增长速度不超过某一指数函数, →+∞ 的增长速度不超过某一指数函数 在常数 M > 0及c ≥ 0, 使得 及 |f (t)|≤ M e ct, 0≤ t <+∞ ≤ ≤ +∞ (t)的拉氏变换 则 f (t)的拉氏变换
f ( n) ( t ) = s n F ( s ) L
( Re s > c ) ( n = 1,2,⋯)
此性质可以使我们有可能将f 的微分方程 此性质可以使我们有可能将 (t)的微分方程 转化为F(s)的代数方程 的代数方程. 转化为 的代数方程
积分变换第二章拉氏变换

La1 f1(t ) a2 f2(t ) a1F1(s) a2F2(s), L1 b1F1(s) b2F2(s) b1 f1(t ) b2 f2(t )
6
例3 求 f (t)=sinkt (k为实数) 的拉氏变换
解 L[sin kt] sin kt estd t 0 1 (ejkt e jkt )e std t 2j 0
f(t)
f(tt)
O
t
t
14
例7
解
求函数 u(t
已知 L[u(t
t)
)] 1 ,
0 1
t t t t
的拉氏变换.
根据延迟性质
s
L[u(t t )] 1 est
s
(Re s 0)
u(tt)
1
O
t
t
15
5.位移性:L f (t) F(s)Re s c,则
10 4
dtL 40 4 2
40
f (t)dt } 4 43
sn
F (s)
n次
例6
求
f
t
t
0
cos
t
dt
的拉氏变换.
解
L
t 0
cos
tdt
1 s
L cos
t
1 s
s2
s
1
1 s2 1
13
4.平移性(延迟性):设L f (t) F(s) ,则
L f (t t ) est L f (t) est F (s) Re s c
(s
积分变换第二章拉氏变换
第一节 Laplace变换概念 第二节 Laplace变换性质 第三节 Laplace逆变换
第一节 Laplace变换的概念
引入
傅里叶变换的前提 绝对可积 在整个数轴上面有意义 工程上用到的函数的特点 非绝对可积 t<0,无意义
第一节 Laplace变换的概念
引入
为了克服傅里叶变换的缺点
考虑两个函数u (t )和e t
对于任意函数(t )
(t ) u (t ) 积分区间(-,+)
(t ) e
t
衰减函数使(t )绝对可积
第一节 Laplace变换的概念
引入
函数(t )先乘以u (t )e ,再取Fourier变换
t
f (t )e dt f (t )e dt
st st 0
0
£+[f(t)]
这样,我们定义拉氏变换时,严格上应为:
F (s) - f (t )e dt (Re(s) 0)
- st 0 ¥
例4 求单位脉冲函数的拉氏变换
f( t)
1
p77
t
第二节 Laplace变换的性质
类似地,可得象函数的积分性质:
£[
f (t )] F (s)ds s t
f (t ) ds F ( s )ds 一般地,£ n s s t n
性质4(位移性质) : 若,F (s) = £ [f (t)],则,
£ [ eat f (t ) ] = F(s-a) ( Re(s-a)>c)
Laplace变换的性质
性质1(线性性质):设, F1(s)= £ [f1(t)] 和 F2(s) = £[f2(t)]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 Laplace变换概念 第二节 Laplace变换性质 第三节 Laplace逆变换
第一节 Laplace变换的概念
引入
傅里叶变换的前提 绝对可积 在整个数轴上面有意义 工程上用到的函数的特点 非绝对可积 t<0,无意义
第一节 Laplace变换的概念
引入
3b
4b
t
拉氏变换中积分下限的讨论
1. 满足拉氏变换存在定理条件的函数f(t) 在t=0处有界时,则下式积分
F ( s)
0
f (t )e st dt (Re(s) 0)
与下限是 0 还是 0无关。即:
£ +[f(t)]= £ -[f(t)] 其中,£+[f(t)]为:
am ( s z1 )( s z 2 )...( s z m ) bn ( s p1 )( s p2 )...( s pn )
A( s) B( s )
1、 n m 且 B(s) 0 无重根,则:
F ( s) k k1 k 2 ... n s p1 s p2 s pn
则有,£ [ f (t ) ] = sF(s) - f(0)
这个性质说明:一个函数求导以后取拉氏 变换等于该函数的拉氏变换乘以s,再减去 函数的初值。 推论 : 若,F (s) = £ [f (t)],
则有,£ [ f (t ) ] = s 2 F (s) sf (0) f (0)
t (2).g (t ) e f ( ) a
at
第三节 Laplace逆变换
Laplace 逆变换定义 前面,我们定义了函数f(t)的拉氏变换为:
F ( s)
0
f (t )e st dt (*)
其中,F(s)称作f(t)的Laplace变换(或象函数, 而f(t) 称作F(s)的Laplace逆变换(或象原函 数),记作:
相应地: f(t) 称作F(s)的Laplace逆变换 (或象原函数),记为
1[F(s)] f(t)=£
结论
拉氏变换存在定理 若函数f(t)满足条件: 1,在t≥0任一有限区间上分段连续; 2,当t→+时, f(t)的增长速度不超过某一指 数函数,即,存在一常数M>0及 c ≥0使:
f (t ) Me , 0 t
1、若B(s)有n个单零点s1,s2,…,sn,有,
A( s ) st A( sk )e sk t Res e , sk B( sk ) B( s)
即:f (t )
k 1
n
A( sk )e , (t 0) B( sk )
sk t
2、若s1是B(s)的一个m级零点,其余的n-m 都是单零点,sm+1,…,sn,有,
1[F(s)] f(t)=£
同时,我们定义f(t)为:
f (t ) 2 j 1
j
j
F ( s)e ds , t 0
st
(#)
上式(#)就是从象函数F(s)求象原函数函 数f(t)的计算公式。右端的积分称为Laplace 反演积分。 注意到,右端积分为一复变函数的积分, 计算该积分时通常比较困难,但当F(s)满足 一定条件时,可以用留数的方法来计算这个 反演积分,特别当F(s)为有理函数时更为简 单。
f (t )e dt f (t )e dt
st st 0
0
£+[f(t)]
这样,我们定义拉氏变换时,严格上应为:
F (s) - f (t )e dt (Re(s) 0)
- st 0 ¥
例4 求单位脉冲函数的拉氏变换
f( t)
1
p77
t
第二节 Laplace变换的性质
1 L[u (t )] s
kt 例2: 求正弦函数 f (t ) e( k为实数)
p69, p71
的Laplace变换。
例3: 求正弦函数余弦函数的laplace变换
周期函数的Laplace变换 一般地,以T为周期的函数f(t) ,当f(t) 在一个周期上是分段连续时,则f(t)的 拉 氏变换式为:
0
f (t )e dt (Re(s ) 0 )
st
2. 若函数f(t) 在t=0处包含脉冲函数时,
则下式积分 F (s) f (t )e st dt (Re(s) 0)
0
0 中必须指明下限是 还是 0 。即:
£ +[f(t)] ≠ £ -[f(t)]
其中:
£-[f(t)]= 0
G ( ) (t )u (t )e
t jt
e
dt
0
f (t )e
( j ) t
dt
s j
F (s)
0
f (t )e dt
st
第一节 Laplace变换的概念
定义 设函数 f (t ) 当 t 0 时有定义,且积分
例3
sin kt 求函数f (t ) t
的拉氏变换。 p82
性质6(相似性质): 若,F (s) = £ [f (t)],a为正整数,则,
1 s £ [ f (at ) ] = F ( ) a a
例4,若F (s) = £ [f (t)],求下列函数g(t)的 拉氏变换。
(1).g (t ) f (at b)u(at b)(a, b为正整数)
ct
成立,则f(t)的Laplace变换(形如式(*)表 示)在半平面Re(s)>c上一定存在,右端的积 分在Re(s) ≥ c1>c上绝对收敛且一致收敛,并 且在Re(s)>c的半平面内,F(s)为解析函数。
举例
1 t 0 例1: 求单位阶跃函数 u (t ) 0 t 0
的Laplace变换。
1 F ( s) 1 e sT
T
0
f (t )e st dt (Re( s) 0)
0t b t , 例3: 求周期性三角波 f (t ) 2b t , b t 2b
且 f (t 2b) f (t ) 的Laplace变换。
f(t)
b
p75
b
2b
n
st 即:f (t ) Re s F ( s ) e , sk , (t 0) k 1
求Laplace逆变换的方法
三种方法求逆变换:
一、留数法 二、部分分式法 三、直接查表法
一、留数法
若函数F(s)=A(s)/B(s),其中A(s),B(s)是不可 约的多项式,B(s)的次数为n, A(s)的次数小 于n,则:
类似地,可得象函数的积分性质:
£[
f (t )] F (s)ds s t
f (t ) ds F ( s )ds 一般地,£ n s s t n
性质4(位移性质) : 若,F (s) = £ [f (t)],则,
£ [ eat f (t ) ] = F(s-a) ( Re(s-a)>c)
结论
定理: 若s ,s , …,sn是函数F(s)的所有奇点 (适当选取β使得这些奇点全落在Re(s)<β 内),且当s→∞时,F(s)→0,则有:
1 2
2 j j
1
j
st F ( s )e st ds Re s F ( s ) e , sk k 1 n
st A( s ) st 1 d m 1 A ( s ) e m ( s s1 ) B ( s ) e (m 1)! lim Res m 1 s s1 ds B ( s ) s1
A( si )e 即:f (t ) i m 1 B( si ) 1 d lim m1 (m 1)! s s1 ds
m 1 st m A( s )e ( s s1 ) , (t 0) B( s )
n
si t
举例
F ( s) 1 s(s 1)2
例1
用留数的方法求 拉氏逆变换。
的
a F ( s) 2 (s a 2 )s 2
二、部分分式法
am s m am 1S m 1 ...a1s ao F ( s) ( n m) n n 1 bn s bn 1s ...b1s b0
Laplace变换的性质
性质1(线性性质):设, F1(s)= £ [f1(t)] 和 F2(s) = £[f2(t)]
则, £[af1(t)+b f2(t)] =a F1(s)+b F2(s)
其中,a,b为常数
注意: Laplace逆变换也有类似的性质
性质2(微分性质) :
若,F (s) = £ [f (t)]
k 1 p1t 1 t e 1 注意:其中 ( s p ) k (k 1)! 1
£
E (s) 其余的 D(s)
按情况1求解即可得到f(t).
2s 1 例 求 的原函数。 s( s 1) 解:首先用部分分式展开法,将所给的象函数展开: 2s 1 A B s( s 1) s s 1 其中,A、B是待定系数,将上式进行通分后可得: A B A( s 1) Bs ( A B) s A s s 1 s( s 1) s( s 1)
一般地 :
n F ( n ) ( s) = (1)n £ [ t f (t )],Re(s)>c
性质3(积分性质) : 若,F (s) = £ [f (t)],则:
