07 特勒根和互易定理
特勒根与互易定理.ppt
0
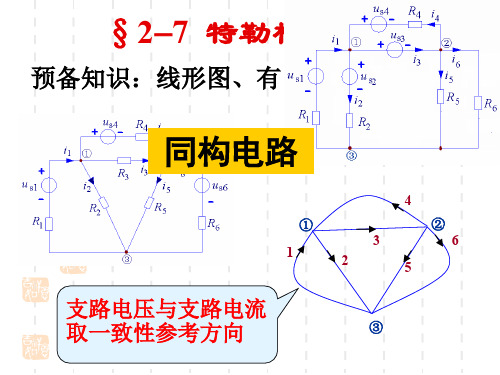
以④节点作为电位参考点,则 ①、②、③节点的电位分别为 v1、v2、v3
i1 i4 i6 0 i2 i4 i5 0 i3 i5 i6 0
u1 v1, u2 v2 , u3 v3 ,
u4
v1
v2 , u5
v2
v3 , u6
v3
v1
对于任一具有nt = n+1个节点、b条支路的电路,其 支路电流、支路电压分别为( i1,i2 ,···,ib )、 ( u1,u2 ,···, ub ),且各支路电压与电流参考方 向相关联,则在任意时刻t,均有
b
ukik 0
k 1
该定理表明,在任意电路中,在任何瞬时t,各支路 吸收功率的代数和恒等于零。也就是说,电路中各独 立源供给功率的总和,等于其余各支路吸收功率的总 和,满足功率守恒。
注意:
(1)该定理要求u(或 uˆ )和i(或 iˆ)应分别满足KVL和KCL。
特勒根定理适用于任何(线性或非线性、有源或 无源、时变或非时变)集中参数网络。 特勒根定理只与考虑电路的联接形式,与元件特性 无关。
(2)每一个支路的电流、电压均取一致的参考方向。
(3)特勒根定理既可用于两个具有相同有向图的不同 网络,k Rkikiˆk
k 1
k 1
b
b
Rkiˆkik uˆkik
k 1
k 1
u11iˆ11 u22iˆ22 uˆ11i11 uˆ22i22
互易定理的第一种形式
因为 则 故
u11 us , u22 0 uˆ22 us , uˆ11 0
I2
第5章 特勒根定理

第五章 特勒根定理5-1 引言特勒根定理是关于电网络拓扑结构的定理,它脱离了元件具体的物理性态,因而具有更普遍的意义。
特勒根定理是B.D.H. Tellegen 在本世纪五十年代初提出的[1、2]。
实际上,在此之前,已出现了许多关于特勒根定理的推导和讨论的文章[3-5]。
最早的工作应追溯到 1883年 O. Heaviside 的论文[6]。
尽管如此,先于Tellegen 的作者们没有指出定理的普遍性及其应用上的灵活性,只是将它用于一个特定的目的,或者只作出说明而没有探讨它的应用。
定理以 Tellegen 的名字命名是因为他是指出定理有普遍意义的第一人。
特勒根定理不仅具有电网络意义,它还具有更一般的应用价值,文[7]在一般数学方程组的基础上提出了广义特勒根定理,并给出了矩阵互易定理,进一步发展了这一理论。
本章介绍特勒根定理。
首先讨论特勒根定理在电网络中的表述,然后给出广义特勒根定理,并进行流图解析,最后是广义特勒根定理的应用举例。
5-2 特勒根定理定理5-1(特勒根定理1):对n 个节点b 条支路的电网络,在标定支路的参考方向后,必有0),,,(02121=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n b T b I I I V V V I V (5.1)其中,b V 和b I 分别是支路电压和支路电流向量。
证明:由第一章网络的关联性可知m Tb b nTa b I K I V K V == (5.2)各符号意义同第一章,于是有b a Tn b T b I K V I V ⋅= (5.3)由基尔霍夫电流定律0=b a I K (5.4)故必有0=b T b I V (5.5)证毕。
定理5-2(特勒根定理2):对于两个网络,若拓扑结构完全相同,且支路标定方向完全一致,必有b b 和0~=b T b I V (5.7)成立。
其中b b I V ,和b b I V ~,~分别属于两个不同网络。
证明:由于两个网络拓扑结构完全相同,并且支路标定方向一致,故在节点、支路及回路编号一致时,两者必然具有相同的关联矩阵a K 和b K ,这样有b a T n b T b I K V I V ~~= (5.8)上式显然为零。
工学07戴维南诺顿特勒根和互易定理电子教案

b
4.3 戴维南定理和诺顿定理
例4 电路如图所示,用戴维南定理求电压U
.
+ 2Ω U
4V_
4
3Ω + U_ 6Ω
.
4.3 戴维南定理和诺顿定理
第1步:求Uoc
.
+ 4V_
2Ω U o c 4
.
.
3Ω +
Uoc
_.
U oc2U 4 oc4U oc8V
4.3 戴维南定理和诺顿定理
第2步:求Req (法一)
U 3 I 2 ( I U ) 4 U 5 I 4 U 1 0 I 8 42
4.3 戴维南定理和诺顿定理
四、诺顿定理
对于任意一个线性含源二端网络NS,就其两个端钮a、b而 言,都可以用一条实际电流源支路对外部进行等效,其中电流 源的电流等于该含源二端网络在端钮处的短路电流iSC,其串联 电阻等于该含源二端网络中所有独立源置零时,由端钮看进去 的等效电阻Req。
UO*C 0.2V
b、求等效电阻Re*q。
1A 1Ω
0.8Ω c a
2Ω
2Ω
R*eq +
1Ω
0.2V
_
b d
32
Re*q
0.82
32
1、先求左边部分电路
1Ω
的戴维南等效电路。
a、求开路电压Uo*c。 1Ω
UO*C 0.2V
b、求等效电阻Re*q。
Req*
320.82 32
2、所以原电路可等效为:
试问:该电路是否可进一步 等效为如右所示的电路?
工学07戴维南诺顿特勒根和互 易定理
4.3 戴维南定理和诺顿定理
4.3 戴维南定理和诺顿定理
2.8 特勒根定理和互易定理

u2 = 0
u s1
−
u1
+
NR
(a )
u2
− 2'
2 +
根据特勒根定理证明: 根据特勒根定理证明:
i2
互易后
ˆ u1 = 0
ˆ i2 i1 = us1 us 2
iˆ2
+
iˆ1
1 +
− 1'
ˆ u1
NR
(b )
ˆ u2
− 2'
2 +
−
us 2
若us1 = us2 ,则i2 = i1.
^
XIDIAN UNIVERSITY 2011年 AM 日星期五12 2011年10月14日星期五12时 GaoJN 西安电子科技大学电路信号与系统实验中心 10/14/2011 12:56:55 10月14日星期五12时 Gao Jianning
第10-5页 10-
■
二、互易定理
对于一个仅含线性电阻的二端 口电路N 口电路 R,在只有一个激励源的情 况下,当激励与响应互换位置时, 况下,当激励与响应互换位置时, 同一激励所产生的响应相同。 同一激励所产生的响应相同。
互易定理有三种形式。详见课本第 页 互易定理有三种形式。详见课本第78页。
4 Ω 3
+
4ˆ ˆ ˆ I × 2 + ∑ uN I N + u × 0 = 0 3 ˆ ∵ ∑ uN IˆN = ∑ uN I N
解得: 解得:
ˆ I = −3 A
NR
U = 2V
−
−
应用齐次性和叠加性, 应用齐次性和叠加性,令:
I = k1 × 10 + k2 × 10
高等数学1 互易定理 -回复

高等数学1 互易定理-回复什么是互易定理?互易定理,也被称为傅里叶互易性质,是高等数学中一个重要的定理。
它描述了一个函数的傅里叶变换与它的自身的傅里叶变换之间的关系。
互易定理被广泛应用在信号处理、图像处理、量子力学等领域。
在本文中,我们将详细介绍互易定理的概念、定义、性质和应用。
1. 互易定理的概念互易定理是傅里叶变换理论的重要内容之一。
傅里叶变换是将一个函数在时域(时间域)上的表达转换为频域上的表达的数学工具。
互易定理表明,一个函数的傅里叶变换与其自身的傅里叶变换之间存在某种变换关系。
2. 互易定理的定义设函数f(t) 的傅里叶变换为F(w),则互易定理可以表述为:F(t) 的傅里叶变换为f(-w)。
换句话说,一个函数在时域上的傅里叶表示对应于另一个函数在频域上的傅里叶表示。
3. 互易定理的性质互易定理具有以下性质:3.1 线性性质:如果f(t) 的傅里叶变换为F(w),g(t) 的傅里叶变换为G(w),那么af(t)+bg(t) 的傅里叶变换为aF(w) + bG(w),其中a和b为常数。
3.2 平移性质:如果f(t) 的傅里叶变换为F(w),那么e^jwtf(t) 的傅里叶变换为F(w - w0)。
即在时域上对函数进行平移,其傅里叶变换在频域上也发生了相应的平移。
3.3 对称性质:如果f(t) 为实函数且f(t) 的傅里叶变换为F(w),那么F(t) 的傅里叶变换为2πf(-w)。
即函数在时域上的对称性对应于其傅里叶变换在频域上的反对称性。
4. 互易定理的应用互易定理在信号处理、图像处理和量子力学等领域有着广泛的应用。
4.1 信号处理中的应用:通过傅里叶变换,我们可以将一个时域上的信号转化为频域上的信号,从而实现频谱分析、滤波等操作。
互易定理可用于说明,对某个信号施加一个变换后,其频域表达将对应于原信号在另一个域中的变换。
4.2 图像处理中的应用:图像可以看作是一个二维函数,通过二维傅里叶变换,我们可以将图像在时域上的表示转化为频域上的表示。
特勒根定理

在稳态情况下,线性电容及电感为互易元件
~ ~ ~ ~ V1I1 V1I1 ZI1I1 ZI1I1 0
不是所有元件都是互易元件, 如晶体管,回转器,独立电源等等
2015-1-15 第6章 特勒根定理 9
互易定理:由互易元件组成的P端口网络一定是互易的
I1
Ip
V1
~ I1
Vp
~ Ip
由特勒根定理得:
b
~ V I k k 0
k 1
b
所有支路(变化前) 所有支路(变化后)
k 1 b
~ (Vk Vk ) I k 0
~ V I k k 0
k 1
~ Vk ( I k I k ) 0
b
k 1
nb
b ~ ~ V I V I k k k k 0 k 1
由基尔霍夫电流定律 Ka I b 0
故必有
T Vb I b
0
K b:回路-支路关联矩阵
功率守恒
T 由网络的关联性可知 Ib Kb Im
T VbT Ib VbT ( Kb Im ) ( KbVb ) Im
T
由基尔霍夫电压定律 故必有
2015-1-15
KbVb 0
VbT I b 0
T T ( I b Zb T T ~ I b Zb ) I b
Vb ZbI b Zb I b
~T Vb I b ~T T T~ T~ I b Z b I b ( I b Vb Vb I b ) T T~ I b Zb I b
T~ ( I b Vb
则称
2015-1-15
N
~ 互为伴随网络 N
特勒根定理(Tellegen’s Theorem)

b
uk i k 0
k 1
或
b
uˆk i k 0
k 1
6
证明:设两个电路的图如下图所示,取结点4为参考结点。
对电路1,可列写KVL方程,有:
u1=-un1 ; u2=un1-un3 ;
电路1 u3=un3 ; u4=un1-un2 ;
中有唯一电压源uj,其在支路k中产生的电流为ikj(图a);若支 路k中有唯一电压源uk,其在支路j中产生的电流为ijk(图b)。
a
uj + – b
线性 电阻 网络 N0
(a)
c ikj
d
a ijk
b
c
线性 电阻 网络
+ uk
N0
–
d
(b)
12
章目录 返回 上一页 下一页
则两个支路中电压电流有如下关系:
i4
+
Λ
i5
+
Λ
i6
+
un3
-
Λ
i2+
Λ
i3
-
Λ
i6
把电路2的KCL方程代入上式,可知:
6
uk
iˆk
0
k 1
此上述证明可推广至任何具有n个 结点和b条支路的电路,即有:
b
uk
iˆk
0
k 1
同理可证明定理的第二部分,即有:
b
uˆk ik 0 8
k 1
章目录 返回 上一页 下一页
4.功率守恒定理:
ukj ujk i j ik
或
ukjik ujk i j
当 ik = jj 时,ukj = ujk 。
实验一 特勒根定理和互易定理

实验一 特勒根定理和互易定理一、实验目的1、加深对特勒根定理的理解;2、加深对线性定常网络中互易定理的理解;3、进一步熟悉稳压源和直流仪表的使用。
二、实验设备1、电工实验装置(DS011)2、万用表三、实验原理1、特勒根定理a 、定理1(又名功率守恒定理):对于一个具有n 个结点和b 条支路的电路,假设各支路的电流和电压取关联参考方向,且)()(321321b b u u u u i i i i ,,,,、,,,,⋅⋅⋅⋅⋅⋅分别为b 条支路的电流和电压,则对如何时刻t ,有∑==bk kk iu 1b 、定理2(又名似功率守恒定理):如果有两个具有n 个结点和b 条支路的电路,它们具有相同的图(拓扑结构),但可以由内容不同的支路构成,假设各支路的电流和电压取关联参考方向,并分别用)()(321321b b u u u u i i i i ,,,,、,,,,⋅⋅⋅⋅⋅⋅和)ˆˆˆˆ()ˆˆˆˆ(321321b b uu u u i i i i ,,,,、,,,,⋅⋅⋅⋅⋅⋅表示两个电路中b 条支路的电流和电压,则对如何时刻t ,有∑==bk kk i u 10ˆ,∑==bk k k i u10ˆ。
2、互易定理:对一个仅含有线性电阻(不含独立源和受控源)的电路(或网络),在单一激励产生响应,当激励和响应互换位置时,响应对激励的比值保持不变。
此时,当激励为电压源时,响应为短路电流;当激励为电流源时,响应为开路电压。
互易定理存在三种形式:a 、定理1:如图4-17(a)与(b)所示电路中,N 0为仅由电阻组成的线性电阻电路,则有S S ui u i ˆˆ12=。
(a)(b)图4-1 互易定理1ui 2S uˆb 、定理2:如图4-18(a)与(b)所示电路中,N 为仅由电阻组成的线性电阻电路,则有SS i u i u ˆˆ12=。
c 、定理3:如图4-19(a)与(b)所示电路中,N 为仅由电阻组成的线性电阻电路,则有S S uui i ˆˆ12=。
互易定理的教学探究
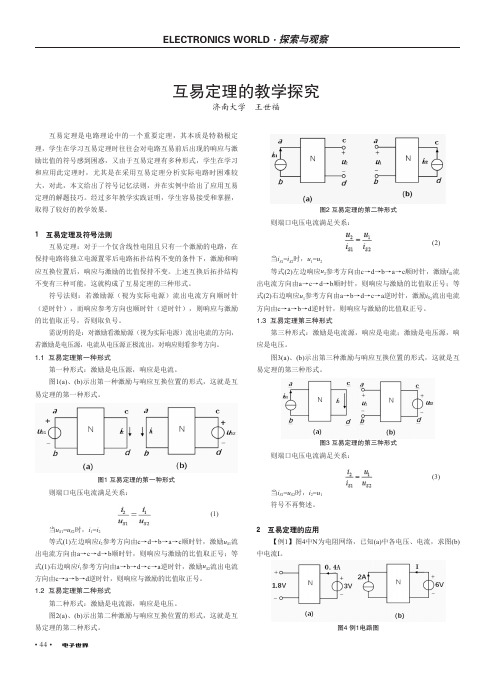
• 44•互易定理是电路理论中的一个重要定理,其本质是特勒根定理,学生在学习互易定理时往往会对电路互易前后出现的响应与激励比值的符号感到困惑,又由于互易定理有多种形式,学生在学习和应用此定理时,尤其是在采用互易定理分析实际电路时困难较大,对此,本文给出了符号记忆法则,并在实例中给出了应用互易定理的解题技巧。
经过多年教学实践证明,学生容易接受和掌握,取得了较好的教学效果。
1 互易定理及符号法则互易定理:对于一个仅含线性电阻且只有一个激励的电路,在保持电路将独立电源置零后电路拓扑结构不变的条件下,激励和响应互换位置后,响应与激励的比值保持不变。
上述互换后拓扑结构不变有三种可能,这就构成了互易定理的三种形式。
符号法则:若激励源(视为实际电源)流出电流方向顺时针(逆时针),而响应参考方向也顺时针(逆时针),则响应与激励的比值取正号,否则取负号。
需说明的是:对激励看激励源(视为实际电源)流出电流的方向,若激励是电压源,电流从电压源正极流出,对响应则看参考方向。
1.1 互易定理第一种形式第一种形式:激励是电压源,响应是电流。
图1(a)、(b)示出第一种激励与响应互换位置的形式,这就是互易定理的第一种形式。
图1 互易定理的第一种形式则端口电压电流满足关系: (1)当u S 1=u S 2时,i 1=i 2等式(1)左边响应i 2参考方向由c →d →b →a →c 顺时针,激励u S 1流出电流方向由a →c →d →b 顺时针,则响应与激励的比值取正号;等式(1)右边响应i 1参考方向由a →b →d →c →a 逆时针,激励u S 2流出电流方向由c →a →b →d 逆时针,则响应与激励的比值取正号。
1.2 互易定理第二种形式第二种形式:激励是电流源,响应是电压。
图2(a)、(b)示出第二种激励与响应互换位置的形式,这就是互易定理的第二种形式。
互易定理的教学探究济南大学 王世福图2 互易定理的第二种形式则端口电压电流满足关系:(2)当i S 1=i S 2时,u 1=u 2等式(2)左边响应u 2参考方向由c →d →b →a →c 顺时针,激励i S 1流出电流方向由a →c →d →b 顺时针,则响应与激励的比值取正号;等式(2)右边响应u 1参考方向由a →b →d →c →a 逆时针,激励i S 2流出电流方向由c →a →b →d 逆时针,则响应与激励的比值取正号。
互易定理和特勒根定理的联系 -回复

互易定理和特勒根定理的联系-回复互易定理和特勒根定理是电路理论中两个重要的定理,它们在电路分析和设计中起到了至关重要的作用。
本文将详细探讨这两个定理之间的联系,并介绍它们的基本原理以及实际应用。
首先,我们来介绍一下互易定理。
互易定理是电路理论中的一个基本定理,它指出两个电路在终端具有相同电压和电流的情况下,它们可以互相替换,不影响电路的性质和特性。
简单来说,互易定理可以帮助我们简化电路的分析和设计。
要理解互易定理的原理,我们先来看看它的数学表达。
设有两个电路A和B,它们在终端具有相同的电压和电流,即Va=Vb和Ia=Ib。
根据互易定理,我们可以得出以下结论:1. 电流互易:如果在电路A中,电压源和电流源的位置对调,且其他元件保持不变,那么电路A和B等效。
2. 电压互易:如果在电路A中,电压源和电流源的位置对调,且其他元件保持不变,那么电路A和B等效。
上述结论是互易定理的基本原理,也是我们应用互易定理进行电路设计和分析的依据。
通过互易定理,我们可以将电路中的电压源和电流源进行互换,从而简化电路的计算。
接下来,我们来介绍一下特勒根定理。
特勒根定理是电路理论中的另一个重要定理,它用于分析和解决电路中的不确定性问题。
特勒根定理可以帮助我们确定由于电路元件参数的变化而引起的电路性能的变化范围。
特勒根定理的原理比较复杂,但可以通过以下步骤来进行分析和计算:1. 首先,我们需要确定电路中的不确定性参数,例如电阻、电感和电容的值。
2. 然后,我们通过对这些不确定性参数进行一定的波动范围设定,例如设定电阻值在±5的范围内变化。
3. 接下来,我们使用特勒根定理来确定电路性能的变化范围。
特勒根定理可以帮助我们确定电路输出的最小值和最大值,以及这些值出现的条件和概率。
4. 最后,根据特勒根定理的计算结果,我们可以进行电路设计和优化,以满足特定的要求和性能指标。
特勒根定理在电路设计和分析中具有广泛的应用。
通过特勒根定理,我们可以确定不同参数变化对电路性能的影响范围,从而对电路进行可靠性分析和优化。
互易定理和特勒根定理的联系 -回复

互易定理和特勒根定理的联系-回复互易定理和特勒根定理作为电路分析中的两个重要定理,是我们理解和解决电路问题的基础。
虽然它们是两个独立的概念,但它们在某种程度上是相互联系的。
本文将一步一步回答互易定理和特勒根定理之间的联系,并探讨它们在电路分析中的应用。
首先,让我们分别介绍一下互易定理和特勒根定理。
互易定理是电路分析中的一个重要定理,它基于基尔霍夫定律,指出一个线性电路中,如果电压源和电流源互换位置,同时将电阻网络也互换位置,电路的行为不会发生改变。
特勒根定理则是基于纯粹电阻网络的,它指出在一个纯粹电阻网络中,如果我们确定了一个特定的电阻已经存在,并且移除这个电阻所造成的影响,不会改变电路的任何其他属性,我们可以通过特定的计算方法,将这个电阻还原到电路中,并求得电路的新的特性参数。
接下来,让我们来看一下互易定理和特勒根定理之间的联系。
互易定理的基本思想是通过对电源和电阻网络的互换来改变电路的形式,而特勒根定理则是通过对电阻网络中的一个特定电阻的移除和还原,来改变电路的特性。
在互易定理中,我们可以通过将电流源和电压源互换位置,同时将电阻网络互换位置,来实现电路的转换。
这意味着我们可以通过使用互易定理,将一个复杂的电路转换为一个等效的简化电路,以更方便地进行分析。
而在这个转换过程中,我们可能会移除一些电阻或者添加一些电阻,这就涉及到了特勒根定理的应用。
特勒根定理要求我们确定一个特定的电阻已经存在,并且在移除这个电阻对电路没有其他影响的情况下,通过一些计算方法将其还原到电路中。
在这个还原过程中,我们需要使用一些杂项电压方法或者杂项电流方法来确定电路中的其他参数。
因此,特勒根定理可以在互易定理中起到一种补充的作用,帮助我们确定电路中的一些参数。
此外,互易定理和特勒根定理在实际应用中也有一些相似之处。
它们都可以被广泛地应用于无源网络和有源网络的分析,并且可以通过使用不同的电路分析技术来求解电路问题。
例如,互易定理和特勒根定理都可以与基尔霍夫定律、欧姆定律和其他电路分析方法相结合,来求解复杂的电路问题。
特勒根定理

特勒根定理特勒根定理是一个不可变定理,它证明了数论中著名的四平方定理。
这个定理由德国数学家威廉特勒根于1825年提出,其原文如下:“任意正整数,用它的四个平方数之和就可以表示成一个形式:a^4+b^4+c^4+d^4。
”特勒根定理的发现让数论的发展取得了重大突破。
因为它所指示的想法使数论定理的推不可断。
因此,对于数论理论家来说,它也是有史以来最重要的定理之一。
特勒根定理给了数论学家们一种攻克数论最难的问题的方法:四平方定理,也就是通过任意正整数的四个平方数之和表示成一个四项式的形式。
证明这一定理,可以使学者们更容易地攻克其它数论问题。
1835年,另一位德国数学家加布里埃尔-哈勒,凭借特勒根定理的基础上,提出了摩根定理,这一定理表明,任意正整数可以表示成一个三项式的形式:a^3+b^3+c^3。
由此可见,特勒根定理曾经是数论领域取得重大成就的根基。
后来,印度数学家兰克尔用数学证明了特勒根定理,这也是数论理论的一个重大里程碑。
仿佛特勒根的定理推开了数论的大门,指出了数论的方向,从而使数论的理论性有了更大的发展。
随着计算机技术的发展,特勒根定理在计算机算法中也发挥了重要作用。
比如,蒙特卡罗算法中,用特勒根定理可以加快算法的求解速度;此外,特勒根定理也被用来解决密码藏和数论组合方面的问题。
特勒根定理也被用来证明数论猜想。
另外,它还被用来解决超级计算机系统和物理学系统中的问题。
以上就是特勒根定理的历史、具体内容及其应用,它的重要性不言而喻,它对数论理论的发展及应用于计算机科学、密码藏、超级计算机系统等方面的影响都不可低估。
特勒根定理的创立,不但让传统的数论发展有了机遇,也引领了数论未来发展的方向。
特勒根定理适用范围

特勒根定理适用范围
特勒根定理,又叫Toeplitz定理,是线性代数中的一个重要定理。
它被广泛运用于数学、物理学、工程学和其他领域中。
特勒根定理可
以解决很多实际问题,因此它的适用范围非常广泛。
特勒根定理主要研究n阶复矩阵,其中每一行都是上一行的旋转。
特别地,对于任何复数序列(a1,a2,...,an),如果矩阵Toepliz
A是其滑动对称矩阵,则A具有均值。
Toeplitz算符是指A将序列映
射到左移的序列并将其与序列的原始版本的乘积的序列求和。
因此,Toeplitz极限定理通常涉及到在n趋于无穷的情况下,尺寸增长到无
穷的Toeplitz矩阵的极限行为发生的现象。
特勒根定理可以应用于信号处理中的很多问题。
在图像处理方面,通过将图像离散化为矩阵,然后将矩阵转换为Toeplitz矩阵,就可以
使用特勒根定理的方法来实现去噪、增强等操作。
在语音识别中,许
多人公式可以直接使用特勒根定理进行计算,以获得较高的精度和速度。
在时间序列分析中,特勒根定理被用来识别周期性变化和趋势性
变化,从而可以预测未来的趋势。
此外,特勒根定理还被广泛用于研究共形场论、天体物理学等领
域中的问题。
它作为一个重要的工具被应用于不同领域中,以研究实
际问题的解决方案。
总结来说,特勒根定理是线性代数中的重要定理,它的适用范围
非常广泛。
它可以应用于信号处理、时间序列分析、共形场论、天体
物理学等众多领域中,并且其被广泛运用以提高计算精度和效率。
因此,深入理解特勒根定理的含义和应用,对于解决实际问题具有重大的指导意义。
第9讲 特勒根定理和互易定理
电压源
开路
KCL
14
对偶电路
is2
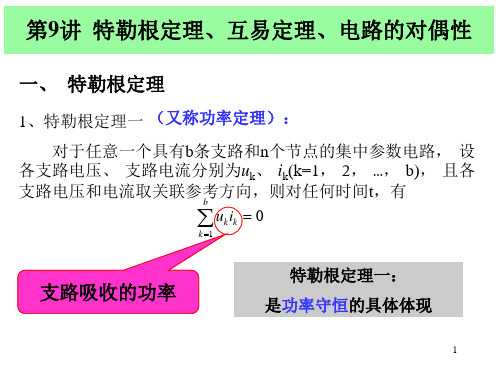
( R1 R2 )i1 R2 i2 us1
R2i1 + ( R3 R2 )i2 us2
(G1 G2 )u1 G2u2 is1
G2u1 + (G2 G3 )u2 -i s2
比较这两组方程, 可看出, 它们的形式相同, 对应变量 为对偶元素, 所以通常把这两组方程称为对偶方程组。电路
u1i1 u2i2 u3i3 u4i4 u5i5 u6i6 u7i7 (u1 u2 u3 )i2 (u4 u5 u7 )i4 u6i6 u6 (i2 i4 i6 ) 0
+ u3 _
i2 i4 i6 0
KVL和KCL可知:
u
k 1
b
k k
i 0
u
k 1
b
k k
i 0
具有功率的量纲, 但不表示任何支路的功 率,称为拟功率。 率,称为拟功率 特勒根定理一是当特勒根定理二中电路N与
3 ^ 为同一电路的特例。 N
证明: 选节点d为参 考节点, 对 独立节点a 、b、 c列出电路的 KCL方程为
i i i 0 1 3 4
中把像这样一个电路的节点方程与另一个电路的网孔方程对
偶的两电路称为对偶电路。
15
第9讲 特勒根定理、互易定理、电路的对偶性
结
束
作业:P123 2-28、2-30 自行学习:P104~117----2.10和2.11 复习:第1 、2章
16
k 1
支路吸收的功率
特勒根定理一:
是功率守恒的具体体现
1
电路定理III-特勒根定理、互易定理、对偶原理

由特勒根定理,得 10 ix 0 i2 ukiˆk 0 3b 0 i1 (5) 1 uˆkik 0 3
ukiˆk ik Rkiˆk ikuˆk
10ix 5 ix 0.5A
返回首页
互易定理 (Reciprocity Theorem)
电路定理
第三讲(总第十四讲)
特勒根定理 互易定理 对偶原理
特勒根定理(Tellegen’s Theorem)
一、具有相同拓扑结构的电路
2
2
+
-
1
4
1
4
3
3
N
+–
2
N 2
2
2
13
13
14
5 3
4 14
5 3
4
6
6
2
2
例:
2
2
13
13
14
5 3
4
14
5 3
4
N6
6
N
*对应支路取相同的参考方向
*各支路电压、电流均取关联的参考方向
(G1+G2)un1- G2 un2 = is1 -(G2 - gm )un1+(G2+G3) un2 = 0
对应元素 网孔电阻阵 CCVS T形
节点导纳阵 VCCS 形
两个电路互为对偶电路。
二、对偶原理 两个对偶电路N,N,如果对电路N有命题
(或陈述)S成立,则将S中所有元素分别以其对应的对偶
k 3
k 3
k 3
a
iˆ2 c
线性电
+
iˆ1 阻网络 uˆS
N
–
b
(b)
特勒根定理和互易定理

特勒根定理和互易定理————————————————————————————————作者:————————————————————————————————日期:特勒根定理和互易定理1、特勒根定理1特勒根定理1内容为:对于一个具有n个结点和b条支路的电路,假设各支路电流和支路电压取关联参考方向,并令、分别为b条支路的电流和电压,则对任何时刻t,有此定理对任何具有线性、非线性、时不变、时变元件的集总电路都适用,它实质上是电路功率守恒的数学表达式。
2、特勒根定理2特勒根定理2内容为:如果两个具有n个结点和b条支路的电路,它们具有相同的图,但由不同的支路构成。
假设各支路电流和支路电压取关联参考方向,并分别用、和、表示两电路中b条支路的电流和电压,则对任何时刻t,有此定理同样对任何具有线性、非线性、时不变、时变元件的集总电路都适用,但它不再是电路功率守恒的数学表达式。
有时称它为“拟功率定理”。
它仅仅是对两个具有相同拓扑的电路中,一个电路的支路电压和另一个电路的支路电流之间所遵循的数学关系。
<?xml:namespace prefix = o />3、互易定理的使用条件1)电路只含有一个独立电源;2)电路中没有受控源;3)电路中的所有无源元件全部为线性电阻。
4、互易定理1互易定理1内容为:对于一个线性无源网络NS,外加激励电压与网络响应电流互换位置时,响应电流相同,如图1所示,即=,则有。
图1互易定理15、互易定理2互易定理2内容为:对于一个线性无源网络N,外加激励电流与网络响应电压互换位置时,响应电压相同,如图2所示,即=,则有。
图2互易定理26、互易定理3互易定理3内容为:对于一个线性无源网络N,若激励在数值上相等,即=,则有,如图3所示。
图3互易定理3。
2-7特勒根定理

• 特勒根定理(Tellegens theorem)是在基尔霍夫定 律的基础上发展起来的一条重要的网络定理。 与基尔霍夫定律一样,特勒根定理与电路元件 的性质无关,因而能普遍适用于任何集中参数 电路。
• 特勒根定理有两条:
(1)特勒根功率定理 (2)特勒根似功率定理
电路的图 (graph) : 线形图(linear graph)
注意:每一个支路的电流、电压均取一致的参考方向。
2. 特勒根似功率定理
设有两个由不同性质的二端元件组成的电路N和
ˆ , 二者的有向图完全相同 。 N
6
ˆ ui ˆ u i ˆ u i ˆ u i ˆ u i ˆ u i ˆ u i k k 11 22 33 44 55 66
k 1
v1 (i1 i4 i6 ) v2 (i2 i4 i5 ) v3 (i3 i5 i6 ) v4 (i1 i2 i3 ) 0
将这一结论推广到任一具有nt = n+1个节点、b条支路的电路,则 有
i
k 1
b
k k
0
这就是特勒根功率定理(Tellegens power theorem)的数学表达式。 该定理表明,在任意电路中,在任何瞬时t,各支路吸收功率的 代数和恒等于零。 用特勒根功率定理可检验电路计算结果是否正确。
将以上结论推广到任意两个具有nt = n+1个节点、b条支路的电路N
ˆ ,当它们所含二端元件的性质各异,但有向图完全相同 时, 和N
则有
ˆ 0 u i kk
k 1
b
ˆ i u
k 1
b
k k
0
这就是特勒根似功率定理(Tellegens quasi-power theorem)的数 学表达式。该定理表明,在有向图相同的任意两个电路中,在 任何瞬时t,任一电路的支路电压与另一电路相应的支路电流的 乘积的代数和恒等于零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④
若选节点4为参考节点,则有:
1 0 0
电路
1 1 0
0 1 0
0 1 1
0 0 1
1 0 1
i1 i 2 i3 0 i4 i 5 i6
KCL 的另一种 形式
Ai = 0
支路,则称图G1为图G的一个子图.
①.
②
.
.③
①.
②
.
.③
①.
②
.
.③
④
.
④
.
图a 如图a、图b均为原图G的子图.
电路
图G
图b
南京理工大学
4.4 特勒根定理
图论基础
连通图:当图G中任意两个节点之间至少存在一条由支路 所构成的路径时,称为连通图,反之称为非连通图.
.
+ Us_
Rs C
M
.
*
RL
*
.
.
求等效电阻的一般方法
开路短路法
+ uoc _
.
N
N
R eq u oc isc
.
isc
注意:uoc与isc的方向在断路与短路支路上关联
电路 南京理工大学
4.3 戴维南定理和诺顿定理
最大功率传输
a
+ Req + U _uOC _
b
I
RL
当 R L R eq 时
电路
p p max
U
2 OC
Aa-完全关联矩阵:反映支路与节点的关联关系.
电路 南京理工大学
4.4 特勒根定理
Aai = 0, Aa-完全关联矩阵, i-支路电流列向量
①
1 6 ② 2 3 5 ④
a jk 1 1 0
4
③
1 0 0 1
1 1 0 0
0 1 0 1
0 1 1 0
R
a R3
R2
+ U _R
4
_b + U2
电路
+ U
_
南京理工大学
(1)
U oc = 1 0 V
R eq = 10
Pm a x =
U oc 4 R eq
2
10
2
4 10
2 .5 W
(2) R = 2.5 , PR 2 m in 0 W
电路
南京理工大学
第4章 电路定理
目 录
i1
i2
N0
图a
+ u 2 i2 _
+
3Ω
u1 _
N0
图b
u2 _ u s2 _
+ +
解: N 0 :
Λ
u 1 u s1 2 0 V , i1 1 0 A , u 2 0,
i2 2 A
N 0 : u 1 4 3 1 2 V , i 1 4 A , u 2 u s2 ? i 2 ?
3
5 ④
1 0 0 1
1 1 0 0
0 1 0 1
0 1 1 0
0 0 1 1
1 0 1 0
i1 i 2 i3 i4 i 5 i6
0
Aai = 0 KCL的矩阵形式
a a N b
iS=iSC
a
NS
iSC
b
a
RS=Req
b N0
b
电路
Req
南京理工大学
4.3 戴维南定理和诺顿定理
求等效电阻的一般方法
外加激励法(原二端网络中独立源全为零值)
i
N0 + u_ N0
i
+ u _ i
R eq
u i
注意:u与i的方向向内部关联
电路 南京理工大学
4.3 戴维南定理和诺顿定理
定理1(功率守恒定理):
定理一、若网络N具有n个节点,b条支路,并设 支路电压向量与支路电流向量分别为:
u i
T
u1 , u 2 , , u b i1 , i 2 , , i b
T
且各支路电压电流为关联参考方向,则:
u i 0 (i u 0 )
作业
4-16
电路
南京理工大学
附加作业1:如图所示电路中,当RL=?时, RL 可获最大功率,并求此功率值.
12Ω
+ 18V _
2Ω 9A 4Ω
电路
+
6Ω
_ 2I RL
I
3Ω
南京理工大学
附加作业2:已知图中N0为线性电阻无 源网络,当us1=10V, us2=0V, Is=4A时, I1=4A, I2=2A; 当us1=0V, us2=0V, Is=2A时, I1=1A, I2=-1A; 问us1=0V, us2=10V, Is=0A时, I1=? I2 I1 + + us1 N0 us2 _ _
这个电路结构所服从的KCL和KVL方程时,一个元件电路
就可以抽象成一个线图.
电路
南京理工大学
4.4 特勒根定理
图论基础 1、图(Graph):用线段代替电路中的支路,并 保留原电路中的节点,如此所构成的点线图, 称为原电路对应的图,用G表示。
R6
①.
②
.
+ Us1 _
R2
Is4
.③
R5
R3
④
.
G
南京理工大学
① 1
6 ② 2 4 ③
② 4 3 5 5 ④
③
3
④ G
如移节点①,支路1,2,6不能保留。
电路 南京理工大学
4.4 特勒根定理
图论基础
③
① 1
6 ② 2 4
节点 1: i 1 i 2 i 6 0 节点 2: i 2 i 3 i 4 0 节点 3: i 4 i 5 i 6 0 节点 4: i 1 i 3 i 5 0
电路
4.4 特勒根定理
图论基础 图反映了支路和节点关联的情况,而不能反映 出各支路的具体元件。
R6
①
.
R2
②
.
+ Us1 _
Is4 R3
.③
R5
①.
②
.
.③
④
.
④
.
G
电路 南京理工大学
4.4 特勒根定理
图论基础
同构电路:具有相同图的电路. R6
①.
②
.
+ Us1 _
R2
Is4
.③
R5
①. ②
R3
i1 i 2 i3 0 i4 i 5 i6
1 0 0
1 1 0
0 1 0
0 1 1
0 0 1
1 0 1
得KVL的矩阵形式:
u A un
T
电路 南京理工大学
4.4 特勒根定理
T T T T
T ˆ ˆT 0, u i 0, i u 0
同理可证:iˆ T u
电路
南京理工大学
4.4 特勒根定理
例: 已知图中N0为线性电阻无源网络,由图a中测得us1=20V, i1=10A, i2=2A, 当图b中 iˆ =4A时,试用特勒根定理求 u ˆ
1
s2
i1 + us1 _ + u1 _
T T
即功率守恒: b
电路
uk ik 0
南京理工大学
k 1
4.4 特勒根定理
特勒根定理
定理 1 证明:
已知支路电压与节点电压之间的关系为:u = ATun
T 则: T i ( A T u n ) T i u n ( A T ) T u
un ( Ai) 0
T
同理可证:T u i
.
ቤተ መጻሕፍቲ ባይዱ
.
非连通图
电路
南京理工大学
4.4 特勒根定理
支路、节点分属两个集合,支路必须落在节点上. 当移去支路时,节点予以保留.
6 ② 2 1 3 5 孤 立 节 点 4 ③
①
①
·
②
4
3 5 ④
③
④
G
如移支路1,2,6,节点①可保留。
电路 南京理工大学
4.4 特勒根定理
当移去节点时,与该点相联的支路全部移去.
4 R eq
南京理工大学
4.3 戴维南定理和诺顿定理
利用戴维南定理分析含受控源的电路
原则 :
1. 控制量和被控量在一个电路中.
(控制量为端口U或I除外)
2. 求Req要用一般方法(外加激励法、开路短路法)
电路
南京理工大学
例:如图所示电路中,在R=10 Ω时,有U=5V, U2=3V,在R=40 Ω时,有U=8V, U2=6V, 试问: (1)当R=?时, R可获最大功率,并求此功率值; (2)当R=?时, R2可获最小功率,并求此功率值; Is R1
Is6④
.
.③
.
①.
②
R1
电路
R2 + Us3
.
.③
R4 R5
④
.
G
_
④
.
南京理工大学
4.4 特勒根定理
图论基础
有向图:在图G中,标出原电路图中各支路电压、电流 关联参考方向的图. i6
