1990年北京市中学生数学竞赛初二年级初赛试题_完美手打版

北师大版八年级上数学竞赛试卷完整版.doc

八年级数学竞赛试卷第1页，共2页八年级数学竞赛试卷一．选择题（每题5分，共30分）1.要从4424333x y x y y x +===的图象得到直线，就要将直线（） A 、向上平移23个单位 B 、向下平移23个单位 C 、向上平移2个单位 D 、向下平移2个单位2.把aa -111-）（中根号外的）（1-a 移入根号内得（） A 、1-a B 、a -1 C 、—1-a D 、—a -13.如果ab ＞0，bc ＜0，那么直线bcx －a b －y =不经过第（）象限.A 、一B 、二C 、三D 、四4. 点P 关于x 轴的对称点1P 的坐标是（4，－8），则P 点关于原点的对称点2P 的坐标是（） A 、（－4，－8） B 、（4，8） C 、（－4，8） D 、（4，－8）5.你一定知道乌鸦喝水的故事吧！一个紧口瓶中盛有一些水，乌鸦想喝，但是嘴够不着瓶中的水，于是乌鸦衔来一些小石子放入瓶中（如图），瓶中水面的高度随石子的增多而上升，乌鸦喝到了水。

但是还没解渴，瓶中水面就下降到乌鸦够不着的高度，乌鸦只好再去衔些石子放入瓶中，水面又上升，乌鸦终于喝足了水，哇哇地飞走了。

如果设衔入瓶中石子的体积为x ，瓶中二．填空题（每题5分，共30分）6.足球比赛的记分规则是：胜一场记3分，平一场记1分，负一场记0分；一支中学生足球队参加了15场比赛，负了4场，共得29分，则这支球队胜了场。

7.已知72π⎡-⎢⎣，，，其中无理数有个。

8.某班有48人准备去西湖划船，每条小船坐3人，租金16元，每条大船坐5人，租金24元，10.在平面直角坐标系中，把直线y=3x 沿y 轴向下平移后得到直线AB ，如果点N （m ，n ）是直线AB 上的一点，且3m ﹣n=2，那么直线AB 的函数表达式为．三．解答题（每题10分，共60分） 11.已知1-a +2)2(-ab =0，求ab 1+)1)(1(1++b a +)2)(2(1++b a +…+)2006)(2005(1++b a 的值。

北京市初二数学竞赛试题

2003年北京市初二数学竞赛试题初赛一、选择题(满分36分)1．2003+2003×2003-2003÷2003的值是(A)4065 (B)2003 (C)4014011 (D)80140172．如图1，在由单位正方形组成的网格图中标出了AB ，CD ，EF ，GH 四条线段，其中能构成一个直角三角形三边的线段是(A)CD ，EF ，GH (B)AB ，CD ，EF(C)AB ，CD ，GH (D)AB ，EF ，GH3．已知a c c b y b a x -=-=-1，则x+y 的值等于 (A)0 (B)一1 (C)1 (D)0．54．平面内的7条直线任两条都相交，交点数最多有a 个，最少有b 个.则a+b 等于(A)42 (B)41 (C)21 (D)225．已知a-b=5且c-b=10，则a 2+b 2+c 2-ab —bc —ca 等于(A)105 (B)100 (C)75 (D)506．存在这样的有理数a ，b ，c 满足a ＜b ＜c ，使得分式+-+-c b b a 11ac -1的值等于 (A)-2003 (B)0(C)2003 (D)2003- 二、填空题(满分64分)1．大、中、小三个正整数，大数与中数之和等于2003，中数减小数之差等于l000．试确定这三个正整数的和．2．在△ABC 中，AB=BC ，高线AD=21BC ，AE 为∠BAC 的平分线，确定∠EAD 的度数。

3．已知a 1，a 2，a 3，a 4，a 5，a 6，a 7是彼此互不相等的正整数，它们的和等于159，求其中最小数a 1的最大值．4．四边形ABCD 中，AD ∥BC ，AB+CD=12，AD+BC=8，M 为∠A 的平分线和∠B 的平分线的交点，N 为∠C 的平分线和∠D 的平分线的交点，求MN 的长．5.若x,y 是实数，且,446422y x y xy x m --+-=确定m 的最小值．6．如图2，四边形ABCD 中，AB=BC=CD ，,150,90 =∠=∠BCD ABC 求BAD∠的度数．7．兄弟二人养了一群羊．当每只羊的价钱(以元为单位)的数值恰等于这群羊的只数时，将这群羊全部卖出．兄弟二人平分卖羊得来的钱；哥哥先取l0元，弟弟再取l0元；这样依次反复进行．最后，哥哥先取10元，弟弟再取不足l0元．这时哥哥将自己的一顶草帽给了弟弟，兄弟二人所得的钱数相等．问这顶草帽值多少钱?8．已知a ，b 均为正数，且a+b=2，求1422+++=b a u 的最小值．复赛一、填空题(满分40分)1. 若,)12(01223344555a x a x a x a x a x a x +++++=-则=+42a a 。

北师大版八年级数学上册竞赛试卷

北师大八年级数学第一学期竞赛试卷一、选择题（每小题4分，共40分）1．如图，已知棋子“卒”的坐标为(－2，3)，棋子“马”的坐标为(1，3)，则棋子“炮”的坐标为( )A ．(3，2)B ．(3，1)C ．(2，2D ．(－2，2)2.下列实数中是无理数的是（）A ．3.14B ．31C ．3D ．93.点P 位于y 轴左侧，x 轴上方，距y 轴3个单位，距x 轴4个单位，则点P 的坐标为( )A ．(3，－4)B ．(－3，4)C ．(4，－3)D ．(－4，3) 4．16的平方根是（）A ．4B ．4±C ．4-D ．2±5．甲、乙两位探险者到沙漠进行探险，某日早晨8：00甲先出发，以6千米/小时的速度向东行走，1小时后，乙出发，以5千米/小时的速度向北行进，上午10：00，甲、乙两人相距( )A ．10千米B ．11千米C ．12千米D ．13千米 6．某单位为鼓励职工节约用水，作出了以下规定：每位职工每月用水不超过10 m 3的，按每立方米m 元水费收费；用水超过10 m 3的，超过部分加倍收费，某职工某月缴水费16m 元，则该职工这个月实际用水为( )A ．13 m 3B ．14 m 3C ．18 m 3D ．26 m 37.若二元一次方程组⎩⎨⎧2x ＋y ＝3，3x －y ＝2和方程2x －my ＝－1有公共解，则m 等于( )A ．－2B ．－1C ．4D ．38.右图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是( )A ．乙前4秒行驶的路程为48米B ．两车到第3秒时行驶的路程相等C ．在0到8秒内甲的速度每秒增加4米/秒D ．在4至8秒内甲的速度都大于乙的速度9.如右图，直线m 是一次函数y ＝kx ＋b 的图象，则k 的值是( )A ．－1B ．－2C ．1D ．210.在如图所示的数轴上，点B 与点C 关于点A 对称，A ，B 两点对班级：姓名：考场：考号：应的实数分别是3和－1，则点C 所对应的实数是( )A ．1＋3 B ．2＋3 C ．23－1 D ．23＋1二、填空题（每小题5分，共40分）11.三只猴子分一堆苹果，老大猴子先拿走了这一堆苹果的一半少一只，老二猴子拿了余下的苹果的一半多一只，小猴子分得了余下的8只苹果，问这堆苹果有只。

北京市初二数学竞赛初赛试题(1992)

初二初赛试题一、选择题(每小题6分，满分36分．)1．已知α是等边三角形的一个内角，β是顶角为30°的等腰三角形的一个底角，γ是等腰直角三角形的一个底角．则( )．(A)α<β<γ (B)γ<α<β (C)β<α<γ (D)α<γ<β2．(-2)4的平方根是( )．(A)-4 (B)±4 (C)2 (D)±23．下面有四个命题：①两个三角形有两边及一角对应相等，则这两个三角形全等；②两个三角形有两角及一边对应相等，则这两个三角形全等；③两个三角形的三条边分别对应相等，则这两个三角形全等；④两个三角形的三个角分别对应相等，则这两个三角形全等．其中真命题是( )．(A)②，③ (B)①，③ (C)③，④ (D)②，④-4．若P是两位的正整数，则可能成立的等式是( )，(A)x2+px+2001＝(x-29)(x-69)(B)x2+px+2001＝(x-23)(x-87)(C)x2+px+2001＝(x+23)(x+87)(D)x2+px+2001＝(x+29)(x+69)5．下面列举的平行四边形的判定条件中，不正确的一个是 ( )。

(A)两组对边分别相等(B)两组对角分别相等(C)一组对边平行，一组对角相等(D)一组对边平行，另一组对边相等6．在1 500年以前，我国古代伟大数学家祖冲之计算出圆周率π的七位小数值是3.1415926<π<3.1415927，并取113355为密率，722为约率，则，113355、π、722之间的正确关系是( )． (A) 722< 113355<π (B) 113355<π<722(C)π<113355<722 (D) 722<π<113355二、填空题(每小题8分，满分64分．)1．p 是负整数，且2001+P 是一个完全平方数，则P 的最大值为 2.如图，四边形ABCD 是正方形，△CDE 是正三角形，则∠AEB 的度数为3，若a 、b 都是正整数，且143a+500b ＝2001,则a+b 的值是 4．若有理数x ，y ，z 满足x +1-y +2-z =21(x+y+z)，则(x-yz)3的值为 5.如图，将边长为12厘米的正方形ABCD 折叠，使得A 点落在边CD 上的E 点，然后压平得折痕FG ，若GF 的长为13厘米，则线段CE 的长为 . 6．化简后=+++++++722-17562-15422-13302-11202-9122-762-522-37.将1～2001这2001个自然数依次写成一行，组成一个新的自然数，新的自然数除以9的余数为 8．已知实数x ，y 满足方程⎪⎩⎪⎨⎧=++=++6y x 232y xy x 22则|x+y+1|的值是参考答案1.B2.B3.A4.D5.D6.C1.-652.30°3. 94.-1255.76. 27. 68.3+22001年北京市初二年级数学竞赛复赛一、填空题(满分40分，每小题8分) 1．已知有理数x 满足方程200111x x 20011=--，则29x 2001x 43+-= 2．如图所示，正方形ABCD 的面积是64 cm 2，正方形CEFG 的面积是36 cm 2，DF 与BG相交于点O ，则△DBO 的面积等于 cm 2．3．已知a 2+b 2=6ab 且a>b>0，则ba ba -+= 4．化简表达式43333 |17160a 131a |17160a 131a 6 `⎥⎥⎦⎤⎢⎢⎣⎡-+--+-+,所得的结果等于． 5．在边长为1cm 的正△ABC 中，P 0为BC 边上一点，作P 0 P 1⊥CA 于点 P 1，作P 1P 2⊥AB 于点P 2，作P 2P 3⊥BC于点P 3．如果点P 3恰与点P 0重合，则△P 1P 2P 3的面积是 cm 2．二、(15分)证明恒等式：a 4+b 4+(a+b)4=2(a 2+ab+b 2)2．三、(15分)在六张纸片的正面分别写上整数l 、2、3、4、5、6，打乱次序后，将纸片翻过来，在它们的反面也随意分别写上1～6这六个整数，然后计算每张纸片正面与反面所写数字之差的绝对值，得出六个数．请你证明：所得的六个数中至少有两个是相同的四、(15分)如图所示，在等腰△ABC 中，延长边AB 到点D ，延长边CA 到点E ，连结DE ，恰有AD=BC=CE=DE ．求证：∠BAC=100°五、(15分)l 与0交替排列，组成下面形成的一串数101，10101，1010101，101010101……请你回答，在这串数中有多少个质数?并请证明你的论断．2002年北京市初二数学竞赛初赛一、选择题(满分36分) 1．计算8008160061400413003120021-+-+( )A ．60061 B ．70073- c 80085 D ．90097-2．2002年8月，将在北京召开国际数学家大会，大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a ，较短直角边为b ，则a 3+b 4的值等于( )．A ．35B ．43C ．89D ．973．若20022002………200215(n 个2002)被15整除，则n 的最小值等于( )． A ．2 15．5 C ．4 D ．54．两个边长为3，4，5的直角三角形纸片，可以拼成n 种不同的凸四边形，则n 的值等于( )． A ．6 B ．5 C4 D ．35．已知三角形三个内角的度数都是质数，则这三个内角中必定有一个内角等于( )． A ．2度 15．3度 C ．5度D ．7度6．a 4+4分解因式的结果是( )．A ．(a 2+2a －2)(a 2—2a+2)B ．(a 2+2a--2)(a 2－2a －2)C ．(a 2+2a+2)(a 2—2a －2)D ．(a 2+2a+2)(a 2—2a+2) 二、填空题(满分64分，每小题8分) 1．计算：(1＋3 )2002—2(1+3)200l－2(1+3)20002．如图所示，AC=10，BC=l7，CD⊥AB 于点D ，CD=8，求△ABC 的面积．3．实数a ，b 满足ab≠O，且使得ba b a b b a a +++=+++111，求a+b 的值． 4．在梯形ABCD 中，下底BC=10 cm ，腰CD=5．5 cm ，如果∠ABC=50°，∠ADC=100°，求上底AD 的长．5．已知实数x ，y,z 满足1=+++++y x z x z y z y x ，求．yx z x z y z y x +++++222的值．6．如图所示，P 是边长为8的正方形ABCD 形外一点，PB=PC ，△PBD 的面积等于48，求△PBC 的面积．7．正数m ，n 满足m+4mn －2m －4n +4n=3，求2002282++-+n m n m 的值．8．一个正整数除以5，7，9及11的余数依次是1，2，3，4．求满足上述条件的最小的正整数．2002年北京市初二数学竞赛初赛一、选择题1．C 2．B 3．B 4．C 5．A 6．D 二、填空题1．0 2．84 3．-2 4．4．5 5．0 6．32 7．4011-8．1731 2002年北京市中学生数学竞赛复赛一、填空题(满分40分，每小题8分)1．已知x 2+y 2+z 2-2x+4y-6z+14=O ，则(x-y-z)2002= ．2．如图所示，A 在线段BG 上，四边形ABCD 和四边形DEFG 都是正方形，面积分别为7 cm 2和11 cm 2，则三角形CDE 的面积等于 cm 2． 3．化简： 3232-++== ．4．如图所示，四边形ABCD 是正方形，E 为BF 上一点，四边形AEFC 恰是一个菱形，则∠EAB= ．5．有6个学生，每人拥有的书中没有相同的，但每两个人都恰好有一本相同的书，每本书也恰好两个学生拥有，则这6个学生共有不同的书本．二、(满分15分)已知abc≠0，证明：四个数,)(,)(,)(,)(3333abcc b a abc b a c abc a c b abc c b a ------++中至少有一个不小于6．三、(满分15分)如图所示，△ABC 是正三角形，△A 1B 1 C 1的三条边A 1B 1、B l C 1、C 1 A 1交△ABC 各边分别于C 2、C 3，A 2、A 3，B 2、B 3．已知A 2C 3=C 2B 3=B 2 A 3，且C 2C 32+B 2B 32=A 2A 32。

北京市初二数学竞赛学生版

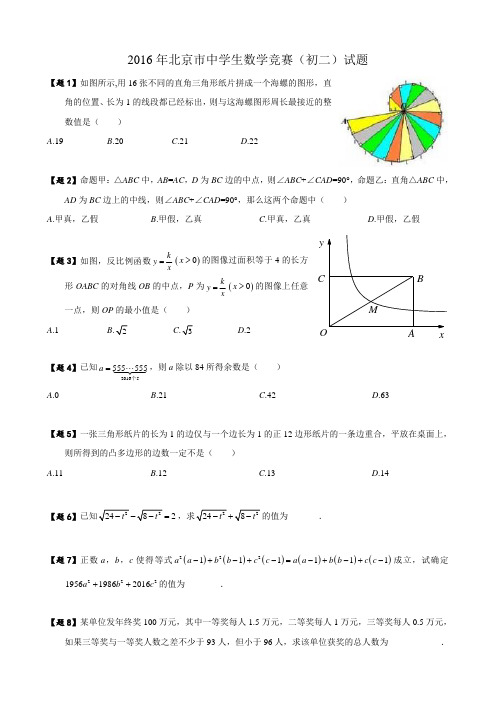
2016年北京市中学生数学竞赛（初二）试题【题1】如图所示,用16张不同的直角三角形纸片拼成一个海螺的图形，直角的位置、长为1的线段都已经标出，则与这海螺图形周长最接近的整数值是（）A .19B .20C .21D .22【题2】命题甲：△ABC 中，AB =AC ，D 为BC 边的中点，则∠ABC +∠CAD =90°，命题乙：直角△ABC 中，AD 为BC 边上的中线，则∠ABC +∠CAD =90°，那么这两个命题中（）A .甲真，乙假B .甲假，乙真C .甲真，乙真【题3】如图，反比例函数ky x=()0x >的图像过面积等于4的长方形OABC 的对角线OB 的中点，P 为ky x=()0x >的图像上任意一点，则OP 的最小值是（）A .1B C D .2【题4】已知20165555555a = 个，则a 除以84所得余数是（）A .0B .21C .42D .63【题5】一张三角形纸片的长为1的边仅与一个边长为1的正12边形纸片的一条边重合，平放在桌面上，则所得到的凸多边形的边数一定不是（）A .11B .12C .13D .14【题6】2=的值为_______．【题7】正数a ，b ，c 使得等式()()()()()()222111111a a b b c c a a b b c c -+-+-=-+-+-成立，试确定222195619862016a b c ++的值为________．【题8】某单位发年终奖100万元，其中一等奖每人1.5万元，二等奖每人1万元，三等奖每人0.5万元，如果三等奖与一等奖人数之差不少于93人，但小于96人，求该单位获奖的总人数为____________．yOC【题9】△ABC 中，∠BAC =45°，∠ABC =60°，高线AD 与BE 相交于H ，若AB =1，求四边形CDHE 的面积_________．【题10】如果正整数x ，y 满足等式22842016x x y ++=，求32x y +的值__________．【题11】已知正整数a ，b ，c ，d 满足ab cd =，求证：2016201620162016a b c d +++是合数．【题12】△ABC 是正三角形，在BC 上取点1A ，2A ，在CA 上取点1B ，2B ，在AB 上取点1C ，2C ，使得凸六边形121212A A B B C C 的边长都相等，如图所示，求证：直线12A B ，12B C ，12C A 相交于．A 1A 2B 1B 2C 2C 1CBA【题13】一个自然数n若能表示为若干个正整数的和，且这些正整数的倒数和也恰等于1，则称n为“金猴数”，比如248822+++=且111112488+++=，22就是一个“金猴数”（1）证明：11与28是两个“金猴数”；（2）证明：如果n是“金猴数”，则22n+、29n+也是“金猴数”；（3）请你判定：2016也是“金猴数”．。

初二数学竞赛试卷及答案.docx

2015年初二下学期数学竞赛试卷本卷满分120分，考试时间120分钟一选择题（5*6=30）1、多项式a? + b~ — 2a — 4b + 5的值总为（）A 、非负数B 、零C 、负数D 、正数2、关于x 的方程2匕 =1的解是正数，则。

的取值范围是（）%-1A 、a > —1B 、a > —1且a H0C 、a v —1D 、av —1 且a H —23•如图，甲、乙两动点分别从正方形ABCD 的顶点，A 、C 同时沿正方形的边开始移动甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的4倍，则它们第2014 次相遇在边（） A. AB 上 B. BC 上 C. CD±D. DA ±k4. 如图，已知梯形ABCO 的底边AO 在兀轴上,BC 〃AO, AB 丄AO,过点C 的双曲线y = —x交OB 于D,且OD : OB=1 : 2,若AOBC 的面积等于3,则k 的值（）3 24A.等于2B.等于一C.等于一D.无法确定4 55. 如图，以RtAABC 的斜边BC 为一边在AABC 的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4, AO=6V2 ,那么AC 的长等于（）A 12B 4A /3C 16D 85/2■D- 乙K 二（第3题）2 9 26•若关于x 的方程x + _ = c +二的解是尢严c,兀严一，则关于x 的方程x + X C C的解是（( 2B. a — 19 --- a-l (5*6=30)小2 Ce Cl 9 a-i------ =a + --------- x — 1 ci — 1a + \ a , ----a-\2A. d f — 二填空题 7•如下图，在直角坐标系中，已知点A （・3, 0）, B （0, 4）,对AOAB 连续作旋转变换，依次 D. A第4题EA（1） ____________________________ 表中第8行的最后一个数是 ,它是自然数的平方，第8行共有 ____ 个数；（2） ____________________________________________ 用含n 的代数式表示：第n 行的第一个数是 _______________________________________ ,最后一个数是 _______ ,第n行共有 _________ 个数；12,设有n 个数X 】，X2, X3 ...••• Xn 它们每个数只能取0, 1, -2,三个数中的一个，且 X1+X2+X3+ … +x n = —5 x 12+x 22+x 32+ • • • +x n 2=19 ,贝lj Xi'+X2‘+X3‘+・・・+Xn'= _______________A J J&已知点卩（兀,y ）位于第二象限，并且y < 2% + 6, x 、y 为整数，则点卩的个数是 ______ o9.如图，AABC 中，点D 、E 、F 分别在三边上，AD 、BE 、CF 交于1（）,如图，P 是平行四边形内一点，过点P 分别作AB,AD 的平行线，交平行四边形四边形的四边于E 、F 、G 、H,若S 四边形PFCG=10, S 四边形AHPE =6,贝|JSA PBD = ________________________________11、如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答。

初二数学竞赛试题A4.docx

初二数学竞赛试题填空题：（第1-20题每题3分，共60分） 1. 如图，已知 AB 〃DE, ZCDE 二2ZABC 二 140° ,则ZBCD= ____ 度. 1 1 1 1 1 1 1 1 2. ------------------------------------------------------------------------------------------- 设S^R —, S 9=l+—, S 3=l+—,……,S n =l+—+ ------------------------------------------- , l 2 22 22 32 32 42 n 2 (n+1)2 +--------------------掘 -----------X!----------- 竦--------------------《)獗HK-《){oeH "#円於料K s DIP 猎凶載於楼 7 . 1 1 3. 设/+i = 3a, Z?2+l=3/7,且QHb,则代数式—+ —的值为 _________________________ • a- 4. 已知一次函数y=ax+b 的图象经过一、二、三象限，且与x 轴交于点（-2, 0）,则不等式 ax>b 的解集是 __________ . 5. 如图，把一个长26cm ,宽14cm 的长方形分成五块，其中两个大正方形和两个长方形分别全等.那么中间小正方形的面积是 ___________ cm 2. 6. 如图是正方体的表面展开图，相对两面数字之和相等，且A+B+C 二14,则6A-2B+3O ___ . （第1颍）（第5题） 7. 已知关于兀的不等式- 2 < 0的负整数解只有-1, -2,则加的取值范圉是 _________________ . 8. 小陈乘坐一辆出租车前往宁波栋社机场，该车起步价10元（路程3km 以内），3km 以上每行驶lkm 增加2元,不足lkni 时按lkm 计算且每次需付燃油附加费1元。

初二数学竞赛题含答案)

初中数学竞赛初二第1试试题一、选择题(每小题7分共56分)1、某商店售出两只不同的计算器，每只均以90元成交，其中一只盈利20%，另一只亏本20%，则在这次买卖中，该店的盈亏情况是( )A 、不盈不亏B 、盈利2.5元C 、亏本7.5元D 、亏本15元2、设20012000,20001999,19991998===c b a ，则下列不等关系中正确的是( ) A 、c b a << B 、b c a << C 、a c b << D 、a b c <<3、已知,511ba b a +=+则b a a b +的值是( ) A 、5 B 、7 C 、3 D 、31 4、已知xB x A x x x +-=--1322，其中A 、B 为常数，那么A ＋B 的值为( ) A 、－2 B 、2C 、－4D 、45、已知△ABC 的三个内角为A 、B 、C ，令B A A C C B +=+=+=γβα,，则γβα,,中锐角的个数至多为( )A 、1B 、2C 、3D 、06、下列说法：(1)奇正整数总可表示成为14+n 或34+n 的形式，其中n 是正整数；(2)任意一个正整数总可表示为n 3或13+n 或23+n 的形式，其中；(3)一个奇正整数的平方总可以表示为18+n 的形式，其中n 是正整数；(4)任意一个完全平方数总可以表示为n 3或13+n 的形式A 、0B 、2C 、3D 、47、本题中有两小题，请你选一题作答：(1)在19991002,1001,1000 这1000个二次根式中，与2000是同类二次根式的个数共有……………………( )A 、3B 、4C 、5D 、6(2)已知三角形的每条边长是整数，且小于等于4，这样的互不全等的三角形有( )A 、10个B 、12个C 、13个D 、14个8、钟面上有十二个数1,2，3，…,12。

将其中某些数的前面添上一个负号，使钟面上所有数之代数和等于零，则至少要添n 个负号，这个数n 是( )A 、4B 、5C 、6D 、7二、填空题(每小题7分共84分)9、如图，XK ，ZF 是△XYZ 的高且交于一点H ，∠XHF ＝40°，那么∠XYZ ＝ °。

第一学期八年级数学竞赛练习题6份

第一学期八年级数学竞赛练习题1 (1)第一学期八年级数学竞赛练习题2 (7)第一学期八年级数学竞赛练习题3 (13)第一学期八年级数学竞赛练习题4 (17)第一学期八年级数学竞赛练习题5 (22)第一学期八年级数学竞赛练习题6 (25)第一学期八年级数学竞赛练习题1(满分120分,时间120分钟)一、选择题(每小题5分,共40分)1．已知一列数a 1，a 2，a 3…a n 中，a 1=0，a 2=2a 1+1，a 3=2a 2+1，…a n+1=2a n +1 ，则a 2004-a 2003的个位数字是（）A. 2B. 4C. 6D. 82. 在△ABC 中，AB=13，AC=15，高AD=12，则BC 的长是（） A.14 B.4 C.14或4 D.以上都不正确3. 如图，四边形ABCD 是正方形，直线l 1，l 2，l 3分别通过A ，B ，C 三点，且a//b//c ，若a 与b 的距离为5，b 与c 的距离为7，则正方形ABCD 的面积等于（）A. 70B.74C.144D.1484.已知对于任意有理数a 、b,关于x,y 的二元一次方程：(a ＋b)x －(a －b)y ＝a －b 都有一组公共解，则这个公共解为（） A.00x y =⎧⎨=⎩ Ｂ.11x y =-⎧⎨=⎩ Ｃ. 12x y =⎧⎨=⎩ D.01x y =⎧⎨=-⎩5. 把自然数n 的各位数字之和记S(n),如：n ＝38,S(n)＝3＋8＝11；n ＝247,S(n)＝2＋4＋7＝13, 若对于某个自然数n 满足:n －S(n)＝2007,则n 的最大值是（） A.2019 B.2021 C.2023 D.20256. 如图是一个由几块相同的小正方体搭成的立体图形的三视图，则这堆立体图形中的小正方体共有（）块。

A. 7B. 8C. 9D. 107. 已知p 、q 均是质数，且满足5p 2+3q=59，则以p+3、1-p+q 、2p+q-4为边长的三角形的形状（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形8. 某校准备开办一些学生课外活动的兴趣班，有计算机班、奥数班、英语口语班和音乐艺术班，结果反映热烈。

1990年北京市初二数学竞赛初赛试题

1990年北京市初二数学竞赛初赛试题一、选择题（每小题7分，共56分） 1. a 是任意实数，则a a --的值为A. 必大于零B. 必小于零C. 必不大于零D. 必不小于零【解析】若0a ≥，则0a a a a --=-=；若0a <，则2a a a a a --=--=-≥0，选D ．2. a 表示一个两位数，b 表示一个四位数，把a 放在b 的左边组成一个六位数，那么这个六位数应表示成A. abB. 10000a b +C. 10010000a b +D. 100a b +【解析】a 作为前两位，b 作为后四位，应该写成0000a b +的形式，即为10000a b +，选B ．3. 如图，在ABC △中，42A ∠=︒，B ∠和C ∠的三等分线分别交于D E ，，则BDC ∠的度数是A. 67︒B. 84︒C. 88︒D. 110︒ 【解析】由“飞镖模型”可知：()13BDC A ABD ACD A ABC ACB ∠=∠+∠+∠=∠+∠+∠ ()121806033A A A =∠+︒-∠=∠+︒ 24260883=⨯︒+︒=︒，选C ．4. 如图，在ABC △中，P 是AC 上一点，取BP 的中点Q ，过CQ 并延长与AB 交于D ，则ABP △的面积ABP S △与ACD △的面积ACD S △的大小关系是A. ABP ACD S S <△△B. ABP ACD S S =△△C. ABP ACD S S >△△D. 不能确定【解析】连接AQ ，记BDQ ADQ BCQ S a S b S c ===△△△，，，则由题意可知 APQ S a b =+△，CPQ S c =△，由“燕尾定理”得a b c bc a++=， ∴1c a b ca b++=>，∴c a >， ∴ABP ACD S S <△△，选A ．5. 设0a b c d >>>>，且X =，YZ =，则X Y Z 、、的大小关系为A. X Z Y <<B. Y Z X <<C. X Y Z <<D. Z Y X << 【解析】22X ab cd ==++22Y ac bd ==++22Zad bc ==++，则()()220X Y ab cd ac bd a d b c -=+--=-->， ()()220Y Z ac bd ad bc a b c d -=+--=-->， ∴2220X Y Z >>>，∴0X Y Z >>>，选D ．6. 在四个实数中，如果任意三个之和都不比另一个小，则下列说法中必定错误的是EDCB AQP DCBAc a+b cb aQP D CBAA. 非零的数不可能只有一个B. 四个数可以都是正数C. 负数有两个D. 如果有零就没有负数【解析】由题意得a b c d ++≥，a b d c ++≥，a c d b ++≥，b c d a ++≥，则0a b c d +++≥，若这四个数中有两个负数，设为c d ，，则a b c d ++≥，此时b c d a ++<，不合题意，选C ．7. x y 、只能取A. 2553029464x y ==，B. 3761526855x y ==，C. 1512332477x y ==，D. 2832628614x y ==，【解析】首先，奇数的平方被8除余1，那么两个奇数的平方和被8除余2，而偶数的平方一定能被4整除，则可以排除B 和C ．其次，一个完全平方数的尾数只可能是0，1，4，5，6，9，而D 中22x y +的尾数为2，也不可能．所以选A ．8. 已知实数a b 、分别满足424230a a--=和4230b b +-=，则代数式4444a b a +的值等于A. 175B. 55C. 13D. 7【解析】根据题意，222b a -、是关于x 的一元二次方程230x x +-=的两个根，且222b a-≠，∴2221b a-+=-，2223b a -=-，()24422422442224422227a b b b b b a a a a a 2⎛⎫+⎛⎫⎛⎫=+=+-=-+--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，选D ．二、填空题（前6个题，每题6分，第7个题8分，共44分）1. =_____________．【解析】原式()()211111119901990119901==--⨯+．2. 设实数x y 、满足2242420x y x y ++-+=，则22y x +_____________．【解析】左边配方得()()221210x y ++-=，∴112x y =-=，，∴221y x +--3. 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分，则这个等腰三角形的底边的长为______________．【解析】设腰长为2x ，底边长为y ，由题意得21221x x x y +=⎧⎨+=⎩或22112x x x y +=⎧⎨+=⎩，解得417x y =⎧⎨=⎩或75x y =⎧⎨=⎩，检验发现第一组解无法构成三角形，不合题意舍去，所以，等腰三角形的底边长为5cm ．4._____________．【解析】2，2=10=5+5，而(22=24255<=，<5. 某厂二月份产量比一月份产量提高12.5%，三月份产量比二月份产量提高20%，那么三月份的产量比一月份产量提高的百分数为______________．【解析】设一月份的产量为x ，由题意可得二月份的产量为()112.5%x +，三月份的产量为()()27112.5%120%20x x ++=，则三月份得产量比一月份产量提高了2735%20x x x ⎛⎫-÷= ⎪⎝⎭．6. 如图，AB BC CD ==，AD AE =，DE BE =，则C ∠的度数为_________．【解析】设BDE EBD x ∠=∠=，则2AED ADE x ∠=∠=，在ADE △中，1804A x ∠=︒-， ∴1804C A x ∠=∠=︒-，又1801803CDB ADB x ∠=︒-∠=︒-，则1803CBD CDB x ∠=∠=︒-，在BCD △中，180C CBD CDB ∠+∠+∠=︒， ∴180418031803180x x x ︒-+︒-+︒-=︒， ∴36x =︒，则180436C x ∠=︒-=︒．7. 如图1，我们规定在边长为1的正方形方格纸上，从格点O 到与它相邻的格点A 、B 、C 、D 、E 、F 、G 、H 的直线运动形成的线段分别记为数码0，1，2，3，4，5，6，7．如以点O 为始点，数码2代表线段OC ，数码7代表线段OH 等等．在图2中画出了从P 点出发，依次按数码001223355的轨线图形.请你在图3的边长为1的正方形方格纸上，从点M 出发，依次按数码006756442312画出相应的轨线图形，___________．图3图2图1【解析】依题意画轨线图形如图所示：的正方形有5个，边长为2的正方形有3的正方形有4个，边EDCBA长为1个，共有534113+++=个．。

初二年级数学竞赛题[含答案解析]

初中数学竞赛初二第1试试题一、选择题(每小题7分共56分)1、某商店售出两只不同的计算器，每只均以90元成交，其中一只盈利20%，另一只亏本20%，则在这次买卖中，该店的盈亏情况是( )A 、不盈不亏B 、盈利2.5元C 、亏本7.5元D 、亏本15元2、设20012000,20001999,19991998===c b a ，则下列不等关系中正确的是( ) A 、c b a << B 、b c a << C 、a c b << D 、a b c <<3、已知,511ba b a +=+则b a a b +的值是( ) A 、5 B 、7 C 、3 D 、31 4、已知xB x A x x x +-=--1322，其中A 、B 为常数，那么A ＋B 的值为( ) A 、－2 B 、2C 、－4D 、45、已知△ABC 的三个内角为A 、B 、C ，令B A A C C B +=+=+=γβα,，则γβα,,中锐角的个数至多为( )A 、1B 、2C 、3D 、06、下列说法：(1)奇正整数总可表示成为14+n 或34+n 的形式，其中n 是正整数；(2)任意一个正整数总可表示为n 3或13+n 或23+n 的形式，其中；(3)一个奇正整数的平方总可以表示为18+n 的形式，其中n 是正整数；(4)任意一个完全平方数总可以表示为n 3或13+n 的形式A 、0B 、2C 、3D 、47、本题中有两小题，请你选一题作答：(1)在19991002,1001,1000 这1000个二次根式中，与2000是同类二次根式的个数共有……………………( )A 、3B 、4C 、5D 、6(2)已知三角形的每条边长是整数，且小于等于4，这样的互不全等的三角形有( )A 、10个B 、12个C 、13个D 、14个8、钟面上有十二个数1,2，3，…,12。

将其中某些数的前面添上一个负号，使钟面上所有数之代数和等于零，则至少要添n 个负号，这个数n 是( )A 、4B 、5C 、6D 、7二、填空题(每小题7分共84分)9、如图，XK ，ZF 是△XYZ 的高且交于一点H ，∠XHF＝40°，那么∠XYZ＝ °。

全国初中数学联赛(初二组)初赛试卷(一)及答案

全国初中数学联赛(初二组)初赛试卷班级：: 姓名：成绩：一、选择题（本题满分42分，每小题7分） 1、()︒---+1|3|4π的值是（）A 、4B 、5C 、8D 、92、若()()222-+=+-bx x a x x ，则=+b a （）A 、1-B 、0C 、1D 、23、如图，已知在ABC ∆中，BO 平分ABC ∠，CO 平分ACB ∠，且AB OM //，AC ON //，若6=CB ，则OMN ∆的周长是（）A 、3B 、6C 、9D 、124、不等式组⎪⎩⎪⎨⎧++≥+23131221x x x x π的解是（） A 、16≤-x π B 、16ππx - C 、16πx ≤- D 、16≤≤-x5、非负整数x ，y 满足1622=-y x ，则y 的全部可取值之和是（）A 、9B 、5C 、4D 、36、如图，已知正方形ABCD 的边长为4，M 点为CD 边上的中点，若M 点是A 点关于线段EF 的对称点，则EDAE等于（） A 、35 B 、53C 、2D 、21二、填空题（本题满分28分，每小题7分）1、已知0|3|22=++-+-y x x ，则_________22=+y x .2、已知31=+x x ，则_____________132=++x x x.MNOACBFE M GDA CB3、设⎩⎨⎧=++=++36542332z y x z y x ，则___________23=+-z y x .4、如图，在ABC ∆中，BC AC =，且︒=∠90ACB ，点D 是AC 上一点，BD AE ⊥，交BD 的延长线于点E ，且BD AE 21=，则_________=∠ABD . 三、（本大题满分20分）先化简后，再求值：244412222+-÷⎪⎭⎫ ⎝⎛++--+-a a a a a a a a ，其中12-=a .四、(本大题满分25分)如图，已知直角梯形OABC 的A 点在x 轴上，C 点在y 轴上，6=OC ，10==OB OA ，AB PQ //交AC 于D 点，且︒=∠90ODQ ，求D 点的坐标。

北京市中学生数学竞赛初二年级竞赛试题.doc

一、（分 25 分，每小只有一个正确答案，答得5 分）1.当 m1，代数式21 5m m 9 mm 3的是（）6 m 2 9 m 2 m 3 m 3A. －1B.1C.1D.1222.一个正八形中最的角等于a ，最短的角等b ，个正八形的面（）A. a 2 b 2B. a 2b 2C.a bD. ab3. 111 1 16 11 26 26 1 1 的是（）.6 11 16 2121 31 31 36A.1B.1C.1D.1183633664.若 n 是正整数， 1×2×3×⋯× n=n! ，比如 1！=1，4！=1×2×3×4=24，等等，若 M=1! ×2！×3！×4！×5！×6！×7！×8！×9！， M 的数中是完全平方数的共有（）A.504 个B.672 个C.864 个D.936 个5.将 2009 表示成两个整数的平方差的形式，不同的表示方法有（）A.16 种B.14 种C.12 种D.10 种二、填空（分 35 分，每小 7 分）1.45.12 13.9 2 45.1 13.9 的等于.31.22.平行四形 ABCD 中，AD= a ，CD=b ，点 B 分作 AD 上的高h a 和 CD 上的高 h b ，已知 h a a ， h b b ，角AC=20 厘米，平行四形 ABCD的面平方厘米 .3. 0 a 1 1 2 3 28 29，并且 a a a a a 18 ，已知30 30 30 30 30则 10a 等于.（其中x 表示不超过 x 的最大整数）4.已知△ ABC 中，∠A，∠B，∠C 的外角度数之比为α∶β∶γ（α，β，γ均为正数），则∠ A ∶∠ B∶∠ C 等于（.用含α，β，γ的式子之比表示）5.当1x 2 时，经化简x 2 x 1x 2 x 1 等于.三、（满分 10 分）已知 a b c 0 ，a2b2c21.（1）求ab bc ca的值（2）求a4b4c4的值四、（满分 15 分）如图所示，六边形ABCDEF 中， AB=BC=CD=DE=EF=FA ，并且∠ A+ ∠C+∠E=∠B＋∠ D＋∠ F，求证∠ A＝∠ D，∠ B=∠E，∠ C=∠ F.五、（满分 15 分）BCA DF E（1）证明：由 2009 个 1 和任意个 0 组成的自然数不是完全平方数；（2）试说明，存在最左边 2009 位都是 1 的形如1111的自然数2009个1（其中 * 代表阿拉伯数码）是完全平方数.。

-1990年全国初中数学联合竞赛试卷

1990年全国初中数学联合竞赛试卷第一试一、选择题本题共有8个小题，每小题都给出了(A)、(B)、(C)、(D)四个结论，其中只有一个是正确的，请把正确结论的代表字母写在题后的圆括号内。

1．31231131144++-++的值是（）（A ）1 （B ）－1 （C ）2 （D ）－22．在△ABC 中,AD 是高,且AD 2 = BD ²CD ，那么∠BAC 的度数是（）（A ）小于90° （B ）等于90°（C ）大于90° （D ）不确定3．方程k k k x k x (02)13(722=--++-是实数)有两个实根α、β，且0＜α＜1，1＜β＜2，那么k 的取值范围是（）（A ）3＜k ＜4；（B ）－2＜k ＜－1；（C ）3＜k ＜4或－2＜k ＜－1 （D ）无解。

4．恰有35个连续自然数的算术平方根的整数部分相同，那么这个相同整数是（）（A ）17 （B ）18 （C ）35 （D ）365．△ABC 中，22=AB ，2=AC ，2=BC ，设P 为BC 边上任一点，则（）（A ）PB PA<2²PC （B ）PB PA =2²PC （C ）PB PA >2²PC （D ）PB PA 与2²PC 的大小关系并不确定 6．若六边形的周长等于20，各边长都是整数，且以它的任意三条边为边都不能构成三角形，那么，这样的六边形（）（A ）不存在（B ）只有一个（C ）有有限个，但不只一个（D ）有无穷多个7．若b a log 的尾数是零，且2log log 1log a b b b a a>>，那么下列四个结论：（）（1）21a b b>> （2）0log log =+a b b a （3）10<<<b a （3）01=-ab 中，正确的结论的个数是（）（A ）1 （B ）2 （C ）3 （D ）48．如图，点P ，Q ，R 分别在△ABC 的边上AB 、BC 、CA 上，且1====RC QR PQ BP ，那么，△ABC 面积的最大值是（）（A ）3 （B ）2 （C ）5 （D ）3二、填空题1．已知82121=+-x x ，则xx 12+= 2． 2223,2,1，…，1234567892的和的个位数的数字是3．方程01)8)((=---x a x ，有两个整数根，则=a4． △ABC 中，2==AC AB ，BC 边有100个不同的点1P ，2P ，…，100P ，记i i i BP AP m +=2²C Pi ( =i 1，2，…，100) 则 ++21m m …100m +=第二试一、已知在凸五边形ABCDE 中，∠BAE = 3α，BC=CD=DE ，且∠BCD=∠CDE=180°－2α，求证：∠BAC=∠CAD=∠DAE二、[]x 表示不超过实数x 的最大整数，令{}[]x x x -=（1）找出一个实数x ，满足{}11=⎭⎬⎫⎩⎨⎧+x x（2）证明：满足上述等式的x ，都不是有理数三、设有n n 22⨯个正方形方格棋盘，在其中任意的n 3个方格中各有一枚棋子。

北京市1990年中学生数学竞赛初中二年级初试试题及答案

北京市1990年中学生数学竞赛初中二年级初试试题及答案岳荫巍
【期刊名称】《数学教学研究》
【年(卷),期】1990(0)4
【总页数】2页(P39-40)
【作者】岳荫巍
【作者单位】
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.北京市1982年中学生数学竞赛初中二年级试题 [J], ;
2.北京市一九九○年中学生数学竞赛初中二年级初试试题 [J], 史树德
3.上海市1990年高三年级数学竞赛试题及答案 [J], 马积祥
4.北京市一九九○年中学生数学竞赛高中一年级初试试题 [J], 岳荫巍
5.北京市1989年中学生数学竞赛高一试题及解答 [J], 周春荔
因版权原因，仅展示原文概要，查看原文内容请购买。

北师大版八年级数学竞赛题

xOAy北师大版八年级数学竞赛试题一、选择题（每小题3分，共27分）1、下列式子正确的是（）A、9)9(2-=- B、525±= C、1)1(33-=- D、2)2(2-=-2、如下是一种电子计分牌呈现的数字图形，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．3、某校八年级8位同学一分钟跳绳的次数分别为：150，164，168，172，176，168，183，185．则由这组数据得到的结论中错误的是（）A．中位数为170 B．众数为168C．平均数为170.75 D．平均数为1704、不能判定四边形ABCD是平行四边形的是 ( )A、AB = CD，AD = BCB、AB∥CD，AB = CDC、AD∥BC，AB = CDD、AB∥CD，AD∥BC5、若点P（m+2,m+1）在y轴上，则点P的坐标为（）A（2,1）B（0,2）C（0,－1）D （1,0）6、若点(m，n)在函数y＝2x＋1的图象上，则2m－n的值是（）A．2 B．－2 C．1 D．－17、如图，函数2y x=和4y ax=+的图象交于点A（m，3），则不等式24x ax+＜的解集为（）A．32x<B．3x<C．32x>D．3x>（第7题）（第8题）8、如图，将一朵小花放置在平面直角坐标系中第三象限内的甲位置，先将它绕原点O旋转180°到乙位置，再将它向下平移2个单位长到丙位置，则小花顶点A在丙位置中的对应点A′的坐标为（）A（3，1）B（1，3）C（3，－1） D （1，1）二、填空题（每小题3分，共21分）学校:班级:姓名:考号:…………………………………………装……………………订………………………线………………………………………9、256的平方根是；10、若532+y xba 与x yb a2425-是同类项，则x= , y = ；11、写出一个y 随着x 的增大而增大的一次函数的解析式：______________12、如图，矩形ABCD 的对角线AC 、BD 相交于点O ，CE ∥BD ，DE ∥AC ．若AC ＝ 4，则四边形CODE 的周长是（12题）（13题）13、如图：矩形ABCD 的对角线AC =10，BC =8，则图中五个小矩形的周长之和为_______ ．14、不等式组的整数解的和是 .15、观察分析下列数据，寻找规律： 0，3，6，3，23，15，32，……那么第10个数据应是 . 三. 解答题（共75分）16、计算（每题5分，共10分）（1）解不等式组：()3228131x x x x -<+⎧⎪⎨-≥--⎪⎩（2）17、（9分）如图，在正方形ABCD 中，对角线AC 、BD 相交于点O ，E 、F 分别在OD 、OC 上，且DE=CF ，连接DF 、AE ，AE 的延长线交DF 于点M ．求证：AM ⊥DF ．x +2＞0，x －1≤218、（6分）长方形ABCD ，长为6，宽为4，建立直角坐标系使其中C 点的坐标（-3，2），并且写出其它顶点的坐标。