3.2 周期信号的傅里叶级数分析
合集下载
第三章――傅里叶变换周期信号的傅里叶级数分析
第三章 傅里叶变换3.1周期信号的傅里叶级数分析（一） 三角函数形式的傅里叶级数满足狄利赫里条件的周期函数()f t 可由三角函数的线性组合来表示，若()f t 的周期为1T ，角频率112T πω=，频率111f T =，傅里叶级数展开表达式为()()()0111cos sin n n n f t a a n t b n t ωω∞==++⎡⎤⎣⎦∑各谐波成分的幅度值按下式计算()0101t T t a f t dt T +=⎰()()0112cos t T n t a f t n t dt T ω+=⎰()()01012sin t T n t b f t n t dt T ω+=⎰其中1,2,n =⋅⋅⋅狄利赫里条件：（1） 在一个周期内，如果有间断点存在，则间断点的数目应是有限个；（2） 在一个周期内，极大值和极小值的数目应是有限个； （3） 在一个周期内，信号是绝对可积的，即()00t T t f t dt +⎰等于有限值。
（二） 指数形式的傅里叶级数周期信号的傅里叶级数展开也可以表示为指数形式，即()()11jn tnn f t F n eωω∞=-∞=∑其中()011011t T jn tn t F f t e dt T ω+-=⎰ 其中n 为从-∞到+∞的整数。
（三） 函数的对称性与傅里叶系数的关系（1） 偶函数由于()f t 为偶函数，所以()()1sin f t n t ω为奇函数，则()()01112sin 0t T n t b f t n t dt T ω+==⎰所以，在偶函数的傅里叶级数中不会含有正弦项，只可能含有直流项和余弦项。
（2） 奇函数由于()f t 为奇函数，所以()()1cos f t n t ω为奇函数，则()0100110t T t a f t dt T +==⎰()()010112cos 0t T n t a f t n t dt T ω+==⎰ 所以，在奇函数的傅里叶级数中不会含有直流项和余弦项，只可能包含正弦项（3） 奇谐函数（()12T f t f t ⎛⎫=-+ ⎪⎝⎭）半波对称周期函数的傅里叶级数中，只会含有基波和奇次谐波的正、余弦项，而不会含有偶次谐波项，这也是奇谐函数名称的由来。
信号与系统王明泉第三章习题解答
（3）周期信号的傅里叶变换；
（4）频域分析法分析系统；
（5）系统的无失真传输；
（6）理想低通滤波器；
（7）系统的物理可实现性；
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零，即：
如果 和 为相互正交的单位矢量，则 和 就构成了一个二维矢量集，而且是二维空间的完备正交矢量集。也就是说，再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示，有
条件1：在一周期内，如果有间断点存在，则间断点的数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有限个。
条件3:在一周期内，信号绝对可积，即
（5）周期信号频谱的特点
第一：离散性，此频谱由不连续的谱线组成，每一条谱线代表一个正弦分量，所以此谱称为不连续谱或离散谱。
第二：谐波性，此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱； (b)周期、离散频谱；
(c)连续、非周期频谱； (d)离散、非周期频谱。
答案：(d)
题7、 的傅里叶变换为
答案：
分析：该题为典型信号的调制形式
题8、 的傅里叶变换为
答案：
分析：根据时移和频移性质即可获得
题9、已知信号 如图所示，且其傅里叶变换为
试确定：
(1)
(2)
(3)
解：
(1)将 向左平移一个单位得到
对于奇谐函数，满足 ，当 为偶数时， ， ；当 为奇数时， ， ，即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
（4）周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说，任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中，经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差，即 。式中， ， 。研究表明， 越大， 越小，当 时， 。
（4）频域分析法分析系统；
（5）系统的无失真传输；
（6）理想低通滤波器；
（7）系统的物理可实现性；
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零，即：
如果 和 为相互正交的单位矢量，则 和 就构成了一个二维矢量集，而且是二维空间的完备正交矢量集。也就是说，再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示，有
条件1：在一周期内，如果有间断点存在，则间断点的数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有限个。
条件3:在一周期内，信号绝对可积，即
（5）周期信号频谱的特点
第一：离散性，此频谱由不连续的谱线组成，每一条谱线代表一个正弦分量，所以此谱称为不连续谱或离散谱。
第二：谐波性，此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱； (b)周期、离散频谱；
(c)连续、非周期频谱； (d)离散、非周期频谱。
答案：(d)
题7、 的傅里叶变换为
答案：
分析：该题为典型信号的调制形式
题8、 的傅里叶变换为
答案：
分析：根据时移和频移性质即可获得
题9、已知信号 如图所示，且其傅里叶变换为
试确定：
(1)
(2)
(3)
解：
(1)将 向左平移一个单位得到
对于奇谐函数，满足 ，当 为偶数时， ， ；当 为奇数时， ， ，即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
（4）周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说，任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中，经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差，即 。式中， ， 。研究表明， 越大， 越小，当 时， 。
信号与系统第三章
T1 t0
1
2 t0 T1
2 t0 T1
2
[ T1
t0
f (t) cos n 1tdt
j T1
t0
f (t) sin n 1tdt]
1 t0 T1
T1 t0 f (t)[cos n 1t j sin n 1t]dt
1 t0 T1 f (t)
T1 t0
2e jn 1t dt
2
1 t0
T1
f (t)e
jn 1t dt
1768年生于法国 1807年提出“任何周
期信号都可用正弦函 数级数表示”
拉格朗日，拉普拉斯 反对发表
1822年首次发表在 “热的分析理论”
一书中
一、频域分析
从本章开始由时域转入变换域分析，首先讨 论傅里叶变换。傅里叶变换是在傅里叶级数正交 函数展开的基础上发展而产生的，这方面的问题 也称为傅里叶分析（频域分析）。将信号进行正 交分解，即分解为三角函数或复指数函数的组合。
t0 T1 t0
f (t)e jn1tdt
n 0,1, 2,3 。
Fn
1 t0
T1
f (t)e
jn 1t dt
T1 t0
n 0, 1, 2, 3 。
为了积分方便，通常取积分区间为：0
~
T1或
T1 2
~
T1 2
推导完毕
f (t)
n
Fne jn 1t F0
Fne jn 1t
n1
1
Fne jn 1t
n
（形式一） f (t) a0 an cos(n1t) bn sin(n1t) n1
傅氏级数展开实质就是确定展开式中各分量系数
确定系数：
f (t) a0 an cos(n1t) bn sin(n1t) n1
1
2 t0 T1
2 t0 T1
2
[ T1
t0
f (t) cos n 1tdt
j T1
t0
f (t) sin n 1tdt]
1 t0 T1
T1 t0 f (t)[cos n 1t j sin n 1t]dt
1 t0 T1 f (t)
T1 t0
2e jn 1t dt
2
1 t0
T1
f (t)e
jn 1t dt
1768年生于法国 1807年提出“任何周
期信号都可用正弦函 数级数表示”
拉格朗日，拉普拉斯 反对发表
1822年首次发表在 “热的分析理论”
一书中
一、频域分析
从本章开始由时域转入变换域分析，首先讨 论傅里叶变换。傅里叶变换是在傅里叶级数正交 函数展开的基础上发展而产生的，这方面的问题 也称为傅里叶分析（频域分析）。将信号进行正 交分解，即分解为三角函数或复指数函数的组合。
t0 T1 t0
f (t)e jn1tdt
n 0,1, 2,3 。
Fn
1 t0
T1
f (t)e
jn 1t dt
T1 t0
n 0, 1, 2, 3 。
为了积分方便，通常取积分区间为：0
~
T1或
T1 2
~
T1 2
推导完毕
f (t)
n
Fne jn 1t F0
Fne jn 1t
n1
1
Fne jn 1t
n
（形式一） f (t) a0 an cos(n1t) bn sin(n1t) n1
傅氏级数展开实质就是确定展开式中各分量系数
确定系数：
f (t) a0 an cos(n1t) bn sin(n1t) n1
周期函数的傅里叶级数分析
周期函数的傅里叶级数分析周期函数的傅里叶级数（Fourier series）由法国数学家傅里叶在19世纪初提出，是周期函数在无穷级数意义下的一种展开形式。
傅里叶级数理论在物理、工程、数学、计算机科学等领域中有广泛的应用。
一、周期函数的定义周期函数是指在某一时间区间内呈周期变化的函数，其周期为T。
即对于任意实数t，都有f(t+T)=f(t)。
周期函数可以是任意形式的，如三角函数、指数函数、幂函数等。
二、傅里叶级数的定义对于一个T周期的函数f(t)，其傅里叶级数定义为：f(t)=a0/2+∑[ancos(nωt)+bnsin(nωt)]，其中：ω=2π/T，a0,an,bn为常数，n为正整数。
公式中a0/2表示周期内的平均值，an和bn分别为以周期为T 的函数f(t)为周期的余弦项和正弦项的系数，即傅里叶系数。
由于正弦和余弦函数互相正交，将它们在一个周期内积分可得到：∫[0,T]cos(nωt)dt=∫[0,T]sin(nωt)dt=0∫[0,T]cos(nωt)cos(mωt)dt=0（n≠m）∫[0,T]sin(nωt)sin(mωt)dt=0（n≠m）∫[0,T]cos(nωt)sin(mωt)dt=0这些正交性质是计算傅里叶系数的重要基础。
三、傅里叶级数的性质1. 周期函数可以展开为傅里叶级数。
2. 傅里叶级数往往使用欧拉公式来表示：eiθ=cosθ+isinθ那么，傅里叶级数也可以表示为：f(t)=∑[cn·ei(nωt)]其中：cn=(an-ibn)/2c*-n=(an+ibn)/23. 傅里叶级数具有线性性质。
即如果f1(t)和f2(t)均为周期为T 的函数，则其线性组合：af1(t)+bf2(t)也为周期为T的函数，且其傅里叶级数：a·∑[c1n·ei(nωt)]+b·∑[c2n·ei(nωt)]即为其线性组合的傅里叶级数。
4. 收敛性质：如果f(t)是具有连续导数的周期函数，其傅里叶级数在其周期内一致收敛于原函数。
信号课件第三章傅里叶变换
• 从本章起，我们由时域分析进入频域分析，在频域分析中， 首先讨论周期信号的傅里叶级数，然后讨论非周期信号的 傅里叶变换。傅里叶变换是在傅里叶级数的基础上发展而 产生的，这方面的问题统称为傅里叶分析。
• 任何周期函数在满足狄义赫利的条件下，可以展成正交函 数线性组合的无穷级数。如果正交函数集是三角函数集或 指数函数集，此时周期函数所展成的级数就是“傅里叶级 数”。
T1 T1 T1 2
f (t) sin n1tdt 0
2 T1
a0 T1
2
an T1
2 T1
T21
2 T1
2
f (t)dt
f (t) c
2f T1 0
osn1tdt
(t)dt
4 T1
T1 2
0
f (t) cosn1tdt
所以，在偶函数的傅里叶级数中不会有正弦项，只可能 含有（直流）和余弦分量。
α>0
F (w) f (t)e jwt dt ete jwt dt 1
0
jw
f (t) 1
t
F(w) 1
2 w2
1/ F( j)
(
)
arctan(
)
( )
/2
/2
2、双边指数信号
f (t)
f (t) e t α>0
1
2/ F()
F (w) f (t)e jwt dt
dt
E
e jnw1t
/2
E
e jnw1 / 2 e jnw1 / 2
T / 2
T
jnw1
T
/ 2
jnw1
Ts
t
2E T
e jnw1 / 2 e jnw1 / 2 2 jnw1
• 任何周期函数在满足狄义赫利的条件下，可以展成正交函 数线性组合的无穷级数。如果正交函数集是三角函数集或 指数函数集，此时周期函数所展成的级数就是“傅里叶级 数”。
T1 T1 T1 2
f (t) sin n1tdt 0
2 T1
a0 T1
2
an T1
2 T1
T21
2 T1
2
f (t)dt
f (t) c
2f T1 0
osn1tdt
(t)dt
4 T1
T1 2
0
f (t) cosn1tdt
所以，在偶函数的傅里叶级数中不会有正弦项，只可能 含有（直流）和余弦分量。
α>0
F (w) f (t)e jwt dt ete jwt dt 1
0
jw
f (t) 1
t
F(w) 1
2 w2
1/ F( j)
(
)
arctan(
)
( )
/2
/2
2、双边指数信号
f (t)
f (t) e t α>0
1
2/ F()
F (w) f (t)e jwt dt
dt
E
e jnw1t
/2
E
e jnw1 / 2 e jnw1 / 2
T / 2
T
jnw1
T
/ 2
jnw1
Ts
t
2E T
e jnw1 / 2 e jnw1 / 2 2 jnw1
傅里叶变换的证明
1 T 1 任何不同的两个函数的 乘积在区间[ T 2 2 ]上的积分为零
1 T nm 2 cos(nw1t ) cos(m w t ) dt 1 0 n m
即有： t
t0 T1
0
t0 T1
t0
1 T nm 2 sin(nw1t ) sin(m w t ) dt 1 0 n m
n
F (nw1)e
jnw1t
n
jnw1t F e n （6）
证明:思路由三角形式→指数形式
f (t ) a0 [an cos(nw1t ) bn sin(nw1t )] （ 7）
n 1
利用欧拉公式:
jnw1t jnw1t 1 cos( nw t ) ( e e ) 1 2 8） jnw1t jnw1t （ 1 e ) sin(nw1t ) 2 j (e
把(10),(11)代入(9)得
f (t ) a0 [ F (nw1 )e jnw1t F (nw1 )e jnw1t ] （ 12 ）
n 1
令a0 F (0)
F ቤተ መጻሕፍቲ ባይዱnw )e
n1 1
jnw1t
n
F (nw )e
1
1
jnw1t
(12)式写为f (t )
an
t0 T1 1 T1 t 0
f (t )dt
信号的平均值、直流分量
是nw1的偶函数 是nw1的奇函数
t0 T1 2 T1 t 0
f (t ) cos(nw1t )dt
2 bn T 1
t0 T1
t0
f (t ) sin(nw1t )dt
1 T nm 2 cos(nw1t ) cos(m w t ) dt 1 0 n m
即有： t
t0 T1
0
t0 T1
t0
1 T nm 2 sin(nw1t ) sin(m w t ) dt 1 0 n m
n
F (nw1)e
jnw1t
n
jnw1t F e n （6）
证明:思路由三角形式→指数形式
f (t ) a0 [an cos(nw1t ) bn sin(nw1t )] （ 7）
n 1
利用欧拉公式:
jnw1t jnw1t 1 cos( nw t ) ( e e ) 1 2 8） jnw1t jnw1t （ 1 e ) sin(nw1t ) 2 j (e
把(10),(11)代入(9)得
f (t ) a0 [ F (nw1 )e jnw1t F (nw1 )e jnw1t ] （ 12 ）
n 1
令a0 F (0)
F ቤተ መጻሕፍቲ ባይዱnw )e
n1 1
jnw1t
n
F (nw )e
1
1
jnw1t
(12)式写为f (t )
an
t0 T1 1 T1 t 0
f (t )dt
信号的平均值、直流分量
是nw1的偶函数 是nw1的奇函数
t0 T1 2 T1 t 0
f (t ) cos(nw1t )dt
2 bn T 1
t0 T1
t0
f (t ) sin(nw1t )dt
信号与系统 第三章 周期信号的傅里叶级数展开
1 T
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
第三章 傅里叶变换
P=a
2 0
1 2
n 1
an2 bn2
c02
1 2
cn2
n 1
n
Fn
2
；
3、一个特别的性质： e jn e jn
3.1.3 函数的对称性与傅里叶系数的关系
1、波形对称分类：（1）、整周期对称，例如偶函数和奇函数，其可决定级数中只可能含有余弦项或正弦项；（2）半 周期对称，例如奇谐函数，其可决定级数中只可能含有偶次项或奇次项。 2、对称条件： （1）、偶函数：若信号波形相对于纵轴是对称的，即满足 f(t)=f(-t),此时 f(t)是偶函数，偶函数的 Fn 为实数。在偶函 数的傅里叶级数中不会含有正弦项，只可能含有直流项和余弦项。 （2）奇函数：若波形相对于纵坐标是反对称的，即满足 f(t)=-f(-t),此时 f(t)是奇函数，奇函数的 Fn 为虚数。在奇函数 的傅里叶级数中不会含有余弦项，只可能含有正弦项。虽然在奇函数上加以直流成分，它不再是奇函数，但在它的 级数中仍然不会含有余弦项。 （3）寄谐函数：若波形沿时间轴平移半个周期并相对于该轴上下翻转，此时波形并不发生变化，即满足：
n2 1 2
) cos n1t
基波和偶次谐波频率分量。谐波幅度以 1 规律收敛。 n2
其中1
=
2 T1
；其频谱只包含直流、
3.2.5 周期全波余弦信号
1、周期全波余弦信号的傅里叶级数为：
f
(t)
2E
4E 3
cos(1t)
4E 15
cos(21t)
4E 35
cos(31t)
2E
4E
1n 1
第三章 傅里叶变换
傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的；
信号与系统第3章傅里叶变换
*本章要点
1.利用傅立叶级数的定义式分析周期信号的离散谱。 2.利用傅立叶积分分析非周期信号的连续谱。 3.理解信号的时域与频域间的关系。 4.用傅立叶变换的性质进行正逆变换。 5.掌握抽样信号频谱的计算及抽样定理
将信号表示为不同频率正弦分量的线性组合意义
1.从信号分析的角度 将信号表示为不同频率正弦分量的线性组合，为不同信号之 间进行比较提供了途径。
发展历史
•1822年，法国数学家傅里叶(J.Fourier,1768-1830)在研究热传导 理论时发表了“热的分析理论”，提出并证明了将周期函数展 开为正弦级数的原理，奠定了傅里叶级数的理论基础。 •泊松(Poisson)、高斯(Guass)等人把这一成果应用到电学中去， 得到广泛应用。 •19世纪末，人们制造出用于工程实际的电容器。 •进入20世纪以后，谐振电路、滤波器、正弦振荡器等一系列具 体问题的解决为正弦函数与傅里叶分析的进一步应用开辟了广 阔的前景。 •在通信与控制系统的理论研究和工程实际应用中，傅里叶变换 法具有很多的优点。 •“FFT”快速傅里叶变换为傅里叶分析法赋予了新的生命力。
一．三角函数形式的傅里叶级数
1.正交三角函数集
三角函数系1, cos x,sin x, cos 2x,sin 2x,..., cos nx,sin nx,...
在区间[-π,π]上正交，是指在三角函数系中任何不同的两个函 数的乘积在区间的积分等于零，即
cosnxdx 0(n 1,2,3,...)
傅里叶生平
1768年生于法国 1807年提出“任何周期信号
都可用正弦函数级数表示” 1829年狄里赫利第一个给出
收敛条件 拉格朗日反对发表 1822年首次发表“热的分析
理论”中
周期函数的傅里叶级数
2
f (t) a0
A e e n jn 1t n
j n1 t n
2 n1 2
§ 周期信号的傅立叶级数
又A-n
A（A 是n的偶函数）
n
n
n
（n n是n的奇函数）
b0 0，A0
a2 0
b02
a， 0
故
f (t)
1 2
Ane
n
j n1
t
n
1 2
Ane
n
j
n
e jn1 t
f t
Fne jn1t 用FS分析是对周期信号进行谐波分解，即
用谐n波 加权和来合成信号，因此，FS分析又称为谐波分析。
周期信号的对称性与付立叶系数的关系。
f (t)的对称条件
展开式中系数特点
f (t)
f (t)，纵轴对称（偶函数 ）
bn
0，an
4 T
t0
T 2
t0
f (t) cos n1tdt
nT
2
n
n
0
Sa( n1 ) 0
2
即 Fn>0
Sa( n1 ) 0 即 Fn<0
2
F e n
1 2
An
j n
§ 周期信号的傅立叶级数
此例中F n
A
T
Sa( n
2
)为一实数。幅度频谱与相位频谱可以合
画在一张图上。
c n
1 2
A n
-4
2
2
4 A
T
1 213141 51
101
第四步：讨论频谱结构与 、T 的关系
§ 周期信号的傅立叶级数
An
信号与系统第3章 傅里叶变换
P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论：周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和，即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 （c三n c角os函(n数1t形 式n )） n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项， 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图：
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1）令 m
2
得
2
m
即在
2
m，m为整数处有零点。
2）
2
2
T1
T1
零点间谱线个数
3) c n值为正，相位为0，值为负，相位为π
4)谱线间隔为 1 带宽
2
T1
，第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1
3.1-2 周期信号的傅里叶级数分析
2 t0 T1 an t0 f (t ) cos n1tdt T1
2 t0 T1 bn t0 f (t ) sin n1tdt T1
an jbn jn1t an jbn jn1t f (t ) a0 e e n1 n1 2 2 F0 Fn e
还得出了关于非周期信号的表示不是成谐波关系的正弦信 号的加权和，而是不全成谐波关系的正弦信号的加权和。和傅 立叶级数一样，傅立叶积分(或变换)仍然是分析LTI系统的最 强有力的工具之一。 当时指定了四位著名的科学家和数学家来评审1807年傅立 叶的论文，其中三位即S.F.拉克劳克斯、G.孟济和P.S.拉普拉 斯赞成发表傅立叶的论文，而第四位J.L.拉格朗日仍然顽固地 坚持他于50年前就已经提出过的关于拒绝接受三角级数的论点。 由于拉格朗日的强烈反对，傅立叶的论文从未公开露过面，为 了使他的研究成果能让法兰西研究院接受并发表，在经过了几 次其它的尝试后，傅立叶才把他的成果以另一种方式出现在 “热的分析理论”这本书中。这本书出版于1822年，也即比他 首次在法兰西研究院宣读他的成果时晚15年。
n1
jn1t
Fn e jn1t
n1 jn1t
F0 Fn e
n1
jn1t
Fn e
n1
又有
F0 Fn e jn1t
n 0
于是，可将上式写成紧凑的形式：
f (t ) Fn e
n
jn1t
（注意n的取值范围与 三角形傅氏级数不同）
到1807年，傅立叶已完成了关于热传理论实质部分的研究， 并于1807年12月21日向法兰西研究院提交了他的研究成果。在 他的研究过程中，傅立叶发现在表示一个物体的温度分布时， 成谐波关系的正弦函数是非常有用的，另外，他还断言“任何” 周期信号都可以用这样的级数来表示！虽然在这一问题上，他 的论述是很有意义的，但是隐藏在这一问题后面的其它很多基 本概念已经被其他科学家们所发现；同时傅立叶的数学证明也 不是很完善的。后来1829年P.L.狄里克雷给出了若干精确的条 件，在这些条件下一个周期信号才可以用一个傅立叶级数来表 示，因此，傅立叶并没有对傅立叶级数的数学理论作出贡献， 然而，他确实洞察出这个级数表示法的潜在威力，并且在很大 程度上正是由于他的工作和断言，才大大激励和推动着傅立叶 级数问题的深入研究。另外，傅立叶在这一问题上的研究成果 比他的任何前驱者都大大前进了一步，这指的是他
周期信号的傅里叶级数分析
实验三周期信号的傅里叶级数分析一、实验目的熟悉连续时间周期信号的傅里叶级数分解原理及方法，掌握周期信号的傅里叶频谱的概念及计算方法，熟悉相应MATLAB 函数的调用格式和作用，掌握利用MATLAB 计算傅里叶级数系数及绘制频谱图的方法。
二、实验原理（一）周期信号的傅里叶级数分析原理按傅里叶分析的原理，任何周期信号都可以用一组三角函数)}cos(),{sin(t n t n ΩΩ的组合表示。
1、三角函数形式的傅里叶级数∑∞=Ω+Ω+=+Ω+Ω+Ω+Ω+=1022110)]sin()cos([2...)2sin()2cos()sin()cos(2)(n n n t n b t n a a t b t a t b t a a t f （1） 式中，n n b a a ,,0称为傅里叶系数。
()dt t f T a TT ⎰-=22012()...3,2,1)cos(222=Ω=⎰-n dt t n t f T a TT n ，(),...3,2,1,)sin(222=Ω=⎰-n dt t n t f T b TT n即可以用一组正弦波和余弦波合成任意的周期信号。
式（1）的三角函数形式傅里叶级数可以写成余弦函数的形式：∑∞=+Ω+=10)cos(2)(n n n t n A A t f ϕ其中：00a A =，22n n n b a A +=,nn n a b arctan -=ϕ 2、指数函数形式的傅里叶分析其中系数3、周期信号的频谱（1）三角函数形式频谱w A n ~关系曲线称为幅度频谱图关系曲线称为相位频谱图（2）指数函数形式频谱 w F n ~关系曲线称为幅度频谱图关系曲线称为相位频谱图（二）周期信号的傅里叶级数的MATLAB 实现例1：试用MATLAB 求如图1所示的周期方波信号的傅里叶级数分解。
解：周期方波信号是一个偶函数，又是一个奇谐函数，因此其傅里叶级数只含有奇次谐波的余弦项，即周期方波信号可以分解为： ()...5,3,1)cos(5.04)cos(244-22=Ω=Ω=⎰⎰-n dt t n T dt t n t f T a TT T T n ， 求傅里叶系数的程序如下：syms t n T;∑∞-∞==n t jn n F t f Ωe )(⎰-=22-Ωd e )(1T T t jn n t t f T F w n ~ϕw n ~ϕy=0.5*cos(n*2*pi/T*t);an=(4/T)*int(y,-T/4,T/4);运行结果为：an=2*sin(1/2*pi*n)/pi/n则此周期方波信号可以分解为：）（,...5,3,1)2sin(2,0===n n n a b n n ππ 将其展开为三角函数形式的傅里叶级数：,...)3,2,1()cos(2sin 2)(...])5cos(51)3cos(31)[cos(2(12==-+-=∑∞-=j nwt n n t f wt wt wt t f j n πππ） 例2：根据例1的结果，试用正弦信号的叠加近似合成一频率为50Hz ，幅值为3的方波。
信号与系统第3章(1)周期信号的傅里叶级数和频谱(3.1,3.2)
变换域分析的基本思想为：将信号分解为 基本信号之和或积分的形式，再求系统对基本 信号的响应，从而求出系统对给定信号的响应 （零状态响应）。 在第二章中我们以 t 为基本信号将任意信号
进行分解
f t f t t
f t d
a0 an cos(nt ) bn sin(nt ) 2 n1 n 1 2 其中 an , bn 称为傅里叶系数， 。 T
那么,傅里叶系数如何求得呢?
a0 1 2 T
T 2 T 2
f ( t )dt
T 2 2 an T f ( t ) cos(nt )dt T 2 T b 2 2 f ( t ) sin( t )dt n n T T 2
f (t )
1 Fn T
n
T 2 T 2
F e
n
jnt
f ( t )e
jnt
e e cos x 2
jx
jx
将上式第三项中的 n 用 n 代换，并考虑到 An 是 n的 偶函数，即 An An ； n 是 n 的奇函数, n n 则上式可写为 :
A0 1 1 j n jnt j n jnt f (t ) Ane e An e e 2 2 n 1 2 n 1 A0 1 1 Ane j n e jnt A ne j n e jnt 2 2 n1 2 n 1
2 T2 (1) si nnt dt T
0
T 2 0
si nnt dt
T 2
, 0 2 1 cosn 4 , n n
第三章-傅里叶变换
三、 三角函数形式的傅里叶级数（3）
f (t) a
(a
cos n t b
sin n t)
0
n1
n
1
n
1
纯余弦形式傅里叶级数
f (t) c
c
co（ s n t ）
0
n1 n
1
n
其中 c a , c
0
0
n
a2 b2 ,
n
n
n
arctg
bn an
c0称为信号的直流分量，cn cos(n1t+ n) 称
为信号的n次谐波分量。 cn0。 可见， 周期信号可分解为直流、基波和各次
谐波的线性组合。
中国民航大学 CAUC
3.2 周期信号的傅里叶级数分析
三、 三角函数形式的傅里叶级数（4）
[例] 求下图所示周期锯齿波的傅里叶级数展开式。
sin n t)
0
n1
n
1
n
1
a0、an、bn—傅里叶系数
1—基本角频率（基频）
a0—信号的直流分量
a b
n
n
a n
b n
n
n
cos1t 、 sin1t —基波
cos(n1t) 、 sin(n1t) — n次谐波
中国民航大学 CAUC
3.2 周期信号的傅里叶级数分析
3.1 信号的正交函数分解
一、正交函数(1)
1. 实变函数：若实函数f1(t) 和f2(t)在(t1 ，t2)上满足
t2 t1
f (t)f (t)dt
1
2
0
则称f1(t)与f2(t)在(t1 ，t2)上正交。 2. 复变函数：若有n个复变函数fi(t) （i=1，…，n） 在区间( t1，t2)上满足
周期信号的傅里叶级数分析
n
2 2e j0t
2e j0t
4e
j
2
e
j
30t
4e
j
2
e
j
30t
j t
j
j ( 3 t )
j ( 3 t )
2 2e 4 2e 4 4e 4 2 4e 4 2
仿真 源码
连续时间信号与系统的频域分析
三、周期信号频谱的特点
f(t) E
-T -/2
/2 T
t
Fn
E T
0 0 20
信号与系统分析
周期信号的傅里叶级数分析 一、三角函数形式的傅里叶级数
若周期信号 的周期f为(t) 角频率 T 狄里赫利条件，即
，且0 满 2足T
（1）在一周期内，若有间断点存在，则间断点的数 目应为有限个。
（2）在一周期内，极大值和极小值的数目为有限个。
（3）在一周期内，信号绝对可积。即 为有限值。
指数型傅 里叶级数
n 为整数，Fn ( jn0 ) 为复傅里叶系数。其中
Fn
(
jn0
)
1 T
t0 T f (t)e jn0t dt
t0
连续时间信号与系统的频域分析
指数型傅里叶系数与三角形傅里叶系数的关系：
F0 a0 A0
Fn ( jn0 )
1 2
(an
jbn )
Fn
e jn
1
Fn
2
an2
二者共同组成信号的复频谱。（双边谱）
连续时间信号与系统的频域分析
单边谱的每条谱线代表一个分量的振幅，而双边谱是 将单边谱的每个频率分量一分为
二、对应到正、负频率处各为一半而得。即
An Fn Fn
典型周期信号的傅里叶级数
d
X(j)ejt
X(jk0)ej0t
x(t)21 X(j)ejtd1
0
2 T
k 0
0
于是,对非周期信号,有傅里叶变换对:
x(t)
1
2
X( j)ejtd 1
反
X( j)
x(t)e jtdt
2正
(e j t )
复 杂 信 号 ＝ 系 数 （ ） 基 本 信 号 （ ）
系 数 （ ） ＝ 复 杂 信 号 （ 与 ） 基 本 信 号 （ ）
F(j)ejtd
F( ) f(t)ejtdt
也是常用的形式
傅立叶变换的理解
周期信号的叶 指级 f数 T(t数 )型 Fn傅 ejn1t表 里明，
n
周期信号可限 以多 分个 解 n 频 1、 为 复率 无 振为 F幅 n的为 指
数分 ejn1t量 的离散和；
非周期信 傅号 里的 叶变 f(t)换 1
周期矩形脉冲信号的三角形式傅里叶级数为
f(t)E T 1 2 T E 1n 1Sa(n 2 1 )cosn1t
F n1 2(anjn b )1 2anE T 1 S(n a 21 )
f(t)的指数形式的傅里叶级数为
f(t)E S(an 1 )ejn 1t
T1 n
2
2、频谱 c0
E T1
规律收. 敛
例1：试将图示周期矩形脉冲信号 展开为(1)三角型和(2)指数型傅里 叶级数。
T
f (t)
A
T
22
t
解(： 1) f (t)是偶函数，故只含 数有 项常 和余弦项。
T
a0T 1
2 T
f(t)d t 2 T
2AdtA
3.2 周期信号的傅里叶级数分析
n=1
1
∞
f (t) = a0 + ∑(an cos nω1t + bn sin nω1t), n为正整数
n=1
∞
1 直流分量： a 0 = T1
∫
t 0 + T1
t0
f ( t ) dt
2 t0 +T1 余弦分量的幅度：n = ∫ a f (t ) cos(nω1t )dt T1 t0
2 正弦分量的幅度： bn = T1
sin(ω1t )
4 T1 a1 = ∫ 2 f (t) cos(ω1t)dt T 0 1
4 T1 b = ∫ 2 f (t) sin( ω1t)dt 1 T 0 1
cos(2ω1t )
sin(2ω1t )
∞
令：Fn = Fn e
∞
jϕn
1 − jϕn 1 = (an − jbn ) F−n = F−n e = (an + jbn ) 2 2
jnwt 1
f (t) = F0 + ∑Fne
n=1
+ ∑F−ne
n=1
∞
− jnwt 1
= ∑Fne
n=0
∞
jnwt 1
+ ∑Fne jnw1t
n=−∞
−1
周期函数: f (t) =
7
周期信号的复数频谱 F0
complex frequency spectrum
F = Fn n − F = c0 0
1 = cn 2
8
周期信号的功率特性
1 t0 +T1 2 周期信号f (t )的平均功率 : P = f (t ) = ∫ f (t )dt T1 t0
2
1
∞
f (t) = a0 + ∑(an cos nω1t + bn sin nω1t), n为正整数
n=1
∞
1 直流分量： a 0 = T1
∫
t 0 + T1
t0
f ( t ) dt
2 t0 +T1 余弦分量的幅度：n = ∫ a f (t ) cos(nω1t )dt T1 t0
2 正弦分量的幅度： bn = T1
sin(ω1t )
4 T1 a1 = ∫ 2 f (t) cos(ω1t)dt T 0 1
4 T1 b = ∫ 2 f (t) sin( ω1t)dt 1 T 0 1
cos(2ω1t )
sin(2ω1t )
∞
令：Fn = Fn e
∞
jϕn
1 − jϕn 1 = (an − jbn ) F−n = F−n e = (an + jbn ) 2 2
jnwt 1
f (t) = F0 + ∑Fne
n=1
+ ∑F−ne
n=1
∞
− jnwt 1
= ∑Fne
n=0
∞
jnwt 1
+ ∑Fne jnw1t
n=−∞
−1
周期函数: f (t) =
7
周期信号的复数频谱 F0
complex frequency spectrum
F = Fn n − F = c0 0
1 = cn 2
8
周期信号的功率特性
1 t0 +T1 2 周期信号f (t )的平均功率 : P = f (t ) = ∫ f (t )dt T1 t0
2
第三章§3.2 周期信号的频谱分析——傅里叶级数
T
2 T 2
T , cos n 1 t cos m 1 t dt 2 0, T , sin n 1 t sin m 1 t dt 2 0,
m n m n m n m n
X
T
2 T 2
请画出其幅度谱和相位谱。
化为余弦形式
f (t ) 1 π 5 cos( 1 t 0 . 15 π ) cos 2 1 t 4
c0 1
三角函数形式的傅里叶级数的谱系数
三角函数形式的频谱图
cn
c1
0 0
5 2 . 236
n
2 . 24 c2
a n
j bn
T
T 0
f ( t ) co s n 1t d t j
T
1 T
T 0
f ( t ) sin n 1t d t
1 T
f ( t )e
0
j n 1t
dt
t 0 T1 t0
因 此 F n 1
1 T
f (t ) e
j n 1t
n
j n 1t
n 0 , 1, 2
jn 1t
f (t )
F (n 1 ) e
4
a
n 1
n
co s n 1t b n sin n 1t
利用欧拉公式
sin n 1 t
co s n 1 t
周期信号
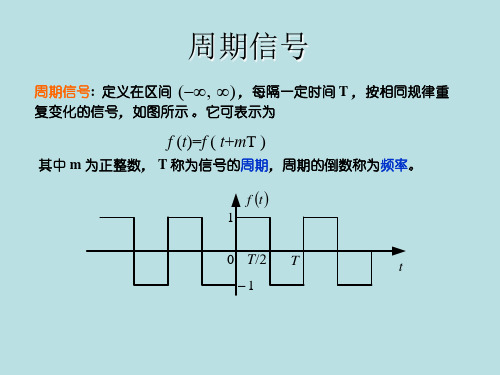
周期信号: 定义在区间 ( , ) ，每隔一定时间 T ，按相同规律重 复变化的信号，如图所示 。它可表示为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
f (t )
n
F e
n
jn1t
E T1
n1 jn1t Sa( 2 )e n
20
E f (t ) T1
n1 jn1t Sa( 2 )e n
E n1 Fn Sa( ) T1 2
2 E n1 cn Sa( ) T1 2 E c0 T1 n0
E cos(n t )dt
2 1 2
2E 2E n1 2 sin(n1t ) sin( ) T1n1 n 2 2
E1
n1 2 E n1 Sa( ) Sa( ) 2 T1 2
E 2 E f (t ) T1 T1
n1 Sa( 2 ) cos(n1t ) n 1
f1 t
f1 (t ) 1 f (t )
1
f (t)
练习P 3 7 171
2
－T
T T 0
2
T 2
T
2T
t
T 2
0 －1
T 2
T
2T
t
注意：不可左右移动，否则改变了 原信号的对称性。
11
四、傅里叶有限级数与最小方均误差
f (t ) a0 (an cos n1t bn sin n1t )
32
1 1 2 2 2 2 2 P a0 (an bn ) c0 cn 2 n 1 2 n 1 1 2 2 2 c0 (2 Fn 2 F n ) 2 n 1 c0 Fn F n
2 2 2 n 1 n 1 n
2 b2 T1
T1 2 T 1 2
f (t ) sin( 21t )dt 0
31
1 P T1
t 0 T1
t0
[a0 (an cos nw1t bn sin nw1t )]2 dt
n 1
1 T1
t 0 T1
t0
[a0 2a0 (an cos nw1t bn sin nw1t )
f (t ) an cos n1t
n 1
只用一项逼近
13
2E n an sin( ) n 2
f (t ) an cos n1t
n 1
用两项逼近
14
2E n an sin( ) n 2
f (t ) an cos n1t
n 1
用三项逼近
15
3.3 典型周期信号的傅里叶级数 一、周期矩形脉冲信号
an cn cosn bn tann an
bn cn sin n
cn an bn
2
2
bn n arctan an
3
f (t ) c0 cn cosn1t n
n 1
cn an bn 幅度谱
2 2
bn n arctan 相位谱 an
1 Fn cn 2 F0 c0
E n1 Fn Sa ( ) T1 2
22
周期信号频谱的特性 1、离散频谱，谱线间隔为基波频率。谱线为 无穷多条。脉冲周期越大，谱线越密。
2、各分量的大小与脉幅成正比，与脉宽成正 比，与周期成反比。 n1 3、各谱线的幅度按 Sa ( )包络线变化。 2
n 1
N
S N (t ) a0 (an cos n1t bn sin n1t )
n 1
误差函数 : N (t ) f (t ) S N (t ) 1 t0 T1 2 方均误差 : E N (t ) N (t )dt T1 t0
2 N
12
2E n an sin( ) n 2 a0 bn 0 n只能取奇数
1 a0 T1 2 bn T1
T1 2 T 1 2
2 f (t ) dt f (t ) dt T1
an jbn an Fn 2 2
29
T1 2 0
T1 2 T 1 2
f (t ) sin n1t dt 0
f (t ) a0 (an cos n1t bn sin n1t )
T1 2 0
f (t ) sin n1t dt
30
cos(1t )
sin(1t )
4 a1 T1
T1 2 0
f (t ) cos(1t )dt
4 b1 T1
T1 2 0
f (t ) sin( 1t )dt
cos(21t )
sin(21t )
2 T1 a2 2 1 f (t ) cos( 21t )dt 0 T T1 2
f (t )在一个周期内的表示式为 : f (t ) E[u (t ) u (t )] 2
2 an T1
T1 2 T 1 2
1 f (t )dt T1
E 2 Edt T1
2
T1 2 T 1 2
2 f (t ) cos(n1t )dt T1
n 1
奇函数
2 T1 an 2 1 f (t ) cos n1t dt 0 T T1 2
1 a0 T1
2 bn T1
T1 2 T 1 2
T1 2 T 1 2
f (t ) dt 0
an jbn bn Fn j 2 2
4 f (t ) sin n1t dt T1
第三章 傅里叶变换
3.2 周期信号的傅里叶级数分析 一、三角函数形式的傅里叶级数
f (t ) a0 (an cos n1t bn sin n1t )
n 1
1 f1 T1
2 1 2 f1 T1
基波频率（基频）
1
f (t ) a0 (an cos n1t bn sin n1t )
2
f (t ) a0 (an cos n1t bn sin n1t )
n 1
1 2 2 P c0 cn Fn 2 n 1 n
2
周期信号的平均功率等于傅里叶级数展开式各谐 波分量有效值的平方和。该式称为帕塞瓦尔定理
8
三、函数的对称性与傅里叶系数的关系 1、偶函数 f t f t 在偶函数的傅里叶级数中不会含有正弦 项，只有余弦项和直流项。Fn为实数。 2、奇函数 f t f t 在奇函数的傅里叶级数中不会含有 余弦项，只有正弦项。Fn为虚数。
n 1
1 t0 T1 a0 f (t )dt T1 t0
2 bn T1
2 t0 T1 an f (t ) cos(n1t )dt T1 t0
t 0 T1
t0
f (t ) sin(n1t )dt
1 1 t 0 ~ t 0 T1通常取(0 ~ T1 )或( T1 ~ T1 ) 2 2
谱线
包络线
周期信号的频谱是离散谱
4
二、指数形式的傅里叶级数
f (t ) a0 (an cos n1t bn sin n1t )
n 1
1 t0 T1 a0 f (t )dt T1 t0
2 t0 T1 an f (t ) cos(n1t )dt T1 t0
F
2
2
n
Fn F n
1 cn 2
cn 2 Fn 2 Fn
2
2
F0 c0
33
不变的情况
T1 5
频带宽度不变 谱线间隔改变
T1 10
34
T1 5
T1不变的情况
T1 10
谱线间隔不变 频带宽度改变
35
Fn F n F0 c0
1 cn 2
17
E 2 E f (t ) T1 T1
n1 Sa( 2 ) cos(n1t ) n 1
E c0 a0 T1
bn 0
2 E n1 cn a n Sa( ) T 2
18
2 E n1 cn Sa( ) T1 2
n0
E c0 T1
26
四、周期半波余弦信号
27
五、周期全波余弦信号
f t E cos 0t
1 0 1 2
28
f (t ) a0 (an cos n1t bn sin n1t )
n 1
偶函数
2 T1 4 T1 an 2 1 f (t ) cos n1t dt 2 f (t ) cos n1t dt T T1 2 T1 0
2
f (t ) a0 (an cos n1t bn sin n1t )
n 1
f (t ) c0 cn cos( n1t n )
n 1
c0 cn cos n1t cos n sin n1t sin n
n 1
a0 c0
2 n 1
{ (an cos nw1t bn sin nw1t )}2 ]dt
n 1
1 2 2 2 a0 (an bn ) 2 n 1
cos n1t , sin n1t为一正交函数集, 任意两项乘
0 积在一个周期内的定积分为 : T1 2 其它 各自的平方
9
3、奇谐函数（半波对称、半周期镜像）
T1 平移半个周期后相对于 f t f t 时间轴对称 2