电工基础学习指导—正弦交流电路
电工基础 第4章正弦交流电

u = U m sin(ωt + u )
i = I m sin(ωt + i )
4.1.2正弦交流电的基本特征和三要素 . . 正弦交流电的基本特征和三要素
两个同频率正弦量的相位角之 差或初相位角之差,称为相位 相位 差,用 表示。 图4.3中电压u和电流i的相位差 为
= (ωt + u ) (ωt + i ) = u i
第4章 正弦交流电路 章
4.1交流电路中的基本物理量 . 交流电路中的基本物理量 4.2正弦量的相量表示 4.3电路基本定律的相量形式 4.4 电阻、电感、电容电路 4.5 谐振电路 . 4.6正弦交流电路中的功率 . 正弦交流电路中的功率
第4章 正弦交流电路 章
4.1交流电路中的基本物理量 . 交流电路中的基本物理量
U m = 220 2V = 311.1V
U= U m 220 2 = V = 220V 2 2
4.1.2正弦交流电的基本特征和三要素 . . 正弦交流电的基本特征和三要素
2.频率与周期 . 正弦量变化一次所需的时间(秒)称为周期T,如图4.2所示。每秒内变化 的次数称为频率f,它的单位是赫兹(Hz)。 频率是周期的倒数,即
电工基础第二章正弦交流电路及应用

U1 sin 1 U 2 sin 2 U1 cos 1 U 2 cos 2
由相量与正弦量之间的对应关系最后得 u u1 u2 2U sin(t ) U1cosψ1+U2cosψ2
三角函数运算由几何分析运算所替代,化复杂为简单!
电工技术
如何把代数形式变 换成极坐标形式?
例:正弦量i=14.1sin(ωt+36.9°)A的最大值相量表示为:
I m 14.1/ 36.9A
其有效值相量为: 10/ 36.9A I 由于一个电路中各正弦量都是同频率的,所以相量只需 对应正弦量的两个要素即可。 即模值对应正弦量的最大值或有效值,
幅角对应正弦量的初相位。
电工技术
复数的运算法则
设有两个复数分别为: A a a1 jb1 A
B B b a 2 jb2
A、B加、减、乘、除时运算公式如下: A B ( a1 a 2 ) j ( b1 b2 )
A B ( a1 a 2 ) j ( b1 b2 ) A B AB a b A A a b B B
补充内容:复数的运算
A 6 j8 B 3 j 4
C 10 30 D 6135
A+B= A-B= A· B=
C+D= C-D= C· D=
A/B=
C/D=
电工技术
(2)正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。 为区别与一般复数,相量的顶上一般加符号“· ”。
正弦量与纵轴相交处若 在正半周,初相为正。
-
正弦量与纵轴相交处若 在负半周,初相为负。
电工技术
模块二、电工基础知识--正弦交流电

阻抗三角形
阻抗:
Z R2 (XL XC )2
arctg X L X C
R 阻抗角
所以p UI sin2ω t
同理,无功功率等于瞬时功率达到的最大值。
QC
UI
I 2XC
U2
XC
单位:乏(var)
例2: 电容器C=0.5μF,外加交流电压U=10V,
i
φ=30°,ω=106rad/s,求i。
+
解: (1)相量图法:先画相量图,
u
C
_
分别求I、 φ。
I
U
UI (1 cos2 t)dt
T0
UI I 2R U 2 / R
ωt
单位:瓦、千瓦 (W、kW)
电压与电流最大值的关系:
Im=URm/R
电压与电流有效值的关系:
I=UR/R
或 UR=IR
电路的功率
瞬时功率:瞬时电压与电流的乘积。 有功功率:瞬时功率的平均值。
P=URI=I2R=UR2/R
UR
R
U UL UC UR
电压三角形
电压与电流的相位差:
arctg U L UC arctg X L XC
UR
R
Z XL XC
R
阻抗三角形
阻抗:
Z R2 (XL XC )2
arctg X L X C
R 阻抗角
Z X XL XC
2.功率关系
由 u 2Usinω t
+
1
u
i 2U sin( ω t 90) (1) 瞬时功率 X C
_
p iu
《电工基础》第5章 正弦交流电路ppt课件

最新课件
11
三、正弦交流电的变化范围
1. 最大值 :正弦交流电在一个周期所能达到的 最大瞬时值,又称峰值、幅值。
用大写字母加下标m表示,如Em、Um、 Im。
2.有效值 :加在同样阻值的电阻上,在相同的 时间内产生与交流电作用下相等的热量的直 流电的大小。
用大写字母表示,如E、U、I。
最新课件
12
最新课件
14
• 用数字万用表测量正弦交流电压时要选择交流
挡,测量的结果是电压有效值;若不慎错用直 流挡,则显示为零。
用直流挡测量市电显示为零
最新课件
15
• 用数字万用表测量直流电压时要选择直流挡, 测量的结果是电压平均值;若不慎错用交流挡, 则显示为零 。
用交流挡测量最叠新层课电件池显示为零
16
(1)同一相量图中,相同单位的相量应按相 同比例画出。
(2)一般取直角坐标轴的水平正方向为参考 方向,逆时针转动的角度为正,反之为负。
(3)用相量图表示正弦交流电后,它们的加、 减运算可按平行四边形法则或三角形法则进行。
最新课件
27
§5-3 单一参数的交流电路
最新课件
28
一、纯电阻电路
• 只含有电阻元件的交流电路称为纯电 阻交流电路。
QCUCICIC 2XCU XC C 2
最新课件
50
§5-4 LC谐振电路
最新课件
51
一、RLC串联电路
• 1.电压三角形 如图所示为RLC串
联电路,为正弦交流 电压,这三个元件流 过同一电流,电流与 各元件电压参考方向 如图所示。
最新课件
52
• 设电流的解析式为
iImsint
• 电阻、电感和电容两端的电压分别为
电工基础-正弦交流电的基本概念

本章介绍了交流电的基本概念以及交流电的表示法。 大小及方向均随时间按正弦规律做周期性变化的电流、 电压、电动势叫做正弦交流电流、电压、电动势。
一、正弦交流电的主要参数 1.周期与频率
交流电完成一次循环变化所用的时间叫做周期 T
2 ; ω
1 周期的倒数叫做频率 f ;角频率与频率之间的关系为 T
i ( t ) = Imsin( t i 0) u ( t ) = Umsin( t u0) e ( t ) = Emsin( t e0)
i ( t ) = Imsin( t i0) u ( t ) = Umsin( t u0) e ( t ) = Emsin( t e0) 式中,Im、Um、Em 分别叫做交流电流、电压、电动势的振幅 (也叫做峰值或最大值),电流的单位为安培(A),电压和电动 势的单位为伏特(V); 叫做交流电的角频率,单位为弧度/秒 (rad/s),它表征正弦交流电流每秒内变化的电角度; i0、u0、 e0 分别叫做电流、电压、电动势的初相位或初相,单位为弧 度 rad 或度( ),它表示初始时刻(t = 0 时)正弦交流电所处 的电角度。 振幅、角频率、初相这三个参数叫做正弦交流电的三要素。 任何正弦量都具备三要素。
二、波形图表示法
图 7-2 正弦交流电的波形图举例
三、相量图表示法
正弦量可以用最大值相量或有效值相量表示,但通常用 有效值相量表示。
1.振幅相量表示法
最大值相量表示法是用正 弦量的最大值做为相量的模(大 小)、用初相角做为相量的幅角, 例如有三个正弦量为 e = 60 sin( t+60 °) V u = 30 sin( t+30 °) V i = 5 sin( t-30°) A 图 7-3 正弦量的振幅相量图举例 则它们的最大值相量图如图 7-3 所示。
电工基础>复习5

设: = 2 I sin ω t i
u i uL i
ωt
O
90°
(1) 频率相同 ) (2) 电压超前电流90° ) 电压超前电流90°
(3)相位差: )相位差: sin(ωt+900)V (
U
∆ϕ =ϕu −ϕi = 90
• L
0
则:uL=Um
& & UL超前I 90°
900
•
作出相量图, 作出相量图,相当于电流相量逆 时针旋转90 时针旋转 0。
加上u=10sin(ωt+300)V 例2:已知:一电阻 :已知:一电阻R=5 ,加上 ( 的电压,求通过的电流i 的电压,求通过的电流i。 解:电阻上电压与电流同相位,所以电流的初 电阻上电压与电流同相位, 相为30 相为 0 求电流的最大值I 求电流的最大值 m:
I
m
=
U R
m
10 = 5
= 2
2、1分钟内交流电变化的次数称频率 ( 、 分钟内交流电变化的次数称频率
× √
)。 。 )
3、交流电变化一周所需要的时间叫周期。( 、交流电变化一周所需要的时间叫周期。(
1 4、周期与频率的关系为( T = 、周期与频率的关系为( f
5、角频率与频率、周期的关系 、角频率与频率、 ( )。 2π ω= = 2πf T
E
Ψ O
T
ωt
e = Em sin(ωt + ϕ)
初相角:决定正弦量起始位置 初相角: 角频率:决定正弦量变化快慢 角频率: 幅值:决定正弦量的大小 幅值:
一、 周期和频率
1 f = Hz) (Hz) 频率f 频率f: T 2 π 角频率: ω = =2 πf (rad/s) rad/s) T i
电工基础 第三章

角频率 1 2 2πf 2 3.14 333rad/s 2091rad/s
(2)最大值 U ml (10 3)V 30V
U m2 (10 2)V 20V
相应的有效值为
U1
Uml 2
30 2
V 21.2V
U2
Um2 2
20 V 14.1V 2
第一节 正弦交流电的基本概念及其表示方法
相同的时间内,两个电阻产生的热量相等,我们就把这个直流电 流的数值定义为交流电流的有效值。电动势、电压和电流的有效 值分别用大写字母E、U、I表示。
第一节 正弦交流电的基本概念及其表示方法
E
Em 2
0.707Em
U
Um 2
0.707U m
I
Im 2
0.707I m
第一节 正弦交流电的基本概念及其表示方法
交流电是指大小和方向均随时间做周期变化的电流、电压 或电动势,分为正弦交流电和非正弦交流电两大类。正选交流 电按正弦规律变化,如图3-1所示;非正弦交流电不按正弦规 律变化,如图3-1d所示。
图3-1 直流电和交流电的波形 a)恒定直流电 b)脉动直流电 c)正弦交流电 d)非正弦交流电
第一节 正弦交流电的基本概念及其表示方法
1MHz 106 Hz
频率和周期的关系是 (3)角频率
f 1 T
指交流电每秒钟变化的弧度数,用ω表示
2π 2πf
t
T
第一节 正弦交流电的基本概念及其表示方法
3.相位、初相位和相位差
(1)相位 电角度(ωt+φ) 为交流电的相位,其单位是弧度或度。相位 反映了交流电变化的进程。
(2)φ表
(3)平均值 交流电的平均值是指由零点开始的半个周期内的平均值,如
电工基础复习4(正弦交流电)

R-L-C 串联电路的阻抗三角形电工基础复习4(正弦交流电)一、正弦交流电的主要参数大小及方向均随时间按正弦规律做周期性变化的电流、电压、电动势叫做正弦交流电流、电压、电动势。
1.周期与频率交流电完成一次循环变化所用的时间叫做周期ωT π=2;周期的倒数叫做频率Tf 1=;角频率与频率之间的关系为 ω = 2πf 。
2.有效值正弦交流电的有效值等于振幅(最大值)的0.7071倍,即mmmmm m 7071.027071.027071.02E E E UUU I I I ======、、3.正弦交流电的三要素:有效值、频率、初相 4.相位差两个正弦量的相位差为 ϕ12 = ϕ01 - ϕ02,存在超前、滞后、同相、反相、正交等。
二、交流电的表示法1.解析式表示法i (t ) = I m sin(ωt + ϕi 0)、u (t ) = U m sin(ωt + ϕu 0)、e (t ) = E m sin(ωt + ϕe 0)2.波形图表示法波形图表示法即用正弦量解析式的函数图象表示正弦量的方法。
3.相量图表示法正弦量可以用振幅相量或有效值相量表示,但通常用有效值相量表示。
振幅相量表示法是用正弦量的振幅值做为相量的模(大小)、用初相角做为相量的幅角;有效值相量表示法是用正弦量的有效值做为相量的模(大小)、仍用初相角做为相量的幅角。
三、 纯电阻电路:只含有电阻元件的交流电路叫做纯电阻电路,如含有白炽灯、电炉、电烙铁等电路。
1、电阻与电压、电流的瞬时值之间的关系服从欧姆定律。
设加在电阻R 上的正弦交流电压瞬时值为u = U m sin(ω t ),则通过该电阻的电流瞬时值为)sin()sin(m m t I t RU Ru i ωω===2、电压、电流的有效值关系:RIU RU I==或3、电阻的两端电压u 与通过它的电流i 同相。
四、纯电感电路1.感抗X L =ωL =2πfL 自感系数L 的国际单位制是亨利(H)2.电感电流与电压的大小关系:LXU I=感抗单位是欧姆(Ω)。
电工电子技术基础知识点详解3-1-单一元件正弦交流电路

单一元件正弦交流电路
1、分析方法
单一元件的正弦交流电路分析方法是相同的,即(1)列出电压电流瞬时值的关系式;
(2)设电压(或电流)为参考正弦量,而后根据电压和电流关系求得电流(或电压),并用三角函数式、正弦波形图、相量图和相量式表示。
(3)比较电压和电流的相位和大小关系。
(4)求出瞬时功率,讨论有功功率和无功功率。
注意:无功功率不是无用的,它是感性负载和容性负载所需要的。
若电路中存在电感或电容元件,则这些元件和电源之间发生能量交换,能量交换的规模也就是无功功率。
2、电量关系
对于单一元件交流电路,电路中电量之间关系如表1所示。
表1单一元件交流电路电量关系
电阻R
电感L
电容C
基本规律Ri u =R t
i
L
u d d L =t
u C
i d d =直流电路RI
U =R 相当于短路
相当于开路
电阻电抗R
fL L X πω2L ==fC C X πω211
C =
=有效值关系
RI
U =R I
X U L L =I
X U C C =
相位关系u R 和i 同相u L 超前i
︒
90u C 滞后i
︒
90相量关系
I R U =R I jX U L L
=I jX U C
C -=
相量图
有功功率R R IU P =0L =P 0C =P 无功功率
R =Q L
R IU Q =C
C IU Q -=。
《电工基础》项目8三相正弦交流电路

模块小结
对称三相电路的计算,可以利用对称关系使计算过程简化 为单相电路的计算。计算的基本公式是:
IP
UP zP
,
arctan
X R
5.中性线能使星形联接的不对称负载的相电压保持对称。这
是不管负载怎样变化,各负载电压都比较稳定。
在负载作星形联接时,若三相负载对称,则中性线电流
为零,可采用三相三线制供电;若三相负载不对称,则中 性线电流不等于零,只能采用三相四线制供电。这时要特 别注意中性线上不能安装开关和保险丝。如果中性线断开, 将造成各相负载两端电压不对称,负载不能正常工作,甚 至产生严重事故。同时在联接三相负载时,应尽量使其对 称以减小中性线电流。
I1
I2
UP ZP
380 10
A 38 A
(3)第三相负载断路时,第一、第二两相负载串联后接在
线电压上,由于两相阻抗相等,所以,相电压为线电压的
一半,即:
380
U1 U2
V 190V 2
于是得到这两相的相电流为:
I1
I2
190 10
A
19A
任务二 学习三相负载联接
二、三相负载的三角形联接
3.无论电源(绕组)或负载都有星形(Y形)和三角形(Δ形) 两种连接方式。但电源(绕组)常接成星形。
模块小结
4、星形联接与三角形联接电路的区别: (1)星形联接
线电压与相电压的关系:数量关系: U线 3U相
相位关系:线电压超前对应相电压30°,线电压等于相电 压 (2)三角形联接 线电流与相电流的关系:线电流等于相电流,数量关系: 相位关系:线电流滞后对应相电流30°
动。 (6)测电容、较长电缆(电感)等设备绝缘电阻后,先将L线
电工电子学-第二讲(正弦交流电路)

解:(1) X L L 106 6 103 6 kΩ
XC
1
C
106
1 0.001 106
1
kΩ
Z R j(X L X C ) 5 j(6 1) 5 245 kΩ
z 0 ,电路呈感性。
由 u 5 2 sin106tV ,得电压相量为:
| Z | R2 X 2
R | Z | cosz
z
arctg
X R
X | Z | sinz
Z
U I
Uu I i
U I
( u
i ) z
0
电压超前电流,感性
| Z | U Um I Im
z u i
z 0 电压滞后电流,容性
z 0 电压电流同相,阻性
dt
I jCU
iC
将U U u 、I Ii 代入上式,得:
I i jCU u CU ( u 90)
+ u - (a) 电容元件
I CU
I
θi
U
i u 90
或
U
j
1
C
I
jX CI
θu
(b) 相量图
容抗:XC=1/ωC,与频率成反比。
复数的四则运算: 设两复数为: A a1 ja2 a1
B b1 jb2 b2 (1)相等。若a1=b1,a2=b2,则A=B。 (2)加减运算:
A B (a1 b1) j(a2 b2 ) (3)乘除运算:
A B ae j1 be j 2 abe j(1 2 ) ab(1 2 )
电工基础5.1 正弦交流电的基本概念

u Um cos(t 60) 当t=0时,所以 u(0) Um cos(60)
(1) Im 为电流i的振幅 (2)Um为电压u的振幅 3.周期,频率和角频率 (1)周期
正弦量变化一次所用的时间称为周期,用T表 示单位为秒(s)。
(2)频率
正弦量单位时间内变化的周期数称为频率。用f表 示,单位为赫兹(Hz). ①周期与频率的关系 f 1 T
②频率的单位
1kHZ 103 HZ
按能量等效的概念定义,以电流为例。设两个相同
电阻R,分别通过正弦电流 i 和直流电流I。
1 有效值
(1)正弦电流 I 通过R在一个周期T里消耗的能量为
Q1 T pdt T i2Rdt R T i2dt
0
0
0
(2)直流电I通过R在相同时间T内产生的能量为
Q2 PT I 2RT
图4-3 例4-1图
解:(1)有波形图可知,T 16ms
2
T
2
16103
125rad / s
f
1 T
16
1 103
62.5HZ
或
2f 2 62.5 125rad / s
由波形图可知,从时间起点到离原点最近的波
形最大值所需的时间为2ms。则初相
随时间按正弦规律变化的交流电流或电压称为 正弦电流或电压。 (2)正弦量
正弦电压、电流统称为正弦量或正弦交流电
二 正弦量的三要素
1.正弦电流i Im cos(t i )
Im , 和 i分别称为振幅,角频率和
初相位。此三个量称为正弦量的三要素。波形 如图4-2所示。
2. 振幅
正弦量在一个周期内的最大值称为振幅。用 Am 表示
《电工电子技术》——正弦交流电路

dt
dt
Im sin(wt 90)
1 电压与电流之间的频率关系 电容元件两端的端电压与电流是同频率的正弦电量。
2 电压与电流之间的数值关系
最大值
Im
wCU m
Um 1 /(wC )
有效值
I wCU U U 1/(wC) X c
X c 等于电压有效值与电流有效值之比,单位为欧[姆],称为容 抗。
计算过程请参考书本,相量图为:
2.3单一参数交流电路
2.3.1单一电阻元件正弦交流电路 一、单一电阻元件正弦交流电路电压与电流之间的关系
i
u
R
i u U m sin(wt u )
R
R
2U R
sin(wt
u
)
单一电阻元件正弦交流电路电压与电流之间有如下几种关系:
1 电压与电流之间的频率关系 在单一电阻电路中,通过电阻元件的电流与其两端电压是 同频率的正弦电量。
I Ie j i I i
I 为有效值
二、相量图
在复数平面上,用几何图形表示正弦量的相量的图,称为相 量图。
已知正弦电压: 相应的电压相量为
u 220 2 sin(wt 45)
U 22045
已知正弦电流: 相应的电流相量为:
i 8 2 sin(wt 30)
字母 T 表示,单位是秒(s)。正弦量在1秒时间内重复变化的
周期数称为频率,用小写字母 f 表示,单位为赫兹(Hz),如 果1秒钟内变化一个周期,频率是1Hz。周期与频率互为倒数关 系:
f 1 T
在我国,发电厂提供的交流电的频率为50Hz,其周期 T 0.02, 这一频率称为工业标准频率,也称工频。
电工基础(第2版)课件:正弦交流电中的电路元件
问题与讨论
1. 电容元件在直流、高频电路中如何?
直流时C相当于开路,高频时C相当于短路。
2. 电感元件和电容元件有什么异同?
L和C上的电压、电流相位正交,且具有对偶关系; L和C都是储能元件;它们都是在电路中都是只交换不耗能。
电路 电路图 基本 参数 (正方向) 关系
i
R u u iR
小结
复数 阻抗
IC
相量图:
电容元件上 iC 超前 uC 90°电角
(在相量关系式中用-j来表示)。
UC
电容元件上的电压、电流关系可归纳为:
(1)频率相同;
(2)uC 相位滞后iC 90º;
(3)有效值关系:IC
UC UC
1 C
XC
或
UC
1 C
IC
X C IC
(4)相量关系: •
1•
•
UC j C IC jX C IC
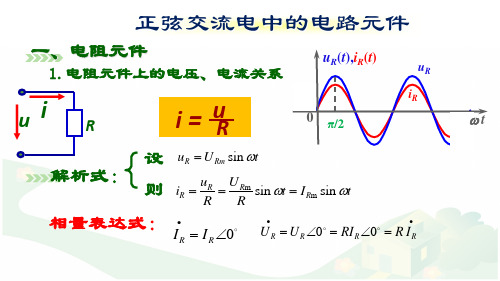
IR UR
正弦交流电路中的电阻元件上的电压、电
流关系为:
(1)频率相同;
(2)相位相同;
(3)有效值关系:
IR
UR R
或
UR IRR
(4)相量关系:
•
•
UR IR R
•
IR
+
•
UR
R
•
IR
•
UR
-
(a)
(b)
图3-16 电阻元件的相量模型及相量图 (a)相量模型;(b)相量图
2. 电阻元件的功率
R
瞬时值
电压、电流关系
有效值
相量图
设
u
则
i
2U cost
2I cost
U IR
电工基础正弦交流电

05
正弦交流电的测量与仪 器
交流电压表与电流表
交流电压表
用于测量正弦交流电压的大小,通常采用电 磁感应原理,将交流电压转换为可测量的直 流电压。
交流电流表
用于测量正弦交流电流的大小,通常采用电 磁感应原理,将交流电流转换为可测量的直
流电流。
功率表与功率因数表
要点一
功率表
用于测量正弦交流电路的功率,可以测量有功功率和无功 功率。
THANKS FOR WATCHING
感谢您的观看
谐振与滤波
谐振
正弦交流电路中的一种特殊状态,当电路的感抗与容抗相等时,电流与电压相位相同, 产生共振现象。谐振时电路的阻抗最小,电流最大,可能会引起过电流和设备损坏。
滤波
通过电路中的电容、电感等元件,将特定频率的信号滤除,实现信号处理和噪声抑制。 在正弦交流电路中,滤波器可以用于分离不同频率的信号,提高电路的稳定性和可靠性。
正弦交流电的三要素
幅值、频率和相位。幅值表示正弦波 的最大值,频率表示单位时间内波动 的次数,相位表示正弦波在某一时刻 所处的位置。
正弦交流电的特点
周期性
01
正弦交流电每秒完成一个周期的波形变化,其频率和周期成反
比。
相位差
02
两个不同频率或不同相位的正弦交流电在合成时会产生相位差。
方向性
03
正弦交流电的电压和电流方向随时间变化,但平均值保持不变。
1
变压器由两个线圈(初级和次级)和一个磁芯组 成。初级线圈输入电压,在磁芯中产生磁场,次 级线圈感应出电压。
2
变压器的工作原理基于电磁感应定律,即变化的 磁场会产生感应电动势,而感应电动势的大小与 磁通量的变化率成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四部份 正弦交流电路一、学习目标与要求1.理解正弦交流电的基本特性、表示方法及其相量表示;2.学习用相量法求解正弦交流电路;3.理解单个参数的正弦交流电路特点,掌握其相量计算方法;4.理解复合正弦交流电路的特点,掌握其相量计算方法;5.理解正弦电路中阻抗、阻抗角的意义及其在电路中的计算;6.理解串联谐振的意义和条件,了解并联谐振的意义和条件;7.理解正弦交流电路的不同功率之间的关系,掌握其计算方法。
二、本章重点内容1.正弦交流电的基本概念正弦交流电流)sin(m ϕω+=t I i ,它可由最大值m I 、角频率ω(或频率f 或周期T ,f T 1=,f πω2=)和初相位ϕ来描述。
正弦交流电的有效值与最大值之间有2mI I =的关系。
两个同频率正弦量的初相位角之差,称为相位差。
两同频率的正弦量有同相、反相、超前和滞后的关系。
正弦交流电可用解析式、波形图和相量图(相量复数式)三种方法来表示。
只有同频率的正弦交流电才能在同一相量图上加以分析。
.2.RLC 串联的交流电路电压电流相量关系:)](j [C L X X R I U -+=&& 复阻抗:==I U Z &&)(j C L X X R -+=ϕ∠Z阻抗模: 阻抗角:R X X C L arctan -=ϕ 3.谐振电路RLC 串联谐振电路:谐振条件:C L X X =或C L ωω1=谐振频率:LC f π210= 4.正弦交流电路的功率有功功率:ϕcos UI P =无功功率:ϕsin UI Q = 视在功率:22Q P UI S +== 5.功率因数的提高一般采用在感性负载两端并联电容器的方法来提高电路的功率因数。
三、本章内容的前后联系在本章中,首先要弄清一个正弦量是如何用一个相量来表示的,它们之间的相互关系是怎样的。
其次,要弄清正弦量用相量表示后,正弦电流电路中电压相量和电流相量的关系。
最后,还要弄清正弦电流电路中功率、能量的关系。
由于电路中含有储能元件,功率关系要比第二章纯电阻电路复杂。
需要引用一些新的概念,如平均功率、无功功率、视在功率及功率因数等,读者不仅要理解它,而且还要能运用它来分析问题。
本章是学习第五章至第六章的基础,非常重要。
对简单的正弦电流电路要能用相量图进行分析。
谐振是正弦电流电路在特定条件下产生的一种特殊物理现象。
四、学习方法指导(一) 学习方法1.图形分析法:本章接触到正弦交流电,对正弦交流电的波形图要非常熟悉才能帮助读者有效地学会交流电路分析方法。
要熟练掌握周期、频率、相位、最大值、有效值等的意义及在波型图上的表示方法。
相量图的使用同样是正弦交流电路分析中常用的图形分析方法,要掌握超前、滞后等在相量图里是如何表示的。
读者要学会利用图形分析帮助解决电路问题。
2.实际应用引申:对谐振电路的应用可帮助读者理解该电路的构成及工作原理。
功率因数的概念也一样,可通过其在电力系统中的应用来加深理解。
3.自学:本章内容多且难,尤其是相量图的分析,要求读者具有一定的自学能力,及一定的知识组织能力,帮助读者更有效地学习。
(二) 学习指导1.工程上常遇到的所谓交流电,是指大小和方向都随时间变动,而在一周内平均值等于零的周期量。
正弦电流是交流电的一种,它在工程上应用极为广泛。
读者在学习本章的第一节时,要弄清正弦量的最大值、有效值、周期、频率、角频率、初相、相位差、超前、滞后、同相、反相等术语的含义。
要注意,相位、初相位和相位差都是角度,但其意义又各不相同。
0ϕω+称为正弦交流电的相位,它反映了正弦量的变化进程;0ϕ称初相位,它表示正弦交流电在计时起点,即t=0时的相位;21ϕϕϕ-=称为两个同频率交流电的相位差,即它们的初相位之差。
两个正弦量的相位差与计时起点无关,与频率也无关,只取决于初相之差。
不同频率的两个正弦量无相位差。
正弦量的有效值与频率、初相无关,读者要了解其与正弦量的最大值有何关系。
2.基尔霍夫定律的相量形式是:0=∑I &,0=∑U &。
为什么不是∑∑==00U I ,?在这里一定要注意相量的特点,要注意相量具有大小和相位两个特征。
3.正弦电流电路中,R 、L 、C 三个元件对电流呈现的阻力是什么?电路参数感抗X L 和容抗X C 的物理意义是什么?它们与频率的关系怎样?为什么电感L 中的电压超前电流900,而电容C 中的情况却相反?读者要掌握感性电路和容性电路的特点。
4.在R 、L 、C 串联电路中,CU U U U &&&&++=L R ,所以,U &、R U &、)(CU U &&+L 组成一个直角三角形。
注意:C L R UU U U ++≠!在教材例题4.11中,电感L 和电容C 上的电压(U L 和U C )都高于电源电压U ,即分电压大于总电压,您感到奇怪吗?在R 、L 或R 、C 或几个相同性质元件的串联电路中,会不会出现这种现象?为什么?在R 、L 、C 并联电路中,又会有什么结论?5.相量图不仅能形象的表征出电路中各量间的关系,而且有时借助它还能方便的定性分析电路中某些特性,因此,掌握相量图的画法是很有用的。
相量图的画法,一般可根据方便,先选择某一相量作为参考相量(串联电路取I &,并联电路取U &);其次,按KCL 、KVL方程,根据R 、L 、C 单个元件上电压相量和电流相量的关系,逐个画出相对应的相量;最后,用矢量平行四边形法则或多角形法则,画出道路的相量图。
6.谐振是正弦电流电路中可能发生的一种特殊现象。
若电路中某一部分的电压与相应的电流同相,而且其中含有储能元件,就说该电路发生了谐振。
谐振可以发生在电路中的某一部分,也可以发生在整个电路。
R 、L 、C 串联电路谐振时,电压与电流同相、无功功率Q =0。
它与电源(或外电路)间没有电磁能量交换。
但由于其中含有储能元件,因此这些储能元件间的能量交换得到平衡。
7.在正弦交流电路中,由于电感和电容的存在,使功率出现一种在纯电阻电路中没有的现象,这就是能量的往返交换。
8.什么是功率因数?为什么要提高功率因数?与感性负载并联电容后,为什么功率因数提高了?提高了负载的功率因数,还是整个电路的功率因数?这时,有功功率有无改变?负载中电流和线路上电流有无改变?并联的电容值应如何考虑?为什么通常不将功率因数提高到1?五、典型例题分析例4.1 幅值为20A 的正弦电流,周期为1mA ,0时刻电流的幅值为10A 。
(a )求电流频率,单位为赫兹。
(b )求电流频率,单位为弧度每秒。
(c )求i (t )的正弦函数表达式,其中ϕ用度表示。
(d )求电流的有效值。
解:(a )由题意知,T =1ms ;因此,Hz T f 10001==。
(b )s rad f /20002ππω==。
(c )由于)()(ϕπ+=t t i 2000sin 20,且i (0)=10A ,所以,030=ϕ,电流i (t )的表达式为:)()(0302000sin 20+=t t i π A (d )A14.14A 2202m ===I I例4.2 写出下列各相量所对应的正弦量解析式,设角频率为ω。
(1)A )3j 4(-=I &(2)V 60220︒∠=U &(3)A 2j =I &(4)V 380=U &解:(1)0229.3643arctan A 5A 34-=-==-+=ϕ,)(I)()(09.36sin 25-=t t i ω A(2)060V 220==ϕ,U)()(060sin 2220+=t t u ωV(3)090A 2==ϕ,I)()(090sin 22+=t t i ω A(4)00V 380==ϕ,Ut t u ωsin 2380=)(V例4.3 图4.1所示的是时间t =0时电压和电流的相量图,并已知U =220V ,I 1=10A ,I 2=25A ,试分别用解析式及复数式表示各正弦量。
解:由图4.1可知:。
,,0u 0i20i104590=-==ϕϕϕ;,)(;,)()(;,)()(V 0220V sin 2220A 4525A 45sin 10A 9010A 90sin 2100002001∠==-∠=-=∠=+=•••U t t u I t t i I t t i ωωω图4.1 例4.3图 例4.4 一电炉电阻为100Ω,接到V )π32sin(311+=t u ω的交流电源上,求电炉电流的瞬时值,有效值,写出电流的相量表达式。
解:电炉属于纯电阻负载,因此,。
0u i 12032===πϕϕA2.2A 10023112m ====R U R U I A 1202.2A 120sin 22.200∠=+=•I t t i ,)()(ω 例4.5 已知H 4.0=L 的电感线圈(R =0)接到V )3π314sin(311+=t u 的交流电源上,试求电流的瞬时值,有效值,写出电流的相量表达式。
解:本题中的电感线圈属于纯电感负载,因此,。
0u i 30213121-=-=-=πππϕϕ Ω=Ω⨯==6.1254.0314L L X ωA 75.1A 6.12523112L m L ====X U X U IA 3075.1A 30sin 275.100-∠=-=•I t t i ,)()(ω例4.6 有一线圈加上30V 直流电压时,消耗有功功率150W ,当加上220V 交流电压时,消耗有功功率为3173W 。
求该线圈的电抗? 解:在直流电源作用时,Ω=Ω==61503022P U R 交流电源作用时,A 23A 63173===R P IΩ=Ω==57.923220L I U X例4.7 图4.2所示电路,已知电路谐振时,表A 1读数为15A ,表A 读数为9A ,求表A 2的读数。
图4.2 例4.7图 图4.3 例4.7相量图解:谐振时的相量图如图4.3所示,因此:A 12A 915222212=-=-=I I I例4.8 某RLC 串联电路中,电阻为40Ω,线圈的电感为233 mH ,电容器的电容为80µF,电路两端的电压u =311sin314t (V )。
求:(1)电路的阻抗值;(2)电流的有效值;(3)各元件两端电压的有效值;(4)电路的有功功率、无功功率、视在功率;(5)电路的性质。
解:(1)Ω=Ω⨯⨯==-2.73102333143L L X ω Ω=Ω⨯⨯==-8.391080314116C C X ωΩ=Ω-+=-+=1.528.392.7340222C L 2)()(X X R Z (2) A 2.4A 1.5223112m ====Z U Z U I(3) V 168V 2.440R =⨯==RI UV 2.167V 2.48.39V4.307V 2.42.73C C L L =⨯===⨯==I X U I X U(4) W 6.70540W 2.422=⨯==R I PVA 924VA 2.42311var3.589var 2.48.392.7322C L =⨯===⨯-=-=UI S I X X Q )()( (5)由于C L X X 〉,电路呈电感性质。
