3.7.2已知两边及夹角作三角形--
八年级数学上册 第2章 三角形2.6 用尺规作三角形第2课时 已知两边及其夹角、两角及其夹边作三角形

第2课时已知两边及其夹角、两角及其夹边作三角形【知识与技能】1.会利用尺规作三角形:已知两角及夹边作三角形,已知两边及夹角作三角形.2.会写出三角形的已知、求作和作法.3.能对新作三角形给出合理的解释.【过程与方法】在用尺规作三角形与已知三角形的过程中,体会、思考作图的合理性及依据.【情感态度】通过师生共同观察、探索、交流、操作,品尝成功的喜悦,形成良好的思维品质,养成科学严谨的学习态度.【教学重点】作图时要做到规X使用尺规,规X使用作图语言,规X地按照步骤作出图形.【教学难点】作图语言的准确应用,作图的规X与准确.一、情景导入,初步认知1.已知:a求作:AB,使AB=a2.已知:∠α求作:∠AOB,使∠AOB=∠α【教学说明】通过作一条线段等于已知线段、作一个角等于已知角的复习,为本节课作三角形打好基础.二、思考探究,获取新知1、如图,已知∠AOB,求作一个角,使它等于∠AOB.如图:作法:①作射线O′A′;②以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;③以O′为圆心,以OC的长为半径画弧,交O′A′于点C′,以OD的长为半径画弧;④以C为圆心,以CD的长为半径画弧,交前弧于D′;⑤过点D′作射线O′B′,则∠A′O′B′为所求作的角.∠α△ABC,使∠B=∠α,BC=a,BA=c.如图:作法:①作∠MBN=∠α;②在射线BM,BN上分别截取BC=a,BA=c;③连接AC,则△ABC为所求的三角形.3.如图,已知∠α,∠β和线段a,求作△ABC,使∠ABC=∠α,∠ACB=∠β,BC=a, 如图:作法:①作线段BC=a;②在BC的同侧,作∠DBC=∠α,∠ECB=∠β,BD与CE相交于点A,则△ABC为所求作的三角形.【教学说明】在完成三个作图后,同学们要比较各自所作的三角形,利用重合等直观的方法观察所作的三角形是否全等.在此基础上,利用已经获得的三角形全等的条件来说明大家所作的三角形一定是全等的,即说明作法的合理性.三、运用新知,深化理解d .(填序号)2.已知:线段c,∠1.求作:△ABC,使∠C=90°,∠A=∠1,AB=c.作法:(1)作∠EAF=∠1.(2)在射线AE上截取AB=c.(3)过点B作BC⊥AF交AF于点C,则△ABC就是所求作的三角形.3.已知两条直角边,求作直角三角形(要求写出已知、求作、作法).解:已知:线段a、b,求作:△ABC,使∠C=90°,AC=b,BC=a.作法:提示,先作∠C=90°.4.如图,已知线段a、b,求作:Rt△ABC,使∠ACB=90°,BC=a,AC=b(不写作法,保留作图痕迹).解:【分析】先作一个直角∠ACB=90°,再作BC=a,AC=b,连接AB就可以.作图如下:5.请你作出一个以线段a为底边,以∠α为底角的等腰三角形(要求:用尺规作图,并写出已知,求作,保留作图痕迹,不写作法和结论).【分析】可先画线段BC=a,进而在BC的同侧作∠MBC=∠α,∠NCB=∠α,MB,交于点A,△ABC就是所求的三角形.已知:线段a,∠α.求作:△ABC,使BC=a,AB=AC,∠ABC=∠α.△ABC就是所求作的三角形.【教学说明】对本节的知识进行巩固练习.考察学生的应变能力,培养学生的转换思想.四、师生互动,课堂小结先小组内交流收获和感想而后以小组为单位派代表进行总结.教师作以补充.布置作业:教材“”中第3、4、5 题.通过练习情况来看,学生对于涉及到作角的作图题掌握的不够好,不知道该在什么地方作角,因此,对此类题型应多加练习.。
已知两边及其夹角作三角形

•
二十八、青少年是一个美好而又是一去不可再得的时期,是将来一切光明和幸福的开端。——加里宁
•
二十九、梦想家命长,实干家寿短。——约·奥赖利
•
三十、青年时准备好材料,想造一座通向月亮的桥,或者在地上造二所宫殿或庙宇。活到中年,终于决定搭一个棚。——佚名
•
三十一、在这个并非尽善尽美的世界上,勤奋会得到报偿,而游手好闲则要受到惩罚。——毛姆
(2)在射线B M上截取BC= a, 在射线B N上截取BA= c, (3)连接AC
则△ABC为所求作的三角形
已知线段AB,用直尺和圆规 作线段AB的垂直平分线
分析:要作线段的垂直平分线,只需找出线段 .垂直平分线上的两个点,这由线段垂直平分 线上点的性质不难得出
1、分别以点A、B为圆心,大于线段AB长 度一半的长为半径画弧,相交于点C、D。
•
九、很多时候,我们富了口袋,但穷了脑袋;我们有梦想,但缺少了思想。——佚名
•
十、你想成为幸福的人吗?但愿你首先学会吃得起苦。——屠格涅夫
•
十一、一个人的理想越崇高,生活越纯洁。——伏尼契
•
十二、世之初应该立即抓住第一次的战斗机会。——司汤达
•
十三、哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅
•
三十六、梦想不抛弃苦心追求的人,只要不停止追求,你们会沐浴在梦想的光辉之中。——佚名
•
三十七、一块砖没有什么用,一堆砖也没有什么用,如果你心中没有一个造房子的梦想,拥有天下所有的砖头也是一堆废物;但如果只有造房子的梦想,而没有砖头,梦想也没法实现。——俞敏洪
•
三十八、如意算盘,不一定符合事实。——奥地利
2、过点C、D作直线CD
直线CD就是线段AB的垂直平分线。
湖南省茶陵县八年级数学《已知两边及其夹角作三角形》教案

课题《已知两边及其夹角作三角形》主备人备课时间周星期第课时备课组长签名教研组长签名教学内容已知两边及其夹角作三角形个性化备课教学目标知识技能掌握已知两边及其夹角作三角形的方法步骤及已知底边上的高作等腰三角形过程与方法在“作一个角等于已知角”的技能的基础上,掌握两个作三角形的作图方法情感态度价值观体会熟练掌握基本作图技巧的价值,感受成功的乐趣。
教学重点已知两边及其夹角作三角形的方法步骤教学难点已知两边及其夹角作三角形的应用于相关作图教学过程一、导入:二、学习目标1、了解尺规作图的含义及其历史背景。
2、在给出的两边夹角的条件下,能够利用尺规作三角形。
3、能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
三、自学指导:要达到本节课的学习目标不是靠老师讲,而是靠大家自学,为了使大家顺利达到本节课的学习目标,并根据自学指导认真看书认真看课本p105面练习前的内容1、看例2你能知道已知两边及其夹角作三角形的依据是什么?2、动脑筋中你知道其实题目中是已知了什么条件,让你求什么问题?3、你能归纳出“已知两边及其夹角作三角形”的两个步骤?下面自学竞赛开始,比一比谁最认真,谁更积极。
6分钟以后,比谁能正确的完成自测题。
四、自学自测1、学生看书、思考,教师巡视,确保每个学生都认真地看书、思考2、完成书本练习105的练习及随堂训练。
五、学生自测、更正、讨论、归纳、总结1、学生自测2、做完之后,给学生一分钟认真看黑板上扮演的内容,如发现错误或有不同解法的同学请举手回答。
1、学生讨论、归纳12、教师点拨、引导、归纳1)根据SAS的话,就得先确定一个直角。
再分别利用方法在两边截取后连接,方可作出直角三角形。
六、小结要会按要求作出图形,一、要熟练掌握基本作图,二、要学会分析利用已经掌握的作三角形的方法七、作业必做题:随堂训练选作题:(1)、利用尺规不能唯一作出的三角形是( D )A、已知三边B、已知两边及夹角C、已知两角及夹边D、已知两边及其中一边的对角(2)、利用尺规不可作的直角三角形是( C )A、已知斜边及一条直角边B、已知两条直角边C、已知两锐角D、已知一锐角及一直角边(3)、以下列线段为边能作三角形的是( D )A、2厘米、3厘米、5厘米B、4厘米、4厘米、9厘米C、1厘米、2厘米、 3厘米D、2厘米、3厘米、4厘米(4)如图,在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=36°,∠C =44°,请你选择适当数据,画与△ABC全等的三角形(用三种方法画图,不写做法,但要从所画的三角形中标出用到的数据)教学反思CAB3.5厘米5厘米3厘米2。
已知两边及其夹角作三角形

A B O 已知两边及其夹角作三角形
学习目标
1、了解尺规作图的含义及其历史背景。
2、在给出的两边夹角的条件下,能够利用尺规作三角形。
体验学习
一、知识链接
如何作一个角使它等于已知角∠A0B
二、自主探究
阅读课本第105页内容,并自主探究下列几个问题:
1. 已知∠α, 和线段a, b
求作: △ABC 使∠C=∠α, BC=a, AC=b
(1)作∠MCN=________
(2)在射线CM, CN 上分别截取CB=___, CA=______
(3)连结_____
△ABC 就是所求作的三角形
2.已知两边及其夹角作三角形是根据全等三角形的________定理作出的
三、合作交流:
根据以上探究过程,请你与小组成员一起交流,解决下列问题:
1. 用尺规作一个等腰三角形,使它的底边长为a, 底边上的高为b. a
2.已知线段a, c,求作Rt △ABC, 使∠C=90°,AC=b, AB=c.
四.实践应用
河流ED 同岸有两个村庄A, B 现在要在河边建一个水泵站给A, B 两村供水,若要使水泵站到两村所用的管道最短,水泵站应建在什么地方?
自主检测
1、利用尺规不能唯一作出的三角形是( )
A 、已知三边
B 、已知两边及夹角
C 、已知两角及夹边
D 、已知两边及其中一边的对角
2.利用尺规不可作的直角三角形是 ( )
A 、已知斜边及一条直角边
B 、已知两条直角边
C 、已知两锐角
D 、已知一锐角及一直角边
3.已知线段a, 和∠β,求作:以a 为斜边,∠β为一锐角的直角三角形
a
E D
a。
已知两边及其夹角作三角形.doc

3.7.2 已知两边及其夹角作三角形课前预习:1、已知三角形的两边及其夹角,求作这个三角形时,第一步应为()A、做一条线段等于已知线段B、作一个角等于已知角C、作两条线段等于已知三角形的两边,并使其夹角等于已知角D、作一条线段等于已知线段或先作一个角等于已知角2、作出∆ABC的高AD,中线AE,角平分线AF,三者中有可能落在∆ABC外部的是()A、ADB、AEC、AFD、都有有可能3、已知线段a、c、∠α,求作∆ABC,使BC=a,AB=c,∠B=∠α,请根据下列作法画出对应的图形.作法:(1)作一条线段BC=a;(2)以B为顶点,以BC为一边作∠DBC=∠α;(3)在射线BD上截取线段AB=c;(4)连接AC,∆ABC就是所求作的三角形.当堂检测:1、已知两边及其夹角作三角形,所用的基本作图是()A、平分已知角B、作线段的中垂线C、作直线的垂线D、作一个角等于已知角及作一条线段等于已知线段2、用尺规作一个直角三角形,使其两条直角边分别等于已知线段时,实际上已知条件是()A、三角形的两条边和它们的夹角B、三角形的两角和它们的夹边C、三角形的三条边D、三角形的三个角3、如左图,已知线段a,b,作等腰∆ABC,使AB=AC,且BC=a,BC边上的高AD=b,张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段b;(4)连结AB,AC,则∆ABC为所作的等腰三角形.上述作法的四个步骤中,有错误的一步.你认为是()A、(1)B、(2)C、(3)D、(4)baa课后练习:1、 已知线段a 和∠α,求作:∆ABC ,使∠C=∠α,AC=a,BC=2a.2、完成下列作图: '如左图,已知A 、B 为直线MN 外两点. (1)过点A 作AC ⊥MN 于C ; (2)延长AC 到'A ,使C 'A =AC ; (3)连结B 'A 交MN 于P .3、已知:线段a.求作:等腰三角形,使AB=AC=a ,且∠A=90︒.a4、如图,MN 是一条公路,A 、B 分别是公路两侧的两个村庄,现在要在公路MN 上修建一个汽车站C ,使汽车站C 到村庄A 、B 的距离都尽可能短,请你帮助设计人员确定汽车站的准确位置,并说明理由.MNABMNAB5、在第7题中,如果村庄A、B是在公路的同侧,如图所示,汽车的准确位置又如何确定呢?请作图说明.6、已知:∠α和线段a.求作:等腰∆ABC,使腰长AB=a,底角=∠α.7、已知:线段a,求作:∆ABC,使AC=BC,∠ACB=90 ,AB边上的中线等于a.a8、已知斜边,一直角边分别为c,a,求作直角三角形.a cM N AB答案:课前预习:1、D ,2、A,3、 解:如图:B C当堂检测:1、D2、A3、C课后练习:1、解:如图:作法:(1)作射线CM ,作∠MCN=∠α;(2)在CM 上截取BC=2a ,在CN 上截取AC=a ;(3)连结A 、B 两点,则∆ABC 就是所求作的三角形. 2、略3、解:作法;(1)作射线AM ,(2)过点A 作直线EF ⊥AM ,(3)在射线AM 和直线AF 上分别截取AB=a ,AC=a. 则∆ABC 为所求作的等腰三角形.4、解:连结AB 与MN 交于点C ,则C 就是汽车站的准确位置,因为连结两点的所有连线中,线段最短. 5、解:先找到A 村庄关于公路MN 的对称点'A ,连结'A A 交于MN 点C ,连结B 'A 交于MN 点D ,则D 为汽车站的位置.因为在∆ABC 和∆ACD 中AD=D 'A ,∠ADC=∠A DC '=90︒,DC=DC ,所以ACD A CD '∆≅∆,所以AC=A C ',AC+BC=A C '+ BC ,而连结两点的所有连线中,线段最短.6、解:已知:∠α和线段a.求作:等腰∆ABC ,使腰长AB=AC=a ,∠ABC=∠ACB=∠α. 作法:(1)作∠MBN=∠α,(2)在射线BM 上截取BA= a ,a(3)以A为圆心,以a为半径作弧交BN于点C,则∆ABC即为所求作的三角形.7、解:作法:(1)作一条直线EF,在直线EF上取一点C,(2)过点C作直线EF的垂线MN,则∠MCF=.90︒(3)作∠MCF的平分线CG,(4)在CG上截取CD=a,(5) 过点D作射线CG的垂线分别交CM、CN于A、B,.则∆ABC即为所求作的三角形.8、解:已知:线段a,c,.求作:直角∆ABC,使得∠C=90︒,BC=a,AB=c.作法:(1)作CB=a,(2)过点C作CB的垂线MN,(3)以B为圆心,以C长为半径画弧交MN于点A,则∆ABC即为所求作的三角形.。
已知两边及其夹角作三角形最新版

湖南教育出版社
湖南教育
复习
已知:∠AOB,求作∠A′O′B′,使 ∠A′O′B′=∠AOB
A
作法:
O
(1)做射线O′B′
B
(2)以O为圆心,任意长为半径画弧,交OA于D点,交OB于C点。
(3)以O′为圆心,OC长为半径画弧,交O′B′于C′点 。
向;我们习惯了飞翔,却成了无脚的鸟。年轻时我们并不了解自己,不知道自己需要什么。不知道什么才是自己最想要的,什么才是最适合自己的,自己又是怎么样的一个 人。”时光叠加,沧桑有痕,终究懂得,漫漫人生路,得失爱恨别离,不过是生命的常态。原来,人生最曼妙的风景,就是那颗没被俗世河流污染的初心。大千世界,有很多 的东西可以去热爱,或许一株风中摇曳的小草,一朵迎风招展的小花,一条弯弯曲曲的小河,都足够让我们触摸迷失的初心。紫陌红尘,芸芸众生,皆是过客。若时光允许, 我愿意一生柔软,爱了樱桃,爱芭蕉,静守于轮回的渡口,揣一颗云水禅心,将寂寞坐断,将孤独守成一帧最美的山水画卷。一直渴盼着,与心悦的人相守于古朴的小院,守 着老旧的光阴,只闻花香,不谈悲喜,读书喝茶,不争朝夕。阳光暖一点,再暖一点,日子慢一些,再慢一些,从容而优雅地老去。浮生荡荡,阳春白雪,触目横斜千万朵, 赏心不过两三枝;任凭弱水三千,只取一瓢饮。有梦的季节,有爱的润泽,走过的日子,都会成为笔尖温润如玉的诗篇。相信越是走到最后,剩下的唯有一颗向真向善向美的 初心。似水流年,如花美眷,春潮带雨晚来急,野渡无人舟自横朝花夕拾,当回望过往,你是此生无憾,还是满心懊悔呢?随着芳华的流逝,我们终究会明白:任何的财富都 比不上精神上的愉悦,任何的快感都不及对初心的执着。愿你不趋炎附势,不阿谀奉迎,不苟且偷生,不虚掷有限的年华,活出属于自己的风采,活在每一个当下,不忘初心,
已知两边与夹角或两角与夹边作三角形PPT授课课件

基础巩固练
5.下列关于噪声的理解,正确的是( D ) A.0 dB是指没有声音 B.0 dB的环境是人类最理想的声音环境 C.长期工作和生活在高分贝噪声环境中可锻炼人的听力 D.噪声使人烦躁不安,有害身心健康
基础巩固练
6.[安徽灵璧校级月考]如图甲所示,摩托车安装消声器是 从噪声的__声__源____处减弱噪声;如图乙所示,道路两 旁的隔音墙是从噪声的_传__播__过__程_中减弱噪声。
16 B
答案呈现
17 B 18 见习题 19 见习题
基础巩固练
1.某市已经明令禁止在城区内燃放烟花爆竹,因为燃放 烟花爆竹除了会造成空气污染外,燃放烟花爆竹时的 巨大声音还是一种___噪__声___(填“乐音”或“噪声”),爆 竹的巨大声音是__空__气____的振动产生的。
基础巩固练
7.[安徽霍邱月考]如图所示,在女子10 m气手枪比赛中,射 击时,很多运动员在耳朵里放一个耳塞或戴上耳罩,这 主要是在___人__耳___处减弱噪声。
HK版 八年级上
第三章 声的世界
第2节 声音的特性
第2课时 噪声的防治
习题链接
提示:点击 进入习题
1 噪声;空气 4 dB;不能
答案呈现
7 人耳 10 见习题
2D
5D
8C
3C
6 声源;传播过程 9 B
基础巩固练
8.[中考·山东潍坊]将教室的门窗关闭,室内同学听到的 室外噪声减弱。对该现象说法正确的是( C ) A.室外噪声不再产生 B.噪声音调大幅降低 C.在传播过程中减弱了噪声 D.噪声在室内的传播速度大幅减小
基础巩固练
3.我们生活在声音的世界里,声音无处不在。 下列声音: ①工厂车间机器刺耳的轰鸣声 ②山间小溪潺潺的流水声 ③清晨公园里小鸟的鸣叫声 ④装修房子时的电钻声 ⑤飞机起飞时的声音 其中属于噪声的是( C ) A.①③④ B.①②⑤ C.①④⑤ D.①②④⑤
已知两角及夹边作三角形

33..77..22已已知知两两角角及及夹夹边边作作三三角角形形章章 节节课课时时分分配配 主主 备备 辅辅备备 第第33章章全全等等三三角角形形 第 33 课课时时1. 使学生进一步熟练尺规作图的步骤:写出已知、求作;会写作法。
2.复习巩固四种基本作图。
3.已知两角及夹边应用基本作图作三角形。
重点:已知两角及夹边作三角形。
难点:确定边与角的作图顺序。
1.上节课学过可利用哪种基本作图画直角?2.已知两边及夹角作三角形:1)先画 ,再画 。
2)基本作图有: 。
3.已知两角及夹边,你能作三角形吗?已知两角及夹边作三角形已知: ∠α,∠ β,线段a ,求作:△ABC ,使BC = a ,∠ABC=∠α, ∠BCA =∠βa α β作法:(略)归纳:已知两角及夹边作三角形1.先画边,再在边的同旁画两个角。
2.基本作图有:作一个角等于已知角;作一条线段等于已知线段请同学们动手仿作思考:请同学们将所作的三角形进行对比,发现它们有什么关系?这是为什么?动脑筋:已知等腰直角三角形的斜边为a,你能用圆规和不带刻度的直尺作出这个三角形吗?作法: 1.作线段AB=a2.作线段AB的垂直平分线MN,交AB于O.AB.3.在MN上截取OC=14.连结AC、BC.⊿ABC为所求作的等腰直角三角形。
例题:已知一直角边和与它相邻的一个锐角,如何作出这个直角三角形呢?已知:锐角∠a和线段a求作:Rt⊿ABC,使∠BCA=90°,AC=a, ∠A= ∠a作法:1.作∠MCN=90°2.在射线CM上截取CA=a3.作∠CAD=∠a,AD交CN于B.⊿ABC即为所求作的直角三角形.分析:练习:作一个直角三角形,使它的斜边a,为一个锐角为∠a这节课你学会了什么?1.已知两边及夹角作三角形2.作线段的垂直平分线基本作图教学中的不足我觉得自己应从以下反思本节的教学:一、教师对学生遇到的问题估计不够学新课前,我们都对旧知识进行了回顾,如何用尺规作线段、角、垂线、余角,并且还进行了演示,但是,总有少数学生记不住或很容易忘记,所以,如何让作图原理在学生脑海中根深蒂固,除了多作外,还要反复提示作图原理。
八年级数学上册《已知三边或两边与其夹角作三角形》教案、教学设计

一、教学目标
(一)知识与技能
1.理解三角形的定义,掌握三角形的特性,如三角形的内角和等于180度,两边之和大于第三边等。
2.学会根据已知条件(三边或两边与其夹角)作出三角形,并能运用这些条件判断三角形的类型(如等腰、等边、直角等)。
3.能够运用勾股定理解决实际问题,如计算三角形的面积、斜边长度等。
(五)总结归纳,500字
在课堂的最后阶段,我会引导学生一起总结本节课的学习内容。我会邀请几名学生分享他们在小组讨论和课堂练习中的心得体会,以及他们是如何解决遇到的问题的。通过这种互动,学生可以加深对知识点的理解,并从同伴的经验中学习。最后,我会对本次课程的重点和难点进行梳理,强调三角形的性质和作法在实际问题中的应用,并鼓励学生在课后继续探索和练习,以便更好地掌握这些重要的数学技能。
(5)拓展:引导学生运用所学知识解决实际问题,培养学生的创新意识和应用能力。
4.教学评价:
(1)注重过程性评价,关注学生在学习过程中的表现,鼓励学生积极参与,勇于表达。
(2)采用多元化的评价方式,如课堂提问、小组讨论、课后作业等,全面评估学生的学习效果。
(3)关注学生的情感态度,鼓励学生克服困难,树立信心,不断提高。
四、教学内容与过程
(一)导入新课,500字
在课堂开始时,我将通过一个生动的情境来导入新课:“同学们,你们在生活中见过三角形吗?它们在哪里出现过?”通过这个问题,引导学生思考三角形在现实世界的存在和应用。接着,我会展示一些图片,如三角形警告标志、建筑物的屋顶、自行车的三角架等,让学生直观地感受到三角形的普遍性。然后,我会提出一个挑战性问题:“如果我们知道三角形的三条边长,我们能否确定一个唯一的三角形?”这个问题将激发学生的好奇心,为接下来的学习打下基础。
已知两边及其夹角作一个三角形29

已知两边夹角作一个三角形(总第29课时)
【学习目标】
1、在给出的两边夹角的条件下,能够利用尺规作三角形。
2、能结合三角形全等的条件与同伴交流作图过程和结果的
合理性。
【学习重点】:在给出的两边夹角的条件下,能够利用尺规作三角形。
【学习难点】:探索作图过程
【学习方法】观察、交流、探索.
【学习过程】:
一、知识链接
1、已知:∠α
求作:∠AOB,使∠AOB=∠α
α
二、自主学习,合作探究:
已知:线段a,c,∠α。
求作:ΔABC,使得BC= a,AB=c,∠ABC=∠α。
作法:
α
三、应用迁移,巩固提高
1、课本P91的动脑筋
已知:
求作:
作法:
2、如图,已知线段a、b、∠α,求作:ΔABC,使得∠A=∠α,
AB=a,BC=b
已知:
求作:
作法:
仔细观察小组内成员所作的图是否相同?为什么?
四、学习小结:
五、当堂检测:
课本P93练习T4、T5
六、教学后记:。
已知两角及其夹边作三角形

已知两角及其夹边作三角形(学案)
学习目标:
1、在给出两角及其夹边的条件下,能够利用尺规作三角形。
2、能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
3、培养学生实际动手能力和合作、自主探究的能力。
学习重点:根据题目的条件作三角形
学习难点:探索作图过程。
学习过程:
一、温故
已知线段a,作一条线段BC,使得BC=a
作法:
二、合作交流
1、已知三角形的两角及其夹边,求作这个三角形.
已知:线段∠α,∠β,线段c 。
求作:ΔABC,使得∠A=∠α,∠B=∠β,AB=c。
作法:(1)作线段BC=
(2) 在BC的同旁,作∠=∠α,
作∠______=∠β,________与_______交于。
ΔABC就是所求作的三角形.
∠α+∠β应满足什么条件,才能作出ΔABC?
2、[动脑筋]
已知等腰直角三角形的斜边为a ,你能用圆规和不带刻度尺的直尺作出这个三角形吗?
作法:
三、尝试应用
已知一直角边和它相邻的一个锐角,如何作出这个直角三角形呢?
αα 已知:锐角∠α 和线段a 如图。
求作:ABC Rt ∆,使∠BCA=90度,AC=a 。
∠A=∠α
应用提高
作一个直角三角形,使它的斜边为a,一个锐角为∠α 作法:。
湘教版八上数学第2课时 已知两边及其夹角、两角及其夹边作三角形

如图,已知∠α,∠β和线段a. 求作△ABC,使∠ABC=∠α,∠ACB=∠β, BC =a.
点击图片 观看视频
试一试
用尺规完成下列作图(只保留作图痕迹,不要求写 出作法). 1. 用尺规作一个角等于90°.
如图所示, ①在直线l以点A、B为圆心,大于PA的任 意长度为半径画弧,两弧相交于点C. ③连接CP,则∠CPA=∠CPB= 90°.
2. 如图,已知线段a,b,求作一个直角三角形,
使它的两直角边分别为a和b.
a 如图所示,
①作∠MCN=90°.
b
②在射线CM上截取CA=a,
在射线CN上截取CB=b.
③连接AB,则△ABC就是所求作的三
角形.
随堂练习
1.如图,已知线段a、b、c,求作以a、b、c为边的三角形.
解:①作一条线段AB=c. ②分别以A、B为圆心,以b、a为半径画弧, 两弧交于C点. ③连接AC、BC.则△ABC就是所求作的三角形.
2
第2课时 已知两边及其夹角、两角及其 夹边作三角形
新课导入
如何作一个角等于已知角? 如图,已知∠AOB,求作一个角,使它等于∠AOB.
点击图片 观看视频
状元成才路
作一个角等于已知角. 已知:∠AOB.
求作:∠DEF,使∠DEF=∠AOB.
B
O
A
作法:(1)在∠AOB上以点O 为圆心, 任意长为半径画弧,分别交OA,OB于 点P,Q; (2)作射线EG,并以点E为圆心,OP 长为半径画弧交EG于点D;
2.已知:一个直角,线段a、b,如图1所示. 求作:△ABC,使∠C=90°,AC=a,BC=b.
如图2所示, ①作∠MCN=90°. ②在射线CM上截取CA=a, 在射线CN上截取CB=b. ③连接AB,则△ABC就是所求作 的三角形.
湖南省茶陵县八年级数学《已知两角及其夹边作三角形》教案

课题《已知两角及其夹边作三角形》主备人
备课时间周星期第课时
备课组长
签名教研组长签名
教学内容已知两角及其夹边作三角形个性化备课
教学目标知识
技能
掌握“已知两角及其夹边作三角形”的方法与技能
过程
与方
法
经历问题情境—建立模型—问题解决—归纳方法—应用的过程达到掌握知识与技能的要求
情感
态度
价值
观
感受基本作图和三角形奠基法在几何作图和实践中的作用
教学重点
已知两角及其夹边作三角形的方法教学难点
已知两角及其夹边作三角形
教学过程一、情境导入
小明做练习时,不小心弄坏了练习本,损坏了画好的△ABC,要另外拿X纸重新画一个一模一样的三角形剪贴在原处,你能帮小明画出来吗?
二、学习目标
1、掌握“已知两角及其夹边作三角形”的方法与技能
2、能够归纳“已知两角及其夹边作三角形”的方法。
3.7.2已知两边及夹角作三角形--

复
习
已知三角形的三边求作 三角形
已知:线段a,b,c
a b c
作法示范
A
求作:△ABC,使BC=a,AC=b,AB=c
作法
(1)做线段BC=a, (2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧 两弧相交于点A
B
C
M
(4)连接AB,AC
则△ABC为所求作的三角形
基本作图 探 究 作线段的垂直平分线 已知线段AB,求作线段AB的垂直平分线。
A
B
C
分析:利用线段的垂直平分线的性质
画法:先连接AB和AC,再作AB和AC的垂直平 分线,两垂直平分线的交点是井应挖之处。
练习
4.如图,某人不小心把一块三角形的
玻璃打碎成三块,现在要到玻璃店去配一块 完全一样的玻璃,那么他最少要(
C
)
A、带①去 B、带②去 D、带①和②去
C、带③去
竞赛趣味题
m
作法:
1.分别以点A,B为圆心,大 于线段AB长度一半的长为半 径画圆弧,相交于点C,D。 2.过点C,D作直线CD。
C
A D
B
直线CD就是线段AB的垂直平分线。 请同学们动手仿作
已知两边及夹角作三角形
例2.已知:线段a, c, ∠α ,求作:△ABC,使BC
= a,AB= c, ∠ABC =∠α
则△ABC为所求的三角形
小结
这节课你学会了 什么?
作业:《每课必练》 P62-63 1-5T
拓展练习
在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=35°,∠C=45°, 请你选择适当数据,画与△ABC全等的 三角形,说一说你有几种办法呢?
知道两个边长及夹角
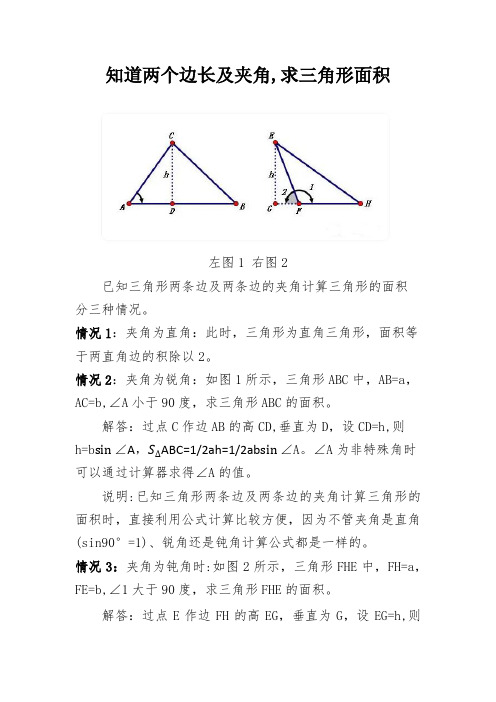
知道两个边长及夹角,求三角形面积
左图1 右图2
已知三角形两条边及两条边的夹角计算三角形的面积
分三种情况。
情况1:夹角为直角:此时,三角形为直角三角形,面积等于两直角边的积除以2。
情况2:夹角为锐角:如图1所示,三角形ABC中,AB=a,AC=b,∠A小于90度,求三角形ABC的面积。
解答:过点C作边AB的高CD,垂直为D,设CD=h,则
h=b sin∠A,S∆ABC=1/2ah=1/2ab sin∠A。
∠A为非特殊角时可以通过计算器求得∠A的值。
说明:已知三角形两条边及两条边的夹角计算三角形的面积时,直接利用公式计算比较方便,因为不管夹角是直角(sin90°=1)、锐角还是钝角计算公式都是一样的。
情况3:夹角为钝角时:如图2所示,三角形FHE中,FH=a,FE=b,∠1大于90度,求三角形FHE的面积。
解答:过点E作边FH的高EG,垂直为G,设EG=h,则
h=b sin∠2=b sin(180°−∠1),S∆FHE=1/2aℎ= 1/2ab sin(180°−∠1)=1/2ab sin∠1,∠1为非特殊角时可以通过计算器求得sin∠1的值。
说明:已知三角形两条边及两条边的夹角计算三角形的面积时,直接利用公式计算比较方便,因为不管夹角是直角(sin90°=1)、锐角还是钝角计算公式都是一样的。
已知两边夹角作一个三角形

α3.7.2已知两边夹角作一个三角形 【教学目标】:1、了解尺规作图的含义及其历史背景。
2、在给出的两边夹角的条件下,能够利用尺规作三角形。
3、能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
【教学重点】:基本尺规作图【教学难点】:在给出的两边夹角的条件下,能够利用尺规作三角形。
【教学准备】:圆规、直尺【教学过程】:一。
知识铺垫已知:∠求作:∠AOB ,使∠AOB=∠二.作一个三角形与已知三角形全等1、已知三角形的两边及其夹角,求作这个三角形.已知:线段a ,c ,∠α。
求作:ΔABC ,使得BC= a ,AB=c ,∠ABC=∠α。
作法与过程:(1)作一条线段BC=a ,(2)以B 为顶点,BC 为一边,作角∠DBC=∠a ;(3)在射线BD 上截取线段BA=c ; α(4)连接AC,ΔABC就是所求作的三角形。
给出示范和作法,让学生模仿,教师可以在黑板上做一次示范,让学生跟着一起操作,并在画完图后,让学生再自己操作一遍.而在下面的作图中,就让学生小组内讨论、交流,通过集体的力量完成,教师再给以一定的指导。
三.巩固练习:课内练习(全体学生完成)四.梳理知识,形成系统。
五.知识提高,拓展练习。
(针对有学有余力的学生)(1)、利用尺规不能唯一作出的三角形是()A、已知三边B、已知两边及夹角C、已知两角及夹边D、已知两边及其中一边的对角(2)、利用尺规不可作的直角三角形是()A、已知斜边及一条直角边B、已知两条直角边C、已知两锐角D、已知一锐角及一直角边(3)、以下列线段为边能作三角形的是()A、2厘米、3厘米、5厘米B、4厘米、4厘米、9厘米C、1厘米、2厘米、3厘米D、2厘米、3厘米、4厘米(4)如图,在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=36°,∠C=44°,请你选择适当数据,画与△ABC全等的三角形(用三种方法画图,不写做法,但要从所画的三角形中标出用到的数据)六.布置作业:基础练习C AB3.5厘米5厘米3厘米。
初中数学第2课时 已知边、角作三角形

第2课时已知边、角作三角形要点感知 1 已知两边及其夹角作三角形,先作一个角等于已知角,然后在角的两边分别以角的顶点为线段的一个端点,截取线段等于已知线段的长度,最后连成三角形即可.预习练习1-1 根据教材填空:已知∠α和线段a,b,如何求作△ABC,使∠C=∠α,BC=a,AC=b呢?(1)作∠MCN=;(2)在射线CM,CN上分别截取;(3),则△ABC为所求作的三角形.要点感知2 已知两角及其夹边作三角形,先作线段等于已知线段,再以线段的两个端点为三角形两角的顶点,在线段的同一侧分别作角等于已知角,此两角的另一边所在的射线相交的交点即为所求作的三角形的另一个顶点.预习练习2-1 已知:∠α,∠β,线段c.求作:△ABC,使得∠A=∠α,∠B=∠β,AB=c.作法:(1)作线段AB=;(2)在BC的同旁,作∠MAB=∠α,作∠NBA=∠,MA与NB交于点.△ABC就是所求作的三角形.知识点1 已知两边及其夹角作三角形1.已知∠α和线段m,n,求作△ABC,使B C=m,AB=n,∠ABC=∠α,作法的合理顺序为(填序号即可).①在射线BD上截取线段BA=n;②作一条线段BC=m;③以B为顶点,以BC为一边,作角∠DBC=∠α;④连接AC,△ABC就是所求作的三角形.知识点2 已知两角及其夹边作三角形2.如图,已知线段a和∠α,求作一直角三角形,使边BC=a,∠B=∠α.3.已知线段a,b,求作△ABC,使BC=a,AC=b,∠C=90°.4.画△ABC,使其两边为已知线段a,b,夹角为β.(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不写作法)已知:求作:参考答案课前预习预习练习1-1 (1)∠α(2)CA=b,CB=a (3)连接AB预习练习2-1 (1)c (2)β C当堂训练1.②③①④2.作图过程如下:(1)作线段BC=a;(2)以B为角的一个顶点,BC为角的一条边,作∠ABC=∠α;(3)过点C作BC的垂线AC,交AB于点A,则三角形ABC就是所求作的三角形.课后作业3.作法:(1)作∠ECD=90°;(2)在CA,CB上分别截取A,B两点,使CA=b,CB=a;(3)连接AB.△ABC即为所求作的三角形.4.已知:线段a,b,∠β(图略).求作:△ABC,使边BC=a,AC=b,∠C=β.所求作的图略.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.上节课我们学过哪些基本的尺规作图? 作一条线段等于已知线段 作一个角等于已知角 作一个角的平分线
复
习
已知三角形的三边求作 三角形
已知:线段a,b,c
a b c
作法示范
A
求作:△ABC,使BC=a,AC=b,AB=c
ห้องสมุดไป่ตู้
作法
(1)做线段BC=a, (2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧 两弧相交于点A
已知:线段m,n,锐角∠α
n α
求作:△ABC,使∠A=∠α,AB=m, , 角平分线AD= n
C
K
D
N P
A
B
M
(3)分别以 B, K为圆心,大于 BK 的距离一半的 交 AM 于 B ,交 AN 于 K ( 1 )作∠ MAN = ∠ α ((5) 2 ) 以 A 为圆心, m 长为半径画弧 在射线 AP 上截取 AD = 连接 BD 并延长交射线 AK 于点 ( 4 )作射线 AP 长为半径画弧,两弧交于P点 n C
已知两边及夹角作三角形
例2.已知:线段a, c, ∠α ,求作:△ABC,使BC
= a,AB= c, ∠ABC =∠α
a c
E
a
D
N
A E′
作法 归纳
已知两边及夹角作三角形 (1)作∠MBN= ∠α 1.先画角,再画角的两边 B (2) 在射线B M上截取BC 2. 基本作图有: D′ C M 作一个角等于已知角 = a,在射线B N上截取 BA= c, 作一条线段等于已知线段 △ABC为所求作的三角形 (3)连接AC
A
G′
B
动脑筋
你能用尺规作一个等腰三角形,使他的底边 长为a,底边上的高为b吗?
a b
分析:先作底边,再作底边上的高
练习
1.书本P105 2.书本P105 1T 2T
练习
3. 有 A, B ,C 三农户准备一起挖
一口井,使它到三农户家的距离相等.这口 井应挖在何处?请在图中标出井的位置,并 说明理由.
A
B
C
分析:利用线段的垂直平分线的性质
画法:先连接AB和AC,再作AB和AC的垂直平 分线,两垂直平分线的交点是井应挖之处。
练习
4.如图,某人不小心把一块三角形的
玻璃打碎成三块,现在要到玻璃店去配一块 完全一样的玻璃,那么他最少要(
C
)
A、带①去 B、带②去 D、带①和②去
C、带③去
竞赛趣味题
m
已知三角形的两角及其夹边,求作三角形
已知: ∠α,∠β ,线段a,用尺规作△ABC,使∠A =∠α, ∠ B= ∠β, AB= a.
F a
a
G F′
β
示范
E
C
D
作法
(1)作一条线段AB=a. (2)以A为顶点,作∠DAB= ∠ α. (3)以B为顶点,在AB的 同侧作∠EBA= ∠ β,DA 与EB相交于点C. 则△ABC为所求作的三角形
则△ABC为所求的三角形
小结
这节课你学会了 什么?
作业:《每课必练》 P62-63 1-5T
拓展练习
在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=35°,∠C=45°, 请你选择适当数据,画与△ABC全等的 三角形,说一说你有几种办法呢?
A
B
5厘米
C
B
C
M
(4)连接AB,AC
则△ABC为所求作的三角形
基本作图 探 究 作线段的垂直平分线 已知线段AB,求作线段AB的垂直平分线。
作法:
1.分别以点A,B为圆心,大 于线段AB长度一半的长为半 径画圆弧,相交于点C,D。 2.过点C,D作直线CD。
C
A D
B
直线CD就是线段AB的垂直平分线。 请同学们动手仿作
