第2章地球体与地图投影
地球、经纬网和投影图

重要特征区域的经纬度
55º E
6º W
100º E
0º 25º N 霍尔木兹海峡 0º 36º N
直布罗陀海峡 28º E
马六甲海峡 180º 66º34′
50º N
40º N
60º
英吉利海峡
土耳其海峡
白令海峡
其他:如麦哲伦海峡、苏伊士运河、巴拿马运河、好望角……
考纲规定的八个国家的经纬度和大陆轮廓
75º E 30º E 40º N 23.5º N
30º N
日本
140º E 10º E 60º N 60º E
印度
140º E 60º N 120º W
埃及
80º W
40º N
50º E
(2)两地经度差不等于180°,则过两点的大圆不是 经线圈,而与经线圈斜交,最短航程不过两极点,而 是过两极地区(或上空),具体又可分为两种情况:
50°N
N
A (10°E,20°S
A B
140°
N
A B
85°
A B
80°
B (175°W,50°N 40° ) 45°
40° 160°
120°
4、两点间实地距离的量算
(1)纬度与距离 所有经线都等长,长度为赤道长度的一半, 即约2万千米 。 任何一条经线上,纬度1°弧长约为111千米。
(2)经度与距离 赤道是最大的纬线圈,长约4万千米(2πR赤= 2π×6378千米),赤道上经度1°弧长约为111千米。 任意一条纬线上经度l°弧长约为111千米×cosφ (φ指所求纬线的纬度)。 南北纬 60°纬线长度是赤道的一半。
第2章-地球体与地图投影ppt课件

北极、南极、赤道、本初子午线地理坐标就是用经线、纬线、经度、纬度表示地面点位的球面坐标。天文经纬度、大地经纬度、地心经纬度
§1 地球体
天文经纬度以铅垂线为依据建立天文纬度ψ:观测点的铅垂线方向与赤道平面间的夹角天文经度λ:观测点子午面与本初子午面间的两面角
§1 地球体
大地经纬度地面点在参考椭球面上大地经度λ:参考椭球面上观测点的大地子午面与本初子午面间的两面角大地纬度ψ:参考椭球面上观测点的法线与赤道面间的夹角
WGS [world geodetic system] 84 ellipsoid:a = 6 378 137mb = 6 356 752.3m
a - b 6378137 - 6356752.3f = —— = ———————— a 6378137
§3 地图投影
§3 地图投影
概念投影:数学上的含义是两个面(平面或曲面)上点与点(或线与线)的对应关系;在一个面上的点,另一个面上只有唯一的点与之对应。地图投影:按照一定数学法则,将地球椭球面上的经纬网转换到平面上,使地面点位的地理坐标与地图上相对应点位的平面直角坐标或平面极坐标间,建立起一一对应的函数关系。
§2 大地测量系统
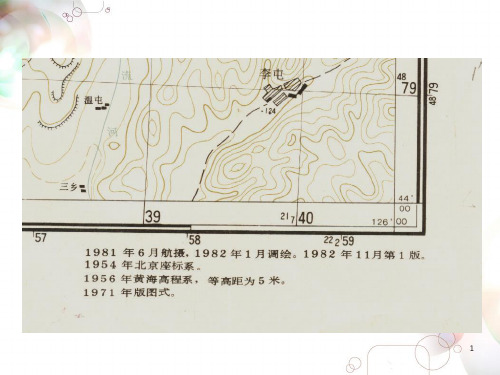
高程控制网中国高程起算面是黄海平均海水面。1956年在青岛观象山设立了水准原点(72.289m),其他各控制点的绝对高程均是据此推算,称为1956年黄海高程系。1987年国家测绘局公布:启用《1985国家高程基准》取代《黄海平均海水面》,其比《黄海平均海水面》上升29毫米。(72.260m) 。
陕西省泾阳县永乐镇北洪流村为 “1980西安坐标系” 大地坐标的起算点——大地原点。
§2 大地测量系统
平面控制网
§2 大地测量系统
平面控制网三角测量:以大地原点为基础,在地面上选择一系列控制点,建立起一系列相连接的三角形,组成三角锁和三角网。
地图投影第二章地图投影方法变形分类

1
2
a b=r2
3
4
CHENLI
a> r,b=r 5
a≠b≠r 6
23
CHENLI
24
三、投影变形的性质和大小
长度比和长度变形:
投影面上一微小线段(变形椭圆半径)和球 面上相应微小线段(球面上微小圆半径,已按规 定的比例缩小)之比。
m表示长度比, Vm表示长度变形
m ds' ds
Vm m 1
Q(0,0),球面上的各点便以新极点Q为原点,以方
位角和天顶距 Z 表示其位置,从而构成球面极坐标系。
CHENLI
32
球面极坐标系
第二节 地理坐标
在地图测制中是把地球表面作为旋转椭球面处理。 地球椭球面上各点的位置,是以地理坐标即经度 和纬度来确定。经纬度是一种绝对的坐标系统。
P,P1—北、南极
CHENLI
2
地图投影,简单的说就是将参考椭球面上的元素 (大地坐标、角度和边长)按一定的数学法则化 算到平面上的过程。
x y
ff12((LL,,BB))
CHENLI
3
二、投影方式: 1.平行投影
CHENLI
4
2.透视投影
CHENLI
5
3. 广义投影
CHENLI
6
三、地图投影实质: 建立平面上的点(用平面直角坐标或极坐标
CHENLI
16
2. 投影变形的概念 地图投影不能保持平面与球面之间在
长度(距离)、角度(形状)、面积等方 面完全不变。
地球仪上经纬线网格和地图上比较:
CHENLI
17
球面经纬网经过投影之后,其几何特征 受到扭曲——地图投影变形:长度(距离)、 角度(形状)、面积。
地图学第二章

第三节 地图投影概述
一. 地图投影的概念 二.地图投影的基本方法 三.地图投影的变形 四.地图投影的分类
沿经线直接展开?
沿纬线直接展开?
沿经线直接展开?
可见,地球椭球面是不可展开的面.无论如 何展开都会产生褶皱,拉伸或断裂等无规律变 形,无法绘制科学,准确的地图.因此解决
球面与平面之间的矛盾—— 地图投影
实际上这种直观的透视投影方法亦有很大的局限性,例如, 只能对一局部地区进行投影,且变形有时较大,同时往往不 能将全球投影下来,多数情况下不可能用这种几何作图的方 法来实现。科学的投影方法是建立地球椭球面上的经纬线网 与平面上相应的经纬线网相对应的基础上的,其实质就是建 立地球椭球面上点的坐标(λ,φ)与平面上对应的坐标(x,y) 之间的函数关系
无级别比例尺地图数据库:
把存储数据的精度和内容的详细程度都有明显高开其 比例尺本身要求的地图数据库,称为无级别比例尺数据 库.
二.比例尺的形式
1 数字比例尺: 2 文字比例尺:”图上1cm相当于实地1km”. 3 图解比例尺:
直线比例尺
斜分比例尺:不是绘在地图上的比例尺,是种地图量算工 具.
1 地理坐标系
(1)天文经纬度:
(2)大地经纬度
(3)地心经纬度
1 地理纬度)的外业以铅垂线为准,大地水准面和 铅垂线是天文地理坐标系的主要面和线。是它沿铅垂线 在大地水准面上投影点的经度和纬度。
以地面某点铅垂线和地球自转轴为基准的经纬度。 天文经度:包含地面某点A的铅垂线和地球自转轴的平面
局部定位:在一定范围内椭球面与大地水准面有最佳
的符合,而对椭球的中心位置无特殊要求;
地心定位:在全球范围内椭球面与大地水准面有最佳
第二章下 常用地图投影

(2)变形规律
切点没变形,离切点越远,变形越 大。 等变形线是以切点为圆心的同心圆。 切点向任意一点的方位角没变形。
斜轴等积方位投影
(3)用途
主要用于绘制水、陆半球,除非洲、南极洲以外的各 大洲(例如亚洲、欧洲、大洋洲、北美洲、南美洲)。 适合中高纬地区呈圆形区域的国家或地区。(例如包 含南海诸岛的中国全国)
(2)经纬线形状
纬线投影成一组平行直 线,经线投影成与纬线垂 直的平行直线。 纬线间距,从赤道向两极 放大,经线间距相等。
(3)变形特点
角度没有变形。 赤道没有变形,离赤道越远,面积变形越大。 等变形线是平行于纬线的直线。
(4)用途
常用于绘制世界时区图、世界交通图。 适合绘制赤道附近沿东西延伸的国家或地区 由于等角航线投影为直线,所以广泛用来绘制 海图。
2、正轴割圆锥投影(南海诸岛作插图的中国全图)
正轴等角割圆锥投影(Lambert conformal projection兰勃特) 正轴等积割圆锥投影(Albers projection亚尔勃斯)
(1)投影的几何概念
以圆锥投影作为投影面,使圆锥面与球面相割 (两条割线为标准线),按等角或等积条件将球面 上的经纬线投影到圆锥面上,然后将圆锥面展为平 面而成。
纬线投影为同心圆弧,经线投影为放射状直线。纬 线间隔从标准纬线向南向北是逐渐缩小的。
(3)变形规律
①两条标准线没有变形,离标 准线越远变形越大。 ②等变形线是平行于纬线的圆 弧。 ③在两条标准线之间,长度比 小于 1 ,为负变形;而在两 条标准线之外,长度比大于 1,为正变形。
中国地图(南海诸岛作插图)的标准线: ϕ 1=25°,ϕ 2=45/47°
地图与地图投影_遥感的概念和基本工作原理_遥感图像在地图中的作用-高中地理知识点

地图与地图投影_遥感的概念和基本工作原理_遥感图像在地图中的作用-高中地理知识点·高中地理地图和遥感一、地图与地图投影地图投影的概念在地球球面和平面之间建立点与点之间函数关系的数学方法。
图投影的意义(1)若不使用地图投影,可用地球仪直接模拟地球,但不细致,不精确,使用不方便,不能满足所有社会需求。
应用上需要把客观世界表现在有限的平面上。
(2)地球表面为不可展曲面,随意展成平面,必然产生无规律变形,因此必须建立科学的投影关系,控制变形和误差。
(3)地图投影尽管不能避免误差,但可求其误差规律,可根据需要,选择适宜的投影方式。
地图投影的变形(1)地图投影变形设想光源的远近对经纬网的影响光源置于球心,纬线间距自极点至赤道由内向外不断拉伸,投影后赤道在无穷远处光源置于无穷远,纬线间距自极点至赤道由内向外不断压缩,赤道附近趋零,纬线被赤道圈围光源置于球心外有限距离,光线弯曲——等距数学函数法,纬线间距不变,投影后赤道半径为子午面上极点至赤道的距离光源置于球心外有限距离,光线弯曲——等积数学函数法,面积不变,纬线间距自极点至赤道由内向外逐步压缩,投影后两纬圈之间的纬度带的面积保持不变几种不同投影的经纬线形式(2)变形椭圆定义:球面上的微小圆,投影后变为椭圆(特殊情况下为圆),这种椭圆叫变形椭圆。
证明椭圆过程地图投影的分类(1)按变形性质分类a.等角投影(正形投影)定义:投影图上没有角度变形,即ω=0的投影。
数学式:a=b形椭圆:为圆,它表明在等角投影中,任一点上的长度比不随方向的改变而改变。
用途:局部图形与实地相似。
航海图、洋流图、风向图等。
b.等积投影定义:没有面积变形,即面积比等于1的投影。
数学式:左右,陆地卫星的卫星轨道高度达910m左右,从而,可及时获取大范围的信息。
(2)获取信息的速度快,周期短。
由于卫星围绕地球运转,从而能及时获取所经地区的各种自然现象的最新资料,以便更新原有资料,或根据新旧资料变化进行动态监测,这是人工实地测量和航空摄影测量无法比拟的。
地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者地基本概念

地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念地球椭球体(Ellipsoid)众所周知我们的地球表面是一个凸凹不平的表面,而对于地球测量而言,地表是一个无法用数学公式表达的曲面,这样的曲面不能作为测量和制图的基准面。
假想一个扁率极小的椭圆,绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体。
地球椭球体表面是一个规则的数学表面,可以用数学公式表达,所以在测量和制图中就用它替代地球的自然表面。
因此就有了地球椭球体的概念。
地球椭球体有长半径和短半径之分,长半径(a)即赤道半径,短半径(b)即极半径。
f=(a-b)/a为椭球体的扁率,表示椭球体的扁平程度。
由此可见,地球椭球体的形状和大小取决于a、b、f 。
因此,a、b、f被称为地球椭球体的三要素。
对地球椭球体而言,其围绕旋转的轴叫地轴。
地轴的北端称为地球的北极,南端称为南极;过地心与地轴垂直的平面与椭球面的交线是一个圆,这就是地球的赤道;过英国格林威治天文台旧址和地轴的平面与椭球面的交线称为本初子午线。
以地球的北极、南极、赤道和本初子午线等作为基本要素,即可构成地球椭球面的地理坐标系统(A geographic coordinate system (GCS) uses a threedimensional spherical surface to define locations on the earth.A GCS includes an angular unit of measure, a prime meridian,and a datum (based on a spheroid).)。
可以看出地理坐标系统是球面坐标系统,以经度/维度(通常以十进制度或度分秒(DMS)的形式)来表示地面点位的位置。
地理坐标系统以本初子午线为基准(向东,向西各分了1800)之东为东经其值为正,之西为西经其值为负;以赤道为基准(向南、向北各分了900)之北为北纬其值为正,之南为南纬其值为负。
新编地图学教程全套完整版

对地球形状 a,b,f 测定后,还必须确定大地水准面与椭球 体面的相对关系。即确定与局部地区大地水准面符合最好的一个 地球椭球体 —— 参考椭球体,这项工作就是参考椭球体定位。
通过数学方法将地球 椭球体摆到与大地水准面 最贴近的位置上,并求出 两者各点间的偏差,从数 学上给出对地球形状的三 级逼近。
新编地图学教程 第2章 地图的数学基础
2.2 中国的大地坐标系统
1.中国的大地坐标系 1980年以前:参见电子教案本章第十三页; 1980年选用1975年国际大地测量协会推荐的参考 椭球: ICA-75椭球参数 a = 6 378 140m b = 6 356 755m f = 1/298.257
陕西省泾阳县永乐镇 北洪流村为 “1980 西安坐标系” 大地 坐标的起算点——大 地原点。
新编地图学教程 第2章 地图的数学基础
§2 地球坐标系与大地定位
地球表面上的定位问题,是与人类的生产活动、科学 研究及军事国防等密切相关的重大问题。具体而言,就 是球面坐标系统的建立。
2.1 地理坐标
—— 用经纬度表示地面点位的球面坐标。
① 天文经纬度 ② 大地经纬度 ③ 地心经纬度
新编地图学教程 第2章 地图的数学基础
2.1 地理坐标 ① 天文经纬度:表示地面点在大地水准面上的位
置,用天文经度和天文纬度表示。
天文经度:观测点天顶子午面与格林尼治天顶 子午面间的两面角。
在地球上定义为本初子午面与观测点之间 的两面角。 天文纬度: 在地球上定义为铅垂线与赤道平面 间的夹角。
椭球体 三要素: 长轴 a(赤道半径)、短轴 b(极半径)和椭球的扁率 f
WGS [world geodetic system] 84 ellipsoid:
地球的地图与地图投影

地球的地图与地图投影地球上有各种各样的地理现象和人文景观,为了更好地理解和呈现地球上的各种信息,人们常常使用地图来描绘地球的形状、地理特征和分布情况。
然而,由于地球是一个近乎球形的体积,将其展示在平面地图上总会产生一定的变形和扭曲。
因此,地图投影成为解决这一问题的重要方法之一。
本文将就地球的地图以及地图投影进行探讨。
第一部分:地球的地图地球的地图是指以地球表面为基准,通过一定的尺度和投影方法将地球上的地理现象表达在平面上的一种图形。
常见的地图类型有三种:等面积地图、等角地图和等距地图。
等面积地图,也被称为等积地图或等积投影地图,是在投影过程中保持地球上各个区域的面积比例不变的地图。
这种地图适用于需要展示地区面积分布、资源分布等以面积为主要参考的情况。
等角地图,也被称为等角投影地图,是在投影过程中保持地球上所有地区的角度关系不变的地图。
这种地图适用于需要更准确地展示地球上各个地区的方向、距离等以角度为主要参考的情况。
等距地图,也被称为等距投影地图,是在投影过程中保持地球上任意两点之间的距离比例不变的地图。
这种地图适用于需要更准确地表示地球上各个地区之间的实际距离的情况。
第二部分:地图投影的原理与方法地图投影是将三维的地球表面映射到二维的平面上的过程。
由于将球体的表面展示在平面上必然会导致形状、方向、面积等的变形和扭曲,因此人们提出了不同的投影方法来解决这一问题。
常见的地图投影方法有:圆柱投影、圆锥投影和平面投影。
圆柱投影是通过将一个圆柱体放置在地球上,将地球的表面映射到圆柱体上,再将圆柱体展开为平面来得到地图。
这种投影方法在赤道附近的地区保持了很好的形状保真度,但随着纬度的增加,变形越来越大。
圆锥投影是通过将一个圆锥体放置在地球上,将地球的表面映射到圆锥体上,再将圆锥体展开为平面来得到地图。
这种投影方法在地球的中纬度地区保持了很好的形状保真度,但极地地区的变形较大。
平面投影是将地球的表面映射到一个平面上,可以选择任意一个点作为投影中心。
地球体与地图投影讲义

b θ n a m
K
有:
m2 + n2 = a2 + b2
m· n· sinq = a· b
椭圆′称内任一条直径d的平行弦中点在椭圆内的轨迹 形成另一直径d ′, 则d为d的共轭直径。
第二章 地球体与地图投影 41
三、地图投影的变形
在分析地图投影时,可借助对变形椭圆和微小圆
的比较,说明变形的性质和大小。椭圆半径与小 圆半径之比,可说明长度变形。很显然,长度变 形随方向的变化而变化,其中有一个极大值,即 椭圆长轴方向,一个极小值,即椭圆短轴方向。 这两个方向是相互垂直的,称为主方向。椭圆面 积与小圆面积之比,可说明面积变形。椭圆上两 方向线的夹角和小圆上相应两方向线的夹角的比 较,可说明角度变形。
第二章 地球体与地图投影 22
三、全球定位系统
地面控制部分由1个主控站,5 个全球监测站
和3 个地面控制站组成。
第二章 地球体与地图投影
23
三、全球定位系统
用户接收部分的基本设备是GPS信号接收机,
其作用是接收、跟踪、变换和测量GPS卫星 所发射GPS信号,以达到导航和定位的目的。
第二章 地球体与地图投影
克拉索夫斯基 1975IUGG WGS-84
a b α e2 e‘2
6 378 245.000 6 356 863.019 1/298.3 0.006 693 422 0.006 738 525
6 378 140.000 6 356 755.288 1/298.257 0.006 694 385 0.006 739 502
x=f1(φ,λ)
y=f2(φ,λ)
第二章 地球体与地图投影 32
三、地图投影的变形
第二章投影及判断和选择

常用方位投影
5.2
正轴方位投影
5.2.3
正轴等距方位投影(波斯托投影)
特点: 由投影中心至任意一点 的距离均与实地相等。即该 投影后长度比 m=1。由于该 投影具有由投影中心至任意 点的距离和方位均保持与实 地的距离和方位不变,因此 在国际上应用的也比较广泛, 多用于两极地区图。
采用正轴等距方位投 影绘制的南极地图
常用方位投影
5.2
正轴方位投影
特点:投影中心为极点, 纬线为同心圆,经线为同 心圆的半径,两经线间的 夹角与实地相等。等变形 线都是以投影中心为圆心 的同心圆,包括等角、等 积、等距三种变形性质。 正轴方位投影主要用于制 作两极地区图。
三种方位投影纬线间隔变化示意图
常用方位投影
5.2
正轴方位投影
°等分,分别交线A于abc…,分别 以abc为圆心,以到C的长度为半径画 圆弧,即得各经线。 B C
①
②
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
经纬线形式:
中央经线为直线,其
它经纬线均是曲线。在中 央经线上纬线间隔相等。
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
非透视方位投影是借助于透视投影的方式,而附加上一定的 条件,如加上等积、等距等条件所构成的投影。在这类投影 中有等距方位投影和等积方位投影。
5.1.3
特点
在投影平面上,由投影中心(平面与球面相切的切点, 或平面与球面相割的割线的同心圆)向各个方向的方位角与 实地相等,其等变形线是以投影中心为圆心的同心圆,该投 影适合作区域轮廓大致为圆形的地图。
§4
地图投影的应用
高斯-克吕格投影(等角横切椭圆柱投影) 通用横轴墨卡托投影——UTM 投影 百万分一地形图投影 方位投影(正轴方位投影、正轴等角方位投影、正轴
地图学投影
18
我国的大地原点
建国初期,我国使用的大地测量坐标系统是从前苏联测过来 的,其坐标原点是前苏联玻尔可夫天文台 。54北京坐标系。
上个世纪70年代,中国决定建立自己独立的大地坐标系统。 通过实地考察、综合分析,最后将我国的大地原点,确定在 咸阳市泾阳县永乐镇北洪流村境内,具体坐标在:34°32′27. 00″N,108°55′25.00″E。 《中华人民共和国大地原点选点报告》:“为了使大地测量 成果数据向各方面均匀推算,原点最好在我国大陆的中部。” 而陕西泾阳县永乐镇石际寺村的确处在祖国大陆的中部。这里 距我国边界正北为880公里,距东北2500公里,距正东1000公 里,距正南1750公里,距西南2250公里,距正西2930公里,距 西北2500公里。同时,这里的地质条件比较理想。
5
6
全国水准网
7
地图投影中的地球体
大地水准面
静止海平面 地球数学表面
1.地球自然表面:地球是一个近似球体,其自然表面是一个极其复杂而 又不规则的曲面。
2. 地球物理表面:是假定海水处于 “完全” 静止状态,把海水面延伸到 (大地水准面)大陆之下形成包围整个地球的连续表面。
• 地球数学表面:假想以一个大小和形状与地球极为接近的旋转椭球面
64
65
2) 条件投影(非几何投影或解析投影)
不是借助于几何承影面,而是根据制图的 具体要求,有条件地应用数学解析的方法确定 球面与平面之间对应点的函数关系,把球面转 换为平面的投影。
66
2) 条件投影(非几何投影或解析投影) (1) 多圆锥投影
设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在 中央经线的延长线上。中央经线为直线,其余经线 投影为对称于中央经线的曲线。
新编地图学期末复习资料

新编地图学复习资料考试题型:判断、填空、解释、简答题、问答题。
第一章导论1.地图的基本特征地理信息的载体、数学法则的结构、有目的的图形概括、符号系统的运用。
2.地图的定义地图是遵循相应的数学法则,将地球(也包括其他星体)上的地理信息,通过科学的概括,并运用符号系统表示在一定载体上的图形,以传递它们的数量和质量在空间和时间上的分布规律和发展变化。
3.地图的功能地图信息的载负功能、地图的传递功能、地图的模拟功能、地图的认知功能4.地图的类型(1)按尺度划分:大比例尺、中比例尺、小比例尺。
(2)按区域范围划分:星球图、地球图、世界图、国家图、海湾图等等。
(3)按地图的图型划分:普通地图和专题地图。
注:我国把比例尺1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5千这8种地形图定为国家基本比例尺地形图(4)按其他指标分类:用途(文化地图)、语言种类(汉字地图)、历史年代(古地图)、出版和使用方式(桌图、挂图)5.《制图六体》——————晋朝、裴秀。
6.地图的成图方法:实测成图和编绘成图。
7.现代地图学:由理论地图学、地图制图学、应用地图学组成。
第二章地球体与地图投影1.大地测量系统(1)我国的大地坐标系统:1980年国家大地坐标系(使用1975年国际测量协会推荐的参考椭球体)、陕西安的大地原点。
(2)大地控制网:平面控制网、高程控制网(3)全球定位系统:GPS\GLONASS\GALILEO\COMPASS\(3S是指遥感、地理信息系统、全球定位系统)2.地图投影概念地图投影是指将地球表面展开成平面的理论和方法,是实现球面到平面的转换,就是地球体的数学模型。
3.地图投影的变形长度(距离)、角度(形状)、面积等等4.投影的分类(1)按地图投影的构成方法分类:几何投影(方位投影、圆柱投影、圆锥投影)、非几何投[根据经纬线形状可以分为(伪方位投影、伪圆柱投影、伪圆锥投影、多圆锥投影)](2)按投影变形性质的分类:等角投影、等积投影、任意投影。
地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念

地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念地球椭球体(Ellipsoid)众所周知我们的地球表面是一个凸凹不平的表面,而对于地球测量而言,地表是一个无法用数学公式表达的曲面,这样的曲面不能作为测量和制图的基准面。
假想一个扁率极小的椭圆,绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体。
地球椭球体表面是一个规则的数学表面,可以用数学公式表达,所以在测量和制图中就用它替代地球的自然表面。
因此就有了地球椭球体的概念。
地球椭球体有长半径和短半径之分,长半径(a)即赤道半径,短半径(b)即极半径。
f=(a-b)/a为椭球体的扁率,表示椭球体的扁平程度。
由此可见,地球椭球体的形状和大小取决于a、b、f 。
因此,a、b、f被称为地球椭球体的三要素。
对地球椭球体而言,其围绕旋转的轴叫地轴。
地轴的北端称为地球的北极,南端称为南极;过地心与地轴垂直的平面与椭球面的交线是一个圆,这就是地球的赤道;过英国格林威治天文台旧址和地轴的平面与椭球面的交线称为本初子午线。
以地球的北极、南极、赤道和本初子午线等作为基本要素,即可构成地球椭球面的地理坐标系统(A geographic coordinate system (GCS) uses a three dimensional spherical surface to define locations on the earth. A GCS includes an angular unit of measure, a prime meridian,and a datum (based on a spheroid).)。
可以看出地理坐标系统是球面坐标系统,以经度/维度(通常以十进制度或度分秒(DMS)的形式)来表示地面点位的位置。
地理坐标系统以本初子午线为基准(向东,向西各分了1800)之东为东经其值为正,之西为西经其值为负;以赤道为基准(向南、向北各分了900)之北为北纬其值为正,之南为南纬其值为负。
2 第二章 地图投影

而是从地图放大系 数的定义入手,来 求有关的表达式。
NIM NUIST
等经纬度网格,没反映麦卡托投影的 放大系数
NIM NUIST
高纬放大系数大
地球表面纬度为处,纬圈的长度为: Ls 2Rs 2a cos
(2.22)
可见,其放大系数是关于赤道成纬向轴对称的。
NIM NUIST
三种地图投影方式总结:
(1)极射赤面投影,在极地和高纬度地区产 生的变形较小,这种投影方式通常用于制作极地 天气图和北半球天气底图。
(2)兰勃托投影,在中纬度地区产生的变 形较小,这种投影方式通常用于制作中纬度地区 的天气图,如亚欧天气底图。
1
cos sin
k
(2.16)
NIM NUIST
可解出
sin
le2/ k le2/ k
l2/k l2/k
(2.17)
根据
m L kl kl
Ls a cos a sin
m
kl
从而有:
a
1
le2 / k le2 / k
l 2/k l 2/k
2
(2.18)
f
2
le2 le2
/ /
k k
l2/k l2/k
(2.19)
NIM NUIST
五、麦卡托投影(Mercator投影)
麦卡托投影,光源位于球心, 映像面是与地球表面相割于南北 纬22.5的圆柱面,标准纬度:
1 22.5 N , 2 22.5 S
NIM NUIST
P70-图2.8
投影后,经线 为等距平行的直线 ,纬线为与经线垂 直的直线。
地球尺度与地图投影方式的选择

地球尺度与地图投影方式的选择地球是我们生活的家园,它的广袤无垠让人们感叹不已。
然而,将地球的真实尺度展示在平面地图上并非易事。
由于地球是一个椭球体,将其展开为平面图就需要进行投影。
然而,不同的投影方式会导致地图上的形状、面积、方向等属性发生变化。
因此,选择合适的地图投影方式对于准确传达地球尺度至关重要。
首先,我们来了解一下地图投影的基本原理。
地图投影是将地球表面的经纬度坐标系映射到平面坐标系上的过程。
由于地球是一个三维球体,而平面是一个二维平面,所以必然会有一定的变形。
这种变形可以通过不同的投影方式来实现。
常见的地图投影方式包括墨卡托投影、兰伯特投影、等距圆柱投影等。
墨卡托投影是最常见的地图投影方式之一。
它以经线和纬线相交的点为基准,将地球表面的每一个点映射到平面上。
墨卡托投影具有保角性质,即在地图上的任意两条线段的夹角与地球表面上的夹角相等。
这使得墨卡托投影在航海、航空等领域具有重要的应用。
然而,墨卡托投影在高纬度地区会出现面积变形的问题,即地图上的面积与实际面积不一致。
兰伯特投影是一种等面积投影方式,它能够保持地球表面上的面积比例。
在兰伯特投影下,地球的每一个点都被映射到平面上,且面积比例不变。
这使得兰伯特投影在统计、地质、气候等领域有着广泛的应用。
然而,兰伯特投影也存在一些问题,例如在极地附近会出现形状的扭曲。
除了墨卡托投影和兰伯特投影外,还有许多其他的地图投影方式,如等角圆锥投影、等距圆柱投影等。
每种投影方式都有其独特的优势和局限性。
选择合适的地图投影方式需要考虑地图使用的目的和地理区域的特点。
在实际应用中,我们可以根据地图使用的目的来选择合适的投影方式。
如果需要强调地图上的角度和方向关系,墨卡托投影是一个不错的选择。
如果需要准确表示地图上的面积比例,兰伯特投影是一个更好的选择。
而对于需要同时兼顾角度和面积比例的地图,可以考虑使用其他投影方式,如等角圆锥投影或等距圆柱投影。
除了投影方式,地图的尺度也是选择的重要考虑因素。
地理信息系统2 地理空间参照系统与地图投影

地理空间既可以是具有属性描述的空间位置的集合(由 一系列的空间坐标值组成);也可以是具有空间属性特
征的实体的集合(由不同实体之间的空间关系构成)。
地理空间的表达是地理数据组织、存储、运算、分析的 理论基础。
地图—传统的地理信息表达方式
现实地理世界抽象模型
点(位置)
高程点, 控制点, 三角点, 地形特征点 水井位, 水泉位, 油井位, 钻井位 站台, 车站, 水文站, 气象站, 天文台, 地震台 乡镇驻地
常用的一些地图投影
各大洲地图投影
亚洲地图的投影:斜轴等面积方位投影、彭纳投影。
欧洲地图的投影:斜轴等面积方位投影、正轴等角圆锥 投影。 北美洲地图的投影:斜轴等面积方位投影、彭纳投影。 南美洲地图的投影:斜轴等面积方位投影、桑逊投影。
澳洲地图的投影:斜轴等面积方位投影、正轴等角圆锥 投影。
地理空间的概念
GIS中的空间概念常用“地理空间”来表达。
地理空间上至大气电离层、下至地幔莫霍面。它是人类活动频 繁发生的区域,是人地关系最为复杂、紧密的区域,是地球上 大气圈、水圈、生物圈、岩石圈和土壤圈交互作用的区域,地 球上最复杂的物理过程、化学过程、生物过程和生物地球化学 过程就发生在这里。
表面(场)
T(Xi ,Yj)
dT / dXi dT / dYj
地图描述地理信息的方式
符号和注记 空间关系隐含
基本地图比例尺
比例尺等级(有级) 1:100, 1:200, 1:500, 1:1 000, 1:2 000, 1:5 000 1:10 000, 1:50 000, 1:100 000, 1:200 000 1:500 000, 1:1000 000, 1:2000 000, 1:4000 000 1:8000 000, 1:10 000 000, 1:20 000 000, 1:50 000 000 1:100 00,通常称地
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
把地图上和地球仪上的经纬线网进行比较,可 以发现变形表现在长度、面积和角度三个方面。
2.变形椭圆
取地面上一个微分圆(小到可忽略地球曲面的 影响,把它当作平面看待),它投影到平面上通常 会变为椭圆,通过对这个椭圆的研究,分析地图投 影的变形状况。这种图解方法就叫变形椭圆。
X' m 为经线长度比; X
WGS [world geodetic system] 84 ellipsoid:
a = 6 378 137m b = 6 356 752.3m equatorial diameter = 12 756.3km polar diameter = 12 713.5km equatorial circumference = 40 075.1km surface area = 510 064 500km2
地面支撑系统:1个主控站,3个注入站,5个监测站。 它向GPS导航卫星提供一系列描述卫星运动及其轨道的参数; 监控卫星沿着预定轨道运行;保持各颗卫星处于GPS时间系 统及监控卫星上各种设备是否正常工作等。
用户设备部分:GPS接收机——接收卫星信号,经数据 处理得到接收机所在点位的导航和定位信息。通常会显示出 用户的位置、速度和时间。还可显示一些附加数据,如到航 路点的距离和航向或提供图示。
椭圆内两共轭半径的平方和等于其长短半径的平方和;两个共 轭半径与它们的交角正弦的乘积等于其长短半径的乘积。
L K O
b θ n
L
根据阿波隆尼定理有: a m
K
m2 + n2 = a2 + b2
m· sinq = a· n· b
特别方向: 变形椭圆上相互垂直的两个方向
• 1.所有经线都是通过两极的大圆且 长度相等;所有纬线都是圆,圆半 径由赤道向两极递减,极地成为一 点。 • 2.经线表示南北方向;纬线表示东 西方向。 • 3.经线和纬线是相互垂直的。 • 4.纬差相等的经线弧长相等;同一 条纬线上经差相等的纬线弧长相等, 在不同的纬线上,经差相等的纬线 弧长不等,由赤道向两极递减。 • 5.同一纬度带内,经差相同的经纬 线网格面积相等,同一经度带内, 纬差相同的经纬线网格面积不等, 纬度越高,梯形面积越小(由低纬 向高纬逐渐缩小)。
在地理学研究及地图学 的小比例尺制图中,通常将 椭球体当成正球体看,采用 地心经纬度。
§2 大地测量系统
1.中国的大地坐标系统
中国1952年前采用海福特(Hayford)椭球体 ; 1953—1980年采用克拉索夫斯基椭球体(坐标原点是前 苏联玻尔可夫天文台) ; 自1980年开始采用 GRS 1975(国际大地测量与地球物理 学联合会 IUGG 1975 推荐)新参考椭球体系,并确定陕西泾 阳县永乐镇北洪流村为“1980西安坐标系”大地坐标的起算 点。
大地水准面的意义
1. 地球形体的一级逼近__大地体:
对地球形状的很好近似,其面上高出与面下缺 少的相当。
2. 起伏波动在制图学中可忽略:
对大地测量和地球物理学有研究价值,但在制 图业务中,均把地球当作正球体。
3. 实质是重力等位面:
它是水准测量的基准面,是高程的其始点,可 使用仪器测得海拔高程(某点到大地水准面的高 度)。
• 导线测量:把各个控制点连接成连续的折线,然 后测定这些折线的边长和转角,最后根据起算点 的坐标和方位角推算其他各点坐标。包括闭合导 线、附合导线、支导线。 • 布设原则:由高级到低级,由整体到局部,步步 有检核。
等级
一等三角锁
边长
20~25km
分布密度
锁与锁间距200km
分布方向
沿经纬线分布
陕西省泾阳县永乐镇北洪流村为 “1980西安坐标系” 大地坐标的 起算点——大地原点。
ICA-75椭球参数
a = 6 378 140m
b = 6 356 755m
f =1/298.257
参考椭球体和大地原点确定之后,便可进 行椭球体定位和精确测定大地原点坐标,进 而再以大地原点坐标为基准,推算其他大地 点坐标。 注意:各国由于采用的参考椭球体及定位方法 不同,因此同一地面点在不同的坐标系中大 地坐标值也不相同。
新 编 地 图 学 教 程
电 子 教 案
第 2 章
地球体与地图投影
第 2 章 地球体与地图投影
§ § § § 1 2 3 4 地球体 大地测量系统 地图投影 地图比例尺
§1
1.1 地球的自然表面
地球体
一 地球体的基本特征
浩瀚宇宙之中 : 地球是一个表面光滑、蓝色美丽的正球体。
机舱窗口俯视大地 : 地表是一个有些微起伏、极其复杂的表面。
North Pole
Polar Axis
b a
Equatorial Axis
Equator
a-b 6378137 - 6356752.3 f = —— = ———————— a 6378137
South Pole
— = 298.257 f
1
对 a,b,f 的具体测定就是近代 大地测量的一项重要工作。
二等三角网
三等三角网
13km
8km
150km2有一控制点(1:10万,1:5 万》3点)
50km2有一控制点(1:5万2~3点)
在一等加密
在二等加密
四等三角网
4km
20km2有一控制点(1:1万~2点)
在三等加密
国家测绘局
高程控制网 : 按统一规范,由精确测定高程的地面点组成,以 水准测量或三角高程测量完成。依精度不同,分为四等。 建立高程控制网的目的是为了精确求算绝对高程,即高程。
Y' n 为纬线长度比 Y
X' m X
2 2
Y' n Y
代入: X + Y = 1,得
X' Y' 2 1 2 m n
2
2
微小圆→变形椭圆
该方程证明: 地球面上的微小圆 ,投影后通常会变为椭圆,即:以O' 为原点,以相交成q角的两共轭直径为 坐标轴的椭圆方程式。
椭圆共轭直径:过椭圆内任一条直径(图中LL)的平行弦 中点的轨迹(图中KK)。 阿波隆尼定理(Apollonius):
2.中国的大地控制网
由平面控制网和高程控制网组成,包括具有精确 测定平面位置和高程的典型的具有控制意义的点,它 是测制地图的基础。
平面控制网 :采用平面控制测量确定控制点的平面位置, 即大地经度(L)和大地纬度(B)。其主要方法是三角测 量和导线测量。依精度不同,分为一等三角锁、二等三角 网、三等三角网、四等三角网四等。 三角测量:在全国范围内将控制点组成一系列的三角形, 通过测定所有三角形的内角,推算出各控制点的坐标。
由于国际上在推求年代、方法及测定的地区不同,故 地球椭球体的元素值定位问题,是与人类的生产活动、科学研 究及军事国防等密切相关的重大问题。具体而言,就是球面 坐标系统的建立。 地理坐标,就是用经线、纬线、经度、纬度表示地 面点位的球面坐标。在大地测量学中,对于地理坐标系 统中的经纬度有三种提法: 天文经纬度
P
Q’
大地纬度 :指参考椭球 面上某点的垂直线(法线) 首子 午线 与赤道平面的夹角。北纬 为正,南纬为负。
L P’
法 B线
Q
③ 地心经纬度:即以地球椭球体质量中心为基点,地 心经度同大地经度l ,地心纬度是指参考椭球面上 某点和椭球中心连线与赤道面之间的夹角y 。 在大地测量学中,常以 天文经纬度定义地理坐标。 在地图学中,以大地经 纬度定义地理坐标。
地球椭球体表面是不可展曲面,要将曲面上的客观事物 表示在有限的平面图纸上,必须经过由曲面到平面的转换。 地图投影:在地球椭球面和平面之间建立点与点之间函 数关系的数学方法。 地图投影的实质:是将地球椭球面上的经纬线网按照一 定的数学法则转移到平面上。
三 地图投影变形
1.投影变形的性质
研究各种投影的变形规律是通过把投影后的经纬线网 与地球仪上经纬线网格比较而实现的。地球仪是地球的真 实缩小。通过比较就会发现地球仪上的经纬网形状与投影 后经纬网的形状是不相同的。为了研究变形,首先让我们 分析一下地球仪上经纬网的特点:
水青 准岛 原观 点象 山
中国高程起算面是黄海平均海水面。
1956年在青岛观象山设立了水准原点(72.289m),其他各控 制点的绝对高程均是据此推算,称为1956年黄海高程系。
1987年国家测绘局公布:启用《1985国家高程基准》取代《 黄海平均海水面》,其比《黄海平均海水面》上升29毫米。 (72.260m)
绝对高程(海拔):地面点到大地水准面的垂直距离。
相对高程:地面点到任一水准面的垂直距离。 高差:某两点的高程之差。
国家测绘局
国家测绘局
国家测绘局
3 全球定位系统 - GPS
授时与测距导航系统/全球定位系统 (Navigation Satellite Timing and Ranging/Global Positioning System--GPS):是
1.3
地球的数学表面
在测量和制图中就用旋转椭球体来代替大地球体,这 个旋转椭球体通常称为地球椭球体,简称椭球体。
它是一个规则的 数学表面,所以人 们视其为地球体的 数学表面,也是对 地球形体的二级逼 近,用于测量计算 的基准面。
椭球体三要素: 长轴 a(赤道半径)、短轴 b(极半径)和椭球的扁率 f
地球椭球体需要4个条件才能达到和大地体最密合:
• 地球椭球体中心和地球的质心重合 • 地球椭球体的短轴和地球的地轴重合 • 地球椭球体起始大地子午面和起始天文子 午面重合 • 在确定长轴a和扁率f时,要满足在全球范围 的大地水准面差距的平方和最小
对地球形状 a,b,f 测定后,还必须确定大地水准面与椭球 体面的相对关系。即确定与局部地区大地水准面符合最好的一个 地球椭球体 —— 参考椭球体,这项工作就是参考椭球体定位。 通过数学方法将地球 椭球体摆到与大地水准面 最贴近的位置上,并求出 两者各点间的偏差,从数 学上给出对地球形状的三 级逼近—— 参考椭球体。
