结构动力学习题解答
结构动力学题解(1)
题图
23 l 3 = 1536 EI
则系统的自振频率
ω=
1 1536 EI = mδ 23ml 3 1 1536 EI = 2 ω 1536 EI − 23ml 3ω 2 1− ω2 1536 EI 23l 3 ⋅ ⋅F 1536 EI − 23ml 3ω 2 1536 EI
2 2 1 l12 l2 l12 k1 + l2 k2 = 1 / m + 3 2 3EI (l + l ) (l + l ) k k mδ 1 2 1 2 1 2
(e) 解，考虑质体水平单位位移时的系统劲度。
k1 = k3 = k2 =
12 EI 2 h3
3EI 2 h3
令 δ t 为两支座弹簧无限刚度时单位力作用下质体的垂直位移
1 1 l1l2 2 l1l2 l12 l22 δt = × (l1 + l2 ) × × = 3 EI (l1 + l2 )2 3 (l1 + l2 )2 2 3EI (l1 + l2 )
总变形： δ = δ t + δ M 其自振频率： ω =
F (t ) = F sin ω t
y0 =
l3 3EI 3EI ml 3
题图
系统自振频率 ω =
动力系数 µ =
1 3EI = 2 ω 3EI − ml 3ω 2 1− ω2 3EI l3 Fl 3 ⋅ ⋅ F = 3EI − ml 3ω 2 3EI 3EI − ml 3ω 2
&& ， Fi1 = Fi 2 = mY
两柱的侧移劲度相等为： k =
3i 3EI = 3 (单位位移下的水平剪力) l2 l
结构动力学习题解析
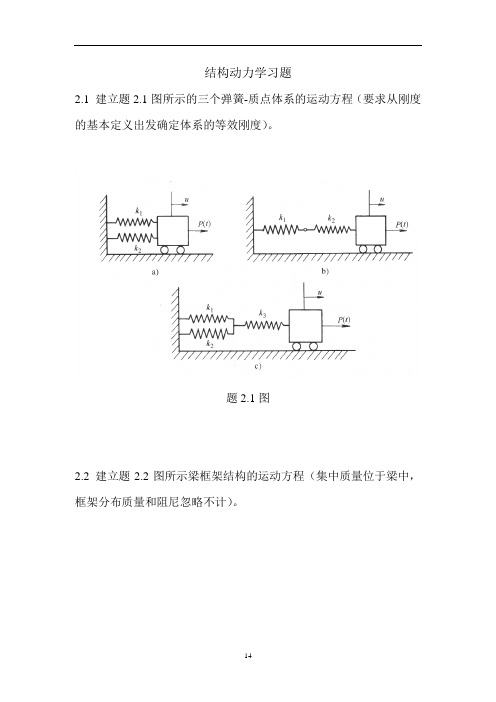
结构动力学习题2.1 建立题2.1图所示的三个弹簧-质点体系的运动方程（要求从刚度的基本定义出发确定体系的等效刚度）。
题2.1图2.2 建立题2.2图所示梁框架结构的运动方程（集中质量位于梁中，框架分布质量和阻尼忽略不计）。
题2.2图2.3 试建立题2.3图所示体系的运动方程，给出体系的广义质量M、广义刚度K、广义阻尼C和广义荷载P(t)，其中位移坐标u(t)定义为无重刚杆左端点的竖向位移。
题2.3图2.4 一总质量为m1、长为L的均匀刚性直杆在重力作用下摆动。
一集中质量m2沿杆轴滑动并由一刚度为K2的无质量弹簧与摆轴相连，见题 2.4图。
设体系无摩擦，并考虑大摆角，用图中的广义坐标q1和q2建立体系的运动方程。
弹簧k2的自由长度为b。
题2.4图2.5 如题2.5图所示一质量为m1的质量块可水平运动，其右端与刚度为k的弹簧相连，左端与阻尼系数为c的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连，摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程（坐标原点取静平衡位置）。
题2.5图2.6如题2.6图所示一质量为m1的质量块可水平运动，其上部与一无重刚杆相连，无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连，m1右端与刚度为k1的弹簧相连，左端与阻尼系数为c1的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连，摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程（坐标原点取静平衡位置，假定系统作微幅振动，sinθ=tanθ=θ）。
计算结果要求以刚度矩阵，质量矩阵，阻尼矩阵的形式给出。
3.1单自由度建筑物的重量为900kN，在位移为3.1cm时（t＝0）突然释放，使建筑产生自由振动。
如果往复振动的最大位移为2.2cm（t ＝0.64s），试求：（1）建筑物的刚度k；（2）阻尼比ξ；（3）阻尼系数c。
3.2 单自由度体系的质量、刚度为m＝875t，k＝3500kN/m，且不考虑阻尼。
结构动力学课后习题答案
结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案，供参考：习题1：单自由度系统自由振动分析解答：对于一个单自由度系统，其自由振动的频率可以通过以下公式计算：\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中，\( k \) 是系统的刚度，\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述，其衰减系数 \( \delta \) 可以通过以下公式计算：\[ \delta = \sqrt{1-\zeta^2} \]习题2：单自由度系统受迫振动分析解答：当单自由度系统受到周期性外力作用时，其受迫振动的振幅可以通过以下公式计算：\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中，\( F_0 \) 是外力的幅值，\( \omega \) 是外力的角频率。
习题3：多自由度系统模态分析解答：对于多自由度系统，可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为：\[ [K]{\phi} = \lambda[M]{\phi} \]其中，\( [K] \) 是系统的刚度矩阵，\( [M] \) 是系统的质量矩阵，\( \lambda \) 是特征值，\( {\phi} \) 是对应的特征向量，即模态形状。
习题4：结构的冲击响应分析解答：对于结构的冲击响应分析，通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱（IRF）来分析，它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5：疲劳分析解答：结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构动力学习题解答一二章
2、 动量距定理法
适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析与动量距分析;
(2) 利用动量距定理J ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:
;
1、7求图1-36所示齿轮系统的固有频率。已知齿轮A的质量为mA,半径为rA,齿轮B的质量为mB,半径为rB,杆AC的扭转刚度为KA,,杆BD的扭转刚度为KB,
解:由齿轮转速之间的关系 得角速度 ;转角 ;
系统的动能为:
CA
;B D
图1-36
系统的势能为:
;
系统的机械能为
;
由 得系统运动微分方程
;
适用范围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为 ,写出系统对于坐标 的动能T与势能U的表达式;进一步写求出拉格朗日函数的表达式:L=T-U;
(2)由格朗日方程 =0,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法
1、2叙述用衰减法求单自由度系统阻尼比的方法与步骤。
用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法与共振法。
方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期与相邻波峰与波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有
,
因为 较小,所以有
。
方法二:共振法求单自由度系统的阻尼比。
;L/2L/2
则固有频率为:
图1-33(b)
结构动力学习题解答
然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
；
再积分求初位移
̇̇ d t == h )d t = 0 ； θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程（6）的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R，质量为 M，作纯滚动。弹簧刚度 为K 。 解：磙子作平面运动， 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ，进一步得到系 dt
统的运动微分方程； （3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个：衰减曲线法和共振法。 方法一：衰减曲线法。 求解步骤： （1）利用试验测得单自由度系统的衰减振动曲线，并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 （2）由对数衰减率定义 δ = ln(
结构动力学1~15
《结构动力学》习题答案1~151． 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1）建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2）进行振型和频率分析对无阻尼自由振动，这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3）求广义质量和荷载依次取每一个振型向量n φ，计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4）求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5）求对荷载的振型反应根据荷载类型，用适当的方法解这些单自由度方程，每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6）振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7）求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然，它反映了各个振型贡献的叠加。
因此命名为振型叠加法。
8）弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时，可以采用另一种弹性力的表达式。
结构动力学作业答案（royr.craig）
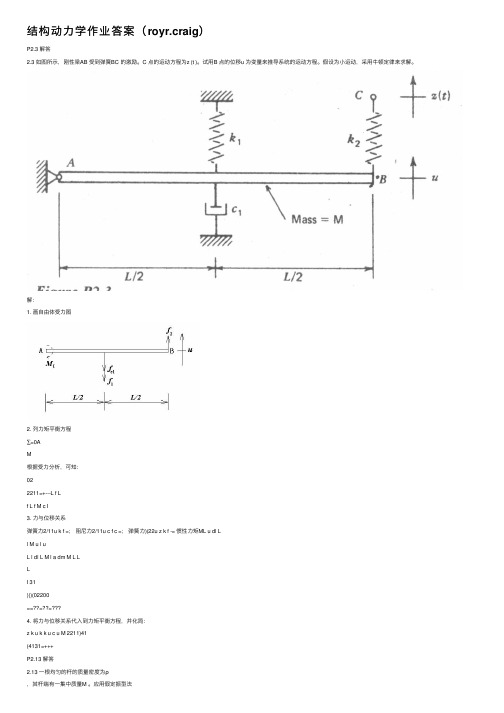
结构动⼒学作业答案（royr.craig）P2.3 解答2.3 如图所⽰，刚性梁AB 受到弹簧BC 的激励。
C 点的运动⽅程为z (t )。
试⽤B 点的位移u 为变量来推导系统的运动⽅程。
假设为⼩运动，采⽤⽜顿定律来求解。
解：1. 画⾃由体受⼒图2. 列⼒矩平衡⽅程∑=0AM根据受⼒分析，可知：022211=+---L f Lf L f M c I3. ⼒与位移关系弹簧⼒2/11u k f =；阻尼⼒2/11u c f c =；弹簧⼒)(22u z k f -= 惯性⼒矩ML u dl Ll M u l uL l dl L M l a dm M L LLI 31)()(02200==??=??=4. 将⼒与位移关系代⼊到⼒矩平衡⽅程，并化简：z k u k k u c u M 2211)41(4131=+++P2.13 解答2.13 ⼀根均匀的杆的质量密度为ρ，其杆端有⼀集中质量M 。
应⽤假定振型法（L x x /)(=ψ）推导如下系统的轴向⾃由振动的运动⽅程。
解：1. 形函数及⼏何边界条件0),0(=t U )()(),(t u x t x U ψ=2. 建⽴虚功⽅程0'=+-=inertia nc W V W W δδδδ因为没有外⼒，所以0=nc W δu LAEudx L u L u AE Udx AEU V LL δδδδ===?)'( 对于惯性⼒⽽⾔，其虚功包括杆本⾝的虚功1inertia W δ和杆端集中质量的虚功2 inertia W δ。
u uALdx x Lu u A Udx UA W LLinertia δρδρδρδ 3)(02201-=-=-=?u u M t L U t L UM W inertia δδδ -=-=),(),(2 3. 化简0)3(=++-u u L AE u M ALδρ因为u δ为虚位移，即0≠u δ，所以运动⽅程为0)3(=++u L AEu M AL ρP3.7 解答3.7 ⼀台机器的质量为70kg ，安装在弹簧上，弹簧的总刚度为15kN/m ，总阻尼为1.2kN.s/m 。
结构动力学试题及答案
结构动力学试题及答案一、选择题1. 在结构动力学中，下列哪项不是描述结构动力响应的参数？A. 自然频率B. 阻尼比C. 静力平衡D. 模态阻尼2. 以下哪个不是结构动力学分析中的常用方法？A. 模态分析B. 时域分析C. 频域分析D. 静力分析二、简答题1. 简述结构动力学中模态分析的目的和重要性。
2. 描述阻尼对结构动力响应的影响。
三、计算题1. 假设一个单自由度系统，其质量为m，刚度为k，初始位移为x0，初始速度为v0。
若外力为F(t) = F0 * sin(ωt)，求该系统在任意时间t的位移响应。
答案一、选择题1. 正确答案：C. 静力平衡解析：静力平衡是静力学的概念，与结构动力学无关。
2. 正确答案：D. 静力分析解析：静力分析是分析结构在静载荷作用下的响应，而结构动力学分析动态载荷下的结构响应。
二、简答题1. 模态分析的目的在于识别结构的自然振动特性，包括自然频率、阻尼比和模态形状。
它的重要性在于：- 预测结构在动态载荷下的响应。
- 为控制结构的振动提供基础数据。
- 优化设计，提高结构的抗震性能。
2. 阻尼对结构动力响应的影响主要表现在：- 减少振动幅度，提高结构的稳定性。
- 改变系统的自然频率和模态形状。
- 影响系统的动态响应时间。
三、计算题1. 单自由度系统的位移响应可以通过以下步骤求解：- 写出系统的动力学方程：m * d²x/dt² + c * dx/dt + k * x = F(t)- 应用初始条件：x(0) = x0, v(0) = v0- 应用外力：F(t) = F0 * sin(ωt)- 通过傅里叶变换或拉普拉斯变换求解方程。
- 应用逆变换得到位移响应的解析解或数值解。
位移响应的一般形式为：x(t) = X * cos(ωt - φ) + Y *sin(ωt - φ)，其中X和Y是与系统参数和初始条件有关的常数，φ是相位角。
具体的数值需要根据系统参数和初始条件进行计算。
结构动力学习题解答(三四章)
第三章 多自由度系统3.1试求图3-10所示系统在平衡位置附近作微振动的振动方程。
图３－１０解：〔1〕系统自由度、广义坐标图示系统自由度N=2，选x1、x2和x3为广义坐标； 〔2〕系统运动微分方程根据牛顿第二定律，建立系统运动微分方程如下：;)(;)()(;)(34233332625323122222121111x K x x K x m x K x K x x K x x K xm x x K x K xm ---=------=---= 整理如下;0)(;0)(;0)(3432333332653212222212111=++-=-++++-=-++x K K x K xm x K x K K K K x K xm x K x K K xm 写成矩阵形式;000)(0)(0)(00000321433365322221321321⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+++--++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x K K K K K K K K K K K K x x x m m m 〔1〕 〔3〕系统特征方程设)sin(,)sin(,)sin(332211ϕωϕωϕω+=+=+=t A x t A x t A x 代入系统运动微分方程〔1〕得系统特征方程;000)(0)(0)(321234333226532222121⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+---+++---+A A A m K K K K m K K K K K K m K K ωωω〔2〕 〔4〕系统频率方程系统特征方程〔2〕有非零解的充要条件是其系数行列式等于零， 即;0)(0)(0)(234333226532222121=-+---+++---+ωωωm K K K K m K K K K K K m K K展开得系统频率方程;0))(())(()))(())(()((21212323432223432265322121=-+--+--+-+++-+ωωωωωm K K K m K K K m K K m K K K K m K K进一步计算得;0;0)()())()(()))(())((())()()(()()()()())(()())(())(())()(())(())(()))(()()())((())(())(()))(())(()((02244662123432265324321236532214321231233224316532214332216321231232123232243226321421434322124321243165322165324323653221653243212121232343222343421221265322165322121212323432223432265322121==++++-+-+++++++++++-++-+++++++++++-=++-++--++++++-++++++++-++++-+++++=-+--+--+++-+++-++++=-+--+--+-+++-+a a a a K K K K K K K K K K K K K K m K K K K K K K K K K m m m K m K m m K K K K m m K K m m K K m m m m m K K K K m K K K K m m m m m K K m m K K K K K K m m m K K K K m K K K K K K m K K K K K K K K K K K K K K m K K K m K K K m K K m m K K m K K K K m K K K K K K m K K K m K K K m K K m K K K K m K K ωωωωωωωωωωωωωωωωωωωωωωωωωω (3)其中;3216m m m a -= ;)()()(316532214332214m m K K K K m m K K m m K K a +++++++=;))(())((36532214321231233222m K K K K K K K K K K m m m K m K a ++++-++-+=);()())()((21234322653243210K K K K K K K K K K K K K K a +-+-+++++=求解方程〔3〕得系统固有频率;)3,2,1(),,,,,,,,,(654321321==i K K K K K K m m m f i i ω 〔4〕 〔5〕系统固有振型 将系统固有频率代入系统特征方程〔2〕得系统固有振型， 即各阶振型之比：)3(3)3(1)3(3)3(2)3(1)3(2)2(3)2(1)2(3)2(2)2(1)2(2)1(3)1(1)1(3)1(2)1(1)1(21,1;1,1,1,1A A A A A A A A A A A A ======γγγγγγ 〔5〕 〔6〕系统振动方程)sin()sin()sin()sin()sin()sin(33)3(1)3(3)3(1)3(2)3(122)2(1)2(3)2(1)2(2)2(111)1(1)1(3)1(1)1(2)1(133)3(3)3(2)3(122)2(3)2(2)2(111)1(3)1(2)1(1321ϕωγγϕωγγϕωγγϕωϕωϕω+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧t A A A tA A A tA A A t A A A t A A A t A A A x x x 〔6〕在方程〔6〕中含有6个待定常数：)1(1A 、)2(1A 、)3(1A 、1ϕ、2ϕ和3ϕ。
结构动力学习题+讲解
&&(t ) + （ω2 – n2 ）S (t) = 0 --------------------------------------------（5） S
1．当 n >ω时（强阻尼） 方程（5）的解为： S (t) = A1sh n − ω t +A2ch n − ω t
2 2 2 2
从而，方程（4）的解为：
若时间 t 不是从 0 开始，而是从τ开始的，则（9）式写为：
y (t ) =
p∆t sinω（t-τ） mω
---------------------------------------（10）
写作： ，记ω2 =
K m
，2n =
C ，又可写作： m
& &(t ) + 2n y & (t ) +ω2 y (t ) = 0 y
利用常数变易法，令 y (t ) = e
− nt
---------------------------------------------（4）
S (t ) 代入方程（4）中 得：
K/2 VBA
48i/7L
2
A
取横梁为研究对象，Σ X=0，得：K= 4）振动方程
24 EI L3
即，
&(t ) - K y(t ) + Psinθt = 0 y - 2 m& &(t ) + y 2 m&
24 EI y(t ) = Psinθt L3
一、 无阻尼的自由振动
振动方程
&(t ) +K y (t ) = 0 ， m& y & &(t ) + y K y (t ) = 0 m
中国大学MOOC结构动力学习题含答案-精品
中国大学MOOC结构动力学习题（含答案）1、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、1B、2C、3D、4答案：22、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、1B、2C、3D、4答案：23、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、0B、1C、2D、3答案：24、在很短时间内，荷载值急剧增大或急剧减小的荷载是（）oA、可变荷载B、偶然荷载C、冲击荷载D、爆炸答案：冲击荷载5、动力自由度的个数（）集中质量的个数。
图所示刚架结构，不计分布质量，动力自由度个数为（）o 此题为多项选择题。
请帮忙给出正确答案和分析，谢谢! •日目•2EI:一.c（A）2个（B）3个（C）4个（D）5个答案：B自由度个数有3个，因此正确答案为（B）。
1、一、单项选择题（每题2分，共6分）答案：ABDAC二.实验探究题（共20分）2、二、填空题（每题2分，共4分）1.相比静力计算，动力计算列平衡方程时，在所考虑的力系中要包括。
2. 爆炸荷载属于。
答案：1、从力系平衡角度建立自由振动微分方程的方法是（）oA、刚度法B、柔度法C、静力法D、动力法答案：刚度法2、忽略杆件的轴向变形和均布质量，各图质点的质量、杆长、质点位置相同，杆件EI相同且为常数。
结构自振频率最大的是（）oA、coaB、3bC、3cD、3d答案：3a3、与单自由度体系自由振动的频率有关的量是（）oA、初速度vOB、初位移yOC、相位角aD、质量m答案：阻尼越大，振幅越大4、按照GB50009-2012《建筑结构荷载规范》，高度为2001Tl的高耸钢筋混凝土结构的基本周期一般为（）0A、0.14sB、1.4sC、14sD、140s答案：1.4s5、yst是指（）oA.自然伽码与电阻率B.方位与井斜C.工具与井斜D.工具面与方位答案：A1、一、填空题（每题5分，共20分）答案：【计分规贝"：Am=K/c2.72X10-268.41X10- 4437.82X10-4；145.94X10-42、二、计算题（每题20分，共80分）答案：【计分规则】：一、回答问题（每题2分、共10分）二、分析（每题10分、共30分）三、计算题（第1题40分, 第2题20分、共60分）1、当。
结构动力学参考答案
m u + c u + ku = Pu (t ) 2.13 一根均匀杆，图 P2.13 其单位体积质量密度 ρ ，并具有顶部质量 M，应 用假定法ψ ( x) = x L 来推导该系统轴向自由振动的运动方程。假定 AE = 常数。 解：
.. 1 EA ( ρAL + M ) u + u = P(t ) 3 L
结构动力学习题 参考答案
1
2.3 一根刚梁 AB，用力在弹簧 BC 上去激励它，其 C 点的运动规定为 Z（t）,如 图 P2.3. 按 B 点的垂直运动 u 来确定系统的运动方程，假定运动是微小的。 解： 4M u + 3c u + (3k1 + 12k 2 )u = 12k 2 Z (t )
.. .
4
4.17 在振动的结构上一个点，已知其运动为 Ζ = Ζ1 cos(Ω1t ) + Ζ 2 cos(Ω 2 t ) =
0.05 cos ( 60π t ) + 0.02 cos(120π t ) 。
（a）用一加速度计其阻尼因数 ξ = 0.70 和 20 KHz 共振频率来确定振动记录 w p (t ) 。 (b) 加速度计是否会引起有效幅值或相位畸变？ 解： （a） w p (t ) = w p1 (t ) + w p 2 (t ) = 6.339 × 10 −11 A1 cos 60π (t − 1.1145 × 10 −5 ) + 6.339 × 10 −11 A2 • cos 120π (t − 1.1146 × 10 −5 ) （b） w p (t ) = C[ A1 cos Ω1 (t − τ ) + A2 cos Ω 2 (t − τ )] A1 , A2 分别表示 Z1 , Z 2 的加速度幅值，所以输出 w p (t ) 与加速度输 入成正比，所以不会发生幅值畸变或相位畸变。 5.2 运送一件仪器设备重 40 1b，是用泡沫包装在一容器内。该容器的有效刚度 k=100 1b/in，有效阻尼因数 ξ = 0.05 ，若整个容器和它的包装以垂直速度 V=150 in/s 碰撞在地面上，求泡沫包装在仪器设备的最大总应力。 （如图 P5.2 所示） 解： f max = 451.739 (1b) 6.5 例 题 4.3 中的 车辆 ， 已知 k = 400 × 10 3 , m = 1200kg , ξ = 0.4。 当满 载时以
第十章 结构动力学解答
为：
72������������
9
���̅���������̈ + ������4 ������ = 2������2 ������������(������)
10.6 求如图所示体系的自振频率。
m
EI1 EI1 m
l/2
l/2
EI
l/2 l/2
l
图 10-6
解：此体系为单自由度体系 (1) 将上图所示的体系转化为下图 10-6-1 所示的体系：
(4) 对位移项系数比较得：
4 ������̈ + 5������ ������1������ = 0
ω
=
√4������1 5������
=
√12������������ 5������������3
10.7 单 自 由 体 系 上 作 用 简 谐 动 荷 载 ， 力 的 幅 值 F0 500N ， 先 后 以 1 10rad / s 和2 17.32rad / s 两种频率分别作用，测得各相应的位移幅值和相 位角为 A1 4.995105 m ， 1 2.55 ； A2 9.823105 m ， 2 10.8 。试求该 体系的质量 m、刚度 k、自振频率 和阻尼比 。
将������1、������������、������������代入(c=0)，得：
������������̈ + ������������ = ������������(������) 4) 求系数 k。在质点处作用单位力所得弯矩图如下图 10-4-5
3
16 ������
1
5 32 ������
3) 将������11、������1������带入，则体系运动方程为
结构动力学试题及答案
结构动力学试题及答案一、选择题（每题2分，共10分）1. 结构动力学中，动力响应分析通常不包括以下哪一项？A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案：C2. 在结构动力学中，下列哪一项不是确定结构动力特性的基本参数？A. 质量B. 刚度C. 阻尼D. 材料强度答案：D3. 单自由度振动系统的动力平衡方程中，下列哪一项是正确的？A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案：A4. 对于多自由度振动系统，下列哪一项不是求解动力响应的方法？A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案：C5. 在结构动力学中，阻尼比通常用来描述阻尼的相对大小，其定义为：A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案：B二、填空题（每题2分，共10分）1. 结构动力学中，当外力作用频率与结构的_________相等时，结构会发生共振。
答案：自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。
答案：位移分布模式3. 动力响应分析中，_________是指在给定的外力作用下，结构的响应随时间变化的过程。
答案：动力响应4. 在结构动力学中，_________是指结构在动力作用下，其响应与外力作用的关系。
答案：动力特性5. 阻尼比越大，结构的_________越小，振动衰减越快。
答案：振幅三、简答题（每题5分，共20分）1. 简述结构动力学中模态分析的目的和意义。
答案：模态分析的目的是确定结构的自振频率和振型，意义在于了解结构的动力特性，为结构设计提供依据，以及评估结构在动力作用下的安全性和稳定性。
结构动力学习题+讲解
结构动力学*本章讨论结构在动力荷载作用下的反应。
**学习本章注重动力学的特征------惯性力。
*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律，从而找出其最大值作为设计的依据。
*动力学研究的问题：动态作用下结构或构件的强度、刚度及稳定性分析。
一、本章重点1．振动方程的建立2．振动频率和振型的计算3．振型分解法求解多自由度体系4．最大动位移及最大动应力二、基础知识1．高等数学2．线性代数3．结构力学三、动力荷载的特征1．大小和方向是时间t的函数例如：地震作用，波浪对船体的作用，风荷载，机械振动等2．具有加速度，因而产生惯性力四、动力荷载的分类1．周期性动力荷载例如：①机械运转产生的动力荷载，②打桩时的锤击荷载。
P（t） Pt t（机械运转荷载）（打桩荷载）2．冲击荷载例如：①爆炸力产生的动力荷载，②车轮对轨道连接处的冲击。
P（t）P（t）P（t）t t t（爆炸力动力荷载）（吊车起吊钢索的受力）（随机动力荷载）3．突加常量荷载例如：吊车起吊重物时钢索的受力。
4．随机动力荷载前3类荷在是时间t的确定函数，称为确定性动力荷载；而地震作用，波浪对船体的作用，风荷载等其作用大小只能用统计的方法获得。
五、动力荷载的计算方法1．原理：达朗贝尔原理，动静法建立方程2．计算工具：微分方程，线性代数，结构力学六、体系振动的自由度---------动力自由度结构具有质量，有质量在运动时就有惯性力。
在进行动力计算时，一般把结构的质量简化为若干质点的质量，整个结构的惯性力就成为各质点的惯性力问题。
1．质点简化的一般要求①简单，②能反映主要的振动特性例如：楼房；质量集中在各层楼板平面内水塔：质量集中在水箱部分梁：无限自由度集中质量（楼房质量集中）（水塔质量集中）（梁的质量集中）2．位移y（t）即指质点的位移y（t），其加速度为y&&)(t3．动力自由度的确定即质点位移数量的确定。
(完整版)结构动力学-习题解答
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
ml 3 T 2.027 ;
EI
m
EI y1(t)
l
l/2 l/2
l/4
7-1（b)试求图示体系的自振频率与周期。
解: 求柔度系数: 用位移法或力矩分配法 求单位力作用引起的弯矩图（图a); 将其与图b图乘，得
48EI 2k
T 2 ( 1 l3 1 )m
48 EI 2k
m
k EI
k
l/2
l/2
7-3 试求图示体系质点的位移幅值和最大弯矩值。
已知 0.6
l
解:
yst
FPl 3 EI
m
y1(t)
1
1
2
/
2
1.5625
位移幅值
A
yst
1.5625
FPl 3 EI
2l
yst
11
5 3
l3 EI
1 11
l
X11 0.4612 ; X12 4.336
X 21
X 22
12 7.965 EI / ml 3
2 2
65.53EI
/
ml 3
1 2.822 EI / ml3
8-6.试求图示刚架的自振频率和振型。设楼面质量分别为m1=120t和m2=100t,
柱的质量已集中于楼面, 柱的线刚度分别为i1=20MN.m和i2=14MN.m,横梁
m 2 A 0.3375 FP
l/2
EI=常数
FP sin t
2l
FP
FPl
结构动力学习题答案
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程： ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时，发生共振有： Rd 1 =
当 w wn = 1 10 时， Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解：
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理： δ Ws
+ δ WI + δ W D +δ W p = 0 得：
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解：
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭
10结构的动力计算习题解答.
1 k2
(a) 刚度系数 习题解 10.5(3)图
k1 EI l3
3EI
(b)
48EI l3
M1
图
，k
2
2
l / 2
3
则
k11 k1 k2
49 EI l3
，
k11 49 EI m ml 3
(4) 求刚度系数，画 M 图，如习题解 10.5(4)图所示。
1
k11 2
11
4
1
1
l l
(a)
M1
1
图 习题解 10.4(3)图 (b)
MP
图
习题 10.5 求习题 10.5 图所示单自由度体系的自振频率。除注明者外， EI＝常数。k1 为弹性支座的刚度系数。
m
m k 1= 3EI/4
l
l /2
l /2
2m
2m
(1)
m k 1=EI /l 3 l /2 l /2
11
2 EI
2 2l 3 1 l l l 2 3 3EI
， =
P
(6) 求柔度系数，绘单位力作用下的 M 图和基本体系 M 图，如习题解
1
10.5(6).(a)、(b)图所示。
1 1 l/5 l 4l /5 2l / 5 l l
(a)
MP
图 习题解 10.5(6)图
EI 0 =∞
EI
(a)
(a)
(b)
(b)
(c)
(c)
(d)
(d)
习题 10.3 图
习题 12-3图
【解】(a) 2；(b) 3；(c) 2；(d) 4，在两个质量上分别附加 2 个支杆。 习题 10.4 不考虑阻尼，列出习题 10.4 图所示体系的运动方程。