结构动力学习题
结构动力计算习题

160结构动力计算习题一.选择题8-1 体系的动力自由度是指( )。
A .体系中独立的质点位移个数B .体系中结点的个数C .体系中质点的个数D .体系中独立的结点位移的个数 8-2 下列说法中错误的是( )。
A .质点是一个具有质量的几何点;B .大小、方向作用点随时间变化的荷载均为动荷载;C .阻尼是耗散能量的作用;D .加在质点上的惯性力,对质点来说并不存在 8-3 图示体系EI =常数,不计杆件分布质量,动力自由度相同的为( )。
题8-3图A .(a )、(b )、(c )B .(a )、(b )C .(b )、(c )D .(a )、(c ) 8-4图示体系不计杆件分布质量,动力自由度相同的为( )。
(b )(c )题8-4图A .(a )、(b )、(c )B .(a )、(b )C .(b )、(c )D .(a )、(c )8-5 若要提高单自由度体系的自振频率,需要( )。
A .增大体系的刚度B .增大体系的质量C .增大体系的初速度D .增大体系的初位移 8-6不计阻尼影响时,下面说法中错误的是( )。
A .自振周期与初位移、初速度无关;B .自由振动中,当质点位移最大时,质点速度为零;C .自由振动中,质点位移与惯性力同时达到最大值;D .自由振动的振幅与质量、刚度无关 8-7 若结构的自振周期为T ,当受动荷载)(P t F =t F θsin 0作用时,其自振周期T ( )。
A .将延长B .将缩短C .不变D .与荷载频率θ的大小有关8-8 若图(a )、(b )和(c )所示体系的自振周期分别为a T 、b T 和c T ,则它们的关系为( )。
(a)(b)(c)题8-8图A .a T >b T >c TB .a T >c T >b TC .a T <c T <b TD .a T =c T <b T 8-9 振幅计算公式βst y A =中的st y 为( )。
在线测试题试题库及解答(第十章)结构动力学

在线测试题试题库及解答第十章结构动力学基础一、单项选择题1、结构的主振型与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案A2、结构的自振频率与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案A3、单自由度体系在简谐荷载作用下,下列哪种情况内力与位移的动力系数相同?A、均布荷载作用B、荷载作用在质点上与质点运动方向垂直C、荷载不作用在质点上D、惯性力与运动方向共线标准答案D4、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案D5、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案D6、当简谐荷载作用于有阻尼的单自由度体系质点上时,若荷载频率远远大于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、重力C、阻尼力D、惯性力标准答案D7、设ω为结构的自振频率,θ为荷载频率,β为动力系数下列论述正确的是A、ω越大β也越大B、θ/ω越大β也越大C、θ越大β也越大D、θ/ω越接近1,β绝对值越大标准答案D8、如果体系的阻尼增大,下列论述错误的是A、自由振动的振幅衰减速度加快B、自振周期减小C、动力系数减小D、位移和简谐荷载的相位差变大标准答案B9、无阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力C、惯性力与弹性力的合力D、没有力标准答案D10、有阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力与弹性力的合力C、惯性力D、阻尼力标准答案D11、当简谐荷载作用于无阻尼的单自由度体系质点上时,若荷载频率远远小于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、阻尼力C、惯性力D、重力标准答案A12、一单自由度振动体系,其阻尼比为ξ,动力系数β,共振时下列结果正确的是A、ξ=0.05,β=10B、ξ=0.1,β=15C、ξ=0.15,β=20D、ξ=0.2,β=25标准答案A13、一单自由度振动体系,由初始位移0.685cm,初始速度为零产生自由振动,振动一个周期后最大位移为0.50cm,体系的阻尼比为A、ξ=0.05B、ξ=0.10C、ξ=0.15D、ξ=0.20标准答案A14、在低阻尼体系中不能忽略阻尼对什么的影响?A、频率B、主振型C、周期D、振幅标准答案D15、单自由度体系受简谐荷载作用,ω为体系自振频率,θ为荷载频率,动位移y(t)与荷载P(t)的关系是A、当θ/ω>1时,y(t)与P(t)同向,当θ/ω<1时,y(t)与P(t)反向。
结构的动力计算习题

《结构的动力计算》习题一、判断题1、图示等效体系的关系是:3211111k k k k ++=。
( )2、结构的动力反应只与初始条件及动荷载有关。
( )3、任何动力荷载作用下均可以采用公式:1221-⎪⎪⎭⎫⎝⎛-=ωθβ计算动力系数。
( ) 4、外界感干扰力只影响振幅、不影响体系的自振频率。
( )5、体系的动力自由度数与质点的个数无关、也与结构静定或超静定无关。
( )6、图示体系各杆自重不计、EA =∞,则该体系在初始时刻的干扰力作用下将做竖向振动。
( )二、选择题1、增加单自由度体系的阻尼、但仍保持为低阻尼体系,其结果是( )。
A 、周期变长 B 、周期不变 C 、周期变短 D 、 周期视具体体系而定2、图示两个等效结构,正确的刚度关系是( )。
A 、k=k 1+k 2 B 、21111k k k += C 、21211k k k k k += D 、2112k kk k k +=3、图示体系不计阻尼,平稳阶段最大动位移y max =4Pl 3/7EI ,其最大动力弯矩为( )。
A 、3Pl /7 B 、4Pl /7 C 、12Pl /7 D 、4Pl /21 4、下列哪句话有错误或不够准确()。
第3题图A、在多自由度体系自由振动问题中,主要问题是确定体系的全部自振频率和相应的主振型; B 、多自由度体系的自振频率不止一个,其个数与自由度个数相等;C 、每个自振频率都有自己相应的主振型,主振型就是多自由度体系振动时各质点的位移变化形式;D 、与单自由度体系相同,多自由度体系的自振频率和相应的主振型也是体系本身的固有性质。
5、图示单自由度体系自振周期的关系为( )。
A 、(a)=(c)B 、(a)=(b)C 、(b)=(c)D 、都不相等6、单自由度振动体系中,若质点在杆的中点,各杆EI 、l 相同,其自振周期的大小排列顺序为(A 、(c)>(a)>(b)B 、(c)>(b)>(a) C 、(a)>(b)>(c) D 、(b)>(c)>(a)三、分析计算题1、梁的抗弯刚度为EI2m3、柱的自重不计,求图示刚架的自振频率。
结构动力学例题复习题
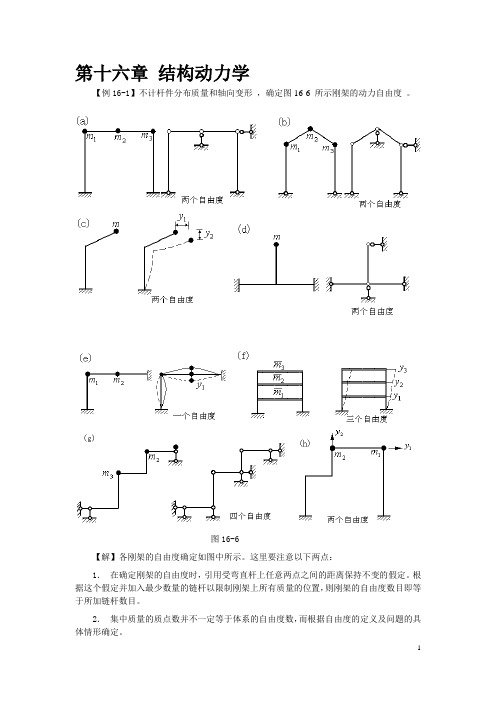
第十六章结构动力学【例16-1】不计杆件分布质量和轴向变形,确定图16-6 所示刚架的动力自由度。
图16-6【解】各刚架的自由度确定如图中所示。
这里要注意以下两点:1.在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。
根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。
2.集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。
【例16-2】 试用柔度法建立图16-7a 所示单自由度体系,受均布动荷载)t (q 作用的运动方程。
【解】本题特点是,动荷载不是作用在质量上的集中荷载。
对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。
设图a 质量任一时刻沿自由度方向的位移为y (向下为正)。
把惯性力I 、阻尼力R 及动荷载)(t P ,均看作是一个静荷载,则在其作用下体系在质量处的位移y ,由叠加原理(见图b 、c 、d 及e ),则)(R I y P D I P +δ+∆=∆+∆+∆=式中,)t (q EI 38454P =∆,EI483=δ。
将它们代入上式,并注意到ym I -=,y c R -=,得)(48)(384534y c y m EIt q EI y --+=图16-7经整理后可得)(t P ky y c y m E =++式中,3EI 481k =δ=,)(85)(t q k t P P E =∆= )(t P E 称为等效动荷载或等效干扰力。
其含义为:)(t P E 直接作用于质量上所产生的位移和实际动荷载引起的位移相等。
图a 的相当体系如图f 所示。
【例16-3】 图16-8a 为刚性外伸梁,C 处为弹性支座,其刚度系数为k ,梁端点A 、D 处分别有m 和3m质量,端点D 处装有阻尼器c ,同时梁BD 段受有均布动荷载)t (q 作用,试建立刚性梁的运动方程。
【解】 因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。
结构动力学试题及答案

结构动力学试题及答案(本文按试题和答案格式进行编写)试题一:1. 请问什么是结构动力学?2. 简述结构动力学的研究对象和主要内容。
3. 结构动力学分析常用的方法有哪些?4. 结构动力学分析中常用的数学模型有哪些?5. 结构动力学的应用领域有哪些?答案一:1. 结构动力学是研究结构在外力作用下的动态响应及其稳定性的学科。
2. 结构动力学的研究对象是各种工程结构,主要内容包括结构的振动、冲击响应、瞬态响应和稳态响应等。
3. 结构动力学分析常用的方法有模态分析法、频率响应分析法、时程分析法等。
4. 结构动力学分析中常用的数学模型有单自由度体系、多自由度体系、连续体系等。
5. 结构动力学的应用领域广泛,包括建筑结构工程、桥梁工程、风力发电机组、地震工程等。
试题二:1. 结构动力学分析中,模态分析的基本原理是什么?2. 简述模态分析的步骤和计算方法。
3. 常用的模态分析软件有哪些?4. 请问什么是结构的固有频率和阻尼比?5. 结构的模态振型对结构动力响应有什么影响?答案二:1. 模态分析是基于结构的振动特性,通过求解结构的固有频率、模态振型和阻尼比等参数,来研究结构的动力响应。
2. 模态分析的步骤包括建立结构有限元模型、求解结构的固有频率和模态振型、计算结构的阻尼比等。
常用的计算方法有有限元法、拉普拉斯变换法等。
3. 常用的模态分析软件有ANSYS、ABAQUS、MSC.NASTRAN等。
4. 结构的固有频率是结构在无外力作用下自由振动的频率,阻尼比是结构振动过程中能量耗散的程度。
5. 结构的模态振型对结构动力响应有很大影响,不同的模态振型会导致不同的振动特性和反应。
试题三:1. 结构动力学分析中,频率响应分析的基本原理是什么?2. 简述频率响应分析的步骤和计算方法。
3. 频率响应分析和模态分析有什么区别?4. 结构的频率响应函数和传递函数有什么区别?5. 频率响应分析在结构设计中的应用有哪些?答案三:1. 频率响应分析是研究结构在单频激励下的响应特性,通过求解结构的频率响应函数,来获得结构的响应。
结构动力学与应用考试试题

结构动力学与应用考试试题一、选择题1. 结构动力学是研究结构在______时的力学响应和形态相互关系的学科。
A. 静力学B. 动力学C. 热力学D. 光力学2. 结构的固有频率是指结构在______下产生共振的频率。
A. 外加荷载B. 自激振动C. 静力平衡D. 温度变化3. 结构动力学分析中常用的求解方法包括有限元法、模态超级法和______法等。
A. 静力平衡法B. 频率响应法C. 换能法D. 变位法4. 结构动力学分析常用的传递函数表示为______。
A. H(ω) = X(ω) / F(ω)B. H(ω) = F(ω) / X(ω)C. X(ω) = F(ω) / H(ω)D. F(ω) = X(ω) / H(ω)5. 结构的阻尼比对于结构动力学响应的影响是______。
A. 提高结构的刚度和强度B. 减小结构的固有频率C. 显著改变结构的失稳现象D. 不影响结构的动力响应6. 结构在动力荷载作用下的振动响应可以通过______分析得到。
A. 弹性力学理论B. 弹塑性力学理论C. 塑性力学理论D. 极限平衡理论7. 结构地震反应的计算方法一般可以分为几种类型?A. 1种B. 2种C. 3种D. 4种8. 结构地震反应计算中常用的几种简化方法包括等效静力法、反应谱法和______法。
A. 位移反应法B. 达比法C. 传递函数法D. 干涉法9. 结构动力学与应用在哪些领域具有广泛的应用?A. 建筑结构设计B. 地震工程C. 桥梁工程D. 所有选项都正确10. 结构动力学的研究对于提高建筑物和桥梁的______具有重要意义。
A. 施工速度B. 建筑安全性C. 建筑造价D. 建筑使用寿命二、填空题1. 结构动力学研究的核心是研究______和______之间的相互关系。
2. 结构固有频率是由结构的______和______决定的。
3. 结构在动力荷载作用下的振动分析可以采用______方法。
4. 结构地震反应计算中的等效静力法是通过将______引入到结构动力方程中进行计算的。
结构动力学习题
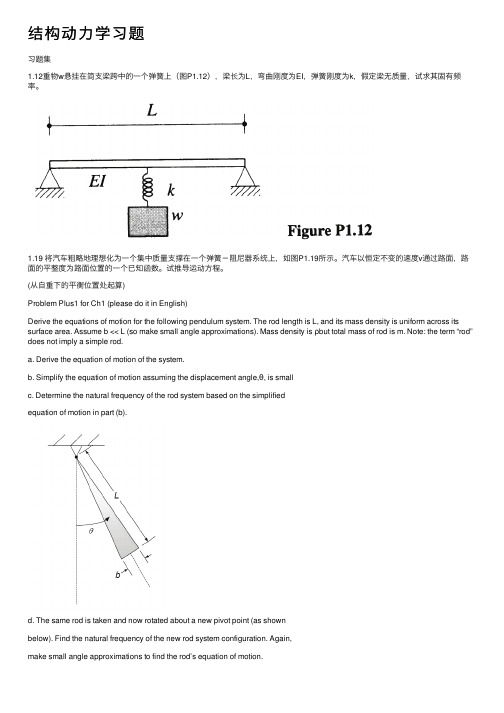
结构动⼒学习题习题集1.12重物w悬挂在简⽀梁跨中的⼀个弹簧上(图P1.12),梁长为L,弯曲刚度为EI,弹簧刚度为k,假定梁⽆质量,试求其固有频率。
1.19 将汽车粗略地理想化为⼀个集中质量⽀撑在⼀个弹簧-阻尼器系统上,如图P1.19所⽰。
汽车以恒定不变的速度v通过路⾯,路⾯的平整度为路⾯位置的⼀个已知函数。
试推导运动⽅程。
(从⾃重下的平衡位置处起算)Problem Plus1 for Ch1 (please do it in English)Derive the equations of motion for the following pendulum system. The rod length is L, and its mass density is uniform across its surface area. Assume b << L (so make small angle approximations). Mass density is ρbut total mass of rod is m. Note: the term “rod”does not imply a simple rod.a. Derive the equation of motion of the system.b. Simplify the equation of motion assuming the displacement angle,θ, is smallc. Determine the natural frequency of the rod system based on the simplifiedequation of motion in part (b).d. The same rod is taken and now rotated about a new pivot point (as shownbelow). Find the natural frequency of the new rod system configuration. Again,make small angle approximations to find the rod’s equation of motion.e. Compare the natural frequency from part (c) and (d). The new pivot point istermed the CENTER of PERCUSSIONProblem Plus2 for Ch1 (please do it in English)Determine the equation of motion of the following system using the Principle of Virtual Work.where()4x c x a=Hint: Be careful with respect to the beam with a distributed mass shown on the left. You caneither consider the rotational inertia about the hinge on the left –OR- you can consider therotational inertia about the beam’s center of mass point. If you go with considering the rotation about the beam’s center of mass, you need to account for the inertia associated with translational movement of that center of mass. In fact, a third valid approach is to not even consider the beam as a rotational element. You could discretize the beam to infinitely small slices with thickness “dx” and find the vertical translational inertia (essentially sum them using integrals). You should convince yourself of the equivalency of both approaches of analysis of the inertial properties of the system shown.2.6 ⼀个仪器的包装可如图P2.6所⽰模拟。
结构动力学试题

结构动力学试题一、选择题1. 结构动力学中的“动力响应”是指:A. 结构在静态载荷下的变形B. 结构在动态载荷下的变形C. 结构的自然频率D. 结构的阻尼比2. 单自由度系统的周期公式为:A. T = 2π√(m/k)B. T = 2π√(k/m)C. T = 2π/mD. T = π√(m/k)3. 多自由度系统的振型分解法是基于以下哪个原理?A. 结构的对称性B. 结构的不确定性C. 结构的线性叠加原理D. 结构的能量守恒原理4. 在地震分析中,反应谱方法的主要优点是:A. 考虑了地震动作用的非线性B. 可以处理任意形状的地震波形C. 能够直接给出结构的响应结果D. 适用于快速评估结构的地震安全性5. 结构阻尼比的增大通常会导致:A. 自然频率的提高B. 振幅的减小C. 周期的延长D. 响应的不稳定二、填空题1. 在结构动力学中,________是用来描述结构在动态载荷作用下的运动状态。
2. 动态载荷下,结构的响应可以通过________方法进行求解,该方法基于结构振动的线性叠加原理。
3. 地震波的________特性对结构的响应有显著影响,因此在进行地震分析时需要特别考虑。
4. 结构的阻尼比可以通过________方法进行实验测定,以评估结构的能量耗散能力。
5. 在进行结构动力分析时,通常需要将结构简化为________自由度系统,以便于计算和分析。
三、简答题1. 请简述单自由度系统与多自由度系统的区别及其各自的适用场景。
2. 描述地震波的基本特性,并解释为什么需要对其进行频谱分析。
3. 说明结构阻尼对动力响应的影响,并讨论如何通过设计来提高结构的阻尼性能。
四、计算题1. 一个单自由度系统的质量为500 kg,刚度为2000 N/m。
请计算该系统的自然频率和阻尼比为0.05时的周期。
2. 假设一个结构在地震作用下的最大加速度为0.3g,其中g为重力加速度(9.81 m/s²),请使用反应谱方法计算该结构在自然频率为2Hz时的响应加速度。
结构动力学试题及答案

结构动力学试题及答案一、选择题1. 在结构动力学中,下列哪项不是描述结构动力响应的参数?A. 自然频率B. 阻尼比C. 静力平衡D. 模态阻尼2. 以下哪个不是结构动力学分析中的常用方法?A. 模态分析B. 时域分析C. 频域分析D. 静力分析二、简答题1. 简述结构动力学中模态分析的目的和重要性。
2. 描述阻尼对结构动力响应的影响。
三、计算题1. 假设一个单自由度系统,其质量为m,刚度为k,初始位移为x0,初始速度为v0。
若外力为F(t) = F0 * sin(ωt),求该系统在任意时间t的位移响应。
答案一、选择题1. 正确答案:C. 静力平衡解析:静力平衡是静力学的概念,与结构动力学无关。
2. 正确答案:D. 静力分析解析:静力分析是分析结构在静载荷作用下的响应,而结构动力学分析动态载荷下的结构响应。
二、简答题1. 模态分析的目的在于识别结构的自然振动特性,包括自然频率、阻尼比和模态形状。
它的重要性在于:- 预测结构在动态载荷下的响应。
- 为控制结构的振动提供基础数据。
- 优化设计,提高结构的抗震性能。
2. 阻尼对结构动力响应的影响主要表现在:- 减少振动幅度,提高结构的稳定性。
- 改变系统的自然频率和模态形状。
- 影响系统的动态响应时间。
三、计算题1. 单自由度系统的位移响应可以通过以下步骤求解:- 写出系统的动力学方程:m * d²x/dt² + c * dx/dt + k * x = F(t)- 应用初始条件:x(0) = x0, v(0) = v0- 应用外力:F(t) = F0 * sin(ωt)- 通过傅里叶变换或拉普拉斯变换求解方程。
- 应用逆变换得到位移响应的解析解或数值解。
位移响应的一般形式为:x(t) = X * cos(ωt - φ) + Y *sin(ωt - φ),其中X和Y是与系统参数和初始条件有关的常数,φ是相位角。
具体的数值需要根据系统参数和初始条件进行计算。
结构动力学典型习题及答案

ω
2 2
=
537.287
1/ s2
{X
}1
=
1 1.870
ω1 = 9.885 1/ s ω2 = 23.179 1/ s
{X }2
=
−
1 0.642
ω12 = 7.965EI / ml3
ω
2 2
=
65.53EI
/
ml 3
ω1 = 2.822 EI / ml3
ω2 = 8.095 EI / ml3
m
EI1 = ∞
EI
2m
EI1 = ∞
2EI
y1
2EI
y2
l 2EI
l
X11 = 0.4612; X12 = −4.336
X 21
X 22
{X
}1
=
1 2.168
m2
EI1 = ∞
i2 m1
y2
i2 4m
k11 − m1ω 2 kδ 21
k12
=0
k22 − m2ω 2
EI1 = ∞
i1
i1y1 4m
X11 = 0.5347; X12 = −1.559
0.012ω 4 − 7.62ω 2 + 630 = 0
X 21
X 22
ω12 = 97.713 1/ s2
=1
=1 3l/16 5l/32 l/2
=1
δ
11
=
l3 192EI
ω = 13.856 EI / ml3
δ11
=
l3 EI
ω = EI / ml3
m
EI m y1
y2
EI
l/2 l/2
l/2 l/2
结构动力学习题
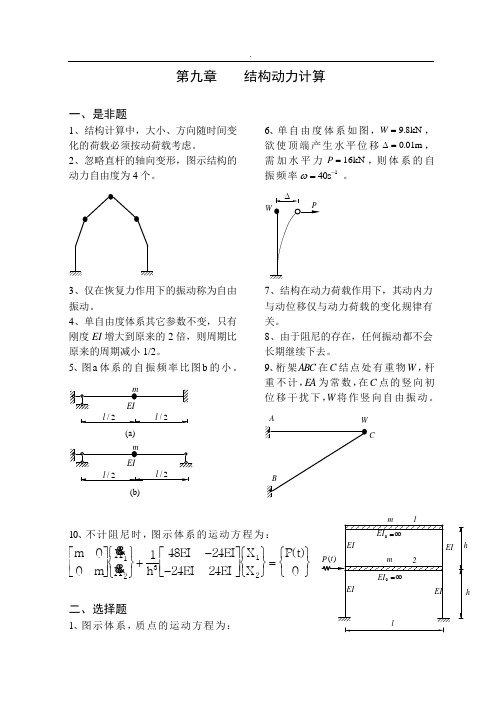
第九章 结构动力计算一、是非题1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形,图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ,W =98.kN ,欲 使 顶 端 产 生 水平 位 移 ∆=001.m ,需 加 水 平 力 P =16kN ,则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ,杆 重 不 计 ,EA 为 常 数 ,在 C 点 的 竖 向 初 位 移 干 扰 下 ,W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ,图 示 体 系 的 运 动 方 程 为 :m m X X h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ,质 点 的 运 动 方 程为 :A .()()()y l P s in m y EI =-77683θ t /;B .()()m y EI y lP s in /+=19273θ t ;C .()()m y EI y l P s in /+=38473θ t ;D .()()()y l P s in m y EI =-7963θ t / 。
ll0.50.52、在 图 示 结 构 中 ,若 要 使 其 自 振 频 率 ω增 大 ,可 以A .增 大 P ;B .增 大 m ;C .增 大 E I ; D .增 大 l 。
第十章 结构动力学(判断填空题)

引起的静位移。
()
9、多自由度体系的自由振动,一般包括所有的振型,所以不可能出现仅按某一个主振型的振动。
()
10、两端固定梁的第一频率比相应简支梁(杆长与截面相同,质量分布也相同)的第
171
一频率高。
(
)11、体系的自振频率与动力荷载的频率有关。
(
)
20、 多自由度体系,刚度系数与柔度系数的关系是:k i j i j =1/δ 。
(
)21、体系质点的初速度越大,则其自由振动频率越高。
(
)22、外界干扰力只影响振幅,不影响自振频率。
(
)
23、只要结构对称(包括质量分布情况),其振型一定是正对称或反对称的。
(
)24、在动力计算中,图a 、b 所示结构的动力自由度相同(各杆均为无重弹性杆)。
()(a)
172
174
变则竖向振动时的自振频率。
175
k为弹簧刚度。
则体系的竖向振2
176。
13结构动力学习题

13结构动⼒学习题1.1 不计轴向变形,图⽰体系的振动⾃由度为2。
1.2 不计轴向变形,图⽰体系的振动⾃由度为1。
1.3 不计轴向变形,图⽰体系的振动⾃由度为2。
1.4 结构的⾃振频率不仅与质量和刚度有关,还与⼲扰⼒有关。
1.5 单⾃由度体系,考虑阻尼时,频率变⼩。
1.6 弹性⼒与位移反向,惯性⼒与加速度反向,阻尼⼒与速度反向。
1.7 如简谐荷载作⽤在单⾃由度体系的质点上且沿着振动⽅向,体系各截⾯的内⼒和位移动⼒系数相同。
1.8 在建⽴质点振动微分⽅程时,考虑不考虑质点的重⼒,对动位移⽆影响。
1.9 图⽰体系在简谐荷载作⽤下,不论频率⽐如何,动位移y(t) 总是与荷载P(t) 同向。
1.10 多⾃由度体系⾃由振动过程中,某⼀主振型的惯性⼒不会在其它主振型上做功。
⼆、单项选择题2.1 在单⾃由度体系受迫振动的动位移幅值计算公式中,yst是A 质量的重⼒所引起的静位移B 动荷载的幅值所引起的静位移C 动荷载引起的动位移D 质量的重⼒和动荷载复制所引起的静位移2.2 ⽆阻尼单⾃由度体系的⾃由振动⽅程:。
则质点的振幅y max=2.3 多⾃由度振动体系的刚度矩阵和柔度矩阵的关系是2.4 图⽰四结构,柱⼦的刚度、⾼度相同,横梁刚度为⽆穷⼤,质量相同,集中在横梁上。
它们的⾃振频率⾃左⾄右分别为ω1,ω2,ω3,ω4,那么它们的关系是2.5 图⽰四结构,柱⼦的刚度、⾼度相同,横梁刚度为⽆穷⼤,质量相同,集中在横梁上。
它们的⾃振频率⾃左⾄右分别为ω1,ω2,ω3,ω4,那么它们的关系是2.6 已知两个⾃由度体系的质量矩阵为,Y22等于A -0.5B 0. 5C 1D -0.252.7 不计阻尼,不计⾃重,不考虑杆件的轴向变形,图⽰体系的⾃振频率为2.8 图⽰四个相同的桁架,只是集中质量m的位置不同,,它们的⾃振频率⾃左⾄右分别为ω1,ω2,ω3,ω4,(忽略阻尼及竖向振动作⽤,各杆EA为常数),那么它们的关系是2.9 设ω为结构的⾃振频率,θ为荷载频率,β为动⼒系数下列论述正确的是A ω越⼤β也越⼤B θ越⼤β也越⼤C θ/ω越接近1,β绝对值越⼤Dθ/ω越⼤β也越⼤2.10 当简谐荷载作⽤于有阻尼的单⾃由度体系时,若荷载频率远远⼤于体系的⾃振频率时,则此时与动荷载相平衡的主要是A 弹性恢复⼒B 阻尼⼒C 惯性⼒D 重⼒2.11 图⽰(a )、(b )两体系中,EI 、EI1及h 均为常数,则两者⾃振频率ωa 与ωb 的关系是2.12 图⽰三个单跨梁的⾃振频率分别为ωa ,ωb ,ωc ,它们之间的关系是2.13 ⼀单⾃由度振动体系,其阻尼⽐为ξ,共振时的动⼒系数为β则ABCD2.14 当荷载频率θ接近结构的⾃振频率ω时A 可作为静荷载处理B 荷载影响⾮常⼩C 引起共振D 可以不考虑阻尼的影响求图⽰体系的⾃振频率ω。
结构动力学试题(一)

结构动力学第1章单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
1.3 叙述用正选弦激励求单自由度系统阻尼比的方法和步骤。
1.4 求图1-33中标出参数的系统的固有频率。
1.5 求图1-34所示系统的固有频率。
图中匀质轮A 半径R,重物B 的重量为P/2,弹簧刚度为k.1.6求图1-35所示系统的固有频率。
图中磙子半径为R,质量为M,作纯滚动。
弹簧刚度为K 。
1.7求图1-36所示齿轮系统的固有频率。
已知齿轮A 的质量为A m ,半径为A r ,齿轮B 的质量为B m ,半径为B r ,杆AC 的扭转刚度为A k , ,杆BD 的扭转刚度为B k 。
1.8已知图1-37所示振动系统中,匀质杆长为l ,质量为m,两弹簧刚度皆为K,阻尼系数为C,求当初始条件000==θθ 时 〔1〕t F t f ωsin )(=的稳态解; 〔2〕t t t f )()(δ=的解;1.9图1-38所示盒内有一弹簧振子,其质量为m,阻尼为C,刚度为K,处于静止状态,方盒距地面高度为H,求方盒自由落下与地面粘住后弹簧振子的振动历程与振动频率。
1.10汽车以速度V 在水平路面行使。
其单自由度模型如图1-39。
设m 、k 、c 已知。
路面波动情况可以用正弦函数sin()y h at =表示。
求:〔1〕建立汽车上下振动的数学模型;〔2〕汽车振动的稳态解。
1.11.若电磁激振力可写为t H t F 02sin )(ω=,求将其作用在参数为m 、 k 、 c 的弹簧振子上的稳态响应。
1.12.若流体的阻尼力可写为3xb F d -=,求其等效粘性阻尼。
第1章1.4 a> ()3314848EIl EI k l mω=+31348k l EImlω+= c>3133k l EIml ω+= d>mk 21=ω1.5ω=1.6ω=1.7ω==1.8 运动微分方程: 366()c k f t m m mlθθθ++= 〔1〕)t θωα=-236c arctgk m ωαω=- 〔2〕()sin nt d d h e t m θωω-=22632d k cm m ω⎛⎫=- ⎪⎝⎭1.9()sin nt d dx t ω-=d ω=1.10 〔1〕)sin()cos(at kh at ach ky y cym +=++ 〔2〕sin()y t ωϕ=- 3222tan()()mc acr k k m c ωϕωω=-+1.110()sin(2/2)2Hx t A t k ωϕπ=--+20220216)4(2ωωωn mHA n +-=2202arctan4n n ωϕωω=-mk m c n n ==2,2ω 1.122243A b c n eq ω=第2章 两个自由度系统2.1 求如图2-11所示系统的固有频率和固有振型,并画出振型。
结构动力学试题及答案

结构动力学试题及答案一、选择题(每题2分,共10分)1. 结构动力学中,动力响应分析通常不包括以下哪一项?A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案:C2. 在结构动力学中,下列哪一项不是确定结构动力特性的基本参数?A. 质量B. 刚度C. 阻尼D. 材料强度答案:D3. 单自由度振动系统的动力平衡方程中,下列哪一项是正确的?A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案:A4. 对于多自由度振动系统,下列哪一项不是求解动力响应的方法?A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案:C5. 在结构动力学中,阻尼比通常用来描述阻尼的相对大小,其定义为:A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案:B二、填空题(每题2分,共10分)1. 结构动力学中,当外力作用频率与结构的_________相等时,结构会发生共振。
答案:自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。
答案:位移分布模式3. 动力响应分析中,_________是指在给定的外力作用下,结构的响应随时间变化的过程。
答案:动力响应4. 在结构动力学中,_________是指结构在动力作用下,其响应与外力作用的关系。
答案:动力特性5. 阻尼比越大,结构的_________越小,振动衰减越快。
答案:振幅三、简答题(每题5分,共20分)1. 简述结构动力学中模态分析的目的和意义。
答案:模态分析的目的是确定结构的自振频率和振型,意义在于了解结构的动力特性,为结构设计提供依据,以及评估结构在动力作用下的安全性和稳定性。
结构动力学习题

结构动力学一、填空题1、右图所示振动体系不计杆件的轴向变形,则 动力自由度数目是 。
2、单自由度体系只有当阻尼比ξ 1时才会产生振动现象。
3、已知结构的自振周期s T 3.0=,阻尼比04.0=ξ,质量m 在0,300==v mm y 的初始条件下开始振动,则至少经过 个周期后振幅可以衰减到mm 1.0以下。
4、多自由度框架结构顶部刚度和质量突然变 时,自由振动中顶部位移很大的现象称 。
二、判断以下说法是否正确.1、凡是大小、方向、作用点位置随时间变化的荷载,在结构动力计算中都必须看作动力荷载。
( )2、超静定结构体系的动力自由度数目一定等于其超静定次数。
( )3、为了避免共振,要错开激励频率和结构固有频率,一般通过改变激励频率来实现。
( )4、求冲击荷载作用下结构的反应谱曲线时一般不计阻尼的影响。
( )5、求静定的多自由度体系的频率和振型,一般采用刚度法比采用柔度法方便。
( )三、选择题1、对单自由度体系的自由振动,下列说法正确的是( B )A C 、振幅和初相角仅与初始条件有关 2、图示(a )、(b A 、b a ωω<B 、∞→EA 时b a ωω≈C 、0→EA 时b a ωω≈D 、b a ωω=3、(1)无阻尼的自由振动(2)不计阻尼,零初始条件下t P θsin 产生的过渡阶段的振动 (3)有阻尼的自由振动(4)突加荷载引起的无阻尼强迫振动 A 、(1)(2)(3) B 、(1)(2)(4)4、右图的单自由度体系,结构的固有频率为ω A 、很小 B 、很大C 、接近静位移st y一、填空题。
(11分)1、2 (3分)2、< (3分)3、14 (3分)4、小鞭梢效应(3分)二、判断以下说法是否正确,对错误的说法加以改正。
(6×3分=18分)1、(×)改正:可简单地在“都是”前加上“不”;或改为“大小、方向、作用点位置随时间变化的荷载,只有使结构的质量产生显著加速度的在结构动力计算中才看作动力荷载。
结构动力学习题

结构动力计算习题习题9-1图示各系统的动力自由度为多少?都是什么?m m m m m m mm(1) (2) (3) (1)①△1x =△2x (2)①△1x =△2x =△3x (3)①△1y =△3y ②△1y ②△1y ②△2y ③△2y ③△3ymmmmmmmmm(4) (5) (6) (4)①△1x (5)①△1y (6)①△1y ②△1y =△2y ②△2x ②△2x ③△3y ③△2y =△3y ③△2y =△3ym m mm mm mm(7) (8) (9) (10) (7)①△1x =△2x (8)①△1x (9)①△1x (10)①△1x ②△2y ②△1y ②△2x ②△2x ③△2x ③△2y ④△2ym m mm m m mm m(11) (12) (13)(11)①△1x =△2x =△3x (12)①△1x =△2x =△3x =△4x (13)①△1x =△2x②△2y ②△1y ②△1y③△4y ③△2ym mm mm mmm(14) (15) (16) (17) (14)①△1x (15)①△1x (16)①△1x (17)①△1x =△2x ②△2x ②△1y ②△1y ②△2y ③△2x ③△2x ④△2y习题9-2图示各系统作强迫振动,已知激振力的频率与系统的自振频率之比,试求系统的动力系数β和最大动弯矩m ax d M 。
2l ltF θsin m2llmFFlM 图(1)32=ωθ, 2211ωθβ-=599411=-=, Fl M d 59m ax =tF θsin mlmlM 图FFl(2)32=ωθ, 2211ωθβ-=33211=-=, Fl M d 3m ax =ltF θsin lmM 图FFl /2(3)53=ωθ, 2211ωθβ-=255311=-=, 45m ax Fl M d = tF θsin mlmlM 图FFl(4)21=ωθ, 2211ωθβ-=22111=-=, Fl M d 2m ax =l /2tF θsin l /2mM 图FFl /4(5)32=ωθ, 2211ωθβ-=33211=-=, 43m ax FlM d =l l /2tF θsin mll /2mFFl /2M 图(6)21=ωθ, 2211ωθβ-=344111=-=, 32max Fl M d =llmtF θsin llmM 图FFl(7)43=ωθ, 2211ωθβ-=44311=-=, Fl M d 4m ax =mtF θsin ll /2M 图FFl /2Fl /2(8)31=ωθ, 2211ωθβ-=233111=-=, 43m ax Fl M d = mtF θsin ll /2mM 图F Fl /2Fl /2(9)31=ωθ, 2211ωθβ-=899111=-=, 169m ax Fl M d = 习题9-3求图示各系统的自振频率。
结构动力学结构动力学试卷(练习题库)(2023版)

结构动力学结构动力学试卷(练习题库)1、结构动力计算与静力计算的主要区别是什么?2、什么是动力自由度,确定体系动力自由度的目的是什么?3、结构动力自由度与体系几何分析中的自由度有何区别?4、结构的动力特性一般指什么?5、什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?6、采用集中质量法、广义位移法(坐标法)和有限元法都可使无限自由度体系简化为有限自由度体系,它们采用的手7、建立运动微分方程有哪几种基本方法?各种方法的适用条件是什么?8、直接动力平衡法中常用的有哪些具体方法?它们所建立的方程各代表什么条件?9、刚度法与柔度法所建立的体系运动方程间有何联系?各在什么情况下使用方便?10、计重力与不计重力所得到的运动方程是一样的吗?11、自由振动的振幅与哪些量有关?12、什么叫动力系数,动力系数大小与哪些因素有关?单自由度体系位移动力系数与内力动力系数是否一样?13、若要避开共振应采取何种措施?14、增加体系的刚度一定能减小受迫振动的振幅吗?15、突加荷载与矩形脉冲荷载有何差别。
16、平断面假定17、弯曲要素18、梁的边界条件19、叠加原理20、三弯矩方程21、平断面假定22、梁的边界条件23、叠加原理24、三弯矩方程25、虚位移原理26、虚力原理27、位能驻值原理28、板条梁29、开口和闭口薄壁杆件。
30、应力的重新分布。
31、几何不变体32、自由度33、多余约束34、超静定结构35、形常数和载常数36、试简述影响线与内力图的区别?37、力法和位移法的解题思路?38、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
39、有多余约束的体系一定是几何不变体系。
40、计算自由度W小于等于零是体系几何不变的充要条件。
41、两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
42、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u c
k
m1
x
L
y
m2
2.1 单自由度建筑物的重量为 900kN,在位移为 3.1cm 时(t=0)突然释放,使建筑产生 自由振动。如果往复振动的最大位移为 2.2cm(t=0.64s) ,试求: (1)建筑物的刚度 k; (2) 阻尼比 ; (3)阻尼系数 c。
2.2 单自由度体系的质量、刚度为 m=875t,k=3500kN/m,且不考虑阻尼。如果初始位 移为 U(0)=4.6cm,而 t=1.2s 时的位移仍为 4.6cm,试求: (1)t=2.4s 时的位移; (2)自由振 动的振幅 u0。
EI b
m
h
P(t )
EI c
EI c
h
EI c / 2
m
EI c
P(t )
EI c
l
l 2h
题 2.2 图
1.3 试建立题 2.3 图所示体系的运动方程,给出体系的广义质量 M、广义刚度 K、广义 阻尼 c 和广义载荷 P(t) ,其中位移坐标 u(t)定义为无重刚杆在端点的竖向位移。
q2 k2 m2 q1
L
1.5 如题 2.5 图所示一质量为 m1 的质量块可水平运动,其右端与刚度为 k 的弹簧相连, 左端与阻尼系数为 c 的阻尼器相连。摆锤 m2 以长度为 L 的无重刚杆与滑块以铰接相连,摆
锤只能在图示船铅垂面内摆动。建议以广义坐标 u 和 θ 表示的体系的运动方程(坐标原点 取静平衡位置) 。
空调机 钢梁
1.2m
1.2m
1.1 建立题 2.1 图所示的三个弹簧-质点体系的运动方程 (要求从刚度的基本定义出发确 定体系的等效刚度) 。
u
P(t )
k1 k2
(a)
k1
k2
P(t )
(b)
u
k1 k2
k3
P(t )
(c)
1.2 建立题 2.2 图所示梁框架结构的运动方程(集中质量位于梁中,框架分布质量和阻 尼忽略不计) 。
2.4 一质量为 m1 的块体用刚度为 k 的弹簧悬挂处于平衡状态(如题 3-4 图所示) 。另一 质量为 m2 的块体由高度 h 自由落下到块体 m1 上并与之完全粘接, 确定由此引起的运动 u(t), u(t)由 m1-k 体系的静平衡位置起算。
m2
h
m1
u (t )
k/2
k/2
2.5 单自由度结构受正弦力激振,发生共振时,结构的位移振幅为 5.0cm,当激振力的 频率变为共振频率的 1/10 时,位移振幅为 0.5cm,试求结构的阻尼比 。
l/2
l
l/2
l l/4 l/4
P(t ) u (t )
无重钢杆
l/2
l/2 k
c
椭圆板
质量 面积
1.4 一总质量为 m1、长为 L 的均匀刚性直杆在重力作用下摆动。一集中质量 m2 沿杆轴 滑动并由一刚度为 k2 的无质量弹簧与摆轴相连,见图题 2.4 图。设体系无摩擦,并考虑大摆 角,用图中的广义坐标 q1 和 q2 建立体系的运动方程。弹簧 k2 的自由长度为 b。
2.3 重量为 1120N 的及其固定在由四个弹簧和四个阻尼器组成的支撑系统上。 在机器重 量作用下弹簧压缩了 2.0cm,阻尼器设计为在自由振动两个循环后使竖向振幅减为初始振幅 的 1/8,确定系统的如下特性: (1)无阻尼自由振动频率; (2)阻尼比; (3)有阻尼自由振 动频率。总结阻尼对自振频率的影响。
2.6 一隔振系统安装在实验室内以减轻来自相邻工厂的地面振动对试验的干扰(题 3.6 图) 。 如果隔振块重 908kg, 地面振动频率为 25Hz, 如果要隔振块的振动降为地面振动的 1/10, 确定隔振系统弹簧的刚度(忽略阻尼) 。
隔振块
k/2
k/2
2.7 重 545kg 空调机固定于两平行简支钢梁的中部(见题 3.7 图) 。梁的跨度 2.4m,每 -6 4 根梁截面的惯性矩为 4.16× 10 m ,空调机转速 300r/min,产生 0.267kN 的不平衡力,假设 体系阻尼比为 1%,并忽略钢梁的自重,求空调机的竖向位移振幅和加速度振幅。 (钢材的 8 2 弹性模量为 2.06× 10 kN/m )
