05空间任意力系
合集下载
材料力学 空间任意力系分析
工程力学
作用线位于不同平面的力系称为空间力系。
z
x
y
2
第五章 空间力系
§5–1 力在空间坐标轴上的投影
§5–2 力对轴的矩 · 力对点的矩
§5–3 空间汇交力系的合成与平衡
§5–4 空间力偶理论
§5–5 空间任意力系
§5–6 空间平行力系的中心 · 物体的重心
习题课
§5-1
力在空间坐标轴上的投影
F X 2 Y 2 Z 2
X Y Z cos ,cos ,cos F F F
Fx
Fz
Fy
6
[例1]已知：F=100N， 30, 60 ，计算图示力 在各坐标轴上的投影。
解：
Y F cos 50 3N
X F sin cos 25N Z F sin sin
的平面，方向用右手螺旋来确定 （右手握住平面的法线，卷曲四
指表示旋转方向，拇指的指向即
为力矩矢的方向）。 力矩矢的大小：
r
O
A
x
h
y
mo ( F ) F h 2AOB
13
空间力对点的矩可用矢积表示：
mO ( F ) F h F r sin rF
mO ( F ) r F i x X j k y z Y Z
z
mo ( F )
F
B
r
A
x
O
b y
a Fxy
力对点的矩矢在过该点的任一轴上的投影等于力对该 轴的矩。
[mo (F )]z mz (F )
15
利用力对点之矩与对通过该点的轴之矩的关系计算力
对点的矩。
mo ( F ) [mo ( F )]x i [mo ( F )]y j [mo ( F )]z k mx ( F )i m y ( F ) j mz ( F )k
作用线位于不同平面的力系称为空间力系。
z
x
y
2
第五章 空间力系
§5–1 力在空间坐标轴上的投影
§5–2 力对轴的矩 · 力对点的矩
§5–3 空间汇交力系的合成与平衡
§5–4 空间力偶理论
§5–5 空间任意力系
§5–6 空间平行力系的中心 · 物体的重心
习题课
§5-1
力在空间坐标轴上的投影
F X 2 Y 2 Z 2
X Y Z cos ,cos ,cos F F F
Fx
Fz
Fy
6
[例1]已知：F=100N， 30, 60 ，计算图示力 在各坐标轴上的投影。
解：
Y F cos 50 3N
X F sin cos 25N Z F sin sin
的平面，方向用右手螺旋来确定 （右手握住平面的法线，卷曲四
指表示旋转方向，拇指的指向即
为力矩矢的方向）。 力矩矢的大小：
r
O
A
x
h
y
mo ( F ) F h 2AOB
13
空间力对点的矩可用矢积表示：
mO ( F ) F h F r sin rF
mO ( F ) r F i x X j k y z Y Z
z
mo ( F )
F
B
r
A
x
O
b y
a Fxy
力对点的矩矢在过该点的任一轴上的投影等于力对该 轴的矩。
[mo (F )]z mz (F )
15
利用力对点之矩与对通过该点的轴之矩的关系计算力
对点的矩。
mo ( F ) [mo ( F )]x i [mo ( F )]y j [mo ( F )]z k mx ( F )i m y ( F ) j mz ( F )k
工程力学-第五章 空间任意力系
22
例题5
由题意有
Fr 0.36 Ft
解方程得
F 10.2 kN Fr 3.67 kN FAx 15.64 kN FAz 31.87 kN FBx 1.19 kN FBy 6.8 kN FBz 11.2 kN
2013-8-2 23
例题5
2. 取工件为研究对象，受力
z
M
0,
Fy r M O 0
11
例题2
水平传动轴上装有两个胶带轮C和D，半径分别是r1=0.4 m ， r2=0.2 m .
套在C 轮上的胶带是铅垂的，两边的拉力F1=3 400 N，F2=2 000 N，套在D轮 上的胶带与铅垂线成夹角α=30o，其拉力F3=2F4。求在传动轴匀速转动时，
3
2）力对轴之矩的计算
A：定义：
力Ｆ对任一z轴的
矩，等于这力在z
轴的垂直面上的投
影对该投影面和z
轴交点O的矩。
2013-8-2 4
R=Fi B：合力矩定理： MZ(R)=MZ(Fi ) 在直角弯的杆C 端作用 着力F，试求这力对坐 标轴的矩。已知:
OA=a=6 m，AB=b=4 m， BC=c=3 m， α=30º 60º ,β= 。
F
x
0,
FAx FBx ( F3 F4 ) sin 30 0
F
z
0,
FAz FBz ( F3 F4 ) cos 30 ( F1 F2 ) 0
M x 0, FAZ 0.25 m FBZ 1.25 m ( F3 F4 ) cos 30 0.75 m 0
例题4
某种汽车后桥半轴可看成支承在
例题5
由题意有
Fr 0.36 Ft
解方程得
F 10.2 kN Fr 3.67 kN FAx 15.64 kN FAz 31.87 kN FBx 1.19 kN FBy 6.8 kN FBz 11.2 kN
2013-8-2 23
例题5
2. 取工件为研究对象，受力
z
M
0,
Fy r M O 0
11
例题2
水平传动轴上装有两个胶带轮C和D，半径分别是r1=0.4 m ， r2=0.2 m .
套在C 轮上的胶带是铅垂的，两边的拉力F1=3 400 N，F2=2 000 N，套在D轮 上的胶带与铅垂线成夹角α=30o，其拉力F3=2F4。求在传动轴匀速转动时，
3
2）力对轴之矩的计算
A：定义：
力Ｆ对任一z轴的
矩，等于这力在z
轴的垂直面上的投
影对该投影面和z
轴交点O的矩。
2013-8-2 4
R=Fi B：合力矩定理： MZ(R)=MZ(Fi ) 在直角弯的杆C 端作用 着力F，试求这力对坐 标轴的矩。已知:
OA=a=6 m，AB=b=4 m， BC=c=3 m， α=30º 60º ,β= 。
F
x
0,
FAx FBx ( F3 F4 ) sin 30 0
F
z
0,
FAz FBz ( F3 F4 ) cos 30 ( F1 F2 ) 0
M x 0, FAZ 0.25 m FBZ 1.25 m ( F3 F4 ) cos 30 0.75 m 0
例题4
某种汽车后桥半轴可看成支承在
第5章 空间任意力系
7
例题
空间任意力系
例题2
解：
由图示可以求出力F 在 各坐标轴上的投影和力F 作 用点C 的坐标分别为：
Fx F coscos
Fy F cos sin
Fz F sin
x= a = 4 m
y= b = 6 m
z= c =－3 m
8
例题
空间任意力系
例题2
则可求得力F 对坐标轴之矩 以及对原点O之矩的大小和方向。
FD 5.8 kN
解方程得 FB 7.777 kN
28
FA 4.423 kN
例题
空间任意力系
例题9
镗刀杆的刀头在镗削工件时受到切向力Fz， 径向力Fy，轴向力 Fx的作 用。各力的大小Fz=5 000 N， Fy=1 500 N， Fx=750 N，而刀尖B 的坐标 x = 200 mm，y = 75 mm，z = 0。如果不计刀杆的重量，试求刀杆根部A 的约束 力的各个分量。
M y 0, F2xl2 Fzr Fx (l1 l2 ) 0
Mz 0, Fyr MO 0
由以上方程可以求出所有未知量。
20
例题
空间任意力系
例题6
水平传动轴上装有两个胶带轮C和D，半径分别是r1=0.4 m ， r2=0.2 m . 套在C 轮上的胶带是铅垂的，两边的拉力T1=3 400 N，T2=2 000 N，套在D轮 上的胶带与铅垂线成夹角α=30o，其拉力F3=2F4。求在传动轴匀速转动时， 拉力F3和F4以及两个径向轴承处约束力的大小。
系统受空间任意力系的作用， 可写出六个平衡方程。
Fx 0,
FAx FBx (F3 F4 ) sin 30 0
空间任意力系
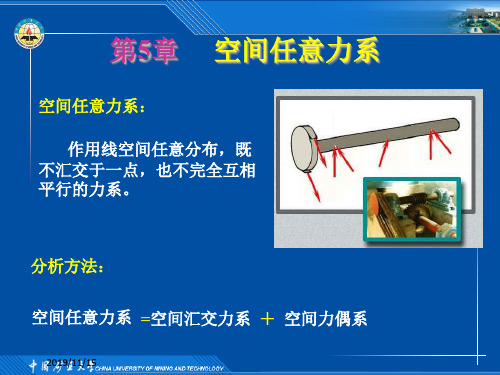
FC
最大载重Pmax是多少。
Q FB
P
D
解: 取起重机为研究对象
A
B,C
My(F)0, FAaco3s0Qa3co3s0Pclos0
MC'x(F)0,
a FA2
FBaQa2P(a2lsin)0
y C
x’
Fz 0, FAFBFCPQ0
A
ED
x
解得: FA=19.3kN， FB=57.3kN， FC=43.4kN
d O1
O
MO MO cos MO MO sin
d MO MO sin
FR
FR
一般情形下空间任意力系可合成为力螺旋
(4) 空间任意力系平衡的情形
● F′R=0，MO=0
2019/11/15
原力系平衡
内容回顾
空间力系的简化与合成
主矢
主矩
最后结果
说
明
FR′ = 0
MO = 0 MO≠0
§5-5 空间任意力系的平衡条件及其应用
1、平衡条件及平衡方程：
平衡条件：
由平衡力系定理可知，空间一般力系平衡的充要条件：力 系的主矢和对任一点的主矩都等于零，即：
平衡方程：
FR Fi 0
M O M O i 0
由主矢与主矩的计算式，有
F R (F x F x i )0 2 i, (F F yy ) i2 i0 ,(F F zz i )i2 0
② 空间任意力系的平衡条件及其应用；
2019/11/15
§5-4 空间任意力系的简化
1. 空间力线平移定理
作用于刚体的力 F 可等效地平移到刚体上的任一点O， 但须附加一力偶，此附加力偶矩 矢M 等于原力对平移点O 的力矩矢MO（F）。
第5章 空间任意力系
求： （5）O 处约束力
研究对象2：工件受力图如图,列平衡方程
F
x
0
FOx Fx 0
F
F
y
0
FOy Fy 0
z
x
0
FOz Fz 0
100FZ M x 0
30 FZ M y 0
100Fx 30 Fy M z 0
M F 0 M F 0
y
M F 0
z
FOx 4.25kN, FOy 6.8kN, FOz 17kN
M x 1.7kN m, M y 0.51kN m, M z 0.22kN m
例5-5
已知：F、P及各尺寸
求： 杆内力
解：研究对象，长方板,列平衡方程
M 0
平衡
§5-2 空间任意力系的平衡方程
1.空间任意力系的平衡方程 空间任意力系平衡的充要条件： 该力系的主矢、主矩分别为零.
F
x
0
0
F
y
0
y
F
z
0
z
M
x
M
0
M
0
空间任意力系平衡的充要条件：所有各力在三个坐标轴 中每一个轴上的投影的代数和等于零，以及这些力对于每一 个坐标轴的矩的代数和也等于零.
列平衡方程
F 0 P P1 FA FB FD 0 M F 0 0.2P1 1.2P 2FD 0
z
x
M F 0
y
0.8P 1 0.6 P 1.2 FB 0.6 FD 0
FD 5.8kN, FB 7.777kN, FA 4.423kN
5第四篇空间任意力系
表示集度大小分布情况及分布力作用方向的图形称为荷载图。 q
A
B
简化结果为合力。 合力作用线位置：
xc x A A,yc y A A
结论：合力通过荷载图的形心。
例题
F12 ql三角形面积
F ql
第三节 一般平行分布力的简化
简化结果为一个合力。 合力作用线位置：
xxV, yyV c V c V
平行分布的面力的合力的大小等于荷载图的体积，合力 通过荷载图体积的形心。
一个力系的主矢量是一常量，与简化中心位置无关，而 主矩一般与简化中心有关。
第一节 空间任意力系的简化
主矢和主矩的解析计算
F R F i F i
( F i) x i ( F i) y j ( F i) z k
F R x F i, x F R y F i, y F R z F iz
F F2 F2 F2
由 Y 0 ;Y A P y 0 , Y A P y 35 (N ) 2 m y 0 ; P z 5 0 10 Q 0 x 0 , Q 74 (N )6
mzA0;30Px05P 0y20X0 B5Q 0co2s000, XB43(N 7) X0;XAXBPxQco2s000, XA72(N 9) mxA0;20ZB 030Pz05Q 0si2n000, ZB20(4N)0 Z0;ZAZBPzQsi2n000, ZA38(N 5)
c
Wc
Wc
W
x x i V i,y y i V i ,z z i V i
c
Vc
Vc
V
对于曲面或曲线，只须在上述公式中分别将ΔVi改为ΔAi (面积)或ΔLi (长度)，V改A为或L，即可得相应的重心坐标 公式。
——形心、对称性
A
B
简化结果为合力。 合力作用线位置：
xc x A A,yc y A A
结论：合力通过荷载图的形心。
例题
F12 ql三角形面积
F ql
第三节 一般平行分布力的简化
简化结果为一个合力。 合力作用线位置：
xxV, yyV c V c V
平行分布的面力的合力的大小等于荷载图的体积，合力 通过荷载图体积的形心。
一个力系的主矢量是一常量，与简化中心位置无关，而 主矩一般与简化中心有关。
第一节 空间任意力系的简化
主矢和主矩的解析计算
F R F i F i
( F i) x i ( F i) y j ( F i) z k
F R x F i, x F R y F i, y F R z F iz
F F2 F2 F2
由 Y 0 ;Y A P y 0 , Y A P y 35 (N ) 2 m y 0 ; P z 5 0 10 Q 0 x 0 , Q 74 (N )6
mzA0;30Px05P 0y20X0 B5Q 0co2s000, XB43(N 7) X0;XAXBPxQco2s000, XA72(N 9) mxA0;20ZB 030Pz05Q 0si2n000, ZB20(4N)0 Z0;ZAZBPzQsi2n000, ZA38(N 5)
c
Wc
Wc
W
x x i V i,y y i V i ,z z i V i
c
Vc
Vc
V
对于曲面或曲线，只须在上述公式中分别将ΔVi改为ΔAi (面积)或ΔLi (长度)，V改A为或L，即可得相应的重心坐标 公式。
——形心、对称性
空间任意力系
B
Fx
mz ( F ) mz ( Fx ) Fx a 25 2 50N .m
x
Fy a 2m
y
11
[练习1] 已知P=2000N, C点在Oxy平面内，求力P对三个 坐标轴的矩。
解：
Pz P sin 45 1000 2N
Pxy P cos45 1000 2 N Px Pxy sin 60 500 6 N Py Pxy cos60 500 2 N
mO ( F ) ( m x ( F )) 2 ( m y ( F )) 2 ( m z ( F )) 2
my (F ) mx ( F ) mz ( F ) cos ,cos ,cos mO ( F ) mO ( F ) mO ( F )
17
§5-3 空间汇交力系的合成与平衡
"
29
⑵ R '∥ M o ; 这种情况力与力偶不能再合成，这就是 力系简化的最终结果，称为力螺旋。如钻孔、攻丝、拧木
螺钉等。
力螺旋中力的作用线称为原力系的中心轴，中心轴过简 化中心。
O·
Mo R'
=
R' · O
O·
R'
Mo
=
· O
R'
右螺旋
左螺旋
力螺旋与力、力偶一样，都是组成力系的基本元素。
30
z
mo ( F )
F
B
r
A
x
O
b y
a Fxy
力对点的矩矢在过该点的任一轴上的投影等于力对该 轴的矩。
[mo (F )]z mz (F )
16
利用力对点之矩与对通过该点的轴之矩的关系计算力
理论力学第5章-空间任意力系
物G = 100 kN的重物，绞车处于平衡状态，结构的几何尺寸如图 所示。试求胶带的拉力和轴承A、B的约束力。
100
z
100
FAz
A y
F
FAx
x
100 FBz
B
（
C
a
FBx
）
G
D
b
F2 F1
解： 取整体为研究对象。
列平衡方程
M y(F) 0
G
D 2
F1
d 2
F2
d 2
0
Mx (F) 0 200FBz 300F1 cos 300F2 cos b 100G 0
(4) FR 0
且 MO 0
FR MO
可进一步简化。
MO O
FR
O FR d FR
O1
FR
O d FR
O1
原力系合成为合力 ，合力矢等于原力系的主矢，
其作用线距简化中心的距离为
d MO FR
由上述分析可知 MO MO (FR ) 而 MO MO(F )
由此得
MO (FR ) MO (F)
F2 200 kN FAz 446.41kN
FBx 1189.23kN FBz 919.62 kN
由于 Fy 0 ，因此本例题只有5个独立的平衡方程。
5.4 平行力系中心 、重心 5.4.1 平行力系中心
设在刚体上的A、B两点，分别作用有同向平行力
F1和F2，。利用平面任意力系的简化理论，可求得它们
5.1.3 力矩关系定理
M z (F ) M O (Fxy ) M O (Fx ) M O (Fy ) xFy yFx
同理得
M x (F ) yFz zFy
100
z
100
FAz
A y
F
FAx
x
100 FBz
B
（
C
a
FBx
）
G
D
b
F2 F1
解： 取整体为研究对象。
列平衡方程
M y(F) 0
G
D 2
F1
d 2
F2
d 2
0
Mx (F) 0 200FBz 300F1 cos 300F2 cos b 100G 0
(4) FR 0
且 MO 0
FR MO
可进一步简化。
MO O
FR
O FR d FR
O1
FR
O d FR
O1
原力系合成为合力 ，合力矢等于原力系的主矢，
其作用线距简化中心的距离为
d MO FR
由上述分析可知 MO MO (FR ) 而 MO MO(F )
由此得
MO (FR ) MO (F)
F2 200 kN FAz 446.41kN
FBx 1189.23kN FBz 919.62 kN
由于 Fy 0 ，因此本例题只有5个独立的平衡方程。
5.4 平行力系中心 、重心 5.4.1 平行力系中心
设在刚体上的A、B两点，分别作用有同向平行力
F1和F2，。利用平面任意力系的简化理论，可求得它们
5.1.3 力矩关系定理
M z (F ) M O (Fxy ) M O (Fx ) M O (Fy ) xFy yFx
同理得
M x (F ) yFz zFy
工程力学05(地大)空间任意力系20页PPT
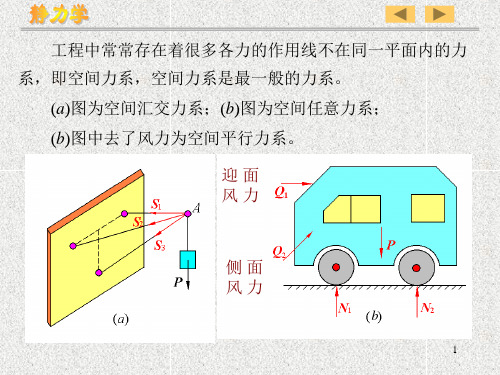
m3 a
Fy
0,YA
YD
0,YD
YA
m3 a
Fz
0,
ZA
ZD
0, Z D
Z A
m2 a
m x1 0 , m 1 bZ D c Y D 0
m 1 bD Z cD Y b ( m a 2) c ( m a 3 ) a b m 2 a c m 3
12
[例3] 已知：AB杆, AD,CB为 绳, A、C在同一垂线上，AB 重80N，A、B光滑接触， ∠ABC=∠BCE=600, 且AD水 平，AC铅直。求平衡时，TA， TB及支座A、B的反力。 解：思路：要巧选投影轴和取 矩轴，使一个方程解出一个未 知数。
所以空间任意力系的平衡方程为：
Fx ,MxF 0 Fy 0,My F 0 Fz 0,Mz F 0
7
空间平行力系的平衡方程，设各力线都 // z 轴。
Fz 0
因为
M z(F ) 0
M x(F ) 0
Fx 0
M y(F ) 0
F y 0 均成为了恒等式。
8
[例1] 已知: RC=100mm, RD=50mm,Px=466N, Py=352N, Pz=1400N 求：平衡时(匀速转动)力Q=？(Q力作用在C轮的最低点）和轴承 A , B的约束反力？
M Ox MO
M xF
MO
cos M O , j
M Oy MO
M y F
MO
cos M O , k
M Oz MO
M zF
MO
6
§4-2 空间任意力系的条件
一、空间任意力系的平衡充要条件是：
FR Fi 0
MO MO i 0
根据： F R F x2 F y2 F z2
工程力学_05空间力系
0, MO 0 时，空间力系为平衡力系。 当 FR
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系向任一点简化可得到一个力和一个力偶。 这个力通过简化中心，称为力系的主矢，它等于各 个力的矢量和，并与简化中心的选择无关。 这个力偶的力偶矩矢称为力系对简化中心的主矩， 并等于力系中各力对简化中心之矩矢的矢量和，并 与简化中心的选择有关。
§5–1 空间任意力系向一点的简化· 主矢和主矩
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系：作用线在空间任意分布的力系。
空间汇交力系
空间任意力系
空间力偶系
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系：作用线在空间任意分布的力系。 一、空间任意力系向一点的简化
其中，各 Fi Fi ，
Fx 0, FAx Fx 0 (1) Fy 0, FAy Fy 0 (2) Fz 0, FAz Fz 0 (3) M x ( F ) 0, M y ( F ) 0, M z ( F ) 0,
FAz MAz
O
z
MAy FAx
FAy Fz
y 200 Fy
MAx
M Ax 0.075Fz 0 M Ay 0.2 Fz 0
x 75 Fx
M Az 0.075Fx 0.2 Fy 0
P 20 kN
§5–2 空间任意力系的平衡条件
解题步骤、技巧与注意问题： 1、解题步骤： ①选研究对象
O
11
§5–1 空间任意力系向一点的简化· 主矢和主矩
三、补充:空间任意力系的简化结果分析（最后结果）
05 空间任意力系[37页]
![05 空间任意力系[37页]](https://img.taocdn.com/s3/m/94b7afaff78a6529647d53f4.png)
主矢：
FR F1 F2 Fn F
主矢的大小： FR Fx 2 Fy 2 Fz 2
主矢的方向余弦：
cosa
Fx FR
cos
Fy FR
cos
Fz FR
5.2 空间任意力系的简化
主矩： MO MO F1 MO F2 MO Fn MO F
主矩的投影：
MOx MO F1 x MO F2 x MO Fn x
Mx F1 Mx F2 Mx Fn Mx F
同理： MOy M y F
MOz Mz F
主矩大小： MO
主矩方向余弦：
cosa M x F MO
Mx F 2 M y F 2 Mz F 2
cos M y F MO
5.2 空间任意力系的简化
（4）主矢 FR 0 ，主矩 MO 0，且 FR MO
MO
O
FR
FR = FR = FR FR
O
d FR
d=
MO
FR
O1
FR
d O1
O
FR
原力系最终简化为一合力。合力的作用线通过 O1。
合力对 O 点的矩矢 MO FR FRd 对 O 点的主矩 MO MO F
B
O
F1
A F2 C
MO F r F
5.1 力对点的矩矢
MO F r F
MO F F r sina Fd
垂直于 F 和 r 所确定的平面 指向由右手螺旋法则 确定
z MO(F)
j
r
x
iO d
k
B
aF A（x, y, z） y
r xi yj zk
F Fxi Fy j Fzk
x
工程力学课后习题答案第五章空间任意力系
第五章 空间任意力系解：cos 45sin 60 1.22x F F KN == cos45cos600.7y F F KN ==sin 45 1.4z F F KN == 6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅5.2 解：21sin cos sin x F F F αβα=- 1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+1sin y M aF β= 121cos cos sin cos sin z y x M F a F a aF aF aF βααβα=-=---解：两力F 、F ′能形成力矩1M1502M Fa KN m ==⋅ 11cos 45x M M =10y M = 11sin 45z M M =1cos 4550x M M KN m ==⋅ 11sin 4550100z z M M M M KN m =+=+=⋅22505C z x M M M KN m =+=⋅63.4α=90β= 26.56γ=5.4 如图所示，置于水平面上的网格，每格边长a = 1m ，力系如图所示，选O 点为简化中心，坐标如图所示。
已知：F 1 = 5 N ，F 2 = 4 N ，F 3 = 3 N ；M 1 = 4 N·m ，M 2 = 2 N·m ，求力系向O 点简化所得的主矢'R F 和主矩M O 。
解：'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α=33.9β=-90γ=5.5 解：120,cos30cos300AxBx X F F T T =+++=∑210,sin30sin300AzBz Z F F T T W =+-+-=∑120,60cos3060cos301000zBx M T T F =---=∑120,3060sin3060sin301000xBz M W T T F =-+-+=∑21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==2a ，AB 长为2b ，列出平衡方程并求解0Bz F =100Az F N =5.7xyz BAFF 140cm60cm40cm20c m20cmBxF BzF AzF AxF解：10,0AxBx X F F F =++=∑0,0AzBz Z F F F =++=∑10,1401000zBx M F F =--=∑10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==-1120,320Bx Bz F N F N =-=-800F N =解：G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑0,sin60sin600Az BG BH Z F F F W =---=∑0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN ===== 5.9。
第5章 空间任意力系
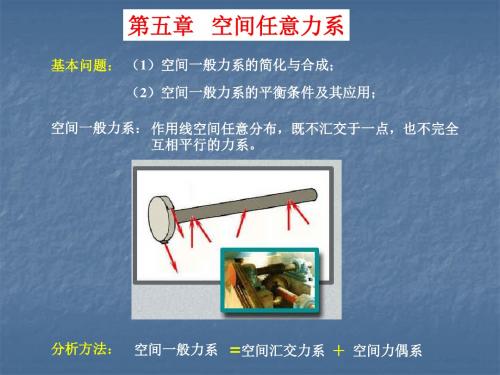
四、空间力系的合力矩定理
定理的表述： 若空间一般力系有合力FR，则合力对作用面内任一点O（或任一轴x）的 矩，等于力系各力对同一点O （或同一轴x）之矩的矢量和（或代数和）。
MO (FR ) MO (Fi ) M x (FR ) M x (Fi )
——对点的合力矩定理
——对轴的合力矩定理
例： 水平传动轴上安装有带轮和 圆柱直齿轮。已知：带轮直径d1= 0.5m，其紧边与松边的拉力分别为 F1和F2，且有F1= 2F2，F2与水平线 夹角θ= 30 ° ；齿轮节圆直径 d2= 0.2 m，Ft=2kN, 啮合角α= 20°； 几何尺寸为：b = 0.2 m，c = e = 0.3 m；零件本身重量不计，设轴处于 平衡状态。求轴承A、B处的反力。 （Fr 与Ft 为齿轮的径向力和圆周力）
F
zi
0:
FA FB FC P 0
（3）
FA P FB FC 1.5 0.35 0.5 0.65kN
第五次作业：
5-1, 5-3(提示）, ５-５, ５-９
若坐标系原点为汇交力系交点O，则有：
(Fi ) 0, M y (Fi ) 0, M z (Fi ) 0
因而空间汇交力系的平衡充要条件或平衡方程为：
F
xi
0, Fyi 0, Fzi 0
三、平衡条件及平衡方程应用：
步骤： （1）选择适当的研究对象； （2）作受力分析，画出受力图； （3）选择适当的投影坐标轴和力矩轴（力矩轴与投影轴可不一致）； （4）列平衡方程，求解未知量。
O
M
主矩的方向： cos( M , x) O
M
x
(Fi ) M y (Fi ) M z (Fi )
第五章空间任意力系
word第五章空间任意力系托架A 套在转轴z 上，在点C 作用一力F = 2000 N 。
图中点C 在Oxy 平面内，尺寸如下列 图，试求力F 对x ， y ， z 轴之矩。
解：F x F cos45 sin60。
1.22KNF y F cos45 cos60 0.7KN FzF sin 45 1.4KN M x F z 60mm 84.85KN mm M yF z 50mm 70.71KN mmM z F x 60mm F y 50mm 108.84KN mm5.2止方体的边长为 a,在其顶用 x ，y , z 上的投影和对轴 x , y , zA 和B 处分别作用着力 R 和F 2,如下列图。
求此两力在轴 的矩。
word解：F x F2 sin F1 cos sinF y F1 cos cosF z F i sin F2 cosM x F z a aF1 sin aF2 cosM y aF sinM z F y a F x a aF^ cos cos aF2sin aF^ cos sin5.3如下列图正方体的外表ABFE内作用一力偶，其矩M = 50 kN •BH作用两力F、F', F = F ' = 50m转向如图。
又沿GA c点的简化结果。
试求该力系向、,2 kN，a = 1m。
解：两力F、F'能形成力矩M1M, Fa 50,2KN mM1x M,cos45M iy 0M1z M1 si n45M x M1 cos45 50KN mM z M1z M M1 sin45 50 100KN mM C .M z2M x250.5KN m63.4 90 26.565.4如下列图，置于水平面上的网格，每格边长 a = 1m，力系如下列图，选O点为简化中心，坐标如下列图。
：F1 = 5 N，F2 = 4 N，F s = 3 N ；M = 4 N • m, M = 2 N • m,求力系向O点简化所得的主矢F R和主矩M。
空间任意力系的简化
1、空间任意力系的平衡充要条件是： R '0 F 0 MO mO ( Fi )0
又 R ' ( X ) 2 ( Y ) 2 ( Z ) 2
M O ( m x ( F )) 2 ( m y ( F )) 2 Байду номын сангаас( m z ( F )) 2
所以空间任意力系的平衡方程为：
空间平行力系的平衡方程，设各力线都 // z 轴。 因为 mz ( F ) 0 Z 0 X 0 m x ( F ) 0 Y 0 m y ( F ) 0
均成为了恒等式。
2、空间约束
观察物体在空间的六种（沿三轴移动和绕三轴转动）可能 的运动中，有哪几种运动被约束所阻碍，有阻碍就有约束反力。
阻碍移动为反力，阻碍转动为反力偶。[例]
1）球形铰链 （前面讲过）
球形铰链
2）向心轴承，滚珠(柱)轴承
绕x和z轴的转动 也同时被约束。
3）滑动轴承
4）止推轴承
第9页，加 两个绕轴 转动的约 束。
5）带有销子的夹板
6）空间固定端
作业：
自学教材例题5-1~5-4.
X 0,m x ( F ) 0 Y 0,m y ( F ) 0 Z 0,m z ( F ) 0
还有四矩式，五矩式和六矩式， 同时各有一定限制条件。
空间汇交力系的平衡方程为：
X 0 Y 0 Z 0
因为各力线都汇交于一点，各轴都通过 该点，故各力矩方程都成为了恒等式。
第五章 空间任意力系
§5-1 空间任意力系的简化
与平面任意力系的简化原理（力的平移定 理）相同，空间任意力系也可以简化为一个主 失和一个主矩。但是由于主矩和主失不在同一 平面，所以不能进一步简化为一个合力。 应当注意，主失仍然与简化中心无关；主矩
又 R ' ( X ) 2 ( Y ) 2 ( Z ) 2
M O ( m x ( F )) 2 ( m y ( F )) 2 Байду номын сангаас( m z ( F )) 2
所以空间任意力系的平衡方程为：
空间平行力系的平衡方程，设各力线都 // z 轴。 因为 mz ( F ) 0 Z 0 X 0 m x ( F ) 0 Y 0 m y ( F ) 0
均成为了恒等式。
2、空间约束
观察物体在空间的六种（沿三轴移动和绕三轴转动）可能 的运动中，有哪几种运动被约束所阻碍，有阻碍就有约束反力。
阻碍移动为反力，阻碍转动为反力偶。[例]
1）球形铰链 （前面讲过）
球形铰链
2）向心轴承，滚珠(柱)轴承
绕x和z轴的转动 也同时被约束。
3）滑动轴承
4）止推轴承
第9页，加 两个绕轴 转动的约 束。
5）带有销子的夹板
6）空间固定端
作业：
自学教材例题5-1~5-4.
X 0,m x ( F ) 0 Y 0,m y ( F ) 0 Z 0,m z ( F ) 0
还有四矩式，五矩式和六矩式， 同时各有一定限制条件。
空间汇交力系的平衡方程为：
X 0 Y 0 Z 0
因为各力线都汇交于一点，各轴都通过 该点，故各力矩方程都成为了恒等式。
第五章 空间任意力系
§5-1 空间任意力系的简化
与平面任意力系的简化原理（力的平移定 理）相同，空间任意力系也可以简化为一个主 失和一个主矩。但是由于主矩和主失不在同一 平面，所以不能进一步简化为一个合力。 应当注意，主失仍然与简化中心无关；主矩
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2）主矩大小和方向
M M M
ox oy oz
v M v M
v M
v o(Fv) o(F )
v o(F )
x y z
v M x(F
v
M
(
y
F
v
M
(
z
F
) ) )
Mo
v
M
(
x
F
) 2
v
M
(
y
F
2
)
v M z(F
) 2
cos
v M
o,
iv
M ox M
cos
v M
o,
vj
M oy M
cos
ij k
y
18
2i 12 j 3
3
0
4 3 2 3 2
9 2i (12 9 2) j (12 9 2)k
16
主主 §矩矢5-1、M空OFR间任148i意2力3i系21的2j j简3化2MkC 9
2i (129
2) j (129
2)k
z
z
B(0,0,2a)
B(0,0,2a)
i 1
作用线过简化中心O
2.特点 主矢的大小和方向与简化中心无关
3.解析计算
(1)主矢投影
n
FR'x Fxi i 1
(2)主矢大小和方向余弦
n
FR'y Fyi i 1
n
FR'z Fzi i 1
FR'
F '2 Rx
F '2 Ry
F '2 Rz
Fxi 2 Fyi 2 Fzi 2
v M
o,
v k
M oz 5M
§5-1、空间任意力系的简化
r FrRx —有效推进力
飞机向前飞行
FrRy —有效升力
飞机上升
FrRz —侧向力
飞机侧移
Mr Ox —滚转力矩
飞机绕x轴滚转
M r
Oy
—偏航力矩
飞机转弯
MOz —俯仰力矩
飞机仰头
6
5-2空间任意力系的平衡条件
7
§5-2、空间任意力系的平衡条件
M Ox yFRz zFRy
由 M Oy zFRx xFRz
M Oz xFRy yFRx
代入
0 2yF 2zF
2Fa z • 0 2xF
2Fa 2xF y • 0
v MO
v FR
D
F3
F5
aO
F2
y
A F1
B F6
x
舍去不独立的方程，
xa
即可得合力作用线方程 y z
过A、D两点的连线
第5章 空间任意力系
1
5-1空间任意力系的简化
2
§5-1、空间任意力系的简化
1． 空间任意力系向一点的简化
其中，各
rr Fi Fi
，各
r rr Mi Mo(Fi )
一空间汇交与空间力偶系等效代替一空间任意力系.
3
§5-1、空间任意力系的简化
主矢 1.定义
FvR'
n
Fvi'
n
v Fi
i 1
主矩方向v v cos(MO , i ) 0
vv
2
cos(MO , j ) 2
vv 2 cos(MO , k ) 2
12
§5-1、空间任意力系的简化
rv
FR • MO = 0 •0+2F •-2Fa 2F •2Fa 0
表明此力系简化的最后结果为一合力。
如何确定合力作用线方程？
C
z F4
M z F 0
F FBx FAx Fx 0 FBy Fy 0
F FBz FAz Fz 0
488 76FBz 76F 388Fz 0
F R Fz r 0
76F 488 76FBx 30Fy 388Fx 205
又： Fr 0.36F , 结果： F 10.2kN,
平衡条件—— F 0 力多边形自行封闭 i
空间汇交力系平衡的充分必要条件是： 力系中所有各力在各个坐标轴中每一轴上的投影的
代数和分别等于零。
空间汇交力系的平衡方程:
Mx 0 My 0 Mz 0
Fx 0
Fy 0
Fz 0
9
§5-2、空间任意力系的平衡条件 2、空间平行力系 空间平行力系的平衡方程
M z F 0 100Fx 30Fy M z 0
结果：FOx 4.25kN, FOy 6.8kN, FOz 17kN M x 1.7kNm, M y 0.51kNm, M z 0.22kNm
27
13
§5-1、空间任意力系的简化 例5-1-2
z B(0,0,2a)
如图，力系中 F1, F2 分
A(0,0,a) 45º
F1
F2
O
C(a,a,0)
x
别作用于点A(0,0,a)和点
B(0,0,2a)，已知：a=3m, y F1=4kN,F2=6kN,求力系
的主矢及力系对点O、点
C(a,a,0)的主矩，并判断力 系简化的最后结果。
14
§5-1、空间任意力系的简化
z B(0,0,2a)
解：F1 4i
A(0,0,a) 45º F1 O
F2
F2 6(
又
r1
3k
2
j
2
2
2
r2 6k
k ) 3 2 j 3 2k
CO 3i 3 j
y 主矢
C(a,a,0)
x
对点O的主矩
FR Fi 4i 3 2 j 3 2k
19
例5-2-1
已知： P=8kN, P1 10kN, 各尺寸如图
求：A、B、C 处约束力
解：研究对象：小车
rr r r r 受力：P, P1, FA, FB , FD ,
列平衡方程
Fz 0 P P1 FA FB FD 0
MxF 0 0.2P 1.2P1 2FD 0
M yF 0 0.8P1 0.6P 1.2FB 0.6FD 0
F6
a
a 2
P
F1
ab 0 a2 b2
r
M FG F 0
Fb
b 2
P
F2b
0
r
M BC F 0
F2
b
b 2
P
F3
cos
45
b
0
F1 0
F2 1.5P
F3
2
2P
21
例5-2-3
已知： F 2000N, F2 2F1, 30, 60, 各尺寸如图
解求：：研F究1, F对2 及象A，、曲B处轴约受束力力：Fr
空间任意力系平衡的充要条件：该力系的主矢、主矩分别为零.
空间任意力系的平衡方程
Fx 0 Fy 0 Fz 0
Mx 0 My 0 Mz 0
空间任意力系平衡的充要条件：所有各力在三 个坐标轴中每一个轴上的投影的代数和等于零，以及这些 力对于每一个坐标轴的矩的代数和也等于零.
8
§5-2、空间任意力系的平衡条件 1、空间汇交力系 空间汇交力系平衡的几何条件
Fx 0 Fy 0
M
n
2
M
ix
n
2
M iy
n
2
M iz
0
i1
i1
i1
Fz 0
空间力偶系平衡的解析条件——平衡方程
Mx =0 My =0 Mz =0
即力偶系各力偶矩矢分别在三个坐标轴投影的代数和等于零。
11
§5-1、空间任意力系的简化
6
v
MOx M x Fi =F2a F4a 0
F1
B(0,0,2a)
r M
45º
A(0,0,a)
F2
OMO
r v 36 2 0 FR • MO 0 左力螺旋
vr
M lFR
O
如何确定力螺旋作用线方程？
r
M
O
rv M O • lFR
v lFR
r
M
O
•
v FvR FR
v FvR FR
rv MO • FR
v2 FR
FR
v FR
FAx 15.64kN,
FBx 1.19kN,
F 3.67kN, FAz 31.87kN, FBy 6.8kN, FBz 11.2kN,
研究对象2：工件受力图如图
列平衡方程
Fx 0 FOx Fx 0
Fy 0 FOy Fy 0
Fz 0 FOz Fz 0 26
M x F 0 100FZ M x 0 M y F 0 30FZ M y 0
v cos(FR'
,
v i)
FR' x FR'
v cos(FR' ,
v j)
FR' y FR'
vv cos(FR' , k )
FR' z FR'
4
§5-1、空间任意力系的简化
主矩
v
v
vv
1.定义
Mo M
M
o(F
)
i
2.特点 在一般情况下，主矩随简化中心位置不同而改变
3.解析计算 （1）主矩投影
由力对点的矩与力对 轴的矩的关系，有
已知： Fx 4.25N, Fy 6.8N, Fz 17N,
Fr 0.36F , R 50mm, r 30mm
各尺寸如图
求：
(1)
r Fr
,
r F
（2）A、B处约束力
（3）O
M M M
ox oy oz
v M v M
v M
v o(Fv) o(F )
v o(F )
x y z
v M x(F
v
M
(
y
F
v
M
(
z
F
) ) )
Mo
v
M
(
x
F
) 2
v
M
(
y
F
2
)
v M z(F
) 2
cos
v M
o,
iv
M ox M
cos
v M
o,
vj
M oy M
cos
ij k
y
18
2i 12 j 3
3
0
4 3 2 3 2
9 2i (12 9 2) j (12 9 2)k
16
主主 §矩矢5-1、M空OFR间任148i意2力3i系21的2j j简3化2MkC 9
2i (129
2) j (129
2)k
z
z
B(0,0,2a)
B(0,0,2a)
i 1
作用线过简化中心O
2.特点 主矢的大小和方向与简化中心无关
3.解析计算
(1)主矢投影
n
FR'x Fxi i 1
(2)主矢大小和方向余弦
n
FR'y Fyi i 1
n
FR'z Fzi i 1
FR'
F '2 Rx
F '2 Ry
F '2 Rz
Fxi 2 Fyi 2 Fzi 2
v M
o,
v k
M oz 5M
§5-1、空间任意力系的简化
r FrRx —有效推进力
飞机向前飞行
FrRy —有效升力
飞机上升
FrRz —侧向力
飞机侧移
Mr Ox —滚转力矩
飞机绕x轴滚转
M r
Oy
—偏航力矩
飞机转弯
MOz —俯仰力矩
飞机仰头
6
5-2空间任意力系的平衡条件
7
§5-2、空间任意力系的平衡条件
M Ox yFRz zFRy
由 M Oy zFRx xFRz
M Oz xFRy yFRx
代入
0 2yF 2zF
2Fa z • 0 2xF
2Fa 2xF y • 0
v MO
v FR
D
F3
F5
aO
F2
y
A F1
B F6
x
舍去不独立的方程，
xa
即可得合力作用线方程 y z
过A、D两点的连线
第5章 空间任意力系
1
5-1空间任意力系的简化
2
§5-1、空间任意力系的简化
1． 空间任意力系向一点的简化
其中，各
rr Fi Fi
，各
r rr Mi Mo(Fi )
一空间汇交与空间力偶系等效代替一空间任意力系.
3
§5-1、空间任意力系的简化
主矢 1.定义
FvR'
n
Fvi'
n
v Fi
i 1
主矩方向v v cos(MO , i ) 0
vv
2
cos(MO , j ) 2
vv 2 cos(MO , k ) 2
12
§5-1、空间任意力系的简化
rv
FR • MO = 0 •0+2F •-2Fa 2F •2Fa 0
表明此力系简化的最后结果为一合力。
如何确定合力作用线方程？
C
z F4
M z F 0
F FBx FAx Fx 0 FBy Fy 0
F FBz FAz Fz 0
488 76FBz 76F 388Fz 0
F R Fz r 0
76F 488 76FBx 30Fy 388Fx 205
又： Fr 0.36F , 结果： F 10.2kN,
平衡条件—— F 0 力多边形自行封闭 i
空间汇交力系平衡的充分必要条件是： 力系中所有各力在各个坐标轴中每一轴上的投影的
代数和分别等于零。
空间汇交力系的平衡方程:
Mx 0 My 0 Mz 0
Fx 0
Fy 0
Fz 0
9
§5-2、空间任意力系的平衡条件 2、空间平行力系 空间平行力系的平衡方程
M z F 0 100Fx 30Fy M z 0
结果：FOx 4.25kN, FOy 6.8kN, FOz 17kN M x 1.7kNm, M y 0.51kNm, M z 0.22kNm
27
13
§5-1、空间任意力系的简化 例5-1-2
z B(0,0,2a)
如图，力系中 F1, F2 分
A(0,0,a) 45º
F1
F2
O
C(a,a,0)
x
别作用于点A(0,0,a)和点
B(0,0,2a)，已知：a=3m, y F1=4kN,F2=6kN,求力系
的主矢及力系对点O、点
C(a,a,0)的主矩，并判断力 系简化的最后结果。
14
§5-1、空间任意力系的简化
z B(0,0,2a)
解：F1 4i
A(0,0,a) 45º F1 O
F2
F2 6(
又
r1
3k
2
j
2
2
2
r2 6k
k ) 3 2 j 3 2k
CO 3i 3 j
y 主矢
C(a,a,0)
x
对点O的主矩
FR Fi 4i 3 2 j 3 2k
19
例5-2-1
已知： P=8kN, P1 10kN, 各尺寸如图
求：A、B、C 处约束力
解：研究对象：小车
rr r r r 受力：P, P1, FA, FB , FD ,
列平衡方程
Fz 0 P P1 FA FB FD 0
MxF 0 0.2P 1.2P1 2FD 0
M yF 0 0.8P1 0.6P 1.2FB 0.6FD 0
F6
a
a 2
P
F1
ab 0 a2 b2
r
M FG F 0
Fb
b 2
P
F2b
0
r
M BC F 0
F2
b
b 2
P
F3
cos
45
b
0
F1 0
F2 1.5P
F3
2
2P
21
例5-2-3
已知： F 2000N, F2 2F1, 30, 60, 各尺寸如图
解求：：研F究1, F对2 及象A，、曲B处轴约受束力力：Fr
空间任意力系平衡的充要条件：该力系的主矢、主矩分别为零.
空间任意力系的平衡方程
Fx 0 Fy 0 Fz 0
Mx 0 My 0 Mz 0
空间任意力系平衡的充要条件：所有各力在三 个坐标轴中每一个轴上的投影的代数和等于零，以及这些 力对于每一个坐标轴的矩的代数和也等于零.
8
§5-2、空间任意力系的平衡条件 1、空间汇交力系 空间汇交力系平衡的几何条件
Fx 0 Fy 0
M
n
2
M
ix
n
2
M iy
n
2
M iz
0
i1
i1
i1
Fz 0
空间力偶系平衡的解析条件——平衡方程
Mx =0 My =0 Mz =0
即力偶系各力偶矩矢分别在三个坐标轴投影的代数和等于零。
11
§5-1、空间任意力系的简化
6
v
MOx M x Fi =F2a F4a 0
F1
B(0,0,2a)
r M
45º
A(0,0,a)
F2
OMO
r v 36 2 0 FR • MO 0 左力螺旋
vr
M lFR
O
如何确定力螺旋作用线方程？
r
M
O
rv M O • lFR
v lFR
r
M
O
•
v FvR FR
v FvR FR
rv MO • FR
v2 FR
FR
v FR
FAx 15.64kN,
FBx 1.19kN,
F 3.67kN, FAz 31.87kN, FBy 6.8kN, FBz 11.2kN,
研究对象2：工件受力图如图
列平衡方程
Fx 0 FOx Fx 0
Fy 0 FOy Fy 0
Fz 0 FOz Fz 0 26
M x F 0 100FZ M x 0 M y F 0 30FZ M y 0
v cos(FR'
,
v i)
FR' x FR'
v cos(FR' ,
v j)
FR' y FR'
vv cos(FR' , k )
FR' z FR'
4
§5-1、空间任意力系的简化
主矩
v
v
vv
1.定义
Mo M
M
o(F
)
i
2.特点 在一般情况下，主矩随简化中心位置不同而改变
3.解析计算 （1）主矩投影
由力对点的矩与力对 轴的矩的关系，有
已知： Fx 4.25N, Fy 6.8N, Fz 17N,
Fr 0.36F , R 50mm, r 30mm
各尺寸如图
求：
(1)
r Fr
,
r F
（2）A、B处约束力
（3）O