八年级几何证明测试卷(教师版)
几何证明选讲(教师版)

BCDO AP1.如图,点P 在圆O 直径AB 的延长线上,且PB=OB=2,PC 切圆O 于C 点,CD ⊥AB 于D 点,则PC= , CD=.2.如图,AB 是⊙O 的直径,P 是AB 延长线上的一点,过P 作⊙O 的切线,切点为C ,,32=PC 若∠CAP =30°,则⊙O 的直径AB =___________答案43.已知圆O 的半径为3,从圆O 外一点A 引切线AD 和割线ABC ,圆心O 到AC 的距离为22,3AB =,则切线AD 的长为 _____。
解:依题意,BC =,∴AC =5,2AD =.AB AC =15,∴AD =154.如图,PA 切O 于点A ,割线PBC 经过圆心O ,OB=PB=1, OA 绕点O 逆时针旋转60°到OD ,则PD 的长为 .解:∵PA 切O 于点A ,B 为PO 中点,∴AB=OB=OA, ∴60AOB ∠=,∴120POD ∠=, 在△POD中由余弦定理,得2222cos PD PO DO PO DO POD =+-⋅∠=1414()72+-⨯-=∴PD 5.如图,在⊙O 中,AB 为直径,AD 为弦,过B 点的切线与ADAD=DC ,则sin ∠ACO=_________解:由条件不难得ABC ∆为等腰直角三角形,设圆的半径为1,则1OB =,2BC =,OC =sin BCO ∠==,s co BCO ∠= ∴ sin ∠ACO=0sin(45BCO -∠)=10106.如图,PT 是O 的切线,切点为T ,直线PA 与O 交于A 、B 两点,TPA ∠的平分线分别交直线TA 、TB 于D 、E 两点,已知2PT =,PB =,则PA = ,TEAD= .;7.已知AB 是圆O 的直径,EF 切圆O 于C ,AD ⊥EF 于D ,AD =2,AB =6,则AC 长为_______. 、23;8.已知AB 是半圆O 的直径,点C 在半圆上,CD AB ⊥于点D ,且4AD DB =,设COD θ∠=,则cos 2θ= .解:()44,AD DB OC OD OC OD =∴+=- 即35OC OD =,22237cos 22cos 12121525OD OC θθ⎛⎫⎛⎫=-=⨯-=⨯-=- ⎪ ⎪⎝⎭⎝⎭9.如图,圆O 是ABC ∆的外接圆,过点C 的切线交AB 的延长线于点D ,CD =3AB BC ==。
初二证明题考试题及答案

初二证明题考试题及答案一、选择题1. 已知在△ABC中,AB=AC,点D在BC上,且BD=DC,那么下列说法正确的是:A. AD是△ABC的中线B. AD是△ABC的角平分线C. AD是△ABC的高线D. AD是△ABC的中线、角平分线和高线答案:D2. 在等腰三角形中,如果顶角的角平分线也是底边的高线,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 不能确定答案:A二、填空题1. 在平行四边形ABCD中,若∠A=60°,则∠B的度数为______。
答案:120°2. 已知等腰三角形的底边长为6cm,腰长为5cm,那么它的高线长度为______。
答案:4cm三、解答题1. 已知在△ABC中,AB=AC,点D在BC上,且BD=DC,求证:AD是△ABC的中线、角平分线和高线。
证明:因为AB=AC,所以△ABC是等腰三角形。
又因为BD=DC,所以D是BC的中点,故AD是△ABC的中线。
在△ABD和△ACD中,有AB=AC,BD=DC,AD=AD,根据SSS(边边边)全等条件,可得△ABD≌△ACD。
因此,∠BAD=∠CAD,所以AD是△ABC的角平分线。
又因为△ABD≌△ACD,所以∠ADB=∠ADC,即AD是△ABC的高线。
综上所述,AD是△ABC的中线、角平分线和高线。
2. 在等腰三角形ABC中,AB=AC,点D是底边BC上的一点,使得AD 是底边BC的高线,求证:BD=DC。
证明:因为AB=AC,所以△ABC是等腰三角形。
又因为AD是底边BC的高线,根据等腰三角形的性质,底边的高线也是底边的中线,所以BD=DC。
因此,BD=DC得证。
初二数学几何证明题(5篇可选)

初二数学几何证明题(5篇可选)第一篇:初二数学几何证明题1.在△ABC中,AB=AC,D在AB上,E在AC的延长线上,且BD=CE,线段DE交BC于点F,说明:DF=EF。
2.已知:在正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直DM于点M,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变,则(1)的结论还成立吗?如果成立,请证明,如果不成立,请说明理由。
3.。
如图,点E,F分别是菱形ABCD的边CD和CB延长线上的点,且DE=BF,求证∠E=∠F。
4,如图,在△ABC中,D,E,F,分别为边AB,BC,CA,的中点,求证四边形DECF为平行四边形。
5.如图,在菱形ABCD中,∠DAB=60度,过点C作CE垂直AC 且与AB的延长线交与点E,求证四边形AECD是等腰梯形?6.如图,已知平行四边形ABCD中,对角线AC,BD,相交与点0,E是BD延长线上的点,且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD,求证四边形ABCD是正方形。
7.已知正方形ABCD中,角EAF=45度,F点在CD边上,E点在BC边上。
求证:EF=BE+DF第二篇:初二几何证明题1如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DCCF.(1)求证:D是BC的中点;(2)如果AB=ACADCF的形状,并证明你的结论AEB第三篇:初二几何证明题初二几何证明题1.已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。
M为AB中点,联结ME,MD、ED求证:角EMD=2角DAC证明:∵M为AB边的中点,AD⊥BC,BE⊥AC,∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、BC的延长线与EF的延长线交于点H、D求证:∠AHE=∠BGE证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:∵E是CD的中点,且EM‖AD,∴EM=1/2AD,M是AC的中点,又因为F是AB的中点∴MF‖BC,且MF=1/2BC.∵AD=BC,∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.∵EM‖AH,∴∠MEF=∠AHF ∵FM‖BG,∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
初中几何证明练习题含答案
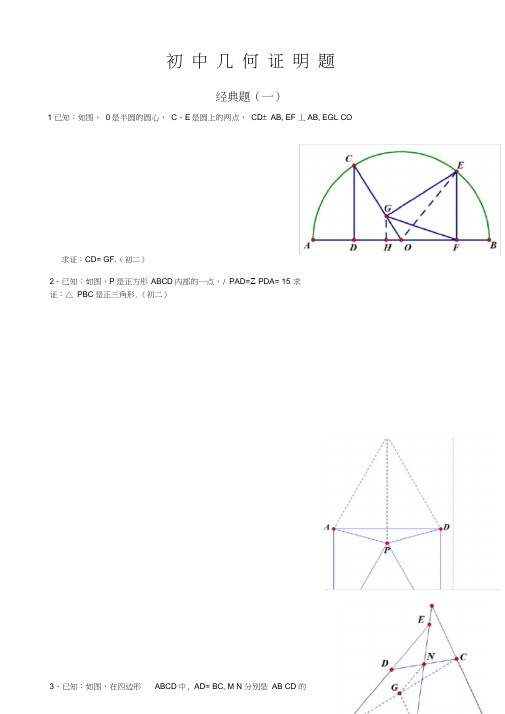
初中几何证明题经典题(一)1 已知:如图,0是半圆的圆心,C、E是圆上的两点,CD± AB, EF丄AB, EGL CO求证:CD= GF.(初二)2、已知:如图,P是正方形ABCD内部的一点,/ PAD=Z PDA= 15 求证:△ PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中, AD= BC, M N 分别是AB CD 的中点,AD BC的延长线交MN于E、F.求/ DEN=Z F.证:经典题(二)1 已知:△ ABC中,H为垂心(各边高线的交点),0为外心,且OM L BC于M(1)求证:AH= 20M(2)若/ BAC= 600,求证:AH= AO (初二)2、设MN是圆O外一条直线,过0作OAL MN于A,自A引圆的两条割线交圆0于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP= AQ3、如图,分别以△ ABC的AB和AC为一边,在厶ABC的外侧作正方形ABFG和正方形ACDE点0是DF的中点,OPL BC求证:BC=20P(初二)L、MN证明:分别过F、A D作直线BC的垂线,垂足分别是•/ OF=OD DIN/ OP// FL••• PN=PL••• OP是梯形DFLN的中位线• DN+FL=2OP•/ ABFG是正方形•••/ ABM丄FBL=90°又/ BFL+Z FBL=90°•••/ ABM2 BFL又/ FLB=Z BMA=90 , BF=AB•△BFL^A ABM• FL=BM同理△ AMC^A CND• CM=DN• BM+CN=FL+DN• BC=FL+DN=2OP经典题(二)1如图,四边形ABCD为正方形, 于F .求证:CE= CF.(初二)DE// AC, AE= AC, AE 与CD相交证明:连接 BD 交AC 于0。
过点E 作EGL AC 于G •/ ABCD 是正方形 ••• BD L AC 又 EGL AC ••• BD// EG 又 DE// AC • 0DEG 是平行四边形 又/ COD=90 • 0DEG1矩形1 1 1 • EG=OD= BD=丄 AC )AE222• / EAG=30 •/ AC=AE• / ACE 玄 AEC=75 又/ AFD=90 -15 ° =75° • / CFE=/ AFD=75 =Z AEC • CE=CF• AE=AF3、设P 是正方形 求证:PA = PF.证明:过点F 作FGL CE 于G, ••• CD L CG ,. HCGF 是矩形•••/ HCF 玄 GCF\ FH=FG • HCGF 是正方形 •CG=GF -AP L FP• / APB+/ FPG=90 -/ APB+/ BAP=90° • / FPG 玄 BAP 又/ FGP 玄 PBA• △ FGP^A PBA 设 AB=x , BP=y , CG=z z : y= (x-y+z ): x 化简得(x-y )• y = (x-y )-x-y 丰 0• y=z 即 BP=FG • △ ABP ^^ PGF2、如图,四边形 ABCD 为正方形,DE// AC 且CE= CA 直线EC 交DA 延长线于F . 求证:AE = AF.(初二) 证明:连接BD,过点E 作EGL AC 于G •/ ABCD 是正方形 • B D L AC,又 EGL AC • B D// EG 又 DE// AC • ODEG!平行四边形 又/ COD=90 • ODEG !矩形 o-/ FAC-/ ACF o1• / CAE / CEA 「/ GCE=152在厶AFC 中/ F =180• EG =OD =丄 BD=! AC 」CE 2 22• / GCE=30 =180 =180 • / F=/ CEA-/ FAC-/ GCE-135 ° -30 ° =15•/ AC=EC ABC [一边BC 上的任一点, PF L AP, CF 平分/ DCE (初二)FH 丄 CD 于 H••• FG: PB=PG AB4、如图,PC 切圆O 于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于 B D. 求证:AB= DC, BC = AD.(初三)..—../证明:过点 E 作EK// BD,分别交 连接OH MH EC •/ EH=FH• OHL EF ,「./ PHO=90 又 PC L OC POC=90• P 、C H O 四点共圆 •••/ HCO M HPO 又 EK// BD HPO M HEK• / HCM N HEM • H C E 、M 四点共圆 • / ECM M EHM 又/ ECM M EFA • / EHM M EFA • HIM/ AC •/ EH=FH经典题(四)1已知:△ ABC 是正三角形,P 是三角形内一点, PA = 3, 求/ APB 的度数.(初二)解:将△ ABP 绕点B 顺时针方向旋转 60°得厶BCQ 连接 则厶BPQ 是正三角形• / BQP=60 , PQ=PB=3在厶 PQC 中, PQ=4, CQ=AP=3 PC=5 • △ PQC 是直角三角形 • / PQC=90• / BQC 2 BQP+Z PQC=60 +90° =150 °• / APB=/ BQC=150 2、设P 是平行四边形 ABCD 内部的一点,且/ PBA=/ PDA求证:/ PAB=/ PCB (初二) 证明:过点P 作AD 的平行线,过点 两平行线相交于点 E ,连接BE•/ PE// AD, AE// PD • ADPE 是平行四边形 • PE=AD又ABCD 是平行四边形 • AD=BC \• PE=BC又 PE// AD AD// BC \• PE// BC• BCPE 是平行四边形 ; • / BEP=/ PCB ••• ADPE 是平行四边形; AC AF 于M K ,取EF 的中点H,1• EM=KM I•/ EK// BD\ • OB竺EM AM KM•OB=ODI又 AO=CO•四边形ABCD 的对角线 ;互相平分•ABCD 是平行四边又/ ADP 玄 ABP •/ AEP=Z ABP • A 、E 、B 、P 四点共圆 •/ BEP=Z PABC•/ ADP玄AEP '3、设ABCD 为圆内接凸四边形,求证: AB- CD+ AD- BC = AC- BD.(初三) 证明:在 BD 上去一点 E ,使/ BCE=/ ACD •/ CD=CD •••/ CAD 2 CBD• B£ BC _AD AC• AD- BC=BE- ACBCE 玄 ACDBCE+Z ACE=/ ACD y ACEBCA=/ ECD • AB AC"DE CD• AB- CD=DE AC4、平行四边形 ABCC 中,设E 、F 分别是BC AB 上的一点,AE 与CF 相交于P,且AE = CF.求证:/ DPA=Z DPC (初二)证明:过点 D 作DGL AE 于G 作DH1 FC 于H,连接DF 、 1 1• S A ADE =2AE • DG S A FDc FqFC • DH 又 AE=CF • DG=DH•••点D 在/ APC 的角平分线上•••/ DPA=Z DPC经典题(五)证明:(1)将厶BPC 绕B 点顺时针旋转60°的厶BEF 连接 •/ BP=BE / PBE=60 • △ PBE 是正三角形。
第19章 专题01几何证明重难点专练(教师版

专题01几何证明重难点专练(教师版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列命题的逆命题是假命题的是()A.全等三角形的面积相等;B.等腰三角形两个底角相等;C.直角三角形斜边上的中线等于斜边的一半;D.在角的平分线上任意一点到这个角的两边的距离相等.【答案】A【分析】先确定每个命题的逆命题,再对每个选项依次判定即可解答.【详解】A.逆命题为:面积相等的三角形是全等三角形,是假命题,符合题意;B.逆命题为:两个角相等的三角形是等腰三角形,是真命题,不符合题意;C.逆命题为:一条边上的中线等于这条边的一半的三角形是直角三角形,是真命题,不符合题意;D.在角的内部到角的两边距离相等的点在这个角的平分线上,是真命题,不符合题意.故选:A.【点睛】此题考查命题,正确的命题是真命题,错误的命题是假命题,正确确定每个命题的逆命题是解此题的关键.2.设D为等腰ABC底边BC上一点,DE∥AB,DF∥AC,则四边形AFDE的周长是()A.2AB B.2AB+BC C.2BC D.AB+BC【答案】A【分析】先证明四边形AFDE是平行四边形,得到DE=AF,AE=DF,再证明BF=DF=AE,问题得解.【详解】解:∵DE∵AB,DF∵AC,∵四边形AFDE是平行四边形,∵DE=AF,AE=DF,∵DF∵AC,∵∵C=∵FDB,∵AB=AC,∵∵B=∵C∵∵FDB=∵B,∵BF=DF,∵BF=DF=AE,∵四边形AFDE的周长等于AE+DE+DF+AF=BF+AF+BF+AF=2AB.故选:A【点睛】本题考查了等腰三角形的判定与性质,平行四边形的性质,熟知相关定理是解题关键.3.下列给出的三条线段中,不能构成直角三角形的是()A.4、8、B.4、8、C.7、24、25D.7、14、15【答案】D【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可.【详解】解:A、∵42+(2=64=82,∵能够成直角三角形,故本选项可构成直角三形;B、∵42+82=80=(2,∵能够成直角三角形,故本选项错误;C、∵72+242=625=252,∵能够成直角三角形,故本选项错误;D、∵72+142=245≠152,∵不能够成直角三角形,故本选项正确.故选:D.【点睛】本题考查的是如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.4.如图,ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,ADC 的周长为9cm,则ABC的周长是()A.12cm B.15cm C.21cm D.18cm【答案】B【分析】由DE是∵ABC中边AB的垂直平分线,根据线段垂直平分线的性质,即可得BD=AD,AB=2AE,又由∵ADC的周长为9cm,即可得AC+BC=9cm,继而求得∵ABC的周长.【详解】解:由DE是边AB的垂直平分线,∵AD=BD,AE=BE,由∵ADC的周长为9cm,∵AC+BC=9,∵AE=3,∵AB=6,∵∵ABC的周长是15cm,故选:B.【点睛】此题考查了线段垂直平分线的性质.此题难度适中,解题的关键是注意等量代换与整体思想的应用.5.下列命题中,假命题是()A.对顶角相等B.同角的余角相等C.面积相等的两个三角形全等D.平行于同一条直线的两直线平行【答案】C【分析】根据对顶角的性质对A进行判断;根据余角的性质对B进行判断;根据三角形全等的判断对C进行判断;根据平行线的传递性对D进行判断.【详解】解:A、对顶角相等,所以A选项为真命题;B、同角的余角相等,所以B选项为真命题;C、面积相等的两个三角形不一定全等,所以C选项为假命题;D、平行于同一条直线的两条直线平行,所以D选项为真命题.故选:C.【点睛】本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.6.下列命题中,是真命题的是()A.对顶角相等B.两直线被第三条直线所截,截得的内错角相等C.等腰直角三角形都全等D.如果a b>,那么22>a b【答案】A【分析】分别利用对顶角的性质、平行线的性质及不等式的性质分别判断后即可确定正确的选项.【详解】解:A.对顶角相等,正确,是真命题;B.两直线被第三条直线所截,内错角相等,错误,是假命题;C.等腰直角三角形不一定都全等,是假命题;D.如果0>a>b,那么a2<b2,是假命题.【点睛】本题考查了命题与定理的知识,解题的关键是了解对顶角的性质、平行线的性质及不等式的性质,难度不大.7.下列命题是真命题的是()A.相等的两个角是对顶角B.好好学习,天天向上C.周长和面积相等的两个三角形全等D.两点之间线段最短【答案】D【分析】根据命题的定义以及几何知识逐一判断即可.【详解】解:A、相等的两个角不一定是对顶角,原命题是假命题;B、好好学习,天天向上,不是命题;C、周长和面积相等的两个三角形不一定全等,原命题是假命题;D、两点之间线段最短,是真命题;故选:D.【点睛】本题考查命题,掌握命题的定义以及对顶角的性质、全等三角形的判定、两点之间线段最短的基本事实是解题的关键.8.下列各命题中,假命题是()A.有两边及其中一边上的中线对应相等的两个三角形全等B.有两边及第三边上高对应相等的两个三角形全等C.有两角及其中一角的平分线对应相等的两三角形全等D.有两边及第三边上的中线对应相等的两三角形全等【答案】B【分析】根据全等三角形的判定定理进行证明并依次判断.【详解】解:A、有两边及其中一边上的中线对应相等的两个三角形全等,可利用证两步全等的方法求得,是真命题;B、高有可能在内部,也有可能在外部,是不确定的,不符合全等的条件,原命题是假命题;C、有两角及其中一角的平分线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;D、有两边及第三边上的中线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;故选:B.【点睛】此题考查全等三角形的判定定理:SSS、SAS、ASA、AAS、HL,灵活判定命题真假,熟记定理并灵活应用解决问题是解题的关键.9.如图,已知正方形ABCD的边长为8,点E,F分别在边BC、CD上,EF=时,AEF的面积是().∠=︒.当845EAFA.8B.16C.24D.32【答案】D【分析】如图:∵ADF绕点A顺时针旋转90°,得到∵ABH,可得AH=AF,∵BAH=∵DAF,进一步求出∵EAH=∵EAF=45°,再利用"边角边"证明∵AEF和∵AEH全等,再根据全等三角形的面积相等,即可解答.【详解】解:如图,将∵ADF绕点A顺时针旋转90°,得到∵ABH,根据旋转的性质可得:AH=AF,∵BAH=∵DAF,∵∵EAF=45°,∵BAD=90°∵∵EAH=∵EAF=45°在∵AEF和∵AEH中AF=Aн∵EAH=∵EAF=45°,AE=AE∵∵AEF∵∵AEH(SAS),∵EH=EF=8,∵SAFE=S∵AEH=-12×8×8=32.故选:D.【点睛】本题考查了正方形和全等三角形的判定与性质,熟记并灵活应用它们的性质并利用旋转作辅助线、构造出全等三角形是解题的关键.二、填空题10.将命题关于某直线对称的两个三角形全等”,改写成“如果…,那么…”的形式:如果___________________________,那么________________________.【答案】两个三角形关于某直线对称;这两个三角形全等.【分析】任何一个命题都可以写成“如果…那么…”的形式,如果是条件,那么是结论.【详解】解:关于某直线对称的两个三角形全等,改写成“如果…,那么…”的形式:如果两个三角形关于某直线对称,那么这两个三角形全等故答案为:两个三角形关于某直线对称;这两个三角形全等【点睛】本题考查了命题与定理,命题是有题设和结论构成.命题都能写成“如果…,那么…”的形式,“如果”后面是题设,“那么”后面是结论.11.将“对顶角相等”改写为“如果...那么...”的形式,可写为__________.【答案】如果两个角互为对顶角,那么这两个角相等【分析】根据命题的形式解答即可.【详解】将“对顶角相等”改写为“如果...那么...”的形式,可写为如果两个角互为对顶角,那么这两个角相等,故答案为:如果两个角互为对顶角,那么这两个角相等.【点睛】此题考查命题的形式,可写成用关联词“如果...那么...”连接的形式,准确确定命题中的题设和结论是解题的关键.12.在Rt ABC中,若∥C=90°,D是BC边上一点,且AD=2CD,则∥ADB=_____°【答案】120【分析】如图,延长DC到E,使EC=CD,连接AE,先证明AC为线段DE的垂直平分线,进而证明∵ADE是等边三角形,得到∵ADE=60°,问题得解.【详解】解:如图,延长DC到E,使EC=CD,连接AE,∵∵ACD=90°,∵AC∵DE,∵AC为线段DE的垂直平分线,∵AD=AE,又∵AD=2CD,CD=CE,∵AD=DE,∵AD=DE=AE,∵∵ADE是等边三角形,∵∵ADE=60°,∵∵ADB=180°-∵ADC=120°.故答案为:120°【点睛】本题考查了线段垂直平分线,等边三角形的判定与性质,根据题意添加辅助线,构造等边三角形是解题关键.13.在Rt ABC中,∥C=90°,∥A的平分线交BC于点D,且BC=8,BD=5,那么点D到AB 的距离是_____【答案】3【分析】作DE∵AB于E点,根据角平分线的性质,即可证得DE=CD,即可求解.【详解】解:如图,作DE∵AB于E点.∵∵A的平分线交BC于点D, ∵C=90°, DE∵AB,∵DE=CD=3.即点D 到AB 的距离等于3.故答案为:3.【点睛】本题考查了角平分线的性质定理,正确证得DE=CD 以及找到点D 到AB 的距离是关键.14.等腰直角ABC 中,90ACB ∠=︒,AH HG ⊥,BG HG ⊥,12HG =,4AH =,则BG =________.【答案】8【分析】先根据等腰直角三角形的定义可得BC CA =,再根据直角三角形的性质可得CBG ACH ∠=∠,然后根据三角形全等的判定定理与性质可得4,CG AH BG CH ===,最后根据线段的和差即可得.【详解】 ABC 是等腰直角三角形,且90ACB ∠=︒,BC CA ∴=,90BCG ACH ∠+∠=︒,,A BG HG H HG ⊥⊥,90G H ∴∠=∠=︒,90BCG CBG ∠∴∠+=︒,CBG ACH ∴∠=∠,在BCG 和CAH 中,G H CBG ACH BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BCG CAH AAS ∴≅,,CG AH BG CH ∴==,12,4H HG A ==,1248BG CH HG CG HG AH ∴==-=-=-=,故答案为:8.【点睛】本题考查了等腰三角形的定义、直角三角形的性质、三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.15.把命题“直角三角形的两个锐角互为余角”改写成“如果…那么…”的形式是________,这个命题是__________(填“真”或“假”)命题【答案】如果一个三角形是直角三角形,那么它的两个锐角互为余角真【分析】找出命题中的题设与结论即可得,根据直角三角形的性质即可得判断真假.【详解】命题“直角三角形的两个锐角互为余角”中的题设是三角形是直角三角形,结论是它的两个锐角互为余角,则改写成:如果一个三角形是直角三角形,那么它的两个锐角互为余角,由直角三角形的性质得:这个命题是真命题,故答案为:如果一个三角形是直角三角形,那么它的两个锐角互为余角;真.【点睛】本题考查了命题、直角三角形的性质,掌握理解命题的概念是解题关键.16.已知“若a>b,则ac>bc”是假命题,请写出一个满足条件的c 的值是_______________.【答案】0(答案不唯一)【分析】举出一个能使得ac=bc或ac<bc的一个c的值即可.【详解】若a>b,当c=0时ac=bc=0,故答案为:0(答案不唯一).【点睛】本题考查了命题与定理,要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.17.把命题“等角的余角相等”改写成“如果…,那么…”的形式为______.【答案】如果两个角相等,那么这两个角的余角相等【分析】把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.【详解】解:命题“等角的余角相等”写成“如果…,那么….”的形式为:如果两个角是相等角的余角,那么这两个角相等.故答案为:如果两个角是相等角的余角,那么这两个角相等.【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.三、解答题18.已知:如图,AB=DE,BC=DF,AF=CE.求证:BC∥DF.【答案】见解析【分析】由AF=CE,得到AC=EF,然后得到∵ABC∵∵DEF,则∵ACB=∵EFD,然后即可证明结论成立.【详解】证明:∵AF=CE,∵AC=EF,在∵ABC和∵DEF中AC=EF,AB=DE,BC=DF,∵∵ABC∵∵DEF∵∵ACB=∵EFD,∵∵BCF=∵DFC,∵BC∵DF;【点睛】本题考查全等三角形的判定和性质,平行线的判定等知识,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.19.已知:如图,在ABC中,AB=AC,AE是外角 CAD的平分线.求证:AE∥BC.【答案】见解析【分析】首先根据角平分线的性质可得∵DAC=2∵DAE,再由AB=AC可得∵B=∵ACB,然后根据内角与外角的关系可得∵DAC=∵B+∵ACB=2∵B,进而可证明∵DAE=∵B,再根据同位角相等,两直线平行可得AE∵BC.【详解】证明:∵AE是∵CAD的平分线,∵∵DAC=2∵DAE,∵AB=AC,∵∵B=∵ACB,又∵∵DAC=∵B+∵ACB=2∵B,∵∵DAE=∵B,∵AE∵BC.【点睛】此题主要考查了等腰三角形的性质,平行线的判定,关键是掌握同位角相等,两直线平行.20.已知:如图,AC=BD,∠1=∠2.求证:AD∥BC.【答案】见解析【分析】根据等角对等边求出OB=OC,再利用已知条件求得AO=OD,进一步利用等腰三角形性质得:∵OAD=∵ODA,再利用内角和定理可得:∠1=∵ODA,即可得到平行.【详解】证明:因为∠1=∠2.所以OB=OC.因为AC=BD.所以OA=OD.所以∵OAD=∵ODA.因为∠1+∠2+∵BOC=180°.∵OAD+∵ODA+∵AOD=180°.∵BOC=∵AOD.所以∠1+∠2=∵OAD+∵ODA.所以2∠1=2∵ODA.即∠1=∵ODA.所以AD∵BC.【点睛】本题利用等腰三角形的性质与判定得到边与角的关系,本题关键找到角与角的关系.21.已知:如图,在∥ABC中,∥A∥∥ABC∥∥ACB=3∥4∥5,BD,CE分别是边AC,AB上的高,BD,CE相交于H,求∥BHC的度数.【答案】135°【分析】先设∵A=3x,∵ABC=4x,∵ACB=5x,再结合三角形内角和等于180°,可得关于x的一元一次方程,求出x,从而可分别求出∵A,∵ABC,∵ACB,在∵ABD中,利用三角形内角和定理,可求∵ABD,再利用三角形外角性质,可求出∵BHC.【详解】解:∵在∵ABC中,∵A:∵ABC:∵ACB=3:4:5,故设∵A=3x,∵ABC=4x,∵ACB=5x.∵在∵ABC中,∵A+∵ABC+∵ACB=180°,∵3x+4x+5x=180°,解得x=15°,∵∵A=3x=45°.∵BD,CE分别是边AC,AB上的高,∵∵ADB=90°,∵BEC=90°,∵在∵ABD中,∵ABD=180°-∵ADB-∵A=180°-90°-45°=45°,∵∵BHC=∵ABD+∵BEC=45°+90°=135°.【点睛】本题利用了三角形内角和定理、三角形外角的性质.解题关键是熟练掌握:三角形三个内角的和等于180°,三角形的外角等于与它不相邻的两个内角之和.22.已知:如图所示ABC,BE,CD相交于O,AB=AC,AD=AE(1)求证:OD=OE(2)联结DE,求证:DE//BC.【答案】(1)见解析;(2)见解析【分析】≅,再由全等三角形对应边、对应角相等解题即可;(1)根据SAS证明ADC AEB≅,(2)先根据AB=AC,整理出BD、EC的数量关系,再由AAS证明BDO CEO最后根据全等三角形对应边相等的性质解题即可.【详解】(1)证明:在ADC和AEB△中AB=AC;∵A=∵A;AD=AE,所以ADC AEB ≅所以∵ABE=∵ACD ,又因为AD=AE ,所以BD=CE ,在BDO △和CEO 中BD=EC∵ABE=∵ACD∵DOB=∵EOC所以BDO CEO ≅所以OD=OE(2)证明:AD AE AB AC ==,AD AE AB AC∴= A A ∠=∠ADE ABC ∴ADE ABC ∴∠=∠//DE BC ∴【点睛】本题考查全等三角形的判定与性质、相似三角形的判定与性质,是重要考点,难度一般,掌握相关知识是解题关键.23.已知:如图,AB=DE ,∠A=∠D ,AC=DF .求证:AC∥DF .【答案】见解析【分析】由边角边证得∵ABC∵∵DEF ,得到∵ACB=∵DFE ,由同位角相等两直线平行即可得证.【详解】证明:在∵ABC 和∵DEF 中,AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩,所以∵ABC∵∵DEF (SAS ),所以∵ACB=∵DFE ,所以AC∵DF.【点睛】本题主要考查三角形全等的判定和性质,要牢固掌握并灵活运用这些知识.24.如图:已知 ∠BAC=30°,AT 平分∠BAC ,TE∥AC .(1)求证:AET △是等腰三角形;(2)若TD AC ⊥,垂足为点D ,AE=4cm ,求TD 的长.【答案】(1)见解析;(2)2cm【分析】(1)根据角平分线可得∵EAT=∵TAD,利用平行可得∵TAD=∵ETA,再利用等量代换即可得到∵EAT=∵ETA,进而证得AET △是等腰三角形.(2)AT 平分∠BAC,依据角平分线定理可得DT=TF 在RT∵TFE 中,ET=4cm,∵FET=30°,则TF=2cm,则TD=2cm .【详解】解:(1)∵AT 平分∠BAC .∵∵EAT=∵TAD.∵TE∵AC.∵∵TAD=∵ETA.∵∵EAT=∵ETA.∵AET△是等腰三角形.(2)过点T作TF⊥AB,垂足点F,⊥.∵AT平分∠BAC,TF⊥AB,TD AC∵据角平分线定理可得DT=TF.∵在RT∵TFE中,ET=4cm,∵FET=30°,则TF=2cm,∵TD=2cm.【点睛】本题考查了等腰三角形的判定,如何利用角平分线性质作出辅助线是解决此问题的关键.25.如图所示,已知点C、P、D在一直线上,∥BAP与∥APD互补,∥1=∥2,试说明∥E=∥F的理由.【答案】∵E与∵F相等,理由见解析.【分析】根据已知可得出AB∵CD,进而由∵1=∵2可证得∵P AE=∵APF,故能得出AE∵FP,即能推出要证的结论成立.【详解】∵E与∵F相等.理由如下:因为∵BAP和∵APD互补,所以AB∵CD(同旁内角互补,两直线平行),所以∵BAP=∵CPA(两直线平行,内错角相等).因为∵1=∵2,所以∵PAE=∵APF,所以AE∵PF(内错角相等,两直线平行),所以∵E=∵F(两直线平行,内错角相等).【点睛】考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.26.已知:如图,AC∥BC ,垂足为C ,∥BCD 是∥B 的余角求证:∥ACD=∥B证明:∥AC∥BC (已知)∥∥ACB=90°( )∥∥BCD 是∥DCA 的余角∥∥BCD 是∥B 的余角(已知)∥∥ACD=∥B ( )【答案】垂直的意义;同角的余角相等.【分析】先根据垂直的意义可得90ACB ∠=︒,从而可得BCD ∠是DCA ∠的余角,再根据同角的余角相等即可得证.【详解】证明:∵AC BC ⊥(已知),∵90ACB ∠=︒(垂直的意义),∵BCD ∠是DCA ∠的余角,∵BCD ∠是B 的余角(已知),∵ACD B ∠=∠(同角的余角相等),故答案为:垂直的意义;同角的余角相等.【点睛】本题考查了垂直的意义、同角的余角相等,掌握理解同角的余角相等是解题关键. 27.如图, AB=AC , E 是AD 上的一点,∥BAE=∥CAE .求证:∥EBD=∥ECD .【答案】见解析【分析】先证明∵ABD∵∵ACD ,得到∵ADB=∵ADC ,BD=CD ,再证明∵BDE∵∵CDE ,问题得证.【详解】证明:在∵ABD 和∵ACD 中AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∵∵ABD∵∵ACD ,∵∵ADB=∵ADC ,BD=CD ,在∵BDE 和∵CDE 中DE DE EDB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩∵∵BDE∵∵CDE ,∵∵EBD=∵ECD .【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理并根据题意灵活选择方法是解题关键.28.如图,在ABC △中,AB AC =,点E ,F 、G 分别在边AB 、BC 、AC 上,CG BF =,BE CF =,O 是EG 的中点,求证:FO GE ⊥.【答案】证明见解析【分析】连结EF 、FG ,根据等腰三角形得到B C ∠=∠,利用SAS 证明∵BEF 与∵CFG 全等,最后利用等腰三角形”三线合一”的性质证明即可.【详解】证明:连接EF 、FG∵AB AC =∵B C ∠=∠.在BEF 与CFG △中,BE CF B C BF CG =⎧⎪∠=∠⎨⎪=⎩,∵BEF ∵CFG △(SAS ).∵EF FG =.∵O 是EG 的中点,∵FO GE ⊥.【点睛】本题考查的是全等三角形和等腰三角形的判定与性质,熟知全等三角形的判定方法是解答本题的关键.29.如图,在已知ABC △中,AB AC =,点D 在BC 上,过D 点的直线分别交AB 于点E ,交AC 的延长线于点F ,且BE CF =.求证:DE DF =.【答案】证明见解析【分析】过点E 作EG AC ∥交BC 于G ,根据平行的性质可得ACB BGE ∠=∠,F DEG ∠=∠,再根据等边对等角可得B ACB ∠=∠,进而得到B BGE ∠=∠,再根据等角对等边可得BE=GE ,从而得到GE=CF ,利用AAS 证得CDF ∵GDE △,根据全等三角形的性质可得DE=DF.【详解】证明:过点E 作EG AC ∥交BC 于G∵ACB BGE ∠=∠,F DEG ∠=∠∵AB AC =∵B ACB ∠=∠∵B BGE ∠=∠∵BE GE =.又∵BE CF =∵GE CF =.∵在CDF 和GDE △中F DEG CDF GDE GE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∵CDF ∵GDE △(AAS ).∵DE DF =.【点睛】本题考查了等腰三角形、全等三角形的判定与性质,构造出全等三角形是解答本题的关键.30.如图,在ABC △中,BAC ∠的角平分线交BC 于D ,且AB AC CD =+.求证:2C B ∠=∠.【答案】证明见解析【分析】在AB 上截取AE AC =,易证∵ACD∵∵AED ,则CD=DE ,∵C=∵AED ,可得DE=BE ,由等边对等角可得:∵EDB=∵EBD ,由三角形外角定理即可得到结论.【详解】证明:在AB 上截取AE AC =,∵AB AC CD =+.∵BE CD =.在ACD 和AED 中AC AE CAD BAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∵ACD ∵AED .∵CD DE =,C AED ∠=∠.∵DE BE =D .∵EDB EBD ∠=∠.∵2EBD B ∠=∠.∵2C B ∠=∠.【点睛】本题考查了全等三角形的判定与性质、三角形外角定理,构造全等三角形、运用等腰三角形的知识是解答本题的关键.31.如图,在ABC △中,已知CA CB =,AD 平分CAB ∠,且AB AC CD =+,求证:AC BC ⊥.【答案】证明见解析【分析】在AB 上截取AE AC =,连结DE ,可得BE=CD ,由角平分线的定义可得∵CAD=∵EAD ,推出∵ACD∵∵ADE ,易得DE=CD 、∵C=∵AED ,即DE=BE ,由等腰三角形的性质可得∵B=∵BDE ,∵CAB=∵B ,进而得到∵C=∵DEB=∵DEA ,即可得到结论.【详解】证明:在AB 上截取AE AC =,连接DE ,∵AB AC CD =+,∵BE CD =.∵AD 平分CAB ∠,∵CAD EAD ∠=∠.在ACD 与ADE 中,AC AE CAD EAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∵ACD ∵ADE .∵DE CD =,C AED ∠=∠.∵DE BE =.∵B BDE ∠=∠.∵AC BC =,∵CAB B ∠=∠.∵C DEB DEA ∠=∠=∠.∵18090DEA ∠=︒=︒.∵90C ∠=︒.∵AC BC ⊥.【点睛】本题考查全等三角形、等腰三角形的判定和性质,作出辅助线构造全等三角形是解题的关键.32.已知AE AB ⊥,DA AC ⊥,AE AB =,AD AC =.直线MN 过点A ,交DE 、BC 于点M 、N .(1)若AM 是EAD 中线,求证:AN BC ⊥;(2)若AN BC ⊥,求证:EM DM =.【答案】(1)详见解析;(2)详见解析.【分析】(1)延长AM 至F ,使MF AM =,易证EMF △∵DMA △,可得DAM F ∠=∠,EF AD =,再根据AD AC =可得EF AC =,再利用∵BAC 、∵BAE 、∵EAD 和∵DAC 四个角和为360°,可得180BAC DAE ∠=︒-∠,利用∵AEF 的内角和可得180AEF DAE ∠=︒-,可得BAC AEF ∠=∠,即可证明ABC △∵EAF △,最后利用等角的余角相等的等量代换以及∵ABN 的内角和为180°可得出结论.(2)过点E 作EF AD ∥交AM 的延长线于F ,则F DAM ∠=∠,根据DA AC ⊥,可得90DAM CAN ∠+∠=︒;AN BC ⊥,可得90CAN C ∠+∠=︒,等量代换得出F DAM C ∠=∠=∠.根据周角等于360°,可得180BAC DAE ∠=︒-∠;根据三角形内角和可得180∠=︒-∠AEF DAE ,可得BAC AEF ∠=∠,则可证明ABC △∵EAF △(AAS ),得到EF AC =;易证EFM △∵DAM △,即可得到EM DM =. 【详解】解:(1)如图,延长AM 至F ,使MF AM =,∵AM 是EAD 中线,∵EM DM =.在EMF △和DMA △中,EM DM EMF AMD MF AM =⎧⎪∠=∠⎨⎪=⎩,∵EMF △∵DMA △(SAS ).∵DAM F ∠=∠,EF AD =.∵AD AC =,∵EF AC =.∵AE AB ⊥,DA AC ⊥,∵360902180BAC DAE DAE ∠=︒-︒⨯-∠=︒-∠. ∵180180180AEF F EAM DAM EAM DAE ∠=︒-∠-∠=︒-∠-∠=︒-, ∵BAC AEF ∠=∠.在ABC △和EAF △中,EF AC BAC AEF AB AE =⎧⎪∠=∠⎨⎪=⎩,∵ABC △∵EAF △(SAS ).∵EAF B ∠=∠.∵AE AB ⊥,∵90EAF BAN ∠+∠=︒.∵90B BAN ∠+∠=︒.在ABN 中,()1801809090ANB B BAN ∠=︒-∠+∠=︒-︒=︒,∵AN BC ⊥. (2)如图,过点E 作EF AD ∥交AM 的延长线于F ,则F DAM ∠=∠,∵DA AC ⊥,∵90DAM CAN ∠+∠=︒.∵AN BC ⊥,∵90CAN C ∠+∠=︒.∵F DAM C ∠=∠=∠.∵AE AB ⊥,DA AC ⊥,∵360902180BAC DAE DAE ∠=︒-︒⨯-∠=︒-∠. ∵180180180AEF F EAM DAM EAM DAE ∠=︒-∠-∠=︒-∠-∠=︒-∠, ∵BAC AEF ∠=∠.在ABC △和EAF △中,BAC AEF F C AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∵ABC △∵EAF △(AAS ).∵EF AC =.∵AD AC =,∵EF AD =.在EFM △和DAM △中,F DAM EMF DMA EF AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∵EFM △∵DAM △(AAS ).∵EM DM =.【点睛】本题考查三角形全等以及角度之间的等量代换,第(1)题通过“倍长中线”这一辅助线做法,构造全等三角形,从而得出角相等,在遇到有中线的题目,并且题中没有全等三角形,那么我们就可以通过延长中线,或者经过中点的线段,构造全等三角形;第(2)题是通过构造平行线,进而得到角相等,构造全等三角形,然后再根据角之间的等量代换,常见的就是等角的余角相等、等角的补角相等,当直角比较多的地方都可以想到这种方法.33.如图,在ABC △中,已知D 是BC 的中点,ED DF ⊥,求证:BE CF EF +>.【答案】证明见解析【分析】延长FD 到M 使MD=DF ,连接BM ,EM.构造出两三角形全等,可得MD=DF ,三角形EFM 中,ED∵MF ,MD=FD ,那么ED 就是MF 的垂直平分线,可得EM=EF ,最后根据三角形三边的关系即可证明.【详解】证明:延长FD 到M 使MD=DF ,连接BM ,EM.∵D 是BC 的中点,∵BD CD =.在MDB △与FDC △中,BD DC MDB CDF FD DM =⎧⎪∠=∠⎨⎪=⎩,∵MDB △∵FDC △(SAS )∵MD DF =.在FMC 中,CF CM MF +>.又∵ED DF ⊥,ED DM =,∵EF FM =.∵CF CM EF +>,即CF BE EF +>.【点睛】本题考查了全等三角形和三角形三边关系;做辅助线构造全等三角形是解答本题的关键.34.如图所示,在ABC ∆中,AC BC =,90ACB ∠=︒,D 是AC 上一点,AE BD ⊥,垂足为E ,BE 交AC 于D ,又12AE BD =.求证:BD 是ABC ∠的平分线.【答案】见解析【解析】【分析】延长AE 、BC 交于点F ,通过证全等得AF=BD ,结合已知条件得E 是AF 的中点,可得BE 是AF 的垂直平分线,根据等腰三角形三线合一即可得.【详解】证明:如图,延长AE 、BC 交于点FAE BE ⊥90BEF ∴∠=︒,又90ACF ACB ∠=∠=︒90DBC AFC FAC AFC ∴∠+∠=∠+∠=︒DBC FAC ∴∠=∠又AC BC =()ASA ACF BCD ≌∴∆∆AF BD ∴=又2BD AE =2AF AE ∴=AE EF ∴=AB BF ∴=BD ∴是ABC ∠的平分线【点睛】本题主要考查全等三角形的判定与性质的综合及等腰三角形的性质,构造全等,即辅助线的引入是解答此题的关键.35.如图1,已知∥ABC 中,AB =BC =1,∥ABC =90°,把一块含30°角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转.(1)在图1中,DE交边AB于M,DF交边BC于N,证明:DM=DN;(2)在这一旋转过程中,直角三角板DEF与∥ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;(3)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN 是否仍然成立?若成立,请给出证明;若不成立,请说明理由.【答案】(1)详情见解析;(2)四边形DMBN面积不发生变化,面积为14;(3)仍然成立,证明见解析.【分析】(1)连接BD,求出BD=DC,∵MDB=∵CDN,∵C=∵ABD,根据ASA证明∵MBD∵∵NCD,进而求证即可;(2)根据全等得出∵MBD与∵NCD面积相等,求出四边形DMBN的面积等于∵BDC的面积,进而求解即可;(3)连接BD,求出BD=DC,∵MDB=∵CDN,∵C=∵ABD,根据ASA证明∵MBD∵∵NCD,进而求证即可.【详解】(1)如图1,连接BD.∵在Rt∵ABC中,AB=BC,AD=DC,∵BD=DC=AD,∵BDC=90°,∵∵ABD=∵C=45°,∵∵MDB+∵BDN=90°,∵CDN+∵BDN=90°∵∵MDB=∵NDC,在∵MBD与∵NCD中,∵∵MDB=∵NDC,BD=DC,∵MBD=∵C,∵∵MBD∵∵NCD,∵DM=DN.(2)四边形DMBN面积不发生变化.由(1)得∵MBD∵∵NCD ,∵S ∵MBD =S ∵NCD ,∵四边形DMBN 面积=S ∵DMB +S ∵BDN = S ∵CND + S ∵BDN =12S ∵ABC =14. (3)DM=DN 仍然成立.如图2,连接BD ,∵在Rt∵ABC 中,AB=BC ,AD=DC ,∵DB=DC,∵BDC=90°,∵∵DCB=∵DBC=45°,∵∵DBM=∵DCN=135°,∵∵NDC+∵CDM=90°,∵BDM+∵CDM=90°,∵∵CDN=∵BDM ,在∵CDN 与∵BDM 中,∵∵CDN=∵BDM ,DC=DB ,∵DCN=∵DBM ,∵∵CDN∵∵BDM ,∵DM=DN.【点睛】本题主要考查了三角形旋转问题与全等三角形的综合运用,熟练掌握相关概念是解题关键.36.如图,在四边形ABCD 中,AB AD =,BC CD =,90ABC ADC ∠=∠=︒,12MAN BAD ∠=∠.(1)如图(1),将MAN ∠绕着A 点旋转,它的两边分别交边BC 、CD 于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明;(2)如图(2),将MAN ∠绕着A 点旋转,它的两边分别交边BC 、CD 的延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?并证明你的结论;(3)如图(3),将MAN ∠绕着A 点旋转,它的两边分别交边BC 、CD 的反向延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明.【答案】(1)详见解析;(2)MN BM DN =-,证明见解析;(3)MN DN BM =-.【分析】(1)延长MB 到G ,使BG DN =,连接AG ,易证ABG ∵ADN △,可得AG AN =,BG DN =,∠=∠NAD BAG ,再根据12MAN BAD ∠=∠,可得∠=∠MAG MAN ,易证AMG ∵AMN ,等量代换可得MN BM DN =+.(2)在BM 上截取BG ,使BG DN =,连接AG ,易证ADN △∵ABG ,可得AN AG =,NAD GAB ∠=∠,所以12MAN NAD BAM DAB ∠=∠+∠=∠,可得MAN MAG ∠=∠,易证MAN △∵MAG △,等量代换即可得出MN BM DN =-. (3)在DC 上截取DF=BM ,易证∵ABM∵∵ANF ,可得AFAM =,∠=∠DAF MAB ,根据12∠=∠+∠=∠MAN NAB BAM DAB ,等量代换可得12∠+∠=∠NAB DAF DAB ,可得∠=∠FAN MAN ,即可证明∵FAN∵∵MAN , 得到=FN MN ,等量代换可得MN BM DN =-.【详解】(1)如图(1),延长MB 到G ,使BG DN =,连接AG .∵90ABG ABC ADC ∠=∠=∠=︒,AB AD =,在∵ABG 与∵AND 中,BG DN NDA GBA AG AD =⎧⎪∠=∠⎨⎪=⎩∵ABG ∵ADN △(SAS ).。
立体几何证明题专题(教师版)

立体几何证明题考点1:点线面的位置关系及平面的性质例1.下列命题:①空间不同三点确定一个平面;②有三个公共点的两个平面必重合;③空间两两相交的三条直线确定一个平面;④三角形是平面图形;⑤平行四边形、梯形、四边形都是平面图形;⑥垂直于同一直线的两直线平行;⑦一条直线和两平行线中的一条相交,也必和另一条相交;⑧两组对边相等的四边形是平行四边形.其中正确的命题是________.【解析】由公理3知,不共线的三点才能确定一个平面,所以知命题①错,②中有可能出现两平面只有一条公共线(当这三个公共点共线时),②错.③空间两两相交的三条直线有三个交点或一个交点,若为三个交点,则这三线共面,若只有一个交点,则可能确定一个平面或三个平面.⑤中平行四边形及梯形由公理2可得必为平面图形,而四边形有可能是空间四边形,如图(1)所示.在正方体ABCD—A′B′C′D′中,直线BB′⊥AB,BB′⊥CB,但AB与CB不平行,∴⑥错.AB∥CD,BB′∩AB=B,但BB′与CD不相交,∴⑦错.如图(2)所示,AB=CD,BC=AD,四边形ABCD不是平行四边形,故⑧也错.【答案】④2.若P是两条异面直线l、m外的任意一点,则()A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面答案B解析对于选项A,若过点P有直线n与l,m都平行,则l∥m,这与l,m异面矛盾.对于选项B,过点P与l、m都垂直的直线,即过P且与l、m的公垂线段平行的那一条直线.对于选项C,过点P与l、m都相交的直线有一条或零条.对于选项D,过点P与l、m都异面的直线可能有无数条.3.已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定A.与a,b都相交B.只能与a,b中的一条相交C.至少与a,b中的一条相交D.与a,b都平行答案C解析若c与a,b都不相交,则c与a,b都平行,根据公理4,则a∥b,与a,b异面矛盾.考点2:共点、共线、共面问题例1.下列各图是正方体和正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的图形是【解析】①在A中易证PS∥QR,∴P、Q、R、S四点共面.②在C中易证PQ∥SR,∴P、Q、R、S四点共面.③在D中,∵QR⊂平面ABC,PS∩面ABC=P且P∉QR,∴直线PS与QR为异面直线.∴P、Q、R、S四点不共面.④在B中P、Q、R、S四点共面,证明如下:取BC中点N,可证PS、NR交于直线B1C1上一点,∴P、N、R、S四点共面,设为α.可证PS∥QN,∴P、Q、N、S四点共面,设为β.∵α、β都经过P、N、S三点,∴α与β重合,∴P、Q、R、S四点共面.【答案】D2.空间四点中,三点共线是这四点共面的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案A3.下面三条直线一定共面的是()A .a 、b 、c 两两平行B .a 、b 、c 两两相交C .a ∥b ,c 与a 、b 均相交D .a 、b 、c 两两垂直 答案 C4.已知三个平面两两相交且有三条交线,试证三条交线互相平行或者相交于一点. 【解析】 设α∩β=a ,β∩γ=b ,γ∩α=c ,由a ⊂β,b ⊂β,则a ∩b =O ,如图(1), 或a ∥b ,如图(2),若a ∩b =O ,O ∈a ,a ⊂α,则O ∈α,O ∈b ,b ⊂γ,则O ∈γ, 又γ∩α=c ,因此O ∈c ;若a ∥b ,a ⊄γ,b ⊂γ,则a ∥γ,又a ⊂α,α∩γ=c ,则a ∥c . 因此三条交线相交于一点或互相平行.5.如图所示,已知空间四边形ABCD 中,E 、H 分别是边AB ,AD 的中点,F ,G 分别是边BC ,CD 上的点,且CF CB =CG CD =23.(1)求证:三条直线EF ,GH ,AC 交于一点.(2)若在本题中,AE EB =CF FB =2,AH HD =CGGD =3,其他条件不变.求证:EH 、FG 、BD 三线共点.【解析】 (1)∵E ,H 分别是AB ,AD 的中点, ∴由中位线定理可知,EH 綊12BD . 又∵CF CB =CG CD =23,∴在△CBD 中,FG ∥BD ,且FG =23BD . ∴由公理4知,EH ∥FG ,且EH <FG .∴四边形EFGH 是梯形,EH 、FG 为上、下两底. ∴两腰EF 、GH 所在直线必相交于一点P . ∵P ∈直线EF ,EF ⊂平面ABC , ∴P ∈平面ABC .同理可得P ∈平面ADC . ∴P 在平面ABC 和平面ADC 的交线上.又∵面ABC ∩面ADC =AC , ∴P ∈直线AC .故EF 、GH 、AC 三直线交于一点. (2)∵AE EB =CFFB =2, ∴EF ∥AC .又AH HD =CGGD =3,∴HG ∥AC ,∴EF ∥HG ,且EF >HG . ∴四边形EFGH 为梯形. 设EH 与FG 交于点P , 则P ∈平面ABD ,P ∈平面BCD . ∴P 在两平面的交线BD 上. ∴EH 、FG 、BD 三线共点.考点3:异面直线的夹角1.在正方体ABCD -A 1B 1C 1D 1中,E 为AB 的中点.求BD 1与CE 所成角的余弦值.【解析】 连接AD 1,A 1D 交点为M ,连接ME ,MC ,则∠MEC (或其补角)即为异面直线BD 1与CE 所成的角,设AB =1,CE =52,ME =12BD 1=32,CM 2=CD 2+DM 2=32.在△MEC 中,cos ∠MEC=CE 2+ME 2-CM 22CE ·ME=1515,因此异面直线BD 1与CE 所成角的余弦值为1515.2.如图,若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为2,高为4,则异面直线BD 1与AD 所成角的正切值是______.答案 53.已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,E 为AA 1中点,则异面直线BE 与CD 1所成角的余弦值为()答案C解析连接BA1,则CD1∥BA1,于是∠A1BE就是异面直线BE与CD1所成的角(或补角),设AB=1,则BE=2,BA1=5,A1E=1,在△A1BE中,cos∠A1BE=5+2-125·2=31010,选C.4.已知正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值为________.【解析】取A1B1的中点F,连接EF,FA,则有EF∥B1C1∥BC,∠AEF即是直线AE与BC所成的角或其补角.设正方体ABCD—A1B1C1D1的棱长为2a,则有EF=2a,AF=2a2+a2=5a,AE=2a2+2a2+a2=3a.在△AEF中,cos∠AEF=AE2+EF2-AF22AE·EF=9a2+4a2-5a22×3a×2a=23.因此,异面直线AE与BC所成的角的余弦值是23.【答案】2 3考点4:直线与平面平行的判定与性质1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.答案⑤⑥解析a∩α=A时,a不在α内,∴①错;直线l与α相交时,l上有无数个点不在α内,故②错;l ∥α时,α内的直线与l平行或异面,故③错;a∥b,b∥α时,a∥α或a⊂α,故④错;l∥α,则l与α无公共点,∴l与α内任何一条直线都无公共点,⑤正确;如图,长方体中,A1C1与B1D1都与平面ABCD 平行,∴⑥正确.2.给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行. 其中正确命题的个数是________个. 答案 1解析 命题①错,需说明这条直线在平面外. 命题②错,需说明这条直线在平面外. 命题③正确,由线面平行的判定定理可知. 命题④错,需说明另一条直线在平面外. 3.已知不重合的直线a ,b 和平面α, ①若a ∥α,b ⊂α,则a ∥b ; ②若a ∥α,b ∥α,则a ∥b ; ③若a ∥b ,b ⊂α,则a ∥α; ④若a ∥b ,a ⊂α,则b ∥α或b ⊂α, 上面命题中正确的是________(填序号). 答案 ④解析 ①若a ∥α,b ⊂α,则a ,b 平行或异面;②若a ∥α,b ∥α,则a ,b平行、相交、异面都有可能;③若a ∥b ,b ⊂α,a ∥α或a ⊂α.4.正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP =DQ .求证:PQ ∥平面BCE .【证明】 方法一 如图所示. 作PM ∥AB 交BE 于M , 作QN ∥AB 交BC 于N , 连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD . 又AP =DQ ,∴PE =QB .又PM ∥AB ∥QN ,∴PM AB =PE AE =QB BD ,QN DC =BQ BD . ∴PM AB =QN DC .∴PM 綊QN ,即四边形PMNQ 为平行四边形. ∴PQ ∥MN .又MN ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE .方法二 如图,连接AQ ,并延长交BC 延长线于K ,连接EK . ∵AE =BD ,AP =DQ , ∴PE =BQ ,∴AP PE =DQBQ .又AD ∥BK ,∴DQ BQ =AQ QK ,∴AP PE =AQQK ,∴PQ ∥EK . 又PQ ⊄平面BCE ,EK ⊂平面BCE , ∴PQ ∥平面BCE .方法三 如图,在平面ABEF 内,过点P 作PM ∥BE ,交AB 于点M ,连接QM .∴PM ∥平面BCE .又∵平面ABEF ∩平面BCE =BE , ∴PM ∥BE ,∴AP PE =AMMB .又AE =BD ,AP =DQ ,∴PE =BQ . ∴AP PE =DQ BQ ,∴AM MB =DQ QB . ∴MQ ∥AD .又AD ∥BC ,∴MQ ∥BC ,∴MQ ∥平面BCE .又PM ∩MQ =M , ∴平面PMQ ∥平面BCE .又PQ ⊂平面PMQ , ∴PQ ∥平面BCE .5.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).<1>求证:MN ∥平面CDEF ; <2>求多面体A —CDEF 的体积.解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2, DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH =2.∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.6.若P 为异面直线a ,b 外一点,则过P 且与a ,b 均平行的平面A.不存在B.有且只有一个C.可以有两个D.有无数多个答案B7.如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.【证明】方法一如右图,作ME∥BC,交BB1于E;作NF∥AD,交AB于F,连接EF,则EF⊂平面AA1B1B.∵BD=B1C,DN=CM,∴B1M=BN.∵MEBC=B1MB1C,NFAD=BNBD,∴MEBC=BNBD=NFAD,∴ME=NF.又ME∥BC∥AD∥NF,∴MEFN为平行四边形.∴NM∥EF.又∵MN⊄面AA1B1B,∴MN∥平面AA1B1B.方法二如图,连接CN并延长交BA的延长线于点P,连接B1P,则B1P⊂平面AA1B1B.∵△NDC∽△NBP,∴DNNB=CNNP.又CM=DN,B1C=BD,CMMB1=DNNB=CNNP,∴MN∥B1P.∵B1P⊂平面AA1B1B,∴MN∥平面AA1B1B.方法三如右图,作MP∥BB1,交BC于点P,连接NP.∵MP∥BB1,∴CMMB1=CPPB.∵BD=B1C,DN=CM,∴B1M=BN.∵CMMB1=DNNB,∴CPPB=DNNB,∴NP∥DC∥AB.∴平面MNP∥平面AA1B1B.∴MN∥平面AA1B1B.8.如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:PA∥平面EFG;(2)求三棱锥P—EFG的体积.解析(1)证明如图,取AD的中点H,连接GH,FH.∵E,F分别为PC,PD的中点,∴EF∥CD.∵G,H分别是BC,AD的中点,∴GH∥CD.∴EF∥GH,∴E,F,H,G四点共面.∵F,H分别为DP,DA的中点,∴PA∥FH.∵PA⊄平面EFG,FH⊂平面EFG,∴PA∥平面EFG.(2)∵PD⊥平面ABCD,CG⊂平面ABCD,∴PD⊥CG.又∵CG⊥CD,CD∩PD=D,∴GC⊥平面PCD.∵PF =12PD =1,EF =12CD =1,∴S △PEF =12EF ·PF =12. 又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.9.如图所示,a ,b 是异面直线,A 、C 与B 、D 分别是a ,b 上的两点,直线a ∥平面α,直线b ∥平面α,AB ∩α=M ,CD ∩α=N ,求证:若AM =BM ,则CN =DN .【证明】 连接AD 交平面α于E 点,并连接ME ,NE . ∵b ∥α,ME ⊂平面ABD ,平面α∩面ABD =ME , ∴ME ∥BD .又在△ABD 中AM =MB , ∴AE =ED .即E 是AD 的中点.又a ∥α,EN ⊂平面ACD ,平面α∩面ADC =EN , ∴EN ∥AC ,而E 是AD 的中点. ∴N 必是CD 的中点,∴CN =DN .10.如图,在三棱柱ABC -A 1B 1C 1中,E 为AC 上一点,若AB 1∥平面C 1EB ,求:AE ∶EC .【解析】 连接B 1C 交BC 1于点F , 则F 为B 1C 中点. ∵AB 1∥平面C 1EB ,AB 1⊂平面AB 1C ,且平面C 1EB ∩平面AB 1C =EF . ∴AB 1∥EF ,∴E 为AC 中点. ∴AE ∶EC =1∶1. 【答案】 1∶1考点5:面面平行的判定及性质1.设m ,n 是平面α内的两条不同直线;l 1,l 2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )A .m ∥β且l 1∥αB .m ∥l 1且n ∥l 2C .m ∥β且n ∥β 答案 B解析 因m ⊂α,l 1⊂β,若α∥β,则有m ∥β且l 1∥α,故α∥β的一个必要条件是m ∥β且l 1∥α,排除A.因m ,n ⊂α,l 1,l 2⊂β且l 1与l 2相交,若m ∥l 1且n ∥l 2,因l 1与l 2相交,故m 与n 也相交,∴α∥β;若α∥β,则直线m 与直线l 1可能为异面直线,故α∥β的一个充分而不必要条件是m ∥l 1且n ∥l 2,应选B.2.棱长为1的正方体ABCD —A 1B 1C 1D 1中,点P ,Q ,R 分别是面A 1B 1C 1D 1,BCC 1B 1,ABB 1A 1的中心,给出下列结论:①PR 与BQ 是异面直线;②RQ ⊥平面BCC 1B 1;③平面PQR ∥平面D 1AC ;④过P ,Q ,R 的平面截该正方体所得截面是边长为2的等边三角形. 以上结论正确的是________.(写出所有正确结论的序号)答案 ③④解析 由于PR 是△A 1BC 1的中位线,所以PR ∥BQ ,故①不正确;由于RQ ∥A 1C 1,而A 1C 1不垂直于面BCC 1B 1,所以②不正确;由于PR ∥BC 1∥D 1A ,PQ ∥A 1B ∥D 1C ,所以③正确;由于△A 1BC 1是边长为2的正三角形,所以④正确.故填③④.3.已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC的重心.<1>求证:平面G 1G 2G 3∥平面ABC ;<2>求S △G 1G 2G 3∶S △ABC .【解析】 (1)如图,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F .连接DE 、EF 、FD .则有PG 1∶PD =2∶3,PG 2∶PE =2∶3.∴G 1G 2∥DE .又G 1G 2不在平面ABC 内,∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC .又因为G 1G 2∩G 2G 3=G 2,∴平面G 1G 2G 3∥平面ABC .(2)由(1)知PG 1PD =PG 2PE =23,∴G 1G 2=23DE .又DE =12AC ,∴G 1G 2=13AC .同理G 2G 3=13AB ,G 1G 3=13BC .∴△G 1G 2G 3∽△CAB ,其相似比为1∶3.∴S △G 1G 2G 3∶S △ABC =1∶9.4.给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题:①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β;②若α∥β,l ⊂α,m ⊂β,则l ∥m ;③若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n .其中真命题为________.答案 ③解析 ①中当α与β不平行时,也能存在符合题意的l 、m .②中l 与m 也可能异面.③中⎭⎪⎬⎪⎫l ∥γl ⊂ββ∩γ=m ⇒l ∥m , 同理l ∥n ,则m ∥n ,正确.5.如图所示,正方体ABCD —A 1B 1C 1D 1中,M 、N 、E 、F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点.求证:平面AMN ∥平面EFDB .【证明】 连接MF ,∵M 、F 是A 1B 1、C 1D 1的中点,四边形A 1B 1C 1D 1为正方形,∴MF A 1D 1.又A 1D 1 AD ,∴MF AD .∴四边形AMFD 是平行四边形.∴AM ∥DF .∵DF ⊂平面EFDB ,AM ⊄平面EFDB ,∴AM ∥平面EFDB ,同理AN ∥平面EFDB .又AM 、AN ⊂平面ANM ,AM ∩AN =A ,∴平面AMN ∥平面EFDB .6.在正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别是C 1C ,B 1C 1,C 1D 1的中点,求证:平面MNP ∥平面A 1BD . 证明 方法一如图(1)所示,连接B 1D 1.∵P ,N 分别是D 1C 1,B 1C 1的中点,∴PN ∥B 1D 1.又B1D1∥BD,∴PN∥BD.又PN⊄平面A1BD,∴PN∥平面A1BD.同理:MN∥平面A1BD.又PN∩MN=N,∴平面PMN∥平面A1BD.方法二如图(2)所示,连接AC1,AC,∵ABCD-A1B1C1D1为正方体,∴AC⊥BD.又CC1⊥平面ABCD,∴AC为AC1在平面ABCD上的射影,∴AC1⊥BD.同理可证AC1⊥A1B,∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN.∴平面PMN∥平面A1BD.7.如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.【证明】①当AB,CD在同一平面内时,由α∥β,α∩平面ABDC=AC,β∩平面ABDC=BD,∴AC∥BD.∵AE∶EB=CF∶FD,∴EF∥BD.又EF⊄β,BD⊂β,∴EF∥β.②当AB与CD异面时,设平面ACD∩β=DH,且DH=AC,∵α∥β,α∩平面ACDH=AC,∴AC∥DH.∴四边形ACDH是平行四边形.在AH上取一点G,使AG∶GH=CF∶FD,又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH.又EG ∩GF =G ,∴平面EFG ∥平面β.∵EF ⊂平面EFG ,∴EF ∥β.综上,EF ∥β.8.已知:如图,斜三棱柱ABC —A 1B 1C 1中,点D 、D 1分别为AC 、A 1C 1上的点.(1)当A 1D 1D 1C 1的值等于何值时,BC 1∥平面AB 1D 1; (2)若平面BC 1D ∥平面AB 1D 1,求AD DC 的值.【解析】 (1)如图,取D 1为线段A 1C 1的中点,此时A 1D 1D 1C 1=1,连接A 1B 交AB 1于点O ,连接OD 1.由棱柱的性质,知四边形A 1ABB 1为平行四边形,所以点O 为A 1B的中点.在△A 1BC 1中,点O 、D 1分别为A 1B 、A 1C 1的中点,∴OD 1∥BC 1.又∵OD 1⊂平面AB 1D 1,BC 1⊄平面AB 1D 1,∴BC 1∥平面AB 1D 1.∴A 1D 1D 1C 1=1时,BC 1∥平面AB 1D 1. (2)由已知,平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O ,因此BC 1∥D 1O ,同理AD 1∥DC 1.∴A 1D 1D 1C 1=A 1O OB ,A 1D 1D 1C 1=DC AD . 又∵A 1O OB =1,∴DC AD =1,即AD DC =1.考点6:线线、线面垂直1.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列四个命题,其中真命题是A .若a ∥α,b ∥α,则a ∥bB .若a ∥α,b ∥β,a ∥b ,则α∥βC .若a ⊥α,b ⊥β,a ⊥b ,则α⊥βD .若a 、b 在平面α内的射影互相垂直,则a ⊥b答案 C解析 与同一平面平行的两条直线不一定平行,所以A 错误;与两条平行直线分别平行的两个平面未必平行,所以B 错误;如图(1),设OA ∥a ,OB ∥b ,直线OA 、OB 确定的平面分别交α、β于AC 、BC ,则OA ⊥AC ,OB ⊥BC ,所以四边形OACB 为矩形,∠ACB 为二面角α-l -β的平面角,所以α⊥β,C 正确;如图(2),直线a 、b 在平面α内的射影分别为m 、n ,显然m ⊥n ,但a 、b 不垂直,所以D 错误,故选C.2.“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件答案 B3.若m ,n 表示直线,α表示平面,则下列命题中,正确命题的个数为① ⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α ② ⎭⎪⎬⎪⎫n ⊥αm ⊥α⇒m ∥n③ ⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n ④ ⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥αA .1B .2C .3D .4答案 C解析 ①②③正确,④错误.4.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA =AB =BC ,E 是PC 的中点.求证:(1)CD ⊥AE ;(2)PD ⊥平面ABE .【证明】 (1)∵PA ⊥底面ABCD ,∴CD ⊥PA .又CD ⊥AC ,PA ∩AC =A ,故CD ⊥平面PAC ,AE ⊂平面PAC .故CD ⊥AE .(2)∵PA =AB =BC ,∠ABC =60°,故PA =AC .∵E 是PC 的中点,故AE ⊥PC .由(1)知CD ⊥AE ,从而AE ⊥平面PCD ,故AE ⊥PD .易知BA ⊥PD ,故PD ⊥平面ABE .5.设l 是直线,α,β是两个不同的平面( )A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若l⊥α,α⊥β,则l⊥βD.若α⊥β,l∥α,则l⊥β答案B解析A项中由l∥α,l∥β不能确定α与β的位置关系,C项中由α⊥β,l⊥α可推出l∥β或l⊂β,D项由α⊥β,l∥α不能确定l与β的位置关系.6.设b,c表示两条直线,α,β表示两个平面,下列命题中真命题是A.若b⊂α,c∥α,则b∥cB.若b⊂α,b∥c,则c∥αC.若c∥α,c⊥β,则α⊥βD.若c∥α,α⊥β,则c⊥β答案C解析如果一条直线平行于一个平面,它不是与平面内的所有直线平行,只有部分平行,故A错;若一条直线与平面内的直线平行,该直线不一定与该平面平行,该直线可能是该平面内的直线,故B 错;如果一个平面与另一个平面的一条垂线平行,那么这两个平面垂直,这是一个真命题,故C对;对D来讲若c∥α,α⊥β,则c与β的位置关系不定,故选C.7. 在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,∠A1DE=90°,求证:CD⊥平面A1ABB1.证明连接A1E,EC,∵AC=BC=2,∠ACB=90°,∴AB=2 2.设AD=x,则BD=22-x.∴A1D2=4+x2,DE2=1+(22-x)2,A1E2=(22)2+1.∵∠A1DE=90°,∴A1D2+DE2=A1E2.∴x= 2.∴D为AB的中点.∴CD⊥AB.又AA1⊥CD,且AA1∩AB=A,∴CD⊥平面A1ABB1.8.如图,长方体ABCD—A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.<1>证明:BD⊥EC1;<2>如果AB=2,AE=2,OE⊥EC1,求AA1的长.【解析】 (1)如图,连接AC ,A 1C 1,AC 与BD 相交于点O .由底面是正方形知,BD ⊥AC .因为AA 1⊥平面ABCD ,BD ⊂平面ABCD ,所以AA 1⊥BD .又由AA 1∩AC =A ,所以BD ⊥平面AA 1C 1C .再由EC 1⊂平面AA 1C 1C 知,BD ⊥EC 1.(2)设AA 1的长为h ,连接OC 1.在Rt △OAE 中,AE =2,AO =2, 故OE 2=(2)2+(2)2=4.在Rt △EA 1C 1中,A 1E =h -2,A 1C 1=2 2.故EC 21=(h -2)2+(22)2.在Rt △OCC 1中,OC =2,CC 1=h ,OC 21=h 2+(2)2.因为OE ⊥EC 1,所以OE 2+EC 21=OC 21.即4+(h -2)2+(22)2=h 2+(2)2,解得h =3 2.所以AA 1的长为3 2.考点7:面面垂直1.△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD ,M 是EA 的中点,求证: ①DE =DA ;②平面BDM ⊥平面ECA ;③平面DEA ⊥平面ECA .【证明】 ①取EC 的中点F ,连接DF .∵BD ∥CE ,∴DB ⊥BA .又EC ⊥BC ,在Rt △EFD 和Rt △DBA 中,∵EF =12EC =BD ,FD =BC =AB ,∴Rt △EFD ≌Rt △DBA ,∴DE =DA .②取CA 的中点N ,连接MN 、BN ,则MN 綊12EC .∴MN ∥BD ,∴N 点在平面BDM 内.∵EC ⊥平面ABC ,∴EC ⊥BN .又CA ⊥BN ,∴BN ⊥平面ECA .∵BN ⊂平面BDM ,∴平面BDM ⊥平面ECA .③∵DM ∥BN ,BN ⊥平面ECA ,∴DM ⊥平面ECA ,又DM ⊂平面DEA ,∴平面DEA ⊥平面ECA .2.已知平面PAB ⊥平面ABC ,平面PAC ⊥平面⊥平面PBC ,E 为垂足.①求证:PA ⊥平面ABC ;②当E 为△PBC 的垂心时,求证:△ABC 是直角三角形.【证明】 ①在平面ABC 内取一点D ,作DF ⊥AC 于F .平面PAC ⊥平面ABC ,且交线为AC ,∴DF ⊥平面PAC .又PA ⊂平面PAC ,∴DF ⊥PA .作DG ⊥AB 于G ,同理可证:DG ⊥PA .DG 、DF 都在平面ABC 内,∴PA ⊥平面ABC .②连接BE 并延长交PC 于H ,∵E 是△PBC 的垂心,∴PC ⊥BH .又已知AE 是平面PBC 的垂线,PC ⊂平面PBC ,∴PC ⊥AE .又BH ∩AE =E ,∴PC ⊥平面ABE .又AB ⊂平面ABE ,∴PC ⊥AB .∵PA ⊥平面ABC ,∴PA ⊥AB .又PC ∩PA =P ,∴AB ⊥平面PAC .又AC ⊂平面PAC ,∴AB ⊥AC .即△ABC 是直角三角形.3.如图所示,在斜三棱柱A 1B 1C 1-ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC .(1)若D 是BC 的中点,求证:AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1,求证:截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥侧面BB 1C 1C 的充要条件吗请你叙述判断理由.【证明】 (1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC .∵底面ABC ⊥侧面BB 1C 1C ,且交线为BC ,∴由面面垂直的性质定理可知AD ⊥侧面BB 1C 1C .又∵CC 1⊂侧面BB 1C 1C ,∴AD ⊥CC 1.(2)方法一 取BC 1的中点E ,连接DE 、ME .在△BCC 1中,D 、E 分别是BC 、BC 1的中点.∴DE 綊12CC 1.又AA 1綊CC 1,∴DE 綊12AA 1.∵M 是AA 1的中点(由AM =MA 1知),∴DE 綊AM .∴AMED 是平行四边形,∴AD 綊ME .由(1)知AD ⊥面BB 1C 1C ,∴ME ⊥侧面BB 1C 1C .又∵ME ⊂面BMC 1,∴面BMC 1⊥侧面BB 1C 1C .方法二 延长B 1A 1与BM 交于N (在侧面AA 1B 1B 中),连接C 1N .∵AM =MA 1,∴NA 1=A 1B 1.又∵AB =AC ,由棱柱定义知△ABC ≌△A 1B 1C 1.∴AB =A 1B 1,AC =A 1C 1.∴A 1C 1=A 1N =A 1B 1.在△B 1C 1N 中,由平面几何定理知:∠NC 1B 1=90°,即C 1N ⊥B 1C 1.又∵侧面BB 1C 1C ⊥底面A 1B 1C 1,交线为B 1C 1,∴NC 1⊥侧面BB 1C 1C .又∵NC 1⊂面BNC 1,∴截面C 1NB ⊥侧面BB 1C 1C ,即截面MBC 1⊥侧面BB 1C 1C .(3)结论是肯定的,充分性已由(2)证明.下面仅证明必要性(即由截面BMC 1⊥侧面BB 1C 1C 推出AM =MA 1,实质是证明M 是AA 1的中点), 过M 作ME 1⊥BC 1于E 1.∵截面MBC 1⊥侧面BB 1C 1C ,交线为BC 1.∴ME 1⊥面BB 1C 1C .又由(1)知AD ⊥侧面BB 1C 1C ,∵垂直于同一个平面的两条直线平行,∴AD ∥ME 1,∴M 、E 1、D 、A 四点共面.又∵AM ∥侧面BB 1C 1C ,面AME 1D ∩面BB 1C 1C =DE 1,∴由线面平行的性质定理可知AM ∥DE 1.又AD ∥ME 1,∴四边形AME 1D 是平行四边形.∴AD =ME 1,DE 1綊AM .又∵AM ∥CC 1,∴DE 1∥CC 1.又∵D 是BC 的中点,∴E 1是BC 1的中点.∴DE 1=12CC 1=12AA 1.∴AM =12AA 1,∴MA =MA 1.∴AM =MA 1是截面MBC 1⊥侧面BB 1CC 1的充要条件.考点8:平行与垂直的综合问题1.如图所示,在直角梯形ABEF 中,将DCEF 沿CD 折起使∠FDA =60°,得到一个空间几何体.(1)求证:BE ∥平面ADF ;(2)求证:AF ⊥平面ABCD ;(3)求三棱锥E —BCD 的体积.【解析】 (1)由已知条件,可知BC ∥AD ,CE ∥DF ,折叠之后平行关系不变.又因为BC ⊄平面ADF ,AD ⊂平面ADF ,所以BC ∥平面ADF .同理CE ∥平面ADF .又因为BC ∩CE =C ,BC ,CE ⊂平面BCE ,所以平面BCE ∥平面ADF .所以BE ∥平面ADF .(2)由于∠FDA =60°,FD =2,AD =1,所以AF 2=FD 2+AD 2-2×FD ×AD ×cos FDA =4+1-2×2×1×12=3.即AF = 3.所以AF 2+AD 2=FD 2.所以AF ⊥AD .又因为DC ⊥FD ,DC ⊥AD ,AD ∩FD =D ,所以DC ⊥平面ADF .又因为AF ⊂平面ADF ,所以DC ⊥AF .因为AD ∩DC =D ,AD ,DC ⊂平面ABCD ,所以AF ⊥平面ABCD .(3)因为DC ⊥EC ,DC ⊥BC ,EC ,BC ⊂平面EBC ,EC ∩BC =C ,所以DC ⊥平面EBC .又因为DF ∥EC ,AD ∥BC ,∠FDA =60°,所以∠ECB =60°.又因为EC =1,BC =1,所以S △ECB =12×1×1×32=34.所以V E -BCD =V D -EBC =13×DC ×S △ECB =13×1×34=312.2.如图1,在Rt △ABC 中,∠C =90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点.将△ADE 沿DE 折起到△A 1DE 的位置,使A 1F ⊥CD ,如图2.<1>求证:DE ∥平面A 1CB ;<2>求证:A 1F ⊥BE ;<3>线段A 1B 上是否存在点Q ,使A 1C ⊥平面DEQ 说明理由.【解析】 (1)因为D ,E 分别为AC ,AB 的中点,所以DE ∥BC .又因为DE ⊄平面A 1CB ,所以DE ∥平面A 1CB .(2)由已知得AC ⊥BC 且DE ∥BC ,所以DE ⊥AC .所以DE ⊥A 1D ,DE ⊥CD ,所以DE ⊥平面A 1DC .而A 1F ⊂平面A 1DC ,所以DE ⊥A 1F .又因为A 1F ⊥CD ,所以A 1F ⊥平面BCDE .所以A 1F ⊥BE .(3)线段A 1B 上存在点Q ,使A 1C ⊥平面DEQ .理由如下:如图,分别取A 1C ,A 1B 的中点P ,Q ,连接PQ ,QE ,PD ,则PQ ∥BC .因为DE ∥BC ,所以DE ∥PQ .所以平面DEQ 即为平面DEP .由(2)知,DE ⊥平面A 1DC ,所以DE ⊥A 1C .又因为P 是等腰三角形DA 1C 底边A 1C 的中点,所以A 1C ⊥DP .所以A 1C ⊥平面DEP .从而A 1C ⊥平面DEQ .故线段A 1B 上存在点Q ,使得A 1C ⊥平面DEQ .3.如图,四棱锥P -ABCD 中,四边形ABCD 为矩形,△PAD 为等腰三角形,∠APD =90°,平面PAD ⊥平面ABCD ,且AB =1,AD =2,E 、F 分别为PC 、BD 的中点.<1>证明:EF ∥平面PAD ;<2>证明:平面PDC ⊥平面PAD ;<3>求四棱锥P —ABCD 的体积.解析 (1)证明:如图,连接AC .∵四边形ABCD 为矩形且F 是BD 的中点,∴F 也是AC 的中点.又E 是PC 的中点,EF ∥AP ,∵EF ⊄平面PAD ,PA ⊂平面PAD ,∴EF ∥平面PAD .(2)证明:∵面PAD ⊥平面ABCD ,CD ⊥AD ,平面PAD ∩平面ABCD =AD ,∴CD ⊥平面PAD .∵CD ⊂平面PDC ,∴平面PDC ⊥平面PAD .(3)取AD 的中点为O .连接PO .∵平面PAD ⊥平面ABCD ,△PAD 为等腰直角三角形,∴PO ⊥平面ABCD ,即PO 为四棱锥P —ABCD 的高.∵AD =2,∴PO =1.又AB =1,∴四棱锥P —ABCD 的体积V =13PO ·AB ·AD =23.。
[必刷题]2024八年级数学下册几何证明专项专题训练(含答案)
![[必刷题]2024八年级数学下册几何证明专项专题训练(含答案)](https://img.taocdn.com/s3/m/ec3edfe7fc0a79563c1ec5da50e2524de418d008.png)
[必刷题]2024八年级数学下册几何证明专项专题训练(含答案)试题部分一、选择题:1. 在△ABC中,若AB=AC,点D是BC的中点,则下列结论正确的是()A. AD垂直于BCB. BD=DCC. ∠BAC=90°D. ∠ABC=∠ACB2. 下列关于平行线的性质,错误的是()A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线平行,则它们的任意一对对应角相等3. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列关于全等三角形的判定,错误的是()A. SASC. AASD. SSD5. 在△ABC中,若∠A=60°,∠B=70°,则边BC与边AC的长度关系是()A. BC > ACB. BC = ACC. BC < ACD. 无法确定6. 下列关于相似三角形的性质,正确的是()A. 对应角相等B. 对应边成比例C. 对应角互补D. 对应边相等7. 若等腰三角形的底角为45°,则其顶角的度数是()A. 45°B. 90°C. 135°D. 180°8. 在平行四边形ABCD中,若AB=6cm,AD=8cm,则对角线AC的长度可能是()A. 4cmB. 10cmC. 12cm9. 下列关于圆的性质,错误的是()A. 圆的半径都相等B. 圆的直径是半径的两倍C. 圆的周长与半径成正比D. 圆的面积与半径成正比10. 在直角坐标系中,点P(a,b)关于y轴对称的点是()A. (a,b)B. (a,b)C. (a,b)D. (b,a)二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
()2. 平行线的同旁内角互补。
()3. 两个等腰三角形的底角相等,则这两个三角形全等。
()4. 在直角三角形中,斜边上的中线等于斜边的一半。
立体几何证明(教师版)
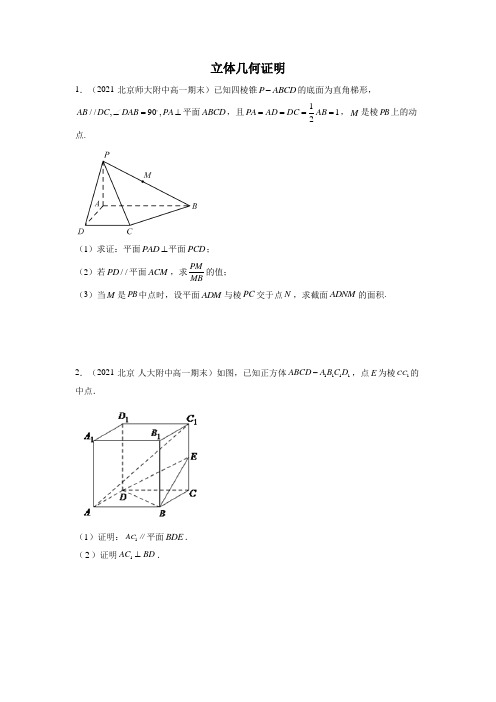
立体几何证明1.(2021·北京师大附中高一期末)已知四棱锥P ABCD -的底面为直角梯形,//,90,AB DC DAB PA ∠=⊥平面ABCD ,且112PA AD DC AB ====,M 是棱PB 上的动点.(1)求证:平面PAD ⊥平面PCD ;(2)若//PD 平面ACM ,求PM MB的值; (3)当M 是PB 中点时,设平面ADM 与棱PC 交于点N ,求截面ADNM 的面积.2.(2021·北京·人大附中高一期末)如图,已知正方体1111ABCD A B C D -,点E 为棱1CC 的中点.(1)证明:1AC ∥平面BDE .(2)证明1AC BD ⊥.3.(2021·北京·汇文中学高一期末)如图1,已知菱形AECD 的对角线AC ,DE 交于点F ,点E 为AB 的中点.将三角形ADE 沿线段DE 折起到PDE 的位置,如图2所示.(1)求证:DE PC ⊥;(2)试问平面PFC 与平面PBC 所成的二面角是否为90︒,如果是,请证明;如果不是,请说明理由;(3)在线段PD ,BC 上是否分别存在点M ,N ,使得平面//CFM 平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.4.(2021·北京·首都师范大学附属中学高一期末)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,O ,M 分别为BD ,PC 的中点.设平面PAD 与平面PBC 的交线为l .(1)求证://OM 平面PAD ;(2)求证://BC l ;(3)在棱PC 上是否存在点N (异于点C ),使得//BN 平面PAD ?若存在,求出PN PC的值;若不存在,说明理由.5.(2021·北京·101中学高一期末)已知正四棱柱1111ABCD A B C D -中,M 是1DD 的中点.(1)求证:1//BD 平面AMC ;(2)求证:1AC BD ⊥;(3)在线段1BB 上是否存在点P ,当1BP BB λ=时,平面11//A PC 面AMC ?若存在,求出λ的值并证明;若不存在,请说明理由.6.(2021·北京师大附中高一期末)在正方体1111ABCD A B C D -中,E 为1CC 中点.(1)求证:1//BC 平面1AD E ;(2)求证:1A D ⊥平面11ABC D .7.(2021·北京·汇文中学高一期末)如图所示,在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .(1)求证://MN 平面ABD ;(2)若MN CD ⊥,BD CD ⊥,求证:平面CBD ⊥平面ABD .8.(2019·北京师大附中高一期末)如图,在三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=,2AB AC ==,1AA ,M N 分别为1,BC CC 的中点,P 为侧棱1BB 上的动点(Ⅰ)求证:平面APM ⊥平面11BB C C ;(Ⅱ)若P 为线段1BB 的中点,求证:1//A N 平面APM ;(Ⅲ)试判断直线1BC 与平面APM 是否能够垂直.若能垂直,求PB 的值;若不能垂直,请说明理由9.(2019·北京师大附中高一期末)如图,已知四棱锥S ABCD-,底面ABCD是边长为2的菱形,60∠=,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,ABCE为线段AD的中点SD平面MAC;(Ⅰ)求证://⊥;(Ⅱ)求证:SE AC-的体积(Ⅲ)求三棱锥M ABC-中,PA⊥平面ABCD,底10.(2019·北京·101中学高一期末)如图,在四棱锥P ABCD部ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.11.(2019·北京·中央民族大学附属中学高一期末)在四面体ABCD 中,CB =CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点,求证:(I )直线EF ACD 面;(II )EFC BCD ⊥面面.12.(2020·北京师大附中高一期末)如图,四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点.(1)求证://CD 平面PAB ;(2)求证://PC 平面BDE ;(3)证明:BD CE ⊥.13.(2021·北京·人大附中高一期末)如图1,已知△ABD 和△BCD 是两个直角三角形,∠BAD =∠BDC =2π.现将△ABD 沿BD 边折起到1A BD 的位置,如图2所示,使平面1A BD ⊥平面BCD .(1)求证:平面1A BC ⊥平面1A CD ;(2)1A C 与BD 是否有可能垂直,做出判断并写明理由.14.(2020·北京·101中学高一期末)如图1,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB AC ==4BC =.将△ADE 沿DE 折起到△1A DE 的位置,使得平面1A DE ⊥平面BCED ,F 为1A C 的中点,如图2.(1)求证://EF 平面1A BD ;(2)求证:平面1A OB ⊥平面1A OC ;(3)线段OC 上是否存在点G ,使得OC ⊥平面EFG ?说明理由.15.(2020·北京师大附中高一期末)如图,在多面体ABCDEF 中,底面ABCD 为矩形,侧面ADEF 为梯形,//AF DE ,DE AD ⊥,DC DE =.⊥;(Ⅰ)求证:AD CEBF平面CDE;(Ⅱ)求证://(Ⅲ)判断线段BE上是否存在点Q,使得平面ADQ⊥平面BCE?并说明理由.-中,平面16.(2020·北京·中国人民大学附属中学朝阳学校高一期末)在三棱锥P ABC⊥.设D,E分别为PA,AC中点.PAC⊥平面ABC,PA AC⊥,AB BCDE平面PBC;(Ⅰ)求证://(Ⅱ)求证:BC⊥平面PAB;(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.答案:1.(1)证明见解析;(2)12;【分析】 (1) 要证平面PAD ⊥平面PCD ,只需证明DC ⊥平面PAD ,利用线面垂直的判定可证DC ⊥平面PAD .(2) 根据题意,作出点M ,再利用相似三角形求PM MB的值 (3) 从四点共面角度出发,利用平面向量基本定理确定点N 的位置,再求截面面积.【详解】(1)证明:因为90DAB ∠=,所以AB AD ⊥,又//AB DC ,所以DC AD ⊥.因为PA ⊥平面ABCD ,DC ⊂平面ABCD ,所以PA DC ⊥.又AD ,PA 在平面PAD 内,且相交于点A ,所以DC ⊥平面PAD . 又DC ⊂平面PCD ,所以平面PAD ⊥平面PCD .(2)如图,连接AC ,BD 相交于点E ,过点E 作//EM PD ,交PB 于点M . 因为//EM PD ,PD ⊄平面ACM ,EM ⊂平面ACM ,所以//PD 平面ACM . 故上述所作点M 为使得//PD 平面ACM 的点M .如图在梯形ABCD 中,有//AB DC ,112AD DC AB === 令()22DE DB DA DC DA DC λλλλ==+=+, 因为A ,E ,C 三点共线,所以21λλ+=,13λ=.即13DE DB =,所以23BE DB =,12DE BE =. 因为//EM PD ,所以BME BPD ,12DE P MB BE M ==. (3)设PN PC μ=, 因为,,,A D N M 四点共面,所以存在实数m ,n ,使得AN mAD nAM =+. 因为()12AN AP PN AP PC AD AB AP μμμμ=+=+=++-,22n n mAD nAM mAD AB AP +=++, 又AD ,AB ,AP 为一组基底, 所以,,2212m n n μμμ⎧⎪=⎪⎪=⎨⎪⎪-=⎪⎩解得23m n ==. 所以2233AN AD AM =+.因为PA ⊥平面ABCD ,AD ⊂平面ABCD ,所以PA AD ⊥. 又AD AB ⊥,PA ,AB 在平面PAB 内,且相交于点A , 所以AD ⊥平面PAB ,又AM ⊂平面PAB ,所以AD AM ⊥. 在四边形AMND 中,AD AM ⊥,1AD =,AM = 因为2233AN AD AM =+,点N 到AM 的距离为2233AD =,点N 到AD的距离为23AM . 所以截面ADNM的面积1121223ADN AMNS S S =+=⨯+2.(1)见解析;(2)见解析【详解】试题分析:(1)连结AC 交BD 于F ,连结EF ,通过正方形对角线的性质以及三角形中位线可得112EF AC ,根据线面平行判定定理可得结果;(2)通过证明BD ⊥平面1ACC 可得结论.试题解析:(1)证明:连结AC 交BD 于F ,连结EF ,正方形ABCD 中,AC 与BD 互相平分,∴F 为AC 中点,在1ACC 中,∵E ,F 分别为1CC 与AC 中点,∴112EF AC ,∵EF ⊂平面BDE ,1AC ⊄平面BDE ,∴EF 平面BDE .(2)证明:在正方形ABCD 中,AC BD ⊥,在正方体1111ABCD A B C D -中, 1CC ⊥平面ABCD ,∵BD ⊂平面ABCD ,∴1CC BD ⊥,∵1AC CC C ⋂=,∴BD ⊥平面1ACC ,∵1AC ⊂平面1ACC ,∴1AC BD ⊥.3.(1)证明见解析;(2)平面PFC 与平面PBC 所成的二面角为90︒,证明见解析;(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明见解析. 【分析】(1)根据线面垂直的判定可证得DE ⊥平面PCF ,由线面垂直性质可证得结论; (2)根据平行关系可证得BC ⊥平面PCF ,由面面垂直的判定可证得两平面垂直,由此得到所成角为90︒;(3)利用平行四边形和三角形中位线性质可证得线线平行关系,由此证得线面平行和面面平行,从而确定存在满足条件的,M N . 【详解】(1)四边形AECD 为菱形,AC DE ∴⊥,即DE PF ⊥,DE CF ⊥, 又,PF CF ⊂平面PCF ,PFCF F =,DE ∴⊥平面PCF ,PC ⊂平面PCF ,DE PC ∴⊥.(2)平面PFC 与平面PBC 所成的二面角为90︒,证明如下:E 为AB 中点且四边形AECD 为菱形,//BE CD ∴,∴四边形BCDE 为平行四边形,//BC DE ∴,由(1)知:DE ⊥平面PCF ,BC ∴⊥平面PCF ,又BC ⊂平面PBC ,∴平面PCF ⊥平面PBC ,即平面PFC 与平面PBC 所成的二面角为90︒.(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明如下:由(2)知:四边形BCDE 为平行四边形,又,F N 分别为,DE BC 中点,//EF CN ∴,∴四边形EFCN 为平行四边形,//CF EN ∴,又EN ⊂平面PEN ,CF ⊄平面PEN ,//CF ∴平面PEN ;,M F 分别为,PD DE 中点,MF ∴为PDE △中位线,//MF PE ∴,又PE ⊂平面PEN ,MF ⊄平面PEN ,//MF ∴平面PEN ,又MFCF F =,,MF CF ⊂平面FCM ,∴平面//CFM 平面PEN .【点睛】本题考查立体几何中线线垂直关系、面面垂直与平行关系的证明问题,涉及到线面垂直的判定与性质、面面垂直的判定、线面平行与面面平行的判定等定理的应用,属于常考题型.4.(1)证明见解析;(2)证明见解析;(3)不存在,理由见解析. 【分析】(1)连接AC , 易知O 为AC 的中点,进而得//AP OM ,再结合线面平行的判定定理即可证明;(2)由题知//BC 平面PAD ,进而根据线面平行的性质定理即可证明//BC l ;(3))假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD ,进而在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E ,故平面//BEN 平面PAD ,进而得//BE AD ,另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾,故不存在. 【详解】解:(1)证明:连接AC ,因为底面ABCD 为平行四边形,O 为BD 的中点, 所以O 为AC 的中点,因为M 为PC 的中点, 所以在APC △中,//AP OM ,因为OM ⊄平面PAD ,AP ⊂平面PAD , 所以//OM 平面PAD(2)因为底面ABCD 为平行四边形, 所以//AD BC ,因为AD ⊂平面PAD ,BC ⊄平面PAD , 所以//BC 平面PAD ,因为平面PAD 与平面PBC 的交线为l ,BC ⊂平面PBC , 所以//BC l(3)假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD , 在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E , 因为EN ⊄平面PAD ,PD ⊂平面PAD ,所以//EN 平面PAD , 因为EN BN N ⋂=,所以平面//BEN 平面PAD , 因为BE ⊂平面BEN ,所以//BE 平面PAD ,又因为BE ⊂平面ABCD ,平面ABCD 平面PAD AD =,所以//BE AD 另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾, 所以在棱PC 上不存在点N (异于点C ),使得//BN 平面PAD .5.(1)证明见解析;(2) 证明见解析;(3)在线段1BB 上存在点P ,当12λ=时,平面11//A PC 平面AMC . 【分析】(1) 利用线面平行的判定定理证明1//BD 平面AMC ;(2) 利用线面垂直的判定定理证明AC ⊥平面11BB D D ,则有1AC BD ⊥; (3) 先确定λ的值,再根据面面平行的判定定理证明两平面平行. 【详解】因为四棱柱1111ABCD A B C D -是正四棱柱,所以底面ABCD 为正方形,侧棱垂直底面,侧面均为矩形.(1)证明:记AC 和BD 相交于点N ,因为ABCD 为正方形,所以N 为BD 的中点.又M 是1DD 的中点, 所以1//MN BD .又1BD ⊄平面AMC ,MN ⊂平面AMC , 所以1//BD 平面AMC .(2)证明:因为ABCD 为正方形,所以AC BD ⊥.因为1D D ⊥平面ABCD ,AC ⊂平面ABCD ,所以1D D AC ⊥. 又BD ,1D D 在平面11BB D D 内,且相交于点D , 所以AC ⊥平面11BB D D .又1BD ⊂平面11BB D D , 所以1AC BD ⊥.(3) 在线段1BB 上存在点P ,当12λ=,即112BP BB =时,平面11//A PC 面AMC . 理由如下:当112BP BB =时,P 为1BB 的中点. 取1CC 的中点G ,连接1PC ,GB ,则有1//PC GB .连接MG ,因为四边形11CC D D 是矩形,M 是1DD 的中点,G 是1CC 的中点, 所以//MG CD ,MG CD =.在正方形ABCD 中,有,//CD AB ,CD AB =.所以//MG AB ,MG AB =,四边形ABGM 为平行四边形. 有//BG AM ,又1//PC GB ,所以1//PC AM ,又1PC ⊄平面AMC ,AM ⊂平面AMC ,所以1PC //平面AMC . 同理可证:1//PA 平面AMC .又1PC ,1PA 在平面11A PC 内,且相交于点P , 所以平面11//A PC 平面AMC . 6.(1)证明见解析;(2) 证明见解析. 【分析】(1)先证明四边形11ABC D 为平行四边形,得到11//BC AD ,再利用线面平行的判定定理证明1//BC 平面1AD E ;(2)先证明11A D AD ⊥,再由线面垂直的性质得到1AB A D ⊥,最后由线面垂直的判定定理证明1A D ⊥平面11ABC D.(1)证明:在正方体1111ABCD A B C D -中, 有//AB CD ,11//CD C D ,所以11//AB C D .又11AB C D =,所以四边形11ABC D 为平行四边形,有11//BC AD . 又1BC ⊄平面1AD E ,1AD ⊂平面1AD E , 所以1//BC 平面1AD E(2)证明:因为1A D ,1AD 为正方形的对角线,所以11A D AD ⊥. 因为AB ⊥平面11AA D D ,1A D ⊂平面11AA D D ,所以1AB A D ⊥. 又1AD ,AB 在平面11ABC D 内,且相交于点A , 所以1A D ⊥平面11ABC D .7.(1)证明见解析;(2)证明见解析. 【分析】(1)由//MN AB ,利用直线与平面平行的判断定理,证明//MN 平面ABD .(2)推导出BA DC ⊥,DC BD ⊥,从而CD ⊥平面ABD ,由此能证明平面ABD ⊥平面BCD . 【详解】(1)∵在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .MN ⊄平面ABD ,AB 平面ABD ,∴//MN 平面ABD(2)∵MN CD ⊥,//MN AB ,∴AB CD ⊥, ∵BD CD ⊥,ABBD B =∴CD ⊥平面ABD , ∵CD ⊂平面BCD ∴平面ABD ⊥平面BCD . 【点睛】本题考查的是空间中平行与垂直的证明,较简单.8.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)直线BC 1与平面APM 不能垂直,详见解析 【分析】(Ⅰ)由等腰三角形三线合一得AM BC ⊥;由线面垂直性质可得1AM BB ⊥;根据线面垂直的判定定理知AM ⊥平面11BB C C ;由面面垂直判定定理证得结论;(Ⅱ)取11C B 中点D ,可证得1//A D AM ,//DN MP ;利用线面平行判定定理和面面平行判定定理可证得平面1//A DN 平面APM ;根据面面平行性质可证得结论;(Ⅲ)假设1BC ⊥平面APM ,由线面垂直性质可知1BC PM ⊥,利用相似三角形得到111C B PB MB BB =,从而解得BP 长度,可知满足垂直关系时,P 不在棱1BB 上,则假设错误,可得到结论.(Ⅰ)AB AC =,M 为BC 中点 AM BC ∴⊥1AA ⊥平面ABC ,11//AA BB 1BB ∴⊥平面ABC又AM ⊂平面ABC 1AM BB ∴⊥ 1,BB BC ⊂平面11BB C C ,1BB BC B = AM ∴⊥平面11BB C C又AM ⊂平面APM ∴平面APM ⊥平面11BB C C (Ⅱ)取11C B 中点D ,连接11,,,A D DN DM B C,D M 分别为11,C B CB 的中点 1//DM AA ∴且1DM AA = ∴四边形1A AMD 为平行四边形 1//A D AM ∴又1A D ⊄平面APM ,AM ⊂平面APM 1//A D ∴平面APM,D N 分别为111,C B CC 的中点 1//DN B C ∴又,P M 分别为1,BB CB 的中点 1//MP B C ∴ //DN MP ∴ 又DN ⊄平面APM ,MP ⊂平面APM //DN ∴平面APM 1,A D DN ⊂平面1A DN ,1A DDN D = ∴平面1//A DN 平面APM又1A N ⊂平面1A DN 1//A N ∴平面APM(Ⅲ)假设1BC ⊥平面APM ,由PM ⊂平面APM 得:1BC PM ⊥设PB x =,x ⎡∈⎣当1BC PM ⊥时,11BPM B C B ∠=∠ Rt PBM ∴∆∽11Rt B C B ∆ 111C B PB MB BB =∴由已知得:MB11C B =1BB=,解得:x ⎡=⎣ ∴假设错误 ∴直线1BC 与平面APM 不能垂直【点睛】本题考查立体几何中面面垂直、线面平行关系的证明、存在性问题的求解;涉及到线面垂直的判定与性质、线面平行的判定、面面平行的判定与性质定理的应用;处理存在性问题时,常采用假设法,通过假设成立构造方程,判断是否满足已知要求,从而得到结论. 9.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)12【分析】(Ⅰ)连接BD ,交AC 于点O ;根据三角形中位线可证得//MO SD ;由线面平行判定定理可证得结论;(Ⅱ)由等腰三角形三线合一可知SE AD ⊥;由面面垂直的性质可知SE ⊥平面ABCD ;根据线面垂直性质可证得结论;(Ⅲ)利用体积桥的方式将所求三棱锥体积转化为14S ABCD V -;根据已知长度和角度关系分别求得四边形面积和高,代入得到结果. 【详解】(Ⅰ)证明:连接BD ,交AC 于点O四边形ABCD 为菱形 O ∴为BD 中点 又M 为SB 中点 //MO SD ∴MO ⊂平面MAC ,SD ⊄平面MAC //SD ∴平面MAC (Ⅱ)SAD ∆为正三角形,E 为AD 中点 SE AD ∴⊥平面SAD ⊥平面ABCD ,平面SAD ⋂平面ABCD AD =,SE ⊂平面SADSE ∴⊥平面ABCD ,又AC ⊂平面ABCD SE AC ∴⊥ (Ⅲ)M 为SB 中点 11112443M ABC M ABCD S ABCD ABCDV V V SSE ---∴===⨯⋅又2AB BC AD CD SA SD ======,60ABC ∠= 2AC ∴=,12222sin 60232ABCDABC SS ∆==⨯⨯⨯=由(Ⅱ)知,SE AD ⊥ SE ∴=11122M ABC V -=⨯∴ 【点睛】本题考查立体几何中线面平行、线线垂直关系的证明、三棱锥体积的求解问题;涉及到线面平行判定定理、面面垂直性质定理和判定定理的应用、体积桥的方式求解三棱锥体积等知识,属于常考题型. 10.(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)见解析. 【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论;(Ⅱ)由几何体的空间结构特征首先证得线面垂直,然后利用面面垂直的判断定理可得面面垂直;(Ⅲ)由题意,利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点. 【详解】(Ⅰ)证明:因为PA ⊥平面ABCD ,所以PA BD ⊥; 因为底面ABCD 是菱形,所以AC BD ⊥; 因为PAAC A =,,PA AC ⊂平面PAC ,所以BD ⊥平面PAC .(Ⅱ)证明:因为底面ABCD 是菱形且60ABC ∠=︒,所以ACD ∆为正三角形,所以AE CD ⊥, 因为//AB CD ,所以AE AB ⊥;因为PA ⊥平面ABCD ,AE ⊂平面ABCD , 所以AE PA ⊥; 因为PA AB A = 所以AE ⊥平面PAB ,AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .(Ⅲ)存在点F 为PB 中点时,满足//CF 平面PAE ;理由如下:分别取,PB PA 的中点,F G ,连接,,CF FG EG , 在三角形PAB 中,//FG AB 且12FG AB =;在菱形ABCD 中,E 为CD 中点,所以//CE AB 且12CE AB =,所以//CE FG 且CE FG =,即四边形CEGF 为平行四边形,所以//CF EG ; 又CF⊄平面PAE ,EG ⊂平面PAE ,所以//CF 平面PAE .【点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力. 11.(I )证明见解析. (II )证明见解析. 【详解】证明:(I )E ,F 分别为AB ,BD 的中点EF AD ⇒}EF ADAD ACD EF ACD EF ACD⇒⊂⇒⊄面面面. (II )}}}EF ADEF BDAD BD CD CB CF BD BD EFCF BD EF CF F⇒⊥⊥=⇒⊥⇒⊥⋂=面为的中点,又BD BCD ⊂面,所以EFC BCD ⊥面面.12.(1)证明见解析;(2)证明见解析;(3)证明见解析. 【分析】(1)根据底面是正方形,得到CDAB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥. 【详解】(1)∵四棱锥P ABCD -的底面是正方形, ∴CDAB ,∵CD CD ⊄平面PAB ,AB 平面PAB ,∴CD ∥平面PAB . (2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.13.(1)证明见解析;(2)1A C 与BD 不可能垂直,证明见解析.【分析】(1)证得1A B ⊥平面1A CD ,结合面面垂直的判定定理即可得出结论;(2)假设1A C 与BD 垂直,然后推出与已知条件11A B A D ⊥矛盾,即可得出1A C 与BD 不可能垂直.【详解】(1)因为平面1A BD ⊥平面BCD ,平面1A BD 平面BCD =BD ,CD ⊂平面BCD ,CD ⊥BD ,所以CD ⊥平面1A BD ,又因为1A B ⊂平面1A BD ,所以CD ⊥1A B ,又因为11A B A D ⊥,1A D CD D =,所以1A B ⊥平面1A CD ,且1A B ⊂平面1A BC ,所以平面1A BC ⊥平面1A CD ;(2)假设1A C 与BD 垂直,又因为CD ⊥BD ,且1AC CD C ⋂=,所以DB ⊥平面1A CD ,又因为1A D ⊂平面1A CD ,所以1DB A D ⊥,这与11A B A D ⊥矛盾,故假设不成立,即1A C 与BD 不可能垂直.23.(1)见解析;(2)见解析;(3)见解析【解析】试题分析:(1)取线段1A B 的中点H ,由三角形中位线性质以及平行四边形性质得四边形DEFH 为平行四边形,即得//EF HD .再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得1A O DE ⊥.再根据面面垂直性质定理得1A O ⊥平面BCED ,即得1CO A O ⊥,根据勾股定理得CO BO ⊥,所以由线面垂直判定定理得 CO ⊥平面1A OB ,最后根据面面垂直判定定理得结论,(3)假设线段OC 上存在点G ,使得OC ⊥平面EFG ,则EO EC =,与条件矛盾.试题解析:解:(1)取线段1A B 的中点H ,连接HD ,HF .因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 //DE BC ,12DE BC =. 因为 H ,F 分别为1A B ,1A C 的中点,所以 //HF BC ,12HF BC =, 所以 //HF DE ,HF DE =,所以 四边形DEFH 为平行四边形,所以 //EF HD . 因为 EF ⊄平面1A BD , HD ⊂平面1A BD ,所以 //EF 平面1A BD .(2)因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 AD AE =.所以11A D A E =,又O 为DE 的中点,所以 1A O DE ⊥.因为平面1A DE ⊥平面BCED ,且1AO ⊂平面1A DE , 所以 1A O ⊥平面BCED ,所以 1CO A O ⊥.在△OBC 中,4BC =,易知 OB OC ==所以 CO BO ⊥,所以 CO ⊥平面1A OB ,所以 平面1A OB ⊥平面1A OC .(3)线段OC 上不存在点G ,使得OC ⊥平面EFG .否则,假设线段OC 上存在点G ,使得OC ⊥平面EFG ,连接 GE ,GF ,则必有 OC GF ⊥,且OC GE ⊥.在Rt △1A OC 中,由F 为1A C 的中点,OC GF ⊥,得G 为OC 的中点.在△EOC 中,因为OC GE ⊥,所以EO EC =,这显然与1EO =,EC =所以线段OC 上不存在点G ,使得OC ⊥平面EFG .14.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析【分析】(I )由AD ⊥DE ,AD ⊥CD 可得AD ⊥平面CDE ,故而AD ⊥CE ;(II )证明平面ABF ∥平面CDE ,故而BF ∥平面CDE ;(III )取CE 的中点P ,BE 的中点Q ,证明CE ⊥平面ADPQ 即可得出平面ADQ ⊥平面BCE .【详解】(Ⅰ)由底面ABCD 为矩形,知AD CD ⊥.又因为DE AD ⊥,DE CD D ⋂=,所以AD ⊥平面CDE .又因为CE ⊂平面CDE ,所以AD CE ⊥.(Ⅱ)由底面ABCD 为矩形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE ,所以//AB 平面CDE .同理//AF 平面CDE ,又因为AB AF A ⋂=,所以平面//ABF 平面CDE .又因为BF ⊂平面ABF ,所以//BF 平面CDE .(Ⅲ)结论:线段BE 上存在点Q (即BE 的中点),使得平面ADQ ⊥平面BCE . 证明如下:取CE 的中点P ,BE 的中点Q ,连接,,AQ DP PQ ,则//PQ BC .由//AD BC ,得//PQ AD .所以,,,A D P Q 四点共面.由(Ⅰ),知AD ⊥平面CDE ,所以AD DP ⊥,故BC DP ⊥.在△CDE 中,由DC DE =,可得DP CE ⊥.又因为BC CE C ⋂=,所以DP ⊥平面BCE .又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE (即平面ADQ ⊥平面BCE ).即线段BE 上存在点Q (即BE 中点),使得平面ADQ ⊥平面BCE【点睛】本题考查了线面垂直、面面垂直的判定与性质定理的应用,线面平行的判定,熟练运用定理是解题的关键,属于中档题.15.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.【分析】(Ⅰ)证明以DE ∥平面PBC ,只需证明DE ∥PC ;(Ⅱ)证明BC ⊥平面PAB ,根据线面垂直的判定定理,只需证明PA ⊥BC ,AB ⊥BC ;(Ⅲ)当点F 是线段AB 中点时,证明平面DEF ∥平面PBC ,可得平面DEF 内的任一条直线都与平面PBC 平行.【详解】(Ⅰ)证明:因为点E 是AC 中点,点D 为PA 的中点,所以//DE PC .又因为DE ⊄面PBC ,PC ⊂面PBC ,所以DE ∥平面PBC .(Ⅱ)证明:因为平面PAC ⊥面ABC ,平面PAC ∩平面ABC =AC ,又PA ⊂平面PAC ,PA ⊥AC , 所以PA ⊥面ABC ,因为BC ⊂平面ABC ,所以PA ⊥BC .又因为AB ⊥BC ,且PA ∩AB =A ,所以BC ⊥面PAB .(Ⅲ)当点F 是线段AB 中点时,过点D ,E ,F 的平面内的任一条直线都与平面PBC 平行. 取AB 中点F ,连EF ,连DF .由(Ⅰ)可知DE ∥平面PBC .因为点E 是AC 中点,点F 为AB 的中点,所以EF ∥BC .又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以EF ∥平面PBC .又因为DE ∩EF =E ,所以平面DEF ∥平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.故当点F 是线段AB 中点时,过点D ,E ,F 所在平面内的任一条直线都与平面PBC 平行.【点睛】本题考查线面平行,考查线面垂直,考查面面平行,考查学生分析解决问题的能力,掌握线面平行、线面垂直、面面垂直的判定定理是关键.16.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)根据底面是正方形,得到CD AB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥.【详解】(1)∵四棱锥P ABCD -的底面是正方形,∴CD AB ,∵CD ⊄平面PAB ,AB平面PAB , ∴CD ∥平面PAB .(2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.。
(完整版)初二数学----几何证明初步经典练习题(含答案)

(完整版)初二数学----几何证明初步经典练习题(含答案)几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是()A、一组锐角对应相等B、两组锐角分别对应相等C、一组直角边对应相等D、两组直角边分别对应相等2、如图,已知AB∥CD,∠A=50°,∠C=∠E.则∠C =()A.20°B.25°C.30°D.40°第2题图第4题图第6题图第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中()A.有两个角是直角B.有两个角是钝角C.有两个角是锐角D.一个角是钝角,一个角是直角4、如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )A.∠2=45°B.∠1=∠3 C.∠AOD+∠1=180°D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18< p="">A.1个B.2个C.3个D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED ⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC 的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE 的交点,则线段BH的长度为()A. B. C.5 D.49、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC 上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对B.仅小亮对C.两人都对D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,?则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC 于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
八年级数学下册《三角形的证明》练习题与答案(北师大版)

八年级数学下册《三角形的证明》练习题与答案(北师大版)一、选择题1.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )A.PQ>5B.PQ≥5C.PQ<5D.PQ≤52.如图,已知在△ABC中,边AB的垂直平分线分别交BC、AB于点G、D,若△AGC的周长为31cm,AB=20cm,则△ABC的周长为( )A.31cmB.41cmC.51cmD.61cm3.如图,在△ABC中,D为BC的中点,AD⊥BC,E为AD上一点,∠ABC=60°,∠ECD=40°,则∠ABE=( )A.10°B.15°C.20°D.25°4.若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为( )A.2 cmB.4 cmC.6 cmD.8 cm5.如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是( )A.20°B.35°C.40°D.70°6.等腰三角形底边上一点到两腰的距离之和等于( )A.腰上的高B.腰上的中线C.底角的平分线D.顶角的平分线7.如图,OP平分∠AOB,PC⊥OA于C,点D是OB上的动点,若PC=6cm,则PD的长可以是( )A.3cmB.4cmC.5cmD.7 cm8.如图,在平面直角坐标系中,以点O 为圆心,适当长为半径画弧,交x 轴于点M ,交y 轴于点N ,再分别以M 、N 为圆心,大于12MN 的长为半径画弧,两弧在第二象限交于点P ,若点P 的坐标为(6a ,2b -1),则a 和b 的数量关系为( )A.6a -2b =1B.6a +2b =1C.6a -b =1D.6a +b =19.如图,在△ABC 中,按以下步骤作图:①分别以点B 和C 为圆心,适当长度(大于BC 长的一半)为半径作圆弧,两弧相交于点M 和N ;②作直线MN 交AB 于点D ,连接CD.若AB =9,AC =4,则△ACD 的周长是( )A.12B.13C.17D.1810.如图,已知在直角坐标系中,点A 在y 轴上,BC ⊥x 轴于点C ,点A 关于直线OB 的对称点D 恰好在BC 上,点E 与点O 关于直线BC 对称,∠OBC =35°,则∠OED 的度数为( )A.10°B.20°C.30°D.35°11.如图所示,在△ABC 中,内角∠BAC 与外角∠CBE 的平分线相交于点P ,BE =BC ,PB 与CE 交于点H ,PG ∥AD 交BC 于F ,交AB 于G ,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )A.1个B.2个C.3个D.4个12.如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )A. 6B. 3C. 2D. 1.5二、填空题13.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是.14.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE周长为14,BC=6,则AB长为 .15.等腰三角形的一个内角为100°,则顶角的度数是________.16.△ABC中其周长为7,AB=3,当BC=时,△ABC为等腰三角形.17.如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF 的周长是 cm.18.如图,∠BOC=9°,点A在OB上,且OA=1.按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=.三、作图题19.如图:求作一点P,使PM=PN,并且使点P到∠AOB的两边的距离相等.四、解答题20.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.21.如图,在△ABC中,AC=DC=DB,∠ACD=100°,求∠B的度数.22.如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A 处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E.请你判断一下,甲、乙两人谁先到达各自的目的地?并说明理由.23.如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连接AF.求证:∠B=∠CAF.24.已知射线AP是△ABC的外角平分线,连结PB、PC.(1)如图1,若BP平分∠ABC,且∠ACB=30°,直接写出∠APB= .(2)如图1,若P与A不重合,求证:AB+AC<PB+PC.25.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.参考答案1.B2.C.3.C.4.A.5.B.6.A7.D.8.B9.B.10.B.11.D.12.D.13.答案为:4.14.答案为:8.15.答案为:100°.16.答案为:1或2.17.答案为:10.18.答案为:9.19.解:如图,点P即为所求.(1)作∠AOB 的平分线OC;(2)连结MN,并作MN 的垂直平分线EF,交OC于P,连结PM、PN,则P点即为所求.20.证明:∵AB=AC=AD∴∠C=∠ABC,∠D=∠ABD∴∠ABC=∠CBD+∠D∵AD∥BC∴∠CBD=∠D∴∠ABC=∠D+∠D=2∠D又∵∠C=∠ABC∴∠C=2∠D.21.解:∵AC=DC=DB,∠ACD=100°∴∠CAD=(180°﹣100°)÷2=40°∵∠CDB是△ACD的外角∴∠CDB=∠A+∠ACD=100°=40°+100°=140°∵DC=DB∴∠B=(180°﹣140°)÷2=20°.22.解:同时到达.理由如下:过点E作EF⊥AC于点F.∵AB =BC ,∠B =90°∴∠C =180°-∠B 2=45°. ∵EF ⊥AC∴∠EFC =90°∴∠CEF =90°-∠C =45°=∠C∴EF =CF.又∵AE 平分∠CAB∴EF =EB.易证得△AEF ≌△AEB得AF =AB可知AB +BE =AF +CF =AC故同时到达.23.证明:∵EF 垂直平分AD∴AF =DF ,∠ADF =∠DAF∵∠ADF =∠B +∠BAD ,∠DAF =∠CAF +∠CAD又∵AD 平分∠BAC∴∠BAD =∠CAD∴∠B =∠CAF.24.解:(1)∵∠DAC =∠ABC +∠ACB ,∠1=∠2+∠APB∵AE 平分∠DAC ,PB 平分∠ABC∴∠1=12∠DAC ,∠2=12∠ABC∴∠APB =∠1﹣∠2=12∠DAC ﹣12ABC =12∠ACB =15°(2)在射线AD 上取一点H ,是的AH =AC ,连接PH.则△APH ≌△APC∴PC =PD在△BPH 中,PB +PH >BH∴PB +PC >AB +AC.25.解:(1)∠EDC =180°﹣∠ADB ﹣∠ADE =180°﹣115°﹣40°=25°∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,∠BDA逐渐变小;故答案为:25°,115°,小;(2)当DC=2时,△ABD≌△DCE理由:∵∠C=40°∴∠DEC+∠EDC=140°又∵∠ADE=40°∴∠ADB+∠EDC=140°∴∠ADB=∠DEC又∵AB=DC=2∴△ABD≌△DCE(AAS)(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形理由:∵∠BDA=110°时∴∠ADC=70°∵∠C=40°∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°∴∠DAC=∠AED∴△ADE的形状是等腰三角形;∵当∠BDA的度数为80°时∴∠ADC=100°∵∠C=40°∴∠DAC=40°∴∠DAC=∠ADE∴△ADE的形状是等腰三角形.。
期中真题几何证明40题专练—2023-2024学年八年级数学上册(沪教版)(解析版)

期中真题几何证明40题专练一.解答题(共40小题)1.(2022秋•宝山区校级期中)五边形ABCDE中,AB=AE,AD平分∠CDE,∠B+∠E=180°,求证:BC+DE=CD.【分析】在DC上截取DF=DE,连接AF,先证△ADF≌△ADE,再证△ACF≌△ACB,即可得证结果.【解答】证明:如图,在DC上截取DF=DE,连接AF,∵AD平分∠CDE,∴∠ADF=∠ADE,在△ADF和△ADE中,,∴△ADF≌△ADE(SAS),∴AF=AE,∠FAD=∠EAD,∵AB=AE,∠BAE=∠CAD,∴AB=AF,∠BAC=∠FAC,在△ACF和△ACB中,,∴△ACF≌△ACB(SAS)∴BC=CF,∵CD=CF+DF,∴CD=BC+DE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解题的关键是准确作出辅助线构造全等三角形.2.(2022秋•虹口区校级期中)如图,△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,且ED ⊥AB于点F,且AB=DE.(1)求证:BD=2EC;(2)若BD=10cm,求AC的长.【分析】(1)根据AAS证明△ABC≌△EDB得BD=BC,再根据E是BC的中点,即可得出结论;(2)根据(1)的结论,结合BD=10,即可求出AC的长.【解答】(1)证明:∵ED⊥AB,∠ACB=∠DBC=90°,∴∠BFE=∠DBC=90°,∴∠BEF+∠ABC=∠BDE+∠BEF=90°,∴∠ABC=∠BDE,在△ABC和△EDB中,,∴△ABC≌△EDB(AAS),∴BD=BC,∵E是BC的中点,∴BC=2CE,∴BD=2EC;(2)解:由(1)知,△ABC≌△EDB,∴BE=AC,∵BD=2CE,即BD=2BE,∵BD=10,∴AC=BE=5cm.【点评】本题考查了全等三角形的判定与性质,证明△ABC≌△EDB是解题的关键.3.(2022秋•静安区校级期中)如图,AD是△ABC的高,∠B=2∠C,BD=5,BC=25,求AB的长.【分析】在线段DC上截取DE=BD,连接AE,根据线段垂直平分线的性质得到AB=AE,求得∠B=∠AEB,根据三角形外角的性质得到∠AEB=∠CAE+∠C,求得AE=CE,于是得到结论.【解答】解:如图:在线段DC上截取DE=BD,连接AE,∵AD⊥BC,∴AB=AE,∴∠B=∠AEB,∵∠B=2∠C,∴∠AEB=2∠C,∵∠AEB=∠CAE+∠C,∴∠C=∠CAE,∴AE=CE,∵BD=5,BC=25,∴DE=BD=5,∴AB=AE=CE=BC﹣BD﹣DE=15.【点评】此题主要考查的是等腰三角形的判定和性质,作出辅助线正确构建出等腰三角形是解答此题的关键.4.(2020秋•杨浦区校级期中)如图,在△ABC中,∠ACB=90°,D是AB上一点,且BD=AD=CD,过B作BE⊥CD,分别交AC于点E、交CD于点F.(1)求证:∠A=∠EBC;(2)如果AC=2BC,请猜想BE和CD的数量关系,并证明你的猜想.【分析】(1)证得∠EBC=∠ACD,∠A=∠ACD,则结论可得出;(2)过点D作DG⊥AC于点G,根据ASA证明△DCG≌△EBC,可得出结论.【解答】(1)证明:∵BE⊥CD,∴∠BFC=90°,∴∠EBC+∠BCF=180°﹣∠BFC=90°,∵∠ACB=∠BCF+∠ACD=90°,∴∠EBC=∠ACD,∵AD=CD,∴∠A=∠ACD,∴∠A=∠EBC;(2)解:CD=BE.过点D作DG⊥AC于点G,∵DA=DC,DG⊥AC,∴AC=2CG,∵AC=2BC,∴CG=BC,∵∠DGC=90°,∠ECB=90°,∴∠DGC=∠ECB,在△DGC和△ECB中,,∴△DCG≌△EBC(ASA),∴CD=BE.【点评】此题主要考查了全等三角形的判定与性质,等腰三角形的性质,关键是掌握全等三角形的判定定理.5.(2020秋•徐汇区校级期中)如图,AD∥BC,点E是AB的中点,联结DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.(1)求证:AD=BF;(2)当点G是FC的中点时,判断△FDC的形状.【分析】(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E 为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE,根据全等三角形的性质即可得解;(2)连接EG,根据题意,结合全等三角形的性质得到GE⊥DF,GE是△FDC的中位线,根据三角形中位线的性质即可得出△FDC是直角三角形.【解答】(1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△ADE和△BFE中,,∴△ADE≌△BFE(AAS),∴AD=BF;(2)解:△FDC是直角三角形,理由如下:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠BFE,由(1)△ADE≌△BFE得:DE=FE,即GE为DF上的中线,∴GE⊥DF,∵点G是FC的中点,DE=FE,∴GE∥CD,∴CD⊥DF,∴△FDC是直角三角形.【点评】此题考查了全等三角形的判定与性质,平行线的性质,以及等腰三角形的判定与性质,利用AAS证明△ADE≌△BFE是解本题的关键.6.(2022秋•静安区校级期中)如图,AB=AC,AD=AE,∠BAD=∠CAE,BE与CD相交于点F.求证:(1)∠ADC=∠AEB;(2)FD=FE.【分析】(1)利用AAS证明△ABD≌△ACE即可;(2)连接DE,利用等腰三角形的性质和判定即可证明结论.【解答】证明:(1)∵∠BAD=∠CAE,∴∠BAD+∠EAD=∠CAE+∠DAE,∴∠BAE=∠CAD,在△ABE与△ACD中,,∴△ABE≌△ACD(SAS),∴∠ADC=∠AEB;(2)连接DE,∵AD=AE,∴∠ADE=∠AED,∵∠ADC=∠AEB,∴∠ADC﹣∠ADE=∠AEB﹣∠AED,∴∠FDE=∠FED,∴FD=FE.【点评】本题主要考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟练掌握等腰三角形的性质和判定是解题的关键.7.(2022秋•杨浦区期中)如图,已知AB=AC,∠BEF=∠CFH,BE=CF,M是EH的中点.求证:FM⊥EH.【分析】根据等腰三角形的性质可求∠B=∠C,根据ASA可证△BEF≌△CFH,根据全等三角形的性质可求EF=FH,再根据等腰三角形的性质可证FM⊥EH.【解答】证明:∵AB=AC,∴∠B=∠C,在△BEF与△CFH中,,∴△BEF≌△CFH(ASA),∴EF=FH,∵M是EH的中点,∴FM⊥EH.ASA证明△BEF≌△CFH.8.(2021秋•浦东新区期中)如图,在△ABC中,BD平分∠ABC,∠A=2∠C,求证:BC=AB+AD.【分析】在BC上截取BE=BA,由“SAS”可证△ABD≌△EBD,可得∠BED=∠A,AB=BE,AD=DE,由外角的性质可得∠C=∠EDC,可证EC=ED,即可得结论.【解答】证明:如图,在BC上截取BE=BA,连接DE,∵BD平分∠ABC,∴∠ABD=∠CBD,在△ABD和△EBD中,,∴△ABD≌△EBD(SAS),∴∠BED=∠A,AB=BE,AD=DE,∵∠A=2∠C,∴∠BED=2∠C,∵∠BED=∠C+∠EDC,∴∠C=∠EDC,∴EC=ED,∴BC=BE+EC=AB+AD.【点评】本题考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键.9.(2021秋•徐汇区校级期中)已知在△ABC中,AB=AC,在边AC上取一点D,以D为顶点,DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB.求证:(1)∠FDC=∠ABD;(2)DB=DF;(3)当点D在AC延长线上时,DB=DF是否依然成立?在备用图中画出图形,并说明理由.【分析】(1)根据角的和差即可得到结论;(2)过D作DG∥BC交AB于G,根据等腰三角形的性质和全等三角形的判定和性质定理即可得到结论;(3)过D作DG∥BC交AB于G,根据平行线的性质得到∠ADG=∠ACB,∠AGD=∠ABC,根据等腰三角形的性质得到∠ABC=∠ACB,根据全等三角形的判定和性质即可得到结论.【解答】(1)证明:∵∠BDC=∠A+∠ABD,即∠BDF+∠FDC=∠A+∠ABD,∵∠BDF=∠A,∴∠FDC=∠ABD;(2)过D作DG∥BC交AB于G,∴∠ADG=∠ACB,∠AGD=∠ABC,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ADG,∴AD=AG,∴AB﹣AG=AC﹣AD,即BG=DC,∵∠ECF=∠ACB=∠AGD,∴∠DGB=∠FCD,在△GDB与△CFD中,,∴△GDB≌△CFD(ASA),∴DB=DF;(3)仍然成立,如图2,过D作DG∥BC交AB于G,∴∠ADG=∠ACB,∠AGD=∠ABC,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ADG,∴AD=AG,∴AG﹣AB=AD﹣AC,即BG=DC,∵∠ECF=∠ACB=∠AGD,∴∠DGB=∠FCD,∵∠ACB+∠BCF+∠FCD=180°,∴∠ACB+∠BCF+∠DGB=180°,∵∠DGB=∠ABC.∴∠ACB+∠BCF∠ABC=180°,∵∠A+∠ABC+∠ACB=180°,∴∠A=∠BCF,∵∠BDF=∠A,∴∠BCF=∠BDF,∴∠CBD=∠CFD,∵∠GBD=180°﹣∠ABC﹣∠CBD=180°﹣∠FCD﹣∠CFD=∠FDC,∴∠GBD=∠FDC,在△GDB与△CFD中,,∴△GDB≌△CFD(ASA),∴DB=DF.【点评】本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.10.(2022秋•浦东新区期中)如图,已知在△ABC中,AB=AC,点D、E分别在AC、AB上,且AD=AE,点F在BC的延长线上,DB=DF.(1)求证:∠ABD=∠ACE.(2)求证:CE∥DF.【分析】(1)由“SAS”可证△ADB≌△AEC,可得∠ABD=∠ACE;(2)由等腰三角形的性质可得∠=∠F,由外角的性质可得∠ACE=∠CDF,可得结论.【解答】证明:(1)∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,在△ADB和△AEC中,,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE;(2)∵DB=DF,∴∠DBF=∠F,∵∠ABC=∠ABD+∠DBC,∠ACB=∠F+∠CDF,∴∠ABD=∠CDF,∴∠ACE=∠CDF,∴CE∥DF.【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,等边三角形的性质,掌握全等三角形的判定方法是本题的关键.11.(2020秋•浦东新区校级期中)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,AC=DF,BF =CE.求证:AB∥DE.【分析】根据线段的和差求出BC=EF,由平行线的性质证得∠ACB=∠DFE,根据SAS定理推出△BAC≌△EDF,根据全等三角形的性质得出∠B=∠E,根据平行线的判定即可证得AB∥DE.【解答】证明:∵BF=CE,∴BF+FC=CE+FC,∴BC=EF,∵AC∥DF,∴∠ACB=∠DFE,在△BAC和△EDF中,,∴△BAC≌△EDF(SAS),∴∠B=∠E,∴AB∥DE.【点评】本题考查了全等三角形的性质和判定,平行线的判定的应用,能推出△BAC和△EDF全等是解此题的关键.12.(2022秋•长宁区校级期中)已知:如图,△ABC中,AD平分∠BAC交BC于点D,CF∥AB且CD平分∠FCA,联结FD并延长交边AB于点E,说明CF=AC﹣AE的理由.【分析】由CF∥AB得∠FCB=∠ABC,由CD平分∠FCA得∠FCB=∠ACB,可得∠ACB=∠ABC,从而得AB =AC,由AD平分∠BAC可得CD=BD,再根据ASA证明△FCD≌△EBD,可得FC=BE,从而可得结论.【解答】解:∵CF∥AB,∴∠FCB=∠ABC,∵CD平分∠FCA,∴∠FCB=∠ACB,∴∠ACB=∠ABC,∴AB=AC,∵AD平分∠BAC,∴CD=BD,在△FCD和△EBD中,,∴△FCD≌△EBD(ASA),∴FC=BE,∵AC=AB=AE+EB=AE+CF,∴CF=AC﹣AE.【点评】本题主要考查了等腰三角形的判定与性质,全等三角形的判定与性质,角平分线的意义等知识,运用ASA证明△FCD≌△EBD是解答本题的关键.13.(2022秋•杨浦区期中)如图1所示,已知点E在直线AB上,点F,G在直线CD上且∠EFG=∠FEG,EF平分∠AEG,如图2所示,H是AB上点E右侧一动点,∠EGH的平分线GQ交FE的延长线于点Q,设∠Q=α,∠EHG=β,(1)若∠HEG=40°,∠QGH=20°,求∠Q的度数;(2)判断:点H在运动过程中,α和β的数量关系是否发生变化?若不变,求出α和β的数量关系;若变化,请说明理由.【分析】(1)先证明,再依据∠HEG=40°,即可得到∠FEG=70°,依据QG平分∠EGH,即可得到∠QGH=∠QGE=20°,根据∠Q=∠FEG﹣∠EGQ进行计算即可;(2)根据∠FEG是△EGQ的外角,∠AEG是△EGH的外角,即可得到∠Q=∠FEG﹣∠EGQ,∠EHG=∠AEG ﹣∠EGH,再根据FE平分∠AEG,GQ平分∠EGH,即可得出,,最后依据∠Q=∠FEG﹣∠EGQ进行计算,即可得到.【解答】解:(1)∵EF平分∠AEG,∴∠AEF=∠GEF,∵∠EFG=∠FEG,∴∠AEF=∠GFE,∴AB∥CD,∵∠HEG=40°,∴,∵QG平分∠EGH,∴∠QGH=∠QGE=20°,∴∠Q=∠FEG﹣∠EGQ=70°﹣20°=50°;(2)点H在运动过程中,α和β的数量关系不发生变化,∵∠FEG是△EGQ的外角,∠AEG是△EGH的外角,∴∠Q=∠FEG﹣∠EGQ,∠EHG=∠AEG﹣∠EGH,又∵FE平分∠AEG,GQ平分∠EGH,∴,,∴∠Q=∠FEG﹣∠EGQ==,即.【点评】本题主要考查了平行线的判定与性质,三角形外角性质的运用,解题的关键是利用三角形的外角性质:三角形的外角等于与它不相邻的两个内角的和.14.(2022秋•宝山区校级期中)如图,在五边形ABCDE中,(1)已知AB=AE,BC=ED,∠B=∠E,F是CD中点,求证:AF⊥CD.(2)已知AB=AE,BC=ED,∠C=∠D,F是CD中点,求证:AF⊥CD.(3)已知∠B=∠E,BC=ED,∠C=∠D,F是CD中点,求证;AF⊥CD.【分析】(1)连接AC,AD,根据全等三角形的判定和性质得出△ABC≌△AED,AC=AD,再由等腰三角形三线合一即可证明;(2)连接BF,EF,BCF≌△EDF,△ABF≌△AEF,∠CFB=∠DFE,∠AFB =∠AFE,结合图形得出∠AFC=∠AFD,即可证明;(3)连接BD,CE交于点G,根据全等三角形的判定和性质得出△BCD≌△EDC,△CGF≌△DGF,∠AFC=∠AFD,结合图形即可证明.【解答】解:(1)如图所示,连接AC,AD,在△ABC与△AED中,,∴△ABC≌△AED(SAS),∴AC=AD,∵F是CD中点,∴AF⊥CD;(2)如图所示,连接BF,EF,∵F是CD中点,∴CF=FD,在△BCF与△EDF中,,∴△BCF≌△EDF(SAS),∴BF=EF,∠CFB=∠DFE在△ABF与△AEF中,,∴△ABF≌△AEF(SSS),∴∠AFB=∠AFE,∴∠AFB+∠CFB=∠DFE+∠AFE,即∠AFC=∠AFD,∵∠AFC+∠AFD=180°,∴∠AFD=90°,∴AF⊥CD;(3)如图所示,连接BD,CE交于点G,∵F是CD中点,∴CF=FD,在△BCD与△EDC中,,∴△BCD≌△EDC(SAS),∴∠CDB=∠DCE,∴CG=DG,在△CGF与△DGF中,,∴△CGF≌△DGF(SAS),∴∠AFC=∠AFD,∵∠AFC+∠AFD=180°,∴∠AFD=90°,∴AF⊥CD.【点评】题目主要考查全等三角形的判定和性质,线段中点的性质及等腰三角形的判定和性质等,理解题15.(2022秋•宝山区校级期中)如图,△ABC和△ABD,AB=AD,点E、F在边BC上,点A、F、D共线,∠BAC=∠AFC,∠EAC=∠FCD,求证:AE=CD.【分析】根据三角形内角和定理得出∠CAD=∠ABC,再由三角形外角的性质及全等三角形的判定和性质即可证明.【解答】证明:∵∠BAC=∠AFC,∴180°﹣∠BAC﹣∠ACB=180°﹣∠AFC﹣∠ACB,即∠CAD=∠ABC,∵∠EAC=∠FCD,∴∠EAC+∠ACB=∠FCD+∠ACB,即∠AEB=∠ACD,在△AEB与△DCA中,,∴△AEB≌△DCA(AAS),∴AE=CD.【点评】题目主要考查全等三角形的判定和性质,三角形内角和定理及外角的性质,熟练掌握全等三角形的判定和性质是解题关键.16.(2022秋•虹口区校级期中)如图,△ABC和△BDE都是等边三角形,且点A、D、E在同一直线上,证明AE=BE+CE.【分析】根据等边三角形的性质,得出∠ABC=∠DBE=60°,AB=CB,BD=BE=DE,再根据角之间的数量关系,得出∠ABD=∠CBE,再根据“边角边”,得出△ABD≌△CBE,再根据全等三角形的性质,得出AD=CE,再根据等量代换,即可得出结论.【解答】证明:∵△ABC和△BDE都是等边三角形,∴∠ABC=∠DBE=60°,AB=CB,BD=BE=DE,∴∠ABC=∠ABD+∠DBC,∠DBE=∠DBC+∠CBE,∴∠ABD=∠CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴AD=CE,∴AE=DE+AD=BE+CE.【点评】本题考查了等边三角形的性质、全等三角形的判定与性质,解本题的关键在熟练掌握相关的性质定理.17.(2022秋•普陀区校级期中)如图,在△ABC中,AD平分∠BAC,E是BC的中点,过点E作FG⊥AD 交AD的延长线于H,交AB于F,交AC的延长线于G.求证:(1)AF=AG;(2)BF=CG.【分析】(1)由FG⊥AD交AD的延长线于H,∠AHF=∠AHG=90°,可根据全等三角形的判定定理“ASA”证明△AHF≌△AHG,得AF=AG;(2)作CL∥AB交FG于点L,则∠AFG=∠CLG,由AF=AG,得∠AFG=∠G,则∠CLG=∠G,得CL=CG,再证明△BEF≌△CEL,得BF=CL,所以BF=CG.【解答】证明:(1)∵AD平分∠BAC,∴∠FAH=∠GAH,∵FG⊥AD交AD的延长线于H,∴∠AHF=∠AHG=90°,在△AHF和△AHG中,,∴△AHF≌△AHG(ASA),∴AF=AG.(2)作CL∥AB交FG于点L,则∠B=∠ECL,∠AFG=∠CLG,∵AF=AG,∴∠AFG=∠G,∴∠CLG=∠G,∴CL=CG,∵E是BC的中点,∴BE=CE,在△BEF和△CEL中,,∴△BEF≌△CEL(ASA),∴BF=CL,∴BF=CG.【点评】此题重点考查全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质等知识,正确地作出所需要的辅助线构造全等三角形是解题的关键.18.(2022秋•浦东新区期中)如图,已知AB=AC,∠BEF=∠CFH,BE=CF,M是EH的中点.求证:∠EFM=∠HFM.【分析】证明△BEF≌△CFH(ASA),△EFM≌△HFM(SSS)即可求解.【解答】证明:∵AB=AC,∠BEF=∠CFH,BE=CF,∴∠B=∠C,在△BEF和△CFH中,,∴△BEF≌△CFH(ASA),∴EF=FH,∵M是EH的中点,∴EM=HM,FM为公共边,∴△EFM≌△HFM(SSS),∴∠EFM=∠HFM.【点评】本题主要考查全等三角形的判定和性质,掌握三角形全等的判定方法和性质是解题的关键.19.(2017秋•上海期中)如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.【分析】(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;(2)根据△BDE≌△CEF,可知∠FEC=∠BDE,∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B即可得出结论,再根据等腰三角形的性质即可得出∠DEF的度数.【解答】(1)证明:∵AB=AC∴∠B=∠C,在△BDE与△CEF中,,∴△BDE≌△CEF(SAS).∴DE=EF,即△DEF是等腰三角形.(2)解:由(1)知△BDE≌△CEF,∴∠BDE=∠CEF∵∠CEF+∠DEF=∠BDE+∠B∴∠DEF=∠B∵AB=AC,∠A=40°∴∠DEF=∠B=70°.【点评】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟知等腰三角形的两个底角相等是解答此题的关键.20.(2022秋•静安区校级期中)已知:如图,AD∥CF,∠A=∠C=90°,DB平分∠ADF,AD+CF=DF.求证:FB平分∠CFD.【分析】在DF上取一点E,使DE=AD,进而利用SAS证明△ADB与△EDB全等,进而证明△FCB与△FEB 全等,进而解答即可.【解答】证明:在DF上取一点E,使DE=AD,∵DB平分∠ADF,∴∠ADB=∠EDB,在△ADB与△EDB中,,∴△ADB≌△EDB(SAS),∴AB=BE,∠BAD=∠BED,AD=DE,∴∠BAD=∠BED=90°,∵AD∥CF,∴∠C=∠A=90°,∵DF=AD+CF,∴EF=DF﹣DE=DF﹣AD=CF,在Rt△BEF与Rt△BCF中,,∴Rt△BEF≌Rt△BCF(HL),∴∠EFB=∠CFB,即FB平分∠CFD.【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.21.(2022秋•静安区校级期中)已知如图,AB=AC,AD=AE,∠BAE=∠CAD,BD与CE相交于点F,求证:FB=FC.【分析】由已知条件证得△ABD≌△ACE,连接BC,要证FB=FC,可利用等式性质来证得.【解答】证明:∵∠BAE=∠CAD(已知),∴∠BAE+∠EAD=∠CAD+∠DAE(等式性质),即∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE(全等三角形对应角相等),连接BC.∵AB=AC(已知),∴∠ABC=∠ACB(等边对等角).∵∠ABD=∠ACE(已证),∴∠ABC﹣∠ABD=∠ACB﹣∠ACE(等式性质),即∠FBC=∠FCB.∴FB=FC(等角对等边).【点评】本题主要考查了两个三角形的判定和性质,关键是根据SAS证得△ABD≌△ACE.22.(2022秋•闵行区校级期中)如图,已知点A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:BC∥EF.【分析】证△ABC≌△DEF(SAS),得∠BCA=∠EFD,再由平行线的判定即可得出结论.【解答】证明:∵AB∥DE,∴∠A=∠D,∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC与△DEF中,,∴△ABC≌△DEF(SAS),∴∠BCA=∠EFD,∴BC∥EF.【点评】考查了全等三角形的判定与性质、平行线的判定与性质等知识,熟练掌握平行线的判定与性质,证明三角形全等是解题的关键.23.(2022秋•杨浦区期中)如图,已知△ABC和△CDE都是等边三角形,点D、A、C在同一直线上,延长BA交边DE于点F,联结AE、BD.(1)试说明△ADB≌△F AE的理由;(2)延长EA交BD于点H,求∠DHE的度数.【分析】(1)证△ADF是等边三角形,得AD=FA=DF,∠DFA=60°,再证CD=BF,则AB=FE,然后证∠BAD=∠EFA,进而证△ADB≌△FAE(SAS);(2)由全等三角形的性质得∠ABD=∠FEA,再证∠DHE=∠FEA+∠FAE,即可得出结论.【解答】(1)证明:∵△ABC和△CDE都是等边三角形,∴AB=AC,∠DAF=∠BAC=60CDE=60°,CD=DE,∴△ADF是等边三角形,∴AD=FA=DF,∠DFA=60°,∴AC+AD=AB+FA,即CD=BF,∴BF﹣FA=DE﹣DF,即AB=FE,∵∠BAD=180°﹣∠DAF=180°﹣60°=120°,∠EFA=180°﹣∠DFA=180°﹣60°=120°,∴∠BAD=∠EFA,在△ADB和△FAE中,,∴△ADB≌△FAE(SAS);(2)解:由(1)得:△ADB≌△FAE,∴∠ABD=∠FEA,∵∠DHE=∠ABD+∠BAH,∠FAE=∠BAH,∴∠DHE=∠FEA+∠FAE,∵∠DFA=∠FEA+∠FAE,∴∠DHE=∠DFA=60°.【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质等知识,熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.24.(2022秋•闵行区期中)如图,点D,E在△ABC的边BC上,AD=AE,BD=CE,求证:∠B=∠C.【分析】方法一:利用全等三角形的性质证明即可.方法二:作AM⊥BC于M.证明AN垂直平分线段BC 即可;【解答】证明方法一:∵AD=AE,∴∠ADE=∠AED,∵∠ADE+∠ADB=∠AED+∠AEC=°,∴∠ADB=∠AEC,在△ABD和△ACE中,∴△ABD≌△ACE(SAS),∴∠B=∠C.证明方法二:作AM⊥BC于M.∵AD=AE,∴DM=EM,∵BD=CE,∴DM+BD=EM+CE,即:BM=CM,又∵AM⊥BC,即AM为BC的垂直平分线,∴AB=AC,∴∠B=∠C.【点评】本题考查全等三角形的判定和性质,等腰三角形的判定和性质,线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.25.(2022秋•普陀区期中)已知:如图,在四边形ABCD中,BC=DC,点E在边AB上,∠EBC=∠EDC.(1)求证:EB=ED.(2)当∠A=90°,求证:∠BED=2∠BDA.【分析】(1)由BC=DC,得出∠CBD=∠CDB,再由∠EBC=∠EDC,推出∠EBD=∠EDB,即可得出结论;(2)由三角形内角和定理得出∠BDA+∠ABD=90°=∠A,再由(1)得∠EBD=∠EDB,则∠BDA+∠EDB=∠A,然后由三角形的外角性质即可得出结论.【解答】证明:(1)∵BC=DC,∴∠CBD=∠CDB,∵∠EBC=∠EDC,∴∠EBC﹣∠CBD=∠EDC﹣∠CDB,即∠EBD=∠EDB,∴EB=ED;(2)∵∠A=90°,∴∠BDA+∠ABD=90°=∠A,由(1)得:∠EBD=∠EDB,∴∠BDA+∠ABD=∠BDA+∠EDB=∠A,∴∠BED=∠A+∠ADE=∠BDA+∠EDB+∠ADE=∠BDA+∠BDA=2∠BDA.【点评】本题考查了等腰三角形的判定与性质、三角形内角和定理、三角形外角的性质等知识,熟练掌握等腰三角形的判定与性质是解题的关键.26.(2021秋•奉贤区校级期中)在△ABC中,AB=AC,点D是直线BC上的一点(不与点B、C重合),以AD为腰右侧作等腰三角形△ADE,且AD=AE,∠BAC=∠DAE,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度.(2)设∠BAC=α,∠BCE=β.①点D是在线段BC上移动时,如图2,则α、β之间有怎样的数量关系?试说明理由.②点D是在射线CB上移动时,则α、β之间有怎样的数量关系?试直接写出结论.【分析】(1)证明△BAD≌△CAE,得∠B=∠ACE,即可证明;(2)①与(1)同理证明△BAD≌△CAE,得∠ABD=∠ACE,则∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°;②同理证明△ADB≌△AEC,得∠ABD=∠ACE,由∠ABD=∠BAC+∠ACB,则∠BAC=∠BCE.【解答】解:(1)∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠B=∠ACE,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①α+β=180°,理由如下:∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠ABD=∠ACE,∵∠BAC+∠ABD+∠BCA=180°,∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,∴α+β=180°;②α=β,理由如下:∵∠DAE=∠BAC,∴∠DAB=∠EAC,在△ADB与△AEC中,,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE,∵∠ABD=∠BAC+∠ACB,∴∠BAC=∠BCE,∴α=β.【点评】本题主要考查了等腰三角形的性质,全等三角形的判定与性质,三角形外角的性质等知识,证明△ADB≌△AEC是解题的关键.27.(2021秋•浦东新区期中)如图,在△ABC中,AD平分∠BAC,DE∥AC,过点E作EF⊥AD于点O,交BC的延长线于F,连接AF,求证:AF=DF.【分析】根据平行线的性质和等腰三角形的判定和性质解答即可.【解答】证明:∵DE∥AC,∴∠EDA=∠DAC,∵AD平分∠BAC,∴∠EAD=∠DAC,∴∠EAD=∠EDA,∴AE=DE,∵EF⊥AD,∴EF垂直且平分AD,∴F在AD的垂直平分线上,∴AF=DF.【点评】此题考查等腰三角形的判定和性质,关键是根据平行线的性质和等腰三角形的判定和性质解答.28.(2020秋•浦东新区期中)如图,已知在△ABC中,AB=AC,D是AB上一点,延长AC至点E,使CE =BD.联结DE交BC于点F,求证:DF=EF.【分析】过点D作DG∥AC交BC于点G,由“AAS”可证△DFG≌△ECF,可得DF=EF.【解答】证明:如图,过点D作DG∥AC交BC于点G,∵AB=AC,∵DG∥AC,∴∠ACB=∠DGB,∠DGF=∠ECF,∴∠ACB=∠DGB=∠B,∴DG=DB,∵CE=BD,∴DG=CE,在△DFG和△EFC中,,∴△DFG≌△EFC(AAS)∴DF=EF.【点评】本题考查了全等三角形的判定和性质、等腰三角形的判定与性质等知识,添加恰当辅助线构造全等三角形是解题的关键.29.(2022秋•奉贤区校级期中)如图,点A、B、C、D在同一直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.【分析】根据BE∥DF,可得∠ABE=∠D,再利用ASA求证△ABC和△FDC全等即可.【解答】证明:∵BE∥DF,在△ABE和△FDC中,,∴△ABE≌△FDC(ASA),∴AE=FC.【点评】此题主要考查全等三角形的判定与性质和平行线的性质等知识点的理解和掌握,此题的关键是利用平行线的性质求证△ABC和△FDC全等.30.(2020秋•普陀区期中)如图,已知AB=AC,BD=CD,过点D作DE⊥AB交AB的延长线于点E、DF ⊥AC交AC的延长线于点F,垂足分别为点E、F.(1)求证:∠DBE=∠DCF.(2)求证:BE=CF.【分析】(1)连接AD,证△ABD≌△ACD(SSS),得∠ABD=∠ACD,即可得出结论;(2)证△BDE≌△CDF(AAS),即可得出结论.【解答】证明:(1)连接AD,如图:在△ABD和△ACD中,,∴△ABD≌△ACD(SSS),∴∠ABD=∠ACD,∴∠DBE=∠DCF.(2)∵DE⊥AB,DF⊥AC,∴∠E=∠F=90°,由(1)得:∠DBE=∠DCF,在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴BE=CF.【点评】本题考查了全等三角形的判定和性质等知识;熟练掌握全等三角形的判定与性质是解题的关键.31.(2017秋•静安区期中)如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.(1)求证:∠E=∠C;(2)如果DF平分∠AFB,求证:AC⊥AB.【分析】(1)根据SAS证明△AED与△BFD全等,再利用等量代换证明即可;(2)根据角平分线的定义和等腰三角形的性质进行证明即可.【解答】证明:(1)∵D为AB的中点,∴BD=AD,在△AED与△BFD中,,∴△AED≌△BFD(SAS),∴∠E=∠DFB,∵DF∥AC,∴∠C=∠DFB,∴∠C=∠E;(2)∵DF平分∠AFB,∴∠AFD=∠DFB,∵∠E=∠DFB,∴∠AFD=∠AED,∵ED=DF,∴∠DAF+∠AFD=90°,∵EF∥AC,∴∠AFD=∠FAC,∴∠DAF+∠FAC=90°,∴AC⊥AB.【点评】本题考查了全等三角形的判定与性质,关键是根据平行线的性质、全等三角形的判定与性质等知识进行解答.32.(2021秋•浦东新区期中)如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE=AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,,∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.33.(2022秋•奉贤区校级期中)(1)已知:如图①,△ABC是等边三角形,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点F,猜想:线段EF、DF之间有怎样的数量关系?并证明你的猜想.(2)已知:如图②,在△ABC中,∠B=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点F,猜想:上述(1【分析】(1)证明△EAC≌△DCA(ASA),可得EC=DA,然后根据线段的和差即可得结论;(2)在CA上截取CG=CD,证明△CDF≌△CGF(SAS),可得DF=GF,∠DFC=∠GFC,再证明△AEF≌△AGF(ASA),可得EF=GF,进而可得结论.【解答】解:(1)EF=DF,证明:∵△ABC是等边三角形,∴∠BAC=∠BCA=60°,∵AD、CE分别平分∠BAC、∠ACB,∴∠FAC=BAC,∠FCA=BCA,∴∠FAC=∠FCA,∴FA=FC,在△EAC和△DCA中,,∴△EAC≌△DCA(ASA),∴EC=DA,∵FA=FC,∴EF=DF;(2)EF=DF仍成立,理由如下:如图,在CA上截取CG=CD,在△CDF和△CGF中,,∴△CDF≌△CGF(SAS),∴DF=GF,∠DFC=∠GFC,∵∠DFC=∠FAC+∠FCA=BAC+BCA=60°,∴∠GFC=60°,∠AFE=60°,∴∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣(BAC+BCA)=180°﹣60°=120°,∴∠AFG=120°﹣60°=60°,∴∠AFE=∠AFG,在△AEF和△AGF中,,∴△AEF≌△AGF(ASA),∴EF=GF,∴EF=DF.【点评】本题考查了角平分线的性质,全等三角形的判定与性质,三角形的内角和定理,遇到角平分线,作角平分线上的点到两边的距离构造出全等三角形是解题的关键.34.(2021秋•台江区期中)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:(1)△ABC≌△AED;(2)OB=OE.【分析】(1)利用SAS ABC≌△AED;(2)根据全等三角形的性质得到∠ABC=∠AED,根据等腰三角形的性质得到∠ABE=∠AEB,得到∠OBE=∠OEB,根据等腰三角形的判定定理证明.【解答】证明:(1)∵∠BAD=∠EAC,∴∠BAD+∠DAC=∠EAC+∠DAC,即∠BAC=∠EAD,在△BAC和△EAD中,,∴△BAC和≌EAD;(2)∵△BAC≌△EAD,∴∠ABC=∠AED,∵AB=AE,∴∠ABE=∠AEB,∴∠OBE=∠OEB,∴OB=OE.【点评】本题考查的是全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.35.(2022秋•宝山区校级期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD =AE.(1)求证:DE∥BC;(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.【分析】(1)根据等腰三角形的性质和三角形内角和证明即可;(2)根据AAS证明△BDE与△EFC全等即可.【解答】证明:(1)∵AB=AC,∴∠ABC=∠ACB,∵AD=AE,∴∠ADE=∠AED,∵∠A=∠A,∴∠ADE=∠ABC,∴DE∥BC;(2)∵∠EBC=∠EFC,∠ABC=∠ACB,∴∠DBE+∠EBC=∠CEF+∠EFC,∴∠DBE=∠CEF,∠DEB=∠EFC,在△BDE与△EFC中,,∴△BDE≌△EFC(AAS),∴DE=CF.【点评】本题考查了等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定语言性质的运用,解答时证明三角形全等是关键.36.(2022秋•浦东新区期中)已知:如图,AB=DC,AC=BD.求证:∠B=∠C.【分析】连接AD,利用SSS判定△ABD≌△DCA,根据全等三角形的对应角相等即证.【解答】解:如图,连接AD,在△ABD和△DCA中,,∴△ABD≌△DCA(SSS),∴∠B=∠C.【点评】本题考查三角形全等的判定方法和三角形全等的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.37.(2022秋•徐汇区校级期中)已知:如图,在△ABC中,∠ACB=90°,AD为△ABC的外角平分线,交BC的延长线于点D,且∠B=2∠D.求证:AB+AC=CD.【分析】过点D作DE⊥AB,垂足为点E,由“在角的平分线上的点到这个角的两边的距离相等”可知DE=DC,再证明Rt△ACD≌Rt△AED,由此可得AC=AE,在证明BE=DE即可.【解答】证明:过点D作DE⊥AB,垂足为点E,又∵∠ACB=90°(已知),∴DE=DC(在角的平分线上的点到这个角的两边的距离相等).在Rt△ACD和Rt△AED中∴Rt△ACD≌Rt△AED(H.L).∴AC=AE,∠CDA=∠EDA.∵∠B=2∠D(已知),∴∠B=∠BDE.∴BE=DE.又∵AB+AE=BE,∴AB+AC=CD.【点评】本题考查了全等三角形的判定与性质,关键是作辅助线使得AB与AC在同一条直线上才好证AB+AC =CD.38.(2021秋•徐汇区校级期中)如图,AB⊥BC,DC⊥BC,垂足分别是点B、C,点E是线段BC上一点,且AE⊥DE,AE=ED,如果BE=3,AB+BC=11,求AB的长.【分析】求出∠A=∠DEC,∠B=∠C=90°,根据AAS证△ABE≌△ECD,推出AB=CE,求出AB+BC=2AB+BE =11,把BE=3代入求出AB即可.【解答】解:∵AB⊥BC,DC⊥BC,垂足分别是点B、C,∴∠B=∠C=90°.∴∠A+∠AEB=90°,∵AE⊥DE,∴∠AED=90°,∵∠AEB+∠AED+∠DEC=180°,∴∠AEB+∠DEC=90°,∴∠A=∠DEC,∵在△ABE和△ECD中,,∴△ABE≌△ECD(AAS),∴AB=CE,∵BC=BE+CE=BE+AB,∴AB+BC=2AB+BE=11,∵BE=3,∴AB=4.【点评】本题考查了全等三角形的性质和判定,三角形的内角和定理,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.39.(2022秋•奉贤区校级期中)△ABC为等边三角形,D为AB边上的任意一点.连接CD.(1)在BD的左侧,以BD为一边作等边三角形BDE(尺规作图,保留作图痕迹,不写作法);(2)连接AE,试说明:CD=AE.【分析】(1)可以分别以B、D为圆心,以BD为半径作弧,相交于E;(2)由已知条件,证明△BCD≌△EAB即可.【解答】(1)解:如图:(2)证明:连接AE,如图,∵在△BCD与△BAE中,,∴△BCD≌△BAE(SAS)∴CD=AE.【点评】此题主要考查等边三角形的作法以及性质的运用,还涉及到全等三角形的判定,综合性强.求得三角形全等是正确解答本题的关键.40.(2022秋•静安区校级期中)如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB 为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.(1)求证:△AMB≌△ENB;。
(完整版)初二上几何证明题100题专题训练(可编辑修改word版)
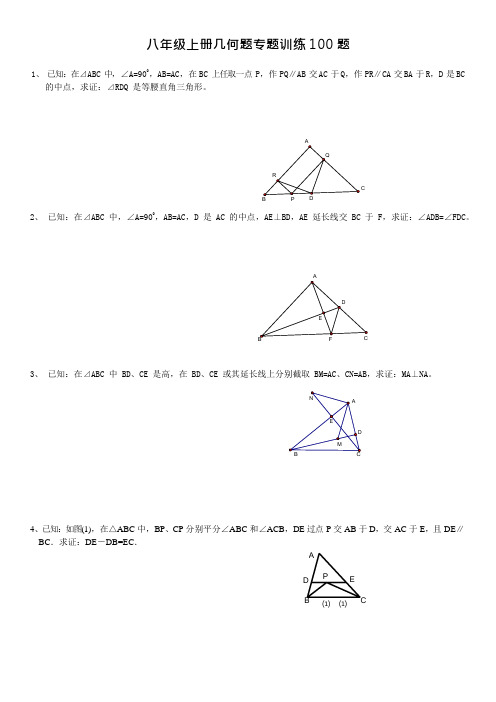
A D P E 八年级上册几何题专题训练 100 题1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在 BC 上任取一点 P ,作 PQ∥AB 交 AC 于 Q ,作 PR∥CA 交 BA 于 R ,D 是 BC的中点,求证:⊿RDQ 是等腰直角三角形。
C2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是 AC 的中点,AE⊥BD,AE 延长线交 BC 于 F ,求证:∠ADB=∠FDC。
3、 已知:在⊿ABC 中 BD 、CE 是高,在 BD 、CE 或其延长线上分别截取 BM=AC 、CN=AB ,求证:MA⊥NA。
4、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点 P 交 AB 于 D ,交 AC 于 E ,且 DE ∥ BC .求证:DE -DB=EC .BC5、在Rt△ABC 中,AB=AC,∠BAC=90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A、B、C 的距离的大小关系(不要求证明);(2)如果点M、N 分别在线段AB、AC 上移动,在移动中保持AN=BM,请判断△OMN 的形状,并证明你的结论。
CNOA M B6、如图,△ABC 为等边三角形,延长BC 到D,延长BA 到E,AE=BD,连结EC、ED,求证:CE=DE7、如图,等腰三角形ABC 中,AB=AC,∠A=90°,BD 平分∠ABC,DE⊥BC 且BC=10,求△DCE 的周长。
8.如图,已知△EAB≌△DCE,AB,EC 分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.9.如图,点 E、A、B、F 在同一条直线上,AD 与BC 交于点 O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠DC DOE B10.如图,OP 平分∠AOB,且OA=OB.(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);(2)从(1)中任选一个结论进行证明.11.已知:如图,AB=AC,DB=DC,AD 的延长线交 BC 于点E,求证:BE=EC。
北师大版八年级数学下册 三角形的证明 单元测试卷(含答案)

北师大版八年级数学下册三角形的证明单元测试卷(时间:120分钟满分:150分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题的四个选项中,只有一个选项正确,请把你认为正确的选项填在相应的答题框内)1.如图,若∠B=30°,∠C=90°,AC=20,则AB=( )A.25B.30C.20 3D.402.如图,已知DE∥BC,AB=AC,∠1=55°,则∠C的度数是( )A.55°B.45°C.35°D.65°3.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )A.∠A=40°,∠B=50°B.∠A=40°,∠B=60°C.∠A=20°,∠B=80°D.∠A=40°,∠B=80°4.以下各组数为三角形的三条边长,其中是直角三角形的三条边长的是( )A.2,3,4B.1,2, 3C.4,5,6D.2,2,45.如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )A.HLB.ASAC.AASD.SAS6.如图,在△AB C中,AB=AC,D为BC的中点,∠BAD=35°,则∠CAD的度数为( )A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为( )A.30°B.45°C.60°D.75°8.如图,D是Rt△ABC的斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β,若α=10°,则β的度数是( )A.40°B.50°C.60°D.不能确定9.如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,DE⊥AB,CD=3,则BD的长为( )A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”,第一步应假设这个直角三角形中( )A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )A.AB=A′B′=5,BC=B′C′=3B.AB=B′C′=5,∠A=∠B′=40°C.AC=A′C′=5,BC=B′C′=3D.AC=A′C′=5,∠A=∠A′=40°12.观察下列命题的逆命题:①有两边相等的三角形是等腰三角形;②到角的两边的距离相等的点在这个角的平分线上;③直角三角形的两个锐角互余;④全等三角形的面积相等.其中逆命题为假命题的个数是( )A.1B.2C.3D.413.如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC=60°,∠ACE=24°,那么∠BCE 的大小是( )A.24°B.30°C.32°D.36°14.如图,直角三角形纸片的两直角边长分别为6,8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE∶S△BDE =( )A.2∶5B.14∶25C.16∶25D.4∶2115.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是( )A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB=150°D.∠APC=135°二、填空题(本大题共5个小题,每小题5分,共25分)16.在直角三角形中,其中一个锐角是22°,则另外一个锐角是.17.如图,某失联客机从A地起飞,飞行1 000 km到达B地,再折返飞行1 000 km到达C地后在雷达上消失,已知∠ABC=60°,则失联客机消失时离起飞地A地的距离为km.18.如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为 .19.如图,已知△ABC的周长是22,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,△ABC的面积是 .20.如图,在等腰△A BC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,点C沿EF折叠后与点O重合,则∠OEC的度数是 .三、解答题(本大题共7个小题,各题分值见题号后,共80分)21.(本题8分)一个机器零件的形状如图所示,在Rt△ABC中,∠BAC=30°,BC=2.5 cm,BD=13 cm,AD=12 cm,求△ABD的面积.22.(本题8分)在加快城镇建设中,有两条公路OA和OB交会于O点,在∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA,OB的距离相等,且到两个蔬菜基地C,D的距离也相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)23.(本题10分)如图,点P为△ABC的BC边上一点,且PC=2PB,∠ABC=45°,∠APC=60°,CD⊥AP,连接BD,求∠ABD的度数.24.(本题12分)如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.(1)判断△CED的形状,并说明理由;(2)若OC=3,求CD的长.25.(本题12分)如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P,PD⊥AB于D,PE⊥AC于E.(1)求证:BD=CE;(2)若AB=6 cm,AC=10 cm,求AD的长.26.(本题14分)如图,在△ABC中,MP,NO分别垂直平分AB,AC.(1)若BC=10 cm,试求出△PAO的周长;(2)若AB=AC,∠BAC=110°,试求∠PAO的度数;(3)在(2)中,若无AB=AC的条件,你能求出∠PAO的度数吗?若能,请求出来;若不能,请说明理由.27.(本题16分)如图,△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动,已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点N第一次到达点B时,M,N同时停止运动.(1)点M,N运动几秒后,M,N两点重合?(2)点M,N运动几秒后,可得到等边三角形△AMN?(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M,N运动的时间.参考答案一、选择题(本大题共15个小题,每小题3分,共45分.在每小题的四个选项中,只有一个选项正确,请把你认为正确的选项填在相应的答题框内)题1 2 3 4 5 6 7 8 9 10 11 12 13 14 15号选D A C B A A C B C D B A C B D项1.如图,若∠B=30°,∠C=90°,AC=20,则AB=(D)A.25B.30C.20 3D.402.如图,已知DE∥BC,AB=AC,∠1=55°,则∠C的度数是(A)A.55°B.45°C.35°D.65°3.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是(C)A.∠A=40°,∠B=50°B.∠A=40°,∠B=60°C.∠A=20°,∠B=80°D.∠A=40°,∠B=80°4.以下各组数为三角形的三条边长,其中是直角三角形的三条边长的是(B)A.2,3,4B.1,2, 3C.4,5,6D.2,2,45.如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是(A)A.HLB.ASAC.AASD.SAS6.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠CAD的度数为(A)A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为(C)A.30°B.45°C.60°D.75°8.如图,D是Rt△ABC的斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β,若α=10°,则β的度数是(B)A.40°B.50°C.60°D.不能确定9.如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,DE⊥AB,CD=3,则BD的长为(C)A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”,第一步应假设这个直角三角形中(D)A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是(B)A.AB=A′B′=5,BC=B′C′=3B.AB=B′C′=5,∠A=∠B′=40°C.AC=A′C′=5,BC=B′C′=3D.AC=A′C′=5,∠A=∠A′=40°12.观察下列命题的逆命题:①有两边相等的三角形是等腰三角形;②到角的两边的距离相等的点在这个角的平分线上;③直角三角形的两个锐角互余;④全等三角形的面积相等.其中逆命题为假命题的个数是(A)A.1B.2C.3D.413.如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC=60°,∠ACE=24°,那么∠BCE 的大小是(C)A.24°B.30°C.32°D.36°14.如图,直角三角形纸片的两直角边长分别为6,8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE∶S△BDE =(B)A.2∶5B.14∶25C.16∶25D.4∶2115.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是(D)A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB=150°D.∠APC=135°二、填空题(本大题共5个小题,每小题5分,共25分)16.在直角三角形中,其中一个锐角是22°,则另外一个锐角是68__°.17.如图,某失联客机从A地起飞,飞行1 000 km到达B地,再折返飞行1 000 km到达C地后在雷达上消失,已知∠ABC=60°,则失联客机消失时离起飞地A地的距离为1__000km.18.如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为7.19.如图,已知△ABC的周长是22,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,△ABC的面积是33.20.如图,在等腰△ABC 中,AB =AC ,∠BAC=54°,∠BAC 的平分线与AB 的垂直平分线交于点O ,点C 沿EF 折叠后与点O 重合,则∠OEC 的度数是108__°.三、解答题(本大题共7个小题,各题分值见题号后,共80分)21.(本题8分)一个机器零件的形状如图所示,在Rt △ABC 中,∠BAC=30°,BC =2.5 cm ,BD =13 cm ,AD =12 cm ,求△ABD 的面积.解:∵Rt△ABC 中,∠BAC =30°,BC =2.5 cm , ∴AB =2BC =5 cm. ∵52+122=132,即AB 2+AD 2=BD 2, ∴△AB D 是直角三角形.∴S △ABD =12AB·AD =12×5×12=30(cm 2).22.(本题8分)在加快城镇建设中,有两条公路OA 和OB 交会于O 点,在图中∠AOB 的内部有蔬菜基地C 和D ,现要修建一个蔬菜转运站P ,使转运站P 到两条公路OA ,OB 的距离相等,且到两个蔬菜基地C ,D 的距离也相等,用尺规作出蔬菜转运站P 的位置.(要求:不写作法,保留作图痕迹.)解:如图所示.23.(本题10分)如图,点P 为△ABC 的BC 边上一点,且PC =2PB ,∠AB C =45°,∠APC=60°,CD⊥AP,连接BD ,求∠ABD 的度数.解:∵∠APC =60 °,CD⊥AP,∴∠PCD =90 °-∠APC =90 °-60 °=30 °. ∴PC =2PD.∵PC =2PB ,∴PB =PD. ∴∠PBD =∠PDB.又∵∠APC =∠PBD +∠PDB,∴∠PBD =12∠APC =12×60 °=30 °.∵∠ABC =45 °,∴∠ABD =∠ABC -∠PBD =45 °-30 °=15 °.24.(本题12分)如图,∠AOB=60°,OC 平分∠AOB,C 为角平分线上一点,过点C 作CD⊥OC,垂足为C ,交OB 于点D ,CE∥OA 交OB 于点E.(1)判断△CED 的形状,并说明理由; (2)若OC =3,求CD 的长.解:(1)△CED 是等边三角形.理由如下:∵OC 平分∠AOB,∠AOB =60 °,∴∠AOC =∠COE =30 °. ∵CE∥OA,∴∠AOC =∠COE =∠OCE =30 °,∠CED =60 °. ∵CD⊥OC,∴∠OCD =90 °. ∴∠EDC =60 °.∴△CED 是等边三角形.(2)∵△CED 是等边三角形,∴C D =CE =ED. 又∵∠COE =∠OCE,∴OE =EC. ∴CD =ED =OE.设CD =x ,则OD =2x.在Rt△OCD 中,根据勾股定理得:x 2+9=4x 2,解得x = 3. 则CD = 3.25.(本题12分)如图,△ABC 的外角∠DAC 的平分线交BC 边的垂直平分线于点P ,PD⊥AB 于D ,PE⊥AC 于E. (1)求证:BD =CE ;(2)若AB =6 cm ,AC =10 cm ,求AD 的长.解:(1)证明:连接BP ,CP.∵点P 在BC 的垂直平分线上,∴BP =CP. ∵AP 是∠DAC 的平分线,∴DP =EP ,在Rt△BDP 和Rt△CEP 中,⎩⎪⎨⎪⎧BP =CP ,DP =EP ,∴Rt△BDP≌Rt△CEP (HL ),∴BD =CE.(2)在Rt△ADP 和Rt△AEP 中,⎩⎪⎨⎪⎧AP =AP ,DP =EP ,∴Rt△ADP≌Rt△AEP (HL ),∴AD =AE.∵AB =6 cm ,AC =10 cm ,∴6+AD =10-AE , 即6+AD =10-AD.解得AD =2 cm.26.(本题14分)如图,在△ABC 中,MP ,NO 分别垂直平分AB ,AC. (1)若BC =10 cm ,试求出△PAO 的周长;(2)若AB =AC ,∠BAC=110°,试求∠PAO 的度数;(3)在(2)中,若无AB =AC 的条件,你能求出∠PAO 的度数吗?若能,请求出来;若不能,请说明理由.解:(1)∵MP,NO 分别垂直平分AB ,AC , ∴AP =BP ,AO =CO.∴△PAO 的周长为AP +PO +AO =BO +PO +OC =BC. ∵BC =10 cm ,∴△PAO 的周长为10 cm.(2)∵AB =AC ,∠BAC =110 °,∴∠B =∠C =12×(180 °-110 °)=35 °.由(1)知AP =BP ,AO =CO.∴∠BAP =∠B =35 °,∠CAO =∠C =35 °.∴∠PAO =∠BAC -∠BAP -∠CAO =110 °-35 °-35 °=40 °. (3)能.理由如下:∵∠BAC =110 °,∴∠B +∠C =180 °-110 °=70 °. 由(1)知AP =BP ,AO =CO. ∴∠BAP =∠B,∠CAO =∠C.∴∠PAO =∠BAC -∠BAP -∠CAO =∠BAC -(∠B +∠C )=110 °-70 °=40 °.27.(本题16分)如图,△ABC 中,AB =BC =AC =12 cm ,现有两点M ,N 分别从点A ,B 同时出发,沿三角形的边运动,已知点M 的速度为1 cm /s ,点N 的速度为2 cm /s .当点N 第一次到达点B 时,M ,N 同时停止运动. (1)点M ,N 运动几秒后,M ,N 两点重合?(2)点M ,N 运动几秒后,可得到等边三角形△AMN?(3)当点M ,N 在BC 边上运动时,能否得到以MN 为底边的等腰三角形AMN ?如存在,请求出此时M ,N 运动的时间.解:(1)设点M ,N 运动x 秒后,M ,N 两点重合, x×1+12=2x ,解得x =12.(2)设点M ,N 运动t 秒后,可得到等边三角形△AMN,如图1, AM =t×1=t ,AN =AB -BN =12-2t.∵三角形△AMN 是等边三角形,∴t =12-2t ,解得t =4. ∴点M ,N 运动4秒后,可得到等边三角形△AMN.(3)当点M ,N 在BC 边上运动时,可以得到以MN 为底边的等腰三角形.由(1)知,12秒时M ,N 两点重合,恰好在C 处.如图2,假设△AMN 是以MN 为底边的等腰三角形,∴AN =AM.∴∠AMN =∠ANM.∴∠AMC =∠ANB .∵AB =BC =AC ,∴△ACB 是等边三角形.∴∠C =∠B.在△ACM 和△ABN 中,⎩⎪⎨⎪⎧∠C =∠B,∠AMC =∠ANB,AC =AB ,∴△ACM≌△ABN (AAS ).∴CM =BN.设当点M ,N 在BC 边上运动时,M ,N 运动的时间y 秒时,△AMN 是等腰三角形.∴CM =y -12,NB =36-2y ,由CM =NB ,得y -12=36-2y ,解得y =16.故假设成立.∴当点M ,N 在BC 边上运动时,能得到以MN 为底边的等腰三角形AMN ,此时M ,N 运动的时间为16秒.。
2024年数学八年级几何证明专项练习题1(含答案)

2024年数学八年级几何证明专项练习题1(含答案)试题部分一、选择题:1. 在三角形ABC中,若∠A = 90°,AB = 6cm,BC = 8cm,则AC 的长度为()。
A. 2cmB. 10cmC. 4cmD. 5cm2. 下列哪个条件不能判定两个三角形全等?()A. SASB. ASAC. AASD. AAA3. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个比例式是正确的?()A. 若a∥b,则∠1 = ∠2B. 若a∥b,则∠1 + ∠2 = 180°C. 若a⊥b,则∠1 = 90°D. 若a⊥b,则∠1 + ∠2 = 180°5. 在等腰三角形ABC中,若AB = AC,∠B = 70°,则∠C的度数为()。
A. 70°B. 40°C. 55°D. 110°6. 下列哪个条件可以判定两个角相等?()A. 对顶角B. 邻补角C. 内错角D. 同位角7. 在平行四边形ABCD中,若AD = 8cm,AB = 6cm,则对角线AC 的长度()。
A. 10cmB. 14cmC. 12cmD. 15cm8. 下列哪个图形是轴对称图形?()A. 等腰三角形B. 等边三角形C. 矩形D. 梯形9. 在三角形ABC中,若a = 8cm,b = 10cm,c = 12cm,则三角形ABC是()。
A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定10. 下列哪个条件不能判定两个直线平行?()A. 内错角相等B. 同位角相等C. 同旁内角互补D. 两直线垂直二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
()2. 在等腰三角形中,底角相等。
()3. 平行线的同位角相等,内错角相等。
()4. 若两个角的和为180°,则这两个角互为补角。
第十九章 几何证明数学八年级上册-单元测试卷-沪教版(含答案)

第十九章几何证明数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题,共计45分)1、如图,在四边形ABCD中,∠C=90°,E,F分别为AB,AD的中点,BC=2,CD=,则EF的长为()A. B. C. D.2、如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆。
设直线AB左边阴影部分的面积为1,直线AB右边阴影部分的面积和为S2,则( )A.S1=S2B.S1<S2C.S1>S2D.无法确定3、如果梯子的底端离建筑物5米,13米长的梯子可以达到该建筑物的高度是()A.12米B.13C.14米D.15米4、下列几组数中是勾股数的是()A. 、、1B.3,4,6C.5,12,13D.0.9,1.2,1.55、如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,①四边形ACED是平行四边形;②△BCE是等腰三角形;③四边形ACEB的周长是10+2 ;④四边形ACEB的面积是16.则以上结论正确的是()A.①②③B.①②④C.①③④D.②④6、如图,点,,,在上,是的一条弦,则().A. B. C. D.7、如图,在△ABC中,DE是边AC的垂直平分线,AE=5cm,△ABD的周长为26cm,则△ABC的周长为()A.29B.32C.36D.388、如图,在▱ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若▱ABCD的周长为20,则△CED的周长为( )A.5B.10C.15D.209、边长为7,24,25的△ABC内有一点P到三边的距离相等,则这个距离是()A.1B.3C.4D.610、如图,四边形,四边形,四边形都是正方形.则图中与相似的三角形为()A. B. C. D.11、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在()A.△ABC的三条中线的交点B.△ABC三边的中垂线的交点C.△ABC 三条高所在直线的交点D.△ABC三条角平分线的交点12、如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点.若的面积为4,,为上一动点,则的最小值为()A.无法确定B.4C.3D.213、如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为()A.6cmB.5cmC.4cmD.3cm14、如图,地面上有三个洞口A、B、C ,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在()A.△ ABC三边垂直平分线的交点B.△ ABC三条角平分线的交点C.△ ABC三条高所在直线的交点D.△ ABC三条中线的交点15、如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为()A. B.4 C. D.6二、填空题(共10题,共计30分)16、如图是一个长,宽,高的无盖的长方体的盒子,在盒子内壁离底的点处有一滴蜂蜜,此时一只蚂蚁正好在盒外壁、离盒子上沿与蜂蜜相对的点处,那么蚂蚁吃到蜂蜜的最短路程是________.17、如图,将矩形绕点旋转至矩形位置,此时的中点恰好与点重合,交于点.若=1,则矩形的面积为________.18、如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为________ cm.19、如图,在矩形中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交于点.若,,则矩形的对角线的长为________.20、如图,在△ABC中,DM、EN分别垂直平分AC和BC交AB于M、N,∠ACB=118°,则∠MCN的度数为________.21、在矩形中,对角线和相交于点O,过点B作的垂线,垂足为E,若,,则线段的长为________.22、如图,在ΔABC中,DE是AC的垂直平分线交BC于D,ΔABC与ΔABD的周长分别为18,12 ,则AE=________.23、如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为4m.则自动扶梯的垂直高度BD=________m.(结果保留根号)24、如图,矩形中,,点为上一点,将沿折叠得到,点为上一点,将沿折叠得到,且落在线段上,当时,则的长为________.25、如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC=________三、解答题(共5题,共计25分)26、如图,方格纸上每个小正方形的面积为1.⑴在方格纸上,以线段AB为边画正方形ABCD,并计算所画正方形ABCD的面积.⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A2B2C2D2,正方形的各个顶点都在方格纸的格点上.27、如图所示,在四边形ABCD中,AB=2 ,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.28、如图,△ABC中,AB=2,BC= ,AC= .分别以A,C为圆心,大于AC长为半径画弧,两弧分别交于点M,N.直线MN分别交AB,AC于点D,E.试求BD的长,29、如图,已知:大风把一颗大树刮断,折断的一端恰好落在地面上的A处,量得BC=3m,AC=4m,试计算这棵大树的高度.30、已知甲村和乙村靠近公路a、b,为了发展经济,甲乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:(1)到两村的距离相等;(2)到两条公路的距离相等.你能帮忙确定工厂的位置吗?参考答案一、单选题(共15题,共计45分)1、D2、A3、A4、C5、A6、D7、C8、B9、B10、B11、D12、D13、C14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)29、。
第十九章 几何证明数学八年级上册-单元测试卷-沪教版(含答案)

第十九章几何证明数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题,共计45分)1、如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为()A.50°B.70°C.75°D.80°2、下列线段的长不能构成直角三角形的是()A.5,12,13B.2,3,C.4,7,5D.1,,3、我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).,图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中,以点 B 为圆心,AB 为半径作 AC,再以CD 为直径作半圆交 AC 于点E,若边长AB=10,则△CDE 的面积为()A.20B.C.24D.4、如图,长方形 OABC 放在数轴上,OA=2,OC=1,以 A 为圆心,AC 长为半径画弧交数轴于 P 点,则 P 点表示的数为()A.2﹣B.﹣C.D.5、如图,在 Rt△ACB 中,∠C=90°, AD 平分∠CAB 交BC平D,DE ⊥AB 交AB于E,则下列结论中不正确的是( )A.BD +ED=BCB.DE 平分∠ADBC.AD 平分∠EDCD.ED+AC>AD6、下列各组数中,是勾股数的是()A.12,8,5B.3,4,5C.9,13,15D. ,,7、已知a,b,c为△ABC的三边长,且a4﹣b4+b2c2﹣a2c2=0,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形8、如图,△ABC中,∠C=Rt∠,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则BE的长为( )A. B. C. D.9、如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程的根,则平行四边形ABCD的周长为( )A. B. C. D.10、如图,有两棵树,一棵高12m,另一棵高4m,两树相距15m,一只鸟从一棵树的树梢飞到另一棵树的树梢,至少飞行()A.8mB.10mC.13mD.17m11、如图,在直角三角形中,是斜边上的中线,已知则的值是()A. B. C. D.12、如图,△ABC中,∠C=90°,ED垂直平分AB,若AC=12,EC=5,且△ACE的周长为30,则BE的长为()A.5B.10C.12D.1313、如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是()A.15B.15+5C.20D.15+514、下列命题中是假命题的是().A.同旁内角互补,两直线平行B.直线,则与相交所成的角为直角C.如果两个角互补,那么这两个角是一个锐角,一个钝角D.若,,那么15、如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为().A. B. C.4 D.6二、填空题(共10题,共计30分)16、一个三角形的三边长分别为6,8,10,则这个三角形最长边上的高是________.17、如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E是AB边上一点.将△CEB 沿直线CE折叠到△CEF,使点B与点F重合.当CF⊥AB时,线段EB的长为________.18、如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O 逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为________.19、如图,已知∠AOB=60°,点P在边OA上,OP=24,点M,N在边OB上,PM=PN,若NM=6,则OM=________.20、在△ABC中,∠C=90°,AC=6,CB=8,则△ABC面积为________,斜边为上的高为________.21、如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,EB=2,则⊙O的半径为________.22、在Rt△ABC中,∠C=90°,BC=6,AC=8,则cos B的值是________.23、某校在一块如图所示的三角形空地上种草皮以美化环境,已知AB=20m,BC=30m,∠B=150°,并且这种草皮每平方米元,则购买这种草皮至少要________元.24、如图,已知正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD 于点E,则BE的长为________.25、如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为________厘米.三、解答题(共5题,共计25分)26、在 Rt△ABC 中,∠C=90°,∠A、∠B、∠C 的对边分别为a、b、c.若a∶c=15∶17,b=24,求a.27、如图是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌的高CD (结果精确到0.1米,参考数据:≈1.41,≈1.73).28、如图,AD、BC垂直相交于点O,AB∥CD,又BC = 8,AD = 6,求:AB+CD的长.29、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求弦DC 的长.30、如图,在中,,,,,垂足为D,求BC,AD的长.参考答案一、单选题(共15题,共计45分)1、B2、C3、A5、B6、B7、D8、A9、A10、D11、C12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
初二下册几何证明练习题

初二下册几何证明练习题几何证明是初中数学中重要的一部分,通过练习证明题可以帮助学生更好地理解几何概念和性质。
本文将为初二下册的学生提供一些几何证明练习题,帮助他们提升证明能力。
一、线段垂直的证明1. 证明:如果两条线段互相垂直,则它们的斜率的乘积为-1。
解答:设线段AB的斜率为k1,线段CD的斜率为k2。
由于线段AB与线段CD互相垂直,所以它们的斜率的乘积为-1,即k1 * k2 = -1。
证明完毕。
二、三角形内角和为180度的证明2. 证明:三角形的内角和为180度。
解答:设三角形的三个内角分别为A、B、C。
我们可以通过将三角形分成两个小三角形来证明这个结论。
以三角形ABC的边AB为分割线,将三角形ABC分成两个小三角形ABD和ACD。
根据直线的性质可知,∠BAD + ∠DAC = 180度。
同时,由于∠BAD = ∠A,∠DAC = ∠C,所以∠A + ∠C = 180度。
再将三角形ABC的边BC为分割线,将三角形ABC分成两个小三角形BAC和BCD。
同理可得,∠B + ∠C = 180度。
由于∠A + ∠C = 180度,∠B + ∠C = 180度,所以∠A + ∠B + ∠C = 180度。
证明完毕。
三、垂直平分线的性质证明3. 证明:一个点到一条线段的垂直平分线的距离等于该点到线段两个端点的距离之差的一半。
解答:设点P在线段AB的垂直平分线上,点P到线段AB的距离为d,点P到A的距离为d1,点P到B的距离为d2。
我们可以通过计算证明d = (d1 - d2) / 2。
根据垂直平分线的性质可知,AP = BP,所以有d + d1 = d + d2。
两边同时减去d,得到d1 = d2。
再将d1 = d2代入d + d1 = d + d2中,得到d + d = 2d1。
两边同时除以2,即得到d = (d1 - d2) / 2。
证明完毕。
通过以上的几何证明练习题,希望可以帮助初二下册的学生巩固几何证明的知识,并提升他们的证明能力。
第十九章 几何证明数学八年级上册-单元测试卷-沪教版(含答案)

第十九章几何证明数学八年级上册-单元测试卷-沪教版(含答案)一、单选题(共15题,共计45分)1、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是()A. B.5 C.6 D.82、图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是()A.51B.49C.76D.无法确定3、如图,正方形网格中,网格线的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得为等腰三角形,则点C的个数有A.4个B.6个C.8个D.10个4、在Rt△ABC中,∠C=90°,AB=10.若以点C为圆心,CB为半径的圆恰好经过AB的中点D,则AC=()A.5B.C.D.65、如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,则FM的长为( )A.2B.C.D.16、如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B在对角线AC 上的点F处,连接DF.若点E , F , D在同一条直线上.给出以下结论:①△ADE≌△FCD;②;③;④当AE=1时,BE=,其中正确的结论共有().A.1个B.2个C.3个D.4个7、下列四组线段中,可以构成直角三角形的是()A.4,5,6B.1.5,2,2.5C.2,3,4D.1,, 38、如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于()A.2B.C.D.9、如图,在△ABC中,∠C=90°,AC=32,AB的垂直平分线MN交AC于点D,连接BD,若sin∠CBD=,则BC的长是()A.16B.8C.4D.810、图中四个阴影的三角形中与△ABC相似的是()A. B. C. D.11、若一个直角三角形的两边长分别为6和8,则第三边长是()A.10B.10或C.10或8D.12、如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE,点B的对应点D 恰好落在BC边上,若DE=2,∠B=60°,则CD的长为()A.0.5B.1.5C.D.113、三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是()A.等边三角形B.钝角三角形C.直角三角形D.锐角三角形14、如图,在正方形网格中,下列正方形网格中的阴影图形与相似的是()A. B. C. D.15、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是()A. B. C.2 D.二、填空题(共10题,共计30分)16、如图,在Rt△ABC中,∠C=90°,AC=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,,则BC边的长为________.17、如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4 ,则BC=________.18、如图,在中,为弦,半径于,如果,那么的半径为________.19、如图,AB∥CD,AC⊥BC,垂足为C.若∠A=40°,则∠BCD=________ 度.20、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是________.21、已知等腰三角形的周长为32.底边长为12,则这个等腰三角形的腰长为________.22、如图,在Rt△ABC中,∠ACB=90°,CA=CB,AD是△ABC的角平分线,过点D作DE ⊥AB于点E,若CD=1,则BD=________.23、如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为________.24、在中, ,的垂直平分线与所在的直线相交所得的钝角为,则等于________ 度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中八年级几何证明阶段性测试卷
(满分100分,限时100分钟)
一、 填空题(每小题3分,共24分)
1、“等腰三角形的两个底角相等”的逆命题是 。
2、已知ABC ∆中,8AB AC cm ==,DE 是AC 的垂直平分线,D 为垂足,DE 与AB 交
于点E ,若BC=6cm ,那么,BCE ∆的周长为 cm 。
3、 在ABC ∆中,AB=AC ,15B ∠=,AB=10,则ABC ∆的面积是 。
4、已知点A 的坐标为()3,5,点B 在x 轴上,且AB=13,那么点B 的坐标为 。
5、以AB 为斜边的直角三角形的直角顶点C
的轨迹
是 。
6、ABC ∆中,60A ∠=,AC=16,2203ABC S ∆=,则AB= 。
7、如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,
则阴影部分的面积和是 。
8、已知:在ABC ∆中,90C ∠=,30A ∠=,BD 平分CBA ∠,且交AC 于点D ,BC=1,那么AD= 。
二、选择题(每小题3分,共6分) 9、下面四个命题:
(1)平行四边形的四个内角之和为360;
(2)有两个内角相等的四边形是平行四边形; (3)平行四边形的四个内角中有两对是相等的; (4)四个内角中有两对相等的四边形是平行四边形; 其中正确的命题个数是( )
(A )4 (B )3 (C )2 (D )1
10、如图所示,点O 为ABC ∆的三条内角平分线的交点,过O 点做DE OA ⊥,与AB 、AC 分别相交于D 、E 两点,则DBO ∠与EOC ∠的大小关系是( ) (A )DBO ∠>EOC ∠ (B )DBO ∠=EOC ∠ (C )DBO ∠<EOC ∠ (D )DBO ∠≠EOC ∠
三、解答题(11—17每小题7分,18题10分,19题11分,共70分) 11、在直角坐标系中,有三点A ()30,、B (0,1)、C (-1,-2),试 判断ABC ∆的形状。
12、1.△ABC 中,∠BAC=2∠B ,AB=2AC ,AE 平分∠CAB 。
求证:AE=2CE 。
13、如图,已知:ABC ∆中,2C B ∠=∠,AH BC ⊥于点H ,D 是AC 的中点,DE AB , 求证:1
2
EH AC =
14、如图,已知:ABC ∆中,CE 交AB 于点E ,AF 平分BAC ∠交CE
于点F ,AD=AC
,连结DF 并延长交AC
于G ,求证:EF=GF
15、如图,已知:ABC ∆中,110BAC ∠=,DE 垂直平分AB ,FG 垂直平分AC ,E 、G 为垂足,求DAF ∠的度数。
16、如图,已知:DA=DB ,60DAC ∠=,1
902
DCA ACB ∠+∠=,求证:DA=AC+CB
17、如图:AB=AC ,AD ⊥BC 于D ,AF=FD ,AE ∥BC 且交BF 的延长线于E ,若AD=9,BC=12,求BE 的长。
18、如图,已知:ABC ∆中,BC=2AB ,AD 是BC 上的中线,AE 是ABD ∆的
中线,求证:AC =2 AE
19、如图,正方形ABCD中,点P为CD上一动点,AP与BC(或BC的延长线)交于E,交BD于M,点N为PE的中点,连结CM、CN。
(1)求证:CM CN
(2)若点P在DC的延长线上,其他条件不变,则上述
结论是否成立?画图并证明。
附:答案
一、 1、“有两个角相等的三角形是等腰三角形” 2、14 3、25 4、(-9,0)或(15,0)
5、以AB 为直径的圆(除去A 、B 两端点)
6、55
7、169
8、2
33
二、 9、C 10、B 三、
11、ABC 是等腰直角三角形 12、取AB 中点M ,连接EM
∵AE 平分∠CAB ∴CAB ∠=∠=∠2
1
21(角平分线意义)
∵∠BAC=2∠B ∴∠2=∠B ∴AE=EB ∴EM ⊥AB ∴∠EMA=90° ∵AB=2AC AB=2AM
∴AC=AM
在△ACE 与△AME 中⎪⎩
⎪
⎨⎧=∠=∠=AE AE AM AC 21
∴△ACE ≌△AME (SAS ) ∴∠EMA=∠C=90°
在Rt △ACB 中,∠1+∠2+∠B=90°
∵∠1=∠2=∠B ∴∠1=30°
∴AE CE 2
1
=
即AE=2CE 。
13、连结DH ,可证DH=DC ,从而有=22DHC C B DEH DEH EDH ∠∠=∠=∠=∠+∠
得DEH EDH ∠=∠ 故有:1
2EH DH AC
==
14、先证:ACF ADF ∆≅∆ 得出ACF ADF ∠=∠ CF=DF 又GFC EFD ∠=∠
可证:GFC EFD ∆≅∆ 即证:EF=GF 15、解:设DAF ∠等于x 度
则根据题意有
()2180B C x ∠+∠+= 110B C x ∠+∠+= 可得:40x =
16、延长AC 到E ,使得CE=CB ,连结DE
D C B D C A A C ∠=∠+∠ 1802A C B D C A
∠=-∠ 所以 DCB DCE ∠=∠
又 DC=DC CB=CE
所以 DCB DCE ∆≅∆ 则 DB=DE=DA 又 60DAC ∠= 所以DAE ∆是等边三角形 即DA=AE=AC+CB 即证
17、∵AD=9 ∴2
9
5.4===FD AF
∵BC=12 ∴BD=CD=6
∵∠BFD=∠EFA AF=FD ∠FDB=∠FAE=90° ∴△AFE ≌△DFB (ASA )
∴FE=FB
在Rt △BFD 中,2
153648122=+=
+=
DF BD BF ∴BE=2BF=15
18、延长AE 到F 使得EF=AE ,连结FD ,可证AFD ACD ∆≅∆ 得到AC=AF=2AE
19、证:(1)
由题意可证ADM CDM ∆≅∆ 得DAM DCM ∠=∠
由直线AD 与BE 平行 可得DAM E ∠=∠
又Rt PCE ∆中,N 为斜边PE 中点 所以:PN=NC=NE 则 NCE E ∠=∠ 即E NCE MCP ∠=∠=∠ 所以 90MCP PCN PCN NCE ∠+∠=∠+∠=
即:CM ⊥CN
(2)同理,可证点P 在DC 延长线上时,结论依然成立。
