矩阵论习题 4.3

合集下载

《矩阵论》习题答案,清华大学出版社,研究生教材习题 4.3

得 x1 1 82 ， x 2 1 136 ， x3 1 35 ， x 4 1 21 .
8. 解：（1） X (3.3,1.2,9) T ；（2） X (3,0.6,10.8) T .
9. 解： X (7.0,23,17) T .可见，当系数矩阵有微小误差（摄动）时，引起了解的较大变化）.
习题 4.3
1. 解： cond ( A) 1010 .
2. 解： cond ( A)1 cond ( A) 12011 .
1 3. 解： A 1
1 1 2 ， A

3 , max(3 , 2) 2,
11. 解：根据圆盘定理知， A 的特征值都在复数平面上的几个圆盘
Z aii Ri
1
(i 1,2, , ai ,i 1 a i ,i 1 ain .所以， A 的四个特征值都落在下列的四个盖尔圆的并集内：
Z 1 1 ； Z 1.5 1.5 ； Z 5 1 ； Z 5i 1 .
10．解：（1） X (1.11,0.228,1.95,0.797) T ；与真解相差较大. （2） X (0.988,1.42,0.428,2.10) T ；与（1）比较，相差较大.
2
（3） X (1.000,0.9995,1.0017,0.9990) T ；与真解靠得较近，说明运算时随着有效数字的增加（摄动减小），解的精度会增加.
是大的，有可能病态.
1
6. 解： H 41
120 240 140 16 120 1200 2700 1680 240 2700 6480 4200 140 1680 4200 2800

矩阵论复习题

矩阵论复习题矩阵论复习题矩阵论作为线性代数的重要分支，涉及到矩阵的性质、运算以及应用等方面。

在学习矩阵论的过程中，复习题是提高理解和巩固知识的重要工具。

本文将通过一些典型的矩阵论复习题，帮助读者回顾和加深对矩阵论的理解。

1. 矩阵的乘法性质与运算规则(1) 证明矩阵的乘法不满足交换律，即AB≠BA。

(2) 若矩阵A是m×n阶矩阵，矩阵B是n×p阶矩阵，证明矩阵乘法满足结合律，即(AB)C=A(BC)。

(3) 证明单位矩阵是矩阵乘法的单位元，即对于任意矩阵A，有AI=IA=A。

2. 矩阵的逆与行列式(1) 若矩阵A可逆，证明其逆矩阵唯一。

(2) 若矩阵A可逆，证明其逆矩阵也可逆，且逆矩阵的逆等于A。

(3) 若矩阵A可逆，证明其转置矩阵也可逆，且转置矩阵的逆等于A的逆的转置。

(4) 证明若矩阵A可逆，则其行列式不为零，即|A|≠0。

3. 矩阵的特征值与特征向量(1) 若矩阵A的特征值为λ，证明矩阵A-λI的行列式为零，即|A-λI|=0。

(2) 若矩阵A的特征向量为v，证明对于任意非零实数k，kv也是矩阵A的特征向量。

(3) 若矩阵A的特征向量v1和v2对应于不同的特征值λ1和λ2，证明v1和v2线性无关。

(4) 若矩阵A的特征向量v对应于特征值λ，证明对于任意正整数n，(A^n)v对应于特征值λ^n。

4. 矩阵的相似与对角化(1) 若矩阵A与矩阵B相似，证明矩阵B与矩阵A相似。

(2) 若矩阵A与矩阵B相似，矩阵B可对角化，证明矩阵A也可对角化。

(3) 若矩阵A可对角化，证明A的特征向量组成的矩阵P可逆，且A=PDP^-1，其中D为对角矩阵。

通过复习以上的矩阵论题目，可以加深对矩阵的性质、运算规则、逆与行列式、特征值与特征向量以及相似与对角化的理解。

同时，通过解题的过程，还可以提高解决问题的能力和运用矩阵论知识的技巧。

希望读者能够充分利用这些复习题，巩固所学的矩阵论知识，为进一步深入学习打下坚实的基础。

矩阵论(华中科技大学)课后习题答案

习题一1.判断下列集合对指定的运算是否构成R 上的线性空间（1）11{()|0}nij n n iii V A a a⨯====∑，对矩阵加法和数乘运算；（2）2{|,}n n T V A A R A A ⨯=∈=-，对矩阵加法和数乘运算；（3）33V R =；对3R 中向量加法和如下定义的数乘向量：3,,0R k R k αα∀∈∈=；（4）4{()|()0}V f x f x =≥，通常的函数加法与数乘运算。

解：（1）、（2）为R 上线性空间（3）不是，由线性空间定义，对0α∀≠有1α=α，而题（3）中10α= （4）不是，若k<0，则()0kf x ≤，数乘不满足封闭性。

2.求线性空间{|}n nT V A R A A ⨯=∈=的维数和一组基。

解：一组基10001010101010000000100..................0010010⎧⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎩⎪⎪⎪⎪⎭dim W =n (n +1)/23.如果U 1和U 2都是线性空间V 的子空间，若dim U 1=dim U 2，而且12U U ⊆，证明：U 1=U 2。

证明：因为dim U 1=dim U 2，故设{}12,,,r ααα为空间U 1的一组基，{}12,,,r βββ为空间U 2的一组基2U γ∀∈，有()12r X γγβββ=而()()1212r r C αααβββ=，C 为过渡矩阵，且可逆于是()()()11212121r r r X C X Y U γγγγβββαααααα-===∈由此，得21U U ⊆又由题设12U U ⊆，证得U 1=U 2。

矩阵论试题及答案

一．（10分）已知n n C ⨯中的两种范数a ⋅和b ⋅，对于n n C A ⨯∈，证明b a A A A +=是n n C ⨯中的范数. 解：⑴非负性：由于b a ⋅⋅,是两种范数，故当A=0时，0,0==b a A A ，所以000=+=+=b a A A A ；当A ≠0时，0,0>>b a A A ，所以0>+=b a A A A⑵齐性：()A A A A A A A A b a b a b a ααααααα=+=+=+= ⑶三角不等式：B A B A B A B A B A B A b b a a b a +=+++≤+++=+二．(每小题10分,共20分)已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=101121103A ,()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=002t e t b , 1. 求At e2. 用矩阵函数方法求微分方程()()()()()⎪⎩⎪⎨⎧-=+=T x t b t Ax t x dt d1,0,10的解.解：1. ()1112113det ----=-λλλλA I ()()3211132-=----=λλλλ显然, )det(A I -λ的一阶子式的公因子为1, 容易知道)det(A I -λ 的二阶子式的公因子为2-λ,所以A的最小多项式为()()()23222-=--=λλλλm ,即()()022=-=I A A m ,设()()()b a g m e f t ++==λλλλλ,则()a te f t =='λλ 对于特征值2=λ有()()⎩⎨⎧=='+==a te f b a e f t t 22222,()⎩⎨⎧+-==ttet b te a 2212 所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----+=+=t t t t t t e bI aA e t At1010122. ()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+=⎰⎰--ds e s s s ss s e e ds s b e x e t x s t s At t As At 001010110102020 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=t t e t e t At 1001012三．(15分)用Givens 变换求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2100421132403100A 的QR 分解. 解：()T01001=β,构造()s c T ,13=,1101sin ,0100cos 22232132223211=+=+===+=+==xx x s x x x c θθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=210031002340421121421132403100100000010010010013A T⎥⎦⎤⎢⎣⎡--=21312A , 构造),(12s c T , ()21sin ,21111cos 222122222211=+==-=+--=+==x x x s x x x c θθ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡---=1052212131111121212A T⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=2/1002/12/1002/10010010013122T T I T ,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-==2/12/100000100102/12/100TT Q ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2/12/522344211R四．(10分)用Gerschgorin 定理证明⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=8110260110410100A 至少有两个实特征值. 解：A 的4个盖尔圆为:{}1|1≤=z z G ,{}2114|2=+≤-=z z G , {}3216|3=+≤-=z z G , {}2118|4=+≤-=z z G ,它们构成的两个连通部分为11G S =,4322G G G S =.易见,1S ,2S 都关于实轴对称且各含有1个和3个特征值,因为实矩阵的复特征值必成对出现, 故1S ,2S 必各含有一个实特征值,从而A 至少含有2个实特征值.五．(20分)已知⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=221221*********A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=44111b 1. 求A 的满秩分解.2. 求+A3. 用广义逆矩阵的方法判别方程组b Ax =是否相容.4. 求方程组b Ax =的极小范数解或极小范数最小二乘解并指出所求解的类型.解 1。

研究生矩阵理论课后答案4,5章习题

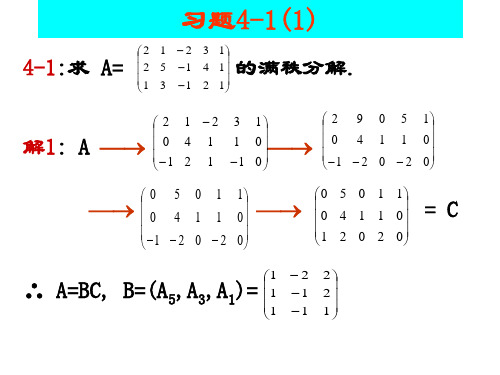
2 1 − 2 3 1 0 4 1 1 0 −1 2 1 −1 0
0 5 0 1 1 0 4 1 1 0 −1 −2 0 −2 0
→
1 1 1 −2 −1 −1
0 5 0 1 1 0 4 1 1 0 1 2 0 2 0
同一向量的三种范数之间的大小关系习题#5-4:对n维线性空间的任意向量x成习题#5维线性空间的任意向量x #5
‖x‖∞ ≤‖x‖2 ≤‖x‖1 ≤ n‖x‖∞ ≤ n‖x‖2 ≤ n‖x‖1 ≤ n2‖x‖∞ ≤ …
立
证: |,…,|x ‖x‖∞= max{|x1|, ,|xn|} ≤(Σi=1n|xi|2)1/2 = ‖x‖2 |+…+|x ≤((|x1|+ +|xn|)2)1/2 = ‖x‖1 |,…,|x ≤ n max{|x1|, ,|xn|} = n‖x‖∞
习题#5是正定矩阵,x ,x∈ 习题#5-6A∈Cn×n是正定矩阵,x∈Cn #5
是向量范数. •证明:‖x‖=(x*Ax)1/2 是向量范数. 证明:‖x‖=(x
解1:因A是正定Hermite矩阵A,故存在可逆矩阵B 是正定Hermite矩阵A,故存在可逆矩阵B Hermite矩阵A,故存在可逆矩阵使得A=B B.则的上述表示式可写为: 使得A=B*B.则x的上述表示式可写为: (Bx)) ‖x‖=(x*Ax)1/2 =((Bx)*(Bx))1/2 =‖Bx‖2 其中‖‖ 是向量2 范数.再注意可逆矩阵B 其中‖‖2 是向量2-范数.再注意可逆矩阵B的性 Bx=0,即可直接推出非负性即可直接推出非负性. 质:x=0 ⇔ Bx=0,即可直接推出非负性. ‖kx‖=‖B(kx)‖2=|k|‖Bx‖2=|k|‖x‖ 推出齐次性;三角不等式则由下式推出: 推出齐次性;三角不等式则由下式推出: ‖x+y‖=‖B(x+y)‖2≤‖Bx‖2+‖By‖2

矩阵论习题答案

自测题一一、解：因为齐次方程0211211=++x x x 的基础解系为T T T )1,0,0,0(,)0,1,0,1(,)0,0,1,1(321=-=-=ααα，所以V 的一组基为⎥⎦⎤⎢⎣⎡-=00111A ，⎥⎦⎤⎢⎣⎡-=01012A ，⎥⎦⎤⎢⎣⎡=10003A ，显然A 1，A 2，A 3线性无关.V a a a a A ∈⎥⎦⎤⎢⎣⎡=∀22211211，有211211a a a --=，于是有 322221112A a A a A a A ++=，即A 可由A 1，A 2，A 3线性表示，故A 1，A 2，A 3为V 的一组基；且dimV=3.二、解：（1）R V X X ∈∈∀λ,.21，有21212122112211(2211)(X X X X X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+⎥⎦⎤⎢⎣⎡=+）=+)(1X )(2X,λλλλ=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=11122112211)(X XX )(1X .又因任意两个二阶方阵的乘积、和仍为二阶方阵，故V V '=，即为从V 到V （自身）的线性算子，所以为线性变换.（2）先求的自然基22211211,,,E E E E 下的矩阵A ：2221121111020020100012211)(E E E E E +++=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=2221121112200)(E E E E E +++=2221121121020)(E E E E E +++=2221121122200)(E E E E E +++=故⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2020020210100101A . 显然, 从自然基到所给基4321,,,E E E E 的过渡过阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000110011101111C ；⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=-10001100011000111C , 所以在4321,,,E E E E 下的矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----==-40200202231201011AC C B .三、解：（1）不是内积. 因为)(,A A tr A A +=)(2)(22211a a A tr +==并不一定大于零.（2）因为1),(10==⎰dt te g f t ,⎰===1021231)(),(dt t f f f ,⎰-===1212212)21()(),(e dt e g g g t,g f g f ⋅≤),( ,即212)21(311-⋅≤e .四、解：（1）2)2)(1(--=-λλλA I ，2,1321===λλλ.行列式因子：1,1,)2)(1(1223==--=D D D λλ ; 不变因子：2321)2)(1()(,1)()(--===λλλλλd d d ; 初等因子：2)2(),1(--λλ .（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2121~21J JJ A ; （3）对T X A I )1,1,0(0)(,1111==-=ξλ得;T X A I )1,0,1(0)2(,2222==-=ξλ得.再求22=λ的一个广义特征向量：由23)2(X X A I -=-得T )1,1,1(3=ξ .取⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-111110111,1111011101P P , :,)(则令SinA A f =[][]⎥⎦⎤⎢⎣⎡===2sin 02cos 2sin )(,1sin )()(22111λλλJ f f J f , 故12211)])([)],([(sin -⋅=P J f J f Pdiag A λλ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1111101112sin 2cos 2sin 1sin 111101110⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+----+=2cos 1sin 1sin 2cos 1sin 2cos 2sin 2sin 1sin 1sin 2sin 1sin 2sin 2cos 2cos 2sin 2cos .五、解：（1）130143014,83,3014max max 31<=⎭⎬⎫⎩⎨⎧==∑=∞j ij ia A ，故0lim =∞→k k A ；（2）∑∞=0k k x 的收敛半径为1，而1<∞A 若在其收敛域内，故∑∞=0k kA绝对收敛，且∑∞=--=01)(k k A I A .六、解：（1）6,5,15,511====∞∞m m A A A A ；又因为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-322232223511A ，571=∞-A . 所以7557)(1=⨯==∞∞-∞A A A cond ；1,5,)1)(5(3212-===+-=-λλλλλλA I .故5lim )(==i iA λρ. （2）因为031221,0121≠-==∆≠=∆，故可分解. （3）-+-r B B B ,,均可取1-B .七、证：设T n T n y y y Y x x x X ),,,(,),,,(2121 ==分别为在两组基下的坐标，则CY X =，当Y X =时有：θ=-X C I )(，则0=-C I ，故C 有特征值1.反之，由于1是过渡过阵C 的一个特征值，设其对应的特征向量为X ，即X CX ⋅=1，由坐标变换公式知，在基1β，2β，n β, 下的坐标CX Y =，故有X Y =.八、证： A 对称正定，∴存在正交矩阵C ，使D diag AC C n T ==),,,(21λλλ其中特征值）n i i ,,2,1(0 =>λ.对θ≠∀X ，有CX Y =，使DY Y y y y AX X T n n T =+++=2222211λλλ ,其中θ≠y .令n nn z y z y z y λλλ1,,1,1222111===.于是θλλλ≠=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=Z BZ Z Y n ,11121故Z Z Z DB B Z DY Y T T T T ==)(. 而)(P B C PZ BZ C Y C X T T T ====令，所以Z Z Z AP P Z AX X DY Y T T T T T ===)(.因Z 的任意性，知I AP P T =，即A 与I 相合.自测题二一、解：I a A a I A I A k k k k k k λλλ===,,,I a a a A a A a A a I a n n k n )(102210λλ+++=++++∀ ,其中R a a a n n ∈+++λλ 10，故取V 的基为I ，1dim =V .二、解：（1）从基2,,1x x 到基22,,1x x x x ++的过渡矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110011001C ，所以在新基下的坐标为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--0111011C .（2）不是线性变换.因为≠++++++=+),,2()(33221121111b a b a b a b b a a βα+)(α)(β.（3）不是内积. 如0341212121<-=-==），），（，（），，（α，不具有非负性.三、解：（1）利用Schmidt 正交化方法，得T e )1,1,1(1=，T e )1,0,1(2-=，T e )61,31,61(3-=.（2）从321,,ααα到321,,e e e 的过渡阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=610021103421C ， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-6003102211C ，故所求⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--==-00000034211AC C B .四、解：（1）由于A 实对称，所以存在正交阵Q ，使⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=∧=n AQ Q T21. 故2)1+=∧==n n AQ Q A F F T F （；n A =)('ρ；n A =2；n A cond =2)(；1)(21=-mA .（2）取⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=000000111A ，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=111 α，得n aA n A ===212,1,α,即有212ααA A >.五、解：（1）3)1(201335212+=+-+---=-λλλλλA I ；1321-===λλλ. 33)1()(+=λλD ，所以,不变因子为3321)1()(,1)()(+===λλλλd d d ；初等因子为3)1(+λ. 故A 的Jordan标准形⎪⎪⎪⎭⎫ ⎝⎛=100110011J .（2）cos A 的Jordan标准形为：J =⎪⎪⎪⎪⎪⎭⎫⎝⎛------)1cos(00)1sin()1cos(0)1cos(21)1sin()1cos(.六、证：（1）因173.01<=A ；故;0lim =∞→kk A（2）因A 有范数小于1，故∑∞=0k k A 绝对收敛；且其和的形式为1)(--A I .七、解：⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--=00032103101~230121121A ；取⎪⎪⎪⎭⎫ ⎝⎛--=302121B ，⎪⎪⎪⎪⎭⎫ ⎝⎛=32103101C ；则有BC A =（最大秩分解）；1)()(12==λλD DT T B B B B 1)(-+=, 1)(-+=T T CC C C ,则 +++=B C A ，所以,方程b AX =的极小范数最小二乘解为b A X +=.八、证：（1）因为A C A AC C A n T 2)1(,=-=-所以，则有,0)1(2>-=n C n 必为偶数.（2）设T n x x x X X AX ],,,[,21 ==λ的分量中绝对值最大者为kx ，则X AX λ=的第k 个方程∑==nj jkj k x a x 1λ；∑∑==≤=nj jkjnj j kj k x a x a x 11λ；∑∑==<≤≤nj nj kj kj kja x x a 111λ，故有1<λ.自测题三一、解：（1）不是. 设B B A A T T -==,，则)(T T B A B A -=+=T T B A B A )()(+≠-（一般情况下），又)()(B A B A B A T +-≠-=+（一般情况下），即V B A ∈+.（2）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++=+++∀001)(111010 n n n n d a d a a D a D a I a⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++++100)(10 n n n n d a d a a ，故得一组基为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100,,001 ，且n V =dim .二、解：（1）123)(22++=x x x,12)(+=x x, 43)1(+=x,在基1,,2x x 下的矩阵为：⎪⎪⎪⎭⎫⎝⎛=411322003A .（2）)5)(1)(3(411322003---=-------=-λλλλλλλA I ,可见矩阵A 有三个不同的单根1，3，5，故 A 可以对角化，即可以对角化.（3）设度量矩阵33)(⨯=ij C C ，则⎰⎰====1010213124114151C dx x C dx x C , ⎰⎰=====1102223121331,31dx x C C dx x C ,⎰⎰=====10331032231,21dx C xdx C C . 故⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=12131213141314151C .三、解：设3322113)(ααααx x x ++=，使得)(1α，)(2α，)(3α是标准正交的.∵)(1α，)(2α已标准正交化，∴（)(1α，)(2α）=（)(2α，)(3α）=0，)(3α=1，即得⎪⎩⎪⎨⎧=++=+-=-+1022022232221321321x x x x x x x x x ；解得：32,32,31321==-=x x x ；即()().22313213αααα++-=.因为)(1α，)(2α，)(3α为标准正交基，且把标准正交基变为标准正交基，故为正交变换, 它在基321,,ααα下的矩阵表示为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=32321323132313232A .四、解：由自测题一中第四题（2）知A 的Jordan 标准形为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2121J ，相似变换矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111101110T . 由T ）321321,,(),,(αααβββ=，求得3V 的一组基为3213312321,,αααβααβααβ++=+=+=，则在该基下的矩阵为J .五、证：当0=X 时，000===F F X α；当θ≠X 时，0≠T X α ;从而0>=FTX X α. ,C k ∈∀FT FTX k kx kX αα()(===X k X k FT=α,FTFTFT T FTY X Y X Y X Y X ααααα+≤+=+=+)(=Y X +，因此 , X 是向量范数. 又因为FT T FTA X AX AX )()(αα==X AA X FFTFT=≤α，因此 , F A 与X 相容.六、解：)6(2-=-λλλA I ，特征根为0,6321===λλλ；则6)(=A ρ.由于A A 62=，故A 可以对角化, 即存在可逆矩阵C ，使1006-⎪⎪⎪⎭⎫⎝⎛=C C A ；1001)(-⎪⎪⎪⎭⎫ ⎝⎛=C C A Aρ. 故得.61001001lim )(lim 11A C C C C A A kk kk =⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛--∞→∞→ρ七、证：⇒设1)(<A ρ，取0)](1[21>-=A ρε，对于矩阵A ，存在矩阵范数⋅，使121)()(<+=+≤A e A A ερ. 1)(<≤⇐A A ρ便得证.八、证：（1）1-====AB B A B A B A T T , 同理，有1-==T T T B A AB .（2）B A B A B A B A B A T T +=+=+--)(11=AB ()AB B A T -=+，得2即有,0=+B A 0=+B A .自测题四一、解：（1）21111011201010011)(E E E E E T +=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=+=，21222011200110101)(E E E E E T+=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=+=，33332200010001000)(E E E E T=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+=，所以在E 1，E 2，E 3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200011011A . (2) 设有一组基321,,e e e ，从E 1 ,E 2 ,E 3到e 1 ,e 2 ,e 3的过渡矩阵设为C ,即C E E E e e e ),,(),,(321321=再设A 在e 1 ,e 2 ,e 3下的矩阵为B ,则AC C B 1-=.要使B 为对角阵，即找一个可逆矩阵C ，使AC C 1-为对角阵. 因为2)2(211011-=-----=-λλλλλλA I ,对0=λ，求得特征向量()T 0,1,1-，对λ=2，求得两个线性无关的特征向量()T 0,1,1，T )1,0,0(.令⎪⎪⎪⎭⎫ ⎝⎛-=100011011C ，得⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-10002121021211C ，则AC C B 1-=为对角阵. 由()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100011011,,,,321321E E E e e e ，可得⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=+-=011001010011211E E e⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=+=011201010011212E E e ⎥⎦⎤⎢⎣⎡==100033E e .二、证：易得()()()122111,,,1,αααααα==0=，()()()()()(),1,,0,,,1,,0,,332332221331======αααααααααααα即11)(α=e ，22)(α=e ，33)(α=e 也是标准正交基，故是正交变换.三、解：（1）令T Y )0,,0,,(21 ηξ=，由Y HX =，知X HX Y ==；取 Y X YX Y X X Y X X --=--=0η ； Y YY 10=，构造初等反射矩阵 T I H ηη2-=，则有Y Y X HX ==0.（2）)3)(5(16)1(12812--=--=--=-λλλλλλA I . 因此3,521==λλ，所以5m ax)(==i iA λρ；因为65)(<=A ρ，故矩阵幂级数收敛.四、解：由正交矩阵行（列）向量组标准正交，得12122=+⎪⎭⎫⎝⎛a12122=+⎪⎭⎫ ⎝⎛b 02=+bc a四组解是：⎪⎪⎪⎩⎪⎪⎪⎨⎧-===212121c b a ，⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==212121c b a ，⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=212121c b a ，⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=-=212121c b a .五、解： (1){}∑====31162,4,6m ax m axi ijja A ；{}∑=∞===3153,4,5m ax m ax j ij ia A;{}9max =⋅=∞ij m a n A.因为()()221--=-λλλA I ，2,1321===λλλ , 故2m ax )(==i iA λρ.（2） 031≠=∆，0521132≠==∆，故可以进行LU 分解 .（3）易得2)(,3)(==B R A R ，所以6)(=⊗B A R ，B 的特征根为2,121==μμ，故B A ⊗的特征根为4,2,4,2,2,1231322122111======μλμλμλμλμλμλ.2)(B A ⊗的特征根为：1，4，4，16，4，16.（4）∵02≠=B ∴B 可逆，且⎥⎦⎤⎢⎣⎡-=-1032211B ，所以-+-r B B B ,,均可取为：⎥⎦⎤⎢⎣⎡-=-1032211B . （5）A 的Jordan标准形为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2121J . （6）对应于11=λ的特征向量T )11,0(，，对应于22=λ的线性无关的特征向量只有一个T )1,0,1(，再求一个广义特征向量T )1,1,1(. 令TT ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111101110，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-1111101111T . 令 AA f 1)(=，则1))((11=λJ f ；⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=214121)((22λJ f . 12211))(),(()(-⋅⋅=T J J diay T A f λλ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111110111210041210001111101110⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=53322211141.六、解：（1）由X AX λ=，即0)(=-X I A λ，若λ不是A 的特征根，则0≠-I A λ，所以0)(=-X I A λ只有零解，故0dim =λV .若λ是A 的特征根，则0=-IA λ，所以0)(=-X I A λ有非零解.设r I A R =-)(λ，则r n V -=λdim .（2）设T I A ωω2-= 其中ω为单位向量1=ωωT .则)2)(2(2T T I I A ωωωω--=T T T T w I ωωωωωωωω422+--=I I T T =+-=ωωωω44.七、证：（1）设()由于二,0≠∈m R X 次型()()0≥==AX AX AX A X BX X TT T T ，所以B 为半正定矩阵.（2）当A 的列向量组线性无关时，若X ≠0，则AX ≠0，故())(AX AX BX X T T =>0 ，即A 为正定矩阵.八、证：（1）λ为非奇异，λ为A 的特征值，故λ≠0 ，而λ1为1-A 的特征值，据特征值上界原理, 有11-≤A λ，即11-≥Aλ. (2) 对0≠∀X ，由已知有BXA X XB A A 11)(--+=+BXA X 1--≥XB A X 1--≥XB A )1(1--=由已知11-<AB , 即11<-A B ,故知0≠∀X , 0)1()(11>-≥+--X B A X B A A ；即对0≠∀X , 有0)(1≠+-X B A A ，即0)(1=+-X B A A 无非零解.故0)(11≠+=+--B A A B A A , 从而0≠+B A ，即A +B 可逆.自测题五一、解：(1) 在V 1中，⎪⎪⎭⎫⎝⎛+-=⎪⎪⎭⎫ ⎝⎛=4324324321x x x x x x x xx x A ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=100101010011432x x x . 令⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=1001,0101,0011321E E E , 因321,,E E E 线性无关，由定义知，它们是1V 的基，且3dim 1=V .(2)[]212，BB L V = 因为21,B B 线性无关； 2dim 2=V .),,,,(2132121B B E E E L V V =+在22⨯R 的标准基下，将21321,,,,B B E E E 对应的坐标向量21321,,,,ββααα排成矩阵, 并做初等变换⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫⎝⎛--=10000031000111001111~13100020102000101111),,,,(21321ββααα，可见4)dim(21=+V V .由维数定理145)dim (dim dim )dim (212121=-=+-+=V V V V V V .二、解：(1) 因为，过渡阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111111C ，且⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-111111C ，所以α在α1，α2，α3下的坐标为=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-3211a a a C ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23121a a a a a .（2）设,21λλV V X ∈则有()X X A 1λ=与()X X A 2λ=，两式相减得()021=-X λλ，由于21λλ≠，所在地只有X=0，故[]0dim 21=λλV V .三、解：取[]3X P 中的简单基,,,,132x x x 由于)1(=,12x-,)(3x x x -=221)(x x +=, 33)(x x x +-= ,则在1，x ，32,x x 下的矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=1010010110100101A . A 的特征值为：2,04321====λλλλ , 相应的特征向量为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1010,0101,1010,0101. 令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=Λ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=2200,1010010110100101C , 则Λ=-AC C 1. 再由()()C x x x f f f f 324321,,,1,,,= , 求得[]3x P 中另一组基：()34233221)(,1)()(,1x x x f x x f x x x f x x f -=-=+=+=，.四、解： (1) ⎰⎰⎪⎪⎭⎫⎝⎛=-1101dt dt de Adt e AtAt)(1I e A A -=-.(2)当j i ≠时0)(=j i εε；故度量矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=n A 21.五、解：（1）,9,1,3,3121====∞m T XX XXX3,4,3===∞∞X X XX XX T m T FT .（2）)1()(23+=λλλD ，易得1)()(12==λλD D . ∴ 不变因子)1()(,1)()(2321+===λλλλλd d d ；初等因子)1(,2+λλ.A 的Jordan标准形为：⎪⎪⎪⎭⎫⎝⎛-=100000010J .六、解：（1）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000001101101112101101011行变换A ，令⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=01101101,211011C B ，则 A=BC . 其中B 为列最大秩矩阵， C 为行最大秩矩阵 .（2）⎥⎦⎤⎢⎣⎡--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==--+121033312111016332)(11TT B B B B ，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎪⎭⎫⎝⎛-==--+1221311251211301111001)(11T T CC C C ，所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-==+++14527533014515112103312213112151B C A .（3）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----==+10111501515151413145275330145151b A X .七、证明提示：类似习题4.1第16题（1）的证明.八、证明：AC A B A ++=⇒因为两边左乘矩阵A ，有C A AA B A AA )()(++=,故 AB=AC .AC AB =⇐因为，设+A 为A 的加号定则，两边左乘+A ，有AC A AB A ++=.自测题六一、解：（1）当V x x x x X ∈⎪⎭⎫⎝⎛=22211211时，由02112=+x x 得⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=011010000001212211X X X X .取 ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=0110,1000,0001321E E E , 因线性无关，则它们是V的一个基.（2）⎪⎪⎭⎫⎝⎛-=-=0110)(111B E E B E T T ；⎪⎪⎭⎫ ⎝⎛=-=0000)(222B E E B E TT ；⎪⎪⎭⎫ ⎝⎛-=-=0220)(333B E E B E TT ；故在基321,,E E E 下的矩阵为：⎪⎪⎪⎭⎫⎝⎛-=201000000A .（3）将A对角化，取⎪⎪⎪⎭⎫ ⎝⎛=110001020C 使⎪⎪⎪⎭⎫⎝⎛=-2001AC C ；设所求基为321,,Y Y Y ，有：()()C E E E Y Y Y 321321,,,,=.得⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛=0110,0112,1000321Y Y Y ，则在基321,,Y Y Y 下的矩阵为对角形.二、解： (1))1(4963752542-=---+---=-λλλλλλA I,A 的特征根1,0321===λλλ；行列式因子)1()(23-=λλλD ，易得1)()(12==λλD D ；不变因子)1()(1)()(2321-===λλλλλd d d ；初等因子1,2-λλ.(2) A 的Jordan 标准形为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100000010J ；(3) ∵01621511,0121≠-=--=∆≠-=∆；∴ A 能进行LU 分解.三、解：（1）.13214,1010,00022322122⎥⎦⎤⎢⎣⎡+=⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=-t t t dt dA t dt dA dt A d .（2）⎥⎦⎤⎢⎣⎡=00032121312x x dX df .四、解：(1) 由)(21I B A +=,得I A A I A B I A B +-=-=-=44)2(,2222,显然, 当且仅当I B =2时，有A A =2.(2) 因B A B BA AB A B BA AB A B A +=+++=+++=+222)(,得,0=+BA AB 即,BA AB -=两端右乘B 得BAB AB -=2, 从而AB B AB )(-=,由于幂等阵B 的任意性，故0=AB .五、解： (1)∵ m x x x 21两两正交的单位向量.∴)(21m x x x A =为列满秩矩阵,故T T T A A A A A ==-+1)(. （2）∵⎪⎭⎫ ⎝⎛=101k A k ，且∑∞=-12)1(k k k与∑∞=-1)1(k kk 都收敛；∴ ∑∞=-12)1(k kk A k 收敛.（3）∵ 762+-=-λλλA I ，而)2()52)(76(37291912222234++++-=+-+-λλλλλλλλ；由于0762=+-I A A ；∴原式⎪⎭⎫⎝⎛-=+=-3217231)2(1I A . （4）∵ A 的特征根为n)2,1(，，i i =；B 的特征根为m )21(，，，j j =λ；∴B A ⊗的特征根为j i λn;2,1(，，i =m)21，，，j =.六、证： (1) 当0=A 时，设A 的最大秩分解为A=BC.则 C B C B B C B C B A A D ~=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛= . 而[]()H HHH B BB B B B B 1~-+⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛=()[][]++-==B B B BB B H HH21211.[]++++++⋅==B B C B C D 21~[]++=A A 21.当A =0时上式也成立.(2) 经计算A a a a A )(2321213++-= . 于是A A a a a AXA =++-=-31232221)(，A a a a X 1232221)(-++-=是A 的一个减号逆.(3)()I e e e e e e A A A A AT A TA A T ===-=-,..,所以因为.故A e 为正交矩阵.七、证：(1) 设R V n ∈∀∈μλβα,,,,，则00),()(ααμβλαμβλαμβλα+++=+k)),(()),((0000ααββμααααλk k +++==λ)(α+μ)(β.所以是线性变换.(2)是正交变换),(),(αααα=⇔T T ,即 ),(),(),(),(2),(0020220αααααααααα=++k k ,得[]0),(2),(0020=+ααααk k .由n V ∈α的任意性，上式等价于0),(20=+ααk ,所以22200212),(2n k +++=-= αα .八、证：由舒尔定理知，存在西矩阵U 及上三角矩阵()ij r R =，使得R AU U H =，因此有H H H R U A U =，从而得H H H RR U AA U =.又因为()()()H H H H RR tr U AA U tr AA tr ==, ①由于R 主对角线上的元素都是A 的特征值，故由①式得2112121ij nj ni ij ni i ni r r ∑∑∑∑====≤=λ, ②而②式端是R 的Frobenius 范数的平方，又因在酉相似（即R AU U H =）下矩阵的F 范数不变，所以211211ij ni ni ijni n i a r ∑∑∑∑=====③综合②、③两式便得到所需证的不等式.又不等式②取等号当用仅当i≠j 时都有0=ij r ，即A 酉相似于能角形矩阵，也就是A 为正规矩阵.自测题七一、解：（1）由02421=-+a a a ，得基础解系)0,0,1,2(1-=α，)0,1,0,0(2=α，)1,0,0,1(3=α；所以V 1的一组基为321,,ααα，且3dim 1=V .因为),(),,(2132121ββαααL L V V +=+),,,,(21321ββαααL =，易知1321,,,βααα是21321,,,,ββααα的一个极大无关组，故4)dim (21=+V V ，21V V +的一组基为1321,,,βααα.（2）251433221121,ββξαααξξk k k k k V V +=++=⇔∈∀ .所以025********=--++ββαααk k k k k . 解此方程组得），，133,2,2(),,,,(54321---=k k k k k . 所以21V V 的一组基为)3,2,21---=，（ξ，且1)dim (21=V V .二、解：（1）211111)(cE aE E +=221212)(cE aE E +=211121)(dE bE E +=221222)(dE bE E +=即⎪⎪⎪⎪⎪⎭⎫⎝⎛=d cd c b a b aE E E E E E E E 00000000),,,(),,,(2221121122211211，故A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡d cd c b a b a000000; (2) 由,B A AB +=得到I I B A AB B A AB =+--=--,0 ,即I I B I A =--))((,显然I A -与I B -均为阶可逆方阵，于是有I I A I B =--))((,即I I B A BA =+--,亦即0=--B A BA , 故B A BA +=,从而AB BA =.三、解：（1）)2()1(2320110012λλλλλλ--=---=-E A ，)2()1()(23λλλ--=D ，1)(2=λD ，1)(1=λD .)2()1()()()(,1)()()(,1)(22331221λλλλλλλλλ--=====D D d D D d d ，所以初等因子为：λλ--2,)1(2.A 的Jordan标准形为⎪⎪⎪⎭⎫ ⎝⎛200010011.（2）()n I A tr dAd=. （3）两边求导数，利用,At AtAe e dtd =且,0Ie = 得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=133131113A .四、解：（1）∑==iij ja A 5m ax 1；∑==∞jij ia A 5m ax .（2）122212221---------=-λλλλA I )5()1(2-+=λλ ,5,1321=-==λλλ；故5m ax )(==i iA λρ；⎪⎪⎭⎫ ⎝⎛--=-3122411B ，故∞-∞∞⋅=1)(B B B cond 54145=⨯⨯=. （3）2,3==rankB rankA ；623)(=⨯=⊗B A rank .)4)(1(26521232--=-+-=----=-λλλλλλλB I ，所以4,121==λλ，故B A ⊗的特征值为：20,4,4,5,1,1'6'5'4'3'2'1=-=-==-=-=λλλλλλ（4） ∵0≠A ，1-A 存在，∴ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===--+-3222322235112221222111A A A .五、解：（1）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000032102101~321043211111A ， BC A =⎥⎦⎤⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32102101102111. （2）∵ 2=rankA ；2):(=b A rank ；∴ b AX =相容.（3）∵⎪⎪⎪⎭⎫ ⎝⎛=142062*********T AA ；⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---==--21103001052152011070)(T T m AA A A ， ∴ 极小范数解⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==-1234101b A X m.六、解：（1）0max≠=x P A 2121022maxmax--≠≠===PAP yy PAP PXPAX XAX x x PP .（2）A 的4个盖尔圆为它们构成的两个连通部分为11G S =， G G G S 322=4.易见，1S 与S 2都关于实轴对称.由于实矩阵的复特征值必成共轭出现，所以S 1中含A 的一个实特征值，而S 2中至少含A 的一个实特征值.因此A 至少有两个实特征值.七．证：（1）设为正交变换，λ为的特征值 , 则有()0()≠=αλαα，),(αα=()(α,)(α)),(),(2ααλλαλα==.∵),(>αα, ∴12=λ,故1±=λ；（2）设λ为的任一特征根，α为的属于λ的一个特征向量，即0,)(≠=αλαα，则1,11)(2,1222-=⇒=⇒==λλααλα.记11=λ的特征子空间为,1V 12-=λ的特征子空间为1-V .对V ∈∀α有=α(+α)(α) 2 + (-α)(α) 2 ，而 (+α)(α) 2∈,1V (-α)(α) 2 ∈1-V ，所以11-+=V V V . 又 ⇒∈∀-11V V α,)(αα=且,)(αα-=；得αα-=，即0=α，故11-⊕=V V V .自测题八{}{}{}{},28,36,24,14321≤-=≤-=≤-=≤=g g G g g G g g G g g G一、解：(1)在已知基)(),(),(321t f t f t f 下的矩阵为：⎪⎪⎪⎭⎫ ⎝⎛------=111323221A ;(2) (⎪⎪⎪⎭⎫ ⎝⎛=321),,1())(2t t t f ；基2,,1t t 且到基)(),(),(321t f t f t f 的过渡矩阵为：⎪⎪⎪⎭⎫ ⎝⎛=101110102C ；则21321234321))(),(,)(())((t t C t f t f t f t f -+-=⎪⎪⎪⎭⎫ ⎝⎛=-.(3) 设度量矩阵33)(⨯=ij d D , 则⎰⎰=====10121121121,11tdt d d dt d ； ⎰⎰=====1012222311331,31dt t d dt t d d ； ⎰⎰=====1014333322351,41dt t d dt t d d ；故⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=51413141312131211D .二、解：(1) 令矩阵,3)(I A A f -=若A 的特征值为λ,则)(A f 的特征值是3)(-=λλf ,故)(A f n 的个特征值为32)2(,,3)6(,1)4(,1)2(-===-=n n f f f f .从而))32(531(3)(-⋅⋅-=-=n I A A f .(2) 2)1)(2(224023638--=+-+---=-λλλλλλA I ；特征根为1,2321===λλλ.行列式因子：23)1)(2()(--=λλλD ，1)()(12==λλD D ; 不变因子：2321)1)(2()(;1)()(--===λλλλλd d d ；初等因子： 2)1(),2(--λλ；故A 的Jordan标准形为⎪⎪⎪⎭⎫⎝⎛=100110002J .三、解：（1）由于A 实对称，所以易求得非奇异矩阵P ，使Λ=-AP P 1，其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=Λ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=2200,1001011001101001P ,于是12211-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=P e e P e t t At=12111000011--⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡P P e P P t =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+--+-+t t ttttt te ee e e e e e 2222222210101100110100121. (2) X ()()Tt t At e e X e t ⎪⎪⎭⎫ ⎝⎛-==22,0,0,0.四、解：（1）6=∞A ；2)4)(2(224)4(31213232-+=--=--=-λλλλλλλλλA I ；特征根为4,2321==-=λλλ；则 4)(=A ρ.（2）2)3(,3)(==R A R∴ 6)(=⊗B A R ；B 的特征根3,421==μμ，∴ B A ⊗的全部特征根为：-8，-6，16，16，12，12. （3）∵⎪⎪⎪⎪⎭⎫ ⎝⎛-=-310125411B ，∴ +-B B l ,可取1-B .五、解：α1()T 4,0,3=，构造⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=3040504035113R ，113140430735A A R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=. 同理，构造R A R R =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=5135165735,3404300055112323.令()==T R R Q 2313⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---012202015012161551, 则A=QR.六、证：（1）∵ A 为对称正定矩阵， ∴≠∀α有：>Aα，当且仅当0≠α时，有0=Aα；对R R ∈∀有：A T AkAk k αααα==；βββαααβαβαβαA A A T T T A++=++=+),(2)()(AAAAβαβα+=+≤2)(, （2）∵ IAA AA AA A A T T T T ==--11))(())((；∴1)(-T T AA A 是A 的右逆.（3）因为1-=A ，且A 为正交矩阵，所以有T T T A I A A I A A AA A I )()(+=+=+=+,则 AI A I A A I T +-=+=+)(，即 0=+A I .故A 一定有特征根-1.七、证：()(),1111A a a A I f n n n n -++++=-=--λλλλλ 因为由()0=A f 得()01111=-++++--I A A a A a A nn n n ,即A ()()I A I a A a A n n n n 112111+----=+++ ,故()()I a A a AAA n n n 12111111--++-+++-=.自测题九一、解：不是. 如取α=（1，2），β=（3，4），()().,4,3,2,1αββααββα⊕≠⊕=⊕=⊕则有.二、解：（1）令⎥⎦⎤⎢⎣⎡--=1111A ，则V X AX X ∈=,)(.V Y X ∈∀,，P k ∈∀，则=+=+)()(Y X A YX )(X +)(Y ，kkX =)()(X ，所以是线性变换. （2）⎥⎦⎤⎢⎣⎡-==0101)(1111AE E ，⎥⎦⎤⎢⎣⎡-==1010)(1212AE E ，⎥⎦⎤⎢⎣⎡-==0101)(2121AE E，⎥⎦⎤⎢⎣⎡-==1010)(2222AE E ，设在基22211211,,,E E E E 下的矩阵为B ，则⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=1010010110100101B . （3）令),,,(4321ββββ=B 其中i β为B 的列向量，由于2)(=B rank ，且21,ββ是4321,,,ββββ的一个极大线性无关组, 所以dim2)(=V ，且),()(21B B L V =，其中⎥⎦⎤⎢⎣⎡-==0101),,,(1222112111βE E E E B ，⎥⎦⎤⎢⎣⎡-==1010),,,(2222112112βE E E E B ，且21,B B 为)(V 的一组基，得dimKer =4-dim (V)=2.令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡00004321x x x x B ，得基础解系⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010,010121ξξ. 记 ⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡==1010),,,(,0101),,,(22221121141222112113ξξE E E E B E E E E B , 则ker),(43B B L =，且43,B B 为Ker的一组基.三、解：非负性.A=0时，A 0,0,0,0;0,0,0〉=〉≠===A A A A A A bHa bHa 从而时从而.相容性. 设A ，B ∈C n n ⨯，则有()()().B A BBAA AB BAAB AB AB bHabHa bHbHaa bHa ⋅=++≤+≤+=同样可验证齐次性与三角不等式.在此A 是矩阵范数.四、解：（1）FG A ，A =⎥⎦⎤⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−→−11101101412101000011101101行. （2）⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--==--+303241012120663)(11TT T F F F F F . ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡==--+11111001313003)(11TT T G GG G G .⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--==+++54131473032410361F G A . （3）b b AA b A T =-=++,)1,1,0,1(，故b AX =有解，极小范数解为T b A X )1,1,0,1(0-==+.五、解：（1）因2,3==rankB rankA ，得623)()()(=⨯=⋅=⊗B rank A rank B A rank .令0)2)(7(=+-=-λλλB I ，特征值2,721-==μμ.所以B A ⊗的所有特征值为：4,14,14,2,7,7161514321=-=-=-='='='λλλλλλ；10976)14()2(3232-=-⋅-==⊗B A B A .（2）∵ B 的特征值2,721-==λλ，∴I B B B f 3)(2+-=的特征值453772'1=+-=λ；113)2()2(2'2=+---=λ.六、解：,11120013221111⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-e ββ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=122212221312,111311111T I H ωωω 令,1102003131⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= A H ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⋅-⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=-⎥⎦⎤⎢⎣⎡=1101110210,11201221e A ββ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=-=⎥⎦⎤⎢⎣⎡-=2011,01102,1121122222A H I H Tωωω 所以取QR A R H H Q =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=得211313,21212222131121.七、证：（1）令),,(11-=n L W αα ，其中11,,-n αα 线性无关.通过标准正交化，将11,,-n αα 变为W 的一个标准正交基11,,-n ηη .由已知可得1,,2,10,-=>=<n i i ηα;因而11,,-n ηη ，α线性无关.把α单位化，令ααη||1=n ，于是{}n n ηηη--,,,11 与{}n n ηηη,,,11- 均为V 的标准正交基.同时，由题设,1,,2,1,)(-==n i i i ηη，而n n ηη-=)(，则把标准正交基{}n n ηηη,,,11- 变为标准正交基，故为正交变换. （2）因为为正交变换，（n ααα,,,21 ）=（n ααα,,,21 ）A ，所以A 为正交矩阵.又 A 的所有特征值n λλλ,,,21 都为实数，故有,T T AA I A A ==即A 为实的正规矩阵，从而存在正交矩阵Q ，使得Λ=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321λλλAQ Q T , 则A =()A Q Q Q Q A Q Q Y TT T T =Λ=Λ=Λ,，即A 为实对称矩阵，故A是对称变换.八、证：（1）设A 的特征根是n λλ,,1 ，令λλ-=1)(f ，则AI A f -=)(的特征根是,1,,11n λλ-- 由题设i λ-1〈1，n i ,,1 =，故,111 --i λ即20 i λ，因此,,,,1,20n i i =λ进而n n 2||||01<<λλ ，然而n d A λλ 1||==，故n n d 2|,|||01<=<λλ .（2）设A 的三个特征根为321,,λλλ，则32132312123213)()(||)(λλλλλλλλλλλλλλλλλ-+++++-=-=A I f ，由于A 是奇数阶正交方阵，且1||=A ，易证奇数维欧氏空间中的旋转变换一定有特征值1，因此不妨设11=λ，则1||32321===A λλλλλ，于是323231213211λλλλλλλλλλλ++=++=++，从而1||)(23-+-=-=λλλλλt t A I f .其中321λλ++=t 为实数（因32,λλ或均为实数或为一对共轭复数）.又由于正交方阵的特征根的模为1.故有22,)(32323232≤+≤-+≤+≤+-λλλλλλλλ,所以31132≤++≤-λλ，即31≤≤-t .由哈密顿－凯莱定理知：023=-+-I tA tA A .自测题十一、解：（1）因为,2=rankA 求得θ=AX 的基础解系()(),9,0,21,2,0,9,24,121T T -=-=ξξ即为V 的一组基，且dimV =2.(2) 设A 为P 上任一n 阶方阵，则)(21T A A +为对称阵，)(21T A A -为反对称阵，且A=)(21T A A ++)(21T A A -，得21V V P n n +=⨯. 又若21V V B ∈∀ , 则有T B B =, 且T B B -=, 从而θ=B , 则{}θ=21V V , 故21V V P n n ⊕=⨯.二、解：（1）∈∀ξ⇒-)(1θθξ=)(.设ξ在基4321,,,εεεε下的坐标为),,,(4321x x x x，则(ξ)在基4321,,,εεεε下的坐标为⎪⎪⎪⎪⎭⎫⎝⎛4321x x x x A .且(ξ)θ=及⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0004321x x x x A , 其中 ⎪⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎪⎭⎫⎝⎛--------=00000000101001011111111111111111A . 得基础解系⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛1010,0101；取)(1θ-中两个线性无关的解向量⎩⎨⎧+=+=422311εεξεεξ, 所以),()(211ξξθL =-，dim2)(1=-θ.（2）由于)(1θ-中有一组基1ξ,2ξ，所以取432121,,,,,εεεεξξ，易知4321,,,εεξξ线性无关，则4321,,,εεξξ构成V 的一组基.设由基4321,,,εεεε到基4321,,,εεξξ的过渡矩阵为C ，则⎪⎪⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎪⎪⎭⎫⎝⎛=-101001010010001,10100101001000011＝C C , 所以在4321,,,εεξξ下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛----=-22002200110011001AC C .三、解：（1）先由rankA=n ，即A 的列向量组线性无关，证A T A 是正定矩阵（见自测题四中第七题），再由习题2-1第7题知，R n 构成一个欧氏空间.（2）令C=A T A =（c ij ），()ij j i j i c C ==εεεε,所以自然基在该内积定义下的度量矩阵为C=A T A.四、（1）证：∵A 是幂收敛的，∴()()B A A A B n n n ===22lim lim lim .（2）解：令⎪⎪⎭⎫ ⎝⎛-==014112B A ，1212<⇒-=-λλλB I , ∴B 是幂收敛.∴原级数和为()⎪⎪⎭⎫⎝⎛-=--04141B I . （3）解：设A的最大秩分解式为：⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛===10010110012AI FG A ,则⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==1002011001010101A A F F H H .显然()⎪⎪⎭⎫⎝⎛==⎪⎪⎭⎫⎝⎛=--1001)(,10021211I GG F F HH,.0102102101010110021)()(1111⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==----+F F F F GG G A H H H五、解：令⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛----=7610,122121211142b A , ⎪⎪⎪⎪⎭⎫⎝⎛----=+561651224112331A ，。

矩阵论试题参考答案(2011年)

从而
cos Atdt
0
1
3t sin t 3t sin t cos t 2sin1 3cos1 3sin1 3cos1 dt . 0 3t sin t 3t sin t cos t 3sin1 3cos1 4sin1 3cos1
A b 0,
故 A 0． 2） C, A C 3） A, B C
n n
n n
，
A
A a A b
2
2

2
Aa
2
2
Ab A ．
2
，记 x
A a B a , y A B , 则 A x 2 , b b
k k k
证法 3．由 A A 可得：k 1 有 A A ，故 lim A A 0 ，因而 A 不是收敛矩阵，从而 A 1, 三、(20 分) 设 A
A a A 1 .
4 3 ． 3 2
1.(6 分) 求
dF x x1 T ，其中 x ， F x x A ； T dx x2

的实轴上， G1 , G2 , G3 的半径依次为
'
'
'
2 3 17 1 3 11 1 2 17 ' ' . , R2 2 , R3 2 2 3 4 12 2 4 16 2 3 36 综合前面的结论可知 A 的 3 个特征值所在的 3 个实数区间分别为
从而 A 只有实特征值，它们分别位于 A 的 3 个 1 知 A 的每个盖尔圆中只有 A 的一个特征值，盖尔圆的实轴上，由此得到 A 的 3 个特征值所在的 3 个实数区间分别为

矩阵论及其应用习题四答案

矩阵论及其应用习题四答案矩阵论及其应用习题四答案矩阵论是数学中重要的分支之一，它研究的是矩阵的性质、运算规律以及在各个学科中的应用。

在学习矩阵论的过程中，习题是不可或缺的一部分，通过解答习题可以加深对矩阵理论的理解和应用。

下面是习题四的答案，希望能对大家的学习有所帮助。

1. 设A、B、C为同阶矩阵，证明：(AB)C=A(BC)解答：我们需要证明(AB)C的每个元素与A(BC)的对应元素相等。

设(AB)C的第i行第j列元素为x，A的第i行第k列元素为a，B的第k行第j列元素为b，C的第k行第j列元素为c。

则有：x = Σ(ai * bk * cj)，其中i、j、k为矩阵元素的下标。

而A(BC)的第i行第j列元素为y，可表示为：y = Σ(ai * bk * cj)，其中i、j、k为矩阵元素的下标。

由于x和y的表达式相同，所以(AB)C=A(BC)。

2. 设A为m×n矩阵，B为n×m矩阵，证明：(AB)A=A。

解答：我们需要证明(AB)A的每个元素与A的对应元素相等。

设(AB)A的第i行第j列元素为x，A的第i行第k列元素为a，B的第k行第j列元素为b。

则有：x = Σ(ai * bk * ak)，其中i、j、k为矩阵元素的下标。

而A的第i行第j列元素为y，可表示为：y = Σ(ai * bk * ak)，其中i、j、k为矩阵元素的下标。

由于x和y的表达式相同，所以(AB)A=A。

3. 设A为m×n矩阵，B为n×m矩阵，证明：(AB)B=B。

解答：我们需要证明(AB)B的每个元素与B的对应元素相等。

设(AB)B的第i行第j列元素为x，A的第i行第k列元素为a，B的第k行第j列元素为b。

则有：x = Σ(ak * bi * bj)，其中i、j、k为矩阵元素的下标。

而B的第i行第j列元素为y，可表示为：y = Σ(ak * bi * bj)，其中i、j、k为矩阵元素的下标。

矩阵论的习题集

其中 aij = a ji = 1, (1 ≤ i ≤ n,1 ≤ j ≤ i ) ，其它元素为 0。 ′, ε 2 ′ ,ε3 ′,ε 4 ′ ] = [ε 1 , ε 2 , ε 3 , ε 4 ] A ，可得 6、[解]由 [ε 1 1 0 −1 ′, ε 2 ′ ,ε 3 ′ ,ε 4 ′] = A = [ε 1 , ε 2 , ε 3 , ε 4 ] [ε 1 0 0 1 0 0 0 1 0 2 = 0 0 1 0 0 0 0 3 0 4 0 1 1 2 2 1 0 3 2 1 2 0 4 1 3 2 2 = 3 1 4 1 1 0 3 1 0 2 0 0 1 1 0 2 0 0 1 0 0 0 0 2
2
3、对于 ∀B, C ∈ V 和 ∀λ ∈ F ，满足 BA = AB ， CA = AC ，并且 A( B + C ) = AB + AC = BA + CA = ( B + C ) A ， A( µB) = µAB = µBA = (µB ) A ，即 B + C ∈ V ， µB ∈ V ，从而由第 1.2 节定理 1 可知，V 是 F n×n 的子空间。满足 trB = 0 ，并且 tr ( B + C ) = trB + trC = 0 ， 4、对于 ∀B, C ∈ V 和 ∀λ ∈ R ， trC = 0 ， tr (λB) = λ tr ( B) = 0 ，从而由第 1.2 节定理 1 可知，V 是 R 2×2 的子空间。 1 0 0 1 0 0 dim V = 3 ，并且 V 的一组基为， 0 − 1 和。 0 0 1 0 5 、对于 ∀B, C ∈ V 和 ∀λ ∈ R ，满足 B = B T ， C = C T ，并且 ( B + C ) T = B T + C T = B + C ， (λB) T = λB T = λB ，从而由第 1.2 节定理 1 可知， V 是 R n×n 的子空间。 dim V = n(n + 1) ，并且 V 的一组基为 Vij = (a ij ) n×n ， 2

矩阵理论习题解答等材料

西南科技大学研究生试题单（B 卷）(2014级高等工程数学A)第一部分矩阵理论（共32分）1、(8分)填空题（1）每个n 阶矩阵都相似于一个矩阵。

（2）n nA C⨯∈，A 为正规矩阵的充要条件是A 对角形矩阵。

（3）正交变换在规范正交基下的矩阵是矩阵。

（4）A 的最小多项式 A 的零化多项式。

2、(6分) 求4R 的子空间1234123412341234{(,,,)|0},{(,,,)|0}V a a a a a a a a W a a a a a a a a =-+-==+++=的交V W I 的一组基。

3、(8分) 已知111111,012A -⎛⎫ ⎪= ⎪ ⎪-⎝⎭计算5432()2822g A A A A A E =-++-。

4、（10分）求矩阵213121242A -⎛⎫⎪= ⎪ ⎪⎝⎭的Doolittle 分解和LDU 分解。

第二部分数值分析（共36分）5、 (4分）解答下列各题设函数2015201420131()5.2015!f x x x x =++,求差商0120142015[2,2,2,2]?f =L 6、（8分）设函数4()f x x =，不直接用拉格朗日插值公式，而用拉格朗日余项公式求出以1,0,1,2x =-为插值节点的三次插值多项式3().L x7、（8分）设有求积公式2120()(0)(1)(2)f x dx af a f a f ≈++⎰试确定系数012,,a a a 使上述公式的代数精度尽量高，且指出其代数精度。

8、（8分）已知方程组123123123102212100.51.931x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩ (1) 构造Jacobi 迭代法的迭代格式，迭代格式是否收敛？说明理由； (2) 取(0)(0,0,0)T x=，用上述迭代法来计算一步迭代值(保留小数点后4位)。

9、（8分）若求解初值问题为24,015(0)1x y y x y y ⎧'=-≤≤⎪⎨⎪=⎩，试写出Euler 方法求解的迭代格式(0.2)h =,并计算(0.2),(0.4)y y 的值(保留小数点后至少8位)。

矩阵理论第4章习题解答 (2)

矩阵理论第四章习题解答1. 习题1问题描述已知矩阵A和B定义如下：A = [1, 2, 3][4, 5, 6][7, 8, 9]B = [9, 8, 7][6, 5, 4][3, 2, 1]求矩阵C = A + B。

解答我们可以直接对A和B对应位置的元素进行相加，得到矩阵C。

A +B = [1+9, 2+8, 3+7][4+6, 5+5, 6+4][7+3, 8+2, 9+1]计算结果为：[10, 10, 10][10, 10, 10]2. 习题2问题描述已知矩阵A和B定义如下：A = [1, 2, 3][4, 5, 6][7, 8, 9]B = [9, 8, 7][6, 5, 4][3, 2, 1]求矩阵D = A - B。

解答我们可以直接对A和B对应位置的元素进行相减，得到矩阵D。

A -B = [1-9, 2-8, 3-7][4-6, 5-5, 6-4][7-3, 8-2, 9-1]计算结果为：[-2, 0, 2][4, 6, 8]3. 习题3问题描述已知矩阵A和B定义如下：A = [1, 2, 3][4, 5, 6][7, 8, 9]B = [2, 0, 1][1, 2, 1][0, 1, 2]求矩阵E = A * B。

解答我们可以通过矩阵乘法的定义来计算E。

矩阵乘法的定义为：矩阵C的第i行第j列的元素等于矩阵A的第i行与矩阵B的第j列对应元素的乘积之和。

对于矩阵A和B，可以计算得到矩阵E。

E = [1*2+2*1+3*0, 1*0+2*2+3*1, 1*1+2*1+3*2][4*2+5*1+6*0, 4*0+5*2+6*1, 4*1+5*1+6*2][7*2+8*1+9*0, 7*0+8*2+9*1, 7*1+8*1+9*2]计算结果为：E = [4, 7, 8][10, 13, 16][16, 19, 22]4. 习题4问题描述已知矩阵A定义如下：A = [1, 2, 3][4, 5, 6][7, 8, 9]求矩阵F = A^T，其中A^T表示A的转置矩阵。

研究生矩阵论课后习题答案(全)习题四

习题四1．求下列微分方程组的通解（1）⎪⎩⎪⎨⎧+=+=;34,2212211x x dt dxx x dt dx （2）⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-+=+=. ,3233212321,x x dt dx x x x dt dxx x dt dx解：(1)设,3421⎪⎪⎭⎫⎝⎛=A ⎪⎪⎭⎫⎝⎛=21x x x ,则原方程组可写为 Ax dtdx=，矩阵A 的特征方程为0)1)(5(3421=+-=----=-λλλλλA I ，则矩阵A 的特征值为51=λ,12-=λ,求得矩阵A 的特征向量分别为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛11,21,令⎥⎦⎤⎢⎣⎡-=1211P ,则⎥⎦⎤⎢⎣⎡-=-1211311P ,有 Λ=⎥⎦⎤⎢⎣⎡-=-10051AP P ,1-Λ=P P A , 则⎥⎦⎤⎢⎣⎡+--+=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-==------Λt t tt t t tt t t t Ate e e e e e e e e e PPe e55555122231121100121131. 故该方程组的通解为⎪⎪⎭⎫⎝⎛--+-++=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡+--+==------t t t t t t ttt t tt At e c c e c c e c c e c c c c e e e e e e e e c e x )2()22()2()(31222312152121521215555其中21,c c 为任意常数.(2)设,110111110⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=A ⎪⎪⎪⎭⎫⎝⎛=321x x x x ,则原方程可写为Ax dtdx=，矩阵A 的特征方程为0)1(2=-=-λλλA I ，则矩阵A 的特征值为01=λ,132==λλ.A 的属于特征值01=λ的特征向量为⎪⎪⎪⎭⎫ ⎝⎛-=1121η,由方程组⎩⎨⎧+==32322ηηηηηA A 解得A 的属于特征值132==λλ的广义特征向量为⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=111,10132ηη.令[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==111101112,,321ηηηP ,则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1113121011P ,有11,100110000--==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=PJP A J AP P ,由于⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t t tJt e te e e 000001, 则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==-1113121010000011111011121t t tJt At e te e P Pe e ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+--+-+-+-=t t tt t tt tt t t tt te e te te e e e e te e te te e 21111222,故方程组的通解为⎪⎪⎪⎭⎫⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+--+-+-+-==32121111222c c c te e te te e e e e te e te te e c e x t t tt t tt tt t t tt At ,其中321,,c c c 为任意常数.2．求微分方程组Ax dtdx=满足初始条件ξ=)0(x 的解：（1）⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=33,3421ξA ，（2）⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=001,102111121ξA .解:(1)由第1题知⎥⎦⎤⎢⎣⎡+--+=----t t t tt t tt Ate e e e e e e e e555522231,故微分方程组Ax dtdx=满足初始条件ξ=)0(x 的解为 ⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+--+==------t t t t t t ttt t tt Ate e e e e e e e e e e e e x 555555423322231ξ. (2)矩阵A 的特征方程为0)1)(3(2=+-=-λλλA I ,故矩阵A 的特征值为31=λ,132-==λλ.A 的属于特征值31=λ的特征向量为⎪⎪⎪⎭⎫ ⎝⎛=2121η,由方程组⎩⎨⎧-=-=32322ηηηηηA A 解得A 的属于特征值132-==λλ的广义特征向量为⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=021,21232ηη,令[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==022211122,,321ηηηP ,则⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=-24025122312811P,有 11,100110003--==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=PJP A J AP P ,又 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=---t t t t Jt e te e e e 000003, 故微分方程组Ax dtdx=满足初始条件ξ=)0(x 的解为 ξξ1-==P Pe e x Jt At ⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=---00124025*******000022211122813t t t te te e e⎪⎪⎪⎭⎫⎝⎛--+=---t t tt t t e e e e e e 44224481333. 3．求)(t Bu Ax dtdx+=满足条件ξ=)0(x 的解：（1）⎪⎪⎭⎫ ⎝⎛==⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛=-21,)(,41,3421c c e t u B A tξ （2）⎪⎪⎪⎭⎫⎝⎛-==⎪⎪⎪⎭⎫ ⎝⎛=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=101,1)(,262,0061011016ξt u B A解:(1)由第1题知⎥⎦⎤⎢⎣⎡+--+=----t t t tt t t t Ate e e e e e e e e555522231, 则⎪⎪⎭⎫⎝⎛--+-++=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡+--+=------t t t t t t ttt t tt Ate c c e c c e c c e c c c c e e e e e e e e e )2()22()2()(31222312152121521215555ξ,⎪⎪⎭⎫⎝⎛++-=⎪⎪⎭⎫⎝⎛-⎥⎦⎤⎢⎣⎡+--+=------------------v t t v t t v v v t v t v t v t v t v t v t v t v t A e e e e e e e e e e e e e e v Bu e6565)()(5)()(5)()(5)()(5)(6636314222231)(故 ⎥⎥⎦⎤⎢⎢⎣⎡+-+--=-----⎰t t t t t ttv t A e e te e e te dv v Bu e 550)(62121631)( 则该方程组的解为⎪⎪⎪⎪⎭⎫⎝⎛++--++---+++=+=-----⎰t t t t t t tv t A At te e c c e c c te e c c e c c dv v Bu e e t x 2])12()122[(312])212()21[(31)()(21521215210)(ξ(2)矩阵A 的特征方程为0)3)(2)(1(=+++=-λλλλA I ,则A 的特征值为11-=λ,3,232-=-=λλ,求得其特征向量分别为⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=231,341,651321ηηη.令⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-139********,2363451111P P ,有 11,300020001--==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=PJP A J AP P ,又 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=---t t t Jt e e e e 32000000, 则ξξ1-=P Pe e Jt At ⎪⎪⎪⎭⎫⎝⎛-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=---101139248111000002363451112132t t te e e ⎪⎪⎪⎭⎫ ⎝⎛+-+-+-=------t t tt t t e e e e e e 32323289121243 , ⎪⎪⎪⎭⎫ ⎝⎛++-++-++-=⎪⎪⎪⎭⎫ ⎝⎛=---------------------)(3)(2)()(3)(2)()(3)(2)(1)()(2663852262)(v t v t v t v t v t v t v t v t v t v t J v t A e e e e e e e e eP Pe v Bu e故 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----+--=----------⎰373236453131)(3232320)(t t t tt t t tt tv t A e e e e e e e e e dv v Bu e则该方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----+--+⎪⎪⎪⎭⎫ ⎝⎛+-+-+-=+=----------------⎰37323645313189121243)()(3232323232320)(t tt tt t t tt t t t t tttv t A At e e e e e e e e e e e e e e e dv v Bu e e t x ξ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+-++-=---------3732212611165313114323232t t t tt t t tt e e e e e e e e e .4．求方程te y y y y -=+'+''+'''6116满足0)0()0()0(=''='=y y y 的解.解:令y x y x y x ''='==321,,,则⎪⎩⎪⎨⎧+---='''='='='-,6116 , ,32133221t e x x x y x x x x x 写成向量方程组为t Be Ax x -+=',其中⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,6116100010B A .对于矩阵A ,有J PAP=-1,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-321,132********,9413211111J P P于是⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=---t tt Jt e e e e 32, 1-=P Pe e Jt At⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-+--+--+--+-+-+-+-=---------------------------t t t tt t t t t t t t t t t t t t t t t t t t tt t e e e e e e e e e e e e e e e e e e e e e e e e e e e 3232323232323232329827325182463491656126238526621由于⎪⎪⎪⎭⎫ ⎝⎛=000)0(x ,则⎰⎰----=+=tv v t A t v v t A At dv Be e dv Be e x e t x 0)(0)()0()(⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+-----+--+--=---------)1(29)1(8)1(23)1(4)1(21)1(221232232232t t tt t t t t t t t t tt t e e e e te e e e e te e e e e te故原方程的解为t t t t t t t t t e e e te e e e e te x y 322321414321)]1(21)1(2[21--------+-=-+--==5．试证明：若A 为2阶方阵，其特征值为21,λλ，特征向量为21,P P ，则方程Ax dtdx= 的解一定能表示成221121P e c P e c x t t λλ+=，其中21,c c 由下式确定:2211)0(P c P c x +=，然后利用这一结论求解定解问题：⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡--=11)0(,651021x x x dt dx 的解,并将这一结论推广到n 阶方阵情形.(1)证明:令],[21P P P =,则,,121211--⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=P P A AP P λλλλ于是x P P dt dx121-⎥⎦⎤⎢⎣⎡=λλ, x P dt dx P 1211--⎥⎦⎤⎢⎣⎡=λλ 令,1x P y -=则dtdxP dt dy 1-=,微分方程化为 y dt dy ⎥⎦⎤⎢⎣⎡=21λλ 其解为⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡=2121c c e e y t tλλ, 故方程Ax dtdx=的解一定能表示成 221121212121],[c e c P e c c c e e P P Py x t t t tλλλλ+=⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡== 若是定解问题,则21,c c 由2211)0(P c P c x +=确定.(2)解:矩阵⎥⎦⎤⎢⎣⎡--6510的特征值为5,121-=-=λλ,特征向量分别为⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=51,1121P P , 则方程组⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡--=216510x x dt dx 的通解为⎪⎪⎭⎫ ⎝⎛--+=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-------t t t t t te c e c e c e c e c e c 52152152155111,由于⎪⎪⎭⎫⎝⎛=11)0(x ,则⎩⎨⎧=--=+1512121c c c c , 解之,得⎪⎩⎪⎨⎧-==212321c c , 故原方程组的解为⎪⎪⎪⎪⎭⎫⎝⎛+--=⎪⎪⎭⎫ ⎝⎛----t t t t e e ee x x 552125232123. (3) n 阶方阵的情形:设微分方程组Ax dtdx=, 其中系数矩阵A 为n 阶可对角化矩阵，其特征值为n λλλ,,,21 ，特征向量分别为n P P P ,,,21 ，则该方程组的通解为n t n t P e c P e c P e c x n t λλλ+++= 221121,其中n c c c ,,,21 为任意常数.若为定解问题,则常数n c c c ,,,21 可由初始条件确定.6．已知),(0t t Φ是方程组)()()(t x t A dtt dx = 的转移矩阵，试证)(),(),(0000t A t t t t dt d ΦΦ-=. 证明:由于I t t t t =ΦΦ),(),(00,两边对0t 求导得,0),(),(),(),(000000=ΦΦ+ΦΦdt t t d t t t t dt t t d , 由于),(0t t Φ是方程组)()()(t x t A dtt dx =的转移矩阵,则 ),()(),(00t t t A dtt t d Φ=Φ, ),()(),(0000t t t A dt t t d Φ=Φ, 故0),()(),(),(),(000000=ΦΦ+ΦΦt t t A t t t t dt t t d , 两边右乘),(),(001t t t t Φ=Φ-,得 0)(),(),(0000=Φ+Φt A t t dt t t d , 即)(),(),(0000t A t t t t dt d ΦΦ-=. 7．求时变系统⎪⎩⎪⎨⎧===00)()()(x t x t x t A dtdx t t 的解，其中0),(x t A 分别如下：（1）⎪⎪⎭⎫ ⎝⎛=-101)(t e t A ，0,1100=⎪⎪⎭⎫ ⎝⎛=t x （2）⎪⎪⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+=111,000)1(100110)(022x t t t A [该题有误: )()()()(1221t A t A t A t A ≠]（3）0,11,21)(00=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=t x t t t A 解:（1）对任意的21,t t ,有)()(101)()(122121t A t A e e t A t A t t =⎥⎦⎤⎢⎣⎡+=--, 故方程组的转移矩阵为+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++=⎰=Φ⎰⎰⎰30200)()(!31)(!21)()0,(0t t t dv v A dv v A dv v A dv v A I e t t由于⎥⎦⎤⎢⎣⎡-=-⎰t e t dv v A t t01)(0, ⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛-⎰22200)1(2!21)(!21t e t t dv v A t t ,⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛-⎰323300)1(3!31)(!31t e t t dv v A t t , ……… ⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛--⎰n t n n n t t e nt t n dv v A n 0)1(!1)(!110 则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++-++++++++=- 323232!31!2110)1)(!31!211(!31!211)0,(t t t e t t t t t t t t Φ ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=-t t t t t t te e e e e e e 010)1(. 故该方程组的解为 ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡-=Φ=t t t t t e e e e e x t t x 121101)0,()(0 (3) 由于)(t A 各元素在区间],0[t 上有界,则该方程组的转移矩阵为⎰⎰⎰++=t v t dv v A dv v A dv v A I t 00221101)()()()0,(Φ ⎰⎰⎰++21033002211)()()(v t v dv v A dv v A dv v A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++++++= 4233428123122181231t t t t t t t t 故该方程组的解为⎪⎪⎪⎪⎭⎫ ⎝⎛+-+-+-++-+-=Φ= 43243208123218121231)0,()(t t t t t t t t x t t x 8．求下列定解问题的解：⎪⎩⎪⎨⎧=+=,00)(),()()()(x t x t u t B t x t A dt dx 其中（1）0,11,1)()(,101)(00=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡=-t x t t u t B e t A t （2）⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+=111,01)()(,000)1(100110)(022x t t u t B t t t A 解:(1)由于系统所对应的齐次系统的转移矩阵为 ⎥⎦⎤⎢⎣⎡-=Φ----00000),(20t t t t t t t e e e e t t , 则该系统的解为⎰Φ+Φ=t dv v Bu v t x t t x 00)(),()0,()( dv v e e e e e e e t v t v v t v t t t t⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡-+⎪⎪⎭⎫ ⎝⎛-⎥⎦⎤⎢⎣⎡-=⎰----10110102 ⎰⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-=----t v t v v t v t t dv e e e ve e 021 ⎪⎪⎪⎭⎫ ⎝⎛---++⎪⎪⎭⎫ ⎝⎛-=-1223211t t t t e t e e e ⎪⎪⎭⎫ ⎝⎛---+=-112321t e e t t。

矩阵论期末试题及答案

矩阵论期末试题及答案1. 选择题题目1：矩阵的秩是指矩阵中非零行（列）线性无关的最大个数，下面关于矩阵秩的说法中，错误的是：A. 若矩阵A的秩为r，则只能确定 A 中有r个行（列）线性无关。

B. 若矩阵A的秩为r，则只能确定 A 中有r个坐标线性无关。

C. 设A，B为n×m矩阵，若A的秩为r，B的秩为s，则AB的秩至少为max{r,s}。

D. 同一矩阵的行秩与列秩相等。

题目2：对于阶梯形矩阵，以下说法正确的是：A. 阶梯形矩阵的行秩与列秩相等。

B. 阶梯形矩阵的行秩等于主元的个数。

C. 阶梯形矩阵的列秩等于主元的个数。

D. 阶梯形矩阵的行秩与列秩之和等于矩阵的阶数。

题目3：设A为n阶矩阵，下列说法正确的是：A. 若A为可逆矩阵，则A的行秩和列秩都为n。

B. 若A的行秩和列秩都为n，则A为可逆矩阵。

C. 若对于非零向量 x，都有Ax=0，则称矩阵A为零矩阵。

D. 若A为可逆矩阵，则方程Ax=b存在唯一解。

题目4：对于实对称矩阵A，以下说法正确的是：A. A一定有n个线性无关的特征向量。

B. A的所有特征值都是实数。

C. 若A的特征向量构成的特征子空间的维数为n，则称A为满秩矩阵。

D. A一定可以对角化。

2. 计算题题目1：已知矩阵A = [1, 2; 3, 4]，求矩阵A的转置矩阵。

解答：转置矩阵的行与列互换，故矩阵A的转置矩阵为：A^T = [1, 3; 2, 4]题目2：已知矩阵B = [2, 1; -1, 3]，求矩阵B的逆矩阵。

解答：逆矩阵满足BB^(-1) = I，其中I为单位矩阵。

对于矩阵B，可以使用伴随矩阵法求解：B^(-1) = (1/(ad-bc)) * [d, -b; -c, a]其中a、b、c、d分别为矩阵B的元素：B^(-1) = (1/(2*3-(-1)*1)) * [3, -1; 1, 2] = [3/7, -1/7; 1/7, 2/7]题目3：已知矩阵C = [1, 2, 3; 4, 5, 6]，求矩阵C的行列式的值。

河海大学研究生矩阵论习题答案

对 k R ，有
kf t 1 kf t dt k f t dt k f t 1
b b a a
对于 g t Ca, b，有
f t g t 1 f t g t dt f t dt g t dt
又已知
T
2

2
0 ，故 T , , 2 2 .
证：（ 1 ）充分性 . 由 C C=I 及坐标变换公式 C 可得
T
16 ．

2 2
T C C T C T C T 2 ，即
M max hi .再由
i

则有
M max hi .对任给正数，取 M ，则当 max hi 时，
i
i
4
结论恒成立. 13．证：（1）设 x1 , 面又有
x2 , , xn ，且 max xi xi 0 ，则
T B T
可得
i j i j ，由
bii bij b ji b jj 2
，
即
bij 0i j, i, j 1,, n ，故有 B=I，也就是 CTC=I.）
(2) 取正交矩阵
1 2 1 C 2 0
n
4 ．证法提示：与上题类似 . 图形在第一象限的部分由 x1 1,
x2 1 和
2 x1 x2 1 所围成. 3
5 ．证：考虑 0, 1 ,
T
1, 0T ，则当 p

矩阵论课后参考答案(第一二三四

;
则 TE 11 E 11ca
b d

a11E 11
a21E 12
a31E 21
a41E 22
即
a0
b 0

a11 a 31
a a
21 41

所以
a 11

a ,a 21
b,a31

0,a 41

0
同理可得： a12 c,a22 d ,a32 0,a42 0
x k11 k22 l11 l22
则
k1 k2 2l1 l2 0
kk212k1kl12k273lll221

l2 0
0

0
，故有
kk12

l2 4l2
l1 3l2
即 x k11 k22 l2 (42 1) l2 (5,2,3,4)
1 1 3 C 1 2 5
1 3 6
17.证明：秩为 1 的 n（n>1）阶阵 A 的最小多项式是 2 (trA) 。
证明：由题知 n 阶矩阵 A 的秩为 1，则说明 A 有 n-1 重 0 特征根
与一个特征根 0 。又因存在特征多项式可写为
n
i tr(A) ，故可知 0 tr( A) ，故 A 的
且对角元全为 0，则其维数为
dim(V ) (n 1) (n 2) 1 (n 1)((n 1) 1) n(n 1)
2
2
其基为 n(n 1) 个 n n 阶的矩阵，故基可写为
2
0 1 0 0 0 0 1 0
1 0
0 0

矩阵论(华中科技大学)课后习题答案

解：（1）、（2）为R 上线性空间（3）不是，由线性空间定义，对0α∀≠有1α=α，而题（3）中10α= （4）不是，若k<0，则()0kf x ≤，数乘不满足封闭性。

2.求线性空间{|}n nT V A R A A ⨯=∈=的维数和一组基。

解：一组基10001010101010000000100..................0010010⎧⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎬⎪⎪⎪⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎩L L L ⎪⎪⎪⎪⎭dim W =n (n +1)/23.如果U 1和U 2都是线性空间V 的子空间，若dim U 1=dim U 2，而且12U U ⊆，证明：U 1=U 2。

证明：因为dim U 1=dim U 2，故设{}12,,,r αααL 为空间U 1的一组基，{}12,,,r βββL 为空间U 2的一组基2U γ∀∈，有()12r X γγβββ=L L而()()1212r r C αααβββ=L L ，C 为过渡矩阵，且可逆于是()()()11212121r r r X C X Y U γγγγβββαααααα-===∈L L L L L L由此，得21U U ⊆又由题设12U U ⊆，证得U 1=U 2。

矩阵论习题 4.3

《矩阵论》习题答案,清华大学出版社,研究生教材 习题 4.3

矩阵论复习题

矩阵论(华中科技大学)课后习题答案

矩阵论试题及答案

研究生矩阵理论课后答案4,5章习题

矩阵论习题答案

矩阵论试题参考答案(2011年)

矩阵论及其应用习题四答案

矩阵论的习题集

矩阵理论习题解答等材料

矩阵理论第4章习题解答 (2)

研究生矩阵论课后习题答案(全)习题四

矩阵论期末试题及答案

河海大学研究生矩阵论习题答案

矩阵论课后参考答案(第一二三四

矩阵论(华中科技大学)课后习题答案

《矩阵论》习题答案,清华大学出版社,研究生教材习题 4.3