黑龙江省哈尔滨市2017-2018学年高一第一学期期中数学试卷

合集下载

2017-2018年黑龙江省哈尔滨三中高一上学期数学期中试卷带答案

2017-2018学年黑龙江省哈尔滨三中高一（上）期中数学试卷一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）给出下列关系：①0∈∅；②∅∈{0，1}；③∅⊆{0}；④{1}∈{1，2}，其中正确的个数是（）A．1 B．2 C．3 D．42．（5分）下列函数中，值域为[1，+∞）的是（）A．B．C．y=x2+x+1 D．3．（5分）函数的单调减区间为（）A．（﹣∞，+∞）B．（﹣∞，1）C．（1，+∞）D．（﹣∞，2）4．（5分）函数的定义域是（）A．（﹣2，0）B．（﹣2，+∞）C．[﹣2，0）∪（0，+∞） D．（﹣2，0）∪（0，+∞）5．（5分）若函数的值域为（0，+∞），则实数m的取值范围是（）A．（1，4） B．（﹣∞，1）∪（4，+∞）C．（0，1]∪[4，+∞）D．[0，1]∪[4，+∞）6．（5分）不等式解集中元素的个数为（）A．1 B．2 C．3 D．47．（5分）函数的值域为（）A．（1，4） B．[1，+∞）C．（3，+∞）D．[4，+∞）8．（5分）已知2a=5b=10，则（+）=（）A．﹣2B．2 C．﹣D．9．（5分）函数y=a x（a＞0且a≠1）与函数y=（a﹣1）x2﹣2x﹣1在同一个坐标系内的图象可能是（）A．B．C．D．10．（5分）已知函数，若0＜x1＜x2＜x3≤2，则由大到小的顺序为（）A．B．C．D．11．（5分）已知f（x）是定义在（﹣∞，+∞）上的偶函数，且在（﹣∞，0]上是增函数，设a=f（log 47），b=f（log3），c=f（0.20.6）则a，b，c的大小关系是（）A．c＜a＜b B．b＜a＜c C．b＜c＜a D．a＜b＜c12．（5分）已知函数f（x）=﹣，若对任意的x1，x2∈[1，2]，且x1≠x2时，[|f（x1）|﹣|f（x2）|]（x1﹣x2）＞0，则实数a的取值范围为（）A．[﹣，]B．[﹣，]C．[﹣，]D．[﹣e2，e2]二、填空题（本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上）13．（5分）设集合A={x|2x2+5x﹣3＞0}，B={x|2x﹣5＜0}，则A∩B=．14．（5分）已知log23=a，log37=b，则log27=（结果用a，b表示）15．（5分）已知函数（a，b为常数，且a≠0）满足f（2）=1，方程f（x）=x有唯一解，则f（f（1））=．16．（5分）已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2．f （x）在[a，b]上的值域为，则a+b=．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（10分）化简求值：（Ⅰ）；（Ⅱ）．18．（12分）设全集U=R，A={x|1≤x≤4}，B={x|2＜x＜5}，C={x|a2≤x≤a+2}．（Ⅰ）求A∩（∁U B）；（Ⅱ）若B∪C=B，求实数a的取值范围．19．（12分）解关于x的不等式：．20．（12分）已知偶函数f（x）的定义域是x≠0的一切实数，对定义域内的任意a，b都有f（ab）=f（a）+f（b），且当x＞1时，f（x）＞0，f（3）=1．（Ⅰ）求证：f（x）在（﹣∞，0）上是减函数；（Ⅱ）解不等式f（x2﹣1）＜2．21．（12分）已知函数（a＞0且a≠1）．（Ⅰ）判断f（x）•g（x）的奇偶性，并说明理由；（Ⅱ）当a=2时，g（x）＜b恒成立，求b的取值范围．22．（12分）已知函数（a，b∈N*）的最大值为，且．（Ⅰ）求函数f（x）的解析式；（Ⅱ）若x，y，z，w＞0，且x+y+z+w=2．求证：．2017-2018学年黑龙江省哈尔滨三中高一（上）期中数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）给出下列关系：①0∈∅；②∅∈{0，1}；③∅⊆{0}；④{1}∈{1，2}，其中正确的个数是（）A．1 B．2 C．3 D．4【解答】解：在①中，0不是∅中的元素，故0∈∅错误；在②中，∅⊊{0，1}，故∅∈{0，1}错误；在③中，∅是{0}的子集，故∅⊆{0}正确；在④中，{1}⊊{1，2}，故{1}∈{1，2}错误．故选：A．2．（5分）下列函数中，值域为[1，+∞）的是（）A．B．C．y=x2+x+1 D．【解答】解：对于A：∵x2+1≥1，∴y=，故A不对；对于B：∵x2+1≥1，∴y=≥1，其值域为[1，+∞），故B对；对于C：y=x2+x+1，其对称轴x=，开口向上，最小值为，其值域为[，+∞），故C不对；对于D：x+1≠0，∴≠0，其值域为（﹣∞，0）∪（0，+∞），故D不对；故选：B．3．（5分）函数的单调减区间为（）A．（﹣∞，+∞）B．（﹣∞，1）C．（1，+∞）D．（﹣∞，2）【解答】解：令t=x2﹣2x﹣3，则函数y=3t，由复合函数的单调性：同增异减，y=3t在R上递增，t=x2﹣2x﹣3在（﹣∞，1）递减，（1，+∞）递增，可得函数的单调减区间为（﹣∞，1）．故选：B．4．（5分）函数的定义域是（）A．（﹣2，0）B．（﹣2，+∞）C．[﹣2，0）∪（0，+∞） D．（﹣2，0）∪（0，+∞）【解答】解：由，解得x＞﹣2且x≠0．∴函数的定义域是（﹣2，0）∪（0，+∞）．故选：D．5．（5分）若函数的值域为（0，+∞），则实数m的取值范围是（）A．（1，4） B．（﹣∞，1）∪（4，+∞）C．（0，1]∪[4，+∞）D．[0，1]∪[4，+∞）【解答】解：函数的值域为（0，+∞），则g（x）=mx2+2（m﹣2）x+1的值域能取到（0，+∞），①当m=0时，g（x）=﹣4x+1，值域为R，包括了（0，+∞），②要使f（x）能取（0，+∞），则g（x）的最小值小于等于0，则，解得：0＜m≤1或m≥4．综上可得实数m的取值范围是{m|0≤m≤1或m≥4}故选：D．6．（5分）不等式解集中元素的个数为（）A．1 B．2 C．3 D．4【解答】解：不等式，即为（3x﹣8）+2（x﹣1）2≤0，且x≠1，（x∈Z），即有2x2﹣x﹣6≤0，且x≠1，（x∈Z），化为（x﹣2）（2x+3）≤0，且x≠1，（x∈Z），解得﹣≤x≤2且x≠1，（x∈Z），可得原不等式的解集为{﹣1，0，2}，则解集的元素个数为3．故选：C．7．（5分）函数的值域为（）A．（1，4） B．[1，+∞）C．（3，+∞）D．[4，+∞）【解答】解：当x≥1时，y=2x﹣1为增函数，则y≥20=1；当0＜x＜1时，y=x+为减函数，此时y∈（3，+∞）．取并集得，函数的值域为[1，+∞）．故选：B．8．（5分）已知2a=5b=10，则（+）=（）A．﹣2B．2 C．﹣D．【解答】解：∵2a=5b=10，∴a=，．则（+）===2．故选：B．9．（5分）函数y=a x（a＞0且a≠1）与函数y=（a﹣1）x2﹣2x﹣1在同一个坐标系内的图象可能是（）A．B．C．D．【解答】解：由函数y=a x（a＞0且a≠1）与函数y=（a﹣1）x2﹣2x﹣1可知，①当0＜a＜1时，此时a﹣1＜0，指数函数y=a x为减函数，而二次函数y=（a﹣1）x2﹣2x﹣1开口向下，且其对称轴为x=＜0，故排除A 与B、D；C选项正确；②当a＞1时，此时a﹣1＞0，指数函数y=a x为增函数，排除C、D；而二次函数y=（a﹣1）x2﹣2x﹣1开口向上，且其对称轴为x=＞0，故B错误，而A不符合题意．故选：C．10．（5分）已知函数，若0＜x1＜x2＜x3≤2，则由大到小的顺序为（）A．B．C．D．【解答】解：∵f（x）=，∴当x＞0时，==在（0，+∞）上是减函数．∵0＜x1＜x2＜x3，∴由大到小的顺序为．故选：A．11．（5分）已知f（x）是定义在（﹣∞，+∞）上的偶函数，且在（﹣∞，0]上是增函数，设a=f（log 47），b=f（log3），c=f（0.20.6）则a，b，c的大小关系是（）A．c＜a＜b B．b＜a＜c C．b＜c＜a D．a＜b＜c【解答】解：∵f（x）是定义在（﹣∞，+∞）上的偶函数，∴b=f（log3）=f（﹣log 23）=f（log23），∵log23=log49＞log47＞1，0＜0.20.6＜1，∴0.20.6＜log47＜log49，∵在（﹣∞，0]上是增函数，∴在[0，+∞）上为减函数，则f（0.20.6）＞f（log47）＞f（log49），即b＜a＜c，故选：B．12．（5分）已知函数f（x）=﹣，若对任意的x1，x2∈[1，2]，且x1≠x2时，[|f（x1）|﹣|f（x2）|]（x1﹣x2）＞0，则实数a的取值范围为（）A．[﹣，]B．[﹣，]C．[﹣，]D．[﹣e2，e2]【解答】解：由任意的x1，x2∈[1，2]，且x1＜x2，由[|f（x1）|﹣|f（x2）|]（x1﹣x2）＞0，则函数y=丨f（x）丨单调递增，当a≥0，f（x）在[1，2]上是增函数，则f（1）≥0，解得：0≤a≤，当a＜0时，丨f（x）丨=f（x），令=﹣，解得：x=ln，由对勾函数的单调递增区间为[ln，+∞），故ln≤1，解得：﹣≤a＜0，综上可知：a的取值范围为[﹣，]，故选：B．二、填空题（本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上）13．（5分）设集合A={x|2x2+5x﹣3＞0}，B={x|2x﹣5＜0}，则A∩B=．【解答】解：∵集合A={x|2x2+5x﹣3＞0}={x|x＜﹣3或x＞}，B={x|2x﹣5＜0}={x|x＜}，∴A∩B=．故答案为：；14．（5分）已知log23=a，log37=b，则log27=ab（结果用a，b表示）【解答】解：∵log23=a，log37=b，∴log27====log23•log37=ab．故答案为：ab．15．（5分）已知函数（a，b为常数，且a≠0）满足f（2）=1，方程f（x）=x有唯一解，则f（f（1））=．【解答】解：∵f（2）=1，∴2a+b=2①，∵f（x）=x有唯一解，∴ax2+（b﹣1）x=0，△=（b﹣1）2=0②，由①②得：a=，b=1，∴f（x）=，∴f[f（x）]=，∴f[f（1）]=；故答案为：．16．（5分）已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2．f（x）在[a，b]上的值域为，则a+b=．【解答】解：设x＜0，则﹣x＞0，∴f（﹣x）=﹣2x﹣（﹣x）2，即﹣f（x）=﹣x2﹣2x，∴f（x）=x2+2x，设这样的实数a，b存在，则a＜b，且，即a，b同号，（1）若a，b同为正；①当0＜a＜b＜1，可得值域为[2a﹣a2，2b﹣b2]，f（x）的值域为，∴，方程组无解；若1＜a＜b，可得值域为[2b﹣b2，2a﹣a2]，f（x）的值域为，∴，方程组无解；若0＜a≤1≤b，可得x=1处取得最大值，f（x）max=f（1）=2﹣1=1，最小值在x=a或x=b处取得，∵当x∈[a，b]时，f（x）的值域为，∴=1，可得a=1，若=2a﹣a2，可得b=1（舍去）；若=2b﹣b2，化简得（b﹣1）（b2﹣b﹣1）=0解得b1=，b2=（舍去），∴a+b=（2）若a，b同为负，由（1）得：a+b=﹣综上可得：a+b=三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（10分）化简求值：（Ⅰ）；（Ⅱ）．【解答】解：（I）原式=﹣+﹣2×+=+1﹣+8﹣+2=；（Ⅱ）原式=×+=+log62×（log66+log63）+4=log63（log63+log62）+log62+4=log63+log62+4=1+4=5．18．（12分）设全集U=R，A={x|1≤x≤4}，B={x|2＜x＜5}，C={x|a2≤x≤a+2}．（Ⅰ）求A∩（∁U B）；（Ⅱ）若B∪C=B，求实数a的取值范围．【解答】解：（Ⅰ）∵全集U=R，A={x|1≤x≤4}，B={x|2＜x＜5}，∴C U B={x|x≤2或x≥5}，A∩（∁U B）={x|1≤x≤2}．（Ⅱ）∵B={x|2＜x＜5}，C={x|a2≤x≤a+2}，B∪C=B，∴B⊇C，当C=∅时，a2＞a+2，解得a＜﹣1或a＞2．当C≠∅时，，解得﹣2＜a＜﹣1．∴实数a的取值范围（﹣∞，﹣1）∪（2，+∞）．19．（12分）解关于x的不等式：．【解答】解：＜a，即﹣a＜0，即＜0，即（x+1）（ax﹣2）＞0，①当a=0时，原不等式转化为x+1＜0，解得x＜﹣1；②当a＞0时，解得x＜﹣1或x＞；③当﹣2＜a＜0时，解得＜x＜﹣1，④当a=﹣2时，不等式无解，⑤当a＜﹣2时，解得﹣1＜x＜；综上所述：①a=0时，解集为（﹣∞，﹣1）；②a＞0时，解集为；③﹣2＜a＜0时，解集为；④a=﹣2时，解集为φ；⑤a＜﹣2时，解集为．20．（12分）已知偶函数f（x）的定义域是x≠0的一切实数，对定义域内的任意a，b都有f（ab）=f（a）+f（b），且当x＞1时，f（x）＞0，f（3）=1．（Ⅰ）求证：f（x）在（﹣∞，0）上是减函数；（Ⅱ）解不等式f（x2﹣1）＜2．【解答】（Ⅰ）证明：设x1，x2是（﹣∞，0）任意两个变量，且x1＜x2，设x2=tx1，（t＞1），则f（x1）﹣f（x2）=f（x1）﹣f（tx1）=f（x1）﹣f（x1）﹣f（t）=﹣f（t）∵当x＞1时，f（x）＞0；∴f（t）＜0，即f（x1）﹣f（x2）=﹣f（t）＞0，∴f（x1）＞f（x2），即y=f（x）在（﹣∞，0）上的单调递减．（Ⅱ）由f（3）=1．那么f（3）+f（3）=f（9）=2．∴不等式f（x2﹣1）＜2．可得f（x2﹣1）＜f（9）．∵f（x）的定义域是x≠0的偶函数∴或解得：x∈．21．（12分）已知函数（a＞0且a≠1）．（Ⅰ）判断f（x）•g（x）的奇偶性，并说明理由；（Ⅱ）当a=2时，g（x）＜b恒成立，求b的取值范围．【解答】解：（Ⅰ）f（x）•g（x）是偶函数：∵f（x）=x．则f（﹣x）=﹣x=﹣f（x），∴f（x）是奇函数．g（﹣x）=1﹣=1====﹣1=﹣g（x），∴g（x）是奇函数．那么f（x）•g（x）是偶函数：（Ⅱ）当a=2时，g（x）＜b恒成立，即＜b恒成立，∵，∴可得g（x）＜1．故得b的取值范围是[1，+∞）．22．（12分）已知函数（a，b∈N*）的最大值为，且．（Ⅰ）求函数f（x）的解析式；（Ⅱ）若x，y，z，w＞0，且x+y+z+w=2．求证：．【解答】解：（I）∵函数（a，b∈N*）∴f（x）=，（a，b∈N*）当x=时，函数取最大值=，即b=又由，得：解得：∈（1，4），故=2，即a=4，b=1即；证明：（II）由（1）得：；不等式可化为：、∵=，令g（x）=，则g′（x）=＜0恒成立，当x=时，可得g（x）=0，故得x=y=z=w=时，取等号．故得原不等式成立．赠送初中数学几何模型【模型一】“一线三等角”模型：图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；xyB CAO2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt△ABC中，∠BAC=90°，AB=AC=2，点D在BC上运动（不与点B，C重合），过D作∠ADE=45°，DE交AC于E．（1）求证：△ABD∽△DCE；（2）设BD=x，AE=y，求y关于x的函数关系式，并写出自变量x的取值范围；（3）当△ADE是等腰三角形时，求AE的长．EB4.如图，已知直线112y x=+与y轴交于点A，与x轴交于点D，抛物线212y x bx c=++与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为(1，0)。

2018年黑龙江省哈尔滨市中考数学试卷含答案

黑龙江省哈尔滨市2018年中考数学试卷一、选择题<共10小题，每小题3分，满分30分）1．<3分）(2018年黑龙江哈尔滨>哈市某天的最高气温为28℃，最低气温为21℃，则这一天的最高气温与最低气温的差为< ）b5E2RGbCAPA．5℃B．6℃C．7℃D．8℃分析：根据有理数的减法，减去一个数等于加上这个数的相反数，可得答案．解答：解：28﹣21=28+<﹣21）=7，故选：C．点评：本题考查了有理数的减法，减去一个数等于加上这个数的相反数．2．<3分）(2018年黑龙江哈尔滨>用科学记数法表示927 000正确的是< ）A．9.27×106 B．9.27×105 C．9.27×104 D．927×103考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于927 000有6位，所以可以确定n=6﹣1=5．p1EanqFDPw解答：解：927 000=9.27×105．故选B．点评：此题考查科学记数法表示较大的数的方法，准确确定a 与n值是关键．3．<3分）(2018年黑龙江哈尔滨>下列计算正确的是< ）A．3a﹣2a=1 B．a2+a5=a7C．a2•a4=a6 D．<ab）3=ab3考点：幂的乘方与积的乘方；合并同类项；同底数幂的乘法．分析：根据合并同类项，可判断A、B，根据同底数幂的乘法，可判断C，根据积的乘方，可判断D．解答：解：A、系数相加字母部分不变，故A错误；B、不是同底数幂的乘法，指数不能相加，故B错误；C、底数不变指数相加，故C正确；D、积的乘方等于每个因式分别乘方，再把所得的幂相乘；故D错误；故选：C．点评：本题考查了积的乘方，积的乘方等于每个因式分别乘方，再把所得的幂相乘．4．<3分）(2018年黑龙江哈尔滨>下列图形中，不是中心对称图形的是< ）A．B．C．D．考点：中心对称图形．分析：根据中心对称图形的概念求解．解答：解：A、是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项正确；C、是中心对称图形，故本选项错误；D、是中心对称图形，故本选项错误；故选B．点评：本题考查了中心对称的知识，中心对称图形是要寻找对称中心，旋转180度后与原图重合．5．<3分）(2018年黑龙江哈尔滨>在反比例函数的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是< ）DXDiTa9E3dA．k＞1 B．k＞0 C．k≥1 D．k＜1考点：反比例函数的性质．分析：根据反比例函数的性质，当反比例函数的系数大于0时，在每一支曲线上，y都随x的增大而减小，可得k﹣1＞0，解可得k的取值范围．RTCrpUDGiT解答：解：根据题意，在反比例函数图象的每一支曲线上，y都随x的增大而减小，即可得k﹣1＞0，解得k＞1．故选A．点评：本题考查了反比例函数的性质：①当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．5PCzVD7HxA6．<3分）(2018年黑龙江哈尔滨>如图的几何体是由一些小正方形组合而成的，则这个几何体的俯视图是< ）jLBHrnAILgA．B．C．D．考点：简单组合体的三视图．分析：找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．解答：解：从几何体的上面看共有3列小正方形，右边有2个，左边有2个，中间上面有1个，点评：本题考查了三视图的知识，俯视图是从物体的上面看得到的视图．7．<3分）(2018年黑龙江哈尔滨>如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD 的度数是< ）xHAQX74J0XA．30°B．25°C．20°D．15°考点：切线的性质．分析：根据切线的性质求出∠OAC，求出∠AOC，根据等腰三角形性质求出∠B=∠BDO，根据三角形外角性质求出即可．LDAYtRyKfE 解答：解：∵AC是⊙O的切线，∴∠OAC=90°，∵∠C=40°，∴∠AOC=50°，∵OB=OD，∴∠ABD=∠BDO，∵∠ABD+∠BDO=∠AOC，∴∠ABD=25°，点评：本题考查了切线的性质，三角形外角性质，三角形内角和定理，等腰三角形性质的应用，解此题的关键是求出∠AOC的度数，题目比较好，难度适中．Zzz6ZB2Ltk8．<3分）(2018年黑龙江哈尔滨>将抛物线y=﹣2x2+1向右平移1个单位，再向上平移2个单位后所得到的抛物线为< ）dvzfvkwMI1A．y=﹣2<x+1）2﹣1 B．y﹣2<x+1）2+3 C．y=﹣2<x﹣1）2+1 D．y=﹣2<x﹣1）2+3rqyn14ZNXI考点：二次函数图象与几何变换．分析：根据图象右移减，上移加，可得答案．解答：解；将抛物线y=﹣2x2+1向右平移1个单位，再向上平移2个单位后所得到的抛物线为y=﹣2<x﹣1）2+3，EmxvxOtOco故选：D．点评：本题考查了二次函数图象与几何变换，函数图象平移的规律是：左加右减，上加下减．9．<3分）(2018年黑龙江哈尔滨>如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为< ）SixE2yXPq5A． 6 B．4C．3D．3考点：旋转的性质．分析：利用直角三角形的性质得出AB=4，再利用旋转的性质以及三角形外角的性质得出AB′=2，进而得出答案．6ewMyirQFL解答：解：∵在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，∴∠CAB=30°，故AB=4，∵△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，kavU42VRUs∴AB=A′B′=4，AC=A′C，∴∠CAA′=∠A′=30°，∴∠ACB′=∠B′AC=30°，∴AB′=B′C=2，∴AA′=2+4=6．故选：A．点评：此题主要考查了旋转的性质以及直角三角形的性质等知识，得出AB′=B′C=2是解题关键．10．<3分）(2018年黑龙江哈尔滨>早晨，小刚沿着通往学校唯一的一条路<直路）上学，途中发现忘带饭盒，停下往家里打电话，妈妈接到电话后带上饭盒马上赶往学校，同时小刚返回，两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，小刚始终以100M/分的速度步行，小刚和妈妈的距离y<单位：M）与小刚打完电话后的步行时间t<单位：分）之间的函数关系如图，下列四种说法：y6v3ALoS89①打电话时，小刚和妈妈的距离为1250M；②打完电话后，经过23分钟小刚到达学校；③小刚和妈妈相遇后，妈妈回家的速度为150M/分；④小刚家与学校的距离为2550M．其中正确的个数是< ）A．1个B．2个C．3个D．4个考点：一次函数的应用．分析：根据函数的图象和已知条件分别分析探讨其正确性，进一步判定得出答案即可．解答：解：①由图可知打电话时，小刚和妈妈的距离为1250M 是正确的；②因为打完电话后5分钟两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，经过5+15+3=23分钟小刚到达学校，所以是正确的；M2ub6vSTnP③打完电话后5分钟两人相遇后，妈妈的速度是1250÷5﹣100=150M/分，走的路程为150×5=750M，回家的速度是750÷15=50M/分，所以回家的速度为150M/分是错误的；0YujCfmUCw④小刚家与学校的距离为750+<15+3）×100=2550M，所以是正确的．正确的答案有①②④．故选：C．点评：此题考查了函数的图象的实际意义，结合题意正确理解函数图象，利用基本行程问题解决问题．二、填空题<共10小题，每小题3分，共计30分）11．<3分）(2018年黑龙江哈尔滨>计算：=．考点：二次根式的加减法．分析：先化简=2，再合并同类二次根式即可．解答：解：=2﹣=．故应填：．点评：本题主要考查了二次根式的加减，属于基础题型．12．<3分）(2018年黑龙江哈尔滨>在函数y=中，自变量x的取值范围是x≠﹣2 ．考点：函数自变量的取值范围．分析：根据分母不等于0列式计算即可得解．解答：解：由题意得，2x+4≠0，解得x≠﹣2．故答案为：x≠﹣2．点评：本题考查了函数自变量的范围，一般从三个方面考虑：<1）当函数表达式是整式时，自变量可取全体实数；<2）当函数表达式是分式时，考虑分式的分母不能为0；<3）当函数表达式是二次根式时，被开方数非负．13．<3分）(2018年黑龙江哈尔滨>把多项式3m2﹣6mn+3n2分解因式的结果是3<m﹣n）2．eUts8ZQVRd考点：提公因式法与公式法的综合运用．分析：首先提取公因式3，再利用完全平方公式进行二次分解．解答：解：3m2﹣6mn+3n2=3<m2﹣2mn+n2）=3<m﹣n）2．故答案为：3<m﹣n）2．点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．sQsAEJkW5T14．<3分）(2018年黑龙江哈尔滨>不等式组的解集是﹣1＜x≤1 ．考点：解一元一次不等式组．分析：分别求出各不等式的解集，再求出其公共解集即可．解答：解：，由①得，x≤1，由②得，x＞﹣1，故此不等式组的解集为：﹣1＜x≤1．故答案为：﹣1＜x≤1．点评：本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．GMsIasNXkA15．<3分）(2018年黑龙江哈尔滨>若x=﹣1是关于x的一元二次方程x2+3x+m+1=0的一个解，则m的值为 1 ．TIrRGchYzg考点：一元二次方程的解．专题：计算题．分析：根据x=﹣1是已知方程的解，将x=﹣1代入方程即可求出m的值．解答：解：将x=﹣1代入方程得：1﹣3+m+1=0，解得：m=1．故答案为：1点评：此题考查了一元二次方程的解，方程的解即为能使方程左右两边相等的未知数的值．16．<3分）(2018年黑龙江哈尔滨>在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为．7EqZcWLZNX考点：列表法与树状图法．专题：计算题．分析：列表得出所有等可能的情况数，找出两次摸取的小球标号都是1的情况数，即可求出所求的概率．解答：解：列表如下：1 2 3 41 <1，1）<2，1）<3，1）<4，1）2 <1，2）<2，2）<3，2）<4，2）3 <1，3）<2，3）<3，3）<4，3）4 <1，4）<2，4）<3，4）<4，4）所有等可能的情况有16种，其中两次摸取的小球标号都是1的情况有1种，则P=．故答案为：点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．17．<3分）(2018年黑龙江哈尔滨>如图，在矩形ABCD中，AB=4，BC=6，若点P在AD边上，连接BP、PC，△BPC是以PB为腰的等腰三角形，则PB的长为5或6 ．lzq7IGf02E考点：矩形的性质；等腰三角形的判定；勾股定理．专题：分类讨论．分析：需要分类讨论：PB=PC和PB=BC两种情况．解答：解：如图，在矩形ABCD中，AB=CD=4，BC=AD=6．如图1，当PB=PC时，点P是BC的中垂线与AD的交点，则AP=DP=AD=3．在Rt△ABP中，由勾股定理得 PB===5；如图2，当BP=BC=6时，△BPC也是以PB为腰的等腰三角形．综上所述，PB的长度是5或6．点评：本题考查了矩形的性质、等腰三角形的判定和勾股定理．解题时，要分类讨论，以防漏解．18．<3分）(2018年黑龙江哈尔滨>一个底面直径为10cm，母线长为15cm的圆锥，它的侧面展开图圆心角是120 度．zvpgeqJ1hk 考点：圆锥的计算．分析：利用底面周长=展开图的弧长可得．解答：解：∵底面直径为10cm，∴底面周长为10π，根据题意得10π=，解得n=120．故答案为120．点评：考查了圆锥的计算，解答本题的关键是有确定底面周长=展开图的弧长这个等量关系，然后由扇形的弧长公式和圆的周长公式求值．NrpoJac3v119．<3分）(2018年黑龙江哈尔滨>如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为 5 ．1nowfTG4KI考点：正方形的性质；勾股定理；等腰直角三角形．分析：由四边形ABCD是正方形，AC为对角线，得出∠AFE=45°，又因为EF⊥AC，得到∠AFE=90°得出EF=AF=3，由△EFC的周长为12，得出线段FC=12﹣3﹣EC=9﹣EC，在RT△EFC 中，运用勾股定理EC2=EF2+FC2，求出EC=5．fjnFLDa5Zo解答：解：∵四边形ABCD是正方形，AC为对角线，∴∠AFE=45°，又∵EF⊥AC，∴∠AFE=90°，∠AEF=45°，∴EF=AF=3，∵△EFC的周长为12，∴FC=12﹣3﹣EC=9﹣EC，在RT△EFC中，EC2=EF2+FC2，∴EC2=9+<9﹣EC）2，解得EC=5．故答案为：5．点评：本题主要考查了正方形的性质及等腰直角三角形，解题的关键是找出线段的关系．运用勾股定理列出方程．tfnNhnE6e5 20．<3分）(2018年黑龙江哈尔滨>如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则的值为．HbmVN777sL考点：相似三角形的判定与性质；全等三角形的判定与性质；角平分线的性质；等腰三角形的判定与性质；平行四边形的判定与性质．V7l4jRB8Hs分析：解题关键是作出辅助线，如解答图所示：第1步：利用角平分线的性质，得到BD=CD；第2步：延长AC，构造一对全等三角形△ABD≌△AMD；第3步：过点M作MN∥AD，构造平行四边形DMNG．由MD=BD=KD=CD，得到等腰△DMK；然后利用角之间关系证明DM∥GN，从而推出四边形DMNG为平行四边形；83lcPA59W9第4步：由MN∥AD，列出比例式，求出的值．解答：解：已知AD为角平分线，则点D到AB、AC的距离相等，设为h．∵====，∴BD=CD．如右图，延长AC，在AC的延长线上截取AM=AB，则有AC=4CM．连接DM．在△ABD与△AMD中，∴△ABD≌△AMD<SAS），∴MD=BD=5m．过点M作MN∥AD，交EG于点N，交DE于点K．∵MN∥AD，∴==，∴CK=CD，∴KD=CD．∴MD=KD，即△DMK为等腰三角形，∴∠DMK=∠DKM．由题意，易知△EDG为等腰三角形，且∠1=∠2；∵MN∥AD，∴∠3=∠4=∠1=∠2，又∵∠DKM=∠3<对顶角）∴∠DMK=∠4，∴DM∥GN，∴四边形DMNG为平行四边形，∴MN=DG=2FD．∵点H为AC中点，AC=4CM，∴=．∵MN∥AD，∴=，即，∴=．点评：本题是几何综合题，难度较大，正确作出辅助线是解题关键．在解题过程中，需要综合利用各种几何知识，例如相似、全等、平行四边形、等腰三角形、角平分线性质等，对考生能力要求较高．mZkklkzaaP三、解答题<共8小题，其中21-24题各6分，25-26题各8分，27-28题各10分，共计10分）21．<6分）(2018年黑龙江哈尔滨>先化简，再求代数式﹣的值，其中x=2cos45°+2，y=2．AVktR43bpw考点：分式的化简求值；特殊角的三角函数值．专题：计算题．分析：原式利用同分母分式的减法法则计算，约分得到最简结果，将x与y的值代入计算即可求出值．解答：解：原式===，当x=2×+2=+2，y=2时，原式==．点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．22．<6分）(2018年黑龙江哈尔滨>如图，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，点E 在BC边上，且点E在小正方形的顶点上，连接AE．ORjBnOwcEd<1）在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点；<2）请直接写出△AEF与四边形ABCD重叠部分的面积．考点：作图-轴对称变换．专题：作图题．分析：<1）根据AE为网格正方形的对角线，作出点B关于AE 的对称点F，然后连接AF、EF即可；<2）根据图象，重叠部分为两个直角三角形的面积的差，列式计算即可得解．解答：解：<1）△AEF如图所示；<2）重叠部分的面积=×4×4﹣×2×2=8﹣2=6．点评：本题考查了利用轴对称变换作图，熟练掌握网格结构并观察出AE为网格正方形的对角线是解题的关键．23．<6分）(2018年黑龙江哈尔滨>君畅中学计划购买一些文具送给学生，为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中，你最需要的文具是什么？<必选且只选一种）”的问题，在全校满园内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据以上信息回答下列问题：2MiJTy0dTT<1）在这次调查中，最需要圆规的学生有多少名？并补全条形统计图；<2）如果全校有970名学生，请你估计全校学生中最需要钢笔的学生有多少名？考点：条形统计图；用样本估计总体；扇形统计图．专题：计算题．分析：<1）由最需要直尺的学生数除以占的百分比求出总人数，确定出最需要圆规的学生数，补全条形统计图即可；gIiSpiue7A<2）求出最需要钢笔的学生占的百分比，乘以970即可得到结果．解答：解：<1）根据题意得：18÷30%=60<名），60﹣<21+18+6）=15<名），则本次调查中，最需要圆规的学生有15名，补全条形统计图，如图所示：<2）根据题意得：970×=97<名），则估计全校学生中最需要钢笔的学生有97名．点评：此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．24．<6分）(2018年黑龙江哈尔滨>如图，AB、CD为两个建筑物，建筑物AB的高度为60M，从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°．uEh0U1Yfmh<1）求两建筑物底部之间水平距离BD的长度；<2）求建筑物CD的高度<结果保留根号）．考点：解直角三角形的应用-仰角俯角问题．分析：<1）根据题意得：BD∥AE，从而得到∠BAD=∠ADB=45°，利用BD=AB=60，求得两建筑物底部之间水平距离BD的长度为60M；IAg9qLsgBX<2）延长AE、DC交于点F，根据题意得四边形ABDF为正方形，根据AF=BD=DF=60，在Rt△AFC中利用∠FAC=30°求得CF，然后即可求得CD的长．WwghWvVhPE解答：解：<1）根据题意得：BD∥AE，∴∠ADB=∠EAD=45°，∵∠ABD=90°，∴∠BAD=∠ADB=45°，∴BD=AB=60，∴两建筑物底部之间水平距离BD的长度为60M；<2）延长AE、DC交于点F，根据题意得四边形ABDF为正方形，∴AF=BD=DF=60，在Rt△AFC中，∠FAC=30°，∴CF=AF•tan∠FAC=60×=20，又∵FD=60，∴CD=60﹣20，∴建筑物CD的高度为<60﹣20）M．点评：考查解直角三角形的应用；得到以AF为公共边的2个直角三角形是解决本题的突破点．25．<8分）(2018年黑龙江哈尔滨>如图，⊙O是△ABC的外接圆，弦BD交AC于点E，连接CD，且AE=DE，BC=CE．asfpsfpi4k<1）求∠ACB的度数；<2）过点O作OF⊥AC于点F，延长FO交BE于点G，DE=3，EG=2，求AB的长．考点：三角形的外接圆与外心；全等三角形的判定与性质；等边三角形的判定与性质；勾股定理．分析：<1）首先得出△AEB≌△DEC，进而得出△EBC为等边三角形，即可得出答案；<2）由已知得出EF，BC的长，进而得出CM，BM的长，再求出AM的长，再由勾股定理求出AB的长．解答：<1）证明：在△AEB和△DEC中，∴△AEB≌△DEC<ASA），∴EB=EC，又∵BC=CE，∴BE=CE=BC，∴△EBC为等边三角形，∴∠ACB=60°；<2）解：∵OF⊥AC，∴AF=CF，∵△EBC为等边三角形，∴∠GEF=60°，∴∠EGF=30°，∵EG=2，∴EF=1，又∵AE=ED=3，∴CF=AF=4，∴AC=8，EC=5，∴BC=5，作BM⊥AC于点M，∵∠BCM=60°，∴∠MBC=30°，∴CM=，BM==，∴AM=AC﹣CM=，∴AB==7．点评：此题主要考查了全等三角形的判定与性质以及等边三角形的性质和勾股定理以及锐角三角函数关系等知识，得出CM，BM的长是解题关键．ooeyYZTjj126．<8分）(2018年黑龙江哈尔滨>荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．BkeGuInkxI<1）求购买该品牌一个台灯、一个手电筒各需要多少元？<2）经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？PgdO0sRlMo考点：分式方程的应用；一元一次不等式的应用．分析：<1）设购买该品牌一个手电筒需要x元，则购买一个台灯需要<x+20）元．则根据等量关系：购买台灯的个数是购买手电筒个数的一半，列出方程；3cdXwckm15<2）设公司购买台灯的个数为a各，则还需要购买手电筒的个数是<2a+8）个，则根据“该公司购买台灯和手电筒的总费用不超过670元”列出不等式．h8c52WOngM解答：解：<1）设购买该品牌一个手电筒需要x元，则购买一个台灯需要<x+20）元．根据题意得=×解得 x=5经检验，x=5是原方程的解．所以 x+20=25．答：购买一个台灯需要25元，购买一个手电筒需要5元；<2）设公司购买台灯的个数为a，则还需要购买手电筒的个数是<2a+8）由题意得 25a+5<2a+8）≤670解得 a≤21所以荣庆公司最多可购买21个该品牌的台灯．点评：本题考查了一元一次不等式和分式方程的应用．解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量<不等量）关系．v4bdyGious27．<10分）(2018年黑龙江哈尔滨>如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B，且点B的横坐标为1．J0bm4qMpJ9<1）求a，b的值；<2）点P是线段AB上一动点<点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间的函数关系式<不要求写出自变量t的取值范围）；XVauA9grYP<3）在<2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR﹣∠BRN=45°时，求点R的坐标．bR9C6TJscw考点：二次函数综合题．分析：<1）利用已知得出A，B点坐标，进而利用待定系数法得出a，b的值；<2）利用已知得出AD=BD则∠BAD=∠ABD=45°，进而得出tan∠BOD=tan∠MPF，故==3，MF=3PF=3t，即可得出d与t的函数关系；pN9LBDdtrd<3）首先利用S△ACN=S△PMN，则AC2=2t2，得出AC=2t，CN=2t，则M<4﹣2t，6t），求出t的值，进而得出△PMQ∽△NBR，求出R点坐标．DJ8T7nHuGT解答：解：<1）∵y=﹣x+4与x轴交于点A，∴A<4，0），∵点B的横坐标为1，且直线y=﹣x+4经过点B，∴B<1，3），∵抛物线y=ax2+bx经过A<4，0），B<1，3），∴，解得：，∴a=﹣1，b=4；<2）如图，作BD⊥x轴于点D，延长MP交x轴于点E，∵B<1，3），A<4，0），∴OD=1，BD=3，OA=4，∴AD=3，∴AD=BD，∵∠BDA=90°，∠BAD=∠ABD=45°，∵MC⊥x轴，∴∠ANC=∠BAD=45°，∴∠PNF=∠ANC=45°，∵PF⊥MC，∴∠FPN=∠PNF=45°，∴NF=PF=t，∵∠DFM=∠ECM=90°，∴PF∥EC，∴∠MPF=∠MEC，∵ME∥OB，∴∠MEC=∠BOD，∴∠MPF=∠BOD，∴tan∠BOD=tan∠MPF，∴==3，∴MF=3PF=3t，∵MN=MF+FN，∴d=3t+t=4t；<3）如备用图，由<2）知，PF=t，MN=4t，∴S△PMN=MN×PF=×4t×t=2t2，∵∠CAN=∠ANC，∴CN=AC，∴S△ACN=AC2，∵S△ACN=S△PMN，∴AC2=2t2，∴AC=2t，∴CN=2t，∴MC=MN+CN=6t，∴OC=OA﹣AC=4﹣2t，∴M<4﹣2t，6t），由<1）知抛物线的解读式为：y=﹣x2+4x，将M<4﹣2t，6t）代入y=﹣x2+4x得：﹣<4﹣2t）2+4<4﹣2t）=6t，解得：t1=0<舍），t2=，∴PF=NF=，AC=CN=1，OC=3，MF=，PN=，PM=，AN=，∵AB=3，∴BN=2，作NH⊥RQ于点H，∵QR∥MN，∴∠MNH=∠RHN=90°，∠RQN=∠QNM=45°，∴∠MNH=∠NCO，∴NH∥OC，∴∠HNR=∠NOC，∴tan∠HNR=tan∠NOC，∴==，设RH=n，则HN=3n，∴RN=n，QN=3n，∴PQ=QN﹣PN=3n﹣，∵ON==，OB==，∴OB=ON，∴∠OBN=∠BNO，∵PM∥OB，∴∠OBN=∠MPB，∴∠MPB=∠BNO，∵∠MQR﹣∠BRN=45°，∠MQR=∠MQP+∠RQN=∠MQP+45°，∴∠BRN=∠MQP，∴△PMQ∽△NBR，∴=，∴=，解得：n=，∴R的横坐标为：3﹣=，R的纵坐标为：1﹣=，∴R<，）．点评：此题主要考查了待定系数法求二次函数解读式以及相似三角形的判定与性质和勾股定理等知识，得出△PMQ∽△NBR，进而得出n的值是解题关键．QF81D7bvUA28．<10分）(2018年黑龙江哈尔滨>如图，在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，∠ADB=∠CAD+∠ABD，∠BAD=3∠CBD．4B7a9QFw9h<1）求证：△ABC为等腰三角形；<2）M是线段BD上一点，BM：AB=3：4，点F在BA的延长线上，连接FM，∠BFM的平分线FN交BD于点N，交AD于点G，点H为BF中点，连接MH，当GN=GD时，探究线段CD、FM、MH之间的数量关系，并证明你的结论．ix6iFA8xoX考点：相似形综合题．分析：<1）根据等式的性质，可得∠APE=∠ADE，根据等腰三角形的性质，可得∠PAD=2β，根据直角三角形的性质，可得∠AEB+∠CBE=90°，根据等式的性质，可得∠ABC=∠ACB，根据等腰三角形的判定，可得答案；wt6qbkCyDE<2）根据相似三角形的判定与性质，可得∠ABE=∠ACD，根据等腰三角形的性质，可得∠GND=∠GDN，根据对顶角的性质，可得∠AGF的度数，根据三角形外角的性质，∠AFG的度数，根据直角三角形的性质，可得BF与MH的关系，根据等腰三角形的性质，可得∠FRM=∠FMR，根据平行线的判定与性质，可得∠CBD=∠RMB，根据相似三角形的判定与性质，可得，根据线段的和差，可得BR=BF﹣FR，根据等量代换，可得答案．Kp5zH46zRk解答：<1）证明：如图1，作∠BAP=∠DAE=β，AP交BD于P，设∠CBD=α，∠CAD=β，∵∠ADB=∠CAD+∠ABD，∠APE=∠BAP+∠ABD，∴∠APE=∠ADE，AP=AD．∵AC⊥BD∴∠PAD=2β，∠BAD=3β．∵∠BAD=3∠CBD，∴3β=3α，β=α．∵AC⊥BD，∴∠ACB=90°﹣∠CBE=90°﹣α=90°﹣β．∵∠ABC=180°﹣∠BAC﹣∠ACB=90°﹣β，∴∠ACB=∠ABC，∴△ABC为等腰三角形；<2）2MH=FM+CD．证明：如图2，由<1）知AP=AD，AB=AC，∠BAP=∠CAD=β，∴△ABP∽△ACD，∴∠ABE=∠ACD．∵AC⊥BD，∴∠GDN=90°﹣β，∵GN=GD，∴∠GND=∠GDN=90°﹣β，∴∠NGD=180°﹣∠GND﹣∠GDN=2β．∴∠AGF=∠NGD=2β．∴∠AFG=∠BAD﹣∠AGF=3β﹣2β=β．∵FN平分∠BFM，∴FM∥AE，∴∠FMN=90°．∵H为BF的中点，∴BF=2MH．在FB上截取FR=FM，连接RM，∴∠FRM=∠FMR=90°﹣β．∵∠ABC=90°﹣β，∴∠FRM=∠ABC，∴RM∥BC，∴∠CBD=∠RMB．∵∠CAD=∠CBD=β，∴∠RMB=∠CAD．∵∠RBM=∠ACD，∴△RMB∽△DAC，∴，∴BR=CD．∵BR=BF﹣FR，∴FB﹣FM=BR=CD，FB=FM+CD．∴2MH=FM+CD．点评：本题考查了相似形综合题，<1）利用了等腰三角形的性质，等腰三角形的判定，直角三角形的性质；<2）相似三角形的判定与性质，直角三角形的性质，三角形外角的性质，平行线的判定与性质，利用的知识点多，题目稍有难度，相似三角形的判定与性质是解题关键．Yl4HdOAA61申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

2018年黑龙江哈尔滨中考数学试卷及答案解析版

)．
【答案】 C． 7．（2018 哈尔滨，7，3 分）如图，在□ABCD 中，AD=2AB，CE 平分∠BCD 交 AD 边于点 E，且 AE=3，则 AB 的长为( )． A． 4 B．3 C． 5 2 D．2
(第 7 题图)
【答案】 B． 8．（2018 哈尔滨，8，3 分）在一个不透明的袋子中，有 2 个白球和 2 个红球，它们只有颜色上的区别，从袋子中随机地摸出一个球记下颜色放回．再随机地摸出一个球．则两次都摸到白球的概率为( )． A． 1 16 B． 1 8 C． 1 4 1 D． 2
【答案】 D．二、填空题(每小题 3 分，共计 30 分) 11．（2018 哈尔滨，11，3 分）把 98000 用科学记数法表示为_______________．【答案】9.8×104． 12．（2018 哈尔滨，12，3 分）在函数 y= 【答案】x≠3． 13．（2018 哈尔滨，13，3 分）计算： 273 =__________________． 2 x 中，自变量 x 的取值范围是_______________． x+3
【答案】 C． 9．（2018 哈尔滨，9，3 分）如图，在△ABC 中，M、N 分别是边 AB、AC 的中点，则△AMN 的面积与四边形 MBCN 的面积比为( )． A． 1 2 1 B． 3 C． 1 4 2 D． 3
【答案】 B． 10．（2018 哈尔滨， 10， 3 分）梅凯种子公司以一定价格销售“黄金 1 号”玉米种子，如果一次购买 10 千克以上(不含 10 千克)的种子，超过 10 千克的那部分种子的价格将打折，并依此得到付款金额 y(单位：元)与一次购买种子数量 x(单位：千克)之间的函数关系如图所示．下列四种说法： ①一次购买种子数量不超过 10 千克时，销售价格为 5 元/千克； ②一次购买 30 千克种子时，付款金额为 100 元； ③一次购买 10 千克以上种子时，超过 10 千克的那部分种子的价格打五折； ④一次购买 40 千克种子比分两次购买且每次购买 20 千克种子少花 25 元钱．其中正确的个数是( )． A． 1 个 B． 2 个 C． 3（2018 哈尔滨，14，3 分）不等式组 3x-1<2，的解集是______________． x+3≥1

XXX2017-2018学年第一学期期末考试高一数学试卷

XXX2017-2018学年第一学期期末考试高一数学试卷XXX2017-2018学年第一学期期末考试高一年级数学试卷第I卷(选择题共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知向量a=(2,1),b=(λ−1,2),若a+b与a−b共线,则λ=（）A.−2B.−1C.1D.2改写：向量a=(2,1)，向量b=(λ-1,2)，若a+b和a-b共线，则λ=（） A。

-2 B。

-1 C。

1 D。

22.已知3sinα+4cosα=2，则1-sinαcosα-cos2α的值是() A。

- B。

C。

-2 D。

2改写：已知3sinα+4cosα=2，求1-sinαcosα-cos2α的值，答案为() A。

- B。

C。

-2 D。

23.已知在△ABC中，AB=AC=1，BC=3，则AB·AC=() A。

1/33 B。

- C。

-2 D。

-改写：在△ABC中，AB=AC=1，BC=3，求XXX的值，答案为() A。

1/33 B。

- C。

-2 D。

-4.在△ABC中，若AB2=AB·AC+BA·BC+CA·CB，则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定改写：在△ABC中，如果AB2=AB·AC+BA·BC+CA·CB，则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定5.已知△ABC中，内角A,B,C所对边的边长分别为a,b,c,且c=7/11，a+b=22/3，XXX-tanA-tanB=3，则△ABC的面积为() A。

3/33 B。

- C。

3 D。

33/2改写：已知△ABC中，内角A,B,C所对边的边长分别为a,b,c，且c=7/11，a+b=22/3，XXX-tanB=3，求△ABC的面积，答案为() A。

3/33 B。

- C。

黑龙江省哈尔滨市2017-2018学年高一第一学期期中英语试卷

2017-2018学年度上学期期中考试高一英语试题本试卷分第一卷（选择题）和第二卷（非选择题）两部分。

共150分。

考试结束后，将本试卷和答题卡一并收回。

第一卷注意事项：1. 答题前，考生先将自己的姓名，准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2. 选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，笔迹清楚。

3. 请按照题号顺序在各题目的答题区域内作答，超出答题区域书写答案无效；在草稿纸、试题卷上答题无效。

4. 保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第一部分听力（共20小题，每小题0.5分，满分10分）第一节听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1 What time is it now?A. 11:15B. 10:30C. 10:152 What has the woman got?A. MilkB. An appleC. Juice3 Which film will the speaker see?A. Fast LifeB. Summer RockC. American Story4 What does the woman mean?A. She is not invited.B. She doesn’t feel well.C. She’ll get a pre sent for Mrs. Lee.5 What does the woman offer to do for the man?A. Call another hotel.B. Change his room.C. Book a double room.第二节听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

黑龙江省哈尔滨市2017_2018学年高一数学上学期期中试题201711080263

2017—2018学年度上学期期中考试高一数学试题考试说明：本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，考试时间120分钟．（1）答题前，考生先将自己的姓名、准考证号码填写清楚；（2）选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色的签字笔书写,字迹清楚；（3）请在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸上答题无效；（4）保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀．一、选择题：（本大题共12小题，每小题5分，共60分）1．集合M{x|x2x60}，集合N{x|3x1}，则N(C M)等于（）R（A）[2,1]（B）(2,1]（C）[3,3)（D）(2,3)2．下列函数中与函数y x相等的函数是（）（A）y(x)2（B）y x2（C）y x（D）2y log2xlog223.设a0.32，b20.3，c log0.3，则a,b,c的大小关系为（）2（A）c a b（B）c b a（C）a b c(D)a c b2x3x44. 函数的定义域是（）yln(x1)（A）(1,1]（B）(1,0)(0,1]（C）[4,1]（D）(1,0)(0,1)x1 35．f(x)的值域是（）31x（A）(3,)（B）(0,3)（C）(0,2)（D）(2,)41x6．函数f(x)的图象（）2x（A）关于原点对称（B）关于直线y＝x对称（C）关于x轴对称（D）关于y轴对称1xa , x 1f (x ) f (x )( )1x7.已知，对任意，都有成立，则实数f xax120 a(4)x 2, x 1xx221 2的取值范围是（）（A ） 1a 8 （B ）1a 4 （C ） 4 a 8 （D ） a 8a a, b8．定义运算若函数,则的值域是( )a bx f2x 2xf (x )b ,ab1（A ） [1,) （B ）(0,) （C ） (0,1]（D ）,1 29．已知 f (x ) 是定义在 R 上的偶函数，当 x [0,)时， f (x ) 2x 2，则不等式f (log 2 x)的解集为（）11（ A ） (0, )（ B ） ( ,1)(2,) （ C ）(2,) （ D ）2 21(0, )(2,)210．若函数 f (x ) ax(a0且a 1) 在(,) 上是减函数，则 g (x )log (x 1) 的大致a图象是（）yyyOO-1 1 -1 1 xO 1 2 x O 1 2 x x（A）（B）（C）（D）11. 已知函数f(x)ln x，若0a b，且f(a)f(b)，则a4b的取值范围是（）（A）(4,)（B）[4,)（C）(5,)（D）[5,)12．函数()log(23)在上是单调递减的，则的取值范围是（）f x2x ax(2,4)a1313（A）（B）（C）（D）(,4][,4][8,)(,4]44二、填空题：（本大题共4小题，每小题5分，共20分）13.计算：．(log9log3)(log2log8)2439214.已知函数f(x)对任意实数a,b，都有f(ab)f(a)f(b)成立，若f(2)2，f(3)3，则f(36)的值为.15.方程2x a22x在x(,0)上有解，则a的取值范围为.x22x,x016.已知函数，函数，若，则实数的f(x)g(x)f(x)g(2a2)g(a)a22x x,x取值范围是.三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明，证明过程或解题步骤）x3B x117．（本题满分10分）已知集合,集合．A x122x2x8（1）求A B；（2）若集合C x a x a1，且(A B)C，求实数a的取值范围．x,x0118．（本题满分12分）已知函数是奇函数f(x)g(x),x（1）求g(x)的解析式；（2）求关于x的不等式x2f(x1)0的解集.319．（本题满分12分）已知关于x的不等式(log x)22log x30的解集为M．22（1）求集合M；x（2）若x M，求函数f(x)[log(2x)](log)的最值．223220.（本题满分12分）已知函数f(x)a x a x（a0且a1）（1）若f(1)0，求a的取值范围；（2）当a2时，f(x)m x在x[1,1]上恒成立，求实数m的取值范围.21.（本题满分12分）已知函数f(x)a x ta x，（a0且a1）是偶函数（1）求实数t的值；（2）当a1时，判断并证明f(x)的单调性.422．（本题满分12分）已知二次函数f x ax2bx c a0满足条件y f x1是偶函数，f(x)的图象被x轴截得的弦长为23，且f(0)1．（1）求f(x)的解析式；（2）若x[1,1]时，f(x)mx2恒成立，求实数m的取值范围.高一数学答案一、选择题：1 2 3 4 5 6 7 8 9 10 11 12B D A B B DC CD A C B二、填空题：13、；14、10；15、16、三、解答题：17、解：（1）————2分（2）18、（1）（2）19、解：（1）（2）设，，当时，即时，5当时，即时，20、解：（1）（2），在上恒成立，在上是增函数当时，21、（1）（2）上增，上减22、解：（1）（2）因为时，设，即恒成立，对称轴当时，即时，所以当，即时，所以当，即时，，所以综上：6。

2017-2018学年哈尔滨高一(上)期末数学试卷((有答案))-(新课标人教版)AlPMMM

2017-2018学年黑龙江省哈尔滨高一（上）期末数学试卷一、选择题（本大题共12个小题，每个小题5分）1．（5分）已知集合A={1，2，3，4，5}，B={x|x2﹣3x＜0}，则A∩B为（）A．{1，2，3}B．{2，3}C．{1，2}D．（0，3））2．（5分）已知角α在第三象限，且sinα=﹣，则tanα=（）A．B．C．D．3．（5分）的值为（）A．B．C．1 D．﹣14．（5分）已知△ABC的三边a，b，c满足a2+b2=c2+ab，则△ABC的内角C为（）A．150°B．120°C．60°D．30°5．（5分）设函数f（x）=，则f（2）+f（﹣log23）的值为（）A．4 B．C．5 D．66．（5分）若sin（）=，sin（2）的值为（）A．B．C．D．7．（5分）已知f（x）=sin2x+2cosx，则f（x）的最大值为（）A．﹣1 B．0 C．1 D．28．（5分）已知函数f（x）=cos2x﹣，则下列说法正确的是（）A．f（x）是周期为的奇函数B．f（x）是周期为的偶函数C．f（x）是周期为π的奇函数D．f（x）是周期为π的偶函数9．（5分）已知f（x）是定义在R上的偶函数，且满足f（x+6）=f（x），当x∈（0，3）时，f （x）=x2，则f（64）=（）A．﹣4 B．4 C．﹣98 D．9810．（5分）函数的图象如图所示，为了得到g（x）=sin（3x+）的图象，只需将f（x）的图象（）A．向右平移π个单位长度B．向左平移π个单位长度C．向右平移个单位长度D．向左平移个单位长度11．（5分）奇函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式x[f（x）﹣f（﹣x）]＞0的解集为（）A．（﹣1，0）∪（0，1）B．（﹣∞，﹣1）∪（0，1）C．（﹣∞，﹣1）∪（1，+∞）D．（﹣1，0）∪（1，+∞）12．（5分）将函数f（x）=2sin（x+2φ）（|φ|＜）的图象向左平移个单位长度之后，所得图象关于直线x=对称，且f（0）＞0，则φ=（）A．B． C．D．二、填空题（本大题共4个小题，每个小题5分）13．（5分）已知f（x）=x+log a x的图象过点（2，3），则实数a=．14．（5分）已知sin，且α∈（0，），则tan的值为．15．（5分）已知f（x）=x2﹣ax+2a，且在（1，+∞）内有两个不同的零点，则实数a的取值范围是．16．（5分）已知△ABC中，内角A，B，C的对边分别为a，b，c，且a=2，cosC=﹣，sinB=sinC，则边c=．三、解答题（本大题共6个小题，共70分）17．（10分）已知函数f（x）=2x﹣sin2x﹣．（I）求函数f（x）的最小正周期及对称轴方程；（II）求函数f（x）的单调区间．18．（12分）若0，0，sin（）=，cos（）=．（I）求sinα的值；（II）求cos（）的值．19．（12分）已知△ABC中，内角A，B，C的对边分别为a，b，c，若（2a﹣c）cosB=bcosC．（I）求角B的大小；（II）若b=2，求△ABC周长的最大值．20．（12分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的最小正周期为π，函数的图象关于点（）中心对称，且过点（）．（I）求函数f（x）的解析式；（II）若方程2f（x）﹣a+1=0在x∈[0，]上有解，求实数a的取值范围．21．（12分）在△ABC中，边a，b，c所对的角分别为A，B，C，且a＞c，若△ABC的面积为2，sin（A﹣B）+sinC=sinA，b=3．（Ⅰ）求cosB的值；（Ⅱ）求边a，c的值．22．（12分）设函数f（x）=a2x+ma﹣2x（a＞0，a≠1）是定义在R上的奇函数．（Ⅰ）求实数m的值；（Ⅱ）若f（1）=，且g（x）=f（x）﹣2kf（）+2a﹣2x在[0，1]上的最小值为2，求实数k 的取值范围．2017-2018学年黑龙江省哈尔滨高一（上）期末数学试卷参考答案与试题解析一、选择题（本大题共12个小题，每个小题5分）1．（5分）已知集合A={1，2，3，4，5}，B={x|x2﹣3x＜0}，则A∩B为（）A．{1，2，3}B．{2，3}C．{1，2}D．（0，3））【解答】解：∵集合A={1，2，3，4，5}，B={x|x2﹣3x＜0}={x|0＜x＜3}，∴A∩B={1，2}．故选：C．2．（5分）已知角α在第三象限，且sinα=﹣，则ta nα=（）A．B．C．D．【解答】解：∵角α在第三象限，且sinα=﹣，∴cosα=﹣．∴．故选：C．3．（5分）的值为（）A．B．C．1 D．﹣1【解答】解：==．故选：B．4．（5分）已知△ABC的三边a，b，c满足a2+b2=c2+ab，则△ABC的内角C为（）A．150°B．120°C．60°D．30°【解答】解：△ABC中，a2+b2=c2+ab，∴a2+b2﹣c2=ab，∴cosC===，C∈（0°，180°），∴C=60°．故选：C．5．（5分）设函数f（x）=，则f（2）+f（﹣log23）的值为（）A．4 B．C．5 D．6【解答】解：∵函数f（x）=，∴f（2）=log22=1，f（﹣log23）==3，∴f（2）+f（﹣log23）=1+3=4．故选：A．6．（5分）若sin（）=，sin（2）的值为（）A．B．C．D．【解答】解：∵sin（）=，∴sin（2）=cos[﹣（2）]=cos（）=cos2（）=．故选：A．7．（5分）已知f（x）=sin2x+2cosx，则f（x）的最大值为（）A．﹣1 B．0 C．1 D．2【解答】解：f（x）=sin2x+2cosx，=1﹣cos2x+2cosx，=﹣（cosx﹣1）2+2，当cosx=1时，f（x）max=2，故选：D8．（5分）已知函数f（x）=cos2x﹣，则下列说法正确的是（）A．f（x）是周期为的奇函数B．f（x）是周期为的偶函数C．f（x）是周期为π的奇函数D．f（x）是周期为π的偶函数【解答】解：函数f（x）=cos2x﹣=（2cos2x﹣1）=cos2x，∴f（x）是最小正周期为T==π的偶函数．故选：D．9．（5分）已知f（x）是定义在R上的偶函数，且满足f（x+6）=f（x），当x∈（0，3）时，f （x）=x2，则f（64）=（）A．﹣4 B．4 C．﹣98 D．98【解答】解：由（x）是定义在R上的偶函数，且满足f（x+6）=f（x），∴f（x）是以6为周期的周期函数，又∵又当x∈（0，3）时，f（x）=x2，∴f（64）=f（6×11﹣2）=f（﹣2）=f（2）=22=4．故选：B．10．（5分）函数的图象如图所示，为了得到g（x）=sin（3x+）的图象，只需将f（x）的图象（）A．向右平移π个单位长度B．向左平移π个单位长度C．向右平移个单位长度D．向左平移个单位长度【解答】解：根据函数的图象，可得A=1，=﹣，∴ω=3，再根据五点法作图可得3×+φ=π，∴φ=，f（x）=sin（3x+）．为了得到g（x）=sin（3x+）的图象，只需将f（x）的图象向左平移个单位长度，故选：D．11．（5分）奇函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式x[f（x）﹣f（﹣x）]＞0的解集为（）A．（﹣1，0）∪（0，1）B．（﹣∞，﹣1）∪（0，1）C．（﹣∞，﹣1）∪（1，+∞）D．（﹣1，0）∪（1，+∞）【解答】解：若奇函数f（x）在（0，+∞）上为增函数，则函数f（x）在（﹣∞，0）上也为增函数，又∵f（1）=0，∴f（﹣1）=0，则当x∈（﹣∞，﹣1）∪（0，1）上时，f（x）＜0，f（x）﹣f（﹣x）＜0；当x∈（﹣1，0）∪（1，+∞）上时，f（x）＞0，f（x）﹣f（﹣x）＞0，则不等式x[（f（x）﹣f（﹣x）]＞0的解集为（1，+∞）∪（﹣∞，﹣1），故选：C．12．（5分）将函数f（x）=2sin（x+2φ）（|φ|＜）的图象向左平移个单位长度之后，所得图象关于直线x=对称，且f（0）＞0，则φ=（）A ．B ．C ．D ．【解答】解：将函数f （x ）=2sin （x +2φ）（|φ|＜）的图象向左平移个单位长度之后，可得y=2sin （x ++2φ）的图象，根据所得图象关于直线x=对称，可得++2φ=kπ+，即 φ=﹣，k ∈Z ．根据且f （0）=2sin2φ＞0，则φ=，故选：B ．二、填空题（本大题共4个小题，每个小题5分）13．（5分）已知f （x ）=x +log a x 的图象过点（2，3），则实数a= 2 ．【解答】解：∵已知f （x ）=x +log a x 的图象过点（2，3），故有2+log a 2=3，求得 a=2，故答案为：2．14．（5分）已知sin ，且α∈（0，），则tan的值为 2 ．【解答】解：由sin ，得，∴sin （）=1， ∵α∈（0，），∴∈（），则=，即，∴tanα=tan ． ∴tan=1+1=2．故答案为：2．15．（5分）已知f （x ）=x 2﹣ax +2a ，且在（1，+∞）内有两个不同的零点，则实数a 的取值范围是（8，+∞）．【解答】解：∵二次函数f （x ）=x 2﹣ax +2a 在（1，+∞）内有两个零点，∴，即，解得8＜a．故答案为：（8，+∞）．16．（5分）已知△ABC中，内角A，B，C的对边分别为a，b，c，且a=2，cosC=﹣，sinB=sinC，则边c=3．【解答】解：△ABC中，a=2，cosC=﹣，sinB=sinC，∴b=c，∴c2=a2+b2﹣2abcosC=22+c2﹣2×2×c×（﹣），化简得5c2﹣3c﹣36=0，解得c=3或c=﹣（不合题意，舍去），∴c=3．故选：3．三、解答题（本大题共6个小题，共70分）17．（10分）已知函数f（x）=2x﹣sin2x﹣．（I）求函数f（x）的最小正周期及对称轴方程；（II）求函数f（x）的单调区间．【解答】解：（Ⅰ）函数f（x）=2x﹣sin2x﹣=（1+cos2x）﹣sin2x﹣=﹣sin2x+cos2x=﹣2sin（2x﹣）；﹣﹣﹣﹣（3分）∴f（x）的最小正周期为π，﹣﹣﹣﹣（4分）对称轴方程为x=+，k∈Z；﹣﹣﹣﹣（6分）（Ⅱ）令+2kπ≤2x﹣≤+2kπ，k∈Z，解得+kπ≤x≤+kπ，k∈Z，∴f（x）的单调递增区间为[+kπ，+kπ]（k∈Z）；﹣﹣﹣﹣（8分）令﹣+2kπ≤2x﹣≤+2kπ，k∈Z，解得﹣+kπ≤x≤+kπ，k∈Z，∴f（x）的单调递减区间为[﹣+kπ，+kπ]（k∈Z）．﹣﹣﹣﹣（10分）18．（12分）若0，0，sin（）=，cos（）=．（I）求sinα的值；（II）求cos（）的值．【解答】解：（Ⅰ）∵0，∴，又sin（）=，∴cos（）=，∴sinα=sin[﹣（）]=sin cos（）﹣cos sin（）=；（Ⅱ）∵0，∴，又cos（）=，∴sin（）=．∴cos（）=cos[（）+（）]=cos（）cos（）﹣sin（）sin（）=．19．（12分）已知△ABC中，内角A，B，C的对边分别为a，b，c，若（2a﹣c）cosB=bcosC．（I）求角B的大小；（II）若b=2，求△ABC周长的最大值．【解答】（本题满分为12分）解：（Ⅰ）∵由（2a﹣c）cosB=bcosC，可得：（2sinA﹣sinC）cosB=sinBcosC，∴2sinAcosB=sinBcosC+cosBsinC，可得：2sinAcosB=sin（B+C）=sinA，∵A∈（0，π），sinA＞0，∴可得：cosB=，∴由B=，B∈（0，π），B=．﹣﹣﹣﹣（4分）（Ⅱ）∵2R==，a=sinA，c=sinC，﹣﹣﹣﹣（6分）∴可得三角形周长：a+b+c=sinA+sinC+2=sinA+sin（﹣A）+2=4sin（A+）+2，﹣﹣﹣﹣（9分）∵0＜A＜，＜A+＜，可得：sin（A+）∈（，1]．﹣﹣﹣﹣（11分）∴周长的最大值为6．﹣﹣﹣﹣（12分）20．（12分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的最小正周期为π，函数的图象关于点（）中心对称，且过点（）．（I）求函数f（x）的解析式；（II）若方程2f（x）﹣a+1=0在x∈[0，]上有解，求实数a的取值范围．【解答】解：（Ⅰ）函数f（x）=Asin（ωx+φ）的最小正周期为T==π，由ω＞0，得ω=2；由函数f（x）的图象关于点（）中心对称，∴2×+φ=kπ，φ=﹣+kπ，k∈Z；又|φ|＜，∴φ=﹣；又f（x）过点（），∴Asin（2×﹣）=1，解得A=2，∴函数f（x）=2sin（2x﹣）；（II）方程2f（x）﹣a+1=0，∴a=4sin（2x﹣）+1；又x∈[0，]，∴2x﹣∈[﹣，]，∴sin（2x﹣）∈[﹣，1]，∴4sin（2x﹣）+1∈[﹣1，5]，∴实数a的取值范围是[﹣1，5]．21．（12分）在△ABC中，边a，b，c所对的角分别为A，B，C，且a＞c，若△ABC的面积为2，sin（A﹣B）+sinC=sinA，b=3．（Ⅰ）求cosB的值；（Ⅱ）求边a，c的值．【解答】解：（Ⅰ）由sin（A﹣B）+sinC=sinA，得sinAcosB﹣cosAsinB+sin（A+B）=sinA即2sinAcosB=sinA，∵sinA≠0，∴cosB=．sinB=（Ⅱ）由余弦定理得：b2=a2+c2﹣2ac•cosB=a2+c2﹣ac⇒a2+c2﹣ac=9…①又∵s=ac•sinB=2，∴ac=6…②△ABC由①②解得，∵a＞c，∴a=3，c=2．22．（12分）设函数f（x）=a2x+ma﹣2x（a＞0，a≠1）是定义在R上的奇函数．（Ⅰ）求实数m的值；（Ⅱ）若f（1）=，且g（x）=f（x）﹣2kf（）+2a﹣2x在[0，1]上的最小值为2，求实数k 的取值范围．【解答】解：（Ⅰ）由题意可得f（0）=0，1+m=0，解得m=﹣1，则f（x）=a2x﹣a﹣2x，f（﹣x）=a﹣2x﹣a2x=﹣f（x），可得f（x）为奇函数，则m=﹣1成立；（Ⅱ）由f（x）=a2x﹣a﹣2x，f（1）=，可得a2﹣a﹣2=，解得a=2，则f（x）=22x﹣2﹣2x，设y=g（x）=22x+2﹣2x﹣2k（2x﹣2﹣x）=（2x﹣2﹣x）2﹣2k（2x﹣2﹣x）+2，设t=2x﹣2﹣x，y=t2﹣2kt+2x∈[0，1]，可得t∈[0，]，当k＜0时，y min=2成立；当0≤k≤时，y min=2﹣k2=2，解得k=0成立；当k≥时，ymin=﹣3k+=2，解得k=不成立，舍去．综上所述，实数k的取值范围是（﹣∞，0]．。

2017-2018学年度第一学期高一第一次月考成绩统计表

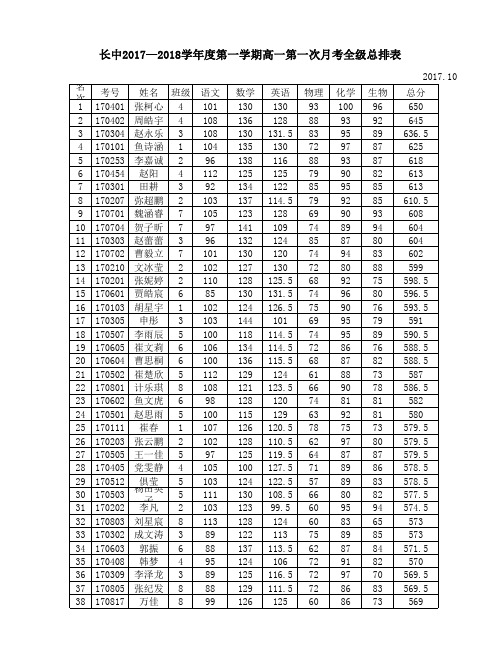
长中2017—018学年度第一学期高一第一次月考全级总排表
2017.10 名次 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 考号 170614 170104 170822 170712 170107 170834 170114 170115 170311 170708 171055 170318 170417 170815 170333 170519 170624 170217 170215 170308 170729 170514 170516 170617 170809 170811 170225 170711 170411 170610 170223 170406 170234 170108 170618 170211 170508 170616 姓名班级司梦晨 6 惠嘉康 1 胡叶叶 8 周逸飞 7 鱼朝阳 1 弥田 8 高金枝 1 尚甜甜 1 陈宝玲 3 李阳 7 杨广 10 杨扬 3 宇文雅 4 郭钾 8 黎佳昊 3 于莹莹 5 全宝婷 6 张晨 2 洪亦璇 2 李昭伟 3 解欣 7 陈雪彤 5 景凡 5 李一杰 6 党佳杰 8 尚国梁 8 罗睿青 2 剡心怡 7 梁娜 4 高星 6 曹亚鹏 2 曹锐洋 4 申岩 2 司帅 1 王帅 6 李煜 2 贾文丽 5 尚丁 6 语文 98 96 89 82 102 103 93 97 90 88 100 88 95 94 87 98 101 95 108 93 102 101 99 94 89 87 91 84 84 107 83 100 92 94 92 90 102 91 数学 117 126 117 119 101 126 112 109 107 120 118 101 103 119 113 115 124 92 97 108 120 116 111 113 138 118 114 123 118 125 123 98 111 102 133 113 112 110 英语 114 100 123.5 89.5 109 105.5 101.5 123 113 98.5 76 113 114.5 81.5 86.5 104 114.5 105.5 106.5 101.5 108 113 78 90.5 87 111.5 99 105 72 79.5 84.5 108.5 73 95.5 109.5 67.5 117 76 物理 57 60 67 67 70 48 66 50 58 65 64 61 63 62 80 59 42 69 47 45 56 42 62 55 44 57 65 56 74 50 62 69 80 68 56 70 52 67 化学 73 85 83 90 73 76 86 82 92 87 82 82 87 86 81 72 72 84 84 89 62 70 86 89 88 80 76 76 95 86 78 76 84 86 80 90 55 95 生物 77 68 54 86 78 74 74 71 71 72 89 83 64 84 79 78 72 79 79 85 72 78 84 78 73 65 72 73 73 68 84 62 73 67 42 82 74 73 总分 536 535 533.5 533.5 533 532.5 532.5 532 531 530.5 529 528 526.5 526.5 526.5 526 525.5 524.5 521.5 521.5 520 520 520 519.5 519 518.5 517 517 516 515.5 514.5 513.5 513 512.5 512.5 512.5 512 512

黑龙江省哈尔滨市四校联考2017-2018学年高一上学期期中考试数学试卷 Word版含解析

2017-2018学年黑龙江省哈尔滨市四校联考高一（上）期中数学试卷一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）设集合A={x|（x﹣1）（x﹣2）2=0}，则集合A中元素的个数为（）A．1个B．2个C．3个D．4个2．（5分）集合A={x|x＜﹣1或x＞2}，B={x|0≤x≤2}，则A∩（C R B）=（）A．{x|x＜2} B．{x|x＜﹣1或x≥2}C．{x|x≥2} D．{x|x＜﹣1或x＞2}3．（5分）在映射f：A→B中，A=B={（x，y）|x，y∈R}，且f：（x，y）→（x﹣y，x+y），则与A中的元素（﹣1，2）对应的B中的元素为（）A．（﹣3，1）B．（1，3）C．（﹣1，﹣3）D．（3，1）4．（5分）若a=20.5，b=log43，c=log20.2，则（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a5．（5分）F（x）=（x3﹣2x）f（x）（x≠0）是奇函数，且f（x）不恒等于零，则f（x）为（）A．奇函数B．偶函数C．奇函数或偶函数D．非奇非偶函数6．（5分）已知幂函数f（x）=x，若f（a+1）＜f（10﹣2a），则a的取值范围是（）A．[﹣1，3）B．（﹣∞，5）C．（3，5）D．（3，+∞）7．（5分）若3x=a，5x=b，则45x等于（）A．a2b B．ab2C．a2+b D．a2+b28．（5分）若函数f（x）=a﹣x（a＞0且a≠1）在（﹣∞，+∞）上是减函数，则g（x）=log a （x﹣1）的大致图象是（）A．B．C．D．9．（5分）若函数f（x）=x2+4x+6，则f（x）在[﹣3，0）上的值域为（）A．[2，6]B．[2，6）C．[2，3]D．[3，6]10．（5分）已知函数f（x）=3log a（4x﹣7）+2（a＞0且a≠1）过定点P，则P点坐标（）A．（1，2）B．（，2） C．（2，2）D．（3，2）11．（5分）已知函数f（x）是定义在R上的偶函数，且在[0，+∞）上单调递增，若f（﹣1）=0，则不等式f（2x﹣1）＞0解集为（）A．（﹣∞，0）∪（1，+∞）B．（﹣6，0）∪（1，3）C．（﹣∞，1）∪（3，+∞）D．（﹣∞，﹣1）∪（3，+∞）12．（5分）函数f（x）=log（x2﹣9）的单调递增区间为（）A．（0，+∞）B．（﹣∞，0）C．（3，+∞）D．（﹣∞，﹣3）二、填空题：（本大题共4小题，每小题5分，共20分）13．（5分）已知集合A={﹣1，a}，B={3a，b}，若A∪B={﹣1，0，1}，则a=．14．（5分）已知函数f（x）=，则f（3）的值为．15．（5分）若幂函数y=（m2﹣2m﹣2）x﹣4m﹣2在x∈（0，+∞）上为减函数，则实数m的值是．16．（5分）函数f（x）=的定义域是．三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明，证明过程或解题步骤）17．（10分）设集合A={x|x2+ax﹣12=0}，B={x|x2+bx+c=0}，且A≠B，A∪B={﹣3，4}，A∩B={﹣3}，求实数b，c的值．18．（12分）已知全集U=R，集合A={x|﹣7≤2x﹣1≤7}，B={x|m﹣1≤x≤3m﹣2}．若A∩B=B，求实数m的取值范围．19．（12分）已知f（x）=1﹣．（1）求证：f（x）是定义域内的增函数；（2）当x∈[0，1]时，求f（x）的值域．20．（12分）已知函数f（x）是奇函数，且定义域为（﹣∞，0）∪（0，+∞）．若x＜0时，f（x）=﹣x﹣1．（1）求f（x）的解析式；（2）解关于x的不等式f（x）＞0．21．（12分）设f（x）=（log2x）2﹣2alog2x+b（x＞0）．当x=时，f（x）有最小值﹣1．（1）求a与b的值；（2）求满足f（x）＜0的x的取值范围．22．（12分）若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．（1）求f（x）的解析式；（2）设g（x）=f（2x），求g（x）在[﹣3，0]的最大值与最小值．2016-2017学年黑龙江省哈尔滨市四校联考高一（上）期中数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）（2016春•长春校级期末）设集合A={x|（x﹣1）（x﹣2）2=0}，则集合A中元素的个数为（）A．1个B．2个C．3个D．4个【考点】集合中元素个数的最值．【专题】计算题；规律型；集合．【分析】求出方程的解，即可得到结合A中元素的个数．【解答】解：（x﹣1）（x﹣2）2=0，可得x=1，或x=2．则集合A中元素的个数为：2．故选：B．【点评】本题考查集合元素个数问题，方程的解是解题的关键．2．（5分）（2016秋•哈尔滨期中）集合A={x|x＜﹣1或x＞2}，B={x|0≤x≤2}，则A∩（C R B）=（）A．{x|x＜2} B．{x|x＜﹣1或x≥2}C．{x|x≥2} D．{x|x＜﹣1或x＞2}【考点】交、并、补集的混合运算．【专题】计算题；方程思想；综合法；集合．【分析】求出B的补集，根据交集的定义即可求出．【解答】解：∵全集为R，B={x|0≤x≤2}，∴∁R B={x|x＜0或x＞2}，∵A={x|x＜﹣1或x＞2}，∴A∩C R B={x|x＜﹣1或x＞2}．故选：D．【点评】本题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．3．（5分）（2012秋•十堰期末）在映射f：A→B中，A=B={（x，y）|x，y∈R}，且f：（x，y）→（x﹣y，x+y），则与A中的元素（﹣1，2）对应的B中的元素为（）A．（﹣3，1）B．（1，3）C．（﹣1，﹣3）D．（3，1）【考点】映射．【专题】计算题．【分析】根据已知中映射f：A→B的对应法则，f：（x，y）→（x﹣y，x+y），将A中元素（﹣1，2）代入对应法则，即可得到答案．【解答】解：由映射的对应法则f：（x，y）→（x﹣y，x+y），故A中元素（﹣1，2）在B中对应的元素为（﹣1﹣2，﹣1+2）即（﹣3，1）故选A【点评】本题考查的知识点是映射的概念，属基础题型，熟练掌握映射的定义，是解答本题的关键．4．（5分）（2016秋•哈尔滨期中）若a=20.5，b=log43，c=log20.2，则（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a【考点】对数值大小的比较；指数函数的图象与性质．【专题】转化思想；函数的性质及应用．【分析】化简成底数相同，如果底数无法化成同底数，则利用中间值0，1，再利用对数函数和指数函数的性质求解．【解答】解：由指数函数的性质可知，底数大于1时，是增函数，指数越大，函数值越大．∵a=20.5＞20=1，∴a＞1由对数函数的性质可知，底数大于1时，是增函数，真数越大，函数值越大．b=log43=log23=log2，∵底数是2大于1，增函数，0.2＜，∴log20.2＜log2＜log22=1，∴1＞b＞c所以：c＜b＜a故选：A．【点评】本题考查了利用对数的运算化简及指数函数和对数函数的性质比较大小，学会利用中间值：0，1进行转化比较是关键．属于基础题，5．（5分）（2016秋•哈尔滨期中）F（x）=（x3﹣2x）f（x）（x≠0）是奇函数，且f（x）不恒等于零，则f（x）为（）A．奇函数B．偶函数C．奇函数或偶函数D．非奇非偶函数【考点】函数奇偶性的判断．【专题】函数思想；定义法；函数的性质及应用．【分析】由F（x）为奇函数，可得F（﹣x）=﹣F（x），进而得到f（﹣x）=f（x），即可判断f（x）的奇偶性．【解答】解：F（x）=（x3﹣2x）f（x）（x≠0）是奇函数，且f（x）不恒等于零，可得F（﹣x）=（﹣x3+2x）f（﹣x）=﹣F（x）=﹣（x3﹣2x）f（x），可得f（﹣x）=f（x），即有f（x）为偶函数．故选：B．【点评】本题考查函数的奇偶性的判断，注意运用定义法，考查化简运算能力，属于基础题．6．（5分）（2016秋•哈尔滨期中）已知幂函数f（x）=x，若f（a+1）＜f（10﹣2a），则a的取值范围是（）A．[﹣1，3）B．（﹣∞，5）C．（3，5）D．（3，+∞）【考点】幂函数的概念、解析式、定义域、值域．【专题】函数思想；转化法；函数的性质及应用．【分析】由幂函数f（x）=在[0，+∞）上单调递增可得0≤a+1＜10﹣2a，从而解得．【解答】解：∵幂函数f（x）=在[0，+∞）上单调递增，又∵f（a+1）＜f（10﹣2a），∴0≤a+1＜10﹣2a，∴﹣1≤a＜3，故选：A．【点评】本题考查了幂函数的性质，属于基础题．7．（5分）（2016秋•哈尔滨期中）若3x=a，5x=b，则45x等于（）A．a2b B．ab2C．a2+b D．a2+b2【考点】对数的运算性质．【专题】计算题；转化思想；定义法；函数的性质及应用．【分析】直接根据指数幂的运算性质化简即可．【解答】解：3x=a，5x=b，则45x=9x•5x=a2b，故选：A【点评】本题考查了指数幂的运算性质，属于基础题．8．（5分）（2016秋•哈尔滨期中）若函数f（x）=a﹣x（a＞0且a≠1）在（﹣∞，+∞）上是减函数，则g（x）=log a（x﹣1）的大致图象是（）A．B．C．D．【考点】对数函数的单调区间．【专题】数形结合；转化思想；函数的性质及应用．【分析】函数f（x）=a﹣x=（a＞0且a≠1）在（﹣∞，+∞）上是减函数，可得，a＞1．则g（x）=log a（x﹣1）的定义域为{x|x＞1}，在定义域内单调递增，且g（2）=0．即可得出．【解答】解：∵函数f（x）=a﹣x=（a＞0且a≠1）在（﹣∞，+∞）上是减函数，∴，∴a＞1．则g（x）=log a（x﹣1）的定义域为{x|x＞1}，在定义域内单调递增，且g（2）=0．其大致图象是A．故选：A．【点评】本题考查了指数函数的定义域与单调性、图象与性质，考查了推理能力与计算能力，属于中档题．9．（5分）（2016秋•哈尔滨期中）若函数f（x）=x2+4x+6，则f（x）在[﹣3，0）上的值域为（）A．[2，6]B．[2，6）C．[2，3]D．[3，6]【考点】二次函数的性质．【专题】函数的性质及应用．【分析】本题利用二次函数的单调性和图象研究函数的值域，得到本题结论．【解答】解：∵函数f（x）=x2+4x+6，∴当x∈[﹣3，0）时，函数f（x）在区间[﹣3，﹣2]上单调递减，函数f（x）在区间[﹣2，0）上单调递增．∵f（﹣2）=2，f（﹣3）=3，f（0）=6，∴2≤f（x）＜6．故选B．【点评】本题考查了二次函数的单调性、图象和函数的值域，本题难度不大，属于基础题．10．（5分）（2016秋•哈尔滨期中）已知函数f（x）=3log a（4x﹣7）+2（a＞0且a≠1）过定点P，则P点坐标（）A．（1，2）B．（，2） C．（2，2）D．（3，2）【考点】函数恒成立问题；对数函数的图象与性质．【专题】规律型；方程思想；定义法；函数的性质及应用．【分析】根据log a1=0恒成立，令真数部分为1，可得定点坐标．【解答】解：当4x﹣7=1，即x=2时，log a（4x﹣7）=0恒成立，∴f（2）=2恒成立，故P点的坐标为（2，2），故选：C【点评】本题考查的知识点是恒成立问题，熟练掌握对数的性质：log a1=0恒成立，是解答的关键．11．（5分）（2016秋•哈尔滨期中）已知函数f（x）是定义在R上的偶函数，且在[0，+∞）上单调递增，若f（﹣1）=0，则不等式f（2x﹣1）＞0解集为（）A．（﹣∞，0）∪（1，+∞）B．（﹣6，0）∪（1，3）C．（﹣∞，1）∪（3，+∞）D．（﹣∞，﹣1）∪（3，+∞）【考点】奇偶性与单调性的综合．【专题】转化思想；数形结合法；函数的性质及应用；不等式的解法及应用．【分析】根据函数奇偶性和单调性的关系进行转化即可．【解答】解：∵f（﹣1）=0，∴不等式f（2x﹣1）＞0等价为f（2x﹣1）＞f（﹣1），∵f（x）是定义在R上的偶函数，且在[0，+∞）上单调递增，∴不等式等价为f（|2x﹣1|）＞f（1），即|2x﹣1|＞1，即2x﹣1＞1或2x﹣1＜﹣1，即x＞1或x＜0，则不等式的解集为（﹣∞，0）∪（1，+∞），故选：A．【点评】本题主要考查不等式的求解，利用函数奇偶性和单调性的性质进行转化是解决本题的关键．12．（5分）（2014秋•湖州期末）函数f（x）=log（x2﹣9）的单调递增区间为（）A．（0，+∞）B．（﹣∞，0）C．（3，+∞）D．（﹣∞，﹣3）【考点】复合函数的单调性；函数的单调性及单调区间．【专题】函数的性质及应用．【分析】设t=x2﹣9，根据复合函数单调性之间的关系即可得到结论．【解答】解：由x2﹣9＞0解得x＞3或x＜﹣3，即函数的定义域为{x|x＞3或x＜﹣3}，设t=x2﹣9，则函数y=log t为减函数，根据复合函数单调性之间的关系知要求函数f（x）的单调递增区间，即求函数t=x2﹣9的递减区间，∵t=x2﹣9，递减区间为（﹣∞，﹣3），则函数f（x）的递增区间为（﹣∞，﹣3），故选：D【点评】本题主要考查函数单调区间的求解，利用换元法结合复合函数单调性之间的关系是解决本题的关键．二、填空题：（本大题共4小题，每小题5分，共20分）13．（5分）（2016秋•哈尔滨期中）已知集合A={﹣1，a}，B={3a，b}，若A∪B={﹣1，0，1}，则a=0．【考点】并集及其运算．【专题】计算题；对应思想；定义法；集合．【分析】利用并集定义及集合中元素的性质求解．【解答】解：∵集合A={﹣1，a}，B={3a，b}，A∪B={﹣1，0，1}，∴，∴a=0．故答案为：0．【点评】本题考查实数的求法，是基础题，解题时要认真审题，注意并集定义的合理运用．14．（5分）（2016秋•哈尔滨期中）已知函数f（x）=，则f（3）的值为．【考点】分段函数的应用．【专题】函数思想；定义法；函数的性质及应用．【分析】根据分段函数的表达式，利用递推法进行转化求解即可．【解答】解：由分段函数的表达式得f（3）=f（3+2）=f（5）=（）5=，故答案为：【点评】本题主要考查函数值的计算，根据分段函数的表达式，利用关系递推是解决本题的关键．比较基础．15．（5分）（2016秋•哈尔滨期中）若幂函数y=（m2﹣2m﹣2）x﹣4m﹣2在x∈（0，+∞）上为减函数，则实数m的值是m=3．【考点】幂函数的概念、解析式、定义域、值域．【专题】计算题；函数的性质及应用．【分析】根据给出的函数为幂函数，由幂函数概念知m2﹣m﹣1=1，再根据函数在（0，+∞）上为减函数，得到幂指数应该小于0，求得的m值应满足以上两条．【解答】解：因为函数y=（m2﹣2m﹣2）x﹣4m﹣2既是幂函数又是（0，+∞）的减函数，所以，⇒，解得：m=3．故答案为：m=3．【点评】本题考查了幂函数的概念及性质，解答此题的关键是掌握幂函数的定义，此题极易把系数理解为不等于0而出错，属基础题．16．（5分）（2015•武汉模拟）函数f（x）=的定义域是{x|﹣1＜x≤2且x≠0} ．【考点】函数的定义域及其求法．【专题】计算题；函数的性质及应用．【分析】由分式中的对数式的真数大于0且不等于1，根式内部的代数式大于等于0，联立不等式组求解x的取值集合即可得到答案．【解答】解：由，解得：﹣1＜x≤2，且x≠0．∴函数f（x）=的定义域是{x|﹣1＜x≤2，且x≠0}．故答案为：{x|﹣1＜x≤2，且x≠0}．【点评】本题考查了函数的定义域及其求法，解答此题的关键是注意分母不等于0，是基础题．三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明，证明过程或解题步骤）17．（10分）（2016秋•哈尔滨期中）设集合A={x|x2+ax﹣12=0}，B={x|x2+bx+c=0}，且A ≠B，A∪B={﹣3，4}，A∩B={﹣3}，求实数b，c的值．【考点】并集及其运算．【专题】计算题；函数思想；方程思想；集合．【分析】利用集合的并集与交集的关系，判断元素与集合的关系，列出方程求解即可．【解答】解∵A∩B={﹣3}，∴﹣3∈A，则9﹣3a﹣12=0，∴a=﹣1，从而A={﹣3，4}，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（3分）由于A≠B，因此集合B只有一个元素﹣3，即x2+bx+c=0有等根．﹣﹣﹣﹣﹣﹣﹣﹣（5分）∴﹣﹣﹣﹣﹣（7分）解之得﹣﹣﹣﹣﹣﹣（9分）所以实数b，c的值分别为6，9．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）【点评】本题考查集合的交集与并集的关系，考查计算能力．18．（12分）（2016秋•哈尔滨期中）已知全集U=R，集合A={x|﹣7≤2x﹣1≤7}，B={x|m ﹣1≤x≤3m﹣2}．若A∩B=B，求实数m的取值范围．【考点】集合的包含关系判断及应用．【专题】定义法；集合．【分析】化简集合A，确定元素范围，根据A∩B=B，建立条件关系即可求实数a的取值范围．【解答】解：由题意：全集U=R，集合A={x|﹣7≤2x﹣1≤7}={x|﹣3≤x≤4}，B={x|m﹣1≤x≤3m﹣2}．∵A∩B=B，∴B⊆A，∴当B=∅时，满足题意，此时m﹣1＞3m﹣2，解得：m＜．当B≠∅时，要使B⊆A成立，需满足：，解得：≤m≤2，综上所得：实数m的取值范围是{m|m≤2}．【点评】本题主要考查集合的基本运算，比较基础．注意空集情况不要漏掉．19．（12分）（2016秋•哈尔滨期中）已知f（x）=1﹣．（1）求证：f（x）是定义域内的增函数；（2）当x∈[0，1]时，求f（x）的值域．【考点】利用导数研究函数的单调性；函数的值域；函数单调性的判断与证明．【专题】证明题；数学模型法；函数的性质及应用．【分析】（1）求导，根据在定义域R上，f′（x）＞0恒成立，可得：f（x）是定义域R上的增函数；（2）由（1）可得当x∈[0，1]时，f（x）为增函数，求出函数的最值，可得函数的值域．【解答】证明：（1）∵f（x）=1﹣．∴f′（x）=．在定义域R上，f′（x）＞0恒成立，故f（x）是定义域R上的增函数﹣﹣﹣﹣﹣﹣﹣（8分）解：（2）由（1）可得当x∈[0，1]时，f（x）为增函数，故当x=0时，f（x）取最小值0，当x=1时，f（x）取最大值，即当x∈[0，1]时，求f（x）值域为[0，]﹣﹣﹣﹣﹣﹣﹣（12分）【点评】本题考查的知识点是利用导数研究函数的单调性，函数的最值，函数的值域，难度中档．20．（12分）（2016秋•哈尔滨期中）已知函数f（x）是奇函数，且定义域为（﹣∞，0）∪（0，+∞）．若x＜0时，f（x）=﹣x﹣1．（1）求f（x）的解析式；（2）解关于x的不等式f（x）＞0．【考点】分段函数的应用；函数奇偶性的性质．【专题】计算题；方程思想；转化思想；函数的性质及应用．【分析】（1）利用函数的奇偶性的定义，直接求解函数的解析式即可．（2）利用分段函数列出不等式求解即可．【解答】解：（1）当x＞0时，﹣x＜0，f（﹣x）=x﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）∵函数f（x）是定义域为的奇函数．∴f（x）=﹣f（﹣x）=1﹣x﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）∴f（x）=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（2）∵f（x）＞0∴或﹣﹣﹣﹣﹣﹣﹣（9分）解得：x＜﹣1或0＜x＜1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）故不等式的解集为：（﹣∞，﹣1）∪（0，1）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）【点评】本题考查函数的解析式的求法，函数的奇偶性以及分段函数的应用，考查计算能力．21．（12分）（2016秋•哈尔滨期中）设f（x）=（log2x）2﹣2alog2x+b（x＞0）．当x=时，f（x）有最小值﹣1．（1）求a与b的值；（2）求满足f（x）＜0的x的取值范围．【考点】对数函数的图象与性质．【专题】函数思想；综合法；函数的性质及应用．【分析】（1）利用配方法，结合x=时，f（x）有最小值﹣1，建立方程组，即可求a与b的值；（2）f（x）＜0即（log2x）2+4log2x+3＜0，即可求出x的范围．【解答】解：（1）f（x）=（log2x）2﹣2alog2x+b=+b﹣a2（x＞0），当x=时，f（x）有最小值﹣1，∴，解得：；（2）由（1）得：f（x）=（log2x）2+4log2x+3，f（x）＜0即（log2x+3）（log2x+1）＜0，解得：＜x＜．【点评】本题考查函数的最值，考查学生解不等式的能力，确定函数的解析式是关键．22．（12分）（2016秋•哈尔滨期中）若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．（1）求f（x）的解析式；（2）设g（x）=f（2x），求g（x）在[﹣3，0]的最大值与最小值．【考点】二次函数的性质．【专题】综合题；函数思想；综合法；函数的性质及应用．【分析】（1）根据待定系数法即可求出函数的解析式，（2）利用换元法和函数的性质即可求出最值．【解答】解：（1）由f（0）=3，得c=3，∴f（x）=ax2+bx+3．又f（x+1）﹣f（x）=4x+1，∴a（x+1）2+b（x+1）+3﹣（ax2+bx+3）=4x+1，即2ax+a+b=4x+1，∴∴∴f（x）=2x2﹣x+3．（2）g（x）=f（2x）=2•22x﹣2x+3，令2x=t，，∴h（t）=2t2﹣t+3，时，g（x）max=h（t）max=h（1）=2﹣1+3=4，g（x）min=h（t）min=h（）=﹣+3=．【点评】本题考查了二次函数的性质和函数最值的问题，考查了学生的计算能力，属于中档题．。

黑龙江省哈尔滨市2017_2018学年高一数学上学期期中试题201711090290

黑龙江省哈尔滨市 2017-2018学年高一数学上学期期中试题考试说明：（1）本试卷分第 I 卷（选择题）和第 II 卷（非选择题）两部分, 满分 150分．考试时间为 120分钟；（2）第 I 卷，第 II 卷试题答案均答在答题卡上，交卷时只交答题卡．第 I 卷（选择题, 共 60分）一、选择题（本大题共 12小题，每小题 5分，共 60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1. 给出下列关系：①0 ；②{0,1}；③{0}；④{1}{1,2}，其中正确的个数是A ．1B ．2C ．3D ．42. 下列函数中，值域为[1,)的是1yy x211 y x 2xA ．B ．C ．D ．x 21yx 1 1f x3x 22x33．函数的单调减区间为A.,B .,1C.1,D.,2(31)xf (x )4. 函数的定义域是x 2A ． (2,0) B ． (2,) C ．[2,0) (0,) D ． (2,0)(0,)1f （0，）(x )5. 若函数的值域为，则实数 m 的取值范围是mx22(m 2)x 1A ． (1, 4)B ． (-,1)(4,)C ． (0,1][4,) D ．[0,1][4,)3x 86. 不等式2 2(x Z ) 解集中元素的个数为(x1)A ．1B ．2C ．3D ．41x2,x1f()x7. 函数2的值域为x,0x1x1A．(1,4)B．[1,)C．(3,)D．[4,)32228．已知2a 5b 10, 则a b2A. 22B. 22C.D.2229．函数y a x（a 0且a 1）与函数y (a 1)x22x 1在同一个坐标系内的图象可能是A. B. C. D.f(1)(x)f(x)x f10．已知函数f(x)4x2,若0x1x2x32,则由大到小的,2,3x x x123顺序为f(x)f(x)f x1(),,23A. B.x x x123f(x3)f()f(x)x,2,1x x x321f1),(),()(x f x f x32C. D.x x x132f(2)f(x)f(x)x,,13x x x21311．已知f x是定义在,上的偶函数，且在,0上是增函数，111aa ,b ,c设(2 ),(3 ),(5 )，则的大小关系是2bf ffc35A. ca b B. c b a C . b a c D. a b ceax12. 已知函数 fx，对于任意的 x 1, x 21,2 ，且1x ，x22 ex[| f (x 1) | | f (x ) |](xx ) 0a恒成立，则实数的取值范围是212222222e ee ee e,,, A.B.C.D.4 4 2 2 3 3e 2,e 2第Ⅱ卷（非选择题, 共 90分）二、填空题(本大题共 4小题，每小题 5分，共 20分．将答案填在答题卡相应的位置上)213. 设集合A {x2x25x 30}，B {x2x 50}，则A B14. 已知log23a,log7b,则log27__________(结果用a,b表示)3xf x)(a 0f(2)1f(x)x15. 已知函数（a，b为常数，且）满足，方程有ax b唯一解，则f(f(1))16. 已知f(x)是定义在R上的奇函数,当x0时, f(x)2x x2. f(x)在[a,b]上的11值域为[,]，则b aa b三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17. （本小题满分10分）化简求值：113211（Ⅰ）33；()81322()3422852438（Ⅱ）3)3log2log3189log2.(log2366618. （本小题满分12分）设全集U R，Ax 1x 4，Bx2x 5，.C x a2x a 2（Ⅰ）求A (C B)；U（Ⅱ）若B C B，求实数a的取值范围．19. （本小题满分12分）a2解关于x的不等式：a.x 120. （本小题满分12分）已知偶函数f(x)的定义域是x0的一切实数，对定义域内的任意a,b都有f(ab)f(a)f(b)x1f(x)0,f(3)1，且当时, .(Ⅰ)求证：f(x)在,0上是减函数；（Ⅱ）解不等式f(x21)2.21．（本小题满分12分）32a0且a1f(x)x,g(x)1已知函数.a1x(Ⅰ) 判断f(x)g(x)的奇偶性，并说明理由；（Ⅱ）当a2时，g(x)b恒成立，求b的取值范围．22.（本小题满分12分）bx11f(x)f(2)（a,b N）已知函数的最大值为，且.a x452(Ⅰ) 求函数f(x)的解析式；（Ⅱ）若x,y,z,w0，且x y z w2.2x22y2z2w x y z w222求证：.a x a y a z a w a x a y a z a w222222224高一数学期中答案一、选择题1-5ABBDD 6-10CBBCA 11-12CB 二、填空题1 5 113.)；14.；15. ；16 (, ab, 3) (2 223 25 三、解答题 21 17.（1）；（2）5218.（1）1,2；（2）(,1) (2,)19.① a0时，解集为(,1)2② a0时，解集为(,1,)) (a 2③ 2 a 0 时，解集为 ( ,1)a④ a2时，解集为2⑤ a2 时，解集为 (1，)a20.（1）略；（2） (10,1) (1,1) (1, 10)21.（1）偶函数；（2）[1,)xf (x )22.（1）；（2）略4 x25。

黑龙江省哈尔滨市2017_2018学年高一英语上学期期中试题

2017-2018学年度上学期期中考试高一英语试题本试卷分第一卷（选择题）和第二卷（非选择题）两部分。

共150分。

考试结束后，将本试卷和答题卡一并收回。

第一卷注意事项：1. 答题前，考生先将自己的姓名，准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2. 选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，笔迹清楚。

3. 请按照题号顺序在各题目的答题区域内作答，超出答题区域书写答案无效；在草稿纸、试题卷上答题无效。

4. 保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第一部分听力（共20小题，每小题0.5分，满分10分）第一节听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

XXX2017-2018学年第一学期高一期末数学试卷

XXX2017-2018学年第一学期高一期末数学试卷XXX2017-2018学年第一学期高一期末数学试卷一、填空题（每题3分，共36分）1、已知全集$U=\mathbb{R}$，集合$A=\{x|y=\pi x\}$，则$C_UA=$ $\{x|x\notin A\}$2、函数$f(x)=x^{-1}$在$(-\infty,0)$内的零点为$x=-1$3、关于$x$的方程$2^x=3$的解集为$\{\log_2 3\}$4、函数$f(x)=\dfrac{1}{x+a}$为奇函数，则实数$a$的值为$0$5、集合$A=\{x|x<a\},B=\{x|x<1\}$，若$A\subseteq B$，则实数$a$的取值范围为$a\leq 1$6、比较两数大小: $2^{e^{5031}}$ $>$ $e^{2^{5031}}$7、函数$y=f(x)$的定义域为$(0,1)$，则函数$y=f(2x)$的定义域为$(0,\dfrac{1}{2})$8、幂函数$y=x^{-2}$的单调递减区间为$(0,+\infty)$9、函数$y=f(x)$过定点$(0,2)$，则函数$y=f(x-2)$过定点$(2,2)$10、不等式$|x|-a\geq 0$ 对任意$x\in[-1,2]$恒成立，则实数$a$的最大值为$a=2$11、若函数$f(x)=\dfrac{x^2-3x+2}{x-2}$，则$f(x)-f(2-x)=\dfrac{4x-10}{x-2}$12、方程$f(x+2018)+f(\dfrac{e-|2-x|}{x-2x-1})-a=0$在$(-\infty,5)$内有两个零点，则实数$a$的取值范围为$a\in(-\infty,4)$二、选择题(每题3分,共12分)13.四个说法中,与“不经冬寒,不知春暖”意义相同的是() C.若知春暖，必经冬寒14、已知实数$x>y$，下列不等式中一定成立的是() B。

人教版2017~2018学年度初三第一学期期末考试数学试题附详细答案

E D CBA2017-2018学年第一学期期末测试卷初三数学一、选择题（本题共30分，每小题3分）1．⊙O 的半径为R ，点P 到圆心O 的距离为d ，并且d ≥ R ，则P 点 A.在⊙O 内或圆周上 B.在⊙O 外C.在圆周上D.在⊙O 外或圆周上2. 把10cm 长的线段进行黄金分割，则较长线段的长（236.25≈, 精确到0.01）是A ．3.09cmB ．3.82cmC ．6.18cmD ．7.00cm 3．如图，在△ABC 中，DE ∥BC ，DE 分别与AB 、AC 相交于点D 、E ，若AD =4，DB =2，则AE ︰EC 的值为 A . 0.5 B . 2 C . 32 D . 23 4. 反比例函数xky =的图象如图所示,则K 的值可能是 A .21B . 1C . 2D . -1 5. 在Rt △ABC 中，∠C =90°，BC =1，那么AB 的长为A ．sin AB ．cos AC ．1cos AD ． 1sin A6．如图，正三角形ABC 内接于⊙O ，动点P 在圆周的劣弧AB 上，且不与A,B 重合，则∠BPC 等于A .30︒B .60︒ C. 90︒ D. 45︒ 7．抛物线y=21x 2的图象向左平移2个单位，在向下平移1个单位，得到的函数表达式为 A . y =21x 2+ 2x + 1 B ．y =21x 2+ 2x - 2C . y =21x 2 - 2x - 1 D. y =21x 2- 2x + 18. 已知二次函数)0(2≠++=a c bx ax y 的图象如图所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ； ④ b c 32<； ⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有 A. 2个 B. 3个C. 4个D. 5个9. 如图所示，在正方形ABCD 中，E 是BC 的中点，F 是CD 上的一点，AE ⊥EF ，下列结论：①∠BAE ＝30°；②CE 2＝AB·CF ；③CF ＝31FD ；④△ABE ∽△AEF .其中正确的有A. 1个B. 2个C. 3个D. 4个10．如图，已知△ABC 中，BC =8，BC 边上的高h =4，D 为BC 边上一个动点，EF ∥BC ，交AB 于点E ，交AC 于点F ，设E 到BC 的距离为x ，△DEF 的面积为y ，则y 关于x 的函数图象大致为A. B. C. D.二、填空题（本题共18分, 每小题3分） 11．若5127==b a ，则32ba -= ． 12. 两个相似多边形相似比为1:2,且它们的周长和为90,则这两个相似多边形的周长分别是 , ． 13.已知扇形的面积为15πcm 2,半径长为5cm ,则扇形周长为 cm ．14. 在Rt △ABC 中，∠C =90°，AC =4, BC =3,则以2.5为半径的⊙C 与直线AB 的位置关系是．15. 请选择一组你喜欢的a,b,c 的值，使二次函数)0(2≠++=a c bx ax y 的图象同时满16. 点是 17.18.如图：在Rt△ABC中，∠C=90°，BC=8，∠B=60°, 解直角三角形.19.已知反比例函数x 1k y -=图象的两个分支分别位于第一、第三象限．（1）求k的取值范围；（2）取一个你认为符合条件的K值，写出反比例函数的表达式，并求出当x=﹣6时反比例函数y的值；20.已知圆内接正三角形边心距为2cm，求它的边长.24.密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物，是美国最高的独自挺立的纪念碑，如图．拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度．25. 如图，已知⊙O 是△ABC 的外接圆，AB 是⊙O 的直径， D 是AB 的延长线上的一点，AE ⊥DC 交DC 的延长线于点E ，且AC 平分∠EAB ．求证：DE 是⊙O 的切线．26. 已知：抛物线y=x 2+bx+c 经过点（2，-3）和（4，5）（1）求抛物线的表达式及顶点坐标；（2）将抛物线沿x 轴翻折，得到图象G ，求图象G 的表达式；（3）在（2）的条件下，当-2<x <2时，直线y =m 与该图象有一个公共点，求m 的值或取值范围.27. 如图，已知矩形ABCD 的边长3cm 6cm AB BC ==，．某一时刻，动点M 从A 点出发沿AB 方向以1c m /s 的速度向B 点匀速运动；同时，动点N 从D 点出发沿DA 方向以2c m /s 的速度向A 点匀速运动，问：（1）经过多少时间，AMN △的面积等于矩形ABCD 面积的19？（2）是否存在时刻t ，使以A,M,N 为顶点的三角形与ACD △相似？若存在，求t 的值；若不存在，请说明理由．()28.（1）探究新知：如图1，已知△ABC 与△ABD 的面积相等，试判断AB 与CD 的位置关系，并说明理由．（2）结论应用：① 如图2，点M ，N 在反比例函数xky =（k ＞0）的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E ，F ．试证明：MN ∥EF ．② 若①中的其他条件不变，只改变点M ，N 的位置如图3所示，请判断 MN 与 EF 是否平行？请说明理由.29. 设a ,b 是任意两个不等实数，我们规定：满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间，表示为[a ,b ]．对于一个函数，如果它的自变量x 与函数值y 满足：当m ≤x ≤n 时，有m ≤y ≤n ,我们就称此函数是闭区间[m .n ]上的“闭函数”．如函数4y x =-+，当x =1时，y =3；当x =3时，y =1，即当13x ≤≤时，有13y ≤≤，所以说函数4y x =-+是闭区间[1,3]上的“闭函数”．（1）反比例函数y =x 2016是闭区间[1,2016]上的“闭函数”吗？请判断并说明理由；（2）若二次函数y =22x x k --是闭区间[1,2]上的“闭函数”，求k 的值；（3）若一次函数y =kx +b (k ≠0)是闭区间[m ,n ]上的“闭函数”，求此函数的表达式（用含 m ，n 的代数式表示）．图 3一、选择题：（本题共30分，每小题3分）二、填空题（本题共18分, 每小题3分）三、计算题：（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分）17. 4sin 304560︒︒︒．解：原式=33222214⨯+⨯-⨯--------------------- 4分 =2-1+3 =4--------------------- 5分18. 解：∵在Rt △ABC 中，∠C =90°，∠B =60°∵∠A=90°-∠B =30°--------------------- 1分∴AB==16--------------------- 3分∴AC=BCtanB=8．--------------------- 5分19. 解：（1）∵反比例函数图象两支分别位于第一、三象限，∴k ﹣1＞0，解得：k ＞1；---------------- 2分（2）取k=3，∴反比例函数表达式为x2y = ---------------- 4分当x=﹣6时，3162x 2y -=-==；---------------------5分（答案不唯一）20. 解: 如图:连接OB,过O 点作OD ⊥BC 于点D ---------------- 1分在Rt △OBD 中,∵∠BOD =︒︒=606360---------------- 2分 ∵ BD=OD ·tan60°---------------- 3分 =23---------------- 4分 ∴BC=2BD=43∴三角形的边长为43 cm ---------------- 5分B21.证明∵△ABC ∽△ADE ，∴∠BAC ＝∠DAE ，∠C ＝∠E ，---------------- 1分 ∴∠BAC －∠DAC ＝∠DAE －∠DAC ，∴∠1＝∠3， ------------------------------ 2分又∵∠C ＝∠E ，∠DOC ＝∠AOE ，∴△DOC ∽△AOE ，----------------------------3分 ∴∠2＝∠3 ， ----------------------------4分 ∴∠1＝∠2＝∠3． ----------------------------5分22. 解：过P 作PD ⊥AB 于D ，---------------- 1分在Rt △PBD 中，∠BDP ＝90°，∠B ＝45°， ∴BD ＝PD ． ---------------- 2分在Rt △PAD 中，∠ADP ＝90°，∠A ＝30°， ∴AD ＝PD ＝PD＝3PD ，--------------------3分 ∴PD ＝13100+≈36.6＞35，故计划修筑的高速公路不会穿过保护区．----------------------------5分23.解：（1）不同类型的正确结论有：①BE=CE ；②BD=CD ；③∠BED=90°；④∠BOD=∠A ；⑤AC//OD ；⑥AC ⊥BC ；⑦222OE +BE =OB ；⑧OE BC S ABC ∙=∆；⑨△BOD 是等腰三角形；⑩ΔBOE ΔBAC ~；等等。

2017年黑龙江省哈尔滨市中考数学试卷(2017)

2017年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）﹣7的倒数是（）A．7 B．﹣7 C． D．﹣【分析】根据乘积是1的两个数互为倒数，可得一个数的倒数．【解答】解：﹣7的倒数是﹣，故选：D．【点评】本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．2．（3分）下列运算正确的是（）A．a6÷a3=a2B．2a3+3a3=5a6C．（﹣a3）2=a6D．（a+b）2=a2+b2【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式=a3，不符合题意；B、原式=5a3，不符合题意；C、原式=a6，符合题意；D、原式=a2+2ab+b2，不符合题意，故选C【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．3．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（）A． B． C． D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、是轴对称图形，不是中心对称图形，不合题意；B、是轴对称图形，不是中心对称图形，不合题意；C、不是轴对称图形，是中心对称图形，不合题意；D、是轴对称图形，也是中心对称图形，符合题意．故选：D．【点评】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．4．（3分）抛物线y=﹣（x+）2﹣3的顶点坐标是（）A．（，﹣3）B．（﹣，﹣3）C．（，3）D．（﹣，3）【分析】已知抛物线解析式为顶点式，可直接写出顶点坐标．【解答】解：y=﹣（x+）2﹣3是抛物线的顶点式，根据顶点式的坐标特点可知，顶点坐标为（﹣，﹣3）．故选B．【点评】此题主要考查了二次函数的性质，关键是熟记：抛物线y=a（x﹣h）2+k 的顶点坐标是（h，k），对称轴是x=h．5．（3分）五个大小相同的正方体搭成的几何体如图所示，其左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看第一层是两个小正方形，第二层左边是一个小正方形，故选：C．【点评】本题考查了简单组合体的三视图，从左边看得到的图形是左视图．6．（3分）方程=的解为（）A．x=3 B．x=4 C．x=5 D．x=﹣5【分析】根据分式方程的解法即可求出答案．【解答】解：2（x﹣1）=x+3，2x﹣2=x+3，x=5，令x=5代入（x+3）（x﹣1）≠0，故选（C）【点评】本题考查分式方程的解法，解题的关键是熟练运用分式方程的解法，本题属于基础题型．7．（3分）如图，⊙O中，弦AB、CD相交于点P，∠A=42°，∠APD=77°，则∠B 的大小是（）A．43°B．35°C．34°D．44°【分析】由同弧所对的圆周角相等求得∠A=∠D=42°，然后根据三角形外角的性质即可得到结论．【解答】解：∵∠D=∠A=42°，∴∠B=∠APD﹣∠D=35°，故选B．【点评】本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等是解答此题的关键．8．（3分）在Rt△ABC中，∠C=90°，AB=4，AC=1，则cosB的值为（）A． B． C． D．【分析】利用锐角三角函数定义求出cosB的值即可．【解答】解：∵在Rt△ABC中，∠C=90°，AB=4，AC=1，∴BC==，则cosB==，故选A【点评】此题考查了锐角三角函数定义，熟练掌握锐角三角函数定义是解本题的关键．9．（3分）如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）A．= B．= C．= D．=【分析】根据相似三角形的判定与性质即可求出答案．【解答】解：（A）∵DE∥BC，∴△ADE∽△ABC，∴，故A错误；（B）∵DE∥BC，∴，故B错误；（C）∵DE∥BC，，故C正确；（D）∵DE∥BC，∴△AGE∽△AFC，∴=，故D错误；故选：C．【点评】本题考查相似三角形的判定与性质，解题的关键是熟练运用相似三角形的性质，本题属于中等题型10．（3分）周日，小涛从家沿着一条笔直的公路步行去报亭看报，看了一段时间后，他按原路返回家中，小涛离家的距离y（单位：m）与他所用的时间t（单位：min）之间的函数关系如图所示，下列说法中正确的是（）A．小涛家离报亭的距离是900mB．小涛从家去报亭的平均速度是60m/minC．小涛从报亭返回家中的平均速度是80m/minD．小涛在报亭看报用了15min【分析】根据特殊点的实际意义即可求出答案．【解答】解：A、由纵坐标看出小涛家离报亭的距离是1200m，故A不符合题意；B、由纵坐标看出小涛家离报亭的距离是1200m，由横坐标看出小涛去报亭用了15分钟，小涛从家去报亭的平均速度是80m/min，故B不符合题意；C、返回时的解析式为y=﹣60x+3000，当y=1200时，x=30，由横坐标看出返回时的时间是50﹣30=20min，返回时的速度是1200÷20=60m/min，故C不符合题意；D、由横坐标看出小涛在报亭看报用了30﹣15=15min，故D符合题意；故选：D．【点评】本题考查由图象理解对应函数关系及其实际意义，应把所有可能出现的情况考虑清楚．二、填空题（本大题共10小题，每小题3分，共30分）11．（3分）将57600000用科学记数法表示为 5.76×107．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥1时，n是非负数；当原数的绝对值＜1时，n 是负数．【解答】解：57600000用科学记数法表示为5.76×107，故答案为：5.76×107．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．（3分）函数y=中，自变量x的取值范围是x≠2．【分析】根据分式有意义的条件：分母不为0进行解答即可．【解答】解：由x﹣2≠0得，x≠2，故答案为x≠2．【点评】本题考查了函数自变量的取值范围问题，掌握分式有意义的条件：分母不为0是解题的关键．13．（3分）把多项式4ax2﹣9ay2分解因式的结果是a（2x+3y）（2x﹣3y）．【分析】原式提取公因式，再利用平方差公式分解即可．【解答】解：原式=a（4x2﹣9y2）=a（2x+3y）（2x﹣3y），故答案为：a（2x+3y）（2x﹣3y）【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．14．（3分）计算﹣6的结果是．【分析】先将二次根式化简即可求出答案．【解答】解：原式=3﹣6×=3﹣2=故答案为：【点评】本题考查二次根式的运算，解题的关键是熟练运用二次根式的运算法则，本题属于基础题型．15．（3分）已知反比例函数y=的图象经过点（1，2），则k的值为1．【分析】直接把点（1，2）代入反比例函数y=，求出k的值即可．【解答】解：∵反比例函数y=的图象经过点（1，2），∴2=3k﹣1，解得k=1．【点评】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．16．（3分）不等式组的解集是2≤x＜3．【分析】分别求出不等式组中两不等式的解集，找出解集的公共部分即可．【解答】解：，由①得：x≥2，由②得：x＜3，则不等式组的解集为2≤x＜3．故答案为2≤x＜3．【点评】此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．17．（3分）一个不透明的袋子中装有17个小球，其中6个红球、11个绿球，这些小球除颜色外无其它差别．从袋子中随机摸出一个小球，则摸出的小球是红球的概率为．【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：∵不透明的袋子中装有17个小球，其中6个红球、11个绿球，∴摸出的小球是红球的概率为；故答案为：．【点评】本题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．18．（3分）已知扇形的弧长为4π，半径为48，则此扇形的圆心角为15度．【分析】利用扇形的弧长公式计算即可．【解答】解：设扇形的圆心角为n°，则=4π，解得，n=15，【点评】本题考查的是弧长的计算，掌握弧长公式l=是解题的关键．19．（3分）四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相交于点O，点E在AC上，若OE=，则CE的长为4或2．【分析】由菱形的性质证出△ABD是等边三角形，得出BD=AB=6，OB=BD=3，由勾股定理得出OC=OA==3，即可得出答案．【解答】解：∵四边形ABCD是菱形，∴AB=AD=6，AC⊥BD，OB=OD，OA=OC，∵∠BAD=60°，∴△ABD是等边三角形，∴BD=AB=6，∴OB=BD=3，∴OC=OA==3，∴AC=2OA=6，∵点E在AC上，OE=，∴当E在点O左边时CE=OC+=4当点E在点O右边时CE=OC﹣=2，∴CE=4或2；故答案为：4或2．【点评】本题考查了菱形的性质、勾股定理、等边三角形的判定与性质；熟练掌握菱形的性质，由勾股定理求出OA是解决问题的关键．20．（3分）如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE ⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为．【分析】由AAS证明△ABM≌△DEA，得出AM=AD，证出BC=AD=3EM，连接DM，由HL证明Rt△DEM≌Rt△DCM，得出EM=CM，因此BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴AB=DC=1，∠B=∠C=90°，AD∥BC，AD=BC，∴∠AMB=∠DAE，∵DE=DC，∴AB=DE，∵DE⊥AM，∴∠DEA=∠DEM=90°，在△ABM和△DEA中，，∴△ABM≌△DEA（AAS），∴AM=AD，∵AE=2EM，∴BC=AD=3EM，连接DM，如图所示：在Rt△DEM和Rt△DCM中，，∴Rt△DEM≌Rt△DCM（HL），∴EM=CM，∴BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得：12+（2x）2=（3x）2，解得：x=，∴BM=；故答案为：．【点评】本题考查了矩形的性质、全等三角形的判定与性质、勾股定理；熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问题的关键．三、解答题（本大题共60分）21．（7分）先化简，再求代数式÷﹣的值，其中x=4sin60°﹣2．【分析】根据分式的除法和减法可以化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．【解答】解：÷﹣===，当x=4sin60°﹣2=4×=﹣2时，原式=．【点评】本题考查分式的化简求值、特殊角的三角函数值，解答本题的关键是明确分式化简求值的方法．22．（7分）如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．（1）在图中画出以AB为底、面积为12的等腰△ABC，且点C在小正方形的顶点上；（2）在图中画出平行四边形ABDE，且点D和点E均在小正方形的顶点上，tan ∠EAB=，连接CD，请直接写出线段CD的长．【分析】（1）因为AB为底、面积为12的等腰△ABC，所以高为4，点C在线段AB的垂直平分线上，由此即可画出图形；（2）首先根据tan∠EAB=的值确定点E的位置，由此即可解决问题，利用勾股定理计算CD的长；【解答】解：（1）△ABC如图所示；（2）平行四边形ABDE如图所示，CD==．【点评】本题考查﹣应用与作图设计、勾股定理、等腰三角形的性质和判定、平行四边形的判定和性质，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，利用数形结合的思想思考问题，属于中考常考题型．23．（8分）随着社会经济的发展和城市周边交通状况的改善，旅游已成为人们的一种生活时尚．洪祥中学开展以“我最喜欢的风景区”为主题的调查活动，围绕“在松峰山、太阳岛、二龙山和凤凰山四个风景区中，你最喜欢哪一个？（必选且只选一个）”的问题，在全校范围内随机抽取了部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题：（1）本次调查共抽取了多少名学生？（2）通过计算补全条形统计图；（3）若洪祥中学共有1350名学生，请你估计最喜欢太阳岛风景区的学生有多少名．【分析】（1）根据条形统计图与扇形统计图求出总人数即可；（2）根据题意作出图形即可；（3）根据题意列出算式，计算即可得到结果．【解答】解：（1）10÷20%=50（名），答：本次调查共抽取了50名学生；（2）50﹣10﹣20﹣12=8（名），补全条形统计图如图所示，（3）1350×=540（名），答：估计最喜欢太阳岛风景区的学生有540名．【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．24．（8分）已知：△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连接AE、BD交于点O．AE与DC交于点M，BD与AC交于点N．（1）如图1，求证：AE=BD；（2）如图2，若AC=DC，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．【分析】（1）根据全等三角形的性质即可求证△ACE≌△BCD，从而可知AE=BD；（2）根据条件即可判断图中的全等直角三角形；【解答】解：（1）∵△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，∴AC=BC，DC=EC，∴∠ACB+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，在△ACE与△BCD中，∴△ACE≌△BCD（SAS），∴AE=BD，（2）∵AC=DC，∴AC=CD=EC=CB，△ACB≌△DCE（SAS）；由（1）可知：∠AEC=∠BDC，∠EAC=∠DBC∴∠DOM=90°，∵∠AEC=∠CAE=∠CBD，∴△EMC≌△BCN（ASA），∴CM=CN，∴DM=AN，△AON≌△DOM（AAS），∵DE=AB，AO=DO，∴△AOB≌△DOE（HL）【点评】本题考查全等三角形，解题的关键是熟练运用全等三角形的判定条件，本题属于基础题型．25．（10分）威丽商场销售A，B两种商品，售出1件A种商品和4件B种商品所得利润为600元；售出3件A种商品和5件B种商品所得利润为1100元．（1）求每件A种商品和每件B种商品售出后所得利润分别为多少元；（2）由于需求量大，A、B两种商品很快售完，威丽商场决定再一次购进A、B 两种商品共34件．如果将这34件商品全部售完后所得利润不低于4000元，那么威丽商场至少需购进多少件A种商品？【分析】（1）设A种商品售出后所得利润为x元，B种商品售出后所得利润为y 元．由售出1件A种商品和4件B种商品所得利润为600元，售出3件A种商品和5件B种商品所得利润为1100元建立两个方程，构成方程组求出其解就可以；（2）设购进A种商品a件，则购进B种商品（34﹣a）件．根据获得的利润不低于4000元，建立不等式求出其解就可以了．【解答】解：（1）设每件A种商品售出后所得利润为x元，每件B种商品售出后所得利润为y元．由题意，得，解得：答：每件A种商品售出后所得利润为200元，每件B种商品售出后所得利润为100元．（2）设购进A种商品a件，则购进B种商品（34﹣a）件．由题意，得200a+100（34﹣a）≥4000，解得：a≥6答：威丽商场至少需购进6件A种商品．【点评】本题考查了列二元一次方程组解实际问题的运用及二元一次方程组的解法，列一元一次不等式解实际问题的运用及解法，在解答过程中寻找能够反映整个题意的等量关系是解答本题的关键．26．（10分）已知：AB是⊙O的弦，点C是的中点，连接OB、OC，OC交AB于点D．（1）如图1，求证：AD=BD；（2）如图2，过点B作⊙O的切线交OC的延长线于点M，点P是上一点，连接AP、BP，求证：∠APB﹣∠OMB=90°；（3）如图3，在（2）的条件下，连接DP、MP，延长MP交⊙O于点Q，若MQ=6DP，sin∠ABO=，求的值．【分析】（1）如图1，连接OA，利用垂径定理和圆周角定理可得结论；（2）如图2，延长BO交⊙O于点T，连接PT，由圆周角定理可得∠BPT=90°，易得∠APT=∠APB﹣∠BPT=∠APB﹣90°，利用切线的性质定理和垂径定理可得∠ABO=∠OMB，等量代换可得∠ABO=∠APT，易得结论；（3）如图3，连接MA，利用垂直平分线的性质可得MA=MB，易得∠MAB=∠MBA，作∠PMG=∠AMB，在射线MG上截取MN=MP，连接PN，BN，易得△APM ≌△BNM，由全等三角形的性质可得AP=BN，∠MAP=∠MBN，延长PD至点K，使DK=DP，连接AK、BK，易得四边形APBK是平行四边形，由平行四边形的性质和平行线的性质可得∠PAB=∠ABK，∠APB+∠PBK=180°，由（2）得∠APB﹣（90°﹣∠MBA）=90°，易得∠NBP=∠KBP，可得△PBN≌△PBK，PN=2PH，利用三角函数的定义可得sin∠PMH=，sin∠ABO=，设DP=3a，则PM=5a，可得结果．【解答】（1）证明：如图1，连接OA，∵C是的中点，∴，∴∠AOC=∠BOC，∵OA=OB，∴OD⊥AB，AD=BD；（2）证明：如图2，延长BO交⊙O于点T，连接PT ∵BT是⊙O的直径∴∠BPT=90°，∴∠APT=∠APB﹣∠BPT=∠APB﹣90°，∵BM是⊙O的切线，∴OB⊥BM，又∠OBA+∠MBA=90°，∴∠ABO=∠OMB又∠ABO=∠APT∴∠APB﹣90°=∠OMB，∴∠APB﹣∠OMB=90°；（3）解：如图3，连接MA，∵MO垂直平分AB，∴MA=MB，∴∠MAB=∠MBA，作∠PMG=∠AMB，在射线MG上截取MN=MP，连接PN，BN，则∠AMP=∠BMN，∴△APM≌△BNM，∴AP=BN，∠MAP=∠MBN，延长PD至点K，使DK=DP，连接AK、BK，∴四边形APBK是平行四边形；AP∥BK，∴∠PAB=∠ABK，∠APB+∠PBK=180°，由（2）得∠APB﹣（90°﹣∠MBA）=90°，∴∠APB+∠MBA=180°∴∠PBK=∠MBA，∴∠MBP=∠ABK=∠PAB，∴∠MAP=∠PBA=∠MBN，∴∠NBP=∠KBP，∵PB=PB，∴△PBN≌△PBK，∴PN=PK=2PD，过点M作MH⊥PN于点H，∴PN=2PH，∴PH=DP，∠PMH=∠ABO，∵sin∠PMH=，sin∠ABO=，∴，∴，设DP=3a，则PM=5a，∴MQ=6DP=18a，∴．【点评】本题主要考查了垂径定理，圆周角定理，全等三角形的判定与性质定理，三角函数的定义等相关知识，作出恰当的辅助线构建全等三角形是解答此题的关键．27．（10分）如图，在平面直角坐标系中，点O为坐标原点，抛物线y=x2+bx+c 交x轴于A、B两点，交y轴于点C，直线y=x﹣3经过B、C两点．（1）求抛物线的解析式；（2）过点C作直线CD⊥y轴交抛物线于另一点D，点P是直线CD下方抛物线上的一个动点，且在抛物线对称轴的右侧，过点P作PE⊥x轴于点E，PE交CD 于点F，交BC于点M，连接AC，过点M作MN⊥AC于点N，设点P的横坐标为t，线段MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，连接PC，过点B作BQ⊥PC于点Q（点Q在线段PC上），BQ交CD于点T，连接OQ交CD于点S，当ST=TD时，求线段MN的长．【分析】（1）首先求出点B、C的坐标，然后利用待定系数法求出抛物线的解析式；=S△AMC+S△AMB，由三角形面积公式可求y与m之间的函数关系式；（2）根据S△ABC（3）如图2，由抛物线对称性可得D（2，﹣3），过点B作BK⊥CD交直线CD 于点K，OG⊥OS交KB于G，可得四边形OCKB为正方形，过点O作OH⊥PC交PC延长线于点H，OR⊥BQ交BQ于点I交BK于点R，可得四边形OHQI为矩形，可证△OBG≌△OCS，△OSR≌△OGR，得到tan∠QCT=tan∠TBK，设ST=TD=m，可得SK=2m+1，CS=2﹣2m，TK=m+1=BR，SR=3﹣m，RK=2﹣m，在Rt△SKR中，根据勾股定理求得m，可得tan∠PCD=，过点P作PE′⊥x轴于E′交CD于点F′，得到P（t，﹣t﹣3），可得﹣t﹣3=t2﹣2t﹣3，求得t，再根据MN=d求解即可．【解答】解：（1）∵直线y=x﹣3经过B、C两点，∴B（3，0），C（0，﹣3），∵y=x2+bx+c经过B、C两点，∴，解得，故抛物线的解析式为y=x2﹣2x﹣3；（2）如图1，y=x2﹣2x﹣3，y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，∴A（﹣1，0），∴OA=1，OB=OC=3，∴∠ABC=45°，AC=，AB=4，∵PE⊥x轴，∴∠EMB=∠EBM=45°，∵点P的横坐标为1，∴EM=EB=3﹣t，连结AM，∵S=S△AMC+S△AMB，△ABC∴AB•OC=AC•MN+AB•EM，∴×4×3=×d+×4（3﹣t），∴d=t；（3）如图2，∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴对称轴为x=1，∴由抛物线对称性可得D（2，﹣3），∴CD=2，过点B作BK⊥CD交直线CD于点K，∴四边形OCKB为正方形，∴∠OBK=90°，CK=OB=BK=3，∴DK=1，∵BQ⊥CP，∴∠CQB=90°，过点O作OH⊥PC交PC延长线于点H，OR⊥BQ交BQ于点I交BK于点R，OG ⊥OS交KB于G，∴∠OHC=∠OIQ=∠OIB=90°，∴四边形OHQI为矩形，∵∠OCQ+∠OBQ=180°，∴∠OBG=∠OCS，∵OB=OC，∠BOG=∠COS，∴△OBG≌△OCS，∴QG=OS，∠GOB=∠SOC，∴∠SOG=90°，∴∠ROG=45°，∵OR=OR，∴△OSR≌△OGR，∴SR=GR，∴SR=CS+BR，∵∠BOR+∠OBI=90°，∠IBO+∠TBK=90°，∴∠BOR=∠TBK，∴tan∠BOR=tan∠TBK，∴=，∴BR=TK，∵∠CTQ=∠BTK，∴∠QCT=∠TBK，∴tan∠QCT=tan∠TBK，设ST=TD=m，∴SK=2m+1，CS=2﹣2m，TK=m+1=BR，SR=3﹣m，RK=2﹣m，在Rt△SKR中，∵SK2+RK2=SR2，∴（2m+1）2+（2﹣m）2=（3﹣m）2，解得m1=﹣2（舍去），m2=；∴ST=TD=，TK=，∴tan∠TBK==÷3=，∴tan∠PCD=，过点P作PE′⊥x轴于E′交CD于点F′，∵CF′=OE′=t，∴PF′=t，∴PE′=t+3，∴P（t，﹣t﹣3），∴﹣t﹣3=t2﹣2t﹣3，解得t1=0（舍去），t2=．∴MN=d=t=×=．【点评】本题是二次函数综合题型，考查了二次函数的图象与性质、一次函数的图象与性质、解方程（方程组）、相似三角形（或三角函数）、勾股定理等重要知识点．。

黑龙江省2017—2018学年高一数学上学期期中考试卷(四)

黑龙江省2017—2018学年高一数学上学期期中考试卷（四）（考试时间120分钟满分150分）一、单项选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1．下列各式：①1∈{0，1，2}；②∅⊆{0，1，2}；③{1}∈{0，1，2}；④{0，1，2}={2，0，1}，其中错误的个数是（）A．1个 B．2个 C．3个 D．4个2．下列四个函数中，在（0，+∞）上为增函数的是（）A．f（x）=3﹣x B．f（x）=x2﹣3x C．f（x）=﹣D．f（x）=﹣|x|3．函数的f（x）=log3x﹣8+2x零点一定位于区间（）A．（1，2）B．（2，3）C．（3，4）D．（5，6）4．sin30°+tan240°的值是（）A．﹣B．C．﹣ +D． +5．已知=﹣5，那么tanα的值为（）A．﹣2 B．2 C．D．﹣6．函数y=f（x）在[0，2]上单调递增，且函数f（x+2）是偶函数，则下列结论成立的是（）A．f（1）＜f（）＜f（）B．f（）＜f（1）＜f（）C．f（）＜f（）＜f（1）D．f（）＜f（1）＜f（）7．已知点P（sinπ，cosπ）落在角θ的终边上，且θ∈[0，2π），则θ的值为（）A．B． C． D．8．函数y=log a（|x|﹣1），（a＞1）的大致图象是（）A． B．C． D．9．某商品零售价今年比去年上涨25%，欲控制明年比去年只上涨10%，则明年比今年降价（）A．15% B．10% C．12% D．50%10．已知函数f（x）=log a（4﹣ax）在（﹣2，2）上是减函数，则a的取值范围是（）A．（0，2）B．（1，2）C．（1，2] D．[2，+∞）11．已知函数f（x）=﹣log2x，若实数x0是函数f（x）的零点，且0＜x＜x0，则函数f（x）的值（）A．等于0 B．恒为正C．恒为负D．不大于012．已知集合，若A∩B≠∅，则实数a 的取值范围为（）A． B． C． D．二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．）13．若f（x）的定义域为，则函数f（lg x）的定义域为．14．经过一刻钟，长为10cm的分针所覆盖的面积是．15．若角α的终边与直线y=3x重合且sin α＜0，又P（m，n）是角α终边上一点，且|OP|=，则m﹣n=．16．已知函数，若f（a）＞f（﹣a），求实数a的取值范围．三、解答题（本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤．）17．（10分）设全集U=R，集合A={x|﹣1≤x＜3}，B={x|2x﹣4≥x﹣2}．（1）求∁U（A∩B）；（2）若集合C={x|2x+a＞0}，满足B∪C=C，求实数a的取值范围．18．（10分）已知任意角α的终边经过点P（﹣3，m），且cosα=﹣（1）求m的值．（2）求sinα与tanα的值．19．（10分）已知函数y=|x|（x﹣4）（1）画出函数的图象；（2）利用图象回答：当f（x）为何值时，方程x，y∈R有一解？有两解？有三解？20．（10分）对于函数f（x）=a﹣（a∈R）．（1）探索并证明函数f（x）的单调性；（2）是否存在实数a使函数f（x）为奇函数？若有，求出实数a的值，并证明你的结论；若没有，说明理由．21．（15分）已知函数f（x），当x，y∈R时，恒有f（x+y）=f（x）+f（y）．（1）求证：f（x）+f（﹣x）=0；（2）若f（﹣3）=a，试用a表示f（24）；时，f（x）＜0，且，试求f（x）在区间[﹣2，6]上的（3）如果x∈R+最大值和最小值．22．（15分）已知二次函数g（x）=mx2﹣2mx+n+1（m＞0）在区间[0，3]上有最大值4，最小值0．（Ⅰ）求函数g（x）的解析式；（Ⅱ）设f（x）=．若f（2x）﹣k•2x≤0在x∈[﹣3，3]时恒成立，求k 的取值范围．参考答案一、单项选择题1．A2．C．3．C．4．D．5．D．6．B7．D．8．D．9．C．10．C．11．B12．B．二、填空题13．答案为：．14．答案为25πcm2．15．答案为2．16．答案为（﹣1，0）∪（1，+∞）三、解答题17．解：（1）由集合B中的不等式2x﹣4≥x﹣2，解得x≥2，∴B={x|x≥2}，又A={x|﹣1≤x＜3}，∴A∩B={x|2≤x＜3}，又全集U=R，∴∁U（A∩B）={x|x＜2或x≥3}；（2）由集合C中的不等式2x+a＞0，解得x＞﹣，∴C={x|x＞﹣}，∵B∪C=C，∴B⊆C，∴﹣＜2，解得a＞﹣4；故a的取值范围为（﹣4，+∞）．18．解：（1）∵角α的终边经过点P（﹣3，m），∴|OP|=．又∵cosα=﹣==，∴m2=16，∴m=±4．（2）m=4，得P（﹣3，4），|OP|=5，∴sinα=，tanα=﹣；m=﹣4，得P（﹣3，﹣4），|OP|=5，∴sinα=﹣，tanα=；19．解：（1）y=，图象如图所示，（2）k＞0或者k＜﹣4方程有一解k=0或者k=﹣4方程有二解当﹣4＜k＜0方程有三解20．解：∵f（x）=a﹣（a∈R）．∴f′（x）=＞0恒成立，∴函数f（x）在R上为增函数（2）由f（0）=a﹣=0，得a=1，∴f（x）=1﹣=，∵f（﹣x）===﹣=﹣f（x）所以当a=1时，f（x）为奇函数．21．解：（1）令x=y=0得f（0）=0，再令y=﹣x得f（﹣x）=﹣f（x），∴f（﹣x）+f（x）=0．（2）由f（﹣3）=af（3）=﹣a，∴f（24）=f（3+3++3）=8f（3）=﹣8a．（3）设x1＜x2，则f（x2）=f[x1+（x2﹣x1）]=f（x1）+f（x2﹣x1）又∵x2﹣x1＞0，∴f（x2﹣x1）＜0，∴f（x1）+f（x2﹣x1）＜f（x1），∴f（x2）＜f（x1）∴f（x）在R上是减函数，∴f（x）max=f（﹣2）=﹣f（2）=﹣2f（1）=1，．22．解：（Ⅰ）∵g（x）=m（x﹣1）2﹣m+1+n∴函数g（x）的图象的对称轴方程为x=1∵m＞0依题意得，即，解得∴g（x）=x2﹣2x+1，（Ⅱ）∵∴，∵f（2x）﹣k•2x≤0在x∈[﹣3，3]时恒成立，即在x∈[﹣3，3]时恒成立∴在x∈[﹣3，3]时恒成立只需令，由x∈[﹣3，3]得设h（t）=t2﹣4t+1∵h（t）=t2﹣4t+1=（t﹣2）2﹣3∴函数h（x）的图象的对称轴方程为t=2当t=8时，取得最大值33．∴k≥h（t）max=h（8）=33∴k的取值范围为[33，+∞）．。

黑龙江省哈尔滨市2016-2017学年高一数学上学期期中试题

黑龙江省哈尔滨市2016-2017学年高一数学上学期期中试题一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知全集U ={0，1，2，3，4}，M ={0，1，2}，N ={2，3}，则（C u M ）∩N =A ．{}4,3,2B ．{}2C ．{}3D ．{}4,3,2,1,02．下列四个集合中，是空集的是（）A ． }33|{=+x xB ． },,|),{(22R y x x y y x ∈-=C ． }0|{2≤x xD ． },01|{2R x x x x ∈=+-3．下面有四个命题：（1）集合N 中最小的数是1；（2）若a -不属于N ，则a 属于N ；（3）若,,N b N a ∈∈则b a +的最小值为2；（4）x x 212=+的解可表示为{}1,1；其中正确命题的个数为（）A ． 0个B ． 1个C ． 2个D ． 3个4．下列表示错误的是（A ）0∉Φ （B ）{}12Φ⊆，（C ）{}{}21035(,)3,4x y x y x y +=-== （D ）若,A B ⊆则A B A ⋂=5．下列函数中,在区间()0,1上是增函数的是（）A ． x y =B ． x y -=3C ． x y 1=D ． 42+-=x y6.设集合{}02M x x =≤≤，{}02N y y =≤≤，给出如下四个图形，其中能表示从集合M 到集合N 的函数关系的是A BC D7．判断下列各组中的两个函数是同一函数的为（）⑴3)5)(3(1+-+=x x x y ，52-=x y ；⑵111-+=x x y ，)1)(1(2-+=x x y ； ⑶x x f =)(，2)(x x g =； ⑷()f x =()F x =；⑸21)52()(-=x x f ，52)(2-=x x f ． A ． ⑴、⑵ B ． ⑵、⑶ C ． ⑷ D ． ⑶、⑸8．若函数y = f （x ）的定义域为[]1,2，则(1)y f x =+的定义域为A ．[]2,3B ．[]0,1C ．[]1,0-D ．[]3,2--9．设()()f x x R ∈为偶函数，且()f x 在[)0,+∞上是增函数，则(2)f -、()f π-、(3)f 的大小顺序是A ．()(3)(2)f f f π->>-B ．()(2)(3)f f f π->->C ．()(2)f f f π-<(3)<-D ．()(2)(3)f f f π-<-<10. 二次函数])5,0[(4)(2∈-=x xx x f 的值域为 A.),4[+∞- B.]5,0[C.]5,4[-D.]0,4[- 11．若函数2()(32)f x k k x b =-++在R 上是减函数，则k 的取值范围为（）A （1,3）B （1,2）C （2,3）D （3,4）12.若函数()f x 为定义在R 上的奇函数，且在(0,)+∞内是增函数，又(2)f 0=，则不等式0)(<x xf 的解集为A ．(2,0)(2,)-+∞ B ．(,2)(0,2)-∞- C ．(,2)(2,)-∞-+∞ D ．)2,0()0,2( -二．填空题（共4题，每题5分，共20分）13．计算4________=14．若集合{}|37A x x =≤<，{}|210B x x =<<，则AB =_____________． 15．函数422--=x x y 的定义域． 16．已知22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪=-<<⎨⎪≥⎩，若()3f x =，则x 的值是三．解答题（共6题，共70分）17．（本题满分10分）已知全集{}{}{}21,2,23,|2|,2,0U U a a A a C A =+-=-=，求a 的值.18.已知全集R U =，集合{}1,4>-<=x x x A 或，{}213≤-≤-=x x B ，求B A 、)()(B C A C U U ；19.集合{}42<<=X X A ，集合{}123+<<=K X X M ,若集合M 是集合A 的子集，求实数k 的取值范围.20.若函数f （x ）在区间（-1,2）上是减函数，求使f （1+x ）<f(2x-1)成立的x 的取值范围21．不用计算器求下列各式的值。

黑龙江省青冈县2017-2018学年高一数学上学期期中试题(A卷)

黑龙江省青冈县2017-2018学年高一数学上学期期中试题（A卷）一、选择题：本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集,集合则( )A.{0}B.{0,1}C.{0,1,4}D.{0,1,2,3,4}2.函数的定义域是( )A.(0,2)B.(1,2)C.D.3.由组成一个集合,中含有个元素,则实数的取值可以是( )A.1B.-2C.6D.24. 已知函数若,则实数的值等于( )A.-3B.-1C.1D.-3或15.指数函数在上的最大值与最小值的和为,则( )A. B. C. D.6.设集合,,则等于( )A. B. C. D.7.若偶函数在区间上是增函数,则( )A. B. C. D.8、若奇函数在上是增函数,且最小值为,则在上是( )A.增函数且最小值是-1B.增函数且最大值是-1C.减函数且最小值是-1D.减函数且最大值是-19. 如果二次函数有两个不同的零点,那么的取值范围是( )A. B. C. D.10.设,则( )A. B. C. D.11.函数的零点所在的一个区间是( )A. B. C. D.12.若关于x的方程＝在区间(0,1)上有解，则实数m的取值范围是( )A.(0,1) B(1,2) C.(-∞,1)U(2,+∞) D.(-∞,0)二、填空题:本大题共4小题,每小题5分,共20分.13.函数是幂函数,则.14.______.15.若函数,且有两个零点,则实数的取值范围是16.若函数定义域为,则的取值范围是. 三解答题（共70分）17、设集合或.分别求满足下列条件的实数的取值范围:(1).(2).18. (1)计算:(2)已知用表示.19、已知,。

(1)求,的值;(2).求的值;(3).求和的解析式。

20.定义在上的奇函数在整个定义域上是减函数,且,求实数的取值范围.21.已知f(x)=(a>0,a≠1)1.求f(x)的定义域;2.若f(x)>0,求x的取值范围。

黑龙江省哈尔滨市2016-2017学年高一数学上册期中考试题

哈尔滨市第六中学2016—2017学年度上学期期中考试高一数学试题考试时间：120分钟满分：150分一、选择题：本大题共12小题，每小题5分，共60分．1．设全集，集合，则＝（）A．ØB．{2} C．{2,5}D．2．设函数,若，则实数等于（）A．－4或－2 B．－4或2 C．－2或4 D．－2或23．若函数的值域是，则函数的值域是（）A．[－5，－1] B．[－2,0]C．[－6，－2] D．[1,3]4．若函数的最小值为，则实数的取值范围是（）A．(1,3) B．(1,3]C．[3，＋∞) D．(3，＋∞) 5．下列函数中，满足“任意且，”的是（）A．B．C．D．6．函数的图象（）A．关于原点对称B．关于直线y＝x对称C．关于x轴对称D．关于y轴对称7．函数的最大值是（）A．45B．54C．34D．438．设，则（）A．B．C．D．9．已知函数（且），当时，，则在R上（）A ．是增函数B ．是减函数C ．当时是增函数，当时是减函数D ．当时是减函数，当时是增函数10．函数的单调递减区间是（）A ．⎝ ⎛⎦⎥⎤－∞，32B ．⎣⎢⎡⎭⎪⎫32，＋∞C ．⎝ ⎛⎦⎥⎤－1，32D ．⎣⎢⎡⎭⎪⎫32，4 11．若不等式对一切恒成立，则的取值范围是（）A ．(－∞，2]B ．[－2,2]C ．(－2,2]D ．(－∞，－2)12．若函数的图象如图所示，其中a ，b 为常数，则函数的大致图象是（）二、填空题：本大题共4小题，每小题5分，共20分．13．如果函数是奇函数，则＝________.14．函数的定义域是________．15．已知幂函数，若，则的取值范围是________．16．直线与曲线有四个交点，则的取值范围是________．三、解答题：本大题共6小题，共70分，解答时写出必要的文字说明，证明过程或解题步骤．17．（本小题满分10分）（1）计算．（2）设，且，求的值．18．（本小题满分12分）若集合，且，求实数的取值范围．19．（本小题满分12分）已知二次函数的最小值为（1）求的解析式，并写出单调区间；（2）在区间上恒成立，求的取值范围．20．（本小题满分12分）函数在区间上的最大值记为．（1）求的解析式；（2）求的最大值．21．（本小题满分12分）已知函数，且．（1）求函数的解析式；（2）证明：，其中．22．（本小题满分12分）已知，（且）．（1）判断的奇偶性并用定义证明；（2）判断的单调性并有合理说明；（3）当时，恒成立，求的取值范围．高一数学答案1 B2 B3 A4B5 C6 D7 D8 B9A10D11C12 D13、2x ＋3 14、(－∞，1)∪(2，＋∞)15、(3,5) 16、1<a <5417（1）＝lg 1100÷110＝－2÷110＝－20 ……5分（2）将两边平方得a ＋a －1＋2＝9即a ＋a －1＝7.将a ＋a －1＝7两边平方有a 2＋a －2＋2＝49，得a 2＋a －2＝47，∴a 2＋a －2＋1a ＋a －1＋1＝47＋17＋1＝6. ……5分 18解：A ＝{－3,2}．……2分对于x 2＋x ＋a ＝0，①当Δ＝1－4a <0，即a >14时，B ＝，成立；……3分②当Δ＝1－4a ＝0，即a ＝14时，B ＝⎩⎨⎧⎭⎬⎫－12，不成立；……3分 ③当Δ＝1－4a >0，即a <14时，若成立，则B ＝{－3,2}，∴a ＝－3×2＝－6. ……3分综上，a 的取值范围为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪ a >14或a ＝－6. ……1分 19解：(1)由题意有f (－1)＝a －b ＋1＝0，且－b 2a ＝－1，∴a ＝1，b ＝2.∴f (x )＝x 2＋2x ＋1，……4分单调减区间为(－∞，－1]，单调增区间为[－1，＋∞)．……2分(2)f (x )>x ＋k 在区间[－3，1]上恒成立，转化为x 2＋x ＋1>k 在[－3，1]上恒成立．设g (x )＝x 2＋x ＋1，x ∈[－3，1]，……4分∴g (x )min ＝.∴ ……2分20解：(1)对区间[t ，t ＋1](t ∈R )与对称轴x ＝2的位置关系进行讨论：①当t ＋1<2，即t <1时，函数f (x )在区间[t ，t ＋1]上递增，此时g (t )＝f (t ＋1)＝－t 2＋2t ＋2；②当t ≤2≤t ＋1，即1≤t ≤2时，函数f (x )在区间[t ，t ＋1]上先增后减，此时g (t )＝f (2)＝3；③当t >2时，函数f (x )在区间[t ，t ＋1]上递减，此时g (t )＝f (t )＝－t 2＋4t －1.综上，g (t )＝⎩⎪⎨⎪⎧ －t 2＋2t ＋2，t <1，3，1≤t ≤2，－t 2＋4t －1，t >2.……7分 (2) 分段求最大值得g (t )的最大值是3. ……5分21解：(1)由于f (－x )＝－f (x )，即log 2(－x ＋1)＋t log 2(1＋x )＝－[log 2(x ＋1)＋t log 2(1－x )]，所以log 2(1－x )＋log 2(1＋x )＋t [log 2(1－x )＋log 2(1＋x )]＝0，所以(1＋t )[log 2(1－x )＋log 2(1＋x )]＝0.(*)欲使(*)在定义域内恒成立，必须有1＋t ＝0，即t ＝－1，故f (x )＝log 2(x ＋1)－log 2(1－x )．……6分(2)证明：因为－1＜x ＜1时，f (x )＝log 2(x ＋1)－log 2(1－x )＝log 21＋x 1－x ，所以f (a )＋f (b )＝log 21＋a 1－a ＋log 21＋b 1－b＝，又因为=，所以f (a )＋f (b )＝f ⎝ ⎛⎭⎪⎫a ＋b 1＋ab . ……6分 22解：(1)因为函数的定义域为R ，所以关于原点对称．又因为f (－x )＝a a 2－1(a －x －a x )＝－f (x )，所以f (x )为奇函数． ……4分(2)当a >1时，a 2－1>0，y ＝a x 为增函数，y ＝a －x 为减函数，从而y ＝a x －a －x 为增函数，所以f (x )为增函数，当0<a<1时，a2－1<0，y＝a x为减函数，y＝a－x为增函数，从而y＝a x－a－x为减函数，所以f(x)为增函数．故当a>0，且a≠1时，f(x)在定义域内单调递增．……4分(3)由(2)知f(x)在R上是增函数，所以在区间[－1,1]上为增函数，所以f(－1)≤f(x)≤f(1)，所以f(x)min＝f(－1)＝aa2－1(a－1－a)＝aa2－1·1－a2a＝－1，所以要使f(x)≥b在[－1,1]上恒成立，则只需b≤－1，故b的取值范围是(－∞，－1]．……4分沁园春·雪<毛泽东>北国风光，千里冰封，万里雪飘。

黑龙江省哈尔滨师范大学附属中学18年-19年学年高一上学期期中考试数学试题 Word版含答案

哈师大附中高一上学期期中考试数学试卷一．单项选择题：（本题共10小题，每小题6分，共60分） 1.已知全集{|2}U x x =≥，集合M {|3}x x =≥，则UM =（）A ．{|23}x x ≤≤B ．{|23}x x ≤<C ．{|3}x x ≤D ．{|2}x x < 2. .设集合={|23}xM x >，{|(1)(3)0}N x x x =-+<，则（） A. M N = B. M N ⊆ C. N M ⊆ D. M N =∅3.下列函数是偶函数，且在0+∞（，）是增函数的是（） A.2()2f x x x =+ B. 2()f x x -= C. ()||f x x = D. ()ln f x x = 4.已知函数2()1f x kx kx =++的定义域为R ，则实数k 的取值范围是（） A. 0k ≠ B. 04k ≤≤ C. 04k ≤< D. 04k << 5.已知函数()f x 为偶函数，当[0,)x ∈+∞时，()1f x x =-，则()0f x <的解集是（） A. 0,1（） B.,1（-1） C.1,0（-） D.∞（-，-1）（0，1）6.若1122(1)(32)a a --+<-，则a 的取值范围是（）A.12(,)23 B. 2(,2)3 C. 23(,)32 D. 3(,)2+∞7.若a b c <<，则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间（）A ．(,b)a 和(b,c)内B ．(,)(,)a a b -∞和内C ．(,)(c,)b c +∞和内D ．(,)(,)a c -∞+∞和内8.已知函数()f x 的定义域为()1,1-，则函数1()()(1)g x f f x x=+-的定义域为（） A. ()1,2 B. ()0,2 C. ()0，1 D. ()1,1-9.已知1322412,log ,log 3,log 53a b c d -====.则( ) A ．a c d b ><> B ．b a c d <<< C ．b a d c <<< D ．c a d b >>> 10.函数243()log (4)f x x x =-的单调递增区间为（）A ．(,2)-∞B ．(2,)+∞C ．(,4)-∞D ． (4,)+∞ 二．填空题：（本题共4小题，每小题5分，共20分） 11.已知函数y =的定义域是___________；12.函数221()2x x f x a-+=+01)a a >≠（且的图像过定点___________； 13.已知函数1(),4()2(1),4xx f x f x x ⎧≥⎪=⎨⎪+<⎩，则2(log 3)f =___________；14.已知函数()()2x xf x a e e -=-+，若(lg3)3f =,则1(lg )3f =___________．三．解答题：（本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 15.(本小题满分10分)计算下列各式：21023213(1)(2)(9.6)(3)(1.5)48-----+7log 29(2)log lg 252lg 27+++16.(本小题满分12分)已知集合22{|20},{|(21)(1)0}A x x x B x x a x a a =--<=-+++<，且B A ⊆,求实数a 的取值范围.17. (本小题满分12分)已知函数2()(0)f x ax bx c a =++≠满足:(0)2,(1)()21f f x f x x =+-=-. (1)求()f x 的解析式；(2)若函数()()g x f x mx =-的两个零点分别在区间(1,2)-和(2,4)内，求m 的取值范围.18. (本小题满分12分)已知函数22(),21x x a af x a R ⋅-+=∈+． (1)当2a =时，判断函数()f x 的单调性,并证明； (2)若()f x 为定义域上的奇函数，求函数()f x 的值域．19. (本小题满分12分)已知函数2()log f x x =的定义域是[2,16].设2()(2)[()]g x f x f x =-. (1)求函数g()x 的解析式及定义域； (2)求函数)(x g 的最值．20. (本小题满分12分)定义在R 上的函数()y f x =.对任意的,a b R ∈.满足:()()()f a b f a f b +=⋅, 当0x >时，有()1f x >，其中12f =（）. (1)求(0)f ，(1)f -的值； (2)判断该函数的单调性，并证明； (3)求不等式(1)4f x +<的解集.哈师大附中高一上学期期中考试数学答案一．单项选择题：（本题共10小题，每小题6分，共60分） 1-5：BDCDB 6-10：CAACD二．填空题：（本题共4小题，每小题5分，共20分） 11.34(,]55 12.(1,3) 13.12414.1 三．解答题：（本题共6小题，共70分，解答题应写出文字说明证明过程或演算步骤） 15. (本小题10分)计算：21023213(1)(2)(9.6)(3)(1.5)48-----+12= …… 5分7log 29(2)log lg 252lg 273+++318= …… 10分 16.(本小题12分)已知集合22{|20},{|(21)(1)0}A x x x B x x a x a a =--<=-+++<，且B A ⊆.求实数a 的取值范围.解：A={|1x 2}x -<< …… 2分{|1}B x a x a =<<+ …… 6分112B Aa a ⊆≥-⎧∴⎨+≤⎩…… 10分11a ∴-≤≤ …… 12分17.(本小题12分)已知函数2()(0)f x ax bx c a =++≠满足(0)2,(1)()21f f x f x x =+-=-(1)求()f x 的解析式；(2)若函数()()g x f x mx =-的两个零点分别在区间(1,2)-和(2,4)内，求m 的取值范围.(1)(0)22f c =∴=解： …… 2分22(1)()(1)(1)2(2)2f x f x a x b x ax bx ax a b+-=++++-++=++ …… 4分22112a ab a b ∴=+=-∴==- …… 6分2()22f x x x ∴=-+ …… 7分2(2)()(2)2g x x m x =-++ …… 8分(1)505(2)22m 012(4)1040g m g m g m -=+>⎧⎪=-<⇒<<⎨⎪=->⎩…… 12分18.(本小题12分)已知函数22(),21x x a af x a R ⋅-+=∈+． (1)当2a =时，判断函数()f x 的单调性,并证明. (2)若()f x 为定义域上的奇函数，求函数()f x 的值域．解:由已知得: 1(1)()2(1)21xf x =-+定义域为R …… 2分 12,x x R ∈任取 12x x <且 121211()()2[(1)(1)]2121x x f x f x -=---++ 121222(21)(21)x x x x -=++ …… 4分 2xy R =在上单调递增 12x x <且 12022xx ∴<<12220x x ∴-<12210210x x ∴+>+>，()()122+12+10x x ∴>12()()f x f x ∴< ()f x ∴-∞+∞在（，）上单调递增 …… 6分2(2)2(2)2,()()002121x x x x a a a a x R f x f x --⋅+-⋅+-∀∈-+=⇔+=++（）对 (22)(21)01xa a ⇔-+=⇔= …… 8分2112211x x x y y y -+==+-由得， 20x > 101yy+∴>- …… 10分 11y ∴-<< ()f x ∴的值域为(-1,1). …… 12分19.(本小题12分)已知函数2()log f x x =的定义域是[2,16].设2()(2)[()]g x f x f x =-.(1)求函数g()x 的解析式及定义域. (2)求函数)(x g 的最值．解：（1）2216216x x ≤≤⎧⎨≤≤⎩ 28x ∴≤≤ …… 3分222()log (2)log 28g x x x x =-≤≤2221log log x x=+-…… 6分（2） 2log [1,3]t xt =∈令…… 8分max 12()1t x g x ∴===即时， …… 10分 min 38()5t x g x ===-即时， …… 12分20.(本小题12分) 定义在R 上的函数()y f x =.对任意的,a b R ∈.满足()()()f a b f a f b +=⋅当0x >时，有()1f x >，其中12f =（） (1)求(0)f ,(1)f -的值； (2)判断该函数的单调性,并证明； (3)求不等式(1)4f x +<的解集.解：（1） 1a =令，0b =，(1)(0)(1)f f f =则(1)1f > (0)1f ∴= …… 2分1a =令，-1b =，则(0)(1)(-1)f f f =⋅12f =（）1(-1)=2f ∴ …… 4分（2）()(,)f x -∞+∞在上单调递增 …… 5分任取1212,(,)x x x x ∈-∞+∞<且210x x ⇒->由题设得21()1f x x ->0x <对任意()()(0)1f x f x f -== 0x ∴-> ()1f x ∴-> ()0f x >x R ∴∈对任意 ()0f x > 1()0f x ∴> ……7分22112111()[()]()()()f x f x x x f x x f x f x =-+=-⋅>()(,)f x ∴-∞+∞在上单调递增 …… 9分（3）(2)(11)(1)(1)4f f f f =+=⋅= ……10分 (1)4(2)121f x f x x +<=+<∴<，1∴-∞不等式的解集为（，） …… 12分。

黑龙江省哈尔滨市2017-2018学年高一第一学期期中数学试卷

2017-2018年黑龙江省哈尔滨三中高一上学期数学期中试卷带答案

最新版黑龙江哈尔滨市高一上学期期中考试数学试题 Word版含答案

2018年黑龙江省哈尔滨市中考数学试卷含答案

2018年黑龙江哈尔滨中考数学试卷及答案解析版

XXX2017-2018学年第一学期期末考试高一数学试卷

黑龙江省哈尔滨市2017-2018学年高一第一学期期中英语试卷

黑龙江省哈尔滨市2017_2018学年高一数学上学期期中试题201711080263

2017-2018学年哈尔滨高一(上)期末数学试卷((有答案))-(新课标人教版)AlPMMM

2017-2018学年度第一学期高一第一次月考成绩统计表

黑龙江省哈尔滨市四校联考2017-2018学年高一上学期期中考试数学试卷 Word版含解析

黑龙江省哈尔滨市2017_2018学年高一数学上学期期中试题201711090290

黑龙江省哈尔滨市2017_2018学年高一英语上学期期中试题

XXX2017-2018学年第一学期高一期末数学试卷

人教版2017~2018学年度初三第一学期期末考试数学试题附详细答案

2017年黑龙江省哈尔滨市中考数学试卷(2017)

黑龙江省2017—2018学年高一数学上学期期中考试卷(四)

黑龙江省哈尔滨市2016-2017学年高一数学上学期期中试题

黑龙江省青冈县2017-2018学年高一数学上学期期中试题(A卷)

黑龙江省哈尔滨市2016-2017学年高一数学上册期中考试题

黑龙江省哈尔滨师范大学附属中学18年-19年学年高一上学期期中考试数学试题 Word版含答案