第四章热力学基础-2

合集下载

第四章热力学第二定律

第四章热力学第二定律§1．热力学第二定律的表述和卡诺定理1．1 自然现象的不可逆性热一律告诉我们:在自然界中,只有遵守能量转化和守恒定律的过程才有可能发生。

第一类永动机，即不需能量而能对外做功，或输入能量小于输出能量的机器是造不成的。

那么，能否说满足热一律的过程就一定能实现呢？自然界中自发进行的过程，如果不加外界条件控制，将沿什么方向演化？热一律对此是无力回答的。

1.1.1 自然现象的自发性和单向性落叶永离，覆水难收。

死灰不能复燃；破镜难以重圆。

人生易老，返老还童只是幻想；生米煮成熟饭，无可挽回。

大量成语表明，自然现象，历史人文，大多是不可逆的。

故孔夫子在川上有“逝者如斯”之叹。

下面我们看几个典型的自然现象。

（1）摩擦生热从热一律看，功和热都是传递的能量，应该是可以相互转换的。

但经验证明，机械功可以通过摩擦全部转化为热，而外界的热却不可能使物体自动地摩擦起来。

即：功可自发地全部转变为热，而热不能自发地转变为功。

（2）电流发热电流通过导体都会发热，但加热一个闭合导体一般却不能在其中产生电流。

（3）热传导热量只能自发地从高温物体流向低温物体，而不可能自发地从低温物体流向高温物体。

（4）气体向真空自由膨胀气体可以自发地向真空自由膨胀，但充满气体的容器不可能在其中自发地将一部分变成真空。

（5）扩散两种流体可以自发地混合在一起，但是却不能自行地分离。

（6）燃烧木材可以通过燃烧自发地变成二氧化碳和灰烬，但二氧化碳和灰烬不可能自发地再变成木材。

另外，像炸弹爆炸、生物生长和进化、天体演化、空气和水的污染……。

只要仔细考察，我们会发现：自然现象的自发进行都具有单向性。

1.1.2 现象分析以上现象分为两类：（1）耗散过程摩擦生热、电流发热、燃烧……等现象说明：机械运动、电磁运动、化学运动等各种运动自发向热运动的转化具有单向性。

（2）非准静态过程热传导（温度不均匀）、自由膨胀（压强不均匀）、扩散（密度不均匀）……等现象说明：当系统内某个强度量在空间分布不均匀时所自发进行的过程具有单向性。

第4章化学热力学

热化学反应方程式

定义：能表示出反应热的化学反应方程式 ex: aA + bB = gG + hH Q=?

怎样书写？
①一般化学反应是在恒压下进行，此时
Q p = △rH
②注明反应温度和压强(标准态: △rH )
③注明物质的聚集状态及晶形或者溶液浓度：
固-s, 液-l, 气-g，水溶液- aq

凝聚体系的相变过程(△T = 0， △P = 0)
VS ≈ VL, △V = 0, △(PV) = 0
则 △H = △U

化学反应(△T = 0)
当反应物和生成物为凝聚体系时
△H = △U [△(PV) = 0]
当反应物或生成物中有气体时 △H = △U + △(PV) △H = △U + △n · RT △n 指气体分子数的变化(生成物 – 反应物)
状态函数：确定体系状态的物理量
特点: 1)状态一定，体系的各状态函数一定 2)状态函数的变化只与始态和终态有关, 与途径无关
3）状态复原时，状态函数也复原，状态函数的改变值为零

状态函数的类别广度性质：状态函数的值与体系内所含物质的量成正比，如体积、质量等

强度性质：状态函数的值与体系内所含物质的量无关，如温度、压强等
体积功的计算公式
可见：P = 0 或 △V = 0 时，W体 = 0
即自由膨胀过程或恒容过程的 W体 = 0

研究的一般化学反应体系，通常在外压作用下进行，都只作体积功，不作非体积功内能(热力学能)、热、功

内能: 体系内一切能量的总和(内能的绝对值目前无法求)
热: 是以微观混乱的形式传递的能量功: 是以规则的形式传递的能量

工程热力学与传热学_第4章_热力学第二定律(1)

0 T T1 T2 0
1 2
v
0
T T1 T2
1 2
v
4 Δs
3
4
3
s
0
Δs
s
卡诺循环
逆向卡诺循环
卡诺制冷循环的制冷系数：

q2 w net q2 q 1 q 2 T
2 2
T 1 T
高温热源 T1
q1 wnet=q1-q2
制冷机热泵
卡诺热泵循环的供热系数：

q1 w net q1 q 1 q 2 T
2 1
整理：
Q2 T2

Q1 T
1
Q1，Q2 改为代数值：
Q1 T1

Q T
2 2
0
对任意不可逆循环：
p
1
s
a
用一组可逆绝热线分割成许多个微元不可逆循环。
对微元不可逆循环abcda：
Q1
T1
b
A
2
B 0
d
c v
Q
T
2
2
0
对全部不可逆循环积分：

Q1
T1

1A2

Q 2
4-3-3 闭口系统的熵方程
不可逆过程中的熵变：
dS dS
dS
Q
T
Q
T
Q
T
dS
g
令：因此：
说明
dS
f

Q
T
f
dS dS
dS g
——闭口系统的熵方程。适用：闭口系统的各种过程和循环。
熵流 dS
ห้องสมุดไป่ตู้

第四章生物热力学要点

测量体核温度的部位通常为直肠、口腔、食管、耳膜以及尿流，但所得的值却各不相同，因而没有一处温度可认为是真正的体核温度。
食管温度: 能间接量度从心脏泵出的动脉血血温。肛温: 直肠热惯性大, 不适于进行变化较快的温度量度。耳膜温度: 耳膜热惯性小，能反映温度变化最快。环境温度为5~30℃时，人体活动时的体核温度只是代谢率的函数，环境温度高于30℃ ，因出现热应激，体核温度上升。
(c) 温度进一步提高到45℃便会造成蛋白变性及死亡。
(2) 体温下降，有可能完全阻止酶的活性。体温下降至 33℃以下，神经功能便会受到抑制且知觉会消失。 30℃以下则会引起调温系统失灵，若降至28℃，更会引起心室纤颤甚至死亡。
4.3.1 体温
1. 体核温度(core temperature) : 人体躯干核心的温度。
Log241=2
Log242=4 Log243=6
Log220=4.322bit
1950s, 物理学家伽莫夫（George Gamov）根据信息论提出三联核苷酸密码编码20种氨基酸的推测。
1960s, 三联核苷酸编码得到证实，并逐一被破译。
第三节
体温与体温的控制
人类生存环境温度: -30 ~ +40℃。人体中央体温: 37±2℃。恒温性：是指机体得热和失热各因素千变万化情况下，机体维持深部温度或体核温度 (即内环境温度) 在一较窄范围内的能力。
等温等压过程，引用态函数吉布斯自由能, G=E+pV-TS 根据热力学第一定律 Q=E+W 及第二定律 dS≥dQ/T，
最大功原理： dG≤pdV-dW 若dV 0，dW ≤ - dG 意义：等温等压过程，系统对外做功≤吉布斯自由能减少（dW为非膨胀功）

4-1 热力学第二定律的表述

❖ 掌握卡诺循环和卡诺定理; ❖ 掌握熵参数,热过程方向的判据; ❖ 掌握孤立系统熵增原理。 ❖ 了解火用的概念。
4—1 热力学第二定律的表述
4-1-1 自发过程的方向性
1. 自发过程 (The natural processes)：不需要任何外界条件的作用而自动进行的过程。
2. 自发过程的方向性（1）功热转化
➢第一类永动机和第二类永动机的区别。
热力学第二定律的上述两种表述只是经验的总结，不是宏观方法所能解释的。
思考题
1. 不可逆性是自发过程的重要特征和属性； 2. 非自发过程就是不能进行的过程； 3. 有人说：“自发过程是不可逆过程，非自发过
程就是可逆过程”。这种说法对吗？ 4. 热力学第二定律可否表述为“功可以完全变为热，而热不能完全变为功。” 5. 第二类永动机不仅违背了热力学第二定律，也违背了热力学第一定律。
4-1-2 热力学第二定律的表述
1. 克劳修斯表述 (The Clausius statement)：不可能将热从低温物体传至高温物体而不引起其它变化。
1850年，克劳修斯从热量传递方向性的角度提出热不可能自发地，不付代价地从低温物体传至高温物体。
低温物体
高温物体
补偿过程
通过热泵，消耗机械能。
非自发过程
自发过程
的进行 + 作补充条件
热量从低温物体传至高温物体
机械能转变为热能
实现
2. 开尔文—普朗特表述 (The Kelvin-Planck statement)：不可能从单一热源取热，并使之全部转变为功而不产生其它影响。
✓1824年，卡诺提出热能转变成机械能的根本条件：凡有温度差的地方都能产生动力。

统计热力学基础

（3）统计热力学基本假设统计热力学基本假设是：当→∞的极限情况下，在实际系统中任何力学量的长时间平均值〈Gt〉等于系综平均值〈G〉，只要统计系综和实际系统的热力学状态及环境完全相同。统计热力学的另一条基本假设：孤立系统(即N，V，E一定)的全部可能达到的量子态是等概率的。
用于N，V，T一定的封闭系统时，该假设还可表述为：在定温热浴中的系统，能量相同的各量子态有相同的概率。
P ( D) WD
Ω

WD WD
D
每一个微态的概率 P
1
Ω
统计热力学中把WD叫分布D的热力学概率。显然热力学概率 WD不同于数学概率P(A)，WD≥1(正整数)，而0≤P(A)≤1。
③WD的计算定域子系统：
gin N! n WD gi N! n ! ni ! i i i
第四章统计热力学基础
1．统计热力学基本概念（1）统计热力学系统的分类 ①独立子系和相依子系（非独立子系）统计热力学将组成系统的分子、原子及离子等统称为粒子或简称子。按照粒子间有无不可忽略的相互作用，系统可分为独立子系（或近独立子系）——子间无相互作用；相依子系（非独立子系）——子间有不可忽略的相互作用。 ②定域子系和离域子系按照粒子的运动是否遍及系统的全体积，系统可分为定域子系——子的运动是定域化的（不遍及系统的全体积）；离域子系（非定域子系）——子的运动是非定域化的（遍及系统的全体积）。
能量守恒: U N P ,i i 粒子数守恒: N ni
ni是布居在能级上的粒子数；Pε,i是粒子分布在各能级εi上的概率；
（4）分布的微态数WD与系统的总微态数任何一种分布，只指出在每个能级(或状态)上有多少个粒子，实现这一分布尚有不同的方式，每一种可区别的方式代表分布 (或系统)的一个可区别的微观状态，简称微态。WD表示分布D 的微态数，用表示系统总的微态数。（5）分布的概率计算分布的概率用古典概型的计算公式。 ① 古典概型又叫等概率模型，既是概率的定义，又是计算概率的基本公式，其特征是： (i)只有有限个基本事件；

热学等温过程和绝热过程分析

V m( 1
p
水蒸气
蒸汽

1
水
)
W pdV pV pm(
E Q W mL pm(
1
蒸汽
1

1
m
)
)
水
水
1
100热源
蒸汽
水
E 1 1 L p( ) 2.09 106 J kg 1 m 蒸汽水
蒸汽 0.598kg m
3
解水汽化所需的热量 Q mL
水汽化后体积膨胀为
水蒸气
m
水
V m(
1
蒸汽

1
水
)
100热源
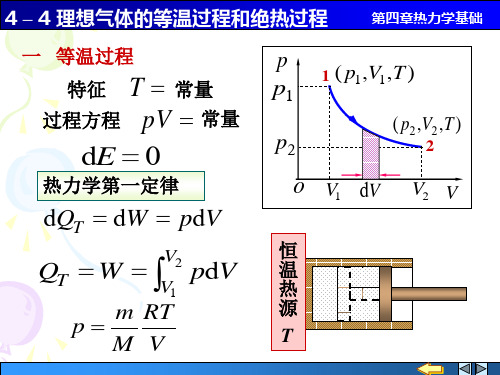
4 – 4 理想气体的等温过程和绝热过程
第四章热力学基础
L 2.26 10 J kg
6
1
水 1040kg m
3
3
蒸汽 0.598kg m
Q0
( p2 ,V2 , T2 ) 2
p2
o
绝热方程
V1
1
V2 V
V T 常量 pV 常量
p T
1

常量
4 – 4 理想气体的等温过程和绝热过程绝热膨胀
第四章热力学基础
绝热压缩
p
p1
1( p1,V1, T1 )
p
p2
2( p2 ,V2 ,T2 )
p2
W
( p2 ,V2 ,T2 ) 2
1( p1,V1, T1 )
p2
W
( p2 ,V2 , T2 ) 2
o V1
V2 V
p1V1 p2V2 m ) 从 pV RT 可得 W CV ,m ( R R M CV ,m p1V1 p2V2 W ( p1V1 p2V2 ) W 1 C P ,m CV ,m

热力学第二定律

讨论：讨论：只取决于T 或 ① ηtc只取决于 1、T2 , T1↑或T2↓→
η tc ↑，，
② ∵T1 < ∞，T2 > 0 ，∴ η tc < 1 ；
（T1受材料限制，T2受环境限制）受材料限制，受环境限制）
η 单一热源） ③ T2＝T1 时， tc = 0 ；（单一热源）
④
ηtc 与工质的性质无关。与工质的性质无关。
1. 卡诺循环（两个可逆等温过程 + 两个等熵过程）卡诺循环（两个可逆等温过程两个等熵过程）可逆
q2 T2 · ∆S T2 =1− =1− 热效率：热效率： ηtc = 1 − q1 T1 · ∆S T1
T1、T2：恒温热源温度，也等于工质的温度（可逆）恒温热源温度，也等于工质的温度（可逆）
由热Ⅰ 由热Ⅰ：w0 = q1 － q2 其中
均取绝对值）（ q1 、q2 均取绝对值）
q2 为吸热量，q1 为放热量 w0 为循环消耗的为吸热量，为放热量, 外功。外功。
经济性指标（适用于任意工质、任意循环）经济性指标（适用于任意工质、任意循环）：
q2 q2 致冷机：致冷机：致冷系数 ε = = w0 q1 − q2
δQ1
T1
+
δQ2
T2
=0
对卡诺循环，可导得卡诺循环，
∫
δQቤተ መጻሕፍቲ ባይዱ
T
=0
根据状态参数的性质，状态参数是全微分，根据状态参数的性质，状态参数是全微分，循环积分为零也是全微分，所以克劳修斯克劳修斯将为零也是全微分，所以克劳修斯将δQ／T定义为状态定义为状态参数熵。参数熵。
第四章热力学第二定律
4－1 热力学第二定律的表述与实质－

第四章经典热学的建立

伽利落验温计
§1.热学现象的初期研究
（二）测温物质的选择和标准点的确定
德国的格里凯（Guericke)曾提出以马德堡地区的初冬和盛夏的温度为定点温度；佛罗伦萨的院士们选择了雪或冰的温度为一个定点，牛或鹿的体温为另一个定点；
1665年，惠更斯建议把水的凝固温度和沸腾温度作为两个固定点；
§1.热学现象的初期研究
3.“热质说”的否定
1798年伦福德(Count Rumford,英国) 由钻头加工炮筒时产生热的现象，得出热是物质的一种运动形式，
1799年，戴维（Humphrey Davy， 1778-1829，英国化学家）作了在真空容器中两块冰摩擦而融化的实验。按热质说观点，热量来自摩擦挤出的潜热而使系统的比热变小，但实际上水的比热比冰的还要大。伦福德和戴维的实验给热质说以致命打击，为热的唯动说提出了重要的实验证据。
§1.热学现象的初期研究
四热本质的认识
1.认为热是运动的表现佛兰西斯•培根从摩擦生热得出热是一种膨胀的、被约束的在其斗争中作用于物体的微小粒子的运动。波义耳认为钉子敲打之后变热，是运动受阻而变热的证明。笛卡尔认为热是物质粒子的一种旋转运动；胡克用显微镜观察火花，认为热是物体各个部分非常活跃和极其猛烈的运动；罗蒙诺索夫提出热的根源在于运动等。
各种温度计
§1.热学现象的初期研究
热力学温标：
19世纪50年代，开尔文注意到：既然卡诺热机与工作物质无关，那么我们就可以确定一种温标，使它不依赖于任何物质，这种温标比根据气体定律建立的温标更具有优越性。
据此，1854年，开尔文(威廉.汤姆逊)提出开氏温标， T=272.3 + t。又称热力学温标，它与测温物质的性质无关，即任何测温物质按这种温标定出的温度数值都是一样的。 1954年国际计量大会决定将水的三相点的热力学温度定为 273.16K。

第4章-化学热力学基础习题

第4章化学热力学基础习题1．选择题4-1下列物质中m f H ∆不等于零的是（）(A) Cl 2(g) (B) O 2(g) (C) C(金刚石) (D) Ne(g) 4-2下列说法中正确的是（）(A) 稳定单质的 m f H ∆、 m f G ∆、m S 都为零(B) 放热反应总是可以自发进行的(C) H 2(g)的标准燃烧热等于H 2O(l)的 m f H ∆ (D) CO 2(g)的 m f H ∆也就是CO(g)的标准燃烧热4-3 下列反应中释放能量最大的是（）(A) CH 4(l) + 2 O 2(g) → CO 2(g) + 2 H 2O(g) (B) CH 4(g) + 2 O 2(g) → CO 2(g) + 2 H 2O(g) (C) CH 4(g) + 2 O 2(g) → CO 2(g) + 2 H 2O(l) (D) CH 4(g) +23O 2(g) → CO(g) + 2 H 2O(l) 4-4 下列叙述正确的是（）(A)m r S ∆＝∑∆θS (生成物)－∑∆θS (反应物)(B) 一个自发进行的反应，体系自由能减少等于体系对环境所做最大功(C) 某气相反应 m r G ∆是指反应物与产物都处于298 K 且气体总压为101.3 kPa 时，该反应的自由能变。

(D) 同类型的二元化合物可用它们的 m f H ∆值直接比较其热力学稳定性。

4-5 已知2 PbS(s) + 3O 2(g) = 2 PbO(s) + 2 SO 2(g)m r H ∆= - 843.4 kJ· mol -1则该反应的Q v 值为（）(A) 840.9 (B) 845.9 (C) -845.9 (D) -840.9 4-6下列物质中，摩尔熵最大的是（）(A) CaF 2 (B) CaO (C) CaSO 4 (D) CaCO 34-7下列反应中 m r S ∆最大的是（）(A) C(s) + O 2(g) → CO 2(g) (B) 2 SO 2(g) + O 2(g) →2 SO 3(g)(C) 3 H 2(g) + N 2(g) →2 NH 3(g) (D) CuSO 4(s) + 5H 2O(l) →CuSO 4· 5H 20(s)4-8下列反应中 m r H ∆等于产物m f H ∆的是（）(A) CO 2(g) + CaO(s) →CaCO 3(s) (B)21H 2(g)+ 21I 2(g) → HI(g) (C) H 2(g) + Cl 2(g) →2 HCl(g) (D) H 2(g)+ 21O 2(g) → H 2O(g)4-9下列反应中 m r G ∆等于产物m f G ∆的是（）(A) Ag +(aq)+Cl -(aq) →AgCl(s) (B) 2Ag(s)+Cl 2(g) →2AgCl(s) (C) Ag(s)+21Cl 2(g) →AgCl(s) (D) Ag(s)+ 21Cl 2(l) →AgCl(s) 4-10对反应CH 4(g) + 2 O 2(g) → CO 2(g) + 2 H 2O(l)的m r H ∆，下列说法中正确的是（）A ． m r H ∆ 是CO 2(g) 生成焓B ．m r H ∆是CH 4(g)的燃烧焓 C ． m r H ∆是正值 D ． m r H ∆－U ∆是正值2．填空题4-11 对某体系做功165 J ，该体系应热量 J ，才能使内能增加100 J 。

相变热力学基础第4章

由两相混合物构成的实际二元材料非常多: 典型的混合物金属二元材料近共析成分高碳钢：铁素体α和渗碳体Fe3C两相混合物组成近共晶成分的高碳铸铁高深冲性能的双相低碳结构钢 40黄铜和双相钛合金二相混合物非金属材料： Si3N4-Al2O3陶瓷 Al2O3-SiO2系莫来石陶瓷材料
各种键的数目nAA, nBB、nAB，可由各种键的键分数得到。
XAA、XBB、XAB：A-A、B-B、A-B键的键分数
A-A键数目nAA=XAAzNa/2 B-B键数目nBB=XBBzNa/2 A-B键数目nAB=XABzNa/2
*
4.2 正规溶体近似
混合前：
*
由NA个A原子和NB个B原子构成1mol的溶体，XA、XB：A、B的原子摩尔分数正规溶体近似
XAB=XAXB , XBA=XBXA ，XAA= XA2, XBB= XB2
正规溶体近似
4.2 正规溶体近似
混合后溶体的内能US：
混合前(含有相同原子数目的纯组元) U0:
正规溶体近似
4.2 正规溶体近似
常压下溶液混合引起的体积变化，可以忽略，即相互作用能IAB（Interaction energy ）: 正规溶体近似
Quasi-chemical model (准化学模型) ：
内能只考虑结合能
内能的变化是最近邻原子的结合键能的变化引起的 ΔUmix =Us(溶体) – U0(混合前含有相同原子数目的纯组元)
如果只考虑最近邻原子间的结合能，内能就是最近邻原子键的键能总和：
从原子角度来考察溶液的形成
*
二元溶体中存在三种类型的原子键： 1．A—A键，每个键的能量为uAA 2．B—B键，每个键的能员为uBB 3．A—B键，每个键的能量为uAB

化工热力学第四章

St ,Vt ,ni
dni
0
H t ni
St , p,ni
U t ni
St ,Vt ,ni
❖ 2）意义： ❖ 化学势体现了不同条件下热力学性
质随构成旳变化，可用以描述相平衡。
❖ §4-3 相平衡准则及相律
❖ 1 相平衡准则相平衡准则能够由均相敞开系统旳热力学关系来推导。
V RT p
ay12 by22 2cy1 y2
dV dy1 2ay1 2by2 2cy1 2cy2
dV V 1 V (1 y1 ) dy1
RT p
ay12 by22 2cy1 y2
(1 y1 )(2ay1 2by2 2cy1 2cy2 )
RT p
a( y12
dni dni( ) dni( ) 0 dni( ) dni( ) (i 1, 2, , N )
dUt T ( )dSt( ) T ( )dSt( )
p( )dVt( ) p( )dVt( )
N
i( )dni( ) i( )dni( ) i
T ( ) T ( ) dSt( ) p( ) p( ) dVt( )
M1
M
(1
x1 )
dM dx1
dM M 2 M x1 dx1
二元混合物旳偏摩尔性质和摩尔性质图示
T,p一定
dM x1 d x1 M
M1
1
x1
d d
M x1
M1
M
M2
M M ( x1 )
M2
0
x1
1
❖ 对于N元系统，各组分旳偏摩尔性质与摩尔性质之间旳关系是：
N M
Mi
M
j1
xj

物理化学第二版习题答案

物理化学第二版习题答案物理化学是研究物质的物理性质和化学性质以及它们之间的相互关系的一门学科。

对于学习物理化学的学生来说，习题是巩固知识、提高能力的重要途径之一。

下面将为大家提供物理化学第二版习题的答案，希望对广大学生有所帮助。

第一章：热力学基础1. 答案：热力学是研究物质在能量转化过程中的规律的科学。

它主要研究能量的转化和守恒规律，以及物质在这个过程中的性质变化。

2. 答案：热力学第一定律是能量守恒定律，即能量可以从一种形式转化为另一种形式，但总能量守恒不变。

3. 答案：热力学第二定律是能量转化过程中的不可逆性原理，即自发过程的方向是从有序向无序的方向进行。

第二章：热力学函数1. 答案：热力学函数是描述物质性质和状态的函数，如内能、焓、自由能等。

2. 答案：内能是系统所拥有的全部能量的总和，包括系统的动能和势能。

3. 答案：焓是系统的内能和对外界做的功之和，常用符号表示为H。

第三章：热力学第一定律的应用1. 答案：热容量是物质吸收或释放热量时的温度变化与热量变化之比。

2. 答案：绝热过程是指在过程中系统与外界没有热交换，即系统的热容量为零。

3. 答案：等温过程是指在过程中系统的温度保持不变，即系统与外界的热交换量为零。

第四章：热力学第二定律的应用1. 答案：熵是描述系统无序程度的物理量，表示系统的混乱程度。

2. 答案：熵增原理是热力学第二定律的数学表达式，它指出孤立系统的熵总是增加的。

3. 答案：卡诺循环是一种理想的热机循环，它由等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程组成。

第五章：相变和化学平衡1. 答案：相变是指物质由一种相转变为另一种相的过程，如固态到液态、液态到气态等。

2. 答案：平衡态是指系统各种性质的变化不再随时间变化，达到动态平衡的状态。

3. 答案：化学平衡是指在封闭容器中，反应物和生成物浓度达到一定比例时，反应速率前后保持不变的状态。

第六章：化学动力学1. 答案：化学动力学是研究化学反应速率和反应机理的学科。

普通化学第四章化学热力学基础

2.液体固体物质的标准状态是在一个标准压力下纯物质的物理状态。
3.溶液中溶质的标准状态是指在标准压力下溶质的
质量摩尔浓度b =1 mol·kg-1的状态。热力学 bθ =1 mol·kg-1。化学计算中，近似处理，标准物质的量浓度cθ =1
mol·L-1 在热力学的有关计算中，状态函数变化需注明其状态，即表明其处于标准状态还是处于非标准状态。
有物质交换敞开系统
有能量交换
经典热力学不研究敞开系统
热力学的基本概念
（2）封闭系统（closed system）系统与环境之间无物质交换，但有能量交换。
环境
无物质交换封闭系统
有能量交换
经典热力学主要研究封闭系统
热力学的基本概念
（3）隔离系统（isolated system）系统与环境之间既无物质交换，又无能量交换，故又称为孤立系统。
△r Hmθ(1)= － 870.3kJ.mol-1
定压反应热，用符号Qp表示。
由热力学第一定律：△U = Qp + W
Qp = △U － W = △U + p△V
热化学
U、p、V都是状态函数，其组合也必为状态函数， U、p、V的组合定义为一新的状态函数——焓，符号为H。
H ≡U + pV Qp = △H
不做非体积功的恒压过程，定压反应热等于化学反应焓变。
这种被划定的研究对象称为系统，也可称为体系。
环境（surroundings）
系统与环境
系统以外与系统密切相关、有相互作用
或影响的部分称为环境。
热力学的基本概念
系统的分类
根据系统与环境之间的关系，把系统分为三类：（1）敞开系统（open system）

第4章热力学基础 [2]

绝热线比等温线更陡
p
PQ 绝热线
P
Q = E + A
PT O V
等温线
(P1,V1,T1) 等温线 (P2,V2,T1) 绝热线 (P2,V2,T2)
V
O
V1
V2
V
2 p nεt 3
3 εt kT 2
pV vRT
等温过程：温度不变，压强降低是由于体积膨胀。绝热过程：压强降低是由于体积膨胀和温度降低。
§4.3.5 几个典型过程的总结及热力学第一定律的应用等容过程等压过程
过程 P 恒量方程 T 内能增量功热量
V 恒量 T
等温过程
绝热过程
E νC v,m (T2 T1 )
0 dE = dQ
i dE RdT 2
p V C1 PV 恒量 T V 1 C 2 p 1 T C 3 i dE RdT 2 0 E νCv,m (T2 T1 )
QT AT pdV
V2 V1
V2 V1
p[Pa] p1
a
7.02 102 J
(吸热)
p1V1 V2 p2 dV p1V1 ln V V1 O
c V1
b V2V[m3]
(2) 在 ac 等容降温和 cb 等压膨胀过程中，因 a、 b 温相同，故 E = 0。
Qacb Aacb Acb p2 V2 V1 5.07 102 ( J )
例 5-2
理想气体经如图所示的直线过程从状态 a
过渡到状态 b。求此过程中系统内能的改变、做功和热传递？（已知 CV , m
p(105Pa) a
5 R） 2

基础化学4第四章化学热力学基础

由于热是途径函数，所以要根据系统状态变化的具体途经将热冠以不同名称，如恒压热、恒容热、气化热、熔化热、升华热等；在进行热量计算时，必须按实际过程（给定的条件）计算，而不能随意假设途径。
热力学中，只讨论三种热：化学反应热；相变热；显热（仅因T变化吸收或放出的热）。
2.功
除热以外，系统与环境之间的其他能量传递统称为功，其符号为W，单位为J或kJ。热力学规定，环境对系统做功时，W＞0；系统对环境做功时，W＜0。功也是过程变量（途径函数），无限小量用δW表示。
系统性质与状态是一一对应的，因此在热力学中又将描述系统状态
的性质称为状态函数。
状态函数的基本特征是：状态一定，状态函数都有一定的值；状态
变化时，状态函数的变化值等于终态值减去始态值，而与所经历的途径
无关。即
△X＝X2－X1
（5-1）
其无限小变化是全微分dX。若系统经历一个循环过程时，所有状态
函数的改变分物质和空间。系统是研究的主体，环境则是辅助部分，按系统和环境之间有无物质及能量传递，可将系统分为三类。
（1）封闭系统与环境只有能量传递，而没有物质传递的系统。（2）敞开系统与环境既有能量传递，又有物质传递的系统。（3）隔离系统与环境既无能量传递，又无物质传递的系统，或称孤立系统。绝对的隔离系统是不存在的，通常将绝热、封闭的保温设备，以及封闭系统中发生的极快变化（如爆炸）等过程
封闭系统的热力学能包括三部分（1）分子的动能是系统温度的函数；（2）分子间相互作用的势能是系统体积的函数；（3）分子内部的能量是分子内各种粒子（原子核、电子等）的能量之和，在不发生化学变化的条件下，为定值。因此，封闭系统的热力学能是温度和体积的函数，即
U＝f（T、V）当系统的状态一定（如物种、nB、T、V一定）时，则系统的热力学能一定，故U为状态函数，广延性质。 U的绝对值无法确定，但可以计算变化量。△U＞0，表示系统的热力学能增加，△U＜0，表示系统热力学能减少。

第4章热力学基础

绝热过程方程:
pV C1
TV

1
C2
C3
T p
1绝热过程
V T降低 p降低更多
p
A
C
V T不变 p降低
等温线、绝热线的斜率分别为：
B
O V
dp p V d V T dp p V dV Q
又因混合后的氮气与压强仍分别满足理想气体状态方程，
由此得：
1 M1 p1 RT V1 ＋V2 M mol 1 1 M2 p RT 2 V1 ＋V2 M mol 2
两者相加即得混合气体的压强：
1 p V1 ＋V2
M1 M2 ＋ M mol 1 M mol 2
RT
解:打开活塞后，原在第一个容器中的氮气向第二个容器中扩散，氩气则向第一个容器中扩散，直到两种气体都在两容器中均匀分布为止。达到平衡后，氮气的压强变为p1'，氩气的压强变为p2' ，混合气体的压强为p= p1' + p2' ；温度均为T 。在这个过程中，两种气体相互有能量交换，但由于容器是绝热的，总体积未变，两种气体组成的系统与外界无能量交换，总内能不变，所以
利用多方方程和状态方程：
dA PdV Rdt /(n 1)
已知
E1 ＋E2 ＝E1 ＋E2 0 M E1 Cv1 T T1 M mol1 M E2 Cv 2 T T2 M mol 2
代入式得：
M M Cv1 T T1 ＋ Cv 2 T T2 ＝ 0 M mol1 M mol 2
M1 M2 Cv1T1 ＋ Cv2 T2 M mol1 M mol 2 T M1 M2 Cv1 ＋ Cv2 M mol1 M mol 2

第四章热力学第一定律~2

这相当于一个隔离系统,在绝热刚性容器中不论发生什么变化,只要没有非体积功,则Q=0,W=0,U=0.但焓不是守恒量 Q=0,W=0,U=0 ,对于气体分子数增加的放热反应,容器中的温度和压力会升高,故H>0. B
3
有一高压钢瓶,打开阀门后气体喷出钢瓶外,当内外压力相等时,关闭阀门,等待一段时间,让瓶内外温度达成平衡,测量瓶内压力与外界相比: A p内>p外 C p内=p外 B p内<p外 D 无法确定
8
在373K和标准压力下,质量为1g的H2O(l)经历如下和标准压力下,质量为的 () 和标准压力下三种不同途径蒸发为同温,同压的H ( ), ),分别求三种不同途径蒸发为同温,同压的 2O(g),分别求各个途径的Q, , 和的值已知: 的值. 各个途径的 ,W,U和H的值.已知:该条件下 H2O(l)的汽化热为 ( )的汽化热为2.259kJ/g.设气体为理想气体, .设气体为理想气体, 凝聚相体积与气体相比可以忽略不计. 凝聚相体积与气体相比可以忽略不计. (1)等温,等压可逆变为H2O(g); 等温,等压可逆变为 ( ); 等温 ),第二步再 (2)第一步等温汽化为第一步等温汽化为50kPa的H2O(g),第二步再 ( ), 第一步等温汽化为的等温可逆变成100kPa的H2O(g) ; 等温可逆变成的 (3)在恒温在恒温373K的真空箱中汽化为在恒温的真空箱中汽化为100kPa的H2O(g). 的 .
6
解: (1)对于单原子理想气体 Cv,m = 3/2 R U = n Cv,m (T2-T1)→T2 = 561.7K V2 = nRT2/p2 = 0.0233 m2 H = n Cp,m (T2-T1) = 6.00KJ W = U – Q = 2.0KJ